
Marc van Zanten
Petra van den Brom-Snijders


Marc van Zanten
Petra van den Brom-Snijders
Reken-wiskundedidactiek
auteurs
Marc van Zanten
Petra van den Brom-Snijders
redactie
Singeling Tekstproducties, Amersfoort
opmaak binnenwerk
Imago Mediabuilders, Amersfoort
ontwerp binnenwerk
Studio Fraaj, Rotterdam
ontwerp omslag
Studio Vlak
beelden omslag
Austris Augusts (Unsplash) / Getty Images
technisch tekenwerk
Imago Mediabuilders, Amersfoort
Over ThiemeMeulenhoff ThiemeMeulenhoff ontwikkelt zich van educatieve uitgeverij tot een learning design company. We brengen content, leerontwerp en technologie samen. Met onze groeiende expertise, ervaring en leeroplossingen zijn we een partner voor scholen bij het vernieuwen en verbeteren van onderwijs. Zo kunnen we samen beter recht doen aan de verschillen tussen lerenden en scholen en ervoor zorgen dat leren steeds persoonlijker, effectiever en efficiënter wordt.
Samen leren vernieuwen.
www.thiememeulenhoff.nl
ISBN 978 90 06 48714 5
Derde druk, eerste oplage, 2025
© ThiemeMeulenhoff, Amersfoort, 2025
Alle rechten voorbehouden. Niets uit deze uitgave mag worden verveelvoudigd, opgeslagen in een geautomatiseerd gegevensbestand, of openbaar gemaakt, in enige vorm of op enige wijze, hetzij elektronisch, mechanisch, door fotokopieën, opnamen, of enig andere manier, zonder voorafgaande schriftelijke toestemming van de uitgever.
Voor zover het maken van kopieën uit deze uitgave is toegestaan op grond van artikel 16B Auteurswet 1912 j° het Besluit van 23 augustus 1985, Stbl. 471 en artikel 17 Auteurswet 1912, dient men de daarvoor wettelijk verschuldigde vergoedingen te voldoen aan Stichting Publicatie- en Reproductierechten Organisatie (PRO), Postbus 3060, 2130 KB Hoofddorp (www.stichting-pro.nl). Voor het overnemen van gedeelte(n) uit deze uitgave in bloemlezingen, readers en andere compilatiewerken (artikel 16 Auteurswet) dient men zich tot de uitgever te wenden. Voor meer informatie over het gebruik van muziek, film en het maken van kopieën in het onderwijs zie www.auteursrechtenonderwijs.nl.
De uitgever heeft ernaar gestreefd de auteursrechten te regelen volgens de wettelijke bepalingen. Degenen die desondanks menen zekere rechten te kunnen doen gelden, kunnen zich alsnog tot de uitgever wenden.
Deze uitgave is volledig CO2-neutraal geproduceerd. Het voor deze uitgave gebruikte papier is voorzien van het FSC®-keurmerk. Dit betekent dat de bosbouw op een verantwoorde wijze heeft plaatsgevonden.
1 Samenhang breuken, decimale getallen, verhoudingen en procenten 9
1.1 Verhoudingen en getallen 10
1.1.1 Overeenkomsten en verschillen 10
1.2 Verschijningsvormen, relaties en begrip 12
1.2.1 Breuken en decimale getallen 14
1.2.2 Breuken en verhoudingen 17
1.3 Absoluut en relatief 20
2 Breuken 23
2.1 Getal, verhouding en bewerking 23
2.1.1 Verschijningsvormen 24
2.1.2 Gelijkwaardigheid en gelijknamigheid 26
2.1.3 Wiskundetaal bij breuken 29
2.1.4 Uit de geschiedenis van breuken 30
3 Breuken op de basisschool 31
3.1 Schets van de leerlijn breuken 31
3.2 Introductie van breuken 33
3.3 Bevorderen van begrip 35
3.3.1 Breukbegrip 35
3.3.2 Gebruik van modellen 37
3.4 Redeneren en rekenen met breuken 46
3.4.1 Vergelijken en ordenen 47
3.4.2 Optellen en aftrekken 53
3.4.3 Vermenigvuldigen en delen 58
3.5 Samenhang met andere leerstof 69
4 Decimale getallen 71
4.1 Uitbreiding van gehele getallen 71
4.1.1 Verschijningsvormen 73
4.1.2 Wiskundetaal bij decimale getallen 75
4.1.3 Uit de geschiedenis van decimale getallen 77
5 Decimale getallen op de basisschool 78
5.1 Schets van de leerlijn decimale getallen 78
5.2 Introductie van decimale getallen 80
5.3 Bevorderen van begrip 81
5.3.1 Begrip van decimale getallen 81
5.3.2 Gebruik van modellen 87
5.4 Redeneren en rekenen met decimale getallen 90
5.4.1 Vergelijken, ordenen en relateren 90
5.4.2 Inschatten, afronden en schattend rekenen 93
5.4.3 Optellen en aftrekken met decimale getallen 94
5.4.4 Vermenigvuldigen en delen met decimale getallen 98
5.5 Samenhang met andere leerstof 106
6 Verhoudingen 108
6.1 Verhoudingen zijn overal 109
6.1.1 Verschijningsvormen 110
6.1.2 Verbanden die geen verhouding zijn 116
6.1.3 Bijzondere verhoudingen 121
6.1.4 Wiskundetaal bij verhoudingen 124
7 Verhoudingen op de basisschool 125
7.1 Schets van de leerlijn verhoudingen 126
7.2 Introductie van verhoudingen 127
7.3 Bevorderen van begrip 128
7.3.1 Begrip van verhoudingen 129
7.3.2 Gebruik van modellen 132
7.4 Redeneren en rekenen met verhoudingen 137
7.4.1 Redeneren en rekenen met de verhoudingstabel 138
7.4.2 Schaal en schaalbegrip 140
7.4.3 Snelheid 143
7.4.4 Andere verschijningsvormen 145
7.4.5 Absolute en relatieve gegevens 147
7.5 Samenhang met andere leerstof 148
8 Procenten 153
8.1 Procenten zie je overal 154
8.1.1 Verschijningsvormen 154
8.1.2 Een gestandaardiseerde verhouding 159
8.1.3 Wiskundetaal bij procenten 161
9 Procenten op de basisschool 164
9.1 Schets van de leerlijn procenten 165
9.2 Introductie van procenten 166
9.3 Bevorderen van begrip 167
9.3.1 Procentbegrip 168
9.3.2 Gebruik van modellen 169
9.4 Redeneren en rekenen met procenten 173
9.4.1 Deel-totaalvraagstukken 174
9.4.2 Toename- en afnamevraagstukken 177
9.4.3 Rekenvormen bij procenten 182
9.5 Samenhang met andere leerstof 189
10 Gelegenheid om te leren: breuken, decimale getallen, verhoudingen en procenten 191
10.1 Leerinhouden en prestatieverwachtingen 191
10.1.1 Functies en waardes van rekenen-wiskunde 192
10.1.2 Gecijferdheid 193
10.1.3 Doelen 194
10.2 Leerprocessen bij rekenen-wiskunde 199
10.2.1 Kennis bij rekenen-wiskunde 199
10.2.2 Leren van rekenen-wiskunde 201
10.2.3 Leertheorieën 204
10.3 Faciliteren van leren 207
10.3.1 Didactische modellen 208
10.3.2 Didactische noties en benaderingen 212
10.3.3 Instructie 218
10.4 Uit de geschiedenis van onderwijs in breuken, decimale getallen, verhoudingen en procenten 222
11 Differentiatie bij breuken, decimale getallen, verhoudingen en procenten 225
11.1 Differentiatie als cyclisch proces 226
11.2 Onderwijsbehoeften vaststellen bij rekenen-wiskunde 229
11.2.1 Zicht op je leerlingen 229
11.2.2 Zicht op leerinhouden 241
11.2.3 Peilen en observeren in groep 1 en 2 242
11.3 Differentiatie naar doelen 243
11.3.1 Gedifferentieerde doelen aan het einde van de basisschool 244
11.3.2 Fundamenteel niveau 1F 246
11.3.3 Hoger dan 1S: niveau 1S+ 248
11.4 Differentiatie in het faciliteren van leren 248
11.4.1 Groeperen van leerlingen 249
11.4.2 Differentiatie in het dagelijkse reken-wiskundeonderwijs 252
Over de auteurs 264
Met dank aan 264
Geraadpleegde bronnen 265
Illustratieverantwoording 273
Register 275
A B C
Rekenen-wiskunde is een kernvak. Het komt op de basisschool elke dag aan bod en is belangrijk voor de voorbereiding op het vervolgonderwijs en voor het functioneren in de maatschappij. De realiteit is doordrenkt met rekenen-wiskunde: bij het boodschappen doen, in de gaten houden van de tijd, plannen van een vakantiereis, lezen van de krant, of als je iemand de weg wijst. Al van jongs af aan komen kinderen rekenen-wiskunde overal tegen: bij het inschatten van afstanden, vergelijken wie het grootste is, onthouden van de weg naar huis en op welk nummer je woont, of het sparen van zakgeld. Op de basisschool leren kinderen met al deze reken-wiskundige zaken omgaan en leren ze ook in meer formele zin rekenen-wiskunde. Daarbij komt de volgende leerstof aan bod: getallen, verhoudingen, meten, meetkunde en verbanden. In dit boek worden breuken, decimale getallen, verhoudingen en procenten behandeld.
Volgens de Kennisbasis wiskunde lerarenopleiding basisonderwijs moeten basisschoolleraren professioneel gecijferd zijn. Dat houdt in dat zij:
■ zelf beschikken over voldoende rekenvaardigheid en gecijferdheid;
■ rekenen-wiskunde betekenis kunnen geven voor kinderen;
■ oplossingsprocessen en niveauverhoging bij kinderen kunnen realiseren;
■ wiskundig denken van kinderen kunnen bevorderen.
De geactualiseerde boekenserie Reken-wiskundedidactiek helpt (aanstaande) leraren om deze kennis, vaardigheden en attitude te verwerven. Naast het voorliggende boek omvat de serie de boeken Hele getallen en Meten, meetkunde en verbanden en een ondersteunende website eDition. De serie is volledig dekkend voor de herziene Kennisbasis wiskunde lerarenopleiding basisonderwijs
De boeken kennen drie invalshoeken voor het leren van (aanstaande) basisschoolleraren:
Activiteiten – ideeën om in de praktijk mee aan de slag te gaan en opdrachten om de leerstof nader te verwerken;
Bronnen – informatie over rekenen-wiskunde in realiteit en theorie, wiskundetaal, leerlijnen, en leren en onderwijzen van rekenen-wiskunde, inclusief differentiatie;
GeCijferdheid – opgaven om te werken aan de eigen professionele gecijferdheid.
Met deze nieuwe editie kunnen (aanstaande) leraren zich goed voorbereiden op de tegenwoordige eisen die worden gesteld op de opleiding en in de onderwijspraktijk. Bovendien zijn in de geactualiseerde boeken recente ontwikkelingen en inzichten opgenomen, zoals rekenen-wiskunde voor burgerschap en kritisch kwantitatief denken, opportunity to learn (gelegenheid om te leren), en de nieuwste tussendoelen en reken-wiskundemethodes. Verder is er nadrukkelijker aandacht voor verschillende instructievormen en de betekenis daarvan voor het leren en onderwijzen van rekenen-wiskunde.
De auteurs
In gesprek over breuken, decimale getallen, verhoudingen en procenten
ABreuken, decimale getallen, verhoudingen en procenten kom je overal tegen. In hoeverre hebben kinderen zicht hierop?
a Noteer voor jezelf situaties waarin mensen te maken hebben met deze concepten.
b Hoe denken kinderen hierover? Kies een van de volgende werkvormen of bedenk zelf een variant. Wissel je ervaringen uit met medestudenten of collega’s.
Groepsgesprek
Vraag aan kinderen uit de bovenbouw waaraan zij denken bij breuken, decimale getallen, verhoudingen en/of procenten. Maak samen met de kinderen een woordveld van dagelijkse situaties die te maken hebben met breuken, decimale getallen, verhoudingen en/of procenten. Waar komen de kinderen zelf mee? Welke situaties breng jij in en wat begrijpen ze van die situaties?
Collage
Laat kinderen op zoek gaan naar breuken, decimale getallen, verhoudingen en/of procenten die ze tegenkomen in hun dagelijks leven en laat ze deze voorbeelden meenemen naar school. Ze kunnen bijvoorbeeld reclamefolders, tijdschriften en kranten doorzoeken, afbeeldingen uit apps verzamelen of foto’s maken in de supermarkt en op andere plekken. Laat ze in groepjes collages maken met verschillende voorbeelden. In een klassikaal gesprek kan het gaan over de betekenis van de gevonden voorbeelden en de verschillen en overeenkomsten tussen de verschillende collages.

Samenhang breuken, decimale getallen, verhoudingen en procenten
Bwiskundetaal
Breuken, verhoudingen en procenten hebben veel met elkaar te maken. Ze zien er verschillend uit, maar je kunt er vaak hetzelfde mee tot uitdrukking brengen. Bijvoorbeeld:
• 1 4 deel van de pabostudenten is een jongen;
• 1 op de 4 pabostudenten is een jongen;
• 25% van de studenten op de pabo is een jongen;
• de verhouding van het aantal mannelijke studenten ten opzichte van het totale aantal studenten is 1 : 4. Maar let op: de verhouding tussen het aantal jongens en het aantal meisjes op de pabo is 1 : 3!
Het gaat hier om verschillende beschrijvingen van dezelfde situatie. Dezelfde verhouding, 1 op elke 4, wordt met verschillende wiskundetaal, weergegeven: met de verwoording ‘1 op de 4’, de notatie ‘1 : 4’, met een percentage en met behulp van een breuk.
Breuken zijn een geval apart. Een breuk kan een verhouding weergeven, zoals hierboven, maar een breuk is ook een getal. Je kunt het getal 1 4 ook als het decimale getal 0,25 noteren. Verder is een breuk ook een bewerking: 1 4 = 1 : 4.
Bnotatiewijze
rationaal getal
Er zijn verschillende overeenkomsten tussen breuken, decimale getallen, verhoudingen en procenten. Breuken en decimale breuken komen in betekenis overeen: het zijn allebei gebroken getallen. Decimale getallen, in het basisonderwijs ook wel kommagetallen genoemd, zijn decimale breuken. Echter de notatiewijze van decimale breuken lijkt meer op die van gehele getallen dan op die van breuken. Hele getallen, breuken en decimale breuken zijn allemaal rationale getallen met verschillende notatiewijzen. Een rationaal getal is het quotiënt van twee hele getallen en is dus te noteren als een breuk (bijvoorbeeld 1 : 4 = 1 4 ). Ook gehele getallen, inclusief 0 en negatieve getallen horen tot de rationale getallen. Zo is bijvoorbeeld 10 te noteren als 10 1 , 0 als 0 1 en -5 als -5 1 .
relatief aspect
Breuken en procenten worden allebei gebruikt om een verhouding aan te geven. Een overeenkomst tussen breuken, verhoudingen en procenten is dat er bij deze concepten een relatief aspect is te onderscheiden. Ze geven namelijk de verhouding aan ten opzichte van een bepaald totaal (meer hierover lees je in paragraaf 1.3). Een breuk geeft de verhouding aan tussen een deel en een geheel. Een percentage geeft de verhouding aan tussen een deel en een totaal dat op honderd is gesteld.
verschijningsvormen
Aan de andere kant kennen breuken, decimale getallen, verhoudingen en procenten elk hun eigen gebruik en verschijningsvormen in de realiteit. Bij notatie van geldbedragen gebruiken we bijvoorbeeld decimale getallen en geen breuken. Procenten kom je veel tegen bij kortingen en rente, terwijl kortingen niet worden uitgedrukt in decimale getallen. In het dagelijks leven gebruiken we
CCverhoudingen, breuken en procenten door elkaar. Bijvoorbeeld in de media, waar ze worden gebruikt om getalsmatige informatie weer te geven. In het bericht hieronder, over vakantiegeld, is dit goed te zien. Verhoudingen worden hier niet alleen geschreven als verhouding, maar ook als percentage en breuk.
Meer vakantiegeld voor werknemers met lager salaris
In mei ontvangen veel werknemers traditioneel hun vakantiegeld. Dit jaar ontvangen vooral werknemers met een lager salaris meer vakantiegeld. Bijna drie op de tien Nederlanders geven hun vakantiegeld deels uit aan iets anders dan de vakantie. De mensen die niet al hun vakantiegeld aan vakanties uitgeven, gebruiken het extraatje liever voor het aflossen van schulden, grote aankopen of voor een extra buffer tegen de hoge inflatie.
Het vakantiegeld in mei moet voor werknemers minimaal 8 procent van het brutoloon van het voorgaande jaar bedragen. In een onderzoek gaf de helft van de deelnemers aan dit bedrag helemaal aan een of meerdere vakanties uit te geven. Voor ruim één op de tien mensen is dat geld noodzakelijk om de vakantie te kunnen betalen. Daar staat tegenover dat 7 procent van de deelnemers aan het onderzoek helemaal niets van het vakantiegeld aan vakanties besteedt.
In het onderzoek komt naar voren dat 27 procent van de Nederlanders goedkoper op vakantie gaat vanwege een krappere financiële situatie. Iets minder dan een vijfde van de respondenten zegt te bezuinigen op andere grote uitgaven om op vakantie te kunnen gaan.
Bron: Het Parool, 3-05-2023
Vakantiegeld
a Geef van alle gegevens in het bericht over vakantiegeld aan om hoeveel personen het gaat.
b Van hoeveel personen is niet duidelijk waaraan het vakantiegeld wordt besteed? Hoeveel procent is dat?
Wat zie je?
a Welke breuken zie je in de figuur?
b Welke verhoudingen zie je in de figuur?
c Hoeveel procent van de figuur is blauw? Hoeveel procent is rood en hoeveel procent is groen?
Samenhang breuken, decimale getallen, verhoudingen en procenten
Om goed te leren redeneren en rekenen met breuken, decimale getallen, verhoudingen en procenten moeten kinderen grip krijgen op de verschijningsvormen ervan en de onderlinge relaties ertussen. Om de samenhang te kunnen doorzien, is het ook nodig dat kinderen leren dat de concepten in de realiteit door elkaar voorkomen, bijvoorbeeld in mediaberichten.

Bron: Pluspunt, groep 8
Daarnaast leren kinderen de betekenis van bewerkingen met verhoudingen en breuken te doorzien, zoals:
• 1 5 × 10 betekent het 1 5 deel nemen van 10;
• ik weet dat 20% ergens van, hetzelfde is als 1 5 deel daarvan nemen, want 100 gedeeld door 5 is 20;
• 1 5 is eigenlijk 1 gedeeld door 5.
rekenfeiten
Op die manier kunnen kinderen ook onderlinge relaties beredeneren, waardoor ze deze niet allemaal afzonderlijk hoeven te leren alsof het losstaande rekenfeiten zouden zijn. Dit helpt ook om gemakkelijk optredende misvattingen te voorkomen, zoals: ‘een vierde deel is hetzelfde als 4%’.
Ook als kinderen al goed zicht hebben op betekenissen en verschijningsvormen van breuken, decimale getallen, verhoudingen en procenten, blijft het helpen om onderlinge relaties te visualiseren, zoals in de voorbeeldopgave hieronder met behulp van het strookmodel.

Bron: Alles Telt Q, groep 7
declaratieve kennis
memoriseren A
productief oefenen
Allerlei relaties moeten uiteindelijk in de vorm van declaratieve kennis beschikbaar zijn. Dit is parate feitenkennis, zoals 1 2 = 5 10 = 0,5 = 1 : 2 en komt overeen met 50%. Deze rekenfeiten moeten uit het hoofd worden geleerd en gememoriseerd, zodat ze snel beschikbaar zijn. Het paraat hebben van zulke rekenfeiten is belangrijk voor het steeds beter kunnen redeneren en rekenen met breuken, decimale getallen, verhoudingen en procenten. Reken-wiskundemethodes bieden daarom hiervoor veel oefenopgaven aan.

Bron: De Wereld in Getallen, groep 8
Sommige rekenfeiten zijn overigens al bekend vanuit informele voorkennis. Veel jonge kinderen weten al dat 50% de helft is en zelfs kleuters hebben vaak al begrip van ‘de helft’. Deze voorkennis omvat vaak meer dan je zou denken.
Kwartetspel
Een actieve vorm van oefenen is kinderen zelf opgaven te laten bedenken. Op deze manier gebruiken ze kennis die ze al hebben, denken ze na over de leerinhoud en oefenen ze tegelijkertijd. Deze vorm van oefenen heet productief oefenen, omdat kinderen zelf opgaven (en rekenfeiten) produceren (zie paragraaf 10.2.2).
Samenhang breuken, decimale getallen, verhoudingen en procenten
Bverschijningsvorm meetgetal
Laat de kinderen van je praktijkgroep een eigen kwartetspel maken met relatieweetjes over breuken, decimale breuken, verhoudingen en procenten. Je zult merken dat ze eerst voor de hand liggende combinaties maken die al eens aan de orde zijn geweest. Zo zullen ze de koppeling tussen 1 2 en de verhouding 1 : 2 eerder maken dan de koppeling tussen 1 2 en de verhouding 3 : 6. Maar als je doorvraagt en kinderen uitdaagt tot het maken van ‘moeilijke’ kwartetsetjes, maken ze ook minder voor de hand liggende combinaties. Laat kinderen samenwerken in groepjes, zodat ze door interactie van elkaar kunnen leren. Sterkere rekenaars zullen op combinaties komen die andere kinderen niet bedenken.
Een verschijningsvorm in de realiteit van zowel breuken als decimale getallen is die van meetgetal. Decimale getallen komen overigens vaker dan breuken voor als meetgetal. Verder zijn er qua verschijningsvormen vooral verschillen: breuken komen bijvoorbeeld vaker voor als deel van een geheel of totaal en deel van een hoeveelheid; decimale getallen bijna nooit.
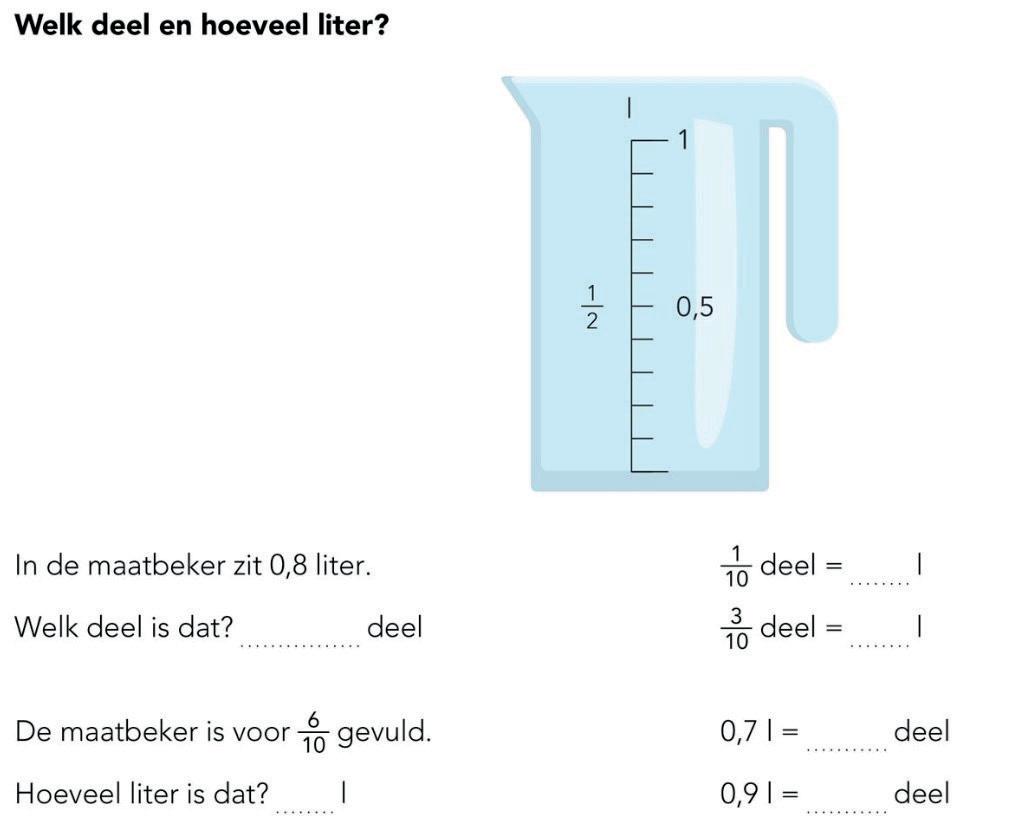
Decimale getallen als meetgetal en breuken als deel van een totaal.
Bron: Pluspunt, groep 7
De overeenkomende verschijningsvorm meetgetal kan worden gebruikt om de relaties tussen breuken en decimale getallen te doorzien en om breuken om te zetten in decimale getallen en omgekeerd. Bijvoorbeeld met behulp van geld, zoals in de opgave hieronder gebeurt. De breuken en decimale
Bbreuk als deling
2 7 , 3 7 , 4 7 , 5 7 , 6 7 en 7 7 dubbele
repeterende breuk repetendum C
getallen kunnen vervolgens op dezelfde plek op de dubbele getallenlijn worden geplaatst, zoals de voorbeeldopgave ook laat zien.

Bron: Pluspunt, groep 7
Van breuk naar decimaal getal
Een andere manier om breuken te schrijven als decimaal getal is door gebruik te maken van het gegeven dat een breuk ook een deling is. Als je bijvoorbeeld 1 : 4 invoert op een rekenmachine, geeft deze als antwoord 0,25. Wanneer je bepaalde breuken, bijvoorbeeld 1 7 , als decimaal getal schrijft door de breuk op te vatten als een deling, kom je tot de ontdekking dat de uitkomst van die deling er bijzonder uitziet. Dat kan je zien met behulp van de rekenmachine: 1 7 = 0,142857142857… en zo verder. Hoe dat komt kan je beredeneren.
Hoeveel zevens gaan er in 1? Dat is 0; noteer een 0 en een komma. Over 1. Nu kijk je naar de tienden. Daarvan heb je er 10, want 1 = 10 10 .
Hoeveel zevens in 10? Dat is 1, over 3.
Hoeveel zevens in 30? Dat is 4, over 2.
Hoeveel zevens in 20? Dat is 2, over 6.
Hoeveel zevens in 60? Dat is 8, over 4.
Hoeveel zevens in 40? Dat is 5, over 5.
Hoeveel zevens in 50? Dat is 7, over 1.
Hoeveel zevens in 10? Dat hadden we zojuist ook al, dus vanaf hier gaat het liedje zich herhalen. Je vindt dus de groep decimalen 142857 die zichzelf herhaalt in 0,142857142857….
De breuk 1 7 heet een repeterende breuk en de groep cijfers 142857 die herhaald worden heet het repetendum.
Repeterende breuken (1)
Reken met behulp van een deling, en wat handig redeneren, het bijbehorende decimale getal van de breuken uit. Noteer steeds 12 decimalen.
Samenhang breuken, decimale getallen, verhoudingen en procenten
Repeterende breuken (2)
Ca Beredeneer waarom het repetendum van een repeterende breuk nooit langer kan zijn dan de waarde van de noemer.
b Hoe ziet het getal 0,2142857… eruit als het als gewone breuk geschreven is? De breuk heeft als repetendum 142857.
c Het getal 0,135135… met repetendum 135 is 5 37 . Laat dit op twee manieren zien.
Van decimaal getal naar breuk
BOmgekeerd kan het ook. Je schrijft het getal dan als een tiendelige breuk die je verder vereenvoudigt. Bijvoorbeeld:
3,152 = 3 + 1 10 + 5 100 + 2 1000 = 3 152 1000
152 en 1000 zijn beide deelbaar door 8, dus de breuk 152 1000 kan worden vereenvoudigd:
3 152 1000 = 3 19 125
Bij een repeterende breuk pas je de volgende werkwijze toe.
Neem bijvoorbeeld 0,461538461538… Vermenigvuldig het getal net zo vaak met 10 als het repetendum lang is. In dit voorbeeld telt het repetendum zes cijfers en vermenigvuldig je dus met 1.000.000. Je krijgt dan
461.538,461538461538….
Trek van deze uitkomst de gezochte breuk af. Dus:
461.538,461538461538….
0,461538461538… –
461.538
Wat overblijft is 999.999 (= 1.000.000 – 1) keer het gezochte getal. In ons voorbeeld is dat 461.538.
Daarmee is de breuk bekend: 461538 999999 en die is te vereenvoudigen tot 6 13
Repeterende breuken (3)
Ca Welke breuken hebben een repetendum als je de breuk schrijft als decimaal getal?
11 20 , 17 25 , 3 32 , 19 57 , 13 125 , 6 75 en 7 75
b Schrijf de breuken als decimale getallen. Rond af, waar van toepassing, op drie decimalen.
1 40 , 7 40 , 7 75 , 3 7 , 1 5 12 , 35 25 , 4 13 en 2 15
Verhoudingen geven altijd een relatief gegeven aan. Procenten zijn een verschijningsvorm van verhoudingen, en geven dus ook altijd een relatief gegeven aan. Breuken kunnen ook een relatief gegeven beschrijven, er staat dan meestal deel bij. Je ziet dat in de voorbeeldopgave (uit het antwoordenboekje) hieronder.

Bron: De Wereld in Getallen, groep 8
Voorkom dat kinderen het idee krijgen dat bijvoorbeeld 20% hetzelfde is als 20 100 en 1 5 . Dat is niet altijd zo, want 20 100 en 1 5 kunnen ook absolute getallen zijn en 20% is altijd een relatief gegeven. Je kunt wel zeggen dat 20% van iets hetzelfde is als het 20 100 deel van iets of het 1 5 deel van iets. Om deze reden moet je ook voorzichtig zijn met het plaatsen van percentages op de getallenlijn tussen 0 en 1, alsof het gebroken getallen zouden zijn. De strook is wel geschikt om percentages te plaatsen en te ordenen, omdat je daarop ook de absolute gegevens kunt plaatsen, en omdat je die kunt begrenzen tot 100%.

Bron: De Wereld in Getallen, groep 7
Samenhang breuken, decimale getallen, verhoudingen en procenten
A CVan breuk naar verhouding en omgekeerd
Hieronder zie je twee opgaven waarbij de relatie wordt gelegd tussen breuken en verhoudingen. Waar zou jij op letten als je deze opgaven zou behandelen in groep 7? Denk bijvoorbeeld aan het volgende.
• Hoe verwoord je de vragen?
• Wat voeg je toe aan de modellen of zou je nog andere modellen toevoegen?
• Welke vragen stel je aan de leerlingen om ze te laten nadenken of om ze op het goede spoor te zetten?
Wissel je ideeën uit met medestudenten of collega’s.

Bron: Alles Telt Q, groep 7

Bron: Getal & Ruimte Junior, groep 7
Verhoudingen op een fotocamera
Op een fotocamera kun je het volgende rijtje getallen aantreffen: 1, 2, 4, 8, 15, 30, 60, 125, 250, 500, 1000. Dit zijn de noemers van breuken die de sluitertijd aangeven, dus 1 1 , 1 2 , 1 4 , 1 8 , 1 15 , 1 30 , enzovoort. De sluitertijd is de tijd
Cdie de sluiter van de camera openstaat, gemeten in seconden. Dus 1 1000 staat voor een sluitertijd van 1 milliseconde. Merk op dat elke sluitertijd in de reeks (ongeveer) de helft van de vorige is.
Een andere reeks die je kunt aantreffen op modellen met meer instelmogelijkheden is: 1, 1.4, 2, 2.8, 4, 5.6, 8, 11, 16, 22.6. Dit zijn de zogeheten diafragmagetallen: een maat voor de grootte van de lensopening. Merk op dat ook hier per stap ongeveer een halvering optreedt. Dit is een halvering van oppervlakte, dus van de hoeveelheid licht die naar binnen kan. Ook deze getallen zijn in feite noemers van breuken.
Beide systemen zijn ontworpen om de hoeveelheid licht die op de gevoelige plaat komt te reguleren (hoewel het effect van een kortere sluitertijd anders is dan van een kleiner diafragma). Door een slimme combinatie van sluitertijd en diafragma te kiezen, kan de fotograaf in vrijwel elke omstandigheid een optimale foto maken. In sommige gevallen voegt de fotograaf nog extra licht toe in de vorm van een flits.
Iemand zegt: ‘De hoeveelheid licht die op de lichtgevoelige cel van je camera valt bij een sluitertijd van 1 125 en diafragma 11 in verhouding tot de hoeveelheid licht die bij een sluitertijd van 1 500 en diafragma 2.8 naar binnen valt, is ongeveer 1 op 4.’
Klopt deze bewering?
Hoeveel blauw?
a Welk deel van de figuur is blauw?
b Wie van de volgende kinderen geeft een correct antwoord?
Jantine zegt: ‘Er zijn 13 blauwe hokjes.’
Petri zegt: ‘De verhouding blauwe en witte hokjes is 13 op 12.’
Mees zegt: ‘ 13 25 deel is blauw.’
Ruud zegt: ‘52% is blauw.’
Pleuni zegt: ‘Ongeveer de helft is blauw.’
c Wat zouden deze kinderen geantwoord hebben bij andere afmetingen, zoals 8 × 8 of 9 × 9?
Samenhang breuken, decimale getallen, verhoudingen en procenten

Bron: Pluspunt, groep 7
absolute gegevens
relatieve gegevens
In deze opgave gaat het om het vergelijken van verschillende situaties, waarbij gevraagd wordt wie de meeste ballen raak gooit. In de opgave staan absolute en relatieve gegevens. Absolute gegevens zijn getallen die naar daadwerkelijke hoeveelheden of aantallen verwijzen. Bijvoorbeeld: 26 ballen (middelste opgave). Bij relatieve gegevens over hoeveelheden of aantallen bekijk je het in verhouding tot iets anders. Het zijn verhoudingsmatige gegevens waaraan je niet direct het daadwerkelijke getal of aantal kunt aflezen. Bijvoorbeeld: 1 2 deel van de ballen. Bij alléén dat laatste weet je het daadwerkelijke aantal ballen nog niet. Om dat te bepalen, heb je het absolute aantal ballen nodig. In dit voorbeeld is het absolute aantal ballen 26. Daarvan is 1 2 deel raak. Dat is dus 26 : 2 = 13 ballen.
AB
gecijferdheid
Verschillende antwoorden mogelijk
a Welke verschillende antwoorden kan je geven op de vraag wie de meeste ballen raak gooit in de vorige voorbeeldopgave?
b Welke oplossingen verwacht je in een groep 7? Wissel je verwachtingen uit met medestudenten of collega’s.
Voor de zich ontwikkelende gecijferdheid van kinderen is het onderscheid tussen absoluut en relatief van groot belang. Zonder begrip van dit onderscheid kun je namelijk veel informatie uit informatiebronnen zoals de media niet goed begrijpen. Juist dit onderscheid tussen absoluut en relatief is erg lastig voor kinderen.
Vrijwilligerswerk.
De gegevens in de volgende tabel komen uit het onderzoek ‘Doe jij vrijwilligerswerk?’, dat Isis (groep 8) heeft gedaan in de bovenbouw van haar school. ja nee totaal
meisjes 39 107 146
jongens 19 79 98
Isis heeft de gegevens ingevoerd in een computerprogramma. Het computerprogramma laat twee stroken zien:
meisjes
jongens
Meester Chahir vraagt: ‘Zijn er verschillen tussen jongens en meisjes?’
Isis antwoordt: ‘Dat kan je niet goed zeggen. Er hebben wel meer meisjes ja gezegd, maar er hebben ook veel meer meisjes meegedaan aan het onderzoek. Je kunt het zo niet vergelijken.
Meester Chahir laat het computerprogramma de gegevens nu in een cirkeldiagram plaatsen:
Samenhang breuken, decimale
jongens meisjes
Isis wijst naar het roodgekleurde stuk bij de meisjes en zegt dat dit inderdaad groter is dan bij de jongens. ‘Maar,’ zegt ze, ‘dat is logisch, want er hebben veel meer meisjes meegedaan aan het onderzoek.’
Met hulp van meester Chahir worden de antwoorden uitgedrukt in breuken: ongeveer een vijfde van de jongens en ongeveer een kwart van de meisjes antwoordt ja. Waarop Isis besluit: ‘Een kwart is meer dan één vijfde, dus de meisjes zeggen iets meer ja, maar dat is ook wel logisch, want er hebben meer meisjes meegedaan aan het onderzoek.’
Isis blijft herhalen dat het logisch is dat er meer meisjes ja antwoorden, omdat er meer meisjes aan het onderzoek meededen. Hieruit kun je afleiden dat zij het relatieve aspect nog niet doorziet, ondanks de verschillende representaties (de strook en het cirkeldiagram). Om kinderen grip te laten krijgen op dit cruciale onderscheid, is het nodig om absolute en relatieve gegevens nadrukkelijk van elkaar te onderscheiden én met elkaar in verband te brengen. Dit kan bijvoorbeeld met het strookmodel.
Voor de opgave wie de meeste ballen raak gooit aan het begin van deze paragraaf zijn hieronder de verschillende situaties getekend in stroken. Bij de stroken staan zowel de absolute gegevens (het aantal keer raak) als de relatie-
verhoudingen en procenten
benoemd
ve gegevens (het percentage). De strook maakt zichtbaar hoe je verschillende relatieve gegevens (het aantal rake worpen in verhouding tot het totale aantal worpen) met elkaar kunt vergelijken: door het totale aantal worpen op 100% te stellen en (dus) de stroken even lang te tekenen.

CSituaties van Tom, Samira en Mo met strookmodel weergegeven.
Om te voorkomen dat kinderen getallen en percentages door elkaar halen, is het verstandig de getallen benoemd te noteren, vooral in het begin van het leerproces. Bijvoorbeeld: zoveel keer raak of zoveel euro. Dit helpt om het onderscheid tussen absolute en relatieve gegevens duidelijk te houden.
Old school
Maak de volgende opgave

De lijst met alle begrippen uit dit hoofdstuk vind je op eDition. Daar vind je ook de uitwerkingen van de C-opgaven uit dit hoofdstuk.
C C C
Getal
a Welke breuk ligt precies in het midden tussen 1 3 en 1 5 ?
b Welke breuk ligt precies in het midden tussen 1 3 en 1 4 ?
Verhouding
Dit jaar gaan 3 op de 5 Nederlanders op vakantie, tegenover 4 op de 7 Belgen. Gaan er relatief gezien meer Nederlanders of meer Belgen op vakantie? En in absolute zin?
Bewerking
a Wat is het verschil tussen 2 : 3 en 2 3 ?
b Wat is het verschil tussen 6 : 2(1+2) en 6 2(1 + 2) ?
B
B quotiënt
Breuken kunnen drie betekenissen hebben: ze kunnen een getal aangeven, een verhouding, en een bewerking. De breuk als getal kan worden geplaatst op de getallenlijn, net zoals hele getallen en decimale getallen. De breuk als verhouding geeft een relatief gegeven aan, bijvoorbeeld ‘een kwart van de jonge basisschoolleraren is man.’ De breuk als bewerking ten slotte, is per definitie een deling.
Rationaal getal
Breuken zijn rationale getallen. Een definitie hiervan is: een rationaal getal is het quotiënt van twee hele getallen, waarvan de tweede niet 0 is. Ook gehele getallen, inclusief 0 en negatieve getallen zijn rationale getallen. De noemer is dan 1. Zo is bijvoorbeeld 10 te noteren als 10 1 , 0 als 0 1 en -5 als - 5 1 Een quotiënt is de uitkomst van een deling. Het quotiënt van 2 en 3, oftewel de uitkomst van 2 : 3, is 2 3 . ‘Ratio’ betekent verhouding. Een breuk is dus een
verhoudingsgetal
verhoudingsgetal, het is de verhouding tussen twee hele getallen (de teller en de noemer).
Bdeel van een geheel deel van een hoeveelheid verdeling
Breuken hebben verschillende verschijningsvormen. Een breuk kan een deel van een totaal aangeven. Dat kan een deel van een geheel zijn, bijvoorbeeld 1 8 deel van een taart of 1 5 deel van een lot. Het kan ook een deel van een hoeveelheid zijn. Bijvoorbeeld 3 4 van het stadion met 12.000 plaatsen is gevuld voor een wedstrijd. Bij beide varianten geeft de breuk een verdeling aan, bijvoorbeeld de verdeling van een taart in acht stukken of de verdeling tussen het aantal bezette plaatsen en lege plaatsen in een stadion.


meetgetal
maat
Net als hele getallen en decimale getallen komen breuken voor als meetgetal. Voorbeelden zijn anderhalve meter, een half uur of, zoals in de afbeelding hieronder, 1 2 inch. De inch is een lengtemaat uit het imperiale systeem (zie het boek Meten, meetkunde en verbanden, hoofdstuk 2). Ook als maat kom je breuken tegen, bijvoorbeeld twee halfjes bruin brood of anderhalve vlaai.


verhouding
De breuk als verhouding komt vaak voor in nieuwsberichten, zoals ‘Een derde van de speeltuinen in Nederland heeft onveilige toestellen’, ‘Driekwart van de schoolleiders is aangemeld in het schoolleidersregister’, en in het bericht hieronder. Het verschil met de verschijningsvorm deel van een hoeveelheid is dat er bij de verschijningsvorm verhouding geen sprake is van een specifieke, bepaalde hoeveelheid (zoals bij deel van een hoeveelheid), maar dat de verhouding kan worden toegepast op verschillende hoeveelheden. Zelfs als je die niet precies weet, zoals ‘alle Nederlandse consumenten’.
‘Achteraf betalen’ verleidt één vijfde van consumenten vaker tot onnodige aankopen
De komst van ‘buy now pay later’ heeft het koopgedrag van consumenten flink veranderd. Ruim één vijfde (22%) van de Nederlandse consumenten doet sindsdien vaker onnodige aankopen. Wat opvalt is dat vooral de jongere generatie hier vatbaar voor is. Een ruime meerderheid (59%) is namelijk tussen de 18 en 34 jaar. Dit in tegenstelling tot de iets oudere generatie van 35 tot en met 54 jaar (31%).
Bron: Baaz.nl, 29-08-2023
De breuk als kans
CBreuken worden ook gebruikt om kansen aan te duiden. Bijvoorbeeld bij dit vraagstuk ‘de kans op een witte bonbon’.
Je hebt drie doosjes met bonbons. In het ene zitten twee witte bonbons, in het andere zitten twee pure bonbons en in het derde doosje zitten een pure en een witte bonbon. Je kiest willekeurig een van de drie doosjes en pakt daaruit ook weer willekeurig een van de twee bonbons. Die bonbon is wit. Wat is nu de kans dat de andere bonbon in het gekozen doosje ook wit is?
1 3 of 1 2 of 2 3 ?
B
rekengetal operator
Ten slotte komen breuken weer net als hele en decimale getallen voor als rekengetal en als operator. Met een rekengetal wordt formeel gerekend, bijvoorbeeld 4 2 3 + 2 3 . Een voorbeeld van de breuk als operator, oftewel bewerker, is 1 4 × 20.
De verschillende verschijningsvormen zijn geen elkaar uitsluitende categorieen. Zo kan de uitkomst van een deling als 2 pizza’s delen met 3 kinderen een deel van een geheel betreffen, namelijk 2 3 pizza. De breuk als punt op de getallenlijn heeft ook een meetaspect: hoe ver is deze breuk verwijderd van nul? In de realiteit van alledag komen voornamelijk eenvoudige breuken voor, zoals in de voorbeelden hierboven. In andere gevallen worden meestal procenten gebruikt, zoals je ook kunt zien in het bericht over achteraf betalen hierboven.
CDe breuk als operator
Waarom is 1 99 × 99 gelijk aan 1?
Allemaal breuken
CIn de afbeelding hieronder zie je breuken in een krantenkop, in reclame, als beeld van de halve maan en als klankduur in de vorm van de muzieknoten.
Welke verschijningsvormen herken je hierin?

Deel van een geheel
Welk deel van de figuren is gekleurd?

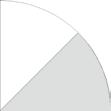

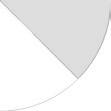


Bgelijkwaardige breuken equivalente breuken vereenvoudigen
Eerlijke verdeling
Jarise verdeelt 5 koeken eerlijk onder 8 personen. Ieder krijgt meer dan een 1 2 koek. Hoeveel meer?
Gelijkwaardige breuken hebben verschillende noemers maar dezelfde waarde. Bijvoorbeeld 3 6 , 5 10 en 500 1000 hebben allemaal dezelfde waarde van een 1 2 en kunnen dus allemaal worden vereenvoudigd tot een 1 2 . In plaats van gelijkwaardige breuken wordt ook wel van equivalente breuken gesproken. Vereenvoudigen van breuken is het zo eenvoudig mogelijk opschrijven van een breuk. Dit kan door de teller en de noemer te delen door hetzelfde getal. Bij bijvoorbeeld 500 1000 kunnen teller en noemer beide worden gedeeld door 100. Dus 500 1000 = 5 10 . Maar 5 10 kan verder worden vereenvoudigd door de teller en de noemer te delen door 5. Dat levert een 1 2 op en die kan niet verder worden vereenvoudigd. Breuken vereenvoudigen kun je dus ook omschrijven als het bepalen van díe schrijfwijze van een breuk waarbij teller en noemer onderling ondeelbaar zijn.
grootste gemene deler (GGD)
Door teller en noemer beide te delen door de grootste gemene deler (GGD) krijg je in één stap een breuk die niet verder te vereenvoudigen is. De GGD is dus het grootste getal waardoor je de teller en noemer allebei kunt delen. Van 500 en 1000 is de GGD 500, dus teller en noemer beide delen door 500 levert in één stap op 500 1000 = 1 2
gelijknamige breuken ongelijknamige breuken
Gelijknamige breuken zijn breuken met dezelfde noemer. Ongelijknamige breuken kunnen altijd gelijknamig worden gemaakt. Bijvoorbeeld 3 4 en 5 6 kunnen gelijknamig worden gemaakt door de tellers en de noemers van beide breuken te vermenigvuldigen met de noemer van de andere breuk.
Dus 3 4 =
kleinste gemene veelvoud (KGV)
en
. Gelijknamig maken van breuken komt van pas bij het vergelijken, ordenen, optellen en aftrekken van breuken. In het voorbeeld van 3 4 en 5 6 is echter ook een kleinere gezamenlijke noemer mogelijk dan 24. Met behulp van het kleinste gemene veelvoud (KGV) kunnen breuken gelijknamig worden gemaakt met een zo klein mogelijke noemer. In dit voorbeeld betekent dat het KGV van 4 en 6 is 12, dus de breuken kunnen onder de kleinste gemeenschappelijke noemer 12 worden gebracht: 9 12 en 10 12
GGD en KGV
Om de breuk 153 255 te vereenvoudigen, ga je op zoek naar de GGD van de teller en de noemer, dus van 153 en 255. Nu wist Euclides (330 v. Chr.) al dat het verschil van 153 en 255, dus 102, dezelfde gemeenschappelijke deler heeft. Nogmaals een paar keer het verschil bepalen (153 – 102 = 51 en 102 – 51 = 51) levert het getal 51 op. Dat is inderdaad de gezochte GGD, want 153 = 3 × 51 en 255 = 5 × 51.
In schema:
102 = 51 + 51 = 2 × 51
153 = 102 + 51 = 3 × 51
255 = 153 + 102 = 5 × 51
Om breuken als 2 153 en 2 255 op te tellen, moet je deze gelijknamig maken. De noemers vermenigvuldigen levert 39.015 op, maar het KGV van 153 en 255 is veel kleiner. We weten dat 153 = 3 × 51 en 255 = 5 × 51 en daarvan kunnen we het KGV afleiden. Dat is 3 × 5 × 51 = 765.
Dus
Meer over de GGD en het KGV lees je in het boek Hele getallen, hoofdstuk 1.
GGD en KGV in groep 8
AVerschillende reken-wiskundemethodes bieden het bepalen van de GGD en het KGV aan in groep 8.
a Zoek uit of de methode van je praktijkschool dit onderwerp aanbiedt. Als het wordt aangeboden, hoe ziet dat er dan uit?
b Probeer met een groepje leerlingen van groep 8 enkele opgaven uit met de GGD en het KGV. Wat zijn de moeilijkheden die leerlingen hierbij ondervinden? Welke ondersteuning kun je bieden?
Deel van een hoeveelheid
C C C
Leroy zegt dat je voor het optellen van breuken eerst een gemeenschappelijk veelvoud moet bepalen. Pas die aanpak van Leroy toe op 1 42 + 8 105 door te denken aan het getal 210. Hoe komt Leroy aan 210?
Autobussen
Twee autobussen, A en B, vertrekken gelijktijdig van een busstation. Bus A is steeds na 1 1 2 uur terug op het busstation, bus B steeds na 1 1 4 uur. Over hoeveel uur treffen ze elkaar weer voor het eerst op het busstation?
Redeneren en rekenen
1 Bereken en schrijf de uitkomst zo eenvoudig mogelijk op.
a 7 2 × 6 3 × 5 4 × 4 5 × 3 6 × 2 7 =
b 1 2 × 2 3 × 3 4 × 4 5 × 5 6 × 6 7 =
c 7 6 × 6 5 × 5 4 × 4 3 × 3 2 × 2 1 =
d 1 1 2 × 1 1 3 × 1 1 4 × 1 1 5 × 1 1 6 × 1 1 7 =
e 1 6 + 1 5 + 1 4 + 1 3 + 1 2 =
2 Welke uitkomst is groter?
a 6 7 × 5 13 of 6 7 + 5 13
b 6 7 : 5 13 of 6 7 –5 13
c 6 7 × 13 5 of 6 7 : 13 5
3 Wat komt op de plaats van de puntjes?
a 1 6 + … = 1 5
b … –1 6 = 1 5
c 13 7 × … = 13
d 1 5 × … = 1 6
e … : 24 25 = 3 5
B CC
In het dagelijks leven kom je veel breukentaal tegen: de helft, een halfje, een half uur, anderhalf uur, een kwart, een kwartier, driekwart, een derde, enzovoort. Kinderen spreken weleens van ‘de grootste helft’, wat wiskundig gezien niet klopt, maar ze geven hiermee het grootste deel aan (als iets in tweeën is verdeeld).
De formele rekentaal omvat de termen ‘teller’, ‘noemer’, ‘breukstreep’, ‘gelijkwaardig’, ‘gelijknamig’ en ‘vereenvoudigen’. De formele notatie van breuken gaat met een horizontale ( 1 5 ) of schuine (1⁄5) breukstreep tussen teller en noemer.
Elk heel getal groter dan 0 kan een noemer zijn. Dus naast gangbare breuken als halven, vijfden, tienden en honderdsten bestaan er ook breuken als drieduizendsten, miljoensten en quadriljardsten. Verschillende breuktypen kennen verschillende benamingen, zoals je in de tabel hieronder ziet.
getal
groter dan 1
Onechte breuk Niet vereenvoudigd gemengd getal
Samengestelde breuk
Uitspraak
Breuk waarvan de teller en noemer zelf ook een breuk zijn
Welke breuken kunnen horen bij de volgende uitspraak: ‘drie-honderd-achttien-duizendste’?
Old school
Maak de onderstaande opgaven met samengestelde breuken voor aanstaande basisschoolleraren.
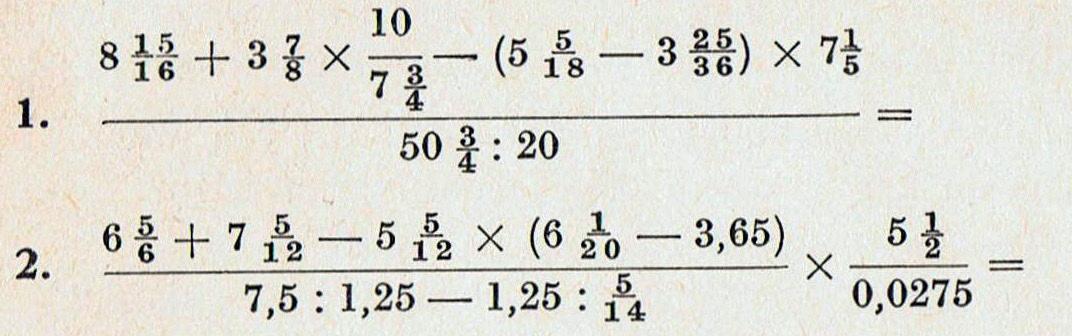
Wij rekenen (1956). Opgaven voor opleidingsscholen
Dankzij verschillende bewaard gebleven papyrusrollen is het een en ander bekend over de rekenkunst in het Egypte van voor onze jaartelling. Een van de bekendste rollen is de Rhind-papyrus. Deze stamt uit ongeveer 1650 tot 1550 voor Christus. Op deze rol staan verschillende wiskundige problemen en de oplossingen daarvan. Daaruit blijkt dat de Egyptenaren toen al breuken kenden. Als een deling niet uitkwam op een heel getal, werkten ze verder met breuken. De Egyptenaren gebruikten voornamelijk stambreuken. Uitzondering daarop was de blijkbaar veelvoorkomende breuk 2 3 en volgens sommige bronnen ook 3 4 .
Een van de opgaven van de Rhind-papyrus is 19 gedeeld door 8. Deze opgave werd opgelost door 8 in te passen in 19. Daarbij werd gebruikgemaakt van verdubbelen en halveren. Dat ging als volgt (hieronder in onze eigen getalsymbolen genoteerd).
1 maal 8 (verdubbelen)
2 maal 16
1 2 maal 4 (halveren)
1 4 maal 2 (halveren)
1 8 maal 1 (halveren)
Daarmee is het getal 19 bereikt: 16 + 2 + 1. De uitkomst van 19 gedeeld door 8 is dus 2 1 4 1 8 (2 + 1 4 + 1 8 ).
Egyptische splitsing
CDe Egyptenaren gebruikten voornamelijk stambreuken. Elke gewone breuk is te schrijven als een som van stambreuken met verschillende noemers. Dat wordt wel een Egyptische splitsing genoemd. Bij 3 8 is dat 1 4 en 1 8 , zoals je hierboven al zag. En bij bijvoorbeeld 4 7 is dat 1 2 + 1 14
a Schrijf de Egyptische splitsing op van 5 6 .
b Schrijf de Egyptische splitsing op van 7 8
c Schrijf de Egyptische splitsing op van 7 15
d Wat is de algemene aanpak om Egyptische splitsingen te vinden?
De lijst met alle begrippen uit dit hoofdstuk vind je op eDition. Daar vind je ook de uitwerkingen van de C-opgaven uit dit hoofdstuk.