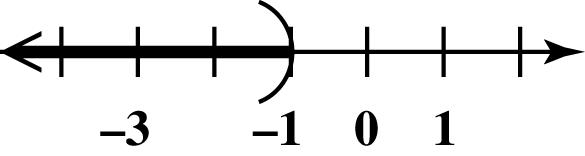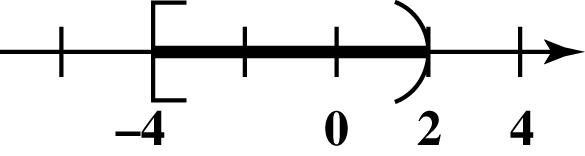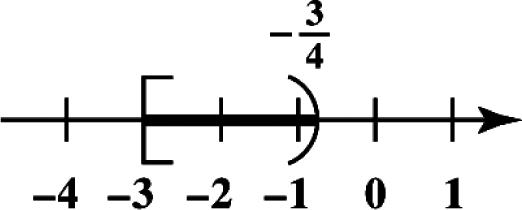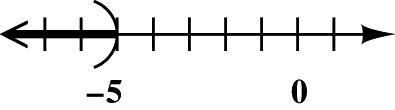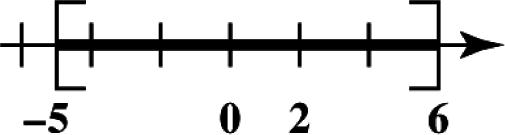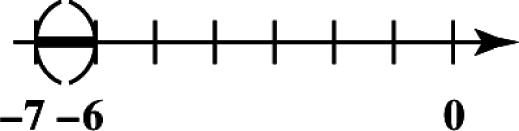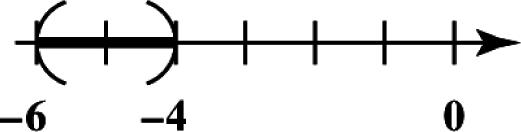Chapter R Review of the Real Number System
R.1 Fractions
Classroom Examples, Now Try Exercises
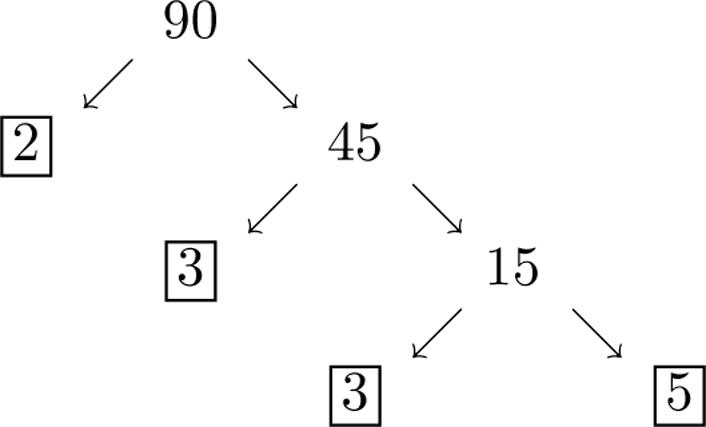
1. 90 is composite and can be written as
Writing 90 as the product of primes gives us 902335
N1. 60 is composite and can be written as
Writing 60 as the product of primes gives us 602235.
2. (a) 12343433 1 20545455
(b) 8811 4868616
(c) 9051855 1 16291899
N2. (a) 30565655 1 42767677
(b) 101011 70710717
(c) 7232433 1 12052455
3. The fraction bar represents division. Divide the numerator of the improper fraction by the denominator. 3 1037 30 7
Thus, 377 3. 1010
N3. The fraction bar represents division. Divide the numerator of the improper fraction by the denominator. 18 592 5 42 40 2
Thus, 922 18. 55
4. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
5315 and 15419
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 419 3. 55
N4. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
31133 and 33235
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 235 11. 33
5. (a) To multiply two fractions, multiply their numerators and then multiply their denominators. Then simplify and write the answer in lowest terms.
518518 925 90 22 925 2 5 5 245 545
(b) To multiply two mixed numbers, first write them as improper fractions. Multiply their numerators and then multiply their denominators. Then simplify and write the answer as a mixed number in lowest terms.
N5. (a) To multiply two fractions, multiply their numerators and then multiply their denominators. Then simplify and write the answer in lowest terms.
(b) Change both mixed numbers to improper fractions. Then multiply by the reciprocal of the second fraction.
(a) To divide fractions, multiply by the reciprocal of the divisor.
(b) To divide fractions, multiply by the reciprocal of the divisor.
(b) To multiply two mixed numbers, first write them as improper fractions. Multiply their numerators and then multiply their denominators. Then simplify and write the answer as a mixed number in lowest terms.
6. (a) To divide fractions, multiply by the reciprocal of the divisor.
7. (a) To find the sum of two fractions having the same denominator, add the numerators and keep the same denominator.
(b) To find the difference of two fractions having the same denominator, subtract the numerators and keep the same denominator.
N7. (a) To find the sum of two fractions having the same denominator, add the numerators and keep the same denominator. 1313 888 4 8 14 24 1 2
(b) To find the difference of two fractions having the same denominator, subtract the numerators and keep the same denominator.
N8. (a) Since 12223 and 8222, the least common denominator must have three factors of 2 (from 8) and one factor of 3 (from 12), so it is 222324.
Write each fraction with a denominator of 24.
55210 1212224 and 339 832 3 84
Now add. 5310910919 12824242424
(b) Write each mixed number as an improper fraction. 1 48 51345 35 48
The least common denominator is 8, so write each fraction with a denominator of 8. 45 8 and 13226 4 13 428
8. (a) Since 30235 and 45335, the least common denominator must have one factor of 2 (from 30), two factors of 3 (from 45), and one factor of 5 (from either 30 or 45), so it is 233590.
Now add. 134526452645 48888 717 , or 8 88
Write each fraction with a denominator of 90. 7321 30 7 39 3 00
and 2224 459 4520
Now add. 7221421425 304590909090
Write 25 90 in lowest terms. 25555 9018518
(b) Write each mixed number as an improper fraction.
9. (a) Since 1025 and 422, the least common denominator is 22520. Write each fraction with a denominator of 20. 3326 1010220
and 1155 45 420
Now subtract. 31651 102020420
(b) Write each mixed number as an improper fraction. 82 31273 31 82
5 63 1297
42 63
The least common denominator is 6, so write each fraction with a denominator of 6. 29 6 and 77214 3326
Now add. 7291429 29 63666 43 6 14 1 , or 7 6
The least common denominator is 8. Write each fraction with a denominator of 8. 27 8 remains unchanged, and 33412 2248
Now subtract. 32712271215 28 , 888 8 27
or 1 7 8
N9. (a) Since 1111 and 933, the least common denominator is 331199. Write each fraction with a denominator of 99.
55945 1111999 and 221122 991199
Now subtract. 52452223 119999999
(b) Write each mixed number as an improper fraction.
151317 42 3636
The least common denominator is 6. Write each fraction with a denominator of 6. 17 6 remains unchanged, and 1313226 3326
Now subtract.
1317261726179 366666
Now reduce. 9333 622 , 3
or 1 1 2
Exercises
1. True; the number above the fraction bar is called the numerator and the number below the fraction bar is called the denominator.
2. True; 5 divides the 31 six times with a remainder of one, so 311 6. 55
3. False; this is an improper fraction. Its value is 1.
4. False; the number 1 is neither prime nor composite.
5. False; the fraction 13 39 can be written in lowest terms as 1 3 since 131311 391333
6. False; the reciprocal of 6 3 2 is 21 63
7. False; Factors of 12 are 1, 2, 3, 4, 6, 12. Factors of 18 are 1, 2, 3, 6, 9, 18. The GCF is 6.
8. False; 2236 , 3339 so 2 3 is equivalent to 6 9
9. 16282 24383
Therefore, C is correct.
10. Simplify each fraction to find which are equal to 5 9 . 355 3 15 2979
655 6 30 5949
22020 237 40 7437 1155 11 55 999 9
Therefore, C is correct.
11. We need to multiply 8 by 3 to get 24 in the denominator, so we must multiply 5 by 3 as well.
55315 88324
Therefore, B is correct.
12. A common denominator for p q and r s must be a multiple of both denominators, q and s. Such a number is qs Therefore, A is correct.
13. Since 19 has only itself and 1 as factors, it is a prime number.
14. Since 31 has only itself and 1 as factors, it is a prime number.
15. 215 23 30 5
Since 30 has factors other than itself and 1, it is a composite number.
16. 50225 255,
so 50 is a composite number.
17. 232 2216 2228 22224 22 4 222 6 2
Since 64 has factors other than itself and 1, it is a composite number.
18. 27 339 8 33 13 33
Since 81 has factors other than itself and 1, it is a composite number.
Copyright © 2025 Pearson Education, Inc.
19. As stated in the text, the number 1 is neither prime nor composite, by agreement.
20. The number 0 is not a natural number, so it is neither prime nor composite.
21. 57319, so 57 is a composite number.
22. 51317, so 51 is a composite number.
23. Since 79 has only itself and 1 as factors, it is a prime number.
24. Since 83 has only itself and 1 as factors, it is a prime number.
25. 262 124 2231,
so 124 is a composite number.
26. 269 138 2323,
so 138 is a composite number.
27. 2250 22125 22525 225 50 55, 0
so 500 is a composite number.
28. 2350 22175 22535 225 70 57, 0
so 700 is a composite number.
29. 21729 27247 271319 3458
Since 3458 has factors other than itself and 1, it is a composite number.
30. 205 1 554 0 1 255
Since 1025 has factors other than itself and 1, it is a composite number.
31. 8181811 1 16282822
32. 141411 1 12343433 4
33. 15353555 1 18363666
34. 164444 2 44 1 545 05 45
35. 903303303 1 15053053055 3
36. 1005 1407 5205205 1 7207207
37. 1811811811 1 9051851855
38. 1611611611 1 64416444 16
39. 14462462466 1 12052452455
40. 132121112111212 1 7117117 777
41. 1 712 7 5 Therefore, 125 1. 77 42. 1 916 9 7 Therefore, 167 1. 99 43. 6 1277 72 5 Therefore, 775 6. 1212 44. 6 15101 90 11 Therefore, 10111 6. 1515
45. 7 1183 77 6
Therefore, 836 7. 1111
46. 5 1367 65 2
Therefore, 672 5. 1313
47. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
5210 and 10313
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 313 2. 55
48. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
7535 and 35641
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 641 5. 77
49. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
81080 and 80383
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 383 10. 88
50. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
31236 and 36238
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 238 12. 33
51. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
51050 and 50151
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 151 10. 55
52. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
618108 and 1081109
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 1109 18. 66
53. 464624 575735
54. 25210 797 5 963
55. 361 1581202 22316 1582060
56. 35151 202142 35115 20212808 152
57. 1121121266 10510525525
58. 1101101255 8724728 87
59. 158158 425425 3542 455 32 5 61 , or1 55
60. 214214 787 374 427 31 , or 8 1 2 2
61. 3213
66. Change both mixed numbers to improper fractions. 311843 37 5656 1843
62.
63. Change both mixed numbers to improper fractions. 12135 31 4343
67. Change both numbers to improper fractions. 121
68. Change both numbers to improper fractions.
64. Change both mixed numbers to improper fractions. 23 33 3 88 21 55 88 5 644 , or 4 1515
65. Change both mixed numbers to improper fractions. 311916 23 8585 1916
69. To divide fractions, multiply by the reciprocal of the divisor. 3 3 772 929 14 27 72
70. To divide fractions, multiply by the reciprocal of the divisor.
74. To divide fractions, multiply by the reciprocal of the divisor.
71. To divide fractions, multiply by the reciprocal of the divisor.
75. To divide fractions, multiply by the reciprocal of the divisor. 331 12 4412
72. To divide fractions, multiply by the reciprocal of the divisor.
76. To divide fractions, multiply by the reciprocal of the divisor.
73. To divide fractions, multiply by the reciprocal of the divisor.
77. To divide fractions, multiply by the reciprocal of the divisor. 365 6 513
78. To divide fractions, multiply by the reciprocal of the divisor.
79. Change the first number to an improper fraction, and then multiply by the reciprocal of the divisor.
82. Change both mixed numbers to improper fractions, and then multiply by the reciprocal of the divisor.
80. Change the first number to an improper fraction, and then multiply by the reciprocal of the divisor.
83. Change both mixed numbers to improper fractions, and then multiply by the reciprocal of the divisor.
81. Change both mixed numbers to improper fractions, and then multiply by the reciprocal of the divisor.
84. Change both mixed numbers to improper fractions, and then multiply by the reciprocal of the divisor.
87. 7171 121212 8 12 24 34 2 3
88. 5351 16161 38 6162
89. Since 933, and 3 is prime, the LCD (least common denominator) is 339. 1133 3339
Now add the two fractions with the same denominator. 51538 93999
90. To add 4 15 and 1 , 5 first find the LCD. Since 1535 and 5 is prime, the LCD is 15. 41413 553 43 1515 1515 43 7 15 15
91. Since 8222 and 623, the LCD is 22224. 3 3339 88324
and 55420 66424
Now add fractions with the same denominator. 3592029 8624244 , 2 or 5 1 24
92. Since 623 and 933, the LCD is 23318. 553 3 15 6618
and 2 22 992 4 18
Now add fractions with the same denominator. 515 , 691818 2419 18
or 1 1 18
93. Since 933 and 1644, the LCD is 3344144. 1680 991 55 6144
and 33927 16169144
Now add fractions with the same denominator. 538027 916144144 107 144
94. Since 422 and 2555, the LCD is 2255100. 332575 4425100
and 66424 25254100
Now add fractions with the same denominator. 36752499 425100010010
95. 1124125 33 88888 11819 22 44444 11259 32 8484
Since 8222 and 422, the LCD is 222 or 8. 112592 32 84842 2518 88 433 , or 5 88
96. 212214 44 1112113 22 2 33333 6 6666
Since 623, the LCD is 6. 3 6 2114213 4 6 2 6326 2813 415 , 66 or 6
97. 1112113 33 44444 44549 11 55555
Copyright © 2025 Pearson Education, Inc.
Since 422, and 5 is prime, the LCD is 22520. 1413594 31 454554 6536 2020 1011 ,or5 2020
98. To add 5 3 4 and 1 1, 3 first change to improper fractions then find the LCD, which is 12. 3123 51 33 23344 4334 6916 12 1 , or 7 12 4 44 12 85 12
99. 72725 9999
100. 8383 11111 5 111 101. 133133 151515 10 15 252 353
113113
103. Since 1243 (12 is a multiple of 3), the LCD is 12. 144 3412
Now subtract fractions with the same denominator. 71743131 123121212434
104. Since 632 (6 is a multiple of 2), the LCD is 6. 1 2 3 3
Now subtract fractions with the same denominator. 5132 5 6666 121 23 23
105. Since 12223 and 933, the LCD is 22336. 3 77321 1212336
and 144 9436
Now subtract fractions with the same denominator. 7121417 129363636
106. The LCD of 12 11111314 and 16 is 48. 1612163124 334 4848 29 48
107. 3316319 44 44444 22527 11 55555
Since 422, and 5 is prime, the LCD is 22520. 3219574 41 454554 9528 2020 677 , or 3 2020
108. Change both numbers to improper fractions then add, using 45 as the common denominator. 4419 31 199135 5995 17165 45 13 5959 45 106 4 16 , o 4 r 55 2
109. 1124125 66 44444 1115116 55 33333
Since 422, and 3 is prime, the LCD is 22312. 112516 65 4343 253164 4334 7564 1212 11 12
110. 33 1115116 55 333 11819 4 2 22 4 22
2 and 3 are prime, so the LCD is 236. 1116293 54 323223 6 3227 6 5 6
111. 74 88 12 4 22722 99999 22214 33333 4
Since 933, and 3 is prime, the LCD is 339. 143 84 33 2274 939 7442 99 35 ,or 3 9 2 9
112. 5584589 1212121212 5524529 66 7 6 44 66 7
Since 12223 and 623, the LCD is 22312. 5589 12612 8 292 74 62 58 12 7 ,or 2 12 9 12 31 12
113. Observe that there are 24 dots in the entire figure, 6 dots in the triangle, 12 dots in the rectangle, and 2 dots in the overlapping region.
(a) 121 242 of all the dots are in the rectangle.
(b) 61 244 of all the dots are in the triangle.
(c) 21 63 of the dots in the triangle are in the overlapping region.
(d) 21 126 of the dots in the rectangle are in the overlapping region.
114. (a) 12 is 1 3 of 36, so Maya got a hit in exactly 1 3 of her at-bats.
(b) 1 is a little less than 1 10 of 11, so Deion got a home run in just less than 1 10 of his atbats.
(c) 9 is a little less than 1 4 of 40, so Christine got a hit in just less than 1 4 of her at-bats.
(d) 8 is 1 2 of 16, and 10 is 1 2 of 20, so Joe and Greg each got hits 1 2 of the time they were at bat.
R.2 Decimals and Percents
Classroom Examples, Now Try Exercises
1. (a) 15 0.15 100
3. (a) 30.21decimal place
0.0523decimal places 604 1510134
1.57044decimal places
(b) 0.062decimal places 0.122decimal places 12 6224
0.00724decimal places
(c) To change the divisor 3.1 into a whole number, move each decimal point one place to the right. Move the decimal point straight up and divide as with whole numbers. 1.21 3137.60 31
We carried out the division to 2 decimal places so that we could round to 1 decimal place. Therefore, 3.763.11.2.
N3. (a) 9.322decimal places 1.41decimal place 3728 932213
13.0483decimal places
(b) 0.61decimal place
0.0043decimal places 24134
0.00244decimal places
(c) To change the divisor 1.3 into a whole number, move each decimal point one place to the right. Move the decimal point straight up and divide as with whole numbers.
We carried out the division to 3 decimal places so that we could round to 2 decimal places. Therefore, 7.3341.35.64.
4. (a) Move the decimal point three places to the right.
19.5100019,500
(b) Move the decimal point one place to the left.
960.11096.01
N4. (a) Move the decimal point one place to the right.
294.72102947.2
(b) Move the decimal point two places to the left. Insert a 0 in front of the 4 to do this.
4.7931000.04793
5. (a) Divide 3 by 50. Add a decimal point and as many 0s as necessary. 0.06 503.00
Therefore, 3 0.06. 50
(b) Divide 11 by 1. Add a decimal point and as many 0s as necessary. 0.090909... 111.000000...
When rounded to the nearest thousandth, this is 0.091 . When rounded to the nearest
hundredth, this is 0.09. When rounded to the nearest tenth, this is 0.1. Note that the pattern repeats. Therefore, 1 0.09, 11
N5. (a) Divide 20 by 17. Add a decimal point and as many 0s as necessary. 0.85 2017.00 160 100 100 0
Therefore, 17 0.85. 20
(b) Divide 2 by 9. Add a decimal point and as many 0s as necessary. 0.222... 92.000...
When rounded to the nearest thousandth, this is 0.222. When rounded to the nearest hundredth, this is 0.22. When rounded to the nearest tenth, this is 0.2. Note that the pattern repeats. Therefore, 2 0.2 9
6. (a) 1 5%5.25% 4 5.25 100 0.0525 (b) 200 200%2.00, 100 or 2
N6. (a) 23 23%0.23 100 (b) 350 350%3.50, 100 or 3.5
7. (a) 0.060.06100%6% (b) 1.751.75100%175%
N7. (a) 0.310.31100%31%
(b) 1.321.32100%132%
8. (a) 85%0.85
(b) 110%1.10, or 1.1
(c) 0.3030%
(d) 0.16516.5%
N8. (a) 52%0.52
(b) 2%02%0.02
(c) 0.4545% (d) 3.53.50350%
9. (a) 65 65% 100 In lowest terms, 6513513 10020520
(b) 1.51.510153 1.5% 100100101000200
N9. (a) 20 20% 100 In lowest terms, 201201 1005205
(b) 160 160% 100 In lowest terms, 16082083 , or 1 10052055
10. (a) 33 100% 5050 3100 % 501 3502 % 50 6%
(b) 11 100% 33 1100 % 31 100 % 3 1 33%, or 33.3% 3
N10. (a) 66 100% 2525 6100 % 251 6254 % 25 24%
(b) 77 100% 99 7100 % 91 700 % 9 7 77%, or 77.7% 9
Exercises
1. 367.9412 (a) Tens: 6 (b) Tenths: 9
(c) Thousandths: 1
(d) Ones: 7
(e) Hundredths: 4
2. Answers will vary. One example is 5243.0164.
3. 46.249
(a) 46.25 (b) 46.2 (c) 46 (d) 50
4. (a) 0.976 (b) 0.865 (c) 0.889 (d) 0.444 5. 4 0.4 10
8. 82 0.82 100
9. 138 0.138 1000
10. 104 0.104 1000
11. 43 0.043 1000
12. 87 0.087 1000
13. 8053805 3.8053 10001000
14. 1665166 5.1665 10001000
27. 12.81decimal place 9.11decimal place 128 1152112 116.482decimal places
28. 34.042decimal places 0.562decimal places 20424 17020224 19.06244decimal places
29. 22.412decimal places 330decimal places 6723 6723202 739.532decimal places
30. 55.762decimal places 720decimal places 11152 39032202 4014.722decimal places
31. 0.21decimal place
0.032decimal places 6123
0.0063decimal places
32. 0.072decimal places
0.0043decimal places 28235
0.000285decimal places
35. To change the divisor 11.6 into a whole number, move each decimal point one place to the right. Move the decimal point straight up and divide as with whole numbers. 2.8 116324.8 232 092 0 000 8 928 0 Therefore, 32.4811.62.8 .
36. To change the divisor 17.4 into a whole number, move each decimal point one place to the right. Move the decimal point straight up and divide as with whole numbers.
4.9 174852.6 696 156 000 6 1566 0 Therefore, 85.2617.44.9 .
37. To change the divisor 9.74 into a whole number, move each decimal point two places to the right. Move the decimal point straight up and divide as with whole numbers. 2.05 9741996.70 1948 4870 4870 0 Therefore, 19.9679.742.05.
38. To change the divisor 5.27 into a whole number, move each decimal point two places to the right. Move the decimal point straight up and divide as with whole numbers. 8.44 5274447.88 4216 2318 2108 2108 2108 0 Therefore, 44.47885.278.44.
39. Move the decimal point one place to the right. 123.26101232.6
40. Move the decimal point one place to the right. 785.91107859.1
41. Move the decimal point two places to the right. 57.1161005711.6
42. Move the decimal point two places to the right. 82.0531008205.3
43. Move the decimal point three places to the right. 0.094100094
44. Move the decimal point three places to the right. 0.025100025
45. Move the decimal point one place to the left. 1.62100.162
46. Move the decimal point one place to the left. 8.04100.804
47. Move the decimal point two places to the left. 124.031001.2403
48. Move the decimal point two places to the left. 490.351004.9035
49. Move the decimal point three places to the left. 23.291000023.2910000.02329
50. Move the decimal point three places to the left. 59.81000059.810000.0598
51. Convert from a decimal to a percent. 0.010.01100%1%
Fraction in Lowest Terms (or Whole Number) Decimal Percent
52. Convert from a percent to a decimal. 2 2%0.02
in Lowest Terms (or Whole Number) Decimal Percent
53. Convert from a percent to a fraction. 5 5%
In lowest terms, 5151 10020520
Fraction in Lowest Terms (or Whole Number) Decimal Percent
54. Convert to a decimal first. Divide 1 by 10. Move the decimal point one place to the left. 1100.1
Convert the decimal to a percent. 0.10.1100%10%
55. Convert the decimal to a percent. 0.1250.125100%12.5%
Fraction in Lowest Terms (or Whole Number) Decimal
56. Convert the percent to a decimal first. 20%0.20, or 0.2 Convert from a percent to a fraction. 20 20%
In lowest terms, 201201 1005205
in Lowest Terms (or Whole Number)
57. Convert to a decimal first. Divide 1 by 4. Add a decimal point and as many 0s as necessary. 0.25 41.00 8
Convert the decimal to a percent. 0.250.25100%25%
Fraction in Lowest Terms (or Whole Number) Decimal Percent
58. Convert to a decimal first. Divide 1 by 3. Add a decimal point and as many 0s as necessary. 0.33... 31.00... 9 10 9 1
Note that the pattern repeats. Therefore, 1 0.3. 3
Convert the decimal to a percent. 0.3330.333100%33.3%, or 1 33% 3
in Lowest Terms (or Whole Number) Decimal
59. Convert the percent to a decimal first. 50%0.50, or 0.5 Convert from a percentl to a fraction. 50 50% 100 In lowest terms, 501501 1002502 Fraction in Lowest Terms (or Whole Number) Decimal
60. Divide 2 by 3. Add a decimal point and as many 0s as necessary. 0.66... 32.00... 18 20 18 2
Note that the pattern repeats. Therefore, 2 0.6. 3
61. Convert the decimal to a percent first. 0.750.75100%75% Convert from a percent to a fraction. 75 75% 100 In lowest terms, 753253 1004254
Fraction in Lowest Terms (or Whole Number) Decimal Percent 3
62. Convert the decimal to a percent. 1.01.0100%100% Fraction in Lowest Terms (or Whole Number)
63. Divide 2 by 5. Add a decimal point and as many 0s as necessary. 0.4 52.0 20 0 0
64. Divide 3 by 5. Add a decimal point and as many 0s as necessary. 0.6 53.0 30 0 0
65. Divide 9 by 4. Add a decimal point and as many 0s as necessary.
69. Divide 5 by 9. Add a decimal point and as many 0s as necessary.
66. Divide 15 by 4. Add a decimal point and as many 0s as necessary.
Note that the pattern repeats. Therefore, 5 0.5, 9 or 0.556 rounded to the nearest thousandth, 0.56 rounded to the nearest hundredth, and 0.6 rounded to the nearest tenth.
70. Divide 8 by 9. Add a decimal point and as many 0s as necessary.
67. Divide 3 by 8. Add a decimal point and as many 0s as necessary.
68. Divide 7 by 8. Add a decimal point and as many 0s as necessary.
Note that the pattern repeats. Therefore, 8 0.8, 9 or 0.889 rounded to the nearest thousandth, 0.89 rounded to the nearest hundredth, and 0.9 rounded to the nearest tenth.
71. Divide 5 by 6. Add a decimal point and as many 0s as necessary. 0.833... 65.000...
Note that the pattern repeats. Therefore, 5 0.83, 6 or 0.833 rounded to the nearest thousandth, 0.83 rounded to the nearest hundredth, and 0.8 rounded to the nearest tenth.
72. Divide 1 by 6. Add a decimal point and as many 0s as necessary. 0.166... 61.000... 6 40 36 40 36 4
Note that the pattern repeats. Therefore, 1 0.16, 6 or 0.167 rounded to the nearest thousandth, 0.17 rounded to the nearest hundredth, and 0.2 rounded to the nearest tenth.
73. 54%0.54
74. 39%0.39
75. 7%07%0.07
76. 4%04%0.04
77. 117%1.17
78. 189%1.89
79. 2.4%02.4%0.024
80. 3.1%03.1%0.031
81. 1 6%6.25%06.25%0.0625 4
82. 1 5%5.5%05.5%0.055 2
83. 0.8%00.8%0.008
84. 0.9%00.9%0.009
85. 0.7979%
86. 0.8383%
87. 0.022%
88. 0.088%
89. 0.0040.4%
90. 0.0050.5%
91. 1.28128%
92. 2.35235%
93. 0.4040%
94. 0.60.6060%
95. 66.00600%
96. 1010.001000%
97. 51 51% 100
98. 47 47% 100
99. 15 15% 100
In lowest terms, 15353 10020520
100. 35 35% 100
In lowest terms, 35757 10020520
101. 2 2% 100
In lowest terms, 2121 10050250
102. 8 8% 100
In lowest terms, 8242 10025425
103. 140 140% 100
In lowest terms, 1407207 , 1005205 or 2 1 5
104. 180 180% 100
In lowest terms, 1809209 , 1005205 or 4 1 5
105. 7.57.51075 7.5% 100100101000
In lowest terms, 753253 1000402540
117. The tip is 20% of $150. The word of here means multiply. 20%of$150
0.20$150$30
The tip is $30, and the total bill is $150 + $30 = $180.
118. The raise is 10% of $15. The word of here means multiply. 10%of$15
0.10$15$1.50
The raise is $1.50 per hour, and the new hourly rate is $1.50 + $15 = $16.50.
119. The discount is 15% of $1000. The word of here means multiply. 15%of$1000
0.15$1000$150
The amount of the discount is $150. The sale price is found by subtracting. $1000$150$850
120. The discount is 25% of $600. The word of here means multiply.
25%of$600
0.25$600$150
The amount of the discount is $150. The sale price is found by subtracting.
$600$160$450
R.3 Basic Concepts from Algebra
Classroom Examples, Now Try Exercises
1. | xx is a natural number greater than 12}
{13, 14, 15, … } is the set of natural numbers greater than 12.
N1. | pp is a natural number less than 6}
{1, 2, 3, 4, 5} is the set of natural numbers less than 6.
2. One answer is | xx is a whole number less than 6.
N2. One answer is | xx is a natural number between 8 and 13.
3. (a) 7 is an integer, a rational number 7 since 7, 1
and a real number.
(b) 3.14, a terminating decimal, is a rational number and a real number.
(c) 42, so it is a whole number, an integer, a rational number, and a real number.
N3. (a) The whole numbers in the given set are in the set {0, 5}.
(b) The rational numbers in the given set are in the set 1 2.4, 1, , 0, 0.3, 5. 2
(c) The irrational numbers in the given set are in the set 5, π.
4. (a) The statement “Some integers are whole numbers” is true since 0 and the positive integers are whole numbers. The negative integers are not whole numbers.
N4. (a) The statement “All integers are irrational numbers” is false. In fact, all integers are rational.
(b) The statement “Every whole number is an integer” is true since the integers include the whole numbers, the negatives of the whole numbers, and 0.
5. (a) |3|3
(b) |3|(3)3
(c) Evaluate the absolute value. Then find the additive inverse.
|3|(3)3 (d) |3|(3)3
(e) Evaluate each absolute value, and then add.
|8||1|819
(f) |81||7|7
N5. (a) |7|(7)7
(b) Evaluate the absolute value. Then find the additive inverse.
|7|(7)7
(c) Evaluate the absolute value. Then find the additive inverse.
|7|(7)7
(d) Evaluate each absolute value, and then subtract.
|4||4|440
(e) 4400
6. Information security analysts: 34.734.7
Word processors and typists: 38.238.2
Since 38.234.7, word processors and typists will show the greater change.
N6. Wind turbine service technicians: 44.344.3
Parking enforcement workers: 37.137.1
Word processors and typists: 38.238.2
Since 37.1 is less than 38.2 and 44.3, parking enforcement workers will show the least change.
(b) The statement “Every real number is irrational” is false. Some real numbers such as 4 , 9 0.3, and 16 are rational. Others such as 2 and are irrational.
Copyright © 2025 Pearson Education, Inc.
7. (a) 25 is true, since 2 is to the left of 5 on a number line.
(b) 84 is false, since 8 is to the left of 4 on a number line, 8 is less than, not greater than, 4.
N7. (a) 51 is false, since 5 is to the left of 1 on a number line, 5 is less than, not greater than, 1.
(b) 76 is true, since 7 is to the left of 6 on a number line.
8. (a) 23 is false, since 2 is to the right of 3 on a number line, it must be greater.
(b) 19 reads “1 is greater than or equal to 9”. This is true, since 1 is to the right of 9 on a number line.
(c) 88 is true. The statement is “8 is less than or equal to 8”. Since 8 is equal to 8, the statement is true.
(d) Since 3(4)12 and 2612, the statement becomes 1212, which is false.
N8. (a) Since 6 is to the left of 5 on a number line, 6 is less than, not greater than 5. The statement is false.
(b) Since 10 is to the left of 2 on a number line, the statement is true
(c) Since the statement is “0.5 is less than or equal to 0.5.” and 0.5 is equal to 0.5, the statement is true
(d) Since 10660 and 8(7)56, the statement becomes 6056, which is true.
Exercises
1. Yes, the choice of variables is not important. The sets have the same description so they represent the same set.
2. (a) The only integer between 6.75 and 7.75 is 7.
(b) There are an infinite number of rational numbers between 1 4 and 3 ; 4 one example is 1 . 2
(c) The number 0 is the only whole number that is not a natural number.
(d) The opposite of any natural number is an integer that is not a whole number; one example is 1.
(e) There are an infinite number of irrational numbers between 4 and 9; one example is 5.
(f) One example is Other answers are possible.
3. The set of natural numbers is {1, 2, 3, … }, so the set of natural numbers less than 6 is {1, 2, 3, 4, 5}.
4. The set is{1, 2, 3, 4, 5, 6, 7, 8}.
5. The set of integers is {,3,2,1,0,1,2,3,}, so the set of integers greater than 4 is {5, 6, 7, 8,… }.
6. The set is {9, 10, 11, 12, …}.
7. The set of integers is {,3,2,1,0,1,2,3,}, so the set of integers less than or equal to 4 is ,4 {,1,0,1,2,3}.
8. The set is {,2,1,0,1,2}.
9. The set of even integers is {,2,0,2,4,}, so the set of even integers greater than 8 is {10, 12, 14, 16, …}.
10. The set is {,7,5,3,1}.
11. This is the set of numbers that lie a distance of 4 units from 0 on the number line. Thus, the set of numbers whose absolute value is 4 is {4,4}.
12. The set is {7,7}.
13. | xx is an irrational number that is also rational}
Irrational numbers cannot also be rational numbers. The set of irrational numbers that are also rational is .
14. The set is , the empty set.
15. {2, 4, 6, 8} can be described by | xx is an even natural number less than or equal to 8.
16. {11, 12, 13, 14} can be described by | xx is an integer between 10 and 15.
17. {4, 8, 12, 16, …} can be described by | xx is a multiple of 4 greater than 0.
18. {,6,3,0,3,6,} can be described by | xx is an integer multiple of 3 .
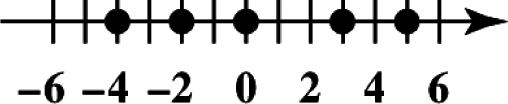
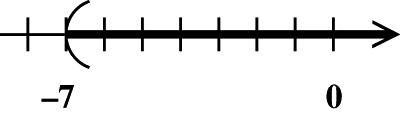
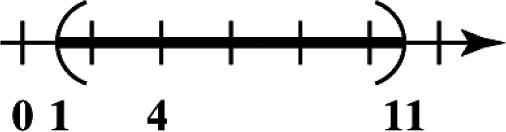
19. Place dots for 4,2,0,3, and 5 on a number line.
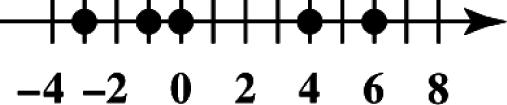
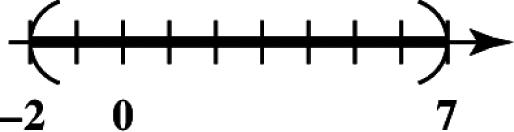
20. Place dots for 3,1,0,4, and 6 on a number line.
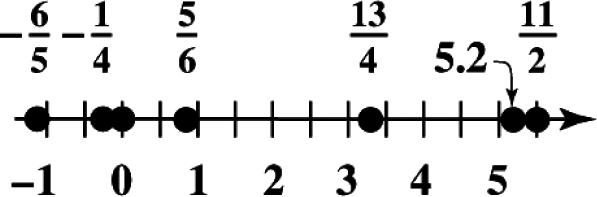
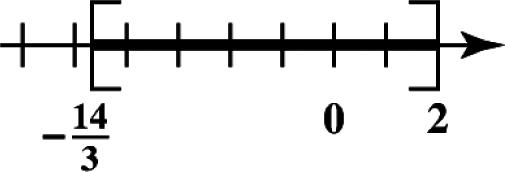
21. Place dots for 61 1.2,0.25,0, 54
513 0.83,3.25,5.2, 64 and 11 5.5, 2 on a number line.
22. Place dots to indicate the points 2 0.6,0, 3
4129 0.8,2.4,4.5, 552 and 4.8 on a number line.
23. (a) The elements 8, 13, and 75 5 (or 15) are natural numbers.
(b) The elements 0, 8, 13, and 75 5 are whole numbers.
(c) The elements 9, 0, 8, 13, and 75 5 are integers.
(d) The elements 6 9,0.7,0, ,4.6, 7 21 8,,13, 2 and 75 5 are rational numbers.
(e) The elements 6 and 7 are irrational numbers.
(f) All the elements are real numbers.
24. (a) The elements 5, 17, and 40 2 (or 20) are natural numbers.
(b) The elements 0, 5, 17, and 40 2 are whole numbers.
(c) The elements 8, 0, 5, 17, and 40 2 are integers.
(d) The elements 313 42 8,0.6,0, ,5,, 17, and 40 2 are rational numbers.
(e) The elements 5,3, and are irrational numbers.
(f) All the elements are real numbers.
25. The statement “Every integer is a whole number” is false. Some integers are whole numbers, but the negative integers are not whole numbers.
26. The statement “Every natural number is an integer” is true. The integers include the natural numbers, their negatives, and zero.
27. The statement “Every irrational number is an integer” is false. Irrational numbers have decimal representations that neither terminate nor repeat, so no irrational numbers are integers.
28. The statement “Every integer is a rational number” is true. Every integer q can be written as 1 q
29. The statement “Every natural number is a whole number” is true. Whole numbers consist of the natural numbers and zero.
30. The statement “Some rational numbers are irrational” is false. No rational numbers are irrational numbers.
31. The statement “Some rational numbers are whole numbers” is true. Every whole number is rational.
32. The statement “Some real numbers are integers” is true. Every integer is a real number.
33. The statement “The absolute value of any number is the same as the absolute value of its additive inverse” is true. The distance on a number line from 0 to a number is the same as the distance from 0 to its additive inverse.
34. The statement “The absolute value of any nonzero number is positive” is true. Every nonzero number is a positive distance from 0.
Copyright © 2025 Pearson Education, Inc.
35. (a) (4)4 (Choice A)
(b) |4|4 (Choice A)
(c) |4|(4)4 (Choice B)
(d) |(4)||4|4 (Choice B)
36. In general ||xa (with 0 a ), is true for two values of a; namely, a and a In this case, ||4 x is true for 4 x and 4. x
37. (a) The additive inverse of 6 is 6.
(b) 60, so |6|6.
38. (a) The additive inverse of 9 is 9.
(b) 90, so |9|9.
39. (a) The additive inverse of 12 is (12)12.
(b) 120, so 12(12)12.
40. (a) The additive inverse of 14 is (14)14.
(b) 140, so 14(14)14.
41. (a) The additive inverse of 6 5 is 6 5
(b) 6 0, 5 so 66 55
42. (a) The additive inverse of 0.16 is 0.16.
(b) 0.160, so 0.160.16.
43. Use the definition of absolute value. 80, so 8(8)8.
44. 19(19)19
45. 3 0, 2 so 33 22
46. 33 44
47. 5(5)5
48. 12(12)12
49. 2[(2)](2)2
50. 6[(6)](6)6
51. 4.5(4.5)4.5
52. 12.4(12.4)12.4
53. 23235
54. 1614161430
55. 109(1)1
56. 126(6)6
57. 93936
58. |10|71073
59. 123123 33 0
60. 731073100
61. (a) The greatest absolute value is 18.418.4. Therefore, Utah had the greatest change in population. The population increased by 18.4%.
(b) The least absolute value is 2.32.3. Therefore, Ohio had the least change in population. The population increased by 2.3%.
62. (a) The greatest absolute value is 2.92.9. Therefore, used cars/trucks showed the greatest change in CPI. It decreased by 2.9%.
(b) The least absolute value is 0.50.5. Therefore, food showed the least change in CPI. It increased by 0.5%.
63. Compare the depths of the bodies of water. The deepest, that is, the body of water whose depth has the greatest absolute value, is the Pacific Ocean 14,04014,040 followed by the Indian Ocean 12,80012,800, the Caribbean Sea 84488448, the South China Sea 48024802, and the Gulf of California 23752375.
64. Compare the heights of the mountains. The shortest, that is, the smallest value, is Point Success 14,16414,164 followed by Rainier 14,41014,410, Matlalcueyetl
14,63614,636, Steele
16,62416,624, and Denali
20,31020,310
65. True; the absolute value of the depth of the Pacific Ocean is 14,04014,040 which is greater than the absolute value of the depth of the Indian Ocean, 12,80012,800.
66. False; the absolute value of the depth of the Gulf of California is 23752375 which is less than the absolute value of the depth of the Caribbean Sea, 84488448.
67. True; since 6 is to the left of 1 on a number line, 6 is less than 1.
68. True; since 4 is to the left of 2 on a number line, 4 is less than 2.
69. False; since 4 is to the left of 3 on a number line, 4 is less than 3, not greater.
70. False; since 3 is to the left of 1 on a number line, 3 is less than 1, not greater.
71. True; since 3 is to the right of 2 on a number line, 3 is greater than 2.
72. True; since 6 is to the right of 3 on a number line, 6 is greater than 3.
73. False; since 33,3 is not greater than 3.
74. False; since 55,5 is not less than 5.
75. The inequality 62 can also be written 26. In each case, the inequality symbol points toward the smaller number so both inequalities are true.
76. 51 is equivalent to 15.
77. 94 is equivalent to 49.
78. 61 is equivalent to 16.
79. 510 is equivalent to 105.
80. 712 is equivalent to 127.
81. “7 is greater than 1 ” can be written as 71.
82. “4 is less than 10” can be written as 410.
83. “5 is greater than or equal to 5” can be written as 55.
84. “6 is less than or equal to 6” can be written as 66.
85. “133 is less than or equal to 10” can be written as 13310.
86. “514 is greater than or equal to 19” can be written as 51419.
87. “50 is not equal to 0” can be written as 500.
88. “67 is not equal to 13” can be written as 6713.
89. 05False
90. 110False
91. 77True
92. 1010True
93. ? 673 610True
The last statement is true since 6 is to the left of 10 on a number line.
94. ? 741 75True
95. ? 2546 1010True
96. ? 8735 1515True
97. ? 33 33True
98. ? 44 44True
99. ? 86 86False
100. ? 104 104False
Copyright
101. 2021: IA15.0, OH10.5, PA8.1
In 2021, Iowa (IA), Ohio (OH), and Pennsylvania (PA) had production greater than 8 billion eggs.
102. IA: 15.015.5;PA: 8.19.0
For Iowa (IA) and Pennsylvania (PA), egg production was less in 2021 than in 2020.
103. 2021: TX6.4,OH10.5 xy
Since 6.410.5, xy is true.
104. 2020: IA15.5,PA9.0 xy
Two inequalities that compare the production in these two states are xy and .yx
R.4 Operations on Real Numbers
Classroom Examples, Now Try Exercises
1. (a) 6(15)(615)21 (b) 1.1(1.2)(1.11.2)2.3
(c) 3535 4848 65 88 11 8
N1. (a) 4(9)(49)13
(b) 7.25(3.57)(7.253.57) 10.82
(c) 2323 510510 43 1010 7 10
2. (a) Subtract the lesser absolute value from the greater absolute value (73), and take the sign of the larger.
3(7)(73)4 (b) 37734 (c) 3.84.64.63.80.8
(d) 3131232 8484288 321 888
N2. (a) Subtract the lesser absolute value from the greater absolute value (157), and take the sign of the larger.
157(157)8 (b) 5121257 (c) 4.6(2.8)4.62.81.8 (d) 5257293518 9797796363 351817 636363
3. (a) 5125(12)7 (b) 12(5)12517 (c) 11.5(6.3)11.56.3 (11.56.3) 5.2
(d) 32323324 43434334 9817 121212
N3. (a) 9159(15)6 (b) 4114(11)15 (c) 5.67(2.34)5.672.34 (5.672.34) 3.33
(d) 43434539 95959559 20277 454545
4. (a) 6(2)816281 4(8)1 121 13
(b) 3[(7)15]6386 116 17
N4. 4(27)124(9)12 4912 512 7
5. 1(8)1877
N5. 10(7)1071717
6. (a) 7(2)14
The numbers have different signs, so the product is negative.
(b) 0.9(15)13.5
(c) 5528(16)10 88
(d) 0(3)0(3)0
The multiplication property of 0 states that any product of any real number and 0 is 0.
N6. (a) 3(10)30
The numbers have the same sign, so the product is positive.
(b) 0.7(1.2)0.84
The numbers have different signs, so the product is negative.
(c) 88311(33)24 1111
(d) 14(0)1400
The multiplication property of 0 states that any product of any real number and 0 is 0.
7. (a) 151 155 33
(b) 2.7 9 0.3
(c) 10 0 is undefined.
(d) 37316344 4164747 3412
(e) 3 311316 8 11 816811 16 3286 81111
(b) 1.5 5 0.3
(c) 0 0 4
6367237 575353 2714 55
Exercises
1. The sum of two positive numbers is a positive number. For example, 18624.
2. The sum of two negative numbers is a negative number. For example, 7(21)28.
3. The sum of a positive number and a negative number is negative if the negative number has the greater absolute value. For example, 1495.
4. The sum of a positive number and a negative number is positive if the positive number has the greater absolute value. For example, 15(2)13.
5. The difference of two positive numbers is negative if the number with the greater absolute value is subtracted from the one with the lesser absolute value. For example, 5127.
6. The difference of two negative numbers is negative if the number with lesser absolute value is subtracted from the one with greater absolute value. For example, 15(3)12.
7. The product of two numbers with the same sign is positive. For example, (2)(8)16 and 2816.
8. The product of two numbers with different signs is negative. For example, 5(15)75.
9. The quotient formed by any nonzero number divided by 0 is undefined, and the quotient formed by 0 divided by any nonzero number is 0. For example, 17 0 is undefined and 0 42 is equal to 0.
10. The sum of a positive number and a negative number is 0 if the numbers are additive inverses. For example, 4(4)0.
11. 6(13)(613)19
12. 8(16)(816)24
13. 156(156)9
14. 179(179)8
15. 13(4)1349
16. 19(13)19136
17. 172222175
18. 121616124
19. 7328919 34121212
20. 541587 69181818
21. The difference between 4.5 and 2.8 is 1.7. The number with the greater absolute value, 4.5 is positive, so the answer is positive. Thus, 2.84.51.7.
22. 3.86.26.23.8 2.4
23. 494(9)5
24. 373(7)4
25. 656(5)(65)11
26. 8178(17)(817)25
27. 8(13)81321
28. 12(22)122234
29. 16(3)16313
30. 21(6)21615
31. 12.31(2.13)12.312.13 (12.312.13) 10.18
32. 15.88(9.42)15.889.42 (15.889.42) 6.46
33. 9494274067 103103303030
34. 333362127 144144282828
35. 8614(14)14
36. 71522(22)22
37. 4955
38. 5611
39. 24242(4)6
40. 1613161316(13)3
41. 759(75)92911
42. 12141821816
43. 6(2)8628880
44. 7(4)11741111110
45. 8(12)2681226 2026 186 12
46. 3(14)6431464 1764 114 7
47. 94(3)6(94)36 1336 106 4
Copyright © 2025 Pearson Education,
48.
49.
50.
102(5)16 102516 10316 1316 3
57. 11572 11572 672 12 1
58. 6348 6348 948 58 3
59. 4 A and 2. B The distance between A and B is the absolute value of their difference.
4266
60. 4 A and 5. C The distance between A and C is the absolute value of their difference.
4599
61. 6 D
and 1 . 2 F The distance between D and F is the absolute value of their difference. 1121 6 222 13 2 131 ,or6 22
62. 3 2 E and 5. C The distance between E and C is the absolute value of their difference. 3310 5 222 13 2 131 ,or6 22
63. It is true for multiplication (and division). It is false for addition and subtraction when the number to be subtracted has the lesser absolute value. A more precise statement is, "The product or quotient of two negative numbers is positive."
64. Because the reciprocal of a number is the quotient of 1 (a positive number) and the number, the reciprocal always has the same sign as the number.
65. The product of two numbers with the same sign is positive, so 8(5)40.
66. The product of two numbers with the same sign is positive, so 20(4)80.
67. The product of two numbers with different signs is negative, so 5(7)35.
68. The product of two numbers with different signs is negative, so 6(9)54.
69. 4(0)400
The multiplication property of 0 states that any product of any real number and 0 is 0.
70. 0(8)080
The multiplication property of 0 states that any product of any real number and 0 is 0.
71. 11 22(0)00
The multiplication property of 0 states that any product of any real number and 0 is 0.
72. 0(4.5)04.50
The multiplication property of 0 states that any product of any real number and 0 is 0.
73. The product of two numbers with different signs is negative, so 33(16)4412. 44
74. The product of two numbers with different signs is negative, so 33(35)5721. 55
75. The product of two numbers with the same sign is positive, so 11 10252. 55
76. The product of two numbers with the same sign is positive, so 11 22(18)299.
77. The product of two numbers with the same sign is positive, so 5125266 2252555
78. The product of two numbers with the same sign is positive, so 9219373 . 7367494
79. The product of two numbers with the same sign is positive, so 324338 1. 8989
80. The product of two numbers with the same sign is positive, so 2222211 1. 1141122
81. The product of two numbers with the same sign is positive, so 0.80.50.4.
82. The product of two numbers with the same sign is positive, so 0.50.60.3.
83. The product of two numbers with different signs is negative, so 0.06(0.4)0.024.
84. The product of two numbers with different signs is negative, so 0.08(0.7)0.056.
85. The quotient of two nonzero real numbers with different signs is negative, so 1411 14277. 222
86. The quotient of two nonzero real numbers with different signs is negative, so 3911 393133. 131313
87. The quotient of two nonzero real numbers with the same sign is positive, so 2411 24466. 444
88. The quotient of two nonzero real numbers with the same sign is positive, so 4511 45595. 999
89. The quotient of two nonzero real numbers with different signs is negative, so 10011 1004254. 252525
90. The quotient of two nonzero real numbers with different signs is negative, so 15011 1505305. 303030
91.
92.
93. Division by 0 is undefined, so 5 0 is undefined.
94. Division by 0 is undefined, so 13 0 is undefined.
95. The quotient of two nonzero real numbers with the same sign is positive, so
71712152613 10610630303015
11343935 1216484848
107. 3591019 812242424
108. 114332053 159454545
109. 723214274422 3045109090909045
110. 8733270929 1562060606060
111. 8524522 251255345315
112. 973373721 20154535455100
594533223 6105232555
495223351 320123225434
814815 315314 2435 327 45 7 20 7
12181225 525518 22355 5233 25 3 101 ,or3 33
2 22212121 3 231323263
3 36313131 4 6414646248
119. 8 828383244 9 2 939292183 3
120. 15 153158 16 3 168163 8 1581205 163482
121.
122.
8.623.7518.623.75132.351
123. 2.5(0.8)(1.5)(2)(1.5)3
124. 1.6(0.5)(2.5)(0.8)(2.5) 2
125. 24.8464.14
126. 32.8484.105
127. 2496(0.52)4800
128. 1875(0.25)7500
129. 1001001 100100100 1 0.01100
130. 60606100 6060 6 0.061006 100 101001000
131. 14.29.814.39
132. 89.4121.32568.085
133. To find the difference between these two temperatures, subtract the lowest temperature from the highest temperature. 100(80)10080 180
The difference is 180°F.
134. 120(29)12029 149
The difference is 149°F.
135. 48.3535.9920.0028.5066.27
12.3620.0028.5066.27
7.6428.5066.27
36.1466.27
30.13
His balance is $30.13.
136. 37.6025.9919.3425.0058.66
11.6119.3425.0058.66
7.7325.0058.66
32.7358.66
25.93
Her balance is $25.93.
137. 382.4525.1034.5045.0098.17 466.02
His balance is $466.02.
(a) To pay off the balance, his payment should be $466.02.
(b) 466.0230024.66190.68 His balance is $190.68.
138. 237.5947.2512.3920.00222.73
Her balance is $222.73.
(a) To pay off her balance, her payment should be $222.73.
(b) 222.7375.0032.06179.79 Her balance is $179.79.
139. (a) 4.9316.278.41(28.46)30.18 31.33
The sum for 2018–2022 was 31.33%. (b) 28.468.4136.87
The difference between the percents from 2021 and 2020 was 36.87%.
(c) 30.1828.4658.64
The difference between the percents from 2022 and 2021 was 58.64%.
140. (a) 14222518577475
The total is $475 thousand, which represents a loss of $475 thousand.
(b) 7718577185 262
The difference was $262 thousand dollars.
(c) 225(142)225142 83
The difference was $83 thousand dollars.
141. Year Difference (in billions)
2001 $1991$1863$128
2006 $2407$2655$248
2011 $2303$3603$1300
2016 $3268$3853$585
2021 $4047$6822$2775
142. There was a surplus in the year 2001. There were defecits in the years 2006, 2011, 2016, and 2021. A positive difference between receipts and outlays indicates a surplus, while a negative difference indicates a deficit.
R.5 Exponents, Roots, and Order of Operations
Classroom Examples, Now Try Exercises
1. (a) 4 22222 77777
(b) (10)(10)(10)(10)3
N1. (a) (3)(3)(3)(3)3
5 tttttt
2. (a) 5 22222232
(b) 2 (0.5)(0.5)(0.5)0.25
(c) 3 (4)(4)(4)(4)64
(d) 4 (4)(4)(4)(4)(4)256
N2. (a) 3 5555125
(b) 4 2222216 55555625
(c) 2 (3)(3)(3)9
3 (3)(3)(3)(3)27
3. (a) 4 33333 933 27381
(b) 4 (3)(3)(3)(3)(3)81
(c) 4 3(3333)81
N3. (a) 2 77749 (b) 2 (7)(7)(7)49 (c) 2 7(77)49
4. (a) 497 because 7 is positive and 2 749.
(b) 12111 819 because 2 11121 , 981
so 12111 . 819
(c) 497 because the negative sign is outside the radical symbol.
(d) 49 is not a real number.
N4. (a) 12111 because 2 11121.
(b) 10010 93 because 2 10100 39
(c) 12111 because the negative sign is outside the radical symbol.
(d) 121 is not a real number.
5. (a) 5924458Multiply. 53Add.
(b) 41242432Divide. 46Multiply. 2Subtract.
N5. 1534215122Multiply. 32Subtract. 5Add.
6. (a) Add and subtract inside parentheses. 2 2 (42)4(83) 645
Evaluate the power.
6165
105Subtract from left to right. 15
(b) 52 61218 43 512218 6 4131 6036 6Multiply. 43
Subtract left from right. 61512 21
N6. (a) Work inside the absolute value bars. 2 510537
Subtract inside the absolute value bars. 2 2 51054 51054Take absolute value. 251054Evaluate the power. 2524Divide. 234Add.
27Subtract.
(b) 25 6916 38 29516 6 3181 1880 6Multiply 38
6610Subtract from left 10to right.
7. 2 1 1069 2 5 1231 6 1 1063 2 Evaluate powers and roots. 5 1291 6 563 Multiply. 1091 13 Add and subtract. 11 2 Undefined 0
N7. 2 2 3643 28328 649 Evaluate powers and roots. 48328 636 Multiply. 42428 30 Add and subtract. 2828 30 Undefined. 0
8. (a) 5 5(12)(3)64 1121 5(12)3(8) 121 6024 121 8484 1313 xzy x
(b) 2323 242(3) 162(27) 16(54) 38 wz
N8. (a) 323724 218 218 29 yx
(b) 22(4)36 33(4)(7) 166 3(4)(7) 166 12(7) 166 84 105 8442 xz xy
Exercises
1. 6 7(777777) 117,649, 6 (7)(7)(7)(7)(7)(7)(7) 117,649
Thus, the original statement, 66 7(7), is false. Note that the statement 66 7(7) is true
2. 5(5)77 is true. 77 (5)5 since (5)7 has an odd number of negative factors.
3. The statement “25 is a positive number” is true. The symbol always gives a positive square root provided the radicand is positive.
4. 3583(58) is true. The order of operations says that multiplication should be done before addition.
5. The statement “(6)7 is a negative number” is true. 7 (6) gives an odd number of negative factors, so the product is negative.
6. The statement “(6)8 is a positive number” is true. (6)8 gives an even number of negative factors, so the product is positive.
7. The statement “The product of 10 positive factors and 10 negative factors is positive” is true. The product of an even number of negative factors is positive.
8. The statement “The product of 5 positive factors and 5 negative factors is positive” is false. The product of 5 positive factors is positive and the product of 5 negative factors is negative, so the product of these two products is negative.
9. The statement “In the exponential expression 5 2, the base is 2 ” is false. The base is 2, not 2. If the problem were written 5 (2), then 2 would be the base.
10. The statement “ a is positive for all positive numbers a” is true.
16. 4 (4)(4)(4)(4)(4)
17. 2 (0.8)(0.8)(0.8)
18. (0.1)(0.1)(0.1)(0.1)(0.1)(0.1)(0.1)6
19. 7 zzzzzzzz
20. 5 aaaaaa
21. (a) 2 864 (b) 2 8(88)64 (c) 2 (8)(8)(8)64
(d) 2 (8)(64)64
22. (a) 3 464 (b) 3 4(444)64 (c) 3 (4)(4)(4)(4)64 (d) 3 (4)(64)64
23. 2 44416
24. 2 66636
25. 3 (0.3)(0.3)(0.3)(0.3)0.027
26. 3 (0.1)(0.1)(0.1)(0.1)0.001
27. 3 11111 5555125
4 11111 66666 11 66661296
4 44444 55555 4444256 5555625
33. 8 (2)(2)(2)(2)(2)(2)(2)(2)(2)
34. 6 (3)(3)(3)(3)(3)(3)(3)729
35. 6 3(333333)729
36. 6 4(444444)4096
37. 4 8(8888)4096
38. 3 10(101010)1000
39. (a) 2 7 is negative because the negative sign is not part of the base.
(b) 2 (7) is positive because the negative sign is part of the base, and the base is squared, so there are an even number of factors.
(c) 3 7 is negative because the negative sign is not part of the base.
(d) (7)3 is negative because the negative sign is part of the base, and the base is cubed, so there are an odd number of factors.
(e) 4 7 is negative because the negative sign is not part of the base.
(f) 4 (7) is positive because the negative sign is part of the base, and the base is raised to the fourth power, so there are an even number of factors.
40. (a) 14412, which is choice B.
(b) 144 is not a real number, which is choice C.
(c) 14412, which is choice A.
41. 819 since 9 is positive and 2 981.
42. 648 since 8 is positive and 2 864.
43. 16913 since 13 is positive and 2 13169.
44. 22515 since 15 is positive and 2 15225.
45. 400400(20)20
46.
900900(30)30
47. 10010 12111 since 10 11 is positive and 2 10100 . 11121
48. 22515 16913 since 15 13 is positive and 2 15225 . 13169
49. 2 0.49(0.7)(0.7)0.7
50. 2 0.64(0.8)(0.8)0.8
51. There is no real number whose square is negative, so 36 is not a real number.
52. There is no real number whose square is negative, so 121 is not a real number.
53. If a is a positive number, then a is a negative number. Therefore, a is not a real number, and aisnotarealnumber
54. If a is a positive number, then a is also a positive number, and a is a negative number.
55. (a) Since 91539514, Student B was correct.
(b) The reasoning was incorrect. The operation of division must be done first, and then the addition follows. The “Order of Process rule” given by Student B is not correct. It just happens coincidentally in this problem that the correct answer was obtained in the wrong way.
56. 77777771497 8497 577 50
57. 12341212Multiply. 24Add.
58. 15521510Multiply. 25Add.
59. 6312418124Multiply. 183Divide. 15Subtract.
60. 94823682Multiply. 364Divide. 32Subtract.
61. 10302310153Divide. 1045Multiply. 55Add.
62. 1224321282Divide. 1216Multiply. 28Add.
63. 2 3(5)(2)(8) 3(25)(2)(8)Evaluatepower. 7516Multiply. 91Subtract.
64. 2 9(2)(3)(2) 9(4)(3)(2)Evaluate power. 366Multiply. 42Subtract.
65. 573(2)3
573(8)Evaluate power. 5218Multiply, change sign. 168Subtract. 8Add.
66. 435(3)3 435(27)Evaluate power. 41527Multiply. 1927Subtract. 8Add.
67. 736(2)(3) 7(6)(2)(3)Evaluate root. 426Multiply. 48Subtract.
68. 864(3)(7)
8(8)(3)(7)Evaluate root. 6421Multiply. 85Subtract.
69. Simplify within absolute value bars. 645243 61243
6(1)243Take absolute value. 68Multiply and divide.
2Subtract.
70. Simplify within absolute value bars. 42482 4282
4(2)82Take absolute value. 816Multiply. 8Add.
71. Simplify within absolute value bars. 2 2 2 65(8)3 11(8)3 11(8)3Take absolute value. 11(8)9Evaluate power. 889Multiply. 97Subtract.
72. Simplify within absolute value bars. 2 2 2 23(9)4 5(9)4
5(9)4Take absolute value. 5(9)16Evaluate power. 4516Multiply. 61Subtract.
73. Simplify within parentheses. 2 2 2 1845(37) 1845(4) 18454Simplify parentheses. 181654Evaluate power. 254Subtract. 74Add. 11Add.
74. Simplify within parentheses. 2 2 2 1029(18) 1029(7) 10297Simplify parentheses. 10497Evaluate power. 697Subtract. 157Add. 22Add.
75. 25 6(9)166(6)10Multiply. 38 010Add. 10Subtract.
76. 35 7(8)127610Multiply. 46 1310Add. 23Add.
77. 2 14(2610) 7 4(1210)Multiply. 42Work inside parentheses. 2Divide.
78. 3 12653 4 9303Multiply. 910Work inside parentheses. 1Subtract.
79. Evaluate root and power in numerator, and subtract in the denominator. (54)22 52 (52)4 7 (3)4 Work inside parentheses. 7 7 Subtract. 7 1Divide.
80. Evaluate root and power in numerator, and subtract in the denominator. (916)32 61 (94)9 7 (5)9 Work inside parentheses. 7 14 Subtract. 7 2Divide.
81. 2 2(5)(3)(2) 831 106 Evaluate power, multiply. 891 4 Add. 11 4 Subtract. 0
Since division by 0 is undefined, the given expression is undefined.
82. 3 3(4)(5)(8) 226 1240 Evaluate power, multiply. 826
28 Add, Subtract. 66
28 Subtract. 0
Since division by 0 is undefined, the given expression is undefined.
83. 33(3)64 3(3)8 98 1 ab
84. 22(3)64 68 2 ab
85. 646(3) 863 14317
bca
bca
86. 646(3) 86(3) 2(3)1
87. 33 424(3)2(6) 4(27)12 1081296
88. 44 333(3)3(6) 3(81)18 24318261
89. 22 2 2()2(36)(3)(6) 2(9)(18) 2(81)18 16218 180
90. 22 2 2 4()4(3)(6)(6(3)) 4(3)(6)(63) 4(3)(6)(9) 4(3)(6)81 7281
91. 22 4644(3) (6) 84(3)
92. 332(3)2(6) 64 272(6) 8 2712 8 15 8 15 8
93. 33 22(6)(3) 464(64)6(3) 12(27) 256(18) 1515 238238
94. 22 33(6)(3) 262(64)6(6) 189 12836 27 92 ca ba
13 848 24 26 8 wyx
96. 1 124(1.25)12 2 56 1 wzy
97. 4 4 311 422 31 816 615 161616 xyy
98. 2 2 313 424 39 816 6915 161616 xyx
99. 23 31 4231.25 42 33 41.25 22 41.25 2.75
100. 653 31 4653(1.25) 42
44.52.53.75 7.25
101. (0.54854850)100031.44
(150,0000.54854850)100031.44 (82,2754850)100031.44
77,425100031.44
77.42531.44
2434.2422434
The owner would pay $2434 in property taxes.
102. (0.54854850)100031.44
(200,0000.54854850)100031.44 (109,7004850)100031.44 104,850100031.44
104.8531.44
3296.4843296
The owner would pay $3296 in property taxes.
103. (a) numberofoz%alcohol0.075body weight inlbhrofdrinking0.015
483.20.07519020.015
(b) 483.20.07519020.015
153.60.07519020.015
11.5219020.015
0.06120.015
0.0610.03
0.031
104. numberofoz%alcohol0.075body weightinlbhrofdrinking0.015
364.00.07513530.015
1440.07513530.015
10.813530.015
0.0830.015
0.080.015 0.035
105. (a) BAC for the man
0.024 BAC for the woman
483.20.075(19025)20.015
364.00.075(13525)30.015
0.023
Increased weight results in lower BACs.
(b) Decreased weight will result in higher BACs. BAC for the man
483.20.075(19025)20.015 0.040
BAC for the woman
364.00.075(13525)30.015 0.053
106. BAC for the man
483.20.07519010.015 0.046
BAC for the woman
364.00.07513520.015 0.05
Decreased time results in higher BACs.
107. 10.39620,893 x
(a) 10.396(2015)20,893$54.9 billion
(b) 10.396(2018)20,893$86.1 billion
(c) 10.396(2021)20,893$117.3 billion
(d) The amount spent on pets more than doubled from 2015 to 2021.
108. (a) Year Average Price (in dollars)
(b) The average price of a movie ticket in the United States increased by $9.55$5.50 $4.05 from 2000 to 2021.
R.6 Properties of Real Numbers
Classroom Examples, Now Try Exercises
1. (a) 4(5)4[(5)] 4()(4)(5) 420 pp p p
(b) Use the second form of the distributive property.
62(62) 4 mmm m
Copyright © 2025 Pearson Education, Inc.
(c) Since there is no common number or variable here, the distributive property cannot be used.
(d) 5(42)5(4)5(2)5() 20105 pqrpqr pqr
N1. (a) 2(3)2[3()] 2(3)(2)() 62 xyxy xy xy
(b) Use the second form of the distributive property.
412[4(12)] 8 kkk k
(c) Since there is no common number or variable here, the distributive property cannot be used.
2. (a) 313Identity property (13)Distributive property 2 xxxx x x
(b) (34)
3(4) 34 p p p p p
1(34)Identity property
1(3)(1)(4)Distributive property
N2. (a) 771Identity property (71)Distributive property 8 xxxx x x
(b) (53)
1(53)Identity prop. 1(5)(1)(3)Distributive prop. 53 pq pq pq pq
3. (See Example 3 for more detailed steps.) 129471 124791 (1247)91 98 bbb bbb b b
N3. (See Example 3 for more detailed steps.) 71034 731104 (731)104 96 xxx xxx x x
4. (a) 12957 (12957) 1 bbbb b b b (b) 6(27)3 6273Distributive property 2673Commutative prop. 24Combine like terms. x x x x
(c) 4(2) [4(2)]Associative property [4(2)]Associative property [4(2)]Commutative property [(42)]Associative property (8)Multiply. (8)Associative property 8 mn mn mn mn mn mn mn mn
(d) 2(3)5(21) 26105Distributive property 21065Commutative prop. 811Combine like terms. xx xx xx x
N4. (a) 3(4)15 31215Distributive prop. 31215Commutative prop. 427Combine terms. tt tt tt t
(b) 742 7142Identity property 742Distributive property 32Subtract. xx xx xx x
(c) 56 [5(6)]Associative property [5(6)]Associative property [5(6)]Commutative property [(56)]Associative property (30)Multiply. 30()Associative property 30 xy xy xy xy xy xy xy xy
(d) 3(57)8(4) 1521832Distributive property 1582132Commutative prop. 753Combine like terms. xx xx xx x
Exercises
1. The identity element for addition is 0 since, for any real number a, 00. aaa Choice B is correct.
2. The identity element for multiplication is 1 since, for any real number a, 11. aaa Choice C is correct.
3. The additive inverse of a is a since, for any real number a, ()0aa and 0. aa Choice A is correct.
4. The multiplicative inverse of a is 1 a since, for any nonzero real number a, 1 1 a a and 1 1. a a Choice D is correct.
5. The distributive property provides a way to rewrite a product such as ()abc as the sum .abac
6. The commutative property is used to change the order of two terms or factors.
7. The associative property is used to change the grouping of three terms or factors.
8. Like terms are terms with the same variables raised to the same powers.
9. When simplifying an expression, only like terms can be combined.
10. The numerical coefficient in the term 2 7 yz is 7.
11. Using the distributive property, 2()22. mpmp
12. 3()33 abab
13. Using the distributive property, 12()12[()] 12()(12)() 1212. xyxy xy xy
14. 10()10[()] 1010 pqpq pq
15. Use the second form of the distributive property. 53(53) 8 kkk k
16. 65(65) 11 aaa a
17. 797(9) [7(9)] 2 rrrr r r
18. 464(6) [4(6)] 2 nnnn n n
19. Since there is no common variable factor here, we cannot use the distributive property to simplify the expression.
20. Since there is no common variable factor here, we cannot use the distributive property to simplify the expression.
21. Use the identity property, then the distributive property.
717 (17) 8 aaaa a a
22. 919Identity property (19) 10 ssss s s
23. 11 (11) 2 xxxx x x
24. 11 (11) 2 aaaa a a
25. (2)1(2) 1(2)(1)() 2 dfdf df df
26. (3)1(3) 1(3)(1)() 3 mnmn mn mn
27. ()1() 1()(1)() xyxy xy xy
28. (34)1(34) 1(3)(1)(4) 34 xyxy xy xy
29. 2(32)22(3)2(2) 264 xyzxyz xyz
30. 8(35)8(3)88(5) 24840 xyzxyz xyz
31. 12432 (12432) 3 yyyy y y
32. 5985 (5985) 11 rrrr r r
33. 654611 641156 (6411)11 111or11 ppp ppp p pp
34. 812359 835129 (835)3 103 xxx xxx x x
35. 3(2)563 36563 35663 (35)663 215 kk kk kk k k
36. 5(3)624 515624 562154 (562)11 911 rrr rrr rrr r r
37. 10(48) 101(48) 1048 42 y y y y
38. 6(95) 61(95) 695 91 y y y y
39. 10(3)()10(3) 30 30 xyxy xy xy
40.
8(6)()8(6) 48 48 xyxy xy xy
41.
22 (12)(7)(12)(7) 33 8(7) 56 wzwz wz wz
55 (18)(5)(18)(5) 66 15(5) 75 wzwz wz wz
43. 3(4)2(1) 31222 32122 14 mm mm mm m
44. 6(5)4(6) 630424 643024 254 aa aa aa a
45. 0.25(84)0.5(62)
0.25(8)0.25(4)(0.5)(6)(0.5)(2) 23 23 (11)23 01 1 pp pp pp pp p p
46. 0.4(105)0.8(510)
0.4(10)0.4(5)(0.8)(5)(0.8)(10) 4248 10 xx xx xx x
47. (25)3(24)2 256122 (262)(512) 27 ppp ppp p p
48. (712)2(47)6 1(712)2(47)6 7128146 526 mmm mmm mmm m
49. 23(25)3(46)8 261512188 612215188 (612)13188 6318 639 zz zz zz z z z
50. 44(43)6(28)7 4161212487 1612412487 457 kk kk kk k
51. 58(58)13Distributive prop. xxxx
52. 96(96)3Distributiveproperty yyyy
53. 5(9)(59)45Associative prop. rrr
54. 4(128)(412)8Assoc. prop. 8816
55. 5995Commutative prop. xyyx
56. 577(5)35Commutative prop.
57. 177Identity property
58. 12012Identity property xx
59. 11 0Inverse prop. 44tyty A number plus its opposite equals 0.
60. 98 1Inverse prop. 89
61. 8(4)8(4)8Distributive prop. 328 xx x
62. 3()333Distributive prop. xyzxyz
63. Use the multiplication property of 0. 0(0.8759)0 xy Zero times any quantity equals 0.
64. Use the multiplication property of 0. 0(0.3512)0 tu
65. Answers will vary. One example of commutativity is washing your face and brushing your teeth. The activities can be carried out in either order. An example of noncommutativity is putting on your socks and putting on your shoes.
66. Answers will vary. One example is waking up and going to sleep. Another example is tying and untying your shoes. These activities are inverses.
67. 9619419(964)19 (100)19 1900
68. 2760274027(6040) 27(100) 2700
69. 333 588(588) 222 3503 (50) 212 150 75 2
70. 888 (17)(13)(1713) 555 830 (30)8 55 8648
71. 8.75(15)8.75(5)8.75(155) 8.75(10) 87.5
72. 4.31(69)4.31(31)4.31(6931) 4.31(100) 431
73. The terms have been grouped using the associative property of addition.
74. The terms have been regrouped using the associative property of addition.
75. The order of the terms inside the parentheses has been changed using the commutative property of addition.
76. The terms have been regrouped using the associative property of addition.
77. The common factor, x, has been factored out using the distributive property.
78. The numbers in parentheses have been added using arithmetic facts to simplify the expression.
Chapter R Test
1.
3.
4. 0.71decimal place 0.042decimal places
places
5. Convert the percent to a decimal first. 4%0.04 Convert from a decimal to a fraction. 41 0.04
6. Convert the fraction to a decimal first.
Convert from a decimal to a percent. 0.830.83100%83.3%
7. Convert the decimal to a percent first. 1.51.5100%150%
Convert from a decimal to a fraction.
Fraction in Lowest Terms (or Whole Number) Decimal Percent
8. 5 {3,0.75,,5,6.3} 3
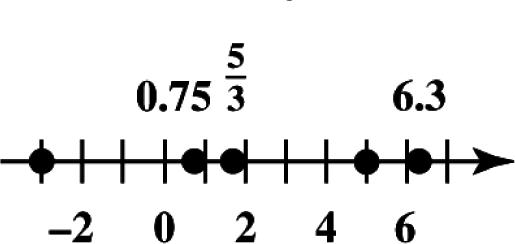
Place dots at 5 3,0.75,1.6,5, 3 and 6.3.
9. The elements 0,3,25(or 5), and 24 2 (or 12) are whole numbers.
10. The elements 1,0,3,25(or 5), and 24 2 (or 12) are integers.
11. The elements 1,0.5,0,3,25(or 5),7.5, and 24 2 (or 12) are rational numbers.
12. All the elements in the set are real numbers except 4.
13. 614(11)(3) 8(11)3 330
14. 51025102 793793 59107221 7997321 457042 636363 457042 63 17 63
15. 10436(4) 1012(24) 2(24)26
16. 22 742(6)(4) 7161216 19
17. 2[3(12)2] 9(3)(2) 2[3(3)2] 3(3)(2) 2[8] 9(2) 1616 77
18. 2 3 84352(1) 3224 84952(1) 3824 32452 2424 11 Undefined 0
19. 19614, because 14 is positive and 2 14196.
20. 225(225)(15)15
21. Since there is no real number whose square is 16,16 is not a real number.
22. Let3, 3,and25kmr 2 2 82 2
8(3)2(3) 252
8(3)2(9) 23 2418 23 66 or 2323 km r
23. 3(24)4(35)24 3(2)(3)(4)4(3) 4(5)24 612122024 612412202 1010 kkk kk k kkk kkk k
24. When simplifying (38)(46), rr the subtraction sign in front of (46) r changes the sign of the terms 4 r and 6. (38)(46) 38(4)6 3846 3486 72 rr rr rr rr
r
25. (a) The answer is B, Inverse property The sum of 6 and its inverse, 6, equals zero.
(b) The answer is D, Associative property The order of the terms is the same, but the grouping has changed.
(c) The answer is A, Distributive property This is the second form of the distributive property.
(d) The answer is F, Multiplication property of 0. Multiplication by 0 always equals 0.
(e) The answer is C, Identity property The addition of 0 to any number does not change the number.
(f) The answer is C, Identity property Multiplication of any number by 1 does not change the number.
(g) The answer is E, Commutative property The order of the terms a and b is reversed.
Chapter 1
Linear Equations, Inequalities, and Applications
1.1 Linear Equations in One Variable
Classroom Examples, Now Try Exercises
1. (a) 9100 x is an equation because it contains an equality symbol.
(b) 910 x is an expression because it does not contain an equality symbol.
N1. (a) 2173xx is an expression because it does not contain an equality symbol.
(b) 2173xx is an equation because it contains an equality symbol.
2. 489171
121710Combine terms. 1217171017Subtract 17. 510Combine terms. 510
Divide by 5. 55 2 xxx xx xxxxx x x x
Check by substituting 2 for x in the original equation. ? ? ? 489171
4(2)8(2)917(2)1Let 2. 8169341 24251 242 .. 4True xxx x
The solution set is
2. N2. 5112133
51113Combine terms. 51113Add. 61113Combine terms. 611111311Subtract11. 624Combine terms. 624 Divide by6. 66 4 xxx xx xxxxx x x x x x
Check by substituting 4 for x in the original equation.
? ? ? 5112133
xxx x
5(4)112(4)133(4)Let 4. 201181312 92112
99Tru .. . .. e
The solution set is {4}.
3. 3453
12353Distributiveprop. 12253Combineterms. 1222532Subtract 2. 1233Combineterms. 123333Add3. 153Combineterms. 153 Divideby3. 33 5 xxx xxx xx xxxxx x x x x x
We will use the following notation to indicate the value of each side of the original equation after we have substituted the proposed solution and simplified.
Check 5:275253True x
The solution set is 5.
N3. 541232 xx 5201232Distributiveprop. 53232Combineterms. 5322322Add2. 7323Combineterms. 73232332Add32. 735Combineterms. 735
Divideby7. 77 5 xx xx xxxxx x x x x x
We will use the following notation to indicate the value of each side of the original equation after we have substituted the proposed solution and simplified.
Check 5:512310True x
The solution set is 5.
4. 6(4)82(35)
648610Distributiveprop. 2210Combineterms. 2210Add. 2310Combineterms. 21031010Add10. 123Combineterms. 123 Divideby3. 33 4 xxx xxx xx xxxxx x x x x x
Check 4:23234True x
The solution set is 4.
N4. 23264136 26184436Dist.prop. 418440Combineterms. 4181844018Add 18. 42240Combineterms. 440224040Subtract 40. 4422Combineterms. 4422 Divideby22. 2222 2 xx xx xx xxxxx x x x x x
Check 2:230436True x
The solution set is 2.
5.
5 32
656LCD is 6. 32 6656Dist. prop. 32 2303Multiply. 230232Subtract 2. 305Combine terms. 305 Divideby5. 55 6 xx xx xx xx xxxxx x x x
7 25 10710LCD is 10. 25 1010710Dist. prop. 25 5702Multiply. 570525Subtract 5. 707Combine terms. 707 Divideby7. 77 10 xx xx xx xx xxxxx x x x
Check 10:572True x
The solution set is 10.
6. Multiply each side by the LCD, 4, and use the distributive property 131 242 131 444 242 2(1)1(3)2 2232 352 33Subtract5. 1Divideby3. xx xx xx xx x x x
Check 21 1:0True 42 x
The solution set is {1}.
N6. Multiply each side by the LCD, 8, and use the distributive property. 424 5 48 424 888(5) 48 2(4)1(24)40 282440 4440 444Add4. 11Divideby4. xx xx xx xx x x x
Check 713 11:5True 44 x
The solution set is 11.
7. Multiply each term by 100. 0.02(60)0.040.03(50)
2(60)43(50) 12041503 4303 30 xx xx xx xx x
Check 30:1.21.22.4True x
The solution set is 30.
N7. Multiply each term by 100. 0.080.12(4)0.03(5)
812(4)3(5) 81248315 448315 4633 637 9 xxx xxx xxx
Check 9:0.720.600.12True x
The solution set is 9.
8. (a) 5(2)2(1)31 5102231 3831 383313 81False xxx xxx xx xxxx
Since the result, 81 is false, the equation has no solution and is called a contradiction. The solution set is
(b) Multiply each side by the LCD, 3, and use the distributive property. 121 333 121 333 333 1231 3131 xx x xx x xxx xx
This is an identity. Any real number will make the equation true. The solution set is {all real numbers}.
(c) 5(31)5 1555 1455Subtract. 140Subtract5. 0Divideby14. xx xx xx x x
This is a conditionalequation.
Check 0:5(1)05True x
The solution set is 0.
N8. (a) 93(4)6(2) 9312612 612612 xxx xxx xx
This is an identity. Any real number will make the equation true.
The solution set is all real numbers.
(b) 3(21)23 6323 833 933Subtract. 90Subtract3. 0Divideby9. xxx xxx xx xx x x
This is a conditionalequation.
Check 0:3(1)3True x
The solution set is 0.
(c) 10212(5)8 10212108 10211010 102110101010 2110False xxx xxx xx xxxx
Since the result, 2110, is false, the equation has no solution and is called a contradiction. The solution set is
Exercises
1. A collection of numbers, variables, operation symbols, and grouping symbols, such as 2815, x is an algebraic expression. While an equation does include an equality symbol, there isnot an equality symbol in an algebraic expression.
2. A linear equation in one variable (here x) can be written in the form 0, axb with 0. a Another name for a linear equation is a first-degree equation, because the greatest power on the variable is one
3. If we let 2 x in the linear equation 259, x a true statement results. The number 2 is a solution of the equation, and 2 is the solution set.
4. A linear equation with one solution in its solution set, such as 259, x is a conditional equation.
5. A linear equation with an infinite number of solutions is an identity. Its solution set is all real numbers.
6. A linear equation with no solution is a contradiction. Its solution set is the empty set .
7. 320 xx can be written as 42, x so it is linear.
949 x is in linear form. Choices A and C are linear.
8. 2 12 x in choice B is nonlinear because the variable is squared.
326 xy in choice D is nonlinear because there are two variables. Choices B and D are nonlinear.
9. 324xx is an equation because it contains an equality symbol.
10. 3244 xx is an equation because it contains an equality symbol.
11. 4(3)2(1)10 xx is an expression because it does not contain an equality symbol.
12. 4(3)2(1)10 xx is an expression because it does not contain an equality symbol.
13. 101243 xx is an equation because it contains an equality symbol.
14. 1012430 xx is an equation because it contains an equality symbol.
15. A sign error was made when the distributive property was applied. The left side of the second line should be 846. xx
122(31)11
126211Distributive property 61011Combine terms.
610101110Subtract 10.
61 1
Divide by 6. 6 x x x x x x
The correct solution is 1 6
17. (a) The true statement 7 = 7 indicates that the solution set is {all real numbers}, choice B.
(b) The final line is x = 0, which is the form of solution for a conditional equation. The solution set is {0}, choice A.
(c) The false statement 7 = 0 indicates that the equation has no solution. The solution set is the empty set , choice C.
18. An equation will have the solution set {all real numbers} if it is an identity. The only equation listed here that is not an identity is choice C: 43 430 0 xx xx x
19. 781 78818Subtract8. 77 77 Divideby7. 77 1 x x x x x
We will use the following notation to indicate the value of each side of the original equation after we have substituted the proposed solution and simplified.
Check 1:781True x
822337
1Subtract 3 and 6. xxx xxx xx xx
84637Distributive property 4637Combine like terms.
The correct solution is 1.
16. The first step should have been to distribute 2 to (31). x
The solution set is {1}.
20. 5421 544214Add4. 525 525 Divideby5. 55 5 x x x x x
Check 5:25421True x
The solution set is 5.
21. 5236 523363Subtract3. 226 22262Subtract2. 28 28 Divideby2. 22 4 xx xxxxx x x x x x
Check 4:202126True x
The solution set is {4}.
22. 9179 917797Subtract7. 219 21191Subtract1. 210 210 Divideby2. 22 5 xx xxxxx x x x x x
Check 5:451359True x
The solution set is {5}.
23. 75158 2158Combineterms. 2158Subtract. 158Combineterms. 1515815Subtract15. 7Combineterms. xxx xx xxxxx x x x
Check 7:49351578True x
The solution set is {7}.
24. 2445 445Combineterms. 345Subtract4. 39Subtract4. 3Divideby3. xxx xx xx x x
Check 3:643125True x
The solution set is 3.
25. 121595359 27434Combine terms. 3044.Add3. 300Add4. 0Divideby30. www ww ww w w
Check 0:9559True w
The solution set is 0. 26. 458464 464Combine terms. 544Subtract6. 50Add4. 0Divideby5. xxx xx xx x x
Check 0:844True x
The solution set is {0}. 27. 3(24)202 612202Distributiveproperty 81220Add2. 832Add12. 4Divideby8. tt tt tt t t
Check 4:3(4)208True t
The solution set is 4.
28. 2(32)4 644Distributiveproperty 654Subtract. 510Subtract6. 2Divideby5. xx xx xx x x
Check 2:2(1)24True x
The solution set is 2. 29. 5(1)3264 553264Distributive prop. 2364Combineterms. 384Add2. 78Subtract4. 7 Divideby8. 8 xxx xxx xx xx x x
Check: Substitute 7 8 for x and show that both sides equal 1.25. The screen shows a typical Check on a calculator.
The solution set is 7 . 8
30. 5(3)4542 5154542Distributive prop. 91042Combineterms. 11104Add2. 116Subtract10. 6 Divideby11. 11 xxx xxx xx xx x x
Check 613524554412 :True 111111111111 x
The solution set is 6 11
31. 2593(4)5 393125 39317 917False xxx xx xx
The equation is a contradiction. The solution set is
32. 62112(23)4 411464 411410 1110False xxx xx xx
The equation is a contradiction. The solution set is
33. 2(3)6(7) 26642 4642 436 9 xx xx x x x
The solution set is 9.
34. 4(9)8(3) 436824 43624 460 15 xx xx x x x
Check 15:4(24)8(12)True x
The solution set is {15}.
35. 3(21)2(2)5 63245 475 42 21 42 xx xx x x x
Check 15:3(0)25True 22 x
The solution set is 1 2
36. 4(2)2(3)6 48266 626 68 84 63 xx xx x x x
Check 4213 :426True 333 x
The solution set is 4 . 3
37. 23(4)2(3) 231226 51226 36 6 2 3 xxx xxx xx x x
Check 2:43(2)2(1)True x
The solution set is {2}.
38. 63(52)4(1) 615644 9644 510 10 2 5 xxx xxx xx x x
Check 2:123(8)4(3)True x
The solution set is {2}.
39. 64(32)5(4)10 612852010 1412530 918 2 xxx xxx xx x x
Check 2:124(7)5(6)10True x
The solution set is {2}.
40. 23(42)2(3)2 2126262 41224 28 4 xxx xxx xx x x
Check 4:83(4)2(1)2True x
The solution set is {4}.
41. 2(3)43(4)2 2643122 310310 xxx xxx xx
The equation is an identity. The solution set is {all real numbers}.
42. 4(27)2253(21) 82822563 828828 xxx xxx xx
The equation is an identity. The solution set is {all real numbers}.
43. 2[(24)3]2(1) 2[243]2(1) 2[1]2(1) 11Divideby2. 121Add. 22Subtract1. 1Divideby2. xxx xxx xx xx xx x x
Check 1:2[123]0True
The solution set is {1}.
44. 4[2(3)5](27) 4[235](27) 4[32](27) 12827 1982Add7. 1910Subtract8. 10 Divideby19. 19 xxx xxx xx xx xx x x
Check 10 : 19 20679532 4True 19191919 x
The solution set is 10 19
45. [2(52)]2(27) [252]227 [32]227 3229 7 xxx xxx xx xx x
Check 7:[1437]221True x
The solution set is {7}.
46. [6(48)]9(63) [648]963 (28)612 28612 84 41 82 xxx xxx xx xx x x
Check 1 :[36]90True 2 x
The solution set is 1 2
47. 365(1)5(24)5 36555245 81179 2 2 xxxx xxxx xx x x
Check 2:6651005True x
The solution set is {2}.
48. 4(2)85392(6) 488539212 4353 6 xxxx xxxx xx x
Check 6:164851890True
The solution set is {6}.
49. 7[2(34)]292(115) 7[234]29230 7[14]2730 7282730 730730 xxx xxx xxx xxx xx
The equation is an identity. The solution set is {all real numbers}.
50. 4[6(12)]102(103)8 4[612]102068 4(52)10202 20810202 202202 xxxx xxxx xxx xxx xx
The equation is an identity. The solution set is {all real numbers}.
51. The denominators of the fractions are 3, 4, 6, and 1. The least common denominator is 12 since it is the smallest number into which each denominator can divide without a remainder.
52. Yes, the coefficients will be larger, but you will get the correct solution. As long as you multiply both sides of the equation by the same nonzero number, the resulting equation is equivalent and the solution does not change.
53. (a) We need to make 0.05 and 0.12 integers. Multiplying by 2 10, or 100, will eliminate the decimal points so that all the coefficients are integers.
(b) We need to make 0.006, 0.007, and 0.0.009 integers. Multiplying by 3 10, or 1000, will eliminate the decimal points so that all the coefficients are integers.
54. 0.06(10)(100) 0.06(100)(10) 6(10)
606Choice B is correct. x x x x
55. 5 2 9 518Multiplyby9. 1818 Divideby5. 55 x x x
Check 18518 :2True 595 x
The solution set is 18 . 5
56. 7 6 8 748Multiplyby8. 4848 Divideby7. 77 x x x
Check 48748 :6True 787 x
The solution set is 48 7
57. 6 1 5 65Multiplyby5. 55 Divideby6. 66 x x x
Check 565 :1True 656 x
The solution set is 5 6
58. 3 5 11 355Multiplyby11. 5555 Divideby3. 33 x x x
Check 55355 :5True 3113 x
The solution set is 55 3
59. Multiply both sides by the LCD, 6.
5 23 656 23 6652Distributive prop. 2 3302 330222Add 2. 5300Combine terms. 53030030Add 30. 530Combine terms. 6Divideby5.
Check 6:352True x
The solution set is {6}.
60. Multiply both sides by the LCD, 20.
1 54 20120 54 202015Distributive prop. 5 4205 420454Subtract 4. 20Combine terms.
Check 20:415True x
The solution set is {20}.
61. Multiply both sides by the LCD, 4.
x x
Check 4:31013True x
The solution set is {4}.
62. Multiply both sides by the LCD, 6. 8 13 32
by13.
Check 6:16313True x The solution set is {6}.
63. Multiply both sides by the LCD, 8. 311 12 428 311 8812 428 311 888812 428 6496 296 296 396 32 xxx xxx xxx xxx xx xxxx x x
Check 32:2416412True x
The solution set is {32}.
64. Multiply both sides by the LCD, 10. 317 3 5210 317 10103 5210 317 101010103 5210 65730 730 730 0630 03063030 306 5 xxx xxx xxx xxx
Check 57 5:33True 22 x
The solution set is {5}.
65. Multiply both sides by the LCD, 35.
11 3242 75 11 35324352 75 5327470Distrib. 151072870Distrib. 81870Combine. 818187018Add 18. 888Combine. 11Div. by 8.
Check 11:532True x
The solution set is {11}.
66. Multiply both sides by the LCD, 12.
11 3133 46 11 12313123 46 3312336Distrib. 932636Distrib. 11336Combine. 1133363Subtract 3. 1133Combine. 3Div. by 11. xx xx xx xx x x x x
Check 3:213True x
The solution set is {3}.
67. Multiply both sides by the LCD, 6. 102 553 102 1515 553 3(10)3(2)5 33065 824 24 3 8 xx xx xx xx x x
Check 72 3:1True 55 x
The solution set is {3}.
68. Multiply both sides by the LCD, 54. 55 6654 55 5454 6654 9595 45945 990 9010 90 9 10 xx xx xx xx xx x x
Check 36459 9:True 545454 x
The solution set is {9}.
69. Multiply both sides by the LCD, 12. 313 3 46 313 1212(3) 46 3(31)2(3)36 932636 11336 1133 3 xx xx xx xx x x x
Check 3:213True x The solution set is {3}.
70. Multiply both sides by the LCD, 35. 324 2 75 324 3535(2) 75 5(32)7(4)70 151072870 81870 888 11 xx xx xx xx x x x
Check 11:532True x The solution set is {11}.
71. Multiply both sides by the LCD, 6.
4153
4153
Check 153 0:True 366 x
The solution set is {0}.
72. Multiply both sides by the LCD, 80.
25318 5216 25318 8080 5216 1625403158 328012040540 328011580 083
Check 11 0:1True 22 x
The solution set is {0}.
73. Multiply each term by 10. 2.735.22 27305220 275052 5025 2 xx xx xx x x
Check 2:5.4310.42True x
The solution set is {2}.
74. Multiply each term by 10. 3.615.15 36105150 366051 6015 4 xx xx xx x x
Check 4:14.4120.45True x
The solution set is {4}.
75. Multiply each term by 100. 0.2510.320.3 251003230 257032 707 10 xx xx xx x x
Check 10:2.513.20.3True x
The solution set is {10}.
76. Multiply each term by 100. 0.450.20.291 452029100 452980 1680 5 xx xx xx x x
Check 5:2.250.21.451True x
The solution set is {5}.
77. Multiply each term by 100. 0.040.060.030.031.46 4633146 46146 4140 35 xxx xxx x x x
Check
35:1.40.061.051.051.46True x
The solution set is {35}.
78. Multiply each term by 100. 0.050.080.060.070.68 586768 118768 460 15 xxx xxx xx x x
Check
15:0.750.080.91.050.68True x
The solution set is {15}.
79. Multiply each term by 1000. 0.0060.020.030.0080.25 620308250 14308250 22220 220 22 10 xxx xxx xx x x x
Check 10:0.060.20.030.080.25True x
The solution set is {10}.
80. Multiply each term by 100. 0.050.10.60.042.22
510604222 5604222 9162 162 9 18 xxx xxx xx x x x
Check 18:0.91.80.60.722.22True x
The solution set is {18}.
81. Multiply each term by 100. 0.050.12(5000)940 512(5000)100(940) 51260,00094,000 1734,000 2000 xx xx xx x x
Check 2000:100840940True x
The solution set is {2000}.
82. Multiply each term by 100. 0.090.13(300)61
100[0.090.13(300)]100(61) 100(0.09)100(0.13)(300)6100 913(300)6100 91339006100 222200 2200 100 22 xx xx xx xx xx x x
Check 100:95261True x
The solution set is {100}.
83. Multiply each term by 100. 0.02(50)0.080.04(50) 2(50)84(50) 10082004 4100 25 xx xx xx x x
Check 25:123True x
The solution set is {25}.
84. Multiply each term by 100.
0.04900.120.06460 1000.04900.121000.06460 490126460 3601227606 36062760 62400 400 xx xx xx xx x x x
Check 400:3.64851.6True x
The solution set is {400}.
85. Multiply each term by 100. 0.050.10(200)0.45 510(200)45 520001045 2000545 200050 40 xxx xxx xxx xx x x
Check 40:21618True x
The solution set is {40}.
86. Multiply each term by 100. 0.080.12(260)0.48 812(260)48 831201248 4312048 312052 3120 60 52 xxx xxx xxx xx x x
Check 60:4.82428.8True x
The solution set is {60}.
87. Multiply each term by 1000. 0.006(2)0.0070.009 6(2)79 61279 3 xx xx xx x
Check 3:0.030.0210.009True x
The solution set is {3}.
88. Multiply each term by 1000. 0.006500.2720.004 6502724 30062724 228 14 xx xx xx x x
Copyright © 2025 Pearson Education, Inc.
Check 14:0.2160.2720.056True x
The solution set is {14}.
1.2 Formulas and Percent
Classroom Examples, Now Try Exercises
1. To solve drt for r, treat r as the only variable.
Divideby. ,or= drt drt t tt dd rr tt
N1. To solve Iprt for p, treat p as the only variable.
() Divideby. ,or Iprt Iprt Iprtrt rtrt II pp rtrt
()Associativeproperty
2. Solve 22 PLW for L 22 22Subtract2. 22 Divideby2. 22 2 ,or 22 PLW PWLW PWL PWP LLW
N2. Solve 2 Pabc for b 2Subtract. 2Subtract. 2 Divideby2. 22 ,or 22 Pabca Pacbc Pacb PacPac bb
3. Solve 1 (3) 2 yx for x. 23Multiplyby2. 23,or23Subtract3. yx yxxy
N3. Solve 2()PLW for L 2() Divideby2. 22 2 Subtract. 2 2 ,or 22 PLW P LW P WLW PPW LWL
4. Solve 277 xy for y. 27272Subtract2. 772 772 Divideby7. 77 722 ,or1 77 xyxxx yx yx x yyx
N4. Solve 5612 xy for y 6125Subtract5. 125 ,Divideby6. 6 5 or2 6 yxx x y yx
5. Use drt Solve for r. Divideby. ,or drt t tt dd rr tt
Now substitute 15 d and 1 3 t 153 1545 1 1 3 r
The average rate is 45 miles per hour.
N5. Use . drt Solve for r. Divideby. ,or drt t tt dd rr tt
Now substitute 21 d and 1 2 t 212 2142 1 1 2 r
The average rate is 42 miles per hour.
6. (a) Let a represent the amount of commission earned.
percentwholepartial
The total amount needed for the down payment is $500.
0.0812,000Let 0.08,12,000. 960Multiply.
apb a
The salesperson earns $960.
(b) The given amount of mixture is 20 oz. The part that is oil is 1 oz.
tial
7. Let a represent the amount spent on vet care/product sales.
The mixture is 5% oil.
(c) The partial amount $22,000 is 80% of the down payment.
percentwholepartial
0.822,000 Let 0.8, 22,000.
0.822,000 Divide by 0.8. 0.80.8 27,50 1 0 2
The total amount needed for the down payment is $27,500.
N6. (a) Let a represent the amount of interest earned.
percentwholepartial
0.0257500Let 0.025,7500. 187.5Multiply. pba apb a
The interest earned is $187.50.
(b) The given amount of mixture is 5 L. The part that is antifreeze is 2 L. 40 100 percentwholepartial Let 5 and 2.
prop.; div. by 5. 55 0.4040% 0.40 1 2 pba pba
The mixture is 40% antifreeze.
(c) The partial amount $450 is 90% of the down payment.
0.90450 Let 0.90, 450. 0.90450 Divide by 0.90. 0.900.90 5 1 2 00 pba bpa b b
percentwholepartial
percentwholepartial
0.278123.6Let 0.278, 123.6. 34.4aMultiply; nearest tenth pba apb
Therefore, about $34.4 billion was spent on vet care/product sales.
N7. Let a represent the amount spent on supplies/live animals/medicine.
percentwholepartial 0.241123.6Let 0.241, 123.6. 29.8aMultiply; nearest tenth pba apb
Therefore, about $29.8 billion was spent on supplies/live animals/medicine.
8. (a) Let x= the percent increase (as a decimal). amountofincrease percentincrease= original amount 13521300 1300 52 1300 0.04 x x x
The percent increase was 4%.
(b) Let x= the percent decrease (as a decimal). amountofdecrease percentdecrease= original amount 54.0051.30 54.00 2.70 54.00 0.05 x x x
The percent decrease was 5%.
N8. (a) Let x= the percent decrease (as a decimal). amountofdecrease percentdecrease= original amount 8056 80 24 80 0.3 x x x
The percent markdown was 30%.
9.
(b) Let x= the percent increase (as a decimal). amountofincrease percentincrease= original amount 689650 650 39 650 0.06 x x x The percent increase was 6%.
Sk
47 90 49.0727 Substitute9.072. 9.07290 0.44 k S
The child has a body surface area of 2 0.44m. N9.
47 90 414.5157 Substitute14.515. 14.51590 0.62 k S k Sk S
The child has a body surface area of 2 0.62m.
10. The surface area of the child is 2 0.44m. The adult dosage is 500 mg.
2 body surface area in m 1.7 0.44 500 1.7 129 CD C C
The child dosage is 129mg.
N10. The surface area of the child is 2 0.62m. The adult dosage is 100 mg.
2 body surface area in m 1.7 0.62 100 1.7
36 CD C C
The child dosage is 36mg.
Exercises
1. A formula is an equation in which variables are used to describe a relationship.
2. To solve a formula for a specified variable, treat that variable as if it were the only one and
treat all other variables like constants (numbers).
3. (a) 35 0.3535% 100 (b) 18 0.1818% 100
(c) 2 0.022% 100 (d) 7.5 0.0757.5% 100 (e) 150 1.5150% 100
4. (a) 60 60%0.6 100 (b) 37 37%0.37 100
(c) 8 8%0.08 100
(d) 3.5 3.5%0.035 100
(e) 210 210%2.1 100
5. Solve Iprt for r. ,or Iprt Iprt ptpt II rr ptpt
6. Solve drt for t. Divideby. ,or drt r rr dd tt rr
7. (a) Solve ALW for W.
Divideby. A WL L
(b) Solve ALW for L.
Divideby. A LW W
8. (a) Solve Abh for b. Divideby. A bh h
(b) Solve Abh for h. Divideby. A hb b
9. Solve 22 PLW for L. 22 22 22 22 2 ,or 22 PLW
10. (a) Solve Pabc for b. Pacabcac Pacb
(b) Solve Pabc for c Pababcab Pabc
11. (a) Solve for VLWH for W. ,or VLWH VLWH LHLH VV WW LHLH
(b) Solve for VLWH for H. ,or VLWH VLWH LWLW VV HH LWLW
12. (a) Solve 1 2 Abh for h.
221 2 2 A bh bb A h b
(b) Solve 1 2 Abh for b.
221 2 2 A bh hh A b h
13. Solve 2 Cr for r. 2 2 Divideby. 22 2 Cr Cr 2 C r
14. Solve 2 Vrh for h. 2 2 2 Divide by . Vrh Vhr r
15. (a) Solve 1 2 AhbB for b. 2()Multiply by 2. 2 Divide by . 2 ,Subtract . 2 or AhbB A bBh h A BbB h AhB b h
(b) Solve 1 2 AhbB for B 2Multiplyby 2 Divideby. 2 Subtract. AhbB2. A bBh h A bBb h AnothermethodtosolveforBisthe following. 2Multiplyby 2Distributiveprop. 2Subtract. 2 Divideby. AhbB2. AhbhB AhbhBhb Ahb Bh h
16. Solve 2 1 3 Vrh for h. 2 2 2 1 3 31 Divide by . 3 Vrh Vhr r
17. Solve 9 32 5 FC for C. 9 32 5 559 32 995 5 32 9 FC FC FC
18. Solve 5 32 9 CF for F.
9959 32Multiplyby. 5595 9 32 5 9 32Add32. 5 CF CF CF
19. (a) Solve 0 axb for x 0 axb axb b x a
(b) Solve 0 axb for a 0 axb axb b a x
20. (a) Solve ymxb for x ymxb ybmx yb x m
(b) Solve ymxb for m. ymxb ybmx yb m x
21. Solve (1)APrt for t (1) 1 1 1 APrt A rt P A rt P A Pt r
This can also be written as AP t Pr
22. Solve (1)MCr for r (1) 1 1 MCr M r C M r C
This can also be written as MC r C 23. 1 2 1 22Multiplyby2. 2 2 2 Divideby. 2 22 1 2ThischoiceisA. 1 2ThisischoiceB. Abh Abh Abh Abh b bb A h b AA bb A b A b
To get choice C, divide 1 2 Abh by 1 . 2 b 1 2 11 22 Abh bb gives us . 1 2 A h b Choice D, 1 2 , A h b can be multiplied by 2 2 on the right side to get , 2 A h b so it is not
equivalent to 2 . A h b Therefore, the correct answer is D.
24. 5 32 9 5160 ThisischoiceA. 99 5160 919 5160 ThisischoiceB. 99 5160 ThisischoiceC. 9 CF CF F C F C F C
Therefore, the correct answer is D.
25. 41 4414 41 xy xyxx yx
26. 39 39 xy yx
27. 26 26 26 6 2 xy xyxx yx x y
Simplified, this is 1 3. 2 yx
28. 520 520 20 5 xy yx x y
Simplified, this is 1 4 5 yx
29. 4911
30. 7811 787117Subtract7. 8711 8711 Divideby8. 88 711 8 711 88 xy xyxxx yx yx x y xabab y ccc
Simplified, this is 711 88yx
31. 325 32353Add3. 235 35 Divideby2. 2 xy xyxxx yx x y
Simplified, this is 35 . 22yx
32. 5312 3512Add5. 512 Divideby3. 3 xy yxx x y
Simplified, this is 5 4. 3 yx
33. 657 65676Subtract6. 567 67 Divideby5. 5 xy xyxxx yx x y
Simplified, this is 67 . 55yx
494114Subtract4. 9411 9411
Divideby9. 99 411 9 411 99 xy xyxxx yx yx x y xabab y ccc
Simplified, this is 411 99yx
34. 834 384Subtract8. 84 Divideby3. 3 xy yxx x y
Simplified, this is 84 33yx
35. 11 1
36. 22 2
by
by
Simplified, this is 5 5. 3 yx
37. Use the formula drt to find the time.
Therefore, a cheetah can run 300 ft (100 yd) in approximately 3.7 seconds.
38. Solve drt for t 10,500 21Let10,500,500. 500 d t
The travel time is 21 hr.
39. Solve drt for r. 54 193Let54,0.28. 0.28 d r
The kick’s speed was approximately 193 feet per second.
40. Solve drt for r 520 52Let520,10. 10 d r t rdt
The driver’s rate was 52 mph.
41. Use the formula 9 32. 5 FC 9 4932Let49. 5 88.232 120.2 FC
The corresponding temperature is 120°F.
42. Use the formula 5 32. 9 CF 5 4132Let41. 9 5 73 9 41 CF
The corresponding temperature is about 41C.
43. Solve 4 Ps for s. 4 P s
To find s, substitute 920 for P. 920 230 4 s
The length of each side is 230 m.
44. Use 2 Vrh Replace r by 35 17.5 2 and h by 588.
2 17.5588 565,722.3 V
To the nearest whole number, the volume is 3 565,722ft.
45. Use the formula 2.Cr (a) 4802Let480. 480 Divideby2. 2 rC r The radius of the circle is 240 inches.
(b) The diameter is twice the radius.
2 2240 480 dr d d
The diameter of the circle is 480 inches.
46. (a) 222.55dr
The diameter is 5 inches.
(b) Use the formula 2.Cr 2 2(2.5)5 Cr C
The circumference is 5 in.
47. Use VLWH Let 187,11,VL and 8.5. W
187118.5 18793.5 2Divideby93.5 H H H
The ream is 2 inches thick.
48. Use VLWH
Let 238, V 8.5, W and 2. H
2388.52 23817 14Divideby17 L L L.
The length of a legal sheet of paper is 14 inches.
49. 18% of 780 is what number? partial amount 0.18780 140.4 a
50. 23% of 480 is what number? partial amount 0.23480 110.4
51. 42% of what number is 294? partial amount
52. 18% of what number is 108? partial amount 108 percent
53. 120% of what number is 510? partial amount
54. 140% of what number is 315? partial amount 315 percent 1.40 225 a p
55. 12 is what percent of 48? partial amount 12 whole amount 48 0.25 25% a b
56. 15 is what percent of 150? partial amount 15 whole amount 150 0.10 10% a b
57. 36 is what percent of 30? partial amount 36 whole amount 30 1.20 120% a b
58. 96 is what percent of 48? partial amount 96 whole amount 48 2.00 200% a b
59. 4 is what percent of 20? partial amount 4 whole amount 20 0.20 20% a b
60. 12 is what percent of 50? partial amount 12 whole amount 50 0.24 24% a b
61. 1239 is what percent of 12? partial amount 9 whole amount 12 0.75 75% a b
62. 301515 is what percent of 30? partial amount 15 whole amount 30 0.5 50% a b
63. The mixture is 36 oz and that part which is alcohol is 9 oz. Thus, the percent of alcohol is 9125 25%.
The percent of water is 100%25%75%.
64. Let x= the amount of pure acid in the mixture. Then x can be found by multiplying the total amount of the mixture by the percent of acid given as a decimal (0.35).
There are 14 L of pure acid. Since there are 40 L altogether, there are 4014, or 26 L of pure water in the mixture.
65. Find what percent $6300 is of $210,000.
6300 0.033% 210,000
The agent received a 3% rate of commission.
66. Solve Iprt for r.
The interest rate on this deposit is 0.75%.
67. The partial amount $1950 is 65% of the total amount needed.
percentwholepartial
0.651950 Let 0.65, 1950.
The total amount needed for the used car is $3000.
68. The partial amount $525 is 70% of the total amount needed.
69. (a) Seattle: 9090 Pct..556 9072162 W WL (b) L.A. Angels: 7373 Pct..451 7389162 W WL
(c) Texas: 6868
6894162 W WL
(d) Oakland: 6060 Pct..370 60102162 W WL
70. (a) San Diego: 8989 Pct..549 8973162 W WL
(b) San Francisco: 8181 Pct..500 8181162 W WL
(c) Arizona: 7474 Pct..457 7488162 W WL
(d) Colorado: 6868 Pct..420 6894162 W WL
71. 35.1million 0.29 121million
In 2021, about 29% of the U.S. households that owned at least one Internet-enabled device owned only a smart TV.
72. 50.8million 0.42 121million
In 2021, about 42% of the U.S. households that owned at least one Internet-enabled device owned only a video game console.
73. 0.16312119.723
0.700.70 7 1 2 50 pba bpa b b
percentwholepartial
0.70525 Let 0.70, 525. 0.70525 Divide by 0.70.
The total amount needed for the deposit is $750.
In 2021, about 19.7 million U.S. households that owned at least one Internet-enabled device owned all three types of Internet-enabled devices.
74. 0.32512139.325
In 2021, about 39.3 million U.S. households that owned at least one Internet-enabled device owned both a video game console and a smart TV.
75. 0.29292,01784,684.93
To the nearest dollar, $84,685 will be spent to provide housing.
76. 0.16292,01746,722.72
To the nearest dollar, $46,723 will be spent to provide child care and education.
77. 0.06292,01717,521.02
To the nearest dollar, $17,521 will be spent on clothing.
78. $52,600 0.1801
$292,017
So the food cost is about 18%, which agrees with the percent shown in the graph.
79. Let x= the percent increase (as a decimal). amountofincrease percentincrease= original amount
The percent increase was 12%.
80. Let x= the percent decrease (as a decimal). amountofdecrease percentdecrease= original amount
The percent discount was 20%.
81. Let x= the percent decrease (as a decimal). amountofdecrease percentdecrease= original amount 1,337,7261,261,726 1,337,726 76,000 1,337,726 0.05681 x
The percent decrease was 5.7%.
82. Let x= the percent increase (as a decimal). amountofincrease percentincrease= original amount 9,509,9349,470,661 9,470,661 39,273 9,470,661 0.0041 x x x The percent increase was 0.4%.
83. amountofdecrease percentdecrease= original amount 17.9916.17 17.99 1.82 0.101 17.99
The percent discount was 10.1%.
84. amountofdecrease percentdecrease= original amount 44.9829.96 44.98 15.02 0.334 44.98
The percent discount was 33.4%.
85. (a) 47 90 4(20)7 (20)90 0.79 k S k S S
A 20 kg child has a body surface area of approximately 2 0.79m. (b) 47 90 4(26)7 (26)90 0.96 k S
A 26 kg child has a body surface area of approximately 2 0.96m.
86. (a) 47 90 4(13.608)7 (13.608)90 0.59 k S k S S
A 30 lb child (13.608 kg) has a body surface area of approximately 2 0.59m.
(b) 47 90 4(11.793)7 (11.793)90 0.53 k S k S S
A 26 lb child (11.793 kg) has a body surface area of approximately 2 0.53m.
87. (a) Recall from exercise 85, part a, that a 20 kg child has a body surface area of approximately 2 0.79m.
A 26 lb child requires a dose of approximately 156 mg.
89. (a) 78 12 3 78 3123 3 7836 x x x
2 body surface area in m 1.7 0.79 250 1.7 116
CD C C
A 20 kg child requires a dose of approximately 116 mg.
(b) Recall from exercise 85, part b, that a 26 kg child has a body surface area of approximately 2 0.96m.
2 body surface area in m 1.7
CD C C
0.96 250 1.7
A 26 kg child requires a dose of approximately 141 mg.
88. (a) Recall from exercise 86, part a, that a 30 lb child has a body surface area of approximately 2 0.59m.
2 body surface area in m 1.7 0.59 500 1.7
A 30 lb child requires a dose of approximately 174 mg.
(b) Recall from exercise 86, part b, that a 26 lb child has a body surface area of approximately 2 0.53m. 2 body surface area in m 1.7
500 1.7
(b) axk t c axk ctc c axktc
90. (a) 7836 788368 x x (b) axktc axkktck
91. (a) 788368 728 x x (b) axkktck axtck
92. (a) 728 728 77 4 x x x The solution set is {4}. (b) axtck axtck aa tck x a
93. In 92(b), the restriction that 0 a must be placed on the variables. This is necessary because if 0 a , then the denominator is 0, which is not allowed.
Copyright © 2025 Pearson Education, Inc.
94. 7 28(13) 2 a
7 2813 2 7(13) 28 2 7(13) 2282 2 567(13) 567(13) 77 813 8131313 5
The solution set is 5
95. () 2 n Sa
() 2 () 2 () 22 2 2() 2() 2 2 22 ,or n Sa Sna Sna Sna Sna
The restriction 0 n must be placed on the variables.
1.3 Applications of Linear Equations
Classroom Examples, Now Try Exercises
1. (a) Thesumofa numberand6is28.
628 x
An equation is 628. x
(b) Theproducttwice ofanumberthe plus12. and7number is 7212 xx
An equation is 7212. xx
(c) Thequotienttwice added ofanumberthe to is and6,number,7.
27 6 x x
An equation is 27, 6 x x or equivalently,
27. 6 x x
N1. (a) Thequotienttwice ofanumberisthe and10number.
2 10 x x
An equation is 2. 10 x x
(b) Theproduct ofanumberdecreased and5,by 7, iszero.
570 x
An equation is 570. x
2. (a) 5327 xx is an equation because it has an equality symbol.
5327 5367Distributiveproperty 267Combineliketerms. 213Add6 13 Divideby2. 2 xx xx x x. x
The solution set is 13 2
Copyright © 2025 Pearson Education,
(b) 532 xx is an expression because there is no equality symbol. 532
xx xx x
536Distributiveproperty 26Combineliketerms.
N2. (a) 3521 xx is an expression because there is no equality symbol.
twice the width, so 22.LW
The perimeter P is 34, so 34. P
Step3
Use the formula for perimeter of a rectangle. 22 342222 PLW WWP34;L2W2
Step4
Solve the equation.
xx xx x
3521
31521Distributiveproperty 516Combineliketerms.
(b) 3521 xx is an equation because it has an equality symbol.
3521
31521Distributiveproperty 5151Combineliketerms.
x x x
516Add15. 16 Divideby5. 5
The solution set is 16 5
3. Step2
The length and perimeter are given in terms of the width W. The length L is 5 cm more than the width, so
5. LW
The perimeter P is 5 times the width, so 5.PW
Step3
Use the formula for perimeter of a rectangle.
52525 PLW WWWPW;LW5
Step4
22
Solve the equation.
52102Distributiveproperty 5410Combineterms. 10Subtract4. WWW WW WW
Step5
The width is 10 and the length is 510515. LW
The rectangle is 10 cm by 15 cm.
Step6 15 is 5 more than 10 and 21021550 P is five times 10.
N3. Step2
The length and perimeter are given in terms of the width W. The length L is 2 ft more than
34442Distributiveproperty 3464Combineterms.
306Subtract4.
5Divideby6. WW W W =W
Step5
The width is 5 and the length is 2210212.LW
The rectangle is 5 ft by 12 ft.
Step6
12 is 2 more than twice 5 and 2122534. P
4. Step2
Let x the number of home runs for Judge. Then 16 x the number of home runs for Schwarber.
Step3
The sum of their home runs is 108, so an equation is 16108. xx
Step4
Solve the equation. 216108 2124Add 16
62Divideby2 x x. x=.
Step5
Judge had 62 home runs and Schwarber had 621646 home runs.
Step6
46 is 16 less than 62, and the sum of 46 and 62 is 108.
N4. Step2
Let x the number of TDs for Stafford.
Then 2 x the number of TDs for Brady.
Step3
The sum of their TDs is 84, so an equation is 284. xx
Step4
Solve the equation.
2284
282Subtract2 41Divideby2 x x x=.
Copyright © 2025 Pearson Education, Inc.
Step5
Stafford had 41 TDs and Brady had 41243 TDs.
Step6
43 is 2 more than 41, and the sum of 41 and 43 is 84.
5. Step2
Let x the Medicare spending in 2010.
Because 53.2%53.20.010.532,0.532 x the additional Medicare spending in 2021.
Step3
Thenumberplustheis692. in2010increase
0.532692xx
Step4
Solve the equation. 10.532692Identityproperty 1.532692Combineliketerms. 451.7Divideby1.532 xx x x.
Step5
The approximate Medicare spending in 2010 was $451.7 billion.
Step6
Check that the increase, 692451.7240.3, is about 53.2% of 451.7, 53.2%451.7240.3, as required.
N5. Step2
Let x the number of Introductory Statistics students in the fall of 2015. Since 700%7000.017,7 x the number of additional students in 2023.
Step3
Thenumberplustheis96. in2015increase 796
Step4
Solve the equation. 1796Identityproperty 896Combineliketerms. 12Divideby8 xx x x.
Step5
There were 12 students in the fall of 2015.
Step6
Check that the increase, 961284, is 700% of 12,700%127000.011284, as required.
6. Let x the amount invested at 2.5%.
Then 34,000 x the amount invested at 2%.
Use Iprt with 1. t
Principal Rate (as a decimal) Interest x 0.025 0.025x 34,000 x 0.02 0.0234,000 x 34,000 Totals 772.50
The last column gives the equation. 0.0250.0234,000772.50 xx
Solve the equation.
0.0256800.02772.50Dist. prop. 0.005680772.50Combine terms. 0.00592.5Subtract680. 18,500Divideby0.005.
xx x x x
The person invested $18,500 at 2.5% and $34,000$18,500$15,500 at 2%.
N6. Let x the amount invested at 3%.
Then 20,000the x amount invested at 2.5%.
Use Iprt with 1. t Make a table to organize the information.
Principal Rate (as a decimal) Interest x 0.03 0.03x 20,000 x 0.025 0.02520,000 x 20,000 Totals 575
The last column gives the equation. 0.030.02520,000575 xx
Solve the equation.
0.035000.025575Dist. prop. 0.005500575Combine terms. 0.00575Subtract500. 15,000Divideby0.005.
xx x x x
The person invested $15,000 at 3% and $20,000$15,000$5,000 at 2.5%.
7. Let x the amount of $8 per lb candy. Then 100 x the amount of $7 per lb candy. Make a table to organize the information.
Number of Pounds Price per Pound Value x $8 8x
7100 x
Copyright © 2025 Pearson Education,
The last column gives the equation.
84007100Dist. prop. 84007700
400700Subtract7x. 300Divideby400. xx xx x x
300 lb of candy worth $8 per lb should be used.
N7. Let x the number of liters of 20% acid solution needed. Make a table.
Liters of Solution Percent (as a decimal) Liters of Pure Acid
5 0.30 0.3051.5 x 0.20 0.20x 5 x 0.24
0.245 x
Acidin30%acidin20%acidin24% + = solutionsolutionsolution.
1.5+0.20=0.24+5 xx
Solve the equation.
1.50.200.241.2 0.30.04 7.5 xx x x
1 7 2 liters of the 20% solution are needed.
Check
30% of 5 is 1.5 and 20% of 7.5 is 1.5; 1.51.53.0, which is the same as 24% of 57.5.
8. Let x the number of liters of water.
Number of Liters Percent (as a decimal) Liters of Pure Antifreeze x 0%0 0
20 50%0.50 0.50(20)
20 x 40%0.40 0.4020 x
The last column gives the equation. 00.50200.4020 100.48
20.4Subtract8. 5Divideby0.4 x x x x
5 L of water are needed.
N8. Let x the number of gallons of pure antifreeze.
Number of Liters Percent (as a decimal) Liters of Pure Antifreeze x 100%1 1x 3 30%0.30 0.30(3) 3 x 40%0.40 0.403 x
The last column gives the equation. 10.3030.403 1.00.90.41.2 0.60.91.2Subtract0.4. 0.60.3Subtract0.9. 0.5Divideby0.6
x x=.
1 2 gallon of pure antifreeze is needed.
Exercises
1. (a) 15 more than a number 15 x (b) 15 is more than a number. 15 x
2. (a) 5 greater than a number 5 x (b) 5 is greater than a number. 5 x
3. (a) 8 less than a number 8 x (b) 8 is less than a number. 8 x
4. (a) 6 less than a number 6 x (b) 6 is less than a number. 6 x
5. Because the unknown number comes first in the verbal phrase, it must come first in the mathematical expression. The correct expression is 7. x
6. Because the unknown number comes first in the verbal phrase, it must be placed in the numerator of the mathematical expression. The correct expression is . 12 n
7. Twice a number, decreased by 13 213 x
8. Triple a number, decreased by 14 314 x
9. 12 increased by four times a number 124 x
10. 15 more than one-half of a number 1 15 2 x
Copyright © 2025 Pearson Education, Inc.
11. The product of 8 and 16 less than a number 816 x
12. The product of 8 more than a number and 5 less than the number 85xx
13. The quotient of three times a number and 10 3 10 x
14. The quotient of 9 and five times a nonzero number: 9 ,0 5 x x
15. The sentence “the sum of a number and 6 is 31” can be translated as 631. x
Solve for x 631
37Subtract6. x x
The number is 37.
16. The sentence “the sum of a number and 4 is 18” can be translated as 418. x
Solve for x 418
22Add4. x x
The number is 22.
17. The sentence “if the product of a number and 4 is subtracted from the number, the result is 9 more than the number” can be translated as 49.xxx
Solve for x 49 49 49 9 4 xxx xxx x x
The number is 9 4
18. The sentence “if the quotient of a number and 6 is added to twice the number, the result is 8 less than the number” can be translated as 28. 6 x xx
Solve for x. 28 6 12648Multiplyby6 13648 748Subtract6. 48 Divideby7. 7 x xx xxx. xx xx x
The number is 48 . 7
19. The sentence “when 2 3 of a number is subtracted from 12, the result is 10” can be translated as 2 1210. 3 x Solve for x. 2 1210 3 36230Multiplyby3. 26Subtract36. 3Divideby2 x x x x.
The number is 3.
20. The sentence “when 75% of a number is added to 6, the result is 3 more than the number” can be translated as 60.753. xx Solve for x. 60.753 60075100300Multiplyby100 60025300Subtract100. 25300Subtract600. 12Divideby25. xx xx. xx x x
The number is 12.
21.
53826 xx is an expression because there is no equality symbol.
53826 5151648Distributiveproperty 1163Combineliketerms.
xx xx x
22. 74136 xx has no equality symbol, so it is an expression.
74136 7281378Distributiveprop. 6106Combineliketerms. xx xx x
Copyright © 2025 Pearson Education, Inc.
23. 5382612 xx has an equality symbol, so this represents an equation. 5382612 515164812Distributiveprop. 116312Combineterms. 1151Subtract63. 51 Divideby11. 11 xx xx x x x
The solution set is 51 11
24. 7413618 xx has an equality symbol, so it is an equation.
7413618 728137818 610618 6124 12462 63 xx xx x x x
The solution set is 62 . 3
25. 113 8 262 xx is an expression because there is no equality symbol. 113 8 262 31316 Commondenom. 6622 213 Combineliketerms. 62 113 Reduce. 32 xx xx x x
26. 111 7 352 xx is an expression because there is no equality symbol. 111 7 352 53114 Commondenom. 151522 813 Combineliketerms. 152 xx xx x
27. Step1
We are asked to find the number of patents each corporation secured.
Step2
Let x the number of patents IBM secured. Then 2316 x = the number of patents that Samsung secured.
Step3
A total of 15,048 patents were secured, so 231615,048 xx
Step4 2231615,048 217,364 8682 x x x
Step5
IBM secured 8682 patents and Samsung secured 868223166366 patents.
Step6
The number of Samsung patents was 2316 fewer than the number of IBM patents. The total number of patents was 8682636615,048.
28. Step1
We are asked to find the number of travelers to each country.
Step2
Let x the number of travelers to Canada (in millions). Then 7.9 x the number of travelers to Mexico.
Step3
A total of 12.9 million U.S. residents traveled to Mexico and Canada, so 7.912.9. 27.912.9 25 2.5 xx Step4x x x
Step5
There were 2.5 million travelers to Canada and 2.57.910.4 million travelers to Mexico.
Step6
The number of travelers to Mexico was 7.9 million more than the number of travelers to Canada. The total number of travelers was 2.510.412.9 million.
29. Step2
Let W the width of the base. Then 265 W is the length of the base.
Step3
The perimeter of the base is 860 feet. Using 22 PLW gives us 22652860. WW
Step4 41302860 6130860 6990 990 165 6 WW W W W
Step5
The width of the base is 165 feet and the length of the base is 216565265 feet.
Step6 2222652165530330860, LW which is the perimeter of the base.
30. Step2
Let L the length of the top floor. Then 1 20 2 L is the width of the top floor.
Step3
The perimeter of the top floor is 520 feet. Using 22 PLW gives us 1 2220520. 2 LL
Step4 240520 340520 3480 160 LL L L L
Step5
The length of the top floor is 160 feet and the width of the top floor is 1 16020100 2 feet.
Step6 2221602100320200520, LW which is the perimeter of the top floor.
31. Step2
Let x= the width of the painting. Then 5.54 x = the height of the painting.
Step3
The perimeter of the painting is 108.44 inches. Using 22 PLW gives us 25.542108.44. xx
Step4 211.082108.44 411.08108.44 497.36 24.34 xx x x x
Step5
The width of the painting is 24.34 inches and the height is 24.345.5429.88 inches.
Step6
29.88 is 5.54 more than 24.34 and 229.88224.34108.44, as required.
32. Step2
Let W= the width of the rectangle. Then 12 W = the length of the rectangle.
Step3
The perimeter, 22, LW is 16 times the width, so 212216. WWW
Step4 224216 42416 2412 2 WWW WW W W
Step5
The width of the rectangle is 2 centimeters. The length is 21214 centimeters.
Step6
The length is 12 more than the width. The perimeter is 2142232, which is 16 times the width, as required.
33. Step2
Let x= the length of the middle side. Then the shortest side is 75 x and the longest side is 375. x
Step3
The perimeter of the Bermuda Triangle is 3075 miles. Using Pabc gives us 753753075.xxx
Step4 33003075 32775Subtract300 925Divideby3. x x x
Step5
The length of the middle side is 925 miles. The length of the shortest side is 7592575850 x miles. The length of the longest side is 3759253751300 x miles.
Step6
The answer checks because 92585013003075 miles, which is the correct perimeter.
34. Step2
Let x the length of one of the sides of equal length.
Step3
The perimeter of the triangle is 931.5 feet. Using Pabc gives us 438931.5. xx
Step4 2438931.5
x x x
2493.5Subtract438 246.75Divideby2.
Step5
The two walls are each 246.75 feet long.
Step6
The answer checks because 246.75246.75438931.5, which is the correct perimeter.
35. Step2
Let x the amount of revenue for Walmart. Then 103 x is the amount of revenue for Amazon (in billions).
Step3
The total revenue was $1043 billion, so (103)1043.xx
Step4 21031043 21146Add103. 573Divideby2.
x x x
Step5
The amount of revenue for Walmart was $573 billion. The amount of revenue for Amazon was 103573103$470 x billion.
Step6
The answer checks because 573470$1043 billion, which is the correct total revenue.
36. Step2
Let x the number of performances of Phantom. Then 3670 x the number of performances of Chicago.
Step3
There were 23,070 total performances, so (3670)23,070.xx
Step4 2367023,070 226,740 13,370 x x x
Step5
There were 13,370 performances of Phantom and 13,37036709700 performances of Chicago.
Step6
The total number of performances is 23,070, as required.
37. Step2
Let x the height of the Eiffel Tower. Then 804 x the height of the Leaning Tower of Pisa.
Step3
Together these heights are 1164 ft, so (804)1164.xx 28041164 21968 984
Step4x x x
Step5
The height of the Eiffel Tower is 984 feet and the height of the Leaning Tower of Pisa is 984804180 feet.
Step6
180 feet is 804 feet shorter than 984 feet and the sum of 180 feet and 984 feet is 1164 feet.
38. Step2
Let x the Mets’ payroll (in millions). Then 24 x the Dodgers’ payroll (in millions).
Step3
The two payrolls totaled $530.2 million, so (24)530.2xx 224=530.2 2=506.2 =253.1
Step4x x x
Step5
In 2017, the Mets’ payroll was $253.1 million and the Dodgers’ payroll was 253.1+24=$277.1 million.
Step6
$277.1 million is $24 million more than $253.1 million and the sum of $277.1 million and $253.1 million is $530.2 million.
39. Step2
Let x number of followers for Nike (in millions). Then 6 x number of followers for National Geographic (in millions).
Step3
There were 506 million total followers, so (6)506.xx
Step4 26506 2500 250 x x x
Step5
Nike had 250 million followers, so National Geographic had 2506256 million followers.
Copyright © 2025 Pearson Education, Inc.
Step6
256 million is 6 million more than 250 million, and the total is 256250506 million followers.
40. Step2
Let x the number of hits Williams got. Then 276 x the number of hits Hornsby got.
Step3
Step4x
Their base hits totaled 5584, so (276)5584.xx 22765584 25308 2654
Step5
Williams got 2654 base hits, and Hornsby got 26542762930 base hits.
Step6
2930 is 276 more than 2654 and the total is 265429305584.
41. Let x the percent increase. amountofincrease original amount 9.88 8 1.8
The percent increase is 22.5%.
42. Let x the percent increase. amountofincrease
The percent increase is approximately 22.0%.
43. Let x the approximate number of users in 2022. Since x is 185.7% more than the 2015 number, solve the equation below to find the number of users in 2022.
7001.857(700) 7001299.9 1999.9 x
To the nearest million, WhatsApp had 2000 million users in 2022.
44. Let x the payroll in 2022. Since x is 12.4% more than the 2020 payroll, solve the equation below to find the payroll in 2022.
42.3 x
37.60.124(37.6) 37.64.6624
To the nearest tenth of a million, the payroll was $42.3 million in 2022.
45. Let x the percent decrease. amountofdecrease original amount
16,000,000350,000 16,000,000 15,650,000 16,000,000 0.978 x
The percent decrease is approximately 97.8%.
46. Let x the percent decrease. amountofdecrease original amount 84.568 84.5 16.5 84.5 0.195 x
The percent decrease is approximately 19.5%.
47. Let x the amount of the receipts excluding tax. Since the sales tax is 9% of x, solve the equation below to find the amount of the tax. 0.092725 10.092725 1.092725 2725 2500 1.09 xx xx x x
Thus, the tax was 0.09(2500)$225.
48. Let x the amount of commission. Since x is 6% of the selling price, 0.06(159,000)9540. x
So after the real estate agent was paid, they had 159,0009540$149,460.
49. We cannot expect the final mixture to be worth more than the more expensive of the two ingredients.
50. Let x the number of liters of 30% acid solution. Make a chart.
Liters of Solution Percent (as a decimal) Liters of Pure Acid x 0.30 0.30x 15 0.50 0.50(15)7.5 15 x 0.60 0.60(15) x
Acidin30%acidin50%acidin60% solutionsolutionsolution.
0.307.50.60(15) xx
Solve the equation. 375690Multiplyby10. 315Subtract6and75. 5Divideby3. xx xx x
The solution, 5, is impossible since the number of liters of 30% acid solution cannot be negative. Therefore, this problem has no solution.
51. Let x the amount invested at 3%. Then 12,000 x the amount invested at 4%.
Complete the table. Use Iprt with 1. t Principal Rate (as a decimal) Interest x 0.03 0.03x 12,000 x 0.04 0.04(12,000) x 12,000 Totals 440
The last column gives the equation. Interestinteresttotal at3%at4%interest.
0.030.04(12,000)440 xx
Multiply by 100. 34(12,000)44,000 348,000444,000 4000 4000 xx xx x x
He should invest $4000 at 3% and 12,0004000$8000 at 4%.
Check $4000at3%$120 and $8000at4%$320;$120$320$440.
52. Let x the amount invested at 2%. Then 60,000 x the amount invested at 3%.
Complete the table. Use Iprt with 1. t
Principal Rate (as a decimal) Interest x 0.02 0.02x 60,000 x 0.03 0.03(60,000) x 60,000 Totals 1600
The last column gives the equation. Interestinteresttotal at2%at3%interest.
0.020.03(60,000)1600 xx Multiply by 100. 23(60,000)160,000
2180,0003160,000 20,000 20,000 xx xx x x
She invested $20,000 at 2% and 60,00060,00020,000$40,000 x at 3%.
Check $20,000at2%$400 and $40,000at3%$1200;$400$1200$1600.
53. Let x the amount invested at 4.5%. Then 21000 x the amount invested at 3%. Use Iprt with 1. t Make a table.
Principal Rate (as a decimal) Interest x 0.045 0.045x 21000 x 0.03 0.03(21000) x
Total 1020
The last column gives the equation. Interestinteresttotal at4.5%at3%interest. 0.0450.03(21000)1020 xx
Multiply by 1000. 4530(21000)1,020,000 456030,0001,020,000 1051,050,000 1,050,000 10,000 105 xx xx x x
She invested $10,000 at 4.5% and 210002(10,000)1000$19,000 x at 3%.
Check $19,000 is $1000 less than two times $10,000. $10,000at4.5%$450 $19,000at3%$570; $450$570$1020.
54. Let x the amount invested at 3.5%. Then 35000 x the amount invested at 4%. Use Iprt with 1. t Make a table.
Principal Rate (as a decimal) Interest
x 0.035 0.035x
35000 x 0.04 0.04(35000) x
Total 1440
The last column gives the equation. Interestinterest 1440. at3.5%at4%
0.0350.04(35000)1440 xx
Multiply by 1000. 3540(35000)1,440,000 35120200,0001,440,000 1551,240,000 1,240,000 8000 155 xx xx x x
He invested $8000 at 3.5% and 350003(8000)5000$29,000 x at 4%.
Check $29,000 is $5000 more than three times $8000. $8000at3.5%$280 and $29,000at4%$1160;$280$1160 $1440.
55. Let x the amount of additional money to be invested at 3%.
Use Iprt with 1. t Make a table.
Use the fact that the yearly return on the two investments is 4%.
Principal Rate (as a decimal)
Interest
12,000 0.06 0.06(12,000) x 0.03 0.03x 12,000 x 0.04 0.04(12,000) x
The last column gives the equation. Interestinterestinterest at6%at3%at4%.
0.06(12,000)0.030.04(12,000) xx
Multiply by 100. 6(12,000)34(12,000) 72,000348,0004 24,000 xx xx x
$24,000 should be invested at 3%.
Check $12,000at6%$720 and
$24,000at3%$720; $720$720$1440, which is the same as ($12,000$24,000)at4%.
56. Let x the amount of additional money to be invested at 5%.
Use Iprt with 1. t Make a table. Use the fact that the yearly return on the two investments is 6%.
Principal Rate (as a decimal) Interest
17,000 0.065 0.065(17,000) x 0.05 0.05x 17,000 x 0.06 0.06(17,000) x
The last column gives the equation. Interestinterestinterest at6.5%at5%at6% 0.065(17,000)0.050.06(17,000) xx
Multiply by 1000. 65(17,000)5060(17,000) 1,105,000501,020,00060 85,00010 8500 xx xx x x
They should deposit $8500 at 6%.
Check
$17,000at6.5%$1105 and $8500at5%$425; $1105$425$1530, which is the same as ($17,000$8500)at6%.
57. Let x the number of liters of 10% acid solution needed. Make a table.
Liters of Solution Percent (as a decimal) Liters of Pure Acid 10 0.04 0.04(10)0.4 x 0.10 0.10x 10 x 0.06 0.06(10) x
Acidin4%acidin10%acidin6% solutionsolutionsolution.
0.40.100.06(10) xx
Solve the equation.
0.40.100.060.6Distributiveprop. 0.40.040.6Subtract0.06.
0.040.2Subtract0.4. 5Divideby0.04. xx xx x x
Five liters of the 10% solution are needed.
Check 4% of 10 is 0.4 and 10% of 5 is 0.5; 0.40.50.9, which is the same as 6% of (105).
58. Let x the number of liters of 14% alcohol solution needed. Make a chart.
Alcoholinalcoholinalcoholin 14%solution50%solution30%solution.
0.14100.30(20) xx
Solve the equation. 14100030(20)Multiplyby100. 14100030600Distributiveproperty 16400Subtract30xand1000. 25Divideby16.
25 L of 14% solution must be added. Check 14% of 25 is 3.5 and 50% of 20 is 10; 3.51013.5, which is the same as 30% of (2520).
59. Let x the number of liters of the 20% alcohol solution. Make a table.
Liters of Solution Percent (as
Alcoholinalcoholinalcoholin 12%solution20%solution14%solution.
1.440.200.14(12) xx
Solve the equation.
1442014(12)Multiplyby100. 1442014168Distributiveproperty 624Subtract14and144. 4Divideby6. xx xx xx x
4L of 20% alcohol solution are needed. Check 12% of 12 is 1.44 and 20% of 4 is 0.8; 1.440.82.24, which is the same as 14% of (124).
60. Let x the number of liters of 10% alcohol solution. Make a chart.
Liters of Solution Percent (as a decimal) Liters of Pure Alcohol x 0.10 0.10x 40 0.50 0.50(40)20 40 x 0.40 0.40(40) x
Alcoholinalcoholinalcoholin 10%soln50%soln40%soln.
0.10200.40(40) xx
Solve the equation. 12004(40)Multiplyby10. 2004160Distributiveproperty 340Subtract4and200. 401or13Divideby3. 33 xx xx xx x
1 13 3 L of 10% solution should be added. Check
50% of 40 is 20 and 10% of 40 3 is 4 ; 3 41 2021, 33 which is the same as 40% of
40 40. 3
61. Let x the amount of pure dye used (pure dye is 100% dye). Make a table.
Gallons of Solution Percent (as a decimal) Gallons of Pure Dye x 1 1xx 4 0.25 0.25(4)1 4 x 0.40 0.40(4) x
Write the equation from the last column in the table.
10.4(4)xx Solve the equation. 10.4(4)
0.60.6Subtract0.4xand1. 1Divideby0.6. xx xx x x
10.41.6Distributiveproperty
One gallon of pure (100%) dye is needed. Check 100% of 1 is 1 and 25% of 4 is 1; 112, which is the same as 40% of (14).
62. Let x the number of gallons of water. Make a chart.
Gallons of Solution Percent (as a decimal) Gallons of Pure Insecticide x 0 0()0 x 6 0.04 0.04(6)0.24 6 x 0.03 0.03(6) x
Insecticideinsecticideinsecticide inwaterin4% solutionin3%solution. 00.240.03(6) x
Solve the equation. 0243(6)Multiplyby100.
2Divideby3. x x x x
24318Distributiveproperty 63Subtract18.
2 gallons of water should be added. Check 4% of 6 is 0.24, which is the same as 3% of (26).
63. Let x the amount of $6 per lb nuts. Make a table. Pounds of Nuts Cost per lb Total Cost
50 $2 2(50)100 x $6 6x
50 x $5 5(50) x
The total value of the $2 per lb nuts and the $6 per lb nuts must equal the value of the $5 per lb nuts.
10065(50) xx
Solve the equation. 10065250 150 xx x
The retailer should use 150 lb of $6 nuts. Check
50 pounds of the $2 per lb nuts are worth $100 and 150 pounds of the $6 per lb nuts are worth $900; $100$900$1000, which is the same as (50150) pounds worth $5 per lb.
64. Let x the number of ounces of 2¢ per oz tea. Make a table.
Ounces of Tea Cost per oz Total Cost x 2¢ or 0.02 0.02x
Costofcostofcostof 2ctea5ctea3ctea. 0.0250.03(100) xx
Solve the equation. 25003(100)Multiplyby100. 25003300Distributiveproperty 200Subtract2and300. xx xx xx
200 oz of 2¢ per oz tea should be used. Check
200 oz of 2¢ per oz tea is worth $4 and 100 oz of 50 per oz tea is worth $5; $4$5$9, which is the same value as (200100) oz of 3¢ per oz tea.
65. (a) Let x the amount invested at 3%.
800 x the amount invested at 6%.
(b) Let y the amount of 3% acid used. 800 y the amount of 6% acid used.
66. (a) Organize the information in a table.
Principal Percent (as a decimal) Interest x 0.03 0.03x
800 x 0.06 0.06(800) x 800 0.0525 0.0525(800)
The amount of interest earned at 3% and 6% is found in the last column of the table, 0.03x and 0.06(800). x
(b) Organize the information in a table.
Liters of Solution Percent (as a decimal) Liters of Pure Acid y 0.03 0.03y
800 y 0.06 0.06(800) y 800 0.0525 0.0525(800)
The amount of pure acid in the 3% and 6% mixtures is found in the last column of the table, 0.03y and 0.06(800). y
67. Refer to the tables for Exercise 66. In each case, the last column gives the equation.
(a) 0.030.06(800)0.0525(800) xx
(b) 0.030.06(800)0.0525(800) yy
68. In both cases, multiply by 10,000 to clear the decimals.
Check
(a) 0.030.06(800)0.0525(800)
300600(800)525(800)
300480,000600420,000
30060,000 200 xx xx xx x x
Jack invested $200 at 3% and 800800200$600 x at 6%.
(b) 0.030.06(800)0.0525(800)
300600(800)525(800)
300480,000600420,000
30060,000
Jill used 200 L of 3% acid solution and 800800200600 L y
of 6% acid solution.
(c) The processes used to solve Problems A and B were virtually the same. Aside from the variables chosen, the problem information was organized in similar tables and the equations solved were the same.
1.4 Further Applications of Linear Equations
Classroom Examples, Now Try Exercises
1. Let x the number of dimes. Then 26 x the number of half-dollars.
Number of Coins Denomination Value
x 0.10 0.10x 26 x 0.50 0.50(26) x Total 8.60
Multiply the number of coins by the denominations, and add the results to get 8.60. 0.100.50(26)8.60 15(26)86Multiplyby10. 1130586 444 11 xx xx xx x x
The child has 11 dimes and 261115 halfdollars.
The number of coins is 111526 and the value of the coins is $0.10(11)$0.50(15)$8.60, as required.
N1. Let x the number of dimes. Then 52 x the number of nickels.
Number of Coins Denomination Value x 0.10 0.10x 52 x 0.05 0.05(52) x Total 3.70
Multiply the number of coins by the denominations, and add the results to get 3.70. 0.100.05(52)3.70
105(52)370Multiplyby100. 102605370 5110
22 xx xx xx x x
The cashier has 22 dimes and 522230 nickels.
Check
The number of coins is 223052 and the value of the coins is $0.10(22)$0.05(30)$3.70, as required.
2. Let x the amount of time needed for the cars to be 420 mi apart.
Make a table. Use the formula , drt that is, find each distance by multiplying rate by time.
Rate Time Distance
Northbound Car 60 x 60x Southbound Car 45 x 45x Total 420
The total distance traveled is the sum of the distances traveled by each car, since they are traveling in opposite directions. This total is 420 mi.
6045420 105420 420 4 105 xx x x
The cars will be 420 mi apart in 4 hr.
Check
The northbound car traveled 60(4)240miles. The southbound car traveled 45(4)180miles, for a total of 240180420, as required.
Copyright © 2025 Pearson Education, Inc.
N2. Let x the amount of time needed for the trains to be 387.5 km apart. Make a table. Use the formula , drt that is, find each distance by multiplying rate by time.
Rate Time Distance
First Train 80 x 80x Second Train 75 x 75x
Total 387.5
The total distance traveled is the sum of the distances traveled by each train, since they are traveling in opposite directions. This total is 387.5 km.
8075387.5 155387.5 387.5 2.5 155 xx x x
The trains will be 387.5 km apart in 2.5, or 1 2 2 hr.
Check
The first train traveled 80(2.5)200km. The second train traveled 75(2.5)187.5km, for a total of 200187.5387.5, as required.
3. Let x the driving rate. Then 12 x the bus rate. Make a table. Use the formula , drt that is, find each distance by multiplying rate by time.
Rate Time Distance
Car x 1 2 1 2 x
Bus 12 x 3 4 3 (12) 4 x
The distances are equal. 13 (12) 24 23(12)Multiplyby4. 2336 36 xx xx xx x
The distance traveled to work is 11 (36)18miles. 22 x
Check
The distance traveled to work by bus is 333 (12)(3612)(24)18miles, 444 x which is the same as we found above (by car).
N3. Let x the driving rate. Then 30 x the bicycling rate.
Make a table. Use the formula , drt that is, find each distance by multiplying rate by time.
Rate Time Distance
Car x 1 2 1 2 x
Bike 30 x 13 1 22 3 (30) 2 x
The distances are equal. 13 (30) 22 13(30)Multiplyby2. 390 902 45 xx xx xx x x
The distance the accountant travels to work is 11 (45)22.5miles. 22 x
Check
The distance the accountant travels to work by bike is 333 (30)(4530)(15)22.5miles, 222 x which is the same as we found above (by car).
4. The sum of the three measures must equal 180°. (61)(27)180 468180 4112 28 xxx x x x
The angles measure 28°, 286189, and 2(28)763.
Check
Since 288963180, the answers are correct.
N4. The sum of the three measures must equal 180°. (11)(336)180 525180 5205 41 xxx x x x
The angles measure 41°, 411152, and 3(41)3687.
Check
Since 415287180, the answers are correct.
Copyright © 2025 Pearson Education, Inc.
5. x the first of the three consecutive integers
1 x the second integer
2 x the third integer
Write the sum of the first and third numbers, 2, xx and set it equal to 49 less than 3 times the second.
223349 22346 246 48 xxx xx xx x x
23149
The three consecutive numbers are 48, 49, and 50.
Check
The sum of the first and third consecutive integers is 485098.
49 less than 3 times the second, yields 3494998, as desired.
N5. x the first of the three consecutive integers
1 x the second integer
2 x the third integer
Write the sum of the first and second numbers, 1, xx and set it equal to 43 less than 3 times the third.
13243 213643 21337 137 38 xxx xx xx x x
The three consecutive numbers are 38, 39, and 40.
Check
The sum of the first and second consecutive integers is 383977. 43 less than 3 times the third, yields 3404377, as desired.
Exercises
1. The total amount is 12(0.10)18(0.25)1.204.50 $5.70.
2. Use , drt or d t r
Substitute 7700 for d and 550 for r. 7700 14 550 t Its travel time is 14 hours.
3. Use , drt or . d r t Substitute 300 for d and 10 for t 300 30 10 r
Their rate was 30 mph.
4. Use 4 Ps or . 4 P s
Substitute 160 for P. 160 40 4 s
The length of each side of the square is 40 in. This is also the length of each side of the equilateral triangle. To find the perimeter of the equilateral triangle, use 3.Ps
Substitute 40 for s. 3(40)120 P The perimeter would be 120 inches.
5. Use 3 Ps or 3 P s
Substitute 27 for P. 27 9 3 s
The length of each side of the triangle is 9 in. This is also the length of each side of the square. To find the area of the square, use 2 As
Substitute 9 for s. 2 (9)81 A
The area would be 81 square inches.
6. Use 2 Ar
Substitute 25 for A. 2 2 25 25 5 r r r
The length of the radius of the circle is 5 ft. This is also the length of each side of the square. To find the perimeter of the square, use 4.Ps
Substitute 5 for s. 4(5)20 P
The perimeter would be 20 feet.
7. The right side of the equation should be 180, not 90. The correct equation is (1)(2)180xxx
Copyright © 2025 Pearson Education, Inc.
33180 3177
59 x x x
The angles measure 59°, 60°, and 61°
8. The number of dimes should be 21 x , not 21 x . The correct equation is 0.050.10(21)14.5 xx
0.052.10.101.45 0.050.65 13 xx x x
There are 13 nickels and 21138 dimes.
9. Let x the number of pennies. Then x is also the number of dimes, and 442 x is the number of quarters.
Number of Coins Denomination Value
x 0.01 0.01x x 0.10 0.10x 442 x 0.25 0.25(442) x
44 Totals 4.37
The sum of the values must equal the total value.
0.010.100.25(442)4.37 1025(442)437 xxx xxx
Multiply both sides by 100. 10110050437 391100437 39663 17 xxx x x x
There are 17 pennies, 17 dimes, and 442(17)10 quarters.
Check
The number of coins is 17171044 and the value of the coins is $0.01(17)$0.10(17)$0.25(10)$4.37, as required.
10. Let x the number of nickels and the number of quarters. Then 2x is the number of half-dollars.
Number of Coins
x
Denomination Value
The sum of the values must equal the total value.
0.050.250.50(2)2.60 52550(2)260 xxx xxx
Multiply both sides by 100. 525100260 130260 2 xxx x x
There were 2 nickels, 2 quarters, and 2(2)4 half-dollars. Check
The number of coins is 2248 and the value of the coins is $0.05(2)$0.25(2)$0.50(4)$2.60, as required.
11. Let x the number of loonies. Then 37 x is the number of toonies.
Number of Coins Denomination Value x 1 1x 37 x 2 2(37) x 37 Totals 51
The sum of the values must equal the total value.
12(37)51
74251 7451 23 xx xx x x
They have 23 loonies and 372314 toonies. Check
The number of coins is 231437 and the value of the coins is $1(23)$2(14)$51, as required.
12. Let x the number of $1 bills. Then 119 x is the number of $5 bills.
Number of Bills Denomination Value x 1 1x 119 x 5 5(119) x 119 Totals 347
The sum of the values equals the total value. 15(119)347 5955347 4248 62 xx xx x x
The cash drawer has 62 $1 bills and 1196257 $5 bills.
Check
Number of bills is 6257119 and the value is $1(62)$5(57)$62$285$347, as required.
13. Let x the number of $10 coins. Then 41 x is the number of $20 coins.
Number of Coins Denomination Value x 10 10x 41 x 20 20(41) x 41 Totals 540
The sum of the values must equal the total value.
1020(41)540 1082020540 10280 28 xx xx x x
The collector has 28 $10 coins and 412813 $20 coins. Check
The number of coins is 281341 and the value of the coins is $10(28)$20(13)$540, as required.
14. Let x the number of two-cent pieces. Then 3x is the number of three-cent pieces.
Number of Coins Denomination Value x 0.02 0.02x 3x 0.03
The sum of the values must equal the total value.
0.020.03(3)2.42 23(3)242 xx xx Multiply both sides by 100. 29242 11242 22 xx x x
The collector has 22 two-cent pieces and 3(22) 66 three-cent pieces. Check 66 is three times 22 and the value of the coins is $0.02(22)$0.03(66)$2.42, as required.
15. Let x the number of adult tickets sold. Then 1460 x the number of student/senior tickets.
Cost of Ticket Number Sold Amount Collected
$25 x 25x
$19 1460 x 19(1460) x Totals 1460 $32,972
Write the equation from the last column of the table.
2519(1460)32,972
2527,7401932,972 65232 872
xx xx x x
872 adult tickets were sold; 1460872588 student and senior tickets were sold.
Check
The number of tickets sold was 8725881460 and the amount collected was $25(872)$19(588)$21,800$11,172 $32,972, as required.
16. Let x the number of student tickets sold. Then 480 x the number of nonstudent tickets sold.
Cost of Ticket Number Sold Amount Collected
$5 x 5x
$8 480 x 8(480) x Totals 480 $2895
Write the equation from the last column of the table.
58(480)2895 5384082895 3945 315 xx xx x x
315 student tickets were sold; 480315165 nonstudent tickets were sold.
Check
The number of tickets sold was 315165480 and the amount collected was $5(315)$8(165)$1575$1320$2895, as required.
17. , drt so 100 8.08 12.37 d r t Her rate was about 8.08 m/sec.
Copyright © 2025 Pearson Education, Inc.
18. , drt so
400 7.77 51.46 d r t
Her rate was about 7.77 m/sec.
19. , drt so
200 10.19 19.62 d r t
His rate was about 10.19 m/sec.
20. , drt so
400 9.12 43.85 d r t
His rate was about 9.12 m/sec.
21. Let t the time until they are 110 mi apart. Use the formula drt Complete the table.
Rate Time Distance
First Steamer 22 t 22t Second Steamer 22 t 22t 110
The total distance traveled is the sum of the distances traveled by each steamer, since they are traveling in opposite directions. This total is 110 mi.
2222110 44110 11051 or2 4422
It will take them 1 2 2 hr.
Check
Each steamer traveled 22(2.5)55miles for a total of 2(55)110 miles, as required.
22. Let t the time it takes for the trains to be 315 km apart. Use the formula drt Complete the table.
Rate Time Distance
First Train 85 t 85t Second Train 95 t 95t 315
The total distance traveled is the sum of the distances traveled by each train, since they are traveling in opposite directions. This total is 315 km.
8595315 180315 31573 or1 18044
It will take the trains 3 1 4 hr before they are 315 km apart.
Check
The first train traveled 85(1.75)148.75 km and the second train traveled 95(1.75)166.25.
The sum is 315 km, as required.
23. Let t Mulder’s time. Then 1 2 t Scully’s time.
Rate Time Distance
Mulder 65 t 65t Scully 68 1 2 t 1 68 2 t
The distances are equal. 1 6568 2 656834 334 341 or11 33 tt tt
Mulder’s time will be 1 11 3 hr. Since he left at 8:30 A M., 1 11 3 hr or 11 hr 20 min later is 7:50 P M
Check
Mulder’s distance was 342 65736 33
miles. Scully’s distance was 341652 6868736, 3263
as required.
24. Let x Lois’ travel time.
Since Clark leaves 15 minutes after Lois, and 151 604 hr, 1 4 x time for Clark.
Complete the table using the formula rtd
Rate Time Distance
Lois 35 x 35x
Clark 40 1 4 x 1 40 4 x
Since Lois and Clark are going in opposite directions, we add their distances to get 140 mi.
1 3540140 4 354010140 75150 2 xx xx x x
They will be 140 mi apart at AMAM. 8..2hr10.
Check
Lois’ distance was 35(2)70. Clark’s distance was 17 4024070. 44
The sum is 140 miles, as required.
25. Let x her average rate on Sunday. Then 5 x her average rate on Saturday.
Time Distance
The distances are equal.
3.6(5)4 3.6184 180.4Subtract3.6. 18 45 0.4 xx xx xx x
Her average rate on Sunday was 45 mph.
Check On Sunday, 4hoursat45mph180miles. On Saturday, 3.6hoursat50mph180miles. The distances are equal.
26. Let x her biking rate. Then 7 x her walking rate.
x
The distances are equal. 21 (7) 35 10(7)3Multiplyby15. 10703 770 10 xx xx xx x x
The distance from her house to the train station is 11 (10)2miles. 55 x
Check
The distance walking is 2 3mphhr2mi. 3
The distance biking is 1 10mphhr2mi. 5
The distances are equal.
27. Let x Anne’s time. Then 1 2 x Johnny’s time.
Rate Time Distance
Anne 60 x 60x Johnny 50 1 2 x 1 50 2 x
The total distance is 80. 1 605080 2 60502580 11055 551 1102 xx xx x x
They will meet 1 2 hr after Anne leaves.
Check
Anne travels 1 6030miles. 2
Johnny travels 11 5050miles. 22 The sum of the distances is 80 miles, as required.
28. Let x her rate (speed) during the first part of the trip. Then 25 x her rate during rush-hour traffic. Make a table using the formula . rtd
Rate Time Distance
First Part x 2 2x
Rush-Hour 25 x 1 2 1 (25) 2 x
The total distance was 125 miles. 1 2(25)125 2 425250Multiplyby2. 5275 55 xx xx x x
The rate during the first part of the trip was 55 mph.
Check
The distance traveled during the first part of the trip was 55(2)110miles. The distance traveled during the second part of the trip was (5525)(0.5)15miles. The sum of the distances is 125 miles, as required.
29. The sum of the measures of the three angles of a triangle is 180°.
(30)(2120)15180
With 90, x the three angle measures become (9030)60, [2(90)120]60, and 1 (90)1560. 2
30. The sum of the measures of the three angles of a triangle is 180°. (15)(1020)(5)180 12180 15 xxx x x
With 15, x the three angle measures become (1515)30, (101520)130, and (155)20.
31. The sum of the measures of the three angles of a triangle is 180°. (37)(94)(41)180 164180 16176 11 xxx x x x
With 11, x the three angle measures become (3117)40, (9114)95, and (4111)45.
32. The sum of the measures of the three angles of a triangle is 180°. (27)(61)180 468180 4112 28 xxx x x x
With 28, x the three angle measures become (2287)63, (2861)89, and 28°.
33. The sum of the measures of the three angles of a triangle is 180°. (336)(11)180 525180 5205 41 xxx x x x
With 41, x the other angle measures become (34136)87, and (4111)52.
34. The sum of the measures of the three angles of a triangle is 180°. (10)(1230)(4)180 1416180 14196 14 xxx x x x
With 14, x the three angle measures become (1410)24, (121430)138, and (144)18.
35. Vertical angles have equal measure. 82717 15 xx x 8152122 and 71517122.
The angles are both 122°.
36. Vertical angles have equal measure. 95253 9252 162 8 xx x x x
95(8)49 and 253(8)49.
The angles are both 49°.
37. The sum of the two angles is 90°. (51)290 7190 791 13 xx x x x
The measures of the two angles are [5(13)1]64 and [2(13)]26.
38. The sum of the two angles is 90°.
(39)690 9990 999 11 xx x x x
The measures of the two angles are [3(11)9]24 and [6(11)]66.
39. Supplementary angles have an angle measure sum of 180°.
(35)(515)180 820180 8160 20 xx x x x
With 20, x the two angle measures become (3205)65 and (52015)115.
40. Supplementary angles have an angle measure sum of 180°.
(31)(749)180 1050180 10130 13 xx x x x
With 13, x the two angle measures become (3131)40 and (71349)140.
41. Let x the first consecutive integer. Then 1 x will be the second consecutive integer, and 2 x will be the third consecutive integer. The sum of the first and twice the second is 17 more than twice the third.
2(1)2(2)17 222417 32221 19 xxx xxx xx x
Since 19, x 120, x and 221. x
The three consecutive integers are 19, 20, and 21.
42. Let x the first consecutive integer. Then 1 x will be the second consecutive integer, and 2 x will be the third consecutive integer. The sum of the first and twice the third is 39 more than twice the second.
2(2)2(1)39 242239 34241 37 xxx xxx xx x
Since 37, x 138, x and 239. x
The three consecutive integers are 37, 38, and 39.
43. Let x the first integer. Then 1, x 2, x and 3 x are the next three consecutive integers.
The sum of the first three integers is 54 more than the fourth.
(1)(2)(3)54 3357 254 27 xxxx xx x x
The four consecutive integers are 27, 28, 29, and 30.
44. Let x the first integer. Then 1, x 2, x and 3 x are the next three consecutive integers.
The sum of the last three integers is 86 more than the first.
(1)(2)(3)86 3686 280 40 xxxx xx x x
The four consecutive integers are 40, 41, 42, and 43.
45. Let x the guest’s room number. Then 2 x will be the room number of the room next to the guest.
The sum of these room numbers will be 2430. (2)2430 222430 22428 1214 xx x x x
The guest’s room number is 1214 and the room next door is numbered 121421216.
46. Let x the first room number. Then 2 x will be the second room number.
The sum of these room numbers will be 1618. (2)1618 221618 21616 808 xx x x x
The two room numbers are 808 and 8082810.
47. Let x the first even integer. Then 2 x and 4 x are the next two consecutive even integers.
The sum of the least integer and the middle integer is 26 more than the greatest integer.
Copyright © 2025 Pearson Education, Inc.
(2)426 2230 230 28 xxx xx x x
The three even integers are 28, 30 and 32.
48. Let x the first even integer. Then 2 x and 4 x are the next two consecutive even integers.
The sum of the least integer and the greatest integer is 12 more than the middle integer.
(4)212 2414 414 10 xxx xx x x
The three even integers are 10, 12, and 14.
49. Let x the first odd integer. Then 2 x and 4 x are the next two consecutive odd integers.
The sum of the least integer and the middle integer is 19 more than the greatest integer.
(2)419 2223 223 21 xxx xx x x
The three even integers are 21, 23, and 25.
50. Let x the first odd integer. Then 2 x and 4 x are the next two consecutive odd integers.
The sum of the least integer and the greatest integer is 13 more than the middle integer.
(4)213 2415 415 11 xxx xx x x
The three even integers are 11, 13, and 15.
51. The sum of the measures of the angles of a triangle is 180°. 260180 360180 3120 40 xx x x x
The measures of the unknown angles are 40° and 280. x
52. Two angles which form a straight line add to 180°, so 18060120. The measure of the unknown angle is 120°.
53. The sum of the measures of the unknown angles in Exercise 51 is 4080120. This sum is equal to the measure of the angle in Exercise 52.
54. The sum of the measures of angles and is equal to the measure of angle .
Summary Exercises Applying ProblemSolving Techniques
1. Let x the width of the rectangle. Then 3 x is the length of the rectangle. If the length were decreased by 2 inches and the width were increased by 1 inch, the perimeter would be 24 inches. Use the formula 22,PLW and substitute 24 for P, (3)2 x or 1 x for L, and 1 x for W.
22
242(1)2(1) 242222 2444 204 5 PLW xx xx x x x
The width of the rectangle is 5 inches, and the length is 538 inches.
2. Let x the width. Then 2x is the length (twice the width).
Use 22 PLW and add one more width to cut the area into two parts. Thus, an equation is shown below. Solve the equation. 22210 2(2)2210 7210 30 LWW xxx x x
The width is 30 meters, and the length is 2(30)60meters.
3. Let x the regular price of the item. The sale price after a 28.57% (or 0.2857) discount was $199.99, so an equation is 0.2857199.99.xx Solve the equation 0.2857199.99. 0.7143199.99 199.99 0.7143 279.98 xx x x x
To the nearest cent, the regular price was $279.98.
Copyright © 2025 Pearson Education, Inc.
4. Let x the regular price of the smart TV. The sale price after a discount of 40% (or 0.40) was $255, so an equation is 0.40255.xx Solve the equation.
0.40255 0.60255 425 xx x x
The regular price of the smart TV was $425.
5. Let x the amount invested at 4%. Then 2x is the amount invested at 5%.
Use Iprt with 1yr. t Make a table.
Principal Rate (as a decimal)
Interest x 0.04 0.04x 2x 0.05 0.05(2)0.10xx
Total 112
The last column gives the equation. Interestat4%interestat5%totalinterest.
0.040.10112 xx
Multiply by 100. 41011,200 1411,200 800 xx x x
$800 is invested at 4% and 2($800)$1600 at 5%.
Check
$800at4%$32 and $1600at5%$80;$32$80$112
6. Let x the amount invested at 3%. Then 2000 x is the amount invested at 4%.
Use Iprt with 1yr. t Make a table.
Principal Rate (as a decimal) Interest x 0.03 0.03 x 2000 x 0.04 0.04(2000) x
Total 920
The last column gives the equation. Interestat3%interestat4%totalinterest.
0.030.04(2000)920 xx
Multiply by 100. 34(2000)92,000 34800092,000 784,000 12,000 xx xx x x
$12,000 is invested at 3% and $14,000 is invested at 4%.
Check $12,000at3%$360 and $14,000at4%$560;$360$560$920
7. Let x the number of points scored by Young in the 2021–2022 season. Then 37 x the number of points scored by DeRozan in the 2021–2022 season. The total number of points scored by both was 4273. (37)4273 2374273 24310 2155 xx x x x
Young scored 2155 points and DeRozan scored 2155372118points.
Check
2118 is 37 fewer points than 2155 points, and 211821554273.
8. Let x the number of films released in 2011. Then 198 x the number released in 2021. A total of 1004 were released in both years. (198)1004 21981004 21202 601 xx x x x
In 2011, 601 films were released. In 2021, 601198403 films were released.
Check
403 is 198 less than 601, and 6014031004.
9. Let t the time it will take until John and Pat meet. Use drt and make a table.
Rate Time Distance
John 60 t 60t Pat 28 t 28t
The total distance is 440 miles.
6028440 88440 5 tt t t
It will take 5 hours for John and Pat to meet.
Check
John traveled 60(5)300miles and Pat traveled 28(5)140miles; 300140440, as required.
10. Let x the length of the side of the square that is being cut from the 12 by 16 sheet of tin. The width of the tin decreases by x at the left and right ends of the tin because small squares have been cut out at each corner. Thus, 122 Wx
is the width of the box made by cutting out the small squares. Similarly, 162 Lx is the length of the box. The length L of the box is twice its width W minus 5. 25 1622(122)5 LW xx
Solve for x 1622(122)5 1622445 162194 23 1 1 2 xx xx xx x x
The length of a side of the square is 1 1cm. 2 x
Check
The length of the box will be 1 162162116313. 2 x
Its width will be 1 12212211239. 2 x
Twice the width minus 5, 2529513, W is equal to the length of the box as desired.
11. Let x the number of liters of the 5% drug solution.
Liters of Solution Percent (as a decimal) Liters of Pure Drug 20
x
Check
10% of 20 is 2 and 5% of 40 3 is 2 ; 3 28 2, 33 which is the same as 8% of 40 20. 3
12. Let x the number of kilograms of the metal that is 20% tin.
Kilograms of Metal Percent Tin (as a decimal) Kilograms of Pure Tin
80 0.70 80(0.70)56 x 0.20 0.20x 80 x 0.50 0.50(80) x Tinin70%tinin20%tinin50%.
560.200.50(80) xx
Multiply by 100. 56025(80) 56024005 1603 1601 or53 33 xx xx x x 1 53 3 kilograms should be added.
Check
70% of 80 is 56 and 20% of 160 3 is 32 ; 3 322 5666, 33 which is the same as 50% of 160 80. 3
13. Let x the number of $5 bills. Then 126 x is the number of $10 bills.
Drugin10%drugin5%drugin8%.
20.050.08(20) xx
Multiply by 100. 20058(20) 20051608 403 401 or13 33 xx xx x x
The pharmacist should add 1 13 3 L.
Number of Bills
Denomination Value
x 5 5x 126 x 10 10(126) x 126 Totals 840
The sum of the values must equal the total value.
510(126)840 5126010840 5420 84 xx xx x x
There are 84 $5 bills and 1268442 $10 bills.
Check
The number of bills is 8442126 and the value of the bills is $5(84)$10(42)$840, as required.
14. Let x the number of $10 tickets sold. Then 2460 x = the number of $13 tickets sold.
Number Sold Cost of Ticket Amount Collected x $10 10x 2460 x $13 13(2460) x 2460 Totals $27,030
Write the equation from the last column of the table.
1013(2460)27,030 1031,9801327,030 34950 1650 xx xx x x
1650 $10 tickets were sold and 24601650810 $13 tickets were sold.
Check
The number of tickets sold was 16508102460. The amount collected was $10(1650)$13(810)$16,500$10,530 $27,030 as required.
15. The sum of the measures of the three angles of a triangle is 180°. (650)(10)180 860180 8240 30 xxx x x x
With 30, x the three angle measures become (63050)130, (3010)20,and30.
16. In the figure, the two angles are supplementary, so their sum is 180°. (107)(73)180 1710180 17170 10 xx x x x
The two angle measures are 10(10)7107 and 7(10)373.
17. Let x the least integer. Then 1 x is the middle integer and 2 x is the greatest integer. “The sum of the least and greatest of three
consecutive integers is 32 more than the middle integer” translates to (2)32(1). 2233 31 xxx xx x
The three consecutive integers are 31, 32, and 33.
Check
The sum of the least and greatest integers is 313364, which is the same as 32 more than the middle integer.
18. Let x the first odd integer. Then 2 x is the next odd integer.
“If the lesser of two consecutive odd integers is doubled, the result is 7 more than the greater of the two integers” translates to 2()7(2).
29 9 xx xx x
The two consecutive odd integers are 9 and 11.
Check
Doubling the lesser gives us 2(9)18, which is equal to 7 more than 11.
19. Let x the length of the shortest side. Then 2x is the length of the middle side and 32 x is the length of the longest side. The perimeter is 34 inches. Using Pabc gives us 2(32)34. 6234
636 6 xxx x x x
The lengths of the three sides are 6 inches, 2(6)12inches, and 3(6)216inches.
Check
The sum of the lengths of the three sides is 6121634inches, as required.
20. Let x the length of the rectangle. Then the perimeter is 43. x
22
4322(10).
43220 23 PLW xxLetW10 xx x
The length of the rectangle is 23 inches.
Check 222(23)2(10)66inches,PLW which is 43 inches more than the length.
1.5 Linear Inequalities in One Variable
Classroom Examples, Now Try Exercises
1. (a) The statement 3 x says that x can represent any number greater than or equal to 3. Graph it by placing a bracket at 3 and drawing an arrow to the right. The bracket shows that 3 is a part of the graph.
This interval is written with a square bracket at 3 as [3,).
(b) The statement 03.5 x says that x can represent any number between 0 and 3.5 with both 0 and 3.5 excluded. Graph it by placing parentheses at both 0 and 3.5. Fill in the points in between them. The parentheses show that 0 and 3 are not part of the graph.
This interval is written with parentheses as (0,3.5).
N1. (a) The statement 1 x says that x can represent any number less than 1 , but x cannot equal 1. Graph it by placing a right parenthesis at 1 and drawing an arrow to the left. The parenthesis shows that 1 is not a part of the graph.
This interval is written with a parenthesis at 1 as (,1).
(b) The statement 42 x says that x can represent any number between 4 and 2 with 4 included and 2 excluded. Graph it by placing a left bracket at 4 and a right parenthesis at 2. Fill in the points in between them.
This interval is written as [4,2).
2. 51
6Add 5. x x Check
Substitute 6 for x in 51. x ? 651 11True
This shows that 6 is the boundary point. Choose 0 and 7 as test points.
51 x ? ? Let0Let7. 051751 51False21True
0isnotinthe7isinthe solutionset.solutionset. x.x
The check confirms that (6,) is the solution set.
N2. 107 3Add10. x x
Check
Substitute 3 for x in 107. x ? 3107 77True
This shows that 3 is the boundary point. Choose 0 and 7 as test points. ?? 107 Let0.Let7. 01077107 107False37True
0isnotinthe7isinthe solutionset.solutionset. x xx
The check confirms that (3,) is the solution set.
3. 5341
31Subtract4. 4Subtract3
xx xx x
Check
Substitute 4 for x in 5341. xx ? 5(4)34(4)1 1717True
So 4 satisfies the equality part of . Choose 5 and 0 as test points.
? 5341
5(5)34(5)1Let5. 2221False xx x
5 is not in the solution set.
? 5(0)34(0)1Let0. 31True x
0 is in the solution set.
The check confirms that [4,) is the solution set.
N3. 415 1Subtract4. 1Equivalentinequality. xx xx x
Substitute 1 for x in 415. xx
? 4(1)15(1) 55True
So 1 satisfies the equality part of Choose 0 and 2 as test points.
? 415 4(0)15(0)Let0. 10True xx x
0 is in the solution set.
? 4(2)15(2)Let2. 910False x
2 is not in the solution set.
The check confirms that (,1] is the solution set.
4. (a) 4100
Divideby40;donot 4100 reversethesymbol. 44 25 x x x
The solution set is the interval (,25].
Linear Inequalities in One Variable
(b) 981
Divideby90; 8181 reversethesymbol. 99 9 x x
The solution set is the interval (9,).
N4. (a) 840
Divideby80;donot 840 reversethesymbol. 88 5 x x x
The solution set is the interval [5,).
(b) 2060 Divideby200; 2060 reversethesymbol. 2020 3 x x x
The solution set is the interval (,3).
5. 6(1)33(2) 66336 9646 1366 130 130 1313 0 xxxx xxxx xx x x x x
The solution set is the interval [0,).
N5. 52(4)114 528114 213114 21311 22 22 22 1 xx xx xx x x x x
The solution set is the interval (,1].
Copyright © 2025 Pearson Education, Inc.
6. Solve the following inequality.
13(3)2(8) 44 13 4(3)24(8)Multiplyby4. 44 (3)83(8) 11324 21124Subtract3. 213Subtract11. Divideby2; 13 reversesymbol. 2 xx xx xx xx xx x x
The solution set is the interval 13 ,. 2
N6. 311(2)(8) 425 311 20(2)20(8)Mult.by20. 425 15(2)104(8) 153010432 1520432 112032Subtract4. 1112Add20. 12 Divideby11. 11 xx xx xx xx xx xx x x
The solution set is the interval 12 ,. 11
7. 425 27Add2toeachpart. x x
The solution set is the interval (2,7).
N7. 123 15Add2toeachpart. x x
The solution set is the interval (1, 5).
8. 5349 9313Add4toeachpart. Divideby3; 9313 reverse symbol. 333 13 3 3 x x x x
The solution set is the interval 13 ,3. 3
N8. 2457 3412Add5toeachpart. Divideby4. 3412 Reverseinequalities. 444 3 3Reduce. 4 3 3Equivalentinequality. 4 x x x x x
The solution set is the interval 3 3,. 4
9. Step2
Let h= the number of hours she can rent the leaf blower.
Step3
She must pay $15, plus $3.50h, to rent the leaf blower for h hours, and this amount must be no morethan $36. Costofisno36 rentingmorethandollars.
153.5036 h
Step4
3.5021Subtract15. 6Divideby3.50. h h
Step5
She can use the leaf blower for a maximum of 6 hr. (She may use it for less time, as indicated by the inequality 6. h )
Step6
Chapter 1 Linear Equations, Inequalities, and Applications Copyright © 2025 Pearson Education,
If Marge uses the leaf blower for 6 hr, she will spend 153.50(6)36, the maximum amount.
N9. Step2
Let x= the number of months she belongs to the health club.
Step3
She must pay $40, plus $35x, to belong to the health club for x months, and this amount must be nomorethan $355. Costofisno355 belongingmorethandollars.
4035355 x
Step4
35315Subtract40. 9Divideby35. x x
Step5
She can belong to the health club for a maximum of 9 months. (She may belong for less time, as indicated by the inequality 9. x )
Step6
If Sara belongs for 9 months, she will spend 4035(9)355, the maximum amount.
10. Let x= the grade the student must make on the fourth test.
To find the average of the four tests, add them and divide by 4. This average must be at least 90, that is, greater than or equal to 90.
929084
90 4
266
90 4
266360Multiplyby4. 94Subtract266.
The student must score at least 94 on the fourth test.
Check 92908494360 90 44
A score of 94 or more will give an average of at least 90, as required.
N10. Let x= the grade the student must make on the fourth test.
To find the average of the four tests, add them and divide by 4. This average must be at least 90, that is, greater than or equal to 90.
829793 90 4 272 90 4
272360Multiplyby4. 88Subtract272.
The fourth test score must be at least 88.
Check 82979388360 90 44
A score of 88 or more will give an average of at least 90, as required.
Exercises
1. 3 x
In interval notation, this inequality is written (,3]. The bracket indicates that 3 is included. The answer is choice D.
2. 3 x
In interval notation, this inequality is written (3,). The parenthesis indicates that 3 is not included. The answer is choice C.
3. 3 x
In interval notation, this inequality is written (,3). The parenthesis indicates that 3 is not included. The graph of this inequality is shown in choice B.
4. 3 x
In interval notation, this inequality is written [3,). The bracket indicates that 3 is included. The graph of this inequality is shown in choice A.
5. 33 x
In interval notation, this inequality is written [3,3]. The brackets indicates that 3 and 3 are included. The answer is choice F.
6. 33 x
In interval notation, this inequality is written 3,3. The parentheses indicate that neither 3 nor 3 is included. The answer is choice E.
7. (a) The optimal category corresponds to an LDL number of “less than 100.”
LDLis less numberthan100.
100 x
(b) The near optimal/above optimal category corresponds to an LDL number between “100–129.” This is represented by the inequality below.
LDL number 100129 x
Copyright © 2025 Pearson Education, Inc.
(c) The borderline high category corresponds to an LDL number between “130–159.” This is represented by the inequality below.
LDL number
130159 x
(d) The high category corresponds to an LDL number between “160–189.” This is represented by the inequality below.
LDL number
160189 x
(e) The very high category corresponds to an LDL number of “190 and above.” This can also be written as “greater than or equal to 190.”
LDLis greater than numberor equal to190.
x
8. (a) The normal category corresponds to a triglycerides number of “less than 150.”
Triglyceridesis less numberthan150.
150 x
(b) The middle high category corresponds to a triglycerides number between “150–199.” This is represented by the inequality below. triglycerides number
150199 x
(c) The high category corresponds to a triglycerides number of “200–499.” This is represented by the inequality below. triglycerides number
200499 x
Triglyceridesis greater than numberor equal to500.
500 x
9. Since 40, the student should not have reversed the direction of the inequality symbol when dividing by 4. We reverse the inequality symbol only when multiplying or dividing by a negative number. The solution set is [16,).
10. The student divided by 2, a negative number, which requires reversing the direction of the inequality symbol. The solution set is (9,).
11. 412 16Add4. x x
The solution set is the interval [16,).
12. 37 10Add3. x x
The solution set is the interval [10,).
13. 3122
321Subtract1. 7Divideby3. k k k
The solution set is the interval (7,).
14. 5676
570Subtract6. 14Divideby5. x x x
The solution set is the interval (,14).
15. 416 4Divideby4. x x
The solution set is the interval (,4).
(d) The very high category corresponds to a triglycerides number of “500 or higher.” This can also be written as “greater than or equal to 500.”
Copyright © 2025 Pearson Education,
16. 210 5Divideby2. x x
The solution set is the interval (5,).
17. 416 x
Divide both sides by 4, and reverse the inequality symbol.
416 44 4 x x
The solution set is the interval (4,).
18. 525 x
Divide both sides by 5, and reverse the inequality symbol.
525 55 5 x x
The solution set is the interval (,5).
19. 3 30 4 x
Multiply both sides by 4 3 and reverse the inequality symbol.
434 30 343 40 x x
The solution set is the interval (,40].
20. 2 12 3 x
Multiply both sides by 3 2 and reverse the inequality symbol.
323 12 232 18 x x
The solution set is the interval [18,).
21. 1.35.2 x
Divide both sides by 1.3, and reverse the inequality symbol.
1.35.2 1.31.3 4 x x
The solution set is the interval (,4].
22. 2.51.25 x
Divide both sides by 2.5, and reverse the inequality symbol.
2.51.25
2.52.5
0.5 x x
The solution set is the interval [0.5,).
23. 5248
550Subtract2. 10Divideby5. x x x
Check that the solution set is the interval (,10].
24. 4131
432Subtract1. 8Divideby4. x x x
The solution set is the interval (,8].
25. 31 5 4 31 44(5)Multiplyby4. 4 3120 321Add1. 7Divideby3. k k k k k
Check Let 7 k in the equation 31 5. 4 k ? ? 3(7)1 5 4 20 5 4 55True
This shows that 7 is the boundary point. Now
1 Linear Equations,
test a number on each side of 7. We choose 0 and 10. 31 5 4 k ?? Let0Let10. 3(0)13(10)155 44 1295False5True 44
0is not in the 10is in the solution set.solution set. k.k
The check confirms that (7,) is the solution set.
26. 56 8 8 56 888Multiplyby8. 8 5664 570Add6. 14Divideby5. x x x x x
Check Let 14 x in the equation 56 8. 8 x ? ? 5(14)6 8 8 64 8 8 88True
This shows that 14 is the boundary point. Now test a number on each side of 14. We choose 0 and 20. ? ? 56 8 8 Let20. Let0. 5(20)6 5(0)6 8 8 8 8 946 6 or118False 8True 88 8 0isinthesolutionset. 20isnotinthe solutionset. x xx
The check confirms that (,14) is the solution set.
and Applications Copyright © 2025 Pearson Education, Inc.
27. Multiply both sides by 4, and reverse the inequality symbol. 25 5 4 25 44(5) 4 2520 215Add5. 15 Divideby2. 2 x x x x x
The solution set is the interval 15 ,. 2
28. Multiply both sides by 5, and reverse the inequality symbol. 32 6 5 3230 328Add2. 28 Divideby3. 3 x x x x
The solution set is the interval 28 ,. 3
29. 3120 321Subtract1. 7Divideby3. k k k
The solution set is the interval ,7.
30. 5629 535Subtract6. 7Divideby5. z z z
The solution set is the interval 7,.
31. 642 840Add2. 84Add4. 41 Divideby8. 82 xx xx x x
The solution set is the interval 1 ,. 2
32. 282 480Add2 48Add8. 8 2Divideby4. 4 xx xx. x x
The solution set is the interval [2,).
33. 2(4)3 283 83 84Add. 2,or2 xxx xxx xx xx xx
The solution set is the interval [2,).
34. 3(1)4 334 234 36Add2 11 ,or 22 xxx xxx xx xx. xx
The solution set is the interval 1 ,. 2
35. (4)2314 42314 4214 412 3Reverse symbol. rr rr r r r
The solution set is the interval (3,).
1.5 Linear Inequalities in One Variable
36. (9)544 9544 1434 318 6 xx xx x x x
The solution set is the interval [6,).
37. 3(6)22
31822Distributive property
520Subtract 2 and 18. 4Reverse symbol. xx xx xx x
The solution set is the interval (,4).
38. 2(4)616 28616 824 3Reversesymbol. xx xx x x
The solution set is the interval [3,).
39. Multiply both sides by 6 to clear the fractions. 23(31)(23) 32 23 6(31)6(23) 32 4(31)9(23) 1241827 623 23 Reverse symbol. 6 xx xx xx xx x x
The solution set is the interval 23 ,. 6
Copyright © 2025 Pearson Education, Inc.
40. 72(101)(65) 53 72 15(101)15(65) 53 21(101)10(65) 210216050 15071 71 150 xx xx xx xx x x
The solution set is the interval 71 ,. 150
41. Multiply each term by 4 to clear the fractions. 13(6)(25)10 42 1(6)6(25)40 6123040 113640 1176 76 11 pp pp pp p p p
The solution set is the interval 76 ,. 11
42. 31(2)(27)3
The solution set is the interval 49 ,.
43. 3(24)423 612423 21223 123True
The statement is true for all values of x
Therefore, the original inequality is true for any real number.
The solution set is the interval (,).
44. 7(4)52(16) 2875322 282322 2832True
This statement is true for all values of x
The solution set is the interval (,).
45. 11 8381 22 42448 248False xx xx
This is a false statement, so the inequality is a contradiction. The solution set is
46. 11 102101 55 220210 2010False xx xx
This is a false statement, so the inequality is a contradiction. The solution set is
47. The goal is to isolate the variable x. 456 455565Add5. 111 x x x
The solution set is the interval (1, 11).
48. The goal is to isolate the variable x 118 111181Subtract1. 27 x x x
The solution set is the interval (2,7).
49. 9515 9555155Subtract5. 1410 x x x
The solution set is the interval [14,10].
Copyright © 2025 Pearson Education,
50. 4310 4333103Subtract3. 77 x x x
The solution set is the interval [7,7].
51. 62416
10212Subtract4. 56Divideby2. x x x
The solution set is the interval [5,6].
52. 153612
21318Subtract6. 76Divide by 3. x x x
The solution set is the interval 7,6.
53. 19351 1436Add5. 14 2Divideby3. 3 x x x
The solution set is the interval 14 ,2. 3
54. 163210
18312Subtract2. 64Divide by 3. x x x
The solution set is the interval (6,4).
55. 4958
193Subtract 5. Divide by 9. 1 Reverse inequalities. 93 x x x
The last inequality may be written as 11 . 39 x
The solution set is the interval 11 39,.
56. 4238
Linear Inequalities in One Variable Copyright © 2025 Pearson Education, Inc.
125Subtract3. Divideby 2. 5 Reverseinequalities. 22 x x x
The last inequality may be written as 51 22 x The solution set is the interval 51 22,.
57. 8426
1044Subtract 2. Divide by 4. 5 1 Reverse inequalities. 2 x x x
The last inequality may be written as 5 1. 2 x
The solution set is the interval 5 1,. 2
58. 126315
15612Subtract 3. Divide by 6. 5 2 Reverse inequalities. 2 x x x
The last inequality may be written as 5 2. 2 x
The solution set is the interval 5 2,. 2
59. 3 36 4
12324Multiply by 4. 48Divide by 3. x x x
The solution set is the interval (4,8).