

INSTRUCTOR’S SOLUTIONS MANUAL
TIM BRITT
Jackson State Community College
A LGEBRA AND T RIGONOM E T RY
TWELFTH EDITION
Michael Sullivan
Chicago State University

Copyright © 2025, 2021, 2017 by Pearson Education, Inc. or its affiliates. All Rights Reserved. Manufactured in the United States of America. This publication is protected by copyright, and permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise. For information regarding permissions, request forms, and the appropriate contacts within the Pearson Education Global Rights and Permissions department, please visit www.pearsoned.com/permissions/
PEARSON and MYLAB are exclusive trademarks owned by Pearson Education, Inc. or its affiliates in the U.S. and/or other countries.
Unless otherwise indicated herein, any third-party trademarks, logos, or icons that may appear in this work are the property of their respective owners, and any references to third-party trademarks, logos, icons, or other trade dress are for demonstrative or descriptive purposes only. Such references are not intended to imply any sponsorship, endorsement, authorization, or promotion of Pearson’s products by the owners of such marks, or any relationship between the owner and Pearson Education, Inc., or its affiliates, authors, licensees, or distributors
3.4
Table of Contents
Chapter 4 Linear and Quadratic Functions
4.1
4.4
4.5
Chapter 5 Polynomial and Rational Functions
5.1
5
5
5.6
5.7
Chapter 6
6.1
6.5
6.6
6.7
6.8
6.9
Chapter 7 Trigonometric Functions
7.1
7.3
7.4
7.5
7.6
7.7
Chapter 8 Analytic Trigonometry
8.1
8.2
8.3
8.4
8
Chapter 9 Applications of Trigonometric Functions
9.1
9.4
9.5
Chapter 10 Polar Coordinates; Vectors
Chapter 11 Analytic Geometry
Chapter 12 Systems of Equations and Inequalities
12.6
Chapter 13 Sequences; Induction;
Chapter R Review
Section R.1
1. rational
2. 4563430331
3. Distributive
4. c
5. a
6. b
7. True
8. False;TheZero-ProductPropertystatesthatifa productequals0,thenatleastoneofthefactors mustequal0.
9. False;6istheGreatestCommonFactorof12 and18.TheLeastCommonMultipleisthe smallestvaluethatbothnumberswilldivide evenly.TheLCMfor12and18is36.
10. True
11. 1,3,4,5,92,4,6,7,8 1,2,3,4,5,6,7,8,9 AB
12. 1,3,4,5,91,3,4,6 1,3,4,5,6,9
13. 1,3,4,5,92,4,6,7,84 AB
14. 1,3,4,5,91,3,4,61,3,4 AC
15.
ABC
16.
ABC
()
1,3,4,5,92,4,6,7,81,3,4,6 41,3,4,6 1,3,4,6
17. 0,2,6,7,8 A
18. 0,2,5,7,8,9 C
19.
AB
1,3,4,5,92,4,6,7,8 40,1,2,3,5,6,7,8,9
BC
20. 2,4,6,7,81,3,4,6 1,2,3,4,6,7,80,5,9
AB
21. 0,2,6,7,80,1,3,5,9 0,1,2,3,5,6,7,8,9
BC
22. 0,1,3,5,90,2,5,7,8,9 0,5,9
23. a. 2,5
b. 6,2,5
c. 1 6,,1.333...,2,5 2
d.
e. 1 6,,1.333...,,2,5 2
()
1,3,4,5,92,4,6,7,81,3,4,6 1,2,3,4,5,6,7,8,91,3,4,6 1,3,4,6
24. a. 1
b. 0,1
c. 5,2.060606...2.06,1.25,0,1 3
d. 5
e. 5,2.060606...2.06,1.25,0,1,5 3
25. a. 1
b. 0,1
c. 1110,1,,,234
d. None
e. 1110,1,,,234
26. a. None
b. 1
c. 1.3,1.2,1.1,1
d. None
e. 1.3,1.2,1.1,1
27. a. None
b. None
c. None
d. 2,,21,1 2
e. 2,,21,1 2
28. a. None
b. None
c. 110.3 2
d. 2,2 e. 1 2,2,10.3 2
29. a. 18.953 b. 18.952
30. a. 25.861 b. 25.861
31. a. 28.653 b. 28.653
32. a. 99.052 b. 99.052
33. a. 0.063 b. 0.062
34. a. 0.054 b. 0.053
35. a. 9.999 b. 9.998
36. a. 1.001 b. 1.000
37. a. 0.429 b. 0.428
38. a. 0.556 b. 0.555
39. a. 34.733 b. 34.733
40. a. 16.200 b. 16.200
41. 325
42. 5210
43. 234 x
44. 322 y
45. 312 y
46. 246 x
47. 26 x
48. 26 y
49. 6 2 x
50. 26 x
51. 942527
52. 643235
53. 6436126
54. 842880
55. 185218108
56. 1001021002080
57. 4112113 333
58. 21413 222
21100374253
73. 3215823 452020
74. 418311 3266
75. 74493281 875656
76. 81516135151 921818
77. 5110313 18123636
2864046 1594545
79. 5825643913 241512012040
80. 32945 14214242
81. 32981 20156060
82. 6312153 35147070
83. 5 1852759359 1118119211 27
5 2153557557 2212732
85. 141741721 1 3721212121
86. 24122222222 35635323532315 25210210212 351515151515 43434 53535
87. 3323363623 2 4814848428 12312315 8888
88. 51351351351 3 62162322322 51514 2 2222
64624 xx
42184 xx
2 44 xxxx
2 43412 xxxx
2121323 333 3636332 3231 2 3322 x
2 2 24428 68 xxxxx
2 2 5155 65 xxxxx
xxxxx
2 2 927271863 21163
98. 2 2 3153155 3145 xxxxx xx
99. 2 2 822816 1016 xxxxx xx
100. 2 2 42248 68 xxxxx xx
101. 2 22 3(5)360 315360 1560 4 xxkxx xxkxx xkx k
102. 2 222 222 222 222 ()(3)412 33412 (3)3412 (3)3412 (2)3412 24 2
xkxkxx xkxkxkxx xxkkkxx xxkkkxx xxkkxx k k
103. 2323 23 5 5 xxxx x x x
104. 23421214 sincemultiplicationcomesbeforeadditioninthe orderofoperationsforrealnumbers.
2345420 sinceoperationsinsideparenthesescomebefore multiplicationintheorderofoperationsforreal numbers.
105. 23421224
23246848
106. 4371 257 ,but 43453220626132.6 251010105
107. Subtractionisnotcommutative;for example:231132
108. Subtractionisnotassociative;for example: 52124521 .
109. Divisionisnotcommutative;forexample: 23 32 .
110. Divisionisnotassociative;for example: 1222623 ,but
122212112
111. TheSymmetricPropertyimpliesthatif2= x, then x =2.
112. Fromthe principleofsubstitution, if5 x ,then
113. Therearenorealnumbersthatarebothrational andirrational,sinceanirrationalnumber,by definition,isanumberthatcannotbeexpressed astheratiooftwointegers;thatis,notarational number
Everyrealnumberiseitherarationalnumberor anirrationalnumber,sincethedecimalformofa realnumbereitherinvolvesaninfinitely repeatingpatternofdigitsoraninfinite,nonrepeatingstringofdigits.
114. Thesumofanirrationalnumberandarational numbermustbeirrational.Otherwise,the irrationalnumberwouldthenbethedifferenceof tworationalnumbers,andthereforewouldhave toberational.
115. Answerswillvary.
116. Since1day=24hours,wecompute 12997541.5416 24
Nowweonlyneedtoconsiderthedecimalpart oftheanswerintermsofa24hourday.Thatis,
0.54162413 hours.Soitmustbe13hours laterthan12noon,whichmakesthetime1a.m. CST.
117. Answerswillvary.
Section R.2
1. variable
2. origin
3. strict
4. base;exponent(orpower)
5. 31.234567810
6. d
7. a
8. b
9. True
10. False;theabsolutevalueofarealnumberis nonnegative.00 whichisnotapositive number.
11. False;anumberinscientificnotationis expressedastheproductofanumber,x, 110 x or101 x ,andapowerof10.
12. True 13.
15. 10 2 16. 56 17. 12 18. 35 2 19. 3.14 20. 21.41
21. 10.5 2
22. 10.33 3
23. 20.67 3
24. 10.25 4
25. 0 x
26. 0 z
27. 2 x
28. 5 y
29. 1 x
30. 2 x
31. Graphonthenumberline:2 x
32. Graphonthenumberline:4 x
33. Graphonthenumberline:1 x
34. Graphonthenumberline:7 x
35. (,)(0,1)1011dCDd
36. (,)(0,3)3033dCAd
37. (,)(1,3)3122dDEd
38. (,)(0,3)3033dCEd
39. (,)(3,3)3(3)66dAEd
40. (,)(1,1)1122dDBd
41. 2223264xy
42. 33(2)3633 xy
43. 525(2)(3)230228 xy
44. 22(2)(2)(3)462 xxy
45. 2(2)4 24 2355 x xy
46. 2311 2355 xy xy
47. 323(2)2(3)6600 22355 xy y
48. 2(2)343 237 333 x y
49. 3(2)11 xy
50. 3(2)55 xy
51. 32325 xy
52. 32321 xy
53. 331 33 x x
54. 221 22 y y
55. 454(3)5(2) 1210 22 22 xy
56. 323(3)2(2)9455 xy
57. 454(3)5(2) 1210 1210 2 2 xy
58. 323322 3322 94 13 xy
59. 21 x x
Part(c)mustbeexcluded.Thevalue0 x must beexcludedfromthedomainbecauseitcauses divisionby0.
60. 21 x x
Part(c)mustbeexcluded.Thevalue0 x must beexcludedfromthedomainbecauseitcauses divisionby0.
61. 2(3)(3) 9 xx xxx
Part(a),3 x ,mustbeexcludedbecauseit causesthedenominatortobe0.
62. 29 x x
Noneofthegivenvaluesareexcluded.The domainisallrealnumbers.
63. 2 21 x x
Noneofthegivenvaluesareexcluded.The domainisallrealnumbers.
64. 33 2(1)(1) 1 xx xxx
Parts(b)and(d)mustbeexcluded.Thevalues 1,and1xx mustbeexcludedfromthe domainbecausetheycausedivisionby0.
65. 22 3 510510 (1)(1) xxxx xxxxx
Parts(b),(c),and(d)mustbeexcluded.The values0,1,and1 xxx mustbeexcluded fromthedomainbecausetheycausedivisionby 0.
66. 22 32 9191 (1) xxxx xxxx
Part(c)mustbeexcluded.Thevalue0 x must
beexcludedfromthedomainbecauseitcauses divisionby0.
67. 4 5 x 5 x mustbeexludedbecauseitmakesthe denominatorequal0.
Domain5 xx
68. 6 4 x 4 x mustbeexcludedsineitmakesthe denominatorequal0.
Domain4 xx
69. 4 x x 4 x mustbeexcludedsineitmakesthe denominatorequal0.
Domain4 xx
70. 2 6 x x 6 x mustbeexcludedsineitmakesthe denominatorequal0.
Domain6 xx
71. 555 (32)(3232)(0)0C 999 CF
72. 555 (32)(21232)(180)100C 999 CF
73. 555 (32)(7732)(45)25C 999 CF
74. 55(32)(432)99 5(36) 9 20C CF
75. 2 (9)(9)(9)81
76. 22 4(4)16
77. 2 2 411 416
78. 2 2 411 416
79. 64642 2 333311 39
80. 23231 44444
90.
313 13 2228
2224
33311333 3 y xyxyxy x
91. 25 235411 34 xyy xyxy xyx
92. 2 211231 23 1 xy xyxy xyxy
93. 253533 37272 315732 221 2 2 (4)()16 (3)27 16 27 16 27 16 27
yxzyxz xyzxyz xyz xyz xz y 94. 21211 344 24111 621 62 4()4 28 4 8 1 2 1 2 xyzxyz xyxy xyz xyz xyz
95. 22 2 33266 13222 3 2339 2
122 2 24 1 x xy y
131 333 22 y xy x
222221415 xy
222221414 xy
2 222124 xy
2 222111 xy 103. 222xx 104.
2 2 xx 105.
222221415 xy 106. 2221213 xyxy 107. 211 2 y x
113. 6 (8.2)304,006.671
114. 5 (3.7)693.440 115. 3 (6.1)0.004
116. 5 (2.2)0.019 117. 6 (2.8)481.890
118. 6 (2.8)481.890
119. 4 (8.11)0.000
120. 4 (8.11)0.000
121. 2 454.24.54210
122. 132.143.21410
123. 0.0131.3102 124. 0.004214.21103
125. 432,1553.215510
126. 4 21,2102.12110
127. 0.0004234.23104
128. 0.05145.14102
129. 4 6.151061,500
130. 3 9.7109700
131. 3 1.214100.001214
132. 4 9.88100.000988
133. 8 1.110110,000,000
134. 2 4.11210411.2
135. 2 8.1100.081
136. 1 6.453100.6453
137. Alw
138. 2 Plw
139. Cd
140. 1 2 Abh
141. 32 4 Ax
142. 3 Px
143. 43 3 Vr
144. 42Sr
145. 3 Vx
146. 62Sx
147. a. If1000, x 40002 40002(1000) 40002000 $6000 Cx
Thecostofproducing1000watchesis $6000.
b. If2000, x 40002 40002(2000) 40004000 $8000 Cx
Thecostofproducing2000watchesis $8000.
148. 210801202560325$98 Hisbalanceattheendofthemonthwas$98.
149. Wewantthedifferencebetween x and4tobeat least6units.Sincewedon’tcarewhetherthe valuefor x islargerorsmallerthan4,wetake theabsolutevalueofthedifference.Wewantthe inequalitytobenon-strictsincewearedealing withan‘atleast’situation.Thus,wehave 46 x
150. Wewantthedifferencebetween x and2tobe morethan5units.Sincewedon’tcarewhether thevaluefor x islargerorsmallerthan2,we taketheabsolutevalueofthedifference.We wanttheinequalitytobestrictsinceweare dealingwitha‘morethan’situation.Thus,we have 25 x
151. a. 110108110225 x 108voltsisacceptable.
b. 110104110665 x 104voltsis not acceptable.
152. a. 220214220668 x 214voltsisacceptable.
b. 22020922011118 x 209voltsis not acceptable.
153. a. 32.9993 0.001 0.0010.01 x Aradiusof2.999centimetersisacceptable.
b. 32.893 0.11 0.110.01 x Aradiusof2.89centimetersis not acceptable.
154. a. 98.69798.6 1.6 1.61.5 x 97˚Fisunhealthy.
b. 98.610098.6 1.4 1.41.5 x 100˚Fis not unhealthy.
155. ThedistancefromEarthtotheMoonisabout 8 410400,000,000 meters.
156. TheheightofMt.Everestisabout 388488.84810 meters.
157. Thewavelengthofvisiblelightisabout 7 5100.0000005 meters.
158. Thediameterofanatomisabout 10 1100.0000000001 meters.
159. Thediameterisabout2 0.04034.0310 inches.
160. Thetiniestmotorislessthan5 0.00004410 millimeterstall.
161. 5112 2 1.86106102.4103.6510
186,000606024365 1012 586.5696105.86569610 Thereareabout12 5.910 milesinonelightyear.
162. 7 2 5 93,000,0009.310510 186,0001.8610 500seconds8min.20sec.
Ittakesabout8minutes20secondsforabeam oflighttoreachEarthfromtheSun.
163. 10.333333...0.333 3 1 3islargerbyapproximately0.0003333...
164. 2 30.666666...0.666 2 3islargerbyapproximately0.000666...
165.
613613 1920 5.24106.5105.246.51010 34.06103.40610
166. 44 6 1010 5 1.62101.62100.3610 4.5 4.51010
167. No.Foranypositivenumber a,thevalue2 a is smallerandthereforecloserto0.
168. Wearegiventhat2110 x .Thisimpliesthat 110 x .Since103.162 x and 3.142 x ,thenumbercouldbe3.15or3.16 (whicharebetween1and10asrequired).The numbercouldalsobe3.14sincenumberssuchas 3.146whichliebetween and10would equal3.14whentruncatedtotwodecimalplaces.
169. Answerswillvary.
170. Answerswillvary. 5<8isatruestatementbecause5isfurtherto theleftthan8onarealnumberline.
Section R.3
1. right;hypotenuse
2. 1 2 Abh 3. 2 Cr
4. similar
5. c 6. b
7. True.
8. True.222 68366410010
9. False;thesurfaceareaofasphereofradius r is givenby2 4 Vr
10. True.Thelengthsofthecorrespondingsidesare equal.
11. True.Twocorrespondinganglesareequal.
12. False.Thesidesarenotproportional.
13. 222 22 5,12, 512 25144 16913 ab cab c
14. 222 22 6,8, 68 3664 10010 ab cab c
15. 222 22 10,24, 1024 100576 67626 ab cab c
16. 222 22 4,3, 43 169 255 ab cab c
17. 222 22 7,24, 724 49576 62525 ab cab c
18. 222 22 14,48, 1448 1962304 250050 ab cab c
19. 222 534 25916 2525
Thegiventriangleisarighttriangle.The hypotenuseis5.
20. 222 1068 1003664 100100
Thegiventriangleisarighttriangle.The hypotenuseis10.
21. 222 645 361625 3641false
Thegiventriangleisnotarighttriangle.
22. 222 322 944 98false
Thegiventriangleisnotarighttriangle.
23. 222 25724 62549576 625625
Thegiventriangleisarighttriangle.The hypotenuseis25.
24. 222 261024 676100576 676676
Thegiventriangleisarighttriangle.The hypotenuseis26.
25. 222 634 36916 3625false
Thegiventriangleisnotarighttriangle.
26. 222 754 492516 4941false Thegiventriangleisnotarighttriangle.
27. 67422 in Alw
28. 94362 cm Alw
29. 112 22(14)(4)28in
Abh
30. 112 22(4)(9)18cmAbh
31. 222 (5)25m 22(5)10m Ar Cr
32. 222 (2)4ft 22(2)4ft Ar Cr
33. 6852403 ft Vlwh
Slwlhwh
2 222 268265285 966080
236ft
34. 9482883 in Vlwh
Slwlhwh
2 222 294298248 7214464 280in
35. 333 222 445005cm 333 445100cm
Vr Sr
36. 333 222 44336f 33 44336ft
Vrt Sr
37. 223 (9)(8)648in Vrh
2 2 2 22 29298 162144 306in
38. 223 (8)(9)576in Vrh
2 2 2 22 28289 128144 272in
39. Thediameterofthecircleis2,soitsradiusis1. 22(1)squareunits Ar
40. Thediameterofthecircleis2,soitsradiusis1. 22 2(1)4squareunits A
41. Thediameterofthecircleisthelengthofthe diagonalofthesquare.
222 22 44 8 822 222 22 d d d r
Theareaofthecircleis:
2222squareunits Ar
42. Thediameterofthecircleisthelengthofthe diagonalofthesquare.
Theareais:
22 2224squareunits A
Section R.3: Geometry Essentials
43. Sincethetrianglesaresimilar,thelengthsof correspondingsidesareproportional.Therefore, weget 8 42 82 4 4 x x x
Inaddition,correspondinganglesmusthavethe sameanglemeasure.Therefore,wehave 90 A ,60 B ,and30 C
44. Sincethetrianglesaresimilar,thelengthsof correspondingsidesareproportional.Therefore, weget 6 1216 616 12 8 x x x Inaddition,correspondinganglesmusthavethe sameanglemeasure.Therefore,wehave 30 A
,75 B ,and75 C
45. Sincethetrianglesaresimilar,thelengthsof correspondingsidesareproportional.Therefore, weget 30 2045 3045 20 135 or67.5 2 x x xx
Inaddition,correspondinganglesmusthavethe sameanglemeasure.Therefore,wehave 60 A
46. Sincethetrianglesaresimilar,thelengthsof correspondingsidesareproportional.Therefore, weget 8 1050 850 10 40 x x x
Inaddition,correspondinganglesmusthavethe sameanglemeasure.Therefore,wehave 50 A ,125 B ,and5 C .
47. Thetotaldistancetraveledis4timesthe circumferenceofthewheel. TotalDistance44()416 64201.1inches16.8feet
48. Thedistancetraveledinonerevolutionisthe circumferenceofthedisk4 Thenumberofrevolutions= dist.traveled2051.6revolutions circumference4
49. Areaoftheborder=areaofEFGH–areaof ABCD222 1061003664ft
50. FG=4feet;BG=4feetandBC=10feet,so CG=6feet.TheareaofthetriangleCGFis: 12 2(4)(6)12ft
51. Areaofthewindow=areaoftherectangle+ areaofthesemicircle. 122 (6)(4)224230.28ft 2
Perimeterofthewindow=2heights+width+ one-halfthecircumference. 1 2(6)4(4)1242 2 16222.28feet
52. Areaofthedeck=areaofthepoolanddeck–areaofthepool. 22 22 (13)(10)169100 69ft216.77ft
Theamountoffenceisthecircumferenceofthe circlewithradius13feet. 2(13)26ft81.68ft
53. WecanformsimilartrianglesusingtheGreat Pyramid’sheight/shadowandThales’ height/shadow: h 126114 240 {{ 2 3
Thisallowsustowrite 2 2403 2240 160
54. Let x =theapproximatedistancefromSanJuan toHamiltonand y =theapproximatedistance fromHamiltontoFortLauderdale.Usingsimilar triangles,weget 1046
5853.5 104653.5 58 964.8 x x x
1046 5857 104657 58 1028.0 y y y
TheapproximatedistancebetweenSanJuanand Hamiltonis965milesandtheapproximate distancebetweenHamiltonandFortLauderdale is1028miles.
55. Convert20feettomiles,andsolvethe PythagoreanTheoremtofindthedistance:
201milefeet20feet0.003788miles 5280feet (39600.003788)396030 5.477miles
222sq.miles
56. Convert6feettomiles,andsolvethe PythagoreanTheoremtofindthedistance:
61mile feet6feet0.001136miles 5280feet (39600.001136)39609 3miles
222sq.miles
57. Convert100feettomiles,andsolvethe PythagoreanTheoremtofindthedistance: 1001milefeet100feet0.018939miles 5280feet
222sq.miles (39600.018939)3960150 12.2miles
Convert150feettomiles,andsolvethe PythagoreanTheoremtofindthedistance: 1501milefeet150feet0.028409miles 5280feet
222sq.miles (39600.028409)3960225 15.0miles
58. Given0,0andmnmn , if2222 ,2and amnbmncmn ,then
and 2 2224224 2 cmnmmnn 222,and abcabc representthesides ofarighttriangle.
Ifyoudoubletheradiusthevolumeis8times theoriginalvolume.
63. Let l= lengthoftherectangle and w =widthoftherectangle. Noticethat 22 ()() [()()][()()] (2)(2)44 lwlw lwlwlwlw lwlwA
Since2()0 lw ,thelargestareawilloccur when l–w =0or l=w;thatis,whenthe rectangleisasquare.But 1000222() 5002 250 lwlw lwl lw
Vrh So,
59. 2 2 3 (10)(4.5) 450ft
3 33 1ft7.48052galso 450ft7.48052gal/ft10,575gal
60. 3 2 2 10000(5.61458)56145.8ft 56145.8(25) 56145.828.6ft 625
61. 2 2 2 2 2 (2) 4 44
Ar Ar r rA
Ifyoudoubletheradius,theareaisfourtimes theoriginalarea.
Thelargestpossibleareais225062500 sqft. Acircularpoolwithcircumference=1000feet yieldstheequation:500 21000rr
Theareaenclosedbythecircularpoolis: 22 22 50050079577.47ft Ar
Thus,acircularpoolwillenclosethemostarea.
64. Considerthediagramshowingthelighthouseat pointL,relativetothecenterofEarth,usingthe radiusofEarthas3960miles.LetPrefertothe furthestpointonthehorizonfromwhichthe lightisvisible.Notealsothat 362362feetmiles. 5280
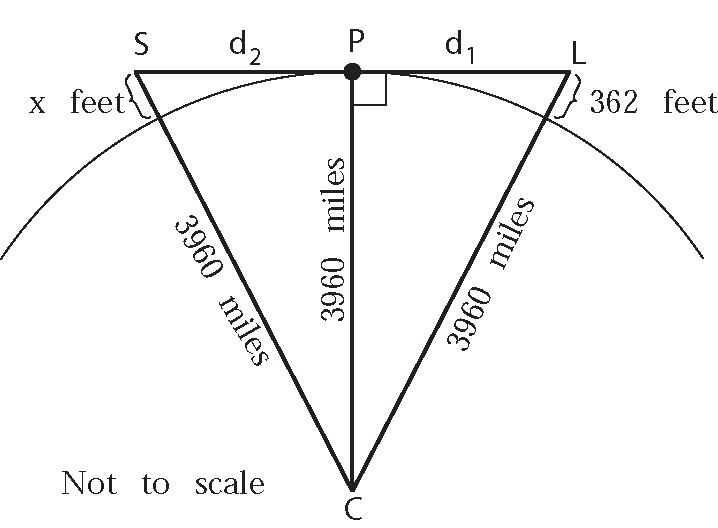
ApplythePythagoreanTheoremto CPL :
2 22 1 39603960362 5280 d
2 22 1 22 1 362 5280 362 5280 39603960 3960396023.30mi. d d
Therefore,thelightfromthelighthousecanbe seenatpointPonthehorizon,wherepointPis approximately23.30milesawayfromthe lighthouse.Brochureinformationisslightly overstated.
Verifytheshipinformation:
LetSrefertotheship’slocation,andlet x equal theheight,infeet,oftheship.
Weneed1240 dd
Since123.30miles d weneed 24023.30=16.70miles. d
ApplythePythagoreanTheoremto CPS :
396016.73960
222 22 22
396016.73960
396016.73960
Theshipwouldhavetobeatleast186feettallto seethelighthousefrom40milesaway.
Verifytheairplaneinformation:
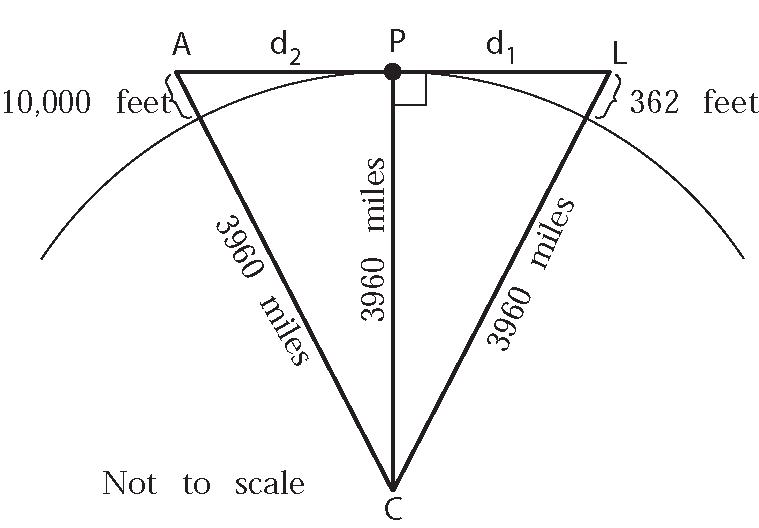
LetArefertotheairplane’slocation.The distancefromtheplanetopointPis2 d Wewanttoshowthat12120 dd Assumethealtitudeoftheairplaneis 10,000feet=10000miles. 5280
ApplythePythagoreanTheoremto CPA :
2 22 2 3960396010000 5280 d
2 22 2 2 2 2 10000 39603960 5280 10000 39603960 5280 122.49miles. d d
61Therefo re,1223.30122.49145.79120. dd
Thebrochureinformationisslightlyunderstated. Notethataplaneatanaltitudeof6233feet couldseethelighthousefrom120milesaway.
Section R.4
False;monomialscannothavenegativedegrees.
False;thedividend=(quotient)(divisor)+ remainder
9. 23 x Monomial;Variable: x ; Coefficient:2;Degree:3
10. 42 x Monomial;Variable: x ;Coefficient: –4;Degree:2
11. 81 8 x x Notamonomial;whenwrittenin theform k ax ,thevariablehasanegative exponent.
12. 23 x Notamonomial;whenwritteninthe form k ax ,thevariablehasanegativeexponent.
13. 22 xy Monomial;Variables:,xy ; Coefficient:–2;Degree:3
14. 523 xy Monomial;Variables:,xy ; Coefficient:5;Degree:5
15. 81 8 x xy y Notamonomial;whenwritten intheform nm axy ,theexponentonthevariable y isnegative.
16. 2 23 3 22 x xy y Notamonomial;when writtenintheform nm axy ,theexponentonthe variable y isnegative.
17. 22 xy Notamonomial;theexpression containsmorethanoneterm.Thisexpressionis abinomial.
18. 2 34 x Notamonomial;theexpression containsmorethanoneterm.Thisexpressionis abinomial.
19. 2 35 x Polynomial;Degree:2
20. 14 x Polynomial;Degree:1
21. 5Polynomial;Degree:0
22. –π Polynomial;Degree:0
23. 325 x x Notapolynomial;thevariableinthe denominatorresultsinanexponentthatisnota nonnegativeinteger.
Section R.4: Polynomials
24. 32 x Notapolynomial;thevariableinthe denominatorresultsinanexponentthatisnota nonnegativeinteger.
25. 3 22 y Polynomial;Degree:3
26. 102zz Polynomial;Degree:2
27. 2 3 5 1 x x Notapolynomial;thepolynomialin thedenominatorhasadegreegreaterthan0.
28. 3 2 321 1 xx xx
Notapolynomial;the polynomialinthedenominatorhasadegree greaterthan0.
29. 22 22 2 (68)(347) (3)(64)(87) 4215
xxxx xxxx xx
30. 322 322 32 (32)(44) (3)(4)(24) 446 xxxx xxxx xxx
31. 322 322 (2510)(243) 2510243 xxxxx xxxxx
322 32 (22)(54)(103) 497 xxxxx xxx
32. 232 232 (34)(35) 3435 xxxxx xxxxx 322 32 (3)(3)(45) 449 xxxxx xxx
33. 53432 542 653 653 xxxxxx xxxx
34. 5232 532 108326 103106 xxxx xxx
35. 22 22 2 (64)3(25) 646315 7311
xxxx xxxx xx
Chapter R: Review
36. 22 22 2 2(1)(52) 22252 73 xxxx xxxx xx
37. 3232 3232 32 6(3)4(23) 6618812 21818 xxxx xxxx xx
38. 323 323 8(431)6(482) 32248244812 xxxx xxxx
32 824484 xxx
39.
40.
222 222 22351 22351 xxxxx xxxxx
2 246 xx
222 222 1452 1452 xxxx xxxx
2 26 xx
41. 22 22 2 75343 73521124 11359 yyy yyy yy
42. 323 323 8141 884444 yyyy yyyy
32 44412 yyy
43. 22432 (25)25 xxxxxx
44. 23532 4(2)448 xxxxxx
45. 2352 2(45)810 xxxx
46. 343 5(34)1520 xxxx
47. 2 22 (1)(24) (24)1(24) xxx xxxxx 322 32 2424 324 xxxxx xxx
48. 2 22 (23)(1) 2(1)3(1) xxx xxxxx 322 32 222333 23 xxxxx xxx
49. 2 2 (2)(4)428 68 xxxxx xx
50. 2 2 (3)(5)5315 815 xxxxx xx
51. 2 2 (27)(5)271035 21735 xxxxx xx
52. 2 2 (31)(21)6321 651 xxxxx xx
53. 2 2 (4)(2)248 28 xxxxx xx
54. 2 2 (4)(2)248 28 xxxxx xx
55. 2 2 (6)(3)6318 918 xxxxx xx
56. 2 2 (5)(1)55 65 xxxxx xx
57. 2 2 (23)(2)2436 26 xxxxx xx
58. 2 2 (24)(31)62124 6104 xxxxx xx
59. 2 2 (34)(2)3468 3108 xxxxx xx
60. 2 2 (31)(1)331 341 xxxxx xx
61. 2 2 (5)(27)210735 21735 xxxxx xx
62. 2 2 (23)(3)6293 239 xxxxx xx
63. 22 22 (2)()22 2 xyxyxxyxyy xxyy
64. 22 22 (23)()2233 23 xyxyxxyxyy xxyy
65. 22 22 (23)(32)6496 6136 xyxyxxyxyy xxyy
66. 22 22 (3)(2)263 273 xyxyxxyxyy xxyy
67. 222 (7)(7)749 xxxx
68. 222 (1)(1)11 xxxx
69. 222 (23)(23)(2)349 xxxx
70. 222 (32)(32)(3)294 xxxx
71. 2222 (4)244816 xxxxx
72. 2222 (5)2551025 xxxxx
73. 2222 (4)244816 xxxxx
74. 2222 (5)2551025 xxxxx
75. 222 (34)(34)(3)4916 xxxx
76. 222 (53)(53)(5)3259 xxxx
77. 222 2 (23)(2)2(2)(3)3 4129 xxx xx
78. 222 2 (34)(3)2(3)(4)4 92416 xxx xx
79. 2 222 ()()() xyxyxyxy
80. 2 222(3)(3)()39 xyxyxyxy
81. 2 222(3)(3)(3)9 xyxyxyxy
82. 2 222(34)(34)(3)4916 xyxyxyxy
83. 222()2 xyxxyy
84. 222()2 xyxxyy
85. 222 22 (2)222 44 xyxxyy xxyy
86. 222 22 (23)22233 4129 xyxxyy xxyy
87. 33223 32 (2)32322 6128 xxxx xxx
88. 33223 32 (1)31311 331 xxxx xxx
89. 33223 32 (21)(2)3(2)(1)3(2)11 81261 xxxx xxx
90. 33223 32 (32)(3)3(3)(2)3(3)22 2754368 xxxx xxx
91. 2 32 32 2 2 41123 2431 48 11 1122 231 2346 45 xx xxxx xx xx xx x x
2 322 32 Check: (2)(41123)(45) 411238224645 431 xxx xxxxx xxx Thequotientis241123 xx ;theremainder is–45.
Chapter R: Review
92. 2 32 32 2 2 3715 232 36 7 714 152 1530 32 xx xxxx xx xx xx x x 2 322 32
Check:
(2)(3715)(32) 37156143032 32 xxx xxxxx xxx
Thequotientis23715 xx ;theremainderis –32.
93. 232 3 2 2 43 431 4 31 3 1 x xxxx x xx x x
Check: ()(43)(1)431 xxxxxx Thequotientis43 x ;theremainderis1 x
232
94. 232 3 2 2 31 32 3 2 2 x xxxx x xx x x
232 Check: ()(31)(2)32 xxxxxx
Thequotientis31 x ;theremainderis2 x
95. 2 2432 42 2 2 513 25031 510 131 1326 27 x xxxxx xx xx x x
Check:
22 422 42 251327 510132627 531 xxx xxxx xxx
Thequotientis2513 x ;theremainderis 27 x
96. 2 2432 42 2 2 511 2502 510 112 1122 20 x xxxxx xx xx x x
Check: 22 422 42 251120 510112220 52 xxx xxxx xxx
Thequotientis2511 x ;theremainderis 20 x
97. 2 35432 52 2 2 2140031 42 1 x xxxxxx xx xx
Check: 322 52252 2121 421431 xxxx xxxxxxx
Thequotientis2 2 x ;theremainderis 21xx
Thequotientis221
22 432322
42 Check: (1)(1)(22) 122 1 xxxxx xxxxxxxx x xx
. 105. 22 323 32 2 22 23 23 00 0 xaxa xaxxxa xax ax axax axa axa
22 322223 33 Check: ()()0 xaxaxa xaxaxaxaxa xa
Thequotientis22 xaxa ;theremainderis0.
106. 432234 54325 54 4 423 0000 xaxaxaxa xaxxxxxa xax ax axax
23 2332 32 324 45 45 0 ax axax ax axax axa axa
Thequotientis432234 xaxaxaxa ;the remainderis0.
108. Theproducts()() xyxy and()() zwzw willeachresultinabinomialthatisthe differenceofsquares.Theproductofthose resultingbinomialswillhave4terms.
109. Whenwemultiplypolynomials 1 px and 2 px ,eachtermof 1 px willbemultiplied byeachtermof 2 px .Sowhenthehighestpoweredtermof 1 px multipliesbythehighest poweredtermof 2 px ,theexponentsonthe variablesinthosetermswilladdaccordingtothe basicrulesofexponents.Therefore,thehighest poweredtermoftheproductpolynomialwill havedegreeequaltothesumofthedegreesof 1 px and 2 px .
110. Whenweaddtwopolynomials 1 px and 2 px ,wherethedegreeof 1 px thedegree of 2 px ,eachtermof 1 px willbeaddedto eachtermof 2 px .Sinceonlythetermswith equaldegreeswillcombineviaaddition,the degreeofthesumpolynomialwillbethedegree ofthehighestpoweredtermoverall,thatis,the degreeofthepolynomialthathadthehigher degree.
111. Whenweaddtwopolynomials 1 px and 2 px ,wherethedegreeof 1 px =thedegree of 2 px ,thenewpolynomialwillhavedegree thedegreeof 1 px and 2 px .
112. Answerswillvary.
113. Answerswillvary.
Section R.5
1. 322 xxx
2. prime
3. c 4. b
5. d
6. c
7. True;24 x isprimeoverthesetofreal numbers.
8. False; 322 3264322 xxxxx
9. 363(2) xx
10. 7147(2) xx
11. 22(1)axaax
12. (1)axaax
13. 322(1)xxxxxx
14. 322(1)xxxxxx
15. 2 222(1) xxxx 16. 2 333(1) xxxx
17. 22 36123(24) xyxyxyxyxy
18. 2232 60487212(546) xyxyxyxyxyx
19. 22211(1)(1)xxxx
20. 22242(2)(2)xxxx
21. 222 41(2)1(21)(21) xxxx
22. 222 91(3)1(31)(31) xxxx
23. 222164(4)(4)xxxx
24. 222255(5)(5)xxxx
25. 2 254(52)(52) xxx
26. 22 3699419(21)(21) xxxx
27. 22 21(1)xxx
28. 22 44(2)xxx
29. 22 44(2)xxx
30. 22 21(1)xxx
31. 22 1025(5)xxx
32. 22 1025(5)xxx
33. 22 441(21) xxx
34. 22 961(31) xxx
35. 22 1681(41) xxx
36. 22 25101(51) xxx
37. 3332273(3)(39)xxxxx
38. 33321255(5)(525)xxxxx
39. 3332273(3)(39)xxxxx
40. 333 2 2 2783(2) (32)(964) 23469 xx xxx xxx
41. 333 2 827(2)3 (23)(469) xx xxx
42. 333 2 2 64274(3) (43)(16129) 3491216 xx xxx xxx
43. 256(2)(3) xxxx
44. 268(2)(4) xxxx
45. 276(6)(1) xxxx
46. 298(8)(1) xxxx
47. 2710(2)(5) xxxx
48. 21110(10)(1) xxxx
49. 21016(2)(8) xxxx
50. 21716(16)(1) xxxx
51. 278(1)(8) xxxx
52. 228(2)(4) xxxx
53. 278(8)(1) xxxx
54. 228(4)(2) xxxx
55. 2 24362(2)3(2) (2)(23) xxxxxx xx
56. 2 33223(1)2(1) (1)(32) xxxxxx xx
57. 2 51535(3)1(3) (3)(51) xxxxxx xx
58. 2 3623(2)1(2) (2)(31) xxxxxx xx
Section R.5: Factoring Polynomials
59. 2 6218283(27)4(27) (27)(34) xxxxxx xx
2 9632332132 3231 xxxxxx xx
60.
61. 2 341(31)(1) xxxx
62. 2 231(21)(1) xxxx
63. 2 297(27)(1) zzzz
64. 2 651(31)(21) zzzz
65. 2 568(54)(2) xxxx
66. 2 3108(34)(2) xxxx
67. 2 568(54)(2) xxxx
68. 2 3108(34)(2) xxxx
69. 2 5228(52)(4) xxxx
70. 2 3148(32)(4) xxxx
71. 2 5188(52)(4) xxxx
72. 2 3108(32)(4) xxxx
73. Since b is10thenweneedhalfof10squaredto bethelastterminourtrinomial.Thus
12 2 22 (10)5;(5)25 1025(5)xxx
74. Since b is14thenweneedhalfof14squaredto bethelastterminourtrinomial.Thus
12 2 22 (14)7;(7)49 1449(7)ppp
75. Since b is-6thenweneedhalfof-6squaredto bethelastterminourtrinomial.Thus
12 2 22 (6)3;(3)9 69(3)yyy
76. Since b is-4thenweneedhalfof-4squaredto bethelastterminourtrinomial.Thus 12 2 22 (4)2;(2)4 44(2)xxx
77. Since b is12thenweneedhalfof12squared tobethelastterminourtrinomial.Thus 2 11111 224416 22 111 2164 ();() ()xxx
78. Since b is13thenweneedhalfof13squaredto bethelastterminourtrinomial.Thus 2 11111 236636 22 111 3366 ();() ()xxx
79. 236(6)(6) xxx
80. 29(3)(3) xxx
81. 22 282(14)21212 xxxx
82. 22 3273(19)31313 xxxx
83. 21110(1)(10) xxxx
84. 254(4)(1) xxxx
85. 2102173 xxxx
86. 268(2)(4) xxxx
87. 22 4832428 xxxx
88. 22 31215345 xxxx
89. 2416xx isprimeovertherealsbecause therearenofactorsof16whosesumis4.
90. 22 1236(6)xxx
91. 22 152(215)(5)(3) xxxxxx
92. 22 146(614) xxxx isprimeoverthe integersbecausetherearenofactorsof–14 whosesumis–6.
93. 22 312363(412) 3(6)(2) xxxx xx
94. 322820(820) (10)(2) xxxxxx xxx
95. 43222 2 1130(1130) (5)(6) yyyyyy yyy
96. 322 318483(616) 3(2)(8) yyyyyy yyy
97. 22 4129(23) xxx
98. 22 9124(32) xxx
99.
22 6822341 2311 xxxx xx
100.
22 8622431 2411 xxxx xx
101. 2 42222 2 819(9)(9) (3)(3)(9) xxxx xxx
102. 2 42222 2 11(1)(1) (1)(1)(1) xxxx xxx
103. 6332 22 222 21(1) (1)(1) (1)(1) xxx xxx xxx
104. 6332 22 222 21(1) (1)(1) (1)(1) xxx xxx xxx
105. 75525(1)(1)(1)xxxxxxx
106. 855352(1)(1)(1)xxxxxxxx
107. 22 1624943 xxx
108. 22 9241634 xxx
109. 22 51616(16165) (45)(41) xxxx xx
110. 22 51116(16115) (165)(1) xxxx xx
111. 2 41615(25)(23) yyyy
112. 2 994(34)(31) yyyy
113. 2442 22 2 189(981) (91)(1) (31)(31)(1) xxxx xx xxx
114. 2442 22 2 41482(472) 2(41)(2) 2(21)(21)(2) xxxx xx xxx
115. (3)6(3)(3)(6) xxxxx
116. 5(37)(37)(37)(5) xxxxx
117.
118.
2 (2)5(2)(2)(2)5 (2)(3) xxxx xx
2 (1)2(1)(1)(1)2 (1)(3) xxxx xx
119.
3 33 2 2 2 3227 323 323323329 359124969 35937 x x xxx xxxx xxx
120.
121.
3 33 2 2 2 511 511 511511511 525101511 525153 x x xxx xxxx xxx
2 2 3102545 3545 5354 53154 5311
122.
123.
2 2 76953 7353 3735 37215 3716 xxx xx xx xx xx
322 2 22(2)12 (2)(1) (2)(1)(1) xxxxxx xx xxx
124.
322 2 33(3)13 (3)(1) (3)(1)(1) xxxxxx xx xxx
125. 433 3 2 1(1)11 (1)(1) (1)(1)(1) xxxxxx xx xxxx
126. 433 3 2 22 1(1)11 (1)(1) (1)(1)(1) (1)(1) xxxxxx xx xxxx xxx
127.
2 234232343 23434233 2343469 234913 xxx xxx xxx xx
128. 2 521562212 21521564 211052024 213019 xxx xxx xxx
129.
130.
2 2252225 225 235 xxxxxx xxx xx
232 2 2 38383838 2498 329 xxxxxx xxx xx
132.
xxx
324 3 3 3 3 3 451521 251215 251225 25133 23511 6511 xxxx xxxx xxxx xxx xxx xxx
2 432434 43438 43438 43123 34341 xxx xxx xxx xx xx
134.
2 23 2 2 2 3342343 334342 334342 33454 xxxx xxxx xxxx
135.
322 2 2 2 235321353212 635212135 635212135 6352154 xxxx xxxx
136.
223 2 2 2 345451452515 24551651545 245513062025 245515031 xxxx xxxx xxxx xxx
137. 4242(1)xxxx
138. 54352 2682(134) xxxxxx
139. 212 22 22 (1)(1)[(1)(1)] (1) (1) xxxxxxxx xxxx xx
140. 1222 2 (3)4(3)(3)[(3)4] (3)(53) xxxxxxxx xxx
141. Thepossiblefactorizationsare 2 1454xxxx or 2 2244xxxx ,noneofwhich equals24 x .
142. Thepossibilefactorizationsare
22 121xxx ,neitherofwhichequals 21xx
143. Answerswillvary.
144. Answerswillvary.
Section R.6
1. quotient;divisor;remainder 2. 32051
3. d 4. a
5. True 6. True
7. 217510 21010 1550
Quotient:255 xx
Remainder:0
8. 11231 114 1145
Quotient:24 xx Remainder:5
9. 33213 93396 3113299
Quotient:231132 xx Remainder:99
10. 24211 82042 4102143
Quotient:241021 xx Remainder:43
11. 3104010 391545138 1351546138
Quotient:432351546
Remainder:138 xxxx
12. 210102 241020 1251022
Quotient:322510xxx Remainder:22
13. 14030105 441122 4411227
Quotient:54324422 Remainder:7 xxxxx
14. 11050010 11666 1166616
Quotient:432666xxxx Remainder:–16
15. 1.10.100.20
0.110.1210.3531
0.10.110.3210.3531
Quotient:20.10.110.321 xx Remainder:–0.3531
16. 2.10.100.2
0.210.441
0.10.210.241
Quotient:0.10.21 x Remainder:0.241
17. 21000032 2481632 1248160
Quotient:43224816xxxx Remainder:0
18. 1100001 11111 111110
Quotient:4321 xxxx
Remainder:0
19. 24384 8104 4528
Remainder=8 ≠ 0.Therefore,2 x isnota factorof324384 xxx
20. 34508 1251153 41751161
Remainder=161 ≠ 0.Therefore,3 x isnota factorof32458 xx
21. 3260721 60021 20070
Remainder=0.Therefore,3 x isafactorof 43 26721 xxx
22. 2401504 81624 48120
Remainder=0.Therefore,2 x isafactorof 42 4154 xx
23. 2500430024 10204061224 3102036120
Remainder=0.Therefore,3 x isafactorof 63 54324 xx
24. 320180109 6180039 2600130
Remainder=0.Therefore,2 x isafactorof 642 2189 xxx
25. 410161019 4160416 140143
Remainder=1 ≠ 0.Therefore,4 x isnota factorof5321619xxx
26. 4101601016 41600416 1400140
Remainder=0.Therefore,4 x isafactor 6421616xxx
27. 131062 3 1002 30060
Remainder=0;therefore1 3 x isafactorof 43 362 xxx
28. 131031 3 1001 30032
Remainder=20 ;therefore1 3 x isnota factorof43331 xxx
29. 21235 2822 141117 32 2 23517 411 22 xxx xx xx
1411179 abcd
30. 23 23 2 1322 3 130 hhhhh hhhh hh 322 3 xxhxh isthequotientand0isthe remainder.
31. 234 233 23 1334 254 12540 yyyyy yyyy yyy
Yes, xy isafactorof 432234 334 xxyxyxyy .
32. Answerswillvary.
Section R.7
1. lowestterms
2. LeastCommonMultiple
3. d
4. a
5. True; 113 33 115 55 355(3) 353(5) x xx x xx xxx xxx
6. False; 322 433 3 2623 64232 2332 xxxx xxxx LCMxxx
7. 2 3(3) 393 9(3)(3)3 xx xxxx
8. 24(2)48 122412(2)3 xxxxx xx
9. 2(2) 2 363(2)3 xxxxx xx
10. 2 22 3(58) 152458 33 xx xxx xxx
11. 22 2 24244 1266(21)21 xxx xxxxx
12. 2 2 (2)2 442 4(2)(2)2 xx xxx xxxx
15. 2 2 (6)(2) 4126 44(2)(2)2
16. 2 2 (1) 2(2)(1)22 xxxxxx xxxxxx
xxxx
254 20 42 54 14 5
18. 2(21)(3) 253(3)3 121(21) xxxx xx xx
19. 222 363(2) 545(2)(2) 3 5(2) x xxx xxxxx xx
20. 2 333 261022(35)4(35) xxx xxxx
23 2 22 2 2 464 162 44416 (4)(4)2 224416 244 2416 4 xx xx xxxx xxx xxxxx xxx xxx
26.
329 627223 541855 229 xx xxxx x
xxxx xxxx xxxx xxxx x x
22 22 625 45215 2355 5153 235 513 xxx xxxx xxxx xxxx xxx xxx
27. 2 2 6 4624 3939 4 24 62(2) (2)(2)3(3) 4 (2)(3) x xxx xx x x xx xxx x xx
32. 3 22 3 3 339 3 99 9 x xxx x xx x
3 3 3 2 3 2 39 333 9 33 9 3 9 3 xx xxx x xx x x x x
33. 2 222 222 2 2 2 712 71271212 1271212 12 (3)(4)(4)(3) (3)(4)(4)(3) (3) (3) xx xxxxxx xxxxxx xx xxxx xxxx x x
34. 2 222 222 2 76 67656 56656 56 (6)(1)(2)(3) (3)(2)(6)(1) (1)(2) (2)(1) xx xxxxxx xxxxxx xx xxxx xxxx xx xx
35. 2 222 222 2 576 23557621320 1514323515143 21320 (53)(2)(25)(4) (1)(25)(53)(31) (2)(4) (1)(31)
xx xxxxxx xxxxxx xx xxxx xxxx xx xx
36.
43. 3524(35)(24) 212121 3524 21 9 21 xxxx
44. 541(54)(1) 343434 541 34 45 34 xxxx
666 11111
47. 737(1)3(3) 31(3)(1)(1)(3) 7739 (1)(3) 416 (1)(3) 4(4) (1)(3)
48. 252(5)5(5) 55(5)(5)(5)(5) 210525 (5)(5) 335 (5)(5) 335 (5)(5) xx xxxxxx xx xx x xx x xx
49. 22 2 23(1)(23)(1) 11(1)(1)(1)(1) 23 (1)(1) 323 (1)(1) xxxxxx xxxxxx xxxx xx xx xx
50.
22 2 323(3)2(4) 43(4)(3)(4)(3) 3928 (4)(3) 5 (4)(3) 51 (4)(3) xxxxxx xxxxxx xxxx xx xx xx xx xx
51. 22 22 34(3)(2)(4)(2) 22(2)(2)(2)(2) 56(68) (2)(2) 5668 (2)(2) 112(112) or (2)(2)(2)(2) xxxxxx xxxxxx xxxx xx xxxx xx xx xxxx
52.
55. 2422 xxx
2212 xxxx Therefore,
56. 21234 xxxx
281644 xxxx Therefore, LCM342 xx .
57. 32111 xxxxxxx
21 xxxx
Therefore, LCM11 xxx .
58. 22 32739333 xxxx 2 215253 xxxx
Therefore, LCM32533 xxx
59.
322 44441 2121 xxxxxx xxx 322 3 221 xxxx x
Therefore, 32LCM21 xx .
60. 3 x
2 32 33 9933 xxxx xxxxxxx Therefore, LCM33 xxx .
61. 32111 xxxxxxx
3222 32 2211 111 xxxxxxxx xxxx
Therefore, 22 LCM111 xxxxx
62. 22 442xxx 322 3 22 2 xxxx x Therefore, 23LCM2 xx
63. 22 22 76224 (6)(1)(6)(4) (4)(1) (6)(1)(4)(6)(4)(1) 45 (6)(4)(1)(6)(4)(1) xx xxxx xx xxxx xxxx xxxxxx xxxxx xxxxxx
64. 2 22 1 3524 1 (3)(3)(8) (8)1 (3)(8)(3)(8) 8171 (3)(8)(3)(8) xx xxx xx xxx xxx xxxx xxxxx xxxx
65. 22 42 46 42 (2)(2)(3)(2) x xxx x xxxx
2 2 2 4(3)2(2) (2)(2)(3)(3)(2)(2) 41224 (2)(2)(3) 4104 (2)(2)(3) 2(252) (2)(2)(3) xxx xxxxxx xxx xxx xx xxx xx xxx
69. 22 22 2 423 228 423 (2)(1)(4)(2) (4)(4)(23)(1) (2)(1)(4)(4)(2)(1) 816(253) (2)(1)(4) 313 (2)(1)(4) xx xxxx xx xxxx xxxx xxxxxx xxxx xxx xx xxx
66. 22 2 2
68.
2 3434 1(1)21(1) 3(1)4 (1)(1)(1) 334 (1) 344 (1) xxxx xxxxx xxx xxx xxx x xx x
22 22 22 22 32 1111 3121 11 3322 11 51 11 xxxx xx xx xx xx x
22 26 2121xxxx
70. 22 232 87(1) xx xxx 2 2 22 2 2 2 232 (1)(7)(1) (23)(1)(2)(7) (1)(7)(1)(1)(7) 23(514) (1)(7) 611 (1)(7) xx xxx xxxx xxxxx xxxx xx xx xx
71. 232 123 xxxxx
2 2 22 2 32 2 32 2 123 11 112131 11 12233 11 253 11 243 11 xxxxx xxxxxx xxx xxxxx xxx xxxx xxx xxx xxx
73. 111111() ()() 1 () () 1 () xxh hxhxhxhxxxh xxh hxxh h hxxh xxh
74. 22 111 () hxhx
22 2222 222 22 2 22 22 22 22 111() ()() 1(2) () 2 () (2) () 2 () 2 () xxh hxhxxxh xxxhh hxxh xhh hxxh hxh hxxh xh xxh xh xxh
78. 2 11 1111 1 21211 1 11 (1) xxx xxxx xxxx xxxx x xx x x
79. 43 21 1 xx xx x
22 2 (4)(1)(3)(2) (2)(1)(1)(2) 1 54(56) (2)(1) 1 1021 (2)(1)1 2(51) (2)(1) xxxx xxxx x xxxx xx x x xxx x xx
80. 2 12 3 xx xx x
22 (2)(2)(1) (1)(2)(2)(1) 3 44() (2)(1) 3 541 (2)(1)3 54 (2)(1)(3) 54 (2)(1)(3) xxxx xxxx x xxxx xx x x xxx x xxx x xxx
81. 21 21 23 1 xx xx xx xx
2 22 22 2 2 2 (2)(1)(1)(2) (2)(1)(1)(2) (23)(1) (1)()(1) 22 (2)(1) (23) (1) 24 (2)(1) 3 (1) 2(2)( (2)(1) xxxx xxxx xxx xxxx xxxx xx xxx xx x xx xx xx xxx xx
2 2 2 2 2 1) (3) 2(2) (2)(3) 2(2) (2)(3) xx xx xxx xx xxx
82. 22 25 3 (1) 33 xx xx xx xx
22 22 3232 2 2 2 (25)(3)() (3)(3) (3)(3)(1) (3)(3)(3)(3) 215 (3) 3(53) (3)(3) 15 (3) 453 (3)(3) 15( (3) xxxx xxxx xxxx xxxx xxx xx xxxxx xx xx xx xx xx xxx xx
2 2 2 3)(3) 453 (15)(3) (453) x xx xxx xxx
83. 1111 111 1 1 1 1 1 1 x xx x x xx x x
84. 111111 1111 111 1111 1 1 xx xxx xx xx xx x x
2 7121 236 (3)7(2)121 3714121 (7)314121 712 5
11 111 1111 121 11 2,1,1 x xx xx xxx xx abc
111111 121121 111 21132 2121 3,2,1 x xx x x xxx xx abc
1121111 132132 1121 11
322153 3232 5,3,2 x xx x x xxx xx abc
Ifwecontinuethisprocess,thevaluesof a, b and c producethefollowingsequences: :1,2,3,5,8,13,21,.... :1,1,2,3,5,8,13,21,..... :0,1,1,2,3,5,8,13,21,.....
a b c Ineachcasewehavea FibonacciSequence, wherethenextvalueinthelistisobtainedfrom thesumoftheprevious2valuesinthelist.
100. Answerswillvary.
Answerswillvary.
21. 33433882 xxxxx
22. 3335322 19264343
xxxxx 23. 444 24381333
24. 44544 4816323 xxxxx
44 41283232 4 xyxyxy 26. 5 5105252 5 xyxyxy
27. 97 44842 3 xy xyxy xy
28. 23 33 42333 3111 81273 27 xy xyxx x
29. 648 xx
30. 542933 xxxxx
31.
444491223 4 234 16223 32 xyxxy xyx
32.
33314103243 3 432 3 405(2) 25 xyxxyy xyxy
33. 222 1557525353 xxxxxxxx
34. 34252010010 xxxx
22233 32333 5959 59581533153
44433 34233 310310 310331003003
3622612643123
51.
445444 44 44 3221622 222 22or22 xxxxx xxx xxxx
32 8350423252 22152 2152 xxxxx xxx xx
52.
39425920 920 xyyxyy xy
53.
4433 3 3333 3 333 3 33 163252 823252 223252 2352 52or52 xyxxyxy xxyxxyyxy xxyxxyyxy xxyxy xyxyxyxy
2233 3 8258852 852 5 xyxyxyxyxyxy xy xy
55. 1122 2222
56. 22323 3333
57. 33515 5555
58. 333266 822222224
59.
60.
3352 525252 352 252 352536 or 2323
2272 727272 272 74 2721422 or 33
61. 2525235
62. 3131233 233233233 623333953 1293
63. 5521 212121 525525 21
64. 3354 545454 35123512 51611 3512 11
65. 33 333 55454 2242
66. 33 333 22323 9933
2 2 2 2 22 xhxxhxxhx xhxxhxxhx xhxxhx xhx xhxxhx xhx xhxxh h
22 22 22 2 2 22 2 xhxhxhxh xhxhxhxh xhxhxhxh xhxh xhxhxh xhxh xxh h
111111111 22111 11110 21112111 5 111
615615615 1515615 6159 901531015 93 3105105
80. 3 3/43 4 161628
3/2 3/233 41111 428 4
3/2 3/233 161111 16464 16
3/2333 33 9933 882222 2727272 8221621622
2 2/32 3 272739 8824
1/31/31/3 36362 xyxyxy
3/43/43/421/33/421/3
1/41/4 21/42 433/21/4
1/41/2
33/21/41/41/2 5/43/4 5/4 3/4 1616 16 2 8 8 xyxy xyxy xy xy xy xy x y
3/23/23/211/33/211/3
3/23/23/2
33/21/2
3/23/2
1/32/31/32/3 1/32/3 2222
2/32/32/32/3
2/31/32/34/3 2/32/3
2/32/32/31/34/32/3
2/312/3 xyxyxyxy xyxy xyxy xy xy xyxy
1/41/21/21/2 221/41/422
3/43/4 223/4
1/41/4
3/23/4
1/413/21/413/4 1/2 1/41/2 1/4 xyxyxyxy xyxy xyxy xy xy y xy x
33/23/21/23/2 31 3 44 4 2 8 8 xyxy xyxy xy xy xy xy xy
1/21/2 1/2 1/21/2 1/2 1/2 1/2 211 21 (1)(1) 21 (1) 22 (1) 32 (1) xxxx x xx xx x xx x x x
102. 1/21/2 1/2 1/21/2 1/21/2 112 22 1231 22 xxxx x xx xxx xx
1/32/3 1 11,1 3 xxxx
106.
33 2233 8121 3,2,8 22481 xx xx xx
22
22
24281 8812 24281 88+12 24281 6482 24281 656 24281 xxxx xx xx xx xx xx xx xx x xx
112.
21/2 2 21/2 2 1 1 ,1or1 x x x xx x
1/21/2222 21/2 2 1/21/2222 21/22 11 1 111 1 xxx x x xxx xx
22 21/22 22 21/22 221/2 11 1 11 1 1 1 xx xx xx xx xx
1/21/2222 2 44 4 xxx x
21/22 21/2 2 1/21/2 222 21/2 2 1/21/2 222 21/22 22 1/223/222 4 4 4 44 4 4 441 44 414 4 44 x x x x xxx x x xxx xx xx x xx
118.
1/223/21/2 1/22 1/22 1/2 688 23()44 234 2(34)(1) xxxxx xxxx xxx xxx
1/23/2 1/2 1/2 6238 23(23)4 2109 xxx xxx xx
119.
4/31/322 1/3 222 1/3 222 1/3 22 34442 4348 43128 41112 xxxx xxx xxx xx
120.
4/31/3 2 1/3 1/3 234434 234342 23454 xxxx xxxx xxx
121.
1/33/24/31/2 4352333523 xxxx
1/31/2 1/31/2 1/31/2 3523423335 3523812915 35231727 xxxx xxxx xxx
3 where 2 x
136. 161222 3222 24.44seconds T
137. 314313 334312 134431
Thequotientis2(34)43 xx Theremainderis1
138. 1219137 126727 1387720
Yes,12 isafactorof329137xxx
139. Answersmayvary.Onepossibilityfollows:If 5 a ,then 225255 aa Sinceweusetheprincipalsquareroot,whichis alwaysnon-negative, 2if0 if0 aa a aa
whichisthedefinitionof a ,so 2 aa
Section R.8: nth Roots; Rational Exponents
Chapter 1
Equations and Inequalities
Section 1.1
1. Distributive
2. Zero-Product
3. 4 xx
4. False.Multiplyingbothsidesofanequationby zerowillnotresultinanequivalentequation.
5. identity
6. linear;first-degree
7. False.Thesolutionis 8 3
8. True 9. b
10. d 11. 721 721
3 x x x
Thesolutionsetis{3}. 12. 624 624 66 4 x x x
Thesolutionsetis{4}. 13. 3150 31515015 315 315 33 5 x x x x x
Thesolutionsetis{5}. 14. 6180 61818018 618 618 66 3 x x x x x
Thesolutionsetis{3}. 15. 230 23303 23 23 22 3 2 x x x x x
Thesolutionsetis3 2
16. 340 34404 34 34 33 4 3 x x x x x
Thesolutionsetis 4 3
17. 17 420 17 44 420 287 205
x x x
Thesolutionsetis7 5
18. 29 32 29 66 32 427 427 44 27 4 x x x x x
Thesolutionsetis27. 4
19.
20.
Thesolutionsetis{2}.
Thesolutionsetis{3}.
21. 263 26636 29 29 39 39 33 3 tt tt tt tttt t t t
Thesolutionsetis{3}.
22. 5618 566186 524 524 624 624 66 4 yy yy yy yyyy y y y
Thesolutionsetis{4}.
23. 629 66296 23 2232 33 33 33 1 xx xx xx xxxx x x x
Thesolutionsetis{1}.
24. 322 32323 21 21 1 1 11 1 xx xx xx xxxx x x x
Thesolutionsetis{1}.
25. 3247 323473 244 24444 24 24 22 2 nn nn nn nnnn n n n Thesolutionsetis{2}.
Chapter 1: Equations and Inequalities
26. 6231 626316 235 23353 55 55 55 1 mm mm mm mmmm m m m
Thesolutionsetis{1}.
30. 7(21)10 72110 8210 828108 22 22 22 1 x x x x x x x
Thesolutionsetis{1}.
27. 3(53)8(1) 15988 9815888 1515815
xx xx xxxx x x Thesolutionsetis{23}.
28. 3(2)21 xx 6321 636216 327 32272 57 57 55 7 5 xx xx xx xxxx x x x
Thesolutionsetis7. 5
29. 8(32)310 xxx 832310 52310 5223102 538 53383 28 28 22 4 xxx xx xx xx xxxx x x x
Thesolutionsetis{4}.
31. 311 2 222 xx 311 222 222 341 34414 33 33 43 43 44 3 4 xx xx xx xx xxxx x x x
Thesolutionsetis3 4
32. 12 2 33 12 332 33 62 2622 36 36 33 2 xx xx xx xxxx x x x
Thesolutionsetis{2}.
33. 13 5 24 13 454 24 2203 220232 20 20 xx xx xx xxxx x x
Thesolutionsetis{20}.
34.
1 16 2 1 2126 2 212 22122 10 10 11 10 x x x x x x x
Thesolutionsetis{10}.
35.
Thesolutionsetis{2}.
36. 114 233 p 114 66 233 328 32383 25 25 22 5 2 p p p p p p
Thesolutionsetis5. 2
37. 0.20.90.5 0.20.50.90.50.5 0.30.9 0.30.9 0.30.3 3
Thesolutionsetis{-3}.
38. 0.91 0.91 0.11 0.11 0.10.1 10 tt tttt t t t
Thesolutionsetis{10}.
39. 12 2 37 xx
12 21212 37 713242 773642 101342 1013134213 1029 1029 1010 29 10 xx xx xx x x x x x
Thesolutionsetis29 10
40. 21 163 3 x x 21 31633 3 21489 2499 249292 497 497 77 7 x x xx xx xxxx x x x
Thesolutionsetis{7}.
Chapter 1: Equations and Inequalities
41. 5111 (3)2(23) 8416 10(3)324(23)11 10303281211
42. 122 3515 (1)3(4) 5(1)456(4)2 55456242 540626
Thesolutionsetis
Since y =2doesnotcauseadenominatorto equalzero,thesolutionsetis{2}. 44. 45 5 2 yy 45 252 2 8105 810858
Since3 10 y doesnotcauseadenominatorto equalzero,thesolutionsetis310
123 24 123 44 24 283 28232 8 x xx x xx xxxx x
Since x =8doesnotcauseanydenominatorto equalzero,thesolutionsetis{8}. 46. 311 36 311 66 36 182 18222 183 183 33 6 x xx x xx xxxx x x x
Since6 x doesnotcauseadenominatorto equalzero,thesolutionsetis{6}.
47. 2 (7)(1)(1) xxx 22 2222 6721 6721 6721 677217 628 62282 48 48 44 2 xxxx xxxxxx xx xx xx xxxx x x x
Thesolutionsetis{2}.
48. 2 (2)(3)(3) xxx 22 2222 669 669 669 66696 615 66156 715 715 77 15 7 xxxx xxxxxx xx xx xx xxxx x x x
Thesolutionsetis15 7
49. 22 2222 (23)(21)(4) 23274 2322742 374 37747 44 44 44 1 xxxx xxxx xxxxxx xx xxxx x x x
Thesolutionsetis{1}.
Section 1.1: Linear Equations
xxxx xxxxxx xx xxxx x x x
50. (12)(21)(2) xxxx 22 2222 2252 222522 52 5525 62 621 663
Thesolutionsetis 1 3
51. 23 33 3333 312 312 312 312 312 4 33
ppp ppp ppppp p p p
Thesolutionsetis{4}.
52. 23 33 3333 (4)8 48 48 48 48 44 2 www www wwwww w w w
Thesolutionsetis{2}.
53. 2 3 22 x xx 2 322 22 322 362 462 46626 48 48 44 2 x xx xx xx xx x x x x x
Since x =2causesadenominatortoequalzero, wemustdiscardit.Thereforetheoriginal equationhasnosolution.
Chapter 1: Equations and Inequalities
54.
Since x =–3causesadenominatortoequalzero, wemustdiscardit.Thereforetheoriginal equationhasnosolution.
Since x =2causesadenominatortoequalzero,wemustdiscardit.Thereforetheoriginalequationhasnosolution.
56.
Since x =3causesadenominatortoequalzero,wemustdiscardit.Thereforetheoriginalequationhasnosolution.
Since x =–6doesnotcauseanydenominatorto equalzero,thesolutionsetis{6}.
Since x =41doesnotcauseanydenominatorto equalzero,thesolutionis{41}.
Since x =–2doesnotcauseanydenominatorto equalzero,thesolutionsetis{2}.
63.
Since1 x doesnotcauseanydenominatortoequalzero,thesolutionsetis{1}.
Since3
Since6 x doesnotcauseanydenominatortoequalzero,thesolutionsetis{14}.
Chapter 1: Equations and Inequalities
69.
Thesolutionsetisapproximately{0.41}.
Thesolutionsetisapproximately{0.94}.
73. ,0axbca axbbcb axbc axbc aa bc x a
74. 1,0 111 1 1 11 axba axb axb axb aa bb x aa
75. ,0,0, () () xxcabab ab xx ababc ab bxaxabc abxabc abxabc abab abc x ab
76. ,0 ab cc xx ab xxc xx abcx abcx cc ab x c
Chapter 1: Equations and Inequalities
77. 2166,if4
4216(4)6 421646 42162 412 412 44 3 xaaxax aaa aaa aa a a a
78. 242,for2 22242(2) 22244 2224 42 4 2 2
bb bb bb b b b
79. 12 111 RRR 1212 12 1221 1221 1221 2121 12 21 111 () () RRRRRR RRR RRRRRR RRRRR RRRRR RRRR RR R RR
80. (1)APrt
APPrt
APPrt APPrt PtPt AP r Pt
82. PVnRT PVnRT nRnR PV T nR
1 Sa r (1)(1) 1 a Srr r SSra SSrSaS SraS SraS SS Sa r S
0 0 0 00 vgtv vvgt vvgt gg
85. AmountinbondsAmountinCDsTotal 300020,000 xx
300020,000 2300020,000 223,000 11,500 xx x x x
$11,500willbeinvestedinbondsand$8500 willbeinvestedinCD's.
86. Sean'sAmountGeorge'sAmountTotal 300010,000 xx
Seanwillreceive$6500andJorgewillreceive $3500.
87. DollarsHoursMoney perhourworkedearned Regular4040 wage
Sandra’sregularhourlywageis$17.50.
88. DollarsHoursMoney perhourworkedearned Regular4040 wage Overtime1.566(1.5) wage Sunday244(2) wage xx xx
Leigh’sregularhourlywageis$19.00.
89. Let x representthescoreonthefinalexam. 8083716195 80 7 3902 80 7 3902560 2170 85
Camilaneedsascoreof85onthefinalexam.
90. Let x representthescoreonthefinalexam. Note:sincethefinalexamcountsfortwo-thirds oftheoverallgrade,theaverageofthefourtest scorescountforone-thirdoftheoverallgrade. ForaB,theaveragescoremustbe80.
1868084902 80 343 13402 80 343 852 80 33 852 3380 33 852240 2155 77.5 x x x x x x x
Alineedsascoreof78toearnaB. ForanA,theaveragescoremustbe90.
1868084902 90 343 13402 90 343 852 90 33 852 3390 33 852270 2185 92.5 x x
Alineedsascoreof93toearnanA.
91. Let x representtheoriginalpriceofthephone. Then0.12x representsthereductionintheprice ofthephone. Thenewpriceofthephoneis$572. originalpricereductionnewprice
xx x x Theoriginalpriceofthephonewas$650. Theamountofthereduction(i.e.,thesavings)is 0.12($650)=$78.
650
92. Let x representtheoriginalpriceofthecar. Then0.15x representsthereductionintheprice ofthecar.
Thenewpriceofthecaris$8000. listpricereductionnewprice
Thelistpriceofthecarwas$21,176.47. Theamountofthereduction(i.e.,thesavings)is 0.15($21176.47)$3176.47
93. Let x representthepricethetheaterpaysforthe candy.
Then2.75 x representsthemarkuponthecandy. Thesellingpriceofthecandyis$4.50. suppierpricemarkupsellingprice
xx x x Thetheaterpaid$1.20forthecandy.
94. Let x representsellingpriceforthenewcar. Thedealer’scostis0.85($24,000)$20,400. Themarkupis$300. sellingprice=dealer’scost+markup 20,400300$20,700 x At$300overthedealer’scost,thepriceofthe careis$20,700.
95. TicketsPriceperMoney soldticketearned Adults7.507.50 Children52004.504.50(5200) xx xx
7.504.50520029,961 7.5023,4004.5029,961 3.0023,40029,961 3.006561 2187 xx xx x x x
Therewere2187adultpatrons.
96. Let p representtheoriginalpricefortheboots. Then,0.30p representsthediscountedamount. originalpricediscountclearanceprice 0.30399 0.70399 570 pp p p
Thebootsoriginallycost$570.
97. Let w representthewidthoftherectangle. Then8 w isthelength. Perimeterisgivenbytheformula22. Plw 2(8)260 216260 41660 444 11 ww ww w w w
Now,11+8=19. Thewidthoftherectangleis11feetandthe lengthis19feet.
98. Let w representthewidthoftherectangle. Then2 w isthelength. Perimeterisgivenbytheformula22. Plw 2(2)242 4242 642 7 ww ww w w
Now,2(7)=14. Thewidthoftherectangleis7metersandthe lengthis14meters.
99. WewillletBbethecaloriesfrombreakfast,L thecaloriesfromlunchandDthecaloriesfrom dinner.Sowehavethefollowingequations: 125 2300 2025 BL DL BLD
Nowwesubstitutethefirsttwointothelastone andsolveforL.
2025(125)(2300) 20254175 22004 550 LLL L L L
NowwesubstituteLintothefirsttwoequations togetBandD. 550125675 2(550)300800 B D
SoHerscheltookin675caloriesfrombreakfast, 550caloriesfromlunchand800caloriesfrom dinner.
100. WewillletBbethecaloriesfrombreakfast,L thecaloriesfromlunch,Dthecaloriesfrom dinnerandSthecaloriesfromsnacks.Sowe havethefollowingequations:
Nowwesubstitutethefirstfourintothelastone andsolveforB. 14800.5(200)(200)700 14803.5620 21003.5 600 BBBB B B B
NowwesubstituteBtogetS. 120600120480 SB
Judypays$10.80andTompays$7.20.
102. Anisoscelestrianglehasthreeequalsides. Therefore:410240318 xxx .Solve eachsetseparately:
Section 1.1: Linear Equations
xx x x xx x xx x x Since22isthelargestofthenumbersthenthe largestperimeteris:
422102224032218266
MultiplybothsidesbytheLCD80toclear fractions. 608488012064 1087258 10716 16 107
104. Ifahexagonisinscribedinacirclethenthesides ofthehexagonareequaltotheradiusofthe circle.LettheP=6rbetheperimeterofthe hexagon.Letrbetheradiusofthecircle. 610 510 2
Thusr=2inchesistheradiusofthecirclewhere theperimeterofthehexagonis10inchesmore thantheradius.
105. Tomovefromstep(6)tostep(7),wedivided bothsidesoftheequationbytheexpression 2 x .Fromstep(1),however,weknow x =2, sothismeanswedividedbothsidesofthe equationbyzero.
106– 107. Answerswillvary.
Chapter 1: Equations and Inequalities
Section 1.2 1.
25661 xxxx 2.
3. 5,3 3 4. True
5.
6. discriminant;negative
7. False;aquadraticequationmayhavenoreal solutions.
8. False;If2 xp then x couldalsobenegative.
9. b
10. d
11.
290 90 xx xx
0or90 0or9 xx xx
Thesolutionsetis{0,9}.
12. 240 (4)0 xx xx 0or40 0or4 xx xx Thesolutionsetis{–4,0}.
13. 2250 (5)(5)0 x xx
50or50 5or5 xx xx Thesolutionsetis{–5,5}.
14. 290 (3)(3)0 x xx 30or30 3or3 xx xx Thesolutionsetis{–3,3}.
15. 260 (3)(2)0 zz zz
30or20 3or2 zz zz Thesolutionsetis{–3,2}.
16. 2760 (6)(1)0 vv vv 60or10 6or1 vv vv Thesolutionsetis{–6,–1}
17. 2 2530 (21)(3)0 xx xx 210or30 1or3 2 xx xx
Thesolutionsetis 1,3 2
18. 2 3520 (32)(1)0 xx xx
320or10 2 or1 3 xx xx
Thesolutionsetis 1,2 3
19. 2 2 51800 5(36)0 5(6)(6)0
w w ww 60or60 6or6
ww ww Thesolutionsetis{–6,6}.
20. 2 2 2500 2(25)0 2(5)(5)0 y y yy
50or50 5or5 yy yy
Thesolutionsetis{–5,5}.
21.
2 3100 3100 (2)50
Section 1.2: Quadratic Equations
25. 2 2 2 6(1)5 665 6560 (32)(23)0 pp pp pp pp
320or230 23 or 32 pp pp
Thesolutionsetis23 , 32
xx xx
xx xx xx 20or50 2or5
Thesolutionsetis 5,2.
22. 2 (4)12 4120 (6)(2)0 xx xx xx
60or20 6or2 xx xx
Thesolutionsetis 6,2.
23. 2 2 2 4912 41290 (23)0 230 3 2 xx xx x x x
Thesolutionsetis 3 2
24. 2 2 2 251640 2540160 (54)0 540 4 5 xx xx x x x
Thesolutionsetis 4 5 .
26. 2 2 2(24)30 4830 (21)(23)0 uu uu uu
210or230 13 or 22 uu uu
Thesolutionsetis13 , 22
27.
2 2 6 65 6 65 656 6560 (32)(23)0 x x xxx x xx xx xx
320or230 23 or 32 xx xx
Neitherofthesevaluescausesadenominatorto equalzero,sothesolutionsetis23 , 32
28. 2 2 12 7 12 7 127 7120 (3)(4)0 x x xxx x xx xx xx
30or40 3or4 xx xx
Chapter 1: Equations and Inequalities
Neitherofthesevaluescausesadenominatorto equalzero,sothesolutionsetis{3,4}.
Neitherofthesevaluescausesadenominatorto equalzero,sothesolutionsetis
32. 236 36 6 x x x
Thesolutionsetis 6,6
33. 2 14 14 12 12or12 3or1 x x x xx xx
Thesolutionsetis 1,3
34. 2 21 21 21 21or21 1or3 x x x xx xx
Thesolutionsetis 3,1
35. 12416 3 1416 3 144 3 1144or44 33 110or8 33 0or24
h h h hh hh hh
Thesolutionsetis 24,0
Neitherofthesevaluescausesadenominatorto equalzero,sothesolutionsetis
31. 225 25 5 x x x
Thesolutionsetis 5,5
36. 2 324 324 322 322or322 34or30 4or0 3
z z z zz zz zz
Thesolutionsetis 0,4 3
37.
Section 1.2: Quadratic Equations
40. 2210 33 xx
Thesolutionsetis7,3.
38.
44 x x xx
The13 solutionsetis,. 44
The1 solutionsetis1,. 3
41. 21 30 2 xx 2 2 2 2 110 36 11 36 1111 336636 17 636 17 636 17 66 17 6 xx xx xx x x x x
The1717 solutionsetis,. 66
42. 2 2310 xx 2 2 2 310 22 31 22 3919 216216 xx xx xx
Chapter 1: Equations and Inequalities
43. 2420xx 2 1,2,13 (2)(2)4(1)(13)2452 2(1)2 2562214114 22
abc x
Thesolutionsetis114,114.
44. 2420xx 2 1,4,2 444(1)(2)4168 2(1)2 48422 22 22 abc x
Thesolutionsetis22,22.
45. 2410xx 2 1,4,1 (4)(4)4(1)(1)4164 2(1)2 42042525 22 abc x
Thesolutionsetis25,25.
46. 2610xx 2 1,6,1 664(1)(1)6364 2(1)2 632642 322 22
abc x
Thesolutionsetis322,322.
47. 2 2530 xx 2 2,5,3 (5)(5)4(2)(3) 2(2) 525245151 444 5151 or 44 64 or 44 3or1 2 abc x xx xx xx
The3 solutionsetis1,. 2
48. 2 2530 xx 2 2,5,3 554(2)(3) 2(2) 525245151 444 5151 or 44 46 or 44 13 or 2 abc x xx xx xx
The3solutionsetis,1. 2
49. 2 420 yy 2 4,1,2 (1)(1)4(4)(2) 2(4) 1132131 88 abc y
Norealsolution.
50. 2 410 tt 2 4,1,1 114(4)(1) 2(4) 1116115 88 abc t
Norealsolution.
51. 2 2 985 9850 xx xx 2 9,8,5 884(9)(5) 2(9) 8641808244 1818 8261461 189
abc x
Thesolutionsetis461461,.99
52. 2 2 212 2210 xx xx 2 2,2,1 224(2)(1)248 2(2)4 21222313 442 abc x
Thesolutionsetis1313,.22
Section 1.2: Quadratic Equations
53. 2 2 49 490 (49)0 xx xx xx 0or490 09 or 4 xx xx
Thesolutionsetis 9 0,. 4
54. 2 2 54 045 0(45) xx xx xx 0or450 05 or 4 xx xx
Thesolutionsetis 5 0,. 4
55. 2 9610 tt 2 9,6,1 (6)(6)4(9)(1) 2(9) 63636601 18183 abc t
Thesolutionsetis 1 . 3
56. 2 4690 uu 2 4,6,9 (6)(6)4(4)(9) 2(4) 6361446108 88 abc u Norealsolution.
57. 2 2 2 3110 442 311 440 442 320 xx xx xx
3,1,2abc
Chapter 1: Equations and Inequalities
2 11432 23 112412515 666 1515 or 66 64 or 66 12 or 3 x xx xx xx
The2solutionsetis,1. 3
58. 2230 3 xx
2 2 2 3330 3 2390 2,3,9 xx xx abc
2 33429 22 397238139 444 3939 or 44 126 or 44 33 or 2 x xx xx xx
The3solutionsetis,3. 2
59. 2 2 2 2 51 33 5133 33 531 5310 xx xx xx xx
2 5,3,1 33451 25 3920329 1010 abc x
Thesolutionsetis329329 , 1010
.
60. 2 2 2 2 31 55 3155 55 351 3510 xx xx xx xx
2 3,5,1 55431 23 52512537 66 abc x
Thesolutionsetis537537 , 66
.
61. 2 2(2)3 2430 xx xx 2 2,4,3 444(2)(3)41624 2(2)4 4404210210 442 abc x
Thesolutionsetis210210,.22
62. 2 3(2)1 3610 xx xx
2 3,6,1 664(3)(1)63612 2(3)6 648643323 663
63. 2 22 2 2 11 40 11 40 410 xx xx xx
equalzero,sothesolutionsetis
64. 2 83 20
Section 1.2: Quadratic Equations
65. 2 22 2 314 2 31(2)4(2) 2 3()(2)48 3248 092 x xx x xxxx xx xxxxx xxxx xx
1,9,2abc 2 (9)(9)4(1)(2) 2(1) 9818973 22 x
Neitherofthesevaluescausesadenominatorto equalzero,sothesolutionsetis 973973 , 22
66. 2 22 2 214 3 21(3)4(3) 3 2()(3)412 23412 02133 x xx x xxxx xx xxxxx xxxx xx
2,13,3abc 2 (13)(13)4(2)(3) 2(2) 131692413145 44 x
Neitherofthesevaluescausesadenominatorto equalzero,sothesolutionsetis 1314513145 , 44
67. 24.12.20xx 2 1,4.1,2.2 4.14.1412.2 21 4.116.818.84.18.01 22 3.47or0.63 abc x xx
Thesolutionsetis 0.63,3.47
Chapter 1: Equations and Inequalities
68. 23.91.80xx
2 1,3.9,1.8 3.93.9411.8 21 3.915.217.23.98.01 22 0.53or3.37 abc x xx
Thesolutionsetis 3.37,0.53.
69. 2330xx
Thesolutionsetis 2.80,1.07
70. 2220xx
2 1,2,2 22412 21 228210 22 0.87or2.29 abc x xx
Thesolutionsetis 2.29,0.87.
71. 20xx
2 2 ,1, 114 2 114 2 1.17or0.85 abc x xx
Thesolutionsetis 0.85,1.17.
72. 220xx
2 2 ,,2 42 2 8 2 0.44or1.44 abc x xx
Thesolutionsetis 1.44,0.44
73. 2 2670 xx 22 2,6,7 4(6)4(2)7365620 abc bac
Sincethe240, bac theequationhasnoreal solution.
74. 2470xx
22 1,4,7 4(4)4(1)7162812 abc bac
Sincethe240, bac theequationhasnoreal solution.
75. 2 930250 xx
22 9,30,25 4(30)4(9)259009000 abc bac
Since240, bac theequationhasone repeatedrealsolution.
76. 2 252040 xx
22 25,20,4 4(20)4(25)44004000 abc bac
Since240, bac theequationhasone repeatedrealsolution.
77. 2 3580 xx
22 3,5,8 4(5)4(3)82596121 abc bac
Since240, bac theequationhastwo unequalrealsolutions.
78. 2 2370 xx
22 2,3,7 4(3)4(2)795665 abc bac
Since240, bac theequationhastwo unequalrealsolutions.
79. 2 2 50 5 5 x x x Thesolutionsetis5,5.
80. 2 2 60 6 6 x x x Thesolutionsetis6,6.
81. 2 16810 41410 410 1 4 xx xx x x
Thesolutionsetis 1 . 4
82. 2 91240 32320 320 2 3 xx xx x x Thesolutionsetis 2 . 3
83. 2 1019150 53250 xx xx 530or250 35 or 52 xx xx
Thesolutionsetis 35 ,.52
84. 2 67200 34250 xx xx
340or250 45 or 32 xx xx
Thesolutionsetis 54 ,.23
Section 1.2: Quadratic Equations
85. 2 2 26 062 03221 zz zz zz
320or210 21 or 32 zz zz
Thesolutionsetis 12 , 23
86. 2 2 26 062 03221 yy yy yy
320or210 21 or 32 yy yy
Thesolutionsetis 21 , 32
87.
2 2 2 2 21 2 1 20 2 1 2220 2 22210 xx xx xx xx
2,22,1abc
2 (22)(22)4(2)1 2(2) 22882216 44 22422 42 x
The2222 solutionsetis,22
88.
2 2 2 2 121 2 1210 2 1 22120 2 2220 xx xx xx xx
1,22,2abc
Chapter 1: Equations and Inequalities
The1515 solutionsetis,. 22
91. 2 271 212
xx xxxx xx xxxx xxxx xxxx xxxx xxx xx xx
Thevalue1 x causesadenominatortoequalzero,sowedisregardit.Thus,thesolutionsetis{5}.
92. 2 3147 212 xx xxxx
2 2 2 3147 21(2)(1) 3147(2)(1)(2)(1)21(2)(1) 3(1)(2)47 33247 32247 3520 (31)(2)0 xx
Thevalue2 x causesadenominatortoequalzero,sowedisregardit.Thus,thesolutionsetis
93. Sincethisisarighttrianglethenwecanusethe PythagoreanTheorem.So 222 222 2 2 (23)(25)(7) 4129420251449 129674 01865 0(5)(13) xxx xxxxxx xxx xx xx
50or130 5or13 xx xx
Thismeansthereare2possiblethatmeetthese requirements.Substituting x intothegivensides gives:
When x =5:5m,12m,13m When x =13:20m,21m,29m Thusthereare2solutions.
94. Sincethisisarighttrianglethenwecanusethe PythagoreanTheorem.So 222 222 2 2 (45)(313) 164025978169 6381440 2(31972)0 2(38)(9)0 xxx xxxxx xx xx xx
Thismeansthereare2possiblesolutionsthat meettheserequirements.Substituting x intothe givensidesgives:
When x =9:41m,40m,9m
When x = 8 3atleastonesideofthetriangle hasanegativemeasurementwhichisimpossible. Thusthereisonly1trianglepossible
95. Let w representthewidthofwindow. Then2 lw representsthelengthofthe window.
Sincetheareais143squarefeet,wehave: 2 (2)143 21430 (13)(11)0 ww ww ww
Discardthenegativesolutionsincewidthcannot benegative.Thewidthoftherectangular windowis11feetandthelengthis13feet.
96. Let w representthewidthofwindow. Then1 lw representsthelengthofthe window.
Sincetheareais306squarecentimeters,we have:(1)306 ww 23060 (18)(17)0 ww ww
Discardthenegativesolutionsincewidthcannot
Chapter 1: Equations and Inequalities
benegative.Thewidthoftherectangular windowis17centimetersandthelengthis18 centimeters.
97. Let l representthelengthoftherectangle. Let w representthewidthoftherectangle. Theperimeteris26metersandtheareais40 squaremeters. 2226 13so13
Thedimensionsare5metersby8meters.
98. Let r representtheradiusofthecircle. Sincethefieldisasquarewitharea1250square feet,thelengthofasideofthesquareis
1250252 feet.Thelengthofthediagonal is2r
UsethePythagoreanTheoremtosolvefor r :
Theshortestradiussettingforthesprinkleris25 feet.
99. Let x =lengthofsideoforiginalsheetinfeet.
Lengthofbox:2 x feet
Widthofbox:2 x feet
Heightofbox:1foot
Discard0 x sincethatisnotafeasiblelength fortheoriginalsheet.Therefore,theoriginal sheetshouldmeasure4feetoneachside.
100. Let x =widthoforiginalsheetinfeet.
Lengthofsheet:2 x
Lengthofbox:22 x feet
Widthofbox:2 x feet
Heightofbox:1foot
2 2 2 42221 4264 026 03 03 Vlwh xx xx xx xx xx
0or3xx
Discard0 x sincethatisnotafeasiblelength fortheoriginalsheet.Therefore,theoriginal sheetis3feetwideand6feetlong.
101. a. Whentheballstrikestheground,the distancefromthegroundwillbe0. Therefore,wesolve
2 2 2 9680160 1680960 560 610 tt tt tt tt
6or1tt
Discardthenegativesolutionsincethetime offlightmustbepositive.Theballwill strikethegroundafter6seconds.
b. Whentheballpassesthetopofthebuilding, itwillbe96feetfromtheground.Therefore, wesolve
2 2 2 96801696 16800 50 50 tt tt tt tt
0or5tt Theballisatthetopofthebuildingattime 0 t whenitisthrown.Itwillpassthetop ofthebuildingonthewaydownafter5 seconds.
102. a. Tofindwhentheobjectwillbe15meters abovetheground,wesolve 2 2 4.92015
Theobjectwillbe15metersabovethe groundafterabout0.99seconds(ontheway up)andabout3.09seconds(ontheway down).
b. Theobjectwillstrikethegroundwhenthe distancefromthegroundis0.Therefore,we solve
Theobjectwillstrikethegroundafterabout 4.08seconds.
c. 2 2 4.920100 4.9201000 tt tt
Thereisnorealsolution.Theobjectnever reachesaheightof100meters.
103. Let x representthenumberofcentimetersthe lengthandwidthshouldbereduced. 12 x =thenewlength,7 x =thenewwidth. Thenewvolumeis90%oftheoldvolume.
2 2 2 (12)(7)(3)0.9(12)(7)(3) 357252226.8 35725.20 198.40 xx xx xx xx
Section 1.2: Quadratic Equations
2 (19)(19)4(1)(8.4)19327.4 2(1)2
0.45or18.55 x xx
Since18.55exceedsthedimensions,itis discarded.Thedimensionsofthenewchocolate barare:11.55cmby6.55cmby3cm.
104. Let x representthenumberofcentimetersthe lengthandwidthshouldbereduced. 12 x =thenewlength,7 x =thenewwidth. Thenewvolumeis80%oftheoldvolume.
(12)(7)(3)0.8(12)(7)(3)
357252201.6 35750.40 1916.80 xx xx xx xx
2 (19)(19)4(1)(16.8)19293.8 2(1)2
0.93or18.07 x xx
Since18.07exceedsthedimensions,itis discarded.Thedimensionsofthenewchocolate barare:11.07cmby6.07cmby3cm.
105. Let x representthewidthoftheborder measuredinfeet.Theradiusofthepoolis5 feet.Then5 x representstheradiusofthe circle,includingboththepoolandtheborder. Thetotalareaofthepoolandborderis
2 (5) T Ax Theareaofthepoolis2(5)25 PA Theareaoftheborderis
2 (5)25
BTP AAAx Sincetheconcreteis3inchesor0.25feetthick, thevolumeoftheconcreteintheborderis
2 0.250.25(5)25 B Ax Solvingthevolumeequation:
2 2 2 0.25(5)2527 102525108 101080 x xx xx
2 2 10(10)4()(108) 2()
2.71or12.71 x xx
31.42100432
6.28
Discardthenegativesolution.Thewidthofthe borderisroughly2.71feet.
Chapter 1: Equations and Inequalities
106. Let x representthewidthoftheborder measuredinfeet.Theradiusofthepoolis5 feet.Then5 x representstheradiusofthe circle,includingboththepoolandtheborder. Thetotalareaofthepoolandborderis
2 (5) T Ax
Theareaofthepoolis2(5)25 PA .
Theareaoftheborderis
108. Let x =thewidthand2x =thelengthofthe patio.Theheightis13footandtheconcrete availableis 827216 cubicfeet.. 2 2 1 (2)216 3 2216 3 32418
2 (5)25
BTP AAAx .
Sincetheconcreteis4inches=13footthick,the volumeoftheconcreteintheborderis
112 33(5)25 B Ax
Solvingthevolumeequation:
2 2 2 1(5)2527 3 10252581 10810 x xx xx
2 2 10(10)4()(81) 2()
2.13or12.13 x xx
31.42100324
6.28
Discardthenegativesolution.Thewidthofthe borderisapproximately2.13feet.
107. Let x representthewidthoftheborder measuredinfeet.
Thetotalareais(62)(102) T Axx
Theareaofthegardenis61060 GA .
feet.
109. Let x =thelengthofa12.9-inchiPadProina 16:9format.
Then 9 16 x =thewidthoftheiPad.Thediagonal ofthe12.9-inchiPadis9.7inches,sobythe Pythagoreantheoremwehave:
Theareaoftheborderis (62)(102)60
BTG AAAxx
Sincetheconcreteis3inchesor0.25feetthick, thevolumeoftheconcreteintheborderis
0.250.25(62)(102)60 B Axx
Solvingthevolumeequation: 2 2 2 0.25(62)(102)6027 6032460108 4321080 8270 xx xx xx xx 2 884(1)(27)8172 2(1)2 2.56or10.56 x xx
Discardthenegativesolution.Thewidthofthe borderisapproximately2.56feet.
Sincethelengthcannotbenegative,thelengthof theiPadis42600.96337inchesandthewidthis 42600.96 337 9 6.32 16 inches.Thus,theareaofthe iPadis42600.96942600.963371633771.11 square inches.
Let y =thelengthofa14.4-inch3:2format MicrosoftSurfacePro.Then 2 3 y =thewidthof theSurfacePro.Thediagonalofa14.4-inch SurfaceProis14.4inches,sobythe Pythagoreantheoremwehave:
Sincethelengthcannotbenegative,thelengthof theSurfaceProis11.98inchesandthewidthis 21866.24 7.99 313 inches.Thus,theareaofthe 14.4-inch3:2formatSurfaceProis 1866.241866.24 2 13313 95.7squareinches.
TheSurfaceProformathasthelargerscreen sinceitsareaislarger.
110. Let x =thelengthofa8.3-inchiPadMiniina 4:3format.
Then3 4 x =thewidthoftheiPad.Thediagonal ofthe8.3-inchiPadis8.3inches,sobythe Pythagoreantheoremwehave:
Sincethelengthcannotbenegative,thelengthof theiPadis6.64inchesandthewidthis
3
4 inches.Thus,theareaofthe iPadis(6.64)(4.98)33.1 squareinches. Let y =thelengthofa8-inch16:10format AmazonFireHD8™.Then 10 16 y =thewidthof theFire.Thediagonalofa8-inchFireis8 inches,sobythePythagoreantheoremwehave:
16384
Sincethelengthcannotbenegative,thelengthof theFireis 16384 6.78399 356 inchesandthe widthis 1016384 4.240 16356 inches.Thus,thearea oftheAmazonFireis
6.783994.24028.8squareinches. TheiPadMini™4:3formathasthelargerscreen sinceitsareaislarger.
111. Let h be1.1.Then 2 2 2 0.04(0.04)4(0.00025)(1.1) 2(0.00025) 1.10.000250.04
00.000250.041.1 35.3ftor124.7ft
xx xx x 124.7ftdoesnotmakesenseinthecontextof theproblem,sotheansweris35.3ft.
112. Sincedisexpressedin1000’swewillsetd=12 andsolveforxusingtheQuadraticFormula. 2 2 2 2 0.26(0.26)4(0.33)(9.71) 2(0.33) 0.2613.0772 0.66 0.330.262.29 120.330.262.29 00.330.269.71
5.085or5.873 dxx xx xx x xx
Sothenearestyearwhentheearningswere12 occurredabout5yearsafter2018or2023.The negativevalue-5.873hasnomeaning.
Chapter 1: Equations and Inequalities
113. Wewillsetg=2.97andsolveforhusingthe QuadraticFormula. 2
0.00060.0153.04
2.970.00060.0153.04
0.015(0.015)4(0.0006)(0.07) 2(0.0006)
0.0150.000393 0.0012
Sotheestimatednumbersofhoursworkedbya studentwithaGPAof2.97is29hours.The value-4.02hasnomeaningsinceitisnegative.
114. Letxbethenumbersofmembersinthe fraternityandsbethesharepaidbyeach member.Then1470 s x . Ifthereare7 memberswhocannotcontributethentheshare goesupby$5.Sowehavethefollowing equation: 51470 7 s x
or
571470sx
Solvingthesetwoequationstogether:
2 5714701470 and 1470571470 10290 14705351470 10290 5350 535102900 sxs x x x x x x x xx
2 535102900 720580 (42)(49)0 42or49 xx xx xx xx
Sincexisthenumberofmembers,itmustbe positivesothenumberofmembersis49.
115. Let a betheagetheindividualisabletostart savingmoney.Thenweneedtofindwherethe modelsareequal.Solvingthesetwoequations together: 2 2 2 2240(2240)4(25)(38540) 2(25)
22401163600 50 252400307001607840 252240385400
22401078.7 50
aa a a a aa aa
22401078.722401078.7 or 5050 66.4or23.2
Since x istheagetostartsaving,itmakessense thattheanswerisapproximateatage23.
116.
2 1365 2 3130 31300 13100 nn nn nn nn 13or10nn
Sincethenumberofsidescannotbenegative,we discardthenegativevalue.Apolygonwith65 diagonalswillhave13sides. 2 1 380 2 3160 31600 nn nn nn 1,3,160abc 2 33411603646 212 n
Neithersolutionisaninteger,sothereisno polygonthathas80diagonals.
117. Therootsofaquadraticequationare
118. Therootsofaquadraticequationare
119. Inordertohaveonerepeatedsolution,weneed thediscriminanttobe0.
121. For20 axbxc : 24 2 bbac x a For20 axbxc :
120. Inordertohaveonerepeatedsolution,weneed thediscriminanttobe0.
122. For20 axbxc : 2 1 4 2 bbac x a and 2 2 4 2 bbac x a
For20 cxbxa :
123. If x =originalwidthand y =originallength,then 11 or xyx y .Theratioofsidelengthsis
2 1 x yy .Foldingalongthelongestsideresults insidesoflength1and2 y x y whoseratiois
Thefirstequationhasthesolutionset 1 whilethesecondequationhasnosolutions.
125. Answerswillvary.Methodsmayincludethe quadraticformula,completingthesquare, graphing,etc.
126. Answerswillvary.Knowingthediscriminant allowsustoknowhowmanyrealsolutionsthe equationwillhave.
127. Answerswillvary.Onepossibility: Twodistinct:23180 xx Onerepeated:214490 xx Noreal:240 xx
128. Answerswillvary.
124. a. 29 x and3 x arenotequivalent becausetheydonothavethesamesolution set.Inthefirstequationwecanalsohave 3 x . b. 9 x and3 x areequivalentbecause 93 .
c. 1212xxx and21 xx are notequivalentbecausetheydonothavethe samesolutionset.
Section 1.3
1. Integers: 3,0
Rationals: 3,0,6 5
2. True;thesetofrealnumbersconsistsofall rationalandirrationalnumbers.
3.
22 3323 232323 323 23 323 43 323
4. real;imaginary;imaginaryunit
5. False;theconjugateof25i is25i .
6. True;thesetofrealnumbersisasubsetoftheset ofcomplexnumbers.
7. False;if23i isasolutionofaquadratic equationwithrealcoefficients,thenits conjugate,23i ,isalsoasolution.
8. b
9. a 10. c
11. (23)(68)(26)(38)85 iiii
12. (45)(82)(4(8))(52) 47 iii i
13. (32)(44)(34)(2(4)) 76 iii i
14. (34)(34)(3(3))(4(4)) 606 iii i
15. (25)(86)(28)(56) 611 iii i
16. (84)(22)(82)(4(2)) 106 iii i
17. 3(26)618 ii
18. 4(28)832 ii
19. 2 3(76)21182118(1) 1821 iiiii i
20. 2 3(34)912912(1)129 iiiiii
21. (34)(2)63842 654(1) 105 iiiii i i
25. 2 1010343040 3434349121216 30403040 916(1)25 3040 2525 68 55 ii iiiiii ii i i
26. 2 1313512 512512512 65156 256060144 6515665156 25144(1)169 65156 169169 512 1313 i iii i iii ii i i
27. 2 2 222 2(1)1212 (1)1 iiiii iiii ii i
28. 2 2 222 222 2(1)121 2(1)22 iiiii iiii ii i
22. (53)(2)105632 103(1) 13
iiiii i i
iiiii
23. (5)(5)25552 25(1) 26
24. (3)(3)9332 9(1) 10 iiiii
29. 2 2 66166 1111 67(1)5757 1(1)222 iiiiii iiiiii iii
30. 2 2 232312233 1111 253(1)1515 1(1)222 iiiiii iiiiii iii
31. 2 1311332 2 224224 13313 (1) 42422 iii ii
Chapter 1: Equations and Inequalities
32. 2 3133112 2 224224 33113 (1) 42422 iii ii
33. 22 (1)1212(1)2 iiiii
34. 22 (1)1212(1)2 iiiii
35.
11 2322122211 (1) iiiiiiii
7 1427(1)1 ii
37. 20 2020210 10 111 () 111 (1)1
i iii
38. 23 2322122211 112 1111 () 111 (1)(1) i iiiiii iii i iii ii
39. 3 62355(1)5156ii
40. 32 444(1)4 iiiii
41. 3532 2 64(64) (64(1))1(10)10 iiii iiii
42. 3222 421421 4(1)2(1)1 421 34 iiiii i i i
43. 32 2 (1)(1)(1)(1)(12)(1) (121)(1)2(1) 2222(1) 22 iiiiiii iiii iii i
44. 44 (3)181181(1)182 ii
45. 7277 (1)(1(1))(0)0 iiii
46. 42 2(1)2(1)(1(1))2(0)0 ii
47.
432 86422222 432 (1)(1)(1)1 1111 0
iiiiiiii 48. 32 753222 32 (1)(1)(1) 0 iiiiiiiiiii iiii iiii
49. 42i
50. 93i
51. 255 i
52. 648 i
53. 124323 ii
54. 189232 ii
55. 2001002102 ii
56. 459535 ii
57. 2 (34)(43)1291612 916(1) 25
5 iiiii i
58. 2 (43)(34)1216912 169(1) 25
5 iiiii i
59. 2 2 40 4 4 2 x x x xi
Thesolutionsetis 2,2. ii
66. 2250xx 22 1,2,5 4(2)4(1)(5)42016 (2)162412 2(1)2 abc bac i xi
Thesolutionsetis 12,12 ii .
60. 240 x (2)(2)0 2or2
Thesolutionsetis2,2.
61. 2160 x 440 4or4
67. 2 251020 xx 22 25,10,2 4(10)4(25)(2)100200100 (10)100101011 505055
abc bac i xi
Thesolutionsetis 1111 , 5555 ii
Thesolutionsetis4,4.
62. 2250 x 225 255
Thesolutionsetis5,5. x xi ii
63. 26130xx 22 1,6,13, 4(6)4(1)(13)365216 (6)166432 2(1)2
Thesolutionsetis32,32. abc bac i xi ii
64. 2480xx 22 1,4,8 444(1)(8)163216 41644 22 2(1)2 abc bac i xi
Thesolutionsetis
65. 26100xx 22 1,6,10 4(6)4(1)(10)36404 (6)4623 2(1)2 abc bac i xi
68. 2 10610 xx 22 10,6,1 464(10)(1)36404 646231 2(10)201010
abc bac i xi
Thesolutionsetis 3131 , 10101010 ii
69. 2 2 512 5210 xx xx 22 5,2,1 424(5)(1)42016 (2)162412 2(5)1055 abc bac i xi
Thesolutionsetis 1212 , 5555 ii .
70. 2 2 1316 13610 xx xx 22 13,6,1 4(6)4(13)(1)365216 (6)166432 2(13)261313
abc bac i xi
Thesolutionsetis 3232 , 13131313 ii .
Chapter 1: Equations and Inequalities
71. 210xx 1,1,1,abc 22414(1)(1)143 131313 2(1)222
bac i xi
Thesolutionsetis1313 , 2222 ii
72. 210xx 1,1,1abc
224(1)4(1)(1)143 (1)31313 2(1)222 bac i xi
Thesolutionsetis1313 , 2222 ii
73. 3640 x 2 2 (4)4160 404 or4160
75. 4 4 16 160 x x 22 2 440 (2)(2)40 xx xxx
2 2 20or20or40 2or2or4 2or2or42 xxx xxx xxxi Thesolutionsetis 2,2,2,2. ii
76. 4 4 1 10 x x 22 2 110 (1)(1)10 xx xxx 2 2 10or10or10 1or1or1 1or1or1 xxx xxx xxxi
Thesolutionsetis 1,1,,. ii
abc bac i xi
xxx xx xx 22 1,4,16 444(1)(16)166448 448443 223 2(1)2
Thesolutionsetis 4,223,223. ii
74. 3270 x 2 2 (3)390 303 or390 xxx xx xx
22 1,3,9 4(3)4(1)(9)93627 (3)27333333 2(1)222 abc bac i xi
Thesolutionsetis3333333,,. 2222 ii
77. 4213360xx 22 22 22 940 90or40 9or4 9or4 3or2 xx xx xx xx xixi
Thesolutionsetis 3,3,2,2. iiii
78. 42340xx 22 2 140 (1)(1)40 xx xxx
2 2 10or10or40 1or1or4 1or1or42 xxx xxx xxxi
Thesolutionsetis 1,1,2,2. ii
79. 2 3340 xx 22 3,3,4 4(3)4(3)(4)94839 abc bac
Theequationhastwocomplexsolutionsthatare conjugatesofeachother.
Section 1.3: Complex Numbers; Quadratic Equations in the Complex Number System
80. 2 2410 xx 22 2,4,1 4(4)4(2)(1)1688 abc bac
Theequationhastwounequalrealnumber solutions.
81. 2 2 234 2340 xx xx 22 2,3,4 434(2)(4)93241 abc bac Theequationhastwounequalrealsolutions.
82. 2 2 62 260 xx xx 22 1,2,6 4(2)4(1)(6)42420 abc bac
Theequationhastwocomplexsolutionsthatare conjugatesofeachother.
83. 2 91240 xx 22 9,12,4 4(12)4(9)(4)1441440 abc bac
Theequationhasarepeatedrealsolution.
84. 2 41290 xx 22 4,12,9 4124(4)(9)1441440 abc bac
Theequationhasarepeatedrealsolution.
85. Theothersolutionis2323. ii
86. Theothersolutionis44. ii
87. 343434346zziiii
88. 8383 83(83) 8383 066 wwii ii ii ii
89. 2 (34)(34) (34)(34) 9121216 916(1)25 zzii ii iii
90. 34(83) 3483 57 57 zwii ii i i
91. 2 2 181834 343434 54723454754 9121216916 5075 23 25 Viii Z Iiii iiii iii i i
Theimpedanceis23i ohms.
92. 12 2 11111(43)(2) 243(2)(43) 626262 8643823112 ii ZZZiiii iii iiiii
So, 2 2 11211262 626262 662212466104 3612124364 701071 4044 iii Z iii iiii iii i i
Thetotalimpedanceis71 44 i ohms.
93. ()() 2 zzabiabi abiabi a () () 2 zzabiabi abiabi abiabi bi
94. zabiabiabiz
95. ()() ()() ()() ()() zwabicdi acbdi acbdi abicdi abicdi zw
Chapter 1: Equations and Inequalities
96. 2 ()() ()() ()() zwabicdi acadibcibdi acbdadbci acbdadbci
2 ()() ()() zwabicdi abicdi acadibcibdi acbdadbci
97.
abiabi aabibiaabibi aabibiaabibi aabibaabib 2222 22 22 () 2()0
22 2222 222222 2222 2()2() 22 22
abab ab abba Anycomplexnumberoftheform aai or aai willwork.
98. Let32 u in320 x sothat330 xu . Then,22()()0 xuxuxu .Fromthefirst factorwefind32 xu .Fromthesecond factor,usethequadraticformulatoget 22 233 ()()41 21 33223 22222
uuu x uuuuii
Thesolutionsetis: 33 3223 2,22
i
99. 2 (5)(5)(); xyxy let5 ux (so 5 xu and5 vy so5 yv . Substitutinggives2 () uvuv or 220 uuvv whichisquadraticinu.Using thequadraticformulagives 223 41 212 vvvvv x .Since x isarealnumber, u mustalsobearealnumber.
Thisisonlypossibleifv=0whichthenmakes u =0.Therefore,055 x and 055 y ,so5510 xy
100 – 102. Answerswillvary.
103. Answerswillvary.Acomplexnumberisthe sumordifferenceoftwonumbers(realand imaginarypartsofthecomplexnumber)justasa binomialisthesumordifferenceoftwo monomialterms.Wemultiplytwobinomialsby usingtheFOILmethod,anapproachwecanalso usetomultiplytwocomplexnumbers.
104. Althoughthesetofrealnumbersisasubsetof thesetofcomplexnumbers,notallrulesthat workintherealnumbersystemcanbeusedin thelargercomplexnumbersystem.Therulethat allowsustowritetheproductoftwosquare rootsasthesquarerootoftheproductonly worksintherealnumbersystem.Thatis, abab onlywhen a and b arereal numbers.Inthecomplexnumbersystemwe mustfirstconverttheradicalstocomplexform. Inthiscasethismeansweneedtowrite9as 19913i .Thenwecanmultiplyto get
2 99339919 iii
False;youcanalsousetheQuadraticFormulaor completingthesquare.
quadraticinform
c
Section 1.4
9. 211 t
Check:2(1)111
Thesolutionsetis{1}.
Check:3(0)442
Thesolutionsetis{0}.
11. 346 t
Sincetheprincipalsquarerootisnevernegative, theequationhasnorealsolution.
12. 532 t
Sincetheprincipalsquarerootisnevernegative, theequationhasnorealsolution.
13. 31230 x
Check:3312(13)32730
Thesolutionsetis{13}.
16.
52551211211 Thesolutionsetis{1}.
42 444 2 2 2 165 165 1625 9 3 x x x x x
Check3:316916255
Thesolutionsetis 3,3.
17.
22 2 2 8 8 64 640 640 xx xx xx xx xx 0or64xx
Check0:080 00 Check64:64864 6464
Thesolutionsetis 0,64
18. 22 2 2 3 3 9 90 90 xx xx xx xx xx 0or9xx
Chapter 1: Equations and Inequalities
Check0:030 00 Check9:939 99
Thesolutionsetis 0,9 19. 152 xx
Check–5:152(5)2555
Check3:152(3)933
Disregard5asextraneous. Thesolutionsetis{3}. x
Check–4:12(4)1644
Check3:123933
Disregard4asextraneous. Thesolutionsetis{3}. x
Check:2221 22
Thesolutionsetis{2}.
xx
22 2 2 2 2 21
Check:22(2)1 22
Theequationhasnorealsolution.
23. 242 xxx
2 22 22 42 444 85 8 5 xxx xxxx x x
Check: 2 88842 555 6482 4 2555 42 255 22 55
Thesolutionsetis
24. 2 32 xxx
8 5
2 22 22 32 344 31 1 3 xxx xxxx x x
Check: 2 111 32 333 3115 393
Sincetheprincipalsquarerootisalwaysanonnegativenumber;1 3 x doesnotcheck. Thereforethisequationhasnorealsolution.
Section 1.4: Radical Equations; Equations Quadratic in Form; Factorable Equations
25. 331xx 22 2 2 313 31(3) 3169 098
0(1)(8) 1or8 xx xx xxx xx xx xx
Check1:33(1)13451
Check8:33(8)132588
Discard1 x asextraneous. Thesolutionsetis{8}.
26. 2122 xx
22 2 2 1222 122(2) 12244 028 (2)(4)0 2or4 xx xx xxx xx xx xx
28.
22 2 2 132 15 1(5) 11025 01124 0(3)(8) 3or8 xx xx xx xxx xx xx xx
Check3:1(3)33211
Check8:1(8)38206
Discard8 x asextraneous. Thesolutionsetis{-3}.
29. 3572 xx
Check2:2+122(2)21662
Check4:2122(4)2444
Discard2 x asextraneous. Thesolutionsetis{4}.
27. 22 2 2 3(10)4 3(10)4 3(10)(4) 330816 0514 0(7)(2) 7or2 xx xx xx xxx xx xx xx
22 22 2 2 2 2 3527 3527 354477 21647 (216)47 46425616(7) 46425616112 4801440 20360 (2)(18)0 xx xx xxx xx xx xxx xxx xx xx xx
2or18xx
Check2:3(2)527 191322
Check18:3(18)5187
49257522
Discard2 x asextraneous. Thesolutionsetis{18}.
Check7:3(710)49417
Check2:3(210)436422
Discard7 x asextraneous. Thesolutionsetis{2}.
Chapter 1: Equations and Inequalities
30. 3721 xx
22 22 2 2 3712 3712 371222 2422 22 (2)2 442 320 (1)(2)0 1or2 xx xx xxx xx xx xx xxx xx xx xx
Check–1:3(1)712 412131
Check2:3(2)722 101011
Discard1 x asextraneous.
Thesolutionsetis{2}.
31. 3112 xx
22 22 2 2 2 3121 3121 314411 2241 (22)41 48416(1) 2144 650 (1)(5)0 xx xx xxx xx xx xxx xxx xx xx
Check1:3(1)111 402022
Check5:3(5)151 1644222
Thesolutionsetis
32. 2311 xx
22 22 2 2 2 2311 2311 231211 121 (1)21 214(1) 2144 230 (1)(3)0 xx xx xxx xx xx xxx xxx xx xx
1or3xx
Check–1:2(1)311 101011
Check3:2(3)331 943211
Thesolutionsetis 1,3
22 32 32 32 23 xx xx xx xx
22 2 2 23 469 0109 019 xx xxx xx xx
1or9xx Check1:Check9: 3211 321 11 11
Discard9 x asextraneous. Thesolutionsetis{1}.
Discard4 x asextraneous.
Thesolutionsetis{25}.
35. 1/2 314 x
1/22
Check: 1/21/2 351164
Thesolutionsetis{5}.
36. 1/2 352 x 2 1/22352 354 39 3 x x x x
Check: 1/21/2 33542
Thesolutionsetis{3}.
37. 1/3 522 x 3 1/33522 528 510 2 x x x x
Check: 1/31/3 52282
Thesolutionsetis{2}.
38. 1/3 211 x 3 1/33211 211 22 1 x x x x
Check: 1/31/3 21111
Thesolutionsetis{1}.
39. 21/295 x
21/222 2 2 95 925 16 164 x x x x
Check4: 21/21/2 49255
Check4: 21/21/2 49255
Thesolutionsetis 4,4
40. 21/2169 x 21/222 2 2 169 1681 97 97 x x x x
Check97: 21/21/2 9716819
Check97: 21/21/2 9716819
Thesolutionsetis 97,97.
Chapter 1: Equations and Inequalities
41. 3/21/2 1/2 30 30 xx xx 1/20or30 0or3 xx xx
Check0:3/21/2030000
Check3:3/21/233333330
Thesolutionsetis 0,3
42. 3/41/4 1/41/2 90 90 xx xx 1/40 0 x x or 1/29 81 x x
Check0:3/41/4090000
Check81:3/41/48198127270
Thesolutionsetis 0,81
43. 42 22 22 540 410 40or10 2or1 xx xx xx xx
Thesolutionsetis 2,1,1,2.
44.
42 22 2 10250 550 50 5 xx xx x x
Thesolutionsetis 5,5.
45. 42 22 6510 6110 xx xx 22 22 610or10 61or1 Notrealor1
xx xx x Thesolutionsetis 1,1.
46.
42 22 25120 2340 xx xx
22 22 230or40 23or4 Notrealor2 xx xx x
Thesolutionsetis 2,2.
47.
63 33 780 810 xx xx 33 33 80or10 8or1 2or1 xx xx xx Thesolutionsetis 2,1.
48.
63 33 780 810 xx xx
33 33 80or10 8or1 2or1 xx xx xx
Thesolutionsetis 1,2.
49. 2 272120xx
Let22 2,sothat2.uxux
27120 340 uu uu
30or40 3or4 23or24 5or6 uu uu xx xx
Thesolutionsetis 6,5.
50. 2 252560 xx Let22 25sothat25.uxux
260 320 uu uu 30or20 3or2 253or252 7 1or2 uu uu xx xx
Thesolutionsetis 7,1. 2
51. 2 491049250 xx
Let22 49sothat49. uxux
Section 1.4: Radical Equations; Equations Quadratic in Form; Factorable Equations
uu u u u x x x
2 2 10250 50 50 5 495 414 7 2
Thesolutionsetis 7 . 2
52. 2 22200 xx
Let22 2sothat2.uxux
2200 540 uu uu
50or40 5or4 25or24 7or2 uu uu xx xx
Thesolutionsetis 2,7.
53. 2 21513 ss
Let22 1sothat1.usus 2 2 253 2530 2130 uu uu uu
210or30 1or3 2 11or13 2 3or2 2 uu uu ss ss
Thesolutionsetis 3,2. 2
54.
2 315120 yy
Let22 1sothat1.uyuy
320or10 2or1 3 12or11 3 5or2 3 uu uu yy yy
Thesolutionsetis 5,2. 3
55. 40 140 xxx xx
1 4 122 4 1 16 0or140 14 xx x x x x
Check:
1111 16161616 111 16164 11 1616 0:04(0)00 00 :40 40 0 00 x x
Thesolutionsetis 1 0,. 16
56. 80xx
22 2 2 8 8 64 064 064 xx xx xx xx xx
0or64xx
Check:0:0800 00 64:648640 64640 x x
Thesolutionsetis 0
Chapter 1: Equations and Inequalities
57. 20 xx
Let2sothat. uxux 2 2 20 200 540 uu uu uu 5040 or 54 or or 54 notorpossible16 uu uu xx x
Check:161620 16420
Thesolutionsetis 16
58. 6 xx Let2sothat. uxux
2 2 6 60 320 uu uu uu
3020 or 32 or or 32 notorpossible4 uu uu xx x
Check:446 426
Thesolutionsetis 4.
59. 1/21/4210tt
Let1/421/2 sothat.utut
2 2 1/4 210 10 10 1 1 1 uu u u u t t
Check: 1/21/4 12110 1210 00
Thesolutionsetis 1
60. 1/21/4440zt Let1/421/2 sothat.uzuz
2 2 1/4 440 20 20 2 2 16 uu u u u z z
Check: 1/21/4 1641640 4840 00
Thesolutionsetis 16.
61. 1/21/4320xx Let1/421/2 sothat.uxux
2320 210 uu uu 1/41/4 2or1 2or1 16or1 uu xx xx
Check: 1/21/4 1/21/4 16:1631620 4620 00 1:13120 1320 00 x x
Thesolutionsetis 1,16.
62. 1/21/4 4940 xx Let1/421/2 sothat.uxux 2 4940 uu 2 (9)(9)4(4)(4)917 2(4)8 u 1/4 4 917 8 917 8 x x
Chapter 1: Equations and Inequalities
Since5415410,isnotreal. 2 x
Since x isafourthroot, 541 2 x isalso notreal.Therefore,wehaveonlyonepossible solutiontocheck:541: 2 x
Check541:
22 2 2 3or2 33or32 Notpossibleor34 340 410 4or1 uu xxxx xx xx xx xx
Check4: x
22 4344346 161216126 161246 66
Check1: x
22 1311316 13136 446 66
Thesolutionsetis 4,1. 66. 22 222 332 Let3sothat3. xxxx uxxuxx
2 2 2 20 120 uu uu uu
22 2 2 1or2 31or32 Notpossibleor34 340 410 4or1 uu xxxx xx xx xx xx
Check4: 43443416124 422
22 22
Check1: 131131134 422 x x
Thesolutionsetis1,4.
34 The43 solutionsetis,. 69. 21 3760 xx
Let122 sothat.uxux
00
Thesolutionsetis341341 , 88
2/31/3 2530 xx Let1/322/3 sothat.uxux
2 2530 2130 uu uu
1/31/3 3 3331/31/3 1or3 2 1or3 2 1or3 2 1or27 8 uu xx xx xx
Check 2/31/3111 :2530 888 11 2530 42 1530 22 330 00
27:2/31/322752730 295330 181530 330 00 x
Thesolutionsetis
1,27 8
Thesolutionsetis
Thesolutionsetis
Thesolutionsetis
20 0 x x or430 43 3 4 x x x
Thesolutionsetis 0,3 4 78.
53 53 32 3 4 40 40 220 xx xx xx xxx 30 0 x x or20 2 x x or20 2 x x
Thesolutionsetis 2,0,2
79.
32 2 200 200 540 xxx xxx xxx 0 x or50 5 x x or40 4 x x
Thesolutionsetis 5,0,4
80.
32 2 670 670 710 xxx xxx xxx 0 x or70 7 x x or10 1 x x
Thesolutionsetis 7,0,1
81.
32 2 2 10 1110 110 1110 xxx xxx xx xxx 10 1 x x or10 1 x x
Thesolutionsetis 1,1
82.
85. 15 44
87. 14 33 1 3 1 3 1 3 3(3)9(3)0 3(3)[13(3)]0 3(3)(139)0 3(3)(38)0 xx xx xx xx
or380 38 8 3 x x x
Thesolutionsetis 8,3 3 . 88. 31 32 32 32 32 3 4(2)(2)0 (2)[4(2)]0 (2)[4(44)]0 (2)[444)]0 (2)(4)0 (2)(4)0 xx xx xxx xxx xxx xxx
3 3 (2)0 10 (2) nosolution x x or0 x or40 4 4 x x x
Thesolutionsetis 4,0. 89.
1/34/322 1/3 22 1/3 22 1/3 22 3230 3230 3260 3250 xxxxx xxxxx xxxxx xxxx
1/3 22 22 30or250 30or250 30or250 05 or3or0or 2 xxxx xxxx xxxx xxxx
Thesolutionsetis 5 0,,3. 2
1/21/2 2222 1/21/2 22 22or22 22or22 22or22 22or22 uu xx xx xx
2 Check22: x
2 2242220 442284220 00 2 Check22: x
2 2242220 442284220 00 Thesolutionsetis
22 22,220.34,11.66 .
92. 2/31/3 1/322/3 420 Letsothat. xx uxux 2420uu 2 444(1)(2) 2(1) 4842222 22 u
1/31/3 33 22or22 22or22 22or22 uu xx xx
3 Check22: x 2/31/333 2 2242220 2242220 442284220 00
221141141,122 1.85,0.17.
2 22 121 Let1sothat1. rr urur
2 2 2 2 ()()4()(2) 2() 8 2 18 2 18 2 u r r
2 22 2222 2 222 22 88 2 22 2888 2 42 22888 2 42
32 32 2 2 312520 3512200 354350 4350 22350 zzz zzz
Thesolutionsetis52,,2 3
101. 433 4123 315 5 ww ww w w
Thesolutionsetis 5
102. 63212 618212 46 3 2 kk kk k k
Thesolutionsetis3 2
Chapter 1: Equations and Inequalities
105.
22521
Thesolutionsetis
xx
470
Thesolutionsetis
Thesolutionsetis17 , 26
Thesolutionsetis
111. 2 2 12 120 kk kk
430kk
Neitherofthesevaluescausesadenominatorto equalzero,sothesolutionsetis 3,5. 2
112. 2 2 328 3280 kk kk
7 37 4 3728 631 315.17 6 k x x xx x x
Neitherofthesevaluescausesadenominatorto equalzero,sothesolutionsetis 1331 ,.56
Chapter 1: Equations and Inequalities
113. Solvetheequation4 41100 ss
Let2,sothat. usus 227544000uu
Thelengthwasapproximately220.7feet.
Since us ,itmustbepositive,so
Thedistancetothewater'ssurfaceis approximately229.94feet.
114. 2 4 25 TLH
Let4 T and10 H
115. 2 32 Tl
118.
Section 1.4: Radical Equations; Equations Quadratic in Form; Factorable Equations
x x x x x x x x
43 4 434 3 3 33 22 710182 710182 7101816 7102 7108 72 74 11
79 2 5510 1449 101010 41 102 4 10 12313 123130 121330 00
xxx xxx xxx xx Tosolve1 2 121330 xx ,let1 2 ux 11 22 Then2121330 (43)(31)0 31 or 43 91 169 uu uu uxx xx
Thesolutionsetis 910,,169
119. 63 33 22 28270 (27)(1)0 (3)(39)(1)(1)0
zz zz zzzzzz 30or10 3or1 zz zz 2 2 1,3,9 33419 2 327333 22 , 1,1,1 11411 2 1313 22
abc x i Also abc x i Thesolutionsetis133333,1,,. 22
120. Answerswillvary.Oneexample:11. x
121. Answerswillvary.Oneexample:20. xx
122. Answerswillvary.
123. Myadidnotcheckhersolutionsandincludedthe extraneoussolution,1 x
2 2 2 2 230 23 23 23 230 310 3or1 xx xx xx xx xx xx xx
Check:
23330 930 330 00
Thesolutionsetis 3
21310 110 110 20
Section 1.5
1. 2 x
2. False.
3. closedinterval
4. multiplicationproperties(forinequalities)
5. True.Thisfollowsfromtheadditionproperty forinequalities.
6. True.Thisfollowsfromtheadditionproperty forinequalities.
7. True;.Thisfollowsfromthemultiplication propertyforinequalities.
8. False.Sincebothsidesoftheinequalityare beingdividedbyanegativenumber,thesense, ordirection,oftheinequalitymustbereversed. Thatis, ab cc .
9. True
10. False;eitherorbothendpointscouldbeanyreal number.
11. d 12. c
13. Interval: 0,2
Inequality:02 x
14. Interval: 1,2
Inequality:12 x
15. Interval: 2,
Inequality:2 x
16. Interval: ,0 Inequality:0 x
17. Interval: 0,3 Inequality:03 x
18. Interval: 1,1
Inequality:11 x
19. a. 35 3353
20. a. 21 2313 54
b. 21 2515 34
c.
3231 63
21 2221 42
21. a. 43 4333 70
b. 43 4535 18
c.
d.
43 3433 129
43 2423 86
22. a. 35 3353 02
b. 35 3555 810
c. 35 3335 915
d.
35 2325 610
23. a. 212 21323 245 x x x
b. 212 21525 243 x x x
c. 212 32132 636 x x x
d.
212 22122 424 x x x
24. a. 125 12353 428 x x x
b. 125 12555 420 x x x
c.
d.
25. [0,4]
125 31235 3615 x x x
125 21225 2410 x x x
26. (–1,5)

Chapter 1: Equations and Inequalities
40. 8 x
41. If5,then50. xx
42. If4,then40. xx
43. If4,then40. xx
44. If6,then60. xx
45. If4,then312. xx
46. If3,then26. xx
47. If6,then212. xx
48. If2,then48. xx
49. If5,then420. xx
50. If4,then312. xx
51. If840,then5. xx
52. If312,then4. xx
53. If13,then6. 2 xx
54. If11,then4. 4 xx
55. If11 05,then05 x x
56. 04,11then0 4 x x
57. 50,11then0 5 x x
58. 010,11 then010 x x
59. 15 1151 4 x x x
4or(,4) xx
60. 61 6616 7 x x x
Thesolutionsetis 7or(,7) xx .
61. 357 510 2 x x x
Thesolutionsetis 2or[2,) xx .
62. 235 33 1 x x x
Thesolutionsetis 1or[1,) xx
63. 372 39 3 x x x
Thesolutionsetis 3or(3,) xx .
64. 251 24 2 x x x
Thesolutionsetis 2or(2,) xx
65. 313 24 2 xx x x
Thesolutionsetis 2or[2,) xx .
66. 223 5 xx x
Thesolutionsetis 5or[5,) xx
67. 2(3)8 268 214 7 x x x x
Thesolutionsetis 7or(7,) xx .
68. 3(1)12 3312 315 5 x x x x
Thesolutionsetis 5or(,5) xx
69. 43(1)3 4333 313 32 2 3 x x x x x
Thesolutionsetis22 or, 33 xx
Section 1.5: Solving Inequalities
70. 84(2)2 8842 42 60 0 xx xx xx x x
Thesolutionsetis 0or,0 xx .
71. 1(4)8 2 128 2 110 2 20 xx xx x x
Thesolutionsetis 20or(,20) xx
72. 1 34(2) 3 3412 33 9122 814 7 4 xx xx xx x x
Thesolutionsetis77or(,)44 xx
73. 1 24 24 34 4 3 xx xx x x
Thesolutionsetis44or,33 xx
Chapter 1: Equations and Inequalities
74. 2 36 212 12 xx xx x
Thesolutionsetis
75. 0375 7312
Thesolutionsetis774or,433

76. 42210 228 14 x x x
Thesolutionsetis
77. 5432 932
Thesolutionsetis223or,333
78. 3329 626 33
Thesolutionsetis
30
Thesolutionsetis111 22 xx
32 04 2 0328 236 22 3 x x x x
Thesolutionsetis222or,233 xx
81. 1 114 2 1 03 2 06or60 x x xx
Thesolutionsetis 60or6,0xx
82. 1 011 3 1 10 3 30or03 x x xx
Thesolutionsetis 03or0,3xx
83. 22 (2)(3)(1)(1) 61 61 5 5 xxxx xxx x x x
Thesolutionsetis
5or,5 xx
84. 22 (1)(1)(3)(4) 112 112 11 11 xxxx xxx x x x
Thesolutionsetis
85. 2 22 (43)(21) 43441 341 1 1 xxx xxxx xx x x
Thesolutionsetis
1or1, xx .
86. 2 22 (95)(31) 95961 561 1 xxx xxxx xx x
Thesolutionsetis
Section 1.5: Solving Inequalities
87. 113 234 6449 245 15 24 x x x x
Thesolutionsetis1515 or, 2424 xx
112 323 2334 131 11 33 x x x x
Thesolutionsetis1111 or, 3333 xx
1 3 1 3
89. 1 420 10 42 420 1 2 x x x x
Thesolutionsetis11 or, 22 xx
90. 1 210 10 21 x x Since10 21 x ,thismeans210 x Therefore, 210 1 2 x x
Chapter 1: Equations and Inequalities
Thesolutionsetis11or,22 xx
91. 1 147 170 14 17(14)0 14 6280 14
x x x x x x
171755 9933 17 5
Interval Number Chosen Valueof Conclusion (,)(,)(,) 21.70 117 f
PositiveNegativePositive
Wewanttoknowwhere()0 fx ,sothe solutionsetis 175 93xxorx or, usingintervalnotation,175 93 [,).Notethat 5 3isnotinthesolutionsetbecause27isnotin thedomainof f
Thesolutionsetis 175 93 ,
Interval(,)(,)(,) Number01 Chosen Valueof6
Thezerosandvalueswheretheexpressionis undefinedare31 144 and xx 3311 141444 22 100 422 33
Conclusion f NegativePositiveNegative Wewanttoknowwhere()0 fx ,sothe solutionsetis 31 144xxorx or,using intervalnotation,31 144 [,).Notethat14isnotin thesolutionsetbecause14isnotinthedomain of f
Thesolutionsetis 31 144 ,
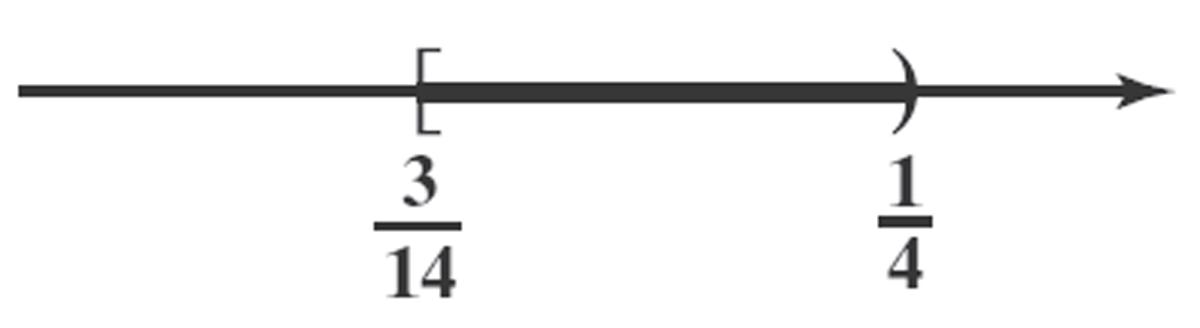
92. 1 2353 230 (35) 23(35)0 2(35) 1790 (35) x x x x x x
Thezerosandvalueswheretheexpressionis undefinedare175 93 and xx
93. 023 5 0223 and 5 x xx
Since20 x ,thismeansthat0 x .Therefore, 23 5 2355 5 103 10 3 x xx x x x
Thesolutionsetis1010or,33 xx
94. 042 3 0442 and 3 x xx
Since40 x ,thismeansthat0 x .Therefore, 42 3 4233 3 122 6 x xx x x x
Thesolutionsetis 6or6, xx
95. 02411 2 011 242 0111 and 24242 x x xx
Since10 24 x ,thismeansthat240 x
Therefore, 11 242 11 2(2)2 112(2)2(2)2(2)2 12 3 x x xx x x x
Thesolutionsetis
3or3, xx
96. 03611 3 011 363 0111 and 36363 x x xx
Since10 36 x
,thismeansthat360 x
Therefore, 11 363 11 3(2)3 113(2)3(2)3(2)3 12 1 x x xx x x x
1or1, xx
Section 1.5: Solving Inequalities
97. If11, x then 14414 345 x x So,3and5. ab
98. If32, x then 36626 964 x x So,9and4. ab
99. If23, x then 4(2)4()4(3) 1248 x x So,12and8. ab
100. If40, x then 11140 222 1 20 2 x x So,2and0. ab
101. If04, x then 2(0)2()2(4) 028 032383 32311 x x x x So,3and11. ab
102. If33, x then 2(3)2()2(3) 626 612161 7125 5127 x x x x x So,5and7. ab
103. If30, x then 34404 144 111 44 111 44 x x x x So,1and1. 4 ab
Chapter 1: Equations and Inequalities
104. If24, x then 26646 462 111 462 111 264 x x x x
So,11 and. 24 ab
105. If6312, x then 222 2 6312 333 24 24 416 x x x x
So,4and16. ab
106. If026, x then 222 2 026 222 03 03 09 x x x x
So,0and9. ab
107. 36 x
Weneed360 36 2 x x x
Tothedomainis 2 xx or 2,.
108. 82 x
Weneed820 28 4 x x x
Tothedomainis 4 xx or 4,.
109. 21<youngadult'sage<30
110. 40 ≤ middle-aged<60
111. a. Let x =ageatdeath. 3052.2
82.2 x x
Therefore,theaveragelifeexpectancyfora 30-year-oldmalein2023willbegreater thanorequalto82.2years.
b. Let x =ageatdeath. 3055.8 85.8 x x
Therefore,theaveragelifeexpectancyfora 30-year-oldfemalein2023willbegreater thanorequalto85.8years.
c. Bythegiveninformation,afemalecan expecttolive85.882.23.6 yearslonger.
112. 20 VT
80º120º
80º120º 20 16002400 T V V
Thevolumerangesfrom1600to2400cubic centimeters,inclusive.
113. Let P representthesellingpriceand C representthecommission.
Calculatingthecommission:
45,0000.25(900,000) 45,0000.25225,000 0.25180,000
Calculatethecommissionrange,giventheprice range: 225,000180,0000.25180,000275,000180,000 900,0001,100,000
0.25(900,000)0.250.25(1,100,000) 225,0000.25275,000
45,00095,000 P P P P C
Theagent'scommissionrangesfrom$45,000to $95,000,inclusive.
45,000 900,000 0.055% to95,0001,100,0000.0868.6%, inclusive.
Asapercentofsellingprice,thecommission rangesfrom5%to8.6%,inclusive.
114. Let C representthecommission. Calculatethecommissionrange: 250.4(200)250.4(3000) 1051225 C C
Thecommissionsareatleast$105andatmost $1225.
115. Let W =weeklywagesand T =taxwithheld. Calculatingthewithholdingtaxrange,giventhe rangeofweeklywages:
Theamountwithheldvariesfrom$1122.50to $1146.50,inclusive.
116. Let x representthelengthoftimeyoushould exerciseonthelasttwodays. 253504015150 115150 35 x x x
Youwillstaywithintheguidelinesbyexercising from35minutestotalonthelasttwodays.
117. Let x representtheamountpaidforinternational minutesandyrepresentthenumberof internationalminutes.Therangeofthebillsis $69.50to$140.75.Therateplanis$60.Thusthe rangeofcostsoftheinternationalminutesis:
9.5080.75 x .Thecostperminis$0.25.
9.5080.75
0.250.25 38323 y y
Theminutesvariesfrom38to323minutes, inclusive.
118. Let C representtheamountpaidforthefares.The rangeofthefareis$20.93to$40.44.ofmiles.The numberofmilesis23. 20.932340.44
0.911.76 x x Thecostpermilevariesfrom$0.91permileto $1.76permile,inclusive.
119. Youhavealreadyconsumed40gramsoffat. LetCrepresentthenumberofcookies.Thenwe havethefollowingequation: 40864 824 3 C C C
Youmayeatupto3cookiesandkeepthetotal fatcontentofyourmealnotmorethan64g.
120. Youhavealreadyconsumed730calories.Let x representthenumberofapplesauceordersyou caneat.Thenwehavethefollowingequation: 73050830 50100 2 x x x
Youmayeatupto2ordersofapplesauceand keepyourcaloriesbeloworequalto830.
121. a. Let T representthescoreonthelasttestand G representthecoursegrade.
Calculatingthecoursegradeandsolvingfor thelasttest: 68828789 5 326 5 5326 5326 GT GT GT TG
Calculatingtherangeofscoresonthelast test,giventhegraderange: 8090 4005450 745326124 74124 G G G T
TogetagradeofB,youneedatleasta74 onthefifthtest.
b. Let T representthescoreonthelasttestand G representthecoursegrade.
Calculatingthecoursegradeandsolvingfor thelasttest: 688287892 6 3262 6 163 3 3163 GT
Calculatingtherangeofscoresonthelast test,giventhegraderange: 8090 2403270 773163107 77107 G G G T
TogetagradeofB,youneedatleasta77 onthefifthtest.
Chapter 1: Equations and Inequalities
122. Let T representthetestscoresofthepeoplein thetop2.5%.
1.96(12)100123.52 T Peopleinthetop2.5%willhavetestscores greaterthan123.52.Thatis,123.52 T or (123.52,).
123. Since ab , and 2222 and 22222222 and 22 abab aaababbb abab ab
So,2ab ab .
124. Fromproblem123,2ab ab ,so 2 ,2222 ababababadaa
and 2 ,2222 ababbabbadbb
Therefore,2ab isequidistantfrom a and b.
125. If0,then ab
22 22 22 0and0 and and ababab ababab ababab
Therefore, aabb
126. Showthat 2 abab .
2 12 22 10,since. 2 ababaabb abab
Therefore,2abab .
127. For1111 0,2 ab hab
11 2 11 2 2 ba hh hab bah ab hab ab
22 22() 2 ()0 ababaabhaa abab abaababa abab aba ab
Therefore, ha . 22 2()2 2 ()0 bhbabbabab abab abbabbab abab bba ab
Therefore, hb ,andwehave ahb .
128. Showthat 2 (geometric2 mean) arithmeticmean1() 2 ab h ab
2 1111 2 211 2 2 1() 2 hab ba habab hab ab habab abab
129. 4235 3 312695 31269and695 33514 114 4
Section 1.6: Equations and Inequalities Involving Absolute Value
Thisisequivalentto14 1 5 x .Thesolution set,inintervalnotation,is14 1,5
.
130. Thelargestvalueof223 x occursatthelargest valuefor x 259 34 43 34or43
x x x xx Thelargestvaluefor223 x is 2 2(4)332329 .
131. Answerswillvary
132. Answerswillvary.Onepossibility:
Nosolution: 46252 xxx
Onesolution: 35231321 xxx
133. Since20 x ,wehave 2 2 101 11 x x
Therefore,theexpression21 x canneverbe lessthan5
134. Answerswillvary.
Section 1.6
1. 22
2. True
3. {5,5}
4. {|55} xx
5. True
6. True 7. d
8. a
9. 315 x 315or315 5or5 xx xx Thesolutionsetis{–5,5}.
10. 312 x 312or312 4or4 xx xx Thesolutionsetis{–4,4}.
11. 235 x 235or235 22or28 1or4 xx xx xx
Thesolutionsetis{–4,1}.
12. 312 x 312or312 33or31 11 or 3 xx xx xx
Thesolutionsetis 1,1 3
13. 14813 145 t t 145or145 44or46 13 or 2 tt tt tt
Thesolutionsetis 1,3 2
14. 1269 123 z z 123or123 22or24 1or2 zz zz zz
Thesolutionsetis 1,2
15. 28 28 x x
28or28 4or4 xx xx
Thesolutionsetis{–4,4}.
Chapter 1: Equations and Inequalities
16. 1 1 x x 1or1xx
Thesolutionsetis{–1,1}.
17. 24 24 2 x x x
Thesolutionsetis{2}.
18. 39 39 3 x x x Thesolutionsetis{3}.
19. 83 7 x 21 8 2121 or 88 x xx
Thesolutionsetis 2121 , 88
20. 39 4 x 12 12or12 x xx Thesolutionsetis{–12,12}.
21. 22 35 x 222or2 3535 5630or5630 524or536 2436 or 55 xx xx xx xx
Thesolutionsetis 3624 , 55
22. 11 23 x 111or1 2323 326or326 38or34 84 or 33 xx xx xx xx
Thesolutionsetis 48 , 33 .
23. 21 2 u Nosolution,sinceabsolutevaluealwaysyieldsa non-negativenumber.
24. 21 v Nosolution,sinceabsolutevaluealwaysyieldsa non-negativenumber.
25. 544 41 41
xx xx
x x x 41or41 11 or 44
Thesolutionsetis 11 , 44 .
26. 1 53 2 12 2 12 2 x x x
112or2 22 4or4 xx xx
Thesolutionsetis 4,4
27. 290 x 2 2 90 9 3 x x x
Thesolutionsetis 3,3
Section 1.6: Equations and Inequalities Involving Absolute Value
28. 2160 x 2 2 160 16 4 x x x Thesolutionsetis 4,4
29. 223xx
22 22 23or23 230or230 3102412 or 2 328 or1ornorealsol. 2 xxxx xxxx xxx xxx
Thesolutionsetis 1,3
30. 212xx
22 22 12or12 120or120 3401148 or 2 3147 or4ornorealsol. 2 xxxx xxxx xxx xxx
Thesolutionsetis 4,3
31. 211xx
22 22 11or11 20or0 120or10 1,2or0,1 xxxx xxxx xxxx xxxx
Thesolutionsetis 2,1,0,1.
32. 2322xx
22 22 2 322or322 34or30 340or30 410or0,3 4,1 xxxx xxxx xxxx xxxx xx
Thesolutionsetis 4,3,0,1
33. 53 2 35 x x
5353 2or2 3535 53235or53235 53610or53610 7or1113 713 or 11
xx xx xxxx xxxx xx xx Neitherofthesevaluescausethedenominatorto equalzero,sothesolutionsetis 13,7. 11 34. 21 1 34 x x
2121 1or1 3434 21134or21134 2134or2134 3or55 3or1 xx xx xxxx xxxx xx xx
Neitherofthesevaluescausethedenominatorto equalzero,sothesolutionsetis 3,1.
35. 2232 xxxx 2222 22 2 32or32 32or32 50or20 0or(21)0 01 or0or 2 xxxxxxxx xxxxxx xxx xxx xxx
Thesolutionsetis 1,0. 2
36. 2226 xxxx 2222 22 2 26or26 26or26 80or240 0or2(2)0 0or0or2 xxxxxxxx xxxxxx xxx xxx xxx
Thesolutionsetis 2,0.
Chapter 1: Equations and Inequalities
37. 28 x
828 44 x x
44or4,4xx
38. 315 x
15315 55 x x
55or5,5xx
39. 742 x 742or742 6or6 xx xx
6or6or,66, xxx

40. 26 x 26or26 3or3 xx xx
3or3or,33,xxx
41. 223 21 x x 121 13 x x
13or1,3xx
42. 435 42 x x 242 62 x x
62or6,2xx
43. 324 t 4324 236 22 3 t t t 222or,233 tt
44. 257 u 7257 1222 61 u u u
61or6,1uu
45. 232 x 232or232 21or25 15 or 22 xx xx xx
1515 oror,, 2222 xxx
46. 342 x 342or342 36or32 22 or 3 xx xx xx
222 oror,2, 33 xxx
47. 1472 145 x x
5145 644 64 44 33 1or1 22 x x x xx
33 122 or1, xx
48. 1241 123 x x 3123 422 42 22 21or12 x x x xx
12or1,2xx
49. 527 x 527or527 212or22 6or1
Section 1.6: Equations and Inequalities Involving Absolute Value
51. 451 451 44 x x x
Thisisimpossiblesinceabsolutevaluealways yieldsanon-negativenumber.Theinequality hasnosolution.
52. 42 42 6 x x x
66 66 x x
|66xx or 6,6
53. 23 23 x x 23or23 33 or 22 xx xx
3333 oror,, 2222 xxx
xx xx xx
1or6or,16, xxx

50. 231 x 231or231 33or31 11 or 3 xx xx xx
11or1or,1,33 xxx
54. 21 x 21or21 1or3 1or3 xx xx xx
3or1xxx or
55. 32521 257 x x 7257 2212 16 x x x
16or1,6 xx

Chapter 1: Equations and Inequalities
56. 123 123 x x
3123
57. 95 x
Thisisimpossiblesinceabsolutevaluealways yieldsanon-negativenumber.Nosolution.
58. 30 x
Absolutevalueyieldsanon-negativenumber,so thisinequalityistrueforallrealnumbers,(,).
59. 51 x
Absolutevalueyieldsanon-negativenumber,so thisinequalityistrueforallrealnumbers,(,).
60. 62 x
Thisisimpossiblesinceabsolutevaluealways yieldsanon-negativenumber.Nosolution.
61. 2311 32 x
62. 311 2 15 2 15 2 x
73 or 22
63. 8413 x
Thisisimpossiblesinceabsolutevaluealways yieldsanon-negativenumber.Nosolution.
64. 749 x
Thisisimpossiblesinceabsolutevaluealways yieldsanon-negativenumber.Nosolution.
65. 720 3 x
Sincetheabsolutevaluecannotbenegative,the onlypossiblesolutionwouldbe:
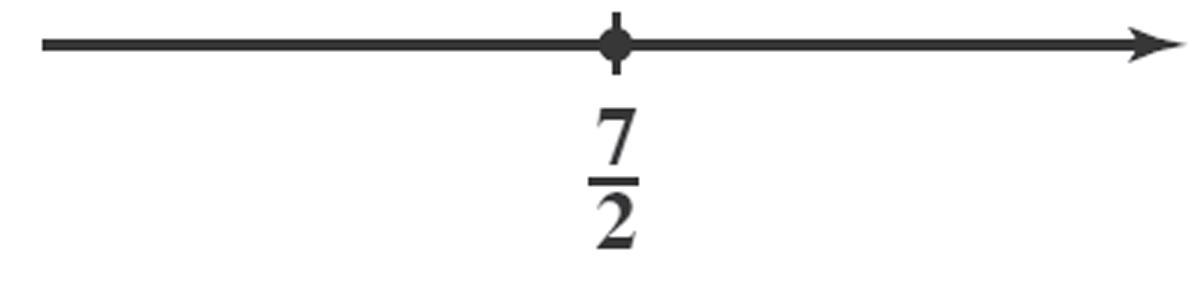
66. 4150 6
Sincetheabsolutevaluecannotbenegative,the onlypossiblesolutionwouldbe:
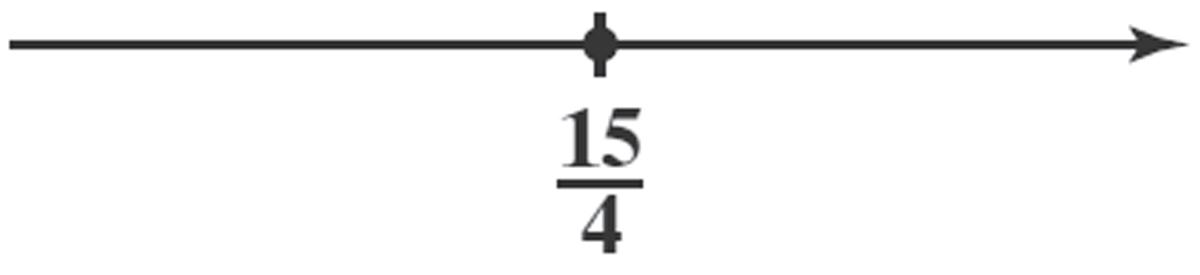
2311 23 x
2312311or1 2323 231231 661or661 2323 3(23)26or3(23)26 6926or6926 676or676 61 xx
or613 113 or 66 x xx
113 or 66 xxx
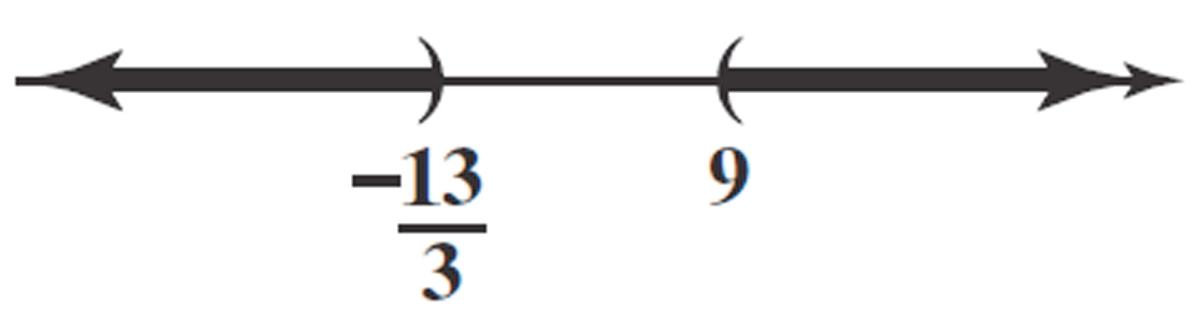
68. 528 9 x 52528or8 99 5272or5272 277or267 7767 or 22
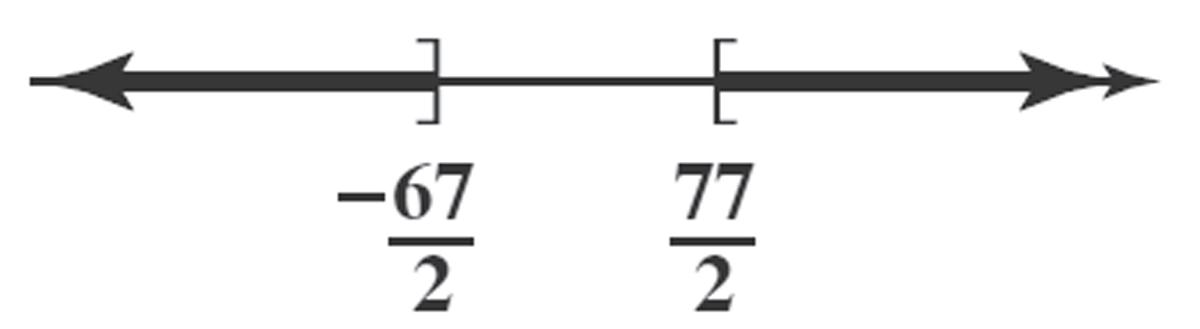
71. Atemperature x thatdiffersfrom98.6 Fbyat least1.5F . 98.61.5 98.61.5or98.61.5 97.1or100.1 x xx xx
Thetemperaturesthatareconsideredunhealthy arethosethatarelessthan97.1˚Forgreaterthan 100.1˚F,inclusive.
72. ThelengthLmustbewithin0.0025of5.375 inches.
5.3750.0025
0.00255.3750.0025
5.37255.3775
Thelengthsmustbebetween5.3725and5.3775 inches,inclusive.
73. Thepercentagemustbewithin3.9percentage pointsof44percent.Theinequalitythat representsthiswouldbe:
443.9 3.9443.9 40.147.9 x x x
Theactualpercentageislikelytofallbetween 40.1%and47.9%,inclusive.
74. Thespeed x variesfrom707mphbyupto55 mph.
a. 70755 x
Chapter 1: Equations and Inequalities
b. 5570755 5570755 652762 x x x Thespeedofsoundisbetween652and762 milesperhour,dependingonconditions.
75. differs1 from3bylessthan2 x . 31 2 11 3 22 57 22 x x x
57 22 xx
76. differsfrom4bylessthan1 x (4)1 41 141 53 x x x x
53xx
77. x differsfrom3bymorethan2. (3)2 32 x x 32or32 5or1 xx xx
|5or1xxx
78. x differsfrom2bymorethan3. 23 23or23 1or5 x xx xx
|1or5xxx
79. 13 x 313 35(1)535 248 x x x 2,8ab
80. 25 x 525 54(2)454 921 x x x 9,1ab
81. 42 x 242 62 1224 15237 x x x x 15,7ab
82. 31 x 131 24 6312 73113 x x x x 7,13ab
83. 27 x 727 59 15101 111 1510 111 1015 x x x x x
1,115 ab
84. 13 x 313 42 157 111 57 111 75 x x x x x 1,1 7 ab
85. Giventhat0,0, ab and ab ,show that ab Notethat bababa . Sincemeans0 abba ,wehave 0 bababa Therefore,0whichmeans. baab
86. Showthat aa Weknow0 a .Soif a <0,thenwehave
Section 1.6: Equations and Inequalities Involving Absolute Value
0whichmeans. aaaa .Now,if 0,then aaa .So aa .
87. Prove abab . Notethat2ababab .
Case1:If0,then, ababab so
abababab aabb aabb ab
22 22 2 2 2 byproblem86
Thus, . abab abab
22
Case2:If 0,then, ababab so
abababab abab aabb aabb ab
22 22 2 2 2 byproblem86
Thus, abab abab
22
88. Prove abab
aabbabb bytheTriangle Inequality,so aabb whichmeans abab Therefore, abab
89. Giventhat a >0,
2 20 0 xa xa xaxa
If xa ,then0 xa and 20xaa .Therefore, 0 xaxa ,whichisacontradiction.
If axa ,then02xaa and 20 axa Therefore, 0 xaxa .
If xa ,then20 xaa and 0 xa .Therefore, 0 xaxa , whichisacontradiction.Sothesolutionsetfor 2is xaxaxa .
90. Giventhat a >0, 2 20 0 xa xa xaxa
If xa ,then0 xa and 20xaa Therefore, 0 xaxa .
If axa ,then02xaa and 20 axa ..Therefore, 0 xaxa ,whichisacontradiction.
If xa ,then20 xaa and 0 xa .Therefore, 0 xaxa
Sothesolutionsetfor2xa is <or.xxaxa
91. 21 11 11 x x x Thesolutionsetis 11xx .
92. 24 44 22 x x x Thesolutionsetis 22xx
93. 29 9or9 3or3 x xx xx
Thesolutionsetis 3or3xxx
94. 21 1or1 1or1 x xx xx
Thesolutionsetis 1or1xxx
Chapter 1: Equations and Inequalities
95. 216 1616 44 x x x
Thesolutionsetis 44xx .
96. 29 99 33 x x x
Thesolutionsetis 33xx .
97. 24 4or4 2or2 x xx xx
Thesolutionsetis 2or2xxx
98. 216 16or16 4or4 x xx xx
Thesolutionsetis 4or4xxx
99. 3214 3214or3214 xx xxxx 3214 3421 xx xx 2134or2134 5or2134 5or53 53 or 5 xxxx xxx xx xx or 3214 3421 xx xx 2134or2134 3or2134 3or55 3or1 xxxx xxx xx xx
Thevalues3and3 5 areextraneous.
Thesolutionsetis 1,5. 100. 322
xx xxxx
322 322 xx xx
322or322 44or322 1or20 1or0 xxxx xxx xx xx
or 322 322 xx xx
322or322 40or322 0or24 0or2 xxxx xxx xx xx
Thevalue2isextraneous.Thesolutionsetis 0,1
101. 2513 2513 18
xx xx x or25(13) 2513 38 8 3
y y y Thevalueof y x islargestusing x =18and y =2, so 21 189
Section 1.7: Problem Solving: Interest, Mixture, Uniform Motion, Constant Rate Job Applications
Therefore11 x .Thesolutionsetin intervalnotationis 1,1.
103 – 105. Answerswillvary.
Section 1.7
1. mathematicalmodeling
2. interest
3. uniformmotion
4. False;theamountchargedfortheuseof principalistheinterest.
5. True;thisistheuniformmotionformula.
6. a
7. b
8. c
9. Let A representtheareaofthecircleand r the radius.Theareaofacircleistheproductof π timesthesquareoftheradius:2 Ar
10. Let C representthecircumferenceofacircle and r theradius.Thecircumferenceofacircle istheproductof π timestwicetheradius: 2 Cr
11. Let A representtheareaofthesquareand s the lengthofaside.Theareaofthesquareisthe squareofthelengthofaside:2 As
12. Let P representtheperimeterofasquareand s thelengthofaside.Theperimeterofasquareis fourtimesthelengthofaside:4Ps
13. Let F representtheforce, m themass,and a theacceleration.Forceequalstheproductofthe masstimestheacceleration: Fma
14. Let P representthepressure, F theforce,and A thearea.Pressureistheforceperunitarea: PF A
15. Let W representthework, F theforce,and d thedistance.Workequalsforcetimesdistance: WFd
16. Let K representthekineticenergy, m themass, and v thevelocity.Kineticenergyisone-half theproductofthemassandthesquareofthe velocity:2 1 2 Kmv
17. C totalvariablecostindollars, x number ofdishwashersmanufactured:150Cx
18. R totalrevenueindollars, x numberof dishwasherssold:250Rx
19. Let x representtheamountofmoneyinvestedin bonds.Then5000 x representstheamountof moneyinvestedinCD's.Sincethetotalinterest istobe$500,wehave:
0.150.07(5000)500 1000.150.07(5000)500100
157(5000)50,000 1535,000750,000 835,00050,000 815,000 1875 xx xx xx xx x x x
$1875shouldbeinvestedinbondsat15%and $3125shouldbeinvestedinCD'sat7%.
20. Let x representtheamountofmoneyinvestedin bonds.Then5000 x representstheamountof moneyinvestedinCD's.Sincethetotalinterest istobe$700,wehave:
0.150.07(5000)700 1000.150.07(5000)700100 157(5000)70,000 1535,000770,000 835,00070,000 835,000 4375 xx xx xx xx x x x
$4375shouldbeinvestedinbondsat15%and $625shouldbeinvestedinCD'sat7%.
21. Let x representtheamountofmoneyloanedat 4%.Then12,000 x representstheamountof moneyloanedat5.5%.Sincethetotalinterestis tobe$600,wehave:
Chapter 1: Equations and Inequalities
0.040.055(12,000)600
$4000isloanedat4%.
22. Let R representtheinterestratefortheloan. Aditiwillowe$16,350attheendoftwoyears. Thiswouldbe$1350ininterestforthetwo years,or$675peryear.Wehave: (15000)675
Herinterestratewouldbe4.5%.
23. Let x representthenumberofpoundsofEarl Graytea.Then100 x representsthenumberof poundsofOrangePekoetea. 64(100)5.50(100) 64004550 2400550 2150
xx xx x
75poundsofEarlGrayteamustbeblendedwith 25poundsofOrangePekoe.
24. Let x representthenumberofpoundsofthe firstkindofcoffee.Then100 x representsthe numberofpoundsofthesecondkindofcoffee. 2.755(100)4.10(100) 2.755005410
2.25500410 2.2590 40
xx xx x x x 40poundsofthefirstkindofcoffeemustbe blendedwith60poundsofthesecondkindof coffee.
25. Let x representthenumberofpoundsof cashews.Then60 x representsthenumberof poundsinthemixture.
156poundsofcashewsmustbeaddedtothe60 poundsofalmonds.
26. Let x representthenumberofcaramelsinthe box.Then30 x representsthenumberof cremesinthebox.
RevenueCostProfit
12.500.250.45(30)3.00
12.500.2513.50.453.00
12.5013.50.203.00
12.5013.500.203.00 1.000.203.00 0.204.00 20 xx xx x x x x x
Theboxshouldcontain20caramelsand10 cremes.
27. Let r representthespeedofthecurrent.
RateTimeDistance
Upstream16
Downstream16 r r r r
2016 1 6033 1516 1 6044
Sincethedistanceisthesameineachdirection: 1616 34 4(16)3(16) 644483 167 162.286 7 rr rr rr
Thespeedofthecurrentisapproximately2.286 milesperhour.
28. Let r representthespeedofthemotorboat.
RateTimeDistance
Upstream3553 Downstream32.52.53 rr rr
Thedistanceisthesameineachdirection: 5(3)2.5(3) 5152.57.5 2.522.5 9 rr rr r
Thespeedofthemotorboatis9milesperhour.
94.50(60)7.75(60) 92707.75465 1.25195
xx xx x x
156
29. Let r representthespeedofthecurrent. RateTimeDistance
Sincethetotaltimeis1.5hours,wehave:
Speedmustbepositive,sodisregard5
Thespeedofthecurrentis5milesperhour.
30. Let r representtherateoftheslowercar.Then 10 r representstherateofthefastercar.
Theslowercartravelsatarateof60milesper hour.Thefastercartravelsatarateof70miles perhour.Thedistanceis(70)(3)=210miles.
31. Let r representKaren’snormalwalkingspeed.
RateTimeDistance
With50walkway2.550
Against50walkway2.550
Sincethetotaltimeis48seconds:
(25)(25)4(12)(75) 2(12) 254225
Speedmustbepositive,sodisregard1.67 r .
Karen’normalwalkingspeedisapproximately 3.75feetpersecond.
32. Let r representthespeedoftheairportwalkway. RateTimeDistance
Walking280with1.5280 1.5
Standing280
Walkingwiththewalkwaytakes60secondsless timethanstandingstillonthewalkway: 2 2 2 28028060 1.5 280280(1.5)60(1.5) 2804202806090 60904200 23140 (27)(2)0
270or20 7or2 2 rr rr
Speedmustbepositive,sodisregard7 2 r
Thespeedoftheairportwalkwayis2metersper second.
33. Let w representthewidthofaregulationdoubles tenniscourt.Then26 w representsthelength. Theareais2808squarefeet: 2 2 2 (26)2808 262808 2628080 314040 (39)(36)0 ww ww ww ww ww
390or360 39or36 ww ww
Thewidthmustbepositive,sodisregard39 w . Thewidthofaregulationdoublestenniscourtis36 feetandthelengthis2(36)+6=78feet.
Chapter 1: Equations and Inequalities
34. l lengthofthecourtand w widthofthe court
Thewidthofthecourtistobetwofeetlessthan halfofitslength.Thus,12 2 wl .Theareaof thecourtis880squarefeet,so:
Sincethelengthcannotbenegativethenthe lengthis44ft.
Theareais880,so: 44880 880 44 20 w w
Thedimensionsofthecourtare44ftby20feet.
35. Let t representthetimeittakestodothejob together.
TimePartofjobdone todojobinoneminute Trent30 Lois20 Together tt 111 3020 2360 560 12 t tt
Workingtogether,thejobcanbedonein12 minutes.
36. Let t representthetimeittakesApriltodothe jobworkingalone.
37. l lengthofthegarden w widthofthegarden
a. Thelengthofthegardenistobetwiceits width.Thus,2lw Thedimensionsofthefenceare4 l and 4 w
Theperimeteris46feet,so: 2(4)2(4)46 2(24)2(4)46 482846 61646 630 5 lw ww ww w w w
Thedimensionsofthegardenare5feetby 10feet.
b. Area51050 lw squarefeet
c. Ifthedimensionsofthegardenarethesame, thenthelengthandwidthofthefenceare alsothesame(4) l .Theperimeteris46 feet,so: 2(4)2(4)46 282846 41646 430 7.5 ll ll l l l Thedimensionsofthegardenare7.5feetby 7.5feet.
d. Area7.5(7.5)56.25 lw squarefeet.
38. l lengthofthepond w widthofthepond
a. Thepondistobeasquare.Thus, lw Thedimensionsofthefencedareaare6 w
Section 1.7: Problem Solving: Interest, Mixture, Uniform Motion, Constant Rate Job Applications
oneachside.Theperimeteris100feet,so: 4(6)100 424100 476 19 w w w w
Thedimensionsofthepondare19feetby 19feet.
b. Thelengthofthepondistobethreetimes thewidth.Thus,3lw .Thedimensionsof thefencedareaare6and6 wl .The perimeteris100feet,so: 2(6)2(6)100 2(6)2(36)100 212612100 824100 876 9.5 3(9.5)28.5 wl ww ww w w w
Thedimensionsofthepondare9.5feetby 28.5feet.
c. Ifthepondiscircular,thediameteris d and thediameterofthecirclewiththepondand thedeckis6 d .
d 3 3
Theperimeteris100feet,so: (6)100 6100 1006 100625.83 d d d d
Thediameterofthepondis25.83feet.
d. 2 square Area19(19)361ft
TimetorunDistance 100yards Def. Back TimeRate Tight12sec End 10sec1010 tt tt
1002525 1233
100 10
Sincethedefensivebackhastorun5yards farther,wehave:
Thecircularpondhasthelargestarea.
39. Let t representthetimeittakesforthedefensive backtocatchthetightend.
Thedefensivebackwillcatchthetightendatthe 45yardline(15+30=45).
40. Let x representthenumberofhighwaymiles traveled.Then30,000 x representsthenumber ofcitymilestraveled.
30,000900 4025 30,000 200200900 4025 5240,0008180,000 3240,000180,000 360,000 20,000 xx xx xx x x x
Thereseisallowedtoclaim20,000milesasa businessexpense.
41. Let x representthenumberofgallonsofpure water.Then1 x representsthenumberof gallonsinthe60%solution.
2 3gallonofpurewatershouldbeadded.
42. Let x representthenumberofliterstobe drainedandreplacedwithpureantifreeze.
Chapter 1: Equations and Inequalities
%liters%liters%liters
10.40(15)0.60(15) 60.409 0.603 5 xx xx x x
5litersshouldbedrainedandreplacedwithpure antifreeze.
43. Let x representthenumberofouncesofwater tobeevaporated;theamountofsaltremainsthe same.Therefore,weget 2 3 0.04(32)0.06(32) 1.281.920.06 0.060.64
0.64643210 0.0663 x x x x
2 3 1010.67 ouncesofwaterneedtobe evaporated.
44. Let x representthenumberofgallonsofwater tobeevaporated;theamountofsaltremainsthe same.
0.03(240)0.05(240) 7.2120.05 0.054.8 4.896 0.05 x x x x
96gallonsofwaterneedtobeevaporated.
45. Let x representthenumberofgramsofpure gold.Then60 x representsthenumberof gramsof12karatgoldtobeused. 12(60)(60)23 300.540 0.510 20 xx xx x x
20gramsofpuregoldshouldbemixedwith40 gramsof12karatgold.
46. Let x representthenumberofatomsofoxygen. 2 x representsthenumberofatomsofhydrogen. 1 x representsthenumberofatomsofcarbon. 2145 444 11 xxx x x
Thereare11atomsofoxygenand22atomsof hydrogeninthesugarmolecule.
47. Let t representthetimeittakesforMiketo catchupwithDan.Sincethedistancesarethe same,wehave: 11(1) 69 322 2 tt tt t
MikewillpassDanafter2minutes,whichisa distanceof1 3 mile.
48. Let t representthetimeofflightwiththewind. Thedistanceisthesameineachdirection: 330270(5) 3301350270 6001350 2.25 tt tt t t
Thedistancetheplanecanflyandstillreturn safelyis330(2.25)=742.5miles.
49. Let t representthetimetheauxiliarypump needstorun.Sincethetwopumpsareemptying onetanker,wehave: 31 49 27436 49 92.25 4 t t t t
Theauxiliarypumpmustrunfor2.25hours.It mustbestartedat9:45a.m.
50. Let x representthenumberofpoundsofpure cement.Then20 x representsthenumberof poundsinthe40%mixture. 0.25(20)0.40(20) 50.48 0.63 305 6 xx xx x x 5poundsofpurecementshouldbeadded.
51. Let t representthetimeforthetubtofillwith thefaucetsonandthestopperremoved.Since onetubisbeingfilled,wehave:
60minutesisrequiredtofillthetub.
52. Let t bethetimethe5horsepowerpumpneeds toruntofinishemptyingthepool.Sincethetwo pumpsareemptyingonepool,wehave:
The5horsepowerpumpmustrunforan additional1.75hoursor1hourand45minutesto emptythepool.
53. Let t representthetimespentrunning.Then 5 t representsthetimespentbiking.
RateTimeDistance
Run66
Bike25525(5) tt tt
Thetotaldistanceis87miles: 625(5)87 61252587 1912587 1938
Thetimespentrunningis2hours,sothe distanceoftherunis6(2)12 miles.The distanceofthebicycleraceis25(52)75 miles.
54. Let r representthespeedoftheeastbound cyclist.Then5 r representsthespeedofthe westboundcyclist.
RateTimeDistance Eastbound66 Westbound566(5) rr rr
Thetotaldistanceis246miles: 66(5)246 6630246 1230246 12216 18 rr rr r r r
Thespeedoftheeastboundcyclistis18miles perhour,andthespeedofthewestboundcyclist is18523 milesperhour.
55. Burke'srateis10012meters/sec.In9.81seconds, Burkewillrun100(9.81)81.75 12 meters.Bolt wouldwinby100-81.75=18.25meters.
56. 2 22 Arrh .Since58.9 A square inchesand6.4 h inches, 2
rr rr rr 2 12.8(12.8)4(2)(58.9) 2(2) 12.8635.04 4 3.1or9.5
Theradiusofthecoffeecanis3.1inches.
57.Lettheindividualtimestocompletetheproject beEforElaine,BforBrian,andDforeither daughter.Usingtherespectiveratesgives 1111111 , 22 EBEDD (or121 2 ED ), and111 4 BD .Fromthefirsttwoequations, 12 BD .Substitutingintothethirdequation gives211 4 DD or 3112hours. 4 D D Then1213hours 122 E E and 1116hours. 124 B B Thecombinedrate ofElaine,Brian,andoneoftheirdaughtersis 1117 361212 projectperhour,soitwilltake them127hourstocompletetheproject.
58. If x =litersoforiginalsolution,thentherewere originally0.2x litersofsaltand0.8litersofpure water.Overtime,thesolutionloses 0.25(0.8)0.2 xx litersofpurewater.Sheadds 20litersofsaltsothetotalamountofsaltis
Chapter 1: Equations and Inequalities
0.220 x liters.Shealsoadds10litersofpure water,sothetotalamountofpurewateris 0.80.2100.610 xxx liters.Theresulting concentrationis331/3%whichmeans 0.22010.2201 or 0.2200.61030.8303 xx xxx or 0.6600.830150 xxx .Therewere initially150litersofsolutioninthevat.
59. Thespeedofthetrainrelativetothemanis30–4=26milesperhour.Thetimeis 5551 secminhh.
Thefreighttrainisabout190.67feetlong.
60. Answerswillvary.
61. Let x betheoriginalsellingpriceoftheshirt. ProfitRevenueCost 40.4020240.6040 xxxx
Theoriginalpriceshouldbe$40toensurea profitof$4afterthesale.
Ifthesaleis50%off,theprofitis: 400.50(40)204020200
At50%offtherewillbenoprofit.
62. Let12 and tt representthetimesforthetwo segmentsofthetrip.SinceAtlantaishalfway betweenChicagoandMiami,thedistancesare equal.
12 12 12 4555 55 45 11 9 tt
TheaveragespeedforthetripfromChicagoto Miamiis49.5milesperhour.
63. Thetimetraveledwiththetailwindwas: 9191.67091hours 550 t
Sincetheywere20minutes 1 3hourearly,the timeinstillairwouldhavebeen:
1.67091hrs20min1.670910.33333hrs 2.00424hrs
Thus,withnowind,thegroundspeedis 919458.53 2.00424 .Therefore,thetailwindis 550458.5391.47knots
64. Itisimpossibletomixtwosolutionswitha lowerconcentrationandendupwithanew solutionwithahigherconcentration.
AlgebraicSolution:
Let x =thenumberoflitersof25%solution. %liters%liters%liters 0.250.48200.5820
0.259.610.60.58
0.331 3.03liters (notpossible)
Chapter 1 Review
1. 28 3 624 18 x x x Thesolutionsetis{18}.
2. 2(53)845 106845 6245 6 xx xx xx x
Thesolutionsetis{6}.
3. 6 15 566 6 x x xx x Since x =6doesnotcauseadenominatorto equalzero,thesolutionsetis{6}.
4. 2 (27)20 2720 2725 2725 725 2
x x x x x Thesolutionsetis725725 , 22
5. 2 2 (1)6 6 06 xx xx xx
2241416 12423 bac
Therefore,therearenorealsolutions.
6. 2 2 (1)6 6 60 (3)(2)0 xx xx xx xx 3or2xx
Thesolutionsetis 3,2.
113 2346 113 1212 2346 6292 811 11 8 x x x x xx x x
Thesolutionsetis 11 8.
8. 1361 432 1361 1212 432 3(13)4(6)6 394246 1327 27 13 xx xx xx xx x x
Thesolutionsetis 27 13.
9. 2 2 (1)(23)3 233 260 (23)(2)0 xx xx xx xx
3or2 2 xx
Thesolutionsetis 2,3 2 .
10. 2 2 2 234 0423 (2)(2)4(4)(3) 2(4) 2522213113 884 xx xx x
Thesolutionsetis113113 , 44
Chapter 1: Equations and Inequalities
11.
12.
32 3 33 2 2 2 12 12 18 9 3 x x x x x
Check3:
3 2 32 3 3 3 13 1(3) 19 8 82 x x x x x
Check2: x
3 123 93 33
13. 2 2 (1)20 20 1(1)4(1)(2)17 2(1)2 xx xx x
Norealsolution. 14.
42 22 22 540 410 40or10 2or1 xx xx xx xx
Thesolutionsetis 2,1,1,2
15. 2 2 233 233 2396 8120 (2)(6)0 xx xx xxx xx xx
2or6xx
Check2:2(2)32123 Check6:2(6)369693 x x Thesolutionsetis 2
16. 4 444 232 232 2316 213 13 2 x x x x x
444
Check13: 2 13 23133162 2 x
Thesolutionsetis 13 2 .
2 222 2 2 2 461 461 461 45 5 4 55 42
Check5: 2 555 4+61 222 0.343560.34356
Check5: 2 555 461 222
x x Thesecondsolutionisnotpossiblebecauseit makestheradicandnegative. Thesolutionsetis5 2
Thesolutionsetis 1,1 2 21.
222 2222 2222 222 2 2 20 120 xmmxnx xmmxnx xnxmxm nxmxm
222 2 2222 2 22 22 22 (2)(2)41 21 2444 21 2422 2121 211 211 mmnm x n mmmmn n mmnmmn nn mnmn nn
2 2 11 1111 or 11 1111 mnmnm x nnnn mnmnm x nnnn
Thesolutionsetis ,,1,1.11 mm nn nn
22.
222 222 102360 5180 5920 axabxb axabxb axbaxb
590 59 9 5 axb axb b x a
or20 2 2 axb axb b x a
Thesolutionsetis 92 5,,0. bb a aa
Chapter 1: Equations and Inequalities
Check9: 5 x 22 9999 37392 5555 81278127 =792 255255 81135175811352252 2525 1214411121220 252555
Thesolutionsetis 9 . 5 24. 237 x 237or237 24or210 2or5 xx xx xx
Thesolutionsetis{–5,2}.
25. 2329 237 x x 237or237 35or39 5or3 3 xx xx xx
Thesolutionsetis 5,3 3
26. 32 32 2 23 230 230 xx xx xx 20or230 03 or 2 xx xx
Thesolutionsetis 0,3 2 .
27.
32 2 2 258200 254250 2540 xxx xxx xx 2 2 250or40 25or4 5or2 2 xx xx xx
Thesolutionsetis 5,2,2 2
28. 23 2 52 2(23)10(2)5 46205 14 14 xx xx xx x x
14or14, xx

29. 23 97 4 362328 33231 3331 22 3133 22 x x x x x
31333133 or, 2222 xx

30. 33 26 12 243372 21369 723 x x x x

31. 1 34 2 11 34 22 97 3 22 37 26 x x x x
3737 or, 2626 xx

32. 259 x 259or259 24or214 2or7 xx xx xx
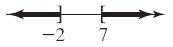
33. 2234 232 2232 430 4 0 3 x x x x x
44 0or0, 33 xx

34. 1234 235 235 235or235 73or33 7 or1 3 7 1or 3 x x x xx xx xx xx
77 1oror,1, 33 xxx
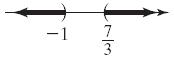
6324623447 iiii 36. 4335212415632 iiiii 37. 2 33393 333933 9393 101010 ii iiiiii i i
38.
12 504824212111 iiiii
32 2 2 232323 412923 51223 10152436 469 iii iii ii iii
Chapter 1: Equations and Inequalities
40. 210xx
Thesolutionsetis 1313 , 2222 ii
41. 2 220 xx
42. 23 xx
2 22 60 1,1,6, 4141612423 123123123 21222
45. Let x representtheamountofmoneyinvestedin bonds.Then70,000 x representstheamount ofmoneyinvestedinCD's. Sincethetotalinterestistobe$5000,wehave:
0.080.05(70,000)5000
1000.080.05(70,000)5000100
8350,0005500,000
3350,000500,000
3150,000 50,000
$50,000shouldbeinvestedinbondsat8%and $20,000shouldbeinvestedinCD'sat5%.
46. Using svt ,wehave3and1100 tv . Findingthedistance s infeet: 1100(3)3300 s Thestormis3300feetaway.
47. 16003600 I 2 2 2 900 16003600 11 16009003600 91 164 31 42 x x
Therangeofdistancesisfrom0.5metersto0.75 meters,inclusive.
48. Let s representthedistancetheplanecantravel. 22 WithwindAgainstwind Rate2503028025030220 Time(/2)(/2) 280220 Dist. ss ss
Sincethetotaltimeisatmost5hours,wehave: /2/2 5 280220 5 560440 11145(6160) 2530,800 1232 ss ss ss s s
Theplanecantravelatmost1232milesor616 milesonewayandreturn616miles.
49. Let t representthetimeittakesthehelicopterto reachtheraft.
RaftHelicopter Rate590
Time Dist.590 tt tt
Sincethetotaldistanceis150miles,wehave: 590150 95150 1.58hours1hourand35minutes tt t t
Thehelicopterwillreachtheraftinabout1hour and35minutes.
50. Giventhat2 12803216 stt ,
a. Theobjecthitsthegroundwhen0 s .
2 2 012803216 2800 1080 tt tt tt
10,8tt
Theobjecthitsthegroundafter8seconds.
b. After4seconds,theobject’sheightis
2 1280324164896 s feet.
51. Let t representthetimeittakesClarissato completethejobbyherself.
ClarissaShawna
Timetodo5 jobalone Partofjob11 done5 in1day Timeonjob66 (days)
Partofjob66 donebyeach5 person tt tt tt
Sincethetwopeoplepaintonehouse,wehave: 2 2 661 5 6(5)6(5) 63065 7300 (10)(3)0 tt tttt tttt tt tt
10or3tt
IttakesClarissa10daystopaintthehousewhen workingbyherself.
52. Let t representthetimeittakesthesmaller pumptoemptythetank.
SmallPumpLargePump Timetodo4 jobalone Partofjob11 done4 in1hr Timeonjob55 (hrs) Partofjob55 donebyeach4 pump tt tt tt
Sincethetwopumpsemptyonetank,wehave: 2 2 551 4 5(4)5(4) 52054 14200 tt tttt tttt tt
Wecansolvethisequationfor t byusingthe quadraticformula: 2 (14)(14)4(1)(20) 2(1) 1411614229 22 72975.385 12.385or1.615(notfeasible) t tt
Ittakesthesmallpumpapproximately12.385 hours(12hr23min)toemptythetank.
53. Let x representtheamountofwateradded.
%saltTot.amt.amt.ofsalt 10%640.1064 0%0.00
2%640.0264 xx xx 0.10640.000.0264
6.41.280.02
256 xx x x x 256ouncesofwatermustbeadded.
5.120.02
Chapter 1: Equations and Inequalities
54. Considerthediagram w w+ 2 10
BythePythagoreanTheoremwehave 222 22 2 2 210 44100 24960 2480 860 ww www ww ww ww
8or6ww
Thewidthis6inchesandthelengthis6+2=8 inches.
55. Let x representtheamountofthe15%solution added.
%acidtot.amt.amt.ofacid 40%600.4060 15%0.15
25%600.2560 xx xx
0.40600.150.2560
90cubiccentimetersofthe15%solutionmustbe added,producing150cubiccentimetersofthe 25%solution.
56. a. Considerthefollowingdiagram:
Thepaintingis6.5inchesby6.5inches. 612.5 s ,sotheframeis12.5inchesby 12.5inches.
b. Considerthefollowingdiagram: w 2w
2262650 ww 1 3 2 3 41221250 626
Thepaintingis283inchesby143inches. Theframeis2143inchesby1103inches.
57. Let x representtheamountScottreceives.Then 3 4 x representstheamountAlicereceivesand 1 2 x representstheamountTriciareceives.The totalamountis$900,000,sowehave:
31900,000 42 31 44900,000 42 4323,600,000 93,600,000 400,000 xxx xxx xxx x x
So, 33400,000300,000 44 x and 11400,000200,000 22 x Scottreceives$400,000,Alicereceives $300,000,andTriciareceives$200,000.
58. Let t representthetimeittakestheolder machinetocompletethejobbyitself.
OldcopierNewcopier Timetodo1 jobalone Partofjob11 done1 in1hr Timeonjob1.21.2 (hrs) Partofjob1.21.2 donebyeach1 copier tt tt tt
Sincethetwocopierscompleteonejob,wehave:
