
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
List all the elements of B that belong to the given set.
1) B = 13, 8, -17, 0, 5 6 ,6 5 , 5.7
Integers
A) {13, 0, 8} B) {13, 0} C) {13, -17, 0}
Answer: C
2) B = 5, 7, -13, 0, 1 5 , - 5, 7.8
Natural numbers
A) 5, 0, - 5
Answer: B
3) B = 6, 7, -17, 0, 0 3
Real numbers
{5}
{5, 0}
{13, -17}
{-13, 0, 5}
A) {6, -17, 0} B) 6, -17, C) 6, -17, 0, 0 3
Answer: D
4) B = 7, 6, -8, 0, 0 8 , 0.3
Rational numbers A) 7, -8, 0, 0 8 , 0.3
Answer: A
5) B = 19, 7, -15, 0, 0 2 , 0.51
Irrational numbers
{ 6}
{7, 0}
6, 7, -17, 0, 0 3
A) { 7, 0.51} B) 7, 0 2
Answer: C
6) B = {16, 8, -24, 0, 7 8 ,8 7 , 8.8, 25 , 0.258258258...}
Integers
{ 7}
,
7, 0 2 , 0.51
A) {16, -24} B) {16, 0, 8} C) {16, 0} D) {16, -24, 0}
Answer: D
7) B = {5, 5, -18, 0, 3 8 ,8 3 , 5.4, 5 , 0.525525525...}
Natural numbers
A) 5, 0,8 3
Answer: C
B) {5, 0}
8) B = {6, 8, -24, 0, 0 9 , 4, 0.84, -8 , 0.444...}
Rational numbers
A) 6, -24, 0, 0 9 , 0.84, 0.444...
C) 6, -24, 0, 0 9 , 4, 0.84, 0.444...
Answer: C
9) B = {20, 6, -13, 0, 0 6 , , 0.09, -6 , 0.161616...}
Irrational numbers
A) { 6}
C) 6, 0 6 , -6
Answer: D
C) {5}
D) {-18, 0, 5}
B) 6, -24, 0, 0 9 , 4, 0.84, -8 , 0.444...
D) 6, -24, 0, 0 9 , 0.84
B) { 6, -6 , 0.161616...}
D) { 6 , -6 }
Given the set sketched on the number line, identify the type of interval (open, closed, half-open, open infinite, closed infinite), write the set using set-builder notation, and write the set using interval notation. 10)
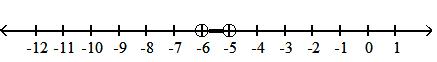
A) half-open interval; {x|-6 x < -5}; [-6, -5)
C) closed interval; {x|-6 x -5}; [-6, -5]
Answer: B
11)
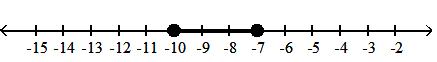
A) half-open interval; {x|-10 x < -7}; [-10, -7)
C) half-open interval; {x|-10 < x -7}; (-10, -7]
Answer: D
12)
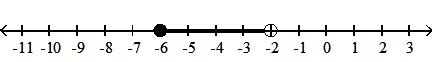
A) half-open interval; {x|-6 x < -2}; [-6, -2)
C) half-open interval; {x|-6 < x -2}; (-6, -2]
Answer: A
B) open interval; {x| -6 < x < -5}; (-6, -5)
D) half-open interval; {x|-6 < x -5}; (-6, -5]
B) open interval; {x|-10 < x < -7}; (-10, -7)
D) closed interval; {x|-10 x -7}; [-10, -7]
B) closed interval; {x|-6 x -2}; [-6, -2]
D) open interval; {x|-6 < x < -2}; (-6, -2)
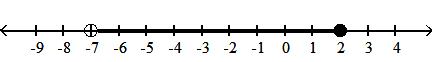
A) half-open interval; {x|-7 x < }; [-7, )
C) half-open interval; {x|-7 < x }; (-7, ]
Answer: C
14)
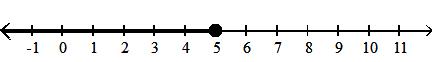
A) closed infinite interval; {x|x 5}; [5, )
C) open infinite interval; {x|x > 5}; (5, )
Answer: B
15)
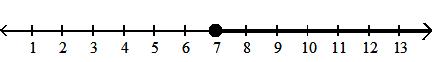
A) open infinite interval; {x|x < }; (, )
C) open infinite interval; {x|x > }; ( , )
Answer: B
16)
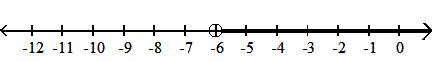
A) closed infinite interval; {x|x -6}; (, -6]
C) closed infinite interval; {x|x -6}; [-6, )
Answer: B
17)
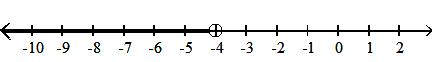
A) open infinite interval; {x|x < -4}; (, -4)
C) open infinite interval; {x|x > -4}; (-4, )
Answer: A
B) closed interval; {x|-7 x }; [-7, ]
D) open interval; {x|-7 < x < }; (-7, )
B) closed infinite interval; {x|x 5}; (, 5]
D) open infinite interval; {x|x < 5}; (, 5)
B) closed infinite interval; {x|x }; [ , )
D) closed infinite interval; {x|x }; (, ]
B) open infinite interval; {x|x > -6}; (-6, )
D) open infinite interval; {x|x < -6}; (, -6)
B) closed infinite interval; {x|x -4}; (, -4]
D) closed infinite interval; {x|x -4}; [-4, )
Write the interval in set-builder notation and graph the set on a number line.
18) -4, 1 2
A) x -4 < x < 1 2
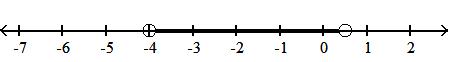
B) x -4 x 1 2
C) x -4 x 1 2
D) x -4 x 1 2
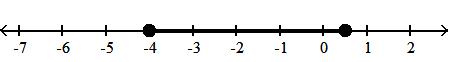
Answer: D
19)1 4 , 3
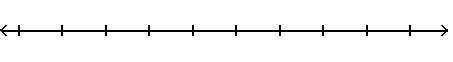
A) x1 4 x < 3 B) x1 4 x < 3 C) x1 4 < x 3 D) x1 4 x < 3

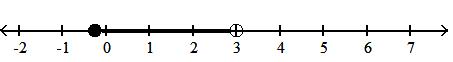
Answer: D
(, -8)

A) {x|x -8}
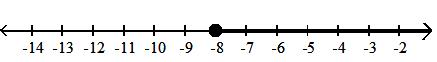
C) {x|x -8}
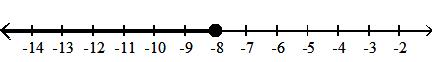
Answer: B
21) [-7, )

{x|x -7}
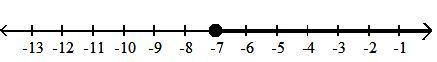
C) {x|x -7}
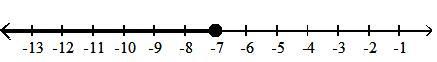
Answer: A
B) {x|x < -8}
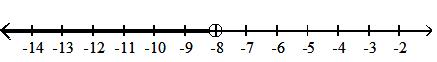
D) {x|x > -8}
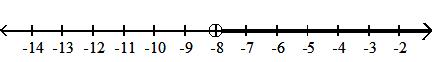
B) {x|x > -7}
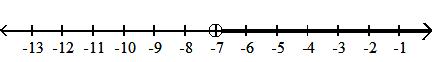
D) {x|x < -7}
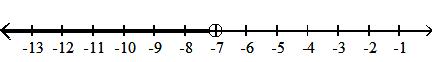
Write the given set in interval notation and graph the set on a number line.
22) x -4 < x < 1 4
A) -4, 1 4
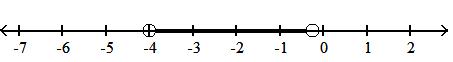
B) -4, 1 4
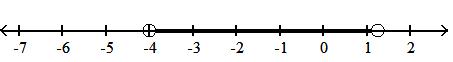
C) -4, 1 4
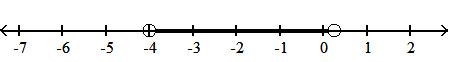
D) -4, 1 4
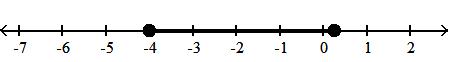
Answer: C
23) x1 4 < x 4
A)1 4 , 4
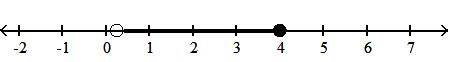
B)1 4 , 4
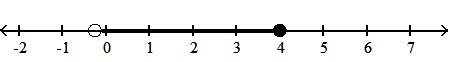
C)1 4 , 4
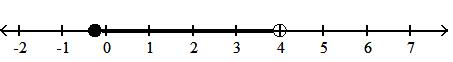
D)1 4 , 4
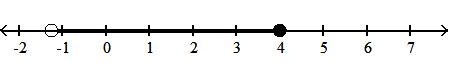
Answer: B

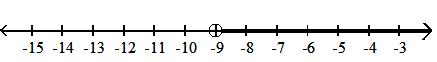
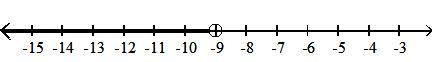
Answer: D

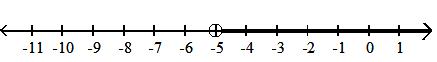
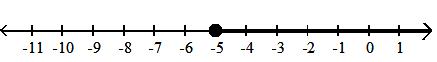
Answer: D
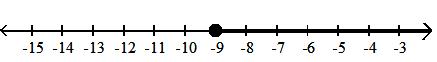
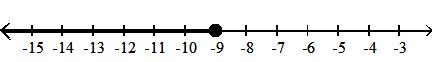
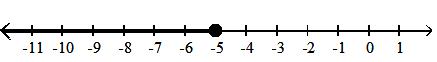
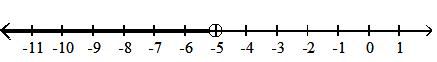
Find the indicated set given A = {-3, 0, 2, 5, 6, 11, 16, 23}, B = {-3, 0, 16, 23}, and C = {-7, -4, 11, 16, 23}.
26) A B
A) {0, 2, 5, 6, 11, 23}
Answer: B
27) C B
A) {16, 23}
B) {-3, 0, 16, 23}
C) {5, 11} D) {-3, 0, 2, 5, 6, 16}
B) {-7, -4, -3, 0, 16, 23}
C) {-7, -4, -3, 0, 11, 16, 16, 23, 23} D) {-7, -4, -3, 0, 11, 16, 23}
Answer: D
28) B C
A) {11, 16, 23}
B) {-7, -4, -3, 0, 11, 16, 23}
C) {16, 23} D) {-4, 16, 23}
Answer: C
Find the union or intersection as indicated.
29) Find A B if A = {x|x -2} and B = {x|x < 7}
A) B) {x|x -2} C) {x|x < 7}
Answer: D
30) Find A B if A = {x|x < -3} and B = {x|x 5} A) B) {x|-3 < x 5} C) {x|x < -3 x 5}
Answer: C
Find the intersection of the given intervals.
{x|-2 x < 7}
{x|x > -3}
31) (, ) [-1, ) A) B) (, -1] C) (, ) D) [-1, ) Answer: D
32) [ , ) (, ] A) [ , ) B) [ , ]
(, ]
(, ) Answer: B
33) (-2, 10] (-7, 4]
A) (-2, 4) B) [-2, 4] C) [-7, 10]
(-7, -2] Answer: B
34) (( , -3) (-3, )) ( , 7] A) ( , -3) B) (-3, 7]
( , -3) (-3, 7]
( , 7] Answer: C
35) ( , 12] [-6, ) ( , 6) A) [-6, ) B) [-6, ) ( , 12] C) [-6, 12]
Answer: A
Evaluate the absolute value expression. 36) -6 - 5
(6, 12]
A) 11 B) -11 C) -1 D) 1
Answer: A
37) -4 + 8
12
Answer: A
38) 6 6 + -4 -4
1
Answer: B
39) 4 8 + 5 -9 A) 13
Answer: C
40) 6 6 - 7 8
92
Answer: D
41) 2 -10 + 4 -3
Answer: B
0
-1
2
-13
77
-77
Find the distance between the given two numbers using absolute value. 42) and -5
7
Answer: A
-7
Multiply and simplify. Assume variables do not cause any denominators to equal 0. 43) 7 8 1 2
4 5
16 7 Answer: B 44) 3 7 1 6
46) 17 26 5
Answer: A 47) 7 2 ·4 3
7 6
Answer: B
48)5 11 ·21 29
8 21
-45 7 5
1 63
-63 Answer: D
36p 25q 5p2 16q
9p 20
Answer: A
Divide and simplify. Assume variables do not cause any denominators to equal 0.
6 7 ÷ 7 3
60) 10x2 33y ÷ 15x 121y
50x3 1331y2
Answer: C
61) 25m 2n ÷ 5mn
5mn
Answer: B
5 2n2
Find the LCD of the given fractions by inspection.
62) 1 5 and 16 14
19
Answer: B
63) 11 4 and 4 20
4
Answer: B
64) 7 10 and 5 35
5
Answer: B
Find the LCD of the given fractions by prime factorization.
65) 7 15 and 5 50 A) 750
Answer: D
66) 7 56 and 2 48
672
Answer: B
67) 7 30 , 1 18 and 4 15
45
Answer: C
-150
2 5
Add or subtract as indicated. Simplify if necessary.
68) 2 5 + 3 10
1 3
Answer: B 69) 5 71 6
Answer: A 70) 9 7 - 4
Answer: D
Answer: C
4 5 + 7
Answer: B
2 8 + 6 14 + 9 15
Answer: A
2 9 + 5 144 7
Answer: A
Use the commutative property of addition to write an equivalent algebraic expression. 75) x + 3
Answer: B
76) 2x + 6y
A) 6y + 2x B) 2x - 6y C) 2y + 6x
Answer: A
Use the commutative property of multiplication to write an equivalent algebraic expression. 77) 8 · x
2x + 6y
A) x + 8 B) 8 x C) 8x D) x 8
Answer: D
78) 2(x + 8)
A) (8 + x)2 B) (x + 2)8 C) (x + 8)2
Answer: C
Use the associative property of addition to write an equivalent algebraic expression. 79) 7 + (3 + x)
A) (7 + 3) + x B) 7(3 + x) C) (7 + 3)x
Answer: A
80) (yz + a) + x A) y(z + a) + x
Answer: C
y + (za + x)
yz + (a + x)
Use the associative property of multiplication to write an equivalent algebraic expression. 81) 7(2x)
A) (7 + 2)x
Answer: D
82) 3(5(a + b)) A) (3 5)(a + b)
Answer: A
(7 · 2) + x
7(2 + x)
2(8 + x)
3(7 + x)
x + (yz + a)
(7 · 2)x
(3 + 5)(ab)
Use the distributive property to multiply the given expressions. 83) 4(x - 9)
A) 4x - 9 B) 4x + 36
Answer: D
84) (a + 4)2 A) 2a + 8
Answer: A
85) 2(3x + 4)
Answer: D
86) (m + 2 - 2n)5
A) m + 10 - 10n
Answer: B
5m + 10 - 10n
3((5a) + b)
(5(a + b))3
x + 36
4x - 36
5m + 10 - 2n
5m + 7 - 7n
87) 7(y - 4x + 9)
A) y - 28x + 63
Answer: D
B) 7y - 28x + 9
C) 7y - 11x + 16
D) 7y - 28x + 63
Use the distributive property to rewrite the sum or difference as a product. Simplify the answer if possible.
88) 9a + 21a
A) a
B) -12a
C) 30a
D) a Answer: C
89) 4c + 7c
A) -3c
Answer: D
90) fx - gx
A) f(x - g)
Answer: C
B) 28c
C) 3c
D) 11c
B) (f - x)g
C) x(f - g)
Write the expression using exponential notation. Then identify the base and the exponent. 91) x x x
A) 3x base: x exponent: 3
B) x3 base: x exponent: 3
C) 3x base: 3 exponent: x
D) x(f + g)
D) x3 base: 3 exponent: x Answer: B
92) (-6x) · (-6x) · (-6x) · (-6x)
A) -6x4 base: -6x exponent: 4
Answer: D
Evaluate.
93) 63
A) -216
B) -6x4 base: 6x exponent: 4
C) (-6x)4 base: 6x exponent: 4
D) (-6x)4 base: -6x exponent: 4
B) -18
C) 216
D) 18 Answer: C
94) -52
A) -10
B) 25
C) -25
D) 10 Answer: C
95) (-4)3
A) -64
B) -12
C) 12
D) 64 Answer: A
96) (11x)2
A) 11x2
B) 22x2
C) 121x2
D) 121x Answer: C
Simplify the expression using the order of operations.
97) 4 + (24 · 21) - 17 A) 32
Answer: C
571
491
98) -1 - (-2 + 9 · 3 + 5) A) -35 B) -21 C) 29
Answer: D
99) 82 - 3 · 9 A) 225
Answer: D
100) 82 - 2(6) + 15 ÷ 3 A) 221
Answer: B
101) 5 - 13 · -12 ÷ (-4)
384
Answer: B
549
360
112
-31
37
57
67 3
21
24
-24
-384
102) (-2 - 6) · (-3 + 8) - 63 A) -256 B) 176 C) 216 D) 5 Answer: A
103) 5 + (-3)2 + 7 · 32 72 · (6 - 4) A) 117 38 B) 11 14
Answer: B
Evaluate the algebraic expression for the indicated variable. 104) 15x - 5y x + 6 for x = 10, y = 7
55 16
Answer: C
105) 9xy + 30 x for x = 5, y = 7
115 13
2
0
115 16
55 13
A) 6 B) 69 C) 93 D) 15 Answer: B
106) -5x2 + 3y2 for x = , y = A) -57 B) -39 C) -3 D) -33
Answer: D
107) -4a2 - 6b + c - 18 for a = 2, b = -4, c = -2
A) -12 B) -24
Answer: A
108) 8a2 - b2 + c for a = -6, b = 0, c = 18
A) 270 B) 66
Answer: C
Simplify the algebraic expression.
109) -7x - 3x A) x
-10 + x
-60
-4
306
-306
-10x
-4x Answer: C
110) x9 + 6x9
x9
Answer: D
x18
111) -5x + 4y - 6x + 3y A) -5x - 6x + 4y + 3y B) -4xy
Answer: C
112) -6(2x - 7) - 4x + 5 A) -16x - 37
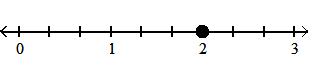
Answer: B
113) 7(8x - 4) - 6(x - 2) A) 50x - 6
Answer: D
-16x + 47
x81
-11x + 7y
x - 11y
14x - 16
50x - 40
50x - 16
Use the laws of exponents to simplify each expression using positive exponents only. Assume all variables represent nonzero real numbers. 114) 45 42
A) 167 B) 47
410 D) 1610 Answer: B
115) x3 · x9 A) x27
27x
x12
12x Answer: C
116) ( x8)(4x7) A) -24x56
Answer: D
x56
117) (-2x6y)(-7x2y3) A) -9x8y3 B) 14x12y3
Answer: C
-24x15
14x8y4
x15
-14x8y3
118) x10 x5
x15
Answer: D
119) (x6)-5 A) -5x30
Answer: D
120) (x-4)-3
1 x7
Answer: D
121) x-8 x-11
- x30
-5x6
Answer: D
122) -5y0
-5
Answer: A
123) (13b)0
1
Answer: A
124) 2-3
8
Answer: C
125) -5-4
Answer: B
-8
-x7
1 x30
13
1 6
126) x4y-6
z-2 A) x4z2 y6
Answer: A
127) x4 x-2
z2 x4y6
x4z6 y2
A)1 x2 B) -x2 C) 1 x2
Answer: D
128) x-7 x4 A) x3
Answer: B
129) 5-3 · 5
Answer: A
130) x-8 x3
1 x5
Answer: B
131) (-4x4y3)2
A) -16x8y6
Answer: B
132) 48x6y13 6x5y-10
A) 8xy23
Answer: A
133) (-2x5y-6)(5x-1y)
A) -10x4y7
Answer: B
y6 x4z2
x2
1 x3
-x3
1 x3
1 x11
B) 16x8y6
1 x24
C) -4x8y6
x11
D) 16x6y5
B) 8xy3
-10x4 y5
C) 8x11y23 D) 48xy23
-10x6 y7
3x4 y5
134) -24x4y8 8x7y-3 3
Answer: A
135) 8x-3y-3z4 2xy-3z-4 -3
Answer: C
Simplify the radical expression. Assume all variables represent positive real numbers. 136) 9
3 511
139) 3 -1000
Simplify the expression. Include absolute value bars where necessary.
143) 9 g9
9 g
g9
-g Answer: C
144) 10 p10 A) p
- p
p
-p Answer: A
145) 9 (-3)9 A) 3
-3
-3 Answer: D
Simplify the exponential expression. Write any negative exponents as positive exponents. Assume all variables represent positive real numbers.
146) 81/3
-2
1 2 Answer: B
147) 7291/3
9 Answer: D
148) 811/4
243
3 Answer: D
149) 1 25 1/2
5
1 5 Answer: D
150) -2431/5
Answer: C
151) 84/3
Answer: D
152) 1 27 2/3
1 4
Answer: D
153) (-64)4/3
A) 4096 B) -256
1 9
1 9
256
not a real number Answer: C
154) 64-3/2 A) -512
Answer: D
155) 8-4/3
1 16
Answer: D
156) x7/8 · x1/8
1 x
Answer: C
512
1 512
1 512
16
1 16
x7/8
x
x7/64
157) x-2/7 x3/7 A) x1/7 B) x7/6
x-1/7
x6/7 Answer: A
158) (x14y7)1/7 A) x2y B) x2|y|
x2
x14y Answer: A
159) (27x6y6)1/3
3x2y
3x2y2
3x6y2 Answer: B
160) (9x8y-16)1/2
3x4y8
Answer: D
3 x4y8
9x4 y8
3x4 y8
161) (9x1/5y1/5)2 A) 81x1/25y1/25
81x2/5y2/5
81x1/10y1/10
81x2y2 Answer: B
162) x1/6 · x5/3 x1/2
Answer: B
163) (3x3/2)2 x-5/2
Answer: B
Multiply. 164) 180 · 5
900
5 6 Answer: C
165) 7x3 7x5
Answer: B 166) 3 4x · 3
Answer: C
Use the product rule to simplify. 167) 180
Answer: A 168) 3 432
Answer: B
169) 147x2
147x
7 3x Answer: B
170) 3 8y6
Answer: B
171) x9
x18 x
x4 x Answer: D
172) 3 -27a8b5
Answer: C
Multiply and simplify. 173) 15 27
Answer: D
175) 15xy 5xy2
Use the quotient rule to simplify. 178) 144 289
Answer: D
Answer: C 180) 3 81x4 3x
186) 3 135 3 5
Answer: A
187) 3 -128x4 3 2x-2
A) -64x8
Answer: B
B) -4x2
C) 4x2
D) -4x6
Determine whether the expression is a monomial. If it is a monomial, state the coefficient and degree.
188) x7
A) monomial; coefficient ; degree 7
C) not a monomial
Answer: A
189) 15 x
A) monomial; coefficient 15; degree 1
C) not a monomial
Answer: C
190) -7x4y5
A) not a monomial
C) monomial; coefficient -7; degree 4
Answer: B
191) 6x4 - 2
A) monomial; coefficient 2; degree 4
C) monomial; coefficient 6; degree 1
Answer: D
B) monomial; coefficient 7; degree 0
D) monomial; coefficient 7; degree 14
B) monomial; coefficient 15; degree -1
D) monomial; coefficient 15; degree 0
B) monomial; coefficient -7; degree 9
D) monomial; coefficient -7; degree 5
B) monomial; coefficient 6; degree 4
D) not a monomial
Determine whether the expression is a polynomial. If it is a polynomial, give its degree.
192) 7x25 x
A) polynomial; degree 1
C) polynomial; degree 2
Answer: B
193) 8
A) not a polynomial
C) polynomial, degree 0
Answer: C
B) not a polynomial
D) polynomial; degree -1
B) polynomial, degree 1
D) polynomial, degree 8
194) -5y5 - 3
A) not a polynomial
C) polynomial; degree 5
Answer: C
195) x4 - 9 x6 + 3
A) polynomial, degree -2
B) polynomial; degree 3
D) polynomial; degree -5
B) not a polynomial
C) polynomial, degree 10 D) polynomial, degree 4
Answer: B
Perform the indicated operations.
196) (-4x2y - xy) + (7x2y + 5xy)
11x2y + 6xy
Answer: D
197) (5x2 - xy - y2) + (x2 + 12xy + 12y2) A) 6x2 + 11xy + 11y2
Answer: A
6x2 + 13xy + 13y2
11x2y + 4xy
Answer: D
199) ( x2 + 9) - (-x3 - 5x2 - 10)
x3 + 4x2 - 1
Answer: C
x3 - 5x2 + 19
200) (6x2y + 6xy + 5xy2) - (2xy + 2xy2 + 2x2y) A) 4x2y + 3xy2 + 4xy B) 4x2y - 3xy2 + 4xy
Answer: A
201) (7x2 + 7x - 9) - (9x2 - 1)
16x2 + 8x - 9
Answer: D
202)9 11 x2y + 2 3 -5 11 x2y1 6
-2x2 + 8x - 9
4 11 x2y + 1 2 B) 4 11 x2y + 1 2
Answer: D
x3 + 14x2 + 19
4x2y - 3xy2 + 8xy
x2y + 5xy2 + 4xy
4 11 x2y + 5 6
4 11 x2y + 5 6
203) (8x2 + 4x - 7) + (8x + 7)
A) 8x2 + 12x - 14 B) 8x2 + 4x + 14
Answer: D
204) (2x2 + 3x - 4) + (8x2 - 7x - 7) A) 10x2 + 4x - 11 B) x2 - 5x - 4
Answer: D
205) (9x2 + 11x - 14) - (6x2 - 19x + 8) A) 3x2 + 30x - 22 B) 3x2 + 30x - 6
Answer: A
206) (5x5 + 7x2) + (8x5 - 3x2) A) 17x14 B) 13x10 + 4x4
Answer: D
207) ( x3 + 4x2) - (-7x3 + 20x2) A) x3 + 24x2
Answer: C
x5
20x3
8x2 + 12x
10x2 - 4x + 11
10x2 - 4x - 11
3x2 + 30x + 22
3x2 + 17x - 6
17x7
13x5 + 4x2
x3 - 16x2
208) (2x5 + 5x3) + (7x5 - 9x3 + 3) A) 9x5 - 4x3 + 3 B) 3x9 C) 2x5 - 7x3 + 3x
Answer: A
x3 + 24x2
3x - 4x5 - 2x3
209) (-10x2 - 8) - (-x3 + 5x2 - 1) A) -9x3 + 5x2 - 7 B) x3 - 15x2 - 7 C) -9x3 - 3x2 + 1 D) x3 - 5x2 - 9
Answer: B
210) (3x6 + 19x3 - 2) - (8x6 - 20x3 + 13)
A) -5x6 + 39x3 - 15 B) -5x6 + 27x3 + 11 C) x9 D) -5x6 + 39x3 + 11
Answer: A
211) (5x5 + 16x4 - 18) - (9x4 + 3x5 - 3) A) x5 + 7x4 - 21 B) x5 + 19x4 - 21 C) x5 + 7x4 - 15 D) -6x9
Answer: C
212) (7x7 - 2x4 - 9x) + (2x7 + 8x4 + 6x) A) 9x7 + 6x4 - 3x B) 12x12 C) -7x7 + 15x4 + 4x D) 9x + 6x7 - 3x4
Answer: A
213) (x2 + 1) - (5x2 + 4) + (x2 + x - 6) A) -5x2 + x - 9 B) -4x2 + x - 9
Answer: C
C) -3x2 + x - 9 D) -3x2 + 5x - 5
Perform the indicated operations. Express the answer as a single polynomial in standard form.
214) -8x( x - 7)
A) -72x2 + 56x B) -72x2 - 7x
Answer: A
215) -3x3(-5x - 12)
C) x2 + 56x D) -16x2
A) x3 B) x4 + 36x3 C) x + 36 D) x4 - 12
Answer: B
216) x6(-4x2 - 2)
A) -20x8 - 10x6 B) -20x8 - 2 C) -20x2 - 10 D) -30x6
Answer: A
217) x7( x4 - 10x2 + 2)
A) 12x11 - 40x9 + 8x7 B) 12x4 - 40x2 + 8 C) 12x11 - 10x2 + 2 D) 12x11 - 40x9
Answer: A
218) (x - 11)(x2 + 4x - 6)
A) x3 + 15x2 + 38x - 66 B) x3 + 15x2 + 50x + 66 C) x3 - 7x2 - 38x - 66 D) x3 - 7x2 - 50x + 66
Answer: D
219) (6y + 11)(10y2 - 2y - 2) A) 60y3 - 12y2 - 12y + 11 B) 60y3 + 122y2 + 34y + 22 C) 170y2 - 34y - 34 D) 60y3 + 98y2 - 34y - 22
Answer: D
Multiply the polynomials using the FOIL method. Express the answer as a single polynomial in standard form. 220) (x + 3)(x + 3)
A) x2 + 9x + 6 B) x2 + 6x + 6 C) x2 + 5x + 9 D) x2 + 6x + 9
Answer: D
221) ( x - 11)(x + 11) A) x2 - 121x + 22 B) x2 + 22x - 121 C) x2 + 22x + 22
Answer: B
222) ( x + 7)( x - 11)
x2 + 20x - 121
A) 8x2 - 30x - 77 B) x2 - 30x - 30 C) 8x2 - 30x - 30 D) x2 - 30x - 77
Answer: A
Multiply the polynomials using a special product formula. Express the answer as a single polynomial in standard form. 223) (x + 7)(x - 7)
A) x2 - 14x - 49 B) x2 - 14 C) x2 + 14x - 49 D) x2 - 49
Answer: D
224) (9x + 11)(9x - 11) A) 81x2 - 198x - 121 B) 81x2 + 198x - 121 C) 81x2 - 121
x2 - 121 Answer: C
225) (x + 8)2
A) x2 + 16x + 64 B) 64x2 + 16x + 64
Answer: A
226) (x - 2)2 A) 4x2 - 4x + 4
Answer: B
x2 - 4x + 4
x2 + 64
x + 64
x2 + 4
227) (7x + 12)2 A) 49x2 + 168x + 144 B) 7x2 + 144 C) 49x2 + 144 D) 7x2 + 168x + 144
Answer: A
228) (9x - 7)2 A) 9x2 - 126x + 49 B) 9x2 + 49
Answer: C
229) (x + 3)3
Answer: B
230) (4x + 5)3
81x2 - 126x + 49
A) 64x3 + 240x2 + 299x + 125 B) 16x2 + 40x + 25
C) 64x3 + 240x2 + 240x + 125 D) 16x6 + 20x3 + 15,625
Answer: A
Find the quotient and the remainder.
231) x2 + 2x - 16 divided by x + 6
A) x - 8; remainder 4 B) x + 4; remainder 8
Answer: C
232) x2 + 6x + 6 divided by x + 4
x - 4; remainder 8
x - 4; remainder 0
A) x + 2; remainder -2 B) x + 3; remainder 0
C) x + 2; remainder 0 D) x + 2; remainder 2
Answer: A
233) 6x3 + 41x2 - 49x + 56 divided by x + 8
A) x2 + 8x + 9; remainder 0 B) 6x2 - 7x + 7; remainder 0
C) x2 + 7x + 6; remainder 0 D) 6x2 + 7x + 7; remainder 0
Answer: B
234) -9x3 + 12x2 - 19x + 24 divided by -3x + 2
A) x2 + 5; remainder -2 B) 3x2 - 2x + 5; remainder 17
C) 3x2 - 2x + 5; remainder 14 D) 3x2 - 2x + 5; remainder 0
Answer: C
235) 5x3 - 7x2 + 7x - 8 divided by 5x - 2
A) x2 - x + 1; remainder 10
C) x2 - x + 1; remainder -6
Answer: C
236) x4 + 3x2 + 7 divided by x2 + 1
x2 + x -1; remainder -6
x2 - x + 1; remainder 6
A) x2 + 2x + 2; remainder 0 B) x2 + 2; remainder 5
C) x2 + 2x + 5 2 ; remainder 5 D) x2 + 2; remainder 0
Answer: B
Add or subtract, if possible. Assume that all variables represent non-negative values. Simplify your answer.
9 11 + 7 11
Answer: D 238) -8 7 - 9 28
Answer: D
7 4 6 + 6 3 6
42 4 36
D
133 x
B
243) 12 + 192
Answer: A
Answer: D
Answer: B
Answer: D
248) 9 3 x3y10 - 2xy 3 8y7
Answer: A
4 256x7 48x 4 81x3 3
Answer: D
Multiply.
252) 3 y( y - 8)
3y - 24 y
Answer: A
253) 2 7x( 11 + 7x) A) 2 11 + 7x
Answer: B
254) 7 3 x2 8 3 x - 2 3 x2
Answer: A
255) (8 2 + 9)(6 2 + 4)
36 + 48 22 + 32 2
132 + 86 2
84 2 + 32 Answer: B
256) ( 7x + 4)( 2x + 3)
x 2 + 12
Answer: C
Answer: B 258) (4 - x)(5 - x)
20 - 8 x
Answer: D
259) (4 x + y)(4 x - y) A) 16x2 -
Answer: B 260) (9 5 - 4)2
Answer: D
261) ( m - 4)(4 + m) A) m - 8 m - 16
m - m + 16
16 - m
m - 16 Answer: D
262) (3 x - 5 y)2 A) 9x + 15 xy + 25y B) 9x - 30 xy + 25y
Answer: B
Rationalize the denominator.
263) 6 5
Answer: D
264) 11 13
Answer: D 265) 18 x
Answer: B
Answer: B
3
Answer: D
4 625 4
Answer: C
Answer: C
Answer: C
Answer: B
Answer: B
Answer: C
Answer: B
Factor out the greatest common factor.
Answer: C
276) 3x2 + 12x
A) 3(x2 + 4x)
Answer: B
277) 18x4 - 6x3 + 8x2
A) 2x2(9x2 - 3x + 4)
Answer: A
278) x(x + 3) + 11(x +3)
A) 3x(x + 11)
C) (x2 + 3x) + (11x + 33)
Answer: B
279) x(6x + 5) - 3(6x + 5)
A) -3x(6x + 5)
Answer: D
280) x2(x - 10) - (x - 10)
A) (x3 - 10x2) - (x - 10)
C) (x - 10)(x2 - 1)
Answer: C
Factor the polynomial by grouping.
281) x2 + 8x + 3x + 24
A) prime
Answer: C
282) 2x2 + 5x + 10x + 25
A) (2x + 5)(2x + 5)
Answer: D
283) 15x2 + 12x - 10x - 8
A) (15x + 2)(x - 4)
Answer: D
284) 15x2 + 10x - 6x - 4
A) (15x + 2)(x - 2)
Answer: D
B) 3x(x + 4)
C) 3x(x + 4x) D) x(3x + 12)
B) 2x(9x3 - 3x2 + 4x) C) x2(18x2 - 6x + 8)
2(9x4 - 3x3 + 4x2)
B) (x +3)(x + 11)
D) 11x(x +3)
B) (6x - 3)(x + 5)
C) (6x + 5)(x + 3) D) (6x + 5)(x - 3)
B) (x - 10)(x2 + 1)
D) x2(x - 10)
B) (x - 8)(x - 3)
C) (x + 8)(x + 3)
D) (x - 8)(x + 3)
B) (2x + 5)(5x + 2)
C) prime
D) (x + 5)(2x + 5)
B) (3x + 2)(5x - 4)
C) (15x - 2)(x + 4)
D) (3x - 2)(5x + 4)
B) (5x + 2)(3x - 2)
Completely factor the polynomial or state that the polynomial is prime.
285) x2 - x - 20
A) (x + 1)(x - 20)
B) (x + 4)(x - 5)
C) (15x - 2)(x + 2)
D) (5x - 2)(3x + 2)
C) (x + 5)(x - 4)
D) prime Answer: B
286) x2 + 6x + 5
A) (x + 1)(x + 5)
Answer: A
B) (x - 1)(x + 1)
C) (x - 1)(x + 5)
D) prime
287) x2 + 8x - 33
A) (x - 11)(x + 3)
Answer: B
288) x2 - x - 40
A) (x + 5)(x - 8)
Answer: D
289) x2 + 25
A) prime
Answer: A
290) 4x2 - 4x - 24
B) (x + 11)(x - 3)
C) (x - 11)(x + 1) D) prime
B) (x - 5)(x + 8)
C) (x - 40)(x + 1) D) prime
B) (x - 5)2
A) prime B) (4x + 8)(x - 3)
Answer: D
291) 2x2 - 12x + 16
A) 2(x - 4)(x - 2)
Answer: A
292) 5x3 + 5x2 - 100x
C) (x + 5)(x - 5) D) (x + 5)2
C) 4(x - 2)(x + 3) D) 4(x + 2)(x - 3)
B) (x - 4)(2x - 4) C) prime D) 2(x - 8)(x + 1)
A) 5x(x - 4)(x + 5) B) (x - 4)(5x2 + 25) C) (5x2 + 20x)(x - 5)
Answer: A
293) (x + 8)2 - 8(x + 8) + 12
A) (x2 + 8x - 2)(x2 + 8x - 6)
5x(x + 4)(x - 5)
B) (x2 - 8x + 2)(x2 - 8x + 6)
C) (x + 6)(x + 2) D) (x + 10)(x + 14)
Answer: C
294) x4 + 7x2 + 10
A) (x2 - 2)(x2 + 1) B) (x2 + 2)(x2 + 5)
C) (x2 - 2)(x2 + 5) D) prime Answer: B
295) 15x2 + 19x + 6
A) prime B) (3x + 2)(5x + 3) C) (3x - 2)(5x - 3) D) (15x + 2)(x + 3)
Answer: B
296) 20y2 + 27y + 9
A) (4y - 3)(5y - 3) B) (20y + 3)(y + 3) C) (4y + 3)(5y + 3) D) prime
Answer: C
297) 12z2 - 7z - 12
A) prime B) (4z - 3)(3z + 4) C) (12z + 3)(z - 4) D) (4z + 3)(3z - 4)
Answer: D
298) 15z2 - 11z - 12
A) (3z + 4)(5z - 3) B) prime C) (15z - 4)(z + 3)
(3z - 4)(5z + 3) Answer: D
299) 9x2 - 6xt - 8t2
A) prime B) (9x - 4t)(x + 2t) C) (3x - 4t)(3x + 2t)
(3x + 4t)(3x - 2t) Answer: C
300) 10z2 - 7z - 12
A) (2z + 3)(5z - 4) B) prime
(2z - 3)(5z + 4)
(10z - 3)(z + 4) Answer: C
301) 27x2 - 117x - 90
A) 9(3x + 2)(x - 5) B) prime C) 9(3x - 2)(x + 5)
(27x + 18)(x - 5) Answer: A
302) 14x2 - 49x - 28
A) 7(2x - 1)(x + 4) B) 7(2x + 1)(x - 4)
(14x - 7)(x + 4)
prime Answer: B
303) 14y2 + 63y - 35 A) prime
7(2y - 1)(y + 5)
(14y - 7)(y + 5)
7(2y + 1)(y - 5) Answer: B
304) 6x2 - 22x + 20
A) 2(3x - 5)(x - 2) B) 2(3x + 5)(x + 2) C) prime
Answer: A
305) 10x3 + 9x2 - 9x
A) x(2x + 3)(5x - 3)
Answer: A
306) 48x2 + 96x + 45 A) 3(4x + 3)(4x + 5)
Answer: A
307) 15(x - 2)2 - 29(x - 2) - 14
(3x + 8)(5x + 17)
Answer: C
308) 9x4 + 12x2 + 4
(3x2 + 2)(3x2 + 2)
Answer: A
309) 15x4 - 4x2 - 4
(3x2 - 2)(5x2 + 2)
Answer: A
(3x - 5)(2x - 2)
x2(2x + 3)(5x - 3)
(2x2 + 3)(5x - 3)
x(5x + 3)(2x - 3)
(4x + 1)(4x + 15)
3(4x + 1)(4x + 15)
3(15x + 3)(x + 5)
(3x + 9)(5x + 4)
(3x - 13)(5x - 8)
(3x + 7)(5x + 2)
(9x2 + 2)(x2 + 2)
(3x2 - 2)(3x2 - 2)
(3x2 + 1)(3x2 + 4)
(15x2 - 2)(x2 + 2)
(5x - 2)(3x + 2)
(3x2 + 1)(5x2 - 4)
310) x2 - 100
A) (x2 + 10)(x2 - 10)
Answer: D
311) 9x2 - 1
A) (3x - 1)(3x + 1)
Answer: A
312) 100 - x2
A) (10 + x)2
Answer: D
313) 4x2 - 49
A) (2x + 7)(2x - 7)
Answer: A
314) x3 - 343
A) (x + 343)(x2 - 1)
C) (x - 7)(x2 + 7x + 49)
Answer: C
315) x3 + 1000
A) (x - 10)(x2 + 10x + 100)
C) (x + 10)(x2 - 10x + 100)
Answer: C
316) 125y3 - 1
A) (5y - 1)(25y2 + 5y + 1)
C) (125y - 1)(y2 + 5y + 1)
Answer: A
317) 216x3 + 1
A) (6x + 1)(36x2 + 1)
C) (6x + 1)(36x2 + 6x + 1)
Answer: B
318) 216 - x3
A) (6 + x)(36 - x2)
Answer: C
319) 729x3 - 512
A) (9x - 8)(81x2 + 72x + 64)
C) (9x - 8)(81x2 + 64)
Answer: A
B) (x + 100)(x - 100)
C) (x - 10)(x - 10)
D) (x + 10)(x - 10)
B) (3x - 1)2
B) (10 - x)2
B) (2x + 7)2
B) (6 + x)(36 - 6x + x2)
C) (3x + 1)2
C) prime
C) (4x + 1)(x - 49)
B) (x + 7)(x2 - 7x + 49)
D) (x - 7)(x2 + 49)
B) (x - 1000)(x2 - 1)
D) (x + 10)(x2 + 100)
B) (5y + 1)(25y2 - 5y + 1)
D) (5y - 1)(25y2 + 1)
B) (6x + 1)(36x2 - 6x + 1)
D) (6x + 1)(36x2 - 6x - 1)
D) prime
D) (10 - x)(10 + x)
D) (2x - 7)2
C) (6 - x)(36 + 6x + x2) D) (6 - x)(36 + x2)
B) (9x + 8)(81x2 - 72x + 64)
D) (729x - 8)(x2 + 72x + 64)
320) 512x3 + 729
A) (8x + 9)(64x2 + 72x + 81)
C) (8x - 9)(64x2 + 72x + 81)
Answer: D
321) 27 - 8x3
A) (3 + 2x2)(9 - 6x + 4x2)
C) (27 - 2x)(1 + 6x + 4x2)
Answer: B
322) x2 + 40x + 400
A) (x + 20)(x - 20)
Answer: D
323) x2 + 4x + 4
A) (x + 2)(x - 2)
Answer: D
324) 25x2 - 60x + 36
B) x2 + 40x + 400
B) (512x - 9)(x2 + 72x + 81)
D) (8x + 9)(64x2 - 72x + 81)
B) (3 - 2x)(9 + 6x + 4x2)
D) (3 - 2x)(9 + 4x2)
C) (x - 20)2 D) (x + 20)2
B) (x - 2)2
C) (x + 4)(x - 4)
A) (5x + 6)(5x - 6) B) (5x + 6)2 C) (5x - 7)2
Answer: D
325) 9x2 + 30x + 25
A) (3x - 5)2 B) (3x + 5)(3x - 5)
Answer: D
326) 3x2 - 75
A) 3(x - 5)2
Answer: D
327) (x + 7)2 - 4
3(x + 5)2
A) (x + 9)(x + 5) B) (x - 5)(x - 9)
Answer: A
328) (x - 8)2 - 9
A) (x + 5)(x + 11)
Answer: C
329) (4x - 1)3 + 216
A) (4x - 7)(16x2 + 16x + 31)
C) (4x + 5)(16x2 - 32x + 43)
Answer: C
(x + 2)2
(5x - 6)2
(3x - 6)2
(3x + 5)2
prime
3(x + 5)(x - 5)
C) (x + 11)(x + 3) D) x2 + 14x + 45
B) (x + 1)(x - 17)
C) (x - 5)(x - 11)
B) (4x + 5)(16x2 + 16x + 31)
D) (4x + 5)(16x2 + 16x + 43)
(x - 11)2
330) (9 - x)3 - x3
A) (9 - 2x)(x2 - 9x + 81)
C) (9 + 2x)(x2 - 9x + 81)
Answer: A
331) 27x2 - 36x + 12
A) 3(3x - 2)2
Answer: A
332) x3 + 24x2 + 144x
B) (9 - x)(x2 - 9x + 81)
D) (9 - 2x)(3x2 - 9x + 81)
B) 3(3x - 2)(3x + 2)
C) 3(3x + 2)2
prime
A) x(x + 12)(x - 12) B) x(x - 12)2 C) x(x + 12)2 D) prime
Answer: C
333) x4 + 4x2 + 4
A) (x + 2)2 B) (x2 - 2)2 C) (x2 + 2)2
Answer: C
Simplify the rational expression.
334) x2 - 36 x - 6
x - 6
Answer: D
335) 2x + 2 10x2 + 16x + 6 A) 2x + 2 10x2 + 16x + 6
Answer: C
336) y2 + 7y + 12 y2 + 9y + 20 A) 7y + 12 9y + 20
Answer: D
337) 3x2 - 22x + 35 x - 5
1 x - 6
(x + 2)(x - 2)
2x + 5 5x + 16
1 5x + 3
2x 5x + 3
7y + 3 9y + 5
y2 + 7y + 12 y2 + 9y + 20
A) 1 x - 5 B) 3x2 - 29 C) 3x - 7
Answer: C
y + 3 y + 5
3x2 - 22x + 35 x - 5
338) x2 + 12x + 32 x2 + 16x + 64
12x + 32 16x + 64
Answer: D
339) 3x2 - 7x - 20 2x2 - 5x - 12
Answer: C
Answer: C
341) y3 - 27 y - 3
y3 - 27 y - 3
Answer: C
Perform the indicated operations and simplify the result. Leave the answer in factored form.
Answer: D 343) 4x - 4 x 2x2 5x - 5
Answer: C
Answer: A
345) x2 + 13x + 36 x2 + 15x + 54 · x2 + 14x + 48 x2 + 12x + 32
A) x + 4 x + 6
Answer: D
346) x2 - 23x + 132 x2 - 10x + 16 x2 - 9x + 8 x2 - 18x + 77
B) x + 6 x + 8 C) 1 x + 8 D) 1
A) (x + 12)(x + 1) (x + 2)(x + 7) B) (x2 - 23x + 132)(x2 - 9x + 8) (x2 - 10x + 16)(x2 - 18x + 77)
C) (x - 12) (x - 7) D) (x - 12)(x - 1) (x - 2)(x - 7)
Answer: D
347) x2 + 12x + 35 x2 + 14x + 45 · x2 + 9x x2 + 4x - 21
x x - 3
Answer: A
348) 9x4 - 72x 3x2 - 12 x2 + x - 2 4x3 + 8x2 +16x
x x2 + 14x + 45
3x(x - 1)(x - 2)2 4(x + 2)2 B) 3x(x + 1) 4
Answer: C
349) x2 + 11x + 28 x2 + 13x + 42 x2 + 6x x2 + 12x + 32 A) x x2 + 13x + 42
Answer: C
350) 10x2 - 3x - 4 5x2 - x - 4 15x2 + 12x 1 - 4x2
x2 + 6x x + 8
1 x - 3
x(x + 9) x - 3
3(x - 1) 4
3x(x - 1) 4
x x + 8
1 x + 8
A) 3x(5x + 4) (1 - 2x)(x - 1) B) (5x + 4)(5x - 4) (1 - 2x)(x - 1)
Answer: C
3x(5x - 4) (1 - 2x)(x - 1)
3x (1 - 2x)(x - 1)
351) 21x - 21 9 ÷ 7x - 7 99
Answer: B 352) 5x - 5 x ÷ 6x - 6 7x2
Answer: C 353) x2 + 10x + 16 x2 + 11x+ 24 x2 + 2x x2 + 6x + 9
Answer: D
Answer: A
Answer: D
(x + 4)(x + 2)
Answer: C
357) 25x2 - 4 x2 - 9 ÷ 5x - 2 x - 3 A) (5x - 2)(25x2 - 4) (x2 - 3)(x -3) B) 5x - 2 x - 3 C) 5x + 2 x + 3
Answer: C
358) x 815 7
x - 15 15
Answer: D
359) 2x + 9 22x - 9 2
x - 15 56
0 B) 9 C) 2x
Answer: B 360) 6x2 x - 16x x - 1
6x B) 6x x - 1
Answer: A
361) 9 11x4 11x
5 22x
Answer: D 362) 1 2x + 1 5x
1
Answer: D
363) -6x - 8 x + 4x + 7 3x A) -14x + 31 3x
Answer: B
x + 3 5x + 2
1
6x(x + 1) x - 1
81
0
-14x - 17 3x C) -22x - 17 3x
-14x - 17 3x2
364) 4 x26 x
2(3x - 2) x
Answer: C
365) 5 x + 7 x - 4
20x - 12 x(4 - x)
Answer: C
366) 5 x + 42 x - 4
3x + 28 (x + 4)(x - 4)
Answer: D 367) 21 x - 4 + 6 x - 4
21(x - 4) 6(x - 4)
Answer: C 368) 8x2 x - 18x x - 1
8x x - 1
Answer: D
369) 7 - x x - 52x - 4 5 - x
x + 3 x - 5
Answer: A
370) x + 8 x - 8x + 8 x + 2
10(x + 8) (x - 8)(x + 2)
Answer: A
2(2 + 3x) x2
2(2 - 3x) x2
2(2x + 3) x2
12x - 20 x(4 - x)
3 (x + 4)(x - 4)
8x(x + 1) x - 1
0
3x - 12 (x + 4)(x - 4)
3x - 28 (x + 4)(x - 4)
8x
x + 11 x - 5
x + 11 x - 5
x + 3 x - 5
0
-10(x + 8) (x - 8)(x + 2)
-6(x + 8) (x - 8)(x + 2)
Answer: B
Answer: C
Answer: D
Answer: C
Answer: B
Answer: B
Answer: A
Answer: B
Answer: A
Answer: C
Answer: A
Answer: D 383) 3 7x - 1 - 3 3 7x - 1 + 3
Answer: B
Answer:
Answer: A
x + 9 x - 9 + x - 9 x + 9
x + 9 x - 9x - 9 x + 9 A) 1 B) (x + 9)2 18x
Answer: D 388) 1 x + 2 + 1 x - 2
Answer: D
(x + 9)3 36x(x + 10)
x2 + 81 18x
Answer: D
Solve the problem.
390) The width of a rectangle can be represented by the ratio A l , where A is the area of the rectangle and l is the length.
Suppose that the area of a rectangle is x2+ 2x - 15 square inches and the length of the rectangle is x + 5 inches.
a. Determine the simplified rational expression that describes the width of the rectangle.
b. What is the width of the rectangle if x = 28 inches?
A) a. (x + 5); b. 33 inches B) a. (x - 3); b. 25 inches
Answer: B
C) a. (x - 5); b. 23 inches
D) a. (x + 3); b. 31 inches
391) On a 608 mile road trip, out to Yellowstone National Park Toby's average speed was x miles per hour. On his return trip, he averaged 15 miles per hour more than his trip to the park. The time that it took Toby to drive to the park can be represented by the rational expression 608 x , while the time it took Toby to return home can be represented by the rational expression 608 x + 15 .
a. Write a simplified rational expression that describes the difference in the time it took Toby to drive to the park and the time it took him to return home.
b. What was the difference in the time it took Toby to drive to the park and the time it took him to return home if he averaged 61 miles per hour on his drive home? Round your answer to the nearest tenth .
A) a. 9120 x2 + 15x ; b. 3.3 hour(s)
Answer: A
B) a. -9120 x2+ 15x ; b. 3.3 hour(s)
Determine if the given solution is correct. If it is not, find the solution.
392) Is -5 the solution to -15 - 2 = x - 10?
A) no; x = -23 B) no; x = -27
Answer: D
393) Is -8 the solution to x + 5 = 4 - 7?
A) no; x = 16 B) no; x = 6
Answer: C
394) Is 14 the solution to -1 + x = 14?
A) no; x = B) yes
Answer: C
C) a. 1216x + 9120 x2+ 15x ; b. 3972.2 hour(s) D) a. 9120 x2 - 15x ; b. 1.3 hour(s)
C) yes D) no; x = -7
C) yes D) no; x = 2
C) no; x = 15
List the terms of the expression. Then identify the coefficient of each term.
395) 4h2 - 9h
A) h2, h; 4, 9
Answer: C
396) 3b - 9t
A) b, t; 3, 9
Answer: D
397) 4m - 2
A) m; 4, -2
Answer: D
398) 5w2 - 2w - ty
A) 5w2, -2w, -ty; 5, 2, 1
C) 5w2, -2w, -ty; 5, -2, -1
Answer: C
D) no; x = -15
B) 4h2, 9h; 4, 9
C) 4h2, -9h; 4, -9
D) h2, h; 4, -9
B) -3b, t; -3,
C) 3b, -9t; -3, 9
D) 3b, -9t; 3, -9
B) 4m; 4
C) 4m, -2; 4, 2
D) 4m, -2; 4, -2
B) 5w2, -2w, -t, y; 5, -2, -1, 1
D) 5w2, 2w, ty; 5, 2, 1
399) 2y3 - 4y2 - y
A) 2y3, -4y2, -y; 2, -4, -1
C) 2y3, -4y2, -y; 2, 4, 1
Answer: A
Identify the like terms in the algebraic expression.
400) 7x + 9y - 44y + 35x
A) 7 and 35; 9 and -44
C) 7 and 44; 9 and 35
Answer: B
401) 3x2 + 8 - 3x + x2 - 5
A) 3x2, x2, and -3x; 8 and -5
C) 3x2 and -3x2; 8 and -5
Answer: D
402) 63p + 7 - 12q + 3 - 13p
A) 63p and 13p
C) 63p and -13p; 7 and 3
Answer: C
403) 5mn - 4m2 + 3n2 - 9m2 + 6mn + 7n2
A) 5mn and 6mn; -4m2 and -9m2; 3n2 and 7n2
C) 5mn and 6mn; -4m2 and -9m2
Answer: A
Determine if the given solution is correct. If it is not, find the solution.
404) Is -13 the solution to -x = 13
A) no; x = 13 B) yes
Answer: B
405) Is 26 11 the solution to 11x = 15
A) yes B) no; x = 15 11
Answer: B
B) 2y3, -4y2, y; 2, -4, 1
D) 2y3, 4y2, y; 2, 4, 1
B) 7x and 35x; 9y and -44y
D) 7x and 9y; -44y and 35x
B) 3x2 and 8; 3x and x2
D) 3x2 and x2; 8 and -5
B) 63p, -13p and -12q; 7 and 3
D) 63p, -13p and -12q
B) 5mn and 6mn; -9n2 and 7n2
D) 5mn and 6mn; -4m2 and 3m2; -9n2 and 7n2
C) no; x = 0 D) no; x = -1
C) no; x = 165
D) no; x = 11 15
Write a fraction to represent the shaded portion of the figure.
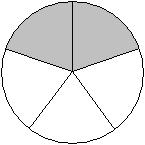
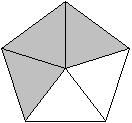
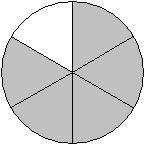

Answer: B
Write a fraction to represent the given information.
410) What fraction of the fuel tank holds fuel?
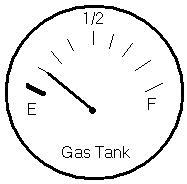
5 8
Answer: B
1 8
Write a mixed number to represent the measurement shown.
3 8
411) Of the 210 students at a college, 57 are juniors. What fraction of the students are juniors?
153 57
Answer: D
2 8
57 153
412) Of the 106 teachers at a school, 81 are women. What fraction of the teachers are men?
Answer: B
413) According to a recent study, 6 out of 21 visits to a hospital emergency room were for an injury. What fraction of emergency room visits were injury-related?
15 6
Answer: C
6 15
6 21
21 6
414) According to a recent study, 11 out of 13 visits to a hospital emergency room were for an injury. What fraction of emergency room visits are NOT injury-related?
2 11
Answer: C
415) In a math class containing 66 students, there are 21 freshman, 11 sophomores, 6 juniors, and 28 seniors. What fraction of the class is NOT juniors?
66 60 B) 60 6 C) 3 4 D) 60 66
Answer: D
Write both an improper fraction and a mixed number or whole number to represent the shaded portion.
416)
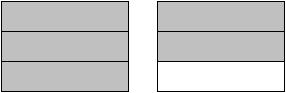
Answer: B 417)
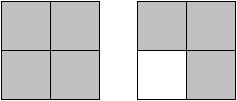
Answer: D
418)
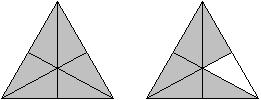
Answer: A
Write a mixed number to represent the measurement shown. 419) What part of the inch is highlighted?
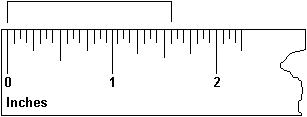
Answer: D
Determine whether the given solution is correct. If it is not, find the solution.
420) Is17 12 the solution for 5x + 9 = -8 - 7x?
A) No; x = B) Yes
Answer: B
421) Is 1 13 the solution for 5x + 4 = -9 + 6x?
A) No; x =11 5
Answer: C
B) Yes
422) Is 5 the solution for -6x + 7 + 4x = -3x + 12?
A) No; x = 12 B) No; x = -7
Answer: D
423) Is 9 the solution for -8x + 4 + 6x = -3x + 9?
A) No; x = 5 B) No; x = -4
Answer: A
Graph the fraction or mixed number on a number line.
424) 1 4
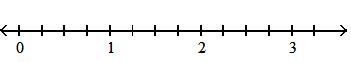
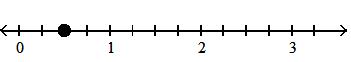
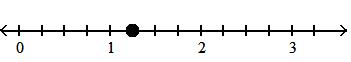
Answer: D
425) 5 8
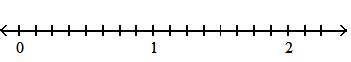
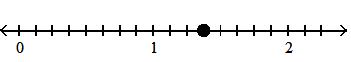
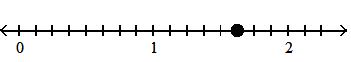
Answer: B
C) No; x = - 2
D) No; x =12 17
C) No; x = 13 D) No; x =1 13
C) No; x = -12 D) Yes
C) Yes D) No; x = -9
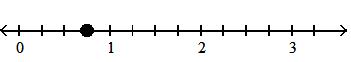
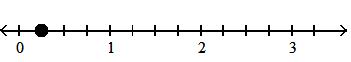
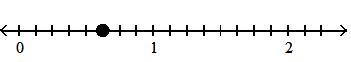
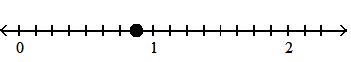
2 3
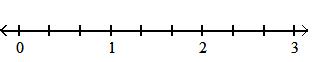
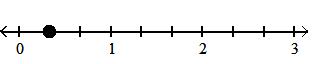

Answer: D
427) 8 5
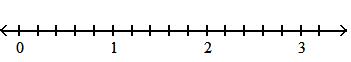

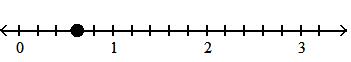
Answer: D
428) 8 3
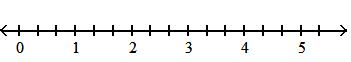

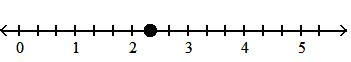
Answer: A
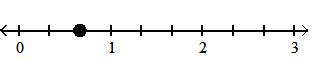
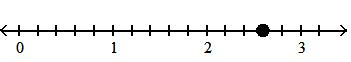


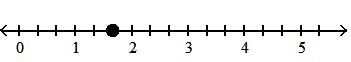
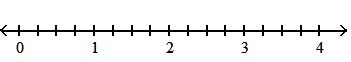
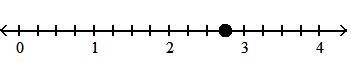

Answer: A
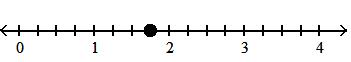
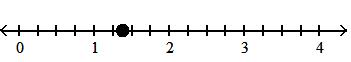
Answer Key
Testname: UNTITLED1
1) C
2) B
3) D
4) A
5) C
6) D
7) C
8) C
9) D
10) B
11) D
12) A
13) C
14) B 15) B
16) B
17) A
18) D
19) D
20) B
21) A
22) C
23) B
24) D
25) D
26) B
27) D
28) C
29) D
30) C
31) D
32) B
33) B
34) C
35) A
36) A
37) A
38) B
39) C
40) D
41) B
42) A
43) B
44) C
45) B
46) A
47) B
48) C
49) A
50) C
Answer Key
Testname: UNTITLED1
51) D 52) C 53) A 54) C
55) D
56) D
57) D
58) B
59) C
60) C
61) B
62) B 63) B 64) B 65) D
66) B 67) C
68) B 69) A
70) D
71) C
72) B 73) A 74) A
75) B 76) A
77) D
78) C
79) A 80) C
81) D
82) A 83) D 84) A 85) D
86) B
87) D
88) C
89) D
90) C 91) B 92) D 93) C 94) C 95) A 96) C 97) C 98) D 99) D
100) B
Answer Key
Testname: UNTITLED1
101) B
102) A
103) B
104) C
105) B
106) D
107) A
108) C
109) C
110) D
111) C
112) B
113) D
114) B 115) C
116) D 117) C
118) D
119) D
120) D
121) D
122) A
123) A
124) C
125) B
126) A
127) D
128) B
129) A
130) B
131) B
132) A
133) B
134) A
135) C
136) B
137) C
138) A
139) A
140) B
141) A
142) B
143) C
144) A
145) D
146) B
147) D
148) D
149) D
150) C
Answer Key
Testname: UNTITLED1
151) D 152) D 153) C
154) D
155) D
156) C
157) A 158) A
159) B
160) D
161) B
162) B 163) B
164) C 165) B
166) C 167) A
168) B 169) B
170) B 171) D 172) C
173) C 174) D
175) B 176) A
177) C
178) D
179) C 180) D
181) D
182) A
183) B
184) A 185) C
186) A
187) B
188) A 189) C
190) B
191) D
192) B
193) C 194) C
195) B
196) D
197) A
198) D
199) C
200) A
Answer Key
Testname: UNTITLED1
201) D
202) D
203) D
204) D
205) A
206) D
207) C
208) A
209) B
210) A
211) C
212) A
213) C
214) A
215) B
216) A
217) A
218) D
219) D
220) D
221) B
222) A
223) D
224) C
225) A
226) B
227) A
228) C
229) B
230) A
231) C
232) A
233) B
234) C
235) C
236) B
237) D
238) D
239) D
240) A
241) A
242) B
243) A
244) D
245) B
246) C
247) D
248) D
249) A
250) D
Answer Key
Testname: UNTITLED1
251) C
252) A
253) B
254) A
255) B
256) C
257) B
258) D
259) B
260) D
261) D
262) B
263) D
264) D
265) B
266) B
267) D
268) C
269) C
270) C
271) B
272) B
273) C
274) B
275) C
276) B
277) A
278) B
279) D
280) C
281) C
282) D
283) D
284) D
285) B
286) A
287) B
288) D
289) A
290) D
291) A
292) A
293) C
294) B
295) B
296) C
297) D
298) D
299) C
300) C
Answer Key
Testname: UNTITLED1
301) A
302) B
303) B 304) A
305) A
306) A
307) C
308) A
309) A
310) D
311) A
312) D
313) A 314) C 315) C
316) A 317) B
318) C 319) A
320) D
321) B 322) D
323) D
324) D
325) D 326) D
327) A
328) C
329) C 330) A
331) A
332) C
333) C
334) D 335) C
336) D 337) C
338) D 339) C 340) C 341) C 342) D 343) C 344) A 345) D 346) D 347) A 348) C
C 350) C
Answer Key
Testname: UNTITLED1
351) B
352) C
353) D
354) A
355) D
356) C
357) C
358) D
359) B
360) A
361) D
362) D
363) B
364) C
365) C
366) D
367) C
368) D
369) A
370) A
371) B
372) C
373) D
374) C
375) B
376) B
377) A
378) B
379) A
380) C
381) A
382) D
383) B
384) B
385) C
386) A
387) D
388) D
389) D
390) B
391) A
392) D
393) C
394) C
395) C
396) D
397) D
398) C
399) A
400) B
Answer Key
Testname: UNTITLED1
401) D
402) C
403) A 404) B
405) B
406) C
407) B
408) A
409) B
410) B 411) D
412) B 413) C
414) C 415) D
416) B 417) D
418) A 419) D
420) B 421) C 422) D
423) A
424) D
425) B 426) D
427) D
428) A
429) A
