PDF Solutions Manual for Engineering Mechanics - Statics 6th Edition by Bedford

Problem2.1 Consider vectors U and V oriented as shown. Their magnitudes are U 8 = and V 3. = Graphically determine the magnitude of the vector UV23

Solution: The vector U 2 has the same direction as U and magnitude 16. The vector V 3 has the direction opposite to V and magnitude 9. We choose a scale and add these vectors to obtain the vector UV23 :

Problem2.2 Suppose that the pylon in Example 2.2 is moved closer to the stadium so that the angle between the forces F AB and F AC is 45 ° Draw a sketch of the structure with the cables in their new orientation. The magnitudes of the forces are F 100 kN AB = and F 60 kN AC = Graphically determine the magnitude and direction of the sum of the forces exerted on the pylon at A by the two cables.

Problem2.3 Two unit vectors e 1 and e 2 are oriented as shown. Graphically determine the magnitude of the vector Uee 23 . 12=+

From the diagram we estimate that +=FF 148 kN ABAC at ° 48 relative to the horizontal.

° 148 kN a t2 8  from horizontal.

Solution: The vector e 2 1 has the same direction as e 1 and magnitude 2. The vector e3 2 has the same direction as e 2 and magnitude 3. We choose a scale and add these vectors to obtain the vector + ee23 : 12

measuring its magnitude, we estimate that +=ee23

Problem2.4 Two unit vectors e 1 and e 2 are oriented as shown. Graphically determine the magnitude of the vector Uee4312=−

Solution: The vector e 4 1 has the same direction as e 1 and magnitude 4. The vector e3 2 has the direction opposite to e 2 and magnitude 3. We choose a scale and add these vectors to obtain the vector ee43 : 12

Problem2.5 Three forces act on the ring. Their sum is zero: FFF0 ABC ++ = The magnitudes

F 100 N B = and F 160 N. C = Graphically determine the magnitude of F A and the angle α

By measuring its magnitude, we estimate that −=

Solution: If the sum of the three forces equals zero, the three force vectors form a closed triangle when placed head-to-tail. We choose a scale and draw the force triangle:

By measuring, we estimate that

Problem2.6 Three forces act on the ring. Their sum is zero: FFF0 ABC ++ = The magnitude F 200 lb C = Graphically determine the value of the angle α for which the magnitude of F A is a minimum. If α has that value, what are the magnitudes of F A and FB ?

Solution: The magnitude and direction of FC are known. The direction of FB is known. If the sum of the three forces equals zero, the three force vectors form a closed triangle when placed head-to-tail. Choosing a scale and drawing the force triangle, we can see that the magnitude of F A is a minimum when it is perpendicular to the line of action of FB Constructing the triangle in this way,

Problem2.7 A T-shaped structural member is suspended from cables. The member is subjected to three forces: the forces F A and FB exerted by the cables and its weight W The weight of the member is W 1000 lb = The sum of the forces is zero. Graphically determine the magnitudes of F A and F . B

Solution: The directions of all three vectors and the magnitude of W are known. If the sum of the three forces equals zero, the three force vectors form a closed triangle when placed head-to-tail. We choose a scale and draw the force triangle:

Problem2.8 A T-shaped structural member is suspended from cables. The member is subjected to three forces: the forces F A and FB exerted by the cables and its weight W. The sum of the forces is zero. Suppose that the magnitude of the force exerted by either cable must not exceed 1200  l b. Graphically determine the largest magnitude of the weight W that can be suspended in this way.

By measuring, we estimate that = F 530  lb, A = F 690  lb. B

FF 530  lb,  6 90  lb. AB

Solution: The directions of all three vectors are known. If the sum of the three forces equals zero, the three force vectors form a closed triangle when placed head-to-tail. We draw the force triangle:

The force FB has the larger magnitude of the two cable forces. It must not exceed 1200  lb. Assuming it has that value and measuring, we estimate that the magnitude of W is 1740  lb. W 1740 lb. =

Problem2.9 The 2700 -k g tractor is at rest on the inclined surface. The angle 30 α =° relative to the horizontal. The forces exerted on the tractor’s tires by the inclined surface are represented by the normal force N, which is perpendicular to the surface, and the friction force f , which is tangential to the surface. The sum of the normal force, the friction force, and the tractor’s weight is zero: NfW0 ++ = Graphically determine the magnitudes of N and f in newtons.

Source: Courtesy of Tka4ko/Shutterstock.

Problem2.10 The 2700 -k g tractor is at rest on the inclined surface. The forces exerted on the tractor’s tires by the inclined surface are represented by the normal force N, which is perpendicular to the surface, and the friction force f , which is tangential to the surface. The sum of the normal force, the friction force, and the tractor’s weight is zero: NfW0 ++ = Graphically determine the value of the angle α relative to the horizontal for which the magnitudes of N and f are equal. What is their magnitude?

Source: Courtesy of Tka4ko/Shutterstock.

Solution: The tractor’s weight is = (2700  kg)(9.81 m/s ) 2 26.5 kN. The directions of all three vectors and the magnitude of W are known. If the sum of the three forces equals zero, the three force vectors form a closed triangle when placed head-to-tail. We choose a scale and draw the force triangle:

Solution: The tractor’s weight is (2700  kg)(9.81 m/s ) 2 = 26.5 kN If the sum of the three forces equals zero, the three force vectors form a closed triangle when placed head-to-tail. The vector f is normal (perpendicular) to the vector N, so these two vectors can be of equal magnitude only if they have the following configuration:

We see immediately that α =° 45 Measuring, we estimate that ==Nf 18.8 kN α =° ==Nf 45 ,  18.8 k N.

Problem2.11 A spherical storage tank is suspended from cables. The tank is subjected to three forces: the forces F A and FB exerted by the cables and its weight W. The weight of the tank is W 800 lb = The vector sum of the forces acting on the tank equals zero. Graphically determine the magnitudes of F A and F . B

Solution: Measuring a vertical distance of 8 units and drawing two lines at ° 20 to where they intersect, we obtain the diagram

Measuring the magnitudes, we estimate that = FFAB = 424 lb.

Problem2.12 The rope ABC exerts forces FBA and FBC of equal magnitude on the block at B. The magnitude of the total force exerted on the block by the two forces is 200  lb. Graphically determine FBA

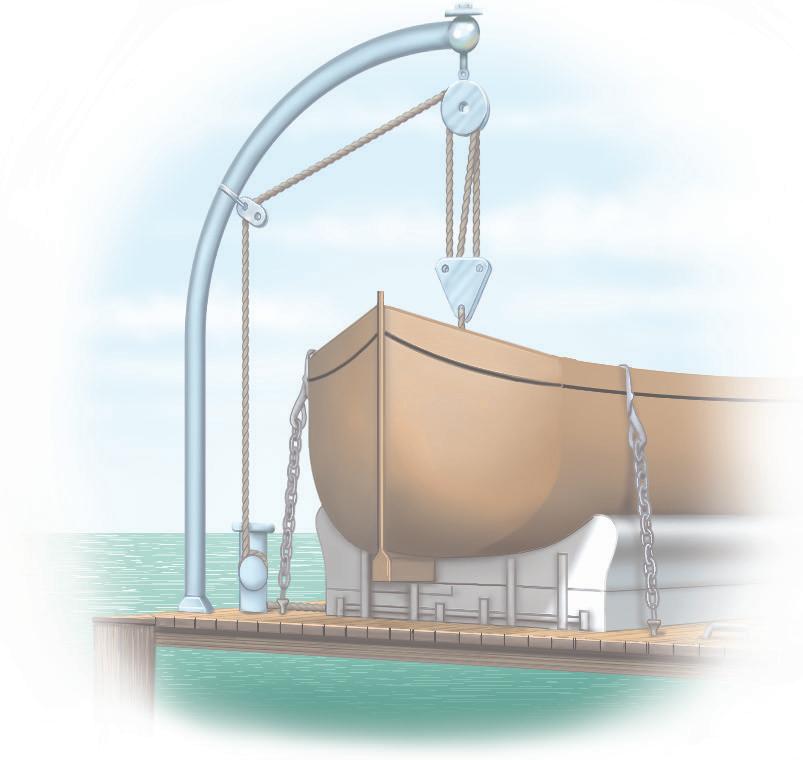
Solution: We know the magnitudes of the forces FBA and FBC are equal, but we don’t know its value. Choose a convenient length, call it L , BA and draw both vectors with that length in their correct directions to graphically determine the sum of the forces FF : BABC +

Now measure the length of the sum FF , BABC + call it L SUM Then the magnitude of FBA is

From our measurements we obtain F 174 lb. BA = F 174 lb. BA =

Problem2.13 Two snowcats tow an emergency shelter to a new location near McMurdo Station, Antarctica. (The top view is shown. The cables are horizontal.) The total force FFAB + exerted on the shelter is in the direction of the line L and has a magnitude of 300  l b. Graphically determine the magnitudes of F A and F . B

Problem2.14 A surveyor determines that the horizontal distance from A to B is 400  m and the horizontal distance from A to C is 600  m . Graphically determine the magnitude of the vector r BC and the angle α

Solution: Measuring a vertical distance of 3 units and drawing two lines at ° 30 and ° 50 as shown to identify where they intersect, we obtain the diagram

Problem2.15 The figure shows three forces acting on a joint of a structure. The magnitude of FC is 60  kN, and FFF0 ABC ++ = Graphically determine the magnitudes of F A and F . B

Measuring the magnitudes, we estimate that ==FF 150 lb, 234 lb. AB

Solution: Using a convenient scale for the given distances, draw lines from point A at 20° and at 60° relative to the East axis. Put point B at 400 m along the 60° line and put point C at 600 m along the 20° line. Then measure the magnitude of the vector r BC and the angle α The results are

Solution: Measuring a vertical distance of 6 units and drawing two lines at ° 40 and ° 15 as shown to identify where they intersect, we obtain the diagram

Measuring the magnitudes, we estimate that

Problem2.16 By drawing sketches of the vectors, explain why

++ =+ + UVWUVW () () .

Solution: Consider three arbitrary vectors:

First we add U and V, then add W:

Problem2.17 Two forces are given in terms of their components by =− Fij 60 20 (l b), A =+ Fij 30 40 (l b) B (a) What are the magnitudes of the forces? (b) What is the magnitude of their sum FF ?

AB + Strategy: The magnitude of a vector in terms of its components is given by Eq. (2.8).

From this diagram we can also see that ++

Problem2.18 Consider three vectors Aij 12 8, =+ BB Bij, xy=+ and CC Cij xy=+ Their sum is zero, ABC0, ++ = and the components of B and C satisfy the relations BB 2 xy =− and CC3.xy = What are the magnitudes of B and C ?

Solution: If the sum of the three vectors is zero, that implies that each component of their sum is zero. That yields the two equations

BC BC 12 0, 80 xx yy ++ = ++ =

Solution: (a)

(60 l b) (2 0  lb) 63.2 lb. (3 0  lb)(40  l b) 50.0 lb. A B 22 22 =+ = =+ = (b)

FFij ij

(6 03 0) (2 04 0)  (lb ) 90 20  (lb ). (9 0  lb)(20  l b) 92.2 lb

Solving these equations together with the two given equations, we obtain Bij Cij 4.8 2.4 , 16.8 5. 6. =− =−

Therefore B C (4.8)( 2.4) 5.37, ( 16. 8) ( 5.6) 17.7. 22 22 =+ = =− +− = ==BC 5.37,  17.7.

Problem2.19 The vector xy rij =+ extends to a point on the curve described by the equation shown. Determine the values of x and y for which the magnitude of the vector is a minimum. What is the minimum magnitude?

We equate the derivative of this expression to zero,

−+ = xx 2 1 4 0, 3

obtaining the roots = x 0 and =± x 8. Substituting these values into the expression for the magnitude in terms of x, we find that = r 4 at = x 0 and = r 3.46 at =± x 8. So the minimum magnitude occurs at =± x 8. At both of these points, = y 2. If we examine a graph of the magnitude as a function of x,

Solution: The magnitude of r is

=+xy r 22

Substituting the relation =− yx 4(1/ 4) 2 into this relation gives

=− + xx r 16 1 16 24

We want to find the value of x for which the magnitude of r is a minimum. We can simplify things a bit by seeking the value of x for which the square of the magnitude of r is a minimum:

=− + xx r 16 1 16 2 24

Problem2.20 The forces Fi 90 (k N) A = and Fj 60 (k N) B = The force c Fij2, C =−() where c is a parameter. Determine the value of c so that the magnitude of the total force exerted on the beam by the three forces is a minimum. What is the minimum magnitude?

we see that this is an interesting case, = x 0 is a stationary point but is not the minimum magnitude.

=± == xy 8,  2, magnitude 3.46.

Solution: The total force is

++ =− +− cc FFFij (9 02 )(60 )  (k N)

ABC Its magnitude is

FFF (9 02 )(60 ) 8100 360 4 3600 120 11,700 480 5.

cc cccc cc

ABC 22 22 2 ++ =− +− =− ++ −+ =− +

We can seek the value of c that makes the square of the magnitude a minimum. We set

−+ =− += d dc ccc (1 1,700 480 5) 480 10 0, 2

obtaining = c 48 kN Substituting this value into the expression for the magnitude gives ++ = FFF 13.4 kN ABC

== c 48 kN, magnitude 1 3.4  kN

Problem2.21 The forces acting on the sailplane are its weight Wj 500 (l b), =− the lift L, and the drag D. The angle between the lift vector L and the vertical y -a xi s is 20 °, and the drag vector is perpendicular to the lift vector. At the instant shown, the sum of the forces on the sailplane is zero: LDW0 . ++ = Determine the magnitudes of L and D

Solution:

Problem2.22 Two unit vectors e 1 and e 2 are oriented as shown. Determine the magnitude of the vector Uee 23 . 12=+

Strategy: Introduce a cartesian coordinate system and express e 1 and e 2 in terms of their components.

Let L and D denote the magnitudes of the lift and drag. Then

We have

LD LDWi j 0 (sin 20 co s2 0) (c os 20 si n2 0 500 l b)

Each component must equal zero, resulting in two equations:

LD si n2 0c os 20 0, co s2 0sin 20 5 00 lb.

Solving, we obtain ==LD 470  lb,  171 lb.

LD 470  lb,  17 1  lb

Solution: We introduce the coordinate system shown: y

The unit vectors have magnitude one, so we can express them as ei eij , co s6 0sin 60 1 2 = =° +°

With these expressions, the vector Uee ij 23 (2 3c os 60 )3 si n6 0. 12=+ =+ °+ ° Its magnitude is U (2 3c os 60 )(3sin 60 ) 4.36. 22 =+ °+ ° = = U 4.36.

Problem2.23 Two forces act on the support. Their magnitudes are F 300 lb , A = F 200 lb B = Determine the magnitude FFAB + of the total force exerted on the support by the two forces.

Solution: Using similar triangles to determine the components, the force F A in terms of its components is

11 (1 1) (5) (3 00  l b) 5 (1 1) (5) (300  l b)

273 12 4  (l b) A 22 22 = + + + =+

The force FB in terms of its components is Fij

7 (7)(5) (200  l b) 5 (7)(5) (200  l b) 163 116  (lb ). B 22 22 =− + + + =− +

The total force is += + FFij 110 240  (lb ), AB and the magnitude of the total force is FF (1 10  l b) (2 40  l b) 265 lb. AB 22 += + =

Problem2.24 The person exerts a 30 -l b force F to push the crate onto a truck. (a) Express F in terms of components using the coordinate system shown. (b) The weight of the crate is 120  l b. What is the magnitude of the sum of the two forces exerted by the person and the crate’s weight?

Solution:

208 x y F Fy

(a) The force F in terms of its components is

ij ij (3 0  lb)c os 20  (30  l b) si n2 0  28.2 10.3  (lb ). xy=+ =° +° =+

(b) The sum of the forces is FWijj ij 28.2 10.3 120  (lb ) 28.2 11 0  (l b) += +− =−

Its magnitude is FW (2 8.2 lb)( 110  l b) 113 lb. 22 += +− = =− Fij (a )  28.2 110  (lb). (b) 113 lb.

Problem2.25 The missile’s engine exerts a 130 -k N thrust F. (a) Express F in terms of components using the coordinate system shown. (b) The mass of the missile is 1800  kg What is the magnitude of the sum of the thrust F and the missile’s weight? y x F 3 4

(a) The thrust F in terms of its components is FF Fij ij ij 4 5 (130  kN ) 3 5 (1 30  kN) 104 78  (kN). xy=+ =+ =+

(b) The missile’s weight is Wm g (1 800 kg)(9.81 m/s ) 17.7 kg. 2 == =

Solution:

The sum of the forces is FWijj ij 104 78 17.7  (kN) 104 60.3  (kN). += +− =+

Its magnitude is FW (1 04  kN )(60.3 kN ) 120  kN. 22 += + = =+ Fij (a )  104 78  (kN). (b) 120  kN

Problem2.26 The magnitude of the force F A is 8 kN. The magnitude of the vertical force FB is 2 kN For what value of the angle α in the range 09 0 α ≤≤ ° is the magnitude of the sum of the two forces equal to 9 kN ?

Solution: In terms of the coordinate system shown, the two forces in terms of their components are αα=+ = Fij Fj (8 kN )(c os si n), (2 kN ). A B

The magnitude of their sum is

FF (8 co s) (8 si n2)  (k N) 68 32 si n  (k N)

AB 22αα α += ++ =+

We want to determine the value of α for which α += += FF 68 32 si n  (k N) 9 kN

AB

Squaring both sides gives the equation α += 68 32 si n8 1.

Solving, we obtain α =° 24.0 α =° 24.0

Problem2.27 The x -a xi s is parallel to the bar AB The x -a xi s ′ is parallel to the bar BC . The magnitude of the vector F is 200  l b. (a) Express F in terms of its components in terms of the xy – coordinate system. Use these components to determine the magnitude of F (b) Express F in terms of its components in terms of the xy –′′ coordinate system. Use these components to determine the magnitude of F

Solution:

(a) The angle between bar AB and bar BC is () =° arctan 5 10 2 6.6

Therefore, the angle between the vector F and the x-axis is °+ °= ° 26.6 40 66.6 The vector F expressed in terms of the xycoordinate system is =° +° =+ Fij ij (200  l b) co s6 6.6 (2 00  l b) sin 66.6 79.5 183.5  (lb ).

Using these components to determine the magnitude of F yields

=+ = F (79.5 l b) (183.5 l b) 200  lb. 22

(b) The vector F expressed in terms of the ′′xy - coordinate system is =° ′ +° ′ = ′ + ′ Fij ij (200  l b) co s4 0(20 0  lb)sin 40 153.2 1 28.6  (lb ).

Using these components to determine the magnitude of F yields

=+ = F (153.2 l b) (128.6 l b) 200  lb. 22

=+ = = ′ + ′ = FijF FijF (a )  79.5 183.5  (lb ), 200  lb.  (b )  153.2 128.6  (lb ), 200  lb.

Problem2.28 Suppose that the magnitude of the component of the vector F parallel to the x -a xi s ′ is 150 lb (a) What is the magnitude of F ? (b) Express F in terms of its components in terms of the xy – coordinate system.

408 10 ft 5 ft A C B x y x9 y9

Solution:

(a) The component of F parallel to the ′ x -axis is ° F co s4 0. Solving

°= F co s4 01 50  l b

for the magnitude of F yields = F 196 lb.

(b) The angle between bar AB and bar BC is () =° arctan 5 10 2 6.6

Therefore the angle between the vector F and the x-axis is °+ °= ° 26.6 40 66.6 The vector F expressed in terms of the xycoordinate system is

=° +° =+ Fij ij (196 l b) co s6 6. 6(196 lb)sin 66.6 77.9 180  (lb ).

== + FFij (a )  196 lb. (b) 77.9 180  (lb ).

Problem2.29 The magnitudes A 12 = and B 10. = (a) Express A in terms of its components in terms of the xy –′′ coordinate system. (b) Express B in terms of its components in terms of the xy – coordinate system.

Solution:

(a) The angle between the vector A and the ′ x -axis is °+ °= ° 20 40 60 The vector A expressed in terms of the ′′xycoordinate system is =° ′ +° ′ = ′ + ′ Aij ij

12 co s6 01 2sin 60

61 0.4

(b) The angle between the vector B and the x-axis is °− °= −° 15 40 25 The vector B expressed in terms of the xycoordinate system is =° −° =− Bij ij

10 co s2 51 0sin 25 9.06 4 .23 = ′ + ′ =− AijBij (a )  61 0.4 . (b) 9.06 4.23

Problem2.30 The magnitudes A 12 = and B 10. = Determine AB +

Solution: To determine the sum of A and B, we must express them in terms of their components in terms of the same coordinate system. The angle between the vector A and the ′ x -axis is °+ °= ° 20 40 60 The vector A expressed in terms of the ′′xy - coordinate system is Aij ij

12 co s6 01 2sin 60

61 0. 4. =° ′ +° ′ = ′ + ′

The vector B expressed in terms of the ′′xy - coordinate system is Bij ij

10 cos1 51 0sin 15 9.66 2 .59 =° ′ +° ′ = ′ + ′

The sum of A and B is

AB (15.7)(1 3.0) 20.3. 22 += + = +=AB 20.3 208 158 408 x y x9 A

ABijij ij (6 10.4 )(9.66 2.59 ) 15.7 1 3.0 += ′ + ′ + ′ + ′ = ′ + ′

Therefore

Problem2.31 In Practice Example 2.3, the cable AB exerts a 900 -N force on the top of the tower. Suppose that the attachment point B is moved in the horizontal direction farther from the tower, and assume that the magnitude of the force F the cable exerts on the top of the tower is proportional to the length of the cable.

(a) What is the distance from the tower to point B if the magnitude of the force is 1000  N ? (b) Express the 1000 -N force F in terms of components using the coordinate system shown.

Solution: In the new problem assume that point B is located a distance d away from the base. The lengths in the original problem and in the new problem are given by

(a) The force is proportional to the length. Therefore

Problem2.32 Determine the position vector r AB in terms of its components if (a) 30 ; θ =° (b) 225 θ =°

(b) The force F is then

80 5  (N).

Solution:

(a) =° +° rij (6 0) cos(30 )(60)sin (3 0) , AB or rij 52.0 30  (mm ). AB =+

(b) =° +° rij (6 0) co s(22 5) (6 0) si n(225 ) AB or rij 42.4 42.4  (mm ). AB =− rijrij (a )  52.0 30  (mm). (b) 42.4 42.4  (mm ). ABAB =+ =−

Problem2.33 In Example 2.4, the coordinates of the fixed point A are (17, 1) ft. The driver lowers the bed of the truck into a new position in which the coordinates of point B are (9, 3) ft. The magnitude of the force F exerted on the bed by the hydraulic cylinder when the bed is in the new position is 4800  lb. Draw a sketch of the new situation. Express F in terms of components.

Solution:

Problem2.34 Using laser instruments, a surveyor determines that the coordinates of point B are = x 120 m, = y 122 m. He knows that r 125 m OA = and r 62 m. AB = Determine the vector rOA

Solution:

).

Problem2.35 The magnitude of the position vector r BA from point B to point A is 6 m and the magnitude of the position vector rCA from point C to point A is 4  m. What are the components of r ?BA

We can apply geometry. The angle β == ° arctan (122 m/120 m) 45.5 The side =+ = b (122 m )(120 m) 171 m , 22 and we are told that ==ac 125 m,  62 m Applying the law of cosines (Appendix A), α =+ caba b 2c os , 22 2 we obtain α = cos 0.956, so α =° 16.3 We can now determine the position vector of A: rij ij (125 m )c os() (125 m )sin () 59.1 11 0  (m ). OA αβ αβ =+ ++ =+ =+ rij 59.1 110  (m) OA

Solution: The coordinates are: AxyBC (,  ),  (0,  0),  (3 m,  0) AA Thus xyxy xyxy rij rij (0)( 0)  (6 m) (3 m )( 0) (4  m )( 3  m) BAAAAA CAAAAA 22 2 22 2 =− +− ⇒= + =− +− ⇒= −+

Solving these two equations, we find == ± xy 4.833 m,  3.55 5  m. AA We choose the “-” sign and find rij 4.83 3 .56  (m) BA =− x y B C 3 m rBA rCA A

Problem2.36 In Problem 2.35, determine the components of a unit vector e CA that points from point C toward point A. Strategy: Determine the components of rCA and then divide the vector rCA by its magnitude. A x y B C 3 m

Problem2.37 The hydraulic cylinder BC exerts a force F on the boom of the crane at C The force points from B toward C , and its magnitude is F 300 kN = Determine the components of F.

Solution: From the solution to the previous problem, we have ij rr 1.83 3 .56  (m), 4 m CACA =− =

Then

The angle α == ° arctan(2.4 /1.2)6 3. 4, so

Fij ij (300 kN )(co ssin ) 134 268  (kN). αα=+ =+

Alternatively, the distance from B to C is += (1.2 m )(2 .4 m) 2.68 m , 22 so

Fij ij 1.2 m 2.68 m (3 0 0 kN )  2.4 m 2.68 m (300 kN ) 134 268  (kN). =+ =+ =+ Fij 134 26 8  (k N) x y B C 3 m rBA rCA A eCA

Problem2.38 The length of the bar AB is 0.6 m. Determine the components of a unit vector e AB that points from point A toward point B

Solution: We need to find the coordinates of point Bxy (,  ) We have the two equations ++ = += xy xy (0.3 m )(0.6 m ) (0.4  m ) 22 2 22 2

Solving we find ==xy 0.183 m,  0 .356 m

Thus e r r ij ij

[(0.183 m )( 0.3 m )] (0.356 m ) [(0.183 m )( 0.3 m )] (0.356 m )

0.806 0.593

0.806 0 .593 AB AB AB 22 AB == + + =+ =+

Problem2.39 The link AC exerts a force F AC on the hydraulic cylinder at C . The force points from C toward A, and its magnitude is F 650 N. AC = Determine the components of F AC

Hydraulic cylinder x y

0.15 m 0.6 m

B D

m Scoop

Solution:

m 0.15 m

The angle α == ° arctan(0.15/ 0.6) 14.0 , so Fij ij (650 N )(sinc os ) 158 63 1  (N).

Alternatively, the distance from A to C is += (0.15 m )(0.6 m) 0.618 m, 22 so Fij ij

0.15 m 0.618 m (6 5 0 N )  0.6 m 0 .618 m (650 N ) 158 63 1  (N). AC =−

Fij 158 63 1  (N).

Problem2.40 The link CD exerts a force FCD on the hydraulic cylinder at C The force points from C toward D, and its magnitude is F 600 N. CD = Determine the components of F . CD

Solution: The angle α == ° arctan(0.4 /1.0)2 1.8 , so

CD αα=+ =+

ij (600 N )(co ssin ) 557 22 3  (N).

Fij

Alternatively, the distance from C to D is

+= (1 m )(0.4 m )1 .077 m , 22

so

CD =+ =+

1.0 m 1.077 m (6 00 N )  0.4 m 1.077  m (600 N ) 557 22 3  (N).

Fij

ij

Fij 557 22 3  (N).

CD

=+

Problem2.41 A surveyor finds that the length of the line OA is 1500  m and the length of the line OB is 2000  m (a) Determine the components of the position vector from point A to point B (b) Determine the components of a unit vector that points from point A toward point B.

Solution: We need to find the coordinates of points A and B

rij

rij 1500 co s6 01 50 0sin 60 750 1299  (m)

OA OA =° +° =+

Point A is at (750, 1299)  (m )

rij

rij 2000 co s3 02 00 0sin 30  (m) 1732 100 0  (m ) OB OB =° +° =+

Point B is at (1732, 1000)  (m )

(a) The vector from A to B is =− +− =− xxyy rij rij () () 982 29 9  (m ). ABBABA AB (b) The unit vector e AB is == =− r e r ij eij 982 29 9 1026.6 0.957 0 .291 AB AB AB AB rijeij (a )  982 29 9  (m ). (b) 0.957 0.291 ABAB =− =−

Problem2.42 The magnitudes of the forces exerted by the cables are T 2800  lb, 1 = T 3200  lb, 2 = T 4000  lb, 3 = and T 5000  l b. 4 = What is the magnitude of the total force exerted by the four cables?

y

Solution: The x -c omponent of the total force is

T T T TTTT co s9 co s2 9c os 40 co s5 1 (2800  l b) co s9 (3 20 0  lb)c os 29 (4000  l b) co s4 0(5000  l b) co s5 1 11,800  l b

x x x 12 34 =° +° °+ ° =° +° +° +° = The y -c omponent of the total force is T T T TTTT si n9 si n2 9sin 40 si n5 1 (2800  l b) si n9 (3 20 0  lb)sin 29 (4000  l b) si n4 0(5000  l b) si n5 1 8450  l b

y y y 12 34 =° +° +° +° =° +° +° +° = The magnitude of the total force is =+ =+ == TT TT (1 1,80 0  lb)(8450  l b) 14,500  l b1 4,500  l b xy 22 22

Problem2.43 The tensions in the four cables are T T , 1 =

T

, 2 =

4 = Determine the value of T so that the four cables exert a total force of 24  kN magnitude on the support.

Solution: The sum of the x components of the forces is

The sum of the y components of the forces is

The magnitude of the total force is += TTT(6.10 )(4 .82 ) 7.78 22

Equating this expression to 24  kN, we obtain = T 3.09 kN

Problem2.44 The rope ABC exerts forces FBA and FBC on the block at B Their magnitudes are equal: FFBABC = The magnitude of the total force exerted on the block at B by the rope is FF 920  N. BABC+= Determine FBA by expressing the forces FBA and FBC in terms of components.

Solution: F F F Fij Fj FFij (c os 20 si n2 0) () (c os 20 [sin 20 1] )

Therefore F (920 N )[(c os 20 °) (sin 20° 1) ]. 22 22=+

Solving, we obtain F 802 N = We see that F 802 N BA

Problem2.45 The magnitude of the horizontal force F1 is 5 kN and FFF0 12 3 ++ = What are the magnitudes of F2 and F3?

Solution: Using components we have FFF FFF :  5 kN co s4 5c os 30 0 :sin 45 si n3 00 x y 23 23 ∑+ °− °= ∑− °+ °=

Solving simultaneously yields:

⇒= = FF 9.66 kN,  13.66 kN 23

Problem2.46 Four groups engage in a tug-of-war. The magnitudes of the forces exerted by groups B, C, and D are FF 800  lb,  1000  lb, BC== and F 900  l b. D = If the vector sum of the four forces equals zero, what are the magnitude of F A and the angle ? α

Solution: The forces in terms of their components are FFij

Fij

Fij

Fij

AA B C D αα =− =− + =+ =−

(c os  sin  ), (800 l b)(c os 70°  sin 70° ), (1000 lb)(c os 30°  sin 30°  ), (900 l b)(c os 20°  sin 20°  )

The sum of the forces is zero, which means that the sums of the x and y components are zero. This yields two equations:

F F co s(800 l b) cos 70° (1000 l b) cos 30° (900 l b) cos 20° 0, si n(800 l b) sin 70° (1000 l b) sin 30° (900 l b) sin 20° 0, A A α α ++

or

F F cos 144 0  lb , sin 944 lb. A A α α = =

Squaring both sides of these two equations and summing them, FF (sin co s) (944 l b) (1440 l b) , AA 2 22 2 22 αα+= =+

We obtain F 1720 lb. A = Then from either of the two equations, we obtain 33.3° α =

F 1720 lb,  33.3° A α ==

Problem2.47 In Example 2.5, suppose that the attachment point of cable A is moved so that the angle between the cable and the wall increases from 40 ° to 55 ° Draw a sketch showing the forces exerted on the hook by the two cables. If you want the total force FFAB + to have a magnitude of 200  l b and be in the direction perpendicular to the wall, what are the necessary magnitudes of F A and F ?B

Solution: Denote the forces exerted by the cables by F A and FB We want the sum of the forces to be FFi 200  (lb ). AB+= Expressing F A and FB in terms of components, we want FiFjFiFji sin 55° co s5 5° sin 20° cos 20° 200  (lb ). AABB ++ −=

This yields the two equations FF FF sin 55° si n2 0° 200  lb, cos 55° co s2 0° 0. AB AB += −=

Solving, we obtain FF 195 lb,  119 lb. AB==

FF 195 lb,  119 lb. AB==

FA

Problem2.48 The bracket must support the two forces shown, where FF 2 kN 12== An engineer determines that the bracket will safely support a total force of magnitude 3.5 kN in any direction. Assume that 09 0. α ≤≤ ° What is the safe range of the angle α ?

Solution: The sum of the forces is

FFiij (2 kN )(2  kN )c os (2 kN )sin 12 αα += ++

The sum Its magnitude is

FF (2  kN )(1c os )sin (2 kN )2 2c os 12 22 αα α += ++ =+

At 0, α = the sum FF 4  kN,  12+= exceeding the safe limit. When the angle has increased to 90° , α = the sum has decreased to FF (2 kN) 2  2 .83 kN, 12+= = below the limit. At what angle is it equal to the limit? Setting

(2 kN )2 2c os 3.5 k N α += and solving, we obtain cos 0.531, α = which gives 57.9° α = The safe range is

57.9° 90°. α ≤≤

Problem2.49 The figure shows three forces acting on a joint of a structure. The magnitude of FC is 80 kN, and FFF0 ABC ++ = What are the magnitudes of F A and F ?B

Solution: Denote the magnitudes of FF  and  AB by A and B Writing the vectors in terms of their magnitudes,

AA BB Fij Fij Fj co s4 0sin 40 , cos1 5sin 15 , (80 kN ). A B C =° +° =− °− ° =−

We know that [] ++ =° −° +° −° −= ABAB FFFij0 (c os 40 cos1 5) si n4 0sin 15 (80 kN ). ABC

If a vector equals zero, each of its components equals zero, so we obtain the two equations

AB AB co s4 0c os15 0, si n4 0sin 15 (8 0 kN )0 °− °= °− °− =

Solving them we obtain == A F 183 kN, A == B F 145 kN B

==FF 183 kN,  1 45 k N. AB 158

Problem2.50 Four coplanar forces act on a beam. The forces FB and FC are vertical. The vector sum of the forces is zero. The magnitudes F 10  kN B = and F 5 kN C = Determine the magnitudes of F A and FD

Solution: Use the angles and magnitudes to determine the vectors, and then solve for the unknowns. The vectors are: =° +° =+ =− =+ =− +

(c os 30 si n3 0) 0.866 0.5 01 0,  0 5,  0 AAAA BCDD

Take the sum of each component in the x - and y - directions:

∑ =− = FFFi (0.86 6) 0 xAD and

∑ =− −=FFj (0.5 (1 05)) 0. yA

From the second equation we get = F 10  kN A Using this value in the first equation, we get = F 8.66 kN. D

Problem2.51 Six forces act on a beam that forms part of a building’s frame. The vector sum of the forces is zero. The magnitudes FFF 20  kN ,  16 kN , BEC == = and F 9 kN D = Determine the magnitudes of F A and F . G

Solution: Let FF ,  ,  AB denote the magnitudes of the forces. The sum of the horizontal components of the forces must equal zero,

FFFF cos 70° co s4 0° cos 40° cos 50° 0, ACDG ++ = and the sum of the vertical components must equal zero,

FFFFFF sin 70° si n4 0° sin 40° sin 50° 0. ABCDEG −+ +− +=

Substituting the given values of the magnitudes and solving, we obtain FF 13.0  kN,  1 5.3 kN AG==

FF 13.0  kN,  15.3 k N. AG==

Problem2.52 The total weight of the man and parasail is W 230  l b. = The drag force D is perpendicular to the lift force L. If the vector sum of the three forces is zero, what are the magnitudes of L and D ?

Solution: Let L and D be the magnitudes of the lift and drag forces. We can use similar triangles to express the vectors L and D in terms of components. Then the sum of the forces is zero. Breaking into components we have

Solving we find ==DL 85.4  lb,  214  l b

Problem2.53 The three forces acting on the car are shown. The force T is parallel to the x-axis and the magnitude of the force W is 14  kN If TWN0, ++ = what are the magnitudes of the forces T and N ?

Solution: Denote the magnitudes of the forces by TWN ,, The sum of the x components is equal to zero, FTN si n2 0° 0, x Σ= −= and the sum of the y components is zero, FWN co s2 0° 0. y Σ= −+ = Setting W 14  kN = and solving, we obtain

Problem2.54 The sum of the three forces acting on the beam is zero: FFF0 ABC ++ = The magnitude F 800 lb . A = Determine the magnitudes of FC and F . B

8

8

Problem2.55 The total force exerted on the top of the mast B by the sailboat’s forestay AB and backstay BC is ij 180 820  ( N). What are the magnitudes of the forces exerted at B by the cables AB and BC ?

Solution: y

8

(0, 1.2) m

(9, 1) m x B (4, 13) m

8

8 x

Let FFF ,  ,  ABC denote the magnitudes of the forces. The sum of the x components of the forces is

Σ= −° −° +° = FFFF co s4 5c os 80 co s5 00 xABC

The sum of the x components of the forces is

Σ= °− °+ °= FFFF si n4 5sin 80 si n5 00 yABC

Solving these two equations, we obtain ==FF 1590  lb,  131 0  lb BC ==FF 1590  lb,  131 0  lb BC

Solution: We first identify the forces: = −+ T Fij ( 4.0  m 11.8 m ) (4 .0  m )(11.8 m ) ABAB 22 = +− T Fij (5 .0  m 12.0  m ) (5.0  m )( 12.0  m )

BCBC 22

Then if we add the force we find

∑− +=FTT : 4 155.2 4 5 16 9 180  N xABBC

∑− −=FTT : 11.8 155.2 4 12 16 9 820  N yABBC

Solving simultaneously yields:

⇒= = TT 226 N,  657  N ABAC B C x y (4, 13) m (0, 1 2) m (9, 1) m FAB FBC A

Problem2.56 The structure shown forms part of a truss designed by an architectural engineer to support the roof of an orchestra shell. The members AB,AC, and AD exert forces FF ,  , ABAC and F AD on the joint A The magnitude F 4k N. AB = If the vector sum of the three forces equals zero, what are the magnitudes of F AC and F ?AD

( 4, 1) m B C D x y ( 2, 3) m

Solution: Determine the unit vectors parallel to each force:

= + + + =− eijij 2 23 3 23 0.5547 0.8320

AD 22 22

= + + + =− + eijij 4 41 1 41 0.9701 0.2425

AC 22 22

= + + + =+ eijij 4 42 2 42 0.89443 0.4472 AB 22 22

The forces are == FFeFFe ,  , ADADADACACAC

== + FFeij 3 .578 1 .789 ABABAB Since the vector sum of the forces vanishes, the x - and y -components vanish separately:

The results: ==FF 2.11 kN, 2.76 kN ACAD FAB FAC FAD A

∑ =− −+ = FFFi ( 0.5547 0.9701 3.578)0, xADAC and

∑ =− ++ = FFFj ( 0.8320 0 .2425 1.789)0 yADAC

Problem2.57 The distance s 45 i n. = (a) Determine the unit vector e BA that points from B toward A (b) Use the unit vector you obtained in (a) to determine the coordinates of the collar C .

Solution:

(a) The position vector from point B to point A is [Fig. (a)]

rijij (14 i n7 5 in)(45 in 12 i n) 61 33  in.

BA =− +− =− +

Dividing this vector by its magnitude, we obtain the desired unit vector:

e r r ijij61 33  i n (6 1  in)(33 i n) 0.880 0.476

BA BA BA 22 == −+ −+ =− +

(b) We can write the position vector from point B to the collar C [Fig. (b)] as

s reij (4 5 i n)( 0.880 0.476 ). BCBA== −+

The position vector of point B relative to the origin is rij 75 12  in. B =+

(4, 2) m x y (14, 45) in (75, 12) in A B eBA rBA

Then the position vector of point C relative to the origin is rrrij 35.4 33.4  in.

These simultaneous equations in two unknowns can be solved by any standard procedure. An HP-28S hand held calculator was used here:

CBBC =+ =+ (35.4 in, 33.4 in). y x s A B C (14, 45) in (75, 12) in

Figure (a) x y A B C (75, 12) in rB rBC rC

Figure (b)

Problem2.58 Determine the x and y coordinates of the collar C as functions of the distance s.

Then the position vector of point C relative to the origin is ss rrrij (7 5 0.88 0) (1 2 0.476 )  in

CBBC =+ =− ++

Solution:

The position vector from point B to point A is [Fig. (a)] rijij (14 i n7 5 in)(45 in 12 i n) 61 33  in.

BA =− +− =− +

Dividing this vector by its magnitude, we obtain a unit vector that points from point B toward point A:

e r r ijij61 33  i n (6 1  in)(33 i n) 0.880 0.476 BA BA BA 22 == −+ −+ =− +

We can write the position vector from point B to the collar C [Fig. (b)] as ss reij (0 .880 0.476 ).

BCBA== −+

The position vector of point B relative to the origin is rij 75 12  in.

B =+ y x s A B C (14, 45) in (75, 12) in

Problem2.59 The vector U can be expressed in terms of its components in terms of either the x–y coordinate system or the x ′ – y ′ coordinate system: =+ = ′ + ′ ′′ UU UU Uij ij xy xy

xsys 75 0.88 0  i n,  12 0.476  in. =− =+

Figure (a) x y (14, 45) in (75, 12) in A B eBA rBA x y A B C (75, 12) in rB rBC rC

Figure (b)

Solution:

It can be shown that the component Ux ′ is given in terms of the components Ux and Uy and the angle θ by UUU co ss in . xxyθθ=+ ′ Determine the component Uy ′ in terms of the components Ux and Uy and the angle θ Strategy: Draw a diagram showing the components U , xU , yU , x ′ and Uy ′ and apply trigonometry to determine Uy ′ Ux Uy9 Ux sinu Uy sinu U x9 y9 x y u u u x9 U x y y9 u

From the diagram, θθ=− UUU co ssinyyx

θθ=− UUU co ssinyyx

Problem2.60 Let r be the position vector from point C to the point that is a distance s meters from point A along the straight line between A and B Express r in terms of components. (Your answer will be in terms of s )

Solution: First define the unit vector that points from A to B =− +− =+ =+ = =+ rijij r eij (10 m 3 m )(9 m 4 m )7 5  (m ). (7  m )(5  m) 74  m 1 74 (7 5)

BA BA / / 22 /

The vector r that points from C to P is then =+ −+ +−ss rij [(3 0.814 )9][(4 0.581 )3]  (m ). =− ++ss rij (0.814 6) (0 .581 1)  (m) x y A (9, 3) m (10, 9) m (3, 4) m B C r s

Let P be the point that is a distance s along the line from A to B The coordinates of point P are () =+ =+ xss 3  m 7 74 (3 0.814 )  m p () =+ =+ yss 4  m 5 74 (4 0.581 )  m. p

Problem2.61 A vector Uijk 34 12 . =− What is its magnitude?

Strategy: The magnitude of a vector is given in terms of its components by Eq. (2.14).

Problem2.62 Two forces are given in terms of their components by Fijk 60 20 30 (l b), A =− + Fijk 30 40 10 (l b) B =+ (a) What are the magnitudes of the forces? (b) What is the magnitude of their sum FF ?AB +

Strategy: The magnitude of a vector in terms of its components is given by Eq. (2.14).

Solution: Use definition given in Eq. (14). The vector magnitude is =+

−= U 3( 4) (1 2) 13 22 2

Solution: (a) The magnitudes of the vectors are

(b) The sum of the vectors is += ++ FFijk 90 20 20  (lb ).

The magnitude of the sum is += ++ = FF (9 0 lb)(20  l b) (2 0  lb) 94.3 lb. AB 222 == +=FFFF (a )  70.0  lb,  5 1.0  lb. (b) 94.3 lb.

Problem2.63 Consider three vectors =+Ai 12 jk81 6, BBB Bijk, xyz=+ + and =+ C Ci x + CCjkyz Their sum is zero, ABC0, ++ = and the components of B and C satisfy the relations BB2,xy =− BB , yz =− and CC3.xy = What are the magnitudes of B and C ?

Solution: The sum of the vectors is zero, which yields the three equations FBC FBC FBC 12 0, 80, 16 0. xxx yyy zzz Σ= ++ = Σ= ++ = Σ= −+ +=

We also have the three given equations BB BB CC 2, , 3. xy yz xy =− =− =

Solving these six equations, we obtain == −=BBB 4.8,  2.4,  2.4, xyz =− =− = CCC 16.8,  5. 6, 13.6. xyz The magnitudes of the vectors are BBB CCC B C

(4.8)( 2.4  l b) (2.4) 5.88, ( 16.8)( 5. 6) (13.6) 22.3. xyz xyz 22 2 22 2 22 2 22 2 =+ + =+ −+ = =+ + =− +− + = ==BC 5.88,  2 2.3.

Problem2.64 A vector UUU Uijk xyz=+ + Its magnitude U 30. = Its components are related by the equations UU 2 yx =− and UU4.zy = Determine the components.

Problem2.65 An object is acted on by two forces Fij 20 30 1 =+ k 24 (k N) and =− + Fi 60 2 + jk 20 40  (kN ). What is the magnitude of the total force acting on the object?

Solution: Substitute the relations between the components, determine the magnitude, and solve for the unknowns. Thus =+ −+ −= UUUU Uijkijk (2 )(4( 2))(12 8) xxxx where U x can be factored out since it is a scalar. Take the magnitude, noting that the absolute value of U x must be taken:

=+ += UU 30 12 8(8.31).xx 22 2

Solving, we get = U 3.612, x or =± U 3.61. x The two possible vectors are Uijk ijk Uijk ijk

=+ +− +− =− =− +− −+ =− ++

3.61 (2(3 .61)) (4(2)(3.61))

3.61 7.2 22 8.9

3.61 (2(3 .61)4(2)( 3.61)

3.61 7.22 28.9

Solution: The sum of the forces is += −+ + +− + =− ++ FFij k ijk (2 0  kN 60  kN) (3 0  kN 20  kN ) (2 4  kN 40  kN ) 40 50 16  (kN), 12

So FF (4 0  kN )(50  kN )(16 kN )6 6  kN 12 22 2 += −+ += 66 kN

Problem2.66 The position vector r AB extends from point A to point B. (a) Express r AB in terms of components. (b) Determine its magnitude r AB

Solution:

(a) The components of r AB are =− −+ +− =− + rijk ijk (1 2  ft (2  ft))( 2  ft 6  ft )(8  ft 3  ft ) 14 85  (ft ). AB

(b) Its magnitude is

=+ −+ = r (1 4  ft )( 8  ft )(5  ft ) 16.9 ft. AB 22 2 =− +=rijkr (a )  14 85  (ft ). (b) 16.9 ft. ABAB y z x A B rAB

Problem2.67 The position vector r AB extends from point A to point B. (a) Determine the direction cosines of r . AB (b) Determine the components of a unit vector that has the same direction as r AB

( 2, 6, 3) ft

( 2, 6, 3) ft

(12, 2, 8) ft

(b) The direction cosines are the components of the desired unit vector. (Notice that the direction cosines are the components of r AB divided by its magnitude.) Therefore, =− + eijk 0.829 0.474 0.296

== −= =− + eijk

(a )  co s0 .829,  cos 0.474,  cos 0.296. (b )  0.829 0.474 0.296 xyz y z x A B rAB

(12, 2, 8) ft

Solution:

(a) The components of r AB are

(1 2  ft (2  ft))( 2  ft 6  ft )(8  ft 3  ft )

=− −+ +− =− + rijk ijk

AB and its magnitude is

14 85  (ft ),

=+ −+ = r (1 4  ft )( 8  ft )(5  ft )

AB 22 2

16.9 ft.

Its direction cosines are

co s 14  ft

16.9 ft 0.82 9,

co s 8  ft

co s 5  ft 16.9 ft 0 .296 x y z

16.9 ft 0.47 4,

Problem2.68 A force vector is given in terms of its components by Fijk 10 20 20  ( N). =− (a) What are the direction cosines of F ? (b) Determine the components of a unit vector e that has the same direction as F

Problem2.69 Express the position vector r BD from point B to point D in terms of components. What are its direction cosines?

Solution: =− Fijk (1 02 02 0)  N =+ −+ −= F (1 0  N) (2 0  N) (2 0  N) 30  N 222 eijk

(a )  co s0 .333,  cos 0.667,  cos 0.667. (b )  0.333 0.667 0.667 xyz

Solution:

(0, 5, 5) m (0, 4, 3) m

(0, 5, 5) m

(4, 3, 1) m

x (4, 3, 1) m

The vector r BD from point B to point D is rij ijk (0 4  m) (5 m 3  m) (5 m 1  m) 42 4  (m ).

=− +− +−

++ Its magnitude is =− ++ = r (4  m )(2 m) (4  m ) 6  m.

22 2 Its direction cosines are co s 4  m 6  m 0.66 7, co s 2 m 6  m 0.33 3, co s 4  m 6  m 0 .667

=− ++

rijk 42 4  (m ),  c os 0.667,  cos 0.333,  cos 0.667. BDx yz

Problem2.70 The cable from B to C exerts a force on the bar AB at B The force points from B toward C and its magnitude is 80 N. Express the force in terms of components.

(0, 4, 3) m

(0, 5, 5) m

(4, 3, 1) m E

Solution:

(0, 4, 3) m rBC

(4, 3, 1) m

The vector r BC from point B to point C is rij ijk (0 4  m) (4  m 3  m) (3 m 1  m) 44  (m) BC =− +− +− =− +−

Its magnitude is r (4  m )(1 m )( 4  m) 5.74  m

22 2 =− ++

By dividing the vector by its magnitude, we obtain a unit vector that points from point B toward point C :

ijk 44  (m) 5.7 4  m 0.696 0.174 0 .696 BC = −+ =− +− y C

(0, 4, 3) m eBC

(4, 3, 1) m

We obtain the force in terms of its components by multiplying the unit vector by 80  N:

Problem2.71* The suspended weight E exerts an 800 -N downward force on bar AB at B The cable from B to C exerts a force on the bar at B that points from B toward C , but its magnitude is unknown. The cable from B to D exerts a force on the bar that points from B toward D, and its magnitude is also unknown. If the weight of bar AB is negligible, the sum of the three forces exerted on it at B is a vector that is parallel to the bar. Use this condition to determine the magnitudes of the forces exerted by cables BC and BD

(0, 4, 3) m

(0, 5, 5) m

(4, 3, 1) m

Solution: y C B

(4, 3, 1) m

(0, 4, 3) m rBC z x

The vector r BC from point B to point C is rij ijk (0 4  m) (4  m 3  m) (3 m 1  m)

BC =− +− +− =− +−

44  (m)

Its magnitude is

r (4  m )(1 m )( 4  m) 5.74  m

BC 22 2 =− ++ = By dividing r BC by its magnitude, we obtain a unit vector that points from point B toward point C : eijk ijk

44  (m)

BC = −+ =− +−

5.7 4  m 0.696 0.174 0 .696

Let FBC be the force exerted at B by the cable BC It can be expressed as

FFe

Fijk ( 0.69 60 .174 0.696 ).

BCBCBC BC = =− +− y D B (4, 3, 1) m

(0, 5, 5) m rBC z x

The vector r BD from point B to point D is

BD =− +− +− =− ++

(0 4  m) (5 m 3  m) (5 m 1  m)

rijk ijk

42 4  (m ).

Its magnitude is

BD 22 2 =− ++ =

r (4  m )(2 m )(4  m) 6  m.

Dividing r BD by its magnitude, we obtain a unit vector that points from point B toward point D: eijk ijk

BD = −+ + =− ++

42 4  (m ) 6  m 0.667 0.333 0.667

Let FBD be the force exerted at B by the cable BD It can be expressed as

FFe

Fijk ( 0.66 70 .333 0.667 ).

BDBDBD BD = =− ++ y A (4, 3, 1) m

(0, 0, 0)

rBA z x

The vector r BA from point B to point A is rijk ijk

BA =− +− +− =−

(0 4  m) (0 3  m) (0 1  m)

43  (m).

2.71 (Continued)

Its magnitude is

r (4  m )( 3  m) (1 m )

5.10  m BA 22 2 =− +− +− =

Dividing r BA by its magnitude, we obtain a unit vector that points from point B toward point A:

eijk

BA = =−

43  (m)

5.1 0  m

0.784 0.588 0.196

ijk

We can write the given condition on the forces at B as

+− = F FFje (8 00  N ), BCBDBA

Problem2.72 Determine the components of the position vector r BD from point B to point D. Use your result to determine the distance from B to D

D (4, 3, 1) m z y x

C (6, 0, 0) m

B (5, 0, 3) m

Problem2.73 What are the direction cosines of the position vector r BD from point B to point D ?

D (4, 3, 1) m z y x A

B (5, 0, 3) m

C (6, 0, 0) m

where F is an unknown constant. Notice that this condition yields three equations. Its i component is

=− F FF 0.696 0.667 0.784 , BCBD its j component is

+− =− F

FF 0.174 0 .333 80 0  N 0.588 , BCBD and its k component is

−+ =− F

FF 0.696 0.667 0.196 BCBD

Solving these three equations yields = F 657 N, BC = F 411 N, BD and = F 932 N

Solution: The position vector from point B to point D is rijk ijk (4 m 5 m) (3 m 0) (1 m 3 m )

BD =− +− +− =− +−

32  (m).

The distance from B to D is the magnitude r (1 m )(3  m) (2  m) 3.74 m BD 22 2 =− ++ −= 3.74 m

Solution: The position vector from point B to point D is rijk ijk (4 m 5 m) (3 m 0) (1 m 3 m )

BD =− +− +− =− +−

32  (m)

Its magnitude is r (1 m )(3  m) (2  m) 3.74 m . BD 22 2 =− ++ −=

Using the definitions of the direction cosines, θθ θ = =− == = =−

co s 2  m 3.74  m 0.535. xy

co s 1  m 3.74  m 0 .267,    co s 3  m 3.74  m 0.802,

θ =− == cos 0.267,    cos 0.802,    cos 0.535. xyz

BCBD : 657 N,  :4 1 1 N x y z rBD D B (5, 0, 3) m (4, 3, 1) m x y z rBD D B (5, 0, 3) m (4, 3, 1) m

Problem2.74 Determine the components of the unit vector e CD that points from point C toward point D

D (4, 3, 1) m z y x

C (6, 0, 0) m

B (5, 0, 3) m

Problem2.75 What are the direction cosines of the unit vector e CD that points from point C toward point D ?

B (5, 0, 3) m C (6, 0, 0) m D (4, 3, 1) m

Solution: The position vector from point C to point D is rijk ijk (4 m 6 m) (3  m 0) (1 m 0)

CD =− +− +− =− ++

23  (m)

Its magnitude is

r (2  m )(3  m) (1 m) 3.74 m .

CD 22 2 =− ++ =

We obtain the desired unit vector by dividing this vector by its magnitude:

e r r ijk 0 .535 0 .802 0.267

CD CD CD == −+ + eijk 0.535 0.802 0.267 . CD =− ++

CD

Solution: Because the magnitude of a unit vector is 1, we can see from the definitions of the direction cosines that the direction cosines of a unit vector are its components. The position vector from point C to point D is rijk ijk (4 m 6 m) (3  m 0) (1 m 0)

CD =− +− +− =− ++

23  (m)

Its magnitude is

r (2  m )(3  m) (1 m) 3.74 m

CD 22 2 =− ++ =

We obtain the unit vector by dividing this vector by its magnitude:

e r r ijk 0 .535 0 .802 0.267 CD CD CD == −+ +

We see that cos 0.535,  co s0 .802,  cos 0.267. xyz θθ θ =− == cos 0.535,  co s0 .802,  cos 0.267. xyz θθ θ =− ==

rCD D (4, 3, 1) m C (6, 0, 0) m eCD

(4, 3, 1) m C (6, 0, 0) m eCD x y

Problem2.76 In Example 2.7, suppose that the caisson shifts on the ground to a new position. The magnitude of the force F remains 600  lb. In the new position, the angle between the force F and the x-axis is 60 ° and the angle between F and the z -axis is 70 ° Express F in terms of components.

Solution: We need to find the angle θ y between the force F and the y-axis. We know that

θθθ ++ = co sc os co s1xyz 222

θθ θ =± =± −° −° =± co s1 co sc os 1c os 60 co s7 0 0.7956 yxz 22 22

θ =± =° ° co s(0.7956)3 7.3  or 142.7 y 1

We will choose θ =° 37.3 y because the picture shows the force pointing up. Now

F F F (600  l b) co s6 03 00  l b (600  l b) cos 37.3 477 lb (600  l b) co s7 02 05 l b

x y z =° = =° = =° =

Thus Fijk 300 477 20 5  (l b) =+ +

Problem2.77 Astronauts on the space shuttle use radar to determine the magnitudes and direction cosines of the position vectors of two satellites A and B The vector r A from the shuttle to satellite A has magnitude 2 km and direction cosines cos 0.768,c os 0.384, xy θθ== cos 0.512. z θ = The vector r B from the shuttle to satellite B has magnitude 4  km and direction cosines cos 0.743,c os 0.557,c os 0.371. xyz θθ θ == =− What is the distance between the satellites?

Solution: The two position vectors are:

The distance is the magnitude of the difference: rrAB

=− +− +− = (1.536 2 .927)(0 .768 2.228)(1.024 ( 1.484)) 3.24  (km ) 22 2

Problem2.78 Archaeologists measure a pre-Columbian ceremonial structure and obtain the dimensions shown. Determine (a) the magnitude and (b) the direction cosines of the position vector from point A to point B

Solution:

(a) The coordinates are A (0 , 16, 14) m and B (10, 8, 4) m.

AB

=− +− +− =− rijk ijk ([10 0] [8 16][41 4] )  m (1 08 10 )  m

(b)

=+ += = r 10 81 0  m 264  m 16.2 m

AB 22 2 = r 16.2 m AB

co s 10 26 4 0 .615

co s 8 26 4 0 .492

co s 10 264 0.615 x y z

Problem2.79 Consider the structure described in Problem 2.78. After returning to the United States, an archaeologist discovers that a graduate student has erased the only data file containing the dimension b But from recorded GPS data he is able to calculate that the distance from point B to point C is 16.61 m. (a) What is the distance b ? (b) Determine the direction cosines of the position vector from B to C

Solution: We have the coordinates + BC (1 0  m, 8  m, 4  m),(10  m b,  0 18 m ).

=+ −+ −+ b rijk (1 0  m1 0  m) (0 8  m) (1 8  m4  m )

BC

=+ −+ b rijk () (8 m )(14  m ) BC

(a) We have =+ −+ b (16.61 m )( 8  m) (1 4  m) 22 22

⇒= b 3.99 m

(b) The direction cosines of r BC are

co s 3.99  m 16.61 m 0.240

co s 8  m 16.61 m 0.482

co s 14  m 16.61 m 0.84 3 x y z

Problem2.80 Observers at A and B use theodolites to measure the direction from their positions to a rocket in flight. If the coordinates of the rocket’s position at a given instant are (4, 4, 2) km, determine the direction cosines of the vectors r AR and r BR that the observers would measure at that instant.

Solution: The vector r AR is given by

=+ + rijk 44 2  km AR

and the magnitude of r AR is given by

=+ += r (4)(4) (2)  km 6  km AR 22 2

The unit vector along AR is given by = urrARARAR

Thus, =+ + uijk 0.667 0.66 70 .333 AR and the direction cosines are

θθ θ == = cos 0.667,  cos 0.667, and  cos 0.333. xyz

The vector r BR is given by

(5, 0, 2) km

xxyyzz rijk ijk () () ()  km

BRRBRBRB =− +− +− =− +− +−

(4 5) (4 0) (2 2)  km

and the magnitude of r BR is given by

=+ += r (1)(4) (0)  km 4.12 km BR 222

The unit vector along BR is given by = rr e BRBRBR

Thus, =− ++ uijk 0.242 0 .970 0 BR and the direction cosines are

θθ θ =− == cos 0.242,  cos 0.970, and  cos 0.0. xyz

Problem2.81 Point p lies in the x–z plane. The line from point p to the tip of the vector r is parallel to the y -a xi s. If rijk 12 61 0(m), =+ + what are the angles φ and ψ in degrees?

Solution: The coordinates of the tip of the vector r are (1 2, 6, 10)  m, so the coordinates of point p are (1 2, 0, 10)  m. The length of the line from the origin to point p is

+= (1 2 m) (1 0  m) 15.6 m : 22

The tangent of ψ is

ψ == ta n 6  m 15.6 m 0.384, which yields θ =° 21.0

The tangent of φ is

φ == ta n 10  m 12 m 0.833, which yields φ =° 39.8

φψ =° =° 39.8 ,  2 1.0

Problem2.82 The height of Mount Everest was originally measured by a surveyor in the following way. He first measured the altitudes of two points and the horizontal distance between them. For example, suppose that the points A and B are 3000  m above sea level and are 10,000 m apart. He then used a theodolite to measure the direction cosines of the vector r AP from point A to the top of the mountain P and the vector r BP from point B to P. Suppose that the direction cosines of r AP are θθ== cos 0.5179,c os 0.6906, xy and cos 0.5048, z θ = and the direction cosines of r BP are cos 0.3743,c os 0.7486, xy θθ =− = and cos 0.5472. z θ = Using this data, determine the height of Mount Everest above sea level.

Solution: Using the given direction cosines, we have rrijk (0.5179 0.6906 0.5048 ), APAP=+ + (1) rrijk (0 .3743 0.7486 0.5472 ). BPBP=− ++ (2)

Let ri (10,000 m ) AB = denote the vector from point A to point B.

We can see that rrr , APABBP =+ and using the expression for the vectors in terms of their components, this gives the three equations

0.5179 10,000 m 0.3743 , 0.6906 0 .7486 , 0.5048 0 .547 2.

Solving these three equations (the second and third equations are redundant), we obtain

rr 11,585 m,  10,687 m . APBP==

To obtain the height of the mountain, we add 3000 m to the z component of r : AP

r 3000 m 0.5048

8848 m (29,030 ft) AP +=

8848 m (29,030 ft)

Problem2.83 The distance from point O to point A is 20  ft. The straight line AB is parallel to the y -axis, and point B is in the x–z plane. Express the vector rOA in terms of components.

Strategy: You can express rOA as the sum of a vector from O to B and a vector from B to A You can then express the vector from O to B as the sum of vector components parallel to the x - and z -axes. See Example 2.8.

Solution: The vector rOA is the sum of the vector r , OB which lies in the xz - plane, and the vertical vector r BA Because the distance from O to A is 20  ft, we can see that the magnitudes r (20 ft) co s3 0° OB = and r (20 ft) sin 30° BA = The vector rOB in terms of its components is rrirk si n6 0° co s6 0° , OBOBOB =+ and the vector r BA in terms of its components is rrj BABA = Therefore

OAOBBA OBOBBA =+ =+ + =+ + =+ + rijk 15 10 8.6 6  (ft) OA =+ +

(20 ft) sin 30° 15 10 8.6 6  (ft)

rirkrj ikj ijk si n6 0° co s6 0° (20 ft) co s3 0° si n6 0° (20 ft) cos 30° cos

Problem2.84 The magnitudes of the two force vectors are F 140  l b A = and F 100  l b. B = Determine the magnitude of the sum of the forces FFAB + .

140  lb([c os 40 si n5 0] [sin 40 ][co s4 0c os 50 ])

(82.2 90.0 6 8.9 )  lb

Solution: We have the vectors =° °+ °+ °° =+ + =− °° +° +° ° =− ++ Fijk Fijk Fijk Fijk

A A B B

100  lb([c os 60 si n3 0] [sin 60 ][co s6 0c os 30 ]) ( 25.0 8 6.6 43.3 )  lb

Adding and taking the magnitude we have

+= ++ FFijk (57.2 176.6 112.2 )  lb AB

+= ++ = FF (57.2 l b) (176.6 l b) (112.2 l b) 217 l b B A 222

+=FF 217 lb AB

y z

Problem2.85 Determine the direction cosines of the vectors F A and FB

Solution: We have the vectors

140  lb([c os 40 si n5 0] [sin 40 ][co s4 0c os 50 ])

A A B B The direction cosines for FA are

(82.2 90.0 6 8.9 )  lb

100  lb([c os 60 si n3 0] [sin 60 ][co s6 0c os 30 ])

( 25.0 8 6.6 43.3 )  lb

co s 82.2 l b 140  l b 0.587,  co s 90.0  l b 140  l b 0.643,

co s 68.9 l b 140  l b 0.49 2

xy z θθ θ == == ==

The direction cosines for FB are

co s 25.0  l b 100  l b 0 .250,  co s 86.6 l b 100  l b 0.866,

co s 43.3 l b 100  l b 0.43 3

xy z θθ θ = =− == ==

F F :c os 0 .58 7,  c os 0.643,  cos 0.492 :c os 0.25 0,  c os 0.866,  cos 0.433

Problem2.86 The positions of two airplanes A and B relative to a control tower are determined by radar. Their distances from the control tower are r 16 km A = and r 12 km . B = Determine the components of the position vector r AB from plane A to plane B (that is, the vector that specifies the position of plane B relative to plane A ). What is the straight-line distance between the two planes?

Solution: The components of r A are rijk ijk (1 6  km )(c os 20 co s3 0sin 20 co s2 0sin 30 ) 13.0 5.4 77 .52  (km ). A =° °+ °− °° =+

The components of are rijk ijk (1 2  km )( co s6 0sin 40 si n6 0c os 60 co s4 0) 3.86 10.4 4.6 0  (k m) B =− °° +° +° ° =− ++

The vector from plane A to plane B is rrr ijk 16.9 4 .92 12.1  (km).

ABBA =− =− ++

The distance between the planes is r (1 6.9 km )(4.92 km )(12.1 km ) 21.3 km. AB 22 2 =− ++ = =− ++ = rijk 16.9 4.9 21 2.1  (km), di stan ce 21.3 km

Problem2.87 An engineer calculates that the magnitude of the axial force in one of the beams of a geodesic dome is P 7.65 kN. = The cartesian coordinates of the endpoints A and B of the straight beam are ( 12.4,  22.0, 18.4)  m and ( 9.2,  24.4, 15.6)  m, respectively. Express the force P in terms of components.

Problem2.88 The cable BC exerts an 8-kN force F on the bar AB at B (a) Determine the components of a unit vector that points from point B toward point C . (b) Express F in terms of components.

Solution: The components of the position vector from B to A are

+− +−

xxyyzz rijk ijk ijk () () ()

(3, 0, 4)

++ −+ −+

12.4 9.2)(22.0 24.4)( 18.4 15.6)

2.4 2. 8  (m ).

Dividing this vector by its magnitude, we obtain a unit vector that points from B toward A:

eijk 0.655 0.492 0.573

Solution:

Problem2.89 A cable extends from point C to point E . It exerts a 50 -l b force T on the plate at C that is directed along the line from C to E Express T in terms of components.

Solution: Find the unit vector e CE and multiply it times the magnitude of the force to get the vector in component form, == −+ −+ −+ −+ xxyyzz xxyyzz e r r ijk () () () () () () CE CE CE ECECEC ECECEC 22 2

The coordinates of point C are (4,4 si n2 0, 4c os 20 ) −° ° or (4, 1.37, 3.76)  (ft) The coordinates of point E are (0,  2,  6)  (ft) = −+ +− ++ =− ++

(0 4) (2 (1 .37)) (6 3.76) 4 3.37 2.24

0.703 0.59 20 .394

50  (lb) 35.2 29.6 1 9.7  (lb) CE CE CE 22 2

Problem2.90 A cable extends from point B to point D

It exerts a 30 -l b force on the bar at B that is directed along the line from B to D Express the force in terms of components.

Solution: The vector r BD from point B to point D is rij ijk

BD =− + −−+ =− +

(1 8  in 8  in)( 8  in 0) (7  in0) 10 87  (in ).

Its magnitude is

14 in 8 in

BD 22 2 =+ −+ =

r (1 0  in)( 8  in)(7  in) 14.6 in.

By dividing this vector by its magnitude, we obtain a unit vector that points from point B toward point D: eijk ijk 10 87  (in ) 14.6 i n 0.685 0 .548 0 .480

BD = −+ =− +

We obtain the force in terms of its components by multiplying this unit vector by 30  lb:

=− + eijk (30 l b) 20. 61 6.4 14.4  (lb ). BD

−+ ijk 20.6 16.4 14.4  (lb ).

(18, 8, 7) in

(8, 0, 0) in (18, 8, 7) in B y x z D eBD

(18, 8, 7) in B y x z D

(8, 0, 0) in

Problem2.91 The cable AB exerts a 200 -l b force F AB at point A that is directed along the line from A to B. Express F AB in terms of components.

Solution: The vector from point A to point B is rijk ijk (0 6 ft) (6 ft0)(8 ft 10 ft) 66 2  (ft).

AB =− +− +− =− +−

0, 10) ft

Problem2.92 The cable CD exerts a 6-kN force on the bar at C that is directed from C toward D Express the force in terms of components.

Solution:

The vector rCD from point B to point D is rijk ijk (1.5 m 0) (0 2 m) (0 (1 m )) 1.5 2  (m ). CD =− +− +− =− + Its magnitude is r (1.5 m )( 2 m) (1 m ) 2.69 m . CD 22 2 =+ −+ = By dividing this vector by its magnitude, we obtain a unit vector that points from point C toward point D: eijk ijk

CD = −+ =− +

1.5 2  (m )

2 .69 m 0.557 0.743 0.371

Its magnitude is r ( 6 ft) (6 ft) ( 2 ft) 8.72 ft.

AB 22 2 =− ++ −=

The unit vector that points from point A toward point B is given by

e r r ijk 0.688 0 .688 0.229

AB AB AB == −+

Then the force F AB in terms of its components is

Feijk (200 l b) 138 138 45.9  (lb ). ABAB== −+

Fijk 138 138 45.9  (lb ). AB =− +− x y z B A rAB eAB (6, 0, 10) ft (0, 6, 8) ft

2, –1)

(0, 2, –1) m

(1.5, 0, 0) m x y z eCD

We obtain the force in terms of its components by multiplying this unit vector by 6  kN: =− + eijk(6 kN)

(kN).

Problem2.93 The 70 -m -tall tower is supported by three cables that exert forces FF ,  , ABAC and F AD on it. The magnitude of each force is 2 kN . Express the total force exerted on the tower by the three cables in terms of components.

Solution: The coordinates of the points are A  (0,  7 0,  0), BCD  (40,  0,  0), (4 0,  0,  40)   ( 60,  0, 60).

The position vectors corresponding to the cables are: =− −+ −+ rijk (6 00)(07 0) (6 00) AD =− rikk 60 70 60 AD =− −+ −+ rijk (4 00)(07 0) (4 00)

−+ rijk 40 70 40

=− +− +− rijk (4 00)(07 0) (0 0)

=− + rijk 40 70 0

The unit vectors corresponding to these position vectors are:

r r ijk ijk 60 11 0 70 11 0 60 110 0.5455 0 .6364 0.5455

The forces are: == −+ FFuijk 0.9926 1.737 0 ABABAB == + FFuij 0.8888 1.5556 0.8888 ACACAC

FFuijk 1.0910 1.2728 1.0910

The resultant force exerted on the tower by the cables is:

+= FFFFijk 0 .9875 4.5648 0.2020  kN RABACAD

Problem2.94 The magnitudes of the two force vectors are F 4.6 kN A = and F 5.2 kN B = Determine the magnitude of the sum of the forces FF . AB + (Notice that the angle between the vector FB and the positive x -a xi s is 180 57 123 °− °= ° )

Solution: The vectors in terms of their direction cosines are

(4.6 kN )(co sc os co s)

AAxAyAz

(4.6 kN )(co s5 0c os 44 co s7 5)

2.96 3 .31 1.1 9  (k N),

(5.2 kN )(co sc os co s)

BBxByBz

(5.2 kN )(cos123 co s4 0c os 70 )

θ =+ + =° +° +° =+ + =+ + =° +° +° =− ++ Fijk ijk ijk Fijk ijk ijk

2.83 3 .98 1.7 8  (k N)

The magnitude of their sum is

FF (2 .96 2.83)(3.31 3.98)(1.19 1.78)  (k N) 7.87  kN

AB 22 2 += −+ ++ + = +=FF 7 .87  kN AB

Problem2.95 The rope BD is attached to the bar ABC at B. The distance from A to B is 3  m. Determine the components of the position vector r BD from point B to point D

The vector from A to D is =− rik 74  (m) AD

Because =+ rrr , ADABBD we obtain

(1 .15 1.54 2.30 )  (m ) 5.85 1.54 1 .70  (m)

=− rijk

1.54 1.7 0  (m ).

Solution: The vector from A to C is =+ rijk 34 6  (m ). AC

Dividing this vector by its magnitude gives a unit vector that points from A toward C We can obtain the vector from A to B by multiplying that unit vector by 3  m: =

AB AC AC 22 2

r r r ijk ijk (3 m ) (3 m ) 34 6  (m ) (3  m )(4 m) ( 6 m ) 1.15 1.54 2.30  (m)

Problem2.96 The rope BD is attached to the bar ABC at B. The distance from A to B is 3  m. The rope exerts a 2-kN force on the bar at B that is directed from B toward D Determine the components of the force.

The vector from A to D is =− rik 74  (m) AD

Because =+ rrr , ADABBD we obtain

BDADAB =− =− −+ =−

ikijk ijk 74 (1.15 1.54 2.30 )   (m) 5.85 1 .54 1.7 0  (m ).

Solution: The vector from A to C is =+ rijk 34 6  (m ). AC

Dividing this vector by its magnitude gives a unit vector that points from A toward C We can obtain the vector from A to B by multiplying that unit vector by 3  m:

r r r ijk ijk (3 m ) (3 m ) 34 6  (m ) (3 m )(4 m )( 6 m ) 1.15 1.54 2 .30  (m)

AB AC AC 22 2 = = +−

Using this result, the force exerted on the bar at B is F r r ijk ijk (2 kN ) (2 kN ) 5.85 1 .54 1.70  (m) (5.8 5  m) (1 .54 m )( 1.70 m ) 1.86 0.489 0.540  (kN).

=− ijk 1.86 0.489 0 .540  (kN). x y z A C D (0, 4, 0) m (4, 0, 2) m ( 3, 0, 6) m

222 = +− +−

4, 0)

2)

Problem2.97 The circular bar has a 4-m radius and lies in the x–y plane. Express the position vector from point B to the collar at A in terms of components.

Solution: The coordinates of point A are [(4 m )c os 20° ,(4 m) sin 20° , 0], and the coordinates of point B are (0,4,3)  m, so the vector from B to A is

=− +− +−

r ijk ijk [(4 m )c os 20° 0] [(4 m )sin 20° 4 m ][0 3 m ] 3.76 2 .63 3  (m ).

ijk 3.76 2 .63 3  (m ).

Problem2.98 The cable AB exerts a 60 -N force T on the collar at A that is directed along the line from A toward B. Express T in terms of components.

Problem2.99 In Practice Example 2.11, suppose that the vector V is changed to Vijk 46 10 =− (a) What is the value of UV ? (b) What is the angle between U and V when they are placed tail to tail?

Solution: The coordinates of point A are [(4 m )c os 20° ,(4 m) sin 20° , 0], and the coordinates of point B are (0,4,3)  m, so the vector from A to B is rijk ijk [0 (4  m )c os 20°][4  m(4 m )sin 20°][3 m 0] 3.76 2.6 33  (m)

AB =− +− +− =− ++

By dividing this vector by its magnitude, we obtain a unit vector that points from A toward B:

e r r ijk 0.686 0.480 0.547

AB AB AB == −+ +

Then the force T in terms of its components is Teijk (60 N )4 1. 12 8.8 32.8  (N)

AB == −+ + Tijk 41.1 28.8 32.8  (N) =− ++ x y z (0, 4, 3) m B

rAB eAB

[(4 m)cos 208, (4 m)sin 208, 0]

Solution: From Active Example 2.4 we have the expression for U Thus

Problem2.100 In Example 2.12, suppose that the coordinates of point B are changed to (6,  4,  4)  m. What is the angle θ between the lines AB and AC ?

Problem2.101 Consider the vectors

1 248 , 68 14 , 88 8. =+

+

Determine the values of the dot products UV, UW, and VW What can you deduce about the three vectors from the results?

Solution: Using the new coordinates we have =+ +=rijkr (2 2)  m,  3  m ABAB =+ +=rijkr (4 52 )  m,  6.71 m ACAC θ = = ++ = rr rr co s ((2)(4)(1)(5)(2)(2)) m (3 m )(6.71 m ) 0.845 ABAC ABAC 2 θ == ° co s(0.84 5) 32.4 1 θ =° 32.4

Solution: Applying Eq. (2.23), the dot products are UV UW VW (1 2)(6)(4)(8)( 8)(1 4) 152, (1 2)(8)(4)(8)( 8)(8) 0, (6)(8) (8)( 8) (1 4)(8) 0. =− ++

WUV 152,  0,  0  and   a re  not perp e ndicular.  is pe rp e ndicular  t o both a nd

Problem2.102 Consider the position vectors P and Q (a) Determine the dot product PQ by using the definition, Eq. (2.18). (b) Determine the dot product PQ ⋅ by using Eq. (2.23).

Solution:

(a) The two vectors in terms of their components are =+ = Pik Qi 12 10  (m), 8  (m ).

Their magnitudes are =+ = = P Q (1 2 m) (1 0  m) 15.6 m , 8  m. 22

The angle between the two vectors is θ () == ° arctan 10  m 12 m 39.8 From Eq. (2.18), =° = PQ (15.6 m )(8  m) co s3 9.8 96 m 2

(b) From Eq. (2.23), =+ + = · PQ (1 2 m)(8 m )(0)(0)(10  m )(0) 96 m 2 = PQ (a ), (b) 9 6  m. 2 x z y (8, 0, 0) m (12, 0, 10) m Q

Problem2.103 Two perpendicular vectors are given in terms of their components by U Uijk 46 x =− + and Vijk 32 3. =+ Use the dot product to determine the component U . x

Solution: When the vectors are perpendicular, ⋅≡UV 0. Thus UVUVUV U UV 0  3 (4)(2) (6)( 3) 0 xxyyzz x ⋅= ++ = =+ −+ −= = U 32 6 x = U 8.67

Problem2.104 The vectors P, Q, and FF Fij xy=+ lie in the x–y plane. The magnitudes of P and Q are 4  m and 5  m, respectively. The dot products PF 50 N-m ⋅= (newton-meters) and QF 60 N-m. ⋅= Determine the components Fx and F y

Solution:

The components of P and Q are Pij Qij (4 m )(c os15 si n1 5), (5 m )(sin 30 co s3 0) =° +° =° +°

The two given conditions are FF FF PF QF (4 m )c os15 (4 m )sin 15 50  N-m , (5 m )sin 30 (5  m )c os 30 60  N-m xy xy

[] =° +° = =° +° =

Solving these two equations, we obtain ==FF 10.9 N,  7.55 N xy

Problem2.105 The magnitudes U 10 = and V 20. = (a) Use Eq. (2.18) to determine UV (b) Use Eq. (2.23) to determine UV. x y

Problem2.106 What is the angle between the ropes OA and OB?

Solution: Let e OA be a unit vector that points from the origin O toward A In terms of the angles shown, its components are =° °+ °− °° eijk co s3 5c os15 si n3 5c os 35 si n1 5. OA

The components of a unit vector e OB that points from O toward B are =− °° +° +° ° eijk co s6 0sin 40 si n6 0c os 60 co s4 0. OB

We can use definition of the dot product to determine the angle between OA and OB: ee ee co s (c os 35 cos1 5)(c os 60 si n4 0) (sin 35 )(sin

obtain

Copyright © 2024, 2008 by Pearson Education, Inc. or its affiliates.

Solution:

(a) The definition of the dot product (Eq. (2.18)) is θ ⋅= UVUV co s. Thus ⋅= °− °= UV (1 0)(2 0) co s(45 30 ) 193.2

(b) The components of U and V are

=° +° =+ Uijij 10(c os 45 si n4 5) 7.07 7.07

=° +° =+ Vijij 20(c os 30 si n3 0) 17.32 10 From Eq. (2.23) ⋅ =+ = UV (7.0 7)(1 7 .32)(7.07)(10) 193.2

Problem2.107 Use the dot product to determine the angle between the forestay (cable AB ) and the backstay (cable BC ) of the sailboat.

13)

Problem2.108 Determine the angle θ between the lines AB and AC (a) by using the law of cosines (see Appendix A); (b) by using the dot product.

Solution: The unit vector from B to A is

The unit vector from B to C is

r ij 0 .385 0 .923

From the definition of the dot product, θ ⋅=ee 11 co s, BABC where θ is the angle between BA and BC Thus θ =− +− co s( 0.321)(0 .385)( 0 .947)( 0.923)

θ = cos 0.750

Solution:

(a) We have the distances:

The law of cosines gives

(b) Using the dot product

(4

⋅= ABAC rr ()() co s ABAC

Problem2.109 The ship O measures the positions of the ship A and the airplane B and obtains the coordinates shown. What is the angle θ between the lines of sight OA and OB ?

y z B (6, 0, 3) km (4, 4, 4) km

Problem2.110 Astronauts on the space shuttle use radar to determine the magnitudes and direction cosines of the position vectors of two satellites A and B The vector r A from the shuttle to satellite A has magnitude 2 km and direction cosines cos 0.768, x θ = cos 0.384, y θ = cos 0.512. z θ = The vector r B from the shuttle to satellite B has magnitude 4  km and direction cosines cos 0.743, x θ = cos 0.557, y θ = cos 0.371. z θ =− What is the angle θ between the vectors r A and r ?B

Solution: From the coordinates, the position vectors are: =+ + rijk 60 3 OA and =+ rijk 44 4 OB The dot product: ⋅= ++ −= rr (6)(4) (0)(4) (3)( 4) 12 OAOB

The magnitudes: =+ += r 603 6.71 km OA 22 2 and =+ += r 444 6 .93 km OA 22 2

From Eq. (2.24) θ = = rr rr cos 0.2581, OAOB OAOB from which θ =± ° 75

From the problem and the construction, only the positive angle makes sense, hence θ =° 75

Solution: The direction cosines of a vector are the components of a unit vector having the same direction as the vector. We are given the components of unit vectors e A and e B having the same directions as the vectors r A and r : B =+ + =+ eijk eijk 0.768 0 .384 0.51 2, 0.743 0.557 0.37 1. A B

From the definition of the dot product, we have ee ee co s (0.76 8)(0 .743)(0.384)(0.557)(0.512)( 0.371) 1 0.595, AB AB θ = = ++ = from which we obtain 53.5° θ =

Problem2.111 Segment AB of the bar is parallel to the x -a xi s. Determine the angle θ between the straight segments AB and BC

Solution: The coordinates of point B are (5,3,1)  m. The vector from B to A is =− ri5  (m ). BA The vector from B to C is rijk

BC =− +− +− =− −+

(2  m 5  m) (0 3  m) (4  m 1  m) 33 3  (m ).

The magnitudes of these vectors are

r r 5  m, (3 m )( 3  m) (3 m ) 5.20  m

BA BC 22 2 = =− +− + =

The value of their dot product is

rr ·  (5 m )( 3  m) (0)( 3  m) (0)(3  m) 15 m BABC 2 =− −+ −+ =

Using the definition of the dot product, rr rr co s ·  15 m (5 m )(5.2 0  m) 0.577.

2 θ = = = This yields θ =° 54.7 5

(0, 3, 1) m (2, 0, 4) m (5, 3, 1) m u

Problem2.112 The person exerts a force

Fij 60 40  (N) =− on the handle of the exercise machine. Use Eq. (2.26) to determine the vector component of F that is parallel to the line from the origin O to where the person grips the handle.

Solution: The vector r from the O to where the person grips the handle is

=+ rijk (250 20 01 50 )  mm, = r 354  m m

To produce the unit vector that is parallel to this line we divide by the magnitude == +− =+ e r r ijkijk (250 20 01 50 )  mm 35 4  mm (0.707 0.566 0.424 )

Using Eq. (2.26), we find that the vector component parallel to the line is

=⋅ =+ −+ FeFeijk () [(0.70 7)(6 0  N) (0.566)( 40  N )](0.707 0.566 0.424 ) p ijk 14.0 11.2 8.4 0  (N). +−

Problem2.113 At the instant shown, the Harrier’s thrust vector is Tijk 4.22 21.6 3.30 (k ip ) =+ and its velocity vector is vijk 24.4 8.86 2.44 (ft/s ). =+ +

(a) Determine the components of the thrust vector parallel and normal (perpendicular) to the velocity vector.

(b) The term Tv is the power being transferred to the plane by its engine. What is the power in horsepower?

Solution:

(a) We divide the velocity vector by its magnitude to obtain a unit vector with the same direction:

+ e v v ijk ijk

24.4 8.8 62 .44 (ft/s)

(24.4  ft/s)(8.86 ft/s)(2.44  ft/s)

0.936 0 .340 0.0936 22 2

The component of T parallel to the velocity vector is ⋅ = TeTe () p

The dot product of e and T is

eT (0.936)(4 .22 ki p) (0.340)(21.6 ki p) (0.0936)( 3.30  ki p) 11.0  kip.

The parallel component is

+

+ TeTe ijk ijk

(11.0  ki p)(0.936 0.340 0.0936 ) 10.3 3.73 1.03  (kip) p

The component of T normal to the velocity vector is

ijk 6.06 1 7.9 4.33  (kip)

(b) The dot product of T and v is

Tv (4.22 ki p)(24.4  ft/s)(21.6 ki p)(8.86 ft/s)( 3.30  ki p)(2.44  ft/s)

286 kip -ft/s

286,000 ft-lb/s

Converting this to horsepower, () =

286,000 ft-lb/s 2 86,000 ft-lb/s 1 horse power 550  ft-lb/s 52 1  ho rsepower

=+ += −+ TijkTijk (a )  10.3 3.73 1.03  (kip),  6.06 17.9 4.33  (kip) (b) 521 horse po wer. pn

Problem2.114 For the three-dimensional truss shown, determine the angle between members AB and AD

The value of their dot product is rr (4  ft)(2  ft) (3 ft)(3 ft) (4)( 4  ft ) 17 ft.

C (5, 0, 6) ft A (4, 3, 4) ft z y F x

Solution: The vector from A to B is =− rijk 43 4  (ft)

AB

D (6, 0, 0) ft

The vector from A to D is rijk ijk

AD =− +− +− =−

(6  ft4  ft) (0 3  ft )(04  ft) 23 4  (ft)

The magnitudes of these vectors are

ABAD 2 ⋅ =− +− −+ = Using the definition of the dot product, rr rr co s 17 ft

BABC BABC 2 θ = = = This yields ° 60.5

(6.40  ft)(5.39  ft ) 0.493.

(4, 3, 4) ft (6, 0, 0) ft

r r (4  ft) (3 ft) (4  ft) 6.40  ft, (2  ft) (3 ft) (4  ft) 5.39 ft.

AB AD 22 2 22 2 =− +− +− = =+ −+ =

Problem2.115 For the three-dimensional truss shown, determine the angle between members AC and CD

y F x

(4, 3, 4) ft

D (6, 0, 0) ft C (5, 0, 6) ft

Solution: The vector from C to A is rijk ijk (4  ft5 ft) (3 ft0)(4  ft 6  ft ) 32  (ft ).

CA =− +− +− =− +−

The vector from C to D is rijk ik

CD =− +− +− =−

(6  ft5 ft) (0 0) (0 6  ft ) 6  (ft)

The magnitudes of these vectors are

The value of their dot product is rr (1 ft)(1 ft) (3 ft)(0)( 2)(6  ft) 11 ft. CACD 2 ⋅ =− ++ = Using the definition of the dot product, θ = = = rr rr co s 11 ft (3.74  ft)(6.08 ft) 0.483.

CACD

(4, 3, 4) ft (6, 0, 0) ft

r r (1 ft) (3 ft) (2  ft) 3.74  ft, (1 ft) (0)( 6  ft ) 6.08 ft.

CA CD 22 2 22 2 =− ++ = =+ +− =

(5, 0, 6) ft rCA rCD u

Problem2.116 The three-dimensional truss is subjected to a force Fijk 25 100 30 (l b) =− at A Determine the components of F parallel and normal (perpendicular) to member AD B

0, 0) ft

The component of F parallel to member AD is = FeFe ()ADAD p

The dot product of e AD and F is eF (0.37 1)(2 5  lb)( 0 .557)(

=+ +−

0, 6) ft

Solution: The vector from A to D is rijk ijk (6  ft4  ft) (0 3  ft )(04  ft)

AD =− +− +− =−

23 4  (ft)

Dividing this vector by its magnitude yields a unit vector that points from A toward D:

AD AD AD

23 4  (ft)

e r r ijk ijk

(2  ft) (3 ft) (4  ft)

22 2 = = +− +− =−

0.371 0.557 0.74 3.

Problem2.117 The rope AB exerts a 50 -N force T on collar A. Determine the vector component of T parallel to the bar CD

Solution: We need to know the coordinates of point A The vector from point D to point C is

DC =− +− +− =+

(0.4 m 0.2 m )(0.3 m 0) (0 0.25 m )

rijk ijk

0.2 0.3 0.2 5  (m ).

Its magnitude (the distance from D to C) is r 0.439 m , DC = so the distance from D to A is 0.239 m The unit vector that points from D toward C is

e r r ijk 0.456 0.684 0.570 DC DC DC == +−

The vector from the origin O to D is rik 0.2 0.25  (m) OD =+ Then the vector from the origin to A is

rreijk (0 .239 m) 0.309 0.163 0.114  (m)

OAODDC =+ =+ +

The vector from A to B is rijk ijk

AB =− +− +− =− ++

(0 0.309 m )(0.5 m 0.163 m )(0.15 m 0.114 m ) 0.309 0.337 0.0360  (m)

The force T in terms of its components is T r r ijk (50 N )3 3.7 36.7 3.93  (N)

AB AB == −+ +

The component of T parallel to the bar is TeTeijk () 3.43 5.14 4.29  (N)

DCDC p =⋅ =+ Tijk 3.43 5.14 4 .29  (N) p =+

Copyright © 2024, 2008 by Pearson Education, Inc. or its affiliates.

The parallel component is FeFe ijk ijk ()

(87.3 l b)(0 .371 0.557 0.743 ) 32.4 48.6 6 4.8  (lb ).

The component of F normal to member AD is FFF

0,

(0 4, 0 3, 0)

Problem2.118 In Problem 2.117, determine the vector component of T normal to the bar CD

Solution: We need to know the coordinates of point A The vector from point D to point C is rijk ijk

DC =− +− +− =+

(0.4 m 0.2 m )(0.3 m 0) (0 0.25 m )

0.2 0.3 0.2 5  (m ).

Its magnitude (the distance from D to C) is r 0.439 m , DC = so the distance from D to A is 0.239 m. The unit vector that points from D toward C is

e r r ijk 0.456 0.684 0.570 DC DC DC == +−

The vector from the origin O to D is rik 0.2 0.25  (m) OD =+ Then the vector from the origin to A is

rreijk (0 .239 m) 0.309 0.163 0.114  (m)

OAODDC =+ =+ +

The vector from A to B is rijk ijk (0 0.309 m )(0.5 m 0.163 m )(0.15 m 0.114 m ) 0.309 0.337 0.0360  (m)

AB =− +− +− =− ++

The force T in terms of its components is T r r ijk (50 N )3 3.7 36.7 3.93  (N)

AB AB == −+ +

The component of T parallel to the bar is

TeTeijk () 3.43 5.14 4.29  (N) DCDC p =⋅ =+

Then the component normal to the bar is TTTijk 37.1 3 1.6 8.22  (N) np =− =− ++

Tijk 37.1 31.6 8.22  (N) n =− ++

Problem2.119 The magnitudes of the two force vectors are F 200 lb A = and F 160 lb B = What is the angle between the two vectors? x

Solution: The components of F A are x y z rDC eDC D B C A rAB (0, 0 5, 0 15) m (0 4, 0 3, 0) m (0 2, 0, 0 25) m

A =° °+ °+ °° =+ +

(200  l b)(c os 40 si n5 0sin 40 co s4 0c os 50 ) 117 129 98.5  (lb ).

Fijk ijk

The components of FB are Fijk ijk (160  l b)(c os 60 si n3 0sin 60 co s6 0c os 30 ) 40.0 139 69.3  (lb ).

B =− °° +° +° ° =− ++

Their dot product is FF (117 l b)(4 0. 0  lb)(129 l b)(139 l b) (98.5 l b)(69.3 l b) 19,9 00  l b. AB 2 ⋅ =− ++ =

Using the definition of the dot product, FF FF co s ·

19,9 00  l b (200  l b)(1 60  l b) 0.623. AB AB 2 θ = = = This yields ° 51.5

Problem2.120 The magnitudes of the two force vectors are F 200 lb A = and F 160 lb B = Determine the components of F A parallel and normal to F . B

Problem2.121 An astronaut in a maneuvering unit approaches the ISS. At the present instant, the station informs him that his position relative to the origin of the station’s coordinate system is rijk 50 80 180  (m) G =+ + and his velocity is vjk 2.2 3.6  (m/s). =− The position of an airlock is rik 12 20  (m) A =− + Determine the angle between his velocity vector and the line from his position to the airlock’s position.

Solution: The components of F A are Fijk ijk

A =° °+ °+ °° =+ +

(200  l b)(c os 40 si n5 0sin 40 co s4 0c os 50 ) 117 129 98.5  (lb ).

The components of FB are Fijk ijk (160  l b)(c os 60 si n3 0sin 60 co s6 0c os 30 ) 40.0 139 69.3  (lb ).

B =− °° +° +° ° =− ++

We divide FB by its magnitude to determine the components of a unit vector with the same direction: e F F ijk ijk 4 0.0 139 69.3  (lb ) ( 40.0  l b) (1 39 l b) (69.3 l b) 0.250 0.86 60 .433 .

B B B 22 2 = = −+ + −+ + =− ++

The dot product of e B with F A is eF ( 0.250)(117 lb)(0.866)(129 l b) (0.433)(98.5 l b) 125 lb.

BA =− ++ =

The component of F A that is parallel to FB is FeFe ijk ijk () (125 l b)(0 .250 0.866 0.433 ) 31.2 108 54.0  (lb ).

ABAB p = =− ++ =− ++

The component of F A that is normal to FB is FFF ijk 149 20.6 4 4.5  (lb ).

AA np

We obtain 19.7° θ = y z x A G =− ++ =+ + FijkFijk 31.2 108 5 4.0  (lb ), 149 20.6 44.5  (lb ). AA pn

Solution: The vector from the astronaut’s position to the airlock is rrrijk 62 80 160  (m) AG=− =−

Let θ denote the angle between his velocity vector and the line from his position to the airlock. Using the definition of the dot product, vr vr cos 0.942. θ = =

Problem2.122 In Problem 2.121, determine the vector component of the astronaut’s velocity parallel to the line from his position to the airlock’s position.

Problem2.123 Point P is at longitude 30 ° W and latitude 45 °N on the Atlantic Ocean between Nova Scotia and France. Point Q is at longitude 60 ° E and latitude 20 °N in the Arabian Sea. Use the dot product to determine the shortest distance along the surface of the earth from P to Q in terms of the radius of the earth R E

Strategy: Use the dot product to determine the angle between the lines OP and OQ; then use the definition of an angle in radians to determine the distance along the surface of the earth from P to Q.

Solution: The vector from the astronaut’s position to the airlock is rrrijk 62 80 160  (m) AG=− =−

We divide this vector by its magnitude to obtain a unit vector that points from the astronaut’s position toward the airlock: e r r ijk 0.328 0.423 0.845

The component of v parallel to e is veveijk () 1 .30 1 .68 3.36  (m/s).

Solution: The vector from O to P is R R rijk ijk (c os 45 °c os 30 °sin 45° cos 45° sin 30° ) (0.612 0.707 0.354 ).

The vector from O to Q is R R rijk ijk (c os 20 °c os 60° sin 20° cos 20° sin 60° ) (0.470 0 .342 0.814 ).

Let θ denote the angle between these two vectors. Using the definition of the dot product, we have rr rr cos 0.242. OPOQ OPOQ

Solving for the angle in radians, this gives 1.33. θ = From the definition of an angle in radians, the desired distance is R 1.33 E

Problem2.124 Consider the vectors Uijk Vijk 1 248 , 68 14 =+ =− ++

(a) Determine the components of the vector WUV. =×

(b) Evaluate the dot products ⋅ UW and ⋅ VW What is the explanation of these two results?

Solution:

(a) The vector W is

+ WUV ijk

(4)(14)( 8)(8)(12)(14)( 8)(6)(12)(8) (4)( 6) 120 12 01 20

ijk 12  4  8 6  8  14

(b) The dot products are UW VW (1 2)(1 20)(4)(1 20)( 8)(120) 0, (6)(12 0) (8)( 12 0) (1 4)(120) 0. ⋅ ⋅ =+ −+

n ition of the cro ss product,

Problem2.125 Two vectors Uij 32=+ and Vij 24 . =+ (a) What is the cross product UV ? × (b) What is the cross product VU ? ×

Solution: Use Eq. (2.34) and expand into 2 by 2 determinants. ×= =− +−

UV ijk ijkk 320 24 0 ((2)(0)(4)(0)) ((3)(0)(2)(0)) ((3)(4)(2)(2)) 8 ×= =− +− =− VU ijk ijkk 24 0 320 ((4)(0)(2)(0)) ((2)(0)(3)(0)) ((2)(2)(3)(4)) 8

UVkVUk (a )  8 . (b) 8 ×= ×=

Problem2.126 Consider the position vectors P and Q (a) Determine the cross product PQ × by using the definition, Eq. (2.28). (b) Determine the dot product ⋅ PQ by using Eq. (2.34).

y (8, 0, 0) m (12, 0, 10) m Q

Solution:

(a) The two vectors in terms of their components are Pik Qi 12 10  (m), 8  (m ). =+ =

Their magnitudes are

P Q (1 2 m) (1 0  m) 15.6 m , 8  m. 22=+ = =

Problem2.127 Consider the position vectors P and Q (a) Determine the cross product QP × by using the definition, Eq. (2.28). (b) Determine the dot product ⋅ QP by using Eq. (2.34).

The angle between the two vectors is θ () == ° arctan 10  m 12 m 39.8

From Eq. (2.28),

×= ° = PQe e (1 5.6 m)(8 m )sin 39.8 (8 0  m) 2

The unit vector e is defined to be perpendicular to P and perpendicular to Q Either j or j satisfies those criteria. The remaining criterion states that PQe ,, form a right-handed system, which requires that = ej Therefore, ×= PQj 80  (m) 2 (b) From Eq. (2.34), ×= =− +− = PQ ijk ij k j 12 m 01 0  m 8  m0 0 [(0)(0)(10  m )(0)][(1 2 m)(0)(10  m )(8  m)] [(12 m )(0) (0)(8  m)] 80  (m) 2

×= PQj (a ), (b) 8 0  (m ). 2

×= QPj (a ), (b) 8 0  (m ). 2 x

Solution:

(a) The two vectors in terms of their components are Pik Qi 12 10  (m), 8  (m ). =+ = Their magnitudes are P Q (1 2 m) (1 0  m) 15.6 m , 8  m. 22=+ =

The angle between the two vectors is θ () == ° arctan 10  m 12 m 39.8 From Eq. (2.28), QPe e (8 m )(15.6 m )sin 39.8 (8 0  m) 2 ×= ° =

The unit vector e is defined to be perpendicular to Q and perpendicular to P Either j or j satisfies those criteria. The remaining criterion states that QPe ,, form a right-handed system, which requires that =− ej Therefore, ×= QPj 80  (m) 2

(b) From Eq. (2.34),

(0)(10  m )(0)(0)(8  m)(1 0  m) (0)(12 m )(8  m)(0)(0)(1 2 m) 80  (m) 2

Problem2.128 Suppose that the cross product of two vectors U and V is UV0 ×= If U 0, ≠ what do you know about the vector V ?

Problem2.129 The cross product of two vectors U and V is UVik 30 40 ×= −+ The vector Vijk 42 3. =− + The vector UU Uijk 4. yz =+ + Determine Uy and Uz

Solution: = VVU Either 0 o r

Solution: From the given information we have

×= UU UV ijk 4 42 3 yz

=+ +− +− UUUUijk (3 2) (4 12)( 84 ) yzzy

×= −+ i UVk (3 04 0)

Equating the components we have += =− −=UUUU32 30,   41 20,    84 40. yzzy

Solving any two of these three redundant equations gives =− = UU 12,  3. yz

Problem2.130 (a) Determine the components of a unit vector e p that is parallel to the line AB and points from A toward B . (b) Determine the components of a unit vector e n that is normal (perpendicular) to the line AB (Make sure your result is a unit vector.) Confirm that it is perpendicular to the line by showing that ee 0. pn ⋅=

Dividing this vector by its magnitude yields the unit vector e p : e r r ijk ijk

41 86  (ft )

Solution:

(a) The position vector from point A to point B is =− −+ +− =− rijk ijk (2  ft( 2  ft )) (6  ft1 2  ft )( 4  ft 2  ft ) 41 86 (ft). AB x ( 2, 12, 2) ft y z (2, 6, 4) ft

–6, –4) ft

AB AB p 22 2 = = +− +− =−

(4  ft) (1 8  ft )( 6  ft )

0.206 0 .928 0 .309

(b) The cross product of e p with any non-zero vector that is not parallel to the line will yield a vector that is perpendicular to the line, from the definition of the cross product. For example, the vector eiijki iijiki kj

(0.20 60 .928 0 .309 )

p ×= × =× −× −× =−

0.20 6( )0 .928() 0.309() 0.928 0.30 9

is perpendicular to e p . However, although it is the cross product of two unit vectors, it is not a unit vector:

ei (0.928)( 0 .309) 0.978 p 22 ×= +− =

To obtain the desired unit vector, we must divide the vector × ei p by its magnitude:

e ei ei

0.309 0.92 8 0.978

jk jk

0.316 0 .949 . n p p = × × = −+ =− +

The dot product of this vector with e p is zero, confirming that the two vectors are perpendicular: ee (0.20 6)(0)( 0 .928)( 0.316) (0 .309)(0.94 9) 0. pn =+ +− = =− =− + eijk ejk

(a )  0.206 0.928 0.309 . (b) For example,  0.316 0.949 p n

Problem2.131 The force Fij 10 4  (N ). =−

Determine the cross product rF AB × y x B A rA B (6, 3, 0) m

(6, 0, 4) m

Problem2.132 By evaluating the cross product UV, × prove the identity θθ θθ −= si n( )s in co s 12 12

θθ co ss in . 12

x y

Solution: The position vector is =− +− +− =− + rijkijk (6 6) (0 3) (4 0) 03 4 AB

The cross product:

×= =− −+ rF ijk ijk 03 4 10 40 (1 6) (4 0) (3 0) AB

=+ + ijk 16 40 30  ( N-m)

ijk rF 16 40 30  (N-m)

AB ×= ++

Solution: Assume that both U and V lie in the xy - plane. The strategy is to use the definition of the cross product (Eq. 2.28) and the Eq. (2.34), and equate the two. From Eq. (2.28) θθ ×= UVUVe si n( ). 12 Since the positive z -axis is out of the paper, and e points into the paper, then =− ek Take the dot product of both sides with e, and note that ⋅=kk 1. Thus

θθ () −= ×⋅ UVk UV si n( ) () 12

The vectors are: θθ θθ =+ =+ UUijVVij (c os si n),  and  ( co ssin ). 12 22

The cross product is θθ θθ ×=UV ijk UU VV  c os sin0  c os si n0 11 22

θθ θθ =− +−ijkUV (0)(0) ()(c os si nc os si n) 12 21

Substitute into the definition to obtain: θθ θθ θθ −= si n( )sin co sc os si n. 12 12 12 Q.E.D.

Problem2.133 In Example 2.15, what is the minimum distance from point B to the line OA ?

Solution: Let θ be the angle between rOA and r . OB Then the minimum distance is

θ = d r si n OB

Using the cross product, we have θ ×= =⇒ = × dd rrrrr rr r si n OAOBOAOBOA OAOB OA

We have

=− + rijk (1 02 3)  m OA

=+ rijk (6 63 )  m OB ×= =− ++ rr ijk ijk 10 23 66 3 (1 24 87 2)  m OAOB 2

Thus = −+ + +− + = d (1 2  m) (4 8  m) (7 2  m) (1 0  m) (2  m )(3  m) 8.22 m 22 22 2 22 2 = d 8.22 m

Problem2.134 (a) What is the cross product rr ?OAOB × (b) Determine a unit vector e that is perpendicular to rOA and r . OB

Solution: The two radius vectors are =+ −= −+ rijkrijk 44 4,  6 23 OBOA

(a) The cross product is

OAOB

×= =− −+ + rr ijk ijk 62 3 44 4 (8 12)( 24 12)(24 8)

=− ++ ijk43 63 2  (m ) 2

The magnitude is

×= ++ = rr 43 63 2 48.33 m OAOB 222 2

(b) The unit vector is

=± −+ + e rr rr ijk  ( 0 .0828 0.7448 0.6621 ) OAOB OAOB

(Two vectors.)

B (4, 4, 4) m x y z O rOB

A (6, 2, 3) m

rrijk ijk

(a )  43 63 2  (m ). (b )( 0.0828 0.7448 0.662 ).

OAOB 2 ×= −+ + ±− ++

Problem2.135 Use the cross product to determine the length of the shortest straight line from point B to the straight line that passes through points O and A.

4, 4) m

Solution: The magnitude of the cross product of rOA and rOB is rr sin. OAOB θ Therefore the length L we seek is

2, 3) m

Problem2.136 The cable BC exerts a 1000 -l b force F on the hook at B. Determine rF. AB ×

Solution: The vector r AB is rijk ijk

AB =− +− +− =− +−

(4 ft1 6  ft )(6 ft0)(0 12 ft) 12 61 2  (ft).

We need to determine the components of the force. The vector r AB is rijk jk (4 ft 4 ft) (0 6 ft) (8 ft0) 68  (ft ).

BC =− +− +− =− +

Then the force is F r r jk (1000 l b) 600 800  (lb ). BC BC == −+

The desired cross product is

rF ijk ijk 12 ft6  ft1 2  ft 06 00  lb 800  l b

AB ×= =− ++

2 400 9600 7200 (ft-l b)

rFijk 2 400 9600 7200 (ft-l b) AB ×= −+ + A

(4, 6, 0) ft (4, 0, 8) ft (16, 0, 12) ft

Problem2.137* The force =+ + Fij 200 180 () k 100 lb Determine the vector component of F that is normal (perpendicular) to the flat plate AC D

(0, 10, 0) ft

C F x A z D (4, 0, 12) ft

Solution:

(4, 0, 12) ft C D A

(0, 10, 0) ft (6, 0, 0) ft

(6, 0, 0) ft

The vector from A to C is =− + rij 61 0  (ft). AC

The vector from A to D is =− + rik 21 2  (ft)

AD

The cross product × rrACAD is perpendicular to the plate.

=+ + rr ijk ijk 61 00 20 12 12 07 22 0(ft ).

2

Dividing this vector by its magnitude yields a unit vector that is perpendicular to the plate: = × × =+ + e rr rr ijk 0.849 0 .509 0.141

From Eq. (2.26), the vector component of F that is parallel to e, and so is perpendicular to the plate, is

+ FeFe ijk ijk () [(0.849)(200  l b) (0.509)(180  l b) (0.141)(10 0  lb)](0 .849 0.509 0.141 ) 234 140 39 (lb)

n =+ + Fijk 234 14 03 9(lb). n

++ +

Problem2.138 The rope AB exerts a 50 -N force T on the collar at A Let rCA be the position vector from point C to point A Determine the cross product rT CA ×

Solution: We define the appropriate vectors.

=− −+ rijk ( 0.2 0.3 0.25 )  m CD

== + r r r ijk (0.2 m )( 0 .091 0.137 0.114 )  m CA CD CD

=+ rjk (0.5 0 .15 )  m OB

=+ rij (0.4 0. 3)  m OC

=− += rrrrijk () (0.61 1.22 0.305 )  m ABOBOCCA

== −+ + T r r ijk (5 0  N) (3 3.7 36.7 3.93 )  N AB AB Now take the cross product

×= =− −+ rT ijl ijk 0 .091 0.137 0.114 3 3.7 36.7 3.93 ( 4.72 3.48

)  N-m CA

×= +− rTijk (4 7.2 3.48 7.96 )  N-m CA

z y A B C D O T

m 0.2 m

m x

Problem2.139 In Example 2.16, suppose that the attachment point E is moved to the location (0.3,  0.3,  0) m and the magnitude of T increases to 600  N What is the magnitude of the component of T perpendicular to the door?

Solution: We first develop the force T. =+ == + rij T r r ij (0.3 0.1 )  m (600  N )(569 190 )  N

CE CE CE

From Example 2.16 we know that the unit vector perpendicular to the door is

=+ + eijk (0.358 0 .89 40 .268 )

The magnitude of the force perpendicular to the door (parallel to e ) is then

=⋅ =+ = TTe (569 N )(0.35 8) (190  N )(0.894) 373 N n = T 373 N n

Problem2.140 The slender bar AB is 14 ft in length and is perpendicular to the flat plate AC D. (a) Determine the components of a unit vector e that is perpendicular to the plate AC D and points in the direction from A toward B (b) Determine the coordinates xyz(, ,)BBB of point B

(0, 10, 0) ft

(6, 0, 0) ft

Solution:

(xB, yB, zB)

The cross product × rrACAD is perpendicular to the plate and points in the direction from A toward B

×= =+ + rr ijk ijk 61 00 20 12 12 07 22 0(ft ).

ACAD 2

Dividing this vector by its magnitude yields the desired unit vector:

e rr rr

ACAD ACAD = × × =+ +

ijk 0.849 0.509 0.14 1.

(b) The bar is 14  ft long, so we obtain the vector from A to B by multiplying e by 14  ft:

Adding the coordinates of point A to the components of this vector, we obtain the coordinates of point B: = xyz(,  ,  ) (1 7. 9, 7 .13, 1.9 8)  ft. BBB =+ + = xyz eijk (a )  0.849 0.50 90 .141 (b )  (,  ,  ) (17.9, 7.1 3, 1.98)  ft BBB y C x A B z D (4, 0, 12) ft

(0, 10, 0) ft

(4, 0, 12) ft C B D A rAC rAB rAD y x z (a) The vector from A to C is =− + rij 61 0  (ft). AC

(6, 0, 0) ft

The vector from A to D is =− + rik 21 2  (ft) AD

re ijk (1 4  ft )

AB = =+ +

11.9 7 .13 1.9 8(ft ).

Problem2.141* Determine the minimum distance from point P to the plane defined by the three points A, B, and C .

Solution: We’ll begin by determining the components of a unit vector e that is normal to the plane and points from P toward the plane. According to the right hand rule, we obtain a vector that has that direction by evaluating the cross product rrACAB × The components of these vectors are rik rij 34  (m), 35  (m), AC AB =− + =− + so we obtain

rr ijk ijk 3  m0 4  m 3  m5 m 0 20 12 15  (m)

ACAB×= =−

We obtain the desired unit vector by dividing this vector by its magnitude:

e rr rr ijk0.721 0.433 0.541 ACAB ACAB = × × =−

The vector rijk 95  (m) PB =−

The component of the vector r PB in the direction of the vector e is normal to the plane. Its magnitude is the perpendicular distance we seek:

er 9.63 m PB ⋅= 9.63 m

Problem2.142 Two cartesian coordinate systems are shown. The unit vectors i′ and j′ of the xyz ′′ ′ coordinate system are given in terms of their components in the xyz coordinate system by iijk jijk

0.743 0.557 0.371 , 0.408 0.816 0.408 . ′ =+ + ′ =− +−

(a) Determine the unit vector k ′ of the xyz ′′ ′ coordinate system in terms of its components in the xyz coordinate system. (b) The force Fijk 40 80 20 (N). =+ + Use the dot product to determine the components of F in terms of the xyz ′′ ′ coordinate system. y9 y F x9 x z z9

(3, 0, 0) m (0, 5, 0) m

(0, 0, 4) m

Solution:

(a) The vector ′ k is ′ = ′ × ′ = =− ++ kij ijk ijk

0.743 0.557 0.371 0.408 0.816 0.40 8 0.530 0 .152 0.834

(b) The ′ x component of F is F Fi

(4 0  N)(0.743)(80  N )(0.557)(20  N )(0.371) 81.7 N, x ⋅ = ′ =+ + = ′ the ′ y component is F Fj

(4 0  N)( 0.408)(80  N )(0.816)(20  N )( 0.408) 40.8 N, y ⋅ = ′ =− ++ = ′ and the ′ z component is F Fk

z ⋅ = ′ =− ++ = ′

(4 0  N)( 0.53 0) (8 0  N)(0.152)(20  N )(0.834) 7.61 N

Therefore = ′ + ′ + ′ Fijk 81.7 40.8 7.6 1  (N).

(a )  0.530 0.152 0.834

(b )  81.7 40.8 7 .61  (N) A x y z B C rAB e P rAC rPB u

′ =− ++ = ′ + ′ + ′ kijk Fijk

Problem2.143 For the vectors =+ Uijk 62 4, =+ Vij 27 , and Wik 32 , =+ evaluate the following mixed triple products:

(a) UVW();⋅×

(b) WVU();⋅×

(c) VWU ()⋅×

Problem2.144 Use the mixed triple product to calculate the volume of the parallelepiped.

Solution: We are given the coordinates of point D From the geometry, we need to locate points A and C The key to doing this is to note that the length of side OD is 200  m m and that side OD is the x-axis. Sides ODAE ,  , and CG are parallel to the x-axis and the coordinates of the point pairs (O and D ), ( A and E ), and (C and D ) differ only by 200  m m in the x coordinate. Thus, the coordinates of point A are (6 0,  9 0,  3 0)  m m and the coordinates of point C are (4 0, 0, 100)  mm. Thus, the vectors rr ,  , OAOD and rOC are == −+ + ririjk 200 mm,  6 09 03 0  mm, ODOA and =− ++ rijk 4 00 100 mm. OC The mixed triple product of the three vectors is the volume of the parallelepiped. The volume is

rrr() 60 90 30 40 0 100 20 00 0

Solution: Use Eq. (2.36).

(a) ⋅× = =− +− −= UVW () 62 4 27 0 30 2  6(1 4) 2(4) (4)( 21) 160

(b) ⋅× = =− −+ −= WVU() 30 2 27 0 62 4  3(2 8) (0)2(4 42) 160

(c) ⋅× = =− −+ = VWU () 27 0 30 2 62 4

2(4)7(1 21 2) (0) 160

UVWWVU VWU (a )  () 160, (b) ( ) 160,  (c )  () 1 60. ⋅× =⋅ ×= ⋅× =

1.8E6 mm. 2 x y z

(140, 90, 30) mm

(200, 0, 0) mm

(160, 0, 100) mm

⋅× = =− ++ =

6 0(0) 90(200)(100)(30)(0)  m m

OAOCOD 3 3

1,8 00,000  m m

Problem2.145 By using Eqs. (2.23) and (2.34), show that

⋅×() =

Solution: One strategy is to expand the determinant in terms of its components, take the dot product, and then collapse the expansion. Eq. (2.23) is an expansion of the dot product: Eq. (2.23):

⋅= ++ UVUVUV UV XXYYZZ Eq. (2.34) is the determinant representation of the cross product: ×=VUUU VVV U ijk Eq. (2.34) XYZ XYZ

Copyright © 2024, 2008 by Pearson Education, Inc. or its affiliates.

For notational convenience, write =× PUV() Expand the determinant about its first row: =− + UU VV UU VV UU VV Pijk YZ YZ XZ XZ XZ XZ

Since the two-by-two determinants are scalars, this can be written in the form: =+ + PPP PijkXYZ where the scalars PP ,  , XY and PZ are the two-by-two determinants. Apply Eq. (2.23) to the dot product of a vector Q with P Thus ⋅= ++ QPQPQP QP XXYYZZ Substitute PP ,  , XY and PZ into this dot product

⋅= −+ Q UU VVQ UU VVQ UU VV QP X YZ YZ Y XZ XZ Z XZ XZ

But this expression can be collapsed into a three-by-three determinant directly, thus:

⋅× = QQQ UUU VVV QUV() XYZ XYZ XYZ This completes the demonstration. y z A B C O F G D E x (140, 90, 30) mm (200, 0, 0) mm (160, 0, 100) mm

Problem2.146 The magnitudes of the two force vectors are F 200 lb A = and F 160 lb B = What is the magnitude of their cross product FFAB × ?

Problem2.147 The magnitude of F is 8 kN Express F in terms of scalar components.

x y (7, 2) m (3, 7) m

Problem2.148 The magnitude of the vertical force W is 600  lb, and the magnitude of the force B is 1500  lb. Given that ++ = ABW0, determine the magnitude of the force A and the angle α

Solution: Let ABW ,  ,  denote the magnitudes of the forces. The forces in terms of their components are AA BB W Aij Bij Wj co ssin , cos 50° si n5 0° , αα =− =+ =−

Solution: The components of F A are Fijk ijk

A =° °+ °+ °° =+ +

(200  l b)(c os 40 si n5 0sin 40 co s4 0c os 50 ) 117 129 98.5  (lb ).

The components of FB are Fijk ijk

B =− °° +° +° ° =− ++

(160  l b)(c os 60 si n3 0sin 60 co s6 0c os 30 ) 40.0 139 69.3  (lb ).

Their cross product is ×= =− −+ FF ijk ijk

1 17 lb 129 lb 98.5 l b 4 0.0  lb 139 lb 69.3 l b 4 740 12,1 00 21,400  (lb ). AB 2

Its magnitude is FF ( 474 0  lb )( 12,100  l b) (2 1,400  l b) 25,000  l b. AB 22 22 22 2 ×= −+ −+ =

×=FF 25,0 00  l b. AB 2

Solution: The unit vector collinear with the force F is developed as follows: The collinear vector is =− +− =− rijij (7 3) (2 7) 45

The magnitude: =+ = r 45 6.40 3  m. 22 The unit vector is

== e r r ij 0.6247 0.7809 The force vector is

FFeij 5 .00 6.25  (kN).

Fij 5.00 6.25  (kN).

This requires that the sums of the i and j components each equal zero, giving two equations that we write as AB co sc os 50°, α = (1) ABW si nsin 50 °. α =− (2)

Dividing Eq. (2) by Eq. (1) gives BW B ta n si n5 0° cos 50° 0.569, α = = from which we obtain 29.7° α = Then Eq. (1) gives A 1110  lb. = A 1110 lb,  29.7°. α ==

The sum of the forces is zero: ABABW ABWij0 (c os cos 50°)( si nsin 50° ). αα ++ =− ++ −+ −= x y W B A 508 a

Problem2.149 The magnitude of the vertical force vector A is 200  lb. If ++ = ABC0, what are the magnitudes of the force vectors B and C ?

Solution: The strategy is to express the forces in terms of scalar components, and then solve the force balance equations for the unknowns. αα =− CCij (c os sin), where

αα == =° ta n 50 70 0 .7143, o r  35.5

Thus =− CCij ( 0.813 70 .581 2) Similarly, =+ BBi, and =+ Aj 200 The force balance equation is ++ = ABC 0. Substituting, −+ = CBi ( 0.8137 )0, and −+ = Cj ( 0.5812 20 0) 0. Solving, ==CB 344.1 lb,  280  l b

Problem2.150 The magnitude of the horizontal force vector D is 280  lb. If ++ = DEF0, what are the magnitudes of the force vectors E and F ?

Solution: The strategy is to express the force vectors in terms of scalar components, and then solve the force balance equation for the unknowns. The force vectors are:

ββ=− EEij (c os si n), where β == ta n 50 100 0.5, or β =° 26.6

Thus =− =− = EEij DiFFj (0.8944 0.4472 ) 280 , and

The force balance equation is ++ = DEF 0. Substitute and resolve into two equations:

−= −+ = EiEFj (0.8944 280)0, and ( 0.4472 )0

Solve: ==EF 313.1 lb,  14 0  lb

Problem2.151 What are the direction cosines of F ?

Solution: Use the definition of the direction cosines and the ensuing discussion.

The magnitude of =+ += FF:2 01 01 0 24.5. 222

The direction cosines are θ == = F F co s 20 24.5 0.8165, x x

θ == = == =− F F F F co s 10 24.5 0 .408 2 co s 10 2 4.5 0.4082 y y z z cos 0.817,  cos 0.408,  cos 0.408. xyz θθ θ

=− x y z A (4, 4, 2) ft B (8, 1, 2) ft F 5 20i 1 10j 10k (lb) u

Problem2.152 Determine the components of a unit vector parallel to line AB that points from A toward B

Solution: Use the definition of the unit vector, we get

The position vectors are: =+ += +− rijkrijk 44 2,  8 12 . AB The vector from A to B is =− +− +− rijk (8 4) (1 4) (2 2) AB =−ijk43 4. The magnitude: =+ += r 43 46 .4. AB 22 2

The unit vector is x y z A (4, 4, 2) ft B (8, 1, 2) ft F 5 20i 1 10j 10k (lb) u == =− e r r ijkijk 4 6.4 3 6. 4 4 6.4

Problem2.153 What is the angle θ between the line AB and the force F ?

Solution: The vector from A to B is =− +− +− =− rijk ijk (8 4) (1 4) (2 2) (ft) 43 4  (ft)

AB

The dot product of this vector with F is =+ −+ = rF (4)(20)( 3)(1 0) (4)( 10)  ft -l b 90  ft-lb

AB

From the definition of the dot product θ = rFrF co s, ABAB

We obtain θ == +− +− ++ = rF rF co s 90 ft-lb (4 ft) (3 ft) (4  ft) (20 l b) (10 l b) (1 0  lb) 0.574. AB AB 22 22 22

This gives θ =° 55.0 . θ =° 55.0

Problem2.154 Determine the vector component of F that is parallel to the line AB.

F 5 20i 1 10j 10k (lb) u x y z A (4, 4, 2) ft

B (8, 1, 2) ft

F 5 20i 1 10j 10k (lb) u x y z A (4, 4, 2) ft

B (8, 1, 2) ft

Problem2.155 Determine the vector component of F that is normal to the line AB

Solution: The vector from A to B is rijk 43 4  (ft) AB =− A unit vector e that points from A toward B is e r r ijk 0.625 0.469 0.625 AB AB ==

The component of F that is parallel to the line from A to B is FeFeijk () 8 .78 6 .59 8.78  (lb ). p =⋅ =−− Fijk 8.78 6 .59 8.7 8  (l b) p =−−

Solution: The vector from A to B is rijk 43 4  (ft) AB =− A unit vector e that points from A toward B is

e r r ijk 0.625 0.469 0.625 AB AB ==

B (8, 1, 2) ft

Problem2.156 Determine the vector × rF, BA where r BA is the position vector from B to A

Solution: The vector from B to A is rijk 43 4  (ft) BA =− ++ The cross product is

BA

BA ×= −+ x y z A (4, 4, 2) ft

70 40 10 0  (ft-lb)

F 5 20i 1 10j 10k (lb) u x y z A (4, 4, 2) ft

The component of F that is parallel to the line from A to B is FeFeijk () 8 .78 6 .59 8.78  (lb ). p =⋅ =−−

Then the component of F that is normal to the line from A to B is FFFijk 1 1.2 16.6 1.22  (lb ). p n =− =+

Fijk 11.2 1 6.6 1.22  (lb ). n =+

ijk ij ijk 43 4 20 10 10 (3 04 0) (4 08 0)  ( 40 60)

rFijk

70 40 10 0  (ft-l b)

Copyright © 2024, 2008 by Pearson Education, Inc. or its affiliates.

B (8, 1, 2) ft F 5 20i 1 10j 10k (lb) u

Problem2.157 (a) Write the position vector r AB from point A to point B in terms of components. (b) A vector R has magnitude = R 200  l b and is parallel to the line from A to B Write R in terms of components.

Solution: rijk ijk

(a )  (8 ft4  ft) (1 ft 4 ft) ( 2 ft 2 ft) 43 4  (ft) AB =− +− +− =− R r r ijk (b )  (200 l b) 125 93.7 125  (lb ).

(a )  43 4  (ft). (b) 125 93.7 125  (lb ).

Problem2.158 The rope exerts a force of magnitude = F 200  l b on the top of the pole at B (a) Determine the vector × rF, AB where r AB is the position vector from A to B. (b) Determine the vector × rF, AC where r AC is the position vector from A to C

Solution: The strategy is to define the unit vector pointing from B to A, express the force in terms of this unit vector, and take the cross product of the position vectors with this force. The position vectors rijkrijk rijkijk 56 1,  3 04 , (3 5) (0 6) (4 1) 26 3. ABAC BC =+ += ++

The magnitude =+ += r 263 7. BC 22 2 The unit vector is

+ e r r ijk 0 .285 70

6 85.74 485.74 514.26

6 85. 74 8 5.7 514.3  (ft -l b)

ijk (a ), (b ) 686 486 514  (ft -l b)

(ft -l b)

(3, 0, 4)

(5, 6, 1) ft

Problem2.159 The pole supporting the sign is parallel to the x -axis and is 6  ft long. Point A is contained in the y–z plane. (a) Express the vector r in terms of components. (b) What are the direction cosines of r ?

Solution: The vector r is =° +° °+ °° rrijk (sin 45 co s4 5sin 60 co s4 5c os 60 )

The length of the pole is the x component of r Therefore

⇒= ° = rr si n4 56  ft 6  ft si n4 5 8.49 ft

(a) =+ + rijk (6.00 5 .20 3.00 )  ft

(b) The direction cosines are

== = cos 0.707,  cos 0.612,  cos 0.354 xyz

Problem2.160 The z component of the force F is 80  lb. (a) Express F in terms of components. (b) What are the angles θ , x θ , y and θ z between F and the positive coordinate axes?

Solution: We can write the force as =° °+ °+ °° FFijk (c os 20 si n6 0sin 20 co s2 0c os 60 )

We know that the z component is 80  lb. Therefore °° =⇒ = FF co s2 0c os 60 80  lb 170  l b

(a) =+ + Fijk (139 58.2 80 )  lb

(b) The direction cosines can be found:

co s 13 9 17 0 35.5

co s 58.2 170 70.0

co s 80 170 6 2.0 x y z 1 1 1 θ θ θ () () ()

Problem2.161 The magnitude of the force vector FB is 2  kN. Express it in terms of components.

Solution: The strategy is to determine the unit vector collinear with FB and then express the force in terms of this unit vector.

The radius vector collinear with FB is

=− +− +− =− +− rijkrijk (4 5) (3 0) (1 3)  or 1 32 BDBD

The magnitude is =+ += r 13 23 .74. BD 22 2

The unit vector is

−+ e r r ijk 0 .2673 0.8018 0.5345 BD BD BD

The force is

FFeeFijk ijk 2  (k N)  0.5345 1.6036 1.0693 0.53 1.60 1.0 7  (kN)

Fijk =  0.53 1 .60 1 .07  (kN). B −+

(5,0,3)

Problem2.162 The magnitude of the vertical force vector F is 6  kN Determine the vector components of F parallel and normal to the line from B to D

Solution: The projection of the force F onto the line from B to D is =⋅ FFee () . PBDBD The vertical force has the component =− Fj6  (kN) From Problem 2.139, the unit vector pointing from B to D is =− +− eijk 0.2673 0 .8018 0.5345 BD The dot product is ⋅=Fe 4.813. BD Thus the component parallel to the line BD is =− =+ −+ Feijk 4.813 1.29 3.86 2.57  (kN ). PBD

The component perpendicular to the line is: =− FFF NP Thus =− Fijk 1.29 2 .14 2 .57  (kN) N FijkFijk 1.29 3.86 2.5 7  (k N),  1.29 2.14 2.57  (kN).

PN =− +=

(4, 3, 1) m

(6, 0, 0) m

(5, 0, 3) m B

Problem2.163 The magnitude of the vertical force vector F is 6  kN. Given that ++ += FFFF0, ABC what are the magnitudes of FF ,  , AB and F ? C =+ += = =+ + =− +− == =− +− =− ++ == =− ++ rijkr eijk rijkr eijk rijkr eijk

(4, 3, 1) m

z Solution:

(6, 0, 0) m (5, 0, 3) m B

The strategy is to expand the forces into scalar components, and then use the force balance equation to solve for the unknowns. The unit vectors are used to expand the forces into scalar components. The position vectors, magnitudes, and unit vectors are:

43 1,  2 6 5.1, 0.7845 0 .5883 0.1961 13 2,  1 4 3.74, 0.2673 0.8018 0.5345 231 ,  14 3.74, 0.5345 0.8018 0.2673 ADAD AD BDBD BD CDCD CD

The forces are: == == FFeFFeFFeFj ,  ,  ,  6  (kN) AAADBBBDCCCD

Substituting into the force balance equation ++ += = ++ =− += FFFF FFFi FFFj FFFk 0, (0.7843 0 .2674 0.5348 )0 (0.5882 0.8021 0 .8021 6)  0(0.1961 0.5348 0.2674 )0

These simple simultaneous equations can be solved a standard method (e.g., Gauss elimination) or, conveniently, by using a commercial package, such as TK Solver®, Mathcad®, or other. An HP-28S hand held calculator was used here: ==FF 2.83 (kN ), 2.49 (kN ), AB = F 2.91 (kN ) C FFF 2.83 (kN), 2.49 (kN), 2.91 (kN). ABC

Problem2.164 The magnitude of the vertical force W is 160 N The direction cosines of the position vector from A to B are θ = cos 0.500, x θ = cos 0.866, y and θ = co s0, z and the direction cosines of the position vector from B to C are cos 0.707,c os0.619,xy θθ== and θ =− cos 0.342. z Point G is the midpoint of the line from B to C Determine the vector × rW, AG where r AG is the position vector from A to G

Solution: The distance from B to G is 0.3 m. Using the given direction cosines, the vector from A to B is rij (0.6 m )(0.50.866 ), AB =+ and the vector from B to G is rijk (0.3 m )(0 .7070.6190.342 ).

BG =+

Then the vector from A to G is rrrijk0.5120.7050.103 (m)

AGABBG =+ =+

The weight Wj160 (N), =− so the desired cross product is rW ijk ik

AG ×= =−

0 .512 m0.705 m0.341 m 01 60 N 0

1 6.481.9 (N-m)

Problem2.165 The rope CE exerts a 500 -N force T on the hinged door. (a) Express T in terms of components. (b) Determine the vector component of T parallel to the line from point A to point B

(0.2, 0.4, 0.1) m

(0, 0.2, 0) m

B C D T

(0.35, 0, 0.2) m

AB

A (0.5, 0, 0) m

Copyright © 2024, 2008 by Pearson Education, Inc. or its affiliates.

rWik 1 6.481.9 (N-m)

AG ×=

Solution: We have =+ == +− rijk T r r ijk

(0.20. 20 .1 )  m (500 N )(333333167 )  N CE CE CE

(a) =+ Tijk (333333167 )  N

(b) We define the unit vector in the direction of AB and then use this vector to find the component parallel to AB =− +

rik e r r ik

Tik ( 0.150.2 )  m ( 0.60.8 ) () ([ 0. 6][333 N ][0.8][ 167 N ])( 0.60.8 ) (20026 7)  N

AB AB AB pABAB p

=− +− −+

TeTeik

TijkTik (a)  333333167 (N). (b)  200267 (N) p =+ −=

Problem2.166 In Problem 2.165, let r BC be the position vector from point B to point C Determine the cross product × rT BC

0.2, 0) m

(0.35, 0, 0.2) m (0.2, 0.4, 0.1) m

0, 0) m

Solution: From Problem 2.165 we know that =+ Tijk (333 333 167 )  N

The vector r BC is =− +− rijk ( 035 0.2 0.2 )  m

The cross product is