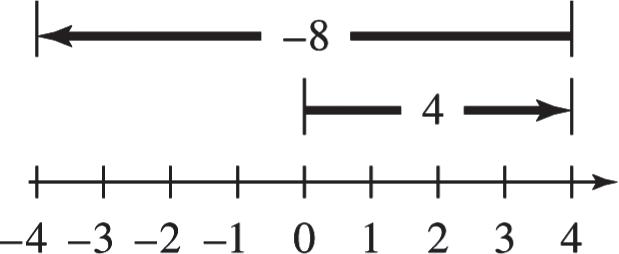Prealgebra Review
R.1 Fractions
Classroom Examples, Now Try Exercises
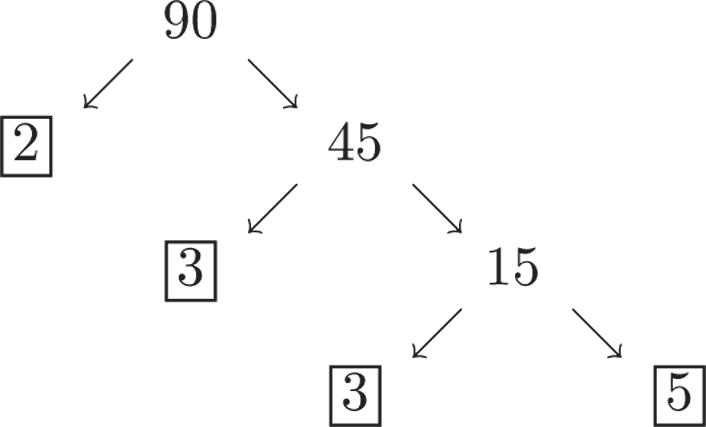
1. 90 is composite and can be written as
Writing 90 as the product of primes gives us 902335
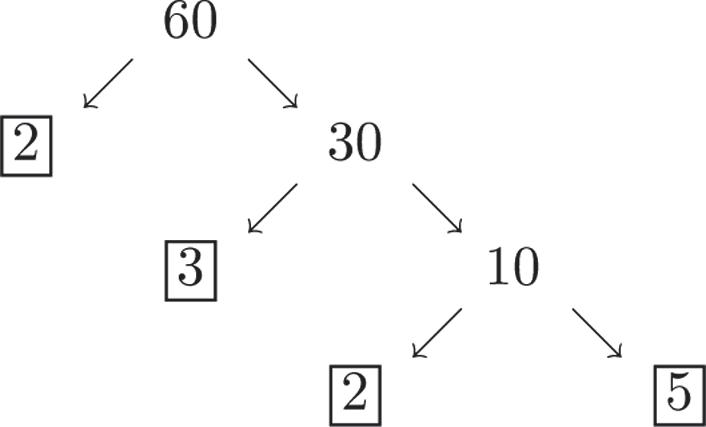
N1. 60 is composite and can be written as
Writing 60 as the product of primes gives us 602235.
2. (a) 12343433 1 20545455
(b) 8811 4868616
(c) 9051855 1 16291899
N2. (a) 30565655 1 42767677
(b) 101011 70710717
(c) 7232433 1 12052455
3. The fraction bar represents division. Divide the numerator of the improper fraction by the denominator. 3 1037 30 7
Thus, 377 3. 1010
N3. The fraction bar represents division. Divide the numerator of the improper fraction by the denominator. 18 592 5 42 40 2
Thus, 922 18. 55
4. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
5315 and 15419
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 419 3. 55
N4. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
31133 and 33235
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 235 11. 33
5. (a) To multiply two fractions, multiply their numerators and then multiply their denominators. Then simplify and write the answer in lowest terms.
518518 925 90 22 925 2 5 5 245 545
(b) To multiply two mixed numbers, first write them as improper fractions. Multiply their numerators and then multiply their denominators. Then simplify and write the answer as a mixed number in lowest terms.
(b) To divide fractions, multiply by the reciprocal of the divisor.
N5. (a) To multiply two fractions, multiply their numerators and then multiply their denominators. Then simplify and write the answer in lowest terms.
(c) Change both mixed numbers to improper fractions. Then multiply by the reciprocal of the second fraction.
(a) To divide fractions, multiply by the reciprocal of the divisor.
(b) To multiply two mixed numbers, first write them as improper fractions. Multiply their numerators and then multiply their denominators. Then simplify and write the answer as a mixed number in lowest terms.
6. (a) To divide fractions, multiply by the reciprocal of the divisor.
(b) To divide fractions, multiply by the reciprocal of the divisor.
(c) To divide fractions, multiply by the reciprocal of the divisor.
7. To find the sum of two fractions having the same denominator, add the numerators and keep the same denominator.
N7. To find the sum of two fractions having the same denominator, add the numerators and keep the same denominator.
8. (a) Since 30235 and 45335, the least common denominator must have one factor of 2 (from 30), two factors of 3 (from 45), and one factor of 5 (from either 30 or 45), so it is 233590.
Write each fraction with a denominator of 90.
Now add. 7221421425 304590909090
Write 25 90 in lowest terms.
25555 9018518
(b) Write each mixed number as an improper fraction.
5 63 1297 42 63
The least common denominator is 6, so write each fraction with a denominator of 6. 29 6 and 77214 3326
Now add. 7291429 29 63666 43 6 14 1 , or 7 6
N8. (a) Since 12223 and 8222, the least common denominator must have three factors of 2 (from 8) and one factor of 3 (from 12), so it is 222324.
Write each fraction with a denominator of 24.
55210
1212224
and 339 832 3 84
Now add. 5310910919 12824242424
(b) Write each mixed number as an improper fraction.
1 48 51345 35 48
The least common denominator is 8, so write each fraction with a denominator of 8. 45 8 and 13226 4 13 428
Now add. 134526452645 48888 717 , or 8 88
9. (a) Since 1025 and 422, the least common denominator is 22520. Write each fraction with a denominator of 20. 3326 1010220
and 1155 45 420
Now subtract. 31651 102020420
(b) Write each mixed number as an improper fraction.
31 82
82 31273
The least common denominator is 8. Write each fraction with a denominator of 8. 27 8 remains unchanged, and 33412 . 2248
Now subtract. 32712271215 28 , 888 8 27 or 1 7 8
N9. (a) Since 1111 and 933, the least common denominator is 331199. Write each fraction with a denominator of 99. 55945 1111999 and 221122 991199
Now subtract. 52452223 119999999
(b) Write each mixed number as an improper fraction. 151317 42 3636
The least common denominator is 6. Write each fraction with a denominator of 6. 17 6 remains unchanged, and 1313226 3326
Now subtract. 1317261726179 366666
Now reduce. 9333 622 , 3 or 1 1 2
10. To find out how long each piece must be, divide the total length by the number of pieces. 121421121 104 221248 , or 5 2 8
Each piece should be 5 2 8 feet long.
N10. To find out how many yards of fabric are needed, add the lengths needed for each piece to obtain the total length. The common denominator is 12. 12138617 1121124 43212121212
Because 175 1 1212 , we have 1755 4415 121212 . A total of 5 5 12 yd of fabric is needed.
11. (a) In the circle graph, the sector for Other is the second largest, so Other had the second largest share of Internet users, 21 . 100
(b) The fraction of Internet users in Other regions can be rounded to 20 , 100 or 1 5
Multiply 1 5 by 5400.
1 54001080million 5
(c) Multiply the fraction from the graph for Other regions by the actual number of users.
21 54001134 million 100
N11. (a) In the circle graph, the sector for Africa is the smallest, so Africa had the least number of Internet users.
(b) The fraction of Internet users in Asia can be rounded to 25 , 50 or 1 2 . Multiply 1 2 by 5400.
1 54002700million 2
(c) Multiply the fraction from the graph for Asia by the actual number of users.
27 54002916 million 50
Exercises
1. True; the number above the fraction bar is called the numerator and the number below the fraction bar is called the denominator.
2. True; 5 divides the 31 six times with a remainder of one, so 311 6. 55
3. False; this is an improper fraction. Its value is 1.
4. False; the number 1 is neither prime nor composite.
5. False; the fraction 13 39 can be written in lowest terms as 1 3 since 131311 391333
6. False; the reciprocal of 6 3 2 is 21 63
7. False; product refers to multiplication, so the product of 10 and 2 is 20. The sum of 10 and 2 is 12.
8. False; difference refers to subtraction, so the difference between 10 and 2 is 8. The quotient of 10 and 2 is 5.
9. 16282 24383 Therefore, C is correct.
10. Simplify each fraction to find which are equal to 5 9 355 3 15 2979
655 6 30 5949
22020 237 40 7437
1155 11 55 999 9
Therefore, C is correct.
11. We need to multiply 8 by 3 to get 24 in the denominator, so we must multiply 5 by 3 as well.
55315 88324
Therefore, B is correct.
12. A common denominator for p q and r s must be a multiple of both denominators, q and s. Such a number is qs Therefore, A is correct.
13. Since 19 has only itself and 1 as factors, it is a prime number.
14. Since 31 has only itself and 1 as factors, it is a prime number.
15. 215 23 30 5
Since 30 has factors other than itself and 1, it is a composite number.
16. 50225 255,
so 50 is a composite number.
17. 227 23 5 9 23 4 33
Since 54 has factors other than itself and 1, it is a composite number.
18. 36218 229 2233,
so 36 is a composite number.
19. 232 2216 2228 22224 22 4 222 6 2
Since 64 has factors other than itself and 1, it is a composite number.
20. 27 339 8 33 13 33
Since 81 has factors other than itself and 1, it is a composite number.
21. As stated in the text, the number 1 is neither prime nor composite, by agreement.
22. The number 0 is not a natural number, so it is neither prime nor composite.
23. 57319, so 57 is a composite number.
24. 51317, so 51 is a composite number.
25. Since 79 has only itself and 1 as factors, it is a prime number.
26. Since 83 has only itself and 1 as factors, it is a prime number.
27. 262 124 2231,
so 124 is a composite number.
28. 269 138 2323, so 138 is a composite number.
29. , 3 2 002150 2275 2325 22355
so 300 is a composite number.
30. 2350 22175 22535 225 70 57, 0
so 700 is a composite number.
31. 8181811 1 16282822
32. 141411 1 12343433 4
33. 15353555 1 18363666
34. 164444 2 44 1 545 05 45
35. 903303303 1 15053053055 3
36. 1005 1407 5205205 1 7207207
37. 1811811811 1 9051851855
38. 1611611611 1 64416444 16
39. 14462462466 1 12052452455
40. 132121112111212 1 7117117 777
41. 1 712 7 5 Therefore, 125 1. 77
42. 1 916 9 7 Therefore, 167 1. 99
43. 6 1277 72 5 Therefore, 775 6. 1212
44. 6 15101 90 11 Therefore, 10111 6. 1515
45. 7 1183 77 6
Therefore, 836 7. 1111
46. 5 1367 65 2 Therefore, 672 5. 1313
47. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
5210 and 10313
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 313 2. 55
48. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
7535 and 35641
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 641 5. 77
49. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
81080 and 80383
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 383 10. 88
50. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
31236 and 36238
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 238 12. 33
51. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
51050 and 50151
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 151 10. 55
52. Multiply the denominator of the fraction by the natural number and then add the numerator to obtain the numerator of the improper fraction.
6848 and 48149
The denominator of the improper fraction is the same as the denominator in the mixed number.
Thus, 149 8. 66
53. 464624 575735
54. 25210 797 5 963
55. 361 1581202 22316 1582060
56. 35151 202142 35115 20212808 152
57. 1121121266 10510525525
58. 1101101255 8724728 87
59. 158158 425425 3542 455 32 5 61 , or1 55
60. 214214 787 374 427 31 , or 8 1 2 2
61. 3213 21 717 213 17 373 17 33 9 1
63. Change both mixed numbers to improper fractions. 12135 31 4343 135 43 655 , or 5 1212
64. Change both mixed numbers to improper fractions. 23 33 3 88 21 55 88 5 644 , or 4 1515
65. Change both mixed numbers to improper fractions.
69. To divide fractions, multiply by the reciprocal of the divisor.
70. To divide fractions, multiply by the reciprocal of the divisor.
66. Change both mixed numbers to improper fractions.
67. Change both
to improper fractions.
71. To divide fractions, multiply by the reciprocal of the divisor.
72. To divide fractions, multiply by the reciprocal of the divisor.
68.
73. To divide fractions, multiply by the reciprocal of the divisor.
77. To divide fractions, multiply by the reciprocal of the divisor.
74. To divide fractions, multiply by the reciprocal of the divisor.
78. To divide fractions, multiply by the reciprocal of the divisor.
75. To divide fractions, multiply by the reciprocal of the divisor.
79. Change the first number to an improper fraction, and then multiply by the reciprocal of the divisor.
76. To divide fractions, multiply by the reciprocal of the divisor.
80. Change the first number to an improper fraction, and then multiply by the reciprocal of the divisor.
81. Change both mixed numbers to improper fractions, and then multiply by the reciprocal of the divisor.
82. Change both mixed numbers to improper fractions, and then multiply by the reciprocal of the divisor.
85. 747411 15151515
86. 25257 9999
87. 7171 121212 8 12 24 34 2 3
88. 5351 16161 38 6162
89. Since 933, and 3 is prime, the LCD (least common denominator) is 339. 1133 3339
83. Change both mixed numbers to improper fractions, and then multiply by the reciprocal of the divisor.
84. Change both mixed numbers to improper fractions, and then multiply by the reciprocal of the divisor.
Now add the two fractions with the same denominator. 51538 93999
90. To add 4 15 and 1 , 5 first find the LCD. Since 1535 and 5 is prime, the LCD is 15. 41413 553 43 1515 1515 43 7 15 15
91. Since 8222 and 623, the LCD is 22224. 3 3339 88324
and 55420 66424
Now add fractions with the same denominator. 3592029 8624244 , 2 or 5 1 24
92. Since 623 and 933, the LCD is 23318. 553 3 15 6618
and 2 22 992 4 18
Now add fractions with the same denominator. 515 , 691818 2419 18
or 1 1 18
93. Since 933 and 1644, the LCD is 3344144.
1680 991 55 6144
and 33927 16169144
Now add fractions with the same denominator. 538027 916144144 107 144
97. 1112113 33 44444 44549 11 55555
Since 422, and 5 is prime, the LCD is 22520. 1413594 31 454554 6536 2020 1011 ,or5 2020
and 66424 25254100
94. Since 422 and 2555, the LCD is 2255100. 332575 4425100
Now add fractions with the same denominator. 36752499 425100010010
95. 1124125 33 88888 11819 22 44444 11259 32 8484
Since 8222 and 422, the LCD is 222 or 8. 112592 32 84842 2518 88 433 , or 5 88
96. 212214 44 1112113 22 2 33333 6 6666
Since 623, the LCD is 6. 3 6 2114213 4 6 2 6326 2813 415 , 66 or 6
98. To add 5 3 4 and 1 1, 3 first change to improper fractions then find the LCD, which is 12. 3123 51 33 23344 4334 6916 12 1 , or 7 12 4 44 12 85 12
99. 72725 9999
100. 8383 11111 5 111
101. 133133 151515 10 15 252 353
102. 113113 121212 12 24 4 8 2 33
Copyright © 2025 Pearson Education, Inc.
103. Since 1243 (12 is a multiple of 3), the LCD is 12. 144 3412
Now subtract fractions with the same denominator. 71743131 123121212434
104. Since 632 (6 is a multiple of 2), the LCD is 6. 1 2 3 3 36
Now subtract fractions with the same denominator. 5132 5 6666 121 23 23
105. Since 12223 and 933, the LCD is 22336. 3 77321 1212336 and 144 9436
Now subtract fractions with the same denominator. 7121417 129363636
106. The LCD of 12 11111314 and 16 is 48. 1612163124 334 4848 29 48
107. 3316319 44 44444 22527 11 55555
Since 422, and 5 is prime, the LCD is 22520. 3219574 41 454554 9528 2020 677 , or 3 2020
108. Change both numbers to improper fractions then add, using 45 as the common denominator. 4419 31 199135 5995 17165 45 13 5959 45 106 4 16 , o 4 r 55 2
109. 1124125 66 44444 1115116 55 33333
Since 422, and 3 is prime, the LCD is 22312. 112516 65 4343 253164 4334 7564 1212 11 12
110. 33 1115116 55 333 11819 4 2 22 4 22
2 and 3 are prime, so the LCD is 236. 1116293 54 323223 6 3227 6 5 6
111. 74 88 12 4 22722 99999 22214 33333 4
Since 933, and 3 is prime, the LCD is 339. 143 84 33 2274 939 7442 99 35 ,or 3 9 2 9
Since 12223
and 623, the LCD is 22312.
113. Observe that there are 24 dots in the entire figure, 6 dots in the triangle, 12 dots in the rectangle, and 2 dots in the overlapping region.
(a) 121 242 of all the dots are in the rectangle.
(b) 61 244 of all the dots are in the triangle.
(c) 21 63 of the dots in the triangle are in the overlapping region.
(d) 21 126 of the dots in the rectangle are in the overlapping region.
114. (a) 12 is 1 3 of 36, so Maya got a hit in exactly 1 3 of her at-bats.
(b) 5 is a little less than 1 2 of 11, so Deion got a hit in just less than 1 2 of his at-bats.
(c) 1 is a little less than 1 10 of 11, so Deion got a home run in just less than 1 10 of his atbats.
(d) 9 is a little less than 1 4 of 40, so Christine got a hit in just less than 1 4 of her at-bats.
(e) 8 is 1 2 of 16, and 10 is 1 2 of 20, so Joe and
Greg each got hits 1 2 of the time they were at bat.
115. Multiply the number of cups of water per serving by the number of servings. 338 8 441 38 41 24 4 6 cups
For 8 microwave servings, 6 cups of water will be needed.
116. Four stove-top servings require 1 4 tsp, or 2 8 tsp, of salt. Six stove-top servings require 1 2 tsp, or 4 8 tsp, of salt. Five is halfway between 4 and 6, and 3 8 is halfway between 2 8 and 4 . 8 Therefore, 5 stove-top servings would require 3 8 tsp of salt.
117. The difference in length is found by subtracting.
1 88
The difference is 1 1 8 inches.
118. The difference in length is found by subtracting.
121. The perimeter is the sum of the measures of the 5 sides.
119. The difference between the two measures is found by subtracting, using 16 as the LCD.
The perimeter is 3 618 4 feet.
122. To find the perimeter of a triangle, add the lengths of the three sides. 111241
difference is 9 16 inch.
120. The difference between the two measures is found by subtracting, using 16 as a common denominator.
The difference is 3 16 inch.
The perimeter of the triangle is 7 22 8 feet.
123. Divide the total board length by 3. 51253 153 881 1251 83 1251 83 1255 , or 5 2424
The length of each of the three pieces must be 5 5 24 inches.
124. Divide the total amount of tomato sauce by the number of servings.
For 1 serving of barbecue sauce, 1 3 cup of tomato sauce is needed.
125. To find the number of cakes the caterer can make, divide 1 15 2 by 3 1 4 . 13317 151 2424 314 27 3122 27 626 , or 8 77
There is not quite enough sugar for 9 cakes. The caterer can make 8 cakes with some sugar left over.
126. Divide the total amount of fabric by the amount of fabric needed to cover one chair.
129. Subtract the heights to find the difference.
The upholsterer can cover 10 chairs. There will be some fabric left over.
127. Multiply the amount of fabric it takes to make one costume by the number of costumes. 3197
For 7 costumes, 5 16 8 yards of fabric would be needed.
128. Multiply the amount of sugar for one batch times the number of batches. 24 24 1
2 10 3 cups of sugar are required to make four batches of cookies.
The difference in heights is 3 3 8 inches.
130. Subtract 3 8 from 11 16 using 16 as the LCD. 1131132 81682 116
Thus, 3 8 inch is 5 16 inch smaller than 11 16 inch.
131. A share of 13 25 can be rounded to 131 . 262 Multiply by the total number of foreign-born people in the U.S., approximately 45 million. , 1145451 452 2122 2 2
There were approximately 1 22 2 million (or 22,500,000) foreign-born people in the U.S. who were born in Latin America. For the actual number: , 13134513 1 117 25 59 45 15 55 5 2
or 23 2 5 The actual number who were born in Latin America was 23 2 5 million (or 23,400,000) people.
132. Multiply the fraction representing the U.S. foreign-born population from Asia, 3 , 10 by the total number of foreign-born people in the U.S., approximately 45 million. , 3327 10 34559 4 5 10 5 112 2
or 13 1 2
There were approximately 13 1 2 million (or 13,500,000) foreign-born people in the U.S. who were born in Asia.
133. Multiply the fraction representing the U.S. foreign-born population from Europe, 1 , 10 by the total number of foreign-born people in the U.S., approximately 45 million. 119 , 45159 4 2 11 01012 5 5
or 4 1 2
There were approximately 4 1 2 million (or 4,500,000) foreign-born people in the U.S. who were born in Europe.
134. Multiply the fraction representing the U.S. foreign-born population from Other regions, 2 , 25 by the total number of foreign-born people in the U.S., approximately 45 million. , 452 25 5 21 4 8 252515 9 5 51
or 3 3 5
There were approximately 3 3 5 million (or 3,600,000) foreign-born people in the U.S. who were born in Other regions.
135. Estimate each fraction. 14 26 is about 1 , 2 98 99 is about 1, 100 51 is about 2, 90 31 is about 3, and 13 27 is about 1 . 2
Therefore, the sum is approximately 11 1237. 22
The correct choice is C.
136. Estimate each fraction. 202 50 is about 4, 99 100 is about 1, 21 40 is about 1 , 2 and 75 36 is about 2.
Therefore, the product is approximately 1 4124 2
The correct choice is B.
R.2 Decimals and Percents
Classroom Examples, Now Try Exercises
1. (a) 15 0.15 100 (b) 9 0.009 1000 (c) 525 2.52 1010
N1. (a) 8 0.8 10 (b) 431 0.431 1000 (c) 58258 2.582 100100
2. (a) 42.830 71.000 3.074 116.904 (b) 32.50 21.72 10.78 (c) 10.000 0.125 9.875
N2. (a) 68.900 42.720 8.973 120.593 (b) 351.800 2.706 349.094 (c) 5.000 0.375 4.625
3. (a) 30.21decimal place 0.0523decimal places 604 1510134 1.57044decimal places
(b) 0.062decimal places
0.122decimal places 12 6224
0.00724decimal places
N3. (a) 9.322decimal places 1.41decimal place 3728 932213 13.0483decimal places
(b) 0.61decimal place 0.0043decimal places 24134
0.00244decimal places
4. (a) To change the divisor 0.37 into a whole number, move each decimal point two places to the right. Move the decimal point straight up and divide as with whole numbers.
We carried out the division to 2 decimal places so that we could round to 1 decimal place. Therefore, 3.763.11.2.
N4. (a) To change the divisor 14.9 into a whole number, move each decimal point one place to the right. Move the decimal point straight up and divide as with whole numbers. 30.3 1494514.7 447 447 447 0 Therefore, 451.4714.930.3.
(b) To change the divisor 1.3 into a whole number, move each decimal point one place to the right. Move the decimal point straight up and divide as with whole numbers.
Therefore, 5.4760.3714.8.
(b) To change the divisor 3.1 into a whole number, move each decimal point one place to the right. Move the decimal point straight up and divide as with whole numbers.
We carried out the division to 3 decimal places so that we could round to 2 decimal places. Therefore, 7.3341.35.64.
5. (a) Move the decimal point three places to the right.
19.5100019,500
(b) Move the decimal point one place to the left. 960.11096.01
N5. (a) Move the decimal point one place to the right.
294.72102947.2
(b) Move the decimal point two places to the left. Insert a 0 in front of the 4 to do this. 4.7931000.04793
6. (a) Divide 3 by 50. Add a decimal point and as many 0s as necessary. 0.06 503.00
Therefore, 3 0.06. 50
(b) Divide 11 by 1. Add a decimal point and as many 0s as necessary. 0.090909... 111.000000...
Note that the pattern repeats. Therefore, 1 0.09, 11 or about 0.091 rounded to the nearest thousandth, about 0.09 rounded to the nearest hundredth, or about 0.1 rounded to the nearest tenth.
N6. (a) Divide 20 by 17. Add a decimal point and as many 0s as necessary. 0.85
Therefore, 17 0.85. 20
(b) Divide 2 by 9. Add a decimal point and as many 0s as necessary.
0.222... 92.000... 18 20 18 20 18 2
Note that the pattern repeats. Therefore, 2 0.2, 9 or about 0.222 rounded to the nearest thousandth, about 0.22 rounded to the nearest hundredth, or about 0.2 rounded to the nearest tenth.
7. (a) 1 5%5.25% 4 5.25 100 0.0525 (b) 200 200%2.00, 100 or 2
N7. (a) 23 23%0.23 100 (b) 350 350%3.50, 100 or 3.5
8. (a) 0.060.06100%6% (b) 1.751.75100%175%
N8. (a) 0.310.31100%31% (b) 1.321.32100%132%
9. (a) 85%0.85 (b) 110%1.10, or 1.1 (c) 0.3030% (d) 0.16516.5%
N9. (a) 52%0.52 (b) 2%02%0.02 (c) 0.4545% (d) 3.53.50350%
10. (a) 65 65% 100 In lowest terms, 6513513 10020520 (b) 1.51.510153 1.5% 100100101000200
N10. (a) 20 20% 100 In lowest terms, 201201 1005205
(b) 160 160% 100 In lowest terms, 16082083 , or 1 10052055
11. (a) 33 100% 5050 3100 % 501 3502 % 50 6%
(b) 11 100% 33 1100 % 31 100 % 3 1 33%, or 33.3% 3
N11. (a) 66 100% 2525 6100 % 251 6254 % 25 24%
(b) 77 100% 99 7100 % 91 700 % 9 7 77%, or 77.7% 9
12. The discount is 30% of $69. The word of here means multiply. 30%of69
0.306920.7
The discount is $20.70. The sale price is found by subtracting.
$69.00$20.70$48.30
N12. The discount is 60% of $120. The word of here means multiply. 60%of120 0.6012072
The discount is $72. The sale price is found by subtracting. $120.00$72$48
Exercises
1. 367.9412
(a) Tens: 6
(b) Tenths: 9
(c) Thousandths: 1
(d) Ones: 7
(e) Hundredths: 4
2. Answers will vary. One example is 5243.0164.
3. 46.249
(a) 46.25
(b) 46.2
(c) 46
(d) 50
4. (a) 0.889 (b) 0.444
(c) 0.976
(d) 0.865
8. 82 0.82 100
9. 138 0.138 1000
10. 104 0.104 1000
11. 43 0.043 1000
12. 87 0.087 1000 13. 8053805 3.8053 10001000
14. 1665166 5.1665 10001000
29.000 8.582 20.418 27. 12.81decimal place 9.11decimal place 128 1152112 116.482decimal places
28. 34.042decimal places 0.562decimal places 20424 17020224 19.06244decimal places
29. 22.412decimal places 330decimal places 6723 6723202 739.532decimal places
30. 55.762decimal places 720decimal places 11152 39032202 4014.722decimal places
31. 0.21decimal place 0.032decimal places 6123 0.0063decimal places
32. 0.072decimal places 0.0043decimal places 28235 0.000285decimal places
35. To change the divisor 11.6 into a whole number, move each decimal point one place to the right. Move the decimal point straight up and divide as with whole numbers. 2.8 116324.8 232 092 0 000 8 928 0 Therefore, 32.4811.62.8
36. To change the divisor 17.4 into a whole number, move each decimal point one place to the right. Move the decimal point straight up and divide as with whole numbers. 4.9 174852.6 696
37. To change the divisor 9.74 into a whole number, move each decimal point two places to the right. Move the decimal point straight up and divide as with whole numbers. 2.05 9741996.70 1948 4870 4870 0 Therefore, 19.9679.742.05.
38. To change the divisor 5.27 into a whole number, move each decimal point two places to the right. Move the decimal point straight up and divide as with whole numbers. 8.44 5274447.88 4216 2318 2108 2108 2108 0 Therefore, 44.47885.278.44.
39. Move the decimal point one place to the right. 123.26101232.6
40. Move the decimal point one place to the right. 785.91107859.1
41. Move the decimal point two places to the right. 57.1161005711.6
42. Move the decimal point two places to the right. 82.0531008205.3
43. Move the decimal point three places to the right.
0.094100094
44. Move the decimal point three places to the right.
0.025100025
45. Move the decimal point one place to the left. 1.62100.162
46. Move the decimal point one place to the left. 8.04100.804
47. Move the decimal point two places to the left. 124.031001.2403
48. Move the decimal point two places to the left. 490.351004.9035
49. Move the decimal point three places to the left. 23.291000023.2910000.02329
50. Move the decimal point three places to the left. 59.81000059.810000.0598
51. Convert from a decimal to a percent. 0.010.01100%1%
54. Convert to a decimal first. Divide 1 by 10. Move the decimal point one place to the left. 1100.1
Convert the decimal to a percent. 0.10.1100%10%
55. Convert the decimal to a percent. 0.1250.125100%12.5%
56. Convert the percent to a decimal first. 20%0.20, or 0.2 Convert from a percent to a fraction. 20 20% 100 In lowest terms, 201201 1005205
52. Convert from a percent to a decimal. 2 2%0.02 100
57. Convert to a decimal first. Divide 1 by 4. Add a decimal point and as many 0s as necessary. 0.25 41.00 8 20 20 0
Convert the decimal to a percent. 0.250.25100%25%
53. Convert from a percent to a fraction.
58. Convert to a decimal first. Divide 1 by 3. Add a decimal point and as many 0s as necessary. 0.33... 31.00... 9 10 9 1
Note that the pattern repeats. Therefore, 1 0.3. 3
Convert the decimal to a percent. 0.3330.333100%33.3%,
or 1 33% 3
59. Convert the percent to a decimal first. 50%0.50, or 0.5
Convert from a percentl to a fraction. 50 50% 100 In lowest terms, 501501
60. Divide 2 by 3. Add a decimal point and as many 0s as necessary.
Note that the pattern repeats. Therefore, 2
61. Convert the decimal to a percent first. 0.750.75100%75%
Convert from a percent to a fraction. 75 75% 100 In lowest terms, 753253
62. Convert the decimal to a percent. 1.01.0100%100%
63. Divide 2 by 5. Add a decimal point and as many 0s as necessary.
64. Divide 3 by 5. Add a decimal point and as many 0s as necessary. 0.6 5 0 0. 3.0 3 0
65. Divide 9 by 4. Add a decimal point and as many 0s as necessary. 2.25
66. Divide 15 by 4. Add a decimal point and as many 0s as necessary.
70. Divide 8 by 9. Add a decimal point and as many 0s as necessary.
67. Divide 3 by 8. Add a decimal point and as many 0s as necessary.
Note that the pattern repeats. Therefore, 8 0.8, 9 or about 0.889, 0.89, or 0.9.
71. Divide 5 by 6. Add a decimal point and as many 0s as necessary.
68. Divide 7 by 8. Add a decimal point and as many 0s as necessary.
Note that the pattern repeats. Therefore, 5 0.83, 6 or about 0.833, 0.83, or 0.8.
72. Divide 1 by 6. Add a decimal point and as many 0s as necessary. 0.166...
69. Divide 5 by 9. Add a decimal point and as many 0s as necessary.
Note that the pattern repeats. Therefore, 5 0.5, 9 or about 0.556, 0.56, or 0.6.
Note that the pattern repeats. Therefore, 1 0.16, 6 or about 0.167, 0.17, or 0.2.
73. 54%0.54
74. 39%0.39
75. 7%07%0.07
76. 4%04%0.04
77. 117%1.17
78. 189%1.89
79. 2.4%02.4%0.024
80. 3.1%03.1%0.031
81. 1 6%6.25%06.25%0.0625 4
82. 1 5%5.5%05.5%0.055 2
83. 0.8%00.8%0.008
84. 0.9%00.9%0.009
85. 0.7979%
86. 0.8383%
87. 0.022%
88. 0.088%
89. 0.0040.4%
90. 0.0050.5%
91. 1.28128%
92. 2.35235%
93. 0.4040%
94. 0.60.6060%
95. 66.00600%
96. 1010.001000%
97. 51 51% 100
98. 47 47% 100
99. 15 15% 100
In lowest terms, 15353 10020520
100. 35 35% 100
In lowest terms, 35757 10020520
101. 2 2% 100 In lowest terms, 2121 10050250
102. 8 8% 100 In lowest terms, 8242 10025425
103. 140 140% 100
In lowest terms, 1407207 , 1005205 or 2 1 5
104. 180 180% 100
In lowest terms, 1809209 , 1005205 or 4 1 5
105. 7.57.51075 7.5% 100100101000
In lowest terms, 753253 1000402540
106. 2.52.51025 2.5% 100100101000
In lowest terms, 251251 1000402540
107. 4441004520 100%%%80% 55515
108. 33 100% 2525 3100 % 251 3425 % 25 12%
109. 77 100% 5050 7100 % 501 7250 % 50 14%
110. 99 100% 2020 9100 % 201 9520 % 20 45%
111. 9991009425 100%%%225% 44414
112. 8881008520 100%%%160% 55515
113. 55 100% 66 5100 % 61 5250 % 23 250 % 3 1 83%, or 83.3% 3
114. 55 100% 1212 5100 % 121 5250 % 26 250 % 6 2 41%, or 41.6% 3
115. 44 100% 99 4100 % 91 400 % 9 4 44%, or 44.4% 9
116. 22 100% 1111 2100 % 111 200 % 11 2 18, or 18.18% 11
117. The word of here means multiply. 50%of320
0.50320160
118. The word of here means multiply. 25%of120 0.2512030
119. The word of here means multiply. 6%of80
0.06804.8
120. The word of here means multiply. 5%of70
0.05703.5
121. The word of here means multiply. 14%of780
0.14780109.2
122. The word of here means multiply. 26%of480
0.26480124.8
123. The tip is 20% of $150. The word of here means multiply.
20%of$150
0.20$150$30
The tip is $30. The total bill is found by adding.
$150$30$180
124. The raise is 10% of $15. The word of here means multiply. 10%of$15
0.10$15$1.50
The amount of the raise is $1.50 per hour. The new hourly rate is found by adding.
$15$1.50$16.50
125. The discount is 15% of $1000. The word of here means multiply. 15%of$1000
0.15$1000$150
The amount of the discount is $150. The sale price is found by subtracting.
$1000$150$850
126. The discount is 25% of $600. The word of here means multiply. 25%of$600
0.25$600$150
The amount of the discount is $150. The sale price is found by subtracting.
$600$150$450
127. The portion of the circle graph showing the carbon dioxide emissions from the United States is 15% of the circle. Find 15% of 36 billion.
15%of36billion
0.1536billion5.4billion
The United States produced 5.4 billion metric tons.
128. The portion of the circle graph showing the carbon dioxide emissions from Asia is 51% of the circle. Find 51% of 36 billion.
51%of36billion
0.5136billion18.36billion
Asia produced 18.36 billion metric tons.
129. First, find the portion of the circle graph that represents the Middle East and Africa.
6%4%10%
The portion of the circle graph showing the carbon dioxide emissions from the Middle East and Africa is 10% of the circle. Find 10% of 36 billion.
10%of36billion
0.1036billion3.6billion
The Middle East and Africa produced 3.6 billion metric tons.
130. First, find the portion of the circle graph that represents Europe and Africa.
11%4%15%
The portion of the circle graph showing the carbon dioxide emissions from Europe and Africa is 15% of the circle. Find 15% of 36 billion.
15%of36billion
0.1536billion5.4billion
Europe and Africa produced 5.4 billion metric tons.
Chapter 1
The Real Number System
1.1 Exponents, Order of Operations, and Inequality
Classroom Examples, Now Try Exercises
1. (a) 2 99981
(b) 4 1111 16 1 is us 1 ed as a factor 4 times. 2 1 22222
(c) 2 (0.5)0.50.50.25
N1. (a) 2 66636
(b) 3 444464 5555125 4 is used as a factor 3 times. 5
2. (a) 1062 103Divide. 7Subtract.
18263 1823Subtract inside parentheses. 186Multiply. 24Add.
(c)
76381 7639Add inside parentheses. 4227Multiply. 15Subtract.
(d) 2 304
(e) 2 1232 12952Apply exponents. 12910Multiply. 310Subtract. 13Ad. 5 d
N2. (a) 1526 1512Multiply. 3Subtract.
(b)
8251 824Subtract inside parentheses. 88Multiply. 16Add.
(c) 62475 6675Add inside parentheses. 3635Multiply. 1Subtract.
(d) 2 14210 14410Apply exponents. 1010Subtract. 20Add.
(e) 810423432 81048316Apply exponents. 8048316Multiply. 20848Divide/multiply. 1248Subtract.
60Add.
3. (a)
9362(48) 9362(12)Add inside parentheses. 93624Multiply inside brackets. 912Subtract inside brackets. 108Multiply.
146Subtrac 6 16 t. 6 20Add.
30Apply exponents.
(b) 2(78)2 351 2(15)2 Add inside parentheses. 351 302 Multiply. 151 3 16 2 Add. Divide 2.
N3. (a)
73(31)4
73(2)4Subtract inside parentheses.
764Multiply inside brackets.
710Add inside brackets.
70Multiply.
(b) 9(144)2
436 9(10)2 Subtract inside parentheses.
436 902 Multiply.
418
88 Subtract and add.
22 4Divide.
4. (a) The statement 126 is true because 12 is greater than 6. Note that the inequality symbol points to the lesser number.
(b) The statement 2847 is false because 28 isequalto 47.
(c) The statement 1 0.1 10 is true because 1 0.1 10
(d) Write the fractions with a common denominator. The statement 11 34 is equivalent to the statement 43 . 1212
Because 4 is greater than 3, the original statement is false.
N4. (a) The statement 12102 is true because 12 isnotequalto 8.
(b) The statement 542 is false because 5 is lessthan 8.
(c) The statement 1 0.25 4 is true because 1 0.25 4
(d) Write the fractions with a common denominator. The statement 57 911 is equivalent to the statement 5563 9999
Because 55 is less than 63, the original statement is false.
5. (a) “Nine is equal to eleven minus two” is written as 9112.
(b) “Fourteen is greater than twelve” is written as 1412.
(c) “Two is lessr than or equal to two” is written as 22.
N5. (a) “Ten is not equal to eight minus two” is written as 1082.
(b) “Fifty is greater than fifteen” is written as 50. 15
(c) “Eleven is less than or equal to twenty” is written as 11. 20
6. 915 is equivalent to 15. 9 N6. 89 is equivalent to 9. 8
Exercises
1. False; 2 3339.
2. False; 1 raised to any power is 1. Here, 3 11111.
3. False; a number raised to the first power is that number, so 1 33.
4. False; 62 means that 6 is used as a factor 2 times, so 2 66636.
5. False; the common error leading to 42 is adding 4 to 3 and then multiplying by 6. One must follow the rules for order of operations.
43(82) 436 418 22
6. False; multiplications and divisions are performed inorderfromlefttoright. 1223 63 18
7. Additions and subtractions are performed in order from left to right.
8. Multiplications and divisions are performed in order from left to right, and then additions and subtractions are performed in order from left to right.
9. Multiplications and divisions are performed in order from left to right, and then additions and subtractions are performed in order from left to right.
10. Multiplications and divisions are performed in order from left to right, and then additions and subtractions are performed in order from left to right. If grouping symbols are present, work within them first, starting with the innermost.
11. Multiplications and divisions are performed in order from left to right, and then additions and subtractions are performed in order from left to right. If grouping symbols are present, work within them first, starting with the innermost.
12. Apply all exponents. Then, multiplications and divisions are performed in order from left to right, and additions and subtractions are performed in order from left to right.
0.90.90.90.81
3 0.40.40.40.40.064
33. The multiplication should be performed before the addition. 82386Multiply. 14Add.
The correct value of the expression is 14.
34. When cubing 2, the correct value is 2228 , not 236 3 16251685Apply exponents. 85Subtract. 13Add.
The correct value of the expression is 13.
35. Divide. 6442162 32Multiply.
36. Divide. 25052502 100Multiply.
37. 13951345Multiply. 58Add.
38. 11761142Multiply. 53Add.
39. 25.212.64.225.23Divide. 22.2Subtract.
40. 12.49.33.112.43D 9. ivide. Subtract 4.
41. 94833624Multiply. 12Subtract.
42. 1141034430Multipl 7 y. Add. 4
43. 151 Multiply. 106 1 LCD 1212 1 Add. 1 211 34612 2 12 3 , r 2 o 4
44. 10 341442 Multiply. 5925155 46 LCD15 1515 Add. 1 2 , or 3 5
45. 2043520125Multiply. 85Subtract. 13Add.
46. 1872618146Multiply. 46Subtract. 10Add.
47. 1040521082Divide. 1016Multiply. 26Add.
48. 1264841284Divide. 204Add. 16Subtract.
49. 182(34) 182(7)Add inside parentheses. 1814Multiply. 4Subtract.
50.
30342 3036Add inside parentheses. 18Multiply. 12Subtrac 30 t
51. 3(42)833683Add. 1824Multiply. 42Add.
52. Add. 7 91 210Multiply. 82 725982 Ad. 5 d
53. 2 184318163Apply exponents. 23Subtract. 5Add.
54. 3 22292289Apply exponents. 149Subtract. 23Add.
55. 23[54(2)]23[58]Multiply. 23[13]Add. 239Multiply. 41Add.
56.
5417354121Multiply. 5422Add. 588Multiply. 93Add.
57. 2 53425[34(4)]Apply exponents. 5(316)Multiply. 5(19)Add. 95Multiply.
58. 62833 62827Apply exponents. 6(2216)Multiply. 6218Add. 1308Multiply.
59. 2 2 2 3[(113)4] 3[144]Add inside parentheses. 3[10]Subtract. 9[10]Apply exponents. 90Multiply.
60.
2 2 2 4 9 [(134)8] 4178Add inside parentheses. 4Subtract. 169Apply exponents. 144Multiply.
61. Simplify the numerator and denominator separately, and then divide.
62. Simplify the numerator and denominator separately, and then divide.
63. Simplify the numerator and denominator separately, and then divide. 22 4(62)8(83)4(8)8(5) 6(42)26(2)2 4(8)8(5) 6(2)4
64. Simplify the numerator and denominator separately, and then divide. 33 6(51)9(11)6(6)9(2) 5(86)25(2)2 3618 108 18 2 9
65. 34242
Listed below are some possibilities. Use trial and error until you get the desired result. (34)2464102
3(424)36182 3(42)432464102 34(24)3461262
66. 281342 281327314342
67. 10736 10(73)1046
68. 2 82100 2 2 82101010100
69. 931116 271116 1616
The statement is true since 1616.
70. 651218 301218 1818
The statement is true since 1818.
71. 5112360 55660 6160
The statement is false since 61 isgreater than 60.
72. 934548 272048 4748
The statement is false since 47 islessthan 48.
73. 012366 03636 00
The statement is true since 00.
74. 10132151 102615 1011
The statement is true since 1011.
75. 452[23(25)]
452[23(7)]
452[221]
452[23] 4546
The statement is false since 45 islessthan 46.
76. 553[43(41)]
553[43(5)]
553[415]
553[19] 5557
The statement is false since 55 islessthan 57.
77. [345(2)]372 [1210]372 [22]372 6672
The statement is false since 66 islessthan 72.
78. 2[753(2)]58 2[356]58 2[29]58 5858
The statement is true since 5858.
79. 35(41) 3
The statement is false since 2 islessthan 3.
80.
7312 2 352 742 2 310 282 2 13 26 2 13 22
The statement is true since 22.
81. 2(51)3(11) 3 5(86)42
2(6)3(2) 3 5(2)8
The statement is true since 33.
82. 3(83)2(41) 7 9(62)1152
3(5)2(3) 7 9(4)11(3) 156 7 3633 21 7 3 77
The statement is true since 77.
83. “5” 17 means “five is less than seventeen.” The statement is true.
84. “8” 12 means “eight is less than twelve.” The statement is true.
85. “5” 8 means “five is not equal to eight.” The statement is true.
86. “6” 9 means “six is not equal to nine.” The statement is true.
87. “7” 14 means “seven is greater than or equal to fourteen.” The statement is false.
88. “6” 12 means “six is greater than or equal to twelve.” The statement is false.
89. “15” 15 means “fifteen is less than or equal to fifteen.” The statement is true.
90. “21” 21 means “twenty-one is less than or equal to twenty-one.” The statement is true.
91. “ 1 3 ” 3 10 means “one-third is equal to threetenths.” The statement is false.
92. “10 6 ” 3 2 means “ten-sixths is equal to threehalves.” The statement is false.
93. “ 7 10 ” 1 2 means “seven-tenths is greather than one-half.” The statement is true.
94. “ 2 3 ” 5 9 means “two-thirds is greater than give-ninths.” The statement is true.
95. 2.52 “” .50 means “two and five-tenths is greater than two and fifty-hundredths.” The statement is false.
96. 1.80 “” 1.8 means “one and eighty-hundredths is greater than one and eight-tenths.” The statement is false.
97. “Fifteen is equal to five plus ten” is written as 15510.
98. “Twelve is equal to twenty minus eight” is written as 12208.
99. “Nine is greater than five minus four” is written as 954.
100. “Ten is greater than six plus one” is written as 1061.
101. “Sixteen is not equal to nineteen” is written as 1619.
102. “Three is not equal to four” is written as 34.
103. “One-half is less than or equal to two-fourths” is written as 12 24
104. “One-third is less than or equal to three-ninths” is written as 13 39
105. 520 becomes 205 when the inequality symbol is reversed.
106. 309 becomes 930 when the inequality symbol is reversed.
107. 43 54 becomes 34 45 when the inequality symbol is reversed.
108. 53 42 becomes 35 24 when the inequality symbol is reversed.
109. 2.51.3 becomes 1.32.5 when the inequality symbol is reversed.
110. 4.15.3 becomes 5.34.1 when the inequality symbol is reversed.
111. (a) Substitute “40” for “age” in the expression for females. 14.7400.13
(b) 14.7400.1314.75.2Multiply 9. Subtract 5.
(c) 85% of 9.5 is 0.85(9.5)8.075. Walking at 5 mph is associated with 8.0METs, which is the table value closest to 8.075.
112. (a) Substitute “55” for “age” in the expression for males. 14.7550.11
(b) 14.7550.1114.76.05M 8 ultiply. Subtract. .65
(c) 85% of 8.65 is 0.85(8.65)7.3525.
Swimming is associated with 7.0 METs, which is the table value closest to 7.3525.
113. (a) Substitute “20” for “age” in the expression for males.
14.7200.11
(b) 14.7200.1114.72.2Mu 12 ltiply. Subtract .5.
(c) 85% of 12.5 is 0.85(12.5)10.625.
Jogging is associated with 10.2 METs, which is the table value closest to 10.6255.
114. (a) Substitute “65” for “age” in the expression for females.
14.7650.13
(b) 14.7650.1314.78.45M 6 ultiply. Subtract. .25
(c) 85% of 6.25 is 0.85(6.25)5.3125.
Ballroom or square dancing is associated with 5.5 METs, which is the table value closest to 5.3125.
115. The states that had a number greater than 14.9 are Alaska (17.6), Texas (15.1), California (23.0), and Idaho (18.1).
116. The states that had a number that was at most 15.1 are Texas (15.1), Virginia (14.9), Maine (12.2), and Missouri (13.2).
117. The states that had a number not less than 14.9, which is the same as greater than or equal to 14.9, are Alaska (17.6), Texas (15.1),
California (23.0), Virginia (14.9), and Idaho (18.1).
118. The states that had a number less than 15.0 are Virginia (14.9), Maine (12.2), and Missouri (13.2).
1.2 Variables, Expressions, and Equations
Classroom Examples, Now Try Exercises
1. (a) 1638Replace with 3. 488Multiply. =4 168 0Subtract. pp
(b) 33 223Replace with 3. 227Cube 3. 54Multiply. pp
N1. (a) 965Replace with 6. 545Multiply. 4 9 9Subtrac. 5 t xx
(b) 2 2 46Replace with 6. 436Square6. 144Multiply. 4 xx
2. (a) 454659 2445Multiply. 69Add. xy
(b) 424629 161 2418 Multiply 6 7 61 Subtract andadd xy
(c) 262222 3681Useexponents. Multiply. 153A 29 2 781 d. 2 d
N2. (a) 343447 1228Multiply. 40Add.
(b) 626427 29279 2414 Multiply. 149 10 2Subtract; reduce. 5 xy y
(c) 2222 4447 41649Use exponents. 6449Multiply. 15Subtract.
3. (a) “The difference of” indicates subtraction. Using x as the variable to represent the number, “the difference of 48 and a number” translates as 48 x
(b) “Divided by” indicates division. Using x as the variable to represent the number, “6 divided by a number” translates as 6 x or 6 x .
(c) “The sum of a number and 5” suggests a number plus 5. Using x as the variable to represent the number, “9 multiplied by the sum of a number and 5” translates as 95. x
N3. (a) Using x as the variable to represent the number, “the sum of a number and 10” translates as 10, x or 10. x
(b) “A number divided by 7” translates as 7, x or 7 x
(c) “The difference between 9 and a number” translates as 9. x Thus, “the product of 3 and the difference between 9 and a number” translates as 3(9. ) x
4. (a) ? ? 8105 8210Replacewith2. 1610Multipl 5 5 65Fae l y s p p
The number 2 is not a solution of the equation.
(b) ? ? 31 2 102 31(5)Replacewith5. 102 31 Multiply. 22 2 2 4 2True 2 x x
The number 5 is a solution of the equation.
(c) ? ? 0.1(3)0.8
translates as 925. xx Now try each number from the set {0, 2, 4, 6, 8, 10}. ? 25 4:49 1321Fals 4 e x ? 25 6:69 1519Fals 6 e x ? 2 8:89 1717True 58 x
0.1(53)Replacewith5.
0.1(8 0.8 0.8 0.80. )Add 8True . x x
The number 5 is a solution of the equation.
N4. (a) ? ? 8559
875Replace with 59 59 7. 565Multiply. 6159False k k
The number 7 is not a solution of the equation.
(b) ? 1 2 ? 625 1 62Replace wit 5 5 h . 2 32Multiply. 55True x x
The number 1 2 is a solution of the equation.
5. Using x as the variable to represent the number, “three times a number is subtracted from 21, giving 15” translates as 21315. x Now try each number from the set {0, 2, 4, 6, 8, 10}.
? 15 0:2130 2115False x ? 15 2:2132 1515True x
? 15 4:2134 915False x
Similarly, 6,8, x or 10 result in false statements. Thus, 2 is the only solution.
N5. Using x as the variable to represent the number, “the sum of a number and nine is equal to the difference between 25 and the number”
Similarly, 0, 2, x or 10 result in false statements. Thus, 8 is the only solution.
6. (a) 31 5 x has no equality symbol, so this is an expression.
(b) 3 1 5 x has an equality symbol, so this is an equation.
N6. (a) 256 x has an equality symbol, so this is an equation.
(b) 256 x has no equality symbol, so this is an expression
Exercises
1. The expression 2 8 x means 8. xx The correct choice is B.
2. If 2 x and 1, y then the value of xy is 212. The correct choice is C.
3. The sum of 15 and a number x is represented by the expression 15. x The correct choice is A.
4. 7 less than a number x is represented by the expression 7 x . The correct choice is D.
5. Try each number in the equation 315 x ? ? 5 0:301 01 15False 5 x ? ? 5 2:321 61 55False 5 x
6. There is no equality symbol in 67 x or 67, x so those are expressions. 67 x and
Copyright © 2025 Pearson Education, Inc.
670 x have equality symbols, so those are equations.
7. The exponent refers only to the 4. 55422 516 80 x
The correct value is 80.
8. Addition in the numerator comes before division. 3103 55 13 5 x
The correct value is 13 5
9. (a) 747 11 x
(b) 767 13 x
10. (a) 343 1 x
(b) 363 3 x
11. (a) 44416 x (b) 44624 x
12. (a) 66424 x
(b) 66636 x
13. (a) 54544 204 16 x
(b) 54564 304 26 x
14. (a) 79749 289 19 x
(b) 79769 429 33 x
15. (a) 22 444 416 64 x
(b) 22 446 436 144 x
16. (a) 22 554 516 80 x
(b) 22 556 536 180 x
17. (a) 141 33 5 3 x
(b) 161 33 7 3 x
18. (a) 242 5 6 5 5 x (b) 262 8 5 55 x
19. (a) 35345 224 125 8 7 8 x x
(b) 35365 226 185 12 13 12 x x
20. (a) 41441 334 161 12 155 124 x x (b) 41461 336 241 18 23 18 x x
21. (a) 22 3344 3164 48452
(b) 22 3366 3366 1086114
22. (a) 22 2244 816 24 xx
(b) 22 2266 1236 48 xx
23. (a) 6.4596.4594 25.836 x
(b) 6.4596.4596 38.754 x
24. (a) 3.2753.2754 13.1 x
(b) 3.2753.2756 19.65 x
25. (a) 83582315 1635 195 24 xy
(b) 83581355 8155 235 28
26. (a) 4274(2)2(1)7 827 17 xy
(b) 4274(1)2(5)7 4107 21 xy
27. (a) 3(2)3(221) 3(22) 3(4) 12 xy
(b) 3(2)3(125) 3(110) 3(11) 33 xy
28. (a)
2(2)2221 241 25 10 xy
(b) 2(2)2215 225 27 14 xy
29. (a) 44 2 1 24 6 x y (b) 44 1 5 54 55 9 5 x y
30. (a) 88 2 1 14 5 y x (b) 1 88 5 58 13 y x
31. (a) 21 2323 62 66 84 63 xy
(b) 15 2323 310 66 13 6 xy
32. (a) 21 454 85 20 5 20 13 20 xy
5 4 20 29 15 454 25 2 0 0 2 xy
33. (a) 242241 525221 44 102 8 12 2 3 xy xy
(b) 242145 525125 220 510 22 15
34. (a) 757(2)5(1) 88(2)1 145 161 19 17 xy xy
(b) 757(1)5(5) 88(1)5 725 85 32 13 xy xy
35. (a) 2222 3321 341 121 13 xy (b) 2222 3315 3125 325 28 xy
36. (a) 2222 424221 4421 162 18 xy (b) 2222 424125 41225 450 54 xy
37. (a) 22 3321 232231 321 43 61 7 7 7 1 xy xy
38. (a)
39. (a) 22 22 0.8410.32 0.84120.321 0.84140.321 3.3640.32 3.684
22 22 0.8410.32 0.84110.325 0.84110.3225 0.8418 8.841 xy
40. (a)
41. “12 times a number” translates as 12, x or 12x
42. “15 times a number” translates as 15, x or 15x
43. “Added to” indicates addition. “9 added to a number” translates as 9. x
44. “6 added to a number” translates as 6. x
45. “2 subtracted from a number” translates as 2. x
46. “7 subtracted from a number” translates as 7. x
47. “A number subtracted from 7” translates as 7. x
48. “A number subtracted from 4” translates as 4. x
49. “The difference between a number and 8” translates as 8. x
50. “The difference between 8 and a number” translates as 8. x
51. “18 divided by a number” translates as 18 . x
52. “A number divided by 18” translates as 18 x
53. “The product of 6 and 4 less than a number” translates as 64. x
54. “The product of 9 and 5 more than a number” translates as 95. x
22 22 0.9410.25 0.94120.251 0.94140.251
3.7640.25 4.014 xy
22 22 0.9410.25
0.94110.255
0.94110.2525
0.9416.25
55. ? ? 426;1 426Let 1. 426 66True 1 m m
Because substituting 1 for m results in a true statement, 1 is a solution of the equation.
56. ? ? 268;1 8Let 1. 268 88True 2(1)6 r r
The true result shows that 1 is a solution of the equation.
57. ? ? ? 14Let 3. 2 23(2)14; 3 23 33114 6314 914False 3(32) y y y
Because substituting 3 for y results in a false statement, 3 is not a solution of the equation.
58.
? ? ? 62314;2 14Let 2. 622514 121014 2214Fals 622(23 e ) xx x
The false result shows that 2 is not a solution of the equation.
59. 1 10911; 5 p ? ? 1 11Let . 5 2911 1111True 1 109 5 p
The true result shows that 1 5 is a solution of the equation.
60. ? ? 1212 58L e 12 5820; 5 et . 20 12820 2020 5 u 5 Tr x x
The true result shows that 12 5 is a solution of the equation.
61. 2 ? 2 ? ? 46Let4. 316246 48246 4646 3246; 4 342 True r r
The true result shows that 4 is a solution of the equation.
62. 2 ? 2 ? ? 19Let 3. 29119 18119 1919True 2119; 3 231 x x
The true result shows that 3 is a solution of the equation.
63. ? ? 31 1;2 84 1Let 2. 3 1 4 31 2 84 1 4 11True x x
The true result shows that 2 is a solution of the equation.
64. ? ? 71 4;5 102 4Let 5. 71 4 2 71 (5) 2 4 10 4e 2 Tru x x
The true result shows that 5 is a solution of the equation.
65. ? ? 0.5(4)80; 20 0.5(204)Let 20. 0.5( 80 80 80F 16) 8alse x x
The false result shows that 20 is not a solution of the equation.
Copyright © 2025 Pearson Education,
66. ? ? 0.2(5)70; 40
0.2(405)Let 40.
0.2( 70 70 770F 35) alse x x
The false result shows that 40 is not a solution of the equation.
67. “The sum of a number and 8 is 18” translates as 818. x Try each number from the given set, {2, 4, 6, 8, 10}, in turn.
818Given equation 2818False 4818False 6818False 8818False 10818True x
The only solution is 10.
68. “A number minus 3 equals 1” translates as 31 x Replace x with each number in the given set. The only true statement results when 4, x since 431. Thus, 4 is the only solution.
69. “One more than twice a number is 5” translates as 215. x Try each number from the given set. The only resulting true equation is 2215, so the only solution is 2.
70. “The product of a number and 3 is 6” translates as 36. x The only true statement results when 2, x since, 326. Thus, 2 is the only solution.
71. “Sixteen minus three-fourths of a number is 13” translates as 61. 3 13 4 x Try each number from the given set, {2, 4, 6, 8, 10}, in turn.
72. “The sum of six-fifths of a number and 2 is 14” translates as 6 214 5 x Replace x with each number in the given set. The only true statement results as follows.
? ? 6 102Let 10. 5 14 12214 1414True x
The only solution is 10.
73. “Three times a number is equal to 8 more than twice the number” translates as 328. xx Try each number from the given set.
328Given equation
3(2)2(2)8False
3(4)2(4)8False
3(6)2(6)8False
3(8)2(8)8True
3(10)2(10)8False
The only solution is 8.
74. “Twelve divided by a number equals one-third of that number” translates as 121 3 x x The only true statement results as follows. ? 121 6Let6. 63 22True x
The only solution is 6.
75. There is no equality symbol, so 324 xx is an expression.
76. There is no equality symbol, so 835 yy is an expression.
77. There is an equality symbol, so 7214 tt is an equation.
78. There is an equality symbol, so 93(4)2 rr is an equation.
79. There is an equality symbol, so 9 xy is an equation.
80. There is no equality symbol, so 9 xy is an expression.
The only solution is 4.
81. 0.138200 0.1382019200 78.6 yx
The life expectancy of an American born in 2019 is about 78.6 years.
82. 0.138200 0.1382010200 77.4 yx
The life expectancy of an American born in 2010 is about 77.4 years.
yx
83. 0.138200 0.1382000200
The life expectancy of an American born in 2000 is 76 years.
84. 0.138200 0.1381980200 73.2 yx
The life expectancy of an American born in 1980 is about 73.2 years.
85. 0.138200 0.1382020200 78.8 yx
The life expectancy of an American born in 2020 is about 78.8 years.
1.3 Real Numbers and the Number Line
Classroom Examples, Now Try Exercises
1. (a) Since Erin spends $53 more than she has in her checking account, her balance is 53.
(b) Since the record high was 134 above zero, this temperature is expressed as 134°.
N1. Since the deepest point is below the water’s surface, the depth is 136.
2. N2.
3. (a) The natural number is 10.
(b) The whole numbers are 0 and 10.
(c) The integers are 5, 0, and 10.
(d) The rational numbers are 38 5,1or, 55
0 0or 1 ,
5 0.45or, 11 5 8 , and 10 since each can be written as the quotient of integers.
(e) The irrational numbers are and 11
(f) All are real numbers.
N3. (a) The natural number is 13.
(b) The whole numbers are 0 and 13.
(c) The integers are 7, 0, and 13.
(d) The rational numbers are 4 7,,0,7 5 , 2. and 13.
(e) The irrational numbers are 3 and
(f) All are real numbers.
4. (a) Since 4 lies to the left of 1 on the number line, 4 is less than 1 Therefore, the statement 41 is false.
(b) Since 1.75 lies to the left of 1.5 on the number line, 1.75 is less than 1.5 Therefore, the statement 1.751.5 is true.
N4. (a) Since 8 lies to the right of 9 on the number line, 8 is greater than 9. Therefore, the statement 89 is false
(b) Since 1 2 lies to the right of 2 3 on the number line, 1 2 is greater than 2 3
Therefore, the statement 12 23 is true.
5. (a) The additive inverse of 100 is 100.
(b) The additive inverse of 100 is 100.
(c) The additive inverse of 0.01 is 0.01.
(d) The additive inverse of 1 5 2 is 1 5. 2
N5. (a) The additive inverse of 9 is 9.
(b) The additive inverse of 9 is 9.
(c) The additive inverse of 1 2 is 1 2
(d) The additive inverse of 0.75 is 0.75.
6. (a) 3232
(b) 323232
(c)
323232
(d) 3223030
N6. (a) |4|4
(b) |4|(4)4
(c) |4|(4)4
(d) 4400
7. The largest positive percent increase from 2019 to 2020 is 20.5, so the category is Medical care.
N7. We must find the negative number with the smallest absolute value. The least decrease from 2019 to 2020 is 6.0 , so the category is Apparel.
Exercises
1. The number 0 is a whole number, but not a natural number.
2. The natural numbers, their additive inverses, and 0 form the set of integers.
3. The additive inverse of every negative number is a positive number.
4. If x and y are real numbers with , xy then x lies to the right of y on a number line.
5. A rational number is the quotient of two integers with the denominator not equal to 0.
6. Decimal numbers that neither terminate nor repeat are irrational numbers.
7. The additive inverse of 5 is 5 , while the additive inverse of the absolute value of 5 is 5
8. If a is negative, then aa
9. (a) |9|9 A
The distance between 9 and 0 on the number line is 9 units.
(b) (9)9 A
The opposite of 9 is 9.
10. The statement “Absolute value is always positive” is not true. The absolute value of 0 is 0, and 0 is not positive. We could say that absolute value is never negative, or absolute value is always nonnegative.
11. The only integer between 3.6 and 4.6 is 4.
12. A rational number between 2.8 and 2.9 is 2.85. There are others.
13. There is only one whole number that is not positive and that is less than 1: the number 0.
14. A whole number greater than 3.5 is 4. There are others.
15. An irrational number that is between 12 and 14 is 13. There are others.
16. The only real number that is neither negative nor positive is 0.
17. True; every natural number is positive.
18. False; 0 is a whole number that is not positive. In fact, it is the only whole number that is not positive.
19. True; every integer is a rational number. For example, 5 can be written as 5 1
20. True; every rational number is a real number.
21. False; if a number is rational, it cannot be irrational, and vice versa.
22. True; every terminating decimal is a rational number.
23. Three examples of positive real numbers that are not integers are 15 28,, and 3 1. 4 Other examples are 0.7, 2 4, 3 and 5.1.
24. Real numbers that are not positive numbers are 0 and all numbers to the left of 0 on the number line. Three examples are , an 3 1,5. 4 d
Other examples are 1 0,5,7, 2 , 1 and 0.3.
25. Three examples of real numbers that are not whole numbers are 12 3, , 23 and 3 7 Other examples are 4.3, 2, and 7.
26. Rational numbers that are not integers are all real numbers that can be expressed as a quotient of integers (with nonzero denominators) such that in lowest terms the denominator is not 1. Three examples are 1 , 2 , 2 3 and 2 7 Other examples are 311 5.6,4,, 4 , 22 and 5.2.
27. Three examples of real numbers that are not rational numbers are 5, , and 3. All irrational numbers are real numbers that are not rational.
28. Rational numbers that are not negative numbers are 0 and all rational numbers to the right of zero on the number line. Three examples are 25 , 36 , and 5 2 Other examples are 11 0,,1,3 24 , and 5.
29. Use the integer 1,256,003 since “increased by 1,256,003” indicates a positive number.
30. Use the integer 174 since “a decrease of 174” indicates a negative number.
31. Use the integer 11,059 since “a decrease of 11,059” indicates a negative number.
32. Use the integer 2809 since “an increase of 2809” indicates a positive number.
33. Use the rational number 85.92 since “closed down 85.92” indicates a negative number.
34. Use the rational number 345.09 since “closed up 345.09” indicates a positive number.
35. Graph 0, 3, 5, and 6.
Place a dot on the number line at the point that corresponds to each number. The order of the numbers from smallest to largest is 6, 5, 0, 3.
36. Graph 2, 6, 2, and 1
The smallest number, 2, will be the farthest to the left.
37. Graph 2, 6, 4, 3, and 4.
38. Graph 5,3,,0, 2 and 4.
39. Graph 11 , 2, 3.8, 4, 42 and 5 1. 8
40. Graph 51 5.25,4,, 932,0 and 2 3 5
41. (a) The natural numbers in the given set are 3 and 7, since they are in the natural number set 1,2,3,.
(b) The set of whole numbers includes the natural numbers and 0. The whole numbers in the given set are 0, 3, and 7.
(c) The integers are the set of numbers {, 3, 2, 1, 0,1, 2, 3,}. The integers in the given set are 9, 0, 3, and 7.
(d) Rational numbers are the numbers that can be expressed as the quotient of two integers, with denominators not equal to 0. We can write numbers from the given set in this form as follows: 915330
9, 1, , 0, 144551 0.1,13597 3, 5.9, and 7. 91101
Thus, the rational numbers in the given set are 13 9, 1, , 0, 0.1, 3, 5.9, 45 and 7.
(e) Irrational numbers are real numbers that are not rational. 7 and 5 can be represented by points on the number line but cannot be written as a quotient of integers. Thus, the irrational numbers in the given set are 7 and 5.
(f) Real numbers are all numbers that can be represented on the number line. All the numbers in the given set are real.
42. (a) The only natural number in the given set is 3.
(b) The whole numbers in the set are 0 and 3.
(c) The integers in the set are 5,1,0, and 3.
(d) The rational numbers are 5.3,5,1, 1 ,0,0.27,1.2, 9 and 3.
(e) The irrational numbers in the set are 3 and 11.
(f) All the numbers in the set are real numbers.
43. (a) The natural number in the given set 11, since it is in the natural number set 1,2,3,.
(b) The set of whole numbers includes the natural numbers and 0. The whole numbers in the given set are 0, and 11.
(c) The integers are the set of numbers {, 3, 2, 1, 0,1, 2, 3,}. The integers in the given set are 0, 11, and 6 .
(d) Rational numbers are the numbers that can be expressed as the quotient of two integers, with denominators not equal to 0. We can write numbers from the given set in this form as follows: 7035 2.3, 0,8, 311 11, 1 31 44 a6 1 6 nd
Thus, the rational numbers in the given set are 73 ,2.3,0, 948,11, and 6 .
(e) Irrational numbers are real numbers that are not rational. 3 and can be represented by points on the number line but cannot be written as a quotient of integers. Thus, the irrational numbers in the given set are 3 and .
(f) Real numbers are all numbers that can be represented on the number line. All the numbers in the given set are real.
44. (a) The only natural number in the given set is 9.
(b) The whole numbers in the set are 9 and 0.
(c) The integers in the set are 9, 12 , and 0.
(d) The rational numbers are 5 1 8 , 0.4 , 9, 12 , 0, and 0.026.
(e) The irrational numbers in the set are 6 and 10.
(f) All the numbers in the set are real numbers.
45. (a) The additive inverse of 2 is found by changing the sign of 2 The additive inverse of 2 is 2
(b) The absolute value of 2 is the distance between 0 and 2 on the number line, so |2|2.
46. (a) The additive inverse of a number is found by changing the sign of a number, so the additive inverse of 4 is 4.
(b) The distance between 4 and 0 on the number line is 4 units, so 44.
47. (a) The additive inverse of 8 is 8
(b) The distance between 0 and 8 on the number line is 8 units, so the absolute value of 8 is 8.
48. (a) The additive inverse of 10 is 10
(b) The distance between 10 and 0 on the number line is 10 units, so 10. 10
49. (a) The additive inverse of a number is found by changing the sign of a number, so the additive inverse of 3 4 is 3 . 4
(b) The distance between 3 4 and 0 on the number line is 3 4 unit, so 3 44 3
50. (a) The additive inverse of a number is found by changing the sign of a number, so the additive inverse of 2 5 is 2 5
(b) The distance between 2 5 and 0 on the number line is 2 5 unit, so 2 55 2
51. (a) The additive inverse of a number is found by changing the sign of a number, so the additive inverse of 5.6 is 5.6.
(b) The distance between 5.6 and 0 on the number line is 5.6 units, so 5.6. 5.6
52. (a) The additive inverse of a number is found by changing the sign of a number, so the additive inverse of 8.1 is 8.1.
(b) The distance between 8.1 and 0 on the number line is 8.1 unit, so 8.1. 8.1
53. Since 6 is a negative number, its absolute value is the additive inverse of 6 — that is, |6|(6)6.
54. 14(14)14
55. 12(12)12
56. 19(19)19
57. 222 333
58. 444 555
59. 6333
60. 9455
61. 6333
62. 9455
63. Since 11 is located to the left of 4 on the number line, 11 is the lesser number.
64. Since 13 is located to the left of 8 on the number line, 13 is the lesser number.
65. Since 2 3 is located to the left of 1 4 on the number line, 2 3 is the lesser number.
66. Since 9 16 is located to the left of 3 8 on the number line, 9 16 is the lesser number.
67. Since 2.8 is located to the left of 2.5 on the number line, 2.8 is the lesser number.
68. Since 1.7 is located to the left of 1.6 on the number line, 1.7 is the lesser number.
69. Since |5|5, 4 is the lesser of the two numbers.
70. Since 33,3 or 3 is the lesser of the two numbers.
71. Since |3.5|3.5 and |4.5|4.5, |3.5| or 3.5 is the lesser number.
72. Since 8.98.9 and 9.89.8,8.9 or 8.9 is the lesser number.
73. Since |6|6 and |4|4, |6| is to the left of |4| on the number line, so |6| or 6 is the lesser number.
74. |2|2 and |3|3, so |3| is to the left of |2| on the number line; 3 or 3 is the lesser number.
75. Since |53||2|2 and |62||4|4, |53| or 2 is the lesser number.
76. Since 7255 and 8177, 72 or 5 is the lesser number.
77. Since 5 is to the left of 2 on the number line, 5 is lessthan 2, and the statement 52 is true.
78. Since 8 is to the left of 2 on the number line, 8 is lessthan 2, and the statement 82 is false.
79. Since (5)5 and 45,45 is true.
80. Since 33 and 63, 63 is true.
81. Since |6|6 and |9|9, and 69, |6||9| is true.
82. Since 1212 and 200, 2 and 12, 20 1220 is true.
83. Since |8|8 and |9|(9)9, |8||9|, so |8||9| is false.
84. Since 1212 and 151515, 1215, so 1215 is false.
85. Since |5|5, |9|9, and 59, |5||9| is true.
86. Since 1212, ,1515 and 1215,1215 is false.
87. Since |65||1|1 and |62||4|4, |65||62|, so |65||62| is false.
88. Since 13855 and 7, 433 18734, so 13874 is false.
89. The number that represents the greatest percentage increase is 6.5, which corresponds to Natural gas service from November to December.
90. The negative number with the largest absolute value in the table is 18.3, so the greatest percentage decrease is Fuel oil from November to December.
91. The number with the smallest absolute value in the table is 0.2, so the least change corresponds to Shelter.
92. The categories with two negative entries (representing a decrease for both time periods) are Fuel oil and Gasoline.
1.4 Adding and Subtracting Real Numbers
Classroom Examples, Now Try Exercises
1. (a) Start at 0 on a number line. Draw an arrow 1 unit to the right to represent the positive number 1. From the right end of this arrow, draw a second arrow 4 units to the right to represent the addition of a positive number. The number below the end of this second arrow is 5, so 145.
(b) Start at 0 on a number line. Draw an arrow 2 units to the left to represent the negative number 2 From the left end of this arrow, draw a second arrow 5 units to the left to represent the addition of a negative number. The number below the end of this second arrow is 7, so 257.
N1. (a) Start at 0 on a number line. Draw an arrow 3 units to the right to represent the positive number 3. From the right end of this arrow, draw a second arrow 5 units to the right to represent the addition of a positive number. The number below the end of this second arrow is 8, so 358.
(b) Start at 0 on a number line. Draw an arrow 1 unit to the left to represent the negative number 1 From the left end of this arrow, draw a second arrow 3 units to the left. The number below the end of this second arrow is 4, so 134.
2. (a) 15419
The sum of two negative numbers is negative.
(b) 1.275.466.73
The sum of two negative numbers is negative.
N2. (a) 61117
The sum of two negative numbers is negative.
(b) 219 5210
The sum of two negative numbers is negative.
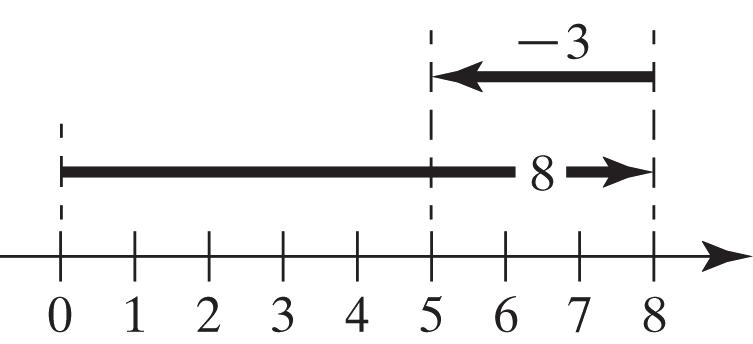
3. Start at 0 on a number line. Draw an arrow 6 units to the right. From the right end of this arrow, draw a second arrow 3 units to the left. The number below the end of this second arrow is 3, so 6. 33
N3. Start at 0 on a number line. Draw an arrow 4 units to the right. From the right end of this arrow, draw a second arrow 8 units to the left.
The number below the end of this second arrow is 4, so 44. 8
4. (a) Since the numbers have different signs, find the difference between their absolute values: 17107. Because 17 has the larger absolute value, the sum is positive: 10177.
(b) Since the numbers have different signs, find the difference between their absolute values: 1091. Because 10 has the larger absolute value, the sum is negative: 9(10)1.
(c) 335 1 488
(d) 3.89.55.7
(e) 25(25)0
N4. (a) Since the numbers have different signs, find the difference between their absolute values: 743. Because 7 has the larger absolute value, the sum is positive:
743.
(b) 21219 2 3939
(c) 5.73.7(5.73.7)2 (d) 10100
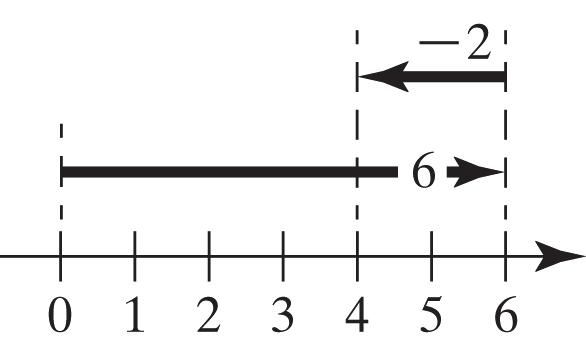
5. Use a number line to find the difference 83.
Step1 Start at 0 and draw an arrow 8 units to the right.
Step2 From the right end of the first arrow, draw a second arrow 3 units to the left to represent the subtraction
The number below the end of the second arrow is 5, so 835.
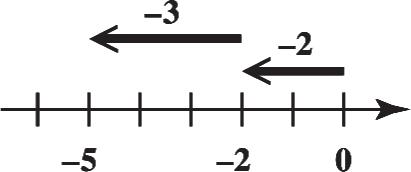
N5. Use a number line to find the difference 62. Step1 Start at 0 and draw an arrow 6 units to the right.
Step2 From the right end of the first arrow, draw a second arrow 2 units to the left to represent the subtraction
The number below the end of the second arrow is 4, so 624.
6. (a) 104104Add the opposite. 6
(b) 410410Add the opposite.
6
(c) 8585Add the opposite. 13
(d) 812812Add the opposite. 4
(e) 5353351247 4747282 , 288
or 19 1 28
(f) 7.59.21.7
N6. (a) 511511Add the opposite.
(b) 415415Add the opposite. 11
(c) 5151 Add the opposite. 7373 157 2121 221 , or 1 2121
(d) 5.25(3.24)5.253.24 8.49
(a)
8[(37)(39)]
8[(4)(3(9))] 8[4(6)] 846 810 8(10) 2
(c) 3|69||412| 3|6(9)||4(12)| 3|3||8| 338 98 1
8. “7 is increased by the sum of 8 and 3” is written 783.
7837512
N8. “The sum of 3 and 7, increased by 10” is written (37)10. (37)1041014
9. (a) “The difference between 5 and 12” is written 512. 512512 7
(b) “2 subtracted from the sum of 4 and 4” is written 42. 4
44202 02 2
N9. (a) “The difference between 5 and 8, decreased by 4” is written [5(8)]4. [5(8)]4[58]4 134 9
(b) “7 less than 2” is written 27. 272(7) 9
10. The difference between the highest and lowest temperatures is given by 79567956 135. The difference is 135F.
N10. The difference between a gain of 226 yards and a loss of 7 yards is given by 226(7)2267 233. The difference is 233 yards.
11. Subtract the enrollment number for 2000 from the enrollment number for 2020. 15.2513.5215.2513.521.73 million
A positive result indicates an increase. N11. Subtract the enrollment number for 2005 from the enrollment number for 2010. 14.8614.910.05 million
A negative result indicates a decrease.
Exercises
1. The sum of two negative numbers will always be a negative number. In the illustration, we have 2(3)5.
2. The sum of a number and its opposite will always be zero (0).
3. When adding a positive number and a negative number, where the negative number has the greater absolute value, the sum will be a negative number. In the illustration, the absolute value of 4 is larger than the absolute value of 2, so the sum is a negative number–that is, 422.
4. To simplify the expression 8235
, one should begin by adding 3 and 5, according to the rules for order of operations.
5. By the definition of subtraction, in order to perform the subtraction 6(8), we must add the opposite of 8 to 6 to obtain 2 .
6. “The difference of 7 and 12” translates as 712, while “the difference of 12 and 7” translates as 12. 7
7. The expression xy would have to be positive since subtracting a negative number from a positive number is the same as adding a positive number to a positive number, which is a positive number.
8. yxyx If x is a positive number and y is a negative number, yx will be the sum of two negative numbers, which is a negative number.
9. ||, xx since x is a positive number. ||, yxyx which is a negative number. (See Exercise 8.)
10. Since y is positive, xy is the sum of two positive numbers, which is positive
11. The sum of two negative numbers is negative.
6(2)8
12. Since the numbers have the same sign, add their absolute values: 9211. Since both numbers are negative, their sum is negative: 9211.
13. Because the numbers have the same sign, add their absolute values: 5712. Because both numbers are negative, their sum is negative: 5(7)12.
14. Because the numbers have the same sign, add their absolute values: 11516. Because both numbers are negative, their sum is negative: 11(5)16.
15. To add 6(4), find the difference between the absolute values of the numbers. |6|6 and|4|4 642 Since |6||4|, the sum will be positive: 6(4)2.
16. Since the numbers have different signs, find the difference between their absolute values: 1183. Since 11 has the larger absolute value, the answer is positive: 11(83. )
17. Since the numbers have different signs, find the difference between their absolute values: 15123. Because 15 has the larger absolute value, the sum is negative: 12(15)3.
18. Since the numbers have different signs, find the difference between their absolute values: 734. Since 7 has the larger absolute value, the sum is negative: 374.
19. Since the numbers have different signs, find the difference between their absolute values: 1679. Since 16 has the larger absolute value, the answer is negative: 1679.
Copyright © 2025 Pearson
20. Since the numbers have different signs, find the difference between their absolute values: 1367. Since 13 has the larger absolute value, the answer is negative: 1367.
21. 6(6)0
22. 11110
23. 145493 = 3151515155
24. 153582 4121212123
25. 121431 636662
26. 61964195 2520254205
27. Since
31. 3.512.412.43.58.9
12.521.321.312.58.8
2.34(3.67)2.343.676.01
1.25(6.88)6.881.258.13
35. 4[13(5)]4[8]12
36. 6[12(3)]6[9]15
37. 8[2(1)]8[3]5
38. 12341275
39. 2[5(1)]2[4]2
40. 892871
41. 6[6(9)]6[3]9
42. 338358
43. [(9)(3)]12[12]120
44. [(8)(6)]14[14]140
45. 6.1[3.2(4.8)]6.1[1.6] 7.7
46. 9.45.87.99.42.1 11.5
47. [3(4)][5(6)][7][1] 8
48. 8346112 13
49. [4(3)][8(1)][7][7] 0
50. 591621414 0
51. [4(6)][3(8)][12(11)] ([10][11])[1] (21)1 20
52. [2(11)][12(2)][18(6)] ([13][14])[12] (27)12 15
53. 474(7)3
54. 8138135
55. 595(9)4
56. 6116115
57. 717(1)8
58. 949413
59. 868(6)14
60. 959514
61. 7(3)7(3)10
62. 929211
63. 6(2)6(2)4
64. 75752
65. 2(35)2[3(5)] 2[2] 2(2) 4
66. 3(411)3[4(11)] 3[7] 3(7) 4
67. 1111 2424 213 444
68. 11415 312121212
69. 3535 4848 65 88 113 , or 1 88
70. 5151 6262 53 66 8 6 41 , or 1 33
71. 513513 824824 523 844 55 84 55 84 510 88 157 ,or1 88
Copyright © 2025 Pearson Education, Inc.
74. 5.711.65.711.6 17.3
75. 6.43.56.4(3.5) 9.9
76. 4.48.64.48.6 13
77. (46)12[4(6)]12 [2]12 10
78.
374374 44 0
79. (81)12[8(1)](12) [7](12) 5
86. 48361435 435 415 19
87. |82||93| |8(2)||9(3)| |10||12| (10)[(12)] 10[12] 2
4281 4281 69 (6)[(9)] 69 3
80.
93159315 615 9
81. 6(83)6(5) 65 11
82.
89584 84 12
83. 2(48)2[4(8)] 2[12] 10
89. 9[(32)(42)] 9[1(2)] 9[12] 93 6
90.
84.
692692 611 5
85. 2|56||92|2|5(6)||11| 2|11||11| 2(11)11 2211 33
92.
84192 8417 857 82 82 10
91. 3[(58)(62)] 3[(5(8))(4)] 3[134] 3[9] 12
4[(121)(19)] 41119 41110 41110 41 5
97. 9.12[4.8(3.25)]
7.621.42.8 7.621.42.8 7.621.4 9.02
99. “The sum of 5 and 12 and 6” is written 5126. 5126[512]6 7613
100. “The sum of 3 and 5 and 12” is written 3512. 3512212 10
101. “14 added to the sum of 19 and 4” is written [19(4)]14. [19(4)]14(23)14 9
102. “2 added to the sum of 18 and 11” is written 18112. 1811272 9
103. “The sum of 4 and 10, increased by 12” is written [4(10)]12. [4(10)]121412 2
104. “The sum of 7 and 13, increased by 14” is written 71314. [7(13)]142014 6
105. 2 “ 7 more than the sum of 5 7 and ” 9 7 is written 592 777
59242 77777 2 7
106. “1.85 more than the sum of 1.25 and 4.75” is written 1.254.751.85.
1.254.751.8561.85 4.15
107. “The difference of 4 and 8” is written 4(8). 4(8)4812
108. “The difference of 7 and 14” is written 74. 1 This expression can be simplified as follows.
7(14)71421
109. “8 less than 2” is written 28. 282(8)10
110. “9 less than 13” is written 139. 13913(9)22
111. “The sum of 9 and 4, decreased by 7” is written [9(4)]7. [9(4)]75(7)2
112. “The sum of 12 and 7, decreased by 14” is written 12714. [12(7)]14514 5(14) 9
113. “12 less than the difference of 8 and 5” is written [8(5)]12. [8(5)]12[8(5)]12 1312 13(12) 1
114. “19 less than the difference of 9 and 2” is written 9219. [9(2)]19(92)19 1119 11(19) 8
115. 5(6)(3)(2)11(3)(2) 14(2) 16
The total score below par is 16, which can be represented by the number 16.
116. 21(5)(2)1(5)(2) 6(2) 8
The total score below par is 8, which can be represented by the number 8.
117. [72][40]5(4) 1
The total score above par is 1, which can be represented by the number 1. 118. [15][0(4)]4(4) 0
The total score is 0, which is exactly par. 119. [1(1)](1)2(1) 3
The total number of seats that Illinois, Minnesota, and New York are projected to lose is 3, which can be represented by the signed number 3
120. 111113
The algebraic sum of these changes can be represented by the signed number 3. 121. 0(130)(54)130(54) 184
Their new altitude is 184 meters below the surface, which can be represented by the signed number 184 m.
122. 34,000210034,0002100 31,900
The new altitude of the plane is 31,900 feet, which can be represented by the signed number 31,900 ft.
123. The lowest temperature is represented by 35F. The highest temperature is represented by 35142, or 107F.
124. To find the temperature, start with 4F and add 49.
44945 The temperature 2 minutes later was 45F.
125. 13F lower than 38F can be represented as 381338(13) 51.
The record low in Michigan is F 51.
126. 36F lower than 19F can be represented as 193619(36) 55.
The record low in Wisconsin is F 55.
127. Add the scores of the four turns to get the final score.
Their final score for the four turns was 17.
128. Add the scores for the five turns to get the final score.
Their final score for the five turns was 28.
129. (a) 12.316.612.3(16.6) 4.3
The change in average personal savings rate from 2020 to 2021 is 4.3%
(b) Answers will vary. Employed U.S. adults may have spent less, thereby saving more in 2020 due to restricted access to restaurants, stores, and other businesses.
130. 236984236984 1220
The difference is $1220 billion.
131. 29,7662326992
32,092992
31,100Subtract. Add.
The average was $31,100.
132. 18834493201434320Subtract. 1754Add.
The average was $1754.
133. Sum of withdrawals:
$35.84$26.14$3.12$61.98$3.12
$65.10
Sum of deposits:
$85.00$120.76$205.76
To obtain the final balance, add the deposits and subtract the withdrawals from the beginning balance.
Final balance
$904.89$65.10$205.76
$839.79$205.76
$1045.55
Their account balance at the end of August was $1045.55.
134. Sum of withdrawals:
$41.29$13.66$84.40$54.95$84.40
$139.35
Sum of deposits:
$80.59$276.13$356.72
To obtain the final balance, add the deposits and subtract the withdrawals from the beginning balance.
Final balance
$537.12$139.35$356.72
$397.77$356.72
$754.49
Their account balance at the end of September was $754.49.
135. Aisha starts with a debt of $870.00, or $870.00. She returns two items, increasing the amount she has by 35.90150.00185.90.
She purchases three items, decreasing the amount she has by 82.5010.0010.00102.50.
Finally, add the payment and subtract the finance charge to calculate how much money she has.
870.00Amountowed 185.90Tworeturncredits
684.10
102.50Threepurchases
786.60
500.00Payment
286.60
37.23Financecharge
323.83
She still owes $323.83.
136. Marcial starts with a debt of $679.00, or $679.00. He returns three items, increasing the amount he has by 36.8929.40113.55179.84.
He purchases four items, decreasing the amount he has by 135.78412.8820.0020.00588.66.
Finally, add the payment and subtract the finance charge to calculate how much money he has.
679.00Amountowed
179.84Threereturncredits
499.16
712.39 He still owes $712.39.
588.66Fourpurchases
1087.82
400.00Payment
687.82
24.57Financecharge
137. The percent return for 2018 is 4.92%, and the percent return for 2019 is 30.77%. Thus, the change in percent returns is 30.77(4.92)30.774.9235.69% (an increase).
138. The percent return for 2019 is 30.77%, and the percent return for 2020 is 17.82%. Thus, the change in percent return is 17.8230.7712.95% (a decrease).
139. The percent return for 2021 is 28.01%, and the percent return for 2022 is 18.55%. Thus, the change in percent return is 18.5528.0146.56% (a decrease).
140. The percent return for 2018 is 4.92%, and the percent return for 2022 is 18.55%. Thus, the change in percent return is 18.55(4.92)13.63% (a decrease).
141. 17,40032,99517,40032,995 50,395
The difference between the height of Mt. Foraker and the depth of the Philippine Trench is 50,395 feet.
142. 14,11023,37614,11023,376 37,486
The difference between the height of Pikes Peak and the depth of the Java Trench is 37,486 feet.
143. 23,37624,72123,37624,721 1345
The Cayman Trench is 1345 feet deeper than the Java Trench.
144. 24,72132,99524,72132,995 8274
The Philippine Trench is 8274 feet deeper than the Cayman Trench.
145. 14,24614,11014,24614,110 136
Mt. Wilson is 136 feet higher than Pikes Peak.
146. 14,24614,11017,400 28,35617,400 10,956
If Mt. Wilson and Pikes Peak were stacked one on top of the other, they would be 10,956 feet higher than Mt. Foraker.
1.5 Multiplying and Dividing Real Numbers
Classroom Examples, Now Try Exercises
1. (a) 4(8)(48) 32
(b) 55 1616 3232 5 2
(c) 101.2101.2 12
N1. (a) 11(9)(119) 99
(b) 11 2020 55 4
(c) 10(2.5)(102.5) 25
2. (a) 12(3)36
(b) 3 106 5
(c) 1.2(1.1)1.32
N2. (a) 8(11)88
(b) 155 7214
(c) 0.80.60.48
3. We want integers, both positive and negative factors, that can be multiplied to obtain 15. The
integer factors of 15 from least to greatest are 15,5,3,1,1,3,5,15.
N3. We want integers, both positive and negative factors, that can be multiplied to obtain 20. The integer factors of 20 from least to greatest are 20,10,5,4,2,1,1,2,4,5,10,20.
4. (a) 16 8 2
N4. (a) 10 2 5 (b) 1.44 12
6. Replace x with 2 and y with 3
5. (a) 342612(12) 1212 0
N6. Replace x with 4 and y with 3
7. (a) “Three times the difference of 4 and 11” is written
3411.
341131545
(b) “Three-fifths of the sum of 2 and 7” is
N7. (a) “Twice the sum of 10 and 7” is written 2107.
2107236
(b) “40% of the difference of 45 and 15” is written 0.4045. 15
0.4045150.43012.
8. “The product of 9 and 2, divided by the difference of 5 and 1” is written
92 51
92 18 3 516
N8. “The quotient of 21 and the sum of 10 and 7” is written
21 107
2121 7 1073
9. (a) “Twice a number is 10” is written 210. x Since 2510, the solution is 5.
(b) “The quotient of a number and 2 is 6” is written 6. 2 x Here, x must be a negative number, since the denominator is negative and the quotient is positive. Since 12 6, 2 the solution is 12.
N9. (a) “The sum of a number and 4 is 7” is written 47. x Here, x must be 4 more than 7, so the solution is 11.
1147
(b) “The difference of 8 and a number is 11” is written 811. x If we start at 8 on a number line, we must move 3 units to the left to get to 11, so the solution is 3.
Exercises
1. The product or the quotient of two numbers with the same sign is positive, since the product or quotient of two positive numbers is positive and the product or quotient of two negative numbers is positive.
2. The product or quotient of two numbers with different signs is negative, since the product or quotient is negative.
3. If three negative numbers are multiplied, the product is negative, since a negative number times a negative number is a positive number, and that positive number times a negative number is a negative number.
4. If two negative numbers are multiplied and then their product is divided by a negative number, the result is negative, since the product is a positive number, and a positive number divided by a negative number is a negative number.
5. If a negative number is squared and the result is added to a positive number, the result is positive, since a negative number squared is a positive number, and a positive number added to another positive number is a positive number.
6. The reciprocal of a negative number is negative, since it is just the number one divided by a negative number, which is negative.
7. If three positive numbers, five negative numbers, and zero are multiplied, the product is 0. Since one of the numbers is zero, the product is zero (regardless of what the other numbers are).
8. The cube power of a negative number is negative. Remember, a negative number raised to an odd power (like 3) is negative.
9. The quotient formed by any nonzero number divided by 0 is undefined, and the quotient formed by 0 divided by any nonzero number is 0. Examples include 1 0 , which is undefined, and 0 , 1 which equals 0.
10. Look for the expression that has 0 in the denominator. The expression 44 44 , or 0 0 , is undefined. The correct response is C.
11. 7(4)(74)28
Note that the product of a negative number and a positive number is negative.
12. 8(5)(85)40
Note that the product of a negative number and a positive number is negative.
Copyright © 2025 Pearson Education,
13.
Note that the product of two negative numbers is positive.
14.
Note that the product of two negative numbers is positive.
15.
16.
19.
30. The integer factors of 36 are 36,18,12, 9,6,4,3,2,1,1,2,3,4,6,9,12,18, and 36.
31. The integer factors of 40 are 40,20,10, 8,5,4,2,1,1,2,4,5,8,10,20, and 40.
32. The integer factors of 50 are 50,25,10, 5,2,1,1,2,5,10,25, and 50.
33. The integer factors of 31 are 31,1,1, and 31.
34. The integer factors of 17 are 17,1,1, and 17.
35. 15533 3 551
36. 35757 7 551
37. 42237 7 623
Note that the quotient of two numbers having different signs is negative.
38. 2847 4 77
Note that the quotient of two numbers having different signs is negative.
39. 3248 8 44
Note that the quotient of two numbers having the same sign is positive.
40. 3557 7 55
Note that the quotient of two numbers having the same sign is positive.
41. 96616 6 1616
42. 38219 2 1919
43. 42.2 8.8 4 2.22.2
44. 4.6 2 2.3
29. Using only positive integer factors, 32 can be written as 132,216, or 48. Including the negative integer factors, we see that the integer factors of 32 are 32,16,8,4,2,1, 1, 2, 4, 8, 16, and 32.
45. Dividing by a fraction is the same as multiplying by the reciprocal of the fraction. 1415 105104 1 8
46. Dividing by a fraction is the same as multiplying by the reciprocal of the fraction. 1719 3937 3
47. 5859 6968 4515 ,or 4816
48. 7374 104103 2814 ,or 3015
49. 0 0, 5 because 0 divided by any nonzero number is 0.
50. 0 0, 9 because 0 divided by any nonzero number is 0.
51. 11.5 0 is undefined, because we cannot divide by 0.
52. 15.2 0 is undefined, because we cannot divide by 0.
53. 736718 11
54. 825810 2
57. 2(5)(4)(2)10(8) 108 2
58. 4(3)(3)(6)12(18) 1218 6
59.
63.
73875 35
54753 15
7241723 76 13
5364532 56 11
4328436 418 22
64. 8457842 88 16
65. 12141423 6
66. 8941218 8
67. 71010436 18
68. 512194715 105
69. 28671067 607 67
70. 9421013210 2610 36
35310157 157
72.
484153211 3211
73. 87(2)6(2)8146(2) 66(2) 66(2) 6(12) 18
74. 53(9)7(4)5277(4) 227(4) 227(4) 22(28)
56 3030 3 919110
125 6060 5 757512
69564 2(3)23 64 5 10 5 2
82. 83281 3(6)36
88.
89.
90. The incorrect answer, 92, was obtained by performing all of the operations from left to right rather than following the rules for order of operations. The multiplications and divisions need to be done in order, before the additions and subtractions.
91.
92.
1515 64 3232 210 210 12
5353 64 6262 56 1
653 665433 016 0
533 563433 170 0
22 22 232433 2163(9) 3227 5
22 22 545644 536416 18064 116
101. 22 545(4)4 6 5(16)4 6 804 6 84 6 14 y x
102.
108. “Twice the product of 8 and 2, subtracted from 1” is written 1282.
109. “9 subtracted from the product of 1.5 and 3.2” is written 1.53.29.
103.
110. “3 subtracted from the product of 4.2 and 8.5” is written 4.28.53.
104.
The expression is undefined.
The expression is undefined.
105. “The product of 9 and 2, added to 9” is written
92. 9
106. “The product of 4 and 7, added to 12” is written 1247.
12471228 40
107. “Twice the product of 1 and 6, subtracted from 4” is written
4216.
4216426 412 412
111. “The product of 12 and the difference of 9 and 8” is written 1298.
12981298 1217 204
112. “The product of 3 and the difference of 3 and 7” is written 337.
337337 310 30
113. “The quotient of 12 and the sum of 5 and 1” is written 12 , 51 and 1212 2. 516
114. “The quotient of 20 and the sum of 8 and 2” is written 20 , 82 and 2020 2. 8210
115. “The sum of 15 and 3, divided by the product of 4 and 3” is written
153 , 43 and
153 12 1. 4312
116. “The sum of 18 and 6, divided by the product of 2 and 4” is written
186 , 24 and
186 24 3. 248
117. “Two-thirds of the difference of 8 and 1” is written 2 81, 3 and
22 8181 33 2 9 3 6
118. “Three-fourths of the sum of 8 and 12” is written 3 812, 4 and
33 81243. 44
119. “20% of the product of 5 and 6” is written 0.2056, and
0.20560.20306.
120. “30% of the product of 8 and 5” is written
0.3085, and
0.30850.304012.
121. “The sum of 1 2 and 5 , 8 times the difference of 3 5 and 1 3 ” is written 1531 , 2853
and 15314595 2853881515
122. “The sum of 3 4 and 1 , 2 times the difference of 2 3 and 1 6 ” is written 3121 , 4236
123. “The product of 1 2 and 3 , 4 divided by 2 ” 3 is written 13
124. “The product of 2 3 and , 1 5 divided by 1 ” 7 is
125. “The quotient of a number and 3 is 3” is written 3. 3 x
The solution is 9, because
126. “The quotient of a number and 4 is 1” is written 1. 4 x The solution is 4, because 4 1. 4
127. “Six less than a number is 4” is written 64. x The solution is 10, because 1064.
128. “Seven less than a number is 2” is written 72. x The solution is 9, because 972.
129. “When 5 is added to a number, the result is 5” is written 55. x The solution is 10, because 1055.
130. “When 6 is added to a number, the result is 3” is written 63. x The solution is 9, because 963.
131. (a) 3,473,986 is divisible by 2 because its last digit, 6, is divisible by 2.
(b) 4,336,879 is not divisible by 2 because its last digit, 9, is not divisible by 2.
132. (a) 4,799,232 is divisible by 3 because the sum of its digits, 479923236, is divisible by 3.
(b) 2,443,871 is not divisible by 3 because the sum of its digits, 244387129, is not divisible by 3.
133. (a) 2,876,335 is not divisible by 4 because the number formed by its last two digits, 35, is not divisible by 4.
(b) 6,221,464 is divisible by 4 because the number formed by its last two digits, 64, is divisible by 4.
134. (a) 9,332,123 is not divisible by 5 because its last digit, 3, is not divisible by 5.
(b) 3,774,595 is divisible by 5 because its last digit, 5, is divisible by 5.
135. (a) 1,524,822 is divisible by 2 because its last digit, 2, is divisible by 2. It is also divisible by 3 because the sum of its digits, 152482224, is divisible by 3. Because 1,524,822 is divisible by both 2 and 3, it is divisible by 6.
(b) 2,873,590 is divisible by 2 because its last digit, 0, is divisible by 2. However, it is not divisible by 3 because the sum of its digits,
287359034, is not divisible by 3. Because 2,873,590 is not divisible by both 2 and 3, it is not divisible by 6.
136. (a) 2,923,296 is divisible by 8 because the number formed by its last three digits, 296, is divisible by 8.
(b) 7,291,623 is not divisible by 8 because the number formed by its last three digits, 623, is not divisible by 8.
137. (a) 2,287,321 is not divisible by 9 because the sum of its digits, 228732125, is not divisible by 9.
(b) 4,114,107 is divisible by 9 because the sum of its digits, 411410718, is divisible by 9.
138. (a) 4,249,474 is not divisible by 3 because the sum of its digits, 424947434, is not divisible by 3. Because a number is not divisible by 12 unless it is divisible by both 3 and 4, this is sufficient to show that the number is not divisible by 12.
(b) 4,253,520 is divisible by 3 because the sum of its digits, 425352021, is divisible by 3. It is also divisible by 4 because the number formed by its last two digits, 20, is divisible by 4. Because 4,253,520 is divisible by both 3 and 4, it is divisible by 12.
139. Add the numbers.
23181348 411348 5448 508 42
140. There are 5 numbers in the group.
141. Divide 42 (the answer for Exercise 139) by 5 (the answer for Exercise 140). 422 8 55
142. To find the average of a group of numbers, we add the numbers and then divide the sum by the number of terms added. The average of the given group of numbers is 422 8 55 .
143. Add the numbers and divide by 4. 15298(6)148(6)
144. Add the numbers and divide by 4. 17349(2)179(2)
145. Add the integers from 10to 14.
1091450
[The 3 dots indicate that the pattern continues.] There are 25 integers from 10to14 (10 negative, zero, and 14 positive). Thus, the average is 50 2. 25
146. Add the integers from 15 to 10
There are 6 integers from from 15 to 10 . Thus, the average is 751 12. 62
Summary Exercises: Performing Operations with Real Numbers
113(4)5(3)11(12)15 111215 2315 2315 8
16.
1.6 Properties of Real Numbers
Classroom Examples, Now Try Exercises 1.
2. (a)
528528
10831083
(a)
937937
549549
3. (a) 246426
While the same numbers are grouped inside the two pairs of parentheses, the order of the numbers has been changed. This illustrates a commutative property.
(b) 132132 553553
The order of the three numbers is the same on both sides of the equality symbol. The only change is in the grouping, or association, of the numbers. This is an example of the associative property.
N3. 576567
While the same numbers are grouped inside the two pairs of parentheses, the order of the numbers has been changed. This illustrates a commutative property.
4. (a)
431726246 60506 432617 1106 1 2 1 46 6
11 67226716767 22
N4. (a)
8547632 8325467 40607 1007
5372052037100373700
5. (a) 505Additiveidentity (b) 11 1Multiplicativeidentity 33
N5. (a) 22 551Multiplicativeidentity
(b) 808Additiveidentity
6. (a) 36312
N6. (a) 1644
22 11 3Associativeproperty 22 30Inverseproperty 3Identityproperty yy yy yy yy
N8. 7
7Identityproperty 11 33 11 7 33 11 7 33 11 33 xx x x x x xx
Orderofoperations
Commutativeproperty
7Associativeproperty 70Inverseproperty
9. (a) 4374347Distributive property 1228Multiply. 40Add.
(b) 5(23)5253 1015 mm m
(c) 22 33(61)[6(1)] 22 33(6)(1) 2 4 3 xx x x
62 6626 6126 xyz xyz xyz
N9. (a) 2(5)225Distributive prop. 210Multiply. pp p
Exercises
1. (a) B, since 0 is the identity element for addition.
(b) F, since l is the identity element for multiplication.
(c) C, since a is the additive inverse of a
(d) I, since 1 a is the multiplicative inverse, or reciprocal, of any nonzero number a.
(e) B, since 0 is the only number that is equal to its negative—that is, 00.
(f) D and F, since 1 has reciprocal
1 1 1
and 1 has a reciprocal 1 1 1 —that is, 1 and 1 are their own multiplicative inverses.
(g) B, since the multiplicative inverse of a number a is 1 a and the only number that we cannot divide by is 0.
(h) A, because the equation 543345 is true by the associative property.
(i) G, since we can consider 54 to be one number, 543 is the same as 354 by the commutative property.
(j) H, because 543 is the same as 5453 by the distributive property.
2. The commutative property allows us to change the order of the addends in a sum or the factors in a product. The associative property allows us to change the grouping of the addends in a sum or the factors in a product.
3. “Washing your face” and “brushing your teeth” are commutative.
4. “Putting on your left sock” and “putting on your right sock” are commutative.
5. “Preparing a meal” and “eating a meal” are not commutative.
6. “Starting a car” and “driving away in a car” are not commutative.
7. “Putting on your socks” and “putting on your shoes” are not commutative.
8. “Getting undressed” and “taking a shower” are not commutative.
9. A “(large deposit) slip” is a slip for a large deposit of money, whereas a “large (deposit slip)” is a large piece of paper onto which a deposit is written.
10. “(Defective merchandise) counter” is a location at which we would return an item that does not work, whereas “defective (merchandise counter)” is a broken place where items are bought and sold.
11.
Since 2117, this example shows that subtraction does not appear to be associative.
23. 415154
The order of the two numbers has been changed, so this is an example of the commutative property of addition: abba
Since 364, this example shows that division does not appear to be associative.
13. In general, a number and its additive inverse have opposite signs. A number and its multiplicative inverse have thesame signs.
14. Jack recognized the identity property of addition.
15. 159915 by the commutative property of addition.
16. 6226 by the commutative property of addition.
17. 8338 by the commutative property of multiplication.
18. 124412 by the commutative property of multiplication.
19. 367367 by the associative property of addition.
20. 236236 by the associative property of addition.
21. 725725 by the associative property of multiplication.
22. 864864 by the associative property of multiplication.
24. 312123
The order of the two numbers has been changed, so this is an example of the commutative property of addition: .abba
25. 51375137
The numbers are in the same order but grouped differently, so this is an example of the associative property of multiplication: abcabc
26. 426426
The numbers are in the same order but grouped differently, so this is an example of the associative property of multiplication:
abcabc
27.
61276127
The numbers are in the same order but grouped differently, so this is an example of the associative property of addition:
. abcabc
28. 81328132
The numbers are in the same order but grouped differently, so this is an example of the associative property of addition:
abcabc
29. 990
The sum of the two numbers is 0, so they are additive inverses (or opposites) of each other. This is an example of the additive inverse property: 0. aa
30. 110
The sum of the two numbers is 0, so they are additive inverses (or opposites) of each other. This is an example of the additive inverse property: 0. aa
31. 23 1 32
The product of the two numbers is l, so they are multiplicative inverses (or reciprocals) of each other. This is an example of the multiplicative inverse property: 1 10.aa a
32. 58 1 85
The product of the two numbers is l, so they are multiplicative inverses (or reciprocals) of each other. This is an example of the multiplicative inverse property: 1 10.aa a
33. 1.7501.75
The sum of a number and 0 is the original number. This is an example of the identity property of addition: 0.aa
34. 8.4508.45
The sum of a number and 0 is the original number. This is an example of the identity property of addition: 0.aa
35. 41733417
The order of the numbers has been changed, but the grouping has not, so this is an example of the commutative property of addition: abba
36. 84121284
The order of the numbers has been changed, but the grouping has not, so this is an example of the commutative property of addition: abba
37. 222 xyxy
The number 2 outside the parentheses is “distributed” over the x and y. This is an example of the distributive property.
38. 999 tsts
The number 9 outside the parentheses is “distributed” over the t and s. This is an example of the distributive property.
39. 55315 99327 3 3 is a form of the number 1. We use it to rewrite 5 9 as 15 27 This is an example of the identity property of multiplication.
40. 77749 1212784
7 7 is a form of the number 1. We use it to rewrite 7 12 as 49 84 This is an example of the identity property of multiplication.
41. 4243423 xyxy
This is an example of the distributive property. The number 4 is “distributed” over 2x and 3y
42. 6567657 trtr
This is an example of the distributive property. The number 6 is “distributed” over 5t and 7r.
43. 97133379731337 10050 150
44.
49199114911991 50200 250
45.
19992181999128 200010 2010
46.
2998321729982317 300020 3020
47.
48.
15912141881591411288 300100
400
1068147210614872 12080
49.
8436274327 8434362727 800600
50.
184612934693 184646129393 18001200
51.
52.
547252471047470
279525791079790
53. 4593545593 20593 10093 9300
54.
225672222567 42567 10067 6700
55.
6863
6863Def. of subtraction
6863Order of operations
8663Commutative property
8663Associative property
803Inverse property
803Orderof operations
83Identity proper
56.
91291
91291Def. of subtraction
91291Order of operations
12991Commutative property
12991Associative property
1201Inverse property
1201Order of operations 121Identi
of operations
property
property
property
Associative
1Inverse property
1Order of operations
01Inverse property
1Identity property
1Inverse property
1Order of operations
01Inverse property
1Identity property
63. When distributing a negative number over a quantity, be careful not to “lose” a negative sign. The problem should be worked in the following way.
3463436 1218 6
64. In the third line, 1 must also be distributed to the number 4.
66. 93333 1 123444
To rewrite 9 12 as 3 , 4 use the fact that 3 3 is another name for the multiplicative identity element, 1.
67. 5985958 4540 85
68. 611861168 6648 114
69. 43443 412 tt t
70. 54554 520 ww w
71. 7878 778 756 zz z z
72.
8686 886 848 xx x x
73.
65. 33339 1 444312
To rewrite 3 4 as 9 , 12 use the fact that 3 3 is another name for the multiplicative identity element, 1.
74.
75.
83883 824 824 rr r r
11411114 1144 xx x
1 83 4 x
11 83 44 13 8 44 3 2 4 x x x
79.
80. 3343334 912
81. 3253235 615 xx x
82. 4324342 128 xx x
83. 0.681.20.680.61.2 4.80.72 xx x
84.
85.
444 12151215 333 44 1215
8345838485 838485 243240 rsyrsy rsy rsy
2537252327 2523(27) 10614 uvwuvw uvw uvw
3834 383334 (38)(33)(34) 24912 xyz xyz xyz xyz
90. 5256xyz
525556 525556 102530 xyz xyz xyz
91.
43143 1413 1413 43 tmtm tm tm tm
92.
9121912 19112 19112 912 xyxy xy xy xy
93. 54154 1514 54 cdcd cd cd
131511315 113115 1315 xyxy xy xy
3581358 131518 358 qrsqrs qrs qrs
1.7 Simplifying Expressions
Classroom Examples, Now Try Exercises
9769176 91716 976 26
3243234 3234 612 xyxy xy xy
4234223 426 462 22 kk k k
2. (a)
59459410 zzzzz (b) 441413 rrrrrr
(d) 2 88xx cannot be simplified. 8x and 2 8 x are unlike terms and cannot be combined.
N2. (a) 4674673 xxxxx (b) 11112 zzzzzz
(c) 109109122222 xxxxx
(d) 2 43pp cannot be simplified because these unlike terms cannot be combined.
3. (a) 3571357 13157 357 32 kkkk kk kk k
102.52102.52 252 25252 2550 xx x x x
361251 36312521 183102 81 yy yy yy y
(d) 21221 10()(10) 5105510
N3. (a) 5634 kk
56134
4. “Twice a number, subtracted from the sum of the number and 8” is written 82. xx
N4. “Four times a number, subtracted from the sum of the number and 5” is written 54. xx
Exercises
1.
The correct response is B.
2. The numerical coefficient of 37 5 xy is 5. The correct response is A.
3. Examples A, B, and D are pairs of unlike terms, since either the variables or their powers are different. Example C is a pair of like terms, since both terms have the same variables (r and y) and the same exponents (both variables are to the first power). Note that we can use the commutative property to rewrite 6yr as 6ry
4. “Six times a number” translates as 6x, and “the product of eleven and the number” translates as 11x Thus, the correct translation of “six times a number, subtracted from the product of eleven and the number” is B, 116. xx
5. The student made a sign error when applying the distributive property.
6. The student incorrectly started by adding 32. First, 2 must be multiplied by 45. x
324532425 3810 87 xx x x
7. 4198411 rr
8. 7184714 tt
9. 7347374 2128 xyxy xy
8298289 1672 pqpq pq
11. 5235223 526 xyxy xy
8368336 8318 stst st
13. 84(36)84(3)4(6) 81224 82412 3212 xx x x x
14. 105(27)105(2)5(7) 101035 103510 4510 yy y y y
15.
2532153 21513 253 73 pp p p p
16.
10714101714 1017114 10714 1714 rr r r r
17.
64386438 1038 1083 23 xx x x x
The correct answer is 116. x
18. 1278612786 586 568 18 xx x x x
19. The numerical coefficient of the term 12k is 12.
20. The numerical coefficient of the term 11 y is 11.
21. The numerical coefficient of the term 2 3m is 3.
22. The numerical coefficient of the term 6 9n is 9.
23. Because x w can be written as 1, xw the numerical coefficient of the term x w is 1.
24. Because pq can be written as 1, pq the numerical coefficient of the term pq is 1.
25. Since 1,xx the numerical coefficient of the term x is 1.
26. Since 1,tt the numerical coefficient of the term t is 1.
27. Since 1 , 22 x x the numerical coefficient of the term 2 x is 1 2
28. Since 1 , 66 x x the numerical coefficient of the term 6 x is 1 . 6
29. Since 22 , 55 x x the numerical coefficient of the term 2 5 x is 2 . 5
30. Since 88 , 99 x x the numerical coefficient of the term 8 9 x is 8 9
31. Since 33 0.50.5, xx the numerical coefficient of the term 3 0.5 x is 0.5.
32. Since 22 1.751.75, xx the numerical coefficient of the term 2 1.75 x is 1.75.
33. The numerical coefficient of the term 10 is 10.
34. The numerical coefficient of the term 15 is 15.
35. 8r and 13r are like terms since they have the same variable with the same exponent (which is understood to be 1).
36. 7 x and 12x are like terms since they have the same variable with the same exponent (which is understood to be 1).
37. 4 5 z and 3 9 z are unlike terms. Although both have the variable z, the exponents are not the same.
38. 5 8 x and 3 10 x are unlike terms. Although both have the variable x, the exponents are not the same.
39. All numerical terms (constants) are considered like terms, so 4, 9, and 24 are like terms.
40. All numerical terms (constants) are considered like terms, so 7, 17, and 83 are like terms.
41. x and y are unlike terms because they do not have the same variable.
42. t and s are unlike terms because they do not have the same variable.
43. 7676 13 yyy y
5252 7 mmm m
6363 9 xxx x
46.
47.
4848 12 zzz z
12121 121 13 bbbb b b
48.
19191 191 20 xxxx x x
38473487 3415 715 kkkk k k
1514215412 1543 193 zzzz z z
51. 53157 yy
513517 5188 488 4 yy y y
52. 275612 kk
257612 250 3 kk k k
53. 2341720 xx
2431720 246 26 xx x x
54. 612416rr
1126416 1126 116 rr r r
55. 165422mmm
162542 14542 147 mmm m m
56. 63252 zzz 65322 1322 17 zzz z z
60. 9.62.78.52.7 9.68.52.72.7 9.68.50 18.1 rr rr r r
61. 4228 3333 tt
4228 3333 4228 3333 66 33 22 tt t t t
62. 5117 6666 xx
5117 6666 617 666 6 1 6 1 xx x x x
63. 2222 2 61186118 9 yyyy y
64. 3333 3 937937 13 mmmm m
57. 2.31.14.20.7
2.34.21.10.7
6.51.8 xx xx x x
2.34.21.8
58.
3.40.82.57.2
65. 23862233 pppp 2233 23 23 2386 2386 514 pppp pp pp
3.47.21.7
3.81.7 pp pp p p
3.47.20.82.5
9.5 xx xx x x
59. 7.25.12.35.1
7.22.35.15.1
7.22.30
66. 56343322 yyyy 3322 32 32 5634 5634 117 yyyy yy yy
67. 246324263 8123 815 xx x x
68. 469746497 24367 2443 yy y y
69. 6447 6 6428 224 47yy y y
70. 4551 453 1 4 61 3 565 5 t t t t
71. 13448134448 131632 1916 pppp pp p
72. 537253732 5216 21 xxxx xx x
73. 35224352224 3548 3 tttt tt t
74. 86331863331 8693 9 pppp pp p
75. 1000.053 x
1000.053 5(3 Associative property Distributive prop ) 5()53 515 . x x x x
76.
1000.065 x
77.
78.
100.582 z
Associative prop. Distributive pr 100.582 5(82) 5(8)52 4010 op. z z z z
79. 559336 yy 55593336 2545918 1663 yy yy y
80.
324824 tt
32348284 6121632 1044 tt tt t
81.
253323 rr
82.
83.
84.
Associative prop.
Distributive pr 1000.065 6(5) 6()65o 630 p x x x x
100.353 x
100.353 3(53) 3(5 Associative prop.
Distributive pr )33 159 op. x x x x
25233233 10669 415 rr rr r
325457 yy
32354547 6152028 1413 yy yy y
82143 kk
821143 82811413 16843 125 kk kk kk k
63251 pp
632151 63621511 181251 1313 pp pp pp p
91. 7.5(24)2.9(36) yy
7.527.542.932.96 15308.717.4 6.312.6 yy yy y
92. 8.4662.439 tt 8.4662.439 8.468.462.432.49
50.450.47.221.6 43.228.8 tt tt tt t
2325635 23215635 2322151635 645635 23 kkk kkk kkk kkk k
94. 234625 2341625 232416125 68625 33 rrr rrr rrr rrr r
95.
4336421 43316421 4343161421 12126421 47 xxx xxx xxx xxx x
96. 58253317 582153317 58521513317 401053317 4810 xxx xxx xxx xxx x
97. “The sum of four times a number, two times a number, eight times a number, and 10” is written 42810. xxx 42810(428)10 (428)10 1410 xxxxxx x x
98. “The sum of three times a number, nine times a number, ten times a number, and 1” is written 39101. xxx 39101(3910)1 (3910)1 221 xxxxxx x x
99. “Five times a number, added to the sum of the number and three” is written 35. xx
3535 53 63 xxxx xx x
100. “Six times a number, added to the sum of the number and six” is written 66. xx
6666 66 76 xxxx xx x
101. “A number multiplied by 7, subtracted from the sum of 13 and six times the number” is written 1367. xx
13671367 1313 xxxx x
102. “A number multiplied by 5, subtracted from the sum of 14 and eight times the number” is written 1485. xx 14851485 143 xxxx x
103. “Six times a number added to 4, subtracted from twice the sum of three times the number and 4” is written 23446. xx
23446 234146 23241416 6846 6684 012 12 xx xx xx xx xx
104. “Nine times a number added to 6, subtracted from triple the sum of 12 and 8 times the number” is written 312869. xx
312869 3128169 312381619 362469 3015 xx xx xx xx x
105. 4832 4832 76 xx xx x
106.
10885 10885 183 tt tt t 107.
5175117 51117 517 48 xxxx xx xx x
233523135 231315 2335 2 xxxx xx xx x
Chapter 1 Review Exercises
1. 4 55555625
2 1111 88864
8513401327
161242161242 1632 192 17
202532028 2016 4
Copyright © 2025 Pearson Education,
9.
10.
11. 1236636360
The inequality becomes 00. Since 00 is true, so is 00, and therefore, the statement “123660” is true.
12. 352331033721
The inequality becomes 2120. Therefore, the statement “352320” is true.
13. 2 481688
The inequality becomes 98. Since 98 is false, the statement 2 “948” is false.
14. “Thirteen is less than seventeen” is written 1317.
15. “Five plus two is not equal to ten” is written 5210.
16. “Two-thirds is greater than or equal to four-sixths” is written 24 . 36
17. 262663 1218 30 xy
434363 4183 415 60 xy
19.
20.
6 443 33 212 14 x y
22363 3336 363 96 39 3 13 x yx
21. “6 added to a number” translates as 6. x
22. “A number subtracted from 8” translates as 8. x
23. “The difference of six times a number and 9” translates as 69. x
24. “Three-fifths of a number added to 12” translates as 3 12. 5 x
25. 53252;2 xx
53252322Let2. 5234 1012 22 xxx
Because the left side, 22, is not equal to the right side, 52, the number 2 is not a solution of the given equation.
26. 21 1;3 93 t 2121 9393(3)Let3. 63 99 9 ,or 1 9
Because the left side and the right side are equal, 3 is a solution of the given equation.
27. “Six less than twice a number is 10” is written 2610. x
Letting x equal 0, 2, 4, 6, and 10 results in a false statement, so those values are not solutions. Since 28616610, the solution is 8.
28. “The product of a number and 4 is 8” is written 48. x Since 428, the solution is 2.
29. 1 4,,0,2.5,5 2
Graph these numbers on a number line. They are already arranged in order from smallest to largest.
30. 12 3,1,,2.25,3 23
31. Since 4 3 is the quotient of two integers, it is a rational number Since all rational numbers are also real numbers, 4 3 is a real number
32. Since the decimal representation of 0.63 repeats, it is a rational number. Since all rational numbers are also real numbers, 0.63 is a real number
33. Since 19 is a natural number, it is also a whole number and an integer. We can write it as 19 , 1 so it is a rational number and, hence, a real number.
34. Since the decimal representation of 6 does not terminate or repeat, it is an irrational number Since all irrational numbers are also real numbers, 6 is a real number
35. Since any negative number is less than any positive number, 10 is the lesser number.
36. Since 9 is to the left of 8 on the number line, 9 is the lesser number.
37. To compare these fractions, use a common denominator.
Since 9 12 is to the left of 8 12 on the number line, 3 4 is the lesser number.
38. Since |23|23 and 230,|23| is the lesser number.
39. The statement 1213 is true since 12 is to the right of 13 on the number line.
40. The statement 05 is true since 0 is to the right of 5 on the number line.
41. The statement 97 is true since 9 is to the left of 7 on the number line.
42. The statement 1313 is true since 1313.
43. (a) The opposite of the number 9 is its negative—that is, 999. (b) Since 90, the absolute value of the number 9 is |9|99.
44. (a) 00 (b) |0|0
45. (a) 66 (b) |6|6
46. (a) 55 77
(b) 555 777
47. |12|1212 48. |3|3
49. |19|1919
50. |92||7|7
51. 1046
52. 14184
53.
8917
54. 454459
55.
57.
688913
58.
59.
60.
61.
62.
66.
14.22
5.67.43.64.82
5.63.84.82
5.63.84.82
5.68.62
67. “19 added to the sum of 31 and 12” is written
3112191919 0.
68. “13 more than the sum of 4 and 8” is written
48131213 1.
69. “The difference of 4 and 6” is written 4646 2.
70. “5 less than the difference of 7 and 5” is written 755755 125 7.
71. 23.7550.0026.25 He now has a positive balance of $26.25.
72. 261610 The high temperature was 10F.
73.
281314281314 281314 1514 29
Her present financial status is $29.
74. 3737 10 The new temperature is 10.
75.
8124281242
The total net yardage is 38.
76. To get the closing value for the previous day, we can subtract the change from the amount at which it closed on January 30.
4.82.110.08
531
646543 3012 3012 18 xz
2 2 555 525 125 x
2 2 3833584 91532 947 423
96. 33(4)(3) 5(5)5 123 0 15 , which is undefined 0 yz x
97. “9 less than the product of 4 and 5” is written
459209 29.
98. “Five-sixths of the sum of 12 and 6” is written
55 1266 66 5.
99. “The quotient of 12 and the sum of 8 and 4” is written
1212 3. 844
100. “The product of 20 and 12, divided by the difference of 15 and 15” is written
2012 240 15151515 240 8. 30
101. “Eight times a number is 24” is written 824. x If 3, x 88324. x The solution is 3.
102. “The quotient of a number and 3 is 2” is written 2. 3 x If 6, x 6 2. 33 x The solution is 6.
103. The statement 606 is an example of an identity property.
104. The statement 515 is an example of an identity property.
105. The statement 23 1 32 is an example of an inverse property.
106. The statement 17170 is an example of an inverse property.
107. The statement 592592 is an example of an associative property.
108. The statement wxywxy is an example of an associative property.
109. The statement 333 xyxy is an example of the distributive property.
110. The statement 123312 is an example of a commutative property.
111. 72772 714 yy y
112. 124124() 12412 4812 tt t t
113. 3253235 615 sysy sy
114. 45145 1415 45 rsrs rs rs
115. 29(29) 11 mmm m
116.
222 2 2 1578 1578 16 ppp p p
117. 5461122 pppp
118.
119.
2 2 51146 162 pp pp
23521 2(3)2(5)2()2(1) 61022 412 kk kk kk k
723284 7(2)7(3)2(8)2(4) 1421168 141629 229 mm mm mm m m
120. 21 154107 55 2211 154107 5555 87 62 55 15 4 5 43 xx xx xx x x
121. “Seven times a number, subtracted from the product of 2 and three times the number” is written 2376713. xxxxx
122. “A number multiplied by 8, added to the sum of 5 and four times the number” is written
Chapter 1 Mixed Review Exercises
1. Complete the first row of the table.
Number
910 2424 910 2424 1 24
9. 22 22
2. Complete the second row of the table.
Number
3. Complete the third row of the table.
Number
4. Complete the fourth row of the table.
Number
5. The repeating decimal 0.6 is a rational number. All rational numbers are real numbers, so it is also a real number.
6.
15.
8417338136
16.
421834
17. 512392222 xyxy
18.
835291157 1157 1135 1135 24
19. 118165118165 47
The lowest temperature ever recorded in Iowa was 47F.
20. 14,49428214,494282 14,776
The difference in elevation is 14,776 ft.
Chapter 1 Test
1.
4207242014 434136
The statement becomes 136135. Since 136135, the statement
is true.
2. 222 2 1212 2323 147 496 2549 3636
Since 2549 , 3636 the statement 1212222 2323
is false.
3.
4. The number 2 3 can be written as a quotient of two integers with denominator not 0, so it is a rational number. Since all rational numbers are real numbers, it is also a real number
5. Simplify 8.
88 8 8
The number 8 is less than 6, and thus 8 is the lesser number.
6. Since 1.277 is located to the left of 0.742 on the number line, 1.277 is the lesser number.
7. “The quotient of 6 and the sum of 2 and 8” is written 6 , 28 and 66 1. 286 8.
251762126 2126 106 4
9. 12118 52 2323 11382 2332 3316 66 175 ,or2 66
3012 932122
18. The difference between the highest and lowest elevations is
6960406960407000 meters.
19. 4 saves (3 points per save)
3 wins (3 points per win)
2 losses ( 2 points per loss)
1 blown save ( 2 points per blown save)
43332212 12942 15points
He has a total of 15 points.
20. 4.056.824.056.822.77 As a signed number, the federal budget deficit is $2.77 trillion.
21. 22 0 33 illustrates an inverse property. The correct response is C.
22. 303xx illustrates an identity property. The correct response is D.
23. 528852 illustrates a commutative property because the order of the numbers is changed, but the grouping is not. The correct response is A.
24. 333 xyxy illustrates the distributive property. The correct response is E.
25. 532532 illustrates an associative property because the grouping of the numbers is changed, but the order is not. The correct response is B.
26. 53 1 35 illustrates an inverse property. The correct response is C.
27.
28.
29.
Chapters R–1 Cumulative Review Exercises
1.
2. To divide fractions, multiply by the reciprocal of the divisor.
5. 0.31decimal place 0.052decimal places 15123 0.0153decimal places
6. Move the decimal point two places to the left. 9.261000.0926
7. Divide the total board length by 3.
3. The LCD of 12 11511354 and 16 is 48. 1612163124 3320 4848
The length of each of the three pieces must be 4 1 4 inches.
8. The discount is 15% of $379. The word of here means multiply. 15%of$379
0.15$379$56.85
The amount of the discount is $56.85. The sale price is found by subtracting.
$379$56.85$322.15
9. Simplify both sides of the inequality.
10554374 1055433 105549 105513 10565
The statement is false because 105 isgreater than 65.
10. Simplify both sides of the inequality.
2 2 641012 2 153 6161012 2 159 6612 2 6 3612 2 6 48 2 6 82
The statement is true because 82.
11. ? ? ? ? 54(27)19; 3 534(237) 534( 19Let 3. 19 19 15(4)19 1119False 67) 534(1) x
Because substituting 3 for x results in a false statement, 3 is not a solution of the equation.
12. ? ? 53 1;4 82 53 1Let 4. 82 2012 1 8 (4 8 8 1 ) True 8 x x
The true result shows that 4 is a solution of the equation.
13. 14. 22 545(4)4(5) 88(4)5 2020 8(16)5 0 1285 0 123 0 xy xy
15. 5.372.762.61 16. 3535 4848 65 88 113 , or 1 88
17. |42||91| |4(2)||8| |6||8| (6)[(8)] 6[8] 2
1214 168168 12 868614
22 3693627 1 31233927
72356 14156 93399 1421 99 35 , or undefined 0
21. 1 41 4
The product of the two numbers is l, so they are multiplicative inverses (or reciprocals) of each other. This is an example of the multiplicative inverse property: 1 10.aa a
22. 112112 233233
The numbers are in the same order but grouped differently, so this is an example of the associative property of addition:
23.
Copyright © 2025 Pearson Education, Inc.
24.
25. 2753552698
The difference between the highest and lowest elevations is 2698 feet.
Equations
and Inequalities in One Variable
2.1 The Addition Property of Equality
Classroom Examples, Now Try Exercises
1. Note: When solving equations we will write “Add 5” as a shorthand notation for “Add 5 to each side” and “Subtract 5” as a notation for “Subtract 5 from each side.” 123Given 1212312Add12.
15Combineliketerms. x x x
We check by substituting 15 for x in the original equation.
N2. 5.77.2
5.75.77.25.7Add5.7. 1.5 x x x
Check 1.5:7.27.2True x The solution set is {1.5}.
3. 12 27 11211Add. 22722 47 Common denominator. 1414 3 14 n n n n
Check 322 :True 1477 n
Check ? 123Originalequation
15123Let15.
33True x x
Since a true statement results, 15 is the solution set.
N1. 134Given 1313413Add13.
17Combineliketerms. x x x
We check by substituting 17 for x in the original equation.
The solution set is 3 . 14
N3. 31 54 33133Add. 55455 512 Common denominator. 2020 7 20 r r r r
Check ? 134Originalequation
17134Let17.
44True x x
Since a true statement results, 17 is the solution set.
2. 4.16.3
4.14.16.34.1Add4.1. 2.2 x x x
Check 2.2:6.36.3True x
This is a shorthand notation for showing that if we substitute 2.2 for x, both sides are equal to 6.3, and hence a true statement results. In practice, this is what you will do, especially if you're using a calculator. The solution set is {2.2}.
Check 711 :True 2044 r
The solution set is 7 20
4. 2216 22161616Subtract16. 38 x x x
Check 38:2222True x
The solution set is {38}.
N4. 1512 15121212Subtract12. 27 x x x Check 27:1515True x The solution set is {27}.
5. 11912 119111211Subtract 11. 9 zz zzzzz z
Check 9:108108True z
The solution set is {9}.
N5. 52
52Subtract . 5Combine terms. xx xxxxx x
Check 5:1010True x
The solution set is {5}.
6. 79 1 22 77977 1Subtract . 22222 1 pp ppppp p
Check 99 1:True 22 p
The solution set is {1}.
N6. 25 4 33 22522 4Subtract 33333 4Combineterms. xx xxxxx x
Check 2020 4:True 33 x The solution set is {4}.
7. 1029Given 102292Add2. 109Combine terms. 1010910Subtract10. 1Combine terms. xx xxxxx x x x
Check 1:1111True x The solution set is {1}.
N7. 12568 1256686Add 6. 128Combine terms. 1212812Subtract12. 4Combine terms. tt ttttt t t t
Check 4:3232True t
The solution set is {4}.
8. 9462547 134124Combine terms. 1341212412Subtract 12. 44Combine terms. 4444Subtract 4. 0Combine terms. rrrr rr rrrrr r r r
Check 0:44True r The solution set is {0}.
N8. 46237510 6353Combine terms. 635535Subtract5. 33Combine terms. 3333Add3. 0Combine terms. www ww wwwww w w w
Check 0:33True w The solution set is {0}.
9. 4(1)(35)1 4(1)1(35)11 44351Distributive prop. 11Combine terms. 1111Add1. 2 xx xxaa xx x x x
Check 2:11True x
The solution set is {2}.
N9. 4(32)(114)3 4(32)1(114)3 4(3)4(2)1(11)1(4)3 1281143 43 4434 7 xx xx xx xx x x x
Check 7:33True x
The solution set is {7}.
Exercises
1. An equation includes an equality symbol, while an expression does not.
2. A linear equation in one variable (here x) is an equation that can be written in the form 0. axb
3. Equations that have exactly the same solution set are equivalent equations.
4. The addition property of equality states that the same expression may be added to or subtracted from each side of an equation without changing the solution set.
5. (a) 5847 xx
This is an expression, not an equation, since there is no equality symbol. It can be simplified by rearranging terms and then combining like terms.
58475487 15 xxxx x
(b) 61275 zz
This is an expression, not an equation, since there is no equality symbol. It can be simplified by rearranging terms and then combining like terms.
6127567125 7 zzzz z
(c) 5847 xx
This is an equation because of the equality symbol.
5847 87 1 xx x x
The solution set is {1}.
(d) This is an equation because of the equality symbol.
61275 125 17 zz z z
The solution set is {17}.
6. Equations that have exactly the same solution sets are equivalent equations. 26 2262Subtract2. 4 x x x
So 26 x and 4 x are equivalent equations. 105 1010510Subtract10. 5 1()1(5)Multiplyby 1. 5 x x x x x
So 105 x and 5 x arenot equivalent equations.
Subtract 3 from both sides to get 6, x so 39 x and 6 x are equivalent equations. Subtract 4 from both sides to get 4. x The second equation is 4, x so 48 x and 4 x arenot equivalent equations. The pairs of equations in A and C are equivalent.
7. Equations C 340 x and D 7639830 xxxx are linear equations in one variable because they can be written in the form 0. axb Note that in a linear equation the exponent on the variable must be 1, and only one variable may be used.
8. Check by replacing the variable(s) in the original equation with the proposed solution. A true statement will result if the proposed solution is correct.
9. 39 3393 12 x x x Check this solution by replacing x with 12 in the original equation. ? 39 1239Let12. 99True x x Because the final statement is true, {12} is the solution set.
10. 98 9989 17 x x x Check 17 x ? 1798Let17. 88True x Thus, {17} is the solution set.
11. 1219 12121912 31 x x x Check 31 x ? 311219Let31. 1919True x Thus, {31} is the solution set.
12. 1822 18182218 40 x x x
Checking yields a true statement, so {40} is the solution set.
13. 69 6696 3 x x x
Checking yields a true statement, so {3} is the solution set.
14. 57 5575 2 x x x
Checking yields a true statement, so {2} is the solution set.
15. 812 88128 4 r r r
Checking yields a true statement, so {4} is the solution set.
16. 711 77117 4 x x x
Checking yields a true statement, so {4} is the solution set.
17. 2617 26261726 9 x x x
Checking yields a true statement, so {9} is the solution set.
18. 4726 47472647 21 x x x
Checking yields a true statement, so {21} is the solution set.
19. 8.42.1 8.48.42.18.4 6.3 x x x
Checking yields a true statement, so the solution set is {6.3}.
20. 15.55.1 15.515.55.115.5 10.4 x x x
Checking yields a true statement, so the solution set is {10.4}.
21. 12.34.6 12.312.34.612.3 16.9 t t t
Checking yields a true statement, so the solution set is {16.9}.
22. 21.513.4 21.521.513.421.5 34.9 x x x
Checking yields a true statement, so the solution set is {34.9}.
23. 11 42 1111 4424 21 44 3 4 x x x x
Check 311 :True 422 x
The solution set is 3 . 4
24. 21 36 2212 3363 14 66 5 6 x x x x
Check 511 :True 666 x
The solution set is 5 6
25. 32 43 3323 4434 89 1212 1 12 k k k k
Check 122 :True 1233 k
The solution set is 1 12
26. 51 92 5515 9929 910 1818 1 18 p p p p
Check 111 :True 1822 p
The solution set is 1 18
27. 73 73 7737 10 r r r r
Check 10:33True r
The solution set is {10}.
28. 84 84 8848 12 k k k k
Check 12:44True k
The solution set is {12}.
29. 215 2151515 13 p p p
Check 13:22True p
The solution set is {13}.
30. 519 5191919 14 z z z Check 14:55True z The solution set is {14}.
31. 414 4141414 10 x x x Check 10:44True x The solution set is {10}.
32. 722 7222222 15 x x x Check 15:77True x The solution set is {15}.
33. 5.24.9 5.24.94.94.9 10.1 z z z Check 10.1:5.25.2True z The solution set is {10.1}.
34. 11.83.6 11.83.63.63.6 15.4 z z z Check 15.4:11.811.8True z The solution set is {15.4}.
35. 13 35 1333 3555 59 1515 4 15 x x x x
Check 4549 :True 15151515 x The solution set is 4 . 15
36. 12 43 1222 4333 38 1212 5 12 x x x x
Check 5358 :True 12121212 x
The solution set is 5 12
37. 839 83898Subtract8. 3 xx xxxxx x
Check 3:8(3)39(3)True x
The solution set is {3}.
38. 647 64676Subtract7. 4 xx xxxxx x
Check 4:6(4)47(4)True x
The solution set is {4}.
39. 625 62555Subtract5. 20 2202Add2. 2 tt ttttt t t t
Check 2:6(2)25(2)True t
The solution set is {2}.
40. 463 46333Subtract 3. 60 666Add 6. 6 zz zzzzz z z z
Check 6:4(6)63(6)True z
The solution set is {6}.
41. 327 32272Subtract2 17or7 xx xxxxx. xx
Check 7:2121True x
The solution set is {7}.
42. 549 54494Subtract4 19or9 xx xxxxx. xx
Check 9:4545True x The solution set is {9}.
43. 1049 104999Subtract9 140 4404Subtract4. 4 xx xxxxx. x x x
Check 4:3636True x The solution set is {4}.
44. 857 85777Subtract7 150 5505Subtract5. 5 tt ttttt. t t t
Check 5:3535True t The solution set is {5}.
45. 27 6 55 22722 6Subtract. 55555 5 6 5 6 ww wwwww w w Check 27 6:(6)6(6)True 55 w The solution set is {6}.
46. 29 2 77 22922 2Subtract. 77777 7 2 7 2 zz zzzzz z z
Check 29 2:(2)2(2)True 77 z The solution set is {2}.
47. 11 5 22 1111 5 2222 50 5505 5 xx xxxx x x x
The solution set is {5}.
48. 14 7 55 1444 7 5555 5 70 5 7707 7 xx xxxx x x x
The solution set is {7}.
49. 5.624.6 5.624.64.64.6 1.020 2202 2 xx xxxx x x x
The solution set is {2}.
50. 9.158.1
9.158.18.18.1 1.050 5505 5 xx xxxx x x x
The solution set is {5}.
51. 1.430.4
1.430.40.40.4 1.030 1.03303 3 xx xxxx x x x
The solution set is {3}.
52. 1.960.9
1.960.90.90.9 1.060 1.06606 6 tt tttt t t t
The solution set is {6}.
53. 3724 372242 74 7747 3 xx xxxx x x x
The solution set is {3}.
54. 9584 958848 54 5545 1 xx xxxx x x x
The solution set is {1}.
55. 8676 867767 66 6666 0 tt tttt t t t
The solution set is {0}.
56. 139129 1391212912 99 9999 0 tt tttt t t t
The solution set is {0}.
57. 7459 745595 79 7797 2 xx xxxx x x x
The solution set is {2}.
58. 36710 3677107 310 33103 7 xx xxxx x x x
The solution set is {7}.
59. 5211 522112 511 55115 16 xx xxxx x x x
The solution set is {16}.
60. 3891 389919 31 3313 4 xx xxxx x x x
The solution set is {4}.
61. 1.240.24 1.240.20.240.2 1.044 4444 0 yy yyyy y y y
The solution set is {0}.
62. 7.766.76 7.766.76.766.7 1.066 6666 0 rr rrrr r r r
The solution set is {0}.
63. 4633 63 6636 9 xx x x x
Check 9:4(9)63(9)3True x
The solution set is {9}.
64. 7864 84 8848 12 xx x x x
Check 12:7(12)86(12)4True x
The solution set is {12}.
65. 3720 70 7707 7 xx x x x
Check 7:3(7)72(7)0True x
The solution set is {7}.
66. 5440 40 4404 4 xx x x x
Check 4:5(4)44(4)0True x
The solution set is {4}.
67. 361022 3422 342222 42 4424 2 xx xx xxxx x x x
Check 2:3(2)6102(2)2True x
The solution set is {2}.
68. 84871 8471 847717 41 4414 3 xx xx xxxx x x x
Check 3:8(3)487(3)1True x
The solution set is {3}.
69. 5326412 (526)316 33163 13
ttt t t t
Check 13: 1616True t
The solution set is {13}.
70. 4636310 613 66136Add6. 19 xxx x x x
Check 19: 1313True x
The solution set is {19}.
71. 6573124 138124 1381212412 84 8848 4 xxx xx xxxx x x x
Check 4:4444True x
The solution set is {4}.
72. 4381112 124112 1241111211 42 4424 2 xxx xx xxxx x x x
Check 2:2020True x
The solution set is {2}.
73. 105741232 153143 1531414314 33 3333 0 xxxx xx xxxx x x x
Check 0:33True x
The solution set is {0}.
74. 74137763 116106 1161010610 66 6666 0 pppp pp pppp p p p
Check 0:66True p The solution set is {0}.
75. 5.24.67.10.94.6 1.94.60.94.6
1.94.60.90.94.60.9 1.04.64.6 1.04.64.64.64.6 0 0 qqq qq qqqq q q q q
Check 0:4.64.6True q
The solution set is {0}.
76. 4.02.79.64.62.7 2.75.64.62.7
2.75.65.64.62.75.6 2.72.7 2.72.72.72.7 0 xxx xx xxxx x x x
Check 0: 2.72.7True x The solution set is {0}.
77. 51222 73575 5142 7357 5214222Add. 7735777 714 Combine terms. 735 11411 1Subtract. 33533 125 LCD15 1515 7 15 xx xx xxxxx x x x x
Check : 722 True 1533 x
The solution set is 7 . 15
78. To solve the equation, follow the simplification steps below. 63411 74576 632415 LCD30 7430730 63291 Add. 74307 63129111Add. 74730777 7329 Combine terms. 7430 332933 1Add. 443044 5845 LCD60 6060 103 60 ss ss ss sssss s s s s
Check 103101101 :True 60140140 s
The solution set is 103 60
79. 532143
5(3)5(2)143 1510143 103 1010310 13 xx xx xx x x x
Check : 1353(13)214(13)3True x
The solution set is {13}.
80. 23457 6857 87 8878 15 xx xx x x x
Check 15:23(15)45(15)7True x
The solution set is {15}.
81. 133244
133(2)3(4)4 136124 64 6646 2 pp pp pp p p p
Check 2:44True p
The solution set is {2}.
82. 214658 2124208 248 2424824 16 ww ww w w w
Check 16:88True w
The solution set is {16}.
83. (56)(34)10 (56)1(34)10 (56)1(3)1(4)10 563410 310 33103 7 yy yy yy yy y y y
Check 7: 1010True y
The solution set is 7.
84. (83)(17)6 83176 26 2262 4 rr rr r r r
Check 4: 66True r
The solution set is {4}.
85. 2(5)(9)3 2(5)1(9)3 2()2(5)1(9)1()3 21093 13 1131 4 pp pp pp pp p p p
Check 4:33True p
The solution set is 4.
86. 4(6)(83)5 424835 165 1616516 21 kk kk k k k
Check 21:55True k The solution set is 21.
87. 6(21)(137)0 6(2)6(1)(137)0 1261370 130 1313013 13 bb bb bb b b b
Check 13: 00True b
The solution set is {13}.
Copyright © 2025 Pearson Education, Inc.
88. 5(33)(161)0 15151610 160 1616016 16 ww ww w w w
Check 16: 00True w
The solution set is {16}.
89. 10(21)19(1) 10(2)10(1)19()19(1) 20101919 201019191919 1019 10101910 29 29 xx xx xx xxxx x x x x
Check 29:570570True x
The solution set is {29}.
90. 2(32)5(3) 64515 6455155 415 44154 11 11 rr rr rrrr r r r r
Check 11: 7070True r
The solution set is {11}.
91. 2(82)3(27)2(42)0 164621840 180 1818018 18 ppp ppp p p p
Check 18: 00True p
The solution set is {18}.
92. 5(12)4(3)7(3)0 5101242170 140 140 14 zzz zzz z zzz z
Check 14:00True z
The solution set is {14}.
93. 4(71)3(25)4(35)6 28461512206 186 1818618 12 xxx xxx x x x
Check 12:66True x
The solution set is {12}.
94. 9(23)4(53)5(4)3 182720122053 673 6767367 64 mmm mmm m m m
Check 64:33True m
The solution set is {64}.
95. Answers will vary. One example is 68 x
96. Answers will vary. One example is 1 1. 2 x
2.2 The Multiplication Property of Equality
Classroom Examples, Now Try Exercises 1. 1575 1575
Divideby15. 1515 5 x x x
Check 5:7575True x
The solution set is 5 N1. 880 880
Divideby8. 88 10 x x x
Check 10:8080True x
The solution set is 10. 2. 820 820
Writeinlowestterms. 82 x x x
Divide by 8. 88 205
Check 5 :2020True 2 x
The solution set is 5 2
3. 5.040.7
Check 18:1212True t
The solution set is 18. N5. 4 16 7 7477 16Multiplyby. 4744 716 1 41 28 z z t t
Check 28:1616True t The solution set is 28. 6.
7 171 1(1)1(7)Multiply by 1. 1(1)7 17 7 p ppp p p p p
Check 7:77True p
The solution set is 7. N6.
9 191 1(1)1(9)Multiplyby1. 1(1)9 19 9 x xxx x x x x
Check 9:99True x
The solution set is 9. 7. 4920 520Combineterms. 520 Divideby5. 55 4 rr r r r
Check 4:2020True r
The solution set is 4.
N7. 9621
321 Divideby3. 33 7 nn n n n
321Combineterms.
Check 7:2121True n
The solution set is 7.
8. 8(21)832
2. Choice C doesn’t require the use of the multiplicative property of equality. After the equation is simplified, the variable x is alone on the left side.
547 7 xx x
8(2)8(1)832Distributive property 168832Multiply.
1632Combine like terms. 1632Divide by 16. 1616 2 x x x x x x
Check 2:3232True x
The solution set is 2.
N8. 3(54)1215
3(5)3(4)1215Distributive prop. 15121215Multiply.
1515Combine like terms. 1515Divide by 16.5 1515 1 x x x x x x
Check 1:1515True x
The solution set is 1.
Exercises
1. (a) multiplication property of equality; to get x alone on the left side of the equation, multiply each side by 1 3 (or divide each side by 3).
(b) addition property of equality; to get x alone on the left side of the equation, add 3 (or subtract 3) on each side.
(c) multiplication property of equality; to get x alone on the left side of the equation, multiply each side by 1 (or divide each side by 1 ).
(d) addition property of equality; to get x alone on the right side of the equation, add 6 (or subtract 6) on each side.
3. Choice B; to find the solution of 3 , 4 x multiply (or divide) each side by 1, or use the rule “If ,xa then xa ”
4. Choice A; to find the solution of 24, x multiply (or divide) each side of the equation by 1, or use the rule “If ,xa then xa ”
5. To get just x on the left side, multiply both sides of the equation by the reciprocal of 4 , 5 which is 5 4
6. To get just x on the left side, multiply both sides of the equation by the reciprocal of 2 , 3 which is 3 2
7. This equation is equivalent to 1 5. 10 x To get just x on the left side, multiply both sides of the equation by the reciprocal of 1 , 10 which is 10.
8. This equation is equivalent to 1 10. 100 x To get just x on the left side, multiply both sides of the equation by the reciprocal of 1 , 100 which is 100.
9. To get just x on the left side, multiply both sides of the equation by the reciprocal of 9 , 2 which is 2 9
10. To get just x on the left side, multiply both sides of the equation by the reciprocal of 8 , 3 which is 3 8
11. This equation is equivalent to 10.75. x To get just x on the left side, multiply both sides of the equation by the reciprocal of 1, which is 1.
12. This equation is equivalent 10.48. x To get just x on the left side, multiply both sides of the equation by the reciprocal of 1, which is 1.
13. To get just x on the left side, divide both sides of the equation by the coefficient of x, which is 6.
14. To get just x on the left side, divide both sides of the equation by the coefficient of x, which is 7.
15. To get just x on the left side, divide both sides of the equation by the coefficient of x, which is 4.
16. To get just x on the left side, divide both sides of the equation by the coefficient of x, which is 13.
17. To get just x on the left side, divide both sides of the equation by the coefficient of x, which is 0.12.
18. To get just x on the left side, divide both sides of the equation by the coefficient of x, which is 0.21.
19. This equation is equivalent to 125. x To get just x on the left side, divide both sides of the equation by the coefficient of x, which is 1
20. This equation is equivalent to 150. x To get just x on the left side, divide both sides of the equation by the coefficient of x, which is 1.
21. 636 636 Divide by 6. 66 16 6 x x
Check 6:3636True x The solution set is 6.
23. 215 215 Divideby2. 22 15 2 m m m
Check 15 :1515True 2 m
The solution set is 15 . 2
24. 310 310 Divideby3. 33 10 3 m m m
Check 10 :1010True 3 m
The solution set is 10 3
25. 315 315
Divideby3. 33 5 x x x
Check 5:1515True x The solution set is {5}.
26. 560 560
Divideby5. 55 12 x x x
Check 12:6060True x
The solution set is {12}.
27. 728 728
Divideby7. 77 4 x x x
Check 4:2828True x
22. 864 864
Divideby8. 88
8 x x x
Check 8:6464True x
The solution set is {8}.
The solution set is {4}.
28. 936 936
Divideby9. 99 4 x x x
Check 4:3636True x
The solution set is {4}.
29. 1036 1036
Divideby10. 1010 3618
Lowestterms 105 t t t
Check 18 :3636True 5 t
The solution set is 18 5
30. 1054 1054
35. 12 1()112Multiplyby 1. 12 x x x
Check 12:1212True x The solution set is {12}. 36. 14 1()114Multiplyby 1. 14 t t t
Check 14:1414True t The
Divideby10. 1010 5427
Lowestterms 105 s s s
Check 27 :5454True 5 s
The solution set is 27 5
31. 672 672
Divideby 6. 66 12 x x x
Check 12:7272True x The solution set is {12}.
32. 464 464
Divideby4. 44 16 x x x
Check 16:6464True x The solution set is {16}.
33. 40 40 Divideby4. 44 0
Check 0:00True r
The solution set is {0}.
Check 333 :True 444 x
The solution set is 3 4
38. 1 2 1 1()1 2 1 2 x x x
Check 111 :True 222 x
The solution set is 1 2
39. 0.28 0.28 0.20.2 40 t t t
Check 40:88True t
The solution set is 40.
34. 70 70 Divideby7. 77
x x x
Check 0:00True x The solution set is {0}.
40. 0.918 0.918 0.90.9 20 x x x
Check 20:1818True x
The solution set is 20.
41. 0.39 0.39 0.30.3
30 x x x Check 30:99True x
The solution set is 30.
48. 3.932.76 3.932.76 3.93.9 8.4 x x x Check 8.4:32.7632.76True x
The solution set is 8.4.
42. 0.520 0.520 Divide by0.5. 0.50.5
40 x x x Check 40:2020True x
The solution set is 40.
43. 0.61.44 0.61.44 Divide by0.6. 0.60.6 2.4 x x x Check 2.4:1.441.44True x
The solution set is 2.4.
44. 0.82.96 0.82.96 Divide by0.8. 0.80.8 3.7 x x x Check 3.7:2.962.96True x
The solution set is 3.7.
45. 9.12.6
9.12.6 Divide by 2.6. 2.62.6 3.5 x x x Check 3.5:9.19.1True x
The solution set is 3.5.
46. 7.24.5 7.24.5 Divide by 4.5. 4.54.5 1.6 x x x
Check 1.6:7.27.2True x
The solution set is 1.6.
47. 2.125.62 2.125.62 Divide by 2.1. 2.12.1 12.2 m m m Check 12.2:25.6225.62True m
The solution set is 12.2.
49. 1 12 4 1 44(12)Multiply by4. 4 148 48 x x x x
Check 48:1212True x
The solution set is 48.
50. 1 3 5 1 55(3)Multiplyby5. 5 15 p p p
Check 15:33True p
The solution set is 15.
51. 12 6 1 12 6 1 6612 6 72 z z z z
Check 72:1212True z
The solution set is 72.
52. 15 5 1 15 5 1 5515 5 75 x x x x
Check 75: 15=15 True x
The solution set is 75.
Check 844 :True 1599 x
63. 6810 210 210 22 5 rr r r
64. 3724
65.
36.
67. 56263 963 963 99 7 mmm m m m
Check 7:6363True m
The solution set is 7.
68. 92768 468 468 44 17 rrr r r r
Check 17: 6868True r
The solution set is 17.
69. 6470 90 90 99 0 xxx x x x
Check 0:00True x
The solution set is 0.
70. 5480 90 90 99 0 xxx x x x
Check 0:00True x
The solution set is 0.
71. 843 53 53 55 3 5 www w w w
Check 3 :33True 5 w
The solution set is 3 . 5
72. 934 74 74 77 4 7 xxx x x x
Check 4 :44True 7 x
The solution set is 4 . 7
73. 111 3 3412 111 3Distributive property 3412 431 3LCD12 121212 1 3Lowest terms
431436 4341436 124436 1236 1236 1212 3 x x x x x x
Check 3:3636True x
The solution set is 3.
74. 21 1 18 20 510 211 18Distributive prop. 51020 821 18LCD20 202020
Check 40:164218True x
The solution set is 40.
75. 0.90.50.13
0.53Combine terms. 0.53 Divideby0.5. 0.50.5 6 www w w w
Check 6:33True w
The solution set is 6.
76. 0.50.60.31 0.21Simplify.
0.21 Divide by 0.2. 0.20.2 5
Check 5:11True x
The solution set is 5.
80.
5321030 53521030 15101030 1530 1530 1515 2 x x x x x x
Check 2:3030True x
The solution set is 2.
42816 442816 48816 416 416 44 4 x x x x x x
Check 4:1616True x
The solution set is 4.
6431848 64631848 24181848 2448 2448 2424 2 x x x x x x
Check 2:4848True x The solution set is 2.
81. Answers will vary. One example is 3 6. 2 x
82. Answers will vary. One example is 10017. x
2.3 Solving Linear Equations Using Both Properties of Equality
Classroom Examples, Now Try Exercises
1. Step1 (not necessary)
Step2 5419
544194Subtract4. 515Combineterms. p p p
Step3 515 Divide by5. 55 3 p p
Step4
Check 3:15419True p
The solution set is 3.
N1. Step1 (not necessary)
Step2 273 27737Add7. 210Combineterms. m m m
Step3 210 Divide by2. 22 5 m m
Step4
Check 5: 1073True m
The solution set is 5.
2. Step1 (not necessary)
Step2 5285 522852Add 2. 5105Combine terms. 551055Add5. 1010Combine terms. xx xxxxx x x x
Step3 1010 Divideby10. 1010 1 x x
Step4
Check 1: 5285True x
The solution set is 1.
N2. Step1 (not necessary) Step2 2349 232492Subtract . 329Combine terms. 39299Add 9. 122Combine terms. qq qqqq2q q q q
Step3 2 12 Divide by 2. 2 2 6 q q
Step4
Check 6: 123249True q
The solution set is 6.
3. Step1
3(1)11516 3311516 Distributive property 314516 Combine terms. xx xx xx
Step2 3141451614 Subtract 14. 352 35525 Subtract 5. 22 xx xx xxxxx x
Step3 22 Divideby2. 22 1 x x
Step4
Check 1: 1111True x
The solution set is 1.
N3. Step1
zzz zzz zz
3(6)577 318577Distributiveproperty 21877Combineterms.
Step2 218187718Add 18. 2725 277257Add 7. 525 zz zz zzzzz z
Step3 525 Divide by 5. 55 5 z z
Step4
Check 5: 2828True z
The solution set is 5.
4. Step1
8(8)25 8825 Distributive property 7825 xxx xxx xx
Step2 782252 Subtract 2. 585
58858Subtract 8. 53 xxxxx x x x
Step3 53 Divide by5. 55 3 5 x x
Step4
Check 31919 :True 555 x
The solution set is 3 5
N4. Step1 5(9)4 594 Distributive property 494 xxx xxx xx
Step2 49949 Add 9. 45 45 Subtract . 35 xx xx xxxxx x
Step3 35 Divide by3. 33 5 3 x x Step4
Check 577 : True 333 x
The solution set is 5 3
5. Step1 23(26)4(1) 261844 Distributive property 41844 zz zz zz
Step2 4184444 Add 4. 184 18444 Subtract 4. 220 zz zz zzzzz z
Step3 220 Divideby22. 2222 0 z z Step4
Check ? 0: 23(2)4(1)8 44 True z
The solution set is 0.
N5. Step1 4(1)244(72) 4424288Distributive property 4448 tt tt tt
Step2 444484Add 4. 48 4484Subtract 4. 04 tt tt ttttt t
Step3 04 Divide by4. 44 0 t t Step4
Check ? 0:244(7)4(1) 44True t
The solution set is 0. 6. 2(5)2414 210210Distr. prop. 2101021010Subtract 10. 22 2222Subtract 2 00True xx xx xx xx xxxxx.
The variable x has “disappeared,” and a true statement has resulted. The original equation is an identity. This means that for every real number value of x, the equation is true. Thus, the solution set is {all real numbers}.
N6. 3(7)321
2. Combine like terms on the left.
321321Distr. prop. 3212132121 Subtract 21. 33
3333Add 3. 00True xx xx xx xx xxxxx
The variable x has “disappeared,” and a true statement has resulted. The original equation is an identity. This means that for every real number value of x, the equation is true. Thus, the solution set is {all real numbers}.
7. 386(1)3
383363Subtract 3. 86False xxx xxx xx xxxxx
38663Distributive prop. 3836Combine terms.
The variable x has “disappeared,” and a false statement has resulted. This means that for every real number value of x, the equation is false. Thus, the equation has no solution and its solution set is the empty set, or null set, symbolized
3. Clear the parentheses by using the distributive property.
4. Use the multiplication property of equality to multiply each side by 1 , 5 or divide each side by 5.
5. (a) 66 (The original equation is a(n) identity.) This goes with choice B, {all real numbers}.
(b) 0 x (The original equation is a(n) conditional.) This goes with choice A, {0}.
(c) 50 (The original equation is a(n) contradiction.) This goes with choice C,
6. 1000.0310310330, xxx so choice D is correct.
7. 3214
322142 Subtract2.
312 Combine like terms.
N7. 4(3)35 41235Distr. prop. 51235Combine.
5125355Subtract 5. 123False xxx xxx xx xxxxx
The variable x has “disappeared,” and a false statement has resulted. This means that for every real number value of x, the equation is false. Thus, the equation has no solution and its solution set is the empty set, or null set, symbolized
8. To find the other number, you would divide 36 by x, so an expression for the other number is 36 x
N8. First, suppose that the sum of two numbers is 18, and one of the numbers is 10. How would you find the other number? You would subtract 10 from 18. Instead of using 10 as one of the numbers, use m. This gives us the expression 18 m for the other number.
Exercises
1. Use the addition property of equality to subtract 8 from each side.
312 Divide by3. 33 4 x x x x x Check 4: 12214True x The solution set is 4.
8. 4327
433273Subtract3. 424Combine like terms.
424 Divideby4. 44 6 x x x x x Check 6: 24327True x The solution set is 6.
9. 5421
525 Divide by 5. 55 5 z z z z z Check 5: 25421True z
544214Add 4. 525Combine like terms.
The solution set is 5.
10. 7410
744104Add 4. 714Combine like terms. 714 Divide by 7.
11. 452
12. 623
13. 2543 254434 Subtract 4.
Check 4: 85163True x
The solution set is
14. 7892 789929 Subtract 9.
Check 5: 4343True p
The solution set is 5.
15. 5873 583733 Subtract 3.
287 28878 Subtract 8. 21 21 Divide by 2. 22 1 2 mm mmmmm m m m m m
Check 11111 : True 222 m
The solution set is 1 . 2
495
Subtract
Check 41627154 :True 33333
17. 125107
12571077 Add7. 5510 555105 Add 5. 515 515 Divide by5. 55 3 xx xxxxx x x x x x
Check 3: 3651021True x
The solution set is 3.
18. 163138 16381388 Add8. 8313 833133 Add 3. 816 816 Divide by8. 88 2 ww wwwww w w w w
Check 2: 3231316True w
The solution set is 2.
19. 125115 125105 Combine terms. 1251010510Subtract 10. 255 25555 Add 5. 210 210 Divide by 2. 22 5 hhh hh hhhhh
Check 5: 5555True h The solution set is 5.
20. 41513 4121 Combine like terms. 211 Add 2. 22 Add 1. 1 Divide by 2. xxx xx xx x x
Check 1: 33True x
The solution set is 1.
21. 75252 2242 222422 222 22222 02 02 22 0 rrrr rr rrrr r r r r r
Check 0:22True r
The solution set is {0}.
22. 946763 5646Combine terms. 66Subtract4. 0Subtract6. pppp pp pp p
Check 0:66True p
The solution set is {0}.
23. 5(1)27 5527 4527 ppp ppp pp 452272 257 25575 22 22 22 1 pppp p p p p p
Check 1:99True p The solution set is {1}.
24. 6(3)227 618227 41827 41827 31827 zzz zzz zz zzzz z
318182718 39 39 33 3 z z z z
Check 3:3030True z The solution set is {3}.
25. 3(42)530xxx 126530 17630 17630 18630 1866306 1824 1824 1818 4 3 xxx xx xxxx x x x x x
Check 48686 :True 333 x
The solution set is 4 3
26. 5(23)4225 10154225Distributive prop. 615225Combine terms. 6210Subtract15. 410Subtract2. 105 Divideby4. 42 mmm mmm mm mm mm m
Check 5 :3030True 2 m
The solution set is 5 2
27. 6(23)1 xxx 6231 321 321 221 22212 23 23 22 3 2 xxx xx xxxx x x
Check 355 :True 222 x
The solution set is 3 . 2
28. 7(32)25 xxx 73225 5325 532252 335 33353 38 38 33 8 3 xxx xx xxxx x x x x x
Check 83131 :True 333 x
The solution set is 8 3
29. 273(51) pp 27351 2752 275525 372 37727 35 35 33 5 3 pp pp pppp p p p p p
Check 53131 :True 333 p
The solution set is 5 3
30. 493(2) 4932Distributiveproperty 495Combine liketerms. 595Add1. 54Subtract9. 4 Divideby5. 5 xx xx xx xx x x
Check 42929 :True 555 x
The solution set is 4 5
31. (82)564 xx 1(82)564
1(8)1(2)564 82564 344 34444 30 30 33 0 xx xx xx x x x x x
Check 0:44True x
The solution set is
32. (75)472 xx
1(75)472 1(7)1(5)472 75472 322 32222 30 30 33 0 xx xx xx x x x x x
Check 0:22True x
The solution set is 0.
33. 6(3)618 xx 186618 18666186 1818 18181818 00 xx xxxx
Because 0 = 0 is true, any real number is a solution. The solution set is {all real numbers}.
34. 9(2)918 pp 189918 18999189 1818 18181818 00 pp pppp
Because 0 = 0 is true, any real number is a solution. The solution set is {all real numbers}.
35. 115(2)65 1151065 61065 6106656 105 xxx xxx xx xxxx
Since 105 is a false statement, the equation has no solution set, symbolized by
36. 64(1)24 64424 2424 44Subtract2. xxx xxx xx x
Since 44 is a false statement, the equation has no solution set, symbolized by
37. 244(72)4(1) tt 2428844 4844 484444 444 44444 40 40 44 0 tt tt tttt t t t t t
Check 0:44True t
The solution set is {0}.
38. 82(2)4(1) 84244 4244 422442 424 20 0 xx xx xx xxxx x x x
Check 0:44True x
The solution set is {0}.
39. 6(35)2(1010) 18302020 183020202020 23020 230302030 210 210 22 5 ww ww wwww w w w w w
Check 5:120120True w
The solution set is {5}.
40. 4(21)6(3) 84618Distributive property 14418Add6. 1414Add4. 1Divideby14. xx xx xx x x
Check 1:1212True x
The solution set is {1}.
41. 10(21)8(21)14 xx 201016814 20101622 201016162216 41022 410102210 432 432 44 8 xx xx xxxx x x x x x
Check 8:150150True x The solution set is {8}.
42. 9(35)12(31)51 2745361251 27453663 45963 189 2 kk kk kk k k k
Check 2:99True k
The solution set is {2}.
43. (42)(35)3 1(42)1(35)3 42353 33 3333 0 0 11 0 xx xx xx x x x x x
Check 0:33True x
The solution set is {0}.
44. (65)(58)3 1(65)1(58)3 65583 33 0 0 kk kk kk k k k
Check 0:33True k
The solution set is {0}.
45. 3(24)6(2) 612612 61266126 1212 12121212 00 xx xx xxxx
The variable has “disappeared.” Since the resulting statement is a true one, any real number is a solution. We indicate the solution set as {all real numbers}.
46. 3(64)2(69) 18121218 1818Add12. xx xx x
Since 1818 is a true statement, the solution set is {all real numbers}.
47. 6(41)12(23) 2462436 24624243624 636 xx xx xxxx
The variable has "disappeared," and the resulting equation is false. Therefore, the equation has no solution set, symbolized by
48. 6(28)4(36) 12481224 4824Subtract12.
xx xx x
Since 4824 is a false statement, the equation has no solution set, symbolized by
49. 4(8)2(26)20 43241220 432432 43244324 3232 xx xx xx xxxx
Since 3232 is a true statement, the solution set is {all real numbers}.
50. 4(3)2(28)4 4124164 412412 1212 xx xx xx
Since 1212 is a true statement, the solution set is {all real numbers}.
51. 9(1)32(31)8 993628 6966 696666 96 vvv vvv vv vvvv
Because 96 is a false statement, the equation has no solution set, symbolized by
52. 8(3)46(21)10 824412610 1224124
Because 244 is a false statement, the equation has no solution set, symbolized by
53. The sum of q and the other number is 11. To find the other number, you would subtract q from 11, so an expression for the other number is 11. q
54. The sum of r and the other number is 34. To find the other number, you would subtract r from 34, so an expression for the other number is 34. r
55. The product of x and the other number is 9. To find the other number, you would divide 9 by x, so an expression for the other number is 9 x
57. If a baseball player gets 65 hits in one season, and h of the hits are in one game, then 65 h of the hits came in the rest of the games.
58. If a hockey player scores 42 goals in one season, and n of the goals are in one game, then 42 n of the goals came in the rest of the games.
59. If Monica is x years old now, then 15 years from now she will be 15 x years old. Five years ago, she was 5 x years old.
60. If Chandler is y years old now, then four years ago he was 4 y years old. Eleven years from now, he will be 11 y years old.
61. Since the value of each quarter is 25 cents, the value of r quarters is 25r cents.
62. Since the value of each dime is 10 cents, the value of y dimes is 10y cents.
56. The product of m and the other number is 6. To find the other number, you would divide 6 by m, so an expression for the other number is 6 m
63. Since each bill is worth 5 dollars, the number of bills is 5 t
64. Since each bill is worth 10 dollars, the number of bills is 10 v
2.4 Clearing Fractions and Decimals When Solving Linear Equations
Classroom Examples, Now Try Exercises
Copyright © 2025 Pearson Education, Inc.