

Part I Solutions to All Exercises
CHAPTER 1
Functions and Their Graphs
Section 1.1 Rectangular Coordinates
1. Cartesian
2. Midpoint Formula
3. The x-axis is the horizontal real number line. Matches (c).
4. The y-axis is the vertical real number line. Matches (f).
5. The origin is the point of intersection of the vertical and horizontal axes. Matches (a).
6. The quadrants are four regions of the coordinate plane. Matches (d).
7. An x-coordinate is the directed distance from the y-axis. Matches (e).
8. A y-coordinate is the directed distance from the x-axis. Matches (b).
9.
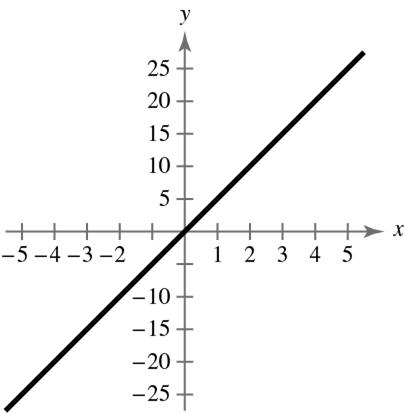
:2,6,:6,2,:4,4,:3,2 ABCD
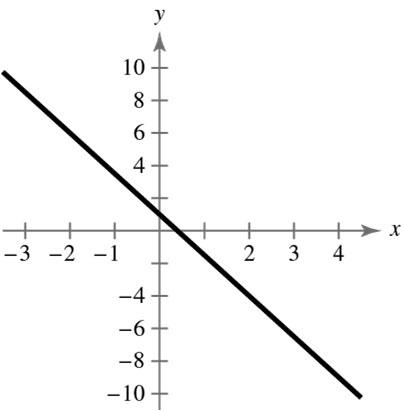
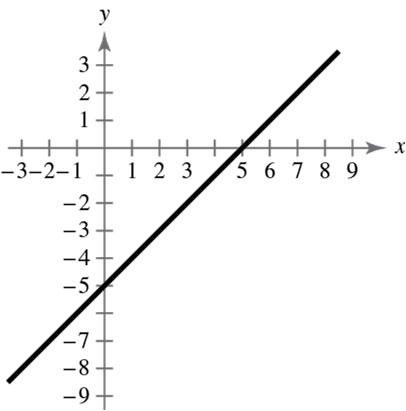
35 22 : ,4; :(0,2); : 3,;:(6,0)ABCD
3,4
12,0 15. 0 x and 0 y in Quadrant IV.
16. 0 x and 0 y in Quadrant III.
17. 4 x and 0 y in Quadrant II.
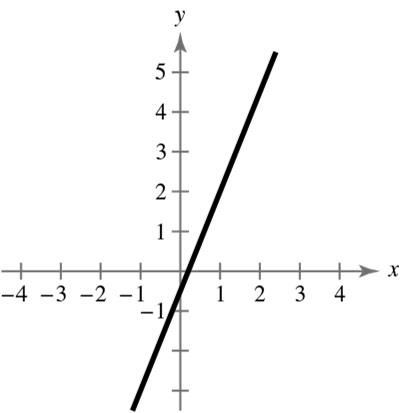
18. 0 x and 7 y in Quadrant II.
19. 0,0,0xyxy means or. xyyx This occurs in Quadrant II or IV.
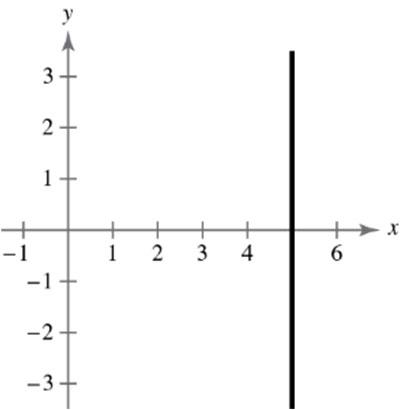
20. ,,0xyxy means x and y have the same signs. This occurs in Quadrant I or III. 21. 22.


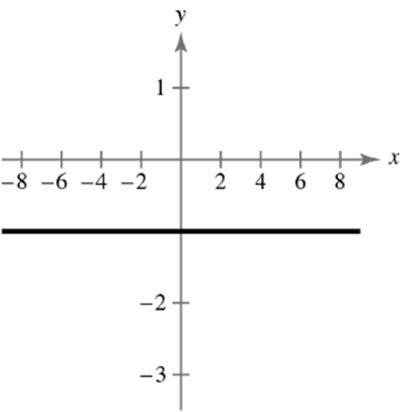
22 2121 2 2 22 3.99.58.22.6 13.410.8 179.56116.64 296.2
30. (a) The distance between
1,1 and 9,1 is 10. The distance between
9,1 and 9,4 is 3.
The distance between 1,1 and 9,4 is
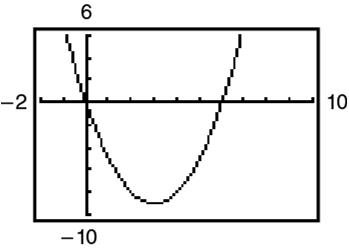
531541620 511336440
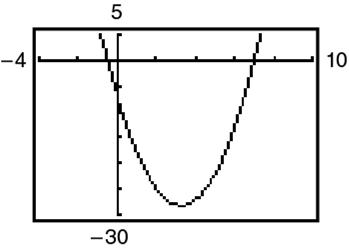
(a)
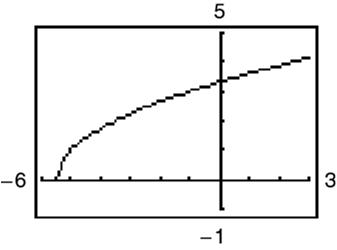
(b) 22 (5(3))(66)648 d (c) 665(3),(6,1) 22
36. (a)
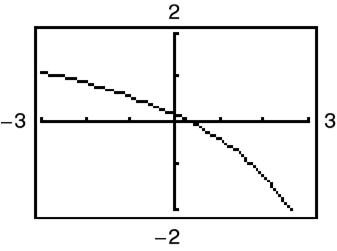
(b) 22 (44)(81)497 d
(c) 18449 ,,4 222
37. (a)
22 9171643610
9171 ,5,4 22
38. (a)
22 161202514413
161207
39. (a)
22 5142364210
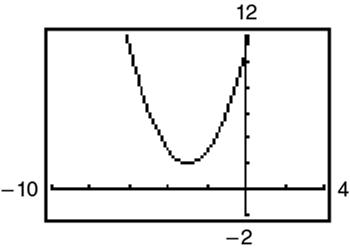
1524
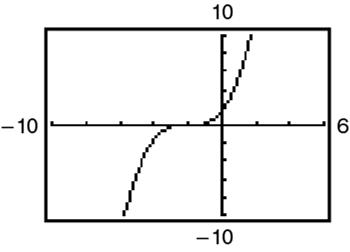
40. (a)
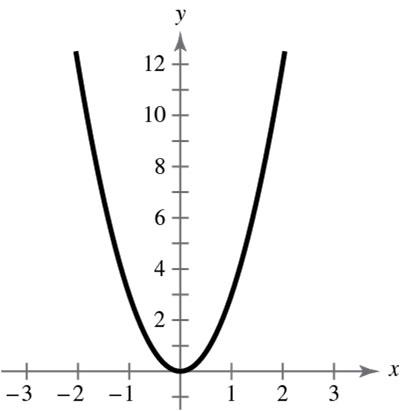
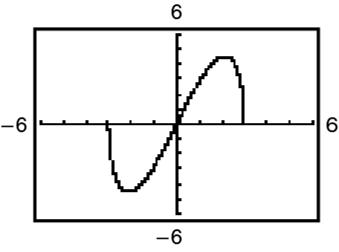
22210102 646482
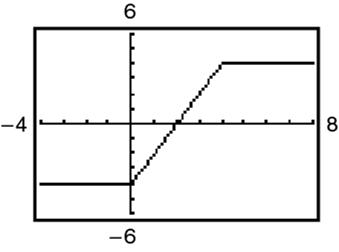
210102 ,6,6 22
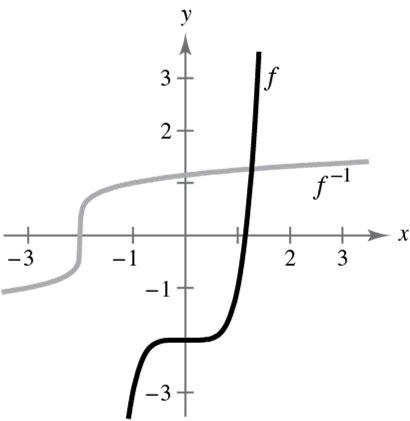
41. (a)
22 16.85.612.34.9 501.7654.76556.52
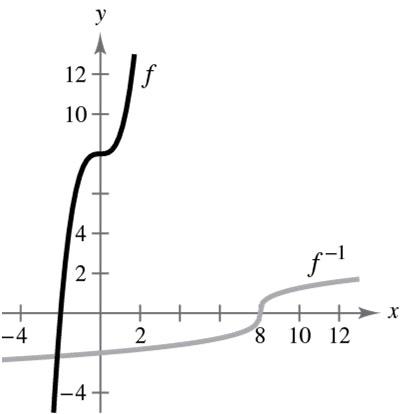
16.85.612.34.9 ,5.6,8.6 22
42. (a)

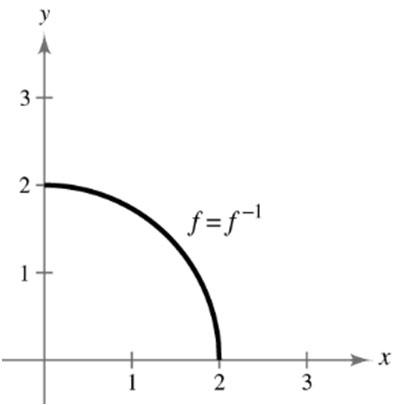
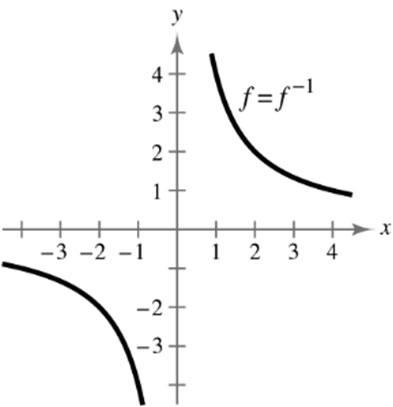
22154 1 223 182 9 93
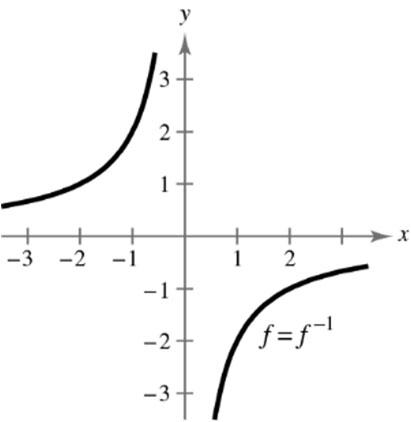
5212431 7 ,1, 226
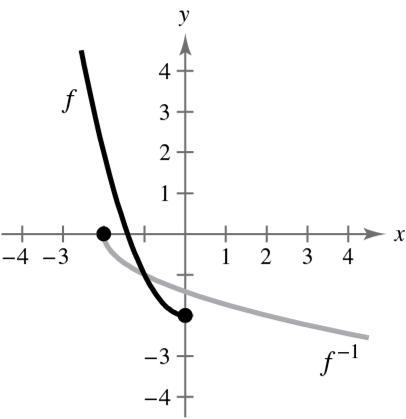
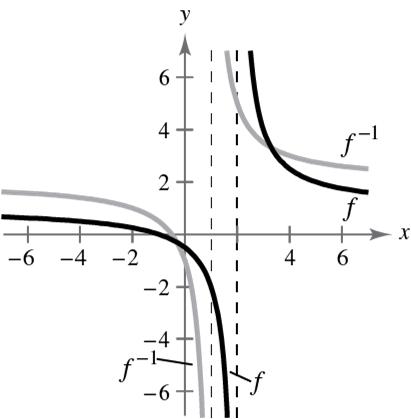
22 22 42185012 2438 2020 2505 45
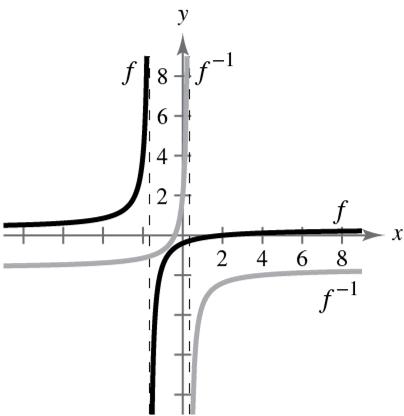
The pass is about 45 meters.
44. 22 120150 36,900 3041 192.09
The plane flies about 192 kilometers.
45.
1212midpoint,22
20162018485.9514.4 , 22 2017,500.15 xxyy
In 2017, the sales were about $500.15 billion.
46. 1212midpoint,22.xxyy
In this problem, you have
2 201720196.16 , 2018,7.57. 22 y
So, 2 2 6.16 7.578.98. 2 y y
In 2019, the earnings per share were about $8.98. 47.
49.
36,633,3 56,331,0 36,033,3 16,335,0
74,283,6 24,282,10 24,482,4 74,483,4
50.
510,865,2 310,667,0 710,663,0
51. True. Because 0 x and 0, y 20 x and 30, y which is located in Quadrant III.
52. False. The Midpoint Formula would be used 15 times.
53. True. Two sides of the triangle have lengths 149 and the third side has a length of 18.
54. False. The polygon could be a rhombus. For example, consider the points
4,0, 0,6, 4,0, and 0,6.
55. The y-coordinate of a point on the x-axis is 0. The x-coordinates of a point on the y-axis is 0.
56. The x- and y-coordinates are switched. For example, 3,2 should be 2,3.
22, 450,1 22, 354,2 12, 151,4
58. The midpoint of the given line segment is
The midpoint between 11 , xy and 1212 , 22 xxyy
The midpoint between 1212 , 22 xxyy
57. Because 12 2 m xx x and 12 2 m yy y we have:
and
22 , xy is 1212 1212 22 33 22,. ,44 22
So, the three points are 1212121233 4422,,,,
and 1212 33 44,.
59. Use the Midpoint Formula to prove the diagonals of the parallelogram bisect each other.
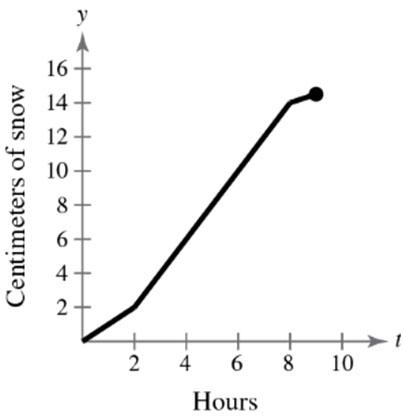
60. (a) Because 00 , xy lies in Quadrant II, 00 , xy must lie in Quadrant III. Matches (ii).
(b) Because 00 , xy lies in Quadrant II, 002,xy must lie in Quadrant I. Matches (iii).
(c) Because 00 , xy lies in Quadrant II,
00 1 2 , xy must lie in Quadrant II. Matches (iv).
(d) Because
00 , xy lies in Quadrant II, 00 , xy must lie in Quadrant IV. Matches (i).
61. (a) First Set
Because 222 345, A, B, and C are the vertices of a right triangle.
Second Set
(b)
A, B, and C are the vertices of an isosceles triangle or are collinear: 101021040.
First set: Not collinear
Second set: Collinear.
(c) A set of three points is collinear when the sum of two distances among the points is exactly equal to the third distance.
62. (a) distance
(b) distance
Answers will vary.
63. 46 x (a)
xxyy yyyy
22 1121 2 2121
xxyy xxxx
22 2111 2 2121
4164610 (b)
406066
64. 97x (a)
97392112
97392130 (b)
65. (a) When 3, x
3 3 22322754. x (b) When 0, x
3 3 2200. x
66. (a) When 0, x 4 4 33 3. 0 x x Division by 0 is undefined. (b) When 2, x
2 2 22xx
32 32 22xxxx
69. 2 222 0 xxxx
72. (a) Time to copy one page: 1 min 50
(b) Time to copy x pages: min 50 x (c) Time to copy 120 pages: 12012 2.4min 505
(d) Time to copy 10,000 pages: 10,000 200min 50
Section 1.2 Graphs of Equations
1. solution or solution point
2. graph
3. intercepts
4. y-axis
5. origin
6. numerical
7. Two other approaches to solve problems mathematically are algebraic and graphical.
12. (a)
? 22 6, 0:26508
? ? 236508 7208 728
No, the point is not on the graph.
(b)
? 22 0, 4: 20548
? ? 205168 0808 808
No, the point is not on the graph.
, hk and
, xy is the radius r
8. Let , xy be any point on the circle. The distance between the center
So,
22 xhykr
9 (a)
? 2 2, 0:23220 ? 4620 00
Yes, the point is on the graph.
(b)
? 2 2, 8:23228 ? 4628 128
No, the point is not on the graph.
10. (a) ? 0, 2:204 2 =2
Yes, the point is on the graph. (b) ? 5, 3:354 ? 39 3 =3
Yes, the point is on the graph.
11. (a) ? 1, 5:5412 ? 541 53
No, the point is not on the graph.
(b) ? 6, 0:0462 ? 044 00
Yes, the point is on the graph.
2022 Cengage Learning. All
yx
16. 2 5 yx
17. x-intercept: 2,0
y-intercept: 0,2
18. x-intercept:
4,0
y-intercepts: 0,2
19. x-intercept: 3,0
y-intercept: 0,9
20. x-intercepts: 2,0
y-intercept: 0,16
y-intercept: 0,6
22. 83 yx
Let 0. y 8 3 083 38 x x x
x-intercept: 8 3,0
-intercept:
0,8 23. 4 yx
4,0
2 xx xx xx
x-intercepts:
322040 00 0 y y y
y-intercept:
0,0 28. 2 1 yx Let 0. y 01 1 x x
x-intercept:
1,0 Let 0. x
2 2 01 1 1 1 y y y y
y-intercepts:
0,1
4
44No -axis symmetry
44No -axis symmetry
44Origin symmetry
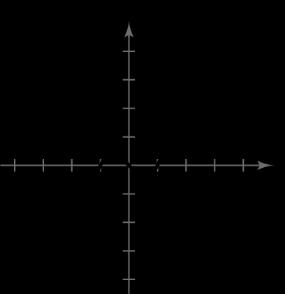
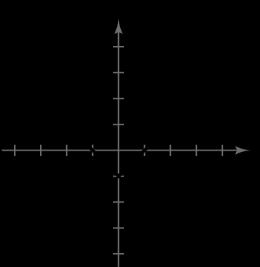
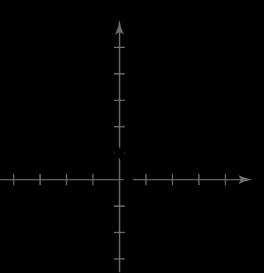
41. 31yx
x-intercept: 1 3,0
y-intercept: 0,1
No symmetry
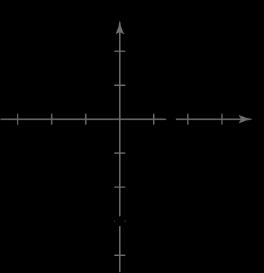
42. 23yx
x-intercept:
3 2,0
y-intercept: 0,3
No symmetry
43. 2 2 yxx
x-intercepts: 0,0,2,0
y-intercept: 0,0
No symmetry
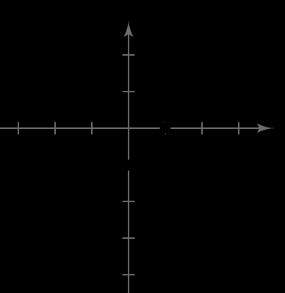
x –1 0 1 2 3
y 3 0 –1 0 3
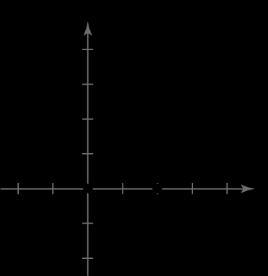
44. 2 2 yxx
x-intercepts: 2,0,0,0
y-intercept: 0,0
No symmetry
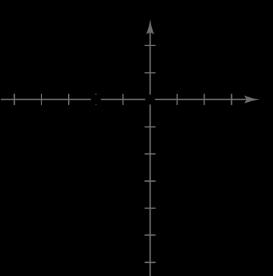
45. 3 3 yx
x-intercept: 3 3, 0
y-intercept: 0,3
No symmetry
x –2 –1 0 1 2
y –5 2 3 4 11
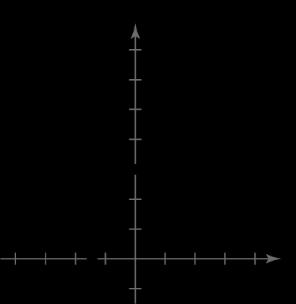
46. 3 1 yx
x-intercept: 1,0
y-intercept: 0,1
No symmetry
47. 3 yx
x-intercept: 3,0
y-intercept: none No symmetry
x 3 4 7 12
48. 1 yx
x-intercept: 1,0
y-intercept: 0,1
No symmetry
49 6 yx
x-intercept: 6,0
y-intercept: 0,6 No symmetry
y 0 1 2 3 x –2 0 2 4 6 8 10
8 6 4 2 0 2 4
50. 1 yx
x-intercepts:
1,0,1,0
y-intercept: 0,1
y-axis symmetry
51. 2 1 xy
x-intercept:
y-intercepts:
1,0
0,1,0,1
x-axis symmetry
x –1 0 3
y 0 ±1 ±2
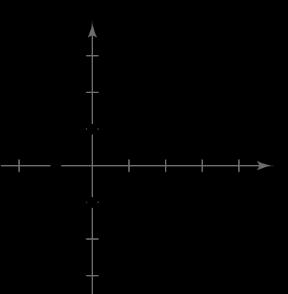
52. 2 5 xy
x-intercept: 5,0
y-intercepts:
0,5,0,5
x-axis symmetry
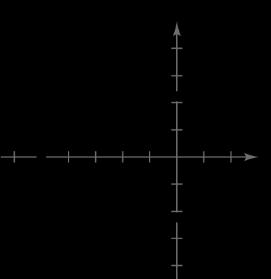
53. 1 2 5 yx

10,0,0,5 54. 2 3 1 yx

3 2 0,1,,0 55. 2 43yxx

Intercepts:
3,0,1,0,0,3 56. 2 2 yxx

Intercepts:
2,0,1,0,0,2 57. 2 1 x y x

Intercept: 0,0

59. 3 1 yx

60. 6 yxx

61. 3 yx


64. Center:
22 2 22 007 49 xy xy
65 Center: 4,5; Radius: 2
66. Center: 1,3; Radius: 11
67. Center: 3,8; Solution point:
9,13
22 2 22 2 22 3813 38169 xhykr xy xy
68. Center: 2,6;Solution point: 1,10
70. Endpoints
Center:


79. (a)


(d) When 2 386 xy yards, the area is a maximum of 1 97511 square yards.
(e) AregulationNFLplayingfieldis120yardslongand 1 353 yardswide. Theactualareais6400squareyards.
80. (a)

The model fits the data well. Each data value is close to the graph of the model.
(b) Using the graph or the model with 40, t The life expectancy is approximately 75.2 years.
(c) The model and the line 70.1 y intersect at 11.1, t corresponding to the year 1961.
(d) The y-intercept is 0,68.0.In 1950 0, t the life expectancy of a child (at birth) was 68.0 years.
(e) Answers will vary.
81. False. The line yx is symmetric with respect to the origin.
82. False. The line 0 y has infinitely many x-intercepts.
83. The test is for symmetry with respect to the x-axis. The statement should read: The graph of 2 3 xy is symmetric with respect to the x-axis because
84. x-axis symmetry:
So, the graph of the equation is symmetric with respect to x-axis, y-axis, and origin.
85. 23yaxbx
(a)
23 23 yaxbx axbx
To be symmetric with respect to the y-axis; a can be any non-zero real number, b must be zero.
Sampleanswer: 1,0ab
(b)
23 23 23 yaxbx yaxbx yaxbx
To be symmetric with respect to the origin; a must be zero, b can be any non-zero real number.
Sampleanswer: 0,1ab
86. The line would rise from left to right, passing through quadrants I, II, and III.

3713731213
91. The least common denominator is
32112321127 7777823,543
174 174541243 54 10 1010101000 10
22 942152811 xxxxx
223 32 411344412 12444 xxxxxx xxx
2 2 297291463 2563 xxxxx xx
22422 42 3513535 385 xxxxx xx
Section 1.3 Linear Equations in Two Variables
1. linear 2. slope 3. point-slope 4. parallel
5. rate or rate of change
6. linear extrapolation
7. They are perpendicular to each other.
9. (a) 2 3 m
Because the slope is positive, the line rises. Matches 2L (b) m is undefined. The line is vertical. Matches 3L (c) 2. m
The line falls. Matches 1L
10. (a) 0. m The line is horizontal. Matches 2L
(b) 3 4 m Because the slope is negative, the line falls. Matches 1L
(c) 1. m Because the slope is positive, the line rises. Matches 3L
13. Two points on the line: 0,0 and 4,6
21 21 63 Slope 42 yy xx
14. The line appears to go through 0,7 and 7,0.
21 21 07 Slope1 70 yy xx
53 Slope:5 -intercept:0,3 yx m y
Slope:1 -intercept:0,10 m y
3 4 3 4 1 Slope: -intercept:0,1 yx m y
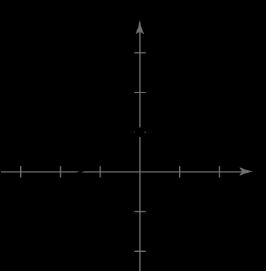
2 3 2 3 2 Slope: -intercept:0,2 yx m y
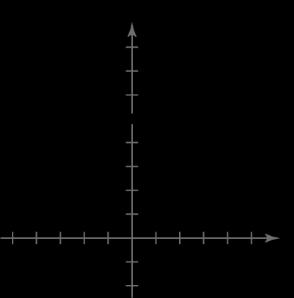
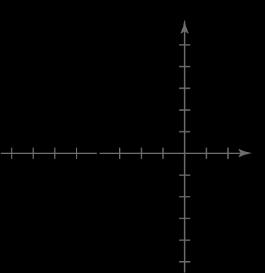
40 4 x x
Slope: undefined (vertical line)
y-intercept: none
21. 2 5 520 ,verticalline x x
Slope: undefined
y-intercept: none 22. 5 3 350 35 y y y
Slope: 0 m
y-intercept:
5 3 0,
23. 7 6 7630 6730 5 xy yx yx
Slope: 7 6 m
y-intercept:
0,5 24. 2 3 239 329 3 xy yx yx
y-intercept: 0,3 25. 0993 6062 m
26. 5051 010102 m
1.63.11.5 0.15 5.24.810 m
35. Point: 5,7, Slope: 0 m Because 0, m y does not change. Three other points are
1,7,0,7, and
4,7.
36. Point: 3,2, Slope: 0 m
Because 0, m y does not change. Three other points are
1,2,10,2, and 6,2.
37. Point: 5,4,Slope: 2 m
Because 2 1 2, my increases by 2 for every one unit increase in x. Three additional points are 4,6, 3,8, and 2,10.
38. Point: 0,9, Slope: 2 m
Because 2, my decreases by 2 for every one unit increase in x. Three other points are 2,5, 1,11, and 3,15.
39. Point: 4,5, Slope: 1 3 m
Because 1 3, m y decreases by 1 unit for every three units increase in x. Three additional points are
19 4 2,7,0,, and 1,6.
40. Point: 3,4, Slope: 1 4 m
Because 1 4, m y increases by 1 unit for every four unit increase in x. Three additional points are
1,5,1,11, and 3,15.
41. Point: 4,3, Slope is undefined.
Because m is undefined, x does not change. Three points are
4,0,4,5, and 4,2.
42. Point: 2,14,Slope is undefined. Because m is undefined, x does not change. Three other points are 2,3,2,0, and 2,4.
43. Point: 0,2;3 m
230 32 yx yx

44. Point: 0,10;1 m
1010 10 10 yx yx yx
45. Point:
3,6;2 m
623 2 yx yx
46. Point: 0,0;4 m
040 4 yx yx
47. Point: 1 3 4,0; m
1 3 14 33 04yx yx
53. Point:
5.1,1.8;5 m
54. Point:
2.5,3.25;0 m
3.2502.5 3.250 3.25 yx y y
51 15 55 3 51 5 3 2 5 yx yx yx
1,0.6,2,0.6
0.60.6 0.61 21 0.410.6 0.40.2 yx yx yx
8,0.6, 2,2.4
2.40.6 0.68 28 3 0.68 10 10638 106324 10318 39 or0.31.8 105 yx yx yx yx yx yxyx
The
The slopes are negative reciprocals, so the lines are perpendicular.
69.
1 1 :0,1,5,9 91 2 50 L m
2 2 :0,3,4,1 131 402 L m
The slopes are negative reciprocals, so the lines are perpendicular.
70.
1 1 :2,1,1,5 51 6 2 123 L m
2 2 :1,3,5,5 538 2 514 L m
The lines are neither parallel nor perpendicular. 71.
1 1 :6,3,2,3 33 0 0 268 L m
11 2 22 11 22 2 :3,,6, 0 0 633 L m
1L and 2L are both horizontal lines, so they are parallel.
72.
1 1 :4,8,4,2 2863 4484 L m
2 2 1 :3,5,1, 3 116 5433 1343 L m
The slopes are negative reciprocals, so the lines are perpendicular.
73. 3 2 423 2 xy yx
Slope: 2 m (a) 2,1,2 m
122 23 yx yx
(b)
1 2 2,1, m
1 2 1 2 12 2 yx yx
573 384 ,, m
357 438 7 8 553 324 241840 24184035 244053 yx yx yx yx yx
337 458 7 8 39 540 403024 40302421 40249 yx yx yx yx yx
77. 50 5 y y
Slope: 0 m
(a) 2,4, 0 4 m y (b) 2,4, isundefined. 2 m x
78. 40 4 x x Slope: m is undefined. (a) 3,2,is undefined. 3 m x (b)
3,2, 0 2 m y
79. 4 4 xy yx
Slope: 1 m (a) 2.5,6.8,1 m
6.812.5 4.3 yx yx
(b) 2.5,6.8,1 m
6.812.5 9.3 yx yx
80. 9 2 629 269 3 xy yx yx
Slope: 3 m
3.9,1.4,3 m
1.433.9 1.4311.7 313.1 yx yx yx
1 3 1 3 1 3 1.43.9 1.41.3 0.1 yx yx yx
1 35 15115 35 53150 xy xy xy
87. (a) 135. m The sales are increasing 135 units per year.
(b) 0. m There is no change in sales during the year.
(c) 40. m The sales are decreasing 40 units per year.
88. (a) The slopes of each line segment are:
182.80170.91229.23215.64 11.8913.59 14131716 233.72182.80265.60229.23 1514181750.92greatest36.37 215.64233.72260.17265.60 18.08least5.43 16151918
The sales increased the greatest between 2014 and 2015. The sales increased the least between 2015 to 2016. (b) 260.17170.9189.26 14.88 19136
The slope of the line is about 14.88. (c) Sales increased an average of about $14.88 billion per year between 2013 and 2019.
89.
90. (a) and (b)
(e) 1 0.0838.3%grade 12 x 300 600 900 1200 1500 1800 2100

(d) Because 1 12, m for every change in the horizontal measurement of 12 meters, the vertical measurement decreases by 1 meter.
91. Using the points 0,32and100,212, where the first coordinate represents a temperature in degrees Celsius and the second coordinate represents a temperature in degrees Fahrenheit, you have 212321809 10001005 m
Since the point 0,32 is the F- intercept, 32, b the equation is 5160 1.832or . 99 FCCF
92. (a) Using the points 1,970and3,1270, you have 1270970300 150. 312 m
Using the point-slope form with 150 m and the point
1,970, you have
11 9701501 970150150 150820. yymtt yt yt yt
(b) The slope is 150. m The slope tells you the amount of increase in the weight of an average male child’s brain each year.
(c)
Let2: 1502820 300820 1120 t y y y
The average brain weight at age 2 is 1120 grams.
(d) Answers will vary.
(e) Answers will vary. Sample answer: No. The brain stops growing after reaching a certain age.
93. Using the points 0,830 and 5,0, where the first coordinate represents the year t and the second coordinate represents the value V, you have 0830 830166830,05. 50 Vttt
94. Using the points
0,24,000and10,2000, where the first coordinate represents the year t and the second coordinate represents the value V, you have 2,00024,00022,000 2200. 10010 m
Since the point 0,24,000 is the -intercept,=24,000,Vb the equation is 220024,000, 010.Vtt
95. (a) TotalCost=costforcostpurchase fuelandfor+cost maintainanceoperator 9.511.542,000 2142,000 Ctt Ct
(b) RevenueRateperhourHours 45 Rt (c) 452142,000 2442,000 PRC Ptt Pt
(d) Let 0, P and solve for t. 02442,000 42,00024 1750 t t t The equipment must be used 1750 hours to yield a profit of 0 dollars.
96. (a)

(b) 21522102850yxxx
Because 8, m each 1-meter increase in x will increase y by 8 meters.
(c)

97. False. The slope with the greatest magnitude corresponds to the steepest line.
98. 8,2 and 1 422 1,4: 187 m 0,4 and 2 74 11 7,7: 707 m
False. The lines are not parallel.
99. Find the slope of the line segments between the points A and B, and B and C
Since the slopes are negative reciprocals, the line segments are perpendicular and therefore intersect to form a right angle. So, the triangle is a right triangle.
Using the Pythagorean Theorem:
101. (a)
(b)
Theslopeis
The -interceptis 0,3,not 0,4. y
102. (a) Matches graph (ii).
The slope is –20, which represents the decrease in the amount of the loan each week. The y-intercept is 0,200, which represents the original amount of the loan.
(b) Matches graph (iii).
The slope is 2, which represents the increase in the hourly wage for each unit produced. The y-intercept is 0,12.5, which represents the hourly rate if the employee produces no units.
(c) Matches graph (i).
The slope is 0.32, which represents the increase in travel cost for each mile driven. The y-intercept is 0,32, which represents the fixed cost of $30 per day for meals. This amount does not depend on the number of miles driven.
(d) Matches graph (iv).
The slope is –100, which represents the amount by which the computer depreciates each year. The y-intercept is 0,750, which represents the original purchase price.
103. The line 4 yx rises most quickly.

The line 4 yx falls most quickly.

The greater the magnitude of the slope (the absolute value of the slope), the faster the line rises or falls.
3377 2 510
3 72 78153 When 2: 1010102
370 7 When 0: 1010
xf (c)
373 727 20 When 3:2 101010
xf (d)
376 7216 209 When 6: 101010
xf 108. 242 433
When 2:0 33
42042 When 0: 33
xg
42345 When 3: 33
4264882 When 6: 333
104. Because 5 2 4, the steeper line is the one with a slope of – 4. The slope with the greatest magnitude corresponds to the steepest line.
2 2 2 2 2 When 2:22426 When 0:000 When 3:33936 When 6:6636630 yxx xy xy xy xy
106. 54 4 x yxyyxy
2 1 When 2: 42 xy
(b) 0 When 0:0 4 xy
(c) 3 When 3: 4 xy
63 When 6: 42 xy
117. 97 97 xx xx
If 90, x then 97216xxx 8, x which is extraneous.
If 90, x then 97, xx which is extraneous.
real solution.
If 360, then 6343100 5202,5
Solutions:2,5
Section 1.4 Functions
1. independent; dependent
2. difference quotient
3. A relation is any set of ordered pairs. A function is a relation in which no two ordered pairs have the same first component and different second components.
4. For () 45,=−gxx to find ()2, + gx substitute2 + x for x, and simplify: ()()2425 43. +=+− =+ gxx x
5. The domain of a piece-wise function must be explicitly described, so that it can determine which equation is used to evaluate the function.
6. The domain of 2 4 =− yx is determined by solving the inequality 2 40. −≥ x
7. Yes, the relationship is a function. Each domain value is matched with exactly one range value.
8. No, the relationship is not a function. The domain value of –1 is matched with two output values.
9. No, it does not represent a function. The input values of 10 and 7 are each matched with two output values.
10. Yes, the table does represent a function. Each input value is matched with exactly one output value.
Input, x −2 0 2 4 6
Output, y 1 1 1 1 1
11. (a) Each element of A is matched with exactly one element of B, so it does represent a function.
(b) Each element of A is matched with exactly one element of B, so it does represent a function.
(c) The element 2 in A is not matched with an element of B, so the relation does not represent a function.
12. (a) The element c in A is matched with two elements, 2 and 3 of B, so it is not a function.
(b) Each element of A is matched with exactly one element of B, so it does represent a function.
(c) This is not a function from A to B (it represents a function from B to A instead).
13. 22 2 44 += =±− xyyx
No, yisnot a function of x
14. 2299 −= =−xyyx
Yes, yis a function of x
15. 2 16 =− yx
Yes, yis a function of x.
16. 5 =+yx
Yes, yis a function of x.
17. 4 =− yx
Yes, yis a function of x.
18. ()44or4=− =−=−− yxyxyx
No, yisnot a function of x
19. 75or750 =−=−+ yyx
Yes, yis a function of x
20. 10 1 −= = x x
No, this isnot a function of x
21. () 2 435=−+gttt
(a) ()()() 2 242325166515 =−+=−+= g
(b) ()()() 2 14131543512 −=−−−+=++= g
(c) ()()() () 2 2 2 242325 444365 41315 +=+−++ =++−−+ =++ gttt ttt tt
22. () 3 4 3 π = Vrr
(a) () () () 3 44 33 332736 ===πππ V
(b) () () () 3 33279 44 232382 ===πππ V
(c) () () () 3 33 32 44 228333 ===πππ Vrrrr
23. () 3 =− fyy
(a) ()4341 =−= f
(b) ()0.2530.252.5 =−= f
(c) ()22 43432 =−=− fxxx
24. () 82=++fxx
(a) ()()88822 −=−++= f
(b) ()() 11825 =++= f
(c) ()()88822 −=−++=+ fxxx
25. () 2 1 9 = qx x
(a) () 2 11 0 099 ==− q
(b) () 2 1 3 39 = q is undefined.
(c) () () 2 2 11 3 6 39 +== + +− qy yyy
26. () 2 2 23 + = t qt t
(a) () () () 2 2 223 8311 2 44 2 + + === q
(b) () () () 2 2 203 0 0 + = q
Division by zero is undefined.
(c) () () () 2 2 2 2 23 23 −+ + −== xx qx xx
or
27. () = x fx x
(a) () 2 21 2 == f
(b) () 2 21 2 −==− f
(c) () 1,if 1 1 1 1 1,if 1 −< −== > xx fx xx
28. () 4 =+fxx
(a) ()2246 =+= f
(b) ()2246 −=−+= f
(c) ()22244 =+=+fxxx
29. () 21,0 22,0 +< = +≥ xx fx xx
(a) ()()12111 −=−+=− f
(b) ()() 02022 =+= f
(c) ()() 22226 =+= f
30. () 2 33,1 21,1 =−−<− +−≥− fxxx xxx
(a) ()()23233 −=−−−= f
(b) ()()() 2 112112 −=−+−−=− f
(c) ()()() 2 112112 =+−= f
31. () ()() ()() ()() ()() ()() 2 2 2 2 2 2 5 2251 1154 0055 1154 2251 =−+ −=−−+= −=−−+= =−+= =−+= =−+= fxx f f f f f x –2 1 0 1 2 ()fx 1 4 5 –4 1
32. () () () () () () 1 2 1 2 11 22 1 2 11 22 1 2 3 5531 443 3330 223 1131 =+ −=−+= −=−+= −=−+= −=−+= −=−+= htt h h h h h t –5 –4 –3 –2 –1 ()ht 1 1 2 0 1 2 1
33. () () 2 1 2 4,0 2,0 =−+≤ −> fxxx xx () () () () () () ()() ()() 2 2 1 2 9 11 222 1 2 2245 1144 0044 1121 2220 −=−−+= −=−−+== =−+= =−= =−= f f f f f
34. () 2 9,3 3,3 =−< −≥ fxxx xx ()() ()() ()() ()() ()() 2 2 1918 2925 3330 4431 5532 =−= =−= =−= =−= =−= f f f f f
35. 1530 315 5 −= = = x x x
36. () 3 2 46 460 46 =+ += =− =− fxx x x x x –2 –1 0 1 2 ()fx 5 9 2 4 1 0 x 1 2 3 4 5 ()fx 8 5 0 1 2
37. 34 0 5 340 4 3 = −= = x x x
38. () 2 2 2 12 8 12 0 8 12 1223 = = = =±=± fxx x x x
39. () 2 2 2 81 810 81 9 fxx x x x =− −= = =±
40. () ()() 2 2 616 6160 820 =−− −−= −+= fxxx xx xx 808 202 −= = += =− xx xx
41. () ()() 3 2 0 10 110 −= −= +−= xx xx xxx 0,1, or 1 ==−=xxx
42. () ()() ()() 32 32 2 2 33 330 1310 130 =−−+ −−+= −−−= −−= fxxxx xxx xxx xx 2 101 303 −= = −= =± xx xx
43. ()() ()() 2 2 2 20 210 = =+ −−= −+= fxgx xx xx xx 2010 21 −=+= ==− xx xx
44. ()() ()() 2 2 21519 3180 630 = ++=+ −−= −+= fxgx xxx xx xx 6030 63 −=+= == xx xx
45. ()() () ()() 422 42 22 2 22 40 40 220 = −= −= −= +−= fxgx xxx xx xx xxx 2 00 202 202 = = += =− −= = xx xx xx
46. ()() ()() 42 60 320 = −=− +−= +−= fxgx xx xx xx 30 3, which is a contradiction, since represents the principal square root. 2024 += =− −= = = xx x xxx
47. () 2 51=+−fxxx
Because ()fx is a polynomial, the domain is all real numbers x
48. () 2 12=− fxx
Because ()fx is a polynomial, the domain is all real numbers x
49. () 6 =+gyy
Domain: 60 6 +≥ ≥− y y
The domain is all real numbers y such that 6. ≥− y
50. () 3 4 =+ftt
Because ()ft is a cube root, the domain is all real numbers t
51. () 13 2 =− + gx xx
The domain is all real numbers x except 0,2.==−xx
52. () () 2 2 6 4 40 40 0 404 = −≠ −≠ ≠ −≠ ≠ hx xx xx xx x xx
The domain is all real numbers x except 0, 4. ==xx
53. () 1 4 = fss s
Domain: 101−≥ ≥ ss and 4 ≠ s
The domain consists of all real numbers s, such that 1 ≥ s and 4. ≠ s
54. () 2 10 + = fxx x 100 10 −> > x x
The domain is all real numbers x such that 10. > x
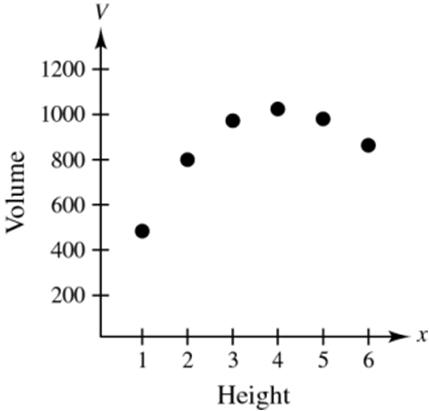
55. (a)
The volume is maximum when4 = x and 1024 = V cubic centimeters. (b)
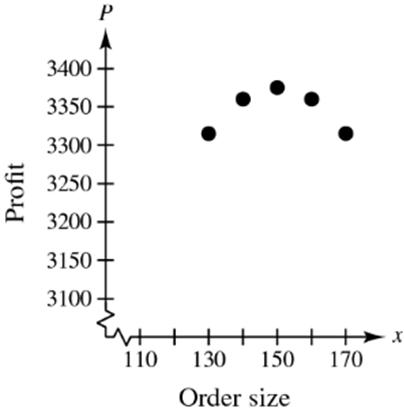
56. (a) The maximum profit is $3375. (b) Yes, P is a function of x (c) () ()() () () 2 2 ProfitRevenueCost pricenumbernumber cost per unitof unitsof units 901000.1560,100 900.151560 1050.1560 1050.1560 450.15,100 =−
57. () ()() 2 2 1 3 1 3 32 883824.67 meters yxx y =−++ =−++≈
(c) The dimensions that will maximize the volume of the package are181836. ×× From the graph, the maximum volume occurs when18. = x To find the dimension for y, use the equation 1084.=− yx () 10841084187236 =−=−−=yx Height,x Volume, V 1 484 2 800 3 972 4 1024 5 980 6 864
V is a function of x. (c) () 2 242=− Vxx
Domain: 012 << x
If the child holds a glove at a height of 1.5 meters, then the ball will be over the child’s head because it will be at a height of 4.67 meters.
58. (a) 2 =⋅⋅=⋅⋅= Vlwhxyxxy where 4108. +=xy So, 1084=− yx and () 22 3 10841084.=−=− Vxxxx
Domain: 027 << x (b)
59. 11 22 == Abhxy
Because ()() 0,,2,1, y and () ,0x all lie on the same line, the slopes between any pair are equal. 101
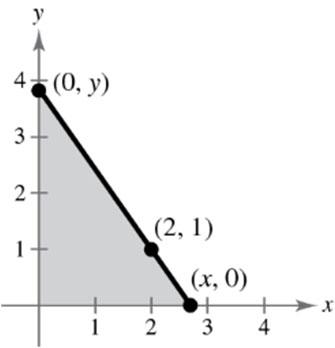
The domain of A includes x-values such that () 2 220. > xx By solving this inequality, the domain is 2. > x
62. () 2 2 4.01176.89586.7,712 14.9470.0,1217
60. ()22=⋅== Alwxyxy
But 2 36,=− yx so 2 236.=− Axx The domain is 06. << x
61. () 1.7658.3,1216 0.9071.5,1618
2012: 121.761258.379.42%
2013: 131.761358.381.18%
2014: 141.761458.382.94%
For 2012 through 2015, use the first equation. ()() ()() ()() ()()
2015: 151.761558.384.70% =+= =+= =+= =+= p p p p
2016: 160.901671.585.90%
2017: 170.901771.586.80%
For 2016 through 2019, use the second equation. ()() ()() ()()
2018: 180.901871.587.70% =+= =+= =+= p p p
74.011776.897586.7245.009$245,009
2008: 84.011876.898586.7228.284$228,284
2009: 94.011976.899586.7219.581$219,581
2010: 104.0111076.8910586.7218.900$218,900
2011: 114.0
For 2007 through 2011, use the first equation. ()()() ()()() ()()() ()()() () 2 2
2012: 1214.941270.0249.28$249,280
2013: 1314.941370.0264.22$264,220
2014: 1414.941470.0279.16$279,160
2015: 1514.941570.0294.1$294,100
2016: 1614.941670.0309.04$309,040
For 2012 through 2016, use the second equation. ()() ()() ()() ()() ()()
2017: 174.26317152.04171030.4322.273$322,273
2018: 184.26318152.04181030.4325.108$325,108
2019: 194.26319152.04191030.4319.417$319,417
For 2017 through 2019, use the third equation. ()()() ()()() ()()() 2 2 2
63. (a)
64. () 52 264910 Fyy =
(a)
The force, in tons, of the water against the dam increases with the depth of the water.
(b)It appears that approximately 7 meters of water would produce 1,000,000 metric tons of force.
(c)
65. (a) Costvariable costsfixed costs 12.30 98,000 =+ =+Cx
Revenueprice
(c)
67. (a) ()
(b) The revenue is maximum when 120 people take the trip.
66. (a) Model: ()()() Total costFixed costsVariable costs =+
Labels: Total cost Fixed cost6000
Variable costs0.95 = = = C x
(a)
Approximately 3.67 million more tax returns were made through e-file each year from 2011 to 2018.
(b)
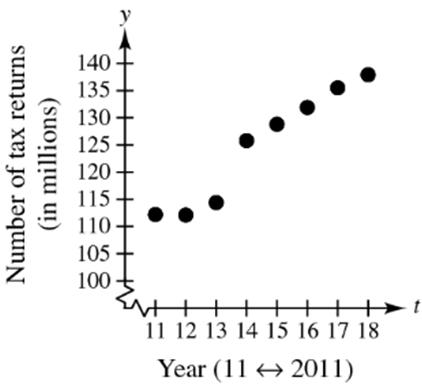
(c) () 3.6771.8,1118
Note that for 11,112.2.
Sampleanswer:Ntt tN =+≤≤ =≈
(d) t 11 12 13 14 15 16 17 18 N
(e) The algebraic model appears to be a good fit for the actual data.
(f) Using a graphing utility, 4.2064.0.Nt=+ The models are similar.
74.
76.
77. False. The equation 22 4 =+yx is a relation between x and y. However, 2 4 =±+yx does not represent a function.
78. True. A function is a relation by definition.
79. False. The range is [ ) 1,.−∞
80. True. The set represents a function. Each x-value is mapped to exactly one y-value.
81. By plotting the points, we have a parabola, so () 2 = gxcx Because () 4,32 is on the graph, you have () 2 324 2. −=− =− cc So, () 2 2. =− gxx
82. By plotting the data, you can see that they represent a line, or () = fxcx Because () 0,0 and () 1 4 1, are on the line, the slope is 1 4. So, () 1 4 . = fxx
83. Because the function is undefined at 0, we have () . = rxcx Because () 4,8 is on the graph, you have 8432.−=− = cc So, () 32. = rxx
84. By plotting the data, you can see that they represent () = hxcx Because 42−= and 11,−= and the corresponding y-values are 6 and 3, 3 = c and () 3. = hxx
85. The domain of () 1 =−fxx includes 1, = x 1 ≥ x and the domain of () 1 1 = gx x does not include 1 = x because you cannot divide by 0. The domain of () 1 1 = gx x is 1. > x So, the functions do not have the same domain.
86. (a) The height h is a function of t because for each value of t there is a corresponding value of h for 02.6. ≤≤ t
(b) Using the graph when 0.5,20=≈th meters and when 1.25,28=≈th meters.
(c) The domain of h is approximately 02.6. ≤≤ t
(d) No, the time t is not a function of the height h because some values of h correspond to more than one value of t.
87. No; x is the independent variable, f is the name of the function.
88. () () ()() 23 23 2323 1 8815 8 154 , 8 888 =+ =+= +−− ==≠ fxx f fxfxx x xxx
89. ()() ()() 32 2 2 330 330 310 3,1 xxx xxx xx x −−+= −−−= −−= =±
90. ()() ()() 32 2 2 2480 2420 240 2 xxx xxx xx x +−−= +−+= +−= =±
91. ()() 2 2 3 2 02715 27150 5230 5, =−−+ +−= +−= =− xx xx xx x
92. ()() 2 5 2 213200 4250 4, −+= −−= = xx xx x
104. () ()() 33 431 64283661 11312122 113113 −+ ==== +−
Section 1.5 Analyzin g Graphs of Functions
1. zeros
2. decreasing
3. average rate of change; secant
93. ()() -intercepts: 2, 0, 1, 0 x () -intercept: 0,2 y
94. ()() -intercepts: 1, 0, 3, 0 x () -intercept: 0, 3 y
95. () () () 3 2 -intercepts: 0, 0, , 0, 6, 0 x
96. x-intercepts: ()() 1,0,3,0±±
97. 2 3.612.86yxx=−+ Using () a graphing utility, the -intercepts are 1.17, 0 x and () 2.44, 0.
98. 321.275.49yxx=++ () Using a graphing utility, the -intercept is 2.30, 0. x
99. ()() 22 3414 1358 4 3122 +−+ ===
100. 3232 9427819 9455 == 101. 111 326 1 64212 == 102. 11 111 94 326 1 945530 −+ −+ === 103. 22 5 12 342512 512 31 5 43 +
===
4. odd
5. No. If a vertical line intersects the graph more than once, then it does not represent y as a function of x.
6. If ()() 22ff ≥ for all x in ()0,3, the () () 2,2 f is a relative maximum of f.
7. Domain: ( ] [ ] 2,2; Range:1,8
(a) ()11 f −=−
(b) ()00 f =
(c) ()11 f =−
(d) ()28 f =
8. [ )( ] Domain: 1,; Range: ,7−∞−∞
(a) ()14 f −=
(b) ()03 f =
(c) ()16 f =
(d) ()30 f =
9. Domain: ()() ,;Range:2, −∞∞−∞
(a) ()20 f =
(b) ()11 f =
(c) ()32 f =
(d) ()13 f −=
10. Domain: ()( ],;Range:–,1−∞∞∞
(a) ()23 f −=−
(b) ()10 f =
(c) ()01 f =
(d) ()23 f =−
11. A vertical line intersects the graph at most once, so yis a function of x
12. yisnot a function of x. Some vertical lines intersect the graph twice.
13. A vertical line intersects the graph more than once, so yisnot a function of x
14. A vertical line intersects the graph at most once, so yis a function of x
15. () ()() 2 2 2730 27300 2560 fxxx xx xx =−− −−= +−= 5 2 250or60 6 xx xx +=−= =−=
16. () ()() 2 2 32216 322160 3280 fxxx xx xx =+− +−=
()
21. () 1 2 21 210 21 21 =− −= = = = fxx x x x x 22. () 2 3 32 320 320 =+ += += −= fxx x x x
27. (a)
Zeros: 0,6 = x (b) () () 2 2 6 60 60 =− −= −= fxxx xx xx 00 606
fxx x x x
23. () 2 2 2 1 10 1 1,1 =− −= =
() ()() 2 2 2 21 210 210 110 1 =++ ++= ++= ++= =− fxxx xx xx xx x 25. () 2 2 3 26 3 0 26 30 3 + = + = += =− fxx x x x x x 26. () ()() 2 2 914 4 914 0 4 720 −+ = −+ = −−= fxxx x xx x xx 707 202 −= = −= = xx xx
(a)
Zeros: 0.5,7 =− x (b) () ()() 2 2 2137 21370 2170 =−− −−= +−= fxxx xx xx 1 2 210 707 += =− −= = xx xx
29. (a)
Zero: 5.5 =− x (b) () 11 2 211 2110 2110 =+ += += =− fxx x x x
30. (a)

Zero:26 = x (b) () 3148 31480 3148 31464 26 =−− −−= −= −= = fxx x x x x
31. (a)
Zero:0.3333 = x (b) () 31 6 31 0 6 310 1 3 = = −= = fxx x x x x x
32. (a)
Zeros: 2.1213 =± x (b) () 2 2 29 3 29 0 3 = = fxx x x x 2 32 2902.1213 2 −= =±=± xx
33. () 3 1 2 =− fxx
The function is decreasing on (),. −∞∞
34. () 2 4 =− fxxx
The function is decreasing on () ,2 −∞ and increasing on () 2,. ∞
35. () 2 1 =−fxx
The function is decreasing on () ,1−∞− and increasing on () 1,. ∞
36. () 3232=−+fxxx
The function is increasing on () ,0 −∞ and () 2, ∞ and decreasing on ()0,2.
37. () 11=++−fxxx
The function is increasing on () 1,. ∞
The function is constant on ()1,1.
The function is decreasing on (),1.−∞−
38. The function is decreasing on () 2,1 and () 1,0 and increasing on () ,2−∞− and () 0,. ∞
39. () 2 21,1 2,1 +≤− = −>− xx fx xx
The function is decreasing on () 1,0 and increasing on () ,1−∞− and () 0,. ∞
40. () 3,0 3,02 21,2 +≤ =<≤ +> xx fxx xx
The function is increasing on () ,0 −∞ and () 2,. ∞
The function is constant on ()0,2.
41. () 3 = fx
Constant on () , −∞∞ x –2 1 0 1 2 ()fx 3 3 3 3 3
42. () = gxx
Increasing on () , −∞∞
gx –2 –1 0 1 2
43. () 2 1 2 3 =−gxx
Decreasing on (),0. −∞
Increasing on () 0,. ∞
gx 1 5
44. () 3642=− fxxx
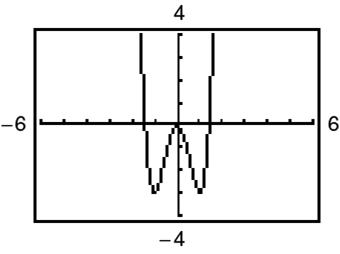
3 5
Increasing on ()() 1,0,1,;−∞ Decreasing on ()() ,1,0,1−∞−
–2 1 0 1 2 ()fx 24 –3 0 –3 24
45. () 1 =− fxx
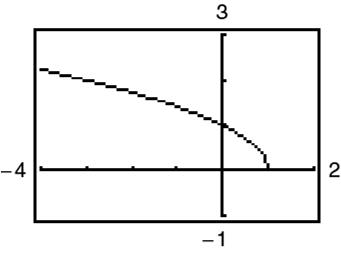
46. () 3 =+fxxx
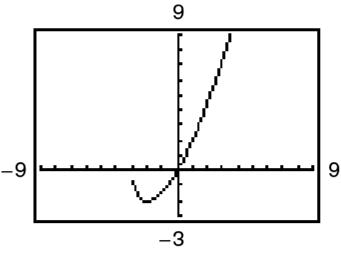
Increasing on ()2,;−∞ Decreasing on () 3,2
Relative minimum: () 1.5,2.25 x –2 1 0 1 2
Decreasing on () ,1−∞
–3 2 –1 0 1 ()fx 2 3 2 1 0 x –3 2 –1 0 1 ()fx 0 –2 –1.414 0 2 x 0 1 2 3 4 ()fx 0 1 2.8 5.2 8
47. () 32 = fxx

Increasing on () 0, ∞
48. () 23 = fxx
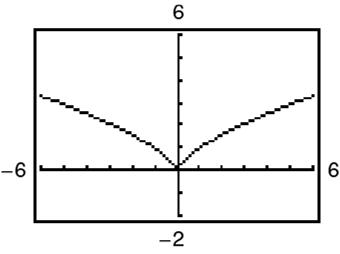
Decreasing on () –,0; ∞ Increasing on () 0, ∞
49. ()() 3 =+fxxx
50. () 2 32=−+−fxxx
Relative maximum: () 1.5,0.25
51. () 32615=−+hxxx
Relative minimum: () 4,17
Relative maximum: () 0,15
52. () 3231=−−+fxxxx
Relative maximum: () 0.15,1.08
Relative minimum: () 2.15,5.08
53. ()() 1 =− hxxx
Relative minimum: () 0.33,0.38
54. () 4 =− gxxx
55. () ()( ] 4 0 on ,4 =− ≥−∞ fxx fx
58. () 2 4 =− fxxx ()( ][ ) () 2 0 on ,0 and 4, 40 40 ≥−∞∞ −≥ −≥ fx xx xx ( ][ ) ,0,4, −∞∞ 4 6 3 2
Relative maximum: () 2.67,3.08
56. () 42=+fxx () ) 1 2 1 2 0 on , 420 42
≥−∞
57. () 2 9 =− fxx () [] 0 on 3,3≥− fx
59. () 1 =−fxx
() [ ) 0 on 1, 10 10 1 ≥∞ −≥ −≥ ≥ fx x x x [ ) 1, ∞
60. () 5 =+fxx
()fx is always greater than or equal to 0. () 0 ≥ fx for all x () , −∞∞
61. () 215=−+fxx
()() 30 915 2 303 ==− ff
The average rate of change from 1 0 = x to 2 3 = x is 2.
62. () 2 28=−+fxxx
()() 51 23716 4 5144 === ff
The average rate of change from 1 1 = x to 2 5 = x is 4.
63. () 32 3 =−− fxxxx
()() () ()2163 3 1 2133 === ff
The average rate of change from 1 1 =− x to 2 2 = x is 1.
64. () 32 6 =−++ fxxxx
()() 61 66 0 615 == ff
The average rate of change from 1 1 = x to 2 6 = x is 0.
65. 2 0.07290.52624.34,1318 =−+≤≤ yttt (a)
(b) ()() 1813 38.4929.82 1.73 18135 ≈≈ yy
The amount of U.S. federal government spent on applied research increased by about $1.73 billion each year from 2013 to 2018.
66. ()() ()() 21 21 Average rate of change 90 90 5400 90 60 feet per second. = = = = stst tt ss
As the time traveled increases, the distance increases rapidly, causing the average speed to increase with each time increment. From0 = t to 4, = t the average speed is less than from4 = t to9. = t Therefore, the overall average from0 = t to9 = t falls below the average found in part (b).
67. 002,19.6 ==sv
(a) 2 4.919.62stt=−++ (b)
(c) ()() 30 16.72 4.9 303 ss ==
(d) The slope of the secant line is positive.
(e) ()02,4.9sm==
Secant line: ()24.90 4.92 yt yt −=− =+ (f)
68. (a) 2 4.9223stt=−++ (b)
(c) The average rate of change from 0 = t to 4: = t ()() 40 12.639.6 2.4 meters 4044 ss === per second
(d) The slope of the secant line through () () 0,0 s and () () 4,4 s is positive.
(e) The equation of the secant line: 2.4,2.43myt==+
(f)
69. 0035,0vs==
(a) 2 4.935 stt =−+ (b)
(c) The average rate of change from 3 to 5: ==tt ()() 53 52.560.98.4 4.2 meters 5322 == −= ss per second
(d) The slope of the secant line through () () 3,3 s and () () 5, 5 s is negative.
(e) The equation of the secant line: 4.2 m =−
Using () () () 5, 55, 52.5 s = we have ()52.54.25 4.273.5. yt yt −=−− =−+
(f)
70. (a) 2 4.925st=−+ (b)
(c) The average rate of change from 1 = t to 2: = t ()() 21 5.420.114.7 14.7 meters 2111 ss ==−=− per second
(d) The slope of the secant line through () () 1,1 s and () () 2,2 s is negative.
(e) The equation of the secant line:14.7 m =−
Using () () () 1,11,20.1 s = we have () 20.114.71 14.734.8. yt yt −=−− =−+ (f)
71. () ()()() () 62 62 62 23 23 23 =−+ −=−−−+ =−+ = fxxx fxxx xx fx
The function is even. y-axis symmetry.
72. () ()()() () 3 3 3 5 5 5 =− −=−−− =−+ =− gxxx gxxx xx gx
The function is odd. Origin symmetry.
73. () ()() () () 5 5 5 =+ −=−−+ =−− ≠ ≠− hxxx hxxx xx hx hx
The function is neither odd nor even. No symmetry.
74. () ()() () 2 2 2 1 1 1 fxxx fxxx xx fx =− −=−−− =−− =−
The function is odd. Origin symmetry.
75. () () () () 32 32 4 4 fss s fs fs = =− ≠ ≠−
The function is neither odd nor even. No symmetry.
76. () ()() () 23 23 23 4 4 4 gss gss s gs = −=− = = The function is even. y-axis symmetry.
77.
The graph of () 9=− fx is symmetric to the y-axis, which implies ()fx is even. () () 9 fx fx −=− =
The function is even.
78. () 53 fxx =−
The graph displays no symmetry, which implies ()fx is neither odd nor even. ()() () () 53 53 −=−− =+ ≠ ≠− fxx x fx fx
The function is neither even nor odd.
79. () 5 fxx=−−
The graph displays no symmetry, which implies ()fx is neither odd nor even. ()() () () 5 5 =−−− =−−− ≠ ≠− fxx x fx fx
The function is neither even nor odd.
80. () 2 4 =−hxx
The graph displays y-axis symmetry, which implies ()hx is even.
()() () 2 2 44 −=−−=−= hxxxhx
The function is even.
81. () 3 4 fxx =
The graph displays origin symmetry, which implies ()fx is odd.
The function is odd.
82. () 3 4 fxx=−
The graph displays no symmetry, which implies ()fx is neither odd nor even.
86. rightleft 2 0 2 =− =− = L y y
87. (a)
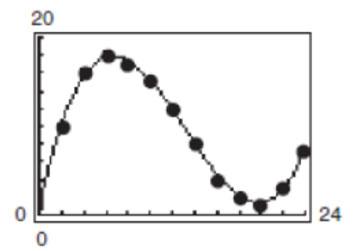
(b) The model is an excellent fit.
(c) The temperature was increasing from 6 A.M. until noon () 0 to 6. ==xx Then it decreases until 2 A M () 6 to 20. ==xx Then the temperature increases until 6 A M () 20 to 24. ==xx
(d) The maximum temperature according to the model is about 18.34°C. According to the data, it is 18°C. The minimum temperature according to the model is about 1°C. According to the data, it is 1°C.
(e) Answers may vary. Temperatures will depend upon the weather patterns, which usually change from day to day.
88.
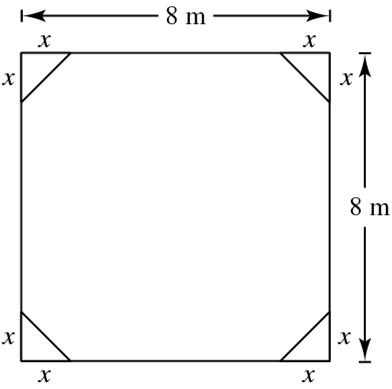
(a) ()() ()()() 2 1 2 884642 =−=− Axxx
Domain:04 ≤≤ x
(b)
The function is neither even nor odd.
Range:3264 ≤≤ A
(c) When 4, = x the resulting figure is a square. By the Pythagorean Theorem, 44222 3242 meters.
89. False. The function () 2 1 =+fxx has a domain of all real numbers.
90. False. An odd function is symmetric with respect to the origin, so its domain must include negative values.
91. The error is that ()33 2525. −−≠−− xx The correct process is as follows. () ()() () 3 3 3 3 25 25 25 25 =− −=−− =−− =−+ fxx fxx x x ()() −≠− fxfx and ()(), −≠ fxfx so the function () 3 25=−fxx is neither odd nor even.
92. (a) Domain: [ ) 4,5; Range: [] 0,9
(b) () 3,0
(c) Increasing: ()() 4,03,5;−∪ Decreasing: () 0,3
(d) Relative minimum: () 3,0 Relative maximum: () 0,9
(e) Neither
93. () 5 3 ,7
(a) If f is even, another point is () 5 3 ,7.
(b) If f is odd, another point is () 5 3 ,7.
94. () 2,2ac
(a) () 2,2ac
(b) () 2,2ac
95. (a) yx = (b) 2 yx = (c) 3 yx = (d) 4 yx = (e) 5 yx = (f) 6 yx =
All the graphs pass through the origin. The graphs of the odd powers of x are symmetric with respect to the origin and the graphs of the even powers are symmetric with respect to the y-axis. As the powers increase, the graphs become flatter in the interval11. x −<<
96.
() 24 is even. fxxx =− () 3 21 is neither. gxx=+ () 53 2 is odd. hxxxx =−+
() 68 2 is even. jxxx =−− () 5422 is neither. kxxxx=−+− () 953 3 is odd. pxxxxx =+−+
Equations of odd functions contain only odd powers of x. Equations of even functions contain only even powers of x. Odd functions have all variables raised to odd powers and even functions have all variables raised to even powers. A function that has variables raised to even and odd powers is neither odd nor even.
97. ()() 1, 3, 4, 0 () 30 Slope: 1 14 014 4 ==− −=−− =−+ m yx yx
98. ()() 2, 6, 4, 9 () () 5 2 5 2 5 2 69 155 Slope: 2462 62 56 1 m yx yx yx === −=−+ =−−+ =−+
101. () 53=−fxx
(a) ()()353315318 −=−−=−−=− f
(b) ()() 353315312 =−=−= f
(c) ()()35335153512 +=+−=+−=+ fxxxx
102. () 2 31=+−fxxx
(a) ()()() 2 223214613 −=−+−−=−−=− f
(b) ()() 2 443411612127 =+−=+−= f
99. ()() 5, 0, 5, 1 011 Slope: is undefined. 550 5 = = m x
100. ()() 6,1, 6,1 () () 11 Slope: 0 66 1 m y == =−
(c) ()()() 2 22 11311213313 −=−+−−=−++−−=+− fxxxxxxxx
103. () 23,1 4,1 +≤ = −+> xx fx xx
(a) ()() 02033 =+= f
(b) ()() 12135 =+= f
(c) ()2242 =−+= f
104. () 1 2 6,4 5,4 −−≤− = +>− xx fx xx
(a) () () 1 2 886462 −=−−−=−=− f
(b) () () 1 2 446264 −=−−−=−=− f
(c) ()0055 f =+=
105. VerbalModel: ()()() Sumfirst numbersecond number =+
Labels: Sum, first number, second number1===+ Snn
Equation: ()121=++=+Snnn
106. VerbalModel: ()()Productfirst numbersecond number =
Labels: Product, first number, second number1===+ Pnn
Equation: () 2 1 =+=+ Pnnnn
Section 1.6 A Librar y of Parent Functions
1. Greatest integer function
2. Identity function
3. Reciprocal function
4. Squaring function
5. Square root function
6. Constant function
7. Absolute value function
8. Cubic function
9. Linear function
10. linear 11.
14. (a) () () () () 3 1 52 3 1 52 , 49 ,, 4,9 ff== () () () () 1 2 3 5 17 1755 2 172172 5 9 4 m = ==⋅= () () () () 5 2 5 2 5 2 94 910 1 fxx fxx fxx −=− −=− =−
(b)
15. () 2.54.25fxx=−
16. () 5 2 63 fxx =−
17. () 2 3 gxx=+
18. () 2 21gxx=−−
19. () 3 1 fxx=−
20. ()()3 12 fxx=−+
21. () 4 fxx=+
22. () 23 hxx=++
23. () 1 2 fx x =
24. () 1 3 3 kx x =+ +
25. () 5 gxx=−
26. () 1 =−fxx
27. () fxx =
(a) ()2.12 = f
(b) ()2.92 = f
(c) ()3.14 f −=−
(d) () 7 2 3 = f
28. () 3 hxx=+
(a) () 211 h -==
(b) () 1 2 3.53 h ==
(c) () 4.27.27 h ==
(d) () 21.618.619 h -=-=-
29. () 21kxx=+
(a) () () 5 11 333211 k =+==
(b) ()() 2.122.113.14 k -=-+=-=-
(c) ()() 1.121.113.23 k =+==
(d) () () 7 22 333212 k =+==
30. () 746gxx=-++
(a) () () 11 88746 74674622 g 1 8 =-++ =-+=-+=
(b) () () 97946 7136713685 g =-++ =-+=-+=-
(c) () () 47446 7067066 g -=--++ =-+=-+=
(d) () () 33 22 1 2 746 75675629 g =-++ =-+=-+=-
() gxx =-
() 4 gxx =
() 1 gxx=-
() 3 gxx=-
35. () 1 2 6,4 4,4 +≤−
xx gx xx
= −>−
36. () 2 4,2 2,2 +≤ = +> xx fx xx
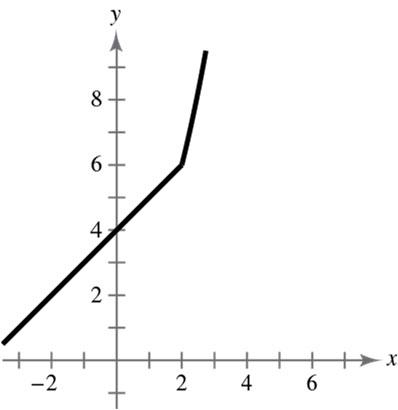
37. () () 2 11,2 2,2 −−≤
fxxx xx
+<
=
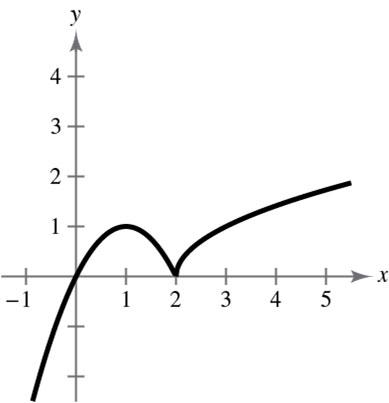
41. () () 11 44 2 sxxx =-
(a)
(b)Domain: (),;−∞∞ Range: [ )0,2
42. () ()2 11 22 4 kxxx =-
(a)
(b)Domain: (),;−∞∞ Range: [ )0,4
38. () 4,0 4,0
xx fx xx
39. () 2 2 4,2 3,20 1,0 −<−
+≥ xx hxxx xx
=+−≤<
43. (a) ()() ()() ()() ()() 301430420 401440560 45214540560665 50215040560770 == == =−+= =−+= W W W W
(b) () () 14, 036 2136504,36 =< ≤
−+> Whhh hh
(c) () () 16, 040 2440640,40 =< ≤ −+>
Whhh hh
44. (a) 0.53 Cx=+ 2.80
9) 2.80 = C )( 1532.800.=+ (0 Note that and C (b)
xx kxxx xx
40. () 2 2 21,1 21,11 1,1 +≤−
45. For the first two hours, the slope is 1. For the next six hours, the slope is 2. For the final hour, the slope is 1 2
1 2 ,02 22,28 10,89
To find () 22,ftt=− use 2 m = and ()2,2. () 22222ytyt −=− =−
To find () 1 2 10, ftt=+ use 1 2 m = and () 8,14. () 11 14822 10 ytyt −=− =+
Total accumulation14.5 centimeters =
46. () 2 fxx = () 3 fxx =
(a)Domain: () , −∞∞
Range: [ ) 0, ∞
(b) x-intercept: () 0,0 y-intercept: () 0,0
(c)Increasing: () 0, ∞
Decreasing: () ,0 −∞
(d)Even; the graph has y-axis symmetry.
(a)Domain: −∞ , ∞ ()
Range: −∞ , ∞ ()
(b) x-intercept: 0,0 () y-intercept: 0,0 ()
(c)Increasing: −∞ , ∞ ()
(d)Odd; the graph has origin symmetry.
47. False. A piecewise-defined function is a function that is defined by two or more equations over a specified domain. That domain may or may not include x- and y-intercepts.
48. False. The vertical line 2 x = has an x-intercept at the point () 2,0 but does not have a y-intercept. The horizontal line 3 y = has a y-intercept at the point () 0,3 but does not have an x-intercept.
49. According to the graph, the domains should be 3 x ≤ and 3. x >
50. When 4 3 , x = 4 3 2,= not –1. So, () 4 3 253. f =−+=
51. (a) Yes. The amount that you pay in sales tax will increase as the price of the item purchased increases.
(b)No. The length of time that you study the night before an exam does not necessarily determine your score on the exam.
52. (a) No. During the course of a year, for example, your
salary may remain constant while your savings account balance may vary. That is, there may be two or more outputs (savings account balances) for one input (salary).
(b)Yes. The greater the height from which the ball is dropped, the greater the speed with which the ball will strike the ground.
53. () ()() 2 2842fxxxxx =−−=−+
x-intercepts: ()() 4,0,2,0 y-intercept: () 0,8
54. () () () 2 2269693gxxxxxx =−+−=−−+=−−
x-intercept: () 3,0
y-intercept: () 0,9
55. () 2 82pxx=−−
x-intercepts: ()() 2,0,2,0
y-intercept: () 0,222
59. ()()
Answers will vary.
56. () 523gxx=−++
x-intercepts: () ()713 55,0,,0
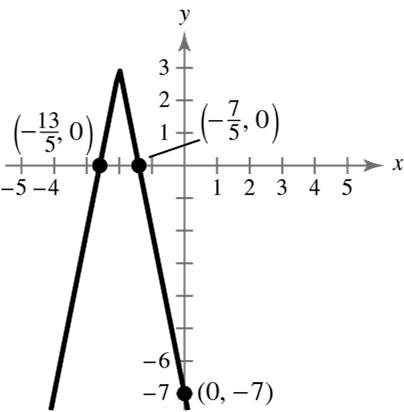
y-intercept: () 0,7
Answers will vary.
60. ()()()()()()
Answers
Section 1.7 Transformations of Functions
1. ()() ; fxfx
2. vertical stretch; vertical shrink
3. The three types of rigid transformations are horizontal shifts, vertical shifts, and reflections.
4. (a) iv
(b) ii
(c) iii
(d) i
5. (a) () fxxc =+ Vertical shifts
() 2: 2 cfxx=−=− 2 units down
() 1: 1 cfxx=−=− 1 unit down
() 1: 1 cfxx==+ 1 unit up
() 2: 2 cfxx==+ 2 units up
(b) () fxxc =− Horizontal shifts
()() 2: 22cfxxx =−=−−=+ 2 units left
()() 1: 11cfxxx =−=−−=+ 1 unit left
()() 1: 11cfxxx ==−=− 1 unit right
()() 2: 22cfxxx ==−=− 2 units right
6. (a) () fxxc =+ Vertical shifts
() 3: 3 cfxx=−=− 3 units down
() 2: 2 cfxx=−=− 2 units down
() 2: 2 cfxx==+ 2 units up
() 3: 3 cfxx==+ 3 units up
(b) () fxxc =− Horizontal shifts
()() 3: 33cfxxx =−=−−=+ 3 units left
()() 2: 22cfxxx =−=−−=+ 2 units left
() 2: 2 cfxx==− 2 units right
() 3: 3 cfxx==− 3 units right
7. (a) () fxxc =+
9. (a) ()yfx =−
Reflection in the y-axis
() 4 yfx=−−
() 4 yfx=+
Vertical shift 4 units
() 2 yfx =
Vertical stretch (each y-value upward is multiplied by 2)
() 3 yfx=−
Reflection in the x-axis and Vertical shift 3 units
() 1 yfx=−−
Reflection in the x-axis and a a horizontal shift 4 units to downward vertical shift 1 unit downward the right (g) () 2 yfx =
Horizontal shrink (each x-value is divided by 2)

10. (a) () 5 yfx=−
Horizontal shift 5 units
(b) () 3 yfx=−+
(c) () 1 3 yfx =
Reflection in the x-axis and a Vertical shrink to the right vertical shift 3 units upward () 1 3 each-valueismultipliedby y
(d) () 1 yfx=−+
(e) ()yfx =−
(f) () 10 yfx=−
Reflection in the x-axis and a Reflection in the y-axis Vertical shift 10 units downward horizontal shift 1 unit to the left
(g) () 1 3 yfx = (h) () 22yfx=−
Horizontal stretch
Vertical stretch by 2 and () each-valueismultipliedby3 x vertical shift 2 units downward
11. Parent function: () 2 fxx =
(a) Vertical shift 1 unit downward () 2 1 gxx=−
(b) Reflection in the x-axis, horizontal shift 1 unit to the left, and a vertical shift 1 unit upward ()() 2 11 gxx=−++
12. Parent function: () 3 fxx =
(a) Shifted upward 1 unit () 3 1 gxx=+
(b) Reflection in the x-axis, shifted to the left 3 units and down 1 unit
()()3 31 gxx=−+−
13. Parent function: () fxx =
(a) Reflection in the x-axis and a horizontal shift 3 units to the left () 3 gxx=−+
(b) Horizontal shift 2 units to the right and a vertical shift 4 units downward () 24 gxx=−−
14. Parent function: () fxx =
(a) A vertical shift 7 units downward and a horizontal shift 1 unit to the left () 17 gxx=+−
(d) Reflection in the x- and y-axis and shifted to the right 3 units and downward 4 units () 34 gxx=−−+−
15. Parent function: () 3 fxx =
Horizontal shift 2 units to the right ()3 2 yx=−
16. Parent function: yx =
Vertical shrink ( each y value is multiplied by ) 1 2 1 2 yx =
17. Parent function: () 2 fxx = Reflection in the x-axis 2 yx =−
18. Parent function: yx = Vertical shift 4 units upward
4 yx=+
19. Parent function: () fxx = Reflection in the x-axis and a vertical shift 1 unit upward 1 yx=−+
20. Parent function: yx = Horizontal shift 2 units to the left 2 yx=+
21. () 2 6 gxx=+
(a) Parent function: () 2 fxx =
(b) A vertical shift 6 units upward (c)
(d) ()() 6 gxfx=+
22. () 2 2 gxx=−
(a) Parent function: () 2 fxx =
(b) A vertical shift 2 units downward
(c)
(d) ()() 2 gxfx=−
23. ()()3 2 gxx=−−
(a) Parent function: () 3 fxx =
(b) Horizontal shift of 2 units to the right and a reflection in the x-axis
(c)
(d) ()() 2 gxfx=−−
24. ()()3 1 gxx=−+
(a) Parent function: () 3 fxx =
(b) Horizontal shift 1 unit to the left and a reflection in the x-axis
(c)
(d) ()() 1 gxfx=−+
25. ()() 2 31gxx=−−+
(a) Parent function: () 2 fxx =
(b) Reflection in the x-axis, a vertical shift 3 units downward and a horizontal shift 1 unit left (c)
(d) ()()13 gxfx=−+−
26. ()() 2 42gxx=−−
(a) Parent function: () 2 fxx =
(b) Reflection in the x-axis, a vertical shift 4 units upward and a horizontal shift 2 units right
(c)
(d) ()()24 gxfx=−−+
27. () 2 21gxx=−+
(a) Parent function: () 2 fxx =
(b) A vertical stretch, reflection in the x-axis and a vertical shift 1 unit upward (c)
(d) ()()21gxfx=−+
28. () 2 1 2 2 gxx=−
(a) Parent function: () 2 fxx =
(b) A vertical shrink and a vertical shift 2 units downward
(c)
(d) () () 1 2 2 gxfx=−
29. () 12 gxx=−+
(a) Parent function: () fxx =
(b) A horizontal shift 1 unit right and a vertical shift 2 units upward
(c)
(d) ()()12 gxfx=−+
30. () 32 gxx=+−
(a) Parent function: () fxx =
(b) A horizontal shift 3 units left and a vertical shift 2 units downward
(c)
(d) ()()32 gxfx=+−
31. () 2 gxx =
(a) Parent function: () fxx =
(b) A horizontal shrink (c)
(d) ()() 2 gxfx =
32. () 1 2 gxx =
(a) Parent function: () fxx =
(b) A horizontal stretch (c)
(d) () () 1 2 gxfx =
33. () 312gxx=−+
(a) Parent function: () fxx =
(b) A horizontal shift of 1 unit to the right, a vertical stretch, and a vertical shift 2 units upward
(c)
(d) ()()312gxfx=−+
34. () 213gxx=−+−
(a) Parent function: () fxx =
(b) A reflection in the x-axis, a vertical stretch, a horizontal shift 1 unit to the left, and a vertical shift 3 units downward
(c)
(d) ()()213gxfx=−+−
35. () 2 gxx =
(a) Parent function: () fxx =
(b) A vertical stretch (each y value is multiplied by 2)
(c)
(d) ()() 2 gxfx =
36. () 1 2 gxx =
(a) Parent function: () fxx =
(b) A vertical shrink ( each y value is multiplied by ) 1 2
(c)
(d) () () 1 2 gxfx =
37. () 9 gxx=−
(a) Parent function: () fxx =
(b) horizontal shift 9 units to the right (c)
(d) ()() 9 gxfx=−
38. () 31gxx=+
(a) Parent function: () fxx =
(b)Horizontal shrink () 1 3 each -value is multiplied by , x vertical shift of 1 unit upward (c)
(d) ()()31gxfx=+
39. () ()() 72 or 72 gxxgxx=−−=−−−
(a) Parent function: () fxx =
(b) Reflection in the y-axis, horizontal shift 7 units to the right, and a vertical shift 2 units downward (c)
(d) ()()72gxfx=−−
40. () 48 gxx=++
(a) Parent function: () fxx =
(b) Horizontal shift of 4 units to the left, vertical shift of 8 units upward
(c)
(d) ()()48 gxfx=++
41. () 21gxx=-
(a) Parent function: () fxx =
(b) A vertical shift of 1 unit downward and a vertical stretch (each y value is multiplied by 2)
(c)
(d) ()()21gxfx=−
42. () 1 gxx=-+
(a) Parent function: () fxx =
(b) Reflection in the x-axis and a vertical shift 1 unit upward
(c)
(d) ()() 1 gxfx=−+
43. () 3 gxx =-
(a) Parent function: () fxx =
(b) Reflection in the x-axis and a vertical shift 3 units upward (c)
(d) ()() 3 gxfx =−
44. () 25gxx=+
(a) Parent function: () fxx =
(b) Horizontal shift 5 units to the left, vertical stretch (each y-value is multiplied by 2)
(c)
(d) ()() 25gxfx=+
45. ()() 2 37 gxx=−−
46. ()() 2 29 gxx=−++
47. () 3 fxx = moved 13 units to the right ()()3 13 gxx=−
48. () 3 fxx = moved 6 units to the left, 6 units downward, and reflected in the y-axis (in that order) ()()3 66 gxx=−+−
49. () 12 gxx=−+
50. () 48 gxx=+−
51. () fxx = moved 6 units to the left and reflected in both the x- and y-axes () 6 gxx=−−+
52. () fxx = moved 9 units downward and reflected in both the x-axis and the y-axis () () 9 9 gxx x =−−− =−−+
53. () 2 fxx =
(a) Reflection in the x-axis and a vertical stretch (each y-value is multiplied by 3) () 2 3 gxx =−
(b) Vertical shift 3 units upward and a vertical stretch (each y-value is multiplied by 4) () 2 43gxx=+
54. () 3 fxx =
(a) Vertical shrink () 1 4 each -value is multiplied by y () 3 1 4 gxx =
(b) Reflection in the x-axis and a vertical stretch () each -value is multiplied by 2 y () 3 2 gxx =−
55. () fxx =
(a) Reflection in the x-axis and a vertical shrink () 1 2 each -value is multiplied by y () 1 2 gxx =−
(b) Vertical stretch (each y-value is multiplied by 3) and a vertical shift 3 units downward () 33gxx=−
56. () fxx =
(a) Vertical stretch (each y-value is multiplied by 8) () 8 gxx =
(b) Reflection in the x-axis and a vertical shrink () 1 4 each -value is multiplied by y () 1 4 gxx =−
57. Parent function: () 3 fxx = Vertical stretch (each y-value is multiplied by 2) () 3 2 gxx =
58. Parent function: () fxx = Vertical stretch (each y-value is multiplied by 6) () 6 g xx =
59. Parent function: () 2 fxx =
Reflection in the x-axis, vertical shrink () 1 2 each -value is multiplied by y
() 2 1 2 gxx =−
60. Parent function: yx = Horizontal stretch (each x-value is multiplied by 2) () 1 2 gxx =
61. Parent function: () fxx =
Reflection in the y-axis, vertical shrink () 1 2 each -value is multiplied by y
() 1 2 gxx =−
62. Parent function: () fxx =
Reflection in the x-axis, vertical shift of 2 units downward, vertical stretch (each y-value is multiplied by 2) () 22gxx=−−
63. Parent function: () 3 fxx =
Reflection in the x-axis, horizontal shift 2 units to the right and a vertical shift 2 units upward
()()3 22 gxx=−−+
64. Parent function: () fxx = Horizontal shift of 4 units to the left and a vertical shift of 2 units downward () 42 gxx=+−
65. Parent function: () fxx =
Reflection in the x-axis and a vertical shift 3 units downward
() 3 gxx=−−
66. Parent function: () 2 fxx =
Horizontal shift of 2 units to the right and a vertical shift of 4 units upward
()() 2 24 gxx=−+
67. (a) (b) () 3 3 3 33 0.00004636 0.00004636 1.61.6 0.00004636 4.096 0.00001131840.00001132 Hxx
xx =
The graph of 1.6 x H is a horizontal stretch of the graph of ()Hx
68. (a) The transformation consists of a vertical shrink by 0.0022, a left shift of 239.16 units, and a vertical shift downward of 17.8 units.
(b) ()() 195 128.82113.35 1.105. 19514 NN =≈
The number of households in the United States increased by an average of 1,105,000 each year from 2005 to 2019.
(c) ()() 2 150.002215239.1617.8124.3 N =+−≈
There were about 124.3 million households in 2015.
69. False. ()yfx =− is a reflection in the y-axis.
70. False. ()yfx =− is a reflection in the x-axis.
71. True. Because , xx =− the graphs of () 6 fxx=+ and () 6 fxx=−+ are identical.
72. False. The point () 2,61 lies on the transformation.
73. ()21 yfx=+−
Horizontal shift 2 units to the left and a vertical shift 1 unit downward ()()() ()()() ()()() 0,102,112,0 1,212,211,1 2,322,310,2 →−−=−
74. (a) Answers will vary. Sample answer: To graph () 2 341fxxx=−+ use the point-plotting method since it is not written in a form that is easily identified by a sequence of translations of the parent function 2 yx =
(b) Answers will vary. Sample answer: To graph ()() 2 216fxx=−− use the method of translating the parent function 2 yx = since it is written in a form such that a sequence of translations is easily identified.
75. Since the graph of ()gx is a horizontal shift one unit to the right of () 3 , fxx = the equation should be ()()3 1 gxx=− and not ()()3 1. gxx=+
76. (a) Increasing on the interval () 2,1 and decreasing on the intervals () ,2−∞− and () 1, ∞
(b) Increasing on the interval () 1,2 and decreasing on the intervals () ,1−∞− and () 2, ∞
(c) Increasing on the intervals () ,1−∞− and () 2, ∞ and decreasing on the interval () 1,2
(d) Increasing on the interval () 0,3 and decreasing on the intervals () ,0 −∞ and () 3, ∞
(e) Increasing on the intervals () ,1 −∞ and () 4, ∞ and decreasing on the interval () 1,4
77. No. () 4 2. gxx=−− Yes. ()() 4 3 hxx=−−
78. (a)
(b) The point () 65,83 represents an entrance exam score of 65.
(c) No. There are many variables that well affect the final exam score.
79. () ()22 21214 xxxxx +++−=+
80. () ()22 2 21212121 2 xxxxxx x +−+−=+−−+ =−+
81. () () 22 2 311311 322 xxxxxx xx +−−−=+−−+ =+−
82. () () 22 3113 xxxx +−+−=
83. () 232 33 xxxx −=−
84. () 22332 1 xxxxxx −=−=−+
85. ()()()()() 2 20.11720.1217 0.234 xxxxx xx −+=−+− =−−
86. () ()()()()33 88 2 9 4 2 9 4 65656 30 30 yyyyy yy yy −=− =− =−+
87. () () () 2 2 3535 35610 610235 15 , 23 xx xxx xxxx x x ++ +÷+== ++ =≠
88. () 2 2 2043 20432043,0 xx xxxxx x −÷==−≠ x y 22 53 29 74 35 57 40 66 44 79 48 90 53 76 58 93 65 83 76 99
Section 1.8 Combinations of Functions: Composite Functions
1. addition; subtraction; multiplication; division
2. composition
3. Since ()() () 2 21fgxxx=+ and () 2 1, fxx=+ () 2,gxx = and ()()()()()() 2.fgxgfxxfx ==
4. Since ()()()() fgxfgx = and ()() () 2 1, fgxfx=+ ()gx must equal 2 1. x +
5. 6.
x 0 1 2 3
f 2 3 1 2
g –1 0 1 2 0
fg + 1 3 3 2 2
x –2 0 1 2 4
f 2 0 1 2 4
g 4 2 1 0 2
fg + 6 2 2 2 6
7. ()() 2, 2 fxxgxx=+=−
(a) ()()()() ()() 22 2 fgxfxgx xx x +=+ =++− =
(b) ()()()() ()() 22 4 fgxfxgx xx −=− =+−− =
(c) ()()()() ()() 2 22 4 fgxfxgx xx x =⋅ =+− =−
(d) () () () 2 2 fx fx x xgxx + ==
Domain: all real numbers x except 2 x =
8. () () 25,2 fxxgxx =−=−
(a) ()() 2523fgxxxx +=−+−=−
(b) ()()() 252 252 37 fgxxx xx x −=−−− =−−+ =−
(c) ()()()() 2 2 252 42105 2910 fgxxx xxx xx =−− =−−+ =−+−
(d) () 25 2 fx x gx =
Domain: all real numbers x except 2 x =
9. ()() 2 ,45fxxgxx==−
(a) ()()()() () 2 2 45 45 fgxfxgx xx xx +=+ =+− =+−
(b) ()()()() () 2 2 45 45 fgxfxgx xx xx −=− =−− =−+
(c) ()()()() () 2 32 45 45 fgxfxgx xx xx =⋅ =− =−
=
(d) () () () 2 45 fx f x ggx x x
=
Domain: all real numbers x except 5 4 x =
10. ()() 2 31,16fxxgxx=+=−
(a) ()()()() 2 2 3116 315 fgxfxgx xx xx +=+ =++− =+−
(b) ()()()() () 2 2 3116 317 fgxfxgx xx xx −=− =+−− =−++
(c) ()()()() ()() 2 32 3116 34816 fgxfxgx xx xxx =⋅ =+− =+−−
+ ==
(d) () () () 2 31 16 fx fx x ggxx
Domain: all real numbers x, except 4 x ≠±
11. ()() 2 6,1 f xxgxx =+=−
(a) ()()()() 2 61 f gxfxgxx x +=+=++−
(b) ()()()() 2 61 f gxfxgxx x −=−=+−−
(c) ()()()() () 2 61 fgxfxgxxx =⋅=+−
+ ===
(d) () () () () 2 2 61 6 1 1 x x fx fx x ggxx x +−
Domain: 1 x <
14. () () 2 21 , 1 fxgx xx ==
(a) ()()
()()
(c) ()()
12. () () 2 4, 2 fxxgxx =−=+
(a) ()() 2 42fgxxx +=−++
(b) ()() 2 42fgxxx −=−−+
(c) ()() () 2 4222fgxxxxx =−+=+−
(d) () 2 4 2 2 fx xx g x ==−
+
Domain of 2 4: x All real numbers x such that 2 x ≤− and 2 x ≥
Domain of 2: x + All real numbers x such that 2 x ≥−
Domain of : f g All real numbers x such that 2 x ≥
13. () () 3 1, x f xgxx x == +
(a) ()() 43 3 11 x xxx fgxx xx ++ +=+= ++
(b) ()() 43 3 11 x xxx fgxx xx −=−= ++
(c) ()() 4 3 11 x x fgxx xx =⋅= ++
(d) () () 3 3 2 1 11 1 1 fxx xx g xxx xx =÷=⋅
++
= +
Domain: all real numbers x except 0 x = and 1 x =−
Domain: all real numbers x, 0, 1. x ≠±
15. ()()()() () () 2 222 2322 7 fgfg +=− =+−− =
16. ()()()() ()()() 2 111 1312 5 fgfg −=− =+−− =
17. ()()()() () () () () () 2 2 2 333 3332 3392 935 fgtftgt tt tt tt −=− =+−− =+−− =−++
18. ()()()() () () () () () 2 2 2 222 2322 1442 33 fgtftgt tt ttt tt +−=−+− =−++−− =++−+− =−+
19. ()()()() () () () () ()() 2 666 6362 934 306 fgfg = =+− = =
20. ()()()() () () () () ()() 2 666 6362 334 102 fgfg−=−− =−+−− =− =−
21. ()()() () () () () () 2 555 5352 8 23 fgfg = =+− =
22. ()()() () () () () () 2 000 0302 3 2 fgfg = =+− =−
or
23. ()() ()() 3 3 3, 10 3 10 x fxxgx x fgxx ==− +=−

For () 02,xfx≤≤ contributes most to the magnitude.
For () 6, xgx > contributes most to the magnitude.
24. () () ()() , 2 2 x fxgxx x fgxx == +=+
()gx contributes most to the magnitude of the sum for () 02.xfx≤≤ contributes most to the magnitude of the sum for 6. x >
25. () () () 32, 5 352 fxxgxx fgxxx =+=−+ +=−++

For () 02,xfx≤≤ contributes most to the magnitude. For () 6, xfx > contributes most to the magnitude.
26. () () ()() 22 2 1 2 3 2 ,31 2 fxxgxx fgxx =−=−− +=−−
For () 02,xgx≤≤ contributes most to the magnitude. For () 6, xgx > contributes most to the magnitude.
or
27. ()() 8, 3 fxxgxx=+=−
(a) ()()()() ()()3385fgxfgxfxxx ==−=−+=+
(b) ()()()() ()()8835gfxgfxgxxx ==+=+−=+
(c) ()()()() ()()3336ggxggxgxxx ==−=−−=−
28. ()() 4 3, f xxgxx ==
(a) ()()()() ()()444 33 f gxfgxfxxx ====
(b) ()()()() ()() 4 4 3381 g fxgfxgxxx ====
(c) ()()()() ()() 4 4416 g gxggxgxxx ====
29. () () 3 3 1, 1 fxxgxx=−=+
(a) ()()()()
30. ()() 3 1 , fxxgx x ==
(b) ()()()() () () () 3 3 3 1 11 11 gfxgfx gx x x x =
(a) ()()()() 3 3 111 fgxfgxf x xx
(b) ()()()() () 3 3 1 gfxgfxgx x ===
(c) ()()()() 1 g gxggxgx x
31. () 4 fxx=+ Domain: 4 x ≥−
() 2 g xx = Domain: all real numbers x
(a) ()()()() ()22 4 fgxfgxfxx===+
Domain: all real numbers x
(b) ()()()() () () 2 444 gfxgfx gxxx = =+=+=+
Domain: 4 x ≥−
(c) ()()()() () () 3 3 3 963 1 11 332 ggxggx gx x xxx = =+ =++ =+++
32. () 3 5 fxx=− Domain: all real numbers x () 3 1 gxx=+ Domain: all real numbers x
(a) ()()()() () 3 3 3 3 3 1 15 4 fgxfgx fx x x = =+ =+− =−
Domain: all real numbers x (b) ()()()() () () 3 3 3 5 51 514 gfxgfx gx x xx = =− =−+ =−+=−
Domain: all real numbers x
33. () f xx = Domain: all real numbers x () 6 gxx=+ Domain: all real numbers x
(a) ()()()() ()66fgxfgxfxx ==+=+
Domain: all real numbers x
(b) ()()()() () 6 gfxgfxgxx ===+
Domain: all real numbers x
34. () 4 fxx=− Domain: all real numbers x
() 3 gxx =− Domain: all real numbers x
(a) ()()()() ()() 3341fgxfgxfxxx ==−=−−=−−
Domain: all real numbers x
(b) ()()()() () () 43434gfxgfxgxxx ==−=−−=−−
Domain: all real numbers x
35. () 1 fx x = Domain: all real numbers x except 0 x =
() 3 gxx=+ Domain: all real numbers x
(a) ()()()() () 1 3 3 fgxfgxfx x ==+= +
Domain: all real numbers x except 3 x =−
(b) ()()()() 11 3 gfxgfxg xx
Domain: all real numbers x except 0 x =
36. () 2 3 1 fx x = Domain: all real numbers x except 1 x =± () 1 gxx=+ Domain: all real numbers x
(a) ()()()() () () 2 22 333 1 2112 11 fgxfgxfx xxxx x ==+=== ++−+ +−
Domain: all real numbers x except 0 x = and 2 x =−
(b) ()()()() 22 2222 33312 1 1111 xx gfxgfxg xxxx +−+
Domain: all real numbers x except 1 x =±
37. () () 1 2 , 4 fxxgxx==−
(a) (b)
38. ()() 2 3, fxxgxx =+=
(a) (b)
39. (a) ()()()()333213fgfg +=+=+=
===
(b) () () () 2 0 20 22 f f gg
40. (a) ()()()()111231fgfg−=−=−=−
(b) ()()()()444400fgfg=⋅=⋅=
41. (a) ()()()() () 2220fgfgf=== (b) ()()()() () 2204gfgfg===
42. (a) ()()()() () 1132fgfgf=== (b) ()()()() () 3322gfgfg===
43. () () 2 2 21hxx=+
One possibility: Let () 2 fxx = and () 21,gxx=+ then ()()() fgxhx =
44. ()()3 1 hxx =−
One possibility: Let () 1 gxx =− and () 3 , fxx = then ()()() fgxhx =
45. () 3 2 4 hxx=−
One possibility: Let () 3 fxx = and () 2 4, gxx=− then ()()() fgxhx =
46. () 9 hxx =−
One possibility: Let () 9 gxx =− and () , fxx = then ()()() fgxhx =
47. () 1 2 = + hx x
One possibility: Let () 1 = fxx and () 2, =+gxx then ()()() = fgxhx
48. () () 2 4 52 = + hx x
One possibility: Let () 52=+gxx and () 2 4 , = fx x then ()()() = fgxhx
49. () 2 2 3 4 −+ = x hx x
One possibility: Let () 3 4 + = + x fx x and () 2 , =− gxx then ()()(). = fgxhx
50. () 3 3 276 1027 + = xx hx x
One possibility: Let () 3 = gxx and () 3 276 , 1027 + = xx fx x then ()()() = fgxhx
51. () 2 1 1 = + hx x
One possibility: Let () = fxx and () 2 1 1, = + gx x then ()() 22 11 11 == ++ fgxf xx
52. () 2 2 4 16 = + x hx x
One possibility: Let () = fxx and () 2 2 4 , 16 = + x gx x then ()() 22 22 44 1616 == ++ xx fgxf xx
53. (a) ()()() 2 11 7127 TxRxBxxx =+=+ (b)
(c) (); Bx As x increases, ()Bx increases at a faster rate.
54. 2 14591.1,=−+ Ctt 3413.2=+ Rt (a) () () 2 2 3413.214591.1 1.112.2196 =−=+−−+ =−++ PRCttt tt
(b)

or
55. (a) () ()() () 100percent change =×= btdt ct pt
(b) () 20 c represents the percent change in the population due to births and deaths in the year 2020.
56. (a) ()()() =+ ptdtct
(b) () 16 p represents the number of dogs and cats in 2016.
(c) () () () ()() () + == ptdtct ht ntnt
()ht represents the number of dogs and cats per capita.
57. (a) () 2 = x rx
(b) () 2 π = A rr
(c) ()()()() 2 22 π
x x ArxArxA ()() A rx represents the area of the circular base of the tank on the square foundation with side length x
58. (a) () () () ()() () () 2 2 2 2 32 10322032600 1091246040600 9060600 303220,06 =+ =+−++
This represents the number of bacteria in the food as a function of time.
(b)Use 0.5. = t () () ()() () 2 0.53030.520.520652.5 =++= NT
After half an hour, there will be about 653 bacteria.
(c) () 2 2 2 3032201500 322050 32300 ++= ++= +−= tt tt tt By the Quadratic Formula, 3.513≈− t or 2.846.
Choosing the positive value for t, you have 2.846 ≈ t hours.
59. False. ()() 61fgxx=+ and ()() 66gfxx=+
60. True. ()() f gc is defined only when () g c is in the domain of f
61. (a) Answer not unique. Sample answer: () 3, fxx=+ () 2 gxx=+ ()()()() () ()()()() () 235 325 fgxfgxxx gfxgfxxx ==++=+ ==++=+
(b) Answer not unique. Sample answer: () 2 , f xx = () 3 g xx = ()()()() () ()()()() () 2 36 3 26 f gxfgxxx g fxgfxxx === ===
62. (a) () : f p matches 2 ; L For example, an original price of $15.00 p = corresponds to a sale price of $7.50. S = (b) () : g p matches 1;L For example an original price of $20.00 p = corresponds to a sale price of $15.00. S =
(c) ()() : g fp matches 4 ; L This function represents applying a 50% discount to the original price p, then subtracting a $5 discount.
(d) ()() f gp matches 3 ; L This function represents subtracting a $5 discount from the original price p, then applying a 50% discount.
63. Let () f x and () g x be two odd functions and define ()()(). hxfxgx = Then ()()() ()() ()() () because and are odd hxfxgx fxgxfg fxgx hx
= =
So, ()hx is even.
Let () f x and () g x be two even functions and define ()()(). hxfxgx = Then ()()() ()() () because and are even hxfxgx fxgxfg hx −=−− = = So, ()hx is even.
64. (a) () ()() 1 2 gxfxfx = +−
To determine if ()gx is even, show ()() gxgx −= () ()()() ()() ()()() 111 22 2 gxfxfxfxfxfxfxgx
() ()() 1 2 hxfxfx =
To determine if ()hx is odd show ()() hxhx −=− () ()()() ()() ()()() 111 22 2 hxfxfxfxfxfxfxhx
65. Let ()fx be an odd function, ()gx be an even function, and define ()()(). hxfxgx = Then ()()() ()() ()() () because is odd and is even . hxfxgx fxgxfg fxgx hx −=−−
So, h is odd and the product of an odd function and an even function is odd.
66. The expression () 3212 x ++ is found using ()() gfx instead of ()() fgx
So, ()()()2321 65. fgxx x =++ =+
67. 2 5 yx=−
() 2255 yxyx =−− =−− No y-axis symmetry
() 2 2 55yxyx−=− =− x-axis symmetry
()() 2 2 55yxyx−=−− =−− No origin
symmetry
68. 2517 xy+=
() 25172517 xyxy−+= −+= No y-axis
symmetry
() 25172517 xyxy +−= −= No x-axis symmetry
()() 25172517 xyxy−+−= −−= No origin symmetry
69. 2 1 yx=+
() 2 2 11yxyx =−+ =+ y-axis symmetry
2211yxyx−=+ =−− No x-axis symmetry
() 2 2 11yxyx−=−+ −=+
2 1 yx=−− No origin symmetry
70. 22 72 xy+=
() 2 222 72 72 xyxy−+= += y-axis
symmetry () 2 222 72 72 xyxy +−= += x-axis
symmetry
()() 22 22 72 72 xyxy −+−= += Origin symmetry
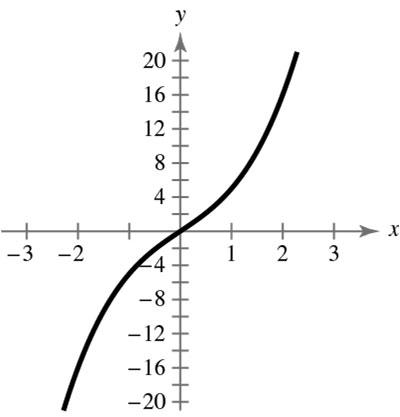
71. 5 yx = () 5 fxx =
()()() 55 fxxxfx −=−=−=− Odd function
72. 2 3 yx = () 2 3 fxx = ()()() 2 2 33 fxxxfx −=−== Even function
Section 1.9 Inverse Functions
1. inverse
2. 1 f
3. range; domain
4. yx =
5. To show that two function f and g are inverse functions, you must show that () () fgxx = and () () gfxx =
6. No. If both the point () 1,4 and () 2,4 lie on the graph of a function, then the function is not one-to-one; it would not pass the Horizontal Line Test.
7. If a function is one-to-one, no two x-values in the domain can correspond to the same y-value in the range. Therefore, a horizontal line can intersect the graph at most once.
10. () () () () () () () () () () 1 1 11 1 3 1 3 11 33 3 33 3 fxx fxx ffxfxxx ffxfxxx = = === === Section 1.9 Inverse Functions
8. Sample answer: () 2 fxx =
9. () () () () () () () 1 1 11 6 1 66 6 66 6 6 6 fxx x fxx xx ffxfx x ffxfxx = ==
13.
14.
15.
16. ()
17. ()()()()
18. () () () () () () () 3 2 28328 4 323 1 244 2 44 248 3 4 23 388 3 3 3 xx fgxf x xx x gfxgx x x x ++
19. () () () () () () 3 3 3 33 3 3 3 4 4 4 4 4 4 44 x fgxfx x x xx gfxg x x == = =
= =
20. ()()()() () () ()()()() () 3 33 33 333 55555 555 fgxfgxfxxxx gfxgfxgxxxx
23. ()() 5, 5 fxxgxx=−=+
(a) () () ()() () () ()() 555 555 fgxfxxx gfxgxx x =+=+−= =−=−+=
(b)
24. ()() 2, 2 x fxxgx==
(a) () () () () () 2 22 2 2 2 xx fgxfx x gfxgxx
25. ()() 1 71, 7 x fxxgx=+=
(a) () () () () () () 11 71 77 711 71 7 xx fgxfx x gfxgxx ==+= +− =+==
(b)
21. 22.
26. () () 3 34, 4 x fxxgx=−=
(a) () () () () () () () 33 34 44 33 334 4 34 44 xx fgxf xx x x gfxgx x
(b)
27. ()() 3 3 , fxxgxx ==
(a) () () () () () () ()() 3 33 33 3 fgxfxxx gfxgxxx === === (b)
28. () () 3 3 , 3 3 x fxgxx ==
(a) () () () () () () 3 3 3 33 3 3 3 3 3 3 33 3 33 x x fgxfxx xx gfxgxx ====
(b)
29. () () 2 5, 5,0fxxgxxx =+=−≥
(a) () () () () () () () () 2 2 2 5, 0 55 5 55 fgxfxx xx gfxgx xx =−≥ =−+= =+ =+−=
(b)
30. ()() 3 3 1,1 fxxgxx =−=−
(a) () () () () () () () ()() 3 33 33 3 3 3 111 11 111 fgxfxx xx gfxgxx xx =−=−− =−−= =−=−− ==
(b)
32. () () 323 , 21
33. No, ()()()()()() {} 2,1,1,0,2,1,1,2,2,3,6,4 does not represent a function. 2 and 1 are paired with two different values.
34. Yes, ()()()()()() {} 10,3,6,2,4,1,1,0,3,2,10,2 does represent a function.
x 3 5 7 9 11 13
()1 f x –1 0 1 2 3 4
36.
x 10 5 0 –5–10–15
() 1 f x –3–2–1 0 1 2
37. Yes, because no horizontal line crosses the graph of f at more than one point, f has an inverse.
38. No, because some horizontal lines intersect the graph of f twice, f does not have an inverse.
39. No, because some horizontal lines cross the graph of f twice, f does not have an inverse.
40. Yes, because no horizontal lines intersect the graph of f at more than one point, f has an inverse.
41. ()() 2 32 gxx=++
g does not pass the Horizontal Line Test, so g does not have an inverse.
42. () ()3 1 5 2 fxx=+
f does pass the Horizontal Line Test, so f does have an inverse.
43. () 2 9 fxxx =−
f does not pass the Horizontal Line Test, so f does not have an inverse.
44. () 4 hxxx=−−
h does not pass the Horizontal Line Test, so h does not have an inverse.
45. (a)
(b)
(c) The graph of 1 f is the reflection of the graph of f in the line yx =
(d) The domains and ranges of f and 1 f are all real numbers. 46. (a) ()
(b)
(c) The graph of 1 f is the reflection of f in the line yx =
(d) The domains and ranges of f and 1 f are all real numbers.
47. (a)
(b)
(c)The graph of 1 f is the same as the graph of f.
(d) The domains and ranges of f and 1 f are all real numbers x such that 02. x ≤≤
48. (a)
(b)
(c) The graph of 1 f is the reflection of f in the line yx =
(d) [ ) 2, −∞ is the range of f and domain of 1 . f
( ],0−∞ is the domain of f and the range of 1 . f
49. (a) () () 1 4 4 4 4 4 4 fx x y x x y xy y x fx x = = = = = = (b)
(c)The graph of 1 f is the same as the graph of f.
(d) The domains and ranges of f and 1 f are all real numbers except for 0.
50. (a) ()
(b)
(c)The graphs are the same.
(d) The domains and ranges of f and 1 f are all real numbers except for 0.
51. (a) ()
(c)The graph of 1 f is the reflection of graph of f in the line yx =
(d) The domain of f and the range of 1 f is all real numbers except 2.
The range of f and the domain of 1 f is all real numbers except 1.
(a)
(c)The graph of 1 f is the reflection of the graph of f in the line .yx =
(d) The domain of f and the range of 1 f is all real numbers except 5 3. x =−
The range of f and the domain of 1 f is all real
numbers x except 1 3 x =
53. (a) ()
(b)
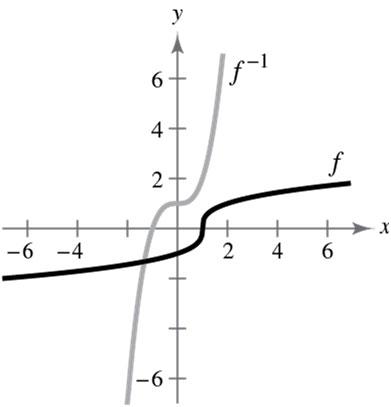
(c)The graph of 1 f is the reflection of the graph of f in the line yx =
(d) The domains and ranges of f and 1 f are all real numbers.
54. (a) ()
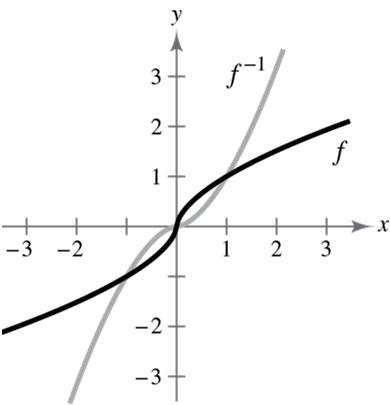
(c)The graph of 1 f is the reflection of the graph of f in the line yx =
(d) The domains and ranges of f and 1 f are all real numbers.
55. ()
56.
This does not represent y as a function of x f does not have an inverse.
This does not represent y as a function of x f does not have an inverse. 57. () 1 6 1 6 1 6 61 61 x gx x y y x xy yx + = + = + = =+ =−
This is a function of x, so g has an inverse. () 1 61gxx=−
58. () 35 35 35 53 5 3 fxx
Because 4 y =− for all x, the graph is a horizontal line and fails the Horizontal Line Test. p does not have an inverse.
60. () 0 0 fx y = =
Because 0 y = for all x, the graph is a horizontal line and fails the Horizontal Line Test. f does not have an inverse.
This is a function of x, so f has an inverse.
62. () 2 2 22,0 2,2,0 2,2,0 2,0,2 2,0,2 fxxxy yxxy xyyx xyxy xyxy =− ≥≥ =−≥≥ =−≥≥ =−≥≥ +=≥≥
This is a function of x, so f has an inverse.
() 12 2,0fxxx=+≥
63. () () () 64 45 64 45 64 45 4564 4564 4654 4654 54 46 54 64 x fx x x y x y x y xyy xyxy xyyx yxx x y x x x + = + + = + + = +
This is a function of x, so f has an inverse. () 1 54 64 x fx x =
64. The graph of f passes the Horizontal Line Test. So, you know f is one-to-one and has an inverse function.
() () ()() () 1 53 25 53 25 53 25 2553 2553 2553 2553 53 25 53 25 x fx x x y x y x y xyy xyxy xyyx yxx x y x x fx x = + = + = +
65. ()() () () 2 2 2 3,30 3,3,0 3,3,0 3,3,0 3,0,3 fxxxy yxxy xyyx xyyx yxxy =+≥− ≥ =+≥−≥ =+≥−≥ =+≥−≥ =−≥≥−
This is a function of x, so f has an inverse. () 1 3,0fxxx=−≥
66. () 2,20 2,2,0 2,2,0 fxxxy yxxy xyyx =−≤ ≥ =−≤≥ =−≤≥ 2or 2 2or 2 xyxy xyxy =−−=− += −=
The portion that satisfies the conditions 2 y ≤ and 0 x ≥ is 2. xy−= This is a function of x, so f has an inverse. () 1 2,0fxxx=−≥
67. () 3,0 6,0 xx fx xx +< = −≥
This graph fails the Horizontal Line Test, so f does not have an inverse.
68. () 2 ,0 3,0 xx fx xxx −≤ = −>
The graph fails the Horizontal Line Test, so f does not have an inverse.
2022 Cengage Learning. All Rights
May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.
69.
So, () 1 10 0.75 x fx = hourly wage,number of units produced xy==
(b) 24.2510 19 0.75 y ==
So, 19 units are produced.
70. (a)
Thus, 091.20. x
In Exercises 71–74, () () –1 =+4,=–4,fxxfxx () () –1 +5 =2–5,=. 2 x gxxgx
71. ()()() () () () 1111 1 4 45 2 1 2 gfxgfx gx x x = =− −+ = + =
72. ()()()() 1111
fgxfgx
73. ()()()() () () 25 254 21 fgxfgx fx x x = =− =−+ =− ()() 1 1 2 x fgx + =
Note: Comparing Exercises 71 and 73, ()() ()() 1 11 fgxgfx =
74. ()()()() () () ()() 1 4 245 285 23 23 23 32 3 2 3 2 gfxgfx gx x x x yx xy xy x y x gfx = =+ =+− =+− =+ =+ =+ −= = =
In Exercises 75–80, () ()() –1 1 =–3,=8+3, 8 fxxfxx ()() 3 3–1 =,=. gxxgxx
75. ()()()() () () 1111 3 1 3 11 1 81332 fgfg f = = =+=
76. ()()() () () () () 1111 1 3 1 33 833 000 gfgf g g −=− =−+ ===
81. False. () 2 fxx = is even and does not have an inverse.
82. True. If ()fx has an inverse and it has a y-intercept at ()0,, b then the point (),0, b must be a point on the graph of () 1 . fx
83. (a)
(b)
x –4–2 0 3 f 3 4 0 –1
The graph does not pass the Horizontal Line Test, so () 1 fx does not exist.
84. (a) ()Cx is represented by graph m and () 1 Cx is represented by graph n.
(b) ()Cx represents the cost of making x units of personalized T-shirts. () 1 Cx represents the number of personalized T-shirts that can be made for a given cost.
85. Let ()()fgxy = Then ()() 1 . xfgy = Also, ()()()() ()() () () ()() 1 11 11 fgxyfgxy gxfy xgfy xgfy = = = = =
Because f and g are both one-to-one functions, () 1 11fggf =
86. Let ()fx be a one-to-one odd function. Then () 1 fx exists and ()() fxfx −=− Letting () , xy be any point on the graph of ()() , fxxy is also on the graph of ()fx and ()() 11 fyxfy −=−=− So, () 1 fx is also an odd function.
87.
There is an inverse function () 1 1 fxx=− because the domain of f is equal to the range of 1 f and the range of f is equal to the domain of 1 f 88. ()fx and () 1 fx are inverses of each other.
x 10 0 7 45
() () 1 f fx –10 0 7 45
() () 1 f fx –10 0 7 45
89. () () () ()() 2 2 2 51 10251 1024 64 yx xx xx xx =−−+ =−−++
Alternate solution: () ()() ()() ()() 2 15 1515 64 64 yx xx xx xx
90. () () () ()() 2 2 2 3412 381612 3812 362 yx xx xx xx =−−
91. ()() ()() 2 2 1325 24 2513 42 513513 2222 49 49 yx x xx xx xx
92. () 2 2 2 2 1363 3 416 11363 3 21616 1120 3 216 115 3 22 5 33 2 yx xx xx xx xx
93. The function is increasing on () 2, ∞ and decreasing on (),2.
94. The function is increasing on () ,2−∞− and decreasing on () 2,.−∞
95. The function is increasing on () ,1−∞− and () 1, ∞ and decreasing on ()1,1.
96. The function is increasing on () 2,1 and () 0, ∞ and decreasing on () ,2−∞− and ()1,0.
97. Relative maximum at () 2,0 Relative minimum at () 0,3
98. Relative minimum at () 1 4 2, No relative maxima
Section 1.10 Mathematic al Modeling and Variation
1. sum of squared differences
2. least squares regression
3. correlation coefficient
4. directly proportional
5. You can say that z varies jointly as x and y, or z is jointly proportional to x and y
6. (a) 4 inverse variation x y =
(b) 12joint variation zxy = (c) 3.5direct variation yx =
(d) 6 combined variation x z y =
7. (a) Model: 1.23151.8, 19ytt =+≤≤
(b) The model is a good fit for the data.
8. (a) Model: 0.4263.42, 29ytt =+≤≤
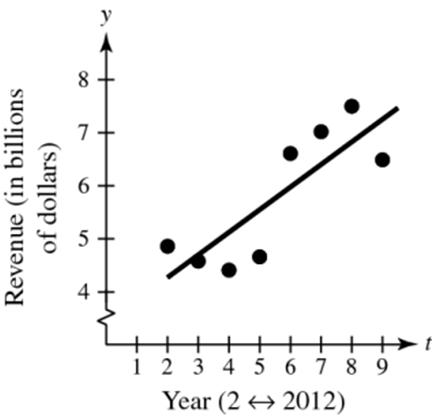
(b) The model is not a good fit for the data.
Sample answer: A cubic model may be a better fit for the data.
9.
Using the point () 0,3 and ()4,4, 1 4 3. yx=+ 10.
The line appears to pass through () 2,5.5 and () 6,0.5, so its equation is 5 4 8. yx=−+
Using the points () 2,2 and ()4,1, 1 2 3. yx=−+
The line appears to pass through () 0,2 and () 3,3 so its equation is 1 3 2. yx=+
The line appears to pass through ()() 2,3 and 4,2 so its equation is 1 2 4. yx=−+
The line appears to pass through ()() 2,3 and 4,4, so its equation is 1 2 2. yx=+
15. (a) and (b)
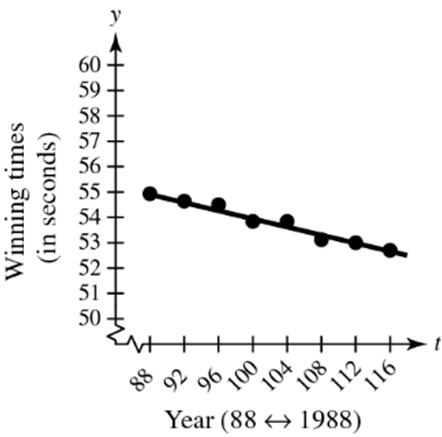
Use the points (88, 54.93) and (116, 52.70).
52.7054.93 0.080 11688
52.700.080116
52.700.0809.28 0.08061.98
(c) 0.08362.30yt=−+
(d)The models are similar.
16. (a) and (c)
The model fits the data well. (b) 1.6632.9yt=+
(c) () F3 or2 209 25, r l 25; 1.6625. 74.4 million toui e sts t ty==+
(d)The slope indicates that each year the number of tourists that visited New York City increased by about 1.66 million.
==
2,1kn== 28. 5,1kn==

25. 1 2 k =
26. 1 4 ,3kn
27.
31. 1 5 5 5 k y x k k y x = = = =
This equation checks with the other points given in the table.
32. 2 5 2 5 25 ykx k k yx = = = =
This equation checks with the other points given in the table.
45. y is directly proportional to the square of x 46. t is inversely proportional to r
47. 1 2 A bh =
The area of a triangle is jointly proportional to its base and height.
48. K is jointly proportional to m and the square of v. 49. ()543 18 18 ykx k k yx = = = =
This equation checks with the other points given in the table.
34. 24 5 120 120 k y x k k y x = = = =
This equation checks with the other points given in the table.
35. 2 A kr =
36. 3 Vkl =
37. 2 k y x =
38. k h s = 39. 2 kg F r = 40. 23zkxy =
57. ()113.753250 0.035 0.035 IkP k k IP = = = =
58. ()31.252500 0.0125 0.0125 IkP k k IP = = = = 59. () 33 13 33 13 3313 ykx k k yx = = = = When 10 x = inches, 25.4 y ≈ centimeters. When 20 x = inches, 50.8 y ≈ centimeters.
63. () 4.81000.048 0.048 dkF kk dF = = = = When the distance compressed is 7 centimeters, we have 70.048 145.83. F F = ≈ No child over 145.83 newtons should use the toy.
65. (a)
(b) The data shows an inverse variation model fits.
69. 0 0 0 T fk lp = where 000 original frequency, original tension, original length of string, and mass density fTlp ====
0 100 f =
(a) The frequency of a string with four times the tension would double the frequency in order to maintain the direct proportion.
Let new new new kT f lp = and new0new0 4, TTll ==
00 new0 00 4 222100200 kTkT f fHz lplp ==⋅=⋅=⋅=
(b) The frequency of a string with two times the length would half the frequency in order to maintain the inverse proportion.
Let new new new kT f lp = and new0new0 2, T llT ==
00 new0 00 111 10050 222 2 kTkT f fHz lplp ==⋅==⋅=
(c) The frequency of a string with four times the tension would double the frequency, and two times the length would half the frequency in order to maintain the inverse proportion. Therefore the frequency would remain the same,
Let new new new kT f lp = and new0new0 4, 2 TTll ==
00 new0 00 42 2 1100100 2 22 kTkT f fHz lplp ====⋅=
70. 2 00 00 0 Load kwd L l == where 0000 original load, width of beam, depth of beam and length of beam Lwdl ====
(a) () () 2 2 0000 0 00 2 Load22 kwdkwd L ll ==⋅=⋅ (b) () () 22 0000 0 00 2 Load44 kwdkwd L ll ==⋅=⋅
The safe load doubles.
(c) () () 22 0000 0 0 0 1 2 Load22 kwdkwd L l l ==⋅=⋅
The safe load doubles.
The safe load is four times as great.
(d) () () () () () () 2 22 11 00 0000 22 0 2 000 1 11 Load 244 kwd kwdkwd L lll ==⋅=⋅=⋅
The safe load is one-fourth as great.
71. True. If 1 ykx = and 2 , x kz = then ()() 1212 y kkzkkz==
72. False. If 1k y x = and 2 , k x z = then 11 2 2 , k z kk y z k == which means y is directly proportional to z.
73. False. In the equation 2 4,Srππ = is a constant, not a variable.
74. (a) The data shown could be represented by a linear model which would be a good approximation.
(b) The points do not follow a linear pattern. A linear model would be a poor approximation. A quadratic model would be better.
(c) The points do not follow a linear pattern. A linear model would be a poor approximation.
(d) The data shown could be represented by a linear model which would be a good approximation.
75. ()()() True. If 2 , f xxpx =− then ()()() 222 20. fp=−=
76. False. For example, the graph of () 3 fxx =− rises to the left, but the leading coefficient is 1.
77. 1212 545454 1 54 1 45 xxxx xxx x x x x −= = + =
78. 3838 222 11 2 xxxx xxx x −+−++ += +++ = +
79. ()() ()() ()() 2 5321 52 1313 2315 13 xxx x xxxx xx xx ++− += −+−+ ++ = −+
80. () ()() ()() 2 2 326 36 2422 3 22 xxx xx xxxx x xx +− −= −−−+ = −+
Review Exercises for Chapter 1
1. 2. 3. 0 x > and 2 y =− in Quadrant IV.
4. 4 xy = means x and y have the same signs. This occurs in Quadrants I and III.
81. () () 344 ,3 2133321 x x xxx + ⋅=≠− +++
82. ()() () 22 2 21 11112 ,0,1 21 xxxx xxxxx x x x + ÷=⋅ −++− =≠−
83. 33 88 is a function of.xyyxx += =−
Domain: all real numbers x
84. is not a function of.xyx =
For example, for 1, 1. xy==±
85. 2 1 is not a function of.yxx−=
For example, for 0, 1. xy==±
86. 33 is a function of.xyyxx = =
Domain: all real numbers except 0 xx =
87. 5 is a function of.yxx =+
Domain: all real numbers such that 5 xx ≥−
88. 22 8232 is not a function of.xyx +=
For example, for 0, 4. xy==±
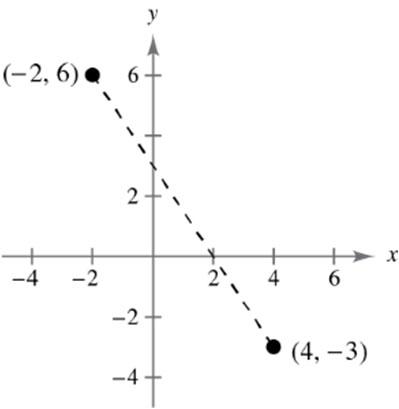
5. (a) (b) ()() 246322 3681117313 d =−−++ =+==
(c) Midpoint: 24633 , 1, 222 −+− =
6. ()() ()() ()() ()() 44, 880, 0 64, 882, 0 44, 380,5 64, 382,5 −−= −−= −−=− −−=−
7. 35yx=−
10. 2 29yxx=−−
8. 1 2 2 yx=−+
9. 2 3 yxx =−
2 -intercept: 034 94 5 0,5 yy y y =−− =− = x –2 1 0 1 2 y –11 –8 –5 –2 1 x –4 2 0 2 4
–2 –1 0 1 2 3
1 –6 –9 –8 –3 6
11. 27yx=+ () 7 2 7 2 -intercept: Let 0. 027 ,0 xy x x = =+ =−
-intercept: Let 0. 207 7 0,7 yx y y = =+ =
12. x-intercept: Let 0. y = 13 013 yx x =+− =+−
For 10,013,or2. xxx +>=+−=
For () 10,013,or4. +<=−+−−= xxx
()() 2,0,4,0 y-intercept: Let 0. x = 13 013or2 yx yy =+− =+−=− () 0,2 13. () 2 34 yx=−−
22 -intercepts: 03434
x
14. 2 4 yxx =− ()()() 2 2 2 -intercepts: 04 040 40 2 0,0,2,0,2,0 xxx xx x x =− =−= −= =± () -intercept: 0400 0,0 yy =⋅−=
15. 41yx=−+
Intercepts: () () 1 4 ,0,0,1 () 4141No -axis symmetry yxyxy =−−+ =+
4141No -axis symmetry yxyxx−=−+ =− () 4141No origin symmetry yxyx−=−−+ =−−
16. 37yx=− x-intercept: () 7 3 7 3 037 73 , 0 x x x =− = = () () -intercept: 307 7 0,7 yy y =− =−
() 3737No -axis symmetry yxyxy =−− =−− () 3737No -axis symmetry yxyxx−=− =−+ () 3737No origin symmetry yxyx−=−− =+
17. 2 6 yx =−
Intercepts: () ()6,0,0,6 ± () () 22 22 2 2 66-axis symmetry
66 No -axis symmetry
66 No origin symmetry yxyxy yxyxx yxyx
18. 2 12 yx=−
Intercepts: () ()23,0,0,12±− () 2 2 1212-axis symmetry yxyxy =−− =−
221212No -axis symmetry yxyxx−=− =−+ () 2 2 1212 No origin symmetry yxyx−=−− =−+
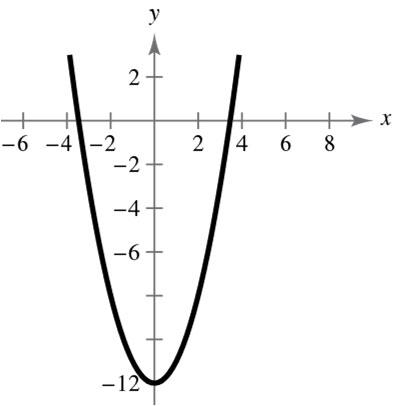
19. 3 5 =+yx
Intercepts: () () 3 5,0,0,5
()3 3 55No -axis symmetry =−+ =−+ yxyxy
−=+ =−− yxyxx
3355No -axis symmetry
−=−+ =− yxyx
()3 3 55 No origin symmetry
20. 3 6 =−− yx
Intercepts: () () 3 6,0,0,6
()3 66 No -axis symmetry =−−− =−+ yxyxy
−=−− =+ yxyxx
33 66No -axis symmetry
−=−−− =− yxyx
()3 3 66No origin symmetry
21. 5 =+yx
Domain: [ ) 5, −∞
Intercepts: () ()5,0,0,5
5No -axis symmetry =−+ yxy
55No -axis symmetry −=+ =−+ yxyxx
−=−+ =−−+ yxyx
22. 9 yx=+
Intercept: () 0,9
55No origin symmetry
99-axis symmetry yxyxy =−+ =+
−=+ =−−
99No -axis symmetry yxyxx
99No origin symmetry yxyx−=−+ =−−
23. 22 9 xy+=
Center: () 0,0
Radius: 3
24. 22 4 xy+=
Center: () 0,0
Radius: 2
25. () () () () 2 2 2 2 2 216 204 xy xy ++= −−+−=
Center: () 2,0
Radius: 4
26. () 2 2 881 xy+−=
Center: () 0,8
Radius: 9
27. Endpoints of a diameter: ()() 0,0and4,6
Center: () () 06 04 ,2,3 22 +− + =−
Radius: ()() 22 20304913 r =−+−−=+=
Standard form: ()() () () ()() 2 2 2 22 2313 2313 xy xy −+−−= −++=
28. 5 4 ,020Fxx=≤≤ (a) (b) (c) When 50 4 10,12.5newtons.xF===
29. 1 2 1 yx=−+
Slope: 1 2 m =− y-intercept: () 0,1
30. 2 3 236 326 2 xy yx yx −= −=−+ =−
Slope: 2 3 m = y-intercept: () 0,2
31. 1 y =
Slope: 0 m = y-intercept: () 0,1
Slope is undefined. y-intercept: none x 0 4 8 12 16 20 F 0 5 10 15 20 25
32. 6 x =−
33. ()() () 5,2, 1,4 42 6 1 156 m ===−
34. ()() () 1,6, 3,2 268 2 314 m ===−
35. () 1 3 6,5, m −= () () 1 3 1 3 1 3 56 52 7 yx yx yx −−=− +=− =−
36. () 3 4 4,2, m −−=− () () () () 3 4 3 4 3 4 3 4 24 24 23 5 yx yx yx yx −−=−−− +=−+ +=−− =−−
37. ()() 6,4, 4,9 () () () () 9451 46102 1 46 2 1 46 2 1 43 2 1 7 2 m yx yx yx yx === −=−− −=+ −=+ =+
38. ()() 9,3, 3,5 () () 53 21 3963 m ===− () () () () 1 39 3 1 39 3 1 33 3 1 6 3 yx yx yx yx −−=−−− +=−+ +=−− =−−
39. Point: () 3,2 5 4 548 2 −= =− xy yx
(a) Parallel slope: 5 4 = m () () 5 4 515 44 523 44 23 2 −−=− +=− =− yx yx yx
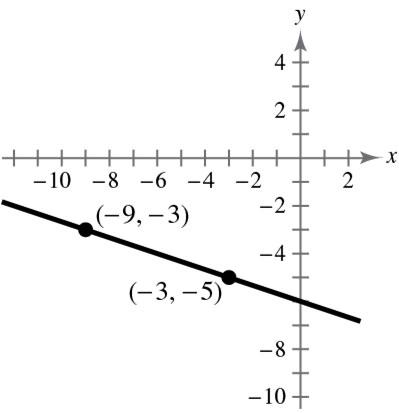
(b) Perpendicular slope: 4 5 =− m () () 12 5 2 5 4 5 4 5 4 5 23 2 −−=−− +=−+ =−+ yx yx yx
40. Point: ()8,3, 235−+= xy 5 2 33 352 =− =− yx yx
(a) Parallel slope: 2 3 =− m () 7 3 2 3 2 3 38 39216 327 −=−+ −=−− =−− =−− yx yx yx yx
(b) Perpendicular slope: 3 2 = m () 3 2 3 2 38 26324 2330 15 −=+ −=+ =+ =+ yx yx yx yx
2022 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.
41. Verbal Model: ()() Sale priceList priceDiscount=−
Labels: Sale price List price
Discount20% of 0.2 = = == S L LL
Equation: 0.2 0.8 =− = SLL SL
42. Verbal Model: ()()() Amount earnedstarting feeper page ratenumber of pages =+⋅
Labels: Hourly wage
Starting fee50
Per page rate2.50
Number of pages = = = = A p
Equation: 2.550=+Ap
43. 4 4 4 160 16 2 xy yx yx −= = =±
No, y is not a function of x. Some x-values correspond to two y-values.
44. 230 23 xy xy −−= −=
Yes, the equation represents y as a function of x
45. 1 yx =−
Yes, the equation represents y as a function of x. Each x-value, 1, x ≤ corresponds to only one y-value.
46. 2 yx=+ corresponds to 2 yx=+ or 2. yx −=+
No, y is not a function of x. Some x-values correspond to two y-values.
47. () 2 1 fxx=+
(a) ()() 2 2215 f =+=
(b) ()() 2 44117 f −=−+=
(c) ()() 2 22411fttt=+=+
(d) ()() 2 2 111 22 ftt tt +=++ =++
48. () 2 hxx=−
(a) ()44266 h −=−−=−=
(b) ()22244 h −=−−=−=
(c) ()00222 h =−=−=
(d) ()222 hxxxx −+=−+−=−=
49. () 2 25 fxx =−
Critical numbers: 5
Test intervals: ,5,5,5,5,
Domain: ()() 2 250 550 x xx −≥ +−≥ ()()() 2
Test: Is 250?
Solution set: 55 x x x =± −∞−−∞ −≥ −≤≤
Domain: all real numbers x such that [] 55,or5,5 x −≤≤−
50. () ()() 2 6 23 x hx xx x xx = = +−
Domain: All real numbers x except 2,3 x =−
51. () () 9.814.7 14.9meters per second vtt v =−+ =
53. () 2 231fxxx=+−
54.
55. () 2 3 yx=−
A vertical line intersects the graph no more than once, so y is a function of x.
56. 4 xy =−−
A vertical line intersects the graph more than once, so y is not a function of x.
57. () 2 31621fxxx=−+ ()() 2 316210 3730 xx xx −+=
58. () 2 541fxxx=+− ()() 2 5410 5110 xx
59. () 1 fxxx=++
f is increasing on () 0,. ∞
f is decreasing on (),1.−∞− f is constant on ()1,0.
60. () () 2 2 4 fxx=−
f is increasing on () 2,0 and () 2,. ∞ f is decreasing on () ,2−∞− and ()0,2.
61. () 2 21fxxx=−++
Relative maximum: () 1,2
62. () 3241fxxx=−−
Relative minimum: () 2.67,10.48
Relative maximum: () 0,1
63. () ()() () 2 84 40124 4 404 fxxx ff =−+− ==
The average rate of change of f from 1 0 x = to 2 4 x = is 4.
64. () 3 21fxxx=++ ()() 31 34430 15 3122 ff ===
The average rate of change of f from 1 1 x = to 2 3 x = is 15.
65. () ()()()() 42 42 42 20 2020 fxxx fxxxxxfx =− −=−−−=−=
The function is even, so the graph has y-axis symmetry.
66. () ()()() () 2 2 2 23 23 23 fxxx fxxx xx fx =+ −=−−+ =−+ =−
The function is odd, so the graph has origin symmetry.
67. (a) ()() 26,13ff=−−=
Points: ()() 2,6,1,3 ()36 9 3 123 m ===− ()() () 632 636 3 3 yx yx yx fxx −−=−− +=−+ =− =− (b)
68. (a) ()() ()() () 05,48 0,5,4,8 85 3 404 ff m =−=−
(b)
69. () gxx =
70. () 53,1 45,1 xx fx xx −≥− = −+<−
71. (a) () 2fxx =
(b) () 2 9 hxx=−
Vertical shift 9 units downward
(c)
(d) ()() 9 hxfx=−
72. (a) () 3fxx =
(b) ()()3 22 hxx=−+
Horizontal shift 2 units to the right; vertical shift 2 units upward
(c)
(d) ()()22 hxfx=−+
73. (a) () fxx = (b) () 4 hxx=−+
Reflection in the x-axis and a vertical shift 4 units upward
(c)
(d) ()() 4 hxfx=−+
74. (a) () fxx = (b) () 35 hxx=+−
Horizontal shift 3 units to the left and a vertical shift 5 units downward
(c)
(d) ()()35 hxfx=+−
75. (a) () 2fxx = (b) ()() 2 23 hxx=−++
Reflection in the x-axis, a horizontal shift 2 units to the left, and a vertical shift 3 units upward
(c)
(d) ()()23 hxfx=−++
76. (a) () 2fxx =
(b) () () 2 1 2 12 hxx=−−
Horizontal shift one unit to the right, vertical shrink, and a vertical shift 2 units downward (c)
(d) () () 1 2 12 hxfx=−−
77. (a) () fxx =
(b) () 6 hxx=-+
Reflection in the x-axis and a vertical shift 6 units upward
(c)
(d) ()() 6 hxfx=−+
78. (a) () fxx =
(b) () 19 hxx=−++
Reflection in the x-axis, a horizontal shift 1 unit to the left, and a vertical shift 9 units upward (c)
(d) ()()19 hxfx=−++
79. (a) () fxx = (b) () 59hxx=-
Horizontal shift 9 units to the right and a vertical stretch (each y-value is multiplied by 5)
(c)
(d) ()() 59hxfx=−
80. (a) () 3fxx =
(b) () 3 1 3 hxx =−
Reflection in the x-axis and a vertical shrink () 1 3 each -value is multiplied by y
(c)
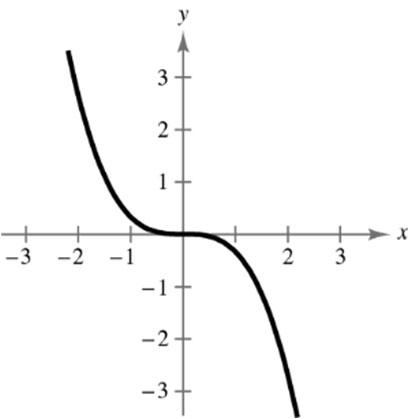
(d) () () 1 3 hxfx =−
81. ()() 2 3,21fxxgxx=+=−
(a) ()() () () 2232122fgxxxxx +=++−=++
(b) ()() () () 2232124fgxxxxx −=+−−=−+
(c) ()() ()()232321263fgxxxxxx =+−=−+−
+ =≠
(d) () 2 31 ,Domain: 212 fx xx gx
82. ()() 2 4,3 fxxgxx =−=−
(a) ()()()() 2 43 fgxfxgxxx +=+=−+−
(b) ()()()() 2 43 fgxfxgxxx −=−=−−−
(c) ()()()() ()() 2 43 fgxfxgxxx ==−−
(d) () () () 2 4 ,Domain: 3 3 fx fx xx ggx x
==<
83. () () 1 3 3,31fxxgxx=−=+
The domains of f and g are all real numbers.
(a) ()()()() () () 1 3 1 3 8 3 31 313 3 fgxfgx fx x x x = =+ =+− =+− =−
Domain: all real numbers
(b) ()()()() () () 1 3 1 3 3 331 91 8 gfxgfx gx x x x = =− =−+ =−+ =−
Domain: all real numbers
84. ()() 3 3 4,7fxxgxx =−=+
The domains of f and g are all real numbers.
(a) ()()()() ()3 3 74 74 3 fgxfgx x x x = =+− =+− =+
Domain: all real numbers
(b) ()()()() () 3 3 3 3 47 3 gfxgfx x x = =−+ =+
Domain: all real numbers
In Exercises 85–86 use the following functions. ()()100,0.95=−= f xx g xx
85. ()()()0.950.95100fgxfxx==− represents the sale price if first the 5% discount is applied and then the $100 rebate.
86. ()()()()1000.951000.9595gfxgxxx =−=−=− represents the sale price if first the $100 rebate is applied and then the 5% discount.
87. ()
88. () 4
89. ()() 2 1 fxx=−
The function is not one-to-one. Some horizontal lines intersect the graph more than once.
90. () 2 3 ht t =
The function is one-to-one. Horizontal lines intersect the graph at most once.
91. (a)
(c) The graph of 1 f is the reflection of the graph of f in the line yx =
(d) The domains and ranges of f and 1 f are the set of all real numbers. 92. (a)
Note: The inverse must have a restricted domain. (b)
(c) The graph of 1 f is the reflection of the graph of f in the line yx =
(d) The domain of f and the range of 1 f is [ ) 1,.−∞
The range of f and the domain of 1 f is [ ) 0,. ∞
93. ()() 2 24fxx=− is increasing on () 4,. ∞ Let ()() 2 24,4fxxx=−> and 0. y >
94. () 2 fxx=− is increasing on () 2,. ∞ Let () 2,2,0.fxxxy=−>> () 1 2 2,0,2 2,0,2 2,0 yx xyxy xyxy fxxx =− =−>> +=>> =+>
95. (a) and (b)
0.5326.5, 1319Ctt=+≤≤
The model fits the data well.
96. () 3 105 3105315 315 k T r k k T r = = == = When 130kmh, r = 315 2.4231hours2hours,25minutes. 130 T ==≈
Problem Solving for Chapter 1
1. (a) 1 0.072000WS=+ (b) 2 0.052300WS=+ (c)
Point of intersection: () 15,000,3050
Both jobs pay the same, $3050, if you sell $15,000 per month.
97. () ()()
When 4 and 25,000, 1250. 25,000 1 12500.2 45 When 5.50, 0.225,000 909 pastries. 5.50 kx d p pxd k k p d = === = == = =≈
98. False. The graph is reflected in the x-axis, shifted 9 units to the left, then shifted 13 units downward.
99. True. If () 3fxx = and () 3 , gxx = then the domain of g is all real numbers, which is equal to the range of f and vice versa.
(d) No. If you think you can sell $20,000 per month, keep your current job with the higher commission rate. For sales over $15,000 it pays more than the other job.
2. Mapping numbers onto letters is not a function. Each number between 2 and 9 is mapped to more than one letter. {()()()()()()()()()()()() ()()()()()()()()()()()()()()} 2,,2,,2,,3,,3,,3,,4,,4,,4,,5,,5,,5,, 6,,6,,6,,7,,7,,7,,7,,8,,8,,8,,9,,9,,9,,9, ABCDEFGHIJKL MNOPQRSTUVWXYZ
Mapping letters onto numbers is a function. Each letter is only mapped to one number. {()()()()()()()()()()()() ()()()()()()()()()()()()()()} ,2,,2,,2,,3,,3,,3,,4,,4,,4,,5,,5,,5, ,6,,6,,6,,7,,7,,7,,7,,8,,8,,8,,9,,9,,9,,9 ABCDEFGHIJKL MNOPQRSTUVWXYZ
3. (a) Let ()fx and ()gx be two even functions. (b) Let ()fx and ()gx be two odd functions.
Then define ()()(). hxfxgx =±
Then define ()()(). hxfxgx =± ()()()
()() () because and are even hxfxgx fxgxfg hx −=−±− =± =
So, ()hx is also even.
()()() ()() () because and are odd hxfxgx fxgxfg hx −=−±− =−± =−
So, ()hx is also odd. ()() () If fxgx ≠
(c) Let ()fx be odd and ()gx be even. Then define ()()() hxfxgx =± ()()() ()() () () because is odd and is even hxfxgx fxgxfg hx hx −=−±− =−± ≠ ≠−
So, ()hx is neither odd nor even.
4. () fxx = () gxx =− ()()ffxx = and ()() ggxx =
These are the only two linear functions that are their own inverse functions since m has to equal 1 m for this to be true.
General formula: yxc =−+
5. ()
So, ()fx is even.
6. It appears, from the drawing, that the triangles are equal; thus ()() ,1.5,2.xy =
The line between () 0.625,0.5 and () 1.5,2 is 124 77yx=−
The line between () 2.375,0.5 and () 1.5,2 is 32 12 77yx=−+
The path of the ball is:
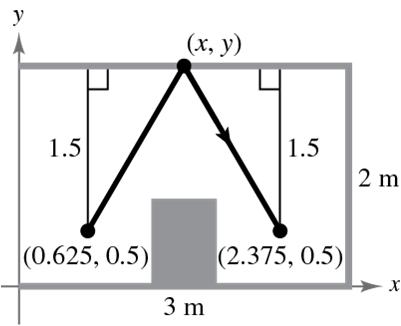
7. (a) April 11:10 hours
April 12:24 hours
April 13:24 hours 2
April 14:23 hours 3 2
Total:81 hours 3 (b) (c) 2028 5470 49 1190
distance3380202819 Speed41 kmh 2 time4949 81 3 ====
8. (a) ()() ()() 21 21 21 10 1 211 fxfxff xx ===
(b) ()() ()() 21 21 1.51 0.750 1.5 1.510.5 fxfxff xx ===
(c) ()() ()() 21 21 1.251 0.43750 1.75 1.2510.25 fxfxff xx ===
Range: 05470 =−+ ≤≤ ≤≤ yx x y (d)
(e) ()() ()() 21 21 1.06251 0.121093750 1.9375 1.062510.625 fxfxff xx ===
(f) Yes, the average rate of change appears to be approaching 2. (g) a. ()() 1,0,2,1,1,1 myx==−
b. ()() 0.75 1,0,1.5,0.75,1.5,1.51.5 0.5 myx ===−
c. ()() 0.4375 1,0,1.25,0.4375,1.75,1.751.75 0.25 myx ===−
Domain: 0 9
d. ()() 0.234375 1,0,1.125,0.234375,1.875,1.8751.875 0.125 myx ===−
e. ()() 0.12109375 1,0,1.0625,0.12109375,1.9375,1.93751.9375 0.0625 myx ===−
(h) () () ()() 1,11,0,2,21,22 fmyxyx =→=−=−
9. (a)–(d) Use () 4 fxx = and () 6. gxx=+
(a) ()()()()646424fgxfxxx =+=+=+
(b) ()() 1 241 6 44 x fgxx==−
(c) () () 1 1 1 4 6 fxx gxx = =−
()()
()() ()()()() ()() () () ()() ()
(f) Answers will vary. (g) Conjecture: ()() ()() 1 11 fgxgfx =
10. (a) The length of the trip in the water is 22 2, x + and the length of the trip over land is () 2 13. x +− The total time is

(d) ()Tx is a minimum when 1. x =
(b) Domain of () :03Txx≤≤
11. () 1,0 0,0 x Hx x ≥
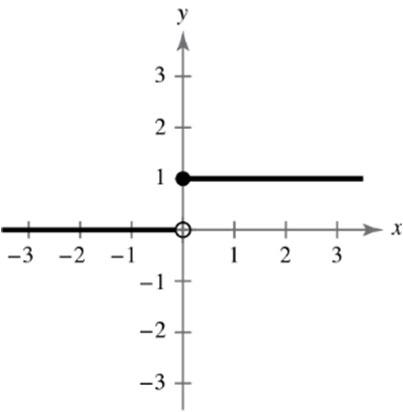
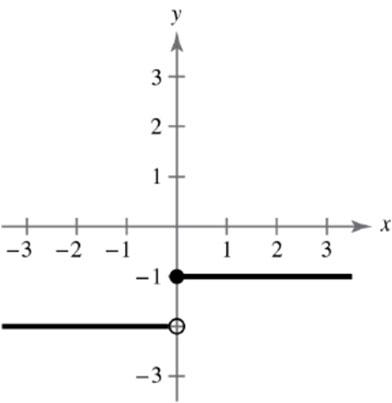
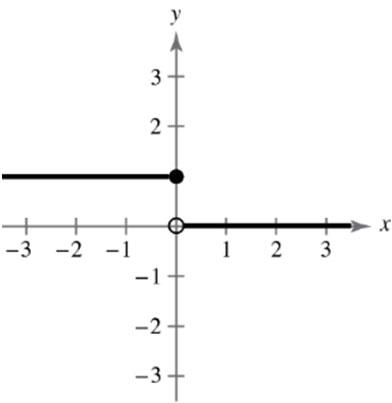
(e) Answers will vary. Sample answer: To reach point Q in the shortest amount of time, you should row to a point one kilometer down the coast, and then walk the rest of the way. The distance 1 = x yields a time of 1.68 hours.
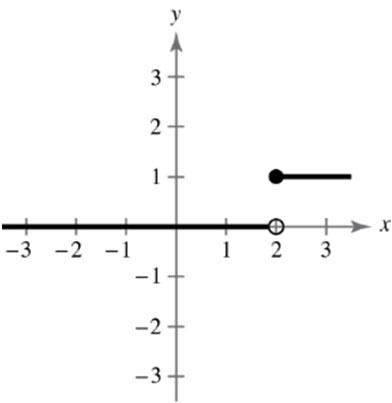
12. () 1 1 fxy x ==
(a) Domain: all real numbers x except 1 x =
Range: all real numbers y except 0 y =
(b) () () 1 1 11 11 1 1 1 1 11 ffxf x x x x xx
Domain: all real numbers x except 0 x = and 1 x = (c) () () () 111 1 1 1 x fffxfx x x x x
The graph is not a line. It has holes at () 0,0 and ()1,1.
13. () ()()()() () () () () ()() () ()()()()() () () () ()()
14. (a) () 1 fx + (b) () 1 fx + (c) () 2 fx
(d) ()fx (e) ()fx
(g) ()fx
()fx
Practice Test for Chapter 1
1. Find the equation of the line through () 2,4 and () 3,1.
2. Find the equation of the line with slope 43 m = and y-intercept 3. b =−
3. Find the equation of the line through () 4,1 perpendicular to the line 230. xy+=
4. If it costs a company $32 to produce 5 units of a product and $44 to produce 9 units, how much does it cost to produce 20 units? (Assume that the cost function is linear.)
5. Given () 2 21,fxxx=−+ find ()3. fx
6. Given () 411,fxx=− find ()() 3 3 fxf x
7. Find the domain and range of () 2 36. f xx =−
8. Which equations determine y as a function of x?
(a) 6540 xy−+=
(b) 22 9 xy+=
(c) 32 6 yx=+
9. Sketch the graph of () 2 5. fxx=−
10. Sketch the graph of () 3. fxx=+
11. Sketch the graph of () 2 21,if0, ,if0. xx fx xxx +≥ = −<
12. Use the graph of () f xx = to graph the following:
(a) () 2 fx +
(b) () 2 fx −+
13. Given () 37fxx=+ and () 2 25,gxx=− find the following:
(a) ()() g fx
(b) ()() fgx
14. Given () 2 216fxxx=−+ and () 23,gxx=+ find () () f gx
15. Given () 3 7, fxx=+ find () 1 f x
16. Which of the following functions have inverses?
(a) () 6 fxx=−
(b) () ,0fxaxba=+≠
(c) () 3 19 fxx=−
17. Given () 3 ,03, x fxx x =<≤ find () 1 f x
Exercises 18–20, true or false?
18. 37yx=+ and 1 3 4 yx=− are perpendicular.
19. () 1 11 f ggf =
20. If a function has an inverse, then it must pass both the Vertical Line Test and the Horizontal Line Test.
