

INSTRUCTOR’S SOLUTIONS MANUAL
GEX INC.
A LGEBRA & T RIGONOMETRY
E NHANCED WITH G RAPHI NG
U TILITIES
NINTH EDITION
Michael Sullivan
Chicago State University
Michael Sullivan, III
Joliet Junior College and Florida SouthWestern State College

Copyright © 2026, 2021, 2017 by Pearson Education, Inc. or its affiliates. All Rights Reserved. Manufactured in the United States of America. This publication is protected by copyright, and permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise. For information regarding permissions, request forms, and the appropriate contacts within the Pearson Education Global Rights and Permissions department, please visit www.pearsoned.com/permissions/
PEARSON and MYLAB are exclusive trademarks owned by Pearson Education, Inc. or its affiliates in the U.S. and/or other countries.
Unless otherwise indicated herein, any third-party trademarks, logos, or icons that may appear in this work are the property of their respective owners, and any references to third-party trademarks, logos, icons, or other trade dress are for demonstrative or descriptive purposes only. Such references are not intended to imply any sponsorship, endorsement, authorization, or promotion of Pearson’s products by the owners of such marks, or any relationship between the owner and Pearson Education, Inc., or its affiliates, authors, licensees, or distributors.
Chapter 1 Graphs, Equations, and Inequalities
1.5
1.6
Chapter 2 Graphs
Chapter 3 Functions and Their Graphs
Chapter 4 Linear and Quadratic Functions
4.1
4.5
Chapter 5
Functions
5.4
5.5
5.6
Chapter 6
6.1
6.3
Chapter 7 Trigonometric Functions
7.1
7.2
7.3
7.4
7.5
7.6
7.7
Chapter 8 Analytic Trigonometry
8.1
8.2
Chapter 9
Chapter 10 Polar Coordinates; Vectors
10.1
Chapter 11 Analytic Geometry
Chapter 12 Systems of Equations and Inequalities
Chapter 13 Sequences; Induction;
Chapter 14 Counting and Probability
Chapter R Review
Section R.1
1. rational
2. 4563430331 +⋅−=+−=
3. Distributive
4. c
5. a
6. b
7. True
8. False;TheZero-ProductPropertystatesthatifa productequals0,thenatleastoneofthefactors mustequal0.
9. False;6istheGreatestCommonFactorof12 and18.TheLeastCommonMultipleisthe smallestvaluethatbothnumberswilldivide evenly.TheLCMfor12and18is36.
10. True
11. { } { } {} 1,3,4,5,92,4,6,7,8 1,2,3,4,5,6,7,8,9 AB∪=∪ =
12. { } { } {} 1,3,4,5,91,3,4,6 1,3,4,5,6,9 AC∪=∪ =
13. { } { } { }1,3,4,5,92,4,6,7,84 AB∩=∩=
14. { } { } { }1,3,4,5,91,3,4,61,3,4 AC∩=∩=
15. {}{} () {} {}{} {} () 1,3,4,5,92,4,6,7,81,3,4,6 1,2,3,4,5,6,7,8,91,3,4,6 1,3,4,6 ABC ∪∩ =∪∩ =∩ =
16. {}{} () {} {}{} {} () 1,3,4,5,92,4,6,7,81,3,4,6 41,3,4,6 1,3,4,6 ∩∪ =∩∪ =∪ = ABC
17. { }0,2,6,7,8 A =
18. { }0,2,5,7,8,9 C =
AB∩=∩ ==
19. {}{} {} {} 1,3,4,5,92,4,6,7,8 40,1,2,3,5,6,7,8,9
BC∪=∪ ==
20. {}{} {} {} 2,4,6,7,81,3,4,6 1,2,3,4,6,7,80,5,9
AB∪=∪ =
21. { } { } {} 0,2,6,7,80,1,3,5,9 0,1,2,3,5,6,7,8,9
BC∩=∩ =
22. { } { } {} 0,1,3,5,90,2,5,7,8,9 0,5,9
23. a. { }2,5
b. { }6,2,5
c. { } 1 6,,1.333...1.3,2,5 2 −−=−
d. {π}
e. { } 1 6,,1.333...1.3,,2,5 2 π −−=−
24. a. { }1
b. { }0,1
c. { }5,2.060606...2.06,1.25,0,1 3 −=
d. { } 5
e. { } 5,2.060606...2.06,1.25,0,1,5 3 −=
25. a. { }1
b. { }0,1
c. { } 1110,1,,,234
d. None
e. { } 1110,1,,,234
26. a. None
b. { }1
c. { }1.3,1.2,1.1,1
d. None
e. { }1.3,1.2,1.1,1
27. a. None
b. None
c. None
d. { } 2,,21,1 2 ππ++
e. { } 2,,21,1 2 ππ++
28. a. None
b. None
c. { }110.3 2 +
d. { } 2,2 π −+
e. { } 1 2,2,10.3 2 π −++
29. a. 18.953 b. 18.952
30. a. 25.861 b. 25.861
31. a. 28.653 b. 28.653
32. a. 99.052 b. 99.052
33. a. 0.063 b. 0.062
34. a. 0.054 b. 0.053
35. a. 9.999 b. 9.998
36. a. 1.001 b. 1.000
37. a. 0.429 b. 0.428
38. a. 0.556 b. 0.555
39. a. 34.733 b. 34.733
40. a. 16.200 b. 16.200
41. 325 +=
42. 5210 ⋅=
43. 234 x +=⋅
44. 322 y +=+
45. 312 y =+
46. 246 x =⋅
47. 26 x −=
48. 26 y −=
49. 6 2 x =
50. 26 x =
51. 942527 −+=+=
52. 643235 −+=+=
53. 6436126 −+⋅=−+=
54. 842880 −⋅=−=
55. 185218108 −⋅=−=
56. 1001021002080 −⋅=−=
57. 4112113 333 + +==
58. 21413 222 −==
59. ()() 63523261521 617 11 −⋅+⋅−=−+⋅
60. ()()
28342328363 28183 2103 203 23 ⋅−⋅+−=⋅−⋅−
61. ()() 495673414423 56423 143 17 ⋅+−⋅+=⋅−+ =−+
62. ()() 1432211222 112 11 −⋅−+=−−+
63. () [ ]
64. ()() [] 25463422061 186 186 12
65. () () 11 5321 22 −==
66. () () 11 5493 33 +==
67. 48126 532 + ==
68. 2421 532 ==−
69. 3103253 521537 ⋅== 25 53 2 77 = 70. 53535 9103352 ⋅ ⋅== 3 ⋅ 335 ⋅⋅ 1 26 = ⋅
71. 610235223 25275539 ⋅== ⋅⋅⋅ 52 553 4 945 =
72. 21100374253 253253 ⋅== 7425 253 28 =
73. 3215823 452020 + +==
74. 418311 3266 + +==
75. 74493281 875656 + +==
76. 81516135151 921818 + +==
77. 5110313 18123636 + +==
78. 2864046 1594545 + +==
79. 5825643913 241512012040 −==−=−
80. 32945 14214242 −==
81. 32981 20156060 −==
82. 6312153 35147070 −==−
83. 5 1852759359 1118119211 27
=⋅== ⋅⋅
3 9 15 21122 = 84. 5 2153557557 2212732 35
=⋅== ⋅⋅
5 7 25 326 =
85. 141741721 1 3721212121 ⋅+=+==
86. 24122222222 35635323532315 25210210212 351515151515 43434 53535 +⋅=+=+=+ + =⋅+=+== ===
87. 3323363623 2 4814848428 12312315 8888 ⋅+=⋅+=+=⋅+ + =+==
88. 51351351351 3 62162322322 51514 2 2222 ⋅⋅ ⋅−=⋅−=−=− ⋅⋅ =−===
89. () 64624 xx+=+
90. () 42184 xx−=−
91. () 2 44 xxxx −=−
92. () 2 43412 xxxx +=+
93. 3131232 222 4242222 2323 1 2222 x xx x x
−=⋅−⋅=−
=−=−
94. 2121323 333 3636332 3231 2 3322 x xx x x ⋅ +=⋅+⋅=+
⋅
⋅ =+=+ ⋅
95. ()() 2 2 24428 68 xxxxx xx ++=+++ =++
96. ()() 2 2 5155 65 xxxxx xx ++=+++ =++
97. ()() 2 2 927271863 21163 +−=−+− =+− xxxxx xx
98. ()() 2 2 3153155 3145 −+=+−− =+− xxxxx xx
99. ()() 2 2 822816 1016 xxxxx xx −−=−−+ =−+
100. ()() 2 2 42248 68 xxxxx xx −−=−−+ =−+
101. 2 22 3(5)360 315360 1560 4 −=− −=− −=− = xxkxx xxkxx xkx k
102. 2 222 222 222 222 ()(3)412 33412 (3)3412 (3)3412 (2)3412 24 2 −+=+− +−−=+− +−−=+− +−−=+− +−=+− = = xkxkxx xkxkxkxx xxkkkxx xxkkkxx xxkkxx k k
103. () () 2323 23 5 5 xxxx x x x +=⋅+⋅ =+⋅ =⋅ =
104. 23421214 +⋅=+= sincemultiplicationcomesbeforeadditioninthe orderofoperationsforrealnumbers.
()2345420 +⋅=⋅= sinceoperationsinsideparenthesescomebefore multiplicationintheorderofoperationsforreal numbers.
105. ()() 23421224 ⋅== ()()()() 23246848 ⋅⋅⋅==
106. 4371 257 + == + ,but 43453220626132.6 251010105 ⋅+⋅+ +=====
107. Subtractionisnotcommutative;for example:231132 −=−≠=− .
108. Subtractionisnotassociative;for example: ()() 52124521 −−=≠=−−
109. Divisionisnotcommutative;forexample: 23 32 ≠
110. Divisionisnotassociative;for example: () 1222623 ÷÷=÷= ,but () 122212112 ÷÷=÷=
111. TheSymmetricPropertyimpliesthatif2= x, then x =2.
112. Fromthe principleofsubstitution, if5 x = ,then ()()()() 2 2 2 55 25 255 30 xx x xx xx = = +=+
113. Therearenorealnumbersthatarebothrational andirrational,sinceanirrationalnumber,by definition,isanumberthatcannotbeexpressed astheratiooftwointegers;thatis,notarational number
Everyrealnumberiseitherarationalnumberor anirrationalnumber,sincethedecimalformofa realnumbereitherinvolvesaninfinitely repeatingpatternofdigitsoraninfinite,nonrepeatingstringofdigits.
114. Thesumofanirrationalnumberandarational numbermustbeirrational.Otherwise,the irrationalnumberwouldthenbethedifferenceof tworationalnumbers,andthereforewouldhave toberational.
115. Answerswillvary.
116. Since1day=24hours,wecompute 12997541.5416 24 = .
Nowweonlyneedtoconsiderthedecimalpart oftheanswerintermsofa24hourday.Thatis, () () 0.54162413 ≈ hours.Soitmustbe13hours laterthan12noon,whichmakesthetime1AM CST.
117. Answerswillvary.
Section R.2
1. variable
2. origin
3. strict
4. base;exponent(orpower)
5. 31.234567810 × 6. d 7. a 8. b
9. True
10. False;theabsolutevalueofarealnumberis nonnegative.00 = whichisnotapositive number.
11. False;anumberinscientificnotationis expressedastheproductofanumber,x, 110 x ≤< or101 x −<≤− ,andapowerof10.
12. True
21. 10.5 2 =
22. 10.33 3 >
23. 20.67 3 <
24. 10.25 4 =
25. 0 x >
26. 0 z <
27. 2 x <
28. 5 y >−
29. 1 x ≤
30. 2 x ≥
31. Graphonthenumberline:2 x ≥− 0 −2
32. Graphonthenumberline:4 x < 4 0
33. Graphonthenumberline:1 x >− −1 0
34. Graphonthenumberline:7 x ≤ 0 7
35. (,)(0,1)1011dCDd==−==
36. (,)(0,3)3033dCAd=−=−−=−=
37. (,)(1,3)3122dDEd==−==
38. (,)(0,3)3033dCEd==−==
39. (,)(3,3)3(3)66dAEd=−=−−==
40. (,)(1,1)1122dDBd=−=−−=−=
41. 2223264xy+=−+⋅=−+=
42. 33(2)3633 xy+=−+=−+=−
43. 525(2)(3)230228 xy +=−+=−+=−
44. 22(2)(2)(3)462 xxy −+=−−+−=−=−
45. 2(2)4 24 2355 x xy ===
46. 2311 2355 xy xy −+ + ===−
47. 323(2)2(3)6600 22355 xy y −+−+ + ==== ++
48. 2(2)343 237 333 x y ===−
49. 3(2)11 xy+=+−==
50. 3(2)55 xy−=−−==
51. 32325 xy+=+−=+=
52. 32321 xy−=−−=−=
53. 331 33 x x ===
54. 221 22 y y ===−
55. 454(3)5(2) 1210 22 22 xy−=−− =+ = =
56. 323(3)2(2)9455 xy+=+−=−==
57. 454(3)5(2) 1210 1210 2 2 xy−=−− =−− =− = =
58. 323322 3322 94 13 xy+=+− =⋅+⋅ =+ =
59. 21 x x
Part(c)mustbeexcluded.Thevalue0 x = must beexcludedfromthedomainbecauseitcauses divisionby0.
60. 21 x x +
Part(c)mustbeexcluded.Thevalue0 x = must beexcludedfromthedomainbecauseitcauses divisionby0.
61. 2(3)(3) 9 xx xxx = −+
Part(a),3 x = ,mustbeexcludedbecauseit causesthedenominatortobe0.
62. 29 x x +
Noneofthegivenvaluesareexcluded.The domainisallrealnumbers.
63. 2 21 x x +
Noneofthegivenvaluesareexcluded.The domainisallrealnumbers.
64. 33 2(1)(1) 1 xx xxx = −+
Parts(b)and(d)mustbeexcluded.Thevalues 1,and1xx==− mustbeexcludedfromthe domainbecausetheycausedivisionby0.
65. 22 3 510510 (1)(1) xxxx xxxxx +−+− = −+
Parts(b),(c),and(d)mustbeexcluded.The values0,1,and1 xxx===− mustbeexcluded fromthedomainbecausetheycausedivisionby 0.
66. 22 32 9191 (1) xxxx xxxx −−+−−+ = ++
Part(c)mustbeexcluded.Thevalue0 x = must
beexcludedfromthedomainbecauseitcauses divisionby0.
67. 4 5 x 5 x = mustbeexcludedbecauseitmakesthe denominatorequal0.
{ }Domain5 xx =≠
68. 6 4 x + 4 x =− mustbeexcludedsineitmakesthe denominatorequal0.
{ }Domain4 xx =≠−
69. 4 x x + 4 x =− mustbeexcludedsineitmakesthe denominatorequal0.
{ }Domain4 xx =≠−
70. 2 6 x x 6 x = mustbeexcludedsineitmakesthe denominatorequal0.
{ }Domain6 xx =≠
71. 555 (32)(3232)(0)0C 999 CF=−=−==°
72. 555 (32)(21232)(180)100C 999 CF=−=−==°
73. 555 (32)(7732)(45)25C 999 CF=−=−==°
74. 55(32)(432)99 5(36) 9 20C CF=−=−− =− =−°
75. 2 (9)(9)(9)81 −=−−=
76. 22 4(4)16−=−=−
77. 2 2 411 416 ==
78. 2 2 411 416 −=−=−
79. 64642 2 333311 39 −−+− ⋅====
80. 23231 44444 −−+ ⋅===
81. () ()() 131 33 44464 ===
82. () ()() 313 13 2228 ===
83. 2 1001010 ==
84. 2 3666 ==
85. () 2 444−=−=
86. () 2 333−=−=
87. ()() 22 4248 9981 == xxx
88. ()21 22 411 44 x xx −==−
89. ()()()2224212142 2 x xyxyxy y =⋅==
90. ()()33311333 3 y xyxyxy x =⋅==
91. 25 235411 34 === xyy xyxy xyx
92. 2 211231 23 1 xy xyxy xyxy ===
93. 253533 37272 315732 221 2 2 (4)()16 (3)27 16 27 16 27 16 27 = =− =− =− yxzyxz xyzxyz xyz xyz xz y
94. 21211 344 24111 621 62 4()4 28 4 8 1 2 1 2 xyzxyz xyxy xyz xyz xyz = = = =
22 2 33266 13222 3 2339 2 3224
xyxxx y yxyy
() () 333 2 22 222 3236 3236 5 56 665 6216 5125 y xx yxy xx yy
==
() () 122 2 24 1 x xy y ===− 98. () () 131 333 22 y xy x −=== 99. ()() 222221415 xy+=+−=+= 100. ()() 222221414 xy =−=⋅= 101. ()()() () 2 222124 xy =⋅−=−= 102. ()() () () 2 222111 xy+=+−== 103. 222xx=== 104. () 2 2 xx== 105. ()() 222221415 xy+=+−=+= 106. 2221213 xyxy+=+=+−=+= 107. 211 2 y x ==
108. () 2 11 x y =−=
109. If2, x = 3232 23542232524 1612104 10 xxx−+−=⋅−⋅+⋅− =−+− = If1, x = 3232 23542131514 2354 0 xxx−+−=⋅−⋅+⋅− =−+− =
110. If1, x = 3232 432413112 4312 8 xxx+−+=⋅+⋅−+ =+−+ =
If2, x = 3232 432423222 321222 44 xxx+−+=⋅+⋅−+ =+−+ = 111. 44 4 4 (666)666381 (222)222 ===
112.
113. 6 (8.2)304,006.671 ≈
114. 5 (3.7)693.440 ≈
115. 3 (6.1)0.004 ≈
116. 5 (2.2)0.019 ≈
117. 6 (2.8)481.890 −≈
118. 6 (2.8)481.890−≈−
119. 4 (8.11)0.000 −≈
SectionR.2: Algebra Essentials
120. 4 (8.11)0.000−≈−
121. 2 454.24.54210 =×
122. 132.143.21410 =×
123. 0.0131.3102 =×
124. 0.004214.21103 =×
125. 432,1553.215510 =×
126. 4 21,2102.12110 =×
127. 0.0004234.23104 =×
128. 0.05145.14102 =×
129. 4 6.151061,500 ×=
130. 3 9.7109700 ×=
131. 3 1.214100.001214 ×=
132. 4 9.88100.000988 ×=
133. 8 1.110110,000,000 ×=
134. 2 4.11210411.2 ×=
135. 2 8.1100.081 ×=
136. 1 6.453100.6453 ×=
137. Alw =
138. () 2 Plw =+
139. Cd π = 140. 1 2 Abh =
141. 32 4 Ax = 142. 3 Px = 143. 43 3 Vr π =
144. 42Sr π = 145. 3 Vx =
146. 62Sx =
147. a. If1000, x = 40002 40002(1000) 40002000 $6000 Cx =+ =+ =+ = Thecostofproducing1000watchesis $6000.
b. If2000, x = 40002 40002(2000) 40004000 $8000 Cx =+ =+ =+ = Thecostofproducing2000watchesis $8000.
148. 210801202560325$98 +−+−−−= Hisbalanceattheendofthemonthwas$98.
149. Wewantthedifferencebetween x and4tobeat least6units.Sincewedon’tcarewhetherthe valuefor x islargerorsmallerthan4,wetake theabsolutevalueofthedifference.Wewantthe inequalitytobenon-strictsincewearedealing withan‘atleast’situation.Thus,wehave 46 x −≥
150. Wewantthedifferencebetween x and2tobe morethan5units.Sincewedon’tcarewhether thevaluefor x islargerorsmallerthan2,we taketheabsolutevalueofthedifference.We wanttheinequalitytobestrictsinceweare dealingwitha‘morethan’situation.Thus,we have 25 x −>
151. a. 110108110225 x −=−=−=≤ 108voltsisacceptable.
b. 110104110665 x −=−=−=> 104voltsis not acceptable.
152. a. 220214220668 x −=−=−=≤ 214voltsisacceptable.
b. 22020922011118 x −=−=−=> 209voltsis not acceptable.
153. a. 32.9993 0.001 0.0010.01 x −=− =− =≤ Aradiusof2.999centimetersisacceptable.
b. 32.893 0.11 0.110.01 x −=− =− =≤ / Aradiusof2.89centimetersis not acceptable.
154. a. 98.69798.6 1.6 1.61.5 x −=− =− =≥ 97˚Fisunhealthy.
b. 98.610098.6 1.4 1.41.5 x −=− = =< 100˚Fis not unhealthy.
155. ThedistancefromEarthtotheMoonisabout 8 410400,000,000 ×= meters.
156. TheheightofMt.Everestisabout 388488.84810 =× meters.
157. Thewavelengthofvisiblelightisabout 7 5100.0000005 ×= meters.
158. Thediameterofanatomisabout 10 1100.0000000001 ×= meters.
159. Thediameterisabout2 0.04034.0310 =× inches.
160. Thetiniestmotorislessthan5 0.00004410 =× millimeterstall.
161. ()()()() 5112 2 1.86106102.4103.6510 186,000606024365 ×××× = 1012 586.5696105.86569610 =×=× Thereareabout12 5.910 × milesinonelightyear.
162. 7 2 5 93,000,0009.310510 186,0001.8610 500seconds8min.20sec. × ==× × =≈ Ittakesabout8minutes20secondsforabeam oflighttoreachEarthfromtheSun.
163. 10.333333...0.333 3 => 1 3islargerbyapproximately0.0003333...
164. 2 30.666666...0.666 => 2 3islargerbyapproximately0.000666...
165. ()()61319 20 5.24106.51034.0610 3.40610 ×× =× =×
166. 44 6 1010 5 1.62101.62100.3610 4.5 4.51010 3.610 × =×=× × =×
167. No.Foranypositivenumber a,thevalue2 a is smallerandthereforecloserto0.
168. Wearegiventhat2110 x << .Thisimpliesthat 110 x << .Since103.162 x <≈ and 3.142 x π >≈ ,thenumbercouldbe3.15or3.16 (whicharebetween1and10asrequired).The numbercouldalsobe3.14sincenumberssuchas 3.146whichliebetween π and10would equal3.14whentruncatedtotwodecimalplaces.
169. Answerswillvary.
170. Answerswillvary. 5<8isatruestatementbecause5isfurtherto theleftthan8onarealnumberline.
SectionR.3: Geometry Essentials
Section R.3
1. right;hypotenuse 2. 1 2 Abh = 3. 2 Cr π = 4. similar 5. c 6. b
7. True.
8. True.222 68366410010 +=+==
9. False;thesurfaceareaofasphereofradius r is givenby2 4 Vr π = .
10. True.Thelengthsofthecorrespondingsidesare equal.
11. True.Twocorrespondinganglesareequal.
12. False.Thesidesarenotproportional.
13. 222 22 5,12, 512 25144 16913 ab cab c == =+ =+ =+ = = 14. 222 22 6,8, 68 3664 10010 ab cab c == =+ =+ =+ = = 15. 222 22 10,24, 1024 100576 67626 ab cab c == =+ =+ =+ = =
16. 222 22 4,3, 43 169 255 ab cab c == =+ =+ =+ = =
17. 222 22 7,24, 724 49576 62525 ab cab c == =+ =+ =+ = =
18. 222 22 14,48, 1448 1962304 250050 ab cab c == =+ =+ =+ = =
19. 222 534 25916 2525 =+ =+ = Thegiventriangleisarighttriangle.The hypotenuseis5.
20. 222 1068 1003664 100100 =+ =+ = Thegiventriangleisarighttriangle.The hypotenuseis10.
21. 222 645 361625 3641false =+ =+ = Thegiventriangleisnotarighttriangle.
22. 222 322 944 98false =+ =+ = Thegiventriangleisnotarighttriangle.
23. 222 25724 62549576 625625 =+ =+ = Thegiventriangleisarighttriangle.The hypotenuseis25.
24. 222 261024 676100576 676676 =+ =+ = Thegiventriangleisarighttriangle.The hypotenuseis26.
25. 222 634 36916 3625false =+ =+ = Thegiventriangleisnotarighttriangle.
26. 222 754 492516 4941false =+ =+ = Thegiventriangleisnotarighttriangle.
27. 67422 in =⋅=⋅=Alw
28. 94362 cm Alw=⋅=⋅=
29. 112 22(14)(4)28in=⋅==Abh
30. 112 22(4)(9)18cmAbh=⋅==
31. 222 (5)25m 22(5)10m Ar Cr =π=π=π =π=π=π
32. 222 (2)4ft 22(2)4ft Ar Cr =π=π=π =π=π=π
33. 6852403 ft ==⋅⋅=Vlwh
()()()()()() 2 222 268265285 966080 236ft =++ =++ =++ = Slwlhwh
34. 9482883 in Vlwh==⋅⋅=
()()()()()() 2 222 294298248 7214464 280in Slwlhwh =++ =++ =++ =
35. 333 222 445005cm 333 445100cm =π=π⋅=π =π=π⋅=π Vr Sr
36. 333 222 44336f 33 44336ft Vrt Sr =π=π⋅=π =π=π⋅=π
37. 223 (9)(8)648in Vrh=π=π=π
2 2 2 22 29298 162144 306in Srrh ππ ππ ππ π =+ =+ =+ =
()()()
38. 223 (8)(9)576in Vrh=π=π=π
()()() 2 2 2 22 28289 128144 272in Srrh ππ ππ ππ π =+ =+ =+ =
39. Thediameterofthecircleis2,soitsradiusis1. 22(1)squareunits Ar=π=π=π
40. Thediameterofthecircleis2,soitsradiusis1. 22 2(1)4squareunits A =−π=−π
41. Thediameterofthecircleisthelengthofthe diagonalofthesquare.
222 22 44 8 822 222 22 d d d r =+ =+ = == ===
Theareaofthecircleis: () 2222squareunits Ar=π=π=π
42. Thediameterofthecircleisthelengthofthe diagonalofthesquare.
222 22 44 8 822 222 22 d d d r =+ =+ = == ===
Theareais: () 22 2224squareunits A =π−=π− 43. Sincethetrianglesaresimilar,thelengthsof correspondingsidesareproportional.Therefore, weget 8 42 82 4 4 x x x = = = Inaddition,correspondinganglesmusthavethe sameanglemeasure.Therefore,wehave 90 A =° ,60 B =° ,and30 C =°
44. Sincethetrianglesaresimilar,thelengthsof correspondingsidesareproportional.Therefore, weget 6 1216 616 12 8 x x x = = = Inaddition,correspondinganglesmusthavethe sameanglemeasure.Therefore,wehave 30 A =° ,75 B =° ,and75 C =° .
45. Sincethetrianglesaresimilar,thelengthsof correspondingsidesareproportional.Therefore, weget 30 2045 3045 20 135 or67.5 2 x x xx = ⋅ = == Inaddition,correspondinganglesmusthavethe sameanglemeasure.Therefore,wehave 60 A =° ,95 B =° ,and25 C =°
46. Sincethetrianglesaresimilar,thelengthsof correspondingsidesareproportional.Therefore, weget 8 1050 850 10 40 x x x = ⋅ = = Inaddition,correspondinganglesmusthavethe sameanglemeasure.Therefore,wehave 50 A =° ,125 B =° ,and5 C =°
47. Thetotaldistancetraveledis4timesthe circumferenceofthewheel. TotalDistance44()416 64201.1inches16.8feet Cd ==π=π⋅ =π≈≈
48. Thedistancetraveledinonerevolutionisthe circumferenceofthedisk4 π Thenumberofrevolutions= dist.traveled2051.6revolutions circumference4 ==≈ ππ
49. Areaoftheborder=areaofEFGH–areaof ABCD222 1061003664ft =−=−=
50. FG=4feet;BG=4feetandBC=10feet,so CG=6feet.TheareaofthetriangleCGFis: 12 2(4)(6)12ft A =⋅=
51. Areaofthewindow=areaoftherectangle+ areaofthesemicircle.
122 (6)(4)224230.28ft 2 A =+⋅π⋅=+π≈
Perimeterofthewindow=2heights+width+ one-halfthecircumference. 1 2(6)4(4)1242 2 16222.28feet P =++⋅π=++π =+π≈
52. Areaofthedeck=areaofthepoolanddeck–areaofthepool. 22 22 (13)(10)169100 69ft216.77ft A =π−π=π−π =π≈
Theamountoffenceisthecircumferenceofthe circlewithradius13feet. 2(13)26ft81.68ft C =π=π≈
53. WecanformsimilartrianglesusingtheGreat Pyramid’sheight/shadowandThales’ height/shadow:
54. Let x =theapproximatedistancefromSanJuan toHamiltonand y =theapproximatedistance fromHamiltontoFortLauderdale.Usingsimilar triangles,weget 1046 5853.5 104653.5 58 964.8 x
TheapproximatedistancebetweenSanJuanand Hamiltonis965milesandtheapproximate distancebetweenHamiltonandFortLauderdale is1028miles.
55. Convert20feettomiles,andsolvethe PythagoreanTheoremtofindthedistance: 222sq.miles
201milefeet20feet0.003788miles 5280feet (39600.003788)396030 5.477miles
56. Convert6feettomiles,andsolvethe PythagoreanTheoremtofindthedistance: 222sq.miles
61mile feet6feet0.001136miles 5280feet (39600.001136)39609 3miles d d =⋅= =+−= ≈ 3960 3960 6ft d
57. Convert100feettomiles,andsolvethe PythagoreanTheoremtofindthedistance: 1001milefeet100feet0.018939miles 5280feet =⋅=
222sq.miles (39600.018939)3960150 12.2miles d d =+−≈ ≈
Convert150feettomiles,andsolvethe PythagoreanTheoremtofindthedistance: 1501milefeet150feet0.028409miles 5280feet =⋅=
222sq.miles (39600.028409)3960225 15.0miles d d =+−≈ ≈
58. Given0,0andmnmn >>> , if2222 ,2and amnbmncmn =−==+ ,then () () 222222 422422 4224 2 24 2 abmnmn mmnnmn mmnn +=−+
and
222,and abcabc∴+=→ representthesides ofarighttriangle.
59. 2 2 3 (10)(4.5) 450ft π π π = = = Vrh So, ()() 3 33 1ft7.48052galso 450ft7.48052gal/ft10,575gal π ≈ ≈
60. 3 2 2 10000(5.61458)56145.8ft 56145.8(25) 56145.828.6ft 625 π π π = = = == Vrh h h
61. 2 2 2 2 2 (2) 4 44 π π π π = = = == Ar Ar r rA
Ifyoudoubletheradius,theareaisfourtimes theoriginalarea. 62.
Ifyoudoubletheradiusthevolumeis8times theoriginalvolume.
63. Let l= lengthoftherectangle and w =widthoftherectangle. Noticethat 22 ()() [()()][()()] (2)(2)44 lwlw lwlwlwlw lwlwA +−− =++−+−− === 122
So4[()()] Alwlw =+−−
Since2()0 lw−≥ ,thelargestareawilloccur when l–w =0or l=w;thatis,whenthe rectangleisasquare.But 1000222() 5002 250 lwlw lwl lw =+=+ =+= ==
Thelargestpossibleareais225062500 = sqft. Acircularpoolwithcircumference=1000feet yieldstheequation:500 21000rrπ π = =
Theareaenclosedbythecircularpoolis: 22 22 50050079577.47ft Arππ ππ
Thus,acircularpoolwillenclosethemostarea.
64. Considerthediagramshowingthelighthouseat pointL,relativetothecenterofEarth,usingthe radiusofEarthas3960miles.LetPrefertothe furthestpointonthehorizonfromwhichthe lightisvisible.Notealsothat 362362feetmiles. 5280 =

ApplythePythagoreanTheoremto

LetArefertotheairplane’slocation.The distancefromtheplanetopointPis2 d Wewanttoshowthat12120 dd+≥ Assumethealtitudeoftheairplaneis 10,000feet=10000miles. 5280
ApplythePythagoreanTheoremto CPAΔ :
2 22 2 2 2 2 10000 39603960 5280 10000 39603960 5280 122.49miles.
()
Therefore,thelightfromthelighthousecanbe seenatpointPonthehorizon,wherepointPis approximately23.30milesawayfromthe lighthouse.Brochureinformationisslightly overstated.
Verifytheshipinformation:
LetSrefertotheship’slocation,andlet x equal theheight,infeet,oftheship. Weneed1240 dd+≥ . Since123.30miles d ≈ weneed 24023.30=16.70miles. d ≥−
ApplythePythagoreanTheoremto
≈ 61Therefo re,1223.30122.49145.79120. dd+≈+=≥ Thebrochureinformationisslightlyunderstated. Notethataplaneatanaltitudeof6233feet couldseethelighthousefrom120milesaway.
Section R.4
4;3
416 x 3. 38 x
a
c
False;monomialscannothavenegativedegrees.
True
False;thedividend=(quotient)(divisor)+ remainder
Theshipwouldhavetobeatleast186feettallto seethelighthousefrom40milesaway.
Verifytheairplaneinformation:
9. 23 x Monomial;Variable: x ; Coefficient:2;Degree:3
10. 42 x Monomial;Variable: x ;Coefficient:–4; Degree:2
11. 81 8 x x = Notamonomial;whenwritteninthe form k ax ,thevariablehasanegativeexponent.
12. 23 x Notamonomial;whenwritteninthe form k ax ,thevariablehasanegativeexponent.
13. 22 xy Monomial;Variables:,xy ;Coefficient: –2;Degree:3
14. 523 xy Monomial;Variables:,xy ;Coefficient: 5;Degree:5
15. 81 8 x xy y = Notamonomial;whenwrittenin theform nm axy ,theexponentonthevariable y isnegative.
16. 2 23 3 22 x xy y −=− Notamonomial;when writtenintheform nm axy ,theexponentonthe variable y isnegative.
17. 22 xy + Notamonomial;theexpression containsmorethanoneterm.Thisexpressionis abinomial.
18. 2 34 x + Notamonomial;theexpression containsmorethanoneterm.Thisexpressionis abinomial.
19. 2 35 x Polynomial;Degree:2
20. 14 x Polynomial;Degree:1
21. 5Polynomial;Degree:0
22. –π Polynomial;Degree:0
23. 325 x x Notapolynomial;thevariableinthe denominatorresultsinanexponentthatisnota nonnegativeinteger.
SectionR.4: Polynomials
24. 32 x + Notapolynomial;thevariableinthe denominatorresultsinanexponentthatisnota nonnegativeinteger.
25. 3 22 y Polynomial;Degree:3
26. 102zz + Polynomial;Degree:2
27. 2 3 5 1 x x + Notapolynomial;thepolynomialinthe denominatorhasadegreegreaterthan0.
28. 3 2 321 1 xx xx +− ++ Notapolynomial;thepolynomial inthedenominatorhasadegreegreaterthan0.
29. 22 22 2 (68)(347) (3)(64)(87) 4215 +++−+ =++−++ =++ xxxx xxxx xx
30. 322 322 32 (32)(44) (3)(4)(24) 446 xxxx xxxx xxx +++−+ =+++−++ =+−+
31. 322 322 (2510)(243) 2510243 xxxxx xxxxx −++−−+ =−++−+− 322 32 (22)(54)(103) 497 xxxxx xxx =+−−+++− =−++
32. 232 232 (34)(35) 3435 xxxxx xxxxx −−−−++ =−−−+−− 322 32 (3)(3)(45) 449 xxxxx xxx =−+++−−+−− =−+−−
33. ()() 53432 542 653 653 xxxxxx xxxx +++−+ =+++
34. ()() 5232 532 108326 103106 xxxx xxx −+−+ =+−+
35. 22 22 2 (64)3(25) 646315 7311 −+++− =−+++− =−− xxxx xxxx xx
ChapterR: Review
36. 22 22 2 2(1)(52) 22252 73 xxxx xxxx xx −+++−−+ =−−−−−+ =−−
37. 3232 3232 32 6(3)4(23) 6618812 21818 xxxx xxxx xx +−−− =+−−+ =−+−
38. 323 323 8(431)6(482) 32248244812 xxxx xxxx −−−+− =−−−−+ 32 824484 xxx =−−+
39. ()()() 222 222 22351 22351 xxxxx xxxxx −++−+−+ =−++−+−− 2 246 xx =−+
40. ()()() 222 222 1452 1452 xxxx xxxx +−+++− =+−−++− 2 26 xx =−+−
41. ()() 22 22 2 75343 73521124 11359 −+−− =−+−+ =−+ yyy yyy yy
42. ()() 323 323 8141 884444 yyyy yyyy −++++ =−++++ 32 44412 yyy =−+++
43. 22432 (25)25 +−=+− xxxxxx
44. 23532 4(2)448 xxxxxx −+=−+
45. 2352 2(45)810 xxxx−+=−−
46. 343 5(34)1520 xxxx −=−
47. 2 22 (1)(24) (24)1(24) xxx xxxxx ++− =+−++− 322 32 2424 324 xxxxx xxx =+−++− =+−−
48. 2 22 (23)(1) 2(1)3(1) xxx xxxxx −++ =++−++ 322 32 222333 23 xxxxx xxx =++−−− =−−−
49. 2 2 (2)(4)428 68 xxxxx xx ++=+++ =++
50. 2 2 (3)(5)5315 815 xxxxx xx ++=+++ =++
51. 2 2 (27)(5)271035 21735 ++=+++ =++ xxxxx xx
52. 2 2 (31)(21)6321 651 xxxxx xx ++=+++ =++
53. 2 2 (4)(2)248 28 xxxxx xx −+=+−− =−−
54. 2 2 (4)(2)248 28 xxxxx xx +−=−+− =+−
55. 2 2 (6)(3)6318 918 −−=−−+ =−+ xxxxx xx
56. 2 2 (5)(1)55 65 xxxxx xx −−=−−+ =−+
57. 2 2 (23)(2)2436 26 xxxxx xx +−=−+− =−−
58. 2 2 (24)(31)62124 6104 xxxxx xx −+=+−− =−−
59. 2 2 (34)(2)3468 3108 −+−=−++− =−+− xxxxx xx
60. 2 2 (31)(1)331 341 xxxxx xx −−+=−−−− =−−−
61. 2 2 (5)(27)210735 21735 −−−−=+++ =++ xxxxx xx
62. 2 2 (23)(3)6293 239 xxxxx xx −−−=−+−+ =−−
63. 22 22 (2)()22 2 xyxyxxyxyy xxyy −+=+−− =−−
64. 22 22 (23)()2233 23 xyxyxxyxyy xxyy +−=−+− =+−
65. 22 22 (23)(32)6496 6136 xyxyxxyxyy xxyy −−+=−−−− =−−−
66. 22 22 (3)(2)263 273 xyxyxxyxyy xxyy −−+=−++− =−+−
67. 222 (7)(7)749 xxxx −+=−=−
68. 222 (1)(1)11 xxxx −+=−=−
69. 222 (23)(23)(2)349 xxxx +−=−=−
70. 222 (32)(32)(3)294 xxxx +−=−=−
71. 2222 (4)244816 xxxxx +=+⋅⋅+=++
72. 2222 (5)2551025 xxxxx +=+⋅⋅+=++
73. 2222 (4)244816 xxxxx −=−⋅⋅+=−+
74. 2222 (5)2551025 xxxxx −=−⋅⋅+=−+
75. 222 (34)(34)(3)4916 xxxx +−=−=−
76. 222 (53)(53)(5)3259 xxxx −+=−=−
77. 222 2 (23)(2)2(2)(3)3 4129 xxx xx −=−+ =−+
78. 222 2 (34)(3)2(3)(4)4 92416 xxx xx −=−+ =−+
79. () 2 222 ()()() xyxyxyxy +−=−=−
80. () 2 222(3)(3)()39 xyxyxyxy +−=−=−
81. () 2 222(3)(3)(3)9 xyxyxyxy +−=−=−
82. () 2 222(34)(34)(3)4916 xyxyxyxy +−=−=−
83. 222()2 xyxxyy +=++
84. 222()2 xyxxyy −=−+
85. () () () 222 22 (2)222 44 xyxxyy xxyy −=+⋅−+ =−+
86. ()()() 222 22 (23)22233 4129 xyxxyy xxyy +=+⋅+ =++
87. 33223 32 (2)32322 6128 xxxx xxx −=−⋅⋅+⋅⋅− =−+−
88. 33223 32 (1)31311 331 xxxx xxx +=+⋅⋅+⋅⋅+ =+++
89. 33223 32 (21)(2)3(2)(1)3(2)11 81261 xxxx xxx +=++⋅+ =+++
90. 33223 32 (32)(3)3(3)(2)3(3)22 2754368 xxxx xxx −=−+⋅− =−+−
91. 2 32 32 2 2 41123 2431 48 11 1122 231 2346 45 xx xxxx xx xx xx x x −+ +−++ + −+ + + 2 322 32 Check: (2)(41123)(45) 411238224645 431 xxx xxxxx xxx +−++− =−++−+− =−++ Thequotientis241123 xx−+ ;theremainder is–45.
ChapterR: Review
92. 2 32 32 2 2 3715 232 36 7 714 152 1530 32 xx xxxx xx xx xx x x −+ +−+− + −+ + 2 322 32
Check: (2)(3715)(32) 37156143032 32 xxx xxxxx xxx +−++− =−++−+− =−+−
Thequotientis23715 xx−+ ;theremainderis –32.
93. 232 3 2 2 43 431 4 31 3 1 x xxxx x xx x x −++ −++ +
232 Check: ()(43)(1)431 xxxxxx −++=−++
Thequotientis43 x ;theremainderis1 x +
94. 232 3 2 2 31 32 3 2 2 x xxxx x xx x x −+− −+−
232 Check: ()(31)(2)32 xxxxxx −+−=−+−
Thequotientis31 x ;theremainderis2 x
95. 2 2432 42 2 2 513 25031 510 131 1326 27 x xxxxx xx xx x x ++−++ + −++ +
Check: ()() () 22 422 42 251327 510132627 531 xxx xxxx xxx +−++ =+−−++ =−++
Thequotientis2513 x ;theremainderis 27 x + .
96. 2 2432 42 2 2 511 2502 510 112 1122 20 x xxxxx xx xx x x ++−+− + −+− +
Check: ()() () 22 422 42 251120 510112220 52 xxx xxxx xxx +−++ =+−−++ =−+−
Thequotientis2511 x ;theremainderis 20 x + .
97. 2 35432 52 2 2 2140031 42 1 x xxxxxx xx xx −++−++ −++
Check: ()()() 322 52252 2121 421431 xxxx xxxxxxx −+−++ =−−++=−++
Thequotientis2 2 x ;theremainderis 21xx −++
Check: ()() () 3252 31232 xxxxxx −+−=−+−
Thequotientis2
SectionR.4: Polynomials
ChapterR: Review
43232 4 Check: (1)(3335)(6) 333533 356 321 xxxx xxxxxx x xx −−−−−+− =−−−−++ ++− =−−−
Thequotientis323335 xxx ;the remainderis–6.
Thequotientis21 xx ;theremainderis
(1)(1)(22) 122 1 xxxxx xxxxxxxx x xx −++−+−+ =+−−−+++ −−+
Thequotientis21 xx+− ;theremainderis 22 x −+ .
22 323 32 2 22 23 23 00 0 xaxa xaxxxa xax ax axax axa axa ++ −++− 22 322223 33 Check: ()()0 xaxaxa xaxaxaxaxa xa −+++ =++−−− =−
Thequotientis22 xaxa ++ ;theremainderis0. 106. 432234 54325 54 4 423 0000 xaxaxaxa xaxxxxxa xax ax axax ++++ −++++− 23 2332 32 324 45 45 0 ax axax ax axax axa axa
108. Theproducts()() +− xyxy and()() +− zwzw willeachresultinabinomialthatisthe differenceofsquares.Theproductofthose resultingbinomialswillhave4terms.
109. Whenwemultiplypolynomials () 1 px and () 2 px ,eachtermof () 1 px willbemultiplied byeachtermof () 2 px .Sowhenthehighestpoweredtermof () 1 px multipliesbythehighest poweredtermof () 2 px ,theexponentsonthe variablesinthosetermswilladdaccordingtothe basicrulesofexponents.Therefore,thehighest poweredtermoftheproductpolynomialwill havedegreeequaltothesumofthedegreesof () 1 px and () 2 px .
110. Whenweaddtwopolynomials () 1 px and () 2 px ,wherethedegreeof () 1 px ≠ thedegree of () 2 px ,eachtermof () 1 px willbeaddedto eachtermof () 2 px .Sinceonlythetermswith equaldegreeswillcombineviaaddition,the degreeofthesumpolynomialwillbethedegree ofthehighestpoweredtermoverall,thatis,the degreeofthepolynomialthathadthehigher degree.
111. Whenweaddtwopolynomials () 1 px and () 2 px ,wherethedegreeof () 1 px =thedegree
of () 2 px ,thenewpolynomialwillhavedegree ≤ thedegreeof () 1 px and () 2 px .
112. Answerswillvary.
113. Answerswillvary.
Section R.5
1. ()() 322 xxx−+
2. prime 3. c 4. b 5. d 6. c
7. True;24 x + isprimeoverthesetofreal numbers.
8. False; () ()322 3264322 xxxxx −−+=−−
9. 363(2) xx+=+
10. 7147(2) xx−=−
11. 22(1)axaax+=+
12. (1)axaax−=−
13. 322(1)xxxxxx ++=++
14. 322(1)xxxxxx −+=−+
15. 2 222(1) xxxx−=−
16. 2 333(1) xxxx−=−
17. 22 36123(24) xyxyxyxyxy −+=−+
18. 2232 60487212(546) xyxyxyxyxyx −+=−+
19. 22211(1)(1)xxxx −=−=−+
20. 22242(2)(2)xxxx −=−=−+
ChapterR: Review
21. 222 41(2)1(21)(21) xxxx −=−=−+
22. 222 91(3)1(31)(31) xxxx −=−=−+
23. 222164(4)(4)xxxx −=−=−+
24. 222255(5)(5)xxxx −=−=−+
25. 2 254(52)(52) xxx −=−+
26. ()22 3699419(21)(21) xxxx −=−=−+
27. 22 21(1)xxx++=+
28. 22 44(2)xxx−+=−
29. 22 44(2)xxx++=+
30. 22 21(1)xxx−+=−
31. 22 1025(5)xxx−+=−
32. 22 1025(5)xxx++=+
33. 22 441(21) xxx++=+
34. 22 961(31) xxx++=+
35. 22 1681(41) xxx++=+
36. 22 25101(51) xxx++=+
37. 3332273(3)(39)xxxxx −=−=−++
38. 33321255(5)(525)xxxxx +=+=+−+
39. 3332273(3)(39)xxxxx +=+=+−+
40. () () 333 2 2 2783(2) (32)(964) 23469 xx xxx xxx −=− =−++ =−−++
41. 333 2 827(2)3 (23)(469) xx xxx +=+ =+−+
42. () () 333 2 2 64274(3) (43)(16129) 3491216 xx xxx xxx −=− =−++ =−−++
43. 256(2)(3) xxxx ++=++
44. 268(2)(4) xxxx ++=++
45. 276(6)(1) xxxx ++=++
46. 298(8)(1) xxxx ++=++
47. 2710(2)(5) xxxx ++=++
48. 21110(10)(1) xxxx ++=++
49. 21016(2)(8) xxxx −+=−−
50. 21716(16)(1) xxxx −+=−−
51. 278(1)(8) xxxx −−=+−
52. 228(2)(4) xxxx −−=+−
53. 278(8)(1) xxxx +−=+−
54. 228(4)(2) xxxx +−=+−
55. 2 24362(2)3(2) (2)(23) xxxxxx xx +++=+++ =++
56. 2 33223(1)2(1) (1)(32) xxxxxx xx −+−=−+− =−+
57. 2 51535(3)1(3) (3)(51) −+−=−+− =−+ xxxxxx xx
58. 2 3623(2)1(2) (2)(31) xxxxxx xx +−−=+−+ =+−
59. 2 6218283(27)4(27) (27)(34) +++=+++ =++ xxxxxx xx
60. ()() ()() 2 9632332132 3231 xxxxxx xx −+−=−+− =−+
61. 2 341(31)(1) xxxx ++=++
62. 2 231(21)(1) xxxx ++=++
63. 2 297(27)(1) ++=++ zzzz
64. 2 651(31)(21) zzzz ++=++
65. 2 568(54)(2) +−=−+ xxxx
66. 2 3108(34)(2) xxxx ++=++
67. 2 568(54)(2) −−=+− xxxx
68. 2 3108(34)(2) xxxx −+=−−
69. 2 5228(52)(4) ++=++ xxxx
70. 2 3148(32)(4) xxxx −+=−−
71. 2 5188(52)(4) +−=−+ xxxx
72. 2 3108(32)(4) xxxx −−=+−
73. Since b is10thenweneedhalfof10squaredto bethelastterminourtrinomial.Thus
12 2 22 (10)5;(5)25 1025(5)xxx == ++=+
74. Since b is14thenweneedhalfof14squaredto bethelastterminourtrinomial.Thus 12 2 22 (14)7;(7)49 1449(7)ppp == ++=+
75. Since b is-6thenweneedhalfof-6squaredto bethelastterminourtrinomial.Thus
12 2 22 (6)3;(3)9 69(3)yyy −=−−= −+=−
SectionR.5: Factoring Polynomials
76. Since b is-4thenweneedhalfof-4squaredto bethelastterminourtrinomial.Thus
12 2 22 (4)2;(2)4 44(2)xxx −=−−= −+=−
77. Since b is12thenweneedhalfof12squared tobethelastterminourtrinomial.Thus 2 11111 224416 22 111 2164 ();() ()xxx −=−−= −+=−
78. Since b is13thenweneedhalfof13squaredto bethelastterminourtrinomial.Thus 2 11111 236636 22 111 3366 ();() ()xxx == ++=+
79. 236(6)(6) xxx−=−+
80. 29(3)(3) xxx−=−+
81. ()() 22 282(14)21212 xxxx −=−=−+
82. ()() 22 3273(19)31313 xxxx −=−=−+
83. 21110(1)(10) xxxx ++=++
84. 254(4)(1) xxxx ++=++
85. ()() 2102173 xxxx −+=−−
86. 268(2)(4) xxxx −+=−−
87. ()22 4832428 xxxx −+=−+
88. ()22 31215345 xxxx −+=−+
89. 2416xx++ isprimeovertherealsbecause therearenofactorsof16whosesumis4.
90. 22 1236(6)xxx++=+
91. 22 152(215)(5)(3) xxxxxx +−=−−−=−−+
ChapterR: Review
92. 22 146(614) xxxx +−=−−− isprimeoverthe integersbecausetherearenofactorsof–14 whosesumis–6.
93. 22 312363(412) 3(6)(2) xxxx xx −−=−− =−+
94. 322820(820) (10)(2) xxxxxx xxx +−=+− =+−
95. 43222 2 1130(1130) (5)(6) yyyyyy yyy ++=++ =++
96. 322 318483(616) 3(2)(8) yyyyyy yyy −−=−− =+−
97. 22 4129(23) xxx++=+
98. 22 9124(32) xxx−+=−
99. () ()() 22 6822341 2311 xxxx xx ++=++ =++
100. () ()() 22 8622431 2411 xxxx xx +−=+− =−+
101. () 2 42222 2 819(9)(9) (3)(3)(9) xxxx xxx −=−=−+ =−++
102. () 2 42222 2 11(1)(1) (1)(1)(1) xxxx xxx −=−=−+ =−++
103. 6332 22 222 21(1) (1)(1) (1)(1) xxx xxx xxx −+=− =−++ =−++
104. 6332 22 222 21(1) (1)(1) (1)(1) xxx xxx xxx ++=+ =+−+ =+−+
105. 75525(1)(1)(1)xxxxxxx −=−=−+
106. 855352(1)(1)(1)xxxxxxxx −=−=−++
107. () 22 1624943 xxx++=+
108. () 22 9241634 xxx−+=−
109. 22 51616(16165) (45)(41) xxxx xx +−=−−− =−−+
110. 22 51116(16115) (165)(1) xxxx xx +−=−−− =−+−
111. 2 41615(25)(23) yyyy −+=−−
112. 2 994(34)(31) yyyy +−=+−
113. 2442 22 2 189(981) (91)(1) (31)(31)(1) xxxx xx xxx −−=−+− =−−+ =−−++
114. 2442 22 2 41482(472) 2(41)(2) 2(21)(21)(2) xxxx xx xxx −−=−+− =−−+ =−−++
115. (3)6(3)(3)(6) xxxxx +−+=+−
116. 5(37)(37)(37)(5) xxxxx −+−=−+
117. [ ] 2 (2)5(2)(2)(2)5 (2)(3) xxxx xx +−+=++− =+−
118. [ ] 2 (1)2(1)(1)(1)2 (1)(3) xxxx xx −−−=−−− =−−
119. () () ()()() () () () () 3 33 2 2 2 3227 323 323323329 359124969 35937 x x xxx xxxx xxx =−− =−−−+−+
=−−++−+ =−−+
120. () () ()()()() () () 3 33 2 2 2 511 511 511511511 525101511 525153 x x xxx xxxx xxx +− =+− =+−++++ =+++++ =++
121. () () ()() ()() ()() ()() 2 2 3102545 3545 5354 53154 5311 xxx xx xx xx xx ++−+ =+−+ =++−
=++− =++
122. () () ()() ()() ()() ()() 2 2 76953 7353 3735 37215 3716 xxx xx xx xx xx −++− =−+− =−−+ =−−+ =−−
123. () 322 2 22(2)12 (2)(1) (2)(1)(1) xxxxxx xx xxx +−−=+−+ =+− =+−+
124. () 322 2 33(3)13 (3)(1) (3)(1)(1) xxxxxx xx xxx −−+=−−− =−− =−−+
125. () 433 3 2 1(1)11 (1)(1) (1)(1)(1) xxxxxx xx xxxx −+−=−+− =−+ =−+−+
126. () 433 3 2 22 1(1)11 (1)(1) (1)(1)(1) (1)(1) xxxxxx xx xxxx xxx +++=+++ =++ =++−+ =+−+
SectionR.5: Factoring Polynomials
127. ()()() ()()()() ()() ()() 2 234232343 23434233 2343469 234913 xxx xxx xxx xx +++⋅+⋅ =++++⋅ =++++ =++
128. ()()() ()()()() ()() ()() 2 521562212 21521564 211052024 213019 xxx xxx xxx xx ++−⋅+⋅ =+++−⋅ =+++− =+−
129. ()()() () () 2 2252225 225 235 xxxxxx xxx xx ++⋅=++ =++ =+
130. ()()() () () 232 2 2 38383838 2498 329 xxxxxx xxx xx −+⋅=−+ =−+ =−
131. ()()()() ()()()()() ()()() ()()() ()()() 322 2 2 2 2 232332 322233 322439 3255 5321 xxxx xxxx xxxx xxx xxx +−++⋅− =+−−++⋅ =+−−++ =+−+ =+−+
132. ()()()() ()()()() () ()()() ()()() ()()() ()()() 324 3 3 3 3 3 451521 251215 251225 25133 23511 6511 xxxx xxxx xxxx xxx xxx xxx +−++⋅− =+−−++ =+−−++ =+−+ =⋅+−+ =+−+
133. ()() ()()() ()() ()() ()() 2 432434 43438 43438 43123 34341 xxx xxx xxx xx xx −+⋅−⋅ =−−+ =−−+ =−− =−−
134. ()() ()()() ()() ()() 2 23 2 2 2 3342343 334342 334342 33454 xxxx xxxx xxxx xxx ++⋅+⋅ =+++ =+++ =++
135. ()()()() ()()()() () ()()() ()()() 322 2 2 2 235321353212 635212135 635212135 6352154 xxxx xxxx xxxx xxx −⋅++−⋅+⋅ =−+++− =−+++− =−+−
136. ()()()() ()()()() () ()()() ()()() 223 2 2 2 345451452515 24551651545 245513062025 245515031 xxxx xxxx xxxx xxx +⋅+++⋅+⋅ =+++++ =+++++ =+++
137. 424244 424 424 42 (1) (1) (1) xxxxxx xxx xx xx −−+ +=+ =+ =+ =+
138. 543 541322 5552 52 268 268 2(34) 2(134) xxx xxxxxxx xxxxx xxx −+ =−+ =−+ =−+
139. 21 22 2 22 22 (1)(1) (1)(1) [(1)(1)] (1) (1) xxxx xxxxx xxxx xxxx xx ++− =++− =++− =++− =+
140. () 122 222 22 2 2 (3)4(3) 3(3)4(3) (3)((3)4) (3)(34) (3)(53) xxxx xxxxx xxxx xxxx xxx +++ =++++ =+++ =+++ =++
141. Thepossiblefactorizationsare ()() 2 1454xxxx ±±=±+ or ()() 2 2244xxxx ±±=±+ ,noneofwhich equals24 x +
142. Thepossiblefactorizationsare () 22 121xxx ±=±+ ,neitherofwhichequals 21xx++
143. Answerswillvary.
144. Answerswillvary.
Section R.6
1. quotient;divisor;remainder 2. 32051 3. d 4. a 5. True 6. True 7. 217510 21010 1550
Quotient:255 xx Remainder:0 8. 11231 114 1145
Quotient:24 xx+− Remainder:5
9. 33213 93396 3113299
Quotient:231132 xx++
Remainder:99
10. 24211 82042 4102143
Quotient:241021 xx −+−
Remainder:43
11. 3104010 391545138 1351546138
16. 2.10.100.2 0.210.441 0.10.210.241
Quotient:0.10.21 x Remainder:0.241
17. 21000032 2481632 1248160
Quotient:43224816++++xxxx Remainder:0
18. 1100001 11111 111110
Quotient:432351546
Remainder:138 xxxx −+−+
12. 210102 241020 1251022
Quotient:322510xxx+++
Remainder:22
13. 14030105 441122 4411227
Quotient:4321 xxxx−+−+
Remainder:0
19. 24384 8104 4528
Remainder=8 ≠ 0.Therefore,2 x isnota factorof324384 xxx−−+
20. 34508 1251153 41751161
Quotient:54324422
Remainder:7 xxxxx +++++
14. 11050010 11666 1166616
Quotient:432666xxxx−+−+ Remainder:–16
15. 1.10.100.20
0.110.1210.3531 0.10.110.3210.3531
Quotient:20.10.110.321 xx−+ Remainder:–0.3531
Remainder=161 ≠ 0.Therefore,3 x + isnota factorof32458 xx −++
21. 3260721 60021 20070
Remainder=0.Therefore,3 x isafactorof 43 26721 −−+xxx
22. 2401504 81624 48120
Remainder=0.Therefore,2 x isafactorof 42 4154 xx
23. 2500430024 10204061224 3102036120
Remainder=0.Therefore,3 x + isafactorof 63 54324 ++xx
24. 320180109 6180039 2600130
Remainder=0.Therefore,2 + x isafactorof 642 2189 xxx−+− 25. 410161019 4160416 140143
Remainder=1 ≠ 0.Therefore,4 + x isnota factorof5321619−−+xxx
26. 4101601016 41600416 1400140
Remainder=0.Therefore,4 x + isafactor 6421616xxx−+−
27. 131062 3 1002 30060
Remainder=0;therefore1 3 x isafactorof 43 362 −+−xxx .
28. 131031 3 1001 30032
Remainder=20 ≠ ;therefore1 3 x + isnota factorof43331 +−+xxx
29. 21235 2822 141117 32 2 23517 411 22 xxx xx xx −++− =−++ ++ 1411179 abcd+++=−+−=−
30. 23 23 2 1322 3 130 hhhhh hhhh hh 322 3 ++− xxhxh isthequotientand0isthe remainder.
31. 234 233 23 1334 254 12540 yyyyy yyyy yyy Yes, + xy isafactorof 432234 334 +−−+ xxyxyxyy
32. Answerswillvary.
Section R.7
1. lowestterms 2. LeastCommonMultiple 3. d 4. a
5. True; 113 33 115 55 355(3) 353(5) + + = + + =⋅= x xx x xx xxx xxx
6. False; () () ()() 322 433 3 2623 64232 2332 xxxx xxxx LCMxxx +=+ +=+ =++
7. 2 3(3) 393 9(3)(3)3 xx xxxx + + == −+−
8. 24(2)48 122412(2)3 xxxxx xx + + == ++
9. 2(2) 2 363(2)3 xxxxx xx ==
10. 2 22 3(58) 152458 33 xx xxx xxx + ++ ==
11. 22 2 24244 1266(21)21 xxx xxxxx ==
12. () 2 2 (2)2 442 4(2)(2)2 xx xxx xxxx ++ +++ == −+−
13. ()() () ()() ()() () 2 22 4977 31821367 77 371 7 31 +− = +− = −+ + = + yyy yyyy yy yy y y
14. ()() ()() 2 2 321 321 3523211 yy yyy yyyyy +− == + ++ ++
15. 2 2 (6)(2) 4126 44(2)(2)2 +− +−+ == −+ xx xxx xxxxx
16. 2 2 (1) 2(2)(1)22 xxxxxx xxxxxx ===− +−++ +−
17. ()() ()() () () 254 20 42 54 14 5 +− +− = +− = =−+ xxxx xx xx x x
18. 2(21)(3) 253(3)3 121(21) xxxx xx xx −+ +− ==−+=−−
19. 222 363(2) 545(2)(2) 3 5(2) x xxx xxxxx xx + + ⋅=⋅ −+ =
20. 2 333 261022(35)4(35) xxx xxxx ⋅=⋅= +++
SectionR.7: Rational Expressions
21. () () () () ()() () 23 2 22 2 2 464 162 44416 (4)(4)2 224416 244 2416 4 xx xx xxxx xxx xxxxx xxx xxx x −++ =⋅ −+ ⋅−++ = −+ ++ = +
22. () () ()() () () 32 2 2 2 12112(1)(1) 42(1)2(21) 2611 2121 61 21 xxxx xxxxxx xxx xxx xx xx +−+ + ⋅=⋅ −+− + ⋅+−+ = +− −+ =
23. () () () ()() 42 481212 3126362 422 312 8 3 xx xxxx x xx x ⋅=⋅ =⋅ =
24. () () 329 627223 541855 229 xx xxxx x ⋅=⋅=
25. ()() ()() ()() ()() 22 22 412432 2481016 6284 8682 4 8 −−+− +−++ −++− =⋅ +−++ = + xxxx xxxx xxxx xxxx x x
26. ()() ()() ()() ()() ()()() ()()() 22 22 625 45215 2355 5153 235 513 xxx xxxx xxxx xxxx xxx xxx +−− +−+− −++− =⋅ +−+− −+− = +−−
27. 2 2 6 4624 3939 4 24 62(2) (2)(2)3(3) 4 (2)(3) x xxx xx x x xx xxx x xx + =⋅ + + =⋅ −+− =
28. 2 22 2 2 12 5201216 520 44 16 12(4)(4) 5(4)4 3(4) 5 x xxx x xx x xxx xx x x + =⋅ + +− =⋅ + =
29. ()() () 2 2 8 181 1010 1 1 81 1110 4 51 x xxx xx x x xx xxx x + =⋅ + + =⋅ −+ =
30. ()() 22 2 4212 4 4444 12 212 422 3 2 x xxx x xxxx x xx xxx x =⋅ −+−+ =⋅ =
31. ()() ()() () 2 2 2 4 4416 444 16 444 44 44 4 4 4 x xxx xxx x xxx xx xx x x x + =⋅ + +− =⋅ + = =−
32. 3 22 3 3 339 3 99 9 x xxx x xx x + + =⋅ ()() ()() () () 3 3 3 2 3 2 39 333 9 33 9 3 9 3 xx xxx x xx x x x x + =⋅ +− = = =−
33. 2 222 222 2 2 2 712 71271212 1271212 12 (3)(4)(4)(3) (3)(4)(4)(3) (3) (3) xx xxxxxx xxxxxx xx xxxx xxxx x x ++ ++−− −+ =⋅ +−−++− ++−+ =⋅ −−+− + = 34. 2 222 222 2 76 67656 56656 56 (6)(1)(2)(3) (3)(2)(6)(1) (1)(2) (2)(1) xx xxxxxx xxxxxx xx xxxx xxxx xx xx ++ ++++ +− =⋅ +−+−+− ++ ++++ =⋅ +−+− ++ = 35. 2 222 222 2 576 23557621320 1514323515143 21320 (53)(2)(25)(4) (1)(25)(53)(31) (2)(4) (1)(31) −−++ +− =⋅ +++−++ ++ +−++ =⋅ −+++ −+ = −+ xx xxxxxx xxxxxx xx xxxx xxxx xx xx
36. 2 222 222 2 932 12529328103 9611252961 8103 (32)(31)(41)(23) (32)(41)(31)(31) (41)(23) (41)(31) xx xxxxxx xxxxxx xx xxxx xxxx xx xx +− +−−− +− =⋅ −++−−+ +−+− =⋅ +−−− +− =
37. 55 222 xx + +=
38. 363633 xxxxx −===−
39. ()() 2222 44 23232323 xxxx xxxx +− −==
40. ()222 393933 21212121 xxx xxxx −==
41. 53253243 4444 +−++−+ +== xxxxx xxxx
42. 25425431 32323232 xxxxx xxxx −+−++− +== ++++
43. 3524(35)(24) 212121 3524 21 9 21 xxxx xxx xx x x x +−− +− −= +−+ = + =
44. 541(54)(1) 343434 541 34 45 34 xxxx xxx xx x x x −−+ −+ −= +++ = + = +
45. 444 22222 xxx xxxxx +=−=
46. 666 11111 xxx xxxxx + −=+=
SectionR.7: Rational Expressions
47. 737(1)3(3) 31(3)(1)(1)(3) 7739 (1)(3) 416 (1)(3) 4(4) (1)(3) +− −=− −+−++− +−+ = +− + = +− + = +− xx xxxxxx xx xx x xx x xx
48. 252(5)5(5) 55(5)(5)(5)(5) 210525 (5)(5) 335 (5)(5) 335 (5)(5) xx xxxxxx xx xx x xx x xx −+ −=− +−+−+− = +− = +− + =− +−
49. 22 2 23(1)(23)(1) 11(1)(1)(1)(1) 23 (1)(1) 323 (1)(1) xxxxxx xxxxxx xxxx xx xx xx −−+ +=+ +−+−−+ −+−− = −+ = −+
50. () 22 2 323(3)2(4) 43(4)(3)(4)(3) 3928 (4)(3) 5 (4)(3) 51 (4)(3) xxxxxx xxxxxx xxxx xx xx xx xx xx +− +=+ −+−+−+ ++− = −+ + = −+ + = −+
51. 22 22 34(3)(2)(4)(2) 22(2)(2)(2)(2) 56(68) (2)(2) 5668 (2)(2) 112(112) or (2)(2)(2)(2) xxxxxx xxxxxx xxxx xx xxxx xx xx xxxx −−++ −+ −=− +−+−−+ −+−++ = +− −+−−− = +− −+ = +−+−
52. 22 22 2321(23)(1)(21)(1) 11(1)(1)(1)(1) 23(21) (1)(1) 2321 (1)(1) 2 (1)(1) 2 (1)(1) xxxxxx xxxxxx xxxx xx xxxx xx xx xx −++− −+ −=− −+−++− = +− −−−++ = +− = +− =− +−
53. () () () ()() 22 22 2 2 2 14 44 24 4 22 22 xxx xxxx x xx x xxx +− += = = −+
54. () () () () () 24 3232 324 32 432 32 111 11 1 1 1 1 xxxxx xxxx xxxx xx xxxx xx −++ += + + −+−+ = + +−+− = +
55. ()() 2422 xxx−=+− ()() 2212 xxxx −−=+−
Therefore, ()()() LCM221 xxx =+−+
56. ()() 21234 xxxx −−=+− ()() 281644 xxxx −+=−−
Therefore, ()() LCM342 xx =+− .
57. () ()() 32111 xxxxxxx −=−=+− ()21 xxxx−=−
Therefore, ()() LCM11 xxx =+− .
58. () ()() 22 32739333 xxxx −=−=+− ()() 2 215253 xxxx −−=+−
Therefore, ()()() LCM32533 xxx =+−+ .
59. () ()() 322 44441 2121 xxxxxx xxx −+=−+ =−− () 322 3 221 xxxx x −=−
Therefore, () 32LCM21 xx =− .
60. 3 x () () ()() 2 32 33 9933 xxxx xxxxxxx +=+ −=−=+−
Therefore, ()() LCM33 xxx =+− .
61. () ()() 32111 xxxxxxx −=−=+− () () () () 3222 32 2211 111 xxxxxxxx xxxx −+=−+=− −=−++
Therefore, ()() ()22 LCM111 xxxxx =+−++
62. () 22 442xxx++=+ () () 322 3 22 2 xxxx x +=+ +
Therefore, () 23LCM2 xx =+ .
63. 22 22 76224 (6)(1)(6)(4) (4)(1) (6)(1)(4)(6)(4)(1) 45 (6)(4)(1)(6)(4)(1) xx xxxx xx xxxx xxxx xxxxxx xxxxx xxxxxx −+−− =− −−−+ +− =− −−+−+− +−+ == −+−−+−
64. 2 22 1 3524 1 (3)(3)(8) (8)1 (3)(8)(3)(8) 8171 (3)(8)(3)(8) xx xxx xx xxx xxx xxxx xxxxx xxxx + +− + =− −−+ + + =− −+−+ +−−+− == −+−+
65. 22 42 46 42 (2)(2)(3)(2) x xxx x xxxx −+− =− −++− 2 2 2 4(3)2(2) (2)(2)(3)(3)(2)(2) 41224 (2)(2)(3) 4104 (2)(2)(3) 2(252) (2)(2)(3) xxx xxxxxx xxx xxx xx xxx xx xxx ++ =− −+++−+ +−− = −++ +− = −++ +− = −++
66. 22 2 2 2 2 2 3434 1(1)21(1) 3(1)4 (1)(1)(1) 334 (1) 344 (1) xxxx xxxxx xxx xxx xxx x xx x −=− −+− =− −−+ = −+ =
67. ()() ()() ()() ()() ()() ()() 22 22 22 22 32 1111 3121 11 3322 11 51 11 xxxx xx xx xx xx x xx + −+−+ ++− = −+ ++− = −+ + = −+
68. ()() ()() 22 26 2121xxxx +−+− ()() ()() ()() ()() () ()() 22 22 22 22 2162 21 22612 21 414 21 227 21 xx xx xx xx x xx x xx −−+ = +− = +− = +− −+ = +−
SectionR.7: Rational Expressions
69. 22 22 2 423 228 423 (2)(1)(4)(2) (4)(4)(23)(1) (2)(1)(4)(4)(2)(1) 816(253) (2)(1)(4) 313 (2)(1)(4) xx xxxx xx xxxx xxxx xxxxxx xxxx xxx xx xxx ++ −−+− ++ =− −++− ++++ =− −+++−+ ++−++ = −++ −++ = −++
70. 22 232 87(1) xx xxx+++ 2 2 22 2 2 2 232 (1)(7)(1) (23)(1)(2)(7) (1)(7)(1)(1)(7) 23(514) (1)(7) 611 (1)(7) xx xxx xxxx xxxxx xxxx xx xx xx =− ++ + −+−+ =− +++ ++ −−−+− = ++ −+ = ++
71. 232 123 xxxxx −+ +− () () ()()()() ()() () ()() ()() ()() 2 2 22 2 32 2 32 2 123 11 112131 11 12233 11 253 11 243 11 xxxxx xxxxxx xxx xxxxx xxx xxxx xxx xxx xxx =−+ + +−−−++ = +− −−+++ = +− −−++ = +− −++ = +−
72. () 232 21 1 xx xxxx + +− () () ()()() () ()() () () () 22 32 22 322 22 3322 22 32 22 21 11 2111 1 2211 1 2421 1 3521 1 xx xxxx xxxxx xx xxxxx xx xxxxx xx xxx xx + =+− +−−+− = +−+−− =
73. 111111() ()() 1 () () 1 () xxh hxhxhxhxxxh xxh hxxh h hxxh xxh +
74. 22 111 () hxhx + 22 2222 222 22 2 22 22 22 22 111() ()() 1(2) () 2 () (2) () 2 () 2 () xxh hxhxxxh xxxhh hxxh xhh hxxh hxh hxxh xh xxh xh xxh
75. 111111 111
76. 22 2222 22 2222 22 22 2 2 414141 313131 41 31 41 31 xx xxxx xx xxxx xx xx x x
77. () () ()() () 212121 13313311 11 11 1 11 42221 1 11 221 xxxxx xxxx xxx xx xx xx x xxx xxx x xx xx ++−− == −++− + +
++ ++ −+ ==⋅ + + + −+ = + 78. 2 11 1111 1 21211 1 11 (1) xxx xxxx xxxx xxxx x xx x x +
+++ + == −+ =⋅ ++ = + 79. 43 21 1 xx xx x +− −+ + 22 2 (4)(1)(3)(2) (2)(1)(1)(2) 1 54(56) (2)(1) 1 1021 (2)(1)1 2(51) (2)(1) xxxx xxxx x xxxx xx x x xxx x xx ++−− −++− = + ++−−+ −+ = + =⋅ −++ = −+
80. 2 12 3 xx xx x +− + () 22 (2)(2)(1) (1)(2)(2)(1) 3 44() (2)(1) 3 541 (2)(1)3 54 (2)(1)(3) 54 (2)(1)(3) xxxx xxxx x xxxx xx x x xxx x xxx x xxx −−+ +−−+ = + −+−+ −+ = + −+ =⋅ −++ −+ = −++ = −++
81. 21 21 23 1 xx xx xx xx + ++ + 2 22 22 2 2 2 (2)(1)(1)(2) (2)(1)(1)(2) (23)(1) (1)()(1) 22 (2)(1) (23) (1) 24 (2)(1) 3 (1) 2(2)( (2)(1) xxxx xxxx xxx xxxx xxxx xx xxx xx x xx xx xx xxx xx −+−+ + ++++ = −+ ++
−−++− ++ = + ++ = −++ + −+ =⋅ ++ 2 2 2 2 2 1) (3) 2(2) (2)(3) 2(2) (2)(3) xx xx xxx xx xxx = −+−− = +−−
SectionR.7: Rational Expressions
82. 22 25 3 (1) 33 xx xx xx xx + + −+ 22 22 3232 2 2 2 (25)(3)() (3)(3) (3)(3)(1) (3)(3)(3)(3) 215 (3) 3(53) (3)(3) 15 (3) 453 (3)(3) 15( (3) xxxx xxxx xxxx xxxx xxx xx xxxxx xx xx xx xx xx xxx xx +− = +−+ −+−+
= +−−−− −+
= ++ −+ =⋅ 2 2 2 3)(3) 453 (15)(3) (453) x xx xxx xxx −+ ++ −−+ = ++
83. 1111 111 1 1 1 1 1 1 x xx x x xx x x −=− =− = = 84. 111111 1111 111 1111 1 1 xx xxx xx xx xx x x −=−=− =−=+ +− = =
85. () () () () () () 1 1 2231 2133111 3213123 2 111 231 1 321 1 x xxxx xx xxx x x x x ++ −+ == −+ + + +− = +− () () () () 2311 1321 231233 321322 31 21 xx xx xx xx x x +− =⋅ −+− +− +− == +−+− = +
86. () () () () () () 1 1 4432 4233222 3123213 1 222 432 2 32 2 x xxxx xx xxx x x x x + +− +++ == + +− + ++ −+ + = −+ + () () () () 4322 232 432436 3232 3232 11 xx xx xx xx xx xx −+ + =⋅ +−+ −+ == −+−− −−+ == −+−
87. ()() () () () 22 2 23335269610 3535 19 35 xxxx xx x +⋅−−⋅ +−+ = =
88. ()() () () () 22 2 415524205208 5252 13 52 xxxx xx x +⋅−−⋅ +−+ = =
89. () () () () ()() () 222 2222 2 22 22 21121 11 1 1 11 1 xxxxx xx x x xx x ⋅−+⋅ = ++ = + −+ = +
90. () () () () ()() 2222 222222 2 22 241244 444 4 22 xxxxxx xxx x xx ⋅−−⋅ −++ == + = +−
91. () () () () () () 222 22 2 2 2 3123623 3131 32 31 32 31 xxxxxx xx xx x xx x +⋅−⋅ +− = ++ + = + + = +
92. () () () () () () 23323 22 32 2 2 2 25326152 2525 415 25 415 25 xxxxxx xx xx x xx x = = =
93. () () () () 222 2222 133423368 11 xxxxxx xx +⋅−+⋅ +−− = ++ () () () ()() () 2 22 2 22 22 383 1 383 1 313 1 xx x xx x xx x −−+ = + −+− = + −+ =− +
94. () () () () () () () 222 2222 2 22 2 22 92252218410 99 21018 9 259 9 xxxxxx xx xx x xx x +⋅−−⋅ +−+ = ++ −++ = + = +
95. 12 111 (1) n fRR =−+
() () () 21 12 12 21 1221 12 21 1(1) (1) 1 (1) (1)
0.1(0.2) (1.51)(0.20.1) 0.020.022 meters 0.5(0.3)0.1515 RR n fRR RR nRR f f RRnRR RR fnRR f + =−
96. 231312 123123 1111 RRRRRR RRRRRRR ++ =++= 123 231312 5410 41051054 20020ohms 11011 RRR R RRRRRR = ++ ⋅⋅ = ⋅+⋅+⋅ ==
97. ()() ()() () 2 2 339333 215(3)(5) 333 (3)(5)(5) 12 5 312 312 4 +−+ +−− = −+ +− −++ = −++ + = + +=+ = = xxkxkxxkxk xxxx xxkxk xxx x x xkx k k
SectionR.7: Rational Expressions
98. 2 7121 236 (3)7(2)121 3714121 (7)314121 712 5 += +− −+ −++=− −++=− +−+=− += = Ax xxxx Axxx AxAxx xAAx so A A
99. 11 11,1,0 xabc xx + += === 11 111 1111 121 11 2,1,1 x xx xx xxx xx abc +=+=+ + + + +++ == ++ === 111111 121121 111 21132 2121 3,2,1 x xx x x xxx xx abc + +=+=+ + + + + + ++++ == ++ === 1121111 132132 1121 11 322153 3232 5,3,2 x xx x x xxx xx abc + +=+=+ + + + + + + ++++ == ++ ===
Ifwecontinuethisprocess,thevaluesof a, b and c producethefollowingsequences: :1,2,3,5,8,13,21,.... :1,1,2,3,5,8,13,21,..... :0,1,1,2,3,5,8,13,21,..... a b c Ineachcasewehavea FibonacciSequence, wherethenextvalueinthelistisobtainedfrom thesumoftheprevious2valuesinthelist.
ChapterR: Review
100. Answerswillvary.
101. Answerswillvary.
Section R.8
1. 9;9
2. 4;44 −=
3. index
4. cuberoot
5. b
6. d
7. c
8. c
9. true
10. False; () 44333−=−=
11. 3332733 ==
12. 4441622 ==
13. () 33 3 822 −=−=−
14. () 33 3 111 −=−=−
15. 84222 =⋅=
16. 7525353 =⋅=
17. 7001007107 =⋅=
18. 32 459535 =⋅⋅⋅= xxxxx
19. 333 328424 =⋅=
20. 333 5427232 =⋅=
21. 33433882 xxxxx−=−⋅=−
22. 3335322 19264343 =⋅⋅= xxxxx
23. 444 24381333 =⋅=
24. 44544 4816323 xxxxx =⋅=
25. ()()44 41283232 4 xyxyxy ==
26. ()5 5105252 5 xyxyxy ==
27. 97 44842 3 xy xyxy xy ==
28. 23 33 42333 3111 81273 27 xy xyxx x ===
29. 648 = xx
30. 542933 xxxxx =⋅=
31. () ()() 444491223 4 234 16223 32 xyxxy xyx = =
32. ()()33314103243 3 432 3 405(2) 25 xyxxyy xyxy −=− =−
33. 222 1557525353 =⋅=⋅⋅⋅= xxxxxxxx
34. 34252010010 xxxx ==
35. () () () 22233 32333 5959 59581533153 = =⋅==⋅=
36. () () () 44433 34233 310310 310331003003 = =⋅=⋅=
37. () () 3622612643123 ==⋅=
38. () () 58331524306 −=−=−
39. () 324234272 +=+=
40. () 654564525 −=−=
41. () 48512163543 43523 4103 63 −+=−⋅+⋅ =−+⋅ =−+ =
42. () 212327243393 4393 493 53 −=⋅−⋅ =− =− =−
43. () () () 2 333133333 3233 23 +−=+−− =+− =
44. () () () 2 5253525356 556 51 −+=−+− =+− =−
45. () 333 3 33 3 3 5225452232 5262 562 2 −=−⋅ =− =− =−
46. () 3333 33 3 3 9248192333 18333 1833 153 −=⋅− =− =− =
47. () () 22 121 21 xxx xx −=−+ =−+
48. () () () () () 222 5255 255 xxx xx +=++ =++
49. () 334333 33 3 162822 222 212 xxxxx xxx xx −=⋅− =− =−
SectionR.8: nth Roots; Rational Exponents
50. () () 445444 44 44 3221622 222 22or22 xxxxx xxx xxxx +=⋅+⋅ =+ =++
51. () 32 8350423252 22152 2152 xxxxx xxx xx −=⋅−⋅ =− =−
52. () 39425920 920 xyyxyy xy +=+ =+
53. () () () 4433 3 3333 3 333 3 33 163252 823252 223252 2352 52or52 xyxxyxy xxyxxyyxy xxyxxyyxy xxyxy xyxyxyxy −+− =⋅−+−⋅ =−− =−− =−−−+
54. () 2233 3 8258852 852 5 xyxyxyxyxyxy xy xy −+=−+ =−+ =
55. 1122 2222 =⋅=
56. 22323 3333 =⋅=
57. 33515 5555 =⋅=
58. 333266 822222224 ==⋅==
59. () () 3352 525252 352 252 352536 or 2323 + =⋅ −−+ + = + + =
60. () () 2272 727272 272 74 2721422 or 33 =⋅ ++− = =
61. 2525235 235235235 4256515 445 19858519 4141 =⋅ ++− −−+ = ==
62. 3131233 233233233 623333953 1293 =⋅ ++− −−+− ==
63. 5521 212121 525525 21 + =⋅ −−+ + ==+
64. 3354 545454 35123512 51611 3512 11 =⋅ ++− −+−+ == =
65. 33 333 55454 2242 =⋅=
66. 33 333 22323 9933 =⋅=
67. ()() () 2 2 2 2 22 xhxxhxxhx xhxxhxxhx xhxxhx xhx xhxxhx xhx xhxxh h +−+−+− =⋅ +++++− +−++ = +− +−++ = +− +−+ =
68. xhxh xhxh ++− +−− ()()() () ()() 22 22 22 2 2 22 2 xhxhxhxh xhxhxhxh xhxhxhxh xhxh xhxhxh xhxh xxh h xxh h ++−++− =⋅ +−−++− ++−++− = +−− ++−+− = +−+ +− = +− =
69. () () 111111111 22111 11110 21112111 5 111 ++− =⋅ == =
70. () () 5435435432543 335433543 1866 3543543543 −−+− =⋅= + + ===− ++ +
71. () 615615615 1515615 6159 901531015 93 3105105 −−+ =⋅ + == ==−
72. 535353 5553 532 515515 ++− =⋅ ==
73. () () 1 −−+ =⋅ + == + −+ xcxcxc xcxcxc xc xcxcxc
74. () () 222 442 41 422 −−+ =⋅ + == + −+ xxx xxx x xxx
75. () () () () 717171 8871 71 871 8 871 1 71 −−−−−+ =⋅ −+ = −−+ = −−+ = −+ xxx xxx x xx x xx x
76. () () () () 494949 252549 16(9) 2549 25 2549 −−−−+− =⋅ +− = −+− = −+− xxx xxx x xx x xx () () 25 2549 1 49 =− −+− =− +− x xx x
77. () 2 2/32 3 8824 ===
78. ()3 3/23 4428 ===
79. ()1/33 64644 −=−=−
SectionR.8: nth Roots; Rational Exponents
80. ()3 3/43 4 161628 ===
81. ()3 3/23 100100101000 ===
82. ()3 3/23 25255125 ===
83. () 3/2 3/233 41111 428 4 ====
84. () 3/2 3/233 161111 16464 16 ====
85. () 3/2333 33 9933 882222 2727272 8221621622 272 32
86. 2 2/32 3 272739 8824
91. 2/32/32 3 2 64125125 1256464 525
93. 3/41/31/2341/31/27/12 xxxxx −+− ==
94. 2/31/21/42/31/21/411/12 xxxxx −+− ==
95. ()()()1/31/31/3 36362 xyxyxy ==
96. ()()()3/43/43/4 484836 xyxyxy ==
97. ()() () ()() ()
1/32/31/32/3 1/32/3 2222
2/32/32/32/3
2/31/32/34/3 2/32/3
2/32/32/31/34/32/3
2/312/3 xyxyxyxy xyxy xyxy xy xy xyxy +−+− = =
98. () () () ()() ()
1/41/21/21/2 221/41/422
3/43/4 223/4
1/413/21/413/4 1/2 1/41/2 1/4 xyxyxyxy xyxy xyxy xy xy y xy x +−+− = = = ==
1/41/4 3/23/4
99. () () ()() () ()
3/43/43/421/33/421/3
1/41/4 21/42 433/21/4 1/41/2
33/21/41/41/2 5/43/4 5/4 3/4 1616 16 2 8 8 xyxy xyxy xy xy xy xy x y = = = = =
100. () () ()() ()
3/23/23/211/33/211/3
3/23/23/2
33/21/2
3/23/2 33/23/21/23/2 31 3 44 4 2 8 8 xyxy xyxy xy xy xy xy xy = = = = =
101. () ()() () 1/21/2 1/2 1/21/2 1/2 1/2 1/2 211 21 (1)(1) 21 (1) 22 (1) 32 (1) xxxx x xx xx x xx x x x +++ ++= ++ ++ = + ++ = + + = +
102. 1/21/2 1/2 1/21/2 1/21/2 112 22 1231 22 xxxx x xx xxx xx +++⋅ += +++ ==
103. () () 1/21/2222 1 2112 2 xxxxx ++⋅+⋅ () () ()() () () () () () 21/23 21/2 1/21/2 223 21/2 1/21/21 2323 1/21/222 21 1 211 1 2121 11 x xx x xxxx x xxxxxx xx + =++ + +⋅++ = + ++++ == ++ () () () () 333 1/21/222 2 21/2 2232 11 32 1 xxxxx xx xx x +++ == ++ + = +
104. () () 1/32/3 1 11,1 3 xxxx ++⋅+≠− () () ()() () () () () () () () 1/3 2/3 2/31/3 2/3 2/31/31 2/32/3 2/32/3 1 31 311 31 3131 3131 3343 3131 x x x xxx x xxxx xx xxx xx + =++ + +++ = + ++++ == ++ +++ == ++
105. 11 435,5 25543 xxx xx +⋅+−⋅> −+ ()() ()() ()() ()() 435 25543 43543525 10543 54325 10543 2015210 10543 225 10543 xx xx xxxx xx xx xx xx xx x xx +− =+ −+ +⋅⋅++−⋅⋅− = −+ ++− = −+ ++− = −+ + = −+
SectionR.8: nth Roots; Rational Exponents
106. () () 33 2233 8121 3,2,8 22481 xx xx xx +− +≠≠− −+ () () () () () () () () () ()() ()() ()() 223333 2233 3333 2233 322 322 322 8818122 24281 8812 24281 88+12 24281 6482 24281 656 24281 xxxx xx xx xx xx xx xx xx x xx +⋅++−⋅− = −⋅+ ++− = −⋅+ +− = −+ ++− = −+ + = −+
1/2 3/2 1 11 2121 11 211 21 1 2(1)1 2(1)1 2 2(1) x xxx xx xx xxx x x xx xx x x +−⋅+− ++ = ++ ++− + = + +− =⋅ + + + = + 108. 2 2 2 2 2 2 2 22 2 22 2 12 21 1 1 1 1 11 11 1 x xx x x x x x x xx x xx x +−⋅ + + +− + = + + +⋅− ++ = + () 22 2 22 2 23/2 1 111 11 1 1 1 xx x xx x x +− + ==⋅ ++ + = +
109. ()() () () () () () () 1/21/2 1/2 1/2 1/2 1/2 1/21/2 424 4 42 4 4 442 44 4 xxx x x x x x xx x xx x +−+ + +− + = +
+ +⋅− ++ = + () () () () 1/2 1/2 3/2 3/2 42 4 4 41 44 4 4 4 4 xx x x x xx x x x x +− + = +
110. ()()1/21/2222 2 99 ,33 9 xxx x x −+− −<< () () ()() () ()() () () () 21/22 21/2 2 1/21/2 222 21/2 2 1/21/2 222 21/22 22 21/22 23/2 9 9 9 99 9 9 991 99 91 99 9 9 x x x x xxx x x xxx xx xx xx x −+
−⋅−+ = −⋅−+ =⋅ −+ =⋅ = 111. () () 21/2 2 21/2 2 1 1 ,1or1 x x x xx x <−> ()() () ()() () 1/21/2222 21/2 2 1/21/2222 21/22 11 1 111 1 xxx x x xxx xx −−⋅− = =⋅ () () () () 22 21/22 22 21/22 221/2 11 1 11 1 1 1 xx xx xx xx xx =⋅ −+ =⋅ = 112. ()()1/21/2222 2 44 4 xxx x +−+ + () () ()() () ()() () () () 21/22 21/2 2 1/21/2 222 21/2 2 1/21/2 222 21/22 22 1/223/222 4 4 4 44 4 4 441 44 414 4 44 x x x x xxx x x xxx xx xx x xx
+− + = +
+⋅+− + = + +⋅+− =⋅ + + +− =⋅= + ++
113. () 2 22 12 2,0 1 x xx x x x + > + () () () () () () () () 2 22 2 22 222 2222 122 2 1 1221 21 14113 2121 xxxx x x xxxx xx xxx xxxx
114. () () () 1/32/3232 22/3 2 211 3,1,1 1 xxxx xx x −+−
() () () ()() () () 21/33 22/3 22/3 1/32/3 223 22/3 22/3 212 31 1 21312 31 1 x xx x x xxxx x x −+
= () () () () () () () () () 1/32/3 23 2/32/322 2333 2/32/34/322 32 4/34/322 6121 311 612662 3131 64232 3131 xxx xx xxxxxx xx xxxx xx + + −+ =⋅ −+ −+ == ==
115. () 3/21/2 1/2 1/2 1/2 3 (1)(1) 2 (1)13 2 5 (1)1 2 1(1)52 2 xxx xxx xx xx ++⋅+ =+++ =++ =++
SectionR.8: nth Roots; Rational Exponents
116. ()() 24/321/3 21/322 21/32 1/3 22 4 (4)(4)2 3 (4)48 3 11 (4)4 3 141112 3 xxxx xxx xx xx ++⋅+⋅ =+++ =++ =++
117. () () () 1/223/21/2 1/22 1/22 1/2 688 23()44 234 2(34)(1) xxxxx xxxx xxx xxx +−− =+−− =−− =−+
118. () () () 1/23/2 1/2 1/2 6238 23(23)4 2109 xxx xxx xx ++⋅ =++ =+
119. ()() ()() () ()() 4/31/322 1/3 222 1/3 222 1/3 22 34442 4348 43128 41112 xxxx xxx xxx xx ++⋅+⋅ =+++ =+++ =++
120. ()() ()() ()() 4/31/3 2 1/3 1/3 234434 234342 23454 xxxx xxxx xxx ++⋅+ =+++ =++
121. ()()()() 1/33/24/31/2 4352333523 xxxx +++++ ()()()() ()()() ()()() 1/31/2 1/31/2 1/31/2 3523423335 3523812915 35231727 xxxx xxxx xxx =+++++ =+++++ =+++ 3 where 2 x ≥−
122. ()()()() 1/33/24/31/2 6614366143 xxxx +−++−
1/31/2 1/31/2 1/31/2 1/31/2 661434361 66143102 66143251 12614351 xxxx xxx xxx xxx =+−−++ =+−−
4 x ≥
123. 1/21/2 3 3,0 2 xxx+> () 1/2 1/2 1/21/2 1/21/21/2 33 2 3236332 222 x x xxxx xxx =+ + ⋅+⋅+ ===
124. 1/32/3 84,0 xxx−≠ () 1/3 2/3 1/32/3 2/32/32/3 84 8484421 x x xxxx xxx =− === 125. 21.41 ≈
234.89 35 + ≈
520.04 24 ≈ +
33522.15 3 ≈
23341.33 2 ≈
133. a. () 296 40120.608 12 15,660.4gallons V =− ≈ b. () 296 4010.608390.7gallons 1 V =−≈
134. a. 2 6440256 16feetpersecond v =⋅+= = b. 2 641601024 32feetpersecond v =⋅+= = c. 2 6424144 12feetpersecond v =⋅+= = 135. 64 2228.89seconds 32 T ππ ==≈
136. 161222 3222 24.44seconds T π ππ π === =≈
137. 314313 334312 134431
Thequotientis2(34)43 +−−xx Theremainderis1
138. 1219137 126727 1387720 +− +−−−
Yes,12 + isafactorof329137−++xxx
139. Answersmayvary.Onepossibilityfollows:If 5 a =− ,then () 225255 aa =−==≠
Sinceweusetheprincipalsquareroot,whichis alwaysnon-negative, 2if0 if0 aa a aa ≥ = −< whichisthedefinitionof a ,so 2 aa =
SectionR.8: nth Roots; Rational Exponents
Section 1.1
Chapter 1 Graphs, Equations, and Inequalities
(f) x-axis

3. x-coordinate; y-coordinate; quadrants
4. False; points that lie in Quadrant IV will have a positive x-coordinate and a negative y-coordinate. The point () 1,4 lies in Quadrant II.
5. d
6. c
7. (a) Quadrant II
(b) x-axis
(c) Quadrant III
(d) Quadrant I (e) y-axis
(f) Quadrant IV

8. (a) Quadrant I
(b) Quadrant III
(c) Quadrant II
(d) Quadrant I (e) y-axis
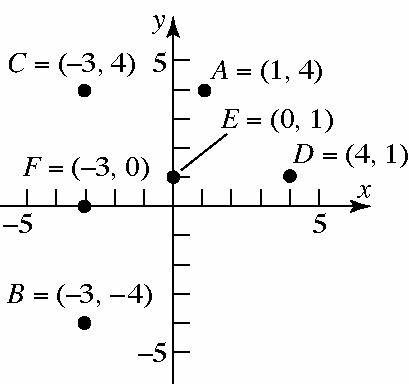
9. The points will be on a vertical line that is two units to the right of the y-axis.

10. The points will be on a horizontal line that is three units above the x-axis.

11. () 1,4 ; Quadrant II
12. (3, 4); Quadrant I
13. (3, 1); Quadrant I
Section 1.1: Graphing Utilities; Introduction to Graphing Equations
14. () 6,4 ; Quadrant III
15. min11 max5
scl1 min3 max6 scl1 X X X Y Y Y =− = = =− = =
16. min3 max7 scl1 min4 max9 scl1 X X X Y Y Y
17. min30 max50 scl10 min90 max50 scl10 X X X Y Y Y
18. min90 max30 scl10 min50 max70 scl10 X X X Y Y Y =− =
=
21. min6 max6 scl2 min4 max4 scl2 X X X Y Y Y
22. min3 max3 scl1 min2 max2 scl1 X X X Y Y Y =− = = =− = = 23. min6 max6 scl2 min1 max3 scl1 X X X Y Y Y =− = = =− = =
24. min9 max9 scl3 min12 max4 scl4 X X X Y Y Y =− =
=− =
19. min10 max110
scl10 min10 max160 scl10 X X X Y Y Y
20. min20 max110 scl10 min10 max60 scl10 X X X Y Y Y
25. min3 max9 scl1 min2 max10 scl2 X X X Y Y Y = =
26. min22 max10 scl2 min4 max8 scl1 X X X Y Y Y =− =−
Chapter 1: Graphs, Equations, and Inequalities
27. 4 y xx=− 4 000 00 =− = 4 111 10 =− ≠ 4 0(1)1 011 =−−− ≠−− (0, 0) is on the graph of the equation.
28. 3 2 y xx=− 3 0020 00 =− = 3 1121 11 =− ≠− 3 1121 11 −=− −=− (0, 0) and (1, –1) are on the graph of the equation.
29. 22 9 yx=+ 22 309 99 =+ = 22 039 018 =+ ≠ 22 0(3)9 018 =−+ ≠ (0, 3) is on the graph of the equation.
30. 3 1 y x =+ 3 211 82 =+ ≠ 3 101 11 =+ = 3 011 00 =−+ = (0, 1) and (–1, 0) are on the graph of the equation.
31. 22 4 xy+= 22 024 44 += = 22 (2)24 84 −+= ≠ 22 224 44 += = () (0,2) and 2,2 are on the graph of the equation.
32. 2244xy+= 22 0414 44 +⋅= = 22 2404 44 +⋅= = () 2 2 1 2 244 54 += ≠ (0, 1) and (2, 0) are on the graph of the equation.
33. (–1, 0), (1, 0)
34. (0, 1)
35. 22,0,,0,(0,1) ππ
36. (–2, 0), (2, 0), (0, –3)
37. () 1,0 , () 0,2 , () 0,2
38. (2, 0), (0, 2), (–2, 0), (0, –2)
39. (–4,0), (–1,0), (4, 0), (0, –3)
40. (–2, 0), (2, 0), (0, 3)
41. 2 yx=+

42. 6 yx=−
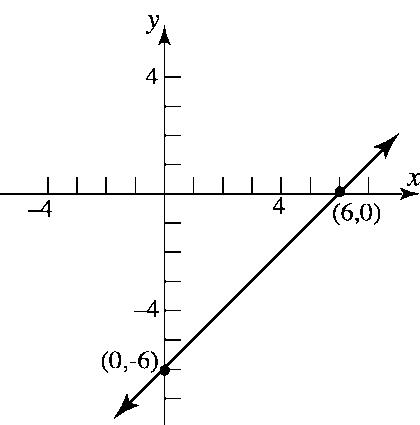
43. 28yx=+

44. 39yx=− 45. 2 1 yx=−


Section 1.1: Graphing Utilities; Introduction to Graphing Equations
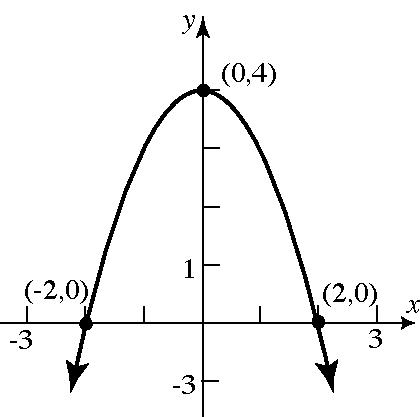
48. 2 1 yx=−+

49. 236 xy+=
46. 2 9 yx=− 47. 2 4 yx=−+
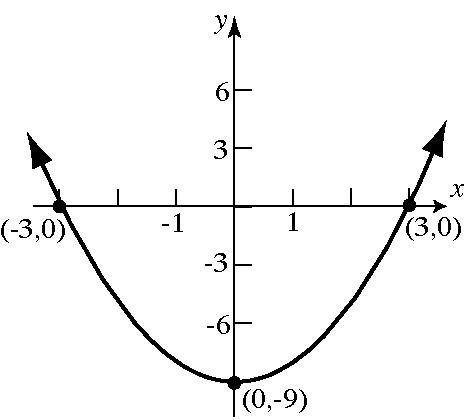
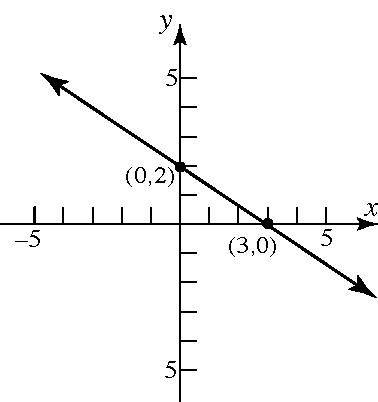

© 2026 Pearson Education,
50. 5210 xy+=
Chapter 1: Graphs, Equations, and Inequalities
51. 2 9436 xy+= 52. 2 44 xy+=


213yx=−

The x-intercept is 6.5 x = and the y-intercept is 13 y =− .
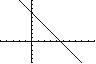
The x-intercept is 4.67 x = and the y-intercept is 14 y =
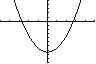

The x-intercepts are 2.74 x =− and 2.74 x = . The y-intercept is 15 y =−
56. 2 319yx=−+

Section 1.1: Graphing Utilities; Introduction to Graphing Equations
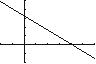
The x-intercepts are 2.52 x =− and 2.52 x = .
The y-intercept is 19 y =
57. 343 3243 or 2 x xyy −==

The x-intercept is 14.33 x = and the y-intercept is 21.5 y =−
The x-intercept is 20.5 x = and the y-intercept is 16.4 y = 59. 2 2 537 5337 or 3 x xyy −+ +==

The x-intercepts are 2.72 x =− and 2.72 x = .
The y-intercept is 12.33 y =
Chapter 1: Graphs, Equations, and Inequalities
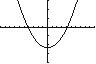
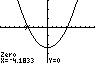
The x-intercepts are 4.18 x =− and 4.18 x = The y-intercept is 11.67 y =−
61. If () 2,5 is shifted 3 units right then the x coordinate would be 23 + . If it is shifted 2 units down then the y-coordinate would be 5(2) +− . Thus the new point would be () 23,5(2)(5,3) ++−=
62. If () 1,6 is shifted 2 units left then the x coordinate would be 1(2)−+− . If it is shifted 4 units up then the y-coordinate would be 64 + . Thus the new point would be ()1(2),64(3,10) −+−+=− .
63. a. 25 feet
b. 23.2 ft; 34.1 ft
c. (0,6), The shot is released at a height of 6 feet; (48.7, 0), the shot hits the ground after traveling a horizontal distance of 48.7 feet.
64. a. 20 meters
b. 12 seconds; 36 meters
c. (0, 2), The discus is released at a height of 2 meters; (18, 0), the discus hits the ground after 18 seconds.
65. a. $19.95; $19.95
b. $182.45
c. (0, 19.95), The membership plan costs $19.95 per month.
66. a. 1.5 miles
b. 1 mile
c. (0, 2), Caleb’s friend lives 2 miles from his house; (28, 0), it takes Caleb 28 minutes to ride home.
67. (1,0),(1,0),(0,1),(0,1)
68. (2,0),(3,0),(0,2),(0,0),(0,2)
69. Answers will vary
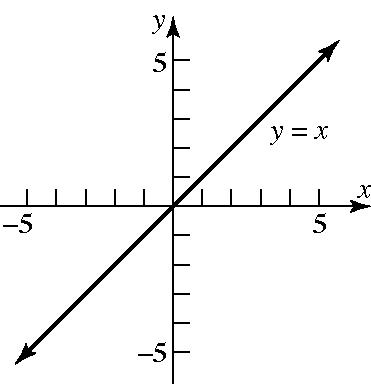
70. a.

Section 1.2: Solving Equations Using a Graphing Utility; Linear and Rational Equations

b. Since 2 x x = for all x , the graphs of 2 and yxyx == are the same.
c. For () 2 yx = , the domain of the variable x is 0 x ≥ ; for yx = , the domain of the variable x is all real numbers. Thus, () 2 only for 0. xxx=≥
d. For 2 yx = , the range of the variable y is 0 y ≥ ; for yx = , the range of the variable y is all real numbers. Also, 2 only if 0. xxx=≥
71. Answers will vary
72. Answers will vary. A complete graph presents enough of the graph to the viewer so they can “see” the rest of the graph as an obvious continuation of what is shown.
73. Answers will vary.
Section 1.2
1. Using the distributive property: () 35315 xx −−=−+
2. () 23512(3)35[(3)1] 635(4)6320 31017 xx−−+=−−+
3. No, 4 x = is not in the domain of 3 4 x because it makes the denominator equal 0.
4. LCM = ()() 32 (1)1333 +−+=+−− x xxxxx
5. b
6. identity
7. linear; first-degree
8. d
9. True; equations that are contradictions have no solution.
10. False; when using a graphing utility, we often obtain decimal approximations to solutions.
11. Divide both sides by 7. The solution set is { }3 .
12. Divide both sides by 6. The solution set is { }4
13. Subtract 35 from both sides, then divide both sides by 5. The solution set is { }7 .
14. Subtract 18 from both sides, then divide both sides by 6. The solution set is { }3
15. Add 3 to both sides, then divide both sides by 2. The solution set is { } 3 2 .
16. Subtract 4 from both sides, then divide both sides by 3. The solution set is { } 4 3 .
17. Multiply both sides by 4. The solution set is 7 5
18. Multiply both sides by 3 2 . The solution set is 27 4
19. 3 420xx−+= ; Use ZERO (or ROOT) on the graph of 3 1 42yxx=−+
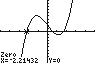

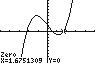
The solution set is { }
.
Chapter 1: Graphs, Equations, and Inequalities
20. 3 810xx−+= ; Use ZERO (or ROOT) on the graph of 3 1 81 y xx =−+


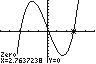
The solution set is { }2.89,0.13,2.76
21. 4 2532 xx −+=− ; Use INTERSECT on the graphs of 4 1 25yx=−+ and 2 32yx=− .

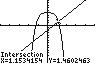
The solution set is { }1.55,1.15
22. 42123xx −+=− ; Use INTERSECT on the graphs of 4 1 1 yx=−+ and 2 2 23yx=−

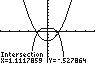
The solution set is { }1.11,1.11 .
23. 43 25840 −+−=xxx ; Use ZERO (or ROOT) on the graph of 43 1 2584 =−+−yxxx
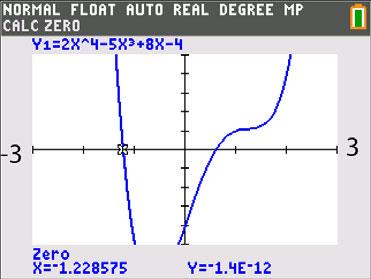

The solution set is { }1.23,0.60
24. 432 3450 xxx−+−= ; Use ZERO (or ROOT) on the graph of 432 1 345yxxx=−+− −10 5 −3 3 −10 5 −3 3
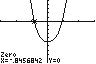
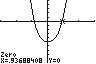
The solution set is { }0.85,0.94 .
25. 3257 20 32 xxx −−++= ; Use ZERO (or ROOT) on the graph of ()()32 1 5/37/22yxxx =−−++



The solution set is { }2.69,0.49,1.51
26. 432715320 32 xxxx −++−+= ; Use ZERO (or ROOT) on the graph of ()()432 1 37/315/22yxxxx =−++−+ .

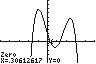
Section 1.2: Solving Equations Using a Graphing Utility; Linear and Rational Equations

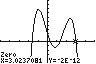
The solution set is { }1.64,0.31,1.31,3.02 .
27. 432 2521 2 3232 xxxx −−+=−+
Use INTERSECT on the graphs of ()() 43 1 2/325/2 yxxx =−−+ and 2 2 (2/3)1/2yx=−+



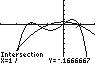
28. 113254 45 xxx−=−
Use INTERSECT on the graphs of 3 1 /45 y xx=− and 2 2 /54 yx=− and a standard viewing window ( 10 to 10 for both x and y).



The solution set is { }4.47,0.80,4.47
29. 4252110 xxx−++=
Use ZERO (or ROOT) on the graph of 42 1 5211yxxx=−++ 15

There are no real solutions.
30. 42 38290 xxx −+−−=
Use ZERO (or ROOT) on the graph of 42 1 3829yxxx =−+−− −15 5 −5 5

There are no real solutions.
31. 34 3444 34 34 24 24 22 2 xx xx xx x xxx x x x += +−=− =− −=−− =− = =−
The solution set is { }2 .
Chapter 1: Graphs, Equations, and Inequalities
32. 295 29959 259 25595 39 39 33 3 xx xx xx x xxx x x x += +−=− =− −=−− −=− = = The solution set is { }3
33. 263tt −=− 26636 29 29 39 39 33 3 tt tt tttt t t t −+=−+ =− +=−+ = = =
The solution set is { }3
34. 5618 y y +=−− 566186 524 524 624 24 6 66 4 yy yy yyyy y y y +−=−−− =−− +=−−+ =− = =−
The solution set is { }4 .
35. 629 66296 23 2232 33 33 33 1 xx xx xx x xxx x x x −=+ −−=+− −=+ −−=+− −= = =−
The solution set is { }1 .
36. ()() 322 32323 21 21 1 111 1 xx xx xx x xxx x x x
= The solution set is { }1 .
37. 3(53)8(1) +=− xx 15988 159158815 9823 988238 23 +=− +−=−− =− −=−− =− xx xx xx x xxx x The solution set is { }23 .
38. 3(2)21 x x −=− 6321 636216 327 32272 57 57 55 7 5 xx xx xx x xxx x x x −=−
= = The solution set is { } 7 5
39. () 832310 832310 52310 5223102 538 53383 28 xxx xxx xx xx xx x xxx x −+=− −−=− −=− −+=−+ =− −=−− =− 28 22 4 x x = =−
The solution set is { }4
40. () 72110
Section 1.2: Solving Equations Using a Graphing Utility; Linear and Rational Equations
41. ()()() 2356334556
42.
Chapter 1: Graphs, Equations, and Inequalities
46.
47.
The solution set is { } 5 2
Section 1.2: Solving Equations Using a Graphing Utility; Linear and Rational Equations
53. 123 24 44123 24 283 28232 8 or 8 x xx x xx xxxx xx +=
The
54. 311 36
The solution set is { }6
55. ()
The solution set is { }2
56. ()()() 2 22 22 2222 233 23669 669 669 669 66696 769 xxx xxxxx xxxx x xxxxx xx xxxx x +−=+ +−−=++ −−=++ −−−=++− −−=+ −−−=+− −−= 76696 715 715 77 15 7 x x x x −−+=+ −= = =−
The solution set is { } 15 7
57. (23)(21)(4) xxxx−=+− 22 2222 23274 2322742 374 37747 44 4 4 1 44 xxxx x xxxxx xx xxxx x x x −=−− −−=−−− −=−− −+=−−+ =− = =−
The solution set is { }1 .
58. (12)(21)(2) xxxx +=−− 22 2222 2252 222522 52 5525 62 621 663 xxxx x xxxxx xx xxxx x x x +=−+ +−=−+− =−+ +=−++ = = =
The solution set is { } 1 3 .
Copyright © 2026 Pearson Education, Inc.
Chapter 1: Graphs, Equations, and Inequalities
59.
60.
This solution is not in the domain of the variable so it must be discarded. The equation has no solution. The solution set is { } or ∅ .
() () () 22 22 22 243 2 44 44243 2 44 2432 2436 2103 510 2 x
This solution is not in the domain of the variable so it must be discarded. The equation has no solution. The solution set is { } or ∅
This solution is not in the domain of the variable so it must be discarded. The equation has no solution. The solution set is { } or ∅
Section 1.2: Solving Equations Using a Graphing Utility; Linear and Rational Equations
67. ()() 72 3103 732310 721620 7641 41 = +− −=+ −=+ =+ = xx xx xx xx x
The solution set is { }41 .
68. ()() 43 46 4634 424312 4312 12 12 xx xx xx xx x x = ++ −+=−+ −−=−− −=−+ −= =−
The solution set is { }12
69. ()()()() 6738 4124 67243841 tt tt tttt ++ = +−=+− 22 22 12142428123238 12102812298 1028298 102920 3920 20 39 20 39 tttttt tttt tt tt t t t +−−=+−− −−=+− −−=− −=+ −= = =−
The solution set is { } 20 39 .
70. ()()()() 22 22 8543 10757 855743107 4025563540302821 408135405821 ww ww wwww wwwwww wwww +− = −+ ++=−− +++=−−+ ++=−+ 81355821 815814 13914 14 139 ww ww w w +=−+ =−− =− =−
The solution set is { } 14 139
71. ()() 437 25 52 xx xx =+ −+ +−
LCD = ()() 25xx−+ () ()() () ()() ()() ()() 4532 7 252552 45327 420367 420313 437 77 1 xx xxxxxx xx xx xx xx x x +−− =+ −+−++− +=−−+ +=−++ +=−+ =−− =− =−
The solution set is { }1
72. ()() 411 231 231 xx xx += +− +−
LCD = ()() 231 xx+− () ()() () ()() ()() ()() 41123 1 231231231 41231 44231 271 26 3 xx xxxxxx xx xx x x x −−+ += +−+−+− −−++= −+++= −+= −=− =
The solution set is { }3 .
73. 235 346yyy += +−+
LCD = ()()() 346yyy+−+ ()()() 235 346 346 yyy yyy +−++= +−+ ()()()()()() ()()() 222 222 22 246336534 22243918512 2448327545560 5 3165560 316560 31566 3666 66 36 11 6 yyyyyy yyyyyy yyyyyy y yyy yy yy y y y −++++=+− +−+++=−− +−+++=−− ++=−− +=−− =−− =− =− =−
The solution set is { }11 6
Copyright © 2026 Pearson Education, Inc.
Chapter 1: Graphs, Equations, and Inequalities
74. 543 511235 zzz +=
LCD = ()()() 511235 zzz
()()() 543 511235 511235 zzz zzz −−−+=
()()()()()() 222 22 523545115351123 106575201442203011199 302092953011199 20929511199 209111196 98196 2 zzzzzz zzzzzz
The solution set is { }2 .
75. 222 410 933 −= −+− xx x xxxx
77. 54 254 25 2 5 yx a a a =+ =+ −= =−
78. 2 2 3 23(2)4610 yxx b =+ =+=+=
79. 236 xy+= 236 326 2 2 3 ab ba ba += =−+ =−+
LCD = ()() 33+−xxx ()() 222 410 33 933 +−−= −+−
xx xxx x xxxx
xxxx xxxx xxxx xx x x x
()()() () 2 22 22 43103 7121030 7121030 7121030 342 14 14 −−−=+ −−+=+
The solution set is { }14
76. 222 143 232 xx xxxxxx ++− −= ++++
LCD = ()() 21xxx++
()() 222 143 21 232 xx xxx xxxxxx ++− ++−= ++++ ()()()()() ()22 22 11423 21683 21683 473 437 7 7 x xxxx xxxxx xxxxx xx xx x x ++−++=− ++−++=− ++−−−=−
The solution set is { }7 .
80. 0(2) 5(0)5 ymxb mb mbb =+ =+ =+→= Therefore, 025 25 5 2 m m m =+ −= =−
81. ,0axbca−=≠ axbbcb axcb axcb aa bc x a −+=+ =+ + = + =
82. 1,0 axba −=≠ 111 1 1 11 axb axb ax b aa bb x aa −−=− −=− = ==
Section 1.2: Solving Equations Using a Graphing Utility; Linear and Rational Equations
83. ,0,0, xx cabab ab +=≠≠≠− () () xx ababc ab bxaxabc x ababc xab abc abab abc x ab +=⋅ += += + = ++ = +
84. ,0 ab cc xx +=≠ ab x xc xx abcx abcx cc ab x c
+= + = + = such that ab ≠−
85. 112 1 x axax += −+− Multiply both sides by the LCD, ()()() 1 xaxax−+− , to get: ()()()()()()
−=− =
where 1,0,1 a ≠−
86. ()()()() bcbc xaxa bcxabcxa bxcxabacbxcxabac bxcxabacbxbxcxabacbx +− = +− +−=−+ +−−=−+− +−−−=−+−− 2 2 22 22 22 cxabaccxabac cxabaccxcxabaccx cxabacabac cxabacabacabacabac cxab cxab cc ab x c −−=−+− −−+=−+−+ −−=− −−++=−++ = = = where 0,0ac≠≠ , and bc ≠±
87. 2166 x aaxa+=+− when 4 x = : () 421646 421646 42162 412 3 aaa aaa aa a a +=+− +=+− +=− = =
88. 242 x bxbx+=−+ when 2 x = : ()222422 22244 2224 42 4 2 2 bb bb bb b bb +=−+ +=−+ +=−+ = = =
89. Solving for R: 12 1212 12 1221 1221 1221 2121 12 12 111 111 () () RRR RRRRRR RRR RRRRRR RRRRR RRRRR RRRR RR R RR =+
=+
=+ =+ + = ++ = +
Chapter 1: Graphs, Equations, and Inequalities
90. Solving for r : (1) A Prt A PPrt APPrt Prt AP PtPt AP r Pt
91. Solving for R: 2 2 2 22 mv F R mv RFR R RFmv RFmvmv R F
92. Solving for T: PVnRT PVnRT nRnR PV T nR = =
93. Solving for r:
94. Solving for t:
95. Let x = amount invested in bonds. Invested in CDs: 3000 x ()3,00020,000 23,00020,000 223,000 11,500 xx x x x
=
$11,500 will be invested in bonds and $8,500 will be invested in CD's.
96. Let x = amount that Sean receives. Amount for Jorge: 3000 x ()3,00010,000 23,00010,000 213,000 6,500 xx x x x +−= −= = = Sean will receive $6,500 and Jorge will receive $3,500.
97. Let x Sandra’s regular hourly wage. ()() 401.58910 4012910 52910 910 17.50 52 += += = == xx xx x x Sandra’s regular hourly wage is $17.50.
98. Let x = Leigh’s regular hourly wage. ()() 4061.5421083 40981083 571083 1083 19 57 ++= ++= = == xxx xxx x x Leigh’s regular hourly wage is $19.00.
99. Let x = final exam score. Compute the final average and set equal to 80. () 1 808371619580 7 xx
Now solve for x:
Camilla needs to score an 85 on the final exam to get an average of 80 in the course.
100. Let x = final exam score.
Ali must score 78 on the final to earn a B.
Following the same approach as above, we get
Ali must score 93 on the final to earn an A.
101. Let x represent the original price of the phone. Then 0.15 x represents the reduction in the price of the phone.
original price – reduction = new price 0.15799 0.85799 940 −= = = xx x x
The original price of the phone was $940. The amount of the savings is 0.15($940) = $141.
102. Let x represent the original price of the car. Then 0.12 x represents the reduction in the price of the car.
original price – reduction = new price 0.1228,160 0.8828,160 32,000 xx x x −= = =
The original price of the car was $32,000.
The amount of the savings is $32,000 – $28,160 = $3,840.
103. Let x represent the price the theater pays for the candy.
Then 2.75 x represents the markup on the candy. The selling price of the candy is $3.00. suppier pricemarkupselling price 2.754.50 3.754.50 1.20 += += = = xx x x
The theater paid $1.20 for the candy.
104. Let x represent the dealer's cost of the new car. 0.85($34,000)$28,900 x ==
If the dealer accepts $100 over cost, then you will pay $28,900 + $100 = $29,000.
105. Let a = number of adult patrons. Child patrons: 3030 a () 12.008.50303027,155 1225,7558.5027,155 3.5025,75527,155 3.501,400 3.501,400 3.503.50 400 +−= +−= += = = = aa aa a a a a
The theater had 400 adult patrons.
106. Let x = original price of the boots. Discount: 0.3 x original pricediscountsale price 0.3399 0.7399 0.7399 0.70.7 570 xx x x x −= −= = = =
The original price of the boots was $570.
107. Let w = width. Length: 8 lw=+ Perimeter: 22 Plw =+ 2260 2(8)260 216260 41660 444 11 lw ww ww w w w += ++= ++= += = =
The rectangle has a width of 11 feet and a length of 19 feet.
Chapter 1: Graphs, Equations, and Inequalities
108. Let w = width. Length: 2 lw = Perimeter: 22 Plw =+ 2242
2(2)242 4242 642 7 lw ww ww w w += += += = =
The rectangle has a width of 7 meters and a length of 14 meters.
109. Let x = the total number of people who owned a smart phone based on the recent survey. Then 0.534 x represents the number of people who owned a smart phone that ran the Google Android OS.
0.534124.4 124.4 233 0.534 = =≈ x x
There were about 233 million people who owned a smart phone at the time of the survey.
110. Let W be the percentage that used WhatsApp. Then: 6222 642 32 =− = = W W W
Therefore, 32% of U.S. adults aged 18-29 used WhatsApp.
111. Let x = amount that Scott gets.
Amount for Alice: 3 4 x
Amount for Tricia: 1 2 x 31 900,000 42 9 900,000 4 4 (900,000) 9 400,000 xxx x x x
++=
=
= Scott receives $400,000; Alice receives $300,000; Tricia receives $200,000.
112. Let x = amount that Judy pays. Amount Tom pays: 2 3 x
= Judy pays $10.80 and Tom pays $7.20.
113. An isosceles triangle has three equal sides. Therefore: 410240318 +=+=+ xxx . Solve each set separately: 410240
Since 22 is the largest of the numbers then the largest perimeter is: ()()() 422102224032218266 +++++= 114. 311114 316 4524205 313134 1
Multiply both sides by the LCD 80 to clear fractions. 608488012064 1087258 10716 16 107 −++=+−
115. If a hexagon is inscribed in a circle then the sides of the hexagon are equal to the radius of the circle. Let the P = 6r be the perimeter of the hexagon. Let r be the radius of the circle. 610 510 2
Thus r = 2 inches is the radius of the circle where the perimeter of the hexagon is 10 inches more than the radius.
116. In order to solve 58 3 33 x xx + += ++ , we multiply each term by the expression “ 3 x + ” to get () () 58 333 33 x xx xx + ++=+ ++
Now, provided 3 x ≠− , we can cancel the denominators to get ()() 5338 5398263 xx xxxx ++=+ ++=+ =− =−
However, we already stated that 3 x ≠− . So we have a contradiction.
117. Answers will vary. One example is 3136 xx+=+
118. Answers will vary. In general, ‘solve’ means to find values for a variable that make the equation true, ‘evaluate’ means to plug in a specific value for a variable in an expression and simplify, and ‘simplify’ means to collect like terms and write an expression in a simpler form.
Ex: Solve () 328 xx+−= .
Solution: () 328 368 268 22 1 xx xx x x x +−= +−= += = =
Ex: Evaluate ()32 x x +− for 2 x =−
Solution: ()()() () 323222 302 2 xx+−=−+−− =+ =
Ex: Simplify ()32 x x +−
Solution: ()32 36 26 x x x x x +− +− +
119. In obtaining step (7) we divided by x – 2. Since x = 2 from step (1), we actually divided by 0.
Section 1.3: Quadratic Equations
Section 1.3
1. ()() 2 5661xxxx −−=−+
2. ()() 2 23231 xxxx −−=−+ 3. { } 5 ,3 3 4. True 5. 2 2 2 2 1552525 5;;5 22244 255 5 42 xx xxx
==++
++=+
6. discriminant; negative
7. False; a quadratic equation may have no real solutions.
8. False; If 2 = x p then x could also be negative.
9. b
10. d
11. () 2 90 90 xx xx −= −= 0 or 90 0 or 9 xx xx =−= ==
The solution set is {0, 9}.
12. 2 40 (4)0 xx xx += += 0 or 40 0 or 4 xx xx =+= ==−
The solution set is {–4, 0}.
13. 2 250 (5)(5)0 x xx −= +−= 50or50 5or5 xx xx +=−= =−=
The solution set is {–5, 5}.
Chapter 1: Graphs, Equations, and Inequalities
14. 2 90 (3)(3)0 x xx −= +−= 30or30 3or3 xx xx +=−= =−=
The solution set is {–3, 3}.
15. 2 60 (3)(2)0 zz zz +−= +−= 30or20 3or2 zz zz +=−= =−=
The solution set is {–3, 2}.
16. 2 760 (6)(1)0 vv vv ++= ++= 60or10 6or1 vv vv +=+= =−=−
The solution set is {–6, –1}
17. 2 2530 (21)(3)0 xx xx −−= +−= 210 or 30 1 or 3 2 xx xx +=−= =−=
The solution set is { } 1 ,3 2
18. 2 3520 (32)(1)0 xx xx ++= ++= 320 or 10 2 or 1 3 xx xx +=+= =−=−
The solution set is { } 2 1, 3
19. 2 2 51800 5(36)0 5(6)(6)0 −+= −−= −+−= w w ww 60or60 6or6 +=−= =−= ww ww
The solution set is {–6, 6}.
20. 2 2 2500 2(25)0 2(5)(5)0 y y yy −= −= +−= 50or50 5or5 yy yy +=−= =−=
The solution set is {–5, 5}.
21. () () 2 3100 3100 (2)50 +−= +−= −+= xx xx xx 20or50 2or5 −=+= ==− xx xx
The solution set is { }5,2 .
22. 2 (4)12 4120 (6)(2)0 xx xx xx += +−= +−= 60or20 6or2 xx xx +=−= =−=
The solution set is { } 6, 2 .
23. 2 2 2 4912 41290 (23)0 230 3 2 x x xx x x x += −+= −= −= =
The solution set is { } 3 2
24. 2 2 2 251640 2540160 (54)0 540 4 5 x x xx x x x += −+= −= −= =
The solution set is { } 4 5 .
25. 2 2 2 6(1)5 665 6560 (32)(23)0 pp pp pp pp −= −= −−= +−= 320 or 230 2 3 or 3 2 p p p p += −= =− =
The solution set is 23 , 32
26. 2 2 2(24)30 4830 (21)(23)0 uu uu uu
210 or230 13 or 22 uu
The solution set is 13 , 22
27. () 2 2 6 65 6 65 656 6560 (32)(23)0 x x x xx x xx xx xx −=
Neither of these values causes a denominator to equal zero, so the solution set is 23 , 32
28. 2 2 12 7 12 7 127 7120 (3)(4)0 x x x xx x x x xx xx +=
Section 1.3: Quadratic Equations
Neither of these values causes a denominator to equal zero, so the solution set is {3, 4}.
29. () () () () () () 42 33 3 3 42 3333 3 3 x xx xx x xxxx xx xx += +−=−
or 2 4 xx xx +=−= =−=
Neither of these values causes a denominator to equal zero, so the solution set is { } 3 ,2. 4
30. 53 4 42xx =+ +− ()() ()() ()()()() () () ()() 2 2 2 2 53 42442 42 5244234 510428312 5104832312 04610 02235 02251 xxxx xx xxxx xxxx xxxx xx xx xx +−=++− +−
=+− =+− =+− 250 or 10 5 or 1 2 xx xx +=−= =−=
Neither of these values causes a denominator to equal zero, so the solution set is { } 5 ,1. 2
31. 2 25 25 5 x x x = =± =±
The solution set is { }5,5
Chapter 1: Graphs, Equations, and Inequalities
32. 2 36 36 6 x x x = =± =±
The solution set is { }6,6
33. () 2 14 14 12 12 or 12 3 or 1 x x x xx xx −= −=± −=± −=−=− ==−
The solution set is { }1,3
34. () 2 21 21 21 21 or 21 1 or 3 x x x xx xx += +=± +=± +=+=− =−=−
The solution set is { }3,1
35. 2 1 416 3 1 416 3 1 44 3 11 44 or 44 33 11 0 or 8 33 0 or 24
+=
+=± +=± +=+=− ==− ==− h h h hh hh hh The solution set is { }24,0
36. () 2
2 2 2 421 44214 225 225 25 25 3 or 7 xx xx x x x x xx += ++=+ += +=± +=± =−± ==− { } The solution set is 7,3. 38. () 2 2 2 613 69139 322 322 322 xx xx x x x −= −+=+ −= −=± =± { } The solution set is 322,322. −+
−= 111 442 11 42 31 or 44 x x xx −=±=± =± ==− { } 13 The solution set is 44,.
Section 1.3: Quadratic Equations
40.
44. 2 420xx++= 2 1,4,2 444(1)(2) 4168 2(1)2 48422 22 22 abc x === −±− −±− == −±−± ===−± { } The solution set is 22,22.−−−+
45. 2 410xx−−= 2 1,4,1 (4)(4)4(1)(1) 4164 2(1)2 420425 25 22 abc x ==−=− −−±−−− ±+ == ±± ===± { } The solution set is 25,25. −+
Chapter 1: Graphs, Equations, and Inequalities
46. 2 610xx++= 2 1,6,1 664(1)(1) 6364 2(1)2 632642 322 22 abc x === −±− −±− == −±−± ===−± { }
49. 2 420 yy−+= 2 4,1,2 (1)(1)4(4)(2) 2(4) 1132131 88 abc y ==−= −−±−− = ±−±− == No real solution.
The solution set is 322,322. −−−+
47. 2 2530 xx−+= 2 2,5,3 (5)(5)4(2)(3) 2(2)
525245151 444 5151 or 44 64 or 44 3 or 1 2 abc x xx xx xx ==−= −−±−− = ±−±± === +− == == == { } 3
50. 2 410 tt++= 2 4,1,1 114(4)(1) 2(4) 1116115 88 abc t === −±− = −±−−±− == No real solution.
The solution set is 1,. 2
48. 2 2530 xx++= 2 2,5,3 554(2)(3) 2(2)
525245151 444 5151 or 44 46 or 44 3 1 or 2 abc x xx xx xx === −±− = −±−−±−± === −+−− == == =−=− { } 3
−± −± == abc x
−±−− = −±+−± ==
51. 2 2 985 9850 += +−= xx xx 2 9,8,5 884(9)(5) 2(9) 8641808244 1818 8261 461 189 ===−
The solution set is 461461 99,. −−−+
52. 2 2 212 2210 x x xx =− +−= 2 2,2,1 224(2)(1) 248 2(2)4 212223 13 442 abc x ===−
−±−− −±+ ==
−±−± −± ===
The solution set is ,1. 2
The solution set is 1313 22,. −−−+
53. 2 2 49 490 (49)0 x x xx xx = −= −= 0 or 490 9 0 or 4 xx xx =−= ==
The solution set is { } 9 0,. 4
54. 2 2 54 045 0(45) xx x x xx = =− =− 0 or 450 5 0 or 4 xx xx =−= ==
The solution set is { } 5 0,. 4
55. 2 9610 tt−+= 2 9,6,1 (6)(6)4(9)(1) 2(9) 63636601 18183 abc t ==−= −−±−− = ±−± ===
The solution set is { } 1 . 3
56. 2 4690 uu−+= 2 4,6,9 (6)(6)4(4)(9) 2(4) 6361446108 88 abc u ==−= −−±−− = ±−±− ==
No real solution.
57. () 2 2 2 311 0 442 311 440 442 320 xx xx xx −−=
Section 1.3: Quadratic Equations
3,1,2abc==−=− ()()()() () 2 11432 23 112412515 666 1515 or 66 64 or 66 2 1 or 3 x xx xx xx −−±−−− = ±+±± === +− == == ==− { } 2 The solution set is ,1. 3
58. 2 2 30 3 xx−−= () 2 2 2 3330 3 2390 2,3,9 xx xx abc
−−= ==−=− ()()()() () 2 33429 22 397238139 444 3939 or 44 126 or 44 3 3 or 2 x xx xx xx −−±−−− = ±+±± === +− == == ==− { } 3 The solution set is ,3. 2
Copyright © 2026 Pearson Education, Inc.
Chapter 1: Graphs, Equations, and Inequalities
59. 2 2 2 2 51 33 3351 33 531 5310 xx xx xx xx −=
()()()() () 2 5,3,1 33451 25 3920329 1010 abc x
The solution set is 329329 , 1010 −+
60. 2 2 2 2 31 55 5531 55 351 3510 xx xx xx xx −=
55431 23 52512537 66 abc x
The solution set is 537537 , 66 −+ .
61. 2 2(2)3 2430 xx xx += +−= 2 2,4,3 444(2)(3) 41624 2(2)4 4404210 210 442 abc x ===− −±−− −±+ == −±−± −± ===
The solution set is 210210 22,. −−−+
62. 2 3(2)1 3610 xx xx += +−= 2 3,6,1 664(3)(1) 63612 2(3)6 648643 323 663 abc x ===− −±−− −±+ == −±−± −± ===
The solution set is 323323 33,. −−−+
63. () 2 22 2 2 11 40 11 40 410 x x xx x x x x +−= +−= +−= 4,1,1abc===− ()() () 2 11441 24 1116117 88 x −±−− = −±+−± ==
Neither of these values causes a denominator to equal zero, so the solution set is 117117 , 88 −−−+ .
64. 2 83 20 ++= x x () ()()()() () 22 2 2 2 83 20 2830 2,8,3 88423 22 86424840 44 8210410 42 ++= ++= === −±− = −±−−± == −±−± == xx x x xx abc x
Neither of these values causes a denominator to equal zero, so the solution set is 410410 , 44 −−−+
65. 2 22 2 31 4 2 31 (2)4(2) 2 3()(2)48 3248 092 x xx x xxxx xx x xxxx x xxx xx += +−=−
+−=− +−=− =−+ 1,9,2abc==−=
2 (9)(9)4(1)(2) 2(1) 9818973 22 x −−±−− = ±−± ==
Neither of these values causes a denominator to equal zero, so the solution set is 973973 , 22 −+
66. 2 22 2 21 4 3 21 (3)4(3) 3 2()(3)412 23412 02133 x xx x xxxx xx x xxxx x xxx xx +=
+−=−
+−=− +−=− =−+ 2,13,3abc ==−= 2 (13)(13)4(2)(3) 2(2) 131692413145 44 x −−±−− = ±−± ==
Neither of these values causes a denominator to equal zero, so the solution set is 1314513145 , 44 −+
67. 2 4.12.20xx−+= ()()()() () 2 1,4.1,2.2 4.14.1412.2 21 4.116.818.84.18.01 22 3.47 or 0.63 abc x x x ==−= −−±−− = ±−± == ≈≈
The solution set is { } 0.63, 3.47
Section 1.3: Quadratic Equations
68. 2 3.91.80xx++= ()()() () 2 1,3.9,1.8 3.93.9411.8 21 3.915.217.23.98.01 22 0.53 or 3.37 abc x x x === −±− = −±−−± ==
The solution set is { }3.37,0.53 .
69. 2 330xx+−= () ()() () 2 1,3,3 33413 21 3312315 22 1.07 or 2.80 abc x xx ===− −±−− = −±+−± == ≈≈− The solution set is { } 2.80, 1.07
70. 2 220xx+−= () ()() () 2 1,2,2 22412 21 228210 22 0.87 or 2.29 abc x xx ===− −±−− = −±+−± == ≈≈−
The solution set is { } 2.29, 0.87 .
71. 2 0 xx ππ−−= ()()()() () 2 2 ,1, 114 2 114 2 1.17 or 0.85 abc x x x ππ ππ π π π ==−=− −−±−−− = ±+ = ≈≈−
The solution set is { } 0.85, 1.17 .
Chapter 1: Graphs, Equations, and Inequalities
72. 2 20 xx ππ+−= ()()() () 2 2 ,,2 42 2 8 2 0.44 or 1.44 abc x x x ππ πππ π πππ π ===− −±−− = −±+ = ≈≈−
The solution set is { } 1.44, 0.44
73. 2 2670 xx−+= () 22 2,6,7 4(6)4(2)7365620 abc bac ==−= −=−−=−=−
Since the 2 40,bac−< the equation has no real solution.
74. 2 470xx++= () 22 1,4,7 4(4)4(1)7162812 abc bac === −=−=−=−
Since the 2 40,bac−< the equation has no real solution.
75. 2 930250 xx−+= () 22 9,30,25 4(30)4(9)259009000 abc bac ==−= −=−−=−=
Since 2 40,bac−= the equation has one repeated real solution.
76. 2 252040 xx−+= () 22 25,20,4 4(20)4(25)44004000 abc bac ==−= −=−−=−=
Since 2 40,bac−= the equation has one repeated real solution.
77. 2 3580 xx+−= () 22 3,5,8 4(5)4(3)82596121 abc bac ===− −=−−=+=
Since 2 40,bac−> the equation has two unequal real solutions.
78. 2 2370 xx−−= () 22 2,3,7 4(3)4(2)795665 abc bac ==−=− −=−−−=+=
Since 2 40,bac−> the equation has two unequal real solutions.
79. 2 2 50 5 5 x x x −= = =± { } The solution set is 5,5.
80. 2 2 60 6 6 x x x −= = =± { } The solution set is 6,6.
81. ()() 2 16810 41410 410 1 4 xx xx x x −+= −−= −= = The solution set is { } 1 . 4
82. ()() 2 91240 32320 320 2 3 xx xx x x −+= −−= −= = The solution set is { } 2 3
83. ()() 2 1019150 53250 xx xx −−= +−= 530 or 250 35 or 52 xx xx +=−= =−=
The solution set is { } 35 52,.
84. ()() 2 67200 34250 xx xx +−= −+= 340 or 250 45 or 32 xx xx −=+= ==−
The solution set is { } 54 23,.
85. ()() 2 2 26 062 03221 zz zz zz += =−− =−+
320 or 210 21 or 32 zz zz −=+= ==−
The solution set is { } 12 , 23
86. ()() 2 2 26 062 03221 yy yy yy =+ =+− =+−
320 or 210 21 or 32 yy yy +=−= =−=
The solution set is { } 21 , 32
87. () 2 2 2 2 1 2 2 1 20 2 1 2220 2 22210 xx xx xx xx += +−= +−=
+−= 2,22,1abc ===− () 2 (22)(22)4(2)1 2(2) 22882216 44 22422 42 x −±−− = −±+−± == −±−± == 2222
The solution set is , 22
88. () 2 2 2 2 1 21 2 1 210 2 1 22120 2 2220 x x xx xx xx =+ −−= −−=
−−= 1,22,2abc ==−=−
Section 1.3: Quadratic Equations
() 2 (22)(22)4(1)2 2(1) 22882216 22 22422 21 x −−±−−− = ±+± == ±± == { }
The solution set is 22,22. −+
89. 2 2 4 40 xx xx += +−= 1,1,4abc===− ()() 2 (1)(1)414 2(1) 1116117 22 x −±−− = −±+−± == 117117
The solution set is 22,. −−−+
90. 2 2 1 10 xx xx += +−= 1,1,1abc===− ()() 2 (1)(1)411 2(1) 11415 22 x −±−− = −±+−± == 1515
The solution set is 22,. −−−+
91. 2 271 21 2 xx xx xx + += −+ 2 2 2 271 21(2)(1) 21(2)(1)271(2)(1)(2)(1) (1)2(2)71 2471 3471 450 (1)(5)0 xx xxxx xx xxxx xxxx xxxx xxxx xxx xx xx + += −+−+ + +−+=−+ −+−+ ++−=+ ++−=+ +−=+ −−= +−=
Chapter 1: Graphs, Equations, and Inequalities
94. Since this is a right triangle then we can use the Pythagorean Theorem. So
92.
The value 1 x =− causes a denominator to equal zero, so we disregard it. Thus, the solution set is {5}.
or
or
The value 2 x =− causes a denominator to equal zero, so we disregard it. Thus, the solution set is 1 3
93. Since this is a right triangle then we can use the Pythagorean Theorem. So
(23)(25)(7)
50 or 130 5 or 13 xx
This means there are 2 possible that meet these requirements. Substituting x into the given sides gives:
When x = 5: 5m, 12m, 13m
When x = 13: 20m, 21m, 29m Thus there are 2 solutions.
This means there are 2 possible solutions that meet these requirements. Substituting x into the given sides gives:
When x = 9: 41m, 40m, 9m
When x = 8 3 at least one side of the triangle has a negative measurement which is impossible. Thus there is only 1 triangle possible
95. Let w represent the width of window. Then 2 lw=+ represents the length of the window.
Since the area is 143 square feet, we have: 2 (2)143 21430 (13)(11)0 ww ww ww += +−= +−= 13 w =− or 11 w =
Discard the negative solution since width cannot be negative. The width of the rectangular window is 11 feet and the length is 13 feet.
96. Let w represent the width of window. Then 1 lw=+ represents the length of the window.
Since the area is 306 square centimeters, we have: (1)306ww += 2 3060 (18)(17)0 ww ww +−= +−= 18 w =− or 17 w =
Discard the negative solution since width cannot be negative. The width of the rectangular window is 17 centimeters and the length is 18 centimeters.
97. Let l represent the length of the rectangle. Let w represent the width of the rectangle. The perimeter is 26 meters and the area is 40
The dimensions are 5 meters by 8 meters.
98. Let r represent the radius of the circle.
Since the field is a square with area 1250 square feet, the length of a side of the square is 1250252 = feet. The length of the diagonal is 2r .
Use the Pythagorean Theorem to solve for r :
The shortest radius setting for the sprinkler is 25 feet.
99. Let x = length of side of original sheet in feet.
Length of box: 2 x feet
Width of box: 2 x feet Height of box: 1 foot
Discard 0 x = since that is not a feasible length for the original sheet. Therefore, the original sheet should measure 4 feet on each side.
100. Let x = width of original sheet in feet.
Length of sheet: 2 x
Length of box: 22 x feet
Width of box: 2 x feet
Height of box: 1 foot
Section 1.3: Quadratic Equations
Discard 0 x = since that is not a feasible length for the original sheet. Therefore, the original sheet is 3 feet wide and 6 feet long.
101. a. When the ball strikes the ground, the distance from the ground will be 0. Therefore, we solve
2 2 2 9680160 1680960 560 610 tt tt tt tt +−= −++= −−= −+= 6 or 1 tt==−
Discard the negative solution since the time of flight must be positive. The ball will strike the ground after 6 seconds.
b. When the ball passes the top of the building, it will be 96 feet from the ground. Therefore, we solve () 2 2 2 96801696 16800 50 50 tt tt tt tt +−= −+= −= −= 0 or 5 tt==
The ball is at the top of the building at time 0 t = when it is thrown. It will pass the top of the building on the way down after 5 seconds.
102. a. To find when the object will be 15 meters above the ground, we solve 2 2 4.92015 4.920150 tt tt −+= −+−= 4.9, 20, 15 abc=−==− ()() () 2 202044.915 24.9 2010620106 9.89.8 t −±−−− = −±± == 0.99 or 3.09 tt ≈≈
Chapter 1: Graphs, Equations, and Inequalities
The object will be 15 meters above the ground after about 0.99 seconds (on the way up) and about 3.09 seconds (on the way down).
b. The object will strike the ground when the distance from the ground is 0. Therefore, we solve () 2 4.9200 4.9200 tt tt −+=
The object will strike the ground after about 4.08 seconds.
c. 2 2 4.920100 4.9201000 tt tt −+= −+−= 4.9, 20, 100 abc=−==−
There is no real solution. The object never reaches a height of 100 meters.
103. Let x represent the number of centimeters the length and width should be reduced.
12 x = the new length, 7 x = the new width. The new volume is 90% of the old volume.
(12)(7)(3)0.9(12)(7)(3)
357252226.8
or 18.55
Since 18.55 exceeds the dimensions, it is discarded. The dimensions of the new chocolate bar are: 11.55 cm by 6.55 cm by 3 cm.
104. Let x represent the number of centimeters the length and width should be reduced. 12 x = the new length, 7 x = the new width. The new volume is 80% of the old volume.
(12)(7)(3)0.8(12)(7)(3)
357252201.6
35750.40 1916.80 xx xx xx xx −−= −+= −+= −+= 2 (19)(19)4(1)(16.8) 19293.8 2(1)2
0.93 or 18.07 x xx
Since 18.07 exceeds the dimensions, it is discarded. The dimensions of the new chocolate bar are: 11.07 cm by 6.07 cm by 3 cm.
105. Let x represent the width of the border measured in feet. The radius of the pool is 5 feet. Then 5 x + represents the radius of the circle, including both the pool and the border. The total area of the pool and border is 2 (5) T Ax=π+ .
The area of the pool is 2 (5)25 AP =π=π
The area of the border is 2 (5)25 BTP AAAx=−=π+−π
Since the concrete is 3 inches or 0.25 feet thick, the volume of the concrete in the border is () 2 0.250.25(5)25 B Ax=π+−π
Solving the volume equation:
2 2 2 0.25(5)2527 102525108 101080 x xx xx π+−π= π++−= π+π−= 2 2 10(10)4()(108) 2() 31.42100432 6.28 2.71 or 12.71 x xx −π±π−π− = π −±π+π = ≈≈−
Discard the negative solution. The width of the border is roughly 2.71 feet.
106. Let x represent the width of the border measured in feet. The radius of the pool is 5 feet. Then 5 x + represents the radius of the circle, including both the pool and the border. The total area of the pool and border is 2 (5) T Ax=π+
The area of the pool is 2 (5)25 AP =π=π
The area of the border is 2 (5)25 BTP AAAx=−=π+−π
Since the concrete is 4 inches = 1 3 foot thick, the volume of the concrete in the border is () 2 11 (5)25 33 B Ax=π+−π
Solving the volume equation: () () 2 2 2 1 (5)2527 3 10252581 10810 x xx xx π+−π= π++−= π+π−= 2 2 10(10)4()(81) 2() 31.42100324 6.28 2.13 or 12.13 x xx −π±π−π− = π
Discard the negative solution. The width of the border is approximately 2.13 feet.
107. Let x represent the width of the border measured in feet.
The total area is (62)(102) AT xx=++
The area of the garden is 61060 AG =⋅=
The area of the border is (62)(102)60 BTG AAAxx =−=++− .
Since the concrete is 3 inches or 0.25 feet thick, the volume of the concrete in the border is () 0.250.25(62)(102)60 B Axx=++−
Solving the volume equation: () 2 2 2 0.25(62)(102)6027 6032460108 4321080 8270 xx xx xx xx ++−= ++−= +−= +−= 2 884(1)(27) 8172 2(1)2
2.56 or 10.56 x xx −±−− −± == ≈≈−
Discard the negative solution. The width of the border is approximately 2.56 feet.
108. Let x = the width and 2x = the length of the patio. The height is 1 3 foot and the concrete available is () 827216 = cubic feet..
Section 1.3: Quadratic Equations
The dimensions of the patio are 18 feet by 36 feet.
109. Let x = the length of a 12.9-inch iPad Pro in a 16:9 format.
Then 9 16 x = the width of the iPad. The diagonal of the 12.9-inch iPad is 9.7 inches, so by the Pythagorean theorem we have:
Since the length cannot be negative, the length of the iPad is 42600.96 337 inches and the width is 42600.96 337 9 6.32 16 ≈ inches. Thus, the area of the iPad is 42600.96942600.96 33716337 71.11 ⋅= square inches.
Let y = the length of a 14.4-inch 3:2 format
Microsoft Surface Pro. Then 2 3 y = the width of the Surface Pro. The diagonal of a 14.4-inch Surface Pro is 14.4 inches, so by the Pythagorean theorem we have:
Chapter 1: Graphs, Equations, and Inequalities
Since the length cannot be negative, the length of the Surface Pro is 11.98 inches and the width is 21866.24 7.99 313 ≈ inches. Thus, the area of the 14.4-inch 3:2 format Surface Pro is 1866.241866.24 2 13313 95.7 square inches. ⋅ ≈ The Surface Pro format has the larger screen since its area is larger.
110. Let x = the length of a 8.3-inch iPad Mini in a 4:3 format.
Then 3 4 x = the width of the iPad. The diagonal of the 8.3-inch iPad is 8.3 inches, so by the Pythagorean theorem we have:
Since the length cannot be negative, the length of the Fire is 16384 6.78399 356 ≈ inches and the width is 1016384 4.240 16356 ≈ inches. Thus, the area of the Amazon Fire is ()() 6.783994.24028.8 square inches.
The iPad Mini™ 4:3 format has the larger screen since its area is larger.
111. Let h be 1.1. Then
0.04(0.04)4(0.00025)(1.1) 2(0.00025) 1.10.000250.04 00.000250.041.1 35.3 ft or 124.7 ft
124.7 ft does not make sense in the context of the problem, so the answer is 35.3 ft.
112. Since d is expressed in billions, we will set d = 12 and solve for x using the Quadratic Formula.
Since the length cannot be negative, the length of the iPad is 6.64 inches and the width is () 3 6.324.98 4 = inches. Thus, the area of the iPad is (6.64)(4.98)33.1 = square inches. Let y = the length of a 8-inch 16:10 format Amazon Fire HD 8™. Then 10 16 y = the width of the Fire. The diagonal of a 8-inch Fire is 8 inches, so by the Pythagorean theorem we have:
or 5.873
So the nearest year when the earnings were 12 occurred about 5 years after 2018 or 2023. The negative value -5.873 has no meaning.
113. We will set g = 2.97 and solve for h using the Quadratic Formula.
0.00060.0153.04
2.970.00060.0153.04
00.00060.0150.07
0.015(0.015)4(0.0006)(0.07) 2(0.0006)
0.0150.000393 0.0012
or 4.02
So the estimated numbers of hours worked by a student with a GPA of 2.97 is 29 hours. The value -4.02 has no meaning since it is negative.
114. Let x be the numbers of members in the fraternity and s be the share paid by each member. Then 1470 s x = . If there are 7 members who cannot contribute then the share goes up by $5. So we have the following equation: 1470 5 7 s x += or ()()571470sx+−=
Solving these two equations together: ()() () 2 1470 571470 and 1470 571470 10290 14705351470 10290 5350 535102900 sxs
2 535102900 720580 (42)(49)0 42 or 49 xx
Since x is the number of members, it must be positive so the number of members is 49.
Section 1.3: Quadratic Equations
115. Let a be the age the individual is able to start saving money. Then we need to find where the models are equal. Solving these two equations together: 2
2240(2240)4(25)(38540) 2(25)
22401163600 50 252400307001607840 252240385400
22401078.7 50
22401078.722401078.7 or 5050
66.4 or 23.2
Since x is the age to start saving, it makes sense that the answer is approximate at age 23.
116. We will set the equation equal to 10 and solve:
0.034.024124 0.006 0.0030.0348.08610 0.0030.0341.9140
0.034(0.034)4(0.003)(1.914) 2(0.003)
0.034.15532 0.006 0.0340.155320.0340.15532 or 0.0060.006 20.22
The percentage will reach 10% approximately 32 years after 1960 which is 1992.
Since the number of consecutive integers cannot be negative, we discard the negative value. We must add 37 consecutive integers, beginning at 1, in order to get a sum of 703.
Chapter 1: Graphs, Equations, and Inequalities
118. () () ()() 2 1 365 2 3130 31300 13100 nn nn nn nn −= −= −−= −+= 13 or 10 nn==− Since the number of sides cannot be negative, we discard the negative value. A polygon with 65 diagonals will have 13 sides.
121. In order to have one repeated solution, we need the discriminant to be 0. ()() 2 2 2 2 2 40 140 140 41 1 4 1 4 11 or 22 bac kk k k k k kk −= −= −= = = =± ==−
Neither solution is an integer, so there is no polygon that has 80 diagonals.
119. The roots of a quadratic equation
120. The roots of a quadratic equation are
122. In order to have one repeated solution, we need the discriminant to be 0. ()()() ()() 2 2 2 40 4140 160 440 bac k k kk −= −−= −= −+= 4 or 4 kk==−
123. For 2 0 axbxc++= : 2 4 2 −±− = bbac x a
For 2 0 axbxc−+= : () 2 2 4 2 4 2 ±−− = −±− =−
bbac x a bbac a
124. For 2 0 axbxc++= : 2 1 4 2 bbac x a = and 2 2 4 2 bbac x a −+− =
For 2 0 cxbxa++= :
Section 1.4: Complex Numbers; Quadratic Equations in the Complex Number System
2 2 == x
126. a. 2 9 x = and 3 x = are not equivalent because they do not have the same solution set. In the first equation we can also have 3 x =− .
b. 9 x = and 3 x = are equivalent because 93 = .
c. ()()() 2 121xxx −−=− and 21 x x −=− are not equivalent because they do not have the same solution set.
The first equation has the solution set { }1 while the second equation has no solutions.
127. Answers will vary. Methods may include the quadratic formula, completing the square, graphing, etc.
128. Answers will vary. Knowing the discriminant allows us to know how many real solutions the equation will have.
129. Answers will vary. One possibility: Two distinct: 2 3180xx−−= One repeated: 2 14490xx−+= No real: 2 40 xx++=
130. Answers will vary.
125. If x = original width and y = original length, then 1 1 or ==xyx y . The ratio of side lengths is 2 1 = x y y . Folding along the longest side results in sides of length 1 and 2 = y x y whose ratio is
Section 1.4
1. True; for example, 2 1 i =−
2. 2 (2)(2)44(1)5 +−=−=−−= iii
3. False; a quadratic equation in the complex number system either has two real solutions, one double root solution, or two complex solutions.
4. real; imaginary; imaginary unit
5. False; the conjugate of 25i + is 25i .
6. True; the set of real numbers is a subset of the set of complex numbers.
7. False; if 23i is a solution of a quadratic equation with real coefficients, then its conjugate, 23i + , is also a solution.
8. b
Chapter 1: Graphs, Equations, and Inequalities
9. a
10. c
11. (23)(68)(26)(38)85 iiii −++=++−+=+
12. (45)(82)(4(8))(52) 47 iii i ++−+=+−++ =−+
13. (32)(44)(34)(2(4)) 76 iii i −+−−=−−+−− =−+
14. (34)(34)(3(3))(4(4)) 606 iii i −−−−=−−+−−− =+=
15. (25)(86)(28)(56) 611 iii i −−+=−+−− =−−
16. (84)(22)(82)(4(2)) 106 iii i −+−−=−−+−− =−+
17. 3(26)618 ii−=−
18. 4(28)832 ii−+=−−
19. 2 3(76)21182118(1) 1821 −+=−−=−−− =− iiiii i
20. 2 3(34)912912(1)129 iiiiii −+=−+=−+−=−−
21. 2 (34)(2)6384 654(1) 105 iiiii i i −+=+−− =−−− =−
22. 2 (53)(2)10563 103(1) 13 +−=−+− =+−− =+ iiiii i i
23. 2 (5)(5)2555 25(1) 26 −−−+=−+− =−− = iiiii
24. 2 (3)(3)933 9(1) 10 iiiii −++=−−++ =−+− =−
25. 2 1010343040 343434 9121216 30403040 916(1)25 3040 2525 68 55 ii iii iii ii i i ++ =⋅= −−+ +−− ++ == =+ =+
26. 2 1313512 512512512 65156 256060144 6515665156 25144(1)169 65156 169169 512 1313 i iii i iii ii i i + =⋅ −−+ + = +−− ++ == =+ =+
27. 2 2 2 22 2(1) 12 12 (1)1 ii iii iii i i i i ++− =⋅= ===−
28. 2 2 222 22 2 2(1) 121 2(1)22 iiiii iii i i i i =⋅= + ===+
29. 2 2 66166 111 1 67(1) 5757 1(1)222 iiiiii iii iii i i i −−−−−+ =⋅= ++− −+− −+− ===−
30. 2 2 232312233 111 1 253(1) 1515 1(1)222 iiiiii iii iii i i i ++++++ =⋅= −−+ +−− ++− −+ ===−+
31. 2 2 131133 2 224224 13313 (1) 42422 iii ii
+=++
=++−=−+
Section 1.4: Complex Numbers; Quadratic Equations in the Complex Number System
32. 2 2 313311 2 224224 33113 (1) 42422 iii ii
−=−+
=−+−=−
33. 22 (1)1212(1)2 iiiii +=++=++−=
34. 22 (1)1212(1)2 iiiii −=−+=−+−=−
35. ()11 2322122211 (1) iiiiiiii + ==⋅=⋅=−=−
36. () 7 1427(1)1 ii==−=−
37. 20 2020210 10 111 () 11 1 1 (1) === === i iii
38. 23 2322122211 112 1111 () 111 (1) (1) i iiiiii iii i iii ii + ==== ⋅⋅ ===⋅===
39. ()3 62355(1)5156 ii−=−=−−=−−=−
40. 32 444(1)4 iiiii +=+⋅=+−=−
41. 3532 2 64(64) (64(1))1(10)10 iiii iiii −=− =⋅−−=−⋅=−
42. 3222 421421 4(1)2(1)1 421 34 iiiii i i i −+=⋅−+ =−−−+ =−++ =−
43. 32 2 (1)(1)(1)(1)(12)(1) (121)(1)2(1) 2222(1) 22 iiiiiii iiii iii i +=+++=+++ =+−+=+ =+=+− =−+
44. 44 (3)181181(1)182 ii+=+=+=
45. 7277 (1)(1(1))(0)0 iiii+=+−==
46. 42 2(1)2(1)(1(1))2(0)0 ii+=+−==
47. ()()() 432 86422222 432 (1)(1)(1)1 1111 0 +−−=+++ =−+−+−− =−+− = iiiiiiii
48. ()() 32 753222 32 (1)(1)(1) 0 iiiiiiiiiii iiii iiii +++=⋅+⋅+⋅+ =−⋅+−⋅+−⋅+ =−+−+ =
49. 42i −=
50. 93i −=
51. 255 i −=
52. 648 i −=
53. 124323 −=⋅=ii
54. 189232 −=⋅=ii
55. 2001002102 −=⋅=ii
56. 459535 −=⋅=ii
57. 2 (34)(43)1291612 916(1) 25 5 iiiii i +−=−+− =−+− =− =
58. 2 (43)(34)1216912 169(1) 25 5 iiiii i +−=−+− =−+− =− =
Copyright © 2026 Pearson Education, Inc.
Chapter 1: Graphs, Equations, and Inequalities
59. 2 2 40 4 4 2 x x x x i += =− =±− =±
The solution set is { } 2,2. ii
66. 2 250xx−+= 22 1,2,5 4(2)4(1)(5)42016 (2)16 24 12 2(1)2 abc bac i xi ==−= −=−−=−=−
−−±− ± ===±
The solution set is { } 12,12 ii−+ .
60. 2 40 x −= {} (2)(2)0 2 or 2
The solution set is 2,2. xx xx +−= =−=
61. 2 160 x −= ()() {} 440 4 or 4
67. 2 251020 −+=xx 22 25,10,2 4(10)4(25)(2)100200100 (10)100 101011 505055 ==−= −=−−=−=−
−−±− ± ===± abc bac i xi
The solution set is 4,4. xx xx +−= =−=
The solution set is { } 1111 , 5555 −+ii
62. 2 250 x += {} 2 25 255
The solution set is 5,5. x xi ii =− =±−=±
63. 2 6130xx−+= {} 22 1,6,13, 4(6)4(1)(13)365216 (6)16 64 32 2(1)2
The solution set is 32,32. abc bac i xi ii ==−= −=−−=−=−
−−±− ± ===± −+
64. 2 480xx++= 22 1,4,8 444(1)(8)163216 41644 22 2(1)2 abc bac i x i === −=−=−=− −±−−± ===−±
The solution set is { } 22,22 ii−−−+ .
65. 2 6100xx−+= 22 1,6,10 4(6)4(1)(10)36404 (6)4 62 3 2(1)2 abc bac i xi ==−= −=−−=−=−
−−±− ± ===±
The solution set is { } 3,3ii−+
68. 2 10610 xx++= 22 10,6,1 464(10)(1)36404 6462 31 2(10)201010 abc bac i x i === −=−=−=−
−±−−± ===−±
The solution set is { } 3131 , 10101010 ii−−−+
69. 2 2 512 5210 x x xx += −+= () 2 2 5,2,1 424(5)(1)42016 (2)16 2412 2(5)1055 abc bac i xi ==−= −=−−=−=−
−−±− ± ===±
The solution set is { } 1212 , 5555 ii−+ .
70. 2 2 1316 13610 x x xx += −+= 22 13,6,1 4(6)4(13)(1)365216 (6)16 6432 2(13)261313 abc bac i xi ==−= −=−−=−=−
−−±− ± ===±
The solution set is { } 3232 , 13131313 ii−+ .
Section 1.4: Complex Numbers; Quadratic Equations in the Complex Number System
71. 2 10 xx++= 1,1,1,abc=== 22414(1)(1)143 1313 13 2(1)222 bac i x i −=−=−=− −±−−± ===−±
The solution set is 1313 , 2222 ii −−−+
72. 2 10 xx−+= 1,1,1abc==−= 224(1)4(1)(1)143 (1)313 13 2(1)222 bac i x i −=−−=−=− −−±−± ===±
The solution set is 1313 , 2222 ii −+
73. 3 640−= x () 2 2 (4)4160 404 or 4160 −++= −=
= ++= xxx xx xx 22 1,4,16 444(1)(16)166448 448443 223 2(1)2 === −=−=−=− −±−−± ===−± abc bac i x i
The solution set is { } 4,223,223. −−−+ii
74. 3 270 x += () 2 2 (3)390 303 or 390 xxx xx xx +−+= += =− −+= 22 1,3,9 4(3)4(1)(9)93627 (3)27 333 333 2(1)222 abc bac i x i ==−=
−−±− ± ===±
The solution set is 333333 3,,. 2222 ii −−+
75. 4 4 16 160 x x = −= ()() () 22 2 440 (2)(2)40 xx xxx −+= −++= 2 2 20 or 20 or 40 2 or 2 or 4 2 or 2 or 42 xxx xxx x xxi −=+=+= ==−=− ==−=±−=±
The solution set is { } 2,2,2,2. ii
76. 4 4 1 10 x x = −= ()() () 22 2 110 (1)(1)10 xx xxx −+= −++= 2 2 10 or 10 or 10 1 or 1 or 1 1 or 1 or 1 xxx xxx x xxi −=+=+=
The solution set is { } 1,1,,. ii
77. 4213360xx++= ()() 22 22 22 940 90 or 40 9 or 4 9 or 4 3 or 2 xx xx xx xx x ixi ++= +=+= =−=− =±−=±− =±=±
The solution set is { } 3,3,2,2. iiii
78. 42340xx+−= ()() () 22 2 140 (1)(1)40 xx xxx −+= −++= 2 2 10 or 10 or 40 1 or 1 or 4 1 or 1 or 42 xxx xxx x xxi −=+=+= ==−=− ==−=±−=±
The solution set is { } 1,1,2,2. ii
79. 2 3340 xx−+= 22 3,3,4 4(3)4(3)(4)94839 abc bac ==−= −=−−=−=−
The equation has two complex solutions that are conjugates of each other.
Copyright © 2026 Pearson Education, Inc.
Chapter 1: Graphs, Equations, and Inequalities
80. 2 2410 xx−+= 22 2,4,1 4(4)4(2)(1)1688 abc bac ==−= −=−−=−=
The equation has two unequal real number solutions.
81. 2 2 234 2340 xx xx += +−= 22 2,3,4 434(2)(4)93241 abc bac ===− −=−−=+=
The equation has two unequal real solutions.
82. 2 2 62 260 x x xx += −+= 22 1,2,6 4(2)4(1)(6)42420 abc bac ==−= −=−−=−=−
The equation has two complex solutions that are conjugates of each other.
83. 2 91240 xx−+= 22 9,12,4 4(12)4(9)(4)1441440 abc bac ==−= −=−−=−=
The equation has a repeated real solution.
84. 2 41290 xx++= 22 4,12,9 4124(4)(9)1441440 abc bac === −=−=−=
The equation has a repeated real solution.
85. The other solution is 2323. ii+=−
86. The other solution is 44. ii−=+
87. 343434346zziiii +=−+−=−++=
88. ()8383 83(83) 8383 066 wwii ii ii ii −=+−+ =+−− =+−+ =+=
89. 2 (34)(34) (34)(34) 9121216 916(1)25 zzii ii iii ⋅=−− =−+ =+−− =−−=
90. 34(83) 3483 57 57 zwii ii i i −=−−+ =−−− =−− =−+
91. 2 2 181834 343434 54723454754 916 9121216 5075 23 25 Viii Z Iiii iiii iii i i +++ ===⋅ −−+ ++++− == + +−− + ==+
The impedance is 23i + ohms.
92. 12 2 11111(43)(2) 243(2)(43) 626262 823112 8643 ii Z ZZiiii iii ii iii −++ =+=+= +−+− === −+− −+− So, 2 2 11211262 626262 662212466104 364 3612124 701071 4044 iii Z iii iiii iii i i −−+ ==⋅ −−+ +−−++ == + +−− + ==+
The total impedance is 71 44 i + ohms.
93. ()() 2 zzabiabi abiabi a +=+++ =++− = () () 2 zzabiabi abiabi abiabi bi −=+−+ =+−− =+−+ =
94. zabiabiabiz =+=−=+=
95. ()() ()() ()() ()() zwabicdi acbdi acbdi abicdi abicdi zw +=+++ =+++ =+−+ =−+− =+++ =+
Section 1.5: Radical Equations; Equations Quadratic in Form; Absolute Value Equations; Factorable Equations
⋅=+⋅+ =+++ =−++ =−−+ 2 ()() ()() zwabicdi abicdi acadibcibdi acbdadbci
96. 2 ()() ()() ()() zwabicdi acadibcibdi acbdadbci acbdadbci
⋅=+⋅+ =−− =−−+ =−−+
Section 1.5
1. True
2. ()3 3 x x =
3. ()() 2 274421 xxxx −−=−+
4. ()() () () ()()() 322 2 4936494 49 433 xxxxxx xx xxx +−−=+−+ =+− =+−+
5. The distance from the origin to 4 on a real number line is 4 units.
6. False; you can also use the Quadratic Formula or completing the square.
7. quadratic in form
8. True
9. a
10. c
11. 64+= y () 2 642 61610 += +=→= y yy
Check: 223255 +==
The solution set is { }22 12. 37 t −= () 2 2 37 34952 t tt −= −=→= {}
Check: 523497
The solution set is 52. −== 13. 211 t −= () 2 2112 211221 t ttt −= −=→=→= {}
Check: 2(1)111
The solution set is 1. −==
14. 342 t += () 2 3422 344300 t ttt += +=→=→=
Check: 3(0)442
The solution set is {0}. +==
15. 346 t +=−
Since the principal square root is never negative, the equation has no real solution.
16. 532 t +=−
Since the principal square root is never negative, the equation has no real solution.
17. 3 1230 x −−= () 3 3 3 3 123 123 122722613 x x xxx −= −= −=→−=→=− 3 3 Check: 12(13)32730
The solution set is {13}. −−−=−=
18. 3 1210 x −−= () 3 3 3 3 121 121 121200 x x xxx −= −= −=→−=→= 3 3 Check: 12(0)1110
The solution set is {0}. −−=−=
Copyright © 2026 Pearson Education, Inc.
Chapter 1: Graphs, Equations, and Inequalities
19. () 4 4 4 4 542 542 5416 520 4 x x x x x −= −= −= = =
Check: () 4 4 544162 −== T
The solution set is { } 4.
20. () () 5 5 5 5 231 231 231 22 1 x x x x x −=− −=−
Check: () 5 5 21311 −=−=− T
The solution set is { }1 .
21. ( ) () () 5 2 5 5 5 2 2 2 2 21 21 21 210 10 10 1 xx xx xx xx x x x +=− +=− +=− ++= += += =−
Check: ()() 2 55 5 1211211 −+−=−=−=− T
The solution set is { }1 22. ( ) () 4 2 4 4 4 2 2 2 165 165 1625 9 3 x x x x x += += += = =±
Check: () () 2 44 4 2 44 4 316916255 316916255 −+=+== +=+== T T The solution set is { }3,3 . 23. () () () 2 2 2 2 8 8 64 640 640 xx x x xx xx xx = = = −= −= 0 or 64 xx==
Check: 080 00 = = T 64864 6488 6464 = =⋅ = T
The solution set is { }0,64 . 24. () () () 2 2 2 2 3 3 9 90 90 xx x x xx xx xx = = = −= −= 0 or 9 xx==
Check: 030 00 = = T 939 933 99 = =⋅ = T
The solution set is { }0,9 25. 152 x x −= () 2 2 22 152 1522150 (5)(3)05 or 3 xx xxxx xxxx −= −=→+−= +−=→=−=
Check –5: 152(5)25 55
Check 3: 152(3)933 The solution set is {3}. −−= =≠− −===
Section 1.5: Radical Equations; Equations Quadratic in Form; Absolute Value Equations; Factorable Equations
26. 12 x x −= () 2 2 22 12 12120 (4)(3)04 or 3 xx xxxx xxxx −= −=→+−= +−=→=−=
Check –4: 12(4)16 44
Check 3: 123933
The solution set is {3}. −−= =≠− −===
27. () 2 2 2 2 3(10)4 3(10)4 3(10)(4) 330816 0514 0(7)(2) 7 or 2 xx xx xx xxx xx xx xx +−= +=+ +=+ +=++ =+− =+− =−=
+−= = = T
The solution set is { } 8 5
30. 2 85xxx−−=+ ( ) () 2 2 2 22 85 81025 1133 3 xxx xxxx x x −−=+ −−=++ −= =−
Check 7: 3(710)49417
Check 2: 3(210)436422 −−+−=−=−≠− +−=−==
Discard 7 x =− as extraneous. The solution set is {2}.
28. () 2 2 2 2 132 15 1(5) 11025 01124 0(3)(8) 3 or 8 xx xx xx xxx xx xx xx −−=+ −=+ −=+ −=++ =++ =++ =−=−
Check: ()() () 2 33835 93835 42 22 −−−−=−+ +−=−+ = = T
The solution set is { }3 .
Check 3: 1(3)33211
Check 8: 1(8)38206 −−−−=−+→−=− −−−−=−+→=−
Discard 8 x =− as extraneous.
The solution set is {-3}.
29. 2 42xxx−−=+ ( ) () 2 2 2 22 42 444 8 85 5 xxx xxxx x x −−=+ −−=++ −=→−=
Check: 2 88842 555 6482 4 2555 42 255 22 55
31. 331 x x ++= () 2 2 2 2 313 31(3) 3169 098 0(1)(8) 1 or 8 xx xx xxx xx xx xx +=− +=− +=−+ =−+ =−− ==
Check 1: 33(1)13451
Check 8: 33(8)132588 ++=+=≠ ++=+==
Discard 1 x = as extraneous. The solution set is { }8 .
Copyright © 2026 Pearson Education, Inc.
Chapter 1: Graphs, Equations, and Inequalities
32. 2122 x x +−= () 2 2 2 2 1222 122(2) 12244 028 (2)(4)0 2 or 4 xx xx xxx xx xx xx −=− −=− −=−+ =−− +−= =−=
Check 2: 2+122(2)21662
Check 4: 2122(4)2444 −−−=+=≠− +−=+==
Discard 2 x =− as extraneous.
The solution set is {4}
33. 3572 xx−−+= () () () 22 2 2 2 2 2 2 3527 3527 354477 21647 (216)47 46425616(7) 46425616112 4801440 20360 (2)(18)02 or 18 xx xx xxx xx xx xxx xxx xx xx xxxx −=++ −=++ −=++++ −=+ −=+ −+=+ −+=+ −+= −+= −−=→==
34. 3721 xx+++= () () () 22 2 2 2 2 3712 3712 371222 2422 22 (2)2 442 320 (1)(2)0 1 or 2 xx xx xxx xx xx xx xxx xx xx xx +=−+ +=−+ +=−+++ +=−+ −−=+ −−=+ ++=+ ++= ++= =−=−
Check –1: 3(1)712 412131
Check 2: 3(2)722 101011 −++−+ =+=+=≠ −−++−+ =+=+==
Check 2: 3(2)527 191322
Check 18: 3(18)5187 49257522 −−+ =−=−=−≠ −−+ =−=−==
Discard 2 x = as extraneous. The solution set is { }18
Discard 1 x =− as extraneous. The solution set is { }2 . 35. 3112 xx+−−= () () () 22 2 2 2 2 2 3121 3121 314411 2241 (22)41 48416(1) 2144 650 (1)(5)01 or 5 xx xx xxx xx xx xxx xxx xx xxxx +=+− +=+− +=+−+− −=− −=− −+=− −+=− −+= −−=→==
Check 1: 3(1)111 402022
Check 5: 3(5)151 1644222 +−− =−=−== +−− =−=−==
The solution set is { }1,5
36.
Section 1.5: Radical Equations; Equations Quadratic in Form; Absolute Value Equations; Factorable Equations
37.
Check –1: 2(1)311101
Check 3: 2(3)331321 −+−−+=−= +−+=−=
The solution set is { }1,3
Discard
Discard 4 x = as extraneous. The solution set is { }25 .
39. ()1/2 314 x += () () () 2 3141/22 31163155 x xxx += +=→=→=
Check: () ()1/2 1/2 3514 164 44 += = = T
The solution set is {5}
40. ()1/2 352 x −= () () () 2 3521/22 354393 x xxx −= −=→=→=
Check: () ()1/2 1/2 3352 42 22 −= = = T
The solution set is {3}
Chapter 1: Graphs, Equations, and Inequalities
41. ()1/3 522 x −= () () () 3 5221/33 5285102 x xxx −= −=→=→=
Check: () ()1/3 1/3 5222 82 22 −= = = The solution set is {2} .
42. ()1/3 211 x +=− () () () 3 2111/33 211221 x xxx +=− +=−→=−→=−
Check: () () () 1/3 1/3 2111 11 11 −+=−
The solution set is { }1 .
43. ()1/2 2 95 x += () () 2 1/2 2 2 22 95 92516 4 or 4 x xx xx
+=
+=→= =−=
Check:
44. ()1/2 2 169 x −= () () 2 1/2 2 2 22 169 168197 97 or 97 x xx xx
−=
−=→= =−= () () 1/2 2 1/2 1/2 97169 97169 819 99
−−=
−= = = () ()
−= = =
The solution set is { } 97,97 .
45. ()() () ()() 4 22 2 160 440 4220 t tt ttt −= +−= ++−= 2 40 has no real solution t += , so we only need to consider 20 2 t t += =− or 20 2 t t −= =
The solution set is { }2,2
46. 4 40 y −= ()() () () () () () 22 2 22 220 2220 202, which is impossible or 2202 yy yyy yy yyy +−= ++−= += =− +−= =±
The solution set is { } 2,2.
47. 42540xx−+= ()() 22 22 410 40 or 10 2 or 1 xx xx xx −−= −=−= =±=±
The solution set is { } 2,1,1,2.
48. 4210240xx−+= ()()22640xx−−= 2 2 60 6 6 x x x −= = =± or 2 2 40 4 2 x x x −= = =±
The solution set is { } 6,2,2,6.
Section 1.5: Radical Equations; Equations Quadratic in Form; Absolute Value Equations; Factorable Equations
49. 42 6510 −−=xx ()() 22 22 2 6110 610 or 10 61 ,which is impossible or 1 +−= +=−= =− =± xx xx x x
The solution set is { } 1,1.
50. 42 25120 xx−−= ()() 22 22 2 2340 230 or 40 23 , which is impossible or 2 xx xx x x +−= +=−= =− =±
The solution set is { } 2,2.
51. 63780xx+−= ()() 33 33 3 3 810 80 or 10 82 or 11 xx xx xx x x +−= +=−= =−→=− =→=
The solution set is { } 2,1.
52. 63780xx−−= ()() 33 33 3 3 810 80 or 10 82 or 11 xx xx xx x x −+= −=+= =→= =−→=−
The solution set is { } 1,2.
53. ()() 2 272120xx++++= () ()() 2 2 2 22 7120 340 30 or 40 3235 or 4246 letpxpx pp pp pp pxx pxx =+→=+ ++= ++= +=+= =−→+=−→=− =−→+=−→=−
The solution set is { } 6,5.
54. ()() 2 252560 xx+−+−= () ()() 2 2 2 2525 60 320 30 20 32531 7 2252 2 letpxpx pp pp porp pxx orpxx =+→=+ −−= −+= −=+= =→+=→=− =−→+=−→=−
The solution set is { } 7 2 ,1.
55. ()() 2 21513 ss+−+= () ()() 2 2 2 2 11 253 2530 2130 210 or 30 113 1 222 or 3132 letpsps pp pp pp pp pss pss =+→=+ −= −−= +−= +=−= =−→+=−→=− =→+=→=
The solution set is { } 3 ,2. 2
56. ()() 2 315120 yy −+−+= () ()() 2 2 2 11 3520 3210 320 or 10 225 1 333 or 1112 letpypy pp pp pp pyy pyy =−→=− ++= ++= +=+= =−→−=−→= =−→−=−→=
The solution set is { } 5 ,2. 3
57. 40xx−= () () () 2 2 22 4 4 16016 0160 or 16016 xx xx x xxx xxx x x = = =→=− =−→= −=→=
Copyright © 2026 Pearson Education, Inc.
Chapter 1: Graphs, Equations, and Inequalities
Check: () 0: 0400 00 16: 164160 16160 00 x x =−= = =−= −= =
The solution set is { }0,16
58. 80xx−= () () () 2 2 22 8 8 64064 0640 or 64 xx xx xxxx xxxx = = =→=− =−→==
Check: 0: 0800 00 64: 648640 64640 x x =−= = =−= −=
The solution set is { }0,64
59. 20 xx+= ()() 2 2 2 20 200 540 50 or 40 5=5 non-real or 4=4=16 letpxpx pp pp pp pp px pxx =→= += +−= +−= +=−= =−→− =→→
Check: 16: 161620 16420 x =+= += The solution set is { }16
60. 6 xx+= ()() 2 2 2 6 60 320 30 or 20 3=3 non-real or 2=24 letpxpx pp pp pp pp px pxx =→= += +−= +−= +=−= =−→− =→→=
Check: 4: 446 426 x =+= +=
The solution set is { }4 .
61. 1/21/4440zt−+= ()() 1/421/2 2 1/4 440 220 20 2216 letpzpz pp pp p pzz =→= −+= −−= −= =→=→=
Check: ()1/4 1/2 16: 1641640 4840 00 z =−+= −+=→=
The solution set is { }16
62. 1/21/4210 tt−+= ()() 1/421/2 2 1/4 210 110 10 111 letptpt pp pp p ptt =→= −+= −−= −= =→=→=
Check: ()1/4 1/2 1: 12110 1210 00 t =−+= −+=→=
The solution set is { }1
Chapter 1: Graphs, Equations, and Inequalities
Check: () () () () 21 21 33 22 42 93 3 : 3760 2 3760 414 60 33 00 111 : 3760 333 x x =−−−−−= −−−= +−= =
()() 397360 272160 00 −−= −−= = The solution set is { } 31 23,.
68. 21 2340 xx−−= 122 2 let 2340 pxpx pp =→= −−= 1 3932341 44 341341 44 p px ±+± == ++ =→= () 1 1 1 341 4 434112441 32 341341 341 8 x x
Equations
Check: () 2/31/3 2/3 111 : 2530 888 11 2530 42 15 30 22 33000 27: 227 x x
+−= −=→= =− () ()() 1/3 52730 295330 181530 33000 −= −−= −−= −=→= The solution set is { } 1 ,27 8
70. 4/32/3 3520 xx+−= ()() 2/324/3 2 let 3520 3120 1 or 2 3 pxpx pp pp pp =→= +−= −+= ==− 2/3 11 33px=→= () 3 3 2/3 2 1 3 113 27279 x xx
=
=→=±=±
Chapter 1: Graphs, Equations, and Inequalities
or () () () 2/3 3/2 3/2 2/3 3/2 22 2 2 which is not a real number px x x =−→=− =− =−
Check: ( ) ( ) () () 334/32/3 99 11 93 3520 3520 15 20 33 00 +−= +−= +−= = ( ) ( ) () () 334/32/3 99 11 93 3520 3520 15 20 33 00 −+−−= +−= +−= =
The solution set is 33 , 99 .
71. 235 x += 235 or 235 22 or 28 1 or 4 xx xx xx +=+=− ==− ==−
The solution set is {–4, 1}.
72. 312 x −= 312 or 312 33 or 31 1 1 or 3 xx xx xx −=−=− ==− ==−
The solution set is { } 1 ,1 3
73. 14813145 tt−+= −= 145 or 145 44 or 46 3 1 or 2 tt tt tt −=−=− −=−=− =−=
The solution set is { } 3 1, 2
74. 1269123 zz−+= −= 123 or 123 22 or 24 1 or 2 zz zz zz −=−=− −=−=− =−=
The solution set is { }1,2
75. 721−= x 721 or 721 3 or 3 −=−=− =−= xx xx
The solution set is {–3, 3}.
76. 1 x −= 1 or 1 xx −=−=−
The solution set is {–1, 1}.
77. 42321 xx−= = 21 or 21 11 or 22 xx xx ==− ==−
The solution set is { } 11 , 22 .
78. 53211 22 x x −= = 11 2 or 2 22 4 or 4 xx xx ==− ==−
The solution set is { }4,4
79. 8 3 7 = x 212121 or 888 =→==−xxx
The solution set is { } 2727 , 22 .
Copyright © 2026 Pearson Education,
Section 1.5: Radical Equations; Equations Quadratic in Form; Absolute Value Equations; Factorable Equations
80. 3 9 4 x = 1212 or 12 xxx=→==−
The solution set is {–12, 12}.
81. 2 2 35 x += 22 2 or 2 3535 5630 or 5630 524 or 536 2436 or 55 xx xx xx xx +=+=− +=+=− ==− ==−
The solution set is { } 3624 , 55 .
82. 1 1 23 x −= 11 1 or 1 2323 326 or 326 38 or 34 84 or 33 xx xx xx xx −=−=− −=−=− ==− ==−
The solution set is { } 48 , 33 .
83. 1 2 2 u −=− impossible, since absolute value always yields a non-negative number.
84. 21 v −=− impossible, since absolute value always yields a non-negative number.
85. 2 90 x −= 2 2 90 9 3 x x x −= = =±
The solution set is { }3,3 .
86. 2 160 x −= 2 2 160 16 4 x x x −= = =±
The solution set is { }4,4
87. 2 23xx−= ()() 22 22 23 or 23 230 or 230 2412 310 or 2 28 no real sol. 2 xxxx xxxx xxx −=−=− −−=−+= ±− −+== ±− = 3 or 1 xx==−
The solution set is { }1,3
88. 2 12 xx+= ()() 22 22 12 or 12 120 or 120 1148 340 or 2 147 no real sol. 2 3 or 4 xxxx xxxx xxx xx +=+=− +−=++= −±− −+== ±− = ==−
The solution set is { }4,3 .
89. () ()() 3 2 90 90 330 xx xx xxx −= −= −+= 0 x = or 30 3 x x −= = 30 3 x x += =−
The solution set is { }3,0,3 .
90. () ()() 42 22 2 810 810 990 xx xx xxx −= −= −+= 2 0 0 x x = = or 90 9 x x −= = or 90 9 x x += =−
The solution set is { }9,0,9
Copyright © 2026 Pearson Education, Inc.
Chapter 1: Graphs, Equations, and Inequalities
91. () ()()
32 2 200 200 540 xxx xxx xxx +−= +−= +−=
0 x = or 50 5 x x += =− or 40 4 x x −= =
The solution set is { }5,0,4
92. () ()() 32 2 670 670 710 xxx xxx xxx +−= +−= +−=
0 x = or 70 7 x x += =− or 10 1 x x −= =
The solution set is { }7,0,1
93. ()() () () ()()() 32 2 2 10 1110 110 1110 xxx xxx xx xxx +−−= +−+= +−= +−+= 10 1 x x += =− or 10 1 x x −= =
The solution set is { }1,1
94. ()() () () ()()() 32 2 2 440 4140 410 4110 xxx xxx xx xxx +−−= +−+= +−= +−+= 40 4 x x += =− or 10 1 x x −= = or 10 1 x x += =−
The solution set is { }4,1,1 .
95. ()() () () ()()() 32 2 2 316480 31630 3160 3440 −−+= −−−= −−= −−+= xxx xxx xx xxx 30 3 x x −= = or 40 4 −= = x x or 40 4 += =− x x
The solution set is { }4,4,3
96. ()() () () ()()() 32 2 2 330 3130 310 3110 xxx xxx xx xxx −−+= −−−= −−= −−+= 30 3 x x −= = or 10 1 x x −= = or 10 1 x x += =−
The solution set is { }1,1,3 .
97. ()() () () ()()() 32 32 2 2 248 2840 214210 2140 21220 x xx xxx xxx xx xxx +=+ −−+= −−−= −−= −−+= 210 21 1 2 x x x −= = = or 20 2 x x −= = or 20 2 x x += =−
The solution set is { } 1 2,,2 2 . 98. ()() () () ()()() 32 32 2 2 342736 3427360 349340 3490 34330 xxx xxx xxx xx xxx +=+ +−−= +−+= +−= +−+= 340 34 4 3 x x x += =− =− or 30 3 x x −= = or 30 3 x x += =−
The solution set is { } 4 3,,3 3
99. 1/2 420xx−+= ; Use ZERO (or ROOT) on the graph of 1 42yxx=−+ 15 5 −5 −1 15 5 −5 −1
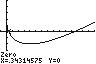
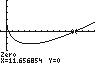
The solution set is { }0.34,11.66
Section 1.5: Radical Equations; Equations Quadratic in Form; Absolute Value Equations; Factorable Equations
100. 2/31/3420xx++= ; Use ZERO (or ROOT) on the graph of 2/31/3 1 42yxx=++
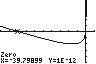
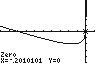
The solution set is { }39.80,0.20
101. 42330xx+−= ; Use ZERO (or ROOT) on the graph of 42 1 33yxx=+−
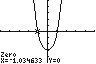
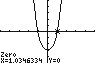
The solution set is { }1.03,1.03 .
102. 42220xx+−= ; Use ZERO (or ROOT) on the graph of 42 1 22yxx=+−


The solution set is { }0.93,0.93
103.
= = or 30 3 x x −= = The solution set is 7 ,3 2
105. ()() () () ()()() 32 32 2 2 545218 5245180 529520 9520 33520 aaa aaa aaa aa aaa −=−+ +−−= +−+= −+= −++= 30 3 a a −= = or 30 3 a a += =− or 520
The solution set is 2 3,,3 5
106. ()() () () ()()() 32 32 2 2 312520 3512200 354350 4350 22350 zzz zzz zzz zz zzz −=−+ +−−= +−+= −+= −++= 20 2 z z −= = or 20 2 z z += =− 350 35 5 3 z z z += =− =− The solution set is 5 2,,2 3
Chapter 1: Graphs, Equations, and Inequalities
107. 35290
114.
115.
The
Section 1.5: Radical Equations; Equations Quadratic in Form; Absolute Value Equations; Factorable Equations
2 2 361 3610 mm mm +=−
3 a
, 6 b = , 1 c = ()() () 2 66431 624 6 23 62636 63 m −±− −± == −±−±
The solution set is 3636 , 33 −−−+
483
The solution set is 2727 , 22 −+
119. 2 11 xx+−= ()() 2 2 11 20 210 2 or 1 xx xx xx xx +−= +−= +−= =−= or () 2 2 11 0 10 0 or 1 xx xx xx xx +−=− += += ==−
The solution set is { }2,1,0,1 120. 2 322xx+−= ()() 2 2 322 340 410 4 or 1 xx xx xx xx +−= +−= +−= =−= or () 2 2 322 30 30 0 or 3 xx xx xx xx +−=− += += ==−
The solution set is { }4,3,0,1
Chapter 1: Graphs, Equations, and Inequalities
Since
126.
Section 1.5: Radical Equations; Equations Quadratic in Form; Absolute Value Equations; Factorable Equations
128. 223283280 kkkk −= −−= ()()470kk+−= 4 3 4 4 3416 13 5 k x x xx x
And since neither of these x values causes a denominator to equal zero, the solution set is { }1331 , 56
129. 8327 xx −=− 8327 3278 515 3 xx xx x x −=− −−=−− −=− =− or 83(27) 8327 3278 1 1 xx xx xx x x −=−− −=−+ −+=−
The solution set is { }3,1
The solution set is 33313 2222,, ii
33313 ,, 3, 1 2222 ii
127. 2212120
And since neither of these x values causes a denominator to equal zero, the solution set is { } 3 ,5 2
130. 53124 x x +=− 53124 54123 99 1 x x xx x x +=− +=− = = or 53(124) 53124 54123 15 x x x x xx x +=−− +=−+ −=−− =−
The solution set is { }1,15 .
131. Graph the equations 1 /4/1100yxx =+ and 2 4 y = ; then use INTERSECT to find the x-coordinate of the points of intersection:
300 5 0 0
The distance to the water's surface is approximately 229.94 feet.
Chapter 1: Graphs, Equations, and Inequalities
132. 2 4
Let
The
133. 2 32 l T π =
The
Since x > 2, the negative solution is extraneous. The solution set is 2231 3 +
The solution set is { }11 136. () 79 2 5510 9 144 101010 41 102 4 10 12313 123130 121330 00 += +−= −+= = = xxx xxx xxx xx To solve 1 2 121330 −+=xx , let 1 2 = ux 11 22 2 Then 121330 (43)(31)0 31 or 43 91 169 −+= −−= === == uu uu uxx xx
The solution set is { } 0,,91 169
137. 63 33 22 28270 (27)(1)0 (3)(39)(1)(1)0 ++= ++= +−++−+= zz zz zzzzzz 30 or 10 3 or 1 +=+= =−=− zz zz
Section 1.6: Problem Solving; Interest, Mixture, Uniform Motion, Constant Rate Job Applications
Section 1.6
1. mathematical modeling
2. interest
3. uniform motion
4. False; the amount charged for the use of principal is the interest.
5. True; this is the uniform motion formula.
6. a
The solution set is
138. Answers will vary, one example is 11 x +=−
139. Answers will vary, one example is 20 xx−−=
140. Answers will vary.
141. x represents the distance from x to the origin. Since distance is never negative, 2 x =− has no real solution.
142. Mya did not check her solutions and included the extraneous solution, 1 x =−
7. b
8. c
9. Let A represent the area of the circle and r the radius. The area of a circle is the product of π times the square of the radius: 2 A r =π
10. Let C represent the circumference of a circle and r the radius. The circumference of a circle is the product of π times twice the radius: 2
11. Let A represent the area of the square and s the length of a side. The area of the square is the square of the length of a side: 2 A s =
12. Let P represent the perimeter of a square and s the length of a side. The perimeter of a square is four times the length of a side: 4 Ps =
13. Let F represent the force, m the mass, and a the acceleration. Force equals the product of the mass times the acceleration: F ma =
14. Let P represent the pressure, F the force, and A the area. Pressure is the force per unit area:
15. Let W represent the work, F the force, and d the distance. Work equals force times distance: WFd =
16. Let K represent the kinetic energy, m the mass, and v the velocity. Kinetic energy is one-half the product of the mass and the square of the velocity: 2 1 2 K mv =
Chapter 1: Graphs, Equations, and Inequalities
17. C = total variable cost in dollars, x = number of dishwashers manufactured: 150 Cx =
18. R = total revenue in dollars, x = number of dishwashers sold: 250 Rx =
19. Let x represent the amount of money invested in bonds. Then 50,000 x represents the amount of money invested in CD's. Since the total interest is to be $6,000, we have:
0.150.07(50,000)6,000
22. Let x represent the interest rate. 16,35015,00015,000()(2) 16,35015,00030,000 1,35030,000 1,350 30,000 0.045 4.5% x x x x x x =+ =+ = = = =
The interest rate was 4.5% per year..
()()()()
1000.150.07(50,000)6,000100
157(50,000)600,000
15350,0007600,000
8350,000600,000
8250,000 31,250
$31,250 should be invested in bonds at 15% and $18,750 should be invested in CD's at 7%.
20. Let x represent the amount of money invested in bonds. Then 50,000 x represents the amount of money invested in CD's. Since the total interest is to be $7,000, we have:
0.150.07(50,000)7,000
23. Let x represent the number of pounds of Earl Grey tea. Then 100 x represents the number of pounds of orange pekoe tea.
64(100)5.50(100)
64004550 2400550 2150 75 +−= +−= += = = xx xx x x x
75 pounds of Earl Grey tea must be blended with 25 pounds of orange pekoe.
24. Let x represent the number of pounds of the first kind of coffee. Then 100 x represents the number of pounds of the second kind of coffee.
()()()()
1000.150.07(50,000)7,000100
157(50,000)700,000
15350,0007700,000
$43,750 should be invested in bonds at 15% and $6,250 should be invested in CD's at 7%.
21. Let x represent the amount of money loaned at 4%. Then 12,000 x represents the amount of money loaned at 5.5%. Since the total interest is to be $600, we have:
0.040.055(12,000)600
0.046600.055600 0.015660600 0.01560 4,000 xx
$4,000 is loaned at 4%.
40 +−= +−= −+= −=− = xx xx x x x
2.755(100)4.10(100) 2.755005410
2.25500410 2.2590
40 pounds of the first kind of coffee must be blended with 60 pounds of the second kind of coffee.
25. Let x represent the number of pounds of cashews. Then 60 x + represents the number of pounds in the mixture.
156 +=+ +=+ = = xx xx x x
94.50(60)7.75(60)
92707.75465 1.25195
156 pounds of cashews must be added to the 60 pounds of almonds.
26. Let x represent the number of caramels in the box. Then 30 x represents the number of cremes in the box.
RevenueCostProfit
12.500.250.45(30)3.00 12.500.2513.50.453.00
12.5013.50.203.00 12.5013.500.203.00
The box should contain 20 caramels and 10 cremes.
27. Let r represent the speed of the current. 2016 1 6033 1516 1 6044
Since the distance is the same in each direction: 1616 34 4(16)3(16) 644483
The speed of the current is approximately 2.286 miles per hour.
28. Let r represent the speed of the motorboat.
RateTimeDistance Upstream3553 Downstream32.52.53 rr rr ++
The distance is the same in each direction: 5(3)2.5(3)
5152.57.5 2.522.5 9 rr rr r r −=+ −=+ = =
The speed of the motorboat is 9 miles per hour.
29. Let r represent the speed of the current. RateTimeDistance 10 Upstream1510 15 10 Downstream1510 15 r r r r + +
Since the total time is 1.5 hours, we have: 2 2 2 2 1010 1.5 1515
10(15)10(15)1.5(15)(15) 15010150101.5(225)
3001.5(225) 200225 250 (5)(5)0 5 or 5 rr rrrr rrr r r r rr rr += −+ ++−=−+
Speed must be positive, so disregard 5 r =− The speed of the current is 5 miles per hour.
30. Let r represent the rate of the slower car. Then 10 r + represents the rate of the faster car.
RateTimeDistance
Slower car3.53.5 Faster car103310 rr rr ++ 3.53(10) 3.5330 0.530 60 rr rr r r =+ =+ = = The slower car travels at a rate of 60 miles per hour. The faster car travels at a rate of 70 miles per hour. The distance is (70)(3) = 210 miles.
31. Let r represent Karen’s normal walking speed.
RateTimeDistance
50 With walkway 2.550 2.5 50 Against walkway2.550 2.5 r r r r + +
Since the total time is 48 seconds: 2 2 2 2 5050 48 2.52.5 50(2.5)50(2.5)48(2.5)(2.5) 501255012548(6.25) 10048300 048100300 0122575
Speed must be positive, so disregard 1.67≈−
Karen’ normal walking speed is approximately 3.75 feet per second.
Chapter 1: Graphs, Equations, and Inequalities
32. Let r represent the speed of the airport walkway. RateTimeDistance
280 Walking with1.5280 1.5
280 Standing still 280 r r r r + +
Walking with the walkway takes 60 seconds less time than standing still on the walkway: 2 2 2 280280 60 1.5
280280(1.5)60(1.5) 2804202806090 60904200 23140 (27)(2)0
270 or 20 7 or 2 2
Speed must be positive, so disregard 7 2 r =−
The speed of the airport walkway is 2 meters per second.
33. Let w represent the width of a regulation doubles tennis court. Then 26 w + represents the length.
The area is 2808 square feet: 2 2 2 (26)2808 262808 2628080 314040 (39)(36)0 ww ww ww ww ww += += +−= +−= +−= 390 or 360 39 or 36 ww ww +=−= =−=
The width must be positive, so disregard 39 w =− . The width of a regulation doubles tennis court is 36 feet and the length is 2(36) + 6 = 78 feet.
34. Let L represent the length of the pickleball court. The width is 2 feet less than half the length, 2 2 L W =−
The area of the court is 880 LW = .
The length must be positive, so disregard 40 L =− The width of the pickleball court is 44 222220 2 W
The dimensions of the court are 44 feet by 20 feet.
35. Let t represent the time it takes to do the job together.
of job done Time to do job in one minute
Working together, the job can be done in 12 minutes.
36. Let t represent the time it takes April to do the job working alone.
Part of job done Time to do job in one hour
Using quadratic formula to solve L,
April would take 15 hours to paint the rooms.
37. l = length of the garden w = width of the garden
a. The length of the garden is to be twice its width. Thus, 2 lw = .
The dimensions of the fence are 4 l + and 4 w + .
The perimeter is 46 feet, so:
2(6)2(6)100
2(6)2(36)100 212612100 824100 876
3(9.5)28.5 wl ww ww w w w l +++= +++= +++= += = = ==
2(4)2(4)46
2(24)2(4)46 482846 61646 630 5 lw ww ww w w w +++= +++= +++= += = =
The dimensions of the garden are 5 feet by 10 feet.
b. Area 51050 lw =⋅=⋅= square feet
c. If the dimensions of the garden are the same, then the length and width of the fence are also the same (4) l + . The perimeter is 46 feet, so:
2(4)2(4)46 282846 41646 430 7.5 ll ll l l l +++= +++= += = =
The dimensions of the garden are 7.5 feet by 7.5 feet.
d. Area 7.5(7.5)56.25 lw =⋅== square feet.
38. l = length of the pond w = width of the pond
a. The pond is to be a square. Thus, lw = The dimensions of the fenced area are 6 w + on each side. The perimeter is 100 feet, so: 4(6)100 424100 476 19 w w w w += += = =
The dimensions of the pond are 19 feet by 19 feet.
b. The length of the pond is to be three times the width. Thus, 3 lw = . The dimensions of the fenced area are 6 and 6 wl++ . The perimeter is 100 feet, so:
The dimensions of the pond are 9.5 feet by 28.5 feet.
c. If the pond is circular, the diameter is d and the diameter of the circle with the pond and the deck is 6 d +
The perimeter is 100 feet, so: (6)100 6100 1006 100 625.83 d d d d π+= π+π= π=−π
The diameter of the pond is 25.83 feet. d. 2 square Area19(19)361 ft
The circular pond has the largest area.
39. Let t represent the time it takes for the defensive back to catch the tight end. 1002525 1233 100 10 Time to run Distance 100 yards Def. Back TimeRate Tight 12 sec End 10 sec1010 tt tt = =
Since the defensive back has to run 5 yards farther, we have: 25 510 3 251530
The defensive back will catch the tight end at the 45 yard line (15 + 30 = 45).
Chapter 1: Graphs, Equations, and Inequalities
40. Let x represent the number of highway miles traveled. Then 30,000 x represents the number of city miles traveled. () 30,000 900 4025 30,000 200200900 4025
Therese is allowed to claim 20,000 miles as a business expense.
41. Let x represent the number of gallons of pure water. Then 1 x + represents the number of gallons in the 60% solution. ()()()()()() () %gallons%gallons%gallons 01(1)0.60(1)
2 3 gallon of pure water should be added.
42. Let x represent the number of liters to be drained and replaced with pure antifreeze. ()()()()()() () %liters%liters%liters
10.40(15)0.60(15) 60.409 0.603 5 xx xx x x += +−= +−= = = 5 liters should be drained and replaced with pure antifreeze.
43. Let x represent the number of ounces of water to be evaporated; the amount of salt remains the same. Therefore, we get 2 3 0.04(32)0.06(32) 1.281.920.06 0.060.64 0.646432 10 0.0663 x x x x =− =− = ==== 2 3 1010.67 ≈ ounces of water need to be evaporated.
44. Let x represent the number of gallons of water to be evaporated; the amount of salt remains the same.
0.03(240)0.05(240)
7.2120.05 0.054.8 4.8 96 0.05 x x x x =− =− = == 96 gallons of water need to be evaporated.
45. Let x represent the number of grams of pure gold. Then 60 x represents the number of grams of 12 karat gold to be used.
12(60)(60) 23
300.540 0.510 20 xx xx x x +−= +−= = = 20 grams of pure gold should be mixed with 40 grams of 12 karat gold.
46. Let x represent the number of atoms of oxygen. 2 x represents the number of atoms of hydrogen. 1 x + represents the number of atoms of carbon. 2145 444 11 xxx x x +++= = =
There are 11 atoms of oxygen and 22 atoms of hydrogen in the sugar molecule.
47. Let t represent the time it takes for Mike to catch up with Dan. Since the distances are the same, we have: 11 (1) 69 322 2 tt tt t =+ =+ = Mike will pass Dan after 2 minutes, which is a distance of 1 3 mile.
48. Let t represent the time of flight with the wind. The distance is the same in each direction: 330270(5) 3301350270 6001350 2.25 tt tt t t =− =− = =
The distance the plane can fly and still return safely is 330(2.25) = 742.5 miles.
49. Let t represent the time the auxiliary pump needs to run. Since the two pumps are emptying one tanker, we have: 3 1 49 27436 49 9 2.25 4 t
The auxiliary pump must run for 2.25 hours. It must be started at 9:45 a.m.
50. Let x represent the number of pounds of pure cement. Then 20 x + represents the number of pounds in the 40% mixture.
0.25(20)0.40(20) 50.48 0.63 30 5 6 xx xx x x +=+ +=+ = ==
5 pounds of pure cement should be added.
51. Let t represent the time for the tub to fill with the faucets on and the stopper removed. Since one tub is being filled, we have: 1 1520 4360
60 minutes is required to fill the tub.
52. Let t be the time the 5 horsepower pump needs to run to finish emptying the pool. Since the two pumps are emptying one pool, we have: 22 1
The 5 horsepower pump must run for an additional 1.75 hours or 1 hour and 45 minutes to empty the pool.
53. Let t represent the time spent running. Then 5 t represents the time spent biking.
RateTimeDistance
Run66 Bike25525(5) tt tt
The total distance is 87 miles: 625(5)87 61252587 1912587 1938 2 tt tt t t t +−= +−= −+= −=− =
The time spent running is 2 hours, so the distance of the run is 6(2)12 = miles. The distance of the bicycle race is 25(52)75 −= miles.
54. Let r represent the speed of the eastbound cyclist. Then 5 r + represents the speed of the westbound cyclist.
RateTimeDistance Eastbound66 Westbound566(5) rr rr ++
The total distance is 246 miles: 66(5)246 6630246 1230246 12216 18 rr rr r r r ++= ++= += = =
The speed of the eastbound cyclist is 18 miles per hour, and the speed of the westbound cyclist is 18523 += miles per hour.
55. Burke's rate is 100 12 meters/sec. In 9.81 seconds, Burke will run 100 (9.81)81.75 12 = meters. Bolt would win by 100-81.75=18.25 meters.
56. 2 22 A rrh=π+π . Since 58.9π = A square inches and 6.4 = h inches, 2
or 9.5 −±−− = −± = ==− r rr .
The radius of the coffee can is 3.1 inches.
Chapter 1: Graphs, Equations, and Inequalities
57. Let x be the side length of the square piece of sheet metal.
Since a 1-foot square is cut from each corner and the edges are turned up, then 2,2,and1LxWxH =−=−=
The volume of the box is 4 LWH =
e ( ,s 2 i ( nc )2) n (1)4 elength cannot be egativ (2)4
The dimensions should be 4 feet by 4 feet.
58. Let x be the width of the rectangular sheet. Then the length is 2x feet.
Since a 1-foot square is cut from each corner and the edges are turned up, then 22,2,1LxWxandH =−=−= .
The volume of the box is 4 LWH = 2 2 (22)(2)(1)4
Since width cannot be zero. So 3 W =
The length of the box, 2(3)6 L ==
The dimensions should be 6 feet by 3 feet.
59. Answers will vary.
60. Let x be the original selling price of the shirt. ProfitRevenueCost
40.4020240.6040 xxxx =− =−−→=→=
The original price should be $40 to ensure a profit of $4 after the sale.
If the sale is 50% off, the profit is: 400.50(40)204020200 −−=−−=
At 50% off there will be no profit.
61. Let 12 and tt represent the times for the two segments of the trip. Since Atlanta is halfway between Chicago and Miami, the distances are equal.
The average speed for the trip from Chicago to Miami is 49.5 miles per hour.
62. The time traveled with the tail wind was: 919 1.67091 hours 550 t =≈ .
Since they were 20 minutes () 1 3 hour early, the time in still air would have been: () 1.67091 hrs 20 min1.670910.33333 hrs 2.00424 hrs +=+ ≈
Thus, with no wind, the ground speed is 919 458.53 2.00424 ≈ . Therefore, the tail wind is 550458.5391.47 knots −=
63. It is impossible to mix two solutions with a lower concentration and end up with a new solution with a higher concentration.
Algebraic Solution:
Let x = the number of liters of 25% solution. ()()()()()() ()() %liters%liters%liters 0.250.48200.5820 0.259.610.60.58 0.331 3.03 liters (not possible) x x x x x x += +=+
Section 1.7
1. 2 x ≥− −2 0
2. True; the absolute value of a number is the distance the number lies from 0 on a real number line. Negative numbers lie to the left of 0 on a real number line, but still have a positive distance from 0.
3. { } ,,,,,,, A Babcdeiou∪=
4. negative
5. closed interval
6. aua−≤≤
7. (,] a −∞
8. True; this follows from the addition property for inequalities.
9. True; this follows from the multiplication property for inequalities.
10. False; since both sides of the inequality are being divided by a negative number, the sense, or direction, of the inequality must be reversed.
That is, ab cc >
11. a 12. c
13. Interval: [ ] 0,2
Inequality: 02 x ≤≤
14. Interval: () 1,2
Inequality: 12 x −<<
15. Interval: [ ) 2, ∞
Inequality: 2 x ≥
16. Interval: ( ] ,0−∞
Inequality: 0 x ≤
Section 1.7: Solving Inequalities
17. Interval: [ ) 0,3
Inequality: 03 x ≤<
18. Interval: ( ]1,1
Inequality: 11 x −<≤
19. a. 35 3353 68 < +<+ < b. 35 3555 20 < −<− −< c. ()() 35 3335 915 < < < d. ()() 35 2325 610 < −>− −>−
20. a. 21 2313 54 > +>+ > b. 21 2515 34 > −>− −>− c. ()() 21 3231 63 > > > d. ()() 21 2221 42 > −<− −<−
21. a. 212 21323 245 x x x +< ++<+ +< b. 212 21525 243 x x x +< +−<− −<−
Chapter 1: Graphs, Equations, and Inequalities
c. ()() 212 32132 636 x x x +< +< +<
d. ()() 212 22122 424 x x x +< −+>− −−>−
22. a. 125 12353 428 x x x −> −+>+ −>
b. 125 12555 240 x x x −> −−>− −−>
c. ()() 125 31235 3615 x x x −> −> −>
d. ()() 125 21225 2410 x x x −> −−<− −+<−
23. [0, 4] 4 0
24. (–1, 5) 1 5 0
25. [4, 6) 6 4 0
26. (–2, 0] −2 0
27. [ ) 4, ∞ 4 0
28. ( ] ,5−∞ 5 0
29. () ,4−∞−
39. If 5, then 50. xx<−<
40. If 4, then 40. xx<−+<
41. If 4, then 40. xx>−+>
42. If 6, then 60. xx>−>
43. If 4, then 312.xx≥−≥−
44. If 3, then 26.xx≤≤
45. If 6, then 212.xx>−<−
46. If 2, then 48.xx >−−<
47. If 840, then 5. <<xx
48. If 312, then 4. xx≤≤
49. If 1 3, then 6. 2 xx −≤≥−
50. If 1 1, then 4. 4 xx −><−
51. 372 39 3 x x x −> > >
{ }3 or (3,) xx >∞ 3 0
52. 251 24 2 x x x +> >− >−
{ }2 or (2,) xx >−−∞ −2 0
53. 3518 515 3 −≤ −≤ ≥− x x x
{ }3 or [3,)≥−−∞ xx

54. 235 33 1 x x x −≤ −≤ ≥−
{ }1 or [1,) xx ≥−−∞ −1 0
55. 313 24 2 x x x x −≥+ ≥ ≥ { }2 or [2,) xx ≥∞ 2 0
56. 223 5 x x x −≥+ ≥
{ }5 or [5,) xx ≥∞ 5 0
Section 1.7: Solving Inequalities
57. 2(3)8 268 214 7 x x x x −+< −−< −< >− { }7 or (7,) xx >−−∞ −7 0
58. 3(1)12 3312 315 5 x x x x −−< −+< < < { }5 or (,5) xx <−∞ 5 0
59. 43(1)3 4333 313 32 2 3 x x x x x −−≤ −+≤ +≤ ≤ ≤ 22 or , 33 xx ≤−∞ 2 3 0 1
60. 84(2)2 8842 42 60 0 x x x x x x x x −−≤− −+≤− ≤− ≤ ≤
{ } ( ] 0 or ,0 xx ≤−∞ 0
61. 1 (4)8 2 1 28 2 1 10 2 20 xx xx x x −>+ −>+ −> <− { }20 or (,20) xx <−−∞− 0 −20
Chapter 1: Graphs, Equations, and Inequalities
62. 1 34(2) 3 12 34 33 9122 814 7 4 xx xx xx x x +>− +>− +>− >− >− 77 or 44(,) xx
63. 1375 6312 24 −≤−≤

64. 42210 228 14 x x x ≤+≤ ≤≤
{ } [ ] 14 or 1,4 xx
1 4 0
65. 5432 932 2 3 3 x x x −≤−≤
≥≥ 22 3 or ,3 33 xx
2 3 3 0
66. 3329 626 33 x x x
{ } [ ] 33 or 3,3 xx
−33 0
67. 21 30 4 12210 1121 111 22 x x x x −<< −<−< −<< −<< 111111 or , 2222
1 2 0 11 2
68. 32 04 2 0328 236 2 2 3 x x x x + << <+< −<< −<< 22 2 or ,2 33 xx
2 3 2 0
69. 1 114 2 1 03 2 06 or 60 x x xx <−< <−< >>−−<< { } () 60 or 6,0 xx−<<− −6 0
70. 1 011 3 1 10 3 30 or 03 x x xx <−< −<−< >><< { } () 03 or 0,3 xx<< 3 0
71. 22 (2)(3)(1)(1) 61 61 5 5 xxxx xxx x x x +−>−+ −−>− −−>− −> <−
{ } () 5 or ,5 xx <−−∞− −5 0
72. 22 (1)(1)(3)(4) 112 112 11 11 xxxx xxx x x x −+>−+ −>+− −>− −>− <
{ } () 11 or ,11 xx <−∞ 11 0
73. 28 x < 828 44 x x −<< −<< { } () 44 or 4,4 xx−<<− −4 4 0
74. 315 x < 15315 55 x x −<< −<<
{ } () 55 or 5,5 xx−<<− 5 −5 0
75. 742 > x 742 or 742 6 or 6 <−> <−> xx xx
{ } ()() 6 or 6 or ,66, <−>−∞−∪∞xxx

76. 26 x > 26 or 26 3 or 3 xx xx <−> <−>
{ } ()() 3 or 3 or ,33, xxx<−>−∞−∪∞ −33 0
Section 1.7: Solving Inequalities
77. 324 t −≤ 4324 236 2 2 3 t t t −≤−≤ −≤≤
−≤≤ 22 2 or ,2 33 tt −≤≤− 2 3 2 0
78. 257 u +≤ 7257 1222 61 u u u −≤+≤ −≤≤ −≤≤ { } [ ] 61 or 6,1 uu−≤≤− 1 −6 0
79. 223 21 x x −+< −< 121 13 x x −<−< << { } () 13 or 1,3 xx<< 13 0
80. 435 42 x x ++< +< 242 62 x x −<+< −<<− { } () 62 or 6,2 xx−<<−−− −2 −6 0
81. 32 x −≥ 32 or 32 1 or 5 xx xx −≤−−≥ ≤≥
{ } ( ] [ ) 1 or 5 or ,15, xxx≤≥−∞∪∞ 5 1 0
82. 42 x +≥ 42 or 42 6 or 2 xx xx +≤−+≥ ≤−≥−
Chapter 1: Graphs, Equations, and Inequalities
{ } ( ] [ ) 6 or 2 or ,62, xxx≤−≥−−∞−∪−∞ −2 −6 0
83. 527 527 −>− −> x x 527 or 527 212 or 22 6 or 1 −<−−> −<−−> ><− xx xx xx
{ } ()() 1 or 6 or ,16, <−>−∞−∪∞xxx

84. 231 231 x x −>− −> 231 or 231 33 or 31 1 1 or 3 xx xx xx −<−−> −<−−>− >< () 11 or 1 or 33,1,xxx
<>−∞∪∞
1 3 1 0
85. 1472 145 x x −−<− −< 5145 644 64 44 33 1 or 1 22 x x x xx −<−< −<−< >> >>−−<<
{ } ()33 22 1 or 1, xx−<<− −1 0 3 2
86. 1241 123 x x −−<− −< 3123 422 42 22 21 or 12 x x x xx −<−< −<−< >> >>−−<< { } () 12 or 1,2 xx−<<− 2 −1 0
87. 952 +<− x
No solution since absolute value is always nonnegative. 0
88. 340 x −≥
All real numbers since absolute value is always non-negative. { } () or , xx−∞<<∞−∞∞ 0
89. 3411 48 2 x x x −< −< >−
{ }|2xx >− or () 2, −∞ −2 0
90. 137 36 2 x x x −≤ −≤ ≥−
{ }|2xx ≥− or ) 2, −∞ −2 0
Copyright © 2026 Pearson Education, Inc.
91.
97. ()() 2 22 4321 43441 1 1 xxx x xxx x x +≤+ +≤++
98. ()() 2 22 9531 95961 561 1 xxx x xxx xx x −≤− −≤−+
Chapter 1: Graphs, Equations, and Inequalities
99. () 1 327 2 1 39 2 x x −−< −< 11 39 22 1719 3 22 1719 66 x x x −<−< << << { } 1719 66 | xx<< or 1719 , 66
100. ()
49 16 47 16
101. 35211 826 43 34 x x x x −<−≤ −<−≤ >≥− −≤< { }|34xx−≤< or ) 3,4
102. () 23218 23228 2128 127 17 22 71 22 x x x x x x ≤−+< ≤−−< ≤−<
7 2 1 2 0
103. 714 13 13 313 24 x x x x x −−> −−>− −< −<−< −<< { }|24xx−<< or () 2,4 −2 4 0 104. 935 34 34 434 71 x x x x x −+≥ −+≥− +≤ −≤+≤ −≤≤ { }|71xx−≤≤ or 7,1 −7 1 0
105. 352 x x −<+< 35 8 8 x x x −<+ −< >− and 52 5 5 x x x x +< < > We need both 8 x >− and 5 x > . Therefore, 5 x > is sufficient to satisfy both inequalities. { }|5xx > or () 5, ∞ 5 0
106. 232 x x <−< 23 5 5 x x x <− < > and 32 3 3 x x x x −< −< >−
We need both 5 x > and 3 x >− . Therefore, 5 x > is sufficient to satisfy both inequalities. { }|5xx > or () 5, ∞ 5 0
107. 2215 x xx+<−< 221 21 3 3 x x x x x +<− <− < > and 215 310 31 1 3 x x x x x −< −−< −< >−
We need both 1 3 x >− and 3 x > . Therefore, 3 x > is sufficient to satisfy both inequalities. { }|3xx > or () 3, ∞ 3 0
108. 213557 xxx −<+<− 2135 15 6 6 x x x x x −<+ −−< −< >− and 3557 257 212 6 xx x x x +<− −+<− −<− >
We need both 6 x >− and 6 x > . Therefore, 6 x > is sufficient to satisfy both inequalities. { }|6xx > or () 6, ∞ 6 0
109. 20.5 x −< 0.520.5 0.520.52 1.52.5 x x x −<−< −+<<+ << { } Solution set: 1.52.5xx<<
110. ()11 x −−< () 111 111 1111 20 x x x x −<−−< −<+< −−<<− −<< { } Solution set: 20xx−<<
Section 1.7: Solving Inequalities
111. ()32 x −−> ()() 32 or 32 32 or 32 5 or 1 xx xx xx −−<−−−> +<−+> <−>− { } Solution set: 5 or 1 xxx<−>−
112. 23 x −> 23 or 23 1 or 5 xx xx −<−−> <−> { } Solution set: 1 or 5 xxx<−>
113. 21 < young adult's age < 30
114. 40 ≤ middle-aged < 60
115. A temperature x that differs from 98.6° F by at least 1.5F ° . 98.61.5 98.61.5 or 98.61.5 97.1 or 100.1 x xx xx −°≥° −°≤−°−°≥° ≤°≥°
The temperatures that are considered unhealthy are those that are less than 97.1˚F or greater than 100.1˚F, inclusive.
116. The length L must be within 0.0025 of 5.375 inches..
5.3750.0025
5.37255.3775 −≤ −≤−≤ ≤≤ L L L
0.00255.3750.0025
The lengths must be between 5.3725 and 5.3775 inches, inclusive.
117. The percentage must be within 3.2 percentage points of 77 percent. The inequality that represents this would be: 773.2 3.2773.2 73.880.2 −≤ −≤−≤ ≤≤ x x x
The actual percentage is likely to fall between 73.8% and 80.2% inclusive.
118. The speed x varies from 707 mph by up to 55 mph. a. 70755 x −≤
Chapter 1: Graphs, Equations, and Inequalities
b. 5570755 5570755 652762 x x x −≤−≤ −≤−≤ ≤≤
The speed of sound is between 652 and 762 miles per hour, depending on conditions.
119. a. Let x = age at death.
122. Let C represent the commission. Calculate the commission range: 250.4(200)250.4(3000) 1051225 C C +≤≤+ ≤≤
The commissions are at least $105 and at most $1225.
3052.2
82.2 −≥ ≥ x x
Therefore, the average life expectancy for a 30-year-old man in 2023 will be greater than or equal to 82.2 years.
b. Let x = age at death.
123. Let W = weekly wages and T = tax withheld. Calculating the withholding tax range, given the range of weekly wages:
3055.8
85.8 −≥ ≥ x x
Therefore, the average life expectancy for a 30-year-old woman in 2023 will be greater than or equal to 85.8 years.
c. By the given information, a woman can expect to live 85.882.23.6 −= years longer.
120. 20 VT =
80º120º
80º120º
The volume ranges from 1600 to 2400 cubic centimeters, inclusive.
121. Let P represent the selling price and C represent the commission. Calculating the commission: 45,0000.25(900,000) 45,0000.25225,000 0.25180,000 CP P P
Calculate the commission range, given the price range:
500312.5312.5700312.5 187.50312.5387.5
0.12(187.5)0.12312.50.12(387.5) 22.500.12312.546.5 1100 1122.501146.50 W W W W W W T +≤−≤+
22.511000.12312.546.51100
The amount withheld varies from $1122.50 to $1146.50, inclusive.
124. Let x represent the length of time you should exercise on the last two days. 253504015150 115150 35 x x x +++++= += = You will stay within the guidelines by exercising from 35 minutes total on the last two days.
125. Let x represent the amount paid for international minutes and y represent the number of international minutes. The range of the bills is $69.50 to $140.75. The rate plan is $60. Thus the range of costs of the international minutes is: 9.5080.75 x ≤≤ . The cost per min is $0.25.
9.5080.75
900,0001,100,000
0.25(900,000)0.250.25(1,100,000)
225,0000.25275,000
225,000180,0000.25180,000275,000180,000
45,00095,000 P P P P C
The agent's commission ranges from $45,000 to $95,000, inclusive.
45,000 900,000 0.055%== to 95,000 1,100,000 0.0868.6%,== inclusive.
As a percent of selling price, the commission ranges from 5% to 8.6%, inclusive.
0.250.25 38323 y y ≤≤ ≤≤
The minutes varies from 38 to 323 minutes, inclusive.
126. Let C represent the amount paid for the fares. The range of the fare is $20.93 to $40.44. of miles. The number of miles is 23. 20.932340.44
0.911.76 x x ≤≤ ≤≤
The cost per mile varies from $0.91 per mile to $1.76 per mile, inclusive.
127. You have already consumed 40 grams of fat. Let C represent the number of cookies. Then we have the following equation: 40864 824 3 C C C +≤ ≤ ≤
You may eat up to 3 cookies and keep the total fat content of your meal not more than 64g.
128. You have already consumed 730 calories. Let x represent the number of apple sauce orders you can eat. Then we have the following equation: 73050830 50100 2 x x
You may eat up to 2 orders of apple sauce and keep your calories below or equal to 830.
129. a. Let T represent the score on the last test and G represent the course grade.
Calculating the course grade and solving for the last test: 68828789 5 326 5 5326 5326 T
Calculating the range of scores on the last test, given the grade range: 8090 4005450
To get a grade of B, you need at least a 74 on the fifth test.
b. Let T represent the score on the last test and G represent the course grade. Calculating the course grade and solving for the last test:
Calculating the range of scores on the last test, given the grade range:
G G G T ≤< ≤< ≤−< ≤<
To get a grade of B, you need at least a 77 on the fifth test.
130. Let T represent the test scores of the people in the top 2.5%.
1.96(12)100123.52 T >+=
People in the top 2.5% will have test scores greater than 123.52. That is, 123.52 T > or (123.52,). ∞
131. Since ab < , and 2222 and 22222222 and 22 abab aaababbb abab ab << +<++<+ ++ << So, 2 ab ab + <<
132. From problem 131, 2 ab ab + << , so 2 , 2222 daaababababa +++−− =−== and 2 , 2222 dbbababbabba ++−−− =−== . Therefore, 2 ab + is equidistant from a and b
133. If 0, then ab<< () () 22 22 22 0 and 0 and and ababab ababab ababab >>>> >> >> Therefore, aabb <<
134. Show that 2 ab ab + < () () 2 1 2 22 1 0, since . 2 ab abaabb abab + −=−+ =−>≠ Therefore, 2 ab ab + <
Chapter 1: Graphs, Equations, and Inequalities
135. 1111 For 0, 2 ab hab <<=+ 11 2 1 1 2 2 ba hh hab ba h ab ab h ab + ⋅=⋅
=
22 2() 2 2 () 0 abaab ab haa abab abaababa abab aba ab −+ −=−= ++ == ++ => +
Therefore, ha > . 22 ()2 2 2 () 0 babab ab bhb abab abbabbab abab bba ab +− −=−= ++ +−− == ++ => + Therefore, hb < , and we have ahb << .
136. Show that
() 2 1111 2 211 2 2 1 () 2 hab ba habab hab ab ab ab h ab ab
=+ + =+= = + =⋅= + +
137. 5 423 3 312695 31269 and 695 33 514 14 1 4 + −<−≤
This is equivalent to 14 1 5 −<≤ x . The solution set, in interval notation, is 14 1, 5 .
138. The largest value of 2 23 x occurs at the largest value for x 259 34 43 34 or 43 ≤−≤ −≤−≤ −≤≤ ≥≥−−≤≤ x x x xx
The largest value for 2 23 x is 2 2(4)332329 −−=−= .
139. Answers will vary. One possibility: No solution: () 46252 x xx+≤−+ One solution: ()() 35231321 xxx +≤++≤+−
140. Answers will vary.
141. Since 2 0 x ≥ , we have 2 2 101 11 x x +≥+ +≥
Therefore, the expression 2 1 x + can never be less than 5
142. Answers will vary.
Chapter 1 Review Exercises
1. 28 3 624 18 x x x −= −= =− The solution set is { }18 2. 2(53)845 106845 6245 6 x x x x x x x −−+=+ −++=+ −=+ =
The solution set is { }6
3. 1 5 31 4312 941 51 xx xx x x −= −= = =
The solution set is { } 1 5
4. 6 15 566 6 x x xx x = =− = Since x = 6 does not cause a denominator to equal zero, the solution set is {6}.
5. 2 2 (1)6 6 06 xx xx xx −= −=
Therefore, there are no real solutions.
6. () () 1361 432 1361 1212 432 3(13)4(6)6 394246 1327 27 13 xx xx xx xx x x −+ =+ −+
The solution set is { } 27 13
7. 2 2 (1)(23)3 233 260 3 (23)(2)0 or 2 2 xx xx xx xxxx −+= +−=
The solution set is { } 3 2, 2 . 8. 2 2 234 0423 2448252 88 2213113 84 xx xx x
±+±
The solution set is 113113 , 44
. 9. ( ) () 3 2 3 3 3 2 2 2 12 12 18 93 x x x xx −= −= −= = =± Check: 3 x =− Check: 3 x =
The solution set is { }3,3 . 10. 2 (1)20 20 11817 22 xx xx x ++= ++= −±−−±− == No real solutions.
11. 2 310 1112111 66 xx x −+= ±−±− == No real solutions.
12. ()() 42 22 22 540 410 40 or 10 2 or 1 xx xx xx xx −+= −−= −=−= =±=± The solution set is { }2,1,1,2
The second solution is not possible because it makes the
18.
()() 63 63 1 Check : 2 1178645680 22
Check 1: 17181780 x x =
The solution set is { } 1 1, 2 .
The solution set is { } ,, 1, 1. 11 mm nn nn ≠≠− −+
19. ()() 222 222 102360 5180 5920 axabxb axabxb axbaxb −−= −−= +−= 590 59 9 5 axb axb b x a += =− =− or 20 2 2 axb axb b x a −= = =
The solution set is { } 92,, 0. 5 bb a aa −≠
20. ( ) ( ) 22 22 22 22 222 2 373920 37392 37392 37394394 66439 xxxx xxxx xxxx xxxxxx xxx ++−−++= ++=−+− ++=−+− ++=−+−−++ −=−−+ () () ( ) ()() 2 2 2 22 22 61439 36211639 3672361648144 xxx xxxx xxxx −=−−+ −+=−+ −+=−+ ()() 2 2 20241080 56270 9 5930 or 3 5 xx xx xxxx −−= −−= +−= =−= 9 Check : 5 x =− 22 9999 37392 5555 81278127 =792 255255 8113517581135225 2 2525 1214411121220 252555 −+−+−−−−++
−+−+++ −+++ =−+ =−+=−+=
Check 3: x = ()() ()()22 333733392 9979992 259222 40 ++−−++ =++−−++ =−+=+ =≠
The solution set is { } 9 5 21. 237 x += 237 or 237 24 or 210 2 or 5 xx xx xx +=+=− ==− ==−
The solution set is {–5, 2}.
©
Chapter 1: Graphs, Equations, and Inequalities
22. 2329 237 x x −+= −= 237 35 5 3 x x x −= −= =− or 237 39 3 x x x −=− −=− =
The solution set is { } 5 ,3 3
23.
The solution set is { } 3 0, 2
The solution set is { } 5 ,2,2 2
26. () 2 29 29 23 23 x x x x −= −=± −=± =± 5 x = or 1 x =−
The solution set is { }1,5 .
27. 3 530xx−+=
Use the Zero option from the CALC menu. 10


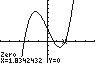
The solution set is { }2.49,0.66,1.83 .
28. 4 321 x x −=+
Use the Intersect option on the CALC menu.

Since 3 does not make any denominator equal to 0, the solution set is { }3 .

The solution set is { }1.14,1.64 .
29. 23 2 52 2(23)10(2)5 46205 14 14 x x x x x x x x +≤ −+≤ −+≤ ≤ ≥ { } [ ) 14 or 14, xx ≥∞

30. 23 97 4 362328 33231 3331 22 3133 22 x x x x x +
31333133 or , 2222 xx

31. 33 26 12 243372 21369 723 x x x x << <−< <−< −>>− { } () 237 or 23,7 xx−<<−−−

32. 1 34 2 11 34 22 97 3 22 37 26 x x x x +<
3737 or , 2626 xx
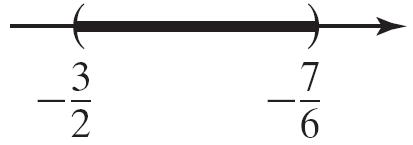
33. 259 x −≥ 259 or 259 24 or 214 2 or 7 xx xx xx −≤−−≥ ≤−≥ ≤−≥ { } ( ][ ) 2 or 7 or ,2 or 7, xxx≤−≥ −∞−∞

34. 2234 232 2232 430 4 0 3 4 0 3 x x x x x x +−≤ −≤ −≤−≤ −≤−≤ ≥≥ ≤≤ 44 0 or 0, 33 xx

Chapter 1: Graphs, Equations, and Inequalities
35. 1234 235 235 235 or 235 73 or 33 7 or 1 3 7 1 or 3 x x x xx x x x x xx −−<− −−<− −> −<−−> <−> <−> <−> () 7 1 or or 3 7 ,1 or , 3 xxx
<−>
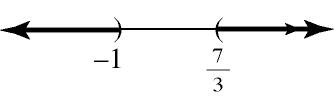
36. ()()()() () 6324623447 iiii +−−=−+−−=+
37. ()() 4335212415632 iiiii −+−+=−−+=−+
38. 2 3339393 33310 933 93 1010 iii iii iii i =⋅== ++− −+− =−
39. () () 12 504824212111 iiiii=⋅=⋅=−=−
40. ()()() () () ()() 32 2 2 232323 412923 51223 10152436 469 iii iii ii iii i +=++ =+++ =−++ =−−++ =−+
41. 2 10 xx++= ()() () 22 1,1,1, 41411143 131313 21222 abc bac i x i === −=−=−=− −±−−± ===−±
The solution set is 1313 , 2222 ii −−−+
42. 2 220 xx+−= ()() () 22 2,1,2, 4142211617 117117 224 abc bac x ===− −=−−=+= −±−± ==
The solution set is 117117 , 44 −−−+
43. 2 3 x x += ()()() () () 2 2 2 30 1,1,3, 4141311211 111 111111 21222 xx abc bac i x i −+= ==−= −=−−=−=− −−±− ± ===±
The solution set is 111111 , 2222 ii −+
44. (1)2xx+= 2 20 (2)(1)02 or 1 xx xxxx +−= +−= =−=
The solution set is { }2,1
45. 2 15 yx=−+ 10 −10 20 −15

46. ()()() 4,0,0,0,2,0 , ()()() 0,2,0,0,0,2 x-intercepts: 4,0,2 y-intercepts: 2,0,2



50. 22 plw =+
51. ()()() 90000.071$630 IPrtI =⋅⋅ ==
52. Let x represent the amount of money invested in bonds. Then 70,000 x represents the amount of money invested in CD's. Since the total interest is to be $5000, we have: ()()()() 0.080.05(70,000)5000 1000.080.05(70,000)5000100 8350,0005500,000 3350,000500,000 3150,000 50,000 xx xx
$50,000 should be invested in bonds at 8% and $20,000 should be invested in CD's at 5%.
53. Using s vt = , we have 3 and 1100 tv== Finding the distance s in feet: 1100(3)3300 s == The storm is 3300 feet away.
54. 16003600 I ≤≤ 2 2 2 900 16003600 11 16009003600 91 164 31 42 x
Chapter 1: Graphs, Equations, and Inequalities
The range of distances is from 0.5 meters to 0.75 meters, inclusive.
55. Let s represent the distance the plane can travel.
22 With windAgainst wind Rate2503028025030220 (/2)(/2) Time 280220 Dist. ss ss +=−=
Since the total time is at most 5 hours, we have: () ()/2/2 5 280220 5 560440 11145(6160) 2530,800 1232 ss ss ss s s +≤ +≤ +≤ ≤ ≤
The plane can travel at most 1232 miles or 616 miles one way and return 616 miles.
56. Let t represent the time it takes the helicopter to reach the raft.
RaftHelicopter Rate590 Time Dist.590 tt tt
Since the total distance is 150 miles, we have: 590150 95150
1.58 hours 1 hour and 35 minutes tt t t += = ≈≈
The helicopter will reach the raft in about 1 hour and 35 minutes.
57. Let d represent the distance flown by the bee traveling at 3 meters per second.
(Times needed to meet are equal.) 150 35 54503 8450 56.25 56.25meters18.75seconds 3 dd dd d dt =
The bees meet for the first time after 18.75 seconds.
The bees will meet a second time on the second lap. The first bee will have traveled 150 + x meters and the second bee will have traveled 150 + (150 – x) meters. Solving for time, we have:
150(150) 150 35 150300 35 75059003 8150
18.75 meters into the second lap 168.75 56.25 seconds 3 x x xx xx x x t +− + = +− = +=− = = ==
The bees meet the second time after 56.25 seconds (37.5 seconds later).
58. Given that 2 12803216 s tt=−− , a. The object hits the ground when 0 s = .
The object hits the ground after 8 seconds. b. After 4 seconds, the object’s height is ()() 2 1280324164896 s =−−= feet.
59. Let t represent the time it takes Clarissa to complete the job by herself.
ClarissaShawna
Time to do 5 job alone
Part of job 11 5 done in 1 day Time on job 66 (days)
Part of job 66 done by each 5 person tt tt tt + + +
Since the two people paint one house, we have: 2 2 66 1 5 6(5)6(5) 63065 7300 (10)(3)010 or 3 tt tttt tttt tt tttt += + ++=+ ++=+ −−= −+= ==−
It takes Clarissa 10 days to paint the house when working by herself.
60. Let x represent the amount of the $8-per-pound coffee.
Add 2 3 6 pounds of $8/lb coffee to get 2 3 26 pounds of $5/lb coffee.
61. Let x represent the amount of water evaporated.
The painting is 6.5 inches by 6.5 inches. 612.5 s += , so the frame is 12.5 inches by 12.5 inches.
b. Consider the following diagram:
51.2 ounces of water must be evaporated.
62. Let the length of leg 1 = x. Then the length of leg 2 = 17 – x By the Pythagorean Theorem we have
the legs are 5 cm and 12 cm long.
63. a. Consider the following diagram:
64. Let t represent the time it takes the smaller pump to finish filling the tank. 3hp Pump8hp Pump Time to do
done in 1 hr Time on job
Since the two pumps fill one tank, we have:
It takes the small pump a total of 2 more hours to fill the tank.
Chapter 1: Graphs, Equations, and Inequalities
65. Let 4 w = . Solve for the length:
The length of the plasterboard should be cut to a length of approximately 6.47 feet.
66. Let x represent the number of passengers over 20. Then 20 x + represents the total number of passengers, and 150.1x represents the fare for each passenger. Solving the equation for total cost, $482.40, we have:
(20)(150.1)482.40 300130.1482.40 0.113182.400 13018240 (114)(16)0114 or 16
Since the capacity of the bus is 44, we discard the 114. Therefore, 201636 += people went on the trip; each person paid () 150.116$13.40 −=
67. Let rS represent Scott's rate and let rT represent Todd's rate. The time for Scott to run 95 meters is the same as for Todd to run 100 meters. () 95100 0.95 0.950.95 ST ST SsTT rr rr dtrtrd =
If Todd starts from 5 meters behind the start: 105 0.950.95(105)99.75 T ST d dd = ===
a. The race does not end in a tie.
b. Todd wins the race.
c. Todd wins by 0.25 meters.
d. To end in a tie: 1000.95(100)
100950.95 50.95 5.263 meters x x x x =+ =+ = =
e. 95 = 0.95(100) Therefore, the race ends in a tie.
f, g, h. Race is a tie.
68. In each problem, we need to use the Least Common Multiple of the expressions 2 2 and 4 xx , namely 2 4. x
a. We use 2 4 x as the LCD in order to combine the given expressions.
b. We multiply each side of the equation by 2 4 x in order to clear out the denominators before solving the equation.
c. We use 2 4 x as the LCD in order to combine the terms on the left hand side before solving the inequality.
Chapter 1 Test
3. 32 2 2 mm −= + LCD: () 2 mm + Restricted values: 2,0mm=−= () () () () () ()() ()() 2 2 2232 2 222 22322 24362 260 2320 mmm m mmmmmm mmmm mmmm mm mm ++ −= +++ +−+= +−−= −−= +−= 3 2 230 m m += =− or 20 2 m m −= =
Since neither solution is a restricted value, the solution set is { } 3 2 ,2 .
4. () 58416 58446 58410 918 2 xx xx xx x x −=−−+ −=−++ −=−+ = =
The solution set is { }2 .
5. 53278 53215 323 b b b −−= −= −= 323 20 0 b b b −= −= = or 323 26 3 b b b −=− −=− =
The solution set is { }0,3
6. 422 42 38 280 xxx xx +=+ −−=
Let 2 ux = . Then () 2 224 uxx == , and we have ()() 2 280 420 uu uu −−= −+= 4 or 2 uu==−
Since we are solving for x, we get 2 4 2 x x = =± or 2 2 2 no real solution x x =− =±−
The solution set is { }2,2 7. 2 420 1,4,2 xx abc −+= ==−= ()()()() () 2 2 4 2 44412 21 4168 2 48 2 422 2 22 bbac x a −±− = −−±−− = ±− = ± = ± = =±
The solution set is { } 22,22 −+ 8. () 2 22 2 2172 2172 630 xxxx xxxx xx +−=++ +−=++ −−= 1,6,3abc==−=− ()()()() () 2 2 4 2 66413 21 63612 2 648 2 643 2 323 bbac x a −±− = −−±−−− = ±+ = ± = ± = =±
The solution set is { }323,323 −+ . 9. 2721 7221 2 3 7 xy yx yx −= −=−+ =− () ()() ()() ()() 2 7 2 7 2 7 3, 77357,5 00330,3 2 77317,1 7 x yxxy y y y =− −=−−=−−− =−=−− =−=−−
Chapter 1: Graphs, Equations, and Inequalities


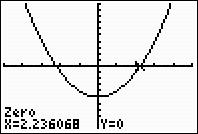
The intercepts are () 0,3 and () 10.5,0
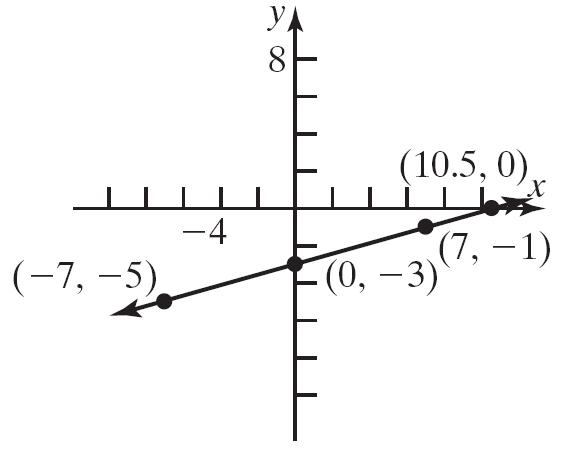
10. 2 5 yx=−
The intercepts are () 0,5 , () 2.24,0≈− , and () 2.24,0 ≈ .

11. 32 2210 xxx−−+= Since this equation has 0 on one side, we will use the Zero option from the CALC menu. It will be important to carefully select the window settings so as not to miss any solutions.
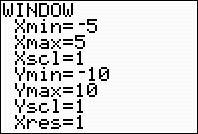

The solutions to the equation are 1 , 0.5, and 1.
12. 42580xx−−=
Since this equation has 0 on one side, we will use the Zero option from the CALC menu.


The solutions, rounded to two decimal places, are 2.50 and 2.50.
13. 327233 xxxx −+−=+−
Since there are nonzero expressions on both sides of the equation, we will use the Intersect option from the CALC menu. Enter the left side of the equation in Y1 and the right side in Y2.
The solutions, rounded to two decimal places, are 2.46 , 0.24 , and 1.70 14. 23 2 4 x + <− () 11 2 23 442 4 238 211 x x x x + ⋅<⋅− +<− =− <−
Solution set: { }11 2 | xx <− Interval: () 11 2 , −∞− 0 11 2 15. 2343 234434 237 x x x +−≥ +−+≥+ +≥ 237 210 5 x x x +≤− ≤− ≤− or 237 24 2 x x x +≥ ≥ ≥
Solution set: { } |5 or 2 xxx≤−≥
Interval: ( ] [ ) ,52, −∞−∪∞ 2 0 −5
Chapter 1: Graphs, Equations, and Inequalities
16. 7358
Solution
Interval:
The solution set is
22. We can use a table to summarize the given information.
per# of cust. in customer1
This leads to the following: ()()() Jamie's rateScott's raterate together
Since 85 65204.63 27 ⋅≈ , it will take Jamie and Scott about 204.63 minutes (3.41 hours) to check out 65 customers working together.
23. Let x = pounds of banana chips. Then the total pounds of the mix will be 40 x + Since there is to be no loss in revenue, we get
The retailer needs to mix 25 pounds of banana chips with the 40 pounds of the original mix.
24. Let x = sale price. We know that the discount is () 0.42275.00115.50 = . Therefore, sale priceoriginal pricediscount
275115.50 159.50 x x =− =− = The sale price is $159.50.
25. Here we need the simple interest formula, I Prt=⋅⋅ . In this case we have 0.04 r = , 3 months1 yr 12 months/yr4 t == , and 10,000 P =
()() () 1 4 10,0000.04
100 IPrt =⋅⋅ = = Mekhi will earn $100.00 in interest after 3 months.
Chapter 1 Project
Internet-based Project – Answers will vary.
Chapter 2
Graphs
Section 2.1
1. () 5388 −−==
2. 22 34255 +==
3. 222 11601213600372161 +=+== Since the sum of the squares of two of the sides of the triangle equals the square of the third side, the triangle is a right triangle.
4. () 0,0
5. 1 2 bh
6. true
7. midpoint
8. False; the distance between two points is never negative.
9. True; 1212 , 22 x xyy M ++ =
10. a
11. 22 12 22 (,)(20)(10) 21415 dPP =−+− =+=+=
12. 22 12 22 (,)(20)(10) (2)1415 dPP =−−+− =−+=+=
13. 22 12 22 (,)(21)(21) (3)19110 dPP =−−+− =−+=+=
14. () 2 2 12 22 (,)2(1)(21) 319110 dPP =−−+− =+=+=
15. () () () 2 2 12 2 2 (,)(53)44 2846468217 dPP =−+−− =+=+==
16. () () () () 2 2 12 2 2 (,)2140 34916255 dPP =−−+− =+=+==
17. () 2 2 12 22 (,)4(7)(03) 11(3)1219130 =−−+− =+−=+= dPP
18. ()() 22 12 22 (,)422(3) 2542529 dPP =−+−− =+=+=
19. () 2 2 12 22 (,)(65)1(2) 131910 =−+−− =+=+= dPP
20. ()() 22 12 22 (,)6(4)2(3) 10510025 12555 dPP =−−+−− =+=+ ==
21. ()() 22 12 22 (,)2.3(0.2)1.1(0.3) 2.50.86.250.64 6.892.62 =−−+− =+=+ =≈ dPP
22. ()() 22 12 22 (,)0.31.21.12.3 (1.5)(1.2)2.251.44 3.691.92 =−−+− =−+−=+ =≈ dPP
23. 22 12 2222 (,)(0)(0) ()() dPPab abab =−+− =−+−=+
24. 22 12 22 222 (,)(0)(0) ()() 22 dPPaa aa aaaa =−+− =−+− =+==
25. (2,5),(1,3),(1,0)ABC =−==− () () () 2 2 22 2 2 22 2 2 22 (,)1(2)(35) 3(2)9413 (,)11(03) (2)(3)4913 (,)1(2)(05) 1(5)12526 dAB dBC dAC =−−+− =+−=+= =−−+− =−+−=+= =−−−+− =+−=+=

Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem: [][][] () () () 222 222 (,)(,)(,) 131326 131326 2626 dABdBCdAC += += += =
The area of a triangle is 1 2 A bh =⋅ . In this problem, [][] 1 (,)(,) 2 11131313 22 13 square units 2 A dABdBC=⋅ =⋅=⋅ =
Section 2.1: The Distance and Midpoint Formulas
26. (2,5),(12,3),(10,11)ABC =−==− () () () 2 2 22 2 2 22 2 2 22 (,)12(2)(35) 14(2) 1964200 102 (,)1012(113) (2)(14) 4196200 102 (,)10(2)(115) 12(16) 144256400 20 dAB dBC dAC =−−+− =+− =+= = =−+−− =−+− =+= = =−−+−− =+− =+= =

Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem: [][][] () () () 222 22 2 (,)(,)(,) 10210220 200200400 400400 dABdBCdAC += += += = The area of a triangle is 1 2 A bh = . In this problem, [][] 1 (,)(,) 2 1 102102 2 1 1002100 square units 2 AdABdBC =⋅⋅ =⋅⋅ =⋅⋅=
