

INSTRUCTOR’S SOLUTIONS MANUAL
GEX INC.
P RECALCULUS
E NHANCED WITH G RAPHI NG
U TILITIES
NINTH EDITION
Michael Sullivan
Chicago State University
Michael Sullivan, III
Joliet Junior College and Florida SouthWestern State College

Copyright © 2026, 2021, 2017 by Pearson Education, Inc. or its affiliates. All Rights Reserved. Manufactured in the United States of America. This publication is protected by copyright, and permission should be obtained from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise. For information regarding permissions, request forms, and the appropriate contacts within the Pearson Education Global Rights and Permissions department, please visit www.pearsoned.com/permissions/
PEARSON and MYLAB are exclusive trademarks owned by Pearson Education, Inc. or its affiliates in the U.S. and/or other countries.
Unless otherwise indicated herein, any third-party trademarks, logos, or icons that may appear in this work are the property of their respective owners, and any references to third-party trademarks, logos, icons, or other trade dress are for demonstrative or descriptive purposes only. Such references are not intended to imply any sponsorship, endorsement, authorization, or promotion of Pearson’s products by the owners of such marks, or any relationship between the owner and Pearson Education, Inc., or its affiliates, authors, licensees, or distributors
Table of Contents
Chapter 2 Functions and Their Graphs
Chapter 3
Chapter 4 Polynomial and
4.1
Chapter 5 Exponential and Logarithmic Functions
5.6
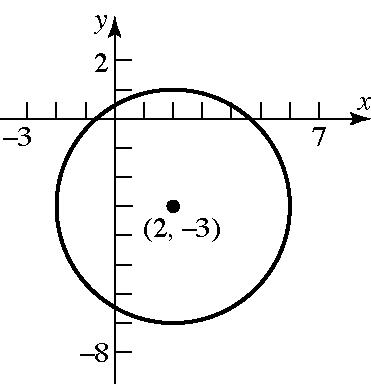
5.7
5.8
Chapter 6 Trigonometric Functions
6.1
6.2
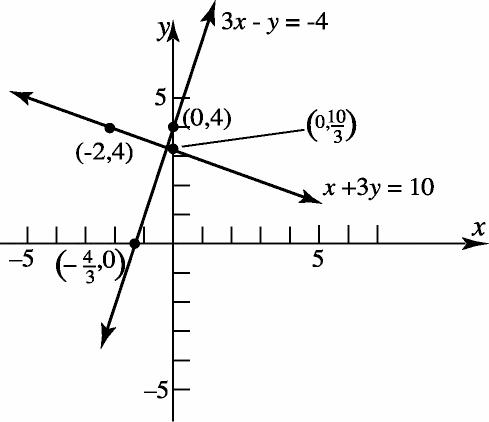
6.3
Chapter
7
Analytic Trigonometry
7.1
Chapter 8 Applications of Trigonometric Functions
8.4
8.5
Chapter 9 Polar Coordinates; Vectors
9.1
Chapter 10 Analytic Geometry
10.2
Chapter 11 Systems of Equations
11.1
11.6
11.7
Chapter 12 Sequences; Induction; the Binomial Theorem
Chapter 13 Counting and Probability
Chapter 14 A Preview of Calculus: The Limit, Derivative, and Integral of a Function
14.1
14.2
Appendix A: Review
A.4
A.5
A.6
A.7
A.8
A.9 Interval Notation; Solving Inequalities
A.10
Chapter 1 Graphs
Section 1.1
1. 0
2. 3. x-coordinate; y-coordinate; quadrants

4. False; points that lie in Quadrant IV will have a positive x-coordinate and a negative y-coordinate.
The point 1,4 lies in Quadrant II.
5. d
6. c
7. (a) Quadrant II (b) x-axis
(c) Quadrant III (d) Quadrant I (e) y-axis (f) Quadrant IV

8. (a) Quadrant I (b) Quadrant III (c) Quadrant II (d) Quadrant I (e) y-axis
(f) x-axis

9. The points will be on a vertical line that is two units to the right of the y-axis.

10. The points will be on a horizontal line that is three units above the x-axis.

11. 1,4 ; Quadrant II
12. (3, 4); Quadrant I
13. (3, 1); Quadrant I
14. 6,4 ; Quadrant III
15. min11 max5
scl1 min3 max6 scl1 X X X Y Y Y
16. min3 max7 scl1 min4 max9 scl1 X X X Y Y Y
17. min30 max50 scl10 min90 max50 scl10 X X X Y Y Y
18. min90 max30 scl10 min50 max70 scl10 X X X Y Y Y
19. min10 max110 scl10 min10 max160 scl10 X X X Y Y Y
20. min20 max110 scl10 min10 max60 scl10 X X X Y Y Y
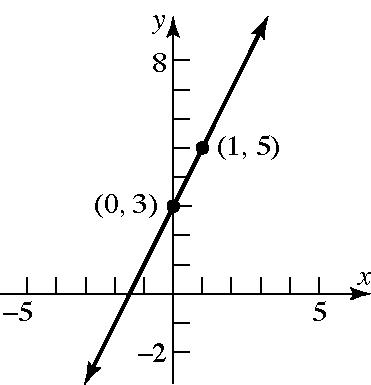
21. min6 max6 scl2 min4 max4 scl2 X X X Y Y Y
22. min3 max3 scl1 min2 max2 scl1 X X X Y Y Y
23. min6 max6 scl2 min1 max3 scl1 X X X Y Y Y
24. min9 max9 scl3 min12 max4 scl4 X X X Y Y Y
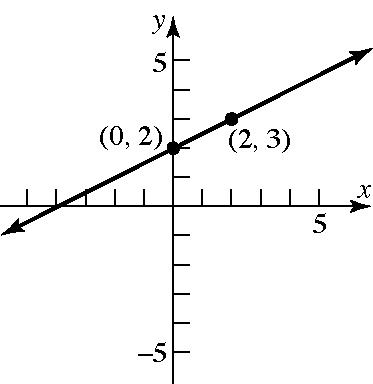
25. min3 max9 scl1 min2 max10 scl2 X X X Y Y Y
26. min22 max10 scl2 min4 max8 scl1 X X X Y Y Y
28.
29.
30.
(0, 1) and (–1, 0) are on the graph of the equation.
31. 22 4 xy 22 024 44
(0,2)and 2,2 are on the graph of the equation.
32. 2244xy 22 0414 44 22 2404
(0, 1) and (2, 0) are on the graph of the equation.
33. (–1, 0), (1, 0)
34. (0, 1)
35. ,0,,0,(0,1)22
36. (–2, 0), (2, 0), (0, –3)
37. 1,0 , 0,2 , 0,2
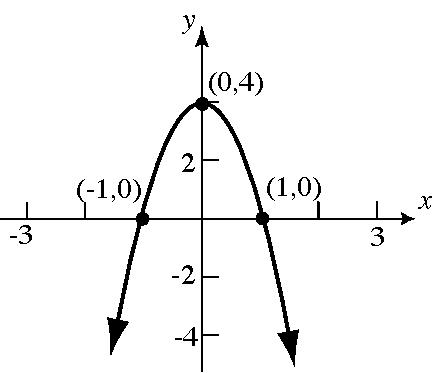
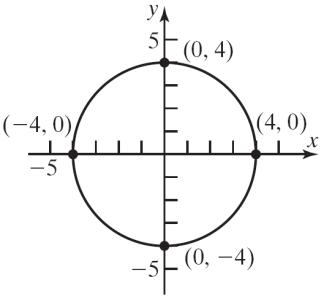
38. (2, 0), (0, 2), (–2, 0), (0, –2)
39. (–4,0), (–1,0), (4, 0), (0, –3)
40. (–2, 0), (2, 0), (0, 3)
41. 2 yx

42. 6 yx

43. 28yx







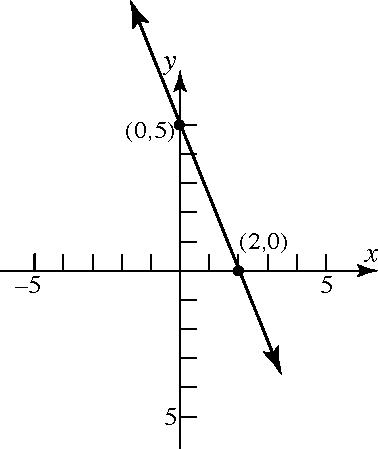

39yx
2 1 yx
2 9 yx
47. 2 4 yx
48. 2 1 yx
49. 236 xy
50. 5210 xy
51. 2 9436 xy
52. 2 44 xy
53. 213yx



The x-intercept is 6.5 x and the y-intercept is 13 y
54. 314yx



The x-intercept is 4.67 x and the y-intercept is 14 y 55. 2 215yx




The x-intercepts are 2.74 x and 2.74 x The y-intercept is 15 y
. 56. 2 319yx




The x-intercepts are 2.52 x and 2.52 x . The y-intercept is 19 y
57. 3243343 or 2 x xyy



The x-intercept is 14.33 x and the y-intercept is 21.5 y .
4582482 or 5 x xyy



The x-intercept is 20.5 x and the y-intercept is 16.4 y
2 2 5337537 or 3 x xyy




The x-intercepts are 2.72 x and 2.72 x
The y-intercept is 12.33 y .
2 2 2335235 or 3 x




The x-intercepts are 4.18 x and 4.18 x The y-intercept is 11.67 y .
61. If 2,5 is shifted 3 units right then the xcoordinate would be 23 If it is shifted 2 units down then the y-coordinate would be 5(2) . Thus the new point would be 23,5(2)(5,3)
62. If 1,6 is shifted 2 units left then the xcoordinate would be 1(2) . If it is shifted 4 units up then the y-coordinate would be 64 . Thus the new point would be
1(2),64(3,10)
63. a. 25 feet b. 23.2 feet; 34.1 feet
c. (0,6), The shot is released at a height of 6 feet; (48.7, 0), the shot hits the ground after traveling a horizontal distance of 48.7 feet.
64. a. 20 meters
b. 12 seconds; 36 meters
c. (0, 2), The discus is released at a height of 2 meters; (18, 0), the discus hits the ground after 18 seconds.
65. a. $19.95; $19.95
b. $182.45
c. (0, 19.95), The membership plan costs $19.95 per month.
66. a. 1.5 miles
b. 1 mile
c. (0, 2), Caleb’s friend lives 2 miles from his house; (28, 0), it takes Caleb 28 minutes to ride home.
67. (1,0),(1,0),(0,1),(0,1)
68. (2,0),(3,0),(0,2),(0,0),(0,2)
69. Answers will vary
70. a.



b. Since 2 xx for all x , the graphs of 2 and yxyx are the same.
c. For 2 yx , the domain of the variable x is 0 x ; for yx , the domain of the variable x is all real numbers. Thus, 2 only for0.xxx
d. For 2 yx , the range of the variable y is 0 y ; for yx , the range of the variable y is all real numbers. Also, 2 only if0.xxx
71. Answers will vary 72. Answers will vary. A complete graph presents enough of the graph to the viewer so they can “see” the rest of the graph as an obvious continuation of what is shown.
73. Answers will vary.
Section 1.2
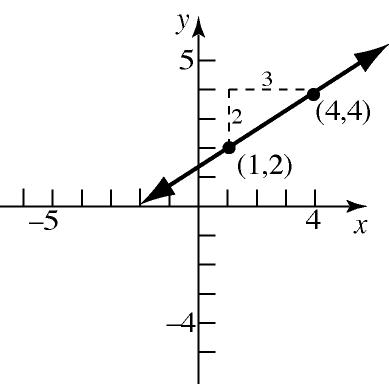
1. 5388
2. 22 34255
3. 222 11601213600372161 Since the sum of the squares of two of the sides of the triangle equals the square of the third side, the triangle is a right triangle.
4. 0,0
5. 1 2 bh
6. true
7. midpoint
8. False; the distance between two points is never negative.
9. True; 1212 , 22 xxyy M
10. a
17.
2 2 12 22 (,)4(7)(03) 11(3)1219130
18.
22 12 22 (,)422(3) 2542529 dPP
dPP
19. 2 2 12 22 (,)(65)1(2) 131910
20. 22 12 22 (,)6(4)2(3) 10510025 12555 dPP
21. 22 12 22 (,)2.3(0.2)1.1(0.3) 2.50.86.250.64 6.892.62
dPP
22. 22 12 22 (,)0.31.21.12.3 (1.5)(1.2)2.251.44 3.691.92
dPP
23. 22 12 2222 (,)(0)(0) ()() dPPab abab
24. 22 12 22 222 (,)(0)(0) ()() 22 dPPaa aa aaaa
25. (2,5),(1,3),(1,0)ABC
2 2 22 2 2 22 2 2 22 (,)1(2)(35) 3(2)9413 (,)11(03) (2)(3)4913 (,)1(2)(05) 1(5)12526 dAB dBC dAC

Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem:
The area of a triangle is 1 2 Abh . In this problem,
(2,5),(12,3),(10,11)
Section 1.2: The Distance and Midpoint Formulas

Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem:
222 22 2 (,)(,)(,) 10210220 200200400 400400 dABdBCdAC
The area of a triangle is 1 2 Abh . In this problem,
AdABdBC
1(,)(,) 2 1102102 2 11002100 square 2units
27. (5,3),(6,0),(5,5)ABC
dAB dBC dAC
130 (,)56(50) (1)5125
2 2 22 2 2 22 2 2 22 (,)6(5)(03) 11(3)1219
26 (,)5(5)(53) 1021004
104 226
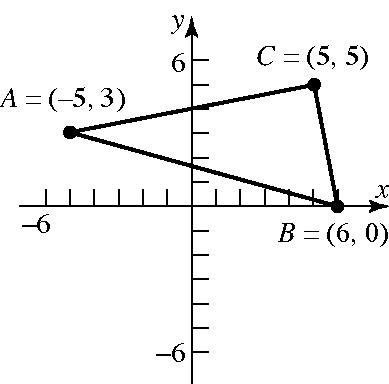
Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem:
222 222 (,)(,)(,) 10426130 10426130 130130 dACdBCdAB
The area of a triangle is 1 2 Abh . In this problem,

Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem:
222 222 (,)(,)(,) 29229145 29429145 29116145 145145 dACdBCdAB
The area of a triangle is 1 2 Abh . In this problem,
AdACdBC
1(,)(,) 2 129229 2 1 229 2 29 square units
29. (4,3),(0,3),(4,2)ABC
22 (,)3(6)(53) 9(8)8164 145 (,)13(5(5)) (4)1016100 116229 (,)1(6)(53) 52254 29 dAB dBC dAC
22
2 2 22 22 22 2 2 22 (,)(04)3(3) (4)0160 16 4 (,)402(3) 451625 41 (,)(44)2(3) 05025 25 5 dAB dBC dAC

Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem:

Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem:
222 2 22 (,)(,)(,) 4225 16420 2020 dABdBCdAC
The area of a triangle is 1 2 Abh . In this problem,
31. The coordinates of the midpoint are: 1212(,),22 44 35 , 22 80 , 22 (4,0) xxyy xy
32. The coordinates of the midpoint are: 1212(,),22 2204 , 22 04 , 22 0,2 xxyy xy
33. The coordinates of the midpoint are:
xxyy xy
1212(,),22 1840 , 22 74 , 22 7,2 2
34. The coordinates of the midpoint are: 1212(,),22 2432 , 22 61 , 22 1 3, 2 xxyy xy
35. The coordinates of the midpoint are: 1212(,),22 7951 , 22 4 16 , 22
xxyy xy
36. The coordinates of the midpoint are:
1212(,),22 4232 , 22 21 , 22 1,1 2 xxyy xy
37. The coordinates of the midpoint are: 1212(,),22 00 , 22 , 22 xxyy xy ab
38. The coordinates of the midpoint are: 1212(,),22 00 , 22 , 22 xxyy xy aa aa
39.
121,3;5,15PP
22 12 22 ,51153 412 16144 160410
The coordinates of the midpoint are: 1212(,),22 15315 , 22 618 , 22 (3,9)
128,4;2,3PP
22 12 22 ,2834 107 10049 149
The coordinates of the midpoint are: 1212(,),22 43 82 , 22 61 , 22 3,1 2
xxyy xy
41.
124,6;4,8PP
42.
The coordinates of the midpoint are: 1212(,),22 6(8) 44 , 22 02 , 22 (0,1)
120,6;3,8
The coordinates of the midpoint are: 1212(,),22 036(8) , 22 32 , 22 3,1 2
43. a. If we use a right triangle to solve the problem, we know the hypotenuse is 13 units in length. One of the legs of the triangle will be 235 Thus the other leg will be:
Section 1.2: The Distance and Midpoint Formulas
b. Consider points of the form 3, y that are a distance of 13 units from the point 2,1 .
22 2121 22 22 2 2 3(2)1 51 2512 226 dxxyy y y yy yy
Thus the coordinates will have an y value of 11213 and 11211 . So the points are 3,11 and 3,13 .
110 11 y y or 130 13 y y
Thus, the points 3,11 and 3,13 are a distance of 13 units from the point 2,1 .
44. a. If we use a right triangle to solve the problem, we know the hypotenuse is 17 units in length. One of the legs of the triangle will be 268 Thus the other leg will be:
222 2 2 817 64289
Thus the coordinates will have an x value of 11514 and 11516 . So the points are 14,6 and 16,6 .
b. Consider points of the form ,6x that are a distance of 17 units from the point 1,2
Thus, the points
14,6 and
16,6 are a distance of 13 units from the point
45. Points on the x-axis have a y-coordinate of 0. Thus, we consider points of the form ,0x that are a distance of 6 units from the point
4,3
2(1) 63644680
325 y or 325 y
Thus, the points 0,325 and 0,325 are on the y-axis and a distance of 6 units from the point 4,3
47. For the x coordinate of B: 2 2 2 2 5 2
For the y coordinate of
433 x or 433 x Thus, the points 433,0 and 433,0 are on the x-axis and a distance of 6 units from the point 4,3
46. Points on the y-axis have an x-coordinate of 0. Thus, we consider points of the form 0, y that are a distance of 6 units from the point 4,3
Thus, the point B is
8,7
48. Let the coordinates of point B be , xy . Using the midpoint formula, we can write 18 2,3, 22 xy
This leads to two equations we can solve.
2 2 22 (,)26(20) (4)2164 2025
22 22 (,)(20)(50) 25425 29
52. Let 12(0,0),(0,4),(,) PPPxy
22 12 22 1 22 22 22 2 22 22 ,(00)(40) 164 ,(0)(0) 4 16 ,(0)(4) (4)4 (4)16 dPP dPPxy xy xy dPPxy xy xy Therefore, 2 2 22 4 816 816 2 yy yyy y y which gives 22 2 216 12 23 x x x Two triangles are possible. The third vertex is 23,2 or 23,2
53. 22 12 22 (,)(42)(11) (6)0 36 6 dPP
2 2 23 22 (,)4(4)(31) 0(4) 16 4 dPP
54.
22 13 22 (,)(42)(31) (6)(4) 3616
Since
22 2 122313 (,)(,)(,) dPPdPPdPP , the triangle is a right triangle.
2 2 12 22 (,)6(1)(24) 7(2) 494
2 2 23 22 (,)46(52) (2)(7) 449 53
2 2 13 22 (,)4(1)(54) 5(9) 2581 106
Since
22 2 122313 (,)(,)(,) dPPdPPdPP , the triangle is a right triangle.
Since 1223 ,, dPPdPP , the triangle is isosceles. Therefore, the triangle is an isosceles right triangle.
55.
22 12 22 (,)0(2)7(1) 2846468
Since 2313 (,)(,) dPPdPP , the triangle is isosceles. Since
22 2 132312 (,)(,)(,) dPPdPPdPP , the triangle is also a right triangle. Therefore, the triangle is an isosceles right triangle. 56.
22 12 22 (,)4702 (11)(2) 1214125 55 dPP
2 2 23 22 (,)4(4)(60) 866436 100 10 dPP
22 13 22 (,)4762 (3)4916 25 5 dPP
Since
22 2 132312 (,)(,)(,) dPPdPPdPP , the triangle is a right triangle.
57. Using the Pythagorean Theorem: 222 2 2 9090 81008100 16200 16200902127.28 feet
58. Using the Pythagorean Theorem: 222 22 6060
360036007200 720060284.85 feet
d
59. a. First: (90, 0), Second: (90, 90), Third: (0, 90)
(0,0) (0,90) (90,0) (90,90) X Y
b. Using the distance formula: 22 22 (31090)(1590) 220(75)54025
52161232.43 feet d
c. Using the distance formula: 22 22 (3000)(30090) 300210134100
30149366.20 feet
60. a. First: (60, 0), Second: (60, 60) Third: (0, 60) (0,0) (0,60) (60,0) (60,60) x y
Section 1.2: The Distance and Midpoint Formulas
b. Using the distance formula: 22 22 (18060)(2060) 120(40)16000
4010126.49 feet
c. Using the distance formula: 22 22 (2200)(22060) 22016074000
20185272.03 feet
61. The Focus heading east moves a distance 60t after t hours. The truck heading south moves a distance 45t after t hours. Their distance apart after t hours is: 22 22 2 (60)(45) 36002025 5625 75miles
62. 15 miles5280 ft1hr22 ft/sec 1 hr1mile3600 sec
2 2 2 10022 10000484feet dt t
100 22t d
63. a. The shortest side is between 1 (2.6,1.5) P and 2 (2.7,1.7) P The estimate for the d 45t 60t
desired intersection point is:
b. Using the distance formula: 22 22 (2.651.4)(1.61.3) (1.25)(0.3) 1.56250.09 1.6525 1.285units
64. Let 1 (2018,232.89) P and 2 (2022,513.98) P The midpoint is:
1212 ,,22 20182022232.89513.98 , 22
4040746.87 , 22 2020,373.44
The estimate for 2020 is $373.44 billion. The estimate net sales of Amazon.com’s e-service in 2020 is lower than the reported value of $386.06 billion
65. For 2008 we have the ordered pair
2008,21211 and for 2022 we have the ordered pair 2022,29417 . The midpoint is
4 y 200820222121129417 , 22 403050628 , 22
2 a 015,21 er, $ 53
The estimate for 2015 is $25,314 billion. The estimate loan debt of an average student for a university graduate in 2015 is lower than the reported value of $29,289 billion.
66. Let 1 0,0 P ,
Since the lengths of the three sides are all equal, the triangle is an equilateral triangle. The midpoints of the sides are
Since the lengths of the sides of the triangle formed by the midpoints are all equal, the triangle is equilateral.
67. Let
1 0,0 P ,
2 0, Ps ,
3 ,0
4 , Pss be the vertices of the square.
and
69. Arrange the parallelogram on the coordinate plane so that the vertices are
1234 0,0,(,0),(,)and (,) PPaPabcPbc
Then the lengths of the sides are:
dPPa aa
22 12 2 (,)000
dPPabac bc
2 2 23 22 (,)()0
dPPbabcc aa and 22 14 22 (,)00 dPPbc bc
2 2 34 2 (,)()
The points 1P and 4P are endpoints of one diagonal and the points 2P and 3P are the endpoints of the other diagonal.
PP
M 23 00 ,, 2222
PP ssss M
The midpoints of the diagonals are the same. Therefore, the diagonals of a square intersect at their midpoints.
68. Let ,2 Paa . Then
13 and PP are the endpoints of one diagonal, and 24 and PP are the endpoints of the other diagonal. The lengths of the diagonals are
dPPabc aabbc and 2 2 24 222 (,)()0 2 dPPbac aabbc
2 2 13 222 (,)()00 2
Sum of the squares of the sides: 22222222 222 ()() 222 abcabc abc
Sum of the squares of the diagonals: y x (0, ) s (0, 0) (, 0)s (, )ss
3. intercepts
4. 0 y


3,4 8. True
9. False; the y-coordinate of a point at which the graph crosses or touches the x-axis is always 0. The x-coordinate of such a point is an x-intercept.
10. False; a graph can be symmetric with respect to both coordinate axes (in such cases it will also be symmetric with respect to the origin). For example: 22 1 xy
11. d 12. c
13. 2 yx x-intercept: y-intercept: 02






21. 236 xy

22. 5210 xy


24. 2 44 xy





= (5, 2)
= (5, 2)
= (5, 2)


Section 1.3: Intercepts; Symmetry; Graphing Key Equations



35. a. Intercepts: 1,0 and 1,0
b. Symmetric with respect to the x-axis, y-axis, and the origin.
36. a. Intercepts: 0,1
b. Not symmetric to the x-axis, the y-axis, nor the origin
37. a. Intercepts: 2 0, ,
0,1 , and 2 ,0
b. Symmetric with respect to the y-axis.
38. a. Intercepts: 2,0 ,
0,3 , and 2,0
b. Symmetric with respect to the y-axis.
39. a. Intercepts: 0,0
b. Symmetric with respect to the x-axis.
40. a. Intercepts: 2,0, 0,2, 0,2, and 2,0
b. Symmetric with respect to the x-axis, y-axis, and the origin.
41. a. Intercepts: 2,0 , 0,0 , and 2,0
b. Symmetric with respect to the origin.
42. a. Intercepts: 4,0 , 0,0 , and 4,0
b. Symmetric with respect to the origin.
43. a. x-intercepts: 2,1 , y-intercept0
b. Not symmetric to x-axis, y-axis, or origin.
44. a. x-intercepts: 1,2 , y-intercept0
b. Not symmetric to x-axis, y-axis, or origin.
45. a. Intercepts: none
b. Symmetric with respect to the origin.
46. a. Intercepts: none
b. Symmetric with respect to the x-axis.
47.




intercepts:
The intercepts are
16,0 ,
0,4 and
0,4
Test x-axis symmetry: Let yy
Test y-axis symmetry: Let xx 2 16yx different
Test origin symmetry: Let xx and yy
yx yx
2 2 16 16 different
Therefore, the graph will have x-axis symmetry.
52. 2 9 yx
x-intercepts: y-intercepts: 2 (0)9 09 9 x x x
The intercepts are 9,0 ,
Test x-axis symmetry: Let yy
and
2 2 9 9 same yx yx
Test y-axis symmetry: Let xx 2 9 yx
different
Test origin symmetry: Let xx and yy .
Therefore, the graph will have x-axis symmetry.
53. 3 yx
x-intercepts: y-intercepts:
3 0 0 x x
The only intercept is 0,0 .
Test x-axis symmetry: Let yy 3 different yx
Test y-axis symmetry: Let xx 33 different yxx
Test origin symmetry: Let xx and yy
3 same yxx yx
Therefore, the graph will have origin symmetry.
54. 5 yx
The only intercept is 0,0
Test x-axis symmetry: Let yy
different yx
Test y-axis symmetry: Let xx
different yxx
Test origin symmetry: Let xx
and yy
Therefore, the is symmetric with respect to the origin.
55. 2 90 xy
x-intercepts: y-intercepts: 2 2 90 9 3 x x x
2 090 9 y y
The intercepts are 3,0 , 3,0 , and 0,9 .
Test x-axis symmetry: Let yy 2 90different xy
Test y-axis symmetry: Let xx
2 2 90 90 same xy xy
Test origin symmetry: Let xx and yy
2 2 90 90 different xy xy
Therefore, the graph has y-axis symmetry.
56. 2 40 xy x-intercepts: y-intercept: 2 2 040 4 2 x x x 2 040 4 4 y y y
The intercepts are
2,0 , and
Test x-axis symmetry: Let yy
2 2 40 40 different xy xy
Test y-axis symmetry: Let xx
2 2 40 40 same xy xy
Test origin symmetry: Let xx and yy
2 2 40 40 different xy xy
Therefore, the graph has y-axis symmetry.
57. 22 254100 xy
x-intercepts: y-intercepts:
2 2 2 2 2504100 4100 25 5 y y y y
The intercepts are 2,0 , 2,0, 0,5, and 0,5
.
Chapter 1: Graphs
Test x-axis symmetry: Let yy
2 2 22 254100 254100 same
xy xy
Test y-axis symmetry: Let xx
2 2 22 254100 254100 same
xy xy
Test origin symmetry: Let xx and yy
22 22 254100 254100 same
xy xy
Therefore, the graph has x-axis, y-axis, and origin symmetry.
58. 22 44 xy
x-intercepts: y-intercepts:
1,0 , 0,2 , and
0,2
Test x-axis symmetry: Let yy
2 2 22 44 44 same xy xy
Test y-axis symmetry: Let xx
2 2 22 44 44 same xy xy
Test origin symmetry: Let xx and yy
22 22 44 44 same xy xy
Therefore, the graph has x-axis, y-axis, and origin symmetry.
59. 3 64 yx
x-intercepts: y-intercepts: 3 3 064 64 4 x x x 3 064 64
y y
The intercepts are
4,0 and 0,64 .
Test x-axis symmetry: Let yy 3 64different yx
Test y-axis symmetry: Let xx
yx yx
3 3 64 64 different
Test origin symmetry: Let xx and yy
yx yx
3 3 64 64 different
Therefore, the graph has no symmetry.
60. 4 1 yx x-intercepts: y-intercepts: 4 4 01 1 1 x x x
The intercepts are
4 01 1 y y
1,0 ,
1,0 , and
Test x-axis symmetry: Let yy 4 1different yx
Test y-axis symmetry: Let xx
4 4 1 1 same yx yx
0,1
Test origin symmetry: Let xx and yy
4 4 1 1 different yx yx
Therefore, the graph has y-axis symmetry.
61. 2 28yxx
x-intercepts: y-intercepts:
2 028 042 4 or2
xx xx xx
y y
The intercepts are 4,0 ,
2 0208 8
2,0 , and
Test x-axis symmetry: Let yy 2 28different
yxx
Test y-axis symmetry: Let xx
yxx yxx
2 2 28 28 different
0,8
Test origin symmetry: Let xx and yy
yxx yxx
2 2 28 28 different
Therefore, the graph has no symmetry.
62. 2 4 yx
x-intercepts: y-intercepts:
2 2 04 4 no real solution x x 2 04 4 y y
The only intercept is 0,4
Test x-axis symmetry: Let yy 2 4different yx
Test y-axis symmetry: Let xx
2 2 4 4 same yx yx
Test origin symmetry: Let xx and yy
2 2 4 4 different yx yx
Therefore, the graph has y-axis symmetry.
63. 2 4 16 x y x x-intercepts: y-intercepts: 2 4 0 16 40 0
x x x x
The only intercept is
0,0
Test x-axis symmetry: Let yy
x y x
2 4 different 16
Test y-axis symmetry: Let xx
x y x x y x
2 2 4 16 4 different 16
Test origin symmetry: Let
x y x x y x x y x
Section 1.3: Intercepts; Symmetry; Graphing Key Equations
The intercepts are
2,0 and
2,0
Test x-axis symmetry: Let yy
Test y-axis symmetry: Let xx
Therefore, the graph has origin symmetry. 64. 2 4 2 x y x x-intercepts: y-intercepts: 2 2 2 4 0 2 40 4 2 x x x x x
Test origin symmetry: Let xx
and yy
Therefore, the graph has origin symmetry.
The only intercept is
0,0
Test x-axis symmetry: Let
Chapter 1: Graphs
There are no intercepts for the graph of this equation.




71. If the point ,4a is on the graph of 2 3 yxx , then we have
2 2 43 034 041 aa aa aa
or 10 1 a a
Thus, 4 a or 1 a
72. If the point ,5a is on the graph of 2 6 yxx , then we have
2 2 56 065 051 aa aa aa
5 a a
or 10 1 a a
Thus, 5 a
or 1 a
73. a. 2 2 05 5 5 x x x
The x-intercepts are 5 x and 5 x .
2 055 y
The y-intercept is 5 y
The intercepts are 5,0 ,
0,5
b. x-axis (replace y by y ): 2 2 5 5different yx yx
y-axis (replace x by x ):
2 2 55yxx
5,0 , and
same origin (replace x by x and y by y ): 2 2 5 5different yx yx
The equation has y-axis symmetry.
c. 2 5 yx
Additional points:
2 2 2 5, 11541,4 1from symmetry1,4 22512,1 2from symmetry2,1 xyxxy y y

74. a. 2 2 08 8 22 x x x
The x-intercepts are 22 x and 22 x .
2 088 y
The y-intercept is 8 y
The intercepts are 22,0 ,
22,0 , and
0,8
b. x-axis (replace y by y ): 2 2 8 8different yx yx y-axis (replace x by x ): 2 2 88yxx same
origin (replace x by x and y by y ):
2 2 8 8different yx yx
The equation has y-axis symmetry.
c. 2 8 yx
Additional points:
2 2 2 8, 11871,7 1from symmetry1,7 22842,4 2from symmetry2,4 xyxxy y

2 09 9 x x
The x-intercept is 9 x
2 2 2 09 9 9 3 y y yy
The y-intercepts are 3 y and 3 y
The intercepts are
9,0 ,
0,3 , and
0,3
b. x-axis (replace y by y ):
2 2 9 9 same xy xy
y-axis (replace x by x ): 2 2 9 9 different xy xy
origin (replace x by x and y by y ): 2 2 2 9 9 9 different xy xy xy
The equation has x-axis symmetry.
c. 2 9 xy or 2 9 xy
Additional points:
2 2 9, 22955,2 2from symmetry5,2 yxyxy x y x (9,0) (,2) (0, ) (, 2) (0,) 5 5 5 2
76. a. 2 04 4 x x
The x-intercept is 4 x . 2 2 04 42 y yy
The y-intercepts are 2 y and 2 y
The intercepts are 4,0 , 0,2 , and 0,2
b. x-axis (replace y by y ):
2 2 4 4 same xy xy
y-axis (replace x by x ): 2 2 4 4 different xy xy
origin (replace x by x and y by y ):
2 2 2 4 4 4 different xy xy xy
The equation has x-axis symmetry.
c. 2 4 xy or 2 4 xy
Additional points:
2 2 4, 14133,1 1from symmetry3,1 yxyxy x

77. a.
2 2 2 09 9 3 x x x
The x-intercepts are 3 x and 3 x .
2 2 2 09 9 3 y y y
The y-intercepts are 3 y and 3 y
The intercepts are 3,0 , 3,0 , 0,3 , and 0,3
b. x-axis (replace y by y ):
2 2 22 9 9same xy xy
y-axis (replace x by x ):
2 2 22 9 9 same xy xy origin (replace x by x and y by y ): 22 22 9 9same xy xy
The equation has x-axis symmetry, y-axis symmetry, and origin symmetry.
Section 1.3: Intercepts; Symmetry; Graphing Key Equations
c. 22 9 xy

78. a. 2 2 2 016 16 4 x x x
The x-intercepts are 4 x and 4 x .
2 2 2 016 16 4 y y y
The y-intercepts are 4 y and 4 y
The intercepts are 4,0 ,
4,0 ,
0,4 , and 0,4
b. x-axis (replace y by y ):
2 2 22 16 16same xy xy
y-axis (replace x by x ):
2 2 22 16 16 same xy xy
origin (replace x by x and y by y ):
22 22 16 16same xy xy
The equation has x-axis symmetry, y-axis symmetry, and origin symmetry.
c. 22 16 xy
3 2 04 04 xx xx
The
intercepts
3 0400 y
The y-intercept is 0 y
The intercepts are
2,0
0,0 ,
2,0 , and
b. x-axis (replace y by y ): 3 3 4 4different yxx yxx
y-axis (replace x by x ):
3 3 4 4different yxx yxx
origin (replace x by x and y by y ):
3 3 3 4 4 4same yxx yxx yxx
The equation has origin symmetry.
c. 3 4 yxx Additional points:
3 3 4, 114131,3 1from symmetry1,3 xyxxxy y

80. a. 3 2 0 01 xx xx
0 x or 2 2 10 1 1 x x x
The x-intercepts are 0 x , 1 x , and 1 x
3 000 y
The y-intercept is 0 y
The intercepts are 0,0 , 1,0 , and
1,0
b. x-axis (replace y by y ): 3 3 different yxx yxx
y-axis (replace x by x ):
3 3 different yxx yxx
origin (replace x by x and y by y ):
3 3 3 same yxx yxx yxx
The equation has origin symmetry.
c. 3 yxx Additional points:
3 3 , 22262,6 2from symmetry2,6 xyxxxy

81. For a graph with origin symmetry, if the point
, ab is on the graph, then so is the point
, ab . Since the point 1,2 is on the graph of an equation with origin symmetry, the point
1,2 must also be on the graph.
82. For a graph with y-axis symmetry, if the point
, ab is on the graph, then so is the point
, ab . Since 6 is an x-intercept in this case, the point 6,0 is on the graph of the equation. Due to the y-axis symmetry, the point 6,0 must also be on the graph. Therefore, 6 is another xintercept.
83. For a graph with origin symmetry, if the point
, ab is on the graph, then so is the point
, ab . Since 4 is an x-intercept in this case, the point 4,0 is on the graph of the equation. Due to the origin symmetry, the point 4,0 must also be on the graph. Therefore, 4 is another x-intercept.
84. For a graph with x-axis symmetry, if the point , ab is on the graph, then so is the point
, ab . Since 2 is a y-intercept in this case, the point 0,2 is on the graph of the equation. Due to the x-axis symmetry, the point 0,2 must also be on the graph. Therefore, 2 is another yintercept. 85.
y-intercepts:
Test y-axis symmetry: Let xx
Test origin symmetry: Let xx and yy
Thus, the graph will have x-axis symmetry.
86. a. 2 16120225 yx
Chapter 1: Graphs
x-intercepts:
2 160120225 0120225 120225 22515 1208 x x x x
The only intercept is 15 ,0 8
b. Test x-axis symmetry: Let yy
2 2 16120225 16120225 same yx yx
Test y-axis symmetry: Let xx
2 2 16120225 16120225 different yx yx
Test origin symmetry: Let xx and yy
2 2 16120225 16120225different yx yx
Thus, the graph has x-axis symmetry.
87. Let 0 y
Test y-axis symmetry: replace x by -x 222222 222222 (())(()) ()() equivalent
xyaxy xyaxy
Test origin symmetry: replace x by -x and y by -y 222222 222222 (()())(()()) ()() equivalent
xyaxy xyaxy
The graph is symmetric by respect to the xaxis, the y-axis, and the origin.
88. Let 0 y
222222 432222 2 (0)(0) 20 (()(()0 0 or or
xaxbx xaxaxbx xxabxab xxab xab Let 0 x 222222 422 2 (00)(0) 0 ()()0 0,, yaby yby yybyb yybyb
xax xax xax xxa xxa xxa xaa
222 222 22 (0)(0) () 0 ()0 0or()0 0 or ,
So the intercepts are (0,0), (a-b,0), (a+b,0), (0,b), (0, b).
Test x-axis symmetry: replace y by -y 2 22222 222222 ()() ()()Equivalent
xyaxbxy xyaxbxy
Let 0 x . 222222 422 422 222 (0)(0) () 0 ()0 0
yay yay yay yya y
(Note that the solutions to 22 0 ya are not real)
So the intercepts are are (0,0), (a,0) and (-a,0).
Test x-axis symmetry: Replace y by -y 222222 222222 (())(()) ()() equivalent
xyaxy xyaxy
Test y-axis symmetry: replace x by -x 2 22222 222222 ()()() ()()Notequivalent
xyaxbxy xyaxbxy
Test origin symmetry: replace x by -x and y by -y 2 22222 222222 ()()()()() ()()Noequivalent
xyaxbxy xyaxbxy
The graph is symmetric with respect to the x-axis only.
89. Answers will vary. One example: y x
90. Answers will vary.
Case 1: Graph has x-axis and y-axis symmetry, show origin symmetry.
, ongraph, ongraph (from-axissymmetry) xyxy x
,on graph,on graph from-axis symmetry xyxy y
Since the point , xy is also on the graph, the graph has origin symmetry.
Case 2: Graph has x-axis and origin symmetry, show y-axis symmetry.
,on graph,on graph from-axis symmetry xyxy x
,on graph,on graph from origin symmetry xyxy
Since the point , xy is also on the graph, the graph has y-axis symmetry.
Case 3: Graph has y-axis and origin symmetry, show x-axis symmetry.
,on graph,on graph from-axis symmetry xyxy y
,on graph,on graph from origin symmetry xyxy
Since the point , xy is also on the graph, the graph has x-axis symmetry.
91. Answers may vary. The graph must contain the points 2,5 , 1,3 , and 0,2 . For the graph to be symmetric about the y-axis, the graph must also contain the points 2,5 and 1,3 (note that (0, 2) is on the y-axis).
For the graph to also be symmetric with respect to the x-axis, the graph must also contain the points 2,5 ,
1,3 ,
0,2 ,
2,5 , and 1,3 . Recall that a graph with two of the symmetries (x-axis, y-axis, origin) will necessarily have the third. Therefore, if the original graph with y-axis symmetry also has xaxis symmetry, then it will also have origin symmetry.
Section 1.4 1. 2 2520 2120 xx xx 210 21 1 2 x x x
or 20 2 x x
The solution set is 1 2, 2
2. 23411 23441 2343 233 26 3 xx xx xx x x x
The solution set is 3 .
3. ZERO (ROOT)
4. False; exact solutions are obtained, in general, if the solution is a rational number. For irrational solutions, approximate answers are typically given, though some utilities can express certain irrational expressions in exact form.
5. 3 420xx ; Use ZERO (or ROOT) on the graph of 3 1 42yxx



The solution set is 2.21,0.54,1.68 .
6. 3 810xx ; Use ZERO (or ROOT) on the graph of 3 1 81yxx



The solution set is
7. 4 2532 xx ; Use INTERSECT on the graphs of 4 1 25yx and 2 32yx .


The solution set is 1.55,1.15
8. 42123xx ; Use INTERSECT on the graphs of 4 1 1 yx and 2 2 23yx


The solution set is 1.11,1.11
9. 432310xxx ; Use ZERO (or ROOT) on the graph of 43 1 231yxxx


The solution set is 1.12,0.36
10. 432 3450 xxx ; Use ZERO (or ROOT) on the graph of 432 1 345yxxx .

The solution set is

0.85,0.94
11. 3257 20 32 xxx ; Use ZERO (or ROOT) on the graph of 32 1 57 2 32 yxxx



12. 432715








The solution set is 2.86,1.34,0.20,1.00
14. 32 1154 45 xxx



15. 4252110xxx

There
16. 42 38290 xxx
Use ZERO (or ROOT) on the graph of 42 1 3829yxxx .

There are no real solutions.
17. 2(32)3(4) xx
64312 6463126 4318 433183 18 xx xx xx xxxx x
The solution set is 4
21. 125 37 12 2121215 37 7736105 xx xx xx
1013105 10131310513 1092 1092 1010 46 5 x x x x x
The solution set is 46 5
22. 21163 3 x x 21 31633 3 21489 2499 249292 497 497 77 7 x x xx xx xxxx x x x
The solution set is 7
26.
27.
2 22 22 2222 233 23669 669 669 669 66696 569 xxx xxxxx xxxx xxxxxx xx xxxx x
56696 515 515 55 3 x x x x
The solution set is 3 .
2 3280 740 xx xx 70 7 x x or 40 4 x x
The solution set is 4,7 .
28.
2 7180 920 xx xx 90 9 x x or 20 2 x x
The solution set is 2,9 .
29. 2 2 344 3440 3220 xx xx xx 320 32 2 3 x x x or 20 2 x x
The solution set is 2 ,2 3
2 .
1. a. 2; 2; 1 b. -2 c. 0 d. ii, iv
e. ii
2. undefined; 0
3. 3; 2 x-intercept: 23(0)6
4. True
5. False; the slope is
d 13. a. Slope101 202
b. If x increases by 2 units, y will increase by 1 unit. 14. a. 101 Slope 202
b. If x increases by 2 units, y will decrease by 1 unit.
15. a. 121 Slope1(2)3
b. If x increases by 3 units, y will decrease by 1 unit.
16. a. 211 Slope2(1)3
b. If x increases by 3 units, y will increase by 1 unit.

2
18. 21 21 422 Slope2 341 yy xx

19. 21 21 1321 Slope 2(2)42 yy xx

20. 21 21 312 Slope 2(1)3 yy xx

21. 21 21 1(1)0 Slope0 2(3)5 yy xx

22. 21 21 220 Slope0 549 yy xx

23. 21 21 224 Slope 1(1)0undefined. yy xx

24. 21 21 202 Slope 220undefined. yy xx


39. 4 Slope41 ; point: 1,2
If x increases by 1 unit, then y increases by 4 units.
Answers will vary. Three possible points are:
112 and246 2,6 213 and6410 3,10
314 and10414 4,14 xy xy xy
40. 2 Slope21 ; point: 2,3
If x increases by 1 unit, then y increases by 2 units.
Answers will vary. Three possible points are:
211 and325 1,5 110 and527 0,7 011 and729 1,9 xy xy xy
41. Slope33 22 ; point: 2,4
If x increases by 2 units, then y decreases by 3 units.
Answers will vary. Three possible points are:
8,13 xy xy xy
224 and437
4,7
426 and7310
6,10
628 and10313
42. 4 Slope3 ; point: 3,2
If x increases by 3 units, then y increases by 4 units.
Answers will vary. Three possible points are:
330 and246 0,6 033 and6410 3,10 336 and10414 6,14 xy xy xy
43. 2 Slope21 ; point: 2,3
If x increases by 1 unit, then y decreases by 2 units.
Answers will vary. Three possible points are:
211 and325 1,5 110 and527 0,7 011 and729 1,9 xy xy xy
44. 1 Slope11 ; point: 4,1
If x increases by 1 unit, then y decreases by 1 unit.
Answers will vary. Three possible points are:
6,1 617 and112 7,2 xy xy xy
415 and110 5,0 516 and011
45. (0, 0) and (2, 1) are points on the line.
Slope101 202 -interceptis0;using : yymxb
1 0 2 2 02 1 20 or 2 yx yx xy xyyx
46. (0, 0) and (–2, 1) are points on the line.
1011 Slope 2022 -interceptis0;using : yymxb
1 0 2 2 20 1 20 or 2 yx yx xy xyyx
47. (–1, 3) and (1, 1) are points on the line.
51. 11 1 (),2yymxxm 1 2(1) 2 11 2 22 15 22 15 25 or 22 yx yx yx xyyx
11 132 Slope1 1(1)2
Using ()yymxx
11(1) 11 2 2 or2 yx yx yx xyyx
48. (–1, 1) and (2, 2) are points on the line.
11 211 Slope 2(1)3 Using ()yymxx
1 1(1) 3 1 1(1) 3 11 1 33 14 33 14 34 or 33 yx yx yx yx xyyx
49. 11(),2yymxxm 32(3) 326 23 23or 23 yx yx yx xyyx
50. 11(),1yymxxm 21(1) 21 3 3 or3 yx yx yx xyyx
52. 11(),1yymxxm 11((1)) 11 2 2or 2 yx yx yx xyyx
53. Slope3 ; containing the point (–2, 3) 11() 33((2)) 336 39 39 or39 yymxx yx yx yx xyyx
54. Slope2 ; containing the point (4, –3) 11() (3)2(4) 328 211 211 or211 yymxx yx yx yx xyyx
55. 1 Slope2 ; containing the point (3, 1) 11() 1 1(3) 2 13 1 22 11 22 11 21or 22 yymxx yx yx yx xyyx
56. 2 Slope3 ; containing the point (1, –1) 11() 2 (1)(1) 3 22 1 33 21 33 21 231 or 33 yymxx yx yx yx xyyx
57. Containing the points (1, 3) and (–1, 2) 2311 1122
m
11() 1 3(1) 2 11 3 22 15 22 15 25or 22 yymxx yx yx yx xyyx
58. Containing the points (–3, 4) and (2, 5) 541 2(3)5
m 11() 1 5(2) 5 12 5 55 123 55 123 523 or 55 yymxx yx yx yx xyyx
59. Slope3 ; -intercept3y 33 33or 33 ymxb yx xyyx
60. Slope2 ; -intercept2y 2(2) 22or 22 ymxb yx xyyx
61. -intercept4x ; -intercept4y
Points are (–4, 0) and (0, 4) 404 1 0(4)4 m 14 4 4or 4 ymxb yx yx xyyx
62. -intercept2x ; -intercept1y
Points are (2,0) and (0,–1) 1011 0222 m 1 1 2 1 22 or1 2 ymxb yx xyyx
63. Slope undefined; containing the point (2, 4)
This is a vertical line.
2 Noslope-interceptform. x
64. Slope undefined; containing the point (3, 8) This is a vertical line.
3 Noslope-interceptform. x
65. Horizontal lines have slope 0 m and take the form yb . Therefore, the horizontal line passing through the point 3,2 is 2 y
66. Vertical lines have an undefined slope and take the form xa . Therefore, the vertical line passing through the point 4,5 is 4 x .
67. Parallel to 2 yx ; Slope2
Containing the point (–1, 2) 11() 22((1)) 22224 24or 24 yymxx yx yxyx xyyx
68. Parallel to 3 yx ; Slope3 ; Containing the point (–1, 2) 11() 23((1)) 23331 31or 31 yymxx yx yxyx xyyx
69. Parallel to 25xy ; 1 Slope;Containing the 2point0,0 11() 11 0(0)22 1 20 or 2 yymxx yxyx xyyx
70. Parallel to 22 xy ; Slope2 Containing the point (0, 0) 11() 02(0) 2 20or 2 yymxx yx yx xyyx
71. Parallel to 5 x ; Containing the point (4,2) This is a vertical line. 4 Noslope-interceptform. x
72. Parallel to 5 y ; Containing the point (4, 2) This is a horizontal line. Slope0 2 y
73. Perpendicular to 1 4; 2 yx Containing the point (1, –2) 2 Slopeofperpendicular 11() (2)2(1) 2222 20or 2 yymxx yx yxyx xyyx
74. Perpendicular to 23yx ; Containing the point (1, –2) 1 Slope of perpendicular2 11() 1 (2)(1) 2 1113 2 2222 13 23 or 22 yymxx yx yxyx xyyx
75. Perpendicular to 25xy ; Containing the point (0, 4) 2 Slopeofperpendicular 24 24or 24 ymxb yx xyyx
76. Perpendicular to 22 xy ; Containing the point (–3, 0) 1 Slope of perpendicular2 11() 113 0((3))222 13 23 or 22 yymxx yxyx xyyx
77. Perpendicular to 8 x ; Containing the point (3, 4) 0 Slopeofperpendicular (horizontal line) 4 y
78. Perpendicular to 8 y ; Containing the point (3, 4) Slope of perpendicular is undefined (vertical line). 3 x No slope-intercept form.
79. 23yx ; Slope2 ; -intercept3y
80. 34yx ;Slope3 ; -intercept4y

81. 1 1 2 yx ; 22yx Slope2 ; -intercept2y

82. 1 2 3 xy ; 1 2 3 yx
; -intercept2y

83. 1 2 2 yx ; 1 Slope2 ; -intercept2y
84. 1 2 2 yx ; Slope2 ; 1 -intercept2y

85. 24xy ; 1 242 2 yxyx

86. 36xy ; 1 362 3 yxyx
Slope3 ; -intercept2y

Section


89. 1 xy ; 1 yx


91. 4 x ; Slope is undefined y-intercept - none

Slope1 ; -intercept1y 90. 2 xy ; 2 yx Slope1 ; -intercept2y
92. 1 y ; Slope0 ; -intercept1y

93. 5 y ; Slope0 ; -intercept5y

94. 2 x ; Slope is undefined y-intercept - none 95. 0 yx ; yx


96. 0 xy ; yx Slope1

97. 230 yx ; 3 23 2 yxyx

320 xy ; 3 23 2 yxyx

2306
The point 3,0 is on the graph.
The point 0,2 is on the graph. b. y x 5 5 5
100. a. x-intercept: 3206
The point 2,0 is on the graph.
The point 0,3 is on the graph.
101. a. x-intercept:
The point

103. a. x-intercept: 72021 721 3 x x x
The point 3,0 is on the graph.

102.
x-intercept:
The
The point 21 0, 2
is on the graph.

104. a. x-intercept: 53018 518 18 5 x x x
The point 18 ,0 5
is on the graph. y-intercept:
The point
0,6 is on the graph.

The point 2,0 is on the graph.
The point 0,3 is on the graph.

2 04 3 4 x x
The

The point 5,0 is on the graph.
The point

The point 0,3 is on the graph.

109. The equation of the x-axis is 0 y (The slope is 0 and the y-intercept is 0.)
110. The equation of the y-axis is 0 x (The slope is undefined.)
111. The slopes are the same but the y-intercepts are different. Therefore, the two lines are parallel.
112. The slopes are opposite-reciprocals. That is, their product is 1. Therefore, the lines are perpendicular.
113. The slopes are different and their product does not equal 1. Therefore, the lines are neither parallel nor perpendicular.
114. The slopes are different and their product does not equal 1 (in fact, the signs are the same so the product is positive). Therefore, the lines are neither parallel nor perpendicular.
115. Intercepts:
2,0 . Thus, Slope1
1,0 . Thus, Slope1
117. Intercepts:
3,0 and
0,1 . Thus, 1 Slope3
1 1 or33 3 yxxy
0,1 and
Since 12 1 mm , the line segments 12PP and 23PP are perpendicular. Thus, the points 1P , 2P , and 3P are vertices of a right triangle.
Each pair of opposite sides are parallel (same slope) and adjacent sides are not perpendicular. Therefore, the vertices are for a parallelogram.
Opposite sides are parallel (same slope) and adjacent sides are perpendicular (product of slopes is 1). Therefore, the vertices are for a rectangle.
Opposite sides are parallel (same slope) and adjacent sides are perpendicular (product of slopes is 1). In addition, the length of all four sides is the same. Therefore, the vertices are for a square.
123. Let x = number of miles driven, and let C = cost in dollars.
Total cost = (cost per mile)(number of miles) + fixed cost
0.6039Cx
When 110 x ,
When 230 x ,
124. Let x = number of pairs of jeans manufactured, and let C = cost in dollars.
Total cost = (cost per pair)(number of pairs) + fixed cost 201200Cx
When 400 x ,
When 740 x ,
204001200$9200 C
207401200$16,000 C
125. Let x = number of miles driven annually, and let C = cost in dollars.
Total cost = (approx cost per mile)(number of miles) + fixed cost 0.286578Cx
126. Let x = profit in dollars, and let S = salary in dollars.
Weekly salary = (% share of profit)(profit) + weekly pay 0.05525Sx
127. a. 0.1317Cx ; 0150 x
b.

c. For 50 miles, 0.135017$23.50 C
d. For 120 miles, 0.1312017$32.60 C
e. For every 1-mile in distance traveled, the cost will increase 13 cents.
128. a. 600.25 Cx
b.

c. For 20 minutes, 600.2520$65.00 C
d. For 60 minutes, 600.2560$75.00 C
e. For every 1-minute increase in international calls the cost will increase by $0.25 (that is, 25 cents).
129. (,)(0,32);(,)(100,212) CFCF slope212321809 10001005 9 32(0) 5 9 32() 5 5(32)9 FC FC CF
If 70 F , then 55(7032)(38)99 21.1 C C
130. a. º273KC b. 5 º(º32) 9 CF 5 (32)2739 5160 º273 99 52297 º 99 KF KF KF
131. a. The y-intercept is (0, 30), so 30 b Since the ramp drops 2 inches for every 25 inches
of run, the slope is 22 2525 m . Thus, the equation is 2 30 25 yx
b. Let 0 y . 2 030 25 2 30 25 25225 30 2252 375 x x x x
The x-intercept is (375, 0). This means that the ramp meets the floor 375 inches (or 31.25 feet) from the base of the platform.
c. No. From part (b), the run is 31.25 feet which exceeds the required maximum of 30 feet.
d. First, design requirements state that the maximum slope is a drop of 1 inch for each 12 inches of run. This means 1 12 m . Second, the run is restricted to be no more than 30 feet = 360 inches. For a rise of 30 inches, this means the minimum slope is 301 36012 . That is, 1 12 m . Thus, the only possible slope is 1 12 m The diagram indicates that the slope is negative. Therefore, the only slope that can be used to obtain the 30-inch rise and still meet design requirements is 1 12 m In words, for every 12 inches of run, the ramp must drop exactly 1 inch.
132. a. Let x represent the percent of internet ad spending. Let y represent the percent of print ad spending. Then the points (0.19, 0.26) and (0.35, 0.16) are on the line. Thus, 162610 0.625 351916
133.
b. x-intercept: 00.62537.875 37.8750.625 60.6
x x x y-intercept: 0.625(0)37.875 37.875 y
The intercepts are (60.6, 0) and (0, 37.875).
c y-intercept: When Internet ads account for 0% of U.S. advertisement spending, print ads account for 37.875% of the spending. x-intercept: When Internet ads account for 60.6% of U.S. advertisement spending, print ads account for 0% of the spending.
d. Let 39 x . 0.625(39)37.87513.5% y
a. Let x = number of boxes to be sold, and A = money, in dollars, spent on advertising. We have the points
11 (,)(100,000,40,000); xA 22 (,)(200,000,60,000) xA 60,00040,000 slope 200,000100,000 20,0001 100,0005 1 40,000100,000 5 1 40,00020,000 5 1 20,000 5 Ax Ax Ax
b. If 300,000 x , then 1 300,00020,000$80,000 5 A
c. Each additional box sold requires an additional $0.20 in advertising.
134. 2xyC Graph the lines: 24 20 22 xy xy xy
yx yx yx
m Using the point-slope formula we have 260.625(19) 260.62511.875 0.62537.875
All the lines have the same slope, 2. The lines
Chapter 1: Graphs
are parallel.

135. Put each linear equation in slope/intercept form. 2523400 25324 1524 2233
xyxyaxy yxyxyax yxyx
If the slope of yax equals the slope of either of the other two lines, then no triangle is formed.
So, 11 22 aa and 22 33 aa
xx x x
Also if all three lines intersect at a single point, then no triangle is formed. So, we find where 1524 and 2233 yxyx intersect. 1524 2233 77 66 1 15 22(1)2
The two lines intersect at (1, 2). If yax also contains the point (1, 2), then 212 aa .
The three numbers are 12 ,, and -2. 23
136. The slope of the line containing , ab and , ba is 1 ab ba
The slope of the line yx is 1.
The two lines are perpendicular
The midpoint of (,)and(,) abba is , 22 abba M .
Since the x and y coordinates of M are equal, M lies on the line yx .
Note: 22 abba
137. The three midpoints are 0000 ,,0,,, 2222222
aaabcabc and 00 ,, 2222
bcbc 1 from (0,0) to,22 0 2 ; 0 2 0(0) abc Line c c m ab ab c yx ab c yx ab
2 from (a, 0) to,22 0 22 22 22 0() 2 2()
bc Line cc c m bba ba a c yxa ba c yxa ba 3 from,0to2(,) 02 2 2 2 0 22 2 22
a Linebc cc m a ba b ca yx ba ca yx ba Find where line 1 and line 2 intersect:
139. (b), (c), (e) and (g)
The line has positive slope and positive y-intercept.
140. (a), (c), and (g)
The line has negative slope and positive y-intercept.
141. (c)
Substitute into line 1: 33
cabc y ab
So, line 1 and line 2 intersect at 33,.
Show that line 3 contains the point , 33
the three lines intersect at 33,.
138. Refer to Figure 69 Assume 12 1 mm Then
Now,
By the converse of the Pythagorean Theorem, AOB is a right triangle with right angle at vertex O. Thus lines OA and OB are perpendicular.
The equation 2 xy has slope 1 and yintercept (0,2). The equation 1 xy has slope 1 and y-intercept (0,1). Thus, the lines are parallel with positive slopes. One line has a positive yintercept and the other with a negative y-intercept.
142. (d)
The equation 22yx has slope 2 and yintercept (0,2). The equation 21xy has slope 1 2 and y-intercept 1 0,. 2
The lines are perpendicular since 1 21 2
. One line has a positive y-intercept and the other with a negative y-intercept.
143 – 145. Answers will vary.
146. No, the equation of a vertical line cannot be written in slope-intercept form because the slope is undefined.
147. No, a line does not need to have both an xintercept and a y-intercept. Vertical and horizontal lines have only one intercept (unless they are a coordinate axis). Every line must have at least one intercept.
148. Two lines with equal slopes and equal y-intercepts are coinciding lines (i.e. the same).
149. Two lines that have the same x-intercept and yintercept (assuming the x-intercept is not 0) are the same line since a line is uniquely defined by two distinct points.
150. No. Two lines with the same slope and different xintercepts are distinct parallel lines and have no points in common.
Assume Line 1 has equation 1ymxb and Line 2 has equation 2ymxb , Line 1 has x-intercept 1b m and y-intercept 1b
Line 2 has x-intercept 2b m and y-intercept 2b .
Assume also that Line 1 and Line 2 have unequal x-intercepts.
If the lines have the same y-intercept, then 12bb 1212 12 bbbb bb mmmm
But 12 bb mm
Line 1 and Line 2 have the same x-intercept, which contradicts the original assumption that the lines have unequal x-intercepts. Therefore, Line 1 and Line 2 cannot have the same y-intercept.
151. Yes Two distinct lines with the same y-intercept, but different slopes, can have the same x-intercept if the x-intercept is 0 x .
Assume Line 1 has equation 1 ymxb and Line 2 has equation 2 ymxb ,
Line 1 has x-intercept 1 b m and y-intercept b
Line 2 has x-intercept 2 b m and y-intercept b
Assume also that Line 1 and Line 2 have unequal slopes, that is 12mm . If the lines have the same x-intercept, then 12 bb mm
. 12 21 21 0 bb mm mbmb mbmb
2112 1212 But 00 0 or 0 mbmbbmm b mmmm
Since we are assuming that 12mm , the only way that the two lines can have the same x-intercept is if 0. b
152. Answers will vary. 153.
21 21 4263 1342 yy m xx
It appears that the student incorrectly found the slope by switching the direction of one of the subtractions.
Section 1.6
1. add; 2 1 2 1025 2. 2 29 29 23 23 x x x x 5 or 1 xx The solution set is {1,5}.
3. a. Center: (0,0) ; radius 1; 22 1 xy
b. 22 9 xy
c. 22 25 xy
d. Center: (2,1); 2 2 2(1)9xy
e. Center: (2,1); 2 2 2(1)9xy
f. Center: (2,2); 2 2 2(2)9xy
g. Center: (5,7);radius 6
4. a. Center: (4,0); 2 2 49xy ;No yintercepts; x-intercepts: 1,7
b. Center: (4,3); 2 2 4(3)9xy ;No y-intercepts; x-intercepts: 4
c. 2 2 4(4)9xy ;No y-intercepts; No x-intercepts
d. One x-intercept
e. No y-intercepts
5. False. For example, 22 2280xyxy is not a circle. It has no real solutions.
6. radius
7. True; 2 93rr
8. False; the center of the circle 22 3213xy is 3,2
9. d
10. a
11. Center(2,1) 22
Radiusdistance from (0,1) to (2,1) (20)(11)42
Equation: 22 (2)(1)4 xy
12. Center(1,2) 22
Radiusdistance from (1,0) to (1,2) (11)(20)42
Equation: 22 (1)(2)4 xy
13. Center = midpoint of (1, 2) and (4, 2)
1422 5 222,,2
2 2 5 2 Radiusdistance from,2to (4,2) 5934(22)242
Equation: 2 2 59 (2) 24xy
14. Center = midpoint of (0, 1) and (2, 3)
0213 ,1,2 22
2 2 Radiusdistance from1,2to (2,3) 21(32)2
Equation: 2 2 1(2)2xy
15. 222()() xhykr 222 22 (0)(0)2 4 xy xy
General form: 22 40 xy

16. 222()() xhykr 222 22 (0)(0)3 9 xy xy
General form: 22 90 xy

17. 222()() xhykr 222 22 (0)(2)2 (2)4 xy xy
General form: 22 22 444 40 xyy xyy

18. 222()() xhykr 222 22 (1)(0)3 (1)9 xy xy
General form: 22 22 219 280 xxy xyx

19. 222()() xhykr 222 22 (4)((3))5 (4)(3)25 xy xy
General form:
22 22 8166925 860 xxyy xyxy

20. 222()() xhykr 222 22 (2)((3))4 (2)(3)16 xy xy
General form: 22 22 446916 4630 xxyy xyxy
21. 222()() xhykr 222 22 (2)(1)4 (2)(1)16 xy xy
General form: 22 22 442116 42110 xxyy xyxy

22. 222()() xhykr
222 22 (5)((2))7 (5)(2)49 xy xy
General form: 22 22 10254449 104200 xxyy xyxy

23. 222()() xhykr 22 2 2 2 11 (0) 22 11 24 xy xy

24. 222()() xhykr
General form: 22 22 11 44 0 xyy xyy

25. 222()() xhykr
2 22 22 (5)((1))13 (5)(1)13
xy xy
General form: 22 22 694420 6470
xxyy xyxy

27. 22 4 xy 222 2 xy
a. Center: (0,0); Radius2 b.
General form: 22 22 10252113 102130
xxyy xyxy

26. 222()() xhykr
2 22 22 (3)(2)25 (3)(2)20
xy xy

c. x-intercepts: 2 2 2 04 4 42 x x x
y-intercepts: 2 2 2 04 4 42 y y y The intercepts are 2,0,2,0, 0,2, and 0,2.
28. 22(1)1xy 222 (1)1xy
a. Center:(0,1); Radius1

a. Center: (–1,1);


31. 22 2440xyxy 22 22
(21)(44)414
a. Center: (1, 2); Radius3
b.

c. x-intercepts:
The intercepts are
32. 22 42200xyxy 22 22 222 4220 (44)(21)2041 (2)(1)5 xxyy xxyy xy
a. Center: (–2,–1); Radius5
b.

c. x-intercepts: 222 2 2 (2)(01)5 (2)125 (2)24 224 226 226 x x x x x x
y-intercepts: 222 2 2 (02)(1)5 4(1)25 (1)21 121 121 y y y y y
The intercepts are 226,0, 226,0, 0,121, and 0,121.
33. 22 22 22 222 4410 441 (44)(44)144 (2)(2)3 xyxy xxyy xxyy xy
a. Center: (–2, 2); Radius3
b. y x
Chapter 1: Graphs
c. x-intercepts: 222 2 2 (2)(02)3 (2)49 (2)5
22 210xyxy 22 22 22 2 21 11 (21)1144 11 (1) 22 xxyy xxyy xy

a. Center: (3, –1); Radius1
b.

c. x-intercepts:
No real solution. The intercept only intercept is



intercepts: 2 22 2 2 022 44 0 0 y y y y The intercepts are 4,0 and


41. Center at (0, 0); containing the point (–2, 3).
22 20304913 r
42. Center at (1, 0); containing the point (–3, 2).
22 31201642025 r
Equation: 2 22 22 (1)(0)20 (1)20 xy xy
43. Endpoints of a diameter are (1, 4) and (–3, 2).
The center is at the midpoint of that diameter:
Center:
1(3)42,1,3 22
Radius: 22 (1(1))(43)415 r
Equation:
2 22 22 ((1))(3)5 (1)(3)5 xy xy
44. Endpoints of a diameter are (4, 3) and (0, 1).
The center is at the midpoint of that diameter:
Center:
47. (c); Center: 1,2 ; Radius2
48. (d) ; Center: 3,3 ; Radius3
49. (b) ; Center: 1,2 ; Radius2
50. (a) ; Center: 3,3 ; Radius3
51. The centers of the circles are: (4,-2) and (-1,5).
The slope is 5(2)77 1455 m . Use the slope and one point to find the equation of the line.
4031 ,2,2 22
Radius: 22 (42)(32)415 r
2 22 22 (2)(2)5 (2)(2)5 xy xy
45. 2 162 8
Cr
2 22 22 (2)((4))8 (2)(4)64
46. 2 2 49 7
Ar r r
2 22 22 ((5))(6)7 (5)(6)49
xy xy
7 (2)(4) 5 728 2 55 510728 7518
yx yx yx xy
52. Find the centers of the two circles: 22 22 22 4640 (44)(69)449 (2)(3)9 xyxy xxyy xy
Center: 2,3
22 22 22 6490 (69)(44)994 (3)(2)4 xyxy xxyy xy
Center: 3,2
Find the slope of the line containing the centers: 2(3)1 325 m
Find the equation of the line containing the centers: 1 3(2) 5 5152 513 5130 yx yx xy xy
53. Consider the following diagram:
(2,2)
Therefore, the path of the center of the circle has the equation 2 y
54. Consider the following diagram:
(7,7)
Therefore the path of the center of the circle has the equation 7 x .
55. Let the upper-right corner of the square be the point , xy . The circle and the square are both centered about the origin. Because of symmetry, we have that xy at the upper-right corner of the square. Therefore, we get
The length of one side of the square is 2x . Thus, the area is
56. The area of the shaded region is the area of the circle, less the area of the square. Let the upperright corner of the square be the point , xy . The circle and the square are both centered about
the origin. Because of symmetry, we have that xy at the upper-right corner of the square. Therefore, we get
The length of one side of the square is 2x . Thus, the area of the square is
2 23272 square units. From the equation of the circle, we have 6 r . The area of the circle is
square units. Therefore, the area of the shaded region is 3672 A
square units.
57. The diameter of the Ferris wheel was 250 feet, so the radius was 125 feet. The maximum height was 264 feet, so the center was at a height of 264125139 feet above the ground. Since the center of the wheel is on the y-axis, it is the point (0, 139). Thus, an equation for the wheel is:
58. The diameter of the wheel is 520 feet, so the radius is 260 feet. The maximum height is 550 feet, so the center of the wheel is at a height of 550260290 feet above the ground. Since the center of the wheel is on the y-axis, it is the point (0, 290). Thus, an equation for the wheel is:
59.

Refer to figure. Since the radius of the building is 60.5 m and the height of the building is 110 m, then the center of the building is 49.5 m above
the ground, so the y-coordinate of the center is 49.5. The equation of the circle is given by 222(49.5)60.53660.25 xy
60. Complete the square to find the equation of the circle representing the formula for the building. 22 222 781521184315213364 (39)58 xyy xy

Refer to figure. The y coordinate of the center is 39. The radius is 58. Thus the height of the building is 583997m
61. Center at (2, 3); tangent to the x-axis. 3 r
Equation: 222 22 (2)(3)3 (2)(3)9 xy xy
62. Center at (–3, 1); tangent to the y-axis. 3 r
Equation: 222 22 (3)(1)3 (3)(1)9 xy xy
63. Center at (–1, 3); tangent to the line 2 y . This means that the circle contains the point (–1, 2), so the radius is 1 r
Equation: 222 22 (1)(3)(1) (1)(3)1 xy xy
64. Center at (4, –2); tangent to the line 1 x
This means that the circle contains the point (1, –2), so the radius is 3 r
Equation: 222 22 (4)(2)(3) (4)(2)9 xy xy
65. a. Substitute 222 into :
222 22222 2222 () 2 (1)20 xmxbr xmxbmxbr mxbmxbr
This equation has one solution if and only if the discriminant is zero.
(1) bmmbr bmbrbmmr brmr brmr rmb
b. From part (a) we know 2222 (1)20 mxbmxbr . Using the quadratic formula, since the discriminant is zero, we get:
The point of tangency is
,.
c. The slope of the tangent line is m The slope of the line joining the point of tangency and the center (0,0) is: 2 2 2 2 0 1 0 r b rb bm mr mr b
The two lines are perpendicular.
66. Let (,) hk be the center of the circle.
The slope of the tangent line is 1 2 . The slope from (,) hk to (0, 2) is –2. 2 2 0 22 k h kh
The other tangent line is 27yx , and it has slope 2
Chapter 1: Graphs
The slope from (,) hk to (3, –1) is 1 2 . 11 32 223 21 12 k h kh kh hk
Solve the two equations in and hk : 22(12) 224 30 0 kk kk k
The center of the circle is (1, 0).
67. The slope of the line containing the center (0,0) and 1,22 is 220 22 10 Then the slope of the tangent line is 12 4 22
So the equation of the tangent line is:
2 221 4 22 22 44 48222 2492
68. 22 4640xyxy 22 22 (44)(69)449 (2)(3)9 xxyy xy
Center: (2, –3)
The slope of the line containing the center and
3,223 is 223(3)22 22 321
Then the slope of the tangent line is: 12 4 22
So, the equation of the tangent line is
2 223(3) 4 232 223 44 48212232 2411212
yx yx yx xy 69. The center of the circle is
. Then the equation of the circle is
70. Complete the square to get
Therefore, the equation of the
Because
Substituting
71. (b), (c), (e) and (g)
We need ,0hk and
72. (b), (e) and (g)
0,0 on the graph.
We need 0 h , 0 k , and hr .
73. Answers will vary.
74. The student has the correct radius, but the signs of the coordinates of the center are incorrect. The student needs to write the equation in the standard form
,3,2
Chapter 1 Review
The slope of the line between the center
b. The coordinates of the midpoint are:
1212(,),22 040242 ,,2,1 2222 xxyy xy
d. When x increases by 2 units, y increases by 1 unit.
Chapter 1: Graphs
b. The coordinates of the midpoint are:
1212(,),22 12 13 , 22 121 ,,1 222
c. 31 44 slope 2133 y x
d. When x increases by 3 units, y decreases by 4 units.
3.
12 4,4 and 4,8 PP a.
2 2 12,4484 014414412 dPP
b. The coordinates of the midpoint are:
1212(,),22 444884 ,,4,2 2222
c.
84 12 slope,undefined 440 y x
d. Undefined slope means the points lie on a vertical line, in this case 4 x





3.87,0 , and
3.87,0 7. 236 326 2 2 3 xy yx yx
x-intercepts: y-intercept:
b.The coordinates of the midpoint are:
1212(,),22 11 23121 ,,,1 22222
c.
d. Slope0
The intercepts are
3,0 and

8. 2 9 yx
x-intercepts: y-intercept:
2 09 033 3 or3 x xx xx

9. 2 2 2 216 216 1 8 2 xy yx yx
x-intercepts: y-intercept:

10. 2 23xy
x-axis:
y-axis:
2 2 23 23different xy xy
2 2 23 23different xy xy
Therefore, the graph of the equation has x-axis symmetry.
11. 22416xy
x-axis: 2 2 22 416 416 same xy xy
y-axis: 2 2 22 416 416 same xy xy
origin:
22 22 416 416 same xy xy
Therefore, the graph of the equation has x-axis, y-axis, and origin symmetry.
12. 4234yxx
x-axis: 42 42 34 34 different yxx yxx
y-axis:
42 42 34 34same yxx yxx
Test origin symmetry: Let xx and yy .
42 42 42 34 34 34different yxx yxx yxx
Therefore, the graph will have y-axis symmetry.
13. 3 yxx x-axis:
3 3 different yxx yxx
y-axis:
3 3 different yxx yxx
origin:
3 3 3 same yxx yxx yxx
Therefore, the equation of the graph has origin symmetry.
14. 22 20xxyy x-axis:
2 2 22 20 20 different xxyy xxyy
Chapter 1: Graphs
15.
origin:
Therefore, the graph of the equation has none of the three symmetries.

17. 4 321xx

16. 3 530xx
Use the Zero option from the CALC menu.


.
Use the Intersect option on the CALC menu.


18. Slope–2 ; containing the point 3,1 . 11() (1)2(3) 126 25 25 or25 yymxx yx yx yx xyyx

19. Slope0 ; containing the point 5,4 .

20. Slope undefined; containing the point 3,4 .
This is a vertical line. 3 x
No slope-intercept form.
21. -intercept2x x- or the point 2,0 ;
Containing the point 4,5

22. -intercept2y y-; containing the point 5,3 Points are 5,3 and 0,2 2(3)11 0555

23. Containing the points 3,4 and 2,1 1(4)55
Chapter 1: Graphs
11 (4)53 4515 511 511or 511 yymxx yx yx yx xyyx

24. Parallel to 234 xy ; 2 Slope ;containing(–5,3) 3 11() 22103((5))3333 219 33 219 2319 or 33 yymxx yxyx yx xyyx

25. Perpendicular to 34 xy ; 1 Slope of perpendicular3
Containing the point 2,4 11() 1 4((2)) 3 12 4 33 110 33 110 310 or 33 yymxx yx yx yx xyyx
26. 222()() xhykr
2 2 2 22 234 2316 xy xy
27. 222()() xhykr
22 2 22 121 121 xy xy
28. 22 2440xyxy 22 22 22 222 244 (21)(44)414 (1)(2)9 (1)(2)3 xxyy xxyy xy xy
Center: (1,–2) Radius3
22 2 024040 240 xx xx 2 22414220 212 225 15 2 x


30. Given the points (2,0),(4,4),(8,5)ABC
a. Find the distance between each pair of points.
360 320 xx xx xx
2 2 2 30360120
222 20125145 20125145 145145
The Pythagorean Theorem is satisfied, so this is a right triangle.
b. Find the slopes:
4042 4(2)2 541 8412 5051 82102
Since the product of the slopes is –1, the sides of the triangle are perpendicular and the triangle is a right triangle.
31. slope15of1; 62 slope11of1 86 AB BC
Since lines AB and BC are parallel, and have a point in common (B), they are the
same line. Therefore, A , B , and C are collinear.
32. A circle with center
1,2 has equation
Therefore the points A, B and C lie on a circle with
33. Endpoints of the diameter are 3,2 and
5,6
The center is at the midpoint of the diameter: Center: 352(6),1,2 22
Radius: 22 (1(3))(22)1616 3242
Equation: 2 22 22 22 (1)(2)42 214432 24270 xy xxyy xyxy
34. Using the distance formula on the points (–3, 2) and (5, y) yields 222 (5(3))(2)64(2)dyy Nowset 10andsolvefor .dy
2 2 22 2 2 1064(2) 1064(2) 10064(2) 36(2) 62 so268 and264 y y y y y yy yy
35. 2 3 Slope , containing the point (1, 2)
36. Answers will vary.
37. a. 0 x is a vertical line passing through the origin, that is, 0 x is the equation of the y-axis.
b. 0 y is a horizontal line passing through the origin, that is, 0 y is the equation of the x-axis.
c. 0 xy implies that yx . Thus, the graph of 0 xy is the line passing through the origin with 1 Slope
d. 0 xy implies that either 0 x , 0 y , or both are 0. 0 x is the y-axis and 0 y is the x-axis. Thus, the graph of 0 xy is a graph consisting of the coordinate axes.
e. 22 0 xy implies that both 0 x and 0 y . Thus, the graph of 22 0 xy is a graph consisting of a single point - the origin.
Chapter 1 Test
1. a. The distance between the two points
2,3 and 4,5 is
b. The midpoint of the line segment connecting the two points is
2721




11541,4 00550,5 11541,4 33543,4

The intercepts are


2.24,0
, and

4. 32 2210 xxx
Since this equation has 0 on one side, we will use the Zero option from the CALC menu. It will be important to carefully select the window settings so as not to miss any solutions.




The solutions to the equation are 1, 0.5, and 1 or 1,0.5,1
5. 42580xx
Since this equation has 0 on one side, we will
use the Zero option from the CALC menu.




The solutions, rounded to two decimal places, are 2.50 and 2.50 or 2.50,2.50
6. 327233xxxx
Since there are nonzero expressions on both sides of the equation, we will use the Intersect option from the CALC menu. Enter the left side of the equation in Y1 and the right side in Y2.





The solutions, rounded to two decimal places, are 2.46, 0.24, and 1.70 or 2.46,0.24,1.70 . 7. a. 21 21 1342 5(1)63 yy m xx
b. If x increases by 3 units, y will decrease by 2 units. 8. 2 yx
9. 2 9 xy x-intercepts: y-intercept: 2 2 09 9 3 x x
The intercepts are
3,0,
3,0, and
Test x-axis symmetry: Let yy
2 2 9 9 different xy xy
Test y-axis symmetry: Let xx
2 2 9 9 same xy xy
0,9.
Test origin symmetry: Let xx and yy
2 2 9 9 different xy xy
Therefore, the graph will have y-axis symmetry.
10. 2 Slope ; containing (3,4) 11() (4)2(3) 426 22 yymxx yx yx yx

11. 222()() xhykr
22 2 22 4(3)5 4325 xy xy
General form:
22 22 22 4325 8166925 860 xy xxyy xyxy
12. 22 22 22 222 4240 424 (44)(21)441 (2)(1)3
Center: (–2, 1); 3 Radius
Chapter 1 Project
Internet-based Project – Answers will vary.
Parallel
Any
Chapter 2
Functions and Their Graphs
Section 2.1
1. 1,3 2.
3. We must not allow the denominator to be 0. 404xx ; Domain: 4 xx .
4. 325 22 1 x x x
5. 52
6. radicals
7. independent; dependent
8. a 9. c
10. False; g 0
11. False; every function is a relation, but not every relation is a function. For example, the relation 22 1 xy is not a function.
12. verbally, numerically, graphically, algebraically
13. False; if the domain is not specified, we assume it is the largest set of real numbers for which the value of f is a real number.
14. False; if x is in the domain of a function f, we say that f is defined at x, or f(x) exists.
15. difference quotient
16. explicitly
17. a. Domain: {0,22,40,70,100} in C Range: {1.031, 1.121, 1.229, 1.305, 1.411} in 3kg/m b.

c. {(0, 1.411), (22, 1.305), (40, 1 229), (70, 1.121), (100, 1.031)}
18. a. Domain: {1.80, 1.78, 1.77} in meters Range: {87.1, 86.9, 83.0, 84.1, 86.4} in kg b.

c. {(1.80, 87.1), (1.78, 86.9), (1.77, 83.0), (1.77, 84.1), (1.80, 86.4)}
19. Domain: {Elvis, Colleen, Kaleigh, Marissa} Range: {Jan. 8, Mar. 15, Sept. 17} Function
20. Domain: {Bob, Darius, Chuck} Range: {Beth, Diane, Imani, Marcia} Not a function
21. Domain: {20, 30, 40} Range: {300, 350, 540, 880} Not a function
22. Domain: {9th-12th grade, High School graduate, Some college, Bachelor’s Degree} Range: {$682, $853, $935, $1432} Function
23. Domain: {-3, 2, 4} Range: {6, 9, 10} Not a function
24. Domain: {–2, –1, 3, 4} Range: {3, 5, 7, 12} Function
25. Domain: {1, 2, 3, 4} Range: {3} Function
26. Domain: {0, 1, 2, 3} Range: {–2, 3, 7} Function
27. Domain: {-4, 0, 3} Range: {1, 3, 5, 6} Not a function
28. Domain: {-4, -3, -2, -1} Range: {0, 1, 2, 3, 4} Not a function
29. Domain: {–1, 0, 2, 4} Range: {-1, 3, 8} Function
30. Domain: {–2, –1, 0, 1} Range: {3, 4, 16} Function
31. Graph 2 234yxx . The graph passes the vertical line test. Thus, the equation represents a function.

32. Graph 3 yx . The graph passes the vertical line test. Thus, the equation represents a function.

33. Graph 1 y x . The graph passes the vertical line test. Thus, the equation represents a function.

34. Graph yx . The graph passes the vertical line test. Thus, the equation represents a function.

35. 22 8 xy
Solve for 2 :8 yyx
For 0,22xy . Thus, 0,22 and 0,22 are on the graph. This is not a function, since a distinct x-value corresponds to two different y-values.
36. 12 yx
For 0,1xy . Thus, (0, 1) and (0, –1) are on the graph. This is not a function, since a distinct xvalue corresponds to two different y-values
37. 2 xy
Solve for : yyx
For 1,1xy . Thus, (1, 1) and (1, –1) are on the graph. This is not a function, since a distinct x-value corresponds to two different y-values
38. 2 1 xy
Solve for :1 yyx
For 0,1xy . Thus, (0, 1) and (0, –1) are on the graph. This is not a function, since a distinct xvalue corresponds to two different y-values.
39. Graph 3 yx . The graph passes the vertical line test. Thus, the equation represents a function.

40. Graph 31 2 x y x . The graph passes the vertical line test. Thus, the equation represents a function.

41. 23yx
Solve for y: 23or (23) yxyx For 1,5or 5xyy . Thus, 1,5 and 1,5 are on the graph. This is not a function, since a distinct x-value corresponds to two different y-values.
42. 2241xy
Solve for y: 22 22 2 2 2 41 41 1 4 1 2 xy yx x y x y
For 1 2, 2 xy . Thus, 1 2, 2
and 1 2, 2 are on the graph. This is not a function, since a distinct x-value corresponds to two different y-values.
43. 2 324fxxx
2 0302044 f
b.
2 1312143241 f
2 21fxxx a.
2 020011 f
2 121112 f
2 121114 f
d.
e.
2 2 2121fxxxxx
22 2121fxxxxx f.
2 2 2 2 12111 22111 242 232 fxxx xxx xxx xx
g.
2 2 22221821 fxxxxx
2 22 22 2()1 221 2421 fxhxhxh xxhhxh xxhhxh
2 11 1 112
2 111 1 112 11
22 1 1 xx fx x
2211 xx fx xx
g.
2 2 21 41 2 2424 x x
a.
c. 114145 f
d. 44fxxx
e. 44fxxx f. 114fxx
g. 22424fxxx
h. 4 fxhxh
48. 2 fxxx
a. 2 00000 f
b. 2 1112 f
c. 2 1111100 f
d. 2 2 fxxxxx
e. 22 fxxxxx
f. 2 2 2 111 211 32 fxxx xxx xx
g. 2 2 22242 fxxxxx
h.
2 22 2 fxhxhxh xxhhxh
2: Functions and Their Graphs
51. ()54fxx
Domain:
52. 2 ()2fxx
Domain: is any real number xx .
53. 2 1 () 28 x fx x
Domain: is any real number xx .
54. 2 2 () 1 x fx x
Domain: is any real number xx
55. 2 () 16 x gx x 2 2 160 164 x xx
Domain: 4,4xxx
56. 2 2 () 4 x hx x 2 2 40 42 x xx
Domain: 2,2xxx .
57. 3 2 () x Fx xx 3 2 2 0 (1)0 0,1 xx xx xx
Domain: 0 xx
58. 3 4 () 4 x Gx xx 3 2 2 40 (4)0 0,4 0,2 xx xx xx xx
Domain: 2,0,2xxxx .
59. ()312hxx 3120 312 4 x x x
Domain: 4 xx .
60. ()1 Gxx 10 1 1 x x x
Domain: 1 xx
61. () 231 x px x 2310 231 231 or 231 2422 21 x x xx xx xx
2,1xxx
62. 1 () 314 x fx x 3140 314 314or314 33 35 5 1 3 x x xx xx xx
Domain: 5 1, 3
63. () 4 x fx x 40 4 x x Domain: 4 xx
64. 2 () x x fx 20 2 2 x x x
Domain: 2 xx
65. 4 () 321 t Pt t
40 4 t t Also 3210 t 3210 321 7 t t t
Domain: 4,7ttt .
66. 3 ()2 z hz z 30 3 z z Also 20 2 z z
Domain: 3,2zzz
67. 3 ()54 fxx
Domain: is any real number xx
68. 3 22 ()7 gtttt
Domain: is any real number tt .
69. 5 2 1 () 514 t Mt tt 2 5140 (2)(7)0 20or70 27 tt tt tt tt
Domain: 2,7ttt .
70. 5 2 () 298 p Np p 2 2 2980 2(49)0 2(7)(7)0 70 or70 77 p p pp pp pp
Domain: 7,7ppp
71. ()34()23 fxxgxx a. ()()342351 fgxxxx
Domain: is any real number xx .
Chapter 2: Functions and Their Graphs
b. ()()(34)(23) 3423 7 fgxxx xx x
Domain: is any real number xx .
c. 2 2 ()()(34)(23) 69812 612 fgxxx xxx xx
Domain: is any real number xx .
d. 34 () 23 fx x gx
3 23023 2 xxx
Domain: 3 2 xx
e. ()(3)5(3)115116 fg
f. ()(4)4711 fg
g. 2 ()(2)6(2)2122421210 fg
h. 3(1)4 347 (1)7 2(1)3231
g
72. ()21()32 fxxgxx
a. ()()213251 fgxxxx
Domain: is any real number xx
b. ()()(21)(32) 2132 3 fgxxx xx x
Domain:
is any real number xx
c. 2 2 ()()(21)(32) 6432 62 fgxxx xxx xx
Domain: is any real number xx .
d. 21 () 32 fx x gx
320 2 32 3 x xx
Domain: 2 3 xx
e. ()(3)5(3)115114 fg f. ()(4)431 fg g. 2 ()(2)6(2)22 6(4)22 242220 fg
h. 2(1)1 213 (1)3 3(1)2321 f g
73. 2 ()1()2 fxxgxx
a. 22 ()()1221 fgxxxxx
Domain: is any real number xx
b. 2 2 2 ()()(1)(2) 12 21 fgxxx xx xx
Domain: is any real number xx .
c. 232()()(1)(2)22 fgxxxxx
Domain: is any real number xx
d. 2 1 () 2 fx x g x
Domain: 0 xx
e. 2 ()(3)2(3)31 2(9)31 183120 fg
f. 2 ()(4)2(4)41 2(16)41 324129 fg
g. 32()(2)2(2)2(2) 2(8)2(4) 1688 fg
h. 2 1100 (1)0 2(1)2 2(1) f g
74. 23 ()23()41 fxxgxx
a. 23 32 ()()2341 424 fgxxx xx
Domain: is any real number xx .
b. 23 23 32 ()()2341 2341 422 fgxxx xx xx
Domain: is any real number xx
c. 23 532 ()()2341 81223 fgxxx xxx
Domain: is any real number xx .
d.
Domain: 3 2 2 xx
e. 32 ()(3)4(3)2(3)4 4(27)2(9)4 108184130 fg
fg
f. 32 ()(4)4(4)2(4)2 4(64)2(16)2 256322222
fg
g. 532 ()(2)8(2)12(2)2(2)3 8(32)12(8)2(4)3 2569683363
h. 2 3 2(1)32(1)3 235 (1)1 4(1)1415 4(1)1
g
75. ()()35 fxxgxx
a. ()()35 fgxxx
Domain: 0 xx
b. ()()(35)35 fgxxxxx
Domain: 0 xx
c. ()()(35)35 fgxxxxxx
Domain: 0 xx
d. () 35 fx x gx 0 and 350 5 35 3 xx xx
Domain: 5 0and 3 xxx
e. ()(3)33(3)5 39534 fg
f. ()(4)43(4)5 21255 fg
g. ()(2)3(2)252 62522 fg
h. 1111 (1) 3(1)53522 f g
76. ()() fxxgxx
a. ()()fgxxx
Domain: is any real number xx
b. ()()fgxxx
Domain: is any real number xx .
c. ()()fgxxxxx
Domain: is any real number xx
d. () x f x gx
Domain: 0 xx
e. ()(3)33336 fg
f. ()(4)44440 fg
g. ()(2)22224 fg
h. 1 1 (1)1 11
77. 11 ()1() fxgx xx
a. 112 ()()11 fgx xxx
Domain: 0 xx
b. 11 ()()11 fgx xx
Domain: 0 xx .
c. 2 1111 ()()1 fgx xxx x
Domain: 0 xx
d. 11 1 1 ()1 11 1 x fxx xx xx gx xx
Domain: 0 xx .
e. 25 ()(3)133 fg
f. ()(4)1 fg
g. 2 11113 ()(2) 2244 (2) fg
h. (1)112 f g
()1()4 fxxgxx
a. ()()14 fgxxx 10and40 1and 4 4 xx xx x
Domain: 14xx
b. ()()14 fgxxx 10and40 1and 4 4 xx xx x
Domain: 14xx .
c. 2 ()()14 54 fgxxx xx 10and40 1and 4 4 xx xx x
Domain: 14xx
d. 11 () 4 4 fxx x gx x 10and40 1and 4 4 xx xx x
Domain: 14xx . e. ()(3)3143 2121 fg
f. ()(4)4144 30303 fg
g. 2 ()(2)(2)5(2)4 41042 fg h. 110 (1)00 413 f g
79. 234 ()()3232 fxgxxx xx
a. ()()2343232 23463 3232 xx fgx xx xxx xx 2 3 320 32 x xx
Domain: 2 3 xx
b.
c.
e. 6(3)3 18321 ()(3)3 3(3)2927 fg
f. 2(4)3835 1 ()(4) 3(4)2122102 fg
g.
2 2 22 ()(2)8(2)12(2) 3(2)2 8(4)243224567 624162 fg
h. 2(1)3 235 (1) 4(1)44
g
80. 2 ()1() fxxgx x
a. 2 ()()1 fgxx x 10and0 1 xx x
Domain: 1,and0xxx
b. 2 ()()1 fgxx x 10and0 1 xx x
Domain: 1,and0xxx
c. 221 ()()1 x fgxx xx 10and0 1 xx x
Domain: 1,and0xxx
d. 11 () 2 2 fxxx x g x
10and0 1 xx x
Domain: 1,and0xxx .
e. 2228 ()(3)31423333 fg
f. 21 ()(4)41542 fg
g. 22123 ()(2)3 22 fg
h. 1112 (1) 22 f g
81. 1 ()31()()62 fxxfgxx 1 631() 2 7 5() 2 ()57 2 xxgx xgx gxx
Chapter 2: Functions and Their Graphs
82. 2 11 ()() fxxfx xg xx
2 2 2 1 1 () 1 1 ()11 1(1)1 11 x x gx xx xx x gx x xx xx xxx xxx
83. ()43fxx
()()4()3(43) 44343 4 4 fxhfxxhx hh xhx h h h
84. ()31fxx ()()3()1(31) 33131 3 3 fxhfxxhx hh xhx h h h
85. 2 ()4fxx
22 222 2 ()() ()4(4) 244 2 2 fxhfx h xhx h xxhhx h xhh h xh
86. 2 ()32fxx 22 222 2 ()() 3()2(32) 363232 63 63 fxhfx h xhx h xxhhx h xhh h xh
87. 2 ()4 fxxx 22 222 2 ()() ()()4(4) 244 2 21 fxhfx h xhxhxx h xxhhxhxx h xhhh h xh
2 326fxxx
2 2 222 2222 326326 32226326 36323632 632 fxhfx h xhxhxx h xxhhxhxx h xxhhhxxhhh hh xh
89.
xhxh hxhxhxhx xhx
97. 2 ()4 fxx
22 2222 22 22 22 222 2 22 22 4()4 4()44()4 4()4 4()(4) 4()4 4(2)(4) 11 2 11 2 4()4 (2) 4()4 fxhfx h xhx h xhxxhx h xhx xhx hxhx xxhhx hxhx xhh hxhx xh xhx xh xhx
98. 1 2 fx x ()() 11 22 22 22 2222 2222 2(2) (2)2(2)2 22 (2)2(2)2 (2)2(2)2 1 (2)2(2)2 fxhfx h xhx h xxh hxxh xxhxxh hxxhxxh xxh hxxhxhx xxh hxxhxhx h hxxhxhx xxhxhx
99. 2 2 1123 028 0(4)(2) 40 or20 4or2 xx xx xx xx xx
The solution set is 2,4
100. 753 1664 735 1646 5712 61616 55 616 563 1658 x x x x x
The solution set is 3 8
101. 32 ()245and (2)5 fxxAxxf 32 (2)2(2)(2)4(2)5 516485 5419 144 147 42 fA A A A A
102. 2 ()34and (1)12 fxxBxf : 2 (1)3(1)(1)4 1234 5 fB B B
103. 38 ()and(0)2 2 x fxf xA (0)3(0)8 2(0) 8 2 28 4 f A A A A
104. 21 ()and(2)342 xB fxf x (2)2(2)3(2)4 14
105. Let x represent the length of the rectangle. Then, 2 x represents the width of the rectangle since the length is twice the width. The function for the area is
106. Let x represent the length of one of the two equal sides. The function for the area is: 2 11 ()22 Axxxx
107. Let x represent the number of hours worked. The function for the gross salary is: ()16 Gxx
108. Let x represent the number of items sold. The function for the gross salary is: ()10100Gxx
111.
c.
b. 32 (15)0.05(15)0.8(15)155(15)500 168.751802325500 $1836.25
c. When 15 hundred smartphones are sold, the profit is $1836.25.
118. a. P is the dependent variable; a is the independent variable
b. 2 (20)0.027(20)6.530(20)363.804 10.8130.6363.804 244.004
There are 244.004 million people in the United States who are 20 years of age or older.
c. 2 (0)0.027(0)6.530(0)363.804 363.804 P
There are a total of 363.804 million people in the United States
Rvv
119. a. 2 2 2 ()0.05 2.20.050.4v15 0.05 ()2.2;0.4v15 ()()() 2.615 Bvv
b. 2 (60)0.05(60)2.6(60)15 18015615 321 D
c. The car will need 321 feet to stop once the impediment is observed.
120. a. 2 hxx
222 hababab hahb
2 hxx has the property.
Chapter 2: Functions and Their Graphs
b. 2 gxx
2 22 2 gababaabb
Since 2222 2 aabbabgagb , 2 () gxx does not have the property.
c. 52Fxx
52552Fababab Since
x x xx x Therefore,
2 23(2)210 f
123. We need 2 1 0 731 x x . Since 2 10 x for all real numbers x, we need 7310 x . 7310 317 7317 8 2 3
x x x x
5525252 ababFaFb ,
52Fxx does not have the property. d.
1 Gx x
111 GabGaGb abab
1 Gx x does not have the property.
The domain of f is 88 |2, or2, 33
xx in interval notation.
124. No. The domain of f is is any real number xx , but the domain of g is 1 xx .
125. 3 3 ( ) xx Hx yourage
126. Answers will vary.
127. 22 (12)16 xy x-intercept (y=0): 22 2 (12)016 (12)16 (12)4 124 16,8 x x x x xx
(16,0),(8,0) y-intercept (x=0): 22 22 2 (012)16 (12)16 16144128 y y y
There are no real solutions so there are no yintercepts.
Symmetry: 22 22 (12)()16 (12)16 xy xy
This shows x-axis symmetry.
128. 2 2 38 3(1)81 yxx y
There is no solution so (-1,-5) is NOT a solution.
2 2 38 3(4)84 481632 yxx y
So (4,32) is a solution.
2 2 38 3(9)89 24324219171 yxx y
So (9,171) is NOT a solution.
129. Let x represent the amount of the 7% fat hamburger added.
% fattot. amt.amt. of fat 20%120.2012 7%0.07 15%120.1512 xx xx
7.5 lbs. of the 7% fat hamburger must be added, producing 19.5 lbs. of the 15%
solution set is:
abxacd aacdbx acdbx dbx a c
(1) 1
132. 2 20.4(0.6) 10 9 rkd k k Thus, 2 2 10 9(1.5) 2.5kg
r m
xy yx yx
133. 31012 10312 36 105
The slope of the line is 3 10 . The slope of a perpendicular line would be 10 3
134. 222 2222 22 22 2 22 2 22 (47)3(35)81221(2440) (47)(47) 12212440 (47) 124021 (47) 124021 (47) xxxxxx xx xxx x xx x xx x
135. Add the powers of x to obtain a degree of 7.
Chapter 2: Functions and Their Graphs
Section 2.2
1. 22416xy x-intercepts:
2 2 2 4016 16 44,0,4,0 x x x
2. False; 22 222 02 0 xy y y y
The point
2,0 is on the graph. 3. vertical
6. False The graph must pass the vertical line test in order to be the graph of a function
7. False; e.g. 1 y x . 8. True
9. c 10. a
11. a. (0)3since(0,3)isonthegraph. f (6)3since(6,3)isonthegraph. f
b. (6)0since(6,0)isonthegraph. f (11)1since(11,1)isonthegraph. f
c. (3)ispositivesince (3)3.7. ff
d. (4)isnegativesince (4)1. ff
e. ()0when 3,6,and 10. fxxxx
f. ()0when 36,and1011.fxxx
g. The domain of f is 611xx or 6,11
h. The range of f is 34yy or 3,4 .
i. The x-intercepts are 3, 6, and 10
j. The y-intercept is 3
k. The line 1 2 y intersects the graph 3 times.
l. The line 5 x intersects the graph 1 time.
m. ()3when 0and 4. fxxx
n. ()2when 5and 8. fxxx
12. a. (0)0since(0,0)isonthegraph. f (6)0since(6,0)isonthegraph. f
b. (2)2since(2,2)isonthegraph. f (2)1since(2,1)isonthegraph. f
c. (3)isnegativesince (3)1. ff
d. (1)ispositivesince (1)1.0. ff
e. ()0when 0,4,and 6. fxxxx
f. ()0when04. fxx
g. The domain of f is 46xx or 4,6
h. The range of f is 23yy or 2,3
i. The x-intercepts are 0, 4, and 6.
j. The y-intercept is 0.
k. The line 1 y intersects the graph 2 times.
l. The line 1 x intersects the graph 1 time.
m. ()3when 5. fxx
n. ()2when 2. fxx
13. Not a function since vertical lines will intersect the graph in more than one point.
a. Domain: 1 or1xxx ;
Range: is any real number yy
b. Intercepts: (1,0),(1,0)
c. Symmetry about the x-axis, y-axis and the origin
14. Function
a. Domain: is any real number xx ;
Range: 0 yy
b. Intercepts: (0,1)
c. None
15. Function
a. Domain: xx ;
Range: 11yy
b. Intercepts: ,0,,0, 22(0,1)
c. Symmetry about y-axis.
16. Function
a. Domain: xx ;
Range: 11yy
b. Intercepts: ,0, ,0,(0,0)
c. Symmetry about the origin.
17. Not a function since vertical lines will intersect the graph in more than one point.
a. Domain: 0 xx ;
Range: is any real number yy
b. Intercepts: (0,0)
c. Symmetry about the x-axis
18. Not a function since vertical lines will intersect the graph in more than one point.
a. Domain: 22xx ;
Range: 22yy
b. Intercepts: (2,0)(2,0)(0,2)(0,2)
Section 2.2: The Graph of a Function
c. Symmetry about the x-axis, y-axis and the origin
19. Function
a. Domain: 03xx ;
Range: <2 yy
b. Intercepts: (1, 0)
c. None
20. Function
a. Domain: 04xx ;
Range: 03yy
b. Intercepts: (0, 0)
c. None
21. Function
a. Domain: is any real number xx ;
Range: 2 yy
b. Intercepts: (–3, 0), (3, 0), (0,2)
c. Symmetry about y-axis.
22. Function
a. Domain: 3 xx ;
Range: 0 yy
b. Intercepts: (–3, 0), (2,0), (0,2)
c. None
23. Function
a. Domain: is any real number xx ;
Range: 3 yy
b. Intercepts: (1, 0), (3,0), (0,9)
c. None
24. Function
a. Domain: is any real number xx ;
Range: 5 yy
b. Intercepts: (–1, 0), (2,0), (0,4)
c. None
25. 2 ()32 fxxx
Chapter 2: Functions and Their Graphs
a. 2 (1)31122 f
The point 1,2 is on the graph of f
b. 2 (2)32228 f
The point 2,8 is on the graph of f.
c. Solve for x : 2 2 1 3 232 03 0310, xx xx xxxx
(0, –2) and 1 3,2 are on the graph of f .
d. The domain of f is is any real number xx .
e. x-intercepts:
fxxx xxxx
2 =0320 2 3210,1 3
f. y-intercept:
2 0=30022 f
26. 2 ()35 fxxx
a.
2 (1)315182 f
The point 1,2 is not on the graph of f
b. 2 (2)3252=22 f
The point 2,22 is on the graph of f.
c. Solve for x : 22 1 3 2353520 3120,2 xxxx xxxx (2, –2) and 1 3,2 on the graph of f
d. The domain of f is is any real number xx
e. x-intercepts:
2 5 3 =0350 3500, fxxx xxxx
f y-intercept: 2 030500 f 27. 2 ()6 x fx x
a. 325 (3)14 363 f
The point 3,14 is not on the graph of f.
b. 426 (4)3 462 f
The point 4,3 is on the graph of f
c. Solve for x : 2 2 6 2122 14 x x xx x (14, 2) is a point on the graph of f
d. The domain of f is 6 xx .
e. x-intercepts: 2 =00 6 202 x fx x xx
f y-intercept: 021 0 063 f
28. 2 2 () 4 x fx x
a. 2 123 (1) 145 f
The point 3 1, 5 is on the graph of f
b. 2 0221 (0) 0442 f
The point 1 0, 2 is on the graph of f
c. Solve for x : 2 2 2 12 424 24 02 1 2100 or 2 x xx x xx xxxx
111 0,and, 222 are on the graph of f .
d. The domain of f is 4 xx
e. x-intercepts:
2 2 2 =0020 4 x fxx x
This is impossible, so there are no xintercepts.
f. y-intercept:
29. 4 2 12 () 1 x fx x
a. 4 2 12(1)12 (1)6 2 (1)1
f The point (–1,6) is on the graph of f.
b. 4 2 12(3)972486 (3) 105 (3)1 f The point 486 3, 5
c. Solve for
(31)(41)0
is on the graph of f.
are on the graph of f
d. The domain of f is is any real number xx
e. x-intercept:
f. y-intercept:
Section 2.2: The Graph of a Function
1 2 112 2 13 23 2 22 f
The point 12 , 23 is on the graph of f
b. 2(4)8 (4)4 422 f
The point 4,4 is on the graph of f
c. Solve for x : 22 122 2 x x xx x (–2,1) is a point on the graph of f
d. The domain of f is 2 xx .
e. x-intercept: 2 =0020 2 0 x fxx x x
f y-intercept: 0 00 02 f
31. a. ()(2)(2)(2)213 fgfg
b. ()(4)(4)(4)1(3)2 fgfg
c. ()(6)(6)(6)011 fgfg
d. ()(6)(6)(6)101 gfgf
e. ()(2)(2)(2)2(1)2 fgfg
f. (4) 11 (4) (4)33 ff gg
32. 2 2 136 2.73.5 x hxx v
a. We want 1510 h 2 2 2 2 13615 2.7153.510 30,600 34 900 30ft/sec v v v v
The ball needs to be thrown with an initial velocity of 30 feet per second.
Chapter 2: Functions and Their Graphs
c. Using the velocity from part (b),
The ball will be 15.56 feet above the floor when it has traveled 9 feet in front of the foul line.
d. Select several values for x and use these to find the corresponding values for h. Use the results to form ordered pairs
, xh . Plot the points and connect with a smooth curve.
c. From part (a) we know the point 8,10.4 is on the graph and from part (b) we know the point 12,9.9 is on the graph. We could evaluate the function at several more values of x (e.g. 0 x , 15 x , and 20 x ) to obtain additional points.
Thus, some points on the graph are
5,13.2 , and
0,3.5 ,
15,10 . The complete graph is given below.

Some additional points are
and
20,3.6 . The complete graph is given below.

No; when the ball is 15 feet in front of the foul line, it will be below the hoop. Therefore it cannot go through the hoop.
In order for the ball to pass through the hoop, we need to have
1510 h
Section 2.2: The Graph of a Function

The ball must be shot with an initial velocity of 30 feet per second in order to go through the hoop.
34. 2 ()41 Axxx
a. Domain of 2 ()41 Axxx ; we know that x must be greater than or equal to zero, since x represents a length. We also need 2 10 x , since this expression occurs under a square root. In fact, to avoid Area = 0, we require 2 0 and10xx
Case1:10and10 1and1 (i.e.11)
1and1 (which is impossible) xx Therefore the domain of A is 01xx .
b. Graphing 2 ()41 Axxx

c. When 0.7 x feet, the cross-sectional area is maximized at approximately 1.9996 square feet. Therefore, the length of the base of the beam should be 1.4 feet in order to maximize the cross-sectional area.
(100)100 130 320,00010081.07 feet 16,900
b. 2 2 32(300) (300)300 130 2,880,000300129.59 feet 16,900
c. 2 2 32(500) (500)500 130 8,000,00050026.63 feet 16,900
The ball is about 26.63 feet high after it has traveled 500 feet. d. 2 2 32 Solving ()0 130 x hxx
Therefore, the golf ball travels 528.13 feet.
Chapter 2: Functions and Their Graphs
e. 2 1 2 32 130 x yx 5 0 150 600

f. Use INTERSECT on the graphs of 2 1 2 32 130 x yx and 2 90 y 5 0 150 600 5 0 150 600


The ball reaches a height of 90 feet twice. The first time is when the ball has traveled approximately 115.07 feet, and the second time is when the ball has traveled about 413.05 feet.
g. The ball travels approximately 275 feet before it reaches its maximum height of approximately 131.8 feet.

h. The ball travels approximately 264 feet before it reaches its maximum height of approximately 132.03 feet.


36. 2 4000 () 4000 Whm h
On Pike's Peak, Amy will weigh about 119.84 pounds.
b. Graphing: 5 0 120 119.5

c. Create a TABLE:


The weight W will vary from 120 pounds to about 119.7 pounds.
d. By refining the table, Amy will weigh 119.95 lbs at a height of about 0.83 miles (4382 feet).


e. Yes, 4382 feet is reasonable. 37. 36000 ()10010 x Cx x
48036000 (480)10010480

c. Graphing:

d. TblStart0; Tbl50

e. The cost per passenger is minimized to about $220 when the ground speed is roughly 600 miles per hour.

38. a. 05000 C
This represents the fixed overhead costs. That is, the company will incur costs of $5000 per day even if no computers are manufactured.
b. 1019,000 C
It costs the company $19,000 to produce 10 computers in a day.
c. 5051,000 C
It costs the company $51,000 to produce 50 computers in a day.
d. The domain is |080 qq . This indicates that production capacity is limited to 80 computers in a day.
e. The graph is curved down and rises slowly at first. As production increases, the graph rises more quickly and changes to being curved up.
f. The inflection point is where the graph changes from being curved down to being curved up.
Section 2.2: The Graph of a Function
39. a. 0$50 C
It costs $50 if you use 0 gigabytes.
b. 5$50 C
It costs $50 if you use 5 gigabytes.
c. 15$150 C It costs $150 if you use 15 gigabytes.
d. The domain is g|030 g . This indicates that there are at most 30 gigabytes in a month.
e. The graph is flat at first and then rises in a straight line.
40. (2) (2)54 3 f g Since 2 (2)(2)4(2) 12
(5)525
42. Answers will vary. From a graph, the domain can be found by visually locating the x-values for which the graph is defined. The range can be found in a similar fashion by visually locating the y-values for which the function is defined.
If an equation is given, the domain can be found by locating any restricted values and removing them from the set of real numbers. The range can be found by using known properties of the graph
of the equation, or estimated by means of a table of values.
43. The graph of a function can have any number of x-intercepts. The graph of a function can have at most one y-intercept (otherwise the graph would fail the vertical line test)
44. Yes, the graph of a single point is the graph of a function since it would pass the vertical line test. The equation of such a function would be something like the following: 2 fx , where
7 x .
45. (a) III; (b) IV; (c) I; (d) V; (e) II
46. (a) II; (b) V; (c) IV; (d) III; (e) I
47.

48.

49. a. 2 hours elapsed; Sobia was between 0 and 3 miles from home.
b. 0.5 hours elapsed; Sobia was 3 miles from home.
c. 0.3 hours elapsed; Sobia was between 0 and 3 miles from home.
d. 0.2 hours elapsed; Sobia was at home.
e. 0.9 hours elapsed; Sobia was between 0 and 2.8 miles from home.
f. 0.3 hours elapsed; Sobia was 2.8 miles from home.
g. 1.1 hours elapsed; Sobia was between 0 and 2.8 miles from home.
h. The farthest distance Sobia is from home is 3 miles.
i. Sobia returned home 2 times.
50. a. Michael travels fastest between 7 and 7.4 minutes. That is, 7,7.4
b. Michael's speed is zero between 4.2 and 6 minutes. That is, 4.2,6
c. Between 0 and 2 minutes, Michael's speed increased from 0 to 30 miles/hour.
d. Between 4.2 and 6 minutes, Michael was stopped (i.e, his speed was 0 miles/hour).
e. Between 7 and 7.4 minutes, Michael was traveling at a steady rate of 50 miles/hour.
f. Michael's speed is constant between 2 and 4 minutes, between 4.2 and 6 minutes, between 7 and 7.4 minutes, and between 7.6 and 8 minutes. That is, on the intervals (2, 4), (4.2, 6), (7, 7.4), and (7.6, 8).
51. Answers (graphs) will vary. Points of the form (5, y) and of the form (x, 0) cannot be on the graph of the function.
52. The only such function is 0 fx because it is the only function for which fxfx . Any other such graph would fail the vertical line test.
53. Answers may vary.
54. 2 2 2 (2)(2)(2)3 (44)23 59
55. 22 22 (13)(0(6)) (2)(6) 43640210
Section 2.3: Properties of Functions
56. 2 4(6) 3 2 44 3 28 3 yx yx yx
57. Since the function contains a cube root then the domain is:
58. 2 1 2(12)36
59.
60. The car traveling north travels a distance or 25t and the car traveling west travels a distance of 35t where t is the time of travel. Using the Pythagorean we have: 222 22 2 2 40(35)(25) 16001225625 16001850 0.8649 0.93 hours
Converting to minutes we have 0.93(60)55.8minutes
61. 347 33 1
x x x and 5213 28 4
The solution set is
62. 2 2 2 (572)(810) 572810 51512
63. 3,10
Section 2.3
1. 25 x
2. 835 slope1 325 y x
3. x-axis: yy 2 2 2 51 51 51 different yx yx yx
y-axis: xx
2 2 51 51 same yx yx
origin: xx and yy
2 2 2 51 51 51 different yx yx yx
The equation has symmetry with respect to the y-axis only.
4.
11 253 253 yymxx yx yx
5. 2 9 yx x-intercepts: 2 2 09 93 x xx
y-intercept:
2 099 y
The intercepts are 3,0 ,
6. increasing
7. even; odd
8. True
9. True
3,0 , and 0,9
Chapter 2: Functions and Their Graphs
10. False; odd functions are symmetric with respect to the origin. Even functions are symmetric with respect to the y-axis.
11. c
12. d
13. Yes
14. No, it is increasing.
15. No
16. Yes
17. f is increasing on the intervals
8,2,0,2,5,7
18. f is decreasing on the intervals:
10,8,2,0,2,5
19. Yes. The local maximum at 2is10. x
20. No. There is a local minimum at 5 x ; the local minimum is 0.
21. f has local maxima at 2and 2 xx . The local maxima are 6 and 10, respectively.
22. f has local minima at 8,0and 5 xxx The local minima are –4, 0, and 0, respectively.
23. f has absolute minimum of 4 at x = –8.
24. f has absolute maximum of 10 at x = 2.
25. a. Intercepts: (–2, 0), (2, 0), and (0, 3).
b. Domain: 44xx or 4,4 ; Range: 03yy or 0,3
c. Increasing: [–2, 0] and [2, 4]; Decreasing: [–4, –2] and [0, 2].
d. Since the graph is symmetric with respect to the y-axis, the function is even
26. a. Intercepts: (–1, 0), (1, 0), and (0, 2).
b. Domain: 33xx or 3,3 ; Range: 03yy or 0,3 .
c. Increasing: [–1, 0] and [1, 3]; Decreasing: [–3, –1] and [0, 1]
d. Since the graph is symmetric with respect to the y-axis, the function is even
27. a. Intercepts: (0, 1).
b. Domain: is any real number xx ; Range: 0 yy or 0, .
c. Increasing: (,) ; Decreasing: never.
d. Since the graph is not symmetric with respect to the y-axis or the origin, the function is neither even nor odd.
28. a. Intercepts: (1, 0).
b. Domain: 0 xx or 0, ;
Range: is any real number yy
c. Increasing: [0,) ; Decreasing: never.
d. Since the graph is not symmetric with respect to the y-axis or the origin, the function is neither even nor odd.
29. a. Intercepts: (,0),(,0),and(0,0)
b. Domain: xx or , ; Range: 11yy or 1,1 .
c. Increasing: , 22 ; Decreasing: ,and, 22 .
d. Since the graph is symmetric with respect to the origin, the function is odd.
30. a. Intercepts: ,0,,0, and 22(0,1)
b. Domain: xx or , ; Range: 11yy or 1,1
c. Increasing: ,0 ; Decreasing: 0,
d. Since the graph is symmetric with respect to the y-axis, the function is even.
31. a. Intercepts: 151 ,0,,0, and0, 322 .
b. Domain: 33xx or 3,3 ; Range: 12yy or 1,2
c. Increasing: 2,3 ; Decreasing: 1,1 ; Constant: 3,1and1,2
d. Since the graph is not symmetric with respect to the y-axis or the origin, the function is neither even nor odd.
32. a. Intercepts: 2.3,0,3,0,and 0,1
b. Domain: 33xx or 3,3 ; Range: 22yy or 2,2 .
c. Increasing: 3,2 and 0,2 ; Decreasing: 2,3 ; Constant: 2,0
d. Since the graph is not symmetric with respect to the y-axis or the origin, the function is neither even nor odd.
33. a. f has a local maximum value of 3 at 0. x
b. f has a local minimum value of 0 at both 2and 2. xx
34. a. f has a local maximum value of 2 at 0. x
b. f has a local minimum value of 0 at both 1and 1. xx
35. a. f has a local maximum value of 1 at 2 x
b. f has a local minimum value of –1 at . 2 x
36. a. f has a local maximum value of 1 at 0. x
b. f has a local minimum value of –1 both at x and x
37. 3 ()4 fxx 33()4()4 fxxxfx Therefore, f is odd.
38. 42 ()2 fxxx 4242()2()()2 fxxxxxfx Therefore, f is even.
39. 2 ()10 gxx 22()10()10 gxxxgx Therefore, g is even.
40. 3 ()35hxx 33 ()3()535 hxxx h is neither even nor odd.
41. 3 ()4 Fxx
33 ()44 FxxxFx Therefore, F is odd.
42. () Gxx () Gxx G is neither even nor odd.
43. () fxxx () fxxxxx f is neither even nor odd.
44. 3 2 ()21fxx
3 22 3 ()2()121 fxxxfx Therefore, f is even.
45. 2 ()1 8 gx x 22 ()11 ()88 gxgx xx Therefore, g is even.
46. 2 () 1 x hx x
22 () ()11 xx hxhx xx Therefore, h is odd.
47. 3 2 () 39 x hx x 3 3 22 () () 3()939 x x hxhx xx
Therefore, h is odd.
48. ()2x Fx x
()2()2x x FxFx xx
Therefore, F is odd.
49. f has an absolute maximum of 4 at 1. x
f has an absolute minimum of 1 at 5. x
f has an local maximum value of 3 at 3. x
f has an local minimum value of 2 at 2. x
50. f has an absolute maximum of 4 at 4. x
f has an absolute minimum of 0 at 5. x
f has an local maximum value of 4 at 4. x
f has an local minimum value of 1 at 1. x
51. f has an absolute minimum of 1 at 1. x
f has an absolute maximum of 4 at x = 3.
f has an local minimum value of 1 at 1. x
f has an local maximum value of 4 at x = 3.
52. f has an absolute minimum of 1 at 0. x
f has no absolute maximum.
f has no local minimum.
f has no local maximum.
53. f has an absolute minimum of 0 at 0. x f has no absolute maximum.
f has an local minimum value of 0 at 0. x
f has an local minimum value of 2 at 3. x
f has an local maximum value of 3 at 2. x
54. f has an absolute maximum of 4 at 2. x
f has no absolute minimum.
f has an local maximum value of 4 at 2. x
f has an local minimum value of 2 at 0. x
55. f has no absolute maximum or minimum. f has no local maximum or minimum.
56. f has no absolute maximum or minimum. f has no local maximum or minimum.
57. 3 32fxxx on the interval 2,2
Use MAXIMUM and MINIMUM on the graph of 3 1 32yxx .


local maximum: (1)4 f
local minimum: (1)0 f
f is increasing on: 2,1and1,2 ; f is decreasing on: 1,1
58. 3235fxxx on the interval 1,3
Use MAXIMUM and MINIMUM on the graph of 32 1 35yxx


local maximum: (0)5 f
local minimum: (2)1 f
f is increasing on: 1,0 and 2,3 ; f is decreasing on: 0,2
59. 53fxxx on the interval 2,2
Use MAXIMUM and MINIMUM on the graph of 53 1


2,0.77 and 0.77,2 ; f is decreasing on:
60. 42fxxx on the interval
Use MAXIMUM and MINIMUM on the graph of 42 1 yxx


local maximum: (0)0 f local minimum: (0.71)0.25 f ; (0.71)0.25 f f is increasing on: 0.71,0 and 0.71,2 ; f is decreasing on: 2,0.71and 0,0.71
61. 32 0.20.646fxxxx on the interval 6,4
Use MAXIMUM and MINIMUM on the graph of 32 1 0.20.646yxxx .


local maximum: (1.77)1.91 f local minimum: (3.77)18.89 f f is increasing on: 3.77,1.77 ; f is decreasing on: 6,3.77 and1.77,4
62. 32 0.40.632fxxxx on the interval 4,5
Use MAXIMUM and MINIMUM on the graph of 32 1 0.40.632yxxx


local maximum: (2.16)3.25 f local minimum: (1.16)4.05 f
f is increasing on: 1.16,2.16 ; f is decreasing on: 4,1.16 and 2.16,5
63. 432 0.250.30.93fxxxx on the interval 3,2
Use MAXIMUM and MINIMUM on the graph of 432 1 0.250.30.93yxxx .



local maximum: (0)3 f local minimum: (1.87)0.95 f , (0.97)2.65 f
f is increasing on:



local maxima: (1.57)0.52 f , (0.64)1.87 f
local minimum: 0,2 (0)2 f f is increasing on: 3,1.57 and 0,0.64 ; f is decreasing on:
1.57,0 and 0.64,2
65. 2 ()24fxx
a. Average rate of change of f from 0 x
1.87,0 and 0.97,2 ; f is decreasing on:
3,1.87 and 0,0.97
64. 432 0.40.50.82fxxxx on the interval 3,2
Use MAXIMUM and MINIMUM on the graph of 432 1 0.40.50.82yxxx .
b. Average rate of change of f from x = 1 to x = 3:
c. Average rate of change of f from x = 1 to
66.
a. Average rate of change of f from
b. Average rate of change of
c. Average rate of change of
c. Average rate of change of h from
b.
a. Average rate of change of f from 1 to 3:
the average rate of change of
b. From (a), the slope of the secant line joining
and
f is 5. We use the
Chapter 2: Functions and Their Graphs
point-slope form to find the equation of the secant line:
41fxx
a. Average rate of change of f from 2 to 5:
73.
b. From (a), the slope of the secant line joining
1,1 g and
2,2 g is 1. We use the point-slope form to find the equation of the secant line:
2 2 hxxx
a. Average rate of change of h from 2 to 4:
Therefore, the average rate of change of f from 2 to 5 is 4
b. From (a), the slope of the secant line joining
2,2 f and
5,5 f is 4. We use the point-slope form to find the equation of the secant line:
2 2 gxx
a. Average rate of change of g from 2 to 1:
Therefore, the average rate of change of g from 2 to 1 is 1.
b. From (a), the slope of the secant line joining
2,2 g and
1,1 g is 1 We use the point-slope form to find the equation of the secant line:
2 1 gxx
a. Average rate of change of g from 1 to 2:
Therefore, the average rate of change of g from 1 to 2 is 1.
Therefore, the average rate of change of h from 2 to 4 is 4.
b. From (a), the slope of the secant line joining
2,2 h and
4,4 h is 4. We use the point-slope form to find the equation of the secant line:
1sec1 042 48 yymxx yx yx
74. 2 2 hxxx
a. Average rate of change from 0 to 3:
30150 3030 155 3 hh
Therefore, the average rate of change of h from 0 to 3 is 5.
b. From (a), the slope of the secant line joining
0,(0) h and
3,(3) h is 5 We use the point-slope form to find the equation of the secant line:
, the function is odd.
76.
b. Since gx is odd then it is symmetric about the origin so there exist a local maximum at 3 x
3 3(3)27(3)278154 g
So there is a local maximum of 54 at 3 x .
3 12 fxxx
a.
3 3 3 12 12 12 fxxx xx xx fx
Since
fxfx , the function is odd.
b. Since fx is odd then it is symmetric about the origin so there exist a local maximum at 2 x
3 2(2)12(2)82416 f
So there is a local minimum value of 16 at 2 x .
77. a. Positive
b. Increasing
c. Positive
d. Negative
e. Decreasing
f. Negative
g. 0
78. a. 4
b. 9
79. 4289Fxxx
a.
42 4 89 89
Fxxx xx Fx Since
FxFx , the function is even.
b. Since the function is even, its graph has y-axis symmetry. The second local maximum value is 25 and occurs at 2 x
c. Because the graph has y-axis symmetry, the area under the graph between 0 x and 3 x bounded below by the x-axis is the
Section 2.3: Properties of Functions
same as the area under the graph between 3 x and 0 x bounded below the x-axis. Thus, the area is 50.4 square units.
80. 4232144Gxxx
Since
GxGx , the function is even.
b. Since the function is even, its graph has y-axis symmetry. The second local maximum is in quadrant II and is 400 and occurs at 4 x
c. Because the graph has y-axis symmetry, the area under the graph between 0 x and 6 x bounded below by the x-axis is the same as the area under the graph between 6 x and 0 x bounded below the x-axis. Thus, the area is 1612.8 square units.
81. 2 0.3212512500Cxxx x
a. 2 1 0.3212512500yxx x

b. Use MINIMUM. Rounding to the nearest whole number, the average cost is minimized when approximately 10 lawnmowers are produced per hour.

c. The minimum average cost is approximately $239 per mower.
82. a.
Chapter 2: Functions and Their Graphs
Graph the function on a graphing utility and use the Maximum option from the CALC menu.

The concentration will be highest after about 2.16 hours.
b. Enter the function in Y1 and 0.5 in Y2. Graph the two equations in the same window and use the Intersect option from the CALC menu.


After taking the medication, the mother can feed her child within the first 0.71 hours (about 42 minutes) or after 4.47 hours (about 4hours 28 minutes) have elapsed.
On average, the population is increasing at a rate of 0.036 gram per hour from
On average, the population is increasing at a rate of 0.1 gram per hour from 4.5 to 6 hours.
c. The average rate of change is increasing as time passes. This indicates that the population is increasing at an increasing rate.


The slope represents the average rate of change of the debt from 2012 to 2019
84. a. b.
c.
c. Average rate of change of f from
d.
e.
f. The average rate of change is increasing.
g.
The debt decreased.
h. Quarantine from Covid19 most likely had a effect on spending habits.
d. Average rate of change of
Average rate of change of f from
f. Graphing the secant lines:




g. The secant lines are beginning to look more and more like the tangent line to the graph of f at the point where 0 x .
h. The slopes of the secant lines are getting smaller and smaller. They seem to be approaching the number zero.
86. 2 () fxx
a. Average rate of change of f from 1 x to 2
b. Average rate of change of f from 1
c. Average
d.
e. Average rate of change of f from 1 x to 1.001 x
f. Graphing the secant lines:





g. The secant lines are beginning to look more and more like the tangent line to the graph of f at the point where 1 x
h. The slopes of the secant lines are getting smaller and smaller. They seem to be approaching the number 2.
()25fxx
b. When 1 x :
sec 0.52hm
sec 0.12hm
sec 0.012hm sec as 0, 2 hm
c. Using the point
1,11,7 f and slope, 2 m , we get the secant line:
721 722 25 yx yx yx
d. Graphing:

The graph and the secant line coincide.
88. ()32fxx
a. sec ()() 3()2(32) 3 3 fxhfx m h xhx h hh
b. When x = 1,
sec 0.53hm
sec 0.13hm
sec 0.013hm
sec as 0, 3 hm
c. Using point
1,11,1 f
and slope = 3, we get the secant line:
131 133 32 yx yx yx
d. Graphing:

The graph and the secant line coincide.
Section 2.3: Properties of Functions
89. 2 ()2 fxxx
a. sec 22 222 2 ()() ()2()(2) 2222 22 22 fxhfx m h xhxhxx h xxhhxhxx h xhhh h xh
b. When x = 1, sec 0.5210.524.5hm sec 0.1210.124.1hm sec 0.01210.0124.01hm sec as 0, 21024 hm
c. Using point
1,11,3 f and slope = 4.01, we get the secant line: 34.011 34.014.01 4.011.01 yx yx yx
d. Graphing:

90. 2 ()2 fxxx
a. sec ()() fxhfx m h
b. When x = 1, sec 0.54120.516hm
Chapter 2: Functions and Their Graphs
c. Using point
and slope = 5.02, we get the secant line:
d. Graphing: 91. 2 ()231 fxxx

b. When x = 1, sec 0.54120.532hm sec 0.14120.131.2hm
sec 0.014120.0131.02hm
sec as 0, 412031 hm
c. Using point 1,11,0 f and slope = 1.02, we get the secant line:
01.021 1.021.02 yx yx
d. Graphing:

92. 2 ()32 fxxx
a. sec ()() fxhfx m h
222 222 2 2 2 (2)33232 233232 3232 23 23 xxhhxhxx h xxhhxhxx h xhxhxx h xhhh h xh
b. When x = 1, sec 0.5210.530.5hm sec 0.1210.130.9hm sec 0.01210.0130.99hm sec as 0, 21031 hm
c. Using point 1,11,0 f and slope = 0.99, we get the secant line: 00.991 0.990.99 yx yx
d. Graphing:

93. ()1fx x
b.
c. Using point
d. Graphing:

c. Using point
and slope = 1.9704, we get the secant line:
d. Graphing:

Chapter 2: Functions and Their Graphs
95. 2 2 (2)20 and(1)8, so (2)(1)124 2(1)3
100. An increasing function is a function whose graph goes up as you read from left to right.
So g is odd.
97. Answers will vary. One possibility follows:
A decreasing function is a function whose graph goes down as you read from left to right.
5 y 3 3
101. To be an even function we need
fxfx and to be an odd function we need
fxfx . In order for a function be both even and odd, we would need
fxfx . This is only possible if 0 fx
102. The graph of 5 y is a horizontal line.


98. Answers will vary. See solution to Problem 97 for one possibility.
99. A function that is increasing on an interval can have at most one x-intercept on the interval. The graph of f could not "turn" and cross it again or it would start to decrease.

The local maximum is 5 y and it occurs at each x-value in the interval.
103.
Chapter 2: Functions and Their Graphs
Section 2.4
y x

y 1 x

3. y x 3 8

y-intercept:
Let 0 x , then 3 088 y
x-intercept: Let 0 y , then 3 3 08 8 2 x x x
The intercepts are 0,8 and 2,0
,0
5. piecewise-defined 6. True
7. False; the cube root function is odd and increasing on the interval
8. False; the domain and range of the reciprocal function are both the set of real numbers except for 0.

Section 2.4: Library of Functions; Piecewise-defined Functions


23. 1 fx x

fxx 25. 3 () fxx 26. 3 fx



27. a. 2 (3)(3)9 f
b. (0)4 f
c. (3)3(3)27 f
28. a. 2326 f
b. 10 f
c. 2 02011 f
29. a. 22240 f
b. 02044 f
c. 12146 f
d. 3 33126 f
30. a. 3 (1)(1)1 f
b. 3 (0)00 f
c. (1)3(1)25 f
24.
31. 2if 0 () 1 if 0 xx fx x
a. Domain:
b. x-intercept: none
y-intercept:
The only intercept is
c. Graph:

Range:
32. 3if 0 () 4 if 0 xx fx x
a. Domain:
b. x-intercept: none y-intercept:
c. Graph:
Range:
33. 23if 1 () 32 if 1 xx fx xx
a. Domain: is any real number xx
b. x-intercept: none
y-intercept:
02033 f
The only intercept is 0,3
c. Graph:

d. Range:
34. 3if 2 () 23if 2 xx fx xx
a. Domain: is any real number xx
x-intercepts: 3 3, 2
y-intercept:
The intercepts are 3,0 , 3 ,0 2
c. Graph:

d. Range: 1 yy ; ,1
35. 3if 21 ()5 if 1 2 if 1 xx fxx xx
a. Domain:
b. 30 3 (notindomain) x x 20 2 2 x x x
x-intercept: 2
y-intercept:
c. Graph:

d. Range: 4,5yyy ;
36. 25if 30 ()3if0 5if0 xx fxx xx
a. Domain:
b. 250 25 5 2 x x x
x-intercept: 5 2 y-intercept:
03 f
The intercepts are 5 ,0 2
and
0,3
Section 2.4: Library of Functions; Piecewise-defined Functions
c. Graph:

d. Range: 5 yy ; ,5
37. 2 1if 0 () if 0 xx fx xx
a. Domain: is any real number xx
b. 10 1 x x 2 0 0 x x
x-intercepts: 1,0
y-intercept: 2 000 f The intercepts are 1,0 and 0,0
c. Graph:

d. Range: is any real number yy 38. 3 1 if 0 () if 0 x x fx xx
a. Domain: is any real number xx
b. 1 0 (nosolution) x 3 0 0 x x
x-intercept: 0
y-intercept: 3 000 f
The only intercept is 0,0
Chapter 2: Functions and Their Graphs
c. Graph:

d. Range: is any real number yy
39. 3 if20 () if0 xx fx xx
a. Domain: 20 and0xxx or
|2,0xxx
b. x-intercept: none
2,00,
There are no x-intercepts since there are no values for x such that 0 fx
y-intercept: There is no y-intercept since 0 x is not in the domain.
c. Graph:

d. Range:
0 yy ;
40. 2if 31 () if 1 xx fx xx
a. Domain: 31 and1xxx or |3,1xxx ; 3,11,
b. 20 2 x x 0 0 (notindomainofpiece) x x
no x-intercepts y-intercept: 0202 f
The intercept is 0,2
c. Graph: y 5 x 5 5 5 (3, 5) (0,2) (4,2)
d. Range: 1 yy ; 1,
xx fxxx
41. 2 if02 ()2 if25 7 if 5
a. Domain: 0 xx ; 0,
b. 2 0 0 (not in domain of piece) x x 20 2 (not in domain of piece) x x 70 (not possible)
No intercepts.
Section 2.4: Library of Functions; Piecewise-defined Functions
c. Graph:

d. Range:
43.
a. Domain:
x-intercept: 5 3
y-intercept:
c. Graph:

d. Range:
44. Answers may vary. One possibility follows: if 10 () 1 if02 xx fx x
45. Answers may vary. One possibility follows: if 0 () 2 if02 xx fx xx
46. Answers may vary. One possibility follows: 22 if 10 () if 0 xx fx xx
(1.7)int2(1.7)int(3.4)3
(2.8)int2(2.8)int(5.6)5 f
c. (3.6)int2(3.6)int(7.2)8 f
48. a. 1.2 (1.2)intint(0.6)0 2 f
b. 1.6 (1.6)intint(0.8)0 2 f
c. 1.8 (1.8)intint(0.9)1 2 f
49. a.

b. The domain is 0,6 .
c. Absolute max: (2)6 f Absolute min: (6)2 f
50. a.

b. The domain is 2,2 .
c. Absolute max: (2)(2)3ff Absolute min: none
51. 0.1317 if0150 0.423.5 if 150 xx C xx
a.
760.137617$26.88 C
b.
1330.1313317$34.29 C
c.
1890.418923.5$52.10 C 52.
33int102 64int224 3648 77824 xx Fxxx x x
a. 0.533int(10.5)3 F Parking for 0.5 hours costs $3.
b.
233int126 F Parking for 2 hours costs $6.
c. 3.2564int23.2514 F
Parking for 3.5 hours costs $14.
d. 836 F Parking for 8 hours costs $36.
53. a. Charge for 2 dozen: 2.00(24) $48.00 C
b. Charge for 120 cupcakes: 1001.5(50) 1001.5(12050) $205 Cx
c. For 050 x : 2 Cx
For 200 x :
1001.550Cx For 200 x : 1001.51501.15(200)
3251.15(200) Cx x
The cost function: 2 if050
1001.5(50) if50200
3251.15(200)if 200
d. Graph:
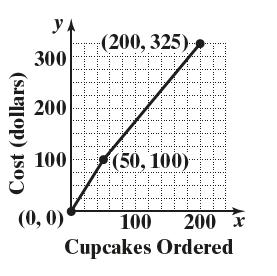
54. a. Taxes for $48,000: 0.08(48000)
$3840 T
b. Taxes for $132,000: 0.08(75000)0.16(57000)
$15,120 T
c. Taxes for $231,000: 0.08(75000)0.16(125000)0.22(31000)
$32,820
d. For 075,000 x : 0.08 Tx
For 75,000200,000 x : 0.08(75,000)0.16(75,000) 60000.16(75,000) Tx x
For 200,000350,000 x : 0.08(75,000)0.16(12,5000) 0.22(200,000) 260000.22(200000)
T x x
For 350000 x : 590000.3(350000)Tx
Section 2.4: Library of Functions; Piecewise-defined Functions
The tax function:
0.08if075,000 60000.16(75,000)if75,000200,000 26,0000.22(200,000)if200,000350,000 59,0000.3(350,000)if350,000

55. For schedule X:
0.1if011,600 11600.12(11,600)if11,60047,150 54260.22(47,150)if47,150100,525 ()17,168.500.24(100,525)if 100,525191,950 39,110.500.32(191,950)if 55,678.500.35(243,725)
191,950243,725 if243,725609,350 183,647.250.37(609,350)if609,350 x x xx
56. For Schedule Y1: 0.1if023,200
23200.12(23,200)if23,20094,300 10,8520.22(94,300)if94,300201,050 ()34,3370.24(201,050)if201,050383,900 78,2210.32(383,900)if383, 111,3570.35(487,450) xx xx xx fx xx x x
900487,450 if487,450731,200 196,669.500.37(731,200)if731,200 x x xx
57. a. Let x represent the number of miles and C be the cost of transportation. 0.50if 0100
0.50(100)0.40(100)if ()100400
0.50(100)0.40(300)0.25(400)if 400800
0.50(100)0.40(300)0.25(400)0(800)if 800960
Chapter 2: Functions and Their Graphs
0.50if 0100
100.40if100400 ()700.25if 400800
270if 800960 xx xx Cx xx x

b. For hauls between 100 and 400 miles the cost is: ()100.40 Cxx
c. For hauls between 400 and 800 miles the cost is: ()700.25 Cxx .
given by
9000 if 659
58. Let x = number of days car is used. The cost of renting is given by
185 if 7
222 if78
259 if89
8250 if660679
5250 if680699
3750 if700719
2250 if720739
1500 if 740
296 if910
333 if1011
370 if1114 x x x Cx x x x

59. a. Let s = the credit score of an individual who wishes to borrow $300,000 with an 80% LTV ratio. The adverse market delivery charge is
b. 725 is between 720 and 739 so the charge would be $2250.
c. 670 is between 660 and 679 so the charge would be $8250.
60. Let x = the amount of the bill in dollars. The minimum payment due is given by
70if1500 xx x fxx x x
if 010
10if 10500
30if 5001000
50if 10001500

61. a. 10 WC
b. (10.451055)(3310) 334 22.04 WC
c. (10.45101515)(3310) 333 22.04 WC
d. 331.5958(3310)4 WC
e. When 01.79 v , the wind speed is so small that there is no effect on the temperature.
f. When the wind speed exceeds 20, the wind chill depends only on the air temperature.
62. a. 10 WC
b.
331.5958331036 WC
63. Let x = the sales made and Sx = the total salary. For 0250,000 x :
$45,0000.04 Sxx
For 250,000500,000 x :
55,0000.06(250,000)Sxx For 500,000 x : 70,0000.09(500,000)Sxx
Sxxx xx
45,0000.04if0250,000 ()55,0000.06250,000if250,0005000,000 70,0000.09500,000if500,000
64. Use intervals
0,8,8,16,16,32,32,38 (exclude 0 and 38 since those would be the walls). Depth for the intervals
8,16 and 32,38 are constant (8 ft and 3 ft respectively). The other two are linear functions. On 0,8 the endpoint coordinates can be thought or as
0,3 and 8,8 8355 3 8088 myx
On 16,32 the endpoint coordinates can be thought of as
16,8 and 32,3 385 321616 5 8(16) 16 13 5 13 16
m b b yx Therefore, 53if 08 8 8if 816 ()5 13if1632 16 3if 3238
xx x dx xx x
65. The function f changes definition at 2 and the function g changes definition at 0. Combining these together, the sum function will change definitions at 0 and 2.
On the interval ,0 : ()()()()(23)(41) 24
fgxfxgxxx x
On the interval
0,2 :
()()()(23)(7) 34 fgxfxgxxx x
On the interval 2, :
Chapter 2: Functions and Their Graphs

66. Each graph is that of 2 yx , but shifted vertically.

If 2 ,0yxkk , the shift is up k units; if 2 ,0yxkk , the shift is down k units. The graph of 2 4 yx is the same as the graph of 2 yx , but shifted down 4 units. The graph of 2 5 yx is the graph of 2 yx , but shifted up 5 units.
67. Each graph is that of 2 yx , but shifted horizontally.

If 2 (),0yxkk , the shift is to the right k units; if 2 (),0yxkk , the shift is to the left k units. The graph of 2(4)yx is the same as the graph of 2 yx , but shifted to the left 4 units. The graph of 2(5)yx is the graph of 2 yx , but shifted to the right 5 units.
68. Each graph is that of yx , but either compressed or stretched vertically.
If ykx and 1 k , the graph is stretched vertically; if and01ykxk , the graph is compressed vertically. The graph of 1 4 yx is the same as the graph of yx , but compressed vertically. The graph of 5 yx is the same as the graph of yx , but stretched vertically.
69. The graph of 2 yx is the reflection of the graph of 2 yx about the x-axis.

The graph of yx is the reflection of the graph of yx about the x-axis.

Multiplying a function by –1 causes the graph to be a reflection about the x-axis of the original function's graph.
70. The graph of yx is the reflection about the y-axis of the graph of yx
Section 2.4: Library of Functions; Piecewise-defined Functions

y x y x
The same type of reflection occurs when graphing 21and 2()1yxyx .

The graph of ()yfx is the reflection about the y-axis of the graph of ()yfx
71. The graph of 3 (1)2yx is a shifting of the graph of 3 yx one unit to the right and two units up. Yes, the result could be predicted.

72. The graphs of , n yx n a positive even integer, are all U-shaped and open upward. All go through the points (1,1), (0,0), and (1,1) . As n increases, the graph of the function is narrower for 1 x and flatter for 1 x

73. The graphs of , n yx n a positive odd integer, all have the same general shape. All go through the points (1,1) , (0,0), and (1,1) . As n
increases, the graph of the function increases at a greater rate for 1 x and is flatter around 0 for 1 x

74. 1 if isrational 0 if isirrational x fx x
Yes, it is a function.
Domain = is any real number xx or ,
Range = {0, 1} or |0or 1 yyy
y-intercept: 0 isrational1xxy
So the y-intercept is 1 y
x-intercept: 0 isirrational yx
So the graph has infinitely many x-intercepts, namely, there is an x-intercept at each irrational value of x
1 fxfx when x is rational;
0 fxfx when x is irrational.
Thus, f is even.
The graph of f consists of 2 infinite clusters of distinct points, extending horizontally in both directions. One cluster is located 1 unit above the x-axis, and the other is located along the x-axis.
75. Answers will vary
76. 6 352610 10 () x xyxy y
77. 22 22 22 222 616 616 (69)169 (3)5 xyy xyy xyy xy
Center (h, k): (0, 3); Radius = 5
Chapter 2: Functions and Their Graphs
78. 45(21)47(1) 4105477 6573
The solution set is: {8}
79. Let x represent the amount of money invested in a mutual fund. Then 60,000 x represents the amount of money invested in CD's. Since the total interest is to be $3700, we have:
$38,000 should be invested in a mutual fund at 8% and $22,000 should be invested in CD's at 3%.
80. 21306 224 1162
Quotient: 2 2
xx Remainder: -2 81. 32 2 i 82. 7 2x
x x The domain is
cannot be negative so: 70 7
Section 2.5
1. a. vertically; up b. vertically; down c. (2,6)
d. (3,5)
2. a. horizontally; right b. horizontally; left c. (6,4)
d. (1,2)
3. a. a; vertically; stretched b. a; vertically; compressed c. (2,12)
d. (5,4)
4. a. 1 a ; horizontal; compression
b. 1 a ; horizontal; stretch
c. (4,5)
d. (12,2)
5. horizontal; right
6. y
7. False
8. True; the graph of yfx is the reflection about the x-axis of the graph of yfx
9. d
10. b
11. B
12. E 13. H
14. D
15. I
16. A
17. L
18. C
19. F
20. J 21. G 22. K
23. 3(4)yx
24. 3(4)yx
25. 3 4 yx
26. 3 4 yx
3 3 yxx
3 yx 29. 3 5 yx
30. 3 3 11 464 yxx
31. 3 3 28 yxx
32. 3 1 4 yx
33. (1)2 yx
(2)2 (3)22 yx
34. (1) yx (2)3 (3)32 yx yx
35. (1)3 yx (2)34 (3)354
yx yx
Section 2.5: Graphing Techniques: Transformations
36. (1)2 yx (2)2 (3)(3)232 yx yxx
37. (c); To go from yfx to yfx we reflect about the x-axis. This means we change the sign of the y-coordinate for each point on the graph of ()yfx . Thus, the point (3,6) would become 3,6 .
38. (d); To go from yfx to yfx , we reflect each point on the graph of yfx about the y-axis. This means we change the sign of the x-coordinate for each point on the graph of yfx . Thus, the point 3,6 would become 3,6 .
39. (c); To go from yfx to 2 yfx , we stretch vertically by a factor of 2. Multiply the y-coordinate of each point on the graph of yfx by 2. Thus, the point 1,3 would become 1,6 .
40. (c); To go from yfx to 2 yfx , we compress horizontally by a factor of 2. Divide the x-coordinate of each point on the graph of yfx by 2. Thus, the point 4,2 would become 2,2 .
41. 2 ()1fxx
Using the graph of 2 yx , vertically shift downward 1 unit.

The domain is , and the range is 1, .
42. 2 ()4fxx
Using the graph of 2 yx , vertically shift upward 4 units.

The domain is , and the range is 4, .
43. ()3 gxx
Using the graph of yx , horizontally compress by a factor of 3

The domain is 0,
and the range is
0,
44. 3 1 () 2 gxx
Using the graph of 3 yx , horizontally stretch by a factor of ½
The domain is , and the range is

45. ()2hxx

Using the graph of yx , horizontally shift to the left 2 units. The domain is 2,
and the range is
0,
.
46. ()1hxx
Using the graph of yx , horizontally shift to the left 1 unit.

The domain is 1, and the range is 0,
47. 3 ()(1)2fxx
Using the graph of 3 yx , horizontally shift to the right 1 unit 3 1 yx , then vertically shift up 2 units 3 12 yx

The domain is , and the range is ,
.
48. 3 ()(2)3fxx
Using the graph of 3 yx , horizontally shift to the left 2 units
3 2 yx
, then vertically shift down 3 units

The domain is , and the range is
49. ()4 gxx
Using the graph of yx , vertically stretch by a factor of 4.

The domain is 0,
and the range is
50. 1 ()2 gxx
Using the graph of yx , vertically compress by a factor of 1 2 .
Section 2.5: Graphing Techniques: Transformations

The domain is 0, and the range is 0,
51. 3 () fxx
Using the graph of 3 yx , reflect the graph about the x-axis.

The domain is , and the range is
52. () fxx
Using the graph of yx , reflect the graph about the x-axis.

The domain is 0, and the range is ,0
53. 2 ()2(1)3fxx
Using the graph of 2 yx , horizontally shift to
Chapter 2: Functions and Their Graphs
the left 1 unit 2 1 yx
, vertically stretch by a factor of 2 2 21yx
, and then vertically shift downward 3 units
2 213yx

The domain is , and the range is
3,
54. 2 ()3(2)1fxx
Using the graph of 2 yx , horizontally shift to the right 2 units
2 2 yx
, vertically stretch by a factor of 3
2 32yx
, and then vertically shift upward 1 unit
2 321yx

The domain is , and the range is 1,
.
55. ()221gxx
Using the graph of yx , horizontally shift to the right 2 units 2 yx , vertically stretch by a factor of 2 22yx
, and vertically
shift upward 1 unit 221yx

The domain is 2, and the range is 1,
.
56. ()313gxx
Using the graph of yx , horizontally shift to the left 1 unit 1 yx
, vertically stretch by a factor of 3 31yx
, and vertically shift downward 3 units 313yx
.

The domain is , and the range is 3,
57. ()2hxx
Using the graph of yx , reflect the graph about the y-axis yx
and vertically shift downward 2 units 2 yx

The domain is ,0
58. 41 ()242hx xx
and the range is 2,

The domain is , and the range is
Stretch the graph of 1 y x vertically by a factor of 4 14 4 y xx
and vertically shift upward 2 units 4 2 y x

The domain is
,00, and the range is
59. 3 ()(1)1fxx
Using the graph of 3 yx , horizontally shift to the left 1 unit
3 1 yx
, reflect the graph about the x-axis
3 1 yx
, and vertically shift downward 1 unit
3 11 yx
60. ()41fxx
Using the graph of yx , horizontally shift to the right 1 unit 1 yx
, reflect the graph about the x-axis 1 yx
, and stretch vertically by a factor of 4 41yx
.

The domain is 1, and the range is ,0 .
61.
()212121 gxxxx
Using the graph of yx , horizontally shift to the right 1 unit 1 yx
, and vertically stretch by a factor or 2 21yx

The domain is , and the range is 0,
62. ()424(2) gxxx
Using the graph of yx , reflect the graph about the y-axis yx , horizontally shift to the right 2 units
2 yx
, and vertically stretch by a factor of 4
42yx

The domain is ,2
63. 1 ()2hx x
and the range is
Using the graph of 1 y x , vertically compress by a factor of 1 2

The domain is ,00, and the range is
,00,
64. 3 ()13fxx
Using the graph of 3 () fxx , horizontally shift to the right 1 unit 3 1 yx , then vertically shift up 3 units 3 13 yx .

The domain is , and the range is ,
65. a. ()()3Fxfx Shift up 3 units.

b. ()(2)Gxfx Shift left 2 units.

c. ()() Pxfx
Reflect about the x-axis.

d. ()(1)2Hxfx Shift left 1 unit and shift down 2 units.

e. 1 ()() 2 Qxfx
Compress vertically by a factor of 1 2

f. ()() gxfx
Reflect about the y-axis.

Section 2.5: Graphing Techniques: Transformations
g. ()(2) hxfx
Compress horizontally by a factor of 1 2 .
66. a. ()()3Fxfx Shift up 3 units.

b. ()(2)Gxfx Shift left 2 units.

c. ()() Pxfx Reflect about the x-axis.

Chapter 2: Functions and Their Graphs
d. ()(1)2Hxfx Shift left 1 unit and shift down 2 units.

e. 1 ()() 2 Qxfx
Compress vertically by a factor of 1 2 .

f. ()() gxfx Reflect about the y-axis.

g. ()(2) hxfx
Compress horizontally by a factor of 1 2

67. a. ()()3Fxfx Shift up 3 units.

b. ()(2)Gxfx Shift left 2 units.
c. ()() Pxfx Reflect about the x-axis.

d. ()(1)2Hxfx Shift left 1 unit and shift down 2 units.

e. 1 ()() 2 Qxfx
Compress vertically by a factor of 1 2

f. ()() gxfx Reflect about the y-axis.

g. ()(2) hxfx
Compress horizontally by a factor of 1 2

Section 2.5: Graphing Techniques: Transformations
68. a. ()()3Fxfx Shift up 3 units.

b. ()(2)Gxfx Shift left 2 units.

c. ()() Pxfx Reflect about the x-axis.

d. ()(1)2Hxfx Shift left 1 unit and shift down 2 units.
Chapter 2: Functions and Their Graphs
e. 1 ()() 2 Qxfx
Compress vertically by a factor of 1 2

f. ()() gxfx Reflect about the y-axis.

g. ()(2) hxfx
Compress horizontally by a factor of 1 2

69. 2 ()2 fxxx 2 2 ()(21)1 ()(1)1 fxxx fxx
Using 2 () fxx , shift left 1 unit and shift down
1 unit.

70. 2 ()6 fxxx 2 2 ()(69)9 ()(3)9 fxxx fxx
Using 2 () fxx , shift right 3 units and shift down 9 units.

71. 2 ()81 fxxx
2 2 ()816116 ()415 fxxx fxx
Using 2 () fxx , shift right 4 units and shift down 15 units.

72. 2 ()42 fxxx
2 2 ()4424 ()22 fxxx fxx
Using 2 () fxx , shift left 2 units and shift down 2 units.
Using 2fxx , shift right 3 units, vertically stretch by a factor of 2, and then shift up 1 unit.

Using 2fxx , shift left 1 unit, vertically stretch by a factor of 3, and shift down 2 units.

Section 2.5: Graphing Techniques: Transformations
Using 2fxx , shift left 2 units, stretch vertically by a factor of 3, reflect about the xaxis, and shift down 5 units.

Using 2fxx , shift left 3 units, stretch vertically by a factor of 2, reflect about the xaxis, and shift up 5 units.

77. a. The graph of 2 yfx is the same as the graph of yfx , but shifted 2 units to the left. Therefore, the x-intercepts are 7 and 1.
b. The graph of 2 yfx is the same as the graph of yfx , but shifted 2 units to
the right. Therefore, the x-intercepts are 3 and 5.
c. The graph of 4 yfx is the same as the graph of yfx , but stretched vertically by a factor of 4. Therefore, the x-intercepts are still 5 and 3 since the y-coordinate of each is 0.
d. The graph of yfx is the same as the graph of yfx , but reflected about the y-axis. Therefore, the x-intercepts are 5 and 3
78. a. The graph of 4 yfx is the same as the graph of yfx , but shifted 4 units to the left. Therefore, the x-intercepts are 12 and 3.
b. The graph of 3 yfx is the same as the graph of yfx , but shifted 3 units to the right. Therefore, the x-intercepts are 5 and 4.
c. The graph of 2 yfx is the same as the graph of yfx , but stretched vertically by a factor of 2. Therefore, the x-intercepts are still 8 and 1 since the y-coordinate of each is 0.
d. The graph of yfx is the same as the graph of yfx , but reflected about the y-axis. Therefore, the x-intercepts are 8 and 1.
79. a. The graph of 2 yfx is the same as the graph of yfx , but shifted 2 units to the left. Therefore, the graph of 2 fx is increasing on the interval 3,3 .
b. The graph of 5 yfx is the same as the graph of yfx , but shifted 5 units to the right. Therefore, the graph of 5 fx is increasing on the interval 4,10
c. The graph of yfx is the same as the graph of yfx , but reflected about the
x-axis. Therefore, we can say that the graph of yfx must be decreasing on the interval 1,5
d. The graph of yfx is the same as the graph of yfx , but reflected about the y-axis. Therefore, we can say that the graph of yfx must be decreasing on the interval 5,1
80. a. The graph of 2 yfx is the same as the graph of yfx , but shifted 2 units to the left. Therefore, the graph of 2 fx is decreasing on the interval 4,5
b. The graph of 5 yfx is the same as the graph of yfx , but shifted 5 units to the right. Therefore, the graph of 5 fx is decreasing on the interval 3,12
c. The graph of yfx is the same as the graph of yfx , but reflected about the x-axis. Therefore, we can say that the graph of yfx must be increasing on the interval 2,7
d. The graph of yfx is the same as the graph of yfx , but reflected about the y-axis. Therefore, we can say that the graph of yfx must be increasing on the interval 7,2
81. a. ()yfx

