

SolutionandAnswerGuide
CONTENTS
ENDOF SECTION SOLUTIONS
EXERCISES1.1
1. Secondorder;linear
2. Thirdorder;nonlinearbecauseof (dy/dx)4
3. Fourthorder;linear
4. Secondorder;nonlinearbecauseof cos(r + u)
5. Secondorder;nonlinearbecauseof (dy/dx)2 or 1+(dy/dx)2
6. Secondorder;nonlinearbecauseof R2
7. Thirdorder;linear
8. Secondorder;nonlinearbecauseof ˙ x2
9. Firstorder;nonlinearbecauseof sin(dy/dx)
10. Firstorder;linear
11. Writingthedifferentialequationintheform x(dy/dx)+ y2 =1,weseethatitisnonlinear in y becauseof y2 .However,writingitintheform (y2 1)(dx/dy)+ x =0,weseethatitis linearin x.
12. Writingthedifferentialequationintheform u(dv/du)+(1+ u)v = ueu weseethatitis linearin v.However,writingitintheform (v + uv ueu)(du/dv)+ u =0,weseethatitis nonlinearin u.
13. From y = e x/2 weobtain y′ = 1 2 e x/2 .Then 2y′ + y = e x/2 + e x/2 =0.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
14. From y = 6 5 6 5 e 20t weobtain dy/dt =24e 20t ,sothat
15. From y = e3x cos2x weobtain y′ =3e3x cos2x 2e3x sin2x and y′′ =5e3x cos2x 12e3x sin2x, sothat y′′ 6y′ +13y =0
16. From y = cos x ln(sec x +tan x) weobtain y ′ = 1+sin x ln(sec x +tan x) and y ′′ =tan x +cos x ln(sec x +tan x).Then y′′ + y =tan x.
17. Thedomainofthefunction,foundbysolving x+2 ≥ 0,is [ 2, ∞).From y′ =1+2(x+2) 1/2 wehave (y x)y ′ =(y x)[1+(2(x +2) 1/2 ] = y x +2(y x)(x +2) 1/2 = y x +2[x +4(x +2)1/2 x](x +2) 1/2 = y x +8(x +2)1/2 (x +2) 1/2 = y x +8
Anintervalofdefinitionforthesolutionofthedifferential equationis ( 2, ∞) because y′ is notdefinedat x = 2.
18. Since tan x isnotdefinedfor x = π/2+ nπ, n aninteger,thedomainof y =5tan5x is {x 5x = π/2+ nπ} or {x x = π/10+ nπ/5}.From y′ =25sec2 5x wehave y ′ =25(1+tan2 5x)=25+25tan2 5x =25+ y 2
Anintervalofdefinitionforthesolutionofthedifferential equationis ( π/10,π/10).Anotherintervalis (π/10, 3π/10),andsoon.
19. Thedomainofthefunctionis {x 4 x2 =0} or {x x = 2 or x =2}.From y′ = 2x/(4 x2)2 wehave y ′ =2x 1 4 x2 2 =2xy 2 .
Anintervalofdefinitionforthesolutionofthedifferential equationis ( 2, 2).Otherintervalsare (−∞, 2) and (2, ∞).
20. Thefunctionis y =1/√1 sin x ,whosedomainisobtainedfrom 1 sin x =0 or sin x =1 Thus,thedomainis {x x = π/2+2nπ}.From y′ = 1 2 (1 sin x) 3/2 ( cos x) wehave 2y ′ =(1 sin x) 3/2 cos x =[(1 sin x) 1/2]3 cos x = y 3 cos x.
Anintervalofdefinitionforthesolutionofthedifferential equationis (π/2, 5π/2).Another oneis (5π/2, 9π/2),andsoon.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
21. Writing ln(2X 1) ln(X 1)= t anddifferentiating implicitlyweobtain
Exponentiatingbothsidesoftheimplicitsolutionweobtain
Solving et 2=0 weget t =ln2.Thus,thesolutionisdefinedon (−∞, ln2) oron (ln2, ∞). Thegraphofthesolutiondefinedon (−∞, ln2) isdashed,andthegraphofthesolution definedon (ln2, ∞) issolid.
22. Implicitlydifferentiatingthesolution,weobtain 2x 2 dy dx 4xy +2y dy dx =0 x 2 dy 2xydx + ydy =0 2xydx +(x 2 y)dy =0
Usingthequadraticformulatosolve y2 2x2y 1=0 for y,weget y = 2x2 ± √4x4 +4 /2= x2 ± √x4 +1 . Thus,twoexplicitsolutionsare y1 = x2 + √x4 +1 and y2 = x2 √x4 +1 .Bothsolutionsaredefinedon (−∞, ∞). Thegraphof y1(x) issolidandthegraphof y2 isdashed.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
23.
InProblems 25–28,weusetheProductRuleandthederivativeofanintegral((
)ofthissection):
Differentiating
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024,
30.
31. From
sothat xy′ 2y =0
32. Thefunction y(x) isnotcontinuousat x =0 since lim x→0 y(x)=5 and lim x→0+ y(x)= 5.Thus, y′(x) doesnotexistat x =0.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
33. Forcethefunction y = emx intotheequation y′ +2y =0 toget (emx)′ +2(emx)=0 me mx +2e mx =0
mx(m +2)=0
Nowsince emx > 0 forallvaluesof x,wemusthave m = 2 andso y = e 2x isasolution.
34. Forcethefunction y = emx intotheequation 3y′ 4y =0 toget 3(e mx )′ 4(e mx)=0 3memx 4emx =0 emx(3m 4)=0
Nowsince emx > 0 forallvaluesof x,wemusthave m =4/3 andso y = e4x/3 isasolution.
35. Forcethefunction y = emx intotheequation y′′ 5y′ +6y =0 toget (emx)′′ 5(emx)′ +6(
Nowsince emx > 0 forallvaluesof x,wemusthave m =2 and m =3 therefore y = e2x and y = e3x aresolutions.
36. Forcethefunction y = emx intotheequation 2
Nowsince emx > 0 forallvaluesof x ,wemusthave m = 5 and m =1/2 therefore y = e 5x and y = ex/2 aresolutions.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
37. Forcethefunction y = xm intotheequation xy′′ +2y′ =0 toget
Thelastlineimpliesthat m =0 and m = 1 therefore y = x0 =1 and y = x 1 are solutions.
38. Forcethefunction y = xm intotheequation 4x2y′′ + y =0 toget
Thelastlineimpliesthat m =1/2 therefore y = x1/2 = √x isasolutions.
39. Forcethefunction
[m 2 8m +15]=0 x m[(m 3)(m 5)]=0
Thelastlineimpliesthat m =3 and m =5 therefore y = x3 and y = x5 aresolutions.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
40. Forcethefunction y = xm intotheequation x2
Thelastlineimpliesthat m =0, m =2,and m =4 therefore y = x0 =1, y = x2 ,and y = x4 aresolutions.
InProblems 41–44,wesubstitute y = c intothedifferentialequationsanduse y′ =0 and y′′ =0
41. Solving 5c =10 weseethat y =2 isaconstantsolution.
42. Solving c2 +2c 3=(c +3)(c 1)=0 weseethat y = 3 and y =1 areconstantsolutions.
43. Since 1/(c 1)=0 hasnosolutions,thedifferentialequationhasnoconstantsolutions.
44. Solving 6c =10 weseethat y =5/3 isaconstantsolution.
45. Substituting y =(x + c1)2 intodifferentialequationyields, dy dx 2 =4y [2(x + c1)]2
Bothsidesofthedifferentialequationarezerowhen y =0.Novalueof c1 inthefamilyof solutionsgives y =0 andthusthetrivialsolution y =0 isasingularsolution.
46. Substituting y =3sin(x + c1) intodifferentialequationyields, dy dx 2 =9 y 2 [3cos(x + c1)]2 =9 (3sin(x + c1))2
Bothsidesofthedifferentialequationarezerowhen y =3.Novalueof c1 inthefamilyof solutionsgives y =3 andthusthesolution y =3 isasingularsolution.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
47. Rewritingthefamilyofsolutions,weget 16 y2 = x c1 and 16 y 2 =(x c1)2 .Using implicitdifferentiationresultsin y dy dx = c1 x.Substituting y dy dx and 16 y2 intothe differentialequationyields,
2 =0 (c1 x)+(x c1)=0
Bothsidesofthedifferentialequationarezerowhen y = ±4.Novalueof c1 inthefamilyof solutionsgives y = ±4 andthusthesolutions y = ±4 aresingularsolutions.
48. Substituting y = x (x c1)2 intodifferentialequationyields,
Bothsidesofthedifferentialequationare 4x 1 when y = x.Novalueof c1 inthefamilyof solutionsgives y = x andthusthesolution y = x isasingularsolution.
49. From x = e 2t +3e6t and y = e 2t +5e6t weobtain
and
Then
50. From x =cos2t +sin2t + 1 5 et and
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
51. (y′)2 +1=0 hasnorealsolutionsbecause (y′)2 +1 ispositiveforalldifferentiablefunctions y = φ(x).
52. Theonlysolutionof (y′)2 + y2 =0 is y =0,sinceif y =0, y2 > 0 and (y′)2 + y2 ≥ y2 > 0
53. Thefirstderivativeof f (x)= ex is ex .Thefirstderivativeof f (x)= ekx is kekx .Thedifferentialequationsare y′ = y and y′ = ky,respectively.
54. Anyfunctionoftheform y = cex or y = ce x isitsownsecondderivative.Thecorrespondingdifferentialequationis y′′ y =0.Functionsoftheform y = c sin x or y = c cos x havesecondderivativesthatarethenegativesofthemselves.Thedifferentialequationis y′′ + y =0
55. Wefirstnotethat 1 y2 = 1 sin2 x = √cos2 x = | cos x|.Thispromptsustoconsider valuesof x forwhich cos x< 0,suchas x = π.Inthiscase
Thus, y =sin x willonlybeasolutionof y′ = 1 y2 when cos x> 0.Anintervalof definitionisthen ( π/2,π/2).Otherintervalsare (3π/2, 5π/2), (7π/2, 9π/2),andsoon.
56. Sincethefirstandsecondderivativesof sin t and cos t involve sin t and cos t,itisplausible thatalinearcombinationofthesefunctions, A sin t + B cos t,couldbeasolutionofthe differentialequation.Using y′ = A cos t B sin t and y′′ = A sin t B cos t andsubstituting intothedifferentialequationweget
=(3A 2B
Thus 3A 2B =5 and 2A +3B =0.Solvingthesesimultaneousequationswefind A = 15 13 and B = 10 13 .Aparticularsolutionis y = 15 13 sin t 10 13 cos t
57. Onesolutionisgivenbytheupperportionofthegraphwithdomainapproximately (0, 2 6) Theothersolutionisgivenbythelowerportionofthegraph, alsowithdomainapproximately (0, 2.6).
58. Onesolution,withdomainapproximately (−∞, 1.6) istheportionofthegraphinthesecondquadranttogetherwiththelowerpartofthegraphinthefirstquadrant.Asecond solution,withdomainapproximately (0, 1 6) istheupperpartofthegraphinthefirstquadrant.Thethirdsolution,withdomain (0, ∞),isthepartofthegraphinthefourthquadrant.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
59. Differentiating (x3 + y3)/xy =3c weobtain
60. Atangentlinewillbeverticalwhere y′ isundefined,orinthiscase,where x(2y3 x3)=0. Thisgives x =0 and
Thus,thereareverticaltangentlinesat x =0 and x =22/3 ,orat (0, 0) and (22/3 , 21/3 ).Since 22/3 ≈ 1.59,theestimatesofthedomainsinProblem50wereclose.
61. Thederivativesofthefunctionsare φ′ 1(x)= x/√25 x2 and φ′ 2(x)= x/√25 x2 ,neither ofwhichisdefinedat x = ±5
62. Todetermineifasolutioncurvepassesthrough (0, 3) welet t =0 and P =3 intheequation P = c1et/(1+ c1et).Thisgives 3= c1/(1+ c1) or c1 = 3 2 .Thus,thesolutioncurve P = ( 3/
passesthroughthepoint (0, 3).Similarly,letting t =0 and P =1 intheequationforthe one-parameterfamilyofsolutionsgives 1= c1/(1+ c1) or c1 =1+ c1 .Sincethisequation hasnosolution,nosolutioncurvepassesthrough (0, 1)
63. Forthefirst-orderdifferentialequationintegrate f (x).Forthesecond-orderdifferential equationintegratetwice.Inthelattercaseweget y = ´ (´ f (x)dx) dx + c1x + c2
64. Solvingfor y′ usingthequadraticformulaweobtainthetwodifferentialequations y ′ = 1 x 2+2 1+3x6 and y ′ = 1 x 2 2 1+3x6 , sothedifferentialequationcannotbeputintheform dy/dx = f (x,y)
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
65. Thedifferentialequation yy′ xy =0 hasnormalform dy/dx = x.Thesearenotequivalentbecause y =0 isasolutionofthefirstdifferentialequationbutnotasolutionofthe second.
66. Differentiatingweget y′ = c1 +3c2 x2 and y′′ =6c2x.Then c2 = y′′/6x and c1 = y′ xy′′/2, so y = y ′ xy′′ 2 x +
andthedifferentialequationis x2y′′ 3
67.(a) Since e x2 ispositiveforallvaluesof x, dy/dx> 0 forall x,andasolution, y(x),ofthe differentialequationmustbeincreasingonanyinterval.
(b) lim x→−∞ dy dx =lim x→−∞ e x2 =0 and lim x→∞ dy dx =lim x→∞ e x2 =0.Since dy/dx approaches0as x approaches −∞ and ∞,thesolutioncurvehashorizontalasymptotestotheleftand totheright.
(c) Totestconcavityweconsiderthesecondderivative
d2y dx2 = d dx dy dx = d dx e x2 = 2xe x2
Sincethesecondderivativeispositivefor x< 0 andnegativefor x> 0,thesolution curveisconcaveupon (−∞, 0) andconcavedownon (0, ∞).
(d) x y
68.(a) Thederivativeofaconstantsolution y = c is0,sosolving 5 c =0 weseethat c =5 andso y =5 isaconstantsolution.
(b) Asolutionisincreasingwhere dy/dx =5 y> 0 or y< 5.Asolutionisdecreasing where dy/dx =5 y< 0 or y> 5.
69.(a) Thederivativeofaconstantsolutionis0,sosolving y(a by)=0 weseethat y =0 and y = a/b areconstantsolutions.
(b) Asolutionisincreasingwhere dy/dx = y(a by)= by(a/b y) > 0 or 0 <y<a/b.A solutionisdecreasingwhere dy/dx = by(a/b y) < 0 or y< 0 or y>a/b.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
(c) Usingimplicitdifferentiationwecompute
d2y dx2 = y( by′)+ y ′(a by)= y ′(a 2by)
Solving d2y/dx2 =0 weobtain y = a/2b.Since d2y/dx2 > 0 for 0 <y<a/2b and d2y/dx2 < 0 for a/2b<y<a/b,thegraphof y = φ(x) hasapointofinflectionat y = a/2b.
(d) y = a/b y = 0 x y
70.(a) If y = c isaconstantsolutionthen y′ =0,but c2 +4 isnever0foranyrealvalueof c.
(b) Since y′ = y2 +4 > 0 forall x whereasolution y = φ(x) isdefined,anysolutionmust beincreasingonanyintervalonwhichitisdefined.Thusitcannothaveanyrelative extrema.
(c) Usingimplicitdifferentiationwecompute d2y/dx2 =2yy′ =2y(y2 +4).Setting d2y/dx2 =0 weseethat y =0 correspondstotheonlypossiblepointofinflection. Since d2y/dx2 < 0 for y< 0 and d2y/dx2 > 0 for y> 0,thereisapointofinflection where y =0.
(d) x y
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
71. In Mathematica use
Clear[y]
y[x_]:=xExp[5x]Cos[2x] y[x]
y‚‚‚‚[x] 20y‚‚‚[x]+158y‚‚[x] 580y‚[x]+841y[x]//Simplify
Theoutputwillshow y(x)= e5xx cos2x,whichverifiesthatthecorrectfunctionwasentered,and0,whichverifiesthatthisfunctionisasolutionofthedifferentialequation.
72. In Mathematica use
Clear[y]
y[x_]:=20Cos[5Log[x]]/x 3Sin[5Log[x]]/x y[x]
xˆ3y‚‚‚[x]+2xˆ2y‚‚[x]+20xy‚[x] 78y[x]//Simplify
Theoutputwillshow y(x)=20cos(5ln x)/x 3sin(5ln x)/x,whichverifiesthatthecorrect functionwasentered,and0,whichverifiesthatthisfunctionisasolutionofthedifferential equation.
EXERCISES1.2
1. Solving 1/3=1/(1+ c1) weget c1 = 4.Thesolutionis y =1/(1 4e x).
2. Solving 2=1/(1+ c1e) weget c1 = (1/2)e 1 .Thesolutionis y =2/(2 e (x+1) ) .
3. Letting x =2 andsolving 1/3=1/(4+ c) weget c = 1.Thesolutionis y =1/(x2 1).This solutionisdefinedontheinterval (1, ∞).
4. Letting x = 2 andsolving 1/2=1/(4+ c) weget c = 2.Thesolutionis y =1/(x2 2). Thissolutionisdefinedontheinterval (−∞, √2).
5. Letting x =0 andsolving 1=1/c weget c =1.Thesolutionis y =1/(x2 +1).Thissolution isdefinedontheinterval (−∞, ∞).
6. Letting x =1/2 andsolving 4=1/(1/4+ c) weget c = 1/2.Thesolutionis y =1/(x2 1/2)=2/(2x2 1).Thissolutionisdefinedontheinterval ( 1/√2 , 1/√2)
InProblems 7–10,weuse x = c1 cos t + c2 sin t and x′ = c1 sin t + c2 cos t toobtainasystemoftwo equationsinthetwounknowns c1 and c2.
7. Fromtheinitialconditionsweobtainthesystem
c1 = 1c2 =8
Thesolutionoftheinitial-valueproblemis x = cos t +8sin t
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
8. Fromtheinitialconditionsweobtainthesystem
Thesolutionoftheinitial-valueproblemis x = cos t
9. Fromtheinitialconditionsweobtain
Solving,wefind c1 = √3/4 and c2 =1/4.Thesolutionoftheinitial-valueproblemis x =(√3/4)cos t +(1/4)sin t.
10. Fromtheinitialconditionsweobtain
Solving,wefind c1 = 1 and c2 =3.Thesolutionoftheinitial-valueproblemis x = cos t+ 3sin t
InProblems 11–14,weuse y = c1ex + c2
equationsinthetwounknowns c1 and c2.
11. Fromtheinitialconditionsweobtain
12. Fromtheinitialconditionsweobtain
x and y′ = c1ex
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
13. Fromtheinitialconditionsweobtain
Solving,wefind c1 =0 and c2 =5e 1 .Thesolutionoftheinitial-valueproblemis y = 5e 1e x =5e 1 x .
14. Fromtheinitialconditionsweobtain
Solving,wefind c1 = c2 =0.Thesolutionoftheinitial-valueproblemis y =0.
15. Twosolutionsare y =0 and y = x3
16. Twosolutionsare y =0 and y = x2.(Also,anyconstantmultipleof x2 isasolution.)
17. For f (x,y)= y2/3 wehave ∂f ∂y = 2 3 y 1/3 .Thus,thedifferentialequationwillhaveaunique solutioninanyrectangularregionoftheplanewhere y =0.
18. For f (x,y)= √xy wehave ∂f/∂y = 1 2 x/y .Thus,thedifferentialequationwillhavea uniquesolutioninanyregionwhere x> 0 and y> 0 orwhere x< 0 and y< 0
19. For f (x,y)= y x wehave ∂f ∂y = 1 x .Thus,thedifferentialequationwillhaveaunique solutioninanyregionwhere x =0.
20. For f (x,y)= x + y wehave ∂f ∂y =1.Thus,thedifferentialequationwillhaveaunique solutionintheentireplane.
21. For f (x,y)= x2/(4 y2) wehave ∂f/∂y =2x2y/(4 y2)2 .Thusthedifferentialequation willhaveauniquesolutioninanyregionwhere y< 2, 2 <y< 2,or y> 2.
22. For f (x,y)= x2 1+ y3 wehave ∂f ∂y = 3x2y2 (1+ y3)2 .Thus,thedifferentialequationwillhavea uniquesolutioninanyregionwhere y = 1.
23. For f (x,y)= y2 x2 + y2 wehave ∂f ∂y = 2x2y (x2 + y2)2 .Thus,thedifferentialequationwillhavea uniquesolutioninanyregionnotcontaining (0, 0)
24. For f (x,y)=(y + x)/(y x) wehave ∂f/∂y = 2x/(y x)2 .Thusthedifferentialequation willhaveauniquesolutioninanyregionwhere y<x orwhere y>x.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
InProblems 25–28,weidentify f (x,y)= y2 9 and ∂f/∂y = y/ y2 9.Weseethat f and ∂f/∂y arebothcontinuousintheregionsoftheplanedeterminedby y< 3 and y> 3 withno restrictionson x.
25. Since 4 > 3, (1, 4) isintheregiondefinedby y> 3 andthedifferentialequationhasa uniquesolutionthrough (1, 4)
26. Since (5, 3) isnotineitheroftheregionsdefinedby y< 3 or y> 3,thereisnoguarantee ofauniquesolutionthrough (5, 3)
27. Since (2, 3) isnotineitheroftheregionsdefinedby y< 3 or y> 3,thereisnoguaranteeofauniquesolutionthrough (2, 3)
28. Since ( 1, 1) isnotineitheroftheregionsdefinedby y< 3 or y> 3,thereisnoguaranteeofauniquesolutionthrough ( 1, 1).
29.(a) Aone-parameterfamilyofsolutionsis y = cx.Since y′ = c, xy′ = xc = y and y(0)= c 0=0.
(b) Writingtheequationintheform y′ = y/x,weseethat R cannotcontainanypointon the y-axis.Thus,anyrectangularregiondisjointfromthe y-axisandcontaining (x0,y0) willdetermineanintervalaround x0 andauniquesolutionthrough (x0,y0).Since x0 = 0 inpart(a),wearenotguaranteedauniquesolutionthrough (0, 0).
(c) Thepiecewise-definedfunctionwhichsatisfies y(0)=0 isnotasolutionsinceitisnot differentiableat x =0.
30.(a) Since d dx tan(x + c)=sec2 (x + c)=1+tan2 (x + c),weseethat y =tan(x + c) satisfies thedifferentialequation.
(b) Solving y(0)=tan c =0 weobtain c =0 and y =tan x.Since tan x isdiscontinuousat x = ±π/2,thesolutionisnotdefinedon ( 2, 2) becauseitcontains ±π/2.
(c) Thelargestintervalonwhichthesolutioncanexistis ( π/2,π/2).
31.(a) Since d dx 1 x + c = 1 (x + c)2 = y 2,weseethat y = 1 x + c isasolutionofthe differentialequation.
(b) Solving y(0)= 1/c =1 weobtain c = 1 and y =1/(1 x).Solving y(0)= 1/c = 1 weobtain c =1 and y = 1/(1+x).Beingsuretoinclude x =0,weseethattheinterval ofexistenceof y =1/(1 x) is (−∞, 1),whiletheintervalofexistenceof y = 1/(1+ x) is ( 1, ∞).
(c) Byinspectionweseethat y =0 isasolutionon (−∞, ∞)
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
32.(a) Applying y(1)=1 to y = 1/ (x + c) gives 1= 1 1+ c or 1+ c = 1
Thus c = 2 and y = 1 x
(b) Applying y(3)= 1 to y = 1/ (x + c) gives
Thus c = 2 and y =
(c) No,theyarenotthesamesolution.Theinterval I ofdefinitionforthesolutioninpart (a)is (−∞, 2);whereastheinterval I ofdefinitionforthesolutioninpart(b)is (2, ∞). Seethefigure.
33.(a) Differentiating 3x2 y2 = c weget 6x 2yy′ =0 or yy′ =3x
(b) Solving 3x2 y2 =3 for y weget y = φ1(x)= 3(x2 1) , 1 <x< ∞, y = φ2(x)= 3(x2 1) , 1 <x< ∞, y = φ3(x)= 3(x2 1) , −∞ <x< 1, y = φ4(x)= 3(x2 1) , −∞ <x< 1
(c) Only y = φ3(x) satisfies y( 2)=3.
34.(a) Setting x =2 and y = 4 in 3x2 y2 = c weget 12 16= 4= c,sotheexplicitsolutionis y = 3x2 +4 , −∞ <x< ∞
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
(b) Setting c =0 wehave y = √3x and y = √3x,bothdefinedon (−∞, ∞)
InProblems 35–38,weconsiderthepointsonthegraphswith x-coordinates x0 = 1, x0 =0,and x0 =1.Theslopesofthetangentlinesatthesepointsarecomparedwiththeslopesgivenby y′(x0) in (a) through (f).
35. Thegraphsatisfiestheconditionsin(b)and(f).
36. Thegraphsatisfiestheconditionsin(e).
37. Thegraphsatisfiestheconditionsin(c)and(d).
38. Thegraphsatisfiestheconditionsin(a).
39. Usingthefunction y = c1 cos3x + c2 sin3x andthefirstboundaryconditionweget
y(0)= c1 cos0+ c2 sin0=0
Therefore c1 =0.Similarlyforthesecondboundaryconditionweget
y(π/6)= c2 sin3(π/6)= 1
Therefore c2 = 1.Thesolutiontotheboundaryvalueproblemis y(x)= sin3x
40. Usingthefunction y = c1 cos3x + c2 sin3x andthefirstboundaryconditionweget
y(0)= c1 cos0+ c2 sin0=0
Therefore c1 =0.Thus y(x)= c2 sin3x.Similarlyforthesecondboundaryconditionweget
y(π)= c2 sin3(π)=0
Butthelastlineissatisfiedforanychoiceof c2 since sin3π =0 thereforethereareinfinitely manysolutionsinthiscase.
41. Thederivativeofthefunction y = c1 cos3x + c2 sin3x is y′ = 3c1 sin3x +3c2 cos3x and usingthefirstboundaryconditionweget
y ′(0)=0+3c2 =0
Therefore c2 =0 Sofarthenwehave y′ = 3c1 sin3x.Similarly,usingthesecondboundary conditionweget
y ′(π/4)= 3c1 √2/2 =0
Therefore c1 =0.Thesolutionisthusthetrivialsolution y =0.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
42. Thederivativeofthefunction y = c1 cos3x + c2 sin3x is y′ = 3c1 sin3x +3c2 cos3x and usingthetwoboundaryconditionsweget
y(0)= c1 +0=1
Therefore c1 =1.Inaddition y ′(π)=0 3c2 =5
Therefore c2 = 5/3.Thesolutiontothisboundaryvalueproblemis y(x)=cos3x 5 3 sin3x.
43. Usingthefunction y = c1 cos3x + c2 sin3x andthefirstboundaryconditionweget
y(0)= c1 cos0+ c2 sin0=0
Therefore c1 =0.Thus y(x)= c2 sin3x.Similarlyforthesecondboundaryconditionweget
c2 sin3(π)=4c2 · 0=40=4
Thelastlineisobviouslyacontradictionandsothereforetheboundaryvalueproblemhas nosolutioninthiscase.
44. Thederivativeofthefunction y = c1 cos3x + c2 sin3x is y′ =
x and usingthefirstboundaryconditionweget
y ′(π/3)=0 3c2 =1
Therefore c2 = 1/3.Similarly,usingthesecondboundaryconditionweget y ′(π)=0 3c2 =0
Therefore c2 =0,whichisacontradictionsotheproblemhasnosolution.
45. Integrating y′ =8e2x +6x weobtain
Setting x =0 and y =9 wehave 9=4+ c so c =5 and y =4e2x +3x2 +5.
46. Integrating y′′ =12x 2 weobtain
Then,integrating y′ weobtain
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
At x =1 the y-coordinateofthepointoftangencyis y = 1+5=4.Thisgivestheinitial condition y(1)=4.Theslopeofthetangentlineat x =1 is y′(1)= 1.Fromtheinitial conditionsweobtain
and
Thus, c1 = 5 and c2 =8,so
47. When x =0 and y = 1 2 , y′ = 1,sotheonlyplausiblesolutioncurveistheonewith negativeslopeat 0, 1 2 ,ortheblackcurve.
48. If y(0)=1,then y =1 when x =0.Therefore, y ′(0)= x 2 + y
2 +12 =1.Differentiating thedifferentialequationwithrespectto x,wehave y ′′ =2x +2yy ′.Therefore, y ′′(0)=2(0)+2(1)(1)=2.
49. Wenotethattheinitialcondition y(0)=0,
issatisfiedonlywhen y =0.Forany y> 0,necessarily
becausetheintegrandispositiveontheintervalofintegration.Thenfrom(12)ofSection 1.1andtheChainRulewehave:
Computingthesecondderivative,weseethat:
Thisisequivalentto
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
50. Ifthesolutionistangenttothe x-axisat (x0, 0),then y′ =0 when x = x0 and y =0 Substitutingthesevaluesinto y′ +2y =3x 6 weget 0+0=3x0 6 or x0 =2.
51. Thetheoremguaranteesaunique(meaningsingle)solutionthroughanypoint.Thus,there cannotbetwodistinctsolutionsthroughanypoint.
52. When y = 1 16 x 4 , y ′ = 1 4 x3 = x( 1 4 x 2)= xy 1/2 ,and y(2)= 1 16 (16)=1.When
,x<
x 2 ,x ≥
1/2 , and y(2)= 1 16 (16)=1.Thetwodifferentsolutionsarethesameontheinterval (0, ∞), whichisallthatisrequiredbyTheorem 1.2.1.
EXERCISES1.3
1. dP dt = kP + r; dP dt = kP r
2. Let b betherateofbirthsand d therateofdeaths.Then b = k1P and d = k2P .Since dP/dt = b d,thedifferentialequationis dP/dt = k1P k2P .
3. Let b betherateofbirthsand d therateofdeaths.Then b = k1P and d = k2P 2.Since dP/dt = b d,thedifferentialequationis dP/dt = k1P k2P 2 .
4. dP dt = k1P k2P 2 h,h> 0
5. Fromthegraphinthetextweestimate T0 =180◦ and Tm =75◦ .Weobservethatwhen T =85, dT/dt ≈−1.Fromthedifferentialequationwethenhave k = dT/dt T Tm = 1 85 75 = 0.1.
6. Byinspectingthegraphinthetextwetake Tm tobe Tm(t)=80 30cos(πt/12).Thenthe temperatureofthebodyattime t isdeterminedbythedifferentialequation
dT dt = k T 80 30cos π 12 t ,t> 0
7. Thenumberofstudentswiththefluis x andthenumbernotinfectedis 1000 x,so dx/dt = kx(1000 x)
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
8. Byanalogy,withthedifferentialequationmodelingthespreadofadisease,weassume thattherateatwhichthetechnologicalinnovationisadoptedisproportionaltothenumberofpeoplewhohaveadoptedtheinnovationandalsotothenumberofpeople, y(t), whohavenotyetadoptedit.Ifonepersonwhohasadoptedtheinnovationisintroduced intothepopulation,then x + y = n +1 and
9. Therateatwhichsaltisleavingthetankis
Thus dA/dt = A/100.Theinitialamountis A(0)=50.
10. Therateatwhichsaltisenteringthetankis Rin = (3L/min) · (2kg/L) =6 kg/min.
Sincethesolutionispumpedoutataslowerrate,itisaccumulatingattherateof (3 2)L/min =1 L/min.After t minutesthereare 300+ t litersofbrineinthetank.Therate atwhichsaltisleavingis Rout = (2L/min) · A 300+ t kg/L
Thedifferentialequationis
11. Therateatwhichsaltisenteringthetankis
Rin = (3L/min) · (2kg/L) =6 kg/min.
Sincethetanklosesliquidatthenetrateof
3L/min 3.5L/min = 0.5 L/min, after t minutesthenumberoflitersofbrineinthetankis 300 1 2 t liters.Thustherateat whichsaltisleavingis
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
12. Therateatwhichsaltisenteringthetankis
Rin =(cin kg/L) (rin L/min)= cinrin kg/min.
Nowlet A(t) denotethenumberofkilogramsofsaltand N (t) thenumberoflitersofbrine inthetankattime t.Theconcentrationofsaltinthetankaswellasintheoutflow is c(t)= x(t)/N (t).Butthenumberoflitersofbrineinthetankremainssteady, isincreased,oris decreaseddependingonwhether rin = rout , rin >rout ,or rin <rout.Inanycase,the numberoflitersofbrineinthetankattime t is N (t)= N0 +(rin rout)t.Theoutputrateof saltisthen
Rout = A N0 +(rin rout)t kg/L · (rout L/min)= rout A N0 +(rin rout)t kg/min
Thedifferentialequationfortheamountofsalt, dA/dt = Rin Rout ,is
dA dt = cinrin rout A N0 +(rin rout)t or dA dt + rout N0 +(rin rout)t A = cinrin
13. Thevolumeofwaterinthetankattime t is V = Aw h.Thedifferentialequationisthen dh dt = 1 Aw dV dt = 1 Aw cAh 2gh = cAh Aw 2gh.
Using Ah = π 2 12 2 = π 36 , Aw =102 =100,and g =32,thisbecomes
dh dt = cπ/36 100 √64h = cπ 450 √h.
14. Thevolumeofwaterinthetankattime t is V = 1 3 πr2h where r istheradiusofthetank atheight h.Fromthefigureinthetextweseethat r/h =3/6 sothat r = h/2 and V = 1 3 π (h/2)2 h = 1 12 πh3 .Differentiatingwithrespectto t wehave dV/dt = 1 4 πh2 dh/dt or dh dt = 4 πh2 dV dt .
FromProblem13wehave dV/dt = cAh√2gh where c =0 6, Ah = π (0 05)2 ,and g =9 8. Thus dV/dt = 0.00664π√h and
dh dt = 4 πh2 0 00664π√h = 0 0266 h3/2
15. Since i = dq/dt and Ld2q/dt2 + Rdq/dt = E(t),weobtain Ldi/dt + Ri = E(t).
16. ByKirchhoff’ssecondlawweobtain R dq dt + 1 C q = E(t).
17. FromNewton’ssecondlawweobtain m dv dt = kv2 + mg
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
18. SincethebarrelinFigure1.3.17(b)inthetextissubmerged anadditional y metersbelow itsequilibriumpositionthenumberofcubicmetersintheadditionalsubmergedportion isthevolumeofthecircularcylinder: π×(radius)2×heightor π(s/2)2y.Thenwehavefrom Archimedes’principle
upwardforceofwateronbarrel = weightofwaterdisplaced =(9810) × (volumeofwaterdisplaced) =(9810)π(s/2)2 y =2452.5πs 2 y.
ItthenfollowsfromNewton’ssecondlawthat
where g =9.81 and w istheweightofthebarrelinnewtons.
19. Thenetforceactingonthemassis F = ma = m
Sincetheconditionofequilibriumis mg = ks,thedifferentialequationis
d2x dt2 = kx.
20. FromProblem19,withoutadampingforce,thedifferentialequationis md2x/dt2 = kx Withadampingforceproportionaltovelocity,thedifferentialequationbecomes
21. Astherocketclimbs(inthepositivedirection),itspendsitsamountoffuelandtherefore themassofthefuelchangeswithtime.Theairresistanceactsintheoppositedirectionof themotionandtheupwardthrust R worksinthesamedirection.UsingNewton’ssecond lawweget
Nowbecausethemassisvariable,wemustusetheproductrule toexpandtheleftsideof theequation.Doingsogivesusthefollowing:
Thelastlineisthedifferentialequationwewantedtofind.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
22.(a) Sincethemassoftherocketis m(t)= mp + mv + mf (t),takethetimerate-of-change andget,bystraight-forwardcalculation,
Thereforetherateofchangeofthemassoftherocketisthesameastherateof changeofthemassofthefuelwhichiswhatwewantedtoshow.
(b) Thefuelisdecreasingattheconstantrateof λ andsofrompart(a)wehave
Usingthegivenconditiontosolvefor c, m(0)=0+ c = m0 andso m(t)= λt + m0. ThedifferentialequationinProblem21nowbecomes
+ m0) dv dt +(k λ)v =
(c) Frompart(b)wehavethat d dt mf (t)= λ andsobyintegratingthisresultweget mf (t)= λt + c.Nowattime t =0, mf (0)=0+ c = c therefore mf (t)= λt + mf (0) . Atsomelatertime tb wethenhave mf (tb)= λtb + mf (0)=0 andsolvingthisequation forthattimeweget tb = mf (0)/λ whichiswhatwewantedtoshow.
23. From g = k/R2 wefind k = gR2 .Using a = d2r/dt2 andthefactthatthepositivedirection isupwardweget d2r dt2 = a = k r2 = gR2 r2 or d2r dt2 + gR2 r2 =0
24. Thegravitationalforceon m is F = kMr m/r2.Since Mr =4πδr3 /3 and M =4πδR3 /3 we have Mr = r3M/R3 and F = k Mr m r2 = k r3Mm/R3 r2 = k mM R3 r.
Nowfrom F = ma = d2r/dt2 wehave m d2r dt2 = k mM R3 r or d2r dt2 = kM R3 r.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
25. Thedifferentialequationis dA dt = k(M A)
26. Thedifferentialequationis dA dt = k1(M A) k2A.
27. Thedifferentialequationis x′(t)= r kx(t) where k> 0.
28. Noticefromthediagramthatthesegmentfromthe waterskiertotheboatistangenttothecurveatthepoint P (x,y).Forthesakeofsimplicity,let’slabelthecoordinates oftheboatonthex-axisas (a, 0).Theequationofthis tangentlineis y = y′(x)(x a) fromwhichweget
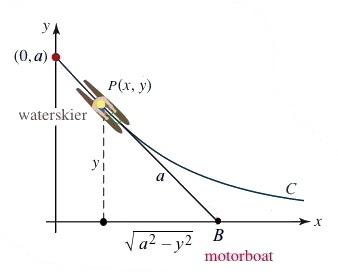
BythePythagoreanTheoremwehave
fromwhichwemakeasubstitution andthensolveforthederivativetoget
Noticethatthesignofthederivativeisnegativebecauseas theboatproceedsalongthe positive x-axis,the y-coordinatedecreases.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
29. Weseefromthefigurethat 2θ + α = π.Thus y x =tan α =tan(π 2θ)= tan2θ = 2tan θ 1 tan2 θ .
Sincetheslopeofthetangentlineis y′ =tan θ wehave y/x =2y′[1 (y′)2] or y y(y′)2 =2xy′ ,whichisthe quadraticequation y(y′)2 +2xy′ y =0 in y′.Usingthe quadraticformula,weget
Since dy/dx> 0,thedifferentialequationis dy dx = x + x2 + y2 y or y dy dx x2 + y2 + x =0
30. Thedifferentialequationis dP/dt = kP ,sofromProblem41inExercises 1 1,aoneparameterfamilyofsolutionsis P = cekt .
31. Thedifferentialequationin(3)is dT/dt = k(T Tm).Whenthebodyiscooling, T>Tm, so T Tm > 0.Since T isdecreasing, dT/dt< 0 and k< 0.Whenthebodyiswarming, T<Tm ,so T Tm < 0.Since T isincreasing, dT/dt> 0 and k< 0.
32. Thedifferentialequationin(8)is dA/dt =6 A/100.If A(t) attainsamaximum,then dA/dt =0 atthistimeand A =600.If A(t) continuestoincreasewithoutreachingamaximum,then A′(t) > 0 for t> 0 and A cannotexceed600.Inthiscase,if A′(t) approaches0 as t increasestoinfinity,weseethat A(t) approaches600as t increasestoinfinity.
33. Thisdifferentialequationcoulddescribeapopulationthat undergoesperiodicfluctuations.
34.(a) AsshowninFigure1.3.23(a)inthetext,theresultantofthe reactionforceofmagnitude F andtheweightofmagnitude mg oftheparticleisthecentripetalforceofmagnitude mω2x.Thecentripetalforcepointstothecenterofthecircleofradius x onwhichthe particlerotatesaboutthe y-axis.Comparingpartsofsimilartrianglesgives
cos θ = mg and F sin θ = mω 2 x.
(b) Usingtheequationsinpart(a)wefind
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
35. FromProblem23, d2r/dt2 = gR2/r2.Since R isaconstant,if r = R + s,then d2r/dt2 = d2s/dt2 and,usingaTaylorseries,weget
Thus,for R muchlargerthan s,thedifferentialequationisapproximatedby d2s/dt2 = g.
36.(a) If ρ isthemassdensityoftheraindrop,then m = ρV and
If dr/dt isaconstant,then dm/dt = kS where ρdr/dt = k or dr/dt = k/ρ.Sincethe radiusisdecreasing, k< 0.Solving dr/dt = k/ρ weget r =(k/ρ)t + c0.Since r(0)= r0, c0 = r0 and r = kt/ρ + r0 .
(b) FromNewton’ssecondlaw, d dt [mv]= mg,where v isthevelocityoftheraindrop.Then
Dividingby 4ρπr3/3 weget
+ 3k ρr v = g or
dt + 3k/ρ kt/ρ
37. Weassumethattheplowclearssnowataconstantrateof k cubickilometersperhour.Let t bethetimeinhoursafternoon, x(t) thedepthinkilometersofthesnowattime t,and y(t) thedistancetheplowhasmovedin t hours.Then dy/dt isthevelocityoftheplowand theassumptiongives
wx dy dt = k, where w isthewidthoftheplow.Eachsideofthisequationsimplyrepresentsthevolumeofsnowplowedinonehour.Nowlet t0 bethenumberofhoursbeforenoonwhenit startedsnowingandlet s betheconstantrateinkilometersperhouratwhich x increases. Thenfor t> t0, x = s(t + t0).Thedifferentialequationthenbecomes dy dt = k ws 1 t + t0 .
Integrating,weobtain
y = k ws [ln(t + t0)+ c ] where c isaconstant.Nowwhen t =0, y =0 so c = ln t0 and
y = k ws ln 1+ t t0
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
Finally,fromthefactthatwhen t =1, y =2 andwhen t =2, y =3,weobtain
Expandingandsimplifyinggives t2 0 + t0 1=0.Since t0 > 0,wefind t0 ≈ 0.618 hours ≈ 37 minutes.Thusitstartedsnowingatabout11:23inthemorning.
38. Attime t,whenthepopulationis2millioncells,thedifferentialequation P ′(t)=0.15P (t) givestherateofincreaseattime t.Thus,when P (t)=2 (millioncells),therateofincrease is P ′(t)=0.15(2)=0.3 millioncellsperhouror300,000cellsperhour.
39. Setting A′(t)= 0 002 andsolving A′(t)= 0 0004332A(t) for A(t),weobtain
40. (1): dP dt = kP islinear (2): dA dt = kA islinear
(3): dT dt = k (T Tm) islinear (5): dx dt = kx (n +1 x) isnonlinear
(6): dX dt = k (α X)(beta X) isnonlinear (8): dA dt =6 A 100 islinear
(10): dh dt = Ah Aw 2gh isnonlinear
(12): d2s dt2 = g islinear
(15): m d2s dt2 + k ds dt = mg islinear
(11): L d2q dt2 + R dq dt + 1 C q = E(t) islinear
(14): m dv dt = mg kv islinear
(16): d2x dt2 64 L x =0 islinear
(17): linearityornonlinearityisdeterminedbythemannerinwhich W and T1 involve x.
CHAPTER1IN REVIEW SOLUTIONS
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
d2
2
4. d dx (c1 cosh kx + c2 sinh kx)= kc1 sinh kx + kc2 cosh kx; d2
7. a,d 8. c 9. b 10. a,c 11. b 12. a,b,d
13. Afewsolutionsare y =0, y = c,and y = ex
14. Easysolutionstoseeare y =0 and y =3.
15. Theslopeofthetangentlineat (x,y) is y′,sothedifferentialequationis y′ = x2 + y2 .
16. Therateatwhichtheslopechangesis dy′/dx = y′′,sothedifferentialequationis y′′ = y′ or y′′ + y′ =0.
17.(a) Thedomainisallrealnumbers.
(b) Since y′ =2/3x1/3 ,thesolution y = x2/3 isundefinedat x =0.Thisfunctionisa solutionofthedifferentialequationon (−∞, 0) andalsoon (0, ∞).
18.(a) Differentiating y2 2y = x2 x + c weobtain 2yy′ 2y′ =2x 1 or (2y 2)y′ =2x 1
(b) Setting x =0 and y =1 inthesolutionwehave 1 2=0 0+ c or c = 1.Thus,a solutionoftheinitial-valueproblemis y2 2y = x2 x 1.
(c) Solvingtheequation y2 2y (x2 x 1)=0 bythequadraticformulaweget y =(2 ± 4+4(x2 x 1))/2=1 ± √x2 x =1 ± x(x 1) .Since x(x 1) ≥ 0 for x ≤ 0 or x ≥ 1,weseethatneither y =1+ x(x 1) nor y =1 x(x 1) is
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
differentiableat x =0.Thus,bothfunctionsaresolutionsofthedifferentialequation, butneitherisasolutionoftheinitial-valueproblem.
19. Setting x = x0 and y =1 in y = 2/x + x,weget 1= 2 x0 + x0 or x 2 0 x0 2=(x0 2)(x0 +1)=0
Thus, x0 =2 or x0 = 1.Since x =0 in y = 2/x + x,weseethat y = 2/x + x isa solutionoftheinitial-valueproblem xy′ + y =2x, y( 1)=1,ontheinterval (−∞, 0) and y = 2/x + x isasolutionoftheinitial-valueproblem xy′ + y =2x, y(2)=1,ontheinterval (0, ∞)
20. Fromthedifferentialequation, y′(1)=12 +[y(1)]2 =1+( 1)2 =2 > 0,so y(x) isincreasing insomeneighborhoodof x =1.From y′′ =2x +2yy′ wehave y′′(1)=2(1)+2( 1)(2)= 2 < 0,so y(x) isconcavedowninsomeneighborhoodof x =1.
21.(a)
(b) When y = x2 +
1 , y′ =2x and (
′)2 =4x2 .When y = x2 +c2 , y′
(c) Pastingtogether
22. Theslopeofthetangentlineis y′ ( 1,4) =6√4+5( 1)3 =7.
23. Differentiating y = x sin x + x cos x weget
and
Anintervalofdefinitionforthesolutionis (−∞, ∞)
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
24. Differentiating y = x sin x +(cos x)ln(cos x) weget
y ′ = x cos x +sin x +cos x sin x cos x (sin x)ln(cos x)
= x cos x +sin x sin x (sin x)ln(cos x)
= x cos x (sin x)ln(cos x) and y ′′ = x sin x +cos x sin x sin x cos x (cos x)ln(cos x)
= x sin x +cos x + sin2 x cos x (cos x)ln(cos x)
= x sin x +cos x + 1 cos2 x cos x (cos x)ln(cos x)
= x sin x +cos x +sec x cos x (cos x)ln(cos x)
= x sin x +sec x (cos x)ln(cos x). Thus y ′′ + y = x sin x +sec x (cos x)ln(cos x)+ x sin x +(cos x)ln(cos x)=sec x.
Toobtainanintervalofdefinitionwenotethatthedomainof ln x is (0, ∞),sowemust have cos x> 0.Thus,anintervalofdefinitionis ( π/2,π/2).
25. Differentiating y =sin(ln x) weobtain y′ =cos(ln x)/x and y′′ = [sin(ln x)+cos(ln x)]/x2 . Then x 2 y ′′ + xy ′ + y = x 2 sin(ln x)+cos(ln x) x2 + x cos(ln x) x +sin(ln x)=0.
Anintervalofdefinitionforthesolutionis (0, ∞)
26. Differentiating y =cos(ln x)ln(cos(ln x))+(ln x)sin(ln x) weobtain y ′ =cos(ln x) 1 cos(ln x) sin(ln x) x +ln(cos(ln x)) sin(ln x) x +ln x cos(ln x) x + sin(ln x) x = ln(cos(ln x))sin(ln x) x + (ln x)cos(ln x) x
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
and y ′′ = x ln(cos(ln x)) cos(ln x) x +sin(ln x) 1 cos(ln x)
+ln(cos(ln x))sin(ln x) 1 x2 + x (ln x)
sin(ln x) x 1 x2
sin(ln x) x + cos(ln x) x 1 x2 (ln x)cos(ln x) 1 x2 = 1 x2 ln(cos(ln x))cos(ln x)+ sin2 (ln x) cos(ln x) +ln(cos(ln x))sin(ln x)
(ln x)sin(ln x)+cos(ln x) (ln x)cos(ln x) .
Then
x 2 y ′′ + xy ′ + y = ln(cos(ln x))cos(ln x)+
sin2 (ln x) cos(ln x) +ln(cos(ln x))sin(ln x) (ln x)sin(ln x)
+cos(ln x) (ln x)cos(ln x) ln(cos(ln x))sin(ln x)
+(ln x)cos(ln x)+cos(ln x)ln(cos(ln x))+(ln x)sin(ln x) = sin2 (ln x) cos(ln x) +cos(ln x)= sin2 (ln x)+cos2 (ln x) cos(ln x) = 1 cos(ln x) =sec(ln x).
Toobtainanintervalofdefinition,wenotethatthedomainof ln x is (0, ∞),sowemust have cos(ln x) > 0.Since cos x> 0 when π/2 <x<π/2,werequire π/2 < ln x<π/2. Since ex isanincreasingfunction,thisisequivalentto e π/2 <x<eπ/2 .Thus,aninterval ofdefinitionis (e π/2,eπ/2).(Muchofthisproblemismoreeasilydoneusingacomputer algebrasystemsuchas Mathematica or Maple.)
InProblems27-30weuse(12)ofSection1.1andtheProductRule. 27.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
31. Usingimplicitdifferentiationweget
32. Usingimplicitdifferentiationweget
Nowfromtheoriginalequation,isolatingthefirsttermleadsto
.Continuing fromthelastlineofourproofwenowhave
Adding1tobothsidesleadstothedesiredresult.
33. Usingimplicitdifferentiationweget
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
Differentiatingthelastlineandrememberingtousethequotientruleontherightside leadsto
Nowsince y′ = 1 y2 +1 wecanwritethelastequationas
whichiswhatwewantedtoshow.
34. Usingimplicitdifferentiationweget
Nowsince y = e xy ,substitutethisintothelastlinetoget yy +(xy +1)y ′ =0 or (1+ xy)y′ + y2 =0 whichiswhatwewantedtoshow.
35. Differentiating y = c1 +cos3x,wehave y ′ = 3sin3x and y ′′ = 9cos3x.Substituting y and y′′ intothedifferentialequationyields,
9cos3x +9(c1 +cos3x)=5
9cos3x +9c1 +9cos3x =5 9c1 =5 c1 = 5 9
36. Differentiating y = c1 + c2x,wehave y ′ = c2.Substituting y and y′ intothedifferential equationyields, c2 +2(c1 + c2x)=3x c2 +2c1 +2c2x =3x
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
37. Differentiating y = ce x +4x 6,wehave y ′ = ce x +4.Addingbothequationsyields,
6
′ + y =4x 2
38. Theinitial-valueproblemthatrepresentsafunctionwhose theslopeat (x,y) is 6 2x and passesthrough (0, 0) is
Thersultingfunction y is
Solvingfor c,wehave
Thus, y(x)=6x x 2 .
39. If y(0)=0 and y′(0)=0,then
subtractingthesecondequationfromthefirstgivesus
c
=4 or c1 =1,andthus c2 = 1. Therefore y = e 3x ex +4x
40. If y(0)=5 and y′(0)= 11,then
subtractingthesecondequationfromthefirstgivesus
. Therefore y =5e 3x +4x.
SolutionandAnswerGuide:Zill,DIFFERENTIALEQUATIONSWithBOUNDARY-VALUEPROBLEMSMETRICVERSION2024, 9798214031958;Chapter#1:IntroductiontoDifferentialEquations
41. If y(1)= 2 and y′(1)=4,then
42. If y( 1)=1 and y′( 1)=1,then
subtractingthesecondequationfromthefirstgivesus
43. Fromthegraphweseethatestimatesfor y0 and y1 are
44. Thedifferentialequationis
,thisbecomes
45. From(17)wehave F = d dt (mv).Theweightoftheropeis w =(1 lb/ft)(x(t) ft)= x lb.The massoftheropeis m = w/g = x/g.Thevelocityatwhichtheropeismovingupwardis thederivativeofthelengthoftheropeor dx/dt.Thefocesactingontheropeisaconstant forceof 5 lbupwardand w = x lbdownward.Thus(17)becomes,
