matematik

Kerstin Olofsson
Verner Gerholm
nivå
1a


Kerstin Olofsson
Verner Gerholm
nivå
1a
Matematik i vardag och yrkesliv 6
1.1 Matematik i vardag och yrkesliv 8 Uppslaget, Samhälle och yrkesliv, Koll på kapitlet 18
Tal i vardag och yrkesliv 22
2.1 Positionssystemet 24
2.2 Bråk 35
2.3 Potenser och prefix 43
Uppslaget, Samhälle och yrkesliv, Koll på kapitlet, Blandade uppgifter, Kapiteltest 52
64
3.1 Formler, uttryck och mönster 66
3.2 Arbeta med uttryck 81
3.3 Ekvationer 97 Uppslaget, Samhälle och yrkesliv, Koll på kapitlet, Blandade uppgifter, Kapiteltest 113
124
4.1 Procent och procentberäkningar 126
4.2 Procentuella förändringar 135
4.3 Procentberäkningar i samhället 143 Uppslaget, Samhälle och yrkesliv, Koll på kapitlet, Blandade uppgifter, Kapiteltest 162
5.1 Enkla slumpförsök 174
5.2 Slumpförsök i flera steg 183 Uppslaget, Samhälle och yrkesliv, Koll på kapitlet, Blandade uppgifter, Kapiteltest 195
6.1 Grafer och koordinatsystem 206
6.2 Linjära funktioner 214
6.3 Exponentialfunktioner 236 Uppslaget, Samhälle och yrkesliv, Koll på kapitlet, Blandade uppgifter, Kapiteltest 247
7.1 Statistiska undersökningar 262
7.2 Tolka och granska statistik 271
7.3 Statistiska samband 281 Uppslaget, Samhälle och yrkesliv, Koll på kapitlet, Blandade uppgifter, Kapiteltest 288
8 Geometri
8.1 Omkrets, area och volym 302
8.2 Vinklar, likformighet och symmetri 318
8.3 Rätvinkliga trianglar och trigonometri 334
8.4 Vektorer 347 Uppslaget, Samhälle och yrkesliv, Koll på kapitlet, Blandade uppgifter, Kapiteltest 358
Matematik Origo är en serie matematikböcker för gymnasiet som gör det lätt att arbeta med problemlösning, resonemang och förståelse. Till Matematik Origo nivå 1a hör en elevbok, en Skriva-bok, en Lärarguide, kopieringsmaterialet Prov, Övningsblad och Aktiviteter och det digitala presentationsverktyget Lärarstöd+. De olika komponenterna ger möjlighet att planera, variera och genomföra undervisningen utifrån elevernas behov.
Elevboken består av åtta kapitel och lyfter särskilt fram matematikens relevans. Här finns tydliga genomgångar på ett lättillgängligt språk och varierade uppgiftstyper på tre nivåer.

Lärarguiden följer elevboken uppslag för uppslag med tips, idéer och inspiration till din undervisning.

Skriva-boken är en version av elevboken där eleverna räknar och skriver direkt i boken. Den riktar sig till elever som behöver en avskalad layout och som siktar på betyget E.

I appen Alva får dina elever hjälp när de ska jobba på egen hand efter lektionerna. Där finns förklarande matematikfilmer och lösningar till vissa uppgifter.
Prov, Övningsblad och Aktiviteter är ett kopieringsmaterial med prov, övningsblad och aktiviteter till varje kapitel i elevboken. Materialet säljs som nedladdningsbara pdf:er.

Lärarstöd+ är ett digitalt presentationsverktyg där vi samlat elevboken, Lärarguiden och Prov, Övningsblad och Aktiviteter på ett ställe. Allt innehåll från elevboken – teoritext, exempel och uppgifter – kan visas separat och klickas fram stegvis.
Algebrans framskjutna ställning inom matematiken är obestridlig. I vardagslivet och yrkeslivet är algebrans roll också betydelsefull, även om den kanske inte är lika tydlig. Elever som läser matematik- eller teknikintensiva program, till exempel El och energi, Industriteknik eller VVS och fastighet, kommer att möta formler i sina yrkesämnen. Även inom privatekonomi finns användbara formler, till exempel för att beräkna sin lön efter skatt eller sin semesterersättning. Egenföretagare inom alla yrkesgrupper kan både effektivisera och underlätta sitt arbete genom att använda formler i kalkylprogram. Inom matematiken är algebran ett viktigt redskap för att bevisa matematiska samband och skapa matematiska modeller. Att lära sig algebrans grunder är ett stort steg mot att förstå matematikens uppbyggnad och struktur.
I det första delkapitlet 3.1 Formler, uttryck och mönster får eleverna börja med att tolka och ställa upp enkla uttryck och formler samt beräkna värdet av dem. Exemplen är såväl inom-matematiska som tagna från vardags- och yrkesliv. Därefter har vi valt att behandla talföljder och mönster eftersom det är en bra träning i att se mönster, formalisera dessa och upptäcka något av matematikens generaliserbarhet. Sist i delkapitlet får eleverna se hur ett kalkylprogram använder formler för att effektivt utföra beräkningar.
I delkapitel 3.2 Arbeta med uttryck börjar vi med att behandla förenklingar av algebraiska uttryck. Vi förklarar sedan vad som menas med uttryck av andra graden och visar hur man multiplicerar uttryck. Avslutningsvis går vi igenom hur man faktoriserar uttryck genom att bryta ut största möjliga faktor.
Delkapitlet 3.3 Ekvationer fokuserar inledningsvis på likhetstecknet och begreppet ekvation. I samband med det introducerar vi övertäckningsmetoden. Därefter behandlar vi den klassiska balansmetoden för lösning av ekvationer och visar hur man kan använda ekvationer vid problemlösning. Sist i kapitlet finns ett avsnitt om att lösa ut variabler ur formler, vilket kan vara nyttig kunskap för vissa program.

När du är klar med kapitlet ska du kunna
u ge exempel på begreppen variabel, konstantterm och koefficient
u beräkna värdet av ett algebraiskt uttryck
u använda formler
u tolka uttryck och formler
u beskriva ett mönster med ord eller med en formel
u skapa och använda formler i kalkylprogram
u förenkla algebraiska uttryck genom att räkna ihop termer av samma sort
u förenkla algebraiska uttryck med parenteser
u faktorisera algebraiska uttryck
u pröva om en lösning till en ekvation är korrekt
u lösa ekvationer av första graden
u använda ekvationer vid problemlösning
u Hantering av formler som är relevanta för arbetslivet.
u Hantering av formler och algebraiska uttryck, däribland faktorisering och multiplicering av uttryck.
u Metoder för att lösa linjära ekvationer.
u Användning av digitala verktyg för att effektivisera beräkningar och komplettera metoder, till exempel vid ekvationslösning.
u Problemlösning som omfattar att upptäcka och uttrycka generella samband.
Kapitelintroduktion
I Lärarguiden får du en bakgrund till varje kapitel och kommentarer kring hur författarna har tänkt när de skapat kapitlets innehåll och strutur. Här finns även kommentarer till kapitlets introduktionsaktivitet.

Algebrakapplöpning
Arbeta två och två eller tre och tre. Ni behöver två spelpjäser per spelare och två tärningar i olika färger, t.ex. en röd och en vit tärning.
u Den första spelaren slår båda tärningarna.
u Värdet på den röda tärningen kallar vi för r och värdet på den vita tärningen kallar vi för v
u I alla rutor utom i hörnen står algebraiska uttryck. Spelaren ska flytta sin pjäs lika många steg som värdet av uttrycket visar.
z Om uttryckets värde är negativt backar pjäsen.
z Om pjäsen hamnar på någon av rutorna i hörnen måste den pjäsen flyttas tillbaka till Start.
u I varje spelomgång flyttar spelaren en av sina pjäser.
Spelaren väljer själv vilken pjäs som ska flyttas.
u Den spelare som först får båda pjäserna i mål vinner.
START/MÅL
Aktiviteten Algebrakapplöpning är en klassisk övning som på ett lekfullt sätt tränar eleverna i att beräkna värdet av ett uttryck. Eleverna behöver två spelpjäser vardera, till exempel färgade gem eller lappar, och två tärningar i olika färger. Har man inte tärningar i olika färger, kan eleverna slå vardera tärningen på ett rött respektive ett vitt papper. För att eleverna ska förstå hur spelet går till kan man inleda med att varje elev bara har en spelpjäs.
I kopieringsmaterialet Prov, Övningsblad och Aktiviteter kan du skriva ut spelplanen i A3. Där hittar du också alternativa spelplaner, som spelas med en respektive tre tärningar. Det gör att du enkelt kan variera spelets svårighetsgrad.
■ Algebrakapplöpning 1
■ Algebrakapplöpning 2
■ Algebrakapplöpning 3
Enheter är något som en del elever uppfattar som svårt. En anledning kan vara att de tror att enhetsomvandlingar är något som måste läras utantill. Naturligtvis underlättar det att ha en viss utantillkunskap, men det är också viktigt att känna till att enhetsomvandlingar kan härledas vid behov.
Ett sätt att inleda en lektion om enheter är att upprätta enhetstabeller på tavlan och låta eleverna fylla i de tomma rutorna. Uppmuntra dem gärna att motivera hur man kan veta att det till exempel går 100 dm2 på 1 m2 eller att 1 cm2 är 0,01 dm2
km2 m2 dm2 cm2 mm2 1 1 200 0,4
Efter att ha arbetat med avsnittet ska eleverna kunna u omvandla mellan vanliga längd-, area- och volymenheter
Yrkesmatematik – enheter
I det här avsnittet fokuserar vi främst på omvandlingar inom metersystemet. I vissa yrkesgrupper kan dock andra enheter vara vanligare. Vid matlagning och inom vården är det till exempel vanligt att man använder litersystemet för att ange volym. Vissa yrkesgrupper kan också ha särskilda volymenheter, till exempel enheten droppe inom vården eller enheten kaffekopp i matlagning.
Undervisningen i geometri ska behandla enheter, enhetsomvandlingar och mätetal som är relevanta i elevernas karaktärsämnen. Undersök vilka enheter och enhetsomvandlingar som är relevanta för just dina elever.
Tips
En del elever skiljer inte på längd-, area- och volymenheter som t.ex. cm, cm2 och cm3. Det kan därför vara givande att diskutera skillnaderna mellan enheterna och varför det är just en upphöjd tvåa i enheterna för area och en upphöjd trea i enheterna för volym. Om man vill, så kan man välja att härleda enheterna så som man ofta gör inom t.ex. fysiken. Utifrån formeln för arean av en rektangel A = b ∙ h kan enheten för arean härledas som [m] ∙ [m] = [m2].
Det är lätt att tro att 1 cl motsvarar 1 cm3 eftersom de båda har prefixet centi. Det kan därför vara bra att särskilt påpeka att 1 ml motsvarar 1 cm3, t.ex. genom att låta eleverna själva härleda sambanden mellan volymenheterna utifrån likheten 1 l = 1 dm3
Enhetsomvandlingar
När vi mäter längder, areor och volymer, kan vi använda olika enheter. Vilken enhet vi väljer beror ofta av situationen. Vi säger till exempel hellre att sträckan till skolan är 4,5 km än att den är 4 500 000 mm. Och vi säger hellre att sprutan innehåller 12 ml medicin än att den innehåller 0,012 l. En nackdel med att det finns så många olika enheter är att vi måste lära oss att omvandla mellan dem. I tabellen här nedanför ser du hur man omvandlar mellan några vanliga enheter.
Omvandlingar inom metersystemet
Längd 1 m 10 dm 100 cm 1 000 mm
Area 1 m2 100 dm2 10 000 cm2 1 000 000 mm2
Volym 1 m3 1 000 dm3 1 000 000 cm3 1 · 109 mm3
Omvandlingar till andra standardenheter
1 mil 10 km
1 ha (hektar) 10 000 m2 1 dm3 1 l 1 cm3 1 ml
Exempel: a) Hur många meter är 37 cm?
b) Hur många kvadratcentimeter är 3,4 dm2?
c) Hur många liter är 0,17 m3?
d) Hur många meter är 5,43 kilometer?
Lösning: a)
Kommentarer och exempel I Lärarguiden finns författarnas kommentarer till teoritexter och exempel. Det finns också kompletterande exempel till varje avsnitt.
Kilo betyder tusen, alltså är 1
I USA har man ett annat måttsystem än det metriska. Där använder man enheterna inch, foot och yard, där 1 yard = 3 feet = 36 inches.
a) 1 inch (in) motsvarar 2,54 cm. Hur många decimeter motsvarar 512 in?
b) 1 foot (ft) motsvarar 30,48 cm. Hur många kvadratmeter motsvarar 1 square foot (ft2)?
c) 1 yard (yd) är 3 ft. Hur många kvadratdecimeter motsvarar 1 yd2?
Lösning/Kommentar
a) 512 in = 512 ∙ 2,54 cm = 1 300,48 cm ≈ 130 dm
b) 1 ft2 = 30,48 cm ∙ 30,48 cm ≈ 929,0 cm2 = 9,290 dm2 = = 0,09290 m2
c) 1 yd2 = 3 ft ∙ 3 ft = 9 ft2 = 9 ∙ 0,09290 m2 = 0,8361 m2 = = 83,61 dm2
Exempel: Kartongen har måtten
40 cm × 15 cm × 25 cm. Hur många liter rymmer den?
Lösning: Metod 1
Svaret ska anges i liter. Eftersom 1 liter = 1 dm3 kan det vara klokt att redan från början göra om kartongens mått till decimeter:
40 cm × 15 cm × 25 cm = 4,0 dm × 1,5 dm × 2,5 dm
V = 4,0 dm ∙ 1,5 dm ∙ 2,5 dm = 15 dm3 = 15 l
Metod 2
Vi kan också välja att göra enhetsomvandlingen i slutet:
V = 40 cm 15 cm ∙ 25 cm = 15 000 cm3 = 15 ∙ 1 000 cm3 =
= 15 ∙ 1 dm3 = 15 l
Svar: Kartongen rymmer 15 liter.
000 cm3 = 1 dm3 = 1
8147 Ungefär hur mycket rymmer en regntunna?
P
Starter
Hur många droppar läsk är det i en läskburk?
Nivå 1
8144 Ange om följande enheter mäter längd, area eller volym.
mm cm2 m3 m2 dl km
8145 Skriv som centimeter
a) 2,75 m b) 129 mm c) 2,1 dm
8146 Skriv som millimeter
a) 4,5 cm b) 1,05 m c) 0,53 dm
A 20 l
B 200 l
C 2 000 l
8148 Ungefär hur mycket rymmer ett dricksglas?
A 20 cm3
B 200 cm3
C 2 000 cm3
8149 Du vet att 1 dm = 10 cm. Rita en bild som förklarar varför a) 1 dm2 = 100 cm2
b) 1 dm3 = 1 000 cm3
8150 Skriv som kvadratmeter a) 10 000 cm2 b) 543 dm2
GEOMETRI u 8.1 OMkRETs, aREa OcH VOlyM 313
Exempel
Tilde, Roman och Pernilla diskuterar hur mycket 3,5 dm3 är.
− Det är lika mycket som 3,5 dl, säger Tilde.
− Nej, det är lika mycket som 0,35 m3, säger Roman.
− Ni har båda fel, säger Pernilla. 3,5 dm3 är lika mycket som 3 500 cl.
Tips till din undervisning
Har någon av dem rätt? Motivera.
Lösning/Kommentar
Eftersom 1 dm3 = 1 liter gäller att
3,5 dm3 = 3,5 liter = 35 dl, så Tilde har fel.
I Lärarguiden hittar du mängder av tips till din undervisning. Det kan vara förslag på inledande problem, kommentarer till kritiska punkter i lärandet, en historisk utvikning eller en matematisk fördjupning.
1 m3 = 1 000 dm3, så 0,35 m3 = 350 dm3. Roman har alltså fel.
3,5 dm3 = 3,5 l = 350 cl, så även Pernilla har fel.
Det kan vara värt att uppmärksamma att omvandlingsfaktorn mellan volymenheterna i metersystemet är 1 000 medan den i litersystemet är 10.
3,5 dm3 = 3 500 cm3 = 3 500 000 mm3
3,5 l = 35 dl = 350 cl = 3 500 ml
Starter
Svar: En droppes storlek kan variera, men i medicinska sammanhang brukar man ge riktvärdet
1 ml ≈ 20 droppar
Om burken innehåller 33 cl = 330 ml, innebär det att den innehåller ungefär 6 600 droppar.
Alternativ starter
Hur många människor får plats på en yta stor som Gotland?
Svar: Gotlands area är ungefär 3 140 km2. Det motsvarar
3 140 000 000 m2. Om vi räknar med att det får plats
4 människor på 1 m2, så får det plats
3 140 000 000 ∙ 4 = 12 560 000 000 människor på Gotlands yta.
Det är mer än hela jordens befolkning!
Låt gärna eleverna undersöka praktiskt hur många människor som får plats på ytan av en kvadratmeter. Det kan de exempelvis göra genom att ställa sig innanför en kvadratmeter som du har tejpat upp på golvet.
För att se hur man kan omvandla längd-, area- och volymenheter kan de här lathundarna vara en hjälp för en del elever.
Längdenheter
1 m = 10 dm = 100 cm = 1 000 mm
· 10 · 10 · 10
m dm cm mm
/ 10 / 10 / 10
Areaenheter
1 m2 = 100 dm2 = 10 000 cm2 = 1 000 000 mm2
· 100 · 100 · 100 m2 dm2 cm2 mm2
/ 100 / 100 / 100
Volymenheter
1 m3 = 1 000 dm3 = 1 000 000 cm3 = 109 mm3
· 1 000 · 1 000 · 1 000 m3 dm3 cm3 mm3
/ 1 000 / 1 000 / 1 000
Kommentarer till uppgifterna
För en del elever kan det vara svårt att beräkna värdet av ett uttryck när variabeln är negativ eller 0. Det får eleverna träna på i 3103, 3108, 3111 och 3117
Uppgift 3105 sätter fokus på skillnaden mellan formel och uttryck.
Uppgifterna 3109 och 3112 liknar Startern och passar bra att genomföra två och två. Uttrycken ger exempel på de osynliga multiplikationstecken som en del elever har svårt för. Elever som snabbt blir klara kan uppmanas att ge ett mer precist svar i c)-uppgiften: För vilka värden på x är värdet av x2 större än värdet av 2x?
3113 är en uppgift som anknyter till vardagslivet, men är särskilt relevant för de elever som utbildar sig inom transport. Det är bra att känna till att bromssträckan fyrdubblas när hastigheten fördubblas. I uppgiften får eleverna visa detta med hjälp av ett räkneexempel. En utvidgning är att låta eleverna motivera tumregeln i b)uppgiften mer generellt, till exempel genom att jämföra uttrycken om man sätter in v respektive 2v i formeln.
I förstoringsglasuppgiften 3115 behöver eleverna uppskatta avståndet och tiden det tar att köra bil från skolan hem till dem. Det är viktigt att eleverna uppmärksammar att tiden ska anges i timmar. Även uppgift 3114 b) är märkt med förstoringsglas, eftersom det finns flera svar.
För att lösa förstoringsglasuppgiften 3116 behöver eleverna ta reda på att höjden av Mount Everest är 8 848 meter. Om eleverna får fel svar i uppgiften kan det bero på att de inte har uppmärksammat att höjden h ska anges i kilometer.
Ledtrådar till uppgifterna
3103 Beräkna värdet av y i formeln y = 20x + 50
om
a) x = 1
b) x = 0
c) x = −0,5
3104 Omkretsen av triangeln kan beräknas med uttrycket 2x + 7. Hur stor är omkretsen om x = 12? 7 x x (cm)
3105 Vilka av alternativen i rutan är
a) formler
b) algebraiska uttryck
y = 2x − 3 2x − 3 U = R ∙ I 3a + 5b
3106 Kostnaden K kronor för att hyra en moped i Thailand x dagar kan man beräkna med formeln K = 150 + 50x
a) Vad kostar det att hyra en moped i 3 dagar?
b) Vad kostar det att hyra en moped i 3 veckor?

Kommentarer och ledtrådar till uppgifterna Till varje avsnitt finns kommentarer till avsnittets uppgifter. Där diskuteras bland annat svårigheter och uppgifternas koppling till olika förmågor. Vi ger också förslag till ledtrådar till utvalda uppgifter.
3109 c) Testa dig fram med olika värden på a. Kom ihåg att värdet på a även kan vara 0 eller negativt.
3110 c) Bestäm något värde på p, t.ex. p = 100. Vilket värde måste a då ha för att I = 100 000 kr?
3112 c) Testa dig fram med olika värden på x. Kom ihåg att x inte måste vara ett heltal.
3114 b) Svaret beror på hur mycket grisarna väger. Du får själv bestämma grisarnas vikt.
3115 Här behöver du själv uppskatta värdet av x och y Hur många kilometer är det från skolan till ditt hus? Hur lång tid (i timmar) tar det att åka taxi från skolan hem till dig?
3116 När vatten väl kokar, ökar inte dess temperatur. För att äggulan ska koagulera måste alltså vattnets kokpunkt vara 70 grader eller mer.
3107 Med hjälp av formeln
beräkna volymen av en cylinder med radien r och höjden h. Vilka två beräkningar ger volymen av cylindern i figuren?
4 3108 Beräkna värdet av uttrycken om a = −3 och b = 6. a) 2a + b b) a
b c) ab d) b a
3109 Uttrycken 3 + a och 3a ser ganska lika ut. a) Vad är skillnaden mellan dem? b) Vad är värdet av uttrycken om a = 5? c) Är värdet av 3a

a + b = 25
Vad är värdet av 2a + 2b + 4?
Lösning/Kommentar
2a + 2b + 4 = a + a + b + b + 4 = (a + b) + (a + b) + 4 = = 25 + 25 + 4 = 54
Den här uppgiften gavs på TIMSS 2011 och löstes av 43,9 % av eleverna i årskurs 8. Uppgiften kräver att eleverna uppmärksammar uttryckets struktur och inser att 2a + 2b = 2(a + b).
Yrkesmatematik – formler
3112 Jämför uttrycken x2 och 2x
a) Förklara vad som skiljer uttrycken åt.
b) Vad är värdet av uttrycken om x = 3?
c) Är värdet av x2 alltid större än värdet av 2x?
3113 Bromssträckan s meter för en personbil med hastigheten v km/h är s = 0,005 ∙ v2
a) Beräkna bromssträckan för en bil med hastigheten 50 km/h.
b) En tumregel säger att om hastigheten fördubblas, så fyrdubblas bromssträckan. Undersök med ett räkneexempel om tumregeln stämmer.
71nn En gris som väger x kg ska enligt Jordbruksverket ha ett utrymme som är minst y m2, där
y = 0,20 + x 84
a) Hur stort utrymme behöver en gris som väger 50 kg?
b) En bonde har ett utrymme på 30 m2 Hur många grisar kan han ha där?
71nn Kostnaden för att åka taxi kan beräknas med formeln
K = 65 + 15x + 600y där K är kostnaden i kronor, x är antalet kilometer och y är tiden i timmar. Vad skulle det kosta att åka taxi från skolan hem till dig?
Nivå 3
3116
Vattnets kokpunkt ändras med höjden över havet. Den kan beräknas med formeln t = 100 · 0,961h där t är kokpunkten i grader Celsius och h är höjden över havet i kilometer. Äggula koagulerar vid temperaturen 70 grader. Är det möjligt att koka och servera ett hårdkokt ägg på toppen av Mount Everest?
3117 Beräkna värdet av uttrycken för x = −2, y = 1 och z = −3.
a) x2 + 3xy − z2
b) 2xz + 5y − z3
c) 4xyz − xz2
Det förekommer en mängd formler, både implicit och explicit, i elevernas yrkesämnen. En elev som läser fysik eller ellära kan stöta på formler som:
U = R ∙ I spänning = resistans ∙ strömstyrka
P = W t effekt = energi tid
P = U ∙ I effekt = spänning ∙ strömstyrka
En elev som studerar VVS och fastighet kan använda en formel för att beräkna transmissionsförluster:
P = A ∙ U ∙ ∆T P = effekt, A = area på byggnadsdelen, U = U-värde för byggnadsdelen, ∆T = inomhustemperatur minus utomhustemperatur
I Lärarguiden lyfter vi matematikens relevans. Här finner du konkreta exempel på hur matematiken används i elevernas yrkesämnen.

ALGEBRA u 3.1 fORmLER, uttRycK Och möNStER
69
Att tänka på
I många yrkesämnen skrivs formler med ord i stället för med variabler, till exempel
intäkt = försäljningsvolym ∙ pris per styck
massa = densitet ∙ volym
mått på bukfetma = midjemått (cm) höftmått (cm)
Diskutera gärna med eleverna vad som är vanligt i deras yrkesämnen, och vilka för- och nackdelar det finns med olika skrivsätt.
Exituppgift
Beräkna värdet av uttrycken om a = 4 och b = −3
a) 2a + 6 b) 5a + 2b
c) 4a − 2b d) a2 − b2
Svar: a) 14 b) 14 c) 22 d) 7
och en elev som arbetar med motorer kan vara intresserad av motorns verkningsgrad:
verkningsgrad = η = nyttiggjord energi tillförd energi
En del formler innehåller fler variabler och är mer komplicerade än de formler som eleverna möter i matematiken. Med den här formeln kan eleverna exempelvis uppskatta det procentuella felet när de använder sig av ett mätverktyg:
Felet = √(mätarfel)2 + (metodfel)2 + (avläsningsfel)2 och i ellära förekommer formeln
IB = P √3 ∙ U ∙ cos φ för att beräkna belastningsström.
Men det är inte bara inom de tekniska yrkesprogrammen som eleverna använder formler. I uppgift 3114 möter eleverna en formel från Jordbruksverket som anger hur stort utrymme ett boskapsdjur ska ha. Även i kurser i företagsekonomi och entreprenörskap förekommer mängder av formler.
marginal (kr) = försäljningspris ex. moms − varukostnad marginal (%) = marginal i kr försäljningspris ex. moms
Låt eleverna ge exempel på formler som de använder i sina yrkesämnen eller be om exempel från elevernas yrkeslärare. Det är ett enkelt sätt att synliggöra hur matematiken används i elevernas yrkesämnen.
Edvard löser 2,5 g druvsocker i en plastflaska med 550 g vatten. Bestäm lösningens sockerkoncentration i promille.
Lösning/Kommentar
Lösningen väger (550 + 2,5) g = 552,5 g
Koncentration: delen det hela = 2,5 g 552,5 g ≈ 0,0045 = 4,5 ‰
Svar: Lösningens koncentration är 4,5 ‰.
Starter
Svar: Det är lätt att jämföra tal som står i samma form. Vi skriver därför alla tal i decimalform.
0,001
800 ppm = 0,0008
0,9 % = 0,009
8 ‰ = 0,008
I storleksordning:
800 ppm 0,001 8 ‰ 0,9 %
Alternativ starter
Vad är mest?
6 ‰ av 2 000 eller 4 ppm av 3 000 000
Svar:
6 ‰ av 2 000 = 6 ∙ 2 000 1 000 = 6 ∙ 2 = 12
Starter
Exempel: För att ett livsmedel ska få kallas glutenfritt, måste andelen gluten ligga under 20 ppm. En maträtt som väger 349 gram innehåller 0,1 gram gluten. Klarar den gränsvärdet?
Lösning: Vi beräknar andelen gluten. andelen = delen det hela = 0,1 349 ≈ 0,000 29 = 290 ppm Mer än gränsvärdet 20 ppm
0,000 29 = 0,000 290
Svar: Nej, maträtten får inte kallas glutenfri.
Skriv talen i storleksordning. Börja med det minsta.
0,001 800 ppm 0,9 % 8 ‰
Nivå 1
4330 Skriv i decimalform
a) 5 ‰ b) 50 ‰
c) 500 ‰ d) 0,5 ‰
4331 Skriv som promille
a) 0,004 b) 0,073
c) 0,0012 d) 0,6 %
4332 Skriv i decimalform
a) 7 ppm b) 38 ppm
c) 905 ppm d) 4 300 ppm
4333 Skriv som ppm
a) 0,000 009 b) 0,000 436
c) 0,000 2 d) 5 ‰
4 ppm av 3 000 000 = 4 ∙ 3 000 000 1 000 000 = 4 ∙ 3 = 12
Talen är lika stora.
Att tänka på
En del elever tror att beräkningar med promille och ppm är något som kräver nya metoder. Det är därför viktigt att betona att procent, promille och ppm bara är olika sätt att beskriva andelar. Om man väljer att använda procent, promille eller ppm beror på andelarnas storlek och vad som är praktiskt. Ibland fungerar det lika bra att använda procent som att använda promille.
■ Promille och ppm
Aktivitet
■ Memory med andelar
4334 Para ihop de tal som är lika stora.
4 ‰
0,4 ‰ 0,000 004 4 ppm
4335 Hur mycket är a) 8 ‰ av 1 000 kr b) 1 ppm av 2 000 000 kr
4336 Beräkna a) 14 ‰ av 3 500 kr b) 2,5 ‰ av 65 000 kr c) 3,5 ppm av 3,5 miljoner kronor
4337
Problemlösningsuppgift
En del elever behöver mer färdighetsträning än vad som erbjuds i läroboken, medan andra elever i stället behöver mer utmanande arbetsuppgifter. Till många avsnitt i läroboken finns därför extra färdighetsträning i form av Övningsblad och mer omfattande uppgifter, inte sällan med en koppling till yrkeslivet, som vi kallar Aktiviteter. Övningsbladen och aktiviteterna säljs separat som nedladdningsbara dokument.
När man dricker alkohol tas den upp av kroppen. Alkoholhalten i kroppen kan uppskattas med formeln:
alkoholhalt (kvinnor) = vikt ren alkohol (kg) kroppsvikt (kg) · 0,55
alkoholhalt (män) = vikt ren alkohol (kg) kroppsvikt (kg)· 0,65
1 ml alkohol väger 0,78 g. Uppskatta alkoholhalten i promille för en man/kvinna som väger lika mycket som du och dricker tre folköl à 0,5 l med alkoholhalten 2,8 %.
Lösning/Kommentar
Alkoholen i 1 500 ml folköl väger:
1 500 ml ∙ 0,028 ∙ 0,78 g/ml = 32,76 g = 0,03276 kg
Vi beräknar alkoholhalten för en man som väger 70 kg: 0,03276
70 ∙ 0,65 = 0,00072 = 0,72 ‰
Svar: Alkoholhalten är ca 0,72 ‰.
4339 Under en influensaperiod drabbades 8,3 ppm av ett lands befolkning av allvarliga följdsjukdomar. Hur många av landets 17,2 miljoner invånare drabbades?
71nn På Polisens webbplats kan man läsa att gränsen för rattfylleri går vid 0,2 ‰ alkohol i blodet. Hur många milliliter ren alkohol har man i blodet vid gränsen för rattfylleri?
4341 Tabellen visar hur barnadödligheten i Sverige har förändrats över tid.
År Dödsfall före 5 års ålder per 1 000 födda barn
1800 381
1900 155
2000 4
2020 3
a) Hur stor var barnadödligheten år 2020 uttryckt i promille?
b) Med hur många procent minskade barnadödligheten mellan år 1900 och år 2020?
Nivå 2
4342 Tabellen visar förekomsten av nickel i några olika tatueringsfärger.
Färg Nickel (mg per kg)
Beast black 666
Divers blue 89
Goth black 110
Hipster pink 7
Purple rain 9
Red as love 100
Enligt EU får andelen nickel i färgen inte överstiga 10 ppm. Vilken eller vilka av färgerna i tabellen klarar gränsvärdet?
4343 I en gruva har man fastställt att det finns
120 gram silver och 0,4 gram guld i 1 ton malm. Beräkna a) silverhalten b) guldhalten

71nn För en få en viss färgnyans behöver man tillsätta 5 droppar färgpigment till 0,5 liter färg. Ungefär hur stor andel färgpigment finns det i den färdiga färgen? Svara i a) procent b) promille c) ppm
4345 Skriv a) 0,85 ‰ som ppm b) 65 000 ppm som promille
4346 Ordna följande tal i storleksordning. Börja med det minsta.
520 ppm 4,2 ‰ 0,05 %
4347 Frida är olycksfallförsäkrad hos ett försäkringsbolag. Årspremien är 1 044 kr vilket motsvarar 1,16 ‰ av försäkringsbeloppet. Hur stort är hennes försäkringsbelopp?
71nn Dricksvatten som innehåller mer än 0,5 mg järn per liter bör renas. Hur många ppm motsvarar det?
PROCENT u 4.3 PROCENTBERäkN NgAR i SAMhällET 153
P
Kommentarer till uppgifterna
Även i det här avsnittet kan man med fördel arbeta med huvudräkning och överslagsräkning. Uppgifterna 4337 och 4338 är exempel på uppgifter som kan lösas utan räknare. I 4339 kan eleverna uppskatta värdet med en överslagsberäkning.
För att lösa uppgift 4340 behöver eleverna veta att man har ca 5 liter blod i kroppen om man väger ungefär 70 kg. Man brukar räkna med att blodet är ca 7–8 % av kroppsvikten.
I förstoringsglasuppgiften 4344 används volymmåttet 1 droppe. En sökning på nätet visar att det går 20 droppar på 1 ml, dvs. 1 droppe = 0,05 ml. När eleverna ska beräkna andelen är det lämpligt att göra dem uppmärksamma på att den totala mängden är 500,25 ml, inte 500 ml. I den här uppgiften syns inte skillnaden i svaret, när man har avrundat till lämpligt antal decimaler, men i andra sammanhang kan denna begreppsliga förståelse vara avgörande. I uppgiften får eleverna uttrycka samma andel på olika sätt och sedan reflektera kring vilket uttryckssätt som är mest lämpligt i sammanhanget.
Uppgift 4346 liknar Startern. Här får eleverna se att en andel given i ppm kan vara större än en annan andel i procent.
I förstoringsglasuppgiften 4348 utnyttjar man att 1 liter vatten väger nästan exakt 1 kilogram.
Ledtrådar till uppgifterna
4340 En människa har ungefär 5 liter blod i kroppen.
4342 Hur många milligram går det på 1 kg? (1 kg = 1 000 g och 1 g = 1 000 mg)
I varje avsnitt ges förslag på uppgifter som du kan använda för att inleda och avsluta lektionen.
4344 1 droppe är ungefär 0,05 ml.
4345 Börja med att skriva talen i decimalform.
4347 Hela försäkringsbeloppet motsvarar 1 000 ‰.
4348 Räkna med att 1 liter vatten väger 1 kg.
Hur mycket är
a) 5 ‰ av 2 000 kg
b) 9 ppm av 3 000 000 kr
Svar:
a) 10 kg b) 27 kr
Uppgifterna på Uppslaget kan användas i slutet av varje kapitel, men de passar också bra att arbeta med under kapitlets gång. I tabellen ser du i vilket avsnitt som uppgifterna passar särskilt bra.
Rubrik Uppgift Delkapitel och avsnitt
Vem har rätt?
1 3.3 Mer om ekvationslösning
2 3.2 Att förenkla uttryck
3 3.1 Mönster och formler
Problemlösning 1, 2, 3 3.3 Problemlösning med ekvationer
Modellering 1 3.1 Ställa upp och tolka formler och uttryck
2 3.1 Ställa upp och tolka formler och uttryck
Matematik i användning
Vem har rätt?
1 tre personer har försökt lösa ekvationen
5(2x − 8) + 30 = 45
Vem har löst ekvationen korrekt?
Vilka fel har de andra gjort?
Agneta 10x − 8 + 30 = 45
10x + 22 = 45
10x = 23
x = 2,3
Beata 10x − 40 + 30 = 45
10x − 10 = 45
10x = 35
x = 3,5
Calle
5(2x − 8) + 30 = 45
5(2x − 8) = 15
2x − 8 = 3
2x = 11
x = 5,5
Fullständiga lösningar
3.1 Formler i kalkylprogram
1 Calle har löst ekvationen rätt.
I Lärarguiden finns svar och lösningar till Resonemang och begrepp, Uppslaget, Samhälle och yrkesliv samt till Kapiteltest Längst bak i Lärarguiden finns även fullständiga lösningar till lärobokens Nivå 3uppgifter.
Agneta utför multiplikationen 5(2x − 8) felaktigt. Hon multiplicerar bara 5 med den första termen i parentesen, men inte med den andra. Därefter stämmer hennes lösning.
Beata subtraherar 10 från högerledet och får 35, i stället för att addera 10 och få 55.
2 a) Robin ersätter bokstaven a med siffran 4, så att 3a blir 34. Han vet inte att 3a betyder 3 ∙ a Ivan tror att a:na tar ut varandra, dvs. att 3a − a + 8 = = 3 + 8. Han vet inte att 3a − a = 2a b) a = 4 ger 3a − a + 8 = 2a + 8 = 2 ∙ 4 + 8 = 16
3 Almas och Toruns formler är rätt, men Bahrams formel är fel.
Alma kan ha tänkt att den nedre raden består av n + 1 rutor och att kvadraten ovanpå består av n2 rutor. Torun kan ha tänkt att om man lägger till n rutor, så får man en kvadrat med sidan (n + 1) rutor. Antalet rutor är därför (n + 1)2 − n
Bahram kan ha tänkt att om man flyttar den övre kvadraten med rutor åt vänster, så får man en rektangel med sidorna n och (n + 1) och en ruta som sticker ut. Antalet rutor är därför n(n + 1) + 1, men Bahram har gjort fel och lagt till n rutor i stället för 1 ruta.
Kommentar: Uppgift 3 kan utvidgas till att algebraiskt visa vilka uttryck som är ekvivalenta. En alternativ ingång till uppgift 3 är att låta eleverna själva finna en formel för antalet rutor i figur n. Den aktiviteten (Problemlösningsuppgifter Algebra, uppgift 3) finns i kopieringsmaterialet Prov, Övningsblad och Aktiviteter
Problemlösning
1 Ett tåg startar från Stockholm.
u I Sala ökar antalet passagerare med 10.
u I Krylbo blir antalet passagerare hälften så stort.
u I Säter minskar antalet passagerare med 5.
Därefter finns det 102 passagerare på tåget. hur många passagerare fanns på tåget när det lämnade Stockholm?
2 Robin och Ivan beräknar värdet av uttrycket
3a − a + 8 för a = 4. De gör på olika sätt.
Robin: 34 − 4 + 8 = 38
Ivan: 3 + 8 = 11
a) Vilka fel har Robin och Ivan gjort? b) Beräkna värdet av uttrycket.
3 Alma, torun och Bahram har skrivit var sin formel för hur många rutor som finns i figur n hur kan de ha tänkt? har någon av dem gjort rätt?
Alma n + 1 + n2
Torun (n + 1)2 − n Bahram n(n + 1) + n n = 1 n = 2 n = 3
2 I en frågesport får du 3 poäng om du ger rätt svar, men ett minuspoäng om du svarar fel eller inte svarar alls. Kan du få 16 poäng om du har svarat på tio frågor?
3 Det är rea på varuhuset. Amanda köper ett par byxor, en tröja och ett par skor och får betala 1 180 kr. Byxorna kostar 100 kr mer än tröjan. Byxorna och tröjan kostar tillsammans 180 kronor mer än skorna. hur mycket kostar varje plagg?
1 Låt x vara antalet passagerare från början. Det ger ekvationen
x + 10 2 − 5 = 102 som har lösningen x = 204
Svar: Det var 204 passagerare på tåget när det lämnade Stockholm.
Kommentar: En alternativ lösningsmetod är att arbeta baklänges. Det kan vara intressant att visa att de beräkningar man gör då, är precis desamma som man gör vid ekvationslösningen.
Eleverna kan få skapa liknande uppgifter till varandra, där de utgår från tåg- eller busstationer i närheten.
2 Anta att antalet rätta svar är x. Då är antalet felaktiga svar 10 − x. Eftersom vi får 3 poäng för rätt svar och −1 för ett felaktigt svar, kommer det totala antalet poäng att ges av uttrycket 3x − 1(10 − x). Vi undersöker om ekvationen
3x − 1(10 − x) = 16 har någon heltalslösning.
3x − 1(10 − x) = 16
3x − 10 + x = 16
4x = 26
x = 6,5
Ekvationen har lösningen x = 6,5 som inte är ett heltal.
Det betyder att resultatet 16 inte är möjligt.
Modellering
1 titi hyr en glasskiosk en sommar. hjälp henne att ställa upp en formel som visar hur hennes vinst beror av antalet glassar hon säljer. Du får själv uppskatta vilka kostnader och intäkter titi har, men listan här nedanför kan ge lite inspiration.
Arbetstid
Timlön
Hyra för lokal
Kostnader för glass och strutar Försäljning av glass

2 med body mass index, BmI, kan man bedöma om en person är underviktig eller överviktig. formeln för BmI är
BmI = m l2
där m är personens vikt i kilogram och l är längden i meter. I uSA bestämmer man BmI med vikt i pounds och längd i inches. Gör om formeln så att den ger samma svar med pounds och inches
Matematik i användning
På många hemsidor kan du få hjälp att göra beräkningar. Du kan exempelvis få hjälp att beräkna din lön efter skatt eller beräkna hur många liter vatten som ryms i en pool med vissa mått. hemsidornas beräkningsverktyg har skapats med hjälp av formler. I den här uppgiften får du hjälpa en förening att skapa sådana formler. En förening hyr ut sin klubbstuga för
2 000 kronor i grundavgift och sedan 150 kronor per gäst och dygn. föreningen vill att de som bokar via hemsidan snabbt ska kunna beräkna vad det kostar att hyra stugan.
u hjälp föreningen genom att ange vilka formler som ska stå i cell B3−B5. Använd gärna ett kalkylprogram för att testa dina formler.
B 1 Antal gäster
2 Antal nätter
3 Total summa
4 Total summa per gäst
5 Total summa per natt för varje gäst
u UPPSLAGET 115
Kommentar: Eftersom antalet frågor är begränsat kan problemet också lösas med en tabell:
3 Anta att tröjan kostar x kr. Då kostar byxorna x + 100 kr och skorna x + (x + 100) − 180 kr = 2x − 80 kr. Det ger ekvationen
x + (x + 100) + (2x − 80) = 1 180 som har lösningen x = 290.
Svar: Tröjan kostar 290 kr, byxorna kostar 390 kr och skorna kostar 500 kr.
Kommentar: Elever som löser uppgiften på det här sättet kan få i uppgift att lösa den på nytt genom att låta byxorna eller skornas pris vara x kr.
1 Vi väljer att göra följande antaganden och uppskattningar:
Kostnader:
Personal: 1 500 kr per person och dag
Hyra: 9 000 kr per månad
Glasskula: 6 kr per styck
Strut: 5 kr per styck
Prissättning:
Strut med 1 kula: 40 kr
Strut med 2 kulor: 50 kr
Strut med 3 kulor: 60 kr
Vinsten för en glass med en kula är 29 kr. För två kulor är vinsten 33 kr och för tre kulor är vinsten 37 kr.
Låt x, y och z vara antalet glassar med en, två respektive tre kulor en dag. Om p är antalet anställda så ges vinsten, V kr per dag, av formeln
V = 29x + 33y + 37z − 1 500p − 9 000 30
Kommentar: Här har vi valt att införa en variabel för varje typ av glass. Formeln blir enklare om man antar att man säljer ungefär lika många glassar av varje sort. Då är vinsten i genomsnitt 33 kr per glass och man behöver bara ha en variabel som anger det totala antalet glassar. Diskutera gärna med eleverna vad som är viktigast − enkelhet eller precision? Det beror kanske på om Titi vill ha en grov uppskattning av om verksamheten går runt, eller om hon vill ha precisa formler till sina budgetberäkningar.
Det är relativt enkelt att anpassa svårighetsgraden genom att lägga till eller dra ifrån parametrar i uppgiften. Vi har till exempel valt att inte ha med några bägare. Eftersom eleverna själva väljer kostnadsposter och intäktsposter, kan de också själva välja hur komplicerad modell de vill göra. Vi har valt att göra vinstberäkningen per dag, men eleverna kan också välja att göra den per månad. Hur ser formeln ut då?
En utvidgning av uppgiften är att låta eleverna implementera sina formler i ett kalkylprogram och undersöka hur många glassar Titi måste sälja för att gå med vinst.
2 1 pound ≈ 0,454 kg och 1 inch ≈ 2,54 cm = 0,0254 m ger formeln
BMI = 0,454m (0,0254l)2 m är vikten i pounds och l är längden i inches
Svar till Matematik i användning
1 Antal gäster 2 Antal nätter
3 Total summa =2000+B1*B2*150
4 Total summa per gäst =B3/B1
5 Total summa per natt för varje gäst =B4/B2
ihop termer av samma sort
förenkla algebraiska uttryck
av första graden 7x − 6 = 3x + 28 Det är flest x i vänstra ledet. Vi samlar därför x-termerna där. 7x − 6 − 3x = 3x + 28 −

Moment Avsnitt Blandade uppgifter
Ge exempel på begreppen variabel, konstantterm och koefficient
Beräkna värdet av ett algebraiskt uttryck
Använda formler
Tolka uttryck och formler
Beskriva ett mönster med ord eller med en formel
Skapa och använda formler i kalkylprogram
3.1 Nivå 1: 8, 9
3.1 Nivå 1: 1, 8, 15 Nivå 2: 29, 30, 31 Nivå 3: 41
3.1 Nivå 1: 8, 10, 11, 12
3.1 Nivå 1: 12, 13, 14, 19, 25 Nivå 3: 42
3.1 Nivå 1: 22, 25 Nivå 2: 37, 38
3.1 Nivå 1: 21 Nivå 2: 39
Moment Avsnitt Blandade uppgifter
Förenkla algebraiska uttryck genom att räkna ihop term av samma sort
Förenkla algebraiska uttryck med parenteser
Faktorisera algebraiska uttryck
Pröva om en lösning till en ekvation är rätt
Lösa ekvationer av första graden
Använda ekvationer vid problemlösning
3.2 Nivå 1: 2, 7
3.2 Nivå 1: 3, 16, 20, 26 Nivå 2: 28, 31, 33 Nivå 3: 40, 41
3.2 Nivå 1: 17 Nivå 2: 32 Nivå 3: 40
3.3 Nivå 1: 4 Nivå 2: 34
3.3 Nivå 1: 5, 6 Nivå 2: 27
3.3 Nivå 1: 12, 13, 18, 23, 24
Nivå 2: 34, 35, 36 Nivå 3: 42
Aktivitet
■ Koll på kapitlet 3
1 Beräkna värdet av uttrycket 5x + 8 om a) x = 5 b) x = −2 c) x = 0
2 Förenkla uttrycken
3 Förenkla uttrycken
a) 10 + (4b − 7)
b) 18m − (13n + 10m)
c) 12x − 3(x + 5)
4 Pröva om x = 4,5 är en lösning till ekvationen 4x + 9 = 32 − x
5 Lös ekvationerna
a) 5x + 3 = 38
b) 12 = 18 − 1,2y
c) 4x 3 = −16
6 Lös ekvationerna
a) 4(x − 3) + 7 = 35
b) 5x − 12 = 24 − x
c) 3x + 17 = 6x + 26
8 Kostnaden K kr per månad för att ringa och skicka sms från Polen till Sverige kan man beräkna med formeln
K = 150 + 1,29x + 0,99y där x är antalet samtalsminuter och y är antalet skickade sms.
a) Vilka variabler finns i formeln? b) Vad blir månadskostnaden om du ringer 35 minuter och skickar 17 sms?
9 Vad i uttrycket 25x + 7y + 4 är
a) variabel
b) konstantterm
c) koefficient
10 Skriv formler som visar följande samband
a) y är 18 mindre än x
b) x är en tredjedel så stort som y
11 Formeln beskriver det n:te talet i en talföljd. Bestäm de tre första talen i talföljden
a) a = 2n b) a = n − 1
c) a = 2n − 1 d) a = n2 + 1
12 Man mäter hastighet i både meter per sekund (m/s) och kilometer i timmen (km/h). För att omvandla mellan enheterna använder man formeln
3,6 ∙ hastigheten i m/s = hastigheten i km/h
a) När det blåser 25 m/s är det storm. Hur många kilometer i timmen är det?
13 Energiåtgången när Pär duschar kan beräknas med formeln E = 0,44 ∙ t där E är energiförbrukningen i kilowattimmar (kWh) och t är tiden i minuter.
a) Hur mycket energi använder Pär om han duschar i 5 minuter?
b) Hur länge har Pär duschat om han använt 6,7 kWh?
14 Kostnaden K kr för att anlita en tekniker i x timmar ges av K = 550x + 400. Vad betyder talen 550 och 400 i formeln?
15 Beräkna värdet av uttrycket x2 − 2x om
a) x = 3 b) x = −3 c) x = 0
16 Utför multiplikationerna
a) x(x + 3) b) 4y(y − 2)
17 Bryt ut största möjliga faktor
a) 6x + 12 b) 10a − a2 c) 22y + 11y2
18 Erik har köpt två påsar med fågelfrön. En av påsarna väger 3 kg mer än den andra. Tillsammans väger påsarna 19 kg. Hur mycket väger den tyngre påsen?

20 Multiplicera och förenkla uttrycken a) (x + 3)(
21 Företaget IceCold säljer is i olika former. De använder ett kalkylprogram för att få koll på sitt lager.
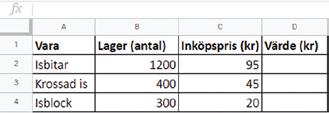
Ta hjälp av ett kalkylblad och beräkna a) det totala värdet av isbitarna b) det sammanlagda värdet av företagets samtliga produkter
22 Titta på talföljden 3, 6, 9, 12, … a) Vilket är nästa tal i talföljden? b) Beskriv talföljden med ord eller med en formel. c) Vilket är det tjugonde talet i talföljden?
23 Lisa arbetar som säljare av mobilabonnemang. Hon får 5 000 kr i månaden och dessutom 150 kr för varje abonnemang hon säljer. Hur många abonnemang måste Lisa sälja för att tjäna minst 12 000 kr per månad?
7 Teckna ett uttryck för fyrhörningens omkrets och förenkla uttrycket så långt som möjligt. x 3x 3x + 1 x + 2
b) Hur många meter per sekund är 72 km/h?
19 I ett skogsområde finns x stycken kaniner och y stycken rävar. Tolka vad det betyder att a) x + y = 110 b) x = 10y
25 Titta på talföljden 5, 8, 13, 20, … Vilken formel beskriver tal nummer n i talföljden? a = 4n + 1 a = 3n + 2 a = n2 + 4 Nivå 1
■ Repetitionsuppgifter kapitel 3
24 Eva och Lina har vunnit 4 300 kr på trav. Eva ska få dubbelt så mycket som Lina, men innan de delar vinsten måste de betala tillbaka 700 kr till Linas mamma. Ställ upp en ekvation och beräkna hur mycket Eva får.
33 Förenkla uttrycken
26 Förenkla uttrycket så långt som möjligt.
(x + 3)(5x − 1) − x2
Nivå 2
27 Lös ekvationerna
a) 12 − 6x = 3,5 − x b) 5x 2 = 19,2 − x 2
28 Vilket tal ska stå i stället för rutan?
a) 5y + 30 = 5(y + )
b) 4xy + 36x = (2xy + 18x)
c) 3x + 6y + 9 = (x + 2y + )
29 Beräkna värdet av uttrycket
−6(2a − 7) − 5(a + 8) för a = 2.
30 Beräkna värdet av uttrycken för a = 3 och
b = −2.
a) a2 − b
b) ab + b2
c) a b + ab2
31 En tomt har formen av en rätvinklig triangel.
x + 2
2x − 4 (m)
a) Skriv ett uttryck för triangelns area.
b) Förenkla uttrycket så långt som möjligt.
c) Beräkna tomtens area om x = 30.
32 Faktorisera uttrycken
a) 12x3 − 20x2
b) −15y2 + 30x2y
c) 8x3 + 2x2 − 4x
(9
c) (3a + 2b)(−b + 4a) − (13ab + 2)
34 Ron har fått uppgiften: ”Albus är 3 år äldre än sin bror Severus.
Minerva är dubbelt så gammal som Albus. Tillsammans är de 29 år. Hur gammal är Albus?”
Ron väljer att lösa uppgiften med hjälp av en ekvation och hans lösning ser ut så här:
x + (x − 3) + 2x = 29 x + x − 3 + 2x = 29 4x − 3 = 29 4x = 32
x = 8
Svar: x = 8
Ge Ron återkoppling på lösningen. Vad har han gjort som är bra? Vad kan förbättras?
35 Maria, Andreas och Patrik springer stafett. Andreas springer på dubbelt så lång tid som Maria och Patrik har 27 minuter längre tid än Andreas. Sammanlagt har de sprungit i 2 timmar och 22 minuter. Hur lång tid behövde var och en på sin sträcka?
36 Summan av tre på varandra följande heltal är 111. Ställ upp en ekvation och bestäm talen.
37 Titta på talföljden 100, 104, 108, … a) Beskriv talföljden med ord eller med en formel.
b) Bestäm det tionde talet i talföljden.
38 De här figurerna består av rutor. 1 2 3
a) Fyll i tabellen. Figurens nummer Antal rutor 1 2 3 4 5
b) Beskriv hur man kan räkna ut antalet rutor om man vet figurens nummer.
c) Skriv en formel för antalet rutor i figur n
d) Hur många rutor finns det i figur 13?
39 Fibonaccis talföljd börjar 1, 1, 2, 3, 5 … Varje tal i talföljden är summan av de två föregående talen. Till exempel får man det tredje talet 2 genom att lägga ihop de två föregående talen, 1 + 1 = 2. Leon vill använda ett kalkylprogram för att bestämma fortsättningen av talföljden.
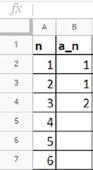
a betecknar det n:te talet talföljden
a) Vilken formel ska Leon skriva i cell B5 för att det fjärde talet i talföljden ska beräknas?
b) Vilket värde har det tjugonde talet i Fibonaccis talföljd?
c) Vilket tal i talföljden är det första som överstiger 1 000 000?
Nivå 3
40 Förenkla uttrycken a) 4x2 − 8x 2x − 4 b) 9y2
Värdet

1 Uttrycket 3x − x + 2y kan förenklas till 1 3 + 2y X 2x + 2y 2 4 + x + y
2 Vilket är värdet av uttrycket 2a + 3b om a = 5 och b = 1?
1 13 X 56 2 11
3 I uttrycket 17a + 2b + 3 är
1 a och b variabler och 3 är en koefficient
X a och b variabler och 3 är en konstantterm
2 a och b koefficienter och 3 är en konstantterm
4 Med formeln V = B h 3 kan man beräkna volymen av en kon. Vilken volym har en kon med B = 10 m2 och h = 4,5 m?
1 45 m3 X 15 m3
2 4,8 m3
5 Uttrycket 4 − (3y − 9) kan förenklas till 1 −3y − 13 X 13 − 3y 2 3y − 5
Del 1
6 Vilket av alternativen är en lösning till ekvationen 7(z − 2) = 21? 1 z = 5 X z = 4 2 z = 3
7 Det n:te talet i talföljden 3, 9, 15, 21, 27, … kan beskrivas med formeln
8 Rektangelns area kan beskrivas med uttrycket 1 x2 + 8x + 15
9 Vilket samband beskriver att x är fyra gånger så stort som y? 1 x = y + 4 X y = 4x 2 x = 4y
10 Uttrycket 6x + x2 kan faktoriseras till 1 6 ∙ x + x x X (6 + x)(x + x) 2 x(6 + x)
11 a) Förenkla uttrycket 2x − 3y + 4x + 5y − 6 b) Beräkna värdet av uttrycket om x = 2 och y = 5.
12 Lös ekvationerna a) 3x − 8 = 14,5 b) 8x − 4 = 3 − (2x + 2)
13 Nino köper godis för 11,90 kr/hg och nötmix för 18,50 kr/hg. Den totala kostnaden för godis och nötter beskrivs av uttrycket 11,90x + 18,50y Vad står x och y för i uttrycket?
14 Formeln I = U R kallas Ohms lag. I formeln är I strömstyrka, U elektrisk spänning och R resistans. Hur förändras strömstyrkan om resistansen fördubblas?
15 Faktorisera uttrycket 5x2 + x
16 Martina är 4 gånger så gammal som Arvid. Arvid är dubbelt så gammal som Vincent. Tillsammans är de 44 år. Vilken av ekvationerna kan du använda för att ta reda på hur gammal Vincent är? x + 2x + 4x = 44 x + 2x + 8x = 44 x + 4x + 8x = 44
17 a) Förenkla uttrycket så långt som möjligt. (x − 3)(4x + 1) − 2x2 b) Beräkna värdet av uttrycket om x = −3.
1 X (2x + 2y)
2 1 (13)
3 X (a och b är variabler och 3 är en konstantterm)
4 X (15 m3)
5 X (13 − 3y)
6 1 (z = 5)
7 2 (a = 6n − 3)
8 1 (x2 + 8x + 15)
9 2 (x = 4y)
10 2 (x(6 + x))
11 a) 6x + 2y − 6 b) 16
12 a) x = 7,5
b) x = 0,5
Del 2
18 Här nedanför ser du ett mönster med rutor. Beskriv med ord eller med en formel hur du kan beräkna antalet rutor om du vet figurens nummer.
n = 1 n = 2 n = 3 n = 4
19 Lös ekvationen 3(2x + 4) − 4(3 − 4x) = 2(x + 7)
20 Viktor och Sanna ska arrangera en fest. De har fasta kostnader på 3 250 kronor och rörliga kostnader på 125 kronor per gäst. a) Ställ upp ett uttryck för den totala kostnaden för festen. b) Ställ upp ett uttryck för kostnaden per person. c) Vilket biljettpris ska de välja om det kommer 65 personer och de varken ska gå med vinst eller förlust?

21 Lisa och Amin bor 20 km ifrån varandra. De startar samtidigt och springer tills de möts. Lisa springer med 11 km/h och Amin med 13 km/h. Var och efter hur lång tid kommer de att mötas?
13 x är antalet hg godis, y är antalet hg nötmix
14 Strömstyrkan halveras när resistansen fördubblas.
15 x(5x + 1)
16 x + 2x + 8x = 44
17 a) 2x2 − 11x − 3 b) 48
18 Antalet rutor a kan beräknas med formeln a = 2n − 1. Med ord: Antalet rutor får du om du multiplicerar figurens nummer med två och sedan subtraherar med 1.
19 x = 7 10 = 0,7
20 a) 3 250 + 125x där x är antalet gäster
b) 3 250 + 125x x där x är antalet gäster
c) 175 kronor
21 De möts efter 50 minuter. Ungefär 10,8 km från Amin och 9,2 km från Lisa.
Prov
■ Prov Kapitel 3
■ E-prov Kapitel 3
nivå
1a
Lärarguiden till Matematik Origo nivå 1a följer elevboken uppslag för uppslag med tips, idéer och inspiration till din undervisning.
Här finns bland annat extra exempel
didaktiska tips och kommentarer förslag på hur du kan inleda och avsluta lektionen lösningar till flera av elevbokens uppgifter
Till Matematik Origo nivå 1a finns även komponenterna elevbok, Skriva-bok, Lärarstöd+ samt kopieringsmaterialet Prov, övningsblad och aktiviteter.
Serien Matematik Origo finns till samtliga gymnasieprogram.