Lärarhandledning
Andreas Ryve
Manuel Tenser
Patrik Gustafsson
Daniel Brehmer
Jannika Lindvall
Hillevi Gavel
Fredrik Blomqvist
3.0 Introduktion
Syftet med kapitel 3 är att befästa och utveckla elevernas förståelse för och färdigheter i räknestrategier och huvudräkning för multiplikation och division Syftet är också att börja utveckla elevernas förståelse för grundläggande aspekter av skriftliga räknemetoder för multiplikation och division�
Sammanfattning
Kapitlet inleds med en repetition av vad multiplikation är, vad multiplikativa situationer innebär och räknestrategier för multiplikation inom ramen för multiplikationstabellernas talområde Därefter görs samma repetition för division
Sambandet mellan multiplikation och division övas sedan genom arbete med strategier för att multiplicera och dividera med hela tiotal och tvåsiffriga tal, vilket lägger grunden för kommande arbete med skriftliga räknemetoder för multiplikation och division
Genom att fokusera på olika strategiers och metoders funktionalitet, hellre än tillvägagångssätten i sig, avser vi träna eleverna i att förstå i stället för att bara mekaniskt göra beräkningar Detta hjälper eleverna att avgöra vilken strategi eller metod som är lämpligast utifrån de ingående talen för den beräkning som ska genomföras Det är viktigt för problemlösning, som bland annat innebär att välja lämplig metod för den givna situationen
I slutet av kapitlet ges en lektion med textuppgifter kopplade till multiplikativa situationer vilka löses med problemlösningsmetoden ALP�
Kapitel avslutas sedan med en repetitionslektion följt av en diagnos�
och dividera med hela tiotal
3.0.1 Multiplikation och division
Räknesätten multiplikation och division bör vara bekant för eleverna från tidigare årskurser. I detta kapitel fokuserar vi därför på att befästa och utveckla elevernas förståelse för och färdigheter i huvudräkning och skriftliga räknemetoder för multiplikation och division. En grundläggande tanke genom hela kapitlet är att vi fokuserar på talförståelse för att förstå de metoder och procedurer som presenteras. Målet med lektionerna är alltså att förstå innehållet och inte att hinna med ett visst antal uppgifter. En förståelseinriktad undervisning (”så här fungerar det”) som bygger på talförståelse har visat sig betydligt mer givande för kommande matematik än procedurinriktad undervisning (”så här gör man”).
Definitioner, terminologi och notation
Multiplikation av heltal kan definieras som upprepad addition, men en mer generell tolkning är att se det som areabestämning för en rektangel. Nedan illustreras ”fyra gånger tre”, 4 3, fyra kolumner med tre i varje, eller arean hos en rektangel med basen 4 längdenheter och höjden 3 längdenheter.

Talen som multipliceras kallas faktorer. Om man vill skilja på dem kallar man den första faktorn för multiplikator, som kan uppfattas som ”så många man ska ta”, och den andra faktorn för multiplikand, som kan uppfattas som ”det man ska ta”. Uttrycket som helhet och också dess värde kallas produkt
Division definieras formellt som motsatsen (inversen) till multiplikation; Om a b = c så är c/b = a. Talet man delar på, här c, kallas täljare, och talet man delar med, här b, kallas nämnare. Uttrycket och dess värde kallas kvot. Kvoten mellan b och c är det tal man ska multiplicera b med om man vill få c.
Notation
Multiplikation betecknas i Sverige med en punkt (till skillnad från många andra länder, som använder ett kryss ×). Om det inte finns någon risk för felläsning använder man ofta ingen symbol alls. T.ex. skrivs ”tre gånger y” ofta som 3y. Vid multiplikation av tal måste multiplikationstecknet skrivas ut, annars kommer det skrivna inte att tolkas som avsett. T.ex. måste ”tre gånger fyra” skrivas 3 · 4 och inte 34 (som utläses ”trettiofyra”).
Division betecknas med bråkstreck, som kan vara horisontellt, som 4/2 (mest lättläst), eller snett, som 4/2 (lättare att infoga i löpande text). Ibland förekommer även divisionstecknet ÷, så man skriver t.ex. 4 ÷ 2 Detta tecken blir dock ofta felaktigt läst som ett plustecken.
Prioritet
Multiplikation och division går före addition och subtraktion, om inte parenteser anger något annat. Så t.ex. 2 + 3 ∙ 4 = 2 + 12 = 14.
Multiplikationen ska utföras innan additionen, trots att additionen står först. Vill man att additionen ska göras först måste man skriva (2 + 3) ∙ 4 = 5 ∙ 4 = 20. Denna regel, prioritetsregeln, är till skillnad från t. ex. de kommutativa lagarna inte något som följer av matematiken utan är en konvention som man har för att det man skriver ska bli entydigt tolkbart. Billiga miniräknare följer inte denna konvention, de mer avancerade följer den.
Räkneregler
Multiplikation har i princip samma räkneregler som addition, vilket medför att division har nästan samma räkneregler som subtraktion.
Kommutativitet
Multiplikation är kommutativ, så att a ⋅ b = b ⋅ a, för alla tal a och b. För resultatets del spelar det ingen roll vilken av faktorerna som står först. Däremot finns ingen kommutativ lag för division; a⁄b är vanligtvis inte samma tal som b⁄a. Exempelvis är 8⁄4 = 2 medan 4⁄8 = 0,5.
Associativitet
Multiplikation är associativ. Ska man multiplicera tre faktorer, vilket innebär att man ska genomföra två multiplikationer, spelar det ingen roll vilken av multiplikationerna som görs först:
5 ⋅ (2 ⋅ 6) = 5 ⋅ 12 = 60 (5 ⋅ 2) ⋅ 6 = 10 ⋅ 6 = 60.
Detta gör att man inte behöver sätta ut några parenteser i denna typ av uttryck, eftersom de inte påverkar slutresultatet.
Division är däremot inte associativ; 8⁄(4/2) = 8⁄2 = 4 medan (8/4)/2 = 2⁄2 = 1. Här brukar man utnyttja typografin för att klargöra vad man menar 8/(4/2) kan t.ex. skrivas
8⁄(4/2) eller 8⁄(4/2).
Multiplikation med 0 – nollfaktorlagen
Detta är en regel som saknar motsvarighet hos addition. Multiplicerar man med 0 är produkten 0, oavsett vad den andra faktorn var. Detta är också enda sättet att få noll som resultat; är en produkt noll så måste minst en av faktorerna vara noll.
Detta har konsekvenser för division: division med noll är odefinierad (något sådant tal finns inte; det går inte att säga vad detta är). 6⁄0 är enligt definitionen ”det tal man ska multiplicera noll med om man vill få sex som resultat”, och något sådant tal finns inte. 0⁄0 är ”det tal man ska multiplicera noll med om man vill få noll som resultat”, och där passar alla tal lika bra så det går inte att säga vad detta är.
Division av noll går däremot bra; 0⁄6 är ”det tal man ska multiplicera sex med om man vill få noll som resultat”, och där passar noll (och inget annat) in.
Multiplikation med 1
Multiplikation med ett fungerar på samma sätt som addition med noll: resultatet är lika med det andra talet: a ⋅ 1 = 1 ⋅ a = a.
För division är konsekvenserna
a/1 = a och a/a = 1 (det sista om a ≠ 0).
Distributiva lagen för multiplikation över addition
Sambandet mellan addition och multiplikation ger upphov till den distributiva lagen för multiplikation över addition: a ⋅ (b + c) = a ⋅ b + a ⋅ c. Detta kan motiveras i bild:

3 ⋅ (3 + 2) = 3 ⋅ 3 + 3 ⋅ 2
Distributiva lagen för multiplikation över addition är också det som utnyttjas då man genomför multiplikationer genom att dela upp i talsorter:
2 ⋅ 46 = 2 ⋅ (40 + 6) = 2 ⋅ 40 + 2 ⋅ 6 = 80 + 12 = 92.
Den har alltså många användningsområden.
Det finns distributiva lagar för andra kombinationer av räknesätt, som union och snitt inom mängdläran, men de brukar inte dyka upp förrän på relativt hög nivå. Man brukar därför bara säga distributiva lagen, utan att specificera vilka räknesätt det handlar om, så länge det inte finns risk för missförstånd. Distributiva lagen för
multiplikation över subtraktion, a
c, brukar räknas som en del av den för addition, eftersom subtraktion här kan ses som addition med ett tal med omvänt tecken.
3.0.2 Undervisa om multiplikation och division
Här beskriver vi övergripande strategiska tankar/kunskaper som är viktiga att förstå då man undervisar om multiplikation och division. Mer detaljerade/specifika metoder beskrivs i texten till de lektioner där de är aktuella och inte här i introduktionen.
Förstå multiplikation och division
I undervisningen om multiplikation låter vi eleverna göra jämförelser mellan olika modeller av multiplikation som
1. lika stora grupper (eller värden),
2. jämförelsesituationer,
3. rektangelformationer/rutnät.
Lika grupper
Dessa situationer kan ses som upprepad addition och kopplar därmed tydligt ihop multiplikation med addition. Exempel: Fyra klasser med 25 elever i varje klass är ett exempel på den multiplikativa situationen lika grupper som kan beskrivas om 4 ⋅ 25. Första faktorn, multiplikatorn (4), beskriver hur många grupper eller delar som är inblandade och den andra faktorn, multiplikanden (25), beskriver storleken/värdet på gruppen. Produkten av dessa (100) beskriver helheten, summan av alla grupper.
Det är viktigt att eleverna får möta lika grupper i kontextuella situationer för att öva sig på att se grupper av objekt som en enda enhet samtidigt som de förstår att varje grupp består av ett givet antal objekt.
Multiplikativa jämförelser
”Ally har två pennor. Emilia har tre gånger så många pennor som Ally.” Detta är ett exempel på en multiplikativ jämförelsesituation där två olika grupper jämförs.
Vid dessa situationer finns det tre olika möjligheter för vad som är okänt:
1. produkten är okänd,
2. gruppstorleken är okänd eller
3. antalet grupper (i bemärkelsen hur många gånger större eller mindre) är okänt.
Den första varianten löses med en multiplikation, medan de andra två hanteras med division.
Rektangelformation, rutnät och area
En äggkartong med fyra rader och sex ägg i varje rad är ett exempel på en rektangelformation. Den kan beskrivas som en lika-grupper-situation med en rektangulär gruppering genom en tvådimensionell struktur. En faktor (4) representerar antalet rader och den andra faktorn (6) antalet i varje rad.

Den tvådimensionella strukturen är en viktig modell för att utveckla en förståelse för multiplikation. Den gör det möjligt att utvidga multiplikation till att gälla andra tal än heltal, som t.ex. bråktal och tal i decimalform. Den synliggör även de kommutativa, associativa och distributiva lagarna för multiplikation. Modellen kan därmed stödja förståelse för såväl huvudräkningsstrategier som algoritmräkning. Dessutom möjliggör den en tydlig koppling mellan multiplikation och area.
Det är viktigt att man i undervisningen synliggör rektangelformationens två dimensioner och låter eleverna koppla ihop de olika faktorerna i situationen med antal kolumner respektive antal objekt i varje kolumn.
Division – lika grupper och delningsdivison
Vi arbetar med division i samband med multiplikation för att öka elevernas förståelse för sambandet mellan multiplikation och division och för att utveckla en djupare förståelse för båda räknesätten. En annan anledning till detta är att eftersom division är inversen till multiplikation går det inte alltid att säga om en situation eller textuppgift är en multiplikations- eller divisionssituation.
Man kan från den multiplikativa modellen lika grupper härleda två olika typer av division. Om antalet grupper är känt men storleken på dem okänd får man delningsdivison: man gör en jämn fördelning på grupperna och ser hur många det blir i varje grupp. Ett exempel är att man vet att man ska göra fem påsar med godisbitar men man vet inte hur många godisbitar det kommer att bli i varje påse. Då fördelar man de godisbitar man har jämnt mellan de fem påsarna och ser hur många det blev per påse.
Om istället storleken på grupperna är känd – det ska vara fem godisbitar i varje påse – medan det är okänt hur många sådana påsar man kan göra, så är det fråga
om innehållsdivision. Operationen kan då ses som att man undersöker hur många påsar med fem godisbitar i varje som det kända totala antalet godisbitar räcker till.
Division med rest
Ofta är kvoten vid division inte ett heltal. Försöker man exempelvis dividera 38 med 5, dvs. hitta vad man ska multiplicera 5 med för att få 38, så finner man att något sådant heltal inte finns. 5 går 7 gånger i 38, men sedan är det 3 över, en rest. Detta problem kan hanteras på olika sätt, men kommer inte att komma upp i det här kapitlet. Om elever inser att problemet finns så kan du tala om att ni kommer att titta på det i senare kapitel.
Problem och kontextuppgifter
Genom att låta eleverna möta intressanta och väl valda kontextuppgifter och problem utifrån deras vardag och erfarenheter istället för enbart nakna uppgifter skapas goda möjligheter att både utveckla elevernas problemlösningsförmåga och stärka deras förståelse för multiplikation och division.
Det är oftast bättre att engagera eleverna ordentligt och djupt i få uppgifter istället för att snabbt öva på att lösa många. Utöver att i varje lektion arbeta utifrån relevanta kontexter så finns i kapitlet en lektion som fokuserar på problemlösning med metoden ALP. Vi rekommenderar att lägga tid på att arbeta med ALP som utgångspunkt och låt eleverna beskriva vad de gör och hur de löst uppgifterna. Uppmuntra gärna eleverna att lösa uppgifter på olika sätt. ALP-metoden beskrivs i detalj i introduktionen till kapitel 2 i denna årskurs.
Växla mellan representationsformer Eleverna får träna på att översätta mellan olika representationsformer som ord, bilder och matematiska uttryck, vilket utvecklar deras begreppsliga förståelse för räknesätten – samtidigt som det kräver en viss förståelse för räknesätten. Att t.ex. kunna tolka en händelse eller situation och teckna ett matematiskt uttryck, i syfte att sedan kunna göra en beräkning, är en central och viktig tillämpning av ens förståelse för räknesätten.
Eleverna behöver utveckla förståelse för sambandet mellan de olika multiplikativa situationerna (både multiplikation och division) och matematiska symboluttryck. Att arbeta med textuppgifter är ett sätt att göra det. Även här är det bättre att engagera eleverna ordentligt och djupt i färre uppgifter genom att använda konkret material, rita bilder och teckna uttryck, än att snabbt öva på att lösa många uppgifter. Låt eleverna beskriva vad de gör och hur de löst uppgifterna. Uppmuntra gärna eleverna att lösa uppgifter på olika sätt.
Automatisering och räkneflyt
Det är viktigt att elever automatiserar alla talkombinationer från 0 · 0 upp till 10 · 10, eftersom det avlastar arbetsminnet och möjliggör att man kan genomföra mer avancerad huvudräkning och skriftliga beräkningar. Det omfattar totalt 121 talkombinationer, men med hjälp av förståelse för räknelagar, tals egenskaper och strukturer så kan inlärningen underlättas. Till exempel så ger den kommutativa lagen för multiplikation i princip en halvering av antalet kombinationer.
För att automatisera dessa kombinationer och uppnå räkneflyt behöver eleverna gå från att beräkna talkombinationerna genom upp- eller nedräkning, med eller utan talföljdsräkning (t.ex. 10-hopp), till att använda räknestrategier för att resonera sig fram till resultatet. Med räknestrategi menas ett sätt att tänka för att utifrån sin förståelse för tals egenskaper, samband mellan tal, känd tabellkunskap och räknelagar, logiskt bestämma en okänd kombination. Genom att använda räknestrategier kommer eleverna så småningom att automatisera talkombinationerna som de beräknar. När man har automatiserat en talkombination kan man direkt plocka fram resultatet ur minnet. Elever som en gång har lärt sig räknestrategier kan då alltid resonera sig fram till svaret, även om en viss kombination skulle ha fallit ur minnet.
Att en förklaring är hållbar betyder att den är lämplig i sitt sammanhang och bygger på talförståelse och logiska resonemang. Förklaringen behöver inte vara ”känd och allmänt använd”, bara den fungerar och är matematiskt korrekt. En hållbar strategi är en strategi som går att utveckla för andra sammanhang. Att resonera utifrån talförståelse är hållbart och går att tillämpa i alla matematiska sammanhang.
Var vaksam på elever som fastnar i talföljdsräkning (”två, fyra, sex, åtta, tio…”) vilket inte är hållbart på lång sikt, och säkerställ att elever går över till hållbara räknestrategier och automatiserade tabellkunskaper. Tänk även på att absolut inte blanda ihop att lära och befästa. Eleverna bör först etablera hållbara strategier innan man övar snabbhet för att befästa.
Multiplikation
Undervisningen i kapitlet är noggrant strukturerad och fokuserar på att eleverna ska lära sig hållbara räknestrategier. Lektionstiden är inte tänkt för färdighetsträning av tabellkunskaper, utan de planerade lektionerna kan varvas med korta, intensiva färdighetsträningspass där eleverna använder strategierna för att beräkna aktuella multiplikationer och divisioner. Passen kan vara 5–10 minuter långa och genomföras dagligen.
Synliggör gärna räknestrategierna med planscher som ni sätter upp på väggarna. Däremot bör du inte sätta upp utskrifter av tabeller med rena talfakta då det kan minska elevers motivation att lära sig räknestrategier.
Vid multiplikation med 3, 6 och 9 kan eleverna tillämpa den distributiva lagen för multiplikation över addition. Lagen är väldigt användbar för att utveckla metodförmågan och stärker även elevernas algebraiska tänkande. Vid multiplikation med 9 tillämpas lagen genom räknestrategin En mängd mindre än 10. Det innebär att man först multiplicerar med 10 istället för 9 och sedan minskar med en ”mängd”. Ett exempel är att vid 9 ⋅ 6 börjar man med att tänka 10 ⋅ 6 = 60 för att sedan minska med en ”mängd”, 60 – 6 = 54, alltså är 9 ⋅ 6 = 54 Vid multiplikation med 3 kan man på liknande sätt tillämpat distributiva lagen genom strategin Dubbelt och en mängd till. Ett exempel är 3 · 7 där man kan tänka dubbelt sju (14) och en sjua till (7) som summeras till 21, alltså är 3 · 7 = 21. Multiplikationer med 6 kan beräknas genom att tänka En mängd mer än 5. Till exempel kan 6 · 7 beräknas genom att först beräkna 5 · 7 (35) och sedan lägga till en sjua till (7) som summeras till 42 (summan av 35 och 7). Alltså är 6 · 7 = 42
Division
När eleverna börjat automatisera multiplikationskombinationerna kan det vara dags att öva på motsvarande divisionskombinationer. Genom räknestrategin Tänk multiplikation kan eleverna använda sig av sambandet mellan division och multiplikation för att beräkna divisionskombinationerna.
När eleven fått undervisning om och kan använda sig av ”tänk multiplikation” bör färdighetsträning ske under korta intensiva pass t.ex. 5 min/dag.
Vanliga svårigheter och missuppfattningar
En vanlig missuppfattning är att någon metod ses som det ”rätta sättet” att beräkna på. Eleven kan då uppvisa motvilja till att använda andra räknemetoder/tankesätt, även om de skulle vara mycket mer effektiva för den specifika uppgiften. Detta hanteras genom att eleven får arbeta med exempel där en annan metod än den som eleven fastnat vid, är mer funktionell. Vid arbetet skall eleverna beskriva hur de tänker när de genomför beräkningarna. Utifrån deras resonemang så kan man då komma fram till att en annan metod kan fungera smidigare för den givna uppgiften.
Kapitel 3 | Multiplikation och division
Vanliga svårigheter och missuppfattningar
Nedan går vi igenom några vanliga svårigheter och missuppfattningar kopplat till multiplikation och division är.
• Elever gör det ibland svårt för sig genom att beräkna t.ex. 37 · 2 · 5 med att beräkna 37 · 2 först istället för 2 · 5 först. Så man sedan kan beräkna 37 · 10. Svårigheten kan grunda sig i att eleven inte förstår kommutativitet i multiplikation, men troligast är att eleven inte tränats i att tänka strategiskt och först analysera uppgiften innan beräkningarna påbörjas.
• Elever kan ibland ”fastna” i att hantera multiplikation som upprepad addition och hanterar t.ex. 7 · 24 som 7 + 7 + 7 … eller 24 + 24 + 24 … vilka båda är ineffektiva metoder. Eleven har då inte uppfattat idén med att kunna multiplicera tiotalen och entalen i 24 var för sig så beräkningarna 20 · 7 = 140 och 4 · 7 = 28 genomförs och sedan adderas till produkten 168.
• Elever ignorerar ibland ”interna nollor” i tal så att 4005 · 9 ”=” 4554 utifrån att 9 · 5 = 45 som skrivs först och sedan 9 · 5 = 54 som skrivs sedan. Alltså, nollorna på tiotalsplatsen och hundratalsplatsen förbises i beräkningen. Svårigheten grundar sig i att eleven inte förstår betydelsen av siffrors olika värden på sina positioner i talet och behöver således mer träning för att förstå just platsvärdens betydelse för siffror i tal.
• Det händer att elever blandar ihop multiplikation med addition och tänker att för t.ex. 28 · 36 beräknas först 20 · 30 = 600, sedan 8 · 6 = 48 och sist adderas dessa till produkten 648. Eleven har då inte förstått den egentliga innebörden av multiplikation och behöver stöd i att förstå hur man kan dela in tal vid multiplikation och matematiskt förstår varför man gör indelningen så.
• Elever missuppfattar ibland division genom att hantera t.ex. 90/15 som 90/10 + 90/5, alltså delar upp nämnaren i delar. Det korrekta är att dela in täljaren i delar som var för sig divideras med den givna nämnaren, t.ex. 60/15 + 30/15. Detta kan avhjälpas med att ta exempel med låga tal och använda konkret material för att illustrera hur de olika fallen kan gestaltas och därigenom se det orimliga i sin missuppfattning.
• Ibland ignorerar elever ”interna nollor” precis som vid multiplikation. Man kan t.ex. se elever som löser 8004/2 genom att dividera 8 med 2 och sedan 4 med 2 och svarar med kvoten 42. Precis som vid multiplikation så grundar sig svårigheten i att eleven inte förstår betydelsen av siffrors olika värden på sina positioner i talet och behöver således mer träning för att förstå just platsvärdens betydelse för siffror i tal.
• Ett vanligt problem är att en elev alltid tänker division som delningsdivision, alltså att täljaren delas upp i det antal som nämnaren anger. Denna strategi fungerar i vissa fall, men försvårar förståelsen för t.ex. 3/0,2 där innehållsdivision fungerar bättre som förståelse, alltså att 0,2 ”får plats 15 gånger i tre”. Det är viktigt att eleven får möjlighet att utveckla förståelse för division som både delningsdivision och som innehållsdivision så de kan använda den tankestrategi som fungerar bäst för den aktuella situationen.
• Eleven kan endast genomföra metoder mekaniskt och inte förstår procedurerna i dem. Detta gäller främst metoden uppställning, vilket inte ingår i detta kapitel, men kan även förekomma i andra metoder och omnämns därför här. Sådana svårigheter hanteras genom att jobba med elevens taluppfattning och betydelsen av positionerna i tal, vilket är grunden för att förstå hur de olika procedurerna fungerar.
• Det är vanligt att elever betraktar någon metod som ”det rätta sättet” att beräkna på. Eleven kan då uppvisa motvilja till att använda andra räknemetoder/ tankesätt, även om de skulle vara mycket mer effektiva för den specifika uppgiften. Detta handlar främst om metoden Uppställning, vilket inte tas upp i detta kapitel, men fenomenet omnämns ändå här i syfte att vara uppmärksam på sådana tendenser utifrån vad eleven kan ha med sig för uppfattningar om vad som är ”rätt metod” t.ex. hemifrån.
3.0.3
Övningsblad
I det här kapitlet finns det övningsblad att dela ut efter lektion 3, 5, 6, 9 och 11. Övningsbladen kan användas som extra färdighetsträning eller som extrauppgifter/ utmaningar till elever som snabbt blir klara.
3.0.4
Referenser
Baroody, A. J., & Purpura, D. J. (2017). Early number and operations: Whole numbers. I C. J. (Red.), Compendium for research in mathematics education (s. 308–354). Reston, VA: National Council of Teachers of Mathematics.
Brendefur, J., Strother, S., Thiede, K., & Appleton, S. (2015). Developing Multiplication Fact Fluency. Advances in Social Sciences Research Journal.
Foegen A., & Dougherty, B. (2017). Instruction that meets the needs of students with mathematical disabilities and difficulties I C. J. (Red.), Compendium for research in mathematics education (s. 893–907). Reston, VA: National Council of Teachers of Mathematics.
Larsson, K. (2015). Multiplikationsundervisning. Nämnaren, 1, 9–13.
Larsson, K., Pettersson, K., & Andrews, P. (2017). Students’ conceptualisations of multiplication as repeated addition or equal groups in relation to multi-digit and decimal numbers. The Journal of Mathematical Behavior, 48, 1–13.
Lemaire, P., LeCacheur, M., & Farioli, F. (2000). Children’s strategy use in computational estimation. Canadian Journal of Experimental Psychology, 54(2), 141–148.
McIntosh, A. (2008). Förstå och använda tal. Göteborg NCM, Göteborgs universitet.
Selter, C. (2001). Addition and subtraction of three-digit numbers: German elementary children’s success, methods and strategies. Educational Studies in Mathematics, 47(2), 145–173.
Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2020). Elementary and middle school mathematics: Teaching Developmentally, Global Edition (10th edition). New York, NY: Pearson Education.
Wallace, A. H., & Gurganus, S. P. (2005). Teaching for mastery of multiplication. Teaching Children Mathematics, 12(1), 26.
Woodward, J. (2006). Developing automaticity in multiplication facts: Integrating strategy instruction with timed practice drills. Learning Disability Quarterly, 29(4), 269–289.
3.1 Multiplikation
Syftet med lektionen är att fördjupa elevernas begreppsliga förståelse för multiplikation genom att låta dem tolka, beskriva och jämföra olika multiplikativa situationer och modeller (rutnät, lika grupper/värden och jämförelsesituationer) för multiplikation�
Lektionsmål
Eleven kan tolka en multiplikativ situation som ges som text eller bild och översätta den till andra representationsformer och visar det t.ex. genom att teckna ett uttryck som passar till situationen.
Eleven kan tolka ett multiplikationsuttryck och översätta till andra representationsformer och visar det t.ex. genom att hitta på en räknehändelse som passar till ett uttryck.
Matematiska begrepp: multiplikation, faktor, produkt, kommutativt
SvA: rutnät, rad, kolumn, grupp
Material: Miniwhiteboard med penna och sudd till varje par
Förberedelser
• Inga särskilda�
Lektionens resurser
Genomgång: Multiplikation
Du går igenom vad ett multiplikationsuttryck är
Genomgång: Multiplikation som rutnät
Du läser en räknehändelse och visar fyra rader med sex burkar i varje rad och eleverna SURRAR om hur man kan visa samma sak med ett uttryck Ni konstaterar att man kan skriva det som 4 − 6 = 24
Genomgång: Kommutativa lagen för multiplikation
Eleverna funderar på om antalet rutor i rutnät ändras beroende på om man räknar rader med ett visst antal rutor i varje rad eller kolumner med ett visst antal rutor� Du visar att multiplikation är kommutativt
Genomgång: Multiplikation som lika grupper
Du visar och förklarar hur man kan förstå multiplikation som ett visst antal lika stora grupper
Genomgång: Multiplikation som jämförelse
Du visar och förklarar hur man kan förstå multiplikation som en jämförelse, t ex tre gånger så många.
Parövning: Teckna multiplikationsuttryck
Du läser en räknehändelse och paren diskuterar för att skriva en multiplikation som passar till händelsen på sina miniwhiteboards Du låter ett par förklara hur deras uttryck passar
Parövning: Skapa räknehändelser
Paren arbetar i elevboken med att skapa en räknehändelse och en bild som passar ett multiplikationsuttryck Därefter skapar de räknehändelse med multiplikation som passar till en bild och skriver ett passande uttryck till det Du låter ett eller flera par redovisa sina räknehändelser�
Sammanfattning:
Vad har vi lärt oss?
Du visar och sammanfattar hur man kan tänka på multiplikation som en jämförelse, som ett antal lika grupper eller som ett rutnät med ett visst antal rader/kolumner med ett visst antal rutor i varje rad/kolumn�
Du sammanfattar också varför multiplikation är kommutativt�


Uppstart
2 Genomgång: Multiplikation 15 min
Peka på multiplikationen 4 ∙ 6 = 24 Berätta att talen som man multiplicerar med i multiplikation kallas faktorer och svaret för produkt Berätta att multiplikationstecknet oftast är en liten punkt men att det ibland kan se ut som bokstaven x, t ex på miniräknare�
3 Genomgång: Multiplikation som rutnät
Läs räknehändelsen: ”Ellen har köpt en kartong med burkläsk Kartongen har fyra rader med sex burkar i varje rad Totalt är det 24 läskburkar�”
Visa en bild på kartongen Repetera att det var fyra rader med sex burkar i varje rad och totalt 24 burkar� Fråga: ”Hur kan man skriva det här som en multiplikation?” Låt eleverna SURRA Visa och förklara att man kan skriva det som en multiplikation med faktorerna 4 och 6 och produkten 24
Klicka så att bilden förändras till ett rutnät� Visa och förklara att multiplikation kan ses som ett rutnät där den första faktorn kan ses som antalet rader och den andra faktorn som antalet rutor i varje rad Multiplikationen 4 ∙ 6 = 24 kan visas med ett rutnät med fyra rader och sex rutor i varje rad Sammanlagt är det 24 rutor

4 Genomgång: Kommutativa lagen för multiplikation
Visa och förklara: ”Om man istället räknar kolumnerna och antalet rutor i varje kolumn, kommer det att vara mer eller mindre än 24 rutor då?” BETÄNKETID Konstatera att antalet rutor inte ändras oavsett hur man räknar dem�
Visa och förklara: ”Precis som addition är multiplikation kommutativt: man kan byta plats på faktorerna utan att produkten ändras: 4 ∙ 6 = 24 och 6 ∙ 4 = 24 Eftersom det här gäller oavsett vilka tal faktorerna är så kan man säga att det är en lag: kommutativa lagen för multiplikation Man kan skriva lagen som a ∙ b = b ∙ a där variablerna a och b står för vilket tal som helst Det spelar alltså ingen roll för resultatet om man multiplicerar a med b eller b med a På samma sätt spelar det ingen roll om man räknar antalet rader och hur många rutor varje rad har, eller antalet kolumner och hur många rutor varje kolumn har Det är fortfarande lika många rutor!”
Visa 3 ∙ 5 = 15 och 5 ∙ 3 = Fråga: ”Om man vet att 3 ∙ 5 = 15, vad är då 5 ∙ 3?” Konstatera att även 5 ∙ 3 = 15�






5 Genomgång: Multiplikation som lika grupper
Läs räknehändelsen: ”Lucas har tre påsar Han lägger sju bullar i varje påse� Tillsammans är det 21 bullar�” Teckna uttrycket
3 ∙ 7 = 21 Förklara: ”Man kan se multiplikation som ett visst antal lika stora grupper� Här visar den första faktorn, 3, att det är tre grupper och den andra faktorn, 7, att det är sju i varje grupp
Tillsammans är det 21 ”
6 Genomgång: Multiplikation som jämförelse
Visa och förklara: ”Multiplikation kan även ses som en jämförelse.
Om Kim har sex enkronor och Julie har tre gånger så många så har hon 18 enkronor� Man kan skriva 1 ∙ 6 = 6 för att visa att Kim har en rad med sex enkronor, vilket totalt är sex enkronor, och
3 ∙ 6 = 18 för att visa att Julie har tre rader med sex enkronor, vilket totalt är 18 enkronor ”
7 – 10 Parövning: Teckna multiplikationsuttryck
Dela in i par och förse paren med miniwhiteboards med penna och sudd� Gör så här:
• Visa och läs räknehändelsen och låt paren diskutera för att skriva en multiplikation som passar� De ska kunna förklara vad i uttrycket som utgör vad i räknehändelsen
• Be paren visa sina tavlor och låt ett par som skrivit en passande multiplikation, 7 ∙ 6 = 42 eller 6 ∙ 7 = 42, förklara hur deras uttryck passar till räknehändelsen Påminn övriga att de kan göra jag med-tecknet för att visa om de har tänkt likadant Ställ frågor för att hjälpa dem vid behov och låt andra återge viktiga saker som sägs
Gör på samma sätt med nästa uppgift�




11 – 12 Parövning: Skapa räknehändelser
Be paren slå upp s 70 i elevboken Förklara att de i uppgift 3�1 ska komma på en räknehändelse som passar till uttrycket 9 ∙ 4 = 36, skriva ned den och sedan rita en bild som passar till räknehändelsen de skapat� I uppgift 3�2 ska de skriva en räknehändelse med multiplikation som passar till bilden och sedan skriva ett passande uttryck
Låt dem börja när alla förstått CIRKULERA Bryt när alla börjar bli klara Låt ett par redovisa sina räknehändelser och hur de hänger ihop med uttrycket Om det finns tid kan du låta fler par redovisa
13 – 14 Sammanfattning: Vad har vi lärt oss? 5 min
Visa och förklara: ”Talen man multiplicerar kallas faktorer, svaret för produkt Man kan tänka på vad multiplikation är på flera olika sätt Ett sätt är att tänka på multiplikation som en jämförelse Om ett barn har tre karameller och ett annat barn fyra gånger så många så har det andra barnet tolv karameller Man kan skriva det som 4 ∙ 3 = 12 ”
Fortsätt: ”Man kan även tänka på multiplikation som lika grupper Om man t ex har fyra skålar och lägger tre äpplen i varje skål så kan detta skrivas som 4 ∙ 3 = 12� Den första faktorn säger hur många grupper det är och den andra hur många det är i varje grupp� Totalt är det tolv äpplen�”
Klicka, och äpplena läggs i en rektangelformation som övergår till ett rutnät� Fortsätt: ”Man kan också tänka på multiplikation, t ex 4 ∙ 3 = 12, som ett rutnät: fyra rader med tre rutor i varje rad där det totala antalet rutor är tolv Då ser man också tydligt att multiplikation är kommutativt: tre kolumner med fyra rutor i varje kolumn är också tolv rutor Man kan alltså byta plats på faktorerna utan att produkten ändras�”
3.1.1 Uppmärksamma och stötta
Det är viktigt att eleverna förstår att man kan tänka på vad multiplikation är på flera olika sätt och att de förstår vad det innebär att multiplikation är kommutativt. Det är inte ovanligt att elever tänker på multiplikation som upprepad addition. Om du märker att många elever har det synsättet är det viktigt att du lägger tonvikt på att se multiplikation som rutnät. Elever som endast ser på multiplikation som upprepad addition blir i längden begränsade i sitt användande av räknesättet, t.ex. kan de få svårt att förstå och ta till sig förklaringsmodeller när man multiplicerar decimaltal eller bråk. Det går exempelvis inte att förstå vad 0,6 ∙ 0,7 innebär om man försöker förstå multiplikationen som upprepad addition.
Vid multiplikation som lika grupper betyder faktorerna i multiplikationen olika saker. Om man tar exemplet 3 ∙ 7 = 21 från steg 5 så anger första faktorn hur många lika stora grupper det är, tre stycken. Den andra faktorn och anger hur många det är i varje grupp, sju stycken. Konkret skulle det kunna handla om tre påsar med sju bullar i varje påse. Totalt är det 21, vilket motsvarar produkten. Ibland kallas första faktorn för multiplikator och den andra faktorn multiplikand (detta förklaras närmare i kapitelintroduktionen), men vi har valt att inte benämna dem på det sättet i lektionerna.
Förenkla
I aktivitetsfasen gör eleverna aktiviteter där de ska tolka räknehändelser och skriva multiplikationsuttryck som passar till dem. De ska också utgå ifrån ett uttryck och en bild och skapa en passande räknehändelse till det. Om du märker att elever har problem med detta kan du förenkla genom att ge mer stöd, t.ex. genom att ställa mer ledande frågor eller genom att ge egna förslag och resonera med eleven om på vilket sätt det passar.
Utmana mer
Utmana elever vid behov att skriva fler räknehändelser till samma uttryck. Vill du utmana dem ännu mer kan du ge dem i uppgift att skapa en räknehändelse som beskriver ett rutnät, en som handlar om ett antal lika grupper och en som handlar om en jämförelse.
Du kan också utmana genom att ge elever fler och mer komplicerade uttryck att skriva räknehändelser till.
3.2 Multiplikation med 0–5 och 10
Syftet med den här lektionen är att säkerställa att eleverna har grundläggande kunskaper om räknestrategier för multiplikation med talen 0–5 samt med 10 Syftet är också att säkerställa att eleverna kan huvudräkna multiplikation med stöd av räknestrategierna och eleverna får färdighetsträna på det för att fortsätta automatisera multiplikationstabellerna 0–5 samt 10:ans multiplikationstabell
Lektionsmål
• Eleven kan huvudräkna multiplikationer med 0–5 och 10 och visar det genom att beräkna produkten utan att hjälpmedel och utan att använda uppenbart ohållbara strategier som t.ex. att räkna på fingrarna samt genom att kunna förklara hur hen tänkte om du frågar.
Matematiska begrepp: multiplikation, faktor, produkt, dubbelt, variabel, uttryck, strategi, kommutativa lagen
SvA: påse, äpple
Material: Sexsidig och tiosidig tärning till varje par (om tärningen är numrerad 0–9 ska 0 räknas som 10)
Förberedelser
• Skriv ut avslutslappar�
• Skriv eventuellt ut winnetkakort till elever som behöver extra färdighetsträning
Lektionens resurser
Repetition: Multiplikation
Du spelar upp den animerade genomgången om multiplikation
Genomgång: Multiplikation med 0
Du går igenom varför multiplikation med 0 alltid ger produkten 0
Genomgång: Multiplikation med 1
Du går igenom varför multiplikation med 1 alltid ger samma resultat som den faktor man multiplicerar med 1
Genomgång och övning: Multiplikation med 2
Du går igenom räknestrategin Dubbelt, dubbelt och eleverna övar på att multiplicera med 2�
Genomgång: Multiplikation med 10
Du går igenom hur man kan tänka tio gånger större när man multiplicerar med 10
Genomgång: Multiplikation med 3, 4 och 5
Du spelar upp animerade genomgångar som förklarar räknestrategier för multiplikation med 3, 4 och 5 och eleverna huvudräknar sedan multiplikationerna med strategierna�
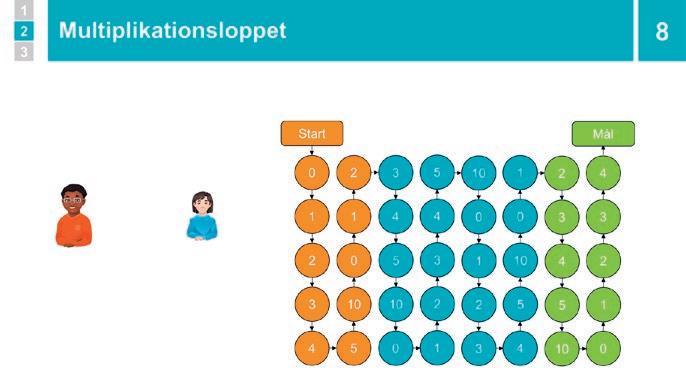
Parövning: Multiplikationsloppet
Eleverna färdighetstränar huvudräkning genom att spela Multiplikationsloppet i par När de är klara färdighetstränar de individuellt i elevboken
Sammanfattning: Vad har vi lärt oss?
Du sammanfattar att ni har gått igenom räknestrategier och använt dem för att huvudräkna multiplikationer� Man måste träna huvudräkning med strategierna tills man kan multiplikationerna utantill� Skulle man senare glömma bort någon kan man alltid använda strategin för att räkna ut svaret� Avslutslapp

Uppstart
2 Repetition: Multiplikation 10–15 min
Talen man räknar med i en multiplikation kallas faktorer och svaret för produkt
Rutnätet har tre rader med sju rutor i varje rad vilket ger multiplikationen 3 ∙ 7 Man kan också se rutnätet som att det har sju kolumner med tre rutor i varje kolumn vilket ger multiplikationen 7 ∙ 3 Båda multiplikationerna har produkten 21 Man kan alltså byta plats på faktorerna utan att produkten ändras (multiplikation är kommutativt)
Man kan även se på multiplikation som lika grupper Här ser vi tre grupper med sju cirklar i varje� Ett tredje sätt att se på multiplikation är som en jämförelse Till vänster ser vi sju cirklar och till höger tre gånger så många
Berätta: ”I den här lektionen ska vi gå igenom räknestrategier för multiplikation, dvs olika sätt att tänka på för att beräkna produkten� Sedan kommer ni få huvudräkna multiplikationer� När man har gjort det tillräckligt många gånger så vet man till slut direkt vad svaret är, utan att behöva räkna ”


3 Genomgång: Multiplikation med 0
Peka på 4 ∙ 0 = 0� Berätta att om man har fyra påsar som alla innehåller noll äpplen så är det totalt noll äpplen Visa uttrycken a ∙ 0 = 0 Peka på variabeln a och repetera att det är en variabel som kan stå för vilket tal som helst
Fråga: ”Vad betyder det här uttrycket?” Låt eleverna SURRA Fördela ordet tills någon säger något i stil med att vilket tal som helst multiplicerat med 0 är lika med 0 Låt då någon annan ÅTERGE det sagda�
Sammanfatta så att alla förstår: ”Det spelar ingen roll vilket tal man multiplicerar med 0, produkten är alltid 0� Om man t�ex� har noll äpplen i varje påse så spelar det ingen roll hur många påsar man har, det är fortfarande noll äpplen�
4 Genomgång: Multiplikation med 1
Peka på 4 ∙ 1 = 4 Berätta att om man har fyra påsar som alla innehåller ett äpple så är det totalt fyra äpplen Visa uttrycket a ∙ 1 = a och några olika multiplikationer med 1 Berätta att när man multiplicerar med 1 är produkten alltid lika med den faktor man multiplicerar med 1� Om det är ett äpple i varje påse så är det lika många äpplen som påsar


5 Genomgång och övning: Multiplikation med 2
Peka på 2 ∙ 6 Berätta att när man multiplicerar med 2 kan man tänka dubbelt: dubbelt så mycket som 6 är 12, alltså är 2 ∙ 6 = 12�
Visa 2 ∙ 8
Fråga: ”Vad är 2 gånger 8 lika med?” BETÄNKETID Konstatera: ”Eftersom dubbelt så mycket som 8 är 16 så är 2 ∙ 8 = 16 ” Gör på samma sätt med resten
6 Genomgång: Multiplikation med 10
Visa och säg: ”När man multiplicerar något med 10 så blir det tio gånger större Om man t ex multiplicerar 3 med 10 så är produkten tio gånger större än 3, alltså 30� Man kan se det som att de tre entalen i talet 3 blir tre tiotal Ett tiotal är tio gånger större än ett ental� Tio ental bildar ett tiotal�”
Fortsätt: ”I talet 3 står siffran 3 på entalsplatsen och visar att talet har tre ental� I talet 30, som är tio gånger större än 3, står siffran istället på tiotalsplatsen och visar att talet har tre tiotal Siffran 0 på entalsplatsen visar att talet 30 har noll ental ”
Visa 4 ∙ 10 Fråga vad produkten är BETÄNKETID. Konstatera att 4 ∙ 10 = 40 eftersom 40 är tio gånger större än 4 Visa multiplikationen med ett rutnät och repetera att multiplikation är kommutativt: 10 ∙ 4 är också lika med 40

7 Genomgång: Multiplikation med 3, 4 och 5
Klicka på ikonen med 3 och titta på den animerade genomgången med berättarröst som förklarar en räknestrategi för multiplikation med 3 Låt sedan eleverna individuellt huvudräkna multiplikationerna med 3 och skriva produkterna på ett kladdpapper� Påminn om JAG MED och låt en elev redogöra för hur hen tänkte ut produkterna med strategin� Sammanfatta själv vid behov�
Klicka på varje uttryck för att visa produkten
Gör på samma sätt med multiplikation med 4 och 5�
Aktivitet
8 Parövning: Multiplikationsloppet 25–30 min
Dela in i par Förse dem med en sexsidig och en tiosidig tärning Be dem slå upp s 71 i elevboken Visa med bildspelet och förklara hur de ska spela Multiplikationsloppet.
Låt paren börja när alla har förstått CIRKULERA När paren är klara arbetar de enskilt i elevboken
Regler för Multiplikationsloppet
Spelare 1 slår den sexsidiga tärningen, går så många steg, slår den tiosidiga tärningen och multiplicerar sedan det tal som blir slaget med talet som hen står på och säger produkten till spelare 2
Spelare 2 kontrollerar om svaret är korrekt� Om det är korrekt står spelare 1 kvar, är det fel backar hen ett steg
Turen går över till den spelare 2 och så fortsätter spelet tills någon kommer i mål�
Avslut


10 Sammanfattning: Vad har vi lärt oss? 10 min
Sammanfatta att ni har gått igenom räknestrategier och använt dem för att huvudräkna multiplikationer med 0–5 och 10 Man måste träna huvudräkning med strategierna tills man kan multiplikationerna med 0–5 och 10 utantill Skulle man senare glömma bort någon kan man alltid använda strategin för att räkna ut svaret�
Visa och förklara: ”Om man t ex inte vet vad 8 ∙ 5 är lika med så kan man huvudräkna produkten genom att tänka så här: jag vet att 8 ∙ 10 = 80 och 8 ∙ 5 måste vara hälften av det, alltså är 8 ∙ 5 = 40�
11 Avslutslapp
3.2.1 Uppmärksamma och stötta
Räknestrategier, huvudräkning och automatisering
En viktig del av matematikundervisningen i åk 1–3 var att eleverna skulle utveckla hållbara räknestrategier, för att kunna resonera sig fram till svaret i beräkningar, och befästa strategierna genom färdighetsträning. Färdighetsträningen bidrog också till att eleverna började automatisera grundläggande talkombinationer, som multiplikationstabellerna.
I början av åk 4 går vi igenom de viktiga räknestrategierna som fokuserar på att alla behärskar några hållbara räknestrategier, och låter dem färdighetsträna för att befästa dem och för att automatisera grundläggande talfakta.
Det kan vara stora variationer mellan olika elever och mellan olika klasser när det gäller förkunskaper och hur långt automatiseringen av grundläggande talfakta har kommit. Var därför beredd att anpassa vid behov.
Behärska strategier innan färdighetsträning
Säkerställ att eleverna har strategier så att de kan resonera sig till svaret på de kombinationer som inte redan är automatiserade innan du låter dem färdighetsträna. Om du ser elever räkna på fingrarna eller använder andra, mindre lämpliga metoder behöver du repetera de strategier som presenteras i lektionen och låta eleven försöka igen.
Produkten tio gånger större vid multiplikation med 10
Var uppmärksam på om någon elev lärt sig att lägga till en nolla vid multiplikation med 10. Det är inte ovanligt att elever har fått lära sig att vid t.ex. 25 · 10 lägger man bara till tians nolla till 25 så svaret blir 250. Den strategin är ibland förknippad med rena felaktigheter, som att nollan liksom flyttas från ett tal till ett annat, även om det till synes fungerar (man får ju ofta rätt svar). Strategin är heller inte hållbar i längden och är vansklig när den inte bygger på förståelse för räknesättet, positionssystemet och talsorterna. Tumregeln om att lägga till en nolla fungerar t.ex. inte vid kommande
decimaltalsberäkningar. Exempelvis skulle 2,5 · 10 med metoden ”lägga till nollan till 2,5” ge svaret 2,50, vilket blir fel. Resonemanget ”lägga till nolla” behöver ersättas med ett resonemang som baseras på förståelse för multiplikation som räknesätt, positionssystemet, talsorternas samband och platsvärde.
Be istället eleven fundera över vad som händer när man multiplicerar något med 10, vad det innebär att produkten är tio gånger så stor som den faktor man multiplicerar med 10, hur man skriver det på matematikspråk och vad de olika siffrorna står för i respektive faktor och i produkten. När eleven väl förstår det kommer hen inte behöva tumregeln om att lägga till en nolla längre.
Förenkla
I spelet Multiplikationsloppet kan du låta eleven slå en sexsidig tärning istället för en tiosidig. På så sätt kan eleven träna på räknestrategierna i ett lägre talområde.
Utmana mer
Du kan låta eleverna använda en 12-sidig eller en 20-sidig tärning i multiplikationsloppet.
Avslutslappen
Avslutslappen visar om eleverna kan använda sig av huvudräkning för att göra några multiplikationer där den ena faktorn är 0–5 eller 10. Om elever gör många fel och/eller tar väldigt lång tid på sig betyder det att de behöver mer färdighetsträning. Se till att de har hållbara strategier innan de exempelvis får färdighetsträna med winnetkakort.
Färdighetsträning
För att elever ska bli säkra på huvudräkning med multiplikation behöver de träna ofta och intensivt i korta pass. Låt dem exempelvis träna runt 10 minuter varje dag. Det finns många appar och program för detta.
I lektionen finns även winnetkakort som du kan skriva ut och ge till eleven. Låt hen klippa isär dem och öva runt 10 minuter per dag. Kombinationer som eleven automatiserat kan eleven lägga åt sidan så att hen fokuserar på de som ännu inte automatiserats.
3.3 Multiplikation med 6–9
Syftet med den här lektionen är att säkerställa att eleverna har grundläggande kunskaper om räknestrategier för multiplikation med talen 6–9 Syftet är också att säkerställa att eleverna kan huvudräkna multiplikation med stöd av räknestrategierna� Eleverna får färdighetsträna på det för att fortsätta automatisera multiplikationstabellerna 6–9
Lektionsmål
• Eleven kan huvudräkna multiplikationer med talen 6–9 och visar det genom att beräkna produkten utan hjälpmedel och utan att använda uppenbart ohållbara strategier som t.ex. att räkna på fingrarna samt genom att kunna förklara hur hen tänkte om du frågar.
Matematiska begrepp: multiplikation, faktor, produkt, dubbelt, variabel, uttryck, strategi, kommutativa lagen, distributiva lagen, talkombinationer
SvA: fem i rad
Repetition: Huvudräkningsstrategier
Du repeterar vad en räknestrategi är�
Genomgång: Multiplikation med 9
Du går igenom räknestrategin En mängd mindre än med 10 och eleverna SURRAR sedan för att beräkna 9 ∙ 9 med den
Genomgång: Multiplikation med 6
Du går igenom strategierna Dubbelt så mycket som multiplikation med 3 och Multiplikation med 5 och en mängd till Sedan SURRAR eleverna för att beräkna 6 ∙ 6 med någon av strategierna
Genomgång: Multiplikation med 7
Du går igenom strategin Multiplikation med 5 och två mängder till�
Genomgång: Multiplikation med 8
Du går igenom strategierna Dubbelt, dubbelt, dubbelt respektive Dubbelt så mycket som multiplikation med 4. Eleverna beräknar 8 ∙ 8�
Material: Två tiosidiga tärningar till varje par (0 räknas som 10)
Förberedelser
• Skriv ut kopieringsunderlaget Multiplikationsspelet (till varje par samt några extra i reserv)�
• Skriv ut avslutslappar�
• Skriv eventuellt ut winnetkakort till elever som behöver extra färdighetsträning
• Övningsblad finns� Skriv ut vid behov�
Lektionens resurser
Parövning: Multiplikationsspelet
Eleverna färdighetstränar huvudräkning genom att spela Multiplikationsspelet i par
Sammanfattning: Vad har vi lärt oss?
Du sammanfattar att ni nu har gått igenom räknestrategier för alla multiplikationer i 0:ans till 10:ans tabeller och förklarar att när man använt en strategi för att tänka ut svaret på en multiplikation tillräckligt många gånger så kommer minns man till slut produkten utantill Avslutslapp
Uppstart




2 Repetition: Huvudräkningsstrategier 10 min
Visa och förklara: ”4 ∙ 6 är ett exempel på en multiplikation som man bör kunna huvudräkna och när man huvudräknar behöver man en bra strategi Vid multiplikation med 4 kan man t ex använda strategin Dubbelt, dubbelt och tänka: Dubbelt så mycket som 6 är 12 och dubbelt så mycket som 12 är 24, alltså är 4 ∙ 6 = 24”
Om man beräknar en multiplikation tillräckligt många gånger så kommer man till slut att kunna svaret utantill Då behöver man inte längre göra någon beräkning, man bara vet svaret� Strategin är ändå bra att kunna för om man någon gång glömmer svaret så kan man alltid resonera sig fram till det igen
Repetera att multiplikation är kommutativt och visa att 6 ∙ 4 också är lika med 24
3 – 4 Genomgång: Multiplikation med 9
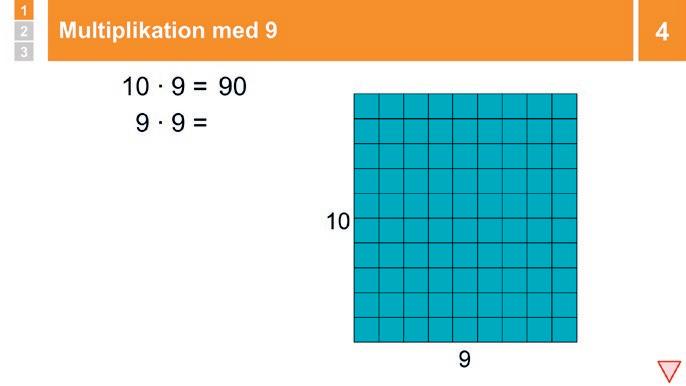
Peka och säg: ”För att beräkna 10 ∙ 6 kan man tänka: vad är tio gånger större än 6? Jo 60! Man kan också tänka: De sex entalen i talet 6 blir sex tiotal och sex tiotal är 60!”
Klicka fram 9 ∙ 6� Säg: ”Om 10 ∙ 6 = 60, vad är då 9 ∙ 6?” Låt eleverna SURRA Fördela sedan ordet tills någon säger något i stil med att 9 ∙ 6 måste vara 6 mindre än 10 ∙ 6, alltså 54 och låt då någon annan elev ÅTERGE det sagda Visa och förklara så att alla förstår
Fortsätt: ”Den här strategin som fungerar vid multiplikation med 9 kallas En mängd mindre än med 10 Om man vill veta vad 9 ∙ 6 är så kan man tänka att det är 6 mindre än produkten av 10 ∙ 6 eftersom man har en sexa mindre (9 stycken istället för 10 stycken sexor)� Alltså är 9 ∙ 6 = 54�”
Visa 9 ∙ 9 Låt eleverna SURRA och beräkna produkten med En mängd mindre än med 10� Låt någon förklara hur de tänkte� Sammanfatta strategin och visa produkten
Gör på samma sätt med 9 ∙ 7 och 9 ∙ 8�
5 – 6 Genomgång: Multiplikation med 6
Visa och förklara: ”För att beräkna multiplikationer med 6 så kan man använda strategin Dubbelt så mycket som multiplikation med 3 Då tänker man så här: Om 3 ∙ 7 = 21 så måste 6 ∙ 7 vara dubbelt så mycket, alltså 42.”
Fortsätt: ”Man kan också använda strategin Multiplikation med 5 och en mängd till Om man ska beräkna 6 ∙ 7 så tänker man då så här: Vad är 7 mer än produkten av 5 ∙ 7? Eftersom 35 + 7 = 42 så är 6 ∙ 7 = 42.”
Visa 6 ∙ 6�
Låt eleverna SURRA och beräkna produkten med valfri strategi Låt någon förklara hur de tänkte Sammanfatta båda strategierna och visa produkten�




7 Genomgång: Multiplikation med 7
Visa och förklara: ”När man beräknar multiplikationer med 7, t ex 7 ∙ 7, så kan man tänka så här: Eftersom 7 ∙ 5 = 35 måste 7 ∙ 7 vara lika med 35 och två mängder med 7 till, alltså 35 + 14. Alltså är 7 ∙ 7 = 35 + 14 = 49. Den här strategin kallas Multiplikation med 5 och två mängder till.”
8 – 9 Genomgång: Multiplikation med 8
Visa och förklara: ”När man multiplicerar något med 8 så kan man tänka dubbelt, dubbelt, dubbelt� Om man ska beräkna t�ex� 8 ∙ 6, och alltså multiplicera 6 med 8, så tänker man ungefär så här: Vad är dubbelt så mycket som 6? 12. Vad är dubbelt så mycket som 12? 24. Vad är dubbelt så mycket som 24? 48. Alltså är 8 ∙ 6 = 48 ”
Fortsätt: ”Man kan också använda strategin Dubbelt så mycket som multiplikation med 4 eftersom faktorn 8 är dubbelt så stor som faktorn 4 Om man vet att 4 ∙ 6 = 24 så förstår man att 8 ∙ 6 måste vara dubbelt så mycket, alltså 48 ”
Visa 8 ∙ 8� Låt eleverna SURRA och beräkna produkten med valfri strategi Låt någon förklara hur de tänkte Sammanfatta båda strategierna och visa produkten�
Aktivitet
10 Parövning: Multiplikationsspelet 25 min
Dela in i par, förse varje par med två tiosidiga tärningar och två olika färgpennor Visa och förklara Multiplikationsspelet
Låt paren börja spela när alla har förstått CIRKULERA
Regler för Multiplikationsspelet
Spelare 1 slår två tiosidiga tärningar� Sedan multiplicerar hen talen som tärningarna visar med huvudräkning och säger produkten till spelare 2
Spelare 2 kontrollerar om svaret är korrekt (du kan låta dem använda miniräknare för att kontrollera svaren så länge de först försöker resonera sig fram till produkten med en räknestrategi)
Om det är korrekt tar spelare 1 sin färgpenna och ringar in produkten på spelplanen� Sedan går turen över till spelare 2� Den som först får fyra i rad vinner

Avslut
11 Sammanfattning: Vad har vi lärt oss? 10 min
Visa multiplikationstabellen Visa hur den fungerar med exemplet 8 ∙ 9 Säg att ni nu har gått igenom räknestrategier för alla multiplikationer i 1:ans till 10:ans tabeller När man använt en räknestrategi för att tänka ut svaret på en multiplikation tillräckligt många gånger så kommer man till slut att veta vad produkten är utantill Det är bra att kunna alla multiplikationer upp till och med 10 ∙ 10 = 100� På så sätt kan man använda sin tankekraft mer för att tänka ut hur man ska lösa en uppgift och mindre på att göra själva beräkningarna� Vid mer avancerade beräkningar använder man ofta skriftliga räknemetoder, eller miniräknare, men det är fortfarande du som måste tänka ut vad som ska beräknas, hur och vad du ska ha svaret till

12 Avslutslapp
Låt eleverna huvudräkna multiplikationerna (läs mer under Uppmärksamma och stötta)
3.3.1 Uppmärksamma och stötta
Från strategi via färdighetsträning till automatiserade tabellkunskaper
I föregående lektion tillsammans med den här lektionen så har ni gått igenom räknestrategier för alla multiplikationer i 1:ans till 10:ans multiplikationstabell och eleverna har fått färdighetsträna huvudräkning med strategierna.
Räknestrategier
Syftet med detta är att alla elever ska ha grundläggande kunskaper om hållbara räknestrategier så att de alltid kan resonera sig fram till rätt svar. Att förstå strategierna är också bra i andra sammanhang (t.ex. för att förstå algebra eller i lägen då man vill använda en strategi, t.ex. göra en huvudberäkning när man handlar. Det är lättare att minnas det man förstår än det man enbart lärt sig) och förståelse för strategierna är tätt kopplat till förståelse för räknesätten och positionssystemet samt en välutvecklad taluppfattning.
När de förstår strategierna är det viktigt att de färdighetstränar med dem, dels för att befästa kunskapen om strategierna och uppnå en högre grad av räkneflyt med dem, dels för att automatisera multiplikationerna i 1:ans till och med 10:ans tabeller.
Att en strategi är hållbar betyder att den är effektiv och lämplig i sitt sammanhang. Den bygger på talförståelse och logiska resonemang och behöver inte vara en ”känd och allmänt använd” strategi, bara den fungerar och är matematiskt korrekt. Om eleven använder en hållbar strategi är risken mindre att hen räknar fel. Det betyder också att den går att utveckla uppåt i ett högre talområde. Att räkna på fingrarna är t.ex. inte en hållbar strategi i längden eftersom det snabbt bli ohållbart när talen man räknar med blir större.
Färdighetsträning
Utöver den färdighetsträning som finns i elevboken kan du vid behov också låta eleverna arbeta med winnetkakort och övningsblad, som finns att skriva ut, eller genom att göra övningar och spela spel som du tar från någon lektion ni har gjort. T.ex. kan eleverna spela Multiplikationsspelet och Multiplikationsloppet flera gånger. Om ni har den möjligheten kan du också låta dem färdighetsträna med lämpliga appar.
Automatiserade tabellkunskaper
När eleven har automatiserat en multiplikation så vet hen direkt vad produkten är och behöver inte göra någon beräkning.
Denna utantillkunskap är viktig eftersom det avlastar arbetsminnet och möjliggör för eleven att fokusera på att analysera uppgifter och tänka ut hur hen ska lösa dem och vad svaret kommer att säga.
Förenkla
Parövningen Multiplikationsspelet i steg 10 kan inte förenklas. Vid behov kan du istället hjälpa elever att resonera sig fram till produkten, i första hand genom att påminna om lämplig strategi och ställa öppna frågor om hur hen kan tänka, och sedan ställa mer ledande frågor om det behövs. Du kan skriva ut en multiplikationstabell som eleverna kan rätta sig med efter att de försökt beräkna produkten. Var uppmärksam på att de verkligen använder det till rättning och inte som en metod att snabbt beräkna svaret.
Utmana mer
Om eleverna behöver utmanas i parövningen Multiplikationsspelet så kan de efter att de kört spelet på det normala sättet köra en omgång till. Den här gången ska de tävla sinsemellan om vem som beräknar multiplikationen först. En elev slår tärningarna och den som först beräknar produkten får fylla i fältet på spelplanen. Detta fungerar bara om eleverna som spelar är jämnstarka.
En annan utmaning är att låta paret ta ett tal i taget på spelplanen och försöka komma på alla multiplikationer som har det talet som produkt. Låt dem sedan göra på samma sätt med andra tal på spelplanen.
Elever som har egna strategier för huvudräkning, alltså tänker på ett annat sätt än de strategier som presenteras i lektionen, bör uppmuntras att beskriva hur dessa strategier fungerar. Du kan också uppmuntra elever som verkar ha lätt för innehållet i lektionen att tänka ut egna strategier för beräkningar och låta dem beskriva hur deras strategi(er) fungerar.
Avslutslappen
Om eleven klarar avslutslappen på relativt kort tid och med få fel så tyder det på att eleven kan huvudräkna multiplikationer med hållbara strategier.
Om eleven gör många fel, eller tar väldigt lång tid på sig, så tyder det på att eleven inte behärskar hållbara strategier som hen kan använda för att huvudräkna multiplikationer i tabellerna 6–9. Prata då med eleven för att undersöka vad felen beror på. Be hen förklara hur hen tänkte för att beräkna några av multiplikationerna. I bästa fall förstår hen strategierna och då behöver hen färdighetsträna mer på dem. Om hen inte förstår strategierna behöver hen få undervisning för det parallellt med den fortsatta undervisningen.
Rik matematik 4A
Lärarhandledning
Rik matematik ger lärare stöd att planera, genomföra och utvärdera rik matematikundervisning. Rik matematikundervisning kännetecknas av aktiva elever och en aktiv lärare där begrepp, resonemang och problemlösning står i fokus. Varje årskurs innehåller mer än 80 strukturerade lektioner med bildspel, vilka hjälper till att visualisera och förtydliga matematiken med pedagogiska animeringar och bilder. Lektionerna har tydliga inledningar och avslutningar där central matematik betonas. Med Rik matematik får läraren stöd att varje lektion bedriva en undervisning som engagerar och utvecklar elevernas matematiska tänkande och bidrar till en djupare förståelse för matematik.
Läromedlet Rik matematik är utvecklat i ett nära samarbete mellan lärare och forskare och noggrant utprovat i klass.
I Rik matematik 4A Lärarpaket ingår utöver den tryckta lärarhandledningen även en digital lärarhandledning med tillgång till förberedda uppdrag i Tomoyo, en digital spelifierad färdighetsträning.
Rik matematik 4A innehåller följande kapitel:
Kapitel 1 – Tals uppbyggnad
Kapitel 2 – Addition och subtraktion
Kapitel 3 – Multiplikation och division
Kapitel 4 – Omkrets, area och skala
