39 minute read
Cuadrantes solares 213 Familiarizándonos con las estrellas y planetas Observación de fenómenos celes-
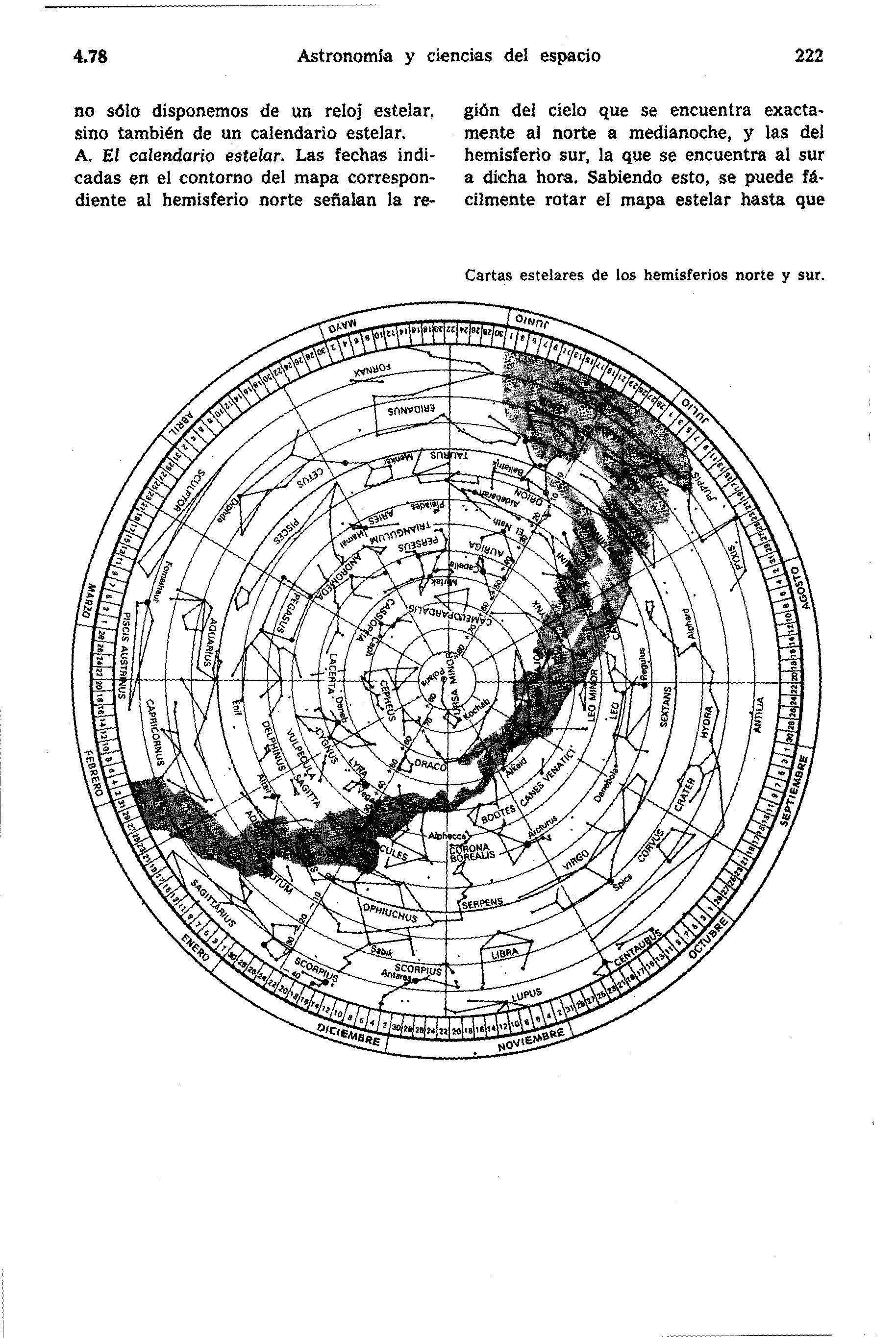
no s6io disponemos de un reloj estelar, gidn del cielo que se encuentra exacta- sino también de un calendario estelar. mente al norte a medianoche, y las del A. Ef calendario esteiar. Las fechas indi- hemisferio sur, la que se encuentra al sur cadas en el contorno del mapa correspon- a dicha hora, Sabiendo esto, se puede fá- diente al hemisferio norte señalan la re- cilmente rotar el mapa estelar hasta que
Cartas estelares de los hemisferios norte y sur.
Advertisement
coincida con lo que.se observa en el cielo. Si el observador se encuentra al norte del ecuador y tiene que hacer girar el mapa 15" en el sentido de las agujas del reloj, a partir de la posición correspondiente a medianoche, la hora será la 1 a.m. Si debe rotarlo 30" en sentido contrario al de las agujas del reloj, serán las 10 horas p.m. En el sur del ecuador, la rotación es en sentido contrario, dado que el observador

se encuenkra mirando al sur. Si debe girar minadas son solares y pueden diferir de el mapa 15" en el sentido de las agujas la hora local adoptada. del reloj a partir de la posición corres- pondiente a medianoche, significará que B. El reloj estelar. A continuación se re- son las 1.1 horas p.m. Las horas así deter- producen juegos separados de diagramas

para 10s hemisferios norte y sur: un reloj para cada mes.
Las posiciones de la manecilla del reloj corresponden a la fecha central de cada mes a las nueve horas en punto. ¿Puede completar dichas posiciones para las nue- ve en punto de mayo, agosto y noviembre y para la medianoche de junio, setiembre y diciembre? En el hemisferio sur deberá localizarse en forma aproximada el polo sur celeste (ver el experimento 4.71).

4.79
Astronomía y cie 4.79 Un modelo de sistema solar Los conceptos referentes al tamaño rela- tivo y distancias de los planetas al Sol pueden ilustrarse haciendo que los alum- nos construyan un modelo del sistema so- lar. Esto puede realizarse: (a) empleando bolas de diversos tamaños que representen al Sol y los planetas; (b) haciendo que los alumnos confeccionen modelos de arcilla o plastilina, empleando plantil!as de pers- pex, o (c) simplemente recortando círcu- los de cartón del tamaño adecuado. Estos pueden disponerse sobre una pared o en el piso o bien en el pizarrón donde podrán dibujarse con tiza las órbitas. La tabla que se reproduce u contimación propor- ciona los datos necesarios para la cons- trucción de un modelo aproximado. Las cifras entre paréntesis expresan la escala de distancias tomando como unidades la distancia media de la Tierra al Sol y el diámetro terrestre. recipiente. Hacer rotar suavemente éste provocando la revolución de los ‘planetas’ formados por las gotas de aceite.
Como el alcohol es menos denso que el agua, flota sobre la misma. El aceite se hunde en el alcohol pero flota en el agua. En este estado ‘libre’, el aceite forma es- feras que permanecen en suspensión en la zona de contacto entre el alcohol y el agua.
Observaci6n de fenómenos celestes
4.82 Observación de las fases lunares Durante el curso de una lunación, o mes lunar, los alumnos efectuarán, noche tras noche observaciones y dibujos de la Luna, comenzando en el novilunio y prosiguien- do en el transcurso de las cuatro fases.
4.83 Determinación de la relación existen- te entre las fases de la Luna y su posición aparente en el cielo Todas las observaciones que comprenden esta serie se efectuarán en un intervalo de dos semanas o más. Comenzarán aproxi- madamente una hora después de la puesta del Sol, observándose en todas las noches despejadas a la misma hora y siempre des- de el mismo lugar. Las observaciones se iniciarán en la fecha en que la Luna en creciente es apenas visible al atardecer, dos o tres días después del novilunio, para lo cual será necesario consultar un alma- naque.
Durante la primera noche se observará y dibujará con exactitud la posición de la Luna con referencia a los accidentes im- portantes del lugar (por ejemplo: si se halla exactamente encima del campanario de la iglesia o a medio pmino entre el campanario y un edificio de oficinas). De- terminar con la mayor exactitud posible su altura en grados sobre el horizonte, empleando el puño o los dedos extendidos. El puño, con el brazo extendido subtiende aproximadamente 10”; la distancia entre el pulgar y el meñique con la mano abierta equivale a unos 20°, etc. Consignar este dato en el dibujo. Observar también la dirección de los cuernos de la Luna y la forma del creciente lo más exactamente posible.
-_..____
Distancia media
__-
Astro al Sol (en millones Didmetro (Km) de Km) Sol Mercurio Venus Tierra Marte Júpiter Saturno Urano Neptuno Plutón
58 (04 108 (0,7) 150 (1,O) 228 (1,5) 778 (5,2) 1.420 (9,5) 2.870 (19,2) 4.490 (30,l) 5.900 (39,5)
1.400.000 (1 10) 4.800 (0,4) 12.000 (1,O) 13.000 (1,O) 6.800 (0,5) 140.000 (1 1,2) 120.000 (9,5) 50.000 (3,7) 53.000 (4,l)
(LO ?>
4.80 La estrella ‘de la mañana’ y ‘de la tarde’ Observar .a Venus y verificar sus salidas y puestas con respecto a las del Sol. 4.81 Demostración de los movimientos de los planetas Se necesitará un recipiente alto y estre- cho, un poco de agua, aceite para motores S. A. E. grado 30, alcohol a 90” y un lápiz. Llenar el recipiente con agua hasta la mi- tad. Verter con cuidado el alcohol sobre el agua procurando no agitar los líquidos ni perturbar la superficie intermedia. Su- mergir el lápiz en el aceite para motores y dejar caer varias gotas en el líquido del

Repetir la observación dos horas más tarde tomando nota de la hora. Efectuar repetidas observaciones de la misma mane- ra cada noche durante dos semanas y redactar un informe detallando éstas. In- dicar específicamente cómo varían de una noche a otra la iluminación de la Luna y su posición aparente; cSmo están orienla- dos sus cuernos o su terminador con res- pecto del Sol que se encuentra por debajo del horizonte occidental; cómo varía la posición de la Luna en el curso de una noche, las razones de dicha variacióil y también de la que se observa en noches sucesivas, ex. En un momento dado, en las cercanías del cuarto menguante (con- sultar previamente el almanaque) se repe- tirán las mismas observaciones pero al amanecer. ¿De qué manera concuerdan es- tas últimas observaciones con las realiza- das al anochecer?

4.84 Observación de un eclipse solar Explicar a !os alumnos que los hombres de ciencia, mediante la observación de los eclipses, los intervalos de tiempo en que se producen y las sombras a que dan lugar, han podido recoger ciertas informa- ciones relativas a la forma, dimensiones y movimientos del Sol, la Luna y la Tierra (observar la figura).
Eclipse de Sol '\. /Y' ,
A 6rbita de la Luna B Tierra c Luna
Preguntar a los alumnos si pueden men- cionar algunos de los procedimientos em- pleados para determinar la forma de la Tierra. indicarles que busquen en diarios o en un almanaque astron6mico las fechas en que se producirán eclipses. Cuando ten- ga lugar un eclipse visible en la zona, dis- poner lo necesario para salir al exterior a observarlo con el curso.
Advertencia: No se debe permitir que los alumnos observen directamente el ec1.p- se porque sus ojos podrían resultar daña- dos. El empleo de un vidrio ahumado o de varias capas de pelicula velada superpurs- tas tampoco es completamente seguro.
Un procedimiento seguro para observar un eclipse es hacerlo en forma indirecta. Los alumnos perforarán un trozo de car- tón y el maestro ies indicará que 10 sos- tengan por encima de su hombro, vueltos de espaldas al Sol de manera que la ima- gen de éste se proyecte a través del ori- ficio sobre un segundo trozo de cartón o papel que el alumno sostendrá frente a sí. Tampoco se les permitirá que observen al Sol directamente a través del agujero riel cartón (ver también el experimento 4.96).
4.85 Observación de un eclipse de Luna En este caso la observación directa es completamente segura. Procurar que los alumnos adviertan la forma del borde de la sombra proyectada por la Tierra cuando cruza el disco de la Luna, prueba de la redondez de la Tierra, aunque también podría ser proyectada por una Tierra con forma de disco (ver la figura) (ver tam- bién el experimento 4.96).
Eclipse de Luna A 6rbita de la Luna B Tierra c Luna
4.86 El período de rotación del Sol Determinar el período de rotación del Sol y la posición de su eje observando los cambios de posición de las manchas sola- res. Se requieren los siguientes elementos: Un pequeño telescopio o en su defecto binoculares (por lo menos de 6 aumentos) ; una caja grande, un tablero deslizable, papel y lápiz.
Advertencia: No permitir que los alum- nos observen directamente el Sol a través del instrumento. Si se emplean binoculares deberán montarse firmemente en el extre- mo anterior de la caja (observar el dibu- jo a). Si se utiliza un telescopio se cons- truirá para el mismo un parasol como pue- de verse en la figura b. Uno de los lados largos de la caja se dejará abierto para observa: por él. Disponer la &a de ma- nera que su extremo posterior sea perpen- dicular a la dirección de los rayos solares. Sobre el mismo se colocará el tablero movible con un papel adosado. El ocular se enfocará en una posición algo diferente a la empleada para la observación directa, la que se determinará mediante ensayos.
4 con binoculares
A

Una vez establecido el diámetro de la ima- gen solar se podrán efectuar todas las ob- servaciones sin variar sus dimensiones, lo que permitirá preparar anticipadamente el papel dibujando en él un círculo del tama- ño adecuado, Conviene tener en cuenta que con unos binoculares de 6 aumentos, a una distancia de 1 metro detrás del ocular se obtendrá una imagen de 5 centímetros de diámetro. Con mayores aumentos se lo- grarán imágenes proporcionalmente más grandes. El tamaño de la imagen es tam- bién proporcional a su distancia desde el ocular. Las observaciones deberán efectuarse diariamente a la misma hora, preferente- mente a mediodía. El papel se orientará siempre de la misma manera. Se marcarán rápidamente en el círculo, con ayuda de un lápiz, las posiciones de .algunas manchas solares y luego se tratará de representar sus dimensiones relativas y su forma apro- ximada. Mientras se realiza esta operación será necesario mover el papel.
A medida que el Sol rota las manchas solares parecerán camb7ar de posición día tras día. Midiendo las diferencias de posi- ción de las manchas en varios dibujos dia- rios se podrá determinar la velocidad del movimiento y SI las observaciones se pro- siguen durante un mes o más podrá verse la reaparición del grupo de manchas luego de haber completado su rotación. Además, en el curso de dicho intervalo puede deca- A parecer una gran mancha y aparecer otras nuevas.
Observacidn de los efectos del movimiento de la Tierra
D
b empleando un telescopio 4.87 Un péndulo de Foucault
Un buen soporte para un péndulo de Fou- cault que servirá para demostrar la rota- ción de la Tierra, puede construirse con
4.86 Observación de los cambios de posición de las manchas solares A hacia el Sol Soporte para el péndulo R tapa cubriendo la segunda abertura de Foucault improvisado c tablero deslizable con una prefisa en forma D imagen del Sol de G
una prensa en forma de G a la que se soldará, en la parte interior de su man- díbula, una bolilla de las empleadas en los cojinetes. Es mejor suspender el péndulo en el interior con la bolilla de cojinete apoyada sobre una hojita de afeitar sólida u otra superficie dura (ver el dibujo). Para suspender el {eso del péndulo, que puede ser una pelota de goma sólida, deberá em- plearse hilo de línea para pescar de nylon no retorcido. La longitud del péndulo no es importante, puede oscilar entre 3 y 30 metros.
Cuando se hace oscilar un péndulo de este tipo el plano üe oscilación parece va- riar en el curso de pocas horas con rela- ción a la marca efectuada en el suelo en el momento en que comenzó a oscilar li- bremente. Por supuesto, la responsable de este fenómeno es la Tierra que rota por debajo del peso del péndulo. Deberá cui- darse que el puntero, improvisado con una aguja de tejer corta introducida en la pe- lota esté perfectamente alineado con el hilo de suspensión. En el piso se puede fijar una línea de referencia, trazada so- bre una cartulina blanca asegurada me- diante chinches de dibujo. Esta deberá colocarse con precisión debajo del puntero cuando la bola esté en reposo.
Para poner el péndulo en movimiento se atará un hilo de algodón a una tachuela fijada en la bola, alineándola de manera que el plano de oscilación coincida con la línea de referencia, luego se quemará el hilo en las proximidades de la tachuela.
No es fácil lograr buenos resultados cuantitativos sin recurrir a muchos refi- namientos, pero no es difícil la observación del efecto.

4.88 Un péndulo de Foucault en miniatura Instálese un péndulo de Foucault pequeño en un soporte colocado sobre una mesa giratoria o una silla de oficina que pueda rotarse. Los alumnos observarán el com- portamiento del péndulo cuando se hace rotar lentamente la mesa.
4.89 La variación en la posición d,e1 Sol en el curso de las estaciones A. Desde una posición fija determínese con precisión el punto del horizonte en que el Sol desaparece al ponerse con refe- rencia a los accidentes del terreno. Repí- tanse las observaciones con intervalos de una semana, por lo menos, durante cuatro semanas y calcúlese la rapidez de dicho cambio en grados por día (para estimar los grados, el puño cerrado con el brazo extendido subtiende aproximadamente 10'). B. Trazar una línea en el piso o en la pa- red de una' habitación iluminada por el Sol, anotando con exactitud el mes, día y hora. Al cabo de una semana se trazará otra línea. Repitiendo la misma operación en el transcurso de un año se obtendrá una se- rie de observaciones interesantes. La va- riación en la posición de la línea de se- mana en semana y de mes en mes es originada por el movimiento de la Tierra alrededor del Sol.
C. En un lugar abierto clavar en el suelo verticalmente una estaca de 150 cm de largo y hacer que los alumnos lleven un registro de la longitud de su sombra, ia que medirán dos o tres veces por día en distintas estaciones del año. Anotarán la posición exacta de la sombra proyectada por la estaca marcando ésta y su longitud. Esta comparación se efectuará al comen- zar el año escolar, en el invierno y la pri- mavera, y al finalizar el período lectivo (véase también el experimento 4.68). D. Se redactará un informe explicando el significado de los oambios observados en función del movimiento de la Tierra.
4.90 Fotografía de trazos estelares Una actividad muy interesante para los alumnos que posean cámaras es la foto- grafía de trazos estelares producidos por la rotación de la Tierra. Se requiere una cámara fotográfica y película, un trípode u otro soporte sólido y un reloj. Se aguar- dará una noche despejada y sin luna y se elegirá un lugar libre de obstáculos que impidan la visibilidad del horizonte, al re- paro de luces extrañas, como faros de automóviles, etc.
La cámara se apuntará lo más exacta- mente posible hacia el polo celeste (o si el observador se encuentra al norte del ecuador, hacia la estrella polar), fijándola
ya sea mediante un trípode o por medio de trozos de madera. Enfocar al infinito y abrir el diafragma a plena abertura; poner el disparador en 'tiempo' e iniciar la ex- posición. Dejar el aparato inmóvil durante dos o más horas evitando toda trepidación de la cámara; luego, cerrar el obturador durante uno o dos minutos cuidando de no mover la cámara. Abrir nuevamente el ob- turador durante un minuto y, finalmente, cerrarlo. Esta última exposición breve ser- virá para identificar el final de la toma. Anotar la hora del comienzo y terminación. Una vez revelada, la película mostrará los trazos estelares como arcos concéntri- cos que tendrán por centro al polo celeste. Los arcos más largos podrán medirse para
Trazos estelares en torno del polo norte celeste determinar la longitud en grados de la rotación y partiendo de este dato se podrá calcular el período de rotación completa.
Se pueden hacer exposiciones similares con la cámara apuntando hacia diversas direcciones y alturas. El estudio de los trazos resultantes indicará que todos ellos demuestran la rotación en conjunto de todo el cielo, 'alrededor de un eje que pasa por los polos celestes, 'como si se tratara de una esfera sólida con las estrellas fijas en su superficie.
La trayectoria aparente de la Luna po- drá mostrarse mediante exposiciones de 1 o 2 minutos, cada una obtenida con intervalos de 10 o 15 minutos, durante un par de horas o hasta que la Luna salga del campo de la cámara. Deberán extremarse !as precauciones para evitar el desplaza- i:iiento de la cámara.
La trayectoria del Sol podrá registrarse durante el día, de la misma manera. Ad- vertencia: Bajo ninguna circunstancia de- berá observarse el Sol a través del visor. Cerrar completamente el diafragma para evitar una exposición excesiva. (Ver tam- bién el experimento 4.75.)

4.91 Trazos estelares en color Las estrellas tienen tanto colorido como los objetos terrestres aunque esto pasa ge- neralmente inadvertido debido a que los ojos adaptados a la oscuridad poseen es- casa sensibilidad al color. Una película para color muy sensible y una cámara fo- tográfica con objetivo de por lo menos f 3,5 registrará B la estrella roja Betelgeuse de la constelación de Orión, o a la amari- lla Capella, de Auriga y la dorada Albireo de Cygnus. En la constelación de Cassio- peia hay dos estrellas azules, una blanca, una dorada y una verde. Una buena cáma- ra con la que se puedan efectuar exposi- ciones largas, un trípode rígido y una pe- lícula rápida son todo lo que se necesita. Las sencillas cartas estelares de este libro ayudarán a identificar las constelaciones. La biblioteca pública local debe contar con libros de astronomía para aficionados que incluyen mapas similares. En algunos paí- ses se pueden obtener también indicadores en forma de disco graduado en el que, haciendo coincidir el mes y el día con la hora, se obtiene la posición de las cons- telaciones visibles.
La Tierra rota a razón de 15' por hora o sea, 1" cada 4 minutos. Para quienes se hallan en la superficie terrestre resulta más fácil apreciar este movimiento par- tiendo de la suposición de que las que se mueven son las estrellas. Además, éstas parecen girar alrededor del polo celeste respectivo. Cada estrella próxima al polo describe en su movimiento un círculo ce- rrado y a medida que aumenta su distan- cia de éste se incrementa el radio de cur- vatura de dicho círculo hasta el extremo de que las estrellas situadas en el ecuador parecen desplazarse en líneas rectas.
Una estrella es una verdadera fuente
puntiforme de luz y no admite ningún movimiento de la cámara, a menos que se desee registrar ‘colas de cerdo’ en vez de imágenes estelares. Podrá evitarse todo movimiento perturbador montando la cá- mara sobre un trípode rígido, cubriendo el objetivo con un trozo de cartón, em- pleando un disparador de cable, largo, pa- ra abrir el obturador en ‘tiempo’ o ‘bulbo’, esperando luego más o menos 3 segundos para que cese toda vibración de la cámara y recién entonces retirando el cartón que cubre el objetivo. Al finalzar 13 t.xposición cubrir nuevamente el objetivo con el car- ‘tón antes de cerrar el alsparador.
Notu: Los laboratorios cornercialcs de
revelado probablemente no reconocerán las imágenes estelares como tales y devolverán los negativos sin copiar, a menos que se los instruya al respecto.
4.92 Fotografía de constelaciones A. La fotografía de las constelaciones agre- ga una motivación estética a la de los trazos estelares. Se pueden lograr hermo- sas copias y diapositivas tanto en blanco y negro como en color y han probado ser un medio de enseñanza muy efectivo.
Existen muchas técnicas para fotografiar las constelaciones, pero una de las prefe- ridas es la siguiente: Elegir una constela- ción determinada, emplazar la cámara, y exponer durante 30 minutos con película en blanco y negro muy rápida (400 ASA) con una abertura del objetivo de f 11, luego cubrir el objetivo durante 2 minu- tos, abrirlo a f 4 y desenfocarlo ligera- mente. Finalmente, descubrir el lente du- rante 3 minutos o más. Una pantalla di- fusora sobre el objetivo durante la expo- sición final producirá el mismo efecto que un leve desenfoque. La fotografia resul- tante mostrará la constelación que apare- cerá como proyectándose en el espacio con todas sus estrellas seguidas por una cola.

B. Las diapositivas de 35 mm subexpuestas y descartadas se pueden perforar con la punta de un alfiler reproduciendo la forma de las diversas constelaciones. Estos ‘sli- des’ pueden proyectarse sobre una pantalla u observarse con un visor para que los alumnos identifiquen las constelaciones. Se pueden también introducir en una ra- nura practicada en un tubo de 105 usados para el envío de correspondencia y ob- servarse colocando el mismo frente 0 una fuente de luz (ver la figura).
‘Slides~ para la enseñanza de las constelaciones con- feccionados con película descactada
4.93 Fotografía de satélites artificiales La fotografía de los satélites constituye un placer. La técnica a emplearse es la descripta más arriba, para los trazos este- lares. Una excelente película para este fin es la Kodak Tri-X Pan. Como revelador se usará el HC-110 de Kodak, diluido 1: 15 durante 4 minutos. El principal problema es saber de antemano hacía dónde apuntar la cámara. Existen diversas fuentes de donde se puede obtener esta iriformación:. muchos periódicos publican diariamente la hora, la altura sobre el horizonte oeste o este expresada en grados y la dirección de la trayectoria de todos los satélites visibles. También los observatorios astro- nómicos locales y asociaciones astronómi- cas de aficionados podrán suministrar los datos requeridos. La fotografía de satélites es particularmente gratificante cuando la trayectoria del satélite pasa a través de una constelación muy conocida o si se tie- ne la fortuna de que dos satélites crucen el campo de la fotografía. Es este factor desconocido el que ejerce una continua atracción sobre el fotógrafo astronómico, tanto aficionado como profesional.
4.94 Determinación de la línea norte-sur por medio del sol A. Si se dispone de un reloj, ajustarlo para que indique el tiempo sohr medio local y proceder como se indica:
Al norte del ecuador: Orientar el reloj de modo que su manecilla horaria apunte hacia el Sol. La bisectriz del ángulo que forma la aguja horaria y las 12 indica la dirección de la línea norte-sur.
A¿ sur del ecuador: Orientar en la di- rección del Sol las 12 del reloj. La posición de la línea norte-sur se determina como en el caso anterior.
B. Si no se dispone de un reloj se puede utilizar en su lugar la sombra proyectada por una estaca clavada verticalmente en el suelo. A medida que el Sol cruza el cielo en el curso del día, la sombra de la estaca rotará y además se acortará durarite la mañana, alargándose nuevamente en Ia tar- de. Cuando la sombra es más corta, cerca del mediodía su extremidad más distante de la estaca apuntará hacia el norte o sur, según la experiencia se efectúe al norte o al sur del ecuador.

Modelos y demostraciones para la enseñan- za de la astronomía
4.95 Fases y eclipses lunares Los materiales necesarios son: Una linter- na enfocable, una pelota blanca y su co- porte para sostenerla, un globo terráqueo y una habitación previamente oscurecida. a propósito de estos aspectos, relacionán- dolos con las fases cambiantes y la ilumi- nación de la Luna verdadera.
Demostrar haciendo rotar el globo cómo las horas de salida y puesta de la Luna están estrechamente relacionadas con las fases.
En el primer cuarto, la Luna sale cerca de mediodía, alcanza su altura máxima en el cielo a la puesta del Sol y se pone cerca de medianoche. Si se observa el globo dirigiendo la visual verticalmente sobre la posición geográfica de la localidad pro- pia, se podrá reproducir la relación de la Luna con el horizonte en sus posiciones
de salida y puesta (ver la figura). .
B. Con ayuda del mismo dispositivo se pueden representar los eclipses. Los eclip- ses lunares, parciales o totales, podrán simularse situando la Luna en la sombra proyectada por el globo terráqueo. Si se la sitúa entre la linterna y el globo SU sombra se proyectará sobre la Tierra de- mostrando que un eclipse solar es visible desde un área mucho menos extensa que aquella desde la que es dable observar un eclipse de Luna -este último es observa- ble desde todo el hemisferio terrestre fren- te al cual se encuentra la Luna- (ver también las figuras correspondientes a los experimentos 4.84 y 4.85).
Las demostraciones relativas a los eclip- ses podrán ,adaptarse como actividades prácticas en las que todos los alumnos construirían modelos de arcilla de la Tie- rra y la Luna iluminándolos con linternas.
A. Fijar la linterna de modo que ilumine plenamente a la pelota e indicar a los alumnos que observen a ésta desde dife- rentes direcciones con lo que verán ‘lunas’ en creciente, en sus cuartos, gibosas y llenas. Pedirles que redacten un informe
4.96 ¿Qué aspecto presentan los eclipses solares?
Desde el punto A de la 0 superficie
rará el eclipse a través de uno de los terrestre, la Luna se observa alta, en Luna el cielo. Un observador situado en B en el mismo instante, la vería mucho más baja El Sol se representará mediante una iám- para eléctrica opaiina que proyecte luz a través de un agujero circular de 5 cm de diámetro practicado en un cartón en- negrecido. En el contorno de este aguje- ro se dibujará con lápiz rojo la corona solar. Una bolilla de madera de 2,5 cm de diámetro clavada en una aguja de tejer representará a la Luna. El observador mi- varios agujeros efectuados con un alfiler en una pantalla situada en la parte delan- tera del aparato (observar la figura). La
corona sólo es visible desde la posición correspondiente a la totalidad del eclipse. La posición de la Luna s,e regula mediante un rayo de bicicleta de alambre rígido fijado en el frente del aparato (ver tunibien el experimento 4.84). fiere, en la hoja de cartón que representa al piano de la órbita terrestre se pueden
practicar ranuras para insertar los discos
de la órbita lunar completa que la mues- tren tanto por debajo como por encima de dicho plano.
Imitación de un eclipse de Sol
4.97 ¿Por qué no se produce un eclipse en cada novilunio o plenilunio? El modelo para esta demostración se cons- truye, como se indicará a continuación, empleando discos de cartón, cuentas, b3- litas, bolillas para cojinetes o modelos de arcilla que representen al Sol, la Tierra y la Luna. La órbita lunar presenta una inclinación suficiente para que la Luna pase generalmente por encima o debajo de la sombra proyectada por la Tierra o

4.97 Modelo para demostrar las circunstancias en que se producen eclipses A ecíipse de Sol B eclipse de Luna c no se producen eclipses
de la región del espacio situada entre la Tierra y el Sol. Todos los discos pequeños, semicirculares, que representan a la órbita lunar, tendrán igual inclinación en el mis- m o sentido, que probablemente deberá exagerarse para que su relación con el fenómeno resulte más evidente. Si se pre- 4.98 La causa de las estaciones Se utilizará una pelota de goma perforada para representar a la Tierra, por ejemplo, una de tenis. A través de la misma se in- sertará un alambre de 15 cm de largo o una aguja de tejer que representará al eje de la Tierra. Sobre un cartón se dibu- jará un círculo de alrededor de 40 c m de diámetro que hará las veces de la órbita terrestre.
A unos 15 cm por encima del centro del cartón se suspenderá una lámpara eléctrica que ocupará la posición del Sol. Puede usarse también una vela encendida. Colocar sucesivamente la pelota que re- presenta a la Tierra en las cuatro posi- ciones que ilustra la figura, con su eje inclinado aproximadamente 23",5. Obser-
var la extensión de la superficie de la pe-
lota que está siempre iluminada. Compro- bar en qué región de la misma inciden
4.98 El invierno y el verano A 20 de Marzo
B 21 de Junio c 23 de Septiembre D 21 de Diciembre
E ecuador
F trópico de Cáncer a trópico de Capri- cornio
H círculo polar ártico J círculo polar an- tártico
perpendicularmente los rayos solares. Ve- rificar en cada una de las cuatro posicio- nes en qué hemisferio los rayos solares inciden en forma inclinada.
Repetir el experimento con la aguja en posición perpendicular a la superficie de la mesa, en cada una de las cuatro posicio- nes y comprobar qué ocurriría si el eje de la Tierra no estuviera inclinado (ver también el experimento 4.70 A.).
4.99 Causas de la desigualdad en la dura- ción del día y fa noche en algunos lugares de la Tierra Trazar un círculo grqde, que representa- rá a la órbita terrestre y dos líneas per- pendiculares entre sí que pasen por su centro En los puntos de intersección de éstas con el círculo, escribir sucesivamente en sentido contrario al de las agujas del reloj: 20 de marzo, 21 de junio, 23 de
C
Desigualdad en la duración del día y la noche A 20 de Marzo E ecuador B 21 de Junio P trópico de Cáncer c 23 de Septiembre O círculo polar ártico D 21 de Diciembre n Sol
septiembre y 21 de diciembre. Estas son las posiciones de la Tierra con respecto del Sol en dichas fechas. Trazar un peque- ño círculo que represente a la Tierra en la posición correspondiente al 21 de junio. El polo norte ocupará una posición ex- céntrica aproximadamente a 1/3 del radio del círculo terrestre en la dirección del Sol. Para cualquier otra fecha o posición orbital de la Tierra (que pueden determi- narse empleando el transportador) la po- siciOn del polo dentro del círculo que re- presenta a la Tierra, permanecerá inva- riable (ver la figura). En éste se podrán trazar el trópico de Cáncer y el ecuador. En consecuencia, el límite entre las zonas diurna y nocturna estará definido por la perpendicular a la línea Tierra-Sol, que pasa por el centro de la Tierra.
Empleando um diagrama de este tipo se puede efectuar una estimación de la ilu- minación solar en diferentes latitudes en una fecha determinada (por ejemplo, me- diante el diagrama se puede verificar que el 19 de agosto, en el círculo polar ártico el Sol estará sobre el horizonte aproxima- damente 18 horas, pero el 1'' de noviembre sólo 6 horas).
4.100 Efectos del ángulo de incidencia de los rayos solares sobre fa cantidad de calor y luz recibida por la Tierra Confeccionar un tubo de sección cuadrada de 2 cm x 2 cm x 32 cm plegando un trozo de cartón y confeccionar con cartón muy rígido una tira de 23 cm de largo por 2 cr.ti de ancho. Pegar esta tira en una de las caras del tubo dejando sobresalir una pro- longación de 15 cm. Apoyar el extremo de ésta sobre la superficie de la mesa e inclinar el tubo de modo que forme un ángulo de aproximadamente 25". *Colocar una linterna o una vela encendida en el extremo superior del tubo y marcar sobre la mesa el área iluminada por la luz ,que pasa a través del mismo. Repetir la expe- riencia dando al tubo una inclinación aproximada de 15" y hacerlo luego nue- vamente con el tubo en posición vertical. Comparar las dimensiones de las tres zo- nas iluminadas y calcular sus áreas. Desta- car la analogía de este experimento con la forma en que los rayos solares inciden en la superficie terrestre. ¿Es mayor la cantidad de calor y luz recibida del Sol por unidad de superficie cuando los rayos inciden en forma inclinada o cuando lo hacen verticalmente?

4.101 Construcción de un espectroscopio, Análisis de sustancias Los científicos frecuentemente pueden ana- lizar la composición de materia situada a grandes distancias mediante el empleo de un instrumento sumamente sensible deno- minado espectroscopio. Este se ha utiliza- do para determinar la composición quími- ca del Sol y otras estrellas y la de la at-
mósfera de diversos planetas. Los astro-
nautas emplearán en el futuro este tipo de instrumento para analizar la composi-
Un espectroscopio construido con una caja de zapatos ción química de sus alrededores inme- diatos.
La luz al penetrar en el espectroscopio es dispersada por una red de difracción desdoblándose en bandas coloreadas deno- minadas espectro. La materia se puede identificar fácilmente porque el espectro de cada elemento químico presenta deter- minadas líneas brillantes características.
Los materiales requeridos para la cons- trucción del espectroscopio consisten en una caja de zapatos, una réplica de red de difracción (consultar los catálogos de pro- veedores de accesorios científicos), un po- co de cinta para enmascarar y una hojita de afeitar partida en dos. En el centro de uno de los extremos de la caja efectuar un agujero de aproximadamente 2 cm de diámetro y fijar sobre el mismo con ayuda de la cinta un trozo de la réplica de la red, por la parte interior de la caja. En el otro extremo de ésta practicar una ranura de 2,5 x 0,5 cm que deberá ser paralela a las líneas de la red. Esta ranura deberá cubrirse por su parte interior con otra ranura más estrecha aiin construida con las dos mitades de la hojita de afeitar dis- puesta con ambos filos enfrentándose. Las dos medias hojitas se mantendrán juntas fijándolas por medio de la cinta engomada. El ancho de la ranura deberá ser igual al espesor de una hojita de afeitar y para asegurar un mejor resultado se ajustará al final (ver la figura). Observar diversos gases luminiscentes a través del espectros- copio, tales como el argón o neón usados en lámparas o letreros luminosos. Exami- nar las líneas luminosas del espectro indi- cadoras de la estructura característica de cada elemento (ver el experimento 2.222).

Modelos para las ciencias del espacio
4.102 Descubriendo la acción y ¿a reacción Este tipo de actividad introducirá a los alumnos en las leyes de Newton acerca del movimiento.
A. Un alumno calzado con patines, levan- tará una pelota grande por sobre su cabeza y la arrojará a un compañero. ¿Se mueve el alumno con patines? ¿En qué dirección? ¿Por qué? Tratar de realizar el experimen- to anterior con dos alumnos, ambos con patines, que traten de cojer al vuelo la pelota. ¿Qué ocurre? (ver asimismo los experimentos 2.249, 2.250 y 2.251). B. Se puede improvisar un sencillo motor a reacción con un globo de goma. Indicar a un alumno que 10 infle y lo sostenga por encima de su cabeza con el pico ce- rrado, soltándolo luego. Pedir a la clase que explique lo ocurrido.
Este experimento puede complementarse haciendo que los alumnos inflen un globo y manteniendo cerrado su pico lo apunten hacia un blanco cualquiera tratando de acertarle. Por lo general no tendrán éxito porque el globo carece de dispositivos de guiaie. Indicarles que le construyan aletas caudales que afectarán el equilibrio del globo y podrán sujetarse al mismo median- te una banda de goma colocada alrededor de su extremidad frontal y en la cual po- drán engancharse pequeños pesos, como por ejemplo broches para papeles. Así se logrará equilibrar el globo dotándolo ade- más de un sistema de guiaje. ¿Pueden aho- ra los alumnos acertar en el blanco?
4.103 Construcción de motores de acción y reacción A. Bote impulsado mediante un globo. Qui- tar uno de sus lados a un envase de cartón
para leche y hacerle un orificio en el fondo, cerca del borde; insertar en dicho agujero un tubito de vidrio y conectarlo al globo ajustándolo con una banca de goma (ver la figura). Inflar el globo y poner el ‘bote’
en una tina con agua; ¿navega? ¿En qué dirección? ¿Varía su velocidad si el extre- m o abierto del tubo de vidrio está debajo, de la superficie ,dd agua? Si no se consi- guen envases de leche del tipo ilustrado en la figura puede confeccionarse un dis- positivo similar con una caja de zapatos.
B. Cohete impulsado por un globo. Por medio de una cinta de celofán un alumno sujetará una pajita para sorber refrescos, lateralmente a un globo de forma alargada, pasando luego por el interior de ésta un alambre fino (ver la figura), uno de cuyos extremos se sujetará a uno de los postes del cerco de la escuela o a la manija de la puerta. Seguidamente, tensará el alambre atando su otro extremo en el lado opues- to de la habitación o patio. Una vez in- flado el globo se lo soltará de improviso. la noción de impulso, al sentir el choque producido por el agua al pasar por la man- guera de riego del jardín. Al aumentar la cantidad de agua que circula por la misma, ésta comienza a moverse; ¿en qué direición se mueve? ¿Qué ocurre con su movimiento a medida que aumenta la presión del agua? Conectar la manguera a un molinete para riego y aumentar gradualmente el caudal de agua observando la velocidad con que gira el molinete: ¿lo hace más rápido o más lentamente?

B. El impulso puede determinarse por me- dio de una balanza (ver la figura). Poner en uno de los platillos pesas (de 10 a 50 g). Sostener firmemente encima del otro platillo un globo inflado dejando W- capar el aire de manera que incida contra éste. ¿A cuántos gramos equivale el im-
¿Qué distancia recorre? Emplear globos de diversos tipos y experimentar con dis- tintas cantidades de aire expresando me- diante cifras y gráficos los resultados que se obtengan aumentando éste. Repetir la experiencia con globos de distintas formas.
Posiblemente los alumnos inventen otros dispasitivos en los gue pueda aplicarse con mayor eficiencia el principio de la acción y reacción.
4.104 Descubriendo los efectos del impulso A. En el patio de la escuela, o la casa, los nifios pueden comen’zar a familiarizarse con pulso producido por el aire proyectado sobre el platillo de la balanza? (Ver tam-
bién los experimentos 2.305 y 4.117.)
C. Los grandes cohetes pueden generar un impulso de 300.000 a 1.000.000 de kg. Analizar con los alumnos el concepto de que el peso de un cohete de 5.000 kg es el empuje hacia abajo, o atracción, ejer- cida sobre éste por la gravedad terrestre con una fuerza equivalente a 5.000 kg de peso. Para poder elevarse, el cohete debe primero superar ese empuje hacia el cen- tro de la Tierra y por lo tanto su impulso debe exceder los 5.000 kg. ¿Cuál de los siguientes cohetes alcanzará mayor altura y por qué?
Peso
Impulso
500.000 kg 500.500 kg 500.000 kg 750.000 kg 500.000 kg 1 .OOO.OOO kg
4.105 Descubriendo la ingravidez Para poder estudiar el movimiento de un cuerpo se requiere un sistema de referen- cia, es decir, algo con respecto al cual se pueda determinar la posición de dicho cuerpo en un instante dado. En muchos experimentos se adopta.un sistema de re- ferencia fijo con relación a la Tierra, como por ejemplo cuando estudiamos la caída de un cuerpo. En dicho sistema, la Tierra se halla en reposo. Si se desean estudiar los cambios estacionales será preferible sin embargo un sistema de referencia en que el Sol se encuentre en reposo y la Tierra en movimiento. describiendo su 6r- bita. Se deduce de lo dicho que la respuesta a la,pregunta de si un objeto está o no en movimiento depende del sistema de refe- rencia que adoptemos.
Del sistema de referencia depende no solamente la posición, sino también el peso de un objeto. El experimento que se descri- be a continuación ilustrará la ingravidez.
A. Atar un piolín del que previamente se habrá suspendido un soldado de juguete u otro objeto de modo que quede unido holgadamente a la parte superior de un armazón formado por tres piezas de ma- dera ensambladas, como indica la figura. Se levantará todo el conjunto tomándolo por el piolín y una vez suspendido e in- móvil se soltará éste. Cuando el soldado cae se comprobará que su posición rela- tiva dentro del armazón permanece inva- riable. Como no está sostenido ni por la cuerda ni por el armazón, se encuentra en estado de ingravidez con relación a sus alrededores, es decir, al sistema de refe- rencia empleado.

B. El peso de un objeto depende también de su posición. Si éste se determina con relación a un sistema de referencia solida- rio con la Tierra, coirkide con la atracción gravitatoria terrestre que actúa sobre dicho cuerpo. Esta fuerza decrece a medida que el objeto se aleja de la Tierra hasta que finalmente se torna insignificante.
Cabe hacer notar que es el peso del cuer- po el que varía bajo las circunstancias señaladas. La masa (o cantidad de materia que contiene, expresada en kg) no varía, en tanto no entremos en el campo de la física relativista donde los objetos se mue- ven con velocidades que se aproximan a la de la luz.
Un astronauta cuya masa en la superfi- cie terrestre sea de 90 kg tendra la misma masa en la superficie de la Luna, pero su peso que en la superficie de la Tierra era de 90 kg-peso será sólo de alrededor de 15 kg-peso en la superficie lunar. Em- pleando las unidades SI, la masa es de m kg, pero el peso es de mg Newtons. Dado que en la Luna g equivale aproxi- madamente a un sexto de su valor terres- tre, el peso de un hombre en la Luna será también alrededor de la sexta parte de su peso en la Tierra (ver los apéndices 1 y 2).
C. Una nave espacial en órbita se halla aún dentro del campo gravitatorio terres- tre. Su peso es exactamente la fuerza re- querida para mantenerla en órbita. Sin embargo, en un sistema de referencia so- lidario con .dicha nave, todo lo que se encuentre en su interior será ingrávido y con un leve impulso contra una de las paredes un tripulante podrá proyectarse a sí mismo contra la pared opuesta.
Más allá de la de la Tierra el efecto de la fuerza gravitatoria se tcrna insigni- ficante y la nave espacial se moverá en
línea recta, a menos que sobre ella actúen fuerzas generadas por su propio motor o por la acción de otros cuerpo;, como por
ejemplo, la Luna (primera ley de Newton) .
Fuera de la nave espacial, un hombre lo suficientemente libre para moverse, po- dría impulsarse a sí mismo hacia cual- quier dirección y no retornar jamás. Para evitar tal posibilidad se fijan cables de seguridad a los trajes espaciales de los astronautas que van a trabajar en el es- pacio.
4.106 Un lanzador de satélites Se necesitan los siguientes elementos: un balde, una pelota de fútbol y una percha de alambre (o un alambre adecuado), una plomada o peso, un piolín y un tubo de ensayo o cierto tipo de tapa adecuada.
Poner ia pelota sobre el balde de manera que quede bien sujeta. Enderezar el alam- bre hasta obtener una varilla recta de unos 30 cm de longitud, y dar forma curva al resto improvisando una base circular en la forma indicada en la figura. Asegu- rar esta base circular sobre la pelota em- pleando cinta de enmascarar, de manera que la porción recta de 30 c m quede en posición perpendicular sobre el centro de la pelota. Atar la plomada o peso al piolín y asegurar el otro extremo de éste mal tubo de ensayo o tapa, por medio de una cinta engomada. Invertir dicho tubo ,sobre el alambre vertícal (observar la figura).
Explicar a los alumnos que la pelota representa a la Tierra y la plomada a un satélite artificial. Para poner la plomada en movimiento hacia cualquier dirección sólo se requiere darle un ligero golpe con el dedo. Dejar que los alumnos descubran por sí mismos que ocurre cuando se lanza un satélite de las siguientes maneras: 1. Aplicando un leve golpe a la plomada hacia arriba e impulsándola afuera de la superficie de la pelota como se ilus- tra en la figura ¿qué ociirre? (La plo- mada se moverá hacia arriba y luego retrocederá cayendo hacia el punto de partida. Reproducirá el movimiento de un cuerpo proyectado verticalmente desde la tierra con escasa velocidad.) 2. Impulsando la plomada hacia afuera mediante un golpe suave pero con cier- to ángulo de inclinación con respecto a la superficie de la pelota. Explicar lo que ocurre mediante un diagrama. (La plomada se aparta de la pelota y luego retrocede nuevamente cayendo a cierta distancia del punto de partida según el ángulo de lanzamiento y la fuerza del golpe.) 3. Proyectando la plomada hacia afuera de la pelota mediante un golpe más fuerte y bajo cierto ángulo. Confec- cionar un esquema de la órbita. (La plomada se apartará de la pelota, des- cribirá círculos y aterrizará. Evidente- mente al completar una órbita pasará por el punto inicial de la misma.)