Jože Berk, Jana Draksler, Marjana Robič
Skrivnosti števil in oblik 9
NOVE SKRIVNOSTI
Samostojni delovni zvezek za matematiko v 9. razredu osnovne šole 1. del
Jože Berk, Jana Draksler, Marjana Robič
Skrivnosti števil in oblik 9
Nove skrivnosti
Samostojni delovni zvezek za matematiko v 9. razredu osnovne šole, 1. del
Uredila: Pika Klopčar
Strokovni pregled: Darja Čermelj
Jezikovni pregled: Renata Vrčkovnik
Fotografije: Natančen seznam je na koncu gradiva.
Direktor produkcije: Klemen Fedran
Izdala in založila: Založba Rokus Klett, d. o. o.
Za založbo: Maruša Dejak
Oblikovanje naslovnice: Beti Jazbec
Oblikovanje notranjosti: Beti Jazbec
Prelom: Danilo Frlež
Tisk: Evrografis, d. o. o.
1. izdaja
Naklada: 1.500 izvodov
Ljubljana, 2025
knjigarna.com
tudi na naslovu www.knjigarna.com
Založba Rokus Klett, d. o. o. (2025). Vse pravice pridržane.
Brez pisnega dovoljenja založnika so prepovedani reproduciranje, distribuiranje, javna priobčitev, predelava ali druga uporaba avtorskega dela ali njegovih delov v kakršnem koli obsegu in postopku, kot tudi fotokopiranje, tiskanje ali shranitev v elektronski obliki. Tako ravnanje pomeni, razen v primerih od 46. do 57. člena Zakona o avtorski in sorodnih pravicah, kršitev avtorske pravice.
Založba Rokus Klett, d. o. o.
Stegne 9 b, 1000 Ljubljana
telefon: 01 513 46 00
e-naslov: rokus@rokus-klett.si www.rokus-klett.si
CIP - Kataložni zapis o publikaciji Narodna in univerzitetna knjižnica, Ljubljana
51(075.2)(076.1)
BERK, Jože Skrivnosti števil in oblik 9. Nove skrivnosti : samostojni delovni zvezek za matematiko v 9. razredu osnovne šole / Jože Berk, Jana Draksler, Marjana Robič ; [fotografije točen seznam je na koncu gradiva]. - 1. izd. - Ljubljana : Rokus Klett, 2025
ISBN 978-961-292-508-6 (komplet) COBISS.SI-ID 239005443
Vsako poglavje
se začne s kratko ponovitvijo snovi iz preteklih let. V rubriki To že znam lahko preveriš, katere pojme, definicije in postopke boš v poglavju uporabljal/-a.
Kako uporabljati
samostojni delovni zvezek

Vsako poglavje se konča s kratkim preverjanjem znanja in ocenjevanjem znanja.
Vdelovnemsamostojnemzvezku
je osnovna razlaga na oranžni podlagi, zgledi pa na modri.
Naloge so razvrščene v dve skupini: Utrdim novo znanje in Rešim še to V prvi skupini naloge rešuješ kar v samostojni delovni zvezek, druge naloge pa v zvezek.
PREVERITE REŠITVE
1. Rešite nalogo v tiskanem samostojnem delovnem zvezku.
2. Poskenirajte QR kodo.
3. Odprite povezavo.
4. Fotografirajte stran v zvezku in fotografijo potrdite.
knjigarna.com

Pravilne rešitve se obarvajo zeleno, nepravilne rdeče. Pri nerešenih primerih se pojavijo vprašaji. Naloge, označene z rdečim okvirčkom, lahko popravite in postopek ponovite.
Pri nalogah odprtega tipa sistem pokaže rešitev in jo nato preverite sami.
1. IZRAZI
Enočleniki in veččleniki
Enočleniki: npr. 3 x, –2ab, 4a2 , –3 4 mn
Podobni enočleniki se ujemajo v spremenljivkah in eksponentu: npr. 3x2y4 in –5x2y4
Koeficient urejenega enočlenika je število, ki stoji pred vsemi spremenljivkami.
Veččleniki: dvočleniki: npr. a – 5, x2 + x, 3x + 2
tričleniki: npr. 3x2 – 7x + 5, 6a + 2b – 3c
štiričleniki: npr. 2a3 + 7a2 – 4a + 6, x – 3y + 5z – 1
Poišči podobne enočlenike in zapiši njihove koeficiente. 3x2, 2x + x2 , –5x, x2 3 , 1 2x, y2 , 2x3 , 1 2 x
Računska zakona
Pri računanju s spremenljivkami veljata isti zakonitosti kot pri številih: Zakon o zamenjavi: pri seštevanju in množenju lahko zamenjamo vrstni red seštevancev oziroma faktorjev.
Primer: a · b = b · a
Zakon o razčlenjevanju: število lahko pomnožimo z dvočlenikom tako, da število pomnožimo z vsakim členom dvočlenika.
Primer:
1.0 Ponovitev računanja z algebrskimi izrazi
knjigarna.com
1.1 Množenje veččlenikov
1.2 Kvadrat dvočlenika
1.3 Produkt vsote in razlike istih dveh členov
1.4 Razstavljanje izrazov
1.5 Algebrski ulomki
Seštevanje in odštevanje enočlenikov
Seštevamo in odštevamo le podobne enočlenike.
Primera: 3a + 5a = 8a 2x + 2
izraz 3,5
Seštevanje in odštevanje veččlenikov
Najprej odpravimo oklepaje, nato seštejemo podobne enočlenike.
Če je pred oklepajem +, ohranimo predznake znotraj oklepaja.
Primer: 5x + (2x – 7) = 5x + 2x – 7 = 7x – 7
Če je pred oklepajem –, spremenimo predznake znotraj oklepaja.
Primer: 3a – (7a – 4) = 3a – 7a + 4 = –4a + 4
Poenostavi izraz 4 – (x – 4) + (2x – 5) – 3x
Množenje enočlenikov
Zmnožimo koeficiente in zmnožimo spremenljivke.
Primer: 3x 4x2 = 12x3
Pomnoži 3x · 2x2 · (3 4 xy).
Množenje veččlenika z enočlenikom
Vsak člen veččlenika pomnožimo z enočlenikom.
Primer: 2a · (3a – 4) = 6a2 – 8a
Pomnoži – 1 2 ab(4ab – 3a2 + 2b2).
Izpostavljanje skupnega faktorja
Kadar vsi členi veččlenika vsebujejo enak faktor, ga lahko izpostavimo.
Primeri: a · b + a · c = a · (b + c) 6x2 + 9x = 3x (2x + 3) 8a2 – 4a = 4a · (2a – 1)
Izpostavi skupni faktor izrazov 3x2 + 12xy2 in 6a5b2 + 4a3b3 – 10a3b2
1.0 Ponovitev računanja z algebrskimi izrazi
Utrdim znanje
1 Izpiši koeficiente danih enočlenikov. enočlenik 3
koeficient
2 Zmnoži oziroma deli enočlenike.
3 Izpostavi največji skupni faktor.
*4 Izpostavi največji skupni faktor, ki je dvočlenik, in poenostavi.
a) 4(x – 2) + a(x – 2) – 3(x – 2) =
b) 5a(3a – 1) – 8a(3a – 1) =
c) (4x – 2)2 + 6x(4x – 2) =
5 Poenostavi izraz.
a) 8x – 3x + 6x – 10x =
c) 6m – 4n – 6m + 9n + m = č) (4x – 5y) + (6x – 3y) = d) 9a – (4b + 2a) =
6 Izračunaj produkt enočlenika in veččlenika. a) (4a – 3b) · 8 =
7 Poenostavi izraz.
a) 2a – 5 · (4a – 8b) =
4a · (5a – 4b + 2) – (9b – 6a) = c) 6x + (–4x) · (9x – 6) =
8 Najprej izraz poenostavi, nato izračunaj njegovo vrednost za dano vrednost spremenljivke.
3(6b – 3) – 9b + 4 =
b = –6 b) 5g + (–4g)(2g – 9) – g2 =
–2(a – 3b) – 4(2a – b) =
g = 1,2
1.1 Množenje veččlenikov
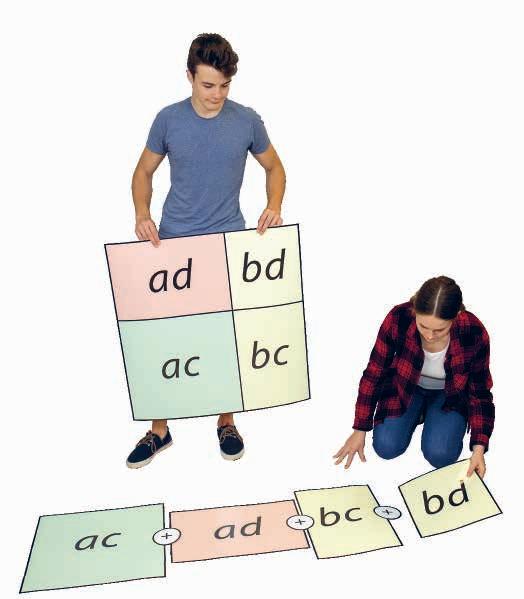
Bojan si je najprej zamislil kvadratno dno zaboja s stranico dolžine x, kasneje se je premislil in eno stranico povečal za 3, drugo pa za 5. Kolikšna je nova ploščina pravokotnega dna?
Če prvotno dolžino stranice kvadrata označimo z x, je dolžina pravokotnika x + 3, širina pa x + 5. Odgovor poiščimo grafično.
1. Narišemo pravokotnik z dolžino x + 3 in širino x + 5.
2. Razdelimo ga na manjše pravokotnike in kvadrate, kot kaže slika.
3. Izračunamo ploščine označenih pravokotnikov in kvadratov in jih seštejemo.
Znali bomo Æ množiti dvočlenik z dvočlenikom, Æ množiti veččlenik z veččlenikom.

Ploščina kvadrata je x2 .
Ploščini zeleno obarvanih p
+ 5x + 3x + 15 pravokotnikov sta 3x in 5x.
Ploščina modrega pravokotnika je 15.
Nalogo rešimo še računsko.
(x + 3)(x + 5) = x · x + x · 5 + 3 · x + 3 · 5 = = x2 + 5x + 3x + 15 = = x2 + 8x + 15
+ 8x + 15
Nova ploščina pravokotnega dna je enaka x2 + 8x + 15, če je stranica prvotnega kvadrata enaka x
Veččlenik množimo z veččlenikom tako, da vsak člen enega veččlenika pomnožimo z vsakim členom drugega veččlenika. (a + b)(c + d) = ac + ad + bc + bd
Rešimo skupaj
Zgled 1 Izračunajmo produkt dvočlenikov a + 3 in b – 2.
Ta korak lahko izpustimo in vsak člen enega veččlenika pomnožimo z vsakim členom drugega veččlenika.
Obarvamo člena prvega veččlenika, drugi veččlenik pa si predstavljamo kot samostojno enoto. (a + 3)(b – 2) =
Drugi veččlenik množimo s prvim členom in nato še z drugim členom prvega veččlenika.
= a · (b – 2) + 3 · (b – 2) = Množimo enočlenik z veččlenikom, kot že znamo.
= a · b + a · (–2) + 3 · b + 3 · (–2) = Pri množenju pazimo na predznake.
= ab – 2a + 3b – 6 = Veččlenik uredimo.
= –2a + ab + 3b – 6
Zgled 2 Izračunajmo produkt dvočlenika 3x + 2 in tričlenika 2x + 3y – 1.
Ta korak lahko izpustimo in vsak člen enega veččlenika pomnožimo z vsakim členom drugega veččlenika.
(3x + 2) (2x + 3y – 1) =
= 3x · (2x + 3y – 1) + 2 · (2x + 3y – 1) =
= 3x · 2x + 3x · 3y + 3x · (–1) + 2 · 2x + 2 · 3y + 2 · (–1) =
= 6x2 + 9xy – 3x + 4x + 6y – 2 =
= 6x2 + 9xy + x + 6y – 2 = 6x2 + x + 9xy + 6y – 2
Utrdim
novo znanje
1 Zmnoži in nato na črto zapiši črko (A–E) pravilnega izraza.
a) (x + 6)(x – 7) =
b) (x – 6)(x + 7) =
c) (x – 6)(x – 7) =
Vsak člen tričlenika pomnožimo z vsakim členom dvočlenika. Množimo enočlenik z veččlenikom, kot že znamo.
Dobimo 6 členov, ker je 2 · 3 = 6.
Podobne člene združimo.
Veččlenik uredimo.
