Issuu

VARIABELSAMMENHÆNGE OG LINEÆRE FUNKTIONER

1. Variable

De store, globale problemer, menneskeheden står overfor, som klimaforandringer, sult og sundhedsproblemer, kan kun løses ved at tage videnskaben til hjælp. Naturvidenskaberne kaldes også de eksakte videnskaber , fordi man konsekvent bygger på data , og fordi man anvender matematik i behandlingen af disse data. Lad os starte med at se på graferne i følgende øvelse – I arbejder sammen i grupper.

Øvelse 1.1

Udviklingen i verdens befolkningstal – med og uden kunstgødning

a) Prøv at beskrive med jeres egne ord, hvad der her illustreres: Start med at repetere, hvilke begreber vi anvender i et koordinatsystem, og hvordan vi aflæser. Fx: Hvad var verdens befolkningstal i 1900, og cirka hvornår passerede det 6 milliarder?

b) Grafen over befolkningstallet bygger her på eksakte data. Men hvad betyder ”estimeret befolkning”? Kan I gennemskue, hvorfor befolkningstallet afhænger af kunstgødning?

Verdens befolkning

Estimeret befolkning uden brug af kunstgødning

Estimeret befolkning afhængig af kunstgødning

c) Fremstilling af kunstgødning blev udviklet af de tyske kemikere Haber og Bosch i årene omkring 1. Verdenskrig, men det var først efter 2. Verdenskrig, at masseproduktionen heraf tog fart. Giver den viden dig en bedre forståelse af graferne over ”estimeret befolkning?”

Befolkningstal i milliarder

Fattige bønder og kunstgødning er jo ikke i sig selv tal, men når vi skal give en matematisk beskrivelse af et fænomen, skal vi kvantificere det, vi vil undersøge. De skal gives talværdier . Når det sker, kalder vi størrelser som befolkningstal og årstal for variable . De varierer.

For omkring 400 år siden begyndte man at indføre symboler for de variable. I matematik bruger vi typisk nogle af de sidste bogstaver i alfabetet, x , y og z , som symboler for de variable. Men vi følger også andre fags traditioner, så tiden betegnes ofte med t , temperatur betegnes T , hastighed betegnes v , osv. I moderne matematikprogrammer kan man også direkte bruge variabelnavnet, fx kunne vi anvende variablen befolkningstal , som varierer med årstallet.

Der er sædvanligvis mange variable, der påvirker en udvikling, og en del af processen i at forstå en udvikling består i at kontrollere de variable og fx udvælge to, der giver mening, i forhold til de spørgsmål, vi ønsker svar på. Dette gør man i alle fag, der arbejder med data – og det kaldes naturligt nok for variabelkontrol .

Øvelse 1.2

Kunstgødning og høstudbytte

Hvis vi tænker videre over kunstgødningens betydning, så kan vi fra landbrugets forsøgscenter have fået disse data:

Her har andre gjort noget af arbejdet for os og valgt to variable ud.

a) Du skal nu afsætte disse datapunkter i et koordinatsystem. Det betyder, du skal vælge, hvilken af de variable, der skal afsættes ud ad 1.-aksen, og hvilken op ad 2.-aksen. Den, som vi afsætter ud ad 1.-aksen, kaldes for den uafhængige variabel, og den, vi afsætter op ad 2.-aksen, kaldes for den afhængige variabel. Det er ofte, men ikke altid helt indlysende, hvor de variable skal afsættes. Diskuter det med din sidekammerat, og prøv fx, om det er meningsfuldt at formulere sætningen: ”Variablen y afhænger af Variablen x ”.

b) Når I er blevet enige om dette, kan I så blot ved at betragte tabellens tal beskrive med ord, hvad disse tal fortæller?

c) Det er måske svært at være meget præcis i besvarelsen af b). Men find nu noget kvadreret papir, tegn et koordinatsystem, og indret akserne, så I kan afsætte datapunkterne. Udtrykker det grafiske billede det samme, som I nåede frem til i b)?

d) Diskuter endelig, hvordan I vil forbinde datapunkterne med en sammenhængende graf.

AUafhængig og afhængig variabel

Ovenfor skulle I selv bestemme, hvad der var den uafhængige og den afhængige variabel.

To andre eksempler kunne være:

• I havet er det sådan, at sigtbarheden afhænger af dybden . Men man kan ikke hævde, at dybden afhænger af sigtbarheden, for der kan være andet på spil.

• I et korndyrkende landbrug ved man, at planternes vækst afhænger af temperaturen. Men man kan ikke hævde, at temperaturen udenfor afhænger af planternes vækst.

I skal nu selv finde på mindst tre andre eksempler. Skriv jeres eksempler op på tavlen, og diskuter derefter, om I er enige.

2. Koordinatsystemet

2. kvadrant (–, +)

3. kvadrant (–, –)

1. kvadrant (+, +)

4. kvadrant (+, –)

Vi vil i dette afsnit kort repetere, hvordan et koordinatsystem er indrettet, og hvilken terminologi (hvilke begreber) vi anvender, når vi taler om noget, der foregår i et koordinatsystem.

De koordinatsystemer, vi anvender, er opbygget af to ortogonale og uendeligt lange rette linjer . Disse linjer er indrettet som tallinjer , og vi angiver med en pil retningen fra negative tal over tallet 0 til de positive tal.

Det er ikke et krav, men hvis ikke andet nævnes, vil de to ortogonale tallinjer skære hinanden i punktet med koordinaterne (0, 0). Dette punkt kaldes også koordinatsystemets begyndelsespunkt , eller i matematik-sprog: origo . De to ortogonale linjer tegnes som vist, og den vandrette kaldes som omtalt for 1.-aksen , den lodrette for 2.-aksen .

De to akser opdeler koordinatsystemet i 4 områder, der navngives som vist på tegningen: 1. kvadrant , 2. kvadrant osv.

Når vi afsætter punkter eller tegner grafer i et koordinatsystem, skal vi altid markere en enhed på hver af akserne.

Øvelse 1.3

Aflæs koordinatsæt for punkter på en graf

Benyt grafen til at aflæse svarene på følgende:

a. Når x = 1, så er y = . . . d. Når y = 12, så er x = . . .

b. Når x = –2, så er y = . . . e. Når y = 0, så er x = . . .

c. Når x = 0, så er y = . . . f. Når y = 4, så er x = . . .

Klasseaktivitet

Øvelse 1.4

Afsæt punkter i koordinatsystem

Tegn et koordinatsystem på et papir, og afsæt følgende punkter: A (2, 5), B (1, –8), C (–3, 4) og D (–2, –6).

3. Repræsentationsformer

Variabelsammenhænge kan optræde på fire forskellige repræsentationsformer . Vi kalder de fire forskellige repræsentationsformer for sprog , tabel , graf og formel . Hver repræsentationsform indeholder forskellige måder at udtrykke variabelsammenhænge på.

BFire repræsentationformer (papir og blyant)

En matematikopgave fra middelalderen går ud på at undersøge, hvornår en hund fanger en hare. I opgaven står hunden og haren på en mark med 150 fods mellemrum, som vist på figuren. Når hunden og haren ser hinanden, løber haren væk fra hunden, og hunden løber efter haren. Hunden løber med en fart på 9 fod pr. spring, og haren med en fart på 7 fod pr. spring. Det er underforstået, at et spring for hhv. hunden og haren tager lige lang tid.

Opgaven løses ved at besvare nedenstående spørgsmål på fire forskellige måder – med hver sin repræsentationsform. I hver repræsentationsform bliver svaret det samme, men opgaven løses på forskellig måde.

Løsning vha. tabel

a) Opstil en tabel, som viser, hvor langt henholdsvis hunden og haren er kommet (målt i fod) efter hvert spring. Hvor langt er hunden efter 0 spring, efter 5 spring, efter 10 spring osv.? Tilsvarende for haren – husk, at haren har et forspring på 150 fod.

b) Benyt tabellen til at aflæse, hvornår hunden indhenter haren, dvs. hvor mange spring foretages, før haren er fanget?

Løsning vha. graf

c) Tegn punkterne for hunden fra tabellen i et koordinatsystem. Vælg antal spring på 1.-aksen og hundens distance på 2.-aksen.

d) Tegn punkterne for haren i samme koordinatsystem.

e) Tegn en graf gennem punkterne for hunden og tilsvarende for haren.

f) Aflæs på grafen det antal spring, der skal til, før hunden indhenter haren. Stemmer resultatet overens med din tidligere fundne værdi fra tabelrepræsentationen?

Løsning vha. formel

g) Benyt opgavens oplysninger til at opskrive en variabelsammenhæng mellem hundens afstand fra dens startpunkt og antallet af spring. Opskriv formlen på papir.

h) Benyt på samme måde opgavens oplysninger til at opskrive en variabelsammenhæng mellem harens afstand fra hundens startpunkt og antallet af spring. Opskriv også den formel på papir.

i) Opstil nu ud fra g) og h) en ligning, der kan bruges til at finde antallet af spring, der skal foretages, før hunden indhenter haren. Løs denne ligning.

j) Stemmer resultatet overens med din tidligere fundne værdi fra grafrepræsentationen?

Løsning vha. sprog

I middelalderen løste man opgaven vha. sproget på følgende måde:

Marken har længden 150 fod. Find halvdelen af 150, som giver 75. Hunden springer 9 fod i hvert spring, og 75 gange 9 er 675; dette er antallet af fod, som den jagende hund må tilbagelægge, før den kan sætte tænderne i haren. Eftersom haren springer 7 fod i hvert spring, skal du gange 75 med 7, hvorved du finder 525. Dette er antallet af fod, som den flygtende hare tilbagelægger, før den er fanget .

k) Forklar, hvorfor løsningen ser ud, som den gør. Hvorfor skal man fx halvere 150?

Øvelse 1.5

Fire repræsentationsformer

I opgaven ovenfor om hunden og haren så vi, hvordan man på fire forskellige måder kunne komme frem til det samme svar på det samme matematiske problem. De fire anvendte repræsentationsformer har hver deres styrker og svagheder, og derfor skifter man i matematik ofte mellem repræsentationsformerne, afhængigt af hvad man vil vise eller løse.

a) Hvilke styrker og svagheder synes du, de fire repræsentationsformer hver især har? Notér dem, og diskuter derefter jeres svar i grupper. I skal inddrage løsningen af opgaven om hunden og haren i jeres argumentation.

3.1 Repræsentationsform: tabel

Når variabelsammenhænge optræder på tabelform, så stilles de to sammenhørende variable overskueligt op i en tabel, som vist herunder. En sådan tabel kaldes også et sildeben . Hvis fx en elev gennemfører en test på en kondicykel, så kan vi beskrive elevens arbejde ved tabellen:

(målt i Watt)

Her er effekten den uafhængige variabel, og pulsen den afhængige. Hvis man benytter et regneark, vil man ofte skrive tabellen lodret, dvs. effekten i den første kolonne og pulsen i den anden kolonne.

3.2 Repræsentationsform: graf

Når variabelsammenhænge optræder på grafisk form, så aflæses den uafhængige variabels talværdier på 1.-aksen ( x -aksen), og den afhængige variabels talværdier på 2.-aksen ( y -aksen). Den grafiske repræsentation viser sammenhængen mellem de to variable på en mere dynamisk og overskuelig måde, end en tabel gør, og kan fx også anvendes til at aflæse sammenhørende værdier af de variable for alle tal og ikke kun hele tal, som vi så i eksemplet med hunden og haren.

Nedenfor til venstre ses et eksempel på et sædvanligt koordinatsystem med begyndelsespunkt origo , dvs. i punktet (0, 0). Nedenfor til højre ses et koordinatsystem med bokskoordinater, hvor akserne lægges, så det giver en bedre visuel fremstilling af det, man ønsker at præsentere. Bemærk, at her er (0, 0) ikke med i billedet.

3.3 Repræsentationsform: formel

Ofte er den afhængige variabel lig med et regneudtryk, hvori den uafhængige variabel indgår. Et eksempel herpå kunne være følgende:

For en bestemt kobbertråd kan sammenhængen mellem de to variable den elektriske modstand i tråden og trådens temperatur udtrykkes ved formlen:

y = 0,218 x + 56

hvor x angiver kobbertrådens temperatur (målt i °C, der læses ”grader Celsius”), og y er modstanden (målt i Ω, der læses ”Ohm”).

Klasseaktivitet

CKendes temperaturen, fx x = 30°, kan modstanden udregnes ved at erstatte variablen x med dens værdi 30, dvs.

y = 0,218 30 + 56 = 6,54 + 56 = 62,54

Konklusion: Når temperaturen er 30°, er modstanden 62,5 Ohm.

Det er ofte en fordel at kunne huske, hvorfra bestemte y -værdier stammer. Det gør vi ved at indføre betegnelsen f ( x ) i stedet for y , så formlen ovenfor skrives:

f ( x ) = 0,218 x + 56, hvor venstre side læses: ”f af x”

Konklusionen på udregningen af modstanden ved temperaturen x = 30° bliver så:

f (30) = 62,54

Her har vi altså i samme udtryk den beregnede y -værdi, og hvor denne kommer fra.

Formlen f ( x ) = 0,218 x + 56 fortæller, hvordan vi kan beregne værdien af den ene variabel ud fra værdien af den anden. Derfor kaldes sådanne formler også ofte for regneforskrifter

Kan du gennemskue, hvordan vi kan svare på et spørgsmål som følgende: Hvor høj er temperaturen, hvis modstanden er 65 Ohm? (Du skal få 41,3°).

Styrken i formelsproget er, at det afdækker en dybere sammenhæng mellem de forskellige variable, end vi umiddelbart kan se af et talmateriale eller en graf. Når sammenhængen er givet i et formelsprog, kan vi forholdsvis let svare på en lang række spørgsmål, som vi så eksempler på.

Men vi skal huske, at vi ikke kan vide, om en matematisk model som den ovenfor gælder for alle temperaturer, eller om der er en begrænsning. Det er en svaghed , som matematikken alene ikke kan svare på.

Funktioner – en aktiv øvelse

I arbejder to og to, og I skal hver have et kvadreret papir, hvor der både er plads til at tegne et koordinatsystem og opskrive en tabel med x- og y-værdier I skal hver opskrive et hemmeligt funktionsudtryk af typen f ( x ) = a x + b , hvor jeres a og b tal holder sig mellem –5 og 5.

På skift kører I nu 5 runder på følgende måde, hvor vi kalder jer for A og B:

1. A giver et tal (input) til B. B udregner funktionsværdien (output) og fortæller svaret til A, der noterer både input og output i en tabel. Derefter skifter I roller, indtil I begge har 5 punkter i en funktionstabel.

2. I plotter punkterne fra hver jeres tabel ind i jeres koordinatsystem og prøver at huske det, I har lært i folkeskolen om, hvordan man kan aflæse a -tallet og b -tallet. Og så komer I med jeres bud på den andens hemmelige formel. Er det den rigtige

3.4 Repræsentationsform: sprog

Når en variabelsammenhæng optræder på sproglig form, så formulerer vi med almindeligt sprog en viden eller en antagelse om en sammenhæng mellem to variable.

De fleste betaler fx for elektricitet efter deres forbrug. I X-købing kommune betaler man en fast årlig afgift på 400 kr. for at være tilsluttet el-nettet samt en pris på 1,75 kr. pr kWh, man forbruger. De to variable er her: forbrug og pris . Vi kan af sammenhængen afgøre, at forbruget er den uafhængige variabel (overvej!), og den vil vi kalde x . Den afhængige variabel er den samlede pris, og den vil vi kalde y . Vi siger, at prisen er en funktion af forbruget.

3.5 Oversættelse mellem repræsentationsformer

Vi har ofte brug for at kunne oversætte fra én af de fire repræsentationsformer til en af de andre.

Øvelse 1.6

Oversættelse mellem repræsentationsformer (brug af computer)

En kylling vejer 40 gram ved udklækningen. De næste måneder tager kyllingen 35 gram på om dagen.

a) Opstil en tabel i et regneark, der viser udviklingen i kyllingens vægt over en periode på 30 dage, idet du kun angiver vægten hver femte dag.

I en model kan kyllingens vægt beskrives ved en funktion f , hvor f ( x ) er vægten (målt i gram), når der er gået x dage efter udklækningen.

b) Benyt de variable til at opstille en formel, der beskriver udviklingen.

c) Tegn en graf, der viser udviklingen.

d) Vi ønsker at besvare spørgsmålet: Hvor meget vejer kyllingen efter 10 dage? Kan du bruge alle fire repræsentationsformer til at besvare spørgsmålet?

Kyllingen bliver slagtet, når den vejer 2500 gram.

e) Vi ønsker nu at besvare spørgsmålet: Hvor gammel bliver kyllingen? Hvilken repræsentationsform foretrækker du til at besvare dette spørgsmål?

Klasseaktivitet

Postløb – oversættelse mellem repræsentationsformer

På bogens website ligger der materiale til et postløb.

Aktiviteten består af fire fysiske poster, som læreren har placeret i hvert hjørne af klasselokalet. Ved hver post ligger der et antal opgaver, som skal løses. Opgaverne handler om oversættelse mellem repræsentationsformerne for lineære funktioner, og hver af de fire poster har særligt fokus på én af de fire repræsentationsformer. Svarene på opgaverne skrives ned på papir. Udover at besvare opgaverne skal det overvejes, hvilke to repræsentationsformer der oversættes imellem.

Klasse- aktivitet

Repræsentationsformer – et aktivt spil

På bogens website ligger der materiale til et spil.

I er inddelt i grupper. Hver gruppe får udleveret en lineær funktion beskrevet ved en af de fire repræsentationsformer. Spillet går ud på at finde de tre andre tilhørende repræsentationer af den samme funktion.

4. Regression – en metode til at afkode sammenhænge

Det danske befolkningstal er de seneste mange år steget jævnt, og vi vil her beskrive sammenhængen mellem antallet af mennesker i Danmark og den tid, der er gået efter år 2000. Vi vil finde en formel, som vi med en rimelig præcision kan anvende til fx at give vores bud på, hvor stor den danske befolkning vil være i fremtiden, hvis den nuværende udvikling fortsætter. Dette udtrykker vi ved at sige, at vi vil opstille en matematisk model , der beskriver befolkningstallet i Danmark som funktion af tiden målt i år efter 2000. Metoden, vi vil gennemgå, kaldes lineær regression , og anvendelsen heraf kræver adgang til et matematikprogram.

Øvelse 1.7

Tabel – punktplot af data

Nedenstående tabel viser udviklingen i befolkningstallet i Danmark efter år 2000.

Hele tabellen findes på bogens website.

Vi er interesserede i at finde en formel, der beskriver udviklingen i befolkningstallet efter 2000, så derfor må vi lave en ny variabel, som omregner årstal til antal år efter 2000.

Befolkningstallet udvikler sig over tid, dvs. variablen befolkningstal afhænger af variablen år efter 2000, som derfor er den uafhængige variabel.

a) Kopier data ind i et regneark.

b) Indfør din nye variabel, år efter 2000, i en ny kolonne, idet du udnytter regnearkets muligheder til automatisk at få beregnet værdierne for denne nye variabel.

c) Importer nu din tabel i dit matematikprogram, og tegn et punktplot over sammenhængen mellem befolkningstal og antal år efter 2000.

d) Ser det ud, som om der faktisk er sket en jævn, positiv tilvækst i befolkningstallet hen over årene efter år 2000? Hvordan er akseinddelingen på den lodrette akse?

e) Indret dit koordinatsystem, så du sammen med datapunkterne kan se koordinatsystemets begyndelsespunkt, dvs. punktet (0,0). Hvordan er akseinddelingen nu på den lodrette akse? Hvilken af de to grafiske repræsentationsformer foretrækker du?

4.1 Regression – bedste rette linje

I stedet for blot at tegne en graf fra datapunkt til datapunkt regner vi i nogle situationer med, at der er en lineær sammenhæng mellem de to variable. For at finde en formel skal vi som nævnt anvende en matematisk metode, som vi kalder lineær regression . Overordnet set går metoden ud på at finde en formel for den lineære funktion, der samlet set beskriver forløbet af punkterne i punktplottet bedst muligt

Træk virksomhederne ind 1

Ticras brug af regression

Se følgende klip fra filmen om TICRA, fra 29.30 til 33.44.

Giv et kort referat af, hvad samtalen mellem Oscar og Casper går ud på.

Lad os med et eksempel illustrere, hvad vi forstår ved bedst muligt . Den dybere matematiske forklaring må vente, til vi har lært differentialregning. Men lineær regression er indbygget i alle matematikprogrammer, og vi kan godt opnå indsigt i metoden allerede nu ved at udnytte de muligheder, som matematikprogrammet tilbyder.

Øvelse 1.8

Bedste rette linje

Når ammoniumnitrat opløses i vand, falder vandets temperatur. Temperaturen er således afhængig af, hvor meget ammoniumnitrat der opløses. I en forsøgsrække benyttes forskellige mængder ammoniumnitrat, der hver gang opløses i 170 g vand. Vandets starttemperatur er 22 ° C. Skemaet her viser opløsningens sluttemperatur:

Lad os betegne mængden af ammoniumnitrat med A og opløsningens temperatur med T . Til højre ses en grafisk fremstilling af de fem målepunkter.

a) Tegn selv et tilsvarende punktplot i dit matematikprogram.

Vi vælger som sagt nu at tro på, at der er en lineær sammenhæng mellem de to variable, dvs. at grafen for sammenhørende værdier med tilnærmelse er en ret linje.

b) Udnyt programmets muligheder til at tilføje en ret linje, som du kan flytte rundt med, indtil du mener, at den rette linje passer bedst muligt til samtlige datapunkter. Du kan med skydere ”skrue på” a - og b -tallene eller anvende flytbare linjer. Noter dine resultater, sammenlign med dine kammeraters, og er der store forskelle, så prøv at indkredse årsagen.

c) Udnyt nu matematikprogrammets muligheder til at udføre lineær regression på datamaterialet. Du skal få en ret linje, der ligner grafen til højre. Sammenlign de værdier, modellen har beregnet, med dem, du selv aflæste.

Matematikprogrammet prøver sig naturligvis ikke frem, som du gjorde ovenfor. Der findes en formel for regressionslinjen , og det er den, programmet anvender. Formlen er lidt indviklet, og vi skal have lært differentialregning, før vi kan forstå, hvor formlen kommer fra – og forstå, hvorfor metoden også kaldes for mindste kvadraters metode .

Træk virksomhederne ind 2

3 Shapes brug af regression

Se følgende klip fra filmen om 3Shape, fra 33.32 til 36.43.

a) Giv et kort referat af, hvad samtalen mellem Søren og Anton går ud på.

b) Søren forklarer, at det er principielt samme metode, de anvender, når de sætter billeder sammen. Kan du forklare, hvad han mener hermed.

Træk virksomhederne ind 3

Et forløb om regression

Hent undervisningsmaterialerne til TICRA.

Kapitel 6, afsnit 6.1 handler om det datamateriale, der historisk set var udgangspunkt for regressionsmetoden. I afsnittet forklares også, hvorfor metoden fik navnet regression, der betyder tilbageskridt. Afsnittet er et kort styret forløb, der giver ekstra indsigt i metoden.

Øvelse 1.9

En matematisk regressionsmodel for Danmarks befolkning

Vend tilbage til dit punktplot fra øvelse 5, der viser, hvordan befolkningstallet udvikler sig som funktion af antal år efter 2000. Metoden med ”flytbar linje” eller at skrue selv på a - og b -tallene er ret omstændelig, og man kan ikke være sikker på, at man finder den bedste rette linje.

a) Benyt i stedet dit matematikprograms faciliteter til at udføre lineær regression på datapunkterne. Du skal få noget, der ligner (afrundet til hele tal):

f ( x ) = 26 929 · x + 5 283 914, hvor x angiver antal år efter 2000, og f ( x )angiver befolkningstallet x år efter 2000.

Vi siger, at vi har fundet en matematisk model, der beskriver udviklingen i befolkningstallet i Danmark i årene efter 2000.

b) Benyt din funktionsforskrift til at beregne befolkningstallet 15 år efter 2000, altså i 2015. Overvej, hvorfor denne værdi ikke stemmer overens med tabelværdien for samme årstal.

Vi vil nu bruge den matematiske model til at forudsige befolkningstallet ud over den periode, vi har data for. Man siger også, at vi udregner en prognose.

c) Hvad bliver befolkningstallet i år 2030 ifølge din model?

d) Beregn f (50), og giv en fortolkning af tallet.

I de foregående spørgsmål regnede vi frem og fandt nogle bud på y -værdier. Vi kan også med den matematiske model besvare spørgsmål af typen: ”Hvilket år vil Danmarks befolkningstal passere 6,5 mio. mennesker?”

e) Spørgsmålet kan løses, ved at man opstiller en ligning. Prøv selv at gøre dette!

f) Løs ligningen ved at anvende en solve-kommando i dit matematikprogram. (Bemærk: Vi vil senere behandle reglerne for løsning af ligninger grundigt).

g) Forklar sprogligt, hvad løsningen fortæller om udviklingen i befolkningstallet. Husk på, at x betegner antal år efter 2000.

4.2 Oversættelse fra matematik til almindeligt sprog

Når vi skal fortælle andre ikke-matematikere om vores matematiske model og især om de spørgsmål, som modellen kan give svar på, så skal vi kunne oversætte mellem matematisk sprog og almindeligt sprog. Funktionsforskriften er jo matematisk sprog, så vi skal forklare i almindeligt sprog, hvad man kan aflæse af formlen. Vi skal derfor fortælle, hvad x og f ( x ) betegner, og vi skal forklare, hvordan konstanterne i forskriften skal fortolkes.

Øvelse 1.10

Hvad fortæller tallene i forskriften?

Besvar følgende spørgsmål ved at formulere hele sætninger, som fortæller noget om Danmarks befolkningstal, som er beskrevet ved funktionen

f ( x ) = 26 929 · x + 5 283 914

hvor f ( x ) betegner befolkningstallet x år efter år 2000.

a) Indsæt x = 0 i din funktionsforskrift, dvs. udnyt matematikprogrammet til at udregne f (0). Kan du genfinde tallet i forskriften?

b) Hvad fortæller b -tallet så om Danmarks befolkningstal ifølge din model?

c) Indsæt x = 1 i din funktionsforskrift, dvs. udnyt matematikprogrammet til at udregne f (1). Hvad får du, hvis du trækker f (0) fra? Kan du genfinde tallet i funktionsforskriften?

d) Udregn på samme måde f (5) – f (4) og f (20) – f (19). Kommenter dit resultat.

e) Konkluder med en sætning, der fortæller, hvad a -tallet siger om Danmarks befolkningstal ifølge din model?

Samtidig med at vi har set en jævn befolkningstilvækst, er Danmarks BNP også vokset. BNP står for bruttonationalprodukt og er det samlede beløb, som et land tjener på alt det, vi producerer og sælger – både varer og tjenester – på ét år. Det er en måde at måle, hvor god en økonomi et land har.

Øvelse 1.11

Danmarks BNP 2000-2025

Tabellen nedenfor viser udviklingen i Danmarks BNP i perioden 2000-2025 målt i mia. kr. Den fulde tabel findes på bogens website.

Kilde: Danmarks Statistik (www.statistikbanken.dk)

a) Tegn et punktplot af data i dit matematikprogram – ser det lineært ud?

b) Bestem ved regression den bedste lineære model, der beskriver udviklingen i Danmarks BNP som funktion af antal år efter 2000. Du skal få noget, der minder om:

g ( x ) = 61 · x + 1245, hvor g ( x ) betegner Danmarks BNP (målt i mia. kr.) x år efter 2000.

c) Aflæs b -tallet i funktionsforskriften, og forklar sprogligt, hvad tallet fortæller om Danmarks BNP.

d) Aflæs a -tallet i funktionsforskriften, og forklar sprogligt, hvad tallet fortæller om Danmarks BNP.

e) Benyt din funktionsforskrift, g ( x ), til at beregne Danmarks BNP i 2020, og sammenlign med tabelværdien – hvorfor er disse to tal ikke ens?

f) Tegn grafen for g .

Vi vil nu bruge formelrepræsentationen for den lineære model til at forudsige

Damarks BNP ud over den periode, vi har data for.

g) Hvad bliver Danmarks BNP i år 2030 ifølge din model? Tjek, at du får det samme ved at aflæse på grafen.

h) Benyt ”solve” til at løse ligningen g ( x ) = 3000, og giv en fortolkning af tallet i relation til Danmarks BNP. Stemmer det overens med grafen?

i) Benyt grafen til at aflæse, hvornår Danmarks BNP overstiger 4000 mia. kr.

FMatematisk analyse af ”signal gennem en kæde af mennesker”

Vi vil undersøge, hvordan et signal kan udbrede sig i en menneskekæde.

Dataopsamling:

a) Stil jer i en lukket ring, og hold hinanden i hånden.

b) På signal (fx ”Klar – parat – start”) startes tiden, samtidigt med at der sendes et håndklem videre fra person til person. Den sidste siger ”Stop”, og tiden måles. Gentag tre gange, og tag gennemsnittet.

c) Udfør forsøget med mindst 5 forskellige kædelængder (fx 5, 10, 15, 20 og 25 personer), og noter gennemsnitstiden i et skema over sammenhængen mellem kædelængde ( n ) og signaltid ( t , målt i sekunder)

Databehandling:

d) Skriv tabellen ind i dit matematikprogram.

e) Tegn et punktplot, der viser signaltider som funktion af kædelængde.

f) Udfør lineær regression på de indtastede data, og opskriv resultatet af regressionen som en funktion af t . Dvs. n ( t ) = . . .

g) Hvad fortæller a -tallet i den lineære funktion om nervesignalets vej gennem kæden?

h) Hvilke usikkerheder er der på vores målinger? Vil resultatet blive bedre, hvis undersøgelsen gentages mange gange?

i) Hvor lang tid vil signalet være om at gennemløbe en kæde af alle elever på din skole?

j) Hvor lang tid vil signalet være om at gennemløbe en kæde af alle mennesker i verden?

4.3 Absolut og relativ afvigelse

Antag, at en variabelsammenhæng mellem to variable, x og y , kan beskrives med følgende lineære model: y = 7,1 · x + 4. Til en bestemt værdi af den uafhængige variabel, x , hører både en forventet y -værdi, beregnet ved modellen, og en observeret y -værdi, fx hentet fra en tabel. Den forventede værdi kaldes også model-værdien. Den observerede værdi kaldes også af og til den sande værdi.

Hvis vi vælger x -værdien x = 1, kan vi beregne den tilhørende forventede værdi ud fra modellen: y model = 7,1 1 + 4 = 11,1. Den observerede værdi er, som vi for eksempel så det med befolkningstallet, ikke nødvendigvis den samme som den forventede. Lad os her antage, at den observerede værdi er: y sand = 10,5. Vi kan nu på to måder bestemme, hvor meget modelværdien afviger fra den sande (observerede) værdi.

Den absolutte afvigelse beregnes således: ansolut afvigelse = y model – y sand = 11,1 – 10,5 = 0,6

Model-værdien kan jo også være mindre end den sande værdi, dvs. den absolutte afvigelse kan blive et negativt tal.

Den relative afvigelse beregnes således = = = = model sand sand 11,1 10 , 5 0 , 6 relativ afvigelse 0 , 057 10 , 5 10 , 5 y y y

Omskrevet til procenttal er den relative procentvise afvigelse 5,7 %.

Om det er en acceptabel eller uacceptabel afvigelse, findes der ikke et fælles svar på. Det afhænger af konteksten. I atomfysik ville det være helt uacceptabelt, i samfundsfag ville det normalt blive opfattet som acceptabelt. I statistik ligger det lige på grænsen.

Øvelse 1.12

Absolut og relativ afvigelse i kontekst

I en model for udviklingen i produktionen af en bestemt type bil gælder følgende sammenhæng:

f ( x ) = 13,1 · x + 256

hvor f ( x ) betegner antallet af producerede biler (målt i tusinde) x år efter 2018.

I år 2020 blev der produceret 311 biler af denne bestemte type.

a) Bestem den absolutte afvigelse mellem den observerede (sande) værdi og modelværdien i 2020, og forklar, hvad den fortæller.

b) Bestem den relative afvigelse mellem den observerede (sande) værdi og modelværdien i 2020, og forklar, hvad den fortæller.

Øvelse 1.13

Forbrug af jordkloder

I en lang periode har vi hvert år brugt mere end én jordklode, forstået på den måde at vi hvert år bruger flere naturlige ressourcer, end jorden kan producere på et år. Nedenstående tabel viser udviklingen i antallet af jordkloder, som vi har brugt hvert år efter 1971. Den fulde tabel findes på bogens website.

Vi vil med lineær regression opstille en matematisk model, der kan give os et bud på, hvordan vores forbrug af jordens ressourcer har udviklet sig efter 1971.

Årstal

a) Hent data ind i et regneark, og opret en ny kolonne til variablen år efter 1971 .

b) Plot tabellens data i dit matematikprogram, og udfør lineær regression.

c) Opskriv forskriften for din regressionsfunktion – giv den selv et navn.

d) Hvor stort var vores forbrug af jordkloder i 2018 ifølge modellen? Og i 2024?

Det oplyses, at vores forbrug af jordkloder i 2024 var 1,75.

e) Bestem de absolutte og de relative afvigelser mellem det observerede forbrug iflg. tabellen og det forventede forbrug, som din model forudsiger.

f) Diskuter, om det er rimeligt at opstille en lineær model til at forudsige forbruget?

g) Diskuter, om det er rimeligt at opstille én samlet model for alle lande. Undersøg selv, hvordan Danmark er placeret – hvor mange jordkloder forbruger vi om året?

4.4 Korrelation og kausalitet

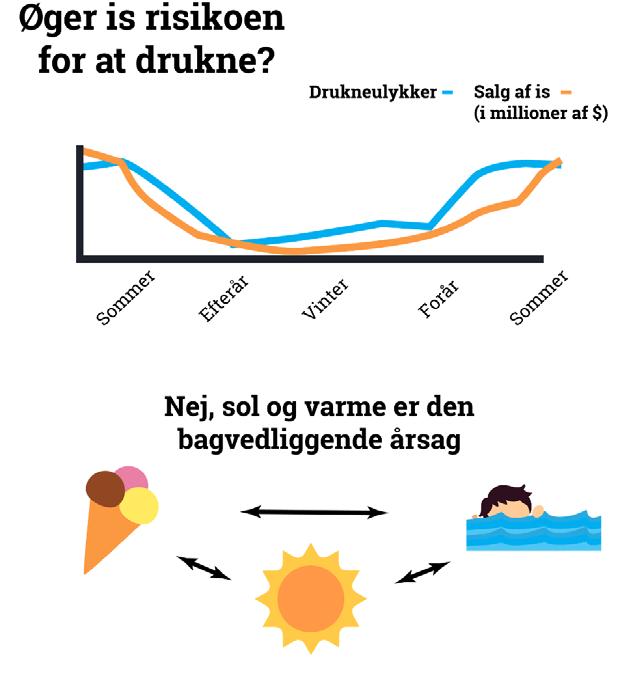
Hvis vi finder en lineær afhængighed mellem to variable, siger vi, at de to variable er korrelerede , eller at der er en korrelation mellem de to variable. En positiv korrelation mellem to variable betyder, at en stigning i den ene variabel forudsiger en stigning i den anden variabel. Omvendt betyder en negativ korrelation mellem to variable, at en stigning i den ene variabel forudsiger et fald i den anden variabel. Korrelationer fortæller os ikke umiddelbart noget om årsagssammenhængen mellem de to variable . Vi kan ikke afgøre om en stigning i den ene variabel rent faktisk forårsager en stigning i den anden variabel – eller om det omvendte gør sig gældende. Vi kan heller ikke vide, om den positive korrelation, vi observerer, i virkeligheden skyldes en tredje, bagvedliggende variabel, som vi ikke kender, eller om den observerede korrelation skyldes en ren tilfældighed. Et eksempel på, at der er en tredje, bagvedliggende variabel i spil, ses på figuren.

Når vi finder korrelation mellem to variable, må vi altså overveje, om der er grund til at tro, at der rent faktisk findes en årsagssammenhæng (kausalitet) mellem de to variable, herunder hvilken retning kausaliteten har. Fx i en undersøgelse af unges sundhedsvaner og computerbrug, er det da troværdigt at sige, at det er computerbrug, der påvirker sundhedstilstanden blandt unge? Eller kunne man argumentere for, at kausaliteten går den anden vej, og at man i virkeligheden sidder foran computeren, fordi man er i dårlig sundhedstilstand. Eller er der en tredje variabel, der kunne spille ind, og som kan være vigtigere end de to, vi faktisk ser på? I arbejdet med kausalitet har vi ofte brug for at trække på viden fra andre fagområder.

Øvelse 1.14

Oplæg til projekt om rygning og sundhed

I dag accepterer de fleste nok, at det er usundt at ryge. Men sådan var det ikke tidligere. Helt op i sidste del af det 20. århundrede var der store diskussioner herom. Der blev gennemført mange undersøgelser, og i en af de mest berømte, fra distriktet Whickham i Newcastle, nåede man frem til, at det var sundt at ryge! På nettet kan man finde mange eksempler på annoncer fra den tid, hvor læger anbefaler bestemte cigaretter, hvis man hoster meget. Men så i perioden 1954-2004 blev der gennemført en omfattende engelsk undersøgelse af sammenhængen mellem rygevaner og levealder, hvis resultater blev publiceret i 2004 i en artikel med titlen: Mortality in relation to smoking. 50 years observation on male British doctors . Grafen her er fra denne undersøgelse.

I projektet kan indgå konkrete spørgsmål som disse:

a) Hvad er det for variable, der indgår? Ved et blåt punkt står der bare 81. Hvad er de præcise koordinater til dette punkt?

b) Se på den blå graf og den røde graf hver for sig. Hvad fortæller disse to grafer?

c) Graferne sammenlignes lodret med en stiplet linje. Hvilken information giver denne? Prøv selv at lægge andre lodrette linjer, og undersøg, om det er samme information, du kan trække ud af de andre lodrette sammenligninger.

d) Graferne sammenlignes vandret med en dobbeltpil, hvorunder der står ’10 years’. Hvad betyder dette? Prøv selv at lægge en sådan pil ind andre steder. Er det samme information?

Men i projektet bør også indgå et referat af datidens diskussion om, hvorvidt rygning er usundt. Hertil skal du hente et dokument, der bla. giver et indtryk af en diskussion mellem to store matematikere/statistikere, der er uenige. Fisher var storryger og argumenterede imod den nævnte undersøgelse, men det er en sober argumentation, som er uden vanskelig matematik.

Træk virksomhederne ind 4

Et forløb om skjulte variable, korrelation og kausalitet

Hent undervisningsmaterialerne til Novo-filmen.

Afsnit 3.2 handler om skjulte variable, korrelation og kausalitet, og afsnittet indeholder et stort antal både sande og opdigtede små cases som grundlag for en drøftelse i grupper om emnet. Der lægges op til, at man selv konstruerer sådanne opdigtede cases om årsagssammenhænge.

Se også afsnittet fra 2.10 til 8.12 af filmen Statistiske metoder i hverdagsliv .

Her fortæller professor Susanne Ditlevsen bl.a. om typiske fejl i analyse af sammenhænge.

5. Lineær funktion med papir og blyant

Vingummibamsefabrikantspillet

Spillet er et rollespil, der spilles parvist med følgende hjælpemidler: kvadreret papir, blyant, lommeregner, vingummibamser. Spillet går ud på at undersøge betydningen af a og b i en lineær funktion, f ( x ) = a · x + b , gennem spørgsmål og svar i et pararbejde.

En udførlig beskrivelse med arbejdsark ligger klar til brug på bogens website.

Vi har tidligere undersøgt betydningen af a og b i en konkret kontekst, og vi vil nu udnytte matematikprogrammets faciliteter til en mere detaljeret undersøgelse af den generelle betydning af a og b . Vi gør brug af et godt undersøgelsesprincip, nemlig variabelkontrol , som betyder, at vi kun skruer på én variabel ad gangen. Når vi ændrer på den ene, så holder vi den anden fast – og omvendt.

Øvelse 1.15

Eksperimentel undersøgelse af betydningen af a og b

a) Tegn grafen for f ( x ) = a · x + b , hvor du anvender skydere for a og b .

b) Variabelkontrol: Sæt skyderen for a på 1, og variér skyderen for b . Observér, hvordan grafen flytter sig.

c) Formulér en sætning om b ’s betydning for grafens forløb, hvor du bruger ordene grafen for f , y -aksen, x er lig med nul , og funktionsværdi i nul .

d) Variabelkontrol: Sæt skyderen for b på 1, og variér skyderen for a . Observér, hvordan grafen roterer omkring grafens skæringspunkt med y -aksen.

e) Formulér en sætning om a ’s betydning for grafens forløb, hvor du bruger ordene grafen for f , stiger/falder/er vandret og a er positiv/negativ/nul

Bemærk, at vi siger om funktionen, at den er voksende/aftagende/konstant, når grafen stiger/falder/er vandret, mens vi bevæger os ud ad den positive del af 1.-aksen. Samlet kalder vi beskrivelsen af grafens forløb for funktionens monotoniforhold .

f) Formulér nu en sætning, hvor du bruger funktionsbetegnelserne, dvs. brug ordene funktionen f og voksende/aftagende/konstant .

5.1 Hældningskoefficient a og konstantled b

I en lineær funktion med forskrift f ( x ) = a · x + b kaldes a -tallet for hældningskoefficienten , og b -tallet kaldes konstantleddet . Vi vil nu se på en mere præcis matematisk betydning af hældningskoefficienten a og konstantleddet b i den lineære funktion f med forskriften f ( x ) = a · x + b .

Øvelse 1.16

Betydning af konstantleddet b

Alle steder på y -aksen er x = 0. Dette kan vi udnytte til at forklare betydningen af konstantleddet b i f ( x ) = a · x + b , hvor y = f ( x ).

a) Sæt x = 0 i funktionsforskriften, og udregn funktionsværdien.

b) Benyt resultatet i a) til at argumentere for, at grafen skærer y-aksen netop i det punkt, hvor y = b , dvs. i punktet (0, b ).

Betydningen af tallet b er altså: Når x -koordinaten er 0, er y -koordinaten lig med b .

Vi ser dernæst på hældningskoefficienten a . Vi tager udgangspunkt i et bestemt punkt, P , på grafen for f og betegner koordinaterne for P ( x 1, y 1), hvor y 1 = f ( x 1).

Så tager vi et andet punkt på grafen, nemlig det punkt, Q ( x 2, y 2), hvor x -koordinaten er netop 1 større end x 1, dvs. x -koordinaten i Q bliver x 2 = x 1 + 1.

Øvelse 1.17

Betydning af hældningskoefficienten a

a) Illustrer sammenhængen ovenfor i et koordinatsystem, dvs. tegn en ret linje, markér x -koordinaterne x 1 og x 2 (som er 1 større end x 1 ) på x -aksen. Afsæt nu de to punkter på linjen, som har koordinatsættene ( x 1 , y 1 ) og ( x 2 , y 2 ). Markér også de to punkters y -koordinater, y 1 og y 2 , på y -aksen. Træk stiplede linjer fra punkterne og vinkelret ud på akserne.

Nu skal vi så finde ud af, hvad y-koordinaten y 2 i det nye punkt bliver, dvs. vi skal udregne y 2 = f ( x 2 ), idet vi udnytter, at x 2 = x 1 + 1. Vi får således:

y 2 = f ( x 1 + 1)

y 2 = a ( x 1 + 1) + b

b) Omskriv nu højresiden af ligningen ovenfor ved at gange a ind i parentesen –husk at gange ind på begge led.

c) Omskriv dit udtryk ved at bytte om på leddene, så du får y 2 = a · x 1 + b + a .

d) Argumenter for, at det betyder, at y 2 = y 1 + a .

e) Benyt resultatet i c) til at argumentere for, at når vi står i et bestemt punkt og lægger 1 til x -koordinaten, så vil det tilsvarende punkt på grafen fremkomme, ved at vi lægger a til y -koordinaten.

Vi husker, at a kan være positiv, negativ eller nul. Derfor fortæller punkt e) i øvelse 18:

• Hvis a > 0 (dvs. a er positiv), så vil y -koordinaten blive større , når x -koordinaten bliver større

• Hvis a < 0 (dvs. a er negativ), så vil y -koordinaten blive mindre , når x -koordinaten bliver større

• Når a er nul, vil en større x -koordinat ikke skabe nogen ændring i y -koordinaten (overvej!).

Vi kan illustrere ovenstående lidt mere overskueligt i en funktionstabel for den lineære funktion f med forskriften f ( x ) = a x + b , idet vi tager udgangspunkt i, at f (0) = b , og lægger a til, hver gang x vokser med 1, og trækker a fra, hver gang x bliver 1 mindre:

Altså: Når x -koordinaten vokser med 1, så ændres y -koordinaten med a .

Øvelse 1.18

Forklar tabellen

Tag udgangspunkt i x = 0 og y = b markeret med rødt i tabellen ovenfor.

a) Hvad sker der, når vi går til højre i tabellen – stemmer det, at vi hver gang får en y -værdi, der er a større end den foregående? Husk, at 2 a = a + a osv.

b) Hvad sker der, når vi går til venstre i tabellen – stemmer det, at vi hver gang får en y -værdi, der er a mindre end den foregående?

c) Fortsæt tabellen i begge retninger: Hvad bliver y -værdien for x = 5? Og for x = 10? Og modsat, for x = –4? Og for x = –8?

Når vi regner med tal, er vi indenfor et område af matematik, der kaldes aritmetik . I øvelserne ovenfor regnede vi med bogstaver og ikke med tal. Der har vi bevæget os ind i det område af matematik, der kaldes algebra . Det kan måske i starten virke lidt sværere at regne med bogstaver end med tal. Men fordi bogstaverne kunne være hvad som helst, så gælder udregningerne, vi gennemførte ovenfor, for alle tal. Det illustrerer styrken i algebra.

En sådan viden som den, vi nu har opnået om lineære funktioner, formulerer vi ofte i det, vi på dansk kalder en matematisk sætning . Det er en lidt mærkelig sprogbrug – på fx engelsk kaldes det a mathematical theorem . Det er ikke så let at lave en sprogbrug om, så vi må vænne os til, at vi samler vores viden op således:

Sætning 1.1

Betydning af a og b for det grafiske forløb

For den lineære funktion f med forskriften f ( x ) = a · x + b giver hældningskoefficienten a og konstantleddet b følgende information om grafens forløb:

b : Grafen skærer 2.-aksen i punktet (0, b ).

a : Hvis x -værdien vokser med 1, så vil y -værdien ændre sig med størrelsen a .

Er a > 0, dvs. positiv, bliver y -værdien altså større , og vi siger, at funktionen er voksende.

Er a < 0, dvs. negativ, bliver y -værdien altså mindre , og vi siger, at funktionen er aftagende.

Er a = 0, dvs. nul , vil y -værdien hverken blive større eller mindre, dvs. funktionen er konstant.

Øvelse 1.19

Konstantled og hældningskoefficient ud fra tabel

I tabellen ses nogle værdier udregnet med forskriften for den lineære funktion f.

a) Hvad er konstantleddet b ?

b) Hvad er hældningskoefficienten a ?

c) Udfyld de tomme felter i tabellen.

Øvelse 1.20

Konstantled og hældningskoefficient ud fra forskrift

Angiv konstantled og hældningskoefficient for følgende lineære funktioner: a) f ( x ) = 7 · x + 23 b) f ( x ) = 4,7 · x + 6,3

( x ) = 0,25 · x d)

( x ) = –2 · x + 5 e)

( x ) = – x + 12 g) f ( x ) = 15 h) f ( x ) = 3 4 x + 8 5 i) f ( x ) = 0

Øvelse 1.21

Hældningskoefficient beregnet ud fra ændring i x og y

Vi betegner ofte en ændring i x -værdi med ∆ x (delta x) og tilsvarende en ændring i y -værdi med ∆ y , som vist på figuren her.

Vi ser igen på tabellen fra øvelsen ovenfor, hvor de tomme felter er udfyldt.

a) Hvad er ∆ y , når ∆ x = 2? Hvad er ∆ y , når ∆ x = 3? Ud regn brøken ∆y ∆x i hvert af de to tilfælde. Hvad ser du?

b) Hvad er ∆x, når ∆y = 4? Hvad er ∆x, når ∆y = 8? Udregn brøken ∆y ∆x i hvert af de to tilfælde. Hvad ser du?

c) Formuler en sætning, der forklarer, hvad brøken ∆y ∆x kan bruges til at beregne, og undersøg, om sammenhængen findes i formelsamlingen.

d) Anvend dit svar i c) til at tegne grafen for funktionen med udgangspunkt i grafens skæringspunkt med y -aksen.

e) Kontroller din graf ved at vise, at et andet af punkterne i tabellen også ligger på linjen.

Øvelse 1.22

Konstantled og hældningskoefficient ud fra graf

Her ses graferne for fire lineære funktioner, f , g , h og k .

a) Aflæs konstantled b og hældningskoefficient a for hver af graferne f , g , h og k her, og anvend de aflæste værdier for a og b til at opskrive en forskrift for hver af de fire funktioner f , g , h og k

Øvelse 1.23

Grafen for en lineær funktion tegnes ud fra a og b

Tegn i hånden graferne for nedenstående funktioner, idet du udnytter dit kendskab til betydningen af konstantled og hældningskoefficient:

Øvelse 1.24

Fortolkning af a og b

CO 2 -indholdet i atmosfæren de senere år kan med god tilnærmelse beskrives ved den lineære funktion f med forskriften

f ( x ) = 2,5 · x + 391,6 hvor f ( x ) er CO 2 -indholdet i atmosfæren (målt i ppm) x år efter 2011.

a) Hvad fortæller tallet 391,6 om CO 2 -indholdet i atmosfæren?

b) Hvor meget vokser CO 2 -indholdet i atmosfæren pr. år ifølge modellen?

6. Regning med lineære funktioner

Vi har tidligere løst opgaver, hvor vi bestemmer y -værdien, når vi kender x -værdien. Dette kalder vi ”at regne frem”. Vi har også omvendt løst opgaver, hvor vi bestemmer x -værdien ud fra y -værdien, hvilket vi vil kalde ”at regne tilbage”. Vi vil her ved hjælp af eksempler finde ud af, hvad strategien er i hvert af de to tilfælde.

Eksempel: ”Regn frem” i en lineær funktion

Der er givet den lineære funktion f med forskriften f (x ) = 2 · x + 3, og vi ønsker at finde y -værdien, når x -værdien er x = 4:

f (x ) = 2 4 + 3

f (x ) = 8 + 3

f (x ) = 11

Dvs. når x = 4, så er y = 11: Punktet (4, 11) ligger på den rette linje, der er graf for f .

Eksempel: ”Regn tilbage” i en lineær funktion

Der er givet den lineære funktion f med forskriften f ( x ) = 2 · x + 3, og vi ønsker at løse ligningen f ( x ) = 9:

f ( x ) = 9

2 · x + 3 = 9 Vi indsætter regneforskriften

2 · x = 6 Vi trækker 3 fra på begge sider

x = 6 2 = 3 Vi dividerer med 2 på begge sider og udregner brøken

Dvs. når y = 9, så er x = 3: punktet (3, 9) ligger på den rette linje, der er graf for f

Øvelse 1.25

Funktionsforskrift og funktionsværdier

Den lineære funktion f har forskriften f ( x ) = –3 · x + 5.

a) Udregn f (4), og forklar, hvad resultatet fortæller om grafen for f

b) Løs ligningen f ( x ) = 32, og forklar, hvad resultatet fortæller om grafen for f .

Øvelse 1.26

Funktionsforskrift – grafens skæring med akserne

Den lineære funktion f har forskriften f ( x ) = 4 x – 20.

a) Udregn f (0), og gør rede for, at svaret er y -koordinaten i grafens skæringspunkt med 2.-aksen.

b) Benyt forskriften for f til at beregne x -koordinaten i grafens skæringspunkt med 1.-aksen.

6.1 Skæring mellem graferne for to lineære funktioner

Øvelse 1.27

Problemløsning – hvilken kaffeleverandør skal caféen vælge?

En café skal købe kaffe i poser med 1 kg og får tilbud fra to leverandører. Den samlede pris hos leverandør A kan beskrives med funktionen

f ( x ) = 64 x + 255

hvor f ( x ) er den samlede pris (i kr.) for x kg kaffe (inklusive levering).

a) Giv en fortolkning af tallene 64 og 250 i forskriften.

b) Hvor meget koster det at købe 10 kg kaffe hos leverandør A?

Hos leverandør B koster kaffen 70 kr. pr. kg, mens der ikke skal betales leveringsgebyr.

Sammenhængen mellem den samlede pris og mængden af kaffe hos leverandør B kan beskrives ved en funktion, g ( x ), hvor g ( x ) er den samlede pris (i kr.) for x kg kaffe.

c) Opskriv en forskrift for funktionen g ( x ). Begrund dit svar.

d) Løs ligningen f ( x ) = g ( x ), og forklar, hvad ligningen og dens løsning fortæller.

e) Tegn graferne for f ( x ) og g ( x ) i det samme koordinatsystem, og kontrollér dit svar i d).

f) Hvor mange kg kaffe skal man købe, før leverandør A er den billigste?

Som øvelsen ovenfor viser, så kan skæring mellem rette linjer anvendes i problemløsning, her i forbindelse med hvilken kaffe en café bør vælge, afhængigt af den mængde kaffe, caféen har brug for. Her så vi på to lineære funktioner, f ( x ) = a · x + b og g ( x ) = c · x + d , hvor tallet d dog var nul.

Vi vil nu se på det generelle tilfælde, hvor vi er interesserede i at bestemme skæringspunktet mellem graferne for de to lineære funktioner f og g , dvs. det ene punkt, S ( x , y ), der ligger på begge de rette linjer (hvis linjerne skærer hinanden). Dette problem kan vi løse ved at løse ligningen:

f ( x ) = g ( x )

a · x + b = c · x + d

hvor venstre side af ligningen er forskriften for den lineære funktion f ( x ), og højre side af ligningen er forskriften for den lineære funktion g ( x ).

Når vi løser ligningen, så svarer det til, at vi beregner x-værdien for S(x, y). For at finde skæringspunktet skal vi efterfølgende bestemme den tilhørende y-værdi.

Eksempel: Skæringspunkt mellem graferne for to lineære funktioner

Der er givet de to lineære funktioner f og g , som har forskrifterne

f (x ) = 2 x + 3 og g (x ) = –3 x – 7,

Vi løser ligningen:

f (x ) = g (x )

2 · x + 3 = –3 · x – 7 Vi indsætter regneforskrifterne.

5 · x + 3 = –7 Vi lægger 3 · x til på begge sider.

5 · x = –10 Vi trækker 3 fra på begge sider.

x = –10 5 = –2 Vi dividerer med 5 på begge sider og reducerer brøken.

Dvs. når x = –2, så har de to funktioner samme y -værdi, men hvilken?

Det skal vi beregne ved at regne frem, dvs. ved at indsætte den fundne x -værdi, x = –2, i en af de to funktionsforskrifter – ligegyldigt hvilken (overvej!). Vi vælger at indsætte x = –2 i g (x ):

g (–2) = –3 · (–2) – 7

g (–2) = 6 – 7 Vi reducerer i første led på højre side.

g (–2) = –1 Vi reducerer højre side.

og det betyder, at når y = –1, så er x -værdien i de to funktioner den samme, nemlig x = –2. Alt i alt har vi altså fundet ud af, at punktet (–2, –1) ligger på både den rette linje, der er graf for f , og på den rette linje, der er graf for g , altså må punktet (–2, –1) være skæringspunktet mellem de to grafer. Overvej: Hvorfor giver det mening, at vi ovenfor taler om skæringspunktet (altså bestemt form), når der er tale om to grafer, der begge er rette linjer?

Øvelse 1.28

Vil graferne for to lineære funktioner altid skære hinanden?

a) På hvilke måder kan to rette linjer ligge i forhold til hinanden? Tegn eksempler.

b) Hvis to linjer er parallelle, hvad gælder der så om deres hældningskoefficienter og konstantled?

c) Hvis to linjer er sammenfaldende (dvs. de ligger oveni hinanden), hvad gælder der så om deres hældningskoefficienter og konstantled?

Øvelsen viser, at vi ved bestemmelse af skæringspunkt mellem graferne for to lineære funktioner, dvs. mellem to rette linjer, altid først bør undersøge og konstatere, at de ikke er parallelle (eller sammenfaldende).

Øvelse 1.29

Parallelle eller sammenfaldende grafer?

Der er givet følgende 6 lineære funktioner

a) Hvilke af disse lineære funktioner har parallelle grafer?

b) Hvilke af disse lineære funktioner har sammenfaldende grafer?

7. Formler, der fastlægger grafen for en lineær funktion

Vi har givet to punkter, P 1( x 1, y 1) og P 2( x 2, y 2), hvor x 1 ≠ x 2, og tegner linjen gennem de to.

Øvelse 1.30

Linjen som graf for en lineær funktion

a) Hvordan ville linjen ligge, hvis vi tillod x 1 = x 2 ?

Linjen gennem de to punkter er graf for en lineær funktion, f ( x ) = a · x + b . Vi ønsker at bestemme formler for hældningskoefficient a og konstantled b . Metoden nedenfor er et eksempel på at løse to ligninger med to ubekendte .

Da punkterne ligger på grafen, må der gælde:

f ( x 2) = y2 og f ( x 1 ) = y 1 , eller opskrevet som et ligningssystem :

a x 2 + b = y 2

a · x 1 + b = y 1

Formel for a og b i f (x) = a · x + b ud fra to punkter på grafen for f

( I arbejder her to og to )

a) Du skal nu skrive forklaringer til de nedenstående omskrivninger af ligningssystemet ovenfor. Du skal skrive dine kommentarer i et skema som det nedenfor.

a x 2 + b = y 2

a x 1 + b = y 1

Husk, at det er a og b , der er de ukendte, mens vi kender x ’erne og y ’erne. ( a x 2 + b ) –

a · x 2 – a · x 1 = y 2 – y 1

a ( x 2 – x 1 ) = y 2 – y 1

a · ( x 2 – x 1) ( x 2 – x 1) = y 2 – y 1 ( x 2 – x 1) a = y 2 – y 1 x 2 – x 1

Når nu vi kender linjens hældning, så mangler vi bare at lægge linjen fast i ét bestemt punkt i koordinatsystemet. Vi har jo allerede to punkter, P1 ( x 1 , y1 ) og

P2 ( x 2 , y2 ), på linjen.

b) Vælg P1 ( x 1 , y1 ), og fortsæt med at forklare omskrivningerne herunder:

Husk, at nu kender vi a , kun b er ukendt.

c) Byt dit udfyldte skema med en kammerat, idet du folder siden, så kun forklaringerne er synlige. Kan din kammerat følge dine forklaringer og skrive beviset linje for linje med formler? Kontrollér jeres udledning af begge formler med hinanden.

Vi samler resultatet af udledningen af de to formler i en sætning, som vi således har bevist :

Sammenhænge

Læg mærke til, at Tælleren i to-punkts-formlen er ændringen i y-værdien :

∆ y = y 2 – y 1.

Nævneren i to-punkts-formlen er ændringen i x-værdien : ∆ x = x 2 – x 1.

Så formlen kan skrives:

som vist på figuren her.

At udtrykke hældningskoefficienten på den måde kan være nyttigt i hurtige aflæsninger, og vi vil senere få brug for notationen i forbindelse med mere avancerede emner.

Øvelse 1.32

Bestemmelse af a og b ud fra sætningen om to-punkts-formlen

Grafen for den lineære funktion

f ( x ) = a · x + b

går gennem punkterne P (2, 18) og Q (5, 27).

a) Benyt sætning 2 til at beregne a -tallet.

b) Benyt sætning 2 til at beregne b -tallet.

Øvelse 1.33

Parallelle grafer – bestemmelse af a og b

Grafen for den lineære funktion

f ( x ) = a · x + b

går gennem punktet P (0, 4) og har hældningskoefficienten a = 2.

a) Angiv b -tallet, og opskriv en forskrift for f .

Grafen for en lineær funktion, g , er parallel med grafen for f , og det oplyses, at g (0) = –3.

b) Opskriv en forskrift for g .

Grafen for en tredje lineær funktion, h , er også parallel med grafen for f , og går gennem punktet Q (6, 3).

c) Beregn b -tallet, og opskriv en forskrift for h

Tarsia – puslespil om lineære funktioner

Tarsia er en slags puslespil, hvor man skal matche brikker, der passer sammen. Det kan fx være en brik med en funktion som f ( x ) = 2 x + 3 og en anden brik med teksten ” Hældningskoefficient 2 ” eller ” Skæring med y-aksen i P (0, 3)”. Når alle brikkerne er sat rigtigt sammen, danner de en figur – fx en stor sekskant. Til aktiviteten ligger et Tarsia-spil til repetition af lineære funktioner klar på bogens website.

Matematik i arbejde B1, kapitel 1

BJØRN GRØN • BODIL BRUUN • OLAV LYNDRUP

KATJA KOFOD SVAN • JES SIXTUS JØRGENSEN • PER ROSENQVIST

MATEMATIK I ARBEJDE B1

Indholdsfortegnelse

Matematik i arbejde

1

VARIABELSAMMENHÆNGE OG LINEÆRE FUNKTIONER

1. Variable

Øvelse 1.1

Øvelse 1.2

2. Koordinatsystemet

Øvelse 1.4

3. Repræsentationsformer

3.1 Repræsentationsform: tabel

3.2 Repræsentationsform: graf

3.3 Repræsentationsform: formel

Funktioner – en aktiv øvelse

3.4 Repræsentationsform: sprog

3.5 Oversættelse mellem repræsentationsformer

Øvelse 1.6

4. Regression – en metode til at afkode sammenhænge

Øvelse 1.7

4.1 Regression – bedste rette linje

Øvelse 1.8

Træk virksomhederne ind 3

4.2 Oversættelse fra matematik til almindeligt sprog

Øvelse 1.10

4.3 Absolut og relativ afvigelse

Øvelse 1.12

Øvelse 1.13

4.4 Korrelation og kausalitet

5. Lineær funktion med papir og blyant

Øvelse 1.15

5.1 Hældningskoefficient a og konstantled b

Øvelse 1.16

Øvelse 1.17

Øvelse 1.18

Sætning 1.1

Øvelse 1.19

Øvelse 1.20

Øvelse 1.21

Øvelse 1.22

Øvelse 1.23

Øvelse 1.24

6. Regning med lineære funktioner

Øvelse 1.25

6.1 Skæring mellem graferne for to lineære funktioner

7. Formler, der fastlægger grafen for en lineær funktion

Øvelse 1.32

Øvelse 1.33