Journal of Automation, Mobile Robotics and Intelligent Systems, vol. 19, no. 1 (2025)

WWW.JAMRIS.ORG pISSN 1897-8649 (PRINT)/eISSN 2080-2145 (ONLINE) VOLUME 19, N° 1, 2025

Indexed in SCOPUS

Journal of Automation, Mobile Robotics and Intelligent Systems

A peer-reviewed quarterly focusing on new achievements in the following fields: • automation • systems and control • autonomous systems • multiagent systems • decision-making and decision support • • robotics • mechatronics • data sciences • new computing paradigms •

Editor-in-Chief

Janusz Kacprzyk (Polish Academy of Sciences, Łukasiewicz-PIAP, Poland)

Advisory Board

Dimitar Filev (Research & Advenced Engineering, Ford Motor Company, USA)

Kaoru Hirota (Tokyo Institute of Technology, Japan)

Witold Pedrycz (ECERF, University of Alberta, Canada)

Co-Editors

Roman Szewczyk (Łukasiewicz-PIAP, Warsaw University of Technology, Poland)

Oscar Castillo (Tijuana Institute of Technology, Mexico)

Marek Zaremba (University of Quebec, Canada)

Executive Editor

Katarzyna Rzeplinska-Rykała, e-mail: office@jamris.org (Łukasiewicz-PIAP, Poland)

Associate Editor

Piotr Skrzypczyński (Poznań University of Technology, Poland)

Statistical Editor

Małgorzata Kaliczyńska (Łukasiewicz-PIAP, Poland)

Editorial Board:

Chairman – Janusz Kacprzyk (Polish Academy of Sciences, Łukasiewicz-PIAP, Poland)

Plamen Angelov (Lancaster University, UK)

Adam Borkowski (Polish Academy of Sciences, Poland)

Wolfgang Borutzky (Fachhochschule Bonn-Rhein-Sieg, Germany)

Bice Cavallo (University of Naples Federico II, Italy)

Chin Chen Chang (Feng Chia University, Taiwan)

Jorge Manuel Miranda Dias (University of Coimbra, Portugal)

Andries Engelbrecht ( University of Stellenbosch, Republic of South Africa)

Pablo Estévez (University of Chile)

Bogdan Gabrys (Bournemouth University, UK)

Fernando Gomide (University of Campinas, Brazil)

Aboul Ella Hassanien (Cairo University, Egypt)

Joachim Hertzberg (Osnabrück University, Germany)

Tadeusz Kaczorek (Białystok University of Technology, Poland)

Nikola Kasabov (Auckland University of Technology, New Zealand)

Marian P. Kaźmierkowski (Warsaw University of Technology, Poland)

Laszlo T. Kóczy (Szechenyi Istvan University, Gyor and Budapest University of Technology and Economics, Hungary)

Józef Korbicz (University of Zielona Góra, Poland)

Eckart Kramer (Fachhochschule Eberswalde, Germany)

Rudolf Kruse (Otto-von-Guericke-Universität, Germany)

Ching-Teng Lin (National Chiao-Tung University, Taiwan)

Piotr Kulczycki (AGH University of Science and Technology, Poland)

Andrew Kusiak (University of Iowa, USA)

Mark Last (Ben-Gurion University, Israel)

Anthony Maciejewski (Colorado State University, USA)

Typesetting

SCIENDO, www.sciendo.com

Webmaster TOMP, www.tomp.pl

Editorial Office

ŁUKASIEWICZ Research Network

– Industrial Research Institute for Automation and Measurements PIAP

Al. Jerozolimskie 202, 02-486 Warsaw, Poland (www.jamris.org) tel. +48-22-8740109, e-mail: office@jamris.org

The reference version of the journal is e-version. Printed in 100 copies.

Articles are reviewed, excluding advertisements and descriptions of products.

Papers published currently are available for non-commercial use under the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 (CC BY-NC-ND 4.0) license. Details are available at: https://www.jamris.org/index.php/JAMRIS/ LicenseToPublish

Open Access.

Krzysztof Malinowski (Warsaw University of Technology, Poland)

Andrzej Masłowski (Warsaw University of Technology, Poland)

Patricia Melin (Tijuana Institute of Technology, Mexico)

Fazel Naghdy (University of Wollongong, Australia)

Zbigniew Nahorski (Polish Academy of Sciences, Poland)

Nadia Nedjah (State University of Rio de Janeiro, Brazil)

Dmitry A. Novikov (Institute of Control Sciences, Russian Academy of Sciences, Russia)

Duc Truong Pham (Birmingham University, UK)

Lech Polkowski (University of Warmia and Mazury, Poland)

Alain Pruski (University of Metz, France)

Rita Ribeiro (UNINOVA, Instituto de Desenvolvimento de Novas Tecnologias, Portugal)

Imre Rudas (Óbuda University, Hungary)

Leszek Rutkowski (Czestochowa University of Technology, Poland)

Alessandro Saffiotti (Örebro University, Sweden)

Klaus Schilling (Julius-Maximilians-University Wuerzburg, Germany)

Vassil Sgurev (Bulgarian Academy of Sciences, Department of Intelligent Systems, Bulgaria)

Helena Szczerbicka (Leibniz Universität, Germany)

Ryszard Tadeusiewicz (AGH University of Science and Technology, Poland)

Stanisław Tarasiewicz (University of Laval, Canada)

Piotr Tatjewski (Warsaw University of Technology, Poland)

Rene Wamkeue (University of Quebec, Canada)

Sławomir Wierzchon (Polish Academy of Sciences, Poland)

Janusz Zalewski (Florida Gulf Coast University, USA)

Teresa Zielińska (Warsaw University of Technology, Poland)

Publisher:

Copyright © by Łukasiewicz

Journal of Automation, Mobile Robotics and Intelligent Systems

VOLUME 19, N˚1, 2025

1

Controllability, Observability and Transfer Matrix

Zeroing of the 2D Roesser Model Tadeusz Kaczorek, Krzysztof Rogowski

DOI: 10.14313/jamris‐2025‐001

7

Integrating Disturbance Handling into Control Strategies for Swing‐up and Stabilization of Rotary Inverted Pendulum

Thi‐Van‐Anh Nguyen, Ma‐Sieu Phan, Quy‐Thinh Dao

DOI: 10.14313/jamris‐2025‐002

17

Formation Control of Multi‐agent Nonlinear Systems using the State‐Dependent Riccati Equation

Saeed Rafee Nekoo

DOI: 10.14313/jamris‐2025‐003

33

Identification of Keywords for Legal Documents Categories Using Som Paulina Puchalska, Kacper Krzemiński, Maksymilian Lis, Rafał Scherer, Paweł Drozda, Kajetan Komar‑Komarowski, Konrad Szałapak, Andrzej Sobecki, Tomasz Zymkowski, Julian Szymański

DOI: 10.14313/jamris‐2025‐004

42

Implementation of Enzyme Family Classification by using Autoencoders in a Study Case with Imbalanced and Underrepresented Classes

Darian Fernández Gutiérrez, Ariadna Arbolaez Espinosa, Deborah Raquel Galpert Cañizares, María Matilde García Lorenzo

DOI: 10.14313/jamris‐2025‐005

49

Design of Fault‐tolerant Structures for Underwater Sensor Networks Based on Markov Chains

Maksim Maksimov, Oleksiy Kozlov, Serhii Retsenko, Viktoriia Kryvda

DOI: 10.14313/jamris‐2025‐006

65

Convolution Neural Network for Face Similarity Estimation

Wojciech Domski, Adam Jankowiak

DOI: 10.14313/jamris‐2025‐007

73

Multi‐Input Melanoma Classification using Mobilenet‐V3‐Large Architecture

Serra Aksoy

DOI: 10.14313/jamris‐2025‐008

Abstract:

CONTROLLABILITY,OBSERVABILITYANDTRANSFERMATRIXZEROING OFTHE2DROESSERMODEL

CONTROLLABILITY,OBSERVABILITYANDTRANSFERMATRIXZEROING OFTHE2DROESSERMODEL

CONTROLLABILITY,OBSERVABILITYANDTRANSFERMATRIXZEROING OFTHE2DROESSERMODEL OFTHE2DROESSERMODEL

Submitted:30th March2024;accepted:8th April2024

TadeuszKaczorek,KrzysztofRogowski

DOI:10.14313/jamris‐2025‐001

Thearticleconsidersthefundamentalpropertiesofthe two‐dimensional(2D)systemdescribedbytheRoesser model.Thecontrollabilityandobservabilityareanalyzed andthesufficientconditionsunderwhichthetransfer matrixiszeroaregiven.Itisshownthatifthematrix ofthestateequationAandBorAandCoftheRoesser modelhasfullrowrank(respectively,fullcolumnrank) thenthereexistsanonsingularmatrixoftransformation suchthatthenewpairofnewmatricesiscontrollable (observable).Thenumericalexamplesaregiventoshow thecorrectnessoftheobtainedconditions.

Keywords: Controllability,Observability,Roessermodel, Transfermatrix,Zeroing

1.Introduction

Two‐dimensional(2D)dynamicalsystemshave beenanactiveareaofresearchformanyyears,owing totheirwidespreadapplicationsinvarious ieldssuch asphysics,biology,engineering,andeconomics.Some interestingpracticalapplicationsofa2Dsystemsthe‐orymaybefoundin[1–5].Themostpopularmodels of2Dlinearsystemsarethemodelsintroducedby Roesser[6],Fornasini‐Marchesini[7,8]andKurek[9]. Anoverviewof2Dlinearsystemstheoryisgivenin [10–13].

Inthisarticle,weexplorethebehaviouroftwo‐dimensionaldynamicalsystems,de inedbytwodif‐ferentialmatrixequationsdescribingthedynamicsin horizontalandverticaldirections.Thisapproachfor 2Dsystemsmodellingwasproposed irstbyRoesser in[6]andthistypeofmodeliscalledbyhisname. Thisclassofsystemsexhibitscomplexbehaviour, sincethereoccursinterferencebetweenthesetwo dimensions.Understandingandanalysingthedynam‐icsofsuchsystemsiscrucialformanyreal‐world applications,includingthedesignandcontrolofphys‐icalsystemssuchasthermalprocesses,distributed parameterssystems,digital ilters,longtransmission linesandmanyothers.

ThedynamicalpropertiesoftheRoessermodel havebeenthesubjectofmanypapers.Thestability problemhasbeensolvedin[14–18].Theasymptotic stabilityofpositive2Dlinearsystemshasbeeninves‐tigatedin[19–22]andtherobuststabilityin[23,24].

Controllabilityandobservabilityarefundamental conceptsinthetheoryofdynamicalsystemsandcon‐troltheory.Controllabilityreferstotheabilitytosteer asystemfromonestatetoanotherusingacontrol input,whileobservabilityreferstotheabilitytoesti‐matethesystem’sinternalstatefromtheavailable measurementsandknownsteering.Theseconcepts areessentialforunderstandinganddesigningcontrol systemsforawiderangeofapplications,including aerospace,robotics,powersystems,andbiomedical engineering.

Controllabilityconditionsforthe2DRoesser modelhavebeenobtainedbyKurek[25].Thesecon‐ditionsarebasedoncheckingtheranksofasystem’s matrices.Next,thecontrollabilityproblemhasbeen consideredin[26–30].Observabilityisadualnotion incomparisonwithcontrollabilityandmaybefound in[29–31].

InthecontextoftheRoessermodel,controllability andobservabilityarecriticalconceptsthatdetermine theeffectivenessofcontrolsystemdesign.Inmany practicalcases,if2Dsystemisunobservableand/or uncontrollable,themostpopularcontrolstrategies cannotbeapplied.Inparticular,acontrollableand observablesystemcanbeeasilystabilizedusingfeed‐backcontroltechniques.Thisisbecausetheinter‐nalstateofthesystemcanbeaccuratelyestimated fromitsoutputmeasurements,andanappropriate controlinputcanbedesignedtostabilizethesystem. Usingtheproposedsimilarityoperationonthematri‐ces �� and ��,wemaytransformoursystemintoa controllableandobservableone.Thismathematical operationopensupthepossibilityofutilizingwell‐knowncontrolalgorithmstodesignadesireddynamic ofthesystem.Finally,throughtheinversetransfor‐mation,wereturntotheoriginalstate‐spacemodel. Theresultspresentedinthemanuscriptexpandthe potentialforachievingbetterdynamicalperformance ofthecontrol2Dsystem.

Anotherimportantconceptincontroltheoryisthe zeroingofthetransfermatrix.Thetransfermatrix ofasystemisamathematicalrepresentationthat describestherelationshipbetweentheinputandout‐putofthesystem.Zeroingthetransfermatrixofa systemreferstotheabilitytomaintaintheoutputof thesystematzero,irrespectiveoftheinput.

Thisconceptisparticularlyrelevantinthedesign ofrobustcontrolsystems,wheretheobjectiveisto ensurethatthesystemremainsstableeveninthe presenceofdisturbances.Thisproblemhasbeencon‐sideredin[32,33].

Inthisarticle,thecontrollability,observability, andthetransfermatrixzeroingoftheRoessermodel willbeconsidered.Itwillbeshownthatforuncon‐trollableandunobservablematricesofthesystem, thereexistsanonsingularmatrixthattransforms thesematricesintocontrollableandobservableones. Suf icientconditionsfortheexistenceofsuchalinear transformationwillbegivenandproved.Moreover, suf icientconditionsforzeroingofthetransfermatrix oftheRoessermodelwillbeestablished.Numeri‐calexampleswillillustratetheobtainedconditions’ utility.

2.ControllabilityandObservabilityofthe RoesserModel

Considerthediscrete2DRoesser‐typemodel describedbythestate‐spaceequationsoftheform

Theorem2. TheRoessermodel (1) isobservableinthe rectangle [(0,0),(��1,��2)] ifandonlyif

rank ����1 ��1 −��11 −��12 −��21 ����2 ��2 −��22 ��1 ��2 =�� (3) forall ��1,��2 ∈ℂ.

Theproofisgivenin[31].

Inthenexttheorem,wewillintroducethelinear transformationofthestateequations(1).

Theorem3. If rank ���� =��

and

∈ℝ��1 isthehorizontalstatevector, ���� ���� ∈ℝ��2 istheverticalstatevector, ������ ∈ℝ�� istheinputvector,������ ∈ℝ�� istheoutputvectorand takesthefollowingforms

��11 ��12 ��21 ��22 ,��= ��1 ��2 ,

11 ∈ℝ��1×��1,��12 ∈ℝ��1

2,��1 ∈ℝ��1 , ��21 ∈ℝ��2×��1,��22 ∈ℝ��2×��2,��2 ∈ℝ��2 , ��= ��1 ��2 ,��1 ∈ℝ��×��1,��2 ∈ℝ��×��2

(1b)

De inition1. TheRoessermodel (1) iscalledcontrollableintherectangle [(0,0),(��1,��2)] ifforevery boundarycondition ��ℎ 0,��, ���� ��,0, ��∈[0,��1], ��∈[0,��2] andeveryvector ���� ∈ℝ�� thereexistsasequenceof inputs ������, (0,0)≤(��,��)<(��1 −1,��2 −1) suchthat ����1,��2 =����.

Theorem1. TheRoessermodel (1) iscontrollablein therectangle [(0,0),(��1,��2)] ifandonlyif

rank ����1 ��1 −��11 −��12 ��1 −��21 ����2 ��2 −��22 ��2 =�� (2) for ��=��1 +��2 andall ��1,��2 ∈ℂ

Theproofisgivenin[31].

De inition2. TheRoessermodel (1) iscalledobservableintherectangle [(0,0),(��1,��2)] ifknowing sequencesofitsinputs ������ andoutputs ������ for (��,��)∈ [(0,0),(��1,��2)] itispossibletocomputeitsuniqueinitialstate ��00 ∈ℝ�� .

(4b)

thenthereexistsanonsingularmatrix ��∈ℝ��×�� such thatthepair (��,��), ��=����, ��=���� (5) iscontrollable.

Proof. Itwillbeshownthatifthepairofmatrices (��,��) satis iesthecondition(4a)thenthereexists anonsingularmatrix�� suchthatthepair(5)iscon‐trollable.From(5)wehave

(6)

Postmultiplying(6)bythematrix ���� �� weobtain

(7)

From(4a)itfollowsthatthematrix ������ +������ is nonsingularandfrom(7)wehave

(8)

Thematrix �� givenby(8)isnonsingularsince rank �� �� =��.

Example1. ConsidertheRoessermodel (1) withthe matrices

(9)

Thepair (��,��) givenby (9) isuncontrollablebutit satis iesthecondition (4a) since rank ���� = rank 1000 −2121 1010 =3=��. (10)

Wearelookingforthenonsingularmatrix ��∈ℝ3×3 suchthatthecorrespondingpair (5) is controllableintheform

��= 101 −210 102 , ��= 0 1 2 (11)

Note,thatcondition (4b) ismet,since

rank ������ +������ =rank 102 −26−2 143 =3. (12)

Using (8), (9) and (11) weobtain ��= ������ +������ ������ +������ −1

101 −210 102 1−21 010 021 + 0 1 2 010

100 −212 101 1−21 010 021 + 0 1 0 010 −1 = 102 −26−2 143 1−21 −2100 102 −1 = 001 21−2 310 (13)

Thematrix (13) isnonsingularsince det��= 001 21−2 310 =−1. (14)

Takingintoaccountthedualityofcontrollability andobservabilityproperty,asimilarapproachmaybe appliedtothepairofmatrices(��,��)

Theorem4. If rank �� �� =�� (15a) and rank ������+������ =��. (15b) thenthereexistsanonsingularmatrix ��∈ℝ��×�� such thatthepair ��,�� , ��=����, ��=���� (16) isobservable.

Proof. Theproofissimilar(dual)totheproofof Theorem2

Remark1. InasimilarwayasintheproofofTheorem 2 itcanbeshownthatthereexistsanonsingularmatrix �� satisfyingtheequality �� ���� = �� �� , (17)

wherethepair (��,��) iscontrollableandthepair (��,��) isuncontrollable.

3.ZeroingoftheTransferMatrixofthe RoesserModel

ConsidertheRoessermodel(1)withthetransfer matrix

1,��2)=

(18)

Suf icientconditionswillbeestablishedforzero‐ingthetransfermatrix(18).

Theorem5. Thetransfermatrix (18) oftheRoesser model (1) isazeromatrixifthefollowingconditionsare satis ied:

1) thepair (��,��) isuncontrollableandthepair (��,��) isunobservable;

2) theproductofthematrices �� and �� iszeromatrix, i.e. ����=0. (19)

Proof. Similarlytothestandardlinearsystem[33]for theproofoftheRoessermodelwehavethefollowing properties:

1)Ifthepair(��,��)isuncontrollableandthepair (��,��) isunobservablethenatleastoneentryofthe adjointmatrix

(20) iszero.

2)Theproduct����choosesinthematrix(20)the zeroentries.

Therefore,ifconditions1)and2)aresatis iedthen thetransfermatrix(18)isazeromatrix.

Example2. ConsidertheRoessermodel (1) withthe matrices

(21) Notethatthepair (��,��) isuncontrollablesince

(22) andthepair (��,��) isunobservablesince

(23)

Therefore,theRoessermodelwith (21) isuncontrollableandunobservable.

Thecondition (19) isalsosatis iedsince

(24)

ThetransferfunctionoftheRoessermodelwiththe matrices (21) iszerosince ��(��1,��2)=

=0,

Thissimpleexamplecon irmstheTheorem5

Theorem6. Thetransfermatrix (18) oftheRoesser model (1) iszeroif 1)

From (24) itfollowsthatthecondition ����=0 isalsosatis ied.Therefore,byTheorem 6 thetransfer matrixoftheRoessermodelwiththematrices (21) is zero.

4.ConcludingRemarks

TheRoessermodelisoneofthemostpopular mathematicalmodelsusedincontrolsystemsengi‐neeringtodescribethedynamicsofprocessestak‐ingplaceintwodimensions.Thisarticleexploresthe conceptsofcontrollability,observability,andzeroing ofthetransfermatrixinthecontextoftheRoesser model.

Zeroingofthetransfermatrixreferstotheability todrivetheoutputofthesystemtozero,irrespective oftheinput.Thisconceptisparticularlyrelevantinthe designofrobustcontrolsystems,wheretheobjective istoensurethatthesystemremainsstableeveninthe presenceofdisturbances.

Inthisarticle,wehaveshownthatforuncontrol‐lableandunobservablematricesofthesystem,there existsanonsingularmatrixthattransformsthese matricesintocontrollableandobservableones.Suf i‐cientconditionsfortheexistenceofsuchlineartrans‐formationhavebeengivenandproved.Moreover,suf‐icientconditionsforthetransfermatrixzeroingof theRoessermodelhavebeenestablished.Numerical exampleshavebeenpresentedthatshowtheuseful‐nessoftheintroducedconditions.

AUTHORS

TadeuszKaczorek –FacultyofElectrical Engineering,BialystokUniversityofTechnol‐ogy,Wiejska45D,15‐351Bialystok,Poland,e‐mail: t.kaczorek@pb.edu.pl.

2) thecondition (19) issatis ied,i.e.

Proof. From(2)and(3)itfollowsthatiftheconditions (27)aresatis iedthentheRoessermodel(1)isuncon‐trollableandunobservable.Therefore,byTheorem5 thetransfermatrix(18)oftheRoessermodel(1)is zero.

Example3. ConsidertheRoessermodel (1) withthe matrices (21).Themodelsatis iesthecondition (27) since

KrzysztofRogowski∗ –FacultyofElec‐tricalEngineering,BialystokUniversityof Technology,Wiejska45D,15‐351Bialystok, Poland,e‐mail:k.rogowski@pb.edu.pl,www: www.we.pb.edu.pl/kair/krzysztof‐rogowski/.

∗Correspondingauthor

ACKNOWLEDGEMENTS

Thisworkwascarriedoutwithintheframeworkof studyNo.WZ/WE‐IA/5/2023and inancedfromthe fundsearmarkedforresearchbythePolishMinistry ofEducationandScience.

References

[1] M.Dymkov,K.Galkowski,E.Rogers,V.Dymkou, andS.Dymkou,“Modelingandcontrolofasorp‐tionprocessusing2Dsystemstheory”.In: The2011InternationalWorkshoponMultidimensional(nD)Systems,Poitiers,France,2011, 1–6.

[2] Q.Y.Xu,X.D.Li,andM.M.Lv,“AdaptiveILC fortrackingnon‐repetitivereferencetrajectory of2‐DFMMunderrandomboundarycondition”,

InternationalJournalofControl,Automationand Systems,vol.14,no.2,2016,478–485.

[3] E.Fornasini,“A2‐Dsystemsapproachtoriver pollutionmodelling”, MultidimensionalSystems andSignalProcessing,vol.2,no.3,1991, 233–265.

[4] C.Chen,J.Tsai,andL.Shieh,“Modelingof variablecoef icientRoessermodelforsystems describedbysecond‐orderpartialdifferential equation”, Circuits,SystemsandSignalProcessing,vol.22,2003,423–463.

[5] C.Ahn,P.Shi,andM.V.Basin,“Two‐dimensional dissipativecontroland ilteringforRoesser model”, IEEETransactionsonAutomaticControl, vol.60,no.7,2015,1745–1759.

[6] R.P.Roesser,“Adiscretestate‐spacemodelfor linearimageprocessing”, IEEETrans.Autom. Contr.,vol.AC‐20,no.1,1975,1–10.

[7] E.FornasiniandG.Marchesini,“State‐spacereal‐izationtheoryoftwo‐dimensional ilters”, IEEE TransactionsonAutomaticControl,vol.AC‐21, 1976,484–491.

[8] E.FornasiniandG.Marchesini,“Doubleindexed dynamicalsystems”, MathematicalSystemsTheory,no.12,1978,59–72.

[9] J.Kurek,“Thegeneralstate‐spacemodelfora two‐dimensionallineardigitalsystems”, IEEE TransactionsonAutomaticControl,vol.AC‐30, 1985,600–602.

[10] N.K.Bose, AppliedMultidimensionalSystems Theory,VanNonstrandReinholdCo:NewYork, 1982.

[11] N.K.Bose, MultidimensionalSystemsTheory Progress,DirectionsandOpenProblems,D.Reidel PublishingCo.:Dordrecht,1985.

[12] T.Kaczorek, Two-DimensionalLinearSystems, SpringerVerlag:London,1985.

[13] K.Galkowski, Statespacerealizationsoflinear2D systemswithextensionstothegeneralnD(��>2) case,SpringerVerlag:London,2001.

[14] J.ZhangandY.Sun,“Practicalexponentialstabil‐ityoftwodimensionalnonlinearswitchedpos‐itivesystemsintheroessermodel”, Journalof SystemsScienceandComplexity,vol.36,2023, 1103–1115.

[15] T.Ooba,“Asymptoticstabilityoftwo‐dimensionaldiscretesystemswithsaturation nonlinearities”, IEEETransactionsonCircuits andSystemsI:RegularPapers,vol.60,no.1, 2013,178–188.

[16] D.D.Tian,S.T.Liu,andW.Wang,“Globalexpo‐nentialstabilityof2Dswitchedpositivenonlin‐earsystemsdescribedbytheRoessermodel”, InternationalJournalofRobustandNonlinear Control,vol.29,no.7,2019,2272–2282.

[17] S.HuangandZ.Xiang,“Delay‐dependentstabil‐ityfordiscrete2Dswitchedsystemswithstate

delaysintheRoessermodel”, Circuits,Systems, andSignalProcessing,vol.32,no.6,2013,2821–2837.

[18] T.KaczorekandK.Rogowski,“Positivityand stabilizationoffractional2Dlinearsystems describedbytheRoessermodel”, Int.J.Appl. Math.Comput.Sci.,vol.20,no.1,2010,85–92.

[19] T.Kaczorek,“Asymptoticstabilityofpositive2D linearsystems”.In: XIIIScienti icConference ComputerApplicationsinElectricalEngineering, April14‐16,Poznan,2008,1–5.

[20] T.Kaczorek,“Asymptoticstabilityofpositive1D and2Dlinearsystems,RecentAdvancesinCon‐trolandAutomation”, Acad.Publ.HouseEXIT, 2008,41–52.

[21] T.Kaczorek,“LMIapproachtostabilityof2D positivesystems”, MultidimensionalSystems andSignalProcessing,vol.20,no.1,2009, 39–54.

[22] M.Twardy,“AnLMIapproachtocheckingsta‐bilityof2Dpositivesystems”, Bull.Acad.Pol.Sci. Techn.,vol.55,no.4,2007,385–395.

[23] M.Buslowicz,“Robuststabilityofpositive discrete‐timelinearsystemswithmultiple delayswithlinearunityrankuncertainty structureonnon‐negativeperturbation matrices”, Bull.Acad.Pol.Sci.Techn.,vol.55, no.1,2007,1–5.

[24] M.Buslowicz,“Robuststabilityofconvexcom‐binationoftwofractionaldegreecharacteristic polynomials”, ActaMechanicaetAutomatica,vol. 2,no.2,2008,5–10.

[25] J.E.Kurek,“Controllabilityofthe2‐DRoesser model”, MultidimensionalSystemsandSignalProcessing,vol.1,1990,381–387.

[26] T.Kaczorek. Controllabilityandminimumenergy controlofpositive2Dsystems,275–309.Springer London,London,2002.

[27] J.Klamka,“Controllabilityof2‐dlinearsystems”. In:P.M.Frank,ed., AdvancesinControl,London, 1999,319–326.

[28] K.Galkowski,E.Rogers,andD.H.Owens, “Matrixrankbasedconditionsforreachabil‐ity/controllabilityofdiscretelinearrepetitive processes”, LinearAlgebraandItsApplications, vol.275‐27,1998,201–224.

[29] E.Rogers,K.Galkowski,andD.H.Owens. Controllability,Observability,PolesandZeros,177–234.SpringerBerlinHeidelberg,Berlin,Heidel‐berg,2007.

[30] R.Eising,“Controllabilityandobservabilityof2‐Dsystems”, IEEETransactionsonAutomaticControl,vol.24,no.1,1979,132–133.

[31] T.Kaczorek, Positive1Dand2DSystems, Springer‐Verlag:London,2001.

[32] J.Tokarzewski. AGeneralSolutiontotheOutputZeroingProblem,65–105.SpringerBerlinHei‐delberg,Berlin,Heidelberg,2006.

[33] T.KaczorekandK.Borawski,“Outputzeroingof thedescriptorcontinuous‐timelinearsystems”.

In:R.Szewczyk,C.Zieliński,M.Kaliczyńska,and V.Bučinskas,eds., Automation2023:KeyChallengesinAutomation,RoboticsandMeasurement Techniques,Cham,2023,3–12.

Abstract:

INTEGRATINGDISTURBANCEHANDLINGINTOCONTROLSTRATEGIESFOR SWING‐UPANDSTABILIZATIONOFROTARYINVERTEDPENDULUM

INTEGRATINGDISTURBANCEHANDLINGINTOCONTROLSTRATEGIESFOR SWING‐UPANDSTABILIZATIONOFROTARYINVERTEDPENDULUM

INTEGRATINGDISTURBANCEHANDLINGINTOCONTROLSTRATEGIESFOR SWING‐UPANDSTABILIZATIONOFROTARYINVERTEDPENDULUM

Submitted:13th January2024;accepted:8th February2024

Thi‑Van‑AnhNguyen,Ma‑SieuPhan,Quy‑ThinhDao DOI:10.14313/jamris‐2025‐002

Therotaryinvertedpendulum(RIP)isanunderactuated mechanicalsystemwithfewerinputcontrolsthanoutput controls.TheapplicationoftheRIPmodelistoinvestigate thecontrolofnonlinearsystems,butisusefulinother fieldsaswell,asitissimpletoanalyzethedynamicsand testdespiteitshighnonlinearity.Thetwofundamental controlissuesintheRIPareachievingthedesiredbalance positionofthependulum,andmaintainingstability.The energy‐basedswing‐upcontrollerisusedforthemodelto bringthependulumtoanuprightposition.Regardingthe issueofstabilitycontrol,theLinearQuadraticRegulator (LQR)linearcontrolleriswell‐knownforitseffectiveness andstability,butitlosesstabilityinthepresenceofdistur‐bance.Theslidingmodecontroller(SMC)isabletoresist theimpactofdisturbancesaffectingthemodel.There‐fore,thispapercombinesbothcontrollerstoaddress thebalancingstabilityproblemoftheRIPsystem.The LQR‐basedSMCcontrollerusestheLQRcontrollerasthe basiccontrollertostabilizethependulum,andemploys theSMCcontrollertoresisttheimpactofdisturbance. Inaddition,itisnecessarytoaccuratelyestimatethe velocityofthependulum,andarminordertoapply themtotherealmodel.Thispaperdesignsanobserver tosolvethisproblem.Thesimulationresultsshowthat theproposedcontrollerperformswellinthepresenceof inputdisturbance.

Keywords: Rotaryinvertedpendulum,Stabilization, Swing‐up,LQRcontroller,Slidingmodecontroller, LQR‐basedSMCcontroller.

1.Introduction

Therotaryinvertedpendulum(RIP)isafascinat‐ingmechanicalsystemthatpresentssigni icantcon‐trolchallengesduetoitsunderactuatedandnonlin‐earnature[3,12–14,17,20].Thissystemhasbeen widelyusedinvarious ieldsforinvestigatingnon‐lineardynamicsandcontrolstrategies[4,8,10,16]. TheprimarycontrolissuesintheRIPinvolveachiev‐ingthedesiredbalancepositionofthependulum andensuringsystemstabilityduringdynamicmotion. Researchershaveexploreddifferentcontrolmethods toaddressthesechallenges,eachwithitsstrengths andlimitations.

Onepromisingcontrolapproachistheenergy‐basedswing‐upcontroller,whichef icientlybringsthe pendulumintoanuprightposition[1,7,14].

However,amorerobustcontrolstrategyisnec‐essarytomaintainstablecontrolinthevicinityof itsunstableequilibrium,aswellasdealwithdis‐turbances.TheLinearQuadraticRegulator(LQR) [15,18,19]isawidely‐recognizedcontroltechnique renownedforitsabilitytoachievestabilityinlin‐earsystems.However,itdoesnotinherentlypossess robustnessagainstdisturbances.Ontheotherhand, theslidingmodecontroller(SMC)[2, 5, 11, 21]is renownedforitsdisturbancerejectioncapabilities, butitschatteringbehaviorcanraisepracticalimple‐mentationconcerns.Toovercomethelimitationsof theseindividualcontroltechniquesandleveragetheir complementaryadvantages,thispaperproposesa novelcontrolstrategyfortherotaryinvertedpendu‐lum:theLQR‐basedSlidingModeControl(LQR‐based SMC)approach.Theobjectiveistoharnessthesta‐bilityadvantagesofLQRwhilebene itingfromthe disturbancerejectioncapabilitiesofSMC.Themain contributionofthisworkliesinthedesignandeval‐uationofanLQR‐basedSMCcontrollerfortherotary invertedpendulum.Byintegratingthesetwocontrol techniques,theproposedapproachaimstoachieve enhancedstabilityandrobustness,allowingthesys‐temtowithstandexternaldisturbancesandparame‐terchanges.

Thisstudyfocusesonaddressingthecontrolchal‐lengesoftheRIPsystem.TheproposedLQR‐based SMCcontrollerisdesignedtostabilizethependu‐lumandeffectivelyresisttheimpactofdisturbances. Throughcomprehensivesimulations,thecontroller’s performanceisevaluated,anditisfoundtooutper‐formthetraditionalLQRcontrollerinthepresence ofdisturbances.TheLQR‐basedSMCcontrollershow‐casesresilienceagainstchangesinmodelparameters, makingitsuitableforrealapplicationswithvarying systemdynamics.However,thepresenceofchattering intheoutputsignalswarrantsfurtherresearchand optimizationeffortstoensuresmoothcontrolaction withoutcompromisingdisturbancerejectioncapabil‐ities.Overall,theinvestigationhighlightsthepoten‐tialoftheLQR‐basedSMCcontrollerasarobustand effectivesolutionforregulatingtherotaryinverted pendulumsysteminthepresenceofdisturbancesand parameteruncertainties,pavingthewayforadvance‐mentsincontrolstrategiesforcomplexandnonlinear systems.

Insummary,thisstudymakesthefollowing notablecontributions:

‐ IntegrationoftheSlidingModeControlapproach intotheLQRcontroller,enablingeffectivehandling ofexternaldisturbancesandvariationsinmodel parametersinarotaryinvertedpendulumsystem.

‐ Implementationofanextendedstateobserverto enhancecontrolperformanceandreducethedepen‐dencyonalargenumberofsensors.

‐ Conductingextensivemulti‐scenariosimulationsto validateanddemonstratetheeffectivenessofthe proposedcontrolapproach.

Thesecontributionscollectivelycontributetothe advancementofcontrolstrategiesfortherotary invertedpendulumsystem,offeringinsightsinto robustandef icientcontroltechniquesforvarious practicalapplications.

2.RotaryInvertedPendulumModelling

Inthisarticle,theRIPmodelisconstructedusing Simscapetodemonstrateitscorrespondencewith physicalreality.Figure 1 displaysaschematicdepic‐tionoftheRIP,comprisingapendulumarmanda pendulumrodoflength ����(��) andmass ����(����) attachedtoit.Thependulumarmhasalengthof ����(��).Here,therotaryarmangleisrepresentedby��, whilethependulumangleisdenotedby��.Intheinitial state,thependulumrodpointsdownwards,andwhen itreachesthedesiredequilibriumstate,thependulum willpointupwardsupright.Thedetailedparameters ofthependulumareprovidedinTable1.

Duetotheuniformityofthependulumrod,the centerofmassislocatedatthemidpointofitslength. Theposition ⃗ ����withinacylindricalcoordinateframe (��−��−��)with3‐unit‐vectors( �� −

�� − ��)canbe representedasfollows[13]:

Takingthederivativewithrespecttotimeonboth sidesoftheequation(1),theabsolutevelocityof

isdetermined:

Squaringbothsidesofequation(2),obtain:

ThekineticenergyoftheRIPincludescontribu‐tionsfromboththevelocityofthependulum’scenter ofmass,aswellastherotationalmotionofboththe pendulumrodandpendulumarm.

Thefollowingexpressiondeterminesthepotential energyoftheRIP:

TheLagrangianequationisrepresentedas:

Thependulumarmischaracterizedbytheviscous frictioncoef icient ����,whereasthependulumrodis associatedwiththeviscousfrictioncoef icient����.The torqueofthemotoris[6]:

ByusingtheEuler‐Lagrangeequation:

Thus,themodelfornonlineardynamicsfortheRIP canbeexpressedasfollows:

Figure1. The3DmodeloftheRIP.

Table1. Theparametersofthependulum.

SymbolDescription

�� Viscousfrictioncoef icientofthependulumrod 9.5×10−3 ‐

�� Viscousfrictioncoef icientofthependulumarm 0.04 ‐

Motortorqueconstant

MotorbackEMFconstant

Selectingthestatevectoras��= ����̇�� �� ⊤ andtheinputas ��=����,theequationscanbepre‐sentedinthefollowingformat:

3.1.LQRcontrol

Inanaturalstate,thependulummaintainsadown‐wardverticalposition,sotobringittoanunstable equilibriumposition,whichisanupwarduprightposi‐tion,aswing‐upcontrolsystemmustbedesigned.To addressthisissue,theenergycontrollawproposed byN.J.Mathew etal. [9]isutilized.Thecontrollawis formulatedasfollowstoattaintherequiredenergy:

(13)

where��representstheaccelerationoftheDCmotor, ��isatuningparameter,��denotesadesignparameter, andthefunctionsat�� referstoafunctionthatsaturates at��

Thesecond‐orderlinearcontrolsystem(LQRcon‐trol)playsarolein indingtheoptimalcontrolsignal tobringthesystemfromtheinitialstatetothe inal statewiththelowestcost.TheLQRcontroller’scost functionisexpressedasfollows:

3.ControlProblems

Inthissection,thediscussionrevolvesaround bringingthependulumtoanuprightposition,along withthecontrollersusedtostabilizethependulum oftheRIPsystem.Anestimatedobserverisalsopro‐posed.

TheobjectiveoftheLQRcontrolleristominimize thecostfunctionasspeci iedinequation(14)inwhich ��������(��) denotesthecontrolinputofthesystemat time��

Modifyingtheelements,thestateweightingmatrix Q andthecontrolcostmatrix R aredesignedaccording tothedesiredperformance.Thematrices Q and R are providedasfollows:

Thestatefeedbackmatrix K isdependentonthe matrices A����, B����, Q,and R.Matrices A���� and B���� are derivedfromlinearizingthesystemdescribedinequa‐tion(10)atthedesiredoperatingpoint.Ontheother hand,theselectionofmatrices Q and R isbasedon desiredperformanceasde inedinequation(15).In MATLAB,thestatefeedbackmatrix K canbedeter‐minedusingtheLQRfunctioninthefollowingmanner:

=������(A����, B����, Q, R) (16)

Theoutputsignalofthe������controlleris:

K �� (17)

3.2.LQR‐basedSlidingModeControl

LQRisalinearcontrolsystemthatissuitable forRIPduetoitsfastsettlingtimes.However,the limitationoftheLQRisitsinabilitytohandleinput disturbances.Toovercomethisdrawback,thepaper proposestheuseofLQR‐basedSMC.

TheSMCisanonlinearcontrol.Thecontrolinput takenfromtheSMCisnotacontinuousfunctionof time.Itswitchesfromonefunctiontoanotherdepend‐ingonthependulum’sposition.Theadditionalterm ��(��)isincorporatedintotheunmodeledplantdynam‐icsandinputdisturbance.

Consideranonlinearinvertedpendulumsystem describedby:

̇��(��)= A��(��)+ B��(��)+��(��) (18)

Thesystem’scontrolinputisspeci iedasfollows:

������ (19)

Typically,

(20)

where ������ istheequivalentcontroland ������ repre‐sentsthediscontinuoushigh‐frequencycontroladded tosuppresstheuncertaintyofsystemandinputdis‐turbances.

Consideringthefollowingslidingsurface: ��(��)= G��(��)+��(��,��) (21)

Inequation(21),gainmatrix G isde inedbytheuser. Therearemultiplemethodstodeterminethegain matrix G,butinthisparticularstudy,theleftinverse oftheinputmatrix B isemployedtocalculate G

WhencombinedwithLQR, �������� isanominal part,while�������� isresponsibleforeliminatingsystem uncertaintiesandinputdisturbances.Therefore: �������� =������ =−��sgn(��(��)) (25)

BycombiningSMCwithLQR,theSMCisexpected toattenuateinputdisturbance,meaningthat B�������� =−��(��).Equation(24)canbeexpressedas:

̇��(��)= G A��(��)+ B��������(��) +��(��,��)=0 (26)

Toensuretheexistenceofslidingmodefromthe beginning(��=0),itisnecessarytohave��(0)=0in (21)andsatisfytheequation(23),hencetheselection:

��(��,��)=−G A��(��)+ B��LQR(��) ��(��,0)=−G��(0) (27) ensures

̇��(��)= GB��������(��)+ G��(��), (28) fromequations(21)and(27),hastheslidingsurface:

G ��(��)−��(0)− �� 0 A��(��)+ B��������(��) ���� (29)

3.3.Stabilityanalysis

TheLyapunovstabilitytheoremisemployedto computethediscontinuouscontrolinputfortheSMC. ConsidertheLyapunovfunctionasfollows:

Foranonlinearsystem,thesuf icientconditionfor stabilityisgivenby:

Formulas(28)in(31),wehave:

Choose ��(��)= B����,where ���� istheinputdistur‐bance,whichisboundedwithinapredeterminedlimit andcombinedwiththeequation(25):

Replace GB =1inequation(22):

Duringsliding,̇��(��)=0 ,therefore:

Ġ��(��)+ ��(��,��)=0 (23)

Replacing(18)and(19)into(23)yields: ̇��(��)= G A��(��)+ B��������(��)+ B��������(��)+��(��) +��(��,��)=0 (24)

Toensuresystemstability,thevalueof Q ischosenas:

(35)

3.4.ExtendedStateObserver

Toapplythistothepracticalmodel,estimatingthe velocityofthependulumandthearmarenecessary. Theobserverestimationalsominimizestheuseof sensorstoavoidwaste.

WhenusinganLQR‐basedSMC,theobserversys‐temisdesignedaccordingtotheExtendedState Observerdesignmethod.AnExtendedStateObserver isasfollows:

wherê�� ��, ��, �� areobserverstates,����,����,���� >0,the ��chosenissuf icientlysmall,ℎisanonlinearfunction, and���� ispracticalvalue. Considering,

Thefollowingequationisobtained

1 =̂��3 + ��1 �� (��1 −̂��1)

2 =̂��4 + ��1 �� (��2 −̂��2)

3 = B����(3,1)���� +̂��5 + ��2 ��2 (��1 −̂��1)

4 = B(4,1)���� +̂��6 + ��2 ��2 (��2 −̂��2)

5 = ��3 ��3 (��1 −̂��1)

6 = ��3 ��3 (��2 −̂��2) (38)

Here,thematrix B���� isobtainedfromsection(3.1); �� istheestimateof ����, ��=1,2,3,4,and ��5 and ��6 are extendedstates.Theparameters ��1,��2,��3,�������� are positive,and��issuf icientlysmall.

4.SimulationandResults

Simulationinmultiplescenariosiscarriedoutto evaluatetheproposedcontroller(LQR‐basedSMC) tostabilizethependulumintheverticallyupright position.ThetraditionalLQRcontrollerischosenas itsencounterineveryscenariosimulation,wherethe pendulumisinitiallysetatthedownrightposition. Bothcontrollersare irstevaluatedintwoscenarios: externaldisturbanceabsentandexternaldisturbance present.Afterthat,thevariationinthephysicalparam‐eterofthemodelisalsodeemedtoverifytheeffective‐nessoftheextendedstateobserver,andthisaffects theproposedcontroller’sperformance.Theparame‐tersoftheLQR‐basedSMCcontrollerare ine‐tunedas follows:

Inthissimulation,theinputdisturbanceisselected withanintensityof ���� =1.Tocompensateforthe in luenceoftheinputdisturbance, Q =1.2ischosen fromequation(35).Thegainmatrix G canbecalcu‐latedusingequation(22)as: G = 003.0819×10−4 2.0546×10−4 (41)

Therefore,thesignalobtainedfromSMCisgiven as:

(42)

CombinedwiththeLQRsignal,theoutputsignalofthe LQR‐basedSMCcontrolleris:

(43)

Todesigntheobserverinsection3.4,theparameters areselectedasfollows:

Usingthematrixvalue Q and R inequation(15)and theabovematrixvalueof A���� and B����,thecalculation oftheLQRgain K isasfollows: K = 15.90821.00002.41581.2119 (40)

Thenextsubsectionspresentthesimulationresults.

4.1.SimulationResultWithoutExternalDisturbance

Inthisparticularscenario,acomparative evaluationisconductedinvolvingboththeproposed controllerandthetraditionalLQRcontroller.These evaluationsarecarriedoutwithidenticalinitial conditionsandsystemsetups,deliberatelyexcluding anyexternaldisturbancesthatcouldaffecttherotary invertedpendulumsystem.Ourprimaryobjectiveis toassesshoweachcontrollerperformsinregulating thesystemdynamicsand,moreimportantly,achieves stabilitybymaintainingthependuluminanupright position.Thisstabilityisacriticalfactorforthe safeandpreciseoperationoftherotaryinverted pendulumsystem.

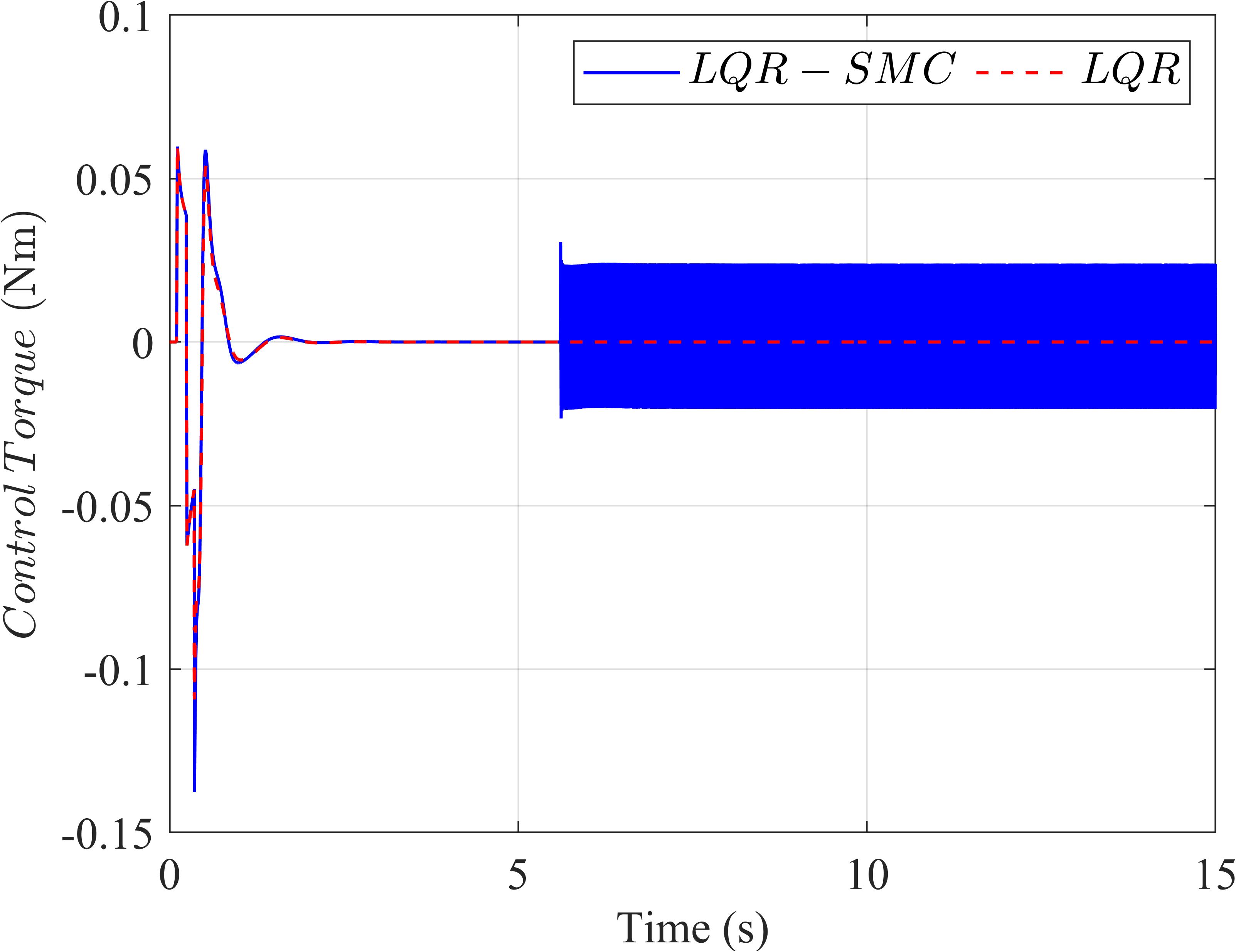
AsillustratedinSub igures2aand2b,itbecomes evidentthatthesignalcontrolledbytheLQRexhibitsa notablyfastersettlingtimewhencomparedtothesig‐nalunderthecontroloftheLQR‐basedSlidingMode Control(SMC)con igurationwhennoinputdistur‐bancesareintroducedintothesystem.Furthermore, Sub igure2cvisuallydemonstratesthatthesignalcon‐trolledbytheLQRisdevoidofthechatteringphe‐nomenonthatisdistinctlyobservableinthesignal governedbytheLQR‐basedSMC.

Itiscrucialtohighlightthefactthattheintro‐ductionoftheSMCcomponentwithintheSMC‐LQR controller,whichisprimarilydesignedtoenhance robustnessagainstexternaldisturbances,appearsto haveanadverseeffectonitsperformanceinscenar‐ioswheredisturbancesareabsent.Thisobservation underscorestheimportanceofcarefullyselectingand con iguringcontrolstrategiesdependingonthespe‐ci icoperationalcontext.

(c)

Figure2. Thecomparisonresultswithoutexternal disturbance:(a)thependulumangle,(b)thearmangle, and(c)thecontrolsignaloftwocontrollers.

Foramorecomprehensiveexamination,Figure 3 offersadetailedcomparativeanalysisoftheestimated valuesandactualvaluesderivedfromtheExtended StateObserverforboththetraditionalLQR(depicted inthetwouppersub igures,labeledasaandb)andthe SMC‐LQRcontrollers(portrayedinthetwolowersub‐igures,designatedascandd).Thisanalysisprovides valuableinsightsintothebehaviorandperformance ofthesecontrollersundervariousoperationalcondi‐tions.

4.2.SimulationResultWhenAnExternalDisturbance Exists

Toevaluatetheperformanceoftheproposedcon‐trollerinthepresenceofexternaldisturbances,aran‐domizedinputwithanamplitudeof 10−2 ���� (Fig‐ure 4a)isintroducedasadisturbancetothesystem after5seconds.Thisallowsustovalidatethecon‐troller’sabilitytohandledisturbancesandassesstheir impactonsystemstability.

AsillustratedinSub igures 4band 4c,the LQR‐basedSMCcontrollerdemonstratesanotable advantagewhendealingwithinputdisturbances. ThesignalscontrolledbytheLQR‐basedSMCexhibit fastsettlingtimesandminimaloscillations,whereas theLQRcontrolleralonefailstostabilizethesystem, leadingtopronouncedoscillations.Sub igure 4d emphasizestheimpactofinputdisturbanceson therotaryinvertedpendulum,withthecontrol signal �������� fromtheLQR‐basedSMCeffectively attenuatingthesedisturbances.However,theoutput signalsexhibitachatteringphenomenonduetothe discontinuousnatureof �������� containingthesign function.Thisabruptswitchinginthecontrolinput mayposechallengesinpracticalapplications.

Similartothepreviousscenario,theestimatedval‐uesoftheExtendedStateObservercloselyapproxi‐matetheiractualsignals,asdepictedinFigure5.This reaf irmstheeffectivenessoftheESOinestimating systemstatesandsupportingthecontroller’sperfor‐manceunderthein luenceofexternaldisturbances.

4.3.TheSimulationResultDuringaChangesinModel Parameters

Itisverydif iculttoobtainthephysicalparame‐tersofanysystemwithhighaccuracy.Thusinthis scenario,theproposedcontrolleristestedwiththe assumptionthatitdeviatesfromthemodel’sparam‐eter.Indetail,thependulumarmisobtainedwitha 15% deviationinmassand 8% deviationinlength fromactualvalues.Thisdeliberatemanipulationof thesystem’sparametersallowsustoexplorethecon‐troller’srobustnessandadaptabilityinthefaceof uncertainties.It’sworthnotingthatthissimulation takesplacewithinthecontextofanenvironmentthat includesexternaldisturbances,aspreviouslystudied inthesecondscenario.Byincorporatingbothparam‐eterdeviationsandexternaldisturbances,ourevalu‐ationaimstoprovideamorerealisticanddemanding testbedforassessingthecontroller’sperformance.

Subsequently,ourobservations,asillustratedin Sub igures6aand6b,revealthebehaviorofthepen‐dulumangleanditsarmangle.Notably,thesystem underthecontroloftheLQRexhibitsapronounced susceptibilitytotheseparameterdeviations.While bothcontrollersdemonstratetheabilitytoeffectively swingthependulumarmupward,onlytheLQR‐based SMCcontrollerexhibitsthecapabilitytostabilize thependulum,effectivelycounteractingtheadverse effectsofparameteruncertainties.Becauseofthese similarconclusions, iguresdepictingcontrolsignals andESO’sstatesforbothcontrollersarenotincluded.

(a)

(b)

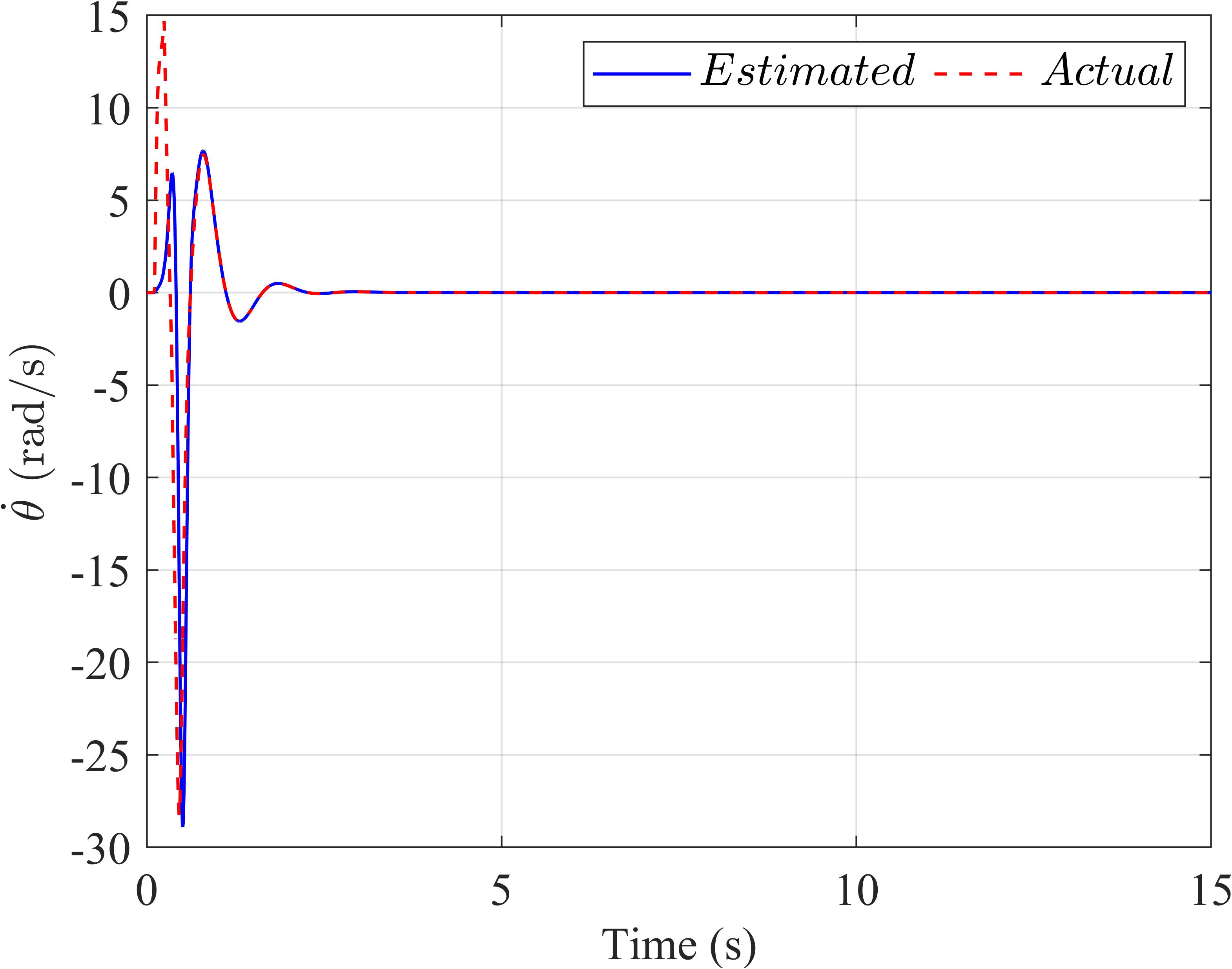
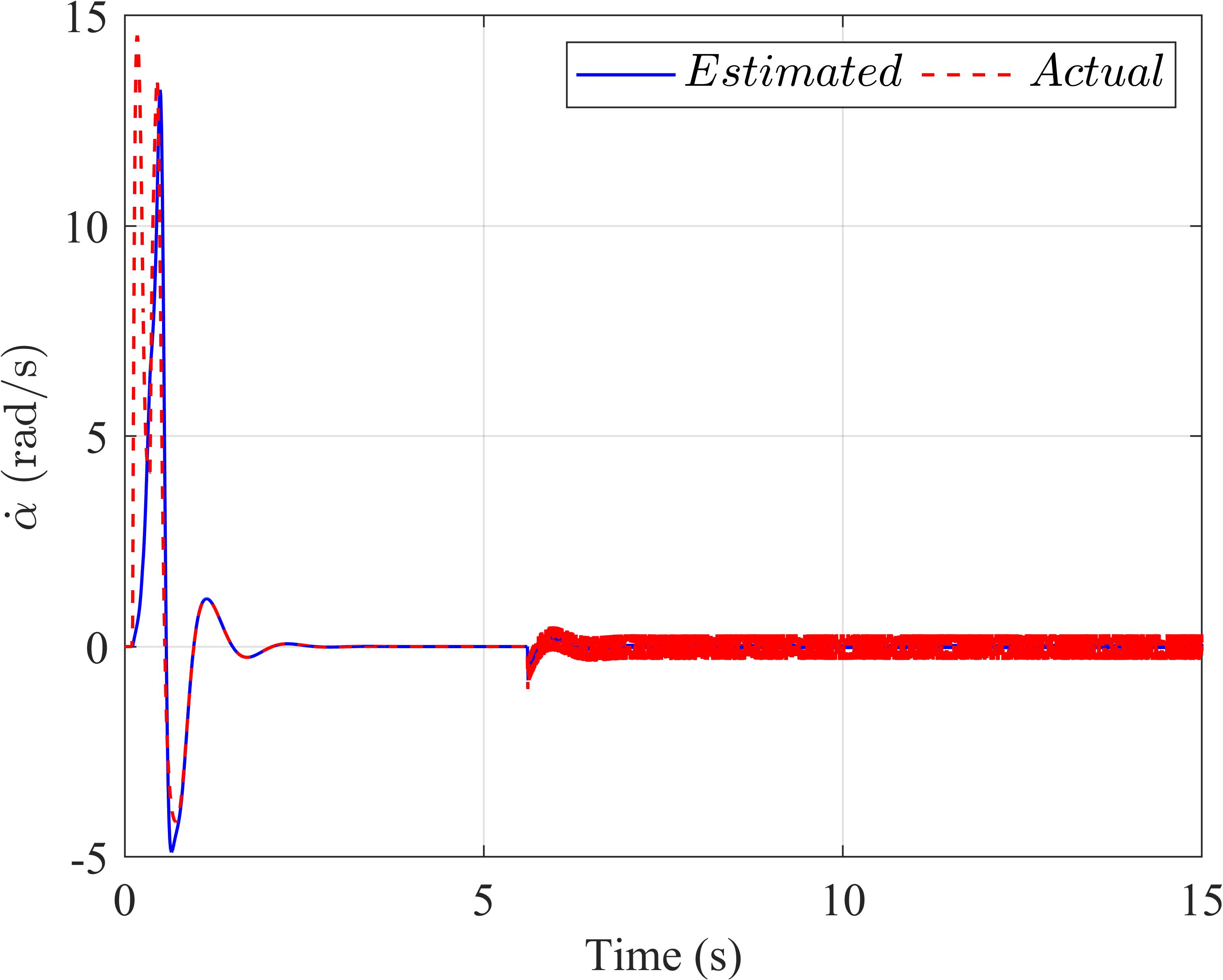
Figure3. TheExtendedStateObserverinthefirstscenario:(a)thependulumanglevelocity,(b)thearmanglevelocityof theLQRcontroller,(c)thependulumanglevelocity,and(d)thearmanglevelocityoftheLQR‐basedSMCcontroller.

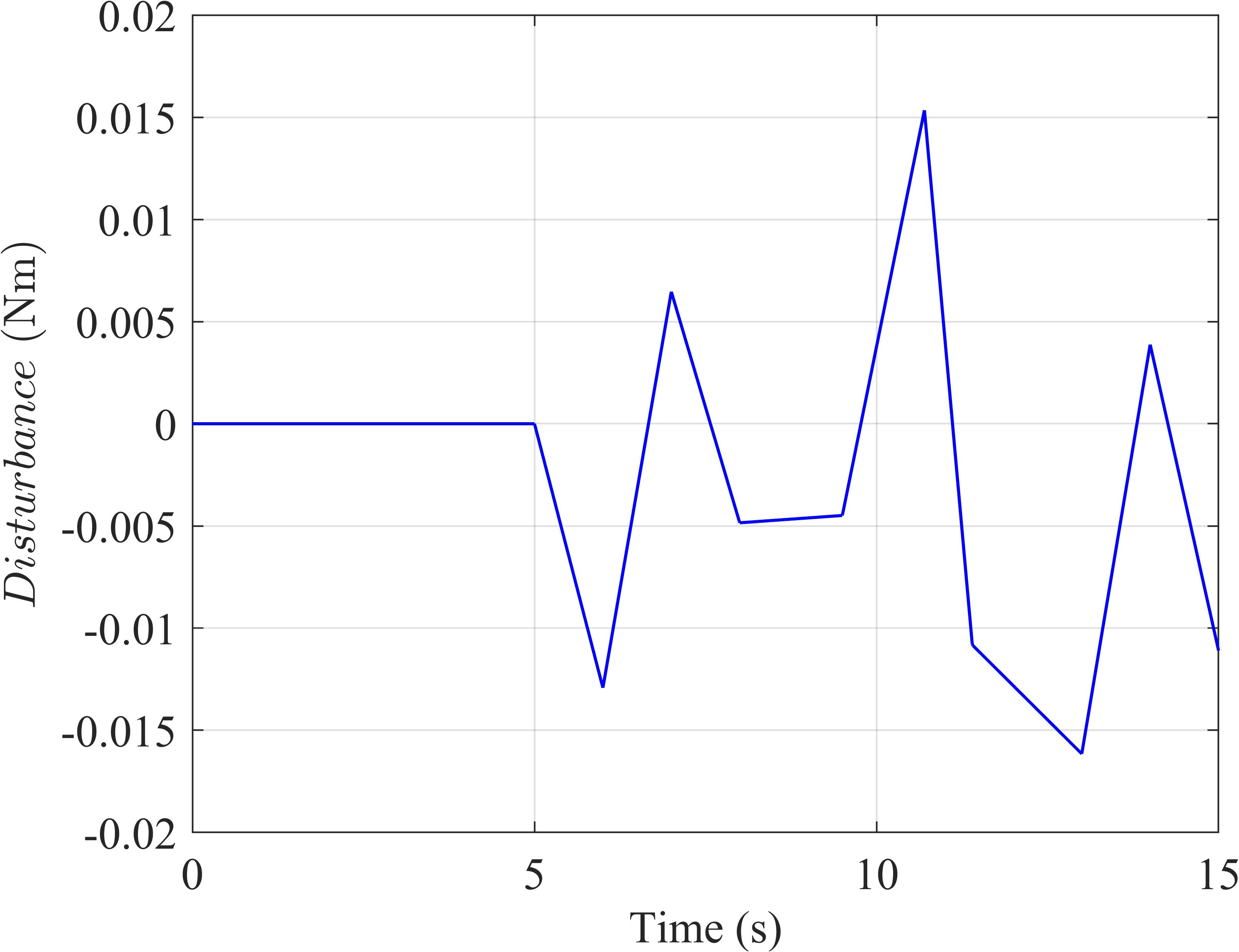
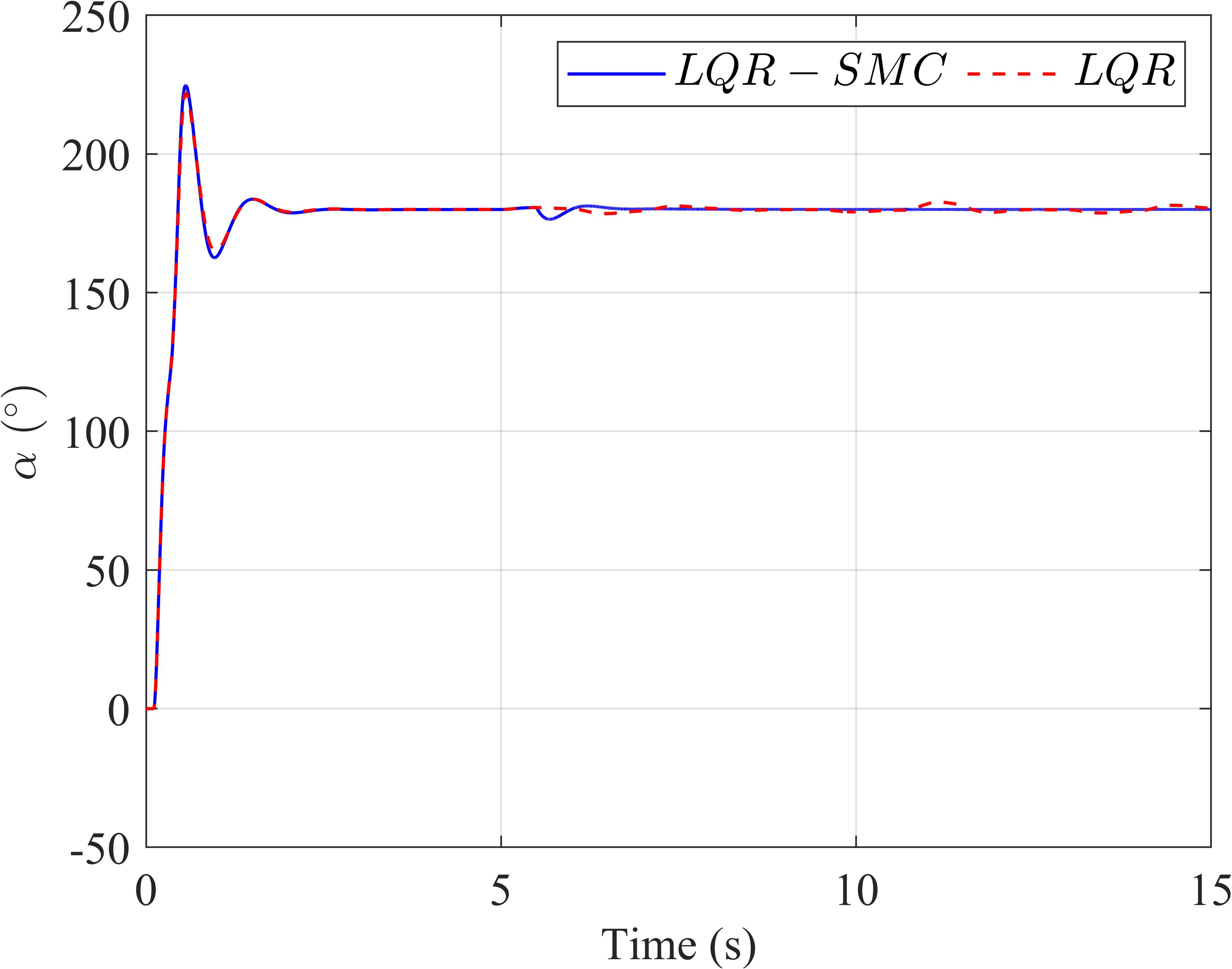
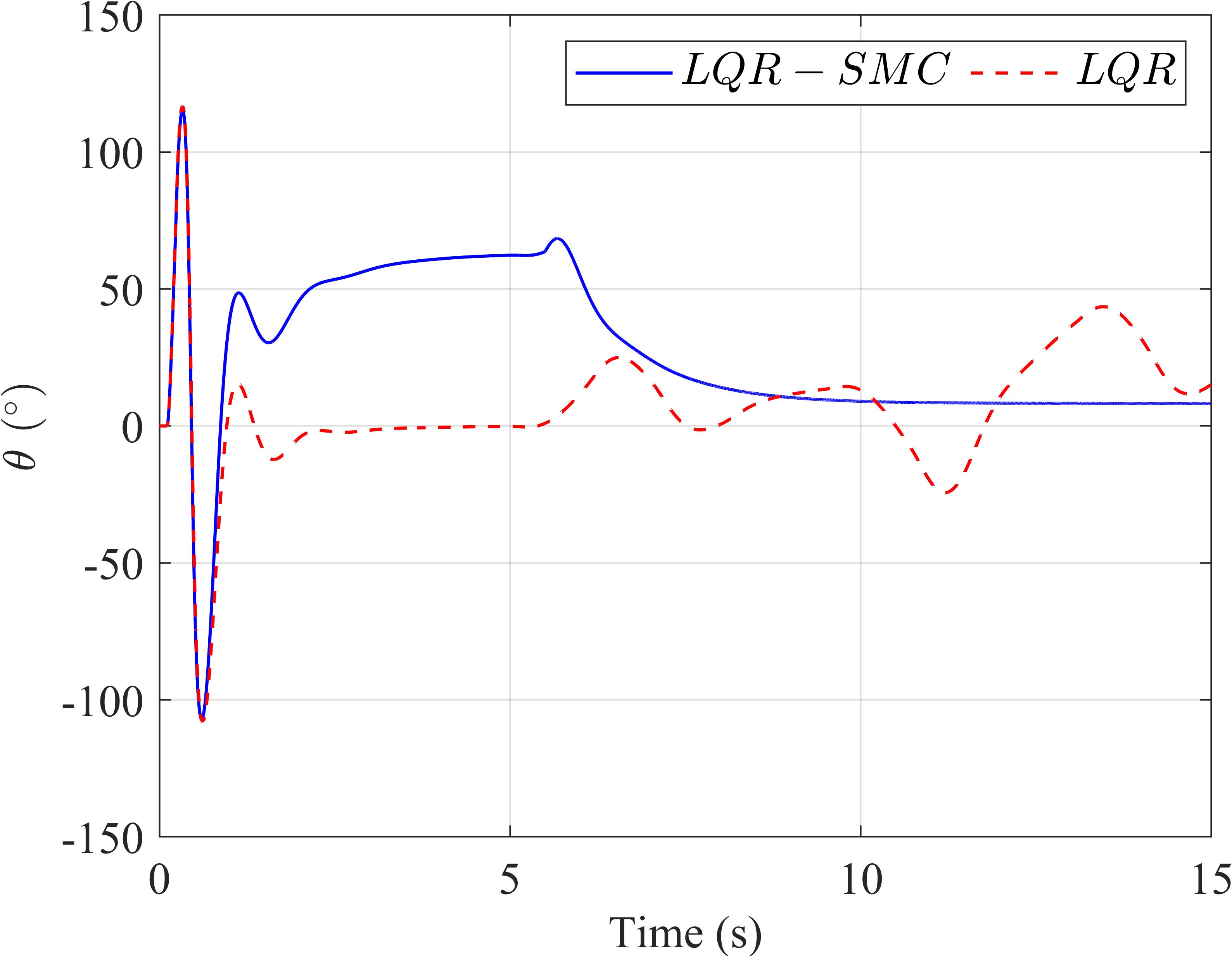
Figure4. Thecomparisonresultswhenthereisexternaldisturbance(a):thependulumangle(b),thearmangle(c),and thecontrolsignaloftwocontrollers(d).

(a)

(b)

(c)

(d)

(a)

(b)

(c)

(d)

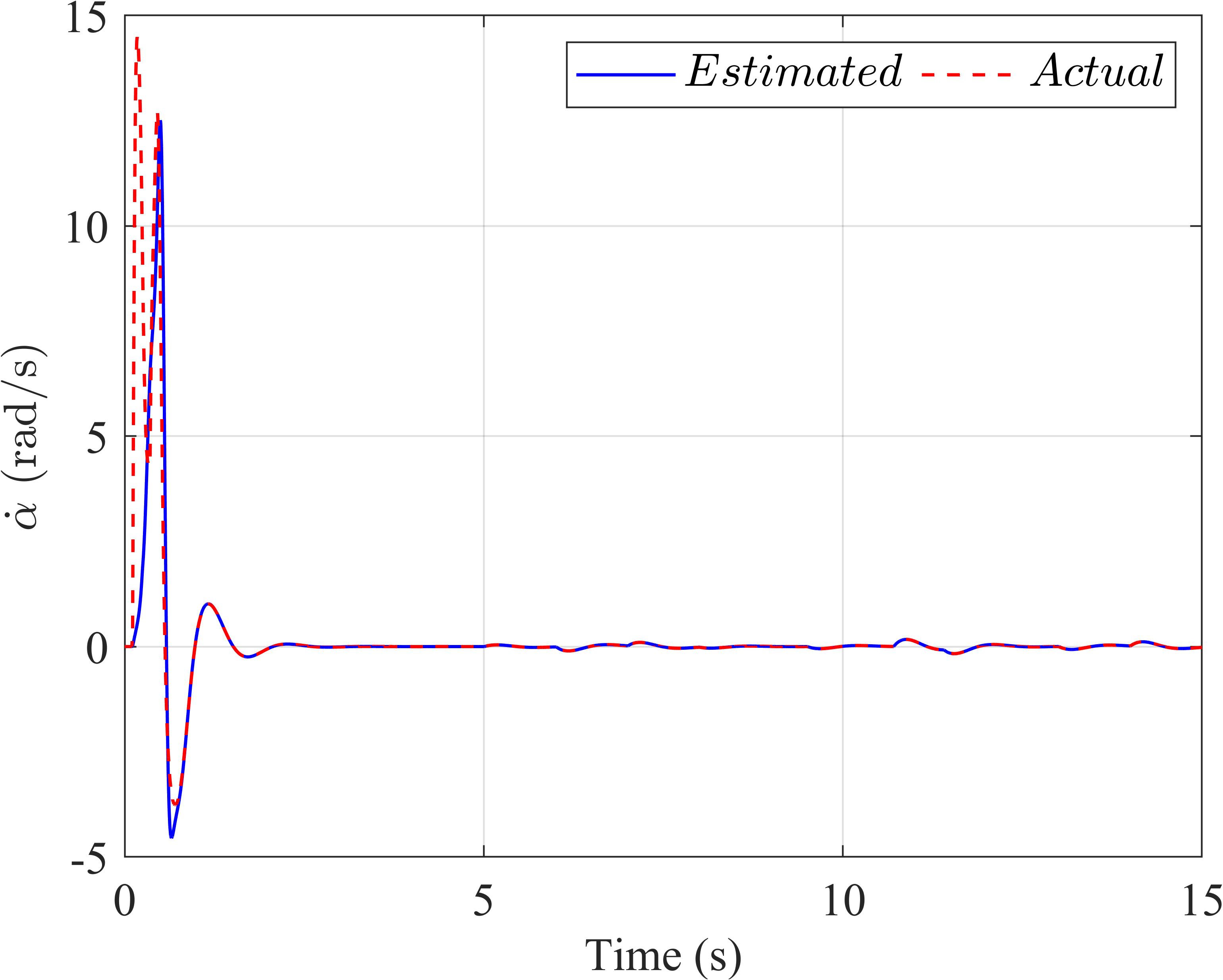
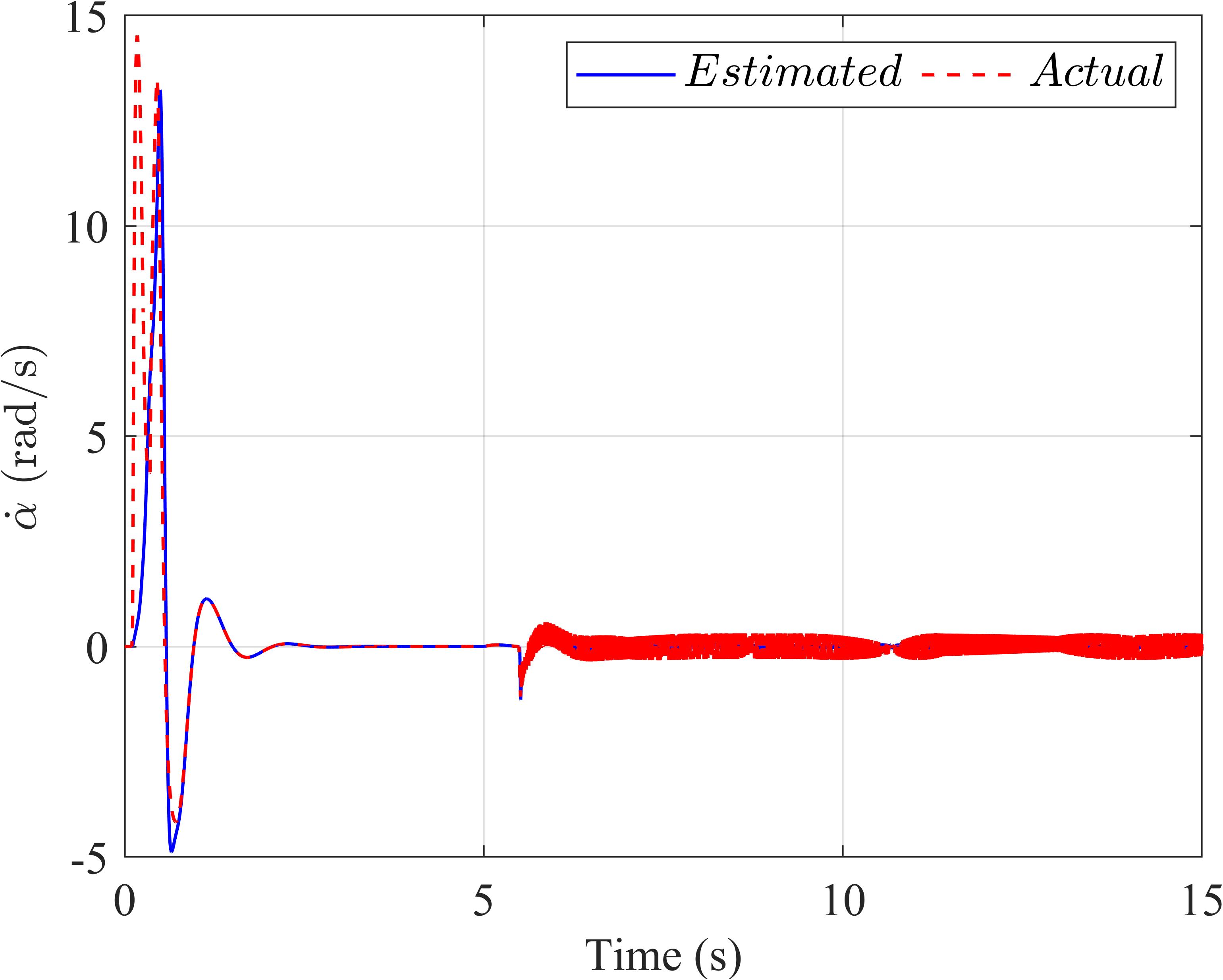
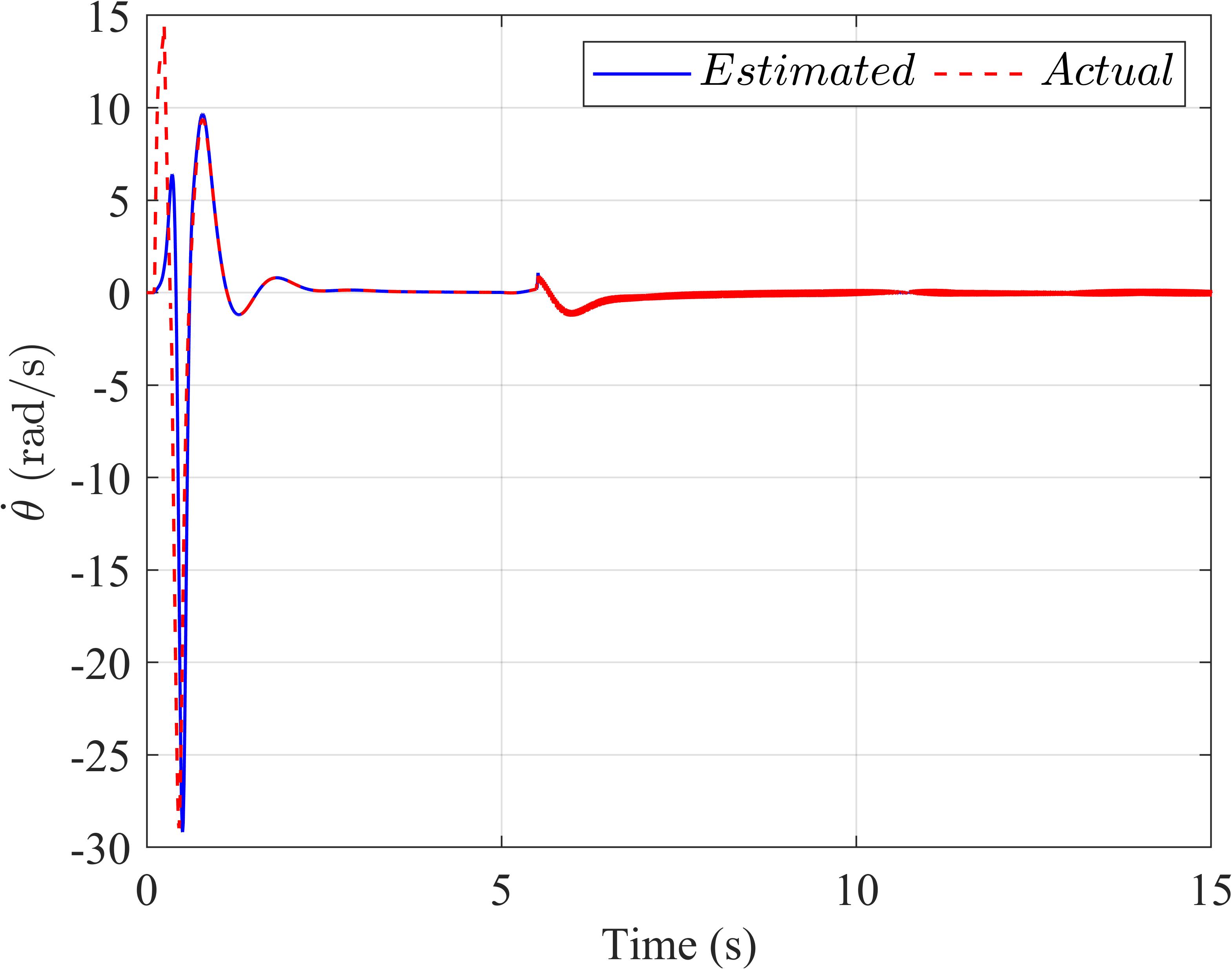
Figure5. TheExtendedStateObserverinthefirstscenario:(a)thependulumanglevelocity,(b)thearmanglevelocityof theLQRcontroller,(c)thependulumanglevelocity,and(d)thearmanglevelocityoftheLQR‐basedSMCcontroller.

Figure6. Thecomparisonresultsduringchangesin modelparameters:(a)thependulumangleand(b)the armangleoftwocontrollers.

5.Conclusions

Inconclusion,ourinvestigationhasdemonstrated therobustnessandadaptabilityoftheLQR‐based SlidingModeControl(LQR‐basedSMC)controllerin dealingwithexternaldisturbancesandvariationsin modelparametersintherotaryinvertedpendulum (RIP)system.Throughcomprehensivesimulations,it wasobservedthattheLQR‐basedSMCcontrollerout‐performedthetraditionalLQRcontrollerinthepres‐enceofexternaldisturbances.TheLQR‐basedSMC controllerexhibitedfastsettlingtimesandminimal oscillations,effectivelyattenuatingtheimpactofdis‐turbancesonthesystem.Thisremarkabledisturbance rejectioncapabilitymakesitavaluablechoicefor applicationswhereuncertaintiesandexternaldistur‐bancesareprevalent.

Furthermore,theLQR‐basedSMCcontrollerdis‐playedresilienceagainstchangesinmodelparame‐ters.Itsuccessfullymaintainedstablecontrol,even whenfacedwithuncertaintiesinthesystemdynamics. Thisadaptabilityisessentialforrealsystems,where modelparametersmayvaryduetoenvironmental conditionsorotherfactors.

However,itisimportanttoacknowledgethatthe introductionoftheSlidingModecomponentinthe controlsignalresultedinachatteringphenomenonin theoutputsignals.Whilethisbehaviordidnotcom‐promisetheoverallstabilityofthesystem,itmayraise practicalimplementationconcerns.Furtherresearch andengineeringeffortsarenecessarytoaddressthis

(a)

(b)

(c)

(d)

(a) (b)

issueandoptimizetheLQR‐basedSMCcontrollerfor smoothercontrolwithoutsacri icingitsdisturbance‐rejectioncapabilities.

Insummary,ourstudyhighlightstheLQR‐based SMCcontrollerasaviableandeffectivesolutionfor regulatingtherotaryinvertedpendulumsystemin thepresenceofexternaldisturbancesanduncertain parameters.BycombiningtheadvantagesofLQR andSlidingModeControl,thiscontrollerdemon‐stratespromisingperformanceandopensavenues foradvancementsincontrolstrategiesforsimilar complexsystems.Lookingtowardsfutureresearch, re iningtheLQR‐basedSMCcontrollerandexploring hybridcontrolapproachesmaypavethewayforeven morerobustandreliablecontrolsolutionsinvarious practicalapplications.

AUTHORS

Thi-Van-AnhNguyen –HanoiUniversityofSci‐enceandTechnology,11615Hanoi,Vietnam,e‐mail: anh.nguyenthivan1@hust.edu.vn.

Ma-SieuPhan –HanoiUniversityofScience andTechnology,11615Hanoi,Vietnam,e‐mail: sieu.pm192053@sis.hust.edu.vn.

Quy-ThinhDao∗ –HanoiUniversityofScience andTechnology,11615Hanoi,Vietnam,e‐mail: thinh.daoquy@hust.edu.vn.

∗Correspondingauthor

References

[1] K.‐Y.ChouandY.‐P.Chen,“Energybasedswing‐upcontrollerdesignusingphaseplanemethod forrotaryinvertedpendulum”.In: 201413th InternationalConferenceonControlAutomation RoboticsandVision(ICARCV),vol.1,no.1,2014, 975–979,10.1109/ICARCV.2014.7064438.

[2] B.A.Elsayed,M.A.Hassan,andS.Mekhilef, “Fuzzyswinging‐upwithslidingmodecontrol forthirdordercart‐invertedpendulumsystem”, InternationalJournalofControl,Automationand Systems,vol.13,2015,238–248,10.1007/s125 55‐014‐0033‐4.

[3] M.F.Hamza,H.J.Yap,I.A.Choudhury,A.I.Isa, A.Y.Zimit,andT.Kumbasar,“Currentdevelop‐mentonusingrotaryinvertedpendulumasa benchmarkfortestinglinearandnonlinearcon‐trolalgorithms”, MechanicalSystemsandSignal Processing,vol.116,2019,347–369,10.1016/j. ymssp.2018.06.054.

[4] J.Huang,T.Zhang,Y.Fan,andJ.‐Q.Sun,“Con‐trolofrotaryinvertedpendulumusingmodel‐freebacksteppingtechnique”, IEEEAccess,vol.7, 2019,96965–96973,10.1109/ACCESS.2019.29 30220.

[5] S.Irfan,A.Mehmood,M.T.Razzaq,andJ.Iqbal, “Advancedslidingmodecontroltechniquesfor invertedpendulum:Modellingandsimulation”,

Engineeringscienceandtechnology,aninternationaljournal,vol.21,no.4,2018,753–759, 10.1016/j.jestch.2018.06.010.

[6] A.KathpalandA.Singla,“Simmechanics™based modeling,simulationandreal‐timecontrolof rotaryinvertedpendulum”.In: 201711thInternationalConferenceonIntelligentSystemsand Control(ISCO),vol.1,no.1,2017,166–172,10 .1109/ISCO.2017.7855975.

[7] V.KumarandR.Agarwal,“Modelingandcontrol ofinvertedpendulumcartsystemusingpid‐lqr basedmoderncontroller”.In: 2022IEEEStudents ConferenceonEngineeringandSystems(SCES), vol.1,no.1,2022,01–05,10.1109/SCES5549 0.2022.9887706.

[8] B.Lima,R.Cajo,V.Huilcapi,andW.Agila,“Mod‐elingandcomparativestudyoflinearandnon‐linearcontrollersforrotaryinvertedpendulum”. In: JournalofPhysics:ConferenceSeries,vol.783, no.1,2017,012047,10.1088/1742‐6596/783 /1/012047.

[9] N.J.Mathew,K.K.Rao,andN.Sivakumaran, “Swingupandstabilizationcontrolofarotary invertedpendulum”, IFACProceedingsVolumes, vol.46,no.32,2013,654–659,10.3182/2013 1218‐3‐IN‐2045.00128,10thIFACInternational SymposiumonDynamicsandControlofProcess Systems.

[10] A.NagarajanandA.A.Victoire,“Optimization reinforcedpid‐slidingmodecontrollerforrotary invertedpendulum”, IEEEAccess,vol.11,2023, 24420–24430,10.1109/ACCESS.2023.3254591.

[11] A.Nasir,R.Ismail,andM.Ahmad,“Performance comparisonbetweenslidingmodecontrol(smc) andpd‐pidcontrollersforanonlinearinverted pendulumsystem”, WorldAcademyofScience, EngineeringandTechnology,vol.71,2010,400–405,10.5281/zenodo.1055423.

[12] S.R.Nekoo,“Digitalimplementationofa continuous‐timenonlinearoptimalcontroller: Anexperimentalstudywithreal‐time computations”, ISATransactions,vol.101, 2020,346–357,10.1016/j.isatra.2020.01.020.

[13] T.‐V.‐A.Nguyen,B.‐T.Dong,andN.‐T.BUI, “Enhancingstabilitycontrolofinverted pendulumusingtakagi–sugenofuzzymodel withdisturbancerejectionandinput–output constraints”, Scienti icReports,vol.13,no.1, 2023,14412.

[14] V.‐A.Nguyen,D.‐B.Pham,D.‐T.Pham,N.‐T. Bui,andQ.‐T.Dao,“Ahybridenergysliding modecontrollerfortherotaryinvertedpendu‐lum”.In: InternationalConferenceonEngineering ResearchandApplications,vol.602,no.1,2022, 34–41,10.1007/978‐3‐031‐22200‐9_4.

[15] L.B.Prasad,B.Tyagi,andH.O.Gupta,“Optimal controlofnonlinearinvertedpendulumsystem

usingpidcontrollerandlqr:performanceanal‐ysiswithoutandwithdisturbanceinput”, InternationalJournalofAutomationandComputing, vol.11,2014,661–670,10.1007/s11633‐014‐0818‐1.

[16] O.Qasem,H.Gutierrez,andW.Gao,“Experimen‐talvalidationofdata‐drivenadaptiveoptimal controlforcontinuous‐timesystemsviahybrid iteration:Anapplicationtorotaryinvertedpen‐dulum”, IEEETransactionsonIndustrialElectronics,vol.1,no.1,2023,1–11,10.1109/TIE.2023.3 292873.

[17] E.Susanto,B.Rahmat,andM.Ishitobi,“Stabiliza‐tionofrotaryinvertedpendulumusingpropor‐tionalderivativeandfuzzycontrols”.In: 20229th InternationalConferenceonInformationTechnology,Computer,andElectricalEngineering(ICITACEE),vol.1,no.1,2022,34–37,10.1109/IC ITACEE55701.2022.9924142.

[18] H.Wang,H.Dong,L.He,Y.Shi,andY.Zhang, “Designandsimulationoflqrcontrollerwiththe

linearinvertedpendulum”.In: 2010international conferenceonelectricalandcontrolengineering, vol.1,no.1,2010,699–702,10.1109/iCECE.20 10.178.

[19] L.Wang,H.Ni,W.Zhou,P.M.Pardalos,J.Fang, andM.Fei,“Mbpoa‐basedlqrcontrollerandits applicationtothedouble‐parallelinvertedpen‐dulumsystem”, EngineeringApplicationsofArtiicialIntelligence,vol.36,2014,262–268,10.101 6/j.engappai.2014.07.023.

[20] J.YuandX.Zhang,“Theglobalcontrolof irst orderrotaryparalleldoubleinvertedpendulum system”.In: 202140thChineseControlConference (CCC),vol.1,no.1,2021,2773–2778,10.23919 /CCC52363.2021.9549400.

[21] J.Zhang,P.Shi,Y.Xia,andH.Yang,“Discrete‐time slidingmodecontrolwithdisturbancerejection”, IEEETransactionsonIndustrialElectronics,vol. 66,no.10,2019,7967–7975,10.1109/TIE.2018 .2879309.

Abstract:

FORMATIONCONTROLOFMULTI‐AGENTNONLINEARSYSTEMSUSINGTHE

FORMATIONCONTROLOFMULTI‐AGENTNONLINEARSYSTEMSUSINGTHE

FORMATIONCONTROLOFMULTI‐AGENTNONLINEARSYSTEMSUSINGTHE

Submitted:10th January2024;accepted:23rd July2024

SaeedRafeeNekoo

DOI:10.14313/jamris‐2025‐003

Thisworkinvestigatestheformationcontrolofamulti‐agentroboticsystemviathestate‐dependentRiccati equation(SDRE).Thesystem’sagentsinteractwitheach otherandfollowaleaderinpoint‐to‐pointmotioncon‐trol(regulation).Thenumberofagentsisunlimitedin conventionalmulti‐agentformationcontrolconsideringa complexdynamicforeachagent,thoughthecomplexities ofthealgorithmsusuallyresultinsmall‐scalesimula‐tions.Hereaformalismisproposedthatconsidersfully couplednonlineardynamicsforroboticsystemsinmulti‐agentsystemformationcontrolwithalargenumberof agents.Theinteractionoftheagentswitheachotherand obstacleavoidanceareembeddedinthedesignthrough theweightingmatrixofstatesintheSDRE.Theinputcon‐straintalsolimitstheactuatorstocreateamorerealistic scenario.Twodynamicalsystemshavebeenmodeledand simulatedinthiswork:wheeledmobilerobots(WMR) andmultirotorunmannedaerialvehicles(UAVs).Thesim‐ulationresultsshowsuccessintheimplementationof atotalof1,089agentsinthedesiredsquareformation shapeintheUAVcasestudy,andafigureof45agentsand 1,050differentialwheeledmobilerobotsinthecircular desiredshape,consideringobstacleavoidanceandalso collisionavoidancebetweentheagents.

Keywords: Multi‐agent,Formation,Control,SDRE, Robotics.

1.Introduction

Thispaperpresentsresearchoncontrollinga highly‐populatedmulti‐agentsystemwithinthe frameworkofthestate‐dependentRiccatiequation (SDRE),whichisanonlinearoptimalclosed‐loop controlpolicy.Amulti‐agentsystemconsistsofa leaderandapopulationoffollowers,playingthe roleofagents.Theagentsinaswarmsystemshow acollectivebehavior,withinteractionsachievinga commongoal[1].Thepreviousreportsonswarm roboticshavebeenquitediverseinsubjectmatter: technologicalaspectsofswarmrobotics[2, 3]; arrangement,formation,andbehavior[4–6];and bio‐inspiration[7,8],amongothers.

Theapplicationofswarmroboticshasbeen reportedinmanyworks,includingmicro‐robotics:the interactionandphysicalcontactbetweentheagents [9–11],nano‐swarmsfordeliveringmedicineorper‐forminganoperationinhumanbody[12],searchand rescue[13–15],monitoringanddatacollection[16, 17],etc.

Multipledecision‐makingagentswithauto nomousoperation,socialabilityinteraction,reactivity perception,andpro‐activenessexhibition,were motivatedbycomplexinherentlydistributedsystems toincreaserobustness.Multi‐agentandswarm systemsaresimilarinthesensethattheyrequire multipleagentsthatcommunicateandcooperate. Eachagentinmulti‐agentsystemscandosome meaningfulpartofatask;however,inswarmsystems, wewouldexpecteachagenttobetoounawareofits environmenttopossiblyevenknowwhatisgoing onaroundit.Thisemphasizestheexistenceofa largenumberofagents,andpromotesscalability, softcollisionsandphysicalcontactsoftheswarmin migration.Thismightnotbethecaseforswarmsin nature,i.e.,inbirds,whichdonotcollide,andalso donotreceiveacommandfromleader[18].Here, inthiscurrentwork,themodelingisnotbasedon bio‐inspiration,sincewearefarawayfromsuch sophisticateddesigninmothernature.

Multi‐agentsystems,orcooperativerobots,can usuallybe itintothesetwocategories:systemsthat consideredcomplexdynamicsforeachagent,though thenumberofagentsissmall[19–24],andsystems withsimpledynamicsoronlykinematicsforeach agentwhenthenumberofagentsislarge[25–32]. Forexample,Yangetal.presentedaformationcon‐trolstrategybasedonastablecontrollawtoguide theagentstowardsaconstraintregionandsimu‐lateditforatotalof155agents[32].Collisionavoid‐anceandobstacleavoidancebetweentheagentsare alsotwoimportantcharacteristicsoftheformation methods.WangandXinpresentedanoptimalcontrol approachforformationcontroltakingintoconsidera‐tionobstacleavoidanceformultipleunmannedaerial vehicle(UAV)systems[33].Kumaretal.presenteda velocitycontrollerforaswarmofUAVswithobstacle avoidancecapability[34].ParkandYooproposeda connectivity‐basedformationcontrolwithcollision‐avoidancepropertiesforaswarmofunmannedsur‐facevessels[35,36].

Table1. Adetailedreportonthepopulationofagentsin SDREinprevious,asliteraturecomparedtothiswork.

context Ref. No.ofagents,typeofagent multi‐agent [37] 5,single‐integrator leader‐follower [38] 2,mobilerobot formation [40] 2,spacecraft [41] 5,single‐integrator [42] 2,spacecraft [43] 3,mobilerobot [44] 2,aircraft [45] 3,spacecraft [46] 2,spacecraft [47] 2,satellite [39] 1024,satellite consensuscontrol [22] 10,crane cooperative [48] 2,manipulator multi‐agents [49] 2,manipulator [50] 3,spacecraft [19] 4,manipulator [51] 4,UAV [52] 3,mobilerobot multi‐agents thiswork 1,089,UAV leader‐follower thiswork 45,mobilerobot thiswork 1,050,mobilerobot

Theapplicationoftheswarmregulationcontrolis devotedtomulti‐copterUAVformationcontrolfora largenumberofagents–1,089–toshowthecapabili‐tiesoftheproposedapproach.Swarmcontrolusing augmentedmethodssuchasgraphtheoryandmulti‐layernetworkdesignisausefulapproach;however, inthiswork,thepurecapacityoftheSDREisusedto controlahighlypopulatedmulti‐agentsystem.This willsimplifythedesignandlimittheformulation topureSDRE.Theadvantagesofthispointofview resultincontrollinglarge‐scalesystemswithcom‐plexdynamics.Afullycoupledsix‐degree‐of‐freedom (DoF)nonlinearmodelofthesystemisconsidered(12 statevariables).Thesecondcasestudyisaleader‐followersystemof45‐wheeledmobilerobots(WMRs) withnon‐holonomicandholonomicconstraintsof wheels.Asmallernumberofrobotswasconsidered tohighlighttheeffectivenessofobstacleandcollision avoidance.SDREhasbeenusedinbothmulti‐agent systems[37–39],andleader‐followercontrol[22,40–47].ThedetailsofthenumberofagentsusingSDRE arereportedonTable1.Themajorityofthesestudies focusedonthecontrolandbehavioroftheleader‐followersystem, irstconsideringtwoagentsandthen sometimesincreasingthenumberofagentsto5or 10.TheonlylargepopulatedsystemusingSDREcon‐trolincluded1,024satellites;obstacleavoidanceand collisionavoidancebetweenagentswerenotconsid‐ered[39].Thelargedistancebetweentheagentsand thepatternofthesatellitesdidnotnecessitatecolli‐sion/obstacleavoidance.Inthiswork,amoremature versionofmulti‐agentSDRE[39]ispresentedtoadd thosecharacteristics,sincetheagentsareworking closetogetherinbothsolvedexamples.

Theswarmformulationincontrolmethodscould besolvedbygraphtheoryfortheformationdesign ofthewholeswarm;inthatcase,anothercontroller mustcontroltheagents,individuallybycheckingthe connectionfortheagentsthroughmultiplelayers[53–55].Thedesignoftheformationusinggraphtheory, andadaptingacontrollerforhandlingthemulti‐agentsystem,mightposedif icultyinimplementa‐tionbecauseacontrollermustincludeotherlayersof designsthroughexternalmethods.

Thereportednumberofagentswas16satellites [53],6agents[54],and90agents[55].Theuseofthe Kroneckerdeltafunctionfortheselectionofinforma‐tionfromaparticularagentlimitstheapplicationof theswarmmulti‐agentformulationtoalimitednum‐ber.IntheSDREmethodparticularly,thesolutionto theRiccatiequationmightbecomeoverlycomplexif theSDREshouldbesolvedfortheentireswarm.In thisapproach,thegainofthetargetedagentwould becollectedfromtheoverallmatrixoftheswarm. Again,thisapproachwouldlimittheimplementation oftheformulationforalargenumberofagents.The reportedSDREagents,usingconsensuscontroland graphtheory,were10[22]and2[38],respectively.

Thefocusofthisworkislarge‐scalemulti‐agent systemsthatneedsimplicityintheirdesign.Thissim‐plicitydoesnotimplyasimplelinearcontroller;on thecontrary,theSDREisanonlinearsub‐optimal controllerwitharelativelycomplexsolution.How‐ever,thepracticalapproachtohandlethemulti‐agent systemreliessolelyontheSDRE’scapabilitiesitself, andusestheweightingmatrixofthestatestohan‐dledistanceconstraintsandobstacleavoidance.As aresult,therewouldnotbefurthercomplexityfor practicalimplementationraisedbytheinteractionof theSDREwithanotherlayerorgraphtheory.Thiscan beviewedasindependentSDREcontrollersworking withneighborcomponentsandtheirleaderthrougha weightingmatrix,whichisinsidetheumbrellaofthe SDRE,notanothersystemaugmentedbythemulti‐agentsorothercomplementarymethods.Thisisthe keytolarge‐scalemodelingandsimulation–whichis simplicityinthecommunicationofthemulti‐agent systemandrelianceonthecapacitiesoftheSDRE itself.

Themaincontributionofthisworkisthepresen‐tationofacontrolstructureforformingamulti‐agent systemwithcomplexdynamicswithobstacleandcol‐lisionavoidancebetweentheagents.Complexsystems withalargenumberofagentsareseldomreported; thisworkpresentsasuitablestructureforthat.This workaddscollisionandobstacleavoidancetoSDRE multi‐agentsystemcontrol,motivatedbytheexample setby[39],whichreportedsolelymulti‐agentsystem SDREwithoutcontactprevention.Forverycrowded systems,contactbetweentheagentshasbeenboth expectedandconsideredintheliterature[30, 32], butthisworkproposesamethodthataddsdistance betweentheagentstoreducecollisionsduringthe controltask.

leader point-topoint trajectory

followers agents, arranged in a predefined shape (arbitrary shape and formation)

Figure1. Aschematicviewofthemulti‐agentsystem,movingfromaninitialrandomly‐distributedformtoafinaldesired shapewitharrangedagentsinanenvironmentwithanobstacle.The2Drepresentationisintendedtoshowmoredetail; itsformationisgeneralandcouldbeappliedto3Dformationaswell.

Thedistance‐basedarrangementofagents,and avoidingcollisionbetweenthem,isbasicallytheidea ofmulti‐agentsystemcontrolmethodsthatusegraph theory,potential ieldmethod,multi‐layerdesigns, andthelike;hereinthiswork,thedistribution,aswell asobstacle,andcollisionavoidance,arestructured withintheSDREformulation–speci ically,theweight‐ingmatrixofstates.

Section 2 presentsthecontrolstructureofthe SDREandmulti‐agentsystemmodeling.Section 3 describesthedynamicsofthetwocasestudiesof thiswork,UAV,andWMR.Thesimulationresultsare presentedinSection4andtheconcludingremarksare summarizedinSection5

2.ControlStructure:SDREforMulti‐agent Systems

2.1.ConventionalController:ABriefPreliminary Formulation

Consider �� numberofagents,randomlydis‐tributedinaprede inedarea,withcontinuous‐time nonlinearsystemsandaf ine‐in‐controlproperties. The��‐thagent’sdynamicisrepresentedinstate‐space formas:

x��(��)= f��(x��(��))+ g��(x��(��), u��(��)), (1) where x��(��)∈ℝ�� isthestatevectorand u��(��)∈ℝ�� is theinputvectorofthe��‐thagent. f��(x��(��))∶ℝ�� →ℝ�� and g��(x��(��), u��(��))∶ℝ��×ℝ�� →ℝ�� in(1)arevector‐valuedsmoothfunctionsthatsatisfythelocalLips‐chitzcondition,withequilibriumpoint f��(0)= 0.The nonlinearsystem(1)istransformedintothestate‐dependentcoef icient(SDC)parameterization:

x��(��)= A��(x��(��))x��(��)+ B��(x��(��))u��(��), (2)

where A��(x��(��))∶ℝ�� →ℝ��×�� and B��(x��(��))∶ℝ�� → ℝ��×�� areheld.

TheSDCparameterization(2)isreferredtoas apparentlinearization;however,itpreservesthe nonlinearityofthesystem.Forexample,consider anover‐actuatedsingle‐degree‐of‐freedomsystemin state‐spaceformwith ��=2 and ��=2,thenthe systemvectors

f(x)= ��2 ��1��2 2 cos��2 +��1����

canpresentasetofSDCmatricesas

f(x)= 0 1 ����1 ��1��2 cos��2 A(x) ��1 ��2 , g(x, u)= 00 ��2 ��1��2 B(x) ��1 ��2

Theresultofmultiplicationof A(x)x and B(x)u willbethesameoriginalvaluesof f(x) and g(x, u); hence,theSDREmethodisanonlinearoptimalcontrol thatkeepsthenonlinearitiesinthecontrolstructure. AnotherpointonSDCmatricesisthattheyarenot uniquerepresentations,andcanshownumerousver‐sions,suchas:

f(x)= 0 1 ����1 +��2 2 cos��2 0 A(x) ��1 ��2 , g(x, u)= 0 0 ��2 +��1��2 ��2 ��1 0 B(x,u) ��1 ��2

B(x, u) inthesecondsetoftheSDCmatricesis notidealbecauseitchangestheproblemintoone withnon‐af ineparameterizationandsingularityin thecaseof��1 =0.Thelimitationandproperselection ofSDCmatricescanbesummarizedincontrollability assumption,asfollows.

Assumption1 Thepairof {A��(x��(��)), B��(x��(��))} isa completelycontrollableparameterizationofnonlinear af ine-in-controlsystem(1)forthestatesofthe ��-th agent x��(��)∈ℝ�� in ��∈[0,∞) [56].

Thecontrolobjectiveistominimizethecostfunc‐tion: ��= 1 2 ∞ 0 {x⊤ �� (��)Q��(x��(��))x��(��)+ u⊤ �� (��)R��(x��(��))u��(��)}d��, (3) where Q��(x��(��))∶ℝ�� →ℝ��×�� and R��(x��(��))∶ℝ�� → ℝ��×�� areweightingmatricesofstatesandinputsof ��‐thagent,respectively. Q�� issymmetricpositivesemi‐de initeand R�� issymmetricpositivede inite.

Assumption2 Thepairof {A��(x��(��)), Q1/2 �� (x��(��))} is acompletelyobservableparameterizationofthenonlinearaf ine-in-controlsystem (1) forthestatesof ��-th agent x��(��)∈ℝ�� in ��∈[0,∞),where Q1/2 �� ,inEq.(3), isCholeskydecompositionof Q�� [57].

ThecontrollawoftheSDREis[56]:

u��(��)=−R−1 �� (x��(��))B⊤ �� (x��(��))K��(x��(��))x��(��), (4) where K��(x��(��)) isthepositive‐de initesymmetric gainofthecontrollaw.Thegain K��(x��(��))isthesolu‐tiontothestate‐dependentRiccatiequation:

A⊤ �� (x��(��))K��(x��(��))+ K��(x��(��))A��(x��(��))+ Q��(x��(��))− K��(x��(��))B��(x��(��)) R−1 �� (x��(��))B⊤ �� (x��(��))K��(x��(��))= 0 (5)

Withoutlossofgenerality,theinputlaw(4)is transformedto:

u��(��)=−R−1 �� (x��(��))B⊤ �� (x��(��))K��(x��(��))e��(��), forcontrollingthesystemtoadesiredconditionin which e��(��)= x��(��)− xdes,��(��)where xdes,��(��)isthe desiredstatevectorof��‐thagent.

2.2.FormationControl

Thede initionofformationcontrolisintroduced byasetoftime‐varyingdesiredconditionsforthe agentstofollowtheleaderofthegroup.The irst agent,��=1,istheleaderandtherestoftheagentsare followers,��=2,...,��.Theleaderisregulated(point‐to‐pointmotion)fromaninitialcondition, x1(0),to thedesiredcondition, xdes,1(��f),inwhich��f isthe inal timeofthecontroltask.Theschematicofthedistribu‐tionoftheagents,andthemigrationfromtheinitialto the inalcondition,areillustratedinFig.1.

Therestoftheagentsfollowtheleaderwhilethey trytokeeptheprede inedgeometricformationduring thetaskandsitattheexactprede inedgeometric formationattheendofthetask:

xdes,��(��)= x1(��)− xf,1 + xf,��,��=2,...,��, (6) where xf,�� representsthedesiredcoordinates (constantvalues)forthe��‐thagentintheprede ined formationshape.Onlytheleaderhasaconstant(time‐invariant)desiredcondition.Equation(6)showsthat thetime‐varyingdesiredconditionsofthefollowers arefedbytheonlinepositionoftheleaderandthe constantdesiredformation.Thatmeansthefollowers trytokeeptheformationoftheoverallpoint‐to‐point trajectoryoftheleaderfromtheinitialtothe inal condition.

Remark1 Itshouldbepointedoutthat xf,��,isastate vector,andonlythe irsttwoorthreestatesaredifferentfromzero(thosethatrepresentthecon igurationspace).Therestofthedesiredstatescouldbeset tozero.CommondynamicsofmultirotorUAVsusually havesixdegreesoffreedomthatprovide12statesfor thesystem.FortheUAVs,onlythreepositionstatesof Cartesiancoordinate(��,��,��)mustbeconsideredinthe formation.Theorientationandvelocitystatesmightbe independentlycontrolled.

2.3.CollisionAvoidanceandObstacleAvoidance BetweenAgents

TheweightingmatrixforthestatesoftheSDRE controllercanincludenonlinearfunctionsofstate variablesinitscomponents.Thispropertyprovides obstacleavoidanceinregulationcontrolbasedonarti‐icialpotential ieldmethod[52,58,59].Thedistance betweenanobstacleandanagentis:

��o,��(��)=‖xp,��(��)− xo‖2, (7) for ��=1,...,�� where xp,��(��) isapartofstatevector, whichincludesthepositioncoordinates, xp,��(��)∈ x��(��),andhas xo asthepositionoftheobstacle.

Thenextstepistode inethedistancebetween twoconsecutiveagentsforcollisionavoidance.The distancebetweenthe��‐thand(��−1)‐thagentis:

����(��)=‖xp,��(��)− xp,��−1(��)‖2, (8) for��=2,...,��,itshouldbenotedthattheleaderdoes notneedtoincludecollisionavoidanceterms.The collisionavoidanceapproachinEq.(8)onlyavoidsthe impactbetweentwoconsecutiveagents.Thetopology oftheagentsisde inedthroughthedistributedpat‐tern(6)wherethemaincharacteristhetime‐varying positionoftheleader.Evidently,thispatternand leaderinformationdoesnotprovideenoughsafety inthemigrationofthemulti‐agentsystem.Hence, thecollisionavoidancetermwasintroduced(8)to addanothersafetyconditionformigrationwithout impact.Thisfeaturecreatescommunicationbetween twoconsecutiveagentsforreadingandsendingthe positiondata.

Theindexisassignedtoagivenagentrandomly; asaresult,twoconsecutiveagentsmightnotbeneigh‐borsattheinitialconditionandcouldevenbefaraway fromeachother.Thisinitializationmightraiseissues. Thecollisionavoidancebetweenneighboragents(8) mightnotbeeffectiveandcollisionmighthappen between ��‐thagentandothermembers.So,itisnot assumedthatagents��and��−1areclosed;however, startingtheregulationcontrol,theyfollowtheleader andthepattern,andtheymergeto indtheirneighbor agentsinashortperiod.Toavoidimpactandcollision inaglobalscheme,thefollowingtermswillbeconsid‐eredaswell.

Toincludethecollisionavoidancebetweenthe��‐th agentandallpreviousmembers,thefollowingcondi‐tionisintroduced:

��s,��(��)= ��tot,��,��(��),��tot,��,��(��)<��min, 1, ��tot,��,��(��)≥��min, (9) for��=3,...,��,and��=1,...,��−1where��tot,��,��(��)= ‖xp,��(��)− xp,��(��)‖2, isthedistancebetweenthe ��‐th agentandthe ��‐thagent,and ��min istheminimum collisionavoidancesafetydistance.Thepseudocodeof Eq.(9)ispresentedas

for ��=3,...,��, for ��=1,...,��−1, ��tot,��,��(��)=‖xp,��(��)− xp,��(��)‖2, if ��tot,��,��(��)<��min, ��s,��(��)=��tot,��,��(��), else, ��s,��(��)=1, end, end, end.

Equation(9)isupdatedateachtimestepofsimu‐lationwhenalltheagentsaremovingfromtheinitial tothe inalcondition.Incasesinwhichthe��‐thagent isclosetooneagent,theterm��s,��(��)isupdatedin(9); otherwise ��s,��(��)=1.Thedifferentdistanceterms (��o,��(��),����(��),and��s,��(��))willbeusedinSection2.4to settheobstacleandcollisionavoidancestrategybased onthemodi icationof Q��(x��(��))matrix.

2.4.DefinitionofWeightingMatrix

Thestate‐dependentweightingmatricesofthe SDREareoneoftheadvantagesofthismethodover alinearquadraticregulator(LQR)controller.The weightingmatricesoftheLQRareconstantandcan‐notincludeparametersrelatedtotrajectoriessuch as–theintroduceddistancetermsinSection 2.3–for obstacleavoidance,collisionavoidance,oradaptive designs.Thede initionsoftheweightingmatricesfor theleaderandfollowersaredifferentinordertogain differentmotionspeeds.Theleadermustbeslower andthefollowersmustbefastertotracktheleader properly.Thefollowingde initionoftheweighting matrixwillprovideforthiscondition.

Theweightingmatrixofstatesfortheleaderonly includesobstacleavoidance:

����,��,1(x1(��))=1+ 1 ��o,1(��), (10)

where����,��,1(x1(��))isthe��‐thdiagonalcomponent of Q1(x1(��))relatedto��‐thpositionstate;��couldbe astatevariableofleader’sdynamics,i.e.thesecond state,generatedby ��2,2,1(x1(��)).Itshouldbenoted thatonlyafewdiagonalcomponentsof Q1(x��(��))are responsibleforobstacleavoidance.Fortheexample presentedinRemark 1,onlythe irsttwodiagonal componentsoftheweightingmatrixinclude(10),and therestofthe10componentsaretunedconvention‐ally.TheUAVpositionvariablesareindeedde inedin ��,��,��,thoughtheobstacleavoidancetermsareset onlyfor��,��;theresultsweresatisfactory.Thechoice iswiththedesigner,andinsomecases,itcanalsobe assignedforallthreeaxesin3Dplatforms.

Remark2 Ifwenoticetheterm 1+ 1 ��o,1(��) in (10), 1 ��o,1(��) mightgainaverysmallvalueifthedistance betweentheobstacleandtheleaderisfar.Theconstant term“1”in ����,��,1(x1(��)) makessurethatthevelocity oftheleaderisproperlyde inedwhen 1 ��o,1(��) →0.

Thefollowers��‐thmustavoidobstacles,aswellas thecollisionbetweentheotheragents,throughthe matrix Q��(x��(��)):

(��))= 1

(��) + 1

��(��) + 1 ��s,��(��), (11) for ��=2,...,��.Ifthedistancetermsbecomesmall, whichshowsthereisaprobabilityofcollisionbetween agentsorobstaclesandanagent,thediagonalcom‐ponentof Q getsbiggerandthatstatedeviatesthe trajectoryofthesystem(inotherwords,itavoids thecollision).Assigningallthepositionstatesforan obstacle,orbetweencollisionavoidancespeedsupall thestatessimultaneouslyandthecollisionavoidance fails.Moredetailscouldberevisitedin[52].Thefol‐lowingishelpfultoclarifythispoint.Imagineamobile robotmovesforwardinastraightlineandthereis anobstacleontheway.Theactuatorsaretwomotors onthewheels.Iftheobstacleavoidancemechanism commandsbothwheelstospeedupatthesametime, therobotjustmovesfasterinastraightline.Inorderto movetherobottooneside,onlyonewheelmustrotate faster!Therefore,avoidancefunctionsareintroduced onlyinoneortwocomponentsrelatedtotheCartesian coordinates.

Inthissection,threedifferentdistancetermswere introduced:��o,��(��),����(��),and��s,��(��).Itmustbenoted thatthesedistancetermswillbeappliedintheweight‐ingmatrixofstates,usingthearti icialpotential ield method.Thedistancetermsincreasethevalueof theweightingmatrix,leadingtheagenttoavoidthe collision.

Figure2. Theschematicviewandaxisdefinitionofa quadrotor.

Eachdistancetermplaysitsownroleinthemigra‐tionofthemulti‐agentsystem.��o,��(��)avoidscollision oftheagentwiththeobstacleintheenvironment; ����(��)avoidscollisionofthetwoneighboragents;and incaseoftheproximityofanypreviousagentsto currentagent, ��s,��(��) willbeactivatedtoavoidthe collision.Insummary,thethreecomponentswillcon‐tributetothesafetyincaseofcollisionoftheagents withtheobstacleandwithotheragents.

Thede initionoftherestofthecomponentsofthe weightingmatrixofstates,aswellastheinputs,could bedonebasedonconventionaltuningmethodsand rules[60].

3.SystemDynamicsandSDCParameterization

3.1.UnmannedAerialVehicle

Thedynamicequationofonequadrotor unmannedaerialvehicle(UAV)ispresentedin thissection.Theschematicviewofthesystem andthecon igurationoftherotorsareillustrated inFig. 2.Theagentsareidenticalandsharethe samedynamics.Thegeneralizedcoordinatesofone systemare {��c,��(��),��c,��(��),��c,��(��),����(��),����(��),����(��)}, where ��1,��(��)=[��c,��(��),��c,��(��),��c,��(��)]⊤(m) de inesthecenter‐of‐mass(CoM)ofthe ��‐th UAVintheCartesiancoordinatesystem,and ��2,��(��)=[����(��),����(��),����(��)]⊤(rad)areitsEuler angles.Thelinearandangularvelocitiesofthedrone arepresented ��1,��(��)=[����(��),����(��),����(��)]⊤(m/s) and ��2,��(��)=[����(��),����(��),����(��)]⊤(rad/s), respectively.Thestatevectorofthesystemis de inedas:

x��(��)=[��⊤ 1,��(��),��⊤ 2,��(��),��⊤ 1,��(��),��⊤ 2,��(��)]⊤ (12)

Thekinematicsrelations

��1,��(��)=R������,��(��2,��(��))��1,��(��), ��2,��(��)=T��(��2,��(��))��2,��(��), (13) areheldforthequadrotorsystem.Consideringthat thequadrotorsystem liesbasedonsmallchangesin theEulerangles,itisnotsupposedtoperformaggres‐siveandaerobaticmaneuvers,andthehoveringstate isassumedforthe lightcondition.

Therefore,thederivativeofstate‐vector(12)gen‐erates

x��(��)=[�� ⊤ 1,��(��),�� ⊤ 2,��(��),̇��⊤ 1,��(��),̇��⊤ 2,��(��)]⊤ .

AssumingsmallchangesinEulerangelsdur‐ing lightcontrol,thederivativeofthekinematics equation(13):

��1,��(��)= R������,��(��2,��(��)) ≈0 ��1,��(��)+ R������,��(��2,��(��)) ≈I 1,��(��), ��2,��(��)= T��(��2,��(��)) ≈0 ��2,��(��)+ T��(��2,��(��)) ≈I ̇�� 2,��(��), showsthatinahoveringstate, ��1,��(��)≈̇��1,��(��) and ��2,��(��)≈̇��2,��(��)arevalid.Asaresult,thestate‐space representationofoneagentis[61]:

R������,��(��2,��)��1,�� T��(��2,��)��2,�� 1 ���� {R������,3,��(��2,��)��B,�� −������e3 Df,����1,��} J−1 �� (��2,��){��

(14) where ����(kg)isthemassofthedrone, ��B,��(��)(N)isthethrustforcein ��c direction (upward), ��=9.81(m/s2) isgravityconstant, e3 =[0,0,1]⊤ , Df,�� = diag(����,����,����)(kg/s) includesdrag,aerodynamiceffects,etc.,and ��B,��(��)=[����,��(��),����,��(��),����,��(��)]⊤(Nm)istheinput torquevector.Moreover,thedetailsof R������,��(��2,��(��)), T��(��2,��(��)), C��(��1,��(��),��2,��(��)),and J��(��2,��(��)) canbe foundinSectionIIIofRef.[61],and R������,3,��(��2,��(��))is thethirdcolumnoftherotationmatrix R������,��(��2,��(��))

ThequadrotorUAVisunderactuated,andthecon‐trolstructureusesacascadedesign,whichcontrols thetranslationpartofdynamics(14)inthe irst layerandtheorientationinthesecondlayer.The translationdynamicsincludesthestates xt,��(��)= [��c,��(��),��c,��(��),��c,��(��),����(��),����(��),����(��)]⊤,expressed inrows1‐3and7‐9ofEq.(14).TheSDCparameteri‐zationconsidersfullactuationfortranslationcontrol:

Thecomponent[R������,3,��(��2,��)��B,��]3×1 inEq.(14) isavectorofthrust,andisdistributedinthetransla‐tiondynamicsbythethirdcomponentoftherotation matrix.BesidestheSDREdesign,thereisacascade controlleraswell,Eq.(17),toaddresstheunder‐actuationconditionofthequadrotor.

Inordertoimplementthecascadedesignand SDREcontrol,inthe irststep,theSDREcontroller mustbeoperatedwiththeassumptionoffullactu‐ationcondition,whichdemandsa Bt,�� = 03×3 1 ���� I3×3 matrixof6×3dimension.Ifthethirdcomponentof therotationmatrixenterstheSDCparameterization,a scalarthrusttermisobtainedasthesingleinputtothe problem,whichcreatesanobstacleinthedesign.This topichasbeenpresentedinpreviousimplementations andexercisedwithdifferentconditions,platforms, andcontrollers[61–63],butitwasoriginallyproposed ascascadecontroldesign;detailscanbeseeninRef. [64].

Assigningweightingmatriceswithproperdimen‐sionsandsolvingtheSDREforthetranslationpart: A⊤ t,��(xt,��)Kt,��(xt,��)+ Kt,��(xt,��)At,��(xt,��)− Kt,��(xt,��)Bt,��R−1 t,�� (xt,��)B⊤ t,��K

,��(xt,��)+

Qt,��(xt,��)= 0, resultsinthesub‐optimalgain Kt,��(xt,��(��)) forthe controllaw:

ut,��(��)=−R−1 t,�� (xt,��(��))B⊤ t,��Kt,��(xt,��(��))et,��(��), (15) where et,��(��)= xt,��(��)− xt,des,��(��)inwhich xt,des,��(��) includesthedesiredtranslationvariables.Thethree componentsofthecontrollaw,in(15),aresubstituted inthethrustequation(16)[61]:

��B,��(��)=����{R⊤ ������,3,��(��2,��(��))(ut,��(��)+��e3)}. (16)

Notethatgravityiscompensatedforin(16),and forthisreason,theSDCmatrix At,��(xt,��(��)) excluded thegravityterm.Thesecondcascadecontrollayer regulatestheorientationofthedronetohelpthe translationpart,basedontwoconstraints[62]:

��des,��(��)=

tan−1��t,1,��(��)cos(��des,��)+��t,2,��(��)sin(��des,��) ��t,3,��(��)+�� , ��des,��(��)=

sin−1��t,1,��(��)sin(��des,��)−��t,2,��(��)cos(��des,��) ��2 t,1,��(��)+��2 t,2,��(��)+(��t,3,��(��)+��)2 , (17) where ��des,��(rad)isthedesiredconstantyawofthe systemandi.e. ��t,2,��(��) isthesecondcomponentof ut,��(��).Thestatevectoroforientationcontrolissetas xo,��(��)=[����(��),����(��),����(��),����(��),����(��),����(��)]⊤,and therelevantdynamicsfororientation,rows4–6and 10–12of(14),providestheSDCmatrices:

Ao,��(xo,��)= 03×3 T��(��2,��) 03×3 J−1 �� (��2,��)C��(��1,��,��2,��) ,

Bo,��(xo,��)= 03×3 J−1 �� (��2,��)

TheSDREfortheorientationcontrolis:

A⊤ o,��(xo,��)Ko,��(xo,��)+ Ko,��(xo,��)Ao,��(xo,��)− Ko,��(xo,��)Bo,��(xo,��)R−1 o,��(xo,��)B⊤ o,��(xo,��) Ko,��(xo,��)+ Qo,��(xo,��)= 0,

whichgeneratesthesub‐optimalgain Ko,��(xo,��(��))for thecontrollaw:

uo,��(��)=−R−1 o,��(xo,��(��))B⊤ o,��(xo,��(��))Ko,��(xo,��(��))eo,��(��),

where eo,��(��)= xo,��(��)− xo,des,��(��) and xo,des,��(��) includesthedesiredorientationvariables.Notethat ��des,��(��)and��des,��(��)in xo,des,��(��)areupdatedineach time‐stepofthesimulationorexperimentby(17).

Theinputthrustandtorquevectortothesystem aregeneratedbyfourrotatingpropellers:

⎡ ⎢ ⎢

��B,��(��)

��,��(��) ����,��(��) ����,��(��)

(18)

where����(��)∈ℝ4 istheangularvelocityvectorofthe rotorsand

isthemixermatrixofthequadrotor,whichisde ined basedonthe“plus”con igurationoftherotorsinFig. 2,inwhich ��(Ns2/rad2) istheliftconstantorthrust factor,��(m)isthedistancebetweenmotorandCoMof thequadrotor,and��(Nms2/rad2)isthedragconstant.

Remark3 Toregulatethesystem(2)tothedesired condition,theequilibriumpointofthesystemshould bezero.Manysystems,suchasroboticmanipulators, multirotorUAVs,etc.,workundertheeffectofgravity, where f��(0)≠ 0.Forthosesystems,thegravitycompensationshouldbeconsideredasshiftingtheequilibriumtozero[65].HereinSection 3.1,thegravitywillbe compensatedforthroughthecascadecontroldesignof theUAVs,whichperformstranslationcontrolinthe irst layerandorientationcontrolinthesecondone[62].

3.2.WheeledMobileRobot

Consider ��‐thwheeledmobilerobotofamulti‐agentsystemwithdifferentialwheelsworkingon {��,��}planarCartesiancoordinates.Thecoordinates, andglobalandlocalaxes,areshowninFig. 3 Thecenterofmassoftherobotisde inedby {��c,��(��),��c,��(��)}(m),andtherotationoftherobot around �� axis,measuredfrom �� axis(counter‐clockwiseindicatespositivedirection),iscalled ����(��)(rad).Thesystemissubjectedtotwoconstraints showingthattherobotcannotmovealongsidethe axisofthewheelsandthatthewheelsonlyhavea purerollingmotion(rollingwithoutslipping).

The irstauxiliaryrelationisfoundbycombining theconstraintsontheleftandrightwheels, ����(��)= �� 2��(��r,��(��)−��l,��(��)).Thisintegrationgeneratesaholo‐nomicconstraint[66]:

��(��)= �� 2��(��r,��(��)−��l,��(��)). (19)

Figure3. Theschematicviewandaxisdefinitionofa differential‐wheelmobilerobot.

Thenon‐holonomicconstraint,derivedfromthe rollingconditionofthewheels,isobtained[67]:

c,��(��)cos����(��)+̇��c,��(��)sin����(��)= �� 2(��r,��(��)+��l,��(��)). (20)

Equation(19)istheholonomicconstraint ofthesystemandequations(̇�� c,��(��)cos����(��)− c,��(��)sin����(��)=0)and(20)arenon‐holonomic constraints,whichcouldberepresentedas A��(q��(��))q��(��)= 0,where

A��(q��(��))= sin����(��) cos����(��)00 cos����(��)−sin����(��) �� 2 �� 2 , (21) inwhichgeneralizedcoordinatevectorofthe��‐thsys‐temis:

q��(��)=[��c,��(��),��c,��(��),��r,��(��),��l,��(��)]⊤ . (22)

Thedynamicsequationofthemobilerobotisthe commonformofasecond‐orderdifferentialequation:

M��(q��(��))q��(��)+c��(q��(��), q��(��))= E����(��)− A⊤ �� (q��(��))����(��), (23)

where M��(q��(��))∶ℝ4 →ℝ4×4 istheinertiamatrix; theCoriolis‐centrifugalvectoris c��(q��(��), q��(��))∶ ℝ4 ×ℝ4 →ℝ4; E =[02×2, I2×2]⊤ , ����(��)= [��r,��(��),��l,��(��)]⊤ istheinputtorquevectortothe wheels; A��(q��(��))∶ℝ4 →ℝ2×4 isconstraintmatrix (21);and ����(��)=[��1,��(��),��2,��(��)]⊤ isthevectorof theLagrangemultipliers.Thedetailsoftheinertia matrixandCoriolisvectorcanbefoundinRef.[67]. OnewaytoomittingunknownLagrangemultipliers fromEq.(23)isto indthenullspaceof A��(q��(��)):

S��(q��(��))= ⎡ ⎢ ⎢ ⎢ ⎣ �� 2 cos(����(��)) �� 2 cos(����(��)) �� 2 sin(����(��)) �� 2 sin(����(��)) 1 0 0 1 ⎤ ⎥ ⎥ ⎥ ⎦ , andpre‐multiplythetransposeof S��(q��(��))to(23)to obtain[66]:

S⊤ �� (q��(��))M��(q��(��))q��(��)+ S⊤ �� (q��(��))c��(q��(��), q��(��))=����(��). (24)

Theangularvelocitiesofthewheelsarearranged inavector v��(��)=[��r,��(��),��l,��(��)]⊤; q��(��)= S��(q��(��))v��(��)isintroduced;thesecondtimederiva‐tiveofthegeneralizedcoordinatesresultsin: q��(��)= S��(q��(��))v��(��)+ S��(q��(��))v��(��). (25)

Thestate‐vectorofthesystemischosenas x�� = [q⊤ �� (��), v⊤ �� (��)]⊤.Substitutionof q��(��) from(24)into (25)willresultinastate‐spacerepresentationofthe system:

InthecontrolschemeofWMR,thecontrolledout‐putofthesystemisapoint Pw(��),aheadoftheCoMof themobilerobot;��s isthedistancebetweentheCoM oftherobot; Pw(��)(seeFig.3).Thepointisrelatedto thestatevariablesoftheWMRthroughakinematics relation.Tocontrolthispoint,theoutput‐andstate‐dependentRiccatiequation(OSDRE)approachis needed[57].Theoutputofthe��‐thWMRisde inedas y��(��)= ��c,��(��)+��scos����(��) ��c,��(��)+��ssin����(��) , andthe irsttwocomponentsof S��(q��(��))v��(��) resultsin

c,��(��)= �� 2(��r,��(��)+��l,��(��))cos����(��), c,��(��)= �� 2(��r

(��). (27)

Substituting(27)into y��(��),andanothertime derivative y��(��)resultsin:

y��(��)=����(x��(��))v��(��)+����(x��(��)), (28) where ����(x��(��))∶ℝ6 →ℝ2×2 and ����(x��(��))∶ ℝ6 →ℝ2 ����(x��(��)) and ����(x��(��)) areanonlinear matrixandvector,respectively,thathavebeengen‐eratedduringthecomputationofthederivativeof theoutput.Thesymbolicrepresentationofthemcan berevisitedin[67].����(x��(��))and����(x��(��))arekine‐matictransformationsthatchangethedynamicsofthe mobilerobotfroma state toan output representation. Substituting v��(��)fromthelowersetof(26)into(28) provides:

Byde ininganewstate‐vectorfortheoutput dynamics(29), z��(��)=[y⊤ �� (��), y⊤ �� (��)]⊤,onecould ind thestate‐spacerepresentationoftheoutputdynamic:

Theoutput‐andstate‐dependentcoef icient parameterizationofsystem(30)isexpressedas[57]:

where y��(��)† ispseudo‐inverseofthevelocityofthe output y��(��).Finally,thecontrollawissetintheform of:

Thenecessaryconditionsoftheoutput,controlla‐bility,andobservabilityoftheOSDRE,andcondition on y��(��)† toavoidasingularityissue,werereported in[57].

4.Simulations

4.1.Multi‐agentsystemsofUAV

Amulti‐agentsystemof ��=1,089 quadrotor agentsisconsideredforasimulationthatrepresents aregulationcasefromaninitialtoa inalconditionin ��f =20(s).Theagentsmustformasquareshapewhen theyarelaunchedandkeeptheshapeduringtheregu‐lation.Astheyapproachthe inalcondition,thesquare shapeandarrangementoftheagentsgetmoreprecise, andtheerrorinregulationalsoconvergestozero.The pseudocodeofthesquarepatternofagentsforthe simulationcaseof1,089drones.Thefollowingloop willde inethelocalarrangementoftheagentsina squareshapeduringtheregulation,presentedinthe pseudocode: for ��=1,...,��n, for ��=1+(��−1)��n,...,��n +(��−1)��n,

��c,f,�� = −(��+��a)

2 +����a −(��−1)��,

��c,f,�� = −(��+��a)

2 +����a,

��c,f,�� =0, end, end,

wherelengthofsquaresideisdenotedby��=30(m), ��n =33 isnumberofrowsandcolumns,and ��a = �� ��n =0.9091(m). Theleaderisthe irstagentofthesystemand guidesthemulti‐agentsysteminpoint‐to‐pointreg‐ulationfromanarbitrarystarttoanendpoint.The 1,089agentsareinitiallyscatteredrandomlyinsidea 10×10(m)squareattheheightof10(m).Theinitial orientationangleandvelocitiesofthetranslationand orientationstatesoftheagentsarezero.Thethree componentsofthepseudocode(��c,f,��,��c,f,��,��c,f,��)are the irstsetofvector xf,�� ∈ℝ12in(6)forthequadrotor multi‐agentsystem.

Figure4. Thetrajectoriesofthemulti‐agentsystemof 1,089quadrotorUAVs.

Thepositionoftheobstacleis (��o,��o,��o)= (15,0.25,6)(m),withasafetyradiusof0.5forcolli‐sionavoidance.The inalpositioncoordinatesforthe leaderare:

xf,1 = ⎡ ⎢ ⎢ ⎣ ��c,des,1 ��c,des,1 ��c,des,1 09×1

⎣ 20+��c,f,1 ��c,f,1 ��c,f,1 09×1

⎥ ⎥ ⎦ , whichisconstantthoughthevaluefortherestofthe agentsistime‐varying,presentedinEq.(6).Thisisa resultoffollowingtheleader.

Thephysicalcharacteristicsoftheagentsaresim‐ilarinthefollowingway.Thedistancebetweenthe motorandtheCoMofthequadrotoris��=0.225(m); theradiusofthepropelleris ��=0.075(m);thelift constantis ��=2.98×10−6(Ns2rad 2);thedrag constantis��=1.14×10−7(Nms2rad 2);additionally ��xx =4.856×10−3(kgm2),��yy =4.856×10−3(kgm2), and ��zz =8.801×10−3(kgm2) aremomentsof inertiaaround ��,��,�� axes.Themassofthedroneis ��=0.468(kg),theaerodynamicsmatrixis Df = diag(0.25,0.25,0.25)(kg/s),theminimumandmax‐imumrotorvelocitiesarealso ��min,max =496.48, 744.73(rad/s)

Themotionofthemulti‐agentsystemisrepre‐sentedinFig.4.Becausetheagentsareverycloseto eachotheratthebeginning,andthecollisionavoid‐anceschemeintuningincreasesthe Q matrixdrasti‐cally,weseearapiddivergenceatthecommencement ofthesimulation.Thebeginningoftheregulationis likean“explosion”ofmultipleagentsescapingfrom collisionswitheachother.TheCartesian‐coordinate errorsoftheagentsin3Dpositioningareillustrated inFig.5forallagents,followedbyazoomedviewthat showstheleader irstconvergingtowardszero,then thefollowerscatchingupwiththeleader.

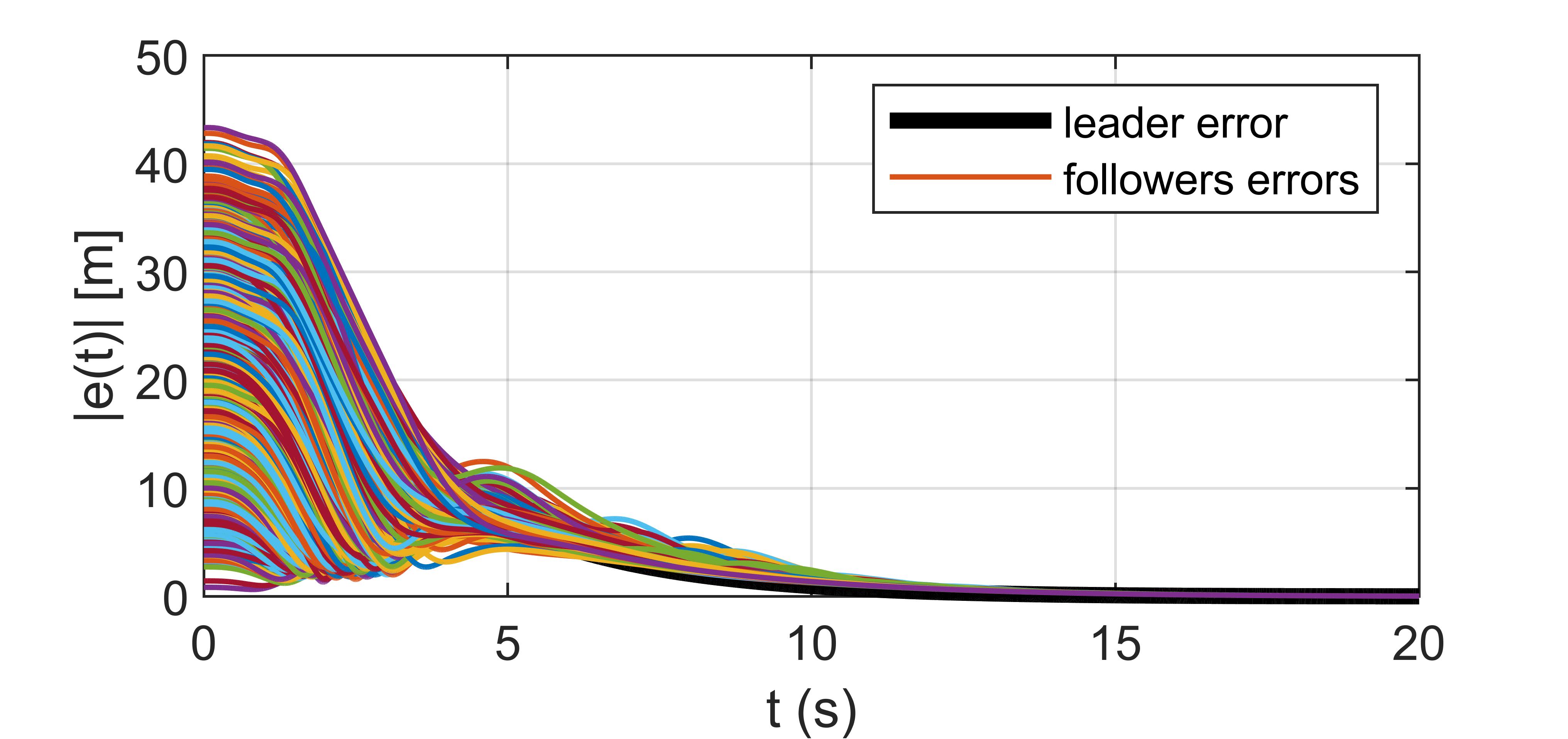
Figure5. Theerrorconvergenceofthemulti‐agent systemof1,089quadrotorUAVs.

Figure6. Thedistancebetweenthedronesandthe obstacleforthemulti‐agentsystemof1,089quadrotor UAVs.

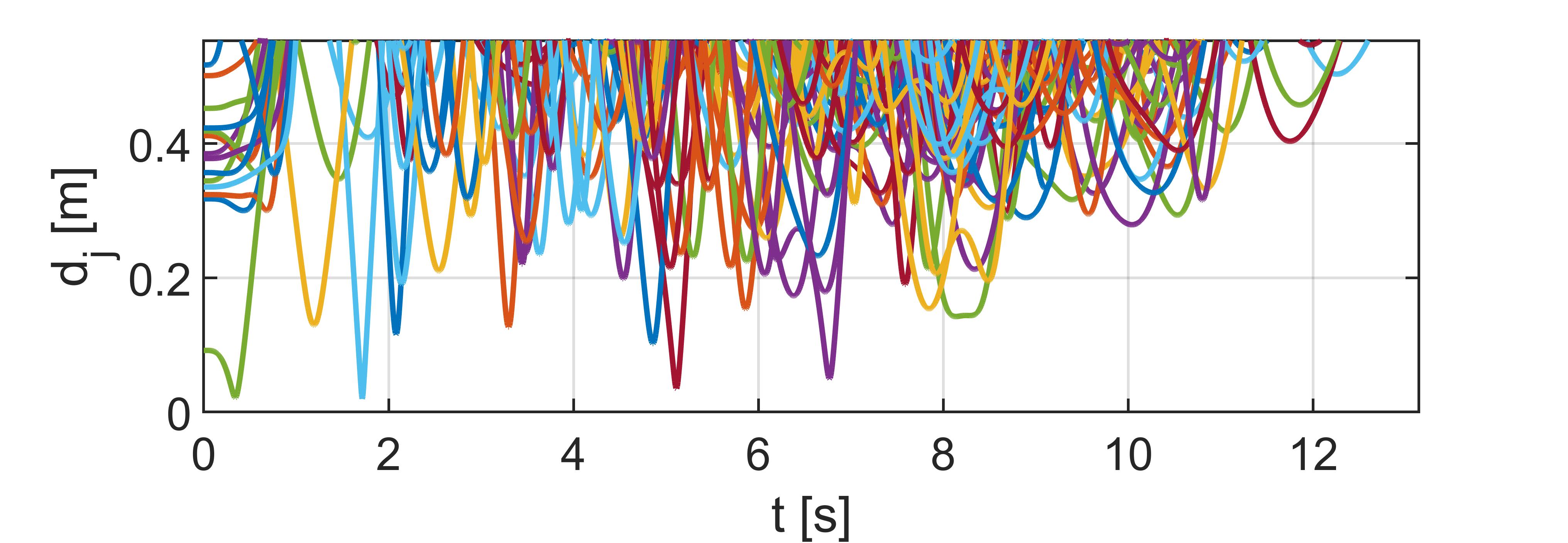
Figure7. Thecollisiondistancebetweenthedronesfor themulti‐agentsystemof1,089quadrotorUAVs.

Figure8. The ��s,��(��) parameterforthemulti‐agent systemof1,089quadrotorUAVs.Samplesareshown theaxesinsteadoftimeasaresultofthemesh presentation.

Theweightingmatricesoftheleaderareselected as:

Theweightingmatricesofthefollowersare:

t,�� = I3×3,

,�� = I3×3, Qt,��(x)=diag(1+��D(x),1+��D(x),1,2,2,5) Qo,�� =diag(21×3, 0.51×3)6×6, where��D(x(��))= 1 ����(x(��)) + 1 ��o,��(x(��)) + 1 ��s,��(x(��)),with ��s,��(x(��))setby(9).

Obstacleavoidancebyembeddinganarti icial potential ieldintotheSDREhasbeenreportedon andanalyzedintheliterature.Ithasbeenstatedthat thismethoddoesnotguaranteeabsoluteobstacle avoidance,thoughitreducesthechanceofimpact signi icantly[52].Figure 6 showsthattheminimum distancebetweensomeagentsandtheobstaclewas 30(cm).Thecollisionavoidancebetweentheagentsis reportedinFig.7.AgroupofdronesinFig.7merged toalmosta30(cm)distance;thosearetheonesatthe beginningofrows,withthepreviousagentslocatedat theendofpreviousrows.Fortherestoftheagents, thecollisionavoidanceterm, ����(��),showsacollision whenitislowerthan 0.48(m).Thereasonforthe collisionbetweentheagentsistheaccumulationof 1,089dronesina10×10(m)attheinitialcondition ofthesimulation.Afterthecommencementofthe simulation,thecollisionavoidanceschemeguidedthe dronesandincreasedthedistancebetweenthemafter 8seconds.

Checkingthecollisionbetweentwoconsecutive agentsdoesnotnecessarilyshowallthecollisions. Otheragentsmightalsohavecollisionsthatare demonstratedinFig.8

Figure9. Thepositionandorientationstatesforthe5th quadrotorUAV.

Figure10. Thelinearandangularvelocitystatesforthe 5thquadrotorUAVofthemulti‐agentsystem.

Contraryto����(��),theparameter��s,��(��)checksthe collisionof ��‐thagentwithallpreviousagents.The behaviorof ��s,��(��) issimilarto ����(��);atthebegin‐ning,thenumberofcollisionsishigher,andmov‐ingtowardsthe inalpattern,thedistancebetween theagentsgetsbigger,startingfrom irsttime‐step andending30,000‐thtime‐steps,discretizedinto20 secondsoftotalsimulationtime(samplesareshown intheaxesinsteadoftimeasaresultofthemesh presentation).Thecollisionoftheagentsisobvious sincetheirarrangementisquiteambitious,leaving only 42(cm) betweentwoagentsinthe inalsquare shape.ItcanbeobservedinFig.7whenthedistance forsomedronesislessthan0.48(m)

Thesimulationof1,089agents,presentedinFig. 4 mightnotrevealthecomplexityofthemulti‐agent systemdynamics,therefore,thedataofthesimula‐tionforthe5thagentispresented.Thepositionand velocitystatesofthe5thdronearepresentedinFigs.9 and10,respectively.Theequationofthemixermatrix (18)presentstheinputangularvelocitiesoftherotors, limitedtothelowerandupperbounds,Fig.11

Figure11. Theangularvelocitiesoftherotorsforthe 5thquadrotorUAV.

4.2.WMR

Agroup ��=45,agentswaschosenforaregu‐lationsimulationover ��f =15(s) withcircular inal arrangementsoftheagents.Thenumberofagents wasselectedsmallerincomparisonwithSection4.1to highlighttheroleofobstacleavoidanceintheresults. Thefollowingalgorithmde inesthearrangementof theagentsinacircularpattern: for ��=1,...,��, ��p =1, ��o =��p, ��c,f,�� =��shift +��pcos (��−1)2�� ��c , ��c,f,�� =��shift +��psin(��−1)2�� ��c , for ��=1,...,��r, if ��> ��(��+1)��c 2 ��o =��o +��p, ��c,f,�� =��shift +��pcos (��−��c −1)2����

p ��c��o , end, end, end, where(��shift,��shift)=(40,20)(m)de inesthecenter ofthecircularpattern;��c =3isthenumberofagents inthe irstcircle; ��r =5 isnumberofrings; ��= ��r(��r+1)��c 2 =45istotalnumberofagents;and��p = 1(m)isthedistancebetweentherings.

Thepositionoftheobstacleissetas (��o,��o) =(25,10)(m)withasafetyradiusof��min =0.5(m). Theagentsarerandomlyscatteredina 10×10(m) squareattheorigin.Theserandomscatteredagents arealmost 40(m) awayfromthedesiredpositionof thepattern.

Table2. Theerrorofthesystemunderdifferent ��s values.

��s(mm) errorleader (mm) error5thfollower(mm)

20 144.3912 911.3158

50 76.4762 345.8130

80 104.3379 388.0787

100

200

300 324.6205 827.9986

400 424.4897 1025.9861

500 524.4070 1223.8401

Thephysicalcharacteristicsofthemobile robotswerechosenasfollows:theradiusofthe wheelsisdenotedby ��=0.08(m);thelengthof thewheels’axisby ��=0.145(m);massofbaseis ��b =6(kg);massofwheelsis ��w =0.32(kg); momentofinertiacomponentsare ��zz,b = 0.06363,��zz,w =0.00006,��yy,w =0.00081(kgm2); andthedistanceofthelook‐aheadcontroltermis selectedas��s =0.1(m).

Theweightingmatricesoftheleaderareset:

start points end points obstacle leader trajectory followers trajectories

051015202530354045 X[m]

Figure12. Thetrajectoriesoftheleaderand45follower agents.

error followers errors

Figure13. Theerrorsoftheleaderand45follower agents.

Theweightingmatricesofthefollowersare selectedas:

Thetrajectoriesoftheleaderandfolloweragents areillustratedinFig.12.Theleaderandthefollowers avoidedtheobstacle,whicharerepresentedinthe trajectories.Theerrorconvergenceofthemulti‐agent systemispresentedinFig. 13.Theobstacleandcol‐lisionavoidancetermsareplottedinFigs.14and15, respectively.Theinputsignalsandstatevariablesof oneagentarepresentedinFigs. 16 and 17,respec‐tively.Theerroroftheleaderand5thfollowerisfound at122.6741(mm)and411.7172(mm)respectively.It isimportanttonoticethattheerrorisafunction ofthelook‐aheadcontrolparameterwhichwasset ��s =0.1(m).Thismeansthattherobotisregulating thelook‐aheadpointtowardsthedesiredcondition, nottheCoMoftherobot.If ��s isreduced,theerror changes.Theovershootandthebehavioroftheregu‐lationalsochangeasthelook‐aheadparametervaries. Acomparativetableispresentedtoclarifythiseffect inTable 2.Anothersimulationwasdonefor 1,050 WMRstoshowthecapacityofthemethodforalarge‐populationmulti‐agentsystem.Forthesakeofbrevity, onlythemigrationofthesystemsfrominitialto inal condition,followingtheleaderandthepattern,isillus‐tratedinFig.18.

Figure14. Theobstacleavoidanceperformanceofthe leader/followersystemofmobilerobots.

4.3.TuningofWeightingMatrices

Therearesomegeneralrulesfortheselectionof weightingmatricesoftheSDRE. Q penalizesthestates and R penalizestheinputs.Sincetheinverseof R isthe irsttermofthecontrollaw,adecreasein R increasestheinputsignal,whichresultsinmore energyconsumption.Increasein Q alsoincreases theprecisionofthestateregulation.Inthiswork, theweightingmatrixofstateshasobstacle/collision avoidancetermsformulti‐agentcontroldesign.The de initionoftheweightingmatricesfortheleaderand followersmustbedifferent.Iftheleaderistoofast, thefollowersmightnotfollowtheleaderwithproper accuracy.

Figure15. Thecollisionavoidanceperformanceofthe leader/followersystemofmobilerobots.

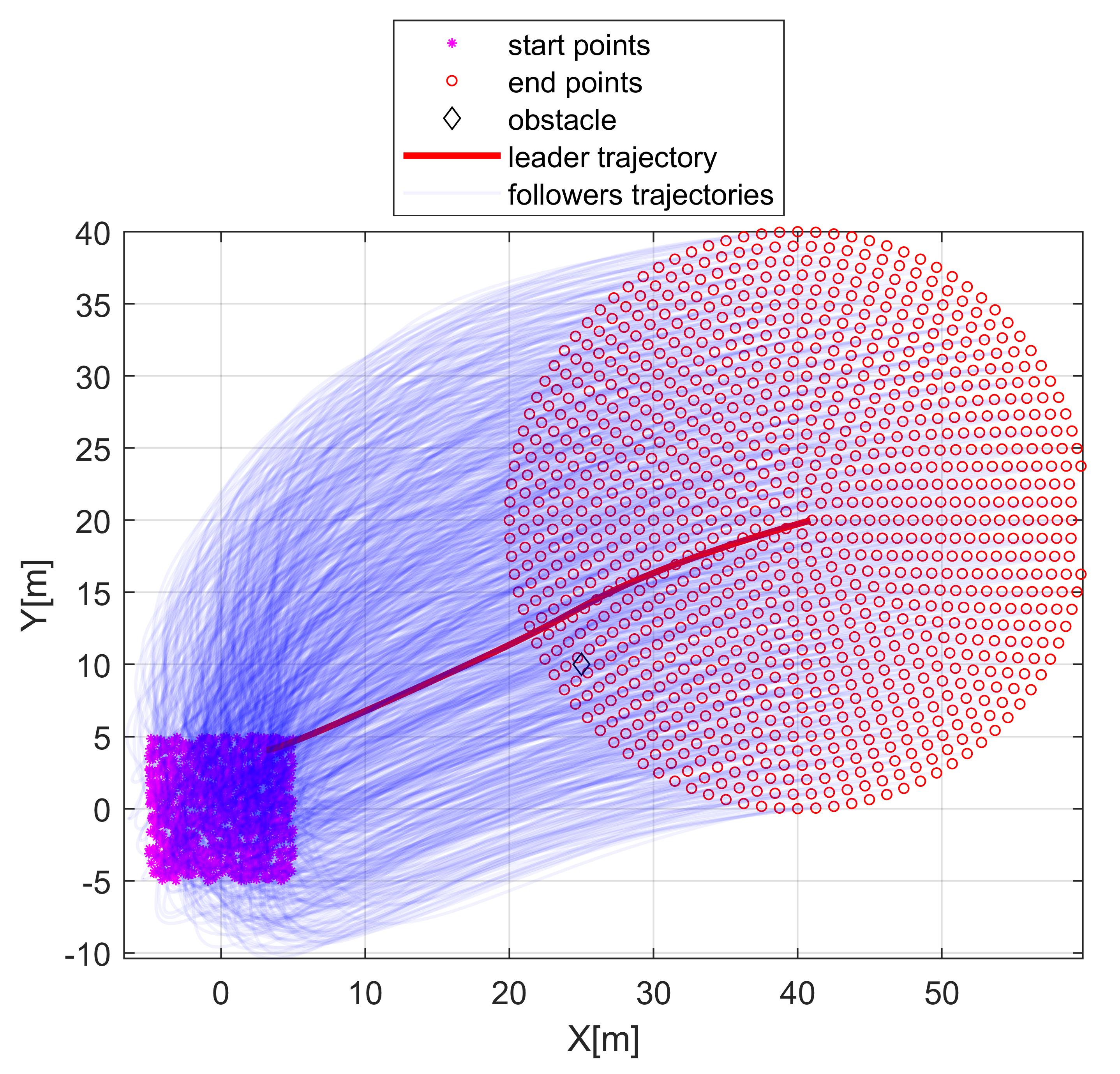
Themigrationof1,050mobilerobotsin leader‐followerformation.

5.Conclusion

Figure16. Theinputsignalsofthewheelsforoneofthe agents.

Figure17. Thestateinformationforoneoftheagents.

Hence,thediagonalcomponentsof Q relativeto thepositioncoordinatesoftheleaderaresmallerthan theonesforthefollowersforbothsimulationsofthe UAVsandWMRs.Anotherimportantpointfortun‐ingtherobotsisthecontrastbetweentheweighting matrices’valueandthedistanceterms!Iflargevalues areselectedfor Q,thechangesduetodistanceterms vanish,andcollision/obstacleavoidancetermsarenot effective.Thesepointswereconsideredinthetuning ofthematricesinthesimulationsections.Considering theaforementionedpoint,itmustbesaidthatseveral trialsanderrorsareneededtotunethecontroller.

ThisworkpresentsanSDREcontroldesign(with‐outaugmentationofothertechniques)forthefor‐mationregulationofamulti‐agentsystemofrobotic systemsthattakesintoaccountthecomplexdynam‐icsoftheagents.Thecommandtothemulti‐agent systemisgiventotheleader,andthefollowerspur‐suetheleaderinaccordancewiththeprede inedpat‐ternofthemulti‐agentsystem.Obstacleandcollision avoidanceamongtheagentswasdesignedthrough themodi icationoftheweightingmatricesofstates andthearti icialpotential ieldmethod.Theappli‐cationoftheproposedmethodwasdevotedtothe controlofunmannedmulti‐coptersystemsanddif‐ferentialwheeledmobilerobots.Ahighlypopulated multi‐agentsystemof1,089agentswassimulatedfor theUAV,andanothersimulationwaspresentedfor theWMRswith45,andthen1,050agentswhichwere successfullyregulatedinthecontroltask,preserving theexpectedformationshapes.

Codeordataavailability

TheMATLABcodesofthesimulationsofthispaper willbepubliclyavailableontheMATLABCentral,File Exchangepageofthecorrespondingauthor(link).

AUTHOR SaeedRafeeNekoo∗ –UniversidaddeSevilla,Spain, e‐mail:saerafee@yahoo.com,ORCID:0003‐1396‐5082.

∗Correspondingauthor

Figure18.

References

[1] G.Beni,“Theconceptofcellularroboticsystem”. Proceedings1988IEEEInternationalSymposium onIntelligentControl,1988,pp.57–58.

[2] V.Genovese,P.Dario,R.Magni,andL.Odetti,“Self organizingbehaviorandswarmintelligencein apackofmobileminiaturerobotsinsearchof pollutants”. ProceedingsoftheIEEE/RSJInternationalConferenceonIntelligentRobotsandSystems,vol.3,1992,pp.1575–1582.

[3] N.Mitsumoto,T.Fukuda,K.Shimojima,and A.Ogawa,“Microautonomousroboticsystem andbiologicallyinspiredimmuneswarmstrat‐egyasamultiagentroboticsystem”. Proceedingsof1995IEEEInternationalConferenceon RoboticsandAutomation,vol.2,1995,pp.2187–2192.

[4] T.Ueyama,T.Fukuda,andF.Arai,“Structure con igurationusinggeneticalgorithmforcellu‐larroboticsystem”. ProceedingsoftheIEEE/RSJ InternationalConferenceonIntelligentRobots andSystems,vol.3,1992,pp.1542–1549.

[5] G.S.Chirikjian,“Kinematicsofametamorphic roboticsystem”. Proceedingsofthe1994IEEE internationalconferenceonroboticsandautomation,1994,pp.449–455.

[6] G.BeniandP.Liang,“Patternrecon iguration inswarms‐convergenceofadistributedasyn‐chronousandboundediterativealgorithm”, IEEE TransactionsonRoboticsandAutomation,vol.12, no.3,1996,pp.485–490.

[7] C.R.KubeandE.Bonabeau,“Cooperative transportbyantsandrobots”, Roboticsand AutonomousSystems,vol.30,no.1‐2,2000,pp. 85–101.

[8] M.J.Krieger,J.‐B.Billeter,andL.Keller,“Ant‐liketaskallocationandrecruitmentincoopera‐tiverobots”, Nature,vol.406,no.6799,2000,pp. 992–995.

[9] L.Yang,J.Yu,S.Yang,B.Wang,B.J.Nelson,and L.Zhang,“Asurveyonswarmmicrorobotics”, IEEETransactionsonRobotics,2021.

[10] L.YangandL.Zhang,“Motioncontrolinmag‐neticmicrorobotics:Fromindividualandmulti‐plerobotstoswarms”, AnnualReviewofControl, Robotics,andAutonomousSystems,vol.4,2021, pp.509–534.

[11] Y.Fu,H.Yu,X.Zhang,P.Malgaretti,V.Kishore, andW.Wang,“Microscopicswarms:Fromactive matterphysicstobiomedicalandenvironmen‐talapplications”, Micromachines,vol.13,no.2, 2022,295.

[12] A.R.Cheraghi,S.Shahzad,andK.Graf i,“Past, present,andfutureofswarmrobotics”. ProceedingsofSAIIntelligentSystemsConference,2021, pp.190–233.

[13] G.A.Cardona,J.Ramirez‐Rugeles,E.Mojica‐Nava,andJ.M.Calderon,“Visualvictimdetec‐tionandquadrotor‐swarmcoordinationcontrol insearchandrescueenvironment”, International JournalofElectricalandComputerEngineering, vol.11,no.3,2021,2079.

[14] G.Kumar,A.Anwar,A.Dikshit,A.Poddar,U.Soni, andW.K.Song,“Obstacleavoidanceforaswarm ofunmannedaerialvehiclesoperatingonpar‐ticleswarmoptimization:Aswarmintelligence approachforsearchandrescuemissions”, JournaloftheBrazilianSocietyofMechanicalSciences andEngineering,vol.44,no.2,2022,pp.1–18.

[15] R.KrzysiakandS.Butail,“Information‐based controlofrobotsinsearch‐and‐rescuemissions withhumanpriorknowledge”, IEEETransactions onHuman-MachineSystems,vol.52,no.1,2021, pp.52–63.

[16] H.Suresha,D.Sumithra,J.Renuka,B.Deepika, andN.Meghana,“Applicationofswarmrobotics systemstomarineenvironmentalmonitoring”, InternationalConferenceonDataScience, MachineLearning,andApplications,2022,pp. 1075–1083.

[17] C.Carbone,D.Albani,F.Magistri,D.Ognibene, C.Stachniss,G.Kootstra,D.Nardi,andV.Trianni, “Monitoringandmappingofcrop ields withUAVswarmsbasedoninformation gain”. InternationalSymposiumDistributed AutonomousRoboticSystems,2021,pp.306–319.

[18] Y.LiuandK.M.Passino,“Swarmintelligence: Literatureoverview”, DepartmentofElectrical Engineering,TheOhioStateUniversity,2000.

[19] M.H.KorayemandS.R.Nekoo,“Controller designofcooperativemanipulatorsusingstate‐dependentRiccatiequation”, Robotica,vol.36, no.4,2018,pp.484–515.

[20] L.Yan,T.Stouraitis,andS.Vijayakumar,“Decen‐tralizedability‐awareadaptivecontrolformulti‐robotcollaborativemanipulation”, IEEERobotics andAutomationLetters,vol.6,no.2,2021,pp. 2311–2318.

[21] J.Hu,P.Bhowmick,I.Jang,F.Arvin,andA.Lan‐zon,“Adecentralizedclusterformationcontain‐mentframeworkformultirobotsystems”, IEEE TransactionsonRobotics,vol.37,no.6,2021,pp. 1936–1955.

[22] B.GeranmehrandE.Khanmirza,“Optimalcon‐sensuscontrolofmulti‐agentsystemsbasedon thestate‐dependentRiccatiequation”, ProceedingsoftheInstitutionofMechanicalEngineers, PartC:JournalofMechanicalEngineeringScience,2022,09544062221091526.

[23] Z.A.AliandH.Zhangang,“Multi‐unmanned aerialvehicleswarmformationcontrolusing hybridstrategy”, TransactionsoftheInstituteof MeasurementandControl,vol.43,no.12,2021, pp.2689–2701.

[24] S.P.HouandC.C.Cheah,“Multiplicativepoten‐tialenergyfunctionforswarmcontrol”. 2009 IEEE/RSJInternationalConferenceonIntelligent RobotsandSystems,2009,pp.4363–4368.

[25] J.Cheng,W.Cheng,andR.Nagpal,“Robustand self‐repairingformationcontrolforswarmsof mobileagents”. AAAI,vol.5,2005.

[26] S.P.Hou,C.‐C.Cheah,andJ.‐J.E.Slotine,“Dynamic regionfollowingformationcontrolforaswarm ofrobots”. 2009IEEEInternationalConferenceon RoboticsandAutomation,2009,pp.1929–1934.

[27] J.A.Preiss,W.Honig,G.S.Sukhatme,andN.Aya‐nian,“Crazyswarm:Alargenano‐quadcopter swarm”. 2017IEEEInternationalConferenceon RoboticsandAutomation(ICRA),2017,pp.3299–3304.

[28] E.Teruel,R.Aragues,andG.López‐Nicolás,“A distributedrobotswarmcontrolfordynamic regioncoverage”, RoboticsandAutonomousSystems,vol.119,2019,pp.51–63.

[29] G.Raja,K.Kottursamy,A.Theetharappan,K.Cen‐giz,A.Ganapathisubramaniyan,R.Kharel,and K.Yu,“Dynamicpolygongenerationfor lexible patternformationinlarge‐scaleUAVswarmnet‐works”. 2020IEEEGlobecomWorkshops(GC Wkshps,2020,pp.1–6.

[30] S.S.Ge,C.‐H.Fua,andW.‐M.Liew,“Swarm formationsusingthegeneralformationpoten‐tialfunction”. IEEEConferenceonRobotics, AutomationandMechatronics,2004.,vol.2,2004, pp.655–660.

[31] D.Grossman,I.Aranson,andE.B.Jacob,“Emer‐genceofagentswarmmigrationandvortexfor‐mationthroughinelasticcollisions”, NewJournal ofPhysics,vol.10,no.2,2008,023036.

[32] Z.Yang,Q.Zhang,andZ.Chen,“Formationcon‐trolofmulti‐agentsystemswithregioncon‐straint”, Complexity,vol.2019,2019.

[33] J.WangandM.Xin,“Integratedoptimalfor‐mationcontrolofmultipleunmannedaerial vehicles”, IEEETransactionsonControlSystems Technology,vol.21,no.5,2012,pp.1731–1744.

[34] S.A.Kumar,J.Vanualailai,B.Sharma,and A.Prasad,“Velocitycontrollersforaswarmof unmannedaerialvehicles”, JournalofIndustrial InformationIntegration,vol.22,2021,100198.

[35] B.S.ParkandS.J.Yoo,“Anerrortransforma‐tionapproachforconnectivity‐preservingand collision‐avoidingformationtrackingofnet‐workeduncertainunderactuatedsurfaceves‐sels”, IEEETransactionsonCybernetics,vol.49, no.8,2018,pp.2955–2966.

[36] B.S.ParkandS.J.Yoo,“Connectivity‐maintaining andcollision‐avoidingperformancefunction approachforrobustleader–followerformation controlofmultipleuncertainunderactuated surfacevessels”, Automatica,vol.127,2021, 109501.

[37] R.BabazadehandR.Selmic,“Distance‐based multiagentformationcontrolwithenergy constraintsusingSDRE”, IEEETransactionson AerospaceandElectronicSystems,vol.56,no.1, 2019,pp.41–56.

[38] M.DavoodiandJ.M.Velni,“Heterogeneity‐aware graphpartitioningfordistributeddeploymentof multiagentsystems”, IEEETransactionsonCybernetics,vol.52,no.4,2022,pp.2578–2588.

[39] S.R.Nekoo,J.Yao,A.Suarez,R.Tapia,and A.Ollero,“Leader‐followerformationcontrolof alarge‐scaleswarmofsatellitesystemusingthe state‐dependentRiccatiequation:Orbit‐to‐orbit andin‐same‐orbitregulation”. 2023IEEE/RSJ InternationalConferenceonIntelligentRobots andSystems(IROS),2023,pp.10700–10707.

[40] H.Rouzegar,A.Khosravi,andP.Sarhadi,“Space‐craftformation lyingcontrolunderorbitalper‐turbationsbystate‐dependentRiccatiequation methodinthepresenceofon–offactuators”, ProceedingsoftheInstitutionofMechanicalEngineers,PartG:JournalofAerospaceEngineering, vol.233,no.8,2019,pp.2853–2867.

[41] R.BabazadehandR.Selmic,“Anoptimal displacement‐basedleader‐followerformation controlformulti‐agentsystemswith energyconsumptionconstraints”. 201826th MediterraneanConferenceonControland Automation(MED),2018,pp.179–184.

[42] M.Tannous,G.Franzini,andM.Innocenti,“State‐dependentRiccatiequationcontrolforspace‐craftformation lyinginthecircularrestricted three‐bodyproblem”. 2018AstrodynamicsConference;AmericanAstronauticalSociety:Springield,VA,USA,2018.

[43] G.Rinaldo,E.Ra ikova,andM.Ra ikov,“Con‐trolofmultiplemobilerobotsindynamicfor‐mations”. InternationalSymposiumonDynamic ProblemsofMechanics,2017,pp.359–369.

[44] S.KumbasarandO.Tekinalp,“Fuzzylogicguid‐anceofformation light”. 2015InternationalConferenceonUnmannedAircraftSystems(ICUAS), 2015,pp.167–175.

[45] L.FelicettiandG.B.Palmerini,“Attitudecoordi‐nationstrategiesinsatelliteconstellationsand formation lying”. 2015IEEEAerospaceConference,2015,pp.1–13.

[46] J.‐I.Park,H.‐E.Park,S.‐Y.Park,andK.‐H.Choi, “Hardware‐in‐the‐loopsimulationsofgps‐based navigationandcontrolforsatelliteformation ly‐ing”, AdvancesinSpaceResearch,vol.46,no.11, 2010,pp.1451–1465.

[47] D.StansberyandJ.Cloutier,“Nonlinearcontrolof satelliteformation light”. AIAAGuidance,Navigation,andControlConferenceandExhibit,2000, 4436.

[48] A.A.KabanovandV.A.Kramar,“Cooperative controlofunderwatermanipulatorsbasedon

theSDREmethod”. 2021InternationalRussian AutomationConference(RusAutoCon),2021,pp. 515–520.

[49] N.Nasiri,A.Fakharian,andM.B.Menhaj, “Anuncertainoptimalfactorizationofcoop‐erativemanipulatorsforrobustoptimalcon‐trolschemes”. 202230thInternationalConferenceonElectricalEngineering(ICEE),2022, pp.582–586.

[50] X.Lin,X.Shi,andS.Li,“Optimalcooperative controlforformation lyingspacecraftwithcolli‐sionavoidance”, ScienceProgress,vol.103,no.1, 2020,0036850419884432.

[51] R.BabaieandA.F.Ehyaie,“Robustoptimal motionplanningapproachtocooperativegrasp‐ingandtransportingusingmultipleUAVsbased onSDRE”, TransactionsoftheInstituteofMeasurementandControl,vol.39,no.9,2017,pp. 1391–1408.

[52] M.H.KorayemandS.R.Nekoo,“TheSDREcon‐trolofmobilebasecooperativemanipulators: Collisionfreepathplanningandmovingobstacle avoidance”, RoboticsandAutonomousSystems, vol.86,2016,pp.86–105.

[53] D.Li,S.S.Ge,W.He,G.Ma,andL.Xie,“Multilayer formationcontrolofmulti‐agentsystems”, Automatica,vol.109,2019,108558.

[54] J.Wu,Q.Deng,T.Han,andH.‐C.Yan,“Bipar‐titeoutputregulationforsingularheteroge‐neousmulti‐agentsystemsonsignedgraph”, AsianJournalofControl,vol.24,no.5,2022, pp.2452–2460.

[55] Z.Pan,Z.Sun,H.Deng,andD.Li,“Amultilayer graphformultiagentformationandtrajectory trackingcontrolbasedonMPCalgorithm”, IEEE TransactionsonCybernetics,vol.52,no.12,2021, pp.13586–13597.

[56] T.Çimen,“State‐dependentRiccatiequation (SDRE)control:Asurvey”, IFACProceedings Volumes,vol.41,no.2,2008,pp.3761–3775.

[57] S.R.Nekoo,“Output‐andstate‐dependentRic‐catiequation:Anoutputfeedbackcontroller design”, AerospaceScienceandTechnology,vol. 126,2022,107649.

[58] S.S.MohammadiandH.Khaloozadeh,“Opti‐malmotionplanningofunmannedgroundvehi‐cleusingSDREcontrollerinthepresenceof obstacles”. 20164thInternationalConference

onControl,Instrumentation,andAutomation (ICCIA),2016,pp.167–171.

[59] M.AsgariandH.N.Foghahayee,“Statedepen‐dentRiccatiequation(SDRE)controllerdesign formovingobstacleavoidanceinmobilerobot”, SNAppliedSciences,vol.2,no.11,2020,pp.1–29.

[60] S.R.NekooandB.Geranmehr,“Nonlinear observer‐basedoptimalcontrolusingthe state‐dependentRiccatiequationforaclassof non‐af inecontrolsystems”, JournalofControl EngineeringandAppliedInformatics,vol.16,no. 2,2014,pp.5–13.

[61] S.Nekoo,J.Acosta,A.Gomez‐Tamm,and A.Ollero,“Optimizedthrustallocationof variable‐pitchpropellersquadrotorcontrol: Acomparativestudyon lipmaneuver”. 2019WorkshoponResearch,Educationand DevelopmentofUnmannedAerialSystems(RED UAS),2019,pp.86–95.

[62] S.R.Nekoo,J.Á.Acosta,andA.Ollero, “Quaternion‐basedstate‐dependentdifferential Riccatiequationforquadrotordrones: Regulationcontrolprobleminaerobatic light”, Robotica,2022,pp.1–16.

[63] S.R.Nekoo,J.Á.Acosta,andA.Ollero,“Fully coupledsix‐dofnonlinearsuboptimalcontrolof aquadrotor:Applicationtovariable‐pitchrotor design”. Robot2019:FourthIberianRobotics Conference:AdvancesinRobotics,Volume2,2020, pp.72–83.

[64] Z.Zuo,“Trajectorytrackingcontroldesignwith command‐ ilteredcompensationforaquadro‐tor”, IETControlTheory&Applications,vol.4,no. 11,2010,pp.2343–2355.

[65] S.R.Nekoo,J.Á.Acosta,andA.Ollero,“Gravity compensationandoptimalcontrolofactuated multibodysystemdynamics”, IETControlTheory &Applications,vol.16,no.1,2022,pp.79–93.

[66] Y.YamamotoandX.Yun,“Coordinatinglocomo‐tionandmanipulationofamobilemanipulator”. Proceedingsofthe31stIEEEConferenceonDecisionandControl,1992,pp.2643–2648.

[67] M.Korayem,S.Nekoo,andA.Korayem,“Finite timeSDREcontroldesignformobilerobotswith differentialwheels”, JournalofMechanicalScienceandTechnology,vol.30,no.9,2016,pp. 4353–4361.

Submitted:27th April2024;accepted:1st November2024

PaulinaPuchalska,KacperKrzemiński,MaksymilianLis,RafałScherer,PawełDrozda,KajetanKomar‑Komarowski, KonradSzałapak,AndrzejSobecki,TomaszZymkowski,JulianSzymański

DOI:10.14313/jamris‐2025‐004

Abstract:

Thisstudyaimstousethedecision‐makingprocess tocategorizelegaldocumentsbyidentifyingkeywords characterizingeachlegaldomainclass.Thestudyuti‐lizestheKohonenSelf‐OrganizingMapmethodandthe GlobalVectorsforWordRepresentation(GloVe)model tocreateanefficientdocumentclassificationsystem. Asaresult,asatisfactoryclassificationaccuracyof 71.69%wasachieved.Thearticlealsodiscussesalterna‐tiveapproachesimplementedtoimproveclassification accuracy,suchastheuseofNamedEntityRecognizer (NER)toolsandtheRoBERTamodel,alongwithacom‐parisonoftheseapproaches’effectiveness.Challenges relatedtotheunevendistributionofcategoriesinthe datasetarealsomentioned,andpotentialdirectionsfor furtherresearchtoenhancetheclassificationresultsof legaldocumentsarepresented.

Keywords: Documentclassification,RoBERTa,NLP, GloVe,NER,SOM

1.Introduction

Documentclassi icationholdssigni icantrele‐vanceacrossvariousdomains,including inance, law,medicine,publicadministrationandcomputer science.Itstandsasafundamentalchallengewithin naturallanguageprocessing(NLP), indingwide applicationintoday’sinformation‐drivenenviron‐ment.Inthisbroadcontext,wherepreciseinforma‐tioncategorizationiscrucial,thisarticlefocuseson theclassi icationoflegaldocumentsintoappropriate categoriesbasedonananalysisofthemostfrequently usedwords.Forthisstudy,adatasetofmorethan 2,700legaldocumentswasused,dividedintonine distinct ields:civillaw,administrativelaw,pharma‐ceuticallaw,laborlaw,medicallaw,criminallaw, internationallaw,taxlawandconstitutionallaw.This studyaimstocreateaneffectivesystemforautomated classi ication,enablingthepreciseallocationofdoc‐umentstotheirrespectivelegalcategories.Addition‐ally,itseekstovisualizethedataset,highlightingthe areasresponsibleforaspeci icclasstogetherwith theirde iningcharacteristics.

Thestructureofthearticlecomprisesanoverview ofexistingsolutionsaddressingthechallengesofdoc‐umentclassi ication,visualization,andfeatureextrac‐tion,alongwithananalysisofthedifferentapproaches andtoolsusedinthis ield.

Thenextsectiondetailsthechosenapproachto solvingtheproblem,togetherwithacharacterization ofthedataset.Followingthis,resultsfromtheimple‐mentedsolutionarepresented,alongsidedescriptions ofadditionalexperimentsaimedatimprovingthe outcomes.Thearticleconcludeswithadiscussionof achievementstodateandoutlinesplansforfuture worktofurtherenhancetheresults.

2.Classification,VisualizationandFeature ExtractionofTextDocuments

Inthissection,wewilldiscussthemostpopu‐larapproachestonaturallanguageclassi icationand analysisandpresentchallengesassociatedwiththem, alongwiththeproposedsolutions.

2.1.Classification

Oneofthemostcommonlyusedalgorithmsfortext classi icationisNaiveBayes,basedontheassumption ofconditionalindependenceoffeaturesforagiven class.Insimplerterms,itassumesthattheproba‐bilityoftheoccurrenceofeachwordisindependent oftheoccurrenceofotherwordsinthesamedocu‐ment,makingthealgorithmfastandef icientinclas‐si icationtasks.However,theauthorsof[10]point outaseriousproblemintheparameterestimation thatleadstoweakerperformancecomparedtoother appliedtextclassi icationalgorithms.Toaddressthis issue,theauthorsproposetheuseoftwoempirical heuristics:textnormalizationandfeatureweighting, whichisparticularlyeffectivewithasmallnumberof trainingdata.Asimilarproblemisaddressedbythe authorsofthepublication NaiveBayesforTextClassiicationwithUnbalancedClasses [6],whoidentifythe classi ier’sdrawbackwhenworkingwithimbalanced datasets.Asasolution,theydemonstratethatnor‐malizingthewordvectorineachclasssigni icantly improvestheclassi ier’sperformance.

Anotherequallypopularmethodislogisticregres‐sion,whichmodelstheprobabilityofadocument belongingtoacertainclassusingalogisticfunction. Thoughitisaneffectiveclassi icationmethod,the authorsof[21]pointoutlimitationsrelatedtohigh‐dimensionaldata.Typically,asparsitythresholdis applied,whichremovessparsefeatures,retainingonly asubsetoftheoriginalones.

However,thismethodalsohaslimitations,asthere isapossibilitythatsomeimportantfeatureswillbe cutoff,introducingbiasintoanycomparisons.Inthe aforementionedpublication[21],tosolvethisissue, theauthorsproposetheuseofregularizedlogistic regression,whichachievessigni icantlybetterresults thanpurelogisticregression.

Analgorithmthatachievesgreateref iciencywith high‐dimensionaldatathanthetwopreviouslymen‐tionedmethodsisadecisiontree.Thismethodmakes hierarchicaldecisionsbasedontheanalysisoftext features,includingdividingthedatasetintosub‐sets,reducingthedimensionalityofthedata,and makingpatternrecognitioneasier.However,despite theirsimplicityandeffectiveness,decisiontreesface challengesrelatedtoover ittingandtheirlackof considerationofdependenciesbetweenvariables.To addresstheseproblems,theauthorsof[12]apply techniquessuchaspruningandpost‐pruning,and presentmoreadvancedalgorithms,suchasIntelligent DecisionTrees(IDA)andC4.5[12],whichachievebet‐terresultsinthetaskofautomatictextclassi ication.

SupportVectorMachines(SVM),appliedto determinetheoptimalhyperplanethatmaximally separatesdifferenttextcategories,havebeenfound tosurpasstheef iciencyoftheaforementioned algorithms.Accordingtotheauthorsof[18],SVM standoutduetotheirabilitytolearnindependently ofdatadimensionality,considerallfeatureswithout priorselection,andhandlesparsedocumentvectors. Despitetheirhigheffectiveness,SVMmayencounter challengesrelatedtoimbalancedtrainingdata,which, accordingtotheauthorsof[16],canbeaddressed throughadvancedthresholdingstrategies.

Inthe ieldofautomatictextclassi ication,more advancedmethodssuchasRecurrentNeuralNet‐works(RNN)arealsoemployed.Thesemethods involveprocessingsequentialinformationintextsby recursivelyupdatingtheirhiddenstatesbasedon previouswords,enablingthemtocapturecontextual dependenciesandinferdocumentclasses[19].How‐ever,evensuchadvancedmethodscannotsolveevery probleminthis ield.Despitetheirabilitytocapture temporalandsequentialdependenciesintext,RNNs faceachallengeknownasthevanishinggradient, whichlimitstheeffectivenessofmodelinglong‐term dependencies.

ComparedtoRNN,LongShort‐TermMemory (LSTM)modelsstandoutfortheireffectiveprocess‐ingoftimesequencesusingmemorymodules,which enablesthemodelingoflong‐termdependenciesin sequentialdata.Despitethisimprovement,LSTMalso facetheproblemofthevanishinggradient,albeittoa lesserextentthantheirpredecessor.However,thanks totheuseofspecialgates,suchastheinputgate, forgetgate,andoutputgate,LSTMcanbetterhan‐dlelong‐termdependenciesandfeatureextraction betweenwordsandsequencesthanthetraditional RNNapproach[22].

Inresponsetothischallenge,theauthorsof[9] proposeanewmodel,SATT‐LSTM,whichcombines theself‐attentionmechanismwithtraditionalLSTMto improvehandlingoflongsequencesintext.

Theself‐attentionmechanismisaninnovative techniquethatenablesthemodeltoassignvarying weightstoindividualelementsinasequencebased ontheircontextualimportance.Itservesasacen‐tralelementinTransformermodels.Thankstothis mechanism,Transformermodelscaneffectivelycon‐siderlong‐termdependenciesandglobalcontextsin text,offeringasigni icantadvantageovertraditional architecturessuchasRNNorLSTM[7].Thispositions Transformermodelsasoneofthemosteffectivemeth‐odsinautomatictextclassi ication.

Themostpopularandadvancedmethodsfortext processingaremodelsbasedontheTransformer architecture,suchasBERTandGPT.TheBidirectional EncoderRepresentationsfromTransformers(BERT) modeldistinguishesitselfwithitsabilitytoanalyze contextualinformationbothprecedingandfollowing agivenwordinasentence.Thiscapability,knownas bidirectionalself‐attention,empowersthemodelto capturesemanticrelationshipswithinthetext[3,13].

Conversely,theGenerativePre‐trainedTrans former(GPT)model,alsobasedontheTransformer architecture,operatesasagenerativemodel,allow‐ingittoproducenewsequencesoftext.Itsprimary strengthliesinitsabilitytopredictsubsequentwords inasentencebasedoncontextualcues,thusfacil‐itatingthegenerationofcoherentandmeaningful texts[20].Bothofthesemodelsrepresentsigni i‐cantadvancementsinnaturallanguageprocessing, enablingmorepreciseparsingandgenerationoftexts acrossvariouscontexts.

2.2.FeatureExtraction

Oneoftheearlyandstraightforwardmethodsfor textfeatureextractionistheBag‐of‐Words(BoW) approach.Itrepresentstextualdocumentsbytreating eachdocumentasasetofwords,whiledisregarding informationaboutgrammarorwordorder[18].Due toitssimplicityandlackofinformationaboutsen‐tencestructureandwordorder,BoWismostcom‐monlyappliedtosmall,uncomplicatedtexts.

AlongsideBoW,anotherapproachistheapplica‐tionofTermFrequency‐InverseDocumentFrequency (TF‐IDF).Inthismethod,weightsareassignedto wordsbasedontheirfrequencyinagivendocu‐mentandtheirrelevancetotheentiretextcorpus [4].Higherweightvaluesindicategreatersigni icance foraword.AlthoughTF‐IDFissimpleandeffective, itresultsinfeaturevectorswithahighnumberof dimensions,potentiallyincreasingtheriskofover it‐tingtheclassi icationmodel.Tomitigatethisissue, variousdimensionalityreductiontechniquesareoften employed.

AmongthesetechniquesareLatentSemanticAnal‐ysis(LSA)andLinearDiscriminantAnalysis(LDA), whicharecommonlyemployedinnaturallanguage processingtasks.

LSAfocusesoncapturinghiddensemanticrela‐tionshipsindata,whileLDA,asaprobabilisticmodel, identi iestopicspresentindocuments.Withthehelp ofthesetechniques,classi icationsystemscanbetter handlediverseandcomplextexts,aswellasanalyze theirsemanticsmoreef iciently[4].

Anotherimportanttechniqueintextanalysisis PrincipalComponentAnalysis(PCA),whichfocuses onreducingthedimensionalityoftextfeatures.PCA involvestransformingdataintoanewsetofuncorre‐latedvariablescalledprincipalcomponents,thereby facilitatingtheanalysisofhigh‐dimensionaltextdata withoutlosingessentialinformation[15].

Moreadvancedmethodsincludewordembed‐dings,anadvancedwordrepresentationtechnique thatassignsnumericalvectorstowordsinaspaceof speci ieddimensionality.Wordembeddingssuchas Word2Vec,GloVe,orFastText[17]storewordseman‐ticsinamannerwherewordswithsimilarmean‐ingsareclosertoeachotherinthisspace[5].This facilitatestherepresentationofcontextandsemantic relationshipsbetweenwords,therebymakingclassi‐icationsystemsutilizingthesemethodsmoreprecise inmodelingthemeaningoftextualdocuments.

Whendealingwithkeywordextraction,several algorithmsenhancetheeffectivenessofclassi ica‐tionsystems,suchastheRapidAutomaticKeyword Extraction(RAKE)methodandthemoreadvanced EmbedRankmethod.RAKEidenti ieskeywordsbased onthefrequencyofwordoccurrenceandtheir co‐occurrencewithotherwordsinthetext.One signi icantadvantageofthisalgorithmisitsdomain andlanguageindependence,althoughitmaynotfully capturethesemanticmeaningoftheextractedkey‐words[14].

AsolutiontothisproblemistheEmbedRank algorithm,whichutilizeswordembeddingsforkey‐wordextraction.Basedonselectedcriteria,suchas frequencyandsemantics,itassignsanappropriate weighttoeachword.However,withthismethod, thereisapossibilityofobtainingredundantkey‐words,whichcandecreasetheirsigni icance.Tomiti‐gatethisredundancy,theauthorsofEmbedRank[1] employedtheMaximalMarginalRelevance(MMR) strategy,whichhelpsselectrelevantanddiversekey‐wordswhileeliminatingredundantones[1].

2.3.Visualization

Textdatavisualizationplaysacrucialrolein understandingandanalyzingtext.Onepopularvisu‐alizationmethodisthewordcloud,whichpresents themostfrequentlyoccurringwordsinadocument, assigningthemasizeproportionaltotheirfrequency. However,wordcloudshavelimitations,suchasthe lackofconsiderationforsemanticsorrelationships betweenwords.Asaresult,theyaremostcommonly usedforstatisticallysummarizingcontent[8].

Anotherpopulartechniqueist‐Distributed StochasticNeighborEmbedding(t‐SNE),anonlinear dimensionalityreductionmethodoftenappliedto visualizehigh‐dimensionaldatainlowerdimensions.

Bymappingdatatoalower‐dimensionalspace,it facilitatestheanalysisandinterpretationofthedata structure.Furthermore,itenablestheobservationof relationshipsbetweendifferenttextfragments,aiding inamorecomprehensiveunderstandingofthecontext oftheanalyzeddocuments[11].

Inourstudy,weutilizedtheSelf‐OrganizingMap (SOM)methodfortextdocumentvisualization.This methodinvolvestransformingmultidimensionaltext dataintoatwo‐dimensionalmapspace,wheredoc‐umentswithsimilarthemesarerepresentedclose toeachother.Byclusteringsimilardocuments,the analysisofthestructureandrelationshipsbetween differentcategoriesbecomesmoreaccessible,and color‐codingareasonthemapassistsinidentifying thematicgroups[2].

3.DescriptionoftheApproach

Weaimtocreateasystemtoautomaticallyclassify documentsintotherelevantlegalcategories.

Inthe irststep,alldocumentsweretransformed intovectorformusingtheKohonenSelf‐Organizing Mapsnetwork.Toderivetheinitialvectorrepre‐sentation,theGlobalVectorsforWordRepresenta‐tion(GloVe)1 modelwasemployed,producingword embeddingsin100‐dimensionalvectorsforwords occurringatleastthreetimesinthecorpus.Thesize oftheKohonennetworkwascon iguredtobe20×20, representingacompromisebetweentaskcomplexity andtrainingtime.Subsequently,eachquery(docu‐ment)wasmappedtotheareaontheKohonenmap (oneof400availableareas)thatbestmatcheditsfea‐tures.Tovisualisethevectorsonatwo‐dimensional plane,a 20×20 gridwascreated.Topreventpoint overlapandenhancevisualizationclarity,eachpoint wasassignedasmallrandomvaluethatwasadded toitscoordinates.Thisway,wewerenotlimitedto just400discretepoints.Theresultisthechaoticand unstructuredmapillustratedinFigure 2,wherethe colorsrepresentthedifferentclasses,accordingtothe legend.Notably,thedistancesbetweendocumentsin thesameclassaresimilartothosebetweendocu‐mentsindifferentclasses.Infuturework,weplan tooptimizethelayoutsothatobjectsfromthesame classaregroupedclosertogether.However,itisworth notingthatprojectingvectorsoflength100ontoa two‐dimensionalplanemaynotbetheperfectmethod ofrepresentingthisdata.

3.1.Dataset

Weutilizedadatasetcomprising2,722unique legalquestionsacrossninedistinctcategoriesoflaw. Eachrecordinthedatasetincludesthelegalarticle numbercorrespondingtothecategory,thecomplete contentofthequestion,themainlegalcategory,and thelegaldepartmentassociatedwiththecategory.An exampleofarecordlooksasfollows:

114Thesubstantiveissue,whetherthehousing communitycanadoptaresolutionregardingthe purchaseofradio-readwatermetersforindividual unitscoveringtheircosts,substantive,substantive,civil law.

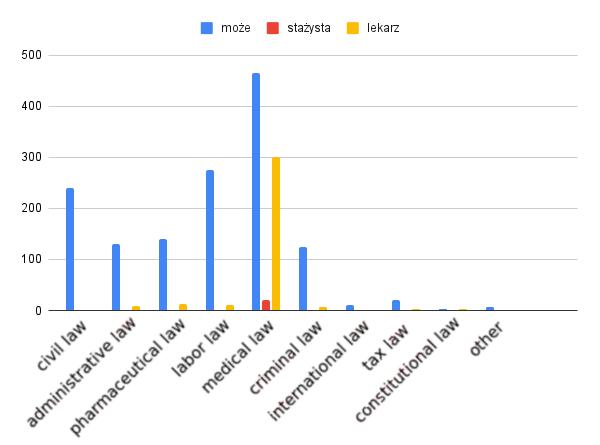
Figure1. Countsofexamplewords“Może”(maybe), “Stażysta”(intern)and“Lekarz”(doctor)ineach category

Speci ically,thenumber114correspondstoanarticle withinpropertylaw,asubsetofcivillaw.

3.2.Pre‐processingData

Tocategorizethedocuments,wordsuniquely linkedtotheirrespectivelegal‐constitutionalcat‐egorieswereextractedfromtheaforementioned dataset.Usingthe SpaCy library(https://spacy.io/)for naturallanguageprocessingandthe pl_core_news_lg databasecontainingPolish‐languageinformation,all documentsfromthedatasetwereanalyzed.Thispro‐cessisshowninTable 2 inthe Before column.Sub‐sequently,10partsofspeechwereremovedfrom thegenerateddictionary,astheirfeatureswere deemedirrelevantfordocumentclassi ication.The followingpartsofspeechwereremoved: numbering, punctuation,interjection,space,auxiliary,subordinatingconjunction,determiner,coordinatingconjunction, pronoun,preposition.Theresultisshownin Step1 columnofTable2.Thenextstepwastoeliminatethe wordsthatappearedonlyonceinacategory,asthese wereconsideredtooweakinthecontextofdocument classi ication.

Inafurtherstep,wordsthatfrequentlyoccurred indifferentcategorieswereremoved,asthiscould signi icantlyreducetheeffectivenessoftheextracted setofwordsinthecontextofmodeltraining.

BycarryingoutananalysisofFigure1,itispossible toidentifythreecategoriesofwords:

‐ “Może”(maybe):

‐ Itappearsinalmostallcategoriesinsigni i‐cantnumbers.Similarlyubiquitouswordsmake ithardertodistinguishbetweenclasses,sosuch wordsareremoved.

‐ “Stażysta”(intern):

‐ Thiswordonlyappearsinonecategoryofdoc‐ument,soitspresenceincreasestheprobability thatadocumentbelongstoaparticularclass.This isthebestpossiblecaseforusingwordsforclass distinction.

Table1. Numberofwordsineachcategorywith differentthresholdsofacceptanceforhowuniquea keywordmustbetoacategory.

Civillaw 587 470 466

Administrativelaw 209 192 191

Pharmaceuticallaw 253 210 210

Laborlaw 358 264 263

Medicallaw

Table2. Numberofwordsineachcategoryduringeach stepofdatapreparation

‐ “Lekarz”(doctor):

‐ Althoughitappearsinmorethanonecategory,the vastmajorityofitsoccurrencesareattributedto medicallaw.Removingitfromthedatasetwould adverselyaffectthequalityofthedata;aseven thoughitisfoundinmanycategories,onlyone ofitsoccurrencesisuntraceable.Therefore,such wordsareassignedtoaspeci iccategoryif90% ormoreofitsoccurrencesareinthatcategory.

Table 1 presentshowthedatasetchangesbased ontheacceptedratesofwordoccurrences.Itspeci ies theminimumpercentageofoccurrencesrequiredfor awordtoberetainedwithinagivencategory.An experimentwasalsoconductedwithathresholdof 100%,whichyieldedthenumberofwordstheset wouldcontainifallduplicateswereremovedfromall categories.Thelowerthepercentage,thehigherthe numberofwordsintheselecteddataset;however,this oftenresultsinlowerquality,asmanywordsbecome lesseffectiveinclassifyingdocumentsasbelongingto theappropriatecategories.Forfurtherwork,athresh‐oldof90%wasadoptedforthedatasetasacompro‐misebetweenthequantityandqualityofwords.

The inalwordcountinthedatasetduringthe preparationprocessisshowninTable2.

Forinternationallawandconstitutionallaw,most ofthewordsextractedfromtheoriginaldatasetwere discardedduringtheeliminationprocessdescribed above.Thisispartlyduetothesmallnumberofdoc‐umentsavailableforthesecategoriesinourdataset (withconstitutionallawcomprising0.15%andinter‐nationallaw0.62%ofthedataset).

TheTF‐IDFmeasurewasusedtoassessthe descriptivenessofthewordsforeachclass.Thismea‐surewascalculatedindividuallyforeachwordinthe class,andthentheaveragewascalculatedtorepresent theentireclasswithasinglemeasure.Table3displays theresultsbeforeandafter ilteringoutstrongkey‐words.

3.3.CreatingaTrainingDataset

Theprocessofcreatingthetrainingdatasetbased onthepreviously‐extracteddataisoutlinedbelow:

1) Extractionofspeci icsentencefragmentsfromthe originaldatasettoserveasthetrainingset.

2) Creationofalistcomprisingthemostfrequently occurringwordsamongtheextractedtokens.

3) Iterationthroughallselectedsentencestoidentify wordspresentinspeci iccategories.

4) Annotationoftheoccurringwordsintheappro‐priateformatandassignmentofcorresponding labels.

Thismethodologyaimedtoconstructatraining setbyextractingrelevantinformationfromsentences, creatingalistoffrequentlyoccurringwords,and appropriatelyannotatingthedata.

3.4.CreatingandTrainingaModel

Usingthegeneratedtrainingset,anewnetwork wastrainedwiththe spaCy library.First,aNamed EntityRecognizer(NER)from spaCy2 wasusedand thepredictionlabelswerede ined(e.g.,“civil_law”, ”administrative_law”).Thetrainingdatawasorga‐nizedtoincludethetextandentitylabelsfordifferent legalcategories.Eachtextwastransformedintoa Doc objectrepresentingthestructureofthedocumentin thegiventextandlabelpair.Alltransformeddocu‐mentswerethencollectedinanoptimizedmannerin the DocBin object.

Wecanassessthequalityofourdatavisualiza‐tionbymeasuringthecoherenceoftheclassesinthe cluster.Todothis,wecomputethedistancesbetween pointsfromthesameclasswithinacertainradius:

3.5.KohonenNetwork

The inalstepoftheexperimentdescribedabove wastovectorizealldocumentscontainedintheinitial datasetusingtheselectedclassi ication.Anexampleof thevectorizationperformedbytheselectedalgorithm isshownbelow.Fortheinputsentence:“Canadoctor beemployedatthehospitalonthebasisofanemploy‐mentcontractforatrialperiod,iftheywerepreviously employedatthislocationasaresident(untiltheendof 2018)?”,theresultingvectortakestheformofanarray of loating‐pointnumbers:

[0.071…,0.035…,0.0,0.0,0.071…,0.0,0.0,0.0,0.0,0.0]

Thearrayhas10differentcharacteristics,eachde in‐ingadifferentlegalcategory;forthecivil,administra‐tiveandmedicallawcategories,thevaluesare0.07, 0.03and0.07,respectively,andforeachoftheother categories,thevalueis0.

Ifallthedocumentsofoneclassareinthesameplace, thequalityequals1.Ifallthepointsarefarfromeach otherbythegivenradiusvalue,thequalitymeasure willbeequalto0.

Thecon igurationoftheNERmodelin spaCy forPolishisbasedonthe TransitionBasedParser.v2 architectureandtokenembeddingusing MaxoutWindowEncoder.v2.Thetrainingprocessincludedtraining datawithNERlabels,utilizingtheAdamoptimizer, andperformingmodelevaluationevery200steps. Keyevaluationmetricsfocusedontheentity‐levelF1 score.

Afterconvertingthedocumentsintovectors,the resultingdatawasfedintotheKohonenNetwork.The network’sparametersremainedconsistentwiththose describedpreviously,wheretheyservedasaninput stageusingGloVerepresentations.Intheinitialstage, theself‐organizingmapwastrainedontheinputdata for1,000iterations.Then,usingthe matplotlib library, theassignmentof“winning”coordinatestoeachdoc‐umentwaspresented.Toimprovethevectorization algorithmused,aweightwasaddedtoeachword, whichwascalculatedbasedonthenumberofoccur‐rencesinthedocument.Thismeansthatawordthat hasoccurred,forexample,300timesinacategoryhas amuchhighervaluethanonethathasonlyappeared afewtimes.Oncetheweightsareaddedtothedoc‐umentvectorizationprocess,thespacepresentedis arrangedintosets,asvisualizedinFigures2and3.

Thenextstepwastocreateatagcloudbasedonthe keywordsforeachofthedocumentspresentedinthe spaceabove.Thisbeganwithextractingthewordsthat characterizedeachdocument.Afterdistributingthese wordsinthespace,thegraphtookontheshapeshown inFigure4.

Figure2. SOMvisualizationusingGloVeembeddings

Table3. Number,coherenceanddescriptivenessofdocumentsbeforeandafterusingexclusivelystrongkeywords

Figure3. SOMvisualizationofdecisionborders,built usingNERmodel

Figure4. AllkeywordsdisplayedonSOM

However,byautomaticallyselectingthe irstword fromtheclassi ication,whenadocumentwasclas‐si iedasbelongingtoemploymentlawduetothe occurrenceof ivewordsfromthiscategory,onlythe irstwordoftheserieswastakenintothetagcloud. Toimprovetheresult,thestrongestwordfromeach document’ssetofkeywordswasselected,andthen duplicateswereeliminated.

Figure5. StrongkeywordsdisplayedonSOM

Afterthesemodi ications,thestructureofthe spacelookedasillustratedinFigure5.Table3shows thatthistreatmentimprovedthecoherenceofthe classesofdocumentsexamined.

4.ResultsandExperiments

4.1.ClassificationAccuracy

Aclassi icationaccuracyof71.69%wasachieved duringourexperiments.Thisresult,intermsof automaticclassi icationoflegaltext,issatisfactory. Acomparisonofthisoutcomewithrandomcategory selection,whichresultedinonly13%accuracy,signi i‐cantlyunderlinestheadvantageofthechosenmethod. Itisworthnotingthatforlessthan2%oftheanalyzed text,itwasnotpossibletoassignanycategory.This indicatesthepresenceofsegmentsthatdonotcontain characteristicwordsforanyofthelegalcategories.

4.2.CharacteristicsoftheDataset

Thedatasetusedtotrainthemodelwassig‐ni icantlyunbalanced.Thecategories“Constitutional Law”and“InternationalLaw”,alongwith“Unde ined”, hadfewerextractedwords,whichmaypotentially havereducedperformance.

Duringtesting,itemsrelatedtothesecategories wereremoved,resultinginaslightincreaseinaccu‐racy,reaching72.03%.

Itisworthnotingthattheobtainedaccuracywas signi icantlyin luencedbythecharacteristicsofthe datasetitself.Thedocumentsinthiscollectionwere unevenlydistributedacrossdifferentlegalcategories. Forinstance,“MedicalLaw”accountedforalmost30% ofthetotalcollection,whiletheshareof“Constitu‐tionalLaw”wasonly0.15%.Thisunevendistribution ofdocumentspresentsapotentialchallengeinthe classi icationprocess,necessitatingfurtheranalysis andoptimizationofthemodel.

4.3.ClassificationBasedonVectorComparison

Thisexperimentwasconductedtothoroughly investigatetheeffectivenessofanapproachbasedon comparingthesemanticsimilarityofwordswithout usingtheNERmodelforentityrecognitioninthe text.Themainobjectivewastocomparethismethod withtraditionalNER‐basedapproachesandexplore whetheritcanbeequally,orevenmoreeffectivein entityrecognition.

Themethodconsistsofthefollowingsteps:

1) DataPreparation: Initialtextprocessing,suchas tokenizationandstopwordremoval.

2) CreationofWordRepresentationVectors: WordsareencodedusingGloVe,withthecreation ofnumericalvectorsforeachword.

3) SemanticSimilarityComparison: Utilizesasim‐ilaritymethodtocomparethesimilaritybetween words.

4) EntityClassi ication: Foreachwordinthedoc‐ument,thewordwiththeclosestmeaningis selected.

5) Evaluation: Similarityresultsforeachcategory areaveraged,andthecategorywiththehighest scoreischosen.

Theresultingaccuracyobtainedwasapproxi‐mately46%,signi icantlylowerthanouroriginal approachusingNER,whichwaswasaround72%. Here,usageofthedomain–orientedtoolforNERmay improvetheprecisionoftheresultsachievedbythe generalpurposeone.

4.4.ClassificationBasedontheVectorRepresentation FromtheRoBERTaTransformer

TheRobustlyOptimizedBERTApproach (RoBERTa)architecturemodelwasused,pre‐trained onaPolishcorpusexceeding200GBinsize.The irst stepinvolvedpassingthenameofeachlegalcategory throughthemodel;theobtainedembeddingshada lengthof1024.Then,foreachquery,thetitleofthe documentwasextendedwiththetext“query:”.The entiresentence,withoutany iltering,wasthenused asinputtothemodeltoobtainanembedding.Using cosinesimilarity,itwaspossibletodeterminewhich categorythe“query”bestmatched.Theoverallresult achievedforallcategories,showninTable 4,was 56.8%.

Table4. ComparisonofaccuracybetweentheNER modelandPolishRoBERTaineachcategoryof document

SOMobtainedfromRoBERTaembeddings

Figure7. StrongestkeywordperqueryfromRoBERTa model

Figure6.

Table5. Coherence(��)anddescriptiveness(��)of classesusingRoBERTaembeddings.

Analyzingtheaccuracyforindividualcategories, onlyinthe“laborlaw”category(59.15%vs.62.88%) wasabetterresultobservedthanwiththeNER model,whichcanbeconsideredananomalysincethe improvementisnotsigni icant.

Sincethevectorsherearesigni icantlylongerthan thoseusedtogeneratethepreviousKohonennet‐works,a40×40mapwasusedinthiscase.Theresult ispresentedbelowinFigure 6.Theclassesonthis diagramaremuchmoreseparatedandvisiblethan inFigure 2,buttheaccuracyoftheresultswasstill inferiortoNER.Extractingkeywordsfromsentence embeddingsisn’taperfectprocess,butbyperform‐ingleave‐one‐outanalysisandseeingwhichword, whenmissing,impactedtherelativecosinesimilarity oftheselectedclasscomparedtothenextbest,the strongestkeywordforeachquerywasextractedand isvisualisedbelowinFigure 7.Thedescriptiveness andcoherenceoftheclassesaresummarizedforeach categoryinTable 5.Whilewestillconsistentlysaw worseresultsthanNER,consideringthatzeropre‐processing, iltering,andadditionaltrainingwereper‐formed,theywereveryimpressive.

5.ConclusionandFutureWorks

Thispaperaimedtodevelopaneffectiveclassi ica‐tionsystemforlegaldocumentsthroughkeywordfre‐quencyanalysis.TheapproachutilizedtheKohonen self‐organizingmapmethodandwordvectorrepre‐sentationusingtheGloVemodel,achievingasatisfac‐toryclassi icationaccuracyof71.69%.

Theresearchconductedrevealedthattheclassi i‐cationprocesscanbeenhancedthroughtheapplica‐tionofvarioustechniques,suchasNERtoolsandthe RoBERTamodel,toachievesimilaraccuracywithout anydomain‐speci ic ine‐tuning.

Challengesencounteredduringtheprocess,such astheunevendistributionofcategoriesinthedataset, highlightedareasforfurtherimprovement.Thus, futureresearchshouldfocusonexperimentingwith AI‐basedmethodsthathandleunbalanceddatamore effectively,andexploringtechniquessuchasgenerat‐ingarti icialdataorresamplingtobalancethedataset.

Notes

1https://nlp.stanford.edu/projects/glove/

2https://spacy.io/api/entityrecognizer

AUTHORS

PaulinaPuchalska –GdańskUniversityofTechnol‐ogy,GabrielaNarutowicza11/12,80‐233Gdańsk, Poland,e‐mail:paulina.puchalska@pg.edu.pl.

KacperKrzemiński –GdańskUniversityofTech‐nology,GabrielaNarutowicza11/12,80‐233Gdańsk, Poland,e‐mail:kacper.krzeminski@pg.edu.pl.

MaksymilianLis –GdańskUniversityofTechnol‐ogy,GabrielaNarutowicza11/12,80‐233Gdańsk, Poland,e‐mail:maksymilian.lis@pg.edu.pl.

RafałScherer∗ –CzęstochowaUniversityofTechnol‐ogy,GenerałaJanaHenrykaDąbrowskiego69,42‐201 Częstochowa,Poland,e‐mail:rafal.scherer@pcz.pl, www:https://kisi.pcz.pl/rscherer.

PawełDrozda –UniversityofWarmiaandMazury inOlsztyn,MichałaOczapowskiego2,10‐718Olsztyn, Poland,e‐mail:pdrozda@matman.uwm.edu.pl,www: wmii.uwm.edu.pl/kadra/drozda‐pawel.

KajetanKomar-Komarowski –LexSecure, Niepodległości723/6,81‐853Sopot,Poland,e‐mail: kkk@lexsecure.com,https://lexsecure.pl/.

KonradSzałapak –LexSecure,Niepodległości723/6, 81‐853Sopot,Poland,e‐mail:ks@lexsecure.com, https://lexsecure.pl/.

AndrzejSobecki –GdańskUniversityofTechnology, GabrielaNarutowicza11/12,80‐233Gdańsk, Poland,e‐mail:andrzej.sobecki@pg.edu.pl, https://pg.edu.pl/p/andrzej‐sobecki‐64426.

TomaszZymkowski –GdańskUniversityofTech‐nology,GabrielaNarutowicza11/12,80‐233Gdańsk, Poland,e‐mail:tomasz.zymkowski@pg.edu.pl.

JulianSzymański –GdańskUniversityof Technology,GabrielaNarutowicza11/12,80‐233 Gdańsk,e‐mail:julian.szymanski@eti.pg.gda.pl, https://julian.eti.pg.edu.pl/.

∗Correspondingauthor

ACKNOWLEDGEMENTS

Thisworkwaspartiallysupportedbyfundsallocated totheprojectof“Asemi‐autonomoussystemforgen‐eratinglegaladviceandopinionsbasedonautomatic queryanalysisusingthetransformer‐typedeepneu‐ralnetworkarchitecturewithmultitaskinglearning,” POIR.01.01.01‐00‐1965/20.

References

[1] K.Bennani‐Smires,C.Musat,A.Hossmann, M.Baeriswyl,andM.Jaggi,“SimpleUnsupervised KeyphraseExtractionusingSentenceEmbed‐dings”, arXive-prints,vol.1,2018,1–9,doi:10.4 8550/arXiv.1801.04470.

[2] T.Y.ChristyawanandW.FirdausMahmudy, “TextClassi icationandVisualizationonNews TitleUsingSelfOrganizingMap”, 2018InternationalConferenceonSustainableInformation EngineeringandTechnology(SIET),2018,doi:10 .1109/SIET.2018.8693189.

[3] J.Devlin,M.‐W.Chang,K.Lee,andK.Toutanova, “BERT:Pre‐trainingofDeepBidirectionalTrans‐formersforLanguageUnderstanding”, CoRR, 2018,doi:10.48550/arXiv.1810.04805.

[4] R.DzisevičandD.Šešok,“TextClassi ication usingDifferentFeatureExtractionApproaches”, 2019OpenConferenceofElectrical,Electronic andInformationSciences(eStream),2019,doi: 10.1109/eStream.2019.8732167.

[5] M.R.Faisal,I.Budiman,F.Abadi,D.T.Nugra‐hadi,M.Haekal,andI.Sutedja,“ApplyingFea‐turesBasedonWordEmbeddingTechniquesto 1DCNNforNaturalDisasterMessagesClassi ica‐tion”, 20225thInternationalConferenceofComputerandInformaticsEngineering(IC2IE),2022, doi:10.1109/IC2IE56416.2022.9970188.

[6] E.FrankandR.R.Bouckaert,“NaiveBayesfor TextClassi icationwithUnbalancedClasses”.In: KnowledgeDiscoveryinDatabases:PKDD2006: 10thEuropeanConferenceonPrinciplesandPracticeofKnowledgeDiscoveryinDatabasesBerlin, Germany,September18-22,2006Proceedings10, vol.1,2006,503–510.

[7] S.X.GaoZhengjie,FengAoandW.Xi,“Target‐DependentSentimentClassi icationWithBERT”, IEEEAccess,2019,doi:10.1109/ACCESS.2019. 2946594.

[8] F.Heimerl,S.Lohmann,S.Lange,andT.Ertl, “WordCloudExplorer:TextAnalyticsBasedon WordClouds”, 201447thHawaiiInternational ConferenceonSystemSciences,2014,doi:10.110 9/HICSS.2014.231.

[9] R.Jing,“ASelf‐attentionBasedLSTMNetworkfor TextClassi ication”, IOPPublishing,2019,doi:10 .1088/1742‐6596/1207/1/012008.

[10] S.‐B.Kim,K.‐S.Han,H.‐C.Rim,andS.H.Myaeng, “SomeEffectiveTechniquesforNaiveBayesText Classi ication”, IEEEtransactionsonknowledge anddataengineering,vol.18,no.11,2006,1457–1466.

[11] K.Kowsari,K.JafariMeimandi,M.Heidarysafa, S.Mendu,L.Barnes,D.Brown,L.Id,andBarnes, “TextClassi icationAlgorithms:ASurvey”, Information(Switzerland),2019,doi:10.3390/info10 040150.

[12] P.S.NavadaArundhati,AnsariAamirNizamand S.Balwant,“Overviewofuseofdecisiontree algorithmsinmachinelearning”, 2011IEEEControlandSystemGraduateResearchColloquium, 2011,doi:10.1109/ICSGRC.2011.5991826.

[13] M.Osowski,K.Lorenc,P.Drozda,R.Scherer, K.Szałapak,K.Komar‐Komarowski,J.

Szymański,andA.Sobecki,“PreviousOpinions isAllYouNeed—LegalInformationRetrieval System”.In: InternationalConferenceon ComputationalCollectiveIntelligence,2023, 57–67.

[14] S.Rose,D.Engel,N.Cramer,andW.Cowley, “AutomaticKeywordExtractionfromIndividual Documents”, TextMining:ApplicationsandTheory,2010,doi:10.1002/9780470689646.ch1.

[15] F.P.ShahandV.Patel,“AReviewonFea‐tureSelectionandFeatureExtractionforText Classi ication”, 2016InternationalConferenceon WirelessCommunications,SignalProcessingand Networking(WiSPNET),2016,doi:10.1109/Wi SPNET.2016.7566545.

[16] A.Sun,E.‐P.Lim,andY.Liu,“OnStrategies forImbalancedTextClassi icationUsingSVM: AComparativestudy”, DecisionSupportSystems, vol.48,no.1,2009,191–201.

[17] A.Talun,P.Drozda,L.Bukowski,andR.Scherer, “FastTextandXGBoostContent‐BasedClassi ica‐tionforEmploymentWebScraping”.In: InternationalConferenceonArti icialIntelligenceand SoftComputing,2020,435–444.

[18] J.W.XuelianDeng,YuqingLiandJ.Zhang,“Fea‐tureSelectionforTextClassi ication:AReview”, MultimediaToolsandApplications,2019,doi:10 .1007/s11042‐018‐6083‐5.

[19] L.Yang,“ABriefIntroductionoftheTextClassi‐icationMethods”, 2022IEEEInternationalConferenceonElectricalEngineering,BigDataand Algorithms(EEBDA),2022,doi:10.1109/EEBD A53927.2022.9744845.

[20] G.Yenduri,M.Ramalingam,G.ChemmalarSelvi, Y.Supriya,G.Srivastava,P.K.R.Maddikunta, G.DeeptiRaj,R.H.Jhaveri,B.Prabadevi,W.Wang, A.V.Vasilakos,andT.R.Gadekallu,“Gener‐ativePre‐trainedTransformer:AComprehen‐siveReviewonEnablingTechnologies,Potential Applications,EmergingChallenges,andFuture Directions”, ArXiv,2023,doi:10.48550/arXiv.2 305.10435.

[21] P.L.YingChenandC.P.Teo,“Regularised TextLogisticRegression:KeyWordDetection andSentimentClassi icationforOnlineReviews”, arXive-prints,2020,doi:10.48550/arXiv.2009. 04591.

[22] Y.Zhang,“ResearchonTextClassi ication MethodBasedonLSTMNeuralNetworkModel”, 2021IEEEAsia-Paci icConferenceonImage Processing,ElectronicsandComputers(IPEC), 2021,doi:10.1109/IPEC51340.2021.9421225.

Submitted:15th April2024;accepted:20th May2024

DarianFernándezGutiérrez,AriadnaArbolaezEspinosa,DeborahRaquelGalpertCañizares, MaríaMatildeGarcíaLorenzo

DOI:10.14313/jamris‐2025‐005

Abstract:

InthefieldofBioinformatics,thescientificcommunity isfullyawareofthechallengesassociatedwithenzyme classification.Inthisstudy,anovelstrategyisproposed basedontheuseofAnomalousAutoencoderstochar‐acterizechitinasesbelongingtoglycosidehydrolases. PythonandTensorFlowprogrammingtechnologieswere employedtoconductthisanalysis.Thedesignedclas‐sifierconsistsoftwolevelsthatdetermineboththe enzymaticnatureofanaminoacidsequenceandits correspondingchitinaseenzymefamily.Theselevelscon‐sideredclassimbalanceandtheunderrepresentationof thoseenzymefamiliesintheCAZy.orgdatabase.Fur‐thermore,acomprehensivecomparisonwasmadewith otheravailablesoftwareinthefield.Torepresentthe aminoacidsequences,embeddingsgeneratedfromthe ProtFlashmodelwereused.Theresultsobtainedinthis studyconfirmtheeffectivenessoftheproposedimple‐mentationcomparedtothemethodsEzyPred,ECPred, andProteinfer.

Keywords: autoencoders,bioinformatics,embeddings, enzymeclassification

1.Introduction

Elucidatingproteinorenzymefunctionsfrom aminoacidsequencesisstillanopen ieldinBioin‐formaticsalthoughveryoutstandingsolutionshave beenreportedinliteratureincludingmachineand deeplearningapproaches[1].Tryingto itthisgen‐eralproblemtotherecognitionofspeci icenzymes wedetectalackofdataaffectingmodelconstruction andvalidation.Ourprojectinvolvestheexploration ofcompleteproteomesofmicroorganismstoidentify potentialchitinaseenzymesbasedontheCAZy,org database,whichcontainsglycosidehydrolases(GH) enzymeswherechitinasesarefoundwithintheGH18 andGH19families.Thecomplexityliesintheclassi‐icationofsequencesthatarenotverysimilartothe annotated(orlabeled)ones,duetotheirlowrepre‐sentativenessinseveralclasses,orsequencesthatare similartotheannotatedones,butbelongtoadifferent class.

Toaddressthis,somemethodshavebeendevel‐opedthatleveragevarioussourcesofinformation, suchasdifferentrepresentationsofk‐mers[2, 3], andthat“learn”fromunlabeledsequencesinasemi‐supervisedapproach,althoughtheaccuracyinclassi‐icationremainsanopenproblem[4,5].

Otherclassi icationmethodsrelyonembedded representationsthatincludeinformationfromprevi‐ousclassi icationsbypretrainingthemwithdatabases ofaminoacidsequences[6–8].Theembeddingstrans‐formthesequencesintonumericalvectorsthrough naturallanguageprocessing(NLP)whileincorporat‐ingheterogeneousdatasources[5].

Inaddition,non‐standardclassi icationmethods withasemi‐supervisedapproachorone‐classlearn‐ing[9]havebeentacklingthelowrepresentative‐nessintheclasses.AnomalousAutoencoderscanbe consideredasaone‐classlearningapproachbecause theyaretrainedusingonlynormaldata[10,11].By exposingthemodeltoanomalousdata,theresulting reconstructionisexpectedtobesigni icantlydifferent fromthenormaldata.Thisdiscrepancycanserveasa measureoftheanomalypresentintheinputdata[12]. Ontheotherhand,classimbalanceisawidely addressedprobleminmachinelearningandhasbeen consideredinenzymeclassi icationbyincorporating informationfromlabeledsequencesintodeepneural networkmodelscombinedwithoversamplingmeth‐odslikeSMOTE[13].

Theproposalofthisworkistodevelopaclas‐si icationmethodusingembeddedrepresentations andAnomalousAutoencoders,consideringunlabeled sequencesorheterogeneoussourcestoachievehigh ef icacyinastudycaseofchitinaseswithlowrep‐resentativenessinthefamilyclasses,whicharealso imbalanced.

2.Content

InthetrainingprocessoftheAutoencoders[14] inthisresearch,sequencedatabelongingtotheGH18 andGH19enzymefamilieswereused(Table1).These sequenceswereobtainedfromtheCAZy.orgdatabase, whichisrecognizedforitsextensiveinformationon enzymesrelatedtocarbohydratedegradation.Allthe trainingsequencesusedfromtheGH18andGH19 familiesexhibitthesameenzymaticactivitywiththe ECnumber3.2.1.14.

Table1. Numberofenzymesperfamily

Family Numberofenzymes

GH18 356

GH19 83

Toconverttheenzymesequencesintonumerical representations,theembeddingtechniqueproposed intheProtFlashstudywasemployed[15].Thistech‐niqueallowedthegenerationoffeaturevectorsof size768,whichcapturerelevantinformationfromthe sequencesandfacilitatetheirfurtherprocessinginthe contextofmachinelearningwork lows.

Theembeddedvectorscanexhibitawidevariation inthevaluestheycanspan,rangingfromverydistant ranges,suchas‐255to55.Toaddressthisdiversity andimprovetheperformanceofneuralnetworks, theMin‐Maxscalingtechniquewasapplied[16].As showninTable 1,thereisanimbalancebetween classesofthefamiliesunderstudy,andingeneral,low representativeness,sopreprocessingtoincreasethe trainingsetcouldimproveclassi ication.Lateron,an experimentationrelatedtothisisshown.

Subsequently,theseresultingfeaturevectorswere usedasinputinthetrainingoftheAutoencoders.In thisway,acompactandmeaningfulrepresentationof theenzymesequenceswasobtained,whichisessen‐tialforsubsequentclassi ication.

2.1.ClassificationoftheEmbeddings

Inthisstudy,asequenceclassi icationapproach forenzymesequencesisemployedusingaclassi ier basedonAutoencoderswithamulti‐levelstructure. Themainobjectiveistoaccuratelyidentifyandthen categorizechitinaseenzymesequences.

Inthe irstleveloftheclassi ier,anevaluationis performedtodetermineifagivensequencecorre‐spondstoanenzyme.Ifthepresenceofanenzymeis con irmed,thesequenceisdirectedtothenextlevelof theclassi ier.Inthissecondlevel,thepredictionofthe enzymefamilytowhichthestudiedsequencebelongs iscarriedout.The lowofprocessesofthemulti‐level classi ierusedinthisworkisillustratedinFig.1

Duetothelimitedrepresentativenessofthe availablesequencesformodelconstruction,the SMOTEmethod[17–19]wasemployed.Thisapproach allowedforthegenerationofsyntheticdata,resulting inimprovedoutcomesasshowninTables 2, 3,and 4.Itisimportanttohighlightthatthenumberof sequencessigni icantlyincreasedfrom439toover 700throughthisstrategy.

2.1.1.FirstLevel

Intheinitialstageoftheclassi ier,ananomalous Autoencoderarchitectureisusedfortheidenti ica‐tionofenzymesequences.ThisAutoencoderhasbeen previouslytrainedusingtrainingsequences(embed‐dings)associatedwiththeGH18andGH19families. TheprimaryfunctionoftheAutoencoderistodeter‐minewhetheragivensequencecorrespondstoan enzymeornot.

Autoencoder‐basedtwo‐levelclassifier

Toful illthispurpose,athresholdisestablished asaclassi icationcriteriontodeterminewhethera vectorreconstructedbytheAutoencodercorresponds toanenzymeornot.Thecalibrationofthisthreshold isperformedwiththeaimofachievingaclassi ication accuracylevelof99%,usingequation(1)tocompare thereconstructeddatawiththetrainingdata.

Where:

����:Thecorrespondingelementatpositioniofthe reconstructeddata��, ����:Thecorrespondingelementatpositioniofthe trainingdata��and ��:sequencelength

ThearchitectureoftheAutoencoderconsistsoftwo parts:theencoderandthedecoder.Theencodertakes theoriginalinputsequence,whichhasadimensionof 768,andtransformsitintoalower‐dimensionallatent representationthroughaseriesofdenselayerswith ReLUactivationfunctions[14,20].Subsequently,the decoderperformsthereverseprocess,reconstructing theoriginalsequencefromthelatentrepresentation. Duringthetrainingprocess,anexhaustivesearch isapplied,whichisatechniqueusedinhyperparam‐eteroptimizationto indtheoptimalcombinationof parametervaluesforamachinelearningmodel.Dif‐ferentvaluesareconsideredforthenumberofepochs (25,50,100,150),batchsize(32,64,128),optimizer (Adam,Nadam),andlearningrate(0.001,0.01,0.1).

Figure1.

Table2. ComparisonofthetrainingsoftheFirstLevel

Thebestvaluesareunderlined.

Figure2. Lossfunction(MSE)ofthefirstlevelclassifier usingSMOTE

Anotherstrategyusedduringmodeltrainingto preventover ittingwasearlystopping,implemented throughthe“early_stopping”object.Thevalidation lossismonitored,andifitdoesnotimproveaftera certainnumberofepochs(inthiscase,5),thetraining isstopped,andthemodelweightsarerestoredtothe bestonesobtained.Thisensuresthatthebestmodel con igurationispreservedandavoidsunnecessary training.

Afterrunningthegridsearchwithallpossible combinationsalongwithearlystopping,thebestval‐ueswerefound:abatchsizeof32,100trainingepochs, alearningrateof0.001,andtheAdamoptimizer[21].

InFig. 2,thegraphicalrepresentationoftheloss functionisshown,whichcorrespondstothemean squarederror(MSE).Itcanbeobservedhowthisloss decreasesthroughoutthe100trainingepochs,indi‐catinganimprovementinthereconstructionofthe autoencoder.

Table 2 showstheresultsobtainedaftertraining the irstlevel,bothbeforeandafterusingSMOTE.It canbeobservedthatthereisanimprovedperfor‐mancewhenusingSMOTE.

2.1.2.SecondLevel

Thesecondleveloftheclassi ierfocusesonpre‐dictingtheenzymefamilytowhicheachenzyme belongs.Thisprocessisdividedintotwostages:Stage 1andStage2[22].

InStage1,thetrainingofAutoencodersiscarried outindividually,whereeachAutoencoderisexclu‐sivelytrainedwithenzymesequencesrelatedtoa speci icfamily.ThisprocessallowseachAutoencoder tolearnlatentrepresentationsofsequencesfromits correspondingfamily.

InStage2,enzymesareclassi iedintotheirrespec‐tivefamiliesusingthereconstructionlossescalculated throughthepre‐trainedAutoencoders(AE1,AE2,..., AEn).Inourcase,onlytwoAutoencoderswerepre‐trained,oneforeachfamily(GH18andGH19).Tocal‐culatetheselosses,eachenzymesequenceispassed throughthepre‐trainedAutoencoders,andtherecon‐structionlossesarecomputedforeachAutoencoder. Theselossesarethenusedasinputsforasigmoidal denselayerclassi ier[14,20],wherethecorrespond‐ingenzymefamilies(F1,F2,...,FN)aretheoutputs. Inotherwords,themodelistrainedtopredictthe enzymefamilybasedonthereconstructionlossesgen‐eratedbytheAutoencoders(Fig.3).

Toachievethis,theweightsofthepre‐trained Autoencodersaresetasnon‐trainable[22].Then,a jointnetworkiscreatedthattakestheinputsequence andpassesitthroughthetwocorrespondingAutoen‐codersfortheGH18andGH19families.Theoutputsof theseAutoencodersareconcatenated,andadropout layerisapplied[23]toregularizethemodel.Next, adenselayerwithReLUactivationisemployedto learnintermediaterepresentations.Finally,asoftmax activationisappliedintheoutputlayerfortheclassi‐icationintooneofthetwoanalyzedenzymefamilies. The inalarchitectureofthetwo‐levelclassi iercanbe seeninFig.4onceimplementedusingtheTensorFlow library.

Forthetrainingprocess,thesamehyperparameter optimizationmethodasinLevel1isused,alongwith earlystopping.Inthiscase,thebestvalueswerea batchsizeof32,50trainingepochs,alearningrateof 0.1,andtheNadamoptimizer[24].Thelossfunction usedduringthisclassi icationstageisthecategori‐calcross‐entropy,whichisshowninFig. 5 over50 epochs.Thisgraphallowsustoobservetheperfor‐manceobtainedduringtraining,whiletheaccuracyis usedastheevaluationmetric.

Table 3 showstheresultsobtainedaftertrain‐ingthesecondlevel,bothbeforeandafterapplying SMOTE.Itcanbeobservedthatthereisanimproved performancewhenusingSMOTE.

2.2.ResultsAnalysis

Toevaluatetheresultsofthedevelopedclassi ier, threeexistingmethodsforenzymeclassi icationwere examined,suchasEzypred[25],ECpred[26]andPro‐teInfer[27].Althoughthesemethodsgenerallyexhibit satisfactoryperformance,thisperformancemightnot remainwhendealingwithsequencesfromimbal‐ancedandpoorlyrepresentedclasses,sincetheydo notaddressclassi icationintosuchkindsoffamilies.

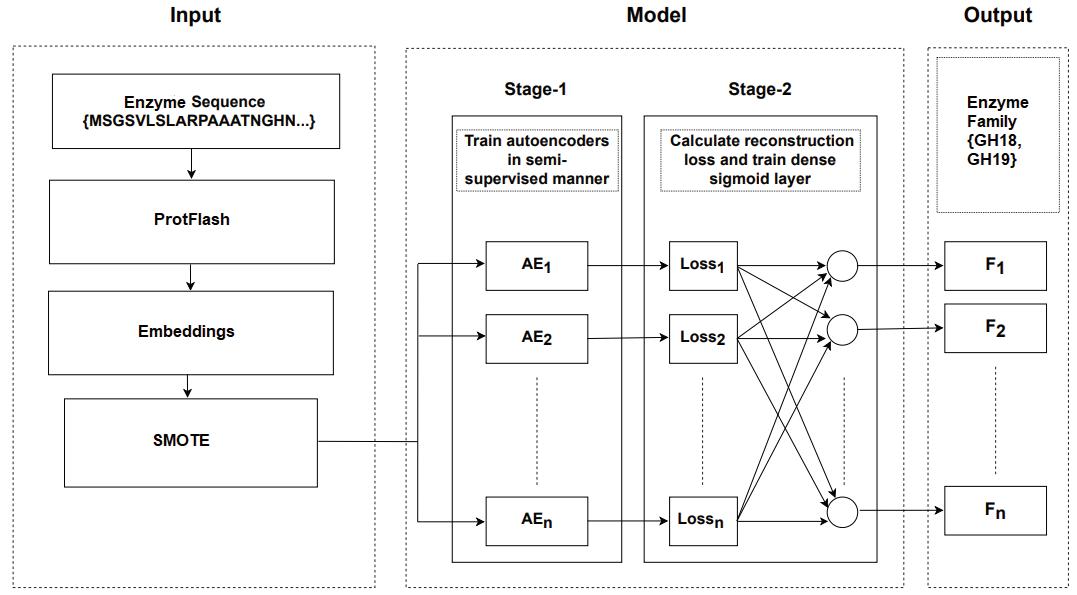
Figure3. Descriptivediagramoftheworkflowofthesecondleveloftheclassifier.TheprocessesAE1,AE2,...,AEn representtheAutoencodersofthecorrespondingenzymefamiliesF1,F2,…,Fn

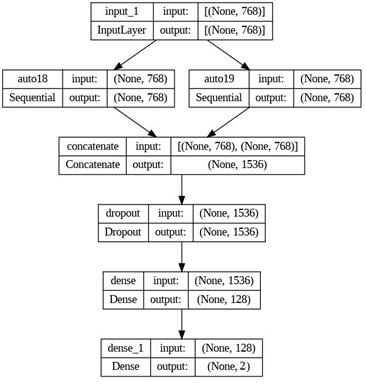
Figure4. Architectureofthetwo‐levelclassifier(the enzymefamilyclassifier)onceimplementedusingthe TensorFlowlibrary

Totestthedifferentsoftware,anexternaltest datasetwasgeneratedconsistingof20enzyme sequencesfromtheGH18andGH19families,10 foreachone.Additionally,10non‐enzymesequences wereincludedinthedataset,whichwereextracted fromthedatabaseUniProt1

Tables 4, 5,and 6 presenttheresultsofthe comparisonofthedifferentselectedsoftware regardingtheclassi icationofsequencesintoenzymes ornon‐enzymes,evaluatedusingthreekeymetrics: precision,recall,andF1‐Score.Thecomparison includesEzyPred,ECPred,Proteinfer,andthenew classi ierusingAutoencoders(AE).

Table3. ComparisonofthetrainingoftheSecondLevel

Bestvaluesareunderlined.

Figure5. Lossfunction(categoricalcross‐entropy)ofthe secondlevelclassifierusingSMOTE

TheresultsindicatethattheAutoencoder‐based classi ierachievedremarkableperformanceinclassi‐fyingsequencesasenzymesornon‐enzymes,surpass‐ingormatchingothersoftwareintermsofallthethree metrics.

Table4. Comparisonofdifferentsoftwaresforthe classificationofsequencesintoenzymesor non‐enzymes(precision)

EzyPred ECPred Proteinfer AE NotEnzyme 0.59 0.57

Bestvaluesareunderlined.

Table5. Comparisonofdifferentsoftwaresforthe classificationofsequencesintoenzymesor non‐enzymes(recall)

EzyPred ECPred Proteinfer AE

Bestvaluesareunderlined.

Table6. Comparisonofdifferentsoftwaresforthe classificationofsequencesintoenzymesor non‐enzymes(F1‐score)

EzyPred ECPred Proteinfer AE NotEnzyme

Bestvaluesareunderlined.

Figure6. ComparisonofAccuracybydifferentsoftware forenzymeclassificationornot

Figure 6 presentstheanalysisoftheaccuracy obtainedbyvarioussoftwareswhenevaluating whetheragivensequencecorrespondstoanenzyme ornot.Theresultsindicatethattheproposedmethod outperformedexistingsoftware,demonstrating itseffectivenessinthetaskofenzymesequence classi icationcomparedtothecompetition.

InTable 7,theresultsobtainedbytheproposed methodusingAutoencodersfortheclassi ication indifferentenzymefamilies,speci icallyGH18and GH19,arepresented.Theclassi ierachievedaremark‐ableresultbyachievinganaccuracyof0.90,indicat‐ingahighef icacyinthetaskofclassifyingenzyme sequencesinthesefamilies.

Table7. Resultsofthefamilyclassification

3.Conclusion

TheuseofAutoencodersinatwo‐levelclassi ier allowsdeterminationofwhetheragivensequence belongstotheenzymecategoryornot.Thisis achievedthroughanAnomalousAutoencoder,which helpsaddressthelackofrepresentativenessof enzymes.Thedevelopedmethodalsoprovides additionalinformationabouttheenzymefamily towhichthesequencebelongs.Toimprovethe performanceofthemodelatthetwolevelsofthe classi ierandreducedeviationsfrompredictionsin relationtotheactualvalues,preprocessingtechniques areapplied,suchasincreasingthenumberoftraining sequencesintheimbalancedclassthroughSMOTE. Theproposedapproach irsttransformsthe sequencesintoembeddingswithpre‐trainedmodels builtfromheterogeneoussourcesandthenapplies Autoencodersfortheclassi icationprocess.Ina comparisonexperimentwithsomeoutstanding enzymeclassi icationsoftwares,thisapproachshows encouragingexternaltestsetaccuracyresults(90%) indetectingwhetherasequenceisanenzymeornot. Additionally,aswementionedbefore,thisapproach providesinformationaboutthepossibleGHfamily towhichthesequencecouldbelong,somethingthat thoseanalyzedsoftwaresdonotoffer.

Notes

1https://www.uniprot.org/

AUTHORS

DarianFernándezGutiérrez∗ –Centerfor InformaticsResearch,FacultyofMathematics, Physics,andComputerScience,CentralUniversity “MartaAbreu”deLasVillas,Cuba,e‐mail: dfgutierrez@uclv.cuhttps://orcid.org/0009‐0001‐5076‐6413.

AriadnaArbolaezEspinosa –Centerfor InformaticsResearch,FacultyofMathematics, Physics,andComputerScience,CentralUniversity “MartaAbreu”deLasVillas,Cuba,e‐mail: ararbolaez@uclv.cuhttps://orcid.org/0009‐0005‐2752‐1986.

DeborahRaquelGalpertCañizares –Center forInformaticsResearch,FacultyofMathematics, Physics,andComputerScience,CentralUniversity “MartaAbreu”deLasVillas,Cuba,e‐mail: deborah@uclv.edu.cuhttps://orcid.org/0000‐0002‐5222‐3324.

MaríaMatildeGarcíaLorenzo –CenterforInfor‐maticsResearch,FacultyofMathematics,Physics,and ComputerScience,CentralUniversity“MartaAbreu” deLasVillas,Cuba,e‐mail:mmgarcia@uclv.edu.cu.

∗Correspondingauthor

References

[1] N.Buton,F.Coste,andY.LeCunff,“Predicting EnzymaticFunctionofProteinSequencesWith Attention,” Bioinformatics,vol.39,no.10,Oct. 2023,doi:10.1093/bioinformatics/btad620.

[2] Y.GonzálezValle,D.Galpert,andR.Molina‐Ruiz, “IntegraciónDeRasgosYAprendizajeSemi‐SupervisadoParaLaClasi icaciónFuncionalDe EnzimasUtilizandoK‐MeansDeSpark,” Revista CubanadeCienciasInformáticas,vol.14,no.4, 2020.

[3] Y.GonzálezValle,D.Galpert,andR.Molina‐Ruiz,“AgrupamientoFuncionalDeEnzimasGH‐70UtilizandoAprendizajeSemi‐SupervisadoY ApacheSpark,” RevistaCubanadeTransformaciónDigital,pp.14–32,2021.

[4] H.Chehili,S.E.Aliouane,A.Bendahmane,andM. A.Hamidechi,“DeepEnz:PredictionOfEnzyme Classi icationByDeepLearning,” Indonesian JournalofElectricalEngineeringandComputer Science,vol.22,no.2,2021,doi:10.11591/ije ecs.v22.i2.pp1108‐1115.

[5] Z.Tao,B.Dong,Z.Teng,andY.Zhao,“TheClas‐si icationofEnzymesbyDeepLearning,” IEEE Access,vol.8,2020,doi:10.1109/ACCESS.202 0.2992468.

[6] N.IbtehazandD.Kihara,“Applicationof SequenceEmbeddinginProteinSequence‐BasedPredictions,”in MachineLearning inBioinformaticsofProteinSequences: Algorithms,DatabasesandResourcesfor ModernProteinBioinformatics,2022.doi: 10.1142/9789811258589_0002.

[7] K.K.Yang,Z.Wu,C.N.Bedbrook,andF. H.Arnold,“LearnedProteinEmbeddingsFor MachineLearning,” Bioinformatics,vol.34,no. 15,pp.2642–2648,Aug.2018,doi:10.1093/bi oinformatics/bty178.

[8] C.Marquetetal.,“EmbeddingsFromProtein LanguageModelsPredictConservationAndVari‐antEffects,” HumGenet,vol.141,no.10,2022, doi:10.1007/s00439‐021‐02411‐y.

[9] M.M.MoyaandD.R.Hush,“NetworkConstraints AndMulti‐ObjectiveOptimizationForOne‐Class Classi ication,” NeuralNetworks,vol.9,no.3, 1996,doi:10.1016/0893‐6080(95)00120‐4.

[10] M.SakuradaandT.Yairi,“AnomalyDetection UsingAutoencoderswithNonlinearDimension‐alityReduction,”in ACMInternationalConference ProceedingSeries,2014.doi:10.1145/2689746. 2689747.

[11] K.PawarandV.Attar,“DeepLearningModel BasedonCascadedAutoencodersandOne‐Class LearningForDetectionAndLocalizationOf AnomaliesFromSurveillanceVideos,” IETBiom, vol.11,no.4,2022,doi:10.1049/bme2.12064.

[12] L.López,N.Acosta‐Mendoza,andA.Gago‐Alonso,“DetecciónDeAnomalíasBasadaEn AprendizajeProfundo,” RevistadeCienciasInformáticas,vol.13,no.3,2020.

[13] M.V.NallapareddyandR.Dwivedula,“ABLE: AttentionBasedLearningForEnzymeClassi ica‐tion,” ComputBiolChem,vol.94,p.107558,2021, doi:https://doi.org/10.1016/j.compbiolchem.2 021.107558.

[14] R.Atienza, AdvancedDeepLearningwithKeras. 2018.

[15] L.Wang,H.Zhang,W.Xu,Z.Xue,andY.Wang, “DecipheringTheProteinLandscapeWithProt‐lash,ALightweightLanguageModel,” CellRep PhysSci,vol.4,no.10,p.101600,2023,doi:https: //doi.org/10.1016/j.xcrp.2023.101600

[16] K.Cabello‐Solorzano,I.OrtigosadeAraujo,M. Peña,L.Correia,andA.J.Tallón‐Ballesteros,“The ImpactofDataNormalizationontheAccuracy ofMachineLearningAlgorithms:AComparative Analysis,”2023.doi:10.1007/978‐3‐031‐4253 6‐3_33.

[17] N.V.Chawla,K.W.Bowyer,L.O.Hall,andW.P. Kegelmeyer,“SMOTE:SyntheticMinorityOver‐SamplingTechnique,” JournalofArti icialIntelligenceResearch,vol.16,2002,doi:10.1613/jair .953.

[18] G.Douzas,F.Bacao,andF.Last,“Improv‐ingImbalancedLearningThroughAHeuristic OversamplingMethodBasedOnK‐MeansAnd SMOTE,” InfSci (NY),vol.465,2018,doi:10.1 016/j.ins.2018.06.056.

[19] H.Han,W.Y.Wang,andB.H.Mao,“Borderline‐SMOTE:ANewOver‐SamplingMethodInImbal‐ancedDataSetsLearning,”in LectureNotesin ComputerScience,2005.doi:10.1007/115380 59_91.

[20] AurélienGéaron, Hands-onMachineLearning withScikit-Learn,KerasandTensorFlow:Concepts,Tools,AndTechniquestoBuildIntelligent Systems.2022.

[21] D.P.KingmaandJ.L.Ba,“Adam:AMethod ForStochasticOptimization,”in 3rdInternational ConferenceonLearningRepresentations,ICLR 2015‐ConferenceTrackProceedings,2015.

[22] R.Dhanuka,A.Tripathi,andJ.P.Singh,“A Semi‐SupervisedAutoencoder‐BasedApproach forProteinFunctionPrediction,” IEEEJBiomed HealthInform,vol.26,no.10,pp.4957–4965, Oct.2022,doi:10.1109/JBHI.2022.3163150.

[23] N.Srivastava,G.Hinton,A.Krizhevsky,I. Sutskever,andR.Salakhutdinov,“Dropout: ASimpleWayToPreventNeuralNetworks

FromOver itting,” JournalofMachineLearning Research,vol.15,2014.

[24] T.Dozat,“IncorporatingNesterovMomentum intoAdam,” ICLRWorkshop,no.1,2016.

[25] H.BinShenandK.C.Chou,“EzyPred:ATop–DownApproachForPredictingEnzymeFunc‐tionalClassesAndSubclasses,” BiochemBiophys ResCommun,vol.364,no.1,pp.53–59,Dec. 2007,doi:10.1016/J.BBRC.2007.09.098.

[26] A.Dalkiran,A.S.Rifaioglu,M.J.Martin,R.Cetin‐Atalay,V.Atalay,andT.Doğan,“ECPred:ATool

ForThePredictionOfTheEnzymaticFunctions OfProteinSequencesBasedOnTheECNomen‐clature,” BMCBioinformatics,vol.19,no.1,Sep. 2018,doi:10.1186/s12859‐018‐2368‐y.

[27] T.Sanderson,M.L.Bileschi,D.Belanger,andL. J.Colwell,“ProteInfer,DeepNeuralNetworksfor ProteinFunctionalInference,” Elife,vol.12,2023, doi:10.7554/eLife.80942.

BASEDONMARKOVCHAINS

Submitted:1st February2024;accepted:4th September2024

MaksimMaksimov,OleksiyKozlov,SerhiiRetsenko,ViktoriiaKryvda

DOI:10.14313/jamris‐2025‐006

Abstract:

Recently,underwatersensornetworks(USN)havegained widespreadadoption,provinginstrumentalindiverse researchendeavorswithinthemarineenvironmentand acrossvariousscientificandtechnologicaldomains. Consideringthechallengingoperationalconditions,a paramountissueinthepresentdayisthecreationof USNswithapredeterminedfaulttolerancemargin.The primaryfocusofthisstudyisthedevelopmentandeval‐uationofadesignmethodforfault‐tolerantstructures ofUSNsusingMarkovchains.Theproposedmethod enablesthecreationofsuitableUSNs’structures,ensur‐ingaguaranteedattainmentofthedesirednumberof operationalcyclesbeforefailureatreasonablecosts.Uti‐lizingthemathematicalframeworkofMarkovchains, coupledwiththestrategyofawell‐selectedsequence ofhierarchylevels,enablestheprecisedeterminationof thenetwork’sactualnumberofoperationcyclesbefore failureaswellasperformingefficientreservationwithout excessiveredundancy.Toevaluatetheefficacyofthe proposedmethod,thisstudyundertakesaspecificcase –thedevelopmentofafault‐tolerantstructureforareal USNwithpredeterminedparameters.Theanalysisofthe resultsobtainedconfirmsthehighfeasibilityofutilizing thedevelopedmethodforcraftingUSNsforvariouspur‐poses,ensuringapredefinedleveloffaulttolerancewhile maintainingacceptablecosts.

Keywords: underwatersensornetwork,faulttoler‐ance,hierarchicalstructure,structuredesigningmethod, Markovchains

1.Introduction

Inthecontinuumoftechnologicalprogress,sensor networks(SN)emergeasapivotalparadigm,ushering inaneweraofpervasivedataacquisitionanddis‐semination[1–3].Comprisingadistributedensemble ofautonomoussensornodesendowedwithdiverse sensingmodalities,thesenetworkshavewitnessed proli icgrowthacrossaspectrumofdisciplines.From ecologicalmonitoringtoindustrialprocesscontrol, healthcareapplicationstourbaninfrastructure,sen‐sornetworkshavebecomeinstrumentalinfurnishing real‐timeinsightsthatunderlieempiricaldecision‐makingandpropeloperationalef icienciesacross multifariousdomains.

Theascendancyofsensornetworkscanbe attributedtotheirinnateadaptabilityandthe expansivenessoftheirapplicationdomain.These networksserveastheindispensablenexusbetween thecorporealandthedigital,engenderingthecapacity togleanandscrutinizedatafromhithertoinaccessible orimpracticableenvirons.Theirdeploymentwithin environmentsasvariegatedasurbanmetropolises, agrarianlandscapes,andsubaquaticrealmsatteststo theirversatilityandunderscorestheirtransformative potential.

Oneofthekeyadvantagesofsensornetworks istheirabilitytoprovidereal‐time,high‐resolution dataoverawidearea[4–6].Theyenabledata‐driven decision‐making,allowingfortimelyresponsesto changingconditions.Moreover,theycanbedeployed inharshorhazardousenvironmentswherehuman interventionmaybeimpracticalorrisky.Sensornet‐worksalsoofferscalability,meaningtheycanbe adaptedtosuitthesizeandrequirementsofaspeci ic application.Additionally,theycontributetoresource conservationandoptimizationbyenablingtargeted interventionsbasedonaccuratedata.

Thefutureofsensornetworksispromising,with ongoingresearchanddevelopmentinseveralkey areas.Advancementsinenergyharvestingtechnolo‐giesareexpectedtofurtherextendthelifespanof sensornodes,reducingtheneedforfrequentbat‐teryreplacements[7, 8].Integrationwitharti icial intelligenceandmachinelearningwillenhancethe capabilitiesofsensornetworksfordataanalysisand decision‐making.Theemergenceoflow‐power,long‐rangecommunicationtechnologieslikeLoRaWANand NB‐IoTisexpandingthereachandapplicabilityofsen‐sornetworks.Additionally,advancementsinsensing technologies,suchasthedevelopmentofmorespe‐cializedandaccuratesensors,willcontributetothe growthandeffectivenessofsensornetworksinvari‐ousindustries.Overall,sensornetworksareatrans‐formativetechnologywithwide‐rangingapplications andsigni icantadvantagesindata‐drivendecision‐makingandresourceoptimization.Ongoingresearch andtechnologicaladvancementspromisetofurther enhancetheircapabilities,openingupnewpossibili‐tiesforinnovationandimpactacrossvariousindus‐tries.

Inturn,sensornetworkshaveawiderange ofapplications,includingenvironmentalmonitoring, industrialautomation,healthcare,agriculture,smart cities,andmore.Inenvironmentalmonitoring,they areemployedtotrackparameterslikeairquality, weatherconditions,andpollutionlevels[9].Inindus‐trialsettings,theyfacilitatereal‐timedatacollec‐tionforprocesscontrolandoptimization[10].In healthcare,sensornetworksareinvolvedinpatient monitoring,falldetection,andotherhealth‐related applications[11].Inagriculture,theyaidinprecision farmingbymonitoringsoilconditions,weather,and crophealth[2,7].Smartcitiesusesensornetworks fortraf icmanagement,wastemanagement,energy conservation,andpublicsafety[12].

Theuseofunderwatersensornetworks(USN) deservesspecialattention[13–15].USNsrepresent atransformativetechnologicalfrontier,designedto navigateandelucidatethedepthsofourplanet’s aquaticenvironments.Thesenetworkscomprise autonomoussensornodes,equippedwithadiverse arrayofspecializedsensors,collectivelytasked withcapturinganddisseminatinginvaluabledata fromunderwaterdomains.Theirsigni icancelies intheircapacitytoaugmentourunderstandingof submergedecosystems,informresourcemanagement strategies,andenablecriticalapplicationsin ieldsrangingfrommarinesciencetomaritime security.TherelevanceofUSNsismanifestacross aspectrumofdisciplines.Inmarinebiologyand oceanography,theyserveasindispensabletools forthestudyofmarinelifebehavior,tracking migratorypatterns,andmonitoringthehealthof delicateecosystems.Furthermore,intherealmof environmentalmonitoring,USNsplayapivotalrole inassessingwaterquality,trackingpollutionlevels, andconductingcomprehensivestudiesofaquatic habitats.Inmaritimeindustries,theycontributetothe optimizationofvesselnavigation,supportoffshore resourceexploration,andfacilitatethemaintenance ofunderwaterinfrastructure.

ParametersmonitoredbyUSNsencompassamul‐titudeofcriticalenvironmentalindicators[15].These includetemperature,afundamentalparameterin lu‐encingmarineecosystemsandclimatepatterns.Salin‐ity,ameasureofwater’ssaltcontent,isessential forunderstandingoceanographicphenomenaand assessingecologicalniches.Pressuremeasurements affordinsightsintooceandepthsandtopography,vital forcomprehensivemarinesurveys.Acousticdata,cap‐turingunderwatersoundscapes,providesawealthof informationonmarinelifebehavior,aswellasanthro‐pogenicnoisepollution.Additionally,sensorsfordis‐solvedoxygen,pHlevels,turbidity,andnutrientcon‐centrationsroundoutthesuiteofinstrumentsutilized inUSNs,providingacomprehensiveperspectiveon theaquaticenvironment.Inachievingtheirmission, USNsemployavarietyofspecializedsensorstailored tothechallengingunderwatermilieu.

Acousticsensors,knownashydrophones,arepiv‐otalincapturingunderwatersounds,enablingthe studyofmarinelifebehavior,aswellasdetectingseis‐micactivity.Temperaturesensors,oftenutilizingther‐mistorsorthermocouples,monitorwatertempera‐tures,whichplayacrucialroleinoceanographicstud‐ies.Conductivitysensors,alongwithtemperatureand pressuresensors,facilitatethecalculationofsalinity levels.Pressuresensorsthemselvesareinstrumen‐talinprovidingdepthmeasurements,contributingto bathymetricmappingandmaritimenavigation.Opti‐calsensors,designedtomeasureparametersliketur‐bidityorlightpenetration,areemployedinenviron‐mentswithsuf icientvisibility.Thesediversesensor modalitiescollectivelyempowerUSNstounravelthe mysteriesofourplanet’ssubmergedecosystemsand contributetoinformeddecision‐makinginarangeof criticalapplications.

Regardlessofthis,USNsfaceuniquechallenges duetotheharshunderwaterenvironment,including limitedcommunicationrange,highpropagationdelay, andtheneedforenergy‐ef icientcommunicationpro‐tocols.Researchersinthis ieldworkondeveloping specializedhardware,communicationprotocols,and deploymentstrategiestoovercomethesechallenges andenhancethecapabilitiesofunderwatersensor networks[14,16,17].However,oneofthemostimpor‐tantproblemsinthisareatodayisthecreationof underwatersensornetworkswithasetfaulttolerance margin[18, 19].Asuccessfulsolutiontothisprob‐lemcanbefoundbydesigninganoptimalnetwork structurewhichwillallowthecreationofUSNswitha speci iedoperatingtimebeforefailure.Toassessfault toleranceandfurthersynthesizethemostsuitable USNstructure,itisadvisabletoapplythemathemat‐icalapparatusofMarkovchains,whichiseffectively usedforcalculatingtherequirednumberofoperation cyclesbeforefailureofvariouscomplexsystems[20].

Thisstudyisdedicatedtothedevelopmentand researchofthedesigningmethodoffault‐tolerant structuresforunderwatersensornetworksbasedon Markovchains.Thesubsequentsectionsofthispaper areorganizedasfollows.Section 2 offersaconcise reviewofpertinentliteratureinthis ield,establish‐ingtheprimaryaimofthisstudy.Section 3 presents astep‐by‐stepmethodfordesigningtheUSNsfault‐tolerantstructures,asproposedinthisresearch.Fol‐lowingthat,inSection4,astudyoftheeffectivenessof thedevelopedmethodiscarriedoutusingtheexample ofthesynthesisofaspeci icnetwork.Finally,Section5 providesconclusionsandoutlinespotentialavenues forfutureresearchendeavors.

2.BriefLiteratureReview

Today,researchonunderwatersensornetworksis intensivelycarriedoutinthefollowingmainareas.

Energy-ef icientcommunicationprotocols. Ongoing researchinunderwatersensornetworksfocuseson thedevelopmentofenergy‐ef icientcommunication protocolstailoredtothechallengesofunderwater acousticchannels[21, 22].Researchersareexplor‐ingadaptiveprotocolsthatcaneffectivelynavigate variablepropagationdelaysandlimitedbandwidth, ensuringoptimaldatatransmissionandprolonged networkoperation.

Localizationandnavigation. Advancementsin accuratelocalizationtechniquesforunderwatersen‐sornodesareveryimportant[23,24].Preciselocal‐izationisessentialforoceanographicstudies,envi‐ronmentalmonitoring,andnavigationofautonomous underwatervehicles.Researchersaredeveloping novelmethodstoenhancetheaccuracyofnodeposi‐tioningindynamicunderwaterenvironments.

Acousticcommunicationandnetworking. The improvementofacousticcommunicationinUSNsis oneofthecriticalareasofexploration[25].Research effortsaredirectedtowardenhancingthereliability, datarates,andrangeofacousticcommunication. Thisincludesinvestigatinginnovativemodulation techniquesandsignalprocessingalgorithmsto overcomethechallengesposedbyunderwater acousticchannels.

Sensingtechnologyandsensorintegration. ResearchinsensingtechnologyforUSNsinvolves thedevelopmentofspecializedandaccurate sensors[26, 27].Thisincludesadvancementsin chemical,biological,andopticalsensorstoexpand thedatacollectioncapabilitiesofUSNs.Integrating diversesensorscontributestoamorecomprehensive understandingofunderwaterenvironments.

Adaptiveandcognitivesensornetworks. Research isdedicatedtocreatingadaptiveandcognitivesensor networksthatcanautonomouslyadjusttochanging underwaterconditions[28,29].Thisinvolvesexplor‐ingself‐con iguring,self‐optimizing,andlearning‐basedapproaches,suchascognitiveradiotechniques, todynamicallyadapttospectrumavailabilityandmit‐igateinterference.

Securityandprivacy. Ensuringthesecurityandpri‐vacyofdatainUSNsisanequallyimportanttaskwhen developingthesenetworks.Scientistsaredesigning securecommunicationprotocolsandencryptiontech‐niquestoprotectdataintransit,addressingtheunique challengesposedbytheunderwaterenvironment [30,31].

BiologicallyinspiredapproachesforUSNsoptimization. Bio‐inspiredalgorithmsandstrategiesarebeing researchedtooptimizeUSNfunctionality[32, 33]. Thisincludestheuseofevolutionaryandswarm intelligencealgorithmstooptimizestructures,energy consumption,routing,nodeaggregation,powercon‐trol,schedulingofsensoractivities,functionality,and more.

Bio‐inspiredintelligentapproaches[34–36],soft computing[37–39]anddifferentmachinelearning algorithms[40–42]haveproventhemselvestobevery effectivetoolsforsolvingdiverseproblemsinvarious ields.

Alongwiththeareasdiscussed,evenmore signi icantisresearchaimedatincreasingthefault tolerance,reliabilityandsurvivabilityofunderwater sensornetworks[43, 44].Theimportanceoffault toleranceinunderwatersensornetworkscannotbe overstated,asthesenetworksoperateinchallenging anddynamicaquaticenvironmentswheresensor nodesaresusceptibletovariousformsoffailure.Fault toleranceiscrucialforensuringthereliabilityand continuousoperationofUSNs,wheresensornodes mayexperiencemalfunctionsduetofactorssuchas harshunderwaterconditions,hardwarefailures,or energydepletion.Giventheremoteandinaccessible natureofmanyunderwaterdeploymentsites, timelymaintenanceandnodereplacementareoften impractical.Fault‐tolerantmechanismsallowUSNsto detect,isolate,andadapttofaults,ensuringthatthe networkcancontinueitsmission‐criticalfunctions eveninthepresenceofnodefailures.Thisresilience isvitalforapplicationsrangingfromenvironmental monitoringandmarineresearchtounderwater infrastructuremaintenanceanddefenseoperations, whereuninterruptedandaccuratedatacollection isparamount.Fault‐tolerantUSNscontributetothe overallrobustnessandeffectivenessofunderwater explorationandmonitoring,providingafoundation forsustainedandreliableperformanceinchallenging underwaterenvironments.

Thequestforenhancingthefaulttoleranceof underwatersensornetworkshasspurredaproli ic bodyofresearch,andacomprehensivereviewofthe methodsrevealsadynamiclandscapeofinnovative approaches.Severalkeystrategieshavebeenexplored tofortifyUSNsagainstthechallengesposedbythe harshunderwaterenvironment[45,46].Theutiliza‐tionofadvancederrordetectionandcorrectionmech‐anisms,includingerror‐correctingcodesandcheck‐sums,hasshownpromiseinmitigatingtheimpactof datatransmissionerrors[20,47].Additionally,adap‐tiveroutingprotocolsdynamicallyreroutedatapaths inresponsetochangingnetworkconditions,offeringa proactiveapproachtofaulttolerance[48,49].Machine learningalgorithmsareincreasinglyemployedfor anomalydetection,allowingUSNstoidentifyandiso‐latefaultynodesbasedondeviationsfromnormal behavior[33,50,51].Energy‐awarestrategies,focus‐ingonef icientpowermanagementandtheutiliza‐tionofenergyharvestingtechnologies,contributenot onlytoprolongingnetworklifespanbutalsotobol‐steringfaulttolerance[52].Moreover,redundancy‐basedmethods,suchasnodeduplicationanddata replication,havebeenprominent,providingresilience byensuringthatcriticalfunctionspersisteveninthe faceofnodefailures[19,53,54].

Inaddition,Markovchainsarequiteeffectively usedtoassesstheobtainedfaulttoleranceandanalyze thereliabilityofthegeneratedarchitecturesofvarious sensornetworks[55–57].

Despitetheconstantincreasingofhardwarerelia‐bility,ef iciencyofroutinganddataprocessing,redun‐dancyofsensors,etc.,thechallengeofcreatingan architectureguaranteedtoprovidetherequirednum‐berofcyclesbeforefailureforeachspeci iccasewith thegivennetworkparametersremainsunsolved.

Hence,itisadvisabletodevelopamethodof designingfault‐tolerantstructuresforunderwater sensornetworksusingMarkovchainsmathematical apparatus.Thisapproachwillensurethecreationof underwatersensornetworksthatexhibittheneces‐sarynumberofoperationcyclesbeforeencounter‐ingfailureforthegivenUSNparameters.Therefore, themainaimofthispaperistodevelopandinvesti‐gateadesignmethodoffault‐tolerantstructuresfor underwatersensornetworksutilizingtheprinciples ofMarkovchains.

Themaincontributionsoftheauthorsareas follows:

a creationofthestep‐by‐stepmethodfordesign‐ingthefault‐tolerantstructuresoftheunderwater sensornetworksbasedonMarkovchains;

b conductionoftheeffectivenessstudyofthedevel‐opedmethodusingtheexampleofthesynthesisof thespeci icunderwatersensornetworkwiththe setparameters.

3.DevelopmentoftheDesigningMethodof Fault‐tolerantStructuresforUnderwater SensorNetworksBasedonMarkovChains

3.1.BasicPropertiesandGeneralizedFunctionalStruc‐tureoftheUnderwaterSensorNetwork

Specializedunderwatersensornetworksareused tocollectvarioustypesofinformationaboutthestate oftheunderwaterenvironment,transmitthisinfor‐mation,andfurtherprocessit.Theprimarycollection ofinformationiscarriedoutfromcertaininforma‐tionsourcesusingspecializedsensorsinstalledinthe underwaterenvironment.Inturn,thenumberofdata sourcesand,accordingly,sensorsisequalto ��0.Sig‐nalsfromthesesensorsaretransmittedtothemain informationprocessingunitusingdatatransmission channels.

Sincethenumberofsensors(initialinformation sources)isquitelarge(cannumberseveralhundreds orthousands),thetransferofdatadirectlyfromthem tothemaininformationprocessingnodethrough communicationchannelsisquitecomplicated.Thisis explainedbythefactthatthesensorswillneedto haveasuf icientlyhighsignaltransmissionpowerand, accordingly,highenergyconsumptiontoensurethe transmissionofalargeamountofinformationover longdistances.

Andthemaininformationprocessingunitwill haveveryhighcomplexityandcost,aswellasfairly lowreliability,which,ofcourse,willsigni icantly increasethecostandreducethereliabilityofthe entiresystem.Therefore,inordertoreducetheover‐allcostandincreasethereliabilityoftheUSN,itis advisabletoformitsstructureaccordingtoahier‐archicalprinciple.Todothis,itisadvisabletouse intermediatedatacollectionnodesthatwillperform functionsofsignalgroupingwithcertaininformation processing.Asaresultofsuchprocessing,thesenodes willtransmitfurthersmalleramountsofinformation whilepreservingallvaluabledata.Thus,intermediate nodesofthe1stlevelofthehierarchywillgroupand processsignalsfromsensorsandsendthemtonodes ofthe2ndlevelofthehierarchy,andsoontothemain nodeofthesystem.

Inthispaperweconsiderthetree‐likeorpyra‐midalarchitecturethatisaspeci ictypeofhierar‐chicalarchitecture.Inthisstructure,nodesareorga‐nizedinatree‐likefashion,withmultiplelevelsand themainsinknodeattheroot.Eachlevelconsists ofnodesthatcommunicatewithnodesinthelevel abovethem,ultimatelyreachingthesinknode.The givenarchitectureishighlyeffectiveandcanprovide reducedenergyconsumptionandimprovedscalabil‐ityaswellasadaptationtovaryingnodedensities. Inparticular,byorganizingnodeshierarchically,the numberofhopsrequiredfordatatransmissiontothe sinknodeisminimized.Thiscanleadtosigni icant energysavings,especiallyfornodeslocateddeeper inthewater.Moreover,thisarchitecturecanbewell‐suitedforlargernetworks,asitprovidesastructured waytomanagecommunicationanddata low.Finally, inenvironmentswithvaryingnodedensities,thetree‐likestructureallowsformoreef icientdatacollection andtransmission.

Thegeneralizedfunctionalstructureofthehier‐archicalunderwatersensornetworkispresentedin Fig.1

Figure1. Generalizedfunctionalstructureofthe hierarchicalunderwatersensornetwork.

Inthissystem,thelowest(zero)levelisthelevel ofunderwatersensors,whichareusedtomeasure variousparameters(pressure,temperature,salinity, pH,currentspeed,etc.).Typically,thesesensorshave built‐inpowersourcesandcontactlesslytransmit measuredinformationtohigherlevelsusingacoustic signals.Thepossibleoperatingtimeofthesesensors dependsonthecapacityofthepowersource,the requiredfrequencyofmeasurementandinformation transmission,aswellasthesignaltransmissionpower toensuredatatransferoverspeci ieddistances.In somecases,sensorscanbepoweredbywire,forexam‐ple,inthepresenceofnearbysourcesofalternative energy(wind,wave,etc.).Inturn,thedatatransmis‐sioncanalsobecarriedoutinthesameway,but wiredconnectionssigni icantlycomplicatetheinitial deploymentandfurthermaintenanceofthenetwork intheeventofabreakdown.

Thenext( irst)levelofthenetworkisimple‐mentedusingunmannedunderwatervehicles(UUVs), whichreceiveinformationfromsensors,processitin acertainwayandtransmititfurthertohigherlevels ofthehierarchy.Moreover,UUVsalsotransmitdata usingacousticsignals;however,duetosome iltering, processingandstructuring,smallervolumesofhigher qualityinformationaretransmitted.

Thismakesitpossibletosigni icantlysavedata transmissionenergywithoutoverloadingthenet‐workwithredundantunnecessaryinformation.These underwatervehiclesmustbereplacedperiodicallyto rechargepowersuppliesandperformmaintenance. AthigherlevelsoftheUSN’shierarchytherearesur‐facebuoysthatreceiveacousticsignalsunderwater fromtheUUVsand,usingradiosignals,transmitinfor‐mationabovethewatertoterrestrialcommunication nodes.Thesebuoyswithradioandacousticcommuni‐cationcanhaveeitherautonomouspowersourcesor bepoweredbynearbyalternativeenergysources.

Inturn,theterrestrialcommunicationnodes transmitinformationusingradiosignalsorbywires. Asaresult,alldata lowsthroughthemainnodeat thehighestlevelofthehierarchytotheterrestrial monitoringstation,wheretheinformationisanalyzed oncomputersandfurtherstoredonservers.Inaddi‐tion,theinformationisalsoprocessedandstructured onthebuoysandterrestrialcommunicationnodes,as ontheUUVs.Thenumberofhierarchylevelsimple‐mentedonUUVs,buoysandterrestrialcommunica‐tionnodesmayvarydependingonspeci iccondi‐tions,theselectednetworktopology,therequireddata transmissiondistance,thedistanceofdatacollection fromtheshoreandthemonitoringstationandmany otherfactors.Herewith,thefewerthehierarchylevels and,accordingly,datatransmissionstages,themore powerfulthesignaltransmitters,powersuppliesand computingcapabilitiesofnodesmustbetosimultane‐ouslyprocessalargeamountofinformationandsend itoverlongdistances.Thiswillsubstantiallyaffectthe overallcostofthenetworkandthesigni icanceofthe lossofitsindividualelements.Ontheotherhand,with asmallernumberofsequentiallyconnectedlevels,

reliabilityandfaulttolerancewillincreaseinacertain way.Thispaperdoesnotconsidercostoptimization ofthenetworkstructure.However,itshouldbeborne inmindthatusingalargenumberofsimpleand cheapelementswillcostlessthanasmallernumber ofexpensiveones,sincethecostofnodesincreases exponentiallywiththeincreaseinthenumberofinput signalsandtherequireddatatransmissionrange.This patternisevenmorepronouncedwhenitisnecessary toreserveelementsofcertainlevelsofthehierarchy.

WhencreatinganUSN,itsstructurecanbe denotedbythevector X withdimension �������� +1, whichcorrespondstothetotal(pre‐selected)num‐berofhierarchylevelsandazerolevel.Eachvariable ofthisvector ���� (��=0,1,…,��max)correspondsto theselectednumberofnodesonthe i‐thlevelofthe hierarchy.Inturn,thenumberofnodes���� atthe i‐th levelofthehierarchycanbechosenaccordingtothe condition(1),

sinceeachnodeofagivenhierarchylevel(exceptzero) musthaveatleast2inputs(���� ≥2,��=1,…,��max), sothatthedimensionofthelevelsdecreasesasinfor‐mationmovestotheupperlevel.Atthesametime, ���� max =1,sincethereisonlyonemainnodeofthe systematthelast(highest)levelofthehierarchy.Also, atthepenultimatelevelofthehierarchy(��max−1),the numberofnodesmustbeatleast2(���� max−1 ≥2).

If ���� nodesareselectedateach i‐thlevelofthe structurehierarchy,thenumberofinputs���� foreach nodecanbecalculatedbasedonthedependence(2)

(2)

Ifthecalculatedvalueof ���� isaninteger,then allnodesatagivenlevelofthehierarchywillhave thegivennumberofinputs.Otherwise,thenumberof nodeinputsiscalculatedasfollows.Atagivenlevel ofhierarchytherewillbenodeswiththenumberof inputsequaltothelargestintegerlessthan ����,and withthenumberofinputsequaltothesmallestinteger greaterthan����.Inthiscase,thenumberofnodeswith thenumberofinputsequaltothesmallestinteger greaterthan ����,asapercentageofthetotalnumber ofnodesofagivenhierarchylevel,willbeequaltothe fractionalpartofthecalculatednumber����

Forexample,thestructureoftheUSNforthenum‐berofinitialsensors(informationsources)��0 =13 andthreehierarchylevels(��max =3)canbeschemat‐icallydepictedinFig.2.

Thenodesofthesystemaresequentiallycon‐nectedbycommunicationchannels,startingfromthe 1stlevelofthehierarchytothelast��max.Atthesame time,nodesofthelevel(��−1)areconnectedonlyto nodesofthelevel i,takingintoaccountthenumberof inputsofthelatter.Theoutputofeachnodeofthelevel (��−1)canbeconnectedtoonlyoneinputofthenode ofthelevel i.

SchematichierarchicalstructureoftheUSN with ��0 =13 and ��max =3

Foragivennetwork,thevector X willhavetheform X ={13,5,2,1}. (3)

Sincethemaincomponentsofthenetworkoper‐ateinharshunderwaterenvironments,wherevarious typesofmalfunctionsandfailuresoccurquiteoften, themostimportanttaskisprovidingthespeci ied fault‐tolerantqualitiestoextendtheUSNlifeandmax‐imizetheeffectiverealizationofitsinternalpotential. Toensuretherequiredfaulttolerancemarginofan underwatersensornetwork,itisnecessarytosyn‐thesizeitshierarchicalstructureusingtheadvanced methodproposedbytheauthors,themainaspectsof whicharediscussedinthenextsubsection.

3.2.BasicAspectsoftheDesigningMethodofFault‐tolerantStructuresforUnderwaterSensorNet‐works

Faulttoleranceofanunderwatersensornetwork istheabilitytomaintainitsfullorpartialfunctionality afterthefailureofoneormoreofitscomponents [56,58].Faulttoleranceisdeterminedbythenumber ofsinglefailuresofthecomponentelements(malfunc‐tions)ofthesystem,aftertheoccurrenceofwhichthe operabilityofthesystemasawholeisstillmaintained. Thebasicleveloffaulttoleranceimpliesprotection againstfailureofanyelement.Therefore,themain waytoincreasefaulttoleranceisredundancy.This approachhasbeensuccessfullyusedtomanagefault toleranceandsurvivabilitybothinUSNsandinanum‐berofothercriticalinfrastructurefacilities[59,60]. Redundancyismosteffectivelyimplementedinhard‐ware,throughreservation.Inthiscase,failuresdue towearandagingarenotconsidered,sinceforthe mainelementsofthesystem,theenergyreserveof thepowersourcesisusedupmuchearlierthanthe intendedoperatinglife.Themainreasonforsystem failurebeforethepowersupplyrunsoutisrandom failurescausedbyharshnetworkoperatingenviron‐ment.

TodeterminethefaulttoleranceofaUSNwitha branchedhierarchicalstructure,itisnecessarytocal‐culatethemaximumnumberofcyclesofitsoperation ��max beforefailureoccursinconditionsofperiodic malfunctionsofitsindividualelements.Ifitisnec‐essarytodeterminethemaximumoperatingtimeof thesystembeforefailure,theoperatingcyclescanbe quiteeasilytranslatedintotime,knowingthedura‐tionofonecycle.BytheUSNfailurewemeanthe inabilitytotransmitacertainnumberofsignals(a certainpercentageofinformation)throughitsnodes andchannels.Forexample,asystemcanbeconsid‐eredoperationalaslongasittransmitssignalsfrom morethan50%oftheinitialmeasurementsensors. Ifinformationistransmittedfromnomorethan50% orlessofthesensors,thenitcanbeconsideredthat asystemfailurehasoccurred.Sincethelevelsofthe USNhierarchyareconnectedtoeachotherinseries, itisobviousthatthefailureoftheentiresystemcan occurasaresultofthefailureofatleastoneofits hierarchylevels.Inturn,thiscanhappenwhen50% ofthenodesorchannels(ornodesandchannels)of agivenhierarchylevelaredownordamageddueto disturbances.

Failureordamageofanyonenode(orchannel)of anyhierarchylevelwillbecalledamalfunctioninthe operationofthishierarchylevel.Thus,afailureofa certainhierarchylevel(thatcorrespondstothefailure ofthewholesystem)canoccurasaresultofsequential malfunctions,thenumberofwhichisequaltothe(pre‐speci ied)criticalnumberofnodes������ ofagiven i‐th hierarchylevel(��=0,1,…,��max).Forexample,when selectingacriticalnumberof50%ofsignalsfromall sensors,foralevelwith10nodes,thefailurewillbe consideredthemalfunctionsof5ormorenodes(������ ≥ 0.5���� ≥5).

Theprobabilityofamalfunctionoccurringateach speci icleveloftheUSN��M�� canbepresetorcalculated basedontheaveragevalueofthenumberofoperation cyclesbetweensinglemalfunctions��M�� (determined experimentally)inaccordancewiththeexpression(4)

(4)

Inturn,theprobability��M�� candiffersigni icantly atdifferenthierarchicallevelsoftheUSN,whichis causedbydifferentpropertiesoftheelementsand differentenvironmentalconditionsinwhichtheseele‐mentsarelocatedandoperate.Forinstance,thelow‐est(zero)levelofthehierarchy,whichincludessen‐sorsfortheinitialmeasurementofquantities,hasthe highestprobabilityofamalfunctionoccurring,since, duetotheharshconditionsofbeingintheunderwater environment,itssensorscanquiteoftenfaildueto mechanicaldamageorlossconnectionswithnodesof higherlevelsofthesystem.Thelevelswithunderwa‐tervehiclesandbuoysarealsolocatedinaggressive underwaterandsurfaceenvironments,respectively; however,theyhavelowerprobabilityvalues ��M�� due totheirhigherinherentreliability.

Figure2.

Figure3. AhomogeneousMarkovchainforcalculating theprobabilityoffailureofthei‐thleveloftheUSN.

Figure4. AhomogeneousMarkovchainforcalculating theprobabilityoffailureofthelast(highest)levelofthe USN.

Asforthelevelswiththeterrestrialcommunica‐tionnodesincludingthehighestlevelwiththemain node,theirprobabilityvalues ��M�� aremuchlower, sincetheyareonthegroundandhaveafairlyhigh reliability.

Tocalculatetheprobabilityoffailure ��F�� ofthe i‐thleveloftheUSN,itisadvisabletouseasimple homogeneousMarkovchain,thestructureofwhichis showninFig.3[61].

Thestate S0 correspondstotheabsenceofamal‐functionwhenperformingthenextoperatingcycle. Ifthe irstmalfunction(afailureofonenode)occurs duringtheoperationofthesystematthe i‐thlevel ofthehierarchy,thenthetransitiontothestate S1 is performed.Theprobabilityofthistransitionis ��M��. Onthenextcycle,withtheprobability ��M��,asecond malfunction(whichcorrespondstotheinoperative stateoftwonodesofthislevel)mayoccuratthislevel ofthehierarchy(transitiontothestate S2)orwiththe probability1−��M�� nomalfunctionwilloccur,which willcorrespondtothepreservationofthestate S1.In turn,returningfromthestate S1 tothepreviousstate S0 isimpossible.Afailureofthewholelevelcorre‐spondstothe S������ state,intowhichthesystemwillfall after������ malfunctionsoccuratthe i‐thhierarchylevel (i.e.,acriticalnumberofnodes������ failsequentiallyfor agivenhierarchylevel).Transitionsfromthestate S������ totheotherstatesarenotpossible.Forthecalculation, weassumethatthesystemmovesfromthestate S������ tothisstatewiththeprobability1.

Herewith,forthelast(highest)leveloftheUSN’s hierarchy,onwhichthereisasinglemainnode(���� = 1),theMarkovchainwillhavetheformpresentedin Fig.4.

Todescribetheprobabilitiesoftransitionsfrom statetostateatthe i‐thlevelofthehierarchy(i =0, 1,…, imax),itisadvisabletousematricesoftransition probabilities R������.Asanexample,forhierarchylevels withacriticalnumberofnodes X���� =2, X���� =3, X���� =4, X���� =5,thesematriceshavetheform:

Theprobabilityoffailure p���� ofthe i‐thlevelof theUSNistheprobabilityoftransitionfromtheinitial state S0 tothestate S������,i.e.isequaltotheconditional probabilitylocatedinthelastcolumnofthe irstrow (upperrightcornerofthematrixoftransitionproba‐bilities)[61].Atthebeginningoftheoperationofthe USN(atthe“zero”operatingcycle),thisprobabilityis zero.

Analyzingexpressions(5)‐(8)itcanbeconcluded thatforacertainlevelofthehierarchy,thematrix oftransitionprobabilitieswillhaveanorderofone greaterthanthecriticalnumberofnodesinagiven hierarchylevel(X���� +1).Thus,forthelast(highest) leveloftheUSNwithasinglemainnode(X�������� =1), thematrixoftransitionprobabilitieswillbeof2nd order:

Inthiscase,forthematrix(9)alreadyatthebegin‐ningofoperation pFimax = pMimax

Inturn,theprobabilityoffailureoftheentiresys‐tem P��Σ canbecalculatedbasedontheexpression (10),sinceallthelevelsofthehierarchyareconnected inseries.

where��F�� istheprobabilityoffailureofthe i‐thlevelof theUSN;��F��max istheprobabilityoffailureofthelast (highest)leveloftheUSN.

To indtheprobabilityoffailureofthe i‐thlevel ofthesystem(i =0,1,…, imax)onthe N‐thcycle,itis necessarytoraiseitsmatrixoftransitionprobabilities tothe N‐thintegerpower:���� ������.

Thus,tocalculatethemaximumnumberofoper‐atingcycles ��imax ofthe i‐thleveloftheUSNbefore failureoccurs,itisnecessarytodeterminethepower towhichthematrixoftransitionprobabilitiesofa givenlevelmustberaisedsothattheprobabilityinthe lastcolumnofthe irstrowofthematrixisequalto one(p���� =1).Toreducecalculations,insteadofone intheupperrightcornerofthematrix,wecanuse aprobabilityof0.999(p���� ≥ 0.999).Forexample,if theprobabilityofamalfunctionatthe i‐thlevelofthe hierarchyis p���� =0.7,thenthevalueofthemaximum numberofoperationcyclesofthislevelforthegiven matrices R1, R2, R3, R4, R5,respectively,willbe:��max =6,��max =9,��max =11,��max =13,��max =15.

Inturn,tocalculatethemaximumnumberofcycles ofoperationbeforefailureoftheentiresystem��Σmax, itisnecessarytodeterminethepowertowhichthe matricesoftransitionprobabilitiesofalllevelsmust beraisedsothattheprobabilityoffailureoftheentire systemisgreaterthanorequalto0.999(����Σ ≥0.999)

Analyzingtheobtainedvalues N��max,itcanbe arguedthatforthesameprobabilityvalue p����,the greaterthecriticalnumberofnodes X���� atthe i‐th levelofthehierarchy,thegreaterthevalueofthe maximumnumberofcyclesbeforefailure N�������� of thislevel.Inaddition,increasingthenumberoflevels ofthehierarchy i������ willsigni icantlyincreasethe probabilityoffailureoftheentiresystem P��Σ

Thus,toincreasethenumberofcyclestofailure, twomainwayscanbedistinguished:1)increasing thecriticalnumberofnodesateachspeci iclevelof thehierarchy;2)reducingthenumberoflevelsofthe systemhierarchy.

Herewith,thesecondwayinsomecasesmaynot givethedesiredresultsduetothepresenceofinitial restrictionsonthedistanceofsignaltransmissionand onthetypesofnetwork’selementsused.Forexample, ifthereisonlyacertaintypeofelements(sensors, UUVs,buoysandothernodes)andagivendistancefor transmittinginformationtoaterrestrialmonitoring station,thentocreateanetworkitwillbenecessaryto formagivennumberofhierarchylevels,whichcannot bereduced.

Therefore,toensureagivennumberoftheUSN operationcycles(oroperatingtime)underdifferent initialconditions,themosteffectivewayistoincrease thecriticalnumberofnodesatspeci icnetwork’slev‐elsthroughredundancy.

Takingintoaccounttheexpression(10),theprob‐abilityoffailureoftheentiresystem P��Σ isalways greaterthantheprobabilityoffailureofeachindi‐viduallevel p����,and,accordingly,thelevel,forwhich thisvalueisthegreatest.Therefore,toincreasethe numberofoperationcycles(oroperatingtime)before failureoftheentiresystem,itis irstnecessaryto reserveelementsofthelevelwiththesmallestvalue ofthisquantity.

Atthesametime,sinceitisunknownwhichnode willfail,inordertoensureastableincreaseinthe criticalnumberofnodesatacertainlevel,itisnec‐essarytoreserveallnodesatthislevel.Forexample, ifthereare10nodesatacertainUSN’slevelandthe criticalnumberofnodesis5(whenchoosing50%), thenforredundancyattheinitialstageitisnecessary toduplicateall10nodes.Then,therewillalreadybe 20nodesatthislevel,andthecriticalnumberofnodes isguaranteedtoincreaseto10.Ifthisnumberwill bestillnotenoughtoensurethegivennumberof operationcycles,thenitisnecessarytocontinueto sequentiallyreservenodes,withstepbystepincreas‐ingtheirnumberto30,40,andsoon.

Next,basedontheaboveprinciples,weformu‐latethemethodfordevelopmentofthefault‐tolerant structuresforUSNs.

3.3.Mainstepsofthedesignmethodoffault‐tolerant structuresforunderwatersensornetworks

Theauthors’proposeddesignmethodoffault‐tolerantstructuresforUSNsconsistsofthefollowing sequentialsteps.

Step1. Initialization.Atthisstep,theinitialUSN structurewithoutredundancyisformed.Thespeci‐iednumberofinitialsensors X0 atthezerolevelisset. Dependingonthecharacteristics(signaltransmission range,frequency,etc.)oftheusedsensorsandother basicnetworknodes,aswellasthespeci iedinforma‐tiontransmissionrangetotheterrestrialmonitoring station,thenumberoflevelsofthenetwork’shier‐archy imax isdeterminedandthenumberofnodes X�� ateach i‐thlevel(i =1,…, imax)isset.Inturn,to buildanetworkwithahierarchicaltree‐likestruc‐turethenumberofnodes X�� atthe i‐thlevelofthe hierarchyshouldbechosenaccordingtothecondition (1).Moreover,thenumberoffaultychannelsfrom initialsensors(inpercentage)isselected,atwhicha network’sfailurewillbeconsidered.Further,based onthisnumberthecriticalnumberofnodes X���� for each i‐thhierarchylevel(i =0,1,…, imax)isde ined. Also,theprobability p���� ofamalfunctionoccurring ateach i‐thlevel(i =0,1,…, imax)oftheUSNisset, thatcanbecalculatedbasedonexpression(4).Finally, therequirednumberoftheUSN’soperationcycles beforefailure��Σmax��,whichmustbeensured,isset. IftherequiredUSN’soperationtimebeforefailureis set,thenitisalsonecessarytosetthedurationofone cycle.

Step2. Calculationoftherealvalueofthemax‐imumnumberofoperationcyclesbeforefailure ��Σmax�� fortheUSNwithagivenstructure.Atthisstep, Markovchainsandcorrespondingmatricesoftransi‐tionprobabilities R������ areconstructedforeach i‐th levelofthesystem(i =0,1,…, i������).Herewith,each matrixhasanorderofonegreaterthanthecritical numberofnodesinacorrespondinghierarchylevel (X���� +1).

Next,thepowerisdetermined,towhichitisnec‐essarytoraisethegivenmatricesofalllevelssothat theprobabilityoffailureoftheentiresystembecomes greaterthanorequalto0.999 (����Σ ≥0.999).The valueofthispoweristherealvalueofthemaximum numberofoperationcyclesbeforefailure ��ΣmaxR for theUSNwithagivenstructure.Inturn,theprobability offailureoftheentiresystem P��Σ iscalculatedbased ontheexpression(10).

Step3. Checkingthecompletionoftheprocessof designingfault‐tolerantstructureoftheUSN.Atthis step,thevaluecalculatedinthepreviousstep��ΣmaxR iscomparedwiththesetinthe irststepvalue��ΣmaxD Ifthecondition��ΣmaxR ≥ NΣmaxD issatis ied,thengo tostep12.Otherwise,gotothenextstep.

Step4. Calculationofthemaximumnumberof operationcyclesbeforefailure��imax foreachindivid‐ual i‐thleveloftheUSN.Atthisstep,foreachindividual i‐thlevel(i =0,1,…, imax),thepowerisdetermined, towhichitisnecessarytoraiseitsmatrixoftransi‐tionprobabilities RXic sothattheprobabilityoffailure ofthislevelbecomesgreaterthanorequalto0.999 (������ ≥0.999).Thevalueofthispoweristhevalue ofthemaximumnumberofoperationcyclesbefore failure��imax

Step5. SelectingtheUSN’slevelswhosemaximum numberofoperationcyclesbeforefailure��imax isless thanthenumber ��ΣmaxD fortheentiresystemsetin step1.Atthisstep,thecalculatedinthepreviousstep values��imax (i =0,1,…, imax)arealternatelycompared withthesetinthe irststepvalue��ΣmaxD.Thoselevels, forwhichthecondition ��imax <��ΣmaxD ismet,are selectedforfurtherreservationinthenextstep.Ifthis conditionissatis iedforatleastonelevel,thengoto step6.Otherwise,gotostep10.

Step6. ReservingoftheUSNlevels’elements selectedatstep5untileachofthemhasamaxi‐mumnumberofoperationcyclesbeforefailure��imax greaterthanthenumber��ΣmaxD fortheentiresystem setinstep1.Atthisstep,astage‐by‐stagereserving ofallelementsofeachselectedleveliscarriedoutto increasethecriticalnumberofnodes������.First,allele‐mentsoftheselectedlevelareduplicatedtoincrease thecriticalnumberofnodes X���� by2times.Ifthisisnot enough,thenoneextraisaddedagaintoeachnodeto increasethecriticalnumberofnodes X���� by3times, andsoon.Afteralllevelshaveamaximumnumberof operationcyclesbeforefailure��imax greaterthanthe number��ΣmaxD fortheentiresystemsetinstep1,the transitiontothenextstepiscarriedout.

Step7. Calculationoftherealvalueofthemaxi‐mumnumberofoperationcyclesbeforefailure��ΣmaxR fortheUSNwithagivenstructure.Thisstepisper‐formedinthesamewayasstep2.

Step8. Checkingthecompletionoftheprocess ofdesigningfault‐tolerantstructureoftheUSN.This stepiscarriedoutinthesamewayasstep3.Ifthe condition ��ΣmaxR ≥��ΣmaxD issatis ied,thengoto step12.Otherwise,gotothenextstep.

Step9. Calculationofthemaximumnumberof operationcyclesbeforefailure��imax foreachindivid‐ual i‐thleveloftheUSN.Thisstepisperformedinthe samewayasstep4.

Step10. SelectingtheUSN’slevelwhosemaximum numberofoperationcyclesbeforefailureisthesmall‐estamongallthelevels.

Step11. ReservingofelementsoftheUSN’slevel selectedatstep10.Atthisstep,oneextranodeis addedtoeachexistingnodeforincreasingthecritical numberofnodes X����.Afterthis,gotostep7.

Step12. Completionoftheprocessofdesigning fault‐tolerantstructureoftheUSN.Afterthis,the implementationandcon igurationoftheUSNwith designedstructurecanbecarriedout.

Theblockdiagramoftheproposeddesigning methodoffault‐tolerantstructuresforUSNsisshown inFig.5.

Tostudytheeffectivenessoftheproposedmethod, thenextsectionpresentstheexampleofdesigning thefault‐tolerantstructureofthespeci icunderwater sensornetwork.

4.DesigningtheFault‐TolerantStructureof theSpecificUnderwaterSensorNetwork

Toconductanumericalexperimentinthissection, aspeci icUSNwasselectedconsistingofazerolevel (initialsensors’level)andfourmainhierarchylevels (unmannedunderwatervehicles’level,buoys’level and2levelsofterrestrialcommunicationnodes).At theinitializationstageoftheproposedmethod(step 1),theUSN’sinitialstructurewasformedwithout redundancyandthemainparametersweresetasfol‐lows.Inturn,thenumberofinitialsensors X0 =16,the numberoflevelsofthenetworkhierarchy�������� =4 Thegivensystemisconsideredoperationalaslongas ittransmitssignalsfrommorethan50%oftheinitial sensors.TherequirednumberoftheUSN’soperation cyclesbeforefailure��ΣmaxD =720.Inthisparticular example,thesignaltransmissionduringthenetwork operationiscarriedoutinsuchawaythatallthe sensorsarepolledonceperhour.Thus,thisrequired numberofworkingcyclesbeforefailure(720)will allowthenetworktooperateuninterruptedlyfor30 days(1month).Forconvenience,themainparameters oftheformedinitialnetwork’sstructure,includingthe totalnumber X�� andcriticalnumber X���� ofnodes,as wellastheprobabilities p���� ofamalfunctionoccur‐ringateach i‐thlevelofthehierarchy,arepresented inTable1

ThusfortheUSNwiththegiveninitialstructure, thevector X hastheform

X ={16,8,4,2,1}. (11)

Atthesecondstepthecalculationoftherealvalue ofthemaximumnumberofoperationcyclesbefore failure ���������� wasperformedfortheUSNwitha givenstructure.

Figure5. Ablockdiagramofthedesigningmethodoffault‐tolerantstructuresforUSNs.

Inparticular,theMarkovchainsandcorrespond‐ingmatricesoftransitionprobabilities R8, R4, R2, R1, and R1′ wereconstructedforeach i‐thlevelofthe system(i =0,1,…,4).Herewith,matrices R1 and R1′ arethesecond‐ordermatricesforthe3rdand4th levelswiththecorrespondingprobabilityvalues p��3 and p��4.Moreover,eachoftheformedmatriceshad anorderofonegreaterthanthecriticalnumberof nodesinthecorrespondinglevels(X���� +1)presented inTable1

Table1. MainparametersoftheinitialUSN’sstructure

i Typeofhierarchylevel pMi Xi Xic

0 Initialsensors 0.025 16 8

1 UUVs 0.0125 8 4

2 Buoys 0.01 4 2

3 Terrestrialcommunication nodes 0.001 2 1

4 Mainterrestrial communicationnode 0.0005 1 1

Table2. MainparametersoftheUSN’sstructureatthe 1stiteration

i Typeof hierarchylevel ������ ���� ������ ��imax

0 Initialsensors 0.025 16 8 781

1 UUVs 0.0125 8 4 1045

2 Buoys 0.01 4 2 924

3 Terrestrial communication nodes 0.001 2 1 6955

4 Mainterrestrial communication node 0.0005 1 1 13914

Then,thepowerwasdetermined,towhichitwas necessarytoraisethegivenmatricesofalllevelsso thattheprobabilityoffailureoftheentiresystem reachedthevalueof0.999(P��Σ ≥0.999).Inturn, usingtheexpression(10)andallconstructedmatrices (R8, R4, R2, R1,and R1′),thisvaluewasfoundtobe ��ΣmaxR =439

Next,atthethirdstep,acomparisonwasmadeof therealvalueofthemaximumnumberofoperation cycles ��ΣmaxR withtherequiredvalue ��ΣmaxD.Since, therealvaluecalculatedatthepreviousstepwasless thantherequiredvalue(��ΣmaxR <��ΣmaxD),thetransi‐tiontothenextstepwasperformed(step4).

Atstep4thecalculationofthemaximumnum‐berofoperationcyclesbeforefailure ��imax wasper‐formedforeachindividual i‐thleveloftheUSNwith agivenstructure.Inthiscase,foreachindividual i‐th level(i =0,1,…,��max),thepowerwasdetermined,to whichitwasnecessarytoraiseitsmatrix�������� sothat theprobabilityoffailureofthislevelreachedthevalue of0.999(������ ≥0.999).Inturn,usingseparatelytaken constructedmatrices(R8, R4, R2, R1,and R1′),these valueswerefoundandsummarizedinTable2.

Atstep5theselectionoftheUSN’slevelswas carriedout,whosemaximumnumberofoperation cyclesbeforefailure��imax waslessthantherequired number��ΣmaxD fortheentiresystem.Since,eachlevel initiallyalreadyhadavalue��imax greaterthan��ΣmaxD (condition ��imax <��ΣmaxD wasnotmet),thenthe transitiontostep10wasperformed.

Next,atthe10thsteptheUSN’slevelwasselected withthesmallestvalueofmaximumnumberof operationcyclesbeforefailureamongallthelevels. Thislevelwasthezerolevel(i =0)oftheinitialsensors with��0max =781(Table2).

Table3. MainparametersoftheUSN’sstructureatthe 2nditeration

Typeof hierarchylevel

Table4. MainparametersoftheUSN’sstructureatthe 3rditeration

Typeof hierarchylevel

Then,atstep11thereservingofelementsofthe USN’szerolevelwascarriedout.Inparticular,one extrasensorwasaddedtoeachexistingsensorto increasethecriticalnumberofnodes ��0�� from8to 16.Afterthat,atransitiontothenextiterationofthe methodwasperformedand,accordingly,areturnto step7.

Calculatedatstep7,therealvalueofthemaximum numberofoperationcyclesfortheentireUSNwiththe newstructurewas��ΣmaxR =535,whichwaslessthan therequiredvalue��ΣmaxD.Therefore,furtherstepsof themethodwereimplemented.

Atstep9thecalculationofthe ��imax valuewas performedforeachindividual i‐thleveloftheUSN withagivenstructure.Thesevalues,aswellasnew USN’sparameters,weresummarizedinTable3

Forthegivennetwork’scon iguration(Table 3), the2ndlevel(buoyslevel)hadthelowestvalueof N������.Afterde iningthislevelatthe10thstep,its elementswerereserved(oneextrabuoywasaddedto eachexistingbuoy)atstep11.Then,atransitiontothe next(3rd)iterationofthemethodwasperformedand, accordingly,areturntostep7.

Thecalculatedvalueatstep,7real��ΣmaxR forthe entireUSNwiththenewstructurewas635,whichwas lessthantherequiredvalue��ΣmaxD.Therefore,further stepsofthe3rditerationwereimplemented.

Atstep9thecalculationofthe ��imax valuewas performedforeachindividual i‐thleveloftheUSN withagivenstructure.Thesevalues,aswellasnew USN’sparametersweresummarizedinTable4.

Table5. MainparametersoftheUSN’sstructureatthe 4thiteration

Table6. Changingofthevector X duringthe implementationofthemethod

Numberofiteration VectorX ��ΣmaxR

1 {16,8,4,2,1}

{32,16,8,2,1}

Forthegivennetwork’scon iguration(Table 4), the1stlevel(UUVs’level)hadthelowestvalueof ��max.Afterde iningthislevelatthe10thstep,its elementswerereserved(oneextraUUVwasaddedto eachexistingUUV)atstep11.Then,atransitiontothe next(4th)iterationofthemethodwasperformedand, accordingly,areturntostep7.

Thecalculatedatstep7realvalue ��ΣmaxR forthe entireUSNwiththenewstructurewas761,therefore thecondition��ΣmaxR ≥��ΣmaxDwassatis ied.Thus,the transitiontostep12wasperformedandtheprocess ofdesigningfault‐tolerantstructureoftheUSNwas completed.

ThusfortheUSNwiththedesignedfault‐tolerant structure,thevector X hastheform

X ={32,16,8,2,1}. (12)

Inturn,forclarity,themainparametersofthe developedfault‐tolerantnetwork’sstructurearepre‐sentedinTable5

Further,toanalyzetheresultsobtained,Table 6 showshowthevector X oftheUSN’sstructure changedoverthecourseofiterationsduringthe implementationofthemethod,aswellasthereal valueofthemaximumnumberofoperationcycles beforefailure��ΣmaxR

Also,thegraphofchangesintherealvalue��ΣmaxR fromiterationsisshowninFig.6

AscanbeseenfromTable 6 andFig. 6,thefault‐tolerantstructurewiththerequirednumberofoper‐ationcyclesbeforefailure(��ΣmaxD =720)forthe givenspeci icUSNwasbuiltin4iterations.Thisfact con irmsthattheproposedmethodallowsthedevel‐opmentoffault‐tolerantstructureswithaguaran‐teedachievementofthedesirednumberofoperation cyclesbeforefailureatrelativelylowcomputational costs.Herewith,reservingtheelementsofthecorre‐spondinghierarchicallevelsintheproperordermade itpossibletosystematicallyincreasetherealvalue ofthemaximumnumberofoperationcyclesbefore failure ��ΣmaxR fromiterationtoiterationuntilthe requiredvalue ��ΣmaxD isachievedwithoutexcessive redundancy.Thiswillminimizethecostofthecon‐structednetworkwiththenecessaryreservationof elements.

Figure6. Changingoftherealvalue ���������� duringthe implementationofthemethod.

Thus,thestrategyofsequentialreservingofele‐mentsinlevelswiththeleastnumberofoperation cyclesbeforefailure,whichisusedintheproposed method,hasafairlyhighef iciency.

Overall,theanalysisoftheresultsobtainedfrom theconductednumericalexperimentindicatesthat theproposedmethodenablesthedesignofunder‐watersensornetworks’structureswiththerequired faulttoleranceandminimalredundancy.Thisaf irms itsviabilityforutilizationinthedevelopmentofUSNs fordiversepurposes,aimingtoenhancereliabilityand reducecosts.

5.Conclusion

Thedevelopmentandeffectivenessstudyofthe methodofdesigningthefault‐tolerantstructures forunderwatersensornetworksbasedonMarkov chainsispresentedinthispaper.Theproposedby theauthorsdesigningmethodmakesitpossibleto createtheproperUSNs’structureswithaguaranteed provisionofthedesirednumberofoperationcycles beforefailureatreasonablecosts.Theemploymentof themathematicalapparatusofMarkovchainsincon‐junctionwiththestrategyofcorrectselectionofthe hierarchylevels’sequenceallowstoquiteaccurately determinethenetworkactualnumberofoperation cyclesbeforefailureaswellasperformtheef icient reservationwithoutexcessiveredundancy.

Theeffectivenessoftheproposedmethodwas assessedthroughaspeci iccasestudy,namelywhen creatingafault‐tolerantstructureofarealunderwater sensornetworkwiththepredeterminedparameters.

Theanalysisoftheobtainedresultsfromthe conductednumericalexperimentrevealsthatreserv‐ingtheelementsofthecorrespondinghierarchical levelsintheproperorderinaccordancewiththe method’smainstepsmakesitpossibletosystemati‐callyincreasetherealvalueofthemaximumnumber ofoperationcyclesbeforefailurefromiterationtoiter‐ationuptotheattainmentoftherequiredvaluewith‐outexcessiveredundancy.Moreover,forthisparticu‐larexample,only4iterationswereneededto indthe USN’sfault‐tolerantstructurewiththedesirednum‐berofoperationcyclesbeforefailure,whichcon irms thehighef iciencyofthemethodatrelativelylowcom‐putationalcosts.Thus,theresearchconductedinthis worksubstantiatesthehighpracticalityofemploying thedevelopedmethodforthecreationofunderwater sensornetworkstailoredtodiversepurposes,ensur‐ingapredeterminedleveloffaulttolerancewhile maintainingmoderatecosts.

Infurtherresearch,itisplannedtoconsider theissuesofoptimizingtheimplementationcostsof underwatersensornetworkswhileadheringtospeci‐iedfaulttolerancemargins.

AUTHORS

MaksimMaksimov –DepartmentofSoftwareand Computer‐integrationTechnologies,OdesaPolytech‐nicNationalUniversity,Odesa,Ukraine,65044,e‐mail: prof.maksimov@gmail.com.

OleksiyKozlov∗ –DepartmentofIntelligent InformationSystems,PetroMohylaBlackSea NationalUniversity,Mykolaiv,Ukraine,54003, e‐mail:kozlov_ov@ukr.net.

SerhiiRetsenko –DepartmentofArmament, UkrainianNavalInstituteNationalUniversity“Odesa MaritimeAcademy”,Odesa,Ukraine,65052,e‐mail: s.s.retsenko@gmail.com.

ViktoriiaKryvda –DepartmentofPowerSupply andEnergyManagement,OdesàPolytechnic NationalUniversity,Odesa,Ukraine,65044,e‐mail: kryvda@op.edu.ua.

∗Correspondingauthor

References

[1] A.Narwaria,A.P.Mazumdar,“Software‐De ined WirelessSensorNetwork:AComprehensiveSur‐vey”, JournalofNetworkandComputerApplications, vol.215,2023,103636.https://doi.org/ 10.1016/j.jnca.2023.103636

[2] M.M.Rahaman,M.Azharuddin,“Wirelesssensor networksinagriculturethroughmachinelearn‐ing:Asurvey”, ComputersandElectronicsinAgriculture, vol.197,2022,106928.https://doi.org/ 10.1016/j.compag.2022.106928

[3] Y.Wu.,etal.,“Epidemicspreadinginwireless sensornetworkswithnodesleepscheduling”, PhysicaA:StatisticalMechanicsanditsApplications, vol.629,2023,129204.https://doi.org/ 10.1016/j.physa.2023.129204

[4] E.Pievanelli,etal.,“Dynamicwirelesssensor networksforrealtimesafeguardofworkers exposedtophysicalagentsinconstructions sites,” 2013IEEETopicalConferenceonWireless SensorsandSensorNetworks (WiSNet),Austin, TX,USA,2013,pp.55–57.doi:10.1109/WiSN et.2013.6488632.

[5] R.Elhabyan,W.Shi,M.St‐Hilaire,“Coverage protocolsforwirelesssensornetworks:Review andfuturedirections”, JournalofCommunicationsandNetworks, vol.21,no.1,2019,pp.45–60.doi:10.1109/JCN.2019.000005.

[6] M.Kumar,etal.,“OptimizationofWireless SensorNetworksInspiredbySmallWorldPhe‐nomenon”, 2015IEEE10thInternationalConferenceonIndustrialandInformationSystems (ICIIS),Peradeniya,SriLanka,2015,pp.66–70. doi:10.1109/ICIINFS.2015.7398987.

[7] R.G.Baldovino,I.C.Valenzuela,E.P.Dadios, “ImplementationofaLow‐powerWirelessSen‐sorNetworkforSmartFarmApplications”, IEEE 10thInternationalConferenceonHumanoid, Nanotechnology,InformationTechnology,CommunicationandControl,EnvironmentandManagement (HNICEM),BaguioCity,Philippines, 2018,pp.1–5,doi:10.1109/HNICEM.2018.86 66262.

[8] H.K.Sethi,etal,“IncrementalModelfor CompleteAreaCoverageinWirelessSensor Networks”, 2015InternationalConferenceon ComputationalIntelligenceandNetworks, Odisha,India,2015,pp.92–97.doi: 10.1109/CINE.2015.27.

[9] R.T.Tse,Y.Xiao,“APortableWirelessSen‐sorNetworksystemforreal‐timeenvironmental monitoring”, 2016IEEE17thInternationalSymposiumonAWorldofWireless,MobileandMultimediaNetworks (WoWMoM),Coimbra,Portugal, 2016,pp.1–6.doi:10.1109/WoWMoM.2016.75 23588.

[10] S.M.Kamruzzaman,etal.,“WirelessPositioning SensorNetworkIntegratedwithCloudforIndus‐trialAutomation”, 2017IEEE42ndConference onLocalComputerNetworks (LCN),Singapore, 2017,pp.543–546.doi:10.1109/LCN.2017.68.

[11] I.A.Sawaneh,I.Sankoh,D.K.Koroma,“Asurvey onsecurityissuesandwearablesensorsinwire‐lessbodyareanetworkforhealthcaresystem”, 201714thInternationalComputerConferenceon WaveletActiveMediaTechnologyandInformationProcessing (ICCWAMTIP),Chengdu,China, 2017,pp.304–308.doi:10.1109/ICCWAMTIP. 2017.8301502.

[12] J.Villadangos,etal.,“DistributedOpportunis‐ticWirelessMapplicationingSystemtowards SmartCityServiceProvision”, 2021IEEESensors, Sydney,Australia,2021,pp.1–4.doi:10.1109/ SENSORS47087.2021.9639791.

[13] S.Li,etal.,“Surveyonhighreliability wirelesscommunicationforunderwater sensornetworks”, JournalofNetworkand ComputerApplications, vol.148,2019,102446. https://doi.org/10.1016/j.jnca.2019.102446

[14] M.Ahmed,M.Salleh,M.I.Channa,“Rout‐ingprotocolsbasedonprotocoloperationsfor underwaterwirelesssensornetwork:Asurvey”, EgyptianInformaticsJournal, vol.19,no.1,2018, pp.57–62.https://doi.org/10.1016/j.eij.2017.0 7.002

[15] K.K.Gola,etal.,“Anempiricalstudyon underwateracousticsensornetworksbasedon localizationandroutingapproaches”, Advances inEngineeringSoftware, vol.175,2023,103319. https://doi.org/10.1016/j.advengsoft.2022.10 3319

[16] G.Yang,etal.,“ChallengesandSecurityIssuesin UnderwaterWirelessSensorNetworks”, ProcediaComputerScience, vol.147,2019,pp.210–216.https://doi.org/10.1016/j.procs.2019.0 1.225

[17] I.F.Akyildiz,D.Pompili,T.Melodia,“Underwater acousticsensornetworks:researchchallenges”, AdHocNetworks, vol.3,no.3,2005,pp.257–279. https://doi.org/10.1016/j.adhoc.2005.01.004

[18] M.Dong,etal.,“Learningautomaton‐based energy‐ef icientandfault‐toleranttopologyevo‐lutionalgorithmforunderwateracousticsen‐sornetwork”, JournalofNetworkandComputer Applications, vol.217,2023,103690.https://do i.org/10.1016/j.jnca.2023.103690

[19] A.P.Das,S.M.Thampi,“Fault‐resilientlocaliza‐tionforunderwatersensornetworks”, AdHoc Networks, vol.55,2017,pp.132–142. https:// doi.org/10.1016/j.adhoc.2016.09.003

[20] R.R.Priyadarshini,N.Sivakumar,“Failure prediction,detection&recoveryalgorithms usingMCMCintree‐basednetworktopologyto improvecoverageandconnectivityin3D‐UW environment”, AppliedAcoustics, vol.158,2020, 107053.https://doi.org/10.1016/j.apacoust.2 019.107053

[21] T.R.Chenthil,P.J.Jayarin,“EnergyEf icientClus‐teringBasedDepthCoordinationRoutingProto‐colForUnderwaterWirelessSensorNetworks”, 2022InternationalConferenceonWirelessCommunicationsSignalProcessingandNetworking (WiSPNET),Chennai,India,2022,pp.370–375. doi:10.1109/WiSPNET54241.2022.9767124

[22] X.Liu,F.Zhou,“Energy‐Ef icientRoutingProto‐colBasedonDataDisseminationforUnderwater WirelessSensorNetwork” OCEANS2023 ‐Limer‐ick,Limerick,Ireland,2023,pp.1–5.doi:10.110 9/OCEANSLimerick52467.2023.10244378

[23] G.Qiao,etal.,“DistributedLocalizationBasedon SignalPropagationLossforUnderwaterSensor Networks”, IEEEAccess, vol.7,2019,pp.112985–112995.doi:10.1109/ACCESS.2019.2934978

[24] A.Sabra,W.‐k.Fung,P.Radhakrishna, “Con idence‐basedUnderwaterLocalization SchemeforLarge‐ScaleMobileSensor Networks”, OCEANS 2018MTS/IEEECharleston, Charleston,SC,USA,2018,pp.1–6.doi: 10.1109/OCEANS.2018.8604878

[25] F.Steinmetz,B.‐C.Renner,“FromtheLong‐RangeChannelintheOceantotheShort‐RangeandVeryShallow‐WaterAcousticChan‐nelinPortsandHarbors”, 2021FifthUnderwaterCommunicationsandNetworkingConference (UComms),Lerici,Italy,2021,pp.1–5.doi:10.1 109/UComms50339.2021.9598094

[26] D.Schützeetal.,“MiniaturizedSensorMod‐ulesforunderWaterApplicationsrealizedby PrintedCircuitBoardEmbeddingTechnology”, 2022IEEE9thElectronicsSystem-Integration TechnologyConference (ESTC),Sibiu,Romania, 2022,pp.49–54.doi:10.1109/ESTC55720.20 22.9939405

[27] G.Sangetal.,“Three‐WavelengthFiberLaser SensorWithMiniaturization,Integrationforthe SimultaneousMeasurementofUnderwaterpH, Salinity,Temperature,andAxialStrain”, IEEE TransactionsonInstrumentationandMeasurement, vol.72,2023,Artno.7006815,pp.1–15. doi:10.1109/TIM.2023.3309356.

[28] B.Mishachandar,S.Vairamuthu,“Anunderwater cognitiveacousticnetworkstrategyforef icient spectrumutilization”, AppliedAcoustics, vol.175, 2021,107861.https://doi.org/10.1016/j.apac oust.2020.107861

[29] H.Doletal.,“EDA‐SALSA:Developmentofaself‐recon igurableprotocolstackforrobustunder‐wateracousticnetworking”, OCEANS2023 ‐Lim‐erick,Limerick,Ireland,2023,pp.1–10.doi:10 .1109/OCEANSLimerick52467.2023.10244330.

[30] H.Li,etal.,“Securityandprivacyinlocalization forunderwatersensornetworks”, IEEECommunicationsMagazine, vol.53,no.11,2015,pp.56–62.doi:10.1109/MCOM.2015.7321972.

[31] X.Feng,Z.Wang,N.Han,“ProtectionResearchof SinkLocationPrivacyinUnderwaterSensorNet‐works”, IEEEINFOCOM2019-IEEEConference onComputerCommunicationsWorkshops (INFO‐COMWKSHPS),Paris,France,2019,pp.1–6.doi: 10.1109/INFOCOMWKSHPS47286.2019.9093 749.

[32] N.V.U.Reddy,“ReducingtheNetworkLatency toMaintainNetworkStabilityinUASNbyUsing Bio‐InspiredAlgorithms”, 2023SecondInternationalConferenceonAugmentedIntelligenceand SustainableSystems (ICAISS),Trichy,India,2023, pp.139–144.doi:10.1109/ICAISS58487.2023.1 0250497.

[33] S.Kaveripakam,R.Chinthaginjala,“Clustering‐baseddragon lyoptimizationalgorithm forunderwaterwirelesssensornetworks”, AlexandriaEngineeringJournal, vol.81,2023,

pp.580–598.https://doi.org/10.1016/j.aej.20 23.09.047

[34] O.V.Kozlov,Y.P.Kondratenko,O.S.Skakodub, “InformationTechnologyforParametricOpti‐mizationofFuzzySystemsBasedonHybridGrey WolfAlgorithms”, SNComputerScience, vol.3,no. 6,2022.463.https://doi.org/10.1007/s42979‐022‐01333‐4

[35] Y.P.Kondratenko,A.V.Kozlov,“Parametricopti‐mizationoffuzzycontrolsystemsbasedon hybridparticleswarmalgorithmswithelite strategy”, JournalofAutomationandInformation Sciences, vol.51,no.12,2019,NewYork:Begel HouseInc.,pp.25–45.DOI:10.1615/JAutomatIn fScien.v51.i12.40

[36] O.V.Kozlov,“OptimalSelectionofMembership FunctionsTypesforFuzzyControlandDeci‐sionMakingSystems”,in:Proceedingsofthe 2ndInternationalWorkshoponIntelligentInfor‐mationTechnologies&SystemsofInformation SecuritywithCEUR‐WS,Khmelnytskyi,Ukraine, IntelITSIS2021,CEUR‐WS,Vol‐2853,2021,pp. 238–247.

[37] “Advancetrendsinsoftcomputing”,M.Jamshidi, V.Kreinovich,J.Kacprzyk,Eds.Cham:Springer‐Verlag,2013.DOIhttps://doi.org/10.1007/978‐3‐319‐03674‐8

[38] J.Kacprzyk,Y.Kondratenko,J.M.Merigo,J.H. Hormazabal,G.Sirbiladze,A.M.Gil‐Lafuente,“A StatusQuoBiasedMultistageDecisionModel forRegionalAgriculturalSocioeconomicPlan‐ningUnderFuzzyInformation”,In:Y.P.Kon‐dratenko,A.A.Chikrii,V.F.Gubarev,J.Kacprzyk (Eds) AdvancedControlTechniquesinComplex EngineeringSystems:TheoryandApplications DedicatedtoProfessorVsevolodM.Kuntse‐vich.StudiesinSystems,DecisionandControl, Vol.203.Cham:SpringerNatureSwitzerland AG,2019,201‐226.DOI: https://doi.org/10.1 007/978‐3‐030‐21927‐7_10

[39] O.Kozlov,G.Kondratenko,Z.Gomolka,Y.Kon‐dratenko,“SynthesisandOptimizationofGreen FuzzyControllersfortheReactorsoftheSpe‐cializedPyrolysisPlants”,KharchenkoV.,Kon‐dratenkoY.,KacprzykJ.(Eds) GreenITEngineering:Social,BusinessandIndustrialApplications, StudiesinSystems,DecisionandControl,Vol 171,2019,Springer,Cham,373–396.https://do i.org/10.1007/978‐3‐030‐00253‐4_16

[40] I.Atamanyuk,J.Kacprzyk,Y.Kondratenko,M. Solesvik,“ControlofStochasticSystemsBased onthePredictiveModelsofRandomSequences”, In:Y.P.Kondratenko,A.A.Chikrii,V.F.Gubarev, J.Kacprzyk(Eds) AdvancedControlTechniques inComplexEngineeringSystems:Theoryand Applications. DedicatedtoProfessorVsevolodM. Kuntsevich. StudiesinSystems,DecisionandControl, vol.203.Cham:SpringerNatureSwitzerland AG,2019,105–128.https://doi.org/10.1007/97 8‐3‐030‐21927‐7_6

[41] Y.P.Kondratenko,O.V.Kozlov,“Mathematical ModelofEcopyrogenesisReactorwith FuzzyParametricalIdenti ication”, Recent DevelopmentsandNewDirectioninSoftComputingFoundationsandApplications, StudiesinFuzzinessandSoftComputing, vol.342,Lot iA.Zadehetal.(Eds.).Berlin, Heidelberg:Springer‐Verlag,2016,439‐451. https://doi.org/10.1007/978‐3‐319‐32229‐2_30

[42] Y.P.Kondratenko,O.V.Korobko,O.V.Kozlov, “FrequencyTuningAlgorithmforLoudspeaker DrivenThermoacousticRefrigeratorOptimiza‐tion”,in:K.J.Engemann,A.M.Gil‐Lafuente, J.M.Merigo(Eds.), LectureNotesinBusiness InformationProcessing,volume115ofModelingandSimulationinEngineering,Economics andManagement, Springer‐Verlag,Berlin,Hei‐delberg:2012,pp.270–279.https://doi.org/10 .1007/978‐3‐642‐30433‐0_27

[43] M.Dong,etal.,“Energy‐savingandFault‐tolerant TopologyforUnderwaterAcousticSensorNet‐works”, OCEANS2022, HamptonRoads,Hampton Roads,VA,USA,2022,pp.1–5.doi:10.1109/OC EANS47191.2022.9977158

[44] M.Hamidzadeh,N.Forghani,A.Movaghar,“A newhierarchalandscalablearchitectureforper‐formanceenhancementoflargescaleunder‐watersensornetworks”, 2011IEEESymposium onComputers&Informatics, KualaLumpur, Malaysia,2011,pp.520–525.doi:10.1109/ISCI .2011.5958970

[45] G.H.Adday,etal.,“FaultToleranceStructuresin WirelessSensorNetworks(WSNs):Survey,Clas‐si ication,andFutureDirections”, Sensors 2022, 22,6041.https://doi.org/10.3390/s22166041

[46] L.Vihman,M.Kruusmaa,J.Raik,“Systematic ReviewofFaultTolerantTechniquesinUnder‐waterSensorNetworks”, Sensors 2021,21,3264. https://doi.org/10.3390/s21093264

[47] N.Goyal,M.Dave,A.K.Verma,“Anovelfault detectionandrecoverytechniqueforcluster‐basedunderwaterwirelesssensornetworks”, Int.J.Commun.Syst. 2018,vol.31,pp.1–14.https: //doi.org/10.1002/dac.3485

[48] Z.Zhou,etal.,“E‐CARP:AnEnergyEf icient RoutingProtocolforUWSNsintheInternetof UnderwaterThings”, IEEESensorsJournal, vol. 16,no.11,pp.4072–4082,2016.doi:10.1109/ JSEN.2015.2437904

[49] Y.Nohetal.,“HydroCast:PressureRoutingfor UnderwaterSensorNetworks”, IEEETransactionsonVehicularTechnology, vol.65,no.1, 2016,pp.333–347.doi:10.1109/TVT.2015.2 395434

[50] N.Desai,S.Punnekkat,“EnhancingFault DetectioninTimeSensitiveNetworksusing MachineLearning”, 2020International ConferenceonCOMmunicationSystems&

NETworkS (COMSNETS),Bengaluru,India,2020, pp.714–719.doi:10.1109/COMSNETS48256. 2020.9027357

[51] A.Shahraki,etal.,“ASurveyandFutureDirec‐tionsonClustering:FromWSNstoIoTandMod‐ernNetworkingParadigms”, IEEETransactions onNetworkandServiceManagement, vol.18, no.2,2021,pp.2242–2274.doi:10.1109/TNSM .2020.3035315

[52] K.Wang,etal.,“AnEnergy‐Ef icientReliableData TransmissionSchemeforComplexEnvironmen‐talMonitoringinUnderwaterAcousticSensor Networks”, IEEESensorsJournal, vol.16,no.11, 2016,pp.4051–4062.doi:10.1109/JSEN.2015. 2428712

[53] Y.Wang,L.Cao,T.A.Dahlberg,“Ef icient FaultTolerantTopologyControlforThree‐DimensionalWirelessNetworks”, 2008 Proceedingsof17thInternationalConferenceon ComputerCommunicationsandNetworks, St.Thomas,VI,USA,2008,pp.1–6.doi: 10.1109/ICCCN.2008.ECP.75

[54] K.A.Alansary,etal.,“NetworkedControlSystem ArchitectureforAutonomousUnderwaterVehi‐cleswithRedundantSensors”, 201911thInternationalConferenceonElectronics,Computersand Arti icialIntelligence (ECAI),Pitesti,Romania, 2019,pp.1–4.doi:10.1109/ECAI46879.2019 .9042033

[55] D.Li,J.Du,L.Liu,“Adataforwardingalgorithm basedonMarkovthoughtinunderwaterwire‐lesssensornetworks”, InternationalJournalof DistributedSensorNetworks, 2017,13(2).doi: 10.1177/1550147717691982

[56] S.Petridou,S.Basagiannis,M.Roumeliotis,“Sur‐vivabilityAnalysisUsingProbabilisticModel Checking:AStudyonWirelessSensorNetworks”, IEEESystemsJournal, vol.7,no.1,2013,pp.4–12. doi:10.1109/JSYST.2012.2224612

[57] M.Martalo,S.Busanelli,G.Ferrari,“Multihop IEEE802.15.4WirelessNetworksWithFinite NodeBuffers:MarkovChain‐BasedAnalysis”, 2008IEEE10thInternationalSymposiumon SpreadSpectrumTechniquesandApplications, Bologna,Italy,2008,pp.644–648.doi:10.1109/ ISSSTA.2008.126

[58] L.Xie,P.E.Heegaard,Y.Jiang,“Non‐Markovian SurvivabilityAssessmentModelforInfrastruc‐tureWirelessNetworks”, 201815thInternational SymposiumonWirelessCommunicationSystems (ISWCS),Lisbon,Portugal,2018,pp.1–5.doi:10 .1109/ISWCS.2018.8491067

[59] S.N.Pelykh,M.V.Maksimov,“Themethodof fuelrearrangementcontrolconsideringfuelele‐mentcladdingdamageandburnup”, Problems ofAtomicScienceandTechnology, vol.87,no.5, 2013,84–90.https://vant.kipt.kharkov.ua/ART ICLE/VANT_2013_5/article_2013_5_84a.pdf

[60] M.V.Maksimov,S.N.Pelykh,R.L.Gontar,“Princi‐plesofcontrollingfuel‐elementcladdinglifetime invariableVVER‐1000loadingregimes”, Atomic Energy, vol.112,no.4,2012,241‐249. https: //doi.org/10.1007/s10512‐012‐9552‐3

[61] I.G.Maysyan,M.V.Maksimov,“Methodologyfor AssessingtheReliabilityofACSTPSoftware UsingFailureRecovery”, BulletinofCherkasy StateTechnologicalUniversity, vol.3,2006, pp.8–13.(InRussian).

Submitted:4th September2024;accepted:5th October2024

WojciechDomski,AdamJankowiak

DOI:10.14313/jamris‐2025‐007

Abstract:

Wepresentaconvolutionneuralnetworkusedtodeter‐minefacesimilaritygiventwoimagesasinput,i.e.aface identificationtask.Themainfocusisontheshapeof theinputdata.Weproposeschemeswheretwopictures areconnectedinfourdifferentways.Theinputsampleis concatenatedhorizontallyandvertically,givingthefirst twoschemes.Theothertwoinputshapesincludethe intertwiningbycolumnandbyrow.Analysisofprecision versusrecallhasbeenprovidedforeachinputschema. Someofthetraditionalapproachesfocusonderiving thefeaturevectorsofanindividualandthencomparing theobtainedvectorswitheachother.Ourpaperoffers anewapproachtofaceidentificationproblemswhere twoimagesofanindividualaredirectlyfedtotheneural network.Then,itisthetaskoftheneuralnetworkto determinethesimilarityscore.

Keywords: CNN,faceidentification,inputshaping

1.Introduction

Solutionscreatedwitharti icialintelligenceare gainingmoreandmoreattention.Forexample,Chat‐GPTisanoptimiseddialoguemodelwhileofferinga human‐likeconversationexperience.AI indsapplica‐tionsinmanydifferentdomainssuchasengineering, medicineand inance.Theuseofarti icialintelligence ismuchbroaderandisnotlimitedtothe ieldsmen‐tioned.Aparticular ieldwheresuchmethodshave proventobeusefuliscomputervision,especially facedetectionandidenti ication[6].This ieldisnot solelyreservedforhumanfacerecognitionbutcanbe appliedtoanimalsaswell[7].Oneofthemethods incomputervisionthatcanbeusedforfacerecogni‐tionistheHaarCascadeClassi ier[15].Itisaclassic objectdetectionalgorithmbasedonHaar‐likefeatures andtheAdaboostalgorithm.Itcanbeadoptedtothe facedetectiontaskbytrainingitonfaceandnon‐faceimages.Itisef icient,butitrequiresapre‐trained database,soitisnotabletoidentifyfacesthatthe algorithmhasnotseenpreviously.Anotherclassical approachtofacedetectionandidenti icationisthe Eigenfacedetector[14].Inthecourseofthisalgo‐rithm,afaceisprojectedonto“facespace”wheredevi‐ationsfromanormalisedpatternsaremeasured.This approachusesprincipalcomponentanalysis(PCA) toextractfeaturesfromimagesandthenusesthose featurestoperformfacerecognition.

Additionally,thisalgorithmcanbeextendedto recognizepreviouslyunseenfacesthroughanunsu‐pervisedlearningprocess.Asimilarapproachto EigenfacesisknownasFisherfaces[2].Itsprojection methodisbasedonFisher’slineardiscriminantand givesresultsinalow‐dimensionalsubspacethatare wellseparable.Researchonthismethodshowedthat itisinvariantorpresentshighrobustnesstoillumina‐tionconditions.

Aseparategroupofalgorithmsisbasedonneural networkssuchasImageNet[5],MTCNN[16],VGGFace [8]andResNet[4].Thesesolutionsarebasedondeep convolutionalneuralnetworks.ImageNetandResNet arenotdirectlyintendedtobeusedasamodelto identifyfacesbutratherasvariousobjectclassi iers thatcouldbeadoptedinordertoperformthistask.In turn,MTCNNandVGGFacearededicatedsolutionsto performfacerecognitiontasks.Itisimportanttoknow theunderlyingdifferencebetweentwoterms:face detectionandfaceidenti ication.Theformerlimitsits scopetothetaskof indingafaceinanimage,whilethe latteriscapableofcomparingtwofacesanddrawing aconclusionifthefacebelongstothesamepersonor not.Whileitisclearthatthefaceidenti icationtask ishardertoperform, indingaperson’sfaceonan imagecannotbeneglectedeither.Moreover,asthe termfacerecognitiongainsmorefriction,itseemsthat isisbeingusedinasimultaneoustaskwhichcombines previoustwo.Inthisarticlewefocusoureffortonthe faceidenti icationtask.Thusweassumefollowingthat apicturecontainingtwofacesisprovided.Through theinferenceprocess,themodeldeterminesproba‐bilitydescribingiftheprovidedimagerepresentsthe sameperson.Themainfocusoftheletterisputonhow structureofinputdataimpactsoverallperformanceof adeepconvolutionneuralnetwork.Wepresentfour similarstructuresoftheinputdatawhichdifferin imagerepresentationandcomparethe inalperfor‐manceofthepresenteddeepCNN.

Inthispaper,wearepresentingresultsobtained duringtrainingofadeepneuralnetworkforthe taskoffaceidenti ication.Thedeepneuralnetwork isprovidedwithtwophotosamples.Thegoalisto determinewhetherthetwopicturesrepresentthe sameperson.Moreover,wefocusoninputdatashape andhowitin luencesaccuracyandperformance.We haveproposedfourdifferentinputdataschemes.The resultsofthetrainedmodelsarepresentedintheform ofprecisionvs.recall.

InSection 2 wediscussfourdifferentimagerep‐resentations.Section 3 containsdescriptionofused neuralnetworkarchitecture.Next,Section4presents detailedinformationgatheredduringtrainingof presenteddeepCNNmodel.Discussionofachieved resultsispresentedinSection5.Additionally,itoffers conclusionandfurtherresearchplans.

2.InputData

Theinputdatasetisthedrivingforceofdeepneu‐ralnetworksolutions.Tofacilitatethis,wehaveused theORL(OlivettiResearchLabs)database[1].This databasecontainsphotographsof40distinctsubjects, 10samplesperperson.Thedatasetwasdividedinto threesubsets:trainingdataset,directlyusedduring trainingprocess;validationdataset,tovalidatenet‐workperformanceduringtraining;and inallytesting datasetthatwasusedduringevaluationofatrained model.Theoriginaldataset(beforedataaugmen‐tation)wasdividedintothreepartswithfollowing shares:

‐ training–32subjects(80%), ‐ validation–4subjects(10%), ‐ testing–4subjects(10%). Therefore,thetrainingdatasetcontainsexactly320 rawsamples.Thesampleswerenotdirectlyfedtothe neuralnetwork.

Thesizeofeachimageis92x112pixelsin8‐bit greyscale.Thedatabasescontainmultipleimagesof thesamesubjectbuttakenunderdifferentconditions. Theseconditionsincludedifferentlightingconditions, facialexpression,andfacialdetails.Thepresented ORLdatabaseisusedinvariousresearchareas[3,10]. InFigure1,9randomlychosenfaceswerepresented.

2.1.DataPreparation

Beforethetrainingdatasetcouldbeconstructed, eachimagehadtobecroppedtoresembleasquare shape.Thiswasachievedbycroppingtheoriginal imagesfrom92x112to92x92pixels.

Afterwards,eachimagewasscaleddownto64x64 pixels.Thisprocesswasrequiredtolimitthenumber ofinputstotheneuralnetwork.Inordertosatisfy deepneuralnetworkwithsuf icientdata,thepost‐processeddatasetwasaugmented.Eachimagewas transformedwithathree‐stagepipeline: ‐ noiseaddition, ‐ rotation,and ‐ zooming. Thisallowedustosigni icantlyenlargethenumber ofsamples.Toeachimage,noisewasaddedbased onnormaldistribution.Additionally,eachimagewas rotatedwithintherangeof[‐5∘,+5∘].Therota‐tionanglewaschosenatrandom.Inaddition,each imagewasslightlyzoomedinorout.Theseopera‐tionsallowedcreationofanautomatedaugmentation pipelinethatproducedanumberofdifferentsamples.

2.2.TrainingSetCuration

Thegoalwastotrainanetworkcapableofdiscov‐eringiftwoimagesbelongtothesameperson,thus performingafaceidenti icationtask.Thisrequires theneuralnetworktobefedwithnotasingleimage butasampleconsistingoftwoimages.Eachsuch sampleisthenlabeledwithazerovaluerepresenting thesituationwhentwopicturesdonotbelongtothe samepersonandvalueofoneotherwise.Through theprocessofdataaugmentationfollowedbyimage concatenation,wehaveextendedourdatasetconsid‐erablyallowingthedeepneuralnetworktobetrained properly.Afterthisprocessthedatasetswereofthe followingmagnitude:

‐ 20160trainingsamples(including10080positive and10080negativesamples),

‐ 2520validationsamples(including1260positive and1260negativesamples),

‐ 2520trainingsamples(including1260positiveand 1260negativesamples).

Inthescopeoftheclassi icationtask(thesameperson ortwodifferentpersons),itisimportanttoensurethat themagnitudeofdatasetsrepresentingpositiveand negativesamplesiscomparable.Therefore,thedata augmentationprocessallowedustosatisfythesetwo requirements.The irstoneconcerningthetotalnum‐berofsamples;alargenumberoftrainingsamples leadstobetterperformance.Thesecondcondition requiresthatthemagnitudeofdatasetsrepresenting eachclassforaclassi icationproblemissimilar,ide‐allyidentical.Basedonthisfact,thenumberofpos‐itivesamples(concatenationofimagesrepresenting thesameperson)ismuchsmallerthanthenumber ofnegativesamples.Fororiginaldatasetthenumber ofpositivesamplescanbecalculatedascombination givenas

Figure1. ExamplefacesfromtheORLdatabase[10]

singleinputsample.Therefore,weproposefourdiffer‑ entsamplerepresentations.The irstschemaisbased onconcatenatingimagestogether,asitwasshownin Fig.2

Thesecondrepresentationissimilartothe irst one,butnowthepicturesofindividualsareconcate‑ natedvertically.TheresultispresentedintheFig.3

Forasinglepersonwith10photographsityields 45positivesamples.Given32individualsthetotal numberofpositivesamplesis1440whichisinsuf i‐cient.Inturn,thenumberofnegativesamplesisfar greaterfortheoriginaldataset.

Thetwoimageswereconcatenatedhorizontally, sotheresultinginputshapewas64x128.Inthecase ofverticalconcatenation,theresultingresolutionis 128x64.Thethirdschemawasbasedonintertwin‑ ingpattern.SeetheexampleinFig.4.Ascanbeseen, theresultingimageisaconcatenationoftwoimages whererowsareintertwined.Theresultingsizeofthe imageis128x64pixels(similartoverticalconcatena‑ tion).

Asalreadymentioned,inordertoachieveface identi ication,twoimageshadtoberepresentedasa singleinputsample.Therefore,weproposefourdiffer‐entsamplerepresentations.The irstschemaisbased onconcatenatingimagestogether,asitwasshownin Figure2.

Thesecondrepresentationissimilartothe irst one,butnowthepicturesofindividualsareconcate‐natedvertically.TheresultispresentedintheFigure3

Thetwoimageswereconcatenatedhorizontally, sotheresultinginputshapewas128x64.Inthecase ofverticalconcatenation,theresultingresolutionis 64x128.Thethirdschemawasbasedonintertwin‐ingpattern.SeetheexampleinFigure 4.Ascanbe seen,theresultingimageisaconcatenationoftwo imageswhererowsareintertwined.Theresulting sizeoftheimageis128x64pixels(similartovertical concatenation).

Similartothethirdinputdataschema,wepropose arepresentationwhereaninputsamplewascreated throughconcatenation,butcolumnswereintertwined insteadofrows.TheresultwasshowinFig.5.There‑ sultingresolutionoftheimageisequaltothe irstrep‑ resentation;thusitisnow64x128pixels.

3.NetworkArchitecture

Theconvolutionnetworkarchitectureispresented inFig.6.Almostthesamenetworkarchitecturewas utilizedforallfourinputschemes.Therefore,thein‑ putlayerwas128x64or64x128.Similarchangeshad

Similartothethirdinputdataschema,wepropose arepresentationwhereaninputsamplewascreated throughconcatenation,butcolumnswereintertwined insteadofrows.TheresultwasshowinFigure5.

Fig.5. Twoimagesintertwinedbycolumn

Conv1 (62x126x32) (31x63x32)

Conv2 (29x61x32) (14x30x32)

MaxPooling2D

BatchNorm Flatten Dense+ReLU

Figure6. Facesimilarityconvolutionnetwork architecture

Fig.6. Facesimilarityconvolutionnetworkarchitecture

Theresultingresolutionoftheimageisequaltothe irstrepresentation;thusitisnow128x64pixels.

3.NetworkArchitecture

tobeadoptedacrossallconvolutionandpoolinglay‑ ers.InFig.6wehavepresentednetworkarchitecture fortheinputlayerwithdimensions64x128,thusfor imageswhichwereconcatenatedhorizontally(sideby side)orintertwinedbycolumn.

ItisworthnotingthattheReLUactivationfunc‑ tionwasusedforthelastoutputlayer.Sincewefocus onvaluesfrom0to1,adifferentactivationfunction couldbeusedforthelastlayer,e.g.thesigmoidfunc‑ tioncouldbeused.However,wehaveobservedthat usingReLUasanactivationlayerforthenetworkout‑ putgavegoodresults.

4.ModelTraining

Theconvolutionnetworkarchitectureispresented inFigure 6.Almostthesamenetworkarchitecture wasutilizedforallfourinputschemes.Therefore,the inputlayerwas128x64or64x128.Similarchanges hadtobeadoptedacrossallconvolutionandpooling layers.InFigure6wehavepresentednetworkarchi‐tecturefortheinputlayerwithdimensions64x128, thusforimageswhichwereconcatenatedvertically (oneundertheother)orintertwinedbyrow.

Wehavetrainedfourmodelswhereeachmodel differsbyshapingofinputsamples.Wepresenttrain‑ ingstatisticssuchasaccuracyandlossduringthe trainingandduringvalidationphase.

ItisworthnotingthattheReLUactivationfunction wasusedforthelastoutputlayer.Sincewefocuson valuesfrom0to1,adifferentactivationfunctioncould beusedforthelastlayer,e.g.thesigmoidfunction couldbeused.However,wehaveobservedthatusing ReLUasanactivationlayerforthenetworkoutput gavegoodresults.

Tobetterunderstandhowthetrainedmodelper‑ forms,itwastestedagainstthetestingdatasetsince itwasnotusedduringtrainingstage.Weprovidetwo metricswhichgiveinsighthowwellitperforms–pre‑ cisionandrecall.Precisionisexpressedas

4.ModelTraining

Precision = TP TP + FP , (2)

where TP aretruepositivesmeaningpositivesamples thatwerecorrectlyclassiiedand FP arefalseposi‑ tivesrelectingnegativesamplesthatweremisclassi‑

Wehavetrainedfourmodelswhereeachmodel differsbyshapingofinputsamples.Wepresenttrain‐ingstatisticssuchasaccuracyandlossduringthe trainingandduringvalidationphase.

Tobetterunderstandhowthetrainedmodelper‐forms,itwastestedagainstthetestingdatasetsince itwasnotusedduringtrainingstage.Weprovidetwo metricswhichgiveinsighthowwellitperforms–precisionandrecall.Precisionisexpressedas

= ���� ����+����, (2)

Figure2. Twoimagesconcatenatedhorizontally

Figure3. Twoimagesconcatenatedvertically

Figure4. Twoimagesintertwinedbyrow

Figure5. Twoimagesintertwinedbycolumn

Fig.2. Twoimagesconcatenatedhorizontally

Fig.3. Twoimagesconcatenatedvertically

Fig.4. Twoimagesintertwinedbyrow

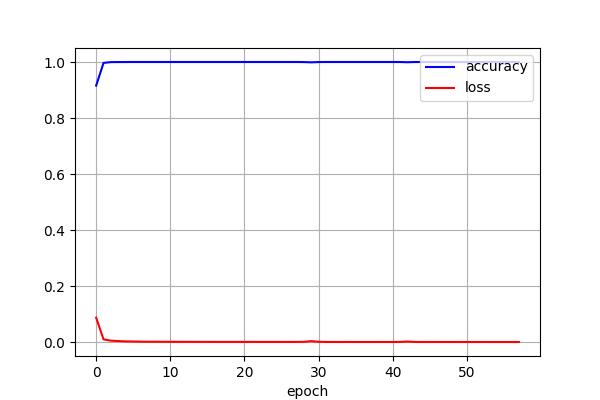
Figure7. Accuracyandlossduringtrainingfor horizontallyconcatenatedpictures

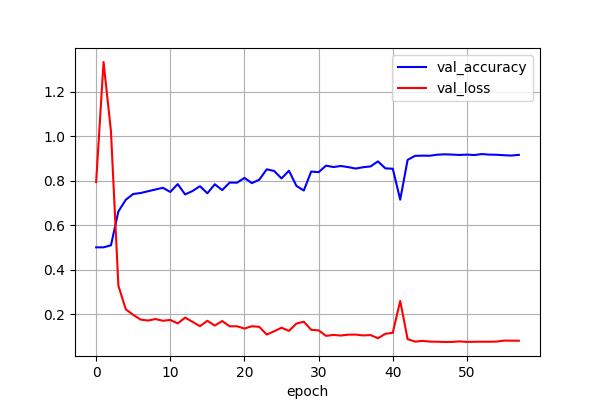
Figure8. Validationaccuracyandlossforhorizontally concatenatedpictures

where����aretruepositivesmeaningpositivesamples thatwerecorrectlyclassi iedand ���� arefalseposi‐tivesre lectingnegativesamplesthatweremisclassi‐iedasnegativesamples.Recallisde inedas

Recall= ���� ����+����, (3)

where����isaspreviously,while����arefalsenegatives re lectingpositivesamplesthatweremisclassi iedas negativesamples.Observinghowprecisionandrecall behaveinafunctionofassumedthresholdallowsus todecidewhichbehaviouroftheclassi ierismore desirable.Dependingontheselectedthresholdwecan decideifthemodelshouldtendtopreferstrongcases whilesomepositivesamplesmightnotbedetected overmorerobustpositiveclassi icationwithsome falsepositives.

Our irstmodelwastrainedonhorizontally concatenateddatawherepictureswerestackedside‐by‐side.InFigure 7 aplotshowsaccuracyandloss functionduringtrainingforthemodelpreparedfor horizontallyconcatenatedimages.Inturn,inFigure8 weshowaccuracyandlossvaluesforthevalidation dataset.

InFigure9recallandprecisionindicatorsforthe irstmodelarepresented.Basedontheplotsthebal‐ancedthresholdisequalto0.72.

Figure9. Precisionandrecallforhorizontally concatenatedpictures

(a)Originaltestdataset (b)Augmented testdataset

Figure10. Confusionmatricesformodeltrainedon horizontallyconcatenatedimages

Figure11. Accuracyandlossduringtrainingfor horizontallyconcatenatedpictures

InFigures 10(a) and 10(b) confusionmatrices havebeenpresentedforour irstmodel.Ascanbe seen,resultsobtainedfortheoriginaltestandthe augmentedtestdatasetsaresimilar.Overallaccuracy forthismodelisaround85%.

Thesecondmodelwastrainedforthesamedataset buttheinputdatawaspostprocessesbyconcatenat‐ingtwopicturesvertically,thusonepictureisabove theotherasalreadybeenpresentedinFigure3.The resultsoftrainingprocessweredepictedinFigure11 wereaccuracyvs.lossfunctionwaspresented.Toget moreinsightfuldatawehavepresentedaccuracyvs. lossfunctioninFigure12.

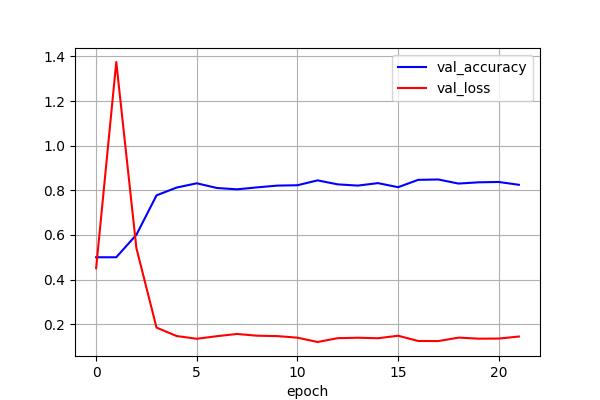
Figure12. Validationaccuracyandlossforhorizontally concatenatedpictures

Figure13. Precisionandrecallforhorizontally concatenatedpictures

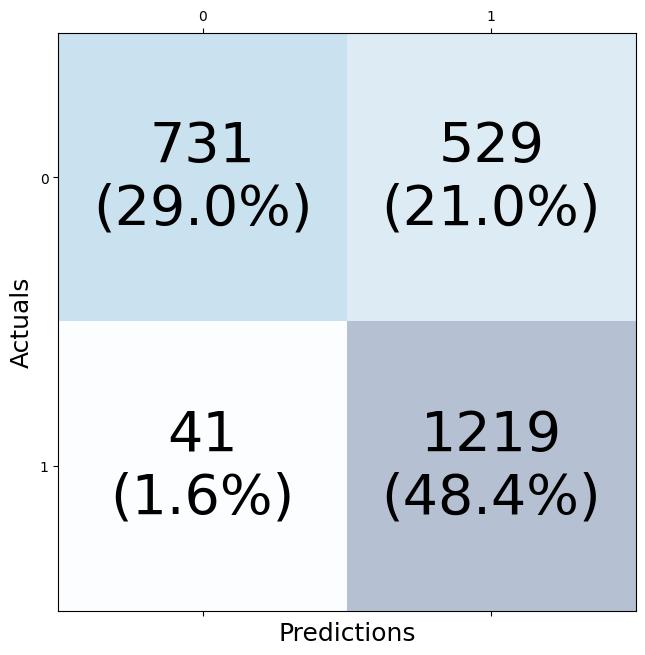
(a)Originaltestdataset (b)Augmented testdataset

Figure14. Confusionmatricesformodeltrainedon verticallyconcatenatedimages

Finally,theprecisionandrecallwerepresentedin Figure13wherethesetwocurveswerecalculatedin afunctionof ixedthresholdfrom0to1.Thebest threshold–providingbalancebetweenrecallandpre‐cisionis0.95. InFigures 14(a) and 14(b) confusionmatrices havebeenpresentedforoursecondmodeltrainedon verticallyconcatenatedimages.Itcanbenoticedthat theoverallperformanceofthismodelisaround80%. Itisslightlylesscomparedtopreviousmodelusing horizontalimageconcatenation.

Figure15. Accuracyandlossduringtrainingforpictures intertwinedbyrow

Figure16. Validationaccuracyandlossforpictures intertwinedbyrow

Figure17. Precisionandrecallforpicturesintertwined byrow

Thesecondgroupofmodelswastested onintertwinedinputdata,thethirdmodel (picturesintertwinedbyrow)andthelastmodel (picturesintertwinedbycolumn).InFigure 15 accuracyvslosswasshownduringtrainingprocess. ValidationresultswerepresentedinFigure 16 showingaccuracyandlossforvalidationdataset.

Inturn,inFigure 17,precisionandrecallforthe modelwithintertwinedrowsarepresented.Thebal‐ancedthresholdbetweenrecallandprecisionforthe modelwascomputedas0.30.

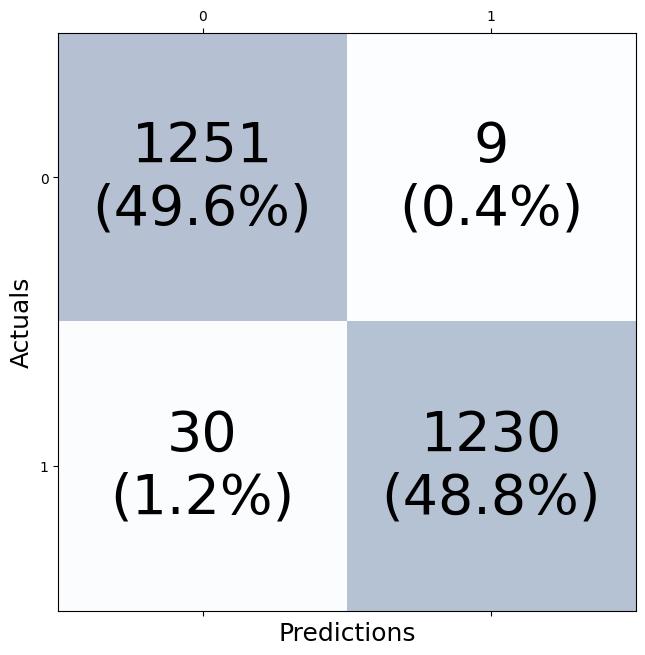
(a)Originaltestdataset (b)Augmented testdataset

Figure18. Confusionmatricesformodeltrainedonrow intertwinedimages

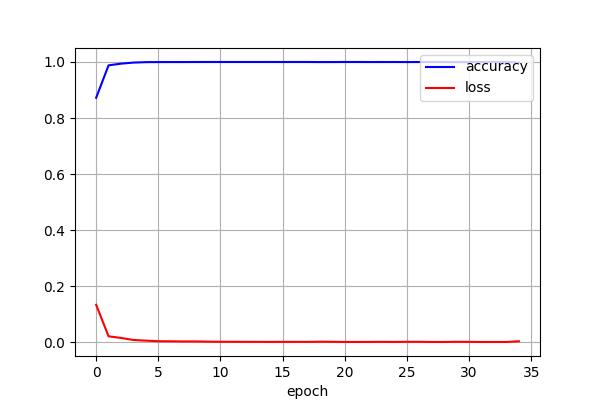
Figure19. Accuracyandlossduringtrainingforpictures intertwinedbycolumn

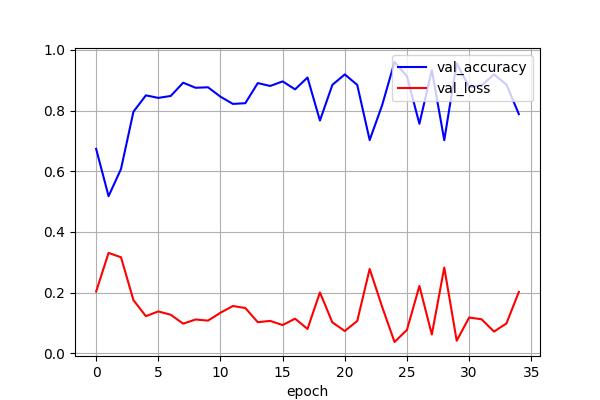
Figure20. Validationaccuracyandlossforpictures intertwinedbycolumn

InFigures 18(a) and 18(b) weshowresultsin theformofconfusionmatricesobtainedwhiletest‐ingmodeltrainedonrowintertwinedimages.Itwas testedonoriginalandaugmenteddatasets.Thereis visible,howeversmall,ca.5%,discrepancybetween resultsobtainedforthesetwodatasets.Thismodelis capableofachievingaccuracyonthelevelof93%.

Similar,tothepreviousmodel,wepresentresults obtainedforinputdatathatwasoriginallyintertwined bycolumn.Inthiscase,thetrainingresultswerepre‐sentedinFigure19.Validationprocesswasconducted alsoonapreviouslyunseenvalidationdataset.The resultswerepresentedinFigure20.

Figure21. Precisionandrecallforpicturesintertwined bycolumn

(a)Originaltestdataset (b)Augmented testdataset

Figure22. Confusionmatricesformodeltrainedon columnintertwinedimages

Tocomplementtheanalysis,wealsopresentrecall andprecisionmetricsachievedonatestingdataset (Figure21).Forthismodelthebalancedthresholdis equal0.66

Wepresentconfusionmatrices(Figures22(a)and 22(b))obtainedduringthetestingroutineforamodel trainedoncolumnintertwinedimages.Asinprevious casesthedifferencebetweenamodeltestedonorig‐inalandaugmenteddatasetsissmall,butlargerthan inthecaseofmodelstrainedonconcatenatedimages. Theoverallperformanceofthismodelisaround87%, whichishighercomparedtomodelstrainedoncon‐catenatedimages.

5.Conclusion

Inthepresentedworkwehavefocusedonawell‐knowproblemoffacerecognition.Therearemany state‐of‐the‐artmethodsandalgorithmsthatfocuson thisproblem[9,11–13].Usually,themethodisbased onobtaininganumericalrepresentationofafacethat isthencomparedtootherrepresentationsusinga prede inedmetric.Inourapproachweinvestigateif aCNNcanlearntodetermineifinputdata,consist‐ingoftwopictures,representsthesameperson.To furtherexaminethiswehaveproposedfourdifferent schemesthatdifferentiateininputdatashape.Two imagesareconcatenated(verticallyorhorizontally) orintertwined(byroworbycolumn).Nosimilarity metricisbeingcomputedotherthantheoutputofthe convolutionneuralnetworkitself.

Theproposedarchitectureallowedustobuilda modelthatiscapableofdifferentiatingbetweentwo photographsofhumanfacesanddeterminingifthe imagesrepresentthesameperson.Researchresults providedinSection 4 showthattheinputprepro‐cessinghassigni icantin luenceonthemodelper‐formance.Itwasshownthatwhentheinputimage isintertwined,eitherbyroworcolumn,itachieves betterclassi icationresults.Thebestmodelachiev‐ing93%accuracywastrainedonintertwinedimages byrow.Whatismore,allmodelsweretestedon twodatasets–anoriginalandanaugmentedtesting dataset.Itisclearthatmodelstrainedonintertwined imageshaveahigheraccuracydispersion.Itisaround 3‐5%whileformodelstrainedwithconcatenated imagestheaccuracydispersionis0.5%‐3%.During thecourseoftheresearchitwasdeterminedthat theintertwinedinputdataperformsbetterthancon‐catenatedinputdata.Itwasshownhowinputdatais shapedhassigni icantimpactonmodelperformance. Itwasdeterminedbyprovidingexactlythesametrain‐ingsetsforeachmodelandutilizingthesamearchitec‐turelayout.

Sincethesystemisnotbasedonmetriccalculation itcouldbedeployedimmediatelyonpremiseswithout additionaladjustments.Themodelprovidedwithtwo images(intertwinedorconcatenated)isabletopro‐videapredictionifthetwoimagesbelongtothesame person.Whatismore,itdoesnotrequireapreexisting databaseofsubjectssinceitcomparestwoimages,so itsmaintenanceislow.However,thedrawbackofsuch systemsisthenecessityofrunninginferencebetween allsubjects,whileametricbasedsystemcouldbe moreef icientintermsofcalculatingonlythedistance betweentwonumericalrepresentationsoffaces.

Infutureresearch,weplantosigni icantlyenlarge theoriginaldataset.Thismightallowustodiscover potentialdiscrepancies.Additionally,weplantointro‐duceadifferentvariantoftheproposedneuralnet‐work.Itwouldbetrainednottoidentifyiftwopictures representthesamepersonbutifthereisanylevel ofkinshipandlateronwhatkindofkinshiplevel itis.Itisachallengingtaskwhichwouldrequirea largedatasetandaspeci icone.Furthermore,since neuralnetworksrequireasigni icantamountofdata itwouldbeworthtoinvestigateifarti iciallyaug‐menteddataset,bythemeansofgenerativeadver‐sarialnetworks(GANs),in luencesaccuracyofsuch architecture.

AUTHORS

WojciechDomski∗ –DepartmentofCyberneticsand Robotics,WrocławUniversityofScienceandTech‐nology,ul.Janiszewskiego11/17,50‐372Wrocław, Poland,ORCID:0000‐0001‐5768‐8051,e‐mail:woj‐ciech.domski@pwr.edu.pl,www:edu.domski.pl. AdamJankowiak –ORCID:0009‐0009‐1587‐7394, e‐mail:adamjankowiak4@gmail.com.

∗Correspondingauthor

References

[1] AT&TLaboratoriesCambridge.“Thedatabaseof faces”,2023. https://cam‐orl.co.uk/facedataba se.html

[2] P.Belhumeur,J.Hespanha,andD.Kriegman, “Eigenfacesvs. isherfaces:recognitionusing classspeci iclinearprojection”, IEEETransactionsonPatternAnalysisandMachineIntelligence,vol.19,no.7,1997,711–720,10.1109/ 34.598228.

[3] A.EleyanandH.Demirel,“Pcaandldabasedface recognitionusingfeedforwardneuralnetwork classi ier”.In:B.Gunsel,A.K.Jain,A.M.Tekalp, andB.Sankur,eds., MultimediaContentRepresentation,Classi icationandSecurity,Berlin, Heidelberg,2006,199–206.

[4] K.He,X.Zhang,S.Ren,andJ.Sun,“Deepresidual learningforimagerecognition”, 2016IEEEConferenceonComputerVisionandPatternRecognition(CVPR),2016,770–778,10.1109/CVPR.201 6.90.

[5] A.Krizhevsky,I.Sutskever,andG.E.Hinton, “Imagenetclassi icationwithdeepconvolutional neuralnetworks”, Commun.ACM,vol.60,no.6, 2017,84–90,10.1145/3065386.

[6] L.Li,X.Mu,S.Li,andH.Peng,“Areviewof facerecognitiontechnology”, IEEEAccess,vol.8, 2020,139110–139120,10.1109/ACCESS.2020. 3011028.

[7] X.Li,Y.Xiang,andS.Li,“Combiningconvo‐lutionalandvisiontransformerstructuresfor sheepfacerecognition”, ComputersandElectronicsinAgriculture,vol.205,2023,107651,https: //doi.org/10.1016/j.compag.2023.107651

[8] O.M.Parkhi,A.Vedaldi,andA.Zisserman,“Deep facerecognition”.In:X.Xie,M.W.Jones,and G.K.L.Tam,eds., ProceedingsoftheBritish MachineVisionConference(BMVC),2015,41.1–41.12,10.5244/C.29.41.

[9] B.S.PengLuandL.Xu,“Humanfacerecogni‐tionbasedonconvolutionalneuralnetworkand augmenteddataset”, SystemsScience&Control Engineering,vol.9,no.sup2,2021,29–37,10.1 080/21642583.2020.1836526.

[10] F.SamariaandA.Harter,“Parameterisationofa stochasticmodelforhumanfaceidenti ication”, Proceedingsof1994IEEEWorkshoponApplicationsofComputerVision,1994,138–142,10.110 9/ACV.1994.341300.

[11] F.Schroff,D.Kalenichenko,andJ.Philbin, “Facenet:Auni iedembeddingforface recognitionandclustering”.In: 2015IEEE ConferenceonComputerVisionandPattern Recognition(CVPR),2015,815–823,10.1109/ CVPR.2015.7298682.

[12] Y.Sun,Y.Chen,X.Wang,andX.Tang,“Deeplearn‐ingfacerepresentationbyjointidenti ication‐veri ication”.In:Z.Ghahramani,M.Welling,

C.Cortes,N.Lawrence,andK.Weinberger,eds., AdvancesinNeuralInformationProcessingSystems,vol.27,2014.

[13] Y.Taigman,M.Yang,M.Ranzato,andL.Wolf, “Deepface:Closingthegaptohuman‐levelper‐formanceinfaceveri ication”.In: 2014IEEE ConferenceonComputerVisionandPattern Recognition,2014,1701–1708,10.1109/CVPR .2014.220.

[14] M.TurkandA.Pentland,“Facerecognition usingeigenfaces”.In: Proceedings.1991IEEE ComputerSocietyConferenceonComputer VisionandPatternRecognition,1991,586–591, 10.1109/CVPR.1991.139758.

[15] P.ViolaandM.Jones,“Rapidobjectdetection usingaboostedcascadeofsimplefeatures”, Proceedingsofthe2001IEEEComputerSocietyConferenceonComputerVisionandPatternRecognition.CVPR2001,vol.1,2001,I–I,10.1109/CVPR .2001.990517.

[16] K.Zhang,Z.Zhang,Z.Li,andY.Qiao,“Jointface detectionandalignmentusingmultitaskcas‐cadedconvolutionalnetworks”, IEEESignalProcessingLetters,vol.23,no.10,2016,1499–1503, 10.1109/LSP.2016.2603342.

DOI:10.14313/jamris‐2025‐008

Abstract:

ARCHITECTURE

ARCHITECTURE

Submitted:24th May2024;accepted:9th July2024

SerraAksoy

Allovertheglobethereexistsaseriousproblemwithskin cancer,mostespeciallymelanoma;amalignancywhich isknowntobehaveaggressivelyandcanmetastasize. Detectingthisearlyisthekeytosavinglives.Thisstudy introducesanewmethodofclassifyingmelanomausing anadvancedmodelknownasMobileNet‐V3‐Large.This techniquediffersfromothersinthatitconsidersboth theimagesoftheskinlesionandtabulardatainclud‐ingfactorsconsistingofthepatient’sapproximateage, genderandthelocationofthelesiononthebodyof thepatient.Suchanapproachempowersthepredictions ofwhethertheskinlesionmaybemalignantorbenign. Testedonahugecollectionconsistingofskinimages combinedwithtabulardata,itwasestablishedthatthis methodoutperformsothersalreadyexisting.Theresults ofthisstudyshowedthatahighaccuracyof99.56%was achievedusingtheproposedmodel.Thisstudyindicates thatutilizingthemulti‐inputmethodwillsubstantially enhancediagnosisformelanomahencereducingmortal‐itiesinthefuture.

Keywords: melanomacancer,benign,malignant,con‐volutionneuralnetwork(CNN),deeplearning(DL),pre‐trainedmodel

1.Introduction

In2023,it’sestimatedthatnearly97,610individ‐ualsintheUSreceivedthedauntingdiagnosisofinva‐sivemalignantmelanoma,whichwasslightlylower thanthe99,780casesreportedin2022.Tragically, thenumberofliveslosttothisdiseaseincreasedfrom 7,650in2022toanestimated7,990in2023[1–3]. Projectionsindicatedthatapproximately89,070cases ofearlyinsitumelanomawouldbeidenti iedin2023. Thesilverliningisthatwhenmelanomasaredetected andtreatedatthisearlystage,there’sachancefor completerecovery.Sincemostmelanomasmanifest visiblyontheskin,itunderscoresthecrucialimpor‐tanceofearlydetectionandtreatment[4].Skincancer, increasinglyprevalenttoday,affectshumanswidely duetotheskin’sstatusasthebody’slargestorgan [5].Whenfacingskincancer,it’simportanttobe proactiveandutilizeallavailableresourcestodetect itearlyandenhancetreatmentoutcomes.Thistypeof cancerencompassestwomaincategories:melanoma andnonmelanomaskincancer[6].Melanoma,though rare,isperilousandoftenfatal,accountingforamere

1%ofcasesyetyieldingahigherdeathtoll.Originat‐ingfrommelanocytes,whichregulateskinpigmen‐tation,melanomacanemergeanywhereonthebody butcommonlyappearsonsun‐exposedareaslikethe hands,face,andneck.Earlydetectioniscrucialfor effectivetreatment;otherwise,melanomacanmetas‐tasize,leadingtodireconsequences.Varioussubtypes exist,includingnodularmelanoma,super icialspread‐ingmelanoma,acrallentiginous,andlentigomaligna. Conversely,nonmelanomaskincancerslikebasalcell carcinoma(BCC),squamouscellcarcinoma(SCC),and sebaceousglandcarcinoma(SGC)aremoreprevalent. Thesecancerstypicallyariseintheouterlayersofthe skinandhavealowertendencytometastasize,making themrelativelyeasiertotreatcomparedtomelanoma [6–12].

Fortunately,technologyplaysacrucialroleinaid‐ingdermatologists.Arti icialintelligenceactsasareli‐ableassistant,swiftlyanalyzingimagesofskinlesions toidentifypotentialsignsofcancerwithgreaterspeed andaccuracy.Additionally,advancedimagingtech‐niqueslikere lectanceconfocalmicroscopyandopti‐calcoherencetomographyprovidevaluableinsights intoskinabnormalitieswithoutinvasiveprocedures [3,13–15].Inthe ieldofmedicalimaging,expertsare hands‐oninassemblingdatasetsandguidingmachine learningresearchersonwhataspectstoconsider.Con‐sidertheHAM10000dataset,forinstance;it’sacol‐lectionofimagesshowingdifferentskinlesions[17]. Since2016,ithasplayedacrucialroleintheInter‐nationalSkinImagingCollaboration(ISIC)challenge, assistinginaddressingvariousskin‐relatedissues [17–19].ThereareotherdatasetslikePH2,featuring 200dermoscopicimagessortedintovariousdiagno‐sisgroups,andtheInteractiveAtlasofDermoscopy, whichoffersover1000clinicalcaseswiththorough annotationsandpathology indings.Theseresources haveproveninvaluableinadvancingcomputer‐aided diagnosis(CAD)research[21].

Segmentationisafoundationalandintricatetask intheautomatedanalysisofskinlesions.Withinclin‐icalcontexts,rule‐baseddiagnosticsystemsheavily relyonpreciselesionsegmentationtoestimatecriti‐caldiagnosticparameterssuchasasymmetry,border irregularity,andlesionsizeaccurately.Thesemetrics serveasfundamentalcomponentsfortheapplication ofestablishedalgorithmsliketheABCDalgorithmand itsderivatives,suchasABCDEandABCDEF.

Table1. Skincancerdetectionmethodologiesandtheirrespectivedatasets

Reference Methodology

[22] Thepreprocessingimagesand ine‐tuning convolutionalneuralnetworkswithtransfer learning,withEf icientNetB4identi iedasthe top‐performingmodel.

[23] AutomatedSkin‐MelanomaDetection(ASMD) systemusingimageprocessingandSVM‐based classi ication,proposingaMelanoma‐Index(MI) forclinicaluse.

[24] Automaticskincancerdiagnosissystemincluding HistogramofGradients(HG)andHistogramof Lines(HL),combinedwithotherfeatures.

[25] SkincancerdetectionsystemutilizingGenetic Programming(GP)forevolvingaclassi ierand featureselection.

[26] Imageprocessinganddeeplearningtechniques, includingConvolutionalNeuralNetworks(CNNs), forskincancerdetectionandclassi ication.

[27] Classi icationofskinlesions,utilizing dynamic‐sizedkernelsandbothReLUand leakyReLUactivationfunctions.

[28] Soft‐Attentionmechanismindeepneural architecturesforskinlesionclassi ication.

[29] MobileNetV3introducingtheImprovedArti icial RabbitsOptimizer(IARO)algorithmtoenhance featureselection

[30] SkinTrans,animprovedtransformernetwork,for skincancerclassi ication,utilizingvision transformers(VIT)withself‐attention mechanism.

TheABCDalgorithmprovidesastructuredframe‐workforevaluatingskinlesions,witheachlet‐terrepresentingkeymorphologicalfeatures.Accu‐ratelesionsegmentationisimperativeforenabling reliableandeffectiveautomateddiagnosticassess‐ments,therebyenhancingclinicaldecision‐making processes.Assuch,robustsegmentationmethodolo‐giesareessentialforensuringtheintegrityandclin‐icalutilityofautomatedskinlesionanalysissystems [30–33].

Intheworldofacademicresearch,three‐ ieldplots (Figure 1)andco‐occurrencenetworks(Figure2) serveasinvaluabletoolsforunderstandingtheintri‐catewebofconnectionswithinscholarlyliterature(93 reviews).Thesevisualizationsprovideinsightsinto howkeywords,universityaf iliations,andauthors’ countriesoforiginintersect.Thesevisualtoolspro‐videasnapshotofhowideasmoveandevolve withinacademia.Conceptualizethesetoolsasarchi‐tecturalschematics,openingthecomplexinterrela‐tionsamongtheseelements.Theheightoftheboxes withinthethree‐ ieldplotsigni iesthevolumeof publicationsassociatedwitheachaf iliation,offering astraightforwardgaugeofresearchoutput.Ataller boxindicatesahighernumberofpublicationsfrom thataf iliation,akeymetricforevaluatingresearch productivity.

Dataset(s)

EvaluationMetrics

HAM10000dataset F1Score:87%, Accuracy:87.91%

DDimagedataset Accuracy:97.50%

HPHdermoscopy databaseandthe Dermo itstandard database

MNIST HAM10000dataset

Accuracy:98.79%(HPH) and92.96%(thestandard Dermo it)

WeightedAverage Accuracy:0.88,Weighted AverageRecall:0.74, WeightedF1‐score:0.77

HAM10000dataset Overallaccuracy:97.85%

HAM10000datasetand ISIC‐2017dataset

PH2,ISIC‐2016,and HAM10000datasets

HAM10000andclinical datasets

Precision:93.7% (HAM10000),sensitivity: 91.6%(ISIC‐2017)

Accuracy:87.17% (ISIC‐2016),96.79%(PH2 dataset),and88.71% (HAM10000)

Accuracy:94.3% (HAM10000)and94.1% (Clinical)

Inresearchpublications,agraphicalrepresenta‐tion(seeFigure2)calledtheco‐occurrencenetwork ofauthorkeywordsshowstheconnectionsbetween differentauthorkeywords.Inthesameresearchdoc‐uments,individualkeywordsarenodeswithinthese networksandedgesthatconnectthesenodesindi‐catetherepeatedco‐occurrenceofsuchwordsoften. Throughtheresearch ieldoraspeci icsetofpubli‐cations,thesenetworkshighlightessentialinforma‐tionbypresentinganelasticpictureoftheunderlying relationships.UponcloserexaminationofFigure1, itisrevealedthatGermany,theUnitedStates,and Australiaprominentlyemergeastheforerunnersin academicendeavorsthatchroniclethestepsmade withinthearti icial‐intelligencedrivenmelanoma.

InFigure 2,speci icallytailoredanalysisofkey‐wordsassociatedwitharti icialintelligenceisoffered, providingacomprehensivebreakdownwithatotalof 30nodes.

Three‐fieldplotanalysis(AU_UN—ID—AU_CO)

Co‐occurrencenetworkofauthorkeywords

2.DifferentPretrainedConvolutionalNeural Networks

Inthisstudythefeatureblocksofthesepre‐trainedConvolutionalNeuralNetworks(CNNs)[35] havebeenusedasthefeatureextractorofthegiven imagedata,andtheyhavebeencomparedaccordingto theclassi icationmetricsofthewholeproposedarchi‐tecture,whichconsistsofthefeatureextractorblock fromthepretrainedmodel,withthatthebestmetrics havebeenobtainedandaclassi icationblockforthe imagedata,aswellasanotherclassi icationblockfor

thetabulardata,andalastclassi icationblockfrom whichthecombinedimageandtabulardatapass.

2.1.ConvNeXtBase

ConvNeXtBase,aninnovativeCNNarchitecture, representsasigni icantadvancementinthe ieldof computervision.Whilenotaswidelyrecognizedas somemainstreamarchitectures,ConvNeXtBasehas garneredattentionforitsrobustfeatureextraction capabilitiesandcomputationalef iciency.

Figure1.

Figure2.

Notableforitsutilizationofgroupedconvolutions, layernormalization,andstochasticdepthregulariza‐tion,ConvNeXtBaseaimstostrikeadelicatebalance betweenmodelcomplexityandperformance.Interms ofperformance,ConvNeXtBasehasdemonstrated promisingresultsinvariousimageclassi icationtasks. Forinstance,researchershaveemployedConvNeXt Basetoclassifycomplexmedicalimages,suchasthose relatedtotumordetectioninmammographyand histopathologicalanalysis.Itsabilitytocaptureintri‐catevisualpatternswhilemaintainingcomputational ef iciencymakesConvNeXtBaseacompellingchoice fordiverseapplications.Architecturally,ConvNeXt BasecomprisesaseriesofCNBlocks,eachfeatur‐inggroupedconvolutions,lineartransformations,and permutations.Theseblocks,augmentedwithstochas‐ticdepthlayers,facilitateenhancedmodelrobustness andgeneralizationcapabilities.Furthermore,Con‐vNeXtBaseleverageslayernormalizationandvari‐ousactivationfunctionstocapturecomplexpatterns effectively.

2.2.MobileNetV3Large

MobileNetV3Largestandsasatestamentto theevolutionoflightweightCNNarchitecturesopti‐mizedformobileandembeddeddevices.Builtupon thesuccessofitspredecessors,MobileNetV3Large prioritizescomputationalef iciencywithoutsacri ic‐ingclassi icationaccuracy.Itsarchitecturaldesign, characterizedbydepth‐wiseseparableconvolutions, invertedresidualblocks,andsqueeze‐and‐excitation modules,enablesef icientfeatureextractionacross diversedatasets.

Inpracticalapplications,MobileNetV3Largehas foundwidespreadadoption,particularlyinscenar‐ioswhereresourceconstraintsposechallenges.For example,ithasbeeninstrumentalinvariousmobile applications,rangingfromreal‐timeobjectdetec‐tiontoimageclassi icationinlow‐powerdevices. Theincorporationofhard‐swishactivationfunc‐tionsanddropoutlayersfurtherenhancesitsper‐formanceandregularizationcapabilities.Architec‐turally,MobileNetV3Largecomprisesahierarchi‐calstructureofdepth‐wiseseparableconvolutions andinvertedresidualblocks,facilitatingef icientfea‐tureextractionandspatialdownsampling.Addition‐ally,squeeze‐and‐excitationmodulesenableadaptive featurerecalibration,enhancingthediscriminative powerofthemodelacrossdifferentinputdomains.

2.3.VGG16

VGG16,aseminalCNNarchitecture,hasleftan indeliblemarkonthelandscapeofimageclassi ica‐tion.Renownedforitssimplicityandeffectiveness, VGG16remainsacornerstoneinthe ielddespitethe emergenceofnewerarchitectures.Itsarchitectural design,characterizedbyrepeatedblocksofconvolu‐tionallayersfollowedbyrecti iedlinearunit(ReLU) activationfunctionsandmax‐poolingoperations,pri‐oritizesfeatureextractionandspatialdownsampling.

Inpractice,VGG16hasbeenextensivelyutilized invariouscomputervisiontasks,rangingfromimage recognitiontoobjectlocalization[6].Itsstraight‐forwarddesignandstrongperformancemakeita popularchoiceforbenchmarkingandexperimenta‐tioninresearchsettings.Architecturally,VGG16com‐prisesahierarchicalstructureofconvolutionallayers, augmentedbyReLUactivationfunctionsandmax‐poolingoperations.Thisdesignfostershierarchical featureextraction,enablingthemodeltocapture increasinglyabstractrepresentationsasinformation traversesdeeperintothenetwork.Additionally,the incorporationofmax‐poolinglayersfacilitatesspa‐tialdownsampling,reducingcomputationalcomplex‐itywhilepreservingdiscriminativeinformation.

2.4.EfficientNetV2S

Ef icientNetV2Semergesasapinnacleinthe realmofscalableandef icientCNNarchitectures, embodyingstate‐of‐the‐artadvancementsinmodel designandoptimization.Withafocusonachieving optimalperformanceacrossvaryingcomputational budgets,Ef icientNetV2Shasgarneredwidespread acclaimforitsadaptabilitytodiversedeployment scenarios.Itsarchitecturaldesign,characterizedby astandardconvolutionallayerfollowedbyfused MobileNetV2(MBConv)blocks,epitomizesef iciency withoutcompromisingclassi icationaccuracy.

Inpracticalapplications,Ef icientNetV2Shas demonstratedremarkableef icacyacrossaspectrum oftasks,fromimageclassi icationtoobjectdetec‐tion.Itshierarchicalstructureandstrategicincor‐porationofstochasticdepthlayerscontributeto enhancedmodelrobustnessandgeneralizationcapa‐bilities.Architecturally,Ef icientNetV2Scomprisesa cascadeofMBConvblocks,eachfeaturingdepth‐wise separableconvolutionsandef icientchannelatten‐tionmechanisms.Thisdesignfostersef icientfea‐tureextractionandaggregation,enablingthemodel tocapturecomplexvisualpatternswhileminimiz‐ingcomputationaloverhead.Additionally,theutiliza‐tionofstochasticdepthlayersenhancesmodelregu‐larization,contributingtoimprovedperformanceon diversedatasets.

2.5.DenseNet161

DenseNet161standsasaparadigmaticshift inCNNarchitectures,distinguishedbyitsdense connectivitypatternthatpromotesfeaturereuseand gradient lowpropagationthroughoutthenetwork. Renownedforitssuperiorperformanceincapturing intricatevisualrepresentations,DenseNet161has becomeacornerstoneinimageclassi icationtasks, particularlyinscenariosrequiringrobustfeature extraction.Inpracticalapplications,DenseNet161 hasdemonstratedremarkableef icacyacrossvarious domains,includingmedicalimageanalysisand remotesensing.Itsdenseconnectivitypatternand hierarchicalstructurefacilitateinformation low, enablingthemodeltocaptureincreasinglyabstract representationsasinformationtraversesdeeperinto thenetwork.

Architecturally,DenseNet161comprisesaseriesof denseblocks,eachfeaturingdenselyconnectedlay‐ersthatreceivedirectinputfromallprecedinglayers withintheblock.Thisdesignpromotesfeaturereuse andgradient lowpropagation,facilitatingef icient trainingandimprovedmodelexpressiveness.Addi‐tionally,transitionlayersandglobalaveragepool‐ingoperationsfurtherenhancefeatureaggregation andclassi icationperformance,makingDenseNet161 aformidablecontenderintherealmofimageclassi i‐cationarchitectures.

3.MaterialandMethod

3.1.DatasetAcquisitionandPreprocessing

Theprimarydatasetutilizedinthisstudyis theSIIM‐ISICMelanomaClassi icationCompetition DatasetsourcedfromKaggle.Thisdatasetcomprisesa comprehensivecollectionofmedicalimagesandcor‐respondingmetadataessentialformelanomaclassi‐icationresearch.Theimagesareprimarilydermo‐scopicimagesofskinlesions,whilethemetadata includescriticalpatientinformationsuchasidenti‐iers,sex,age,anatomicalsite,diagnosis,andmalig‐nancystatus.

Uponacquisition,thedatasetunderwentextensive preprocessingtoensureuniformityandcompatibility withthemodelarchitecture.Theimageswereini‐tiallyavailableinmultipleformats,includingDICOM, JPEG,andTFRecord.Tofacilitateeaseofprocessing andanalysis,allimageswereconvertedtoastandard format,namelyJPEG.Additionally,theimageswere resizedtoauniformresolutionof224x224pixelsto ensureconsistencyacrossthedataset.

3.2.DataAugmentationandTransformation

Toenhancethediversityandrobustnessofthe trainingdataset,variousdataaugmentationtech‐niqueswereapplied.Leveragingthetransformsmod‐ulefromthePyTorchlibrary,augmentationssuchas randomverticalandhorizontal lipswereperformed ontheimages.Theseaugmentationshelpthemodel generalizebetterbyintroducingvariationsinthe trainingdata,therebyreducingover ittingtendencies.

Furthermore,normalizationwasappliedtothe imagedatatostandardizethepixelvalues.Thisnor‐malizationprocessinvolvedscalingthepixelvaluesto astandardrange,typicallybetween0and1,tostabi‐lizethetrainingprocessandaccelerateconvergence.

3.3.ProposedDeepLearningModel

ConvolutionalNeuralNetworks(CNNs)have becomeintegralinvariousdomains,particularly incomputervisiontasks,duetotheiref icacyin learningandextractingfeaturesfromvisualdata. CNNsareadeptatdiscerningintricatepatternsand structureswithinimages,makingthemsuitablefor taskslikeimageclassi ication,objectdetection,and segmentation.

Table2. Numberoftabularandimagedatatakenfrom SIIM‐ISICDataset

Class Total Training Testing

Malignant 571 461 110

Benign 579 459 120

Total 1150 920 320

Inthisstudy,CNNsareutilizedtotacklethecrucial taskofclassifyingbenignandmalignantskinlesions indermatology.TheobjectiveistoleverageCNNs toidentifyunderlyingpatternsandstructureswithin skinlesionimagesaccuratelydistinguishingbetween benignandmalignantcases.

Thedataset(Table 2)incorporatesbothtabular data,whichconsistsofpatientdemographics(sex, approximateage)andlesionlocation,andimagedata characterizedbythreechannelsanddimensionsof 224x224pixels.Theimagedataundergoesasequen‐tialprocess,startingwithconvolutionallayers,fol‐lowedbybatchnormalizationlayers,andthenHard‐wishactivationlayersfromtheMobileNetV3Large Model’sFeatureBlock,toextractpertinentfeatures. Subsequently,itpassesthroughlinear,batchnormal‐ization,anddropoutlayerstoprepareitforclassi i‐cation.Meanwhile,thetabulardataundergoestrans‐formationsviamultiplelinearandReLUlayers.These twosetsofdataarecombinedandprocessedthrough alinearlayer.Forclassi ication,thecombineddata thenproceedsthroughasigmoidactivationfunction andisroundedas inalclassi ication.

3.4.ProposedDeepLearningModelArchitecture

IncorporatingMobileNetV3’sfeatureextraction mechanism,thismodelharnessestheef iciency andsophisticationofmodernCNNarchitectures. MobileNetV3’sfeatureextractorispivotalindistilling intricatepatternsfromskinlesionimages.Comprising multiplelayers,asshowninFigure 3 MobileNetV3 initiateswithaconvolutionallayer,followedby batchnormalizationforstabilizationandHardswish activationfornon‐linearity.Thisisparticularly effectiveincapturingdiversefeaturesacrossvarious skinlesiontypes.Subsequently,MobileNetV3’s architectureintegratesInvertedResidualblocks,each composedofdepthwiseseparableconvolutionsand pointwiseconvolutions.Theseintricatestructures enablethemodeltoef icientlycapturespatial hierarchiesandsemanticinformationwithinthe imagedata.

TheimagefeaturesextractedbyMobileNetV3 arethenfurtherre inedthroughtheimageclassi‐iercomponent.Thisclassi iercomprisesmultiple layers,startingwitha latteningoperationtocon‐vertthemulti‐dimensionalfeaturemapsintoaone‐dimensionaltensor.Subsequently,the lattenedfea‐turesareprocessedthroughasequenceoflinear transformations,ReLUactivations,batchnormaliza‐tionforfeaturescaling,anddropoutregularizationto mitigateover ittingrisks.

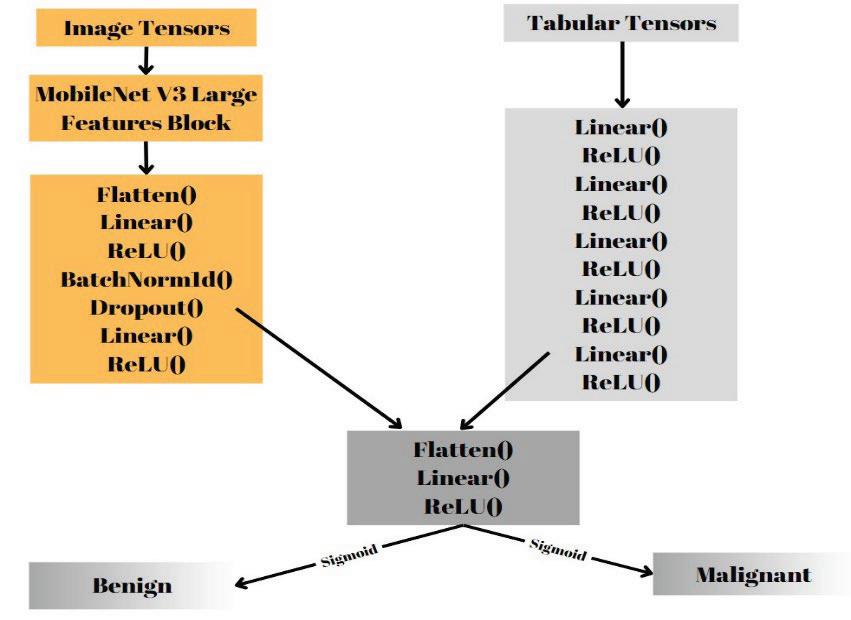
Theseoperationscollectivelyfacilitatethelearn‐ingofdiscriminativefeaturesessentialforaccurate lesionclassi ication.Concurrently,thetabulardata undergoesprocessingthroughadedicatedtabular classi iercomponent.Similartotheimageclassi ier, thiscomponentcomprisesmultiplefullyconnected layersaugmentedwithReLUactivationfunctions. Theselayersenablethemodeltocaptureintri‐caterelationshipswithinthetabulardata,leverag‐ingpatientdemographicsandmedicalhistoryfor improvedlesionclassi icationaccuracy.

Finally,thefusedfeaturesfromboththeimage andtabularclassi iersareconcatenatedandpassed throughthefusionlayer.Thislayerconsistsofa lat‐teningoperationfollowedbyalineartransformation. Whilesimplerinstructurecomparedtotheclassi iers, thefusionlayersynthesizestheextractedfeatures frombothmodalities,facilitatingaholisticanaly‐sisoftheinputdataandultimatelycontributingto enhancedclassi icationperformance.Byintegrating bothimageandtabulardatasourcesandleveraging sophisticatedfeatureextractionmechanismsandclas‐si icationcomponents,thismodelpresentsacompre‐hensiveapproachtoskinlesionclassi ication.

3.5.ExperimentalSetup

Forconductingtheexperiments,acomputational setupconsistingofanIntelCorei9processorandan NVIDIAGeForceRTXGPUwasutilized.Theexperi‐mentswereexecutedwithintheVSCodeJupyterNote‐bookinterfaceleveragingthePyTorchframeworkfor modelimplementation.Thetrainingprocessspanned over35epochsandtookapproximately28minutesto completeontheaforementionedhardwarecon igura‐tion.Thearchitectureoftheproposedmethodologyis showninFigure4

Theexperimentalsetupencompassedtheevalu‐ationofmultipleneuralnetworkarchitectures.Loss andaccuracycurvesweregeneratedforeacharchitec‐ture,asdepictedinthefollowing igures.

Inthestudyofskinlesionclassi ication,theexper‐imentalprocessisinitiatedwiththecollectionoftwo distincttypesofdata.ImageData,whichconsistof skinlesionimages,andTabularData,whichencom‐passpatientdemographicsandclinicalinformation. Thedatathenundergoesapreprocessingstage.This stageismultifacetedandincludestheremovalof anynullvaluespresentinthedata,theelimina‐tionofzerovaluesfromthe‘age_approx’column, andthecustomencodingofthe‘sex’and‘anatomi‐cal_site_general_challenge’columns.

Figure3. Proposedmodelarchitecture

Proposedmethodology

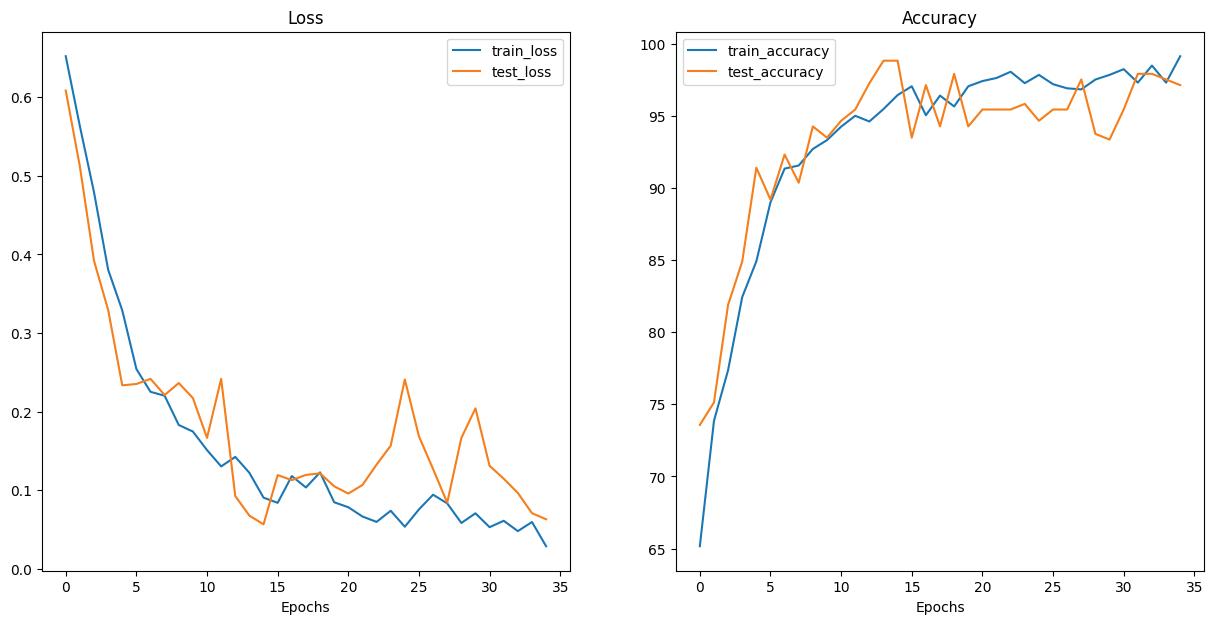
Densenet161lossandaccuracycurves

Additionally,dataselectionisperformedbasedon thetargetvalue,selectingalldatawithamalignanttar‐getvalueandsamplinganequalamountofdatawith abenigntargetvalue.Theimagesarethenprocessed, resizedtoastandardsizeof(224,224,3),augmented toincreasethediversityofthedataset,normalized, andconvertedtotensorswitha loatdatatype.

Concurrently,‘sex’,‘age_approx’,and‘anatomi‐cal_site_general_challenge’areextractedasindepen‐dentvariablesfromthetabulardata.TheImageTen‐sorsandTabularTensorsarethenutilizedtotrain themodel.TheImageTensorsareprocessedthrough anMobileNetV3Largemodelforfeatureextraction, whiletheTabularTensorsareprocessedthrougha MultilayerPerceptron.Thetrainingprocessinvolved iterativelyoptimizingthemodelparametersusing theAdamoptimizerwithalearningrateof0.01.

Figure4.

Figure5.

Figure7. Mobilenet_v3_largelossandaccuracycurves

ThelossfunctionemployedwastheBinaryCross‐EntropywithLogitsLoss(BCEWithLogitsLoss),which iswell‐suitedforbinaryclassi icationtaskssuchas melanomaclassi ication.

Finally,themodelisevaluatedusingaseparate testset,outputtingapredictionofeither‘Benign’ or‘Malignant’foreachskinlesion.Toevaluatethe performanceofthetrainedmodel,acomprehensive suiteofevaluationmetricswasemployed.Thepri‐marymetricsusedweretheconfusionmatrixand theclassi icationreport.Theconfusionmatrixpro‐videsadetailedbreakdownofthemodel’spredictions, includingtruepositives(TP),truenegatives(TN),false positives(FP),andfalsenegatives(FN).Fromthe confusionmatrix,metricssuchasaccuracy,precision, recall(sensitivity),andF1‐scorecanbederived.

4.ResultsandDiscussion

TheresultsofthisstudyhighlightMobileNetV3 Largeastheoptimalpretrainedmodelforskinlesion classi ication,offeringsuperioraccuracyandrobust‐ness.These indingsunderscorethepotentialofdeep learningmodelsinenhancingdiagnosticaccuracyand guidingclinicaldecision‐makinginmelanomadetec‐tion.Theresultsobtainedfromtheevaluationonthe testsetaresummarizedinTable 3,whileTable 4 providesthecorrespondingconfusionmatrix.

Figure6. Convnext_baselossandaccuracycurves

Figure8. VGG16lossandaccuracycurves

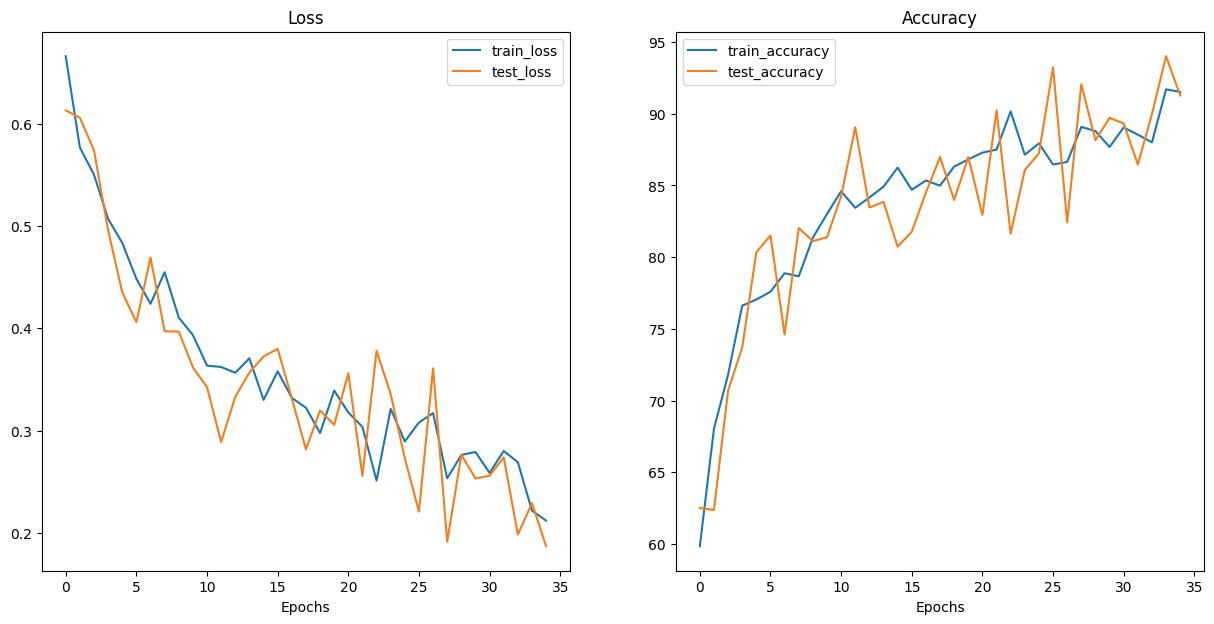
Figure9. Efficientnet_v2_slossandaccuracycurves

Table3. Performanceonthetestset

Thisstudyinvestigatedtheperformanceofdiffer‐entpretrainedmodelsasfeatureextractorsfordis‐tinguishingbenignandmalignantskinlesions.Among

themodelsexamined,MobileNetV3Largedemon‐stratedthehighestaccuracy,achievinganoutstanding 99.56%.

Table4. Confusionmatrixonthetestset

icientnet_v2_s 105 106 15 4 Convnext_base 87 91 33 19

Adetailedcomparisonofthemodels’perfor‐mancemetrics,encompassingaccuracy,precision, recall,andF1‐score,ispresentedinTable3.MobileNet V3Largeexhibitedsuperiorperformanceacross allmetrics,indicatingitseffectivenessincapturing discriminativefeaturesfromskinlesionimages.With precisionandrecallscoresof1.00forbenignand malignantlesions,respectively,MobileNetV3Large demonstratedexceptionalaccuracyinidentifying bothclasses.

Ef icientNetV2SmallandVGG16alsoyieldedcom‐petitiveresults,achievingaccuraciesof91.74%and 87.39%,respectively.However,theydisplayedslightly lowerprecisionandrecallcomparedtoMobileNet V3Large.Conversely,modelssuchasConvNextBase exhibitedrelativelylowerperformance,suggesting limitationsinfeatureextractionfromskinlesion images.

TheconfusionmatricesprovidedinTable 4 offer insightsintothemodels’classi icationperformance, depictingTP,TN,FP,andFN.MobileNetV3Large achievedthehighestTPrateforbothbenignand malignantlesions,withonlyoneFNandnoFP instances.Thisunderscoresitsrobustnessinaccu‐ratelesionclassi ication,minimizingmisclassi ica‐tions,andmitigatingtheriskoffalsediagnoses.

Inconclusion,thechoiceofapretrainedmodelas afeatureextractorsigni icantlyimpactstheperfor‐manceofskinlesionclassi icationtasks.MobileNetV3 Largeemergedastheoptimalmodel,offeringsuperior accuracyandrobustnessindistinguishingbetween benignandmalignantlesions.Futureresearchcould exploreensemblemethodsor ine‐tuningstrategiesto furtherenhancemodelperformanceandgeneraliza‐tioncapabilities.

5.Conclusion

Concludingthisstudyemphasizestheseverityof theglobalskincancerissue,particularlymelanoma, duetoitsaggressivebehaviorandpotentialtospread. Earlydetectionispivotalincombattingthisdisease andsavinglives.Theintroductionofanovelapproach tomelanomaclassi icationutilizingtheMobileNet‐V3‐Largemodelrepresentsasigni icantadvancement inthis ield.

Byintegratingskinlesionimageswithpertinent patientdatasuchasage,gender,andlesionloca‐tion,thismethoddemonstratesenhancedpredictive capabilitiesfordistinguishingbetweenmalignantand benignlesions.

Thecomprehensiveanalysisofavastdatasetcon‐irmsthesuperiorityofthisapproachoverexisting methods,asevidencedbyanimpressiveaccuracyrate of99.56%.

These indingsholdpromiseforrevolutioniz‐ingmelanomadiagnosisandsubsequentlyreducing mortalityratesassociatedwiththisdisease.Byhar‐nessingthepowerofmulti‐inputmethodology,clin‐icianscananticipatemoreaccurateandtimelydiag‐noses,therebyfacilitatingpromptinterventionand improvedpatientoutcomes.Thisresearchheraldsa newerainmelanomadetection,underscoringthe potentialofinnovativetechnologiestomitigatethe impactofthisdeadlydiseaseonglobalhealth.

Futureresearchattemptsshouldprioritizethe re inementandoptimizationofmulti‐inputmodels, theintegrationofemergingimagingtechnologies,and thedevelopmentofuser‐friendlyAI‐drivendiagnostic tools.Additionally,extensivevalidationstudiesand clinicaltrialsareimperativetocon irmthereal‐world effectivenessofnoveldiagnosticapproaches.Further‐more,thereisapressingneedtoexplorepersonalized medicinestrategiestailoredtoindividualpatientchar‐acteristics,whilesimultaneouslyaddressingglobal disparitiesinaccesstoadvanceddiagnosticandtreat‐mentmodalities.Byfollowingthesepaths,the ield canstrivetowardsmoreaccuratediagnosis,person‐alizedtreatmentregimens,andequitablehealthcare access,ultimatelyleadingtoimprovedoutcomesand reducedmortalityratesforindividualsaffectedby melanomaworldwide.

Authorcontribution

SAhelpedinconceptualization,software,valida‐tion,writing—originaldraft,resourcesanddatacura‐tion.SAhelpedinmethodology,writing—review& editing,supervision,revision,fundingacquisitionand formalanalysis.

Dataavailability

Allthedatasetsusedinexperimentationareavail‐ableonlineontheInternet.

Conflictofinterest

Authorsdeclarethattheyhavenoknowncompet‐ing inancialinterestsorpersonalrelationshipsthat couldhaveappearedtoin luencetheworksubmitted forpublication.

AUTHOR

SerraAksoy∗ –LudwigMaximilianUniversity ofMunich(LMU),Munich,Geschwister‐Scholl‐Platz1,80539,Germany,e‐mail: Serra.Aksoy@campus.lmu.de.

∗Correspondingauthor

References

[1] R.L.Siegel,K.D.Miller,H.E.Fuchs,andA.Jemal, “Cancerstatistics,2022,” CAACancerJClinicians, vol.72,no.1,pp.7–33,Jan.2022,doi:10.3322/ caac.21708.

[2] R.L.Siegel,K.D.Miller,N.S.Wagle,andA.Jemal, “Cancerstatistics,2023,” CAACancerJClinicians, vol.73,no.1,pp.17–48,Jan.2023,doi:10.3322/ caac.21763.

[3] S.Aksoy,P.Demircioglu,andI.Bogrekci, “EnhancingMelanomaDiagnosiswithAdvanced DeepLearningModelsFocusingonVision Transformer,SwinTransformer,andConvNeXt,” Dermatopathology,vol.11,no.3,pp.239–252, Aug.2024,doi:10.3390/dermatopathology 11030026.

[4] A.K.Nambisanetal.,“ImprovingAutomatic MelanomaDiagnosisUsingDeepLearning‐BasedSegmentationofIrregularNetworks,” Cancers,vol.15,no.4,p.1259,Feb.2023,doi: 10.3390/cancers15041259.

[5] R.Ashrafetal.,“Region‐of‐InterestBasedTrans‐ferLearningAssistedFrameworkforSkinCan‐cerDetection,” IEEEAccess,vol.8,pp.147858–147871,2020,doi:10.1109/ACCESS.2020.3014 701.

[6] M.Elgamal,“AutomaticSkinCancerImagesClas‐si ication,” IJACSA,vol.4,no.3,2013,doi:10.145 69/IJACSA.2013.040342.

[7] F.Xiang,R.Lucas,S.Hales,andR.Neale,“Inci‐denceofNonmelanomaSkinCancerinRelation toAmbientUVRadiationinWhitePopulations, 1978‐2012:EmpiricalRelationships,” JAMADermatol,vol.150,no.10,p.1063,Oct.2014,doi: 10.1001/jamadermatol.2014.762.

[8] A.Stratigosetal.,“Diagnosisandtreatmentof invasivesquamouscellcarcinomaoftheskin: Europeanconsensus‐basedinterdisciplinary guideline,” EuropeanJournalofCancer,vol. 51,no.14,pp.1989–2007,Sep.2015,doi: 10.1016/j.ejca.2015.06.110.

[9] D.Koh,H.Wang,J.Lee,K.S.Chia,H.P.Lee,and C.L.Goh,“Basalcellcarcinoma,squamouscell carcinomaandmelanomaoftheskin:analysisof theSingaporeCancerRegistrydata1968‐97,” Br JDermatol,vol.148,no.6,pp.1161–1166,Jun. 2003,doi:10.1046/j.1365‐2133.2003.05223.x.

[10] L.Faniaetal.,“BasalCellCarcinoma:FromPatho‐physiologytoNovelTherapeuticApproaches,” Biomedicines,vol.8,no.11,p.449,Oct.2020,doi: 10.3390/biomedicines8110449.

[11] L.Faniaetal.,“CutaneousSquamousCellCar‐cinoma:FromPathophysiologytoNovelThera‐peuticApproaches,” Biomedicines,vol.9,no.2,p. 171,Feb.2021,doi:10.3390/biomedicines9020 171.

[12] S.K.T.Que,F.O.Zwald,andC.D.Schmults, “Cutaneoussquamouscellcarcinoma,” Journalof

theAmericanAcademyofDermatology,vol.78, no.2,pp.237–247,Feb.2018,doi:10.1016/j.ja ad.2017.08.059.

[13] M.Rubattoetal.,“Classicandnewstrategiesfor thetreatmentofadvancedmelanomaandnon‐melanomaskincancer,” Front.Med.,vol.9,p. 959289,Feb.2023,doi:10.3389/fmed.2022.95 9289.

[14] S.R.Waheed,N.M.Suaib,M.S.MohdRahim,M. MundherAdnan,andA.A.Salim,“DeepLearning Algorithms‐basedObjectDetectionandLocal‐izationRevisited,” J.Phys.:Conf.Ser.,vol.1892, no.1,p.012001,Apr.2021,doi:10.1088/1742‐6596/1892/1/012001.

[15] S.R.Waheedetal.,“MelanomaSkinCancerClas‐si icationbasedonCNNDeepLearningAlgo‐rithms,” Mal.J.Fund.Appl.Sci.,vol.19,no.3,pp. 299–305,May2023,doi:10.11113/mjfas.v19n3 .2900.

[16] F.PereiraDosSantosandM.AntonelliPonti, “RobustFeatureSpacesfromPre‐TrainedDeep NetworkLayersforSkinLesionClassi ication,” in 201831stSIBGRAPIConferenceonGraphics, PatternsandImages(SIBGRAPI),Parana:IEEE, Oct.2018,pp.189–196.doi:10.1109/SIBGRA PI.2018.00031.

[17] P.Tschandl,C.Rosendahl,andH.Kittler,“The HAM10000dataset,alargecollectionofmulti‐sourcedermatoscopicimagesofcommonpig‐mentedskinlesions,” SciData,vol.5,no.1, p.180161,Aug.2018,doi:10.1038/sdata.2018 .161.

[18] D.Gutmanetal.,“SkinLesionAnalysistoward MelanomaDetection:AChallengeattheInterna‐tionalSymposiumonBiomedicalImaging(ISBI) 2016,hostedbytheInternationalSkinImaging Collaboration(ISIC),”2016,doi:10.48550/ARX IV.1605.01397.

[19] N.Codellaetal.,“SkinLesionAnalysisToward MelanomaDetection2018:AChallengeHosted bytheInternationalSkinImagingCollaboration (ISIC),”2019,doi:10.48550/ARXIV.1902.03368.

[20] B.Cassidy,C.Kendrick,A.Brodzicki,J.Jaworek‐Korjakowska,andM.H.Yap,“AnalysisoftheISIC imagedatasets:Usage,benchmarksandrecom‐mendations,” MedicalImageAnalysis,vol.75,p. 102305,Jan.2022,doi:10.1016/j.media.2021.1 02305.

[21] M.Combaliaetal.,“BCN20000:Dermoscopic LesionsintheWild,”2019,doi:10.48550/ARX IV.1908.02288.

[22] K.Ali,Z.A.Shaikh,A.A.Khan,andA.A.Laghari, “Multiclassskincancerclassi icationusingEf i‐cientNets–a irststeptowardspreventingskin cancer,” NeuroscienceInformatics,vol.2,no.4,p. 100034,Dec.2022,doi:10.1016/j.neuri.2021.1 00034.

[23] K.H.Cheongetal.,“Anautomatedskin melanomadetectionsystemwithmelanoma‐indexbasedonentropyfeatures,” Biocybernetics andBiomedicalEngineering,vol.41,no.3, pp.997–1012,Jul.2021,doi:10.1016/j.bbe. 2021.05.010.

[24] N.AlfedandF.Kheli i,“Baggedtexturalandcolor featuresformelanomaskincancerdetectionin dermoscopicandstandardimages,” ExpertSystemswithApplications,vol.90,pp.101–110,Dec. 2017,doi:10.1016/j.eswa.2017.08.010.

[25] Q.UlAin,BingXue,H.Al‐Sahaf,andM.Zhang, “Geneticprogrammingforskincancerdetection indermoscopicimages,”in 2017IEEECongress onEvolutionaryComputation(CEC),Donostia, SanSebastián,Spain:IEEE,Jun.2017,pp.2420–2427.doi:10.1109/CEC.2017.7969598.

[26] R.Garg,S.Maheshwari,andA.Shukla,“Decision SupportSystemforDetectionandClassi ication ofSkinCancerusingCNN,”2019,doi:10.48550 /ARXIV.1912.03798.

[27] T.H.H.Aldhyani,A.Verma,M.H.Al‐Adhaileh,and D.Koundal,“Multi‐ClassSkinLesionClassi ica‐tionUsingaLightweightDynamicKernelDeep‐Learning‐BasedConvolutionalNeuralNetwork,” Diagnostics,vol.12,no.9,p.2048,Aug.2022,doi: 10.3390/diagnostics12092048.

[28] S.K.Datta,M.A.Shaikh,S.N.Srihari,andM.Gao, “Soft‐AttentionImprovesSkinCancerClassi ica‐tionPerformance,”2021,doi:10.48550/ARXIV .2105.03358.

[29] M.AbdElaziz,A.Dahou,A.Mabrouk,S.El‐Sappagh,andA.O.Aseeri,“AnEf icientArti‐icialRabbitsOptimizationBasedonMutation StrategyForSkinCancerPrediction,” ComputersinBiologyandMedicine,vol.163,p.107154, Sep.2023,doi:10.1016/j.compbiomed.2023.10 7154.

[30] C.Xinetal.,“Animprovedtransformernetwork forskincancerclassi ication,” ComputersinBiologyandMedicine,vol.149,p.105939,Oct.2022, doi:10.1016/j.compbiomed.2022.105939.

[31] S.Gupta,N.Sharma,R.Tyagi,P.Singh, A.Aggarwal,andS.Chawla,“Cognitive Inspired&Computationally‐IntelligentEarly MelanomaDetectionUsingFeatureAnalysis Techniques,” JAIT,Oct.2023,doi:10.37965/ jait.2023.0334.

[32] K.Kachare,N.Bhagat,andP.Raundale, “AdvancementsinMelanomaSkinCancer DetectionUsingDeepLearning:ACompre‐hensiveReview,”in 20237thInternational ConferenceOnComputing,Communication, ControlAndAutomation(ICCUBEA),Pune,India: IEEE,Aug.2023,pp.1–6.doi:10.1109/ICCU BEA58933.2023.10392174.

[33] K.Tomar,U.Panwar,andR.Gupta,“Amelanoma skincancerdetectionandanalysisusing dermoscopyimageprocessing,”presentedatthe MACHINELEARNINGANDINFORMATION PROCESSING:PROCEEDINGSOFICMLIP 2023,Ranchi,India,2023,p.080007.doi: 10.1063/5.0168906.

[34] R.Mittal,F.Jeribi,R.J.Martin,V.Malik,S.J. Menachery,andJ.Singh,“DermCDSM:Clinical DecisionSupportModelforDermatosisUsing SystematicApproachesofMachineLearningand DeepLearning,” IEEEAccess,vol.12,pp.47319–47337,2024,doi:10.1109/ACCESS.2024.3373 539.

[35] S.Aksoy,P.Demircioglu,andI.Bogrekci, “AdvancedArti icialIntelligenceTechniquesfor ComprehensiveDermatologicalImageAnalysis andDiagnosis,” Dermato2024,vol.4,no.4,pp. 173–186,doi:10.3390/dermato4040015.