
5 minute read
3.4.1 TEORIA DE GRAFOS
from Seminario de la Presentación Final de mi tutorada y futura profesionista Matemática Matilde Juárez J
by PDLM
En general, una cadena de Markov es un sistema en un tiempo discreto, que en cada instante se encuentra en un estado distinto. La cantidad total de estados es finita, y en cada instante se pasa de un estado a otro con unas probabilidades fijas que dependen sólo del estado actual, y no del resto de la historia del sistema.
Es habitual disponer los posibles estados del sistema en un grafo, y poner una arista entre dos vértices �� y �� cuando el sistema puede evolucionar del estado �� al estado �� en un sólo instante de tiempo, con probabilidad positiva.
Advertisement
Los estados de las Cadenas de Markov se clasifican en:
Estado alcanzable. Dados dos estados �� y ��, una trayectoria de �� a �� es una secuencia de transiciones que comienza en �� y termina en ��, tal que cada transición en la secuencia tiene una probabilidad positiva de ocurrir. Un estado �� es alcanzable desde el estado �� si hay una trayectoria que conduzca de �� a ��. Estados que se comunican. Se dice que dos estados �� y �� se comunican si �� es alcanzable desde ��, y de igual manera �� es alcanzable desde ��.
Conjunto cerrado. Un conjunto de estados �� de una Cadena de Markov es cerrado si ningún estado fuera de �� es alcanzable desde algún estado en ��.
Estado absorbente. Es un estado en el que ������ = 1 ������ = 0. Siempre que se entra en un estado absorbente, no se sale de él; un estado absorbente es un conjunto cerrado que contiene sólo un estado.
FIGURA 6. ESTADO ADSORBENTE
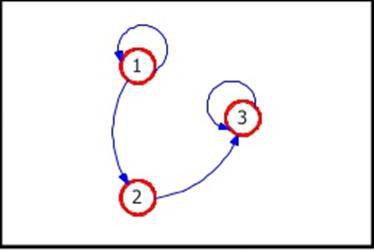
Figura 6. Estado adsorbente. El estado 3 es adsorbente. (Tomado Wikipedia. Imágenes)
UnADM | DCEIT| PT2 28

Estado transitorio. Un estado �� es transitorio si existe un estado �� que es alcanzable desde ��, pero el estado �� no es alcanzable desde el estado ��.

FIGURA 7. ESTADO TRANSITORIO
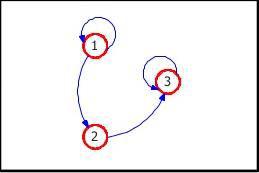
Figura 7. Estado transitorio. El estado 2 es transitorio. (Tomado de Wikipedia. Imágenes).
Estado recurrente. Es un estado que no es transitorio.
FIGURA 8 ESTADO RECURRENTE
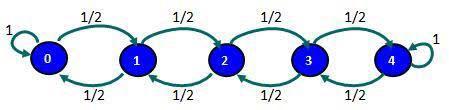
Figura 8. Estado recurrente. Los estados 1,2,3 son recurrentes. (Tomado Wikipedia).
Estado periódico. Un estado �� es periódico con periodo �� > 1 si �� es el número más pequeño tal que las trayectorias que conducen al estado �� de regreso al estado �� tienen una longitud que es un múltiplo de ��. Si un estado recurrente no es periódico, se conoce como aperiódico (Winston, 2008).
FIGURA 8. ESTADO PERIÓDICO
Figura 9. Estado periódico. Cadena de período 3. (Tomado Wikipedia Imágenes).
UnADM | DCEIT| PT2 29

3.4 MODELO O PROCESO ESTOCÁSTICO

El conocer los diferentes conceptos matemáticos que se mencionan en esta investigación nos ayuda a comprender de una manera más clara respecto al uso de las cadenas de Markov en la predicción de ciertos fenómenos , como es el caso de la deserción escolar.
En la teoría de la probabilidad, un proceso estocástico es un concepto matemático que sirve para usar magnitudes aleatorias que varían con el tiempo o para caracterizar una sucesión de variables aleatorias (estocásticas) que evolucionan en función de otra variable, generalmente el tiempo.
Cada una de las variables aleatorias del proceso tiene su propia función de distribución de probabilidad y pueden o no estar correlacionadas entre sí. Cada variable o conjunto de variables sometidas a influencias o efectos aleatorios constituye un proceso estocástico.
Un proceso estocástico ���� puede entenderse como una familia uniparamétrica de variables aleatorias indexadas mediante el tiempo t. Los procesos estocásticos permiten tratar procesos dinámicos en los que hay cierta aleatoriedad.
3.4 .1 MODELO MATEMÁTICO ESTOCÁSTICO
Uno de los conceptos matemáticos que puede causar cierta confusión puede ser lo referente a la modelación de procesos estocásticos ya que sus términos no son de uso común, pero que al ser diseñados resultan de gran apoyo para predecir en cierta forma la evolución o el comportamiento de eventos relacionados con nuestra vida cotidiana. Entonces se dice que:
Un modelo matemático estocástico es una abstracción matemática de un proceso empírico cuyo desarrollo está gobernado por leyes probabilísticas. El proceso empírico se estudia como un modelo probabilístico que evoluciona en el tiempo y genera secuencias de valores numéricos.
Un modelo matemático estocástico tiene por lo menos una variable de este es tomada como un dato al azar y las relaciones entre variables se toman por medio de funciones probabilísticas.
UnADM | DCEIT| PT2 30

Sirven por lo general para realizar grandes series de muestreos, quitan mucho tiempo en el computador son muy utilizados en investigaciones científicas. (Modelode.com, 2021). Para poder modelar de forma correcta un proceso estocástico es necesario comprender numerosos conceptos de probabilidad y estadística.

Los modelos estocásticos poseen elementos aleatorios los cuales se encuentran distribuidos dentro del modelo, es así como es más fácil predecir el valor calculado, como también la cantidad en términos de probabilidad de ocurrencia; este modelo matemático también puede ser definido como los modelos cuantitativos en los que existe más de un estado de la naturaleza y donde cada estado debe encontrarse estimado.
3.4.1 TEORIA DE GRAFOS
La teoría de grafos resulta de gran importancia dentro del estudio de las cadenas de Markov ya que al proyectar de manera gráfica las diferentes probabilidades de transición que sigue nuestra variable aleatoria dentro de un determinado tiempo nos ayudara a tener una mejor proyección de los diferentes eventos que ocurren con dicha variable. Por lo que el conocimiento de algebra será un complemento perfecto para adentrarse en el tema de Cadenas de Markov.
Definición:
�������������������� ����������, ��,���� ������ ���������������� �������������� ������ ���� ���������������� ������������ ���� ������í��, ��, �� ���� ����������������, ��,���� ���������� ���� ���������������� ���� ������������������ ������ ����������. �� �������� ���������������� ���������� ��é������������ �� ���������� ������ ����������. �� ������á ���� ���������������� ���� ������ �������������� �� ���������� ������ ����������. ������������������������ ���� ������������ó�� �� =(��, ��) �������� ���������������� ���� ���������� ���������� ������������������ ���� ��é������������ �� �������������� ������, ������������������������������,(����). A cualquier arista de un grafo se le puede asociar una pareja de vértices de este. Si �� �� �� son dos vértices de un grafo y la arista a está asociada con este par, escribiremos �� =���� Por ejemplo:
���� �� ={��1, ��2, ��3, ��4, ��5} �� �� ={��1��2, ��1��3, ��1��4, ��2��4, ��2��5}
UnADM | DCEIT| PT2 31



