Osnove kriptografije

Ilma Gusinac i Nerma Fazlibašić maturantice Prve bošnjačke gimnazije

Kriptografija (kriptos - skriven i grafo - pisati) je nauka koja se bavi lingvističkim i matematičkim načinima zaštite informacija u komunikaciji.

Kriptogram je vrsta slagalice koja se sastoji od kratkih komada šifrovanog teksta. Kriptoanaliza je obrnuti inžinjering kriptografije - pokušaj prepoznavanja slabosti različitih kriptografskih algoritama i njihovih implementacija. Kriptologija obuhvata kriptografiju i kriptoanalizu i promatra matematičke probleme koji su u njihovoj osnovi.

Slika 1. Podjele kriptografije

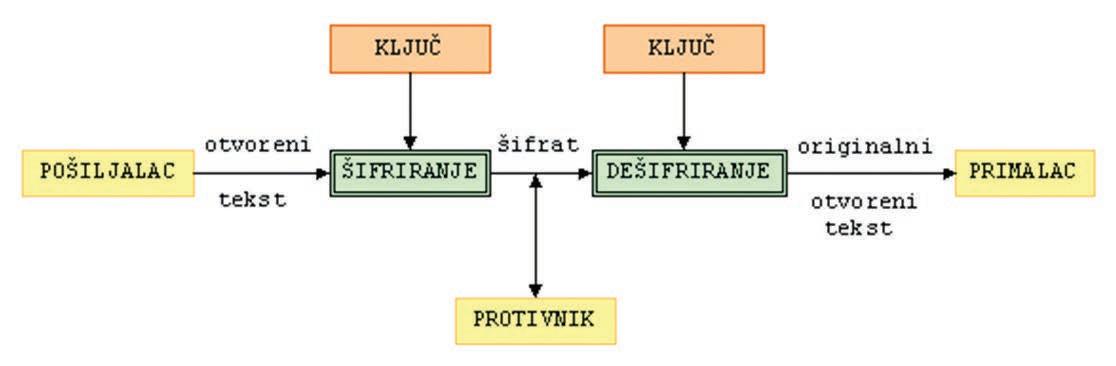
Kriptografija se bavi lingvističkim i matematičkim načinima zaštite informacija u komunikaciji. Kako bi poruke ostale tajne, korištene su matematičke metode koje bi zbunile i obeshrabrile svakog neželjenog primatelja poruke. Najviše su utjecaja u klasičnoj kriptografiji imale matematičke metode supstitucije i transpozicije. Razvojem računara u 20. stoljeću stvara se mogućnost implementacije novih matematičkih metoda u kriptografiji. Kako bi sistemi bili sigurni, a kako bismo sebi olakšali život pri računanju i stvaranju strukture algoritma, kriptografi se koriste modularnom aritmetikom u svim novijim sistemima.

Transpozicija

Metoda šifriranja koja se naziva transpozicija koristi se anagramima koji se dobijaju premještanjem slova otvorenog teksta. U slučaju korištenja malog broja slova, ova je metoda nesigurna za slanje poruka zbog malog broja kombinacija kojim se originalna poruka može dešifrirati.

Primjer 1.

Otvoreni tekst: OVA Broj mogućih transpozicija: 6 (3 faktorijela 1 )

Moguće transpozicije: OVA, VAO, AVO, OAV, AOV, VOA.

1 Matematička funkcija kojom se izračunava proizvod prirodnih brojeva od 1 do nekog određenog prirodnog broja n, označeno kao n!.

Supstitucija

Supstitucija se definira kao matematička metoda kojom svako slovo ili znak mijenja svoj identitet ali zadržava svoje mjesto. Tehnika je jednostavno definirana nasumičnim povezivanjem slova abecede, nakon čega se znakovi sparuju (slova otvorenog teksta se zamjenjuju nasumično odabranim parovima).

Primjer 1. Otvoreni tekst: MATEMATIKA

Supstitucija: M → G, A → R, T → N, E → O, I → P, K → L

Šifrat: GRNOGRNPLR

Cezarova šifra

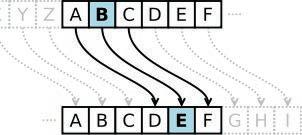
Šifra nastaje pomicanjem abecede za 3 mjesta. Svakom slovu otvorenog teksta odgovara jedinstveno slovo abecede koje ga zamjenjuje, te zbog toga ovaj tip šifre nazivamo i monoalfabetska šifra.

Neka je otvoreni tekst označen oznakom x, dok je šifrirani tekst y, a ključ oznakom k tada možemo zapisati: x,y,z ∈�� 26 .

Iz toga možemo zaključiti:

Enkripcija: �� �� (x)≡ x + k mod 26

Dekripcija: �� �� (y)≡ y – k mod 26

Primjer 2. Otvoreni tekst = DISKRETNA

Ključ k = 12

DISKRETNA = �� 1 , �� 2 , �� 3 .... �� 9 = 3, 8, 18, 10, 17, 4, 19, 13, 0. Slika 2. Cezarova šifra

Šifrat je tada izračunat kao: �� 1 , �� 2 , �� 3 .... �� 9 = 15, 20, 4, 22, 3, 16, 5, 25, 12 = PUEWDQFZM

Fibonaccijev brojni sistem

Fibonaccijevi kodovi atraktivniji su u odnosu na ostale univerzalne kodove jer omogućuju lako određivanje polaznih podataka i jednostavnu, zahvalnu manipulaciju. Zbog tog zanimljivog svojstva Fibonaccijevi kodovi često nalaze svoju primjenu u programiranju i analizi tržišta kapitala.

U binarnom sistemu svaki niz varijabli 0 i 1 predstavlja neki broj. Pogreška bilo koje vrste, poput nedostatka neke varijable, opet daje valjani prikaz nekog drugog broja, stoga lako može proći neopaženo. Fibonaccijev sistem pretvara brojeve u nizove varijabli nula i jedinica, u kojem se nikada dvije jednice ne mogu pojaviti zajedno u toku. Kada je god 0 koja prethodi 1, slučajno zamijenjena s 1, takva se pogreška lako uočava. Ovo svojstvo Fibonaccijeva sistema daje Fibonaccijevu kodu veliku prednost u odnosu na druge postojeće kodove. Oštećeni niz podataka ne postaje beskoristan, nego se tokom procesa dekodiranja gube najviše tri varijable.

Šifre toka

Šifre toka (engl. Stream Ciphers) šifriraju svaki bit zasebno. Za ključ ove šifre se koristi nizovni ključ koji je stvoren od niza bitova.

Prikaz osnovnih funkcija u šifri toka:

Enkripcija: ���� = ������ = ���� + ���� mod 2

Dekripcija: ���� = ������ = ���� + ���� mod 2

Prvo što možemo zaključiti iz funkcije enkripcije i dekripcije je da sabiramo u obje funkcije. U dosadašnjim primjerima kriptografije uvijek je postojala razlika, odnosno u dekripciji se koristio suprotni operator od enkripcije.