9 minute read
proizvoljnih funkcija Zadaci i rješenja za Kantonalnog
Zadaci i rješenja za Kantonalnog takmičenja
1. 1. 1. 1. 1.
Advertisement
2. 2. 2. 2. 2.
učenika IX razreda 2018. godine Neka su ��������i ��������različiti realni brojevi takvi da je 2����������������+ 1≠0i neka su: Neka su ��������i ��������različiti realni brojevi takvi da je 2����������������+ 1≠0i neka su: Neka su ��������i ��������različiti realni brojevi takvi da je 2����������������+ 1≠0i neka su: Neka su Neka su �������� �������� i i �������� �������� različiti realni brojevi takvi da je 2���������������� različiti realni brojevi takvi da je 2���������������� 6�������� 2 �������� 2 +���������������� −1 �������� ( �������� 2 ��������= 6�������� 2 �������� 2 +���������������� −1 2����������������+ 1 ; ��������= �������� ( �������� 2 ��������= 6�������� 2 �������� 2 +���������������� −1 2����������������+ 1 ; ��������= �������� ( �������� 2 + 1≠0i neka su: + 1≠0i neka su: −1 ) − �������� ( �������� 2 −1 ) −1 ) − �������� ( �������� 2 −1 ) �������� − �������� −1 ) − �������� ( �������� 2 −1 ) �������� − �������� ��������= 6�������� 2 ��������= 6�������� 2 ��������= Odrediti koji je broj veći, Odrediti koji je broj veći, �������� �������� 2 2 �������� �������� 2 +���������������� − 2 +���������������� − ����������������+ 1 ����������������+ 1 ili ��������. ili ��������. 1 1 ; ; ; �������� �������� �������� = = = �������� �������� ( �������� ( �������� 2 2 − − 1 ) − �������� ( �������� 1 ) − �������� ( �������� �������� − �������� �������� − �������� 2 2 − − 1 1 ) ) Odrediti koji je broj veći, 2 �������� ���������������� ili + 1 ��������. �������� − �������� Odrediti koji je broj veći, Rješenje: Rješenje: ��������ili ��������. Odrediti koji je broj veći, Rješenje: ��������ili ��������. Rješenje: Sređivanjem datih algebarskih razlomaka dobijamo: Sređivanjem datih algebarskih razlomaka dobijamo: Rješenje: Sređivanjem datih algebarskih razlomaka dobijamo: Sređivanjem datih algebarskih razlomaka dobijamo: Sređivanjem datih algebarskih razlomaka dobijamo: 6�������� 2 �������� 2 + 3���������������� −2���������������� − ��������= 6�������� 2 �������� 2 + 3���������������� −2���������������� − 2����������������+ 1 ��������= 6�������� 2 �������� 2 + 3���������������� −2���������������� − 2����������������+ 1 1 1 1 ��������= = ��������= = = ( 2 ��������= = = ( 2 = = ( 2 = = ( 2 6�������� 2 �������� 2 + 3���������������� −2���������������� −1 2����������������+ 1 3���������������� ( 2����������������+ 1 ) − ( 2����������������+ 1 ) 2����������������+ 1 6�������� 2 �������� 2 + 3���������������� −2���������������� −1 2����������������+ 1 3���������������� ( 2����������������+ 1 ) − ( 2����������������+ 1 ) 2����������������+ 1 ����������������+ 1 )( 3���������������� −1 ) = 3���������������� − 2����������������+ 1 3���������������� ( 2����������������+ 1 ) − ( 2����������������+ 1 ) 2����������������+ 1 ����������������+ 1 )( 3���������������� −1 ) 2����������������+ 1 = 3���������������� − 3���������������� ( 2����������������+ 1 ) − ( 2����������������+ 1 ) 2����������������+ 1 ����������������+ 1 )( 3���������������� −1 ) 2����������������+ 1 = 3���������������� − 3���������������� ( 2����������������+ 1 ) − ( 2����������������+ 1 ) 2����������������+ 1 ����������������+ 1 )( 3���������������� −1 ) 2����������������+ 1 = 3���������������� − 1 1 1 1 Analogno dobijamo i Analogno dobijamo i = ( 2����������������+ 1 )( 3���������������� − 2����������������+ 1 1 ) = 3���������������� −1 Analogno dobijamo i 2����������������+ 1 Analogno dobijamo i Analogno dobijamo i �������� ( �������� 2 −1 ) − �������� ( �������� ��������= �������� ( �������� 2 −1 ) − �������� ( �������� �������� − �������� ��������= �������� ( �������� 2 −1 ) − �������� ( �������� �������� − �������� 2 2 2 − − − 1 1 1 ) ) ) = = �������� �������� �������� 3 3 3 − �������� − �������� − �������� − �������� �������� − �������� − �������� − �������� �������� − �������� 3 3 3 + + + �������� �������� �������� = = ( �������� ( �������� ( �������� 3 3 3 − �������� 3 ) − ( �������� − �������� − �������� 3 ) − ( �������� − �������� �������� − �������� − �������� 3 ) − ( �������� − �������� �������� − �������� ) ) ) ��������= �������� ( �������� 2 −1 ) − �������� ( �������� 2 −1 ) �������� − �������� = �������� 3 − �������� − �������� 3 +�������� �������� − �������� = ( �������� 3 = ( �������� − �������� )( �������� 2 − ����������������+�������� 2 ) − ( �������� − �������� ) �������� − �������� = ( �������� − �������� )( �������� 2 − ����������������+�������� 2 −1 ) =�������� 2 − ����������������+�������� 2 −1 ��������= �������� ( �������� 2 −1 ) − �������� ( �������� 2 −1 ) �������� − �������� = �������� 3 − �������� − �������� 3 +�������� �������� − �������� = ( �������� 3 = ( �������� − �������� )( �������� 2 − ����������������+�������� 2 ) − ( �������� − �������� ) �������� − �������� = ( �������� − �������� )( �������� 2 − ����������������+�������� 2 −1 ) �������� − �������� =�������� 2 − ����������������+�������� 2 −1 ��������= �������� − �������� = �������� − �������� = = ( �������� − �������� )( �������� 2 − ����������������+�������� 2 ) − ( �������� − �������� ) �������� − �������� = ( �������� − �������� )( �������� 2 − ����������������+�������� 2 −1 ) �������� − �������� =�������� 2 − ����������������+�������� 2 −1 = ( �������� − �������� )( �������� 2 − ����������������+�������� 2 ) − ( �������� − �������� ) �������� − �������� = ( �������� − �������� )( �������� 2 − ����������������+�������� 2 −1 ) �������� − �������� =�������� 2 − ����������������+�������� 2 −1 Kako bi odredili koji je broj veći, posmatrajmo razliku brojeva = ( �������� − �������� )( �������� 2 − ����������������+�������� 2 ) − ( �������� − �������� ) �������� − �������� = ( �������� − �������� )( �������� 2 − ����������������+�������� 2 −1 ) �������� − �������� =�������� 2 − ����������������+�������� 2 −1 Kako bi odredili koji je broj veći, posmatrajmo razliku brojeva − �������� 3 ) − ( �������� − �������� �������� − �������� − �������� 3 ) − ( �������� − �������� �������� − �������� �������� − �������� �������� i ��������. �������� i ��������. ) ) �������� − �������� Kako bi odredili koji je broj veći, posmatrajmo razliku brojeva �������� i ��������. Kako bi odredili koji je broj veći, posmatrajmo razliku brojeva �������� − ��������= ( �������� 2 − ����������������+�������� 2 −1 ) − ( 3���������������� − �������� − ��������= ( �������� 2 − ����������������+�������� 2 −1 ) − ( 3���������������� − �������� i 1 ) 1 ) ��������. Kako bi odredili koji je broj veći, posmatrajmo razliku brojeva �������� − ��������= ( �������� 2 − ����������������+�������� 2 −1 ) − ( 3���������������� − =�������� 2 −2����������������+�������� 2 = ( �������� − �������� ) 2 ≥0 =�������� 2 −2����������������+�������� 2 = ( �������� − �������� ) 2 ≥0 �������� 1 i ) ��������. �������� − �������� = = �������� 2 ( �������� − 2 2 − ���������������� ����������������+ + �������� 2 �������� 2 = −1 ) − ( �������� − �������� ( 3���������������� − ) 2 ≥0 1 ) Budući da je Budući da je Budući da je �������� ≠ �������� �������� ≠ �������� �������� ≠ �������� �������� − ��������= ( �������� 2 − ���������������� =�������� 2 −2����������������+ =�������� 2 −2����������������+ , zaključujemo da je �������� , zaključujemo da je �������� , zaključujemo da je �������� +�������� 2 �������� 2 = �������� 2 = <��������. <��������. <��������. −1 ) − ( �������� − �������� ( �������� − �������� ( 3 ) 2 ) 2 ���������������� − ≥0 ≥0 1 ) Budući da je �������� ≠ ��������, zaključujemo da je Odrediti trocifren broj ������������������������, ( �������� ≠0, Odrediti trocifren broj ������������������������, ( �������� ≠0, ��������< �������� ≠ �������� ≠ �������� 0, 0, . �������� ≠ �������� ≠ 0 0 ) ) za koga važi za koga važi �������� �������� + + �������� �������� + + �������� �������� = 9 = 9 Naučno-istraživački matematički klub Prve bošnjačke gimnazije Sarajevo Budući da je �������� ≠ ��������, zaključujemo da je ��������<��������. Odrediti trocifren broj ������������������������, ( �������� ≠0,�������� ≠0,�������� ≠0 ) za koga važi �������� Odrediti trocifren broj ������������������������, ( �������� ≠0,�������� ≠0,�������� ≠0 ) za koga važi �������� 9�������� 2 + 9�������� 2 + 9�������� 2 −6������������������������ ≤ �������� 3 +�������� 3 +�������� 3 . 9�������� 2 + 9�������� 2 + 9�������� 2 −6������������������������ ≤ �������� 3 +�������� 3 +�������� 3 . + + �������� �������� + + �������� �������� = 9 = 9 Odrediti trocifren broj ������������������������, ( 9�������� 2 + 9�������� 2 + 9�������� 2 −6������������������������ ≤ �������� 3 9�������� 2 + 9�������� 2 + 9�������� 2 −6������������������������ ≤ �������� 3 �������� ≠ +�������� +�������� 0,�������� ≠ 3 +�������� 3 3 +�������� 3 . . 0,�������� ≠0 ) za koga važi ��������+��������+��������= 9 i i i i i
Limes Budući da je �������� ≠ ��������, zaključujemo da je ��������<��������.
2.
Odrediti trocifren broj ������������������������, ( �������� ≠0,�������� ≠0,�������� ≠0 )
9�������� 2 + 9�������� 2 + 9�������� 2 −6������������������������ ≤ �������� 3 +�������� 3 +�������� 3 . za koga važi ��������+��������+��������= 9 i
Rješenje:
Datu nejednakost možemo napisati u obliku
�������� 2 ( 9− �������� ) +�������� 2 ( 9− �������� ) +�������� 2 ( 9− �������� ) 6������������������������
odnosno zbog ��������+��������+��������= 9dobijamo
�������� 2 ( ��������+�������� ) +�������� 2 ( ��������+�������� ) +�������� 2 ( ��������+�������� ) 6������������������������
Nakon dijeljenja gornje nejednakosti sa ������������������������> 0, imamo
�������� �������� �������� �������� �������� �������� �������� + �������� + �������� + �������� + �������� + �������� ≤6
Kako na osnovu poznate nejednakosti vrijedi da je �������� + �������� ≥2, za sve ��������,�������� ∈ ℝ + �������� �������� dobijamo �������� + �������� ≥2, �������� + �������� ≥2, �������� + �������� ≥2, te nakon sabiranja ovih nejednakosti imamo �������� �������� �������� �������� �������� �������� �������� �������� �������� �������� �������� �������� �������� + �������� + �������� + �������� + �������� + �������� ≥6 ( ∗∗ )
Sada iz ( ∗ ) i ( ∗∗ ) zaključujemo da vrijedi samo jednakost
�������� �������� �������� �������� �������� �������� �������� + �������� + �������� + �������� + �������� + �������� = 6
u slučaju kada je ��������=��������=��������.
Tada je ��������+��������+��������= 3�������� ( = 3��������= 3�������� ) , odnosno ��������=��������=��������= 3.
Dakle, u pitanju je broj ������������������������=333.
Limes ���������������� ���� ���� ���� ���������������� �������� ����
�������� ൌ �������� �������� ʹ ���� �������� ���������������� �������� �������� ൌ �������� ʹ �������� �������� ൌ �������� ൌ�������� ʹ ����������������
�������� ʹ
����ൌͳʹǢ ����ൌͳ͵ ����ൌͳʹǢ ����ൌͳ͵ ʹ
ʹ ͳǡʹǡ Ǥ Ǥ Ǥ ǡ����
ͳǡʹǡ Ǥ Ǥ Ǥ ǡ����
Rješenje:
a) Broj 12 je lijepje što potvrđuje ovaj raspored brojeva na krugu
b)
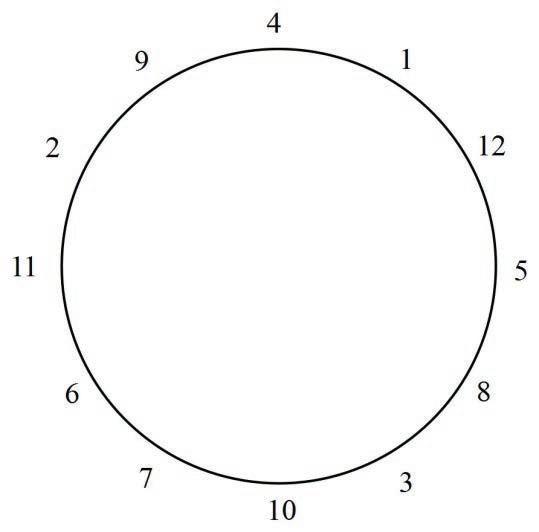
Dokazat ćemo da broj 13 nije lijep.
Među brojevima 1, 2, . . . ,13 nalazi se 7neparnih i 6parnih brojeva.
Zbog toga ćemo, ma kako rasporedili ovih 13 brojeva na krug, po Dirihleovom principu imati 2 susjedna neparna broja na krugu.
Njihov zbir je sigurno paran broj i veći ili jednak od 4pa ne može biti prost broj pa broj 13 nije lijepbroj.