Recomendaciones metodológicas para incorporación del cambio climático en el diseño de obras

norte de Chile

Recomendaciones metodológicas para la incorporación del cambio climático en el diseño de obras hidráulicas en la zona norte de Chile.

Programa de las Naciones Unidas para el Desarrollo, Chile.

Inscripción N°: 218815

ISBN: 978-956-6057-45-1

Representante Residente del Programa de las Naciones Unidas para el Desarrollo en Chile . Georgiana Braga-Orillard.

Edición

Maria Colmenares, Área de Medio Ambiente y Desarrollo Sostenible, PNUD-Chile.

Esteban Delgado, Área de Medio Ambiente y Desarrollo Sostenible, PNUD-Chile.

Anahí Encina Araya, Coordinadora Nacional de Proyecto AdaptaClima, Chile.

Claudia Apaz Huck, Ingeniera Asesora en Cambio Climático AdaptaClima, Chile.

Paulina Hunt Vergara, Apoyo Comunicacional AdaptaClima, Chile.

Consultores:

Ximena Vargas Mesa.

Eduardo Muñoz Castro.

Joaquín Jorquera Fernández.

Diseño:

Paula Oyarzun Fadic

Colaboran:

Ministerio de Obras Públicas.

• Dirección de Obras Hidraúlicas.

• Dirección General de Obras Públicas.

Copyright © PNUD (2025). Recomendaciones metodológicas para la incorporación del cambio climático en el diseño de obras hidráulicas en la zona norte de Chile. Todos los derechos reservados.

Santiago de Chile. 2025

Recomendaciones metodológicas para la incorporación del cambio climático en el diseño de obras hidráulicas en la zona norte de Chile

El cambio climático sugiere una serie de desafíos para la humanidad, donde la planificación estratégica a corto, mediano y largo plazo es clave para asegurar la pertinencia, factibilidad y sostenibilidad de las soluciones que se propongan para afrontarlos. A pesar de reconocerse esta necesidad, a nivel nacional aún existen vacíos en cuanto a recomendaciones técnicas y prácticas para la implementación del cambio climático en el diseño de infraestructura hidráulica. Si bien existen algunas experiencias a nivel nacional respecto a la incorporación del cambio climático en el diseño de obras, estas son altamente dependientes de la experiencia del consultor, consideran supuestos estacionarios y carecen de propuestas para la reducción y cuantificación de la incertidumbre. En términos internacionales, lineamientos metodológicos disponibles en diferentes regiones reconocen la necesidad de adoptar diferentes métodos de acuerdo con el tipo de obra, se apoyan en productos meteorológicos grillados, la estacionariedad es un supuesto ampliamente cuestionado y se promueve el uso de conjuntos de simulaciones futuras para efecto de cuantificar de manera adecuada la incertidumbre.

Con el objetivo de alinear las metodologías adoptadas a nivel nacional en materia de diseño hidrológico en un contexto de clima cambiante respecto a las experiencias reportadas en la literatura internacional, en el presente trabajo se presentan algunas recomendaciones y lineamientos para tratar las precipitaciones extremas y la consiguiente generación de escorrentía superficial. Se aborda la escala temporal y espacial de precipitación y temperatura, y se presentan metodologías para estimar caudales en cuencas con y sin información fluviométrica, en particular mediante métodos de modelación dinámica, métodos estadísticos, y relaciones empíricas precipitación-escorrentía del tipo hidrograma unitario sintético. Además, se presentan ejemplos aplicados que ilustran la incorporación del cambio climático en la estimación de caudales máximos, precipitaciones extremas y curvas intensidad-duración-frecuencia, con énfasis en la macrozona norte de Chile, aunque los métodos pueden aplicarse globalmente

Los resultados del estudio indican que la modelación hidrológica entrega resultados más consistentes con los observados en la realidad cuando se analiza el periodo histórico, lo que permite suponer que sus proyecciones de cambio hidrológico (i.e., en contexto de clima cambiante) tendrían una menor incertidumbre asociada. El carácter dinámico permite considerar la interacción entre factores como la humedad del suelo previa y durante los eventos de crecida, la posición de línea de nieve, entre otros. En el caso del norte de Chile, se recomienda emplear modelos espacialmente distribuidos o semidistribuidos, que puedan capturar la heterogeneidad espacial de los eventos extremos, los cuales no siempre afectan toda la cuenca de manera uniforme. El desafío viene dado por la transferencia

de parámetros cuando no se cuenta con registros fluviométricos, lo cual sugiere desafíos en esta materia. Por otro lado, los métodos estadísticos y de hidrograma unitario sintético, aunque más simples y de menor complejidad, presentan limitaciones significativas. Estos métodos se desarrollan a partir de relaciones establecidas entre datos históricos de precipitación y escorrentía, lo cual podría condicionar su aplicabilidad en contexto futuro y, adicionalmente, no consideran la heterogeneidad espacial de las precipitaciones. En consecuencia, si bien estos métodos pueden ser útiles en las fases preliminares de análisis, no se recomienda su uso exclusivo para la estimación de crecidas en un contexto de cambio climático sin aplicar algunas modificaciones.

Finalmente, se destaca que, para abordar los futuros cambios en el clima, es necesario adoptar enfoques transdisciplinarios flexibles y apoyados en modelación de los sistemas hidrológicos y el entendimiento de los procesos que condicionan su respuesta ante eventos hidrometeorológicos extremos.

Tabla de contenido

1 Introducción

1.1 Motivación y contexto

1.2 Objetivos y alcances

2 Revisión de antecedentes

2.1 Sobre la importancia de la inclusión del cambio climático

2.2 Normativa y lineamientos para el diseño hidrológico actual en Chile

2.3 Incorporación de la variable cambio climático en el diseño de obras

2.3.1 Experiencias a nivel internacional

2.3.2 Oportunidades y desafíos

2.4 Oportunidades y desafíos

3 Recomendaciones metodológicas para la incorporación del cambio climático en el diseño de obras hidráulicas

3.1 Descripción general

3.1.1 Resumen de decisiones metodológicas

3.1.2 Zona de estudio

3.2 Análisis de estadísticas de eventos hidrometeorológicos extremos

3.3 Estimación de precipitaciones representativas del dominio de estudio

3.3.1 Precipitación total y efectiva

3.3.2 Distribución temporal de precipitación

3.3.3 Área pluvial y nival durante eventos de precipitación extrema

3.4 Uso de regresiones lineales para estimaciones de crecidas

3.5 Modelación hidrológica

4

3.6 Selección de escenarios y modelos de cambio climático

3.7 Selección de ventanas futuras de evaluación

3.8 Escalamiento y corrección de sesgo

3.9 Cálculo de crecidas en clima cambiante

3.10

Cuantificación de incertidumbre

3.11 Alcances y limitaciones

Ejemplos de aplicación de las recomendaciones metodológicas

4.1

Estimación de crecidas mediante modelación hidrológica

4.2 Estimación de frecuencia de crecidas mediante métodos estadísticos

4.3 Estimación de crecidas mediante método de hidrograma unitario sintético (HUS)

4.4

Estimación de curvas intensidad-duración-frecuencia

5 Consideraciones y pertinencia de la incorporación del cambio climático en el diseño de infraestructura hidráulica

5.1 La necesidad de actualización de ajustes y relaciones estadísticas

5.2 El valor informativo de las estadísticas pasadas para proyectar el futuro

5.3 El uso de percentiles para cuantificar incertidumbre y sus implicancias prácticas

5.4

Impactos metodológicos en la estimación de caudales máximos de crecida

5.5 El valor agregado de enfoques transdisciplinarios

6 Síntesis y conclusiones

Índice de Tablas

Tabla 2.1: Periodos de retorno para diseño y verificación.

Tabla 2.2: Resumen de normativa y lineamientos para el diseño hidrológico en Chile.

Tabla 4.1: Promedio de las eficiencias de los caudales diarios obtenidas mediante la técnica de transferencia de parámetros.

Tabla 4.2: Cuencas seleccionadas para la regresión.

Tabla 4.3: Valores curva número promedioa escala de cuenca para condición seca, normal y húmeda extraídos desde GCN250 para la cuenca del río Lluta en Panamericana y sus subcuencas con controles fluviométricos.

Tabla 4.4: Coeficientes de duración (CD) para diferentes duraciones asociados a las cuencas en el río Lluta.

Tabla 4.5: Parámetros para la configuración del hidrograma unitario sintético (HUS) SCS asociado a las subcuencas controladas del río Lluta.

Tabla 4.6: Caudales máximos instantáneos para las cuencas del río Lluta en el periodo histórico y proyecciones futuras derivadas de 29 GCMs del CMIP6 en escenario ssp5-8.5 escaladas y corregidas por sesgo usando el método MBCn y el producto grillado CR2Met v2.5 como referencia climática.

Tabla 4.7: GCMs con diferencias porcentuales absolutas menores al 25% en el análisis de frecuencia en el periodo histórico 1991-2020 respecto a CR2Met. En negrita se identifican los modelos recomendados por Gateño et al. (2024) para la macrozona Norte Grande de Chile.

Tabla 5.1: Resultados de los caudales medios diarios máximos obtenidos mediante los métodos de Modelación Hidrológica, Regresión e Hidrograma Sintético Unitario en periodo histórico.

Índice de Figuras

Figura 2.1: Factores que determinan impactos ambientales de un proyecto.

Figura 2.2: Conceptualización de los elementos en la estimación de caudales de crecida.

Figura 2.3: Consideraciones clave para el desarrollo de factores de cambio delta (Δ) en Canadá.

Figura 2.4: Esquema metodológico del enfoque tradicional para el estudio de crecidas, donde el orden del análisis de probabilidad y el cálculo de la precipitación promedio puede cambiar según el autor.

Figura 3.1: Esquema general de las decisiones a considerar en el desarrollo de un estudio hidrológico orientado a la estimación de precipitaciones extremas y crecidas en un contexto de clima cambiante.

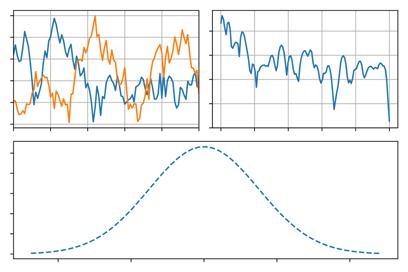
Figura 3.2: Atributos fisiográficos y climáticos promedio en el período 1980-2014 para Chile continental: (a) elevación, (b) precipitación anual, (c) temperatura media, (d) fracción de nevadas, (e) índice de aridez, y (f) p-seasonality (estacionalidad de la precipitación).

Figura 3.3: Ejemplo de valores curva número (CN) para condiciones antecedentes de humedad seca (Tipo I), normal (Tipo II) y húmeda (Tipo III) obtenidos desde el producto GCN250. Se incluyen los contornos de las cuencas (de norte a sur) del río Copiapó, Huasco y Elqui en sus controles fluviométricos más próximos a la desembocadura.

Figura 3.4: Coeficiente de duración (CD) estimados para duraciones de a) 1, b) 6, c) 12, d) 24 y e) 48 hrs.

Figura 3.5: Coeficientes para la estimación de coeficiente de duración (CD) asociados a la transformación de máxima precipitación diaria (Pd) en máxima precipitación en “D” horas en el Norte de Chile.

Figura 3.6: Clúster de distribuciones temporales de precipitación representativas del dominio de estudio.

Figura 3.7: Ejemplo de distribuciones de precipitación propuestas para eventos de duración 24 hrs en clúster 1.

Figura 3.8: Incorporación de cambios en la línea de nieve según temperaturas durante los eventos de precipitación, gradiente de temperatura durante el evento o teórico para la zona, isoterma cero y curva hipsométrica.

Figura 3.9: Esquema de escenarios de trayectorias socioeconómicas compartidas (SSPs) del proyecto CMIP6 y comparación con escenarios del proyecto CMIP5 (RCPs).

Figura 3.10: Representación del paradigma de la “cascada de incertidumbre” y opciones metodológicas clave para la evaluación de los impactos del cambio, y cómo se combinan sus incertidumbres en una envolvente proyectada.

Figura 4.1: Cuenca del Río Lluta, utilizada como zona de estudio para la modelación

hidrológica y las proyecciones de impactos del cambio climático en caudales máximos de crecida. Las líneas y puntos indican las delimitaciones de la cuenca y su estación fluviométrica.

Figura 4.2: Eficiencias obtenidas con cada modelo, tanto para calibración como validación.

Figura 4.3: Flujo base previo a las crecidas máximas anuales, obtenido mediante la modelación hidrológica.

Figura 4.4: Resultados de las eficiencias calculadas mediante la técnica de regionalización en periodos de calibración y validación para cada modelo.

Figura 4.5: Simulación suponiendo que no existiese información fluviométrica. A modo de ejemplo se presenta la simulación de una crecida ocurrida en 2012.

Figura 4.6: Máximos caudales medios diarios anuales derivados de la modelación hidrológica utilizando 29 GCMs.

Figura 4.7: Caudales medios diarios máximos según diferentes periodos de retorno según escenario SSP5-8.5 y 29 GCMs, para periodo estival e invernal.

Figura 4.8: Cuencas seleccionadas para la regresión junto con sus diferentes atributos: a) corresponde a la precipitación media anual, b) corresponde a la escorrentía media anual, c) corresponde al índice de aridez, d) corresponde al área total, e) corresponde a la elevación media, y, f) corresponde al porcentaje de cobertura de nieve de cada cuenca.

Figura 4.9: Resultados de la regresión. Los colores indican el periodo de retorno utilizado, mientras que la línea azul corresponde a la regresión exponencial es escala logarítmica.

Figura 4.10: Resultados de la regresión. Los colores indican el periodo de retorno, mientras que la línea azul representa el ajuste perfecto con una banda de confianza del 20%.

Figura 4.11: Errores de la verificación de la regresión en términos de porcentaje de error de cada cuenca (a) y de manera general (b).

Figura 4.12: Valores curva número espacialmente distribuidos para condición seca (Tipo I), normal (Tipo II) y húmeda (Tipo III) extraídos desde GCN250 para la cuenca del río Lluta en Panamericana.

Figura 4.13: Distribuciones de precipitación representativas para la cuenca del río Lluta en Panamericana y sus subcuencas. Considerando que la mayor parte de la cuenca se asocia al cluster 2, se considera este como representativo del dominio completo.

Figura 4.14: Comparación entre máxima precipitación diaria total y efectiva en el periodo 1991-2020 para la cuenca río Colpitas en Alcérreca. (a) Comparación entre valores máximos anuales, (b) Comparación entre precipitaciones asociadas a periodos de retorno.

Figura 4.15: Resultados análisis de frecuencia de máxima precipitación diaria anual efectiva para el periodo histórico y proyecciones futuras en las subcuencas del río Lluta.

Figura 4.16: Hidrograma de escorrentía directa asociados a precipitaciones en 24 horas, percentil 50% de la distribución de precipitación, y periodo de retorno 100 años.

Figura 4.17: Ejemplo de series de máxima precipitación anual en diferentes bloques de duración obtenidas a partir de la interpolación de ERA5 a la estación Antofagasta para el periodo 1950-2023.

Figura 4.18: Curvas IDF derivadas mediante ERA5 para la estación Antofagasta en periodo 1991-2020.

Figura 4.19: Resultados de análisis de frecuencia de máxima precipitación diaria anual en el periodo histórico (1991-2020), futuro cercano (2035-2064) y lejano (20652094) para la estación Antofagasta según producto de referencia CR2Met v2.5 y 29 GCMs CMIP6 para el escenario ssp5-8.5.

Figura 4.20: Diferencia entre resultados de análisis de frecuencia para el periodo histórico asociado a CR2Met y los diferentes GCMs estudiados interpolados a la estación Antofagasta.

Figura 4.21: Resultados de análisis de frecuencia de máxima precipitación diaria anual en el periodo histórico (1991-2020), futuro cercano (2035-2064) y lejano (20652094) para la estación Antofagasta según producto de referencia CR2Met v2.5 y 14 GCMs CMIP6 para el escenario ssp5-8.5 filtrados según sesgo en periodo histórico.

Figura 4.22: Ejemplo de curvas IntensidadDuración asociadas a periodos de retorno 10 y 100 años en la estación Antofagasta para el

periodo histórico (1991-2020), futuro cercano (2035-2064) y lejano (2065-2094).

Figura 5.1: Parámetros de ajuste de curvas IDF para la estación Antofagasta calculados para subperiodos móviles de 30 años entre 1950 y 2023 a partir de las estadísticas derivadas de ERA5.

Figura 5.2: Máximas precipitaciones diarias (Pd) por periodo de retorno en el periodo 19712020 estimadas para los subperiodos 19712000, 1981-2010, y 1991-2020. a) Resultados absolutos en mm, b) diferencias porcentuales respecto al periodo 1971-2020.

Figura 5.3: GCMs asociados a los percentiles 25,50 y 75% según diferentes periodos de retorno y subperiodos para las estadísticas en la estación Antofagasta. La inexistencia de círculos (NA) se refiere a la correspondencia del GCM con percentiles diferentes a los de interés.

Figura 5.4: Esquema de la conexión entre la producción de conocimiento científico y manejo de los problemas sociales a través de la transdisciplinariedad.

Glosario

AF

Análisis de frecuencia.

CMIP

Proyecto de Intercomparación de modelos acoplados (siglas en inglés).

CMP

Crecida Máxima

Probable (generada por la precipitación máxima probable).

DEM

Modelo de elevación digital (siglas en inglés).

EPE

Evento de precipitación extrema.

FDP

Función de densidad de probabilidad (PDF en inglés).

PEA

Probabilidad de excedencia anual (AEP en inglés)

PMP

Precipitación

FDPA

Función de densidad de probabilidad acumulada (CDF en inglés).

Máxima Probable. RCP

Trayectorias de concentraciones representativas (siglas en inglés).

GCM

Modelo de circulación general (siglas en inglés).

SSP

Trayectorias socioeconómicas compartidas (siglas en inglés).

Instituciones:

DGA : Dirección General de Aguas, Ministerio de Obras Públicas, Chile.

DGOP : Dirección General de Obras Públicas, Ministerio de Obras Públicas, Chile.

DOH : Dirección de Obras Hidráulicas, Ministerio de Obras Públicas, Chile.

IPCC : Grupo Intergubernamental de Expertos sobre el Cambio Climático (siglas en inglés).

MMA : Ministerio del Medio Ambiente, Chile.

MOP : Ministerio de Obras Públicas, Chile.

PNUD : Programa de las Naciones Unidas para el Desarrollo (UNDP por sus siglas en inglés).

SEA : Servicio de Evaluación Ambiental, MMA, Chile.

SEIA : Sistema de Evaluación de Impacto Ambiental, SEA, MMA, Chile.

WMO : OMM – Organización Meteorológica Mundial (siglas en inglés).

01 INTRODUCCIÓN

1.1 Motivación y contexto

Para adaptarse al cambio climático es necesario una planificación estratégica a corto, mediano y largo plazo, la cual debe considerar diferentes escenarios futuros posibles para asegurar la pertinencia, factibilidad y sostenibilidad de las soluciones que se propongan. Desde hace algunas décadas el Grupo Intergubernamental de Expertos sobre el Cambio Climático (IPCC por sus siglas en inglés) y la comunidad científica internacional han trabajado en el desarrollo (y actualización) de potenciales trayectorias de las emisiones de gases de efecto invernadero y, con ello, anticiparse a la evolución del clima futuro, de manera tal de contar con lineamientos respecto a los impactos de cambios en el clima.

En 2013, el IPCC presentó una gama de escenarios de Trayectorias Representativas de Concentración (RCP por sus siglas en inglés) de gases de efecto invernadero, los cuales abarcan desde una condición de mayor severidad y menor acción de mitigación (i.e., RCP 8.5) a una de menor severidad y mayor acción de mitigación (i.e., RCP 2.6). Estos escenarios han servido como insumo para diferentes centros de investigación (e.g., NCAR, EE. UU.; BCC, China), los cuales han empleado dichas directrices para generar simulaciones del sistema atmosférico apoyados en modelos numéricos denominados Modelos de Circulación General (GCM, por sus siglas en inglés) y, así, proyectar cambios en diferentes variables meteorológicas como, por ejemplo, temperaturas extremas, precipitación, entre otras. Para facilitar el estudio del cambio climático, las simulaciones generadas por los diferentes centros de investigación se incluyen en la quinta fase

del Proyecto de Intercomparación de Modelos Acoplados – CMIP5 (Taylor et al., 2012). En 2021, se presentan los resultados de la sexta fase del proyecto, CMIP6 (IPCC, 2021; O’Neill, 2016), donde se introducen trayectorias socioeconómicas que, junto a trayectorias de concentración representativas, originan los escenarios SSP, siendo el SSP5–8.5 de mayor gravedad un escenario de desarrollo futuro basado en el uso de combustibles fósiles.

La variabilidad natural del clima y los futuros cambios climáticos que puedan alterar la intensidad de las precipitaciones o la duración de las tormentas tendrá consecuencias para la infraestructura hidráulica diseñada bajo el supuesto de estacionariedad (Teegavarapu, 2013). Para Chile y el mundo, diferentes estudios muestran un futuro de condiciones extremas (e.g., Bambach et al., 2021; MMA, 2014; Trenberth, 2011), donde, por ejemplo, se proyectan aumentos de temperaturas, aumentos en la intensidad de precipitación, aumentos en la ocurrencia y persistencia de sequías meteorológicas, entre otras. En este contexto, aumentos de la intensidad de precipitación pueden traer consigo la ocurrencia de crecidas y, de darse las condiciones, flujos aluvionales. Así, el cambio climático constituye una amenaza que puede poner en riesgo la seguridad de un territorio de no tomarse las medidas de adaptación adecuadas.

Si bien los modelos de cambio climáticos permiten evaluar los cambios de diferentes variables meteorológicas dados diferentes escenarios de emisiones de gases de efecto invernadero y decisiones socioeconómica y políticas asociadas a la acción climática (i.e., mitigación y adaptación), estos no son pronósticos, sino que potenciales trayectorias futuras. En consecuencia, resulta importante identificar qué modelos son más adecuados para caracterizar la climatología histórica y futura de un

sector de interés, lo cual sugiere adoptar estrategias para su selección. Asimismo, al contar con diferentes casos de estudio (i.e., diferentes modelos combinados con diferentes escenarios), los análisis vinculados a cambio climático no pueden entregar un resultado único y es necesario incluir la incertidumbre asociada, lo cual se propaga en los diferentes niveles de la cadena de análisis de cambio climático y, sin lugar a duda, a las decisiones que se deben adoptar. Así, la incorporación de la incertidumbre atribuida al cambio climático es clave en el diseño de las nuevas obras hidráulicas y, a la vez, la verificación de la seguridad de la infraestructura hidráulica existente, diseñada usando los antecedentes históricos bajo el supuesto de estacionariedad.

En Chile, se reconoce la necesidad de incorporar la componente cambio climático y sus impactos en la disponibilidad de recursos hídricos, eventos extremos de precipitación y crecidas, vegetación, flora y fauna, entre otros. A muestra de ello, desde la suscripción de Chile a la Convención Marco de las Naciones Unidas sobre el Cambio Climático (CMNUCC) en la cumbre de Río 1992, se han elaborado diferentes acuerdos a nivel nacional (e.g., planes de acción, estrategias de adaptación), comunicaciones a la CMNUCC, y estudios mandatados por organismos públicos para analizar los potenciales impactos del cambio climático en el país, así como propuestas de alternativas para su mitigación y adaptación. Sin perjuicio de lo anterior, y a pesar de los avances a la fecha, no existen recomendaciones para la incorporación de cambio climático orientado al diseño de infraestructura hidráulica.

Ante la necesidad de contar con lineamientos que permitan incorporar la componente cambio climático en el diseño y verificación de infraestructura hidráulica, el Programa de las Naciones Unidas para

el Desarrollo (PNUD o UNDP por sus siglas en inglés) ha impulsado un proyecto orientado al desarrollo de dichos lineamientos, el cuál debe estar alineado con las recomendaciones a nivel internacional y los avances científico-tecnológicos. Considerando la dificultad que representa por la escasez de información hidrometeorológica, las diferencias en la fisiografía de sus cuencas, y los patrones meteorológicos que condicionan la generación de eventos de precipitación extremos y crecidas (e.g., precipitaciones frontales y/o convectivas dependiendo de la ubicación), el presente documento considera como caso de análisis la zona norte de Chile. De este modo, se busca entregar recomendaciones metodológicas para la incorporación del cambio climático en el diseño de obras hidráulicas aplicados de manera práctica a la zona norte de Chile (17°S – 32°15’S), que comprende las Regiones de Arica y Parinacota, Tarapacá, Antofagasta, Atacama y Coquimbo.

1.2 Objetivos y alcances

El objetivo general del presente documento radica en entregar recomendaciones metodológicas a especialistas, consultores, profesionales institucionales y tomadores de decisiones para la incorporación de la variable cambio climático en el diseño de obras hidráulicas. En términos específicos, además de las recomendaciones metodológicas, se busca realizar una revisión de antecedentes a nivel internacional y nacional en materia de diseño hidrológico en contexto de clima cambiante, así como la implementación de las recomendaciones en casos

prácticos de estudio. Considerando los desafíos que sugiere la zona, los ejemplos de aplicación se centran en la macrozona Norte de Chile.

El documento no constituye una “receta” para la incorporación del cambio climático en el diseño de infraestructura hidráulica desde el punto de vista hidrológico, sino que entregar recomendaciones que puedan orientar la toma de decisiones metodológicas. Esto, reconociendo que los avances científicos y tecnológicos pueden ofrecer nuevas y mejores alternativas para abordar el problema, y la propuesta de recomendaciones fijas atenta contra el principio de adaptabilidad que sugiere un futuro en contexto de clima cambiante.

02 Revisión de antecedentes

Esta sección da cuenta de los antecedentes principales de una selección de trabajos desarrollados a nivel internacional y nacional ilustrativos de las estrategias adoptadas a la fecha para la incorporación del cambio climático al diseño de infraestructura hidráulica. Con esto, se espera entregar una visión general del estado del arte del tema en cuestión y, así, poder destacar algunas oportunidades de mejora y desafíos pendientes asociados a la materia. Se debe tener en cuenta que, considerando la vasta disponibilidad de documentos, esta revisión de antecedentes no está orientada a entregar definiciones de cambio climático, sino que a ilustrar como dicha componente se traduce desde la teoría a la práctica en el diseño de obras.

2.1 SOBRE LA IMPORTANCIA DE LA INCLUSIÓN DEL CAMBIO CLIMÁTICO

A pesar de la necesidad y el deseo de incorporar la componente de cambio climático tomando en consideración la amenaza que este sugiere a la infraestructura hidráulica, a la fecha, no existen lineamientos claros en el contexto nacional de cómo hacerlo. Más aún, la diversidad hidroclimática de Chile sugiere desafíos adicionales enfocados en la búsqueda de una estrategia que sea generalizable a todo el territorio. A continuación, se revisan algunos casos de aplicación reportados en estudios impulsados por agencias gubernamentales y experiencias internacionales. Cabe mencionar que la revisión se concentra en el diseño hidrológico y la generación de crecidas, no obstante, existen otros extremos meteorológicos que pueden condicionar la seguridad de la infraestructura hidráulica y que debiesen ser estudiados. Ejemplo

de ello es la velocidad de viento, variable empleada para el cálculo de la revancha por oleaje en embalses. Asimismo, la ocurrencia conjunta de diferentes eventos hidrometeorológicos extremos (e.g., precipitaciones intensas combinado con condiciones cálidas en cuencas con influencia nival) podría aumentar los impactos asociados a estos, razón por la cual es importante considerar la naturaleza multivariada de, en el caso de interés, las crecidas.

2.2 NORMATIVA Y LINEAMIENTOS PARA EL DISEÑO HIDROLÓGICO ACTUAL EN CHILE

En Chile existen diferentes lineamientos para el diseño hidrológico, los cuales, desafortunadamente, se consideran como guías normativas que, si bien garantizan un estándar mínimo, limitan la aplicación de nuevas alternativas para abordar la estimación de precipitaciones y caudales para el diseño de infraestructura. Uno de los principales documentos corresponde al denominado “Manual de cálculo de crecidas” (DGA, 1995), el cual tuvo por objetivo mejorar la estimación de caudales extremos en cuencas del país con escasa o nula información fluviométrica. Esto mediante el empleo de fórmulas o procedimientos sencillos pero confiables, que pudieran ser aplicados con facilidad en el diseño de obras hidráulicas de pequeña a mediana envergadura. Allí se analizaron distintos métodos de uso habitual en el país, con el objetivo específico de probarlos, seleccionarlos y validar los más adecuados. Entre estos, se incluyó el análisis de frecuencias regional tanto para caudales máximos como mínimos y la fórmula racional y de Verni y King para caudales máximos de origen pluvial. Para cada uno de estos métodos se validaron

los parámetros que los definen, y entregaron recomendaciones para la determinación de sus valores. Es interesante notar la determinación de zona homogéneas para el análisis de frecuencia regional, que se realizó sobre los valores de caudales medios diarios máximos anuales en los períodos pluvial y deshielo, definiendo a base de un coeficiente regional su transformación a caudal máximo instantáneo. Adicionalmente, se realizó el análisis de la estimación de hidrogramas de origen pluvial usando como función de transferencia los hidrogramas unitarios tipo Linsley y tipo Gray. Dado lo determinante que resulta en la generación de la escorrentía directa la infiltración de la lluvia, se propuso una metodología para estimar el monto de precipitación efectiva de una tormenta mediante el empleo del Método de la Curva Número. A pesar de los años transcurridos, la mayor cantidad de información disponible y los avances tecnológicos, el documento sigue vigente sin modificaciones ni actualizaciones desde su publicación.

Otro de los documentos importantes en materia de diseño hidrológico corresponde al Volumen N°3 del

Manual de Carreteras (MOP, 2024), documento que se actualiza parcialmente año a año. En particular, en el volumen se presentan políticas, criterios, procedimientos, instrucciones y recomendaciones involucrados en un diseño vial. La sección de Hidrología presenta metodologías y criterios de estimación de caudales de diseño de obras de drenajes de la carretera y de la faja de camino. Se incluyen los criterios de diseño, sus hipótesis, posibilidades de aplicación y limitantes, de manera que el proyectista deba escoger los métodos apropiados al problema y característica del lugar e información disponible. Los procedimientos incluidos en el manual se refieren principalmente a la estimación de crecidas provocadas por lluvia sin incluir el derretimiento de nieve (i.e., crecidas pluviales). Se indican, según el tipo de obra, los periodos de retorno asociados al diseño y verificación, considerando el riesgo de falla según la vida útil (ver Tabla 2.1).

Tabla 2.1: Periodos de retorno para diseño y verificación.

Tipo de Obra Tipo de Ruta

Puentes y Viaductos(1)

Alcantarillas (S>1,75 m2) o H terraplén ≥10 m y estructuras enterradas(2)

Alcantarillas (S<1,75m2)

Drenaje de la Plataforma

Defensas de Riberas

Carreteras

Caminos

Carreteras

Caminos

Carreteras Caminos Carreteras Caminos

Periodo de Retorno (T; años)

Vida útil supuesta (n; años)

(1) En el caso de viaductos el cálculo de caudales en crecidas está destinado a calcular la socavación en las fundaciones de las pilas. Iguales T se emplearán para el cálculo de socavaciones en puentes.

(2) Las alcantarillas de drenaje construidas bajo terraplenes de altura≥10 m deben diseñarse para estos períodos de retorno cualquiera que sea su sección. En esta misma categoría se clasificarán las estructuras proyectadas bajo nivel del terreno natural circundante, destinadas al cruce desnivelado de dos vías.

(3) Para la etapa de diseño de puentes y defensas de riberas, la revancha mínima asociada a la cota de aguas máximas para el período de retorno de diseño debe ser de 1,0 m.

(4) Para la verificación hidráulica de puentes se considerará que la revancha asociada a la cota de aguas máximas para el periodo de retorno de verificación puede reducirse a 0,3 m.

Fuente: MOP (2024).

En el Manual de Carreteras (MOP, 2024) se enfatiza la necesidad de contar con información histórica para estimar la recurrencia de estos eventos durante la vida útil de la obra (i.e., periodo futuro). Así, se describen las observaciones y registros que se pueden realizar (y utilizar) para el estudio de probabilidades de las variables hidrológicas, indicando que los procedimientos correspondientes se encuentran en el Volumen N°2 del mismo documento. Parte de la sección de Hidrología también está dedicada a describir la metodología para realizar el análisis de frecuencias de las variables hidrológicas de interés. También se incluyen definiciones y conceptos asociados a la obtención de las curvas Intensidad-DuraciónFrecuencia (curvas IDF). Allí se presentan tanto las intensidades de lluvia asociadas a periodos de retorno (T) entre 10 y 100 años, para lluvias de duración entre 1 y 24 horas como los coeficientes de duración para T=10 años y los coeficientes de frecuencia hasta T=200 años, en 36 estaciones distribuidas a lo largo del país. Adicionalmente, el documento muestra la relación entre lluvia máxima diaria (Pd) y lluvia máxima en 24 horas (P24) sugiriendo, a base de los registros en 14 estaciones pluviográficas ubicadas entre la Región de Coquimbo y la Región de Los Lagos, el valor 1,1 para estos efectos (i.e., P24 = 1,1*Pd). Por otra parte, para la estimación de lluvias e intensidades con duración menor que 1 hora se sugiere el uso de la fórmula de Bell que data del año 1969, mostrando su aplicabilidad en el país. También se presenta el método racional para ser aplicado en cuencas pequeñas (áreas menores a 25 km2) incluyéndose los valores del coeficiente de escorrentía para T=10 años. A su vez se presentan los métodos descritos en el Manual de cálculo de crecidas (DGA, 1995) y se agregan otros métodos de análisis regional como el del USG y el de momentos ponderados por probabilidad.

En términos de hidrología urbana, la principal referencia corresponde al “Manual de drenaje urbano” (DOH, 2013). Dicho documento apunta a orientar el desarrollo de los proyectos de drenaje urbano en el país, incluyendo elementos como la planificación, diseño, construcción, conservación y operación de las redes de drenaje de aguas lluvias. Para la caracterización climática, en particular relacionada a precipitaciones de diseño, se presentan las condiciones medias de algunas variables en ciudades con Planes Maestros de Aguas Lluvias, a base de documentos que datan de 1987 a 2001. También se mencionan los efectos del transporte de sedimentos considerando la morfología de los sistemas fluviales, la capacidad de transporte de sedimentos, los efectos de la urbanización y el transporte de sedimentos en las redes de drenaje, zonas inundables y riesgos naturales. Igualmente se definen las propiedades de las tormentas (i.e., duración, magnitud, intensidad, hietograma, variación espacial y probabilidad de ocurrencia) y describe la metodología de determinación de curvas IDF usando los coeficientes de duración y frecuencia generalizados propuestos por DGA (1991) en zonas donde no se cuenta con registros de precipitación, sugiriendo que, para lluvias menores a 1 hora, se adopte la fórmula de Bell.

En materia de cambio climático, si bien se reconoce la necesidad de su incorporación, los lineamientos existentes abordan esta componente desde una perspectiva conceptual y holística. El primer documento oficial en esta materia corresponde a la Guía metodológica para la consideración del cambio climático en el Sistema de Evaluación de Impacto Ambiental (SEIA; SEA, 2023a). Allí se busca entregar criterios e instaurar una metodología para la evaluación ambiental de proyectos y actividades en un contexto de cambio climático y adaptación y

mitigación climática. En el documento se presentan de manera complementaria antecedentes del cambio climático y los alcances generales de la evaluación de impacto ambiental, incluyendo la siguiente metodología para incorporar consideraciones de cambio climático previo al ingreso al SEIA. Asimismo, se destaca la importancia de la descripción del proyecto e identificación de los factores generadores de impacto los que, como se muestra en la Figura 2.1, incluyen localización, temporalidad, extracción y uso de recursos naturales, mano de obra, suministro y transporte, descarga de contaminantes al medio ambiente, y objetivo del proyecto.

En línea con la publicación de la guía Servicio de Evaluación Ambiental (SEA, 2023a), se publicó la guía “Criterio de evaluación en el SEIA: Cambio climático

en la evaluación ambiental del recurso hídrico” (SEA, 2023b). Dicho documento tuvo por objetivo entregar una metodología para proyectar los cambios de precipitación y temperatura producto del cambio climático, estableciendo para ello una zonificación de Chile y los porcentajes de cambio de precipitación para cada zona. Así, tomando como base las series de precipitación y temperatura del periodo histórico (1980-2010) y futuro (20352065) proyectadas por los Modelos de Circulación General (GCM por sus siglas en inglés) incluidos en la plataforma ARClim, se recomienda seleccionar el valor asociado a las probabilidades p25 o p75, dependiendo de con cual de estos se produce una mayor magnitud o duración del impacto que se pretende proyectar. Adicionalmente, se hace notar que los valores expuestos corresponden a los efectos del cambio climático sobre la magnitud

Figura 2.1: Factores que determinan impactos ambientales de un proyecto. Figura 2.1: SEA (2023a).

LOCALIZACIÓN Y TEMPORALIDAD

Partes del proyecto

OBRAS

Requerimientos para la ejecución:

Mano de Obra Suministros

Extracción y uso de RRNN Transporte

Emisiones

Enfluentes

Residuos

ACCIONES

Objetivo del proyecto:

Productos Servicios

debe revisar la forma en que se está abordando este desafío tanto a nivel internacional como nacional a modo de proveer recomendaciones alineadas con las experiencias allí reportadas. a escala temporal de años, entonces se podrá, justificadamente, utilizar supuestos para determinar variaciones a dichos valores y, también, será posible utilizar otras alternativas para determinar proyecciones de las variables hidrometeorológicas, con la debida justificación. Además, se destaca que la metodología y valores presentados serán válidos mientras este documento no sea actualizado, independiente de potenciales actualizaciones en ARClim.

En conclusión, los antecedentes presentados muestran que no existen recomendaciones para la incorporación del cambio climático en el diseño de obras hidráulicas y en el estudio de eventos hidrometeorológicos extremos a nivel nacional (ver resumen en Tabla 2.2). Más aún, se deja entrever la rigidez y dificultad que existe para la actualización de ciertos lineamientos metodológicos, a pesar del transcurso del tiempo, la aparición de nuevas metodologías, herramientas de análisis, avances científico-tecnológicos y desafíos a nivel nacional e internacional. En este sentido, en vez de asegurar procedimientos mínimos, los documentos antes mencionados limitan la implementación y desarrollo de nuevos enfoques. Considerando la forma en que se estructuran estos manuales y la necesidad de incorporar la componente cambio climático para aumentar la resiliencia de las obras hidráulicas, se

2.3 INCORPORACIÓN DE LA VARIABLE CAMBIO CLIMÁTICO EN EL DISEÑO DE OBRAS

Los cambios en la magnitud de los caudales de diseño en un contexto de clima cambiante tienen impactos directos sobre la estimación de parámetros de diseño asociados diferentes elementos de la infraestructura hidráulica. Ejemplo de ello corresponde a la estimación de las velocidades de flujo y aceleración a través de un puente, los cuales son definidos principalmente por el caudal máximo, y condicionan la socavación y erosión alrededor de los pilares y estribos de los puentes, considerada la principal causa de fallas en estos. Así, resulta importante considerar esta componente en el diseño hidráulico a modo de aumentar la resiliencia de estas obras. A continuación, se revisan experiencias internacionales y nacionales vinculadas a la incorporación de la componente cambio climático en el diseño de infraestructura hidráulica.

Documento Objetivo principal

Métodos de estimación de caudales

Manual de cálculo de crecidas (DGA, 1995)

Mejorar la estimación de caudales extremos en cuencas con escasa o nula información fluviométrica.

Análisis de frecuencia regional para caudales máximos y mínimos. Fórmula racional. Fórmulas de Verni y King. Método Curva Número.

Manual de Carreteras, Volumen N°3 (MOP, 2024)

Diseño hidrológico para obras viales.

Manual de drenaje urbano (DOH, 2013)

Orientar el desarrollo de proyectos de drenaje urbano.

Métodos de análisis de frecuencias para curvas IDF. Método racional para cuencas pequeñas. Fórmula de Bell. Métodos del Manual DGA 1995 y otros.

Curvas IDF basadas en DGA (1991). Fórmula de Bell para lluvias menores a 1 hora.

Incorporación del cambio climático

Nivel de detalle metodológico

No incluido. Moderado. Incluye ecuaciones generales, pero falta personalización a nivel de microcuencas.

Aplicabilidad en zonas específicas

Enfocado en zonas rurales y cuencas naturales; escaso enfoque en áreas urbanas.

Restricciones reconocidas Oportunidades de mejora

No incorpora variaciones climáticas ni efectos dinámicos de urbanización.

Actualizar el enfoque incorporando simulaciones continuas y análisis físico para mejorar precisión, incluyendo cambio climático.

Perspectiva conceptual, incorpora zonificación y porcentajes proyectados (SEA, 2023).

Alto. Detalle en las curvas IDF, pero con limitada cobertura espacial.

Funciona mejor en zonas viales con datos históricos sólidos; limitado en áreas rurales sin estaciones.

Curvas IDF pueden no ser representativas en escenarios de cambio climático severo.

Implementar simulaciones con modelos climáticos para IDF proyectadas, especialmente para eventos extremos poco frecuentes.

No incluido, aunque se reconoce necesidad futura.

Bajo. Falta desarrollo metodológico para áreas urbanas complejas con alta heterogeneidad.

Enfocado en zonas urbanas planificadas; restringido en áreas densamente urbanizadas y de crecimiento no controlado.

No aborda escenarios dinámicos de urbanización futura ni efectos de infraestructuras ya construidas.

Incorporar factores de cambio delta para escenarios urbanos futuros y adaptar métodos a proyecciones más finas de eventos de precipitación intensa.

Tabla 2.2: Resumen de normativa y lineamientos para el diseño hidrológico en Chile.

Guías SEIA (SEA, 2023a, SEA, 2023b)

Incorporar cambio climático en la evaluación ambiental de proyectos.

Proyecciones basadas en modelos de circulación general (GCM). Selección de valores p25 y p75 según mayor impacto.

Fuente: Elaboración propia

Incorporado como componente central. Alto. Presenta alta flexibilidad y capacidad para adaptar metodologías a diferentes condiciones.

2.3.1 EXPERIENCIAS A NIVEL INTERNACIONAL

2.3.1.1 LINEAMIENTOS PRÁCTICOS PARA LA INCORPORACIÓN DEL CAMBIO CLIMÁTICO EN EL DISEÑO DE OBRAS

En materia de lineamientos prácticos para la incorporación del cambio climático en la estimación de caudales de crecida, el trabajo realizado por Wasko et al. (2021) es, a la fecha, el más completo pues comparan los lineamientos disponibles en diferentes regiones del mundo (e.g., Australia, El Salvador, Vietnam, Inglaterra, Bélgica, etc.). Según Wasko et al. (2021), y la evidencia reportada en la literatura, la incorporación de la variable cambio climático sugiere la alteración de las probabilidades estimadas a partir de información del pasado o “histórica”, pudiendo desplazar dichas probabilidades fuera de la envolvente de la variabilidad histórica (i.e., eventos asociados a una misma probabilidad de ocurrencia podrían tener mayor/menor magnitud en el futuro respecto a los registros históricos). Destacan que la incorporación de escenarios de cambio climático posee una “incertidumbre profunda” que (por definición) no

Amplia aplicabilidad, pero con dependencia a los datos climáticos disponibles para cada región.

Falta estandarización para escenarios extremos e incertidumbre asociada a modelos climáticos.

Avanzar hacia la integración de incertidumbre profunda en evaluaciones de impacto y realizar análisis de sensibilidad con escenarios extremos modelados.

se puede caracterizar mediante distribuciones de probabilidad. En consecuencia, la incertidumbre total se propaga dentro de la cadena de decisiones que se deben realizar para llegar a la estimación final de crecidas, proceso que, a su vez, es iterativo (ver Figura 2.2).

Reconociendo la necesidad de actualización continua de las recomendaciones dados los avances científicos y tecnológicos en materia de cambio climático, destacan que ellas deben: i) contar con evidencia científica sólida y defendible, ii) ser prácticas, iii) incorporar la caracterización de la incertidumbre, y iv) ser de fácil actualización. Adicionalmente, Wasko et al. (2021) sintetizan diferentes enfoques para la incorporación de las diferentes fuentes de incertidumbre, estimación de las crecidas de diseño e incorporación del cambio climático en dicha estimación. Dichos enfoques se presentan a continuación:

1. Métodos para incorporar incertidumbre en la estimación de crecidas de diseño

1.1 Basado en factores: un único valor de diseño basado en los manuales o lineamientos disponibles

Figura 2.2: Conceptualización de los elementos en la estimación de caudales de crecida.

Paradigma de la incertidumbre

Aleatoria | Epistémica | Profunda

Las fuentes de incertidumbre influenciarán el enfoque adoptado. El peligro de crecidas es usualmente considerado un proceso aleatorio, pero el cambio climático introduce incertidumbre profunda.

Enfoque de toma de decisiones

Estándares | Riesgo | Robusta | Adaptativa

Si se puede suponer estacionariedad, los enfoques de diseño tradicionales son aplicables. No obstante, la incertidumbre profunda supone adaptarlos enfoques de diseño para ser más apropiados.

Información disponible

Datos | Cuenca | Contexto del problema

Los datos disponibles, la naturaleza del problema de diseño y el presupuesto disponible definirán el método de estimación de caudales de crecidas que deberá usarse.

Método de estimación de crecidas

Frecuencia | Evento | Continua | Razonamiento físico

La estimación de caudales de crecida debe incorporar tanto la incertidumbre aleatoria como epistémica. En la toma de decisiones adaptativa, estas estimaciones deben ser actualizadas a medida que se tenga disponible nueva información.

Fuente: Traducido de Wasko et al. (2021).

(por ejemplo, 1% PEA o 75% de la CMP). A veces se incluye un factor de seguridad para tener en cuenta la incertidumbre epistémica.

1.2 Basado en riesgos: un valor de diseño único basado en un nivel específico de riesgo considerado tolerable a partir de algún tipo de análisis costebeneficio.

1.3 Basado en escenarios: un único valor de diseño basado en múltiples escenarios “plausibles” de forma no probabilística. Los análisis de sensibilidad son una herramienta útil en el marco de la toma de decisiones robusta, ya que ayudan a explorar las implicaciones de supuestos alternativos sobre el resultado deseado.

1.4 Adaptativo: un plan flexible/dinámico que se actualiza y revisa a medida que mejora la comprensión de los cambios futuros. Se evalúan múltiples opciones en función de plazos y puntos de decisión críticos.

2. Métodos de estimación de crecidas de diseño

2.1 Análisis de frecuencia (AF): consiste en ajustar una distribución de probabilidades a los valores máximos de las crecidas (o precipitaciones).

2.2 Enfoques basados en eventos: combinar la precipitación de diseño de intensidad-duraciónfrecuencia (IDF) con factores dependientes para producir la inundación de diseño utilizando modelos de precipitación-escorrentía.

2.3 Simulaciones continuas: los registros de precipitaciones (y otras variables meteorológicas dependiendo del caso) de larga duración se convierten en registros de caudales para el posterior análisis de la frecuencia de las crecidas.

2.4 Razonamiento físico: informa las estimaciones de la precipitación máxima probable (PMP) que, utilizando un modelo de precipitación-escorrentía, da como resultado una estimación de la crecida máxima probable (CMP o PMF por sus siglas en inglés).

3. Métodos para la estimación de crecidas de diseño incorporando cambio climático

3.1 Enfoques heurísticos: buscan incorporar la componente cambio climático basados en razonamientos físicos como, por ejemplo, un cambio medio global en las precipitaciones medias del 2%/°C basado en el balance energético de la Tierra y del 6-7%/°C para los fenómenos de precipitaciones extremas basado en la capacidad de la atmósfera para retener más humedad.

3.2 Proyección de tendencias históricas: si el clima se ha calentado, por ejemplo, aproximadamente 1 °C desde la era preindustrial, y se ha observado no estacionariedad en las observaciones o en los parámetros que modelan las observaciones, se puede realizar una extrapolación hacia el futuro suponiendo que la relación causal no cambia. Esto supone que cualquier no estacionariedad observada se debe únicamente al cambio climático y no, por ejemplo, a la variabilidad interanual (como El Niño Oscilación del Sur) o a la urbanización.

3.3 Proyecciones basadas en modelos de clima global: son la principal herramienta utilizada por los climatólogos para elaborar proyecciones de los cambios futuros. Dado que modelan cambios climáticos a gran escala, su uso en la estimación de crecidas de diseño requiere una reducción de escala (estadística o dinámica) para transferir la información a la escala de cuenca.

Otro ejemplo de recomendaciones para incorporación del cambio climático corresponde al trabajo realizado por CSA Group (2024), quienes se enfocan en el diseño de puentes en un contexto de cambio climático en Canadá. Allí se destaca que, aunque los mecanismos de las causas subyacentes generadoras de crecidas pueden estar cambiando, el desarrollo de “curvas límite” (o envolventes) y “factores de cambio delta” (Figura 2.3) puede justificarse comparando los caudales máximos de ventanas climáticas históricas y futuras modeladas. Los factores de cambio delta se podrían aplicar para estimar flujos máximos

conservadores en condiciones futuras en otros lugares dentro de la misma región hidrológica. Los factores de cambio delta proporcionarían la base para un diseño resiliente (es decir, baja probabilidad de excedencia) en ausencia de evaluaciones hidrológicas detalladas y específicas del sitio basadas en parámetros climáticos futuros.

2.3: Consideraciones clave para el desarrollo de factores de cambio delta (4) en Canadá.

Fuente: Adaptado de CSA Group (2024).

Zona de Seleccionar Corregir

Figura

2.3.1.2

MÉTODOS PARA LA ESTIMACIÓN DE CAUDALES DE CRECIDA

En cuencas no controladas (i.e., sin registros de caudal), el análisis de caudales de crecida se aborda, en general, a partir de métodos precipitación-escorrentía. Este tipo de métodos apunta a transformar, mediante diferentes relaciones matemáticas, la precipitación asociada a un determinado evento en la crecida que este podría generar. Así, la proyección de cambio climático y sus impactos en la generación de crecidas recae principalmente en los cambios de la magnitud de precipitación. Dentro de estos enfoques se puede mencionar el método racional (Chow et al., 1988) y los métodos de hidrograma unitario sintéticos (HUS). Los HUS corresponden a formas aproximadas de un hidrograma teórico generado por una precipitación unitaria, los cuales se obtienen a partir del análisis de hidrogramas de crecida observados y su relación con atributos geomorfológicos de las cuencas, lo cual permite derivar expresiones basadas solo en estos últimos. Singh et al. (2014) distinguen cuatro formulaciones de HUS: (a) modelos tradicionales o empíricos (e.g., Snyder, SCS); (b) modelos conceptuales (e.g., Clark, Nash); (c) modelos probabilísticos (e.g., Gray-2PGD, Croley-2PGD); y (d) modelos geomorfológicos (e.g., GIUH, GCIH, GANN). Allí discuten que, aunque los métodos tradicionales de Snyder y SCS se utilizan ampliamente, presentan varias incoherencias, mientras que la sólida base matemática y conceptual de los modelos probabilísticos y los basados en geomorfología, podrían posicionarlos como el enfoque más útil y atractivo para la hidrología en cuencas no controladas. Otros autores han demostrado que la implementación de hidrogramas unitarios sintéticos locales (i.e., ajustados y/o desarrollados con información de la zona de estudio) entregan mejores resultados en comparación a formulaciones genéricas

recomendadas en la literatura como, por ejemplo, los HUS de Snyder o SCS (e.g., Shaikh et al., 2022). En zonas con influencia nival, los fenómenos de deshielo y de lluvia sobre nieve pueden convertirse en los procesos impulsores que generan las crecidas de diseño, lo que requiere métodos diferentes, como la modelación hidrológica (i.e., simulaciones continuas) y/o análisis de frecuencia (Martel et al., 2021).

En cuencas urbanas o rurales, las curvas Intensidad-Duración-Frecuencia (IDF) se posicionan como una herramienta útil para el estudio de precipitaciones extremas y las crecidas asociadas. Las curvas IDF son modelos estadísticos de las precipitaciones, que dependen del tiempo y, a su vez, del clima, las cuales pueden ser específicas de un emplazamiento o regionales (Schlef et al., 2023). La intensificación observada y prevista de las precipitaciones extremas diarias y subdiarias desafía la aplicabilidad de las curvas IDF históricas, que no consideran una potencial no estacionariedad, en el diseño de infraestructuras en condiciones climáticas futuras (Martel et al., 2021). En esta línea, se han propuesto alternativas para actualizar estas curvas incluyendo la componente de cambio climático. A partir de revisión de más de 100 artículos publicaciones científicas entre 2001 y 2021 enfocadas en la propuesta de curvas IDF en contexto de cambio climático, Kourtis et al. (2022) realizan las siguientes recomendaciones:(i) adquisición de observaciones de alta resolución, al menos cada hora durante al menos 20 años; (ii) uso de un conjunto que incorpore varios GCMs (General Circulation Models), RCMs (Regional Circulation Models) y escenarios climáticos o uso de un conjunto multimodelo a partir de CPMs (Convection-Permitting Models); (iii) uso de más de una técnica estadística de corrección del sesgo de la reducción de escala; (iv) uso de más de un enfoque de desagregación temporal; (v) cuantificación de

la incertidumbre y estimaciones y comunicación de los intervalos de confianza (por ejemplo, 95, 90%) para las curvas IDF actuales y futuras; (vi) evaluación de la reducción espaciotemporal y comparación con las observaciones. En caso de que se disponga de proyecciones climáticas de alta resolución procedentes de CPMs y se empleen para la actualización de la IDF, podrán omitirse los pasos (iii y iv).

En consecuencia, los cambios en los caudales se crecida en contexto de cambio climático se basan, en general, en el cambio asociado a las precipitaciones extremas. En algunos casos se pueden incorporar cambios en la distribución temporal de los eventos extremos (hietograma), el área pluvial aportante en cuencas con influencia nival, la permeabilidad de la cuenca y su condición antecedente de humedad.

2.3.1.3 DEFINICIÓN DE PERIODOS DE RETORNO: ESTACIONARIEDAD VS NO ESTACIONARIEDAD

Dado que las proyecciones de cambio climático y su impacto en los caudales de crecida se suelen abordar a partir de los eventos de precipitación extrema, el análisis de frecuencia es un paso metodológico clave. Esto pues el diseño hidrológico apunta a caracterizar la probabilidad de recurrencia promedio de eventos extremos de cierta magnitud (i.e., periodo de retorno). Sin embargo, las obras de infraestructura que se construyen para, por ejemplo, proteger a las comunidades de los impactos de los fenómenos climáticos extremos, se han diseñado en gran medida basándose en conceptos como el periodo de retorno suponiendo la estacionariedad en los procesos que se modelan para la estimación de eventos extremos asociados a algún riesgo (Obeysekera et al., 2020).

El periodo de retorno (T) es un concepto ampliamente utilizado en ingeniería (particularmente en hidrología) para la estimación de eventos extremos. Teóricamente corresponde al tiempo promedio en que un evento hidrológico de magnitud x es igualado o excedido, recíproco de la probabilidad de excedencia P de tal evento. Por ende, se define como: (2.1) P = 1 T

En el caso de inundaciones, se estudia la probabilidad de excedencia de un evento, es decir: (2.2)

F (x) := P { x > x } = 1 - F(x)

La ecuación es conocida como tail function. Luego, el periodo de retorno T en función de x se define como: (2.3) T (x) = 1 1-F (x)

Donde F(x) es la probabilidad de no excedencia de x, es decir, su distribución acumulada. El modelo para estimar la distribución acumulada puede ser teórico o bien empírico, siempre que esté justificado. Stöwhas (2016), remarca que el periodo de retorno no debe asociarse a un comportamiento cíclico de los eventos hidrológicos. Esto, ya que los eventos de cada año se asumen independientes entre sí, y, por ende, puede darse el caso de que un evento de

periodo de retorno igual a 100 años se exceda más de un año seguido.

Además, está el supuesto de estacionariedad. El supuesto de estacionariedad hace referencia a una invariabilidad en los parámetros estadísticos de algún proceso. Es decir, un proceso se llama estacionario cuando sus parámetros estadísticos se mantienen constantes en el tiempo. Por ende, F(x) no cambia en el tiempo ante algún cambio τ , cumpliendo que: (2.4)

Al contrario, un proceso es no-estacionario si sus parámetros estadísticos sí varían en el tiempo. En geociencias ambas visiones son aplicables cuando están bien fundamentadas.

Las amenazas naturales se caracterizan por su variabilidad temporal y los procesos aleatorios que controlan la aparición de sucesos individuales (Vogel et al., 2024), lo cual puede tener consecuencias sobre los supuestos de estacionariedad que tradicionalmente se adoptan. Además, el uso de modelos no estacionarios concuerda con las proyecciones de cambio climático (Cheng et al., 2014; De Paola et al., 2018; Hosseinzadehtalaei et al., 2020; Towler et al., 2010; Xavier et al., 2019). Una suposición errónea sobre la (no) estacionariedad puede dar lugar a una infraestructura inadecuada y vulnerable a los fallos (subdimensionamiento) o a un aumento en los costos producto de un sobredimensionamiento (Schlef et al., 2023).

Generalmente, la incorporación de la no estacionariedad se limita a una de segundo orden, cuando solo cambian el primer momento estadístico del proceso estocástico subyacente (media y desviación estándar). Una de las razones de esta limitación es que los registros hidrometeorológicos suelen ser breves y no permiten una estimación sólida del cambio en momentos estadísticos superiores (Schlef et al., 2023). La literatura indica que la distribución que mejor describe los procesos de eventos extremos es la distribución de Valores Extremos Generalizada, particularmente la de Tipo I (El Adlouni et al., 2008; Hossain et al., 2022). En este contexto, la media se define como variable en función del tiempo, ya sea mediante metodologías de inferencia bayesiana o simulaciones Monte Carlo.

2.3.1.4

DISTRIBUCIÓN TEMPORAL DE PRECIPITACIONES EXTREMAS (HIETOGRAMAS DE DISEÑO)

Los hietogramas de diseño son representaciones gráficas de la distribución temporal de las precipitaciones. Sin embargo, la resolución temporal de las estaciones y mediciones son a menudo a escala diaria. Los métodos de desagregación de precipitación son técnicas utilizadas para convertir datos de precipitación de baja resolución temporal, como datos diarios o mensuales, en series de tiempo de alta resolución, como datos a escala de horas o minutos. Estos métodos son esenciales para el análisis de sistemas hidrológicos y la gestión de riesgos de inundación, ya que las precipitaciones intensas y de corta duración pueden tener un impacto significativo en estos entornos. Existen dos enfoques principales para la desagregación de precipitación: los modelos condicionales y los incondicionales. La principal diferencia entre los modelos condicionales e incondicionales radica en la manera en que manejan los datos originales y en sus objetivos de precisión y representatividad estadística. Los modelos condicionales desagregan los datos de lluvia manteniendo la consistencia con los valores de precipitación originales. Esto significa que la suma de la precipitación desagregada en intervalos más cortos coincide con el valor total del intervalo original (por ejemplo, un día), mientras que los modelos incondicionales, no buscan reproducir los valores de lluvia originales, sino generar series temporales sintéticas que reflejan las estadísticas generales observadas.

En términos aplicados, la metodología propuesta por Huff (1967) es una alternativa rápida y sencilla que permite definir hietogramas representativos

en base a la distribución temporal de tormentas de las cuales se tenga registro a nivel horario. Esta metodología se basa en la clasificación de tormentas según el cuarto del tiempo de duración donde se concentra la mayor fracción de precipitación (e.g., 4 bloques de 6 horas para un evento de 24 hrs.). Así, se agrupan eventos de precipitación en cuantiles de tiempo para definir tipos de distribución de precipitación (i.e., Tipo I, concentradas en el primer cuartil, a Tipo IV, concentradas en el último cuarto de duración) y, del total de tormentas clasificadas, se estiman los percentiles 10, 50 y 90%. A pesar del tiempo transcurrido desde la publicación del método, este todavía sigue vigente y ha sido empleado para definir hietogramas de precipitación representativos de diferentes lugares. Ejemplo de ello es Chile y las denominadas “Distribuciones de Varas” (Varas, 1985), las cuales se recomiendan en la literatura nacional (e.g., MOP, 2024; DGA, 1995). Varas (1985) replica la metodología propuesta por Huff utilizando los registros de tormentas recuperadas de cuatro estaciones pluviográficas ubicadas entre 30,41 a 36,50°S (i.e., aproximadamente entre La Serena y Concepción). Allí analiza tormentas de duración 4h, 6h, 8h y 12h, las cuales agrupa según la metodología propuesta por Huff y luego estima una envolvente superior (P90%), promedio (P50%) y envolvente inferior (P10%) para cada tipo. No obstante, considerando la base de datos empleada (e.g., registros en zona centro-sur, duraciones menores a 12 hrs.), se puede cuestionar la representatividad de estas distribuciones para todo el territorio nacional, más aún tomando en cuenta las diferencias en la naturaleza de los eventos de precipitación en las diferentes macrozonas de Chile continental. Sin embargo, las distribuciones propuestas por Varas (1985) y su amplio uso en la ingeniería nacional

permiten ejemplificar la utilidad del método propuesto por Huff (1967) y abrir oportunidades a actualizaciones basadas en este enfoque.

Recientemente, Vorobevskii et al. (2024) presenta las metodologías: WayDown y LetItRain. WayDown es un método condicional que utiliza cadenas de Markov de primer orden para simular la ocurrencia de eventos de lluvia y copulas empíricas para modelar la distribución de la lluvia dentro de esos eventos. Este enfoque permite una representación detallada de las estadísticas de la lluvia, pero puede ser computacionalmente intensivo y depende de la calidad y disponibilidad de los datos de referencia de alta resolución. El método LetItRain es un método no condicional que se enfoca en generar datos sintéticos que reflejan las estadísticas globales de la lluvia observada, como la media, la varianza y la proporción de periodos húmedos. Utiliza una distribución gamma para modelar la intensidad de las celdas de lluvia y algoritmos de barajado para captar la autocorrelación de las tormentas y eventos prolongados, lo que permite simular una amplia gama de escenarios de lluvia. El modelo LetItRain ha sido validado con datos de estaciones en Alemania y Corea del Sur, mostrando una buena concordancia con las estadísticas de lluvia observadas. Su aplicación a proyecciones climáticas demuestra su capacidad para evaluar cambios futuros en las precipitaciones y proporcionar información crítica para el análisis de riesgos de inundaciones urbanas y la planificación de infraestructuras resilientes al clima. Al capturar tanto las características medias como extremas de la lluvia, LetItRain se convierte en una herramienta valiosa para la gestión y adaptación frente a fenómenos climáticos extremos. De igual forma, WayDown demostró ser útil para evaluar tendencias en estadísticas y extremos de precipitación a

escalas sub-horarias, proporcionando información valiosa para la planificación y adaptación a futuros escenarios climáticos.

2.3.1.5 FACTORES QUE CONDICIONAN LA GENERACIÓN DE CRECIDAS

Varios factores que interactúan entre sí pueden intensificar la aparición de procesos naturales potencialmente adversos, lo cual complica aún más la cuantificación de los impactos (Vogel et al., 2024). Asimismo, diferentes cuencas tendrán diferentes respuestas hidrológicas a eventos meteorológicos de similares características. Por ejemplo, Yi et al. (2022) demostraron que el contenido de humedad del suelo era un factor significativo que afectaba a la generación de caudal, especialmente en la cuenca dominada por la escorrentía tipo saturación-exceso. En particular, durante un evento de crecidas se deben tener en consideración diferentes componentes que impactan directamente en las características de los eventos (e.g., duración, magnitud, etc.); algunas de ellas son la distribución temporal y espacial de la tormenta, la magnitud de precipitación, las condiciones antecedentes de humedad del suelo (AMC por sus siglas en inglés), la capacidad de infiltración de la cuenca y la posición de la línea de nieve cuando existe una contribución nival en la cuenca. En este contexto, diferentes configuraciones pueden entregar como resultado el mismo caudal de crecida. En términos prácticos, esto implica que el periodo de retorno de un caudal de crecida no necesariamente será el mismo que, por ejemplo, el periodo de retorno de la precipitación que lo genera, sino que existen otros factores que pueden atenuar o intensificar la crecida en cuestión.

2.3.1.6 ESTIMACIÓN DE LA PRECIPITACIÓN MÁXIMA

PROBABLE

La estimación de la precipitación máxima probable (PMP), definida como la precipitación máxima teórica para una duración determinada en condiciones meteorológicas que, en el caso más desfavorable podría convertirse en la crecida máxima probable (WMO, 2009), se realiza mediante dos enfoques: i) hidrometeorológico y ii) estadístico. El primero de estos métodos considera la representación de los mecanismos que intervienen en la generación de una tormenta, estableciendo que esta será máxima cuando se maximice el contenido de agua precipitable y la velocidad de convergencia de dicha humedad al lugar donde se centra la tormenta (WMO, 2009). El segundo método se basa en el método propuesto por Hershfield (1965), quien define un límite superior para la precipitación por medio del ajuste de un factor de frecuencia. Esta fórmula también ha tenido algunas modificaciones de acuerdo con ajustes locales y/o regionales (e.g., Stowhas, 1983). Recientemente, en un estudio elaborado por The National Academies (2024), se discute sobre la necesidad de modernizar la definición

y métodos de estimación de la PMP. Esto, debido tanto a las debilidades de las bases científicas de su estimación como a los avances que existen en el entendimiento, observaciones y modelación de eventos extremos. Considera que las debilidades principales son: i) el supuesto de que exista un límite en la precipitación; ii) inexistencia de procedimientos para incorporar el cambio climático en los extremos de precipitación; iii) el muestreo temporal y espacial de los eventos extremos de precipitación es incompleto; iv) la subjetividad de los procesos de transposición de tormentas; v) la ausencia de bases científicas sólidas para maximizar la humedad; vi) los factores de corrección empíricos utilizados para tener en cuenta los efectos del terreno complejo sobre las precipitaciones extremas; vii) la ausencia de procedimientos para tener en cuenta la incertidumbre estadística de las estimaciones de PMP. Ellos proponen que a base de modelos probabilísticos es factible estimar la precipitación con una probabilidad de excedencia extremadamente baja en climas actuales y futuros, en el espacio y escalas de tiempo relevantes para el diseño y el análisis de seguridad de infraestructura crítica en la próxima década.

2.3.1.7

INCORPORACIÓN DE LA INCERTIDUMBRE

Las incertidumbres asociadas con el cambio climático futuro, junto con las limitaciones de los modelos de cambio climático y las incertidumbres en las proyecciones, introducen complejidades adicionales en el diseño hidrológico utilizando precipitaciones extremas futuras (Teegavarapu, 2013). Las cuencas son sistemas únicos, dinámicos, altamente no lineales, sensibles a pequeñas variaciones en las condiciones de borde, y están constantemente cambiando. Las principales fuentes de incertidumbre son: a) errores en la medición de los datos, b) uso de modelos sobre parametrizados, c) representación inapropiada de los cambios temporales y espaciales de los datos de entrada del modelo, d) inapropiada identificación de las condiciones de borde, e) datos de ajuste/calibración sin información sobre todo el sistema de las cuencas, f) uso de estadística inapropiada en los criterios de ajuste, g) debilidades en los algoritmos de optimización, y, h) supuestos inconsistentes sobre los parámetros constantes en el tiempo, es decir, no consideran los cambios de la cobertura del suelo o del clima.

2.3.2 EXPERIENCIAS A NIVEL NACIONAL

La incorporación del cambio climático en el diseño de obras hidráulicas es un tema que ha tomado importancia a nivel nacional, razón por la cual diferentes instituciones públicas y privadas se encuentran actualmente exigiendo su consideración. No obstante, no existen recomendaciones sobre cómo abordar este desafío y la metodología queda sujeta a los requerimientos del mandante o bien a las sugerencias que pueda realizar quien desarrolla el estudio en cuestión.

Esto puede resultar contradictorio si se toman en los lineamientos técnicos para la incorporación del cambio climático en estudios hidrológicos desarrollados durante los últimos años en Chile (e.g., SEA 2023b, 2023a), sin embargo, estos se encuentran orientados al diseño de obras o, en particular, a eventos hidrometeorológicos extremos. A pesar de lo anterior, a nivel nacional existen algunas experiencias relacionadas a la incorporación del cambio climático en el diseño de obras. Por ejemplo, en el “Marco estratégico para la adaptación de la infraestructura al cambio climático” (MOP, 2013), además de presentarse una metodología para determinar la necesidad de incorporar o no la componente cambio climático en el diseño de obras y la forma de hacerlo aplicada a tres ejemplos, destacan la necesidad de adaptar la infraestructura en Chile al cambio climático, flexibilizando barreras normativas, manuales y estándares, y considerando la incertidumbre asociada. Allí se concluye que la integración de consideraciones de cambio climático en la planificación, diseño y operación de infraestructuras es crucial para garantizar su resiliencia y sostenibilidad a largo plazo, lo cual a su vez requiere mejorar la coordinación interinstitucional, desarrollar metodologías específicas para infraestructuras críticas, y establecer sistemas de monitoreo continuo para adaptarse proactivamente a las condiciones climáticas cambiantes.

Otro de los esfuerzos a nivel nacional corresponde al proyecto ARClim (Atlas de Riesgo Climático para Chile; Pica-Téllez et al., 2020), orientado a fortalecer las capacidades de gestión frente a los desafíos del cambio climático en el país. El proyecto desarrolló mapas de riesgos relacionados con el cambio climático para Chile, incorporando proyecciones climáticas históricas (período 1980-2010) y futuras (periodo multidecadal de 30 años, centrado en

2050, bajo un escenario de altas emisiones de gases de efecto invernadero, RCP8.5). En este informe se describen los aspectos metodológicos empleados en el proyecto los que dan soporte a la información y datos, espacialmente explícitos, que se presentan en la plataforma web de este proyecto (https:// arclim.mma.gob.cl/). Si bien el riesgo es el foco principal del proyecto, se da especial énfasis a la definición de amenaza como aquella condición climática cuya potencial ocurrencia puede resultar en pérdidas de vidas, accidentes y otros impactos en salud, como también en pérdidas de propiedad, infraestructura, medios de subsistencia, provisión de servicios, ecosistemas y recursos medio ambientales. La información base es el producto grillado CR2Met (Boisier et al., 2018), que proporciona las forzantes meteorológicas, precipitación y temperatura, en el periodo histórico (1980-2010) a base de las cuales se caracterizan las condiciones del clima histórico y futuro (centrado en el año 2050). Para tener en cuenta la incertidumbre se consideró el promedio entre 25 simulaciones en base a los modelos de circulación general (GCMs), los que se escalan y corrigen estadísticamente usando la metodología Quantil Mapping (QM). Con esto, se proyectan los cambios futuros en variables meteorológicas como precipitación, temperatura media y extremas (mínima y máxima), velocidad de viento, entre otras, así como productos derivados de ellas (e.g., recurrencia olas de calor/frio, máximas precipitaciones anuales).

La actualización hidrológica del embalse Aromos en la Región de Valparaíso (DOH, 2020) es otra experiencia importante pues, además de la estimación actualizada de caudales de diseño y verificación de las obras de excedencia del embalse, se realiza un análisis de los estudios previos y la estimación de la PMP y CMP mediante métodos estadísticos e hidrometeorológicos. Como parte del análisis de antecedentes, se identifican

las metodologías empleadas generalmente para el estudio de crecidas (Figura 2.4). Así, se define el “enfoque tradicional” como aquel donde dada una cierta estadística de precipitación, se procede al análisis de eventos extremos para determinar el valor asociado al caudal máximo instantáneo de una crecida, generada por una tormenta con un cierto periodo de retorno y duración. La propuesta metodológica del estudio radica en la utilización del producto grillado de base observacional CR2Met (Alvarez-Garreton et al., 2018; Boisier et al., 2018) y productos grillados globales de tipo reanálisis atmosféricos, en particular, ERA5 (Hersbach et al., 2020) para analizar las series máximas de precipitación en 24, 48 y 72 horas. Dichas series son analizadas según diferentes pruebas estadísticas a modo de establecer el cumplimiento (o no) de los supuestos base de un análisis de frecuencia “tradicional”: 1) homogeneidad, 2) independencia, 3) representatividad, y 4) estacionariedad. Las precipitaciones vinculadas a diferentes periodos de retorno son utilizadas para estimar los caudales máximos instantáneos (QMI) mediante métodos precipitación-escorrentía. Adicionalmente, se incorpora un ajuste aplicado a los periodos de retorno según la probabilidad de recurrencia de condiciones antecedentes de humedad (i.e., probabilidad conjunta). Para incorporar la componente de cambio climático se seleccionan modelos de circulación general (GCM) representativos del dominio de estudio siguiendo cuatro criterios: 1) representación de señal estacional de precipitación y temperatura en el periodo histórico 1979-2005, 2) preservar el signo de la correlación observada/referencial entre la precipitación e índices asociados al fenómeno de El Niño Oscilación del Sur (ENOS), 3) señal de cambio climático futuro, y 4) correspondencia entre las curvas de distribución de probabilidad empírica de la máxima precipitación diaria anual observada/ referencial y del GCM escalado y corregido por

sesgo. Para efecto de incorporar el flujo base en la estimación de caudales de crecida, se adiciona a los hidrogramas de crecida un 10% del caudal máximo instantáneo según criterio experto aplicado en estudios similares.

En cuanto a diseño de obras, el estudio para Actualización de obras de control aluvional quebrada Bonilla Norte y Sur de la Región de Antofagasta (MOP, 2022a) propone una alternativa concreta para la incorporación del cambio climático en este contexto. Considerando el producto grillado CR2Met y el reanálisis atmosférico ERA5, y los modelos de cambio climático seleccionados en el proyecto de Actualización del Balance Hídrico Nacional (BHN; DGA, 2023, 2019b, 2019a, 2018, 2017) y los escenarios

RCP2.6 y RCP8.5, se estiman precipitaciones máximas en bloques de 1 a 72 horas. Se estiman coeficientes de duración para vincular la máxima

precipitación diaria anual respecto a la magnitud de precipitación concentrada en dichos bloques, se aplican pruebas estadísticas para analizar la estacionariedad de las series, y se realizan análisis de frecuencia tanto para el periodo histórico (1979-2020) como futuro (hasta 2100). A partir de los caudales máximos estimados mediante el método racional, se definen los caudales de diseño según la condición más desfavorable entre el periodo histórico y futuro. El estudio destaca la alta incertidumbre en las proyecciones, subrayando la importancia de no justificar la inacción debido a dicha incertidumbre, así como la importancia de evaluar diferentes escenarios de emisiones, pues un escenario RCP más desfavorable no necesariamente implica ser más desfavorable en cuanto a eventos extremos de precipitación. Siguiendo una metodología similar, el proyecto de “Actualización plan maestro de evacuación

Figura 2.4: Esquema metodológico del enfoque tradicional para el estudio de crecidas, donde el orden del análisis de probabilidad y el cálculo de la precipitación promedio puede cambiar según el autor.

Estadísticas

•Serie de máximos

•e.g., Pd , P24h

Análisis prob.

•Método gráfico

• Método de los momentos

Fuente: MOP (2020).

Precip. promedio

• Promedio Simple

• Polígonos de Thiessen

• Isoyetas

Distrib. Temporal de Precip.

•Distribución centrada

•Bloques alternados

•Tormentas registradas

Precip. Efectiva

Caudal máx. instantáneo

• Método Curva Numero SCS

• Método de Horton

• Índice Phi

• Tormentas registradas

• Métodos empíricos

• Hidrograma Unitario

• Hidrograma

Unitario Sintético

y drenaje de aguas lluvia Antofagasta” (MOP, 2022b), desarrollado en el contexto del proyecto “Reducción de la Vulnerabilidad Climática y riesgo de inundación en áreas urbanas y semiurbanas costeras en ciudades de América Latina” del Programa de las Naciones Unidas para el Desarrollo (PNUD), concluye que: i) en general, las máximas precipitaciones anuales ocurren, al menos desde el punto de vista diario, de manera simultánea sobre la zona de estudio, ii) existen diferencias en los patrones de precipitación sobre el dominio, donde existe un aumento en las magnitudes de precipitación hacia la parte sur del dominio y la cabecera de las quebradas, iii) las proyecciones de cambio climático apuntan, en general, a un aumento en la intensidad media de los eventos de precipitación, independiente de su duración o periodo de retorno. Así, se recomienda diseñar con las curvas IDF estimadas en el periodo histórico de referencia para el sector correspondiente, e incluir la componente de cambio climático para la verificación del diseño.

Uno de los documentos más recientes orientados al diseño hidrológico en contexto de cambio climático es el “Estudio para la incorporación del cambio climático en el plan de reconstrucción” (MOP, 2023), el cual se centró en puentes afectados durante eventos de precipitación ocurridos en junio y agosto de 2023, en particular en las regiones Metropolitana, O’Higgins, Maule y Ñuble. En términos metodológicos, dicho estudio entrega las siguientes recomendaciones:

Información meteorológica: Se propone la utilización conjunta de registros insitu y productos grillados como, por ejemplo, CR2Met y ERA5. Considerando la base observacional de CR2Met, se utiliza dicho producto para estimar patrones de distribución espacial de la precipitación y temperatura en la zona de interés. No obstante, previo a dicho paso, se

destaca la necesidad de evaluar el desempeño del producto de referencia (i.e., CR2Met) en cuanto a la representación de las observaciones locales (i.e., estaciones). Tomando en cuenta las diferencias intrínsecas a las escalas punto-píxel, se proponen análisis discretos y continuos para precipitación y continuos para temperaturas extremas, poniendo énfasis en la representación de la temporalidad. De manera complementaria, se utiliza el reanálisis ERA5 para determinar los hietogramas de diseño aplicando una metodología análoga a lo propuesto por Varas (1985) y se determinan coeficientes de duración para expresar la máxima precipitación diaria en máximas precipitaciones vinculadas a diferentes bloques de duración (e.g., 24 horas, P24h).

Selección y uso de modelos climáticos (GCMs): Se destaca la necesidad de incorporar procesos de selección de GCMs, así como los escenarios de emisiones climáticas y horizontes futuros de evaluación, según los propósitos del estudio. Asimismo, se pone como una exigencia mínima la verificación de la representatividad de los GCMs de la climatología histórica del dominio de interés como un elemento clave en la reducción de la incertidumbre y remover modelos que no logren capturar dicha componente climatológica y que puedan sesgar las proyecciones futuras. Este enfoque va en línea con lo realizado previamente en el proyecto de actualización del balance hídrico nacional (DGA, 2023, 2019b, 2019a, 2018, 2017), donde se seleccionan cuatro modelos climáticos globales (GCMs) que poseen distinta sensibilidad climática (bajas, moderadas y altas) y que representan adecuadamente la respuesta regional a modos globales de variabilidad climática (fenómeno del Niño, ENSO, y la oscilación Antártica, SAM)

Escalamiento espacial y corrección de sesgo de GCMs: Se reconoce la necesidad de incorporar procesos de escalamiento y corrección de sesgo para ajustar las escalas a

las cuales se desea trabajar. En este contexto, considerando que se trabaja con cuencas donde existe una componente nival, se propone la utilización de un método de corrección de sesgo multivariado como MBCn, el cual permite preservar (hasta cierto punto) la codependencia que existe entre variables meteorológicas como la precipitación y temperatura.

Modelo precipitación-escorrentía: Para la estimación de caudales y volúmenes de crecida se utiliza el hidrograma unitario sintético de Linsley recomendado en DGA (1995). El cálculo de las precipitaciones extremas asociadas a diferentes periodos de retorno incorpora una modificación que no se había reportado de manera previa en la literatura. Allí, a modo de incorporar los impactos la posición de la línea de nieve en la precipitación aportante durante un evento de precipitación, se calcula un volumen de precipitación aportante mediante el cálculo de la precipitación por bandas de elevación hasta la posición de la línea de nieve. El análisis de frecuencia se realiza sobre dicha variable y luego, para retomar la variable de precipitación, se utilizan dos condiciones de posición de línea de nieve (i.e., área pluvial aportante) determinadas mediante un análisis estadístico para dividir el volumen pluvial aportante asociado a diferentes periodos de retorno y recuperar unidades de precipitación. Estas precipitaciones son utilizadas para forzar el hidrograma unitario y estimar los volúmenes y caudales máximos de escorrentía directa. Cabe mencionar que no se realiza un análisis del flujo base durante la crecida ni se incorpora esta componente en los valores reportados.

De este modo, se deja de manifiesto que han existido esfuerzos para incorporar el cambio climático como una componente del diseño de infraestructura hidráulica en Chile. En general, estos enfoques se han apoyado del uso de productos climáticos grillados tanto locales como globales, y métodos precipitación-escorrentía para expresar las precipitaciones extremas en términos de caudal máximo instantáneo. Sin embargo, ninguno de estos enfoques se ha adoptado como una recomendación de procedimientos mínimos para orientar el diseño y verificación de infraestructura hidráulica en un contexto de cambio climático, lo cual deja entrever oportunidades de mejora y desafíos en dicha materia.

2.4 OPORTUNIDADES Y DESAFÍOS

Los documentos revisados dan cuenta que, tanto a nivel nacional como internacional, la incorporación del cambio climático en la estimación de diferentes variables hidroclimáticas y ambientales proyectadas en un horizonte futuro es parte de los requerimientos mínimos. Sin embargo, no existen lineamientos únicos sobre cómo incorporar esta componente y cómo la incertidumbre asociada a la metodología se propaga en la cadena de cuantificación de impactos del cambio climático y las propuestas de mitigación y adaptación al mismo. Más aún, en materia nacional, el principal enfoque recomendado para la incorporación del cambio climático es del tipo holístico (e.g., percentiles y enfoque delta), a pesar de que existen estudios donde se incluyen enfoques basados en proyecciones climáticas. No obstante, la forma en que se trabajan estas proyecciones depende del consultor y no siguen un criterio común y comparable entre ellas, pudiéndose adoptar metodologías que, en base a lo reportado en la literatura, podrían considerarse obsoletas. Adicionalmente, no se pone énfasis en los diferentes mecanismos de generación de escorrentía, y en particular de crecidas (e.g., precipitación frontal/convectiva, crecida pluvial/

nival, etc.), que podrían tenerse en las diferentes cuencas del territorio. Esto realza la necesidad de contar con un documento con recomendaciones y lineamientos mínimos para la incorporación del cambio climático en el estudio de los recursos hídricos y los eventos extremos como, por ejemplo, crecidas.

En términos hidroclimáticos, existe consenso respecto a un futuro con extremos intensificados producto de los cambios en el clima, lo cual podría conducir a precipitaciones más intensas, eventos de crecidas, deslizamientos de tierra, aluviones, sequías más intensas y persistentes, entre otros. Si bien los impactos dependen de la zona de estudio (i.e., caso a caso), para Chile continental la literatura coincide en un futuro de extremos, más cálido y seco, lo cual tendrá impactos directos sobre, por ejemplo, la infraestructura hidráulica, que se verá sometida a eventos extremos de manera más recurrente, y la disponibilidad hídrica, dados cambios en los regímenes de escorrentía, menor cantidad de precipitación y mayores temperaturas respecto al periodo histórico. Esto sugiere, sin lugar a duda, desafíos en materia de proponer soluciones que puedan mitigar los impactos del cambio climático y, asimismo, adaptar la infraestructura y la sociedad a un futuro diferente. Dichos desafíos deben ser abordados con soporte técnico y científico acorde al desarrollo internacional,

entendiendo el tipo de obra, la fase del proyecto, y la zona de emplazamiento, razón por la cual se hace indispensable disponer de un documento con recomendaciones para la incorporación de la variable cambio climático en el dimensionamiento y diseño de infraestructura hidráulica y, en particular, de obras que deben responder a eventos extremos de precipitación y caudal (e.g., obras de evacuación de crecidas, pilas y estribos en puentes, colectores de aguas lluvias, etc.). Adicionalmente, se debe tener en consideración la incertidumbre intrínseca vinculada a las proyecciones de cambio climático y la necesidad de propuestas metodológicas que sean adaptativas y permitan su actualización a medida que se desarrollan avances científicotecnológicos en la materia.

De la revisión de antecedentes se desprende que los métodos de estimación de caudales de crecida actualmente disponibles (e.g., método racional, hidrogramas unitarios sintéticos, modelación hidrológica, etc.), siguen siendo válidos en la actualidad y en un contexto de clima cambiante. Sin embargo, algunos de ellos debiesen ser actualizados a la luz de, por ejemplo, las nuevas bases de datos disponibles (e.g., mapas de cobertura de suelo, reanálisis atmosféricos, etc.), e incorporar elementos que permitan mejorar la cuantificación de incertidumbre asociada a sus estimaciones. Así, la aplicación de la fórmula racional en cuencas pequeñas (A < 10-15 km2) puede ser aplicada en el futuro considerando nuevas curvas IDF definidas con concepto factor delta o curvas límites. Usar modelación hidrológica en cuencas sin control fluviométrico y pluviométrico para, usando modelos de reanálisis para la estimación de precipitación horaria a nivel espacial y su distribución temporal, aplicar técnicas de transferencia de parámetros por

similitud hidrológica para recuperar simulaciones continuas que permitan considerar la combinación de diferentes mecanismos de generación de crecidas (e.g., crecidas pluviales y nivales). Respecto a curvas IDF, el uso de modelo bayesiano para su estimación podría aportar a superar la limitación de cantidad de datos históricos requeridos y, a su vez, reducir la incertidumbre y entregar una medida de ella.

Existen nuevos modelos de cambio climático como, por ejemplo, los modelos climáticos que permiten la convección (CPM por sus siglas en inglés), que permitirían mejorar las estimaciones de precipitaciones extremas y su distribución espaciotemporal (e.g., Fosser et al., 2024; Dallan et al., 2023). Esto permitiría analizar los cambios en la intensidad de precipitación futura a nivel temporal horario, lo cual se podría complementar con los registros derivados de estaciones climáticas automáticas de la red hidrometeorológica nacional, las cuales registran datos históricos a escala horaria y podrían ser utilizadas para la corrección de sesgos y análisis de la representatividad de las distribuciones en el periodo de referencia. Asimismo, estos modelos más refinados permitirían caracterizar de mejor forma precipitaciones de diferente naturaleza, como las convectivas y de origen frontal, e incorporar información más reciente para su construcción. En este sentido, para proponer una metodología, más allá de definir de manera estricta las bases de datos y/o modelos que deben ser utilizados para un determinado estudio, se debe priorizar la descripción de una estrategia para la evaluación de los nuevos modelos y productos que se publiquen en el tiempo pues estas actualizaciones sugieren mejoras en la caracterización de los procesos atmosféricos y

cómo se representa la evolución de las variables climáticas en el futuro.

En materia de diseño hidrológico, existe consenso en la necesidad de diseñar obras según los criterios más desfavorables. Ahora bien, en materia de proyecciones de eventos hidrometeorológicos extremos, cambio climático y escenarios futuros, un escenario más desfavorable en cuanto a emisiones y acciones de mitigación y adaptación al cambio climático (i.e., ssp5-8.5), no implica necesariamente un caso más desfavorable (i.e., crecidas más severas). De este modo, se deben incorporar múltiples escenarios a modo de identificar cuáles son los que reportan la condición más desfavorable. Se propone el diseño con escenarios medios y verificación con escenarios más desfavorables.

Adicionalmente, se debe poner énfasis en que el cambio climático puede afectar, potencialmente, algunos supuestos de estacionariedad sobre las series de tiempo, lo cual exige la verificación de estos supuestos y la incorporación de enfoques no estacionarios cuando corresponda. Finalmente, se destaca que los cambios asociados a diferentes periodos de retorno no son únicos y/o constantes en todos los sistemas, y que se debe poner especial atención en mantener la seguridad de la obra más que los periodos de retorno en sí.

Recomendaciones metodológicas para la incorporación del cambio climático en el diseño de obras hidráulicas

3.1 DESCRIPCIÓN GENERAL

3.1.1 RESUMEN DE DECISIONES

METODOLÓGICAS

La realización de un estudio de crecidas involucra diferentes decisiones metodológicas como, por ejemplo, la estimación de variables meteorológicas representativas del dominio de interés, identificación de eventos extremos, caracterización de la capacidad de infiltración de la cuenca, entre otros.

La Figura 3.1 resume algunas de esas decisiones clave al momento de realizar este tipo de estudios, donde además se incluye la componente cambio climático dentro del flujo de decisiones.

Los enfoques para abordar cada una de estas componentes dependerá estrechamente de la disponibilidad de información, capacidades de cómputo, objetivos del estudio (i.e., prefactibilidad, diseño, etc.), experiencia del equipo consultor y requerimientos del mandante, entre otros. No obstante, es importante recalcar la constante actualización de algunas metodologías como, por ejemplo, técnicas de modelación hidrológica o corrección de sesgo en modelos de cambio climático, o nuevos productos grillados de variables meteorológicas tanto para el periodo histórico como proyecciones futuras, que sugieren la necesidad de una constante revisión de los procedimientos actualmente adoptados.

3.1.2 ZONA DE ESTUDIO

El presente documento se desarrolla considerando como zona de interés Chile continental (Figura 3.2), en particular la macrozona Norte (17°S – 32°15’S). Marcado por un gradiente de precipitaciones (temperaturas) que aumentan (disminuyen) de norte a sur y de mar a cordillera (Figura 3.2 b-c respectivamente), y una cordillera que disminuye su elevación hacia la zona sur del país, Chile alberga diferentes climas y condiciones hidrológicas, así como también diferentes tipos de ríos y cuenca. La Figura 3.2e muestra la transición desde condiciones hiper-áridas en la zona norte (índices de aridez mayores a 10) a húmedas en la macrozona austral, mientras que si bien las precipitaciones en la zona cordillerana del norte grande se concentran en los meses de diciembre-marzo (verano), en la zona centro-sur se concentran entre abril- agosto (otoño-invierno) y en la zona austral se distribuye de manera uniforme durante el año, lo cual queda representado por los valores de p-seasonality de la Figura 3.2f.

Figura 3.1: Esquema general de las decisiones a considerar en el desarrollo de un estudio hidrológico orientado a la estimación de precipitaciones extremas y crecidas en un contexto de clima cambiante.

Caracterización meteorológica

Periodo histórico

Observaciones locales

Productos grillados (locales/globales)

Precipitación Temperatura

Serie de EPE según duración

Temperatura durante EPE de interés

Condiciones antecedentes de humedad

Posición de la línea de nieve

Patrones espaciales (e.g., gradientes, mapas)

Distribución temporal (hietogramas)

Periodo futuro

Escenarios SSP

Modelos Climáticos

Escalamiento

Corrección de sesgo

Registros de caudal

Modelación Hidrológica

Caudales máximos

Análisis de Frecuencia (AF)

Caudales de diseño

Caracterización geomorfológica

Delimitación de cuenca

Parámetros geomorfológicos

Cobertura de suelo

Capacidad de infiltración

Curva hipsométrica

Métodos indirectos precipitación-escorrentía

Caracterización de eventos de precipitación extrema (EPE)

Fuente: Elaboración propia

Figura 3.2: Atributos fisiográficos y climáticos promedio en el período 1980-2014 para Chile continental: (a) elevación, (b) precipitación anual, (c) temperatura media, (d) fracción de nevadas, (e) índice de aridez, y (f) p-seasonality (estacionalidad de la precipitación).

a) Elevación b) Precipitación c) Temperatura

d) Fracción de nevadas e) Índice de aridez

f) p-seasonality

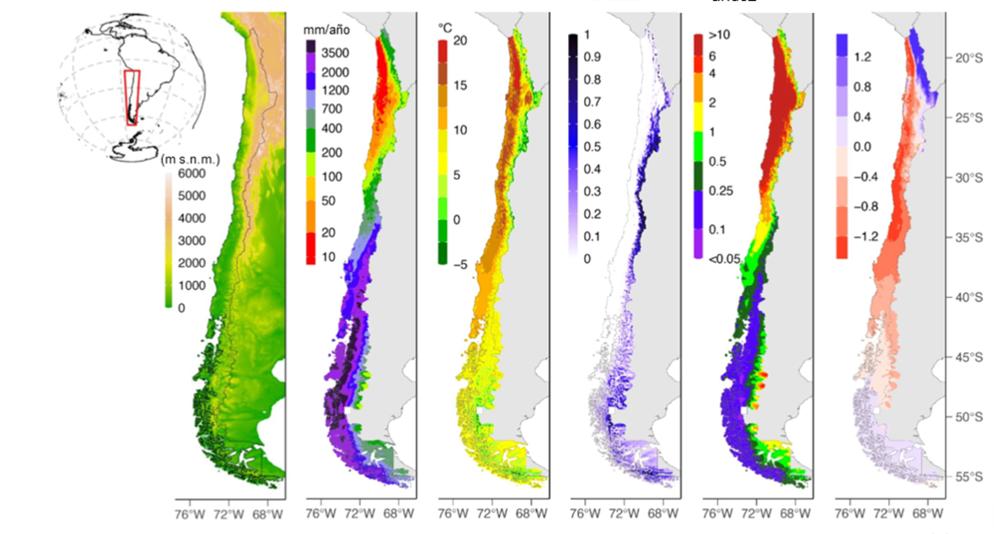
Fuente: Vásquez et al. (2024).

Si bien la diversidad de condiciones hidroclimáticas y atributos geomorfológicos de sus cuencas posiciona a Chile continental como una interesante zona de estudio de procesos hidrológicos y, en particular, los cambios que estos podrían tener en un contexto de clima cambiante, el dominio de interés se acota, como se mencionó anteriormente, a la macrozona norte. Dicha zona también cuenta con algunos desafíos adicionales pues, además de tener una menor densidad de estaciones meteorológicas y fluviométricas en comparación a la zona central, durante los eventos extremos de precipitación también se tienen precipitaciones de tipo convectivas (i.e., corta duración, espacialmente concentradas e intensas).

3.2 ANÁLISIS DE ESTADÍSTICAS DE EVENTOS HIDROMETEOROLÓGICOS

EXTREMOS

Para poder estimar la probabilidad de ocurrencia de eventos extremos en función de la frecuencia con la que han ocurrido en el pasado se utiliza la técnica del análisis de frecuencia. Para esto, el primer paso es la recopilación y selección de serie de datos. La serie de datos puede ser de máximos anuales o de excedencias sobre un umbral. Luego, un ajuste de un modelo de distribución de probabilidad debe llevarse a cabo, siempre y cuando las series se asuman independientes, homogéneas y estacionarias. Finalmente, se estima la probabilidad en base al modelo.

La elección de series de datos ya sea de máximos anuales o excedencias sobre un umbral dependerá de la decisión del hidrólogo. La primera selecciona los valores máximos registrados para cada año hidrológico dentro de una serie temporal, siendo un enfoque más clásico y congruente con la teoría del periodo de retorno. Por otra parte, las series de excedencia consisten en valores que exceden un umbral que el hidrólogo estime pertinente, como, por ejemplo, un valor estadístico como el percentil 95 o 99, que por lo general busca igualar el número de datos al número total de años de observaciones.

Para la elección de modelos de distribución de probabilidad se recomiendan las distribuciones de cola larga, tales pueden ser: valores extremos (tipo I, tipo II, tipo III o generalizada), Pearson Tipo III, logPearson Tipo III, log-Normal o Pareto Generalizada.

Para ajustar el modelo a las series, comúnmente se utilizan los métodos de Máxima Verosimilitud y el método de los L-Momentos. El primero se busca maximizar la probabilidad de observar los datos reales dado un conjunto de parámetros, mientras que el segundo busca igualar los parámetros estadísticos del modelo con los de la serie. El método de Máxima Verosimilitud es sensible a series cortas (caso común en series hidroclimáticas), por lo que se recomienda el uso de los L-Momentos.

Si las series de tiempo se consideran estacionarias, los parámetros estadísticos son fijos en el tiempo. Si embargo, si se supone que las series son no-estacionarias, los parámetros estadísticos son sometidos a un análisis de sensibilidad. Particularmente, la distribución de valores extremos destaca en este aspecto para modelar eventos hidroclimáticos extremos para escenarios futuros de cambio climático, variando el parámetro de forma. En caso de ser necesario, existen tests para verificar la hipótesis de estacionariedad en las series, tales como la prueba Dickey-Fuller aumentada, Kwiatkowski-Phillips-Schmidt-Shin (KPSS) o la prueba Phillips-Perron.

Para verificar el ajuste del modelo de distribución de probabilidad se pueden realizar pruebas de bondad de ajuste no paramétricas, tales como Kolmogorov-Smirnov o Anderson-Darling con un 0,05 de nivel de significancia.

3.3 ESTIMACIÓN DE PRECIPITACIONES

REPRESENTATIVAS DEL DOMINIO DE ESTUDIO

3.3.1 PRECIPITACIÓN TOTAL Y EFECTIVA

Para determinar la precipitación efectiva asociada a un evento de precipitación extrema se recomienda utilizar el método de la curva número, CN, considerando mapas de cobertura de suelo locales o regionales (e.g., Zhao et al., 2016) y textura, a partir de lo cual se pueden establecer equivalencias con los valores CN definidos por el método (mayor detalle en Chow et al., 1988). En caso de no contar con esta información a nivel local, se recomienda utilizar productos grillados globales de alta resolución como, por ejemplo, GCN250 (Jaafar y otros, 2019), el cuál sigue el mismo principio mencionado anteriormente (i.e., equivalencia cobertura de suelo y CN) a una escala global.

GCN250 está construido a partir de los productos de textura de suelo HYSOGs250m (Ross et al., 2018) y cobertura de suelo de la agencia espacial europea (ESA-CCI; Bontemps et al., 2013), tiene una extensión global, resolución espacial de 250 m y permite estimar directamente el valor CN asociado la condición de humedad antecedente seca (Tipo I), normal (Tipo II) y húmeda (Tipo III). Esto pues se tiene disponible un mapa para cada condición. Adicionalmente, dentro de la base de datos se encuentra publicado un código que permite cambiar el mapa de cobertura de suelo base y

recalcular los valores CN bajo el mismo enfoque metodológico. Esto resulta interesante cuando se busca proyectar cambios de cobertura de suelo vinculadas a escenarios de cambio climático y su impacto en la generación de crecidas.

En la Figura 3.3 se visualiza, a modo de ejemplo para las cuencas delimitadas por los controles fluviométricos Río Copiapó en Angostura (cód. BNA 3453001), Río Huasco en Huasco Bajo (cód. BNA 3826001) y Río Elqui en La Serena (cód. BNA 4335001), la información que se puede extraer del producto GCN250. A partir de dicha información se pueden estimar los valores curva número equivalentes (i.e., suma ponderada) representativos de la cuenca completa o subcuencas en su interior, así como una medida de la heterogeneidad espacial en ella.

3.3.2 DISTRIBUCIÓN TEMPORAL DE PRECIPITACIÓN

3.3.2.1 COEFICIENTES DE DURACIÓN (CD)

En general, las estadísticas de precipitación disponibles a nivel nacional hacen referencia a valores de precipitación diaria (i.e., registradas de 8 a.m. a 8 a.m.). Así, es necesario estimar coeficientes que permitan transformar la máxima precipitación diaria (Pd) en la máxima precipitación en un bloque de, por ejemplo, 24 horas (P24). Dichos coeficientes, denominados “Coeficientes de Duración” (CD), pueden ser estimados directamente a partir de los registros de precipitación intradiaria de una determinada estación. No obstante, cuando no se

Figura 3.3: Ejemplo de valores curva número (CN) para condiciones antecedentes de humedad seca (Tipo I), normal (Tipo II) y húmeda (Tipo III) obtenidos desde el producto GCN250. Se incluyen los contornos de las cuencas (de norte a sur) del río Copiapó, Huasco y Elqui en sus controles fluviométricos más próximos a la desembocadura.

Fuente: Elaboración propia

cuenta con dicha información o su accesibilidad es compleja, la utilización de productos grillados de resolución temporal intradiaria puede ser de gran utilidad (e.g., IMERG, Huffman et al., 2020; ERA5, Hersbach et al., 2020).

Considerando que el reanálisis atmosférico ERA5 permite extraer, además de la precipitación, otras variables meteorológicas importantes para la estimación de eventos extremos de precipitación (e.g., temperatura, humedad relativa, velocidad de viento, etc.) se recomienda utilizar dicho

producto como insumo para la estimación de los coeficientes de duración. En caso de contar con otro tipo de producto grillado de mejor resolución que permita obtener, a lo menos, series subdiarias de precipitación y temperatura (e.g., simulaciones provenientes del modelo WRF; Schumacher et al., 2020; Morroni et al., 2017), se sugiere evaluar la posibilidad de recalcular los coeficientes para la zona de interés.

A partir de las series horarias derivadas del reanálisis ERA5, para cada pixel asociado al dominio de

interés se identifican de manera independiente los eventos de máxima precipitación anual en bloques de diferentes duraciones, los cuales se contrastan con los valores de máxima precipitación diaria anual (i.e., agregadas de 8 a.m. a 8 a.m. hora local). Así, para cada duración de interés se ajusta una regresión lineal de la forma definida por la Ec. (3.1) para efecto de estimar el CD representativo.

Notar que en la ecuación Pd corresponde a la máxima precipitación diaria anual, CD(t = D) es el coeficiente de duración asociado a “D” hrs, y P(t = D) la precipitación asociada a dicha duración.

P (t = D) = CD (t = D)Pd

(3.1)

Aplicando de manera sucesiva la metodología propuesta a los píxeles identificados en la zona de interés, se obtienen resultados como los presentados en la Figura 3.4, la cual resume los coeficientes de duración de 1, 6, 12, 24 y 48 hrs de manera espacialmente distribuida.

Si para la determinación de los CD se realiza el análisis con paso de tiempo horario (i.e., 1, 2, 3, …, N hrs), dada la resolución temporal de ERA5, se puede ajustar una curva continua entre los coeficientes de duración y la duración asociada según la Ec. (3.2). Mediante el análisis independiente y ajuste de la función para cada píxel, se puede obtener un producto grillado de coeficientes de ajuste para la estimación continua de coeficientes de duración. Dicho producto se presenta en la Figura 3.5.

3.4: Coeficiente de duración (CD) estimados para duraciones de a) 1, b) 6, c) 12, d) 24 y e) 48 hrs.

Fuente: Elaboración propia

Figura

3.3.2.2 HIETOGRAMAS DE TORMENTA

CD (t=D) = A+B ∙ln In (D)

(3.2)

En caso de requerir una mayor resolución, se recomienda realizar una interpolación bilineal de los coeficientes de duración asociados a la grilla de ERA5 (i.e., ecuación evaluada en el D requerido) a la grilla o resolución espacial de interés (e.g., grilla CR2MET).

Cuando se trabaja con métodos indirectos precipitación-escorrentía para la estimación de caudales máximos instantáneos de crecida pluvial como, por ejemplo, los Hidrogramas Unitarios Sintéticos (HUS), resulta necesario contar con una distribución temporal de precipitación.

Figura 3.5: Coeficientes para la estimación de coeficiente de duración (CD) asociados a la transformación de máxima precipitación diaria (Pd) en máxima precipitación en “D” horas en el Norte de Chile.

Fuente: Elaboración propia

En la literatura nacional existen diferentes recomendaciones asociadas a distribuciones de precipitaciones para la estimación de caudales de crecidas y el diseño hidrológico, tales como las propuestas por Benítez y Verni (1985), Varas (1985), entre otras. Sin perjuicio de la utilidad de ellas, su representatividad es limitada pues no consideran, necesariamente, precipitaciones extremas, no incluyen estaciones fuera de la zona centro del país, o se desarrollan considerando tormentas cortas y luego extendiendo su validez a duraciones mayores.

Para efecto de estimar las distribuciones de precipitación representativas de la zona de interés, aquí se recomienda replicar la propuesta metodológica desarrollada por Varas (1985), utilizando las series horarias derivadas del reanálisis atmosférico ERA5. Varas (1985) sigue la metodología propuesta por Huff (1967), quien agrupa tormentas según el cuarto de duración donde concentran la mayor precipitación acumulada y luego las analiza estadísticamente para obtener distribuciones adimensionales. Así, tanto Huff (1967) como Varas (1985) clasifican cuatro tipos de distribuciones de precipitación: Tipo I, cuando se concentra en el primer cuarto de duración (temprana); Tipo II, si se concentra en el segundo cuarto (centrada-temprana); Tipo III en caso de estar concentrada en el tercer cuarto (centrada-tardía); y Tipo IV cuando se concentra en el último cuarto de duración (tardía). Notar que esta sugerencia se basa en la disponibilidad de otros antecedentes meteorológicos que pueden complementar este tipo de análisis. No obstante, en caso de contar con un producto de precipitaciones espacialmente distribuido con una mejor resolución espaciotemporal y desempeño en contraste a registros locales, se sugiere reestimar las distribuciones temporales de precipitación para la zona de interés.

A modo de identificar zonas homogéneas en términos de la distribución de precipitación durante eventos de precipitación extrema, se propone realizar una agrupación (o clusterización) considerando la ubicación geográfica los píxeles del dominio de interés y la recurrencia de los tipos de distribución de precipitación para duraciones de 6, 12, 24, 48 y 72 hrs. Para ello, se utiliza el algoritmo K-means (Hartigan y Wong, 1979) y el método “Gap statistic” (Tibshirani et al., 2001) para la estimación del número de clústeres óptimo. En términos generales, K-means busca agrupar “puntos” en un espacio definido por el número de variables empleadas para la agrupación, minimizando la distancia entre ellos y la varianza al interior cada grupo (i.e., entre miembros). Posterior a la identificación de clústeres, se realiza un suavizado para combinar aquellos clústeres pequeños (e.g., “islas”) de manera consistente con los ubicados a su alrededor.

La Figura 3.6 muestra la distribución y extensión espacial de los seis clústeres de distribuciones de precipitación extrema definidos para la zona norte de Chile. Cabe mencionar que, por construcción, las distribuciones de precipitación dentro de un clúster son relativamente similares entre sí, y distinguiblemente diferentes de otro clúster. Para cada duración de interés y clúster, se realiza el análisis y clasificación de eventos de precipitación extrema según la metodología propuesta por Huff (1967). A modo de ejemplo, la Figura 3.7 muestra las distribuciones de precipitación extrema estimadas para una duración de 24 horas para el clúster 1, las que a su vez se contrastan con las distribuciones de Varas (1985). Allí queda de manifiesto los problemas que puede conllevar el uso de estas últimas en regiones para las cuales no fueron ajustadas.

Figura 3.6: Clúster de distribuciones temporales de precipitación representativas del dominio de estudio.

Fuente: Elaboración propia

En caso de contar con proyecciones de cambio climático a resolución temporal subdiaria, escaladas y corregidas por sesgo a la escala espacial de interés, se recomienda replicar el análisis propuesto considerando periodos futuros y evaluando la sensibilidad de las distribuciones de precipitación representativas del dominio de estudio en un contexto de clima cambiante.

3.3.3 ÁREA PLUVIAL Y NIVAL DURANTE EVENTOS DE PRECIPITACIÓN EXTREMA

Como se ha mencionado en acápites anteriores, la magnitud de una crecida pluvial no depende sólo de la precipitación e intensidades asociadas al evento, sino que la condición antecedente de humedad del sistema, la presencia de nieve, la fracción de cuenca donde ocurre precipitación sólida y líquida (i.e., posición de línea de nieve), entre otras (pre)condiciones, también juegan un rol importante. Particularmente, en el caso de crecidas pluviales en cuencas con influencia nival, resulta necesario estimar la fracción de cuenca aportante durante el evento, lo cual se conoce como área pluvial aportante.

Una forma de estimar de manera práctica la fracción de cuenca aportante durante eventos de precipitación extrema corresponde a la esquematizada en la Figura 3.8 donde, a partir de un gradiente de temperatura (TGRAD) y la temperatura “Tref” registrada a una elevación “H” (e.g., en una estación patrón), se estima la elevación de la isoterma cero (i.e., elevación donde la temperatura es 0°C). Con ello, aplicando la

Figura 3.7: Ejemplo de distribuciones de precipitación propuestas para eventos de duración 24 hrs en clúster 1.

Distribuciones de precipitación propuestas

Tipo I

Fracción de precipitación acumulada (-)

Cluster 1 - Tormentas con duración de 24 hrs 0.0

Tipo II

Tipo III

Referencia

Estudio Actual Varas (1985) --

Tipo IV

Fracción de tiempo transcurrido desde el inicio del evento (-)

Fuente: Elaboración propia

aproximación propuesta por Garreaud (1993) para estimar la línea de nieve y posicionando dicho valor sobre la curva hipsométrica de la cuenca, se puede determinar el área pluvial aportante durante la crecida. Un enfoque similar ha sido aplicado en

DGOP (2024), permitiendo la incorporación de los cambios en la posición de la línea de nieve en la estimación de crecidas pluviales de una manera rápida y práctica a través de métodos tradicionales como, por ejemplo, hidrograma unitario sintético.

Figura 3.8: Incorporación de cambios en la línea de nieve según temperaturas durante los eventos de precipitación, gradiente de temperatura durante el evento o teórico para la zona, isoterma cero y curva hipsométrica.

1

Estimación de elevación de isoterma cero y línea de nieve 2

T(H) = Tref + TGRAD * (H - Href)

(a) Elevación de la isoterma cero (i.e., T(H) = 0°C)

Ho = Href + Tref / TGRAD

(b) Posición de la línea de nieve (Garreaud, 1993)

HLN = Ho - 300

Notas:

• En caso de contar con productos grillados o más de 3 estaciones, TGRAD puede estimarse:

• Para cada evento de precipitación.

• Promedio (u otro estadístico) derivado del conjunto de eventos.

• Supuestos razonables:

• TGRAD = -5,5 °C/km | -6,5°C/km

Fuente: Elaboración propia

Cabe mencionar que la estimación del área pluvial aportante según el método propuesto i) no considera el aporte asociado al derretimiento de nieve ubicada bajo la línea de nieve (i.e., eventos de lluvia sobre nieve o “rain-on-snow”), y ii) al aplicarse a precipitaciones diarias, se omite la variabilidad intradiaria que puede tener la línea de nieve, la cual en combinación con la intensidad de precipitación podría condicionar sub/sobreestimaciones de la precipitación líquida aportante durante el evento. Estas limitaciones pueden traer consigo sub/ sobreestimaciones del caudal máximo instantáneo. Sin embargo, tanto los eventos de lluvia sobre nieve

Estimación del área pluvial aportante durante la crecida

Determinación de área pluvial aportante durante el evento mediante la curva hipsométricay el área total de la cuenca.

Anival Atotal = Anival + Apluvial = Atotal + ( 1 - fnival)

Precipitación Sólida Precipitación Líquida

fnival

Fracción de área por sobre la elevación (-)

y variabilidad intradiaria de la línea de nieve durante eventos de precipitación extrema son temas que, en la literatura científica, aún no se encuentran completamente estudiados y caracterizados. Así, el enfoque propuesto permite estimar de manera práctica la línea de nieve en términos dinámicos dependiendo de la temperatura registrada durante los eventos de precipitación extrema y gradientes de temperatura. Para abordar la incertidumbre del método se sugiere sensibilizar las estimaciones según gradientes de temperatura en un rango plausible para la zona de estudio.

3.4 USO DE REGRESIONES LINEALES PARA ESTIMACIONES DE CRECIDA

El uso de regresiones lineales para estimar crecidas a partir de datos de precipitación es una herramienta fundamental en hidrología. Este método busca establecer una relación estadística entre las precipitaciones (como variable independiente) y los caudales de crecida o eventos de inundación (como variable dependiente). La relación se basa en datos históricos y puede proporcionar estimaciones de caudales máximos esperados durante eventos de lluvia intensa. El método consiste en ajustar una función de regresión, usualmente de tipo potencia, a los datos que se tengan, para diferentes periodos de retorno, de caudales y precipitaciones máximos.

A nivel nacional, destacan el trabajo realizado por Verni y King (1977), en donde, mediante el teorema de Buckingham (análisis dimensional), se logró establecer ecuaciones para estimar diversos periodos de retorno asociados a caudales de crecida.

Para aplicar el teorema de Buckingham, se deben suponer las variables fundamentales que determinan el valor del caudal máximo, las cuales usualmente son: precipitación que genera la crecida (P), tiempo de duración de la precipitación (t), área de la cuenca (A) y la longitud del cauce principal (L). De ellas, se obtiene la siguiente relación aplicando el teorema de Buckingham:

Donde:

. t A 1.5 =f P A 0.5 , L A 0.5

Q : caudal máximo de la crecida [m3/s]

t : tiempo de duración de la precipitación [días]

A : área pluvial de la cuenca [km2]

P : precipitación que genera la crecida [mm]

L : largo del cauce principal [km]

Para efectos del cálculo de la crecida máxima diaria, t es igual a 1. Respecto a L, el trabajo de Verni y King concluye que esta variable es despreciable para efectos del cálculo de la relación. La regresión se realiza mediante una transformación logarítmica.

Sin embargo, como se mencionó anteriormente, cada cuenca es única con sus propios procesos dominantes. Por ende, el hecho de homogeneizar las respuestas de las cuencas para eventos extremos incrementa la incertidumbre en las estimaciones, al no considerar la unicidad de cada cuenca. Además, los métodos de regresión podrían fallar en cuencas que no fueron utilizadas para ajustar el modelo. Es por esto, que los métodos de regresión lineal deben ser considerados con el cuidado correspondiente, que es estar al tanto de las cuencas que fueron utilizadas para tal regresión. De esta forma, se recomienda el uso solo para etapas preliminares.

3.5 MODELACIÓN HIDROLÓGICA

La modelación hidrológica alude a la construcción de un esquema o modelo que, de forma simplificada, represente un sistema hidrológico en particular. En otras palabras, busca balancear lo que entra y sale de una cuenca y el estado del sistema. Existen una variedad de modelos hidrológicos, los cuales pueden ser clasificados en 3 categorías: conceptuales, basados en física y basados en datos (Liu et al 2017). Los modelos hidrológicos conceptuales han sido identificados como los preferidos para efectos prácticos de las ciencias del agua (Thyer et al., 2023), esto pues los modelos hidrológicos conceptuales permiten simular de manera continua (i.e., dinámica) los procesos de generación de escorrentía y analizar cómo cambios en, por ejemplo, las forzantes climáticas se traducen en cambio en la hidrología de cuenca. Los modelos conceptuales identifican de manera parcial y simplificada los principales procesos hidrológicos, a escala concentrada o semi-ditribuida. A diferencia de los modelos completamente distribuidos y basados en física, estos pueden entregar mejores resultados a un costo computacional menor para la calibración (Jehanzaib et al. 2022). Los modelos hidrológicos permiten además realizar proyecciones futuras, ya sea de oferta hídrica o estudios de contingencia

de eventos extremos dadas diferentes forzantes climáticas.

Para aplicar un modelo hidrológico en una cuenca en específico, este modelo debe calibrarse (sección 3.2.2). Esto vuelve a los modelos hidrológicos dependientes a datos empíricos (por ejemplo, de caudales en el tiempo). Esto se debe principalmente a que no existe un modelo hidrológico universal, ya que cada cuenca es única, lo que se conoce como, “uniqueness of place” (Beven, 2000).

Por otro lado, cada modelo es imperfecto en estructura (al ser una representación simplificada del complejo sistema hidrológico). Esto genera lo que se conoce como incertidumbre estructural. Para poder cuantificar esta incertidumbre las metodologías de los multi modelos son la técnica preferida (Horton et al 2022), particularmente, la técnica multi modelo de los pesos iguales (Block et al., 2009; Gupta y Govindaraju, 2023).

Ya que es común el no contar con datos empíricos para calibrar el modelo, i.e., lo que entra y sale de la cuenca, el último siglo en lo que respecta al estudio de la hidrología superficial se ha centrado en la predicción de cuencas sin información fluviométrica. De hecho, la asociación internacional de ciencias hidrológicas embocó una década para centrarse en este tópico. Los principales avances de la década se detallan en Hrachowitz et al. (2013). Para poder simular escorrentía en cuencas sin información fluviométrica, es posible regionalizar

mediante una donación de parámetros de algún modelo hidrológico. Para esto, se deben clasificar las cuencas mediante criterios de similitud, ya sea (Mendoza et al., 2021):

• Proximidad espacial (i.e., cuenca más cercana).

• Similitud física.

• Similitud climática.

• Similitud física-climática.

• Cuenca más cercana entre candidatas climáticamente similares.

• Cuenca más similar en clima, entre candidatas climáticamente similares.

• Cuenca más similar en atributos físicos, entre candidatas climáticamente similares.

• Cuenca más similar en atributos físicos y climáticos, entre candidatas climáticamente similares.

• Cuenca más cercana entre candidatas físicamente similares.

• Cuenca más similar en clima, entre candidatas físicamente similares.

• Cuenca más similar en atributos físicos, entre candidatas físicamente similares.

• Cuenca más similar en atributos físicos y climáticos, entre candidatas físicamente similares.

Vásquez et al. (2021) realizaron una clasificación de cuencas a nivel nacional encontrando que las cuencas del extremo norte pertenecen a un mismo tipo, lo que facilita el proceso de selección de candidatas para regionalizar en caso de buscar similitudes distintas a la proximidad espacial. En la misma línea, Acuña y Pizarro (2023) mostraron que, a nivel nacional, las cuencas más cercanas usualmente entregan mejores resultados al regionalizar.

3.2.1 SELECCIÓN DE MODELOS HIDROLÓGICOS

Y MODELOS RECOMENDADOS PARA LA ZONA

NORTE DE CHILE

Para seleccionar un modelo hidrológico adecuado para una cuenca en particular, el modelo debe ser capaz de identificar los procesos que gobiernan la generación de escorrentía en particular. En el caso del norte de Chile, al ser este una zona árida, es dominante la generación de escorrentía superficial mediante exceso de infiltración. Por esto, los modelos a utilizar debiesen tener componente de generación de escorrentía superficial mediante dicho proceso. Por ejemplo se recomienda:

IHACRES (Littlewood et al., 1997; Ye et al., 1997; Croke and Jakeman, 2004)

SIMHYD (Chiew et al., 2002)

MODHYDROLOG (Chiew, 1990; Chiew and McMahon, 1994)

Variable Infiltration Capacity (VIC; Liang et al., 1994)

e.

f.

Climate and Land-use Scenario Simulation in Catchments model (CLASSIC; Crooks and Naden, 2007)

Large-scale catchment water and salt balance model element (LASCAM; Sivapalan et al., 1996)

Estos modelos son solo recomendaciones, al tener componente de generación de escorrentía por exceso de infiltración, y haber sido elaborados para representar las complejidades de las recargas de aguas subterráneas. Son lo suficientemente parsimoniosos y al mismo tiempo complejos para obtener buenas simulaciones. De todas formas, el modelador hidrológico es libre de incluir más modelos en caso de ser necesario, siempre y cuando se justifique para sus fines.

3.2.2 CALIBRACIÓN Y VALIDACIÓN DE UN MODELO

Como se mencionó anteriormente, los modelos hidrológicos deben calibrarse con datos empíricos, lo cual no es trivial. Si bien inicialmente estos eran calibrados manualmente, hoy en día es posible calibrar modelos hidrológicos utilizando algoritmos computacionales robustos como la covariance matrix adaptation evolution strategy (CMA-ES; Hanser et al., 2003) o el shuffled complex evolution (SCA-UA) method (Duan et al., 1993). La calibración se lleva a cabo optimizando algún índice de eficiencia (maximización) u error (minimización). Existen varias opciones de funciones objetivos, pero más utilizadas para la calibración de modelos hidrológicos son las eficiencias de Nash y Sutcliffe (NSE; Nash y Sutcliffe, 1970) y las eficiencias de Kling y Gupta (KGE; Gupta et al., 2009). Para validar los

resultados de las simulaciones, se utiliza la técnica del split-sample (Klemes, 1986). La técnica consiste en dividir las series de tiempo en dos ventanas, una con datos utilizados para calibrar el modelo y otra ventana para validar el modelo, es decir, hacerlo correr con datos como si estos aún no ocurriesen. El periodo de calibración y validación usualmente sigue la proporción 2/3 y 1/3 de las series de datos. Sin embargo, entre mayor sean los datos de calibración, el modelo podría contar con información crucial para eventos futuros. Por esta razón es importante abordar una filosofía de adaptación a medida que se obtienen más datos empíricos de eventos extremos.

Los resultados que un modelo hidrológico pueda entregar son sensibles a la función objetivo. Por ejemplo, si el modelador busca poner más peso en modelar caudales bajos, la función objetivo puede ser la versión inversa del KGE (i.e., utilizando 1/Q). Para la estimación de eventos extremos, Pizarro y Jorquera (2024) estudiaron el uso de una nueva variante del KGE utilizando Kmomentos (KGE KMoments), a nivel nacional encontrando mejoras para la simulación de eventos extremos (percentil 95), lo que indica ser una alternativa recomendable. El uso de la variante KGE KMoments también ha sido validado en una cuenca de China bajo escenarios de cambio climático (Yan et al., 2024). Una modelación idealmente debiese tener un valor cercano al máximo valor posible que función objetivo pueda tomar, sin embargo, esto es en muchos casos algo muy difícil o imposible de lograr. Por ende, para efectos de rechazar o no un modelo en base a la eficiencia obtenida, el modelador puede establecer un umbral de aceptación. Para efectos de NSE y KGE KMoments, una simulación se considera satisfactoria si esta es mayor a 0, y para el KGE si esta es mayor a –0.41. Para tales casos, las simulaciones se consideran mejores que la media de las series observadas.

3.2.3

CONSIDERACIONES IMPORTANTES

Como se mencionó anteriormente, las cuencas son sistemas únicos. Estos sistemas son complejos y conllevan, a la fecha, una serie de incertidumbres epistémicas, es decir, que escapan del conocimiento y comprensión del fenómeno en cuestión. Los modelos hidrológicos, y particularmente los conceptuales, son una gran herramienta para poder estudiar el balance hídrico del ciclo hidrológico. De todas formas, es necesario comprender que estas son simplificaciones del complejo sistema natural. También, es necesario comprender que los datos empíricos que alimentan a los modelos están sujetos a incertidumbres, ya sea por errores en la medición, insignificante representación espacial de alguna estación meteorológica (de P, T), errores en los parámetros de la curva de descarga, errores estructurales de los modelos climáticos o poca cantidad de datos, especialmente de escorrentía durante eventos de crecidas.

Otra fuente de incertidumbre son los parámetros de algún modelo hidrológico en particular. Los parámetros que se utilicen son dependientes a la función objetivo y al método de optimización de esta. Al mismo tiempo, la calibración de modelos hidrológicos puede llevar a lo que se conoce como “equifinalidad de parámetros”, que refiere a la existencia de más de un set de parámetros que ofrezcan un valor de eficiencia similar.

El modelador es libre de considerar tantas incertidumbres como estime necesario, siempre y cuando estén argumentadas. Sin embargo, es necesario tener en cuenta que el poder computacional requerido aumenta. Por ejemplo, para considerar las incertidumbres que puedan de las funciones objetivos se recomienda el uso de calibraciones multi objetivos. Para considerar la “equifinalidad”, se puede realizar un análisis de sensibilidad, mediante simulaciones Montecarlo con distintos sets de parámetros.

3.6 SELECCIÓN DE ESCENARIOS Y MODELOS DE CAMBIO CLIMÁTICO

En las últimas décadas, el IPCC ha promovido activamente iniciativas para unificar los escenarios de proyecciones futuras, así como de esquemas de modelación que faciliten la comparación entre diferentes modelos climáticos. La Figura 3.9 muestra de manera esquemática la versión más

reciente de escenarios de emisiones de gases de efecto invernadero (GEI) y decisiones sociopolíticas y económicas respecto a mitigación del cambio climático, denominados SSP, y la versión anterior basada en cambios en las forzantes radiativas de acuerdo con aumentos en emisiones de GEI, denominados RCP.

Estos escenarios son utilizados para forzar los modelos climáticos y proyectar la evolución del clima futuro. Así, para efecto de considerar los impactos en el clima de un caso optimista, intermedio y pesimista en término de las emisiones de gases

Figura 3.9: Esquema de escenarios de trayectorias socioeconómicas compartidas (SSPs) del proyecto CMIP6 y comparación con escenarios del proyecto CMIP5 (RCPs).

Trayectorias socioeconómicas compartidas

Fuente: O’Neill et al. (2016).

Ens: conjunto de condiciones

Escenarios anteriores

de efecto invernadero, y decisiones sociopolíticas y económicas en torno a la mitigación del cambio climático, se recomienda el uso de los escenarios

SSP2-4.5, SSP3-7.0 y SSP5-8.5. Se debe precisar que un escenario más o menos desfavorable en términos de, por ejemplo, aumentos en las forzantes radiativas, no implican necesariamente condiciones hidrometeorológicas locales más extremas que otro escenario. Sin embargo, en caso de limitaciones computacionales u otros, se sugiere utiliza los escenarios más desfavorables (e.g., SSP58.5) considerando que a escala global representan condiciones hidrometeorológicas en promedio más severas que escenarios más favorables.

La selección de los modelos de cambio climático dependerá del objetivo del estudio y de la capacidad del mismo de representar (sin previa corrección de sesgo) los patrones climáticos de la zona de interés. Así, es necesario definir algunos indicadores que permitan evaluar ciertas características de los GCMs previo a su uso en proyecciones de cambio hidrológico. Por ejemplo, se puede 1) evaluar la correlación entre las anomalías de temperatura media mensual (o precipitación) del GCM y la referencia, 2) comparar curvas de distribución de probabilidad empírica asociadas a eventos de precipitaciones extremas del GCM y la referencia en el periodo histórico, 3) analizar tendencias del GCM y la referencia, entre otros. Todos estos análisis requieren la descarga y manipulación de datos.

Otra forma sugerida para seleccionar modelos corresponde a la revisión de literatura y experiencias previas. Por ejemplo, el proyecto de Actualización del Balance Hídrico Nacional (DGA, 2017) seleccionó cuatro GCMs del proyecto CMIP5 (CCSM4, CSIROMk3-6-0, IPSL-CM5A-LR, MIROC-ESM) que permitían representar modos de variabilidad de gran escala,

patrones climatológicos locales y capturar la incertidumbre en las proyecciones futuras a escala nacional. Gateño et al. (2024) realiza una selección por macrozona hidroclimática de GCMs del proyecto CMIP6 adecuados para Chile continental basado en el desempeño de los modelos en la representación de patrones climáticos locales en el periodo histórico. En consecuencia, existe evidencia que permite justificar la selección de ciertos modelos que podrían ajustarse mejor a la climatología del territorio nacional o una localidad específica.

Es importante destacar que los modelos de cambio climático están orientados a capturar patrones climáticos y no representan la temporalidad del periodo histórico. Esto quiere decir que no se puede comparar una fecha particular entre modelo de cambio climático y producto de referencia.

3.7 SELECCIÓN DE VENTANAS FUTURAS DE EVALUACIÓN

La selección de ventanas futuras debe considerar no solo el período de tiempo relevante para la aplicación específica, sino también las características dinámicas de un clima en constante cambio. Tradicionalmente, los análisis climáticos se han basado en ventanas de al menos 30 años, ya que estas permiten reducir la influencia de la variabilidad natural del clima y proporcionar una visión más estable de las tendencias climáticas. Sin embargo, en un contexto de cambio climático, donde los patrones climáticos están en evolución, las ventanas fijas de 30 años pueden no representar

adecuadamente las condiciones futuras. Por ello, se recomienda complementar este enfoque con el uso de ventanas móviles, que permiten capturar mejor las transiciones climáticas a lo largo del tiempo. Asimismo, considerar períodos más cortos, de 10 a 20 años, puede ser útil para analizar la variabilidad natural del clima y las tendencias emergentes en el corto plazo, factores clave para adaptarse a un entorno en rápida transformación.

En el caso específico del diseño de infraestructura hídrica, como puentes, cuya vida útil típica se extiende a 50 años, es esencial integrar ventanas de análisis que equilibren las proyecciones a mediano y largo plazo. En este contexto, para un estudio orientado a proyectar cambios futuros en, por ejemplo, máximas precipitaciones diarias anuales hasta finales de siglo, se recomienda seleccionar y analizar ventanas de 30 años como, por ejemplo, 2035-2064, 2050-2079, o 2065-2094. Esta elección busca capturar tanto las condiciones climáticas proyectadas para el futuro cercano como las tendencias más amplias que podrían afectar la resiliencia de las infraestructuras diseñadas.

3.8 ESCALAMIENTO Y CORRECCIÓN DE SESGO

Los modelos de cambio climático están orientados a reproducir patrones climáticos globales, razón por la cual su escala difiere de lo que tradicionalmente se requiere para efectos de la realización de estudio hidrológicos. Mientras lo GCM y RCM tienen escalas del orden de cientos y decenas de kilómetros respectivamente, los estudios hidrológicos requieren de una escala espacial representativa de la escala

de cuenca, lo cual se traduce en la necesidad de grillas en torno a los 5-10 km. En consecuencia, para efecto de homologar las escalas, se requiere realizar una transferencia desde una escala espacial gruesa a una más fina, proceso que se conoce en la literatura como “downscaling”. Este puede ser dinámico, cuando se utilizan modelos climáticos, o estadísticos, cuando se utilizan, por ejemplo, funciones lineales y/o métodos geoestadísticos. Tomando en cuenta el costo computacional asociado al escalamiento dinámico, en general se procede mediante métodos estadísticos como, por ejemplo, interpolaciones bilineales.

El proceso de escalamiento sólo permite ajustar las escalas espaciales, pero se mantienen sesgos intrínsecos a las diferencias de escalas. Así, resulta necesario aplicar métodos de corrección de sesgo a los productos escalados. Actualmente existen diferentes métodos de corrección de sesgo, cada uno con sus respectivas ventajas y limitaciones, los cuales se pueden clasificar, además de por su naturaleza (e.g., basados en cuantiles, machine learning, regresivos, etc.), en univariados y multivariados.

Si bien no existe un consenso generalizado sobre cual o cuales son los mejores métodos de corrección de sesgo, los métodos multivariados toman una cierta ventaja pues permiten preservar (hasta cierto punto) la co-dependencia entre variables meteorológicas como precipitación y temperatura. La omisión de estas interacciones puede conducir a sesgos en las estimaciones de, por ejemplo, precipitación sólida (e.g., DGA, 2022) u otras variables hidrológicas, o disminuir el desempeño de modelos hidrológicos en la representación del periodo histórico forzado con series corregidas por sesgo, principalmente en cuencas con influencia nival (Dionizis et al., 2021). En base a la experiencia

nacional (e.g., DGA, 2022), se recomienda el uso del método multivariado MBCn (Cannon et al., 2018), el cual es una generalización del método de mapeo de cambios en cuantiles (QDM; Cannon et al., 2015). Además, el método MBCn se encuentra implementado en la plataforma de programación R, lo cual lo hace accesible y de fácil uso.

Finalmente, resulta necesario realizar la verificación del proceso de corrección de sesgo. Para ello, se pueden utilizar las series de tiempo asociadas a subperiodos de tiempo históricos no considerados para efecto del ajuste de las funciones de corrección de sesgo. Otra alternativa es comparar los resultados de los modelos de cambio climático en el periodo histórico definido para la corrección de sesgo y compararlo con el producto de referencia empleado. Notar que la verificación mínima a realizar corresponde a la representación de los patrones estacionales promedio en el periodo histórico de los modelos de cambio climático en comparación al producto de referencia. Verificaciones complementarias pueden estar orientadas a evaluar aspectos de interés sobre la serie de datos como, por ejemplo, la representación en el periodo histórico de las distribuciones empíricas de probabilidad de las máximas precipitaciones diarias anuales, temperaturas extremas, recurrencia de periodos secos, normales, húmedos, entre otros.

3.9 CÁLCULO DE CRECIDAS EN CLIMA

CAMBIANTE

En un contexto de clima cambiante, se propone considerar los siguientes enfoques para la estimación de crecidas dependiendo de la información disponible para ello:

Estimaciones basadas en el concepto de elasticidad: según cambios en el caudal máximo dados cambios en, por ejemplo, temperatura y precipitación en el periodo histórico de referencia, estimar un coeficiente que dé cuenta de la elasticidad del caudal a dichas variables. Con ello, las proyecciones futuras de cambio en extremos de caudal se limitan a cuantificar los cambios futuros en precipitación, temperatura u otra variable que se incluya dentro del análisis.

Métodos indirectos precipitaciónescorrentía: siguiendo las recomendaciones de, por ejemplo, el Manual de cálculo de crecidas (DGA, 1995), aplicar un método indirecto (e.g., hidrograma unitario sintético) forzado por proyecciones de máxima precipitación diaria futura asociada a diferentes periodos de retorno y GCMs. Se recomienda para casos sin control fluviométrico o registros de corta extensión o incompletos.

Modelos estadísticos y dinámicos: Utilización de regresiones lineales múltiples, métodos machine learning (e.g., Random Forest), modelos hidrológicos, u otros, para transformar forzantes meteorológicas en caudales de crecida. Para efectos de ajustar los modelos, se requiere información asociada a caudales a una escala temporal, a lo menos, diaria, pero idealmente subdiaria para efecto de estimar los caudales máximos instantáneos y caracterizar los hidrogramas de crecida asociados.

Es importante mencionar que algunos métodos como los hidrogramas unitarios sintéticos sólo entregan estimaciones asociadas al caudal máximo y volumen de escorrentía directa, razón por la cual

en cauces con flujo permanente se debe incluir el flujo base durante el evento. En un contexto de clima cambiante se puede plantear la hipótesis de que la contribución del flujo base podría cambiar y, para incluir dicho aspecto, se recomienda apoyarse en la literatura.

3.10 CUANTIFICACIÓN DE INCERTIDUMBRE

La estimación de caudales de crecida, así como cualquier otro tipo de análisis basado en datos o modelos, tiene asociada incertidumbre, la cual proviene de las diferentes decisiones y supuestos que deben realizarse para concretar dicha estimación. Así, cuando se incorpora cambio climático, también se agregan nuevas fuentes de incertidumbre generando lo que en la literatura se conoce como “cascada de incertidumbre”. La Figura 3.10 muestra de manera esquemática dicho paradigma, donde se representan diferentes fuentes de incertidumbre en la cadena de estimación de impactos de cambio climático en el ciclo hidrológico (notar que pueden existir otras fuentes de incertidumbre). En este contexto, resulta necesario adoptar técnicas que permitan reducir (e.g., selección de escenarios de emisiones y modelos de cambio climático) y cuantificar la incertidumbre (e.g., cálculo de la dispersión de los caudales máximos proyectados en un contexto de clima cambiante).

En el contexto de estimaciones de proyecciones de cambio hidrológico, eventos hidrometeorológicos extremos, y la cuantificación de incertidumbre, se propone considerar las siguientes opciones al

final de la cadena de modelación (e.g., posterior al análisis de frecuencia independiente para cada serie de máximas precipitaciones anuales derivada de cada GCMs): Promedio y desviación estándar sobre el conjunto de resultados: a partir de, por ejemplo, caudales máximos por periodo de retorno para diferentes GCMs, presentar como resultado final el promedio por periodo de retorno entre ellos y la banda de dispersión asociada a más menos una desviación estándar.

Percentiles sobre el conjunto de proyecciones: a partir de, por ejemplo, caudales máximos por periodo de retorno para diferentes GCMs, presentar como resultado final el percentil 25 y 75% asociado al conjunto de valores por periodo de retorno.

Selección de modelos de acuerdo con representación del periodo histórico u otro criterio: evaluar el desempeño histórico de los GCMs en cuanto a, por ejemplo, representación de anomalías estacionales promedio de precipitación y temperatura de los modelos crudos respecto a una referencia (e.g., estación meteorológica), filtrar un conjunto de modelos adecuados para la zona de estudio. En forma alternativa o complementaria, seleccionar modelos de acuerdo con recomendaciones de la literatura para la zona de interés (e.g. Gateño et al., 2024; DGA, 2022). Al final de la estimación de la variable de interés (e.g., precipitaciones o caudales máximos anuales), reportar promedio y desviación estándar u otros estadísticos.

Análisis de acuerdo entre proyecciones: cuantificar cuántos de los GCMs pertenecientes al conjunto utilizado para el estudio proyectan la misma señal de cambio. Por ejemplo, si se tienen 15 modelos, de los cuales 10 (5) proyectan un aumento (disminución) en máximas precipitaciones anuales futuras, se tendrá un acuerdo (desacuerdo) del 67% (33%), lo cual deja entrever una señal de cambio más robusta que un caso en que dicha partición sea más cercana al 50%.

Es importante recalcar que estas recomendaciones, algunas complementarias, pueden ser aplicadas al final de la cadena de modelación y no en otras etapas donde se pueda sesgar los resultados y alterar su variabilidad, lo cual tendría impacto directo en, por ejemplo, el análisis de frecuencia de los valores extremos. En caso de buscar reducir la dimensionalidad del problema durante análisis intermedios, evaluar el impacto que tiene la utilización de estadísticos en la proyección

Figura 3.10: Representación del paradigma de la “cascada de incertidumbre” y opciones metodológicas clave para la evaluación de los impactos del cambio, y cómo se combinan sus incertidumbres en una envolvente proyectada.

Escenario(s) de emisiones Modelos

Condiciones

Fuente: Mendoza (2015).

de cambio hidrológico y si la naturaleza de esos resultados es o no comparable entre sí (e.g., series de precipitación entre GCMs no necesariamente tienen relación entre sí).

3.11 ALCANCES Y LIMITACIONES

En el contexto de diseño de obras hidráulicas resilientes, especialmente en zonas áridas o semiáridas como el norte de Chile, es fundamental considerar la incorporación de los efectos del cambio climático. Este fenómeno intensifica la frecuencia y magnitud de eventos extremos, como lluvias torrenciales, que a su vez incrementan el transporte de sedimentos y la probabilidad de flujos aluvionales. Por lo tanto, las metodologías deben ser adaptadas para incluir esta componente, no solo en la estimación de caudales máximos, sino también en la evaluación del riesgo asociado al transporte sólido.

Las metodologías actualmente propuestas para a la estimación de caudales máximos de crecida solo consideran la componente líquida, es decir, no toman en cuenta el aporte de causal sólido producto de arrastre de sedimentos o, en un caso extremo, flujos aluvionales.

Para estos efectos es necesario referirse a la modelación hidráulica. Los modelos hidráulicos unidimensionales, por ejemplo, permiten realizar estudios de inundaciones, cálculos de ejes hidráulicos y diseño de obras hidráulicas. Los modelos bidimensionales pueden tener en cuenta las variaciones en la velocidad y dirección del flujo de agua en diferentes partes del cuerpo de agua y la propagación del agua en diferentes direcciones

durante eventos de inundación. Finalmente, con los modelos 3D es posible analizar fenómenos hidráulicos complejos, por ejemplo, fenómenos multifase, donde el agua y el aire deben ser modelados en conjunto. Pueden citarse los modelos HEC-RAS (https://www.hec.usace.army.mil/), FLO-2D (https://flo-2d.com/), IBER (https://www.iberaula. es/) y el Modelo Numérico OpenFoam (https://www. openfoam.com/).

Otro tipo de análisis complementario orientado a evaluar, por ejemplo, soluciones para gestionar las amenazas hidrometeorológicas y su impacto en la infraestructura hidráulica corresponde a la elaboración de modelos físicos a escala. Ejemplo de ello son los trabajos realizados por el Instituto Nacional de Hidráulica (INH; https://inh.cl/wp/), quienes han elaborado modelos físicos para estudiar la operación de evacuadores de crecidas en embalse y la socavación generada por crecidas asociadas a diferentes periodos de retorno, las cuales se estiman a partir de métodos como hidrogramas unitarios sintéticos.

Es importante destacar la necesidad de mejorar la red de monitoreo de variables hidrometeorológicas de manera tal de i) mejorar nuestra comprensión de los procesos hidrometeorológicos, ii) mejorar su predictibilidad (e.g., pronósticos), iii) calibrar y evaluar de mejor forma modelos hidrológicos y relaciones empíricas para utilizarlos en proyecciones futuras, entre otros.

Si bien las recomendaciones metodológicas propuestas se orientan a la incorporación de la componente cambio climático en el diseño de obras hidráulicas en la zona norte de Chile, su aplicación puede extenderse al resto de Chile continental u otra región.

Ejemplos de aplicación de las recomendaciones metodológicas

4.1 ESTIMACIÓN DE CRECIDAS MEDIANTE

MODELACIÓN HIDROLÓGICA

Para ejemplificar la estimación de crecidas futuras, el proceso de modelación hidrológica de una cuenca sin información fluviométrica mediante regionalización de parámetros se presenta para el río Lluta en Arica y sus tributarios. El objetivo es lograr estimar las respuestas hidrológicas a eventos extremos futuros suponiendo que no existiesen datos fluviométricos, utilizando 29 modelos climáticos basados en el escenario SSP5-8.5. Para efectos de validación del modelo hidrológico, se propone estudiar la inundación ocurrida el 4 de enero y 15 de febrero del año 2012, para luego simular caudales futuros.

Respecto a la cuenca de estudio, el río Lluta es uno de los cursos de agua más importantes del extremo norte de Chile. Ubicado en la Región de Arica y Parinacota, este río nace en la cordillera de los Andes y recorre aproximadamente 147 kilómetros antes de desembocar en el océano Pacífico, cerca de la ciudad de Arica. La cuenca del río Lluta drena 3340 km2. En promedio, escurren 25 mm de los 275 mm que precipitan anualmente en la cuenca. A pesar de encontrarse en una de las regiones más áridas del mundo, i.e., el desierto de Atacama, el río Lluta juega un papel crucial en el suministro de agua para la agricultura y las comunidades locales. Es vital para las comunidades indígenas que habitan la región, quienes han desarrollado sistemas de riego tradicionales para aprovechar sus aguas en la agricultura. Es una fuente esencial de vida en una de las regiones más secas del planeta. Sin embargo, una característica distintiva del río Lluta es su régimen altamente variable, condicionado por

las precipitaciones esporádicas en la alta montaña andina. Durante los eventos climáticos extremos, el río puede experimentar crecidas repentinas que generan inundaciones y aluviones, poniendo en riesgo las zonas agrícolas y las infraestructuras en su valle. Además, la cuenca del río Lluta es conocida por su susceptibilidad a los procesos de erosión y sedimentación, lo que aumenta la complejidad de la gestión de sus recursos hídricos.

Los datos que alimentan los modelos hidrológicos fueron obtenidos de 4 estaciones fluviométricas, mostradas en la Figura 4.1, que son: Río Lluta En Panamericana (ID: 1211001), Río Lluta en Alcérreca (ID: 1201003), Río Colpitas En Alcérreca (ID: 1201001) y Río Colpitas En Humapalca (ID: 1201005). Los datos hidroclimáticos de la cuenca se obtuvieron desde la base de datos de CAMELS-CL (Alvarez-Garreton et al., 2018; https://camels.cr2.cl/) a escala diaria, abarcando desde 1979 hasta el año 2020. CAMELS-CL proporciona, de manera fácil y abierta, información sobre 516 cuencas con información fluviométrica en Chile. Además, entrega información hidroclimática a escala diaria y concentrada a escala de cuenca de precipitación (P), temperatura (T) y evapotranspiración potencial (PET), e información sobre atributos físicos de cada cuenca.

Los datos de P, T y PET obtenidos de CAMELS-CL corresponden a productos grillados concentrados a escala de cuenca. El producto grillado de precipitación CR2MET (Boisier, 2023) fue elegido para este estudio, esto ya que CR2MET es un producto grillado de base observacional. La evapotranspiración potencial que ofrece CAMELSCL se calcula en base a la ecuación de HargreavesSamani (1985).

Una vez obtenidos los datos de las cuencas, es posible seleccionar algunos modelos hidrológicos pertinentes a utilizar. Como se mencionó anteriormente, los modelos conceptuales son de gran utilidad debido a que entregan información de los procesos que ocurren en las cuencas, y en consiguiente de los cambios que estas puedan experimentar. Para este estudio de ejemplo se consideran los 7 modelos recomendados en la

sección 3.5, junto con 5 modelos más: GR4J (Perrin et al., 2003), Plateau (Savenije, 2010), New Zealand v2 (Atkinson et al., 2003), Penman (Wagener et al., 2002). y TOPMODEL (Beven y Kirkby, 1979).

En total, 12 modelos son utilizados. El uso de una variedad de modelos permite considerar la incertidumbre estructural inminente de cada uno de estos, junto con evaluar la posibilidad de considerar

Figura 4.1: Cuenca del Río Lluta, utilizada como zona de estudio para la modelación hidrológica y las proyecciones de impactos del cambio climático en caudales máximos de crecida. Las líneas y puntos indican las delimitaciones de la cuenca y su estación fluviométrica.

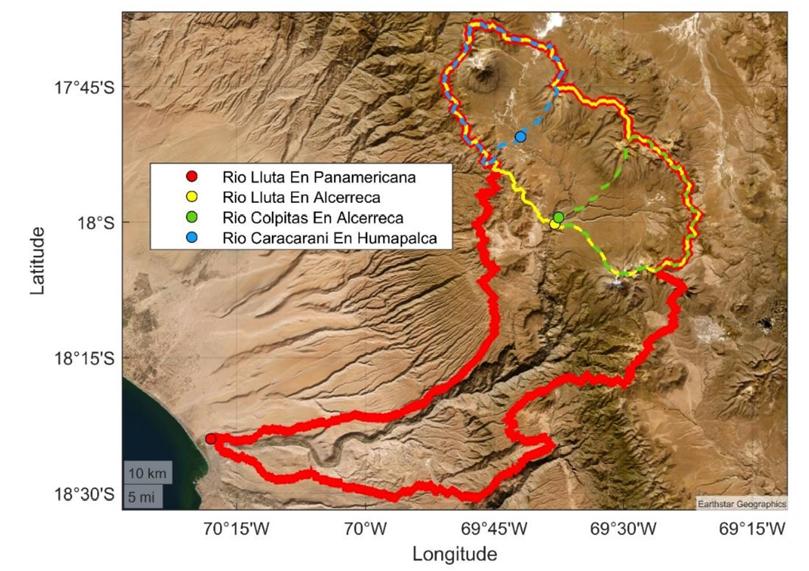
Fuente: Elaboración propia con base en Google Earth.

o rechazar algún modelo. Para calibrar los modelos se utiliza el algoritmo “Covariance matrix adaptation evolution strategy” (CMA-ES; Hanser et al., 2003) y la eficiencia KGE KMoments (Pizarro y Jorquera, 2024), mencionada anteriormente, como función objetivo. Para esto, se utilizan 30 de los 40 años disponibles de datos. De estos 30 años, 2 años son utilizados para un calentamiento (i.e., “warm-up”) de los modelos, es decir, 2 años para que el modelo adquiera las condiciones de borde deseadas.

Una síntesis de las eficiencias a nivel diario obtenidas con cada modelo se muestra en la Figura 4.2. Se puede observar que los modelos con mejores eficiencias en validación, en términos de su mediana, son: IHACRES, SIMHYD y CLASSIC. Para este

caso, se decide que un KGE KMoments mayor a 0 se considera aceptable. Al ser todas las eficiencias de los modelos mayores a 0, estas se consideran para efectos de regionalización. Si algún modelo hubiese entregado eficiencias menores a 0 en validación, se hubiese rechazado. El modelador es libre limitar la restricción de modelos aceptados, por ejemplo, a eficiencias mayores a 0,5.

A su vez, la modelación hidrológica permite la estimación del flujo base previo a los eventos extremos. Para esto, se identifican los máximos anuales de cada simulación con la finalidad de identificar el flujo base de este (flujo previo a la crecida). Como se cuenta con más de una simulación, se obtienen los promedios de caudal

Figura 4.2: Eficiencias obtenidas con cada modelo, tanto para calibración como validación.

Calibración

periodo 01/04/1982 - 31/03/2010

Validación

periodo 01/04/2010 - 31/04/2020

Fuente: Elaboración propia

base para cada crecida de cada año de registro. El flujo base obtenido para cada cuenca se muestran en la Figura 4.3a, mientras que el porcentaje que aporta el flujo base a la crecida se muestran en la Figura 4.3b. Para tomar un valor representativo de flujo base, se puede utilizar el promedio o la mediana de estos valores.

Luego de calibrar y aceptar los 12 modelos para cada cuenca que será donante, se procede a regionalizar las 4 cuencas de estudio, cada una con 3 cuencas donantes, con cada uno de los 12 modelos. Es esperable entonces, que, por cada

modelo y cuenca, se tengan 3 simulaciones distintas procedentes de 3 cuencas donantes, las cuales se promedian. En consecuencia, para cada cuenca, se tienen 12 simulaciones de caudales regionalizados.

La síntesis de eficiencias obtenidas para la regionalización utilizando cada modelo se muestra en la Figura 4.4. Se puede apreciar que los modelos que mejor desempeño tuvieron en calibración destacan en la eficiencia de regionalización. A ellos se les suma también los modelos HYMOD y MODHYDROLOG.

Fuente: Elaboración propia

Figura 4.3: Flujo base previo a las crecidas máximas anuales, obtenido mediante la modelación hidrológica.

Figura 4.4: Resultados de las eficiencias calculadas mediante la técnica de regionalización en periodos de calibración y validación para cada modelo.

Regionalización: calibración periodo 01/04/1982 - 31/03/2010

Regionalización: validación periodo 01/04/2010 - 31/04/2020

KGE KMoments

GR4JHYMODPENMANNEWZEALANDIHACRESSIMHYDTOPMODELPLATEAUVIC CLASSIC MODHYDROLOGLASCAM

Fuente: Elaboración propia

Como se mencionó anteriormente, el uso de más de un modelo tiene por finalidad considerar la incertidumbre estructural de estos y evaluar la consideración de un modelo u otro. Como valor final, es posible utilizar la media o mediana de las 12 simulaciones (técnica multi modelo de los mismos pesos). Finalmente, las eficiencias obtenidas para cada cuenca se muestran en la Tabla 4.1.

Ya que para todas las cuencas la eficiencia obtenida en validación es mayor a 0, es posible considerarlas exitosas. La crecida de estudio se muestra en la Figura 4.5 para las 4 cuencas de estudio. Los resultados muestran concordancias entre simulado y observado para la crecida de

KGE KMoments

GR4JHYMODPENMANNEWZEALANDIHACRESSIMHYDTOPMODELPLATEAUVIC CLASSIC MODHYDROLOGLASCAM

Tabla 4.1: Promedio de las eficiencias de los caudales diarios obtenidas mediante la técnica de transferencia de parámetros.

Fuente: Elaboración propia

Figura 4.5: Simulación suponiendo que no existiese información fluviométrica. A modo de ejemplo se presenta la simulación de una crecida ocurrida en 2012.

A. Cuenca 1211001

2012

2012

3 /s] B. Cuenca 1201003

Ene 2012

C. Cuenca 1201001

Fuente: Elaboración propia

D. Cuenca 1201005

Incertidumbre estructural Q obs Q sim (media) Precipitación

febrero del 2012, pero discrepancias para las crecidas de enero del mismo año. Esto se debe, posiblemente, a incertidumbres que escapan de la metodología, tales como incertidumbres de datos de entrada, de parámetros de los modelos, función objetivo, o incertidumbres epistémicas.

Para la estimación de los caudales de diseño futuros, se utilizan 29 modelos climáticos de precipitación y temperatura para alimentar los 12 modelos hidrológicos previamente calibrados para simular caudales que van desde enero de 1950 hasta el año diciembre del año 2099. De las simulaciones, se obtienen 348 series de tiempo de caudales simulados (i.e., 12 modelos hidrológicos x 29 GCMs). De estas series de tiempo de caudales medios diarios simulados, se identifican los valores máximos anuales asociados a cada simulación. Una vez identificados los caudales medios diarios

máximos anuales, se procede a analizar el desempeño de cada uno de los 29 modelos CGM. Para esto, se consideran los percentiles P25, P50 y P75 de los caudales obtenidos con los 12 modelos.

Para efectos prácticos, se consideran dos casos, estos son: con datos de escorrentía (caudales simulados con un modelo calibrado con datos de la zona) y sin datos de escorrentía (caudales simulados con la técnica de regionalización). Los percentiles de los máximos anuales obtenidos utilizando los 29 modelos climáticos se muestran en la Figura 4.6 en río Lluta en Panamericana (ID: 1211001), con y sin datos fluviométricos. Los límites de la banda de incertidumbre corresponden al promedio de los P25 y P75 de cada CGM, mientras que las líneas corresponden a las medianas.

Figura 4.6: Máximos caudales medios diarios anuales derivados de la modelación hidrológica utilizando 29 GCMs.

Q obs

Q sim con datos

Q sim sin datos Banda de incertidumbre

Fuente: Elaboración propia

Para calcular los caudales asociados a periodos de retorno desde 2 a 500 años, se utilizan las 348 series de máximos anuales obtenidas anteriormente, el modelo de distribución de probabilidad de Pearson Tipo III ajustado mediante el método de Máxima Verosimilitud, y una prueba de bondad de ajuste no paramétrica Kolmogorov-Smirnov. Los resultados para río Lluta en Panamericana se muestran en la Figura 4.7, junto con su respectiva banda de

incertidumbre, para valores de periodo de retorno T = 2, 5, 10, 25, 50, 100, 200 y 500 años. Para este caso se volvió a considerar como límites de la banda de incertidumbre los percentiles P25 y P75 de los máximos caudales medios diarios, por modelo CGM. Los puntos corresponden a la mediana de los caudales asociados a cada período de retorno de los datos simulados.

Figura 4.7: Caudales medios diarios máximos según diferentes periodos de retorno según escenario SSP5-8.5 y 29 GCMs, para periodo estival e invernal.

A. Cuenca 1211001

Con datos fluviométricos

Periodo Abril - Septiembre

150

Pearson; p = 0,55

Empírico (simulado)

Banda de incertidumbre

C. Cuenca 1211001

Con datos fluviométricos

Periodo Octubre - Marzo 300

Pearson; p = 0,49

Empírico (simulado)

Banda de incertidumbre

B. Cuenca 1211001

Sin datos fluviométricos

Periodo Abril - Septiembre

Pearson; p = = 0,44

Empírico (simulado)

Banda de incertidumbre

D. Cuenca 1211001

Sin datos fluviométricos

Periodo Octubre - Marzo

Pearson; p = 0,49

Empírico (simulado)

Banda de incertidumbre

Fuente: Elaboración propia

De las distribuciones utilizadas, se observa que estas alcanzan valores p aceptables. Sin embargo, los modelos discrepan en valores a medida que el periodo de retorno aumenta. Esta discrepancia debe tomarse con atención, ya que podría llevar a un sobredimensionamiento de diseño. Dado esto, es recomendable utilizar tantos modelos como sea necesario, aceptando los mejores y rechazando los peores.

De los resultados obtenidos respecto a la estimación para cuencas sin información fluviométrica, se observa que la metodología de regionalización tiende a sobreestimar las crecidas para este caso en particular, como se observa en las Figura 4.5 y Figura 4.6. También puede darse el caso que la regionalización de parámetros subestime los valores reales. Debido a esto, es imprescindible llevar a cabo una consideración y estimación de la incertidumbre. En este caso, se consideró la incertidumbre estructural de los modelos al considerar más de uno para la modelación.

Respecto de las proyecciones futuras considerando el caso más pesimista dadas las emisiones de dióxido de carbono, se observa en la Figura 4.6 que las inundaciones podrían ser más severas para la segunda mitad de siglo. Realizando un análisis de frecuencia de eventos extremos, se pudo estimar la probabilidad de excedencia para los eventos extremos y su respectiva banda de incertidumbre. Sin embargo, la Figura 4.7 muestra que la incertidumbre aumenta a medida que la probabilidad de excedencia se minimiza, tanto como para el periodo Abril – Septiembre como Marzo – Octubre, siendo este último el periodo con mayor aumento de incertidumbre. Importante de destacar es también que la incertidumbre aumenta para el caso sin datos fluviométricos.

4.2 ESTIMACIÓN DE FRECUENCIA DE CRECIDAS MEDIANTE MÉTODOS ESTADÍSTICOS

El uso de métodos estadísticos como las regresiones, comentadas en el acápite 3.1.1, tiene por finalidad establecer relaciones generalizadas para la estimación de crecidas teniendo en cuenta solo datos empíricos. Los métodos estadísticos no buscan formular el proceso físico detrás del fenómeno de la generación de escorrentía. Como se comentó anteriormente, dado que cada cuenca es única con sus propios procesos dominantes, los métodos de regresiones que homogenizan una zona tienden a entregar errores en su estimación de caudales. Además, se ha demostrado que la precipitación de un periodo de retorno T no necesariamente es la que genera una crecida de mismo periodo de retorno, ya que las crecidas son sensibles a la condición de humedad del suelo que exista antes de la crecida. Debido a lo anterior, estos métodos pueden incurrir en grandes incertidumbres.

A continuación, se presenta un ejemplo para la estimación de crecidas mediante el método de regresión, introducido en la sección 3.4, para estimar una ecuación generalizada para periodos de retorno T = 2, 5, 10, 100, 500 y 1000 años en la zona norte de Chile. Para generar la regresión se tomaron datos de 42 cuencas que abarcan desde las latitudes 17°S hasta 32°S, mostradas en la Tabla 4.2, mientras que la Figura 4.8 muestra de forma visual las cuencas seleccionadas junto con precipitación media anual, escorrentía media anual, índice de aridez, área, elevación media y cobertura de nieve. Las cuencas fueron seleccionadas en base a su “p-seasonality”, descriptor climático disponible en CAMELS-CL.

Tabla 4.2: Cuencas seleccionadas para la regresión.

Fuente: Elaboración propia

Rio Chalinga en La Palmilla

Estero Pupio en El Romero

Figura 4.8: Cuencas seleccionadas para la regresión junto con sus diferentes atributos: a) corresponde a la precipitación media anual, b) corresponde a la escorrentía media anual, c) corresponde al índice de aridez, d) corresponde al área total, e) corresponde a la elevación media, y, f) corresponde al porcentaje de cobertura de nieve de cada cuenca.

Fuente: Elaboración propia

Para estimar las precipitaciones diarias máximas y caudales medios diarios máximos, se ajustó el modelo de distribución de probabilidad de Valores Extremos y Pearson Tipo III, evaluadas con un test de bondad de ajuste Kolmogorov-Smirnov, seleccionándose la que presenta un mayor valor p. Una vez obtenidas las precipitaciones y caudales máximos, se procede a generar el gráfico en escala log-log de las variables de interés utilizando la relación obtenida con el teorema de Buckingham, mostrado en la sección 3.4, a los cuales se les ajusta el modelo de regresión exponencial, como se muestra en la Figura 4.9. Para simplificar el ejemplo, el área pluvial de cada cuenca se consideró igual al área total de cada una.

El valor del coeficiente de correlación R mayor a 0,7 indica que los datos presentan una correlación positiva fuerte. De la regresión y de la relación del teorema de Buckingham, se obtiene la siguiente ecuación: (4.1)

QT=0,0005502 . PT 1,2922 . A0,8539

Donde QT y PT son el caudal medio diario máxima y precipitación diaria máxima para un periodo de retorno T y Ap es el área pluvial de la cuenca. Para evaluar la ecuación obtenida, se simulan los caudales utilizando la ecuación y se comparan

Figura 4.9: Resultados de la regresión. Los colores indican el periodo de retorno utilizado, mientras que la línea azul corresponde a la regresión exponencial es escala logarítmica.

Fuente: Elaboración propia

y = 0.00055002 x1.2922

T = 2 años

T = 5 años

T = 10 años

T = 100 años

T = 500 años

T = 1000 años

Regresión

con los caudales observados. Los resultados se muestran en la Figura 4.10.

La Figura 4.10 muestra cómo los resultados para las cuencas no son homogéneos en términos de errores, como es de esperar. Además, se observan grandes errores para algunas cuencas. Con la finalidad de verificar los resultados obtenidos, se realiza una validación mediante el método leaveone-out, el cual consiste en repetir el proceso de la regresión dejando una cuenca fuera, y evaluando el desempeño de la regresión obtenida en la cuenca

no considerada. Para cuantificar el desempeño de la regresión con respecto a la cuenca que se deja fuera de la muestra, se calcula la raíz del porcentaje de error entre el caudal simulado y el caudal observado de la cuenca, con la finalidad de visualizar si la regresión subestima o sobrestima los valores de caudales de crecidas. Los resultados se muestran en la Figura 4.11 los errores en la estimación de caudales para cada cuenca cuando esta es dejada fuera de la regresión (a) y en términos de boxplot para los periodos de retorno en estudio (b).

Figura 4.10: Resultados de la regresión. Los colores indican el periodo de retorno, mientras que la línea azul representa el ajuste perfecto con una banda de confianza del 20%

T = 2 años

T = 5 años

T = 10 años

T = 100 años

T = 500 años

T = 1000 años

Regresión

Fuente: Elaboración propia

Figura 4.11: Errores de la verificación de la regresión en términos de porcentaje de error de cada cuenca (a) y de manera general (b).

Fuente: Elaboración propia

Se puede observar cómo la metodología incurre en errores que incrementan a medida que la probabilidad de excedencia aumenta (T disminuye), encontrándose los mayores errores en la cuenca ID: 2103002, la cuenca ID: 2105005 y la cuenca ID: 4502001. Como se mencionó anteriormente, es de esperar que la metodología incurra en errores. Para el caso del norte de Chile, los errores pueden ser de gran consideración, debido a la vastedad del territorio desértico e incertidumbres hidrológicas en la distribución espacial de las precipitaciones.

Respecto a este último punto, los resultados entregados obedecen al input de precipitación diaria extraído del producto grillado distribuido de precipitación CR2Met. Es importante recordar que tal producto es también el resultado de un modelo, el cual puede presentar incertidumbres estructurales. De esta forma, las ecuaciones de la regresión son sensibles también al input de precipitación que se considera. Debido a esto, como se comentó en la sección 3.4, el método de la regresión debe ser utilizado solo para etapas preliminares.

4.3 ESTIMACIÓN DE CRECIDAS MEDIANTE MÉTODO DE HIDROGRAMA UNITARIO

SINTÉTICO (HUS)

La implementación del método de hidrograma unitario sintético (HUS) requiere, además de los parámetros geomorfológicos que dan forma al hidrograma unitario de escorrentía directa, la estimación de la precipitación efectiva y la distribución temporal de la precipitación. En el presente documento se propone la estimación de la precipitación efectiva mediante el método curva número y la distribución de precipitaciones extremas a partir de valores representativos a escala regional derivados del análisis de tormentas extremas recuperadas de ERA5. En cuanto al estudio de precipitaciones con diferentes duraciones, se

plantea la utilización de coeficientes de duración para expresar la precipitación diaria en términos de una duración determinada. Así, el análisis se reduce a obtener las máximas precipitaciones diarias asociadas a ciertos periodos de retorno y sub-periodos (e.g., histórico y futuro cercano) de tiempo de interés. Para ejemplificar la aplicación de esta metodología, se consideran las cuencas con control fluviométrico y buena extensión de registros ubicadas en el río Lluta, las cuales fueron utilizada anteriormente para el análisis de la modelación hidrológica como herramienta para la estimación de crecidas en cuencas no controladas (ver Figura 4.1).

Como se indicó en el acápite 3.3.1, para estimar la precipitación efectiva mediante el método curva número, se utiliza como insumo base el producto grillado GCN250. La Figura 4.12 muestra los valores CN para la cuenca del Río Lluta en Panamericana

Figura 4.12: Valores curva número espacialmente distribuidos para condición seca (Tipo I), normal (Tipo II) y húmeda (Tipo III) extraídos desde GCN250 para la cuenca del río Lluta en Panamericana.

Fuente: Elaboración propia

Tipo I Tipo II Tipo III

Valor Curva Número - CN (-)

y, en consecuencia, la cuenca de interés, la cual se encuentra anidada en esta. De manera complementaria, la Tabla 4.3 resume los valores CN equivalentes para las diferentes condiciones antecedentes de humedad y una medida de la dispersión de dicho valor a modo de cuantificar la heterogeneidad en las características de infiltración de la cuenca.

En cuanto a la distribución de precipitación (i.e., hietograma de diseño), la Figura 4.13 muestra, a modo de ejemplo, las distribuciones en 24 horas representativas estimadas para la cuenca de

interés, las cuales a su vez se comparan con las distribuciones de Varas (1985). Allí se puede ver que el uso de las distribuciones de Varas en la zona de estudio puede introducir sesgos en la intensidad de la precipitación, las cuales serían más suaves que lo estimado en el presente trabajo. Esto resalta la importancia de la estimación de distribuciones de precipitaciones representativas de la zona de interés y los riesgos de transferir estas desde dominios que no presentan los mismos patrones de precipitación.

Tabla 4.3: Valores curva número promedio a escala de cuenca para condición seca, normal y húmeda extraídos desde GCN250 para la cuenca del río Lluta en Panamericana y sus subcuencas con controles fluviométricos.

Fuente: Elaboración propia

Figura 4.13: Distribuciones de precipitación representativas para la cuenca del río Lluta en Panamericana y sus subcuencas. Considerando que la mayor parte de la cuenca se asocia al cluster 2, se considera este como representativo del dominio completo.

a) Clusteres asociados a zona de interés

b) Distribuciones de precipitación para el cluster 2 según una duración de 24 hrs.

Referencia Estudio

(1985) --

Fracción de precipitación acumulada (-)

Fuente: Elaboración propia

Fracción de tiempo transcurrido desde el inicio del evento (-)

Los coeficientes de duración se obtienen a partir de la Figura 3.5 y la Ec. (3.2), la cual se aplica de manera recursiva para cada píxel perteneciente a la cuenca y luego se promedian espacialmente. La Tabla 4.4 resume los valores obtenidos para la cuenca y algunas duraciones de interés, donde se desprende que no existe una gran dispersión entre los resultados asociados a las cuencas de interés (CV < 2%). En consecuencia, se propone adoptar el

valor promedio entre cuencas. Notar que, si bien la baja dispersión entre cuencas se puede atribuir a la resolución de ERA5, los resultados permiten tener nociones sobre la correspondencia entre la máxima precipitación diaria y las duraciones de interés a una escala regional.

Tipo I

Tipo II

Tipo III

Tipo IV

Tabla 4.4: Coeficientes de duración (CD) para diferentes duraciones asociados a las cuencas en el río Lluta.

Elaboración propia

Las máximas precipitaciones diarias anuales para el periodo histórico se obtienen de CR2Met v2.5 y para el periodo futuro del producto desarrollado por Vásquez y Mendoza (2024). Considerando que la generación de una crecida pluvial no solo depende de la precipitación asociada, para cada evento de máxima precipitación diaria anual (i.e., Pd) se estima la precipitación efectiva asociada (i.e., Peff) a modo de aplicar el análisis de frecuencia sobre dicha variable. La Figura 4.14a compara la serie de precipitación diaria anual máxima total y efectiva para la cuenca río Colpitas en Alcérreca, mientras que la Figura 4.14b compara los resultados obtenidos del análisis de frecuencia de ambas asociadas a CR2Met en el periodo 1991-2021. Allí queda de manifiesto la no linealidad que existe

entre ambas variables, lo cual sugiere la necesidad de incorporar estos factores que condicionan los montos de precipitaciones que posteriormente serán utilizados para el análisis de crecidas pluviales. Es importante notar que la máxima precipitación diaria anual puede no corresponder, necesariamente, con la máxima precipitación diaria efectiva anual, pues en esta última interactúan otros factores que condicionan su valor (e.g., condiciones antecedentes de humedad y posición de línea de nieve).

Fuente:

Figura 4.14: Comparación entre máxima precipitación diaria total y efectiva en el periodo 1991-2020 para la cuenca río Colpitas en Alcérreca. (a) Comparación entre valores máximos anuales, (b) Comparación entre precipitaciones asociadas a periodos de retorno.

antecedente de humedad

diaria total (mm)

Fuente: Elaboración propia

A las series de máxima precipitación diaria anual (i.e., CR2Met y 29 GCMs) se aplica un análisis de frecuencia considerando los subperiodos 19912020 (histórico), 2035-2064 (futuro cercano) y 2065-2094 (futuro lejano). Los resultados obtenidos para los periodos de interés derivados del análisis de frecuencia aplicados a la serie de máxima precipitación diaria efectiva (Peff) se presentan en la Figura 4.15.

Una vez estimadas las máximas precipitaciones diarias efectivas asociadas a diferentes

periodos de retorno y subperiodos de tiempo, la implementación del hidrograma unitario es directa una vez aplicado el coeficiente de duración de interés a la precipitación total. Aquí se supone que la distribución de precipitación total es una buena aproximación de la distribución de precipitación efectiva, lo cual podría ser diferente en algunos casos. Los parámetros requeridos para la configuración del HUS-SCS se resumen en la Tabla 4.5.

Figura 4.15: Resultados análisis de frecuencia de máxima precipitación diaria anual efectiva para el periodo histórico y proyecciones futuras en las subcuencas del río Lluta.

Colpitas Alcérrecaen

Lluta en Alcérreca Periodo de retorno (años)

Caso

CR2Met GCMs

Fuente: Elaboración propia

Periodo

Histórico (1991-2020)

Futuro Cercano (2035-2064)

Futuro Lejano (2065-2094)

Dispersión entre GCMs

Histórico (1991-2020)

Futuro Cercano (2035-2064)

Futuro Lejano (2065-2094)

Lluta en Panamericana

Tabla 4.5: Parámetros para la configuración del hidrograma unitario sintético (HUS) SCS asociado a las subcuencas controladas del río Lluta.

Fuente: Elaboración propia

Caracarani en Humapalca

Figura 4.16: Hidrograma de escorrentía directa asociados a precipitaciones en 24 horas, percentil 50% de la distribución de precipitación, y periodo de retorno 100 años.

Hidrograma de crecida precipitación de 24 hrs asociada a T=100 años

Distr. Tipo I

Distr. Tipo II

Distr. Tipo III

Distr. Tipo IV Caudal instantáneo de escorrentía directa durante el evento (m 3 /s)

en Humapalca

Colpitas Alcérrecaen

Lluta en Alcérreca

Lluta en Panamericana

Caso

Periodo

Histórico (1991-2020)

Futuro Cercano (2035-2064)

Futuro Lejano (2065-2094)

Dispersión entre GCMs

Histórico (1991-2020)

Futuro Cercano (2035-2064)

Futuro Lejano (2065-2094)

Fuente: Elaboración propia

Caracarani

Replicando el análisis con los GCMs, la Tabla 4.6 resume los resultados más desfavorables de caudal máximo instantáneo de escorrentía directa de crecida pluvial por GCM para los tres subperiodos de interés (histórico, futuro cercano y lejano) y diferentes periodos de retorno de precipitación efectiva (i.e., considerando interacción precipitación e infiltración). Es importante notar la dispersión que existe entre el conjunto de GCMs para las diferentes cuencas y periodos de retorno, lo cual refuerza la idea de seleccionar modelos a modo de reducir la incertidumbre asociada a sus proyecciones.

Por ejemplo, si se considera una tormenta de 24 horas, la cual tiene asociado un coeficiente de duración (CD) igual a 1,22 y la precipitación diaria efectiva de periodo de retorno 100 años en el periodo histórico de referencia (i.e., CR2Met; 16 mm). Este caso tendrá como resultado una precipitación efectiva máxima en 24 hrs de 19,5 mm, lo cual dependiendo de la distribución de precipitación se traduce en los hidrogramas de crecida ilustrados en la Figura 4.16 para el percentil 50% asociado a las distribuciones propuestas (ver Figura 3.6). Para la cuenca del río Lluta en Panamericana, por ejemplo, estos muestran que, dependiente del tipo de distribución de precipitación, los caudales máximos instantáneos de crecida pueden variar entre 793 y 958 m3/s. Asimismo, se puede observar que, en general, i) el caso más desfavorable se obtendría para la distribución de precipitaciones tipo IV (tardía), ii) existe mayor dispersión y casos más extremos para el futuro cercano, y iii) el promedio de los GCMs es más desfavorable para el futuro lejano.

Tabla 4.6: Caudales máximos instantáneos para las cuencas del río Lluta en el periodo histórico y proyecciones futuras derivadas de 29 GCMs del CMIP6 en escenario ssp5-8.5 escaladas y corregidas por sesgo usando el método MBCn y el producto grillado CR2Met v2.5 como referencia climática.

GCMs 2035-2064

Fuente: Elaboración propia

[66,5 - 199,6]

[89,7 - 248,9]

[44,9 - 422,1]

[307,3 - 832,2]

[299,2 - 1053,2]

[193,8 - 2006,8]

[123,4 - 401]

[160 - 694,5]

[109,1 - 773]

[579,6 - 1640,4]

[561,8 - 2956,6]

[459,5 - 3353,6]

[173,5 - 1078]

[138,4 - 963]

[239,7 -

[698,5 - 2096,7]

[635,1 - 4584,1]

[579,6 - 3921,9]

[941,2 - 4330,6]

[852,5 - 18641,6]

[982,2 - 7704,5]

Cabe mencionar que los resultados presentados utilizan las proyecciones de cambio climático aplicadas a enfoques actualmente vigentes a nivel nacional. No obstante, estos enfoques suponen, en general, una correspondencia directa entre el periodo de retorno de precipitación y la crecida que esta genera, lo cual no necesariamente ocurre. Factores como la distribución de precipitación y condición antecedente de humedad modulan la respuesta de la cuenca ante un evento de precipitación extrema. Así, crecidas con igual precipitación podrían tener caudales máximos instantáneos de crecida con diferentes periodos de retorno.

Para abordar dicha limitación, en el presente estudio se ha considerado el análisis de frecuencia asociado a la precipitación efectiva derivada de la máxima precipitación diaria anual para evitar realizar supuestos sobre la condición antecedente

de humedad en la estimación de caudales máximos instantáneos de escorrentía directa de crecida pluvial. Sin embargo, allí subyace el supuesto de que la máxima precipitación diaria anual podría generar el máximo caudal instantáneo anual de crecida pluvial, lo cual no necesariamente ocurre.

Siguiendo el método curva número, precipitaciones de menor magnitud con una condición antecedente húmeda podrían generar crecidas pluviales de mayor magnitud que una precipitación mayor en condiciones antecedentes secas. Así, considerar este tipo de enfoques, así como la propuesta metodológica presentada en DGOP (2023) con el “volumen de precipitación de crecida pluvial” o bien la propuesta de análisis de eventos presentada por Astudillo et al. (2024), donde los análisis se independizan de los supuestos asociados posición de línea de nieve y/o condiciones antecedentes de humedad, permitiría reducir la incertidumbre a las

estimaciones de crecidas pluviales. Esto puede ser extendido utilizando un remuestreo estadístico en base a las recurrencias de, por ejemplo, condiciones antecedentes de humedad y distribuciones de precipitación similar a lo presentado por MuñozCastro et al (2024) en el caso denominado QMI-STAT, lo cual permite prescindir de supuestos asociados a dichas condiciones a costo de suponer condiciones de recurrencia estacionarias en el futuro si es que estas no se pueden recalcular.

4.4 ESTIMACIÓN DE CURVAS

INTENSIDAD-DURACIÓN-FRECUENCIA

Las curvas Intensidad-Duración-Frecuencia (IDF) se construyen a partir del análisis de múltiples tormentas con registros intradiarios disponibles. Como ya se ha mencionado anteriormente, en general, la precipitación diaria es la variable de más fácil acceso pues, por ejemplo, para el análisis del periodo histórico, obtener los registros horarios puede involucrar ciertos esfuerzos burocráticos (e.g., solicitar la información a

las agencias correspondientes) y demoras en el envío/ recepción de estos. En contexto de cambio climático, por temas de gestión de almacenamiento de las variables a nivel global, existen solo unos pocos GCMs que tienen disponibles para la descarga valores intradiarios de precipitación, y en general es la precipitación diaria la variable reportada. En consecuencia, para el estudio de eventos de precipitación extrema resulta clave presentar metodologías que consideren la máxima precipitación diaria como punto pivote para el estudio de diferentes duraciones.

Para este ejemplo, se considera la estación meteorológica Antofagasta (ID: 2710003), ubicada en la ciudad de Antofagasta en la región homónima. A partir del reanálisis atmosférico ERA5 se pueden obtener las series horarias de precipitación interpoladas a la estación y, a partir de ellas, se pueden analizar las máximas precipitaciones anuales en bloques de diferente duración. La Figura 4.17 muestra algunos ejemplos de máxima precipitación en diferentes duraciones entre los años 1950 y 2023 obtenidas desde las series de ERA5, donde a su vez se incluye la máxima precipitación diaria anual.

Figura 4.17: Ejemplo de series de máxima precipitación anual en diferentes bloques de duración obtenidas a partir de la interpolación de ERA5 a la estación Antofagasta para el periodo 1950-2023.

Fuente: Elaboración propia

Para cada duración, se realiza de manera independiente un análisis de frecuencia y luego se ajusta el modelo de Aparicio (1997) para determinar la intensidad de precipitación asociada a un periodo de retorno “T” y duración “D”. Dicho modelo se expresa según la Ec. (4.2), donde el objetivo es determinar los coeficientes de ajuste k, m y n. La selección de este modelo radica en su utilización es estudios previos realizados en Chile a escala de macrozona centro-sur (UNESCO, 2007) y la interpretabilidad que tienen sus coeficientes de ajuste dada la formulación del modelo.

Al ajustar las curvas IDF se obtienen los resultados presentados en la Figura 4.18a. Para expresar los resultados respecto a la máxima precipitación diaria, se normalizan las curvas IDF dividiendo por la precipitación diaria asociada al periodo de retorno correspondiente (Figura 4.18b). Este procedimiento permite expresar las curvas IDF en términos similares a los coeficientes de duración, pero incluyendo el periodo de retorno como factor.

La Figura 4.19 muestra los resultados del análisis de frecuencia de la máxima precipitación diaria para la estación Antofagasta a partir de las series derivadas de CR2Met v2.5 en el periodo 1991-2020, y los 29 GCMs CMIP6 según escenario ssp5-8.5 para el periodo histórico (1991-2020), futuro cercano (2035-2064) y lejano (2065-2094).

4.18: Curvas IDF derivadas mediante ERA5 para la estación Antofagasta en periodo 1991-2020.

Fuente: Elaboración propia

Figura

Es importante destacar la dispersión que existe entre los resultados derivados de los GCMs, lo cual resalta la importancia de seleccionar modelos representativos a modo de reducir la incertidumbre asociada a las proyecciones futuras.

Como se mencionó en el acápite 3.10, existen diferentes alternativas para reducir y cuantificar la incertidumbre asociada a las proyecciones de cambio climático. Para efecto del presente caso de estudio, se propone evaluar los resultados del análisis de frecuencia en el periodo histórico

Figura 4.19: Resultados de análisis de frecuencia de máxima precipitación diaria anual en el periodo histórico (19912020), futuro cercano (2035-2064) y lejano (2065-2094) para la estación Antofagasta según producto de referencia CR2Met v2.5 y 29 GCMs CMIP6 para el escenario ssp5-8.5.

Precipitación diariaPd (mm/d)

Caso

CR2Met GCMs

Fuente: Elaboración propia

Periodo de retorno (años)

Periodo

Histórico (1991-2020)

Futuro Cercano (2035-2064)

Futuro Lejano (2065-2094)

Dispersión entre GCMs

Histórico (1991-2020)

Futuro Cercano (2035-2064)

Futuro Lejano (2065-2094)

asociado a los 29 GCMs y la referencia dada por CR2Met. Dicha diferencia se muestra en la Figura 4.20, donde se propone, de manera arbitraria, una tolerancia de ±25% para filtrar modelos que representen de buena forma, según este criterio,

la referencia. De manera complementaria, la Tabla 4.7 resume aquellos modelos que pasan dicho filtro (14/29), entre los cuales se encuentran algunos de los recomendados por Gateño et al. (2024).

Figura 4.20: Diferencia entre resultados de análisis de frecuencia para el periodo histórico asociado a CR2Met y los diferentes GCMs estudiados interpolados a la estación Antofagasta.

Diferencia entre Pd por periodo de retorno estimada según series de GCMs y CR2Met para el periodo 1991-2020 (%)

ACCESS-CM2

ACCESS-ESM1-5

BCC-CSM2-MR CanESM5

CMCC-ESM2

CNRM-CM6-1

CNRM-CM6-1-HR

Fuente: Elaboración propia

CNRM-ESM2-1

E3SM-1-0

EC-Earth3

EC-Earth3-CC

EC-Earth3-Veg

EC-Earth3-Veg-LR

FGOALS-g3

GFDL-CM4

GFDL-ESM4

INM-CM4-8

INM-CM5-0

IPSL-CM6A-LR

KACE-1-0-G

KIOST-ESM

MIROC-ES2L

MIROC6

MPI-ESM1-2-HR

MPI-ESM1-2-LR

MRI-ESM2-0

NESM3

NorESM2-MM

TaiESM1

Tabla 4.7: GCMs con diferencias porcentuales absolutas menores al 25% en el análisis de frecuencia en el periodo histórico 1991-2020 respecto a CR2Met. En negrita se identifican los modelos recomendados por Gateño et al. (2024) para la macrozona Norte Grande de Chile.

Diferencia respecto a análisis de frecuencia con CR2Met para el periodo 1991-2020

Modelo

Veg

IPSL-CM6ALR

Fuente: Elaboración propia

A partir de los 14 GCMs filtrados por su desempeño representado las máximas precipitaciones diarias asociadas a diferentes periodos de retorno en el periodo histórico, la Figura 4.19 puede ser actualizada. Así, la Figura 4.21 muestra los resultados a partir del filtro aplicado, donde se puede ver que se reduce la dispersión de los resultados. Es importante notar que no se puede eliminar dicha dispersión pues es parte de la incertidumbre de las proyecciones futuras. Asimismo, la selección de un GCM más optimista por sobre otro más pesimista no puede ser a priori y debe justificarse a partir de, por ejemplo, otros filtros basados en el desempeño de los GCMs en el periodo histórico. Esto pues las proyecciones de cada modelo pueden considerarse técnicamente como equiprobable (incertidumbre profunda).

Figura 4.21: Resultados de análisis de frecuencia de máxima precipitación diaria anual en el periodo histórico (19912020), futuro cercano (2035-2064) y lejano (2065-2094) para la estación Antofagasta según producto de referencia CR2Met v2.5 y 14 GCMs CMIP6 para el escenario ssp5-8.5 filtrados según sesgo en periodo histórico.

Caso

CR2Met GCMs

Periodo de retorno (años)

Periodo

Histórico (1991-2020)

Futuro Cercano (2035-2064)

Futuro Lejano (2065-2094)

Dispersión entre GCMs

Histórico (1991-2020)

Futuro Cercano (2035-2064)

Futuro Lejano (2065-2094)

Fuente: Elaboración propia

A partir del enfoque propuesto para la estimación de las curvas IDF en un contexto de clima cambiante, usando los 14 GCMs seleccionados y considerando los periodos de retorno 10 y 100 años, se obtienen las curvas IDF presentadas en la Figura 4.22. Allí es

importante notar que, de manera consistente con los resultados presentados en la Figura 4.21 y en estudios previos (e.g., MOP 2022a, 2022b), el futuro cercano reporta cambios mayores respecto al periodo histórico en comparación al futuro lejano.

Figura 4.22: Ejemplo de curvas Intensidad-Duración asociadas a periodos de retorno 10 y 100 años en la estación Antofagasta para el periodo histórico (1991-2020), futuro cercano (2035-2064) y lejano (2065-2094).

Duración (hrs)

Cercano (2035-2064)

Futuro Lejano (2065-2094)

Dispersión entre GCMs

Histórico (1991-2020)

Futuro Cercano (2035-2064)

Futuro Lejano (2065-2094)

Fuente: Elaboración propia

Cabe mencionar que, si bien utilizar ERA5 como base para el análisis supone que las distribuciones de tormenta no cambiarán en un contexto de cambio climático, los cambios en la intensidad de precipitación estarán dados por los cambios en las máximas precipitaciones diarias anuales en el futuro.

Consideraciones y pertinencia de la incorporación del cambio climático en el diseño de infraestructura hidráulica

5.1 LA NECESIDAD DE ACTUALIZACIÓN DE AJUSTES Y RELACIONES ESTADÍSTICAS

Uno de los principales documentos con recomendaciones para el diseño hidrológico en Chile corresponde, como se ha mencionado en acápites anteriores, al denominado Manual de Cálculo de Crecidas (MOP, 1995). Dicho documento se ha utilizado durante las últimas tres décadas sin considerar actualizaciones en las metodologías propuestas ni en los coeficientes de ajuste asociados a los métodos de base estadística que

allí se presentan. Esto supone de manera implícita la estacionariedad del sistema climático y la respuesta de las cuencas a eventos hidrometeorológicos extremos.

El sistema climático es dinámico y existen ciertos modos de variabilidad global que en Chile influyen en, por ejemplo, los montos de precipitación anual o las precipitaciones extremas en un determinado periodo de tiempo (e.g., ENOS, SAM, PDO; DGA, 2022). Las emisiones de gases de efecto invernadero de origen antrópico incluyen una dimensión adicional a esta dinámica y agregan incertidumbre a la evolución futura del sistema. En este contexto, el supuesto de estacionariedad podría verse afectado.

Figura 5.1: Parámetros de ajuste de curvas IDF para la estación Antofagasta calculados para subperiodos móviles de 30 años entre 1950 y 2023 a partir de las estadísticas derivadas de ERA5.

Fuente: Elaboración propia

Año central del subperiodo de 30 años 2000

Por ejemplo, si se consideran las estadísticas en el periodo histórico 1950-2023 derivadas de ERA5 y, de manera análoga a lo presentado en el acápite 4.4, se ajustan las curvas IDF para la estación Antofagasta usando ventanas móviles de subperiodos de 30 años, se obtienen los resultados presentados en la Figura 5.1. Allí queda en evidencia la variabilidad asociada a los parámetros de ajuste de las curvas IDF según la estadística empleada para su estimación. En el caso particular del ejemplo, se observan cambios en torno al valor promedio 1950-2023 que, aproximadamente cada 10-15 años, pasan de ubicarse a un lado de la media (e.g., k entre 1965-1978) a ubicarse en torno a la misma (e.g., k entre 1979-1987) y, posteriormente, al otro lado de ella (e.g., k entre 1988-1999) para luego repetir el ciclo inverso.

Este ejemplo, que solo incluye los registros “observados” o de referencia, deja de manifiesto la necesidad de actualizar de manera periódica (510 años) las relaciones estadísticas ajustadas para determinadas regiones. Esta idea cobra mayor importancia cuando se piensa en cambio climático, pues podrían acentuarse y/o acelerarse los cambios en las estadísticas, comprometiendo la validez de estimaciones y/o ajustes realizados a partir de los registros históricos. Asimismo, al considerar los avances científico-tecnológicos en materia de proyecciones de cambio climático y la mejora en la comprensión de los procesos y mecanismos asociados, las metodologías para la incorporación de la variable cambio climático también debiesen ser revisitadas a modo de comprobar su validez y/o actualizarlas.

5.2 EL VALOR INFORMATIVO DE LAS ESTADÍSTICAS PASADAS PARA PROYECTAR EL FUTURO

En el diseño de infraestructura hidráulica, los conceptos de operación y vida útil de la obra son aspectos claves para la determinación del periodo de retorno requerido para el dimensionamiento de estas. En un contexto de diseño hidrológico en clima cambiante, estos conceptos debiesen orientar la selección de los subperiodos de tiempo con los cuales se realizará, por ejemplo, la estimación de las precipitaciones y caudales de diseño de una determinada obra.

El diseño hidrológico “tradicional” considera las estadísticas pasadas para efectos de la estimación de los valores a adoptar para el dimensionamiento de una obra que operará en un horizonte futuro. Esto considerando, lógicamente, que se desconoce con certeza lo que ocurrirá en el futuro. No obstante, esto puede conllevar a una sub o sobrestimación de los parámetros de diseño y, consecuentemente, un sub o sobredimensionamiento de la obra.

A modo de ejemplo, si se consideran las máximas precipitaciones diarias anuales asociadas a la estación Antofagasta para el periodo 1971-2020 derivadas de CR2Met v2.5 y se contrastan los subperiodos 1971-2000, 1981-2010 y 1991-2020 (Figura 5.2), se puede observar que existen diferencias en las magnitudes asociadas a los diferentes

periodos de retorno. Específicamente, se puede notar que existe un punto de cambio en el signo de la diferencia (i.e., de positivo a negativo) en torno al periodo de retorno 30 años donde, en comparación con el subperiodo 1971-2000, los subperiodos pasan de tener magnitudes mayores para periodos de retorno menores (e.g., ~20% para T=2 años al comparar 1991-2020 respecto a 19712000) a magnitudes menores (e.g., ~-5% para T=100 años al comparar 1991-2020 respecto a 19712000). Esto es una muestra de los cambios en las propiedades estadísticas de las series de datos (i.e., no estacionariedad) y cómo pueden afectar en los valores de diseño de infraestructura hidráulica.

Buscando una analogía con un caso práctico, esto podría reflejar el uso de las estadísticas de precipitación (y/o caudales máximos) para el

diseño de las obras de excedencia de un embalse y el tiempo que transcurre la etapa de estudios, el inicio de la operación de la obra y su vida útil.

En la actualidad, la incorporación del futuro en el diseño hidráulico puede realizarse a partir del uso de proyecciones de cambio climático las que, si bien tienen asociada una incertidumbre y no se pueden interpretar como un pronóstico bajo ningún caso, permiten tener una idea de cómo podría evolucionar el clima y sus impactos en, por ejemplo, la magnitud de eventos hidrometeorológicos extremos. Sin embargo, una pregunta que debiese realizarse en este contexto es cómo se traduce la incertidumbre en el diseño. Una propuesta que se podría adoptar es diseñar la infraestructura considerando casos ubicados dentro de los más desfavorables (e.g., percentiles iguales o superiores

Figura 5.2: Máximas precipitaciones diarias (Pd) por periodo de retorno en el periodo 1971-2020 estimadas para los subperiodos 1971-2000, 1981-2010, y 1991-2020. a) Resultados absolutos en mm, b) diferencias porcentuales respecto al periodo 1971-2020.

Fuente: Elaboración propia

al 75%) y utilizar los casos más desfavorables para la verificación del diseño incorporando soluciones no estructurales para gestionar el riesgo asociado a dichos eventos. Esto sugiere la adaptación de algunas normativas para efectos de definir cómo se incluye el cambio climático en el diseño, donde la idea propuesta en DOH (2020) de una “revancha por variabilidad climática futura”, determinada a partir del análisis de las diferencias positivas (i.e., casos más desfavorables para el diseño) de diversas proyecciones futuras (i.e., escenarios y modelos) respecto al periodo histórico, surge como una alternativa que debiese ser explorada.

5.3 EL USO DE PERCENTILES PARA

CUANTIFICAR INCERTIDUMBRE Y SUS

IMPLICANCIAS PRÁCTICAS

Documentos oficiales (e.g., SEA, 2023b) recomiendan el uso de percentiles para incorporar los efectos del cambio climático en estudios asociados a recursos hídricos. Sin embargo, la correspondencia entre un percentil y un GCM puede cambiar según el periodo de retorno y subperiodo de interés (ver Figura 5.3)

Figura 5.3: GCMs asociados a los percentiles 25,50 y 75% según diferentes periodos de retorno y subperiodos para las estadísticas en la estación Antofagasta. La inexistencia de círculos (NA) se refiere a la correspondencia del GCM con percentiles diferentes a los de interés.

Histórico (1991-2020)

Futuro Cercano (2035-2064)

Futuro Lejano (2065-2094)

ACCESS-CM2

ACCESS-ESM1-5

BCC-CSM2-MR

Can ESM5

CMCC-ESM2

CNRM-CM6-1

CNRM-CM6-1-HR

CNRM-ESM2-1

E3SM-1-0

EC-Earth3

EC-Earth3-CC

EC-Earth3-Veg

EC-Earth3-Veg-LR

FGOALS-g3

GFDL-CM4

GFDL-ESM4

INM-CM4-8

INM-CM5-0

IPSL-CM6A-LR

KACE-1-0-G

KIOST-ESM

MIROC-ES2L

MIROC6

MPI-ESM1-2-HR

MPI-ESM1-2-LR

MRI-ESM2-0

NESM3

NorESM2-MM

TaiESM1

Percentil asociado

P25%

P50%

P75%

NA

Fuente: Elaboración propia

En este sentido, no queda claro cómo seleccionar aquella trayectoria que representa el percentil de interés, más aún cuando se busca trabajar con enfoques dinámicos (e.g., modelación hidrológica) donde los estados del sistema son una consecuencia de los impactos acumulados de eventos hidrometeorológicos. Si se considera el caso de, por ejemplo, máximas precipitaciones diarias, simplificar el análisis al uso de percentiles calculados por periodo de retorno podría generar inconsistencias con el resto de los periodos de retorno producto de la independización de estos valores respecto a las condiciones que lo acompañan, limitando la comparabilidad de los resultados obtenidos. Esto podría tener aún mayores impactos en el contexto de estimación de crecidas dadas las interacciones asociadas a este tipo de eventos (e.g., posición línea de nieve, condición de humedad antecedente).

Una alternativa al uso directo de percentiles podría ser la selección de modelos (i.e., serie completa de estadísticas) que consistentemente se ubiquen dentro de uno de los cuartiles de interés y que sean diferentes en términos estadísticos del resto de los miembros del conjunto de GCMs. Esto se podría evaluar con pruebas estadísticas tipo KolmogorovSmirnov y reducir el número de simulaciones a partir de la selección de casos que cubran el rango de dispersión de las proyecciones futuras.

5.4 IMPACTOS METODOLÓGICOS EN LA ESTIMACIÓN DE CAUDALES MÁXIMOS DE

CRECIDA

Los métodos presentados anteriormente para la estimación de crecidas están sujetas a diversas fuentes de incertidumbres, tales pueden ser estructurales del modelo, de las variables (y su proveniencia) que se utilizan para alimentar al modelo, o bien epistémicas. De esta forma, es necesario aclarar cuál de los métodos presentados es el que permite un mejor manejo y, en consiguiente, una reducción de la incertidumbre. A modo de comparación, se presentan en la Tabla 5.1 los caudales estimados para los periodos de retorno T = 10, 100 y 1000 años, utilizando el método de modelación hidrológica (caso sin datos fluviométricos), regresión e hidrograma unitario. Es importante mencionar que los métodos de MH y regresión fueron trabajados con caudales medios diarios máximos, a diferencia del método del HUS que trabaja con caudales máximos instantáneos diarios. Debido a esto, el caudal máximo instantáneo entregado por el HUS fue transformado a caudal medio diario utilizando la fórmula de Füller (1914), mostrada en la ecuación 5.1:

Donde IPF corresponde al caudal máximo instantáneo (m3/s), referido como QMI en otras secciones del presente documento, MDF corresponde al caudal medio diario máximo (m3/s) y A corresponde al área de la cuenca (km2). Además, para el método del HU se consideró el flujo base previo a la crecida, estimado mediante la modelación hidrológica de la zona, promediando los flujos bases que se tienen en las crecidas máximas anuales de las series de tiempo de caudales simulados en el periodo histórico. En consecuencia, se consideró un flujo base igual a 2 m3/s.

Es posible observar que el método que ofrece un menor error porcentual es el método de la modelación hidrológica. Los modelos hidrológicos tienen la ventaja de poder capturar las condiciones de borde de cada crecida, lo que entrega un resultado modelado de mayor precisión. En base a esto, es necesario aclarar que el hecho de que una precipitación asociada a un periodo de retorno T no necesariamente implica que será la misma precipitación que cause una crecida de mismo periodo de retorno, debido a la importancia de la humedad del suelo en la generación de escorrentía. A pesar de las incertidumbres que traen consigo los inputs de la modelación, sobre todo considerando la alta heterogeneidad espacial en las precipitaciones

de la zona norte de Chile, los modelos hidrológicos logran simular la hidrología de las cuencas.

Por otro lado, los modelos de Regresión y HUS, son sensibles a las variables de entrada y su procedencia. Desde esta perspectiva, es importante aclarar que existirán inminentemente discrepancias en los valores de precipitación que entreguen diversos modelos de productos grillados, debido a las altas incertidumbres del tipo espacial en los instrumentos de medición. Además, el hecho de concentrar los datos podría soslayar eventos puntuales y aislados de precipitación con magnitudes considerables. Considerando además que la zona norte de Chile es caracterizada por zonas áridas de altas elevaciones, la incertidumbre incrementa. La aridez de la zona compromete las mediciones satelitales de precipitación debido a la alta evaporación que existe en la zona. Por otro lado, las altas elevaciones dificultan la extrapolación de las mediciones de precipitación, considerando la falta de instrumentación en zonas de difícil acceso. Además, como se mencionó anteriormente, cada cuenca es única, con sus propios procesos dominantes, por lo que homogeneizar un conjunto de cuencas, bajo el supuesto de que cada una responde igual, conlleva inminentemente a mayores incertidumbres.

5.1: Resultados de los caudales medios diarios máximos obtenidos mediante los métodos de Modelación Hidrológica, Regresión e Hidrograma Sintético Unitario en periodo histórico.

Fuente: Elaboración propia

Tabla

Otro aspecto de importancia es la distribución espacial de las tormentas, aspecto que no es considerado por ninguno de los métodos empleados. En el caso de los modelos hidrológicos concentrados, la calibración de parámetros compensa la falta de esta representación espacial de la precipitación, la cual dadas las características de la zona se concentra en su parte alta. Esto podría explicar los sesgos asociados al método HUS aplicado a Lluta en Panamericana, pues el método supone una precipitación que se distribuye en toda la cuenca, lo cual no es el caso particular del dominio. La recomendación en estos casos sería estudiar la distribución espacial de las precipitaciones y aplicar el HUS a las cuencas en la parte alta (e.g., Lluta en Alcérreca y Colpitas en Alcérreca) y luego hacer el rastreo de la onda de crecida hacia el punto de interés mediante, por ejemplo, el método de Muskingum u otro.

Las cuencas son sistemas dinámicos, sujetos a cambios en el tiempo en su hidrología. Además, la toma de datos de calidad es difícil debido a las discrepancias en los modelos de precipitación y la falta de instrumentación en zonas de altas elevaciones. Son los modelos hidrológicos las únicas herramientas, que, de momento, se cuenta para poder simular la dinámica en la generación de escorrentía de las cuencas. Los modelos hidrológicos permiten calibrarse a sí mismos acorde a la cuenca que se desea modelar con las variables de entrada con la procedencia que el hidrólogo considere pertinente.

5.5 EL VALOR AGREGADO DE ENFOQUES

TRANSDISCIPLINARIOS

El cambio climático es materia de interés tanto a nivel científico como social por los impactos que este puede tener sobre el mundo que conocemos. A pesar de este interés compartido, en general, el problema se aborda desde enfoques separados. En este contexto, la interacción entre el campo de la ciencia y la práctica (i.e., diferentes actores sociales) a través de enfoques de trabajo transdiciplinarios (ver Figura 5.4) podría aportar en el desarrollo de soluciones con mayor impacto para hacer frente a los desafíos que sugiere un futuro de clima cambiante. Esto pues, por ejemplo, al combinar ambas fuentes de conocimiento y experiencia, se puede mejorar la definición del problema englobando diferentes aristas de este.

La pura comunicación de resultados (i.e., transferencia de conocimiento), a pesar de reconocerse como uno de los enfoques de inclusión de partes interesadas en el proceso de generación de conocimiento (e.g., Reed et al., 2018; Knaggård et al., 2019), no es suficiente para lograr cambios en los enfoques que actualmente se adoptan para proyectar los impactos del cambio climático en nuestra sociedad. En particular, la incorporación del cambio climático en el diseño de infraestructura hidráulica debiese considerar aristas adicionales a

lo que es las proyecciones de cambio hidrológico y sus impactos en los caudales de diseño. Aspectos normativos (e.g., DS 90), operativos (e.g., ¿cómo abordarán los consultores y organismos públicos estos nuevos criterios?), constructivos, entre otros, sugieren la necesidad de incluir otras disciplinas, así como partes interesadas (“stakeholders”) y tomadores de decisiones, en la producción de conocimiento que se ajuste a las necesidades de la sociedad y trasciendan el puro ejercicio académico. En este contexto, los consultores que han desarrollado el presente documento han orientado los análisis y discusión según su

experiencia profesional como consultores en proyectos públicos y privados (i.e., práctica), así como su experiencia académica en proyectos de investigación (i.e., ciencia), con el fin de entregar lineamientos hidrológicos para la incorporación del cambio climático en el diseño de infraestructura hidráulica. No obstante, el desafío pendiente radica en revisitar estas propuestas y recomendaciones metodológicas incluyendo otras disciplinas en la co-producción del conocimiento para, entre otros beneficios, facilitar la implementación de estas.

5.4: Esquema de la conexión entre la producción de conocimiento científico y manejo de los problemas sociales a través de la transdisciplinariedad.

Campo de la ciencia, rigor y comprensión (es esto verdad?)

TRANSDISCIPLINARIEDAD:

Colaboración funcional y dinámica entre disciplinas y actores sociales para investigar y resolver un problema.

Campo de la práctica, relevancia y diseño (es esto funcional?)

La ciencia investiga el problema

Definición del problema

Análisis del problema

Análisis de impactos

La sociedad maneja/resuelve el problema

Figura

Fuente: Traducido y adaptado de Pohl et al. (2017).

06 Síntesis y conclusiones

El cambio climático supone cambios en los patrones de precipitación y temperatura, y, en consiguiente, cambios en la generación de escorrentía, lo cual podría afectar la seguridad la infraestructura hidráulica. Con el objetivo proporcionar un conjunto de directrices y metodologías para integrar los impactos del cambio climático en los análisis de eventos hidrometeorológicos extremos y la estimación de parámetros de diseño hidrológico, en el presente documento se han revisado y sintetizado diferentes consideraciones y experiencias técnicas y científicas reportadas tanto en la literatura nacional como internacional. A partir de ello, se han presentado algunos ejemplos aplicados de la incorporación del cambio climático en la estimación de caudales máximos medios diarios e instantáneos de crecidas pluviales, precipitaciones máximas, y curvas intensidad-duración-frecuencia. Si bien los ejemplos consideran cuencas ubicadas en la macrozona norte de Chile, los procedimientos pueden ser utilizados en cualquier zona de Chile y otras regiones del mundo.

Los resultados muestran que el método de la modelación hidrológica es el que entrega resultados más similares a los derivados del análisis de observaciones, debido a su enfoque basado en procesos y componente dinámica, capaz de considerar condiciones de borde distintas para cada evento de crecida, tales como la humedad de suelo en momentos anteriores y durante el evento, y su interacción con otros elementos del sistema hidrológico como la precipitación sólida (i.e., línea de nieve). De esta forma los modelos conceptuales son capaces de considerar (hasta cierto punto) los cambios en las cuencas. Para la zona de estudio (i.e., Norte de Chile) se recomienda explorar el uso de modelos espacialmente distribuidos o semi-

distribuidos a modo de incluir dentro de la cadena de modelación la heterogeneidad espacial que puede existir durante eventos de precipitación extrema, la cual podría concentrarse sólo en una fracción menor de la cuenca y no en todo su dominio. Esta es una de las principales limitaciones detectadas para métodos del tipo hidrograma unitario sintético, pues en la zona norte de Chile no es directo suponer que un evento de precipitación extrema se distribuye homogéneamente en la cuenca, algo que potencialmente podría suponerse en cuencas en la zona centro-sur para eventos durante invierno, por lo que se recomienda realizar los análisis por subcuencas e incorporar esquemas de rastreo desde aguas arriba hacia el punto de interés, enfoque similar al incorporado en HEC-HMS.

Respecto a los métodos estadísticos, estos incurren en incertidumbres que no son menores, pues se busca relacionar precipitaciones de una duración específica asociada a cierto periodo de retorno con crecidas de igual periodo de retorno. Sin embargo, se debe reconocer que una precipitación de cierta magnitud no necesariamente causa una crecida del mismo periodo de retorno, ya que existen otros procesos que condicionan la generación de una crecida pluvial. Así, dada su incertidumbre y supuestos, se recomienda el uso de estos métodos sólo para las fases preliminares en la estimación de crecidas.

Ante la falta de disponibilidad registros de caudales a nivel intradiario (e.g., horarios) que permitan estimar el caudal máximo instantáneo durante crecidas, que corresponde a la variable de interés para el diseño hidrológico, se recomienda adoptar la fórmula de Füller (1914) o bien los valores propuestos en DGA (1995). En caso de contar con registros

intradiarios en cuencas cercanas al dominio de interés, se recomienda estimar los coeficientes de ajuste según alguna metodología disponible (e.g., Füller (1914)) y transferirlos en base a algún criterio de similitud (e.g., proximidad espacial) a la cuenca de estudio.

Finalmente, se destaca la necesidad de adoptar enfoques transdisciplinarios para el estudio de eventos hidrometeorológicos extremos y su utilización para el diseño de infraestructura hidráulica. Esto, a modo de desarrollar propuestas de lineamientos metodológicos que sean vinculantes, se encuentren respaldadas tanto por la comunidad científica como consultores, así como todas las partes interesadas, y consecuentemente tengan un mayor impacto en la comunidad.

Referencias

Acuña, P., & Pizarro, A. (2023). Can continuous simulation be used as an alternative for flood regionalisation? A large sample example from Chile. Journal of Hydrology, 626, 130118.

Alvarez-Garreton, C., Mendoza, P.A., Pablo Boisier, J., Addor, N., Galleguillos, M., Zambrano-Bigiarini, M., Lara, A., Puelma, C., Cortes, G., Garreaud, R., McPhee, J., Ayala, A. (2018). The CAMELS-CL dataset: Catchment attributes and meteorology for large sample studiesChile dataset. Hydrol. Earth Syst. Sci. 22, 5817–5846. https://doi.org/10.5194/hess-22-5817-2018

Aparicio, F. (1997). Fundamentos de hidrología de superficie. Editorial Limusa, Grupo Noriega Editores. ISBN 968-18-3014-8.

Astudillo, V. (2024). Metodología para la incorporación del cambio climático en el análisis de eventos extremos de precipitación aplicado al diseño de obras hidráulicas. Memoria para optar al título de Ingeniera Civil, Facultad de Ciencias Físicas y Matemáticas (FCFM), Universidad de Chile. Profesor guía: Eduardo Muñoz-Castro; Comisión examinadora: Oscar MuñozCastro, Franco Ricchetti, Ximena Vargas.

Atkinson, S., Sivapalan, M., Woods, R., and Viney, N. (2003). Dominant physical controls on hourly flow predictions and the role of spatial variability: Mahurangi catchment, New Zealand, Advances in Water Resources, 26, 219–235, https://doi.org/10.1016/ S0309-1708(02)00183-5, URL https://linkinghub. elsevier.com/retrieve/pii/S0309170802001835, 2003.

Bambach, N. E., Rhoades, A. M., Hatchett, B. J., Jones, A. D., Ullrich, P. A., Zarzycki, C.M. (2021). Projecting climate change in South America using variable-resolution Community Earth System Model: An application to Chile. Int. J. Climatol, https://doi.org/10,1002/joc.7379

Benítez, A., Verni, F., 1985. Distribución porcentual de las precipitaciones de una duración «t», para 12 h < t < 72 h, in: VII Congreso Nacional de Ingeniería Hidráulica, SOCHID. Departamento de Ingeniería Civil, Facultad de Ingeniería, Universidad de Concepción, Concepción, Chile.

Beven, K. J. and Kirkby, M. J.: A physically based, variable contributing area model of basin hydrology / Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant, Hydrological Sciences Bulletin, 24, 43–69, https://doi.org/10.1080/02626667909491834, URL http://www.tandfonline.com/doi/ abs/10.1080/02626667909491834, 1979.

Beven, K. J. (2000). Uniqueness of place and process representations in hydrological modelling. Hydrology and earth system sciences, 4(2), 203-213.

Block, P. J., Souza Filho, F. A., Sun, L., & Kwon, H. H. (2009). A streamflow forecasting framework using multiple climate and hydrological models 1. JAWRA Journal of the American Water Resources Association, 45(4), 828-843.

Boisier, J. P., Alvarez-Garretón, C., Cepeda, J., Osses, A., Vásquez, N., & Rondanelli, R. (2018). CR2MET: A highresolution precipitation and temperature dataset for hydroclimatic research in Chile. In EGU general assembly conference abstracts (p. 19739).

Boisier, J. P. (2023). CR2MET: A high-resolution precipitation and temperature dataset for the period 1960-2021 in continental Chile. (Version v2.5) [Dataset]. Zenodo. https://doi.org/10.5281/zenodo.7529682

Cannon, A. J. (2018). Multivariate quantile mapping bias correction: an N-dimensional probability density function transform for climate model simulations of multiple variables. Climate dynamics, 50(1), 31-49.

Cannon, A. J., Sobie, S. R., & Murdock, T. Q. (2015). Bias correction of GCM precipitation by quantile mapping: how well do methods preserve changes in quantiles and extremes?. Journal of Climate, 28(17), 6938-6959.

Cheng, L., Aghakouchak, A., Gilleland, E., Katz, R.W. (2014). Non-stationary extreme value analysis in a changing climate 353–369. https://doi.org/10.1007/ s10584-014-1254-5

Chiew, F. H. S.: Estimating groundwater recharge using an integrated surface and groundwater model, PhD thesis, University of Melbourne, 1990.

Chiew, F. and McMahon, T.: Application of the daily rainfall-runoff model MODHYDROLOG to 28 Australian catchments, Journal of Hydrology, 153, 383–416, https://doi.org/10.1016/0022-1694(94)902003, URL https://linkinghub.elsevier.com/retrieve/ pii/0022169494902003, 1994.

Chow, V.T., Maidment, D.R. and Mays, L.W. (1988) Applied Hydrology. International Edition, McGraw-Hill Book Company, New York.

Cressman, G.P. (1959). An operational objetive analysis system. Mon. Weather Rev. 87, 367–374. https://doi.org/10.1175/1520-0493(1959)087<0367:AOO AS>2.0.CO;2

Croke, B. and Jakeman, A.: A catchment moisture deficit module for the IHACRES rainfall-runoff model, Environmental Modelling & Software, 19, 1–5, https://doi.org/10.1016/j.envsoft.2003.09.001, URL https://linkinghub.elsevier.com/retrieve/pii/ S1364815203002123, 2004.

Crooks, S. M. and Naden, P. S.: CLASSIC: a semidistributed rainfall-runoff modelling system, Hydrology and Earth System Sciences, 11, 516–531, https://doi.org/10.5194/hess-11-516-2007, URL https:// hess.copernicus.org/articles/11/516/2007/, 2007.

CSA Group. (2024). Peak Flow Assessment under a Changing Climate: Recommendations for the Canadian Highway Bridge Design Code. Standards Research. Authors: T. Stadnyk and J. van der Eerden.

Dallan, E., Marra, F., Fosser, G., Marani, M., Formetta, G., Schär, C., and Borga, M. (2023). How well does a convection-permitting regional climate model represent the reverse orographic effect of extreme hourly precipitation?, Hydrol. Earth Syst. Sci., 27, 1133–1149, https://doi.org/10.5194/hess-27-1133-2023, 2023.

De Paola, F., Giugni, M., Pugliese, F., Annis, A., & Nardi, F. (2018). GEV Parameter Estimation and Stationary vs. Non-Stationary Analysis of Extreme Rainfall in African Test Cities. Hydrology, 5(2), Article 2. https:// doi.org/10.3390/hydrology5020028.

DGA (2022) Homologación del cálculo hidrológico para la estimación de la oferta natural de agua histórica y futura en Chile. S.I.T. 524 Ministerio de Obras Públicas. Dirección General de Aguas. División de Estudios y Planificación. Santiago. Chile. Elaborado

por: Universidad de Chile. Facultad de Ciencias Físicas y Matemáticas.

DGA (2019b). Aplicación de la metodología de actualización del balance hídrico nacional en las cuencas de la parte sur de la Macrozona Austral e Isla de Pascua, SIT N° 444. Elaborado por: Universidad de Chile. Facultad de Ciencias Físicas y Matemáticas.

DGA (2019a). Aplicación de la metodología de actualización del balance hídrico nacional en la macrozona sur y parte norte de la macrozona Austral, SIT N° 441. Elaborado por: Universidad de Chile. Facultad de Ciencias Físicas y Matemáticas.

DGA (2018). Aplicación de la metodología de actualización del balance hídrico nacional a las macrozonas Norte y Centro, SIT N° 435, Dirección General de Aguas, División de Estudios y Planificación. Elaborado por UNTEC en UTP con la P.U. Católica de Chile.

DGA (2017). Actualización del Balance Hídrico Nacional, SIT N° 417, Ministerio de Obras Públicas, Dirección General de Aguas, División de Estudios y Planificación, Santiago, Chile. Elaborado por: Universidad de Chile & Pontificia Universidad Católica de Chile.

DGA. (1995). Manual de cálculo de crecidas y caudales mínimos en cuencas sin información fluviométrica. Dirección General de Aguas, Ministerio de Obras Públicas.

Dionizis D., Ojeda P., Quezada, S., Lagos, M., Monserrat, S. (2021). Implicancias de la elección del método de escalamiento estadístico de modelos de circulación general en proyecciones de cambio climático. Sociedad Chilena de Ingeniería Hidráulica. XXV Congreso Chileno de Ingeniería Hidráulica.

DOH (2013) Manual de Drenaje Urbano. Ministerio de Obras Públicas. Dirección de Obras Hidráulicas

El Adlouni, S., Bobée, B., & Ouarda, T. B. M. J. (2008). On the tails of extreme event distributions in hydrology. Journal of Hydrology, 355(1), 16–33. https://doi. org/10.1016/j.jhydrol.2008.02.011.

Fosser, G., Gaetani, M., Kendon, E. J., Adinolfi, M., Ban, N., Belušić, D., ... & Tölle, M. H. (2024). Convectionpermitting climate models offer more certain extreme rainfall projections. npj climate and atmospheric science, 7(1), 51.

Füller, W.E., 1914. Flood flows. Trans. Am. Soc. Civ. Eng. 77, 564–617.

Garreaud, R. (1993). Impacto de la variabilidad de la línea de nieve en crecidas invernales en cuencas pluvio-nivales de Chile central. XI Congreso Chileno de Ingeniería Hidráulica (pp. 271-285).

Gateño, F., Mendoza, P. A., Vásquez, N., Lagos-Zúñiga, M., Jiménez, H., Jerez, C., ... & Montserrat, S. (2024). Screening CMIP6 models for Chile based on past performance and code genealogy. Climatic Change, 177(6), 87.

Ghorbani, M. A., Kashani, M. H., &amp; Zeynali, S. (2013). Development of synthetic unit hydrograph using probability models. Research in Civil and Environmental Engineering, 1(1), 54-66.

Gupta, H. V., Kling, H., Yilmaz, K. K., & Martinez, G. F. (2009). Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. Journal of hydrology, 377(12), 80-91.

Gupta, & Govindaraju, R. (2023). Uncertainty quantification in watershed hydrology: Which method to use? Journal of Hydrology, 616, 128749.

Gupta, H. V., Kling, H., Yilmaz, K. K., & Martinez, G. F. (2009). Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. Journal of Hydrology, 377(1), 80–91. https://doi.org/10.1016/j.jhydrol.2009.08.003

Hansen, N., Müller, S. D., & Koumoutsakos, P. (2003). Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evolutionary Computation, 11(1), 1–18.

Hargreaves, G. H., & Samani, Z. A. (1985). Reference crop evapotranspiration from temperature. Applied Engineering in Agriculture, 1(2), 96–99.

Hartigan, J. A. and Wong, M. A. (1979). Algorithm AS 136: A K-means clustering algorithm. Applied Statistics, 28, 100--108. 10.2307/2346830.

Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., Nicolas, J., Peubey, C., Radu, R., Schepers, D., Simmons, A., Soci, C., Abdalla, S., Abellan, X., Balsamo, G., Bechtold, P., Biavati, G., Bidlot, J., Bonavita, M., De Chiara, G., Dahlgren, P., Dee, D., Diamantakis, M., Dragani, R., Flemming, J., Forbes, R., Fuentes, M., Geer, A., Haimberger, L., Healy, S., Hogan, R.J., Hólm, E., Janisková, M., Keeley, S., Laloyaux, P., Lopez, P., Lupu, C., Radnoti, G., de Rosnay, P., Rozum, I., Vamborg, F., Villaume, S., Thépaut, J.N. (2020). The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049. https://doi.org/10.1002/ qj.3803.

Horton, P., Schaefli, B., & Kauzlaric, M. (2022). Why do we have so many different hydrological models? A review based on the case of Switzerland. WIREs Water, 9(1), e1574. https://doi.org/10.1002/wat2.1574

Hossain, I., Khastagir, A., Aktar, M. N., Imteaz, M. A., Huda, D., & Rasel, H. M. (2022). Comparison of estimation techniques for generalised extreme value (GEV) distribution parameters: A case study with Tasmanian rainfall. International Journal of Environmental Science and Technology, 19(8), 7737–7750. https://doi. org/10.1007/s13762-021-03693-5

Hershfield, D. (1965). Method for Estimating Probable Maximum Rainfall. J. Am. Waterworks Assoc. 57, 965–972.

Hosseinzadehtalaei, P., Tabari, H., &amp; Willems, P. (2020). Climate change impact on short-duration extreme precipitation and intensity–duration–frequency curves over Europe. Journal of Hydrology, 590, 125249.

Hrachowitz, M., Savenije, H. H. G., Blöschl, G., McDonnell, J. J., Sivapalan, M., Pomeroy, J. W., ... & Cudennec, C. (2013). A decade of Predictions in Ungauged Basins (PUB)—a review. Hydrological sciences journal, 58(6), 1198-1255.

Huff, F. A. (1967). Time distribution of rainfall in heavy storms, Water Resour. Res., vol. 3, no. 4, pp. 1007–1019, 1967.

Huffman, G.J., Bolvin D., Braithwaite, D., Hsu, K., Joyce, R., Kidd, C., Nelkin, E., Sorooshian, S., Stocker, E., Tan, J., Wolff, D., Xie, P. (2020). Integrated Multi-satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG). In: Levizzani, V., Kidd, C., Kirschbaum, D.B., Kummerow, C.D., Nakamura, K., Turk, F.J. (eds) Satellite Precipitation Measurement. Advances in Global Change Research, vol 67. Springer, Cham. https://doi. org/10.1007/978-3-030-24568-9_19

IPCC. (2023). Summary for Policymakers. In: Climate Change 2023: Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change [Core Writing Team, H. Lee and J. Romero (eds.)]. IPCC, Geneva, Switzerland, pp. 1-34, doi: 10.59327/IPCC/AR6-9789291691647.001

IPCC. (2019). Summary for Policymakers. In: Climate Change and Land: an IPCC special report on climate change, desertification, land degradation, sustainable land management, food security, and greenhouse gas fluxes in terrestrial ecosystems [P.R. Shukla, J. Skea, E. Calvo Buendia, V. Masson-Delmotte, H.- O. Pörtner, D. C. Roberts, P. Zhai, R. Slade, S. Connors, R. van Diemen, M. Ferrat, E. Haughey, S. Luz, S. Neogi, M. Pathak, J. Petzold, J. Portugal, P. Vyas, E. Huntley, K. Kissick, M. Belkacemi, J. Malley, (eds.)].

IPCC. (2017). Meeting Report of the Intergovernmental Panel on Climate Change Expert Meeting on Mitigation, Sustainability and Climate Stabilization Scenarios [Shukla, P.R. J. Skea, R. van Diemen, K. Calvin, Ø. Christophersen, F. Creutzig, J. Fuglestvedt, E. Huntley, F. Lecocq, M. Pathak, J. Portugal-Pereira, J. Rogelj, J. Roy, J. Scull, R. Schaeffer, R. Slade, D. Ürge-Vorsatz, D. van Vuuren.]. IPCC Working Group III Technical. Support Unit, Imperial College London, London, the United Kingdom.

IPCC. (2013). Summary for Policymakers, in: Intergovernmental Panel on Climate Change (Ed.), Climate Change 2013 - The Physical Science Basis. Cambridge University Press, Cambridge, pp. 1–30. https://doi.org/10.1017/CBO9781107415324.004.

IPCC. (2021) Resumen para responsables de políticas. En: Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel

on Climate Change [Masson-Delmotte, V., P. Zhai, A. Pirani, S. L. Connors, C. Péan, S. Berger, N. Caud, Y. Chen, L. Goldfarb, M. I. Gomis, M. Huang, K. Leitzell, E. Lonnoy, J. B. R. Matthews, T. K. Maycock, T. Waterfield, O. Yelekçi, R. Yu y B. Zhou (editores)]. Cambridge University Press. Jehanzaib, M., Ajmal, M., Achite, M., & Kim, T. W. (2022). Comprehensive review: Advancements in rainfallrunoff modelling for flood mitigation. Climate, 10(10), 147.

Knaggård, Å., Slunge, D., Ekbom, A., Göthberg, M., & Sahlin, U. (2019). Researchers’ approaches to stakeholders: Interaction or transfer of knowledge?. Environmental Science & Policy, 97, 25-35.

Kourtis, I. M., & Tsihrintzis, V. A. (2022). Update of intensity-duration-frequency (IDF) curves under climate change: a review. Water Supply, 22(5), 49514974.

Littlewood, I. G., Down, K., Parker, J., and Post, D. A.: IHACRES v1.0 User Guide, Tech. rep., Centre for Ecology and Hydrology, Wallingford, UK & Integrated Catchment Assessment and Mangament Centre, Australian National University, 1997.

Liang, X., Lettenmaier, D. P., Wood, E. F., and Burges, S. J.: A simple hydrologically based model of land surface water and energy fluxes for general circulation models, Journal of Geophysical Research, 99, 14 415, https://doi.org/10.1029/94JD00483, URL http://doi. wiley.com/10.1029/94JD00483, 1994.

Liu, Z., Wang, Y., Xu, Z., & Duan, Q. (2017). Conceptual Hydrological Models. In Q. Duan, F. Pappenberger, J. Thielen, A. Wood, H. L. Cloke, & J. C. Schaake (Eds.), Handbook of Hydrometeorological Ensemble Forecasting (pp. 1–23). Springer. https://doi. org/10.1007/978-3-642-40457-3_22-1

Machado, M. J., Botero, B. A., López, J., Francés, F., DíezHerrero, A., &amp; Benito, G. (2015). Flood frequency analysis of historical flood data under stationary and non-stationary modelling. Hydrology and Earth System Sciences, 19(6), 2561-2576.

Martel, J. L., Brissette, F. P., Lucas-Picher, P., Troin, M., & Arsenault, R. (2021). Climate change and rainfall intensity–duration–frequency curves: Overview of science and guidelines for adaptation. Journal of Hydrologic Engineering, 26(10), 03121001.

Mendoza, P. A., Muñoz-Castro, E., Vásquez, N., Lagos, M. A., & Vargas, X. USO DE PRINCIPIOS DARWINIANOS PARA CARACTERIZAR EL BALANCE HÍDRICO NATURAL EN CHILE. RUTAS HIDROLÓGICAS, 7.

Mendoza, P. A (2015). Impacts of climate change on hydrologic processes in the Colorado River basin. PhD Thesis, Department of Civil, Environmental, and Architectural Engineering. Thesis directed by Professor Balaji Rajagopalan.

MMA (2014). Plan Nacional de Adaptación al Cambio Climático. Tercera comunicación nacional (Chile). Ministerio del Medio Ambiente.

MOP. (2024). Manual de Carreteras. Volumen N°3: Instrucciones y criterios de diseño. Dirección de Vialidad, Ministerio de Obras Públicas. Edición 2024. Ministerio de Obras Públicas.

MOP. (2023). Estudio para la incorporación de la variable Cambio Climático en el plan de reconstrucción. Dirección General de Obras Públicas (DGOP), Ministerio de Obras Públicas. Elaborado por Ximena Vargas Mesa, Franco Ricchetti Campos, Eduardo Muñoz Castro y Catalina Jerez Toledo.

MOP. (2022b) Actualización plan maestro de evacuación y drenaje de aguas lluvia Antofagasta. APRISA, PNUD, MOP.

MOP. (2022a) Actualización del diseño de obras de contención aluvional de Quebrada Bonilla, Antofagasta. APRISA, PNUD, MOP.

MOP. (2020). Actualización Hidrológica Embalse Aromos. Región de Valparaíso. Santiago, Chile. Elaborado por: Universidad de Chile. Facultad de Ciencias Físicas y Matemáticas.

MOP. (2013). Marco estratégico para la adaptación de la infraestructura al cambio climático. Elaborado por: Pontificia Universidad Católica de Chile (PUC), Centro de Cambio Global UC, Centro Nacional de la Investigación para la Gestión Integrada de Desastres Naturales (CIGIDEN), Instituto de Hidráulica Ambiental de Cantabria, y Universidad de Valparaíso.

Morroni, G. Y., Gironás, J., Caneo, M., & Delgado, R. (2017). Using Weather Research and Forecasting (WRF) model for extreme precipitation forecasting in an Andean region with complex topography. European Water, 59, 85-90.

Muñoz-Castro, E., Merino, M., Ojeda, D., Vargas, X. (2024). Estimación de crecidas pluviales ajustadas por probabilidad de ocurrencia de eventos conjuntos. XXXI Congreso Latinoamericano de Ingeniería Hidráulica, Medellín, Colombia.

Nash, J. E., & Sutcliffe, J. V. (1970). River flow forecasting through conceptual models part I — A discussion of principles. Journal of Hydrology, 10(3), 282–290. https://doi.org/10.1016/0022-1694(70)90255-6

National Academies of Engineering and Medicine (2024). Modernizing Probable Maximum Precipitation Estimation. Report prepared by Board on Atmospheric Sciences and Climate and the Water Science and Technology Board. National Academies Press (800) 624-6242 | www.nap.edu | https://nap. nationalacademies.org/catalog/27460.

Obeysekera, J. T., & Salas, J. D. (2020). Hydrologic designs for extreme events under nonstationarity. In Engineering Methods for Precipitation under a Changing Climate (pp. 63-82).

O’Neill, B. C., Tebaldi, C., van Vuuren, D. P., Eyring, V., Friedlingstein, P., Hurtt, G., Knutti, R., Kriegler, E., Lamarque, J.-F., Lowe, J., Meehl, G. A., Moss, R., Riahi, K., and Sanderson, B. M. (2016). The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6, Geosci. Model Dev., 9, 3461–3482, https://doi. org/10.5194/gmd-9-3461-2016, 2016.

Perrin, C., Michel, C., & Andréassian, V. (2003). Improvement of a parsimonious model for streamflow simulation. Journal of Hydrology, 279(1), 275–289. https://doi.org/10.1016/S0022-1694(03)00225-7

Pica-Téllez, A., Garreaud, R., Meza, F., Bustos, S., Falvey, M., Ibarra, M., ... & Silva, I. (2020). Informe Proyecto ARClim: Atlas de Riesgos Climáticos para Chile. Centro de Ciencia del Clima y la Resiliencia, Centro de Cambio Global UC y Meteodata para el Ministerio del Medio Ambiente a través de La Deutsche Gesellschaft für Internationale Zusammenarbeit (GIZ). Santiago, Chile.

Pizarro, A., & Jorquera, J. (2024). Advancing objective functions in hydrological modelling: Integrating knowable moments for improved simulation accuracy. Journal of Hydrology, 634, 131071. https://doi. org/10.1016/j.jhydrol.2024.131071

Pohl, C., Krütli, P., & Stauffacher, M. (2017). Ten reflective steps for rendering research societally relevant. GAIAEcological Perspectives for Science and Society, 26(1), 43-51.

Reed, M. S., Vella, S., Challies, E., De Vente, J., Frewer, L., Hohenwallner-Ries, D., ... & Van Delden, H. (2018). A theory of participation: what makes stakeholder and public engagement in environmental management work?. Restoration ecology, 26, S7-S17.

Salas, J. D., & Obeysekera, J. (2014). Revisiting the concepts of return period and risk for nonstationary hydrologic extreme events. Journal of hydrologic engineering, 19(3), 554-568.

Savenije, H. H. G.: HESS Opinions; Topography driven conceptual modelling (FLEXTopo), Hydrology and Earth System Sciences, 14, 2681–2692, https://doi. org/10.5194/hess-14-2681-2010, URL https://hess. copernicus.org/articles/14/2681/2010/, 2010.

Schlef, K. E., Kunkel, K. E., Brown, C., Demissie, Y., Lettenmaier, D. P., Wagner, A., ... & Yan, E. (2023). Incorporating non-stationarity from climate change into rainfall frequency and intensity-durationfrequency (IDF) curves. Journal of Hydrology, 616, 128757.

Schumacher, V., Fernández, A., Justino, F., & Comin, A. (2020). WRF high resolution dynamical downscaling of precipitation for the Central Andes of Chile and Argentina. Frontiers in Earth Science, 8, 328.

SEA (2023b). Criterio de evaluación en el SEIA: Cambio climático en la evaluación ambiental del recurso hídrico. Primera edición. Servicio de Evaluación Ambiental, 2023.

SEA (2023a). Guía metodológica para la consideración del cambio climático en el SEIA. Segunda edición, Santiago, Chile. Servicio de Evaluación Ambiental, 2023.

Shaikh, M. P., Yadav, S. M., & Manekar, V. L. (2022). Assessment of the empirical methods for the development of the synthetic unit hydrograph: A case study of a semi-arid river basin. Water Practice & Technology, 17(1), 139-156.

Sivapalan, M., Ruprecht, J. K., and Viney, N. R.: Water and salt balance modelling to predict the effects of land-use changes in forested catchments. 1. Small catchment water balance model, Hydrologic Processes, 10, 1996.

Stowhas, L. (2016). Fundamentos de Hidrología Aplicada. Valparaíso, Chile, Editorial USM.

Stowhas, L. (1983). Precipitaciones Máximas Diarias en Chile, in: VI Congreso Nacional Sociedad Chilena de Ingeniería Hidráulica.

Taylor, K. E., Stouffer, R. J., & Meehl, G. A. (2012). An overview of CMIP5 and the experiment design. Bulletin of the American meteorological Society, 93(4), 485498.

Teegavarapu, R. S. (2013). Climate change-sensitive hydrologic design under uncertain future precipitation extremes. Water Resources Research, 49(11), 78047814.

Thyer, M., Gupta, H., Westra, S., McInerney, D., Maier, H. R., Kavetski, D., Jakeman, A., Croke, B., Simmons, C., Partington, D., Shanafield, M., & Tague, C. (2024). Virtual Hydrological Laboratories: Developing the Next Generation of Conceptual Models to Support Decision Making Under Change. Water Resources Research, 60(4), e2022WR034234. https://doi. org/10.1029/2022WR034234

Tibshirani, R., Walther, G. and Hastie, T. (2001). Estimating the number of data clusters via the Gap statistic. Journal of the Royal Statistical Society B, 63, 411–423. https://doi.org/10.1111/1467-9868.00293

Towler, E., Rajagopalan, B., Gilleland, E., Summers, R.S., Yates, D., Katz, R.W. (2010). Modeling hydrologic and water quality extremes in a changing climate: A statistical approach based on extreme value theory. Water Resour. Res. 46, 1–11. https://doi. org/10.1029/2009WR008876

Trenberth, K. E. (2011). Changes in precipitation with climate change, Clim. Res. 47, 123–138, https://doi. org/10.3354/cr00953

UNESCO. (2007). Curvas Intensidad – Duración –Frecuencia, para la zona centro sur de Chile. Roberto Pizarro Tapia, Dayanna Aravena Garrido, Karina Macaya Pérez, Alejandro Abarza Martínez, Mariela Cornejo Espinoza, Mauricio Labra Lorca, Marcelo Pavez Vidal, Leonardo Román Arellano. Editorial Universidad de Talca, Chile. Documentos Técnicos del PHI-LAC, Nº7.

Vásquez, N. A., Mendoza, P. A., Knoben,W. J. M., Arnal, L., Lagos-Zúñiga, M.,Clark, M., & Vargas, X. (2024a). The key role of temporal stratification for GCM bias correction in climate impact assessments. Earth’s Future, 12,e2023EF004242. https://doi. org/10.1029/2023EF004242

Vasquez, N. & Mendoza, P. A. (2024b) “Statistically downscaled and bias corrected CMIP6 models for Continental Chile under scenario SSP5-8.5”, https:// doi.org/10.7910/DVN/O3YBOT, Harvard Dataverse, V1.

Varas, E. (1985). Hietogramas de tormentas de diseño, in: VI Congreso Nacional Sociedad Chilena de Ingeniería Hidráulica. Departamento de Ingeniería

Civil, Facultad de Ingeniería, Universidad de Concepción, Concepción, Chile, pp. 533–548.

Vásquez, N., Mendoza, P. A. & Vargas, X. EXPLORANDO LA RELACIÓN ENTRE SIMILITUD HIDROLÓGICA, CLIMÁTICA Y FISIOGRÁFICA MEDIANTE CLASIFICACIÓN DE CUENCAS. RUTAS HIDROLÓGICAS, 19

Verni, F., & King, H. (1977). Estimación de crecidas en cuencas no controladas. III Coloquio, Sociedad Chilena de Ingeniería Hidráulica. Santiago, 357-374.

Vogel, K., Sieg, T., Veh, G., Fiedler, B., Moran, T., Peter, M., ... & Bronstert, A. (2024). Natural hazards in a changing world: Methods for analyzing trends and non-linear changes. Earth’s Future, 12(5), e2023EF003553.

Vorobevskii, I., Park, J., Kim, D., Barfus, K., and Kronenberg, R. (2024). Simulating sub-hourly rainfall data for current and future periods using two statistical disaggregation models: case studies from Germany and South Korea, Hydrol. Earth Syst. Sci., 28, 391–416, https://doi.org/10.5194/hess-28-391-2024, 2024.

Vrugt, J. A., Gupta, H. V., Bouten, W., & Sorooshian, S. (2003). A Shuffled Complex Evolution Metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters. Water resources research, 39(8).

Wagener, T., Lees, M. J., and Wheater, H. S.: A toolkit for the development and application of parsimonious hydrological models, in: Mathematical Models of Small Watershed Hydrology - Volume 2, pp. 91–139, Water Resources Publications LLC, USA, edited by singh, frevert, and meyer edn., 2002.

Wasko, C., Westra, S., Nathan, R., Orr, H. G., Villarini, G., Villalobos Herrera, R., & Fowler, H. J. (2021). Incorporating climate change in flood estimation guidance. Philosophical Transactions of the Royal

Society A, 379(2195), 20190548.

WMO (2009). Manual on Estimation of Probable Maximum Precipitation (PMP). World Meteorological Organization

Xavier, A.C.F., Blain, G.C., de Morais, M.V.B., Sobierajski, G. da R. (2019). Selecting “the best” nonstationary generalized extreme value (Gev) distribution: On the influence of different numbers of GEV-models. Bragantia 78, 606–621. https://doi.org/10.1590/16784499.20180408

Yan, B., Gu, Y., Li, E., Xu, Y., & Ni, L. (2024). Runoff Prediction of Tunxi Basin under Projected Climate Changes Based on Lumped Hydrological Models with Various Model Parameter Optimization Strategies. Sustainability, 16(16), 6897.

Ye, W., Bates, B. C., Viney, N. R., Sivapalan, M., and Jakeman, A. J.: Performance of conceptual rainfallrunoff models in low-yielding ephemeral catchments, Water Resources Research, 33, 153–166, https:// doi.org/10.1029/96WR02840, URL http://doi.wiley. com/10.1029/96WR02840, 1997.

Yi, B., Chen, L., Zhang, H., Singh, V. P., Jiang, P., Liu, Y., ... & Qiu, H. (2022). A time-varying distributed unit hydrograph method considering soil moisture. Hydrology and Earth System Sciences, 26(20), 5269-5289.