Volume5,Issue1
MathematicsSociety MathematicsPublicationCCA
April2025
Credits Firstofall,wewouldliketoexpressoursinceregratitudetothefollowingcontributorstoVolume5Issue1 ofNLCSJejuAnnualJournalofMathematics.
TheMathematics Society
Chair
JeffSuhyukCho(12)
DerekYejunYoo(12)
PublicityOfficer
SoulPark(11)
Secretary JaydenJunseokLee(11)
Y12Leaders
AustinTaehongHa(12)
SeanTaehoonKim(12)
LinkTeachers
MsDuyguBulut
MrWilliamHebbron
LATEXEditors&Managers JeffSuhyukCho(12)
DerekYejunYoo(12)
RyanHanjinLee(12)
JaydenJunseokLee(11)
AustinTaehongHa(12)
SeanTaehoonKim(12)
SoulPark(11)
ElliottHyunseokLee(12)
Wewouldalsoliketoexpressoursinceregratitudetoourlong-servingformerHeadoftheMathsDepartment, Ms.Bulut,whoserelentlesssupportandenthusiasmhavebeenaconstantsourceofinspiration.Thisjournal wouldnothavebeenpossiblewithouther.Wishingyouallthebestonyournextchapter,Ms.Bulut.
© CopyrightbytheNLCSJejuJournalofPureandAppliedMathematics EditedbytheJPAMEditingTeam
Editor’sNote WelcometoanotherremarkableeditionofJPAM,acollectionofrigorousmathematicalarticleswrittenbythebrilliantmindsofNLCSJeju!This year’sselectionfeaturessomeofthemostintriguingandthought-provoking topicstheMathsSocietyhaseverexplored.Butdon’tbeintimidated: whetherit’stheRiemannzetafunctionoranotherabstractconcept,you aresuretofindsomethingfascinatingwithinthesepages.Andifsomearticlesseemtoochallengingnow,revisittheminafewyears—youmightjust discoveryournewfavouritepieceofmathematics!
JPAMliesattheheartoftheMathsSociety,acherishedtraditionpassed downthroughtheyearsandonethatwillundoubtedlycontinueinthefuture. Whileaspectsofthejournalhaveevolved,likeoursleeknewcoverdesign, itscoremissionremainsunchanged:tosharethevaluableinsightsofour school’smathematiciansandtoignitecuriosityinallreaders,regardlessof theirinterests,backgrounds,orexpertise.Thisjournalisnotaboutshowcasingability;rather,itexistsforanyoneeagertoexpandtheirknowledge, eventotheslightestdegree.
Asyouread,keepthisinmind:ifyougraspaconcept,fantastic!Ifnot, simplymoveontothenextarticle.Mathematics,likeallsubjects,isajourney.Understandingdoesn’talwayscomeinstantly.Thetopicscoveredhere areindeedadvanced,extendingbeyondthestandardcurriculum,butifeven asinglearticlebroadensyourperspective,wewillhaveaccomplishedourgoal.
Pleaseenjoy.
JeffSuhyukCho ChairofPureMathematics, Co-LeaderoftheJPAMEditingTeam
VietaJumping Doyeon(Alex)Kim Year10
Email:dykim28@pupils.nlcsjeju.kr
Reviewer
Hanjin(Ryan)Lee∗
RecommendedYearLevel:KS5
Keywords:NumberTheory
1Introduction 1988IMOP6
Letaandbbepositiveintegerssuchthatab+1divides a2 + b2.Showthat a2+b2 ab+1 isasquareofaninteger.
ThequestionaboveisthelastquestionfromIMO(InternationalMathematicalOlympiad)1988.Nobodyofthesix membersoftheAustralianproblemcommitteecouldsolve it.Sinceitwasanumbertheoreticproblemitwassenttothe fourmostrenownedAustraliannumbertheorists.Theywere askedtoworkonitforsixhours.Noneofthemcouldsolve itintime.Theproblemcommitteesubmittedittothejuryof theXXIXIMOmarkedwithadoubleasterisk,possiblytoo hardtopose.Afteralongdiscussion,thejuryfinallyhadthe couragetochooseitasthelastproblemofthecompetition. Elevenstudentsgaveperfectsolutions.Then,whatwasthe perfectsolution?Itusesanumbertheoretictechniquecalled “VietaJumping”orinotherwords,“RootFlipping”.
2WhatisVietaJumping?
VietajumpingisusedtosolveDiophantineEquations (anindeterminateequationwithintegerroots),inequalities orcongruenceswherethesolutionshavearecursivestructure.
ItreliesonVieta’sformulasfortherootsofaquadratic equationandinvolvessystematically”jumping”fromonesolutiontoanother.VietaJumpingisnotatheoremlikeFermat’slittletheoremorStewart’stheorem.Itisatechnique usedtoprovepropositions.
1.Startwiththegivenequation:Typically,theproblem involvesanintegerequation,oftensymmetricalinsome way
2.Assumeaninitialsolution:Findorassumeoneintegersolution(oftenthesmallestpositivesolution)tothe givenequation.
3.Formaquadraticequation:Usethegivenequationto constructaquadraticequationwhereonevariable(x)is treatedasarootwhiletheother(sayy)istreatedasa parameter.
4.ApplyVieta’sFormula:Asyoualreadyknowonesolutionwhichwouldbetheintegersolutionyouwouldalso knowtheothersolutionwhichwouldalsobeaninteger.
5.Jumptoanewsolution:Usingthepropertiesofthe quadraticequation,you”jump”toanothersolutionby replacingoneroot(x)withtheother(x’),whichisguaranteedtobeanintegerifthecoefficientsareintegers.
6.Iterateandfindsmallersolutions:Byrepeatedlyjumping,youeitherreducetheproblemtoasimpleroneor reachacontradiction,provingsomethingaboutthenatureofthesolutions(e.g.,minimality).
7.Concludetheproof:Theprocessoftenprovesastatementbyshowingthatnosmallerpositivesolutionexists, oritarrivesatacontradiction.
AsVietajumpingisnotatheorem,ratheraprooftechnique,showinganexamplewouldbeamoreeffectiveway ofexplainingit.
31988IMOExample(ClassicalVietaJumping) 1988IMOP6
Letaandbbepositiveintegerssuchthatab+1divides a2 + b2.Showthat a2+b2 ab+1 isasquareofaninteger.
Assumethat a2+b2 ab+1 = k(k ∈ N wherekisnotaperfect square.Fixkandletthesetofpositiveintegersolutions (a,b)thatsatisfy a2+b2 ab+1 = k betset S.Duetowell-ordering principle,inset S,therewillexist(a,b)s.t.a+bisminimised. Letthissetof(a,b)be(A,B).W.L.O.G. A ≥ B > 0
Denotethetworootsof 1 ⃝ by x1 and x2 1 ⃝ willahvean integerrootAandifweapplyVieta’sformula,
x1 + x2 = kB
x1x2 = B2 k
W.L.O.G.Let x1 = A.Ifso, x2 = kB A = B2 k A
As kB A isaninteger, B2 k A ∈ Z
IF x2 = 0,then k = B2 −→ contradictionIf x2 < 0,then x2 2 kBx2 +(B2 k)= x2 2 + B2 k(Bx2 + 1) > 0 −→
contradiction(x2 2 kBx2 + B2 k = 0) x2 > 0 −→ (x2, B) ∈ S
x2 = B2 k A < B2 A ≤ A −→ x2 < A −→ x2 + A < A + B −→ contradictionasA+B(Minimality)Otherwise,wecancontinue, using (b, x2) insteadof (A, B).Wegetadecreasingsequence ofpositiveintegers.
[a1, a2, a3]=[a, b, b2 k a ...]
Forall n(n ∈ N),thepair (an, an + 1) willsatisfy
an 2+an+12
anan+1+1 = k.Asthissequencecannotcontinueindefinitely, atsomepointoneofthenumberswillbe0,provingthatkis aperfectsquare.
4Anotherexample
Whena,b,cisanaturalnumber,a,b,csatisfies0 < a2 + b2 abc ≤ c.Showthat a2 + b2 abc isaperfectsquare.
Let’sdenote a2 + b2 abc as k(0 < k ≤ c)
W.L.O.G.Let a ≤ b(symmetrical)
As a2 + b2 abc = k ←→
a2 + b2 = abc + k ←→
abc < a2 + b2 = abc + k ≤ ab + b2
ac < a + bb > a(c 1)
Then,therewillbelargelytwocasespossible, Case1) b > ac Case2) b ≤ ac
Case1)
If b > ac, b canbeexpressedas b = ac + t(t ∈ N)
a2 + b2 abc = ... 1 ⃝.Ifwesubstitute b = ac + t into equation 1 ⃝, a2 + a2c2 + 2act + t2 a2c2 tac = k ⇔a2 + act + t2 = k ≤ c−→ contradiction(a,t ∈ N)
Case2)
if b ≤ ac, b canbeexpressedas b = ac s(s ∈ N) a2 + b2
abc = k 1 ⃝⇔b2 ac × b +(a2 k)= 0... 2 ⃝
Let’sdenotethetworootsofthequadraticequationof 2 ⃝ as b1 and b2.IfweapplyVieta’sFormula, b1 + b2 = acb1b2 = a2 k Howeve,a s = ac b,wecanrecognise s asanotherformof b s = a2 k b < a.Cahgningtheform, a2 acs + s2 k = 0.
If s = 0, k = a2,thusaperfectsquare.
If s = 0, a2 csa + s2 k = 0.Let’sdenotethetwo rootsofthequadraticequation a1 and a2.IfweapplyVieta’s formula,
a1 + a2 = cs
a1a2 = s2 kcs a isalsoasolutiontotheequation. r = s2 k a < s.If (a, b) established,therewillexistapair (r, s) Ifweassumethat a + b isminimised,as a + b > r + s −→ contradiction(minimalism).
Therefore, k = a2.As k = a2 + b2 abc, a2 + b2 abc isa perfectsquare.
5ConstantDescentVietaJumping TherearealsovariationsinVietaJumping.Themethod ofconstantdescentVietajumpingisaprooftechniqueoften usedtoestablishstatementsinvolvingaconstantkandthe relationshipbetweenaandb.UnliketraditionalVietajumping,thismethoddoesnotrelyoncontradictionandconsists ofthefollowingfoursteps:
1.Provethecasewhereequalityholds,allowingtheassumptionthat a > b
2.Fixthevaluesof b and k,thenrewritetherelationship between a, b,and k asaquadraticequationwithcoefficientsinvolving b and k.Onerootofthisquadraticis a, whiletheotherrootisdeterminedusingVieta’sformulas.
3.Forallpairs (a, b),beyondacertainbasecase,demonstratethat o < x2 < b < a,andthat x2 isaninteger. Thenreplace(a,b)with (b, x2),repeatingthisprocess untilreachingthebasecase.
4.Provethestatementforthebasecase.Since k remains constantthroughouttheprocess,thestatementisvalid forallorderedpairs (a, b).
Thisensuresthevalidityofthestatementforallrelevant cases.Asaforementioned,asVietaJumpingisaprooftechnique,notatheory,anexamplewillexplaintheabovemore intuitively.
Let a and b bepositiveintegerssuchthat ab divides ab + 1.
Provethat3ab = a2 + b2 + 1.
If a = b, ab|ab + 1 ⇔ a2|2a2 + 1,as a2|2a2 forall a ∈ Z, thisimpliesthat a2|1.
Hence, a and b willbothbe1and32 = 12 + 11 + 1.
So,W.L.O.G.assumethat a > b
Forany (a, b) satisfyingthegivenconditions,let a2+b2+1 ab = 3.Ifwerearrangethisandsubstitute,wecangetthefollowingquadraticDiophantineequation.
x2 (kb)x +(b2 + 1)= 0... 1 ⃝
IfweapplyVieta’sformula,
x1 + x=kb
x1x2 = b2 + 1
Asonerootofthequadraticequationisa,theotherroot, x2 = kb a = b2+1 1 ∈ Z.Thefirstequationshowsthat x2 is anintegerandthesecondthatitispositive.As a > b and because a, b ∈ Z, a ≥ b + 1andhence ab ≥ b2 + b.If b > 1, ab > b2 + b wouldalwayshold,andtherefore x2 = b2+1 a < b Thus,whilemaintainingthesame k,wemayreplace (a, b) with (b, x2) andrepeatthisprocessuntilwearriveatthebase case.
Asthebasecaseiswhen b = 1,for (a, 1) tosatisfythegiven
condition, a shoulddivide a2 + 2.Yet a|a2 forall a ∈ Z, a|2. Ifso, a shouldbeafactorof2,makinga1or2.
Thefirstcaseiseliminated −→ contradiction(a=byeta¿b)
Inthesecondcase, k = a2+b2+1 ab = 6 2 = 3. As k hasremainedconstantthroughoutthisprocessof Vietajumping,thisissufficienttoshowthatforany (a, b) satisfyingthegivencondition, k = 3.
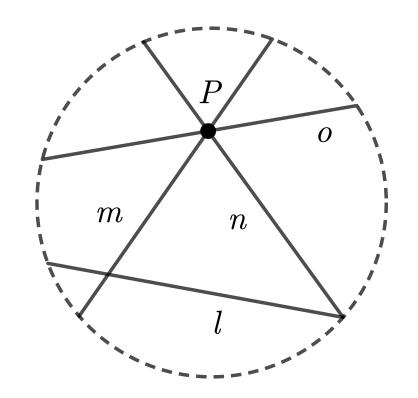
6GeometricalInterpretationofVietaJumping Vietajumpingisconsideredtobeanumbertheorictechniquewithincludespartsofalgebra.However,Vietajumpingcanalsobeinterpretedgeometrically.Thegeneralprocedureisasfollows:
1.Usingthegivencondition,derivetheequationofafamilyofhyperbolasthatremainunchangedwhen x and y areswapped,makingthemsymmetricabouttheline y = x
2.Provethepropositionfortheintersectionsofthehyperbolasandtheline y = x
3.Assumethereissomelatticepoint (x, y) onsomehyperbolaandW.L.O.G.assumethat x < y.ThenbyVieta’s formulas,thereisacorrespondinglatticepointwiththe samex-coordinateontheotherbranchofthehyperbola, andbyreflectionthrough y = x anewpointontheoriginalbranchofthehyperbolaisobtained.
4.Showthatthisprocessgenerateslatticepointsprogressivelyloweronthesamebranchandcanberepeateduntilaspecificcondition(suchas x = 0)isreached.Substitutingthisconditionintotheequationofthehyperbola, thestatementcanthenbeproven.
Let’sgobacktothe1988IMOP6,andinterpretthe solutionintermsoflatticepointsonhyperbolasinthefirst quadrant.
1988IMOP6
Let a and b bepositiveintegerssuchthat ab + 1divides a2 + b2.Showthat a2+b2 ab+1 isasquareofaninteger.
Let a2+b2 ab+1 = q where q isnowafixedvalue.If q = 1, q isapefectsquare.if q = 2,theredoesnotexist (a, b) where a, b ∈ Z.Thus,when q > 2,theequation
x2 + y2 qxy 1 = 0
Defineshyperbola H,and(a,b)representsanintegrallatticepointon H
If (x, x) isanintegrallatticepointon H where x > 0, then x = 1as q ∈ Z
Thepropositionistrueforthepoint (x, x)
Let P =(x, y) bealatticepointon H,where x, y > 0and x = y.Duetosymmetry(oftheline y = x),assume x < y.
IfweapplyVieta’sformula, (x, qx y),isalatticepointon thelowerbranchof H.
Let y′ = qx y.From H,1 + xy′ > 0andsince x > 0, y′ ≥ 0. Hence (x, y′) isonthefirstqudrant(exceptwhen y′ = 0).Due tosymmetry, (y′ , x) isalsoon H onthefirstquadrant.
IfweapplyVieta’sformula, yy′ = x2 q,and y′ = x2 1 y y′ = x
Let Q =(y′ , x) andthus Q willbeanewlyconstructedpoint inthefirstquadrantonthehigherbranchof H,andwith smaller x,and y-coordinatesthanthepoint P westartedwith. Ifwerepeatthisprocess,the x-coordinatewillformasequenceofdecreasingnon-negativeintegers.Thiscanonly berepeateduntil Q =(0, y′) as x ∈ Z Bysubstitution, q = y2 .
7Conclusion WhenVietaJumpingwasfirstintroducedin1988,itwas unheardofandthusitbecameveryfamousveryquickly. However,asmorethan30yearshavepassed,thistechnique isnowstandardisedandthusitdoesnotseemtoappearin Olympiadsoften.ThisisbecausetheproblemsthatuseVieta Jumpinghavesolutionsthatarebasicallythesame(asseen inthe3examplesabove)andalsoitisquiteeasytorecognise.Furthermore,althoughitiscalledVietaJumping,inthe end,itusesalargeaspectofFermat’smethodofinfinitedescent,whileFermat’smethodofinfinitedescentdependson theWell-orderingprinciplewhichisoneofthemostimportanttheoriesinnumbertheory.Yet,thistechniquewasonce knownasoneofthemostbeautifulwaystoproveaquadratic Diophantineequation.
8Bibliography 1.Brilliant.org.(2025).VietaRootJumping—BrilliantMathScienceWiki.[online]Availableat: https://brilliant.org/wiki/vieta-root-jumping/[Accessed 23Jan.2025].
2.Tat-Wing,L.(2005).TheMethodofInfiniteDescent.[online]Availableat: https://www.math.hkust.edu.hk/excalibur/v10n4.pdf [Accessed19Oct.2024].
Figure1.SketchofhyperbolaH.
TheTaylorSeries J.Y.Seol
Year10
Email:jyseol28@pupils.nlcsjeju.kr
Editor Hanjin(Ryan)Lee
RecommendedYearLevel:KS4 Keywords:Taylorseries, MaclaurinSeries
1Introduction
Thetaylorseriesisafundamentalmethodtoapproach afunctionincalculus.Thisconceptrepresentsfunctionsas aninfinitesum,andmodelstheclosestapproximationtothe originalfunction.
2TheTaylorSeries
Thetaylorseriesisakeyconceptincalculus,andisa representationofacontinuous,differentiablefunctioninto aninfinitesumofpolynomials.
Thisisaninfinitesumoftermsthatareexpressedin termsofthefunction’sderivativesatasinglepoint.
2.1TheMaclaurinSeries
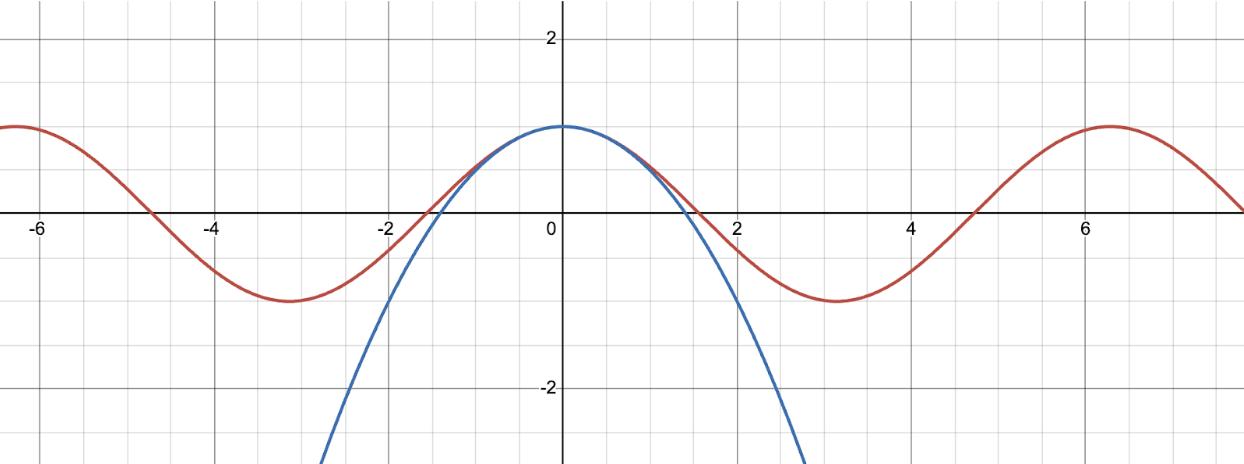
TheMaclaurinseriesisasubsetofthetaylorseries wherethefunction’sderivativeisconsideredissetat0.Takingthegraph cos(x) asanexample.Letafunctionbe P(x), where P(x)= c0 + c1x + c2x2,andourgoalistomakethis polynomialaclosestapproximationto cos(x).
Tomakethispolynomialsimilartothegraph cos(x) as possible, c0,the y-interceptmustequatetothe y-interceptof thegraph cos(x).Therefore, c0 = 1.Thegradientof P(x) shouldalsoequatetothelocaltangentslope.Thederivative of cos(x) equalsto sin(x),and x = 0.Therefore,thelocal tangentslopeofthefunctionis0.Takingthederivativeof P(x),
d dx (x0 + x1x + c2x2)= 0
c1 + c2x = 0
x = 0
c1 + c2(0)= 0
c1 = 0 P(x)= 1 +(0)x + c2x2
∗
Nowsolvingfor c2,Thesecondderivativeof cos(x) equatesto cos(x). x = 0,thereforeitis 1.Takingthe secondderivativeof P(x):
d2 dx2 (c0 + c1x + c2x2)= 1
2c2 = 1
c2 = 1 2
P(x)= 1 +(0)x +( 1 2 )x2
Graphing P(x))alongwith cos(x) showsanapproximation
near x = 0:
Figure1.P(x)andcos(x)sketched
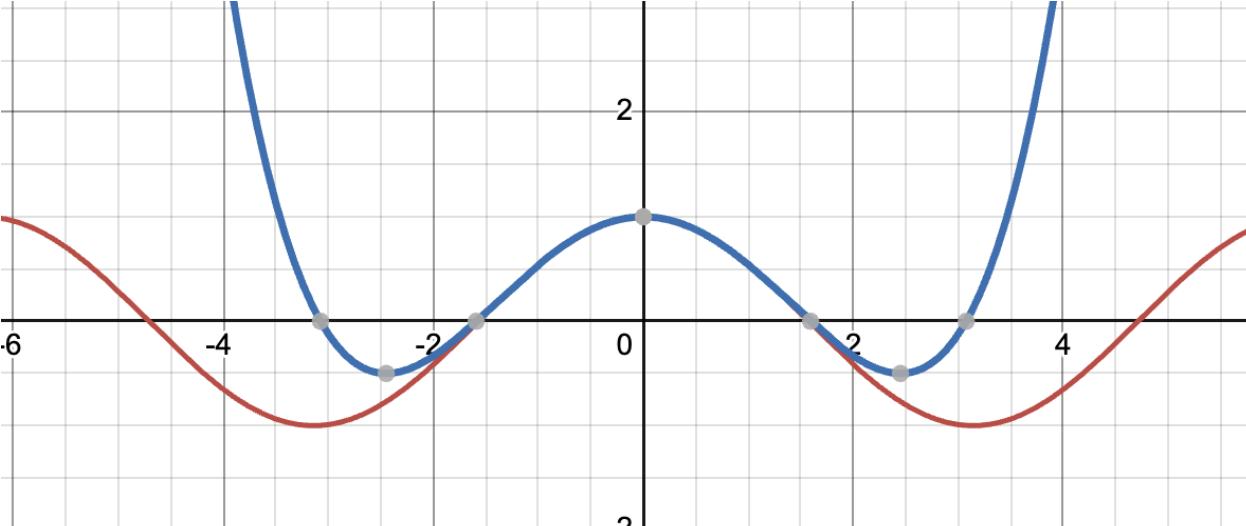
LetthepolynomialP(x)havemoretermswithlarger exponents:
P(x)= 1 +(0)x +( 1 2 )x2 + c3x3 + c4x4
Applyingthethirdandthefourthderivative,
d3 dx3 cos x = sin x sin0 = 0
d3 dx3 (1 +(0)x +( 1 2 )x2 + c3x3 + c4x4)= 0 0 + 1 × 2 × 3 × c3 = 0
c3 = 0
d4 dx4 cos x = cos x cos0 = 1 d4 dx4 (1 +(0)x +( 1 2 )x2 +(0)x3 + c4x4)= 1
0 + 1 × 2 × 3 × 4 × c4 = 1 c4 = 1 24
P(x)= 1 +(0)x +( 1 2 )x2 +(0)x3 + 1 24 x4
Figure2.developedversionofP(x)(blue)andcos(x)(red)sketched
Thegraphaboveillustratesamuchaccurateestimation tothegraph cos(x) near x = 0.Here,onemustrecognise thatcoefficient cn equalstothederivativevalueover n!.For instance,the4thderivativeoftheterm c4x4 equalledto1 × 2 × 3 × 4 × c4,whichequalsto4! × c4 .Moreover,onemust notethataddingnewtermsdonotinfluencethevaluesofthe otherterms.Thisisbecausesubstituting x as0alwaysoccur inthisprocess.Forinstance,thesecondderivativeof P(x) doesnotinterferewiththeotherterms,becausetheprevious termsallbecome0andthetermsafteritcancelsoutas x becomes0,shownbelow.
0 +( 1 2 )+ c3(0)1 + c4(0)2
Thecoefficientsofthetermsarethenthderivativesofof thefunction P(x) when x is0.Therefore,foreachterm,a generalisedexpressioncouldbe:
Forconvenience,letusdefine fn(0) asthenthderivative of f at0,thereforetheexpressionbeing:
( f n(0) n! )xn
Giventhatthefunction P(x) getsclosertotheinitial function cos(x) whenmoretermsareadded,itispossible toacquireinfiniteamountoftermsinorderforthefunction P(x) tobethemostsimilarwiththefunction cos(x)
Therefore,usingthegeneralisedexpression,aninfinite sumofthetermsarerepresentedas:
3TheEulerFormula Thefamouseulerformulawhere eix = cosx + isinx is oftenrecognisedasthemostbeautifulformulainmaths because:
eiπ + 1 = 0when x = π Thisformulaisprovenfromthe taylorseriesitself.Letusfirstconsiderthederivativesof eix toobtainthetaylorseriesof ex ex isaveryconvenient exampleasthederivativeof ex equalstoitself.Therefore, onecanassumethatthecoefficientsofthetermsareall1. Hence,thetaylorseriesof ex is:
Replacing x with ix gives:
Since i is √ 1, i2 resultsin 1.Henceforth,thetaylor seriesfor eix becomes:
2.2TheTaylorSeries...Again
Thetaylorseriesisamoregeneralisedformulawhere thederivationpointisabletochange.
Let a bearealorcomplexnumbersothat x a isthe derivationpoint.
Therefore,byreplacing0with a,since f n isthe nth derivativeof f evaluatedatacertainpoint,andbychanging x to x a inthemaclaurinseries:
Thisexpression,whichisthetaylorseriesisobtained.
Groupingtheimaginarypartgives:
Calculatingthederivativesof cosx andusingthemaclaurinseriestoset x = 0: d dx cos x = sin x = 0 d2 dx2 cos x = d dx ( sin x)= cos x = 1 d3 dx3 cos x = d dx ( cos x)= sin x = 0 d4 dx4 cos x = d dx (sin x)= cos x = 1
Anditrepeats.
Therefore,onecanacknowledgethatthecoefficientforthe termsareinfinitecyclesin0, 1, 0, and1.
Knowingthis,thetaylorseriesforcosxis: cos(0)+(0) x 1! +( 1) x2 2! +(0) x3 3! +(1) x4 4! +
Whichsimplifiesto: 1 x2 2! + x4 4! +
Lookingbacktothetaylorsereisof eix,whichwas: 1 x2 2! + x4 4! + + i(x x3 3! + x5 5! + )
showsthatthetaylorseriesfor cosx equalstoacertainpartof theTaylorseriesfor eix.Replacingthefirstsequencegives: eix = cos x + i(x x3 3! + x5 5! + )
Calculatingthederivativesof sinx andusingthe Maclaurinseriestoset x = 0:
Anditrepeats.
Therefore,onecanacknowledgethatthecoefficientforthe termsareinfinitecyclesin1, 0, 1, and0.
Knowingthis,thetaylorseriesforsin x is:
+(1)
Whichsimplifiesto:
Lookingbacktothetaylorseriesof eix:
Showsthatacertainpartofthetaylorsseriesequatestothe taylorseriesofsin x
Replacinggives:
4Limitations
TheTaylorseriesisapowerfulmathematicaltoolused toapproximatefunctionsusinganinfinitesumofterms derivedfromthefunction’sderivativesatasinglepoint. However,ithaslimitations.
Onekeylimitationisitsrelianceonthefunctionbeing infinitelydifferentiableatthepointofexpansion.
Pointingouttheobvious,Ifthefunctionisnotsufficientlysmooth,suchashavingdiscontinuities(since differentiationonlyappliesoncontinuousfunctions,the taylorserieswouldobviouslynotwork)orundefinedhigherorderderivatives,theTaylorseriesmayfailtoconvergebut diverge.
Anotherlimitationarisesfromtheconvergenceofthe series.Evenforsmoothfunctions,theTaylorseriesmaynot convergetotheactualfunctioneverywhere.
Forinstance,theseriesexpansionfor f (x)= e 1 x2 /x2 at x = 0yieldsaTaylorseriesequalto0forall x asany derivativeofthisfunctionis0.Thisisbecause e 1 x2 dominates thecoefficients,tendingto0faster.
Thisdiffersfromthefunction’struevalueof f (x) > 0 for x = 0.
pointbetween a and x
Thismeasureshowfaristhetaylorpolynomialfromthe actualfunctionatthenextterm, n + 1,andisoftenreferred toastheLagrangeErrorBound.
If Rn(x) doesnotapproach0as n −→ ∞,theseriesfails toapproximatethefunctionaccurately.
5Bibliography 1.MathisFun.(2017).TaylorSeries.Mathsisfun.com. https://www.mathsisfun.com/algebra/taylor-series.html
2.Dawkins,P.(2020,May26).CalculusII -TaylorSeries.Tutorial.math.lamar.edu. https://tutorial.math.lamar.edu/classes/calcii/TaylorSeries.aspx
3.Taylorseries—Chapter11,Essenceof calculus.(n.d.).Www.youtube.com. https://www.youtube.com/watch?v=3d6DsjIBzJ4abchannel=3Blue1Brown
4.Ault,Shaun.“APCalculusBCReview:Lagrange ErrorBound.”MagooshBlog—HighSchool,10 Aug.2017,magoosh.com/hs/ap/ap-calculus-bc-reviewlagrange-error-bound/.
5.“TaylorSeries-ErrorBounds—BrilliantMath ScienceWiki.”Brilliant.org,brilliant.org/wiki/taylorseries-error-bounds/.
If f (x) isexpandedabout x = a,theerrorinthen-thdegreeTaylorpolynomial Tn(x) isexpressedastheremainder: Rn(x)= f (x) Tn(x)= f n+1(c) (n+1)! (x
Where c issome
RecommendedYearLevel:KS3,KS4
Keywords:irrational,graph,inequality
JunyoungKim Year10 Email:jy2kim27@pupils.nlcsjeju.kr
Editor TaehongAustinHa
1Introduction
Theconstants π and e arefundamentalinmathematics,appearingacrossvariousareassuchasgeometry, calculus,andnumbertheory.Oneintriguingquestion thatarisesisthecomparisonoftheirexponentialforms: πe and eπ
Thisarticleprovidesaseriesofproofsandinsights intotherelationshipbetweenthesetwoexpressions, sheddinglightontheirfascinatingandunexpectedbehaviour.
2BackgroundInformation
Thenumberpi,writtenas π istheratioofthecircumferenceofanycircletoitsdiameter.Itisafundamentalconstantinmathematics,appearinginvarious formulasingeometry,trigonometry,andcalculus.More formally, π isdefinedas:
3Method
Therearethreemainproofspresented.Thefirst twoproofsinvolvegraphicalanalysis,whilethethird utilizestheMeanValueTheorem(MVT)toprovidean alternativeperspectiveontheinequality.
3.1Proofusingthegraph y = xe e x Let’sbeginbydefiningf(x)asfollows:
y = xe · e x
Thegraphof y = f (x) increaseswhen 0 <x<e and decreaseswhen x>e
Fig.1: y = xe e x
Thisdefinitioncomesfromthelimitofaninscribed polygonwithnsides,buthasnumerousotherrepresentationsandappearancesinmathematics.
Thenumber e isthebaseofthenaturallogarithm. Itisdefinedastheuniquerealnumbersuchthatthe derivativeofthefunction f (x)= ex isthesameas ex itself,makingitthebase ofexponentialgrowth.Moreformally, e canbedefined bythefollowinglimit:
Fromthegraph, f (e)=1,π e e 1 < 1
whichcanberearrangedinto
π e <eπ
Therefore, πe <eTπ
3.2Proofusingthegraph y = 1 x Thegraph y = xe e x mightbeabithardto sketch,soanotherproofusingagraphisprepared.
Let’sdefine f (x) asfollows: f (x)= 1 x
Fig.2: y = 1 x
Fromthegraphabove,wecanknowthat
Since
)
And 1 e (π e)= π e 1
Wecansubstituteandrearrangetheinequalityto get
ln π< π e e ln π<π
ln π e <π π e <eπ (1)
4Proofusingmeanvaluetheorem Themeanvaluetheoremstatesthatwhenafunction f (x) iscontinuousontheclosedinterval [a,b] and differentiableontheopeninterval (a,b) where a<b, thereexistsatleastone c in (a,b) suchthat:
f ′(c)= f (b) f (a) b a
For f (x)=ln x,themeanvaluetheoremtellsusthat forsome c ∈ (e,π),
f ′(c)= f (π) f (e) π e
Whichbecomes 1 c = ln π ln e π e = ln π 1 π e
Since e<c<π 1 c < 1 e (2)
Sowehave:
ln π 1 π e < 1 e
ln π 1 < π e e
ln π< 1+ π e e
ln π< π e e ln π<π ln π e <π π e <eπ (3)
5Conclusion
Inthisarticle,weexploredthefascinatinginequalitythroughthreedistinctapproaches:graphicalanalysesandaproofleveragingtheMeanValueTheorem. Eachmethodoffersauniqueperspectiveontherelationshipbetweenthesetwoexponentialexpressions,ultimatelyleadingtothesameconclusion.
Theinequality πe <eπ servesasaremarkableexampleofhowseeminglyabstractconstantslike e and π,
whichoriginateinentirelydifferentareasofmathematics,interactinwaysthatarebothsurprisingandbeautiful.Theseresultsnotonlydeepenourappreciation fortheinterconnectednessofmathematicalconceptsbut alsohighlightthepowerofdiversemathematicaltools andtechniquesinuncoveringsuchrelationships.
6Bibliography
1. Artelius,J.2010."AQuestion Comparing π to e]pi."Mathematics StackExchange.October20,2010. <https://math.stackexchange.com/questions/337565/aquestion-comparing-pie-to-e-pi>
2. Rayc20.2020."WhichisGreater,etothePower of π or π tothePowerofe?"Tistory.February17, 2020<https://rayc20.tistory.com/14>
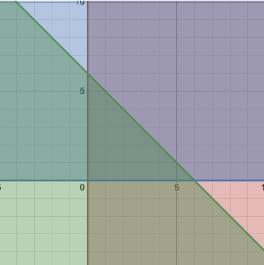
ExploringtheRelationshipBetweenConstraints andFeasibleRegionGeometryinLinear Programming Juwon(John)Yu Year11
Email:jwyu27@pupils.nlcsjeju.kr
Editor Junseok(Jayden)Lee
RecommendedYearLevel:KS4
Keywords:LinearProgramming,FeasibleRegion, Convexity
1Abstract
Linearprogrammingisamathematicalmethod usedtooptimizeanobjectivefunction,subjecttoaset ofconstraints.Itiswidelyappliedinareaslikeeconomics,engineering,andlogistics.Thefeasibleregion, definedasthesetofallpossiblesolutionsthatsatisfyall givenconstraints,playsacriticalroleintheoptimizationprocess.Thegeometryofthisregionisinfluenced bytheconstraints,whicharetypicallyrepresentedby linearequationsorinequalities.Akeypropertyofthe feasibleregionisconvexity,meaningthattheregionis well-structured,andoptimalsolutionsareguaranteedto lieatitsvertices.Thisjournalexaminestherelationship betweentheconstraintsandthegeometryofthefeasibleregion,focusingonhowtheconstraintsinfluence itsshape,structure,andconvexity.Byunderstanding thesegeometricproperties,thejournalprovidesinsights intohowconstraintsimpacttheoptimizationprocessin linearprogramming.
2Hypothesis Thehypothesisisthattheconstraintsnotonlydeterminethesizeandshapeofthefeasibleregionbutalso controlitsconvexityandtheplacementofitsvertices. Asthenumberofconstraintsincreases,thefeasibleregionisexpectedtoshrinkorbecomemorecomplex,but itsconvexitywillbepreserved.Additionally,thepositioningandinteractionoftheconstraintswillinfluence thegeometryoftheregioninwaysthatarecrucialfor
identifyingoptimalsolutionsinlinearprogramming.
3Methodology 1. SetupofTestProblems: Constructabaseproblemintwodimensions,startingwithnon-negativity constraints:
x1 ≥ 0,x2 ≥ 0
Incrementallyintroduceadditionallinearconstraints(forexample, x1 + x2 ≤ 6 or 2x1 + x2 ≤ 8) toobservechangesinthefeasibleregion.
2. GeometricAnalysis: Ploteachconstraintasa line(in2D)oraplane(in3D)tovisualizehow thefeasibleregionisalteredwhennewconstraints areadded.Identifyverticesforeachversionofthe problemtoseewhetheroptimalsolutions,whenan objectiveisapplied,lieatthosecornerpoints.
3. ConvexityVerification: Checkthatforany twopointsinsidethefeasibleregion,thelinesegmentconnectingthemstaysentirelywithinthatregion.Examinewhethertheadditionofconstraints changestheoverallshapewhilepreservingconvexity.
4. ObservationofRedundancyandContradiction: Identifyconstraintsthatdonotfurtherlimit thesolutionspace(redundant)orconstraintsthat leadtonofeasiblesolutions(contradictory).Note howredundantconstraintsdonotchangethegeometry,whilecontradictoryconstraintscaneliminate thefeasibleregionaltogether.
Toinvestigatehowconstraintsinfluencethegeometryofthefeasibleregion,asystematicapproachwas used,beginningwithaminimalsetofconstraintsand graduallyaddingormodifyingthem:
BaseCase:MinimalConstraints Startingwith x1 ≥ 0 and x2 ≥ 0 confinestheregiontothefirst quadrantofthe x1- x2 coordinateplane.Thisunboundedregion(thefirstquadrant)isconvex:any twopointsinthefirstquadranthaveaconnecting linesegmentthatremainsinthatquadrant.
AddingaSingleLinearConstraint Theintroductionof x1 + x2 ≤ 6 restrictsthefeasibleregionto atriangularshapewithverticesat(0,0),(6,0),and (0,6).Thisshapeisstillconvex,andthevertices areclear.
Fig.1:Thetriangularshapeofthefeasibleregionshown above
IncrementalConstraints Additionalconstraints suchas 2x1 + x2 ≤ 8 or x1 ≤ 4 furtherrefinethe feasibleregion,“cuttingoff”partsoftheexisting region.Theseconstraintsmaytransformthetriangleintoapentagonoranotherpolygonalshape,but theregionremainsconvexunlesstheconstraintsare contradictory.
TestingConvexityToverifythatagivenfeasible regionisconvex,astandardapproachistocheck whether,foranytwopointswithintheregion,everypointonthelinesegmentconnectingthemremainsinsidetheregion.Whileconvexitycanbevisuallyinterpretedbyobservingtheshapeofthefeasibleregion,analgebraicapproachprovidesamore preciseandreliablemethod,especiallyforanalyzingtheconvexityofcomplexshapes.Let (x1,x2) and (x′ 1,x′ 2) betwofeasiblepoints,andtheexpressionbelowrepresentsthelinesegment/pointsbetweenthetwofeasiblepointswhere λ ∈ [0, 1] f (λ)= (λx1 +(1 λ)x′ 1), (λx2 +(1 λ)x′ 2) If f (λ) conformstoallconstraintsforevery λ ∈ [0, 1],thentheregionisconvexForourcase,the constraintswere x1 ≥ 0, x2 ≥ 0, x1 + x2 ≤ 6 andthe verticesofthetriangularregionare(0,0)(6,0)and (0,6).Points(2,2)and(4,1)werechosenarbitrarily.Thelinesegmentconnectingthesepointswas thenevaluatedtodeterminewhetherallintermediatepointssatisfythegivenconstraints.
(λ)=(λ(2)+(1 λ)(4),λ(2)+(1 λ)(1))
Expanding:
Overall: x1 =4 2λ ≥ 0 (alwaystruefor λ ∈ [0, 1])
2 =2λ +1 ≥ 0 (alwaystruefor λ ∈ [0, 1]) (4 2λ)+(2λ +1)=5 ≤ 6 (alwaystrue) Thustheregionisconvex.
4Conclusion Thisjournalexploredtherelationshipsbetweenconstraintsandthegeometryofthefeasibleregioninlinearprogramming,withaparticularfocusonconvexity. Throughmathematicalanalysis,itwasdemonstrated thatincreasingthenumberofconstraintsaltersthesize andshapeofthefeasibleregionwhilepreservingitsconvexity,providedtheconstraintsremainconsistent.The convexitytestconfirmedthatanylinesegmentbetween twofeasiblepointsremainswithintheregion,reinforcingthefundamentalpropertyoflinearprogramming thatoptimalsolutionslieatvertices.Understanding thesegeometricpropertiesisessentialforoptimization, asitensuresthatfeasibleregionsmaintainawell-defined structure,allowingforefficientsolution-findingmethods suchastheSimplexalgorithm.
GoldenRatioinHigherDimensions MinjaeKang Year10
Email:mjkang28@pupils.nlcsjeju.kr
RecommendedYearLevel:KS4,KS5
Keywords:GoldenRatio,analysis,expansion
Editor TaehongAustinHa
1IntroductiontotheGoldenRatio
Thegoldenratio,denotedbytheGreekletter ϕ is amathematicalconstantthathasintriguedmathematicians,artists,andscientistsforcenturies.Algebraically, itcanbesolvedby a + b a = a b (a>b> 0)
Whichleadsto x 2 = x +1
Whichsimplifiesto x 2 x 1=0
Usingthequadraticformulatosolveforx,wefind thetwosolutions
x = ( 1) ± ( 1)2 4(1)( 1) 2
Thepositiverootofthisequation, 1+ 5 2 isthe goldenratio.Indecimals,thisvalueisapproximately 1.618.
Thisvaluerepresentstheratiooftwoquantitiesthat areaestheticallypleasing,appearingfrequentlyinmany artformsandevennature.
Whilemostdiscussionsofthegoldenratiofocuson twoandthreedimensionalobjects,ithasfurtherimplicationsinhigher-dimensionalspacesaswell.Inthese spaces,thegoldenratioisusedtodescribeproportions thatmaximisesymmetryandbalance,contributingto structuralstability.
Thearticlewillexploreonhowthegoldenratiocan beappliedtohigher-dimensionalspacesusingtheidea of“goldenboxes”,whicharemultidimensionalobjects whereeachdimensionisscaledaccordingto ϕ.The focuswillbeondeterminingthestabilityoftheboxes byexaminingthesurfaceareatovolumeratiosbasedon thefactthatstabilityisachievedwhenthesurfacearea tovolumeratioisminimised.
2N-dimensionalgoldenbox
Letthen-dimensionalgoldenboxhavesidelengths thatfollowthegoldenratio
Ifweletthesidelengthofthefirstdimension, x1 ,tobea,thesidelengthofdimensionwillbegivenby
xk = a ϕk 1 for k =1, 2....n
3Volumeofthen-dimensionalgoldenbox
Thevolume,V,ofthen-dimensionalgoldenboxis theproductofitssidelengthsofdifferentdimensions
V = x1 x2 xn
Substitutingeach xk with a ϕk 1
V =(a ϕ) (a ϕ2).... (a ϕn 1)
Usingtheformulaforthesumof n 1 integers, 0+ 1+2+ .... +(n 1)= n(n 1) 2 ,thissimplifiesto an ϕ n(n 1) 2
4Surfaceareaofthen-dimensionalgoldenbox
Thesurfaceareaofann-dimensionalboxrefersto thesumofallareasofthen-1dimensionalfaces.
Foreachdimensionk,therearetwofaceswitharea givenbytheproductofallsidelengthsexcept xk Summingtheareasofallthesefacesweget:
SurfaceArea=
5Surfaceareatovolumeratio
Therefore,ratioRofthesurfaceareatovolumeof n-dimensionalgoldenboxisasfollows:
7Applicationofn-DimensionalGoldenBoxes
Duetoitsrelativestability,thegoldennboxin higherdimensionscanbeusefulinvariousfields.Two ofthefieldsarearchitectureandnaturalsciences.
7.1Architecture
Inarchitecture,theideaofn-dimensionalgolden boxescanaffectthedesignofcomplexstructures.The constantproportionalityinthesegoldenboxesenables evenstressdistributionacrossstructures,ensuringbalanceanddurability.Furthermore,stability,orminimizingthesurfaceareatovolumeratio,reducestheamount ofmaterialrequired,presentingapossibleopportunity tolessenthecostburdenforarchitects.
7.2NaturalSciences
Thegoldenratiohaslongbeenassociatedwith naturalgrowthpatterns.Theintroductionofndimensionalspacescanprovidedeeperinsightintohow creaturesmaintainstabilityandefficiencyinsurvival. Specifictopicsforresearchincludecellulargrowth, moleculararrangements,oreventheorganizationof ecosystemsinhigher-dimensionalspaces.
8Conclusion Thegoldenratio,widelyknownforitsaesthetic qualities,continuestorevealitssignificanceinmultidimensionalspaces.Thiscanbeshownbytheinvestigationofn-dimensionalgoldenboxes,whichrevealsthat thesurfaceareatovolumeratioisconstant,andthus isstableinhigherdimensionsaswell.Thismakesita usefultoolfordesigningsystemsthatrequirestructural integrity.
Thisindicatesthat,foraconstantinitialdimension lengthofa,thesurfaceareatovolumeratioisrelativelystableasdimensionsincrease,andthusthegolden n-boxesproportionallymaintainefficiencyinhigherdimensions.
6Stability
Stabilityisachievedwhensurfaceareatovolume ratioisminimised.Extendingthisconcepttohigherdimensionalspaces,theconstancyof R ingoldenboxes indicatesstability.Therefore,itcanbeusefulinstructuresinmultipledimensionsthatrequireuniformityand balance.
Euler’sProofofTheInfinitudeofPrimeNumbers SeongminHong Year12 Email:smhong26@pupils.nlcsjeju.kr
RecommendedYearLevel:KS4,KS5
Editor Suhyuk(Jeff)Cho
Keywords:Primenumbers,Riemannzetafunction, Numbertheory
1Introduction
Iamcertainthatmostpeoplereadingthisarticle willhaveencounteredEuclid’sProofoftheInfinitudeof PrimeNumbers,beingaclassicexampleofa reductio adabsurdum.Assumingotherwise,andthatafinite numberofprimesexist,Euclidproposedthattheremust existaset P ofprimesfrom p1 upto pn (where p1 = 2,p2 =3,...).Thatmeansthat
= n i=1
+1=(
mustbeindivisiblebyanyoftheprimeswithinthe setofprimesthatwe’veestablished,meaningthere hastoexistanewprimenumber,meaningthrough contradiction,therecannotexistafinitesetofprimes. Hence,Euclid’sargumentguaranteesthata’largest’ primenumbercanneverexist.
Forexample,ifweweretoassumethatthelargest primenumbertoexistwas11,thentheproductof ourprimes q =(2 × 3 × 5 × 7 × 11)+1=2311 wouldbe indivisibleby 2, 3, 5, 7 and 11.Andhenceitstandsto reasonthat 2311 isaprimenumber(whichitinfact is!),orthereexistsanotherprime pn+1 < 2311 which isnotinoursetofallprimenumbers.Eitherway,a contradictionoccurswithourinitialassumption,and hence 11 isnotthebiggestprimenumbertoexist,and norisanyotherprimenumberbythesamelogicalflow.
Whilsttheeleganceofthisproofiscleartosee,it disappointswhenattemptingtoestimatingthedensity ofprimes.Thisargumentstatesthatthenextprime
numberafter p1 to pn couldbeasbigas q = n i=1 pi +1
Fortunately,Eulerstrengthensthedensityofprimes throughcomingupwithadistinctprooffortheinfinitudeofprimenumbers,usingwhatwouldlaterbe knownastheRiemannzetafunction,andevenpaves thepathforthePrimeNumberTheorem.
2Euler’sProof Eulerarguedthat
where P isthesetofallprimes,and a ∼ b as s → 1+ means a and b areasymptoticallyequivalent,or a b approaches 1 as s tendsto 1+ fromabove.
TheRiemannzetafunction,alsoknownasthe Euler-Riemannzetafunction,isafunctionofacomplex variable,andhasmanyuseswithinanalyticnumbertheory(themostfamousofwhichistheRiemannhypothesis,whichisaboutthezeroesoftheRiemannzetafunction).Itisdefined(ignoringtheintegralform,complex natureandtheanalyticalcontinuationforRe(s) < 1)as being
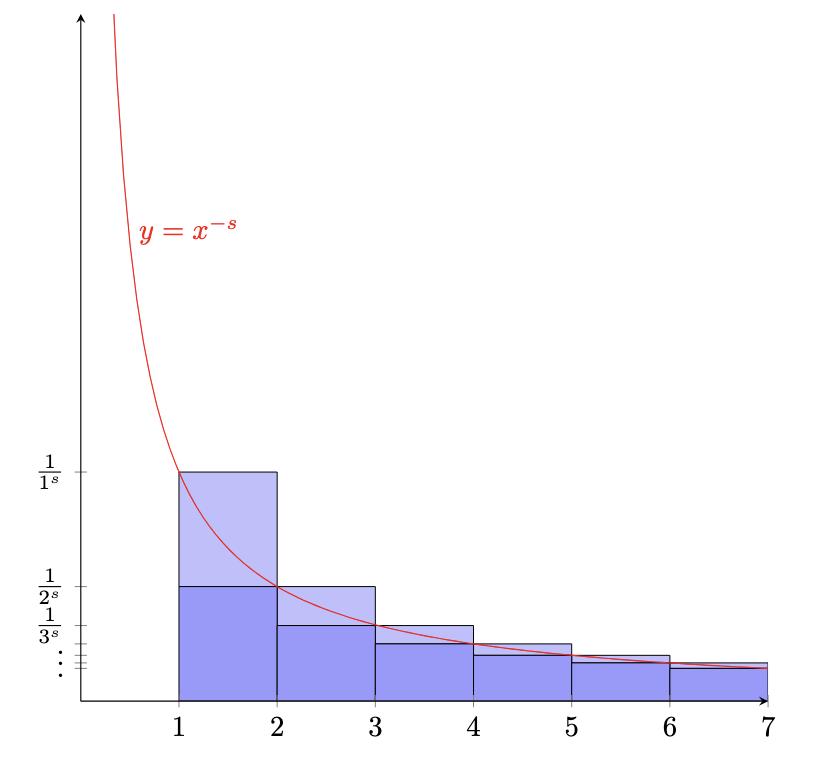
Wewanttolinkthezetafunctiontothefraction 1 s 1 ,sincethisfractionappearsin(1),andthiscanbe foundinthebyanalysingtheareaunderthecurveof y = 1 xs throughintegration.
Fig.1:Themodularcurve
Fromthegraphabovewecanseethatthearea underthecurveof x s isclearlylinkedtotheRiemann zetafunction.Thesumoftheareasofthebluelesser shadedrectangle ( 1 1s + 1 2s + 1 3s + 1 4s + ) isostensibly equaltotheRiemannzetafunction,butalsogreater thantheintegralofthecurve ∞ 1 x sds,sincethese boxesareanoverestimation.Thesumoftheareasofthe blueheavilyshadedrectangle ( 1 2s + 1 3s + 1 4s + 1 5s + ) is similarlyequaltotheRiemannzetafunctionminus 1, butalsolesserthantheintegralofthecurve ∞ 1 x sds, sincetheseboxesareanunderestimation.
Thatmeansthataninequalitymaybeformedbetweenfromthis:
Hence,takingthenaturallogarithmofbothsides,
Itmustbenoticedthattherighthandsideof(1)is equaltotherighthandsideof(3).Hence,itissatisfactorytoprovethat
Thegivenboundsimplythat
Consequently,bythesqueezetheorem,thisshows that
Subtractingtheaboveequationfrom(2),weget
Noticethatthedenominatoroftheaboveequation containnomultiplesof2.Thatmeansthat
Withthesameprocess,subtractingtheaboveequationfromtheequationpriortoit,weget
Similarly,thedenominatoroftheabovetheequationnowcontainnomultiplesof2or3.Whathappens whenwerepeatthisprocessinfinitelybymultiplying bythereciprocalofeveryprimetothepowerofs,ina mannersimilartothesieveofEratosthenes?
Dividingbothsidestoonlygetthezetafunctionon thelefthandside,
Therefore,takingthenaturallogarithmofboth sides
ln(ζ(s))=ln
SincetheMaclaurinexpansionofthenaturallogarithmintheformfoundaboveis
ln(1 x)= x
TheMaclaurinexpansionaboveisonlyapplicableifthe itpassestheratiotest.Hence,
SubstitutingtheMaclaurinexpansionof ln(1 x),
ln(ζ(s))=
Sincewearetryingtoprove(4),weneedtoshow thatthefinalpartoftheaboveequationisextremely smallcomparedtotheothertwotermsintheequation as s tendsto 1+.First,notethat:
As s tendsto 1+,thevalueofthelefthandside willalwaysbelessthan 1,butbothindividualterms willgrowto ∞.Thisproves(4),whichinturnwas aconditionsatisfactorytoprovetheinfinitudeofthe primenumbers.
Then,wemayfindthattheinnersumcanbeexpressedasageometricseries.
As s → 1+ , ln 1 s 1 willtendto ∞,andsince p∈P 1 ps isasymptoticallyequivalent,itwillalsotend to ∞.Iftherewereafinitenumberofprimes,thesum foundabovewouldconverge,sinceafiniteseriescannot diverge.Hence,thereareaninfinitenumberofprimes.
3ThePrimeNumberTheorem Inthepaperthatcontainedtheaboveproof,called Variaeobservationescircaseriesinfinitas,or"Various observationsaboutinfiniteseries",Eulerstates"Atque illiussummaesthuiussummaequalilogarithmus""Andthesumofthat(thereciprocalsoftheprimes) isthelogarithmofthissum(ofthereciprocalsofthe naturalnumbers)".Thisismathematicallysuggesting that
Hence,
Noticethefirstinequalityholdsasaresultoftheset ofprimenumbersbeingasubsetofthesetofnatural numbers,andthesecondinequalityholdssince ns(ns 1) >n(n 1) ⇒ 1 ns(ns 1) < 1
.Uponexpansion,
However,hisprooffoundwithinthebookwasnot rigorous,anditisnotknownwhetherhecouldproveit rigorously.
Letusanalysewhatthisobservationleadsto though.Toestimatethedensityoftheprimes,wecan differentiatebothsideswithrespecttonusingthechain rule.
dn ln(ln n)= d ln(ln n) d ln n d ln n dn = 1 n ln(n) 1 n = 1 n ln(n)
Thisshouldshowushowmuchthesumisexpected toincreasewhenincrementingfromanygiven n to n+1 Considerthelefthandsideof(6).If n wereprime, thenthelefthandwouldbeexpectedtoincreaseby 1 n
andifotherwise,itwouldbeexpectedtoincreaseby 0 Sincethederivativeoftherighthandsideis 1 n ln(n) ,the probabilityof n beingprimemustbe 1 ln(n) .Thismeans that
π (x)= p∈P,p<n 1 ∼ x ln(x))
⇐⇒ π (x) x ∼ 1 ln(x)) forlargervaluesof x (7)
andsince π(x) representsthenumberofprimesless thanorequalto x, π(x) x mustrepresenttheprobability of x beingaprimenumber,whichgivesasacorollary thePrimeNumberTheorem.
Thediscoveryoftheprimenumbertheoremcould becreditedtoLegendre,whopositedthetheoremin 1798,orGaussinhisnotebookpriorto1800,andwas laterprovenin1896usingsomerigorousmathematics. However,itwouldn’tbeastretchtosaythattheprime numbertheoremwouldhavebeenaneasycorollaryby Eulerifhehadtrulyobservedandproven(6).
4EndingRemarks
WhetherEulerdidreallyobserve(6)willneverbe certain,buttheproofof(1) (=(5)) wasstilloneof thebiggestadvancementsmadeinthefieldofprime numberssinceEuclid’sproofoftheinfinitudeofprime numbersovertwomilleniaprior,inspiringmanytocontinuedownhispathintoprimenumbersandanalytical numbertheory.Notonlyisthisproofthefirstever appearanceoftheEuler-ProductformulafortheRiemannzetafunction,butitwasthetoolwhichDirichlet modifiedtoproveanevenstrongerresultaboutprime numbers,knownasDirichlet’stheorem.
5Bibliography
1. Conrad,K.(2023).Theinfinitudeofthe primes.[online]kconrad.math.uconn.eduAvailable at:https://kconrad.math.uconn.edu/blurbs/ugrad numthy/infinitudeofprimes.pdf
2. WolframMathWorld.(2018)RiemannZetaFunction.[online]mathworld.wolfram.com.Availableat: https://mathworld.wolfram.com/RiemannZetaF unction.html
3. ThinkingInMath(2022).Euler’s Proof-ThereAreInfiniteManyPrimes [video]youtube.com.Availableat: https://www.youtube.com/watch?v=DEmoPfeAA KA
Fermat’sLittleTheorem Taewon(Ryan)Kim Year10
Email:twkim28@pupils.nlcsjeju.kr
Editor SoulPark
RecommendedYearLevel:KS4
Keywords:ModularArithmetic,PrimeNumbers, CompositeNumbers,PrimalityTesting,Carmichael Numbers,BinomialTheorem
1Introduction
In1679,oneFrenchmathematicianintroducedan innovativeconceptwhichlateronwasincorporatedin provingnumeroustheories;thisisFermat’slittletheorem.Thetheoremstipulatesthatif p isaprimenumber, thenforanyintegera,
Theequationaboveindicatesthattheremainderof ap dividedby p iscongruent—equal—totheremainder ofadividedby p.Anotherequationdrivenbythefirst onewiththeconditionthataiscoprimeto p is,
p 1 ≡ 1(modp)
Whentheequationaboveissatisfied,aslongasa and p arecoprime,theremainderof a(p 1) divided bypalwaysresultsas1.Hence,thetheoremcanbe implementedtoderivewhetheracertainintegerisa compositenumberbydeterminingifthecertaininteger satisfiestherelationornot,ortoderivetheremainder ofanumberforparticularcases.
2BackgroundInformation
PierredeFermat,arenownedmathematicianinthe 1600s,introducednumerousproofsandvaluablemathematicalinsightstotheworldbackthen,whichgreatly
contributedtothedevelopmentoftheparticularfield. Throughouthiswell-respectedlife,Fermathadrather apersonalmethodofshowcasinghisnewfoundknowledge.Insteadofovertlypublishinghisproofsandtheoremstothepublic,histheoremswerepresentedmainly throughlettersormessagesinaprivatemanner,devoid ofmathematicalproofs.Famously,Fermatpresenteda theorythatwasdubbedFermat’sLastTheoreminhis book,which,however,onlyencompassedtheprinciples ofthetheoremwithoutproofs,sayingthattherewasn’t enoughspacetowriteitdown:"Ihavediscovereda trulymarvellousproofofthispropositionthatthismarginistoonarrowtocontain(Fermat’sLittleTheorem wasalsofirstintroducedinalettersenttohisfriend). Duetosuchabluntmannerofintroducingstatements andwiththeabsenceofproof,alotofmathematicians duringhistimeandinlatercenturiesquestionedhis work.However,asfuturemathematicianssucceededin corroboratingFermat’sstatementsonebyone,hisabsolutemathematicalingenuitywaswidelyrecognisedin thepresentday.
3Proof 3.1CombinatorialProof(ProofbyCounting Necklaces)
ThefollowingproofisanadaptationofGolomb’s proofofFermat’sLittleTheorem,whichcanbemost explicitlydisplayed.
Firstofall,imagineanecklace,andletthenumber p,apositiveinteger,bethenumberofbeadsofthe necklace.Theaiminthiscontextistofullycolourthe beadsofthenecklaceonebyone.Letanotherpositive integer,a,bethenumberofcoloursavailable.Ifall possiblecombinationsofstringswhereeachstringis constructedofpnumberofalphabetswithdifferent possiblealphabetsweretobecalculated,thetotal numberofthosestringswouldbeapaccordingtothe ruleofproduct.
Forexampleifp=5anda=2,therewouldbe25 =32strings.
Fig.1:32Strings
However,thestringsthatconsistofasinglesymbolwouldberemovedfromthislist,astheabovehas restrictedthedifferentpossiblealphabetsto2.Anyelementthatunsatisfiestheconditionistoberemovedin thisproof.Inthecaseabove,AAAAAandBBBBB, whichare2strings—a numberofstrings—wouldbe deleted.Henceforth,theremainingnumberofstrings wouldresultasap-a,wheretherestofthestringscan bearrangedintogroupscontainingpnumberofstrings.
Fig.2:30Strings
Inthecircumstanceabove,therefinedlistcontains 25 2=30 stringswhereeachgroup,column,isconstructedof5strings.Therefore,itcouldbestatedthat it ap a isdivisibleby p,inthiscase 30/5=6,corroboratingtheequationwhichargues ap ≡ a(modp).
3.2ProofusingtheBinomialTheorem
AnotherformofproofforFermat’sLittleTheorem incorporatestheconceptsofthebinomialtheorem. Usinginduction,thisproofwillcorroboratethetheorem forallintegers a ≤ 0
Firstandforemost,assignit p asaprimenumber. Thefirststepoftheproofisobvious 0p ≡ 0(modp),as 0 multiplyingordividingbyanynumberalwaysgives 0.Itisnowrequisitetoprovethatifthetheoremis trueforallothervaluesofa.Assumethestatement ap ≡ a(modp) istrue.Whenthebinomialtheoremis appliedfor (a +1)p ,
Accordingtotheoriginalbinomialtheorem,
Inthiscase,since p isaprimenumber, p!= p(p 1)!, and p divides p! ,butdoesnotdivide k! or (p k)! for 1 ≤ k ≤ p 1
Therefore, p k isdivisibleby p forall 1 ≤ k ≤ p 1
Furthermore,itcouldbestatedthatfor k =0 and k = p,1 p k equalsto 1.
Hence,theexpansionof (a +1)p simplifiesto
a +1)p ≡ ap +1(modp) (5)
As ap ≡ a(modp),itfollowsthat (a +1)p ≡ a +1(modp) (6)
Inessence,byinduction, ap ≡ a(modp) istruefor alltheintegersof a.
4FermatPseudoprimes
PseudoprimesareacaseofFermat’sLittleTheorem where p isacompositenumberintherelationap 1 ≡ 1(modp),where a and p arecoprimenumbers,and ap 1 1 isdivisibleby p.Ifthenumber p satisfies alltheconditionsabove, p iscalledaFermatpseudoprimetobase a.Forexample,let p intherelation be 341 341 isacompositenumberas 341=11x31 Normally,anycompositenumbersshouldfailtosatisfy Fermat’sLittleTheorem,asthetheoremisknownto betrueonlyforprimenumbers.Although 341 isnot truewhensubstitutedintherelation ap ≡ a(modp) → 3341 1 =3(mod341),itperfectlysatisfiestheotherrelation, ap 1 ≡ 1(modp).Therefore, 341 canbesaidthatit isacompositenumberaswellasaFermatPseudoprime.
5ConverseandCarmichaelNumbers
Longstoryshort,theconverseforFermat’sLittle Theoremdoesnotexist.Thisisduetoaparticular setofnumbersdubbedastheCarmichaelNumbers. Innumbertheory,aCarmichaelnumberisacompositenumber n inwhichmodulararithmeticsatisfies
Fermat’sLittleTheorem.Inotherwords,Carmichael numbersareatypeofpseudoprimes,which,whenpin thecongruencerelation, ap ≡ a(modp),isnotaprime number,unlikepreviouscaseswherepwasalways assumedtobeone;Carmichaelnumbersaretrue whensubstitutedintobothequationsofthetheorem. SomeexamplesofCarmichaelnumbersencompass 561(3 ∗ 11 ∗ 17), 1105(5 ∗ 13 ∗ 17),and 1729(7 ∗ 13 ∗ 19)
AlthoughFermat’sLittleTheoremcancorrectlydeterminetheprimalityforsomepseudoprimesasmostof themfailtosatisfybothrelationsofthetheorem,forexample, 341,thisisnotthecaseforCarmichaelnumbers. Unfortunatelyenough,Carmichaelnumberseasilysatisfybothrelationsofthetheorem,leadingtopotential inaccuraciesduringtheprimalitytestofthetheorem. Henceforth,themereexistenceofthissetofnumbers functionsasacounterexampleoftheclaimthatonly primenumberswouldsatisfyFermat’sLittleTheorem, becauseCarmichaelnumberswouldstillsatisfytherelationeventhoughtheyarenotprimenumbers.
6Implementations
AlthoughFermat’sLittleTheoremsporadically failsduringprimalitytests,itneverthelesscanbe utilisedtoaccuratelyderivetheremainderofacertaininteger.Usingthetheoremforexample,the remaindersforinconceivablylargenumberssuchas 39(299999986043 1) dividedby 299999986043,since 39 and 299999986043 arebothprimeandcoprimeto eachother,theremainderissimply, 1.
Furthermore,Fermat’sLittleTheoremplaysakey roleinmodernaffairssuchascryptographyandalso actedasacrucialpartinprovingtheoriesoffuture mathematicianssuchastheEulertheorem.
7Conclusion
Inconclusion,Fermat’sLittleTheorem,partofthe numbertheory,suggests2relations.Firstofall,
remaindersfornumbersincertaincircumstances.Fermat’sLittleTheoremhasbeenoneofthefoundational notionsofthenumbertheorywhichgreatlyinspiredand provokedthefieldofmathematicsbyencouragingfurtherresearchandaidingtocorroboratefuturetheories.
8Bibliography
1. Brilliant."Fermat’sLittleTheorem:BrilliantMath&ScienceWiki."Brilliant, brilliant.org/wiki/fermats-little-theorem/.
2. Caldwell,C.K."ProofofFermat’s LittleTheorem."ThePrimePages, t5k.org/notes/proofs/FermatsLittleTheorem.html.
3. "Fermat’sLittleTheorem."Artof ProblemSolving,artofproblemsolving.com/wiki/index.php/Fermat’s_Little_Theorem.
4. "Fermat’sLittleTheorem." WolframMathWorld,mathworld.wolfram.com/FermatsLittleTheorem.html.
5. GeeksforGeeks."Fermat’sLittleTheorem." GeeksforGeeks,geeksforgeeks.org/fermats-littletheorem/.
Essentially,itcouldbeprovenbyimplementingcombinatorics,thebinomialtheorem,andmany more.Althoughitpossessessomelimitationsregarding Carmichaelnumbersduringprimalitytests,thetheoremdemonstratesunparalleledpowerwhendetermining
ExploringtheEvolutionofGeometry SoulPark Year11
Email:sopark27@pupils.nlcsjeju.kr
Editor SoulPark
RecommendedYearLevel:KS4
Keywords:Geometry,Euclidean,Non-Euclidean, Hyperbolic,Riemann,Postulate
1IntroductiontoEuclideanGeometry
Geometryistheareaofmathematicsrelatedtothe studyofpointsandfiguresandtheirproperties.This fieldisessentialbecauseofitsundetachableapplication intherealworld.Euclid,theGreekmathematician alsoknownasthefatherofgeometry,foundedgeometry.
Euclidfurtherorganisedthemathematicalcontent inastrictlogicalsequencewithEuclid’scommon notionsandpostulates,takenfromtheElementsas follows:
CommonNotion:
1. Thingswhichequalthesamethingalsoequalone another.
2. Ifequalsareaddedtoequals,thenthewholesare equal.
3. Ifequalsaresubtractedfromequals,thentheremaindersareequal.
4. Thingswhichcoincidewithoneanotherequalone another.
5. Thewholeisgreaterthanthepart.
Postulate:
1. Astraightlinesegmentcanbedrawnjoiningany twopoints.
2. Anystraightlinesegmentcanbeextendedindefinitelyinastraightline.
3. Givenanystraightlinesegment,acirclecanbe drawnhavingthesegmentastheradiusandone endpointasthecentre.
4. AllRightAnglesarecongruent.
5. Iftwolinesaredrawnthatintersectathirdinsuch awaythatthesumoftheinneranglesononeside islessthantwoRightAngles,thenthetwolines inevitablymustintersecteachotheronthatsideif extendedfarenough.
Thefifthpostulateisequivalenttowhatisknown astheParallelPostulate,whichisthemostcontroversialoneandledtothedevelopmentofnon-Euclidean geometries.
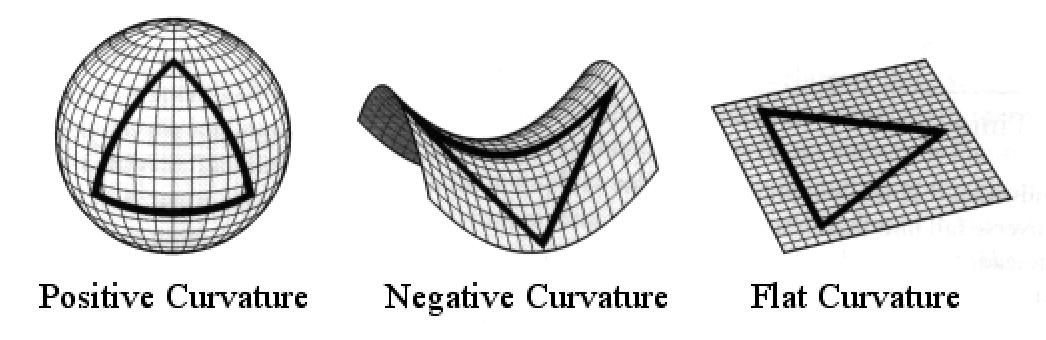
2Non-EuclideanGeometry Inthe19thcentury,theGreekgeometersviewed theparallelpostulateasatheoreminvolvingmany difficultiesasitsproofrequiredanumberofdefinitions andtheorems.ComparedtootherEuclid’spostulates, theparallelpostulatewasunclearandcomplicated.
Non-Euclideangeometryisusedtostatethetheory ofrelativityincurvedspaceandisappliedtocelestial mechanics.ThemajordifferencebetweenEuclidean geometryandnon-Euclideangeometryisdependenton thenumberofparallellines.Ifthereisexactlyoneparallelline,itisEuclideangeometry,andnon-Euclidean geometryiswhenthereisnoparallellineormorethan one.
WiththenumerousattemptsofProclus’andWallis’proofoftheparallelpostulatefromtherecognitionofthesignificanceofexponents,RussianNikolay LobachevskyandtheHungarianJánosBolyaipublished adescriptionofgeometrythatsatisfiedallofEuclid’s postulatesexceptfortheparallelpostulate,calledas thehyperbolicGeometry.
Fig.1:Non-EuclideanDiagram
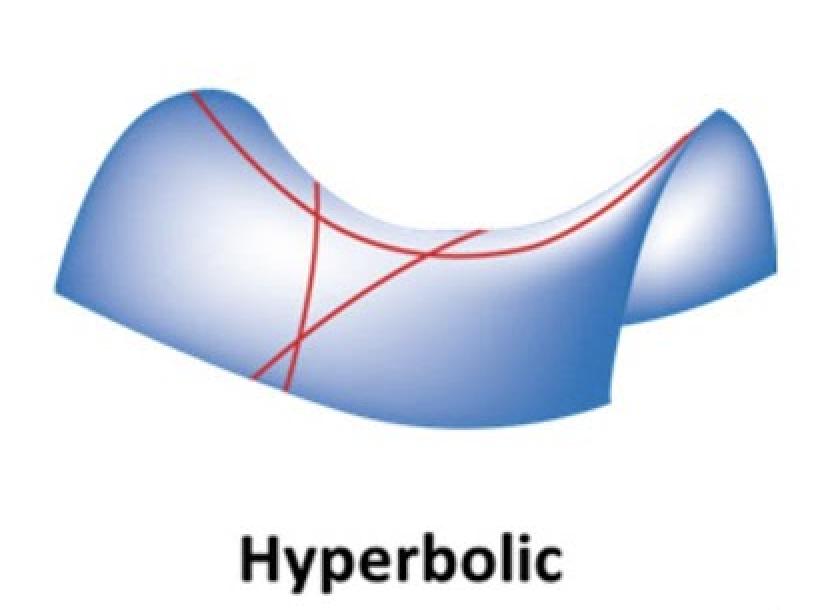
3HyperbolicGeometry In1868theItalianmathematicianEugenioBeltramidescribedasurfacecalledapseudospherethathas constantnegativecurvature.Thepseudosphereisnot acompletemodelforhyperbolicgeometry,asstraight linesmayintersectthemselves,unlikethehyperbolic postulate.Hence,in1901,theGermanmathematician DavidHilbertprovedthatacompletehyperbolicsurface cannotbedefinedusingrealanalyticfunctionsandwas notdiscussedfor54years.ThentheDutchmathematicianNicolaasKuiperprovedtheexistenceofacomplete hyperbolicsurface,andlaterinthe1970s,theAmericanmathematicianWilliamThurstondescribedhowit isconstructed.
Fig.2:CurvatureDiagram
HyperbolicGeometryisthefirstpublishedwork thatinterpretstheexistenceofhyperbolicandother non-Euclideangeometries.Theparallelpostulateof EuclideangeometryisreplacedwiththeHyperbolic parallelpostulate:
ForanygivenlineLandapointPnotonL,there existatleasttwolinesthroughPthatdonotintersectL.
Thekeypropertiesofhyperbolicgeometryincludes:
1. Thesumoftheinterioranglesofatriangleisless than180degrees.
2. Therearenosimilartrianglesofdifferentsizes
3. Linesthatappearparalleldiverges
ThiscontrastswiththeEuclideanpostulateasit statesthattwoparallellinesareequidistant.Unlikethe Euclidean,whenthesumoftheanglesinatriangleis equaltotworightangles;inhyperbolic,thesumisless thantworightangles.Consequently,polygonsofdifferingareascanbesimilarinEuclidean;andinhyperbolic, similarpolygonsofdifferentareasdonotexist.
Fig.3:EuclideanDiagram
Fig.4:HyperbolicDiagram
4HyperbolicModels
Later,hyperbolicmodelswerediscoveredinthe 19thcenturytoaidtheunderstandingofhyperbolicgeometryandvisualiseit.Thesemodelsareusedtoexpresstheanglesofparallelisminhyperbolicgeometry.
4.1Klein-BeltramiModel
From1869to1871BeltramiandtheGerman mathematicianFelixKleindevelopedthefirstcomplete modelofhyperbolicgeometry.Itisalsocalledtheprojectivemodel,Kleindiskmodel,andtheCayley–Klein modelinwhichpointsarerepresentedbythepointsin theinterioroftheunitdiskandthelinesarerepresented bythechords.
Fig.5:Klein-BeltramiModel
4.2PoincaréDiskModel
In1882,aFrenchmathematician,HenriPoincaré (1854-1912),studiedtwotypesofmodelsonthehyperbolicplane.Thefirstmodel,thePoincaréDisk,has overlappingsimilaritieswiththeKlein-BeltramiModel
yetwithasignificantadvantagethatmakesitmoresuitabletoworkwiththeEuclideananglebetweentwointersectinghyperboliclines.ItisconsideredastheimprovedmodelfromtheKlein-BeltramiModel.
Fig.6:PoincaréDiskModel
4.3PoincaréUpperHalf-PlaneModel
AnothermodelisthePoincaréhalf-planemodel, whichisthemostcommonlyusedmodel.Thismodel providesabettervisualisationcomparedtoothermodels,asitissuitableformorevariouscalculations.For thismodel,theEuclideanplanehasafixedlineinstead ofacircle,calledtheabsoluteline.Theabsolutelineis usedtorepresentthehyperbolicplane.
Fig.7:PoincaréUpperHalf-PlaneModel
5RienmannianGeometry
RiemanniangeometryoriginatedbyBernhard Riemann,aGreekmathematician,whofurtherextendedthenotionoftheparallelpostulateintotwoand three-dimensionalplanes.
InRiemanniangeometry,therearenolinesparallel tothegivenline.Euclid’ssecondpostulateis:thata straightlineoffinitelengthcanbeextendedcontinuouslywithoutbounds.However,Riemannmodifiesthe secondpostulate:astraightlineoffinitelengthcanbe extendedcontinuouslywithoutbounds,butallstraight linesareofthesamelength.
6Conclusion Theevolutionofgeometryhasbeenstartedfrom thefoundationalworkofEuclidtothedevelopment ofthenon-Euclideangeometrieswiththeparallelpostulate.TheexplorationofthefifthpostulateofEuclid’sElementshasextendedtowardshyperbolicgeometry.Throughthediscoveryofhyperbolicgeometry, ithasemergedtofindexpressionsinmodelslikethe Klein-BeltramiandPoincarémodels.Furthermore,RiemanniangeometryexpandedupontheseideasbychallengingEuclid’ssecondpostulatewiththeideaofall straightlineshavingafinitelength.Thishighlightshow themathematicalapproachtounresolvableproblemsreshapestheunderstandingoffundamentalconceptsof geometry.
7Bibliography 1. Britannica.“HyperbolicGeometry.”Britannica, www britannica com/science/hyperbolicgeometry
2. Britannica.“Non-EuclideanGeometry.”Britannica, www britannica com/science/nonEuclidean-geometry
3. Britannica.“TheHistoryofHyperbolicGeometry.”Britannica, www britannica com/science/ hyperbolic-geometry#:~:text=The%20first% 20published%20works%20expounding
4. “Euclid’sElements.”OxfordReference, www.oxfordreference.com/display/10.1093/ acref/9780199235940 001 0001/acref9780199235940
5. Heath,T.H. TheThirteenBooksofEuclid’sElementsTranslatedfromtheTextofHeibergwith IntroductionandCommentary.DoverPublications,1956.GoogleBooks, books.google.co.kr/ books?id=HxhEBgAAQBAJ
6. “HistoryofHyperbolicGeometry.”MathosUniversity, www mathos unios hr/~mdjumic/uploads/ diplomski/PRO21 pdf
7. “HyperbolicGeometry.”StudySmarter, www studysmarter co uk/explanations/math/ geometry/hyperbolic-geometry/
8. “HyperbolicGeometryHistoryandApplications.”Study.com, study com/learn/ lesson/hyperbolic-geometry-historyapplications.html.
9. Milnor,John.“HyperbolicGeometryand ItsParallelPostulates.”RutgersUniversity, sites math rutgers edu/~cherlin/History/ Papers2000/eder html
10. Schombert,James.“HyperbolicGeometryinCosmology.”UniversityofOregon, pages uoregon edu/jschombe/cosmo/lectures/ lec15 html
11. Stillwell,John.“EuclidandBeyond.”Harvard University, people math harvard edu/~ctm/home/ text/class/harvard/113/97/html/euclid.html.
PrimeNumbersandGoldbach’sConjecture Woojin(Roy)Han Year10
wjhan28@pupils.nlcsjeju.kr
Editor Suhyuk(Jeff)Cho
RecommendedYearLevel:KS4
Keywords:Goldbach’sConjecture,PrimeNumbers, Pairs
1Introduction
Primenumbersaremorethanjustabasiccuriosityfrommathematicians.Theyarethesolidfoundation formoderncryptography,computerscience,andeven physics.Fromprotectingonlineactionsperformedin ourdailylivestoconstructingmachinelearningalgorithms,primenumbersplayanessentialroleinourdigitalworld.Unfortunately,asoneofthemostdifficult andinterestingtopicsinmathematics,primenumbers havepuzzledmanymathematiciansthroughouthistory. TheseproblemsultimatelyincludeGoldbach’sConjecture,themostfamousandprominent.
2InfiniteStateofPrimeNumbers BeforewetackleGoldbach’sconjecture,itisnecessaryforustodemonstratethatprimenumbersarein aninfinitestate,sinceiftheywerefinite,atsomepoint largeevennumberswouldlosetheirprimepairs,contradictingtheconjecture.Therefore,weuseEuclid’s Theoremofprimenumbers.
2.1Divergenceoftheharmonicseriesofprime numbers
ProvenbyEuler,itisstatedthatthesumofthe reciprocalsofallprimenumbersdiverges.
Iftherewereonlyafiniteamountofprimespresent, thissumwouldconvergetoacertainnumber.Forexample,let’ssupposethatthereareonly5numbersof primes:
Thesumoftheirreciprocalsarethefollowing:
Whichshowsthatthevalueconvergesatonepoint. However,ifmorevaluesofprimesareadded,
Thismeansthataswesummoretermsof1/p,the sumgrowscontinuously.
Asshown,thesevaluesneversettleonafinitevalue. Thegraphicalimplementationisshown:
Figure1showshowthecumulativesumofreciprocalsofprimesincreasesasmoreprimesareincluded. Itdemonstratesthatthesumdoesnotconvergetoa finitelimit;instead,itkeepsincreasingindefinitely, supportingEuler’sproofthatthereareinfinitelymany primes.
Fig.1:Cumulativesumofreciprocals
3Goldbach’sConjecture
Nowthattheinfinityofprimenumbershasbeen proven,wecannowsuggestwhetherthereisaninfinite setofevennumbersshownbyaddingappropriateprime numbersets.Inotherwords,theGoldbach’sConjecture statesthatanyevennumberNthatisbiggerthan2,can berepresentedbytwoprimenumberspandq,sothat
3.2Heuristicjustification Goldbach’sConjecturecanbesupportedheuristicallyusingprobabilisticnumbertheory.Thecentral ideaisthatthenumberofwaystoexpressaneven integerNasasumoftwoprimescanbeestimated usingthePrimeNumberTheorem.
ThedensityofprimenumbersaroundNisapproximately: 1 ln(x)
Therefore,theprobabilitythatarandomlychosen numbernear N 2 isprimeisabout:
Forinstance,whenN=4,6,8,10,theycanbe representedas
4=2+2 6=3+3
8=3+5
10=3+7=5+5
Currently,thepatternhasbeentesteduptoatleast 4 × 1018,confirmingtheconjecturecomputationallybut notanalytically.
3.1Computation
Eventhoughtheconjectureisstillnotanalytically proven,thereareefficientalgorithmstoverifytheconjectureuptoaspecificpoint.Asimplebrute-forcealgorithmcanbeused:
Sinceweareselectingtwoindependentprimes,the expectednumberofprimepairsthatsumtoNcanbe approximatedby:
Whatthissumsuggestsisthatforasufficiently largeN,thereshouldbemanyvalidprimepairs,which makesancounterexamplehighlyunlikely.
Hereisagraphshowingthenumberofprimeparis forvariousevennumbersN:
Fig.3:y-axis:NumberofPrimepairs(p,q).x-axis: EvennumberN
Figure3showsthenumberofprimepairs(p,q)for eachnumberNupto2000.AsNincreases,thenumber
Fig.2:Abrute-forcealgorithm
ofvalidprimepairsalsogrows,whichsupportstheidea thateveryevennumberhasatleastonevalidprime pair.
3.3TwinPrimeConjecture
Goldbach’sconjectureiscloselyrelatedtothe TwinPrimeConjecture,whichstatesthatthereare infinitelymanyprimepairs(p,p+2).Thistheory strengthensGoldbach’sconjecture,sincetwinprimes canmakeupforGoldbachpairsforsmallevennumbers.
OneapproachtoprovingtheTwinPrimeConjectureinvolvestheHardy-Littlewoodconjecture,which predictsthenumberoftwinprimesuptox.
3.4Goldbach’sWeakConjecture
TheWeakGoldbach’sConjecturestatesthatevery oddnumbergreaterthan7canbeexpressedasthesum of3primenumbers:
4Conclusion Goldbach’sConjectureremainsasanunsolvedmysterythathumanityshouldstillattempt.Although heuristicarguments,partialresults,andcomputation stronglysuggestitstruth,theproofisbeyondourreach. However,astheworldofmathematicsdevelopsandadvances,finalproofswillfittogether.
5Bibliography 1. rlagks05(2023).Exploringmathematicalconcepts relatedtoprimes.[online]NaverBlog.Availableat: https://m.blog.naver.com/rlagks05/223218483152
2. Wikipedia(n.d.).Goldbach’sconjecture-Heuristic justification.[online]Wikipedia.Availableat: https://en.wikipedia.org/wiki/Goldbach%27s_con jecture#Heuristic_justification
3. Wikipedia(n.d.).Divergenceofthe sumofthereciprocalsoftheprimes. [online]Wikipedia.Availableat: https://en.wikipedia.org/wiki/Divergence_of_the _sum_of_the_reciprocals_of_the_primes
Thisversionwasfinallyprovenin2013byHarald Helfgott,makingitonestepclosertoprovingthe conjecture.
Thistheorystatesthatthedensityofprimes ensuresthattheprobabilityofforminganoddnumber usingthreeprimesremainshigh.
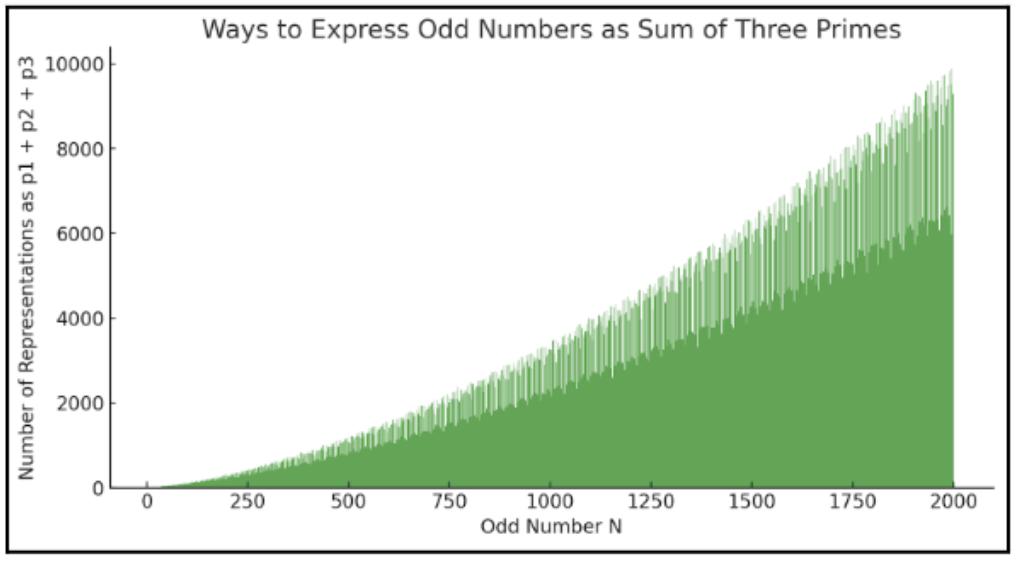
Hereisahistogramshowingthenumberofwaysin whichdifferentoddnumberscanbeexpressedasasum of3primes.
Fig.4
Figure4showsthatthenumberofwaysdifferent oddnumberscanbeexpressedasthesumof3primes. Sinceasthenumbersincrease,thenumberoftriples grows,whichfurtherstrengthensGoldbach’sconjecture.
Tetrations Seoha(David)Kim Year10
seohakim28@pupils.nlcsjeju.kr
Editor
Suhyuk(Jeff)Cho
RecommendedYearLevel:KS4,KS5
Keywords:Hyperoperations,Fractals,Spirals
1Introduction
Additionisconsideredtobeoneofthemostfundamentalyetarcaneideologiesinmathematicsthatformulatetheabsolutefoundationofthefield.Ostensibly, theoperatorisn’tregardedwithsuchprominencewithin modernsociety,butwithoutthefunctionsoftheadditionoperator,mathematicswillremainasunapproachabletheory,aninfeasibleconceptonlyeverdreamtof. However,thisisnotthecase,andmankindhassuccessfullyflourishedinmathematicssuchthatmodern technologyandscientificfeatswerenotpossiblewithouttheimplementationofthesubject.Theconceptto bepresentedinthisjournalisthe‘tetration’,anobscure operationnottaughtinschoolcurriculums.
2The4thHyperoperation
Weallhavebeenwellacquaintedwiththeaddition symbol(‘+’)eversinceourfirststepsinoureducational expedition.Thisisconventionallyreferredtoasthefirst hyperoperation;thus,thisimpliesthatmoreistofollow. Whenadditionisrepeatedlyperformedonanumber,we callitmultiplication(‘×’).Subsequently,theiterated performanceofmultiplicationresultsinthepowersymbol(‘bn’).Thecontinuationofthissequenceproceeds tobecomethefourthhyperoperation,officiallynamed ‘tetration’.Amereminorityisexposedtothissymbol, visuallyexpressedas nb.Thisoperationisanextensionofthesequentialprogressionoftheprecedingoperations.Inpracticalterms,3+4is7,3×4is3+3+3+3 whichequatesto12, 34 is3 ×3×3×3,whichresultsin 81,andultimately, 43 is 3333 ,whichroughlycalculates to1.25×103,638,334,640,024.Seeingasitexceeds3trilliondigits,nopracticalapplicationsseemplausibleat
thispoint.Thisforeignmathematicaloperationdoesn’t possessastandardnotationforexpression,andnounifiedsymbolexistsincasesforutilisationinproofs.The notation nbcanalsobefoundinthetransfiguredform ofb ↑↑ n.Thefactthatthesequenceofnumbersmoved from7to12to81toanumbernodifferenttoinfinity intriguedmathematicians,andeventuallytheyfounda patternthroughvisualisationofthegivendata.
3Implementation 3.1 ∞3
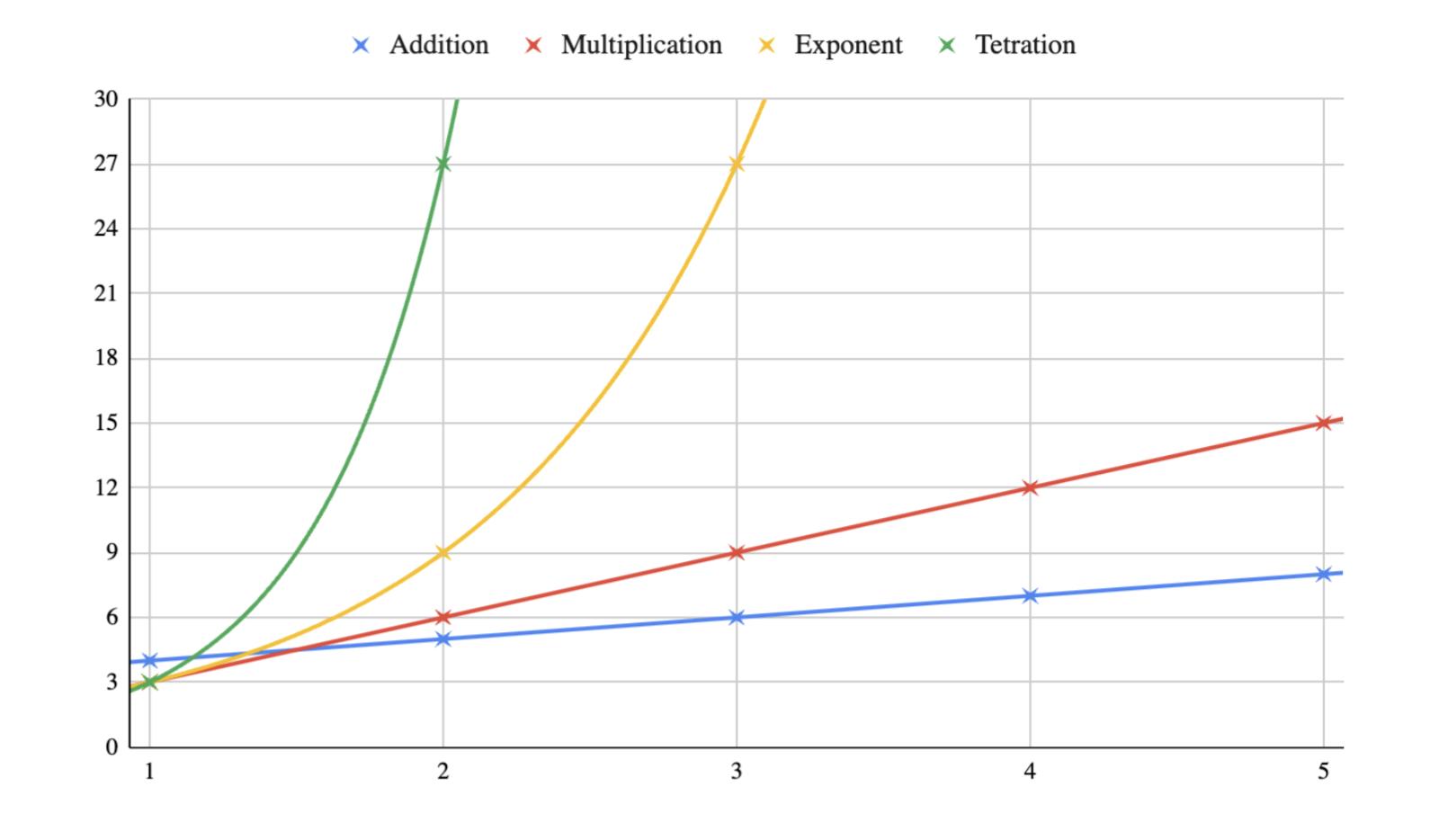
Fig.1:AVisualRepresentationoftheFourHyperoperations
Thefollowingisagraphshowingthevalueswhen eachofthefourhyperoperationswereperformedonthe number3(y=x+3,y=3x,y=3x,y= x3).The resultsareasexpected,andthefourlines,despiteall tendingtoinfinity,approachitatvariedrates,shown bythevariedgradients(andthevariedinstantaneous gradients)ofthegraphs.Thissetofgraphsisatypical exampleofthetetrationoperatorabidingbytheconventions.However,willthetrendbesustainedwhenthe
subjectofthegraphisalteredtoanirrationalnumber, say √2?
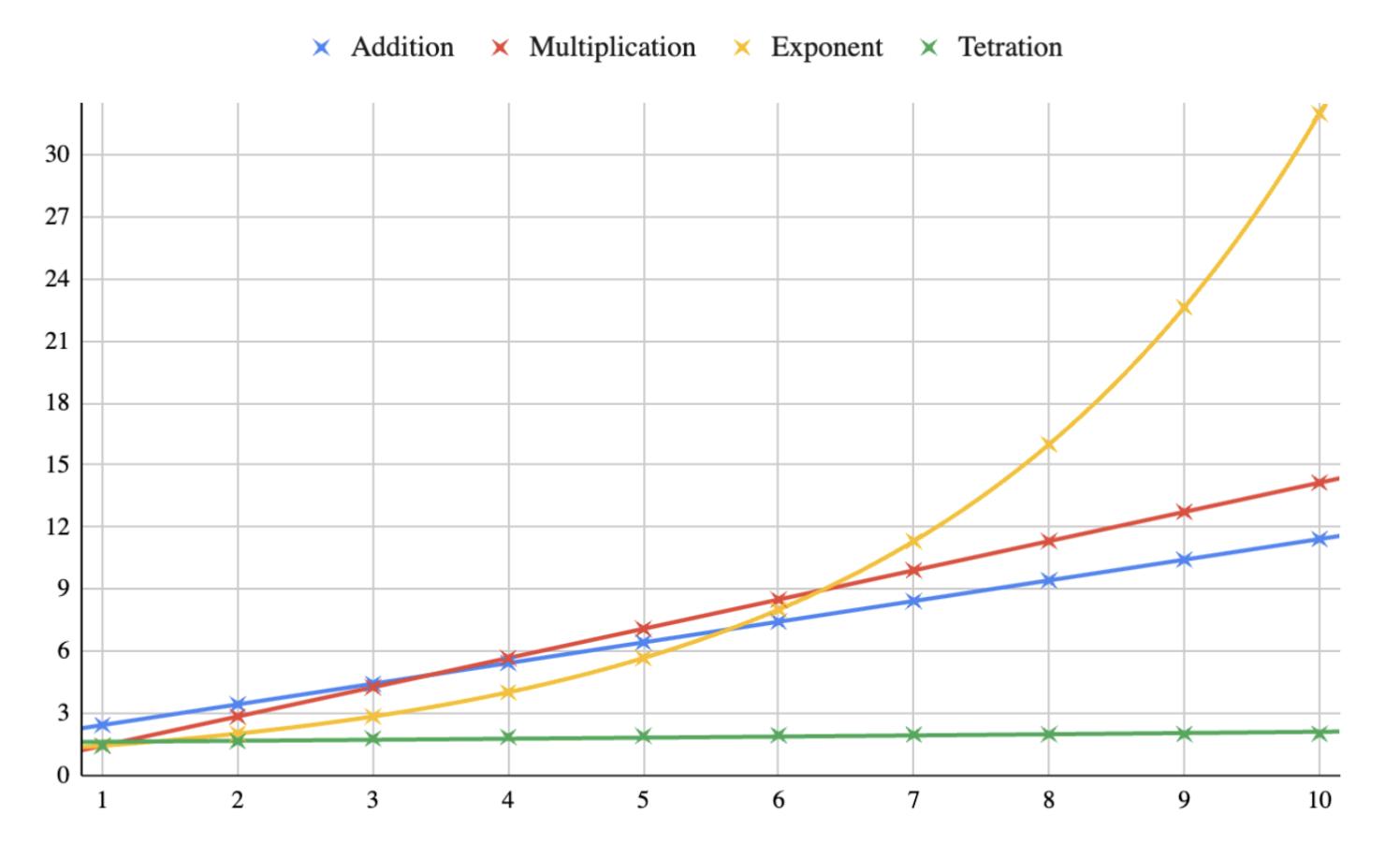
3.2 ∞√2
Fig.2:AVisualRepresentationoftheFourHyperoperations
Unsurprisingly,thefirstthreehyperoperationsdo notshowanydeviationfromthestandardconventions setinthepreviousgraph.However,thetetrationshows apatternwhichwaslaterfoundtotendto2; ∞√2, otherwiseknownas √2√2√2 ,hadavalueof2.Bothalgebraicandgraphicalmethodologiesexisttoprovethis.
Algebraically,toprovethat ∞√2 isrational(ideally 2),itiscrucialtoshowthatthesequence an= n √2 ismonotoneincreasing,i.e.strictlyincreasingand possessesnocrucialpoints,andalsoisboundedabove (meaningitconverges).Althoughitisalreadyshown throughthegreenlineinFigure2,algebraandsimple logicoutputtheconclusionthatsequentially,theupper boundis2.Regardingthetetrationofthesquareroot of2,thesequencewillbeassuch: √2, √2√2 , √2√2√2 Focusingonthesecondterm, √2√2 issmallerthan √2 2,justbythecomparisonoftheirindices.This means √2√2√2 willbesmallerthan2,sincetheindex ofthisnumber,asaforementioned,issmallerthan2, or √2 2.Thisiscarriedoncontinuously,eventually settlingupontheconclusionthatgiven ak=√2ak 1 , ak-1 willneverbegreaterthan2,andthusak will alwaysbelessthan √2 2.Theupperboundforthis sequenceisthereforesetto2.
Movingontothelatterportionoftheproof,let x=√2√2√2 .Throughsubstitution, x = √2x,and √2x x =0.Formulatinganequationregardingthis, f (x)= √2x x,and x isarootofthisequation.The relativemaximum/minimumcanbefoundbyderiving
theequationandsettingtheresultto0.Thestepsare asfollows:
f ′(x)= d dx 2 x 2 d dx (x)
f ′(x)=ln(2) × 2 x 2 × d dx x 2 1
f ′(x)=ln(2) × 2 x 2 × 1 2 × d dx (x) 1
f ′(x)=ln(2) × 2 x 2 × 1 2 × 1 1
f ′(x)=2 x 2 1 × ln(2) 1 (1)
Whentheequationissetto0,thex-valueofthe criticalpointis x = log√2( 2 ln(2) ),whichisapproximately3.06.Thenumericalvalueofthisequation doesnotpossessanysignificance;themerefactthat onerootexistsconveysgreatermeaning.Thus,itis foundthattheequationof x possesseseither2orno roots,butthroughobservation,itisevidentthat2 and4aretherootsforthisequation.Despitethis, asaforementioned, x isalwayslessthanorequalto 2,leadingtotheconclusionthattheanswerwouldbe2.
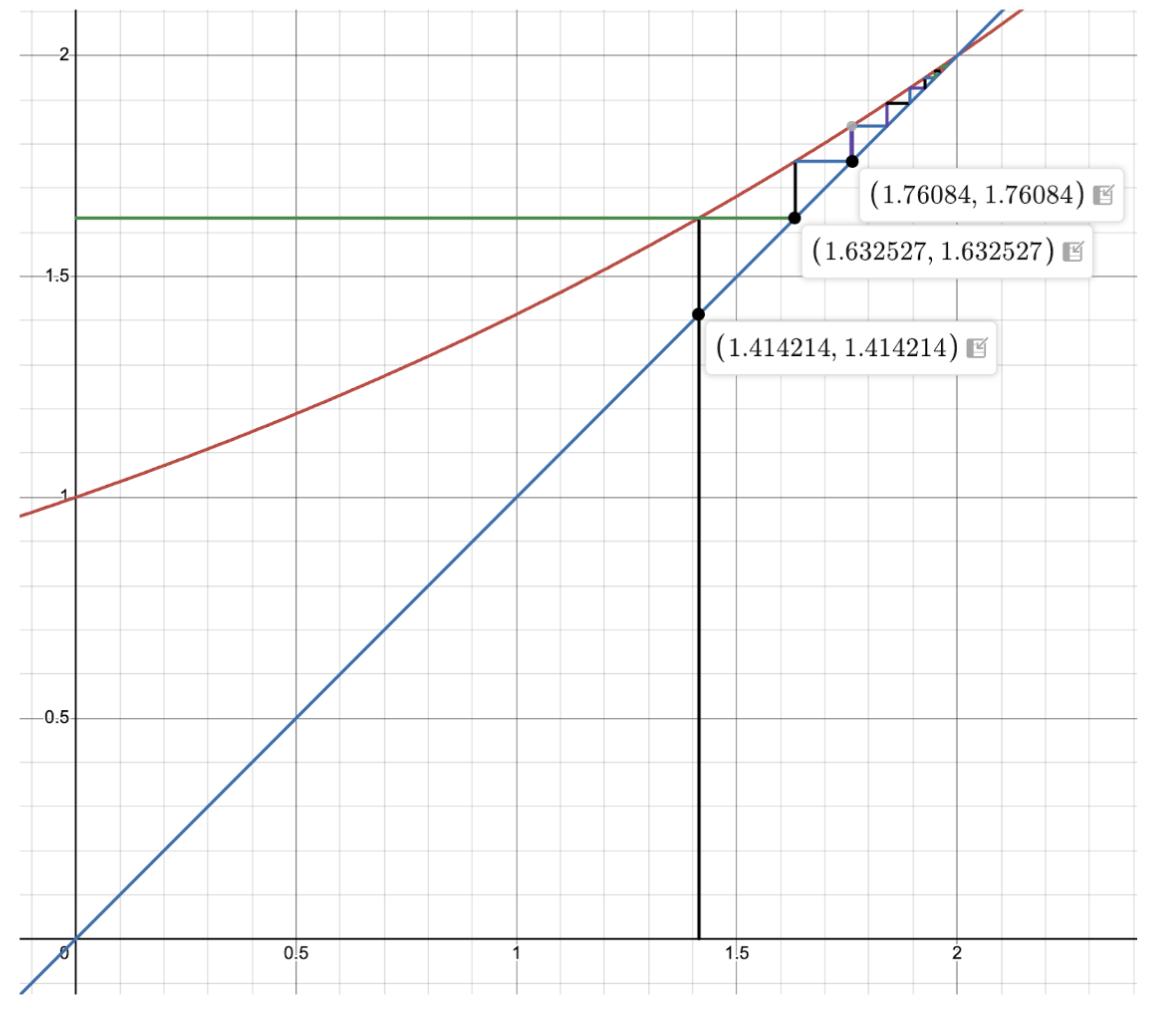
Agraphicalmethodthatrefrainsfromutilisingcalculusalsoexists.Thefollowingisagraphof y = x and y = √2x,alongwithadditionalguidelinestoassistthe explanation.
Fig.3:AGraphof y = x and y = √2x
Asclearlyshowninthegraphbelow,boththe x and y valuestendto2,whichistheconstantthat ∞√2 tendsto.Thiscontinuousstaircasewasconstructedby initiallysetting x to √2 andidentifyingthecorresponding y valueontheliney = √2x (colouredinred).These valuesarethevaluesof n √2 ,where n isanaturalnumberbeginningfrom1andsequentiallyincreasingasit tendstoinfinity.The x and y valueseventuallytendto 2,asshownintheintersectionbetweenthetwographs. Thiswasshownearlierwhentheequation x = √2x was introduced.Thus, ∞√2 is2.
3.3 ∞i
Whatwilloccurwhenthesubjectoftheoperation isalteredtoanimaginarynumber, i?Thevalueof i,whenprocessedwithtetration,producesvisually appealingresults.
Togetthebasicgistoftheoperation, 2i,or i i ,can becalculatedusingEuler’sidentity,oneofthemost renownedandeccentricformulasthatexistwithinthe fieldofmathematics,asitconnectsoneofthemostfundamentalrealandimaginarynumbersintoanequation. Now,proceedingwiththeproof,theEuler’sequation willbemanipulatedalgebraicallyassuch:
iπ +1=0
Finally,repeatingthetetrationwithanewvalue utilisingthesamemethodologies,itwasfound,after someresearchandexperimentation,thatthevalue 3i returnedresultsthatwerefairlyunexpectedanddeviatedfromthenorm.
Thefactthatthepowerofanimaginarynumberto animaginaryoneresultedinarealnumberastonished andpuzzledmany.However,whenthisprogressionis continued,agraphofextremeaestheticsandmathematicalsignificanceisproduced,asshownbelow.
i (y= x i)
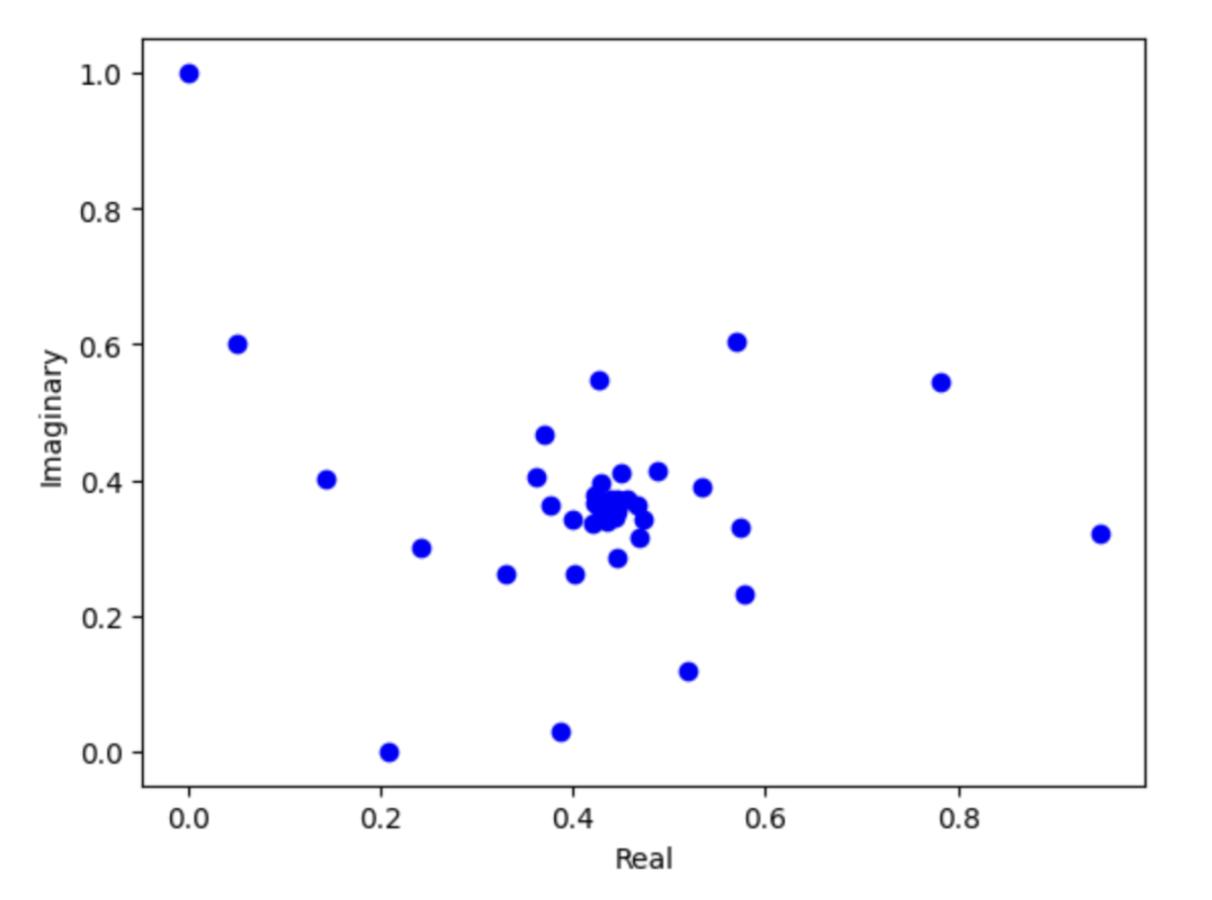
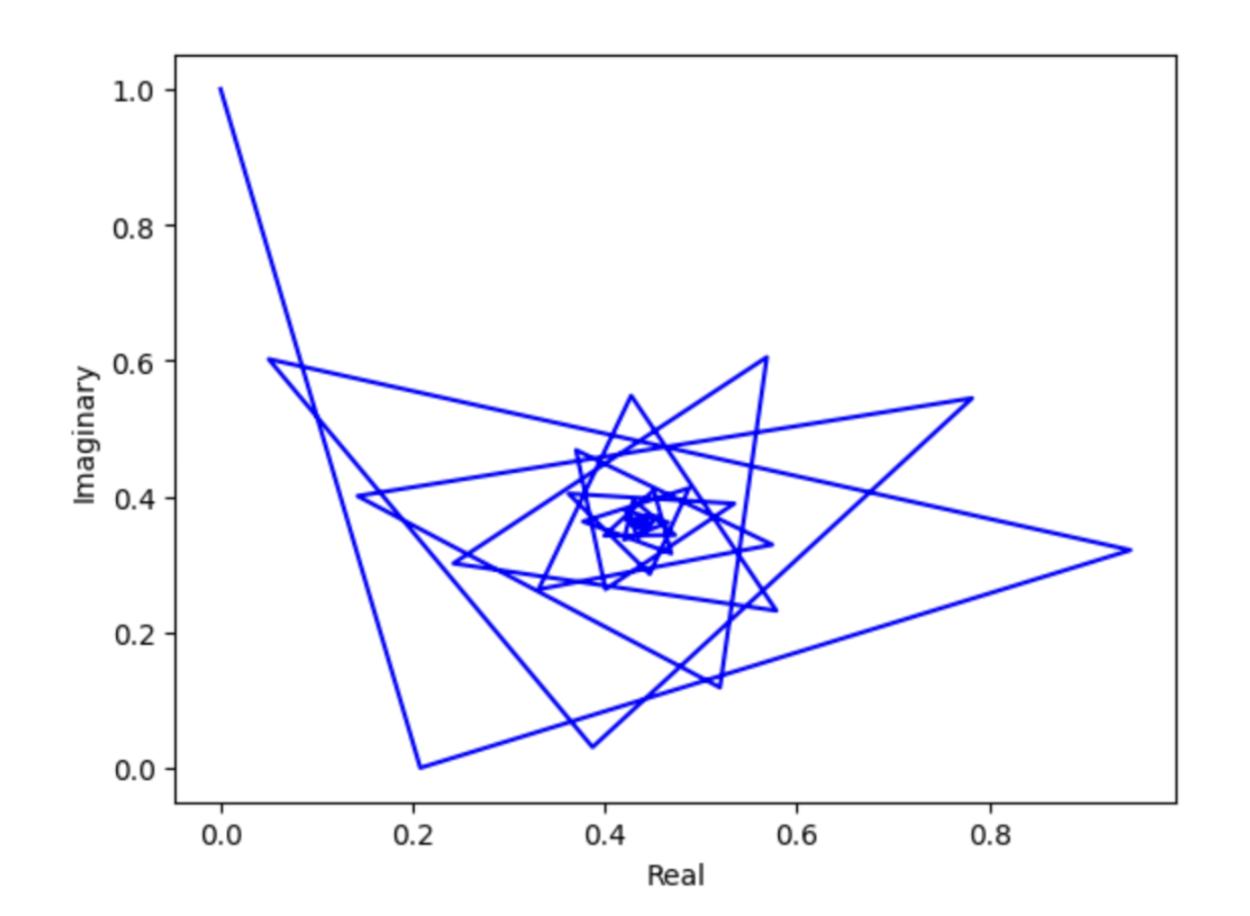
Thefollowingcanbedescribedasaspiralfractal, wherethevaluestendto0.44+0.36i,aseeminglyarbitraryvalue.Thisspiralcouldalsobefoundinthenaturalenvironment,includingtheformationofthegalaxy. Additionally,suchpatternscanbefoundontheleaves ofplants,wheretheleavesformaspiralshapethatrolls continuouslyinwards.
∞3i
3i (y= x 3i)
Thefollowingwastheresultofthetetrationfor thevalue 3i.Initially,thefirstterm, 3i,wassolely imaginary,butasadditionaldatapointswereplotted, thegraphresembledatriangularshapethatperpetually repeated.Theverticesofthetrianglecorrespondedto thethreepoints0,1and0.08+3.06i.Duetothis,itis extremelychallengingtoidentifywherethegraphitself ‘tends’to,asnoendpointexists.Toberatherspecific, theendpointsdoexist,withtheproblembeingthatthe graphtendstohavethreepoints,whichwasnotthe caseforanyofthenumbersinvestigatedpriortothis one.
Throughtheseobservations,itbecomesclearthat
Fig.4:Alinegraphofthetetrationof
Fig.5:Ascatterplotofthetetrationof i (y= x i)
Fig.6:Alinegraphofthetetrationof
thevalueof ∞3i neitherconvergesnordivergesatone point.Keepinginmindthatthevalueof ∞ isconstant aslongasafinitenumberissubtractedfromit,itcan benotedthatifpoint 1 issetto ∞3i,thevalue 0 willbe ∞−13i and 0.08+3.06i as ∞−23i.Allvalues, ∞, ∞ -1 and ∞ -2areallnumericallyequivalentto ∞,meaning that ∞3i consistsofthethreevaluesaforementioned0,1and0.08+3.06i.Again,0.08+3.06iisyetanother arbitraryvaluethatpossessesnomathematicalsignificancewhatsoever.Withinthescientificrealm,thisis consideredstructurallysimilartotheideologiesinvolvingquantummechanics,whichdealswiththepossibility ofhavingmultipleoutputsforasingleinput.Suchare epitomesofhowmathematicscanoverrideconventions oflife.
4Fractals Arecurringthemethatwasprevalentamongsttwo oftheexampleswerefractals,whichareself-repeating structureswhichtheoreticallyhavethepotentialto exceedtopologicaldimensionsandpossesscomplexity thatcannotbeillustratedthroughsimplesketchesand drawings.Suchfractalscanbeidentifiedwithinthe naturalworld,ascountlesslymentionedwithexamples likethegalaxy.Fractalscanalsobeobservedonplants andtheformationoftheirleaves.
Figure3showsastaircasefractal,whichrepeats continuouslyandgraduallydecreasesinsizeasittends toafinitepointonthegraph,2.Thisrepetitionwas formedbydrawingtheguidelinesinthegraph;the graphitselfismerelyacurve,alongwithastraight line.However,inthemidstoftheprocessofreaching 2,thisfractalwasformed.
Toelucidate,thepointbeganatthesquareroot of2,andthevalueof √2 inthegraph y = √2x ,or just y = √2√2 Withthesubstitution,thefirstoutput ofthetetrationwasrevealed 2 √2.Next,thehorizontal segmentofthestaircasemovedthe x valuesuchthat itisequaltothe y valuebyutilisingthegraphof y = x.Afterthis,theprocessisrepeated,suchthat x isnowthefirstoutputofthetetration, √2x ,and √2√2√2 .Theprocesseventuallysettlesatthepoint (2,2),suggestingthattheinfinitetetrationof √2 is2. Itwasfairlyintriguingthattheprocessofreachingthe answerresultedinafractal.
Theotherfractalformulawasshowninthetetrationoftheimaginarynumber i,onthecomplexplane. Thispatternthenrevealsthevaluesfor -1 i and 0 i as0 and1respectively,asmovingback,thespiralcanbe made.Thereareproofstowhyaspiralwasformed, andsuchproofsareintricatetoagreatextent.Thus, theunnecessaryexplanationswereomittedwithjust thecoreinformationremaining.
Notethatthegraphconsistsofa129º shiftateach point,formingaspiral.Anexact120º wouldresultina triangularshape,resemblingtheshapeshowninFigure 5.The9º offsetcreateddifferencesbetweeneverythird point.Additionally,ifalgebraicmeanswereutilisedto identifythepointofconvergence,theprincipalbranchof theLambertWfunctionwouldbeusedontheformula W = W ( ln(x)) ln(x) .Thisfunctioncanbeusedtoidentify theinfinitetetrationofanumber,andcanalsobeused toidentifywhetherthisvalueissignificantlyhigh(which suggeststhenumber’sinfinitetetrationdiverges).Based onthefollowing,thevaluefor i tetratedwas 0 438+ 0 361i,asidentifiedearlier.Thisformsaconverging spiral.
5FinalGraph Shouldtherealmoftetrationceasehere,mathematicianswouldlosethepointinthepointinstudying thisoperation.Yet,onefinalgraphremainstoastound thosewhoseeit.
Asshownthroughthepreviousexamples,thereare caseswhentheinfinitetetrationofanumberresults intheconvergenceorthedivergenceoftheoutput. Whenthesevaluesarenotedandplottedonagraph dependingontheirattributesofbeingconvergentor divergent,therearepatternsthatarerevealed.Thisis knownasthetetrationfractal.
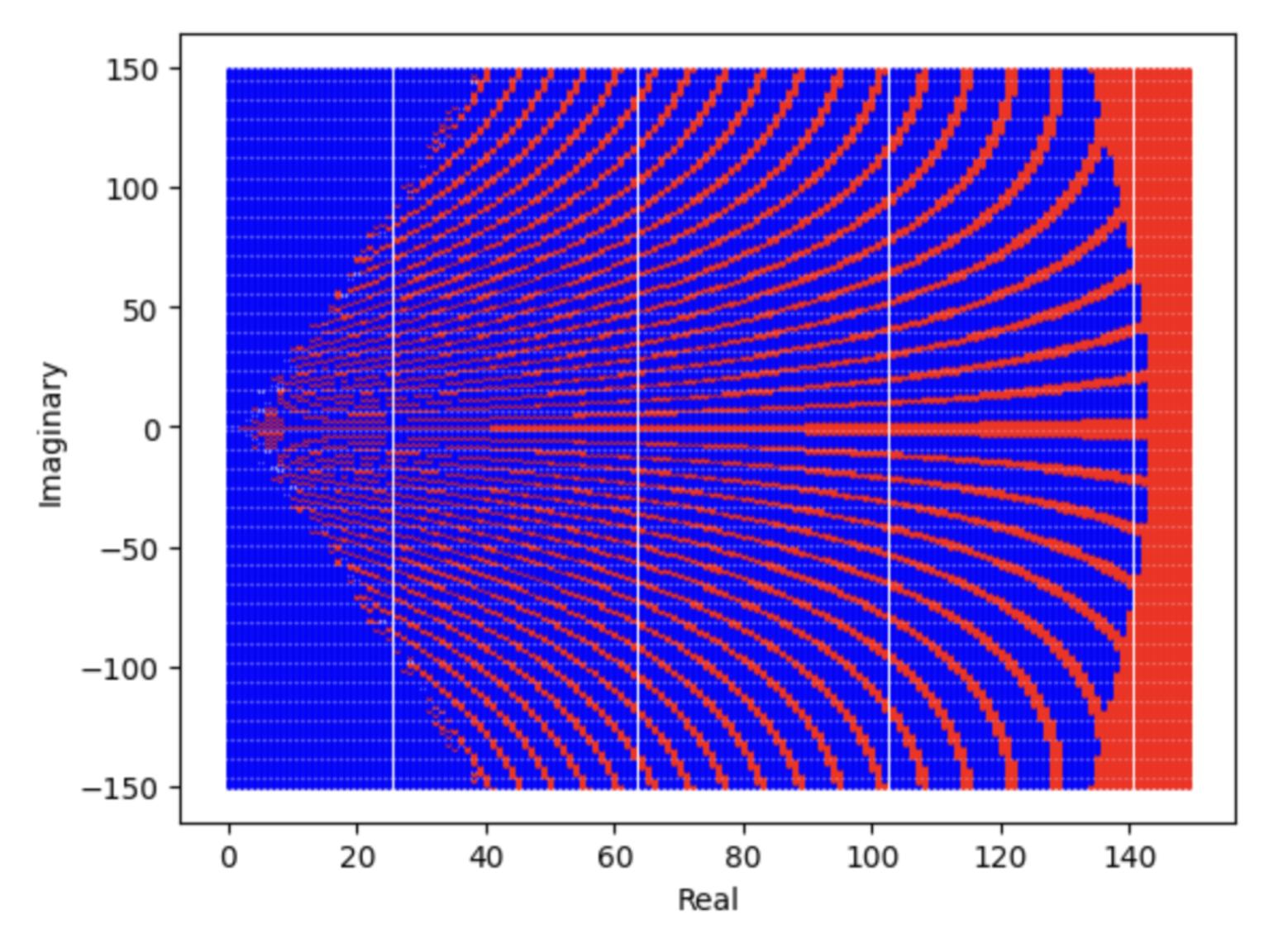
Duetothecharacteristicsofafractalbeinginfinite andrepeating,therearevariousshapesandpatterns thatcanresultfromzoominginandcapturingdifferent centresatvariedrangesofthe x and y values.The followingfractalbelowhasanupperthresholdofthe overflowlimitinPython,andwasformedfromthepoint (0,-150)to(150,150).
Admittedly,thefollowingisnotatypicalparadigm forthetetrationfractal,butcanalsobefound.For reference,atypicalfractallooksasfollows,andcontinuesinalldirectionseternally.Thefollowingimagewas madefromprofessionalgraphingsoftware,specialised forsuchtasks.
Fig.7:Ascatterplotofthetetrationfractal
Fig.8:Atypicalexampleofthetetrationfractal
6ComputerScience Whenvisualisingdata,itisvitaltoensurethe dataismeaningful,andthatitcanbevisualised.All thefiguresillustratedaboveareuniqueproductions fromtheauthor,withtheexceptionofFigure8, whichwasfoundontheofficialwebsiteoftetration fractals.Figures1and2utilisedGoogleSheetsandits associatedfunctions,Figure3wasascreenshotfrom Desmos,agraphingcalculator,andFigures4to7were codedwithPython,ageneral-purposeprogramming language.Tomakevisualisationpossiblehere,this articleusedthenumpyandmatplotlibpackageofthe Pythonlanguage.Thecodeusedisasfollows:
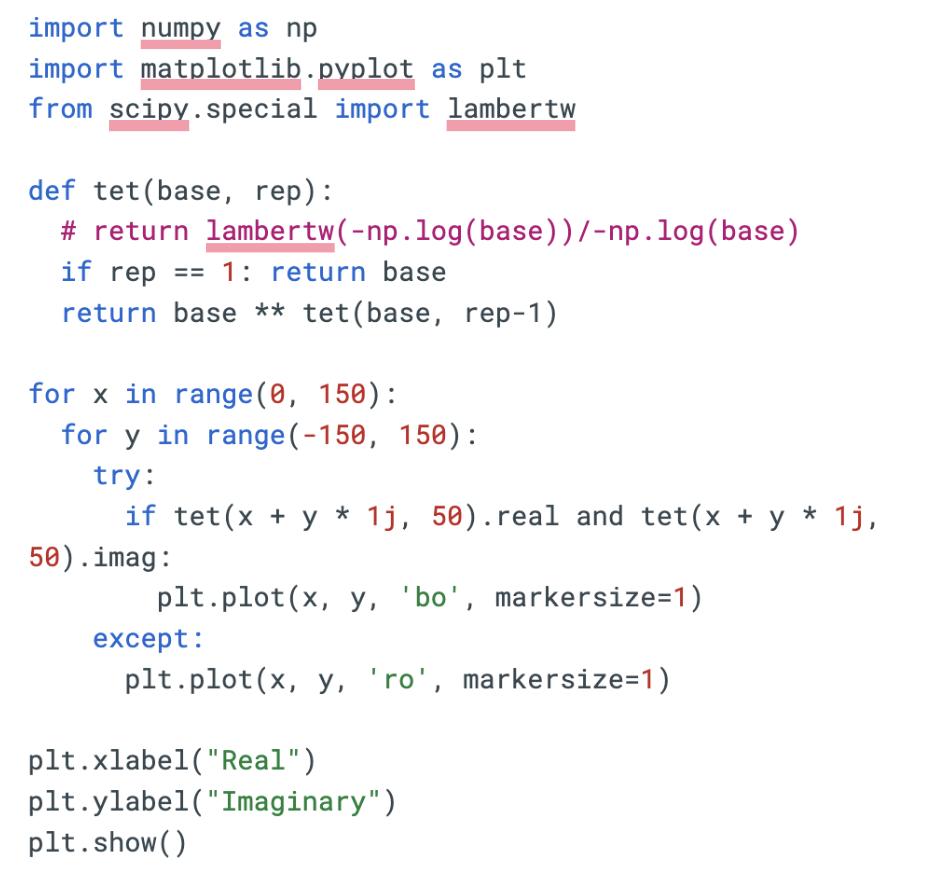
Fig.9:Thegeneralcodeusedtodrawgraphs(Figs.4 6)
resultinaRecursionError,duetothelimitinthe maximumrecursiondepthofPythonfunctions.The basewaschangedbyadjustingthe‘1j’online8.Note that‘j’inPythonistheequivalentof‘i’inmathematics.
Movingon,thesecondsnippetofcodeusedthe sameprinciples,andalsohadatryandexceptfunction tocatchOverflowErrors.
Fig.10:Thecodeusedtocreatethetetrationfractal (Fig.7) 7Conclusion
Althoughthisarticleissolelyconsideredtetration, thereissuperfluouscontentregardingthefifthandsixth hyperoperations,anditcontinuessystematically.The materialintroducedinthispieceoftextwas,however, justameagreportionofthebiggerpicture,reservedfor thosewithgreaterinterestinthisfieldofmathematics. Itishopedthatthisarticleinspiresreaderstodofurther researchorfurtherstudies.
8Bibliography
1. Bourke,P.(2013).Tetrationfractal. [online]Paulbourke.net.Availableat: https://paulbourke.net/fractals/tetration/
2. Geisler,D.(2019).Tetration.org-Tetration.[online]Tetration.org.Availableat: https://tetration.org/original/Tetration/index.html
Tobrieflyexplainthefollowingcode,recursionwas usedtoraisethebasetothepoweroftheprevious term,withthepatternrepeated.Whenthetetration indexis1,thevaluewillalwaysbethebaseitself.The datawaslimitedto959points,as960orabovewould
3. SciPy(2008).lambertw—SciPyv1.15.0 Manual.[online]Scipy.org.Availableat: https://docs.scipy.org/doc/scipy/reference/generated/scipy.special.lambertw.html
RecommendedYearLevel:KS5
Derek(Yejun)Yoo Year12
Email:yjyoo26@pupils.nlcsjeju.kr
Editor Derek(Yejun)Yoo
Keywords:Optimization,LagrangeMultiplier,NumericalMethods,PersonalFinance,DecisionTheory
1Introduction
Seollal,theKoreanLunarNewYear,isaculturallysignificanteventcelebratedbymillions.Itisatime whenfamiliescometogethertohonorancestors,share traditionalmeals,andexchangegoodwishes.Oneof themostanticipatedaspectsofSeollal,especiallyfor youngergenerations,isthecustomofreceivingmonetarygiftsfromelders.Thesefinancialgifts,oftengiven inneatlypackedenvelopes,provideanexcellentopportunityforrecipientstoengageinfinancialplanning.
Jeff,astudentwithakeeninterestinmathematics andfinance,findshimselfwithaconsiderablesumofSeollalmoney.Unlikemanyofhispeerswhomighthastily spenditongadgets,fashion,orentertainment,Jeffsees thisasanopportunitytoapplymathematicalprinciples tomakerationalfinancialdecisions.Thechallengehe facesisnotjustaboutspendingorsavingbutabout makinganoptimalallocationthatbalancesthreekey financialobjectives:security,growth,andliquidity.
Thisproblemnaturallylendsitselftothestudyof **constrainedmultivariableoptimization**,amathematicalframeworkusedineconomicsandfinanceto findthebestpossibleoutcomegivenspecificlimitations. Jeff’sgoalistomaximizehisfinancialwell-beingbydistributinghismoneyamongsavings,investments,and immediateexpenditureswhileadheringtoreal-worldfinancialconstraints.
2MathematicalFormulationoftheProblem Jeffdecidestodistributehismoneyacrossthreeprimarycategories:
1. Savings (x):Alow-riskaccountofferingstablebut modestreturns.
2. Investments (y):Stocksorotherhigh-returnfinancialinstruments,whichcomewithanassociated levelofrisk.
3. ImmediateSpending (z):Thiscoversday-to-day expensesanddiscretionarypurchasesthatofferinstantutility.
ThetotalutilityJeffderivesfromhismoneyisrepresentedbythefunction:
where:
Theterms 0 03x and 0 08y reflectlinearreturnson savingsandinvestments,respectively.
Thequadraticterm 0 01y2 modelsdiminishingreturnsoninvestments,capturingtheideathathighriskassetsdonotalwaysyieldproportionalrewards. Thelogarithmicterm 0 5ln(z) ensuresthatspendingcontributestoutilitybutexhibitsdiminishing marginalbenefits.
Jeffalsofacesseveralreal-worldconstraints:
x + y + z ≤ 300 (Totalbudgetconstraint)(2)
0 05y ≤ 10 (Riskconstraint,limitingexposuretovolatileassets) (3)
z ≥ 50 (Minimumliquidity,ensuringhehasenoughcashforessentials) (4)
3OptimizationUsingLagrangeMultipliers TheLagrangemultipliermethodisapowerful mathematicaltechniqueusedtofindthelocalmaximaandminimaofafunctionsubjecttoequalityconstraints.InJeff’sscenario,heaimstomaximizehis utilityfunction U (x,y,z),representingthesatisfaction derivedfromallocatinghisSeollalmoneyintosavings (x),investments(y),andimmediatespending(z).This optimizationissubjecttoconstraintssuchashistotal budgetandrisktolerance.
ToapplytheLagrangemultipliermethod,wefirst definetheconstraintfunction g(x,y,z) thatrepresents thelimitationsJefffaces.Forinstance,abudgetconstraintcanbeexpressedas:
TheLagrangianfunctionisformulatedas:
L(x,y,z,λ)= U (x,y,z) λ(x + y + z 300) (5)
WethenconstructtheLagrangianfunction, L, whichcombinestheoriginalutilityfunctionandtheconstraintusinganewvariable λ (theLagrangemultiplier):
L(x,y,z)= U (x,y,z) λg(x,y,z) (6)
Thenextstepinvolvestakingthepartialderivatives of L withrespecttoeachvariable(x,y,z)andtheLagrangemultiplier λ,andsettingthemequaltozero:
Step1:DefinetheProblem Jeff’sutilityfunctionwasgivenby:
Solvingthissystemofequationsyieldsthevaluesof x,y,z, and λ thatmaximizeJeff’sutilitywhilesatisfying theconstraint.
Geometrically,thismethodensuresthatthegradientoftheutilityfunction ∇U isparalleltothegradientoftheconstraintfunction ∇g attheoptimalpoint. Thismeansthatthedirectionofthesteepestascentof theutilityfunctionisalignedwiththedirectionofthe constraintsurface,ensuringthatanymovementalong theconstraintdoesnotincreasetheutility,indicating anoptimalallocation.
TheLagrangemultiplier λ itselfprovidesvaluable economicinsight;itrepresentstherateatwhichthe maximumvalueoftheutilityfunctionincreasesasthe constraintisrelaxed.InJeff’scase, λ indicateshow muchhismaximumutilitywouldincreaseifhisbudget constraintwereslightlyexpanded,providingameasure ofthemarginalutilityofadditionalresources.
ByapplyingtheLagrangemultipliermethod,Jeff cansystematicallydeterminetheoptimalallocationof hisSeollalmoneyacrosssavings(x),investments(y), andspending(z),ensuringthatheachievesthehighest possiblesatisfactionwithinhisfinancialconstraints.
Withtheconstraintbeing:
TosolvethisusingtheLagrangemultipliermethod, wecombinetheutilityfunctionandtheconstraintinto asinglefunction,theLagrangian:
Step2:ComputethePartialDerivatives
Wecalculatethepartialderivativesof L withrespecttoeachvariable(x,y,z,and λ).
1. Withrespectto x: δL δx =0 03 λ =0 (11)
2. Withrespectto y: δL δy =0 08 0 02y λ =0 (12)
3. Withrespectto z: δL δz = 0 5 z λ =0 (13)
4. Withrespectto λ: δL δλ = (x + y + z
Step3:SolvetheSystemofEquations
Thesystemofequationstosolveis:
1. λ =0 03 (from δL δx =0)
2. λ =0.08 0.02y (from δL δy =0)
3. λ = 0 5 z (from δL δz =0)
4. x + y + z =300 (fromtheconstraint)
Step4:SubstitutingValues
1. Fromequation(1),substitute λ =0 03 intoequation (2): 0 03=0 08 0 02y (15)
Solvingfor y: y = 0.08 0.03 0 02 =2 5 (16)
2. Substitute λ =0 03 intoequation(3): 0 03= 0 5 z (17)
Solvingfor z:
3.Usethebudgetconstrainttosolvefor x:
(18)
Step1:ComputetheGradientof U (x,y,z) Thegradientof U (x,y,z) isthevectorofpartial derivatives:
U (x,y,z)= δU δx , δU δy , δU δz
Forthegivenutilityfunction:
Step2:InitializeStartingValues
Chooseinitialguessesfor x,y,z: x0 =100,y0 =100,z0 =100
Then,setalearningrate(α)tocontrolthesizeof eachstep.Forthisproblem,let α =0 1
Step3:IterativeUpdates
Ateachiteration,update x,y, and z usingthegradientascentformulas:
x +2 5+16 67=300 x =300 2.5 16.67=280.83
FinalSolution
x =280 83,y =2 5,z =16 67,λ =0 03
4NumericalOptimizationApproach
Method2:NumericalOptimizationusingthe Gradient-basedMethod
Numericaloptimizationisapracticalandpowerful approachtosolvingconstrainedoptimizationproblems, particularlywhenanalyticalmethodsliketheLagrange multiplierarechallengingorinfeasible.Unlikeanalyticalmethods,whichaimtofindanexactsolution,numericaloptimizationiterativelysearchesfortheoptimal solutionbyapproximatingthemaximumorminimum oftheobjectivefunction.InJeff’scase,numericaloptimizationhelpsdeterminethebestallocationofhisSeollalmoney(x,y,z)acrosssavings,investments,andimmediatespending,subjecttobudget,risk,andliquidity constraints.
Afterupdatingthevalues,checkwhetherthedata constraintsaresatisfied:
1. If x + y + z> 300,adjustthevariablestoensurethe budgetconstraintismet.
2. If y> 200,set y =200
3. If z< 50,set z =50.
Step4:Convergence
Repeattheupdatesuntilthechangesin x,y, and z betweeniterationsareverysmall(e.g.,lessthan0.01), indicatingthatthesolutionhasconvergedtotheoptimalallocation.
WhyNumericalOptimization?
1. Handlesnon-linearfunctionslike U (x,y,z) effectively.
2. Accommodatescomplexconstraintsinastraightforwardmanner.
3. Providesapproximatesolutionswhenexactanalyticalsolutionsareimpractical.
1
ForJeff,thismethodnotonlyfindsthebestallocationofhismoneybutalsohighlightstheroleof constraintsinshapinghisdecision-makingprocess.By iteratingtowardtheoptimalsolution,numericaloptimizationoffersaclear,adaptableapproachtoreal-world problems.
Method3:Python 2 # Define the utility function and its gradient
3 def utility(x,y,z):
4 return 0.03*x+0.08*y-0.01*y**2+ → 0.5*np.log(z)
5
6 def gradient(x,y,z):
7 grad_x=0.03 # Partial derivative with → respect to x
8 grad_y=0.08-0.02*y # Partial → derivative with respect to y
9 grad_z=0.5/z # Partial derivative with → respect to z
10 return np.array([grad_x,grad_y,grad_z])
11
12 # Gradient ascent with constraints
13 def optimize_budget(initial_x,initial_y, → initial_z,budget,alpha,max_iter, → tolerance):
14 x,y,z=initial_x,initial_y,initial_z
15 for in range (max_iter):
16 # Calculate gradient
17 grad=gradient(x,y,z)
18
19 # Update variables using gradient → ascent
20 x_new=x+alpha*grad[0]
21 y_new=y+alpha*grad[1]
22 z_new=z+alpha*grad[2]
23
24 # Apply constraints
25 if x_new+y_new+z_new>budget: # → Budget constraint
26 excess=(x_new+y_new+z_new)→ budget
27 total=x_new+y_new+z_new
28 x_new-=(x_new/total)*excess
29 y_new-=(y_new/total)*excess
30 z_new-=(z_new/total)*excess
31
32 y_new= min (y_new,200) # Risk → constraint
33 z_new= max (z_new,50) # Liquidity → constraint
34
35 # Check convergence
36 if abs (x_new-x)<tolerance and abs ( → y_new-y)<tolerance and abs ( → z_new-z)<tolerance:
37 break
38
39 # Update variables for the next → iteration
40 x,y,z=x_new,y_new,z_new
41
42 return x,y,z
43
44 # Parameters for optimization
45 initial_x=100
46 initial_y=100
47 initial_z=100
48 budget=300
49 alpha=0.1
50 max_iter=1000
51 tolerance=0.01
52
53 # Solve for optimal allocation
54 optimal_x,optimal_y,optimal_z= → optimize_budget(initial_x,initial_y, → initial_z,budget,alpha,max_iter, → tolerance)
55
56 optimal_x,optimal_y,optimal_z
Listing1:GradientAscentOptimizationforBudget Allocation
5Conclusion Jeff’sfinancialdilemmaisaclassicexampleofconstrainedoptimizationinaction.Whetherusing**Lagrangemultipliers**or**numericaloptimization**, thiscasestudydemonstrateshow**mathematicsprovidesastructuredapproachtofinancialdecisionmaking**.
PoissonDistributionandHowIt’sUsedinSports Betting RyanLee Year12
Email:hj2lee26@pupils.nlcsjeju.kr
Editor Hanjin(Ryan)Lee∗
RecommendedYearLevel:KS4+
Keywords:Poissondistribution,Numberofsuccess,Probability
1Introduction
Weoftenseepeoplebettinginsports,withmanypeopleattemptingtopredicttheoutcomeofmatches,oftenrelyingheavilyonintuitionandpersonalbias.Thesesubjective guesseseasilyleadtobettingaddictionandmassivefinanciallosses.Whatiftherewereawaytomakemoreinformed andreasonedpredictionsthroughmathematicalanalysis?By leveragingdataandstatisticalmodels,itbecomespossibleto enhancetheaccuracyofsportspredictions,reducingreliance ongutfeelings.
2IntroductiontoPoissondistribution
Forourprediction,weturntofootballdataandapply thePoissondistribution.ThePoissondistributionisaprobabilitydistributionthatpredictshowmanytimesaneventis likelytooccurwithinagiventimeperiod.ForarandomdiscretevariableXthatfollowsthePoissondistribution,andis theaveragerateofvalue,thentheprobabilityofXtimesof eventsisgivenby:
x=numberofsuccesses
λ =rateofsuccess
e=Euler’snumber(2.71828)
Inthiscontext,successreferstoscoringagoal,andthe rateofsuccessrepresentstheaveragenumberofgoalsscored byateampermatch.
APoissondistributioncanbeappliedunderthefollowingconditions:
1.Eachevent(goal)occursindependently,meaningthe likelihoodofonegoaldoesnotaffecttheprobabilityof another.
2.Theaveragenumberofeventsoveraperiodisconstant andknown(representedby λ (lambda)).
3ManchesterCityvManchesterUnited
TodemonstratetheapplicationofthePoissondistribution,let’sanalyzeamatchupbetweenManchesterCityand ManchesterUnitedinthePremierLeague.Byexamining theirhead-to-headrecordsince2017,wecanpredictpotentialoutcomesoftheirnextmatch.
MCI MNU
GamesPlayed 22 22 Goalspergame 38 26
Withtheaveragegoalspergamecalculated,wecanapplythePoissondistributiontoestimatetheprobabilityof eachteamscoringaspecificnumberofgoals(e.g.0to5 ormore).
Thevisualizationsofcalculationcarriedoutforeach teamarethefollowing.
Figure1.PoissonDistributionoftheScoringProbabilitiesofManchesterCity
Figure2.PoissonDistributionoftheScoringProbabilitiesofManchesterUnited
Then,Aheatmapcanbecreatedtovisualizeallpotential scorecombinations,showingtheprobabilityofeachpossible outcome.Eachboxontheheatmaprepresents,ofcourse, theproductofthegoalprobabilitiesforManchesterCityand ManchesterUnited.
Figure3.AheatmapofpossibilitiesforthepossiblescorecombinationsbetweenCityUnited
Thevisualizationgenerallyrevealsthatlow-scoring games(0-2goalsperteam)arethemostlikelyoutcomes. TheheatmapalsoindicatesthatManchesterCityisstatisticallymorelikelytowin,withthesecondmostprobable outcomebeinga2-1winforCity.
Basedonthisanalysis,themostrationalbetswouldfocusona1-1drawora2-1winforManchesterCity,ifyou alsogobythecommonsensethatCityisobjectivelyabetter teamthanUnited.
4Extension GiventhatthePoissondistributioncandealwiththe numberofoccurrencesinagiventimeperiod,itisalsopossibletocalculatethenumberofgoalsinthefirsthalfandthe separatehalf.Thiscanbehelpfulinevaluatingtheoffensive consistencyofteamsacrossthefullgame,allowingforbetter strategicdecisions.
Additionally,itcanpredictthetotalnumberofgoalsa teammayscoreoverthecourseofa38-gamePremierLeague season.
Byapplyingthesamemethodology,predictionscanbe extendedtoindividualplayers’goal-scoringorassiststatistics.Althoughattackersnaturallyhaveahigherprobability ofscoring,thismightcauseissuessuchastheattackerbeing thefavoritetoscoreallthetime,whichiscertainlynotthe caseinreality.However,thePoissonmodelself-corrects.If anattackerfailstoscore,theirsuccessrate()decreasesover time,redistributingtheprobabilitytootherplayers,leading toamoreaccuratemodel.
5Limitations However,stillthisisafairlyunprofessionalandoversimplifiedanalysisofafootballgamethatignoresmany importantfactors,suchasthesquadquality,injuries, home/awayadvantage,orhumanitarianelementssuchas playerfatigueorintenseschedules.
Themodelreliesprimarilyonpastperformanceand assumesthathistoricalgoaldatareflectsthevariableslike theonesabovethatcannotbeexplicitlymeasured.Consequently,whilethePoissondistributionoffersausefultoolfor prediction,itshouldbecoupledwithamuchbroaderanalysis.
6Conlcusion ThePoissondistributionprovidesasimpleapproachto predictingsportsoutcomes.Althoughthismethodsimplifiesmanycomplexitiesofreal-worldsports,itopensthedoor forfurtherrefinementandintegrationwithadditionalpredictivefactors,suchasplayerform,injuries,andotherdynamic variables.Whilenotfoolproof,Poissondistributionoffersa valuablefoundationformoreinformedsportspredictions.
Bayes’TheoremandPsychology:AreOur PerceptionsofProbabilityMisguided? Suhyuk(Jeff)Cho Year12
Email:shcho26@pupils.nlcsjeju.kr
Editor
Suhyuk(Jeff)Cho
RecommendedYearLevel:KS4,KS5
Keywords:Conditionalprobability,Representationof probabilities,Bayes’Theorem,Psychology
1Introduction
Eveninyourmostmundaneday,youarelikely toencountertheconceptofprobability,regardlessof whetheryouareconsciousofit.Youunconsciously makenumerousdecisionsbasedontheprobabilityand likelihoodofdifferentevents,whicharenaturallycalculatedinsideyourbrain.Butwhenpeopleinitially comeupwithahypothesisandthenareintroduced tonewinformation,quiteoftenthisleadstoanirrationaldecision,heavilyinfluencedbythelatestknowledge.Inotherwords,ratherthan‘updating’thehypothesisheldbeforebeinggiventheinformation,peopledisregardorprioritisethenew,whichmakesthem makeachoiceratherthanirrational.TheBayes’theoreminsteadshowshowtheprobabilitychangesgivena certainconditionandhowtheoutcomecandifferfrom theinitialhypothesis.Itallowspeopletodeterminethe conditionalprobabilityofanevent.
2Bayes’theorem
2.1Thebasics
Considerthisverybasicexample:Infrontofyou are50vehicles,whichareeitheracaroramotorcycle. Outofthe50vehicles,30arecars,and20aremotorcycles.
Arichmancomesbyandsaysthathewantsto randomlyselectavehicleandbuyit.Whatisthe probabilitythathewillbuyacarorthathechoosesa motorcycle?
Fig.1:Case1
Theanswerisverysimple.Sincethereare30cars and20motorcycles,theprobabilityofchoosingacaris 60%whilechoosingamotorcycleis40%. Fig.2:Simplerepresentationofcase1
Butthistime,outofthe30cars,15areblue,and outofthe20motorcycles,only5areblue.
Therichmannowwantstobuyabluevehicleand hewantstodothisrandomly.Doestheprobabilityof selectingacarorselectingamotorcyclechange?
Fig.3:Case2
Yes,itwillchange.Duetothisnewrestriction,the probabilityofchoosingacarincreasedto75%whilethe probabilityofchoosingamotorcycledecreasedtoonly 25%.
Fig.4:Simplerepresentationofcase2
Whenweweremakingthiscalculationweonlyconsideredadescriptiongivenfromthepoolofbluevehicles thatrestrictedthenumberofcarsormotorcyclesthat hadthepossibilityofbeingchosen.
2.2Case-specificformula Liketheaforementionedexample,ifnewinformation(bluevehicle)isintroducedtoaninitialhypothesis (60%car:40%motorcycle),theoverallprobability canchangeandthereforea’update’tothepreliminary probabilityshouldbemadeinaccordancewiththis.
Whengiventheinitialhypothesisthatoutof50 vehicles,30arecarsand20aremotorcycles,theprobabilityofrandomlyselectingacarcanbecalculatedby theformula
p(c)= Numberofcars n (1)
Thisgoessamewiththemotorcycles.
p(m)= Numberofmotorcycles n (2)
wherenisthetotalnumberofvehicles
So,ifweformanewformulabasedonthe‘update’ thatthereare15bluecarsand5bluemotorcycles,and
trytoworkouttheprobabilityofselectingabluecar outofallbluevehicles(condition),
where
p(b|c)=Theprobabilityofchoosingabluecarout ofallcars
p(b|m)=Theprobabilityofchoosingablue motorcycleoutofallmotorcycles
Inotherwords,theprobabilityofchoosingablue carisequaltothenumberofbluecarsoverthenumber ofbluecarsaddedtothenumberofbluemotorcycles (whichisultimatelythenumberofbluevehicles).
Tohelpwiththeunderstanding,theformulaabove isthesameas
p(c|b)= Numberofbluecars Numberofbluecars + Numberofbluemotorcycles (4)
Fromhere,wecanobtainthefollowingvalues:
n=50(vehicles)
p(c)=0.6
p(m)=0.4
Sincethereare15bluecarsoutofall30cars, p(b|c)=0.5
Sincethereare5bluemotorcyclesoutof20all motorcycles, p(b|m)=0.25
Ifwesubstituteinthesevalues, p(c|b)= 50 0.6 0.5 50 0 6 0 5+50 0 4 0 25 =0 75 =75% (5)
2.3GeneralFormula
Amoregeneralformulawithstandardisednotations canrepresentasimilarsituation.Rememberthatweare usingtheconceptofhypothesis(representedasH)and
Evidence(meaningthenewlyintroducedinformation, representedasE).
p(c|b)= n (H) P (E|H) n (H) P (E|H)+ n P (¬H) P (E|¬H) (6)
where
p(H|E)=Theprobabilitythatthehypothesis holds given thattheevidenceistrue(thisisthesame astheprobabilityofchoosingabluecaroutofall blue vehicles)
n=Thetotalnumberofcases
p(H)=Thepriorprobability(notgiventhenew evidence)ofthehypothesis
P(E|H)=Theprobabilitythattheevidenceholds given thatthehypothesisistrue(theprobabilityof choosingabluecaroutofallcars)
¬H=Whenthehypothesis isn’t true(themotorcycles,sincetheyarenotcars)
Thetotalnumberofvehicles n canbedividedfor boththenumeratorandthedenominator.Fromhere, theexpressionleftinthedenominatorcanbereplaced byp(E),since
p(E)=Thetotalprobabilityofseeingtheevidence (theprobabilityofchoosinga bluevehicle)
Hence,amoresimplifiedformulaoftheBayes’theoremwouldbe
portfolios.Numerousfactorsareaccountedforin thecalculations,hencetheyallcorrespondtothe ‘evidence’oftheBayes’theoremwhichmodifiesthe probabilities.
3. MedicalDiagnosis:Basedonpriorknowledge andtestoutcomes,theprobabilityofbeingacertain diseaseoraconditioncanbecalculatedbymatching withthepatient’ssymptomsandtestresults.
3Linktopsychology 3.1KahnemanandTversky’sexperiment In2011,DanielKahneman,awidelyacclaimedpsychologist,publishedthebook Thinking,FastandSlow whichdiscusseshumandecision-makingandrationality basedonhissetofpsychologicalexperimentsthat showedthathumanintuitionisimperfect.Heclaimed thatthechoicesandjudgementsahumanmakescan deviatefromthenormativestatisticalmodels,which canoftenresultinirrational,nonstatisticalandflawed decisions.
OneveryfamousexperimentKahnemanandhis partnerAmosTverskyconductedwastogiveabrief descriptionofamannamed Steve
“Steve isvery shyandwithdrawn,invariably helpfulbutwithverylittleinterestinpeopleorthe worldofreality.A meekandtidy soul,hehasaneed fororderandstructure,andapassionfordetail.Is Stevemorelikelytobea librarian ora farmer ?”
Afterhearingthisdescription,mostansweredthat Steve ismorelikelytobea librarian.Whenquestioned why,thetwomostpopularreasonswerethetwo descriptivephrasesabouthim:‘shyandwithdrawn’ and‘meekandtidy’.Sincethesedescriptionsarelikely tobeassociatedmorewithastereotypicallibrarian thanafarmer,thisisdirectlyajudgementthat Steve ismorelikelytobealibrarian.
2.4Applications
Albeititssimplisticnature,Bayes’theoremisfrequentlyusedinvariousfieldsandistreatedasthe basisfordeterminingandcalculatingcomplexconditionalprobabilities.Somenotableapplicationsofthe Bayes’theoremareasfollows.
1. Spamfiltering:Althoughtheprocessrequires greatercomplexity,thebasisofidentifyingandremovingspamisbyspottingtheoccurrenceofcertainwordsorphrases,andthencalculatingthelikelihoodoftheemailbeingspambasedonthetrained dataset.
2. Financialforecasting:Historicmarketdataand economicindicatorsareanalysedtomatchand projectthepossibleoutcomeofanyinvestments, whicharetheninreturnusedtocreateinvestment
Butthisdecision,accordingtoKahneman,is irrational.Nearlyeveryonewhoparticipatedinthe experimentdisregardedthefactthattherearesignificantlymorefarmersthanlibrariansintheUnited States(wheretheexperimentwasconducted).The ratiobackthenwas20:1,whichshowsthatAmerican citizenswouldhavealreadyknownthedifferenceinthe numberoffarmersandlibrariansbutjustproceededto ignorethisknowledge.
Here,torationallydeterminethelikelihoodof Steve beingeitherafarmeroralibrarian,Bayes’theorem canbeused.The‘hypothesis’wediscussedbeforeis nowthepreconditionthatthereexist20timesmore farmersthanlibrarians,andthe‘evidence’whichalters theprobabilityisthelikelihoodofalibrarianora farmerbeing‘shyandwithdrawn’and‘meekandtidy’.
Whileitistruethatthesequalitiesarestereotypically associatedwithalibrarianmorethanafarmer,the initialhypothesismakesitextremelydifficultfor Steve tobemorelikelytobealibrarian.
For Steve,ameekandtidyman,tohaveanequal probabilityofbeingeitherafarmeroralibrarian,
Ifweassumethat all librariansare‘meekandtidy’, andthenumberof‘meekandtidy’farmersis x,
“Lindaisthirty-oneyearsold,single,outspoken, andverybright.Shemajoredinphilosophy.As astudent,shewasdeeplyconcernedwithissuesof discriminationandsocialjustice,andalsoparticipated inanti-nucleardemonstrations...”
Therespondentswereaskedtoranktheorderof likelihoodofLindabeing:
a)anelementaryschoolteacher
b)activeinthefeministmovement
c)abankteller
d)aninsurancesalesperson
e)abanktelleralsoactiveinthefeministmovement
Quitesurprisingly,85%oftherespondentsranked e)higherthanc).Althoughatfirstglancethismight feelreasonable,thiscompletelyignoresthebasicrules ofprobability:e,abanktelleralsoactiveinthefeminist movement,isasubsetofc,abankteller.Inotherwords, eventhoughafeministbanktellerstillisabankteller, mostpeoplemadetheirrationaldecisionofrankingit aboveabroaderterm.
Hence,whatthismeansisthatevenundertheextremecircumstancethatalllibrariansintheUnited Statesare‘meekandtidy’,for Steve tohavea50:50 chanceofeitherbeingalibrarianorafarmer,there shouldexistatmostonefarmerforeverytwentyfarmerswhoisrelevanttothedescriptionof Steve.Which, consideringthevariouspersonalitiesofdifferentpeople, isalmostimpossible.
3.2Humanmindandprobability
Atthispoint,onemightquestionwhetherthis psychologicalexperimentbecomesrelevantonlyand iftherespondenthaspriorknowledgeoftheratio betweenthenumberoflibrariansandfarmersinthe UnitedStatesatthattime.However,thisisnotthe focusofthisexperiment.Themostimportantpartis whethertheparticipanthasevenconsideredusingthis informationtoformhis/herjudgement.Withouteven accountingforapieceofinformationthatcanseverely changetheanswer,itiscorrecttosaythatinmaking decisionsforthesetypesofquestions,we,ashumans, areirrational.
Butdowealwaysmakeirrationaldecisions?Or, aretherecertainmomentswherebiaseskickinwhen makingdecisions?
Onewayourintuitionofprobabilitychangesisin thelanguageandhowwerepresentaprobability.
Considerthisexamplefromanotherexperiment conductedbyKahnemanandTversky.
Fig.5:Venndiagramofthetwooccupations
Butwhenthequestionwasrephrased,noonemade thesamemistake.
“100peoplefitthisdescription.Howmanyare:”
a)Banktellers?_outof100
b)Banktellersandactiveinthefeministmovement?_outof100
Eachrespondentputalargernumberforathan b,whichwerecorrectdecisionstakingintoaccountthe factthatfeministbanktellersareasubsetofbank tellers.
Althoughwecananalysethisdrasticdifference injudgementsusingvariouspsychologicalfactorslike whatKahnemanandTverskydid,asimplerfocuscan bemadetowardshowprobabilityisrepresentedineach case.
Itisundeniablethatgraphicalmethodsofrepresentingprobabilitiesarebyfarthemostintuitive
method,andbyusingthis,itisveryunlikelythata personwouldfallintothe‘trap’likewhatKahneman andTverskyhadsetupforbothexamples Steve and Linda.Onthecontrary,thereisatendencyforphrases thatdonotincludeanydefinitenumericalvalueslike ‘morelikely,’,or‘haveagreaterlikelihoodof...’to causepeopletohaveblindnessoveranystatistical factorsthatshouldhavebeentakenintoaccountto maketheirdecisions.
Afterall,anycalculationsorevenroughestimates givenaconditionalprobability(whichrequiresBayes’ theoreminourheads)aremadeafterrealisingboththe ‘hypothesis’andthe‘evidence’,notwhenthefocusis madeononlyoneofthem.
4Conclusion
Throughthisarticle,wefirstinvestigatedwhat Bayes’theoremisanditsapplications,withanextensionintotherelationshipbetweenthehumanmind andprobability.AlthoughBayes’theoremlookscomplicatedfromtheoutside,itisasimplecalculationwe makeinourheadswhenencounteringanyconditional probability.Butassaidinsection3,thesecalculations donotoccurwhenwecannotrecognisethatthereare boththehypothesisandtheevidencetoaproblem, withsometimesonehiddeninthephrasingwhich hindersusfrommakingrationaldecisionsintheend.
Hence,thenexttimeyouencounteranyproblems orsituationsthatsuspiciouslyguideyoutowardsone choice,rememberthatyoumightberestrictingyourselffromthebroaderperspectivethatcancompletely transformyourfinalchoice.Youdon’twanttorepeat thesamemistakeyouhavemadefor Steve!
5Bibliography
1. StanfordEncyclopediaofPhilosophy(2003).Bayes Theorem.[online]plato.stanford.edu.Availableat: https://plato.stanford.edu/entries/bayes-theorem/ 2. Tversky,A;Kahneman,D.(1974).JudgmentunderUncertainty:HeuristicsandBiases.[online]psych.ubc.ca.Availableat: https://www2.psych.ubc.ca/schaller/Psyc590Re adings/TverskyKahneman1974.pdf
3. Kuter,K.(2021).ConditionalProbabilityand Bayes’Rule.[online]libretexts.org.Available at:https://stats.libretexts.org/Courses/SaintMary’s-College-Notre-ame/MATH-345Probability(Kuter)/23A-ComputingProbabilities/2.23A-Conditional-Probabilityand-Bayes’-Rule
CryptographyandFermat’sLastTheorem Minseong(Eric)Ko
Year10
Email:msko28@pupils.nlcsjeju.kr
Editor Junseok(Jayden)Lee
RecommendedYearLevel:KS4
Keywords:Fermat’sLastTheorem,NumberTheory, Cryptography
1Introduction
Onemighthavewonderedhowmathematicsisused incryptography.Inordertoknowthat,thestorybegins 400yearsago.
“Itisimpossibleforanynumberwhichisapower greaterthanthesecondtobewrittenasasumoftwo likepowers.Ihaveatrulymarvelousdemonstration ofthispropositionwhichthismarginistoonarrowto contain.”Thisenigmaticwordscribbleddownin1637by PierredeFermatgaverisetooneofthemostinfuriating brainteasersinthedevelopmentofmathematics:Fermat’sLastTheorem.Accordingtothetheorem,forany integervalueof n> 2,theredon’texistthreepositive integers x, y and z suchthat:
reasoning.Witheachfailedattempt,themystiqueof thetheoremgrewtohintathiddenconnectionsbetween apparentlyquitediverseareasofmathematics.
Thisdeceptivelysimplestatement,ageneralization ofthePythagoreantheorem,willbewitchmathematiciansforoverthreecenturies.Fermatpuffedthathe possesseda"trulymarvelousdemonstration,"butone cannotbecertainthatheeverdidhavesuchademonstration.Intheend,hischallengeencouragedcenturies ofmathematicianstopushthelimitsofnumbertheory.
2EarlyProgress ThebeautyofFermat’sLastTheoremwasbuta partoftheinnocuous-soundingstatementwithwhich itfacedresistanceuntilitsproofwasfound.Itshonelike abeacon,luringbrilliantmindsdeepintomathematical
TheproofofFermat’sLastTheoremwasindeed ajourneyofwho’swhoinmathematicalhistory.The proofbroughtinnewinsightsintothesurprisingdepth andcomplexityofthistheoremonebyone.Fermat himselfprovedthecasefor n =4 byusinghismethodof infinitedescent.Thistechniqueinitseleganceandsimplicitywouldproveinfluentialinmanylaterattempts. Thecaseof n =3 wastreatedbyLeonhardEuler,the indefatigable18th-centurymathematician,whoseproof, althoughitcontainedgapsthatwerelaterfilledbyothers,showedthatthetheoremwasresistanteventothe greatestmindsoftheage.Theearly19thcenturysaw abrilliantbreakthroughbySophieGermain.Herwork onprimenumberslaidthegroundtoprovethetheorem foraninfiniteclassofprimeexponents.Germain’stheoremstandsasatestamenttoperseveranceintheface ofsocietalbarriers,assheinitiallyhadtoworkundera malepseudonymtobetakenseriouslyinthemathematicalcommunity.ErnstKummer’swork,inthemiddle ofthe19thcentury,generalizedthistothetheoryof idealnumbers,whichallowedforuniquefactorization incertainnumberfields.Thisasastrongtool,infact, enabledKummertoproveFermat’sLastTheoremfora largeclassofprimeexponentsandbroughtmathematicianstantalizinglyclosetoageneralproof.
3BreakthroughsinEllipticCurvesandModularForms TheproofofFermat’sLastTheoremhadacompletelysurprisingbreakthrough:thetheoryofelliptic curvesandmodularforms.Thesolutionopeneddoors tocenturies-oldproblems.However,thisparticularcorrelationwastheonethatwasfirstperceivedtheother wayaround.YutakaTaniyamaandGoroShimura,two mathematiciansfromJapan,alongwithAndréWeil, putforwardafamoustheoryduringthe1950sthatcon-
nectedthetwoconcepts.Theyclaimedthatthemodularformwasaspecializedtransformationoftheelliptic formandthat a = y2 and b = x3 + ax + b
ThesevariablesbarenoresemblancetoFermat’s equationbutthefunctionalconnectioniswhatMathematicianslatercalledtheModularTheorem.Gerhard Freymadeastrongargumentin1984tobacktheclaim, statingthatifthetheoremwasproven,itwouldposeas asolutiontotheFermat’sLastTheorem.Hisevidence wasstrongasoneproblemwouldyieldmanysolutions andgivebirthtoaspecialtypeofellipticcurve.This specificcurve,knownasthemodulartype,wouldsolve manyotherequationssoifthetheoremwasprovenfalse, itwouldposeaproblemonitsown.In1986,KenRibet strengthenedthetheoryfurtherbyclaimingthatifthe ModularTheoremwasfalseforthatclassofcurves,it wouldstrengthenFrey’sargument.
EnterAndrewWiles,whosinceagetenhadbeen captivatedbyFermat’sLastTheorem.Wile’sintuitiontoldhimthatinRibet’sworktherewassomethingworthbuildingaproofoftheModularityTheoremforsemistableellipticcurves.Thenheworkedfor aboutsevenyearsinnear-secretconditions,combining techniquesthatcamefromalgebraicgeometry,number theory,andcomplexanalysisinwaysnobodyhadpreviouslydone.TheannouncementoftheproofbyWilesin 1993sentshockwaveswithinthemathematicalcommunity.Whileagapindeedwasfound,Wiles,alongwith hisformerstudentRichardTaylor,fixedthegapina year.Thefullproof,publishedin1995,provedmuch morethanFermat’sLastTheorem;itmarkedconsiderableadvancesinalgebraicnumbertheoryandarithmeticgeometry.
4Fermat’sLastTheoremandCryptography WhileFermat’sLastTheoremitselfdoesn’thavedirectapplicationsoutsideofpuremathematics,thetools developedforitsproofdohavesurprisingusefulnessin theworldofcryptography.Thestudyofellipticcurves isattheveryheartoftheproofbyWilesandnowadaysformsthegroundforsomereallysecureencryption methods.TheideabehindECCisthatit’spublic-key cryptographythatbasesitsfoundationonthealgebraic structureofellipticcurvesoverfinitefields.
Itfindsitsresistanceonthehardnessassumptionof theECDLPproblem,whichisconsideredtobemuch intractablethantheintegerfactorizationproblem,used inthetraditionalRSAcryptography.InECC,thepublickeyisapointontheellipticcurve,whiletheprivate keyissomerandomnumber.Inotherwords,thepublickeyisobtainedbymultiplicationoftheprivatekey withageneratorpointonthecurve.Thestrengthof ECCliesinthefactthatwhileitisrelativelyeasyto performthismultiplication,it’scomputationallyinfeasibletodeterminetheprivatekeygiventhepublickey andthegeneratorpoint.TheadvantagesofECCover traditionalcryptographicsystemsareasfollows:
Smallerkeysizes,whereinforthesamestrengthof thekey,ECCcanhaveverysmallkeysizescomparedto RSA.Forinstance,a256-bitECCkeywouldhavecomparablesecurityasthatofa3027-bitRSAkey.Faster computationsduetothesmallerkeysizeresultinlow powerconsumption,whichmakesECCverysuitablefor resource-constraineddevicessuchassmartphonesand IoTdevices.
Bandwidthefficiency:
ThekeysizeandsignatureinECCaremuch smaller,reducingbandwidthusage;hence,thisisuseful overnetworkcommunication.
Thesebenefitscomewithareason,whichiswhy mostsecurityprotocolsandsystemsareusingittoday:
TransportLayerSecurityorTLS:
MostwebsitesnowuseECCaspartoftheirTLSto establishsecureHTTPS.
Bitcoinandcryptocurrencies: Bitcoinprotocolemploysthe"secp256k1"elliptic curveinitspublickeycryptography.
Fig.1:TheSecp256k1EllipticCurve
SecureShell(SSH):
OpenSSHsupportsECCforkeyexchangeanddigitalsignatures.Governmentsystems:TheNSAhasrecommendedECCtoprotectclassifiedinformation.
5Conclusion
TheresolutionofFermat’sLastTheoremisoneof thegreattriumphsofmathematicsinthe20thcentury.Notonlydiditsealapageoutofmathematics book,butdoorsfornewinvestigationswereopened,and deepconnectionsbetweenseeminglyrelativelydisparate branchesofmathematicswererevealed.
FromFermat’smarginalnotetotheproofgivenby Wiles,centuriesofmathematicaldevelopmentwereinvolvedinnumbertheory,algebraicgeometry,andcomplexanalysis.Itwasatestimonytothewaymathematicsprogressesingeneral:eachgenerationelaborateda bitfurtherwherethepreviousonehadstopped.
Theunexpecteduseofellipticcurvesinthenewer formsofcryptographyisagainmerelyafurtherinstanceoftheways-sometimesentirelyunexpected-in which‘pure’mathematicspaysitsdividend.Continue aswemayintothefrontiersofmathematics,wecanonly speculatewhatotherdeepinterconnectionsandapplicationswillbeuncovered.
Fermat’sLastTheoremisareminderofthepersistenceofmathematicalcuriosityandthefantasticinsightsthatmayresultfromwhat,atfirstglance,was apparentlyanabstractproblem.Itremainsasinspirationforbothmathematiciansandscientistsintackling, withpersistencecreativity,andaspiritofcollaboration, problemswhichmostresistsolution.
Butintheend,Fermat’sLastTheoremisatale notsomuchofamathematicalstatementbutrather ofhumaningenuity,beauty,andevenunexpectedfruits thatarisethroughthemathematicalargumentationof abstractconceptionsaboutrealityandourtechnological capabilityintheworld.Fromahumblemarginalnoteto theverybedrockofmoderncryptography,Fermat’sLast Theoremhascontinuedtobeguileandchallengeusein itsinvitationtotheendlessfrontiersofmathematical discovery.
6Bibliography
1. “WhatIsEllipticCurveCryptography?Definition FAQs.”VMware,www.vmware.com/topics/ellipticcurve-cryptography.Accessed23Jan.2025.
2. “Fermat’sLastTheorem.”Wikipedia, WikimediaFoundation,21Jan.2025, en.wikipedia.org/wiki/Fermat
3. CryptographyandFermat’sLastTheorem,ieeexplore.ieee.org/document/10315806.Accessed23 Jan.2025.
4. Broad,WilliamJ.“MathThatHelped SolveFermat’sTheoremNowSafeguards theDigitalWorld.”TheNewYorkTimes, TheNewYorkTimes,31Jan.2022, www.nytimes.com/2022/01/31/science/fermatelliptic-curves-encryption.html.
5. Dawar,Harshit.“Fermat’sTheoreminItsCore!” Medium,AnalyticsVidhya,17Oct.2020,
ArithmeticSequenceandGeometricSequencein Music SeohyunJey Year8
Email:shjey30@pupils.nlcsjeju.kr
Editor
SoulPark
RecommendedYearLevel:KS3
Keywords:Arithmeticsequence,Geometricsequence, Frequency,Octave
1Introduction
Thestructureofamelodyoftenfollowssequences, particularlyarithmeticorgeometricsequences.Forinstance,whenamelodyrepeatsorchangesatspecific intervals,thoseintervalsformasequence,whichplaysa crucialroleincontrollingthepredictabilityandmusical tensionofthemelody.
2Definition
2.1ArithmeticSequence
Anarithmeticsequenceinvolvesaseriesofnumbers whereeachtermincreasesbyaconstantdifference.In musicalterms,thisconceptisexemplifiedintheharmonicseries,whereeachovertoneisanintegermultiple ofafundamentalfrequency.
Fig.1:FundamentalFrequency
2.2GeometricSequence
Ageometricsequenceconsistsofnumberswhere eachtermismultipliedbyaconstantratio.Inmusic,thisisobservedintherelationshipbetweenpitches acrossoctaves.
Here, an representsthe n-thtermofasequence, a1 isthefirstterm, d denotesthecommondifference(forarithmeticsequences),and n indicatesthepositionoftheterminthesequence.
Thissequence(f, 2f, 3f, 4f,... )representsanarithmeticprogressionwhereeachtermincreasesbythefundamentalfrequency f .Theseharmonicscontributeto thetimbreofmusicalinstruments,enrichingthesound byaddingovertonesatintegermultiplesofthefundamentalpitch.
Here, an representsthe n-thtermofasequence, a1 isthefirstterm, r denotesthecommonratio(for geometricsequences),and n indicatesthepositionof theterminthesequence.
Ifanotehasafrequencyf,thenoteoneoctave higherhasafrequency 2 f
Twooctaveshigher: 22 f =4f
Threeoctaveshigher: 23 f =8f
Thissequence(2f, 4f, 8f,... )formsageometric progressionwithacommonratioof2.Thisexponentialrelationshipdefineshowpitchesareperceivedand organised,ensuringthateachoctavespansafrequency rangethatdoublesthepreviousone.
a
2.3InterplayBetweenArithmeticandGeometricSequences
Theinteractionbetweenthesesequencesisfundamentaltomusicalharmonyandscaleconstruction. Whiletheharmonicseries(arithmetic)definestheovertonestructureofasinglepitch,theoctaverelationships (geometric)determinehowthesepitchesarespaced acrossthemusicalspectrum.
2.3.1ExampleQuestion Amusicianiscomposingapiecebasedona sequenceofnotesandwantstocombinearithmeticand geometricprogressionstocreateauniquemelody.The musicianstartswithanoteat 200Hz (A3).
• Eachsuccessivenoteinthe arithmeticsequence increasesby 55Hz forthefirst4notes
• Afterthe4thnote,a geometricsequence is applied,wheretheratiobetweensuccessivefrequencies is 3 2 (perfectfifthinterval)
1.Writethefrequenciesofthefirst8notesinthe sequence.
2.Determinewhetherthefinalfrequencyiswithin thesameoctaveasthestartingfrequency,assumingan octavedoublesthefrequency.
Theformulaforthe n-thtermofanarithmetic sequenceis: an = a1 +(n 1)d
• a1 =220Hz
• a2 =220+(2 1) · 55=220+55=275Hz
• a3 =220+(3 1) 55=220+110=330Hz
• a4 =220+(4 1) · 55=220+165=385Hz
Thefirst4notesare: 200Hz, 275Hz, 330Hz, 385Hz
Theformulaforthe n-thtermofageometric sequenceis: an = a1 rn 1
Here, g1 =385Hz (lastnoteofthearithmetic sequence),and r = 3 2
• g1=385Hz
• g2 =385 · ( 3 2 1)=385 · 1 5=577 5Hz
• g3 =385 ( 3 2 2)=385 2.25=866.25Hz
• g4 =385 ( 3 2 3)=385 3 375=1299 375Hz
Thefirst4notesare: 385Hz, 577 5Hz, 866 25Hz, 1299.375Hz.
Itisnotwithinthestartoctave.Anoctavedoubles thefrequency.Thestartingfrequencyis220Hz.The octaveboundariesare:
• 220Hz to 440Hz :A3toA4
• 440Hz to 880Hz :A4toA5
• 880Hz to 1760Hz :A5toA6
• 220Hz :A3(originalpitch)
• 275Hz :A3
• 330Hz :A3
• 385Hz :A3
• 577 5Hz :A4
• 866 25Hz :A4
• 1299 375Hz :A5
2.3.2ActualExamplesinMusicHistory
ClassicalExamples:Bach’s“PreludeinCMajor” featuresascendingsequencesthatbuildintensityand leadthelistenerthroughintricatemelodicdevelopment. Vivaldi’s“Winter”fromTheFourSeasonsshowcasesdescendingsequencesthatreplicatefallingsnow andenhancethethematicelementsofthepiece.
ModernExamples:TheBeatles’’LetItBe’incorporatesascendingsequencesinthepianoaccompaniment, addingemotionalupliftandreinforcingthesong’shopefulmessage.
Radiohead’s“KarmaPolice”employsadescending sequenceinthechorus,creatingasomber,contemplativemoodthatcomplementsthelyrics.
3Conclusion Arithmeticsequencescandefinerhythmicpatterns, melodicprogressions,orharmonicstructures.Besides, geometricsequencesarefundamentalintuningsystems andpitchrelationships.Bothconceptshighlightthe profoundrelationshipbetweenmusicandmathematics, providingcomposersandperformerswithtoolstocreate structuredandharmonicallyrichmusic.
4Extension Hereareadditionalexamplesofhowalgebraic mathematicsareappliedinmusic.Mathematicsplaysa significantroleinvariousaspectsincludingmusic,where ithelpsstructureandenrichcreativeprocesseslikemusiccompositionandanalysis.
4.1Transformation
Inmusic,transformationsallowamelodyormotiftobedevelopedandvariedwhileretainingitscore identity.Thesetransformationsareakintoalgebraicoperationsinmathematics,whereabasicformisaltered accordingtoaspecificrule.Here’sadeeperlookinto eachtypeoftransformation:
4.1.1Transposition
• Definition:Transpositioninvolvesshiftinga melodyormotifupordownbyaspecificinterval.This doesnotchangetheinternalrelationshipsbetweenthe notesbutchangestheirabsolutepitch.
• MathematicalView:Ifthemelody’snotesarerepresentedas{x1,x2,x3,... }thenatranspositionbyan intervalresultsin{x1 + k,x2 + k,x3 + k,... }
• UseinMusic:Transpositionisessentialinmodulation(keychanges),makingamotifadaptabletodifferentharmoniccontexts.
4.1.2Inversion
• Definition:Inversionflipsamelodyaroundacentralaxis,effectivelyreversingthedirectionofeachinterval.Ascendingintervalsbecomedescendingonesand viceversa.
• MathematicalView:Ifthemelody’snotesare {x1,x2,x3,... }inversiontransformsthemto{c x1,c x2,c x3,... }wherecistheaxisofsymmetry.
• UseinMusic:Inversioncreatescontrastwhile maintainingaconnectiontotheoriginaltheme.It’s commonincounterpointandfugues(e.g.,J.S.Bach).
4.2Symmetry
Symmetryinmusicreferstothebalanceandproportioncreatedwhenonesectionofamelodymirrors orcomplementsanother.Thiscanbeachievedthrough reflectiveorrotationalsymmetry.
4.2.1ReflectiveSymmetry
• Definition:Reflectivesymmetryoccurswhenone partofamelodymirrorsanotherpartacrossacentral axis.
• MathematicalView:Ifthemelody’snotes are{x1,x2,x3,... }reflectivesymmetrycreatesanew melody{xn,xn 1,xn 2,... }
• UseinMusic:Reflectivesymmetryenhancesbalance,oftenusedincompositionslikepalindromicstructures(e.g.,Bartók’s"MusicforStrings,Percussion,and Celesta").
4.2.2RotationalSymmetry
• Definition:Rotationalsymmetryinvolvesrepeatingamelodyormotifincycles,butstartingatdifferent points,similartorotatingashapeingeometry.
• UseinMusic:Rotationalsymmetrycreatesvariationwhilepreservingthecoreidentityofthemelody, commonlyseeninminimalism(e.g.,SteveReich’s works).
5Bibiliography
1. CMUSE."ClassicalPieceswiththeGoldenRatio." CMUSE,www.cmuse.org/classical-pieces-with-thegolden-ratio.
2. ProMusicianHub."WhatIsSequenceinMusic?" ProMusicianHub,promusicianhub.com/what-issequence-music/.
3. AudioApartment."SequenceinMusic:MusicTheoryandComposition."AudioApartment,audioapartment.com/music-theory-andcomposition/sequence-in-music/.
4. Fiveable."Motive,MotivicDevelopment,andPitchTransformation."Fiveable,library.fiveable.me/ap-music-theory/unit6/motive-motivic-pit-transformation/studyguide/z0DJQvgjoByphnhSnztH.
5. Vaia."MusicalSymmetry:Music Composition."Vaia,www.vaia.com/enus/explanations/music/musiccomposition/musical-symmetry/.
Volume5,Issue1
MathematicsSociety MathematicsPublicationCCA
April2025