
VOL. 4 | ISSUE 1 | 2024 MAR
THE NLCS JOURNAL OF URE AND PPLIED MATHEMATICS
P A
Volume4,Issue1
MathematicsSociety
MathematicsPublicationCCA
March2024

PureandAppliedMathematics
TheNLCSJejuJournalof
Credits
Firstofall,wewouldliketoexpressoursinceregratitudetothefollowingcontributorstoVolume4Issue1 ofNLCSJejuAnnualJournalofMathematics.
TheMathematics Society
Chair
EmmaChaeeunChung(12)
TerryTaehoonKim(12)
PublicityOfficer
DerekYejunYoo(11)
Secretary
SuhyukJeffCho(11)
JuneKim(12)
JeanKim(12)
Members
AshleySiyeonJung(9)
AustinTaehongHa(11)
ChloeNayeonKim(10)
CollinYoungjaeSeo(10)
DavidSeohaKim(9)
JamesChoisungPark(10)
JamesJiminLim(11)
JaydenJunseokLee(10)
JungseoPark(10)
LukeJungyoonHan(12)
LynnKim(10)
MaxMinjaeKo(10)
MinjaeKang(9)
PeterSeunghyeonKim(10)
RyanHanjinLee(11)
SeanTaehoonKim(11)
SeongminHong(11)
SiwoolUm(10)
TimofeiKudinov(11)
TonyXinhengLi(9)
LinkTeachers
MsDuyguBulut
MrWilliamHebbron
LATEXEditors&Managers
EmmaChaeeunChung(12)
DerekYejunYoo(11)
RyanHanjinLee(11)
JaydenJunseokLee(10)
AustinTaehongHa(11)
SeanTaehoonKim(11)
Also,wewouldliketothankthefollowingcontributorsthatarenotpartofthemathematicssocieties,but haveassistedusinvariousways.
MarketingDepartment forhelpinguswiththeprintingandpublicizingourjournal. MrTamlyn forcoordinatingsocietiesinourschool.
© CopyrightbytheNLCSJejuJournalofPureandAppliedMathematics FormattingbyEmmaChaeeunChung(’25)
EditedbytheJPAMEditingTeam
4
Editor’sNote
Thisisit:thefirstissueoftheJournalofPureandAppliedMathematics (JPAM)ofthe2023-2024academicyearisout!
FormembersoftheMathematicsSociety,ithasbeenanothermathematicallyenriching,unbelievablyeventful,andacademicallyfulfillingyear. Despitealltheupsanddowns,we’vebeenabletoproduceaninspiringfourth issueoftheschool’sofficialannualMathematicsJournal.Ourjournalshave beenlongregardedashigh-qualitypublicationswrittenbytheschool’smost enthusiasticstudentmathematiciansacrossadiverserangeofyeargroups, andwehopethisissuewillnotfailtomotivatestudents(andevenstaff!)to pursueorcontinuetheirjourneyinthebottomlessandfascinatingfieldof mathematicsyetagain.
Thisissueinparticularmaybeourmostambitiouspublicationupto thisdate.Over20studentwritershavecontributedtothisjournal,whomI wouldliketothankimmenselyfortheiroriginal,thought-provokingworks. Itisnoteasytoconductindividualresearchonanextra-curriculartopic,not tomentionmakeitdistinctivefromothers.Theyhaveworkedforanextensiveperiodofapproximately5months,somehowfindingthetimeamidst theirjam-packedacademicschedule,activelyacceptingthefeedbackfrom thesociety’sleadershipteam,andimprovingtheirarticlesinwayswecould notimagine.Welldone!
Itwouldbecriminaltoforgetoureditingteam,agroupoftirelessLatex expertswhohaveeditedandformattedevery.single.word.andequation. inthisjournal.Thiswasonlythesecondyearwerecruitedaformalteam ofeditors,andit’sgreattoseethataneditingteamisspeedingupthepublicationprocesstremendously.Workingbehindthescenesdoesn’talways comewithcompletecredit,andnonetheless,oureditingteamhasworked diligentlyandconsistentlywithoutcomplaints.They,infact,deservehuge creditfortheirmeticulouslabourandsleeplessenergy-drink-fuellednights. Itwaspersonallyagreatpleasuretoworkwiththem.Acosmicthankyou to:AustinHa,DerekYoo,HanjinLee,JaydenLee,andSeanKim.
Andabigthankyoutoourleadershipteam-Chairs,Secretary,and PublicityOfficer.Theyaretheoneswhoinitiatedthisprojectandmadeit happen.Overseeingtheprogressofthisprojectandofferingsupportforthe writers,theyhaveundoubtedlyplayedanintegral(mathpununintended) partinthispublication.
IwouldalsoliketoexpressmysinceregratitudetoMsBulutforoffering theMathematicsSocietyandJPAMunconditionalsupport.MsBuluthas themostcreativeideasandagenuinepassionformathsthatinspiresstudentseverywhere.ShehasdrivennotonlyJPAMbutalsotheMathsSociety towhereitisnow.
Additionally,thankyouAaronJoonseokKang(‘24)andJamesDaewoongKang(‘24),formerleadersoftheMathematicsSociety,fordeveloping astrongfoundationforJPAM,helpingwithediting,andasmoothhandover.
Lastbutnotleast,YOU,thereader!Youarethereasonwhywecreate JPAM.
Havefunreading!
EmmaChaeeunChung -ChairofAppliedMathematics, LeaderoftheJPAMEditingTeam
Contents PureMathematics8 1TypesofMean AshleySiyeonJung(Y9) 9 2BoundsontheRamseyNumbers AustinTaehongHa(Y11) 12 3Pascal’sTriangleandCombination ChloeNayeonKim(Y10) 14 4SetTheory CollinYoungjaeSeo(Y10) 16 5Paradoxes DavidSeohaKim(Y9) 19 6Howtosketchanyfunctionstepbystep DerekYejunYoo(Y11) 23 7MathematicsBehindRubik’sCube JamesChoisungPark(Y10)27 8EigenvaluesofCirculantMatrices JaydenJunseokLee(Y10) 30 9ForecastingHighDimensionalSpace MaxMinjaeKo(Y10) 33 10PappusLine PeterSeunghyeonKim(Y10)35 11PiApproximation RyanHanjinLee(Y11) 38 12DivisionbyZero SeanTaehoonKim(Y11) 43 13TwinPrimesConjecture SeongminHong(Y11) 51 14FourierSeriesanditsApplicationinAtomicorbitals TerryTaehoonKim(Y12) 54 AppliedMathematics57 7
15MathematicalAnalysisoftheMechanismoftheGlobalPositioningSystem(GPS) EmmaChaeeunChung(Y12)57 16KMPAlgorithm JamesJiminLim(Y11) 61 17Penney’sGame JeffSuhyukCho(Y11) 67 18BlockchainandHashFunction JungseoPark(Y10) 69 19MathematicalModelandSimulationofSIRModelforCovid-19OutbreakinKorea LukeJungyoonHan(Y12) 73 20LotteryMathematics LynnKim(Y10) 78 21ThePrisoner’sDilemmaandNashEquilibrium MinjaeKang(Y9) 81 22MathinMinecraft SiwoolUm(Y9) 83 23MathematicsinSudoku TimofeiKudinov(Y11) 86 24ProbabilityinBlackjack TonyXinhengLi(Y9) 88 8
TypesofMean
Siyeon(Ashley)Jung Year9
Email:syjung28@pupils.nlcsjeju.kr
Editor
Derek(Yejun)Yoo
RecommendedYearLevel:KS3andabove
Keywords:ArithmeticMean,GeometricMean
1IntroductiontoArithmeticmean
1.1Whatisanarithmeticmean?
Itisafundamentalconceptinstatisticsandmathematics, anditisbetterknownasanaverageofasetofnumbers. Itcanbecalculatedbydividingthesumofacollectionof numbers.Ifthisisrepresentedusingaformula,itis
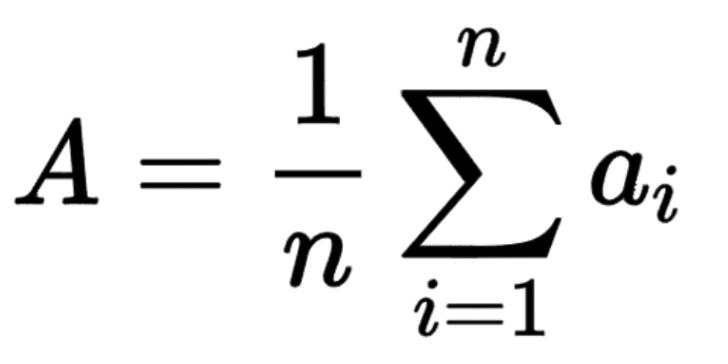
Whennisthenumberofvaluesandaiisthedatasetvalues. Aistheaverage(arithmeticmean).
1.2Typicalrepresentation
Insteadofusingtheformula,thereisasimpleformula forarithmeticmeanofasetthatcontainstwovalues:
a+b 2
Thisisfurtherrelatedtoothertypesofmean,andcanbe convenientlyusedwhenonlyrequiringtwovariables.
1.3Usesofarithmeticmean
Thisconceptiswidelyusedineverydaylife;calculatingaveragespeedwhiledriving,orthebattingaverageofa baseballplayer.Whenthereareextremedifferences(range) betweenthevalues,arithmeticmeanishugelyinfluenced, andmayproduceunsuitableresultsthatmaynotbeableto representthecollectionofdata.
2IntroductiontoGeometricmean
2.1Whatisageometricmean?
Geometricmeanisnotasfrequentlyusedasthearithmeticmean,butitisanotherwaytorepresentagroupof
data.Infact,itisatypeofaveragethat,inasetofnnumbers,multipliesallthevaluesandfindsthenthrootofthe product.
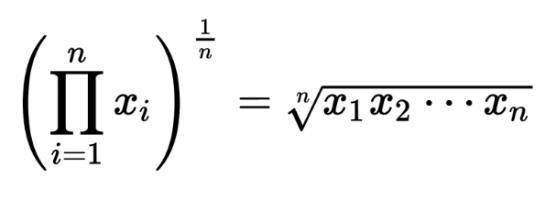
Thisistherepresentationofageometricmeanwhereisthe geometricmean,nisthenumberofvaluesintheset,andxi isthevaluestoaverage.
2.2Typicalrepresentation
Whenthereare2valuesinaset,thegeometricmeanof thatsetcanberepresentedusingthisformula:
√ab
Thiscanbemanipulatedandappliedtoaninequalitythat willbefurtherdescribedlater.
2.3Usesofgeometricmean
Geometricmeanissuitableforrepresentingasetof growthfiguresbecauseitconsidersthecompoundingthat occursfromtimetotime.Thiscanbeappliedtousessuch aspopulationgrowth,financialinvestmentportfolio,theannualexpansionoftheeconomyandevencalculatingtherise andfallofstockmarketprices.Oneadvantageofgeometricmeanisthatitisnotheavilyinfluencedbytheeffectof extremevalues.
2.4Arithmetic-geometricmeaninequality 2.5Idea
TheideaoftheAM-GM(arithmeticmean-geometric mean)inequalityisthatthearithmeticmeanofasetofnumbersisalwaysgreaterorequaltothegeometricmeanofit. Thisarticlecontainstheproofofwhythisisso,typically whentherearetwovaluesinthesetofnumbers.
2.6Proofbyalgebraicmethod
Therepresentationoftheinequalityis
9
a+b 2 ≥ √ab
andthisisthealgebraicmethodtoprovethe inequality.
a+b
2 ≥ √ab
a + b ≥ 2√ab
(a + b)2 ≥ (2√ab)2
a2 + 2ab + b2√4ab
a2 2ab + b2√0
(a + b)2 ≥ 0
∴ a+b 2 ≥ √ab
Here,sinceaandbarerealnumbers,thefinalinequalityis true.ThereforetheAM-GMinequalityisalwaystrueaslong asthetwovaluesaandbarepositiverealnumbers.
2.7Proofbygeometricmethod
Thereisanotherproofthatusesacircleanditsradius. Beforewegettotheproof,readersshouldbefamiliarwith theconceptoftherelationshipbetweenthehypotenuseand theheightofarightangledtriangle.Imaginethataperpendicularline,representingtheheight,isdrawnfromtheright angletothehypotenuseinarightangletriangle.Inthissituation,theproductofthetwosections,dividedbytheheight, isequaltothesquareoftheheight.Usingthisapplication, letusproceedtothegeometricalproofoftheAM-GMinequality.
Thisisanimagefromamathematicalbookcalled “Proofswithoutwords”,writtenbyRogerB.Nelsen.
Source:Nelsen,R.B.,“Proofswithoutwords”
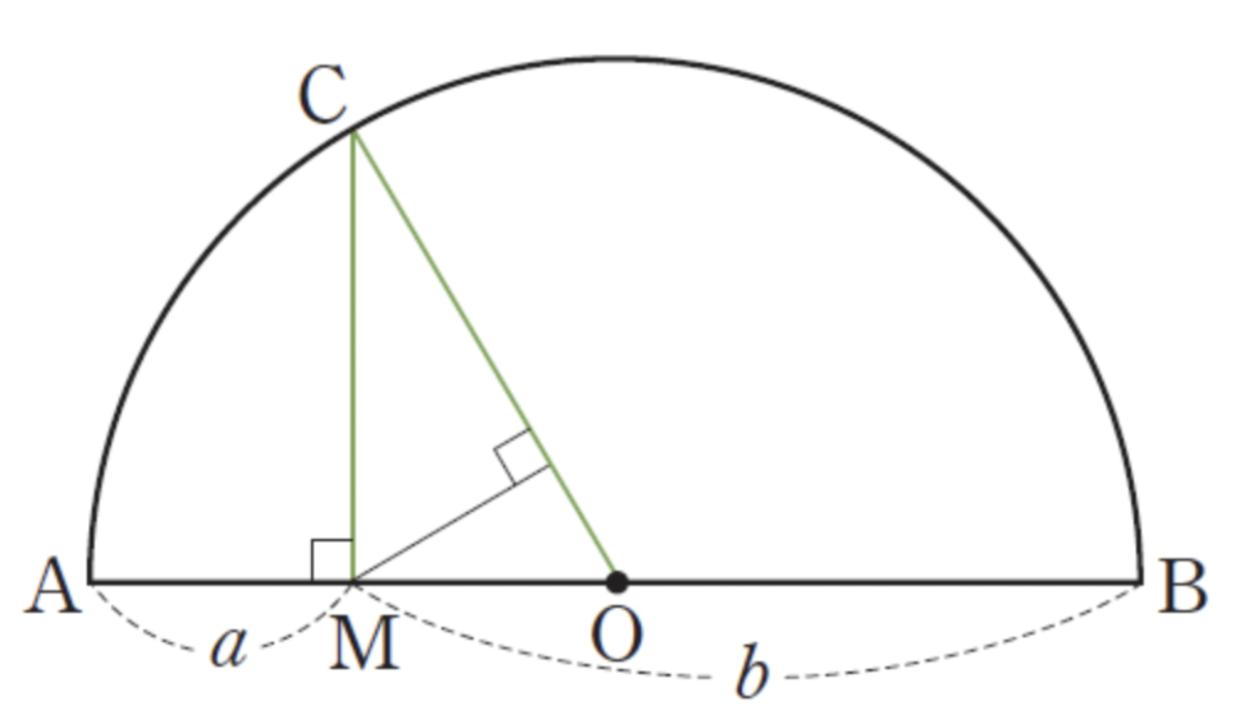
Asmentionedabove,thediameterofthesemicircleis AB,andsincetheinscribedangleofasemicircleisalways 90degrees,triangleABCisalwaysarighttriangle.Then, thesquareofCMisequaltotheproductofAMandBM, whichisab.Ifthisisrearranged,CMisequaltothesquare rootoftheproductofAMandBM(sincelengthispositive), whichis √ab.Becausethediameteris a + b,itisevident thattheradiusis a+b 2 .SincethelargestCMcanbeisthe radius, a+b 2 ≥ √ab istrue.Additionally,aslengthisalways apositivenumber,theinequalitysolelyistruewhenthetwo numbersarepositive.Theequalsigncomestruewhena=b, whichisalsowhenCMisequaltotheradius,andaandbare eachequaltothelengthsoftheradius.
3AM-GMInequalityinreal-lifecontext
3.1BasicQuestion question
Given x > 0, y > 0andxy=3,findtheminimumof 4x+3y.
solution
Since x > 0, y > 0,referringtotheAM-GMinequality, 4x + 3y ≥ 2√36 = 12(Theequalsignisappliedonlywhen 4x=3y)Hence,theminimumof4x+3yis12.
3.2AdvancedQuestion question
Usinga60cmwire,fourcongruentrectanglesare formedlikethediagrambelow.Findthemaximumareaof thelargestrectangleandthecorrespondinglength.

solution
Letthelengthandthewidthofthelargestrectanglebex cmandycmrespectively.Then,theareaofitwillbe xycm2 Sincethetotallengthofthewireis60cm,2x + 5y = 60
As x > 0and y > 0,usingtheAM-GMinequality, 2x + 5y ≥ 2√2x ∗ 5y = 2√10xy,60 ≥ sqrt10xy, 30 ≥ 10xy Hence,xy90(theequationistruewhen 2x=5y)Consequently,themaximumofthearea oftherectangleis90cm2.Theareaofthelargest rectangleisthebiggestwhen2x=5y,sosubstituting2x=5yinto2x+5y=60,2x+2x=60,x=15Thus, thelengthis15cmwhentheareaismaximum.
4Outro
4.1Conclusion
Inthispieceofarticle,youhavelearnedabout thetwomajortypesofmean,andtheequationthat canbeobtainedusingthetwo.Therewerereal lifeexamplesthatcouldhelpreadersunderstand howthesecanbeused.TheAM-GMinequalityis provenusingvariousmethods,i.e.,geometricand arithmetic,anditcanbemanipulatedforfurther usessuchascalculatingtheideallengthforaminimumprice,etc.
Iappreciateyoureadingthisarticlewithpatience.Ihopeyoulearnedsomethingthatinterestedyou,andperhapsyoucouldusethisopportunitytoexploremoreaboutthistopic.Ifyouwant
10
toresearchaboutthisfurther,Irecommendyou findthecorrelationbetweentheAM,GMandHM ofaset.HMistheharmonicmean,anditisnot asfrequentlyusedasAMandGM.However,it wouldbegreatandhighlyadvancedifyoucould provetherelationshipbetweenthethreetypesof mean.Remember,learningisatreasurethatwill followitsownereverywhere.Thankyou.
11
BoundsontheRamseynumbers
Taehong(Austin)Ha Year11
Email:thha26@pupils.nlcsjeju.kr
Editors
TaehongAustinHa, Emma(Chaeeun)Chung
RecommendedYearLevel:KS4,KS5
Keywords:Ramsey’stheorem,Ramsey’snumbers
1WhatisRamsay’stheoremandRamsay numbers?
Ramsay’stheoremstatesthatonewillfind monochromaticcliquesinanyedgelabellingofasufficientlylargecompletegraph.
Insimpleterms,itmeansthattherewillalwaysbe aminimumnumberofnodes(points)allinterconnected toeachotherthatacertainsetofnodesthatareall interconnectedwiththesamelabel(colourorstate).A ramseynumberistheminimumnumberthatthiscertainsizeofasetmustbepresent.
AfamousexampleofaRamsaynumberisR(3,3).
TheRfunctionistheramseyfunctionthatgeneratestheramseynumbergivenacertaininput.(Inthis article,wewillbeonlydiscussingtheramseynumber with2inputsbutpleasenotethatitcanextendtoany numberofinputs.)
Thefirst3representsthattherewillbeasetofthree nodesthatareallconnectedtoeachotherwithstate1 connections.(Atriangle)
Similarly,thesecond3representsasetofthree nodesthatareallconnectedtoeachotherwithstate 2connections.
ValueR(3,3)meanstheminimumsetofnodesthat hasatleastonetrianglewithallstate1connectionsor state2connections.
EvaluatingR(3,3)ismorewellknownastheparty problemphrasedas‘Ifyouthrowaparty,howmany peopleensuresthat3peopleknoweachotherornot knoweachother?”
Thevalueiselegantlyprovedtobe6.Here’sthe proof;
Sofor5nodes,theouterconnectionscanbe colouredinred(state1).Andthestarshapeddiagonals canbecolouredblue(state2).Therearenotriangles formed.
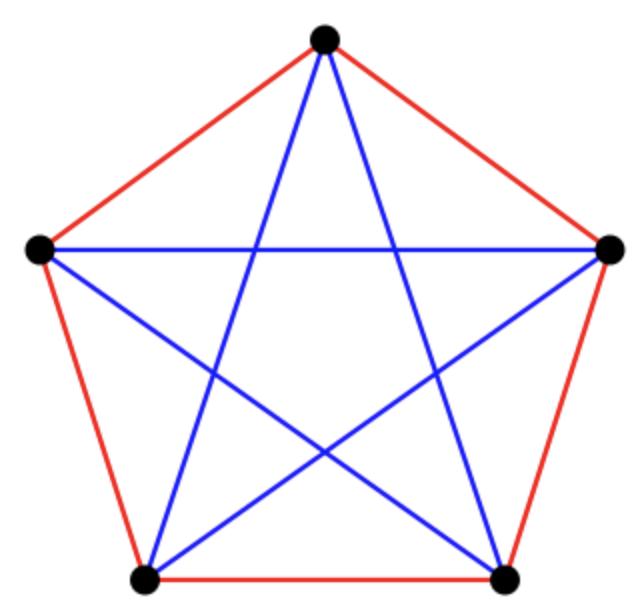
However,for6nodes,theremustbeatriangle. Imaginefromtheperspectiveofanode.Ofthe5nodes connectedtoit,theremustbeatleast3redconnects or3blueconnections.Takethemajority.Ofthe3 connections,the3othernodesmustbecolouredoppositecolourstoitsconnectwiththefirstnode.Thenan oppositecolouredtriangleformed.
Mymethod:Inthispaperweplantoestimatethe valueofR(5,5).
Firstthingsfirst,thelowerboundrequiresbrute forcingalgorithms.Sincetheonlywaytolookfor lowerboundsisfindingcounterexamples,thispaperwill mostlyfocusonfindingupperbounds.Wewilldiscuss brieflyaboutbruteforcingalgorithmslater.
Sofirst,letusfigureout(estimate)thevalueof R(n+1,n+1)whenR(n,n+1)isgiven.
Let’sputR(n,n+1)asanarbitraryvalueX.
SaywewanttotestforavalueX+Yandseeifit meetsR(n+1,n+1)
Fig.1
12
Intheperspectiveofanode,ifthereareatleast Xnodeswithstate1connections.Thenwecanensure thatthereisan+1sizedinterconnectedgraphsince thereiseitheransizedinterconnectedstate1graph whichwecanincludethefirstnodeorthereisan+1 sizedinterconnectednode.
Applyingsimilarlogic,ifthereareatleastX nodeswithstatetoconnections,wecanensurethere isan+1sizedinterconnectedgraphsinceR(n,n+1)and R(n+1,n)arethesameduetosymmetry.
Then,wecanconcludethatforgraphssized2X, theremustbean+1sizedinterconnectedgraphwitha singletypeofconnectionsinceoutof2X-1connections with1node,theremustbeatleastonestatewithat leastXconnections.Thenweputalooseupperbound onR(5,5)as2*R(4,5).Whichis50.
ThisproofcanbegeneralisedtoR(k+1,n+1)<= R(k,n+1)+R(k+1,n)usingthesamelogic.
WecantightentheupperboundofR(5,5)witha littlebitofelaborationonthislogic.
Ifwehave2X-1nodes,tonotimmediatelyensurefor theconditionstobemet,theremustbeX-1connections intheperspectiveofasinglenode.Andthisshould bealltrueforallnodes.Thisleadstobrute-forcingall again.However,wecanuseRamseynumberswithmore inputstopushthisboundarydrastically.
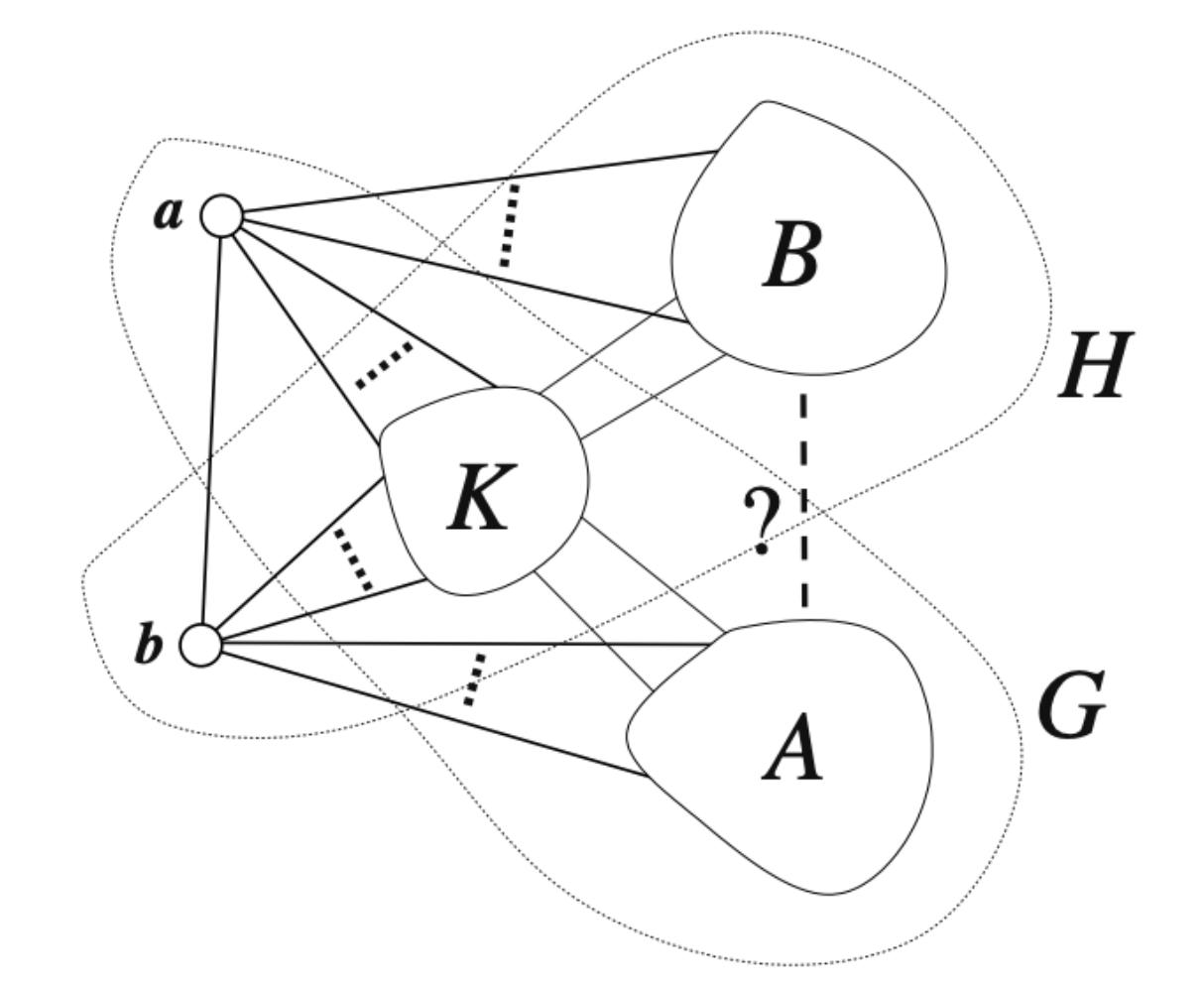
UsingtheknowledgethatR(4,5,24)is352366,we candraw2graphsGandHforR(4,5,24)andlabelK astheoverlappingregion.
Now,wecandefineaasalltheverticesthatare borderingHandbasalltheverticesthatarebordering G.
Thebiggraphasawholecanbedefinedas R(4,4,48).
Foreach K ∈ R(3, 5,d) with d ≤ 11 andforeachpair (G,a),(H,b)R(4,5,24,K).Bruteforceallthepossible
waysofglueingGandHwithK.
Sinceitisimpossibletoaddonevertexwhilestaying withinR(5,5),noneofthegraphsthatwerecreatedare subgraphsofR(5,5,48)
ThesestepsinturnprovethatR(5,5)islessthan orequalto48.
Thecounterexamplecanbedescribedasfollowing:
Arrange43pointsequallyspacedaroundacircle andlabelthemfrom0to42inclockwiseorderandin modulo43(sothatforallintegersa,thevertexaisthe sameasvertexa‘43).Foranytwodistinctverticesa, bwedefinethedistancebetweenthemasthelengthof theminorarcbetweenthevertices(wherewedefinethe minorarclengthbetweenadjacentverticestobe1).
Forallintegersisuchthat0<=i<=42,the5-tuple ofvertices(i,i+1,i+2,i+22,i+23)formsagraphsized5 inredcyclic(43).Thisyields43distinctred K5’s.
Thenextstepistodeletevertex0,producingacolored K42 withonly435=38red K5s.Finally,changethe followingedgesfromredtoblue:11←→32and j←→j+1 for j=4,5,6,7,13,14,15,16,23,24,30,33,39,40,41.
Onecanverifywithacomputerthatthiscoloring of K42 is K5-free.
Fig.2
13
Pascal’sTriangleandCombination
ChloeNayeonKim
Year10
Email:nkim27@pupils.nlcsjeju.kr
Editor
RyanHanjinLee
RecommendedYearLevel:KS4
Keywords:pascal’striangle,tetrahedral,binomial expansion
1Introduction
Mostmathematiciansnolongerexpandbinomial expansiononebyone.Theydon’tspendalongperiodoftimeexpandingmillionsofbrackets.Instead, theyusethesmartestandinnovativewaytosolvethe binomialexpansionproblem,whichisPascal’sTriangle.
2BackgroundInformation
ManypeoplemayhaveheardofBlaisePascal;a Frenchmathematicianandphysicistwhodiedinan earlyageof39.However,inspiteofhisyounglife, hewasasignificantfigureinthefieldofmathematics andphysics.Hewasthefoundationofthemoderntheoryofprobabilitiesaswell,formulatingwhatcameto beknownasPascal’sprincipleofpressure.Moreover, besidesthetheoriesthathediscovered,heinventedPascal’scalculator,mechanicalcalculator,addingmachine etc...Despitehismanyinventionsanddiscoveries, hisnameismostlywellknowntothemathematicians throughhistheoryofPascal’sTrianglethatpeopleused forcenturies.
3Method/Analysis
3.1HowtocreatePascal’striangle
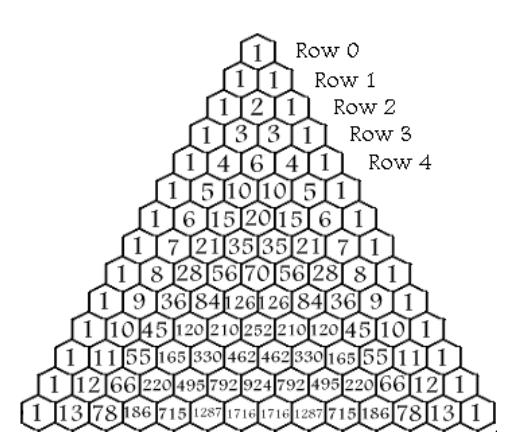
Thissimplymaylooklikeaneatlyarrangedstackof numberstopeoplewhodon’tknowaboutit.However, itisactuallyamathematicaltreasuretrovethatwas highlyregardedinthehistoryofMathematics.Indian mathematicianscalledittheStaircaseofMouthMeru. InIran,it’stheKhayyamTriangle,andinChina,itis knownasYangHui’sTriangle.IntheWesternworld,it
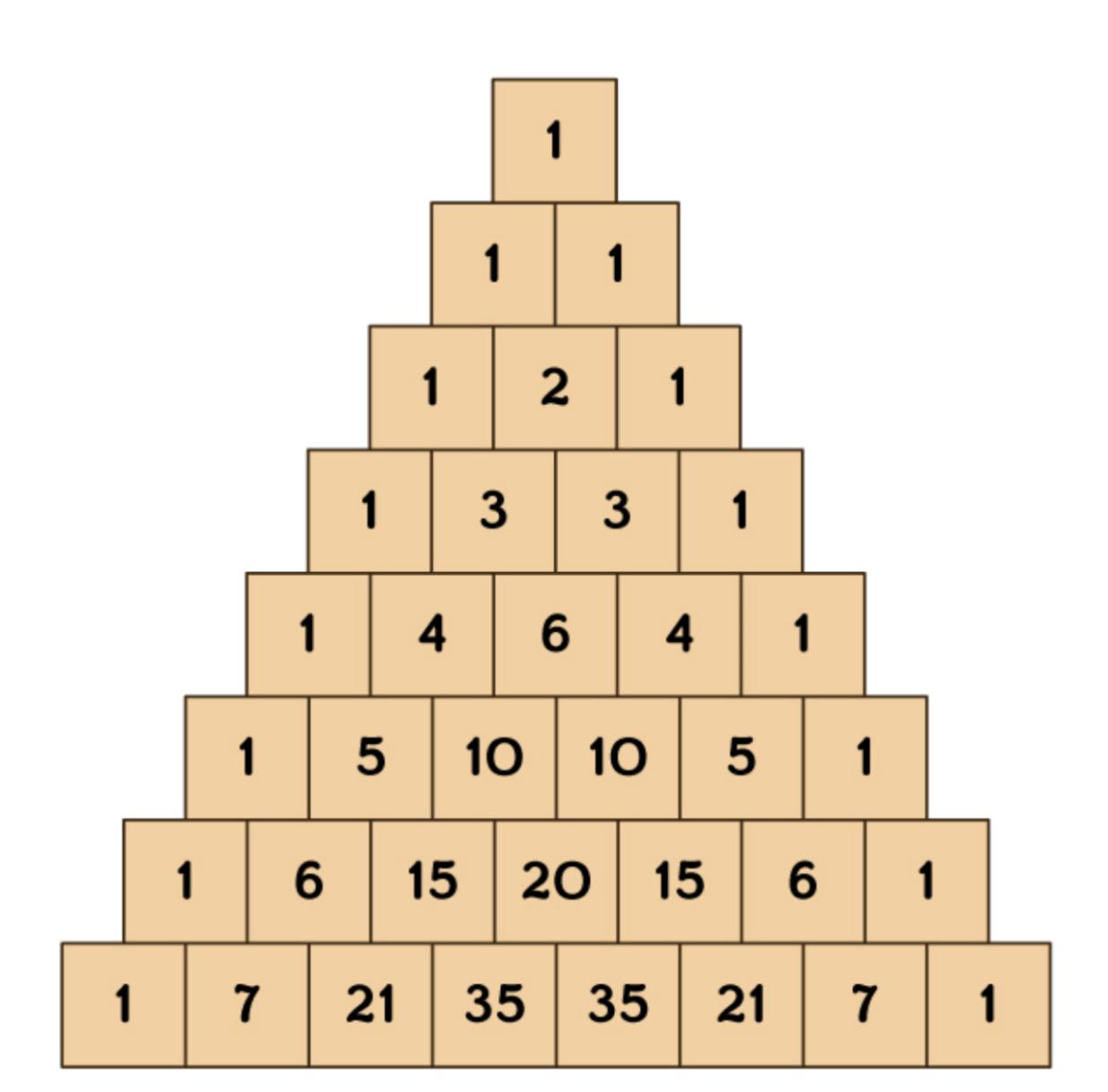
iswellknownasPascal’sTriangle.ThisPascal’sTriangleisfullofpatternsandsecretsbehind.Thepattern underneaththistriangleisverysimple.Staringwith oneandimagininginvisiblezerosoneithersideofthe numberone.Addthemtogetherinpairs,andyouwill beabletogeneratethenextrow.Continueandkeep goingwiththisprocessoverandoveragainasthePascal’sTrianglegoesoninfinitely.Then,nowwehaveto knowwhatthesenumbersmean.So,eachrowcorrespondstothecoefficientofabinomialexpansionofthe form (x + y)n wherenisthenumberoftherowstart countingfrom0.Forexample,ifyoumakentobe3, andexpandit,youwillget
(x + y)(x + y)(x + y)
whichis:
Ifwelookcarefullyintoit,thecoefficient,ornumber infrontofthevariables,arethesameasthenumbers inthatrowofPascal’sTrianglewherethetriangle isaquickandsimplestwaytolookupallofthese coefficients.
3.2Power
Moreover,notwiththebinomialexpansion,butif youaddupthenumbersineachrowitwillalwaysbea
Figure1:Pascal’striangle
x 3 +3x 2 +3xy 2 + y 3
14
successivepowerof2.Forexample,row2,whenweadd upallofthenumbersitis4whereitis2tothepowerof 2.Inthesameway,thesumofthenumbersinrow5is 32,whichisalso2tothepowerof5,asshowninfigure2.
Also,lookinginadifferentway,let’stakeeachrow asanindividualnumberinsteadofahorizontalarrangementofonedigitnumbers.Forinstance,forrow2it is
(1 × 1)+(2 × 10)+(1 × 100)
whichequals121; 112 Anotherexample,forrow5,it willbe:
(1 × 1)+(5 × 10)+(10 × 100)
+(10 × 1000)+(5 × 10000)+(1 × 100000),
whichis 115 Inthiscase,itisnoticeablethatrown willresultas11tothepowerofn.

3.3Tetrahedral
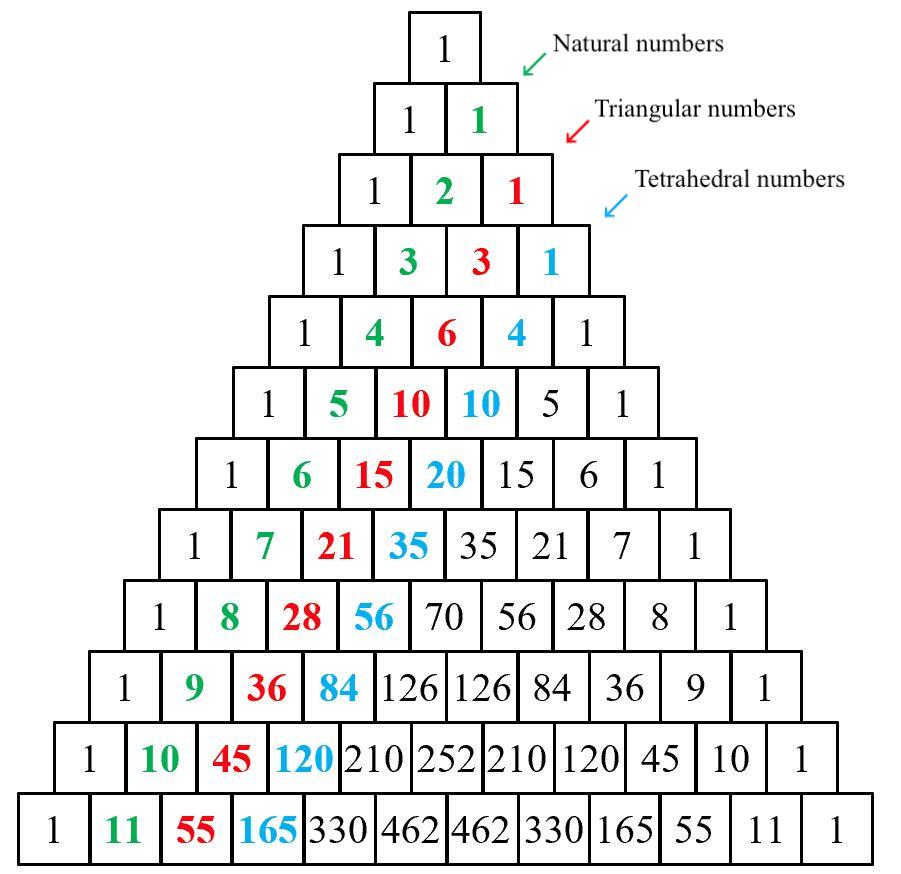
Movingontotheaspectofgeometricapplications. Thediagonalsofthetriangleareimportant.Thefirst twodiagonalsaren’tsointerestingorcaptivatingasthey areallonesandthenthepositiveintegersarealsocalled naturalnumbersbutfromthethirddiagonal,itbecomes fascinating.Thenumbersonthethirddiagonalare knownasthetriangularnumbersbecauseifthenumbersarealltakenoutandstackthemup,theycanbe stackedupinequilateraltriangles.Thenextdiagonalis tobeknownastetrahedralnumbersbecausesimilarly, itcanbestackedupintotetrahedral.
3.4Sketchingalloddnumbers
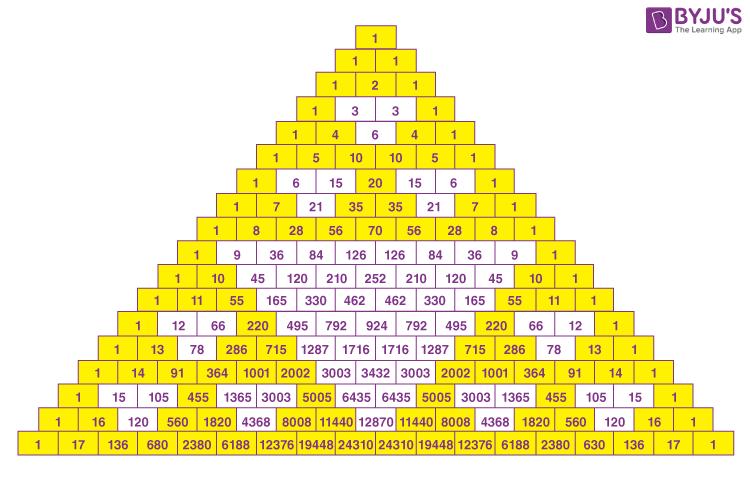
Anothergeometricapplicationcanbeseenby shadingineveryoddnumber.Afterathousandrows, thefractalknownasSierpinski’sTriangleappears. Thisisveryusefulinthesenseofprobabilityand
calculationsinthedomainofcombinatorics.Sofor example,ifafamilycalledAislookingfor3girls and2boysastheirdreamchildren,inthebinomial expansion,itwillbasicallycorrespondto(boy+girl)5. Thenwhenwelookatrow5,itis1x5+5x4y+10x3y2 +10x2y3+5xy4+1y5wherethefirstrefersto5girls andthelastrefersto5boys.Butasthefamilywants 3girlsand2boys,theonethattheyarelookingforis 10x3y2.Tocalculatethepossibility,itwouldbe10out ofthesumofallthenumbersintherowwhichmeans 10/32being31.25%of3girlsand2boys.
4Conclusion
ThroughthediscoveryofPascal’sTriangle,itwas mucheasierforpeopletosolvebinomialexpansionsin ashorteramountoftime.
5Extension
Combination (nCr) isusedtocountthenumberof differentgroups/terms/collections/setsetc...that canbeformedusingrobjectsselectedfromndifferent objectsnotconsideringtheorder.Theformulaofcombinationis
nCr =(n!)/(n r)!(r!)
Thisisusefulinawaytosolvethebinomialexpansion problem.Thewayweusecombinationsinbinomialexpansionisfairlysimpleifweexactlyknowhowto.
Figure2:Pascal’striangleandthepowerof2
Figure3:TetrahedralinPascal’striangle
Figure4:OddnumbersshadedinPascal’striangle
15
RecommendedYearLevel:KS4
Keywords:settheory,infinity
SetTheory
Youngjae(Collin)Seo Year10
Email:yjseo27@pupils.nlcsjeju.kr
Editor
Taehong(Austin)Ha
1Introduction
Intheworldofsettheory,wheremathematicsexploresinfinity,comparingthesizesofsetsisthecentral focus.Inthissense,settheorymaybeinterpretedas challengingthefundamentalsofmathematics,asitquestionsaverybasicbutcomplicatedconcept–theideaof infinity.ThisarticledivesintotheenigmaoftheContinuumHypothesis,firstsuggestedbyGeorgCantor,in thelate19thcentury.Thisarticleaimsforajourney throughthehistoryofsettheory,discussingCantor’s ideaofsets.SettheoryandContinuumHypothesis reachesthelimitofmodernmathematicalknowledge, wherefiguringoutthesizesofsetsmeetsapuzzlethat cannotberesolved.
3TheTheoryofTransfiniteNumbers
SettheorybeganwiththeworkofGeorgeCantor. In1874,GeorgeCantorprovedthatthesetofalgebraic numbersiscountable,meaningthattheyshowabijection(1to1correspondence)betweenthemselvesandthe setofnaturalnumbers.Thealgebraicnumbersreferto complexsolutionsofpolynomialequationsoftheform:
2KeyTerminologies/Definitions
1.Card(X):thenumberofelementsoftheset.
2.CardinalityofanemptysetisZero.
3.Countablesetsreferstothesetthatcanbe countedasasubsetofnaturalnumbersanduncountablesetsreferstothesetsthatcannotbeexpressedas asubsetofnaturalnumbers
4.Thecardinalityofsetsaredefinedtobethe same,whentheyshowaonetoonerelationship (bijection).
Wherethecoefficients ai areintegersand an isnon-zero. Givensuchanequation,letthisequation:
|+|a0|+n
beitsindex,k.Itisclearthatforeveryk>0there areonlyafinitenumberofequationsofindexk.Forinstance,thereareonly4equationsofindex3withstrictly positivean,namely X 2 =0,2X=0,X+1=0and X-1=0,whichhavesolutions0,1,and1.Itfollows thatforallk>0,therearefinitely-manysolutionsof equationsofindexk.Thus,wecanenumerateallalgebraicnumbersbyenumeratingallsolutionsofequations ofindex1,followedbyallnewsolutionsofequationsof index2,andsoon.
3.1ComparingtheSizesofIntegerandNatural number
Manystudentsbelievethattheintegerhasgreater cardinalitythanthenaturalnumber.Thismayseem obviousasintegerisasetthatcontainsthesetofnaturalnumbers.However,throughthefollowingfunction, itcanbeeasilyproventhatthecardinalityofnaturalnumbersandintegersarethesame,indicatingthat theyhavethesamenumberofelements,nonetheless, thefactthatthenaturalnumberisapartofinteger.
anXn+an 1Xn 1
+ + a1X+a0
an|+|an1
|
16
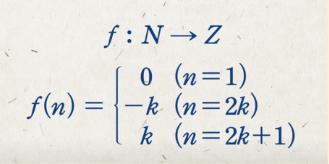
Throughthefunctionabovebijectionisshownbetweentheintegerandnaturalnumbers.Thestatement thattheirsizesofinfinityarethesame,hasbeenproven. Therefore,
card(N)=card(Z)
3.2ComparingtheSizesofNaturalNumbers andRationalNumbers
Inasimilarmanner,therationalnumbersarealso expectedtohavegreatercardinalitythanintegerand naturalnumbers.However,thisisalsoamisconception thatcanbedisapprovedofeasily.

Whenarrangedinthewaypresentedabove,bijectionexistsbuthowever,the1to1correspondence cannotbecheckedfully,asthefirstlinedoesnotend.

Byrearrangingthesetsinsuchamanner,presented above,wecancheckthebijectionbetweenthesetsdiagonally.Thefractionsorthevaluesthathavebeen countedcanberejectedintheprocess,andthisenablestocheckthecorrespondencethroughouttheset; notonlythefirstline.Thus,ithasalsobeenproven thatthesizeofrationalnumbersortheinfinityofrationalnumbersequalstheinfinityofNaturalnumbers. Thus:
card(N)=card(Q)
3.3ComparingtheSizesofNaturalNumbers andIrrationalNumbers
Accordingtothelogicpresentedin3.1and3.2,it mightbeobvioustothinkthatthenaturalnumbersand theirrationalnumbershavethesamecardinalityaswell (hereirrationalnumberreferstothewordthatcannot beexpressedinfractions).However,surprisingly,this isnotthecasefortheirrationalnumbers.

Bylookingatthenumberarrangementsabove,it iseasytobelievethatthenaturalnumbersandthe irrationalnumbersshowabijectionbetweenthem.

However,oncethenumbersarearrangedinsuch amannerandifdifferentdigitsarebroughtfrom thenumbersandiftheyaremadeintooneirrational number,1beingaddedoneverydigitbelowdecimal point,anumberthatdoesnotoverlapcanbemade. Thisproveshow,nonethelesstheamountofirrational numbercorrespondingtothenaturalnumber,there isalwaysanirrationalnumberthatcannotbecorresponded.Thusthisshowsthattheirrationalnumbers havegreatercardinalitythanthenaturalnumbers.As aresult,
17
card(n) = card(Qc) card(n)<card(Qc)
4CountabilityofInfinites
GeorgCantordefinesthesizeofthenaturalnumber ortheinfinityofnaturalnumbersascountable.Considerthefunction f(n)=n.Apparently,thisisaninjectivefunctionsinceforevery n ∈ S=N andthereisan f(n) inNaturalnumbers.SonaturalnumberswereconsideredcountablebyCantor.Duetothisthefollowing statementswereproved:
card(N)=countable ∞
card(Z)=countable ∞
card(Z)=countable ∞
However,therealnumbercannotbedefinedas countable,astherealnumbersaredefinedas
R=Q ∪Qc
Asshown,realnumbersconsistoftwodifferent numbers–rationalandirrationalnumbers.Although therationalnumbersarecountable,becausetheirrationalnumbersareuncountabletherealnumberscannot beconsideredascountable.Thus,
card(Z)=uncountable ∞
5SizesofInfinity:IntroducingAleph Cantor,whileinvestigatingandcomparingthesizes ofthesets,hewonderedwhetherthesizesofinfinitycan beexpressedassymbolsorcanbemeasured.Herethe introductiontoAlephtakesplace.
ℵ
ThroughtheintroductionofAlephnull,expressing thesizesofinfinityasanexpressionbecamepossible. Basedonthecalculationofthenumberofsubsetsofa set,sizesofsetscouldbedetermined.
n(P(x))= 2n(x)
BytheusageofAleph,Cantordefinedthesmallest sizeofinfinityortheset,asAlephnull,whichisthesize andcardinalityofnaturalnumbers.
card(N)= ℵ0
Thusaccordingtothis,bydefiningthesizeofreal numbersasthenumberofsubsetsofnaturalnumber, thecardinalityofrealnumbercanbeexpressedasfollowing:
card(R)= 2ℵ0
6AbsoluteInfinity
Accordingtothelogicofthenumberofsubsets, utilisedondeterminingthecardinalityofrealnumbers, Cantorquestioned“Thenwhatisthebiggestcardinality?”
Asthiscontinuesthesizeofinfinitygrowsinfinitely bigger.Cantordefinesthisasabsoluteinfinity,whichis expressedasthesymbolOmega.
Defining Ω orfiguringoutanumericalvaluetois consideredamystery,tothecurrentunderstandingsof mathematics.
7ContinuumHypothesis
AlthoughCantorhadremovedmanybarriersbetweenhumanityandmathematics,thereisahypothesis whereitcouldnotbeprovennorbeproven.Although thissoundsawkward,thisisthetruth.
ℵ0 <x< 2ℵ0 2ℵ0 = ℵ1
ℵn+1 = 2ℵn
Thecontinuumhypothesis,suggestedbyCantor, statesthatthereisnosuchcardinalitybetweenthose twocardinalities.ThishypothesisisalsooneofGodel’s incompletenesstheorems,whichindicatesthatitcannotbeprovednordisproved.Regardlessofthehypothesisbeingrightorwrong,itdoesnotcauseanymathematicalparadoxesorproblems.Thereasonwhythis isnamedasacontinuumhypothesisisbecause,ifthere isnocardinalityexistingbetween ℵ0 <x< 2ℵ0 , 2ℵ0 is thenextsmallestcardinality.Andinthismanner,the cardinalityisbelievedtocontinueincreasinguntilthe absoluteinfinity().Thus,asitisbelievedtoincrease likeafunction,itisnamedastheContinuumHypothesis.
8Conclusion
Settheoryestablishesthebasicsandthefundamentalsofmathematics.Havinganinsightonsettheory givesabetterunderstandingofmathematics,notonlyas asubjecttakeninschool,butasanareaofstudy.However,althoughthesettheoryandCantor’sinsightreply tomanyquestions,thereisstillanareathatcannotbe understood,bythecurrentunderstandingofmathematics.ContinuumHypothesisiswherehumanityreaches theirlimit.AlthoughtheContinuumHypothesiswas provedthatitcannotbedisproved,thisarticlefirmly believesthatthereisacardinalityexistingbetweenthe sizeofnaturalnumbersandrealnumbers.Thisarticle alsobelievesthattheanswertothishypothesisisthe keytothefuture,whichwillsolvemysteriesofmathematicsandphysics.Solvingthis,isthemissionassigned bytheseniormathematicians,tothefuturegenerations.
ℵ0, 2ℵ0 , 22ℵ0 , 222ℵ0 ,........
Ω
18
RecommendedYearLevel:KS4
Paradoxes
Seoha(David)Kim Year9
Email:seohakim28@pupils.nlcsjeju.kr
Editor Taehong(Austin)Ha
Keywords:Paradox,thoughtexperiments,antimony anddialethia
1Introduction
AsthewriterofthenewspaperLittleJourneyonce said,“Lifeisaparadox”.FromwhenSocratesandhis contemporarieswerealivetothemodernInformation Paradox,paradoxesencompassvariousfields,radiatingtheirpresencetomankind,thequestionoftheir acknowledgementputaside.However,thefundamentalsregardingparadoxesarenotfrequentlydiscussed, whichwouldbethemainobjectiveofthisarticle.The vaguedefinitionofparadoxesconsistsofanystatement oranideathatcontradictsitself,commonlyaccepted knowledge,orotherseemingly“true”ideas.Themathematical(philosophical)wordconveysthesameideas, althoughtheyarelimitedtomore‘field-specific’ones.
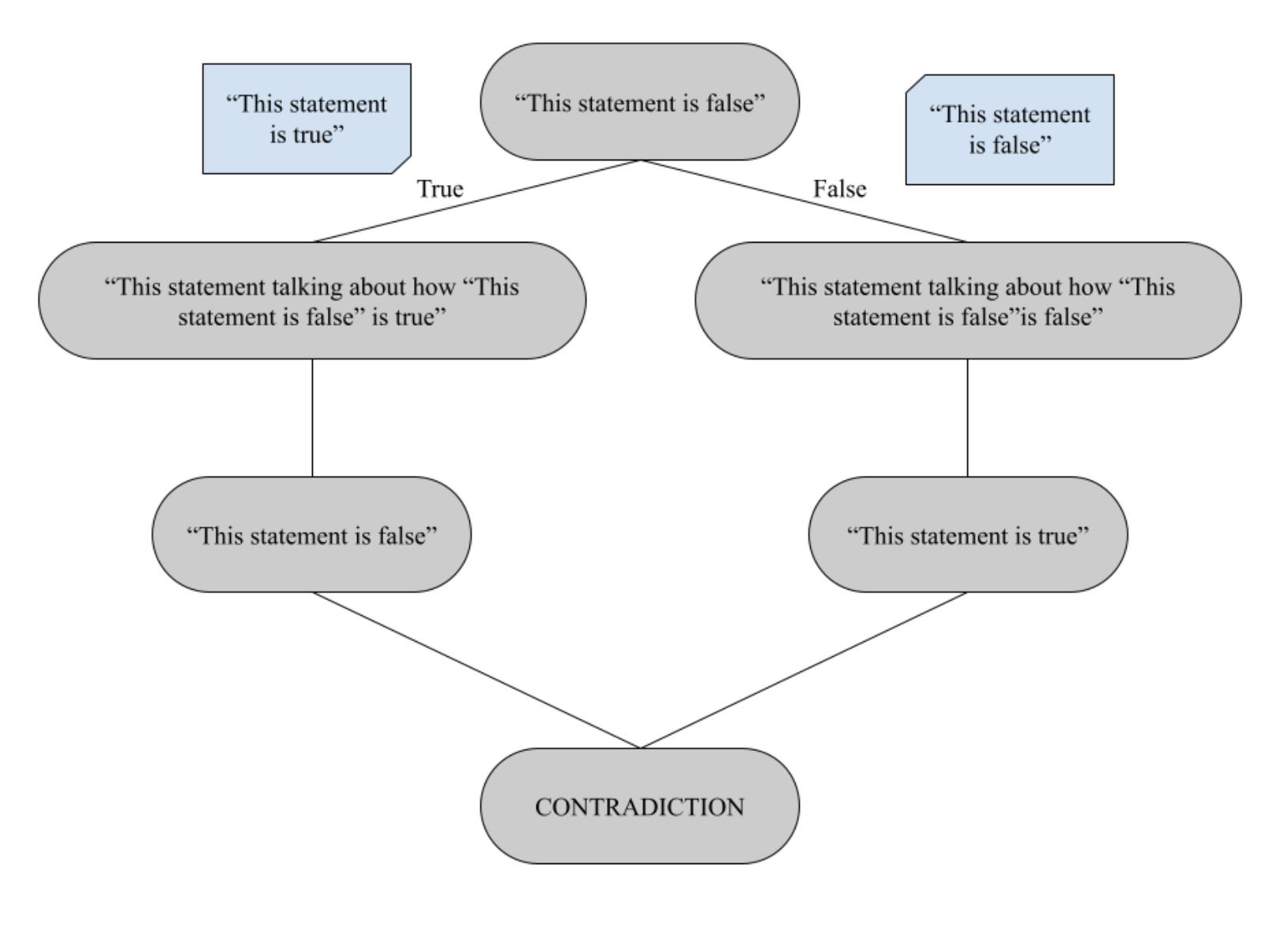
3ThoughtExperiments(Gedankenexperiments)
2PatrickHughes’ThreeLawsofParadoxes
Someelementsareessentialwhilecreating(or analysing)aparadox:self-reference,contradiction,and viciouscircularity.Theliarparadoxisbothoverused andaperfectexampleofallthreeconstituents.The axiomoftheparadoxliesinitself,whichiscommonly theoriginofconfusion.Thisalsofitsnicelywitha clearthemeofcontradiction,sincethestatementistrue ifitisfalseandviceversa,thusresultinginanambiguousvalueofsomewherebetweentrueandfalse. Theultimateattribute,viciouscircularity,isquiteselfexplanatory;ifastatementistrue,thenitstrivestobe itsopposite,infinitelyregressing
Thisisthepartwhereitgets(arguably)themostintriguingandcomplex.Thereisanindistinguishablebarrierbetweenthoughtexperiments,philosophyandparadoxes,andthesebarriersarefrequentlydisregarded. Thoughtexperimentsgenerallyformamiddeepcontemplation,recreatingassumedworldsandaxioms.Ludwig Wittgenstein(b.1889,d.1951)isaprominentphilosopherwhotookontheuntouchedroadof“expressing pain”.Hiswordsareasfollows:
“Imagineaworldwhereeveryindividualisprovided withabeetleinabox.Anyinformationregarding morphologyorcharacteristicsistoberestrictedto anythinginsidetheirbox.Thiswouldsuggestthat conversationordescriptionwouldbemeaningless,as whatoneseeswoulddifferfromanother.”
Usingthesameconceptastheonethatcanbedepictedfromtheexperimentabove,itwouldbelogicalto statethatpaincannotbedescribedthroughanalogies. Painisanelementthatcannotbeconsideredrelatively.
Fig.1:AvisualrepresentationoftheLiarParadox
19
4Quine’sclassification
WillardQuine(b.1908d.2000),anotablephilosopherofthe20thcentury,categorisedparadoxesbased ontheir interiorandexterior absurdity.Twomainideas branchoffinhisclassification-veridicalandfalsidical paradoxes.Whenlogicfitsinneitherorbothcategories, itisdefinedasantimonyanddialetheiarespectively.
4.1Veridicalparadoxes
Veridicalparadoxesseemabsurd,yettheytend tocontraveneconceptions.Thisabsurdityoriginates mostlyfromhastyassumptionsorincorrectlyconceptualisingacertainoutcome.TheMontyHalldilemmais anabstractwayofvisualisingit
Inagameshow,youareaskedtochooseadoorout ofthree,twoofwhichconcealagoatandtheremaining withacar.Thenadoorwithagoatisdisclosed,and onceagain,youareaskedtoreconsideryourchoices.It iseitheryoustickorchange,itisessentialtomaximise profit.
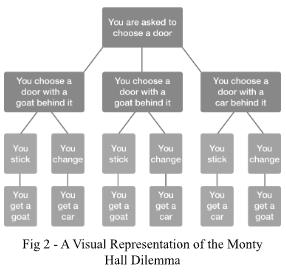
Althoughthechancesofgettingacarwhenyoustick orchangedon’tseemtobeaffected,theprecedingtree diagramsignifiesotherwise.Changingyourchoiceresultsina 2 3 chanceofsuccess.
Surprisingly,thisparadoxlacksthehiddenrequirementofone;itsolelyreliesonsociety.Ifsocietydoesn’t haveaunifiedbeliefthattheresultsareunexpected,it losesitsidentityasaparadox.
MarilynvosSavant(b.1946a.77)fitsinthatcategory.Shearguedthatgiventwogoats,thealternative wouldbringinaconsequenceoftwocars.Thisexplanation,althoughacceptable,doesnotprovideappropriate evidenceforwhytheopposingargumentiscontradictory.
4.2Falsidicalparadoxes
Afalsidicalparadox,justasitsnameimplies,retainsitsqualityasaseeminglylookingandabsurdparadox.Itoftenconveysaxioms,whicharelogicallyproven concepts,toreachacertainconclusionthatisandseems absurd.Itisoftenthecasethataflawinreasoningis whatcausedthefallacy.
Arenownedexampleofafalsidicalparadoxwould be Curry’sParadox,wherearbitraryclaimsareusedto proveacertainassertionbothinfinitelyprovableand unprovablesimultaneously.Belowistheformalproof forthisparadox.
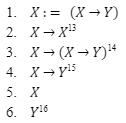
Writingoutthesemathematicalsymbolswould resultinthefollowing:
GiventhatXis“Thissentence”andYis“Germany bordersChina”,thesentenceinfinitelyreiterateswhilst returningtheanswerasY.
Theparadoxcanbedisprovedinthefollowingway:
∀A, ∃X,X = A
Thisisthestandardwayofdefiningunusedvariables.However,thisleadstothefollowing:
f(X → Y)=X → Y
Theproofdidnotbeginwiththisstatementand thereforeincorrectlyconcludedthewaysofdefiningY. Thiswastheideaofafalsidicalparadox,illustrated throughformalproof.
4.3Antimony&Dialetheia
Notethatthefollowingtwotopicsareofsevereambiguity.Antimonyanddialetheiaeachrefertoparadoxespossessingnoneorbothveridicalorfalsidical properties.Toelaborate,dialetheiacanbeconsidereda specialcaseofantimony,wherethenegationofacertain propositionisalsoasvalidastheformer.
heintroductionofanotherparadoxwillbenecessaryherefortheexplanationofthesenotions. TheGrelling–Nelsonparadoxintroducestwocrucial words,‘autological’and‘heterological’.Theyrefer toadjectivesthatdoanddonotdescribethemselves respectively.Althoughclassifyingthesewordsdoesn’t
20
seemlikeaproblem,multiplearisewhenputtingthe word‘heterological’in.
“Isheterologicalaheterologicalword?”
Bothcasesprovideawronganswer,successfully stayingoutoftherealmofbothveridicalandfalsidicalparadoxes.Iftheanswerisno,thenheterological wouldbeanautologicalword,meaningheterologicaldescribesitself.Thiscontradicts.Iftheanswerisyes, thenheterologicalisaheterologicalword,meaningthat heterologicaldoesn’tdescribeitself.Likewise,thisis contradictory.
Dialetheia,surprisingly,ismerelyabeliefthat therearecaseswhereboththenegationanditsreverse argumentarevalid.Noexamplesexistregardingthis topic,asthethesishasnotyetbeenverified.
5Implementation
Withalltheanalogiesandexplanationssettled,let usviewthereal-lifeapplicationsofparadoxes.
Assumeyouaretotravelxkm.Ifyouaretravellingatotaldistanceofxkm/h,commonsensereveals thefactthatitwilltakeexactlyonehourtoreachthe destination.
However,afractionofasecondlater,youarefaced withthesamesituationoftravellingalittlelessthan xkm.Assumethatyourspeeddecreaseslinearlyin correlationwiththedistanceleftyettotravel.
Fromthis,itcanbeconcludedthatyouwillalways betravelling.However,atanypointduringthejourney, itwasalsoshownthatonehourwillalwaysbeleftof thejourney.Ifbothaxiomsaretrue,astatementcan bemadehere:
Thetravellerwillneverreachtheirdestination.
Thiscontradictscommonknowledge,sincexwill alwaysbereasonablybig,andthetravellerwillalways beinastateofconstantmotion.Thetravellershould reachtheirdestinationatsomepoint.
Therearemultiplewaysthisparadoxcanbeproven logicallyincorrect.Theflawherecanbesolvedwiththe conceptoflimits.
Thesituationcanbecondensedtothefollowing equation,giventhatxisthetimetakenatacertain frame,yisthedistancetobetravelledandAisthe non-inclusivesetofallrealnumbersbetweentherange ofyand0.:
resultsinanerrorandcannotbecomputed.
6Conclusion
Withthis,thestoryoftherealmofparadoxescomes toanend,leavingbehindnothingbutambiguityand perplexity.Paradoxes,despitetheiranonymityamongst laymen,havetheirusageinlife;theyindicatethefact thatourphilosophicalnotionsandourwaysoffixed mindsetsareflawed.Thisarticleshouldhavehopefully providedreaderswithinsightintohowparadoxessettled theirplaceinreallife,supportingtheoriesandengaging learnerswithcriticalthinking.Itishopedthatallarein completeagreementthatparadoxesarethefoundation ofproofsandthattheyprovidetheinspirationforthe formulationofone.
7Appendix
Althoughthisequationcanbewrittenonhand,the ideaofinfinity,addedontosetAbeinguncountable,
Considerthetwotablesbelow.
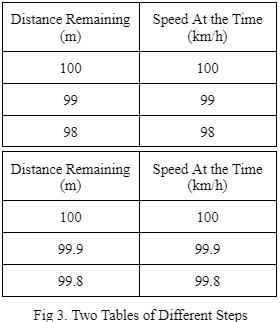
Lookingatthetableabove,aswetravelthefirst metre,ittakes distance rate = 1m 100km/h =0 01 secondsuntil thespeedisthendepreciated.Thetablebelowillustratesthesameidea,onlythattheequationisslightly alteredinto 0 1m 100km/h =0 001 secondsbeforethespeed changes.Asthisprocessiscontinued,alimitequation canbeformed,asthemostpreciseversionofthisequationwouldbe 10−∞ 100km/h =0.01.Hencethefirstequation.
However,thiswasmerelythefirststep.Eachtime thedistanceisdecreased,thetimeittakesbeforethat minusculeamountofspeeddecreaseshastobecalculatedandaddedup.Thesummationsymbolcomes inhere,addingupallthevaluestobecomputed,and
f (x)= y∈A lim x→−∞ 10x y
f (x)= y∈A lim x→−∞ 10x y
21
changingthevalueofy,whichwilldecreaseagainbyan infinitesimalvalue.
Addingallthesevaluestogetherresultsinthefinal equationaforementioned.
22
Howtosketchanyfunctionstepbystep
Yejun(Derek)Yoo Year11
Email:yjyoo26@pupils.nlcsjeju.kr
Editor
Emma(Chaeeun)Chung
RecommendedYearLevel:KS4,KS5
Keywords:Functions,graphing,derivatives
1Introduction
Knowinghowtosketchafunctionisafundamental skillthathasbroadapplicationsinmathematics,science,engineering,andbeyond.Byacquiringsucha virtuewouldenableonetovisualiserelationshipsbetweenvariables.Accordingly,itnotonlyhelpsyouunderstandandcommunicatemathematicalideasbutalso fosterscriticalthinkingandproblem-solvingskillsthat arevaluableinmanyaspectsoflife.
Inthisjourneyfordiscovery,Iwouldliketocreateasystematicapproachtowardscreatingtheultimate “sketcher”.
Thisjournalwouldnotincludeanydifficultjargon orrequireanyknowledgeoutoftheIGCSEcurriculum. Yet,itwouldbedonesolelybymydiscoveries.
Theidealreaderofthisarticleshouldbeableto utilisebasicdifferentiation.
2Step-by-step
Astepbystepapproachwouldbeshownwithan example: y
2.1EndBehaviours
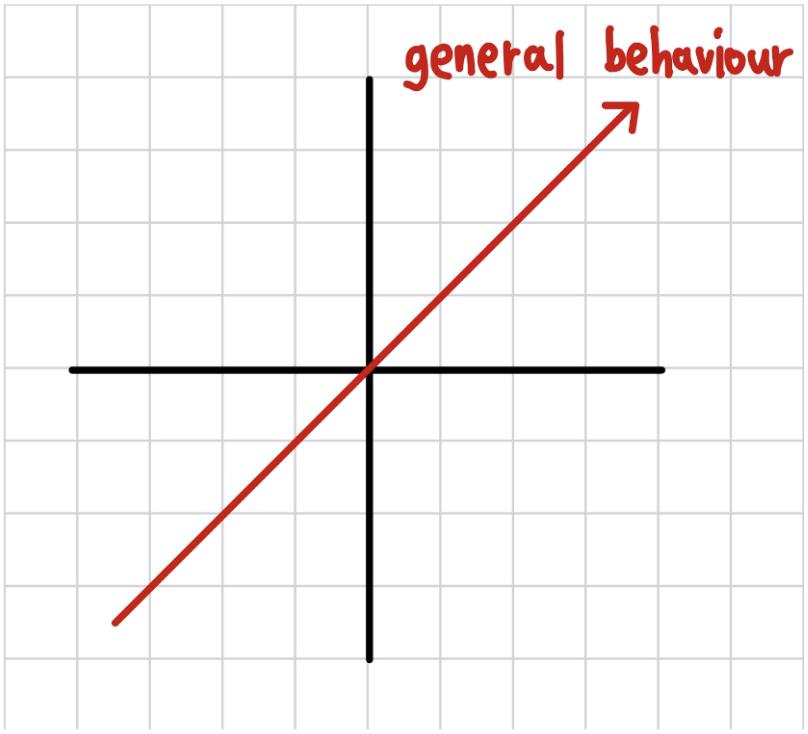
First,wewillhavetoimagineatypicalcartesian planeandimaginetheextremes:
Arigorouswaytodosowouldbeusinglimits,but inthiscaseitdoesnotseemnecessary.Asthexgets
bigger,thefirsttermxwouldincreaseincreasingly.Althoughthesecondtermwouldgetsmallerasxgetsbigger,itwouldstillbeaddingasmallbittothefirstterms. Therefore:
Similarly,thesamelogicapplieswhenxgetsinfinitely small.Making:
Atthisstage,onewouldimagineagraphcoming fromthethirdquatraintowardsthefirstquatrain.
2.2Checksforasymptotes
Afunctioncanhaveasymptotes,meaningthatthe functionmightinfinitelygetclosertoalinewithout touching.Theasymptotemightexistintheformofhorizontal,verticalandslant.Horizontalasymptotescan beeasilyfoundinthenextstep,butverticalasymptotes followthefollowingrule.
= x + 1 x (1)
x → +∞ and x →−∞ (2)
x →∞ : y →∞
(3)
x →−∞ : y →−∞
(4)
Fig.1:generalbehaviour
f (x)= axn + bxm + (5) 23
1. If n < m,thehorizontalasymptoteisthe x axis
2. If n=m,thehorizontalasymptoteis y = a b
3. If n>m,nohorizontalasymptote
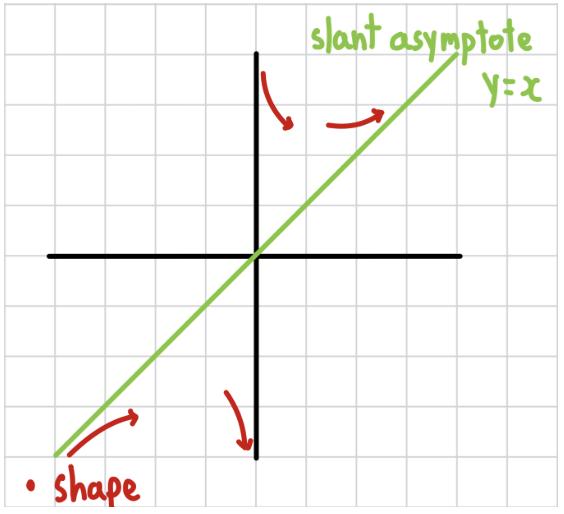
Then,thepresenceofaslantasymptotecanbe determinedby:
If g(x) istheslantasymptote,
lim x→∞ f (x) g(x)
(6)
Forthisfunction,theslantasymptotecanbefound by:
lim x→∞ x + 1 x = x
(7)
Theequationrepresentsthatasxgetsbiggeror smaller,theincrementordecreaseof 1 x wouldbeinsignificantmakingtheequationtheoreticallygetting moresimilartoy=x.Inotherwords,theslantasymptotewouldbey=x.
2.3Checkdomain
Second,onewouldbelookingforvaluesofxwhere theyvalueisundefined.Inotherwords,whereaconstantorvariablehastobedividedby0.Inthiscase:
x =0: y = UND
(8)
Atthisstage,wecaninferthatatthispointthe graphwouldshowaverticalasymptoteorapiecewise graph.
2.4Derivatives
Third,onewouldusethefirstandsecondderivative ofthefunctiontoderivecriticalpoints,pointofinflection,andthegeneralshapeofthegraphbeingconcave upordown.
Thefollowingarethefirstandsecondderivativeof thefunctionwearetryingtosketch.
dy dx =1 1 x2
d2y
dx2 = 2 x3
(9)
Sincethevalueofthefirstderivativeindicatesthe gradientattheinstance,therootsofthefunctionare thecriticalpointsofthefunction.Inthiscase,x= ± 1wouldbethecriticalpointsofthegraph.Inother words,eachwouldbeeitherthemaximumorminimum point.
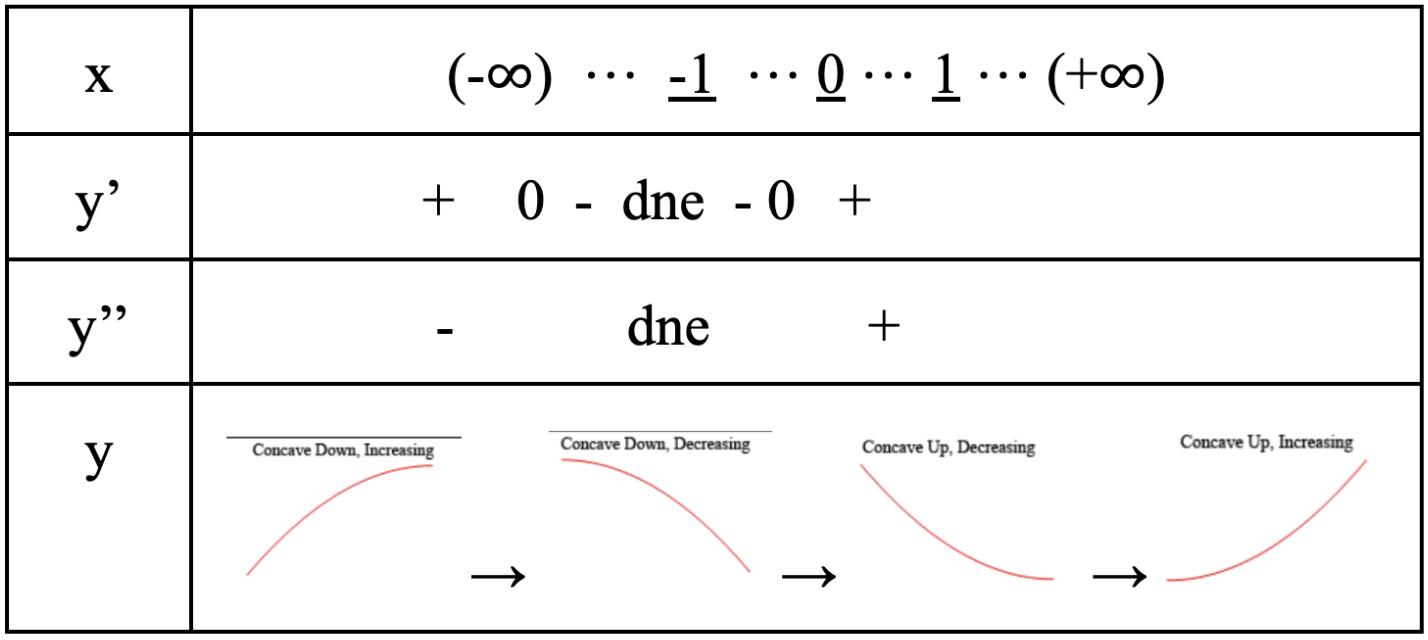
Atthispoint,Ifoundoutthatmakingatablewith suchinformationwouldbeeffective.Thefollowingstep illustratesthethoughtprocessoneshouldbeundertakingwhencreatingatable.
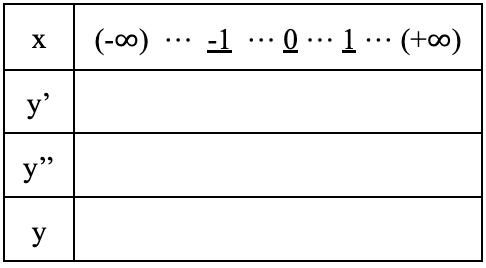
Fig.3
Likewise,thefirstrowshouldalwayscontainanegativeinfiniteandpositiveinfiniteoneachsideofthe imaginaryxaxis.Then,accordingtothepreviousstep, ifthefunctionhasanyundefineddomainorcritical point,additintheaxis(underlinedinthetable).


Then,asthegradientstayspositiveornegativeunlessitpassesacriticalpointwhichisalreadyindicated,
Fig.2:ThoughtProcess
Fig.4
Fig.5
24
wecanlabelthegradientpositiveornegativethroughoutthedomain.
Ontopofthat,wesimilarlyaddthesameforthe secondderivative.
Finally,withalltheinformation,wecansuccessfully imaginetheshapeofthefunction:Thegraphwouldbe concavedownforxssmallerthan0andconcaveupfor xsbiggerthan0.
Ultimately,combiningtheinformationfromthetwo derivatives,wecandecideupontheshapeofeachpart ofthegraph.
2.5Labellingessentialinformation
Ageneralsketchfortheshapeandconcavityshould havebeendoneatthispoint.Inturn,atthisstep,one wouldsimplylabeltheso-called“essential”pointsofthe graph.
Foremost,ifanx-interceptispresent,onecanfind suchbysolvingtheequationwheref(x)is0.Considering therequiredknowledgeofdifferentiation,Iwillassume thereaderiscapableofsimplealgebra.
Similarly,ifany-interceptispresent,thecoordinatescanbefoundbyconsideringxas0.
Then,thecriticalpoints(stationarypoints)would belabelled.Thecriticalpointsarewherethefirst derivativeequal0.
Moreover,thepointswherethesecondderivatives equal0areusuallycalledthepointofinflection;insome cases,anundulationpointexists.
3PracticeFunctions
Thefollowingarethemostfrequentlyusedgraphs outofconvention.
Haveagoinsketching:
4Challenge
Nowlet’strytosketchthissomewhatchallenging function.Thestepswon’tbejustifiedorexplained;this
Fig.6
Fig.7
Fig.8
Fig.9
• y = e x x • y = 1nx x • y = e x +e x 2 • y = e x e x 2 • y = x 1 x • y = 1 1+x2 • y = 1 1 x2 • y = 1 1+x2 • y =sin x +cos x • y = x sin x • y =sin x + x
y = x2 + x +1 x2 x +1 (10)
25
sectiondemonstrateshowonecouldgainmomentum andideallyworkitoutintheirmind.
4.1EndBehaviours
Thiscanbeknownbysanity,buttoaddrigor:
4.2Checksforasymptotes
Ithasahorizontalasymptoteofy=1.Thisisdone usingtheformulamentionedinpart2.2.
4.3Checkdomain
Allvaluesof x correlatetoaspecific y value.The denominator x2 -x+1doesnothaveanyroots,inotherwordsnotallowingasituationdividing0.
4.4Derivatives
First,derivethederivatives.
Then,findzerosofthefirstderivativetobeinserted inthetable(underlined).

Repeatthestepsinpart2.d. Eventually,asketchlikesuchcanbeproduced.
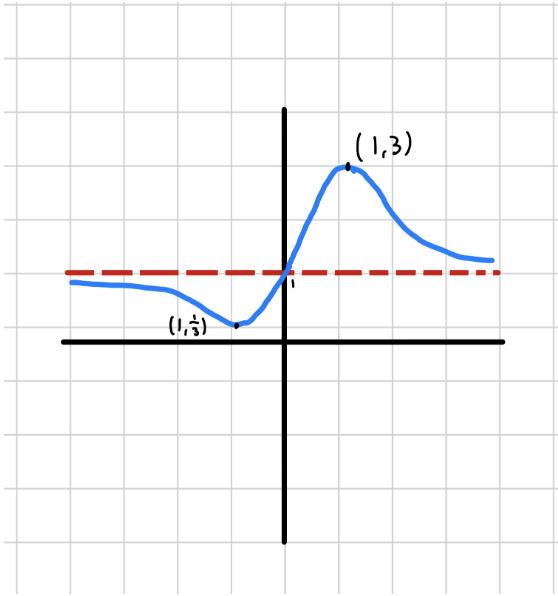
x → +∞ : y → 1 x →−∞ : y → 1 (11)
lim x→+∞ x2 + x +1 x2 x +1 =lim x→+∞ 1+ 1 x + 1 x2 1 1 x + 1 x2 =1 (12)
{x : x ∈ R} (13)
f ′(x)= 2x2 +2 (x2 x +1)2 f ′(x)= 4 x3 +3x 1 (x2 x +1)3 (14)
2x2 +2 (x2 x +1)2 =0 x =1, 1 (15)
Fig.10
26
Fig.11
MathematicsBehindRubik’sCube
James(Choisung)Park Year10
Email:cspark27@pupils.nlcsjeju.kr
Editor
Emma(Chaeeun)Chung
RecommendedYearLevel:KS5
Keywords:Rubik’scube,grouptheory,combination permutation
1Introduction
Inventedin1974byaHungarianarchitect,Ernő Rubik,theRubik’sCubeisa3-dimensionalpuzzleconsistingof26uniqueminusculecubes,oftencalled“cubies”or“cubelets”.Thecubeisusedasatoywhere theaimistoreassemblethecubesothat9cubbieson eachfacedisplaythesamecolor.Inordertoefficiently accomplishsuchaim,awiderangeofpeopleattempted toinvestigatethemostefficientmethodtoreassemble thecube.Asaresult,notwithstandingthatnearlya halfdecadehaspassedsinceitsinvention,theintriguingquestionyetremains:whydoestheprobabilityof solvingitconvergeto1/12?
2Rubik’sCube
Rubik’sCubeismadeupof271x1x1cubes,often referredtoas"cubies"or“cubelets”:7centercubbies, whichdonotmove,12edgecubieseachwith2sides outward,and8cornercubieswith3sidesoutward.20 cubbiesfacingoutwardincludeconcealedinwardextensionsthatinterlockwiththeothercubes,allowingthem tomovetodifferentlocations.However,thecentercube ofeachofthesixfacesisasinglesquarefaçade,allsix ofwhichareaffixedtothecorecentercubbies.Such arrangementallowsothercubbiestofitintoandrotate around.
3Notation
Throughoutthepaper,thenotationsbelowwillbe usedtoindicatethespecificsides.
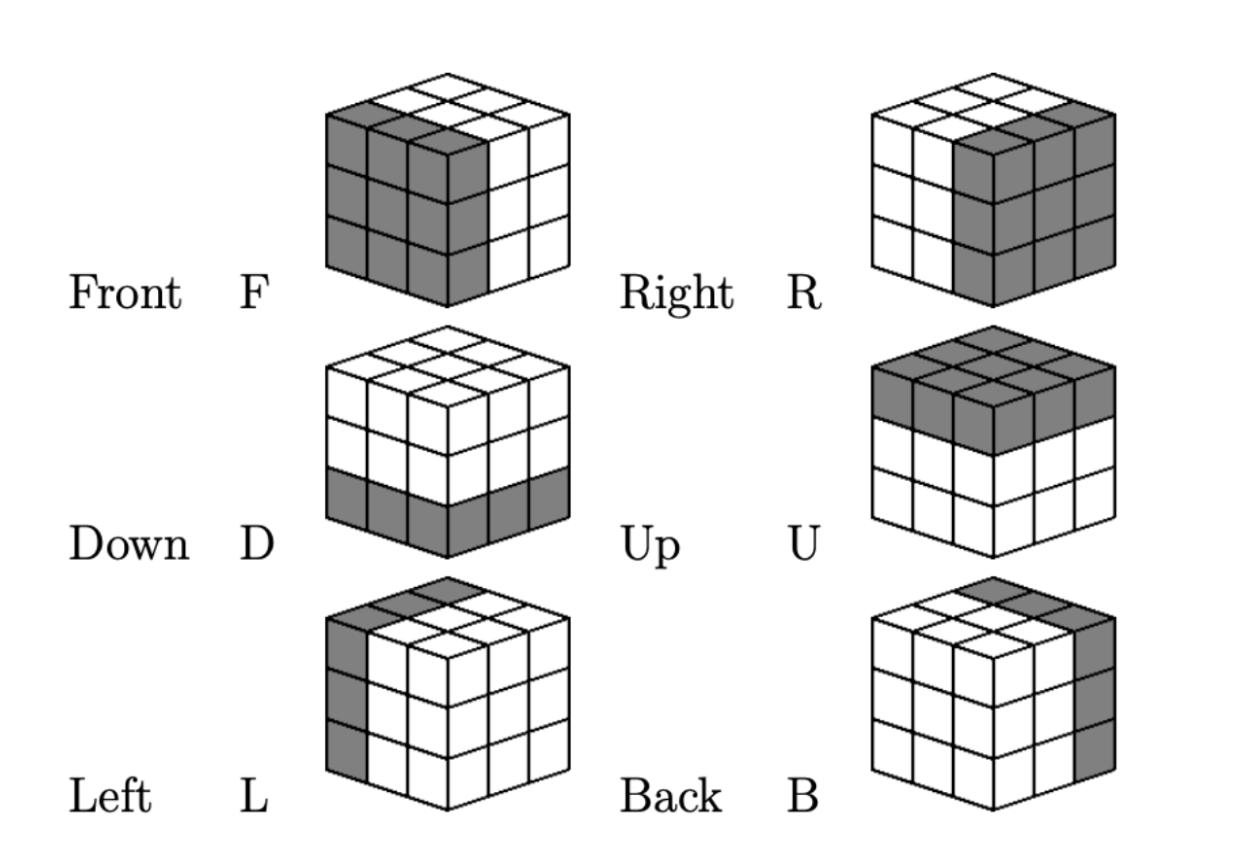
1. F(Front):Thesidefacingthepersonwhois currentlysolvingthecube.
2. B(Back):ThesidelocatedoppositetotheFside
3. U(Up):Thetopsurface,thesurfacefacingupwards D(Down):ThesidelocatedoppositetheUside, thebottomsideofthecube
4. L(Left):Thesideimmediatelytotheleftofyou whenlookingattheFside.
5. R(Right):Thesideimmediatelytotherightofyou whenlookingattheFside.
TheRubik’sCubeisdeeplyrootedingrouptheory,abranchofabstractalgebra.Thesetofallpossiblemovesonthecubeformsamathematicalstructure knownasagroup.Grouptheoryhelpsdescribethe cube’ssymmetriesandaidsinunderstandinghowits piecesmoveandinteractduringsolving.
Fig.1:SidesofaRubik’sCube
27
4PermutationGroups
Apermutationofcornerpiecesorvertexpiecesis oddifthetotalnumberofrotationsisodd,andeven ifthetotalnumberofrotationsiseven.Thisisfundamentaltounderstandingthemathematicalpropertiesof Rubik’sCubeandsimilarsequentialmovementpuzzles.
Thesmallestunitofrotationofthecubeisoneturn. Everypossiblepermutationofthecubecanberepresentedbyanexchangeofpieces.
8cornercubbiesthatcanbearrangedin8!ways, eachofwhichcanbearrangedin3orientations,giving 38possibilitiesforeachpermutationofthecornercubies.Thereare12edgepieceswhichcanbearrangedin 12!ways.Eachedgepiecehas2possibleorientations,so eachpermutationofedgepieceshas212arrangements. ButintheRubik’scube,only13ofthepermutations havetherotationsofthecornercubiescorrect.Only1 2ofthepermutationshavethesameedge-flippingorientationastheoriginalcube,andonly12ofthesehave thecorrectcubie-rearrangementparity,whichwillbe discussedlater.Thisgives
3
possiblecombinationsofthecube.
Itonlylooksatthepermutationanddoesnotcare aboutthedirectionalityofthepieces.Inconclusion, thepermutationofedgepiecesorvertexpiecesbecomes oddpermutationwhenthetotalnumberofrotationsis odd,andevenpermutationwhenthetotalnumberof rotationsiseven.Thisbecomesbasicknowledgewhen consideringthemathematicalpropertiesofaRubik’s Cubeorsimilarsequentialmovementpuzzle.Therefore, theminimumunitforrotatingacubeisonerotation. Allpossiblepermutationsofacubecanberepresented byexchangingpieces.
5OrientationofCubes
Demonstratingpropertiesrelatedtoorientationinvolvescoloringthespotsofeachpiece.Thecriterionfor apiecetobeconsideredorientedisthatitspink-colored sidealignswiththepink-coloredspotinthefigureon theleft.Assumingnoaxisrotation,asanyrotationis achievablewithafixedaxisandappropriateviewpoint adjustments,weassigneachpieceavalueof1ifitspink sidealignswiththepinksideinthereferencefigure, and-1ifitalignswiththegrayside.Observingthe figurerevealsthatU,D,R,L,F2,andB2rotations consistentlymaintaintheorientationofcornerpieces. However,FandBrotationsresultintheflipoforientationforsomecornerpieces.Notably,onlyaneven numberofcornerpiecesconsistentlyexhibitthecorrect orientation.Thisimpliesthatonlyanevennumberof cornerpieceswillconsistentlyhaveamisorientedstatus.Forinstance,considerF.Ifthefourcornerpieces
ontheFsidewereassigneda1,theywillbechanged to-1,andifassigneda-1,theywillbechangedto1. Eachofthefourcornerpiecesistherebymultipliedby -1.Multiplyingall12cornerpiecesbytheirassigned numbersconsistentlyyieldsaproductof1,maintaining aconstantstate.Sincetheproductwas1inthesolved state,itcanbeconcludedthatitwillalwaysbe1.Itis evidentthatonlyanevennumberofcornerpieceswill alwaysbeoriented,meaningonlyanevennumberofcornerpieceswillconsistentlybemisoriented.Therefore,if cornerpiecesareflipped,anevennumberofthemwill alwaysbeflipped.
6EvenandOddPermutations
Intheoriginalpermutationofndifferentthings,the stateformedbyexchanging2positionsanoddnumber oftimesiscalledanoddpermutation,andthestate formedbyexchanginganevennumberoftimesiscalled anevenpermutation.
Thisiscalledtheoddnessofthepermutation. Ifthenumberofpermutationsofnobjectsisn,the numberofevenandoddpermutationsisn/2.
Example) Originalpermutation:(1,2,3,4) Numberofpermutations=4!
Numberofevenandoddpermutations=4!/2 Oneexchange-(2,1,3,4)>oddpermutation
Threeexchanges-(2,3,4,1)>oddpermutation
Swaptwice-(2,3,1,4)>evenpermutation Swapfourtimes-(4,3,2,1)>evenpermutation
7Swapsand4-cycles
1. 1swap:swappingthepositionsof2pieceswitheach other.
2. 4-cycle:swappingthepositionsof4piecesoneby onetotheside.
3. A4-cyclecanberepresentedby3swaps:abcd → bacd → bcad → bcda
Lookingatthecornerpiecesalone,onerotationresultsinthree(odd)exchanges.Thesameistruefor thevertexpieces.Intheoriginalstate,anoddnumber of4-cycleswouldresultinanoddpermutation,andan evennumberofpermutationswouldresultinaneven permutation.However,sinceeachrotationisasingle applicationofthe4-cycletoeachofthecornerandvertexpieces,theresultisthatthepermutabilityofeachof thecornersandverticesisaligned,withanoddnumber ofrotationsresultinginanoddpermutationandaneven numberofrotationsresultinginanevenpermutation.
Ifeach90-degreerotationoftheouterlayerisa
2)
(1)
8 × 8! × 212 × 12! (3 × 2 ×
=43, 252, 003, 274, 489, 856, 000
28
rotation,thenanoddnumberofrotationsinthealigned statewillresultinanoddpermutation,andaneven numberofrotationswillresultinanevenpermutation. Thisistrueforcornersandvertices.
Becauseoddandevenpermutationsaredistinct,an oddpermutationcanalwaysbesolvedwithanoddnumberofrotationsandanevenpermutationcanalwaysbe solvedwithanevennumberofrotations.
29
EigenvaluesofCirculantMatrices
Junseok(Jayden)Lee
Year10
Email:jslee27@pupils.nlcsjeju.kr
Editor
Taehong(Austin)Ha
RecommendedYearLevel:KS4
Keywords:Eigenvalues,matrix,circulantmatrices
1Introduction
Theconceptofcirculantmatricescanbetracedback tothe19thcenturywhenmathematiciansbegan studyingmatricesandtheirproperties.However,the explicituseandidentificationofcirculantmatrices asadistinctclassemergedintheearly20thcentury, particularlywiththedevelopmentofmoderncomputationalmethodsandFourieranalysis.Thedefining characteristicofcirculantmatrices,whereeachrowis acyclicpermutationoftheoneabove,madethema naturalfitforproblemsinappliedmathematics,especiallythoseinvolvingperiodicityandsymmetry. Therealsurgeintheapplicationandunderstandingof circulantmatricescoincidedwiththedevelopmentof fastcomputationalalgorithmsinthemid-20thcentury. TheintroductionoftheFFTalgorithmbyCooleyand Tukeyin1965wasapivotalmoment.FFTmadeit computationallyfeasibletousecirculantmatricesin awiderangeofapplications,particularlyindigital signalprocessing,wheretheyareusedforefficientconvolutionandcorrelationcalculations.
Inparallel,thefieldofnumericallinearalgebrasaw agrowinginterestincirculantmatricesduetotheir uniquealgebraicproperties.TheirabilitytobediagonalizedeasilyusingdiscreteFouriertransforms, andthesimplicityincalculatingtheireigenvalues andeigenvectors,madethemanattractivesubjectof study.Thisinterestwasnotjusttheoretical;practical applicationsinimageprocessing,communications,and solvinglarge-scalelinearsystemsemergedassignificantareaswherecirculantmatricesprovidedefficient solutions.
Thelatterpartofthe20thcenturyandtheearly21st centurysawtheapplicationofcirculantmatricesextendintomoreadvancedfields.Inthesedomains,the propertiesofcirculantmatricesareleveragedtode-
velopnewalgorithmsandunderstandcomplexsystems.Thisperiodalsowitnessedadeepermathematicalexplorationofcirculantmatrices,linkingthem withothermathematicalconceptssuchasToeplitz matricesandgrouptheory.
2BackgroundKnowledge
Themathematicalexpressionforacirculantmatrix C ofsize n × n canbegivenas:
Aneigenvectorofacertainmatrixisanon-zerovectorthat,whenthematrixismultipliedbythisvector, resultsinavectorthatisascalarmultipleoftheoriginalvector.Thisscalarisknownastheeigenvalue. Insimpleterms,whenalineartransformationrepresentedbythematrixisappliedtotheeigenvector,it stretchesorshrinksthevectorbutdoesnotchangeits direction.
3Aims
Theaimofthisarticleistoprovideademonstration ofoneofthemostcommonwaysoffindingtheeigenvaluesofacertainmatrixthroughageneralisedapplicationofthemethodforacertaintypeofmatrix, whichis,inthiscase,acirculantone.
4Preliminaries
Throughoutthispaper,whileacirculantmatrix C of size n × n canbedefinedas:
C = c0 cn 1 c2 c1 c1 c0 cn 1 c2 . c1 c0 . . cn 2 . . cn 1 cn 1 cn 2 ··· c1 c0
30
forthesakeofsimplicity,wewilloccasionallyusethe matrix
Sincewewantnontrivialsolutions, (P λI) hastobe non-invertible,asotherwiseyouget x =(P λI) 1 × 0=0,whichisclearlyatrivialsolution.Thus,
where I istheIdentitymatrix:
Bysubstitutingweobtain:
instead,asallcirculantmatricesareinherentlysquare andcanalsoberepresentedentirelyfromitsfirstrow, sinceeachrowisacyclicshiftofthepreviousrowto theright.
Theterm ω =exp 2πi n willbeusedtorepresentthe n-throotofunity.
Theeigenvaluesofcirculantmatricesexhibitstructuredpatternsandcanbeefficientlycomputedusing theDiscreteFourierTransform(DFT).Foracirculantmatrix C,itseigenvaluesarecloselyrelatedtothe Fouriertransformofitsfirstrow.
Whencalculatingtheeigenvaluesofacirculantmatrix,wewillusematricesofsize 4 × 4 forsimplicity.
λ willbeusedtodenotetheeigenvaluesofbothcirculantandpermutationmatricesintheMainResults,as permutationmatriceswillbeusedpurelyforderiving theeigenvalueofthecirculant.
5Mainresults
5.1ProducingEigenvalues
Webeginwithaconcretemethodforfindingthe eigenvaluesofacirculantmatrix.
Let P beapermutationmatrixofsize 4:
If λ isusedtorepresenttheeigenvalueofthispermutationmatrix,thenwewantnontrivialsolutionsto thisequation:
Therefore:
Thismeansthatthereare4possibleeigenvaluesfor P : λ =1, 1,i, i
Assuch,itisknownthattheeigenvaluescanbegeneralizedbytherootsofunity ω:
Togeneralizethisconceptforapermutationmatrixof size5,let’sconsiderasimilarpattern.Apermutation matrixofsize5wouldbe:
C = c0 cn 1 c2 c1 c1 c0 cn 1 . c2 . c1 c0 . cn 1 cn 2 c1 cn 1 cn 2 ··· c1 c0
C = c0 cn 1 c2 c1
P = 0001 1000 0100 0010
Px = λ⃗x ⇒ (P λI)⃗x = ⃗ 0
det(P λI)=0
I = 1000 0100 0010 0001
0001 1000 0100 0010 λI =0 ⇒ det λ 001 1 λ 00 01 λ 0 001 λ =0
λ4 1=0
λk = ω k 4 = e 2πki 4
P = 00001 10000 01000 00100 00010 31
Again,wewanttofindtheeigenvalues λ ofthismatrix.Asbefore,weusethecharacteristicequation det(P λI)=0,where I istheidentitymatrixofthe samesize.Forasize5matrix,theidentitymatrixis:
Notehowthisisnottheeigenvalueofthecirculant matrix,buttheeigenvaluesofapermutationmatrixof thesamesize.However,wecaneasilyfindtheeigenvaluesofacirculantmatrixbynotingthatacirculant matrixismadeofthesumofseparatepermutation matricesmultipliedbyitsvalue.
Consideringthefactthatrightmultiplicationbya permutationmatrixrearrangesthecolumns,theeigenvaluesofacirculantmatrix C are:
Substitutingtheseintotheequation,weget:
ormoresimply:
Thisleadstothematrix:
λ 0001 1 λ 000 01 λ 00 001
Tofindtheeigenvalues,wecalculatethedeterminant ofthismatrixandsetitequaltozero.Thiswillgive usanequationintermsof λ
Thedeterminantofacirculantmatrixlikethisone iseasiertocalculatethanageneralmatrix.Forthis 5x5permutationmatrix,thecharacteristicpolynomial turnsouttobe:
λ5 1=0
Thisequationimpliesthattheeigenvaluesof P arethe 5throotsofunity.Thesecanbeexpressedas:
Note λ isusedheretodenotetheeigenvaluesofacirculantmatrixratherthanapermutationmatrixas before.Thisispurelyforsimplicityasthereisnoneed foranyuseofpermutationmatricesfrombeyondthis point,and λ iscommonlyusedtodenoteeigenvalues.
6Conclusion
Thispaperhasexploredthepropertiesofcirculant matrices,particularlyinthecontextofeigenvalue computation.Theuniquestructureofcirculantmatrices,witheachrowbeingacyclicpermutationofthe precedingone,allowsforasimplifiedandefficientcalculationoftheireigenvalues.Wehavedemonstrated thisusingtherootsofunityforeasyrepresentation. Thesignificanceofcirculantmatricesextendsfarbeyondthetheoreticalrealm,asevidencedbytheirapplicationinvariousfieldslikedigitalsignalprocessing, imageprocessing,andlinearalgebra.Theabilityto easilycomputetheireigenvaluesisnotonlyofmathematicalinterestbutalsoofpracticalimportancein theseareas.
.Thesecorrespondto1, acomplexroot,itsconjugate,andtwomorecomplex rootsthatareconjugatesofeachother.
Apermutationmatrixofsize n × n haseigenvalues definedby:
λk = ω k n
I =
10000 01000 00100 00010 00001
λI =0
00001 10000 01000 00100 00010
λ 0
λ
0001
λk = ω k 5 = e 2πki 5
k
, 1, 2, 3
1
2πi 5 ,e 4πi 5
6πi 5 , and e 8πi 5
for
=0
, 4.Therefore,theeigenvaluesare
,e
,e
λj = c0 +c1ωj +c2ω 2j + +cn 1ω(n 1)j ,j =0, 1,...,n 1
λj = n 1 k=0 ckωkj
32
ForecastingHighDimensionalSpace
Minjae(Max)Ko
Year10
Email:mjko27@pupils.nlcsjeju.kr
Editor
Junseok(Jayden)Lee
RecommendedYearLevel:KS3
Keywords:Dimensions,ThoughtExperiments, Tesseracts
1Introduction
Throughouthumanhistory,theimprovementoftechnologyhasgreatlyreliedonpeople’slongingtoexplore theunknownaspectsoftheworldanddiscovertheunrevealedtruthbeyondcurrentcomprehension.This ishowhumanitywasabletoconquerthisplanet,and significantlyenhanceourlife.
Now,humanityislookingforwardtochallengingand conqueringconceptsbeyondtheirknowledge,such asthebirthoftheuniverseorquantummechanics. Amongstthem,themostintriguingyetthemostincomprehensiblemaybethestudyofthefourthdimension.Thestudyofthisunfathomabletopicdatesback tothe18thcentury,andhasbeendevelopedovertime withthehopesofopeningnewpossibilitiesforgreat improvementofourtechnology.Thisjournalwillattempttoforeshadowthisdimensionofthebeyond.
2BackgroundKnowledge
Themostbasicunderstandingofthefourthdimension couldbeattainedbythecharacteristicsofthelower dimensions.Dimensionsinmathematicsreferstothe minimumnumberofcoordinatesrequiredtoidentify anypointswithinthespace.Eachdirectionshould beperpendiculartooneanothertobecomeadimension.Forexample,ourworldisthreedimensionalasit consistsofaminimumnumberofthreeaxes:xaxis, yaxis,andzaxis,orlength,width,andheightfor simplification.Alldimensionscurrentlyidentifiedall followthesamelogic.Thisindicatesanewdirection thatisperpendiculartoallthreeaxesofourdimension,whichiscompletelyincomprehensibletoourvery humanminds.Thus,thegeneralmethodcarriedout inordertoshapeourunderstandingofthefourthdi-
mensionistoconductasimulationonthelowerdimension,andapplyittothefourthdimension,just likethebook‘Flatland’thatwaspublishedin1884.In fact,thereisavisualisationofthefourthdimensional figuredevisedbythemathematicianHowardHinton backinthe19thcentury.
Thisisahypercube,oralsoknownasthetesseract. Itisafourthdimensionalanalogueofthecube,butit stillisn’ttheperfectdepiction.Itsdepictiononlylies withintheseconddimensionasoureyesperceivethe surroundingsasseconddimension.Yet,itisoneofthe farmostaccuratedepictionsthatpeoplewereableto comeupwith.
Thus,thisjournalwillbeusingthegeometriccharacteristicsofthedimensionstosimplyforecastthe fourthdimension.
3Aim
Theaimofthisjournalistovisualisethefourthdimensionasmuchaspossible.However,thisjournal maynotbeabletoprovidethemostsatisfyingoutcomeasthisdimensionisfarbeyondourperception, thusallowingonlyafewfragmentsoftheoriesfrom variousmathematiciansandscientists.Thus,instead ofexplainingtheentirefourthdimension,theultimateaimofthisjournalistoforeshadowthesights ofhigherdimensionalspace,suchastheshapeofour bodyfromthefourthdimensionandwhatitwouldbe liketobelivinginafourthdimensionalspace.
4Method
Inordertocarryoutthisforecast,Iwillplayaround withtheseveralthoughtexperiments,mostlybasedon thenobel‘Flatland’,andapplythesimulationstothe hypercube.Then,theconclusionwillbemodifiedso theforecastmaybeappliedtoourcomprehension.For example,basedonourunderstandingofdimensions, wecouldputourowneyestomuchlowerdimensions,
33
andtrytocomprehendthehigherdimensionswith ourlimitedcomprehensionofthelowerdimensions. Thehypercubewillprovidethegeneralpathofour simulations.
5Experiment
Imagineouruniverseasaflat,two-dimensionalspace withoutheightperception.Inthisscenario,wecan onlyseeaone-dimensionalline,similartohowour retinascapturetwo-dimensionalimageswithdepth. Despiterecognizingdepth,ourviewislimited.Introducingthetesseractconcept,droppingacubic shapeintoour2Dworldlooksextraordinary.Astwodimensionalbeings,westruggletofullyvisualisethe objectduetotheabsenceofthez-axis.Thisislike tryingtounderstandathree-dimensionalobjectusing onlyone-dimensionalfragments.Inahypotheticalscenariowherewe,as2Dbeings,gainaccesstothethird dimension,itwouldbecomparabletoobservingthe insidesofobjects,similartolookingatprokaryotesin reallife.
6DataAnalysis
Nowlet’sapplythisthoughtexperimenttothefourth dimension.Inthefourthdimension,thebeing’sperceptionswouldbedisplayedasthreedimensional.For instance,whatthe3Dprinterdoescanbedoneby merelydrawingonpaper,andthecomputerscreen willdisplaythreedimensionalobjectsthatyoucan actuallytouch.Ourownbodieswill–obviously–look verydifferent.Our4Dselveswillconsistofour3D selves,meaningthataninfiniteamountofourselves willbeconnectedbythefourthaxes.Thisiswhy tesseractappearstobeconstantlychangingitsshapes. Similarly,ourbodieswouldappeartobestretched out,probablyfromtheveryinsideofourcellstoour entireoutline.Thus,ourinsideandoutsidescanbe seenatthesametime.Notlimitedtoourownbodies, themajorityofobjectswillappeartobestretchedout endlessly,anditsshapeswillbesotwistedthatyou couldactuallyinteractwiththeitemsinsidetheobjectswithouttouchingtheobjectitself.Tosimplify, everysingleshapewillshowbothitsinteriorandexterior,whilebeingstretchedoutfromitssmallestform tothelargestform.
7Conclusion
Inconclusion,exploringthefourthdimensionposes challengestohumanperception.Inspiredbymathematicallogic,simulations,andvisualisationslikethe hypercube,thisjourneyforeseesthecomplexitiesof higherdimensions.Applyingathoughtexperiment tothefourthdimensionenvisionsperceptionsdisplayedinthreedimensions,transformingactionslike 3Dprintingintotangibleobjectsonascreen.Inthis
4Drealm,bodiesstretchinfinitely,revealinginteriors andexteriorssimultaneously.Thetesseractexemplifies theconstantshape-changingnatureof4Dentities.Everydayobjectsappeartwistedandstretched,allowing interactionwithouttouch.Thisconciseexploration providesinsightintotheextraordinarylandscapesof ahigher-dimensionalreality,pushingtheboundaries ofimagination,whileacknowledgingthespeculative natureofsuchvisualisations.
8Extension
Inextendingthisexploration,delvingintotherealm ofquantummechanicsandconsideringthephysicist’s perspectiveonthefourthdimensionastimeoffersa promisingavenueforfurtheranalysis.Theconceptualalignmentbetweenthecharacteristicsdescribed inthefourthdimensionandtheprinciplesgoverningthequantumworldraisesintriguingquestions abouttheinterconnectednatureofthesedomains. Byincorporatinginsightsfromquantummechanics, wemaydeepenourunderstandingofthefourthdimension,particularlyinrelationtotimeasadynamic component.Exploringhowquantumphenomenaand thetemporaldimensionintersectcouldunveilnovel perspectivesonthenatureofrealityandprovidea morecomprehensiveframeworkforvisualisinghigherdimensionalspaces.Thisinterdisciplinaryapproach, combiningthetheoreticalunderpinningsofthefourth dimensionwithquantumprinciples,opensavenues forrefiningouranalysisandbroadeningthescopeof knowledgeinthisfascinatingfieldofstudy.
9References
1. carlsagandotcom(2009).Cosmos-Carl Sagan-4thDimension.YouTube.Availableat: https://www.youtube.com/watch?v=UnURElCzGc0 [Accessed13Dec.2023].
2. SIDE,B.(2020).WhatWillYouLookLikein 4thDimensionalSpace.YouTube.Availableat: https://www.youtube.com/watch?v=tD_yeG3QLuI.
3. TED-Ed(2013).Exploringotherdimensions-AlexRosenthalandGeorge Zaidan.YouTube.Availableat: https://www.youtube.com/watch?v=C6kn6nXMWF0.
4. TED-Ed(2016).Whatisavector?DavidHuynh.YouTube.Availableat: https://www.youtube.com/watch?v=ml4NSzCQobk [Accessed27Apr.2020].
34
RecommendedYearLevel:KS4
PappusLine
Seunghyeon(Peter)Kim Year10
Email:sh2kim27@pupils.nlcsjeju.kr
Editor Junseok(Jayden)Lee
Keywords:Geometry,IntersectionPoints,Lines
1Introduction
Whenweconnecttheoreticalzero-dimensional points,wemakeaone-dimensionalline,withnowidth orheight,butonlylength.Inourlives,wecomeacross theusageofthislineinvariousways:measuringsomething’slength,drawingabeautifulshape,orcreating delicatestructureswithcomplexplansinvolved.But forthemajorityofthetime,wedrawalinebyconnectingtwopoints.Intheworldofmathematics,aquestion hadtobeansweredandproved.
Qs:Aretherewaystoplot3linesthatareperfectly collinearsothattheyformaflawlesslinewhenconnected?
Thisancientyetdifficultproblemwassolvedbyagreat Greekmathematiciansofantiquity,PappusofAlexandria,from290to350AD.Thisproblem,sosimplesuperficiallybutsocomplexinternally,wassolvedthrough themostadvancedmathematicsandgeometryatthat time.Henamedthisperfectlineconnectingthree points,thepappusline.
2PlottingaPappusLine
2.1Apparatus
Arulerisnecessary,asplottingpappuslinesrequiresadvancedgeometricshapes.Whenconnecting pointsinthemethodutilizingarulerisnecessarytosee theproperresults.
2.2Method
1.Draw2lines.Theydonothavetobeparallel andcanintersecteachother,buttoseeandidentifythe pappuslineclearlyfirstmakingthelineasmuchparallel
aspossiblecanhelp.Makingthemeasilyintersectwill makecomplexpolygons,whichisoneoftheapplications ofthepappusline.
2.Choosethreepointsoneachline.Theydonot havetobeevenlydistanced;theycanbeanypointon thedrawnline.Theycannotbeonthesamedot.
3.Connectthecorrespondingpointsfollowingthe rulebelow.(Thefirstandsecondarejustfordifferentiatingtwolines,orderdoesnotmatter.)

4.Locatethespecificintersectionpoints.There are7intersectionswhendrawnparallelorsimilarto parallel.3inthemiddleand2eachtopandbottom. The3inthemiddleiswhatwearelookingfor.Plot pointsontheintersections.
5.Connectthethreeplottedpointswitharuler. Theconnectedlineswillbecollinear;theywillbethe sameline.Thatlineisthepappusline.
35
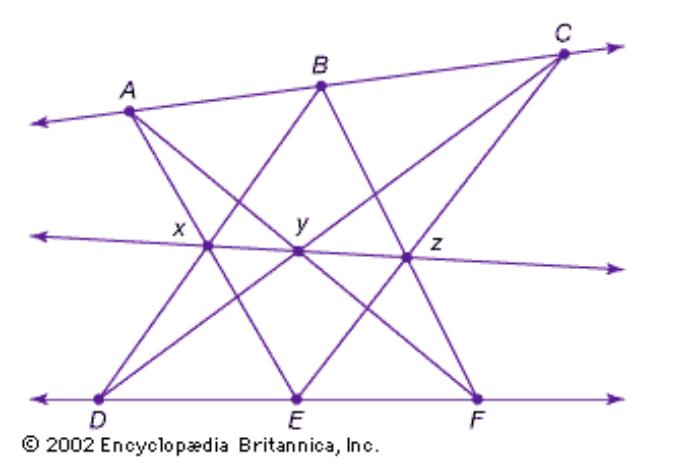
Fig.1:Diagramofapappuslinedrawn
AsshowninFigure1,byplotting6pointsA,B,C, D,E,andFandconnectingtheminaspecificmanner, intersectionsx,y,andzcanbeplotted.Whenx,y,and zareconnected,aperfectcollinearlineismade.
2.3Variations
3Proof
3.1UsingMenelaus’theorem
WhenprovingthePappustheorem,wecanusethe Menelaustheoremtoshowthecollinearityofdifferent pointsinFigure5andlogicallyjointhem.
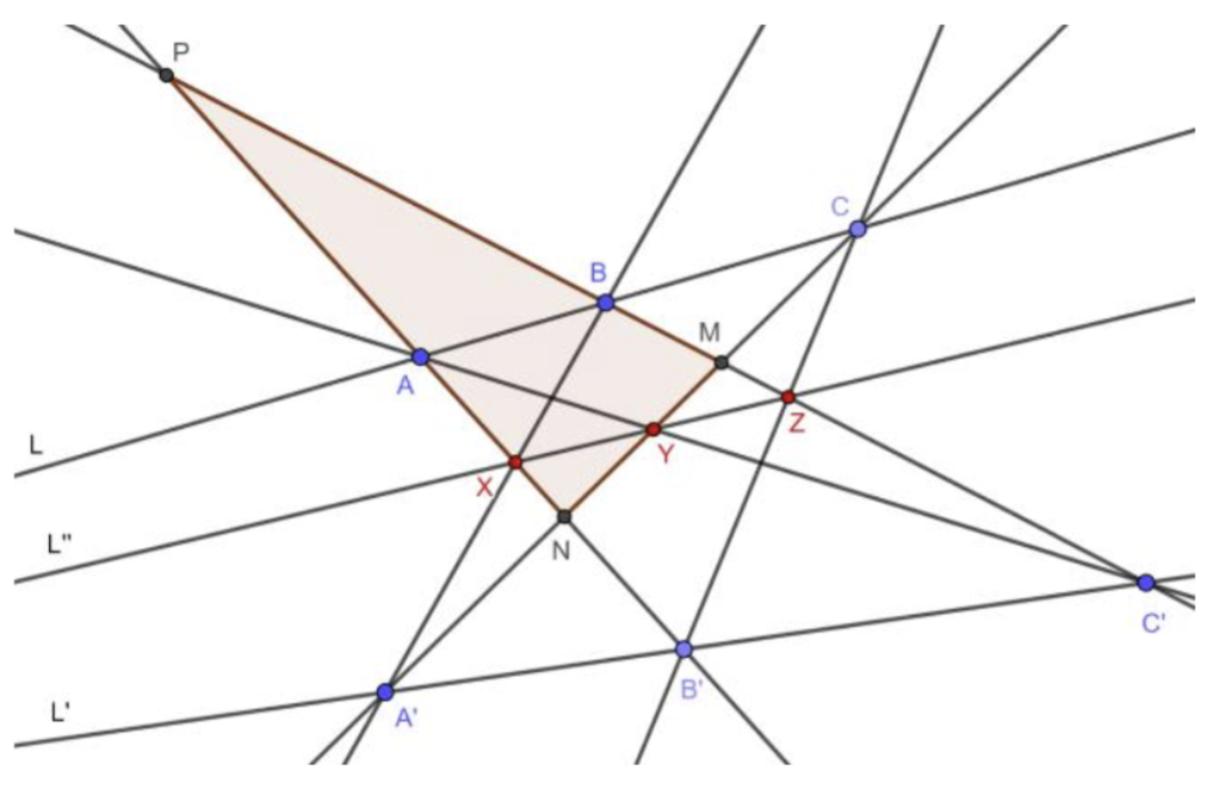
InFigure5,wearesupposingthatAB’,BC’,and A’CareformingatriangleNPM.
Now,dividetheproductofthefirstthreeexpressionsbytheproductofthelasttwoexpressions.
 Fig.2:Pappuslinewiththefoundationlinesintersecting
Fig.3:Morecomplexconjunctions
Fig.4:Pappuslinediagram
Fig.2:Pappuslinewiththefoundationlinesintersecting
Fig.3:Morecomplexconjunctions
Fig.4:Pappuslinediagram
[SX (N,P )SB (P,M )SA′ (M,N )] [SB′
N,P )SZ
P,M
C
)] · [SA(N,P )SC′ (P,M )SY
M,N )] =( 1) ( 1) ( 1) ⇒ NX XP PB BM MA′ AN NB′ B′P PZ ZM MC CN NA AP PC′ C′M MY YN = 1 (1) [SA(N,P )SB (P,M )SC (M,N )] [SB′ (N,P )C′(P,M )SA′ (M,N )]=( 1) ( 1) ⇒ NA AP PB BM MC CN NB′ B′P PC′ C′M MA′ A′N =1 NX XP PB BM MA′ A′N NB′ B′P PZ ZM MC CN NA AP PC′ C′M MY YN NA AP PB BM MC CN NB′ B′P PC′ C′M MA′ A′N = 1 1 36
(
(
)S
(M,N
(
ByusingtheManelustheorem,pointX,Y,andZ iscollinear,andformsthepappusline.
4Real-lifeUsage
4.1Blueprints
Usingprojectivegeometryanditswell-knownapplications,Pappustheorem,areusedinconstructingblue printsin3D.Computingitgivesusthemostaccurate blueprints,andusingthepappustheoremwecancreate3pointsthatarecollinearperfectly,andusethem inastrotechnologyandotherapplicationswherethe extremeaccuracyisrequired.
4.2LightProjection
Inmoderntechnology,projectivegeometryisused incomputationsthatallowdifferenttypesoflens,like onesinourglasses,tobeaccurate.Itcanalsobeusedas predictionofshadowsandusingtheminadvantageous ways.
5Conclusion
Pappuslineisthetheoreminprojectilegeometry thatcansuccessfullyplot3collinearpoints.Ithasvarietyofapplicationisthefundamentaltheoriesthatare usedinvariouscoordinatesystemsandcomputational program.
6References
1. https://www.britannica.com/science/Pappussprojective-theorem
2. https://en.wikipedia.org/wiki/Pappus%27s_hexagon_theorem
3. https://www.researchgate.net/figure/Pappustheorem-in-classical-projective-geometry-The-linesa-b-and-c-are_fig13_2107629
4. https://www.researchgate.net/figure/The-Pappustheorem-if-A-1-A-2-A-3-and-B-1-B-2-B-3-are-twocollinear-triples-of_fig18_305401152
5. https://math.uchicago.edu/˜may/REU2021/REUPapers/Roscoe.pdf
6. https://www.mathinactionjournal.com/pappusdesargues
7. https://www.cut-theknot.org/pythagoras/Pappus.shtml
⇒ NX XP PZ ZM MY YN = 1 ⇒ Sx(N,P )Sz(P,M )Sy(M,N )= 1
37
PiApproximation
Hanjin(Ryan)Lee Year11
Email:hj2lee26@pupils.nlcsjeju.kr
Editor
Emma(Chaeeun)Chung
RecommendedYearLevel:KS4,KS5
Keywords:Pi,BinomialTheorem,Integration
1Introduction
Pi,denotedasthegreekletter π,isamathematicalconstantthathascaptivatedthemindsofmany mathematicians.Definedastheratioofacircle’scircumferencetoitsradius,thedecimaldigitsofpiextendendlesslyas3.14158265...,lackingaperceivable pattern.Drivenbythesignificancethattherenowned constantholdsinthefield,orperhapspurecuriosity derivedfromitsnever-endingnature,mathematicians haveattemptedtomanuallycalculatepiasaccurately aspossibleforlong;however,mostremainedunsuccessful.ThispaperaimstodiscussNewton’sapproach,one ofthefewfruitfulattempts,tothisproblem,alongside theevaluationofhowhismethodtookprimitivemathematicstoadifferenttrajectory.
2BackgroundInformation
Atfirst,accordingtothedefinitionofpi,people couldeasilyfindoutthatthenumericalvalueofpiwas inbetween3and4bythefollowingprocess;
1. Inscribearegularhexagonwithasidelengthof1
2. Splitthehexagoninto6equilateraltriangles.This givesthediameterofthecircle,whichis2.
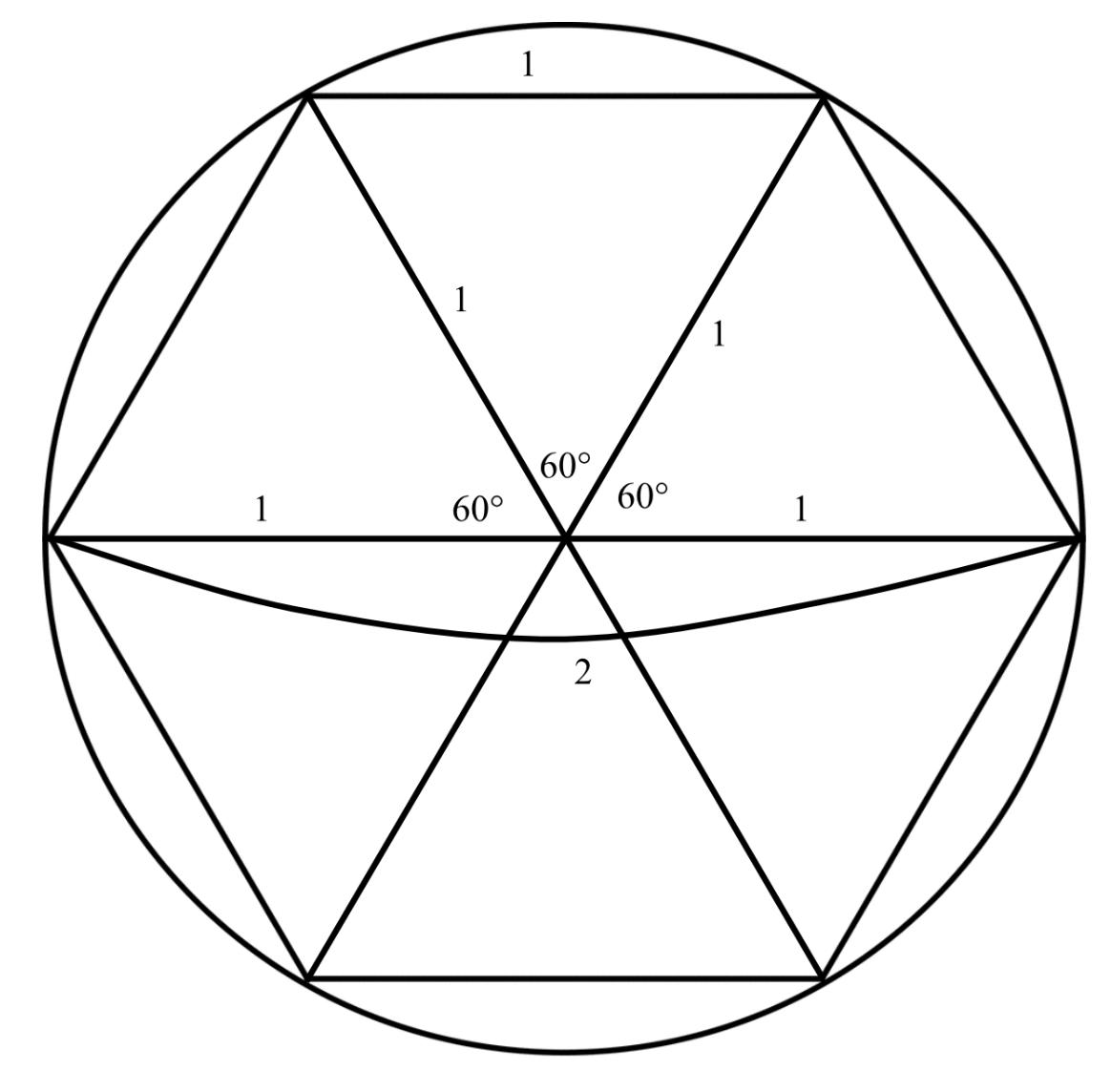
3. Theperimeteroftheinscribedhexagonisthen6, meaningthatthecircle’scircumferencehastobe larger.
4. Therefore, π> 6 2
5. Inthisway,thecircleisinscribedtoasquare.This givestheperimeterofthesquare,8,whichislarger thanthecircumference.Therefore, π> 8 2 .
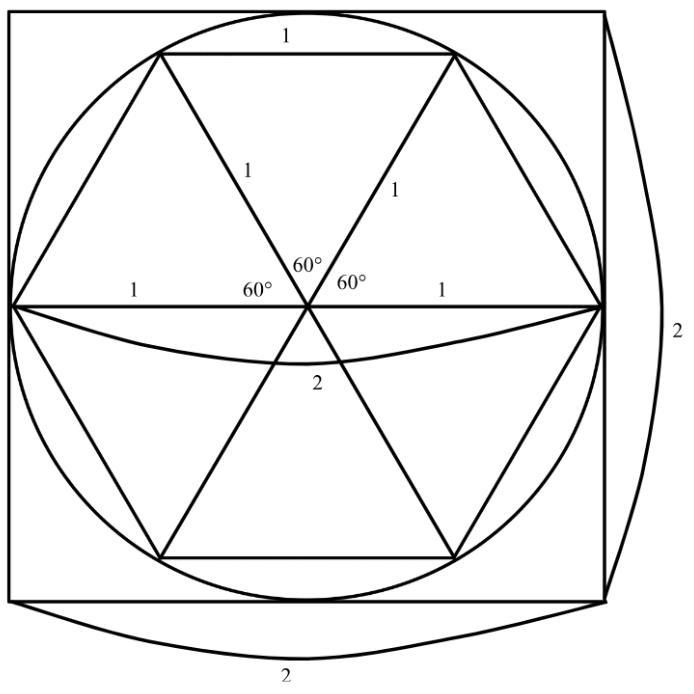
However,Archimedesexpandeduponthismethod further.Heinsteaddrewtangentialandcyclicpolygons ofthecircle,graduallyincreasingtheirnumberofsides andcalculatingtheirperimeters;heknewthatregular polygonsfollowtheshapeofacircleasmoresidesare addedandsignificantlynarrowedtherangeofpossible
insideacircle.
Fig.1:Hexagoninscribedinacircle
Fig.2:Hexagonsplitinto6equilateraltriangles
Fig.3:Thecircleisinscribedinasquare
38
pivalues.Inthisway,althoughthecalculationprocess oftheircircumferenceswascomplexandtedious,itwas stillpossibletodeduceapreciseenoughrangeofpi, eventuallyreachingtheconclusionthatpimustbein between3.1429and3.1408aftercalculatingtherange withpolygonsof96sides.
Precisionforpracticalpurposeswasalreadycomplete;still,mathematiciansacrosstheglobeattempted toobtainevengreateraccuracy,nowasamediatopubliclyexpresstheirmathematicaltalent.Eventually,after25yearsofdevotion,LudolphVanCeulenmanaged tocomputetheperimeterofa 262 sidedpolygon,just tocalculate35decimalsofpi.Despitetheeffortsthat manymathematiciansputinto,itwasapparentthat Archimedes’methodwasincrediblyinefficient.
3Pascal’sTriangleandBinomialTheorem
TheBinomialTheorem,whichmayseemirrelevant tothediscussion,infact,isanintegralconceptwhen understandingNewton’scalculationofpi.Pascal’striangleandthebinomialtheoremwasalreadywellknown evenbackinNewton’sera.
Pascal’strianglecanbecreatedbyaddingthetwo adjacentnumberstocalculatethenumberbelowit, whenthestartingnumbersaretwo1s.
Giventheequation (1+ x)2,itsexpandedformis 1+2x+x2.Inthesameway, (1+ x)3 is1+3x+3x2+x3 whenexpanded.Inthisway,forallexpansionsofbinomialsraisedtothepowerofnwhennisanon-negative integer,theircoefficientscanbearrangedasPascal’s triangle.
Usingthisinformation,peoplecalculatedthegeneralisedformulaofthenthrowofthepascal’striangle, whichturnedouttobe:
Thisisalsoknownasthe binomialtheorem
4Binomialtheorembeyondnaturalnumbers
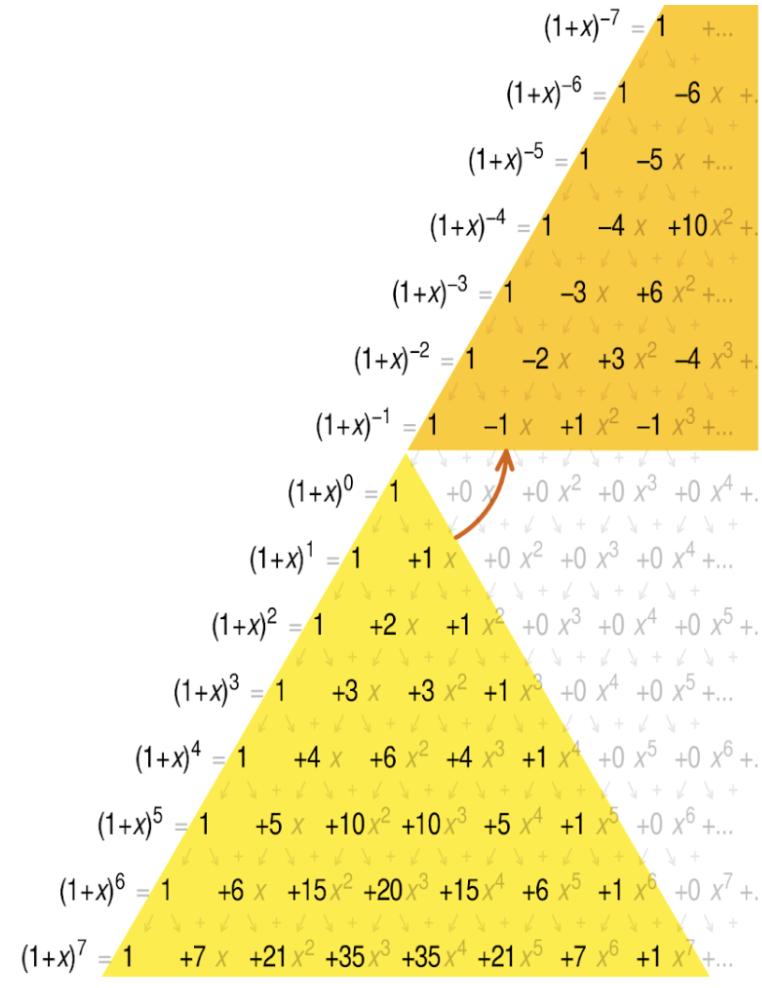
This“BinomialTheorem”wasfirmlybelievedthat itonlypermittednaturalnumbersasn,astheformula wasdeducedinthefirstplacetofindthe“nthrow”of Pascal’striangle,whichisaconceptinwhichonlypositiveintegersworkwith.Despitethisaxiomaticprinciple,Newtondecidedtoput-1,anegativeinteger,asn, riskingthefailureoftheformula.
Theproblemwhennisanegativeintegerwasthe following.Originally,giventhatnisanonnegativeinteger,asthecoefficientsofthetermsaren,n(n-1)/2!, n(n-1)(n-2)/3!...andsoon,atacertainpointwhenone ofthefactorsbecomes0dueton-n.Thetermsafterwill turnto0aswell,leavingafinitesum.Forinstance,if n=3,n(n-1)(n-2)(n-3)/4! X 4 Willequalto0asn-3=0, andsowillthetermsthatcomeafterwards,asallof themincluden-3asafactoroftheircoefficient.This explainswhythepascal’striangleisatriangleinthe firstplace,insteadofeveryrowextendingendlessly.
However,fornegativeintegers,representedby-1, thatisn’tthecase;negativeintegerminuspositiveintegercanneverequal0,making (1+ x)n (n ∈ Z ) an infiniteseries.Ifn=-1,theresultingbinomialexpansion isthefollowing.
Fig.4:Inscribedpolygons
Fig.5:Pascal’sTriangle
(1+x)n =1+nx+ n(n 1) 2! x 2 + n(n 1)(n 2) 3! x 3 + ∞ (1)
(1+ x) 1 =1+( 1)x + 1( 1 1) 2! x 2 + 1( 1 1)( 1 2) 3! x 3 + 1( 1 1)( 1 2)( 1 3) 4! x 4 =1 x + x 2 x 3 + x 4 (2) (1+ x) 1 becomesaninfinitesequence.However,if 39
Newtonwasconvincedthatthebinomialtheorem willworkwiththerestofthenegativeintegersaswell. Thiswasanimplicationthatthepascal’strianglecould beextendedabove0,startingwiththerow0,1,-1,1,-1, andsoon.Thismakessense,astheimpliedextension ofnthrows (n ∈ Z+) isendless0s,and1-1or-1+1are both0.Assumingthatnegativeintegersworkwiththe binomialtheorem,ifnegativeintegerswereputinthe formulaandarrangetheinfinitecoefficientsinPascal’s triangle,surprisingly,theextensionabove0isidentical totherotatedPascal’striangleofthepositiveside,if negativesignsareignored.Inaddition,thenegative rowsalsodonotdivergefromthefundamentalruleof Pascal’striangle,whichwasaddingtheneighboursto obtainthevaluebelow,provingthevalidityofnegative integersinthebinomialtheorem.
5Expansiontorationalnumbersunitcircle
Conjecture:Newtonnowattemptedtoputnumbers thatwerenotintegers.Bydoingso,heaimedto:
1. Expandtherangeofpermittednvaluestorational numbers.
2. Usethebinomialtheoremtogetasequencethat isequivalenttotheunitcircleequationarranged abouty.
3. Integratethesequence.
Infact,aPascal’striangleofitsowncouldbe formedwith.5binomialexpansions,inwhichnoneof

therowshasintegerpowers;inthesamewayofthe originaltriangle,theruleofaddingtwoadjacentnumberstocalculatetheonebelowappliedtothenewly createdtriangleaswell.
Again,thisshowsthatthebinomialtheoremcan operatewithrationalnumbersingeneral.
Amongthenon-integersNewtonwasallowedtoput asn,heputthefocusonthenumber 1 2
Why?
Theequationforaunitcircleis x2+y2=1.If theequationisrearrangedabouty,itbecomes y = 1 x2 1 2 .Iftheequationisplottedonax-yplane, itdrawsasemicircle:
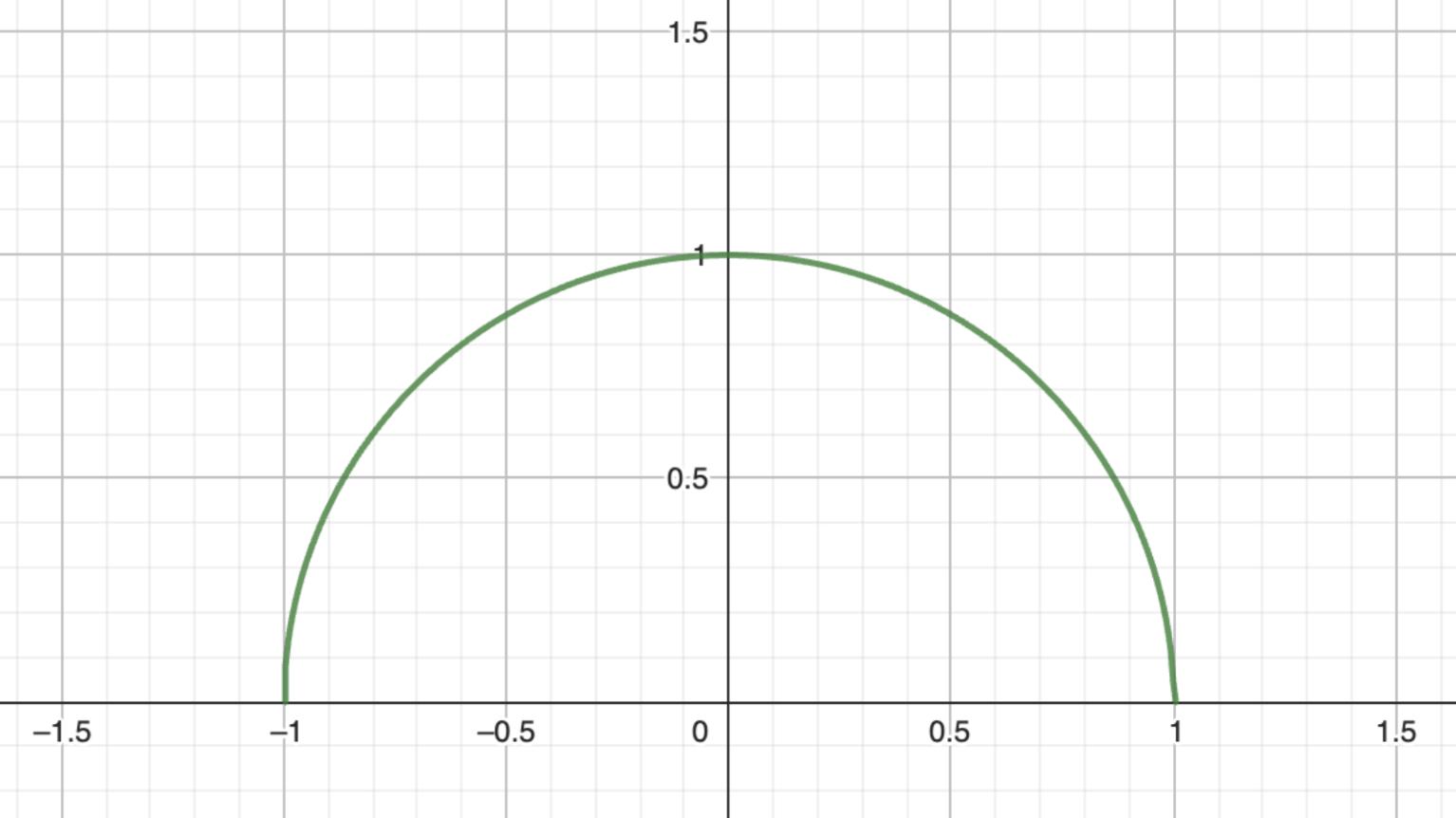
Fig.8: y = 1 x2 1 2
Essentially, y = 1 x2 1 2 isequivalenttothebinomialtheoremformulawheren= 1 2 andxisreplacedwith x2,meaningthat
1 1+ x (1+ x)=1 = 1 x + x 2 x 3 + x 4 (1+ x) =1+ x x x + x 2 + x 3 x 3 x 4 + x 4 + x =1 (3)
(1+x)ismultipliedonbothsides,
Fig.6:NegativeIntegersintheBinomialTheorem
Fig.7:.5BinomialExpansions
(1+ x) 1 2 =1+ 1 2 x + 1 2 1 2 1 2! x 2 + 1 2 1 2 1 1 2 2 3! x 3 + 1 2 1 2 1 1 2 2 1 2 3 4! x 4 =1+ 1 2 x 1 8 x 2 + 1 16 x 3 5 128 x 4 (4) 40
y
isasemicircle;ifthecurveisintegratedasxgoesfrom0to1,followingthefundamental rulesofintegration,theareaunderthecurvecanbe calculated.Therangeof0from1ishalfofanoriginal semicircle;therefore,theintegrationof
Nowthatthetermsconvergetotheintegrated constantquicker,thenumericalvalueof 1 2 0 1 x2 1 2 whichthesequenceconvergestohastobecalculated. Thefollowingimageisthevisualisationof f (x)=
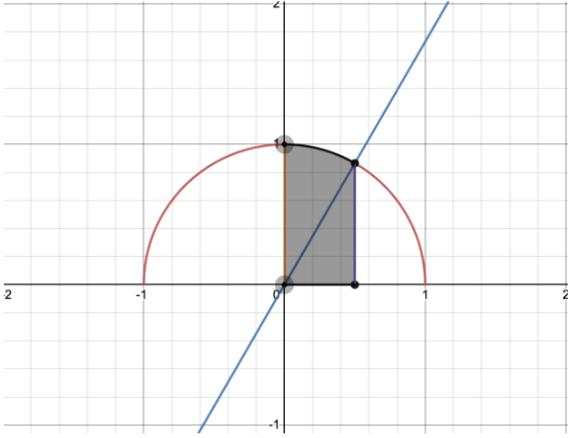
Theintegratedareacanbedividedintotwosections:asectorwithanangleof π 6 ,andarighttriangle. Now,theareaoftheshadedregioncanbecalculated:
6Experiment:Integrationfrom0to ½
Itistruethatthesequenceconvergestopifaster thantheprimitivemethodsofbisectingregularpolygons,butitcertainlydoeslackspeedforittobea ground-breakinginnovation.
Toconvergetopifaster,asimplesolutioninterms ofintegrationistointegrateasmallerfractionofthe function.Becausethevaluethatthesequenceapproachesisultimatelysmaller,intuitively,thesizeof thetermsofthesequencewilldiminishfasteraswell, resultinginafasterconvergence.Therefore,thistime, theequation y = 1 x2 1 2 canbeintegratedinasmaller range:from0to ½.
Now,thesequenceconvergestoaconstantthatcontainspi.Theconstantnowhastobearrangedwith respecttopi.
Inthisway,thesumofonlythefirstfourtermsendsup being:3.14161.
7Conclusion
Newton’sinventionwastrulyamathematicalsensation.Fromitsadvent,noonededicatedtheirentire livesjusttocalculatethefiftiethdecimalofpithatcould
1 x 2 1 2 =1+ 1 2 x 2 1 8 x 2 2 + 1 16 x 2 3 5 128 x 2 4 ... =1 1 2 x 2 1 8 x 4 1 16 x 6 5 128 x 8 (5)
= 1 x2 1
y = 1 x2 1 2 , whichisalso 1 1 2 x2 1 8 x4 1 16 x6 5 128 x8 ,isequal to 1 2 × π 2 = π 4 π 4 = 1 0 1 x 2 1 2 = 1 0 1 1 2 x 2 1 8 x 4 1 16 x 6 5 128 x 8 ...dx = x 1 2 x3 3 1 8 x5 5 1 16 x7 7 5 128 x9 9 1 0 =(1) 1 2 (1)3 3 1 8 (1)5 5 1 16 (1)7 7 5 128 (1)9 9 ... =1 1 6 1 40 1 112 5 1152 ∴ π =4 1 1 6 1 40 1 112 5 1152 (6)
2
1 2 0 1 x 2 1 2 dx = x 1 2 x3 3 1 8 x5 5 1 16 x7 7 5 128 x9 9 ... 1 2 0 (7)
1 2 0 1 x2 1 2 dx : Fig.9:Visualisationof f (x)= 1 2 0 1 x2 1 2 dx
f (x)= 1 x2 A = r 2θ 1 2 +0 5 f (0 5) ∴ A =(1)2 · π 6 · 1 2 +0 5 · (1 0 52) = π 12 + √3 8 ∴ 1 2 0 1 x 2 1 2 = π 12 + √3 8 = 1 2 1 48 1 1280 1 14336 5 589824 (8)
π 12 + √3 8 = 1 2 1 48 1 1280 1 14336 5 589824 π 12 = 1 2 1 48 1 1280 1 14336 5 589824 √3 8 π =12 1 2 1 48 1 1280 1 14336 5 589824 √3 8 (9)
41
bedoneinamatterofdays.Itcontributedtotheexpansionofthescopeofapplicationofpiinreallife,as therequiredaccuracyforpitobeapplicableincomplex real-lifesituationscouldeasilybeachievedthroughsimplecalculations.Although,twomaindisappointments existedintheprocessofanalysinghismethod:
1. Atthisstageoftheacademiccourse,itwashard toperfectlyprovethevalidityofbinomialfunction withallrationalnumbersotherthanbygivingexamplessuchas ½ ordisplayingasmallfractionof pascal’strianglethatfollowedthetrend.
2. Thetermsofthesequencearequitearbitrary,withoutanoticeablecommonratioordifference;forthe samereason,thesequencecouldnotbegeneralised toamoreintuitiveformat,wherethenexttermcan easilybederived.
ItisstillworthrememberingthatNewton’smethod setsitsbasisonaverysimplemathematicalconceptthat everyonewasawareof:thebinomialtheorem.After all,hisbreakthroughrootsfromtheslightesttwistof convention,whichendedupbeingoneofthegreatest inspirationsofitstime.
8Bibliography
1. Insearchof:Exploringtheuniverse. TimesofMalta.(2022,October25). https://timesofmalta.com/articles/view/In-searchof-exploring-the-universe.628886
2. JJO’Connor.(2009,April).LudolphvanCeulen-Biography.Maths History.https://mathshistory.standrews.ac.uk/Biographies/VanCeulen/
3. Pascal’striangle.AllYouEverWantedto KnowAboutPascal’sTriangleandmore.(n.d.). https://ptri1.tripod.com/
4. Cmglee.(2021).Pascaltriangleextended.
42
DivisionbyZero
Taehoon(Sean)Kim Year11
Email:thkim26@pupils.nlcsjeju.kr
Editor
Derek(Yejun)Yoo
RecommendedYearLevel:KS4
Keywords:zero,division,limits
1Introduction
We’vebeenindoctrinatedbythemathdepartment, specifically,Ms.Bulut,toaccepttheunprovedmathematical propertiesthatdivisionbyzeroisindeterminate.WhenIhad inquiries,theytoldmethatdividingby0wassimplyimpossible.Evenworse,Ms.Buluttreatsthemavericksthatare brazenenoughtoquestionsuchnormsasignorant,ostentatious,andun-additional-mathable-useless-set-5-ishmuppets. Fromhere,myinstincttodisobeyMs.Bulutpromptlyarises: isdivisionbyzeroimpossible?
2InheritContradictionsofdivisionby0
Thereasonwhydivisionby0isprohibited,orleftundefinedinmathematicsisbecausetheallowanceof0division devastatestheprinciplesandregulationsofmathematics,especiallyarithmetics.
3IntuitiontoArithmetics
Thefoundationofarithmeticistheassumptionthatthere areobjectscalledrealnumbers.Itisassumedthatthese realnumberscanbemodifiedbyadditionandmultiplication, whichtaketworealnumbersandoutputinathird:
Addition
∀a, b ∈ ℜ, ∃a + b ∈ ℜ
Multiplication
∀a, b ∈ ℜ, ∃ab ∈ ℜ
Thoseoperationsareassumedtosatisfycertainaxioms, whichcannotbeproven,includingstandardcommutative, associative,anddistributivelawsforarithmetic.Among
thoseaxioms,thedefinitionofinverseoperationsaredenoted:
Additiveinverse:
Multiplicativeinverse:
Fromhere,theasymmetryofadditiveandmultiplicative inverseisevident:additiveinverseisdefinedinallsetsof realnumberswhereasmultiplicativeinverseisdefinedforall non-zeronumbers.Consideringthattheinverseofaddition andmultiplicationisalsoknownassubtractionanddivision respectively,whyis0excluded?
4DefinitionofDivision
Theaxiomsofarithmeticareonlydefinedforaddition andmultiplicationoperations,thusthesubtractionanddivisionaredefinedaftertheaxiomsarestated.
Division:
canbesatisfied.Hence,multiplicationisnotdefinedfor0as thereisno0 1 :0doesnothaveamultiplicativeinverse.
∀a ∈ ℜ, ∃− a ∈ ℜ, a +( a)= 0
∀a ∈ ℜ −{0}, ∃a 1 ∈ ℜ, a · a 1 = 1
∀a, b ∈ ℜ, b = 0, a ÷ b = a × b 1 (1)
5 ÷ 4 = 5 1 4 = 5 4 1 (2)
forinstance,
43
5Indefinitenatureof 0 1
Theorem1: ∀x ∈ R, 0x = 0Proof:
1 + 0 = 1
Multiplyingbothsidesby x,
x(1 + 0)= 1x
Usingthedistributivelaw,
1x + 0x = 1x
Usingtheaxiomthat1x = x, x + 0x = x
Adding x tobothsides, x +(x + 0x)= x
Usingtheassociativelaw, ( x + x)+ 0x = x + x
Usingtheaxiomofadditiveinverse,
0 + 0x = 0(∵ x + x = 0)
∴ 0x = 0
SeeAppendixAforaxiomforfieldsSupposethat a = 0 1.Then,inaccordancewiththedefinitionofmultiplicativeinverse,
0a = 1
However,substituting z totheorem1lendstheequation of
0a = 0
Thissuggeststhat0 = 1,anevidentcontradiction. Therefore,assigninganyrealnumberto0 1 ismathematicallyimplausiblewithoutcontradictingthepre-established axiomofarithmetics.Attempttodefine0 1 innon-realnumbersisawholedifferentstory.Consideringthat0 1 maydisobeythecurrentrulesofarithmetics,mathematiciansmust figureoutseveralnewruleswhichcouldsatisfythecalculationof0 1 withoutanycontradiction.However,theusefulnessof0 1 highlyquestionable:itismuchsimplertoadmit that0doesnothaveitsmultiplicativeinverse.
6Intuitiononreversibility
Asaninverseoperationofmultiplication,divisionaninvertibleoperation-mustbereversibleinthefollowing sense:Ifa,b,csatisfiestheequation,
∀a, b, c ∈ ℜ, ab = c, b = 0(3)
themultiplicandacouldbeexpressedby
a =
Subsequently,ifweassumethatb=0,
theequationitselfdoesnotofferanyinformationaboutmultiplicand:multiplyingby0isanon-invertibleoperation. Also,simplysubstitutinganynon-zeronumberforawould createacontradiction.
7Absenceofdefinition
Asaforementioned,theorem1hasprovedthat
istrueforeveryrealnumbera.Thenusingthisequation,the valueof00canbededucedasfollowing:
Unfortunately,defining0 ÷ 0asanyrealnumberdisobeysthedefinitionofalgebraicalarithmetics:thecalculationbetweentworealnumbersmustproduceasingledefined value.Inparticular,3+3=6and3+3=2cannotbesatisfiedsimultaneously.Aseverymathematiciancannotreachthereasonabledefinitionof0 ÷ 0divisionby0remainsundefined underanycircumstances.
8Intuitivelimitarguments
Referringbacktothedefinitionofdivision,
c b
a = c 0 0a = c
∀a, 0 × a = 0(4)
0 ÷ 0 = a ∈ ℜ (5)
∀a, b ∈ ℜ, b = 0, a ÷ b = a × b 1 (6)
1 ÷ 1 n = 1 × n 1 1 = n (7) 44
canbesubstantiated.Fromtheequationabove,itisevident thatifthedividendis1,thedecreaseinthedivisorincreases thequotient.
Theequationaboveshowswhennreachesinfinity.As limn→∞ n 1 getsinfinitelycloserto0asnreaches,canwe define10=?Beforediscussing,itissignificanttonotethat ∞ referstotheconceptofcontinuousandlimitlessincrease, notadefinitenumber.Therefore,thecalculationbetween numbersmustproduceadefinitenumber,notasymbolthat representsanambiguousconcept.Evenifweassumethat 1 ÷ 0 = ∞ istrue,thecontradictionisunavoidable.Fromthe previousequation,justchangethesignofthedivisor.
Infact,thoseindeterminateformdoesnotactuallycalculate0or ∞.Rather,itapproachesthecalculationoflimits byexploringtheratiobetweenfunctions.Simply,assume thatthevalueofnon-zeroaexistsandaisextremelyclose to0.Then,thefractionalformcanbesimplifiedbydividingboththedenominatorandnumeratorbyanumberthatis extremelycloseto0yetnot0.
Supposethatthenreachesinfinity,then 1 n willconvergeto 0whilethe1 ÷ 0 = ∞.Here,wecouldconcludethat
Thisishowtheindeterminateform,specifically 0 0 iscalculated.Therefore,theresultoftheindeterminateformcannot betheactualcalculationofdivisionby0.Forinstance,supposethattherearetwofunctions
Thenwhenxapproaches0,
whichisaclearcontradiction
Thisproblemiswhythefunction f (x)= 1 x doesnothave extremevaluewhenxapproaches0.
9Calculationofindeterminateform
Asthedivisionisacumulativeandcontinuousprocess, especiallyinlimits,0mustbeconsideredcarefully.Inparticular,indeterminateformssuchas 0 0 or ∞ ∞ mightintuitively provideinsightfordivisionbyzero-yetdoesitreally?
Theratiobetweenf(x)andg(x)altersandproducesacontradictionwhere 2 3 = 4 3 .Evenifthefunctionsconvergeto 0,dependingonthefunctions’convergencespeed,thevalue coulddivergeorconverge:
Therefore,divisionby0orthefunctionthatconvergesto0 mustbetakenextremelycarefullytoavoidanypossibilities ofcontradiction.
10Divisionby0
Aspreviouslymentioned,divisionby0isprohibitedas ithindersthebasicprinciplesofmathematics.Then,whatif divisionby0couldbecalculatedwhilepreservingthebasic rulesofmathematics?
11Group,Ring,andField
11.1Group
Group ⟨G, ⊕ > isasetthatisclosedundertheonebinary operation,anoperationthatreceives2inputsandoutputsone result, ⊕ :
lim n→∞ 1 ÷ 1 n = lim n→∞ n → ∞ (8)
1 ÷ 1 n = 1 × n 1 1 = n (9)
10 = ∞ = ∞ (10)
∃a > 0, a → 0, 2a 3a = 3 2 (11)
f (x)= 2x 2 , f (0)= 0 g(x)= 3x 2 , g(0)= 0 (12)
lim x→0 f (x) g(x) = lim x→0 2x2 3x2 = 2 3 (13)
lim x→0 sin x x = 1 lim x→0 x tan x sin x = ∞ (14)
∀a, b ∈ G, a ⊕ b ∈ G 45
Forinstance,naturalnumbersareclosedundermultiplicationasthemultiplicationoftwonaturalnumbersalways producesthenaturalnumbers.
∀a, b ∈ K , a · b ∈ N
However,naturalnumbersarenotclosedunderdivision asthedivisionofnaturalnumbersdoesnotnecessarilyresult innaturalnumbers.
∀a, b ∈ N , a ÷ b / ∈ ℵ ⇒ b ∤ a
Also,thegroupmustsatisfythefollowingaxioms:associativeproperty,identityelement,andinverseelement.Associativepropertyiswhentheresultofthebinaryoperation ofmorethanthreenumbersremainsthesameirrespective ofhowtheyaregrouped.Itcanbeexpressedasfollows:
∀a, b, c ∈ G, a ⊕ (b ⊕ c)=(a ⊕ b) ⊕ c Theidentityelementis whenexecutionofbinaryoperationdoesnotcausethealterationofanelement’svalueinacertainset.
∀a ∈ G, ∃e ∈ G, a ⊕ e = e ⊕ a = a
Inparticular,themultiplicativeidentityelementofinteger set, ⟨Z, x >,is0as
∀a ∈ Z, a × 1 = 1 × a = a
Theinverseelementiswhenperformingagivenbinary operationresultsintheidentityelementofthegivenelement.
∀a ∈ G, ∃x ∈ G, a + x = x + a = e
Forinstance,theinverseelementofadditionisthevalue thatresultsintheadditiveidentityelement:0
∀a, a ∈ Z, a +( a)=( a)+ a = 0
Hence,foranintegerset,theadditiveinverseelementis alwaysthenegativevalueofanumber.Examplesofgroups arefollowing:
< Z, + >,< Zn′ + >,< Q, + >,< R∗ , x >
Incontrast, ⟨Z, x > isnotconsideredasagroupalthough itsatisfiesassociativepropertyandtheidentityelementexists becausetheinverseelementisincludedinthesetofintegers.
∀a ∈ Z, a × 1 = 1 × a = a a × 1 a = 1, 1 a / ∈ Z
11.1.1Abeliangroup
Intheaxiomsofthegroup,thegivensetandthebinary operationdoesnothavetosatisfythecommutativeproperty. Ifthegroupsatisfiesthecommutativeaxiom,itiscalledan abeliangroup.Forinstance, < Z, + > or ⟨Z, x > satisfiesthe commutativeaxiom,henceitisanabeliangroup.
∀a, b ∈ Z, a + b = b + a
∀a, b ∈ Z, ab = ba
Asacounterexample,althoughthesetofallinvertible 2 × 2matricesformagroupunderthematrixmultiplication, < M2(Q), × >,
det(A B)= det(A) det(B)
(A B) C = A (B C)
A I = I A = A
AA 1 = A 1A = I
asgeneralmatrixmultiplicationdoesnotsatisfythecommutativelaw,itisnotanabeliangroup.
let A = ab cd , B = ef gh
A B = ab cd ef gh = ae + bgaf + bh
ce + dgcf + hd
B A = ef gh ab cd = ea + fceb + fd ga + hcgb + hd
∴ A B = B A
11.2Ring
(15)
Unlikeagroup,whichisdefinedforonlyonebinary operation,theringisdefinedforbothadditionandmultiplication.Interestingly,theringisconsideredasemi-groupin multiplication:identityandinverseelementsarenotessential.Ring, ⟨R, +, x⟩,isclosedunderadditionandmultiplicationandsatisfiesthefollowingaxioms: < R, + > isabelian group
∀a, b, c ∈ a (b c)=(a b) c
∀a, b, c ∈ R, a (b + c)=(a b)+(a c) (a + b) · c =(a · c)+(b · c)
11.3Field
Fieldisdefinedwhenaringhasanidentityelementand aninverseelementofmultiplication.Field ⟨F, +, x⟩ therefore shouldbering, ⟨R, +, x⟩,andsatisfyadditionalproperties:
∀
1 a = 1
Fieldformsanabeliangroupforaddition,andmultiplicationsexcept0.Examplesoffieldsare ⟨Q, +, x > , ⟨ℜ, +, x >,and ⟨C, +, x >.
−{
a ∈ F, ∃1 ∈ F, 1 · a = a · 1 = a ∀a ∈ F
0}, ∃a 1 ∈ F, a a 1 = a
46
12Arithmetics
Contrarytoourgeneralknowledgeofarithmetics,which includesaddition,subtraction,multiplication,anddivision, fieldandringareonlydefinedforadditionandmultiplication.Thisisbecausetheadditiveinverseelementcouldreplacesubtractionanddivisionissubtractionandthemultiplicativeinverseelementisdivision.Therefore,theideaof divisibilityinacertainfieldtransferstotheexistenceofmultiplicativeinverse.Forfield < F, +, × >,
However,itisimportanttonotethatthezeroringisa specializedoccasionthatcouldforceustodefinethedivisionbyzero.Therefore,thiscannotbeappliedtogeneral mathematicsasthemultiplicativeinverseof0isindeterminate:0 1 = 0isuselessexceptfortheuniquecharacteristic thatthezeroringpossesses.
14Wheeltheory
Previously,Ihavediscussedthatdefining
couldbeproblematicintermsoflimit,evenifweassumethat theconceptofinfinityisanumber,thesignoftwoinfinity wouldbedifferent:
Also,theinverseofanelementisalwaysunique.This canbesubstantiatedbyproofbycontradiction:forgroup ⟨G, ∗⟩ , ∀a, b, c ∈ G.let a′ betheinverseofasupposethat anotherinverse ∃a′′ = a′ Then, a a′
Thiscontradictsouroriginalassumption ∃a′′ = a′,hence theuniquenessoftheinverseisproved.Therefore,defining 1 0 canbededucedtofindingtheuniquemultiplicativeinverse of0.
13ZeroRing
Theset Z = {0},alsoknownaszeroring,isaspecializedringthatcoulddefinethedivisionbyzero.The setitselfformsanabeliangroupforaddition,andformsa semigroupformultiplication:itisconsideredasaring:for < {0}, +, x >,
Then,whatifweassumethat ∞ = ∞ ?Theideaof wheeltheoryoriginatesfromhere.Inmathematics,there isauniquewaytolimitinfinityinafiniteform:one-point compactification.Thissimplifiesthecomplexproblemsusingone-to-onecorrespondence.Supposethatthesetofreal numberscouldberepresentedasanendlessstraightline, xaxis.Fromhere,acircle
Therefore,0isanadditiveandmultiplicativeidentity elementsimultaneously:zeroringistheuniquecasewhere theadditiveandmultiplicativeidentityelementarethesame. Fromhere,giventhat0isthemultiplicativeidentityelement, zeromultipliedbythemultiplicativeinversemustresultina multiplicativeidentityelement,zero.
couldbedrawn.Then,astraightlinethatstartsfrom P(0, 1) andcrossesanypointonacirclemustinterceptwith x-axis. Asthestraightlineonlycrossesthe x-axisonce,itisevident thatthepointonacircleandthe x-axisisone-to-onecorresponding.Forinstance,adiagraminFigure1-2showsthat pointAcorrespondstopointEonacircle,pointBcorrespondstopointG,andpointFcorrespondstopointFitself. Hence,ifthecirclewithout P(0, 1) isdenotedas S 1 ,
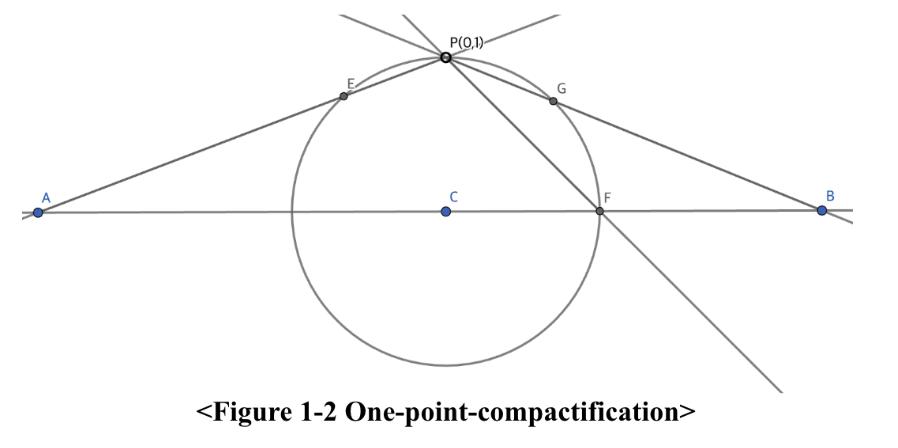
Therefore,applyingtheaforementionedlogic,
ℜ
However,theset S 1 P(0, 1) isconsideredasbounded yetnotclosed.Giventhataboundedandclosedsetin T2 iscompact,wecouldclosethesetbyaddingonepointto
∀a ∈ F, a 1 a = 1 a a 1 = 1 a 1 = 1 a
∴ a ′ = a ′′ ∵ a a ′ = a a ′′
= e, a a′′ = e
0 + 0 = 0 0 × 0 = 0
0 × 0 = 0
0 1 = 0 ∴ 0 0 = 0
lim n→∞ 1 ÷ 1 n = 1 ÷ 0 = ∞
1 ÷ 0 = 1 ÷ ( 0)= ∞ = ∞
f (x, y)= x 2 + y 2 = 1
∼ = S 1 P(0, 1)
47
facilitatetheoverallprocess.As P(0, 1) wasexcludedona circle,wecouldaddpoint P anditscorrespondingpoint:
ℜ ∪{∞} ∼ = S1
Ifthisdefinitionisconfusing,imaginethatbothends oftheline-thatrepresentsthesetofrealnumbers-areconnectedinacircularformwiththepoint ∞ = ∞.Sincethe linecontainsinfinitelymanypoints,andasetofrealnumbersdoso,thenumberofpointsonacirclewitharadiusof1 willcorrespondone-to-onetothestraightlinewithinfinitely manypoints.
Atthispoint,althoughnowitbecameevidentthat ∞ =
∞,defining1 ÷ 0 = ∞ isyetimpossible:todefinedivisionby0asatypeofoperation,wemustfigureoutwhether theoperationsatisfiestheconditionsoffield,ring,orgroup. Therefore,theproofstartsbydefiningthecalculationsasfollows:supposethat
*Note:0 ÷ 0couldbedenotedasbottomsymbol, ⊥,orlunateepsilon, ε,oretc.
AccordingtotheWheelsonDivisionbyZero (J.Carlstrom,2001)set ⟨H, 0, +⟩ isacommutativemonoid (monoid:agroupthatdoesnotsatisfytheinverseelementorsemigroupthatsatisfiestheidentityelement)and ⟨H, 1, ×, ÷ > iscommutativemonoidwithinvolution(involution:afunctionoroperatorthatwhenappliedtwice,brings onebacktothestartingpoint).Fromhere,severaloperations couldbedefined.
However,theproblemarisesastheinverseelementof infinity, 1 0 ,is0whereas 0 0 remains 0 0 evenifweexecuteinverseoperations.
Distributivity
Rulesfor0terms
Therefore,wemustaddanewpointto S1,acurrentcircularsetofrealnumbers:ifwedefine
(a, b)= a b
wecouldaddapoint (0, 0) toacirclewithradiusof 1:theexpansionofthesetofrealnumberswouldlooklike acirclewithapointinthecentre(figure1-3)-ashapethat lookslikeawheel,andthatiswhythistheoryiscalledwheel theory!
Iftheoperationisdefinedasfollows,divisionbyzeroispossible.
1 ÷ 0 = ∞ 0 ÷ 0 = ε
a b + c d = ad + bc bd a b c d = ac bd a b = a b a b = 1 b a
1 0 0 = 1 0 0 = 0 0 ∴ 0 0 = 1 0
H = S1 ∪ (0, 0)
∀x, y, z ∈ H
(x + y)z + 0z = xz + yz x y + z + 0y = x + yz y
0 × 0 = 0 (x + 0y)z = xz + 0y /(x + 0y)= /x + 0y x + 0 0 = 0 0
0 0 = ε = 1 0 = ∞ = ∞ 48
TheadditionandmultiplicationwithinHarealsopossible.
Subtractionanddivisionoperatorsareexecutedbyusing theinverseelement.Forinstance, ∞ ∞ couldbecalculated usingthetableabove.
byzero.https://ee.usc.edu/stochastic-nets/docs/divide-by-ze ro.pdf
Hamblin,J.(2017,January3).Algebraic structures:Groups,rings,andfields.YouTube. https://www.youtube.com/watch?vvvfyUUprh9s
Carlstrom,J.(2001).WheelsonDivisionbyZeroSU. https://www2.math.su.se/reports/2001/11/2001-11.pdf
Kim,R.(2023a,September19).0.Ray. https://rayc20.tistory.com/322figure1-1:Bennett,M.(n.d.). F(x)= 1/x.GeoGebra.https://www.geogebra.org/m/knGkv f8E
EpicMath.(2019,August5).Wheeltheory-anintroduction.YouTube.https://www.youtube.com/ watch?v = aVqQ3XKWRUA
17AppendixA
1)Commutativelaw: a + b = b + a, ab = ba
2)Associativelaw: (a + b)+ c = a +(b + c), (ab)c = a(bc)
3)Distributivelaw: a(b + c)= ab + ac
4)Existenceof0,additiveidentity:
∀a ∈ ℜ, ∃0, a + 0 = a
15Conclusion
Assuch,thereisnosuchthingas‘never’intheinfinitefieldofmathematics.Eventhedivisionbyzeroisdefinedbyintroducingspecialisedsets:wheeltheoryandzero rings.Inelementaryschool,teachersclaimthatsubtraction betweengreatersubtrahendandsmallerminuendisimpossible.Whentheconceptofrealnumbersisintroduced,teachersarguethatanegativenumberinsquarerootisimpossiblesoon,teachersintroduceanewconceptof i = √ 1.Division byzero,andthefieldofmathematicsresentschallengingthe pre-existingaxiomsorproperties.Ihopethatthisarticlehas providedaninterestinginsightintomathematics.Always, wheneveryourteacherintroducesmathematicalproperties, questionandchallengeitasthepurebeautyofmathematics reliesonquestioningthegeneralnormsofmathematics.
16Bibliography
Neely,M.J.(n.d.).1whywecannotdividebyzero -universityofsoutherncalifornia.Whywecannotdivide
5)Existenceof1,multiplicativeidentity:
∀a ∈ ℜ, ∃1, a × 1 = a
6)Additiveinverse:
∀a ∈ ℜ, ∃− a ∈ ℜ, a +( a)= 0
7)Multiplicativeinverse:
∀a ∈ R −{0}, ∃a 1 ∈ ℜ, a · a 1 = 1
8)0notequalto1 0 = 1
∀x, y ∈ H −{0, ε, ∞}
∞ ∞ = ∞ ( ∞)= ∞ + ∞ = ε
49
18AppendixB
x + y = x + y x + 0 = x x + ∞ = x + 1 0 = x 1 + 1 0 = 0 · x + 1 · 1 1 0 = 1 0 =∝ x + ε = x 1 + 0 0 = 0 1 + 0 x 1 · 0 = 0 0 = ε 0 + y = y 0 + 0 = 0 0 + ∞ = ∞ 0 + ε = ε ∞ + y = 1 0 + y 1 = 1 1 + 0 y 0 1 = 1 0 = ∞ ∞ + 0 = ∞ ∞ + ∞ = 1 0 + 1 0 = 1 0 + 1 0 0 · 0 = 0 0 = ε ε + ε = 1 0 + 0 0 = 1 0 + 0 0 0 0 = 0 0 = ε ε + y = 0 0 + y 1 = 0 y + 0 1 0 1 = 0 0 = ε ε + 0 = 0 0 + 1 0 = 1 0 + 0 0 0 0 = 0 0 = ε ε + ∞ = 0 0 + 1 0 = 0 · 0 + 1 · 0 0 0 = 0 0 = ε ε + ε = 0 0 + 0 0 = 0 0 + 0 0 0 0 = 0 0 = ε 19AppendixC x y = xy x 0 = 0 x ∞ = x 1 1 0 = 1 1 x 1 0 = 1 0 = ∞ x ε = x 1 0 0 = 1 1 x 0 0 = 0 0 = ε 0 y = 0 0 0 = 0 0 ∞ = 0 1 1 0 = 0 0 = ε 0 ε = 0 1 0 0 = 0 0 = ε ∞ · y = 1 0 · y 1 = 1 0 · 1 1 y = 1 0 = ∞ ∞ · 0 = 0 ∞ ∞ = 1 0 1 0 = 1 0 = ∞ ∞ ε = 1 0 0 0 = 0 0 = ε ε y = 0 0 y 1 = 0 0 1 1 y = 0 0 = ε ε 0 = 0 0 0 1 = 0 0 = ε ε ∞ = 0 0 1 0 = 0 0 = ε ε ε = 0 0 0 0 = 0 0 = ε 50
TwinPrimesConjecture
SeongminHong
Year11
Email:smhong26@pupils.nlcsjeju.kr Editor Emma(Chaeeun)Chung
RecommendedYearLevel:KS4,KS5
Keywords:primenumbers,conjecture,proof
1Abstract ThisarticlewilldiveintotheTwinPrimeConjecture,statedbymathematicianAlphonsedePolignac.
2ResearchPaper
Theexplorationofprimenumbersstandsasacornerstoneintheancientrealmofmathematics,having beenapursuitwhichhascapturedtheattentionof mathematiciansfeelingdrawntowardsthefundamentalbuildingblocksofthenaturalnumbersystem.Despitethemillenniumssincewhichprimenumberswere discovered,itwasonlyrecentlydiscoveredthepracticalapplicationsofprimenumberswiththeinventionof thecomputerinthe20thcentury.Nowbeforewebegin withtheseveraldifferentapproachestothisproblem,we shouldfirstdefineacoupleoffundamentalkeywords.
3Definitions
1. Definition1:Aprimenumberisapositiveinteger withexactlytwopositivedivisors.
2. Definition2:Aprimetwinisapairoftwoprime numbers(p,q)suchthatbothofthesubsequent conditionsareapplicable:pandqaretwooddconsecutiveintegers(thusqis2lessthanp),pandq arebothprimenumbers
3. Definition3:Thedifferencebetweenaprimenumberandthesubsequentprimenumberiscalledthe “primegap”.
Theproofoftheinfinitudeofprimenumbersby Euclid(325–265b.c.e.)issomethingmostofthe peoplereadingthisarticlehavelikelyencountered inoneshapeoranother.
4Preposition4
Thereareaninfinitenumberofprimenumbers. Proof:
1. AssumethereareafinitesetofprimenumbersP= P1,P2...Pn.
2. LetN=P1 × P2 × ...Pn
3. SinceNistheproductofalloftheprimenumbersin setP,N+1isnotdivisiblebyanyofthenumbers suchthattheyarewithinsetP.
4. Thereforewecanconcludethateither:
(a) N+1isprimeitself=>contradictsassumptionmadeinstep1.
(b) N+1isdivisiblebyaprimenumbernotinset P=>contradictsassumptionmadeinstep1.
5. Thus,theoriginalassumptionthatthereareafinite numberofprimenumbersisprovenwrongthrough contradiction.
5Conjecture5(TwinPrimeConjecture
Thetwinprimeconjecturepositsthattherearean infinitenumberofprimetwins.

51
Fig.1

Eventhoughthetwinprimeconjecturewasstated almosttwocenturiesago,in1846byFrenchmathematicianAlphonsedePolignacinhisconjecture(called “Polignac’sConjecture”),itisstillyettobesolved.De Polignacstatedinhisconjecturethatforeverynatural numberk,thereareaninfinitenumberofprimenumbersp,suchthatp+2kisalsoprime.Thecaseofk =1ofdePolignac’sconjectureleadstothetwinprime conjecture.
Thereareseveralwaystotacklethisproblemofthe twinprimeconjecture.Toprovethetwinprimeconjecture,youwillhavetodemonstratethatthereisno largestprimetwin,whichwouldusuallybedonethrough proofbycontradiction.Orontheotherhand,todisproveit,itwouldtypicallybedonethroughshowing thatthereisanupperboundbeyondwhichnomore primetwinsexist.
6HeuristicApproach
Aheuristicapproachtothetwinprimeconjecture wouldinvolverecognisingtheintuitiveconnectionbetweentheinfinitudeofprimenumbers(asreferencedin proposition4),andthepotentialexistenceofaninfinite numberoftwinprimes.Wecanbasethisapproachoff oftheassumptionthatasweexplorelargerandlarger setsofnumbers,thefrequencyofprimenumberswill alsoincrease.
Consideringtheideathatthereareaninfinitenumberoftwinprimenumbers,thelikelihoodofencounteringprimetwinsshouldremainhighacrosslargerintervals.Theintuitionwithwhichwecanconcludethatif therangeofnumbersincreases,sodoestheprobability offindingprimetwins.
However,althoughthisapproachsuggeststheplausibilityofaninfinitenumberofprimetwins,likeother heuristicapproaches,itfallsshortwhencomingupwith arigorousproof.Thereisachallengeinestablishinga definitiveconnectionbetweentheinfinitudeofprimes andthecertaintyofaninfinitesetofprimetwins.
7Approach2.ExtensionofEuclid’sProof
Averyintuitivewayofapproachingthetwinprime conjectureisbyextendingEuclid’sprooftoapplyto thetwinprimeconjecture.Ifweassumethesamesteps fromuptostep3intheaforementionedformofEuclid’s
proofoftheInfinitudeofPrimeNumbers,thenwewill beabletoconcludethatN+1isprimeandN-1is prime,meaningthatthereareaninfinitenumberoftwin primeswiththis.
HoweverthisisonlywiththeassumptionthatN+ 1andN-1isprime,andifeitherN+1orN-1is divisiblebyaprimenumberwhichisabovethehighest numberinthesetestablishedinstep1,thenthisproof isdismantled.
Wecanfindacounter-examplewhichalsoproves thatthisisnotapplicablebylettingthesizeoftheset instep1asbeingequalto4,whichmeanstheelements ofthesetwillbe2,3,5and7.Theproductofthese willbeN=210.N+1=211isprimehoweverN-1 =209=11 × 19.
8Approach3.InfiniteSeriesProof
Apossiblewayofapproachingthisproblemwould bebyusinganinfiniteseries,anideaderivedfrom Dirichlet’sTheorem(withtwoprimenumbers(a,b) suchthatgcd(a,b)=1,thereareinfinitelymanyprime numbersoftheforma+nbwhere n ∈ Z+ 0 ).Ifyoucan provethatthesumofthereciprocalsoftwinprimesdiverge,youareabletoconclusivelyprovethataninfinite seriesofprimesexist(buttheoppositeisnottrue).
ViggoBrun’ssievecanbeusedhere,whichstates thatthenumberoftwinprimeslessthanNdoesnot exceed CN (log N )2 foraconstantC>0.Usingamathematicalproofwhichistoocomplicatedtodemonstrate here,Brunshowedthatthesumofthereciprocalsof thetwinprimesconvergedtoaconstant,whichisnow knownasBrun’sconstant,or B2
Youmaynowbethinkingthatthisisadisproofof theconjecture.However,thatisnottrueeither.The convergenceofthesumdoesnotimplytheexistenceof
Fig.2
Fig.3:pictureofbrun’sconstantconvergingtothis point
52
alimittothenumberofprimetwins.Asnincreases, thenumberoftwinprimesbecomesparse,andsimultaneously,thereciprocalsoftheselargernumberswill becomesmaller.Thus,itcanleadtoanincreasingly negligibleandsmallernumberwhichwillcontributeto thesuminsuchaminisculeamountaninfiniteamount oftimes.
9ComputationalProof
Anotherblatantmethodthatcomestomindwould bethroughtheusageofcomputeralgorithmstotryand solvefortheprimetwinconjecture.
Whatpeoplemayfirstthinkofisbytryingtofind anunfathomablyhighprimetwin.Averysimplebut unoptimisedpieceofcodeforthiswouldbelikesuch:
Thehighestprimetwinfoundis2996863034895 × 21290000 ± 1,whichisanumberwithover388342digits.
However,thereisaverybigproblemwiththisapproach-it’snotrigorous.Findinganunequivocally highprimetwindoesnotmeanthatthereareaninfinitenumberofprimetwins.It’snotenoughtofinda highprimetwin,oneneedstoshowthatthereisnolimit totheoccurrenceofsuchpairs.Additionally,thismatterofgeneralisationdoesn’tprovideavalidproofofall cases,asamathematicalproofhastocoverallpossible primefactors.
10Progress
Whilsttherehasn’tbeenacompleteanalyticalproof ofthisconjectureyet,ithasgainedsomeprogressin thepastdecadeorso,whichwaskickstartedbyYitang Zhang’spaperontheBoundedGapsbetweenPrimes. Hedemonstratedthat liminf n→∞ (pn+1 pn) < 7×107 , orthatthereISanumberbetween2and70million
whichappearedastheprimegapinfinitelyoften.Then, thisboundof70millionwasreducedinsubsequentyears byJamesMaynardandYitangZhangto600and246 respectively.Thesedevelopmentsinrecentyearshave givenhopetomathematiciansgloballyandwemaybe abletoseeacompleteproofforthisconjecture,ora weakerconjectureatleast,intheupcomingyears.
11Bibliography
1. https://www.britannica.com/science/twin-primeconjecture
2. https://collections.dartmouth.edu/archive/object /dcdis/dcdis-klyve2007?ctx=dcdis?length=12start= 0view=listrdatonlyu=nordatu=yescol=dcdisoc0=maintitleod0=asv=Brun27s+constant
3. https://annals.math.princeton.edu/wp-content/ uploads/annals-v179-n3-p07-s.pdf
Fig.4
Fig.5
53
FourierSeriesanditsApplicationinAtomic Orbitals
Taehoon(Terry)Kim Year12
Email:th3kim25@pupils.nlcsjeju.kr
Editor
Emma(Chaeeun)Chung
RecommendedYearLevel:KS5
Keywords:FourierSeries,ConvolutionTheorem, CompactGroups
1Introduction
Despiteitsunfamiliarname,theFourierseriescan bewidelyobservedaroundusasanaturalphenomenon. Itisusedtomodelsingleharmonicmotionoranytype ofmotion,includingtheformulationofsinusoidalor non-sinusoidalwaves.However,itsapplicationisnot limitedtothewavefunctionequation.Inthecondition thattheseriesisacompactRiemannianmanifold,the Laplace–Beltramioperatorcanbeusedtoconjugatethe Fourierseriesinmodellingtheatomicorbitals.
2Background
Fourierseriesisanexpansionofaperiodicfunction intoasumoftrigonometricfunctions.Themostsimplisticformattakestheformof
topologicalgroupwhosetopologyrealizesitasacompacttopologicalspace(whenanelementofthegroupis operatedon,theresultisalsowithinthegroup).This willbefurtherdiscussedlater.
3Objective
ThispaperaimstoinvestigatetheFourierseriesand itsvisualisationinRiemannianmanifolds,thusderiving theatomicmodel,whichisknowntohaveasimilar morphologicalpropertyasthesphericalharmonics.
4Investigation
4.1ConvolutionTheorem
Inmathematics,theconvolutiontheoremstates thatundersuitableconditions,theFouriertransformof aconvolutionoftwofunctions(orsignals)isthepointwiseproductoftheirFouriertransform.Tosimplify, convolution-mathematicaloperationontwofunctions (fandg)thatproducesathirdfunction-inonedomain (e.g.,timedomain)equalspoint-wisemultiplicationin another(e.g.,frequencydomain).Thisisregardingthe Fourierseriesservesasapivotalconcept,asitheavily contributestotheproductionofthecompactgroup.
Byexpressingafunctionasasumofsinesand cosines,itisviabletomodelawiderangeofharmonic datausingtheFourierseries.Thiscanbeobservedin variouscasesofearlymodellingattemptsofnaturalphenomena,includingJosephFourier’sattempttofindsolutionstotheheatequation.Thisapplicationisbasedon thesimplicityofthederivativeofatrigonometricfunction.Amongthesetheoremsandattempts,thecompact groupsoftheFourierserieshavethegreatestrangeof applications.Thecompactgroup,bydefinition,isa
Theproofofthefundamentalconvolutiontheorem canbeconducted.
ConsidertwofunctionswithFouriertransforms U and V :
SN (x)= D0 + N n=1 Dn cos 2π n p x φn (1)
U ≡ F {u}f = ∞ −∞ u(x)e 2iπfxdx,f ∈ R V ≡ F {u}f = ∞ −∞ u(x)e 2iπfxdx,f ∈ R (2) 54
FmeanstheFouriertransformoperator
r(x)= {u ∗ v}(x) ≡ ∞ −∞
u(τ )v(x r)dr = ∞ −∞ u(x τ )v(τ )dr (3)
Theconvolutiontheoremstates R(f ) ≡ F {r}(f ) = U (f )V (f ), f ∈R
ApplyingtheinverseFouriertransform F 1 producesthecorollary:
r(x)= {u ∗ v}(x)= F 1{U V } (4)
Given P -periodicfunctions sp and rp Fourierseries coefficients S[n]R[n], n ∈ Z,thepointwiseproductwill be:
hp(x) ≡ sp(x) rp(x), (5)
whichisalsoperiodicgivingthefunctionbythe discreteconvolutionofthe S and R sequencesas H[N ]= {S ∗ R}[n]
Theperiodicconvolutionwillbe:
hp(x) ≡ p sp(τ ) rp(x τ )dτ, (6)
whichcanbeagainrearrangedintoP-periodicwith Fourierseriescoefficient
H[N ]= P S[n] R[n] (7)
4.2CompactGroups
OneoftheinterestingpropertiesoftheFourier transformisthefactthatitcarriesconvolutionsto pointwiseproducts.Ifthatisthepropertywhichwe seektopreserve,onecanproduceaFourierserieson anycompactgroup.
Compact(topological)groupisatopologicalgroup whosetopologyrealizesitasacompacttopological space(whenanelementofthegroupisoperatedon, theresultisalsowithinthegroup).Compactgroups areanaturalgeneralizationoffinitegroupswiththe discretetopologyandhavepropertiesthatcarryoverin significantfashion
ThisgeneralizestheFouriertransformtoallspaces oftheform L2(G),where G isacompactgroup,insuch awaythattheFouriertransformcarriesconvolutions topointwiseproducts.TheFourierseriesexistsand convergesinsimilarwaystothe [ π,π] case.
4.3RiemannManifolds
Ifthedomainisnotagroup,thenthereisno intrinsicallydefinedconvolution.Nonetheless,ifX isacompactRiemannManifoldcompactRiemannian manifold,ithasaLaplace–Beltramioperator.The Laplace–Beltramioperatoristhedifferentialoperator thatcorrespondstoLaplaceoperatorfortheRiemannianmanifoldX.
ThesphereisisometricallyembeddedintoRnasthe unitspherecentredattheorigin.Thenforafunctionf onSn1,thesphericalLaplacianisdefinedby:
∆sn 1 f (x)=∆f (x/|x|) (8)
Asweadd {ϕ,ξ} tothesphericalcoordinateonthe spherewithrespecttoaparticularpoirpofthesphere (the"northpole"),thatisgeodesicpolarcoordinates withrespectto p,theequationwouldbe:
∆sn 1 f (ξ,ϕ)=(sin ϕ)2 n ϑ ϑϕ (sin ϕ)2 n ϑf ϑϕ +(sin ϕ) 2 (9)
SinceFourierarrivedathisbasisbyattemptingto solvetheheatequation,thenaturalgeneralizationisto usetheeigensolutionsoftheLaplace–Beltramioperator asabasis.ThisgeneralizesFourierseriestospacesof thetype L2(x),where X isaRiemannmanifold.The Fourierseriesconvergesinwayssimilartothe [ π,π] case.Ifwetake X tobethespherewithusualmetric, theFourierbasiswillconsistofsphericalharmonists, whichisabasicmodellingofequationtodeterminethe atomicorbitaloftheatom.
5Conclusion
HoweverunlikemyinitialattempttoderivetheaccuratesphericalharmonicsmodelusingFourierseries, theRiemannmodelratherfocusontheproductionof theFourierseriesonthesphere“usingharmonicmodel” toderivethesphericalmodeloftheFourierseries.This wouldrequirebacktrackingoftheequations,whichwas apparentlybeyondmymodel.
Nonetheless,thefactthattheFourierserieshad asignificantdevelopmentonsphericalharmonicscannotbedenied.Whereasthetrigonometricfunctions inaFourierseriesrepresentthefundamentalmodes ofvibrationinastring,thesphericalharmonicsrepresentthefundamentalmodesofvibrationofasphere inmuchthesameway.Manyaspectsofthetheory ofFourierseriescouldbegeneralizedbytakingexpansionsinsphericalharmonicsratherthantrigonometric functions.Moreover,analogoustohowtrigonometric functionscanequivalentlybewrittenascomplexexponentials,sphericalharmonicsalsopossessanequivalent formascomplex-valuedfunctions.
Therefore,consideringthisrelation,thefinalinvestigationwouldsimplyintroducetheuseofsphericalhar-
55
monics,whichtakesimilarform/structuretotheFourier series.
6Extension
Rhemodeloftheelectronsfollowsthetrajectory providedintheSchrodingerequation.This,converted inreferencetotheenergywouldbe
Thiscanbewrittenas
Thiscanbeconvertedagainusingsphericalharmonicstoderivefunctionof
Y
fortheequationoftheatomicorbitals.
7Bibliography
1. Libretexts.(2023,July12).8.7:Quantumnumbersandelectronorbitals.ChemistryLibreTexts. https://chem.libretexts.org/Bookshelves/General Chemistry/Map3A-General-Chemistry-(Petrucciet-al.)/083A-Electrons-in-Atoms/8.073AQuantum-Numbers-and-Electron-Orbitals
2. Umanitoba.(n.d.).http://www2.physics.umanitoba. ca/rogers/phys2380/files/slides-Hydrogen atom.pdf
3. WikimediaFoundation.(2022,October18).CompactGroup.Wikipedia. https://en.wikipedia.org/wiki/Compactgroup
4. WikimediaFoundation.(2023a,December5).Sphericalharmonics.Wikipedia. https://en.wikipedia.org/wiki/Sphericalharmonics
5. WikimediaFoundation.(2023b,December5).Sphericalharmonics.Wikipedia. https://en.wikipedia.org/wiki/Sphericalharmonics
6. WikimediaFoundation.(2023c,December21).Riemannianmanifold.Wikipedia. https://en.wikipedia.org/wiki/Riemannianmanifold
7. WikimediaFoundation.(2024a,January 21).Convolutiontheorem.Wikipedia. https://en.wikipedia.org/wiki/Convolutiontheorem Periodicconvolution(Fourierseriescoefficients)
8. WikimediaFoundation.(2024b,February15).Fourierseries.Wikipedia. https://en.wikipedia.org/wiki/Fourierseries
9. WikimediaFoundation.(2024c,February22). Tableofsphericalharmonics.Wikipedia. https://en.wikipedia.org/wiki/Tableofspherical harmonicsSphericalharmonics
P 2 r 2me + L2 2mer2 Ze2 4πϵ0r = E. (10)
E = εr + L2 2mer2 , (11) where εr = P 2 r 2me Ze2 4πϵ0r (12)
11(θφ)= (3/8π)1/2 Sin θeiφ ,
1 1(θφ)=(3/8π)1/2 Sin θe iφ ,
10(θφ)= (3/4π)1/2 cos θ (13)
Y
Y
56
MathematicalAnalysisoftheMechanismofthe GlobalPositioningSystem(GPS)
RecommendedYearLevel:KS5
Emma(Chaeeun)Chung Year12
Email:cechung25@pupils.nlcsjeju.kr
Editor
Emma(Chaeeun)Chung
Keywords:GlobalPositioningSystem,Trilateration
1Introduction
TheGlobalPositioningSystem(GPS)isaradio navigationsystemthatprovidesuserswithpositioning, navigation,andtimingworldwide.Inthepresentday, majorcommunicationnetworks,bankingsystems,and financialmarketsdependheavilyonGPSforpreciselocationandtimesynchronisation.
2RoleofGPSComponents
TheGPSSystemConsistsofthreesegments:the spacesegment,thecontrolsegment,andtheusersegment.Thespacesegmentisasatelliteconstellation thattransmitsradiosignalstousers.Foursatellites areplacedineachcircularorbitevenlyspacedevery60º aroundtheEarth;24satellitesorbittheEarthandat least4satellitesareavailableforsendingsignalstoany pointonEarth.Currently,therearethreeextrasatellites,makingup27.
Thecontrolsegmentisanetworkofgroundfacilitiesthattrack,monitor,andsendcommandstoGPS satellites.Intheusersegment,theGPSequipment’sreceiverreceivessignals,whicharethenusedtocalculate theuser’slocationandtimeinthethirddimension.
Thispaperwillfocusonthemechanismofthecommunicationbetweenthespacesegment’ssatellitenetworkandausersegment,oraGPSreceiver.
3ThePrinciplesofTrilateration
GPSreceiversusetrilaterationtodeterminethepositionoftheGPSreceiver.Trilaterationisamethodof surveyingthatreliessolelyondistancemeasurements.
Whentwomeasurementsaremadeattwodistinct points,twopointswillexistaspossiblelocationsofthe pointofinterest.Atleastthreedistancesarerequiredto determineanunknownpositioninthe2nddimension, asthereisamaximumofonepointwherethreecircles intersect.
Fig.1:TheGPSsatellitenetwork
Fig.2:Twomeasurementsfromtwopoints
57
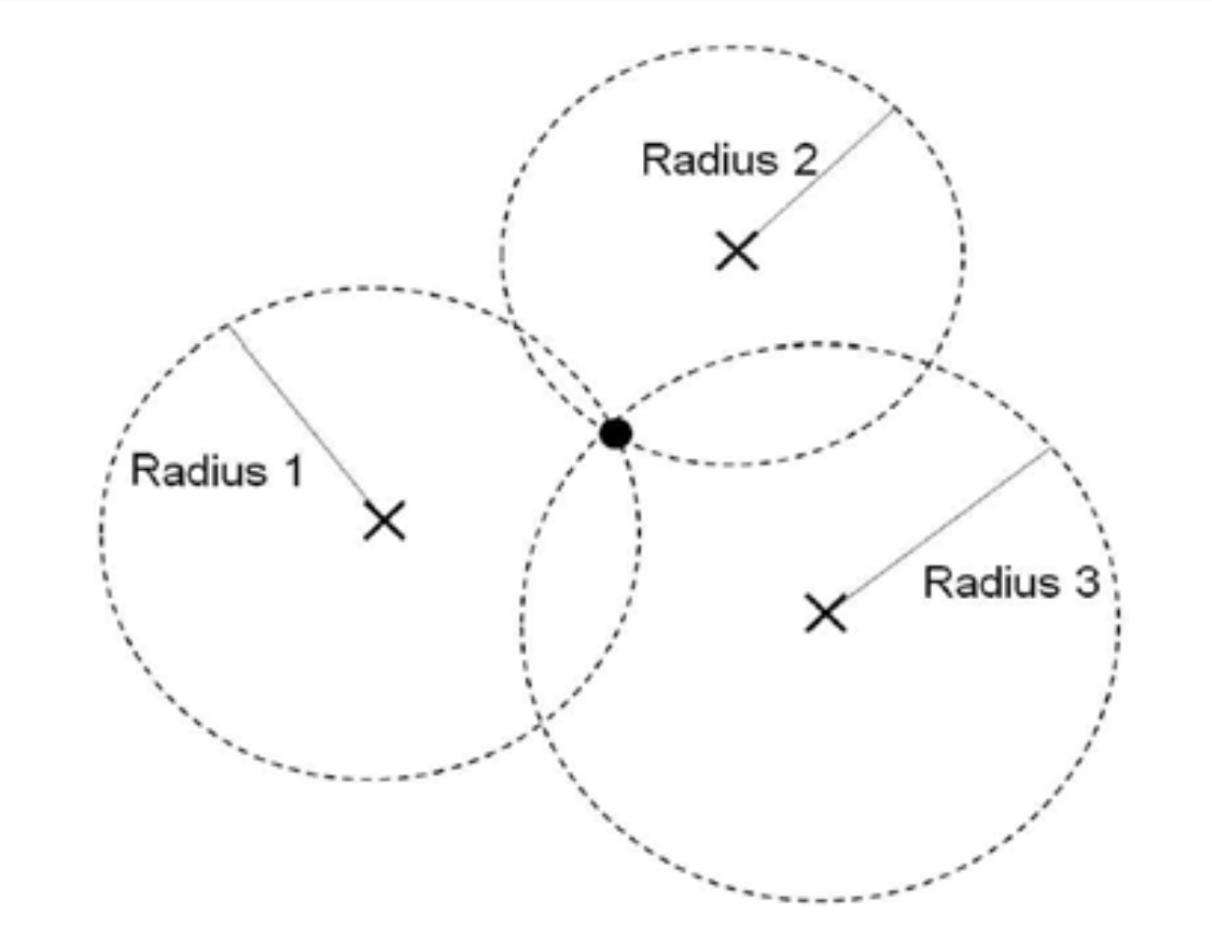
4ApplicationsofTrilaterationinGPS
Itseemsthesamewouldapplyinthe3rddimension ofouruniverse,inwhichspheresareconsideredinplace ofcircles.Assumingnospheresaretangent,thereare threepairsofspheresandsoatmostthreecirclesof intersection.Inthiscase,thereisamaximumof2points thatallspheresintersect.InGPS,onepointcanbe ruledoutusingadditionalcriteriasuchaswhenonly onelocationliesontheEarth’ssurface.
AGPSreceiveronEarthreceivesthelocationalinformationofthreesatellites.Indoingso,italsorecords thetimedifferencebetweenthetimethesignalswere sentandreceived.Thenthereceivercancalculateits distancefromeachofthesatellites’positions,andultimately,itsownpositiononEarth.
5TheWatchError
However,thisidealmechanismonlyfunctionswhen GPSsatellitesandreceiverscontainhighlysynchronized clocks.Thelevelofaccuracycanonlybeachievedby usingatomicclocks,whichareveryexpensive.
Considerthescenariobelowinthe2nddimension. Theobjectiveistofindunknowncoordinatesthatare insidethelargestcircle,givenitsdistancefromthree pointsonthelargestcircle’scircumference.
Usingtwopointsgivesonepossiblecoordinate.Usingthreedistancesresultsinhigheraccuracy-ifthe calculateddistancesarecorrect,theunknowncoordinateswouldbetheintersectionofthreecircles.Yet,as
Fig.5:2nddimensiondemonstrationofawatcherror
thefigureontherightshows,thethreecirclesdonot intersectatasinglepoint.
Thistellsusthattherehasbeenanerrorindistance measurement,andweshouldusethreeinsteadoftwo distancemeasurementsastheycanindicatewhetheror notanerrorhasoccurred.Themostlikelycauseofthis errorinGPSisthewatcherror:theclockonthereceiver andthesatellitesarenotsynchronized.
Thefigureaboveillustratestheeffectsofvarious watcherrors.Let E representthewatcherror,inwhicha positive E denotesthattheclockoftheunknowncoordinatesisfasterthanthesatellites’clocks,andanegative E denotesthattheclockoftheunknowncoordinatesis slowerthanthesatellites’clocks.
Assumingthatthewatcherrorissteadyandfixed (i.e.,sloworfastbyaconstantamountoftime),the radiusofthecirclesinthefigureisinerrorbythesame amount.Thereforetheprecisecoordinatesofunknown pointcanbedeterminedwhenthethreecirclesintersect atasinglepoint,suchaswhen E=5secinthefigure above.
AsimilarappliestoGPScoordinatesonEarth. Thoughtheoretically,threesphericaldistancesmaybe sufficient,fourareusedtocheckforaccuracy,avoiding theneedtousecostlyatomicclocks.Thesystemof
Fig.3:Threemeasurementsfromthreepoints
Fig.4:Max.of2pointsofa3-sphereintersection
Fig.6:Effectsofvariouswatcherrors
58
equationswouldbesimilartobelow:
(
(
wheresatellitenumber i islocatedat(
), sendingasignalattime ti.Also,
Repeattheprocesswiththeremainingthreeother satellites.Theequationsareasfollows:
where T ′ i istimeofsignalreception,and ∆ti isthe timedifference.Hence,d(∆ti, E)isthedistanceofthe unknowncoordinates(x0, y0, z0)fromsatellite i.
6AnAlgebraicSolutiontoanExampleCase
Thissectionwillguidethroughtheillustratedprocessusingthebelowexamplenumericalvalues.
Letthesignal’sreceptiontimebe t andthetime oftransmission19.9,andthespeedofthesignal0.047. Thenthedistanceis:
Subtractthefirstequationfromeachoftheother three,leavinguswith:
Sincethereare3equationsand4unknowns,three unknownsfrom x, y, z, t canbeexpressedintermsofthe fourth,givingusaquadraticequationinonevariable. Formulatethislinearsystemasanaugmentedmatrix:
whichisequalto:
Thevaluesabovehavebeenrounded,althoughtin reallife,computationsutilisemoredigits.Asaresultof Gaussianelimination,thereducedrowechelonformis:
givingthegeneralsolution:
Returningtoourprevious
x0 X1)2 +(y0 Y1)2 +(z0 Z1)2 = d (∆t1,ε)2
(
x0 X2)2 +(y0 Y2)2 +(z0 Z2)2 = d (∆t2,ε)2
x0 X3)2 +(y0 Y3)2 +(z0 Z3)2 = d (∆t3,ε)2
x0 X4)2 +(y0 Y4)2 +(z0 Z4)2 = d (∆t4,ε)2 , (1)
(
xi, yi, zi
T
(2)
∆ti = T ′ i
i,
Satellite Position Time 1 (1,2,0) 19.9 2 (2,0,2) 2.4 3 (1,1,1) 32.6 4 (2,1,0) 19.9
d =0 047(t 19 9) (3)
d = (x 1)2 +(y 2)2 +(z 0)2 (4)
(x 1)2 +(y 2)2 + z 2 =0 0472(t 19 9)2 (5)
2x +4y 2(0 0472)(19 9)t =12 +22 0 0472(19 9)2 + x 2 + y 2 + z 2 0 0472t2 (6)
whensatellite1’spositionissetas(1,2,0),leading totheequation:
Expansionandappropriaterearrangementgives:
2x +4y +0z 2 0.0472 (19.9)t =12 +22 +02 0.0472(19.9)2 + x 2 + y 2 + z 2 0.0472t2 4x +0y +4z 2 0 0472 (2 4)t =22 +02 +22 0 0472(2 4)2 + x 2 + y 2 + z 2 0 0472t2 2x +2y +2z 2 0 0472 (32 6)t =12 +12 +12 0 0472(32 6)2 + x 2 + y 2 + z 2 0 0472t2 4x +2y +0z 2 0 0472 (19 9)t =22 +12 +02 0 0472(19 9)2 + x 2 + y 2 + z 2 0 0472t2 (7)
2x 4y +4z +2(0 0472)(17 5)t =8 5+0 0472(19 92 2 42) 0x 2y +2z 2(0 0472)(12 7)t =3 5+0 0472(19 92 32 62) 2x 2y +0z +2(0 0472)(0)t =5 5+0 0472(19 92 19 92) (8)
2 440 0773 86 0 22 0 056 3 47 2 2000 (9)
1000 0955 41 0100 0955 41 0010.0673.67 (10)
x =5 41 0 095t, y =5 41 0 095t, z =3.67 0.067t (11)
= 59
(x 1)2 +(y 2)2 + z2
Thereforethetwosolutionsare43.1and50.0,respectively(x, y, z)=(1.317,1.317,0.790)or(0.667, 0.667,0.332).Thefirstsolutionimpliesthat r≈2earth radii,whichisimpossibleforaGPSposition.The coordinatesofinterestarethesecondsolution,giving r≈0.9997earthradii;onthesurfaceoftheearth.

7Bibliography
1. ReferencelistGPS.GOV(2021).GPS.gov:GPS Overview.[online]Gps.gov.Availableat: https://www.gps.gov/systems/gps/.
2. Kalman,D.(2002).AnUnderdetermined LinearSystemforGPS.TheCollegeMathematicsJournal,[online]33(5),p.384. doi:https://doi.org/10.2307/1559010.
3. Thompson,R.B.(1998).GlobalPositioning System:TheMathematicsofGPSReceivers. MathematicsMagazine,71(4),pp.260–269. doi:https://doi.org/10.1080/0025570x.1998.11996650.
4. Trilateration|measurement|Britannica.(2019). In:EncyclopædiaBritannica.[online]Availableat: https://www.britannica.com/science/trilateration.
5. WolframCloud.(n.d.).Trilaterationandthe IntersectionofThreeSpheres.[online]Availableat: https://www.wolframcloud.com/objects/demonstra tions/TrilaterationAndTheIntersectionOfThreeSpheressource.nb.
ASimulationofIntersectionofSpheresinWolframMathematica



0472(t 19 9)2
(5 41 0 095t 1)2 +(5 41 0 095t 2)2 +(3 67 0 067t)2 =0 0472(t 19 9)2 , 0 02t2 1 88
+43
0
withthesesubstitutions,
t
56=0 (12)
60
KMPAlgorithm
Jimin(James)Lim
Year11
Email:jmlim26@pupils.nlcsjeju.kr
Editor
Emma(Chaeeun)Chung
RecommendedYearLevel:KS5andabove
Keywords:algorithm,search,pattern,optimisation, string
1Introduction
1.1Introductiontoalgorithms
Humanshavecountlesslyattemptedtorefinetheir codestobeexecutedatanunimaginablespeed,butonly failedmiserably.Whathumanshaveinventedafterfailuresafterfailurestoaidhumanityinwritingnewand bettercodesarealgorithms.
Algorithmsaredefinedasasetsequenceofprogrammingsyntaxandinstructionstocarryoutacertain taskatanotablyhigherspeedthananaiveimplementation.Anaiveimplementationinthiscontextrefersto acodethatistooslowtobeused.However,thereare somecaveatstothisdefinition;forexample,bruteforce algorithmistheslowestpossiblealgorithmyoucanuse foranyquestions.Hence,itisverydifficulttospecify theexactdefinitionofalgorithm,butisratheravague ideaofagroupofmethodsofhowtoapproachaquestion.
1.2KMPAlgorithm
Amongstthemanyalgorithms,somearespecialised insearching,especiallyinastringoranarray.There aredifferentvariantsofstringsearchalgorithms,butthe mostfamousandwidelyusediswhenyouhavetofind alloccurrencesofasub-stringinagivenstring.Hereisa simpleranalogy.Imagineyougointoawikipediaarticle andpressctrl+fandsearchforaphrase“searching algorithm”.Instantaneously,thebrowserwillshowyou everyinstancewherethearticlementionedthephrase “searchingalgorithm”.ThisiswhentheKMPalgorithm isused.
KMPalgorithm,theabbreviationofKnuth-Morris-
Prattalgorithm,isastring-searchingalgorithmmade bythreecomputerscientists-DonaldKnuth,James MorrisandVaughanPratt-in1970.Similartothe Boyer-MooreandRabin-Karpalgorithm,itfindsand usespatternstoefficientlysearchthroughastringina relativelyshorttime.
Thisarticlewillexploretheoptimisationofthe KMPalgorithmandtheapplicationsindifferentcases.
2BackgroundInformation
2.1TimecomplexityandbigOnotation
Beforemakinganin-depthexplanationaboutthe processofoptimisation,itisnecessarytounderstand theconceptoftimecomplexityandthebigOnotation. Timecomplexityisaterminologyusedtoshowhowfast acodeisexecuted,anditisachievedbyusingthebigO notation.ThebigOnotationhasauniversalformatof O(...),wherethenumberorexpressioninthebrackets representthespeedorthe“numberofexecutions”ofa code.
BigOnotationbecomesespeciallyusefulwhenone ormoreloopsareused.Forexample,givenanarray withlengthn,iteratingthroughallindexesofthefor loopwillgivethetimecomplexityofO(N ).Taking anotherexample,ifthereisthereare2forloopsnested, thetimecomplexitywillincreasetoO(N 2).However,if thetwoloopsarenotnestedandareseparate,thetime complexitywillreducetoO(2N ).
Justbyobservingthedifferenttimecomplexities,it isquitedifficulttovisualisethedifferenceinthetime ittakesforthedifferentcodestobeexecuted.The graphaboveshowshowdifferenttimecomplexitiesvary asN,orthevariableusedinthebigOnotationincreases(towardsinfinity).Fromthegraph,itisnoticeablethatthereisahugedifferenceintimecomplexities ofO(N),O(NlogN)andO(N 2),whichshowsthesignificanceofoptimisingcodesandimplementingnecessary algorithmstoreducethetimecomplexity.
61

2.2Prefixandsuffix
Theseconceptsarerathersimpleandmorefriendly tomostpeople.PrefixesofastringintheKMPalgorithmareconsideredallsubstringsstartingfromthe index0.Ifastringhasalengthofn,therewouldbe ncorrespondingprefixesofthestring.Forexample, thestring“apple”willhaveprefixes“a”,“ap”,“app”, “appl”and“apple”
Suffixesworktheexactsamewaywithprefixes,but juststartfromtheendofthestringincontrasttoprefixes.Suffixesstartfromtheindex-1andworktheir wayback.Usingthesamestring“apple”,itwillhave suffixes“e”,“le”,“ple”,“pple”,“apple”.Also,itisimportanttonotethatprefixesandsuffixesofastringboth canincludethestringitself.
2.3FailureTable
Thefailuretable,alsoknownasthepartialmatch table,isaone-dimensionalarraythatisthekeytooptimisingthetimecomplexityofalinear-stringsearch. Theindexiofthefailuretablecontainsthemaximum lengthwherethesuffixwillbeequaltotheprefixof thesubstringfromindex0toi.Thevalueofthefailuretableisoftenreferredtopi[i]:theithvalueofthe array,wherethearrayisnamedpuforthesakeofsimplicity.Anexampleofafailuretableofthestring “AABABAABAABA”isasthefollowing.
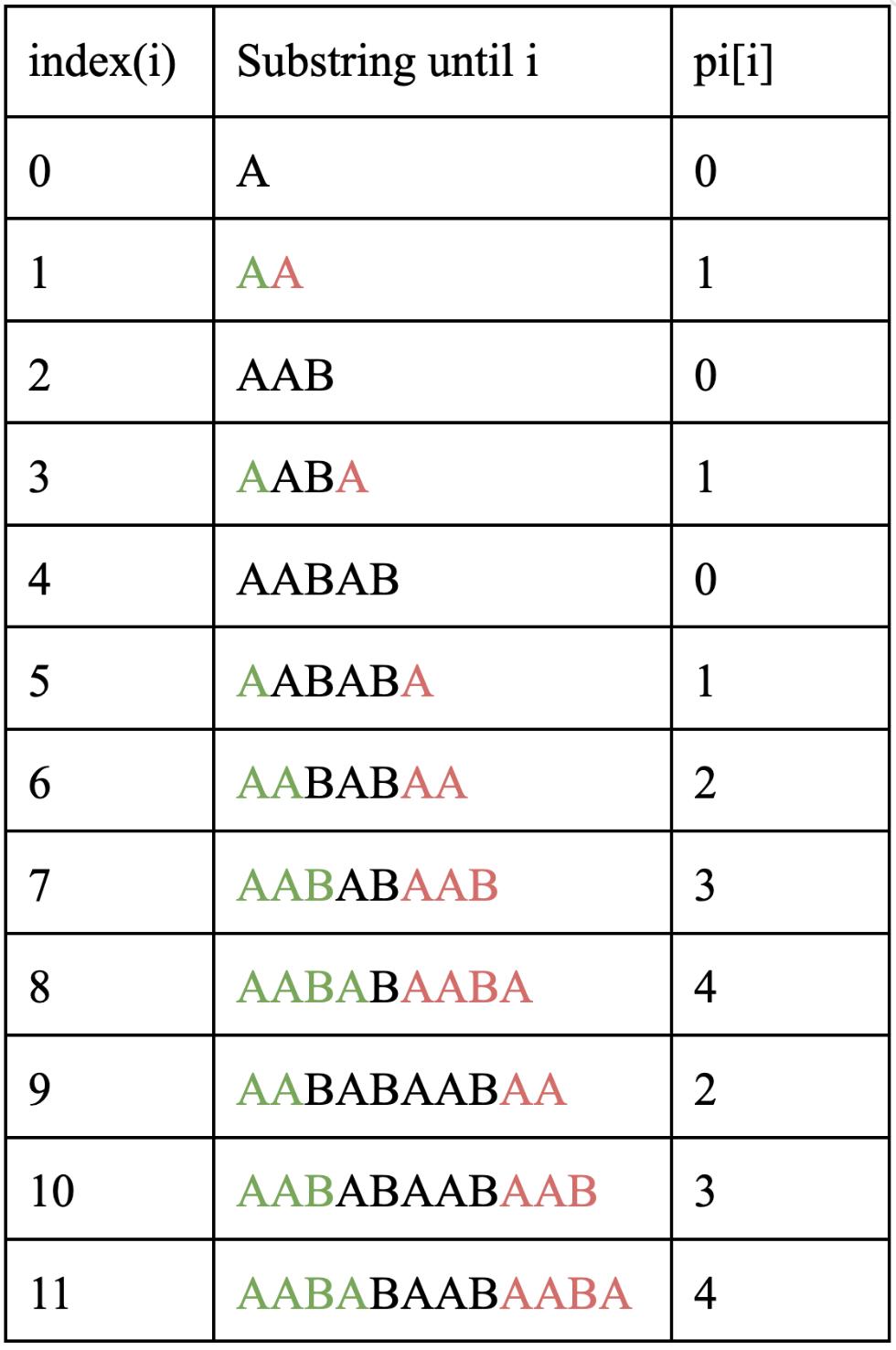
Fig2aboveshowsanexampleofafailuretableof astringandthematchingsuffixandprefixarecoloured toshowaclearrepresentationofhowitworks.Also, theprefixateachcolumnofthefailuretablemustnot equalthesubstringitself.Howexactlythefailuretable isutilisedandexploitedwillbefurtherelaboratedlater oninthisarticle.
3OptimisationofKMP
3.1BeforeOptimisation
Toreduceanyconfusion,thelengthofthefull string(text)willbereferredasN,andthelengthof thewantedsubstring(pattern)tobesearchedwillbe referredasM.
3.2Naivesolution
Themostinstinctiveimplementationwillbebrute forcingeverysubstringandcountingthenumberofcorrespondingsubstrings.Thismethodisstillvalid,but willwastetoomuchtime.Throughthisimplementation,thecodewilliteratethroughallofthesubstrings oflengthM,andcomparethesubstring,resultingina timecomplexityofO(NM).Thiswilleventuallybecome aproblemasthetimecomplexitywillincreaseexponentiallyeventhoughnandmitselfincrementsbyasmall number.
3.3Makingthefailuretable
3.3.1Naiveapproach
Solelycreatingthefailuretableshouldnotbeunderestimatedasitalsorequiresitsownoptimisation.The failuretablecanalsobeimplementedbyusingabrute forcealgorithm,butwillresultinatimecomplexityof O(M 3),whichismuchworsethanthesolutionin3.2, despitebeingonlythepreprocessingstage.Therefore, anothermethodmustbeusedtoreducethiscomplexity tounderO(M 3).
3.3.2Optimisationoffailuretableandits mechanism
Infact,thereisanelegantwayofreducingthetime complexityallthewaytoO(M).Asmentionedearlier on,theKMPalgorithmusespatternstoreducethetime complexity,andthisworksjustthesameforthisoptimisation.Thetablebelowisatracetablewhenthe patternis“ABABBAB”.
Thegeneralruletofollowforcreatingthefailure tableisthatifpattern[i]andpattern[j]arethesame,i andjarebothincremented,butiftheyaredifferent,iis settopi[i-1].Whenpattern[i]andpattern[j]aredifferent,thisimpliesthatweareoverestimatingthepotential correspondingprefixthatmatchesthesuffix,therefore willhavetodecreasethelengthoftheprefix.However, sincedecrementingtheprefixby1isnotenoughtogive
Fig.1:Timecomplexitychart
Fig.2:Failuretableexample
62
Fig.3:Tracetableoffailuretable
anoticeablechangeinthetimecomplexity,thealgorithmusespreviouspivaluestojumpmultipleindexes atonce.Thisistruebecausethevalueofpi[i-1]tells usthataprefixwithalengthofpi[i-1]existstwiceas italsoincludesthesuffix.Therefore,movingpointer itothep[i-1]guaranteesthatthesearchingprefixwill bethesame.Forexample,ifpi[i-1]hasavalueof2, therewillbeaprefixandasuffixwiththesamepatternwithbothlengthof2,meaningthatpointerican takeashortcutfromitopi[i-1],ratherthantraversing 1indexatatime.Duetothisspecificflowofthealgorithm,whenpattern[i]andpattern[j]arethesame,we cansimplyadd1toi(indexstartsfrom0)andadditto thepiarray.
Insimpleterms,thefailuretableiscreatedbyskippingunnecessarysearchesbyrecognisingdifferentpatternsandsamenessofthesubstringsinthegiventext. Moreover,ithasbeenpreviouslymentionedthatthe timecomplexityifO(M),butthecodeexplicitlyshows anestedforloopandawhileloop.AcursoryexaminationwilldeduceatimecomplexityofO(M)inthe worstcasescenario.However,everytimejincrements by1,themaximumvalueicansubsequentlyincreaseis 1.Therefore,thisprovesthatthetimecomplexitywill notgoovertwiceofM,andwillultimatelyconvergeto O(M).
3.4Matchingstage:usingthefailuretable
Oncethefailuretableiscreated,thepreprocessing isdone,andthematchingstageofthealgorithmisready tobeexecuted.Ifyouseethecodeofthematching stage,youcanobservethatthematchingalgorithmis almostexactlythesameasthepreprocessingstage.The matchingalgorithmalsousestwopointersiandj,but theonlydifferenceisthatbothpointersstartfromthe index0.Thepointeriinthispieceofcodereferstothe indexofthepattern,whilepointerjreferstotheindex ofthetext.
Thealgorithmstartswithcomparingpattern[i]and text[j].Ifthetwolettersarethesame,thealgorithm incrementsbothiandjby1tocheckthenextindex. Theprogramiteratesthesameprocedureuntilpointeri
reachesthelengthofthepatternorpattern[i]andtext[j] doesnotmatch.Beforethispointisreached,thereare twopossiblecases:whenthepointerireachesthelength ofthepatternanddoesn’t.Forbothcases,pointeriis incrementedby1.However,ifthispointisreached,the codewillmakeextrastepstoincrementthecountand setitopi[i-1].Thereasonwhyiissettopi[i-1]isalmostthesamefortheexplanationusedinoptimising thefailuretable.Thepi[i-1]valuetellsusthatthereare 2occurrencesoftheprefixwithlengthofpi[i-1],meaningthatifpointeriissettopi[i-1],thecodewillreduce thenumberofrequirediterationswithoutskippingtoo muchtotheextentthatacertainnumberofoccurrences ofthepatterninthetextisskipped.However,ifpattern[i]andpattern[j]aredifferentinthefirstplace,iis settopi[i-1]toskipcolumnsinthemiddleofthesearch asmuchaspossible.
Totakeanexample,thetracetableofthematchingalgorithmforthetext“ABBABABBABABABABBAB”andpattern“ABABBAB”isasshownbelowto aidinthevisualrepresentationofthecode.
TheoveralltimecomplexityforthematchingalgorithmisO(N)ratherthanO(NM)orO(N 2)forthe similarreasonforthetimecomplexityofthefailuretable.Pointeriiteratesthroughthepatternandpointer jiteratesthroughthetextitself.Althoughpointeriis bothincrementalanddecrementalwhennecessary,the amountofindexesitdecrementsroughlycancelsout withtheamountofindexesincremented.Thismeans
Fig.4:Tracetableofmatchingalgorithm
63
thattheoveralltimecomplexitywillnevergoover O(2N),whichisconsideredtobeconvergingtoO(N). ThisresultsinaoveralltimecomplexityofO(N+M)includingthepreprocessingstageandthematchingstage.
4Analysis
4.1AdvantagesofKMP
ThemainandmostevidentbenefitoftheKMPalgorithmisthatitsuccessfullyreducesthetimecomplexityfromO(NM)toO(N+M).Thisisveryimportantas otherstringsearchingalgorithmssuchasrabin-karpalgorithmdohavetimecomplexityofO(N+M),butmight haveworsttimecomplexityofO(NM)duetofrequent hashcollisions.
Otherthanthegeneraltimecomplexity,theKMP algorithmisalsopowerfulinthesensethatitdoesn’t requireanyelementofbacktracking.Thistraitnot onlyshortensthecodethatisneededtobewritten, butalsomakesitveryfavourableforbrowserstoimplementKMPalgorithmsforsearchinginlargetextfiles ordocuments.
4.2LimitationsofKMP
ThebiggestlimitationoftheKMPalgorithmisthat inspiteofitsefficiencyinstringmatching,itsflexibility toadapttoperformingvarioustasksotherthanstring matchingisfairlypoor.Unliketheboyermoorealgorithm,KMPalgorithmisnotageneral-purposealgorithm,soitsfunctionwillbestrictlylimitedtostring matching.
Also,onelimitationthatthemajoritytendtooverlookisthattherestillaresomespacesforimprovements. AlthoughtheKMPalgorithmissaidtohavethetime complexityofO(N+M)intheworstcase,theactual timecomplexityisclosertoO(2N+2M).Asthepointersareslidedtowardstheendofthetext,thealgorithm doesmakematchesandcomparisonsthatarenotfully necessary.Anewlyproposedalgorithmasasuccessor oftheKMPalgorithmistheL-I-KMPalgorithm.
Thisnewalgorithmworksinasimilarwaytothe KMPalgorithmbyrelyingonthemismatchofthepatternandthetext,butinsteadusesanewdatastructure calledalast-identicalarray.TheL-I-KMPalgorithm alsohasapreprocessingandamatchingstage,where thepreprocessingstagecreatesthelast-identicalarray andthematchingstageusesittomakealinearsearch throughthetext.TheL-I-KMPalgorithmdoesnotdifferinthelevelofefficiencywiththeKMPalgorithm withsmalldatasets,butwillhaveabiggergradualdifferencewhenthedatasetbecomesextremelylarge.
5Applications
DespitethefactthattheKMPalgorithmisnota general-purposealgorithm,thisdoesn’tthwartthealgorithmitselfbeingappliedinotherfieldsandscenarios.
OneinterdisciplinaryusageoftheKMPalgorithmisin theareaofbioinformatic,especiallyinDNAsequencing. DNAsareoftenrepresentedasauniquestringwhere eachletterrepresentsabaseofanucleotide.Sincethere are4typesofnucleotides-adenine(A),cytosine(C), thymine(T)andguanine(G)-DNAincomputerscience isnothingmorethanapieceoftext.Therefore,givena strandofDNA,wecancomputetofindthenumberor positionoftheoccurrenceofaDNApattern.Thisapplicationisparticularlyusefulintheareaofmedicine. Forexample,doctorscanusethealgorithmtoreveal certainmutatedgenomesequencesthatcanpotentially causeadiseaseandmakeearlypreventions.
TheKMPalgorithmisalsousedinanti-virussoftwares.Thereasonwhythesesoftwaresusesthisalgorithmistheneedtoidentifythevirussignatures.Virus signaturesarealgorithmsorhashesthatarestoredin thedatabaseofamalware.Duetothisproperty,malwaressuchasvirusescanbedetectedbydetectingthe signatureofthemalware.Thus,theanti-virussoftware willbeabletoscanthroughthedatabaseandeachfile andscanfortheknownvirussignatures.Sincethesignaturesareonlyinstalledintheinfectedfilesandnot intheuninfectedfiles,detectingthesignaturewilleasilyaidthesoftwaretoeradicateandkillthemalwares inthecomputer.Althoughadvancedtypesofviruses aregraduallyemergingthatcanobfuscatetheirsignaturesandremainundetected,usingtheKMPalgorithm stilleliminatesnumerousrudimentarymalwaresandis anecessaryprocessanti-virussoftwaresshoulduse.
Otherthanthetwoareasofapplications,theKMP algorithmisalsousedinfilecompression,networksecurityandevenAIsastheyneedtheabilitytorecognise patternsinimagesandspeeches.
6Conclusion
Inanutshell,thisarticleexploredtheprocessof optimisingtheKMPalgorithm,evaluatedthestrengths andweaknessesofthenatureofthealgorithmitselfand finallydiscussedtheapplicationofthealgorithmand howitbranchesintodifferentfields.
TheKMPalgorithmhassurprisinglyinfiltratedour dailylivesaftertheadventofmoderntechnologywithoutbeingnoticedbyhumansourselves.Eventhough thecomplexityveilsitselffrombeingknownbymany people,acknowledgingandappreciatingtheeleganceof thealgorithmisadutywemustallcarry.
7Bibliography
1. Xianglu,Y.(2019).TheAnalysisofKMP AlgorithmanditsOptimisation[online]
https://iopscience.iop.org/article/10.1088/17426596/1345/4/042005/pdf
2. Anonymous.(2016).KMP[online]
https://bowbowbow.tistory.com/6
64
3. Everton,G.(2023).EfficiencyinString
Searching:AnIn-DepthAnalysisofthe Knuth-Morris-Pratt(KMP)Algorithm[online]
https://medium.com/@evertongomede/efficiencyin-string-searching-an-in-depth-analysis-of-theknuth-morris-pratt-kmp-algorithm-2adb07b6bc60
4. LogicFirst.(2019).Knuth-MorrisPratt(KMP)algorithm|StringMatchingAlgorithm|SubstringSearch[online]
https://www.youtube.com/watch?v=4jY57Ehc14Y
5. Gyongi.(2022).KMPalgorithm[online]
https://yiyj1030.tistory.com/495
6. Hwan.(2021).KMPalgorithm[online]
https://velog.io/@hwan2da/
7. Ghanshyam,C.(2018).PatternMatching AlgorithminDNASequenceAnalysis[online]
https://ijcrt.org/papers/IJCRT1801645.pdf
8. Yodi,P.(2010).ImplementationofPatternMatchingAlgorithmonAntivirus forDetectingVirusSignature[online]
https://informatika.stei.itb.ac.id/rinaldi.munir/ Stmik/2013-2014/Makalah2013/MakalahIF22112013-062.pdf
9. Alexey,M.(2016).Antivirusfundamentals:Viruses,signatures,disinfection[online]
https://www.kaspersky.com/blog/signature-virusdisinfection/13233/
ANaivesolutioncode
import sys
input =sys.stdin.readline
n,m= map( int , input ().split())
text= input ().strip()
pattern= input ().strip() count=0
for i inrange (n m+1): if text[i:i+m]==pattern: count+=1
print (count)
BFailuretable(naive)
import sys
input =sys.stdin.readline
n,m= map( int , input ().split())
text= input ().strip()
pattern= input ().strip() count=0
pi=[0 for inrange (m)]
for i inrange (m): temp_p=0 for j inrange ((i+1)//2): if pattern[:j+1]==pattern[i j:i+ → 1]: temp_p=j+1
pi[i]=temp_p print (p)
CFailuretable(optimised)
import sys
input =sys.stdin.readline
n,m= map( int , input ().split())
text= input ().strip() pattern= input ().strip() count=0
pi=[0 for inrange (m)] i=0
for j inrange (1,m): while i>0 and pattern[j]!=pattern[i]: i=pi[i 1]
if pattern[j]==pattern[i]: i+=1 pi[j]=i
print (pi)
DMatchingstage
import sys input =sys.stdin.readline
n,m= map( int , input ().split()) text= input ().strip() pattern= input ().strip() count=0
pi=[0 for inrange (m)]
i=0 for j inrange (n): while i>0 and pattern[i]!=text[j]: i=pi[i 1]
if pattern[i]==text[j]: i+=1 if i==m: count+=1 i=pi[i 1]
EFullKMPalgorithmcode import sys input =sys.stdin.readline
n,m= map( int , input ().split()) text= input ().strip() pattern= input ().strip() count=0
pi=[0 for inrange (m)] i=0
for j inrange (1,m): while i>0 and pattern[j]!=pattern[i]: i=pi[i 1]
65
i=0
if pattern[j]==pattern[i]:
i+=1
pi[j]=i
for j inrange (n): while i>0 and pattern[i]!=text[j]: i=pi[i 1]
if pattern[i]==text[j]:
i+=1
if i==m: count+=1 i=pi[i 1]
print (count)
66
Penney’sgame
Jeff(Suhyuk)Cho Year11
shcho26@pupils.nlcsjeju.kr
Editor
Derek(Yejun)Yoo
RecommendedYearLevel:KS4andKS5
Keywords:Treediagram
1Introduction
Ifyoutossacoin,whatistheprobabilityofthecoin landingoneitherside?50%itis,unlessthecoinawkwardly landsonitsedge,aprobabilitysounlikelythatwecanignoreit.Whatifwethrowacointhreetimesanditalways landsonheads?Well,thatisa12.5%chancefollowingbasic probabilitycalculations.Aprobabilitynotextremelyhigh, buthighenoughtobeoccurringonceineighttimes.
Supposeweplayasimplegame:youcomeupwitha sequencepredictingthreeconsecutivethrowsofacoin.You mightsayHeads,Heads,Tails,orTails,Heads,Tails...and soon.Then,Ialsopickasequencebasedonyoursequence andwestarttossingacoinuntiloneofoursequencescomes out.Theonewiththeirsequencefirstappearinggetstowin. WhatifItellyouthatI,choosingmysequenceafteryou,alwayshaveahigherchanceofwinningjustbyusingasimple method?
2Examples
Let’sstartwithaneasyexample.Saythatyouchose HHH.IchooseTHH.
TheprobabilityofthesequenceHHHshowingupafter threeconsecutivecointossesis 1 8 ,asstatedbefore.Similarly, theprobabilityofthesequenceTHHshowingupafterthree consecutivecointossesisalso 1 8 .WhywouldIhavechosen suchasequence,andhowdoesitmakethesituationinfavour ofme?
Theanswerissimple.Wearenottossingthecoinjust threetimes,butwearetossingthecoinuntiloneofthesequencescomesout.Whenthreeheadscomeoutinarow, whichisa12.5%probability,congratulations,youhavewon thegame.Butassoonastailscomeout,thingschange.In orderforyoutowin,youwouldneedthreeheadsaftertails comeout.ButmysequencewasTHH,henceevenbefore
youhavecompletedyoursequence,Ifinishedmine.Therefore,anysequenceexceptHHHwouldeventuallymakeme win,whichisa 7 8 probability.
Thiswasbyfarthesimplestexample.Let’smoveinto morecomplicatedscenarios:
Thistime,annoyedbymyvictory,youchooseHHT.I willchooseTHH.
Iftailscomeoutfirst,Iwin.Why?Youneedtwoheads inarowtocompleteyoursequence,andbeforeyoufinish yours,Icompletemine(twoheadsfollowingatail).Bearin mindthattailscomeouthalfofthetime,sofornow,Ihave atleast50%chanceofwinningalready.
Ifheadscomeoutfirst,itbecomesadifferentstory.Two consecutiveheadswouldmeanthatyouwin,asIneedtails tocompletemysequencebutthiswouldmakeyouwinbeforeme.Iftailsfollowheads,Iamdefinitelygoingtowin, followingthesamelogicfromwhentailscomeoutfirstin theparagraphabove.
Referringtothetreediagram,wecancalculatetheprobabilityofyouwinningthegame,whichisonly 1 2 ∗ 1 2 = 1 4 .It isthreetimesmorelikelyformetowinthanyou.
Onelastexample:thisoneshouldbethetoughestofall. YouchooseHTH,andIchooseHHT.
Iftailscomeoutfromthestart,neitherofthesequences wouldbeinfavouroftheothersincebothsequencesstart withheads,nottails.Soweneedtoonlyconsiderwhenthe startofthecointossisheads.
Headscomeout,andnowwearebacktoa50-50chance ofgettingeitherheadsortailsinoursecondtoss.Firstconsiderwhenthetwoconsecutivethrowsfromthestartareboth heads.ThenHHTisgoingtowin,asHTHneedsonemore
67
headsaftertails,andbythenHHTwouldhavefinishedthe sequence.
Ifthesecondtossistails,fulfillingthefirsttwoofthesequenceHTH,weneedtoconsiderthethirdcointossaswell. Ifthethirdcointossisheads,thereyougo,youwin.You wereverylucky,sincethefirstthreetosseswereH-T-H.But ifthethirdcointossistails,wehavetogobacktothestart again,sincebothsequencesdonotincludetailsfollowedby tails.
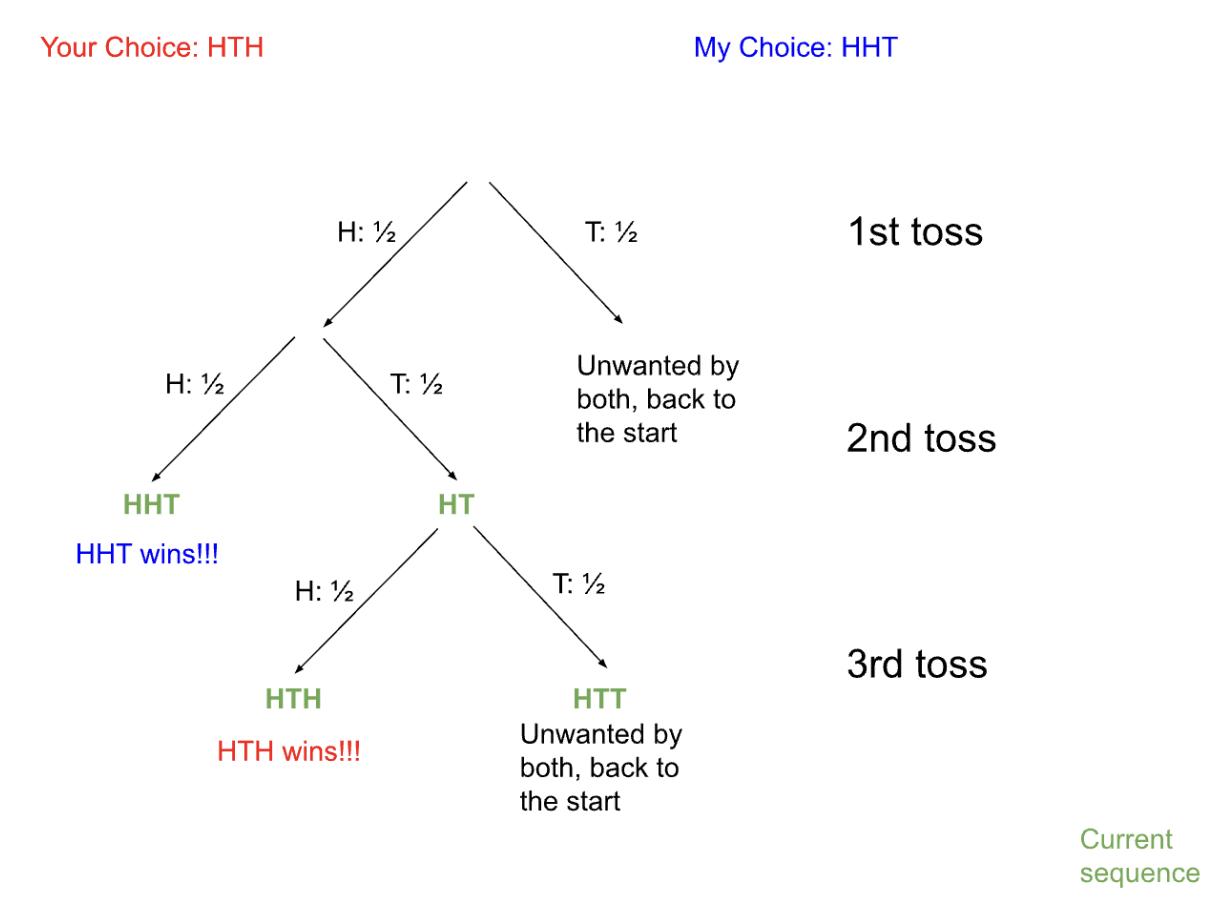
Here,youcanseethatmychanceofwinningistwiceof yours,sinceHHTwins 1 4 ofthetimewhileHTHwins 1 8 of thetime.Hence,theprobabilityofHHTwinningis 2 3 ,while thechanceofHTHwinningis 1 3
Afterworkingoutallthecombinationsofsequences, hereisthecompletetableshowingtheoddsofwinning:
3Thestrategy
Foralloftheseexamples,Ihaveahigherprobabilityof winningthanyou.Haveyouwonderedwhy?Whatkindofa strategyamIusingtoputmeinanadvantage?
Asyoucanseefromtheexamples,Iamconstantly changingyoursecondguessandplacingitasmyfirstguess, andthenmysecondguessandmythirdguessarethesame asyourfirstandyoursecondguess.

Thereasonwhywelookedattheexamplesbeforeisbecausethesecondpersonaimstomakeitimpossibleforthe firstperson’ssequencetocompleteoncethesecondperson’s firstguesshasbeencompleted.

Fromhere,thesecondpersonnowonlyneedstocopy thefirstperson’sfirstguessandthesecondguesstocomplete beforetheotherperson.
68
BlockchainandHashFunction
JungseoPark
Year10
Email:js2park27@pupils.nlcsjeju.kr
RecommendedYearLevel:KS4,KS5
Editor
Emma(Chaeeun)Chung
Keywords:Blockchain,Hashfunction,Birthday
Paradox
1Introduction
Thehistoryofthehashfunctionhasprogressed alongwiththedevelopmentofcryptographyandcomputerscience,andhasdevelopedinresponsetothe needsofsafetyandsecurityaspects.Thehashfunction,whichisstillbeingcontinuouslyresearchedand developedinthefieldofcryptographyandsecurity,also playsalargeroleinblockchaintechnology,whichhas recentlyreceivedalotofattention.Next,wewilllook atthedefinitionandcharacteristicsofthehashfunction anditsuseinblockchain.
2BackgroundInformation
2.1HistoryofHashFunctions
Theconceptofhashfunctionsemergedinthe1950s, butitsrootsextendfurtherbackwhendatatransformationandcompressionmethodswereemployedforefficientdatastorageandretrieval.Hashfunctionsbecame pivotalincryptographyandcomputerscience,gaining prominenceinthe1970s.TheMerkle-Damgardstructure,afundamentalhashfunctionframework,surfaced in1979,leadingtothedevelopmentofvarioushashalgorithms.Sincethe1990s,heightenedconcernsabout hashfunctionsecurityledtothecreationofMD5,SHA1,andSHA-256,utilisedacrossdataintegritychecks, encryption,andblockchainfortheircryptographicrobustness.Yet,evolvingsecurityunderstandingshaverevealedvulnerabilitiesinsomehashfunctions,prompting theongoingdevelopmentandadoptionofmoreresilient alternatives.
2.2DefinitionofHashFunction
Ahashfunctionisafunctionthattakesdataofarbitrarylengthasinputandoutputsafixed-lengthvalue, thatis,ahashvalue.Sincethehashvalueisderived fromtheinputdata,thesameinputwillalwayshavethe samehashvalue (Thevaluereturnedbyahashfunction isalsocalledahashvalue,hashcode,digest,orsimply hash).
Modulooperation,orremaindercalculation,isone oftheeasiestandmostintuitiveexamplesofahash function.Therestofthecalculationsaresimplefunctionsthatconvertonerandomnumbertoanother,and canbeviewedasakindofhashfunction.
Forexample,let’ssaywehaveadatasetofnumbersfrom0to9.Andlet’sassumethatweusethe operationofdividingtheinputnumberby5andtaking theremainderasahashfunction.Usingthisremaining calculationasahashfunction,eachnumberinthedata setisconvertedtoahashvaluewithafixedrangefrom 0to4.
Forexample,whenyouapplythenumber7toa hashfunction,theremainderof7dividedby5,whichis
Fig.1:Exampleofasimplehashfunction
69
2,isoutputasthehashvalue.Likewise,thehashvalue forthenumber8isoutputas3,andthehashvalue forthenumber9isoutputas4.Usingahashfunction inthiswayallowsyoutogenerateafixed-lengthhash valuefortheinput,alwaysfollowingthesamerules.
Therestofthecalculationsareverysimpleandpredictablehashfunctions.However,complexhashfunctionsthatareactuallyusedusebitoperations,nonlinear functions,andcomplexalgorithmstoensuresafetyand collisionresistanceandperformsaferdataconversion.
3CharacteristicsofHashFunctions
3.1Unidirectional
Thehashfunctionisunidirectional,soconversion frominputdatatohashvalueiseasy,butreverseconversionfromhashvaluetooriginaldataisalmostimpossible.Thisisanimportantfeatureforthehashfunction toensuretheintegrityofdataandtobeusedforsecurity purposes.
Onemeasureofthisunidirectionalityispreimage resistance.Excellentanti-phaseresistancemeansthat itisdifficultforanyhashfunctiontofindaninputvalue thatoutputsaspecificvalue.Manycryptographichash functionscurrentlyusedinsecurityreturncompletely differentoutputsfordifferentinputs,makingitverydifficulttoinfertheirinputs.

Fig.2:Exampleofacryptographichashfunctionthat producescompletelydifferentoutputvaluesevenwith similarinputvalues
aninputbthathasthesamehashvalueasthehashvalue ofinputa.
→ Anti-phaseresistance,collisionresistance,and secondanti-phaseresistancearefactorsthatevaluatethe safetyofthecryptographichashfunction.
3.3Fixedresultvaluelength
Thehashfunctionalwaysoutputsaresultofacertainlength.Evenifthesizeoftheinputdataisdifferent,italwaysreturnsahashvalueofthesamelength, soitisusefulforensuringdataconsistencyandefficient processingindistributedsystemssuchasblockchain.
Forexample,whencheckingwhetheralargeamount ofdatahasbeentamperedwith,itiseasiertocheck whethertamperinghasoccurredbycomparingthehash valueofthedataratherthancomparingallthedataone byone.Thismethodofcheckingiscalleddataintegrity checking.
Fig.3:Hashfunctionusedtochecktheintegrityoflarge amountsofdata
4CryptographicHashFunction
Thishashfunctioncannotbeappliedtoproof-ofworkorchains.Acryptographichashfunctionthat requiresdifferentpropertiesfromgeneralhashfunctions isneeded.
Hashfunctionsinevitablycausehashcollisions.A hashcollisionoccurswhentheinputvaluesaredifferent buttheoutputvaluesarethesame.
1. AninputvaluecalledxentersthehashfunctionH andhasanoutputvaluecalledH(x).
3.2HashCollisions
Ahashfunctioncanoutputthesamehashvalue fordifferentinputs.Thisiscalledahashcollision.A goodhashfunctionshouldminimisecollisions,anda securehashfunctionshouldensureaverylowcollision probability.
Thescaleforevaluatingthiscanbeexpressedascollisionresistance.Goodcollisionresistancemeansthat itisdifficultforanyhashfunctiontofindtwodifferent inputsthatcollide.
Whatissecondpreimageresistance?Thisisa casewherecollisionresistanceandanti-phaseresistance worktogether,indicatingthatitshouldbedifficulttofind
2. AninputvaluecalledyentersthehashfunctionH andhasanoutputvaluecalledH(y).
3. Atthistime,ifH(x)=H(y),ahashcollisionoccurs.
Acryptographichashfunctionisahashfunctionin whichitisverydifficulttofindsuchhashcollisions.It hasthreecharacteristics:‘collisionresistance’,‘reverse phaseresistance’,and‘secondreversephaseresistance’.
4.1CollisionResistance
Thecharacteristicisthatitisverydifficulttofind twoinputvalueswiththesamehashvalue.Itisdifficult tofindx=ysuchthatH(x)=H(y).
70
4.2Pre-imageResistance
Whenahashvalueisgiven,itisdifficulttodeterminetheinputvaluethatgeneratesthehashvalue. Givenh,theinputvaluexsuchthath=H(x)isdifficult tocalculate.
4.3SecondPre-imageResistance
Itisacharacteristicthatitisimpossibletofind anotherinputvaluethathasthesamehashvalueasan inputvalue.
GivenaninputvaluexandanoutputvalueH(x), itisdifficulttofindanotherinputvalueysuchthat H(x)=H(y)
5CryptographicHashFunctionRelationship
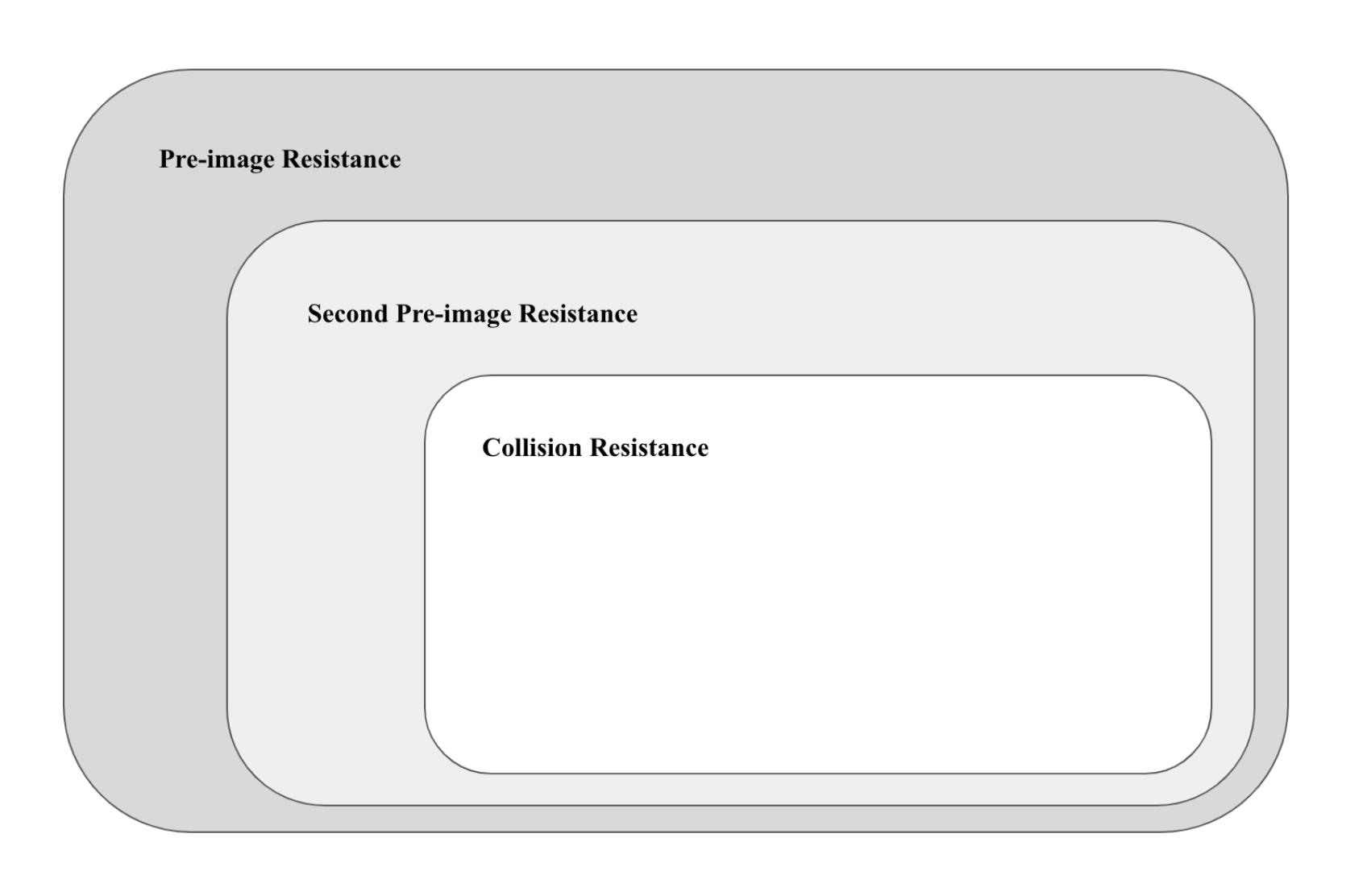
Ifitisacollisionresistancehashfunction,itcanbe asecondpre-imageresistancehashfunctionorapreimageresistancehashfunction.
1. First,selectaandcalculateH(a).
2. Calculatethepre-imagexforH(a)throughanalgorithmthatcanfindthepre-image.Thereisahigh probabilitythatxandaaredifferentvalues.
3. FindxsuchthatH(x)=H(a).Itisthesecondpreimage.Inotherwords,itisahashcollision.
Therefore,ifyoucanfindthepre-image,youcan findthecollision.Ifwetakethetreatmenthere,ifwe don’tfindtheconflict,wecan’tfindthereverseimage either.Therefore,ifitisacollisionresistancehashfunction,itcanalsobeanpre-imageresistanthashfunction.
6Outputlengthandstability
Whydocryptographichashfunctionsuseoutput valuesaslongas256bits?Thisisrelatedtothebirthday issue.Thebirthdayproblemistofindtheprobability thattwopeopleamongrandomlycollectedpeoplehave thesamebirthday.
Beforelookingatthebirthdayproblem,let’slook atthepigeonholeprinciple.
6.1PigeonholePrinciple
Theprincipleisthatwhenn+1objectsareputinto nboxes,atleastoneboxcontainstwoormoreobjects.
Proofbythelawofreductio:Supposetherearenpigeonholesandn+1pigeons.Ifeachpigeonholecontains lessthanonepigeon,thenthereareatmostnpigeonsin allpigeonholes.However,sincetherearen+1pigeons intotal,thereisacontradiction.Therefore,thereare twoormorepigeonsinanypigeonhole.
6.2BirthdayParadox
Thereare365daysinayear,sothereareatotal of365birthdays.Ifmorethan366peoplegather,there mustbetwopeoplewiththesamebirthdayaccording tothepigeonholeprinciple.
Let’scalculatethecasewheretherearelessthan 365people.Iftherearenpeopleandtheprobability thattwoormoreofthemhavethesamebirthdayis p(n),thentheprobabilitythatallpeoplehavedifferent birthdaysp(n)is-p(n).First,let’sfindp(n).Sincethe birthdayofthesecondpersonmustbedifferentfromthe firstperson,andthebirthdayofthethirdpersonmust bedifferentfromboththefirstandsecondpersons,we canobtainthefollowingequation.
Theprobabilityoftwopeoplehavingthesame birthdayis 1 365 ,soyoumightthinkthatitwouldtake 365peopletohavethesamebirthday,butifyoucalculatetheaboveequation,
Evenifthereareonly23people,thereisa50%
Fig.4:CryptographicHashFunction
p(n)=1 × 1 1 365 × 1 × 1 2 365 ×···× 1 × 1 n 1 365 = 365 × 364 × 363 ×···× (365 n +1) 365n = 365! 365n(365 n)! (1) Thereforep(n)is p(n)=1 365! 365n(365 n)! (2)
Fig.5
71
chancethatsomeonewillhavethesamebirthday.
8Conclusion
23canberoughlyconsideredtobethesquareroot of365.Let’ssaywehaveahashfunctionwhoseoutput is256bits.Ifanyofthesehavethesamevalue,i.e.to findaconflict,ittakesabout 2 n 2 =2 256 2 =2128.Makethe outputbitslongenoughbecausecollisionscanbefound bycalculatingonly 2128 times.
Incryptography,itisusuallysaidthatifittakes morethan 280 times,itissafe.Therefore,theoutput lengthissufficientlylong,about256bits,tomakeit muchmoretransparent.
7Usinghashfunctionsinblockchain
7.1Reasonsforusinghashfunctionsin blockchain
Theapplicationofhashfunctionswithinblockchain isfundamentaltoitsdecentraliseddistributedsystem, prioritisingthesafetyandintegrityofdata.Through theconversionofblockchaindataintouniquehashvaluesusinghashfunctions,thisapproachofferssignificant advantagessuchasestablishingidentity,ensuringdata integrity,andfortifyingoveralldatasecurity.
7.2Exampleofusingblockchainhashfunction
7.2.1TransactionHash
Transactions,whichareunitsofdatatransmittedbetweennetworkparticipantsinablockchain,go throughahashfunctionandareconvertedintoahash valueofacertainlength.Thismakesiteasytoidentifyandensuresintegritybecausewhentransactiondata changes,thehashvaluealsochanges.Additionally,since hasheddataisdifficulttorestoretotheoriginaldata, thestabilityofdatastoredintheblockchainincreases.
7.2.2BlockHash
Eachblockhasauniquehashvaluebasedonthe datacontainedintheblock.Thisallowsblockstobe distinguishedfromeachother,andhashvaluescanbe usedtofindorverifyspecificblocks.Additionally,when calculatingthehashofeachblock,thehashvalueofthe previousblockisalsoincludedtoensuretheintegrityof thechain.
7.2.3MerkleTree
MerkleTreeisacoredatastructureforverifyingthe integrityofblockchain.AMerkletreeisadatastructure thatrepresentsmultipledataasasinglehashvalueby applyingahashfunctionstepbystep.Simplyput,itis adatastructurethatturnsmultipledataintoonehash value.
Inconclusion,hashfunctions,particularlycryptographicones,areindispensabletoolsfordataintegrity andsecurity.Theyenablevariousapplications,notably inblockchain,byprovidinguniqueidentifiers,ensuring dataconsistency,andenhancingoverallsystemsecurity. Continuousresearchanddevelopmentinthisdomainremainimperativetoaddressevolvingsecuritychallenges.
9Bibliography
1. Wang,M.,Duan,M.andZhu,J.,2018,May. Researchonthesecuritycriteriaofhash functionsintheblockchain.InProceedings ofthe2ndACMWorkshoponBlockchains, Cryptocurrencies,andContracts(pp.47-55). https://dl.acm.org/doi/abs/10.1145/3205230.3205238
2. Kuznetsov,A.,Oleshko,I.,Tymchenko,V.,Lisitsky,K.,Rodinko,M.andKolhatin,A.,2021.Performanceanalysisofcryptographichashfunctions suitableforuseinblockchain.InternationalJournal ofComputerNetworkInformationSecurity,13(2), pp.1-15.
3. DiPierro,M.,2017.Whatistheblockchain?. ComputinginScienceEngineering,19(5),pp.92-95. https://ieeexplore.ieee.org/abstract/document/8024092
4. Preneel,B.,1994.Cryptographichash functions.EuropeanTransactionson Telecommunications,5(4),pp.431-448. https://onlinelibrary.wiley.com/doi/abs/10.1002/ ett.4460050406
n ≈ 1 17√365 ≈ 22 3 ≈ 22 3 (3)
72
MathematicalModelandSimulationofSIRModel forCovid-19OutbreakinKorea
Jungyoon(Luke)Han Year12
Email:jyhan25@pupils.nlcsjeju.kr
Editor
Emma(Chaeeun)Chung
RecommendedYearLevel:KS5
Keywords:Mathematicalmodelling,SIRModel, differentiation
1Introduction
EversincethefirstincidentinNovember2019, Covid-19hasposedasignificantglobalchallengeworldwide,with354confirmedcasesand24,503deathsreportedasofMay4,2020.Worldwide,lockdowns,socialdistancing,andmaskusagehavebecomewidespread measurestocombattherapidtransmissionofthevirus. Korea,alsofacinganoutbreak,implementedpolicies regardingsocialdistancinginordertomitigatethe widespreadofthevirus,includingtemporarysuspensionoffacilityoperations.Despitetheseefforts,the numberofcovid-19caseshasincreasedatanunprecedentedrate,recordingatotalinfectionof621,328people adayin2022March16th.Althoughrecentlyboththe policieswithinthenationandthenumberofinfected peoplehavesignificantlydecreased,itisundeniablethat Korea’sattempttohandlethediseasehasfailed,reachingatotalof34,571,873infectionsand35,934deaths by2023December8th.Thereisaneedtoanalysethe covid-19pandemicexperienceinordertoallowthoroughexaminationforenhancedpreparednessforfuture challenges.
Thusinthisstudy,anepidemicmodelbasedonSIR methodofCovid19isusedtoquantifyandvisualisethe spreadofthediseaseinKorea.TheSIRmodelusedhas threedifferentialequationswhicharecomplicatedand timeconsuming,henceEuler’smethodhasbeenusedto solvethesethreeequations.Theobjectiveofthisstudy istoquantifythenumberofcasesinKoreainvarious timeperiods,anddevelopanSIRmodeltocompare thecalculateddatawithreal-timedatatoshowhow
accuratethemodelis,andpossiblyfindouttheending stageofcovid-19.
2SIRModel
TheSIRmodel,shortforSusceptible,Infectiveand Recoverymodel,wasintroducedbyKermackandMcKendrickin1927.Havingbeensuccessfulinseveral diseasesincludingCholera,MERS,Influenza,theSIR modelcanpredictactivitiesofoutbreakdiseasesincludingendandpeakofepidemicdiseaseandfuturepredictions.
Considerthepopulationremainsconstantregarding thestudyinKorea.Theconductedpopulationofthe studywaschosentobeinMay2020.Thetotalcovid-19 populationisdividedintothreeparts.
1. S(t):Thenumberofpopulationwhoaresusceptible tothediseaseatthetime
2. I(t):Thenumberofpopulationwhoareinfectedto thediseaseatthetime
3. R(t):Thenumberofpopulationwhohasrecovered fromorpassedawayduetotheinfectionatthetime period
Withoutconsideringtheevolutionoftheviruses,a simplediagram(Fig1)canbedrawntodescribetheSIR ModelofCovid-19outbreak.

Fig.1:DiagramofSIRmodeldescriptionwithoutconsideringvirusevolution
ThediagramisdefiningthatpeoplewhoareinR(n), orwhohaverecoveredfromtheinfectionwillnolonger
73
beinfectedwiththediseaseagain.Butasotherviruses, covid-19hasevolvedmultipletimes.Henceconsidering thedevelopmentofcovid-19,thediagram(Fig2)illustratesadescriptionoftheSIRmodelincludingrecoveredpopulationreturningintosusceptiblepopulations.
3Methodology
Threedifferentialequationsareusedforthestudy anddiscussionsforthecovid-19infectioninKorea.
S′(t)= rSI I′(t)= rSI aI
R′(t)= aI (1)
Thevariablesrandaaretheinfectionrateandrecoveryrateofthedisease.Inthisstudytheaverage timeofcovid-19incubationperiodis14days.These valuesareusedforsolvingthethreedifferentialequationsofcovid-19outbreaks.Thesecanalsobewritten asshown.
dS dt = rSI dI
dt = rSI aI dR dt = aI
(2)
becalculated
Thethreedifferentialequationswhichwillbeused intheSIRmodelisalsoknownastheKermackMCKendrickSIRmodel.Itisusefulforanalysingthe dataofcovid-19occurrencesinKorea.Additionofthe equationsprovidedcanbeconvenientforthedataanalysis.
dR dt + dR dt + dR dt = rSI + rSI aI + aI =0 dS + dI + dR =0
NisaconstantwhichmeasuresthetotalsizeofpopulationforKoreaduringthepandemicsituation.The valueisconstantalltime,boththeinitiallevelaswellas afterthepandemic.TheinitialvaluesoftheSIRmodel areshownas S(0)=S0, I(0)=I0, R(0)=R0
Asthepopulationisconsideredconstant,therecoveredpopulationofcovid-19canbecalculatedbythe givenformula
(3)
Byintegratingtheequation,arelationshipbetween thevariablesandthetotalnumberofpopulationscan
Withthesedifferentialequations,aquantitativeapproachhasbeenusedtosolvetheequationsoftheSIR model.
Accordingtotheequations,ifS(t)isconsistently negativeforalltandI(t)isconsistentlypositive,providedthat S0 exceeds a r ,weobserveatrend.Toclarify,ifthe S0 surpasses a r therewillbeaninitialincrease,reachingamaximumgrowthrate(rmax).However,overtimethisgrowthratewillgraduallydecrease andapproachzero,duetothedecreasingin S0 value. Bythis,severalassumptionscanbemade.
1. Case1:If S0 islessthan a r ,thentheinfectionrate oftheCOVID-19outbreakinKoreawilldecrease andbecomezeroaftersometime.
2. Case2:If S0 ismorethan a r ,thentheinfection rateofCOVID-19willexhibitanepidemicpattern, orwillincreaseandpersistovertime.
Bythetwoassumptions,thebehaviourofcovid-19 outbreakdependsonthevalueofn.nisreferredtoas thethresholdnumber.
Rn = S(0)r a (6)
Rn isdefinedasreproductivenumber.Thisisthe numberofsecondaryinfectivesofcovid-19producedby oneprimaryinfectiveinthesusceptiblepopulation.By regardingthevalue Rn,twocasescanbeassumed:
1. Case1:If Rn islessthanone,itpimplesthatthe covid-19outbreakwilldiminishoutofKorea
2. Case2:If Rn isgreaterthanone,itpimplesthatthe Covid-19outbreakisstillprevalentandinepidemic stateinKorea.
4ExperimentalResultConduction
Inordertoanalysethecovid-19outbreakofKorea,itisnecessarytosolvethedifferentialequationof
Fig.2:DiagramofSIRmodeldescriptionwithconsideringvirusevolution
S′ + I′ + R′ = N or S{t} + I{t} + R{t} = N
(4)
R(t)= N (S(t)+ I(t)) (5)
74
theSIRmodel.Considerapopulationsusceptibleto theCOVID-19outbreakalongwithasmallnumberof infectedindividuals.ThequestionofwhetherthepopulationofCOVID-19infectiveswillsubstantiallyincrease inIndiacanbeansweredbysolvingthesystemofdifferentialequationsprovidedabove.Althoughtheseconsist ofthreeunknownvariables,bycombiningtheequations, asingledifferentialequationwithonlyoneunknown variablefortheproposedSIRmodelcanbeobtained.
Accordingtothechainrule,
dI dS = dI/dt dS/dt = rSI aI rSI = rSI rSI aI rSI = a rS 1
dI dS = a rS 1
dI = a rS 1 dS
Integratingeachsidewillgive:
dI = a rS 1 dS I = a r ln S S + C
(7)
equationisshown:
Here 0 < S∞ < K thatispastthepopulationofKoreaescapestheCOVID-2019infective.Inthisproposed study,itisverydifficulttoestimatetheparametersof r andabecausethesedependondiseasebeingstudiedand onsocialandbehaviouralfactorsofthatcountry.The population S∞ and S0 canbeestimatedbyserological studiesbeforeandafteroftheCOVID-2019outbreak andusingthisdata,thebasicreproductionnumberis givenbythefollowingformula:
(8)
Byinputtingthevaluesofinitialconditionsofeach variableintheequation,itbecomes:
I(0)= a r ln S(0) S(0)+ C
C = I(0)+ S(0) a r ln S(0)
(9)
Considerthepopulationsizeofsusceptiblecaseof covid-19asK,whichisapproximatelyequaltotheinitialpopulationS0.Thenumberofinfectivesinthepopulationisconsideredsmall,hence
S(0)= K,I(0)=0,Rn = rK a (10)
If I(t)=0 as t →∞ and S0 < a r then V(S0, I0)= V(S0),givinganexpression
K a r ln S(0)= S(∞) a r ln S(∞)
Where S∞ istheamountofsusceptiblepopulationifthe infectivecaseiszero.Aftersimplification,thefollowing
Themaximumnumberofcovid-19infectivescanbe obtainedbyusingthefollowingformula:
Byimplementingaformulafromabove,themaximumnumberofcasescanbecalculatedasshown:
Thedifferentialequationcalculatedcanbesolved byusingEuler’smethod.
AMATLABsoftwarehasbeenusedtosolvethe differentialequations.Theexpressionsforthesoftware areprovidedbelow.
TheSIRmodelhasasystemoffirstorderdifferentialequations,andeuler’smethodispurelynumerical methodforsolvingthefirstorderdifferentialequations
ln
(0) a r ln S(∞) K S(∞)= a r [ln S(0) ln S(∞)] K S(∞)= a r ln S(0) S(∞) r a = ln S(0) S(∞) K S(∞) (11)
K S(∞)= a r
S
Rn = rK a (12)
S = a r , I=Imax (13)
I = a r ln S S + C C = I(0)+ S(0) a r ln S(0) I(max)= a r ln a r + S + I(0) a r a r ln S(0) (14)
75

Fig.3
thusthecalculationwillbeusingeuler’smethod.Considerthedifferentialequation dy dx = f (x,y).Thesolution isprovidedbelow.
y(n +1)= y(n)+∆tf (x(n),y(n)) (15)
The ∆t isasmallstepinthetimedomainand the f (xn,yn) istheslopeofthecurve.Thewanted dependentvariablesareS,IandR.Thus,thedependent variablescanbeimplementedintotheequation
S(n +1)= S(n) rI(n)S(n)∆t
I(n +1)= I(n)+[rI(n)S(n) aI(n)]∆t
R(n +1)= R(n)+ aI(n)∆t (16)
Inthestudy,theinitialdatasetofcovid-19isfrom September4th2020(Mostformerdata).Thustheinitial values,or S0, I0,and R0 canbeshownas:
S0 =5 18417, I0 =0 20842, R0 =0 16114 (17)
Thevalueofrecoveryrate(r)wouldbe
InfectedPopulation
r =
SusceptiblePopulation = 20842 518417 r =0 04020315691 ≈ 0 040203 (18)
byusingequationsabove.
(20)
a
≈ 0 0714,
1407 (19)
(max)= a r ln a r + S + I(0) a r a r ln S
(0) (23)
K
S(0) S(∞)
14 ,astheincubationtimeofcovid-19
= 1
∆t=0
S1 =S0 rI0 S0∆t S1 =5 18417 (0 040203 ∗ 0 20842 ∗ 5 18417 ∗ 0 1407) S1 =5 178058
Withthesevalues, S1,I1 and R1 canbecalculated I1 =I0 +(rI0 S0 aI0)∆t I1 =0 20842+(0 040203 ∗ 0 20842 ∗ 5 18417 0 0714 ∗ 0 20842)0 1407 I1 =0 21243 (21) R1 =R0 +aI∆t R1 =0 16114+(0 0714 ∗ 0 20842)0 1407 R1 =0 16323 (22)
Thismethodcancontinueevenfurtherusingasimplealgorithm. Fig.4
ThiscodewillprovidethevaluesoftheSIRmodel fromSeptember4th2020toDecember13th2020.It alsoshowsthedateofwhenthereisthemostnumber ofinfectivecases,andwhenthecovid-19outbreakwill stopinKorea.Themaximumnumberofinfectivescases ofcovid-19canbecalculatedusingtheformulafrom above: I
ln
76
where a r canbecalculatedby r a =
S(∞) .ByimplementingthevaluescalculatedbytheSIRmodel,these aretheresultsshown.
5Conclusion
BasedonthedataasofSeptember4th,2020,the SIRmodelindicatesthatthecovid-19outbreakwill peakonOctober28th2020,andwillofficiallyendon December7th2023.However,thesearestrictlyconsideredonquantitativefactors,andbasedonthefactthat thepoliciesregardingsocialdistancingandtemporary suspensionsoffacilitieswerenotcompliedwellenough, thereallifevaluesaredifferentcomparedtothecalculatedvalues.Therefore,thestudyimpliesthatifall policieswerekeptastheinitialstate,covid-19would likelybeextinct,andwouldalsostatethattheKorean governmentshouldtrytheirbesttokeeptheircitizens strictlyfollowingtheirregulationsinordertoendthe situationasfastaspossible.
77
RecommendedYearLevel:KS4
LotteryMathematics
LynnKim Year10
Email:lkim28@pupils.nlcsjeju.kr
Editor Emma(Chaeeun)Chung
Keywords:Lottery,Gametheory,probability
1Introduction
Everyonehasadreamofbecomingamillionaireand escapingfromschoolorwork.Thereareamyriadof waysthiscanbeachieved–workinghard,doingbusiness,investingstock–andlotteryisoneofthesemethods.“Wellitsnonsense!Gettinghitbylightningwill bemuchmorelikely!”.Mostpeoplebelievethatwinningthelotteryisjustoutofpureluck.But,isthis thetruth?Tofindthisout,thispaperinvestigateslotterymathematicsandhowtoincreasethepercentageof winning.
2Aim
Thispaperaimstofindawaytoincreasetheprobabilityofwinningalotteryorfindingaholeinthelottery inwhichifoneusesacertainamountofmoney,thereis a100%chanceofearningprofit.
3TypesofLottery
Lotterydoesnotonlyexistasoneform:thereare multifariouskindsoflotteries,alluniquefromoneanother.Tolimittheamountofvariables,thisarticlewill bemajorlytalkingaboutthelotteriesinSouthKorea.
SouthKoreahas4majortypesoflotteries:online lottery,scratchofflottery,pensionlotteryandinternet lottery.Onlinelotteryisagamelinkedtothenetwork wheretheuserelectsacertainnumberfromacertain numberrange.Thesecondtypeisscratchofflottery,a lotteryinwhichyouscratchathinlayeroffasmallcard toseeifthosehiddennumbersmatchthewinningnumbers.Thethirdtypewouldbethepensionlottery,or inotherwords,drawinglottery.Thistypeoflotteryis
themostwellknownone.Thecustomerpurchasesticketsandchoosestheirnumbersandonaspecificdate, randomnumbersareselectedasthewinningnumber. Thusthewinnerneedstohavethesamenumbercombination.ThelastbutnotleastistheInternetlottery whichisquitesimilartoonlinelottery,buthasabiggerboundaryasitincludesalllotteriesontheinternet. However,therearevariationsinthesetypesoflottery whichmayhaveadistinctiveruleorcharacteristicsfrom eachother.
Totalkaboutincreasingthechanceofwinninga lottery,somekindsoflotterieswillnotbeincludedin thispaper–forexample,scratchofflottery–andwill mostlybefocusedonpensionlottery.
4LotteryMathematics
Firstoff,itisnecessarytocalculatetheprobability ofwinningthelottery.Beforecalculation,wemustdefineNastherangeinthelotteryandRastheamount ofwinningnumbersandassumethatrepetitioncannot happen.
Whenchoosingthefirstnumber,thereareatotal ofNpossiblenumbersthatcanbeselected.Thesecond numberwouldbeN–1asrepetitionisnotallowed. ThismeansthatthethirdisN–2,fourthisN–3,fifth isN–4andonandon.ThiswillleaveuswithN+1 –Rpossibilitiesforthelastone.
Then,wewillneedtomultiplyalltheseoutcomes leadingustogetN!/(N–R)!whichisthepermutation
Fig.1:definingR
78
equation.However,wemustdividethisoutcomebyR! astheorderdoesnotmatterinthiscase.
Thisleadstothenumberofpossibleoutcomesofthe lotterybeingN!/R!(N-R)!whichisaverysimplemathematicscalledcombinations!Byutilisingthisformula, Icreatedatableshowingtheprobabilityofwinninga lotterywithdifferentvariables.

ThedataaboveshowsthatthesmallertheNand thesmallertheRis,theratiogapissmaller.Thisconcludesthatchoosinglotterieswithsmallernumbersresultsinahigherpercentageofwinningthelottery.
Now,let’ssupposethatyouhavealreadywonthe lotteryandyouwanttofurtherincreasetheamountof moneyyouareabletoearn.Lotteryisnotjustabout winning.Formostlotteries,themoneyisdividedupon theamountofpeoplewhowonfirstplace.Thismeans thatthemorepeoplehaveidenticalnumbersasyou,the lessmoneyyoureceive.Onewayyoucanavoidcases likethisistolookatstatistics.
Peopletendtohavetheir“luckynumbers”–which arenumbersusuallyconsistingtheirbirthdates–andselectnumbersusingitorchoosethenumbersinacertain sequenceofacertainshape.Byavoidingthis(choosing numberslargerthan12or31,choosingarandomorder andmore)youmayhaveanastoundingamountofprize moneyonceyouwin.
5SpecificCases
Therearecertaincaseswheremathematicscould befurtherusedtoincreasetheprobabilityofwinning thelottery.OnegoodexamplewouldbetheWinfall.
TheWinfalllotteryiswhereifthejackpotreaches$5 millionandtherewerenowinners,themoneyisdivided andlendedtothelowerplacedwinners.Amathematical couplesawthislotteryandcalculatedthatiftheyinvest acertainamountofmoney,thegainwillbelargerthan theloss.Tohaveabetterview,wecouldseethatwhen buyingNamountoftickets,itissurethatyouwillbe oneofthe4numberwinnersandtheprizeoverweighs thecostofbuyingNamountoftickets.
6Experiment
Myquestionisthatcanwe100%gainprofitby winningthelotteryinSouthKorea?Tofindthisout,I wenttoSouthKorea’sofficiallotterywebsiteDongHang Lottery.InSouthKorea,thereare2drawinglotteries calledLotto6/45andPensionlottery720+.
Lotto6/45isdonebyfillingout6numbersoutof1 to45justasthenametellsus.Thetablebelowshows thewaysofwinningandtheprizemoneyforeachplace.
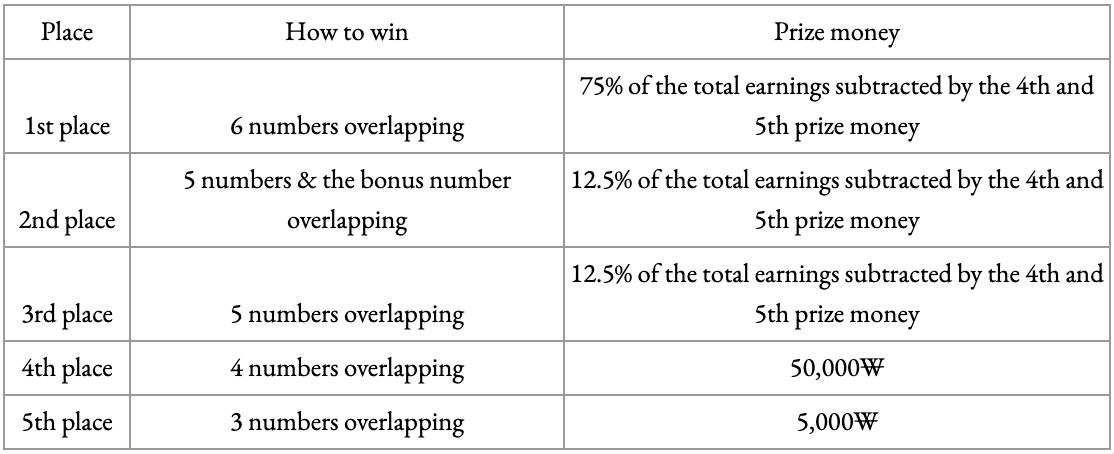
WhenLotto6/45hasnowinners,theprizeisadded ontothenextfirstplacewinner.However,thisisonly allowedtwicesoonthethirdtime,themoneywillbe movedtothesecondwinnerjustliketheWinfallLottery.Buttheproblemhereisthatthemoneyearntby the3rd,2ndand1staredistributedequallybythepeoplewhohavethesamenumbersinLotto6/45.This meansthathavinga100%profitcannotbecalculated withoutstatistics.
Now,IwillbemovingontothePensionlottery 720+.Thislotteryworksquitedifferentlywiththe onesstatedabove.Thefirstplacegets7,000,000₩ each monthfor20years.Andunlikeotherlotterieswhich thewinnerneedstopay33%taxifthewinningprize isover300,000,000₩,thewinnerofthePensionlottery 720+onlyneedstopay22%taxwhichusuallythetax forprizemoneyunder300,000,000₩.
So,howdoweselectthenumbersforthislottery? Inthislottery,youchoose7numbersbutitisn’tout ofacertainrangeofnumbers.Thereare2sections forchoosingit.Youfirstneedtoselectyour’jo’which isfrom1to5.Thenyouneedtochoose6numbers inwhicheachdigitcanbefrom1to9.Moreover,a
((N ) · (N 1) · (N 2) · (N 3) · · (N R +1)) · R! N !/R!(N R +1 1)! N !/R!(N R)! (1)
Fig.2:variablesandprobabilityofwinning
Fig.3:waysofwinningandprizemoney
79
sequenceofnumberscanonlybeselectedonce,thus eachindividualwillhavedifferentnumbers.
Thisisn’ttheonlyuniquethingaboutthislottery. Towinthelottery,theorderheavilymatters.Evenif yougetthesamesequence,theyneedtofollowtheorder ofthewinningnumbers.
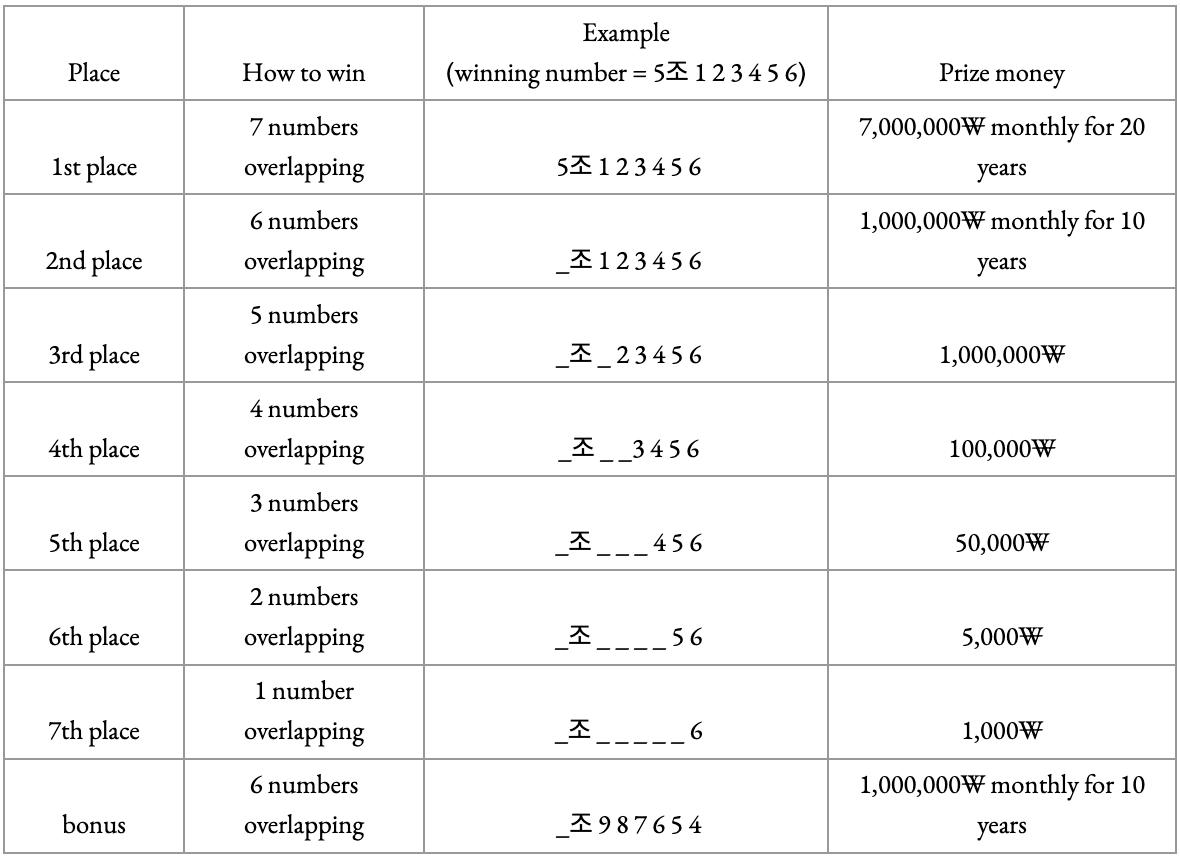
Now,letuscalculatehowtogetasurewin.For the7thplace,youwouldneedtobuy9tickets,costing 9,000₩.Forthe6thplaceyouwouldneedtobuy9 × 9tickets,costing81,000₩...Thistablebelowindicates thenumberofmoneyyouhavetospendtohaveasure win.
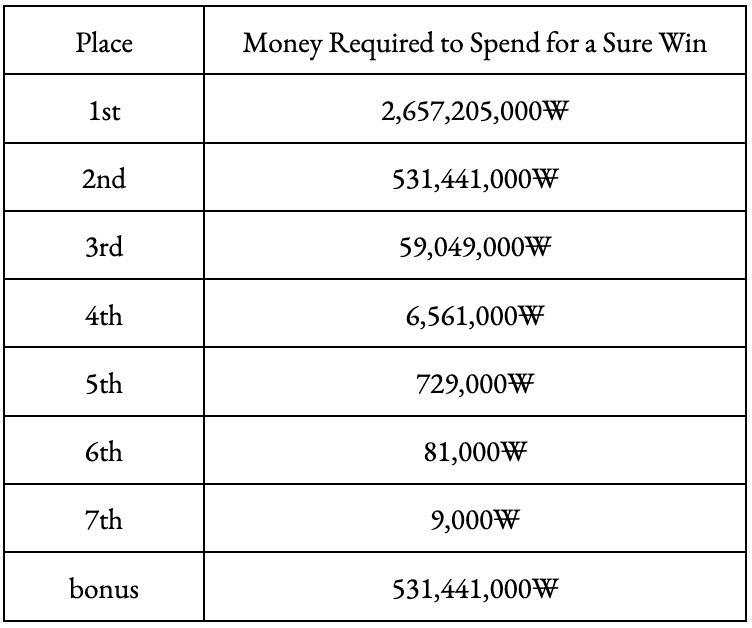
So,howmuchmoneydoyouhavetospendtogain profit?Youmaythinkthatthefirstplacewillonly gain1,680,000,000₩,secondplace120,000,000₩and
etcthustherewillbenowaytogainprofitfromit. Howeverluckily,theDongHangLotteryallowsreceivingtheprizemoneyforeveryticketyouwin.Insimpler words,itmeansthatifyoubuytickets1’jo’234567and 3’jo’234567andthewinningnumberis1’jo’234567, youcanreceiveboththeprizes.Wealsoneedtoconsiderthetax(1st&2nd&bonus=22%tax)forit.Now, recalculatingitthereisahigherprofitforeachcase.
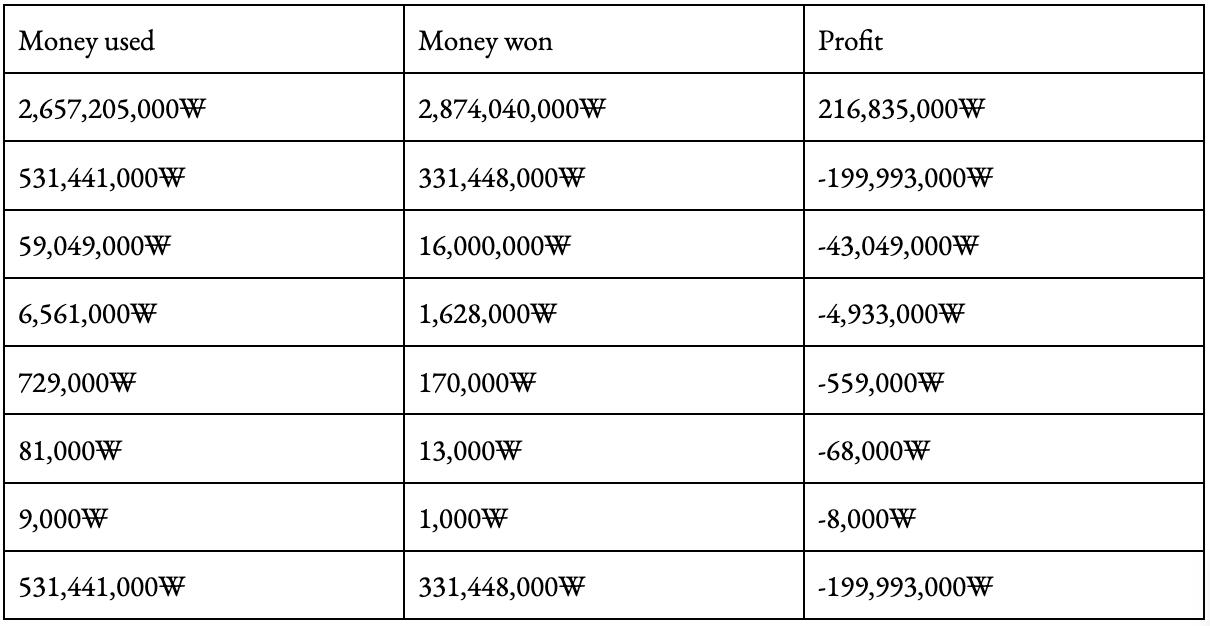

Thisshowsthatbuyingallthelotteryticketswill lendyoua100%profitof216,835,000₩.
7Conclusion
Thisdatashowsthatlotteryisnotjustpureluck andthatthereisawaytogaina100%profitinlotteries.MygoalwhenIwasalittlekidwastoimplement basicmathsknowledgetowinthelottery,andthisresearchhelpedmetogetastepclosertoitandbetter understandaboutlotteriesandmaths.
8Bibliography
1. StatisticsandProbabilityinLotteryof“WINFall”
https://www.jofamericanscience.org/journals/amsci/0201/06-lihao-0106.pdf
2. DongHanglottery
https://dhlottery.co.kr/common.do?method=main
3. HowtoWintheLotteryAccordingtoMath
https://lotterycodex.com/how-to-win-the-lotterymathematically/
Fig.4:howtowinthePensionlottery720+
Fig.5:moneyrequiredforasurewin
Fig.6:moneyused,won,andprofit
Fig.7:theworkingoutprocess
80
ThePrisoner’sDilemmaandNashEquilibrium
MinjaeKang
Year9
Email:mjkang28@pupils.nlcsjeju.kr
Editor
Emma(Chaeeun)Chung
RecommendedYearLevel:KS4
Keywords:Prisoner’sDilemma,Gametheory,Nash Equilibrium
1Introduction
Theprisoner’sdilemmaisoneofthebestknown sectionsofgametheorywhichillustratesaconflicting situationbetweenindividualrationalityandcollective rationality.Itdealswiththesituationwheretwopeople havecompetingincentivesthatleadthemtochoose asuboptimaloutcome.Thetheorywasfirstdevised byRANDCorporationscientistsMerrillFloodand MelvinDresherin1950,butwasfurtherdevelopedand eventuallypublishedbyAlbertW.Tucker,aPrinceton Mathematician.Thesetupfollowsthe5following assumptions:
1. Eachplayerremembersgivencontextforthechoice
2. Eachplayerdoesnotconsidertheeffectofactions ontheothers
3. Eachplayerisinterestedinmaximisingtheirutility orpayoff.
4. Eachplayerknowsthepreferencesandstrategiesof theotherplayers.
5. Eachplayerhasthesameunderstandingofhowthe gameis.
Theinitialproposalisstraightforward:“Youhave twochoices:confessorremainsilent.Ifbothdeny,you willallspendonly1yeareach.Ifyouconfessandthe otherdoesn’tyouwillbefreeofjailtimewhiletheaccomplicewillget10years.Viceversa,youwillget10 yearsandtheaccomplicewillgetofffree.Ifbothconfess,youbothget8years.”
Thetheorydirectlycorrelatestothe“NashEquilibrium”,astablestateofasystemthatinvolvesseveral

interactingparticipantsinwhichnoparticipantcangain byachangeofstrategygiventheopponent’stacticas longasalltheotherparticipantsremainunchanged.It isabroaderconceptwhichcanbeappliedtoanalyse varioustypesofinteractionsingametheory,including theprisoner’sdilemma.TheexistenceoftheNashequilibriumintheprisonerdilemmacanbeprovedbythe tableabove:theonlypairunabletolessenthetime injailbychangingone’scooperationattitudeiswhen theybothconfess.Thefactthatalldominantstrategyequilibriumstaketheshapeof“Nashequilibrium” isnotable.
Inanysituationinvolvingtheformatoftheprisoner’sdilemma,thedominantstrategyischoosingconfessing.Adominantstrategyreferstoachoicethat producesthebestpayoffforthatplayerregardlessof thestrategiesemployedbyotherplayers.Accordingto thetable,ifprisoner1confesses,theyeithergofreeor get8yearsinprison.However,iftheydonotconfess, theyeithergetoneyearor10yearsinprison.Theaveragejailtimeislowerintheformer.Itisthesamein areciprocalmanner.Thesituationshowsthedominant strategyequilibriumisbothconfessing(8,8).However, the“dominant”strategyisnotthe“optimal”strategy,
Fig.1:Possibleoutcomesofnumberofyearsinprison
81
whichraisesa“dilemma”.
2Experiment
Areal-lifeexperimentdemonstratestheconceptof theprisoner’sdilemma.ApairofNLCSJejustudents arepartoftheexperiment.
Procedure:
1. Suggestasituation:“Youcaneitherdoagroup projectindividuallyorasagroup.Ifbothcollaborate,youbothgeta6onbothindividualandteam criteria.Ifbothdonot,youbothgeta5onthe criterias.Ifyouchoosetoworktogetherbutyour partnerdoesnot,yougeta4onindividualmarks but7onteam.Viceversa,yourpartnergetsa4."
2. Distributedecisioncardstoeachstudent.Onesays “collaborate”andtheotherstates“individual”.
3. Inprivate,eachstudentdecideswhethertocollaborateorworkindividuallyandhandsintheirdecision card.
4. Collectthedecisioncardswithoutrevealingthe choices.
5. Announcethedecisionssimultaneously.

Fig.2:Aresulttableshowingthepossibleoutcomesof theexperimentabove
analysedecisionsinanaturalsetting.Repeatingtheexperimentseveraltimestocalculatethemeanandthus increaseaccuracyofinformationwilladdupcredibility totheexperiment.Iintendtoexplorethepsychologicalfactorsofthesuboptimalchoicesoftheprisoner’s dilemmaaswell.
3Analysis
Theexperimentsuccessfullydemonstratedtheprisoner’sdilemmaanditsconnectiontothenashequilibrium.
Fortheindividual,workingindividuallymayseem appealingforgettingaveryhighgrade,butitresultsin aloweroverallgroupprojectgradewhenbothindividualschoosetoworkindividually.However,theoptimal choiceiswhenbothcollaborate,makingita“dilemma”. Inthiscase,theNashequilibriumwhenbothindividualschoosetoworkindividually.Theexamplepairin theexperimentdemonstratedasuboptimaldecisionor thenashequilibrium(showninred).
4Extension
Althoughtheexperimentwell-supportedthetheory,therewerealsocertainlimitations.Incontrived,or lessrealistic,situations,people’sinstinctiveandnatural judgementwaslikelytobeclouded.Iaimtoobserveand
82
RecommendedYearLevel:KS4
MathinMinecraft
SiwoolUm Year9
Email:swum28@pupils.nlcsjeju.kr
Editor RyanHanjinLee
Keywords:momentum,velocity,elevationmomentum
1Introduction
ThisarticlewillintroduceaspectsofMinecraftto determinewhethera5blockjumpispossibleornot.
2BackgroundInformation
MinecraftisapopularsandboxgameoriginallydevelopedbyMarkusPerssonandlatertakenoverbyMicrosoftwithover160millionactiveusersinamonth(as ofAugust2023)andover10millionpeakplayersaday. throughhistheoryofPascal’sTrianglethatpeopleused forcenturies.
3Aim
Asitisasimulationofathree-dimensionalworld withauniquegame-enginedevelopedbythedeveloperhimselfinsteadofimportingorimplementingpreexistinggame-enginesusingothersoftwaresuchasUnrealandUnity,thecodecanbeanalysedtodetermine howthephysicsofthegamework,hencefiguringout ifa5blockjumpwithoutanygimmicks(potioneffects, damageboosts,ice,slime,glitches,etc.)ispossibleor not.
4Power
Incountlessdifferentgames,jumpingisakeyelement.Minecraftisnoexception.
InMinecraft,aplayercanjump1.252blocks(1.249 blocksinversionslowerthan1.9,butthisarticlewill refertothevalueof1.252)andlastsfor12in-game tickswhichisequivalentto0.6seconds.Accordingto theMinecraftParkourWiki,whenaplayerjumps,the verticalvelocityissetto0.42.Duringajump,the
verticalvelocityisdecreasedby0.08andmultiplied by0.98everytick,–duetogravityandairresistance respectively–or0.05seconds.Whentheplayerhitsa ceiling,theverticalvelocityissetto0.
Whichmeansthat:
Sotheresultsare:
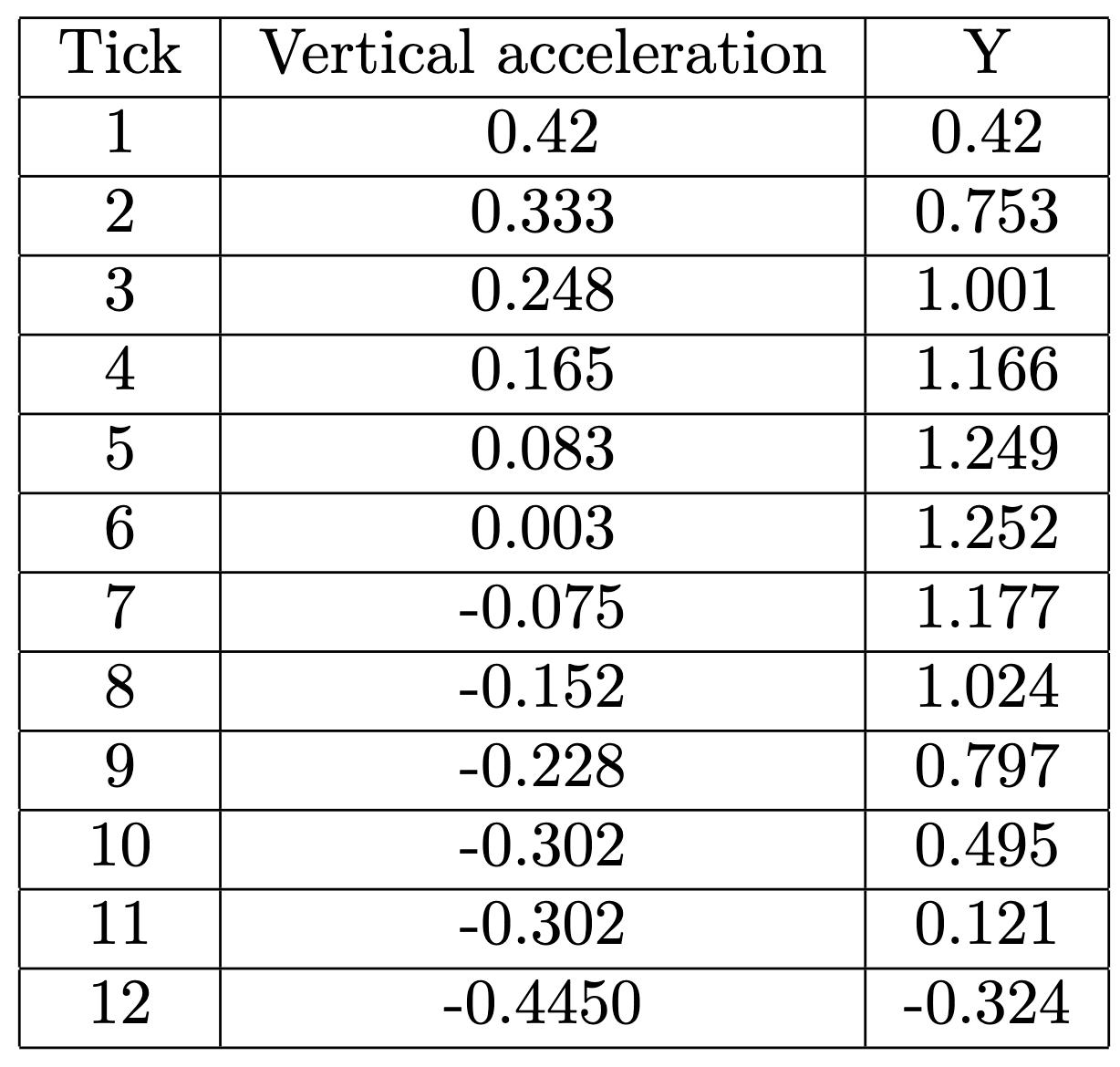
Figure1:Verticalaccelerationonflatgroundwhenthe playerjumps
Intheair,91%oftheplayer’sspeedisconserved everytick(duetodrag),whichissignificantlymore thanwhenjustrunningonground.Thismakes sprint-jumping(wheretheplayerholdsjumpwhile sprinting)amoreeffectivewaytoconservemomentum sincesprintingis30%fasterthanwalking.
Asforthehorizontalmovementoftheplayer,itis thefollowing:
Vy(1)=0.42 and Vy(t)=(Vy(t 1) 0 08) × 0 98
83

Thismeansthatthejumpdistancecanbegivenby:
75bjump
Animportantthingtonoteisthata5bjumpisnot actually5blocksinlength.Theplayer’shitbox(abox aroundtheplayerusedtocheckcollision)is0.6b.Soa 5bjumponlyrequirestheplayertojump4.4b.Using theequationfromearlier,wecanseethattherequired initialspeedbeforethejumphastobegreaterthanor equalto0.332232069.(SeeFigure4)
(Thevaluesareonlyaddedfromt=0tot=11because theplayerisnotairborneatt=12)
Whichalsomeansthattheinitialspeedatthetimeof thejumpisakeyfactorwhichdeterminesthejump distance.
5ParkourNomenclature
Beforecontinuing,herearethelistoftermsbeing usedinlatersections:
b-blocks bc-blockceiling bm-blockmomentum
(E.g.a4blockjumpwitha3blockceilingwith 1blockavailableformomentumwillbereferredtoasa 4b3bc1bmjump)
645◦ Strafes
45◦ Strafesaretechniquesusedtoincreasethevelocityoftheplayer.Whenstrafing,theaccelerationgets multipliedby1insteadof0.98.(SeeFigure2)
Figure4:Speedneededfora5bjump(Using45◦ strafe)
Tick12isnotcountedinthesumbecausethejump endsatt=12.
However,simplysprint-jumping(using45◦ strafes)is notenoughtogaintherequiredmomentumforthejump becausethenthevalueof
after1sprint-jumpwillbeapproximately0.256128.2 sprint-jumpswillresultin0.305685;3sprint-jumps, 0.315273;4sprint-jumps,0.317129;andsoon.However,thereisalimittoapplyingconsecutivesprintjumpcycles.At9,10,and11jumps,thespeedsforall ofthemare0.315574;thevaluebeingincreasedistoo smalltomakeanoticeablechangefromafterthispoint. (SeeFigure5foralgebraicexplanation.Notethatthis oneusedsprint-jumpswith45◦ strafes.Thistechnique shouldhaveboostedtheplayer’sspeedbyabout2
8Conclusion
Fromthis,wecanconcludethata5bjumpisnot possibleonflatgroundandbysprint-jumpchains.
9Extension
However,thereareothermethodsofgaining momentum.Elevationmomentumisanexampleof
Figure2:Player’shorizontalspeed
Σ1 n=01Vh(t0 + n)]
Figure3:Applicationof45◦ StrafesinBridging
VH
84
Figure5:Limitationsofsprint-jumpchains
this.Insteadofa11-tickjumpcycle,itallowsa8-tick jumpcycle.Inthissetup,eachjumpis+1.125from thepreviousone,andthehorizontalgapbetweenthe jumpsare2b,whichmeansthattheplayerismaking 2b+1.125jumpswitheachsprint-jump.
Byusingelevationmomentum,thefollowingresults canbeobtained:
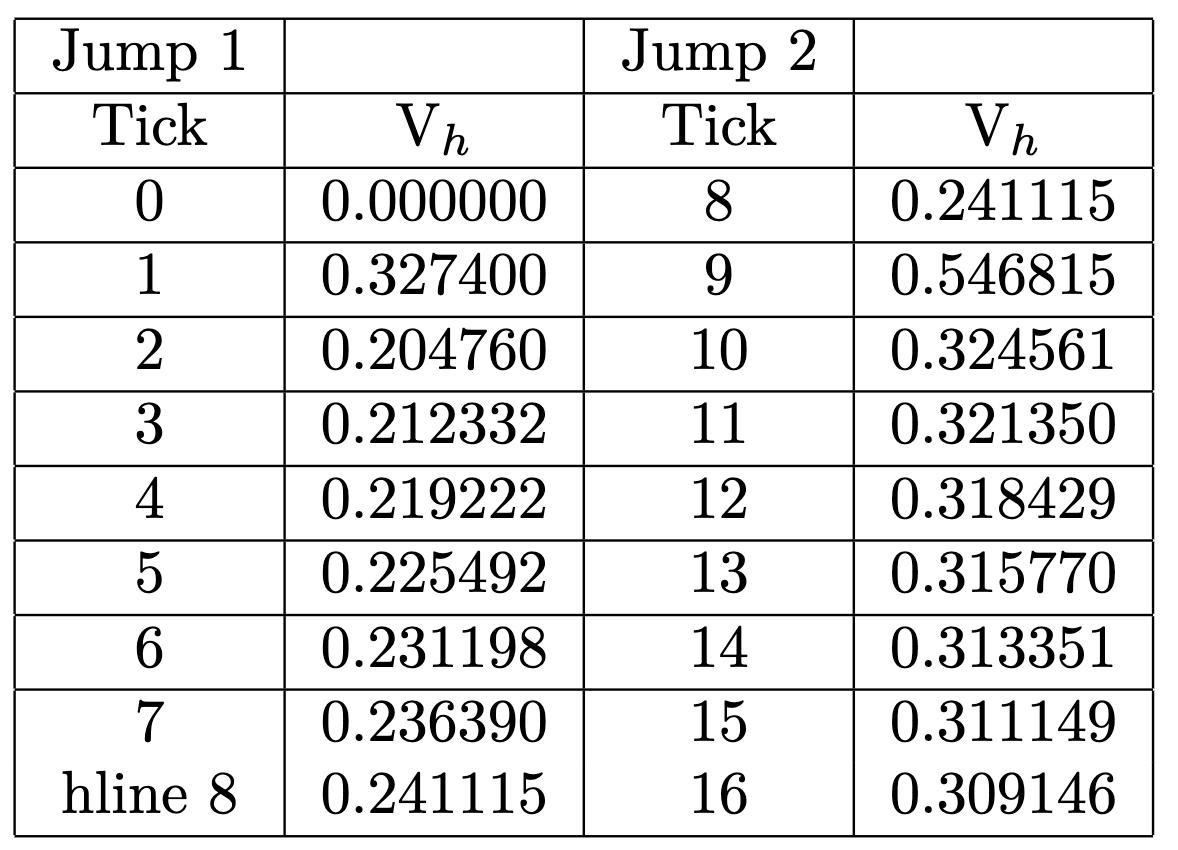
Wecanclearlyseethatinonly4consecutivejumps, theplayerisabletogainenoughmomentumtomakea 5bjump.
Anothermethod,andprobablyoneofthemosteffectivewaystogainmomentumisthehead-hittermomentum.Morespecifically,thetdhh,whichisshortof trapdoorhead-hitter(or1.8125bctiming).Thisshortensthejumpcycletoonlylast2tickssincethejump isresetwhenevertheplayerhitstheceiling.Sincethe playeris1.8btall,thereisonly0.125bofspacebetween theceilingandtheplayer.
Usingthismethod,theplayerisabletomakethe 5bjumpinonly3jumps(SeeFigure7)
However,itisimpossiblefortheplayertogain enoughmomentumfora5bjumpwith1bm,unlikethe 4bjump.
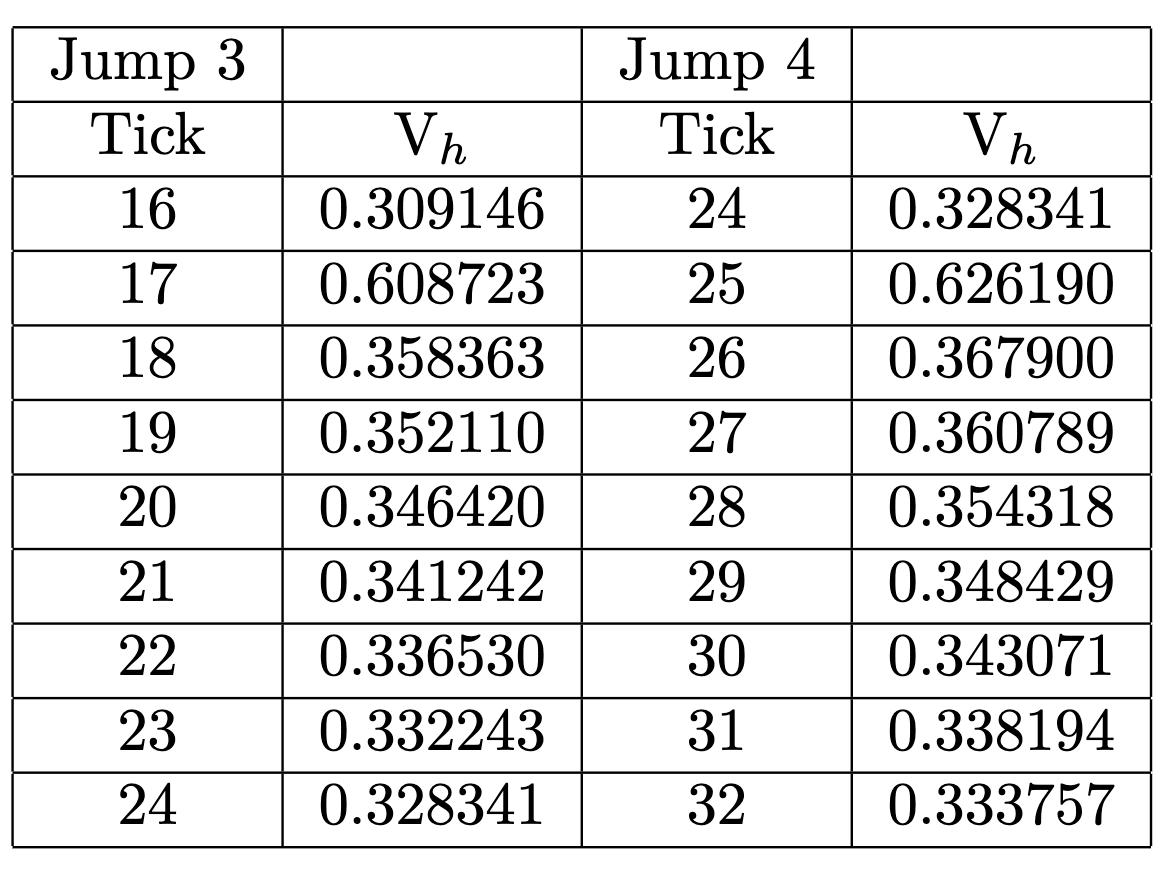
Figure6:Elevationmomentum
Figure7:TimingJumpcycle
10Bibliography
Spreadsheet:
https://docs.google.com/spreadsheets/d/16kFgIAzdyKDi9KY lfdEOD2zWMK06-dBkmmow9W7KBbc/edit?usp=sharing
References:
1. https://www.youtube.com/watch?v=qUFzMkDYsXc
2. https://www.mcpk.wiki/wiki/ParkourNomenclature
3. https://www.mcpk.wiki/wiki/MovementFormulas
4. https://www.mcpk.wiki/wiki/Jumping
85
MathematicsinSudoku
TimofeiKudinov
Year11
Email:tkudinov26@pupils.nlcsjeju.kr
Editor
RyanHanjinLee
RecommendedYearLevel:KS4,KS5
Keywords:Sudoku,combinatorics,grouptheory, symmetry
1Introduction
Sudokuinvolvesdifferentmathematicsaspectssuch ascombinatoricsandgrouptheory,whichcouldbeused toaddressfundamentalquestionsabouttheirstructure, solutions,andsymmetries.Theamalgamationofthese mathematicaldisciplinesenablesarigorousanalysisof Sudoku.
2Filledgridenumeration.
Oneoftheprimaryinquiriesisdeterminingthe numberoffilledSudokugrids.Fortheclassical9x9Sudoku,thecountreachesanastonishing 6,670,903,752,021,072,936,960 (6 671Ö10šź),which,afterfactoringinvalidity-preservingtransformations,reducesto5,472,730,538essentiallydistinctsolutions. Whilethereare26possibletypesofsymmetry,their occurrenceisinonlyabout0.005%ofallfilledgrids.
3Minimumcluesforavalidpuzzle.
Theminimumnumberofcluesrequiredforavalid puzzlewasdeterminedbyGaryMcGuire,BastianTugemann,andGillesCivario,intheir2012paper.Through computersearches,theyestablishedthataproperSudokupuzzle,withauniquesolution,necessitatesaminimumof17clues.
4SymmetryinSudoku
AnotheraspectofSudokuissymmetry.Sudoku withtwo-waydiagonalsymmetry,equivalenttoa180° rotationalsymmetry,anddiagonalsymmetry,introducesaSudokuwith24clues.However,whetherthis
numberofcluesistheminimalrequirementforthisspecificclassofSudokupuzzlesisstillnotdetermined.
TheextensionofSudokutodifferentsizes,suchas 6x6and8x8grids,bringsforthvariationsintheminimumnumberofcluesneeded.Fora6x6Sudoku,the fewestcluesrequiredare8,whilean8x8Sudokudemandsaminimumof14clues.
5Thenumberofminimalpuzzles
Theconceptofminimalpuzzles,wherenocluecan beremovedwithoutsacrificingtheuniquenessofthesolution,introducesarealmofcomplexityinSudokuanalysis.Statisticaltechniquescombinedwithacontrolledbiasgeneratorestimateapproximately 3 10Ö1037 distinctminimalpuzzles,offeringaglimpseintothevast landscapeofpotentialpuzzleswithintheconstraintsof minimality.Additionally, 2 55Ö1025 minimalpuzzles areidentifiedasnotpseudo-equivalent,emphasizingthe intricateinterplayofdigitarrangementsinSudokupuzzles.
6Sudokuvariants
Sudokuvariants,characterizedbysizeandregion shape,furtherdiversifythemathematicallandscape. Whetherit’srectangularSudokuwithregionsofrowcolumndimensionR×CorjigsawSudokuwithnonsquareregions,eachvariantpresentsuniquechallenges andopportunitiesformathematicalexploration.The mathematicalcontextofSudoku,encompassinggraph coloringproblemsandLatinsquares,establishesconnectionstobroadermathematicalconcepts,illustrating thepuzzle’sembeddedcomplexity.
7Complexity
TheNP-completenatureofsolvingSudokupuzzles on n2 × n2 gridsunderscoresthecomputationalchallengesinherentinfindingsolutions.ExpressingSudoku asagraphcoloringproblem,theaimistoconstructa
86
9-coloringofaparticulargraph,subjecttospecificconstraints.TheSudokugraph,with81verticesrepresentingcells,imposesconstraintsbasedoncolumn,row,and 3 × 3 cellrelationships.Thisgraphcoloringperspective opensavenuesforleveraginggraphtheoryinSudoku problem-solvingstrategies.
8Latinsquares
Theutilizationofgrouptables,akintoLatin squares,unveilsamethodforconstructingSudokus.By employing(addition-or)multiplicationtablesoffinite groups,Sudokusandrelatedtablesofnumbersemerge. Subgroupsandquotientgroupsplayacrucialrolein thisconstruction,emphasizingtheinterconnectedness ofgrouptheoryandSudoku.
9JigsawSudokus
JigsawSudokus,whereregionsarenotnecessarily squareorrectangular,introduceadditionalchallenges. ThetilingofanN×Nsquare,especiallywhenNisprime, requiresirregularN-ominoes.ForsmallerNvalues,the waystotilethesquarehavebeencomputed,revealinginstanceswheresometilingsareincompatiblewith Latinsquares,leadingtoSudokupuzzleswithnosolutions.
10Enumeratingsolutions
TheenumerationofSudokugridsinvolvesdistinguishingbetweenallsolutionsandessentiallydifferentsolutions.Thecomplexityarisesfromconsidering symmetriesandpermutations.Thefirstcompleteenumeration,postedbyQSCGZ,revealedanastounding 6,670,903,752,021,072,936,960distinctsolutions.FelgenhauerandJarvis,ina2005study,confirmedthis resultthroughananalysisofbandpermutations.However,thefocusshiftedtoessentiallydifferentsolutions, consideringthesudokusymmetrygroupandapplying Burnside’slemma.Theculminationoftheseefforts yieldedthecountof5,472,730,538essentiallydifferent solutions,providinganuancedunderstandingofthediversesolutionspaceinSudoku.
11GroupTheoryandSudoku
In2008,AvivAdlerandIlanAdlerdemonstrated thecompletenessoftheSudokusymmetrygroup,showcasingthatallsolution-preservingcellrearrangements arecontainedwithinthegroup,evenforgeneral n2 × n2 grids.ThissignificantresultsolidifiestheconnectionbetweenSudokupuzzlesandgrouptheory,furtherestablishingSudokuasarichplaygroundformathematical exploration.
12Conclusion
Inconclusion,themathematicalanalysisofSudoku opensupaworldofintricacies,fromthequestforminimalpuzzlestotheexplorationofdiversesymmetries andvariants.Combinatorics,grouptheory,andgraph theoryinunderstandingSudokushowcasesthemultifacetednatureofthisseeminglystraightforwardgame. Asresearcherscontinuetounveilnewinsights,Sudoku remainsacaptivatingsubjectformathematicalexplorationanddiscovery.
87
ProbabilityinBlackjack
Xinheng(Tony)Li Year9
Email:xhli28@pupils.nlcsjeju.kr
Editor DerekYoo
RecommendedYearLevel:KS4,KS5
Keywords:blackjack,gametheory
1Introduction
Blackjackisagamethatisplayedeverywhere.You justneedtoknowtherulesandprepareadeckofcards. Often,peoplethinkthatcardgames(especiallygamblinggames)arejustluckgames,buttheyareactually wrong.Cardgames,forexample,poker,blackjack,etc., arefullofprobabilities.Andinthisjournal,wewant todiscovertheprobabilitiesofgettingtheidealcard thatyouwanttomaximiseyourchancesofwinningthe game.
2Background
2.1Whatisblackjack?
cardgameinwhichplayerstrytoacquirecardswith afacevalueascloseaspossibleto21withoutgoingover.
2.2RulesofBlackjack
1. Alltheplayersmakeabetwiththeirchipsbefore thecardshavebeenhandedout.
2. Thedealergivesacardtoeachplayeraswellas themselves.
3. Thedealerhandsoutasecondcardtoeveryplayer.
4. Theplayertotheleftofthedealerstartsgameplay.
5. Decideifyouwanttostayorhit.
(a) Staying:Youdon’twantthedealertogiveyou anothercardthat’llgetaddedtoyourtotal.
(b) Hitting:you’dlikethedealertoaddanother cardtoyourhandthat’llgetaddedtoyour total
(c) Split:Ifyoursecondcardisidenticaltoyour first,youhavetheoptionto“split”yourhand intotwoseparateones.Evenifonehand
busts,youstillcontinueplayingwithyour otherhand.
6. Cyclethrougheachplayeruntilthey’veeachfinishedtheirturn.
7. Thedealerrevealstheirsecondcard,andwinners aredetermined.
2.3WhatisProbability?
Probabilityisdefinedasthelikelihoodofsomething happeningorbeingthecase.
2.4GameTheory
Gametheoryisabranchofappliedmathematics thatprovidestoolsforanalysinginterdependentsituations.Accordingtothistheory,eachsideconsidersthe other’spossibledecisionsfortheplayers,andtheresults maydifferregardingtheirfindings.
Gametheoryhaswideapplications,especiallywhen players’choicesaffecteachother’spossibleoutcomes. Therearetwokeywordsingametheorythatneedtobe defined:
1. Game:Asetofcircumstancesinwhichtheresult dependontheactionsofdecision-makers(moreor equalto2)
2. Players:Strategicdecision-makerswithinthecontextofthegame
3. DependentEvent:Thepastaffecttheprobability what’sgoingtohappennext
3Aim
Inthisjournal,weaimtocalculatehowtomaximise theprobabilityofwinninginblackjackandhowyou shouldactwhenyoumeettheactualsituationswhere youhavesimilarcards.Also,weaimtocalculatethe averagepercentageofwinninginareal-lifeblackjack game.
88
4Method
Themethodthat’sgoingtobeusedtocalculatethe probabilityofwinninginblackjack:BasicSetRules:
1. Therewillbetwopeopleplayinginthegame.1 dealer,1player
2. Nosurrenderingisallowedinthisgame
3. Aiscountedas11,wewillallow1
4. Iftherearetwo21sappearing,thereisnowinor lose
5. Nodouble-downisallowed
6. Onlyonehitwillbeallowedineachround
7. Thegameisplayedusingonlyonedeckofcards.
8. Ifitisadraw,theplayerwins.
Method1:P(x)=Numberoffavourableoutcomes toA/Totalnumberofpossibleoutcomes
UsingthecheatsheetsonGoogle,wewillbeexplainingwhyweshouldbedoingthisinwhichsituation. Furthermore,weplantofindoutthereasonhiddeninsidethecheatsheets.
BlackjackStrategyChart:Thebasicblackjack strategychartwilloutlinethebestpossibledecisionfor thosewhodon’tcountcards.Itgoeswithoutsaying thatthecardsthatconstituteahand,withouttheinclusionofanace,willhaveanimpactonthechancesof makingacorrectdecisionincertainscenarios.However, thisisonlyapplicableinahandfulofscenarioswhere theblackjackvariationusesonedeckofplayingcards.
5Experiment
5.1Total=17,Dealer’scard=2
Whenyourtotalsumis17,thisindicatesthatyour cardiseither6+11,7+10,or8+9,andthedealerhasa 2.
Inthissituation,thecardthathelpsyoureachnear 21butdoesn’tbustisAce,2,3,4.Thecardthathelps youwillbea+,andthecardthatdoesn’thelpyouwill bea-.Ifadealerhasahiddencardof+,itmeans theprobabilityofyougettingwhatyouwantisgoing todecrease.Andifthedealerhasahiddencardof,theoppositethingwillhappen.Now,letusdothe calculations.
Cardsremaining:49+Cards:15-Cards:34If Dealer’scardis+,theprobabilityofgettinga+card is15/49*14/48=5/56IfDealer’scardis-,theprobabilityofgettinga+cardis34/49*15/48=85/392 Probabilityofwinning=5/56+85/392=15/49= 30.61%ProbabilityofDealerwinning=69.39%Inthis situation,itisbettertostay.
5.2Repeating
Ifwerepeatthismethod,wecanhavea chartofthefollowing:Dealer’srevealedcard
6DataAnalysis
Wecanseethatithassimilarformsastheothercharts.
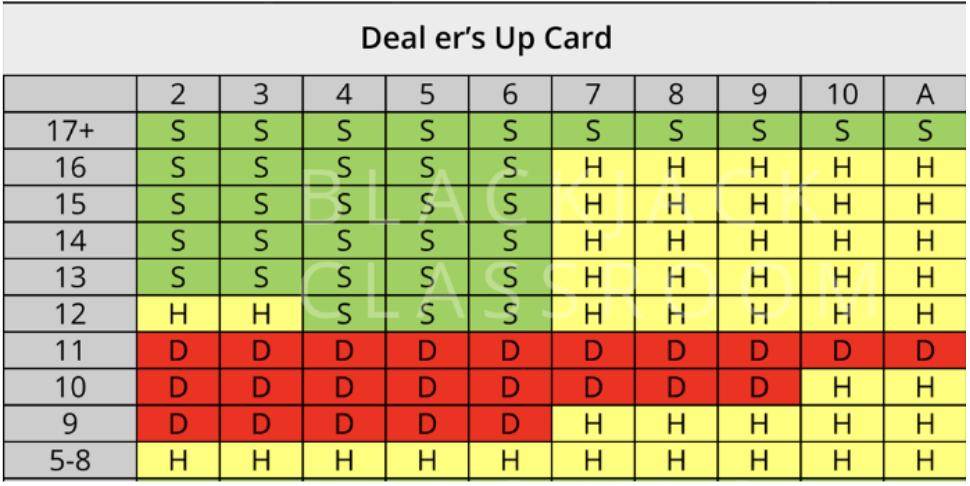
7Conclusion
Fromthisjournal,wehavelearnedandactuallycalculatedandmadeacheatsheet(aka.BlackjackBasic Strategy).Thehorizontalaxisistheonecardthatthe dealerisrevealing,andtheverticalaxisisthesumof yourtwocards.Thiscantelluswhenweareactually playingthegame,wecanapplythischarttomaximise yourrateofwinning.Ortherateofmakingmistakes duringthegame.
8Extension
Thereisalsoawayofcalculating.Itisdoneby usingthecountingmethod.Thelinkbelowcanteach ushowtousecardcountingandhowtocalculatehow muchyouwillbetaccordingtothecountingvalue.
https://www.youtube.com/watch?v=GS o72lFNIUabchannel = WIRED
9Bibliography
1. “HowtoPlayBlackjack:Rules,GameplayMore.” wikiHow,www.wikihow.com/Play-Blackjack.Accessed22Jan.2024.
89
2. “AMust-ReadGuidetoBlackjackOddsand Probability.”PlayToday.Co,10Jan.2024, playtoday.co/blog/blackjack-odds/::text=Classic
3. “BlackjackStrategyCharts-HowtoPlayPerfectBlackjack.”BlackjackApprenticeship,2June 2022,www.blackjackapprenticeship.com/blackjackstrategy-charts/.
4. “BlackjackExpertExplainsHowCardCountingWorks|Wired.”YouTube,6Mar.2017, www.youtube.com/watch?v=GSo72lFNIUabchannel=WIRED.
90


JPAM 2024 Design by Emma C (‘25)



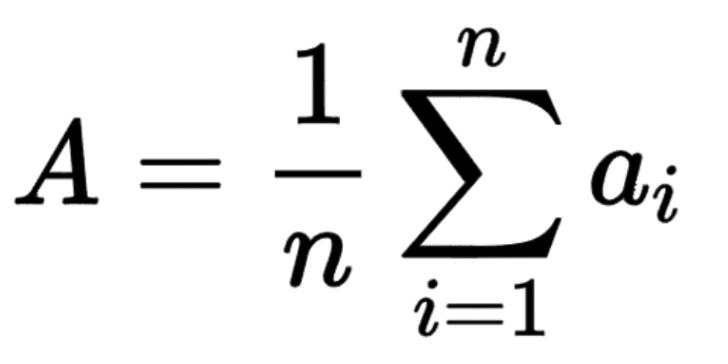
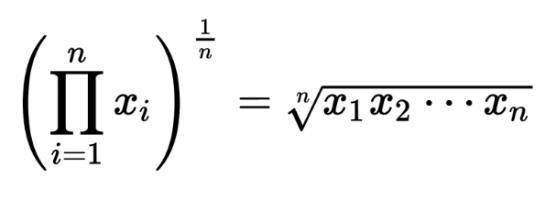








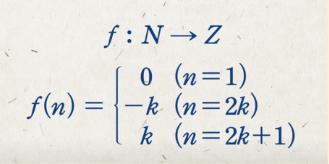























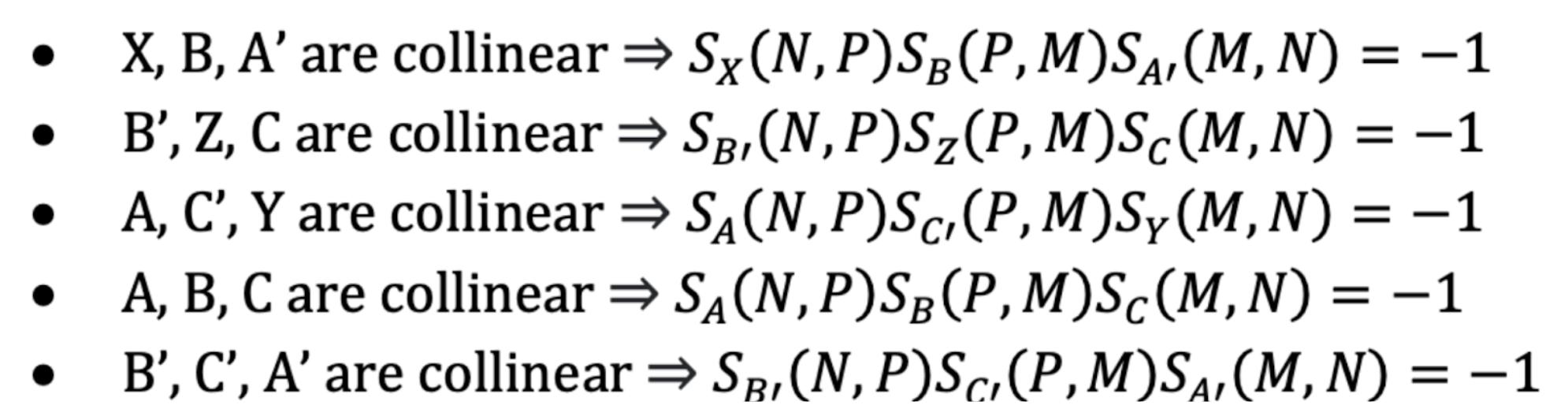
 Fig.2:Pappuslinewiththefoundationlinesintersecting
Fig.3:Morecomplexconjunctions
Fig.4:Pappuslinediagram
Fig.2:Pappuslinewiththefoundationlinesintersecting
Fig.3:Morecomplexconjunctions
Fig.4:Pappuslinediagram

































































