UNIVERSIDAD MARIANO GÁLVEZ DE GUATEMALA
LICENCIATURAEN EDUCACIÓN DE LA FÍSICAY MATEMÁTICA
CURSO:
ESTRATEGIAS DE EVALUACIÓN PARAMEJORAR LAPRÁCTICADOCENTE DE LA MATEMÁTICAY LAFÍSICA
CATEDRÁTICO:
LIC. INGRID ORTÍZ DE WEST
TAREA: PROYECTO FINAL
POR: MIGUELANGEL CORDERO MONZÓN
CARNÉ: 9613-08-2690
FECHADE ENTREGA: 1 DE NOVIEMBRE DE 2024
La planificación y evaluación en la educación son componentes esenciales para el desarrollo efectivo de las competencias de los estudiantes, especialmente en áreas como la matemática y la física, donde el aprendizaje conceptual y práctico se interrelacionan estrechamente. Este proyecto presenta un enfoque integral sobre las estrategias de evaluación en el contexto educativo, destacando la importancia de una planificación adecuada para mejorar la práctica docente y asegurar que las evaluaciones no solo midan el conocimiento, sino que también promuevan el desarrollo de habilidades analíticas y de resolución de problemas en los estudiantes.Através de un análisis de diversos métodos de evaluación y su relación con las competencias específicas, se propone una serie de actividades que facilitan una evaluación formativa y sumativa. Estas estrategias están diseñadas para fomentar un aprendizaje significativo y adaptarse a los distintos niveles de dominio de los estudiantes, optimizando así el proceso de enseñanza y aprendizaje en áreas clave del conocimiento.
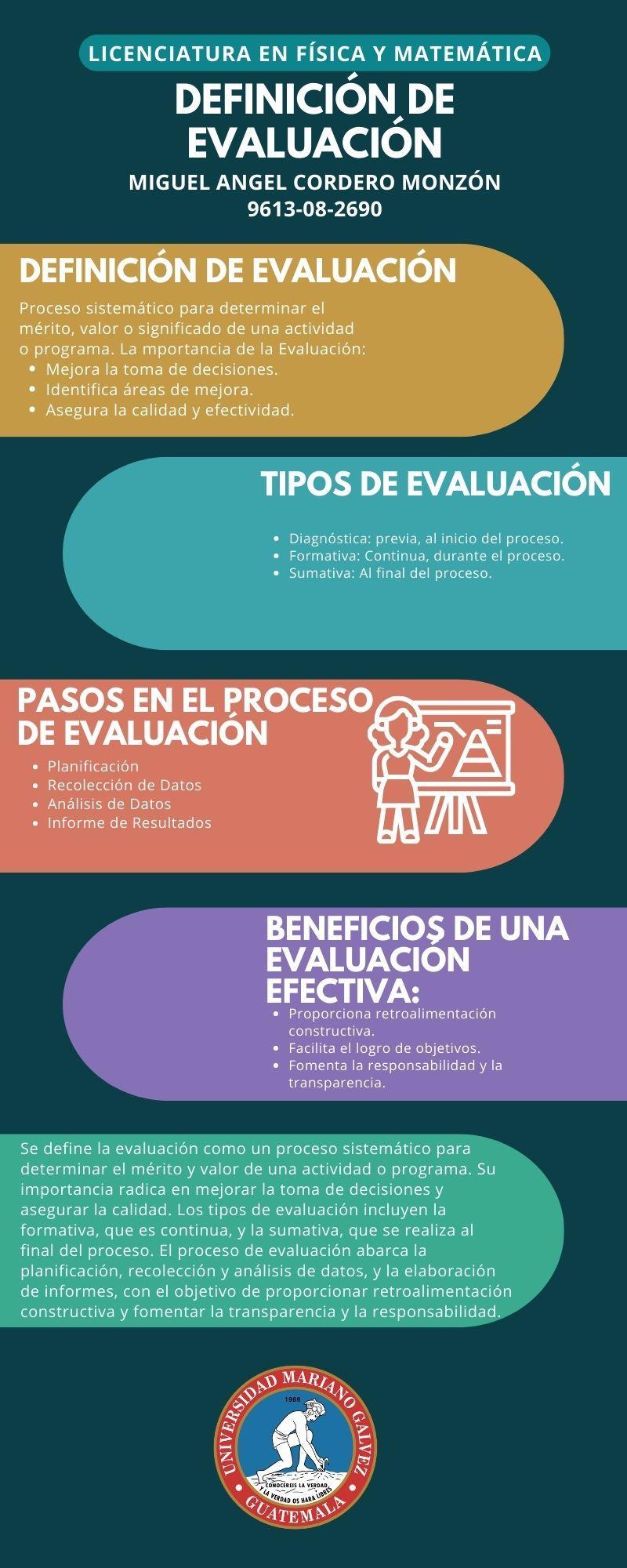
Nivel de la taxonomía de Bloom
Actividad de evaluación
Conocimiento (Recordar) Realizar una lista de fórmulas matemáticas para resolver ecuaciones cuadráticas.
Comprensión Explicar en sus propiaspalabrascómo se resuelve una ecuaciónlineal.
Características
Requierequelosestudiantes memoricen y recuperen información específica sin necesidaddecomprendersu usoocontexto.
Implicaquelosestudiantes entiendanelprocesoysean capaces de describirlo usando su propio lenguaje, demostrando comprensión conceptual.
Aplicación Resolver problemas matemáticos utilizando el Teorema de Pitágoras en diferentescontextos.
Análisis Descomponer una función cuadrática para identificar sus raíces, vértice y concavidad.
Los estudiantes deben aplicar sus conocimientos del Teorema de Pitágoras para resolver problemas prácticos, demostrando su capacidad de uso en situacionesnuevas.
Requierequelosestudiantes analicen una función cuadráticayladesglosenen sus componentes básicos, identificandocaracterísticas clave.
Síntesis (Crear) Crear un modelo matemático para representar un problema del mundo real, como la predicción de la trayectoria de un proyectil.
Evaluación Justificar la elección del método para resolver sistemas de ecuaciones lineales: sustitución, eliminaciónométodos gráficos.
Involucralacreacióndeun nuevo modelo matemático que integra diferentes conceptos para resolver un problema práctico, demostrando habilidades creativasydesíntesis.
Implica evaluar diferentes métodos para resolver sistemas de ecuaciones y justificarlaeleccióndeuno de ellos basándose en criterios matemáticos y de eficiencia.
Justificación
Esta actividad se clasifica en el nivelde Conocimiento porquese centra en la memorización de fórmulasmatemáticas,locualno implica comprensión o aplicación, sino simplemente recordarinformaciónbásica.
Clasificada en Comprensión porque requiere que los estudiantesentiendanyexpliquen el proceso matemático, lo que muestra su capacidad para interpretar y comunicar ideas, más allá de solo recordar información.
Estaactividadpertenecealnivel de Aplicación porque implica usarunconocimientomatemático conocido en situaciones nuevas, resolviendo problemas que requieren la aplicación de una fórmulaespecífica.
Clasificada en Análisis porque losestudiantesdebendividiruna función compleja en partes más simples y entender cómo estas partes contribuyen al todo, mostrando habilidades analíticas y de descomposición de información.
Esta actividad se clasifica en Síntesis porque los estudiantes deben combinar elementos de diferentesáreasmatemáticaspara desarrollar un nuevo modelo, lo que requiere creatividad, innovación y una comprensión profundadelosconceptos.
Clasificada en Evaluación porque requiere que los estudiantesjuzguenlaeficaciade varios métodos matemáticos y tomen una decisión informada sobre cuál es el mejor para un escenario dado, demostrando habilidadescríticasyevaluativas.
Temas:
✓ Electricidad: Ley de Ohm.
Estructura de la Evaluación
Elemento Descripción de laActividad Recursos TIC
Indicador de Logro Identificar la relación entre voltaje, corriente y resistencia en un circuito eléctrico (Ley de Ohm). Socrative
Descripción de laActividad Los estudiantes resolverán tres problemas de aplicación de la Ley de Ohm para calcular el voltaje, la corriente y la resistencia.
Recursos Computadora, conexión a internet, software de simulación de circuitos, Socrative student.
Aplicación y tipo de evaluación:
Uso de simuladores (PhET para simulaciones de circuitos eléctricos). Ley de Ohm (colorado.edu)
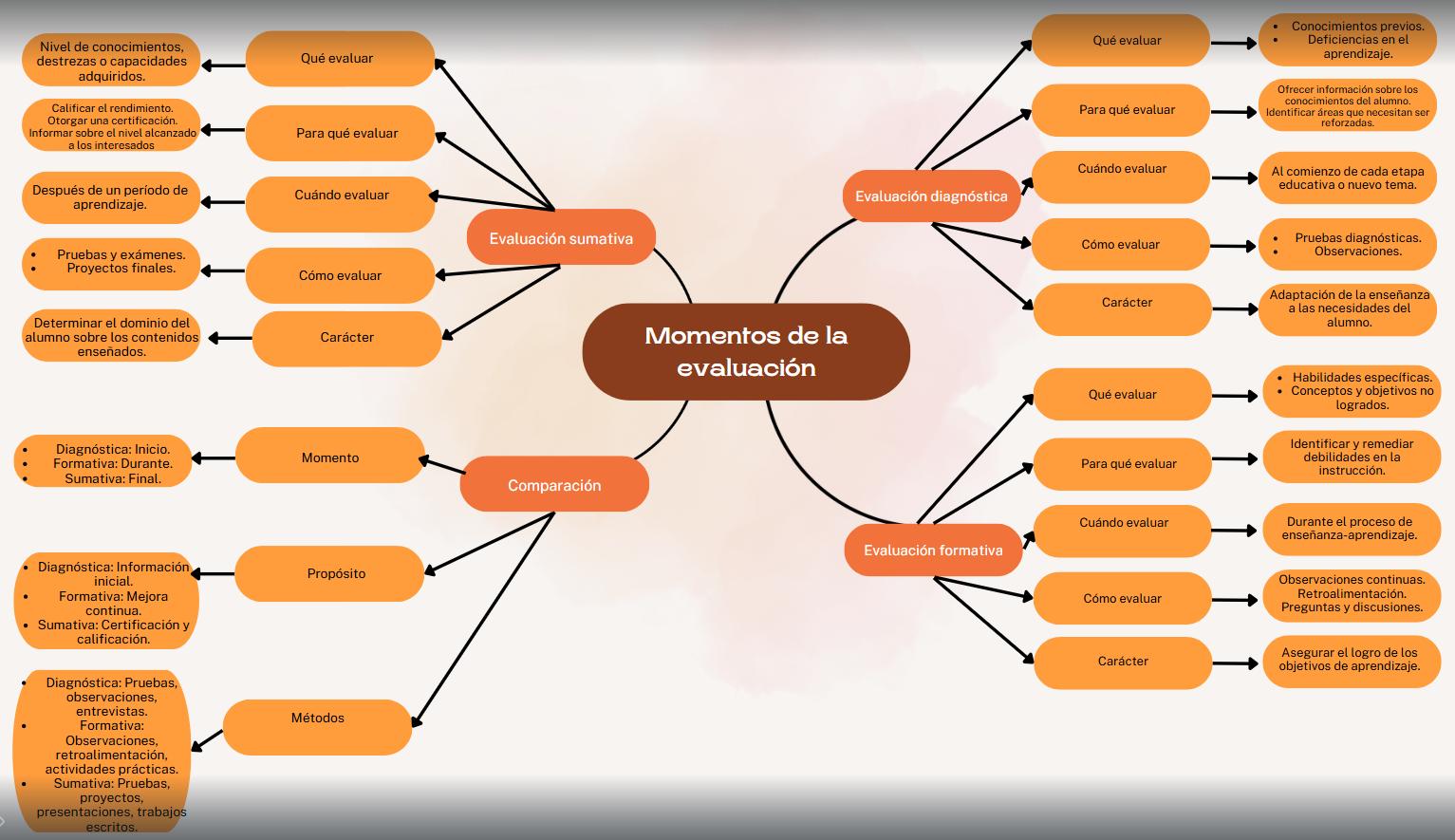
1. Evaluación Diagnóstica: Se inicia con una breve evaluación en Socrative student para verificar el nivel previo de conocimientos en el tema de Ley de Ohm. La evaluación consistirá en preguntas de selección múltiple para diagnosticar el punto de partida de los estudiantes.
2. Evaluación Formativa: A lo largo de la actividad, se les proporcionarán simulaciones virtuales (PhET) para que interactúen con circuitos eléctricos y comprendan visualmente cómo afectan el voltaje, la corriente y la resistencia. Aquí, se utilizarán rubricas para evaluar el progreso y las interacciones en los simuladores.
3. Evaluación Sumativa: Al final del módulo, los estudiantes completarán un cuestionario de opción múltiple en Socrative student con preguntas que les obliguen a aplicar lo aprendido. Las respuestas correctas proporcionarán retroalimentación automática, ayudando a consolidar conceptos.
Rúbrica para la Evaluación Formativa: Ley de Ohm
Criterio Excelente (4 pts)
Comprensión de la Ley de Ohm
Resolución de Problemas
Demuestra una comprensión clara y completa de la relación entre voltaje, corriente y resistencia. Explica correctamente con ejemplos.
Resuelve todos los problemas planteados correctamente, muestra los cálculos detallados y usa las fórmulas apropiadas sin errores.
Uso del Simulador de Circuitos
Representación
Gráfica de Resultados
Usa el simulador de manera eficiente, realiza experimentos virtuales variados y recopila datos precisos sobre voltaje, corriente y resistencia.
Presenta gráficos claros y precisos que muestran la relación entre las variables (V, I, R). Los gráficos están correctamente etiquetados y son fáciles de entender.
Participación y Reflexión
Participa activamente en las discusiones, reflexiona sobre sus resultados y propone mejoras o preguntas adicionales sobre la ley de Ohm.
Bueno (3 pts)
Entiende la relación entre voltaje, corriente y resistencia, pero con una leve confusión en detalles menores.
Resuelve la mayoría de los problemas correctamente, pero comete pequeños errores en los cálculos o la aplicación de las fórmulas.
Usa el simulador adecuadamente, pero tiene algunos problemas con la precisión de los datos o los experimentos virtuales.
Presenta gráficos comprensibles, pero puede faltar precisión en algunos puntos o etiquetas.
Suficiente (2 pts) Insuficiente (1 pt)
Tiene una comprensión parcial de la ley de Ohm, algunos conceptos básicos están mal interpretados.
Resuelve algunos problemas correctamente, pero presenta errores significativos en la mayoría de los cálculos.
Usa el simulador con ayuda, pero no explora todas las funciones y presenta dificultades para recopilar datos.
Presenta gráficos con errores significativos o incompletos, lo que dificulta la interpretación de los datos.
Participa en las discusiones, pero con reflexiones limitadas sobre los resultados o sin proponer mejoras significativas.
Participa mínimamente, sin reflexionar sobre sus resultados o sin aportar nuevas ideas o mejoras.
Muestra poca o ninguna comprensión de la ley de Ohm y no puede explicar la relación correctamente.
No puede resolver los problemas o los resultados son incorrectos debido a errores graves.
No usa el simulador correctamente o no lo utiliza, y no puede completar los experimentos virtuales.
No presenta gráficos o los gráficos son incomprensibles y no muestran la relación entre las variables.
No participa en las discusiones ni reflexiona sobre los resultados obtenidos en los experimentos.
✓ Nombre del trabajo: Proyecto Final de Estrategias de Evaluación
✓ Lo que más me gustó de este trabajo fue: La oportunidad de profundizar en las diferentes estrategias de evaluación y su impacto en el desarrollo de competencias en los estudiantes.
✓ Lo que menos me gustó de este trabajo fue: La dificultad inicial para integrar todos los aspectos teóricos en una propuesta práctica y aplicable.
✓ Lo que aprendí al realizarlo fue: La importancia de planificar cuidadosamente las evaluaciones para asegurar que estén alineadas con las competencias y objetivos de aprendizaje, así como los beneficios de usar diversas herramientas de evaluación.
✓ Lo que podría mejorar es: Incorporar ejemplos más concretos y detallados de cada estrategia de evaluación en el contexto de matemáticas y física.
✓ Lo puedo aplicar: En la creación de evaluaciones más efectivas y alineadas con las competencias en mis clases, para facilitar el aprendizaje significativo y el desarrollo integral de los estudiantes.
Fecha: 1 de noviembre de 2024
Nombre o firma del estudiante: MiguelAngel Cordero Monzón