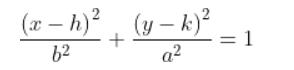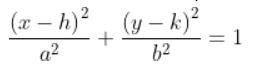02 SECCIONES CÓNICAS

Las secciones cónicas son curvas resultantes de las diferentes intersecciones entre un cono y un plano, cuando ese plano no pasa por el vértice del cono. Existen cuatro tipos de secciones cónicas: la circunferencia, la elipse, la parábola y la hipérbola.


‘Come cuanto le doy. Le gustan las naranjas mandarinas, las uvas moscateles, todas de ámbar; los higos morados, con su cristalina gotita de miel…’
Cónicas:
Las cónicas son figuras que pueden definirse como lugares geométricos en un plano.La intersección entre un plano y un cono doble genera figuras llamadas secciones cónicas.
Las figuras que pueden ser generadas por los cortes de un cono son: Líneas, puntos, circunferencias, parábolas, elipses,hipérbolas.
- Ej. de elipse de Juan Ramón Jiménez
04 CIRCUNFERENCIA ELEMENTOS EJERCICIOS
Centro: punto central que está a la misma distancia de todos los puntos pertenecientes a la circunferencia.
Radio: pedazo de recta que une el centro con cualquier punto perteneciente a la circunferencia
Cuerda: pedazo de recta que une dos puntos cualquiera de una circunferencia.
Diámetro: mayor cuerda que une dos puntos de una circunferencia. Hay infinitos diámetros y todos pasan por el centro de la circunferencia.
ecta secante: recta que corta dos puntos cualesquiera de una circunferencia.

Recta tangente: recta que toca a la circunferencia en un solo punto y es perpendicular a un radio.

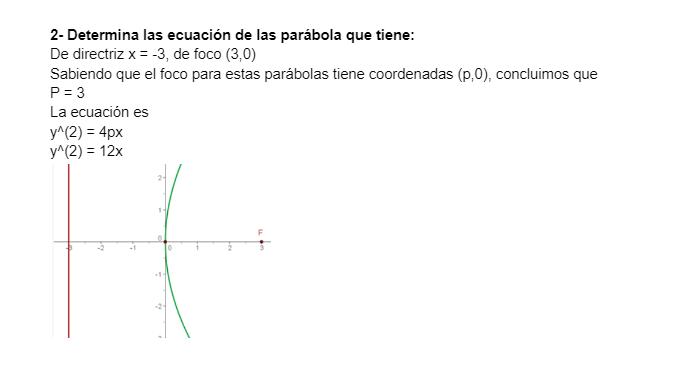
05 PARÁBOLA
Una parábola queda definida por el conjunto de los puntos del plano que equidistan de una recta fija y un punto fijo.
Elementos de la parábola:


Foco: Es el punto fijo F.
Directriz: Es la recta fija D.
Parámetro: A la distancia entre el foco y la directriz de una parábola se le llama parámetro p.
Eje: La recta perpendicular a la directriz y que pasa por el foco recibe el nombre de eje. Es el eje de simetría de la parábola.
Vértice: Es el punto medio entre el foco y la directriz. También se puede ver como el punto de intersección del eje con la parábola.
Radio vector: Es el segmento que une un punto cualquiera de la parábola con el foco.

EJERCICIOS
07 HIPÉRBOLA
Una hipérbola es una representación gráfica de funciones homográficas, un ejemplo común y sencillo es la gráfica de la función f(x)=1/2.
Una hipérbola es una curva abierta de dos ramas, obtenida cortando un cono recto mediante un plano no necesariamente paralelo al eje de simetría, y con ángulo menor que el de la generatriz respecto del eje de revolución.
Tipos de hipérbola:
Hipérbola horizontal: Se la denomina de esta forma, debido a que la línea imaginaria en la que se ubicaran sus componentes, siempre será paralela al eje x. Independientemente de encontrarse su centro en el origen de coordenadas o fuera de este. Sus ecuaciones son las siguientes: x2/a2-y2/b2=1 ó (x-h)2/a2-(y-k)2/b2=1
Hipérbola equilátera: Se las denomina de esta forma cuando los semiejes a y b vienen a ser iguales,dejando a su ecuación de la siguiente forma: x2-y2=a2
Elementos de la hipérbola:
1. Focos: Son los puntos fijos F y F'.
2. Eje principal o real: Es la recta que pasa por los focos.
3. Eje secundario o imaginario: Es la mediatriz del segmento FF'.
4. Centro: Es el punto de intersección de los ejes.

5. Vértices: Los puntos A y A' son los puntos de intersección de la hipérbola con el eje focal.
Los puntos B y B' se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y de radio c.
6. Radios vectores: Son los segmentos que van desde un punto de la hipérbola a los focos: PF y PF'.
7. Distancia focal: Es el segmento de longitud 2c.
8. Eje mayor: Es el segmento de longitud 2a.
9. Eje menor: Es el segmento de longitud 2b.
10. Ejes de simetría: Son las rectas que contienen al eje real o al eje imaginario.
11. Asíntotas: Son las rectas de ecuaciones:
Ejercicios:



07 HIPÉRBOLA
Ejercicios:


07 HIPÉRBOLA
Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante.
Elementos de la elipse:
. Focos: Son los puntos fijos F y F'.
Eje focal: Es la recta que pasa por los focos
. Eje secundario: Es la mediatriz del segmento FF'.
. Centro: Es el punto de intersección de los ejes.
. Radios vectores: Son los segmentos que van desde un punto de la elipse a los focos: PF y PF'.
Distancia focal: Es el segmento de longitud 2c, c es el valor de la semi distancia focal.
. Vértices: Son los puntos de intersección de la elipse con los ejes: A, A', B y B'.
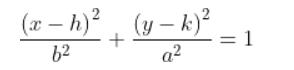
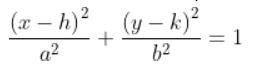
.
.
Eje mayor: Es el segmento de longitud 2a, a es el valor del semieje mayor.
Eje menor: Es el segmento de longitud 2b, b es el valor del semieje menor. Ejes de simetría: Son las rectas que contienen al eje mayor o al eje menor
. Centro de simetría: Coincide con el centro de la elipse, que es el punto de intersección de los ejes de simetría.
Tipos de elipse:
-Elipse con el eje mayor horizontal: Sea el punto C de coordenadas (h,k) el centro de la elipse, la longitud del eje mayor es 2a y la longitud del eje menor igual a 2b, con a > b. La ecuación de esta elipse es:
-Elipse con el eje mayor vertical: Con los mismos parámetros de la elipse con eje mayor horizontal, la elipse con eje mayor vertical se escribe como:
En ambos casos, la distancia del foco al centro c está relacionada con los semiejes mayor y menor mediante: c2 = a2 b2.
08 ELIPSE


08
ELIPSE


08
ELIPSE