El área de las Coordenadas Polares
Edición Nro. 1
R. M. Leonardo Javier
La lógica tras el recurso Matemático
6 de Agosto de 2023
Ciencia Numérica:
El área de las Coordenadas Polares
La elaboración de la siguiente Área de las Coordenadas Polares, se busca explicar, desarrollar, ejemplificar y abordar con fines académicos y científicos, los fundamentos requeridos para la aplicación de diversos universos matemáticos tales como las antes mencionadas Coordenadas Polares, Coordenadas Paramétricas, Curvas en coordenadas rectangulares, cálculo de volúmenes de sólidos de revolución y aplicaciones en la ingeniería de las integrales definidas.
Fomentar de manera práctica el estudio y la investigación del universo matemático es el pie para el desarrollo de un futuro avanzado e inteligente donde, la capacidad numérica y humana, serán las que puedan conducir el prosperar de la humanidad.
Esperamos con suma gratitud que la información aquí presentada, sirva de guía para aquel estudiante que desea aprender de forma inmersiva, algunos de los diversos temas fundamentales del cálculo y la matemática, siempre buscando y asegurando el entendimiento y sobre todo, el disfrute fundamental de la materia.
El material expuesto en esta revista es solo con fines informativos y no desea perjudicar ni desprestigiar cualquier prejuicio del tema abordado a continuación. TODOS LOS DERECHOS RESERVADOS. Las imágenes, logos y menciones utilizadas en esta revista pertenecen a sus debidos autores. La publicación sin autorización de este material se considerará una falta grave a la ley de los derechos de autor, este material es presentado solamente con fines educativos y de entretenimiento.
Contacto: 0424-7256440
Correo Electrónico: tuMaTematica@gmail.com
Publicación inscrita el 06 de agosto de 2023
Venezuela - San Cristóbal, Estado Táchira
Coordenadas Polares .......................................................................................................... 6 Coordenadas Paramétricas ............................................................................................... 7 Longitud de Curvas .............................................................................................................. 8 Volumen Sólido de Revolución ........................................................................................ 9 Método de los discos ......................................................................................................... 10 Método de los anillos ........................................................................................................ 11 Aplicación a la Ingeniería de Integrales Definidas ................................................... 12 Conclusión ............................................................................................................................. 13
Índice
Introducción
A lo largo del tiempo se ha sido testigo del inmenso poder y recurso que la matemática ha brindado a la humanidad, desde la resolución de problemas complejos que han servido para el descubrimiento de nuevas ciencias, hasta la posibilidad de poder optimizar y reducir tiempos en el desarrollo de nuevas tecnologías y acertar cálculos sobre disyuntivas nunca antes cuestionadas.
Cálculo gra´fico de Regiones en una Coordenada Polar
Por ello, se ha escogido una ligera recopilación de teoremas
matemáticos importantes, los cuales pueden ser fundamentales para diversas ramas de la ingeniería, por ello, se pretende estudiar, analizar, comprender y ejemplificar los siguientes temas matemáticos:
´ Cálculo de Coordenadas Polares
Cálculo de Coordenadas
paramétricas
Longitud de curvas en coordenadas rectangulares
Comportamiento de una gráfica
Polar vista en el plano
Volumen de discos solidos de revolución
Aplicaciones a la ingeniería de Integrales Definidas
Coordenadas Polares
El sistema de coordenadas polares es un sistema de coordenadas bidimensional en el cual cada punto del plano se determina por un ángulo y una distancia.
La forma de determinar un punto del plano se describe mediante dos números:
r, que es la distancia del punto al extremo de la semirrecta, llamado polo. el ángulo que forma el eje polar (que es horizontal) con el segmento que une el punto con el polo, este ángulo debe medirse en sentido opuesto a las manecillas del reloj.
El ángulo polar se puede dar en cualquier medida angular pero lo más frecuente es usar grados sexagesimales o radianes.
Es posible calcular el area bajo la siguiente ´ fórmula:
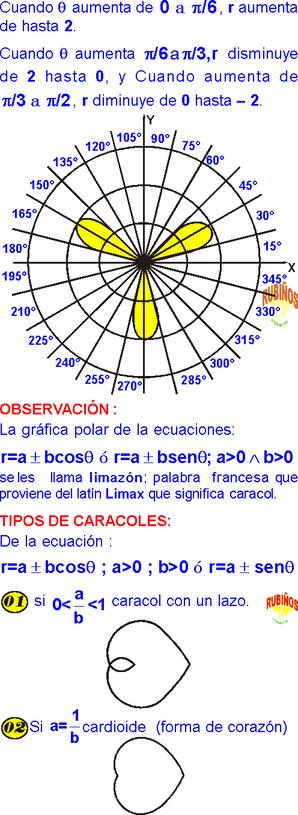
Siendo que se trata de 1/2 de la Integral definida desde B hasta a de F de Tita al cuadrado todo en función de la derivada de Tita, de esta manera se obtiene el area en una coordenada polar
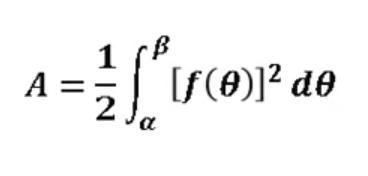
Representación Gráfica de una coordenada polar
Las coordenadas polares son usadas para el posicionamiento aéreo, debido a una versión ligeramente modificada de las coordenadas polares para la navegación. La dirección de desplazamiento se pueden dar como un ángulo y distancia del objeto que está siendo considerado.
6
θ
Coordenadas Paramétricas
Las ecuaciones paramétricas son útiles para describir curvas que no son necesariamente funciones. El parámetro es una variable independiente que tanto x como y depende de él, y a medida que aumenta el parámetro, los valores tanto de x como de Y trazan una trayectoria a lo largo de una curva plana.
El área de la región que está debajo de una curva y = f(x) en el intervalo [a, b], donde f(x) >= 0 para todo x que pertenezca al intervalo [a,b] se define como:
[
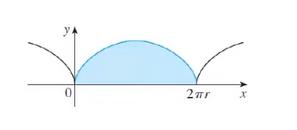
Ahora, si esta curva puede representarse mediante las ecuaciones paramétricas x = f(t) & y = g(t) donde t está definida en el intervalo , entonces es posible definir una fórmula para calcular el área usando un cambio de variable como:
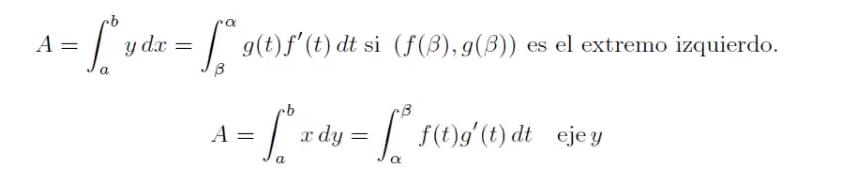
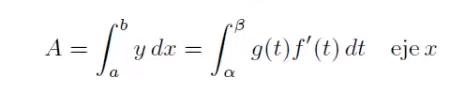
O en caso que el limite de integración sea invertido
Cicloide delimitado por una región
7
α,β]
Y
En matemática, la longitud de arco, es la medida de la distancia o camino recorrido a lo largo de una curva o dimensión lineal. La misma viene definida por la fórmula:
Es decir, la formula consiste de: Longitud será igual a la integral definida desde b hasta a de la Raíz Cuadrada de 1 + (Derivada de Y sobre Derivada de X) al cuadrado todo en Función de la Derivada de X
Bajo esta fórmula y aplicando los teoremas fundamentales del cálculo orientado a las derivadas definidas, es posible calcular y obtener la longitud de una curva dado un límite de integración
Longitud de Curvas 8
El calculo de longitud de curvas es muy útil en diversas ramas como la física, la geometría y la ingeniería
Volumen Sólido de Revolución
Un sólido de revolución es un sólido que puede obtenerse mediante la rotación de una curva plana alrededor de una recta que está contenida en su mismo plano. Dicha recta se denomina eje de revolución. La superficie creada por esta rotación y que encierra el sólido se denomina superficie de revolución. En principio, cualquier cuerpo con simetría axial o cilíndrica es un sólido de revolución.
La formulación del solido dependerá del eje estudiado en el disco, ya que la misma varía según su orientación, ya sea respecto al eje X o respecto al eje Y, de igual forma, estas formulaciones se llaman
El método de los discos
El método de los anillos
Cada una comprende el análisis del volumen del solido de revolución enfocado en un eje específico
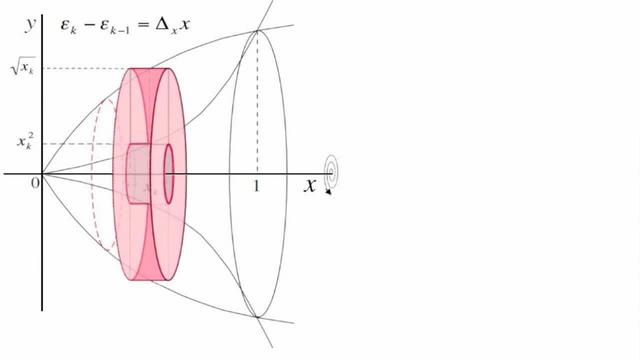
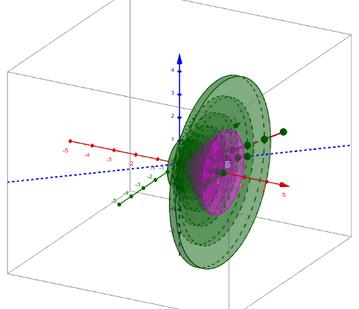
Visión Gráfica de un sólido de Revolución en el plano, delimitada por una región
9 El volumen de un sólido de revolución de forma indirecta aplica una visión 3D sobre un plano 2d
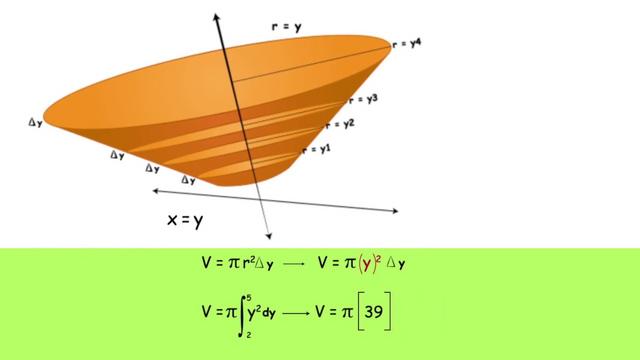
Método de los discos
El método de discos es una forma de calcular el volumen de un sólido de revolución mediante el cálculo integral. Consiste en dividir la figura en infinitos discos o porciones circulares, haciendo una sumatoria de sus volúmenes. Para utilizar este método, se hace rotar la gráfica de la función sobre algún eje para obtener un sólido de revolución que pueda modelarse como la suma de discos.
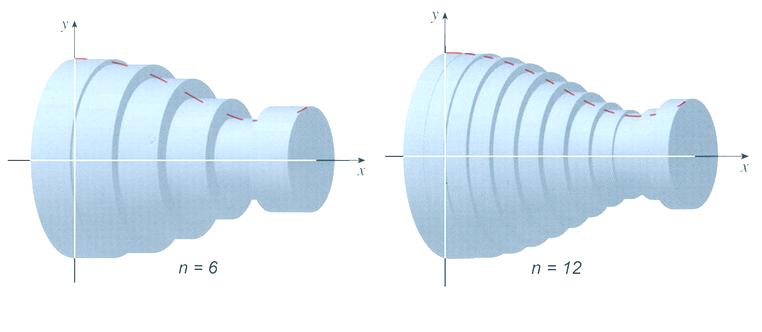
Este método utiliza la siguiente fórmula para poder calcular el volumen en una función dada:
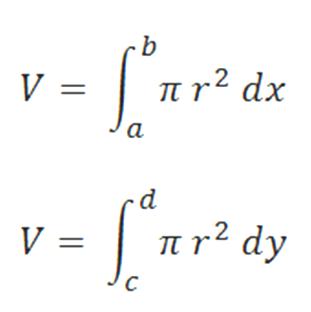
Comportamiento gráfico de una función al segmentarse por discos
Ejemplificación Gráfica:
El método de los discos y los anillos son formas de obtener el mismo resultado segun las condiciones
10
Método de los anillos
El método de los anillos es similar al método del disco, pero se usa cuando se gira una región limitada por dos curvas alrededor de un eje, en lugar de girar una curva. El objetivo es buscar el volumen encerrado entre las dos curvas. Un gráfico de anillos se usa para representar los porcentajes de un conjunto de datos, de manera que la parte del anillo que ocupa cada valor es proporcional a su frecuencia. Si una región del plano se hace girar alrededor de un eje paralelo al eje, de tal forma que se genera un sólido de revolución cuyas secciones transversales, perpendiculares al eje de rotación, son anillos con centro en el eje de revolución, entonces el volumen del sólido está dado por el método de anillos.
Dicha teoría se fundamenta usando la siguiente fórmula:
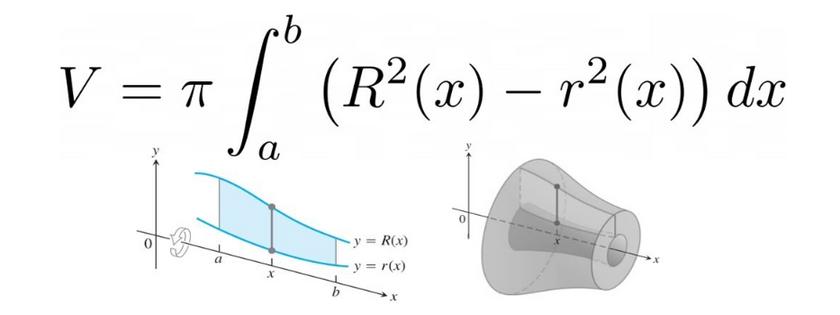
Dicho de otra forma, el volumen de un sólido usando el método de los anillos consta de calcular:
Pi * La Integral definida desde b hasta a de R de X al Cuadrado menos el Radio al cuadrado de X todo en función de la derivada de X
11
Aplicación a la ingeniería de Integrales Definidas
Como bien es sabido, todo teorema tiene su aplicación práctica en alguna otra subrama de la que provenga, por esto se lista un par de Aplicaciones vistas en diversas ingenierías con el fin de ejemplificar el uso del cálculo de áreas en las ingenierías:
Ingeniería civil: el cálculo integral en la ingeniería civil se emplea en toda ocasión en la que haga falta la medición de un área. Por ejemplo, el cálculo de las fuerzas internas en una viga o el cálculo de la capacidad de carga de un puente son ejemplos de aplicaciones del cálculo integral en esta área.
Ingeniería mecánica: el cálculo de áreas es importante para calcular la resistencia de materiales y el análisis de estructuras.
Ingeniería eléctrica: el cálculo de áreas se utiliza para calcular la capacidad de carga y la distribución de corriente en circuitos eléctricos.
Ingeniería química: el cálculo de áreas se utiliza para calcular la cantidad de sustancias que reaccionan en un proceso químico y para diseñar equipos y procesos.
Ingeniería industrial: el cálculo integral se utiliza para medir los costos totales involucrados en un proceso de producción.
Ingeniería aeroespacial: el cálculo de áreas se utiliza para calcular la resistencia y capacidad de carga de estructuras aeroespaciales.
Ingeniería ambiental: el cálculo de áreas se utiliza para calcular la cantidad de contaminantes liberados al medio ambiente y para diseñar sistemas de tratamiento y control.
12
Conclusión
El cálculo de áreas en coordenadas polares y paramétricas, así como la longitud de curvas en coordenadas rectangulares y el cálculo de volúmenes de sólidos de revolución, son herramientas matemáticas importantes en la ingeniería. Estos conceptos permiten a los ingenieros calcular áreas, longitudes y volúmenes de objetos con formas complejas, lo que es esencial en el diseño y análisis de estructuras y sistemas. Además, las integrales definidas son una herramienta poderosa en la ingeniería para resolver problemas de resistencia de materiales y análisis de estructuras. Por ejemplo, en la ingeniería civil, el cálculo de las fuerzas internas en una viga o el cálculo de la capacidad de carga de un puente son ejemplos de aplicaciones del cálculo integral. Tras haber visualizado, ejemplificado y entendidas las formulas presentes para la aplicación del calculo del área en diversos escenarios, será más sencillo poder evaluar diversos ejercicios de esta índole.
13
