Coordenadas Paramétricas

Las ecuaciones paramétricas son útiles para describir curvas que no son necesariamente funciones. El parámetro es una variable independiente que tanto x como y depende de él, y a medida que aumenta el parámetro, los valores tanto de x como de Y trazan una trayectoria a lo largo de una curva plana.

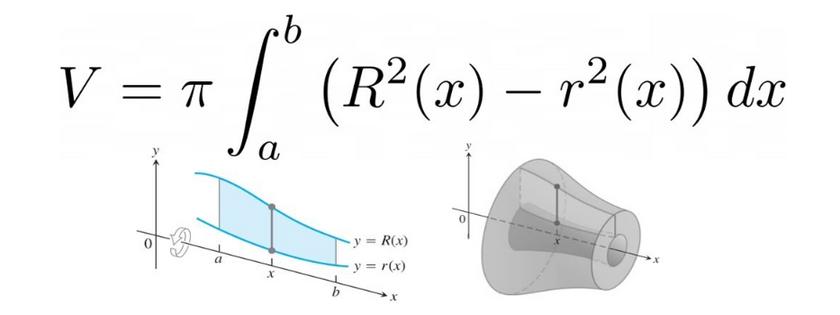
El área de la región que está debajo de una curva y = f(x) en el intervalo [a, b], donde f(x) >= 0 para todo x que pertenezca al intervalo [a,b] se define como:

[

Ahora, si esta curva puede representarse mediante las ecuaciones paramétricas x = f(t) & y = g(t) donde t está definida en el intervalo , entonces es posible definir una fórmula para calcular el área usando un cambio de variable como:

O en caso que el limite de integración sea invertido

Cicloide delimitado por una región

En matemática, la longitud de arco, es la medida de la distancia o camino recorrido a lo largo de una curva o dimensión lineal. La misma viene definida por la fórmula:

Es decir, la formula consiste de: Longitud será igual a la integral definida desde b hasta a de la Raíz Cuadrada de 1 + (Derivada de Y sobre Derivada de X) al cuadrado todo en Función de la Derivada de X

Bajo esta fórmula y aplicando los teoremas fundamentales del cálculo orientado a las derivadas definidas, es posible calcular y obtener la longitud de una curva dado un límite de integración