CONSTRUCTION OF NONASSOCIATIVE GRASSMANN ALGEBRA by IRJET Journal

CONSTRUCTION OF NONASSOCIATIVE GRASSMANN ALGEBRA

Dr. Saad Salman Ahmed

University of Technology and Applied Sciences-Muscat Branch

Department of Computing and Mathematics

Section of mathematics

AL-KHUWAIR 133, Box 74, Muscat, Oman ***

Abstract: One of the main sources of algebraic structures that illustrates basic concepts of modern algebra, is theoretical physicswheretherearemanywell-knownalgebraicstructuresusedastheLiegroups,rotationgroups,and“Algebraofcolor” proposed by Domokos as a candidate for the algebra obeyed by quantized field describing quark and leptons. We wish to investigate the nonassociative Grassmann and symmetric algebras. Z. OZIEWIOZ and C. SITARCZYK in [8], (non-published) started with the pair of the mutually dual Grassmann and symmetric algebras with the full set of the interior and exterior Grassmann and symmetric (bosonic) multiplications. They investigate the non-associative Grassmann algebra by combining the exterior and interior products for the Grassmann and symmetric algebra in one product on the Z-graded vector space (withnopositivegradation).Inthispaper,wederivedanewmultiplicationruleforthisalgebraandgavethecompletetables ofmultiplicationindimensions3,7,and 15.

Keywords: Grassmann Algebra, nonassociative Algebra, Z-graded vector spaces, The th p exterior power V p  of finite–dimensionalvectorspace.

Literature Review: HermanGrassmann wasa schoolteacher in StettinGermany whodid remarkable work inmathematics and the theory of languages. He created an algebra of Geometry which we are concerned with here. Grassmann wrote two books on the subject, one in 1844 and the second one in 1862. They were “The Theory of Extension”(meaning extension to higher dimensions in space. These two books received little notice before his death in 1877 when he received an Honorary Ph.D. a year before his death. Nevertheless, since then many good mathematicians have taken notice of Grassmann’s work. WilliamCliffordknewitandwroteavariantnowcalledCliffordAlgebra[3].Alfred NorthWhiteheadstudieditandwrote“A TreatiseonUniversalAlgebrawhichwasanexpositionofGrassmann’sworkinEnglish.ElieCaratanuseGrassmann’sexterior producttodevelopdifferentialformsandexteriorderivativesandappliedthemtodifferentialgeometry.WillardGibbsknew and admired Grassmann’s algebra but helped devise a different vector Analysis that became the mainstay of technical educationforoveracentury.JohnBrownewasdoinganengineeringPh.D.whenhediscoveredGrassmannAlgebraandfellin lovewithit.HeswitchedtothemathematicsdepartmentandhisthesistoGrassmannalgebra.Itwasvotedthebestthesisof theyear.Johnspenttherestofhislifedeepening,extending,andclarifyingGrassmann'salgebrawherehewrotethreebooks, [14,15,16].JohndiedinJune2021.

Introduction: LetVbeavectorspaceoverafieldF.TheGrassmannalgebraofV,denotedby V ,isthelinearspan(overF) ofproducts r v v v    ..... 2 1 where .V vi  Eachterminamemberof V hasadegree,whichisthenumberofvectorsin theproduct: . ) ... deg( 2 1 r v v v r     Weagreethat,bydefinition,theelementsofthefieldF willhavedegreeequalto0. The product is associative and bilinear, also it is very nilpotent: . 0 V v all for v v    Furthermore, the product is anticommutativethatis . , V w v all for v w w v     WewishtoinvestigatethenonassociativeGrassmannandsymmetric algebra. We start with the pair of the mutually dual Grassmann and symmetric algebras with the full set of the interior and exteriorGrassmannandsymmetric(bosonic)multiplication.Thesymmetricalgebrasarerelatedbythepermanent,in theanalogytotheGrassmanncasewherethemutuallydualGrassmannalgebrasarerelatedby thedeterminant.Ourstudyis motivatedbythesymplecticCliffordalgebraswhichhasbeenintroducedbyAlbertCrumeyrollein1975,infullanalogytothe usualpresentationofCliffordalgebrasforthepseudo-Riemannianstructures.

Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056 Volume: 10 Issue: 08 | Aug 2023 www.irjet.net p-ISSN:2395-0072

International

1. THE CREATION:

Throughout this paper we consider .... , lg , etc ebras a spaces vector   , (for simplicity)howeverallresultsarevalidforreasonablyany ring  (unitary, associative, and commutative). The Grassmann (exterior) FG and symmetric ebras a GB lg , are generated by the , , B F L and L spaces vector  where the subscript F refers to the fermionic (skew-symmetric) case and B denotesthebosoniccase.Oftenwewillomitthesubscripts and then G and his generating vector spaces L could refer to both (skew-symmetric and symmetric) cases. The generating space L could be interpreted as linear space of all one-fermion ( FL ) or one-boson ( BL ) states, however, wedonotfixyetanyoftheHilbertorHermitianstructures on L. The subspaces 1G , of degree one element in the algebra G, and , 1 G G  coincide with the generating space, 1G = L in both F and B cases. We denote the dual space by  

volumeoftheparallelograms,andthereforeplaythemost important role in the multiple integral calculus. (Whitney 1957).Wecanlookto(1)intwodualways:firstasforthe external products(symmetric )or external skewsymmetric(Grassman), and second as an external tensor product:

Weneedtochoosethepropernotationforthemaps(2).In the skew-symmetric case the multiplication (2) has been invented by Hermann Grassman in 1844 and nowadays is denotedbythewedge  :

 

G and L Hom L G ) , ( 1 denoting thesetofzero-degreeelements.Weintroducetheunusual negative gradation for the dual space and we put , 1 1   G if grad   the dual space L as the interpretation of the space of one-antiparticle quantum states. For each,   k we will define the linear spaces ), , ( ) ( *    k k k k G Hom G G and G to be interpreted as the state spaces of K-particles or Kantiparticles. We start with the 2K-  -linear evaluation mapwithvalueeitherinthedeterminantforthefermionic caseorwiththevalueinthepermanentforthebosonic,or justwiththevalueinthetraceforthetonsorialcase,

Inwhatfollowswewilldenotethemap(2)by (c)whichis short for the creation, and we will differentiate the different cases by a subscript ( ) , T B F c and c c .Now the subsets:

Here per is short for permanent. Both cases of the determinantforfermionsandofthepermanentforbosons are discussed in lectures by Feynman(1972). We will use for either case the symbol as ev the short for the evaluation, with the meaning that . det, trace

In the case of fermions, the evaluation map (1) also has the geometrical meaning of the oriented measure of the k-dimensional

arereferredtoasthesubsetsofsimpleordecomposablekparticle and k-anti-particle states. We will refer also to ) ( L c v K   the k-vector and the k-covector. This terminology is common for F and B cases, however, for T cases we have no obvious particle interpretation. In quantum theory, the decomposable states are called the pure states. The subset (4) generates freely  linear spaces ). ,

If thestate or v isnotdecomposablethenwesaythatthe particularone-particle(orone anti-particle)states,from which ) (  or v hasbeenbuilt usingthecreation(2),are virtualforv.

Both creators, of particles and anti-particles, are denoted bythesamesymbolc.Foreach, k G t  wehave:

Hereweinvertedtwicethemappingargument(theduality principle). The first inversion 1  k is non-injective and

 

det ) ,..., , ),( ( ) ( 2 1 * 2 1 j vi K K K k tr per v v v L L                                   



 

.........(1)

per ev

T B F   

ev and

).........................(2) , ( ) , (           L L L L L L K K K K

) , ( ) ,......... ( ).................(3) , ( ) ,..... ( 2 1 1 2 1 1                    L L v v v L v v similarly L L v v v L v v K k K k K k K k

) , ( ) ( ) , ( ) (           L L L c L L L c K K K K …………….(4)

, (        L L G and L L G K K K K

( )

k and G v k v k K       

For each . deg ,deg

........(5) ) ,....., ( , ) ,..... ( ,..., ,.... 1 1 1 1 k k v v t v v k k c i t c v v t and v v t   

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056 Volume: 10 Issue: 08 | Aug 2023 www.irjet.net p-ISSN:2395-0072

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 10 Issue: 08 | Aug 2023 www.irjet.net p-ISSN:2395-0072

coincideswiththecreatormapping(2).Thisonecanseeas follows:

The second inversion in (5) gives the pair of monomorphisms

skew-symmetricGrassmanncase.Theybuiltupgfromthe usual external and internal Grassmann multiplications for fermions and anti-fermions i.e. from four different creation-annihilationoperators.Firstoneshouldstartwith the definition of the (left) Grassmann creation operators. Thecreationoperatorswereidentifiedwiththecasewhen, (dega)(degb)≥0,then

For , dim

one can show easily that I in (6) is an isomorphism (because the vector spaces  G and their dual has the same dimension). We identify the universal property of the creator mapping (2) with the existence of the monomorphism (6). Therefore the universal property, accordingto(5),meansthat

commutativeandassociative

2. Nonassociative Grassmann Algebra:

We have started with 2 k-linear evaluation maps (1), determiningthepairofcreators:

is well-defined by (12)onlyfor

Thanks to the universal property (6), we get the bilinear evaluation:

NowweconsidertheZ-gradedvectorspaceoverZ:

F B G and G referred to as the Fock spaces of the multi-bosons and anti-bosons states (for B) and analogously for fermions chose the convention that if 0  k then –k denotes the number of antiparticles if k>0 then k denotes the number of particles then they put deg a=k

Their task was to make the vector space G into the nonassociativegradedcommutativealgebra.Theydefinea homomorphism g ) , ( EndG G Hom  which makes the space G into the algebra (G, g) and they consider only the

C * (not yet in

, ( G End G Hom is the annihilation operator,

b C define we and C a a a

The annihilation operator was defined when a * * a C G C   and they define b C a * for all 0 ) )(deg (deg  b a demanding in addition to (3), that 0 *  b C a for 0 ) )deg( (deg * e i b C a a  0 ) )(deg (deg ) (deg 2   b a a Both above multiplications are known as the “external and “internal” Grassmann Multiplications and are denoted correspondingly by ) ( creation emision external C      , and ) (int* annhilition absorption ernal i     .

Using this notation, they define the full Grassmann nonassociativemultiplicationoperatorgas

). ,..., ( ) ,..., ( ) ,...., , ,.... ( 1 ,..., 1 ,... 1 1 1 1 k v v k k k k k c v v c v v ev        

)...........(6) , (     G Hom G I k



.......(8) )......... , ( ) , ( ..(7) (6) , 1                  L L G G Hom mappings back Herebystarwedenotethepull id i c that short in or t c thati such i G t k k c k G t k k  

.(9) * k c k k G L or L    

0G G G k k   

......... ........ 2 1 0 1 2           G G G G G G G K Z k This

gradationisnotusual;itisnotpositive.Inquantumtheory

 

. k

p q p a C q G a G b a b C G b a         ) ( and ( deg deg ) b a b C a   ……(10)

( 0  pq ) is graded

a C b C b b a a ) )(deg (deg) (  ………………(11) deg deg ) deg( , ) ( ). ( ...(12) ) ( ) ( ) ( , 0 ) )(deg (deg 0 deg deg deg 0 Z f a f C and C C C of back pull the denote C Here b f C b C f G b C f then b a and f b a let a a a a a a a a                 

 *

)................(13) ) (deg ) )(deg (deg 0 ) )deg( (deg 2 * a f a f C a a   

The above multiplication

It is important to realize that G C a

))

  0 (deg ) (deg * *   b

for

a all

g is “self-adjoin” * g g  The creation of particles is associative,however,annihilationisnotassociative.

The nonassociative Grassmann algebra means, just the pair (G, g), the Grassmann Z- graded linear space G with the above Grassmann multiplication (11). The most importantpropertyofGrassmannproductsis

dimensional case, we have also and G n  n G . In the oppositeoftheparticular(fermions)case,theannihilation of the anti-holes is the associative operation (external Grassmann multiplication) as the hole creation is not the associativeoperator”I”.

3. The new multiplication of the Algebra:

We will givea multiplicationtable forthis algebra over IR (which makes sense over any field of characteristics not two).

Some basic definitions:

Equation(15)isessentiallyequivalenttothe associatively of the usual Grassmann exterior product (10-11). One can mention that for the finite-dimensional case, important in the nuclear shell theory, when    L n dim , the definition (14) should be complemented by the additional condition 0  b g a for n b a   deg deg and for

n b a   deg deg

this means that 0  b g a for

n b a   ) )(deg (deg a deg

2) (deg a and for

n b a  ) )(deg (deg ) (deg a 2) (deg a ………………………………………………….…(16)

From(14)wehavenon-zeroterms

Definetion1: The th p exterior power V p  of finite–dimensionalvectorspace V isthedualspaceofthevector space of alternating multi-linear forms of degree P onV Elements of V p  are called vectors p The subspace in r V r 0,1,...,) (   V generated by the elements of theform ) ,..., ( , 1 1 V isbasisof e whene

Saidtobether-thexteriorpowerofthespaceV.Wehave:

By simple check, we can show that 17.1 and 17.4 are not compatible with 0 ) )(deg (deg  b a and that 17.2 and 17.3arenotcompatiblewith 0 ) )(deg (deg  b a

Therefore (15) follows at once. Also, the relation (15) contains the usual four different anti-commutative relations for the creation operators of Fermions and antifermions (17.1), and for the annihilation operators of fermions and anti-fermions (17.4). In the finite-

The elements of the space 0,1,...,) (   r V r are said to be r-vectors, which are closely connected with rdimensionalsubspacesinV.

Definition 2:Thek-thexteriorpowerofVdenoted V k  is the vector subspace V spanned by the elements of the form

If k i V x x x x i k 1,2,... , , 2 1

, canbeexpressedasanexteriorproductofkelements ofV,then  issaidtobedecomposable.

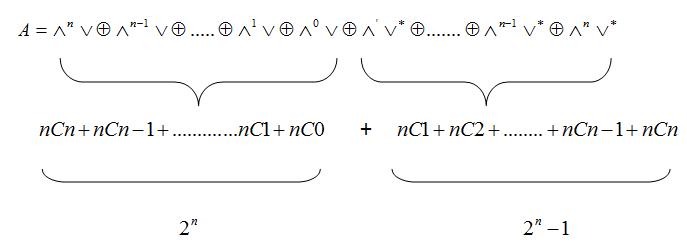
Definition 3:Any element of the exterior algebra can be writtenasasumofk-vectors.Hence,asavectorspace,the exterioralgebraisadirectsum:

e e

i i r  

. , 1) ( 3 0 2 0,..., , dim 1 V v V u if u v v u n r if v n r r n V s r rs r r                     

     





V k

. , , 1 0 2 1 0 V V and K V wher V V V V V n               (14) (15) 17.1 17.2 17.3 17.4

Journal of

and

(IRJET) e-ISSN:2395-0056 Volume:

Issue: 08 | Aug 2023 www.irjet.net p-ISSN:2395-0072

International Research

Engineering

Technology

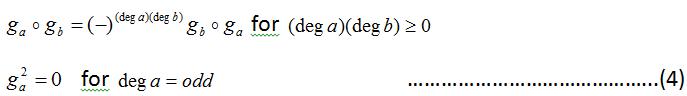
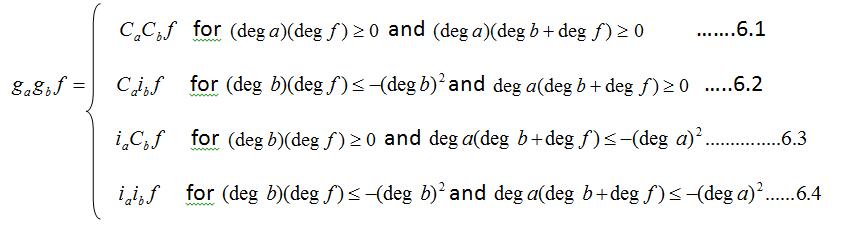
And therefore its dimension is equal to the sum of binomialcoefficients,whichis2 n MoreoverifKisthebase field, the exterior product is graded anticommutative, meaning that if . 1) (  

kp p k then and V

Definition 4: Let kV V V V ,......., , , 3 2 1 be k-vectors in nIR

Define the exterior product kV V V    ..... 2 1 by stipulatingthat:

(i) 0   V V ,foranyvector n IR V 

(ii) V W W V    1) ( ,foranyvectorVandWin nIR

(III) With the exception of (i) and (ii) all algebraic rules whichapplyto“ordinarymultiplication”alsoapplyto“  ”

Remark: and IR e Let n k   (0,0,0,0.....0,1,0.....0)

Byconsequence,ifHandKaretwocomplementspartsof the interval

We now have vector spaces   p of dimension ) , ( p n C , naturally associated with V. The space   ' is by definitionthedualspaceofthespaceoflinearfunctionson V

by converting we have

1 we also have a corresponding vector

,......., , , 3

and the notation suggests that there should be a product so thatwecanremovethebrackets:

are two sequences of elements of H and K respectively given in increasingorder,thenfor

1, of IN, and

Now, consider a finite-dimensional vector space V with dimensionnandtheZ-gradedvectorspaceoftheexternal direct sums and we consider a vector space A with coefficients taken from an algebraic field F (For practical purposes,Fmaybethefieldforrealorcomplexnumber):

Corollary: If n V

Proof: Since n v

dim then

| ISO 9001:2008 Certified Journal | Page476

8.226

 

 

 

   



 

                              n i i ik n i i i n i i i k e a e a e a V V V 1 1 2 1 1 2 1 = ik i i k i I i i i i i e e e a a a n k n k     .... ,..... , 2 ) ,.... , ( 2 1 1 2 1 2 1 = ) ( ...................... , ,1 .... ,..... , 2 ) ,.... , ( 2 1 1 2 1 2 1 i byapplying k i i e e e a a a ik i i k i I i i i i i n k n k            = ) ( ) ,..... , ( .... ,..... , 1) ( 2 1 2 ,... ( 2 1 1 2 1 2 1 ii byapplying I i i i e e e a a a n k k ik i i k i i i i i i n k       



ki i i    ..... 2 1

then n I

1,2,3

When

denotes the number of transportations required toobtain

, so       '' '

F   

V V V 

      p p V V V ..... 2

q p q p v v v u u u v v v u u u            ,.... ) ,.... ( ) ( 2 1 2 1 2 1 2 1

. Given

vectors V Vp

n

p n k i k p n i n j i     ) ,( ) (

ip i i H x x x X     ...... 2 1 and ) ( 2 1 ...... p n j j j K x x x X     Wehave n K H x x x X X      ...... 1) ( 2 1  ,



theorderpairs   K H j i   ,

where

is the numberof

suchthati>j.

* * 1 1 0 1 1 .....                         n n n n A

V= n

  n e

2 1

set  n i i i e e e k ik i i         .... /1 .... 2 1 2 1

a basis for

  k

 0    k ,fork>n,and     1

If the dim

and

e e ,.... ,

is a basis of V, then the

. By counting the basis elements, the dimension   k is the binomial coefficient ) , ( k n C . In particular,

1 2 1 2 2 dim 1    n n n A

 dim ,then



When     * and     1

e-ISSN:2395-0056

Issue: 08 | Aug 2023 www.irjet.net p-ISSN:2395-0072

International Research Journal of Engineering and Technology (IRJET)

Volume: 10

Any element of A can be written as a sum of multisector.Hence,asavectorspace,Acanbewrittenasa directsum

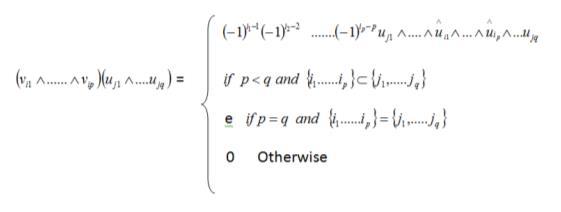
Definition 5: Now we can define nonassociative Grassmann Algebra by “composing” the exterior product and the interior product of exterior Algebra and SymmetricAlgebrainoneproductoverthevectorspaceA. As a result, we get a nonassociative Grassmann Algebra withthefollowingmultiplication:

© 2023, IRJET | Impact Factor value: 8.226 | ISO 9001:2008 Certified Journal | Page477 ) , ( dim n n C n    , 1) , ( dim 1    n n C n ,………. ) , ( dim * n n C    , ,0) ( dim 0 n C    So 1 2 1 2 2 dim 1    n n n A Henceif n   dim then 1 2 dim 1  n A

* * 1 1 0 1 1 ....                         n n n n A

have we v v v and u u u for n jq j j n ip i i              ) ..... ( ) ( 2 1 2 1 andtheexteriorProduct 4. EXAMPLES: 1 dim dim dim * 1 0 1          and 3 1 2 dim 1 1    A ,andthetableofmultiplication isgivenby: e 1e 2e e e 1e 2e 1e 1e 0 e 2e 2e e 0 multiplicationisgivenby: International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056 Volume: 10 Issue: 08 | Aug 2023 www.irjet.net p-ISSN:2395-0072 Example 1:Supposethat1dim  then *101 A and 712dim 12   A ,thetableof and .1dim 2    ,2dim 1   ,1dim 2  ,2dim 1  ,1dim 0   21012 A

2:Supposethat 2dim  then

Example

Example 3: Suppose that 3 dim



' 1 0 1 2 3 A 1, dim 3    3, dim 2    3, dim 1    1, dim 0    3, dim 1     3, dim 2    1, dim 3     and 15 1 2 dim 1 3    A ,andthetableofmultiplicationisgivenby: e1 e2 e3 e1 ^ e2 e1ê3 e2 ^ e3 e1^ e2ê3 e p1 p2 p3 p1^p2 p 1^p3 p 2^p3 p1^p 2^p3 e1 0 e1ê2 e1 ^ e3 0 0 e1^ e2ê3 0 e1 0 0 0 p2 p3 0 p 2^p3 e2(e1ê2) 0 e2 ^ e3 0 -(e1^ e2ê3) 0 0 e2 0 e 0 -p1 0 -p3 -(p 1^p3) e3(e1ê3) -(e2ê3) 0 e1^ e2ê3 0 0 0 e3 0 0 e 0 p1 p2 p1^p2 e1ê2 0 0 e1^ e2ê3 0 0 0 0 e1ê2 0 0 0 e 0 0 -p3 e1ê3 0 -(e1 ^ e2ê3) 0 0 0 0 0 e1ê3 0 0 0 0 e 0 -p2 e2ê3 e1^ e2ê3 0 0 0 0 0 0 e2ê3 0 0 0 0 0 e p1 e1^ e2ê3 0 0 0 0 0 0 0 e1^ e2ê3 0 0 0 0 0 0 e e e1 e2 e3 e1 ^ e2 e1ê3 e2 ^ e3 e1^ e2ê3 e p1 p2 p3 p1^p2 p 1^p3 p 2^p3 p1^p 2^p3 p1 e 0 0 e2 e3 0 e2ê3 p1 0 p1^p2 p 1^p3 0 0 p1^p 2^p3 0 p2 0 e 0 -e1 0 -e3(e1ê3) p2 -(p 1^p2) 0 p 2^p3 0(p1^p2^p3) 0 0 p3 0 0 e 0 e1 e2 e1ê2 p3 -(p 1^p3) -(p 2^p3) 0 p1^p2^p3 0 0 0 p1^p2 0 0 0 e 0 0 -e3 p1^p2 0 0 p1^p2^p3 0 0 0 0 p 1^p3 0 0 0 0 e 0 -e2 p 1^p3 0 -(p1^p 2^p3) 0 0 0 0 0 p 2^p3 0 0 0 0 0 e e1 p 2^p3 p1^p 2^p3 0 0 0 0 0 0 p1^p 2^p3 0 0 0 0 0 0 e p1^p 2^p3 0 0 0 0 0 0 0 1e 2e 2 1 e e  e 1p 2p 2 1 p p  1e 0 2 1 e e  0 1e e 0 2p 2e - ) ( 2 1 e e  0 0 2e 0 e - 1p 2 1 e e  0 0 0 2 1 e e  0 0 e e 1e 2e 2 1 e e  e 1p 2p 2 1 p p  1p e 0 2e 1p 0 2 1 p p  0 2p 0 e - 1e 2p -( 2 1 p p  ) 0 0 2 1 p p  0 0 e 2 1 p p  0 0 0   32* International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056 Volume: 10 Issue: 08 | Aug 2023 www.irjet.net p-ISSN:2395-0072

 then

Conclusion:

The present paper is devoted to the formalism of the Grassmann and symmetric algebras We combine the exterior and interior products for both algebras in one product on the Z-graded vector space which gives the nonassociative Grassmann algebra(definition 5) which incorporates the full set of the creation and annihilation operators for both particles and antiparticles.We also gave some exaples in different dimensions with their tables of multiplication. We compare the fermionic case (related to determinant)with the bosonic one (related to permanent).In futureresearch,wecanstudysomepropertiesofthisalgebra as a non-associative algebra.

References:

1-M.BARNABEI,A.BRINI,andG.ROTA,ontheexteriorcalculus ofinvarianttheory,Algebra96(1985),120-160.

2-J.S.R. CHISHOLN and A.K. COMMON,” Clifford Algebras and their applications in mathematical physics” D.Reidel Dordrecht,1986.

3-A.CRUMRYROLLR,’SymplecticCliffordAlgebras“printedin (ChisholmandCommon,1986).

4-R.P.FEYNMAN,” Statistical Mechanics. A set of lectures”. Benjamin,NewYork,1972.(Ch6).

5-N.L.MICHELSOHN, Clifford and Spinor Cohomology of Kahier Manifolds, American Journal of Mathematics 102(1980),1083-1146.

6-N.E.SWEEDLER,”HopfAlgebras”,Benjamin,NewYork,1969.

7-H.WHITNEY,” Geometric Integration Theory”, Princeton, 1957

8-Z.OZIEWIOZandC.SITARCZYK“NonassociativeGrassmann Algebra”(nonpublished),November1987.

9-Rafal Ablamowicz.Computations with Clifford Algebra and Grassmann Algebra, Advances in Applied Clifford Algebra 19,499(2009).

10-Daniel Alpay, and others, Mathematical Methods in the AppliedSciences,Volume45,Issue1,Jan2022.

11. L. Ceentrone, The G-graded identities of the Grassmann Algebra,ArchivumMathemticum,2016.dml.cz.

12 Divincenzo, O.M., Koshlukov,p.da Silva, V.R.T: on Algebra,Commun.Algebra45(1),343-356(2017).

gardedZ P identities and characters of the Grassmann

13-Carla Rizzo, The Grassmann Algebra and Differential Identities, Algebra, and Representation Theory 23,125134(2020)

14. John Brown, Grassmann Algebra, Volume 1:Foundation.Exploring extended vector algebra with Marhematica.2012

15. Jhon Brown, Multiplanes and Multispheres.Notes on a GrassmannAlgebraApproachwithMathematica.2020

16. John Brown.Grassmann Algebra, Volume 2:Etensions, HypercomplexandAssociativeAlgebras.2021.

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056 Volume: 10 Issue: 08 | Aug 2023 www.irjet.net p-ISSN:2395-0072 © 2023, IRJET | Impact Factor value: 8.226 | ISO 9001:2008 Certified Journal | Page479