Analysis of Hysteresis and Eddy Current losses in ferromagnetic plate induced by time-varying electr by IRJET Journal

Analysis of Hysteresis and Eddy Current losses in ferromagnetic plate induced by time-varying electromagnetic field

G. D. Kedar1 , B. B. Balpande2

1,2 Department of Mathematics, RTM Nagpur University, Nagpur-440033, Maharashtra, India,

Abstract - Whenever electric devices are exposed to timevaryingelectromagnetic field, it brings outtwoimpactsonthe devices: Firstly, conducting currents appears in the device, which ultimately gives rise to Joule’s heat which rises the temperature of the device in terms of Eddy current loss, and, secondly due to the time lag between magnetization and demagnetization of the ferromagnetic plate some amount of energyis lost which is termed Hysteresis loss. Inthis paper,we have treated this total loss as the heat source for the problem. Based on Maxwell’s equations a three-dimensional mathematical model for the magnetic field, temperaturefield, and elastic field in the plate was established. Then the governingequations for determining magnetic fieldintensity, temperature, and stresses inside the plate were solved by integral transform technique. The results obtained are displaced graphically to illustrate the influence of wave frequency, skin depth, electrical conductivity, magnetic permeability, hysteresis loss, and Eddy current loss of steel plate on the various fields considered in the problem.

Key Words: Eddy current, hysteresis loss, time-varying electromagnetic field, magneto-thermoelasticity, integral transform

1.INTRODUCTION

In many electromagnetic equipment such as magnetic circuits of motors, generators, inductors, magnetically levitated high-speed terrestrial vehicles, energy storage devices in electromagnetic fields, fusion reactors, and devicesusingelectro-magneticpropulsionetc,ferromagnetic materials are widely used. Analogous to conventional structures which experience mechanical loads, the ferromagneticstructuresinsidethestrongmagneticfields typically are exposed to the magnetic force arising due to mutual interaction between time-varying magnetic fields andthemagnetizationofferromagneticmaterials. Dueto this strong magnetic force, the ferromagnetic structures undergodeformationwhichaffectstheirstabilitydrastically [1].

Eddy current induced in conducting mediums (such as metallic plates) by time-varying magnetic field and its consequencesisofgreatpracticablesignificanceduetoits magnificentroleinavastrangeoftechnicalandindustrial applications.Manymechanicalstructuresgetactivatedwhen immersed in the electromagnetic field. Such structures or conducting mediums, when moving through the

***

electromagneticfieldorwhenexposedtothetime-varying electromagneticfield,Eddycurrentsareinduced.Thiseddy current creates an internal magnetic field that exactly opposestheexternalmagneticfield.Thisgivesrisetoaskin effectinwhichthecurrentdensityneartheoutsideofthe conducting medium becomes higher than the inside. The eddy current creates a kind of power loss in the medium known as Eddy current loss. The heat produced by Eddy currentisusedinvariousapplicationslikeheattreatmentof metalproducts,inductionfurnaces,Inductionhardeningin steel parts, induction welding/brazing as a way of connectingmetalcomponents,orinductionannealingwhich canselectivelysoftenaregionofasteelportion,etc.[2-5]. The estimationofEddycurrent isalsousedforone ofthe inspectionmethodswhichisnon-destructivetestingwhich serves for a variety of purposes, including flaw detection, measuringmaterialandcoatingthicknessanddetermining andlayingouttheheattreatmentconditionforconducting materials.

Magneto-thermoelasticityisa subjectwhere westudythe interactions between magnetic, thermal, and mechanical fieldsinathermoelasticsolidinthepresenceofamagnetic field. The theories like heat conduction theory, classical elasticity theory, and electromagnetic theory which are appliedtosolvethecouplingproblemsoftemperaturefield, electromagneticfield,andelasticfieldofconductiveelastic solids are also included in Magneto-thermoelasticity. The theoreticalideaofmagneto-thermoelasticitywasintroduced by [6-7] and later on was developed by [8]. Paria [9] consideredathermo-elasticsolidinsideamagneticfieldand studied the propagation of the plane waves and gave a theoretical framework for the advancement of magnetothermoelasticity. Wilson [10] studied the propagation of magneto–thermoelastic waves in a non-rotating medium. The above studies were based on the theory of classical coupled thermoelasticity, with interaction among the electromagneticfield,thethermalfield,andtheelasticfield, aswellasthedispersionrelation,takenintoconsideration. Nayfehetal.[11]usedthePerturbationtechniquetostudy theeffectofsmallcouplingsrelatedtothermoelasticityand magneto-elasticity of an unbounded isotropic medium. Sheriefetal.[12]discussedaone-dimensionalthermalshock problemofgeneralizedthermoelasticelectricallyconducting half-spacepermeatedbyaprimaryuniformmagneticfield withthermalrelaxation.Biswasetal.[13]exemplifyathreedimensional electro-magneto-thermoelastic coupled problem for homogeneous orthotropic thermally and

electrically conducting solid subjected to time-dependent thermal shock. Xu et al. [14] proposed an approximate analytical solution method to investigate the behavior of three-dimensionalsimplysupportedrectangularplateswith variable thickness subjected to thermo-mechanical loads. Baksietal.[15]studiedthethree-dimensionalproblemsof magneto-thermoelasticity in the infinite rotating elastic mediumwiththermalrelaxationandheatsource.Thestudy oftheinteractionbetweenthemagneticfieldandthestrain field in a thermoelastic solid is receiving considerable attention in recent years due to its wide range of applicationsinvariousfields.Especiallyinnuclearfields,the extremelyhightemperaturesandtemperaturegradients,as wellasthemagneticfieldoriginatinginsidenuclearreactors, influencestheirdesignandoperations.Roychoudhuri[16] studiedmagnetoelasticplanewavesinrotatingmediawith uniform angular velocity. Othman et al. [17] developed a three-dimensionalmodeloftheequationsofthegeneralized thermoelasticity to study the effect of magnetic field and thermalrelaxationforahomogeneousisotropicelastichalfspace solid in the context of Lord-Shulman theory in the absence of body forces or heat source. Ezzat et al. [18] developedanewmathematicalmodelfortheequationsof thetwo-temperaturemagneto-thermoelasticitytheory.Das etal.[19]investigatedtheinteractionofahomogeneousand isotopicallyperfectconductinghalf-spacewithrotation,in the context of Lord-Shulman theory. Bawankar et al. [20] studied a two-dimensional problem of a thermosensitive conducting plate with eddy current loss in the context of magneto-thermoelasticity. Higuchi et al. [21] studied the stresses aroused due to transient magnetic fields in an infinite conducting plate using the theory of magnetothermoelasticity.Mitiketal.[22]haveobtainedJoule’sheat asathermalloadingofathinelastic,isotropic,ferromagnetic plate subjected transversally to the homogeneous, timevaryingmagneticfield.Mitik[23]hasstudiedtheinfluence ofplatethickness,wavefrequency,andhysteresisfactoron thetemperaturefieldofthethinmetallicpartiallyfixedplate whichisinducedbyHarmonicElectromagneticwave.

The present article is an attempt to study the effect of eddycurrentloss(arousedduetoJouleheatgeneratedby Eddycurrent)andHysteresisloss(arousedduetotimelag between magnetization and demagnetization) on a threedimensional ferromagnetic plate placed in time-varying electro-magneticfieldasanextensiontotheresearchwork byBawankaretal.[20].Thevariousdeterminedexpressions areobtainednumericallyforsteelmaterialandresultsare introduced graphically. Effects of Eddy current loss along withHysteresislossandmagneticfieldquantitiesarealso analyzed.Theintegral transformtechniqueis usedtofind thetemperaturesolution.

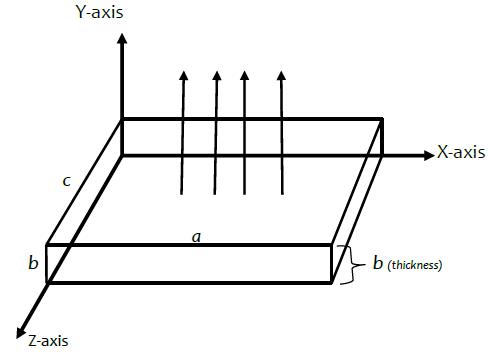
2. PROBLEM FORMULATION

Weconsideranisotropic,homogeneous,thermally, and perfectlyconductingelasticthinrectangularferromagnetic platewithlength a width c andthickness b occupyingthe

space :0,0,0 Dxaybzc  asshowninfigure1. The plate is subjected to time-dependent exponentially varyingmagneticfield 0 t He uniformlydistributedalongXandZ-directionandactsontheplateinapositiveY-direction asshowninthefigure.Here 0H isthemagneticfieldstrength at the outer surface of the plate and  is the angular frequencygivenby 2/2Tf  .Letthemagneticfield be given by  0,,0 y HH  where 0 t y HHe  and the inducedelectricfieldvectorbegivenby   ,0,.xzEEE  Ampere-Maxwell’s equation which states two possiblewaysofgenerationofmagneticfield:oneisdueto electriccurrentandtheotherisduetochangingelectricfield (calledthedisplacementcurrent)isgivenby:

The component form (in the absence of displacement current) of the Ampere-Maxwell’s equation takes the followingform:

Thedisplacementvector u hasthecomponents:

Following[24],weconsideredthemodifiedOhm’slawwhich outlines the impact of temperature gradient and charge density ignoring the seemingly small consequence of temperaturegradientontheconductioncurrent J as:

Using(2)thecomponentformoftheaboveequationcanbe writtenas:

Similarly,thecomponentof magneticfluxdensityisgiven by:

D HJ t    (1)

, yy xz HH JJ zx    (2)

Fig -1: Geometry of the problem.

,, xyz uuvuwu 

(3)

 JEuB   (4)

    , xxyzzy JEBwJEBu   (5)

yyBH  

(6)

Solving (1) and (4) we obtain the components of electric fieldintensityas:

Faraday’s law of electromagnetism which describes how time-varyingmagneticfieldinducesanelectricfieldgives:

Using(6)and(7),theaboveequationreducesto:

generated when this kind of work done is performed by magnetizingforce.Thisextraheatgeneratedresultsinthe wastageof energyintheformofheatcalledasHysteresis loss.ItisknownthatHysteresisloss HystW isproportionalto thesquareofmagneticfieldamplitudeandfrequency[23], thereforeitisgivenby

Neglectingthecouplingterm  between the temperature andthedeformationfields[22],thegoverningequationof the temperature field along with the boundary and initial conditionsisgivenby:

Equation (9) represents the uncoupled equation of the magneticfield.Using 00(,,), t yrHxztHe

in (9), weobtain:

where 002/,2/ zzrxxr   ,aretheskin depth in the z-axis and x-axis directions respectively. In particular, for isotropic material xz  , hence

withthis,Eq.(10)modifiesto:

Thepre-requisiteboundaryconditionsareconsideredas:

Theterm (,,,) TotalTotal WWxyzt  istreatedastheheatsource oftheproblem.Also,itconsistsoftwopartsthehysteresis loss and Joule’s Heat (responsible for Eddy Current loss). Botharetakenwithintheplatefor 0 t  subjecttotheinitial and boundary conditions prescribed for the problem considered.Thus

Apart from Eddy current loss and Hysteresis loss the metallic plate placed in a time-varying magnetic field also sufferstheLorentzforce.ThecomponentsofLorentzforce aregivenbytheexpressions:

As a result of a time-varying electromagnetic field conductingcurrentsappearintheplatematerial,referredto as Eddy current. Eddy current produces the resistive deprivationthatconvertssomeformofenergy,forexample, kineticenergyintoheatenergywhichisknownasJouleheat. Joule heat diminishes the efficiency of the conducting material. Joule heat gives rise to the Eddy current loss . EddyW FortheconsideredproblemthedistributionofJoule’s heatintermsofEddycurrentlossgivenby[23]

The constitutive equation for stress-displacementtemperature relation and strain-displacement relation is givenby[9]:

When a magnetization force is applied to a magnetic material,themoleculesofthemagneticmaterialarealigned in one particular direction. Switching of magnetic force in the opposite direction causes the internal friction of the molecularmagnets.Thisfriction,infact,resiststhechangein the direction of magnetism which finally gives rise to the MagneticHysteresis.Todefeatthisresistancecauseddueto internalfriction,apartofthemagnetizingforceisutilized which results in the work done by the force. Heat is

Using(24),thecomponentsofthestressfieldarewrittenas:

11 , yy xz HH EE zx    (7)

B E t    (8)

22 22 yyy HHH t xz      (9)

 

22 22 22 2 zx HH H xz    

(10)

2/ xzr  

xz     (11)

222 2 HH H

0 (0,,)(,,) HztHaztH  (12) 0 (,0,)(,c,) HxtHxtH  (13)

22 Eddyxz WJJJ    (14)

22 11

2 (,) HystHy WztkfH   (15)

2 0 TotalW CT T t      (16)     0,,,,,,0TyztTayzt (17)     ,0,,,,,0TxztTxbzt (18) 0, 0 zc T z        (19)   ,,,00Txyz  (20)

  ,,, TotalEddyHyst WxyztWW  (21)

 2 2 xy fH x     (22)  2 2 zy fH z     (23)

2(eT) ijijij e   (24) uvw eu xyz    (25)   ,, 1 2 ijijji euu  (26)

2eT xx u x     (27)

The displacement equation of the theory of elasticity, consideringtheLorentzforcetakesthefollowingform:

For considered three-dimensional problem, the above equationsgive:

ApplyingdoublefiniteFouriersinetransform[21]

weobtain:

We now apply the inverse of double finite Fourier sine transformto(44)toobtain:

Using(45)in(40),weobtaintheexpressionforthemagnetic fieldas:

Consequently, the magnetic field intensity inside the rectangularplateatanytimetisgivenby:

Currentdensityexpressionsaremodifiedto:

3. SOLUTIONS

3.1 Determination of Magnetic field

To find the solution to the magnetic field described in (11), (12) and (13), we need to transform the inhomogeneous boundary conditions into homogeneous ones.Forthis,weassumethesolutionof(11)as

Using(40)in(11)to(13)weobtain:

Using(14)and(15),theexpressionsforEddycurrentand Hysteresislossesaregivenby:

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 10 Issue: 07 | July 2023 www.irjet.net p-ISSN: 2395-0072 © 2023, IRJET | Impact Factor value: 8.226 | ISO 9001:2008 Certified Journal | Page1174 2eT, yy v y     (28) 2eT zz w z     (29) xy uv yx       (30) xz uw zx       (31) yz vw zy       (32)

2 2 () iik i k u JB x t       (33)

  222 2 T 2 uvw u xyxzx x              2 2 y H x    (34)   222 2 2 vuwT v yxyzy y             (35)   222 2 2 wuvT w zxzyz z              2 2 y H z    (36) Weconsidertheplateisatrestbefore 0, t  andwesuppose thatthesurfacesaretractionfreei.e. 0 xxzz  (37) And the mechanical boundary conditions and the initial conditions are: 0,0, 0, 2 xazc yb uvw T xyz                 (38)       000 0 ttt uvw   (39)

0 (,,)(,) HxzthxzH  (40)

  22 0 222 2 hh hH xz     (41) (0,,)(,,)0 hzthazt (42) (,0,)(,c,)0 hxthxt (43)

0 2 2 (,) mn hmnH    (44)

(41)

    1 11 (,)sinsinmnmm mn hxzcxz      (45)

    01 11 (,)sinsinmnmm mn HxzHcxz      (46)

    01 11 (,)sinsin t mnmm mn HxzHcxze        (47)

    2 11 (,)sincos t xmnmm mn Jxzacnxze         (48)     2 11 (,)cossin t zmnmm mn Jxzccmxze         (49)

    2 2 3 11 sincos Eddymnmn mn n Wcxz c              2 2 cossin t mn m xze a           (50)     2 2 01 11 sinsin t HystHmnmm mn WkfHcxze         (51) where 00 12222 84 ,,,,mn HH mn cc ac acac        2 0 3 2 (1)1(1)1 8,, mn mn H c ac mn            22 2 222 2 / mnmn mn ac          

3.2 Dimensionless Quantities

It is more convenient to introduce the dimensionless variablesasbelow:

3.4 Determination Displacement and Stresses

Simplifying (34)-(36) further and dropping the inertia term,weobtain:

3.3 Determination of Temperature Field

Thetemperaturefieldalongwiththeinitialandboundary conditionsindimensionlessformisexpressedas(fromhere onwards we drop the bar notation for the sake of convenience):

ApplyingdoublefiniteFouriersine[25]transformto(53), weobtain:

Following[21],thequasi-staticsolutionsofdisplacement duetotemperaturechangeandLorentzforceintermsofits thermalandmagneticcomponentsaregivenby:

Applying Laplace Transform to the above equation with respecttotimeco-ordinate,weobtain:

Usingtheaboveequationsalongwith(25)in(27)-(32),we obtain:

Applying the inverse Laplace transform, inverse finite Fourier cosine and inverse double finite Fourier cosine transformtotheaboveequationweobtain:

2 0 ,,,,,, y y H xyzcHxyzct bbbbH b    2 22 00 00 ,,, x zEH xz EH H bJ bJbWW JJWW HH HkfH        222 000 , ,,, /2 ij xz xzij bff CT Tff HHH      (52)

222 45 222 (,) TTTT cWzc xyz       (53)     0,,,1,,,0TyzTyz (54)     ,0,,,1,,0TxzTxz (55) 0,1 0 z T z        (56)   ,,,00Txyz  (57) where 2 45 2 00 , acC cc H    

  2 222 45 2 ˆˆ ˆˆ (,) TT mnTcWzc z       (58)

toz,   2 2222 45 2 ˆˆ ˆˆTT mnpTcWc z       (59)

We now apply the Finite Fourier cosine transform with respect

   ** 6 1 ˆˆ (,,,) 2 mnp TmnpscW scs        (60)

  6 111 (,,,)2cos Totalmnmnp mnp TxyzcWIIpz             sinsinmxny   (61) Where   2 222 6 22 00 ,, mnp a ccmnp C H     ,0 [(2)2] [(2)2] 00 , mnp mnp cu cu mnpmn IeduIedu        

      2 2 2 T 222 y u H xx x       (62) 2 2 2 vT y y       (63)     2 2 2 222 y wT H zz z       (64) Theexpressionsfordisplacementcomponentsaregivenby:      2 222,,,,, x uuTxyzdxHxzdx      (65)   ,,, 2 y vuTxyzdy       (66)      2 222,,,,, z wuTxyzdzHxzdz      (67)

  ,,,, 2 T uTxyzdx       (68)    2 ,, 22 M uHxzdx       (69)   ,,, 2 M vTxyzdy       (70)   ,,,, 2 T wTxyzdz       (71)    2 ,, 22 M wHxzdz       (72)

  2 ,,, 2 TT xxzz Txyz      (73)    2 ,, 2 MM xxzz Hxz       (74)   2 ,,, 2 T yy Txyz      (75)  2 ,, 2 M yy Hxzt      (76)

4. NUMERICAL RESULTS AND DISCUSSION

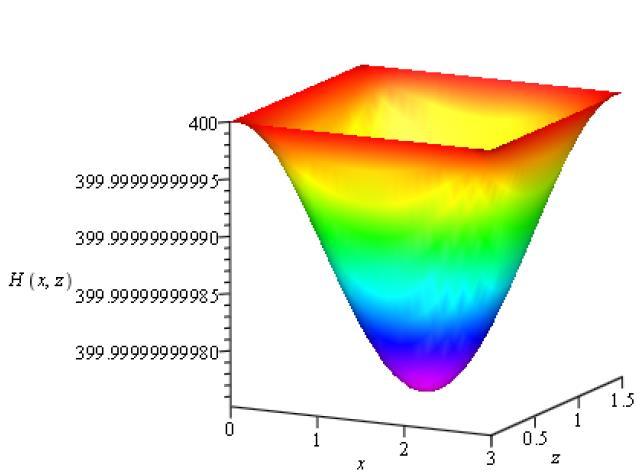
To illustrate and compare the theoretical results obtained, we now present some numerical results which depict the variations of displacement, temperature, and stresscomponents.Thematerialchosenforthepurposeof numerical evaluations is steel, for which we take the followingvaluesofthedifferentphysicalconstants,usingthe physical data given in [22]. Figure 2, shows the magnetic field inside the rectangular plate. It is found that the magnetic field intensity is symmetric in both directions. Figure 3, shows the variations of specific heat losses with frequency. Frequency has a huge impact on both Eddy current loss and Hysteresis loss as well as on the general properties of ferromagnetic materials. At high frequency, eddy current losses are dominating whereas at low frequency, hysteresis losses are determining. At low frequency,theHysteresislossisabitlargerthantheeddy currentloss(seeFigure3),whilethemagneticfluxdensity remainsthesame.Meanwhile,whenthefrequencyreaches above110 Hz,eddycurrentlossispredominantascompared to hysteresis loss. Further, as frequency increases slowly, bothlossesalsoincrease.

frequency.Figure4,showsthatthetotalheatlossesincrease whenmagneticfluxdensityincreases,whereasfrequencyis keptasconstant.Italsoshowsthatthetotalheatlossgets largerandlargerasthefrequencyofinputsupplyincreases, meanwhile, the magnetic flux density remains constant. Thus,steadygrowthisobservedintotal heatloss with an increase in magnetic flux density and the frequency increases from 50250. HztoHz This is because as per equation(17)thetotalheatlosstermconsistsoftwoparts, Heat loss due to Eddy current and due to Hysteresis phenomenon.AndEddycurrentlossisdirectlyproportional to the frequency of the supply whereas Hysteresis loss is proportional to the square of the frequency (see equation (14)). Therefore, this will lead to an increase in total heat losswithanincreaseinfrequency.Figure5showstheeffect of the resistivity of the material on the variation of Eddy current loss. Resistivity is the main factor that affects the Eddy current loss of the electrical machines which work under the time-varying electromagnetic field. The Eddy current loss mainly depends on the resistivity of the thin lamination platesof insulationmaterial whichareused in the machines like transformers where the thermal effect produced by the Eddy current loss affects the working environmentofthemachinedrastically.

Eddycurrentlosseshaveapowerfulimpactontotalheat loss.However,Hysteresislossesareimportantpartsoftotal heatlossesatlowfrequencies.Thegraphofhysteresislossis linearasitisproportionaltothefrequencywhiletheeddy current losses are proportional to the square of the

Itisalsoobservedthatthe highertheresistivityofthe insulation/laminationmaterialthelessertheEddycurrent lossproduced.Mostoftheceramicswhicharenon-metals like porcelain have a high tendency to resist the flow of electric current. With the use of such high resistivity materialsforinsulationonecanreducetheEddycurrentloss completely.Eddycurrentlossisgreatestonthesurfaceand decreaseswhenwegodeepinsidetheplatematerial.Thisis becauseofthephenomenonso-calledas“SkinEffect”.The non-uniform distribution of the Electric current over the surfaceorskinofthematerialplatecarryingthecurrentis calledtheSkineffect.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 10 Issue: 07 | July 2023 www.irjet.net p-ISSN: 2395-0072 © 2023, IRJET | Impact Factor value: 8.226 | ISO 9001:2008 Certified Journal | Page1176       2 1 ,,2,,, 2 xxzz HxzTxyz          (77)     2 ,,2,,, 2 yy HxzTxyz        (78) ,,xyxz uvuw yxzx       yz vw zy       (79)

Physical Constants Value Permeabilityofvacuum(µ0) 1.26×10-4 H/m Lame’sconstant(µ) 79.3GPa Electricconductivity(σ) 7.7×106 S/m SpecificHeat(C) 502.416J/kgK Density(ρ) 7663kg/m3 CoefficientofThermalIntensity(κ) 1.4×10-3m2/sec Poisson’sRatio(ν) 0.28 ThermalDiffusivity(α) Heatconductioncoefficient(λ0) Electricfieldintensity(E) 12×10-6 K-1 50W/mK 205GPa

Table -1: MaterialConstants Fig -2:Distributionofmagneticfieldintensityalongxand zdirection

Fig-3: VariationofSpecificheatlossesversusfrequency

Fig-6: VariationofSkindepthwithfrequency

Fig-4: DistributionofTotalHeatLossversusfluxdensity

Fig-7: B-HCurveforSteel,IronandAir

Fig-5: EffectofResistivityonEddyCurrentloss

The skin depth   of the magnetic material defines a certaindistancetowhichthestrengthoftheelectromagnetic fieldsufferstheresistanceintheamplitudeanditreducesto 1/ e ofitsoriginalamplitude.

Fig-8: Timevariationofnon-dimensionaltemperature alongthethicknessoftheplate

Orinotherwords,skindepthdefinesthedistancebelow thesurfaceofthecurrent-carryingconductorwherethe amplitudeoftheelectromagneticfieldstrengthdecreases to1/eofitsvalueatthesurface.

This decrease is referred to as the decay of one Naper (0.368).Theoretically,itisgivenby[23]:

At higher frequencies, the electromagnetic waves can penetrateonlynearthesurfaceoftheplatematerialandthe strengthofelectromagneticwavesdecreasesexponentially withanincreaseinthethicknessoftheplatematerial.Figure 6 shows the variation of skin depth with the frequency of electromagnetic waves for various values of magnetic permeability. It shows that at higher frequencies the skin depthbecomesmuchsmaller.Therefore,theEddycurrent loss or heating aroused due to it can be controlled to any requireddepthofthematerialsimplybychangingthesupply of input frequency. Figure 7 represents the variation of Magnetic fluxdensity(B) withtheMagneticfieldstrength (H)forSteel,Iron,andAir. Fromthefigure,wecannotice thatvariationinmagneticfielddensityisproportionaltothe Magneticfieldstrengthuntilitreachesacertainvaluefrom

Fig-9: Timevariationofnon-dimensionaltemperaturefor differentvaluesoffrequency Fig-10: Variationofdisplacementcomponent u alongthe thicknessofplatefordifferentvaluesoftime Fig-11: Variationofdisplacementcomponent v alongthe thicknessofplatefordifferentvaluesoftime Fig-12: Variationofdisplacementcomponent w alongthe thicknessofplatefordifferentvaluesoftime Fig-13: Variationofstresscomponentalongthethickness ofplatefordifferentvaluesoftime

1 f    (80)

which it does not increase anymore and becomes almost constant and steady while the Magnetic field strength continuestoincrease.Fromthefigure,itcanbeseenthatfor Steelthemagneticfluxdensityincreasesupto1.5Tandthis pointinthegraphisreferredtoasthe Magnetic Saturation. Thus, Magnetic Saturation is the point of maximum flux density attained by the ferromagnetic material in the B-H Curve.Figure8showsthetimevariationoftemperaturefor thedifferentvaluesofthickness.Itcanbeobservedfromthe figurethattemperaturefirstincreasesandthenitbecomes steady with time. Also, since wave frequency is inversely proportional to the skin depth of the plate material, therefore as soon as the plate thickness increases the temperatureoftheplatedecreases.Fromthefigure,itcanbe observedthatforhigherplatethicknessthetemperatureis lowerascomparedtothatforsmallplatethicknesses.Figure 9showsthetimevariationoftemperatureatthemiddleof theplatewithdifferentvaluesoffrequency.Duetotheeffect ofwavefrequencytheplateheatsupgraduallytoattainthe maximum temperature then after a few seconds, the temperature becomes steady. Figure 10 displays the distribution of the displacement component u versus distance y . The displacement component always begins fromzeroforthefourvaluesoftimecoordinateandsatisfies the boundary condition at 0 y  as well as the initial condition at 0.   For 2,3,4sec   the displacement component u decreases for the range 00.06 x  and 0.20.26 x  while it increases in the range 0.060.2 x  and 0.260.38. x 

It can be observed that thedisplacementcomponent u decreasesastimeincreases. Anditisshowingoscillatorybehaviorandfinallyconverging towardszerowiththeincreaseof y .InFigure11and12, variation of v and w with respect to y is presented for variousvaluesoftimecoordinate.Itisnoticedthat v and w decrease with time. Displacement components exhibit oscillatory behavior and tend towards zero with the increment in y . Figure 13 shows the variation of Stress components along the thickness of the plate for different valuesoftime.

5. CONCLUSIONS

In this paper, a three-dimensional model of Magnetothermo-elasticity under the influence of time-varying magnetic field is established. Taking Steel plate as an exampleofferromagneticmaterial,aseriesofanalyseswere carriedout.Accordingtotheresultsobtainedinthispaper, thefollowingconclusionscanbeobtained:

1. ThesubjectofthispaperisobtainingEddycurrentloss and Hysteresis loss as the total heat loss of the ferromagneticplate.

2. ThedistributionfunctionofMagneticfieldintensityina rectangular plate of steel material is expressed in context of Maxwell’s equations using Double finite Fouriersinetransform.

3. It is observed that the time-varying electromagnetic field is responsible for the generation of Joule heat whichultimatelygivesrisetoEddycurrentloss.

4. Theinfluenceofthefrequency,magneticfieldintensity, and the plate thickness on the total heat loss is discussed.

5. One of the very suitable methods for solving the problem as discussed in this paper is the integral transformtechnique(Finite Fouriercosinetransform, Double finite Fourier Sine transform and Laplace transform).

6. It is found that the temperature increases with an increase in wave frequency and decreases with an increaseinplatethickness.

7. The conductivity of the material affects the depth of penetrationsignificantly.

REFERENCES

[1] F. C. Moon, Magneto-solid mechanics, WileyInterscience,1984

[2] N. Tsopelas and N. J. Siakavellas, “Influence of some parameters on the effectiveness of induction heating,” IEEE Transactions on magnetics 44, 4711–4720,2008.

[3] Rudnev, V., Loveless, D., and Cook, R. L, Handbook of inductionheating,MarcellDekkerInc.,NewYork,2003.

[4] I.-H.Park,I.-G.Kwak,H.-B.Lee,K.-S.LeeandS.-Y.Hahn, “Optimal design of transient eddy current systems driven by voltage source,” IEEE TransactionsonMagnetics33,1624–1629,1997.

[5] B.Ebrahimi,M.B.KhameseeandF.Golnaraghi,“Anovel eddy current damper: theory and experiment, Journal of Physics D: Applied Physics 42, 075001,2009.

[6] L. Knopoff, “The interaction between elastic wave motionandamagneticfieldinElectricalconductors,”J. ofGeophysicalResearch,60,441–456,1955.

[7] P. Chadwick, “Elastic wave propagation in a magnetic field,” Proceedings of the Int. Congress of Applied Mechanics,Brussels,Belgium,143–153,1957.

[8] S. Kaliski, J. Petykiewicz, “Equation of motion coupled with the field of temperature in a magnetic field involving mechanical and electrical relaxation for anisotropicbodies,”ProceedingsofVibrationProblems, vol.4,1–12,1959.

[9] G. Paria, “On magneto-thermo-elastic plane waves,” ProceedingsoftheCambridgePhilosophicalSociety,58, 527–531,1962.

[10] A.J.Wilson,“Thepropagationofmagneto-thermoelastic plane waves,” Math. Proc. Cambridge Philos. Soc. 59, 438–488,1963.

[11] A. H. Nayfeh, S. Nemat-Nasser, “Electromagnetothermoelastic plane waves in solids with thermal relaxation,”J.ofAppliedMechanics,TransactionsASME, 39,1,108–113,1972.

[12] H.H.Sherief,M.A.Ezzat,“Athermal-shockproblemin magneto-thermoelasticitywiththermalrelaxation,”Int. J.ofSolidsandStructures,33,30,4449–4459,1996.

[13] S.Biswas,SMAbo-Dahab,“Three-dimensionalThermal ShockprobleminMagneto-ThermoelasticOrthotropic Medium,”J.ofSolidMechanics,12(3),663–680,2020.

[14] Y.Xu,D.Zhou,K.Liu,“ThreeDimensionalThermoelastic AnalysisofRectangularPlateswithVariableThickness Subjected to Thermomechanical Load,” J. of Thermal Stresses,33:1136-1155,2010.

[15] A. Baksi, R. K. Bera, L. Debnath, “A study of magnetothermoelastic problems with thermal relaxation and heat sources in a three-dimensional infinite rotating elasticmedium,”Int.J.ofEngineeringScience,43,19-20, 1419–1434,2005.

[16] S. K. Roychoudhuri, “Magnetoelastic plane waves in rotating media in thermoelasticity of type II (GN model),” International Journal of Mathematics and MathematicalSciences,3917–3929,2004.

[17] M.I.A.Othman,S.Y.Atwa,A.W.Elwan,“Theeffectof MagneticfieldandThermal relaxationTimeonthreedimensional thermal shock problem in Generalized Thermoelasticity,” Int. J. of Innovative Research in Science, Engineering and Technology, 4(4), doi: 10.15680/IJIRSET.2015.0404069.

[18] M.A.Ezzat,A.S.El-Karamany,A.A.El-Bary,“Magnetothermoelasticity with two fractional order heat transfer,”J.ofAssociationofArabUniversitiesforBasic and Applied Sciences, 27, doi: 10.1016/j.jaubas.2014.06.009.

[19] B.Das,S.Chakraborty,A.Lahiri,“GeneralizedMagneto thermoelasticInteractionforaRotatingHalfSpace,”Int. J.ofAppliedandComputationalMathematics4(3),doi: 10.1007/s40819-018-0523-9.

[20] L. C. Bawankar, G. D. Kedar, “Magneto-Thermoelastic ProblemwithEddyCurrentLossofaThermosensitive ConductivePlate,”AdvancesinMathematics:Scientific Journal,doi:10.37418/amsj.10.1.55,2021.

[21] M. Higuchi, R. Kawamura, Y. Tanigawa, H. Fujieda, “Magneto-thermoelasticStressesInducedbyaTransient

Magnetic Field in an Infinite Conducting Plate,” J. of MechanicsofMaterialandStructures,2,113–130,2007.

[22] V.Miloševic-Mitić, D. Kozak,T.Maneski,N. Anđelić,B. Gaćeša, M. Stojkov, “Dynamic nonlinear temperature fieldinaferromagneticplateinducedbyhighfrequency electromagnetic waves,” Strojarstvo52, (2), 115-124, 2010.

[23] V. Miloševic-Mitić, “Temperature and Stress Fields in ThinMetallicPartiallyFixedPlateinducedbyHarmonic Electromagnetic wave,” FME transactions 31, 49-54, 2003.

[24] H. Parkus, “Electromagnetic Interactions in Elastic Solids”,Springer-Verlag,1979.

[25] F.Pasquel,“DoubleFiniteFourierSineTransformand ComputerSimulationforBiharmonicEquationofPlate Deflection,”EuropeanInternational JournalofScience andTechnology,8(3),59-64,2019.