Modified Mountain Gazelle Optimizer Based on Logistic Chaotic Mapping and Truncation Selection
Abdul-Fatawu Seini Yussif1 , Elvis Twumasi2 , Emmanuel Asuming Frimpong31,2,3 Department of Electrical and Electronic Engineering, Kwame Nkrumah University of Science and Technology, Kumasi, Ghana
Abstract - In this study, a Modified Mountain Gazelle Optimizer (MMGO) algorithm is presented. The proposed algorithm was designed to improve the ability of MGO in solving high-dimensional problems, increase convergence speed, and enhance stability. The modification is based on the application of a logistics chaotic mapping at the initialization stage, a modified Migration pattern in the Search of Food (MSF) phase for diversity maintenance, and a controlling factor at the Territorial and Solitary Males (TSM) phaseusing the truncation selection technique. The proposed algorithm was implemented in MATLAB software and its performance was tested on 23 benchmark functions, and a real-life engineering problem to prove its efficiency and adaptability. The results of the MMGO were compared with those of the basic Mountain Gazelle Optimizer (MGO), Particle Swarm Optimization (PSO), and Gravitational Search Algorithm (GSA). The findings of the work indicated that the MMGO outperformed the other state-of-the-artalgorithmsintermsof both optimization accuracy and computationalefficiency. The results demonstrated the effectiveness and robustness of the proposed MMGO algorithm, in solving high-dimensional optimization problems in engineering and other fields.
Key Words: Mountain Gazelle Optimizer (MGO), logistics chaotic mapping, truncation selection technique, highdimensionalproblem,optimization.
1. INTRODUCTION
The use of metaheuristic algorithms in finding optimal solutionstocomplexproblemshasseenwideapplicationsin various fields such as engineering, finance, and computer science[1,2].However,asthecomplexityanddynamismof the problem increase, metaheuristic algorithms often struggle to find the global optimum solution within a reasonabletimeframeanditerations[3-5].Toaddressthis limitation, researchers have proposed modifications to metaheuristicalgorithmstoenhancetheirperformancein solving complex optimization problems [6-8]. These modifications can improve the search efficiency of the metaheuristic algorithms, thereby enabling them to find bettersolutions.Onesuchmodificationistheincorporation ofproblem-specificoperators[9].For instance,Ogun et al proposed a modified bull optimization algorithm for continuous optimization problems based on genetic operators[10],andBingetalimprovedtheSparrowSearch
Algorithm (SSA) with a mutation strategy for global optimization[11].

Thoughtheseimprovedalgorithmsofferapromisingavenue forsolvingcomplexproblems,researchersarestillinsearch ofnovelalgorithmsthatexhibitrobustness,flexibility,and the ability to handle diverse problem domains. Also, the dynamicnatureofmanyreal-worldproblemsnecessitates newly developed algorithms that are adaptive and can quicklyrespondtochangingorevolvingproblemconditions [9,11].TheMountainGazelleOptimizer(MGO)developedby Benyaminetal[12]in2022isoneofsuchalgorithms.The MGOhasbeenproventohandleproblemscharacterizedby high nonlinearity, and combinatorial complexity and has exhibitedgoodperformancewhentestedonsomestandard benchmarktestfunctionsandreal-lifeengineeringproblems. However,similartosomeothermetaheuristicalgorithms,it stillsuffersfromoptimizationaccuracy,slowconvergence, and entrapment in suboptimal solutions when applied to complex high-dimensional optimization problems [12]. These high-dimensional and large-scale problems often exhibit a large number of variables, constraints, and interactions,makingitdifficultfortheMGOtogetanexact solutionduetotheexponentialgrowthofthesearchspace.
Thisismainlyassociatedwiththepoorqualityoftheinitial population, lack of proper diversity maintenance mechanism,andlackofeffectiveconvergencecontrolinthe algorithmderivation[12].However,inordertoensurethe holisticapplicationofthisessentialalgorithmwhichisbased onthesocialintelligenceofmountaingazellesinthewildlife, there needs to be an improvement of its parameters to ensureitsexplorationandexploitationabilitytodealwith highdimensionalproblems.
Therefore,thispaperproposesaModifiedMountainGazelle Optimizer(MMGO),animprovementoftheMGOalgorithm to enhance its performance in solving high-dimensional engineeringproblems.Threemodificationsareincorporated. Firstly, a Logistic Chaotic mapping [13][14] is utilized to replace the random initialization in MGO to improve the quality of the initial population. Secondly, an operator is modifiedtomaintaindiversityinthepopulationduringthe execution process to avoid suboptimal solutions [15]. Thirdly,aTruncationSelectionTechnique[16]isadoptedto determine the value of the newly introduce parameter to control the convergence speed. The effectiveness of the
proposedMMGOalgorithmisestablishedbybenchmarking itsperformanceagainsttheoriginalMGOandotherstate-ofthe-artoptimizationalgorithms,includingPSO[8],andGSA [17].
Theremainderofthispaperisarrangedasfollows:thebasic MGOalgorithmisbrieflydescribedinsection2.Insection3, a detailed description of the three modifications is presented.Section4containsthetestbenchmarkfunctions andtheengineeringproblem,togetherwithtestparameters. Section5:theresultsarepresentedanddiscussed.Finally, the conclusion and recommendations are presented in section6.
2. MOUNTAIN GAZELLE OPTIMIZER (MGO)
2.1 Inspiration
Themountaingazelleisatypeofgazellethatisnativeto theArabianPeninsulaandsurroundingareas[12].Although it has a large distribution range, its population density is quitelow.Thespeciesiscloselyassociatedwiththehabitatof the Robinia tree species. Mountain gazelles are highly territorial and their territories are located at a significant distancefromoneanother.Theyformthreetypesofgroups, including mother-offspring herds, young male herds, and single males withtheir territories.Male gazelles engagein regularbattles,withthestruggleforresourcesbeingmore dramatic than the battles for the possession of females. Immature males use their horns more often in fights than adultsorterritorialmales.Mountaingazellesmigratemore than 120 km in search of food. They have a high running speed,withtheabilitytorunahundredmetersat80km/h.
2.2 Mathematical Model of MGO
The MGO optimization algorithm is derived from the social behavior and habitats of mountain gazelles and is based on a mathematical model that incorporates key aspectsofthegazelles’grouplife,includingthebehaviorof bachelor male herds (BMH), maternity herds (MH), territorialandsolitarymales(TSM),andmigrationpattern in search of food (MSF) [12]. They are modelled mathematically,asfollows.
Territorial Solitary Males (TSM):
Adult mountain gazelles create and protect their territoriesbyengaginginabattle,andthisphenomenonis modeledintoequation1asfollows.
Xra isarandomsolution(youngmale)intherangeof ra Mpr is the average number of search agents randomly selected. N is the number of gazelles, and r1 and r2 are randomvaluesfromarangeof0and1.

N1 is a random value in the problem dimension determinedusingastandarddistribution, Iter,and MaxIter representstheiterationcounterandthemaximumiterations respectively.
Inequation(4), a iscalculatedusingequation(5).also, r3 and r4 arerandomvaluesselectedfromarangeof0to1. N2, N3,and N4 arerandomnumbersinthenormalrangeofthe searchspaceandhavetheproblemdimension.
Where; ri1 and ri2 arerandomintegers1or2,malegazelle represents the position vector of the global solution (best malegazelle),and HB, F, Cofr aregiveninequations(2),(3), and(4)respectively.
Maternity Herds (MH):
Maternity herds play an important role in mountain gazelles’lifeasthemotherprovidesimmediateprotection and grooming to her young ones. This is modelled in Equation6below.
Xrand is a random vector position of a gazelle from the entirepopulation, ri3 and ri4 areintegersrandomlyselected fromeither1or2.
Bachelor Male Herds (BMH):
Uponmaturity,youngadultmalescreatetheirterritories andturntoengageinabattlewiththeadultmalesforthe possession of the female gazelles. This is formulated into equation(7).
X(t) is the position vector of the gazelle in the current iteration, ri5, and ri6 are integers of either 1 or 2. D is determined using equation (8), where r6 is a randomly selectedvaluefromarangeof0to1.
Where; rj isarandomlychosenvaluefromtherangeof3.5to 4, x0 is the initial value of xj chosen as 0.5. Below is the pseudocodefor XCh.
Initialize xo (xo =0.5), d, lb, ub, and N.
Migration in Search of Food (MSF):
Mountaingazellescontinuouslylookforfoodbytraveling overlongdistances.Thisrandommovementismodelledin Equation(9)below.
For i=1:N
For j=1:d
Update the value Ch X according to equation (11).
Update the value i X according to equation (10).
Where; lb, and ub arethelowerandupperboundsofthe searchspacerespectively,and r7 isarandomlydetermined value(0,1).
Algorithm 1: Pseudo-code of MGO
Inputs:thepopulationsizeN,andmaximumiterations
Output:Gazelle’slocationandfitnesspotential
Createarandompopulation,Xi(i=1,2,..N)
CalculateGazelle’sfitnesslevel.
While (thestoppingconditionisnotmet) do for (eachGazelle(Xi)) do
CalculateTSMusingequation(1)
CalculateMHusingequation(2)
CalculateBMHusingequation(3)
CalculateMSFusingequation(4)
Calculate the fitness values of TSM, MH, BMH, andMSF end for
Sorttheentirepopulationinascendingorderaccording tofitness.
end while
ReturnXbestGazelle ,theBestFitnessvalue.
3. PROPOSED MODIFICATION
To modify the basic mountain gazelle optimizer (MGO) to improve its performance in handling high-dimensional optimizationproblems,threeapproacheswereused.Firstly,a logistic chaotic mapping [13] is adopted to generate the initial population of the algorithm in place of the random approach used in the traditional MGO. This is given in Equation(10)below.
Also,theupdateoperatorattheterritorialandsolitarymale (TSM)phase,thatisequation(12),ismodifiedtoincrease theconvergencespeedoftheMGOalgorithmbyintroducing a controlling factor whose value is determined using the truncationselectiontechniqueinthegeneticalgorithm[16]. Theupdatedoperatorisshowninequation(12).
Where 0,1 isacontrollingfactordeterminedusingthe truncation selection technique based on the pseudocode givenbelow.
Start
Select n, the sample size. For i=1: n (); i xrand
Evaluate the performance of ix

Sort all values of x according to the performance from best to worst.
Select 1x , where 1x is the best x value.
Finally,theupdateoperator atthemigratingtosearchfor food(MSF)phaseismodifiedbychangingittoenhanceits abilitytosearchthoroughlywithinthesearchspaceforthe continuous maintenance of good divergence in the population for high dimensional problems. The adopted approachhasbeenappliedin[5,15].Itisgiveninequation (13)below.
Where; Xch isasetofvaluesgeneratedfromtherange0to1 withtheproblemdimensionusinglogisticchaoticmapping byequation(11).
Where lb and ub, are the lower and upper bounds of the search space, and r7 is a random value selected from the range0to1.
TheflowchartoftheproposemodifiedMGOisshowninfig1 below
Initialize population N using equation (10), Iter, and MaxIter

Calculate TSM, MH, BMH, and MSF using the modified eq (12), eq(6), eq(7), and eq(13) respectively
Calculate the fitness of TSM, MH, BMH, and MSF from the modified equations
Update and sort entire population in ascending order according to their fitness values
In addition to the above details, the proposed MMGO algorithmwasimplementedinMATLAB2019aversionusing thestandardparametersinreference[12].Theseincluded 500 iterations and 30 runs for each test function. The following statistical information was extracted from the resultsandcomparedtothatoftheoriginalMGO,PSO,and GSA; best solution (Best), worst solution (Worst), mean solution (Mean), and standard deviation of the solutions (STD).
4. TESTING OF PROPOSED MMGO
Twenty-three(23)Standardbenchmarktestfunctionsand theparameterestimationforFMsoundwaveoptimization problem[12],wereusedtotesttheproposedmodificationto ascertaintheeffectivenessofitsperformance.Thetwentythree(23)standardbenchmarktestfunctionsthatconsistof third-teen (13) high-dimensional problems, and ten (10) fixed-dimensional problems were tested on. The results were compared to other three optimization algorithms, including original MGO [12], Particle Swarm Optimization (PSO) [8], and Gravitational Search Algorithm (GSA) [17]. ThedetailsofthefunctionsaregiveninTable1.
ToassesstheperformanceoftheproposedMMGOalgorithm onhandlinghighdimensionalengineeringproblems,itwas testedonthestandardParameterEstimationofFMSound Waveoptimizationproblemwhichisoneofthechallenging high-dimensional and multimodal engineering problems [12] The proposed MMGO algorithm was tested on it to establish its superiority over other algorithms by comparisonoftheirsolutions.
The best solution of the problem is 0 sol fX , where
The mathematical representation of the problem used as objectivefunctionispresentedinequation14
5. RESULTS AND DISCUSSIONS
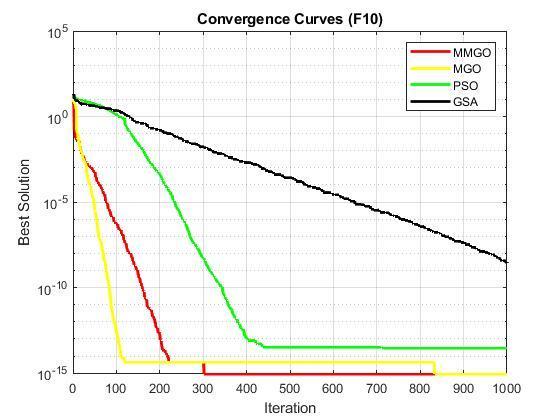
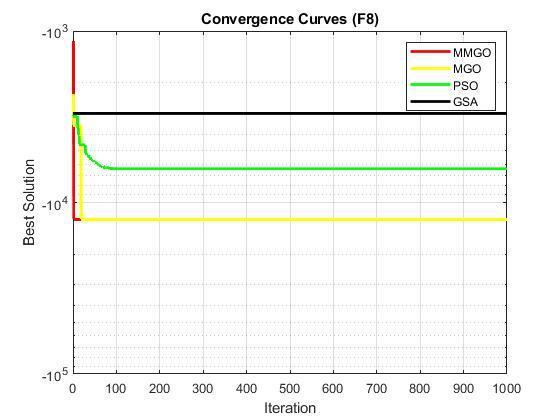
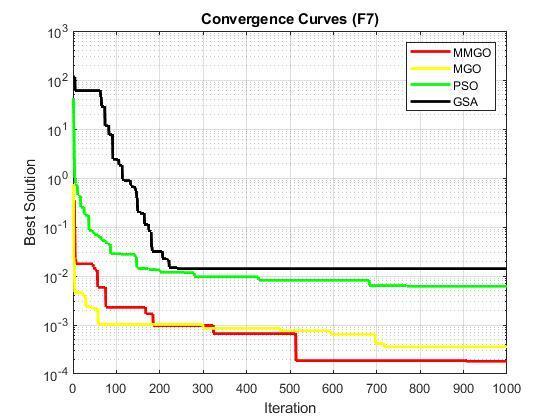
The outcome of the tests is as shown in table 2. Table 2 contains the simulation results of the proposed MMGO algorithmandotherstate-of-the-artoptimizationalgorithms (MGO,PSO,andGSA).Thecomparisonisbasedonthebest results, worst results, mean, and standard deviation from repeated runs of thirty times. The proposed MMGO significantlyoutperformedMGO,PSO,andGSAinF1,F2,F3, F4,F5,F6,F7,F8,F9,F10,F11,F12,andF13.Thesefunctions arehigh-dimensionaloptimizationtestfunctions,implying that the proposed MMGO would outperform the others in realhigh-dimensionalproblems.

Table – 2:ResultsComparisonofTestFunctions
Also,MMGOmaintainedthebestresultsproducedbyMGO, and improve the worst value, mean value, and standard deviationinF14,F15,F16,F17,F18,F19,F20,F21,F22,and F23. These consist of fixed-dimensional optimization benchmark functions, and this implies that the proposed MMGOhasthepotentialtoperformefficientlyonrealfixeddimensionalproblems.

Inaddition,theconvergencecharacteristicsofMMGO,MGO, PSO,andGSAareplottedonthehigh-dimensionalfunctions andpresentedasF1toF12.Itisobservedinthecurvesthat MMGOconvergesveryfastandproducedthebestoroptimal solutions with fewer iterations compared to the other optimizationalgorithms(MGO,PSO,andGSA).Thisconfirms thattheproposedMMGOissuitableforreal-lifeoptimization problemsthatrequirefastconvergencewithlessiteration.
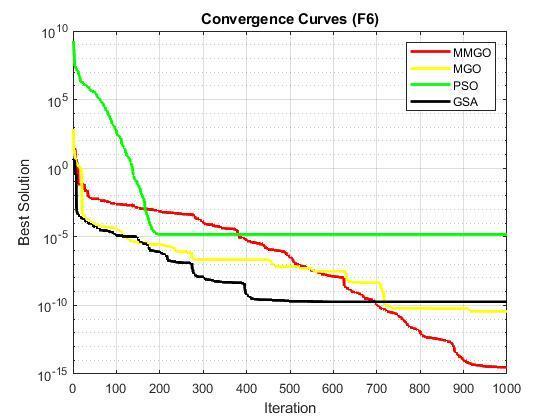

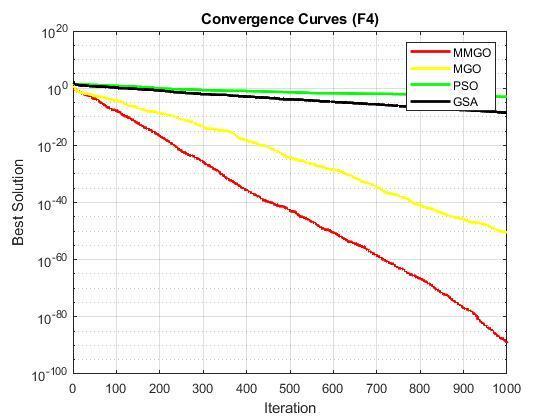
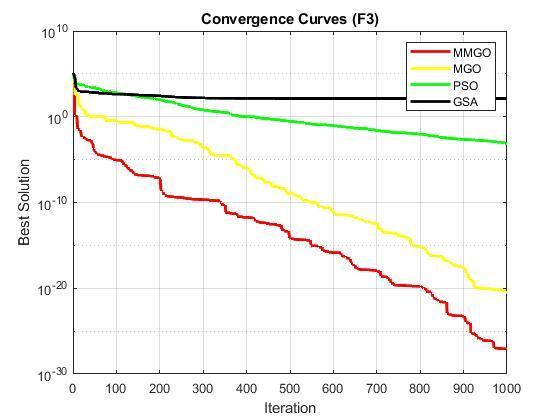
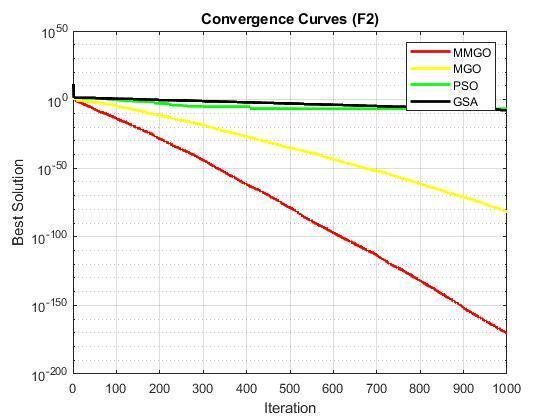

Finally,theresultfromthetestontheparameterestimation of FM sound wave is presented in Table 3 below. It is compared with that of the original MGO, PSO, and GTO pickedfromliterature[12],anditisshownfromtheresults thatMMGOoutperformedthemwithcompetitiveresults.




6. CONCLUSION
AnimprovedversionofthetraditionalMGOalgorithmcalled modifiedmountaingazelleoptimizer(MMGO)ispresented. The modified MGO introduces three modifications at the initialization,themigrationtosearchforfood(MSF)phase, and the territorial and solitary male (TSM) phase. The proposedMMGOhasbeencomparedwiththeoriginalMGO, PSO,andGSAon23standardbenchmarktestfunctions.The proposedMMGOoutperformedtheotheralgorithmsonall 23 test functions in terms of quality results, fast convergence,andstability.Italsoavoidedstagnationinlocal optimalorsuboptimalsolutions.
The proposed MMGO algorithm is recommended for application in solving high-dimensional engineering problems, such as optimal integration of shunt compensatorsindistributionsystems,optimalintegrationof distribution generations, and optimal placement of sectionalizingswitchesinpowersystems.Also,MMGOcan beappliedtooptimizationproblemsinthefieldofcontrol systemsthatrequirefastconvergence.
REFERENCES
[1] T.Li,G.Shao,W.Zuo,andS.Huang,“Geneticalgorithm forbuildingoptimization-State-of-the-artsurvey,”ACM Int.Conf.ProceedingSer.,vol.PartF1283,pp.205–210, 2017,doi:10.1145/3055635.3056591.
[2] N. Eslami, S. Yazdani, M. Mirzaei, and E. Hadavandi, “Aphid–Ant Mutualism: A novel nature-inspired metaheuristic algorithm for solving optimization problems,”Math.Comput.Simul.,vol.201,pp.362–395, 2022,doi:10.1016/j.matcom.2022.05.015.
[3] P. Trojovský and M. Dehghani, “Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for EngineeringApplications,”Sensors,vol.22,no.3,2022, doi:10.3390/s22030855.
[4] M. O. Okwu and L. K. Tartibu, “Grey Wolf Optimizer,” Stud. Comput. Intell., vol. 927, pp. 43–52, 2021, doi: 10.1007/978-3-030-61111-8_5.
[5] D.K.SambariyaandR.Fagna,“AnovelElephantHerding Optimization based PID controller design for Load frequency control in power system,” 2017 Int. Conf. Comput.Commun.Electron.COMPTELIX2017,pp.595–600,2017,doi:10.1109/COMPTELIX.2017.8004039.
[6] Z.Peng,K.Dong,H.Yin,andY.Bai,“Modificationoffish swarm algorithm based on lévy flight and firefly behavior,”Comput.Intell.Neurosci.,vol.2018,2018,doi: 10.1155/2018/9827372.
[7] K. Hussain, M. N. Mohd Salleh, S. Cheng, and Y. Shi, “Metaheuristicresearch:acomprehensivesurvey,”Artif. Intell. Rev., vol. 52, no. 4, pp. 2191–2233, 2019, doi: 10.1007/s10462-017-9605-z.
[8] M. Jain, V. Saihjpal, N. Singh, and S. B. Singh, “An Overview of Variants and Advancements of PSO Algorithm,”Appl.Sci.,vol.12,no.17,pp.1–21,2022,doi: 10.3390/app12178392.
[9] D. Kwegyir, E. A. Frimpong, and D. Opoku, “Modified Local Leader Phase Spider Monkey Optimization Algorithm,”vol.5,no.2.pp.1–18,2021.
[10] O.Findik,“Bulloptimizationalgorithmbasedongenetic operators for continuous optimization problems,” Turkish J. Electr. Eng. Comput. Sci., vol. 23, pp. 2225–2239,2015,doi:10.3906/elk-1307-123.
[11] B.Maetal.,“EnhancedSparrowSearchAlgorithmwith MutationStrategyforGlobalOptimization,”IEEEAccess, vol. 9, pp. 159218–159261, 2021, doi: 10.1109/ACCESS.2021.3129255.

[12] B.Abdollahzadeh,F. S.Gharehchopogh, N. Khodadadi, and S. Mirjalili, “Mountain Gazelle Optimizer: A new Nature-inspired Metaheuristic Algorithm for Global OptimizationProblems,”Adv.Eng.Softw.,vol.174,no. May, p. 103282, 2022, doi: 10.1016/j.advengsoft.2022.103282.
[13] C. Han, “An image encryption algorithm based on modifiedlogisticchaoticmap,”Optik(Stuttg).,vol.181, no. December 2018, pp. 779–785, 2019, doi: 10.1016/j.ijleo.2018.12.178.
[14] F. B. Demir, T. Tuncer, and A. F. Kocamaz, “A chaotic optimization method based on logistic-sine map for numericalfunctionoptimization,”NeuralComput.Appl., vol. 32, no. 17, pp. 14227–14239, 2020, doi: 10.1007/s00521-020-04815-9.
[15] G.G.Wang,S.Deb,andL.D.S.Coelho,“ElephantHerding Optimization,”Proc.-20153rdInt.Symp.Comput.Bus. Intell. ISCBI 2015, pp. 1–5, 2016, doi: 10.1109/ISCBI.2015.8.
[16] K.JebariandM.Madiafi,“SelectionMethodsforGenetic Algorithms,”Int.J.Emerg.Sci.,vol.3,no.4,pp.333–344, 2013.
[17] E. Rashedi, E. Rashedi, and H. Nezamabadi-pour, “A comprehensive survey on gravitational search algorithm,”SwarmEvol.Comput.,vol.41,no.January, pp.141–158,2018,doi:10.1016/j.swevo.2018.02.018.
