BSCM, 34-1

BUTLLET Í

DE LA SOCIETAT CATALANA DE MATEMÀTIQUES

Institut d’Estudis Catalans

Volum 34 ● Número 1 ● Juny 2019

©delsautorsdelsarticles

EditatperlaSocietatCatalanadeMatemàtiques filialdel’Institutd’EstudisCatalans

CarrerdelCarme,47 08001Barcelona

Textrevisatlingüísticament

perlaUnitatdeCorrecciódelServeiEditorialdel’IEC.

Imprèsa Open Print,SL

ISSN:0214-316-X

DipòsitLegal:B19272-1987

Sónrigorosamentprohibides,sensel’autoritzacióescritadelstitularsdel copyright,lareproducciótotaloparciald’aquestaobraperqualsevolprocedimentisuport,incloent-hilareprografia ieltractamentinformàtic,ladistribuciód’exemplarsmitjançantllogueroprésteccomercial,la inclusiótotaloparcialenbasesdedadesilaconsultaatravésdexarxatelemàticaod’Internet. Lesinfraccionsd’aquestsdretsestansotmesesalessancionsestablertesperleslleis.

ButlletídelaSocietatCatalanadeMatemàtiques Vol.34,núm.1,2019

Índex

MiriamAlcaláVicente

L’inicidelageometrianoeuclidianaaItàlia.........................................5

CristinaDalfóiMiquelÀngelFiol

Elmètodedeleslíniesperalaresoluciónumèricad’equacions enderivadesparcials................................................................33

MercèVillanuevaiCristinaFernández-Córdoba

Codisdetectorsicorrectorsd’errorsialgunesdelessevesaplicacions alasocietatdelainformació.......................................................53

Englishsummaries......................................................................91

ButlletídelaSocietatCatalanadeMatemàtiques Vol.34,núm.1,2019.Pàg.5–32. DOI:10.2436/20.2002.01.84

L’inicidelageometrianoeuclidianaaItàlia

MiriamAlcaláVicente

Resum: Lageometrianoeuclidianaés,probablement,lateoriamatemàticamésrevolucionàriadelsegle xix.Desprésdepassardesapercebudadurantmésdetrentaanys, el1860s’iniciaunprocésderenaixença,quevaserimpulsatperlalabordedos matemàtics,G.JulesHoüeliGiuseppeBattaglini.

Enaquestarticletractaremelprocésdedifusió,desenvolupamentiacceptació delanovageometria,centrant-nosenelcontextitalià.Enparticular,mostraremque l’aportaciódeBattaglinienaquestcampvamésenllàdeladivulgació.Alfinaldel seuarticle«SullageometriaimmaginariadiLobatschewsky»enstrobemambuna inesperadacoincidènciaentreladescripcióquefadelplanoeuclidiàielmodeldel discdonatméstardperEugenioBeltrami.Ensproposemjustificarlasemblançaentre lesduesinterpretacions.

Paraulesclau: històriadelageometria,geometrianoeuclidiana,Hoüel,Battaglini, Beltrami.

ClassificacióMSC2010: 01A55,51-03,53-03.

1Introducció

Enssituemenelmomentdelarenaixençadelageometrianoeuclidiana,que esvainiciaraEuropal’any1860.Aquestprocésculminaamblapresentació delmodeldeldiscdeBeltrami,el1868,idelmodelprojectiudeKlein,el1871, quevanaportarlesraonsnecessàriesperadmetrelavalidesadelanova teoria,jaqueconstitueixenunaprovadelasevaconsistènciarelativaala geometriaeuclidianaoprojectiva,respectivament.L’acceptaciódelageometria noeuclidianavasuposaruntrencamentambelpensamentmatemàticanterior ivaprovocarunacrisienelsfonamentsdelesmatemàtiques,quenovaser resoltafinsafinalsdesegleamblareformulaciódelageometriadonadaper Hilbert.Podríemdir,doncs,queestractadeladescobertaméstranscendent delsegle xix,nonomésenl’àmbitmatemàtic,sinótambéfilosòfic.

MiriamAlcaláVicente

L’objectiud’aquestarticleseràveurecomarriba,delamàdeG.J.Hoüel1 i G.Battaglini,2 lanovageometriaaItàliaielseuposteriordesenvolupamenten elstreballsd’E.Beltrami.3 Alavegada,explicaremlesdiferentsposicionsenel debatsobrelasevaacceptació.

Ladata,1860,quehapassataconsiderar-seelcomençamentd’aquesta renaixençavedonadaperserl’anyenquèescomençaapublicarlacorrespondènciadeC.F.Gauss.4 Lescartesdelcèlebrematemàticvandesvelarque s’haviaocupatdurantmoltsanysdelpostulatdelesparal.leles,totinohaver publicatmaires,5 iquelessevesrecerquescoincidienamblespublicadesper J.BolyaiiN.I.Lobatxevski.6 Nonomésaixò,tambédeclaralasevaaprovació iadmiraciópelstreballsdelsdosgeòmetres7 is’inclinaaacceptarlanova geometria.8

1 GuillaumeJulesHoüel(Thaon,1823-Périers,1886)vaestudiarprimeraCaenidesprés aRollin,abansd’ingressaral’Écolenormalesupérieurel’any1843.Enacabarelseusestudis vaensenyarmatemàtiquesadiferentsliceusfinsque,el1855,finalitzaelseudoctoraten mecànicacelestealaFacultatdeCiènciesdelaSorbonadeParís.El1859obtélacàtedrade matemàtiquespuresdelaFacultatdeCiènciesdeBordeus,succeintLeBesgue,idonantclasse decàlculinfinitesimal.Amésdelessevesaportacionsengeometria,ésdestacablelasevafeina enlacreacióirevisiódetaulesdecàlcul.

2 GiuseppeBattaglini(Nàpols,1826-1894)vaassistiral’escolaprivadadematemàtiquesde Tucciid’Angelis,deixeblesdeFergola,onesvaprepararperal’admissióalaRegiaScuoladi PontieStrade,enlaqualesvallicenciarl’any1848.Dosanysméstardcomençacomaalumne enl’ObservatorideCapodimonte,feinaqueaviatesveuràobligatadeixarpernegar-seasignar lapeticiódelreiBorbóperabolirlaconstitució.L’any1854espresentaalconcursperauna càtedraalaUniversitatdeNàpols,senseaconseguirlaplaça.Donarà,llavors,classesal’estudi deTuccifinsal’expulsiódelsBorbonsl’any1860,quanvapassaraocuparlanovacàtedrade geometriasuperioralaUniversitatdeNàpols.El1871estraslladaalaUniversitatdeRoma,fins al1885,quantornaaladeNàpols.

3 EugenioBeltrami(Cremona,1835-Roma,1900)provéd’unafamíliadereconegutsidealsdel Risorgimento,perlaqualcosavivienunasituaciódifícilsotaelgovernaustríac.Vacomençara estudiarmatemàtiquesalaUniversitatdePavia,peròvahaverd’abandonarelsestudisabansde llicenciar-seperqüestionseconòmiques.Obligatatreballarenfeinesadministrativespera l’enginyerDiday,descobreixlasevavocaciómatemàticairefàdeltotlasevaeducaciócientífica. El1862,BrioschielfanomenarperdecretprofessorextraordinarialaUniversitatdeBolonya. Unanyméstard,E.BettiliofereixlacàtedradegeodèsiaalaUniversitatdePisa.Degutala insistènciadeCremona,quevaserelseuamicimentordurantmoltsanys,tornaalaUniversitat deBolonya,el1866,iestraslladadesprésaRoma,el1873.Descontentalacapitaliperlasalut delasevadona,intentaràuntrasllatalaUniversitatdePàdua,quefracassàperl’oposicióde Cremona.L’any1876aconsegueixlacàtedradefísicamatemàticaalaUniversitatdePavia,on trobaràelseuamicFeliceCasorati,peròlamortprematurad’aquestelfaràdecidiratornara Romael1891.

4 Laprimeradepublicar-sevaserlaquemanteniaambSchumacher,editadaperC.A.F.Peters ensisvolumsqueapareguerenentreelsanys1860–1865[41].

5 VegeulacartadeGaussaSchumacherambdata17.5.1831editadaperPeters,a[41,1861, vol.2,p.261]oa Werke [24,1900,vol.8,p.212].

6 Hoüel,enlasevatraducciódel’articledeBattaglini[5,p.217],afirmaapeudepàginaque, defet,seriamésjustanomenaralateoriadelesparal.lelesdeLobatxevskilateoriadeGauss,ja quelacorrespondènciamostraquevaserelprimerainventar-la.

7 Vegeu,perexemple,sobreeltreballdeJanosBolyai,lacartadeGaussaGerlingdel14.2.1832 (aSchaefer[45,p.387]oa Werke [24,1900,vol.8,p.220]),ol’escritaalparedeJanos,Farkas, el6.3.1832(a Werke [24,vol.8,p.220–221],oalatranscripciódigitalitzadaa https://gauss. adw-goe.de).SobreeltreballdeLobatxevski,vegeuperexemplelacartaaSchumacherdel 28.11.1846(aPeters[41,1863,vol.5,p.246–247]oa Werke [24,1900,vol.8,p.239]).

8 Gaussreconeixperprimercopquenotrobaresd’absurdenlahipòtesinoeuclidianaala

Gauss,deliberadament,novaferpúbliquesaquestesopinions;nomésleshaviacompartitambalgunsamicsicol.leguesinteressatsenlaqüestió,conscient quelacomunitatmatemàtica,fortamentinfluenciadaperlafilosofiakantiana, noacceptarialesnovesidees.9 SenseelsuportdeGauss,lesmassainnovadoresrecerquesdeJ.BolyaiiN.I.Lobatxevskinovantenirlarepercussióque caliaesperardavantlasoluciód’unproblemaquehaviamantingutocupatsels matemàticsdesdelamateixaapariciódels Elements d’Euclides.

Recordemque,enaquestarecopilació,elmatemàticgrecconstrueixtotel coneixementgeomètricdel’èpocademanerarigorosa,fentservirladeducció lògicaipartintdecincpostulatsoaxiomesquehaviendesertanevidentsque ningúnoenpoguésdiscutirlaveracitat.Peròlacomplexaredacciódelcinquè postulat,eldelesparal leles,quecontrastaamblasenzillesadelsquatreanteriors,vaportaralacreençaqueesdeviapoderdemostrarapartirdelsaltres,i vapassaraserconsideratcomunteorema.10 Durantelsseglesposteriorsmolts matemàticsvanintentardemostrarelteoremasenseèxit,arribantsempreauna petitioprincipii,ésadir,enalgunmomentdelaprovasuposavencomacertun fet,aparentmentevident,queenelfonseraunenunciatequivalentalpostulat. Enelsseustreballs,independents,BolyaiiLobatxevskiparteixendelanegació delpostulatdelesparal leles,iaconsegueixenconstruirunsistemageomètric sensecapcontradicciólògica.D’aquestamanera,considerenquehanprovatla impossibilitatdedemostrarelpostulatapartirdelsanteriors,alavegadaque hantrobatunanovageometriapossiblediferentdel’euclidiana.11

Aquestresultatdesveladorvapassarpràcticamentdesapercebut,enpart, perquèelsautorsnoesmovienenelsprincipalscerclesacadèmics,peròsobretot,combésabiaGauss,perquècontradeial’epistemologiadeKant.Enla seva Críticaalaraópura,Kantexplicaquenototelconeixementprovéde l’experiència,hihaconceptesquesóninnatsalaraóhumana.L’ésserhumà, enobservarlarealitat,organitzalessevespercepcionsenl’espaiieltemps. Aquestessón,doncs,duescondicions apriori del’experiènciasensible.La geometriaeuclidiana,endescriurelespropietatsdel’espai,ésunconeixement apriori,éslanostramaneradepercebrelarealitat,pertant,ésl’únicageometriapossible.L’apariciód’unageometriabasadaenlanegaciód’unaxioma ilògicamentcoherentdesmuntacompletamentlavisiókantianadelmón.La sevacartaaGerlingdel’11.4.1816(aSchaefer[45,p.122],oa Werke [24,vol.8,p.168–169]),i esmostracadavegadamésconvençutenlacorrespondènciaposterior.Vegeuperexemplela cartaaSchumacherdel12.7.1831(aPeters[41,1861,vol.2,p.269]oa Werke [24,1900,vol.8, p.215–218]).

9Abardia,ReventósiRodríguez,a«WhatdidGaussreadintheAppendix?»[1],mostrenque Gaussintentavabuscarunasuperfíciequefeselpaperd’esferaimaginàriaenelseuestudide superfíciescorbes.Segurament,ennotrobar-la,noesvadecidirapublicarressobrelaqüestió, jaquenoteniaunasolucióconvincent.

10 Defet,jaentempsd’Aristòtil,hihaviadiscussionssobreelpostulatdelesparal.leles.Aquesta ésprobablementlaraóperlaqualEuclidesvaelaborarunenunciattancomplexivadecidir, encertadament,incloure’lentreelsaxiomes.Vegeul’articled’ImreToth«Non-EuclideanGeometry beforeEuclid»[47].

11 El3denovembredel1823,Bolyaiescriualseupare:«delno-reshecreatununiversnou». PodemllegirlaversióanglesadelacartaaBonola[15,p.98]ilatraduccióalcatalàa Unalectura del Disquisitiones,deReventósiRodríguez[42,p.110].

MiriamAlcaláVicente

realitatpodrianosereuclidiana,desprésdetot.Iencaraquehofos,noméses podriacorroborarmitjançantl’experiència,veientquinadelesduesgeometries s’adaptamilloralarealitatsensible.ComdiuLobatxevski,«resnoautoritza,a partdelesobservacionsdirectes,asuposarqueenuntrianglelasumadels anglesésigualadosanglesrectes».12

Laqüestiódelesparal lelesvacaureenl’obliti,durantelsanyssegüents, elpostulatvapassaraconsiderar-sedelamateixamaneraquelaquadratura delcercleoelmovimentperpetu,problemesques’hanmantingutirresolubles alllargdelahistòria.Lareferènciaaaquestsproblemesclàssics13 mostra,però, uncanvidementalitat;entreelsmatemàticsesvacomençarainstaurarla ideaqueelcinquèpostulatnoespodiademostrarapartirdelsaltresquatre, cosaquevadonarunacertapredisposicióaacceptarlesnovesideesproposades perBolyaiiLobatxevski.

L’autoritatdeGaussvadespertarràpidamentl’interèsperlespocconegudesobresd’aquestsautors.14 Aviatvanaparèixerlestraduccionsfrancesesi italianes,fetesrespectivamentperG.J.HoüeliG.Battaglini.15 Aquestsdos matemàticsvanimpulsarelprocésderenaixençadelanovageometria,no nomésamblessevestraduccions,sinótambéambladivulgacióielsuportque vandonaralesnovesidees.Elseupapervaserfonamentalenelposterior desenvolupamentdelageometrianoeuclidiana.

2ContextpolíticisocialaItàlia

EnstrobemenelsúltimsanysdelRisorgimento(1815–1870),quevafinalitzar amblaunificaciódelsdiferentsestatsitaliansenunsolpaís,sotaelgoverndel reiVíctorManuel.Moltsmatemàticsitaliansvanparticiparenaquestmoviment, formantpartdelesrevoltescontraelrègimpolíticestablert,16 icompartien l’idealdelaconstrucciódelnouestat.Amblaunificació,vanpassaraocupar càrrecsalesnovesinstitucions,desd’onesvanpoderimplicarenlesreformes del’educaciópúblicailauniversitatquevainiciarelnougovern.Elsmatemàtics

12 «...j’aiatâchédeprouverquerienn’autorise,sicenesontlesobservationsdirectes,de supposerdansuntrianglerectilignelasommedesangleségaleàdeuxanglesdroits...»A «Géométrieimaginaire»[36,p.295].

13 VegeuR.Baltzer, DieElementederMathematik [3,p. iii],iG.J.Hoüel,«Quelquesréflexions ausujetdelalignedelongueurminimumsurlasphère»[28,p.78].

14 Voelke,a[48,p.50],assenyalalescartesdeGaussaSchumacherambdates28.11.1846i 12.7.1831(aPeters[41,1863,vol.5,p.246–247i1861,vol.2,p.269]oa Werke [24,1900,vol.8, p.238–239ip.215–218])comelsprincipalsdesencadenantsdelarenaixençadelageometriano euclidiana;Battagliniesrefereix,amés,aladel17.5.1831(aPeters[41,vol.2,p.258–261])enla sevacartaaGenocchidel14.5.1867,a[19,p.167–168].Elpesdel’opiniódeGaussveconfirmat pelscomentarisdeBaltzerenelprefacide DieElementederMathematik [3,p. iii],ideHoüelen Surl’axiôme xi d’Euclide [27,nota vi del’apèndix,p.72].

15 El1866espublicalatraducciódel GeometrischeUntersuchungenzurTheoriederParallellinien deLobatxevskialfrancès[37],il’anysegüentladela«Pangeometria»al’italià[38].Les traduccionsdel’Appendix deBolyai,francesa[14]iitaliana[13],sónde1868.

16 Perexemple,CremonavaparticiparenladefensadelaRepúblicadeVenèciafinsalaseva rendiciól’agostdel1849;BrioschivalluitaralesCincJornadesdeMilà,enlesqualselshabitants insurgentsvanvèncerlestropesocupantsdelgovernaustríac;Bettivapertànyeralbatallódels universitarispisansalabatalladeCurtatoneiMontarael1848;iBeltramivaseracomiadatde l’administracióferroviàrialombardovènetael1859,perlessevesideespolítiques.

mésinfluentsenl’àmbitpolíticvanserLuigiCremona(1830–1903),17 Francesco Brioschi(1824–1897)iEnricoBetti(1823–1892).18

ElGovernvacreartambénouscentresderecercainovescàtedres,com lesdegeometriasuperior,assignadesperreialdecretaCremonaaBolonya iaBattagliniaNàpols.Vanaparèixerescolestècniquesdestinadesaformar enginyers,comelPolitecnicodiMilano,fundatperBrioschiel1863,ilaScuola diApplicazionipergliIngegneriaRoma,dirigidaperCremona,ontambé vandonarclasseBattagliniiBeltrami.Ladarreraformavapartdelprojecte deconvertirlarecentproclamadacapitalenelprincipalcentrecientíficide formaciódelpaís.Ambaquestaideaesvacreartambéunaescolanormal performarprofessors,19 iesvacridarelspersonatgesmésil.lustresireputats atreballaralauniversitat.Roma,però,noesvaacabarimposantcomacentre derecercamatemàticaaItàlia.20

Elprojecteperpromoureeldesenvolupamentdelamatemàticavaseguir diverseslíniesd’actuació,21 entrelesqualslainternacionalitzaciódelarecerca italiana.Ambaquestpropòsit,allotjatsacasadePlacidoTardy,aGènova,en lesvacancesdePasquadel1858,estrobenGenocchi,BettiiBrioschi;elsdarrers esvanconèixerenaquellmoment.Lareunióeraperparlardelanovarevista AnnalidiMatematicaPuraedApplicata,queescomençariaaeditaraquell any.Ambl’entradadelstresmatemàticsenladirecció,lapublicacióhaviade substituirels Annalidiscienzematematicheefisiche,queespublicavendes del1850sotaladirecciódeBarnabaTortoliniiquejadifoniengranpartdela recercafetaaItàlia.L’objectiueramantenirelsmatemàticsinformatstambé sobrelarecercaqueesduiaatermeforadelseupaís,iniciantunafeina detraduccióidivulgaciódelesprincipalsobreseuropees.Lainiciativaera compartidapel GiornalediMatematiche,dirigitperBattagliniaNàpols,quees vaconvertirenlaprincipalviadedifusiódelageometrianoeuclidiana.

Enlatrobada,Betti,BrioschiiGenocchiprojectenferunviatgealesprincipalsuniversitatsestrangeres.Pretenen,principalment,conèixerlesúltimes novetatsenrecercapertaldepublicar-lesalanovarevistaiposar-lesal’abast delsmatemàticsitalians,aixícompresentarlesinvestigacionsdelsdarrers. Alviatge,hivaacabaranantFeliceCasorati(1835–1890),llavorsassistentde Brioschi,enllocdeGenocchi,ivanvisitar,entreelsmesosdesetembreinovembre,lesprincipalsuniversitatsdeFrançaiAlemanya,païsosdeconsiderable tradicióenlaformaciódegransmatemàtics.AAlemanya,vananaraGöttingen, onvanconèixerDedekindiRiemann,perònoelsvaserpossibletrobar-seamb Dirichlet.TambévanviatjaraBerlín,onvanconèixerWeierstrass,Kummeri Kronecker,aLeipzigiaDresden.AParís,vanconèixerBertrandiHermite,però malauradamentnovanpodertrobar-seambLiouville.

17Vasersenador,ministred’InstruccióPúblicaivicepresidentdelSenat.

18 Totsdosvanserdiputats,senadorsisecretarisgeneralsdelMinisterid’InstruccióPública.Lasevacol laboracióésconsideradaelprincipalpotenciadordeldesenvolupamentdeles matemàtiquespostunitàries,vegeu«NewperspectivesonBeltrami’slifeandwork»[46,p.469]. 19VegeulacartadeBeltramiaHoüel,Bolonya8.10.1873,a[12,p.176].

20 EnlescartesdeBattagliniaHoüels’evidencienelsproblemesquesorgiren;vegeu,per exemple,ladel25.1.1872,a[19,p.126–127].

21 R.Tazziolienumeraleslíniesd’actuacióqueesvanduratermea«Newperspectiveson Beltrami’slifeandwork»[46,p.469].

MiriamAlcaláVicente

BettiquedàforçaimpressionatdelatrobadaambRiemann.Deseguida vatraduirlaseva Inauguraldissertation,del1851[43],iesvaencarregarde promocionarlessevesidees.Entreelsdosmatemàticsvasorgirunagran amistatiRiemannvapassarllarguestemporadesalaUniversitatdePisa convidatperBetti.Durantaquestsanys,Beltramieraprofessordegeodèsia alamateixauniversitatperò,comconfesaaHoüel,22 enlessevesfreqüents xerrades,Riemannmainovaparlardelesinnovadoresideesexposadesala sevamemòriapòstuma.23

Elsmatemàticsitaliansvanmantenirelcontacteamblesuniversitatsestrangeresiesvanesforçaraenviar-hielsjovesaespecialitzar-se.Vaser,per exemple,elcasdeGregorioRicci-Curbastro(1853–1925)iLuigiBianchi(1856–1928),quevanassistiralesclassesdeKleinalaUniversitatdeMunic,oUlisse Dini(1845–1918),alumnedeBetti,quevaestudiarunanyaParísambHermite. Elsesforçosperpotenciarlainvestigacióvancomportarl’oberturadenous campsderecercaivanpropiciarunentorncientíficqueaconseguíformar unanovageneraciódematemàticsitaliansreconegudainternacionalment.Pertanyenaaquestageneració,acavallentreelssegles xix i xx,Ricci-Curbastroiel seudeixebleTullioLevi-Civita(1873–1941),formatsalaScuolaNormaleSuperioredePisa,dirigidaperBetti.Tambévasermoltdestacablel’escolaitaliana degeometriaalgebraica,iniciadaperCorradoSegre(1863–1924)iEugenioBertini(1846–1933)seguintlalíniadelstreballsdeCremona,quetécomamàxims representantsGuidoCastelnuovo(1865–1952),FederigoEnriques(1871–1946), FrancescoSeveri(1879–1961)iGiuseppeVeronese(1854–1917).

Lareformaenl’educacióvaportaraunarevisiódel’ensenyamentdeles matemàtiquesalesescoles.SeguintlesindicacionsdeCremona,el1867,el ministred’educacióproposatornarautilitzarels Elements d’Euclidesper ensenyarlageometria.24 Aquellmateixany,BettiiBrioschipubliquenuna revisiódels Elements [11],ambalgunscomentarisiunasèried’exercicisalfinal decadallibre,25 pensatperquèesfesservircomallibredetext.Elmanual seguiaunestilpuramenteuclidià,conservantelllenguatgecaracterísticisense ferúsdel’àlgebraodel’aritmètica.Lasevaintencióeracontraposar-seals tractatscomunsqueseguienlalíniadels ElementsdeLegendre. 26 L’úsde mètodesexclusivamentgeomètricshaviaestatreivindicatperHoüelal’Essai critique, 27 queinsistiaenlanecessitatd’abandonarlametodologiadeLegendre enconsiderarqueelsprocedimentsmodernsques’introdueixensóndeltot innecessarisenl’exposició.

22VegeulacartadeBeltramiaHoüel,Bolonya4.12.1868,a[12,p.69].

23 Estractadel’Habilitationsvortrag,ladissertaciófetaperRiemann,el1854,perobtenirla qualificaciópostdoctoralnecessàriaperdonarclassealesuniversitatsalemanyes,titulada«Über dieHypothesen,welchederGeometriezuGrundeliegen»[44].Lamemòriaesvapublicarper primercopel1868,dosanysdesprésdelamortdeRiemann.

24 EstrattodalDecretoCoppino(10.10.1867), SupplementoallaGazzettaUfficialedelRegno d’Italia,Florència24d’octubrede1867.

25 SegonsexplicaFortiaHoüelalasevacartadel3.12.1867,queestrobaal DossierHoüel dels Archivesdel’AcadémiedesSciencesdeParís.

26Talcomelsmateixosautorsespecifiquenalprefaci[11,p. vi–vii].

27 Hoüelexposalessevesopinionssobrecomhauriad’estructurar-sel’ensenyamentdeles matemàtiquesalanota Réflexionssurl’enseignementdelagéométrieélémentaire del’apèndixde l’Essaicritique,a[27,p.81–85]oa[32,p.88–91].Alseumanual,BettiiBrioschiesrefereixenal treballdeHoüelendiversesocasions.

Eltextnovatenir,però,unabonaacceptacióentreelprofessorat,degutala sevacomplexitatialamancad’aportacionsdidàctiques,ivapassaraengrandir ladiscussió,encetadapeldecretministerial,entrepartidarisidetractorsdefer servirels Elements comallibredetext.Elsprimersdefensavenelrigord’Euclides,queconsideravenperdut,icreienqueeraunabonamanerad’ensenyar elraonamentlògic.Elssegonselconsideravenantiquat,perquènoincloïaels descobrimentsrecentsques’havienfetenaquestadisciplina,ipelllenguatge complicatques’hiutilitza.

LapolèmicaesvarevifaramblatraducciódelamemòriadeJ.M.Wilson, «Euclidasatext-bookofelementarygeometry»,28 publicadaal Giornaledi Matematiche sotalasignaturaR.R.,darrerelaquals’amagavaelprofessor RaffaeleRubini,delaUniversitatdeNàpols.29 L’escritfaunacríticacontundent deltextd’Euclidesiconclouqueés«antiquat,artificial,il lògiciinapropiat» comallibreperal’ensenyament.30 Lareacciódelspartidarisdeltextd’Euclides noesvaferesperar.Battaglinipublicaràal Giornale larèplicadeBrioschii Cremona,defensantlamesuragovernamental[16]iunfragmentdelacartaque varebredeHoüel[29].Totiaixí,semblaquel’editorcompartiaméslesopinions deRubini.31 EnlessevescartesaHoüel,Battagliniacceptalanecessitatdel rigorlògiciquecaldesenvoluparelsconceptessenserecórreral’àlgebra,32 peròtambédiuqueeltextd’Euclidess’hauriadeferservirnomésen«primer lloc»,sempresuposantqueselidonésunformatmoderniquefosrectificaten algunspunts.33 Creiemqueelqueenrealitatestàdient,ambmoltadiplomàcia, ésqueconsideraeltextantiquatiqueeltrobainsuficientperaconèixeren profunditatlageometria,seguramentpensantenelsnousdescobriments.La nostrainterpretacióesconfirmaenlacartaqueelnapolitàescriuaGenocchi, onesmostracontundentenelseudesacordambl’úsdeltextd’Euclides:

...nonhoritegnoadireche,contuttorispettopelmeritodell’Euclide,ritengo isuoiElementicomelibroinadattoall’insegnamento,tantosesihainmiral l’ammaestramentonella Geometria (perlapovertàdiquellibro)quantosesi riguardailsololatoeducativo,poichécredochequellibrosiapiùadattoad addormentarelamentedeiragazzi,cheasvolgerelelorofacoltà.34

[...notincreservesadirque,ambtotelrespectepelmèritd’Euclides,considero elsseus Elements comallibreinadequatperal’ensenyament,tantpelquefa alconeixementdela Geometria (perlapobresad’aquestllibre)comsiesmira noméselcantópedagògic,jaquecrecqueaquestllibreésmésadequatper adormirlamentdelsnoisquenopasperdesenvoluparlessevesfacultats.]

[BattagliniaGenocchi,7.2.1869]

28 TheEducationalTimes,1868,p.125–128.

29 TalcomrevelaFortiaHoüelalasevacarta,Pisa25.2.1869,queestrobaal DossierHoüel dels Archivesdel’AcadémiedesSciencesdeParís.

30VegeulatraducciódeRubini,a[49,p.368].

31 SegonsdiuBeltramienlasevacartaaHoüelambdataBolonya23.1.1870,a[12,p.126–127].

32CartadeBattagliniaHoüel,Nàpols19.7.1871,a[19,p.116].

33CartadeBattagliniaHoüel,Nàpols2.2.1869,a[19,p.78].

34A[19,p.169–170].

MiriamAlcaláVicente

Aquestadeclaraciópotsemblarmoltradicalenaquestcontext,peròsi pensemqueelllibreanavadestinataestudiantsd’institutd’entre10i15anys, laposiciódeBattaglinise’nsrevelaforçaequilibrada.

Mésendavant,Beltrami,quicomparteixlaposiciódeCremona,35 enformar partd’algunesinspeccionsalsinstituts,tindràl’oportunitatdeconèixerels resultatsqueestavatenintlamesuradelgovern,ivalorarqueelsprofessors reticentsacanviardemètodeerendeltipusquenomésdemanenestereotipar l’ensenyament.Alavegada,esqueixadelamancademanualsdequalitatdes delpuntdevistacientíficididàcticidelapocapreparaciódelprofessorat delesescolessecundàries.36 Conscientsd’aquestsproblemes,elsmatemàtics italiansesvanocuparenlatraducciódemanualseuropeusienlacreació denous.Tambés’instauraran,l’any1875,lesescolesdemagisteripertalde donarconeixementsactualitzatsalprofessoratiunentrenamentapropiaten qüestionspedagògiques.

3ElpaperdeG.J.Hoüel

Enlarecercahistòrica,lacorrespondènciaentreelsprotagonistestéuninterès especial.Enlessevespàginess’expressenintuïcionsencaranoconcretes,es plantegeniesresolendubtes,sesegueixendiscussions...endefinitiva,ens permetenconèixerelspensamentsdelsmatemàticsdelasevapròpiamà.La figuradeG.JoulesHoüelesrevela,peraquestaraó,moltrellevantenlahistòria delageometrianoeuclidiana.Elfrancèsescartejavaambunallargallistade matemàtics,moltsd’ellsitalians,iesconservaunagranquantitatdecartes rebudesperBattagliniiBeltrami.37

LasevacontribucióésreconegudaperlestraduccionsdelesobresdeBolyai iLobatxevski,amblesqualsvaintroduirlanovageometriaaFrança.També vamantenirelsmatemàticsfrancesosinformatssobreeldesenvolupament delaqüestiótraduintelstreballsdeBattaglini,BeltramiiKlein.Peròlaseva aportaciónoésnomésladedivulgador;elsseusescritssobreelsfonaments delesmatemàtiquesproporcionenunsuportfilosòficperacceptarlanova geometria.Defet,Hoüelvaserelprincipaldifusoridefensordelageometria noeuclidianaaFrança,on,engeneral,esvanrebreambbastantaapatiai reticència.Lareacciódelsmatemàticsfrancesosesdeviaalagraninfluència d’A.-M.Legendre(1752–1833),quihaviapresentatunaprovanovadelpostulat acadascunadelessuccessivesedicionsdelsseus Elémentsdegéométrie,la primeradel1794.

Elsanyscomaprofessord’institutvanportarHoüelainteressar-seperla geometriaelementalipelseuensenyament.Veientunadebilitataxiomàticaen elstractatsdegeometria,enl’«Essaid’uneexpositionrationnelledesprincipes fondamentauxdelagéométrieélémentaire»[26],del1863,esproposarevisar elsfonamentsperestablirunabasesòlidasobrelaqualconstruiraquesta disciplina.Els Essaicritique del1867idel1883,[27]i[32],seranversionsmés

35VegeulacartadeBeltramiaHoüelambdataBolonya23.1.1870,a[12,p.126–127].

36VegeulacartadeBeltramiaHoüelambdataBolonya12.6.1870,a[12,p.141–142].

37 LescartesrebudesperHoüelestrobenal DossierHoüel delsArchivesdel’Académiedes sciencesdeParis,tretd’algunesd’inèditesquevampoderconsultaralaBibliotecaMunicipalde CaeniqueactualmentestrobenalaBibliotecaAlexisdeTocquevilledelmateixmunicipi.

completesd’aquestprimertreball,enquèjaparlaràdelesaportacionsde LobatxevskiiBolyaisobrelateoriadelesparal.leles.

LesprimeresreflexionsdeHoüelsobrelageometriadeLobatxevskiles trobemenunesanotacionsfetesenelsobred’unacartatimbradal’any1866, queestrobaintercalatalespàginesd’unaversiódel’Essai. 38 Hoüelvaconèixer l’existènciadelstreballsdelgeòmetrarusideBolyaiperR.Baltzer,39 quihavia introduïtperprimercoplesnocionsnoeuclidianesauntractatdegeometria elemental.40 Eljuliold’aquellany,l’alemanyliescriuperproposar-lidivulgara Françaaquestesideesdesconegudes.41 Hoüelpublicaràdeseguidaels Études géométriquessurlathéoriedesparallèles deN.I.Lobatxevski[37].Latraducció del’Appendix deBolyai[14]trigarà,encanvi,unparelld’anys,degutales dificultatsquehihaviaperfer-seambunexemplar.Vasergràciesal’arquitecte hongarèsFranzSchmidt42 quevaaconseguir-neduescòpies,ienvaenviaruna aBattaglini.43 Schmidthaviatrobat,percasualitat,unacòpiadel’Essai del1863 i,volentcontinuarambelsseusestudisdematemàtiques,livaescriureper demanar-liconsell.Enlasevaresposta,Hoüellidemanaajutperaconseguirla rarapublicaciódelsBolyaiimaterialperalessevesbiografies,quevaacabar escrivintelmateixSchmidt.

Manuscritdels Étudesgéométriques ArchiveHoüel, BibliotecaAlexisdeTocqueville,Caen.

38 BrunelsituaelmanuscritalabibliotecauniversitàriadeBordeus,itranscriulesanotacions delsobrea[18,p.25–31].

39Comexplicaenaquestmanuscritial’Essaicritique [27,p. vii].

40Enlasegonaedicióde DieElementederMathematik [3].

41CartadeBaltzeraHoüel19.7.1866,citadaperVoelkea[48,p.60,n.3].

42 Vegeulanotadeltraductora Lascienceabsoluedel’espace [14]ilabiografiadeHoüelescrita perHalsted[25,p.100–101].

43 VegeulescartesdeBattagliniaHoüel,Nàpols13.6.1867i17.6.1867,onliagraeixqueles hagienviat,a[19,p.66–67].

MiriamAlcaláVicente

Alcontrariquelacomunitatcientíficadelseupaís,Hoüelacceptaimmediatamentlageometrianoeuclidiana.Lasevapredisposicióafavordelesnoves ideesprovédelasevarecercasobreelsfonaments,quejal’haviaportatacreurequeelpostulatdelesparal lelesnoespodiademostrar.Al’Essai del1863 valoraque,silesrecerquesdetants«esperitseminents»nohavienarribatacap resultatsatisfactori,era,probablement,perquèestavenescometentun«problemairresoluble».44 Enl’opuscledeLobatxevskiveuràconfirmadadefinitivament aquestaimpressió.45

Enelsseustreballs,Hoüelassenyalaques’estàpartintd’un«falspuntde vistametafísic»enconsiderarquelageometriaésunaciènciaderaonament pur,46 iquel’experiènciasíqueintervéenlatriadelsaxiomes.Lespropietatsgeomètriquesse’nsrevelenpermitjàdelssentits,peròcomquealgunes ensresultentanclares,hemacabatcreient-lesinnatesal’intel.lectehumài declarantquesónaxiomes apriori.Lesciènciesexactesesbasenenprimer llocenl’observació,queenspermetestablir,perinducció,leslleisiprincipis «indefiniblesiindemostrables»apartirdelsqualsesdeduiran,mitjançantla lògica,fetsnous.47 Partirdelreconeixementquelageometrianoésunaciència apriori suposaunadiferènciaepistemològicafonamentalperpoderacceptar lateoriadeLobatxevski,jaquesignificaquel’euclidiananohadeserl’única geometriapossible.

Hoüelcontinuaadmetentque,enpartirdel’observacióexperimental,que noésd’unaexactitudrigorosa,espodriadonarelcasqueestriésunaxioma equivocat.L’errorelreconeixeríemquan,enseguirlesdeduccionslògiques, arribéssimaresultatsqueestanen«desacordamblarealitatobjectiva».48 Aquestaés,precisament,lasituacióenlaqualenstrobemquanesprencom aaxiomalanegaciódelpostulatdelesparal.leles,cosaqueportaaconcloure quelageometrianoeuclidianaésfísicamentfalsa.Però,puntualitzaHoüel, aixònovolpasdirquenosigui«absolutamentcerta».Elquerealmentimporta enunaciènciaracionaliabstractaésqueelsaxiomesinicials,quepodenser triatsarbitràriament,siguincompatibles,ésadir,nocontradictorisentreells,i independentselsunsdelsaltres,garantintamés,queelnombreseleccionat siguielmínimpossible.Qualsevolciènciaconstruïdaambaquestabaseique obtéelsseusresultatsseguintladeducciólògicaéscertadesdelpuntdevista abstracte,totiquenoconcordiambelsfetsrealsquepreteniarepresentar.49 Arabé,sielqueesvolésaplicaraquestateoriacientíficaaunadeterminada realitatiquecondueixiaresultatspràctics,llavorselsprincipiss’handetriar enconformitataaquestarealitatobservada.Lageometrianoeuclidianaés, pertant,certa,peròcomquenosemblaqueespuguiaplicaral’espaiqueens

44Enlaintroducció[26,p.171].

45VegeulacartadeHoüelaDeTillydel21.2.1875,citadaperVoelkea[48,p.61].

46Introducciódel’«Essai»del1863[26,p.171–178].

47 Durôledel’expériencedanslessciencesexactes,lanotaesrecullal’apèndixdelasegona ediciódel’Essaicritique,1883[32,p.63–70].

48 Durôledel’expérience [32,nota i del’apèndix,p.63].

49 Durôledel’expérience [32,nota i del’apèndix,p.66].Vegeutambéelsfragmentsdeles cartesdeHoüelaDeTilly,ambdates9.12.1873i4.1.1873,citadesperVoelke,a[48,p.71].

envolta,l’hemdeconsiderarcomunateoriaabstractaquenomésexisteixal nostrepensament,50 elseuinterèséspuramentfilosòfic.51 Ésadir,Hoüelfa unadistincióclaraentrelaconsistèncialògicad’unateoriaabstractailaseva validesaexperimental.52

4LageometriaimaginàriadeG.Battaglini

LalabordeGiuseppeBattaglinicomadifusordelageometrianoeuclidiana aItàliahaestatsovintreconegudapelshistoriadors.Vatraduirlesobresde LobatxevskiiBolyai,quelivaproporcionarHoüel,53 isotalasevadirecció, el GiornalediMatematiche eralarevistaquemésarticlespublicavasobre laqüestió.Però,comveurem,lasevacontribucióaldesenvolupamentdela geometrianoeuclidianavamoltmésenllà.

BattaglinimostraunràpidinterèsperlesideesdeLobatxevskiiaccepta immediatamentlanovageometria,entrantenconflicteambelsseuscol.legues alafacultatdeNàpols,onlarebudanovasergensfavorable.Enlasevacartaa Genocchiperinformar-losobrelanovageometria,escriu:

...sono inguerra contuttalafacoltàdimatematicadiNapoli,peressermi fattopropugnatorediquestenuoveidee... 54

[...estic enguerra ambtotalafacultatdematemàtiquesdeNàpols,per haver-mefetdefensord’aquestesnovesidees...]

Aquestesposicionsoposadesesfonamentavenenlesduestendènciesfilosòfiquesquellavorscoexistienalauniversitat,elpositivismedeComtei l’idealismeabsolutdeHegel.55

ElsuportinqüestionablealanovageometriaperpartdeBattaglini,que trobemenlacorrespondència,malauradamentnoveacompanyatd’arguments queeljustifiquin.Lessevesraonsse’nsdesvelaran,però,enentendrelesidees implícitesenelseuarticle«SullageometriaimmaginariadiLobatschewsky»,56 publicatpocdesprésdetraduirLobatxevski,ienalguneslíniesdelesseves cartes.

50 Lobatxevskivaarribaraaquestamateixaconclusiódesprésderealitzarunasèried’experimentspercomprovarsienlarealitatescompliaelpostulatdelesparal.lelesolasevanegació,i peraixòvaposaralanovageometriaelnomde geometriaimaginària

51 Surl’axiome xi (ditpostulatum)d’Euclide, Essaicritique,1867[27,p.77–78]o1883[32,p.85].

52 D’aquestadiferènciaenparlaalacartaaDeTillyambdata21.8.1876,citadaperVoelkea [48,p.70–71].

53VegeulescartesdeBattagliniaHoüelescritesentreabrilijulioldel1867,a[19,p.66–67],i lesdel21.07.1867,23.11.1867,2.4.1868,1.8.1868,a[2,p.211–212,214–216].

54BattagliniaGenochi,Nàpols14.5.1867,a[19,p.167-168].

55 Elpositivismed’AugustComtecreuenelmètodecientíficcomaviadeconeixement,basat enlapercepcióobjectivailainducció.D’altrabanda,lafilosofiadeHegeltéunconceptedel’a priori pròximaldeKant.

56 Espublicarana Rendicontidell’AccademiadelleScienzediNapoli,vol. vi (1867),157–173ial GiornalediMatematiche [4].

MiriamAlcaláVicente

El1854,enlasevacartadepresentacióaBetti,Battaglinihaviaexpressat quecreiaquelageometriaprojectivaéslateoriamésgeneral,iqueambella estenentotselsmitjansperestudiarlespropietatsdel’espai.57 Defet,el napolitàvaser,juntambCremona,delsprimersitaliansainteressar-seper laprojectiva.Eneldebatentrepartidarisdelmètodesintèticodel’analític, Battaglinis’inclinapelprocedimentanalític,seguintlalíniadelsseusmestres al’EscoladePontsiCamins,TucciiDeAngelis,queescontraposavaala fortatendènciasintèticaques’imposavaalaUniversitatdeNàpolsdeguta lainfluènciadel’escoladeFergola.Comparteix,doncs,lamateixaposicióque RiemanniBeltrami,oenelcasconcretdelaprojectiva,queMöbiusiPlücker. Així,enelseuarticle«Sullageometriaimmaginaria»,esproposaestudiar lageometriaimaginàriadeLobatxevskifentservirleseinesdelageometria projectivaiseguintunametodologiaanalítica.Aquestplantejamentmostraper primercoplapossibilitatdeconsiderarlanovageometriacomainclosaenla projectiva.

Laprincipaldificultatqueunestrobaenlalecturadel’articleéslacomplexitatdelasevaexposició,quehafetqueseliatribuísfaltaderigor.Perexemple, elseualumneD’Ovidiovaloraelprocedimentcoma«mésfeliçquerigorós»58 ielmateixBattaglinireconeixaHoüelquecaldriaqueeldesenvolupésamb mésclaredat.59 Enunaopiniómésrecent,Voelkequalificaelraonamentde «matemàticamentinsatisfactori»iconsideraqueestà«seriosamenthipotecat desdelprincipi».60 Elseuargumentésqueladeducció,queexposaremacontinuació,delafórmula (1),apartirdelaqualBattaglinidedueixgranpartdels seusresultats,ésincorrecta.

sinh mω sinh ωn = λ sin M Ω sin ΩN (1)

Mencionemprimerquel’articles’iniciapartintdelarotaciód’unarecta Ω entornaunpunt p.Lafunció F(z) queexpressaaquestarotacióhadeser periòdicaicompleix,amés,lapropietat F(x + y) = F(x)F(y),ésadir,ésuna funcióexponencial.Pertalquelafuncióexponencialsiguiperiòdicacalprendre l’exponencialcomplexa F(z) = eikz,introduintaixílavariablecomplexacom Lobatxevski.Lesfuncionscircularslesdefiniràfentservireldesenvolupament deTaylordelafuncióexponencial.

Battagliniconsidera,llavors,elsistemadepunts ω delarecta L iles corresponentsrectes Ω queelsuneixenambunpunt p,exterioralarecta.

57VegeulacartadeBattagliniaBetti,Nàpols8.11.1874,a[19,p.179–180].

58«InveritàpiùfelicecherigorosopuòdirsiilprocedimentodelBattaglini».A[21,p.588].

59 «JesaisquemaNotesurlaGéométriedeLobatschewskyauraitbesoind’êtreplusclairement développée.»BattagliniaHoüel,Nàpols6.8.67,BibliotecaAlexisdeTocqueville,Caen;transcripció a[2,p.212].

60 Voelkeésquihaaprofunditmésenl’anàlisidel’article«LaméthodedeBattagliniest mathématiquementinsatisfaisante»,a[48,p.75].«LaméthodedeBattagliniestsérieusement hypothéquéedèsledébut»,a[48,p.77].

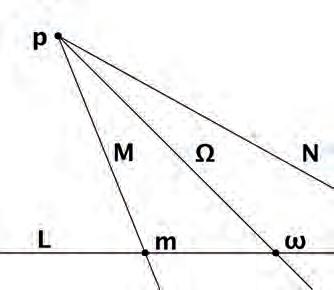
p Lmω n M Ω N

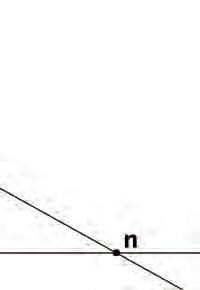
Figura 1: RepresentaciódelasituaciódescritaperBattaglini.

Prenentduesposicionsfixadesdelspunts n i m ilesrespectivesrectes M i N,comesmostraalafigura1,s’obtenenlesbijeccionssegüents:61

ω ←→ sinh mω sinh ωn =: r(ω),

Ω ←→ sin M Ω sin ΩN =: R(Ω),

ω ←→ Ω.

Lacomposiciód’aquestesfuncionsensdonaunabijeccióentrelesduesraons, queensporta,segonsBattaglini,«evidentment»,alarelació:

r(ω) = λR(Ω), ésadir,alafórmula(1).

Certament,l’equacióplantejamésdificultatsdelesqueacceptaBattaglini. ElmateixHoüelesvaencallarenaquestpuntivademanarmésexplicacionsa Battaglini,quienlasevacartadel6d’agostdel186762 lienviaràunasèriede càlculsperjustificar-neelresultat.

61 L’últimabijeccióresultaòbviaperlamateixaconstrucció.Lesduesprimeresafirmenque cadaunadelesduesraonstindràunvalorúnicideterminatsegonslaposiciódelpunt ω ola recta Ω,iviceversa.Espodendemostrarfentservirlesdefinicionsdesinuscircularihiperbòlic mitjançantl’exponencial.

62 Lacartainèditaestrobaal’ArchiveHoüel,BibliotecaAlexisdeTocqueville,Caen.Vegeu-nela transcripcióa[2,p.212–213].

MiriamAlcaláVicente

CartadeBattagliniaHoüel,Nàpols6.8.1867. ArchiveHoüel, BibliotecaAlexisdeTocqueville,Caen.

Elsaclariments,ambelvistiplaudel’autor,63 apareixeranalatraducció francesa[5]enquè,amés,se’nsremetaunteorema64 queconsideremque resollaqüestiódelaveracitatdelafórmula.Pertald’aplicar-localquelafunció departidasiguibijectivaiholomorfa.Enl’exposicióquedaclaralabijectivitat, perònoesfamencióal’holomorfia.NosabemsiBattagliniesdeviaparara demostrar-la,peròésclarqueescompleix,jaqueestractadefraccionsentre funcionshiperbòliquesicirculars,onlesúniquessingularitatsestrobarienquan s’anul lenelsdenominadors,quesónjustamentelscasoslímitcontemplatsen elsaclarimentsfetsaHoüel.65

BattagliniarribaalconceptefonamentaldelateoriadeLobatxevskiconsiderantlesrectesquepassenperunpunt p exterioraunarectadonada L,i trobantlesfórmulessegüentsperaladistànciadelpuntdetallamb L alpeu delaperpendicularper p:

(3) on Θ ésl’anglequeformalarectaquepassaper p amblaperpendiculari k ∈ R.

63VegeulacartadeBattagliniaHoüel5.8.1868,a[19,p.74].

64 Totafunciómonòdromaimonògena,queadmetunnombrelimitatd’infinits,ésunafracció racional,teoremaenunciatalmanualdeBriotiBouquet, Théoriedesfonctionsdoublement périodiques [17,capítol4delllibre i,p.40].

65 Peramésdetalls,vegeu«EldesenvolupamentdelageometrianoeuclidianaaItàlia»[2, p.121–126].

Quanelvalordeladistànciaésinfinitobtélesduesparal.lelesdeLobatxevski,queseparenlesrectesquetallenenpuntssituatsadistànciareal finita,donadaperlafórmula (2),delesquehofanenpuntssituatsadistància ideal,donadaperlafórmula (3),talcomesmostraalafigura2.Elsdarrersels consideracomapuntsdelarectaqueestan«mésenllàdel’infinit».

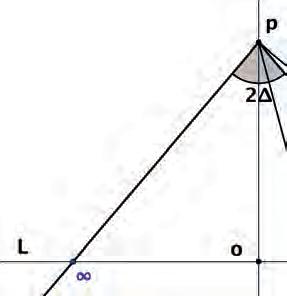
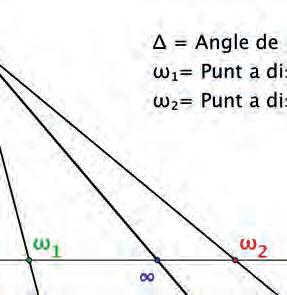
∆ = 0p∞= angledeparal lelisme

ω1 = puntadistànciareal

ω2 = puntadistànciaideal

Figura 2: ElsdiferentstipusderectasegonsladescripciódeBattaglini.

Observant,llavors,quelageometriaeuclidianaestàinclosaenlaimaginària, assenyalaquelaprincipaldiferènciaentrelesduesgeometriesésque,en l’euclidiana,lesrectessóncomcercles,jaqueelsdospuntsal’infinitsón coincidents,mentrequeenlaimaginàriasóndiferentsientreellsestroben infinitspuntsideals.66 Battaglininonomésintrodueixelconcepteprojectiude puntal’infinit,sinóqueaméshaafegitelsanomenats puntsidealsalarecta. Al’article,tambéapareixelconcepteprojectiudepold’unarecta,definitcom elpuntenquèestallentoteslessevesperpendiculars.

Al’inicidelaúltimaseccióse’nspresentaunaidead’allòmésinteressant. Battaglinipassalessevesobservacionssobrelarectaalpla,fentgirarelfeixde rectesquepassenperunpuntexterioralarectadonada,talcomil.lustrala figura3,ifalasorprenentobservaciósegüent:

NelsistemadellaGeometria non-euclidiana ilpianoèunasuperficieindefinita essendoisuoipuntiall’infinitotutti distinti traloroedappartenentiaduna circonferenzadicircolo,chehapercentrounpunto qualunque delpianoedil raggioinfinito;similmenteperlospazio,ipuntiall’infinitosonotutti distinti traloroedappartengonoaduna superficiesferica,chehapercentrounpunto qualunque edilraggioinfinito.67

[Enelsistemadelageometria noeuclidiana elplaésunasuperfícieindefinida, totselsseuspuntsdel’infinitsón diferents entresiipertanyenauna circumferènciadecercle,quetépercentreunpunt qualsevol delplairadiinfinit; anàlogamentperal’espai,elspuntsdel’infinitsóntots diferents entresi ipertanyenauna superfícieesfèrica quetépercentreunpunt qualsevol i radiinfinit.]

66«Sullageometriaimmaginaria»[4,p.223].

67A«Sullageometriaimmaginaria»[4,p.229].

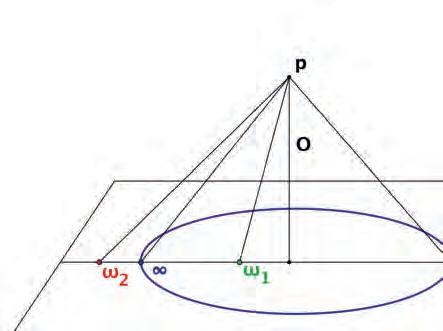
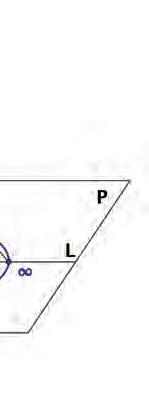
Figura 3: RepresentaciógràficadeladescripciódeBattaglinidelpla hiperbòlic.

Ladescripciódelplanoeuclidiàcomlaregiólimitadaperuncerclesense fronteradinsdelplaeuclidiàcoincideix,clarament,ambelsmodelsdonatsper BeltramiunsmesosdesprésiKleinunsanysméstard.

AquestareflexiódeBattaglininohaestatanalitzadaenprofunditat,tot ique,enlanostraopinió,portaapreguntar-sequinarelacióhihaentreels estudisdelstresautors.L’enigmaelresoldremenelsegüentapartat.Veurem queelplantejamentdeBattaglininovasuposarunainfluènciaeneltreballde Beltrami,totiqueJ.M.Montesinosaixíhocreu.68 Beltramiparteixd’unaltre enfocament.Klein,encanvi,síquesegueixlalíniaprojectiva,iseràenlaseva recercaontrobaremlajustificaciódelasimilitudentrelestresdescripcions delplahiperbòlic.

5Lainterpretaciódelageometrianoeuclidianad’E.Beltrami iF.Klein

Lacontribuciód’EugenioBeltramialageometrianoeuclidianaésdelesmés destacablesenlahistòriad’aquestamatèria.Lasevainterpretaciódelageometrianoeuclidiana,comlaquefaràKleinunsanysméstard,espotreformular segonselqueactualmentanomenem teoriademodels,solucionantelproblemadelasevaconsistència.Enlamatemàticamoderna,esconsideraqueuna teoriaabstractaésvàlidasiesconstrueixseguintdeduccionslògiquesapartird’unconjuntd’axiomesindependentsiconsistents.Laconsistènciaqueda demostradasiespotproporcionarunmodelonsónvàlidselsaxiomesdela teoria,jaque,sihihaguésunacontradiccióalanovateoria,tambéesdonaria enelmodel,iaquests’hafetapartird’unateoriaquejaesconsideraacceptada.

68 Vegeuelseuarticle«Lacuestióndelaconsistenciadelageometríahiperbólica»[40,p.221].

ElpuntclauperentendreelstreballsdeBeltramiésllegir-losenelcontextde lageometriadiferencial,introduïdaperGaussal«Disquisitionesgeneralescirca superficiescurvas»[23].LagranaportaciódeGaussésqueproposaestudiar lessuperfíciessensepensar-lescomainclosesenl’espaireal,sinódemanera intrínseca,ésadir,comhofarienhabitantsbidimensionalsquevisquessindins delasuperfície.AquestaideaseràdesenvolupadaposteriormentperRiemann iéselprincipienquèesfonamental’obradeBeltrami.

Lageometriaintrínsecadelessuperfíciestractalespropietatsquenovarien endoblegarunasuperfíciesenseestirar-lanitrencar-la.Aquestespropietats venendeterminadesperlafórmuladel’elementdelongitud,queéslaque defineixcommesurenelshabitantsdelasuperfície.Posem,perexemple,un plaiuncilindre;podemdoblegarelplaperferuncilindreoobrirelcilindre sobreelpla,sónlocalmentdesenvolupablesl’unsobrel’altre.Pertant,tindran elmateixelementdelongitudilamateixageometriaintrínseca;diemquesón superfíciesisomètriques.

UnadelespropietatsinvariantsperflexionséslacurvaturadeGauss.Si unasuperfícieesdesenvolupasobreunaaltra,lacurvaturadeGaussenpunts corresponentséslamateixa.Elrecíprocnoméséscertquanlacurvaturaés constant:siduessuperfíciestenenlamateixacurvaturadeGaussconstant, llavorsespotdesenvoluparlocalmentl’unasobrel’altra.Elplaielcilindre tenen,doncs,lamateixacurvatura,zero,iqualsevolaltrasuperfíciequetingui curvaturazeroespodràdesenvoluparlocalmentsobreunplaitindràcoma geometriaintrínsecal’euclidiana.Delamateixamanera,toteslessuperfíciesde curvaturaconstantpositivaesdesenvolupenlocalmentsobreunaesferaitenen comageometriaintrínsecal’esfèrica.LagenialitatdeBeltramiseràdescobrir quelageometriadeLobatxevskiésladelessuperfíciesdecurvaturaconstant negativa,queellanomena«pseudoesfèriques».

DurantelsanysquevaserprofessordegeodèsiaalaUniversitatdePisa (1864–1866),Beltramiesvadedicaral’estudidelescartesgeogràfiques.Un comentarifetperLagrange69 elvaportaraplantejar-selapossibilitatde representarunasuperfíciesobreunplademaneraquelesgeodèsiquesdela superfícieescorresponguinambrectesdelpla.Beltramitrobal’elementde longituddelessuperfíciesquecompleixenaquestapropietat,iencalcular apartird’elllacurvatura,veuquehadeserconstant.70 Segonsexplicaala sevacorrespondència,ésaquestestudielqueelconduiràatopar-seamb lageometrianoeuclidianagairebépercasualitat.71

Enel«Saggiod’interpretazionedellageometrianoneuclidea»[7],publicat el1868,72 parteixdel’elementdelongitudquehaviatrobatperal’esferai 69Al’article«Surlaconstructiondescartesgéographiques»,del1779[35].

70 Al’article«Risoluzionedelproblema:“Riportareipuntidiunasuperficiesopraunpianoin modochelelineegeodetichevenganorappresentatedalineerette”»[6].

71 EnlasevacartaaD’Ovidiodel25.12.1872,Beltramiexplicadetalladamentlasevaviade descobriment.VegeuelfragmentcitatperG.Loriaa[39,p.421–423];lacartavaserpublicada perprimercopperD’OvidioalasevacommemoraciódeBeltrami[22].Vegeutambélacartade BeltramiaHoüel,Bolonya18.11.1868,a[12,p.65].

72 Totiqueelvaescriureunanyabans,Beltraminoesdecidiaapublicar-lodegutaunaobjecció

MiriamAlcaláVicente

canvialaconstant R delradiper iR,iobtéunacurvaturaconstantnegativa iguala 1/R2 .

Beltramiveullavorsquelageometriaintrínsecadefinidaperaquestamètrica ésprecisamentladesenvolupadaperLobatxevski.Desprésmostracomaquestessuperfíciespseudoesfèriquesespodenrepresentarenelplamitjançantun disc,demaneraquelesgeodèsiquesdelasuperfícies’apliquenalescordes deldisc.Obté,així,unmodeldelaplanimetrianoeuclidiana.

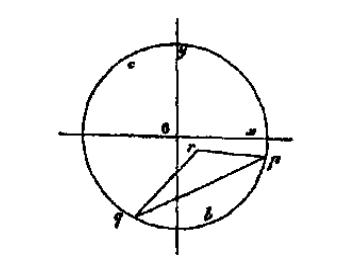
Figura 4: ModeldeldiscpresentatperBeltramial«Saggio».

Continuaveientqueespotaplicarunapartdelasuperfíciepseudoesfèrica enlasuperfíciederevoluciógeneradaperlacorbatractiu,conegudaambel nomde pseudoesfera.Beltramiesvapreocupardeconstruirmaterialment aquestasuperfícieperpoderestudiar-nemillorlespropietats.

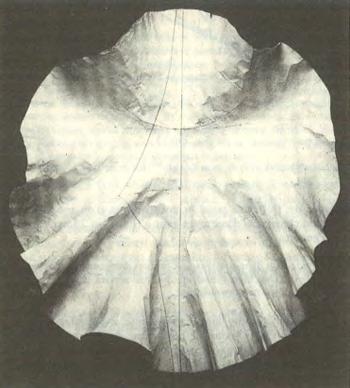
ConstrucciómaterialdelapseudoesferafetaperBeltrami. ModelconservatalDepartamentdeMatemàtiquesdelaUniversitatdePavia.

fetaperCremona,referidaasiespodiautilitzarl’anàlisiordinària,fonamentadaenlageometria euclidiana,pertractarnocionsdegeometrianoeuclidiana.Lessevesreticènciesdesapareixeran quanllegeixilamemòriapòstumadeRiemann.BeltramihoexplicaalessevescartesaGenocchi del9.6.1868idel23.7.1868,a[39,p.415–416],iaHoüeldel18.11.1868,a[12,p.66].

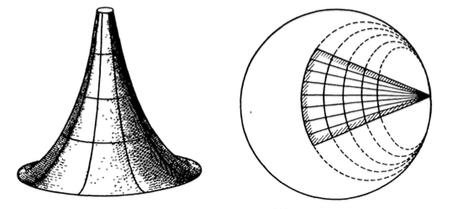
Figura 5: DibuixdeKleinpermostrarl’aplicacióentrelapseudoesfera ieldisc,presentatenel VorlesungenüberNicht-EuklidischeGeometrie, del1928.

Lapseudoesfera,però,noméséslocalmentisomètricaalasuperfíciepseudoesfèricadequèparlaBeltrami.Ésadir,podemtallar-laiobrir-laiposar-la sobreuntrosdeldiscdeBeltrami,delamateixamaneraquepodemtallari obriruncilindreidirqueésigualqueuntrosdepla,peròuncilindrenoés unpla!Nos’hadeconfondre,doncs,lasuperfícieabstractadeBeltrami,que avuianomenaríem varietatdeRiemanndedimensió 2 decurvaturaconstant negativa,amblapseudoesfera,queésunasuperfíciedel’espaireal.Aquesta confusióeramoltcomunaentreelsseuscontemporanis,quenohaviencomprèscompletamentlesteoriesdeGaussiRiemann,compodemveureenles moltescartesaHoüelondonaexplicacionssobreeltema.73

Beltramifinalitzal’articlereflexionantquenoéspossibledonarunainterpretaciórealperal’estereometrianoeuclidianadelamateixamaneraque hoacabadeferamblaplanimetria,ésadir,noespottrobarunmodel.No obstant,veupossibledonarunainterpretacióanalítica,sensesuportgeomètric, simplementintroduintunavariablemésenlamètricainicial.Així,a«Teoria fondamentale»[8],el1869,esténelsresultatsperasuperfíciesdecurvatura constantnegativadedimensióarbitrària,iconcloudientque«lateoriade Lobatxevskicoincideix,tretdelnom,ambladel’espaidetresdimensions decurvaturaconstantnegativa».74

PocsanysdesprésdelespublicacionsdeBeltramiapareixenlesduesmemòriesdeKlein«UeberdiesogenannteNicht-EuklidischeGeometrie»[33]i[34], el1871iel1873,respectivament,onl’alemanyaportatambéunnoumodelper alageometrianoeuclidiana,aquestavegadaseguintelpuntdevistaprojectiu suggeritperBattaglini.75

73 Vegeu,perexemple,leseditadesa[12],ambdates13.3.1869,p.79;1.4.1869,p.87–88; 22.4.1869,p.92;12.10.1869,p.100;25.10.1869,p.102–103;19.12.1869,p.108. 74«[...]lateoriadiLobatschewskycoincide,salvoneinomi,collageometriadellospazioatre dimesionidicurvaturacostantenegativa»[8,p.425].

75 SabemqueKleinhaviallegitel«Sullageometriaimmaginaria»,jaqueelcitaatribuinta Battaglinilaintroducciódelconceptedepuntidealil’observacióquelesperpendicularsauna rectasónconcurrentsenelpold’aquestarespectealacònicafonamental.Vegeu[33,p.290].

MiriamAlcaláVicente

Elsseusestudisparteixendelateoriadel’Absolutd’ArthurCayley(1821–1895).Recordemquelageometriaprojectivaestudialesposicionsrelatives entreelselementsgeomètrics,enllocd’estudiarlespropietatsmètriques,com falageometriaeuclidiana,jaquelesdarreresnoesconservenenferprojeccions iseccions.Alasevamemòriadel1859,«Asixthmemoiruponquantics»[20], elbritànicaportavaunamètricaalageometriaprojectiva,definintladistància demaneraquequedainvariantperatransformacionsquedeixenfixauna cònicaqueanomena Absolut.Veia,llavors,quelageometriaeuclidianaéselcas particularenquèl’Absolutésunacònicadegeneradaformadaperunparellde punts.

Kleindonaràunanovadefiniciódedistànciaapartirdelaraódoble,un invariantprojectiu,idistingiràtambéelscasosenquèl’Absolutésreali imaginari,queescorresponenamblageometriadeLobatxevskiilageometria esfèrica,respectivament.D’aquestamanera,demostraquelestresgeometries decurvaturaconstant,queellanomena parabòlica, hiperbòlica i el.líptica,es podenestudiarcomacasosparticularsd’unateoriamésgeneral,lageometria projectiva.Enprendreelspuntsinteriorsdelacònicarealdel’Absolut,Klein obtéelmodeldeBeltrami,liproporciona,amés,unafórmulaperaladistància iassenyalaqueeldisctambépodriaserunael.lipse.

El1873,Beltramiescriul’«Osservazione»[9],enquèrelacionatambéels seusestudisanteriorsamblateoriadel’AbsolutdeCayley.Larealitat,però, ésquefeiatempsqueeraconscientd’aquestvincleentrelessuperfíciesde curvaturaconstantilageometriaprojectiva.El1869escriuaHoüel,sobreun afegitquevoldriaferalessevesmemòries,siaconseguísconcretarlaidea:

C’estlaconjectured’uneétroiteanalogie,etpeut-êtreidentité,entrelagéométriepseudosphériqueetlathéoriedeM.Cayleysurl’origineanalytiquedes rapportsmétriques,àl’aidedelaconique(oudelaquadrique) absolue.Jene connaissaispresquepascettethéorie,quandl’identitédecertainesformesm’a vivementfrappé.76

[Estractadelaconjecturad’unaestretaanalogia,ipotseridentitat,entrela geometriapseudoesfèricailateoriadelSr.Cayleysobrel’origenanalíticde lesrelacionsmètriques,ambl’ajutdelacònica(oquàdrica) absoluta.Amb proufeinesconeixiaaquestateoria,quanlaidentitatdecertesformesm’ha impressionatprofundament.]

[BeltramiaHoüel,29.7.1869]

RecordemaraelcerclelímitdescritperBattaglinienelparàgrafquehem destacatabansdel«Sullageometriaimmaginaria»,iobservemquenoésaltra cosaquelacònicarealdel’Absolut.Ésprobableque,precisamentpernotenir gairesconeixementsenprojectiva,Beltraminoveiésaquestaal lusióimplícitaa l’AbsolutfetaperBattaglini.

76A[12,p.96–97].VegeutambélacartaaD’Ovidiodel25.12.1872,esmentadaanteriorment.

CartadeBeltramiaHoüel,Bolonya29.7.1869. DossierHoüel, Archivesdel’AcadémiedesSciences,París.

LaqüestióquehomesplantejaimmediatamentéssiBattaglinijatenia alcap,llavors,elmodelprojectiudeKlein,comsuggereixMontesinos.77 La respostalatrobemenlessegüentslíniesescritesaHoüelquantreballavaen l’article:

Ilm’estréussi(avecdesprincipesdeGéométrieiperbolique[sic])àétablirdes relationsdonnéesparLobatschewskyentrelesanglesetlescôtésd’untriangle rectiligne;onpeutmêmearriveràcesformulesensuivantlaméthodede Cayley(Asixthmemoiruponquantics,Philos.Trans)pourétablirlesrelations métriquesducontinuàdeuxdimensions,ensupposant(lorsqueonparledu plan)quel’Absolu soituneformequadratique quelconque,tandisquedansla Géométrieeuclidiènnecetteformesedécomposeendeuxfacteurslinéaires. J’espèrelemoisprochainpouvoircommuniquermesrecherchesàl’Académie desSciencesdeNaples.78

[Heaconseguit(ambelsprincipisdegeometriahiperbòlica)establirlesrelacions entreelsanglesielscostatsd’untrianglerectilinidonadesperLobatxevski; tambéespotarribaraaquestesfórmulesseguintelmètodedeCayley(«Asixth memoiruponquantics», Philos.Trans)perestablirlesrelacionsmètriquesdel continuenduesdimensions,suposant(quanparlemdelpla)quel’Absolut sigui unaformaquadràtica qualsevol,mentrequeenlageometriaeuclidianaaquesta formaesdescomponendosfactorslineals.Esperopodercomunicarlesmeves recerqueselmesqueveal’AcadèmiadelesCiènciesdeNàpols.]

[BattagliniaHoüel,Nàpols21.5.1867]

77Vegeu«Lacuestióndelaconsistenciadelageometríahiperbólica»a[40,p.218]. 78A[19,p.63–64].

MiriamAlcaláVicente

CartadeBattagliniaHoüel,Nàpols21.5.1867. DossierHoüel, Archivesdel’AcadémiedesSciences,París.

Observemquetambéfaservirelterme geometriahiperbòlica,quedesprés utilitzaràKlein.Segurament,l’alemany,ambelsseusconeixementsdegeometriaprojectiva,síquevaentendreelnouenfocamentdeBattaglini,isembla bastantprobablequeveiésquelacircumferènciadepuntsal’infinitéslacònica realdel’Absolut.

6L’acceptaciódelageometrianoeuclidiana

Enaquestapartatpresentarembreumentlareacciódelacomunitatmatemàtica davantlareapariciódelageometrianoeuclidianaidelesnovesaportacions deBeltrami.LadifusiófetaperHoüeliBattaglinidelanovageometriava desencadenaruninteressantdebatsobresihaviadeserreconegudaonocom unateoriavàlida.Ladiscussióesvaprolongarfinsitotdesprésdelapublicació delstreballsdeBeltrami,quevanrebremoltescrítiques.

Desd’uninicielsprincipalsdefensorsvanserHoüeliBattaglini.Comveurem,BeltraminoméslavaacceptarcompletamentdesprésdellegirRiemann. PerquèBattaglinivaacceptardemaneratanimmediatalanovageometria,és unaqüestióque,enunprincipi,semblanoestarclara,jaque,adiferènciade Hoüel,mainoexplicaconcretamentlessevesraons.Unpotpensar,simplement, queeraunhomed’acordambelmomenthistòric,obertaideesnovesirevolucionàries...Arabé,l’anàlisiqueexposemenelsapartatsanteriorsdelseu articleidelasevacorrespondènciamostraquelarespostaaaquestapregunta estàsòlidamentbasadaenargumentsmatemàtics.Enlanostralecturadel «Sullageometriaimmaginaria»hemvistqueBattaglinidecideixestudiarla novageometriadesdelpuntdevistaprojectiu.Descobrimamés,enlaseva cartaaHoüel,queeraplenamentconscientquecorresponalcasparticularen

quèlacònicadel’Absolutésreal.Pertant,enentendrequelageometriano euclidianaestàinclosaenlaprojectiva,queésunateoriatotalmentacceptada, deseguidavaveureforadedubtelasevavalidesainoésestranyquel’aprovéssenserecances.Defet,lessevesinquietudsestanmésaviatrelacionades amblesrepercussionsquepottenirlanovateoria.Conscientquesuposauna rupturaambelpensamentmatemàtictradicional,Battagliniassenyalaquecal unreplantejamentdeladoctrinadel’espai.Enaquestanovaconcepcióes mostrapartidarideseguirelcamíproposatperRiemann.79 Tambécreuque ésfonamentaldisposard’uns Elements delageometrianoeuclidianapertal d’introduir-laal’ensenyament.Lasevapersonalitatidealistalifasentirlaresponsabilitatd’ensenyarlarevoluciócientífica,dedonaralsjovesinstruments pertrencaramblesmetodologiesestablertesimantenirlamentobertadavant novesviesderecerca.

Eneldebat,superadalainfluènciakantiana,escontraposavenduesposicions:ladeHoüel,partidarid’acceptar-lacomacertaaunnivellabstracte,i ladelsrealistes,queconsideravenquelaveritats’haviadefonamentarenla realitatinopasenlaconsistèncialògica.

AFrança,elprincipaldefensord’aquestadarreraopinióeraJosephBertrand. Eldesembredel1869vapresentaral’AcadémiedesSciencesunademostració delpostulatfetaperJulesCarton,80 que,naturalment,esbasaenunapeticióde principiensuposarqueleslíniesrectesnoesdesvienencapmoment,ique vasuscitarforçapolèmica.Davantlescrítiques,Bertrandargumentaque,en elcasdelpostulat,calrecórreral’«evidència».Lademostracióés,enelfons, innecessària,jaqueésl’observaciólaqueenselmostracomacert.Elquees pretén,endonarunaprovarigorosa,ésconvènceraquellsquenoelveuentan evidentcomlarestad’axiomes.Pertant,Cartonaconsegueixelpropòsiten partirnomésd’unaevidènciatotalmentirrecusable.81 Lademostració,però, vaproduirjustamentl’efectecontrarienelreconegutgeòmetraGastonDarbouxque,enanalitzar-laiveure’neldefecte,esvaacabardeconvèncerdela impossibilitatdedemostrarelpostulat.82

TambéaItàlia,reconegutsmatemàtics,comGiustoBellavitisiAngeloGenocchi,compartienl’opiniódeBertrand.83 EnlesnombrosescartesaHoüel, Bellavitisexposalasevaposició,dientquenopotadmetreunmóncreatnomés apartirdelraonament;laciènciaserveixperexplicarlarealitat,ilarealitatés laqueés.Laideade«monspossibles»liresultaincomprensible;lescoseso sóncertesosónimpossibles.84

79VegeulacartadeBattagliniaHoüelambdataNàpols5.8.1868,a[19,p.74].

80 «Nouveaumoyendeleverladifficultédelathéoriedesparallèles», ComptesRendushebdomadairesdesséancesdel’AcadémiedesSciencesdeParis,69(1869),p.44.

81Vegeu«Surlasommedesanglesd’untriangle»[10,p.1265–1266].

82VegeulacartadeDarbouxaHoüelcitadaperVoelkea[48,p.9].

83 VegeulacartadeBellavitisaHoüeldel20.3.1870,al DossierHoüel,Archivedel’Académiedes Sciences,París.BeltramitambéhodiualacartaaHoüeldel8.7.1870,a[2,p.220–221].D’altra banda,HoüeldiuaDeTillyel9.10.1873,a[48,p.184–185],queGenocchicomparteixl’opinióde Bellavitis.

84 VegeulacartadeBellavitisaHoüelambdata2.7.1872,p.4,al DossierHoüel,Archivesde l’AcadémiedesSciences,París.

MiriamAlcaláVicente

L’apariciódel«Saggio»deBeltramiresponaaquestacridaatrobaruna interpretaciórealdelanovateoria,quealgunsreclamavenperacceptar-la.El mateixBeltramil’haviaconsideratnecessària,iveientquenopodiadonaruna interpretaciógeomètricadel’estereometrianoeuclidianacomlaquehavia aconseguitperalaplanimetria,inicialmentnol’haviaacceptat.85 Vaseren llegirlamemòriadeRiemannqueesvaadonarquenonecessitavatrobaruna interpretaciód’aquesttipus.Lesnovesaportacionsdelmatemàticalemanyli proporcionavenunfonamentanalíticperexplicarlageometrianoeuclidiana enqualsevoldimensió;aquestanoésmésquelageometriaintrínsecad’una varietat n-dimensionaldecurvaturaconstantnegativa.

SeguintelnouconceptedevarietatdeRiemann,n’hihaproudedonar unaexpressióquadràticadelescoordenades,quesiguil’elementdelongitud aunasuperfícieabstracta,perpoderfergeometria.Nocalpreocupar-sede comseriaaquestasuperfícieenlarealitat,odesiespotonorealitzarcom unasuperfíciede R3.Peraaquellsquenocomprenienelpuntdevistade Riemann,encanvi,l’acceptaciódelageometrianoeuclidianadepeniadetrobar unasuperfícierealdel’espaionescomplissinlespropietatsdelageometriano euclidiana.SegonsAbardia,ReventósiRodríguez,Gausshaviaintentattrobar aquestasuperfíciesenseèxit.86 BellavitisiGenocchi,simplement,nocreienque poguésexistiri,comdemostraràHilbertunanydesprésdelamortdeBeltrami, noanavenequivocats.Elmésproperquepodemaconseguiraunarealització desuperfíciedecurvaturaconstantnegativaéslapseudoesfera,perònomésés localmentisomètricaalplanoeuclidià,pertant,comassenyalavaGenocchi, presentatotaunasèriedeproblemes.

PerBeltrami,però,l’existènciaonodelarealitzacióenl’espairealno afectaenabsolutlavalidesadelageometrianoeuclidiana.Lessuperfícies pseudoesfèriquesexisteixenenelsentitdonatperRiemann.Lageometria diferencial,delaqualnoesdiscuteixlacertesa,englobalestresgeometries: euclidiana,esfèricaipseudoesfèrica.Ladarrera,doncs,ésexactamentigualde vàlidaquelageometriaintrínsecadequalsevolaltrasuperfície.

Amblaintencióderesoldredefinitivamentlaqüestió,Hoüelpublica,afinals del’any1870,«Notesurl’impossibilitédedémontrerparuneconstruction planeleprincipedesparallèles,ditPostulatumd’Euclide»,87 enquèaclareixper quènoéspossibledemostrarelpostulatd’Euclides.Esremettambéalstreballs deBeltrami,assegurantquedissipenqualsevoldubtequeespuguitenirsobre l’acceptaciódelanovageometria.Defet,desprésdelespublicacionsdeBeltrami,nomésalgunsmatemàtics,generalmentpertanyentsalageneracióanterior, continuarenveientlanecessitatdetrobarunasuperfícierealonesdonésla geometrianoeuclidiana.Larestan’haviatingutprouqueesfonamentésen unateoriaacceptada.

85 VegeulesduescartesaGenocchiambdatesBolonya9.6.1868i23.7.1868citadesperG.Loria a[39,p.415–416],ilacartaaHoüeldel18.11.1868,a[12,p.65–66].

86 Comdèiemalanota9delapàgina7.Vegeul’article«WhatdidGaussreadintheAppendix?»[1].

87 AmbelmateixtítolHoüelvapublicarenvuitrevistesdiferents,peròhihanomésdues versionsdel’article;nosaltresleshemconsultatenles MémoiresdelaSociétédessciences physiquesetnaturellesdeBordeaux [30],ienels Nouvellesannalesdemathématiques [31].

Agraïments

Elpresentarticleesbasaenlatesidoctoraldel’autora,«Eldesenvolupament delageometrianoeuclidianaaItàlia»,presentadaeljunydel2017irealitzada sotaladirecciódelprofessorAgustíReventósiTarrida,aquiagraeixoelseu suportilessevesinestimablesaportacions.

Referències

[1] Abardia,J.;Reventós,A.;Rodríguez,C.J. «WhatdidGaussreadinthe Appendix?». HistoriaMath.,39(3)(2012),292–323.

[2] Alcalá,M. «EldesenvolupamentdelageometrianoeuclidianaaItàlia». Tesidoctoral.UniversitatAutònomadeBarcelona,2017.

[3] Baltzer,R. DieElementederMathematik.Vol.2.2aed.Dresden:B.G. Teubner,1867.

[4] Battaglini,G. «SullageometriaimmaginariadiLobatschewsky». Giornale diMatematiche,5(1867),217–231.

[5] Battaglini,G. «SurlagéométrieimaginairedeLobatcheffsky». Nouvelles annalesdemathématiques,2esérie,7(1868),209–221,265–277.[Traduccióde[4]perJ.Hoüel]

[6] Beltrami,E. «Risoluzionedelproblema:“Riportareipuntidiunasuperficiesopraunpianoinmodochelelineegeodetichevenganorappresentate dalineerette”». AnnalidiMatematicaPuraedApplicata,serie i,7(1865), 185–204.

[7] Beltrami,E. «Saggiod’interpretazionedellageometrianoneuclidea». GiornalediMatematiche,6(1868),284–312.Tambédisponibleenlíniaa: http://www.caressa.it/pdf/beltrami01.pdf.

[8] Beltrami,E. «Teoriafondamentaledeglispaziidicurvaturacostante». AnnalidiMatematicaPuraedApplicata,serie ii,2(1868–69),232–255.

[9] Beltrami,E. «OsservazionesullaprecedenteMemoriadelsig.rprof.Schläfli». AnnalidiMatematicaPuraedApplicata,serieii,5(1871–73),194–198.

[10] Bertrand,J. «Surlasommedesanglesd’untriangle». ComptesRendus hebdomadairesdesséancesdel’AcadémiedesSciencesdeParis,69(1869), 1265–1269.

[11] Betti,E.;Brioschi,F. GliElementid’Euclide,connote,aggiunteedesercizi adusode’ginnasiede’licei.Florència:LeMonnier,1867.

[12] Boi,L.;Giacardi,L.;Tazzioli,R. Ladécouvertedelagéométrienon euclidiennesurlapseudosphère:Leslettresd’EugenioBeltramiàJules Hoüel(1868–1881).París:AlbertBlanchard,1998.

[13] Bolyai,G. «Sullascienzadellospazioassolutamentevera,edindipendente dallaveritàodallafalsitàdell’assioma xi diEuclide(giammaidapotersi decidereapriori)». GiornalediMatematiche,6(1868),97–115.[Traducció deG.Battaglini]

[14] Bolyai,J. Lascienceabsoluedel’espaceindépendantedelavéritéoudela faussetédel’Axiôme xi d’Euclide(quel’onnepourrajamaisétablirapriori); suivedelaquadraturegéométriqueducercle,danslecasdelafuassetéde l’Axiôme xi.París:Gauthier-Villars,1868.[TraducciódeJ.Höuel]

[15] Bonola,R. Non-EuclideanGeometry.ACriticalandHistoricalStudyofits Developments.NovaYork:Dover,Inc.,1955.[TraduccióambapèndixsaddicionalsperH.S.Carslaw.Suplementqueconté«Thetheoryofparallels», deN.Lobachevski«Thescienceofabsolutespace»,deJ.Bolyai]

[16] Brioschi,F.;Cremona,L. «AlsignorDirettoredelGiornalediMatematiche adusodeglistudentidelleUniversita’italiane—Napoli». Giornaledi Matematiche,7(1869),51–54.

[17] Briot,M.;Bouquet,M. Théoriedesfonctionsdoublementpériodiqueset, enparticulier,desfonctionselliptiques.París:Mallet-Bachelier,1859.

[18] Brunel,G. «Noticesurl’influencescientifiquedeGuillaume-JulesHoüel». MémoiresdelaSociétédessciencesphysiquesetnaturellesdeBordeaux, 3esérie,1ercahier,4(1888),1–78.

[19] Castellana,M.;Palladino,F. GiuseppeBattaglini.Raccoltadilettere (1854–1891)diunmatematicoaltempodelRisorgimentod’Italia.Bari: Levante,1996.

[20] Cayley,A. «Asixthmemoiruponquantics». PhilosophicalTransactionsof theRoyalSocietyofLondon,149(1859),61–90; TheCollectedMathematical Papers.Vol.2.Cambridge:CambridgeUniversityPress,1889.

[21] D’Ovidio,E. «CommemorazionedelSocioGiuseppeBattaglini». Mem. RealeAccad.LinceiCl.Sci.Fis.(5),1(1895),558–610.

[22] D’Ovidio,E. «EugenioBeltrami». AttidellaRealeAccademiadellescienze diTorino,35(1900),541–546.

[23] Gauss,C.F. «Disquisitionesgeneralescircasuperficiescurvas». CommentationesSocietatisRegiaeScientarumGottingensisRecentioresClassis Mathematicae, vi (1828),99–146.[Presentatel8d’octubredel1827.Vegeu també[24,vol.4,p.217–258]]

[24] Gauss,C.F. CarlFriedrichGaussWerke.Vol.1–12.B.G.Teubner,Leipzig: KöniglichenGesellschaftderWissenschaftenzuGöttingen,1870–1927. [LescartesdeGaussespodenconsultartambéa: https://gauss.adwgoe.de]

[25] Halsted,G.B. «Biography:GuillaumeJulesHoüel». Amer.Math.Monthly, 4(4)(1897),99–101.

[26] Hoüel,G.J. «Essaid’uneexpositionrationnelledesprincipesfondamentauxdelagéométrieélémentaire». ArchivderMathematikundPhysik,40 (1863),171–211.

[27] Hoüel,J. Essaicritiquesurlesprincipesfondamentauxdelagéométrieélémentaireoucommentairesurles xxxii premièrespropositionsdesÉléments d’Euclide.París:Gauthier-Villars,1867.

[28] Hoüel,J. «Quelquesréflexionsausujetdelalignedelongueurminimum surlasphère». Nouvellesannalesdemathématiques,2esérie,7(1868), 73–78.

[29] Hoüel,J. «EstrattodiunaletteradelProf. Hoüel alredattore». Giornaledi Matematiche,7(1869),50.

[30] Hoüel,J. «Notesurl’impossibilitédedémontrerparuneconstruction planeleprincipedesparallèles,ditPostulatumd’Euclide». Mémoiresdela SociétédessciencesphysiquesetnaturellesdeBordeaux,8(1867),11–18.

[31] Hoüel,J. «Notesurl’impossibilitédedémontrerparuneconstructionplaneleprincipedesparallèles,ditPostulatumd’Euclide». Nouvellesannales demathématiques,2esérie,9(1870),93–96.

[32] Hoüel,J. Essaicritiquesurlesprincipesfondamentauxdelagéométrieélémentaireoucommentairesurles xxxii premièrespropositionsdesÉléments d’Euclide.París:Gauthier-Villars,1883.

[33] Klein,F. «UeberdiesogenannteNicht-EuklidischeGeometrie». MathematischeAnnalen,4(4)(1871),573–625.[TraducciófrancesadeM.L.Laugel, «Surlagéométrieditenoneuclidienne». AnnalesdelafacultédessciencesdeToulouse,1resérie,11(4)(1897),G1–G62;traduccióanglesade J.Stillwell, SourcesofHyperbolicGeometry.Providence,RI:AmericanMathematicalSociety;Londres:LondonMathematicalSociety,1996.(History ofMathematics;10)]

[34] Klein,F. «UeberdiesogenannteNicht-EuklidischeGeometrie.(Zweiter Aufsatz.)». MathematischeAnnalen,6(2)(1873),112–145.

[35] deLagrange,J.L. «Surlaconstructiondescartesgéographiques».(Nouveauxmémoiresdel’Académieroyaledessciencesetbelles-lettresdeBerlin, année1779). Œuvrescomplètes.Vol.4.París:Gauthier-Villars,1867–1892, 637–692.

[36] Lobatschewsky,N. «Géométrieimaginaire». JournalfürdieReineund AngewandteMathematik.[Crelle’sJournal],17(1837),295–320.

[37] Lobatschewsky,N.I. Étudesgéométriquessurlathéoriedesparallèles París:Gauthier-Villars,1866.[Traducciódel’alemanyperJ.Hoüel]

[38] Lobatschewsky,N. «Pangeometria,osuntodigeometriafondatasopra unateoriageneraleerigorosadelleparallele». GiornalediMatematiche,5 (1867),273–336.[TraducciódeG.Battaglini]

[39] Loria,G. «EugenioBeltrami elesueoperemathematiche.(MitBildnis.)». BibliothecaMathematica,3esérie,2(1901),392–440.

[40] MontesinosAmilibia,J.M. «Lacuestióndelaconsistenciadelageometría hiperbólica».A: Historiadelamatemáticaenelsiglo xix.Parte2.Madrid: RealAcademiadeCienciasExactas,FísicasyNaturales,1994,213–232.

[41] Peters,C.A.F.(ed.). BriefwechelzwischenC.F.GaussundH.C.Schumacher 6vol.Altona:G.Esch,1860–1865;Hildesheim;NovaYork:G.Olms,1975. [Versiódigitaldelescartesa: https://gauss.adw-goe.de]

[42] Reventós,A.;Rodríguez,C.J. Unalecturadel Disquisitionesgenerales circasuperficiescurvas deC.F.Gauss.Barcelona:Institutd’EstudisCatalans.SocietatCatalanadeMatemàtiques,2006.201p.(Publicacionsde laSCM;4)

[43] Riemann,B. «Fondamentidiunateoricageneraledellefunzionidiuna variabilecomplessa». AnnalidiMatematicaPuraedApplicata,2(1)(1859), 288–304.[Títoloriginal: GrundlagenfüreineallgemeineTheoriederFunctioneneinerveränderlichencomplexenGrösse.Inauguraldissertation,Göttingen,1851]

[44] Riemann,B. «ÜberdieHypothesen,welchederGeometriezuGrunde liegen».Habilitationsvortrag(1854); AbhandlungenderKönigl.Gesellschaft derWissenschaftenzuGöttingen,13(1868),309–326.

[45] Schaefer,C. BriefwechselzwischenCarlFriedrichGaussundChristian LudwigGerling.Berlín:O.Elsner,1927.[Reimpressió:Hildesheim;Nova York:G.Olms,1975.Versiódigitaldelescartesa: https://gauss.adw -goe.de]

[46] Tazzioli,R. «NewperspectivesonBeltrami’slifeandwork–considerationsbasedonhiscorrespondence».A: Coen,S. (ed.). Mathematiciansin Bologna1861–1960.Basilea:Birkhäuser,2012,465–517.

[47] Toth,I. «Non-EuclideanGeometrybeforeEuclid». ScientificAmerican, 221(5)(1969),87–101.

[48] Voelke,J.-D. Renaissancedelagéométrienoneuclidienneentre1860 et1900.Berna:PeterLang,2005.

[49] Wilson,J.M. «Euclidecometestodigeometriaelementare». Giornaledi Matematiche,6(1868),361–368.

malcalavi@gmail.com

ButlletídelaSocietatCatalanadeMatemàtiques Vol.34,núm.1,2019.Pàg.33–51. DOI:10.2436/20.2002.01.85

Elmètodedeleslíniesperalaresoluciónumèrica d’equacionsenderivadesparcials

CristinaDalfóiMiquelÀngelFiol

Resum: Enaquesttreballesdescriuunmètodenumèricsemidiscretperalaresolució d’untipusd’equacionsenderivadesparcials.Ésconegutcomel mètodedeleslínies (MOL,perlessiglesenanglès),iesbasaenladiscretitzaciódetoteslesvariables involucrades,excepteuna.Il.lustreml’aplicaciódelMOLamblaresoluciódel’equació deLaplaceencoordenadescartesianes.Elsconceptesmatemàticsquehiapareixen escomparenambelscorresponentsalmètodeanalíticdeseparaciódevariables.A més,mostremqueelsresultatsobtingutsambelMOLsónbonesaproximacionsdeles solucionsanalítiques.

Paraulesclau: equacionsenderivadesparcials,discretitzaciód’unavariablecontínua, anàlisinumèrica.

ClassificacióMSC2010: 65M20.

1Introducció

Elmètodedeleslínies,tambéanomenat mètodedesemidiscretització per Zuazua[14],ésunmètodeperalaresoluciód’equacionsenderivadesparcials(EDP)ambcondicionsdecontornienregionsambunacertasimetria.Es basaadiscretitzartoteslesvariables,excepteuna(sielproblemahopermet, sovintesdiscretitzenlesvariablesespacialsiesmantécontínualavariabletemporal).Aixòcondueixaunsistemad’equacionsdiferencialsordinàries(EDO), lesqualsespodenresoldrepelsmètodesnumèricshabitualsperaEDOamb condicionsinicials.Aquestmètodevaserintroduïtaprincipisdelsanysseixantai,desdellavors,lasevaexactitudiestabilitathanfetqueesgeneressin unabonaquantitatd’articles(vegeu,perexemple,Zafarullah[13]iVerweri Sanz-Serna[11]).

Pertant,el mètodedeleslínies (MOL)ésunenfocamentdiferencialide diferènciesfinitesperresoldreequacionsenderivadesparcials.Aquestmètode témoltesaplicacionsenlaresoluciódeproblemesenfísicaienginyeria.Per exemple,haestatusatàmpliamentperexpertsentècniquescomputacionals

CristinaDalfóiMiquelÀngelFiol

enproblemesd’electromagnetisme;vegeu,perexemple,BerardiiVurro[1], Diestel[4],Sadiku[6,capítol9],SadikuiObiozor[7],oShakeriiDehghan[9].

Enaquesttreballil.lustremelmètodedeleslíniesambl’equaciódeLaplace enelpla,persimplicitat.Elprocésaseguirconstadelspassossegüents:

1. Discretitzaciódel’equaciódiferencialenunadirecció:contracciódela regiódesolucionsaunconjuntdelínies,iaproximaciódelesderivades corresponents.

2.Obtenciód’unsistemad’equacionsdiferencialsordinàriesacoblades.

3. Transformacióperobtenirunsistemad’equacionsdiferencialsordinàries desacoblades.

4.Resoluciódelesequacionsdiferencials.

5.Transformacióinversaiintroducciódelescondicionsdecontorn.

6.Resoluciódelsistemad’equacionslinealsobtingutenelpasanterior.

Amésdelessevesmúltiplesaplicacions,perexemple,comjas’hadit,en electromagnetisme,aquestmètodeinvolucramoltesidees,conceptesitècniquesdelamatemàticadiscreta,juntamentambelsmètodesbàsicsdel’anàlisi diferencial.Defet,eneldesenvolupamentdelmètodeenstrobemambelsconceptesielsresultatssegüents:lesequacionsdiferencialsenderivadesparcials (el.líptiques,parabòliquesihiperbòliques),amblessevesaplicacions;l’estudi delsproblemesdecontorn(ambcondicionsdeDirichletodeNeumann);les tècniquesnumèriquesd’interpolaciópolinòmicail’aproximaciódederivades; lateoriadematriustridiagonalssemidefinidespositives(lesqualstambéapareixenenelsgrafsdistància-regulars);lateoriadematriuscirculantsilaseva relacióambelsgrafsdeCayleysobregrupscíclics;ladiagonalitzaciódematrius ielsalgorismesdelcàlculdelsvalorspropisivectorspropis;elteoremadels cerclesdeGershgorin(perlocalitzarelsvalorspropis);elspolinomisortogonals devariablediscreta(tambéimportantsenelsgrafsdistància-regulars);l’estudidecondicionsd’ortogonalitatenelcasdiscretrespectedelcascontinu;les transformacionsdiscretes(canvisdebase)com,perexemple,latransformada discretadeFourier(DFT);laresoluciódelesrecurrèncieslinealsilesdiferències finites;laresoluciód’equacionsdiferencialsordinàries(EDO)lineals;l’aproximacióicàlculd’errors;i,finalment,larepresentaciógràficailainterpretació delessolucions.

2Elmètodedeleslínies(MOL):l’equaciódeLaplace

Latransferènciadecaloral’estatestacionariensòlidssegueixl’equacióde Laplaceihaestatresoltadirectamentperdiversosmètodesnumèrics,comel mètodesuccessiudesobrerelaxació,elmètodeimplícitdedireccióalternativa ielmètodedetransitorisfalsos.AquestsmètodessónalternatiusalMOL, queveuremacontinuacióiqueconsisteixadiscretitzartoteslesvariables excepteuna.Devegades,elMOLtambéésanomenat mètodesemianalític (vegeu SubramanianiWhite[10]).

Elmètodedeleslíniesperalaresoluciónumèricad’EDP 35

2.1L’equaciódeLaplaceenundominirectangular Considereml’equaciódeLaplaceperalafunciópotencial V(x,y) enunaregió rectangular a × b. ∇2V = ∂2V ∂x2 + ∂2V ∂y 2 = 0,x ∈ (0,a),y ∈ (0,b), (1) ambcondicionsdefronteraque,persimplicitat,establimcoma

V(0,y) = V(a,y) = 0,y ∈ (0,b), (2)

V(x, 0) = 0,V(x,b) = f(x),x ∈ (0,a). (3)

Elprimerpasésdiscretitzarlavariable x ∈ (0,a) enels N punts xj = j∆x, pera j = 1, 2,...,N,onel«pas» h = ∆x = a N+1 corresponaladistànciaentre duesdeles N líniesresultantsdeladiscretització,segonsmostremalafigura1. y b

Figura 1: Discretitzaciódelavariable x

Araitereml’aproximaciólinealdeladerivadaendospuntssuccessius,

V (xj ) V(xj+1) V(xj ) h , iobteniml’anomenada aproximaciócentrada delasegonaderivada

V (xj ) V (xj ) V (xj 1) h

V(xj+1) 2V(xj ) + V(xj 1) h2 ,

amberror | j |≤ Ch2,perauna C constant,quecorresponaunmètodede segonordre.Ambnotaciósimplificada,

2 , (4) on Vj denotalafunció V(xj ,y).Sisubstituïm (4) a (1),obtenimles N equacions diferencials

∂2V ∂y 2 + 1 h2 (Vj+1 2Vj + Vj 1) = 0,j = 1,...,N. (5)

Aleshores,sireemplacem V(x,y) pelvectorcolumna V = (V1,...,VN ) , podemescriure(5)enformamatricialcoma

on Q ésunamatriutridiagonal,ésadir,

onelsvalors ql i qr depenendelescondicionsdecontorna x = 0i x = a. SilacondiciódecontornésdeDirichletperl’esquerra(respectivament,per ladreta),aleshores ql = 2(respectivament, qr = 2);silacondiciódecontorn ésdeNeumannperl’esquerra(respectivament,perladreta),aleshores ql = 1 (respectivament, qr = 1).

Perresoldreelsistema (6) d’equacionsdiferencialsordinàries(EDO)lineals desegonordreacobladesnecessitemtransformar-loenunsistemad’EDO desacoblades.Aleshores,lasolucióésdiagonalitzarlamatriu Q.Enaquest sentit,notemque Q éssimètricai,pertant,elsseusvalorspropis λ1,...,λN sónreals.Amés,elteoremadeGershgorin1 ensasseguralanonegativitat,ja quehandecomplir |λk 2|≤ 2,demaneraqueutilitzaremlanotació λk = ω2 k pera k = 1,...,N.Defet,coms’explicaalasubsecció3.2,lamatriu tridiagonal Q tétotselsvalorspropisdiferents,idonallocaunasuccessióde Sturmdepolinomisortogonals,elsqualsestanrelacionatsestretamentamb elscorresponentsvectorspropis(vegeu,perexemple,Godsil[5,§8,5]).

Pertant,tenimque T QT = D,on T éslamatriuortogonal(ambcolumnes ortonormalscorresponentsalsvectorspropisde Q),ésadir, T 1 = T ,i D éslamatriudiagonaldelsvalorspropisde Q.Aleshores, Q = TDT que,si substituïma(6),ensdona

1 RecordemqueelteoremadeGershgorinafirmaque,donadaunamatriu A = (ajk) ∈ Mn(C), siesdefineixenelscercles D1,...,Dn ambcentre ajj iradi rj = k≠j |ajk|,elsvalorspropisde lamatriu A estrobenenlauniódels Dj

Elmètodedeleslíniesperalaresoluciónumèricad’EDP 37

iutilitzantel potencialtransformat V := T V ,tenim

2

2 1 h2 D V = 0. (8)

Pertant,obtenim N equacionsdiferencialsordinàries(enlavariable y),del tipus V j = 1 h2 ω2 j ,j = 1,...,N,

ambsolucions(elpolinomicaracterísticés s2 = ω2 j h2 ,ambarrels s1,2 =± ωj h ) V j = αj e ωj h y + βj e ωj h y = Aj cosh ωj y h + Bj sinh ωj y h ,j = 1,...,N. (9)

Pertrobarelvectordepotencialsperacada j = 1,...,N,noméscalrealitzar la transformadainversa de V ,osigui, V = T V .

Finalment,imposemlescondicionsdecontorniresolemlesequacions resultantsperdeterminarlesconstants αj , βj ,o Aj , Bj

3Diagonalitzaciódelamatriu Q iortogonalitat

3.1Valorsivectorspropis

Abansderesoldreunexempleconcret,enaquestasecciódiscutimladiagonalitzaciódelamatriu Q ilespropietatsd’ortogonalitatinvolucrades.Elsresultats obtinguts,elsvalorspropis λk = ω2 k ilesmatriusdevectorspropis T = (Tjk), esmostrenalataula1,segonslescondicionsdecontorna x = 0i x = a

Esquerra Dreta

Neumann

Taula 1: Componentsdelamatriu T ivalorspropis λk = ω2 k segonsles condicionsdecontorna x = 0i x = a

Peralcàlculprocedimdelamanerasegüent.L’equacióaresoldreés

d’on (ql λ)u1 u2 = 0, (11) (2 λ)uj uj 1 = uj+1,j

(13)

on,peralsvalorsusatsde ql i qr ,elteoremadeGershgorinielfetquela matriuéssimètricaimpliquenqueelsvalorspropisestanal’interval [0, 4]

Perresoldrel’equacióendiferències (12) podríemusarlasolució uj = sj , peròs’obtéunresultatméscompacteamb uj = eijα (ésadir,agafant s = eiα = cos α + i sin α).Sisubstituïmaquestvalora (12) idividimper ei(j 1)α obtenim

(14)

Pertant,l’equaciócaracterísticaés λ = 2(1 cos α) = 4sin2 α

cosaquesignificaque,peracadavalorpropi λ,tenimdospossiblesvalors de α:

Així,amb α = α1,lasoluciógeneraldelarecurrènciaés

Pertrobarelspossiblesvalorsdelesconstants A, B,i α,imposemles «condicionsinicials» (11) i (13).SuposemquetenimcondicionsdeDirichletper ladretail’esquerra,ésadir, ql = qr = 2.(Elsaltrescasosesresolendemanera similar.)Delaprimeraequació,s’obtéque (2 λ)u1 u2 = 2cos α(Aeiα + Be iα) Aei2α Be i2α = 0 ⇒ A + B = 0, onhemaplicat cos α = eiα+e iα 2 i sin α = eiα e iα 2i .Pertant, B =−A i,llevatd’una constantmultiplicativa,podemsuposarque uj = sin(jα),j = 1,...,N.

Elmètodedeleslíniesperalaresoluciónumèricad’EDP 39

D’altrabanda,de(13)s’obté

(2 λ)u1 u2 = 2cos α(AeiNα + Be iNα) Aei(N 1)α Be i(N 1)α) = 0 ⇒ sin((N + 1)α) = 0.

Pertant,elspossiblesvalorsde α són αk = kπ N+1 ,pera k = 1,...,N,ambla qualcosaobtenimelsvalorspropis λk = 4sin2 kπ 2(N + 1) ,k = 1,...,N, (17) elsqualscompleixenque λ1 <λ2 < <λN ,ambelsrespectiusvectors propis

uk = (ujk) = sin kπ N + 1 , sin 2kπ N + 1 ,..., sin Nkπ N + 1 . (18)

Finalment,comquelescolumnesde T handeserortonormals,tenim uk 2 = N j=1 sin2 jkπ N + 1 = 1 2 N j=1 1 cos 2jkπ N + 1 =···= N + 1 2 ,

onhemusatque sin2 x = 1 2 (1 cos(2x)) ilasumad’unasèriegeomètrica N j=1 r j = r(1 r N ) 1 r .Concloemquelescomponentsdelamatriu T són Tjk = (ujk) = 2 N + 1 sin jkπ N + 1 ,j,k = 1,...,N, (19) coms’indicaalataula1.

3.2Ortogonalitat

Consideremaralespropietatsd’ortogonalitatqueapareixenenelMOL,iles comparemamblescorresponentsdelmètodeanalític.Enprimerlloc,notem que,perserunamatriusimètrica,elselementsdelessubdiagonalsdela matriu Q = (qjk) satisfan qj,j+1qj+1,j > 0pera j = 1,...,N i,pertant,donenllocaunafamíliadepolinomisortogonals p0,p1,...,pN 1 devariable discreta.2 Aquestéstambéelcas,perexemple,delamatriuquocientd’un grafdistància-regular,elspolinomisortogonalsdelqualcorresponenalsanomenats polinomisdistància.Elsdetallsd’aquestaaplicació,ialtresdetipus combinatori,podentrobar-seal’articledeCámara,Fàbrega,FioliGarriga[2].

2 Ésadir,polinomisortogonalsrespected’unproducteescalardiscretenelspuntsd’una malla x1,...,xN ∈ R: f,g = N j=1 wj f(xj )g(xj ) peraunscerts«pesos» wj > 0.Elspolinomis ortogonalsespodenobtenirambelmètodedeGram-Schmidtapartirde1,x,x2,...,xN 1 amb lanormalitzacióadequada.

Elspolinomis p0,p1,...,pN 1 constitueixenunasuccessiódeSturm(vegeu Godsil[5,§8.5]oChihara[3])isatisfanunarelacióderecurrènciadetres termes(comal’expressió(12))

pk+1(x) = (2 x)pk(x) pk 1(x),k = 1,...,N 2, (20) inicialitzadaamb p0(x) = 1i p1(x) = 2 x.Amés, pN (x) = (2 x)pN 1(x) pN 2(x) corresponalpolinomicaracterísticdelamatriu Q i,pertant,lesseves arrelssónelsvalorspropis λk,ambvectorspropis

uk = (p0(λk),p1(λk),...,pN 1(λk)) ,k = 1,...,N, trobatsanteriormenta (17) i (18) (aquestsúltimsllevatd’unaconstantmultiplicativa).L’ortogonalitatesmentadas’obtérespected’unproducteescalardiscret enelspuntsdelamalla λ1,λ2,...,λN ,amb λ1 <λ2 < <λN .Pertant,un copnormalitzemelsvectors uk,ésadir, uk = uk/ uk ,obtenimdenouels elementsdelamatriu T donatsa(19):

Tj,k = (vk)j ,j,k = 1,...,N, ésadir,

Tj,k = 2 N + 1 sin jkπ N + 1 = pj 1(λk) N 1 j=0 p2 j (λk) 1 2 ,j,k = 1,...,N. (21)

Compareulesfuncionspròpiesdelaprimeraigualtatde (21) amblesdelcas analític(23).Observeuque(21)espotentendrecomlaversiódiscretade(23).

Enaquestcontext,observemqueelpotencialtransformat V = T V noés mésqueelvectordecoeficientsdeFourierobtingutenexpressar V entermes d’unspolinomisortogonals(que,enelspuntsdelamalla,tenenelsvalors donatspercadafilade T ).

Perexemple,enelcasdelamatriu Q a (10) amb N = 5i ql = qr = 2, s’obtenenelspolinomis p0(x) = 1, p1(x) = 2 x, p2(x) = x2 4x + 3, p3(x) =−x3 + 6x2 10x + 4, p4(x) = x4 8x3 + 21x2 20x + 5, p5(x) =−x5 + 10x4 36x3 + 56x2 35x + 6

Elsvalorspropisde Q (lesarrelsde p5(x))són: λ1 = 2 3,λ2 = 1,λ3 = 2,λ4 = 3,λ5 = 2 + 3.

Elmètodedeleslíniesperalaresoluciónumèricad’EDP 41

Alafigura2esmostrenlesgràfiquesde pj (x),pera j = 0,..., 4.Noteules paritats(parellsisenars)d’aquestspolinomisrespectede x = λ3 = 2,induïdes perlescorresponentssimetriesdelamatriu

Figura 2: Elspolinomisortogonals pj (x) (degrau j),pera j = 0,..., 4.

4Unexemple

Aravegemcoms’aplicaelMOLalaresoluciód’unproblemaconcret:resoldre l’equaciódeLaplace(potencial)

ambcondicionsdecontorndetipusDirichlet V(0,y) = V(a,y) = V(x, 0) = 0 i V(x,b) = 100,amb a = b = 1alaregiórepresentadaalafigura3.També volemcalcularelvalordelpotencialenelspuntsindicatsenaquestafigura.

y 1 3/4 1/2 1/4 1/41/23/41 x

Figura 3: Regióonvolemresoldrel’equaciódeLaplaceambelMOL.

Lamatriu Q tévalorspropis ω2 k = 4 sin2 kπ 2N+2 ,pera k = 1, 2,...,N,ila matriudevectorspropis T técomponents Tjk = 2 N+1 sin jkπ N+1 (vegeulataula1).

Siescollim N = 15,resultaque h = x = 1 16 ,ilesabscissesdelspuntson volemcalcularelpotencialsón x4 = 1 4 , x8 = 1 2 i x12 = 3 4

De Vj = N k=1 TjkV k,pera i = 1, 2,...,N,obtenimlasolució

Ara,perdeterminarlesconstants Aj i Bj ,imposemlescondicionsdecontorn: • V(x, 0

d’on Aj = 0,pera

• V(x, 1) = 100

Elmètodedeleslíniesperalaresoluciónumèricad’EDP 43

Figura 4: Gràficadelspotencials Vj (y) = V(xj ,y),amb xj = jh i j = 1,..., 15,pera V(x, 1) = 100.

d’on

Pertant,

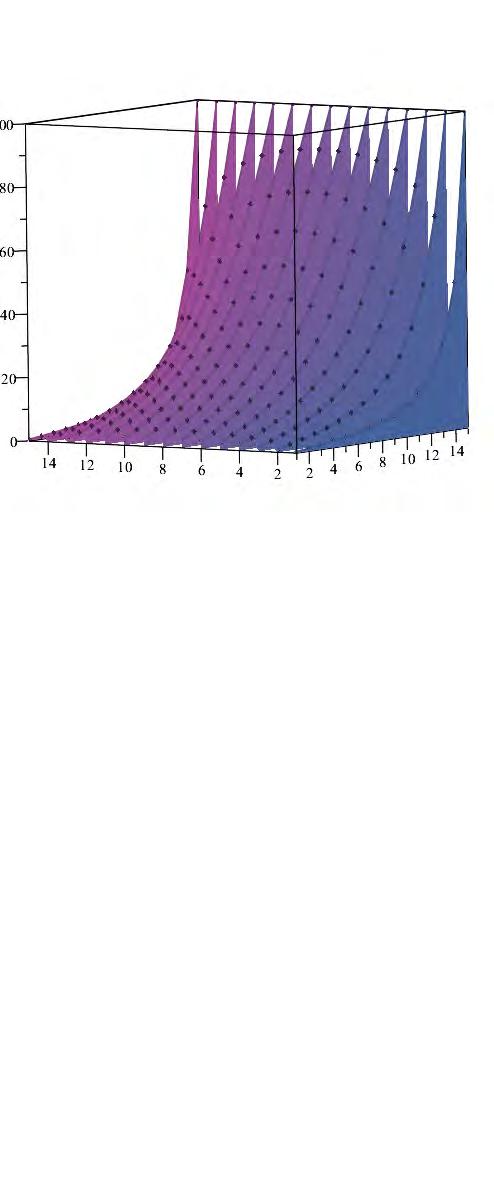
Així,arribemal’aproximació V(xj ,y) de V(xj ,y): V(xj ,y) = N

laqualestàrepresentadaalafigura4.

Enelspuntsqueensinteressen,elsvalorsques’obtenenambelMOL (calculatsambelprogramadelasecció7)són

que,comparatsambelsvalorscalculatsanalíticamentaplicantlafórmula (24) delasecció5,

demostrenserbonesaproximacions.

5Elmètodeanalític

Aravolemresoldreelproblemaanteriorambelmètodeanalític,perpoder-lo compararambelresultatobtingutambelMOL.Ésadir,jaquepodemconèixer lasolucióanalítica,empreml’equaciódeLaplacecomatestpelmètodedeles línies.

Considerem,doncs,denoul’equació

pera x ∈ (0,a) i y ∈ (0,b),ambcondicionsdecontorn V(0,y) = V(a,y) = V(x, 0) = 0, V(x,b) = f(x), comesveualafigura5.

Figura 5: Regióonvolemresoldrel’equaciódeLaplaceambelmètode analític.

Lasolucióanalíticas’obtéperseparaciódevariables,ésadir,suposant queelpotencialésdelaforma V(x,y) = X(x)Y(y),d’ontrobemque X i Y satisfanlesequacions X (x) + ω2X(x) = 0, Y (y) ω2Y(y) = 0

Elmètodedeleslíniesperalaresoluciónumèricad’EDP 45

Imposantlescondicionsdecontornhomogènies,resultaque ω = ωk = kπ a pera k = 1, 2,... iobtenimlesfuncions

X(x) = B sin kπ a x ,

Y(y) = C sinh kπ a y ,

amb B i C constants.Pertant,lessolucionsdelproblemahomogenisón:

Vk(x,y) (23)

Consideremaraunasolucióenformadesèrie

V(x,y) =

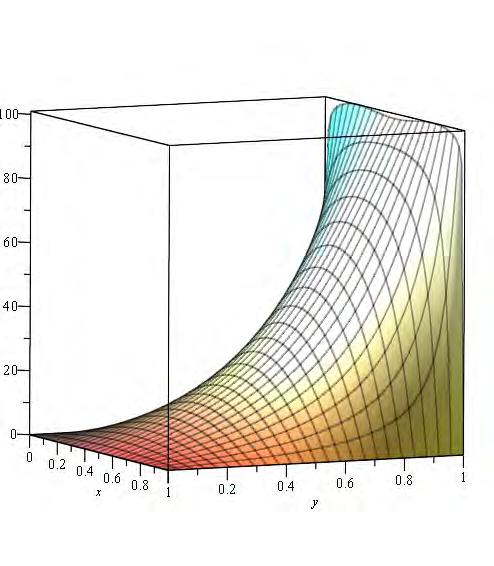
Figura 6: Gràficadelpotencial V(x,y) enelcas a = b = 1, V(0,y) = V(a,y) = V(x, 0) = 0i V(x,b) = 100.

Siimposemlacondiciódecontornnohomogènia

V(x,b) = f(x) = ∞ k=1 Ak sinh kπ a b sin kπ a x ,

iconsideremque sin kπ a x : k = 1, 2,... ésunabaseortogonala (0,a), obtenimelcorresponentdesenvolupamentensèriedeFourierde f(x),amb coeficients αk = Ak sinh kπ a b = 2 a a 0 f(x) sin kπ a x dx.

Pertant,lasolucióanalíticaés

V(x,y) = ∞ k=1 αk sinh kπ a y sinh kπ a b sin kπ a x .

Observemquelescondicionsdecontorn iguals azeroa x = 0i x = a donen solucionsperiòdiquesen sinus,mentrequelescondicionsdecontorn diferents a y = 0i y = b donensolucionsnoperiòdiquesen sinushiperbòlics. Enl’exempleanterior,utilitzantelMOL,consideràvemelcasparticular a = b = 1i f(x) = 100.Enaquestcas,araobtenimque αn = 400 nπ pera n senar i αn = 0pera n parell.Aleshores,lasolucióanalíticaés

V(x,y) = 400 π ∞ k=1 1 2k 1 sinh((2k 1)πy) sinh((2k 1)π) sin((2k 1)πx), (24) larepresentaciógràficadelaqualesmostraalafigura6.

6Sobrel’error

Podemcalcularl’errorcomèsquanutilitzemelmètodedeleslínies,simplement ambladiferènciaentreelsresultatsobtingutsambelMOLielmètodeanalític. Defet,sesapque,sotacondicionsgeneralsderegularitatdelessolucions, l’errordelmètodedeleslíniesésdel’ordredeO(h2) (vegeu,perexemple, Schiesser[8]oZuazua[14,15]).

Nosaltresestudiemprimerelcomportamentdel’errorenelcasdel’exemple anterior(secció4).Alafigura7esrepresentenelserrorsdelesaproximacions de V(xj ,y) pera j = 1,..., 8;perbéque N = 15,persimetriaenlescondicions decontorn,hihasetfuncionsd’errorquesesuperposenaunesaltresset.

y

Figura 7: Gràfiquesdelserrorsabsolutscomesosencalcularelpotencialambelmètodedeleslíniesenl’exempledelasecció4encomparacióambelmètodeanalític(secció5).

Elmètodedeleslíniesperalaresoluciónumèricad’EDP 47

Observemquetenim8funcionsd’error(pera xj = j/16, j = 1,..., 8)malgrat que N = 15perquè,persimetriaenlescondicionsdecontorn,hiha7funcions d’errorquesesuperposenaaltres7(ienquedaunasensesuperposar).Com erad’esperaracausadeladiscontinuïtatenlescondicionsdecontorn,els errorssónméspetitsquansommésapropdelcentredelagràfica(ésadir, pera x8 = 1/2).

Perobtenirresultatsmésprecisos,consideremaraunaltreexemplemés senzill,elqualenspermetdonarlasoluciónumèricaambunafórmulatancada. Així,suposemaraquelescondicionsdecontornsón V(0,y) = V(1,y) = V(x, 0) = 0,comabans,ique V(x, 1) = sinh(π) sin(πx).Aleshores,pertrobar lasolucióanalíticanocalferl’últimpasdeldesenvolupamentensèriede Fourier,is’obté

V(x,y) = sinh(πy) sin(πx), (25) lagràficadelaqualesmostraalafigura8.Pelquefaalmètodedeles línies,esmentemprimerqueaquestcasvaserresoltcomputacionalmentper SubramanianiWhite[10]utilitzantmatriusexponencials,encaraquesense arribaraunaexpressiótancada.Encanvi,lestècniquesdescritesaquíens permetenobtenirlasoluciócompactasegüent

V(xj ,y) (26) on xj = jh, j = 1,...,N,i sinc .Vegeulafigura9.Notemque,com que limh→0 sinc(h) = 1,quan V(xj ,y) → V(x,y),comerad’esperar.Defet,enaquestcasésfàcilcomprovarque,per acada y,l’error = V(xj ,y) ,comjahem comentat.

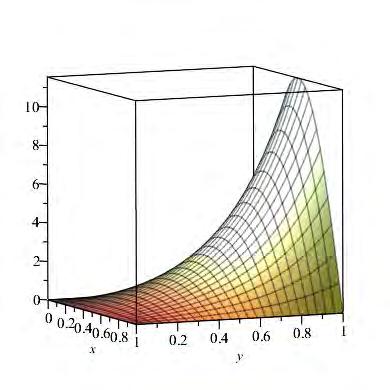
Figura 8: Gràficadelpotencial V(x,y) enelcas a = b = 1, V(0,y) = V(a,y) = V(x, 0) = 0i V(x,b) = sinh(π) sin(πx).

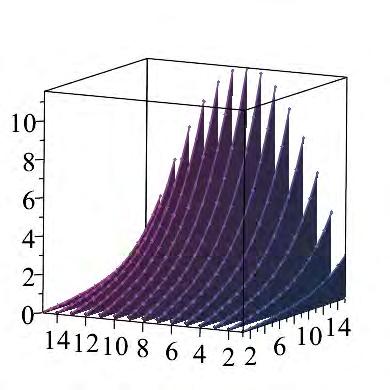
Figura 9: Gràficadelpotencial Vj (y) = V(xj ,y), xj = jh, j = 1,..., 15, pera V(x,b) = sinh(π) sin(πx).

7ProgramaenMATLAB

Acontinuació,escrivimenelllenguatgedelprogramaMATLABlesinstruccions percalcularelvalordelpotencialenelstrespuntsinteriorsqueesconsideren al’exempledelasecció4.

>>AA=1; >>BB=1; >>N=15; >>%Determinemelvectoralpha >>H=AA/(N+1); >>LAMBDA=2*sin((1:N)*pi*0.5/(N+1)); >>ALPHA=LAMBDA/H; >>%Calculemlamatriudetransformació >>S=sqrt(2/(N+1)); >>T=zeros(N,N); >>forJ=(1:N) forK=(1:N)

T(J,K)=S*sin(J*K*pi/(N+1)); end end

>>V=100*ones(N,1); >>C=inv(T)*V; >>A=ALPHA’; >>B=C./sinh(BB*A); >>%CalculemVenelspuntsdonats >>V1=0;V2=0;V3=0; >>forK=1:N

Elmètodedeleslíniesperalaresoluciónumèricad’EDP 49

V1=V1+T(4,K)*B(K)*sinh(ALPHA(K)*0.75);

V2=V2+T(8,K)*B(K)*sinh(ALPHA(K)*0.5);

V3=V3+T(12,K)*B(K)*sinh(ALPHA(K)*0.25); end

>>diary

>>V1,V2,V3

V1=43.1008

V2=24.9644

V3=6.7984

>>diaryoff

8AltresexemplesresolublesambelMOL

Finalment,detallemalgunsaltresexemplesqueespodenresoldreambel mètodedeleslínies.

1. L’equaciódeLaplaceenlaregióquadrada1×1ambcondicionsdecontorn:

(a)Dirichlet-Neumann. (b)Neumann-Dirichlet.

(c)Neumann-Neumann.

(Elsvalorsautilitzardelamatriu T ielsvalorspropis ω2 k sónalataula1.)

2. L’equaciódeLaplaceencoordenadescilíndriques ρ

2 = 0, amblescondicionsdecontorn V(ρ,φ) = 0pera0 ≤ ρ ≤ a i V(ρ,φ) = V0 pera a<ρ ≤ b,ambladiscretitzaciódelacoordenadaangular φ.La solucióanalíticaés V(ρ) = V0 ln( ρ a ) ln b a .

3. L’equaciód’ona ∂2 v ∂t2 ∂2 v ∂x2 = q(x,t),amb0 ≤ x ≤ L i0 ≤ t ≤ T ,les condicionsinicials v(x, 0) = f1(x) i ∂v ∂t (x, 0) = f2(x) pera0 ≤ x ≤ L, lacondiciódecontorndeDirichlet v(0,t) = g1(x) ilacondiciónolocal L 0 v(x,t)dx = g2(x) pera0 ≤ t ≤ T .Alataulasegüenthihaalguns casosparticularsamblacorresponentsolucióanalítica.

L T q(x,t) f1(x) f2(x) g1(t) g2(t) v(x,t) analítica

1 4 0 0 π cos(πx) sin(πt) 0 cos(πx) sin(πt)

1 5 2(x t)e x t 0 0 xe x 0 0 2te t 1+ +te t xte x t xte x t

1 4 0 cos(πx) 0 cos(πt) 0 1 2 cos(π(x + t))+ + 1 2 cos(π(x t))

1 5 2x5 + 2x3 2x2 (20x3 + 6x 2) (t2 t) 0 x5 x3 + x2 0 t(t 1) 12 (x5 + x3 x2)· (t2 t)

9Conclusions

Elmètodedeleslínieshademostratserunabonaeinaperresoldrealguns tipusd’equacionsenderivadesparcialsambcondicionsdecontorn.Comquees basaadiscretitzartoteslesvariablesexcepteuna,espotutilitzardirectament enl’equaciódeLaplace,laqualhemfetservircomaexempleil lustratiu.Una alternativaésaplicarelmètodedelesfalsestransicions,afegintunaderivada temporalidiscretitzantlesvariablesespacials.Siestemalpla xy,l’error d’aquestmètodealternatiuésdel’ordrede ∆2 x + ∆2 y .Pertant,ésmilloraplicar elmètodesemidiscret(osemianalític),queéselquehemaplicat,ienelqual hemvistquel’errorésdel’ordrede ∆2 x .

Perunaaltrabanda,espotestudiarcomcanvial’errorsi,encomptes deprendrelíniesequiespaiades,consideremlíniessituadesalszerosdels polinomisdeTxebixov(elsqualstenenunmillorcomportamentrespectede l’error).Enaquestcontext,espotconsultareltreballdeYoussefiShukur[12]. Finalment,proposemelsegüentproblemaobert:Estudiarlessemblancesiles diferènciesentreelMOLilaintegracióalllargdelesrectescaracterístiquesde l’equacióenderivadesparcialsdeprimerordre ∂V ∂t + c ∂V ∂x = f(x,t),amb c> 0.

Agraïments

Elsautorsvolenagrairelscomentarisisuggerimentsdelrevisoranònim,els qualshancontribuïtconsiderablementamilloraraquesttreball.

Aquesttreballhaestatparcialmentfinançatperl’AGAURdelgoverncatalàambelprojecte2017SGR1087ipelMICINNdelgovernespanyolambel projectePGC2018-095471-B-I00.

LaprimeraautoratambéhaestatparcialmentfinançadapelMICINNambel projecteMTM2017-83271-RipelprojectedelaUnióEuropeaMarieSkłodowskaCurie734922dinsdelprogramaHorizon2020.

Referències

[1] Berardi,A.;Vurro,M. «ThenumericalsolutionofRichards’equationby meansofmethodoflinesandensembleKalmanfilter». Math.Comput. Simulation,125(2016),38–47.

[2] Cámara,M.;Fàbrega,J.;Fiol,M.A.;Garriga,E. «Somefamiliesof orthogonalpolynomialsofadiscretevariableandtheirapplicationsto graphsandcodes». Electron.J.Combin.,16(1)(2009).(ResearchPaper;83, 30p.)

[3] Chihara,T.S. AnIntroductiontoOrthogonalPolynomials.NovaYork; Londres;París:GordonandBreachSciencePublishers,1978.(Mathematics anditsApplications;13)

[4] Diestel,H. «Analysisofplanarmulticonductortransmission-linesystems withthemethodoflines». Arch.Elektron.Übertragungstech.,41(3)(1987), 169–175.

Elmètodedeleslíniesperalaresoluciónumèricad’EDP 51

[5] Godsil,C.D. AlgebraicCombinatorics.NovaYork:Chapman&Hall,1993. (ChapmanandHallMathematicsSeries)

[6] Sadiku,M.N.O. ComputationalElectromagneticswithMatlab.4aed.Boca Raton;Londres;NovaYork:CRCPress,2018.

[7] Sadiku,M.N.O.;Obiozor,C.N. «Asimpleintroductiontothemethodof lines». Int.J.Elec.Eng.Educ.,37(3)(2000),282–296.

[8] Schiesser,W.E. TheNumericalMethodofLines.IntegrationofPartial DifferentialEquations.SanDiego,CA:AcademicPress,Inc.,1991.

[9] Shakeri,F.;Dehghan,M. «Themethodoflinesforsolutionoftheonedimensionalwaveequationsubjecttoanintegralconservationcondition». Comput.Math.Appl.,56(9)(2008),2175–2188.

[10] Subramanian,V.R.;White,R.E. «Semianalyticalmethodoflinesfor solvingellipticpartialdifferentialequations». Chem.Eng.Sci.,59(4)(2004), 781–788.

[11] Verwer,J.G.;Sanz-Serna,J.M. «Convergenceofmethodoflinesapproximationstopartialdifferentialequations». Computing,33(3–4)(1984), 297–313.

[12] Youssef,I.K.;Shukur,A.M. «Thelinemethodcombinedwithspectral Chebyshevforspace-timefractionaldiffusionequation». Appl.Comput. Math.,3(6)(2014),330–336.

[13] Zafarullah,A. «Applicationofthemethodoflinestoparabolicpartial differentialequationswitherrorestimates». J.Assoc.Comput.Mach.,17 (1970),294–302.

[14] Zuazua,E. «Introducciónalanálisisnuméricodeecuacionesenderivadas parcialesdeevolución».Notesd’uncursintroductorialcàlculnumèric d’equacionsdiferencials.UniversidadAutónomadeMadrid,2003. http:// verso.mat.uam.es/web/ezuazua/documentos public/archivos/personal/ comites/1 anedpde2.pdf.

[15] Zuazua,E. «Métodosnuméricosderesolucióndeecuacionesenderivadas parciales».BasqueCenterforAppliedMathematics(BCAM),2009.Notes.

CristinaDalfó DepartamentdeMatemàtica UniversitatdeLleida Igualada(Barcelona),Catalunya cristina.dalfo@matematica.udl.cat

MiquelÀngelFiol DepartamentdeMatemàtiques

BarcelonaGraduateSchoolofMathematics UniversitatPolitècnicadeCatalunya Barcelona,Catalunya miguel.angel.fiol@upc.edu

ButlletídelaSocietatCatalanadeMatemàtiques Vol.34,núm.1,2019.Pàg.53–89. DOI:10.2436/20.2002.01.86

Codisdetectorsicorrectorsd’errorsialgunesde lessevesaplicacionsalasocietatdelainformació

MercèVillanuevaiCristinaFernández-Córdoba

«Maleïtsigui!Silesmàquinespodendetectarunerror,perquènopodemlocalitzarla posiciódel’erroricorregir-lo?»,1947.

RichardW.Hamming(1915–1998)

Resum: Enlestransmissionsdigitalsd’informaciód’unemissoraunreceptora travésd’uncanal,normalmentesprodueixenerrors.Enaquestarticles’exposenels conceptesiresultatsmésimportantsdelateoriadecodisdetectorsicorrectorsd’errors, queestudiamètodeseficientspergarantirunatransmissióexactadelainformació. Primeresdescriuenalgunsexemplesquotidiansdecodisdetectorsd’errorsinclosos enelDNI,l’ISBN,l’IBANil’EAN.Acontinuació,espresentalateoriaclàssicadelscodis correctorsd’errors,queinclouelscodislinealsi,dinsd’aquests,elscodiscíclics,que resultenméseficientsal’horadecodificar.Tambéesdescriuenlesduesfamíliesmés importantsdecodiscíclics,elsBCHiReed-Solomon,quepermetendescodificartambé deformaeficient.Finalment,esmostrenduesaplicacionshistòriques,enlesmemòries d’ordinadorienlatransmissiódefotografiesal’espai,iduesaplicacionsmésrecents, enelscodisQRienl’emmagatzematgedistribuït.

Paraulesclau: detecciód’errors,correcciód’errors,codislineals,codiscíclics,BCH, Reed-Solomon,aplicacions.

ClassificacióMSC2010: 94B05,94B15,11T71.

1Introducció

Capal’any1948,ClaudeE.Shannonvaformularenelsseustreballselproblemadelatransmissiód’informacióentermesestadístics,utilitzantmodels probabilísticsperalesfontsd’informacióielscanalsdecomunicació[41].Amb aqueststreballsvanéixerunnoucampanomenat teoriadelainformació [1], dinsdelqualestrobalateoriamatemàticadelacomunicaciódigital,queestudialatransmissiódelainformacióentreunemissoriunreceptoratravésd’un

canal.Enmoltscasos,elscanalsqueesfanservirsóninsegursiambsoroll, com,perexemple,enlacomunicacióentredostelèfonsmòbilsviasatèl.lit,on lainformacióviatjaperl’espaiatravésd’ones.

Així,engeneral,lainformaciópotserinterceptadaimanipuladapertercers. Amés,espodenproduirerrorsiinterferènciesquealterenelsenyaltransmès, cosaquefaqueelreceptornorebiexactamentlamateixainformacióquehavia enviatl’emissor.Altresexemplesdecomunicaciódigitalestrobenenlatelevisió digital,l’emmagatzematgededadesendiferentsdispositius(memòries,CD, Blu-ray,etc.),Internet,Internetdelescoses(IoT),etc.

Enlatransmissiód’informacióesconsiderendiferentsmecanismes,de maneraqueespuguigarantirquelacomunicacióentrel’emissorielreceptor siguieficient,seguraiexacta.Lafigura1mostraunesquemagenerald’un sistemadecomunicaciódigitalatravésd’uncanalinseguriambsoroll.Pertal quelatransmissiósiguiméseficient,s’aplicauncompressorquepermetreduir lamidadelesdadesquevolemenviaraprofitantlaredundànciaqueaquestes presenten.Tambéespotrealitzarunprocésdexifratge(tambéconegutcoma encriptació)pertald’evitarqueuntercerpuguiaccediralesdadesigarantir aixílasevaconfidencialitati/oautenticitat.Finalment,perassegurarunacomunicaciófiableiexacta,escodifiquenfentservircodiscorrectorsd’errors.Ésen aquestadarrerafase,estudiadadinsdel’anomenada teoriadelacodificació, enlaqualenscentraremenaquestarticle.

Emissor Compressió

Xifratge

Soroll

Espia

Descompressió Receptor

Codificació Canal Descodificació Desxifratge

Figura 1: Sistemadecomunicaciódigital.

Inicialment,lateoriadelacodificacióestrobavadinsdel’àmbitdel’enginyeriaelectrònicaoinformàtica.Amés,elscanalsconsideratserenbinaris i,pertant,elscodisestudiatsestavendefinitssobreelcos Z2.Apocapoc, lateoriadelacodificaciós’haanatendinsantmésenl’àmbitmatemàtic.Per unabanda,s’haanatdotantelscodisdecertaestructuraalgebraicaqueha anatfentméseficientelprocésdecodificaridescodificar;i,perunaaltra banda,s’hanconsideratcodissobrealfabetsdiferents.Primer,esvancomençar aestudiarcodissobrecossosfinits.Apartirdel1994,arrandel’article[18], onesvanestudiarcodissobre Z4,vancomençaratenirmésimportànciaels codissobreanellsengeneral.Tambés’hanconsideratcodissobrealfabets mixtos(lescoordenadesestrobenendiferentsanells)[5].Actualment,dins delcampdelateoriadelacodificació,hihaunavessantmésd’enginyeria queestudial’aplicaciódemètodesdecodificacióidescodificacióadiferents

sistemesdecomunicació,iunaaltravessantmésmatemàticaqueestudiales diferentsestructuresalgebraiques,geomètriquesicombinatòriesdelscodis,la construcciódenouscodis,l’existènciadecodisambcertespropietats,ilaseva classificació.

Durantlatransmissiódedadesdigitals(normalmentenformadeseqüència debits)atravésdecanalsambsoroll,espodenproduirerrorsi,pertant,no rebrealasortidadelcanalexactamentlesmateixesdadesques’havienenviat. Perexemple,pothaver-hisorolltèrmicgeneratperl’equipamentelectrònic. Elscodiscorrectorsd’errorstenencomaobjectiudetectaraquestserrorsi corregir-los.Aquestprocéspermet,perexemple,rebrebonesimatgesdesdels satèl.lits,ogaudirdelamúsicaemmagatzemadaenunCDencaraqueeldisc estiguiratllat.Elpreuques’hadepagarpercorregirelserrorsésafegiruna certaredundànciaalesdadesqueesvolentransmetre.

Nonomésenlestransmissionsd’informació,onelcanalésuncable,l’aireo l’espai,ésnecessaridisposardemecanismesquepuguinpermetreladetecciói, siéspossible,lacorrecciód’errors.Siconsiderem,perexemple,queelcanal éselpaperoundiscdur,enspodemplantejarsienescriureiemmagatzemaralgunnúmerollarg,volempoderdetectarpossibleserrors.Enaquests canals,elserrorsmésfreqüentssónequivocar-seintroduintalgundígitobé intercanviantdosdígits.Perpoderdetectaraqueststipusd’errors,usualment s’afegeixredundànciaincorporantunnousímbolalnúmero.Aixíéscoms’han dissenyatcodistanquotidianscomelcodideldocumentnacionald’identitato DNI,l’InternationalStandardBookNumber oISBNdelsllibres,l’International BankAccountNumber oIBANielCodideCompteCorrentoCCCdelscomptes bancaris,il’EuropeanArticleNumber oEAN,queformenpartdelsconeguts codisdebarres,quedescriuremenlasecció2.

Enlasecció3,introduiremelsconceptesdelateoriaclàssicadelscodis correctorsd’errors.Primerenscentraremenelscodislinealsbasatsenconceptesd’àlgebra.Acontinuació,descriuremelscodislinealscíclicsocodis cíclicsquepermetencodificarlainformaciódeformaméseficient.Finalment, presentaremlesduesfamíliesmésimportantsdecodiscíclics,elscodisBCHi Reed-Solomon,quepermetentambédescodificardeformaeficientique,per tant,sónelsqueesfanservirenmoltessituacionsenquèésnecessaripoder corregirerrorsievitarunaretransmissiódelesdades.

Elsprimerscodislineals,elscodisdeHamming,s’expliquenenlasecció4, onesveulasevaaplicacióenlesprimeresmemòriesd’ordinador.Enlasecció5,esdescriuenelscodisdeReed-Mullerdeprimerordre,conegutstambé coma codisdeHadamard.Amés,esmostracomalgunsd’aquestscodises vanutilitzarpermillorarlatransmissiódefotografiesal’espai.Enlasecció6, enscentraremenl’aplicaciódelscodisBCHiReed-Solomondinsdelsconeguts codisQR (QuickResponse),querepresentenunaevoluciódelscodisdebarres, d’unaaduesdimensions.Finalment,enlasecció7,veuremunaaplicaciórecent delscodiscorrectorsd’errorsenelcampdel’emmagatzematgedistribuït.

2Exemplesquotidiansdecodisdetectorsd’errors

Enaquestasecció,descriuremalgunsdelscodisdetectorsd’errorsmésconeguts,jaesmentatsenlaintroducció:elcodiassociatalDNI,l’ISBNdelsllibres, l’IBANielCCCdelscomptesbancaris,il’EANocodidebarres.Totsellssón forçaquotidiansienselstrobemtotsovinteneldiaadia.Amés,totsestan basatsenl’aritmèticamodularidetecten,perònopermeten,corregirelserrors. Apartd’aquests,n’hihamoltsmés,comelsqueapareixenenlestargetesde crèdit,elsbitlletsd’avióoelsserveisdemissatgeria,entred’altres.

2.1CodiDNI

Elcodideldocumentnacionald’identitat(DNI)consisteixenunnúmerode 8xifresdecimalsseguitd’unalletra.Aquestalletra,defet,representalaredundànciaquepermetràdetectarelserrorsmésfreqüentsenescriureelnúmero. Lalletras’assignasegonselvalorqueresultadecalcularelnúmerodelDNI a Z23,oelqueéselmateix,segonselresiduques’obtéendividir-loper23, d’acordamblesequivalènciesqueesmostrenenlataula1.

01234567891011

TRWAGMYFPDXB 1213141516171819202122

NJZSQVHLCKE

Taula 1: AssignaciódelletresperalDNI.

Elcàlculesrealitzaa Z23.Esprenunnúmeroprimerpertaldetreballaren uncosfinit.Amés,s’exclouenleslletresI,OiU,perquèaquestesespoden confondremésfàcilmentambl’1,el0ilalletraV,respectivament.Podem simplificarelscàlculssitenimprecalculadeslespotènciesde10a Z23.Així, comque102 = 8,103 = 11,104 = 18,105 = 19,106 = 6i107 = 14a Z23, calcularelnúmerodelDNIa Z23 equivalacalcular x0 + 10x1 + 8x2 + 11x3 + 18x4 +19x5 +6x6 +14x7 a Z23,on x7x6x5x4x3x2x1x0 = 7 i=0 10ixi representa elnúmerodelDNI.

Exemple 1. LalletradelDNIcorresponentalnúmero34149351ésD,jaque 34149351 = 9a Z23,oequivalentment,14 · 3 + 6 · 4 + 19 · 1 + 18 · 4 + 11 · 9 + 8 · 3 + 10 · 5 + 1 = 9a Z23,ilalletracorresponentalvalor9ésDd’acordamb lataula1.

AquestcodipermetdetectarsihihahagutunerrorenundelsdígitsdelDNI, obésihihahagutunatransposicióentredosdígits[6].Encanvi,sin’hiha dosomés,nosempreespodendetectar.Tambépermetrecuperarundels dígitssiaquestnoesvisualitzacorrectament,simplementresolentunaequació lineala Z23.

Exemple 2 ContinuantambelDNIdel’exemple1,quèpassasienescriure elDNIensequivoquemenundígitiescrivim,perexemple,34249351D?Com

que34249351 = 5a Z23 ilalletracorresponental5éslaM,podemdetectarque hihahagutunerror,irepassarl’escripturad’aquestDNI.

Isiensequivoquemendosdígitsques’hanintercanviatdeposició,iescrivim,perexemple,34419351D?Enaquestcas,denou,encalcular34419351 = 12a Z23,podemdetectarl’errorjaque12corresponalalletraN.

Finalment,quèpodemfersiundelsdígitsésborrós,perexemple,sitenim 341493✷1Donelsetèdígitnoesreconeix?Enaquestcas,podemplantejar l’equaciólinealsegüenta Z23,14 3+6 4+19 1+18 4+11 9+8 3+10 x1+1 = 9, osigui10x1 = 4a Z23.Comquel’inversde10és7,tenimque x1 = 4·7 = 28 = 5 a Z23.Pertant,eldígitdelaposiciósetenaés5iobtenimelDNI34149351D.

2.2CodiISBN

Cadallibreportaassociatunidentificadorúnic,l’anomenat InternationalStandardBookNumber (ISBN)[27],queconsisteixenunaseqüènciade10símbols enquècadascunpotserunelementde {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, X} iXrepresenta el10.Lesoperacionsesrealitzena Z11,adiferènciadelcodiDNI,queeren a Z23.Eldarrersímbolrepresentalaredundànciaiescalculaapartirdelsanteriors.Aquestcoditambépermetdetectarsi,durantlatranscripciód’aquest identificador,s’haproduïtunerrorenalgundelsseusdígitsolatransposició dedosd’ells[6,12].

Exemple 3. Elsidentificadors0-444-85010-4i84-732-9114-Xcorresponenals codisISBNdelsllibres TheTheoryofError-CorrectingCodes,deFlorence J.MacWilliamsiNeilJ.A.Sloane,enl’editorialNorth-Holland,i Miralltrencat, deMercèRodoreda,enl’editorialClubEditor,respectivament.

Dels10símbols,elsqueapareixenabansdelprimerguiófanreferènciaa l’idioma/país,elssímbolsentreelprimerielsegonguióidentifiquenl’editorial, elssegüentsidentifiquenelllibredinsdel’editorial,ifinalmenteldarrer representalaredundància.Apartirdelsnouprimerssímbols,denotatsper x1, x2, x3, x4, x5, x6, x7, x8, x9,escalculalaredundància x10 coma x10 = x1 + 2x2 + 3x3 +···+ 9x9 a Z11.Sielresultatés10,escrivimelsímbolX.

Exemple 4. ContinuantambelprimerISBNqueapareixenl’exemple3,sien escriure’lensequivoquemenunsímboliescrivim,perexemple,0-444-855104,aleshoresencalcular x10 obtenimque x10 = 6encomptesde4.Pertant, podemdetectarquehihahagutunerror,irepassar-nelatranscripció.Deforma similar,siensequivoquemendossímbolsconsecutiusques’hanintercanviat deposició,iescrivimperexemple,0-444-58010-4,denouencalcular x10 obtenimque x10 = 7 = 4iaixídetectemquehihahagutalgunerror.Finalment, ésfàcilveurequesiundelssímbolsnoesreconeix,podemobtenir-loresolent unaequaciólineala Z11

2.3CodiIBANiCCC

Elscomptesbancaristenenassociatuncodi,anomenat InternationalBank AccountNumber (IBAN),queconsisteixenunaseqüènciad’unmàximde34ca-

ràctersalfanumèricsqueidentifiquen,deformaúnica,uncomptebancarid’una determinadaentitatfinancera[24].Elsdosprimerscaràctersidentifiquenel país.Elsdossegüentssóndígitsdecontrolqueescalculenapartirdelaresta, comveuremtotseguit.Larestacorresponenalnúmerodecomptebancarii permetenidentificartambél’entitatil’oficina,enlamajoriadepaïsos.

Exemple 5. LaseqüènciaBG18RZBB91550123456789corresponalcodiIBAN d’unpossiblecomptebancariaBulgària,ilaseqüènciaES021234567806011155 5555aunaEspanya.ABulgàriatotselscodisIBANtenenexactament22caràctersiaEspanyaentenen24.

Percalcularelsdosdígitsdecontrol,situatsenlesposicionsterceraiquarta delaseqüència,esprocedeixdelaformasegüent.Lesduesprimereslletres corresponentsalpaísestraslladenalesduesdarreresposicions,s’eliminen elsdosdígitsdecontrolis’afegeixendoszerosalfinal.Elscaràcterssesubstitueixenperunnúmerodeduesxifresd’acordamblataula2iescalculael númeroobtinguta Z97.Finalment,perevitarutilitzarcomadígitsdecontrol el00i01,esrestaelvalorobtinguta98,is’obtenenelsdosdígitsdecontrol.Si elresultatcontéunúnicdígit,s’afegeixunzeroaldavant.

10111213141516171819202122

ABCDEFGHIJKLM 23242526272829303132333435

NOPQRSTUVWXYZ

Taula 2: Assignaciónumèricaperal’IBAN.

Exemple 6 Elsdosdígitsdecontroldel’IBANBG18RZBB91550123456789 són18.Acontinuaciócomprovemqueéscorrecte.Primer,trasllademles duesprimereslletresalfinal,eliminemelsdosdígitsdecontroliafegimdos zerosalfinal,pertant,obtenimRZBB91550123456789BG00.Acontinuació, substituintelscaràcterspervalorsnumèricssegonslataula2,arribemal número2735111191550123456789111600,queésiguala80a Z97.Elsdígits decontrolsónefectivament98 80 = 18.

Comenelsdoscodisanteriors,elDNIil’ISBN,elcodiIBANtambépermet detectarpossibleserrorsproduïtsenunaúnicaposicióotransposicionsde doscaràcters,aixícomrecuperar-neunqueapareguiil.legible.

AEspanya,elcodiIBANesvaimplantardefinitivamentl’1defebrerdel2014 aprofitantl’anticcodidecomptecorrent(CCC).Defet,elcodiIBANesconstrueixapartirdelcodiCCC,queté20xifresdecimals,afegintaldavantelsdos caràctersEScorresponentsalpaísielsdosdígitsdecontrolquehemexplicat abans,finsacompletarels24caràcters.

ElcodiCCCestàformatper20dígits.Els4primersdígitsidentifiquen l’entitatbancària,els4següentsidentifiquenl’oficina,els2següentssóndígits decontrol,ifinalmentelsdarrers10descriuenelnúmerodecomptebancari.

Així,aquestcodielpodemrepresentardelamanerasegüent:

Elprimerdígitdecontrol c1 escalculaapartirdels8dígitsanteriors, d’acordambl’equaciósegüent c1 =−

2x7 + 4x8 + 8x9 + 5x10 a Z11,ielsegon c2,apartirdels10dígitssegüentscoma c2 =− 10 i=1 2i 1yi = 10y1 +9y2 +

y

a Z11.Sienferaquestscàlculsobtenimun10a Z11,assignemeldígit1.Fixemnosqueenelsdoscasoslafórmulaéslamateixaconsiderantque x1 = x2 = 0 peralcàlculde c1.Aquestscodistenenlesmateixespropietatsperdetectar errorsocorregirunesborrall(dígitborrósquenoesreconeix)queelscodis anteriors,excepteenalgunscasosenquèenferelscàlculsobtenim ci ∈{1, 10}.

Exemple 7 ElcodiCCC,corresponentalcodiIBANES02123456780601115555 55,és12345678060111555555,on1234representariaunaentitatbancària i5678unaoficinad’aquestaentitat.Sial’horadetranscriureaquestcompte bancari,escrivim12345678060111655555,aleshoresencalcularelsdígitsde control c1 i c2 obtenimque c1 = 0però c2 = 1encomptesde6.Pertant, hauremdetectatquehihaalgunerror,iqueaquestestrobadinsdelsdarrers 10dígits.

2.4CodiEAN

Lamajoriadelsproductescomercialsportenassociatunnúmerode13xifres decimalsanomenat EuropeanArticleNumber (EAN)o,mésrecentment, InternationalArticleNumber.L’EANapareixjustasotad’uncodidebarresqueserveix perfacilitar-nelalectura.Elsdosotresprimersdígitsidentifiquenl’estato associacióalaqualestàregistratelfabricant,elssegüentsde5a8dígits identifiquenl’empresa,elssegüentsfinsal12è,elproducte,ifinalmentel darreréseldígitdecontrol[25,20].

Eldígitdecontrolescalculaapartirdelsanteriors.Sil’EANde13xifres eldenotemper x1x2 ...x13,aleshores x13 escalculadelamanerasegüent: x13 =− 6 i=1(x2i 1 + 3x2i) = 9x1 + 7x2 +

9x9 + 7x10 + 9x11 + 7x12 a Z10.Igualqueelscodisdetectorsquehemvistenles subseccionsanteriors,elcodiEANpermetdetectarsis’haproduïtunerroren undelsdígits,peròencanvinopermetdetectarsemprelatransposiciódedos dígits.Concretament,sis’intercanviendosdígitsdiferents, xi i xj ,talsque i i j tenenlamateixaparitat,obé xi xj = 5,latransposiciónoesdetecta[6, 20]. Tambéésfàcilveurequepodemrecuperarundígitil.legible,jaquel’1iel3(o equivalentment,elsseusoposats,el9iel7)sóninvertiblesa Z10.

Exemple 8 Sil’empresautilitzaelcodiEANdel’AssociacióEspanyolade CodificacióComercial(AECOC),elsdosprimersdígitssón84.Encanvi,en altrespaïsoscomAlemanyaelsprimersdígitssónnúmerosdel400al440.

Sitenimelnúmerosegüent1512345678909,de13xifres,podemcomprovar fàcilmentqueésuncodiEANvàlid.Siesprodueixunerrorenundelsdígits,i obtenimperexemple1518345678909,podemdetectarl’error,jaqueeldígit decontrolhauriadeser1enllocde9.Sis’intercanviendosdígitsnosemprees detecta.Perexemple,siobtenim1512340678959degutaunintercanvientre lesposicions7ai12a,podemcomprovarqueeldígitdecontroléscorrecte ipertantl’errornoesdetecta.Encanvi,sil’intercanviesprodueixentreles posicions1ai6a,esdetectaria,jaque 4512315678909hauriadetenirel5com adígitdecontrol.

3Teoriaclàssicasobrecodiscorrectorsd’errors

Enlasubsecció3.1,veuremelsconceptesbàsicsdelateoriadelscodiscorrectorsd’errors.Descriuremelstresparàmetresmésimportantsquedefineixenun codiiespecificaremquanaquestésòptim.Acontinuació,enlasubsecció3.2, enscentraremenelscodisquesónlinealsielsmètodesgeneralspercodificar idescodificaraquestscodis.Enlasubsecció3.3,descriuremelscodislineals cíclicsquepermetencodificaridescodificardeformaméseficient.Finalment, enlasubsecció3.4,enscentraremenduesfamíliesimportantsdecodiscíclics:elsanomenats codisBCH i Reed-Solomon.Siesvolaprofundirenaquesta teoriaclàssicadelscodiscorrectorsd’errors,espotconsultar,perexemple, [23,31,38].

3.1Codis q-arislinealsinolineals

Comhemdit,sivolemdetectari/ocorregirelspossibleserrorsqueesprodueixenenlestransmissionsatravésdecanalsambsoroll,hemd’afegircerta redundànciaalainformacióquevolemtransmetre,expandint-ladeformaque hihagicerta«distància»entreduesinformacionsdiferents,queseràlaqueens permetràcorregirerrorsiaconseguiraixíunatransmissióalmésfiableiexacta possible.

Exemple 9. Suposemquevolemtransmetreunaseqüènciadebitsatravésd’un canalbinarisimètricambprobabilitatd’error p, BSC(p),on p éslaprobabilitat queelbitdesortidasiguidiferentald’entradaisatisfàque0 <p< 1/2. Pertaldereduiraquestaprobabilitat p,encomptesd’enviarun0oun1, enviem000o111,respectivament.Perexemple,sivolemtransmetre1101,enviem111111000111atravésdelcanal BSC(p).Suposemquealasortidadel canalrebem101100001111.Acontinuació,descodifiquemsegonselnombre dezerosiunsquehihaencadablocde3bits.Perexemple,sirebem101, comquehihamésunsquezeros,descodifiquemper111.Així,obtenim 111000000111,osigui1001.Observemquealgunserrorss’hancorregitialtresno.Entotcas,aquestmètodepermetreduirlaprobabilitatd’errorfins a p = p3 + 3p2(1 p) = p2(3 2p).Perexemple,si p = 0.02,aleshores p = 0 001184,idiemquehemobtingutunguanyde10 log10(p/p ) ≈ 12 28 dB.Elpreuquepaguemésquehemtriplicatelnombredesímbolsques’envien pelcanalipertantesfaméslentalatransmissió.

Consideremunalfabetamb q elements.Normalmentestriaque q siguiuna potènciad’unnombreprimeril’alfabetuncosfinit Fq.Un codi q-ari C ésun conjuntfinitdevectorsoseqüènciessobre Fq,anomenades paraulescodi.Si toteslesseqüènciessóndelamateixalongitud n,aleshoresdiemque C és un codibloc delongitud n.Enaquestcas, C ⊆ Fn q ,on Fn q ésunespaivectorial sobre Fq.Apartird’araenscentraremenelscodisblocisuposaremquela informacióatransmetreestàrepresentadaperunaseqüènciad’elementsde l’alfabet Fq.Enunatransmissiófentservircodisbloc,lainformacióquevolem transmetreesdivideixprimerenblocsde k símbolsde Fq.Després,acadascun d’aquestsblocs,seliassignaunaparaulacodidelongitud n delcodi q-ari C. Pertant, C had’estarformatperunmínimde qk paraulescodi;enparticular, calque k ≤ n.Aquestprocésd’assignaciós’anomena codificació. Ésfàcilveurequecommésseparadesestiguinaquestesparaulescodi entreelles,méserrorspermetràcorregirelcodi.Així,esdefineixla distància (deHamming) entredosvectors v = (v1,...,vn) i w = (w1,...,wn),que denotaremper dH (v,w),comelnombredecoordenadesquetenendiferents. El pes(deHamming) d’unvector v = (v1,...,vn),denotatper wtH (v),ésel nombredecoordenadesdiferentsdezeroi,pertant, wtH (v) = dH (v, 0),on 0 éselvectorzero.LadistànciadeHammingdefineixunamètricaa Fn q [38, p.114].Ladescodificaciópermínimadistànciatrialaparaulacodiméspropera alvectorrebut,d’acordambaquestadistància.Aquestmètodeminimitzala probabilitatmitjanad’error,icoincideixambladescodificaciópermàxima versemblança[38,p.128],sicadasímboldel’alfabettélamateixaprobabilitat d’error p ilamateixaprobabilitatd’aparèixer.Uncanalambaquestesdues propietatss’anomena canal q-arisimètric.Quan q = 2,s’anomena canalbinari simètric oBSC(p).

La distànciamínima d’uncodi q-ari C és d(C) = min{dH (v,w) : v,w ∈ C, v = w}.Engeneral,calcularladistànciamínimad’uncodiéscomputacionalmentdifícilis’hademostratqueésunproblemaNP-difícil[44].Siuncodi q-ari C delongitud n sobre Fq conté M paraulescodiitédistànciamínima d = d(C),diremqueésuncodi q-ari (n,M,d).La taxadetransmissió de C és R = logq(M)/n imesuralaproporciód’informacióquecontécadaparaula codi.

Trobaralgorismesdedescodificacióeficientsésunadelesàreesd’investigaciómésimportantsenlateoriadecodisateseslessevesaplicacionspràctiques. Sienenviarunaparaulacodi c ∈ C esrepelvector w ∈ Fn q ,diemque e = w c ésel vectord’error.Ladescodificacióconsisteixatrobarelvectord’error e apartirde w,queequivalatrobarlaparaulacodi c enviada.Entretotsels possiblesvectorsd’errorstriemeldepesmenor,queequivalatriarlaparaula codiamenordistànciade w

Diremqueuncodi C detecta elvectord’error e siinoméssi c +e ∉ C pera qualsevol c ∈ C,idiremque corregeix elvectord’error e siinoméssiper atot c ∈ C, c + e ésméspropera c queaqualsevolaltraparaulacodi.Si uncodi C corregeixtotselsvectorsd’errordepescomamolt t,inoenpot corregircomamínimundepes t + 1,diremqueés t-corrector oque t ésla capacitatcorrectora de C.Deformasimilaresdefineixla capacitatdetectora.

Elvectorrebut w ∈ Fn q ,apartd’errors,potconteniresborralls.Diremque hihaun esborrall enunacoordenadade w sinos’hapogutdeterminarquin símbolde Fq s’haviaenviat.Laposiciód’unerrordinsdelvector w noes coneix,mentrequelad’unesborrallsíqueésconeguda.Sinodiemelcontrari, suposemsemprequenohihahagutesborrallsenlatransmissió.

Apartirdeladistànciamínimad’uncodi,veuremquepodemcalcular lasevacapacitatdetectoraicorrectora,tantd’errorscomd’esborralls.Per examinarelsvectorsqueestanméspropersaunaparaulacodi,introduïmel conceptedebolaalvoltantd’unaparaulacodi.Unaboladeradi r centradaen elvector c ∈ Fn q ,denotadaper Sr (c),contétotselsvectorsquesónadistància menoroigualque r de c,osigui, Sr (c) ={v ∈ Fn q : dH (v,c) ≤ r }.Percorregir finsa t errors,ésnecessariquelesbolesderadi t alvoltantdecadaparaula codisiguindisjuntesduesadues,talcomesmostraenlafigura2.

Teorema 10 ([38,p. 117]). Uncodi q-ari C potdetectarfinsa d(C) 1 errors. Elcodipermetcorregirfinsa t errorsi s esborrallssiinoméssi 2t + s<d(C). Amés,lacapacitatcorrectoraés t = (d(C) 1)/2

d(C) d(C)

Figura 2: Bolesderadi t centradesenlesparaulescodideC.

Exemple 11. Elcodidel’exemple9, C1 ={(0, 0, 0),(1, 1, 1)},ésuncodi2-ari (binari) (3, 2, 3),pertant,potdetectarfinsadoserrorsocorregirfinsaun error.Lasevataxadetransmissióés R = 1/3 ≈ 0 33.Elcodi C2 ={(0, 0, 0, 0), (1, 2, 1, 2), (2, 1, 2, 1), (1, 1, 2, 2), (2, 2, 1, 1)} ésuncodi3-ari(ternari) (4, 5, 2) quepermetdetectarunerror,perònoenpotcorregircap.Enaquestcas, R = log3(5)/4 ≈ 0.36.Elcodi C3 ={(0, 0, 0, 0, 0), (2, 1, 0, 2, 0), (1, 2, 0, 1, 0), (2, 1, 1, 1, 2), (1, 2, 2, 2, 1), (1, 2, 1, 0, 2), (2, 1, 2, 0, 1), (0, 0, 1, 2, 2), (0, 0, 2, 1, 1)} ésuncoditernari (5, 9, 3) amblamateixacapacitatdetectoraicorrectora que C1,peròambmillortaxadetransmissió R = 2/5 = 0.4.

Pelteorema10,pertaldecorregirelmàximnombred’errorsnecessitem queelvalordeladistànciamínima d = d(C) siguigran.Almateixtemps,però, volemquelalongitud n siguipetitapertalquelatransmissiósiguiràpida,

iqueelnombredeparaulescodi M tambésiguigranpercodificarelmajor nombredemissatges.Aquestescondicionsnoespodenassolirtotesalhora ateseslesrelacionsquehihaentreaquestsparàmetres.Perexemple,tenim que M ≤ qn.Tambéescompleixl’anomenada fitadeSingleton, M ≤ qn d+1;i la fitadeHamming, M t i=0 n i (q 1)i ≤ qn , (1)

on t = (d 1)/2 éslacapacitatcorrectoradelcodi[31,p.20].Esdiuque uncodiés òptim sitéelsmillorsparàmetrespossibles n, M, d, q,ésadir,al mateixtempsnoespotincrementar M peravalorsde n, d, q fixats,inoes potincrementar d peravalorsde n, M, q fixats.

3.2Codislineals

Diremqueuncodi q-ari C delongitud n sobreuncosfinit Fq és lineal siés unsubespaide Fn q .Defet,qualsevolsubespaide Fn q ésuncodi q-arilineal.Si k = dim(C) i d = d(C),diremqueésuncodi [n,k,d]q o [n,k]q encomptes d’uncodi q-ari (n,qk,d).Enaquestcas,lataxadetransmissióés R = k/n,ja que M = qk.Amés,ésfàcilveurequesi C éslineal,aleshores d = min{wtH (v) : v ∈ C,v = 0},osigui,ladistànciamínimacoincideixambelpesmínim[38, p.125].

Unamatriuquadradasobre Fq és monomial sitéexactamentunaentrada diferentdezeroencadafilaicolumna.Diemquedoscodislineals C i C sobre Fq delamateixalongitud n són equivalents siexisteixunamatriu monomial M demida n × n sobre Fq iunautomorfisme γ de Fq talque C = {γ(cM) : c ∈ C},on γ s’aplicacoordenadaacoordenada[23,p.24].Ésclarque sidoscodissónequivalents,aleshorestenenelsmateixosparàmetres [n,k,d]q i R.

Si C ésuncodilineal [n,k]q,una matriugeneradora G de C ésunamatriu k × n sobre Fq quecontécomafilesunabasede C.Enlacodificaciófent servircodislineals,acadavectord’informació i ∈ Fk q lipodemassignarla paraulacodi c = iG ∈ C ⊆ Fn q .Silamatriu G contélamatriuidentitatdemida k comasubmatriu,aleshoreslescoordenadesde i apareixenenlescoordenades de c = iG,exactamentenlesmateixesposicionsonestrobenlescolumnesdela matriuidentitatdinsde G.Enaquestcas,diremquelamatriu G és sistemàtica oquelacodificacióés sistemàtica enaquestescoordenades.

Sigui G unamatriugeneradorad’uncodi C lineal [n,k]q.Observemque totamatriuquetinguiperfilesunabasede C ésunamatriugeneradorade C. Pertant,semprepodemtriarunamatriugeneradorade C sistemàtica.Encanvi, sipermutemlescolumnesde G,obtenimunanovamatriu G quegeneraun noucodi C equivalentalcodi C.Ésfàcilveurequequalsevolcodilineal C és equivalentauncodi C generatperunamatriudelaforma G = (Ik A),on Ik éslamatriuidentitatdemida k i A ésunamatriu k × (n k) sobre Fq.En aquestcas,diremquelamatriu G estàen formaestàndard iquelacodificació

éssistemàticaenles k primerescoordenades.Lautilitzaciódelcodi C amb matriugeneradora G simplificaelprocésd’obtenirlainformaciódesprésdela correcciód’errors,jaqueaquestaestàlocalitzadadirectamentenlesprimeres k coordenades.

Exemple 12. Delscodisdel’exemple11,tenimque C1 ésuncodilineal [3, 1, 3]2 ambmatriugeneradora G1 = (111).Encanvi,elcodi C2 noéslineal,jaque (1, 2, 1, 2) + (1, 1, 2, 2) = (2, 0, 0, 1) ∉ C2.Elcodi C3 éslinealambparàmetres [5, 2, 3]3 ipotsergeneratapartirdelamatriugeneradorasegüent:

G3 = 21020 21112

Així,abansd’enviaratravésd’uncanalternarilaseqüènciad’informació, primerladividimenblocsde k = 2elementsde F3 iacontinuaciómultipliquemcadablocper G3 iobtenimblocsde n = 5elements.Perexemple,si lainformacióés10212211,enviem (1, 0)G3, (2, 1)G3, (2, 2)G3 i (1, 1)G3,o sigui21020001222120112102,atravésdelcanal.Ésfàcilveureque C3 és equivalent(permutantla2ai3acoordenadesirealitzantcombinacionslineals defiles)auncodi C3 generatperlamatriusegüentenformaestàndard:

G3 = (I2 A) = 10210 01022 .

Sicodifiquemlamateixainformació,utilitzantlamatriu G3,obtenim10210 211122210111202.Fixem-nosque,enaquestcas,lacodificacióéssistemàtica enlesduesprimerescoordenades,osigui,lainformacióestàlocalitzadaenles duesprimerescoordenadesdecadaparaulacodi.

Perdescriureelmètodegeneraldedescodificacióperacodislineals,necessitemdefinirelcodiortogonal(odual)ilamatriudecontrol.Elproducteescalarentredosvectors, v = (v1,...,vn) i w = (w1,...,wn),és v,w = n i=1 viwi.El codiortogonal (o dual)d’uncodi C lineal [n,k]q,denotatper C⊥,és C⊥ ={v ∈ Fn q : v,c = 0 ∀c ∈ C}.Ésfàcilveureque C⊥ ésun codilineal [n,n k]q.Qualsevolmatriugeneradora H delcodi C⊥ s’anomena matriudecontrol de C.Amés,si G = (Ik A),aleshoresunamatriudecontrol és H = ( At In k),on At denotalamatriutransposadade A.Tambétenim que,apartird’unamatriudecontrol,espotdeterminarladistànciamínima d’uncodi,talcommostralaproposició13.Totiaquestresultat,calcularla distànciamínimad’uncodilinealcontinuasentunproblemaNP-difícil[44].

Proposició 13 ([38,p. 125]). Ladistànciamínimad’uncodilineal C coincideix ambelmínimnombredecolumneslinealmentdependentsquehihaenuna matriudecontrolde C.

Exemple 14 Enl’exemple12,hemvistqueelcodi C3 ésequivalentalcodi C3 generatperlamatriu G3 = (I2 A) enformaestàndard.Pertant,elcodi ortogonal C3 ⊥ estàgeneratperlamatriusegüent:

queéstambéunamatriudecontrolde C3.Comquehemobtingut C3 apartir de C3 permutantla2ai3acoordenades,podemobtenirunamatriudecontrolde C3,desfentlapermutacióquehavíemfet;ésadir,permutantla2aila 3acolumnesde H3.Així,lamatriusegüentésunamatriudecontrolde C3:

Comqueelmínimnombredecolumneslinealmentdependentsde H3 és3,perexemple,lescolumnes1,2i4,podemveureque d(C3) = 3perla proposició13.

Elmètodegeneralperdescodificarcodislinealss’anomena descodificació viasíndrome [23,p.61].Comqueuncodilineal C espotveurecomunsubgrup delgrupadditiu Fn q ,lesdiferentsclassesd’equivalència C + v representenuna particióde Fn q en qn k conjuntsdemida qk.Dosvectors v1 i v2 estanenla mateixaclassesiinoméssi v1 v2 ∈ C.Suposemqueenviemunaparaula codi c ∈ C irebemelvector w = c + e ∈ Fn q .Enladescodificació,volemtrobar laparaulacodi c mésproperaa w,oequivalentment,elvectord’error e de pesmínimdinsdelaclasse C + w queconté w.Unvectordepesmínimen unaclasses’anomena líderdelaclasse inonecessàriamentésúnic.Elvector zeroésl’úniclíderdelaclasse C.Deformamésgeneral,sielpesdellíderde laclasseésmenoroigualalacapacitatcorrectora t,aleshoresaquestlíderés únic.

La síndrome d’unvector v ∈ Fn q ,respecteaunamatriudecontrol H d’un codilineal C,éselvector Hv t ∈ Fn k q .Elsvectorsquetenencomasíndromeel vectorzerosónexactamentelscorresponentsatoteslesparaulescodi.Comque H térang n k,qualsevolvectorde Fn k q ésunasíndrome.Amés,comquetots elsvectorsd’unamateixaclassetenenlamateixasíndrome,existeixunabijecció entrelesclassesmòdul C ilessevessíndromes.Pertant,podemconstruir l’anomenada tauladesíndromes,queassignaacadasíndromeunlíderdela classecorresponent(sinoésúnicse’ntriaundeformaaleatòria).Fixem-nos queladescodificacióviasíndromerequereixunataulaamb qn k entrades,que potsermoltmenorcomparatambunataulaamb qn vectorsmostrantquina paraulacodiéslamésproperaacadavectordel’espai.

Enunadescodificaciócompletas’assignaunaparaulacodiacadavector rebut w ∈ Fn q .Peraixò,primercalculemlasíndromede w.Siészero,sabem

quenohihahagutcaperror.Encanvi,siésdiferentdezero,utilitzemlataula desíndromespertrobarl’error e ilaparaulacodi c = w e ∈ C.Enuna descodificacióincompletapodemreduirlatauladesíndromesconsiderant nomésaquellessíndromesquetenenunlíderambpesmenoroigualala capacitatcorrectora t,osiguiquanellíderdelaclasseésúnic.Enaquest cas,quanlasíndromedelvectorrebutnoestrobaenlataula,esdemana retransmetreaquestvector.

Exemple 15. Consideremelcodi C3 donatal’exemple12ilasevamatriude control H3 donadaal’exemple14.Perdescodificar,utilitzantaquestamatriu decontrol H3,primerconstruïmlataula3desíndromes. lídersíndrome

Taula 3: Tauladesíndromesperalcodi C3 ambmatriudecontrol H3

Suposemquehemcodificatlainformacióutilitzantlamatriu G3.Comque lacapacitatcorrectorade C3 és t = 1,sielvectord’errortépes1,l’errores corregeix.Encanvi,sielvectord’errortépes2,segonsquinsigui,potpassar queelvectorrebutesdescodifiquicorrectamentoqueesdescodifiquicomsi s’haguésproduïtunaltreerrordepes1o2.Enlataula3,apareixenmarcats ambun ∗ aquellslídersquenosónúnics.

Sivolemtransmetrelainformació10212211,enviematravésdelcanal laseqüènciacodificada10210211122210111202calculadaal’exemple12. Suposemquealasortidadelcanalrebem 202102001222211 01002.Pera cadabloc w delongitud n = 5calculemlasíndrome,elvectord’error e a partirdelataula3,ilaparaulacodi c corresponent:

cew = c + e síndromelíder e c = w e 1021010000202101201000010210 2111202200200122220220021112 2210100110222111102020002011 1120220100010020100001001022

Taula 4

Observemqueenelsdosprimersblocsl’errors’hacorregit,tanteldepes1 comeldepes2,jaqueelslídersdelesduesclassescorresponentssónúnics. Eneltercerbloc,ellíderdelaclassenoésúnicisen’hatriatundediferental del’errorreal e peralaconstrucciódelatauladesíndromes.Enelquartbloc, ellíderésúnicperòelvectord’error e depes2télamateixasíndromeque undepes1,iestriaeldemenorpes,osiguiunaparaulacodiamenysdistància delvectorrebut.Finalment,desprésd’intentarcorregirelserrors,s’obtéla informacióassociadaacadaparaulacodi,queenaquestcasestàsituadaenles duesprimerscoordenades,jaques’hacodificatamblamatriugeneradora G3 queestàenformaestàndard.Osigui,obtenimquelainformacióenviadaera 1021 02 01.

Hihamoltscodisimportantsques’obtenenmodificantocombinantaltres codis.Aixòespotferdediversesmaneres,iacontinuacióendescriuremalgunes.Perexemple,éspossiblecrearcodismésllargs,afegintnovescoordenades. Concretament,donatuncodi C lineal [n,k,d]q,elseu codiestès (extended code),denotatper C,éselcodi

Elcodiestès C ésuncodilineal [n + 1,k, d]q,on d ∈{d,d + 1} [23,p.15]. Aquestprocéstambéesconeixcomafegirundígitdecontroldeparitat.Fixemnosquesi C ésuncodibinari,aleshorestoteslesparaulescodide C tenen pesparell.Pertant, d = d si d ésparelli d = d + 1si d éssenar.Engeneral, podemobtenirunamatriugeneradorade C afegintaunamatriugeneradora de C unacolumnaextra,deformaquelasumadetoteslescoordenadesde cadafilasiguizero.Si H ésunamatriudecontrolde C,aleshoreslamatriu H següentésunamatriudecontroldelcodi C:

El codipunxat (puncturedcode)enla j-èsimacoordenadad’uncodi C lineal [n,k,d]q,denotatper C j ,éselcodiformatperlesparaulescodide C desprésd’eliminarlacoordenada j-èsimadecadauna.Aquestésuncodilineal [n 1,k,d ]q,on d ∈{d,d 1},si d> 1[23,p.13].Si G ésunamatriu generadorade C,aleshorespodemobtenirunamatriugeneradorade C j eliminantlacolumna j (ieliminanttambépossiblesfilesrepetidesodezeros) de G.

Finalment,perdefinirel codiescurçat (shortenedcode)enla j-èsimacoordenadad’uncodi C lineal [n,k,d]q,denotatper C j 0 ,definimprimerelsubcodi C0 ⊆ C formatperlesparaulescodide C quetenenun0enlacoordenada

j-èsima.Elcodi C j 0 éselcodi C0 desprésd’eliminarla j-èsimacoordenadade toteslessevesparaulescodi,osigui,éselcodipunxatde C0 enlacoordenada j-èsima.Amés,fixem-nosqueésunsubcodide C j ,ésadir, C j 0 ⊆ C j ,iésun codi [n 1,k ,d ]q,on k ∈{k 1,k} i d ≤ d [23,p.16].

Exemple 16. Sigui C elcodi [7, 3, 3]2 amblamatriugeneradorasegüent:

Elcodiestès C éselcodi [8, 3, 4]2 generatper G;elcodipunxat C 5 en la5acoordenadaéselcodi [6, 3, 2]2 generatper G5,ielcodiescurçat C 5 0 enla 5acoordenadatéparàmetres [6, 2, 4]2 iestàgeneratper G5 0 ,on

3.3Codiscíclics

Donatunvector v = (v1,...,vn) ∈ Fn q ,definimlasevapermutaciócíclica π(v) comelvector π(v) = (vn,v1,...,vn 1).Diremqueuncodi q-arilineal C de longitud n és cíclic silapermutaciócíclicadequalsevolparaulacoditornaa serunaparaulacodi,osigui, π(c) ∈ C peratot c ∈ C.Fixem-nosque,per linealitat,éssuficientveurequelapermutaciócíclicadequalsevolfilad’una matriugeneradorapertanyalcodiperafirmarsiuncodilinealéscíclicono.

Exemple 17. Consideremelscodis C1, C2 i C3 del’exemple11.Elcodilineal C1 éscíclic,jaque π(c) = c ∈ C1 peratot c ∈ C1.Elcodi C2 noéslineal,talcom s’havistal’exemple12,i,pertant,nopotseruncodicíclic.Finalment,el codilineal C3,ambmatriugeneradora G3 donadaenl’exemple12imatriu decontrol H3 calculadaenl’exemple14,noéscíclic.Siconsiderem,perexemple, laparaulacodi c corresponentalaprimerafilade G3, π(c) = π(2, 1, 0, 2, 0) = (0, 2, 1, 0, 2) ∈ C3 jaque H3(0, 2, 1, 0, 2)t = (2, 1, 0)t = (0, 0, 0)t

Uncodi q-aricíclicdelongitud n espotdescriureentermesmésalgebraics, relacionant-loambl’anelldepolinomis Rq,n = Fq[x]/(xn 1).Perfer-ho, consideremlabijecciósegüent: Fn q → Rq,n v = (v1,v2,...,vn) → v(x) = v1 + v2x +···+ vnxn 1 .

Fixem-nosqueelpolinomiassociatalapermutaciócíclicad’unvector v ∈ Fn q , π(v)(x),és xv(x).Sigui C ⊆ Fn q uncodi q-ariqualsevol.Apartir d’ara, C denotaràindistintamenttantelcodia Fn q comlasevaimatgeper labijeccióanterior.Així,tenimqueuncodilineal C éscíclicsiinoméssi xc(x) ∈ C peratot c(x) ∈ C.Perlinealitat,tambétenimque C éscíclicsii noméssi a(x)v(x) ∈ C peratot a(x) ∈ Rq,n.Pertant,elscodiscíclicsa Fn q es corresponenambelsidealsde Rq,n.

Sabemqueelsidealsdel’anell Rq,n sónprincipals[30]i,pertant,estan generatspernomésunelement.Si C ésuncodicíclic,aleshoresexisteixun únicpolinomimònic g(x) ∈ Fq[x] talque g(x) | (xn 1) i C = g(x) [23, capítol4].Aquestpolinomis’anomena polinomigenerador de C icoincideix ambl’únicpolinomimònicdegraumínimdelcodi.

Teorema 18 ([23,capítol 4]). Sigui C uncodi q-aricíclicdelongitud n i g(x) ∈ Fq[x] elpolinomigeneradorde C.Aleshores, (i)ladimensióde C és k = n grau(g(x)), (ii)unabasede C és {g(x),xg(x),...,xk 1g(x)},i (iii)unamatriugeneradorade C és

Ésfàcilveurequesi C ésuncodicíclic,aleshoreselseucodiortogonal, C⊥ , tambéhoés.Acontinuació,veiemqueunamatriugeneradoraielpolinomi generadorde C⊥ espodendonarenfunciódelpolinomigeneradorde C. Definimelpolinomi h(x) = (xn 1)/g(x).Diemque h(x) = h1 + h2x + ···+ hk+1xk ésel polinomidecontrol de C,jaque c(x) ∈ C siinoméssi h(x)c(x) = 0a Rq,n.Apartird’aquestadarreraigualtatdepolinomis,tenim queunamatriudecontrolde C és

(3) El polinomirecíproc de h(x),denotatper h∗(x),éselpolinomimònicque téelsmateixoscoeficientsque h(x),peròenordreinversidividitsper h1; ésadir, h∗(x) = xkh(x 1)/h1.Comque H tambéésunamatriugeneradorade C⊥,tantelconjunt {h1h∗(x),h1xh∗(x),... , h1xn k 1h∗(x)} com elconjunt {h∗(x),xh∗(x),...,xn k 1 h∗(x)} sónunabasede C⊥.Pertant,el

MercèVillanuevaiCristinaFernández-Córdoba

polinomi h∗(x) ésdefeteldivisorde xn 1quegeneraelcodi C⊥,osigui C⊥ = h∗(x) [38,p.146].

Exemple 19. Elpolinomi g(x) = 1 + x + x3 divideix x7 1 ∈ F2[x].Aleshores, C = g(x) ésuncodibinaricíclicdelongitud7idimensió7 3 = 4.El polinomidecontroldelcodiés h(x) = (x7 1)/(1 + x + x3) = 1 + x + x2 + x4 ielpolinomigeneradorde C⊥ és h∗(x) = 1 + x2 + x3 + x4.Apartird’aquests polinomis,obtenim,respectivament,lesmatriusgeneradoraidecontrolde C següents:

Utilitzarcodiscíclicssuposaunavantatgeenelprocésdecodificarrespecte delscodislineals,tantdesdelpuntdevistadel’espaidememòriacomde lasevaimplementaciófísicaatravésdelscircuitsLFSR(linearfeedbackshift register)[38,p.148].Sigui C = g(x) ⊆ Rq,n uncodicíclici i = (i1,...,ik) ∈ Fk q unvectord’informacióquevolemcodificar.Acontinuació,veuremdiverses maneresdecodificarlainformació i,ésadir,d’assignara i unaparaulacodi de C

Atèsque C ésuncodilineal,espotcodificarmultiplicantperunamatriu generadora.Perexemple,podemassignara i laparaulacodi c = iG,on G és lamatriu (2).Tambépodemfercombinacionslinealsperfilesenlamatriu G finsaobtenirunamatriugeneradora G enformaestàndard,iassignara i la paraulacodi c = iG .Aquestaseriaunacodificaciósistemàticaenlesprimeres k coordenades.

Tambéespotcodificarutilitzantelpolinomigenerador g(x).Considerem elpolinomiassociatalvectord’informació, i(x) = i1 + i2x +···+ ikxk 1 . Perexemple,podemassignara i laparaulacodi c corresponentalpolinomi c(x) = i(x)g(x) ∈ Rq,n.Enaquestcas,lacodificacióde i seriaiguala l’obtingudafent iG.Encanvi,sivolemunacodificaciósistemàtica,aleshores podemassignara i laparaulacodi c corresponenta c(x) = i(x)xn k r(x), on r(x) éselresidudedividir i(x)xn k per g(x).Aquestadarreracodificació s’anomenaCRC(cyclicredundancycheck),ésfàcilveurequeéssistemàtica enlesdarreres k coordenadesiespotimplementarfàcilmentfentservircircuitsLFSR.

Finalment,podemcodificarutilitzantelpolinomirecíprocde h(x), h∗(x) = h∗ 1 +h∗ 2 x+···+h∗ k xk 1+xk.Apartirdelaigualtat Hct = 0,on H éslamatriu (3), obtenimquepodemassignara i laparaulacodi c = (i1,...,ik,ck+1,...,cn),on ci =− k j=1 h∗ j ci k+j 1 per i ∈{k + 1,...,n} [23,p.129].Clarament,aquesta codificacióéssistemàticaenlesprimeres k coordenades.

Exemple 20 Consideremelcodi C = g(x) ,on g(x) = 1 + x + x3,del’exemple19.Acontinuació,codifiquemelvectord’informació i = (1, 0, 1, 1) de diversesmaneres.

Apartirdelamatriugeneradora G donadaenl’exemple19,lacodificació de i seria c = iG = (1, 1, 1, 1, 1, 1, 1).Aquestacoincideixambmultiplicar i(x) per g(x) a Rq,n,jaque i(x) = 1 + x2 + x3 i c(x) = i(x)g(x) = 1 + x + x2 + x3 + x4 + x5 + x6.Arabé,sifemservirelmètodeCRCtenimque r(x) = 1i c(x) = (1+x2 +x3)x3 1 = 1+x3 +x5 +x6,queescorresponambelvector c = (1, 0, 0, 1, 0, 1, 1).Podemveurequeenaquestcaslacodificacióéssistemàtica enlesquatredarreresposicions.Finalment,fentservir h∗(x) = 1+x2 +x3 +x4 , tenimque c = (1, 0, 1, 1,c5,c6,c7) i,aplicantlafórmula ci =− 4 j=1 h∗ j ci+j 5, per i ∈{5, 6, 7},obtenim c5 = 1, c6 = 0i c7 = 0.Així,elvectorcodificatés c = (1, 0, 1, 1, 1, 0, 0).

Hemvistqueelscodiscíclicsdelongitud n sónidealsdel’anell Rq,n iel polinomigeneradorés,defet,unpolinomimònicdivisorde xn 1a Fq[x] Pertant,peral’estudid’aquestscodis,s’utilitzalafactoritzacióde xn 1 a Fq[x] [30].

Sigui m l’enterpositiuméspetittalque n | qm 1;osigui,l’ordremultiplicatiude q mòdul n.Així, Fqm éselmínimcosdecaracterística q queconté toteslesarrelsde xn 1is’anomena cosdedescomposició de xn 1.Les arrelsde xn 1formenunsubgrupcíclicdelgrupmultiplicatiude Fqm .Per tant, xn 1 = n 1 j=0 (x αj ),on α ∈ Fqm ésunaarrel n-èsimaprimitivadela unitat[23,31].

Araquejatenimlafactoritzacióde xn 1a Fqm [x],donaremlaseva factoritzacióa Fq[x].Donatunenter s,0 ≤ s ≤ n 1,la classe q-ciclotòmica de s mòdul n és Cs ={s,sq,sq2,...,sqm 1},on sqm ≡ s(mod n).Elconjunt {0,...,n 1} espotescriurecomlauniódisjuntadeclasses q-ciclotòmiques.El polinomimínimde αs , Mαs (x),éselpolinomimònicdemenorgrau a Fq[x] queté αs comaarrel.Tenimque Mαs (x) = j∈Cs (x αj ) ésirreductiblea Fq[x].Pertant,qualsevolpolinomi g(x) | (xn 1) a Fq[x] espotescriure coma g(x) = j∈K (x αj ),on K éslauniódeclasses q-ciclotòmiques.

Exemple 21. Consideremelpolinomi x7 1 ∈ F2[x].Enaquestcas,l’ordre multiplicatiude2mòdul7és m = 3.Pertant,elcosdedescomposicióde x7 1 és F8.Sigui F8 = F2[x]/(1 + x + x3) i α unaarrelde1 + x + x3 queés tambéunaarrel7-èsimaprimitivadelaunitat.Així,lafactoritzacióa F8[x] és x7 1 = 6 j=0(x αj ).Lesclasses2-ciclotòmiquesmòdul7són C0 ={0}, C1 ={1, 2, 4} i C3 ={3, 5, 6}.Pertant,lafactoritzacióa F2[x] és x7 1 = M1(x) · Mα(x) · Mα3 (x) = (1 + x)(1 + x + x3)(1 + x2 + x3) Continuantambl’exemple19,consideremelcodibinaricíclic C = g(x) , on g(x) = 1 + x + x3.Tenimque g(x) = (x α)(x α2)(x α4),osigui, g(x) = Mα(x) ienaquestcas K = C1.Delamateixamanera,siconsideremel codibinaricíclic C⊥ quehemvistqueestàgeneratpelpolinomi h∗(x) = 1 + x2 +x3 +x4,tenimque h∗(x) = (x 1)(x α)(x α2)(x α4) = M1(x)·Mα(x) i K = C0 ∪ C1.

Sigui C = g(x) uncodicíclic,on g(x) = j∈K (x αj ).Pelteorema18,la dimensióde C és n −|K|,itenimque c(x) ∈ C siinoméssi c(αj ) = 0pera

tot j ∈ K.Aquestapropietatenspermetdefinirlasegüentmatriudecontrol de C apartirdelesarrelsdelpolinomigenerador g(x):

on K ={j1,...,jn k}.

Elfetdeconsiderarelpolinomigeneradord’uncodicíclictenintencompte lessevesarrelsa Fqm permetdissenyarcodiscíclicsambunadistànciamínima superioroigualaunvalorfixat, δ,anomenat distànciamínimaprevista,tal commostraelresultatsegüent.

Teorema 22 ([23,p. 151]). Sigui C = g(x) uncodi q-aricíclicdelongitud n, amb g(x) = j∈K (x αj ),on α ∈ Fqm ésunaarrel n-èsimaprimitivadela unitati m l’ordremultiplicatiude q mòdul n.Si K conté δ 1 entersconsecutius, aleshoresladistànciamínima d satisfà d ≥ δ.

Exemple 23 Consideremdenouelcodibinaricíclic C delongitud7generat per g(x) = 1 + x + x3 del’exemple19.Comhemvistal’exemple21,les arrelsde g(x) a F8 són α, α2 i α4.Pertant,comquehihaduesarrelsamb exponentsconsecutius,podemassegurarqueladistànciamínimade C és d ≥ 3 pelteorema22.Enaquestcas,defet,tenimqueladistànciamínimaés d = 3, jaqueperexemplelaprimerafiladelamatriugeneradora G ésunaparaula codidepes3.

3.4CodisBCHiReed-Solomon

DuesfamíliesimportantsdecodiscíclicssónelscodisBCHiReed-Solomon.Els codisBCHvanserintroduïtsperHocquenghemi,independentment,perBosei Chaudhuri,el1960.Elmateixany,vanserintroduïtselscodisReed-Solomon oRSperReediSolomon.Totsaquestscodisespodenconstruirfentservir elteorema22perassegurarqueladistànciamínima(i,pertant,lacapacitat correctora)siguicomamínimunvalorfixat.ElscodisRS,amés,satisfanla fitadeSingletonambigualtati,pertant,esdiuquesóncodisMDS(Maximum DistanceSeparable).Aquestapropietat,que d = n k + 1,nolacompleixenen generalelscodisBCH.

Sigui n unenter, n ≥ 1,i m l’enterpositiuméspetittalque n | qm 1.Sigui α ∈ Fqm unaarrel n-èsimaprimitivadelaunitat.Definimel codi q-ari BCH (o RS)ambdistànciamínimaprevista δ ≥ 1iparàmetres(m,δ)comelcodicíclicsobre Fq (o Fqm )generatpelpolinomidemenorgrausobre Fq[x] (o Fqm [x]), quetécomaarrels, αb,αb+1,...,αb+δ 2,peralgunenter b ≥ 1.PeralscodisBCH,elpolinomigeneradorés g(x) = mcm(Mαb (x),...,Mαb+δ 2 (x)) ∈ Fq[x].Aquestpolinomitambéespotescriurecoma g(x) = j∈K (x αj ), on K = Cb ∪···∪ Cb+δ 2.EnelcasdelscodisBCH,ladistànciamínima d satisfà d ≥ δ.D’altrabanda,peralscodisRS,elpolinomigeneradorés

Codisdetectorsicorrectorsd’errors

g(x) = b+δ 2 j=b (x αj ) ∈ Fqm [x] iladistànciamínimaés d = δ.Finalment, peralsdoscasos,quan b = 1,elcodis’anomena BCH o RSensentitestricte,i quan n = qm 1,s’anomena BCH o RSprimitiu.Enaquestdarrercas,lataxa detransmissióéslamàximaentretotselscodisBCHoRSamblamateixa capacitatcorrectora.

Exemple 24 ConstruïmelcodibinariBCHambparàmetres (4, 7) primitiui ensentitestricte.Comque q = 2i m = 4,consideremelcosfinit F16 = F2[x]/(1 + x + x4) ={0,α0,α,...,α15},on α ésunaarrel15-èsimaprimitiva delaunitat.Lataula5mostraelsvectorsde F16 enformapotencial.

potencialvectorial potencialvectorial

α−∞ = 0 (0, 0, 0, 0)

7 (1, 1, 0, 1) α0 (1, 0, 0, 0) α8 (1, 0, 1, 0)

1 (0, 1, 0, 0) α9 (0, 1, 0, 1) α2 (0, 0, 1, 0) α10 (1, 1, 1, 0) α3 (0, 0, 0, 1)

11 (0, 1, 1, 1) α4 (1, 1, 0, 0) α12

α5 (0, 1, 1, 0) α13

(1, 1, 1, 1)

(1, 0, 1, 1)

α6 (0, 0, 1, 1) α14 (1, 0, 0, 1)

Taula 5: Representaciópotencialivectoriala F16 = F2[x]/(1 + x + x4).

Comquevolemuncodiprimitiu,lalongitudhadeser n = 24 1 = 15. Lesclasses2-ciclotòmiquesmòdul15són C0 ={0}, C1 ={1, 2, 4, 8}, C3 = {3, 6, 12, 9}, C5 ={5, 10} i C7 ={7, 14, 13, 11}.Comquevolemuncodiensentit estrictei δ = 7,llavors K = 6 i=1 Ci = C1 ∪ C3 ∪ C5 ={1, 2, 3, 4, 5, 6, 8, 9, 10, 12} i g(x) = j∈K (x αj ).Tambépodemobtenir g(x) apartird’algunspolinomismínims,jaque g(x) = mcm(Mα(x),...,Mα6 (x)),on Mα(x) = Mα2 (x) = Mα4 (x) = 1+x +x4 , Mα3 (x) = Mα6 (x) = 1+x +x2 +x3 +x4 i Mα5 (x) = 1+x + x2.Així,elpolinomigeneradorés g(x) = Mα(x) Mα3 (x) Mα5 (x) = 1+x+x2 + x4 + x5 + x8 + x10 ∈ F2[x] ielcodiBCHés C = 1 + x + x2 + x4 + x5 + x8 + x10 . Volemcodificarelprimervectord’informaciódelaseqüènciabinària101101 00 ... Comqueelcodi C télongitud n = 15ielgraude g(x) és n k = 10, aleshoresladimensiódelcodiés k = 5ielprimervectord’informacióés i = (1, 0, 1, 1, 0).Lacodificacióde i(x) = 1 + x2 + x3 fentservirelmètodeCRC és c(x) = i(x)x10 r(x),on r(x) = x + x3 + x8 + x9 i c(x) = x + x3 + x8 + x9 + x10 + x12 + x13.Pertant,lacodificacióde i = (1, 0, 1, 1, 0) és c = (0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0).

Exemple 25. ConstruïmelcodibinariRSambparàmetres (4, 7) primitiuien sentitestricte.Comque q = 2i m = 4,consideremtambéelcosfinit F16 comenl’exemple24.Perquèsiguiprimitiu,lalongituddelcodihadeser n = 24 1 = 15.Comquehadeserensentitestrictei δ = 7,elpolinomigenerador és g(x) = 6 j=1(x αj ) = α6 +α9x+α6x2 +α4x3 +α14x4 +α10x5 +x6 ∈ F16[x]

MercèVillanuevaiCristinaFernández-Córdoba

Volemcodificarelprimervectord’informaciódelaseqüènciabinària101101 0000101101001011100001000111110101 ... Enaquestcas,comquelalongitudés n = 15ielgraude g(x) és n k = 6,ladimensiódelcodiés k = 9.Percodificarnecessitemunvectord’informaciódelongitud9a F16,oequivalentment, unaseqüènciabinàriade4·9 = 36bits.Prenemels36primersbitsdelaseqüènciaacodificar,agrupatsenblocsde4bits1011010000101101001011100001 00011111,iconsideremelscorresponentselementsa F16 d’acordamblataula5: α13

.Així,tenimque i(x) = α13 + αx + α2x2 + α

.CodificantambelmètodeCRC tenimque c(x) =

.Així,lacodificaciódels36primers bitséslaseqüènciabinàriadelongitud60,010000001001 ... 00011111, corresponentalaparaulacodi c delongitud15sobre F16

Ladescodificacióperacodiscíclicséstancomplexacomladescodificació peracodislinealsengeneral.Encanvi,peralscodisBCHiRSexisteixunmètode eficientdedescodificació,àmpliamentutilitzaticonegutcomaalgorisme deBerlekamp-Massey,queestàbasatenl’algorismed’Euclidesestès[32].A continuació,veuremcoms’aplicaaquestmètodealscodisBCHiRSprimitiusi ensentitestricte.

Suposemqueenlatransmissiód’informaciód’unaparaulacodi c delongitud n esprodueixenerrors.Esrepelvector u,oequivalentmentelpolinomi u(x),queconsisteixenlaparaulacodienviadaméselserrorsques’han produït.Sis’hanproduïtesborralls,aleshoressesubstitueixcadascund’ells perunvalorarbitraridelcos,perexemple,el0.Apartirde u(x),calculem el polinomisíndrome S(x) = u(α) + u(α2)x +···+ u(αδ 1)xδ 2.Comque α,α2,...,αδ 1 sónarrelsdelpolinomigeneradordelcodi,tenimque S(x) = 0 siinoméssi u corresponaunaparaulacodii,pertant,nos’haproduïtcap error.

Si S(x) = 0,aleshoreselvectorrebut u contéerrorsquevolemcorregir. Sigui J elconjuntquecontéelsvalors j talsques’haproduïtunerrora lacoordenada (j + 1)-èsimai J elconjuntquecontéelsvalors j talsque s’haproduïtunesborrallalacoordenada (j + 1)-èsima.Definimel polinomi localitzadord’esborralls σb(x) = j∈J (1 αj x) iel polinomilocalitzadord’errors σe(x) = j∈J (1 αj x).Així,el polinomilocalitzadord’errorsiesborralls és σ(x) = σb(x) · σe(x).Apartirde S(x) i δ,plantegeml’equaciósegüent, anomenada equacióclau: w(x) = σ(x)S(x)(mod xδ 1).

Fentservirl’algorismed’Euclides,estèsapartirdelspolinomis S(x) i xδ 1 , podemresoldreaquestaequacióiobtenirdospolinomis σ(x) i w(x) tals que mcd(σ(x),w(x)) = 1,0 < grau(σ(x)) ≤ (δ 1)/2 i grau(w(x)) ≤ (δ 1)/2 [38,p.179].Elpolinomi w(x) s’anomena polinomiavaluador d’errorsiesborralls.Acontinuació,calculemlesarrelsde σ(x) a Fqm ila derivadade σ(x), σ (x).Peracadaarrel α j de σ(x),elcoeficientde xj del

polinomi e(x) és ej =− w(α j ) σ (α j ) .Finalment,apartirde e(x) obtenimelvector d’error e i,pertant,laparaulacodienviadaés c = u e.Enaquestprocésde descodificació,elméscostóscomputacionalmentésl’obtenciódelesarrels de σ(x) a Fqm .

Exemple 26 ConsideremelcodiBCHambparàmetres (4, 7) del’exemple24. Suposemquealasortidadelcanalrebem101000110101100,corresponent aunvector u delongitud15.Elpolinomiassociatés u(x) = 1 + x2 + x6 + x7 + x9 + x11 + x12.Apartirde u(x),calculemelpolinomisíndrome S(x) = u(α)+u(α2)x +···+u(α6)x5.Tenimque u(α) = 1+α2 +α6 +α7 +α9 +α11 + α12 = α14 , u(α2) = α13 , u(α3) = α, u(α4) = α11 , u(α5) = α5 i u(α6) = α2

Pertant,elpolinomisíndromeés S(x) = α14 + α13x + αx2 + α11x3 + α5x4 + α2x5.Comque S(x) = 0,sabemques’hanproduïterrors.Aleshores,resolem l’equacióclau w(x) = σ(x)S(x)(mod x6).Aplicantl’algorismed’Euclides estès,obtenimque σ(x) = α11 + α10x + α10x2 i w(x) = α10.Laderivada de σ(x) és σ (x) = α10.Lesarrelsde σ(x) són α7 = α 8 i α9 = α 6 i,pertant, elscoeficientsdiferentsdezerode e(x) sónelscorresponentsa x8 i x6.Els valorsd’aquestscoeficientssón e8 = w(α 8 ) σ (α 8 ) = α10 α10 = 1i e6 = w(α 6 ) σ (α 6 ) =

10 α10 = 1. Així, e(x) = x6 + x8,elvectord’errorés e = (0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0) ilaparaulacodienviadaés c = u e = (1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0).Si s’hacodificatutilitzantelmètodeCRC,aleshoreslainformacióestrobaenles darreres k = 5coordenades,osigui,és01100.

Exemple 27. ConsideremelcodiRSambparàmetres (4, 7) del’exemple25. Suposemquealasortidadelcanalrebemunaseqüènciabinàriadelongitud60 corresponentaunparaulacodiambpossibleserrors.Fentblocsde4bits,i considerantelscorresponentselementsa F16 d’acordamblataula5,obtenim unvector u delongitud15a F16.Considerem u(x) elpolinomiassociat.Igual queal’exemple26,calculemelpolinomisíndrome S(x) iresoleml’equació clau w(x) = σ(x)S(x)(mod x6).Apartirdelesarrelsdelpolinomilocalitzadord’errors σ(x),obtenimlesposicionsdelescoordenadesdiferentsdezero delvectord’error.Apartirdelpolinomiavaluadord’errors,obtenimelsvalors d’aquestescoordenades.Així,construïmelvectord’error e a F16.Finalment, calculemlaparaulacodia F16, c = u e,itornemaconsiderarcadacoordenada de c com4bitsd’acordamblataula5.Sis’hacodificatutilitzantelmètodeCRC, aleshoreslainformacióestrobaenelsdarrers4k = 4 · 9 = 36bits.

ElscodisBCHiRSs’utilitzenenmoltsàmbits[46].Apartdelesaplicacions enelcampdelesmemòriesdelsdispositiuselectrònics,lescomunicacionsespacials,larepresentaciód’informacióenformadecodisdebarresbidimensionals il’emmagatzematgedistribuït,queescomentaranenlesproperesseccions, aquestscodistambéesfanservirenl’emmagatzematgededadesdelsdiscs òptics.Enaquestcas,lacodificacióicorrecciód’errorspermetenlalecturade lesdadesencaraqueeldiscòpticnoestiguienperfecteestat.Inicialment,es vanemprarperal’escripturadedadesenelsCDi,posteriorment,s’haestès alarestadedispositiusd’emmagatzematgeendiscsòptics,comelDVDiel Blu-ray.

UnageneralitzaciódelscodisBCHiRSsónelscodisalgebraicsgeomètrics, queesdefineixenusantcorbesalgebraiquessobrecossosfinits[35,capítol10].

Entreaquests,caldestacarelscodisdeGoppa,que,enelcasbinari,s’han aplicatensistemescriptogràficsdeclaupúblicabasatsencodis,comper exempleelcriptosistemadeMcElieceieldeNiederreiter.Dinsdel’estudidela criptografiapostquàntica,s’hademostratqueaquestsalgoritmescriptogràfics sónsegursenversatacsefectuatsmitjançantcomputacióquàntica[2,40].

4CodisdeHammingenlesmemòriesd’ordinadors

El1947,pertaldemillorarlafiabilitatdelsordinadorsdel’èpocainohaver dereiniciarelsprogramesdesdezeroquanesdetectavaunerror,Richard W.Hammingvaplantejarperprimeravegadalanecessitatnonomésdedetectar errorssinódecorregir-los.Ellvaserquivaconstruirelprimercodicorrector, elcodilineal [7, 4, 3]2,queapareixpublicattresanysméstard[17],jaqueels LaboratorisBellontreballavavansol.licitar-nelapatent.Aquestcodivaser generalitzatperMarcelJ.E.Golayl’any1949ivadonarllocalsconeguts codis deHamming [14].

EnaquestasecciódescriuremelscodisdeHammingin’analitzaremles propietats.Veuremquepermetencorregirunúnicerror,peròlacorreccióes potrealitzardeformamolteficient,tantentempscomenmemòria.També mostraremqueelcodiestèsd’uncodideHamming,amésdecorregirunerror, permetdetectarfinsadoserrors,icomaquesttipusdecodis’aplicaenles memòriesd’ordinador.

Diemqueuncodilinealsobre Fq ésun codideHamming silescolumnesdelasevamatriudecontrolformenunconjuntmaximaldevectorsde longitud t ≥ 2sobre Fq linealmentindependentsdosados.Perlaproposició13,aquestacondiciógaranteixqueladistànciamínimaés d = 3i,per tant,sóncodis1-correctors.Perconstrucció,sóncodislineals [n,n t, 3]q,on n = (qt 1)/(q 1).Amés,d’entretotselscodis1-correctors,aquestssón elsquetenenlamajorlongitud n i,pertant,tambélamajortaxadetransmissió R = (n t)/n.Donatuncosfinit Fq iunnombreenter t ≥ 2,ésfàcilveure queexisteixunúniccodideHamming,denotatper Hq,t ,llevatd’equivalències. Exemple 28. Enelcasbinari,si t = 3,aleshoresunamatriudecontrolperal codideHamming H2,3,quetéparàmetres [7, 4, 3]2,podriaserlasegüent:

Encanvi,sil’alfabetés F4 i t = 2unamatriudecontrolperalcodide Hamming H4,2,quetéparàmetres [5, 3, 3]4,podriaser

1 αα2 01 , on α ésunelementprimitiudelcosfinit F4.

AlgunsdelscodisdeHammingtambéespodenconsiderarcomacodis cíclics.Defet,elcodideHamming Hq,t ésequivalentauncodicíclicsiinomés sielsvalors t i q 1sóncoprimers[4,p.114].D’aquestfetesdesprènquetot codibinarideHammingésequivalentauncodicíclic.

ElscodisdeHammingsónperfectesenelsentitquecompleixenlafitade Hamming (1) ambigualtat.Peraixò,noméscalveurequelesbolesderadi1 centradesencadascunadelesparaulescodirecobreixentotl’espai Fn q [23, p.48].Aquestfetfacilitalaconstrucciódelatauladesíndromes,jaqueel conjuntdesíndromescoincideixamblescolumnesdelamatriudecontroli elsseusmúltiples.Amés,toteslesclassesd’equivalènciadiferentsdelaclasse delzerotenenunúniclíderqueésdepes1,ielconjuntdelíders(diferentsde zero)coincideixambelconjuntdetotselsvectorsdepes1.

Lacorrecciód’errorstambéresultaeficient,jaqueenaquestcas,uncop rebemunvector w ∈ Fn q ,calculem Hwt ibusquemenquinacolumnadela matriudecontrol H estrobaaquestasíndromeounmúltipleseu.Així,si Hwt = rhi,on r ∈ Fq i hi éslacolumna i-èsimade H,diremquel’errorés elvectordepes1,amb r enla i-èsimacoordenadaizerosenlaresta.Enel casbinari,noméscaltrobarlacolumnade H quecoincideixiamblasíndrome. Pertant,siordenemlescolumnesde H demaneraquelacolumna i-èsima coincideixiamblarepresentacióenbase2de i,ladescodificacióésmésràpida.

Elcodiestèsd’uncodideHammingésuncodilineal [n + 1,n t, 4]2,on n = (qt 1)/(q 1).Aquestcodicontinuasent1-corrector,peròadiferència delcodideHamming,amésdecorregirunerror,potsimultàniamentdetectarnedos.Fixem-nosquelesclassesd’equivalènciadiferentsdelaclassedelzero tenenobéunlíderdepes1queésúnic,obéunlíderdepes2quenoésúnic. Enaquestcas,sioptemperunadescodificaciócompleta,podemdecidirper exemplequeellíderdepes2siguielquetinguiun1enladarreraposició.

Exemple 29. ElcodiestèsdelcodideHamming [7, 4, 3]2,ambmatriudecontrol H donadaenl’exemple28,éselcodi [8, 4, 4]2 quetélamatriudecontrol següent:

Suposemquehemcodificatlainformacióambaquestcodiiquerebemelvector w = (1, 1, 0, 0, 0, 1, 1, 1).Perdescodificar,calculem Hwt=(1, 0, 1, 0).Comque (1, 0, 1, 0) coincideixambla2acolumnade H,l’errorés e = (0, 1, 0, 0, 0, 0, 0, 0) i,pertant,laparaulacodiés c = w e = (1, 0, 0, 0, 0, 1, 1, 1).Enaquestcas, comquelescolumnesde H estanordenades,enspodemestalviarlacerca dinsdelamatriu H.Apartirde (1, 0, 1, 0),eliminantelprimerbit,comque 010ésel2enbase2,sabemquel’errorestàenla2aposició.Encanvi,si rebemelvector w = (0, 0, 0, 1, 0, 1, 1, 1),comquelasíndromeés (0, 1, 0, 1) inocoincideixambcapdelescolumnesde H,podemdetectarques’han produïtdosoméserrors.Tambéésfàcildeveure-hoanalitzantlaparitatdel

vectorrebut:siéssenar,diremques’haproduïtunerrorqueespodràcorregir; isiésparell,detectaremquen’hihahagutcomamínimdos.Siapliquem unadescodificaciócompleta,comlaquehemdefinitabans,l’errorassociatal vector w seria e = (0, 0, 0, 0, 1, 0, 0, 1),jaque101és5enbase2.Pertant,la paraulacodiseria c = w e = (0, 0, 0, 1, 1, 1, 1, 0).

Lesmemòriesdelsordinadorsestanconstruïdesapartirdexipsdesilici. Unxipdememòriaésbàsicamentunamatriuquadradadecel lesqueemmagatzemenbits.Perexemple,unxipde64kilobitsemmagatzema64 · 210 = 216 bits, ounde256kilobitsemmagatzema218 bits.Enelde64kilobits,elsbitss’organitzenenunamatriude28 × 28.S’accedeixacadabitapartirdedosvalorsde0 a28 1 = 255querepresentenlafilailacolumna.Comqueelsvalorsde0a255 espodenrepresentarapartirde8bits,esnecessiten8 + 8 = 16bitsperdescriurelaposiciód’unbitenelxip.Enunxipde256kilobitsesnecessitarien 18bitsperlocalitzarlaposiciód’unbit.

Elbitques’emmagatzemaenunaposiciódelxipesrepresentaapartirde lapresènciaol’absènciadecàrregaelèctricanegativa.Quans’emmagatzema un0,elforatdelpotencialdel’electróésomplertambelectrons,iquan s’emmagatzemaun1,esdeixabuit.Esconsideraquehihaun0si,mesurant lasevacàrreganegativa,aquestaéssuperiorauncertvalorllindar.Pertant, siunaposicióperdlasevacàrreganegativa,aleshoresesllegeixdeforma incorrectaidiemques’haproduïtunerror.Aqueststipusd’errorssónforça freqüentsinoespodenevitar.

4xips

Figura 3: Esquemadeconfiguracióenmemòriesd’ordinadors.

Pertaldecorregirelserrorsdescrits,inicialmentesvanferservircodis deHammingestesosdelaformasegüent.Perexemple,sitenim128xipsde 64kilobits,aquestss’organitzenen4filesde32xipscadascuna.Lainformació esdivideixenparaulesde32bits,oncadascundels32bitss’extreud’undels 32xips.Percorregirelserrors,s’afegeixen7xipsalfinaldecadascunadeles 4filesde32xips,obtenintuntotalde128 + 7 4 = 156xips.Així,dels39xips

quecontécadascunadeles4files,elsdarrers7contenenlaredundànciaisón utilitzatspercorregirelserrors.Lafigura3mostraunesquemad’aquestaconfiguració.Enaquestcas,s’utilitzaelcodibinariestèsdeHamming [64, 57, 4]2, encaraquenoméss’aprofiten32dels57bitsd’informació.

Partdelainformaciósobreaquestaaplicaciós’haextretde[29].L’aplicació d’altrescodisendiferentstipusdememòriesd’ordinadoridispositiuselectrònicsespottrobar,perexemple,a[42,capítols2i3]o[47].Enaquestàmbit,a partdelscodisdeHamming,esfanservirelscodisBCHiRS,imésrecentment elscodisLDPC(low-densitiyparity-check).

5CodisReed-Mullerperalatransmissiódefotografies al’espai

Enaquestasecciódescriuremalgunscodisquevanaparèixerpocdesprésdels codisdeHamming.Amés,veuremcomalgunsesvanaplicarpermillorarla qualitatdelesfotografiesdelsplanetesdelsistemasolarenviadesalaterraa travésdesondesespacials.

Sigui Hq,t elcodideHamming [n,n t, 3]q,on n = (qt 1)/(q 1). L’ortogonald’uncodideHamming, H ⊥ q,t ,s’anomena codisimplex iésuncodi ambparàmetres [n,t,qt 1]q,ontoteslesparaulescodidiferentsdezero tenenpes qt 1.El codiReed-Mullerdeprimerordre,tambéanomenat codi deHadamardlineal,éselcodi (Hq,t )⊥,osiguil’ortogonaldelcodiestèsde Hamming.Aquestcoditéparàmetres [n + 1,(n + 1)q,(qt + q 2)/q]q,per tant,pera q = 2sóncodislineals [2t ,t + 1, 2t 1]2 [21,p.83].Engeneral,els codisReed-Mullerd’ordre r ,1 ≤ r ≤ n,vanserdescritsperprimeravegada perDavidE.Mullerel1954[33];elmateixany,IrvingS.Reedvaproposarel primeralgorismeeficientperdescodificar-los[36].

RecordemqueelscodisdeHammingsóncodisperfectesenelsentitque compleixenlafitadeHamming (1) ambigualtat.Defet,totselscodis1-perfectes linealssóncodisdeHamming.Comquesóncodis1-correctors,tambées diuquesóncodis1-perfectes.Engeneral,esdiuqueuncodiés t-perfecte sisatisfàlafitadeHammingambigualtat,oequivalentment,sitotvector w ∈ Fn q estàadistànciacomamàxim t d’exactamentunaparaulacodi.Per definició,elscodis t-perfectessóncodis t-correctors.El1973,esvademostrar queelsúnicscodisperfectesnotrivialssónelssegüents:elscodis q-arisde repetició [n,q,n]q amb n senar;elscodis q-aris1-perfectes(nonecessàriament lineals);elcodibinarideGolay [23, 12, 7]2,ielcoditernarideGolay [11, 6, 5]3; vegeu[43, 49].Totsaquests,excepteels1-perfectesnolineals,sónúnicsllevat d’equivalències[31].Encanvi,hihamoltscodis1-perfectesnolinealsqueno sónequivalentsentreells[11,19,34].

El1962vancomençarlesprimeresmissionsespacialsperfotografiarels planetesMercuri,VenusiMart,atravésdelprogramaMariner.Inicialmentles imatgesesvandividiren200 × 200elementsopíxels,iacadascund’aquests seliassignavaunvectorbinaridelongitud6perindicarunnivellenl’escala

degrisos,del000000querepresentavaelblancal111111querepresentava elnegre.Comquelaprobabilitatd’errord’unbitenviatatravésdel’espai era p = 0.05,laprobabilitatd’errord’unpíxelera1 (1 p)6 ≈ 0.265.O sigui,mésdel26 % delaimatgeconteniaerrors.Aquestpercentatgeeraforça inacceptableiesvaestudiarlamaneradereduir-lo.

ApartirdeldissenydelessondesespacialsMariner6i7,llançadesel1969 perfotografiarelplanetaMart,esvancomençaraincorporarcodiscorrectors d’errors.Calia,però,tenirencomptecertesrestriccionsdepes,consumd’energia,emmagatzematgeicapacitatdecomputació.Peraixò,comqueesvan dividirlesimatgesen700 × 832píxels,aquestspíxelsjacodificatsnopodien excedirde30bitsaproximadament.Tambécaliaqueelprocésdecodificació idescodificaciófosràpidperpoderaixíredirigirlacàmaraapartirdeles fotografiesrebudes.

Finalment,esvadecidirferservirelcodideHadamardlineal [32, 6, 16]2 que permetcorregirfinsa (16 1)/2 = 7errorscada32bits.D’aquestamanera,es vaaconseguirreduirl’errorenlesimatgesd’un26 % aun0.01 %,jaquelaprobabilitatd’errord’unpíxelesvareduirfinsa1 7 i=0 32 i pi(1 p)32 i ≈ 0 00014. Lacodificacióperacodislinealsresultavaràpidainorequeriamemòria.La descodificacióespodiaaccelerarutilitzantlatransformadaràpidadeFourier queesvaimplementardinsdelacircuiteriadelasonda,conegudacoma «GreenMachine»(nopelseucolor,sinópelseudisenyador,R.R.Green).Més informaciósobreaquestaaplicaciódelscodisespotconsultarambdetalla[35, capítol25]obreumenta[29, 21].A[21]esdescriuenmoltesaltresaplicacions delscodisdeHadamard.

EnlasondaMariner9,llançadael1971,lesdadesinstrumentalsquerequerienunamajorprotecciócontraelserrorsvansercodificadesafegintabansde formaconcatenadauncodiRS [6, 4] sobre F26 .Esconsideraqueaquestvaserel primerdissenyd’unsistemadecodisconcatenats.EnlessondesVoyager1i2, llançadesel1977perenviarfotografiesencolordeJúpiteriSaturn,partdeles dadesesvancodificarfentservirelcodiestèsdeGolay [24, 12, 8]2 concatenat ambuncodiconvolucional.Apartirdel1968,amblamissióespacialPioneer9

LasondaMariner9.

peral’estudidelsol,esvancomençaraferservircodisconvolucionalscoma partd’unexperiment.Posteriorment,dinsdelsestàndardsdetransmissióper l’espaiCCSDS(ConsultativeCommitteeforSpaceDataSystems),s’handissenyat sistemesdecodisconvolucionalsconcatenatsambcodisRS.Peramésinformaciósobrecodisaplicatsenaquestcamp,espotconsultar[35,capítol25]o[46, capítol3],iperamésinformaciósobrecodisconvolucionalsoconvolucionals Reed-Solomon,[35,capítol12]o[10],respectivament.

6CodisBCHiReed-SolomonenelQR

Enlasecció2s’haexplicatelcodiEAN,utilitzatperidentificarproductes comercials.Aquestésuntipusdecodidebarresunidimensional(1D)olineal. Engeneral,tépocacapacitatinoméspermetdetectarerrors.Encanvi,els codisbidimensionals(2D)omatricialstenenméscapacitat,osigui,permeten representarmésquantitatdedades,ialhoracorregirerrors,desd’un5 % finsa un35 % segonseltipus.Dinsdelscodis2DtrobemelMaxiCode,elHanXin,el DataMatrix,l’HCC2DielQR,entred’altres[3].Enaquestasecciódescriuremels codisQR,jaquesónelsmésconegutsiutilitzats,iamésunsdelsmillorstant desdelpuntdevistadelacapacitatperrepresentardadescompercorregir errors.

ElcodiQR(del’anglès QuickResponse)vasercreatel1994perlacompanyia japonesaDensoWaveivaserestandarditzatel2000[26].Actualment,elseu úsésdecaràcterpúblic,jaquel’empresavarenunciaralsseusdretsd’autor. Inicialment,aquestcodiesvautilitzarperferelseguimentdelespecesen lafabricaciódevehicles.Avuiendia,però,s’utilitzaenmoltsllocs,tanten l’àmbitcomercialcomparticular.Espotferservirpermostrarunmissatgede text,obrirunapàginaweboungestordecorreu,afegiruncontactealmòbil, etc.

Figura 4: Exempled’unQRamblaURLd’unapàginaweb.

EnelscodisQRlaunitatmínimaperrepresentarlesdadeséselmòdul, unquadratquerepresentaun1a Z2 quanésnegreoun0quanésblanc.La versióoriginalomodel1eracapaçderepresentarnomésfinsa1167caràcters numèricsambunamatriude73 × 73mòduls.Actualment,s’utilitzaelmodel2,

MercèVillanuevaiCristinaFernández-Córdoba

quepermetrepresentarfinsa7089caràctersnumèricsambunamatriude 177 × 177mòduls.Dinsd’aquestmodel,enpodemtrobarversionsdiferents. Laversió1estàformadaper21 × 21mòdulsilaversió40per177 × 177.Per passard’unaversióalasegüents’incrementenen4elnombredemòdulsde cadacostat.

Cadaversiódisposadequatrenivellssegonslacapacitatcorrectora:el nivell L téunacapacitatcorrectorad’aproximadamentel7 %,el M téuna capacitatdel15 %,el Q entéunadel25 % ifinalmentel H entéunadel30 %. Lacapacitatmàximadepèndelaversióielnivelldecorrecció.Perexemple,el màximqueespotrepresentarambuncodiQRsón7089caràctersnumèrics(o 4296d’alfanumèrics)amblaversió40delnivell L

Lafigura4mostraunexempled’uncodiQR(versió2ambnivelldecorrecció L)amblaURLdelapàginawebdel ButlletídelaSocietatCatalanade Matemàtiques.Fixem-nosqueestàformatper25 × 25mòduls,jaquecorrespon auncodidelaversió2.Amés,elnivelldecorreccióéselmésbaix,osigui, permetcorregirnomésun7%delsmòduls,aproximadament.

5: Estructurad’unQRdelaversió2.

ElscodisQRestanformatsperdiferentsparts,incloent-hilaquecontéla informacióqueesvolrepresentar.Enlafigura5esmostral’estructuradelQR delafigura4amblesdiferentspartsqueconté.AlvoltantdelcodiQRhiha unazonalliuredemarquesd’unaampladade4mòduls.Alescantonades superiorsiinferioresquerrahihatrespatronsidènticsdedetecciódeposició quepermetenqueespuguillegirencaraqueestiguirotatohihagiunareflexió. Alllargdelafila7idelacolumna7estrobenelspatronsdesincronització,que estanformatspermòdulsnegresiblancsdeformaalternadaiqueserveixen comareferènciaperdeterminarlescoordenadesdelsmòdulsdedades.Els patronsd’alineaciósónsemblantsalsdedeteccióperòsónméspetits,també serveixenperalinearelcodiielseunombredepèndelaversió.Lainformació sobrequinéselnivelldecorreccióoformatescodificaambuncodibinariBCH, esduplicaisesituaendosotresllocsdiferentssegonslaversió.Lainformació sobrequinaéslaversiótambéescodificaambuncodibinariBCH,esduplicaise situaenduesubicacionsdiferents.Finalment,lainformacióqueesvolincloure

Figura

enelQRescodificaambuncodiRSsobreelcosfinit F28 ,enfunciódelnivell decorreccióiversió,is’organitzaengrupsde8bitscadascuncorresponenta unelementde F28 .

Enleszonesdestinadesaindicarelnivelldecorreccióoformatilaversió s’utilitzauncodibinariBCH.Concretament,elformatesrepresentaamb5bits (2perindicarundels4nivellsdisponiblesi3peraplicarunamàscarapertal d’evitaralgunesseqüènciesdebitsdemésdifícillectura)queescodifiquenamb unBCH [15, 5]2.Aquestainformacióapareixduplicadaisituadaendosotres llocsdiferentssegonslaversió.Elnúmerodeversióesrepresentaamb6bits, queescodifiquenambunBCH [18, 6]2.Aquestainformaciónoméss’incloua partirdelaversió7,itambéapareixduplicadaiubicadaendosllocsdiferents.

PeralesdadesquevolemincloureenelQRs’utilitzendiferentscodisRS, segonsquinsiguielnivelldecorreccióilaversió.Perexemple,enelnivell H delaversió4,comquehiha100bytesdisponibles,s’inclouen4paraulescodi, codificadesambunRS [25, 9, 17]28 .Enaquestcas,comqueladistànciamínima és d = 17,aquestcodipermetcorregir8bytespercadaparaulacodi,pertant, untotalde4 · 8 = 32bytesdels4 · 25 = 100bytestotals,osigui,el32%.

ElscodisQRhanevolucionatendiversesdireccionsatravésdelamateixa empresaqueelsvacrear.El1998esvancrearelscodismicroQR,mésapropiats peraaplicacionsonlesdadesil’espaisónreduïts,mantenintlamateixafacilitat delectura.El2007vanaparèixerelsSQRC(securityQRcode),preparatsper inclouredadesencriptadesdeformaqueaquestesnoméssónaccessibles peralslectorsautoritzats,osigui,quetinguinlesclausperdesencriptar. Entreel2009iel2011esvanpresentarelscodisiQR,que,comparatsamb elscodisQR,permetenrepresentarmésinformació(finsa40637caràcters numèrics),reduirl’espaiperaunamateixaquantitatd’informacióicorregirmés errorsambunnounivell S,quecorregeixaproximadamentel50 % delsmòduls. Amés,aquestscodistambépermetencomprimirlesdadesisergeneratsen formarectangular.

7Codisperal’emmagatzematgedistribuït

Enaquestaseccióveuremunaaplicaciódelscodiscorrectorsd’errors(ocorrectorsd’esborralls)enelcampdel’emmagatzematgedistribuït.Concretament, veuremalternativesal’emmagatzematgefentservirrèpliques,elsproblemes quecomportenialgunesdelessolucionsproposadesrecentment.

Ésevidentqueestemtotalmentimmersosdinsdelanovaeradigital.Avuien dia,lamajoriadelsobjectessóndigitalsoendepenenengranmesura.El2011, laInternationalDataCorporationvaestimarquelaquantitattotaldedades almóncreixeriael2012finsals2 7zettabytes(unzettabytesón1021 byteso 109 terabytes)i,pertant,suposariaunincrementdel48 % respecteal2011[7]. Mésrecentment,laprediccióésquecreixeràdels33zettabytesel2018als175 el2025[37].Aixòimplicaquecadadiahihamésimésdadesdigitalsquees creeniquecalemmagatzemar.Amés,volemqueestiguinsempredisponibles desdequalsevollloc,iquesiguindefàciliràpidaccés.

Actualment,peremmagatzemargransquantitatsdedadesesfanservir sistemesdistribuïts(distributedstoragesystems).Osigui,lesdadess’emmagatzemenenmoltsservidorsdiferentsqueenconjuntescomportencomunúnic sistemad’emmagatzematge,conegutcoma centrededades.Així,lesdades d’unfitxeresdivideixenidistribueixenendiversesunitatsd’emmagatzematge, anomenades nodes,que,simplificant,podenassociar-seambelsdiscsdurs.Un nodeodiscdurpotnecessitarserreparatperdiversosmotius.Perexemple, elnodepotfallar(laprobabilitatqueundiscdurdeixidefuncionarestàentreel2 % iel4 % l’any),opotestarocupatambaltrespeticionsoenfasede manteniment.

Unaprimerasolucióaaquestproblemaconsisteixafercòpiesdeseguretat (tambéconegudescoma backups),osigui,replicar n copslesdadesdecada node.Aixòespotveurecomsienrealitats’estiguésfentserviruncodide repetició,comeldescritenl’exemple9amb n = 3.Siunnodefalla,podem accediralesdadesd’unadelescòpies,descarregar-lesirestaurarelnode.El nombredenodesquepodenfallarsensequehihagicappèrduad’informació enelsistemas’anomena tolerànciaafallades,ienaquestcasésiguala n 1. Normalments’assumeixqueelsnodesfallendeformaindependent.Finalment, caldestacarqueaquestmètodeésforçaineficient,jaquesuposaunelevatcost entermeseconòmicsid’espai.

Unaprimeraalternativaconsisteixaferserviraltrescodislinealsdiferents delcodiderepetició.Engeneral,siesfaserviruncodilineal [n,k]q,lesdades esdivideixenen k nodesis’afegeixen n k nodesderedundànciadeforma queassignemcadascundels n símbolsdelaparaulacodiacadascundels n nodes.Siunnodefalla,aixòésequivalentadirquehihaunesborrallen unadelescoordenades.Noesconsideraunerror,jaqueespotsaberenquin node,osiguienquinacoordenada,s’haproduït.Siladistànciamínimadelcodi és d,elcodipermetcorregirfinsa d 1esborralls,pertant,latolerànciaa falladesdelsistemaseria d 1.Aquestvalorpotserinferioral’obtingutamb uncodiderepetició [n, 1]q,peròl’avantatgeésqueespotreduirelnombrede nodesredundants,passantde n 1a n k.D’aquestaformaespodenobtenir sistemesamblamateixafiabilitat,peròmillorantsignificativamentl’espaiiels costosd’emmagatzematge.

Enlaindústria,s’hananatreemplaçantelssistemesinicialsbasatsenla rèplicad’informaciópersistemesonesfanservircodiscorrectorsd’esborralls (erasurecodes).Normalments’utilitzencodisReed-Solomoncomelsdescrits enlasubsecció3.3,jaquesónMDS(vegeulasubsecció3.4).Així,ladistància mínimai,pertant,lacapacitatpercorregiresborrallséslamàximapossible fixatselsvalorsde n i k.Amés,podemrecuperarlesdadesemmagatzemades connectant-nosaqualssevolsubconjuntde k nodesdels n nodes.Perexemple, enelsistemad’emmagatzematgedeLinuxRAID-6esfaserviruncodiRS [10, 8] ienelGoogleColossusunRS [9, 6] [8].TambéFacebookenelseusistemade fitxersvaincorporarunRS [14, 10] [45].Ladarreraversiódelsistemadefitxers distribuïtsHadoop,Hadoop3.0,incorporal’opciód’utilitzaraquestscodis[48].

Malgratelsseusavantatgesrespectealssistemesbasatsenlarèplicad’informació,elssistemesbasatsencodiscorrectorsd’esborrallstenenelgran inconvenientque,quanunnodefalla,elsistemahad’accedira k nodes,i descarregar k vegadeslaquantitatdedadesquecontéelnodequevolem restaurar.Pertant,ésineficienttantdesdelpuntdevistadelaquantitatde dadesquehemdedescarregar(repairbandwidth)comdelaquantitatdenodes queintervenenenlareparació(repairdegree).Aquestproblemahadonatlloca duesnovesfamíliesdecodis:elscodisregeneratius(ReGenerating oRG)[9] ielslocalmentrecuperables(LocallyRecoverable oLR)[15].EnelscodisRG l’objectiuésminimitzarlaquantitatdedadesquehemdedescarregar,mentre queenelscodisLResbuscaminimitzarelnombredenodesnecessarisenla reparaciód’unnode.Tambés’hancombinatlesideesd’aquestesduesfamílies pertaldeminimitzarelsdosparàmetresambelsanomenats codislocalment regeneratius (LocallyRegeneratingCodes oLRG)[28].Altresautorshanbuscat alternativespermillorarlareparacióambelscodisReed-Solomon[16,8].

ElscodisLRjaestrobenimplementatsensistemesd’emmagatzematgecom elWindowsAzure[22]ienl’emmagatzematgedelesdadesaFacebook[39].A continuació,descriurembreumentlaprimerad’aquestesduesaplicacions.

Exemple 30. Talcoms’explicaa[22],enelsistemad’emmagatzematgeWindowsAzure,lesdadesinicialmentesvanincorporantaunfitxerfinsaarribar aunacertamida,perexemplefinsaobtenirunfitxerd’1gigabytequejano potsermodificat.Durantaquestprocés,esvanmantenintsempretrescòpies d’aquestfitxer.

Uncopelfitxers’haomplert,esdivideixen k = 6partsques’emmagatzemen en6nodes, x0, x1, x2, y0, y1, y2.Acontinuació,s’afegeixen n k = 4nodes deredundància, p0, p1, px , py ,talcomesmostraenlafigura6.Elsdos primersnodesderedundànciaescalculenapartirdels6nodesd’informaciói s’anomenen paritatsglobals.Elsaltresdosnodesderedundàncias’anomenen paritatslocals.Elnode px escalculaapartirde x0, x1, x2 i py apartirde y0, y1, y2 x0 x1 x2 y0 y1 y2

Figura 6: Esquemad’unexempledecodilocalmentrecuperable.

AquestcodiLRseriacomparableambuncodiReed-Solomon [9, 6] entermes delcostd’emmagatzematge(storageoverhead),jaqueelcodiLRtéuncost de10/6 = 1 66ielRSde9/6 = 1 5.Enl’LRhihauria4nodesderedundància

MercèVillanuevaiCristinaFernández-Córdoba

encomptesdels3quehihaenl’RS.Acanvi,siunnodefalla,esnecessitarien només3nodesperrecuperarlesdades,enllocdels6quecalenambelcodiRS. Finalment,aquestcodiRSpottolerarfinsalapèrduadequalssevol3nodes, mentrequeelcodiLRpottolerarlapèrduadequalssevol3nodesialguns patronsde4nodes.Perexemple,sifallenelsnodes x0, x1, y0, y1 síquees podrienrecuperarapartirdelaresta,perònosifossinelsnodes x0, x1, x2, px .

Pertaldereduirelcostd’emmagatzematgerespectedelcodiRS [9, 6],s’ha utilitzatunaltrecodiLRsemblantal’anterior,peròamb14nodesd’informaciói 4deredundància.AquestcodiLRéscomparableambl’RSrespectealnombrede nodesnecessarisperreparar-neun(repairdegree),jaquese’nnecessiten7en llocde6.Acanvi,s’hareduïtelcostd’emmagatzematged’1.5al’RSa18/14 = 1.29al’LR,fetquehasuposatunestalvidemilionsdedòlarsaMicrosoft[13].

Agraïments

LesautoresvolenagrairespecialmentalscompanysdelgrupderecercaCombinatorics,CodingandSecurityGroup(CCSG)delDepartament,JoaquimBorges, JaumePujoliJosepRifà,elsseuscomentarisiaportacionsenlamilloradel redactatfinaldel’article.Lesautorestambéhantingutl’ajutdelprojecte MINECO(AEI/FEDER,UE)númeroMINECOTIN2016-77918-Pidelprojectenúmero2017SGR-00463delaGeneralitatdeCatalunya.

Referències

[1] Ash,R. InformationTheory.NovaYork;Londres;Sydney:Interscience PublishersJohnWiley&Sons,1965.(InterscienceTractsinPureand AppliedMathematics;19)

[2] Bernstein,D.J.;Buchmann,J.;Dahmen,E.(ed.). Post-quantumCryptography.Berlín:Springer-Verlag,2009.

[3] BhaskarRaj,A.S. BARCODES:TechnologyandImplementation.Nova Delhi:TataMcGraw-HillEducation,2001.

[4] Biahut,R.E. AlgebraicCodesforDataTransmission.NovaYork:CambridgeUniversityPress,2003.

[5] Borges,J.;Fernández-Córdoba,C.;Pujol,J.;Rifà,J.;Villanueva,M. «Z2Z4-linearcodes:generatormatricesandduality». Des.CodesCryptogr., 54(2)(2010),167–179.

[6] BrunatBlay,J.M.;VenturaCapell,E. Informacióicodis.Barcelona: EdicionsUPC,2001.

[7] BusinessWire.«IDCpredicts2012willbetheyearofmobileandcloud platformwarsasITvendorsvieforleadershipwhiletheindustryredefines itself»(1desembre2011). https://www.businesswire.com/news/home /20111201005201/en/IDC-Predicts-2012-Year-Mobile-Cloud-Platform

[8] Dau,H.;Duursma,I.;Kiah,H.M.;Milenkovic,O. «RepairingReedSolomoncodeswithtwoerasures».A: Proceedingsof2017IEEEInternationalSymposiumonInformationTheory(ISIT).NovaYork:IEEE,2017, 351–355.

[9] Dimakis,A.G.;BrightenGodfrey,P.;Wu,Y.;Wainwright,M.J.;Ramchandran,K. «Networkcodingfordistributedstoragesystems». IEEE Trans.Inform.Theory,56(9)(2010),4539–4551.

[10] Ebert,P.M.;Tong,S.Y. «ConvolutionalReed-Solomoncodes». BellSystem Tech.J.,48(1969),729–742.

[11] Etzion,T. «Nonequivalent q-aryperfectcodes». SIAMJ.DiscreteMath., 9(3)(1996),413–423.

[12] Gallian,J.A. «Errordetectionmethods». ACMComput.Surveys,28(3) (1996),504–517.

[13] Gantenbein,D. «Abetterwaytostoredata».MicrosoftResearch Blog(5setembre2012). https://www.microsoft.com/en-us/research/ blog/better-way-store-data/.

[14] Golay,M.J.E. «Notesondigitalcoding». ProceedingsoftheIRE,37(6) (1949),657.

[15] Gopalan,P.;Huang,C.;Simitci,H.;Yekhanin,S. «Onthelocalityof codewordsymbols». IEEETrans.Inform.Theory,58(11)(2012),6925–6934.

[16] Guruswami,V.;Wootters,M. «RepairingReed-Solomoncodes». IEEE Trans.Inform.Theory,63(9)(2017),5684–5698.

[17] Hamming,R.W. «Errordetectinganderrorcorrectingcodes». BellSystem Tech.J.,29(1950),147–160.

[18] Hammons,A.R.,Jr.;Kumar,P.V.;Calderbank,A.R.;Sloane,N.J.A.; Solé,P. «The Z4-linearityofKerdock,Preparata,Goethals,andrelated codes». IEEETrans.Inform.Theory,40(2)(1994),301–319.

[19] Heden,O. «Asurveyofperfectcodes». Adv.Math.Commun.,2(2)(2008), 223–247.

[20] Hernández,L.;Martín,A. «Codificacióndeinformaciónmediantecódigosdebarras». Bol.Soc.Esp.Mat.Apl.SeMA,27(2004),29–48.

[21] Horadam,K.J. HadamardMatricesandtheirApplications.Princeton,NJ: PrincetonUniversityPress,2007.

[22] Huang,C.;Simitci,H.;Xu,Y.;Ogus,A.;Calder,B.;Gopalan,P.;Li,J.; Yekhanin,S. «ErasurecodinginWindowsAzureStorage».A: Proceedings ofthe2012USENIXAnnualTechnicalConference.Boston:USENIXAssociation,2012,15–26.

[23] Huffman,W.C.;Pless,V. FundamentalsofError-CorrectingCodes.Cambridge:CambridgeUniversityPress,2003.

[24] ISO 13616-1:2007 Financialservices-Internationalbankaccountnumber(IBAN)-Part1:StructureoftheIBAN.1aed.Suïssa:International OrganizationforStandardization,març2007.

[25] ISO/IEC 15420:2009(en) Informationtechnology-Automaticidentificationanddatacapturetechniques-EAN/UPCbarcodesymbologyspecification.2aed.Suïssa:InternationalOrganizationforStandardization, desembre2009.

[26] ISO/IEC 18004:2015(en) Informationtechnology-Automaticidentification anddatacapturetechniques-QRCodebarcodesymbologyspecification. 3aed.Suïssa:InternationalOrganizationforStandardization,febrer2015.

[27] ISO 2108:2017,ISO 2108:2005 Informationanddocumentation-InternationalStandardBookNumber(ISBN).7aed.Suïssa:InternationalOrganization forStandardization,desembre2017.

[28] Kamath,G.M.;Prakash,N.;Lalitha,V.;Kumar,P.V. «Codeswithlocal regenerationanderasurecorrection». IEEETrans.Inform.Theory,60(8) (2014),4637–4660.

[29] Key,J.D. «Someerror-correctingcodesandtheirapplications».A: Shier, D.R.;Wallenius,K.T.(ed.). AppliedMathematicalModeling:AMultidisciplinaryApproach.BocaRaton:Chapman&Hall/CRC,1999,276–299.

[30] Lidl,R.;Niederreiter,H. Finitefields.2aed.Cambridge:Cambridge UniversityPress,1997.(EncyclopediaofMathematicsanditsApplications; 20)

[31] MacWilliams,F.J.;Sloane,N.J.A. TheTheoryofError-CorrectingCodes. I.Amsterdam;NovaYork;Oxford:North-HollandPublishingCo.,1977. (North-HollandMathematicalLibrary;16)

[32] Massey,J.L. «Shift-registersynthesisandBCHdecoding». IEEETrans. InformationTheory,IT-15(1969),122–127.

[33] Muller,D.E. «ApplicationofBooleanalgebratoswitchingcircuitdesign andtoerrordetection». TransactionsoftheI.R.E.ProfessionalGroupon ElectronicComputers,EC-3(3)(1954),6–12.

[34] Phelps,K.T.;Rifà,J.;Villanueva,M. «Kernelsand p-kernelsof pr -ary 1-perfectcodes». Des.CodesCryptogr.,37(2)(2005),243–261.

[35] Pless,V.S.;Huffman,W.C.(ed.). HandbookofCodingTheory.Vol.II. Holanda:ElsevierScienceB.V.,1998.

[36] Reed,I.S. «Aclassofmultiple-error-correctingcodesandthedecoding scheme». Trans.I.R.E.,PGIT-4(1954),38–49.

[37] Reinsel,D.;Gantz,J.;Rydning,J. «Dataage2025:Thedigitization oftheworld.Fromedgetocore».A: InternationalDataCorporation. WhitePaper,US44413318(novembre2018),1–28. https://www.seagate. com/files/www-content/our-story/trends/files/idc-seagate-dataagewhitepaper.pdf.

[38] Rifà,J.;Huguet,Ll. Comunicacióndigital:teoríamatemáticadelainformación,codificaciónalgebraica,criptología.Barcelona:Masson,1991. (ColecciónTécnicayCientíficadeTelecomunicaciones)

[39] Sathiamoorthy,M.;Asteris,M.;Papailiopoulous,D.;Dimakis,A.G.; Vadali,R.;Chen,S.;Borthakur,D. «XORingelephants:Novelerasure codesforbigdata».A: Proceedingsofthe39thInternationalConferenceon VeryLargeDataBases.RivadelGarda:CurranAssociates,2013,325–336.

[40] Sayols,N.;Xambó,S. «Codiscorrectorsd’errorsicriptografiapostquàntica». ButlletídelaSocietatCatalanadeMatemàtiques,33(2)(2018), 147–171.

[41] Shannon,C.E. «Amathematicaltheoryofcommunication». BellSystem Tech.J.,27(3)(1948).379–423.

[42] Stievano,I.(ed.). FlashMemories.Londres:IntechOpen,2011.

[43] Tietäväinen,A. «Onthenonexistenceofperfectcodesoverfinitefields». SIAMJ.Appl.Math.,24(1973),88–96.

[44] Vardy,A. «Theintractabilityofcomputingtheminimumdistanceofa code». IEEETrans.Inform.Theory,43(6)(1997),1757–1766.

[45] Wang,W.;Kuang,H. «SavingcapacitywithHDFSRAID». Facebook Core (5juny2014). https://code.fb.com/core-data/saving-capacity -with-hdfs-raid/.

[46] Wicker,S.B.;Bhargava,V.K.(ed.). Reed-SolomonCodesandtheirApplications.NovaYork:Wiley-IEEEPress,1994.

[47] Zhang,L.;Tan,Y.-A.;Zhang,Q.-K. «IdentificationofNANDflashECC algorithmsinmobiledevices». DigitalInvestigation,9(1)(2012),34–48.

[48] Zhang,Z.;Wang,A.;Zheng,K.;Maheswara,G.;Vinayakumar,B. «IntroductiontoHDFSerasurecodinginApacheHadoop». ClouderaEngineeringBlog (23setembre2015). https://blog.cloudera.com/blog/2015/ 09/introduction-to-hdfs-erasure-coding-in-apache-hadoop/

[49] Zinov’ev,V.A.;Leont’ev,V.K. «NonexistenceofperfectcodesoverGalois fields». ProblemsofControlandInformationTheory,2(1973),123–132.

Departamentd’EnginyeriadelaInformacióidelesComunicacions UniversitatAutònomadeBarcelona merce.villanueva@uab.cat,cristina.fernandez@uab.cat

ButlletídelaSocietatCatalanadeMatemàtiques Vol.34,núm.1,2019.Pàg.91–92

Englishsummaries

MiriamAlcaláVicente

Thebeginningofnon-EuclideangeometryinItaly

Non-Euclideangeometryisprobablyoneofthemostrevolutionarytheories ofthe19thcentury.Afterremainingunnoticedforover30years,from1860 itunderwentaRenaissanceprocess,whichwasdrivenbytheworkoftwo mathematicians:JulesHoüelandGiuseppeBattaglini.

Thisarticleisabouttheprocessofdissemination,developmentandacceptance ofthenewgeometry,focusingontheItaliancontext.Inparticular,wewillshow thatthecontributionofG.Battaglinitothisareagoesfarbeyondthedisclosure. Attheendofhisarticle«SullageometriaimmaginariadiLobatschewsky»,we findanunexpectedcoincidencebetweenhisdescriptionofthenon-Euclidian planeandthesubsequentBeltrami’sdiskmodel.Ourpurposeistojustifythe similaritiesbetweenthesetwointerpretations.

Keywords: historyofgeometry,non-Euclideangeometry,Hoüel,Battaglini, Beltrami.

MSC2010SubjectClassification: 01A55,51-03,53-03.

CristinaDalfóandMiquelÀngelFiol

Themethodoflinesfornumericalsolutionsofpartialdifferentialequations

Inthispaper,wedescribeasemi-discretemethodforanumericalresolutionof atypeofpartialdifferentialequationscalledthemethodoflines(MOL).This methodisbasedonthediscretizationofallbutoneofthevariablesofthe problem.WeillustratethismethodbysolvingtheLaplaceequationinCartesian

coordinates.WecomparetheconceptsusedbytheMOLwithrespecttothe analyticalmethodofvariableseparation.Weshowthattheresultsobtained withtheMOLareverygoodapproximationsoftheanalyticalsolutions.

Keywords: partialdifferentialequations,discretizationofacontinuousvariable, numericalanalysis.

MSC2010SubjectClassification: 65M20.

MercèVillanuevaandCristinaFernández-Córdoba

Errordetectingandcorrectingcodesandsomeoftheirapplicationsintheinformationsociety

Indigitaltransmissionsofinformationfromasendertoareceiverthrough achannel,errorsmayoccur.Inthisarticle,themostimportantconceptsand resultsofthetheoryoferrordetectingandcorrectingcodesarediscussed. Thistheorystudiesefficientmethodstoguaranteeaccuratetransmissionof information.First,someeverydayexamplesoferrordetectingcodesaredescribed,suchasthecodesincludedinDNI,ISBN,IBANandEAN.Next,theclassical theoryoferrorcorrectingcodesispresented,particularlyconsideringlinear codesand,withinthem,cycliccodes,whicharemoreefficientforencoding. Thetwomostimportantfamiliesofcycliccodes,theBCHandReed-Solomon codes,whichalsomakeitpossibletodecodeefficiently,arealsodescribed. Lastly,twohistoricalapplications,incomputermemoriesandthetransmission ofphotographsinspace,andtwomorerecentapplications,inQRcodesand distributedstorage,areshown.

Keywords: errordetection,errorcorrection,linearcodes,cycliccodes,BCH, Reed-Solomon,applications.

MSC2010SubjectClassification: 94B05,94B15,11T71.

Instruccionsperalsautors

Elsarticlessotmesosapublicaciós’hand’enviaralseditorsoaqualsevol membredelcomitèeditorialpercorreuelectrònic,preferentmentenformat PDF.Elsoriginalshandecontenirlaversióanglesadeltítol,unresumbreuen catalàienanglès,paraulesclauencatalàienanglèsielscodisdelaclassificació permatèriesMSC2010.

Lesversionsdefinitivesdelsarticlesacceptatss’handepresentarencodiTEX,preferentmentenl’estilLATEXpropidel Butlletí.Aquestestilespot obteniralespàgineswebdelaSocietatCatalanadeMatemàtiques(SCM).Fem notarqueenaquestapublicaciós’utilitzapreferentmentelpuntperaseparar decimals,enllocdelacomarecomanadaperl’IEC,perapoderfacilitarla comprensiódelesexpressionsmatemàtiques.Pertald’accelerarelprocésde producció,espregaalsautorsquesegueixinlesindicacionscontingudesenel documentd’exemple.

Laversióenpaperdel Butlletí s’imprimeixenblancinegre.Quanun articlecontinguifiguresencoloriesconsidericonvenient,l’autorproporcionarà unaversiódelsgràficssubstituintelcolorpertonsdegrisosilíniesdegruix variable.Aixímateix,modificaràelscomentarisquefacinreferènciaalcolorde lesfigures.Enqualsevolcas,el Butlletí publicaràl’originalencolorenelseu formatelectrònic.

Lapropietatintel lectualdelsarticlesésdelsrespectiusautors.

Elsautors,enelmomentdelliurarelsarticlesal Butlletí perasol licitar-ne lapublicació,acceptenelstermessegüents:

—ElsautorscedeixenalaSCM(filialdel’Institutd’EstudisCatalans)els dretsdereproducció,comunicaciópúblicaidistribuciódelsarticlespresentats peraserpublicatsal Butlletí

—ElsautorsresponendavantlaSCMdel’autoriail’originalitatdelsarticles presentats.

—Ésresponsabilitatdelsautorsl’obtenciódelspermisosperalareproducciódetotelmaterialgràficinclòsenelsarticles.

—LaSCMestàexemptadetotaresponsabilitatderivadadel’eventual vulneraciódedretsdepropietatintel.lectualperpartdelsautors.

CadaautorrebràunacòpiaenPDFd’altaqualitatdelaversiódigitaldelseu articleiunexemplarimprèsdelnúmerodel Butlletí enelqualespubliqui.

Lacorrespondènciaadministrativarelacionadaambel Butlletí s’had’adreçaralaSCM.

Pelquefaalaprotecciódedadespersonals,l’Institutd’EstudisCatalans(IEC) compleixelqueestableixelReglamentgeneraldeprotecciódedadesdelaUnió Europea(Reglament2016/679,del27d’abrilde2016).Deconformitatamb aquestanorma,s’informaque,ambl’acceptaciódelesnormesdepublicació, elsautorsautoritzenquelessevesdadespersonals(nomicognoms,dadesde contacteidadesdefiliació)puguinserpublicadesenelcorresponentvolum del Butlletí.

Aquestesdadesseranincorporadesauntractamentqueésresponsabilitat del’IECamblafinalitatdegestionaraquestapublicació.Únicaments’utilitzaranlesdadesdelsautorsperagestionarlapublicaciódel Butlletí ino serancedidesatercers,niesproduirantransferènciesatercerspaïsosoorganitzacionsinternacionals.Uncoppublicatel Butlletí,aquestesdadeses conservarancomapartdelregistrehistòricd’autors.Elsautorspodenexercir elsdretsd’accés,rectificació,supressió,oposició,limitacióeneltractament iportabilitat,adreçant-seperescrital’Institutd’EstudisCatalans(carrerdel Carme,47,08001Barcelona),obéenviantuncorreuelectrònical’adreça dades.personals@iec.cat,enquès’especifiquidequinapublicacióestracta.

Comitèeditorial

AntoniGuillamon(editorencap)

DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya antoni.guillamon@upc.edu

CarmeCascante

Dep.deMatemàtiquesiInformàtica UniversitatdeBarcelona cascante@ub.edu

BartomeuColl

Dep.deMatemàtiquesiInformàtica UniversitatdelesIllesBalears tomeu.coll@uib.cat

NúriaFagella

Dep.deMatemàtiquesiInformàtica UniversitatdeBarcelona fagella@maia.ub.es

ArmengolGasull

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona gasull@mat.uab.cat

GáborLugosi

ICREAiDepartamentd’Economia UniversitatPompeuFabra gabor.lugosi@upf.edu

RosaCamps(editoraadjunta)

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona rcamps@mat.uab.cat

MarcNoy

DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya marc.noy@upc.edu

FrancescPlanas

DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya francesc.planas@upc.edu

JoanSaldaña

Dep.d’Informàtica,Mat.AplicadaiEstadística UniversitatdeGirona joan.saldana@udg.edu

MartaSanz-Solé

Dep.deMatemàtiquesiInformàtica UniversitatdeBarcelona marta.sanz@ub.edu

GilSolanes

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona solanes@mat.uab.cat

Durantelprocésd’elaboraciód’aquestnúmeros’haproduïtelcanvid’editor encapdel Butlletí.AgraïmaJuliàCufí,anticeditorencap,latascarealitzadaduranttotsaquestsanysi,enconcret,enlaprimeraetapadelaconfecció d’aquestnúmero.

SocietatCatalanadeMatemàtiques

La SocietatCatalanadeMatemàtiques(SCM) ésunasocietatfilialdel’Institutd’EstudisCatalans,quecontinualesactivitatsdelaSecciódeMatemàtiques delaSocietatCatalanadeCiències,quefoufundadaperl’Institutl’any1931. Lesfinalitatsdela SCM són:elconreudelesciènciesmatemàtiques,l’extensió delseuconeixementenlasocietatcatalana,elfomentdelseuensenyament idelasevainvestigacióteòricaiaplicada,aixícomlapublicaciódetotamena detreballsques’adeqüinaaquestsobjectius.La SCM desenvolupalesseves activitatsenlesterresdellenguaiculturacatalanes.Elcatalàés,doncs,la llenguapròpiadela SCM ilaqueésusadanormalmententotselsseusactesi publicacions.

La SCM editalespublicacionsperiòdiques SCM/Notícies i Butlletídela SocietatCatalanadeMatemàtiques.Elssocisdela SCM reben,gratuïtament, aquestesduespublicacions.

La SCM téconvenisdereciprocitatambdiversessocietatsmatemàtiques d’arreudelmón,mitjançantelsqualselssocisdela SCM obtenenunareduccióenlaquotadesocid’aquestessocietats.Aixímateix,elssocisdela SCM podenfer-sesocisdelaSocietatMatemàticaEuropeapagantunaquota complementària.

LaJuntaDirectivadela SCM estàconstituïdaperlespersonessegüents:

Presidenta:DolorsHerberaiEspinal

Vicepresident:JosepVivesiSanta-Eulàlia

Adjuntala vicepresidència:AbrahamdelaFuentePérez

Secretària:ImmaculadaBaldomáiBarraca

Tresorer:AlbertGranadosiCorsellas

Vocals:AlbertAvinyóiAndrés,NúriaFagellaiRabionet,Josep GranéiManlleu,CarlesRomeroiChesa,AleixRuizdeVilla,Manel UdinaiAbelló

Delegadadel’IEC:PilarBayeriIsant

L’adreçadela SCM éscarrerdelCarme,47,08001Barcelona.Telèfon: 933248583.Fax:932701180.Correuelectrònic: scm@iec.cat.Adreçaweb: http://scm.iec.cat.