BSCM, 29-1

BUTLLETÍ

DE LA SOCIETAT LA SOCIETAT CATALANA

DE DEDE DE MATEMÀTIQUES MATEMÀTIQUES

Institut d’Estudis Catalans Institut d’Estudis Catalans

Volum 29 ● Número 1 ● Juny 2014

©delsautorsdelsarticles

EditatperlaSocietatCatalanadeMatemàtiques filialdel’Institutd’EstudisCatalans CarrerdelCarme,47 08001Barcelona

Textrevisatlingüísticament perlaUnitatdeCorrecciódelServeiEditorialdel’IEC.

ImprèsaLimpergraf,SL PolígonindustrialCanSalvatella CarrerdeMogoda,29-31 08210BarberàdelVallès

ISSN:0214-316-X DipòsitLegal:B.19272-1987

Sónrigorosamentprohibides,sensel’autoritzacióescritadelstitularsdel copyright,lareproducciótotaloparciald’aquestaobraperqualsevolprocedimentisuport,incloent-hilareprografia ieltractamentinformàtic,ladistribuciód’exemplarsmitjançantllogueroprésteccomercial,la inclusiótotaloparcialenbasesdedadesilaconsultaatravésdexarxatelemàticaod’Internet. Lesinfraccionsd’aquestsdretsestansotmesesalessancionsestablertesperleslleis.

ButlletídelaSocietatCatalanadeMatemàtiques Vol.29,núm.1,2014

Índex

ÁlvaroCorraliFrancescFont-Clos Processosderamificació,criticitatiautoorganització: aplicacióalsdesastresnaturals......................................................5

MercèRomero-Gómez,PatriciaSánchez-MartíniJosepJ.Masdemont Comlesvarietatsinvariantsformenespiralsianellsengalàxiesbarrades.......51

CarlesSimó

Aplicacionsquadràtiquesquepreservenl’àreaa R2 ...............................77

Englishsummaries.....................................................................109

ButlletídelaSocietatCatalanadeMatemàtiques Vol.29,núm.1,2014.Pàg.5–49. DOI:10.2436/20.2002.01.52

Processosderamificació,criticitati autoorganització:aplicacióalsdesastresnaturals

ÁlvaroCorraliFrancescFont-Clos

Noméselsbeneits,elsxarlatansielsmentidersprediuenterratrèmols.

C.F.Richter

Resum: L’estadísticadelsdesastresnaturalscontémoltsresultatsantiintuïtius.Fent servirelsterratrèmolscomaexemple,mostraremquel’energiaradiadaperaquests esdevenimentssegueixunadistribuciódetipusPareto,ésadir,unalleidepotències. Aixòimplica,enteoria,queelvaloresperatdel’energiaésinfinit,ialapràctica,quela mitjanad’unconjuntfinitdedadesmainoésrepresentativadeltotaldelapoblació.A mésamés,aquestadistribuciópresentainvariànciad’escalai,pertant,ésimpossible definirunaescalacaracterísticaperal’energia.Unmodelsimplecapaçdereproduir aquestapeculiarestadísticasónelsanomenatsprocessosderamificació;perexemple, ellliscamentodesplaçamentd’unsegmentdefallapotconduiraldesplaçament d’altressegments,ambcertaprobabilitat.Totiqueinicialmentelssismòlegsnon’eren conscients,aquestmodelésuncasparticulardelprocésestocàsticestudiatperGaltoni Watsonunsegleenrere,enaquellcasperamodelarl’extinciódelesfamílies(benestants). Obtindremlespropietatsprincipalsd’aquestsmodelsmitjançantelformalismede lesfuncionsgeneratriusdemoments.Sorprenentment,ladistribuciódepotènciaper al’energiapotrecuperar-setansolsenuncasmoltparticular:quanelprocésde ramificacióestrobajustentrel’atenuacióilaintensificació,ésadir,enlacriticitat.Per adonarsentitaaquestfet,introduiremelsmodelsdecriticitatautoorganitzada,enels qualsmitjançantunmecanismederetroalimentaciól’estatcríticesdevéunatractoren l’evoluciódelsistema.Alllargdeltextesmostrenalgunesanalogiesambconceptes bàsicsdefísicaestadística.Lamajorpartdelmaterialésautocontingut,excepteelque téaveureambconeixementselementalsdeteoriadeprobabilitat.

Paraulesclau: processosderamificació,modeldeGalton–Watson,criticitat,autoorganització,lleisdepotències,lleideGutenberg–Richter.

ClassificacióMSC2010: 60J80,60J85.

Aquestarticleésunatraduccióabreujadade[7],ques’hapublicatcomacapítold’unllibre dedicatíntegramentalacriticitatautoorganitzada.

1L’estadísticadelsdesastresnaturals

Desdelsinicisdelstemps,lahumanitathaviscutsotal’amenaçadelsdesastres naturals:inundacions,erupcionsvolcàniques,tsunamis,terratrèmols,huracans, etc.Estracta,d’algunamanera,d’unaespasadeDàmoclesdelaqual,enple segle xxi,lesnostressocietatsencaranohanpogutdesfer-se.Arabé,aquests fenòmenstotalmentcapritxosossónobradelafúriadelsdéus,oamaguen potsercertesregularitats?Laprimeravisióhadominatelpensamenthumà durantmoltssegles,ifinsfapocnos’hacomençataconsolidarunaperspectiva mésracional.

1.1LalleideGutenberg–Richter

Unadelesprimereslleisperquantificarl’ocurrènciad’undesastrenaturalva serproposadapelsfamosossismòlegsBenoGutenbergiCharlesF.Richter,cap al’any1940,totaprofitanteldesenvolupamentrecentdelaprimeraescala demagnitudsperpartdelmateixRichter.LalleideGutenberg–Richteréssorprenentmentsimple:sicomptemelnombredeterratrèmolsaqualsevolregió sísmicamentactivadelmóndurantunperíodedetempssuficientmentllarg, trobaremquepercada100terratrèmolsdemagnitud M ≥ 4hiha,aproximadament(demitjana),10terratrèmolsamb M ≥ 5,1terratrèmolamb M ≥ 6,i aixísuccessivament[11, 17].Pertant,lagranmajoriad’esdevenimentssónels méspetitsi,persort,nomésunamínimapartpodenserdevastadors;esmanté sempreunaproporcióconstantentreelseunombre.

Totiquenoéspossiblemesurartotselsterratrèmolsdelplaneta,enalgunes àreesonl’activitatsísmicaesmonitoritzaambmoltaprecisiós’havalidatlallei deGutenberg–Richterfinsalamagnitud 4;aixòcorresponapetitesesquerdes otrencamentsenroquesdepocscentímetres(lesmagnitudsnegativess’han introduïtperapodertreballarambterratrèmolsméspetitsqueelsdemagnitud0).I,persinofosprou,enexperimentsdenanofracturesallaboratori,la lleis’havalidatfinsamagnitudsinferiorsa 13.Peraltrabanda,l’escassetatde gransesdeveniments(escassetatquelapròpialleiprediu),impedeixdeterminar quinaéslafitasuperiordevalidesad’aquestallei.

TotiqueGutenbergiRichternohomencionenenelseuarticle[11],un estudiantdeprobabilitatiestadísticas’adonaràimmediatamentquelalleide Gutenberg–Richterimplicaunadistribucióexponencialperalamagnituddels terratrèmols,ésadir,

DM (M) ∝ 10 bM ,

on DM (M) éslafunciódedensitatde M, b ésunparàmetrepropera1i elsímbol ∝ indicaproporcionalitat;laconstantdeproporcionalitatespot determinaramblacondiciódenormalitzacióde DM (M). Nomésdonaremunparelldepistessobrecomespotdeduirlarelacióanterior:partintdelnombredeterratrèmolssuperiorsaunacertamagnitudes potestimarlafunciódedistribucióacumuladacomplementària,definidacom laprobabilitatdetenirmagnitudmésgranoigualqueuncertvalor M.Com

Processosderamificació,criticitatiautoorganització

BenoGutenberg CharlesRichter ElssismòlegsBenoGutenbergiCharlesF.Richter (fotosextretesde seismo.berkely.edu). queaquestamagnitudresultaserexponencial,proporcionala10 bM ,laseva derivadatambéhoserà,iaquestaés,excepteunsigne,lafunciódedensitat.En equacions,

DM (M) =− d dM P(magnitud ≥ M) ∝ d10 bM dM ∝ 10 bM

PeròquinéselsignificatdelalleideGutenberg–Richter,amésdeproporcionarunareglafàcilderecordarperalesabundànciesrelativesdelsterratrèmols? Lainterpretaciódepèn,òbviament,delsentitdelterme magnitud,quefinsara hemevitatdefinir.Defet,lamagnitudnoésunavariablefísicaadequada—al capialafi,notéunitats.Peraaprofundirunamicamés,éspreferiblefixar-se enl’energia E radiadaperunterratrèmol,queésunafuncióexponencialdela sevamagnitud[17],ésadir,

E ∝ 103M/2 , demaneraqueunaugmentd’1enlamagnitudsuposaunaugmentenenergiad’unfactor √1000 32.Aixòsignificaqueunterratrèmoldemagnitud9 radiatantaenergiacom1000terratrèmolsdemagnitud7,o106 demagnitud5. ArapodemreformularlalleideGutenberg–Richterentermesdel’energia. Defet,laprobabilitatd’unesdevenimentés«independent»delavariableque s’usiperadescriure’l,ipertant,perunsenzillcanvidevariables,

DE (E) = DM (M) dM dE ,

on DE (E) éslafunciódedensitatdel’energia.Aquestcanvidevariablesimplica que

E (E) ∝ 1 Eα , on α = 1 + 2b 3 , iaquestaéslafamosadistribuciódepotències,odistribuciódePareto[22], ambexponent α alvoltantd’1 67quan b éspropera1.Observeuqueperquè DE (E) siguirealmentunafunciódedensitatcalqueestiguidefinidanomésper sobred’unvalormínimd’energia Emin > 0jaqueencascontrari(si Emin = 0) nopotnormalitzar-se.Alapràctica,aquestvalornoespotmesurar(ésmassa petit),peròaixònoésunproblema,jaquerealmentnohihacappropietatdels terratrèmolsqueendepengui.

Lafigura1mostralafunciódedensitatdelmomentsísmicperaterratrèmols d’arreudelmón[16];aquestavariableesconsideraproporcionalal’energia (peròésmoltmésfàcildemesurar),ipertanttambéhauriadeteniruna distribuciódepotènciaambelmateixexponent.Lalíniarectaés,òbviament,el tretquecaracteritzaleslleisdepotènciesenescalalogarítmicadoble,jaque log DE (E) = C α log E.

Figura1: Estimaciódelafunciódedensitatdelmomentsísmicpera terratrèmolssuperficialsd’arreudelmón,utilitzantelcatàlegconegut perCMT[16].L’ajustamentd’unalleidepotènciesdónaunexponent α = 1.68.L’energiaradiadahauriadetenirelmateixcomportamentdellei depotències.Lesdesviacionsperavalorspetitsdelmomentsísmic s’atribueixenalanocompletesadelcatàleg.

1.2Propietatsdelesdistribucionstipuslleisdepotències

Algunespropietatsd’aquestesdistribucionsmereixenatencióespecial.D’entrada,podemcalcular-nelamitjana,ésadir,elvaloresperatde E,quevedonat per

Observeuquedenotemelvaloresperatper E ,talcomfanelsfísicsino per E[E],comfarienelsprobabilistes.Laraóésqueestemmésinteressatsen lesaplicacions,onlaprimeraopcióéslaméshabitual.Esfàcilcomprovarque, enelcasdel’energiadelsterratrèmols,aquestaintegraldivergeixi,pertant, enrigor,elvaloresperatdel’energiaésinfinit.Aquestadivergènciaésdeguda alfetquel’exponentdelalleidepotènciesésméspetitque2.Òbviament l’energiaque,demitjana,radiaunterratrèmolnopotserinfinita(alcapiala fi,laTerracontéunaquantitatfinitad’energia),pertanthideuhaveralgun problemaenextrapolarlalleidepotènciesfinsal’infinit.Sitinguéssimuna distribuciónormal,ounaexponencial,podríemextrapolar-lafinsal’infinitsense cappor,perquèlaintegralnodivergiria.Peròcalremarcarqueestemdavant d’unproblemafísic,nomatemàtic—silanostravariablefos,perexemple,el tempsd’esperaentreesdeveniments,eltempsmitjàpodriaperfectamentser infinit.

Pertant,perraonsfísiques,had’existirunafitasuperiorperalavalidesa delalleideGutenberg–Richter;perònotenimniideadelvalord’aquestafita. Alapràctica,elfetqueelvaloresperatdel’energiadivergeixiimplicaqueles mitjanesdel’energiaqueespodencalcularusantconjuntsfinitsdedadesno convergeixen,siguiquinsiguielnombrededades.Enresum,elssismòlegs ignorencompletamentquinaésl’energiamitjanaradiadapelsterratrèmols,a causadelespropietatsinusualsdeleslleisdepotències.

Totiqueencomençaraquestarticleheminterpretatpositivamentelfet quelamajorpartdeterratrèmolssónpetits,inomésunsquantssóndevastadors, lasituaciócertamentnoéstanfavorable.Elproblemaésqueelsesdeveniments rarsigrans,totisermoltpocs,sónelsresponsablesdeladissipaciód’energia enelsistema.Peralvalorparticularde α quetractem,ésfacilverificarque l’ordredemagnitudmésgranqueesconsideri(ladècadamésgran)contribueix mésaltotalquetoteslesquetépersotajuntes.Matemàticament, c Emin

EDE (E) dE< 10c c EDE (E) dE, siguiquinsiguielvalorde c.Podeutrobarlademostracióal’apèndix.

Unaaltrapropietatcuriosadeleslleisdepotèncieséslainvariànciad’escala. Peraintroduirelconceptedetransformaciód’escalaconsideremprimeruna funcióqualsevolqueanomenarem D(E).Laidead’unatransformaciód’escala ésmirarlafunció D(E) aunaaltraescala,comsitinguéssimunmicroscopi matemàtic.Podríemtenirunavisióde D(E) al’escalademetres(si E i D(E) fossindistàncies)itractard’esbrinarquinaspectetéal’escaladecentímetres.

Perafer-ho,utilitzemunatransformaciód’escala,quedenotemambl’operador T actuantsobre D(E), T D(E) = c2D(E/c1),

on c1 i c2 sónelsanomenatsparàmetresd’escala,responsablesdelestransformacionslinealsen E i D.Enelcasdemetres-centímetres,perexemple,tindríem c1 = c2 = 100.

Engeneral,gairebétoteslesfuncionscanviensotaunatransformaciód’escala;sivolemtrobarl’excepció,hemdedeterminarlafuncióofuncionsque compleixenlacondiciósegüent: D(E) = c2D(E/c1).

Éstrivialcomprovarquelasolucióéslalleidepotències

amb α donatper

Ésadir,unalleidepotènciesambexponent α nocanviasotaunatransformació d’escalasielsfactorsd’escalamantenenlarelació

Lafigura2il.lustraaquestasituació,amb c1 = 10, c2 =√10,i D(E) =√E.Cal destacarquelaconstantdeproporcionalitat,quedefetestàcontigudaenel símbol ∝,notécappaperenaquestesrelacions.

Figura2: Unatransformaciód’escalaactuantsobrelasevacorresponent funcióambinvariànciad’escala.Lafunciós’expandeixenelsfactors c1 = 10i c2 = √10,detalmaneraqueelpetitrectangledelapartesquerrade lafiguraesdevélapartdretasencera.Lafuncióenquestióés D(E) = √E

Processosderamificació,criticitatiautoorganització 11

Encaramés,nosolamentespotdemostrarquelalleidepotènciesésuna solució,sinóqueésl’únicasolucióvàlidaperatotselsvalorsde c1 (reals positius)si c1 i c2 mantenenlarelacióanterior[22, 6].Enresum,lacondició d’invariànciad’escalaimposaque

D(E) = c2D(E/c1) peratotsels c1 realspositius i,aleshores,l’únicasoluciópossibleésunalleidepotències.Espotverificar quealtressolucions,comperexemple D(E) = sin(ln E),nomésfuncionenper aunsvalorsdeterminatsde c1 i c2.

Lainvariànciad’escalaés,defet,lasimetriaassociadaalestransformacions d’escala,aixícomlainvariànciarotacionaléslasimetriacorresponentalesrotacions.Siteniminvariànciad’escalanopodemdefinirunaescalacaracterística peralavariable E,demaneraanàlogaalfetque,siteniminvariànciarotacional enunsistema,noelpodemferservirperasenyalardireccions.Elsistemeson no hihainvariànciad’escalapermetendefinirescalescaracterístiques,comper exemplelesfuncionsexponencialsquedefineixenladesintegracióradioactiva, quepermetendefinirlaunitatdetempsentermesdelasemivida.

Detotamanera,calremarcarunpuntimportant:si D(E) representauna densitatdeprobabilitat,comenelcasdel’energiaradiadapelsterratrèmols, aleshores D(E) nopotserunalleidepotènciesperatot E ≥ 0,perquèaleshores nopodrianormalitzar-se(laintegralde0a ∞ divergiria).Comjahemdit,cal introduirunafitainferiordevalidesa Emin perevitaraquestasituació.Amés, tambéhemvistquelalleinopotestendre’sfinsal’infinitperraonsfísiques. Pertant,lainvariànciad’escalaabsolutanoéspossibleentrelesdistribucions deprobabilitat;nomésespotaspiraraunainvariànciad’escalarestringida.Ara bé,comqueenelcasdelsterratrèmolscapdelesfites,lasuperiorilainferior, noespotobtenirapartird’observacions,lainvariànciad’escalasíqueexerceix unpaperreal.

Lainvariànciad’escalaenl’energiadelsterratrèmolstéconseqüènciesantiintuïtives.Imaginem,perexemple,quearribemaunpaís,iestempreocupatspels terratrèmols.Aleshoresdecidimacostar-nosaalgúifer-lilapreguntasegüent: comsóndegranselsterratrèmols,aquí? Totiquepotsemblarunapregunta moltinnocent,acausadelainvariànciad’escalanoespotdefinirunaescala característicaperal’energiai,pertant,lapreguntanopottenirresposta.

Peracabaraquestasubseccióvolemremarcarqueladistribucióenlleide potènciesnoésunacaracterísticasolamentdelsterratrèmols:s’haafirmatque moltsaltresdesastresnaturalsestandistribuïtssegonsunalleidepotències,toti quel’exponentpotvariar:tsunamis[5],esllavissamentsicaigudesderoques[19], erupcionsvolcàniques[21],huracans[8],pluja[27],aurores[9],incendisforestals[20],flamaradessolars[3],cràtersdemeteorits(alaLluna)[3]…

Talcomellectorjas’imagina,partdelqueexplicaremacontinuaciópensant enelsterratrèmolstambéespotaplicaraalgunsd’aquestsfenòmens,però potsernoatots.Defet,ésunproblemaobertdistingirentreaquestscasos. Peraunreculldelleisdepotènciaenaltresàmbits,amésdelageociència, recomanem[22].

1.3Unprimermodeldegeneraciódeterratrèmols

Elprimerintentqueconeixemdedesenvoluparunmodelperalsterratrèmols queexpliquilalleideGutenberg–RichtervaserobradeMichioOtsukaals inicisdeladècadade1970[ ].Otsukautilitzavacomametàforaeljoc xinèsdelgo,perònosaltrespresentaremelmodelfentreferènciaaldòmino, queseràmésfamiliarperalslectors(iperalsautors!).Enllocdejugaral dòminodeveritat,enfaremservirlespecesperjugaraunaltrejoc.Estracta deveuresilespeces,posadesdretes,fancaurelesunesalesaltres,comen elsfamososconcursosiintentsdesuperarelrècordGuiness,peròambdues diferènciessubstancials.Primer,lespecesnoesdisposenenfila,sinóque formenunaespècied’arbre.Segon,quanunapeçacau,nosabemquèpassaràa continuació,sifaràcaurealgunaaltrapeçaono,niquantes.Ésadir,quetenim unprocésestocàsticencascadaque,enprincipi,imitalesrupturesquetenen llocalesfallessísmiquesdurantunterratrèmol.L’arbredepecesdedòminofa elpaperdefalla,icadapeçacorresponaunpetitfragmentdefalla,oelement. Elterratrèmol,alseutorn,corresponalasuccessiódepecesquecauen(ésa dir,fragmentsqueestrenquenillisquen).

Figura3: Representacióesquemàticadelmodeld’Otsukaperaruptures enterratrèmols.Elscerclesblancsrepresentenlapropagaciódelaruptura, ielsnegresindiquenpuntsterminals[24].

Concretament,Otsukavasuposarquel’arbrequerepresentavalafallateniaunnombrefixdebranquesacadaposicióonode,iquelescaigudeses propagavend’unabrancaal’elementsegüentambunaprobabilitatfixa,independentmentdequalsevolaltravariable.Perexemple,enlafigura3elnombre debranquesperelementés2.Així,elnombretotaldepostcaigudesoramificacionsoriginadesperunsolelementseguiriaunadistribucióbinomial[29].Si associemunacertaquantitatfixaelementald’energiaallliscamentdecadaelement,podemobtenirl’energiaalliberadaenaquestprocésapartirdelnombre totald’elementsquellisquen,iaixòpermetriacompararladistribuciód’energia almodelamblalleideGutenberg–Richter.

Pertant,lapropagacióderupturesesconsideraunfenomenprobabilístic, enelsentitquequancomençaunterratrèmolnoéspossiblesabercomarribarà aserdegran.Desprésveuremqueaquestaafirmacióésmoltmésfortadel quearaenssembla.Eltípic efectedòmino,onunacaigudasempreindueixla següent,correspondriaalpolèmicconceptedeterratrèmolcaracterístic,un esdevenimentqueespropagasemprealllargdetotalafallaosistemadefalles ique,pertant,semprealliberarialamateixaquantitatd’energia.Així,hade quedarclarquel’efectedòminonoescorrespondriaambelnostremodel.

Processosderamificació,criticitatiautoorganització 13

Ésmoltsignificatiuqueelmodelqueacabemd’explicar,novedósioriginal engeofísica,introduïtperOtsukaalsanyssetanta,jaeraconegutperalguns matemàticsmésdecentanysabans.Esmerçaremlesproperespàginesaexplicar ladistribuciód’energiadelmodel.

2ElprocésdeGalton–Watson

Apartdelesapostes,moltsprobabilistes tambés’haninteressatenlareproducció.

G.GrimmettiD.Stirzaker

Enstrasllademaraal’Anglaterravictorianadelsegle xix.Allà,SirFrancis Galton,polímata,paredelsconceptesestadísticsdecorrelacióiregressióicosí deCharlesDarwin,s’ocupavad’afersmoltdiversos.Amésd’estudiarl’estatura delsfillsenrelacióambladelspares,tambéestavapreocupatpeldeclivi,ifins itotl’extinció,delesfamíliesprominentsdel’època,ipersiaquestdeclivi eraconseqüènciad’unadisminuciódelafertilitatprovocadaperl’augmentdel confort.Siaixòfosaixí,aleshoreslapoblacióesmantindriaperlacontribució delesclassespopulars[34].Peraentendremillorelproblema,vacrearun modelmínimonelnombredefillsvaronsdecadahomeeraaleatori(enaquella època,l’abundànciadedonesnoesconsideravaunproblema).Totil’aparent simplicitatdelmodel,Galtonnovapoderresoldre’l,ivadecidirferunacrida públicad’ajuda(uncasprecursor,segonscom,delqueactualmentesconeix comaintel.ligènciadistribuïda).Lacridanovafructificar,iGaltonesvaadreçar almatemàticireverendHenryWilliamWatson.

SirFrancisGalton Rev.HenryWilliamWatson

ElsparesdelprocésdeGalton–Watson(fotosextretesdelaWikipedia ide www.wolframalpha.com,respectivament).

2.1DefiniciódelprocésdeGalton–Watson

Consideremuns«elements»quepodengenerarunsaltreselements,iaixí successivament.Aquestselementspodenrepresentarhomesdel’aristocràcia britànicaquetenendescendentsmasculins—o,enunareinterpretaciómés actual,donesd’arreuquedonenallumlessevesfilles;opotsermésapropiadamentbactèriesqueesrepliquen—,neutronsqueemetend’altresneutrons enunareacciónuclearencadenaofragmentsdefallesquellisquendurantun terratrèmol.ElprocésdeGalton–Watsonpressuposaquecadascund’aquests elementsdónallocaunnombrealeatori K d’elementsnous,descendentsde l’anterior,detalmaneraquecada K ésindependentdeladelsaltreselements,i totesles K’sestanidènticamentdistribuïdes,ambprobabilitats P(K = 0) = p0, P(K = 1) = p1 ].(Naturalment, lacondiciódenormalitzacióimposaque

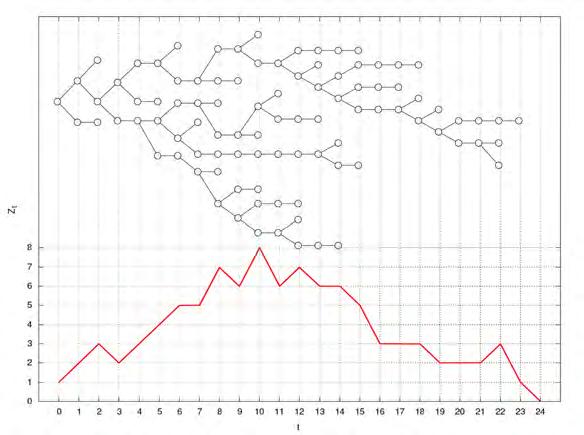
Figura4: UnarealitzaciódelprocésdeGalton–Watson.Adaltesmostra l’arbreassociatalprocés,començantperl’esquerra(Z0 = 1).Asota, l’evoluciódelnombred’elementsnascutsacadageneració t.Elmodel ésbinomialpera P(K = k),amb n = 2i p = 1/2,cosaquecorresponal cascrític.

Elmodelparteixinicialmentd’unúnicelement,ques’anomenalageneració0 delprocés,talcommostralafigura4.Els K descendentsd’aquestprimerelement constitueixenlaprimerageneració.Sigui Z0 = 1elnombred’elementsdela generació0, Z1 elnombred’elementsdelageneració1,etc.Òbviament,per construcció P(Z1 = k) = pk.Elnombred’elementsdelageneració t + 1s’obté

apartirdel’anteriormitjançant

amb t ≥ 0,on Ki corresponalnombrededescendentsdecadaelementdela generació t.Aquestaequaciósenzillapotusar-sedirectamentpersimularel procés,iseràmoltimportanttambéeneltractamentanalíticdelmodel(per exemple,quancalculemladistribuciódeprobabilitatde Zt peraun t qualsevol). Algunslectorsprobablements’hanadonatquelesvariables Z0,Z1,... formen unacadenadeMarkov,peròaixònotindràcaprellevànciaperalqueens interessa.

2.2Funcionsgeneratrius

Unaeinamatemàticaextremamentútilseràlafunciógeneratriudeprobabilitats[10].Aquestaesdefineix,peralavariablealeatòria K,com fK (x) ≡ ∞ k=0 pk

onelsclaudàtorsangularsindiquenvaloresperat.Lacondiciódenormalització ensgaranteixque fK (x) sempreestàdefinida,comamínim,al’interval [ 1, 1], totiqueanosaltresnomésensinteressaràl’interval [0, 1]. Òbviament,lamateixadefiniciós’aplicaaqualsevolaltravariablealeatòria queprenguivalorsentersnonegatius;enelcasparticularde K (querepresenta elnombrededescendentsd’unelement)podemometreelsubíndex,ésadir, escriure fK (x) = f(x).Algunespropietatssimplesiútilssónlessegüents:

1. fK (0) = P(K = 0);

2. fK (1) = 1(normalització);

3. fK (1) = k pkk = K ≡ m;

4. fK (x) ≥ 0per x ≥ 0(funciónodecreixent);

5. fK (x) ≥ 0pera x ≥ 0(funciónoconvexamirant-la«desdedalt»); onlesprimesdenotenderivades(derivadesperl’esquerraa x = 1),ionla propietat3òbviamentnoméstésentitquanelprimermomentnodivergeix. Calrecordarque,totiqueestemil.lustrantaquestespropietatsperalavariable aleatòria K,sónvàlidesperaqualsevolfunciógeneratriu.Pertant,lagràfica d’unafunciógeneratriuentre0i1estàforçacondicionada.Japodemanticipar queenstrobaremdosgranscasos,segonssielvaloresperatde K és m< 1 o m> 1.Aixòésmoltnatural,jaqueelprimercascorresponaunapoblació que,demitjana,disminueixd’unageneracióalasegüent,iencanvienelsegon caslapoblació,demitjana,creix.

Unaaltrapropietat,potsernotandirecta,ésquelafunciógeneratriudela sumade N variablesindependentsiidènticamentdistribuïdes, Ki (amb N fixat),

éslapotènciaenèsimadelafunciógeneratriude K.Ésadir,quesi Σ = N i=1 Ki,

aleshores fΣ(x) = fK (x)N .

Defet,

onelsvalorsesperatsfactoritzenacausadelaindependènciaestadísticaentre lesdiferents Ki.

Engeneral,silesvariablesaleatòriesnofossinidènticamentdistribuïdes (peròsíindependents),lafunciógeneratriudelasevasumaseriaelproductede lescorresponentsfuncionsgeneratrius.Lademostració,defet,ésessencialment lamateixa:noméscalmodificarlanotacióperdiferenciarlesdiversesfuncions generatrius.

Elpassegüentconsisteixaconsiderarque N tambéésunavariablealeatòria, independentde K,ambfunciógeneratriu fN (x).Aleshores,

fΣ(x) = fN fK (x)

Observeuqueaquestafórmulanoésmésqueunageneralitzaciódel’anterior, ésadir,aracalculemelvaloresperatdepotènciesde fK (x) quedepenendels valorsque N potprendre.Enqualsevolcas,ésfàcildedemostrar:sidenotem elvaloresperatrespecteles Ki per · Ki ,ielvaloresperatrespecte N per · N , tenimque

fΣ(x) = xΣ = xΣ Ki N = fK (x)N N = fN fK (x) ,

onladarreraigualtatéssimplementladefiniciódelafunciógeneratriude probabilitatdelavariablealeatòria N,avaluadaalpunt fK (x).Remarquem, però,queaquestargumentnecessitalacondiciód’independència.

2.3Distribuciódelnombred’elementspergeneració

SiararecuperemelprocésdeGalton–Watson,ésadir,femservirque Zt+1 = Zt i=1 Ki,podemidentificar Zt+1 amb Σ i Zt amb N.Pertant, fZt+1 (x) = fZt fK (x) = fZt f(x) ,

obviantelsubíndex K.Comque fZ1 (x) = f(x),espotveureperinduccióque lafunciógeneratriude Zt vedonadaper

fZt (x) = f f ...f(x) = f t (x),

Processosderamificació,criticitatiautoorganització 17

onelsuperíndex t denotacomposició t vegades.Aixòésvàlidpera t = 1, 2,... ; pera t = 0tenim,òbviament,que fZ0 (x) = x (jaque Z0 = 1ambprobabilitat1). Enresum,lafunciógeneratriudelnombred’elementsdecadageneraciós’obté mitjançantcomposicionssuccesivesdelafunció f(x).Aquestresultatno elementalelvaprovarperprimercopWatsonl’any1874[12].

2.4Elnombreesperatd’elementspergeneració

Arapresentemunresultatcertamentil.luminador,queensfaràserveimés endavant.Totique,generalment,lescomposicionssuccesivesdelafunció generatriuportenaexpressionsmatemàtiquesmoltcomplicades,elsmoments de Zt espodencomputard’unaaltramanera,moltméssenzilla[12].Fentservir lapropietat3delapàgina15ilacomposiciódefuncionsgeneratrius,tenim queelvaloresperatde Zt és

t = d dx f t (x) x=1

Siescrivim

aleshores,perinducció d dx f t (x) =

Prenent x = 1,iobservantqueenaquestpunttoteslesfuncionsgeneratrius valen1,arribema

Zt = f (1)t = mt .

Pertant,quan m< 1elnombreesperatd’elementspergeneraciódecreix exponencialment,iencanviquan m> 1aquestnombrecreix.Aixòconstitueix, defet,unarealitzacióestocàsticadelcreixementmalthusià.Ésperaixòque,de vegades, m s’anomenalaraóderamificació.Quan m = 1lamidamitjanadela poblacióésconstant,peròdesprésveuremqueaixònoimplicaquelapoblació assoleixiunestatestable.Elsmomentsd’ordresuperiorespodencalcularde manerasimilar,perònosóntanútilscomlamitjana.

Tambéésinteressantestudiarelvaloresperatdelnombred’elementsd’una generaciócondicionatalvalordelageneracióanterior,ésadir, Zt+1 | Zt = zt Comquequan Zt ésfix, Zt+1 = zt i=1 Ki,prenentelvaloresperattenimque

Zt+1 | Zt = zt = zt m.

Aquestresultatpotusar-seperrelacionarelsprocessosderamificacióambles martingales[10],peròaixòaranoenshadepreocupar.

2.5Laprobabilitatd’extinció

ElprocésdeGalton–Watsonesconsideraextingitquan Zt = 0perprimera vegada(ésadir,peralageneracióquedónalloca Zt = 0perprimercop).

Aleshores,totesles Z’sposteriorssónòbviamenttambézero,ienaquestsentit l’extincióespotconsiderarun«estatabsorbent»delsistema.Araveuremque, peralprocésdeGalton–Watson,laprobabilitatd’extincióés1(extinciósegura)pera m ≤ 1,iencanviésméspetitaque1quan m> 1.Aixòhova demostrarperprimercopJ.F.Steffensencapal1930[12].Defet,l’extinció espotdonaralaprimerageneració, Z1 = 0,oalasegona, Z2 = 0,etc.Com {Zt = 0} incloutotselsesdeveniments {Zi = 0} pera i = 1,...,t,aleshores P(Z1 = 0,...,Zt = 0) = P(Zt = 0).Pertant,laprobabilitatd’extinció Pext ve donadaper

Pext = lim t→∞ P(Z1 = 0o Z2 = 0o ... o Zt = 0) = lim t→∞ P(Zt = 0) = lim t→∞ f t (0), ésadir,perlaiteracióinfinitadelpunt x = 0atravésdelafunciógeneratriu f(x) (aquí,defet,femservirquelaprobabilitatdelvalor0éselvalorde lafunciógeneratriualpunt0,iquelafunciógeneratriude Zt vedonadaperla t-èsimacomposicióde f(x)).

Figura5: Funciógeneratriudeprobabilitats f(x) delnombrededescendentsperelementiiteraciódelpunt x = 0mitjançantlessuccessives composicionsde f(x).Elspuntsfixoscorresponenalspuntsdetallamb ladiagonal;elsméspropersazerosóntambéatractors.Al’esquerra,cas subcrític.Aladreta,cassupercrític.Elmodelésbinomial,amb n = 2.

Calculemaralaiteració f t (0).Al’interval [0, 1] lafunció f(x) ésnodecreixentinoconvexa(miradadesdedalt)inomésprenvalorsentre p0 i1.Siel pendentde f(x) a x = 1,quevedonatper m = K = f (1),ésméspetito igualque1,aleshores f(x) noméspottallar(otocar)ladiagonala x = 1(sino, f(x) hauriadeserconvexaenalgunpunt),ilaiteraciódelpunt x = 0acabaal

Processosderamificació,criticitatiautoorganització 19

punt x = 1(queésl’atractor;vegeulafigura5).Enconseqüència,

Pext = lim t→∞ f t (0) = 1,

ésadir,l’extincióésinevitablesi m ≤ 1.Detotamanera,hihaunaexcepció trivial,quecorresponalcaspatològic p1 = 1(i0peralaresta);estractad’una situaciómoltensopida,ontotelementtésempreunúnicdescendent(pot correspondre,perexemple,alasuccessiódereisoreinesenunamonarquia, sinotenimencomptelesrevolucions).Enaquestcas, f(x) = x,ipertant lim f t (0) = 0,cosaqueimplica,òbviament,quelaprobabilitatd’extincióés zero.

Sielpendentde f(x) a x = 1és m> 1(cosaquenoméspotpassarperauna funciógeneratriudeprobabilitatsnolineal,ésadir, p0 +p1 < 1),aleshores f(x) hadetallarladiagonalenalgunpunt x∗ méspetitque1,queseràl’atractoral quallaiteraciótendeix(vegeunovamentlafigura5).Matemàticament,

Lademostracióesdesenvolupaambmésdetallal’apèndix.Enresum,

amb x∗ < 1,excepteenelcastrivial p1 = 1,on m = 1però Pext = 0.

Aixòmostraclaramentcom,engeneral,elpunt m = 1separadoscomportamentsdiferents:extincióasseguradapera m ≤ 1,ilapossibilitatde supervivència(extinciónoassegurada)pera m> 1.Pertant, m = 1correspon alcascríticqueseparaaquestsdoscomportaments,anomenatsconseqüentmentsubcrític(m< 1)isupercrític(m> 1).

2.6Laprobabilitatd’extincióperalcasbinomial

Peraposarunexempleil lustratiu,consideraremuncasconcretisenzill:una distribucióbinomial[10,29], pk = P(K = k) = n k pk(1 p)n k , pera k = 0,...,n.

Aixòcorresponasuposarquecadaelementdisposanomésd’uncertnombre n d’intentsdegenerardescendència,iquecadascund’aquestsintentstéuna probabilitatfixa p deserexitós.Resultaque,fentservirelteoremabinomial,la funciógeneratriudeprobabilitatprenlaformasegüent: f(x) = n k=0 n k (1 p)n kpkxk = (1 p + px)n

Consideremcomaexempleelcasméssimple, n = 2,idefinim q = 1 p.Com jahemvist,laprobabilitatd’extincióvindràdonadaperlasolucióméspetita a [0, 1] de

Pertant,

peròl’arrelquadradaespotescriure 1

2 = (1 2p), ialeshores,

=

Pertant,l’arrelméspetitadepèndesi p estàpersobreopersotade1/2:

Comque(peraladistribucióbinomialamb n = 2)elvaloresperatés m = 2p, elcascrític m = 1corresponòbviamenta p = 1/2,cosaqueencaixaambel comportamentde Pext.

2.7Inestabilitatdelapoblació

Totiqueaquestasubsecciócontéunresultatmoltinteressantquepotajudara entendreelcomportamentd’unprocésdeGalton–Watson,espotsaltar,jaque noésnecessàriaperallegirlarestadel’article.

Laiteraciódelpunt x = 0,defet,ésil.lustrativadelquelipassaatota lafunciógeneratriude Zt quan t →∞.Defet,delamateixamaneraqueala subsecció2.5,podríemcomprovarque

f t (x) = 1si m ≤ 1, peròencanvi lim t→∞ fZt (x) = lim t→∞ f t (x) = x∗ < 1si m> 1, exceptepera x = 1(vegeulafigura6).

Recordemqueunafunciógeneratriuplanacorresponaprobabilitatsiguals azero,excepteperalvalorzero,ésadir,

lim t→∞ P(Zt = k) = 0, exceptepera k = 0.

Així,pera m ≤ 1,tenimque limt→∞ P(Zt = 0) = 1,ilapoblaciós’extingeix, peròpera m> 1hemvistque limt→∞ P(Zt = 0) = x∗ < 1;icomquequalsevol

Processosderamificació,criticitatiautoorganització 21

Figura6: Composicionssuccesivesdelafunció f(x),peratot x,que donenllocalafunciógeneratriudeprobabilitatsde Zt ,començantper t = 1(líniamésclara)finsa t = 15(líniamésfosca).Quan t creixs’obtenen funcionsmésplanes,cadacopmésapropdelpuntfix.D’esquerraadreta, casossubcrític,críticisupercrític,peraunmodelbinomialamb n = 2.

altrevalorfinitde K téprobabilitatzero,aixòimplicaque Zt →∞ quan t →∞, ésadir,que Zt nopotmantenir-sepositivaifitada:l’únicestatestableés l’extinció.Òbviament,elprocésdeGalton–Watsonenaquestlímitnoésrealista, enelsentitquealtresfactorsexternspodrienevitarquelapoblaciócreixés indefinidament.Peròaixònoenshadepreocupar,semprequetinguemclares leslimitacionsdelmodel.

2.8Transiciódefasedeno-equilibri

Passemaraaanalitzarmésdetalladamentquèsucceeixalvoltantdel«punt detransició» (m = 1).Talcomacabemdeveure,laprobabilitatd’extincióve donadaperlasolucióde Pext = f(Pext).Quan m ≤ 1,l’únicasolucióa [0, 1] és Pext = 1(excepteperalcastrivial p1 = 1).Quan m> 1,hemdeprendrela solucióméspetitade Pext = f(Pext) a [0, 1].Reescrivint-hototentermesde laprobabilitatdeno-extinció, ρ = 1 Pext,hemdetrobarelvalorde ρ mésgran quesiguisolucióde

al’interval [0, 1].Enscentremenelcason Pext éspropera1,ipertant ρ és properazero,i,usantelteoremabinomial,trobeml’expansió (1 ρ)k = 1 kρ + k(k 1)ρ2/2 +··· ,laqualenscondueixa

onhemintroduïtlamitjana m ielsegonmomentfactorial µ = K(K 1) ,que suposemqueexisteixenisónfinits(pertant,suposemqueelsmomentsdetots elsordressónfinits).Aixídoncs,finsasegonordreen ρ,hemderesoldre

1 2 µρ + 1 m ρ 0.

Òbviament,unasolucióés ρ = 0,idefetésfàcilveurequeaquestasolució ésexactaperaqualsevolordreen ρ.L’altrasolucióés ρ 2(m 1)/µ,però calpararatencióalvalorde µ,quepotescriure’s µ = σ 2 + m(m 1),amb σ 2 = (K m)2 = K2 − m2,ésadir,lavariància.Suposantque σ 2 = 0,

2(m 1) µ = 2(m 1) σ 2[1 + m(m 1)/σ 2] = 2(m 1) σ 2 1 m(m 1) σ 2 +··· (onhemusatlafórmuladelasumad’unasèriegeomètrica),amb m(m 1)<σ 2 sienstrobemsuficientmentapropdelpuntcrític,ipertantcomque ρ alvoltant dezeroimplica m alvoltantd’1,podemescriurelasegonasoluciódelamanera següent

ρ 2(m 1) σ 2 , queestrobaalrangqueensinteressapera m> 1.

Enresum,tenimque

ρ = 0si m ≤ 1, ρ 2(m 1)/σ 2 si m> 1, si ρ ésproupetita.Pera m> 1,aquestlímitésequivalenta m → 1.Elcas particularde σ 2 = 0,defet,nomésesdónaperalasoluciótrivialon p1 = 1 (altrament,lamitjananopodriaacostar-sea1).

Així,hemobtingutuncomportamentanàlegald’unatransiciódefasecontínuaenequilibritermodinàmic,onlavariaciód’unparàmetredecontrol,per exemplelatemperatura,indueixuncanvibrusc(continuperòambderivadadiscontínua)enun«paràmetred’ordre»,diguem-nelamagnetizacióenl’exemple d’unsistemamagnètic.Identificant m ambelparàmetredecontrol(latemperaturao,essentmésexactes,l’inversdelatemperatura)i ρ ambelparàmetre d’ordre(lamagnetització),ipensanten ρ comafuncióde m,podemescriure aquestarelaciódelamateixamaneraqueesfaalestransicionsdefase,on mc representaràelpuntdetransició,

ρ = 0persotade mc , ρ ∝ (m mc )β persobreperòapropde mc .

Seguintambl’exempledelssistemesmagnètics, mc correspondriaalafamosa temperaturadeCurie,elvalorprecísdelatemperaturaperalqualtélloc latransicióabrupta,queseparaunafasenomagnètica,peratemperatures

Processosderamificació,criticitatiautoorganització 23

altes,d’unafasemagnètica(oferromagnètica,ambmagnetizacióespontània nonul la)peratemperaturesbaixes.Acabemdedemostrarqueelprocésde Galton–Watsons’ajustaaaquestafenomenologia,amb

mc = 1i β = 1, onsuposemquelavariànciade K noesfa0alpuntdetransició.

Podemcompararelresultatanteriormésgeneral, ρ 2(m 1)/σ 2,pera m persobreperòapropd’1,ambelresultatquehemtrobatperalcasbinomial amb n = 2,on

quan p ≥ 1/2.Fentservirque,enaquestcas, m = 2p i σ 2 = 2pq (vegeu[29]),

jaque q = 1 p p pera p 1/2.Pertant,ambdósresultatssóncoincidents propdelpuntdetransició.

Figura7: Esquerra:probabilitatdeno-extinció ρ comafunciódelnombre mitjàdedescendentsperelement, m.Leslíniesdiscontínuescorresponen al’aproximacióques’explicaaltext.Elcanviabrupteen ρ éslamarca delacasad’unatransiciódefasecontínua.Ladistribuciódenombrede descendentsésbinomial,amb n = 2.Dreta:elmateix,peròcomafunció deladistànciaalpuntcríticreescalada,2(m 1)/σ 2,on σ 2 indicala variànciaa m = 1.Tambés’himostrenlesdistribucionsdePoissoni geomètrica.

Japeracabar,iencaraquesiguinomésenprodelacompletesa,podemjugar ambuncasnou,diferentdel’anterior,elquecorresponalvalorpatològic σ 2 = 0 (peralqualnosónvàlideslesderivacionsdedalt).Consideremprimerelsegüent model: p0 = 1 λ1, p1 = λ1 (i0altrament),amb λ1 ≤ 1.Aleshores, m = λ1,ija

sabemque ρ = 0.Consideremara p1 = 1 λ2, p2 = λ2,i,pertant, m = 1 + λ2. Enaquestcas,elpuntdetalldelafunciógeneratriuambladiagonalésper a ρ = 1sempre.Quanconsideremlavariaciódelesprobabilitatsdonades pelsdosmodelsconjuntamentobtenimunatransiciódefasediscontínua,ode primerordre.

2.9Ladistribuciódelamidatotaldelapoblació:distribucióbinomiali arbresambarrel

Enaquestasubseccióenscentraremenelcàlculdelamidatotal S delapoblació quanfemlasumarespectedetoteslesgeneracions,ésadir,

Aquestaquantitatcorresponalnombretotald’individusques’hanoriginato alnombretotaldeneutronsqueparticipenenunareacciónuclearencadena o,enelnostremodeldelsterratrèmols,al’energiatotalradiadadurantun esdeveniment.

Recuperemuncopméselcasparticulardeladistribucióbinomial pk = P(K = k) = n k pk(1 p)n

Enaquestcas,ladistribuciódelamidatotalespotcalcularfentservirprobabilitaticombinatòriabàsiques.Elpuntclauéslacorrespondèncianaturalentreels processosderamificacióiels arbres (ésadir,elsgrafsconnectatssensecicles). Cadaindividucorresponaunnode,icadabrancaoarestadelgrafcorrespon aunarelaciódedescendènciaentredosnodes.Òbviament,totselsnodestenen unasolabrancaentrant(unsol«pare»),excepteelnodequecorresponala generaciózero(que,enaquestcontext,s’anomenal’arrel del’arbre).Pertant,el nombredebranqueséselnombredenodesmenys1.Comquelamida s d’un arbreéselseunombredenodes,elnombredebranquesserà s 1,ielnombre debranquesabsents(intentsdereproducciónofavorables)serà ns (s 1) (jaqueelnombretotaldepossiblesbranquesapartirde s nodesés ns)[6].Per tant,cadaarbreconcretdemida s apareixambprobabilitat ps 1(1 p)(n 1)s+1 , ilaprobabilitatdetenirunarbrequalsevoldemida s s’obtésumantrespecte totselsarbresdemida s.Peralcas n = 2elnombred’arbresbinarisdemida s corresponalnúmerodeCatalan Cs = 1 s + 1 2s s ; vegeul’apèndixperalcàlculcomplet.Pertant,

Processosderamificació,criticitatiautoorganització 25

FentservirlafunciógeneratriudelsnúmerosdeCatalanespotcomprovarque aquestaexpressióestànormalitzadapera p ≤ 1/2perònopera p> 1/2,i que,defet, ∞ s=1

P(S = s) = Pext; novament,vegeul’apèndix.

Detotesmaneres,l’expressió (1) noensajudagaireacomprendreelcomportamentdeladistribució P(S = s) (sinoésquetenimunagranintuïcióper alcomportamentdelscoeficientsbinomials).Peròfentservirl’aproximacióde Stirling[1,7]podemobtenirunresultataproximatperòmésinformatiu[6]:

Aquestaexpressió,vàlidaperamidesgrans,ésunaexponencialcreixenten s,i elterme s3/2 nosemblatenirunpaperimportant,asimptòticament.Arabé,en introduirelfactor ps 1(1 p)s+1,resulta

P(S = s) ∼ 1 p √πp [4p(1 p)]s s3/2 .

Comque p(1 p) ≤ 1/4,eltermeexponencialesdevédecreixentexcepteper a p = 1/2,ondesapareixtotalment.Defet,podemanarunpasmésenllàsi posem [4p(1 p)]s = es ln[4p(1 p)] = e s/ξ(p) ,

on ξ(p) ésunamidacaracterísticaquedepènde p,definidaper

ξ(p) = ln 1 4p(1 p) 1 , ifinalment

P(S = s) ∼ 1 p √πp e s/ξ(p) s3/2 .

Pertant,pera s granperòconsiderablamentméspetitaque ξ(p),ladistribució deprobabilitatdelamidatotaldelapoblacióésessencialmentunalleidepotènciesambexponent3/2;ipera s encaramésgran,eldecreixementexponencial domina.Enaquestsentit, ξ(p) ésunaescalacaracterística.L’excepcióesdóna pera p = 1/2,on ξ(p) →∞,eltermeexponencialdesapareixiladistribucióes converteixenunalleidepotènciespura.Enaquestcas,l’exponent3/2ésun exponentcrític.Peratenirunaideadelabondatdel’aproximacióquehemdut aterme,vegeulafigura8.

p=0.35, exact p=0.35, asymptotic p=0.47, exact p=0.47, asymptotic p=0.50, exact p=0.50, asymptotic

P(S=s)

Figura8: Distribuciódeprobabilitatdelamidatotaldelapoblació S peradiferentsvalorsdelparàmetre p enuncasbinomialamb n = 2.Es mostrenelcassubcríticielcascrític;enaquestdarrerlalleidepotències puraesfabenpalesa.Tambéesmostralasolucióasimptòticapera s gran.

Deladivergènciadelamidacaracterística ξ(p) sorgeixunaltreexponent crític[6].Introduïntladesviaciórespecteelpuntcrític ∆ ≡ p pc ,ienelnostre exemple ∆ = p 1/2,podemescriure

, ipertant,apropdelpuntcrític(ésadir,pera ∆ petit),

ipertant

(fentservireldesenvolupamentdeTaylordellogaritmealvoltantde1),illavors

=

Enparaules,quanelsfísicsdiuenquelamidacaracterística ξ(p) divergeixal puntcríticcomunalleidepotències,ambexponentiguala2,estandientel

Processosderamificació,criticitatiautoorganització 27

queexpressal’equacióanterior.Amés,aquestaequacióenspermetescriure d’unamaneraméssenzillalafórmulaasimptòtica(s gran)peraladistribució delamidatotal,alvoltantdelpuntcrític:

Noteuqueladistribuciótélamateixaformatantpersobrecompersotadel puntcríticsiesmantéladistànciaaaquest, |p pc |,il’únicadiferènciaestroba enlaconstantmultiplicativa,quedepènde p directament.Aixòésperquèper sobredelpuntcríticladistribuciónoestànormalitzada(acausadelamassa al’infinit;vegeul’apèndix).Arasí,desprésd’aquestesúltimesconsideracions, queestrobena[6],japodemdiralgunacosadeladistribuciódeprobabilitatdel’energiaenelmodeld’Otsuka(modelque,debensegur,elsnostres lectorsjahanidentificatcomuncasparticulardelprocésdeGalton–Watson). Siprenem p< 1/2,ladistribucióqueobtenimtéunacuaexponencial,amb unaescalacaracterísticadonadaper ξ(p).Aixòsignificaqueelsterratrèmols s’atenuen,os’extingeixen,iquedecapmanerapodendissiparenergiesper sobrede ξ(p) (laprobabilitatd’obtenirunesdevenimentdemidasuperior a10ξ(p) ésextraordinàriamentpetita).Aquestéselcassubcrític.

Encanvi,si p> 1/2hihadostipusdeterratrèmols.Elsprimerssónsemblantsaldelcassubcrític:tenenunamidalimitadaperl’escalaquedefineix ξ(p), peròelssegonssóndiferents,sónterratrèmolsinfinits(recordemque Pext < 1 enaquestcas!).Peraaquestsegontipusdeterratrèmol,lapertorbacióinicial (lacaigudad’unasolapeçadedòmino)dónallocauncreixementexponencial. Aquestsegonéselcassupercrític.Arabé,nielcassubcríticnielcassupercrític sóncompatiblesamblalleideGutenberg–Richter,laqualpresentaunadistribuciód’energiesenlleidepotències,sensecapescalacaracterística.Únicament elcascrític, p = 1/2,éscapaçdereproduiraquestaestadística.Pertant,la propagaciód’unterratrèmolalllargd’unafallaésunfenomenestocàsticno nomésenelsentitquenosabemquèpassaràdesprésqueunfragmentllisqui sinóque,moltpitjor,enelcascríticlaprobabilitatquetél’activitatdecréixeri ladedecréixersóniguals.

Calremarcarquelaconcordançadelsresultatsésqualitativa,perònoquantitativa,jaqueelmodeldóna α = 3/2 = 1.5iencanviperaterratrèmolsreals s’hatrobatque α 5/3 1.67.Alasubsecciósegüentexpliquemqueelvalor3/2ésrobust,iquealtresversionsdelprocésdeGalton–Watsoncondueixen almateixexponent.YanKaganhaestudiatafonsaquestadiscrepànciaentrela modelitzacióielsterratrèmolsreals[16],iconclouqueelsmesuramentsempírics(elsquepermetenobtenirelmomentsísmic,ol’energia)contenenunasèrie d’artificisoperacionalsquefanqueelvalordel’exponentperaterratrèmols creixi,ipertant,segonsaquestautor,ambdósexponentsserienrealmentmés propersiprobablementcompatibles.

2.10Lafunciógeneratriudelamidatotaldelapoblació

EnsmovemaraalsEstatsUnits,enplenaSegonaGuerraMundial.Mentreels soldatsmorienalcampdebatallaielscivilspatienelshorrorsdela«barbàrie», ungrupdecientíficsesreunienenlatranquil.litatdeLosÁlamos,NouMèxic,amb l’objectiudeferrecercaidesenvoluparlesprimeresbombesnuclears.Undels integrantsd’aquestgrupdeprivilegiatseraelgranmatemàticpolonèsStanislaw Ulam,contractatpelseufamóscol.legaJohnVonNeumann[33].Juntament ambDavidHawkins—filòsofdelaciènciaielmatemàticamateurambmés talentquemaivaconèixerUlam—esdedicavenainvestigarlamultiplicació deneutronsenreaccionsnuclearsencadena,fentservirelquearaanomenem processosderamificació.Semblaquedesconeixienpercompletelstreballs pionersdeGaltoniWatson.

Figura9: ElmatemàticpolonèsStanislawUlam,alcostatdelaversióactualdelaprimerapàginade[13],desprésquefosdesclassificada.Aquesta feina,quecontédeduccionsifórmulesimportantsperalsprocessosde ramificació,vaformarpartdel’anomenatprojecteManhattan.

HawkinsiUlamvanprovar,entred’altrescoses,quelafunciógeneratriude probabilitats g(x) delamidatotaldelapoblació S = t≥0 Zt compleix,enels casossubcríticicrític,que

g(x) = xf(g(x)), on,comdecostum, f(x) éslafunciógeneratriudelnombrededescendents d’unsolelement.Elquesegueixacontinuacióestàbasatenaquellstreballsdel projecteManhattan[13],peròlanostradeduccióés,segonscom,méssenzilla.

Processosderamificació,criticitatiautoorganització 29

Elqueperanosaltreséslamidatotaldelapoblaciócorresponalnombretotal deneutronsgeneratsdurantunareacciónuclear.

Primerdetotensseràmésútilconsiderarlamidadelapoblaciódesdela generació1finsala τ (pertant,sensecomptardemomentlageneraciózero). Ésadir,

ambprobabilitats q(τ) s = P(Sτ = s) ifunciógeneratriu ˜ gτ (x) = s≥0 q(τ) s xs .

Unamidatotal s entrelesgeneracions1finsa τ espotdescompondreenuna mida k alaprimerageneració,ambprobabilitat pk,iunamida s k enles restants τ 1generacions(dela2ala τ),peròamb k elementsinicials;aixòpassa ambprobabilitat q(τ 1,k) s k (fixeu-vosque,amblanotacióactual, q(τ) s = q(τ,1) s ).

Aleshores,perlalleidelesprobabilitatstotals[26] q(τ) s = s k=1 pkq(τ 1,k) s k ,

exceptepera s = 0,on q(τ) 0 = p0.Siaramultipliquemper xs isumempera tot s,desde0finsa ∞,obtindremalcantóesquerrelafunciógeneratriude Sτ , queresultaser

gτ (x) = p0 + ∞ s=1 s k=1 pkq(τ 1,k) s k xs = p0 +

k=1 pk

s=k q(τ 1,k) s k xs k

xk

Ara,eltermeentreclaudàtorséslafunciógeneratriudelamidaacumulada entrelesgeneracions1i τ,peròamb k elementsinicials(ésadir, Z1 = k enlloc de Z0 = 1).Comquelesevolucionsdels k individusinicialssónindependentsentresi,lamidaresultantseràlasumade k variablesaleatòriesindependents, cadascunad’ellesambfunciógeneratriu ˜ gτ 1,ipertantlafunciógeneratriu totalcorresponentserà [ ˜ gτ 1(x)]k: gτ 1(x) k = ∞ s k=0 q(τ 1,k) s k xs k .

Substituintadalt,obtenim gτ (x) = p0 + ∞ k=1 pk

τ 1(x) k xk = f xgτ 1(x) , onhemintroduïtladefinicióde f(x) = fK (x)

Finalment,sivolemcomptarlageneraciózero,hemd’afegirunavariable aleatòriaambfunciógeneratriu x (jaque Z0 prenelvalor1ambprobabilitat1), ipertantlafunciógeneratriudelamidaacumuladaentrelesgeneracions0i τ seràelproducte gτ (x) = x ˜ gτ (x).Aixòensportaa gτ (x) = xf gτ 1(x) .

Tornantalamidatotal S = ∞ t=0 Zt ,

lasevafunciógeneratriués g(x) = limτ→∞ gτ (x).Silaprobabilitatd’extinció és1,ésadir,sielsistemanoéssupercrític,aixòésequivalenta limτ→∞ gτ 1(x), ipertanttenimque

g(x) = xf g(x) .

Aixídoncs,lasoluciód’aquestaequació,on f(x) ésconeguda,éslafunció generatriuquebuscàvem.Engeneralnopodremresoldreaquestaequació,però peraobtenirelsmomentsde S defetnoenscaldrà.Derivantrespecte x tenim que

g (x) = f g(x) + xf g(x) g (x), iprenent x = 1iaïllant, S = g (1) = 1 1 f (1) = 1 1 m , quetendeixainfinitquan K = m = f (1) tendeixa1,ésadir,alpuntcrític. Òbviament,comjahemdit,aquestresultatnoespotaplicaralcassupercrític, m> 1,onlapoblaciópotcréixerfinsal’infinitambprobabilitatnonul la.Si continuemderivant,obtenimdemanerasimilarelsmomentsd’ordresuperior. Aquestresultat,defet,l’hauríempogutobtenirdirectament,jaque

S = Z0 +Z1 +Z2 +··· = Z0 + Z1 + Z2 +···= 1+m+m2 +···= 1 1 m , onladarreraigualtatnomésésvàlidaenelcassubcrític,jaquealtrament S divergeix.

L’equaciópera g(x) espotresoldrefàcilmentenalgunscasos(moltpocs). Tornantalnostrecasbinomialamb n = 2,on f(x) = (1 p + px)2,tenimque g(x) = xf g(x) = x 1 p + pg(x) 2 , ipertant g(x) = 1 2pqx ± 1 4pqx 2p2x ,

amb q = 1 p.Ara,desenvolupantperTaylorl’arrelquadrada, 1 4pqx = 1 2pqx ∞ s=1 (2s 1)!!2s+1 (s + 1)! (pqx)s+1 ,

observemquehanaparegutnovamentelsnúmerosdeCatalaniobtenim(vegeu l’apèndixperalsdetalls), g(x) = q p ∞ s=1 Cs (pqx)s

Processosderamificació,criticitatiautoorganització 31

Noteutambéqueúnicamentelcasdesignemenysdavantdel’arrelensproporcionarealmentunavertaderafunciógeneratriu.Pertant,elscoeficientsde xs ensportena

P(S = s) = Cs ps 1qs+1 ,

pera s ≥ 1.Aquestresultatésexactamentelmateixquehemobtingutanteriorment.Aquestvegada,però,nohemhagutdecomptararbres,perquèels númerosdeCatalanhanaparegutdeformanaturalenfereldesenvolupament ensèrie(defet,noeranecessariniconèixer-los!).

Pertant,hemconfirmatqueelmodeld’Otsukaambunadistribucióbinomial i n = 2portaaunalleidepotènciesambexponent3/2peraladistribució delamidatotaldelapoblació.Peròelquerealmentensagradariaésestudiar comésderobustaquestexponent,jaquedefetelmodelés,comtots,una simplificaciódelarealitat,ipertantnovoldríemque,enmodificarelmodel, s’obtinguessincomportamentstotalmentdiferents.

Totiqueobtenirlalleidepotènciesperaladistribucióde S ésforçarebuscat (alcapialafi,calajustarelparàmetre p a1/2),siconsideremaltrescasos mésenllàdelbinomial,elcomportamentasimptòticenelcascríticsegueix sentunalleidepotènciesambexponent3/2.Aixòespotdemostrarfent servirlafórmuladeCauchyenelplacomplexisuposantúnicamentvariància finita,1 vegeu[12, 25].Pertant,mésenllàdelarobustesa,s’acostumaaparlar d’universalitatperareferir-seaaquestainvariància.

3Autoorganitzacióicriticitat

Lateoriadelapiladesorra—lacriticitat autoorganitzada—ésirresistiblecomametàfora.

AlGore

Araestemencondicionsd’acceptarlacorrespondènciaentreunprocésde ramificaciócríticil’ocurrènciadeterratrèmols,nonomésqualitativamentsinó també,siseguimelscomentarisdeKagan[16],quantitativament.Perafer coincidirelnostremodelamblarealitat,simplementhemd’agafar p = 1/2(per almodeld’Otsukabinomial),o m = 1(engeneral),il’ajustamentésrealment satisfactori,idefetpodríemfinalitzaraquílanostracercad’unmodel.

Peròtambépodemanarunpasmésenllàipreguntar-nos:comésque elssistemestectònics(ialtresgeosistemesrelacionatsamblescatàstrofes naturals)estansempreenunestataparentmentcrític?Pottractar-sed’unapura coincidència?Peralcasdelareproducciód’éssersvius,hompodriaempescarseunargumentdetipusevolucionista.Imaginemunasèried’illes,totalment aïlladesentresi,icadascunahabitadaperunapoblacióquesegueixunprocésde Galton–Watson,peròambunvalordiferentdelparàmetre p (o m).Sensdubte, 1Aquestresultat,però,noesmantéperalcasdevariànciainfinita;vegeu[30].

lesillesambpoblacionssubcrítiquesquedarandesertesalcapdecertnombre degeneracions.Pelquefaalespoblacionssupercrítiques,obés’extingirano béexplotaranexponencialment,ienaquestcassuposemquelapoblacióes col lapsaràperl’exhaurimentdelsrecursos(aquestingredientnoformapart delmodeloriginaldeGalton–Watson).Enelcascríticlespoblacionstambé s’extingiran,peròperaalgunes(poques)d’aquestesilleslapoblaciópodrà sobreviuredurantmoltdetemps,moltíssimmésqueenelsaltresdoscasos.Per tant,alcapd’uncerttempsnoméstrobaríempoblacionscrítiques,queserien lesmésadaptadesal’entornqueelshihemproporcionat.

3.1Procésderamificacióautoorganitzat

Detotamanera,l’escenarievolutiutotjustdescritnoespotaplicarasistemes tectònics,peralsqualsquanunprocés(elterratrèmol)s’extingeix,tardod’hora encomençaundenou.Lasituaciódelsterratrèmolscorrespondria,mésaviat, atrobartotselsmaterialsmagnèticsdelaTerraalllindardelamagnetització, oequivalentmentatrobarcadamaterialalasevacorresponenttemperatura deCurie.Aleshores,potserpensaríemquealgunmecanismeestàforçantla criticitat,fentvariarlatemperaturaenfunciódelamagnetitzacióimantenint aquestaalvoltantdelatransició.Enresum,sospitaríemquealgunmecanisme deretroalimentacióinterrelacionaelsdosparàmetres[28].

Zapperi etal. [35]proposenunmodeld’aquesttipus.Comencenambun procésderamificacióestàndard,peròintrodueixenalgunesmodificacionsimportants:

• Limitenelnombredegeneracionsaunmàximde τ,pertant0 ≤ t ≤ τ. Aixòvoldirquedesprésdelageneració τ elprocésjanocontinua.

• Quanelprocéss’acaba,béenarribaralageneració τ béperquès’extingeix abans,estornaagenerarunprocésnou,començantnovamentambunúnic element,osigui, Z0 = 1.Aquestprocésnouconstituiràelqueanomenarem unanovarealització,queenumeraremambl’índex T .Laclaud’aquest modelésqueelsparàmetrespodencanviarderealitzacióenrealització. Aixòesfadetalmaneraquequanelprocésessubcrític(m< 1),la mitjana m delnombrededescendentsperelementtinguitendènciaa augmentar;iencanviquanelprocéséssupercrític(m> 1),lamitjana m tendeixiadisminuir.Laideaéstransformarelcascrític m = 1enun atractordelsistema.

Comaexempleconcret,tornemalnostrecasparticular,ladistribucióbinomialambdosintentsdereproduccióiunaprobabilitat p d’èxitassociada acadaintent.Comjasabem, p< 1/2, p = 1/2i p> 1/2corresponenals casossubcrític,críticisupercrític,respectivament.Ladinàmicaproposadaper Zapperi etal. a[35]estàbasadaen Zτ ,elnombred’elementsaladarrerageneració τ.Aquestadinàmicaconsisteixafervariar p derealitzacióenrealització mitjançantlafórmula

p(T + 1) = p(T) + 1 Zτ (p(T),T) N ,

Processosderamificació,criticitatiautoorganització 33

essent T l’índexdiscretquecomptaelnombrederealitzacionsdelprocés(ique calnoconfondreamb t)i N unnúmeromoltgran(N τ demoment).Pertant, sielprocéss’extingeixabansd’arribaraladarrerageneraciópossible, Zτ és0i elparàmetre p augmentaen1/N,unaquantitatmoltpetitaenellímit N →∞ Peraltrabanda,sielnombred’elementsalageneració τ ésmésgranque1, p disminueixen (Zτ 1)/N

Sabentqueelvaloresperatde Zτ és mτ ,on m éslamitjanadeladistribució dedescendència(m = 2p enelnostrecasbinomialparticular),introduïmara untermedesoroll η peratenirencomptelesfluctuacionsde Zτ alvoltant delamitjana,ésadir, η = Zτ mτ .Òbviament, η = 0perconstrucció.Si, perunsmoments,ignoremeltermedesorollal’equacióde p(T + 1),lapart deterministaés

p(T + 1) = F p(T) = p(T) + 1 2p(T) τ N .

Aixònoésmésqueunsistemadinàmicdiscret,ounmapa[2],quetéunpunt fixdonatperlasolucióde p∗ = F(p∗) queresultaser p∗ = 1/2.Amésamés, elpuntfixésunatractor[2],jaque |F (p∗)| < 1,pelfetque τ N.

Pera N moltgraneltermedesoroll η/N tindràunefectenegligible,i pertantelsistemaestocàsticevolucionaràcapalpuntfixprevistperlapart determinista,mésalgunespetitesfluctuacionsaleatòriesentornseu.Noteuque aquestpuntfixcorresponalpuntcríticdelprocésderamificació.L’evolució espontàniad’unsistemacapaunestatambunacertaestructuraoordre s’anomenaautoorganitzacióihihaexemplesbenconeguts(elspatronsde conveccióalsfluidsol’autoregulaciódelsmercats).Enelnostrecasparlem deprocésderamificacióautoorganitzat;mésendavantveuremquinordreo estructuraestàassociatal’estatcrític.

Detotamanera,s’hadepagarunpreuperobtenircriticitatdemanera espontània.Comqueelprocéss’interrompalageneració τ,ladistribucióde lagrandàriadelprocés, P(S = s),janoseràexactamentunalleidepotències, totiqueelprocéssiguicrític,sinóquetindremdesviacionspelsvalorsmés gransde s.Finsitot,si τ fosmoltpetit,ladistribucióresultanttindriapoca veureambunalleidepotències.Noobstantaixò,fent τ prougranenspodrem aproximartantcomvulguemalalleidepotències.

Resumint,elqueZapperi etal. vanintroduirésunprocésderamificació ques’autoorganitzacapaunestatcrític,totiqueladinàmicaqueproposen semblamésaviatarbitrària.Correspondria,enl’exempledelesilles,atenir undéucreadorque,quanunapoblaciós’extingeix,encreaunaaltraperò modificantadequadamentlasevatassadereproducció,finsaacabararribanta unapoblaciócrítica,osigui,enequilibrientrel’extincióil’explosiódemogràfica. Arabé,comespodriaimplementaraquesttipusdecontrolglobal(quefacanviar elsparàmetres p detotselselementsalhora)enunsistemareal,onhomespera quelesinteraccionsentreelementssiguinpuramentlocalsinohihagicap controladoromniscient?

3.2Criticitatautoorganitzada

ElprocésderamificacióautoorganitzatdeZapperi etal. defets’emmarcade maneranaturalenlanociódecriticitatautoorganitzada,creadaperPerBaki elsseuscol laboradorsalsanysvuitantadelseglepassat[4, 14, 6].Totiqueara noésrellevantperalsnostrespropòsits,vallapenadirqueaquestsautorsno estaveninteressatsenelproblemadeleslleisdepotènciesendesastresnaturals (jaquenoelconeixien),sinóqueelspreocupavenaltresproblemessimilars enfísicadelamatèriacondensadacomaralesonesdedensitatdecàrrega,el sorolldeltipus«1/f »ilaubiqüitatdelesestructuresfractalsalanatura.Però avuidialacriticitatautoorganitzadaésmoltmésacceptadacomaexplicació defenòmenscatastròfics(tantageociènciacomperalesflamaradessolars, l’extinciódelesespècies,etc.[4])quepelquevaseroriginalmentproposada. Llavors,malgrateldesconeixementinicialdelsautors,aquestsvantrobarun mecanismemoltfactibleperreproduirl’estadísticadelsdesastresnaturals. Comhemvistalllargd’aquestarticle,semblaquelafaltad’informacióésuna característicacomunaenl’evoluciódelaciència.

Perail.lustrarlessevesidees,Bak etal. vanutilitzarlametàforadelapilade sorra.Hemdereconèixerquelapiladesorraamblaqualtractaremnosaltresés unamicaesotèrica;mésendavantjustificaremperquèiquanpotrepresentar unapiladesorrareal.Consideremunsistemaformatperungrannombrede cel.les,oncadacel.lapotemmagatzemaruncertnombredepaquetsdiscrets (opartícules),demaneraquequansesuperaaquestmàximalgunspaquetses distribueixenentreelsveïns(demomentnocalentrarendetalls,peròperveïns entendremlescel.lesmésproperesaunadonada).Lasituacióésanàlogaalque passaalesoficinesd’unministeriounaconselleria:cadaburòcratatéunasèrie dedocumentsopapers(elspaquets)alasevataula,peròquanelnombrede documentsésmassagran,decideixsolucionar-hosimplementpassantalguns delsdocumentsalscompanysdelestaulesdelcostat,iaixísuccessivament (vegeufigura10).Inesperadament,aquestcomportamenttansenzilldonarà llocaunadinàmicamoltinteressant.

Pertaldeconcretarunamica,consideremunreticlehipercúbicen d dimensionsoncadacel lapotemmagatzemarnomésunpaquet;siarribaun segonpaquet,lacel.lareenviaràelsdospaquetsaaltrescel.les,escollidesaleatòriamentiindependententreels2d veïnsméspropers(queseranlescel.les adjacents).Si,desprésd’aquestprocés,elnombredepaquetsencaraéssuperior a1(cosaquepotpassarsilacel.lahaviarebutmésd’unpaquet),elprocéses repeteix.Toteslescel lesduenatermeaquestprocésdemanerasimultània,és adir,seguintunrellotgecomúquemarcaeltemps t,elqueesconeixcoma actualitzacióenparal lel.Amésamés,elsistemaésobert:pothaver-hiuna pèrduadepaquetscapal’exterior(foradelreticle).Aixòpassaquanunacel.la delafronteraseleccionacomadestíd’unpaquetunaaltracel.laqueestàfora delslímitsdelsistema;enelcasdelsburòcratestenimelmateixquanalgú d’ellsllençaundocumentperlafinestra.

Figura10: Il.lustraciódelmodeldepiladesorraentèscomunaparòdia delaburocràcia.DelllibredeBak[4].

Òbviament,aquestprocéspotengegarunaallaudetransferènciesdepaquets, quenoméss’aturaquantoteslescel.lestenenunpaquetcomamolt.Quan s’arribaaaquestpunt,elsistemaéspertorbatafegintunpaquetaddicionala unacel.laescollidademaneraaleatòria,cosaquereactivaladinàmica,ono. Mentrenohihagiactivitat(toteslescel lesestanpersotadelllindar)esvan afegintpaquetsacel.lesaleatòries.D’aquestamaneraesdefineixunanova escalatemporal,quedenotaremper T (talcomfèiemalasubseccióanterior);o sigui, T comptaelnombredepaquetsafegits.Notemquetenimduesescales temporalsbenseparades:l’escalaràpida,assenyaladaper t,quecomptaels passosdel’allau,il’escalalenta,marcadaper T .

Lesreglestotjustdescritesverbalmentpodentambéexpressar-sematemàticament,ésclar.Siguin j, k, n,vectorsqueidentifiquenlescel lesalreticle d-dimensionalisigui zj laquantitatdepaquetscontingutsalacel.la j.Amés, nn(j) representadosveïnsaleatorisdelacel.la j,triatsuniformementiindependententreels2d veïnsméspropers;perlasevabanda, rand representauna cel.ladelreticletriadaaleatòriament,demanerauniformesobretotelreticle. Lestriesaleatòriess’actualitzenacadapas,demaneraindependent.Lesfletxes finesindicaranqueunavariablepassaaprendreunaltrevalor,talcomes programariaenunordinadorambelsigned’igualtat.Llavorslesreglessón: si zj ≥ 2 ⇒ zj → zj 2, znn(j) → znn(j) + 1, si zk < 2 ∀ k ⇒ zn → zn + 1amb n = rand, queespodeniterar adinfinitum.Laprimeraregla,ladelarelaxació,defineix l’escaladetempsràpida,donadaper t,mentrequelasegona,ladel’addició, defineixl’escalalenta,donadaper T .L’existènciadeduesescalesdetemps fafarragosalanotacióiperaixòprescindimd’etiquetestemporals.Repetim quelaregladerelaxaciós’had’aplicarenparal.lel,simultàniament,atotesles cel.les j queverifiquinlacondicióllindar.

Aquestesreglesdefineixenunautòmatcel.lular:unsistemadinàmicon l’espai,eltempsilavariabledefinidasobreaquestssóntotsdiscrets;aquests autòmatspodendonarllocacomportamentsd’unagrancomplexitat.Defet, enstrobemdavantd’unsistemacomplex,enelsentitqueestàconstituïtper moltselements(lescel.les)queinteraccionenentresidetalmaneraqueel comportamentcol.lectiu,detotelsistema,seràmésquelasimplesumadels comportamentsindividuals,comjaveurem.Tenimexemplesdesistemescomplexosengairebéqualsevolestructurarealmentinteressant:lacèl.lula,elcervell, elsecosistemes,l’economia,lesxarxessocials,elclima…Laciènciaemergent delssistemescomplexostractad’aportarunanovaperspectivaal’estudid’aquestamenadesistemes.Hompotendevinarqueestractad’unadisciplina claramenttransversal.

Tornantalnostremodel,seguintlessevesreglessenzilles,elnombretotal depaquetsalsistemaevolucionadelamanerasegüent,entreunapertorbació T ilasegüent T + 1:

M(T + 1) = M(T) + 1 drop(T), on«drop»éselnombredepaquetsqueelsistemaexpulsa.Ésadir,entrecada addiciódepaquetsilasegüent,lamassa M delsistemas’incrementapelpaquet quehemafegitidisminueixpelnombredepaquetsquesurtenperlafrontera durantl’allau(siaquestatélloc).Elparàmetrecentrald’aquestmodelés p, definitaquíperacadacel.lacomlaprobabilitatdetenirunsolpaquet(just abansd’afegirunpaquet,osigui,quanlatransferènciadepaquetshacessat).

Veuremcom p esrelacionaamb M.Enunprincipi, p depèndelaposiciódecada cel laalreticle(lesqueestanmésapropdelcontorntindranunaprobabilitat diferentdelesquenohoestan)ihauríemd’afegir-liuníndexespacial.

Noobstantaixò,perapodertractarmatemàticamentelsistema,treballarem enl’anomenadaaproximaciódecampmitjà[6],onveuremque p esdevéun paràmetregenèricdetotelsistema.Enrealitat,l’aproximaciódecampmitjà, mésqueunaaproximacióésunaredefiniciódelsistema,quefacanviaralguna característicad’aquestperòsensealterar-nel’essència.Arahoveurem.Una manerad’implementarelcampmitjàésconsiderarqueelreticle d-dimensional ésdedimensióinfinita,osigui,enellímit d →∞ (totiqueelsistemaqueens interessipuguitenir d = 2,comalafigura10).Unaaltraopcióéssuposarqueels veïnsnosónelsméspropersalacel.lasinóqualsevolcel.latriadaaleatòriament entretoteslesdelsistema,is’actualitzenaquestestriesaleatòriescadavegada. Ambdueseleccionssónequivalentsperquèlapropagaciódelspaquetsalsistema noformaràbucles:laprobabilitatqueunpaquettornialacel lad’onvenia tendeixazeroenaquestsdoscasos(sielsistemaéssuficientmentgranen elcasdetriarlaversiódeveïnsaleatoris);igualment,laprobabilitatquedos paquetsarribinalamateixacel.latendiràazero.

Llavors,enl’aproximaciódecampmitjànohihacorrelacióentrel’estatde lescel.les,iaquestessónequivalents,ipertantlaprobabilitatqueunacel.la qualsevolcontinguiunpaquetvindràdonadapelnombredepaquets M dividit pelnombredecel.lesdelsistema,queanomenemaquí N,osigui, p = M/N (les

Processosderamificació,criticitatiautoorganització 37

cel.lesotenenunpaquetonoentenencap,quannohihaactivitat).Aquesta probabilitat,perlesreglesdelmodel,ésigualalaprobabilitatqueunacel la deixianardospaquetsquanenrepun,osigui,esrelaxi.Aixòespotconsiderar unintentdereproduccióexitós,peròaquestacel lanoseràlacel lamaresinóla filla,ésadir,aquestacel.laseràfilladelacel.laquelivatransferirelspaquets. Lacel.lafillapodràdonarllocadescendènciaono,depenentdesilescel.lesque desprésrebinelspaquetsesrelaxinono.Veiem,doncs,quelesrelaxacionses propaguenpelsistemacomunprocésderamificacióbinomialambparàmetre p, iambnomés0,1o2filles.Sidividiml’equaciódelamassaalsistemaper N, obtenim

p(T + 1) = p(T) + 1 drop(T) N ,

queéspràcticamentidènticaal’equacióintroduïdaperZapperi etal. [35]en elprocésderamificacióautoorganitzatdelasubseccióanterior,iqueensdiu que,enaquestmodeldecampmitjà,laprobabilitatdereproduccióencada intentevolucionad’aquestamanera(al’escaladetempslenta).Osigui,enuna allaulesrelaxacionsespropaguencomunprocésderamificacióperò,amés amés,entreallauiallau,elparàmetre p canviadelamaneraproposadaper Zapperiielsseuscol.laboradors.Calremarcar,però,queaixòs’haaconseguit senseactuarglobalmentsobretoteslescel.les.Éstotelsistemaelqueregula elseupropivalorde p,atravésdelbalançentrel’addiciódepaquetsilaseva sortidapelscontorns.

Talcomhemanalitzatalasubseccióanterior,elsistematendirà,excepteper apetitesfluctuacions,aunestatenelqualelnombremitjàdepaquetsquesurtin sigui drop = 1.Llavors,al’aproximaciódecampmitjàhemd’implementaro redefinirlescondicionsdecontorndetalmaneraqueelpuntcríticcorrespongui aaquestasituació.SimplementpodemagafarlamateixareglaqueZapperi etal., queésquelesallausesdissipinespontàniamentdesprésd’unnombrefixat τ depassosdetemps.Osigui,lescel.lesqueesrelaxenalageneració τ envien elsseuspaquetsforadelsistema.Aixòfaque drop = 2 Zτ = 2mτ = 1,que dóna m = 1/21/τ iquetendeixialpuntcrític m = 1quan τ tendeixainfinit.De totamanera,aquestatriaperalescondicionsdecontornnoésl’únicapossible.

Aixídoncs,l’aproximaciódecampmitjàenspermetrelacionarelmodelsde piladesorraambunprocésderamificaciócrític,ipertant,ladistribució delagrandàriadelesallausaaquestaversiódelapilaseguiràunalleide potències,ambexponent3/2.Defet,comhemdit,esperemalgunapetita desviaciórespecteaaquestcomportament,acausadelsefectesintroduïtsper lescondicionsdecontorn,queequivalenatenirunagrandàriadelsistemafinita. Llavors,sielsistemaésfinit,nopodemtenirallausarbitràriamentgrans,però enshipodremacostarmolt.Peralmodeldepiladesorraoriginal,sensefer l’aproximaciódecampmitjà(ambinteraccionslocalsiambdimensiópetita),els resultatsserandiferents.Peròsimul.lacionsperordinadormostrenqueelcamp mitjàdónaunaexplicacióqualitativadelcomportamentdelapila;enparticular, s’obténormalmentunadistribuciódelleidepotènciesperòambexponent diferentde3/2.Amés,lesreglesd’interacciólocaldonenllocacorrelacions

espacialsiaestructures,iperaixòtésentitparlard’unaautoorganitzaciócapa lacriticitat,perl’existènciaprecisamentd’aquestesestructuresalsistema.

3.3Modelsdepilesdesorra

Hemparlattotal’estonadepilesdesorra,peròquètéaveurelatransferència depaquetsdescritaambunapilareal?Laclauésqueelspaquetsqueestransfereixennosóngransdesorra,sinóunitatsdependentd’unapilabidimensional. Si j ésuníndexdeposicióquevad’1a L (on L éslagrandàrialinealdelsistema), definiml’alçadadelapilaalaposició j coma hj = hj+1 + zj ,començantpel valorde j mésgranamb hL = zL.Recordemque zj eraelnombredepaquetsa laposició j,iararesultaqueesdevéelpendentdelapilaenaquestaposició. Femnotarquesentlapilabidimensional(vegeufigura11),lesvariables zj i hj estandefinidessobreunadimensió,ipertant, d = 1.

Pertenirl’equivalènciaambunahipotèticapiladesorracalencaraunapetita modificaciódelesregles:encomptesquequanunacel.la j esrelaxaaquesta enviadospaquetsaveïnstriatsaleatòriament,arafemques’enviïunpaquetal veí j 1iunaltreal j + 1,pertant, nn(j) s’haderedefinircoma nn(j) = j ± 1 (aquestcanvinoalteraelcomportamentdecampmitjàdelmodel,perquèa campmitjàesredefineixenelsveïns).Llavors,ésimmediatcomprovarqueles reglesresultenserlessegüents:

Tenimllavorsunautòmatcel.lularquerepresentaunapiladegransdetal maneraquequanelpendenta j ésmésgranoigualque2,ungrasaltade j a j + 1(capaladreta,segonslafigura).Noteuqueperconstrucciódelmodel maiarribaremalasituaciósimètrica,pendentméspetitoiguala 2,iaixí elfluxdegranssempreseràcapavalorsde j mésgrans,osigui,d’esquerra adreta.Lacondiciódecontornobertaperalpendent z a j = L nodónauna condiciódecontorncreïblepera h,iésmésconvenientcanviar-la.Pertenirla situacióexperimentald’unapilaobertaperladreta(segonslafigura),donada per hL+1 = 0resultaqueobtenimperalarelaxacióa j = L laregla zL → zL 1 (elpendentpassariaaconservar-sealcontorndret).Defet,aquestacondiciója estavaimplícitaalatria hL = zL

Unaltrecanvipossiblealmodelpotserafegirnomésungradesorradurant l’addició(encomptesd’unpaquet,osigui,unaunitatdependent);aixòés, hn → hn + 1illavors zn → zn + 1peròamb zn 1 → zn 1 1.Existeixen moltíssimesvariantsd’aquestesreglesquedefineixendiferentsmodelsdepiles desorra,avegadesambpocaconnexióambelquehauriadeserunapilade sorrareal.Recordem,alfinal,queaquestsmodelspretenenserenelfonsuna metàforadel’aparicióespontàniadecriticitatalanatura,ienprincipinohiha uninterèsespecíficaestudiar perse elsmedisgranulars.Aixòseriaunaaltra història.

Processosderamificació,criticitatiautoorganització 39

Aquestsmodelspodenserútilsperdescriureunaltretipusdefenomen:el creixementdesuperfícies(perexemple,unfluidquepenetraenunaltremedi). Sifemquelavariable Hj comptielnombretotalderelaxacionsalaposició j (desdel’instantinicial)isilacondicióinicialdelapilaésbuida(hj = 0pera tot j)il’addiciódegransesfanomésa 1,llavorslavariable Hj defineix l’avençd’unainterfaseestiradadesde 1.Elgradientd’aquestainterfase dónal’alçadadelapila,aixòés, ,osigui,elnombre totaldegransafegits.Ambaquesttemapodríemseguirmoltmésperòse’ns acabal’espaiieltemps…

Figura11: La«metàfora»delapiladesorra,peralcasbidimensional, s’haarribataestudiarexperimentalment.Lainstal.laciódelafotografia (cortesiadeK.Christensen)utilitzadosplafonsperaconstrenyirlapila (defet,duespiles),iarròsencomptesdesorra.

4Conclusions

Hemcomençataquestarticlemostrantalgunespropietatsestadístiquesinteressantsdel’ocurrènciadeterratrèmols,ihemacabatjugantambpilesdesorra d’infinitesdimensionsquemodelenlacriticitatautoorganitzada.I,mentrestant, hemtinguttempsd’aprendrequatrecosesdelsprocessosderamificació.Potser araéselmomentderecapitular,deposarelscontingutsenperspectivaid’esbossaralgunesconclusionsperalnostreobjected’estudiinicial:elsdesastres naturals.

D’entrada,senseferreferènciaacapmodel,nomésmirantlesdadesja podemdirforçacoses:elsterratrèmolsialtresdesastresnaturalssegueixenuna distribuciótipuslleidepotènciesperlamidadelasevagrandària,encaraqueen algunscasosambunadisminucióexponencialafegidaacausadel’efectedela finituddelsistema(laTerraésfinita!).Iencaramés:peralsvalorsdelsexponents ques’hantrobat,aquestadistribucióimplicaqueelsgransesdeveniments,tot iquepocfreqüents,sónelsqueméscontribueixenaladevastacióglobal.

Pelquefaalmodeld’Otsuka,hemmostratcomespodenrecuperarles propietatsestadístiquesdel’ocurrènciarealdeterratrèmols(id’altresdesastres naturals)mitjançantunprocésestocàsticencascadaraonablementsimpleper alesdinàmiqueslocalsdelssegmentsdelesfallestectòniques,iambl’ajuda delformalismematemàticdelsprocessosderamificació.Ésmoltimportant remarcaraquestpunt,perquèconstitueixunpontentreduesescalesobservacionalsdiferents:lamicroescaladeladinàmicalocalilamacroescaladel comportamentestadísticglobal.

Arabé,elmodeld’Otsukanoésmésqueuncasparticulardelprocésde ramificaciódeGalton–Watson.Ésperaixòque,primerament,hempresentat demaneraplaneraelsprincipalsresultatsconegutsperaaquesttipusde processos(principalssegonselsnostresinteressos,ésclar).Hemexplicat com,mitjançantlamaquinàriadelesfuncionsgeneratrius,espottrobaruna fórmulaperal’activitat(opoblació)aqualsevolgeneraciódelprocés.Enel límitd’infinitesgeneracionss’obtélaprobabilitatd’extinció,quemostraun brusccanvidecomportamententredosrègimsclaramentdiferenciats:extinció seguraquanelnombremitjàdedescendentsésinferiora1,ilapossibilitatde noextincióquanéssuperiora1.Tambéhemobtingutunaexpressióperala probabilitatdelamidatotaldelprocés,ésadir,lapoblacióquehanascuten total,o,equivalentment,l’energiatotalradiadaperunterratrèmol.Ésjustament alafronterad’aquestsdosrègims,ésadir,alpuntcríticdelatransiciódefase, ons’obtenendistribucionscompatiblesamblesdadesrealsdeterratrèmols ialtresfenòmens.Enelnostrecas,apareixunadistribuciódepotènciesamb exponent3/2;peròllavorscalexplicarquinmecanismeseriaelresponsablede conduirlaTerracapaaquestestatcrític.

Enaquestsentit,hemmostratcomespottransformarelpuntcríticenun atractordelsistema,fentservirunmecanismederetroalimentacióforçasenzill. Calqueunacondicióglobal,relacionadaambladissipacióalafrontera,actui sobrelaprobabilitatd’activació,demaneraquequanaquestaprobabilitatés massabaixa,augmenti,iquanésmassaalta,disminueixi.Elsmodelsdepilesde sorra,enellímitideald’infinitesdimensions,implementendemaneranatural aquestmecanismemitjançanteltransportdepartículesatravésdelsistema finsalafrontera,onesdissipen.Elnombredepartículesregulal’activitatdel sistema.

Finalment,calcomentarquelagènesidesistemacomplexquehemexplicat (començantperunsimpleprocésderamificacióicomplicant-hofinsaarribar aunmodeldepiladesorraambmoltselementsqueactuenlocalment)no constitueixlamaneranaturalcomesdesenvolupenaquestesidees.Mésaviat

Processosderamificació,criticitatiautoorganització 41

ésalcontrari;onitansolsaixò,mésaviatnoespotferlaconnexióentre unsistemacomplexiunadinàmicasimple.Engeneral,perleslimitacions inherentsqueplantegenelssistemescomplexos,elsmodelsenaquestcamp nopodensermésqueunacaricaturadelesinteraccionsrealsalsistema.Tot iaixò,nomésimposantamésamésl’aproximaciódecampmitjàhompot establirlaconnexióambunsistemasimple.Peròl’aproximaciódecampmitjà enlamajoriadelscasosresultaestarbenallunyadadelmodelinicial,almenys quantitativament.Resoldremodelsreticulars,ambinteraccionsnoglobals, ésterriblementcomplicat,iaramateixelsinvestigadorss’handerefiarde simulacionsnumèriques,jaquenohiharesultatsanalíticsexactesdisponibles, exceptecomptadesexcepcions(unconjuntdemesuranul la,segurament).Però tambééscertqueaixòfaencaramésinteressantselsproblemesmatemàticsque plantegenaquestssistemes.Sensdubte,elsinvestigadorsencarasen’hauran d’ocupardurantdècades!

AApèndix

A.1Dissipaciód’energiaalesescalesmésgrans Consideremunadistribuciódepotènciescontínua,definida,persimplificar peròsensepèrduadegeneralitat,entre1i ∞,ambfunciódedensitat

D(x) ∝ 1 xα .

Demostraremque,donat r> 2,existeixenvalorsde α talsquelacontribuciód’uninterval1 ≤ x<c alvaloresperatde x éssempremenorquela contribucióde c ≤ x<rc,independentmentdelagrandàriade c Lacontribuciódel’interval a ≤ x<c alvaloresperatde x és c a xD(x) dx ∝ c2 α a2 α , i,pertant, rc c xD(x) dx ∝ c2 α(r 2 α 1).

Pertalqueladarreraintegralsiguimésgranquel’anteriorseràsuficient demanarque (r 2 α 1)c2 α >c2 α

Pertant, r 2 α > 2iaixòimplicaque

α< 2 logr 2.

Pera r = 10,lacondiciósuficientresultaser α< 1 699.Enelcasdel’energia radiadapelsterratrèmols, α 1 + 2b/3 1.667,ipertantlacondicióes compleix.Aixòsí,valorsde α lleugeramentsuperiorsviolarienlacondició.

Totiaixò,latriade r = 10notéresd’especial(noéscapnúmeromàgic!)i lacondicióescompleixperavalorsde r mésgrans.Pera r = 2lacondició dictariaque α< 1,cosaquenoésunexponentacceptableperaunalleide potències(noserianormalitzable).

A.2Demostraciórigorosadelaprobabilitatd’extinció Mésenllàd’argumentsgràfics(vegeulafigura5),volemdonarunaprovatotalmentrigorosadelcàlculdelaprobabilitatd’extincióenunprocésdeGalton–Watson,quevedonadaper

Pext = lim t→∞ f t (0),

on Pext nomésestàbendefinidaquanellímitexisteix.Peraveurequeaixò semprepassa,observemque Zt = 0 ⇒ Zt+1 = 0.Pertant, {Zt = 0}⊂{Zt+1 = 0} i P(Zt = 0) ≤ P(Zt+1 = 0),ipertant f t (0) ≤ f t+1(0) o,ditd’unaaltra manera, (f t ) ésunasuccessiócreixent.Comque f [0, 1] ⊂ [0, 1],podem concloureque f t (0) estàfitadaipertanttélímit.Percontinuarlanostra demostració,seràconvenienttractarperseparatelscasos m ≤ 1i m> 1.

A.2.1Elcas m ≤ 1: Comquelafunció f(x) éscòncavapera x ≥ 0,sempre estàpersobredequalsevolrectatangentaaquesta[31].Enparticular,si consideremlatangenta f(x) pelpunt (1, 1),tenimque f(x)> 1 + m(x 1)>x.

Pertant f(x)>x pera0 ≤ x< 1.Ésfàcilcomprovar,també,que f(Pext) = Pext, f lim

f t (0) = lim

f f t (0) = lim

iòbviament0 ≤ Pext ≤ 1.Pertant,tenimque f(Pext) = Pext amb0 ≤ Pext ≤ 1.Resumint, Pext ésunpuntfixde f(x) al’interval [0, 1],però f(x)>x (estrictament)a [0, 1).Quedaclar,doncs,quel’únicaopcióquerestaés Pext = 1.

A.2.2Elcas m> 1: Enaquestcas,començaremdemostrantque Pext ≠ 1. Talcomacabemdeveure, (f t ) ésunasuccessiócreixent.Amés,comque f(x) éscontínuai f (1) = m> 1,tenimque f(x)<x pera x ∈ (1 , 1) peraun cert > 0.Pertant, f t (0) ∉ (1 , 1) peratot t (jaquellavorsdecreixeria). Aixòvoldriadirquel’únicamaneraenquè f t (0) pottenirlímit1seria«saltar persobre»del’interval (1 , 1),ésadir,mitjançantun y< 1 talque f(y) = 1.Peròaquest y nopotexistir,perquèaleshores f (x)< 0enalgun puntentre y i1.

Acontinuacióveuremquel’equació f(x∗) = x∗ téunaúnicasolucióa l’interval [0, 1).Jasabemquehihad’haver,comamínim,unasolució,jaque f(0)> 0,i f(x)<x a (1 , 1) (aquíusemelteoremadeBoltzanopera f(x) x).

Processosderamificació,criticitatiautoorganització 43

Peraveurequelasolucióésúnica,suposemquen’hihadues,0 ≤ x1 <x2 < 1. Comque f(1) = 1,elteoremadeRolleimplicariaqueexisteixendospunts, y1, y2,talsque f (y1) = f (y2) = 1i x1 <y1 <x2 <y2 < 1.Peròaixòés impossiblejaque f >(x) ≥ 0a [0, 1],ipertant f (x) éscreixentiinjectiva a [0, 1].

Pertant,si Pext ≠ 1però f(Pext) = Pext,aleshores Pext hadeserl’única solucióde f(x∗) = x∗ a [0, 1)

Sivolguéssimsertotalmentrigorosos,hauríemdetractarperseparatalguns casospatològics,peròhoometremperquèsónsempresituacionssenseinterès real.Perexemple,elcas f(x) = x òbviamentnotéunaúnicasolució,ipertant lademostraciónos’hiaplica,peròcorresponaunasituaciógensinteressant: p1 = 1i pk = 0peratot k ≠ 1.Detotesmaneres,aquestscasospatològics semprecorresponenalcas p0 + p1 = 1;encascontrarilaconcavitatestà garantida.Mésdetallsengeneraldelademostraciód’aquestapèndixestroben al’articledeJolis[15].

A.3ElsnúmerosdeCatalan

ElsnúmerosdeCatalannodeuenelseunomacaphomenatgealnostrepaís, sinóalmatemàticfrancobelgadelsegle xix EugèneCharlesCatalan(totique, defet,ésraonablesuposarquevateniralgunavantpassatcatalà).Els«seus» númerospermetencomptarunagranvarietatd’objectes[32],incloent-hiels arbresambarrelqueapareixenenl’estudidelsprocessosderamificacióquan elnombredebranquesnoméspotser0,1o2.

Unarbredemida s espotdescompondreenl’arrel(quecorresponala generaciózero)ielsrestants s 1nodes.Aquests,alseutorn,espoden classificarsegonsaquinabrancapertanyin,ipertanttenimunaquantitat variabledenodesalaprimerabranca,0, 1,...,s 1ilarestaalasegona, s 1,s 2,..., 1, 0respectivament.Pertant,elnombred’arbresdemida s, Cs , compleixque,

, onprenem C0 = 1,jaquehihaunasolamaneradetenirmida0.D’aquíobtenim

ipertantaquestasenzillarecursiógeneratotselsnúmerosdeCatalan.Peral lectorcuriósheminclòslafigura12,onesmostrentotselspossiblesarbres ambarrelambnomésdeduesbranquespernode,finsalamida4.

C1 = 1

C2 = 2

C3 = 5

C4 = 14

Figura12: Totselsarbresambarrelambunmàximdeduesbranques pernode,finsalamida s = 4.Elnombred’arbresdemida s vedonat per Cs ,l’s-èsimnúmerodeCatalan.

Arabé,sielquebusquemésunformaexplícitapera Cs ,caldràdefinir-nela funciógeneratriu

h(x) = C0 + C1x + C2x2 +···= ∞ s=0 Cs xs .

Éspossibleobtenirunaexpressiópera h(x) fentservirnoméslespropietats delsnúmerosdeCatalan.Eltrucconsisteixacalcular elquadrat de h(x): h(x) 2 =

s=0 Cs+1xs+1 = h(x) C0 x ,

i,fentservirque C0 = 1,arribema

h(x) = 1 ±√1 4x 2x .

Unad’aquestesduesfuncions(segonselsignede ±)hadeser,pertant,la funciógeneratriudelsnúmerosdeCatalan.Elquepretenemaraés,simplement, recuperaraquestsnúmerosapartirdelasevafunciógeneratriu.Fentservirel desenvolupamentdeTaylorde √1 x alvoltantde x = 0isubstituinta h(x) ésfàcilveurequenoméselsignemenyspotcorrespondrealafunciógeneratriu, ipertant h(x) =

d’onobtenimlanostraprimeraexpressióexplícitaperalsnúmerosdeCatalan,

Sivolemunaexpressiómésagradable,podemferservirque

ialeshoresarribema

queésl’expressióméshabitualperalsnúmerosdeCatalan,vàlidaarapera tot s ≥ 0.

A.4Normalitzacióino-normalitzaciódeladistribuciódelamidatotal Passemaraail.lustrarcomladistribuciódelamidatotaldelprocés, P(S = s), estànormalitzadanomésenelscasossubcríticicrític.Peraladistribuciódel nombrededescendentsutilitzaremcomaexempleladistribucióbinomialamb k = 0,1i2.Alasecció2.9hemvistque

P(S = s) = 1 s + 1 2s s ps 1(1 p)s+1 amb s = 1, 2,...

FentservirlafunciógeneratriudelsnúmerosdeCatalan,éspossiblecomprovar queaquestaexpressiónomésestànormalitzadapera p ≤ 1/2,perònoper p> 1/2.Peraveure-ho,consideremnovamentlafunciógeneratriudelsnúmeros deCatalan,queacabemd’obteniralaseccióanteriordel’apèndix: h(x) = ∞ s=0 Cs xs = 1 √1 4x 2x

Aleshores,introduint q = 1 p, ∞ s=1 P(S = s) = q p ∞ s=1 Cs (pq)s = q p h(pq) 1 ,

ifentservirl’expressiópera h(x),resulta h(pq) = 1

Arapodemdistingirdoscasos.Elprimer, p ≤ 1/2,peralqual h(pq) 1 = 1 q 1 = p q = min{p,q} max{p,q} , iperalcascontrari, p ≥ 1/2,és h(pq) 1 = 1 p 1 = q p = min{p,q} max{p,q}

Conseqüentment,

1pera p ≤ 1/2 q p 2 pera p ≥ 1/2 ,

cosaqueensrecordaelnostreresultatsobrelaprobabilitatd’extincióperal casbinomial ∞

s=1 P(S = s) = Pext, expressióqueclaramentnoestànormalitzadapera p> 1/2.Tambééspossible arribaralsmateixosresultatsfentservir g(x),lafunciógeneratriudelamida totaldelapoblació,peròdeixemaquestcàlculcomaexerciciperallector.

Agraïments

VoldríemdedicaraquesttreballalpintoresccientíficPerBak,coincidintamb el25èaniversaridelasevainvenciódelacriticitatautoorganitzada,iamb el10èaniversaridelasevaprematuramort.Aquestarticleneix,enpart,de la LorenzLecture queundelsautorsvadonarl’any2011al FallMeeting de l’AmericanGeophysicalUnion.Enrelacióambaixò,donemlesgràciesaArmin Bunde,itambéaTomDavis,perpenjarlessevesnotessobreelsnúmerosde Catalanpúblicamentainternet,aAnnaDelucaiGunnarPruessnerpelsseus comentarisinteressants,aCecíliaM.Closperassistir-nosenl’ediciógràficaia JosepMariaFontiRosalbaGarcíaperl’ajutenlatraduccióalcatalà.Aquest treballhaestatfinançatpelMinisteriodeCienciayTecnología(FIS2009-09508), elMinisteriodeEconomíayCompetitividad(FIS2012-31324)ilaGeneralitatde Catalunya(2009-SGR-164),quetambéfinançaFrancesFont-Closatravésdela beca2012FI_B00422.

Referències

[1] Abramowitz,M;Stegun,I.A. (ed). Handbookofmathematicalfunctions withformulas,graphs,andmathematicaltables.Washington,DC:U.S. GovernmentPrintingOffice,1964.(NationalBureauofStandardsApplied MathematicsSeries;55)

[2] Alligood,K.T.;Sauer,T.D.;Yorke,J.A. Chaos.Anintroductiontodynamicalsystems.NovaYork:Springer-Verlag,1997.(TextbooksinMathematical Sciences)

[3] Aschwanden,M.J. «SOCsystemsinastrophysics».A: Aschwanden,M.J. (ed). Self-OrganizedCriticalitySystems.Berlín:OpenAcademicPress,2013, 439–478.

[4] Bak,P. Hownatureworks.Thescienceofself-organizedcriticality.Nova York:Copernicus,1996.

[5] Burroughs,S.M.;Tebbens,S.F. «Power-lawscalingandprobabilistic forecastingoftsunamirunupheights». PureAppl.Geophys.,162(2005), 331–342.

[6] Christensen,K.;Moloney,N.R. Complexityandcriticality.Londres:ImperialCollegePress,2005.(ImperialCollegePressAdvancedPhysicsTexts;1)

[7] Corral,A.;Font-Clos,F. «Criticalityandself-organizationinbranching processes:applicationtonaturalhazards».A: Aschwanden,M.J. (ed). Selforganizedcriticalitysystems.Berlín:OpenAcademicPress,2013,183–228.

[8] Corral,A.;Ossó,A.;Llebot,J.E. «Scalingoftropical-cyclonedissipation». NaturePhys.,6(2010),693–696.

[9] Freeman,M.P.;Watkins,N.W. «Theheavensinapileofsand». Science, 298(2002),979–980.

[10] Grimmett,G.R.;Stirzaker,D.R. Probabilityandrandomprocesses.3aed. NovaYork:OxfordUniversityPress,2001.

[11] Gutenberg,B.;Richter,C.F. «FrequencyofearthquakesinCalifornia». Bull.Seismol.Soc.Am.,34(1944),185–188.

[12] Harris,T.E. Thetheoryofbranchingprocesses.Berlín:Springer-Verlag, 1963.(DieGrundlehrenderMathematischenWissenschaften;119)

[13] Hawkins,D.;Ulam,S. «TheoryofmultiplicativeprocessesI».LANLreport, LA-171.

[14] Jensen,H.J. Self-organizedcriticality.Emergentcomplexbehaviorinphysicalandbiologicalsystems. Cambridge:CambridgeUniversityPress,1998. (CambridgeLectureNotesinPhysics;10)

[15] Jolis,M. «Desapareixeràelteucognom?». MATerialsMATemàtics,treball núm.4(2010),29p.

[16] Kagan,Y.Y. «Earthquakesizedistribution:Power-lawwithexponent β ≡ 1/2?» Tectonophys.,490(2010),103–114.

[17] Kanamori,H.;Brodsky,E.E. «Thephysicsofearthquakes». Rep.Progr. Phys.,67(8)(2004),1429–1496.

[18] Kanamori,H.;Mori,J. «Microscopicprocessesonafaultplaneandtheir implicationsforearthquakedynamics».A: Problemsingeophysicsforthe newmillennium.Bolònia:EditriceCompositori,2000,73–88.

[19] Malamud,B.D. «Tailsofnaturalhazards». Phys.World,17(8)(2004), 31–35.

[20] Malamud,B.D.;Millington,J.D.A.;Perry,G.L.W. «Characterizing wildfireregimesintheUnitedStates». Proc.Natl.Acad.Sci.USA,102(2005), 4694–4699.

[21] McClelland,L.;Simkin,T.;Summers,M.;Nielsen,E.;Stein,T.C. (ed.) Globalvolcanism1975–1985.EnglewoodCliffs:PrenticeHall,1989.

[22] Newman,M.E.J. «Powerlaws,ParetodistributionsandZipf’slaw». Cont. Phys.,46(2005),323–351.

[23] Otsuka,M. «Asimulationofearthquakeoccurrencepart2.Magnitudefrequencyrelationofearthquakes». Zisin,24(1971),215–227.[Enjaponès]

[24] Otsuka,M. «Achain-reaction-typesourcemodelasatooltointerpretthe magnitude-frequencyrelationofearthquakes». J.Phys.Earth,20(1972), 35–45.

[25] Otter,R. «Themultiplicativeprocess». Ann.Math.Statistics,20(1949), 206–224.

[26] Papoulis,A. Probability,randomvariables,andstochasticprocesses.2aed. NovaYork:McGraw-HillBookCo.,1984.(McGraw-HillSeriesinElectrical Engineering.CommunicationsandInformationTheory)

[27] Peters,O.;Deluca,A.;Corral,A.;Neelin,J.D.;Holloway,C.E. «Universalityofraineventsizedistributions». J.Stat.Mech.,P11030.

[28] Pruessner,G.;Peters,O. «Self-organizedcriticalityandabsorbingstates: LessonsfromtheIsingmodel». Phys.Rev.E,73(2006),025106(R).

[29] Ross,S.M. Afirstcourseinprobability.2aed.NovaYork:MacMillan PublishingCo.,1984.

[30] Saichev,A.;Helmstetter,A.;Sornette,D. «Power-lawdistributionsof offspringandgenerationnumbersinbranchingmodelsofearthquake triggering». PureAppl.Geophys.,162(2005),1113–1134.

[31] Spivak,M. Calculus.Berkeley,Califòrnia:PublishorPerish,Inc.,1980.

[32] Stanley,R.P. Enumerativecombinatorics.Vol.2.Cambridge:Cambridge UniversityPress,1999.(CambridgeStudiesinAdvancedMathematics;62)

[33] Ulam,S.M. Adventuresofamathematician.NovaYork:CharlesScribner’s Sons,1976.

[34] Watson,H.W.;Galton,F. «Ontheprobabilityoftheextinctionoffamilies». J.Anthropol.Inst.GreatBritain,4(1875),138–144.

Processosderamificació,criticitatiautoorganització 49

[35] Zapperi,S.;Lauritsen,K.B.;Stanley,H.E. «Self-organizedbranching processes:Mean-fieldtheoryforavalanches». Phys.Rev.Lett.,75(1995), 4071–4074.

CentredeRecercaMatemàticai

DepartamentdeMatemàtiquesdelaUAB EdificiC,CampusBellaterra UniversitatAutònomadeBarcelona 08193Bellaterra,Barcelona {acorral,fontclos}@crm.cat

ButlletídelaSocietatCatalanadeMatemàtiques Vol.29,núm.1,2014.Pàg.51–75. DOI:10.2436/20.2002.01.53

Comlesvarietatsinvariantsformenespiralsianells engalàxiesbarrades

MercèRomero-Gómez,PatriciaSánchez-MartíniJosepJ.Masdemont

Resum: L’espectacularitatdelesgalàxiesbarradesconsisteixnosolamentenla presènciadelabarra,allargadaenelcentredelagalàxia,sinótambéenelsbraços espiralsoanellsqueesdesenvolupenenlespartsexteriors.Nohihaunateoriaclara peralaformaciód’anellsi,finsfapoc,nomésn’hihaviaunaqueexplicaval’origendels braçosespiralsengalàxiesnobarrades.Enelsdarrersanyshemdesenvolupatunateoria basadaenelssistemesdinàmicsquerelacionaelsbraçosespiralsielsanellsambles varietatsinvariantshiperbòliquesassociadesaòrbitesperiòdiquesiquasiperiòdiques alvoltantdepuntsd’equilibricolinealsdelsistema.

Paraulesclau: sistemesdinàmics,varietatsinvariants,estructuraidinàmicadegalàxies.

ClassificacióMSC2010: 37D10,85A05.

1Introducció

Desdelstempsd’EdwinP.Hubble(1889–1953)quelesgalàxiesesclassifiquen segonslasevaforma,bàsicament,enel líptiquesiespirals.Idinslesespirals,en espiralsnormals(figura1esquerra),onlesespiralsesformendesdelcentrede lagalàxia,iespiralsbarrades(figura1dreta),onalcentredelagalàxiahihauna sobredensitatallargadaenformadecigaromésomenysel.lipsoïdal,anomenada barragalàctica,ilesespiralsesformenalfinaldelabarra.Actualmentsabem quealmenysel66%delesgalàxiesespiralssónbarrades(Sheth etal. [35]),la qualcosahaimpulsatelsastrònomsiteòricsaestudiar-nelescaracterístiques afons.Defet,lesgalàxiesbarradesnoescaracteritzennoméspertenirespirals sinóquemoltesd’aquestespresentenanellsenllocd’espirals(vegeulaprimera filadelafigura9).

Dinsdelesespiralsbarradesexisteixunasubclassificaciósegonssiels braçosespiralsestanmoltenrotllatsalabarraipresentenunnuclicentralmolt brillantosisónmésobertsielnuclicentralésmoltfeble.Sónlesgalàxiesde tipusprimerencidetipustardà,respectivament.

MercèRomero-Gómez,PatriciaSánchez-MartíniJosepJ.Masdemont

Figura1: Galàxiesespirals.Esquerra:Galàxiaespiralnormal(nobarrada)M74(cortesiaNASA).Dreta:GalàxiaespiralbarradaNGC1300 (cortesiaNASA,ESA,iTheHubbleHeritageTeamSTScI/AURA).

Pelquefaalsanells,unagalàxiaenpotpresentarmúltiplesidediferents tipussegonslaclassificaciómorfològica[8, 9, 38].Unanellintern, r ,properi encerclantlabarraianellsexternsambdiferentsorientacionsrespectelabarra imésaviatallargats.Sielsemieixmajordel’anellexternésperpendicularal semieixmajordelabarra,esdiuquelagalàxiatéunanelldetipus R1.Siaquest anellnoestàcomplets’anomenapseudoanelliesdenotaper R1.Sielsemieix majordel’anellésparal lelalsemieixmajordelabarra,esdiuquel’anellés detipus R2.Finalment,hihagalàxiesquepresentenelsdosanellsalavegada; aleshoresdiemquetenenunanell R1R2.Aquestaclassificaciólavarealitzar observacionalmentR.J.Buta[7]enelsanysvuitantaambunamostrademés de1000galàxies.MésendavantButamateixa[8]classificaunamostrademés de3500galàxiessegonselstipusd’anells,lasevaorientacióilasevamida.

Apartdeclassificarelsbraçosielsanellssegonslasevaforma,ésimportantsabertambécoms’hanformatenlesgalàxiesbarrades.Peraaixò s’hand’entendreelsmodelsactualsqueexpliquenelseuorigen.Finsfapoc, escreiaqueelsbraçosespiralserenonesdedensitatiqueelsanellsestan associatsaressonànciesdelabarraambeldiscdelagalàxia,ésadir,queles espiralsielsanellstenienunorigendiferent.Lateoriad’onesdedensitatlavan desenvoluparalsanyssetantaelsastrònomsLin&Shu([20, 21])i,agranstrets, descriuelsbraçosespiralscomunalleugerapertorbacióenformad’espiral moltenrotlladaenlacomponentgasosadeldisc.Quanlesestrellesielsnúvols degasqueviatgenpeldiscestrobenaquestapertorbació,esprodueixenels xocsqueoriginennovesestrelles.Segonsaquestateoria,elsbraçosespirals sónestructuresglobalsdellargavidaeneldisc,ésadir,laformadelbraçes mantéconstanteneltemps.Peròlateoriad’onesdedensitatnoexplicaquin éselmecanismegeneradord’aquestesones.

Pelquefaalsanells,escreuquel’anellinternestàassociatalafreqüència decorotació(puntsonlabarrailesestrellesdeldiscgirenalamateixavelocitat

Varietatsinvariantsformenespiralsianellsengalàxiesbarrades 53

angular)iquel’anellexternestàassociatalafreqüènciaexteriordeLindblad (puntsonlabarragiraduesvegadesmésràpidquelesestrellesdeldisc).En lesregionsdelagalàxiaonesprodueixenaquestesressonànciestéllocuna acumulaciód’estrellesqueformenanells(Schwarz[32,33,34]).

Enelsdarrersanys,hemdesenvolupatunanovateoria(vegeu[29, 30])que unificalaformaciódelsbraçosespiralsianellsengalàxiesbarrades.Aquesta teorianomésnecessital’existènciadelabarraperformaraquestesestructuresi esbasaenlesvarietatsinvariantshiperbòliquesassociadesaòrbitesperiòdiques iquasiperiòdiquesalvoltantdelspuntsd’equilibricolinealsdelsistemagalàctic (vegeu[29, 30]).Lesvarietatsinvariantsdefineixenl’esqueletprincipaldela dinàmicadetransportenelssistemesdinàmicsienelcampgalàctichitrobem unexemplebonicd’aplicació.

2Lamodelitzaciód’unagalàxiabarrada

Perestudiarladinàmicademovimentdinsd’unagalàxiacalbuscarunadistribuciódedensitatdemassaqueaproximibélasevalluminositat.Enlesgalàxies, aixòesfadescomponentenmodelsdedensitatlessevescomponentsprincipals: eldiscdelagalàxia,labarra,elbulbcentralil’haloquelaformen.D’aquestes components,eldisc,elbulbil’haloesmodelitzenmitjançantunadistribució axisimètrica,mentrequelabarraésunacomponentallargadaambunaforma aproximadad’el.lipsoide.Unpuntimportantquecalremarcarésquenoutilitzaremunadistribuciódedensitatespecíficaperalsbraçosespiralsoanells. Aquestesestructuressortirandemaneranaturaldeladinàmicadelsistema.

Enlaliteraturaespodentrobardistintesdistribucionsdedensitatque s’hanutilitzatperamodelarlesdiferentscomponentsd’unagalàxia.Llavors, apartirdeladistribuciódedensitat,espotcalcularelpotencialmitjançant l’equaciódePoisson: ∆Φ = 4πGρ,on G éslaconstantdegravitació, ρ ésla distribuciódedensitati Φ,elpotencialdesitjatcorresponent.

Percomençardescriuremelspotencialsilesdistribucionsdedensitatmés utilitzades.Eldiscdelagalàxiaescaracteritzaperserunadistribucióde densitatambunacaigudaexponencialdesdelcentredelagalàxiacapales partsmésexteriors.ElspotencialsméscomunssónelsdeMiyamoto-Nagai[26] ieldeKuz’min/Toomre(Kuz’min[19],Toomre[37]).L’expressiódelpotencial deMiyamoto-Nagaiéslasegüent:

on Md éslamassadeldisc, ad i bd sónleslongitudsd’escalaradialivertical, respectivament.ElpotencialdeKuz’min/Toomres’acostumaadonarentermes dedensitatsuperficial:

MercèRomero-Gómez,PatriciaSánchez-MartíniJosepJ.Masdemont

onelsparàmetres Vd i rd fixenlesescalesdelavelocitatielradi,respectivament.Elbulbcentral,juntamentambl’haloestel lar,esmodelautilitzantuna distribuciódedensitatdeltipus

on ρs i rs determinenlasevadensitatcentralil’anomenatfactord’escala, respectivament.Esferoidesambunaconcentracióaltatindranvalorsaltsde ρs ivalorspetitsde rs ,mentrequeelcontraripassaenelcasd’esferoidesamb unaconcentracióbaixa.Encaraqueintroduïmcomponentsaxisimètriques separades,ésimportantemfatitzaraquíqueelqueimportaéslacorbade rotaciódetotalacomponentaxisimètricainoladescomposiciódelacorba segonscadacomponent.Lacorbaderotació,moltempradapelsastrònoms,és lagràficadelmòduldelavelocitatqueportariaunaestrellaenunahipotètica òrbitacircularsituadaauncertradidelcentredelagalàxia.Seguintelmodel keplerià,lescorbesderotaciócreixendemaneralinealfinsauncertradii despréshauriendedecréixercom1/√r itendirasimptòticamentazerojaque lallumvisibledelagalàxiatambédecreix.Alapràctica,s’haobservatqueles corbesderotaciódegalàxiesexternesestornenplanes(vegeulafigura2)a radisgrans,encaraquelamatèriavisibles’hagiextingit(Bosma[6]).Aquestfet hainduïtelsastrònomsaintroduirlamatèriafoscaenelsseusmodels.Enel nostremodel,ajustemelsparàmetresquecomponenelpotencialdemanera quelaformadelacorbaderotaciós’assemblialescorbesobservades.

Figura2: CorbesderotacióperaunmodelambdiscdeKuz’min/Toomre, esferoideibarraFerrersambíndexdeconcentració n = 0(líniadiscontínua)i n = 1(líniacontínua).ElradiestàmesuratambKpcilavelocitat enkm/s.

Varietatsinvariantsformenespiralsianellsengalàxiesbarrades 55

Peramodelitzarlabarra,tanttrobempotencialsfísics,queprovenend’una distribuciódedensitat,commodelsadhoc,anomenatsaixíperquèesconstrueixenafiquesatisfacinunescertespropietatsosupleixinmancancesd’altres models.Elsmésutilitzatssónl’el lipsoidedeFerrers[15],comapotencialfísic, ielspotencialsdetipusquadrupol,comapotencialsadhoc.Ladistribucióde densitatassociadaalpotencialdeFerrerséslasegüent:

on m2 = x2/a2 + y 2/b2 + z2/b2,i a i b sónelssemieixosmajorimenorsde l’el.lipsoide,respectivament.Elparàmetre n mesuraelgraudeconcentració delabarrai ρ0 mesuralasevaconcentraciócentral.Aquestparàmetreestà relacionatamblamassadelabarramitjançantl’expressió Mb = 22n+3πab2ρ0Γ (n

on Γ éslafunciógammad’Euler.Elspotencialsdetipusquadrupols’obtenenen ferunadescomposiciódeFourierdetotelpotencialiretenirlacomponent m = 2.D’aquestamaneraelspotencialsdequadrupoltenenlaforma

Φb(r,θ) =−A(r) cos(2θ), (6)

on A(r) ésunafuncióquedepèndelradiideterminalamidail’amplituddela barra.Unexempleclàssicpodriaser

= Ab

(7)

on Rb determinalamidai Ab determinal’amplitud[14, 16].Enresum,doncs, elpotencialgalàcticglobalambelqualtreballaremvindràdonatperlasuperposiciód’aquestspotencials: Φ = Φd + Φh + Φb,on Φd éselpotencialdedisc, Φh represental’haloestel.lari Φb descriulabarra.

3Lesequacionsdemovimentiladinàmicaalvoltantdels puntsd’equilibri

Consideremunsistemadereferènciaonlabarradelagalàxiagiricomunsòlid rígidalvoltantdel’eixdeles z ambunavelocitatconstant,anomenadavelocitat delpatró, Ωp = (0, 0, Ωp).1 Lesequacionsdelmovimentenelsistemanoinercial onlabarraestàfixaestandescritesenformavectorialcoma(vegeu[5]) ¨r =−∇Φeff 2(Ωp × ˙r), (8)

1Lesvariablesennegretadenotenvectors.

56

MercèRomero-Gómez,PatriciaSánchez-MartíniJosepJ.Masdemont

on r = (x,y,z) éselvectorposició, Φeff = Φ 1 2 Ω2 p(x2 + y 2) éselpotencial efectiuenelsistemanoinerciali Φ = Φaxi + Φb éselpotencialtotaldelsistema, considerantque Φaxi comprènlescomponentsaxisimètriquesi Φb denotael potencialdebarradescritsenlasecció2.

Elspuntsd’equilibridelsistema (8) elstrobemallàons’anul.laelgradient delpotencialefectiu.Hihacincpuntsd’equilibri,denotatsper Li, i = 1 5, totslocalitzatsenelplagalàctic, z = 0,idistribuïtstalcomveiemalafigura3. L’estabilitatd’aquestspuntstindràunpaperimportantiladescriuremmés endavant.

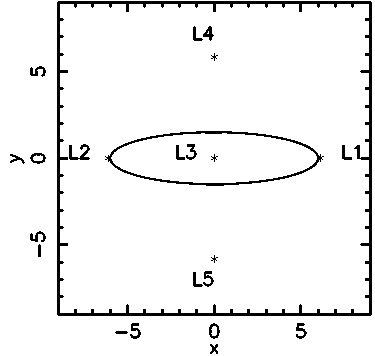
Figura3: Posiciódelspuntsd’equilibrienelplagalàctic.Elscincpunts deLagrangeestanassenyalatsambunasterisc,mentrequelalíniamés gruixudaassenyalalaposicióilallargadadelabarra.

Lesequacionsdelmoviment (8) tenentambéunaintegralprimera,anàloga al’energiaenelsistemainercial,anomenada energiadeJacobi o constantde Jacobi idefinidaper

Peraunvalord’energiafixat,aquestaequaciódefineixunasuperfíciedevelocitatzeroi,eltalld’aquestaambelplagalàctic, z = 0,defineixlescorbesde velocitatzero: Φeff (x,y) = EJ .Notemque,acausadelvalornonegatiuqueha detenirl’energiacinèticaa (9),elspunts (x,y) del’espaideconfiguracions talsque Φeff (x,y)>EJ constitueixenregionsprohibidesperalnivelld’energia considerat.Mentrequelesregionson Φeff (x,y) ≤ EJ sónpossiblesllocsde movimentques’anomenenregionsdeHill.

També,comqueladensitatassociadaalpotencials’esténmoltmésenel plagalàcticqueenladireccióvertical,icomqueelplagalàcticésinvariant,és comúrestringirl’estudidelproblemaenaquestpla.Alafigura4podeuveure lesregionsdeHillperalproblemaplasegonselsvalorsd’energiaconsiderats.

Varietatsinvariantsformenespiralsianellsengalàxiesbarrades 57

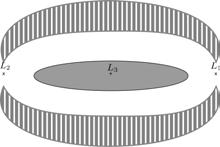
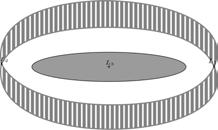
Figura4: RegionsdeHilla z = 0segonselnivelld’energia EJ considerat. Sidenotemper ELi l’energiadelspuntsd’equilibri L1 i L2 (EL1 = EL2 ), lestresfiguresensdescriuenlaformaiconnectivitatdelesregionsde Hillquetenimquan EJ >ELi , EJ = ELi i EJ <ELi dinselrangd’energiesdelnostreinterès.Depenentdesil’energiaésmésgranomés petitaquel’energiadelspuntsd’equilibri L1 i L2,lesregionsdeHill estanconstituïdesperunaoduescomponentsconnexesqueformen elcomplementarideleszonesprohibides,representadesperleszones ratllades.Arabé,jasiguienelcasdeduescomponentsconnexes,o enelcasd’unaúnicacomponentconnexa,enelnostrerangd’energies d’interèssempreesdelimitenduespossibleszonesdemoviment.Una d’interior,onhihalabarra(representadaperunael lipseengris),iuna altrad’exteriorqueenvoltarialesregionsprohibides.Enelcasonnomés tenimunaúnicacomponentconnexacomaregiódepossiblemoviment, lesregionsdeHillinterioriexteriorquedenconnectadesper«uncoll d’ampolla»al’entorndelaposiciódelspuntsd’equilibri L1 i L2 (vegeu tambélafigura6).

3.1Puntsd’equilibrilagrangiansidinàmicaalvoltantseu Talcomveiemalafigura3,dosdelspuntsd’equilibri,elsquedenotemper L1 i L2,estansituatsalllargdelsemieixmajordelabarra(queenaquestarticle consideremqueestrobadamuntl’eix x)isóndeltipuscentre × sella.Alcentre delagalàxia,iorigendelnostresistemadecoordenades,hitrobemelpunt L3, mentrequealllargdelsemieixmenordelabarra(damuntdel’eix y ioposats ensigne)hihaelspunts L4 i L5.Elstresdarrerspuntssónlinealmentestables idetipuscentre × centre.Notemtambél’analogiad’aquestspunts,anomenats puntsdeLagrange,ambelsd’altresmodelscomelproblemarestringitdetres cossos(vegeu[36]).

Associadaacadacentredecadaund’aquestspuntsd’equilibrihihauna famíliad’òrbitesperiòdiques,itambéòrbitesquasiperiòdiquesencasdetenir mésd’unacomponentcentral.Lesòrbitesalvoltantdelpuntd’equilibri L3 han estatbenestudiadesalaliteratura.Aquestesòrbitessónestablesperaunrang grand’energiesiperaixòesconsideraquepodenatraparmatèriaalvoltant seu.D’aquestamaneraescaracteritzenperformarl’esqueletdelabarra(vegeu lafigura5ielstreballsdeContopoulos&Papayannopoulos[13],Pfenniger[28], Patsis,Skokos,Athanassoula[27],Contopoulos[12],percitar-nealguns).

MercèRomero-Gómez,PatriciaSánchez-MartíniJosepJ.Masdemont

Figura5: Alafiguradel’esquerraesrepresentenunconjuntd’òrbites periòdiquesestablesalvoltantdelpunt L3 (figura7adePatsis,Skokos& Athanassoula[27]).Enaquestcas,elsemieixmajordelabarracoincideix ambl’eixdeles y.Alafiguradeladretaesmostralabarradela galàxiaNGC4314extretadeDigitalSkySurvey.

Lesòrbitesalvoltantde L4 i L5 sóntambélinealmentestablesis’acostumen aanomenaròrbites banana,peròlasevaformanorepresentacapcaracterística delagalàxia[27].Lesòrbitesalvoltantdelspunts L1 i L2 sóninestablesi,per aquestfet,nopodenatraparmatèriaalseuvoltantdurantllargsperíodesde temps.Ésperaixòquenos’havienestudiatmaiambprofunditatfinsalstreballs quehemdesenvolupata[29, 30, 31],ontambéincloeml’anàlisidelpaperque exerceixenlessevesvarietatsinvariants.

3.2Elpaperdelesvarietatsinvariants

Denotemper X = (x,y, ˙ x, ˙ y) unestatdelnostremodelplaiper Ψt (X) l’òrbita que,pera t = 0,tél’estat X (Ψ0(X) = X).Comésbensabut,donadaunaòrbita periòdica γi enunentornde L1 ode L2,onlafamíliaésinestable,hitenim associadeslessevesvarietatsestableiinestablequeesdefineixenper

W s γi = X ∈ R4 | lim t→∞

0 , onladoblebarradenotadistànciaeuclidianaal’espaidefase.Ésadir,quela varietatinvariantestable(respectivament,inestable)estàformadapelconjunt d’òrbitesasimptòtiquesquetendeixenal’òrbitaperiòdica γi quaneltemps tendeixamésinfinit(respectivament,amenysinfinit).

Lesòrbitesde W s γi i W u γi tenenlamateixaenergiaquel’òrbitaperiòdica γi i, pertant,pertanyenalamateixavarietatenergètica3-dimensionalqueconté γi.A més,topològicament, W s γi i W u γi espodendescriurecomacilindres2-dimensionalsqueformen,peracadavarietat,duesbranquesqueestrobenal’òrbita

Varietatsinvariantsformenespiralsianellsengalàxiesbarrades 59

periòdicad’unamanerasimilaralcomportamentd’unpuntdesella(enaquest caselpuntésuncercle S 1),talcomesveualafigura6.Notemquepera cadaparelldebranquesunaesdirigeix,oprové,delacomponentinteriora lacorbadevelocitatzero,mentrequel’altrahofarespectedelacomponent exterior.També,dinselnivelld’energia,aquestscilindresseparendiferents comportamentsdepenentdesiunestatestrobaadins,aforaoaldamuntseu, talcomespotveurealstreballsiniciatsperConleyperalproblemarestringit (vegeu[11,17,18]).

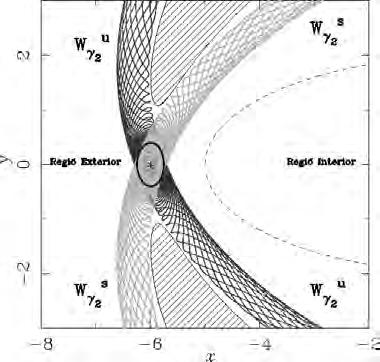
Figura6: Varietatsinvariantsestableiinestabled’unaòrbitaperiòdica alvoltantdelpunt L2.Engrisclar,lesduesbranquesdelavarietatinvariantestable, W s γi ,iengrismésfosc,lesduesbranquesdelavarietat invariantinestable, W u γi .Lesregionsprohibidesesrepresentenperles zonesratlladesmentrequelalíniadiscontínuadelaregióinteriorassenyalalaposiciódelabarrailacorbanegraalvoltantdelpuntd’equilibri represental’òrbitaperiòdica, γi.Lescomponentsdinàmiquesesfaran visiblesenunagalàxiaencasquelessevesòrbitescontinguinestrelles.

Unabonamaneradevisualitzarientendreaquestesvarietats3-dimensionals éspermitjàdeseccionsdePoincaré.Enelnostrecas,prenemlasuperfíciede secció S definidaper y = 0, x> 0amb y< 0.Ésadir,consideremlesòrbites entallarlapartpositivadel’eix x amblacomponentdevelocitat y negativa.

Enaquestasecció S consideraremlesinterseccionsdelesvarietats W s γ2 i W u γ2 .Sortintdel’òrbitaperiòdica γ2 iintegranttempsendavantpera W u γ2 (resp.tempsenrerepera W s γ2 )obtenimelprimertalldelavarietatamb S,que anomenem W u,1 γ2 (resp. W s,1 γ2 ).

Talcomveiemalafigura7,onrepresentemlaprojecció (x, x) de W u,1 γ2 i de W s,1 γ2 dinsde S, W u,1 γ2 i W s,1 γ2 sónduescorbestancades.Éstambéimportant

MercèRomero-Gómez,PatriciaSánchez-MartíniJosepJ.Masdemont

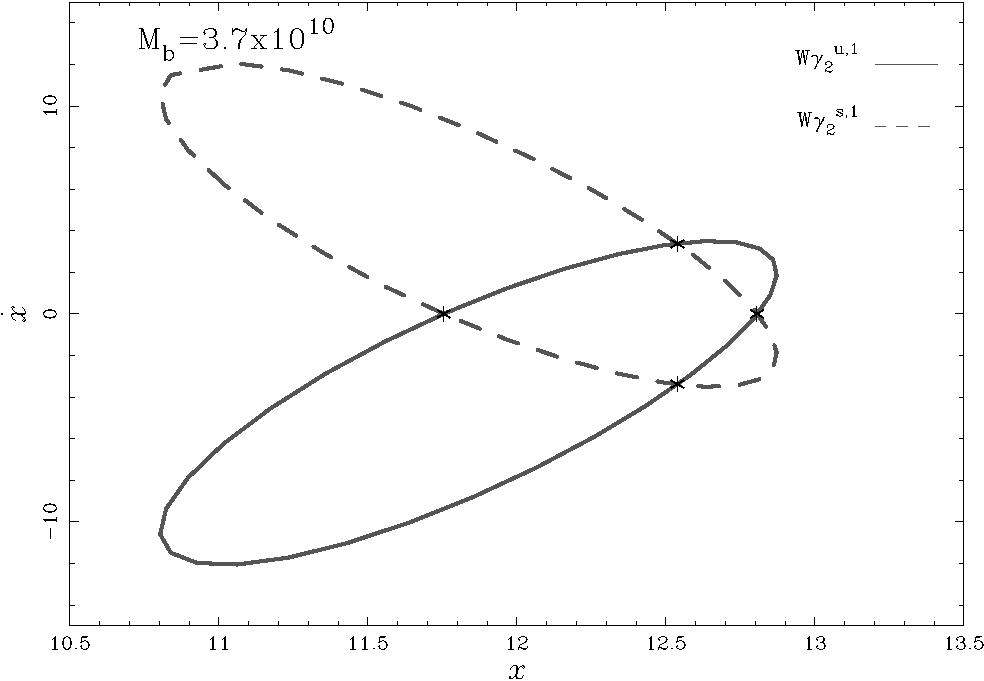
Figura7: Talldelesvarietatsinvariantsestableiinestabled’unaòrbita periòdicaalvoltantdelpunt L2 amblasecció S.Enlíniadiscontínua,el primertalldelabrancadelavarietatinvariantestable, W s γ2 ,ienlínia contínua,elprimertalldelabrancadelavarietatinvariantinestable, W u γ2 . Elspuntsmarcatsambunasterisccorresponenaòrbiteshomoclíniques.

notarqueunaparella (x, x) a S representaunaòrbitademaneraúnicaencas quel’energiaestiguifixada,jaquel’estat (x,y, x, y) escompletaamb y = 0 ilacoordenada y< 0s’obtéimposantlarestriccióquel’estatpertanyiala varietatdenivelld’energiadonat.

Arribatsaaquestpuntenscalrecordaralgunsconceptespelquefaaòrbites asimptòtiquestempsendavantitempsenrerealavegada:unaòrbita ψ esdiu queéshomoclínicasi ψ ∈ W u γi ∩ W s γi , i = 1, 2.Anàlogamentesdiuque ψ és heteroclínicasi ψ ∈ W u γi ∩ W s γj , i,j = 1, 2, i = j.Tenim,pertant,queunpuntde W u,1 γ2 ∩ W s,1 γ2 representatalaprojecció (x, x) de S escorresponambunaòrbita homoclínica.Al’exempledelafigura7hihaquatrepuntsperò,comésnatural, laformaiposiciórelativade W u,1 γ2 i W s,1 γ2 variadepenentdel’energiaidelmodel galàcticconsideratiipodentallar-seono.

Lesinterseccions,olamancad’interseccions,devarietatsestablesiinestablesdeterminenl’esqueletfonamentaldeladinàmicaiclassifiquen,d’alguna manera,conjuntsdetrajectòriesatenentalseucomportamentpassatifutur, talcomvaintuirPoincaréidesprésSmaleimoltsaltresvanformalitzariestudiar.Enuncontextsemblantalqueensocupaespodentrobardescripcionsi anàlisisdetalladesa[18,22,25]peralcasdelproblemapla,ia[17]peralcas delproblemaespaial.Però,pelquefaal’aplicacióconcretadel’exempleque representemalafigura7,referital’estudideformaciódebraçosianellsen galàxiesbarrades,nomésnotaremelsfetssegüents:

• Talcomhemdit,elspuntsde S queestrobendamuntde W s,1 γ2 ode W u,1 γ2 corresponenaòrbitesasimptòtiquesa γ2 jasiguitempsendavantotemps enrere.

Varietatsinvariantsformenespiralsianellsengalàxiesbarrades 61

• Elspuntsde S queestrobenal’interiordelacorba W s,1 γ2 escorresponen aòrbitesdinsdelcilindre W s γ2 que,tempsendavant,passaranpel«coll d’ampolla»quehihaentrelesregionsdeHilldelacorbadevelocitatzero propde γ2 itransitaran,d’aquestamanera,delaregiògalàcticaexteriora lainterior,onestrobalabarra.

• Elspuntsde S queestrobenal’exteriordelacorba W s,1 γ2 escorresponen ambòrbitesforadelcilindre W s γ2 lesquals,tempsendavant,laprimera vegadaqueestrobinapropdelmateix«colld’ampolla»notransitaran sinóqueromandranalaregióexterior.

• Peralspuntsde S quehihaalesregionsinterioroexterioralacorba W u γ2 elcomportamentéstotalmentanàlegperòconsideranteltempsenrere. Ésadir,demanerarespectiva,obévénendetransitarpelcolld’ampolla, obéladarreravegadaquehanpassatapropdelcolld’ampollanohan transitat.

Atenentaaquestsfets,diferentsregionsde S quedenclassificadessegonsel seucomportamentpassatifutur.Ésclarque«perveure»mésendavantenel futur,omésenrereenelpassat,caldriaconsiderarmésinterseccions(W s,j γ2 , W s,j γ2 , j = 2, 3,... )itambéelpaperde W s,j γ1 , W s,j γ1 ,(j = 1, 2,... )lesqualsespoden intersecarentresi,itambéamblesde γ2,laqualcosadónacomportaments homoclínicsoheteroclínicscomplexos.

Alafigura8representemalgunsexemplespossibles:alapart(a)tenim unaòrbitahomoclínicaa γ2 iquepodriacorrespondreaalgundelspunts d’intersecciódelafigura7.L’òrbitasurtde γ2,notransitaquanestàpropde L1 (ésadir,estariaforad’unacorba W s,1 γ1 calculadaperexempledamuntd’una seccióposadaa x = 0, y> 0)idesprésdeferlavoltatornaa γ2.Alapart(b) tenimunaòrbitaheteroclínicaquesurtdel’òrbitadeLyapunovapropde L2 i arribaalaLyapunovapropde L1 iquepodriaestarcalculadaintersecantles corresponentsvarietatsenunaseccióposadaa x = 0.Finalmentalapart(c) tenimunaòrbitadetrànsitque,d’estarpropdelabarraalaregióinterior, passapelcolld’ampollaisurtalaregióexteriorenespiral.

Aqueststrestipusd’òrbitesesdevenenl’esqueletdelesestructuresd’anells iespiralsobservadesenlesgalàxies.Enelcasqueelsparàmetresdelmodel siguinelsadequats,elsistemapresentaràòrbitesheteroclíniquesilamorfologia globalresultantseràlad’anelldetipus rR1,ésadir,unagalàxiaambelsdos anells r i R1 presentsalavegada;enelcasqueelsparàmetresdelmodelfacin queelsistemapresentiòrbiteshomoclíniques,lamorfologiaglobalseràd’anell detipus R1R2.Finalment,peracertsparàmetres,elsistemanoméstéòrbites detipustrànsiti,aleshores,depenentdel’angledecargolamentdelavarietat invariant,lamorfologiaglobalseràd’anell R2 odebraçosespirals.Alasecció següentanalitzemquinssónelsparàmetresquediferencienunamorfologia d’unaaltra.

MercèRomero-Gómez,PatriciaSánchez-MartíniJosepJ.Masdemont

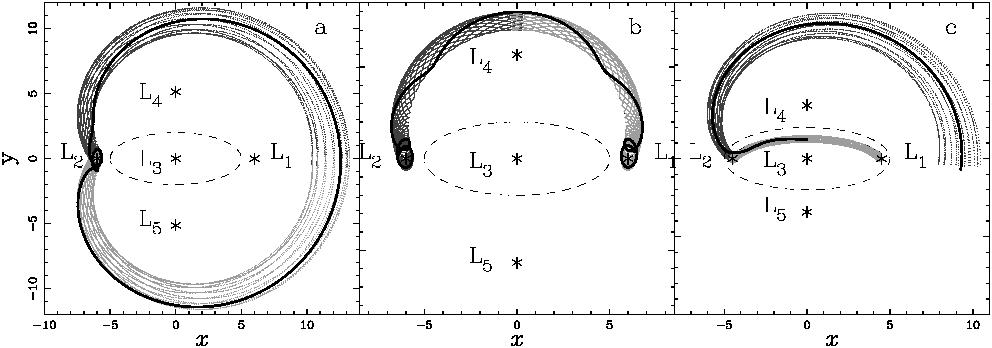
Figura8: Varietatsinvariantsestableiinestabled’unaòrbitaperiòdica alvoltantdelspuntsd’equilibri L1 i L2.Engrisclarrepresentemlesvarietatsinvariantsestables, W s γi ,iengrismésfosc,lesvarietatsinvariants inestables, W u γi .Elsasteriscsmarquenlaposiciódelspuntsd’equilibrii leslíniesdiscontínuesenformad’el.lipseassenyalenlaformadelabarra. Lesòrbitesmésgruixudesennegredecadaquadreescorresponenamb òrbites:(a)homoclíniques,(b)heteroclíniquesi(c)detrànsit.

3.3Estudimorfològicenfunciódelsparàmetresgalàctics

Enaquestaseccióvolemestudiarcomdepènelllocgeomètricdelesvarietats invariants,ipertant,l’existènciad’òrbiteshomoclíniques,heteroclíniquesi detrànsit,delsparàmetresdelabarra.Consideraremduesfamíliesdemodels lleugeramentdiferents.Elprimer,queanomenaremmodelA,tindràundiscde Kuz’min/Toomre (2),unesferoide (3) iunabarradeFerrers (4).Elsegon,que anomenemmodelB,tindràlamateixacomponentaxisimètricaqueelmodelAi unabarraquadrupol (6).ElsmodelsdetipusAtenenquatreparàmetreslliures principals:lasevaconcentraciócentral ρc ;elquocientdelssemieixosdelabarra, a/b;lamassadelabarra, Mb (5),ilavelocitatangular, Ωp (parametritzada mitjançantelradideLagrange2 rL).A[29]vàremcomprovarquenomésla massadelabarraielradideLagrangetenenunainfluènciaenregionsexteriors, ipertant,limiteml’estudiaaquestsdosparàmetres.PelquefaalmodelB, noméstédosparàmetreslliuresquesónl’amplituddelpotencialdebarra, Ab, ielradideLagrange.Larestadeparàmetresdelsmodelsrestaranfixats.Pera cadascundelsmodels,construïmunagraellaonencadaquadreconsiderem unsvalorsrellevantsperaaquestespaideparàmetres: (rL,Mb) peralmodelA i (rL,Ab) peralmodelB(vegeuelspanellssuperioriinferior,respectivament, delafigura10).Cadafilacorresponaunvalordelaforçadelabarraicada columna,aunvalordelavelocitatangulardelpatró.

2 Definim rL comladistànciaentreelspuntsd’equilibri L1 i L2 alcentredelagalàxia.Aquesta distànciaestàrelacionadaamblavelocitatangulardelpatrómitjançant: Ω2 p = rL

Φ(r)

rL , (10) on Φ(r) éselpotencialenelplagalàctic.

Varietatsinvariantsformenespiralsianellsengalàxiesbarrades 63

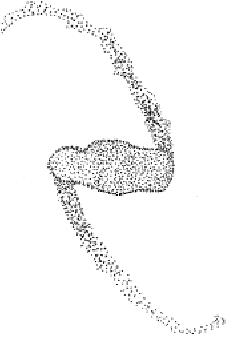
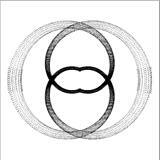
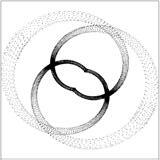
NGC 1365NGC2665NGC2935NGC1079

Braçosespirals

R1

R2

R1R2

Figura9: Morfologiesd’anellsidebraçosespirals.Aladarrerafila tenimquatregalàxiestipus:espiral, R1, R2 i R1R2.Laprimerafilamostra dibuixosesquemàticsd’aqueststipusrealitzatsperButaiCrocker[10]. Alesfilescentralsveiemcomlesvarietatsinvariantspodenreproduir morfologiessemblants.Concretamentalasegonafilarepresentemles varietatsalplaialatercerafila,unaprojeccióadequada.

64 MercèRomero-Gómez,PatriciaSánchez-MartíniJosepJ.Masdemont

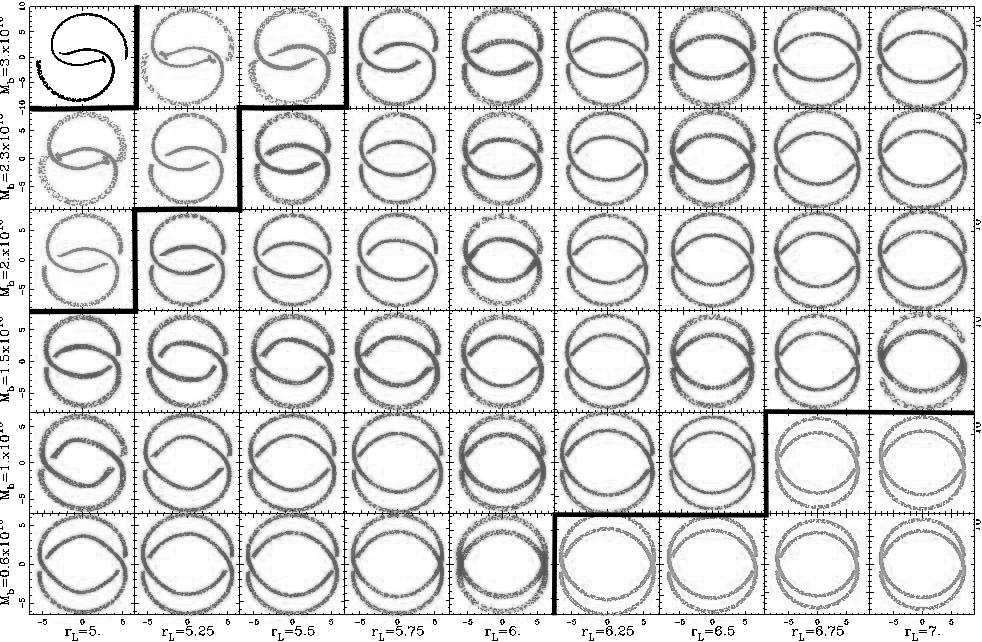
Figura10: Morfologiesenfunciódelsparàmetresprincipalsdelamodelització: rL i Mb peralmodelA(quadresuperior)i rL i Ab peralmodelB (quadreinferior).Lestransicionsestandescriteseneltext.

Varietatsinvariantsformenespiralsianellsengalàxiesbarrades 65

Tenintencomptesicadacaspresentaòrbiteshomoclíniques,heteroclíniques odetrànsit,hemtrobaticlassificatlesmorfologiesdelesbranquesexteriorsde lesvarietatsenespirals,anells R1,anells R2 ianells R1R2.Atenentalsquadres delafigura10obtenimunaclaratendènciaenelpla(força,velocitatangular). Diferentsmorfologiesestanagrupadesendiferentspartsdelplaformant, demaneraaproximada,bandesdiagonals.Així,enelmodelAobservemuna transició,viaanells R1,desdelagalàxiaespiraldel’extremsuperioresquerraa l’extreminferiordret,onelsbraçosexteriorsformenpràcticamentunsolanell circular.EnelmodelBs’observenduesbandesdegalàxiesespiralsseparades perunabandad’anells R2 i R1R2 ,mentrequealapartinferiord’aquestafigura hihaunatranscióenverselsanells R1 deladarrerafila.

Notemtambéladiferènciaentreelsdosmodels.ElmodelAésmésfísici aquestfetensrestringeixelrangdevalorsperalamassadelabarra.Encanvi, elmodelBésunmodeladhocienspermetampliarelrangdelparàmetre d’amplituddelabarra.Ladiferènciaentreelsdosquadresensindicaqueel rangdemassadelmodelAcorresponaunpetitrangdelparàmetre Ab del modelB,entre726i2420.L’exploraciódelparàmetre Ab enelmodelBreflecteix lesdiferentsmorfologiesdelesvarietatsinvariants.

4Comparacióamblateoriadelesonesdedensitat

Comhemapuntatenlaintroducció,enlateoriad’onesdedensitatelsbraços espiralsesformenacausadepetitespertorbacionsenlacomponentgasosa. Segonsaquestateoria,elsnúvolsdegasquegireneneldiscestrobenaquesta pertorbació,escreaunasobredensitatquefaqueesprodueixinxocsiformació estel.larilesestrellesformadesevolucionenicontinuengiranteneldisc.Per tant,lesestrellestravessenelbraçespiraltransversalment.Elsentitdecirculació delesestrellesésunadelesdiferènciesmésimportantsentrelesduesteories. Enlateoriadelesvarietatsinvariants,lespartículescirculenperdinselstubs delesvarietats,ésadir,resseguintelbraçespiral.Enlafigura11veiemquina éslacirculaciónaturalenunmodeldevarietatsinvariants.Partintdelapart internadelagalàxia,lespartículesseguirienlabrancainteriordelavarietat estable,s’acostarienalpuntd’equilibriiescapariencapenforaseguintlabranca exteriordelavarietatinestable.Aquestacirculació,però,portad’algunamanera implícitelfetquelespartículesdelsbraçosprovenendelcentredelagalàxiai quelabarrafadereservaperalsbraços.Tenintencomptequelessimulacions de N-cossoshandemostratquelabarranoésunaestructuraestablesinó queevolucionaeneltempsallargant-seifrenant-se(e.g.Widrow etal. [39] ireferènciesal’interior),semblaquealallargas’hauriendeveuregalàxies onlabarrabrillimenysqueelsbraços,iaquestfetnos’observa.Mitjançant simulacionsdepartículestest,hempogutcomprovarquenototeslespartícules quepoblenelsbraçosespiralsprovenendelcentredelabarra.Amesuraquela barraesvaformanteneldiscdelagalàxia,lesvarietatstambévanapareixenti partículesamblaposicióivelocitatadequadaqueinicialmentestavenenles partsexternesdeldisc,arasegueixenlesvarietats.

MercèRomero-Gómez,PatriciaSánchez-MartíniJosepJ.Masdemont

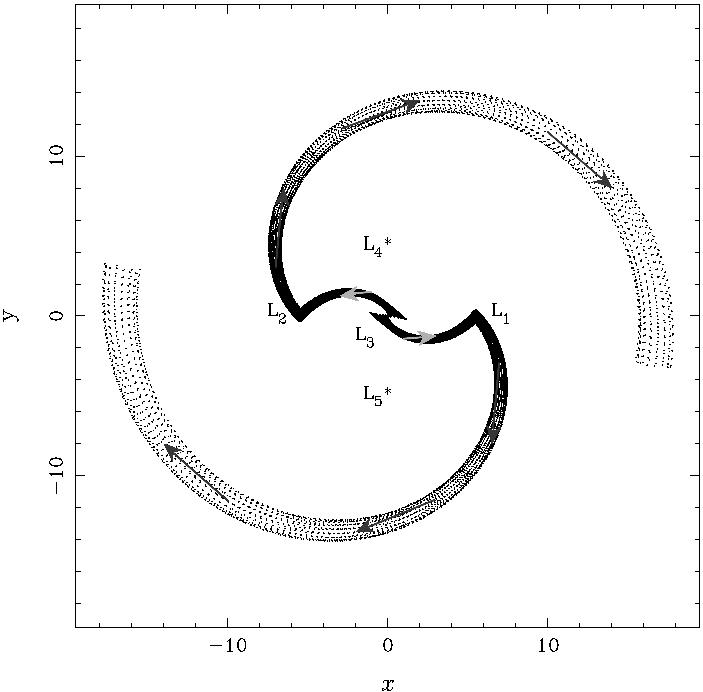
Figura11: Sentitdecirculaciódelespartículesalllargdelesvarietats invariants.Lesvarietatsestablesesdisposenalapartinteriordelafigura ilesinestablesalapartexterior.

Unaaltradiferènciaambelsbraçosoriginatsmitjançantonesdedensitatfa referènciaalamorfologia.Lateoriadelesonesdedensitatconsisteix,agrans trets,apertorbarladinàmicadeldiscmitjançantunafuncióque,descomposta ensèriedeFourier,recullelmode m = 2itéunllocgeomètricimposatque, demaneraestàndard,ésd’unaformalogarítmica.Ésadir,elsbraçosespirals generatsperlateoriad’onesdedensitattenenunaformalogarítmica,imposada perlespròpiesequacions.Aquestaformas’hadeduïtaforçadedeprojectaruna mostradegalàxiesespiralsnormalsicomprovarquelamajoriadelesespirals espodenajustarmitjançantunafunciólogarítmica(vegeu[23]).Aquestestudi, però,nomésincloulesespiralsnormals,sensebarra.Engalàxiesbarrades s’apreciacoml’espiralnoespiralacapenforasinóques’expandeixfinsaassolir unradimàximidesprésretornaalaregiódelabarra,comperexemplea lagalàxiaNGC1365representadaalafigura12.Aquestfenomentambéel podenreproduirlesvarietatsinvariants.Observemlamateixafigura12,onen elquadredel’esquerraesdetectalasobredensitatdelsbraçosenlagalàxia NGC1365ieneldeladreta,lasobreposemamblesvarietatsinvariantsd’un modeldetipusBamb rL = 5i Ab = 1210,enelpla(ln(r),θ).Enaquestpla,un braçlogarítmicesrepresentariaambunalíniarecta.

Tambéhihacertsparàmetresdelsmodelsquepermetenquelesvarietats invariantstinguinunaformaaproximadamentlogarítmica.Estudiemcomvaria l’angled’enrotllamentdelsbraçosobtingutsmitjançantvarietatsinvariantsen funciódelaforçadelabarra,expressadacomaquocientdelaforçatangencial delabarraenelradideLagrangeilaforçaradialdelacomponentaxisimètrica. Encadamodellaformadelesvarietatsinvariantss’haajustataunaespiral logarítmica.Elresultatreprodueixl’obtingutperSchwarz[33]mitjançantsimulacionsdinàmiquesambpartículestestitambélesdadesobservacionals obtingudesperMartínez-García[24]apartird’unamostradegalàxiesexternes idonadaalafigura13.

Varietatsinvariantsformenespiralsianellsengalàxiesbarrades

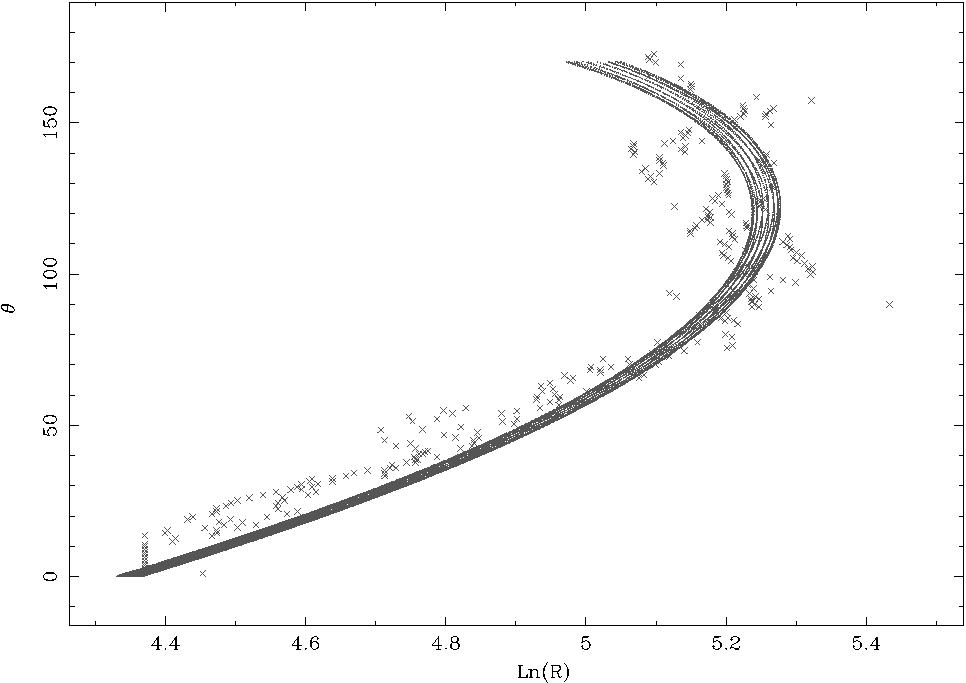
Figura12: Enelpanelldel’esquerraesrepresentalagalàxiaNGC1365 i,marcatsambpunts,lasobredensitatdonadapelsbraçosespirals.En elpanelldeladreta,sobreposemelspuntscorresponentsalafigura del’esquerraamblesvarietatsinvariantscorresponentalmodelBamb rL = 5i Ab = 1210,enelpla(ln(r),θ).

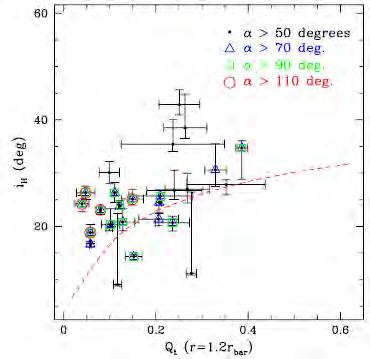
Figura13: Variaciódel’angled’enrotllamentenfunciódelaforçatangencialdelabarraavaluadaenelpuntdeLagrange L1 peraunamostra degalàxiesdescritaen[24].Lalíniadiscontínuaindicalaprediccióde lesvarietatsinvariants.

MercèRomero-Gómez,PatriciaSánchez-MartíniJosepJ.Masdemont

5Comparacionsobservacionalsambgalàxiesexternes

Enlasèried’articles[29, 30, 31],fetsamblacol laboraciód’investigadorsde l’ObservatorideMarsella,hemaplicatlateoriadelssistemesdinàmicsielcàlcul devarietatsinvariantsaunpotencialgalàctic,totcomprovantqueaquestes tenenl’estructuraadequadaperdescriureelsbraçosielsanellsdegalàxies barrades.Aixímateixhemestudiatquinésl’efectedelgasacumulatenaquestes òrbitesiquinaéslacinemàticainduïda(vegeu[1,2,3]).

Laformadelsanellsesmanténonomésperalsmodelsbarratsestàndards, sinótambéquanlabarraésdetipus«ansae».Aquesttipusdebarraescaracteritzapertenirunessobredensitatsdeformamésomenysesfèricaalcapdavallde labarra,iperquèobservacionalmentsemblennansesenganxadesalsextrems delabarra.Podemmodelitzarlesbarresnansaafegintalpotencialdelabarra dosdiscsidèntics,cadascuncentratenlaposiciódelpuntsdeLagrange L1 i L2. Aixòfaquecanviïlatopologiadelescorbesdepotencialisoefectiudelamanera següent:elspunts L1 i L2 esdevenenmínimsdelpotenciald’onesbifurquen dospuntsdesella,unacadacostatdelmínim.Elsanomenem Li j i Lo j (j = 1, 2) (vegeuelquadresuperioresquerredelafigura14).Tenimllavorsquealvoltant d’aquestspuntsd’equilibriexisteixunafamíliainestabled’òrbitesperiòdiques amblesvarietatsinvariantscorresponents.Ladinàmicaquedescriuenila sevaformaglobal,representadaalarestadequadresdelafigura14,ésmés complexa,peròespotdescriureamblesmateixesideesquehempresentatala secció3.

Pelquefaalaformadelsanells,hemcalculat,peratotalamostrade modelsconsiderats,quinaéslarelaciódelssemieixosdelsanellsqueserveix alsastrònomsperalessevesclassificacions: do/Do,on do éselsemieixmenor del’anellexteriori Do éselsemieixmajordel’anellexterior,aixícomel quocientdelssemieixosdel’anellinterior, di/Di,definitdemaneraanàloga.En lamostradegalàxiesambanellsdelcatàlegdeButa[8],aquestsvalorsestan entre0.82 ± 0.07i0.81 ± 0.06,respectivament.Alafigura15elsrepresentem segonslaforçadelabarra,descritaenfunciódelaforçatangencial,coms’ha mencionatanteriorment.L’escaladegrisosielssímbolsdelspuntsrepresenten lesmorfologies(R1 engrisfosci R1 engrismésclar)ielsdiferentsmodels utilitzatsenl’estudi(rombes,modelA,iasteriscs,modelB).Notemlaforta correlacióentreelquocientdelssemieixosilaforçadelabarra:commés fortaéslabarra,mésexcèntricssónelsanells.Notemtambéquepràcticament totselsvalorsformenpartdelazonaombrejadaquecoincideixambelrang observacionalquehemmencionat.

Unaltrefetobservacionalquecaltenirencompteésquelamajorpartdels braçosespiralsestanformatspergasi,pertant,ésnaturalpreguntar-sequin seràl’efectedelgasenlesòrbitesatrapadesperlesvarietatsinvariants.Per estudiaraquestefecte,ensremetemaltreballdeSchwarz[33],ons’utilitzensimulacionsdepartículestest.Encertesposicionsaleatòrieseneldiscessimulael xocdepartículesfentperdreunacertaquantitatd’energiacinèticaalapartícula. Enelsnostrestreballs[2, 3]utilitzemunatècnicasemblant:prenemcondicions

Varietatsinvariantsformenespiralsianellsengalàxiesbarrades 69

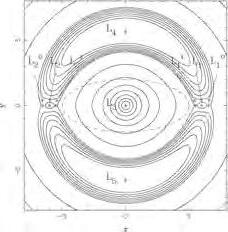
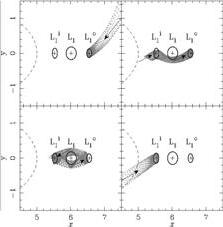
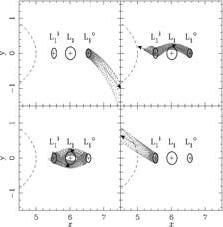
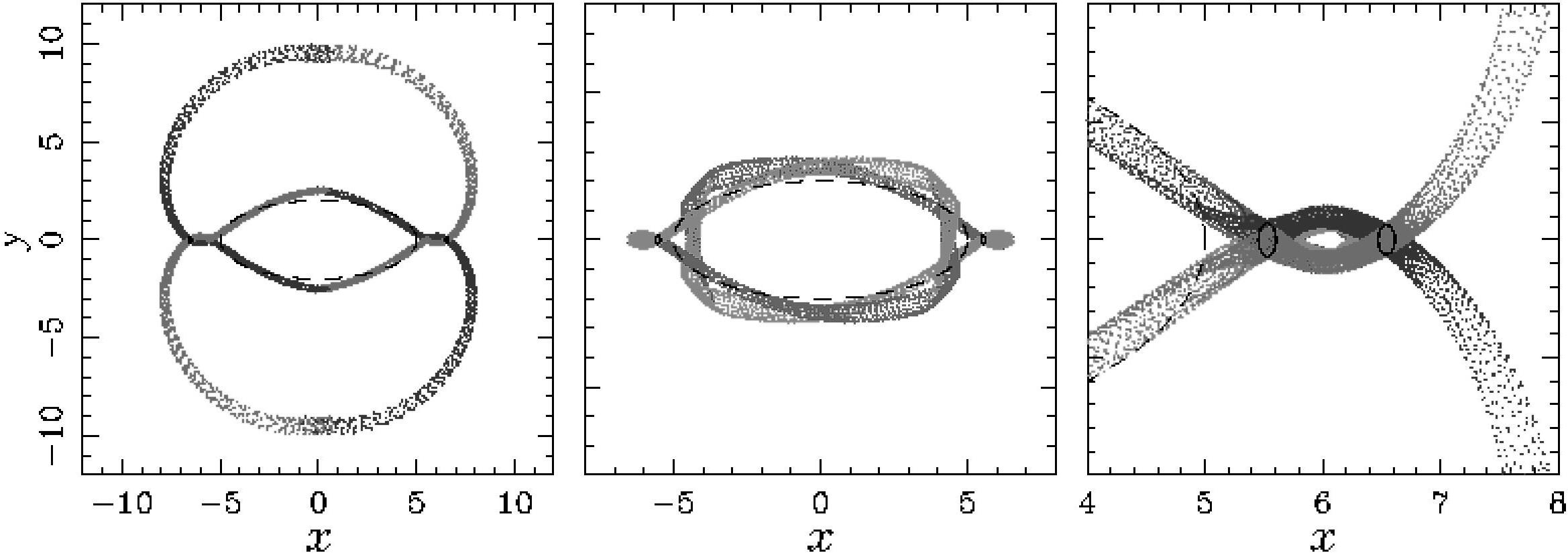
Figura14: Dinàmicaalvoltantdelspuntsd’equilibrialfinaldelesbarra nansa.Superioresquerra:Corbesdepotencialisoefectiuiposiciódels puntsd’equilibri.Superiorcentreidreta:Òrbitesperiòdiquesivarietats invariantsalvoltantdelsnouspuntssella Li 1 i Lo 1 .Inferioresquerra:les varietatsassociadesalpunts Lo 1 i Lo 2 mantenenlaformaglobald’anell.

Inferiorcentre:Lesvarietatsinvariantsassociadesalspunts Li 1 i Li 2 donen unaformamésrectangularal’anellinterior.Inferiordreta:Ampliacióde lazonadelspuntsd’equilibriemfatitzantlaformadenansa.

inicialsd’òrbitesatrapadesperlesvarietatsinvariantsienunaposicióaleatòria alllargdemitjarevoluciólifemperdreenergiacinèticaicontinuemintegrant. Llavorscomparemduescoses:lestrajectòriesoriginalsilestrajectòriesamb xoc,icomprovemquelesòrbitesambxocestan,comsidiguéssim,perdinsdels cilindresdelesòrbitesoriginals.Ésadir,enferperdreenergiaalapartícula, aquestas’hamogutdelavarietatinvariantoriginalaunaòrbitaconfinadaper lavarietatcorresponentdel’energiafinal.L’efecteglobalésqueelsbraços ambxocsónmésestretsidensosenlapartcentral(vegeuelquadreesquerre delafigura16).Lasegonacomprovacióéslacomparaciódelesvarietats invariantsambelresultatdelespartículestestdeSchwarz.Comprovemqueles sobredensitatsdonadesperlessimulacions(puntsennegre)ilesdonadesper lesòrbitesambxocs(zonesombrejadesengrisclar)sesolapenperfectament, talcomveiemalquadredretdelafigura16.

70 MercèRomero-Gómez,PatriciaSánchez-MartíniJosepJ.Masdemont

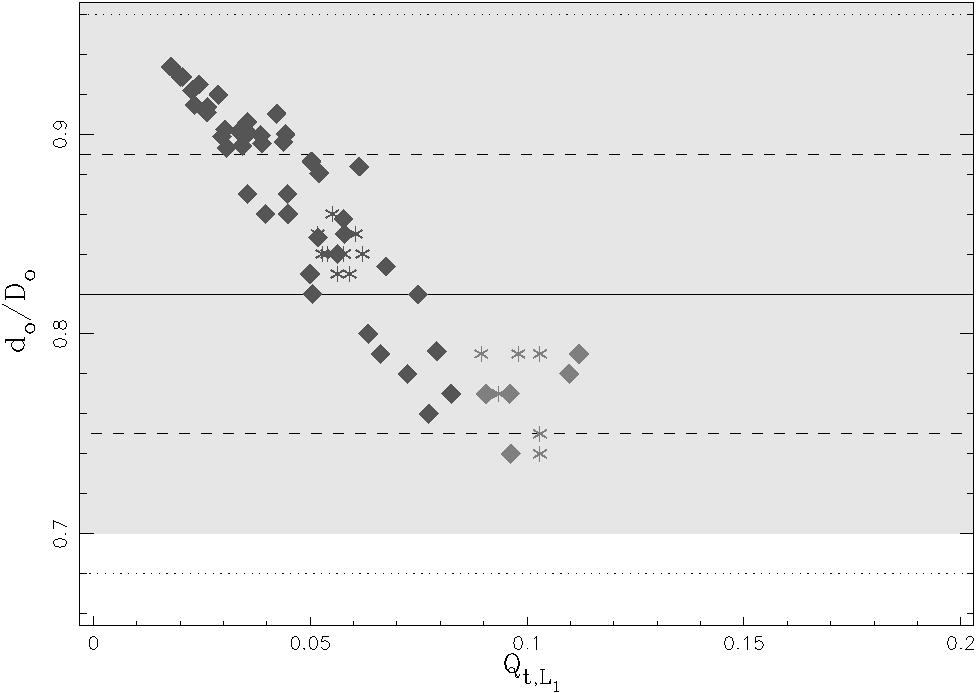
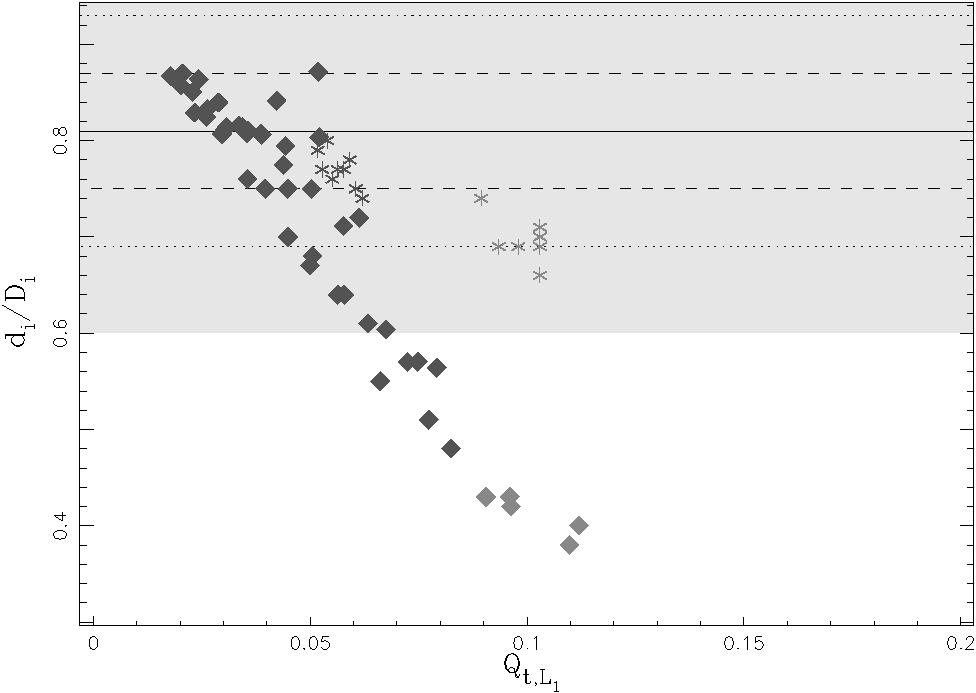
Figura15: Quocientdelssemieixosdel’anellexterior(figuraesquerra)i del’anellinterior(figuradreta)enfunciódelaforçatangencialavaluada enelpuntd’equilibri L1.Lalíniahoritzontalsòlidamarcalamitjana observacional;ladiscontínuaassenyalaelrangdinsladesviacióestàndardilapuntejada,elrangdinsduesvegadesladesviacióestàndard.La zonaombrejadaassenyalaelrangobservacionalobtingutperButa[8]. L’escaladegrisosdelspuntsdenoteneltipusdemorfologia(grisfoscper aanells R1 igrisclarperapseudoanells rR1),mentrequeelsdiferents símbolsdenotenelsdiferentsmodels(rombesperalmodelAiasteriscs peralmodelB).

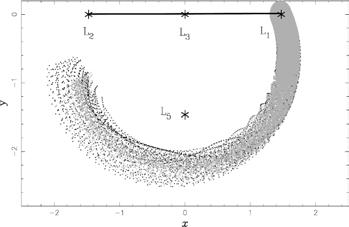
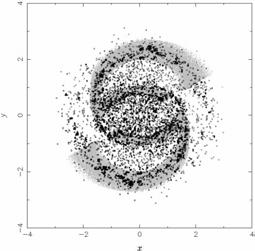
Figura16: Efectesdelgasenlesòrbitesatrapadesperlesvarietats invariants.Panellesquerre:Comparaciódelesvarietatsinvariants(en negre)ilesòrbitesafectadespelsxocs(ombrejadesambgrisclar).Els astericsmarquenlaposiciódelspuntsd’equilibri,ilalíniarectasuperior marcalaposiciódelabarra.Panelldret:Comparaciódelesòrbites afectadespelsxocs(ombrejadesengrisclar)amblespartículestestde lessimulacionsdeSchwarz(ennegre).

Varietatsinvariantsformenespiralsianellsengalàxiesbarrades 71

Finalment,calculemlavelocitatalllargdelalíniadevisióendiferentspunts del’espiralidelsanellsexteriors(vegeufigura17).Ésadir,projectemelvector velocitatdecadapartículaenelsistemainercialalllargdelalíniaqueuneixla posiciódel’observadoriladelapartícula.Cadascundelsquadresrepresenta unangledevisiódiferent;aixòvoldirquelaposiciódel’observadorrespectela galàxiaésdiferentencadascundelsquatrecasosconsiderats.Enconseqüència podemgeneralitzarelresultatalesdiferentsconfiguracionsdegalàxiesque enspodemtrobaralcel.L’eixdeles x represental’anglealllargdelavarietat invariantdefinitdemaneramatemàticail’eixdeles y,laprojeccióalllargde l’eixdelavisiódelvectordevelocitatsenelsistemainercial.Comprovemque enelcasquelamorfologiasiguid’anell R1,lapodemajustarperunacorba sinusoïdal(corbavermella),mentrequeenelcasd’espirals,maiespotajustar perunsinus.Lafunciósinuséslaquenormalments’utilitzapercalcularl’eix principaldelagalàxiaideprojectar-la.

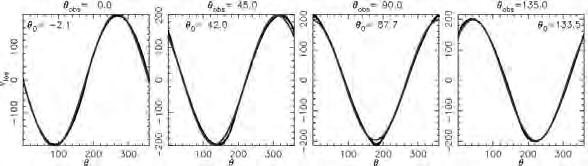
Figura17: Velocitatsalllargdelalíniadevisiópresaambquatreangles diferents.D’esquerraadreta:0◦,45◦,90◦ i135◦.Alesrepresentacions superiors,lamorfologiacorresponaunanell R1,mentrequeenles inferiors,lamorfologiaésdebraçosespirals.Encadacas,apareixen ambuntraçmésgruixutennegrelesvelocitatsdonadesperlesòrbites atrapadesperlesvarietatsinvariantsenfunciódel’anglealllargdela varietat,iperunalíniagrisal’ajustperunacorbasinusoïdal.Elvalor θ0 indicalaposicióenlaquallavelocitatenlalíniadevisiós’anul.la.

6Conclusionsirecercaactual

Lateoriadesistemesdinàmicsi,enparticular,elpaperdelesvarietatsinvariants modelitzademaneraprecisaelsproblemesdedinàmicagalàctica.Mentreque lesteoriesanteriorssobrelaformaciódebraçosespiralsi/oanellsengalàxies barradesnoconsiderenunorigencomú,lesvarietatsinvariantsassociadesa

MercèRomero-Gómez,PatriciaSánchez-MartíniJosepJ.Masdemont

lesòrbiteshiperbòliqueslocalitzadesalsextremsdelabarrasíqueproveeixen aquestapossibilitat.

Endiversostreballshemdesenvolupataquestateoriaconsiderantdiferents potencialsgalàcticsiatenentalsmésusatspelsastrònomsafidemodelitzargalàxiesambbarra.Totstenenunacomponentaxisimètrica,quemodelitzaeldisc, bulbihalodelagalàxia,iunacomponentnoaxisimètrica,quemodelitzala barra.Hihabàsicamentdostipusdepotencialspermodelitzarunabarra.Un, enelqualelpotencialesderivad’unadistribuciódedensitatiqueésmés«físic» enelsentitqueprovéd’unadensitatonlabarraestàbendefinida,ésadir,té unallargada,unaamplada,unamassa.Mentrequelasegonaopcióésutilitzar elsegonmodedeladescomposiciódeFourierdetotelpotencialglobaldela galàxia.Aquestsdarrerstipusdepotencials’anomenenquadrupoloadhoc perquènoprovenend’unadistribuciódedensitatdonadaapriori.

Peracadascund’aquestsmodels,hemrealitzatcomparacionsambobservacionsi/ohemproporcionateinesdepredicciópertaldecomprovarsilateoria ésplausible.Enelstestsreferentsalamorfologiadelsanellsiespiralshem comprovatquelesprediccionss’ajustenbéalarealitat.Tambéhemcomprovat quel’efectedelgasenlesespiralsnoafectalaformadelesvarietatsinvariantsde manerainadequada,sinóqueprecisamentfaquesiguinmésestretes.Finalment, hemcomprovatquelavelocitatenlalíniadevisióperamorfologiesdetipus anellespotajustarambunacorbasinusoïdal,mentrequesilagalàxiatédos braçosespirals,noespotajustarperunsinus.Aquestfettéconseqüènciesen elprocésdecàlculdel’angledeposiciód’unagalàxia.

Pelquefaamorfologiesmésespecials,laformaciódelsansaealsextrems delabarrailadinàmicaassociadatambéquedadescritaenunmarccomú. Actualmentestemusantlateoriaperaexplicarlaformaciódelsanomenats warps.Aquestssóndeformacionsdeldiscidelsbraçosespiralsenladirecció z, ésadir,foradelpla,talcompassaalagalàxiadelsigneintegralquepodem veurealafigura18.Perlessimulacionsfetes,semblaqueaquestfenomen estariaassociatalaprecessiódelabarra[4].

Figura18: Esquerra:Vistatansversaldel’anomenada galàxiadelsigneintegral (UGC3697)enlaqualpodemapreciarlacurvaturadelsbraçosenla direcció z.Dreta:Unasimulacióonlesvarietatsinvariantsquedencorbadesrespectedelabarraiobservacionalmentreproduirienelmateixpatró.

Varietatsinvariantsformenespiralsianellsengalàxiesbarrades 73

Agraïments

AquesttreballhaestatparcialmentfinançatpelsajutsMINECO-FEDERAYA200914648-C02-01,AYA2010-12176-E,AYA2012-39551-C02-01,MTM2009-06973, MTM2012-31714,perl’AGAUR2009SGR-D-D859-EipelCONSOLIDERCSD200700050.Agraïmtambél’ajutdel’AgrupacióAstronòmicadeManresa.

Referències

[1] Athanassoula,E.;Romero-Gómez,M.;Bosma,A.;Masdemont,J.J. «Ringsandspiralsinbarredgalaxies-II.Ringandspiralmorphology». MonthlyNoticesRoy.Astronom.Soc.,400(4)(2009),1706–1720.

[2] Athanassoula,E.;Romero-Gómez,M.;Bosma,A.;Masdemont,J.J. «Ringsandspiralsinbarredgalaxies-III.Furthercomparisonsandlinks toobservations». MonthlyNoticesRoy.Astronom.Soc.,407(3)(2010), 1433–1448.

[3] Athanassoula,E.;Romero-Gómez,M.;Masdemont,J.J. «Ringsandspiralsinbarredgalaxies-I.Buildingblocks». MonthlyNoticesRoy.Astronom. Soc.,394(1)(2009),67–81.

[4] Barajas,D. «Precessingmodelsandeventuallinkswithgalaxywarps». MàsterTesi.FacultatdeMatemàtiquesiEstadística,UPC,Barcelona,2011.

[5] Binney,J.;Tremaine,S. Galacticdynamics.2aed.Princeton,NovaJersey: PrincetonUniversityPress,2008.(PrincetonSeriesinAstrophysics)

[6] Bosma,A. «21-cmlinestudiesofspiralgalaxies.I-Observationsofthe galaxiesNGC5033,3198,5055,2841,and7331.II-Thedistributionand kinematicsofneutralhydrogeninspiralgalaxiesofvariousmorphological types». Astronom.J.,86(1981),1791–1846.

[7] Buta,R.J. «Thestructureanddynamicsofringedgalaxies.I-Themorphologyofgalaxyrings,andstatisticsoftheirapparentshapes,relativesizes, andapparentorientationswithrespecttobars». Astrophys.J.,61(1986), 609–630.

[8] Buta,R.J. «Thecatalogofsouthernringedgalaxies». Astrophys.J.Suppl., 96(1995),39–116.

[9] Buta,R.J.;CorwinJr,H.G.;OdewahnS.C. TheVaucouleursAtlasof Galaxies.Cambridge:CambridgeUniversityPress,2007.

[10] Buta,R.J.;Crocker,D.A. «TheouterLindbladresonanceandthemorphologyofearlytypediskgalaxies». Astronom.J.,102(1991),1715–1723.

[11] Conley,C.C. «Lowenergytransitorbitsintherestrictedthree-body problem». SIAMJ.Appl.Math.,16(1968),732–746.

[12] Contopoulos,G. Orderandchaosindynamicalastronomy.Berlín:Springer-Verlag,2002.(AstronomyandAstrophysicsLibrary)

[13] Contopoulos,G.;Papayannopoulos,Th. «Orbitsinweakandstrong bars». Astronom.andAstrophys.,92(1–2)(1980),33–46.

MercèRomero-Gómez,PatriciaSánchez-MartíniJosepJ.Masdemont

[14] Dehnen,W. «TheeffectoftheouterLindbladresonanceoftheGalactic baronthelocalstellarvelocitydistribution». Astronom.J.,119(2)(2000), 800–812.

[15] Ferrers,N.M. «Onthepotentialsofellipsoids,ellipsoidalshells,elliptic laminaeundellipticringsofvariabledensities». Quart.J.,14(1876),1–22.

[16] Fux,R. «Orderandchaosinthelocaldiscstellarkinematicsinducedby theGalacticbar». Astronom.andAstrophys.,373(2)(2001),511–535.

[17] Gómez,G.;Koon,W.S.;Lo,M.W.;Marsden,J.E.;Masdemont,J.;Ross, S.D. «Connectingorbitsandinvariantmanifoldsinthespatialrestricted three-bodyproblem». Nonlinearity,17(5)(2004),1571–1606.

[18] Koon,W.S.;Lo,M.W.;Marsden,J.E.;Ross,S.D. «Heteroclinicconnections betweenperiodicorbitsandresonancetransitionsincelestialmechanics». Chaos,10(2)(2000),427–469.

[19] Kuz’min,G.G. «Astationarygalaxymodeladmittingtriaxialvelocitydistribution». AstronomicheskiiZhurnal,33(1956),27–45.[Enrus]

[20] Lin,C.C.;Shu,F.H. «Onthespiralstructureofdiskgalaxies». Astrophys. J.,140(1964),646–655.

[21] Lin,C.C.;Shu,F.H. «Onthespiralstructureofdiskgalaxies,II.Outline ofatheoryofdensitywaves». Proc.Nat.Acad.Sci.U.S.A.,55(2)(1966), 229-234.

[22] Llibre,J.;Martínez,R.;Simó,C. «TranversalityoftheinvariantmanifoldsassociatedtotheLyapunovfamilyofperiodicorbitsnear L2 inthe restrictedthree-bodyproblem». J.DifferentialEquations,58(1)(1985), 104–156.

[23] Ma,J.;Zhao,J.L.;Shu,C.G.;Peng,Q.H. «Somestatisticalpropertiesof spiralgalaxies». Astronom.andAstrophys.,350(1999),31–37.

[24] Martínez-García,E. «Testingtheoriesinbarred-spiralgalaxies». Astrophys.J.,744(2)(2012),92–105.

[25] McGehee,R.P. «Somehomoclinicorbitsfortherestrictedthree-body problem».Tesidoctoral.UniversitatdeWisconsin-Madison,1969.

[26] Miyamoto,M.;Nagai,R. «Three-dimensionalmodelsforthedistribution ofmassingalaxies». PublicationsoftheAstronomicalSocietyofJapan,27 (1975),533–543.

[27] Patsis,P.A.;Skokos,Ch.;Athanassoula,E. «Orbitaldynamicsofthreedimensionalbars-IV.Boxyisophotesinface-onviews». MonthlyNotices Roy.Astronom.Soc.,342(1)(2003),69–78.

[28] Pfenniger,D. «The3Ddynamicsofbarredgalaxies». Astronom.and Astrophys.,134(2)(1984),373–386.

[29] Romero-Gómez,M.;Athanassoula,E.;Masdemont,J.J.;García-Gómez,C. «Theformationofspiralarmsandringsinbarredgalaxies». Astronom.andAstrophys.,472(1)(2007),63–75.

Varietatsinvariantsformenespiralsianellsengalàxiesbarrades 75

[30] Romero-Gómez,M.;Masdemont,J.J.;Athanassoula,E.;García-Gómez,C. «Theoriginof rR1 ringstructuresinbarredgalaxies». Astronom. andAstrophys.,453(1)(2006),39–45.

[31] Romero-Gómez,M.;Masdemont,J.J.;García-Gómez,C.;Athanassoula,E. «Theroleoftheunstableequilibriumpointsinthetransferofmatter ingalacticpotentials». Commun.NonlinearSci.Numer.Simul.,14(12) (2009),4123–4138.

[32] Schwarz,M.P. «Theresponseofgasinagalacticdisktobarforcing». Astrophys.J.,247(1981),77–88.

[33] Schwarz,M.P. «Howbarstrengthandpatternspeedaffectgalacticspiral structure». MonthlyNoticesRoy.Astronom.Soc.,209(1984),93–109.

[34] Schwarz,M.P. «Are-examinationofsomebar-drivenmodelsofspiral structure». MonthlyNoticesRoy.Astronom.Soc.,212(1985),677–686.

[35] Sheth,K.[etal.]. «EvolutionofthebarfractioninCOSMOS:quantifyingthe assemblyoftheHubblesequence». Astrophys.J.,675(2)(2008),1141–1155.

[36] Szebehely,V.G. Adventuresincelestialmechanics.Afirstcourseinthe theoryoforbits.Austin,TX:UniversityofTexasPress,1989.

[37] Toomre,A. «Onthedistributionofmatterwithinhighlyflattenedgalaxies». Astrophys.J.,138(1963),385–392.

[38] DeVaucouleurs,G. «Classificationandmorphologyofexternalgalaxies».A: AstrophysicsIV:StellarSystems.Berlín-Heidelberg:Springer,1959, 275–310.(HandbuchderPhysik;53)

[39] Widrow,L.M.;Pym,B.;Dubinski,J. «Dynamicalblueprintsforgalaxies». Astrophys.J.,679(2)(2008),1239–1259.

MercèRomero-Gómez Departamentd’AstronomiaiMeteorologia InstitutdeCiènciesdelCosmos(ICC) UniversitatdeBarcelona(IEEC-UB) MartíiFranquès,1 08028Barcelona mromero@am.ub.es

PatriciaSánchez-Martín,JosepJ.Masdemont IEEC-UPCiDepartamentdeMatemàticaAplicadaI UniversitatPolitècnicadeCatalunya Diagonal,647(ETSEIB) 08028Barcelona

patricia.sanchez.martin@upc.edu,josep@barquins.upc.edu

ButlletídelaSocietatCatalanadeMatemàtiques Vol.29,núm.1,2014.Pàg.77–108. DOI:10.2436/20.2002.01.54

Aplicacionsquadràtiquesquepreservenl’àreaa R2

CarlesSimó

Resum: Consideroladescripció,explicacióipredicciódelespropietatsdelesòrbites d’unsistemadonatcomundelsobjectiusprincipalsdelssistemesdinàmics.Enaquesta lliçóenscentremenlesaplicacionsquadràtiquesquepreservenl’àrea(APM)a R2.Hiha diversesraonsperaaquestaelecció.Enprimerlloc,sónunmodelparadigmàtic.Amés, moltsproblemesreferentsal’existènciadecorbesinvariantsdifeomorfesauncercle, elpaperdelesvarietatsinvariantsdepuntsfixosoperiòdicsdetipushiperbòlicicom portenal’existènciadecaos,elsmecanismesgeomètricsqueportenaladestruccióde corbesinvariants,imesuresquantitativesdelesdiferentspropietatsd’APMgenerals espodenentendregràciesalnostreconeixementdelcasquadràtic.Enaquestarticle passemrevistaaalgunsd’aqueststemes.Alfinalespresentendiversesqüestions obertesiextensionsadimensiósuperior.

Paraulesclau: aplicacionsquadràtiquesquepreservenl’àrea,corbesinvariants,varietatsinvariants,caos,mesuresquantitatives.

ClassificacióMSC2010: 37E30,37A05,37E40,37C29.

1Introducció

Donadaunaaplicació F : R2 → R2 esteminteressatsenelcomportamentdels iteratsdelspuntsde R2 (od’algunsubconjuntconnexde R2).Si z0 = (x0,y0) ∈ R2 ésunpuntinicialqualsevol,volemveurequinéselcomportamentdels iterats zk+1 = F(zk).Elconjunt {zk,k ∈ N} s’anomenal’òrbitade z0. Hihadiversesmaneresd’obtenirunsistemadinàmicdescritperunaaplicació F .Podemdonarexplícitamentl’aplicacióobéconsiderarunaequació diferencialordinàriaautònoma(EDO) dz/dt = f(z) idefinir F(z) comlaimatge d’unpunt z pelfluxdel’EDOdesprésd’untemps τ fixat: F(z) = ϕ(τ,z) o, simplement, ϕτ (z),ques’anomena l’aplicaciótemps-τ.

Aquestarticleesbasaenlalliçóinauguraldelcursacadèmic2013–2014delaFacultatde MatemàtiquesdelaUniversitatdeBarcelona,impartidaperl’autor.Unaprimeraversiód’aquest text,enanglès,vaaparèixeralesPublicacionsdelaUniversitatdeBarcelona.Lapresentacióestà disponibleal’enllaç http://www.maia.ub.es/dsg/2013/ AgraïmaNarcísMigueliArturoVieirolatraduccióalcatalàdel’articleoriginal.

CarlesSimó

Unaaltramanerainteressantd’arribaraunaaplicació F ésusantl’anomenada aplicaciódePoincaré.PeraunaEDO, dw/dt = f(w),en R3 (oenunsubconjunt connexd’aquestespai,oenunavarietat3D),sigui Σ unasuperfícieen R3 definida,perexemple,per g(w) = 0,onsuposemque g ésprouregular.Siel fluxdel’EDOinterseca Σ transversalment(ésadir, f(w) noéstangenta Σ en cappunt w ∈ Σ)podemferelsegüent.Prenemunpuntinicial w ∈ Σ ibusquem lasolució ϕ(t,w) queté w comacondicióinicial.Siexisteix t = t(w)> 0 peralqual ϕ(t(w),w) ∈ Σ i ϕ(t,w) ∉ Σ pera0 <t<t(w),definimaquest punt ϕ(t(w),w) comlaimatge P(w) de w perl’aplicaciódePoincaré P. Aquestaaplicacióestàdefinidasobrelavarietat Σ,queés2D. Caldestacarelcasenquèelcampvectorial f provéd’unhamiltoniàamb 2grausdellibertat,enunnivelld’energiafixat.Un sistemad’equacionshamiltonià amb n grausdellibertatihamiltonià H(q,p) ésdelaforma dqi dt = ∂H ∂pi , dpi dt =− ∂H ∂q

pera (q,p) ∈ Rn × Rn (oenvarietatsadequades).Sesegueixdemanera immediataqueelvalorde H(q,p) espreservaalllargdelessolucionsdel’EDO. Aaquestvalorse’lconeixperl’energia.Pera n = 2,siconsideremunvalor del’energiafixat,tenimunaEDOen3D.Siaméspodemdefinirunaaplicacióde Poincarécomabans,obtenimunaaplicaciósobreunavarietat2D, Σ.

Enaquestcas,l’aplicació P téunapropietatimportant: preserval’àreaa Σ Així,d’araenendavantpodemsimplificarlapresentació.Considerarem R2 en comptesd’unasuperfíciegeneral Σ,denotareml’aplicaciósimplementper F i, amés,suposaremquepreserval’àrea.Aixòimplicaque det(DF(z)) = 1pera tota z ∈ R2,on DF representaladiferencialde F .Persimplificarlanotacióens referiremalesaplicacionsquepreservenl’àreaambeltermeAPM(delesseves siglesenanglès, areapreservingmaps).

D’entretotesaquestesaplicacions,elcasméssimpleéseld’aplicacions polinomials F degrau1.Sóndelaforma F(z) = Mz + b, b ∈ R2,on M ésuna matriu2 × 2.Llevatdelscasostrivialsenquè M téunvalorpropidobleigual a1,espotsuposarque b = 0,traslladantl’origen.Elsvalorspropisde M són delaforma

1)exp(±iα), α ∈ (0,π),casconegutcom ellíptic,

2) λ,λ 1 , λ> 1,casconegutcom hiperbòlic, 3) 1doble,però M noespotdiagonalitzar,casconegutcomde cisallament

Hihadosaltrescasosquepodenaparèixer:unaparelladevalorspropis λ, λ 1 , λ< 1(casconegutcom hiperbòlicambreflexió),i 1doble,de nouamb M nodiagonalitzable.Esredueixenals2)i3)anteriorscomponent l’aplicacióamblasimetriacentral Idoprenent F 2 encomptesde F .

Enelstrescasosconsiderats,desprésd’uncanvidecoordenades,lamatriu M espotreduiraunadelesformessegüents: cos(α) sin(α) sin(α) cos(α) , λ 0 0 λ 1 , 11 01 . (2)

Aplicacionsquadràtiquesquepreservenl’àreaa R2 79

Enelcasel.líptic,segons (2),ladinàmicaésessencialmentunarotació.Tots elspuntstenenòrbitesacotades,confinadesenel lipses.Calnotarquesi α ésde laforma α = m n 2π , m n ∈ Q, (m,n) = 1, llavorstotselspuntssónfixosper F n , unasituacióextremamentdegenerada.Ésadir,totselspuntssónperiòdics ambperíodeminimal n.Recordemqueunpunt z esdiuqueés periòdicamb períodeminimal n> 1si F n(z) = z i F k(z) ≠ z pera k = 1, 2,...,n 1.

Enelcashiperbòlic,ladinàmicaésdetipussella.Escrivint F(x,y) = (λx,λ 1y),segons (2),totselspuntsamb x0 ≠ 0s’escapenal’infinit,mentre queaquellsamb x0 = 0tendeixenal’origen.

Enelcasdecisallament,pera b = 0id’acordamb (2),podemescriure l’aplicació F com F(x,y) = (x + y,y).Totselspuntsamb y0 ≠ 0tendeixena infinit,mentrequeelspuntsamb y0 = 0sónfixos.

Lafigura1mostraelstrescasos,ambunpuntinicialrepresentatper0,iles imatgesrespectivesrepresentadesper1,2,3, ... Ésmoltimportantnotarque enaquestcaslineal totselsiteratspertanyenacorbes quesónsoluciód’una EDOlineal,quepreserval’àrea.Ésadir,l’EDOestàassociadaaunhamiltonià quadràtic.Defet,hihaunhamiltoniàtalquel’aplicació F coincideixamb l’aplicaciótemps-1delfluxhamiltonià.

Figura1: Exemplesdeladinàmicadelstresmodelsd’aplicacionslineals. D’esquerraadreta:rotació,sellaicisallament.Lesformesnormalsde lesmatriuscorresponentssónlesdonadesa(2).

Siperaunaaplicaciógeneral F de R2 existeixunafunciónoconstant G que ésinvariantper F ,ésadir G(F(z)) = G(z),diemquel’aplicacióés integrable. Elprimerquese’nsacutéselcasdeles aplicacionsquadràtiques definidesper F(x,y) = (F1(x,y),F2(x,y)),onlesfuncions F1 i F2 sónpolinomisquadràtics en (x,y).Aquestcasésextremamentrellevant,perquè

a) Permetferunareduccióquefadecréixerdemaneramoltimportant elnombredeparàmetresinvolucratsenl’aplicació.Amés,téalgunes simetriesrellevantsiunainterpretaciógeomètricamoltsimple.Aquestés elcontingutdelasecció2.

b) Apareixdemaneranaturalcomunaaproximaciómoltbonaenalgunes partsde R2 quanconsideremunaAPMarbitrària.Enparticular,quan estudiemaplicacionsdePoincarédehamiltoniansamb2grausdellibertat.

c) Ésunmodelparadigmàtic.Moltsproblemesrelacionatsambl’existència decorbesinvariantsdifeomorfesa S1 (secció4),comaraelroldeles varietatsinvariantsdepuntshiperbòlics,fixosoperiòdics,icomduen al’existènciadecaos(secció5),elsmecanismesgeomètricsqueduena ladestrucciódecorbesinvariants(secció6),imesuresquantitativesde diversespropietats(seccions7i8)peraAPMgenerals[26],espoden entendregràciesalconeixementactualdelcasquadràtic.

Finalment,ésinteressantressaltarquelesAPMquadràtiquessón analítiques, fetquepermetusarresultatsútilsperaaplicacionsanalítiques,iencaramés: són aplicacionsenteres.Peraunadiscussiócompletadelespropietatsde diferentstipusd’aplicacionsd’Hénonialgunesaplicacions,vegeu[19].Diverses figuresiideesqueaquíespresentens’hanextretd’aquestarticle.Enelque segueix,perfixaridees,toteslesAPMesconsiderarananalítiques.

Diversesqüestionsromanenencaraobertes,ialgunesd’aquestesespresentenalasecció9.

2Reduccióisimetries

Afinalsdelsseixanta,MichelHénon[13]vainiciarl’estudidelesAPMquadràtiques.Méstard,amitjansdelsetanta,vaestudiarelcasdissipatiu[14].Enel casquevaconsiderar,eljacobiàésconstant,peròambvalorabsolutméspetit que1.Aquíapareixelpopular atractord’Hénon.

Unfetremarcable,quenoésdifícildeprovar,ésquelacondiciódetenir jacobiàconstantpermet,viaescalatsadequatsdelesvariablesitraslladant l’origendeformaadient,escriureunaaplicacióquadràticagenèricade R2 dela forma:

F : (x,y) → (1 ax2 + y,bx) (3) peracertesconstants a, b.Quan a tendeixa0,l’escalats’hadeferdemanera lleugeramentdiferent.Òbviament,eljacobiàésiguala b i,pertant,elcas conservatius’obtépera b =−1.

Elcasconservatiutéunainterpretaciógeomètricamoltsimple.Estracta delacomposiciódeduesaplicacions.Laprimeraés (x,y) → (x,y + 1 ax2), unadelesanomenadesaplicacionsde deJonquières,mentrequelasegonaés simplementunarotaciód’angle π/2.Lafigura2mostra,pera a =−1/2,el quadrat [ 3, 3]2 (engrismoltfosc),lasevaprimeraimatge(engrisfosc)ipart delesduesimatgesconsecutivessegüents(engrisigrisclar,respectivament). Enspodempreguntarsi,eniterar,totselspuntss’escaparan.Comarespostaa aquestapregunta,dibuixemennegreelconjuntdepuntsqueromanenacotats peraqualsevolnombred’iteracions,peralvalorde a seleccionat.Aquestés eltipusd’objectesquevolemestudiar,aixícomlasevaevolucióenfunciódel paràmetre.

Aplicacionsquadràtiquesquepreservenl’àreaa R2 81

Figura2: Elquadrat [ 3, 3]2 (engrismoltfosc)ilessevestresprimeres imatgesperl’aplicaciód’Hénonamb a =−0.5, b =−1,mostradesen grisfosc,grisigrisclar,respectivament.Lesduesúltimestenenparts foradelrangmostrat.Elconjuntennegreéselconjuntinvariantde puntsqueromanenacotatsperqualsevolnombred’iteracions.

Unarepresentaciómillordel’APMquadràtica,queusaremd’araenendavant, és

Fc x y → x + 2y + c 2 (1 (x + y)2) y + c 2 (1 (x + y)2) , (4) onéssuficientconsiderar c> 0.Aquestanovaformas’obtéambunapetita modificaciódelaversióusadaen[34].Elsubíndex c de Fc l’escrivimperemfatitzarquel’aplicaciódepènd’aquestparàmetre.L’aplicaciótédospuntsfixos. Unestàsituata ( 1, 0) iéshiperbòlicperaqualsevol c> 0.L’altreestàa (1, 0) iésel lípticpera0 <c< 2, parabòlic (defet,decisallament)pera c = 2i hiperbòlicambreflexiópera c> 2.

Espotcomprovarfàcilmentquelainversadel’aplicació Fc espotexpressar per F 1 c = SFc S,on S éslasimetria S(x,y) = (x, y).Així,sidefinim R = SFc , queéstambéunainvoluciócom S,tenim Fc = SR i F 1 c = RS.Lesdues aplicacions S i R s’anomenen reversors.Podemconsiderarconjuntsdepunts fixospelsdosreversors,ésadir,punts z = (x,y) talsque S(z) = z (quesón elspuntsamb y = 0),obéunspuntsperalsquals R(z) = z,quepertanyena unaparàbola.

L’existènciadereversorsd’unaaplicació F téunaconseqüènciaimportant: si K ésunreversori z∗ ésunpuntdelconjunt Fix(K) depuntsfixosde K, llavors,siexisteix m ∈ N talque F m(z∗) ∈ Fix(K),elpunt z∗ ésperiòdicper F Òbviament,si F m(z∗) = z∗,téperíode m,isi F m(z∗) ≠ z∗,téperíode2m.És clarqueunpuntfixtambéespotconsiderarcomaperiòdicdeperíode1.

CarlesSimó

Peraestudiarlespropietatslocals(lineals)d’unpuntperiòdic z∗ deperíode m,éssuficientconsiderarl’aplicaciólinealdefinidaper DF m(z∗) iusar ladescripciódeladinàmicadonadaalasecció1.D’acordambaixò,elpunt s’anomenaràel líptic,hiperbòlic,hiperbòlicambreflexióo,sielsvalorspropis de DF m(z∗) són +1dobleo 1doble,parabòlic.

3Unfluxlímit:comparacióamblesaplicacionsdiscretes

Unprocedimentútilperal’estudipreliminardeladinàmicad’unaaplicació F , enelcasqueaquestasigui properaalaidentitat,consisteixabuscarl’existència d’unaEDOdetalmaneraquel’aplicaciótemps-1associadaalfluxsiguiuna bonaaproximacióde F .Laformade (4) suggereixintroduirnovesvariables (ξ,η) = (x, 2y/√c).Ara,enlesvariables (ξ,η), Fc difereixdelaidentitat enunaquantitat O(√c).Éselementalquesiconsiderem Fc ,queenspassa delesvariables (ξ,η) alesvariables (ξ,η),llavors ξ = ξ + √cη +O(c), η = η + √c(1 ξ2) +O(c).Lavariaciódelesvariables (ξ,η) perunitatdetempsés (√cη, √c(1 ξ2) +O(c).Unescalatdeltemps,tambépelfactor √c,ifertendir c capazero,ensproporcional’EDO

dt = η, dη dt = 1 ξ2 , (5) queéshamiltonianaamb H(ξ,η) = 1 2 η2 ξ + 1 3 ξ3 (vegeu (1)).Així,lessolucions estancontingudesenlescorbesdenivellde H.Ladinàmicade (5) éselementali lessevespropietatsprincipalss’il.lustrenalafigura3,esquerra.Tambété ( 1, 0) i (1, 0) comapuntsfixos,elsqualssónhiperbòliciel.líptic,respectivament.

Elnivell H = 2/3delpuntfixhiperbòliccontéduesbranquesnoacotades(la superiorés,defet,unabrancade W s,+,la varietatestable delpuntfix,mentre quelainferiorésunabrancade W u, ,la varietatinestable d’aquestpunt)i unabrancaacotadaquetancaundominide R2.Aquestaúltimabrancade lesvarietatsinvariantsesconeixper separatriu,iestàformadaperlesdues altresbranquesdelesvarietatsque,defet,coincideixen: W s, = W u,+.Totsels puntsnoacotatsperlaseparatrius’escapenal’infinit,aexcepciódelspunts de W s,+.Elspuntsdinsdelconjuntacotatperlaseparatriuesmouenenòrbites periòdiquesdel’EDOalvoltantdelpuntel.líptic.Aquestesòrbitesfolienaquest dominiacotat.

Laseparatriuéslasolucióde (5) ambcondicióinicial (2, 0) pera t = 0i vadesde ξ =−1finsa ξ = 2.Elvalormésgranquepren |η| és 8/3.Amés, caldirqueaquestasolucióéselcaslímitd’unafuncióel.lípticaquetendeixa ( 1, 0) pera t →±∞ iquetéuna singularitat en t = iπ/√2.

Elperíodedelesòrbitesperiòdiquesalvoltantdelpuntfix (1, 0) tendeix a √2π quanaquestess’acostenalpuntfix,itendeixa ∞ quans’apropenala separatriu.Elperíodecreixdemaneramonòtona,laqualcosaésconseqüència d’algunespropietatssimplesdelesfuncionsel.líptiques.

Aplicacionsquadràtiquesquepreservenl’àreaa R2 83

Figura3: Al’esquerra:espaidefasedelsistema (5).Elspuntsfixoses mostrenennegre,aixícomlesvarietatsinvariantsdelpunthiperbòlic. Lesòrbitesperiòdiquesesmostrenengrisclar.Vegeuelcosdeltextper alsdetallssobrelesòrbitesperiòdiquesqueesmostrenengrisfosc.A ladreta:lesbranquesdeladretadelesvarietatsinvariantsdelpuntfix hiperbòlici(partde)lesòrbitesde Fc peradiversescondicionsinicials, pera c = 0 2.

Comespotcompararelcomportamentdescritambelde Fc pera c petita? Aladretadelafigura3,prenentcondicionsinicialsenl’eixdeles x ambvalors 1 01 (0 04) 1 93,peralvalor c = 0 2,esmostren5000puntsdecadaòrbita de Fc ,desprésd’untransitoride106 iterats.

Lesseparatriusdel’aplicaciósemblencoincidents,peròenrealitatnoho són(vegeusecció5).Lesòrbitesqueesmostrensemblaqueestiguinsobre corbesinvariants.Probablementlamajoriapertanyinaunad’aquestescorbes, peròsiesfancàlculsambcura,espotcomprovarquehihaunpetitintervalde puntsinicialsapropde x = 1.7412624214onalgunesòrbitessemblenser caòtiques.Ésclarquesiesprenencondicionsinicialsenelcostatoposatdel puntfixel líptic,enelrang [ 0 08343, 0 08246] aproximadament,lesòrbites noestansobrecorbesinvariantsalvoltantdelpuntel.líptic.

Elqueprovocaaquestadificultatal’horad’interpretarelques’observaal gràficdeladretadelafigura3iquinaésladinàmicarealesdiscutiràales seccions4,5i6.

Unacaracterísticaimportantdelspuntsl’òrbitadelsqualsésunacorba invariantésel númeroderotació.Aquestmesuralamitjanadelafraccióde revolucióquegiraunpuntperacadaiterat.Considerantelsanglesrespectedel puntfixel.líptic(mesuratenelsentitdelesagullesdelrellotge)noa S1,sinó enl’aixecament a R,sidenotemper θk l’angledel k-èsimiterat,elnúmerode rotacióesdefineixcom ρ = 1 2π lim k→∞ θk k

(6)

Aquestnúmerosempreexisteixinodepèndelacondicióinicialsobrela corba.Ésclar,però,queelvalorde ρ depèndelacorbainvariant.Silescorbes invariantsesparametritzenpelpunt x enquèintersequenl’eixdeles x ala

CarlesSimó

dretadelpuntel.líptic,podemescriure ρ = ρ(x).Hihamoltsmètodespera calcular ρ,ilamajorianodepenennidel’existènciad’unpuntcentral(coms’ha consideratabans)nideladimensiódel’espaionestiguidefinidal’aplicació. Vegeu[11,12,24].

Enelcasdelflux,podemdefinirl’aplicaciótemps-1associada, ϕ1,coms’ha fetalasecció1.Elnúmeroderotacióésl’inversdelperíode.Perpoderveurela bonaconcordançaentrelespartsdretaiesquerradelafigura3,enlafigura4 esmostraelnúmeroderotacióenelsdoscasos,comafuncióde x, x> 1.El númeroderotaciódelfluxs’haescalatpertenirencomptel’escalatdeltemps, is’haaplicatunapetitacorreccióalvalorinicialde x pertenirencompte, també,quelesvarietatsdel’aplicació Fc intersequenl’eixdeles x enunpunt lleugeramentpersotade2.

Figura4: Comparacióentre ρ peral’aplicació Fc , c = 0 2,enpuntsgris clar,ambelvalorperalcamp (5),comalínianegra,desprésd’haver escalatadequadament.Noteulaconcordançaexcel.lentaaquestnivell deresolució.

Tornantalcasdelflux,hemtriatunpunt(elsituatmésaladreta,d’entre elsgrisosfoscos)delgràficdel’esquerradelafigura3quedefineixunaòrbita periòdicadeperíode5.Aquestpunttéperíode5per ϕ1,iésclarquetots elspuntsenaquestaòrbitaperiòdicadelfluxtenenperíode5per ϕ1.Els altrespuntsengrisfoscsónlesimatgesdelsituatmésaladreta,per (ϕ1)k , k = 1, 2, 3, 4.

Quèpassariasihaguéssimconsideratl’aplicació Fc ,pera c petita,coma pertorbació O(√c) del’aplicació ϕ1 delflux,ibusquéssimpuntsambperíode n periteracióde Fc ?Unpunt n-periòdiccompleixlacondició G(z) = F n c (z) z = 0. Siescrivim F n c = ϕn 1 +O(√c) ibusquemsolucionsde G(z) = 0usantel teoremadelafuncióimplícitaenstrobaremquenopodremfer-ho,perquèla diferencialde ϕn 1 Idéssingular.Pertant,calusaraltresmètodes.

Mésgeneralment,podempreguntar-nossi,peral’aplicació Fc ,existeixuna EDO(properaperòdiferenta (5))talquel’aplicació ϕ1 associadacoincideix amb Fc .Finsitotenspodemplantejaraixòmateixenelcasd’aplicacions F arbitràriessuposantquesónproperesalaidentitat(bélamateixa F ouna potènciad’ellaenundominiadequat).

Aplicacionsquadràtiquesquepreservenl’àreaa R2 85

Aquestúltimcaséseldelesfuncions F detipusAPMalvoltantd’unpunt fixhiperbòlic.Lesòrbitesdel’aplicació ϕ1 d’unaEDO(queespotprovarque existeixiéscalculabledemaneraefectiva)coincideixenamblesde F mentre estiguinenunentorndelpuntcitat.Aquestéselcontingutdelaconeguda forma normaldeBirkhoff (BNFdelessevessiglesenanglès);vegeu,perexemple,[25].A més,enunentornd’unpuntfixel.líptic,espotcalcularunaBNFfinsaqualsevol ordre,però,engeneral, noseràconvergent.Les formesnormals sóneinesmolt útilsquedonenmoltainformació[1].Laideaclauésintroduirunasuccessió detransformacionsqueconverteixinelproblemaoriginalenunaltrequesigui moltmésfàcild’estudiar.

Concretament,enelcasd’unpuntfixhiperbòlic,existeixuncanvidevariables analític,quepassaaunesvariables (ξ,η) enlesqualsl’aplicaciós’escriu (ξ,η) → (λ(ξη)ξ,η/λ(ξη)), on λ(ξη) = n≥0 λj (ξη)j (convergent)ionelvalorde λ0 éselvalorpropi dominantenelpuntfix.Notemque λ(ξη) solsdepèndelproductedeles variables.Aquestproducteésconstantperl’aplicaciódinsd’uncertentorndel puntfix.Òbviament,enaquestentorn,elsiteratsesmouensobrehipèrbolesde manerasemblantalcaslineal.

Enelcasd’unpuntfixel.lípticisuposantquenohiharessonància,ésa dir,quesilapartlinealésunarotaciód’angle α0 llavors α0 ∉ 2π Q,hihauna successiódecanvisanalíticsqueredueixenl’apliacióaformesdeltipus

ξ η → RαN (ξ,η) ξ η +O(||(ξ,η)||2N+1),

on RαN (ξ,η) voldirunarotaciód’angle αN (ξ,η) quedepèndelesvariables delaforma αN (ξ,η) = N j=0 αj (ξ2 + η2)j .Peròperaqualsevolentorndelpunt fix,lasuccessióderesidusdelaformanormal, O(||(ξ,η)||2N+1),notendeix azerosi N →∞,llevatdecasosmoltdegenerats.Nohihaconvergènciaen general.Elscoeficients αj s’anomenencoeficientsdeBirkhoffimoltesvegades s’escriuen bj enrecorddeBirkhoff.

Ésimmediatescriureelscampselfluxtempsunitatdelsqualsreprodueix elques’obtédelaformanormal.Enelcashiperbòlicés ˙ ξ = log(λ(ξη))ξ, η =− log(λ(ξη))η,ienelcasel.líptic,encoordenadespolars (r,θ),tindrem r = 0, θ = αN (r 2)

Siesteminteressatsenl’existènciad’unaEDOdetalmaneraquel’aplicació ϕ1 associadacoincideixiglobalment,ésadir,enundominicompacte K fixat, ambunaaplicacióproperaalaidentitat F ,tambéhiharesultatsbasatsen tècniquesdemitjanes[20, 28].Perfixaridees,suposemque F(z) = Fε(z) = z + εF1(z,ε).Elprimerpasconsisteixaconstruiruna suspensió,ésadir,unaequació diferencialordinàriaquedepenguiperiòdicamentdeltemps(perexemple,amb període1)demaneraquelasevaaplicaciótemps-1,desde t = 0finsa t = 1, coincideixiambl’aplicació Fε [4].Aixòéssemprepossiblesi ε éspetit.Llavors calaplicaruna successiódetransformacions pertaldecancel.larladependència

CarlesSimó

deltempsdel’EDO[20, 28].Engeneralaixònoéspossible.Lasuccessióde campsvectorialsnoconvergeixauncampautònom,peròsis’aturaelprocés enelmomentadequat,quedepènde ε,espotobteniruncampautònomtal quelasevaaplicaciótemps-1difereixde Fε(z) enunaquantitatacotadaper c1 exp( c2/ε),peratota z ∈ K iperacertesconstants c1 i c2 positives.Vegeula secció5peratemesrelacionats,queincloueneltipusdedivergènciad’aquesta successiódetransformacions.

Figura5: Algunesòrbitesdel’aplicació Fc pera c = 0.762.Comabans, prenempuntsinicialsiil.lustrem5000iteratsdecadaund’ellsdesprés d’untransitoride106 iterats.Aralescondicionsinicialsen y = 0són0.98 ( 0 02) 0 02.Elspuntsforadeldominiqueesmostras’escapena l’infinitapropant-sealabranca W u .

Alafigura5s’il lustralasituacióqueestrobaperavalorsmésgransde c Encarasemblaquehihamoltescorbesinvariantsalvoltantdelpuntfixellíptic.Llunyd’aquestpunthitrobemalgunes illes alvoltantdepuntsel líptics periòdicsdeperíode5.Propdeleszonesonunaillas’apropaalessevesveïnes, éspossibledetectar-hiunaòrbitahiperbòlicaperiòdicadeperíode5.Enun entornd’aquestesòrbitesperiòdiques,ladinàmicasemblacaòtica:aparentment lesòrbitesomplenunconjuntdemesurapositiva,ijanoestansobrecorbes. Propdelaperifèria,enstrobemunaaltravegadaambméscorbesinvariants envoltantlesillesdeperíode5i,finalment,algunescadenesd’illesmoltpetites. AquestaestructuraéstípicaperaAPMdequalsevoltipus.

Calnotar,també,quelesillesdeperíode5intersequen y = 0(elconjunt Fix(S))al’esquerradelpuntfixel.líptic,perònoaladreta,onpodemintuir quehihauràunpunthiperbòlicdeperíode5.D’altresillesnoméspodentenir interseccióaladretaialgunesnoteneninterseccióamb Fix(S),peròpoden

Aplicacionsquadràtiquesquepreservenl’àreaa R2 87

tenir-neamb Fix(R).Perferevidentl’existènciad’illes,alafigura6representem elvalordelnúmeroderotacióenfuncióde x perapuntsinicialstriatsa Fix(S) (esquerra)itambéperapuntsinicialstriatsa Fix(R) (dreta)peralvalor c = 0.7. Enl’últimcasnomésusemdadesinicialsal’esquerrade x = 1.Enambdós casoss’observaqueelmàximde ρ s’assoleixen x = 1.Arabé,comveuremmés endavant,aixòpotcanviarenvariarelvalorde c.Alafigura6,esdestaquen ambpuntsnegresleszoneson ρ éslocalmentconstant,quecorresponena illes.Enelsllocsonhihapuntsperiòdicshiperbòlicsaprop,elvalorde ρ no estàdefinit,acausadelamancadecorbesinvariantsidel’existènciadepunts homoclínicstransversals(vegeuseccions5i6),i ρ tésalts.

Elnúmeroderotaciós’hacalculatdesprésd’untransitoride106 iterats usantels106 iteratssegüentsiunmètodebasatenl’ordreenquèelsiteratses distribueixensobrelacorbainvariant.S’hanignoratelsvalorsde x perals qualselsiteratss’escapenonoestansobrecorbesinvariants(fetqueesdetecta automàticamentambaquestmètode;simplement,simireml’ordredelsangles ques’obtenenconsiderantelsiteratsencoordenadespolarsalvoltantdel puntel.líptic,elsvalorssuccessiusqueprenennosónelsquecorresponena unarotaciórígida:unraonamentpuramenttopològic).Elsnúmerosderotació racionalsdetectatsusantvalorsde x delaforma k × 10 3 , k ∈ Z,d’esquerra adretaalail lustraciódel’esquerra,són3/17,25/141,13/73,7/39,11/61, 15/83,23/127,2/11,5/27,1/5,4/21,2/11,8/45,14/79,10/57i4/23,totsamb denominadorsenar.Alail.lustraciódeladreta,són1/6,7/40,13/74,17/96, 11/62,5/28,9/50,17/94,29/160,33/182i3/16,totsambdenominadorparell.

Figura6: Nombrederotaciócomafuncióde x,pera Fc , c = 0.7.A l’esquerra:s’hanprespuntsinicialsen y = 0.Aladreta:s’hanconsiderat puntsinicialsenelconjunt Fix(R) ambelvalorde y méspetit.Elspunts negresindiquenelsvalorsperalsqualselnúmeroderotacióésracional icorresponenailles.Vegeueltextperamésdetalls.

CarlesSimó

4L’existènciadecorbesinvariants

Araensinteressemperresultatsqueassegurinl’existènciadecorbesinvariants; nonomésperaAPMquadràtiques,sinótambéperaAPMgenerals.Considerarem corbesalvoltantd’unpuntfixel.lípticdetalmaneraque,encoordenadespolars centradesenaquestpunt,elradiespuguiexpressarcomafunciódel’angle r = r(θ) o,simplement,corbesdefinidesenun dominianular quetinguitambé lapropietatqueelradiespuguiexpressarcomafunciódel’angleusantun puntcentraladequat.

Primercalqueintroduïmlesanomenades aplicacionstwist,lesqualssón aplicacionsintegrables (queadmeten,pertant,una foliació formadapercorbes invariantsenundominianular).Suposemque,pera θ = 0,elradi r0 variaen undomini ra <r0 <rb idenotemper ρ(r0) elnúmeroderotaciócorresponent. EsdiuqueunaAPMd’aquesttipussatisfàla condiciótwist si dρ(r0)/dr0 ≠ 0. Usaremelsímbol T perreferir-nosaaquesttipusd’aplicacions.PeraunaAPM F donada,espodenobteniraplicacionstwistcomaaplicacionstemps-1d’unflux queaproximal’aplicació(bésiguialvoltantd’unpuntel.líptic,enunanell,bé usantalgunaformanormal).

Suposemquel’aplicacióenquèesteminteressatsésuna pertorbació d’una aplicaciótwist: Fε = T + εP ,on P ésunafunciónormalitzadademaneraque tinguialgunanormaiguala1.Perhipòtesi, T técorbesinvariants.Podem assegurarque subsisteixen pera Fε?Elresultatvedonatpelconegut teorema deltwistdeMoser

Teorema. Consideremunapertorbació Fε = T + εP d’unaaplicaciótwist T .Si tenimunacorbainvariantde T ambnúmeroderotaciódiofàntic γ,aquestacorba subsisteix,lleugeramentdeformada,per Fε sempreque ε siguisuficientment petit.

Enaquestmomentcalqueintroduïmunadefinició:lade nombrediofàntic.És clarquequalsevolnombreirracional γ espotaproximarpernombresracionals tantcomvulguem.Elproblemaésquepertenirunabonaaproximaciónecessitemracionalsamb denominadorsgrans.Així,si p/q, q> 0,ésunaaproximació racionalde γ,podemmesurarquinaésladiferènciacomparant-laambuna potènciade1/q.Mésconcretament,diemque γ satisfàuna (C,τ)-condició diofàntica (persimplificar (C,τ)-DCosimplementDC,delessiglesenanglès dediophantinecondition),si |γ p/q| >C/qτ peracerts C> 0i τ ≥ 2i peraqualsevol p/q ∈ Q.Ésfàcilcomprovarquesifixem τ> 2,elconjuntde γ ∈ R quenosatisfanuna (C,τ)-DCperacap C> 0témesurazero.Entreels nombresdiofàntics,elmillorésla raóàuria, g = (√5 1)/2,enelsentitque satisfàunaDCamb τ = 2(queéselvalormínimquepotprendre τ),ielvalor màximde C que,peraracionalsambdenominadorquetendeixia ∞,tendeixa 1/√5 ≈ 0.4472136.Elpitjorvalorde C pera g s’assoleixpera p/q = 2/3.En aquestcas, C = (9√5 21)/2 ≈ 0 4376941.

Així,tenimtrescondicionsqueensgaranteixenque Fε tindràunacorba invariantdeltipusdesitjat:

Aplicacionsquadràtiquesquepreservenl’àreaa R2 89

a)Hadeseruna pertorbació d’unaaplicaciótwist T .

b)Elseunúmeroderotació γ hadeser diofàntic.

c)Had’estarsuficientmentapropde T ,ésadir, ε hadeser petit

Calcomentarunamicaquinaéslafunciódecadaunad’aquestescondicions.Consideremla representaciódeFourier delacorbainvariantde T amb númeroderotació γ: r(θ) = j∈Z aj exp(ijθ).Sigui rε(θ) = j∈Z bj exp(ijθ) larepresentaciódelacorbadesitjada,invariantper Fε.La condiciód’invariància s’expressa(encoordenadespolars)per Fε(θ,rε(θ)) = (θ + 2πγ,rε(θ + 2πγ)) Ésclarquepodemfixarl’origendelsanglesdemaneraarbitrària.

Quanintentempassardelscoeficients aj als bj fentunasuccessiódecanvis devariabledemaneraque,desprésdel k-èsimcanvi,tinguemunaaproximació ambunerror O(ε2k ) delacorbainvariantamb ρ = γ de Fε,elqueestemfentés aplicarel mètodedeNewton enl’espaidelessèriesdeFourier.Acadapas,hemde resoldreunaequaciódelaforma G(θ+2πγ) G(θ) = R(θ),l’anomenada equació homològica,on R(θ) estàrelacionatambl’errordel’aproximacióanteriorité mitjanazero,unacondiciónecessàriaperpoderresoldrel’equació.

UsantrepresentacionsdeFourierpera G i R: G = j∈Z gj exp(ijθ),R = j∈Z rj exp(ijθ),r0 = 0,ésfàcilobtenirque gj = rj /(exp(ij2πγ) 1), j ≠ 0. Arabé,eldenominadoranteriorésproperazerosi jγ ésproperaunenter. Aquestésl’anomenat problemadelsdivisorspetits.LaDCenspermetcontrolar elcomportamentdelscoeficientsde G demaneraque,si R ésanalíticaenuna certabandacomplexaalvoltantdelarectadevalorsrealsde θ, G tambéés analítica(potser,però,enunabandalleugeramentmésestreta).

Concretament,sienunpasdelprocéstenimunafunció R ambbandad’analicitatd’amplada ∆,lesdesigualtatsdeCauchyensdonencotesdelaforma |rj |≤ M exp( ∆|j|).Si γ satisfàunaDC,llavors jγ distadelsentersunaquantitat acotadainferiormentper C/|j|τ 1.Eldenominador exp(ij2πγ) 1téuna cotainferiordel’ordrede1/|j|τ 1 (amblaconstantquetoqui).Aixòfaque |gj | estiguiacotatperunaquantitatdel’ordrede exp( ∆|j|)×|j|τ 1 que,alaseva vegada,espotacotarperunaexponencialambunvalorunamicaméspetitque ∆ (iquetambépotinclourel’efectedelesconstantsquehananatapareixent).

Elproblemaésquel’errorenl’aproximaciósegüent notinguimitjanazero inopuguemresoldrel’equacióhomològicasegüent.Aquestamitjanaespot cancel.larmodificanteltermeindependentinicial a0 (o,equivalentment,triant unvaloradequatde g0)iaixòéspossiblegràciesalacondiciótwist.Ésconvenientexpressarlacondiciótwistenlaforma dρ/da0 ≠ 0,ésadir,entermes delamitjanadelacorbainicial.Finalment,elfetque ε siguipetitéscondició necessàriapergarantirlaconvergènciadelprocésdeNewton.Noteuque,fixada γ,commésgransiguilacondiciótwist(ésadir,lamagnitud |dρ/da0|), mésgranssónelsvalorsde ε admissibles.

Calmencionar,també,quelademostraciódel’existènciadecorbesinvariantsperaunaaplicacióiun ρ donatsespotferdemaneraconstructiva, produintcotesrigorosesdelserrorsacadapasusant demostracionsassistides perordinador (CAP,delessiglesenanglèsdecomputerassistedproofs).

Figura7: Lail lustraciómostra,enfuncióde c,elsvalorsde x pera puntsde Fix(S) peralsqualss’hacalculatelnúmeroderotació.Elspunts engrismoltclarcorresponenapuntsamb ρ ∉Q,mentrequeelsaltres tonsdegriscorresponena ρ ∈ Q.Pera ρ = m/n i n = 3, 5, 7, 9, 11,els grisossóncadavegadamésfoscos.Usemelnegreperaaltresvalors racionals.

Figura8: Lail.lustraciómostra,enfuncióde c,elsvalorsde x pera puntsde Fix(S) peralsqualss’hacalculatelnúmeroderotació.Elspunts engrismoltclarcorresponenapuntsamb ρ ∉Q,mentrequeelsaltres tonsdegriscorresponena ρ ∈ Q.Pera ρ = m/n i n = 2, 4, 6, 8, 10,els grisossóncadavegadamésfoscos.Usemelnegreperaaltresvalors racionals.

Aplicacionsquadràtiquesquepreservenl’àreaa R2 91

Tornantal’APMquadràtica,ésinstructiucalcularnúmerosderotaciópera valorsde c prenentcondicionsinicialsa Fix(S) (y = 0)oa Fix(R),perveure onpodemesperartrobar,respectivament, corbesinvariants,illesperiòdiques, zonescaòtiques o,simplement, escapament.Elresultatesmostraalesfigures7 i8.Noteuquelamajoriadelesllengüetesassociadesambillesarribena x = 1, peròsónextremamentestretes;persotadelaresoluciódepíxel.Comque elsnombresracionalssóndensos,elsdominisengrismoltclarenaquestes figurestenen,defet,una estructuradetipuscantoriana.Hihaunconjuntdens dellengüetesquecaltreuredeldominigrismoltclar,peròaquesttémesura positiva(i,defet,relativamentgran).Aixòestàrelacionatambelfetqueel conjuntdenúmerosquesatisfanuna (C,τ)-DC,pera τ> 2i C moltpetita fixades,ésunconjuntdeCantoramb mesuragairebétotal. Caldirquealgunsdelsdominisd’illesenlesfiguresanteriorsnosurtende x = 1.Estanrelacionatsamb satèl.lits (isatèl.litsdesatèl.litsiaixísuccessivament)delesillesprincipals.Encertamanera,l’estructuraalvoltantdecadailla ialvoltantdelessevesillessatèl litrepeteixl’estructuradelconjuntsencer, comun objectefractal. Arribatsaaquestpunt,potserinstructiuveurecomlesillesd’uncertnúmero derotaciódonatevolucionenquan c canvia.Lesillesambnúmeroderotació p/q neixendelpunt (1, 0) quan c = 1 cos(2πp/q).Aquestaevolucióesveualapel.lícula movie1,queespottrobara http://www.maia.ub.es/dsg/QuadraticAPM. Laqüestiósegüentsorgeixdemaneranatural:quèpassasil’aplicacióintegrableaproximada perdlasevacondiciótwist ?Alafigura9mostremlavariació de ρ enfuncióde x pera c = 1.35.Silacomparemamblafigura6veiemque, enprimerlloc,alafigura9elvalorde ρ en x = 1ésunmínimlocalencomptes d’unmàxim.Tambéveiemunmàximpera x< 1(elmàximpera x> 1està relacionatambaquest).Lacondiciótwistesperdperòcontinuenexistintcorbes invariants;vegeulafigura10.Sónlesanomenades corbesmeandre,queno espodenrepresentarcomagràficdelradienfunciódel’anglevistdesdel puntel liptic.Lescorbesespleguen(formantmeandres),peròhihaeinesper provar-nel’existència[29].

Figura9: Similaralafigura6,peròpera c = 1 35.Esrepresentaelvalor de ρ = ρ(x) perapuntsinicialsen y = 0(esquerra),ien Fix(R) (dreta). Ennegreesmarquenelspuntsamb ρ ∈ Q.Noteuqueara,tantaladreta comal’esquerrade x = 1,lafunció ρ janoésmonòtona.

Figura10: Al’esquerraesmostrenunparelld’òrbitespera c = 1.3499, queestanenundominion ρ passaperunmàxim.Aquestesòrbitesestan sobrecorbesinvariants,anomenadesmeandres.Aladretase’nmostra unamagnificació.Entreelsdiferentsmeandresengrisfosc,espoden veureduescorbesinvariantsordinàries(dinsifora),iennegre,illesque pertanyenaduescadenesd’illesdiferentsdenúmeroderotació4/13.

Aquesttipusdecorbesexisteixendesde c = 5/4finsa c ≈ 1.4123.Elseu númeroderotacióprenvalorsenl’interval I = (cos 1( 1/4)/(2π) ≈ 0 29022 , ≈ 0.32846).Estanrelacionadesamblacoexistènciadeduesillesdiferents ambelmateixnúmeroderotació.Peraqualsevolnúmeroracional ρ ∈ I es repeteixelmateixfenomen,peròendominisextremamentestretssi ρ téun denominadorgran.

5Lesvarietatsinvariantsdelspuntshiperbòlicsielseu paperenlacreaciódecaos

Amésdelescorbesinvariantsd’unaAPMhihaaltresobjectesinvariants moltimportantsquetenenunpaperclauenladinàmica(elmateixvalper aaplicacionsmésgeneralsifluxosenqualsevoldimensió).Estractadeles varietatsinvariantsestableiinestabledelspuntsfixoshiperbòlics,queespoden considerarunageneralitzaciódelesrectesinvariantsmostradesalgràficdel centredelafigura1.Unprimerexempleesmostraenelgràficdeladreta delafigura3.Hemmencionatqueenaquellafiguralesbranques W u,+ i W s, (aquellesquecomencenaladretade x =−1)semblencoincidentsperòque, defet,nohosón.Alafigura11,esquerra,reproduïmaquestesvarietatsinvariantspera c = 0.2ialaimatgedeladretamostremunaampliaciódelretorn d’aquestesaunentorndelpunt ( 1, 0),desprésd’havergiratensentithorari alvoltantde (1, 0) enconsiderariteracionsper Fc (puntsgrisos)oensentitantihorariiterant F 1 c (puntsnegres).Veiempetitesoscil lacionsdemida O(10 3) Lafigura12mostravarietatssimilarspera c = 0.3iaralesoscil.lacionssón deuvegadesmésgrans,laqualcosafaquefinsitotespuguindetectarenla representaciódel’esquerra,moltapropde ( 1, 0).Objectessimilarsapareixen si,enllocdepuntsfixos,consideremòrbitesperiòdiqueshiperbòliques.

Aplicacionsquadràtiquesquepreservenl’àreaa R2 93

Figura11: Varietatsinvariantsinestable(engris)iestable(ennegre)del puntfixhiperbòlicpera c = 0.2.Aladretaesmostraunaampliaciódel gràficdel’esquerraapropdelpuntfix.Algràficdel’esquerrasembla quelesvarietatscoincideixen.L’escissióésbastantpetita.

Aquestsobjectesesdiueninvariantsjaqueesrequereixqueelspuntsen unad’aquestescorbes(W u o W s )s’apliquinapuntsdelamateixacorbaquan elsiteremper Fc iper F 1 c .Encaramés,elspuntsde W s tendeixenalpuntfix hiperbòlicoal’òrbitaperiòdicaquans’iterenper Fc ielmateixelssucceeixals puntsde W u quans’iterenper F 1 c .Lacondiciód’invariànciatambéenspermet obtenirdesenvoupamentslocalsd’aquestesvarietats[27].

Figura12: Similaralafigura11,pera c = 0.3.Enelgràficdel’esquerraes començaaveurequelesvarietatssónlleugeramentdiferents.L’escissió d’aquesteséspetita.

Perquèsónrellevants?Aquestesvarietatstenenuna intersecciótransversal quancreuenlarecta y = 0aladreta,propde x = 2.Defet,acausadel’existència delreversor S,satisfan W s = S(W u).Elspuntsonlavarietatinvariantestable iinestabled’unpuntfixoperiòdichiperbòlics’intersequenesconeixenper puntshomoclínics.Potpassartambé,comveuremalasecció6,quelavarietat inestabled’unpunt(fixoperiòdichiperbòlic) Z1 intersequilavarietatestable

CarlesSimó

d’unaltrepunt(fixoperiòdichiperbòlic) Z2.Enaquestcas,lainterseccióés coneixper puntheteroclínic.Ésclar,acausadelainvariància,quesiunpuntés homoclínic(respectivament,heteroclínic),totesles imatgesipreimatges per F tambésónpuntshomoclínics(respectivament,heteroclínics).

Amesuraques’incrementa c lamancadecoincidènciade W u i W s esfa mésevident.Lafigura13mostraaquestesvarietatspera c = 0.77,1.0i1.5.

Figura13: Similaralesfigures11i12esquerra,peròpera c = 0 77,1 0 i1.5,d’esquerraadreta.L’escissiódelesvarietatsésclaramentvisiblei creixent.Notemque,almateixtemps,eldominialvoltantdelpuntfix el líptic (1, 0),quenoquedarecobertperlesoscil lacionsdelesvarietats, esvafentméspetit.

Unamesuradelamancadecoincidènciadelesvarietatsestableiinestable és l’angled’escissió,queesdefineixcoml’angleentrelesduesvarietatsenun punthomoclínicdonat.Enelcasd’APMquadràtiquesqueconsiderem,podem mesurarl’angleenla primeraintersecció delesvarietatsamb y = 0aladreta de x = 1,iveurecomevolucionaenfuncióde c.Perfixaridees,denotemaquest angleper σ(c).Alapartsuperiordelafigura14representemelvalorde σ(c) demaneresdiferents.Enelgràficdel’esquerra,totiquel’escissióésdiferent dezeroperatot c> 0,veiemqueúnicamentpera c> 0 2començaaser visible.Pertaldeveureelquesucceeixperavalorsde c petits,enelgràficde daltaladretarepresentem log(σ) contra log(c).Caltenirencompteque,ja pera c = 0.05,elvalorde σ(c) ésmenorque10 15 i,pertant, negligibleen qualsevolaplicaciópràctica.

Sigui λ(c) elvalorpropidominantdelpuntfixhiperbòlicque,pera Fc ,és iguala1 + c + √2c + c2.Unparàmetreessencialenl’estuditeòricdelproblema és h(c) = log(λ(c)),jaque,usantrepresentacionsadequadesdelesvarietats,és possibleveurequel’escissióadmetcotessuperiorsdelaforma exp( η/h),on η estàrelacionatamblapartimaginàriadelasingularitatdelaseparatriudel fluxlímit,coms’haesmentatalasecció3.Aquesttipusderesultatéscertper a APManalítiquesgeneralsproperesal’aplicacióidentitat [7, 8].Defet,peral problemapresentespotdemostrarunresultatmésprecís.L’angled’escissióté laforma

σ(c) = 9 2 × 106π 2h(c) 8 exp

2π 2 h(c) × Ω(h), (7)

Aplicacionsquadràtiquesquepreservenl’àreaa R2 95

onelterme Ω(h) s’anomena factorcorrector iincloul’efectedelstermesno dominants(ésadir,nilapartexponencialmentpetitanilespotènciesde h(c)). Típicamentesdemostraqueaquesttermeespotacotarperunaconstantmés unterme

Figura14: Adalt:Diferentsrepresentacionsdel’angled’escissió σ(c) entrelesvarietatsenlaprimerainterseccióamb y = 0, x> 1.Al’esquerra: σ enfuncióde c,mostrantque σ semblanegligiblepera c< 0.2.Ala dreta: log(σ) enfuncióde log(c),quepermetveurecomésdepetit σ(c) quan c tendeixazero.Abaixal’esquerra: log(σ) + 2π 2/ log(λ(c)) com afuncióde log(log(λ(c))),mostrantunadependènciagairebélineal ambpendent 8,d’acordamblateoria.Abaixaladreta:elsvalorsde log10(ω2m(2π 2)2m/(2m + 6)!) enfuncióde m,pertaldedonaruna evidènciadelcaràcterGevreyde Ω(h).

Elgràficdebaixal’esquerradelafigura14il.lustralespropietatsde (7). Aquílavariabledel’eixhoritzontalés log(h(c)) mentrequeenl’eixverticales representa log(σ(c)) + 2π 2/h(c).D’acordamb (7),elqueesrepresentahauria deser(simenyspreemelterme O(h) enlacotade Ω(h);vegeuelparàgraf següent)unarectaambpendent 8,queconcordaperfectamentamblesdades.

Elfetquecalculemvalorsbastantpetitsde σ(c) noéspasunproblema.El paquetPARI/GP[3]ésútilperaaquestsproblemessenzills.

Enelcasdel’aplicaciód’Hénon,enlaformulaciópresent,s’observaexperimentalmentqueelterme Ω(h) espotdesenvoluparenpotènciesde h2: Ω(h) = m≥0 ω2mh2m.Eltermeconstantielsprimerstermesdeldesenvolupamentde Ω(h) podenésserdeterminatsnumèricament(vegeu-neelsmètodes

CarlesSimó

a[10, 30])demaneraacurada(finsitotambmilersdexifrescorrectes)iels primersdígitsde ω0 són2.48931280293671.Noobstantaixò,lasèrieque defineix Ω(h) és divergent,peròensproporcionaunabonaaproximacióper acadavalorde h siestruncalasumaenellloccorrecte.Hihaevidèncianumèricaquelasèrieésde classeGevrey-1,ésadir,totiserdivergent,lasèrie associada m≥0 ωmh2m/(2m)!ésconvergent.Elgràficdesotaaladretade lafigura14mostraaquestaevidència.Deladeterminaciónumèricade Ω(h) peradiferentsvalorsde h espodenobtenirelscoeficients ω2m.Alafigura representem log10(ω2m(2π 2)2m/(2m+6)!) enfuncióde m,quesemblaque tendeixaunaconstant.

AquestcaràcterGevreytambés’had’esperaren lamajoriadelesconstruccionsformalsdefluxos enlesqualsl’aplicaciótemps-1aproximaunaAPM donada(ofinsitotunaaplicaciógeneral)properaalaidentitat.

Perexplicar lageneraciódecaos degutal’existènciadepuntshomoclínics transversals,tornemunmomentalafigura5.Ésclarqueentrelesillesde període5hihaunaòrbitaperiòdicahiperbòlicadelmateixperíode.Substituint Fc per F 5 c elspuntsdel’òrbitaperiòdicaesconverteixenenpuntsfixos. Siensfixemenunadelesilles,perexemplelaqueestàmésal’esquerra,i enlesvarietatsdelspuntsfixosdelvoltant,veiemquel’estructuraéssimilar aladel’espaidefased’un pèndol,peròaralesseparatrius nocoincideixen: lavarietatestableilainestables’intersequentransversalmentenl’eix y = 0. Espotveurequeaquestasituacióéstopològicamentequivalental patróde figuravuit mostratal’esquerradelafigura15[35].Espodenveurelespetites oscil lacionsdelesbranquesde W u alvoltantde W s apropde p iviceversa. Notemqueelpatrómostratenlafigura15noeltrobaremenl’aplicacióde Hénon,sinóenaltresfamílies,com l’aplicaciódeDuffingconservativa oalguna representacióde l’aplicacióestàndard.

Figura15: Al’esquerra:unpuntfixhiperbòlic p delamenaqueles sevesvarietatsgenerenduesvoltes(ounavoltadelafiguravuit).També esmostrendospuntsfixosel.líptics, e+ i e ,juntamentamblescorbes invariantsalvoltantd’aquests, γ+ i γ ,iunacorbainvariantexterna Γ .A ladreta:detalldelretorndelspunts A i B aunentornde p,com Φ(A) i Φ(B),quepermetentendrel’origendelcaos.Vegeueltextperalsdetalls.

Elgràficdeladretaésunaampliaciódeldel’esquerra.Consideremdospunts comsón A i B,propersa W u,+ però encostatsdiferents de W s,+.Podenestartan properscomesvulgui.Desprésdediversesiteracions,diguem-ne m,idefinint

Aplicacionsquadràtiquesquepreservenl’àreaa R2 97

Φ = F m,elspuntsretornenapropde p com Φ(A) i Φ(B).Comqueestanen costatsdiferentsde W s,+ elsiteratssuccessiusdelpunt Φ(A) esmouran cap aladreta ielsde Φ(B) esmouran capal’esquerra.Elsistematé sensitivitat respectelescondicionsinicials.Aquestprocésesrepeteixcadavegadaqueels iteratsdelpunttornenapropde p.Defet,donadaunaseqüènciabiinfinita desímbols (left)i r (right),delaforma {..., , ,r,r,r, ,r, ,r,... },espot demostrarquehihapuntsquerealitzenaquestaseqüènciaenelspassatges successiusapropde p.Ésadir,ladinàmicaés impredictible.Elsistemaés determinista peròmostra dinàmicacaòtica.

6Elmecanismededestrucciódecorbesinvariantsiels

conjuntsdeCantorassociats

Talcoms’hacomentatalasecció4,sielnúmeroderotacióésmassaproper aunracional(ensentitdiofàntic)osilacondiciótwistésmassadèbilosila pertorbaciórespected’unaaplicacióintegrableésmassagran,lacorbainvariant noexisteix.Aquestespropietatsanalítiquestenenalhorauna interpretació geomètrica.Abansd’entrarenelsdetallsesproposaveurel’animació movie2 a http://www.maia.ub.es/dsg/QuadraticAPM,queproporcionaunaevidènciade la destrucciódelescorbesinvariants queenvoltenlesillesdeperíode6,5i4, quan c augmenta.Elspuntsenvermelldelesimatgesestrobensobrecorbes invariants,mentrequeelspuntsenverdtenendinàmicacaòtica.Notemque aquestsúltimsestan confinats sihihauna corbainvariantqueelsenvolti.Quan aquestacorbaesdestrueixelsiteratsdelspunts s’escapen

Pertald’il.lustrarelmecanismequecomportala destrucció delescorbes invariants,consideremlafigura16.S’hageneratpera c = 0.63imostralapart esquerradelconjuntdepuntsquetenenòrbitesacotades.Elcasdelafigura16 éssimilaraldelafigura5,peròaralesillesprincipalssóndeperíode6.En negrerepresentemduescadenesd’illesambnúmeroderotació3/19i4/25. Consideremlesòrbitesperiòdiqueshiperbòliquesassociades,ladeperíode4/25 ésvisiblesobrel’eixdeles x ielsdospuntssimètricsdel’òrbitahiperbòlicade númeroderotació3/19estanapropde x =−0.2,foradel’eixdeles x.Les varietatsd’aquestesòrbitesperiòdiquesdonenlloca connexionsheteroclíniques, delamaneracomesdescriuenlallegenda.

Aquestesconnexionsheteroclíniquessón obstruccions peral’existència delescorbesinvariantsquepodriensepararlescadenesd’illes.Enrealitat, siconsideremunacorbaformadaperuntrosdelavarietatinvariantdesdel puntperiòdichiperbòlicinterior(elquetéperíode25)finsalpuntheteroclínic, seguitdeltrosdelavarietatinvariantdelpuntperiòdichiperbòlicextern (eldeperíode19),desdelpuntheteroclínicfinsalpuntperiòdic,lescorbes invariants haurandecreuar-la.Això ésimpossibleacausadelainvariància Defet,esconclouquenopodenexistircorbesinvariantsambnúmerode rotacióenl’interval (3/19, 4/25).Així,elmecanismegeomètricresponsablede ladestruccióésl’existènciadeconnexionsheteroclíniquesqueobstrueixenles possiblescorbes[21,23].

Figura16: Unail lustraciódelmecanismededestrucciódecorbesinvariantspera c = 0 63.Ennegre:partdelesduescadenesd’illesde períodes19(laqueinterseca y = 0)i25.Engrisclarientraçgruixuti primesmostrenlesvarietatsestableiinestable, W s 25 i W u 25,respectivament,d’unaòrbitaperiòdicahiperbòlicadeperíode25.Engrisfoscitraç gruixutiprimlesvarietatsestableiinestable, W s 19 i W u 19,respectivament, d’unaòrbitaperiòdicahiperbòlicadeperíode19.Noteuque W u 25 i W s 19 (i, simètricament, W s 25 i W u 19)tenenpuntsheteroclínicstransversals.Això representaunaobstruccióperal’existènciadelescorbesinvariantsque podriensepararlescadenesd’illes.Vegeuelsdetallseneltext.

Noésnecessariqueunaconnexióheteroclínicasiguitransversalperimpedir l’existènciadecorbesinvariants.Éssuficienttenir contactetangencial,ésadir, quelesvarietatsestableiinestablerelacionadessiguintangents.Ésbastant comúque,variantelsparàmetres,duesvarietatsqueestavenallunyadescomencinaacostar-sefinsquesóntangentsi,després,esdevinguintransversals, amblaqualcosaescreenpuntshomoclínicsoheteroclínics.Algunesòrbites periòdiquesespodencrear propdelatangència i,enparticular,podenserde tipusel.lípticidonarllocaillesperiòdiques.Denou,elmodelperentendreel comportamentpropdelatangènciaésl’aplicaciód’Hénon.Unexamendetallat delprocésrevelaque,peraaplicacionsanalítiques,elspuntshomoclínicsja existienabansdelatangència,peròpertanyiena l’espaidefasecomplex.Això comportaconsiderarl’aplicaciód’Hénon(od’altresaplicacionsanalítiques)no a R2 sinóa C2.Enelmomentdetangència,aquestspuntssimplement aterren alsreals [15].

Comescomentaràalasecció8,pera c ≈ 0 6204janohihacorbesinvariants envoltantlesillesdeperíode6.Enparticular,s’handestruïtlescorbesentre lesillesdeperíode19i25delafigura16.Perònoméscomencemaveure connexionsheteroclíniquesenlafigurapera c = 0.63.Gràficssemblantsper a c = 0 625o c = 0 628,perexemple,noevidencienl’existènciadepunts heteroclínics.Lesraonsd’aixòsónsimples:

Aplicacionsquadràtiquesquepreservenl’àreaa R2 99

a) Lalongitudd’arcdelesvarietatsdelafigura16éscurta.Siesrepresenten partssimilarsdelesvarietatspera c = 0.628,lavarietatentraçgrisclar gruixutnotocaladetraçgrisfosciprim,nilavarietatengrisclariprim notocalarepresentadaentraçgrisfoscgruixut(acausadelasimetria). Peròpartsmésllarguesdelesvarietatss’intersequen.Enparticular,hiha arcsdelavarietatinvariantques’escapenal’infinit(periteracióde Fc per a W u ide F 1 c pera W s ).

b) Entrelescadenesd’illesmostradesalafigura16hihamoltesaltres òrbitesperiòdiqueshiperbòliques(defet,unainfinitat).Aixíéspossible trobaruna cadenadeconnexionsheteroclíniques entrealgunesd’aquestes òrbites,queproporcional’obstrucciódesitjada.Alseutornaixòimplica l’existènciadeconnexionsheteroclíniquesentrelesòrbitesdeperíodes19 i25.

Siguicomsigui,hihaobjectesinvariantsambnúmeroderotacióenl’interval mencionatprèviament.S’hademostratqueaquestsobjectesestan fora deles varietatsdel’òrbitaperiòdicahiperbòlicaamb ρ = 4/25i dins delesvarietats del’òrbitaperiòdicahiperbòlicaamb ρ = 3/19.Lesconnexionsheteroclíniques d’aquestesvarietatscreen forats que hiimpedeixenl’existènciadepuntsde l’objecteinvariant.Comaconseqüènciad’això,aquestobjecteésun conjuntde Cantor [17,18,22]iestàdemostratqueté mesurazero.

Pertant,elspuntsambdinàmicacaòticaqueestavenconfinatsquanlacorba invariantencaraexistia,espodenescaparquanlacorbahaestatdestruïdaiés substituïdaperunconjuntdeCantor.Noobstantaixò,sielsforatsd’aquest conjuntsónrelativamentpetits,serànecessariun tempsllarg perquèelsiterats trobinlamanerad’escapar-se.Aixòesveuràenlasecció8.

7Mesurantlaquantitatdecaos:exponentsdeLyapunovi entropia

Perestudiarlespropietatsd’estabilitatlineald’unpuntfixod’unpunten unaòrbitaperiòdicadeperíode k,quedenotarem z∗,perunaaplicació F ,cal calcularsimplement DF(z∗) o DF k(z∗) imirarelsvalorspropis,talcoms’ha descritalasecció1.Laqüestióéscomprocedirpera òrbitesgenerals,comles quetenimenelcasdepuntsencorbesinvariantsoambdinàmicacaòtica.

Laideabàsicaésferservirla mitjanadelataxadecreixementdeladistància entreelspuntsdel’òrbitaielsd’unaòrbitaarbitràriamentpropera[5].En general,podemconsiderarquel’aplicació F actuaenunavarietat Σ.Sigui z ∈ Σ unpuntiniciali ξ unvectorenl’espaitangenta Σ en z: TzΣ.Amés,suposem que ξ ténormaiguala1.Aleshorescalculem DF m(z)(ξ) imiremlataxade creixementdellogaritmedelanormapertaldedefinirelnúmero

Λ(z,ξ) = lim m→∞ 1 m log |DF m(z)(ξ)|, (8) queesconeixper l’exponentdeLyapunov de z enladireccióde ξ.S’hademostrat queellímitexisteixperagairebétot ξ ∈ TzΣ iperagairebétot z ∈ Σ.Elvalor

CarlesSimó

màximde Λ(z,ξ) quan ξ variaenelfibrattangentunitaria TzΣ esconeixper l’exponentdeLyapunovmaximal delpunt x: Λ(z).Peragairebétot ξ ∈ TzΣ es téconvergènciacapa Λ(z).

Perobtenirunaestimacióde Λ(z) s’handereescalarelsvectors DF m(z)(ξ) (altramentlanormapodriacréixermassa)iusardiferentsestratègiespertalde poderconfiarenl’estimació[31, 16].Peraòrbitesenunacorbainvariantamb ρ irracional(aquestesòrbitessóndenses)elvalorde Λ(z) észero,mentreque lesòrbitesambdinàmicacaòticadonen,genèricament,valorspositiusde Λ(z). Hihaòrbitescaòtiquesquedonen Λ(z) = 0,peròsónbastantexcepcionals[9].

Tornantal’APMquadràtica Fc ,hemcalculatl’exponentdeLyapunovmaximal peramoltsvalorsde c iunaxarxafinadepunts.Unaseparaciótípicaenles coordenades x i y enlaxarxaés0.0005.Enmoltsdelscasosprimercalculem untransitoride106 iteratsabansdecomençaracalcular Λ(z).D’aquesta maneradetectemmoltsdelspuntsques’escapen.S’hautilitzattambéunvalor de m = 106 a (8) perobtenirunaestimacióde Λ(z).Sielvalorobtingutésmenor que2 × 10 5,l’òrbitade z ésconsideradaregular.Altrament,ésconsiderada caòtica.Enaquestúltimcas,continuemfentiteracionsaddicionals(finsaun totalde108 ienalgunscasosfinsa1010)percomprovarsipodemconsiderarel caosconfinatosil’òrbitade z finalments’escapa.Algunsresultatss’il.lustren enlasecció8.

Unaindicacióglobaldelespropietatsregularsocaòtiquesdelsistemaensla dóna l’entropiamètrica hm(F).Hihadiversesmaneresequivalentsdedefinir-la, peròlaméssimpled’implementaréslaintegraldel’exponentdeLyapunoven elconjuntd’òrbitesacotades;vegeu[16].Ensdiucomésde caòtica l’aplicació globalment

8Canvisenlamesuradelconjuntdepuntsquenos’escapen

Elgràficdela mesura µ(c) delconjunt d’òrbitesacotades enfuncióde c per l’aplicació Fc ,donadaper (4),ésbastantinstructiu.Caldestacarquehiha moltsaltresmodelsconservatiusmésgenerals(p.ex.sistemeshamiltonians amb2o3grausdellibertat,comelproblemarestringitdetrescossos,oones viatgeresd’algunesEDP,comelsistemadeMichelson[32, 6])quetenen moltes característiquesencomú amblesqueusemperail lustrarelcasdel’aplicació d’Hénonconservativa.

Amés,peraAPMenunavarietat2D,cadavegadaqueesprodueixuna tangènciahomoclínica(ésadir,peraalgunpuntfixoòrbitaperiòdica, W u i W s tenentangència)unestudilocalpropdelatangènciaproporcionaaplicacionssimilarsalad’Hénonambpropietatsglobalssemblants,talcoms’ha esmentatalasecció6.

Alafigura17esrepresentalamesura µ(c) delconjuntd’òrbitesacotadesen funcióde c,iunaampliaciód’aquestafigura.Noteuelsdecreixementsbruscos delamesuraperaalgunsvalorsde c.Dedretaaesquerra,espotveureun primerdecreixementpropde c = 1.5.Peraaquestvalordelparàmetreelpunt el.líptictévalorspropis 1/2 ± i√3/2iés(dèbilment)inestable. Noexisteixen

Aplicacionsquadràtiquesquepreservenl’àreaa R2 101

corbesinvariantsquel’envoltin.L’àreapetitaconfinadapera c = 1.5ésdeguda al’existènciad’illesdiminutesdeperíode3.Acontinuacióveiemunaseqüència decanvisbruscosde µ(c) quecorresponenaladestrucciódetoteslescorbes invariantsqueenvoltenlesillesdeperíodes4,5,6,etc.

Figura17: Al’esquerra:mesura µ(c) delconjuntdepuntsconfinatsen funcióde c.Aladreta:unaampliacióenelrang c ∈ [0 77, 0 97] per donarevidènciadelespropietatsd’autosimilitudd’aquestamesura.

L’ampliacióqueesmostraaladretadelafigura17dónaunafortaevidència delquepassaalesillesdeperíodemésaltiil.lustralespropietatsd’autosimilitudde µ(c).Perexemple,elgransaltapropde c = 0.91escorresponal trencamentdelescorbesinvariantsqueenvoltenlesillesdenúmeroderotació2/9(compareu-hoambeldominisuperiorgrisfoscdelafigura7),mentre queelsaltques’observapocdesprésde c = 0.96corresponaltrencamentde lescorbesinvariantsqueenvoltenlesillesdenúmeroderotació3/13.Noés difícilidentificartotselssaltsqueesveuenenaquestesgràfiques.Comque hihasaltsde µ(c) peracadapetitcanvide c,estéunaevidènciaqueésuna funciótotalmentdiscontínua.

Esproposaferuncopd’ullala movie3 quetrobareua http://www.maia.ub.es/ dsg/QuadraticAPM perveureelscanvisnonomésdelamesura,sinótambéde laformadelconjuntd’òrbitesacotades.

Entreelspuntsambòrbitaacotadan’hiha,noobstantaixò,algunsque mostrenuncomportamentcaòtic.L’exponentdeLyapunovenspermetdetectarlos.Unaqüestiónaturalés,pertant,sabercomvarialamesurad’aquestconjunt respectealvalorde c.Aquestavariaciós’il.lustraenlafigura18.Elgràficmostra uncanvibastantbruscenelcomportament.Caliaesperaraixòatesalainfinitud decadenesd’illesenelsistema(n’hihaperacada ρ ∈ Q ∩ (0, 1/2]).Cada cadenad’illestéunaòrbitaperiòdicahiperbòlicaassociadaquegenerauna certaquantitatdecaos,elqualestàconfinatfinsquelescorbesinvariants queenvoltenaquestesòrbitescaòtiquesesdestrueixen.Totiqueelscàlculs ques’il.lustrenenlafigura18hanestatrealitzatsambunpasde10 3 en c,una exploraciódetalladadelesdadesenspermetdetectaralgunscentenarsdepics.

CarlesSimó

Figura18: Mesuradelconjuntdepuntsconfinatsambdinàmicacaòtica enfuncióde c

Alafigura19se’nmostrentresampliacions.Escorresponenambelque passadesprésdeltrencamentdelescorbesinvariantsqueenvoltenlesillesde període6,5i4,respectivament.Perara,noconsideremelspetitssaltsd’aquestes corbes,nomésunamenademitjana.Elgràficdel’esquerraésconseqüència delcanvidemidadelazonacaòticacreadapelspuntshomoclínicsassociatsa l’òrbitaperiòdicahiperbòlicadeperíode6.Peròaquestaòrbitaneixpera c = 0 5. Aixídoncs,perquècostatantveurequelamidad’aquestazonaésrellevant? Larespostaéssimilaraladiscussiódelasecció5sobreelcanvidelamidade l’angled’escissió σ(c) enfuncióde c.Enaquestsentit,tambéensreferimala figura14,especialmentalgràficdedaltal’esquerra.

Figura19: Ampliaciódelafigura18corresponentaltrencamentdeles corbesinvariantsqueenvoltenlesillesdeperíode6(esquerra),període5 (centre)iperíode4(dreta).

Allíensvamadonarqueelcanvien c desdelcomençamentdel’existència d’unangled’escissiónonulfinsqueaquestcomençaaservisibleera,coma mínim,iguala0.2.Alafigura19,esquerra,lasituacióéssimilar.Totique

Aplicacionsquadràtiquesquepreservenl’àreaa R2 103

l’escissiódelesvarietatsdelesòrbitesdeperíode6començaa c = 0.5,només peravalorsde c propersa0.6estornavisible.Enelsgràficsdelcentreidela dretadelafigura19lasituacióésbastantsimilar.Volemdestacarúnicament quel’òrbitaperiòdicahiperbòlicadeperíode5s’hacreaten c = 1 cos(2π/5) ≈ 0.690983iqueladeperíode4s’hacreaten c = 1.Així,enaquestsdoscasos l’evoluciódel’escissiórespectede c ésmésràpida.

Elsaltqueesveuenelgràficdel’esquerrapocdesprésde c = 0.61es corresponexactamentambelmateixtipusdefenomen,peròcausatperl’òrbita periòdicadenúmeroderotació ρ = 3/19.Lamesuradelazonacaòticaassociada aaquestaòrbitaperiòdicas’had’afegir,d’algunamanera,alazonacaòticamés grandegudaal’òrbitadeperíode6.

Eneldominionesfaevidentl’existènciadecaosespodentrobarilles diminutes.Unaprovad’aquestfetusantargumentsanalíticsigeomètricses pottrobara[33].

Unaltrepuntquevolemil.lustrarés comn’ésderàpid,enfuncióde c, l’escapamentdelspuntsd’unazonacaòticaquanlescorbesinvariantsque l’envoltens’hantrencat.Sigui cp/q el valorcrític peralqualesprodueixel trencamentdelescorbesinvariantsenvoltantlesillesdenúmeroderotació ρ = p/q.Aleshores,quan c>cp/q,elspuntsdelazonacaòticaassociadaespoden escapar.Peròésclarquesi ∆c = c cp/q éspetit,elsforatsenelsconjunts deCantorqueenvoltenlazonacaòticasón estrets iserànecessari,perterme mitjà,un nombregrand’iterats pertalqueesprodueixil’escapament.

Lafigura20mostraexemplesenaquestsentit.Elsvalorscríticsaproximats peralesòrbitesperiòdiquesdelafigurasón c1/6 ≈ 0 6204, c1/5 ≈ 0 7649 i c1/4 ≈ 1.0141.Analitzem,perexemple,elgràficdel’esquerra.Peraunvalor com c = 0 625,lafracciódepuntsqueromanendesprésde105 iteratsés relativamentgranenfrontd’aquellsquehofandesprésde106 iterats.De fet,d’acordamblafigura,un8%mésgran(corbaengrisclar).Siensfixem enaquellsqueromanendesprésde106 iteratsielscomparemambaquells quehofandesprésde107 iterats,l’excésésdel’1%aproximadament(corba grisa).Finalment,lamesuradelspuntsqueromanendesprésde107 iteratsen comparacióambaquellsqueromanendesprésde108 iteratsésquasinegligible (corbanegra).Aixòvoldirqueunagranpartdelspuntsen òrbitescaòtiquesno confinades s’escapendesprésde106 iteratsin’hihamoltpocsquerequereixen mésde108 iteratsperfer-ho.

Elsvalorscanvienquanestudiemdiversosvalorsde c.Peraunvalorcom c = 0 63lamajoriadepuntsjas’escapenper105 iterats,mentrequepera c = 0 621 gairebénohihapuntsques’escapinabansde107 iteratsilamajoriarequereixen 108 iteratsomés.

Sitornemalafigura17o18,veuremqueelssaltssóninstantanis:obé existeixencorbesinvariantscircumdantsinohihapossibilitatd’escapament obénon’existeixenitotselspuntsdelazonacaòticarelacionadas’escapen. Notem,però,quelessimulacionsesduenatermeambunnombrefinitd’iteracions(que,coms’hadit,variaentre108 i1010 iterats,depenentdelafigura). Elsresultatsperadiferentsperíodesmostratsenelsgràficsdelcentreide

CarlesSimó

l’esquerradelafigura20sónbastantsimilars.Elmateixcomportaments’ha d’esperarenlamajoriadecasos.

Figura20: D’esquerraadretaesmostrenelsresultatsrelatiusal’escapamentdepuntsdesprésdeladestrucciódelescorbesqueconfinenal voltantdelesillesdeperíodes6,5i4,respectivament.Si Mn denotael conjuntdepuntsambdinàmicacaòticaquenos’hanescapatdesprés de n iterats,lescorbesengrisclar,grisinegremostrenl’excésrelatiu M105 /M106 1, M106 /M107 1i M107 /M108 1,respectivament.

9Algunsproblemesoberts

Elquesabemactualmentsobreladinàmicad’APMquadràtiques,itambésobre APMmésgenerals,permetunacomprensióbastantcompletadelsdiferentstipus decomportament,elsmecanismesgeomètricsilesestimacionsanalítiques.

Totiaixòencarahihaalgunsproblemesclàssicsque romanenoberts.A continuacióenmencionemalguns,elsqualssón llunydeserelementals ihan resistitdiversosintentsfinsara.

a) LesAPMquadràtiquessónuncasespecialdelesanomenades aplicacions deCremona.Aquestessónaplicacionspolinomialsenqualsevoldimensió: z → T(z) ∈ Rm,ontoteslescomponentsde T sónpolinomialsambgrau maximal n.Suposemqueeljacobiàde T ésconstant: det(DT(z)) = a, peratot z ∈ Rm,amb a ≠ 0unnúmeroreal.Noésrestrictiusuposar que a = 1,altramentcomponem T ambunaaplicaciólinealadequada. L’anomenada conjecturajacobiana plantejalaqüestiósegüent:éscert quel’aplicacióinversa T 1 éstambéunaaplicaciópolinomial?Elgraude T 1 nohadesernecessàriamentelmateixqueelgraude T . Sabemque,peraaplicacionsdeCremonaquadràtiques,larespostaés sí,ilainversatambéésquadràtica.Aixòésconseqüènciadelformatde l’equació (4) idel’existènciadelreversor S peraAPMquadràtiques,que implicaquelainversade Fc ésconjugadade Fc . Aquestaconjecturahaestatdemostradaperagrau2ihiharesultats queredueixenelproblemaademostrar-laenqualsevoldimensiópera aplicacionspolinomialsdegrau3.Hihaaltresresultatsquefanreferència aalgunscasosespecials,peròelproblemageneralrestaobert.

Aplicacionsquadràtiquesquepreservenl’àreaa R2 105

b) Hemvistquelesòrbitesperiòdiquestenenunpaperdestacatenl’organitzaciódeladinàmicad’APMquadràtiquesielmateixéscertperaAPM generals.

Unaantigaconjecturadegudaa Poincaré és:considereuelconjuntd’òrbitesacotadesd’unaAPM.Éscertquelesòrbitesperiòdiquessóndensesen aquestconjunt?

c) Enlesseccions7i8hemparlatdelamesuradelconjuntdepuntsamb exponentdeLyapunovpositiuitambédel’entropiamètrica,comala integraldel’exponentdeLyapunovmaximal.Totil’evidèncianumèricahi haunaqüestióbàsicaquerestaoberta,queésconegudaambelnomde conjecturad’entropiamètricapositiva.Ésl’entropiamètricad’unaAPMno integrableestrictamentpositiva?

Unaqüestióequivalentpotserexpressadadelamanerasegüent.Considereulavarietatinvariantestableolainestabled’unpuntfixoperiòdic z∗ . ÉslamesuradeLebesguedelaclausurad’aquestavarietatestrictament positiva?

d) Enlasecció4s’hanfetalgunscomentarissobreelsnombresdiofàntics ilespropietats òptimes delaproporcióàuria g.Les (C,τ)-DCespoden expressarcom |qγ p| >C/qτ 1 peraqualsevol (p,q) ∈ Z2 , q ≠ 0.

Passema dimensiósuperior.Siguin n> 1i ω = (ω1,...,ωn) ∈ Rn.Diem queelvector ω satisfàuna (C,τ)-DCsi | n i=1 ωiki k0| >C/(||k||2)τ 1 , peraqualsevol k = (k1,...,kn) ∈ Zn,on ||k||2 éslanormaeuclidiana, quesuposempositiva,iperatot k0 ∈ Z

Pera n> 1donat,quinéselvector òptim,enelmateixsentitquehem usatpera g?

Unaltreproblemabastantgeneralapareixenlesperspectivesdelasecció següent.

10Perspectivesiconclusions

Lesaplicacionsquadràtiquesquepreservenl’àrea,totiserlaprimeraextensió delcaslinealaserconsiderada,mostrenuna dinàmicaextremamentrica. Leseinesanalítiques,geomètriquesitopològiquesenspermetenteniruna bonacomprensiódeladinàmica itrobarexplicacionspera(quasi)totselsfets numèricamentobservats.

Algunsaspectesrequereixenencaraunacombinaciód’einesanalítiquesi numèriques,comaralapredicciódequanestrencaranlesdiferentscorbes invariantsobélapredicciódepropietatsestadístiquesglobals.

Amés,l’estudidelcasquadràticpotserconsideratun paradigma quees potusarperdescriurelespropietatsd’APMmésgenerals.

Unapreguntaclauésquèsucceeixquan augmentemladimensió Les aplicacionssimplèctiques sóngeneralitzacionsnaturalsd’APMenvarietatsdedimensióparell(diguemdimensió2n).Suposemqueusem coordenadeslocals (x1,x2,...,xn,y1,y2,...,yn) iconsideremla2-forma

CarlesSimó

ω = dx1 ∧dy1 +dx2 ∧dy2 +···+dxn ∧dyn.Unaaplicaciósimplècticaésuna transformacióquepreserva ω.Ésclarquesi n = 1laformanoésresmésque l’elementd’àrea.Aquestestransformacionsapareixendemaneranaturalcoma aplicacionsdePoincaréensistemeshamiltoniansamb n+1grausdellibertat. Quèespotdirdeladinàmicadelesaplicacionssimplèctiques?Hihadiversos resultatsparcials,comaral’existènciadetorsinvariants n-dimensionals(que generalitzenlescorbesinvariantsquetrobemenAPM).Resultatssemblantshan estatdemostratsperalssistemeshamiltonianspropersaunsistemaintegrable, untemaestudiatperla teoriaKAM (vegeu,perexemple,[2]).L’últimproblema obertdelsmencionatsabansestàrelacionatamblespropietatsdeltorinvariant méspersistent.Però,finsitotperalcas n = 2,encaranoesdisposad’unabona descripciódelespropietatsglobalsdeladinàmica.Aixòpodriaserunbontema d’investigacióperalspropersanys.

Agraïments

Larecercadel’autorhaestatfinançadaalllargdelsanyspersubvencions europees,espanyolesicatalanes.L’autoragraeixprofundamentlacontribució demúltiplescol.laboradorsal’horadeclarificardiversostemes.Enparticular, N.MigueliA.Vieiro,ambquicol.laboraenlamateixaàread’estudi.S’hanusat lesfacilitatscomputacionalsdelGrupdeSistemesDinàmicsdelaUniversitat deBarcelonaperalesil lustracionsnumèriquespresentadesenaquestesnotes. EsvolagrairtambéeltreballeficientdeJ.Timonedacomaadministradordel clúster.

Referències

[1] Arnold,V. Lesméthodesmathématiquesdelamécaniqueclassique.Moscou:ÉditionsMir,1976.[TraduïtdelrusperDjilaliEmbarek]

[2] Arnold,V.I.;Avez,A. Problèmesergodiquesdelamécaniqueclassique París:Gauthier-Villars,1967.(MonographiesInternationalesdeMathématiquesModernes;9)

[3] Batut,C.;Belabas,K.;Bernardi,D.;Cohen,H.;Olivier,M. Users’guide toPARI/GP. http://pari.math.u-bordeaux.fr/.

[4] Broer,H.;Roussarie,R.;Simó,C. «InvariantcirclesintheBogdanovTakensbifurcationfordiffeomorphisms». ErgodicTheoryDynam.Systems, 16(6)(1996),1147–1172.

[5] Cincotta,P.M.;Giordano,C.M.;Simó,C. «Phasespacestructureof multi-dimensionalsystemsbymeansofthemeanexponentialgrowth factorofnearbyorbits». Phys.D,182(3–4)(2003),151–178.

[6] Dumortier,F.;Ibáñez,S.;Kokubu,H.;Simó,C. «Abouttheunfolding ofaHopf-zerosingularity». DiscreteContin.Dyn.Syst.,33(10)(2013), 4435–4471.

[7] Fontich,E.;Simó,C. «Invariantmanifoldsfornearidentitydifferentiable mapsandsplittingofseparatrices». ErgodicTheoryDynam.Systems,10(2) (1990),319–346.

Aplicacionsquadràtiquesquepreservenl’àreaa R2 107

[8] Fontich,E.;Simó,C. «Thesplittingofseparatricesforanalyticdiffeomorphisms». ErgodicTheoryDynam.Systems,10(2)(1990),295–318.

[9] Garrido,L.;Simó,C. «Someideasaboutstrangeattractors».A: Dynamical systemsandchaos.Berlín;NovaYork:Springer,1983,1–28.(LectureNotes inPhys.;179)

[10] Gelfreich,V.;Simó,C. «High-precisioncomputationsofdivergentasymptoticseriesandhomoclinicphenomena». DiscreteContin.Dyn.Syst.Ser.B, 10(2–3)(2008),511–536.

[11] Gómez,G.;Mondelo,J.M.;Simó,C. «AcollocationmethodforthenumericalFourieranalysisofquasi-periodicfunctions.I.Numericaltestsand examples». DiscreteContin.Dyn.Syst.Ser.B,14(1)(2010),41–74.

[12] Gómez,G.;Mondelo,J.M.;Simó,C. «AcollocationmethodforthenumericalFourieranalysisofquasi-periodicfunctions.II.Analyticalerror estimates». DiscreteContin.Dyn.Syst.Ser.B,14(1)(2010),75–109.

[13] Hénon,M. «Numericalstudyofquadraticarea-preservingmappings». Quart.Appl.Math.,27(1969),291–312.

[14] Hénon,M. «Atwo-dimensionalmappingwithastrangeattractor». Comm. Math.Phys.,50(1)(1976),69–77.

[15] Lazutkin,V.F.;Simó,C. «Homoclinicorbitsinthecomplexdomain». Internat.J.Bifur.ChaosAppl.Sci.Engrg.,7(2)(1997),253–274.

[16] Ledrappier,F.;Shub,M.;Simó,C.;Wilkinson,A. «Randomversusdeterministicexponentsinarichfamilyofdiffeomorphisms». J.Statist.Phys., 113(1–2)(2003),85–149.

[17] Mather,J.N. «Minimalmeasures». Comment.Math.Helv.,64(3)(1989), 375–394.

[18] Mather,J.N. «Actionminimizinginvariantmeasuresforpositivedefinite Lagrangiansystems». Math.Z.,207(2)(1991),169–207.

[19] Miguel,N.;Simó,C.;Vieiro,A. «FromtheHénonconservativemaptothe Chirikovstandardmapforlargeparametervalues». Regul.ChaoticDyn., 18(5)(2013),469–489.

[20] Ne˘ıshtadt,A.I. «Theseparationofmotionsinsystemswithrapidly rotatingphase». J.Appl.Math.Mech.,48(2)(1984),133–139(1985).[Traduït delrusde Prikl.Mat.Mekh.,48(2)(1984),197–204]

[21] Olvera,A.;Simó,C. «Anobstructionmethodforthedestructionofinvariantcurves». Phys.D,26(1–3)(1987),181–192.

[22] Olvera,A.;Simó,C. «ThedynamicsnearinvariantCantoriansetsof perturbedtwistmaps».A: Velarde,M.G. (ed). Synergetics,orderand chaos.Teaneck,NovaJersey:WorldSci.Publ.,1988,698–705.

[23] Olvera,A.;Simó,C. «Ellipticnon-Birkhoffperiodicorbitsinthetwist maps». Internat.J.Bifur.ChaosAppl.Sci.Engrg.,3(1)(1993),165–185.

CarlesSimó

[24] Sánchez,J.;Net,M.;Simó,C. «ComputationofinvarianttoribyNewtonKrylovmethodsinlarge-scaledissipativesystems». Phys.D,239(3–4) (2010),123–133.

[25] Siegel,C.L.;Moser,J.K. Lecturesoncelestialmechanics.NovaYorkHeidelberg:Springer-Verlag,1971.(DieGrundlehrenderMathematischen Wissenschaften;187)

[26] Simó,C. «Anoverallviewonconservativemapsoftheplane».A: Alsina,C. etal. (ed). EuropeanConferenceonIterationTheory.Teaneck,NovaJersey: WorldSci.Publ.,1989,56–73.

[27] Simó,C. «Analyticalandnumericalcomputationofinvariantmanifolds». A: Benest,D.;Froeschlé,C. (ed). Modernmethodsincelestialmechanics Gif-sur-Yvette:EditionsFrontières,1990,285–330.

[28] Simó,C. «Averagingunderfastquasiperiodicforcing».A: Hamiltonian mechanics.NovaYork:Plenum,1994,13–34.(NATOAdv.Sci.Inst.Ser.B Phys.;331)

[29] Simó,C. «Invariantcurvesofanalyticperturbednontwistareapreserving maps». Regul.ChaoticDyn.,3(3)(1998),180–195.

[30] Simó,C. «Analyticalandnumericaldetectionofexponentiallysmallphenomena».A: Proceedingsoftheconference,Equadiff’99.Singapur:World Scientific,2000,967–976.

[31] Simó,C. «Globaldynamicsandfastindicators».A. Globalanalysisof dynamicalsystems.Bristol:Inst.Phys.,2001,373–389.

[32] Simó,C. «Somepropertiesoftheglobalbehaviourofconservativelowdimensionalsystems».A: Foundationsofcomputationalmathematics.Cambridge:CambridgeUniv.Press,2009,162–189.(LondonMath.Soc.Lecture NoteSer.;363)

[33] Simó,C.;Treschev,D. «Stabilityislandsinthevicinityofseparatrices ofnear-integrablesymplecticmaps». DiscreteContin.Dyn.Syst.Ser.B, 10(2–3)(2008),681–698.

[34] Simó,C.;Vieiro,A. «Resonantzones,innerandoutersplittingsingeneric andloworderresonancesofareapreservingmaps». Nonlinearity,22(5) (2009),1191–1245.

[35] Simó,C.;Vieiro,A. «Dynamicsinchaoticzonesofareapreservingmaps: closetoseparatrixandglobalinstabilityzones». Phys.D,240(8)(2011), 732–753.

DepartamentdeMatemàticaAplicadaiAnàlisi

ButlletídelaSocietatCatalanadeMatemàtiques Vol.29,núm.1,2014.Pàg.109–110

Englishsummaries

ÁlvaroCorralandFrancescFont-Clos

Criticalityandself-organizationinbranchingprocesses:applicationtonatural hazards

Thestatisticsofnaturalcatastrophescontainsverycounter-intuitiveresults. Usingearthquakesasaworkingexample,weshowthattheenergyradiatedby sucheventsfollowsapower-laworParetodistribution.Thismeans,intheory, thattheexpectedvalueoftheenergyisinfinite,andinpractice,thatthemean ofafinitesetofdatainnotrepresentativeofthefullpopulation.

Also,thedistributionpresentsscaleinvariance,whichimpliesthatitis notpossibletodefineacharacteristicscalefortheenergyAsimplemodelto accountforthispeculiarstatisticsisabranchingprocess:theactivationorslip ofafaultsegmentcantriggerothersegmentstoslip,withacertainprobability, andsoon.

Althoughnotrecognizedinitiallybyseismologists,thisisaparticularcase ofthestochasticprocessstudiedbyGaltonandWatsononehundredyearsin advance,inordertomodeltheextinctionof(prominent)families.Usingthe formalismofprobabilitygeneratingfunctionswewillbeabletoderivethemain propertiesofthesemodels.

Remarkably,apower-lawdistributionofenergiesisonlyrecoveredinavery specialcase,whenthebranchingprocessisattheonsetofattenuationand intensification,i.e.,atcriticality.Inordertoaccountforthisfact,weintroduce theself-organizedcriticalmodels,inwhich,bymeansofsomefeedbackmechanism,thecriticalstatebecomesanattractorintheevolutionofsuchsystems Alongthetext,analogieswithbasicstatisticalphysicsconceptsaredrawn.

Thebulkofthematerialpresentedhereisself-contained,withtheexception ofsomebasicconceptsinTheoryofProbability.

Keywords: branchingprocess,Galton–Watsonmodel,criticality,self-organization, powerlaws,Gutenberg–Richterlaw.

MSC2010SubjectClassification: 60J80,60J85.

MercèRomero-Gómez,PatriciaSánchez-Martín,andJosepJ.Masdemont

Howinvariantmanifoldsformspiralsandringsinbarredgalaxies

Thespectacularityofbarredgalaxiesresidesnotonlyinthepresenceoftheir bars,extendedinthecenterofthegalaxy,butalsointheringsandspiral armsdevelopedintheexteriorregions.Thereisnocleartheoryontherings formationand,untilrecently,therewasonlyoneexplainingtheoriginofspiral armsinnon-barredgalaxies.Inrecentyears,andbasedondynamicalsystems, wehavedevelopedatheorythatrelatesringsandspiralarmswithhyperbolic invariantmanifoldsassociatedwithperiodicandquasiperiodicorbitsabout thecollinearpointsofthesystem.

Keywords: dynamicalsystems,invariantmanifolds,galaxystructure,galactic dynamics.

MSC2010SubjectClassification: 37D10,85A05.

CarlesSimó

Quadraticareapreservingmapsin R2

Iconsiderthedescription,explanationandpredictionofthepropertiesofthe orbitsofagivensystemasoneofthemaingoalsofDynamicalSystems.In thislecturewefocusonthequadraticAreaPreservingMaps(APM)in R2.There areseveralreasonsforthischoice.Itisaparadigmaticmodel.Manyproblems concerning:theexistenceofinvariantcurvesdiffeomorphictoacircle;the roleofinvariantmanifoldsofhyperbolicfixedorperiodicpointsandhow theyleadtotheexistenceofchaos;thegeometricalmechanismsleadingto thedestructionofinvariantcurves;andquantitativemeasuresofdifferent propertiesforgeneralAPM,canallbeunderstoodthankstoourknowledgeof thequadraticcase.Areviewofthesetopicsispresentedinthelecture.Several openquestionsandextensionsareshownattheendofthelecture.

Keywords: quadraticareapreservingmaps,invariantcurves,invariantmanifolds, chaos,quantitativemeasures.

MSC2010SubjectClassification: 37E30,37A05,37E40,37C29.

Instruccionsperalsautors

Elsarticlessotmesosapublicaciós’hand’enviaralseditorsoaqualsevol membredelcomitèeditorial,percorreuelectrònic,preferentmentenformat PDF.Elsoriginalshandecontenirlaversióanglesadeltítol,unresumbreuen catalàienanglès,paraulesclauencatalàienanglèsielscodisdelaclassificació permatèriesMSC2010.

Lesversionsdefinitivesdelsarticlesacceptatss’handepresentarencodiTEX,preferentmentenl’estilLATEXpropidel Butlletí.Aquestestilespot obteniralespàgineswebdelaSocietatCatalanadeMatemàtiques(SCM).Per tald’accelerarelprocésdeproducció,espregaalsautorsquesegueixinles indicacionscontingudeseneldocumentd’exemple.

LaversióenpaperdelButlletís’imprimeixenblancinegre.Quanunarticle continguifiguresencoloriesconsidericonvenient,l’autorproporcionarà unaversiódelsgràficssubstituintelcolorpertonsdegrisosilíniesdegruix variable.Aixímateixmodificaràelscomentarisquefacinreferènciaalcolorde lesfigures.EnqualsevolcaselButlletípublicaràl’originalencolorenelseu formatelectrònic.

Elsautorsdelsarticlespublicatsal Butlletí enreteneneldretdecòpia (copyright)iautoritzenl’IECadifondre’ls,tantatravésdelapublicacióimpresa commitjançantelsportalsdigitalspropisod’altresambquès’estableixinels convenisoportunsaaquestefecte.Ésresponsabilitatdelsautorsassegurar queesdisposadelsdretsdereproducciódelsgràficsidelesfiguresquehi apareguin.CadaautorrebràunacòpiaenPDFd’altaqualitatdelaversiódigital delseuarticleiunexemplarimprèsdelnúmerodel Butlletí enelquales publiqui.

Lacorrespondènciaadministrativarelacionadaambel Butlletí s’had’adreçaralaSCM.

Comitèeditorial

JuliàCufí(editorencap) DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona jcufi@mat.uab.cat

BartomeuColl Dep.deMatemàtiquesiInformàtica UniversitatdelesIllesBalears tomeu.coll@uib.cat

NúriaFagella Dep.deMatemàticaAplicadaiAnàlisi UniversitatdeBarcelona fagella@maia.ub.es

JosepMariaFont Dep.deProbabilitats,LògicaiEstadística UniversitatdeBarcelona jmfont@ub.edu

ArmengolGasull

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona gasull@mat.uab.cat

GáborLugosi

ICREAiDepartamentd’Economia UniversitatPompeuFabra gabor.lugosi@upf.edu

RosaCamps(editoraadjunta) DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona rcamps@mat.uab.cat

JorgeMateu DepartamentdeMatemàtiques UniversitatJaumeI mateu@mat.uji.es

MarcNoy DepartamentdeMatemàticaAplicadaII UniversitatPolitècnicadeCatalunya marc.noy@upc.edu

FrancescPlanas DepartamentdeMatemàticaAplicadaI UniversitatPolitècnicadeCatalunya francesc.planas@upc.edu

AgustíReventós DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona agusti@mat.uab.cat

MartaSanz-Solé Dep.deProbabilitats,LògicaiEstadística UniversitatdeBarcelona marta.sanz@ub.edu

SocietatCatalanadeMatemàtiques

La SocietatCatalanadeMatemàtiques(SCM) ésunasocietatfilialdel’Institutd’EstudisCatalans,quecontinualesactivitatsdelaSecciódeMatemàtiques delaSocietatCatalanadeCiències,quefoufundadaperl’Institutl’any1931. Lesfinalitatsdela SCM són:elconreudelesciènciesmatemàtiques,l’extensió delseuconeixementenlasocietatcatalana,elfomentdelseuensenyament idelasevainvestigacióteòricaiaplicada,aixícomlapublicaciódetotamena detreballsques’adeqüinaaquestsobjectius.La SCM desenvolupalesseves activitatsenlesterresdellenguaiculturacatalanes.Elcatalàés,doncs,la llenguapròpiadela SCM ilaqueésusadanormalmententotselsseusactesi publicacions.

La SCM editalespublicacionsperiòdiques SCM/Notícies i Butlletídela SocietatCatalanadeMatemàtiques.Elssocisdela SCM reben,gratuïtament, aquestesduespublicacions.

La SCM téconvenisdereciprocitatambdiversessocietatsmatemàtiques d’arreudelmón,mitjançantelsqualselssocisdela SCM obtenenunareduccióenlaquotadesocid’aquestessocietats.Aixímateix,elssocisdela SCM podenfer-sesocisdelaSocietatMatemàticaEuropeapagantunaquota complementària.

LaJuntaDirectivadela SCM estàconstituïdaperlespersonessegüents:

President:JoandeSolà-Morales

Vicepresident:JoaquimOrtega-Cerdà

Secretari:AlbertRuiziCirera

Tresorera:MarionaPetitiVilà

Vocals:NúriaFagellaiRabionet,JosepGranéiManlleu,Agustí ReventósiTarrida,CarlesRomeroiChesa,OriolSerraiAlbó,Esther Silberstein,ManelUdinaiAbelló,EnricVenturaiCapell

Delegatdel’IEC:JoanGirbauiBadó

L’adreçadela SCM éscarrerdelCarme,47,08001Barcelona.Telèfon: 933248583.Fax:932701180.Correuelectrònic: scm@iec.cat.Adreçaweb: http://scm.iec.cat.

El Butlletí de la Societat Catalana de Matemàtiques publica, en llengua catalana, exposicions matemàtiques de qualitat, que puguin interessar a un nombre elevat de lectors. Es donarà prioritat a aquells treballs en què destaquin la claredat d’exposició i l’interès general del tema. El Butlletí està obert a tots els camps de la matemàtica i també als aspectes matemàtics de les ciències experimentals, la tecnologia, l’economia, etc., així com a altres àrees, com la història, la didàctica i la filosofia, sempre que els treballs tinguin un component matemàtic important. També tenen cabuda al Butlletí aquells articles que desenvolupin un aspecte significatiu de la problemàtica de la professió matemàtica al nostre país.

El Butlletí publica un volum a l’any, dividit en dos números, que es trameten gratuïtament a tots els socis. El Butlletí es publica també en format electrònic. L’edició electrònica del Butlletí pot obtenir-se des del portal de revistes científiques en línia de l’IEC o al servidor http://scm.iec.cat.

La correspondència administrativa s’ha d’adreçar a la Societat Catalana de Matemàtiques.

Editor en cap

Julià Cufí

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Comitè editorial

Bartomeu Coll

Dep. de Matemàtiques i Informàtica

Universitat de les Illes Balears

Núria Fagella

Dep. de Matemàtica Aplicada i Anàlisi

Universitat de Barcelona

Josep Maria Font

Dep. de Probabilitats, Lògica i Estadística

Universitat de Barcelona

Armengol Gasull

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Gábor Lugosi

ICREA i Departament d’Economia

Universitat Pompeu Fabra

Societat Catalana de Matemàtiques

Carrer del Carme, 47 - 08001 Barcelona tel. 933 248 583 - fax 932 701 180

scm@iec.cat - http://scm.iec.cat

Editora adjunta

Rosa Camps

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Jorge Mateu

Departament de Matemàtiques

Universitat Jaume I

Marc Noy

Departament de Matemàtica Aplicada II

Universitat Politècnica de Catalunya

Francesc Planas

Departament de Matemàtica Aplicada I Universitat Politècnica de Catalunya

Agustí Reventós

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Marta Sanz-Solé

Dep. de Probabilitats, Lògica i Estadística Universitat de Barcelona