

1.DISPOSICIONESGENERALES
Lasedificacionesindustrialesdiseñadas bajolanormachilenaNCh2369.OF2003 debencumplirdosnivelesdediseño, estasson:seguridaddevidayla continuidaddelasoperaciones. Parapoderalcanzarestosnivelesde diseñolanormativasehapropuestolos siguientesobjetivos:Evitarelcolapsode lasestructuras,estoconlafinalidadde evitarincendios,derramestóxicos, explosionesydesastresmedio ambientales;protegeryasegurarla operacióndevíasdeescape;minimizar lostiemposdeinactividaddelos procesosindustrialesygarantizarque procesosyserviciosesencialesse mantenganoperativos.
1.1Alcanceycampodeaplicación LanormaNCh2369OF2003,se complementaconlanormativade DiseñoSísmicodeEdificios NCh433OF96Modif.2012.Porloque, todoslosrequerimientosquenoson modificadosdirectamenteenla NCh2369.OF2003sonaplicables.
1.1.1Alcance

Estructurasindustrialestanto livianascomopesadas.Las estructuraspesadascomprenden
todasaquellasedificaciones industrialessusceptiblesasufrir dañosporterremotos,debidoaque soportanoposeenunagran cantidaddemasa.Recordemosla terceraleydeNewton�=��;a mayormasa,mayorserálafuerza queafectaalaedificacióndurante uneventosísmico.Lasestructuras livianasestáncompuestasportodas aquellasedificacionescuyamasaes muypequeñaenrelaciónalvolumen queocupan,porejemplo,los galponesdeaceroestructuralcon cubiertaslivianas.Estasnaves industrialessonsusceptiblesasufrir dañosporcargascíclicasdetipo eólica.
SistemasdeductosycañeríasEn estoscasossedeberealizaranálisis deflexibilidaddelascañeríasydelos sistemasdesoportecomorackso soportessuspendidos.Sedeben tomartodaslasmedidasnecesarias paragarantizarsufuncionamiento unavezpasadoelterremoto.Eluso desistemasdeamortiguamientode movimientocomoloscolgadoresde resorte(quesirvenparaequilibrarlos desplazamientosverticalesinducidos porelsismo),yloscompensadores demovimientoenunionesdelas tuberías(estasjuntassirvenpara absorbermovimientosenzonasde cambiosderigidezodedirecciónde lastuberías)sonsiempreopcionesa
considerarparagarantizarelcorrecto funcionamientodeestossistemas.
Equiposdeproceso,mecánicosy eléctricoysusanclajes.Sedebe garantizarlacontinuidadde operacióndelosequiposo maquinariadespuésdelterremoto. Serecomiendaverificardemanera adecuadaconlosproveedoresde equipos,losrequisitosmínimosde resistenciaylímitesde deformacionesydesplazamientos, paraasegurarqueestosvaloresson adecuadosparacumplirconel rendimientoesperado.Esnecesario realizarunanálisisporvolcamiento delosequiposydiseñaranclajes suficientementedúctilespara soportarlascargascíclicasinducidas poreleventosísmico
Estructurasdebodegasorecintos devocaciónindustrialComprende todaslasedificacionesdealmacenaje deproductos,piezas,químicos,etc. Tambiéncentralesdemonitoreoy oficinasqueesténcontenidasdentro delasinstalacionesindustrialestanto pesadascomolivianasSedeben evitarderrames,fugas,explosionesy garantizarelfuncionamientodelas víasdeescape
Construccionesestructuradascon columnasenvoladizoEstetipode configuraciónconsisteencolumnas opilaresempotradasenlabasecon

movimientolibreenelextremo superiordelamisma.Suusodebe realizarsedemaneramuydetalladay sistemáticadebidoaque,son sistemasquedependendeunbuen diseñodelempotramientobase.Se puedenverestetipodesistemasen taqueselevados,tolvas,chimeneas deacero.Ensistemasestructurales comonavesindustriales(galpones) podemosverlosenestructuras dondelospilaressostienenuna estructuradetechoquesolose apoyademaneraarticuladaenel pilar. 1.1.2Restriccionesdeuso
Lassiguientesestructurasestánfuera delrangodeaplicabilidaddela normaNCh2369OF2003:
Edificiosqueapesardeestardentro deunáreaindustrialpuedanser asimilablesausohabitacional.Como, edificiosdeoficinas,casinos,etc. CentralesNucleares. CentralesdeEnergíaEléctricaylíneas detransmisión. Presas. Tranquesderelaves. Puentes. Túneles. MuelesGravitacionales. MurosdeContención. Líneasdeductosenterrados
1.2Referenciasnormativas
Setomanvariasreferencias normativastantonacionalescomo internacionales.
Lanormatambiénrecomienda investigarlaposibilidaddeaplicarlas edicionesmásrecientesdelas referenciasnormativasAdemás,da laposibilidaddecitarlasnormas extranjerasqueseestimennecesarias.
1.3Términos,definicionesy simbología
Lostérminosydefiniciones establecidosenlanorma NCh2369.OF2003,complementanlos yaestablecidosenlanorma NCh433OF96Modif.2012.
1.4Disposicionesdeaplicación general
1.4.1Principiosehipótesisbásicos

Comosehamencionado anteriormenteLasedificaciones industrialesdiseñadasbajolanorma chilenaNCh2369OF2003deben cumplirdosnivelesdediseño: seguridaddevidaenlaindustriayla continuidaddelasoperaciones industriales.
Paracumplirconestas especificacionesdediseño,dicha normaestablecequelossistemas resistentesdebenteneramplia reservaderesistenciay/oser capacesdeabsorbergrandes cantidadesdeenergía,másalládel límiteelástico,antesdefallarEsta filosofíadediseñoesdiferenteala establecidaenlanorma ASCE7/AISC341Estaestableceque lasedificacionessismorresistentes debenhacerusodelaductilidad provistaporcadasistemaestructural, estoselograconundetallamiento dúctilmuyestricto.
LanormaNCh2369.OF2003, estableceparámetrosdediseñoque garanticeedificacionesindustriales conaltosnivelesde sobreresistencia,peroconla ductilidadsuficienteparagarantizar unadecuadocomportamientosila estructuraincursionaenelrango inelásticodedeformacionesen eventossísmicosseveros.Porloque, lasestructurasdiseñadasbajola normaNCh2369OF2003requieren undetallamientodúctilmenos estrictoqueelindicadoenlanorma ASCE7/AISC341
Sedebenlimitarlasincursionesen elrangoinelásticode deformacionessiestasponenen peligrolacontinuidaddelas
operacionesenlaindustriay/olas operacionesdeescapeyrescatedel personalindustrial.
1.4.2ClasificacióndeEstructurasy equipossegúnsuimportancia
Lasestructurasyequiposse clasificanencategoríasyacadauna deellaslescorrespondeun coeficientedeimportanciaI, establecidosenlaTabla1.4.2
Clasificación I
C1.Obrascríticas. Vitales:paracontrolarincendios, explosiones,dañoecológico, primeros auxiliosalosafectados Peligrosas:incendio,explosión, envenenamientodelaireolas aguas Esenciales:detenciones prolongadasypérdidasserias deproducción
1.20 C2.Obrasnormales. Puedentenerfallasmenoresde reparaciónrápida,nocausan detencionesprolongadas,no ponenenpeligrootrasobrasde lacategoríaC1.
100 C3.Obrasyequiposmenores oprovisionales. Sufallanoocasionadetenciones prolongadas,niponeenpeligro otrasobrasdelascategoríasC1 yC2
0.80 Tabla1421CoeficientedeImportancia“I”
1.4.3CombinacionesdeCarga

Lascombinacionesdecargasiempre representanunaspectocriticoenel diseñodeestructuras.Esimportante asegurarsedequeestáaplicando correctamentelascombinacionesde cargapertinentesparagarantizarlos requisitosmínimosdediseño normativos
LanormaNCh2369establece distintostiposdesobrecargasse debehacerusandolasreglasde superposiciónparacombinarloscon lasaccionessísmicasy gravitacionales.Acontinuación,se muestranlasecuacionesestablecidas enelcapítulo4delanorma NCh2369: TensionesAdmisibles:
SA=Sobrecargasaccidentalesde operación. SH=SismoHorizontal. SV=SismoVertical. a=factorqueafectaala sobrecargaSC. b=factordeamplificacióndelas cargassísmicasVerTabla 1.4.2.3. Elfactor“a”debeconsiderarse igualalaunidadalmenosquese realiceunanálisisenconjuntoal profesionaldeprocesosindustriales yseestablezcaquepuedeserun valormenor.Siembargo,nodebe sermenoralosmostradosenla Tabla1.4.2.2 TipodeRecinto a Bodegasyengeneralzonasde acopioconbajatasaderotación0.50 Zonasdeusonormal, plataformasdeoperación0.25 Diagonalesquesoportancargas verticales 1.00 Pasarelasdemantencióny techos 0.00 Tabla1.4.2.2.Valoresmínimosdel“a”. MaterialdeConstrucciónb Estructurasoequiposdeacero1.10 Estructurasoequiposde hormigón 1.40 Tabla1.4.2.3.Valoresde“b”. Enloquerespectaalassobrecargas especialesyaccidentalesde
operación“SO”y“SA”sedebe realizarunanálisisparaverificarla ocurrenciadelasmismasdurante uneventosísmico.
Porejemplo,lasobrecargaSOes muyprobablequeestéocurriendoal iniciarseelsismodebidoaqueson accionesdinámicasprovenientesdel usonormaldelasinstalaciones.Por lotanto,sedebeconsiderarque actúanenconjuntoconelsismode diseño,almenosqueexistaalgún medioomecanismoquegaranticela interrupcióndelosprocesosal iniciarseelsismo.
LomismoocurreconSAque dependedirectamentedela ocurrenciadelsismoAcontinuación, semuestraenlaTabla1.4.2.4los tiposdefenómenosycaracterísticas delassobrecargasSOySA

Alobservardetenidamentelas ecuacionesA4.1alA4.4,vemosque enlasmismaslascomponentes sísmicasestánafectadasporel signo±.Estoestáorientadoatomar ambasdireccionesdelacomponente sísmicaaanalizar.Enelcasodela cargasísmicaverticalsedebetomar encuentaloestablecidoenlaTabla 1.4.2.5
CombinacióndelSV Eq

Lossignos+óparaelsismo verticalsedebenaplicarde mododeobtenerunefectoque sesumealproducidoporlas cargasCPySC
A4.1 A4.3 Lossignos+óparael sismoverticalsedebenaplicar demododeconseguirelefecto inverso,esdecir,disminuir elefectodelascargasCPySC
A4.2 A44 Tabla1425ElsignodelSVenlas combinacionesdediseño
2.ANALISISSÍSMICO
2.1SismoVertical

Lasondassísmicassepropagan desdeelhipocentroentodas direcciones,provocandoel movimientodelosdepósitosde suelotantoenformahorizontal comovertical.
Elefectodelacargasísmicavertical dependesignificativamentedela distanciaepicentralEnlas edificacionescercanasalafuente,la componenteverticaldelmovimiento esmuchomayorquelas componenteshorizontales.A medidaquelasondassedesplazan, lascomponentesverticalesse atenúanylascomponentes horizontalesseamplificanyel movimientosevuelveoscilatorio LanormaNCh2369,esunodelos pocoscódigosanivelmundialque consideraelefectodela aceleraciónsísmicaenla componentevertical
Acontinuación,semuestranlos casosendondesedebeconsiderarel efectodelasaceleracionessísmicas verticalesdemaneraobligatoria segúnlanorma:
Barrasdesuspensióndeequipos colgantesysuselementos soportantesyvigasdeacerode construcciónsoldada,laminadao plegada,conosinlosa colaborante,ubicadasenzona sísmica3,enlasquelascargas permanentesrepresentanmásdel 75%delacargatotal.
Estructurasyelementosde hormigón precomprimido (pretensadoypostensado).
Fundacionesyelementosde anclajeyapoyodeestructurasy equipos.
Cualquierotraestructurao elementoenquelavariacióndela acciónsísmicaverticalafecteen formasignificativasu dimensionamiento,comopor ejemplo,lasestructuraso elementosenvoladizo.
Estructurasconaislaciónsísmica sensitivasalosefectosverticales.
2.2SismoHorizontal
Engeneral,lanormapropiciaeluso desistemasestructuralessimples, simétricosysinirregularidades torsionales.
Sedebeprocurarqueladistribución delasmasassealomásuniforme posible,tantoenplantacomoen altura.Lavariacióndelasmasaspiso apisodebesersimilaralavariación delarigidezparaevitar concentracionesdeesfuerzos.
Evitarlasconfiguraciones geométricasenL,H,U,Toplanta encruzEstodebidoaqueestas configuracionesinducenefectos torsionalesqueoriginanproblemas enloselementosubicadosenlas esquinascomolospilares.Porotro lado,tiendenaproducirvariaciones derigidezy,portanto,movimientos diferencialesentrelaspartesdelde laedificación,causandouna concentracióndeesfuerzos perjudicialesparalaestructura.
Pararesistirlosefectosdelatorsión enplantaesconvenientetener elementosresistentesenel perímetrodelaedificación.Cuanto másalejadodelcentroderigidezde laplantaseubiqueunelemento, mayoreselbrazodepalanca respectoaesecentro,ymayorserá elmomentoresistentequepueda generar
Serecomiendautilizar configuracionesestructuralesconla mayorcantidaddeelementos
verticalesenlabasedelaedificación continuosdesdelospisossuperiores.
Sedebenevitargrandes dimensionesenplanta,unaumento delalongituddeledificioincrementa losesfuerzosenunnivelque funcionacomoundiafragmade distribuciónhorizontal.Larigidezdel pisopuedeserinsuficientepara redistribuirlacargahorizontal originadaporunsismo.Además,los esfuerzoscausadosporvariaciones detemperatura,oprovocadospor terremotossonmayoresenedificios congrandesdimensionesenplanta.

Alutilizarsistemasestructurales sinirregularidades,noesnecesario combinarlosefectosdebidosalas doscomponenteshorizontalesdela acciónsísmica.Sepuedeproceder comosidichosefectosnofueran concurrentesy,enconsecuencia,los elementossepuedendiseñarpara elsismoactuandosegúncadauna delasdireccionesdeanálisis consideradaseparadamente.
Enlasestructurasquepresentan notorias irregularidades torsionalesoquetienenenambas direccionesmarcosrígidoscon columnascomunesadoslíneas resistentesqueseinterceptan (distribucionesenplataenL,H,U, Toencruz).Entalescasos,los
elementossedebendiseñarparalos esfuerzosobtenidosdeconsiderar el100%delasolicitaciónsísmica que actúaenunadirecciónmáslos esfuerzosobtenidosdeconsiderar el30%delasolicitaciónsísmica actuandoenladirecciónortogonal alaanterior,yviceversa.
2.3Masasísmicaparaelmodelo estructural

Paraelcálculodelasfuerzasde inerciahorizontalesduranteunsismo, lassobrecargasdeoperaciónse puedenreducirdeacuerdoasu probabilidaddeocurrencia simultáneaconelsismodediseño. Lassobrecargasdeusosepueden reducirmultiplicándolasporel coeficiente“FR”establecidosenla Tabla2.3.1. Recinto FR Techos,plataformasypasarelas tantodeoperacióncomode mantención 000 Bodegasdealmacenamiento, salasdearchivoysimilares050 Tabla231Coeficientedereducción
Parafinesdedeterminarlosefectos delsismovertical,nosedebe considerarreduccióndelascargas verticales,salvolasindicadasenel capítulo8delanorma
NCh1537.OF2009paralas sobrecargasdeuso.
2.4AnálisisLinealElásticoEstático
Elanálisislinealocupalarelación entrecargasydesplazamientos resultanteseslineallocualse cumpleelprincipiode superposición:siseduplicala magnituddelacargaseobtieneel doblederespuestadelmodelo Basadoenlahipótesisde comportamientoelástico-linealde losmaterialesconstituyentesyenla consideracióndelequilibriooenla estructurasindeformar.
Paralaampliacióndelanálisis elásticoestáticosegúnlaNCh2369la edificaciónalaquesequiereaplicar dichoanálisisdebecumplirconlas siguientescondiciones:
Estructurascuyaalturaseacomo máximo20m.
Larespuestasísmicasepueda asimilaraladeunsistemadeun gradodelibertad
Paralaelaboracióndelmodelo matemáticodelaestructura,las edificacionesquecuentancon sistemasdelosasdeentrepisoque puedan asimilar el
comportamientodeundiafragma horizontalrígido,sepuedeemplear unmodelocontresgradosde libertadporpisoysedeben incorporarlosefectosdelatorsión naturalylatorsiónaccidental.Por otrolado,alnocontarcon diafragmasrígidos,sedebedefinir unnúmerosuficientedegradosde libertadnodalesasociadosamasas traslacionalesCuandoseanecesario, sedebenconsiderarademáslas masasrotacionales.
Elefectodelatorsiónaccidentalse puedeanalizarcómoseindicaa continuación: Considerandolasposibles variacionesenladistribuciónde pesospropiosysobrecarga. Encasoquenoexistan antecedentespararealizarlo anterior,sedebeusarla disposición6.2.8deNCh433.Of96. Sedebenaplicarmomentosde torsiónencadanivel,calculados comoelproductodelasfuerzas estáticasqueactúanenesenivel porunaexcentricidadaccidental dadapor:
Engeneral,losmodelosmatemáticos debenconsiderarlainteracciónde losequipos,tantolosqueson soportadoscomolosqueestán suspendidos,deestosúltimosse debeincluirlainterconexiónentre elequipoylaestructura.
2.4.1CálculodelCortanteBasal

Elcálculodelcortebasalhorizontal, permitedeterminarlafuerza lateraltotalaplicadaenlabasedela estructura,comoconsecuenciadelas fuerzasinerciaqueseinduceaun sistemaestructural,distribuyéndolo posteriormentealolargodelas diferentesalturasdeentrepisode laestructura.
Elesfuerzodecortehorizontalen labasesedebecalcularsegúnla expresiónsiguiente: �0=��� (�4.3) Donde:
I=coeficientedeimportanciaI especificadoenlaTabla1.1.2.1. P=pesototaldeledificiosobreel nivelbasal,calculadoenlaforma indicadaenlaTabla2.3.1. C=coeficientesísmico.
Elcálculodelcoeficientesísmico vienedadoporlasiguiente ecuación:
Donde:
A0=aceleraciónefectivamáxima definidaenTabla2.6.1segúnla zonificaciónsísmicaestablecida enelanexoBZSalfinaldeeste capítulo.
T′,n=parámetrosrelativosaltipode suelodefundación,quese determinandelaTabla2.6.2 segúneltipodesuelo establecidoenelanexoBTSal finaldeestecapítulo.

T*=períodofundamentalde vibraciónenladirecciónde análisis. R=factordemodificacióndela respuesta
ξ=razóndeamortiguamientoque seestableceenTabla2.6.3. Cmax=Coeficientesísmicomáximo establecidoenlaTabla2.6.4 1.Distribuciónenaltura
Lasfuerzassísmicassedeben distribuirenlaalturasegúnla expresiónsiguiente:
Donde:
Fk=fuerzahorizontalsísmicaenel nivelk. Pk=pesosísmicoenelnivelk. Ak=parámetroenelnivelk(k=1es elnivelinferior) n=númerodeniveles. Q0=esfuerzodecortebasal. Zk,Zk1=alturasobrelabasedelos niveleskyk−1; H=alturadelnivelmásaltosobreel nivelbasal. 2.4.2EjemploB4.1
Setieneunaedificaciónde05 nivelesincluyendoeltechocon alturadeentrepisoconstantede 3.00m,ubicadaenlaComunade LampaenlaRegiónMetropolitana. Laestructuraconsisteenmarcos rígidossinarriostramientosenla dirección“Y”yarriostradosenla dirección“X”,conconexiones apernadas.Cadaentrepiso incluyendoeltecho,están compuestasporunalosade encofradocolaborantetipoPC6 conterminaciónafinadode15cm deespesorincluyendoelnervio.Los pilaresylasvigassonigualesen
todoslospisos.Enlaestructurano existeningúntipodetabiqueríao divisiones.Laedificaciónsoporta equiposmecánicosquesoncríticos paralasoperacionesdelaindustria.
Seconocequeelperíodo fundamentaldevibraciónenla dirección“Y”esde0.10segundosy enladirección“X”esde0.25 segundosLaMecánicadesuelos sugieretomarunsueloTipoIII.
Sepidedeterminarlasfuerzas sísmicashorizontalesporpisoy distribuirlasenplanta.


FiguraB4.1b.MarcoA=B=C.EjemploB4.1

FiguraB4.1a.Planta.EjemploB4.1
FiguraB4.1c.Marco1=2=3.EjemploB4.1

Dirección“X”
ZonaSísmica=3 A0=040g,segúnTabla261 A0=3.92m/s2 R=5 T’=0.62s,segúnTabla2.6.2 n=1.80 T*=0.25s =0.03,SegúnTabla2.6.3 Cmax=0.23,SegúnTabla2.6.4a 392 4�9.81≤ 275�392 9.81�5 062 0.25 18005 0.03
0.4 ≤0.23 001≤138≤023

ElvalordeCx=0.23
Dirección“Y”
ZonaSísmica=3 A0=0.40g,segúnTabla2.6.1 A0=3.92m/s2 R=5
04 ≤0.23 0.01≤7.19≤0.23 ElvalordeCy=0.23 Cálculodelpesototaldela edificación“P” Paraellosedeterminaelpesototal delaedificaciónporencimadel sistemadefundaciones. CargasPermanentes“CP”
un10%delpesototaldela
paralasoperaciones,porloque,la estructuraseclasificacomoC1.El coeficientedeImportanciaI=1.20.

1���

ElcálculodelaFuerzaLateralFkse obtuvodividiendoelvalordeAk*Pk decadanivelporeltotal1 4�����.
ElesfuerzodecortebasalQkse calculaatravésdelacantidadde FuerzaLateralFkcorrespondientea cadanivel Laimagenmatemáticadela edificaciónparaladistribuciónde losesfuerzosQkesladeun voladizo,porlotanto,amedidaque nosacercamosalabasedela edificaciónsevanacumulandolas fuerzaslaterales.Esdecir,enelnivel TechoelvalordeQkesdirectamente elvalordelafuerzalateralFk,luego elnivelsubsiguientequeesestecaso eselcuatro(4)eslasumadela fuerzaFkdelnivelTechoyelnivel cuatro(4)yasísucesivamente.


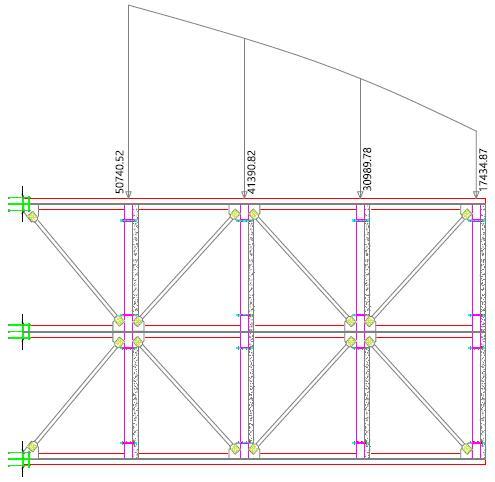
RigidezLateraldeMarcos
Paraelcálculodelarigidezlateral, utilizaremoselMétododeWilbur. Estemétodosebasaenladefinición derigidezpornivel,lacualesla relaciónentrelafuerzacortante absorbidaporunmarcorígidoo muro,enunnivelyel desplazamientohorizontalrelativo entrelosdosnivelesquelolimitan
Idealmenteparalaaplicaciónde estemétodo,sedebedefinirqué tipodecomportamientoacargas lateralesgobiernaladeformación horizontaldelsistemaestructural. Sepuedendefinirdostiposde estructuras:estructurasdecortante, dondelarigidezdeentrepisoes independientedeladistribuciónde cargaslaterales(FiguraB4.3a)y estructurasdeflexióndondeno existeindependenciaentrelarigidez deentrepisoyladistribuciónde cargasaplicadas(FiguraB4.3b).
FiguraB43bEstructurasdeFlexión
deformaciónlateralgobiernael comportamientoglobalenelsistema estructuralsepuedeemplearel ÍndicedeRotación
.Este parámetroseobtieneatravésdelas siguientesecuaciones:

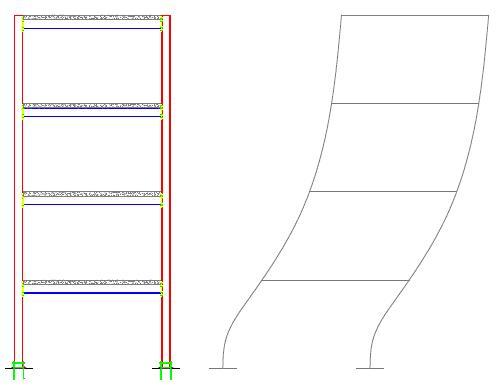
FiguraB4.3a.EstructurasdeCortante.

estructura.Además,elMomentode Inerciadecadaelementodebeser constante.
Elcasodeestructurasgobernadas porflexión,porlogeneralnoson recomendables,debidoaquelas vigassondemasiadoflexiblesen comparaciónalospilares.
Enelcasodeestructuras intermedias,sepuedeobtenerla rigidezatravésdemétodos matriciales
LaRigidezlateraldemarcosrígidos seobtienenatravésdelassiguientes ecuaciones:
PrimerNivelconpilaresempotrados
UltimoNivel
MarcosArriostrados
Ladeterminacióndelacontribución delarigidezhorizontaldelsistema dearriostramientosseobtiene igualandoladeformaciónproyectada yelcortanteproyectadoporla accióndelacargaaxialsobrelos arriostramientos.
FiguraB4.4.DCLdeArriostramientos. RevistaInternacionaldeIngenieríade EstructurasVol.18,1,123(2013).


Porlotanto,
Donde: n=cantidaddearriostramientos. Ad=Áreadelarriostramiento. Ld=Longituddelarriostramiento




indicaquesedebenverificarlosdos posiblessentidosdelafuerza.
Cuandoserealizaunanálisispor marcosintomarencuentaelaporte delosmarcosperpendiculares conectadosaeste,Lafuerza horizontaltotalsobrecadamarcoes lasumaenvaloresabsolutostanto deQkyQT.
Siporelcontrarioserealizaun análisisentresdimensiones, considerandoelaportedelos marcosinterconectados,sedebe analizarsimulandolatorsión,por ejemplo,enelmarco“A”conelcorte +QTmientrasqueelmarco“C”sele asignaelcorteQT.
2.5AnálisisLinealElástico
Dinámico
Elobjetivoprimordialdelestudio dinámicodeunaestructuraconsiste entratardepredecirel comportamientodelamismapara establecerelgradodeseguridad frentealcolapso.
Enelanálisisdelsismoesnecesario estudiarlasfuerzasdeinercia generadasalproducirseuna aceleraciónenlacimentacióndela estructura.Paraellosedebe determinarcuáleslahistoriade
aceleracionesenunalocalización determinada,yanalizarcomolas mismassetrasmitenenformade fuerzas.
Elanálisismodalesunproceso medianteelcualsedescribeuna estructuraentérminosdesus propiedadesdinámicaso parámetrosmodalesquesonla frecuencia,elamortiguamientoy losmodosdevibración.Todaslas estructurasposeenfrecuencias naturalesymodosdevibración,que dependenbásicamentedelamasay delarigidezdelaestructura.
Eneldiseñoesnecesarioidentificar estasfrecuenciasyconocercómo afectanalarespuestadela estructuracuandounafuerzaactúa sobrelamisma.
2.5.1Espectrodediseño

Elmétodomodalespectraleselmás usadouniversalmentepara determinarlasfuerzassísmicas, debidoaquelosespectrossísmicos sonfácilmentegeneralizablesy normalizables.
Además,elmétodopermite determinarespectrosenvolventes querepresentenlasismografíade unazonageográficayevitarealizar
múltiplescombinacionesapartirde cálculosevolutivossobremúltiples acelerogramasdecálculo.
Elanálisismodalespectralsedebe hacerparaelespectrodediseño siguiente:
Ensistemasestructuralescon presenciadediafragmas horizontalesrígidos,seconsideran tresgradosdelibertaddinámica pornivel.Dostraslasionalesyuno torsional.
Enloquerespectaalperiodo fundamentaldevibracióndeun edificioesunparámetroclaveparael diseñosísmicodeunaestructura
Donde: T=períododevibracióndelmodo considerado
Elanálisisdebeincluirsuficientes modosdevibrarparaquelasuma delasmasasequivalentes,encada direccióndeanálisis,seaigualo superioral90%delamasatotal.
Unmododevibraciónesunpatróno formacaracterísticaenelquevibrará unsistema.Losmodosdevibración yperiodossonparámetros intrínsecosdeunaestructura,no dependendirectamentedelas accionesalaqueestaestásujetala estructura,perosídelamasaquese definiódeesasaccionesydelos elementosquelaconstituyen.Una estructuratendrátantosmodosde vibraciónyrespectivosperiodos, tantocuantosgradosdelibertad dinámicosposeadichaestructura.
Estecorrespondealperiododel mododevibracióndonde interactúalamayorcantidadde masaantelacargacíclica.Sedebe configurarlaestructuradetalforma queelperiodofundamentalseade tipotraslacional.Idealmenteun mododevibracióndeinvolucre torsióndebeexcitarlamenor cantidaddemasaposible;estoconla finalidaddeevitarfallasgravesenla edificación.
2.5.2Usodelespectrodediseño

Elespectrodediseñoseutilizacomo métodograficoparaobtenerlas fuerzassísmicasmínimasque afectanalaestructuradeuna edificación,yaseaexistenteono.
Porlotanto,sedebeconstruirun gráficoqueestáenfuncióndeltipo dedepositodesuelodondesevaa
fundarlaestructura,delmaterial queconformalaestructura,del sistemaestructuralautilizar,del usodelaedificaciónydel amortiguamientodelaestructura.
Paraconstruirelgrafico correspondientealespectrode diseñosedebeutilizarlaecuación B5.1.Lasvariablesestánfunciónde lodescritoanteriormenteSegrafica enfuncióndelperiodoT,elcual vamosvariandoyobteniendovalores deSa
Unavezobtenidoelespectrode diseñosedebencalcularlos periodosdelosmodosde vibraciónparaloscuales interactúanalmenosel90%dela masasísmica.
Concadaunodeestosperiodos, vamosalgráficoyobtenemosun valorSacorrespondienteacada mododevibración.ElvalordeSa estáenfuncióndelaaceleración degravedad.Recordemosentonces laterceraleydeNewton�=��, dondelamasacorrspondeaalpeso delaedificaciónylaaceleración correspondealvalordeSaPorlo queseobtieneunafuerzabasal horizontalparacadamodode vibración
2.5.3EjemploB5.1
TomaremoselejemploB4.1parael desarrollodelespectrodediseñoyel calculodelasfuerzassísmicas.
ParámetrosSísmicosDirección“X”
ZonaSísmica=3 A0=040g,segúnTabla261 A0=3.92m/s2 R=5 T’=0.62s,segúnTabla2.6.2 n=1.80 =0.03,SegúnTabla2.6.3 I=1.20,SegúnTabla1.4.2.1 Cmax=0.23,SegúnTabla2.6.4a �� = 2.75�0� � � ' �
�0.05 �

04 ≤������ �� = 275�392�120 5 062 �
180005 003
180 ≤2.71
04 ≤1.20�9.81�0.23 ��=3.18 062 �
Luegoseprocedeagraficarelvalor deSaenfuncióndeTqueesuna funcióndetiporacionaldelimitada porunvalormáximode2.71.
GráficoB51Espectrodediseñoen“X”
ParámetrosSísmicosDirección“Y”
ZonaSísmica=3 A0=0.40g,segúnTabla2.6.1 A0=3.92m/s2 R=5 T’=0.62s,segúnTabla2.6.2 n=1.80 =0.03,SegúnTabla2.6.3 I=1.20,SegúnTabla1.4.2.1 Cmax=0.23,SegúnTabla2.6.4a
GráficoB52Espectrodediseñoen“Y”

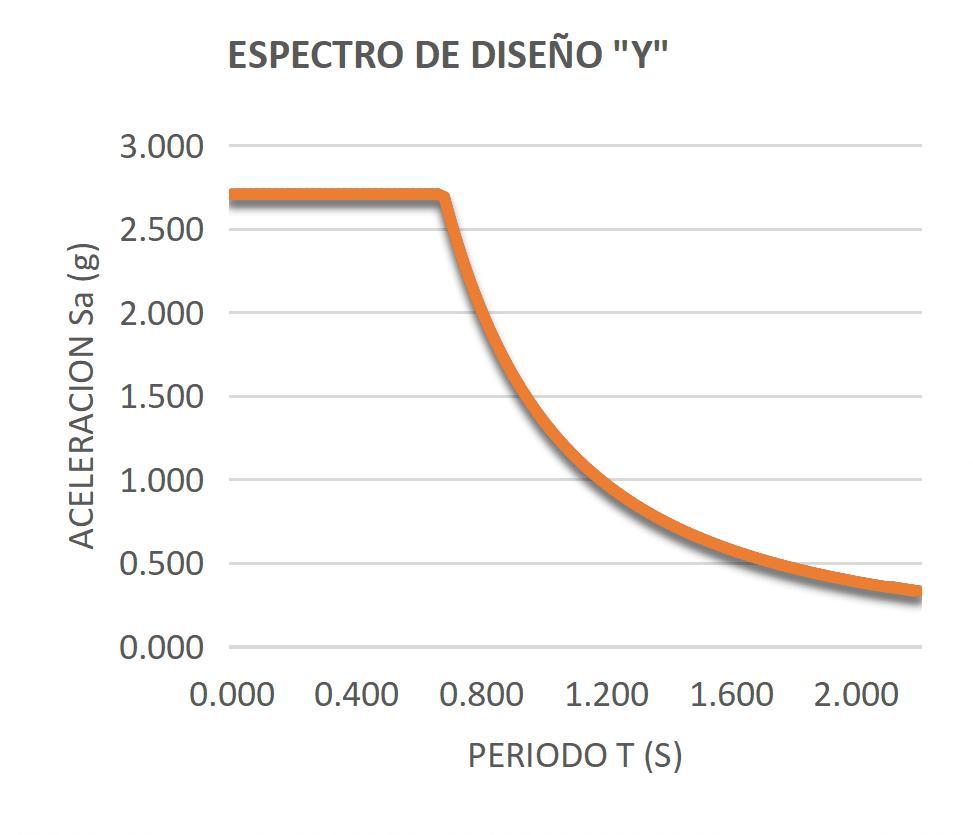

Paraestaedificaciónelespectrode diseñoesigualenambasdirecciones.
PeriodosdeVibración
Paraellodebemosdeterminarla cantidaddeperiodosdevibración queinteractúenconalmenosel90% delamasadelaedificación.
Seconsiderantresgradosdelibertad porniveldebidoalapresenciadela placacolaboranteencadaniveldela edificaciónquesirvedediafragma rígido.Setienencuatro(04)nivelesy tresgradosdelibertaddinámicos porcadaunodeellos,porlotanto, sedebenconsideraralmenos12 modosdevibración.
FiguraB5.1.Modelo3D

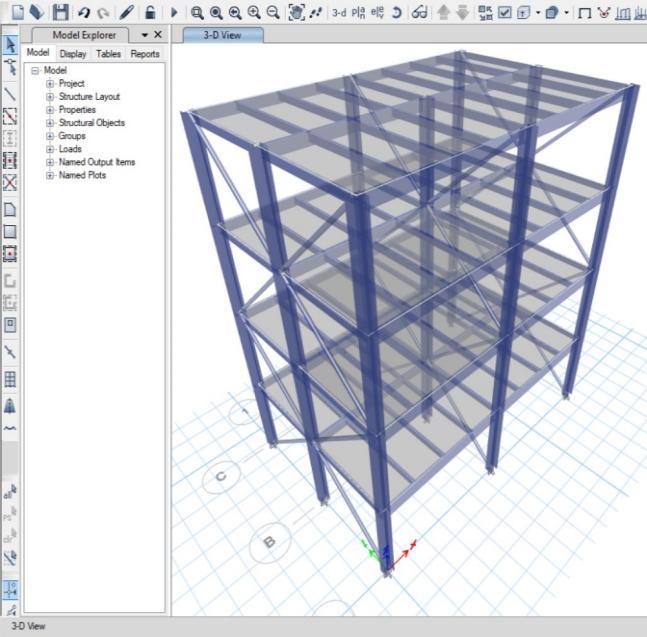

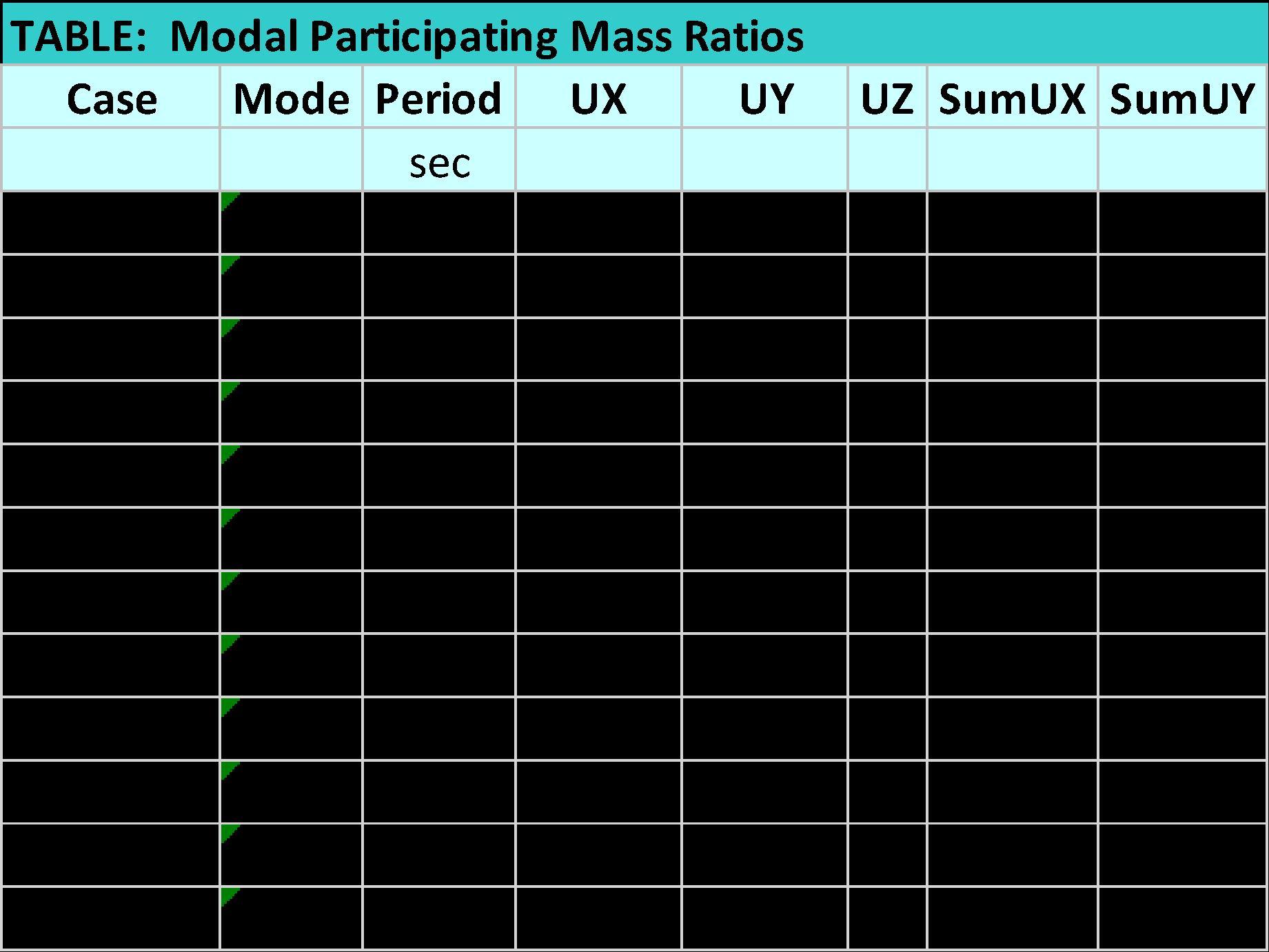
TablaB5.1.MasaParticipativa.
Paraunprimeranálisisconsiderando solo12periodosdevibraciónenla dirección“Y”soloparticipael83.74% delamasadelaedificación.Porlo tanto,sedebeaumentarlacantidad demodosdevibraciónhasta garantizarqueinteractúealmenosel 90%delamasaenambas direcciones.
TablaB52MasaParticipativa
Alduplicarlacantidaddemodosde vibración,esposibleconseguiruna cantidadsuficienteparaque interactúehastaun98%delamasa enambasdirecciones.Nóteseque paraefectosnormativosessuficiente conconsiderar12modosde vibración,enladirección“X”y17en elsentido“Y”.
2.5.4Superposiciónmodal
Losesfuerzosydeformaciones sísmicassedebencalcular superponiendolosvaloresmáximos modalesporelmétododela SuperposiciónCuadráticaCompleta Estemétodoquefuepublicadoen 1981porWilson,DerKiureghian,y
Bayoen“AreplacementfortheSRSS Methodinseismicanalysis”, EarthquakeEngineeringand StructuralDynamics.Estábasadoen lateoríadevibraciónaleatoria.
amortiguamientoatravésdel términoC
enlacombinacióndelas respuestasmodales.Estecriterio consideralaposibilidadde acoplamientoentrelosmodosde vibración.
deexcitacióncriticoqueafectala edificación.
1.EjemploB5.2
TomaremoselejemploB4.1parael desarrollodelasuperposiciónModal. Sepidedeterminarelcortantebasal máximoencadadirecciónyelagulo
TablaB5.3.Cortantebasalparacada mododevibración.
CortanteBasalDirección“X”
Paraecalculodelcortantetotalpor elmétododesuperposiciónmodal serealizamediantelaecuaciónB5.2. �= �� ���������
Enelcasodecálculodeconbinacion defuerzasenunadirección,se convierteenlasoluciónparticularde laraízcuadradadelasumadelos cuadrados(SSRS,porsussiglasen ingles)estodebidoaqueelvalorres igualalaunidad.Esdecir:


SistemaResistente
Mantodeacerosoldado. chimeneas,silos,tolvas,tanques apresión,torresdeproceso, cañerías,etc 002
Mantodeaceroapernadoo remachado 003
Marcosdeacerosoldadoscono sinarriostramiento 002
Marcosdeaceroconunionesde terrenoapernadas,conosin arriostramiento 0.03
Estructurasdehormigón armadoyalbañilería005
Estructurasprefabricadasde hormigónarmadopuramente gravitacionales 005
Estructurasprefabricadasde hormigónarmadoconuniones húmedas,nodilatadasdelos elementosnoestructuralese incorporadosenelmodelo estructural
0.03
Estructurasprefabricadasde hormigónarmadoconuniones húmedasdilatadasdelos elementosnoestructurales 0.03
Estructurasprefabricadasde hormigónarmadoconuniones secas,dilatadasynodilatadas, conconexionesapernadasy conexionesmediantebarras embebidasenmorterode relleno
0.03

Estructurasprefabricadasde hormigónarmadoconuniones secas,dilatadasynodilatadas: conconexionessoldadas 0.02
Otrasestructurasnoincluidaso asimilablesalasdeestalista0.02
Tabla2.6.3.Razonesdeamortiguamiento

