
Diseño por estabilidad de losas de fundación para equipos pesados y robustos. NCh 2369
01 INTRODUCCIÓN
Para el diseño de estos equipos la NCh 2369 en su disposición 5.6 establece que las solicitaciones sísmicas se pueden diseñar mediante el método de análisis estático con un coeficiente sísmico horizontal de 0.7 A/g y de 0.5 A/g para la componente vertical con fuerzas aplicadas en el centro de gravedad del equipo.
Cabe destacar que esta disposición es aplicable para equipos cuyo periodo fundamental propio es menor o igual a 0.006 s, incluyendo el efecto del sistema de conexión a la fundación.
Se recomienda para este tipo de sistemas que el área de contacto de la fundación con el suelo de soporte sea del 100 % para todos los casos de carga. Esto con la finalidad de evitar deformaciones y giros excesivos en el equipo que pudiesen originar un incorrecto funcionamiento de este.
02 OBJETIVO
El presente documento está referido diseño de losas de fundación para soportar equipos pesados y robustos.
03 BASES PARA EL DISEÑO
NCh 2369.Of2003 -Diseño Sísmico de Estructuras e Instalaciones Industriales.
NCh 1537.Of2009 -Diseño Estructural -Cargas Permanentes y Cargas de Uso.
NCh 3171.Of2010 -Diseño Estructural -Disposiciones Generales y Combinaciones de Carga. Normas
Diseño por estabilidad de losas de fundación para equipos pesados y robustos. NCh 2369
04
CALIDAD DE LOS MATERIALES
Esfuerzo del fluencia del acero de refuerzoNCh 204 Tabla 1 ≔ f y 420 M P a
Resistencia a la compresión del Hormigón ≔ f c 20 M P a
4.1
PARAMETROS DEL SUELO
4.2
PARAMETROS DEL HORMIGON
Tensión vertical admisible
σ s 1.9 k g f c m 2
Peso unitariohormigón armado
γ c 2500 k g f m 3 Ángulo de fricción interna ≔ ϕ 30 d e g
4.3 PARAMETROS DEL ACERO DE REFUERZO Cohesión
c 0 k g f m 2
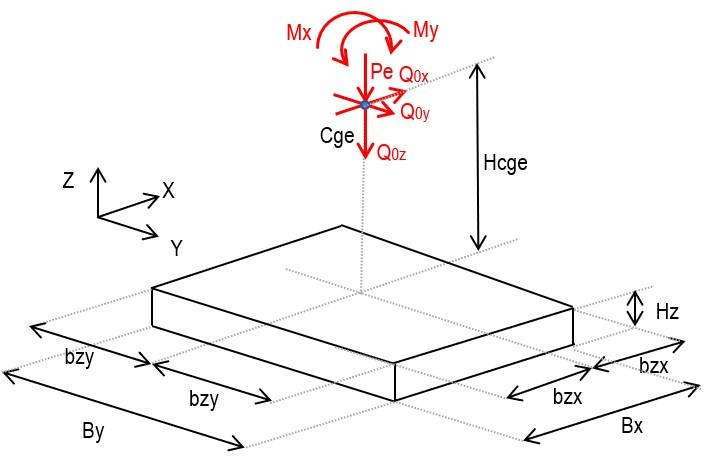
05 GEOMETRÍA
5.1 LOSA DE FUNDACIÓN
Longitud de la zapata en X ≔ B x 2500 m m
Longitud de la zapata en Y ≔ B y 3000 m m
Altura de la zapata ≔ H z 500 m m
Long. de la zarpa en X ≔ b zx = B x 2 125 c m
Long. de la zarpa en Y ≔ b zy = B y 2 150 c m
5.2 EQUIPO
Peso unitarioacero ≔ γ a ⋅ 7850 k g f m 3
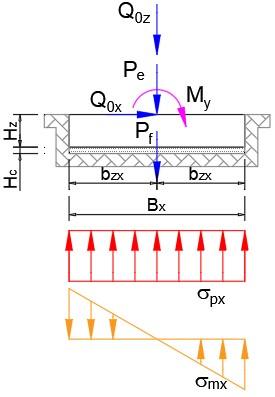
Figura 1. Geometría de la fundación
Altura del centro de gravedad del equipo ≔ H cge 2000 m m
06 SOLICITACIONES ACTUANTES EN CENTRO DE GRAVEDAD DEL EQUIPO
6.1 SOBRECARGA SÍSMICA
Acción sísmica Horizontal
Peso del equipo ≔ P e 8000 k g f
Clasificación o categoría de la estructura Art. 4.3.1 NCh 2369 Of.2003 ≔ C at C1
Zona sísmica Fig. 5.1 y 5.2 NCh 2369 Of.2003 ≔ Z s 2
Aceleración efectiva máxima Tabla 5.2 NCh 2369 Of.2003 = A 0 0.3
Coeficiente de importancia Art. 4.3.2 NCh 2369 Of.2003 = I 1.2 ≔ C xy = 0.7 A 0 0.21
Coeficiente sísmico Art. 5.6 NCh 2369 Of.2003 by Ing Angel Manrique
Diseño por estabilidad de losas de fundación para equipos pesados y robustos. NCh 2369

Coeficiente sísmico Art. 5.6 NCh 2369 Of.2003
Esfuerzo de corte basal Art. 5.3.2 NCh 2369 Of.2003
Acción sísmica vertical
Coeficiente sísmico Art. 5.6 NCh 2369 Of.2003
NCh 2369
0.21
⎛ ⎜ ⎝ ++ 1 ⋅ 6 e x B x
⎞ ⎟ ⎠ 0.487
k
⋅ 6 e y B y g f c m 2
Factor de seguridad de la presión de contacto máximo ≔ FS pc = σ s σ cmax 3.898 = FS “OK”
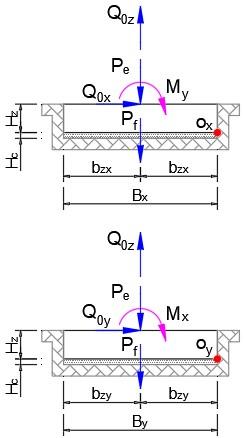
7.3 VERIFICACION DE ESTABILIDAD AL VOLCAMIENTO
Momento estabilizador en X ≔ M ex = ⋅ ⎛ ⎝ - + P f P e Q 0z ⎞ ⎠ b zx 19918.8 ⋅ k g f m
Momento de volcamiento en X ≔ M vx = + M y ⋅ Q 0x H z 5040 ⋅ k g f m
Punto de volcamiento , o x o y
if else
Factor de seguridad al volcamiento en X ≔ F sx = M ex M vx 3.952 = | | | | | | |
≥ F sx 1.5 ‖ ‖ “OK” ‖ ‖ “FAIL”
“OK”
Momento estabilizador en Y ≔ M ey = ⋅ ⎛ ⎝ - + P f P e Q 0z ⎞ ⎠ b zy 23902.5 ⋅ k g f m Figura 4. DCL Volcamiento
Momento de volcamiento en Y ≔ M vy = + M x ⋅ Q 0y H z 5040 ⋅ k g f m
Factor de seguridad al volcamiento en Y ≔ F sy = M ey M vy 4.743 = | | | | | | |
if else
≥ F sy 1.5 ‖ ‖ “OK” ‖ ‖ “FAIL”
“OK”
Momento estabilizador en X-Y ≔ M exy = ⋅ ⎛ ⎝ - + P f P e Q 0z ⎞ ⎠ 0.5 ⎛ ⎝ 2 + B x 2 B y 2 ⎞ ⎠ 31114.1 ⋅ k g f m Momento de volcamiento en X-Y ≔ M vxy = + 2 + M x 2 M y 2 ⋅ ⎛ ⎝ 2 + Q 0x 2 Q 0y 2 ⎞ ⎠ H z 7127.6 ⋅ k g f m
7.4 VERIFICACION DE ESTABILIDAD AL DESLIZAMIENTO by Ing Angel Manrique Página 6 de 11
Diseño por estabilidad de losas de fundación para equipos pesados y robustos. NCh 2369
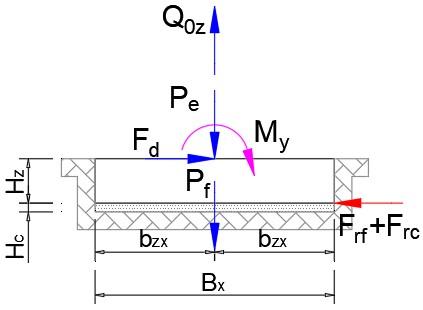
7.4 VERIFICACION DE ESTABILIDAD AL DESLIZAMIENTO
Área en Compresión ≔ A c = ⋅ B x B y 75000 c m 2
Fuerza Deslizante ≔ F d = 2 + Q 0x 2 Q 0y 2 2851.1 k g f
Factor de reducción de resistencia por fricción ≔ ϕ f 0.77

Factor de reducción de resistencia por cohesión ≔ ϕ c 0.33 Figura 5. DCL Deslizamiento
Angulo de rozamiento terreno -zapata ≔ ϕ d = ⋅ 2/3 ϕ 20 d e g
Fuerza resistente por fricción ≔ F rf = ⋅ ⋅ ϕ f ⎛ ⎝ - + P f P e Q 0z ⎞ ⎠ tan ⎛ ⎝ ϕ d ⎞ ⎠ 4465.9 k g f
Fuerza resistente por adherencia ≔ F rc = ⋅ ⋅ ϕ c A c c 0 k g f
Fuerza resistente ≔ F r = + F rf F rc 4465.9 k g f
≥ F sd 1.5 ‖ ‖ “OK” ‖ ‖ “FAIL” 08
SOLICITACIONES SOBRE LA FUNDACION
8.1 HIPOTESIS DE CÁLCULO NCh 3171 Of.2010
if else
“OK”
Capacidad resistente D: Carga Permanente (Pe, Pf) E: Carga Sísmica NCh 2369 (Qox, Qoy, Qoz) b = 1.1 Factor de amplificación de cargas sísmicas (Art. 4.5b NCh 2369 Of. 2003)
1) 1.4D 5a) 1.2D + 1.4bEx+ 0.3bEy + bEz 5b) 1.2D + 1.4bEy+ 0.3bEx + bEz
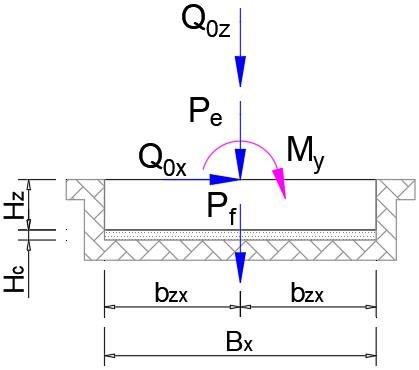
8.2 SOLICITACIONES SENTIDO X
Momento actuante máximo
Carga distribuida originada por las fuerzas verticales
≔ σ
Página 7 de 11
≔ σ
Figura 6. DCL Refuerzo X
Diseño por estabilidad de losas de fundación para equipos pesados y robustos. NCh 2369
Carga distribuida originada por el momento de volcamiento y cortante ≔ σ mx = ⋅ ⋅ ⋅ 31.41.1 ⎛ ⎝ + M y ⋅ Q 0x H z ⎞ ⎠ 2 B x 2 1862.784 k g f m
Momento actuante máximo ≔ M actx max ⎛ ⎜ ⎝ , ⋅ σ px1 b zx 2 2 + ⋅ σ px2 b zx 2 2 ⋅ 2 σ mx b zx 2 6 ⎞ ⎟ ⎠ = M actx 8178.825 ⋅ k g f m
Cortante actuante máximo
Recubrimiento llenado contra terreno ≔ rz 7.5 cm
Altura útil de la sección transversal sentido X ≔ d = - H z r z 42.5 c m
Cortante actuante máximo ≔ V actx max ⎛ ⎜ ⎝ , ⋅ σ px1 ⎛ ⎝ - b zx d ⎞ ⎠ + ⋅ σ px2 ⎛ ⎝ - b zx d ⎞ ⎠ ⋅ ⎛ ⎜ ⎝ + ⋅ σ mx d b zx σ mx ⎞ ⎟ ⎠ ⎛ ⎝ - b zx d ⎞ ⎠ 2 ⎞ ⎟ ⎠ = V actx 8641.962 k g f
8.3 SOLICITACIONES SENTIDO Y
Momento actuante máximo
Carga distribuida originada por las fuerzas verticales ≔ σ py1 = 1.4 ⎛ ⎝ + P f P e ⎞ ⎠ B y 8108.333 k g f m ≔ σ py2 = + 1.2 ⎛ ⎝ + P f P e ⎞ ⎠ ⋅ 1.41.1 Q 0z B y 7689.2 k g f m
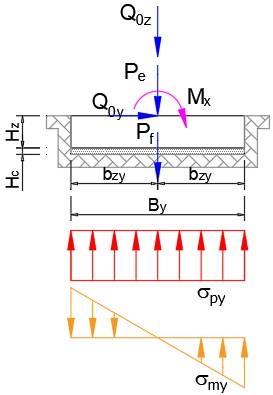
Carga distribuida originada por el momento de volcamiento y cortante Figura 7. DCL Refuerzo Y ≔ σ my = ⋅ ⋅ ⋅ 31.41.1 ⎛ ⎝ + M x ⋅ Q 0y H z ⎞ ⎠ 2 B y 2 1293.6 k g f m
Momento actuante máximo ≔ M acty max ⎛ ⎜ ⎝ , ⋅ σ py1 b zx 2 2 + ⋅ σ py2 b zy 2 2 ⋅ 2 σ my b zy 2 6 ⎞ ⎟ ⎠ = M acty 9620.55 ⋅ k g f m
Cortante actuante máximo
Cortante actuante máximo ≔ V acty max ⎛ ⎜ ⎝ , ⋅ σ py1 ⎛ ⎝ - b zy d ⎞ ⎠ + ⋅ σ py2 ⎛ ⎝ - b zy d ⎞ ⎠ ⋅ ⎛ ⎜ ⎝ + σ my b zy dσ my ⎞ ⎟ ⎠ ⎛ ⎝ - b zy d ⎞ ⎠ 2 ⎞ ⎟ ⎠ = V acty 9158.205 k g f
Diseño por estabilidad de losas de fundación para equipos pesados y robustos. NCh 2369 = V acty 9158.205 k g f
CAPACIDAD RESISTENTE A FLEXIÓN DE LA ZAPATA
9.1 ACERO DE REFUERZO LONGITUDINAL SENTIDO X
Factor de minoración Tabla 21.2.2 ACI318-19 ≔ ϕb 0.9
Diámetro de barra de refuerzo ≔ D bz 16 m m Numero de barras de refuerzo ≔ N zy 16 Recubrimiento llenado contra terreno = r z 7.5 c m
Separación de barras de refuerzo ≔ S by = - B y ⋅ 2 r z - N zy 1 19 c m Acero de refuerzo mínimo Art. 8.6.1.1 ACI318-19 ≔ A smin = ⋅ ⋅ 0.0018 B y H z 27 c m 2
Acero de refuerzo ≔ A sx = ⋅ B y S by
⋅ π D bz 2 4 31.747 c m 2 = | | | | | | |
if else
≥ A sx A smin ‖ ‖ “OK” ‖ ‖ “Aumentar As”
“OK” Altura útil de la sección transversal sentido X ≔ d x = - - H z r z D bz 2 41.7 c m
Profundidad equivalente del bloque comprimido ≔ a = ⋅ A sx f y ⋅ ⋅ 0.85 f c B y 2.614 c m Momento resistente sentido X ≔ M rx = ⋅ ⋅ ⋅ ϕ b A sx f y ⎛ ⎜ ⎝ - d x a 2 ⎞ ⎟ ⎠ 49427.9 ( ( ⋅ k g f m ) )
Factor de Utilización a flexión sentido X ≔ F ufx = M actx M rx = | | | | | | |
9.2 ACERO DE REFUERZO LONGITUDINAL SENTIDO Y
Factor de minoración Tabla 21.2.2 ACI318-19 = ϕ b 0.9
Diámetro de barra de refuerzo = D bz 16 m m
Numero de barras de refuerzo ≔ N zx 13 Recubrimiento llenado contra terreno = r z 7.5 c m
if else
≤ F ufx 1 ‖ ‖ “OK” ‖ ‖ “FAIL”
“OK”
Separación de barras de refuerzo ≔ S bx = - B x ⋅ 2 r z - N zx 1 19.583 c m
Acero de refuerzo mínimo Art. 8.6.1.1 ACI318-19 ≔ A smin = ⋅ ⋅ 0.0018 B x H z 22.5 c m 2
Acero de refuerzo mínimo Art. 8.6.1.1 ACI318-19
Diseño por estabilidad de losas de fundación para equipos pesados y robustos. NCh 2369 ≔ A smin =⋅⋅ 0.0018 B x H z 22.5 c m 2
Acero de refuerzo ≔ A sy = ⋅ B x S bx
⋅ π D bz 2 4 25.667 c m 2 = | | | | | | |
if else
≥ A sy A smin ‖ ‖ “OK” ‖ ‖ “Aumentar As”
Altura útil de la sección transversal sentido Y ≔ d y = - - H z r z ⋅ 3 2 D bz 40.1 c m
Profundidad equivalente del bloque comprimido ≔ a = ⋅ A sy f y ⋅ ⋅ 0.85 f c B x 2.537 c m
“OK”
Momento resistente sentido Y ≔ M ry = ⋅ ⋅ ⋅ ϕ b A sy f y ⎛ ⎜ ⎝ - d y a 2 ⎞ ⎟ ⎠ 38418.6 ( ( ⋅ k g f m ) )
Factor de Utilización a flexión sentido Y ≔ F ufy = M acty M ry = | | | | | | |
10 CAPACIDAD RESISTENTE A CORTANTE DE LA ZAPATA
10.1 CORTANTE SIMPLE SENTIDO X
Cortante resistente del Hormigón
Factor de minoración ≔ ϕ v 0.75 Tabla 21.2.1 ACI318-19
if else
≤ F ufy 1 ‖ ‖ “OK” ‖ ‖ “FAIL”
“OK”
if else
≤ F uvx 1 ‖ ‖ “OK” ‖ ‖ “FAIL”
“OK”
Cortante resistente del hormigón ≔ V rx1 = ⋅ ⋅ ⋅ ⋅ ⋅ ϕ v 0.660.0018 1 3 B y d x 2 ⋅ f c M P a 34351.7 k g f Tabla 22.5.5.1 ACI318-19 Av < Av,min ≔ V rmax = ⋅ ⋅ ⋅ ⋅ ϕ v 0.42 B y d x 2 ⋅ f c M P a 179705.8 k g f ≔ V rx = min ⎛ ⎝ , V rx1 V rmax ⎞ ⎠ 34351.7 k g f Factor de Utilización cortante X ≔ F uvx = V actx V rx = | | | | | | |
10.2 CORTANTE SIMPLE SENTIDO Y
Cortante resistente del Hormigón
Factor de minoración al corte = ϕ v 0.75 Tabla 21.2.1 ACI318-19
Cortante resistente del hormigón ≔ V ry1 = ⋅ ⋅ ⋅ ⋅ ⋅ ϕ v 0.660.0018 1 3 B x d y 2 ⋅ f c M P a 27528 k g f Av < Av,min Tabla 22.5.5.1 ACI318-19
V rmax =⋅⋅⋅⋅ ϕ v 0.42 B x d y 2 ⋅ f c M P a 144008.9
Diseño por estabilidad de losas de fundación para equipos pesados y robustos. NCh 2369 Av < Av,min ≔ V rmax = ⋅ ⋅ ⋅ ⋅ ϕ v 0.42 B x d y 2 ⋅ f c M P a 144008.9 k g f ≔ V ry = min ⎛ ⎝ , V ry1 V rmax ⎞ ⎠ 27528 k g f
Factor de Utilización cortante Y ≔ F uvy = V acty V ry = | | | | | | |
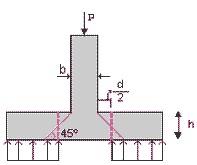
10.3 CORTANTE POR PUNZONAMIENTO
if else
≤ F uvy 1 ‖ ‖ “OK” ‖ ‖ “FAIL”
“OK”
Altura útil de la sección ≔ d v = - - H z r z D bz 40.9 c m Cortante actuante ≔ V pa ⋅ max ⎛ ⎝ , 1.4 ⎛ ⎝ + P f P e ⎞ ⎠ + 1.2 ⎛ ⎝ + P f P e ⎞ ⎠ ⋅ 1.41.1 Q 0z ⎞ ⎠ ⋅ B x B y ⎛ ⎝ - ⋅ B x B y d v 2 ⎞ ⎠ = V pa 23782.452 k g f
Perímetro de punzonamientomínimo ≔ b 0 = + ⋅ 2 ⎛ ⎝ d v ⎞ ⎠ ⋅ 2 ⎛ ⎝ d v ⎞ ⎠ 163.6 c m
, 1 2 2 + 1 ⋅ ⋅ 0.004 d v c m 10
Relación del lado largo al lado corto ≔ β = max ⎛ ⎝ , B x B y ⎞ ⎠ min ⎛ ⎝ , B x B y ⎞ ⎠ 1.2
⎞ ⎟ ⎟ ⎟ ⎠
Factor de modificación por efecto de tamaño ≔ λ sz = min ⎛ ⎜ ⎜ ⎜ ⎝
0.871
Cortante resistente del hormigón ≔ V rp1 = ⋅ ⋅ ⋅ ⋅ ϕ v b 0 d v 0.33 λ sz 2 ⋅ f c M P a 65783.7 k g f Tabla 22.6.5.2. ACI318-19 ≔ V rp2 = ⋅ ⋅ ⋅ ⋅ ⋅ ϕ v b 0 d v 0.17 ⎛ ⎜ ⎝ + 1 2 β ⎞ ⎟ ⎠ λ sz 2 ⋅ f c M P a 90369.6 k g f ≔ V rp3 = ⋅ ⋅ ⋅ ⋅ ⋅ ϕ v b 0 d v 0.083 ⎛ ⎜ ⎝ + 2 ⋅ 40 d v b 0
⎞ ⎟ ⎠ λ sz 2 ⋅ f c M P a 198547.2 k g f ≔ V rp = min ⎛ ⎝ , , V rp1 V rp2 V rp3 ⎞ ⎠ 65783.7 k g f
≤ F up 1 ‖ ‖ “OK” ‖ ‖ “FAIL” by Ing Angel Manrique Página 11 de 11
if else
“OK”
