COLD-FORMED STEEL N4. Resistencia a flexión de secciones tubulares. AISI S100-07

COLD-FORMEDSTEELN°4 DICIEMBRE,

Serie: Perfiles conformados o doblados en frio.

RESISTENCIA A FLEXIÓN DE SECCIONES TUBULARES O

AISI S100-07 -NorthAmerican Specification for the Design of Cold-Formed Steel Structural Members, 2007.

MÉTODO DE LOS ESTADOS LIMITES, LRFD

Angel Manrique

Ingeniero Civil Especialista en Estructuras

2022

01

INTRODUCCION

Los elementos de acero cuya sección transversal se logra mediante el plegado o doblado de planchas de acero al carbono a temperatura ambiente, se denominan perfiles conformados o laminados en frio.

Los perfiles tubulares se caracterizan por ser una pieza hueca de metal de contorno redondo, cuadrado o rectangular. Al tener una sección transversal cerrada presentan un buen comportamiento al pandeo torsional. Además, tienen una notable mejora en cuanto a la estética de las estructuras, esto debido en parte a que son elementos que permite que las uniones puedan realizarse mediante soldaduras directa entre perfiles. Sin embargo, este tipo de uniones requiere una revisión exhaustiva sobre todo en sistemas sismorresistentes.

Las propiedades mecánicas que se requieren para los perfiles tubulares conllevan a que la forma más común de fabricarlos sea sin costura. También se tienen perfiles fabricados con costura longitudinal y con una soldadura helicoidal o en espiral que recorre el tubo.

02OBJETIVO

El presente documento está referido al diseño mediante el método de los estados limites por de capacidad resistente y de servicio, para vigas con sección transversal tipo tubular.

03BASESPARAELDISEÑO

Normas Nacionales 1. 2. 3.

NCh 1537.Of2009 - Diseño Estructural - Cargas Permanentes y Cargas de Uso.

NCh 2369.Of2003 - Diseño Sísmico de Estructuras e Instalaciones Industriales.

NCh 3171.Of2010 - Diseño Estructural - Disposiciones Generales y Combinaciones de Carga.

Normas Internacionales

1. 2. 3.

AISI S100-07. North American Specification for the Design of Cold-Formed Steel Structural Members, 2007.

ANSI/AISC 360-10. Specification for Structural Steel Buildings

ASCE/SEI7. Minimum Design Loads and Associated Criteria for Buildings and Other Structures

DocumentosTécnicos

1. 2.

CIDECT 7 Guía de diseño para la fabricación ensamble y montaje de estructuras de perfiles tubulares

Publicación ICHA “Especificaciones Norteamericanas para el Diseño de Miembros Estructurales Conformados en Frío”, 2009).

04

2. Publicación ICHA “Especificaciones Norteamericanas para el Diseño de Miembros Estructurales Conformados en Frío”, 2009).

CALIDADDELOSMATERIALES.ACEROESTRUCTURAL

Esfuerzo del fluencia

fys 250 MPa Modulo de elasticidad

Es 200000 MPa Peso unitario del acero

γa 7850⋅ kgf m 3 Modulo de Poisson

μ 0.3 Modulo de corte ≔ Gs = Es 2 ( (1+μ) ) 76923.08 MPa

05GEOMETRÍAYCONDICIONESDEAPOYO

5.1. CONDICIONES DEAPOYO

Separación entre apoyos de la viga

Lx 6000 mm Figura 1. Condiciones de apoyo de costanera de techo Numero de arriostramientos laterales ≔ Nlat 1

PERFILES ESTRUCTURALES

7) Viga central

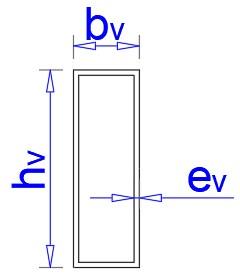
hv 150 mm

bv 50 mm

ev 3 mm Área neta = Av 17.41 cm 2 Área Esquinas = Aesqv 6.85 cm 2 Modulo elásticoY = Svy 7 cm 3 Peso por ml = Pvml 13.67 kgf m Radio de giro X = rvx 4.14 cm

Modulo elástico X = Svx 39.78 cm 3 Radio de giro polar = r0v 57.23 mm

CARGASYSOLICITACIONES

6.1. CARGAS MAYORADAS

Carga de diseño sentido fuerte (Incluye peso propio) ≔ qcrf 169.1 kgf m

Carga de diseño sentido débil (Incluye peso propio) ≔ qcrd 27.5 kgf m

Carga de diseño por deflexión (Incluye peso propio) ≔ qcs 89.48 kgf m

6.2. SOLICITACIONES

Sentido fuerte

Momento actuante máximo de diseño sentido fuerte ≔ Macf = ⋅ qcrf Lx 2 8 760.95 ⋅kgf m

Cortante actuante máximo de diseño sentido fuerte ≔ Vacf = ⋅ qcrf Lx 2 507.3 kgf

Sentido débil

Momento actuante máximo sentido débil = Nlat 1 ≔ Macd = ⋅ qcrd Lx 2 32 30.94 ⋅kgf m

Cortante actuante máximo sentido débil = Nlat 1 ≔ Vacd = ⋅ 0.62⋅qcrd Lx 102.3 kgf

DISEÑOPORCAPACIDADRESISTENTE

7.1. CONSIDERACIONES GEOMÉTRICAS

Limitaciones y consideraciones sobre las dimensiones

Relacióndeesbeltezdeloselementos

Relación entre el ancho plano de las alas y su espesor Art. B.1.1aAISI 2007 ≔Rala ≤ - bv ev ev 60 = Rala “OK”

Relación entre la profundidad del alma y su espesor Art. B.1.2aAISI 2007 ≔Ralma ≤ - hv ev ev 100 = Ralma “OK”

Efectodecortediferido.Tramoscortosquesoportancargasconcentradas

Ancho del ala que se proyecta más allá del alma ≔ Wfc =b 38 mm

Altura de la viga = hv 150 mm Espesor del perfil = ev 3 mm

Ancho limite del ala Eq. B1.1-1AISI 2007 ≔ Wf = Wfc 38 mm

Coeficiente de pandeo de placas ≔ ksl 4

Ancho real plano del ala ≔ wslf =b 38 mm

Figura 3. Ancho de ala

⎞ ⎟ ⎠

Tensión de pandeo elástico de la placa Eq. B2.1-5AISI 2007 ≔ Fcrslf = ⋅ ⋅ ksl ⋅ π 2 Es 12⋅⎛ ⎝1-μ 2 ⎞ ⎠ ⎛ ⎜ ⎝ ev wslf

2 4506.53 MPa

Factor de esbeltez Eq. B2.1-4AISI 2007 ≔ λsl = 2 fys Fcrslf 0.24

⎛ ⎜ ⎝ 10.22 λsl

Factor de reducción local Eq. B2.1-3AISI 2007 ≔ ρsl =

⎞ ⎟ ⎠ λsl 0.28

Ancho efectivo de diseño del ala = bsl 38 mm

Relación entre la longitud de la viga y ancho de ala ≔ RLWf = Lx Wf 157.89

Relación entre el ancho efectivo de diseño y ancho real ≔ Rbw = bsl wslf 1 = Rbwadm 1

Relación admisible entre ancho efectivo de diseño y ancho real Tabla B1.1cAISI 2007 by Ing Angel Manrique .com

Relación admisible entre ancho efectivo de diseño y ancho real Tabla B1.1cAISI 2007 = Rbwadm 1

Factor de corte diferido ≥ ＝ Fsl Rbwadm Rbw = Fsl “OK”

7.2. VERIFICACIÓN POR PANDEO LOCAL

Ala en compresión rigidizadas

Tensión de pandeo elástico de la placa Eq. B2.1-5AISI 2007 = Fcrslf 4506.53 MPa

Pandeo local del ala en compresión ≥ ＝ Pandeof Fcrsl fys = Pandeof “OK”

Almas rigidizadas con gradiente de tensiones

Coeficiente de pandeo de placas = ksl 4 Alto real plano del alma ≔ wslw =a 138 mm

Figura

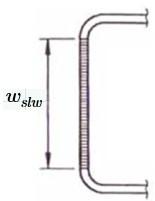
4. Alto de alma

⎞ ⎟ ⎠

Tensión de pandeo elástico de la placa Eq. B2.1-5AISI 2007 ≔ Fcrslw = ⋅ ⋅ ksl ⋅ π 2 Es 12⋅⎛ ⎝1-μ 2 ⎞ ⎠ ⎛ ⎜ ⎝ ev wslw

2 341.71 MPa

Pandeo local del alma ≥ ＝ Pandeow Fcrslw fys = Pandeow “OK”

7.3. INCREMENTO DE LARESISTENCIADEBIDOALCONFORMADO EN FRIO

Las propiedades mecánicas del acero en la zona de las esquinas cambia de manera significativa debido en mayor medida a que reciben mas esfuerzo durante el proceso de doblado. Se tiene entonces un incremento en el esfuerzo de fluencia y de la tensión ultima , pero este ultimo fys Fu en menor medida, por tanto, se reduce de manera significativa la ductilidad del perfil. Las partes planas también sufren una incremento del esfuerzo de fluencia y de tensión ultima, pero en menor medida al incremento originado en las esquinas.

Figura 5. Efectos del conformado en frío sobre el límite elástico. Fuente: ICHA. Doc. Tec Ref. 1

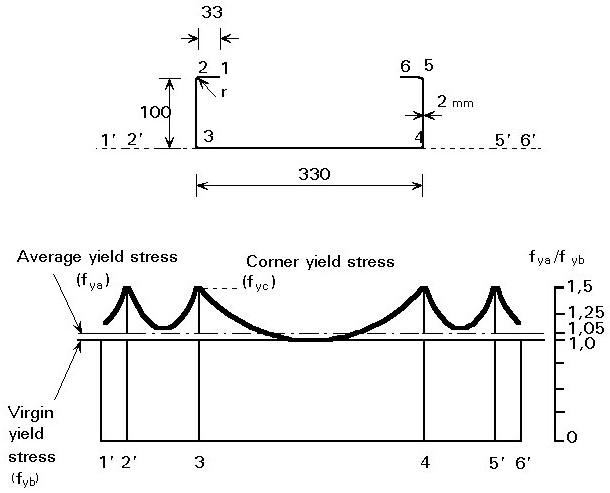
El esfuerzo de fluencia medio de la sección depende entonces del número de esquinas y del ancho de los elementos planos.

Razón entre el área de las esquinas y el área total de la sección transversal ≔ Cc = Aesqv Av 0.39

Tensión de fluencia del material virgen ≔ Fyv = fys 250 MPa

Tensión ultima del material virgen = Fuv 400 MPa

⎞ ⎟ ⎠ 0.819⋅ ⎛ ⎜ ⎝ Fuv Fyv

⎞ ⎟ ⎠

Factor Bc (Eq.A7.2-3AISI 2007) ≔ Bc = - - 3.69⋅ ⎛ ⎜ ⎝ Fuv Fyv

2 1.79 ?

Factor m (Eq.A7.2-4AISI 2007) ≔ mc = - 0.192⋅ ⎛ ⎜ ⎝ Fuv Fyv

⎞ ⎟ ⎠ 0.068 ? Radio interno de plegado ≔R = rple 4.5 mm

Tensión de fluencia a tracción promedio de las esquinas (Eq.A7.2-2AISI 2007) ≔ Fyc = ⋅ Bc Fyv ⎛ ⎜ ⎝ R ev

⎞ ⎟ ⎠

mc 457.72 MPa

Condición CC1 ≥ Fuv Fyv 1.2 =CC1 “OK”

Condición CC2 ≤ R ec 7 =CC2 “OK”

Condición CC3 ≤ θcc 120 deg =CC3 “OK”

¿Aplica incremento de resistencia? =INC.RES “SI”

7.4. CAPACIDAD RESITENTE SENTIDO FUERTE

Capacidad resistente al momento flector

Resistencia nominal a momento por fluencia

Tensión de fluencia de cálculo (Art. C3.1.1AISI 2007) by Ing Angel Manrique .com

if else

＝INC.RES “SI” ‖ ‖ + ⋅ Cc Fyc ⋅ ⎛ ⎝1-Cc⎞ ⎠ Fyv ‖ ‖fys = Fyav 331.72 MPa

Tensión de fluencia promedio de la sección total (Eq.A7.2-1AISI 2007) ≔ Fyav | | | | | | |

Módulo elástico de la sección efectiva calculado con la fibra extrema comprimida o traccionada a Fy (Art. C3.1.1AISI 2007) = Svx 39.78 cm 3 = Fyav 331.72 MPa

Tensión de fluencia de cálculo (Art. C3.1.1AISI 2007) = Fyav 331.72 MPa

Momento de fluencia efectivo en base a la resistencia de la sección (Ec. C3.1.1-1AISI 2007) ≔ Mvf1 = ⋅ Svx Fyav 1345.64 ⋅kgf m

Resistencia nominal a momento por pandeo lateral torsional

Factores de longitud efectiva Tabla C-A-7.1AISC 360-16 ≔ Kxv 1.00 ≔ Kyv 1.00 ≔ Ktv 1.00

Figura 6. Tabla C-A-7.1 AISC 360-16

Longitud no arriostrada del elemento eje fuerte ≔ Lxv = Lx 6000 mm

Longitud no arriostrada del elemento eje débil ≔ Lyv = Lx + Nlat 1 3000 mm

Longitud no arriostrada del elemento torsión ≔ Ltv = Lyv 3000 mm

Radio de giro polar Ec. C3.1.2-13AISI 2007 = r0v 5.72 cm

Momento ubicado a un cuarto del segmento no arriostrado ≔ MA = ⋅ ⋅ qcrf Lyv 8 ⎛ ⎜ ⎝ - Lxv Lyv 4 ⎞ ⎟ ⎠ 332.92 ⋅kgf m

Momento ubicado en el centro del segmento no arriostrado ≔ MB = ⋅ ⋅ qcrf Lyv 4 ⎛ ⎜ ⎝ - Lxv Lyv 2 ⎞ ⎟ ⎠ 570.71 ⋅kgf m

Momento ubicado tres cuartos del segmento no arriostrado ≔ MC = ⋅ ⋅ qcrf 3 Lyv 8 ⎛ ⎜ ⎝ - Lxv 3 Lyv 4 ⎞ ⎟ ⎠ 713.39 ⋅kgf m

Coeficiente de flexión ≔ Cbv = 12.5⋅Macf + + + 2.5⋅Macf 3⋅MA 4⋅MB 3⋅MC 1.3

2 ⋅ ⋅ ⋅ Es Gs Jv Ivy 30341.53

kgf

elástico crítico Eq. C3.1.2.2-2AISI 2007

Tipo de pandeo lateral torsional =T.PAND “Nopresentapandeotorsional”

if else

≥ Fevf 2.78 Fyav ‖ ‖Fyav ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖

if else

> > 2.78 Fyav Fevf 0.56 Fyav ‖ ‖ ‖ ‖ ⋅ ⋅ 10 9 Fyav ⎛ ⎜ ⎝ 110⋅Fyav 36⋅Fevf

Tensión crítica de pandeo lateral torsional ≔ Fcvf | | | | | | | | | | | | |

⎞ ⎟ ⎠ ‖ ‖Fevf = Fcvf 3382.56 kgf cm 2

Momento de resistencia nominal al pandeo lateral Ec. C3.1.2-1AISI 2007 ≔ Mvf2 = ⋅ Svx Fcvf 1345.64 ⋅kgf m

Resistencia nominal a momento sentido fuerte

Factor de minoración a flexión ≔ ϕbv 0.90

Momento resistente máximo ≔ Mvf = ⋅ ϕbv min⎛ ⎝ , Mvf1 Mvf2⎞ ⎠ 1211.07 ⋅kgf m

Tipo de Falla = T.FALLAf “PandeoLateral”

Resistencia nominal al corte sentido fuerte Coeficiente de pandeo por corte ≔ kvv 5.34

Factor de minoración al corte ≔ ϕvv 0.95

⎞ ⎟ ⎠ by Ing Angel Manrique .com Página 10 de 14

≔ Fvvf

| | | | | | | |

2 3287.02 kgf cm 2

if ≤ hv e 2 ⋅ Es

vv f

⎞ ⎟ ⎠

≔ Fvvf

if else

≤ hv ev

|

7.5. CAPACIDAD RESITENTE SENTIDO DÉBIL

Capacidad resistente al momento flector

Resistencia nominal a momento por fluencia

2 ⋅ Es kvv fys ‖ ‖Fvvf1 ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖

≤ < 2 ⋅ Es kvv fys

if else

hv ev 1.51⋅ 2 ⋅ Es kvv fys ‖ ‖Fvvf2 ‖ ‖Fvvf3 = Fvvf 150 MPa

Resistencia nominal al corte ≔ Vvf = ⋅ ⋅ ⋅ ϕvv Fvvf 2 hv ev 13077.86 kgf

| | | | | | | | |

Módulo elástico de la sección efectiva calculado con la fibra extrema comprimida o traccionada a Fy (Art. C3.1.1AISI 2007) = Svy 7 cm 3

Tensión de fluencia de cálculo (Art. C3.1.1AISI 2007) = Fyav 3382.56 kgf cm 2

Momento de fluencia efectivo en base a la resistencia de la sección (Ec. C3.1.1-1AISI 2007) ≔ Mvd1 = ⋅ Svy Fyav 236.89 ⋅kgf m

Resistencia nominal a momento por pandeo lateral torsional

Factores de longitud efectiva Tabla C-A-7.1AISC 360-16 = Kxv 1 = Kyv 1 = Ktv 1

Longitud no arriostrada del elemento eje fuerte = Lxv 6000 mm

Longitud no arriostrada del elemento eje débil = Lyv 3000 mm

Longitud no arriostrada del elemento torsión = Ltv 3000 mm

Coeficiente de flexión ≔ Cbvd 1

Esfuerzo elástico crítico Eq. C3.1.2.2-2AISI 2007 ≔ Fevd = ⋅ ⋅ Cbvd π ⋅ ⋅ Kxv Lxv Svy

2 ⋅ ⋅ ⋅ Es Gs Jv Ivx 158154.58 kgf cm 2

Página 11 de 14

Tipo de pandeo lateral torsional

=T.PAND “Nopresentapandeotorsional”

Tensión crítica de pandeo lateral torsional ≔ Fcvd

if else

≥ Fevd 2.78 Fyav ‖ ‖Fyav ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖

if else

> > 2.78 Fyav Fevd 0.56 Fyav ‖ ‖ ‖ ‖ ⋅ ⋅ 10 9 Fyav ⎛ ⎜ ⎝ 110⋅Fyav 36⋅Fevd

⎞ ⎟ ⎠ ‖ ‖Fevd = Fcvd 3382.56 kgf cm 2

Momento de resistencia nominal al pandeo lateral Ec. C3.1.2-1AISI 2007 ≔ Mvd2 = ⋅ Svy Fcvd 236.89 ⋅kgf m

Resistencia nominal a momento sentido débil

Factor de minoración a flexión = ϕbv 0.9

Momento resistente máximo ≔ Mvd = ⋅ ϕbv min⎛ ⎝ , Mvd1 Mvd2⎞ ⎠ 213.2 ⋅kgf m Tipo de Falla = T.FALLAd “PandeoLateral”

Resistencia nominal al corte sentido débil

Coeficiente de pandeo por corte = kvv 5.34 Factor de minoración al corte = ϕvv 0.95

| | | | | | | |

⎞ ⎟ ⎠

5998.43 kgf cm 2 ≔ Fvvd3 = ⋅ ⋅ π 2 Es kvv ⋅ 12⋅⎛ ⎝1+μ 2 ⎞ ⎠ ⎛ ⎜ ⎝ bv ev

2 29583.2 kgf cm 2

⎞ ⎟ ⎠ ≔ Fvvd | | | if ≤ bv e 2 ⋅ Es kvv f by Ing Angel Manrique .com Página 12 de 14

if else

≤ bv ev

Diseño a flexión biaxial

2 ⋅ Es kvv fys ‖ ‖Fvvd1 ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖

≤ < 2 ⋅ Es kvv fys

≔ Fvvd | | | | | | | | | | | | | | | |

bv ev 1.51⋅ 2 ⋅ Es kvv fys ‖ ‖Fvvd2 ‖ ‖Fvvd3 = Fvvd 150 MPa

if else

| | | | | | | | |

Resistencia nominal al corte ≔ Vvd = ⋅ ⋅ ⋅ ϕvv Fvvd 2 bv ev 4359.29 kgf

7.6. RESUMEN DE DISEÑO POR CAPACIDAD RESISTENTE DE COSTANERAS

Momento actuante máximo de diseño sentido fuerte = Macf 760.95 ⋅kgf m = Macf Mvf 0.63 Momento resistente máximo sentido fuerte = Mvf 1211.07 ⋅kgf m

Momento actuante máximo sentido débil = Nlat 1 = Macd 30.94 ⋅kgf m = Macd Mvd 0.15 Momento resistente máximo sentido débil = Mvd 213.2 ⋅kgf m

Factor de utilización a momento ≔FUM = + Macf Mvf

Macd Mvd 0.77 = FUM “OK”

Diseño a corte

Cortante actuante máximo de diseño sentido fuerte = Vacf 507.3 kgf

Resistencia nominal al corte sentido fuerte = Vvf 13077.86 kgf

Diseño a cortante ≔FUV = Vacf Vvf 0.04 = FUV “OK”

DISEÑOPORCAPACIDADDESERVICIO

8.1. DISEÑO POR DEFLEXIÓN

La norma NCh427/1 2016 especifica en su disposición L1 que para los estados límites de servicio, las cargas y las combinaciones de carga apropiadas se encuentran en el documento Minimum Design Loads andAssociated Criteria for Buildings and Other Structures (ASCE/SEI7),Anexo C

Sentido fuerte

Deformación limite Anexo C ASCE/SEI7 ≔ Dlim = Lx 240 25 mm

Deformación máxima de la viga ≔ Dmax = ⋅ 5⋅qcs Lx 4 ⋅ 384⋅Es Ivx 24.82 mm

Factor de utilización por deflexión ≔FUD = Dmax Dlim 0.99 = FUD “OK”