VIVES - graduaat onderhoudstechnieken - elektrotechniek (Basis)

Elektrotechniek(Basis)

Studiegebied Technology

Opleiding Onderhoudstechnieken

Opleidingsfase Fase1

Legende van de gebruikte iconen

Denkvraag

Leerdoelen

Formule

Extra informatie

Niet vergeten

Opdracht/Oefening

Presentatie (PowerPoint)

Rekenblad (Excel)

Samenwerking

Studeeraanwijzingen

Tijdsinschatting

Toledo

Beeld/geluidsfragment

Voorbeeld

Tools/Apps

Website

Zelfstudie (Zelf)toets

3.4.1

4.1.3

4.1.4

4.1.7

4.1.8

4.1.9

6.5.2

6.5.3

12.1.2

12.1.3

12.2.1

13.4.4

13.4.5

13.4.7

13.4.8

13.5

13.5.1

13.5.2

13.5.3

13.5.4

13.6

13.6.1

13.6.2

13.6.3

13.6.4

13.6.5

Inleiding

Wat is de bedoeling van dit opleidingsonderdeel (OPO). Waarom werd dit OPO opgenomen in het curriculum van diverse graduaatsopleidingen? Voorbeeld in de Elektromechanische Systemen, onderhoudstechnieker, of HVAC.

In deze opleidingen verwelkomen we alle studenten die goesting hebben voor techniek. Een onderhoudstechnicus moet verschillende vaardigheden ontwikkelen. Daarom onze drie grote pijlers in deze opleiding : elektriciteit – mechanica en onderhoud. Een technicus HVAC moet ook op meerdere domeinen beschikken over de juiste skills.

Sommigen zijn vanuit een vorige opleiding reeds vertrouwd met een of meerdere van deze domeinen. We willen geen stappen overslaan en in deze module wordt vooral kennis gemaakt met het elektrische domein.

Om iedereen dezelfde kansen te bieden wordt gestart met een aantal kleine, praktische projecten. Deze worden uitgevoerd en soms zal dit in een verder OPO opnieuw behandeld worden.

Wanneer je door deze cursus bladert , ontmoet je in eerste instantie enkele basislichtschakelingen. In dit OPO worden deze uitgevoerde en alle schema’s die hier zinvol zijn worden geschetst..

Tijdens de uitvoering wordt ook aandacht geschonken aan de technologie, het materiaal, en de technieken om dit efficiënt uit te voeren.

Dit OPO is een actieve OPO.

Deze cursus werd samengesteld door Luc De Ruytter in samenspraak met Michaël De Loof en Mathieu Himpe.

Benodigheden

Om de leerstof efficiënt te kunnen volgen moeten steeds volgende zaken aanwezig zijn in de lessen:

 Velleman experimenteerkit EDU01.

 9V blokbatterij (deze wordt niet voorzien in de Velleman experimenteerkit).

 Knoopcelbatterij 2032.

 Wasknijper (zorg ervoor dat deze volle bekken heeft – draad moet op batterij gekneld kunnen worden ).

 Multimeter.

 Rekenmachine.

1 De elektrische kring

Een elektrische kring bestaat altijd uit een aantal elementen die zeker nodig zijn om de elektriciteit te kunnen laten vloeien.

1.1 Voeding

Een stroombron zorgt voor elektrische energie. Voorbeelden van stroombronnen zijn batterijen, het elektrisch net, …

1.2 Leidingen

Een geleider zorgt voor transport van de elektrische energie naar de verbruiker. Een geleider is meestal vervaardigd van koper met daaromheen de isolatie.

1.4 Schakelaar

Een schakelaar is "verbinder" waarbij vaak twee geleidende delen met elkaar verbonden worden. Omgekeerd kan een schakelaar de stroomkring juist verbreken (kortweg breken).

De bekendste is de lichtschakelaar in huis waarmee een lamp "aan (1)" of "uit (0)" gedaan kan worden.

Er zijn 6 soorten basisschakelaars:

 Enkelpolige schakelaar

 Dubbelpolige schakelaar

 Serie-schakelaar

 Wisselschakelaar

 Kruisschakelaar

 Dubbelpolige wisselschakelaar

1.5 Verbruiker

Een verbruiker verbruikt de elektrische energie van de bron. Het verbruik kan onder allerlei vormen gebeuren, zoals licht, warmte en beweging

1.6 Gebruik van symbolen

Symbolen worden gebruikt in iedere omgeving. Er zijn elektrische–, pneumatische–, verkeer..

Alle symbolen hebben als voornaamste doel EENVORMIGHEID en een EENDUIDIGE betekenis.

Uit deze voorbeelden blijkt dat het veel eenvoudiger is om de toestellen voor te stellen door een symbool dat hun functie weergeeft dan het toestel te tekenen.

1.7

Gebruik van symbolen

Door symbolen van verschillende onderdelen te verbinden worden vlot schema’s getekend.

De bovenste figuur links is een foto van een eenvoudige opstelling. De figuur er rechts van is een vertaling naar een schema. Uit dit schema blijkt dat de lamp continu brandt.

Der derde schakeling (onderaan links) geeft een parallelschakeling weer. Wanneer de schakelaar wordt bedient dan zullen alle drie de lampen oplichten.

De laatste schakeling is een uitbreiding waarbij de weerstanden de stroom, doorheen de lampen, beperken.

Een schema leert hoe een schakeling werkt.

1.8 Schema’s

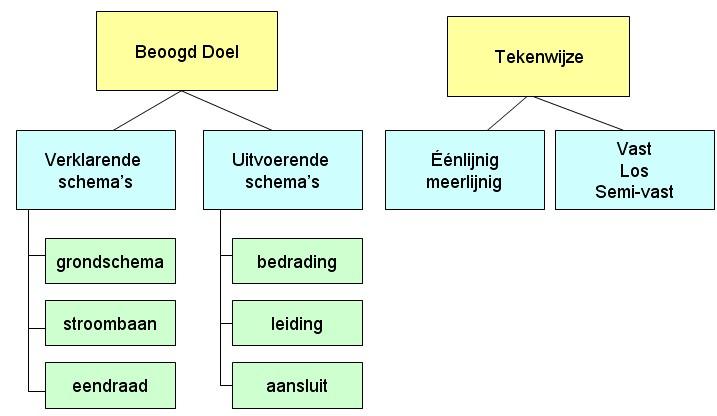
Elektriciteit en de installatie ervan kent zijn toepassing in veel domeinen. Afhankelijk van de toepassing zijn andere plannen en schema’s gewenst. De besturing van een vliegtuig is niet te vergelijken met het bedienen van een handboormachine. Zelfs bij huisinstallaties met klassieke schakelelementen zijn anders dan een huis met domotica.

Verklarende schema’s zijn schema’s waarbij de werking van een toestel of een installatie wordt verduidelijkt.

Uitvoerende schema’s zijn hulpmiddelen bij de realisatie van de installatie.

2 Basis lichtschakelingen

Niet elk lichtpunt is gemaakt voor bediening vanop 1 plaats en niet alle omstandigheden staan toe dat we een bepaald type schakelaar kunnen gebruiken. Zoals we in het vorige hoofdstuk zagen bestaan er 6 soorten schakelaars. Die zullen we nu één voor één van naderbij bekijken.

2.1 Enkelpolige schakelaar voor de studentenkamer

Deverlichtingvolgenseenopgavemoetworden uitgevoerd.De architectbezorgde hetplan.Voorbeeld een studentenkamer.

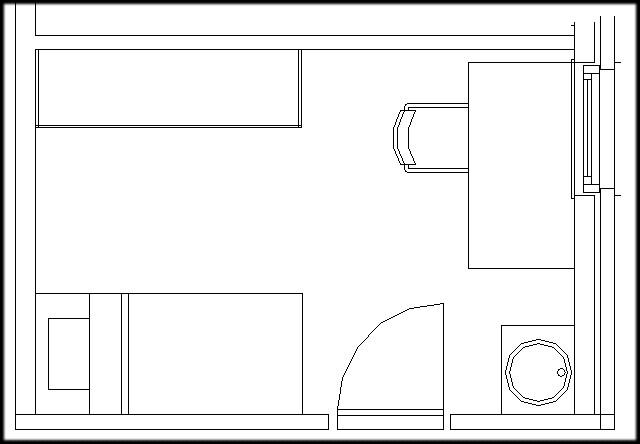
De elektrieker wordt gevraagd om hier een centraal lichtpunt en een lichtpunt boven de wastafel te voorzien. In het lichtpunt boven de wastafel is een schakelaar voorzien. We houden daar momenteel geen rekening mee en schakelen beiden lichtpunten samen. Dit gebeurt van bij de deur.

2.1.1

Theoretische oplossing

Op de plattegrond worden de symbolen geplaatst van de toestellen. Dit is een enkelpolige lichtschakelaar, een lichtpunt en een wandverlichting.

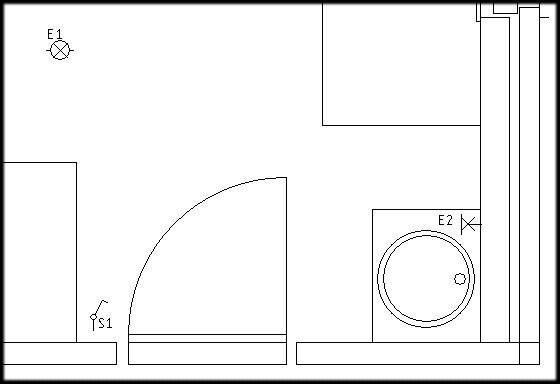
Voor het verlichten van het toilet, berging,….wordt een enkelpolige schakeling gebruikt.

Doel : vanaf 1 plaats wordt één of meerdere lichtpunten samen bediend.

Eenlijnig symbool

Meerlijnig symbool

Volgens het AREI moet naar ieder lichtpunt een beschermingsgeleider voorzien zijn (PE). Die beschermingsgeleider wordt in het stroomkringschema niet getekend, wel op het bedradings- en leidingschema.

Bij de zekeringkast vertrekt dan één leiding naar de schakelaar. De verbinding wordt in de vloer verwerkt.

Van de schakelaar wordt een leiding naar het eerste lichtpunt en van daar verder naar het tweede gelegd.

Er zijn andere mogelijkheden. De keuze maakt u in de toekomst zelf.

Deze leidingen worden getekend. Om de onderdelen te verduidelijken werden telkens figuurtjes bij geplaatst.

Vanaf deze situatie kunnen nu de overige schema’s getekend worden.

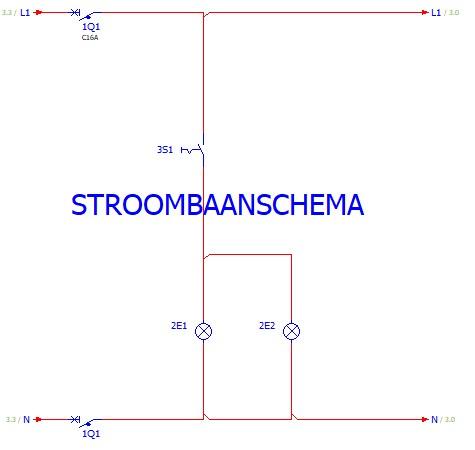
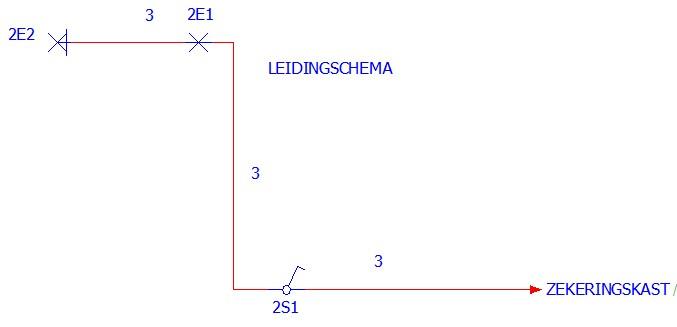
De enkelpolige schakeling is bedoeld om één lichtpunt aan en uit te schakelen.

2.2 Dubbelpolige schakelaar

2.3 Serieschakelaar

Bij een serieschakeling heeft de schakelaar twee wippen. In feite is een serieschakelaar niets anders dan één behuizing met daarin twee aparte schakelaars met ieder een enkelpolige schakeling.

U heeft twee aansluitpunten, waarop u twee zwarte draden zet, die beiden naar een verschillende lamp(fitting) gaan. Op het rode contact zet u de bruine stroomdraad. (Fase/P)

2.4 Wisselschakelaar

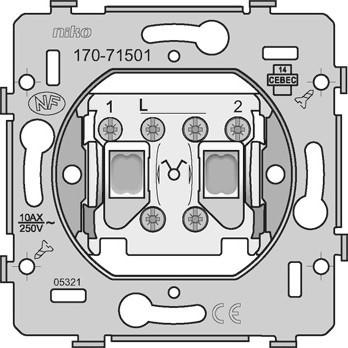
Bij een wisselschakeling gebruikt u altijd twee schakelaars, bijvoorbeeld één beneden aan de trap en één boven. Zo kunt u beneden de lamp aandoen en boven weer uitdoen, of andersom.

De wisselschakelaar heeft twee aansluitpunten voor de zwarte draad. Deze beide zwarte draden verbindt u met de twee aansluitpunten op de andere wisselschakelaar. Op het rode (P) contact van de eerste schakelaar sluit u de bruine stroomdraad aan, de zogenaamde fasedraad (P). Vanaf het rode contact van de tweede schakelaar gaat u met een zwarte draad naar de lampfitting. Op het tweede contact van de fitting wordt de blauwe 0-draad aangesloten.

3 De elektrische schakelkast

3.1 Zekeringen

Er bestaan automatische zekeringen & niet-automatische zekeringen.

Ze vormen het zwakste punt van de kring

Ze beveiligen tegen kortsluiting en overbelasting



Kortsluiting:

Een verbinding tussen twee actieve geleiders zonder tussenschakeling van een verbruiker met een zeer grote stroom tot gevolg.



Overbelasting:

Een abnormaal grote stroom in de geleiders, meestal te wijten aan het in dienst zijn van te veel verbruikers op hetzelfde ogenblik

In alle nieuwe installaties wordt momenteel gebruik gemaakt van automatische schakelaars. Deze moeten altijd een C-karakteristiek hebben bij residentieel gebruik.

De meest voorkomende automaten zijn 16A, 20A, 25A en 32A

3.2 Voorbeelden van zekeringskasten

3.3 Smeltveiligheden

Smeltveiligheden bestaan uit een geleidend “smeltbaar gedeelte” dat in serie geschakeld wordt met de te beveiligen verbruikers.

De wet van Joule stelt dat het vermogen evenredig is met het kwadraat van de stroom. Dit vermogen door een geleider veroorzaakt een warmteontwikkeling. Dit betekent dat bij het overschrijden van een bepaalde stroomsterkte een veel te hoge warmteontwikkeling ontstaat waardoor de geleider doorsmelt.

We zoeken nu een metaallegering met een laag smeltpunt. Hieruit vervaardigen we een dunne draad of platte stroken. Deze draden of stroken kunnen we gebruiken bij het beveiligen van een stroomkring. Volgens de samenstelling en de doorsnede bekomen we smeltveiligheden die smelten bij enkele mA tot honderden Ampère.

De patronen bestaan in snelle, gewone en trage uitvoering.

Voorbeeld: wordt een snelle 10 A zekering belast met 50 A dan zal deze in 0,1 s doorsmelten, een trage zal pas na 1,5 s doorsmelten.

Snel : Wordt gebruikt voor het beveiligen van stroomkringen zoals die van verlichting, contactdozen, signalisatie.....

Traag : Wordt gebruikt voor het beveiligen van motoren daar de aanloopstroom van een motor merkelijk hoger ligt dan de nominale stroom. Een smeltdraad van een snelle zekering zou reeds doorgesmolten zij voor de motor op toeren is.

Het verband tussen de draaddoorsnede van de beschermde geleiders en de nominale stroomsterkte van de penveiligheid wordt aangegeven in de tabel en is herkenbaar volgens een welbepaalde kleurencode.

3.4 Installatieautomaten

3.4.1

Inleiding

Defecten in elektrische leidingen en toestellen kunnen de stroomsterkte door die geleiders en de opgenomen stroom in die apparaten doen toenemen waardoor oververhitting ontstaat. Blijft die oververhitting aanhouden dan kunnen niet alleen de geleiders en toestellen worden beschadigd maar er kan ook brand ontstaan.

Om brand te vermijden plaatsen we in serie met de leidingen smeltzekeringen of installatieautomaten.

Deze onderbreken de stroomkring automatisch bij doorgang van een te hoge stroomwaarde.

Het doorsmelten van een gekalibreerde smeltdraad wordt gebruikt bij smeltpatronen. Het principe berust op het Joule-effect

Het automatisch openen van een schakelaar wordt gebruikt bij een installatieautomaat. Deze techniek vinden we praktisch in alle recente huisinstallaties terug.

Afspraken en normen gelden in de elektrische wereld voor allerhande toepassingen. Er is dus ook een huishoudelijke norm NBN C61-898. Deze is in overeenstemming met de Europese norm 60-898.

3.4.2 In.

De normale stroom, uitgedrukt in Ampère, waarvoor de smeltveiligheid of patroon gebouwd is. Deze stroom wordt op het beveiligingstoestel geplaatst. Deze stroom mag oneindig.lang doorheen dit toestel vloeien zonder doorsmelten of uitschakelen te veroorzaken.

3.4.3 Ue.

De gebruiksspanning uitgedrukt in Volt. Deze spanning bedraagt 230 of 400 V

3.4.4 Uitschakeltijd tu .

Dit is de tijd in honderdsten, tienden van een seconden of seconden die nodig is om een uitschakeling ten gevolge van een overbelasting of een kortsluiting te veroorzaken.

3.4.5

Uitschakelcurven .

De NBN norm C-1-898 omschrijft de eisen die gesteld worden aan de automatische schakelaars voor het beveiligen van huishoudelijke en aanverwante installaties.

Deze norm bepaalt wanneer een automatische schakelaar bij welke stroom niet mag en bij welke stroom wel moet onderbreken.

Niet onderbreken:

Bij een belastingsstroom In * 1,13 tot In *1,45 mag de schakelaar de stroom niet onderbreken binnen het uur.

Deze stroom wordt de conventionele niet–uitschakelstroom genoemd. Een ander gebruikte naam is de thermische uitschakeldrempel.

Wel onderbreken:

Bij een belastingsstroom In * 2,55 is de uitschakeltijd tussen 1 seconde en maximaal 1 minuut bij schakelaars tot 32A. Deze tijd wordt verdubbeld voor schakelaars met In > 32A.

Het breed gearceerde gedeelte is het gedeelte waarbij uitschakelen ALTIJD MOET gebeuren.

De eerste uitvoering (B):

Deze beveiliging word gebruikt voor het beveiligen van verlichting en verwarming. De automaat zal uitschakelen bij een In van 3 tot 5.

De tweede uitvoering (C):

Hier zal de automaat in beveiliging treden bij een In van 5 tot 10. Deze C uitvoering gebruiken we onder andere voor het beveiligen van motoren. Het nadeel van de B uitvoering is dat bij het aanlopen van een motor de aanloopstroom te groot zou worden en dat dan deze automaat doet afschakelen. Bij residentiele schakelingen wordt altijd een C-type gebruikt.

De derde uitvoering (D):

Bij deze uitvoering zal de automaat uitschakelen bij een In van 10 tot 20, hij wordt gebruikt voor het beveiligen van netten en stroombannen bij grote motoren met een grote aanloopstroom.

Bij de keuze van een installatieautomaat mag je eenzelfde stroomkring beveiligen met één kalibernummer hoger dan die van de normale smeltveiligheid.

4 Residentiële verlichting

4.1 Overzicht

4.1.1 Basisschakelingen met schakelaars

4.1.2 Basisschakelingen met drukknopbediening

4.1.3

Basisschakelingen met schakelaars verlicht versie 1

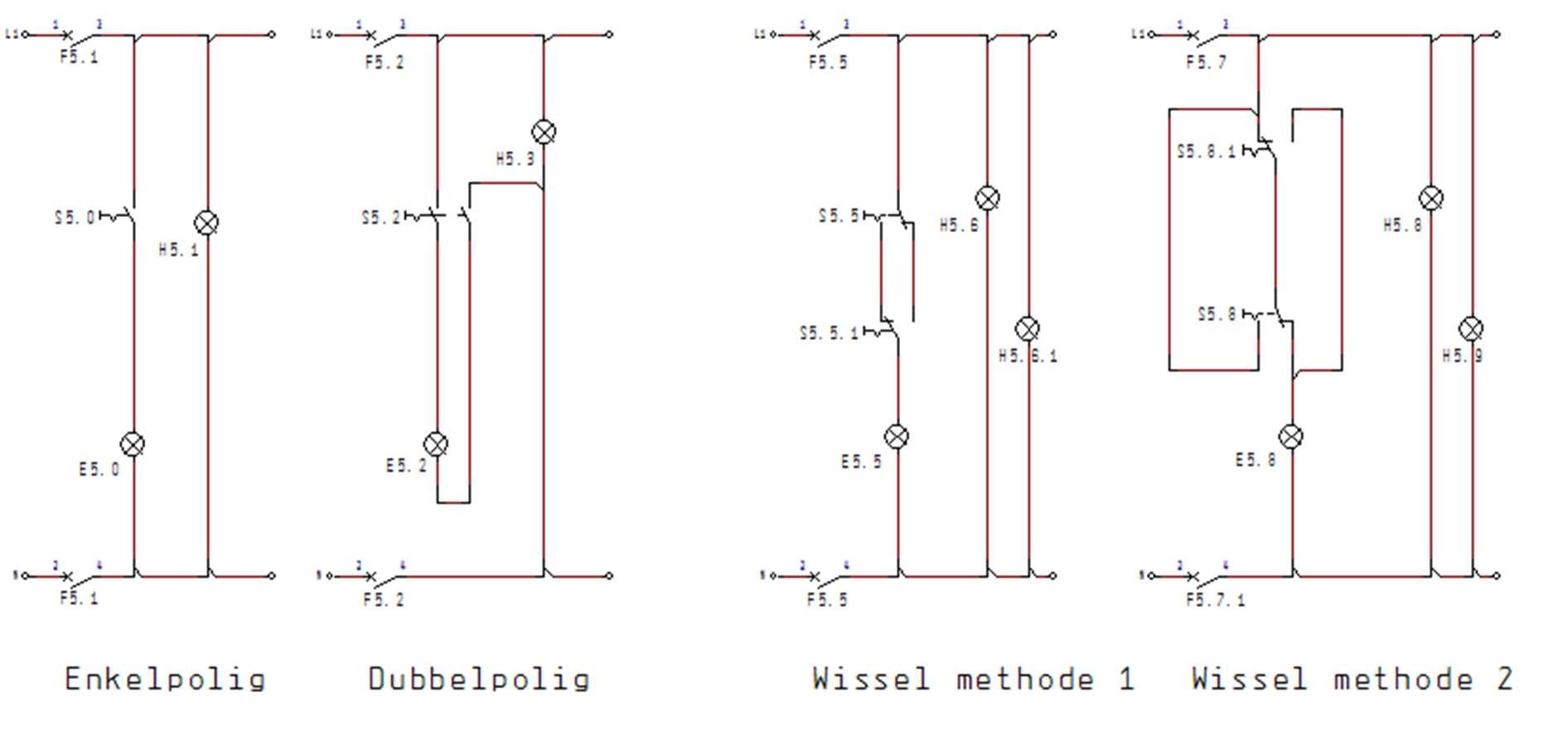
4.1.4

Basisschakelingen met schakelaars verlicht versie 2

4.1.5 Basisschakelingen met schakelaars controle

4.1.6 Impulsrelais en trappenhuis op 230V verlicht methode 1

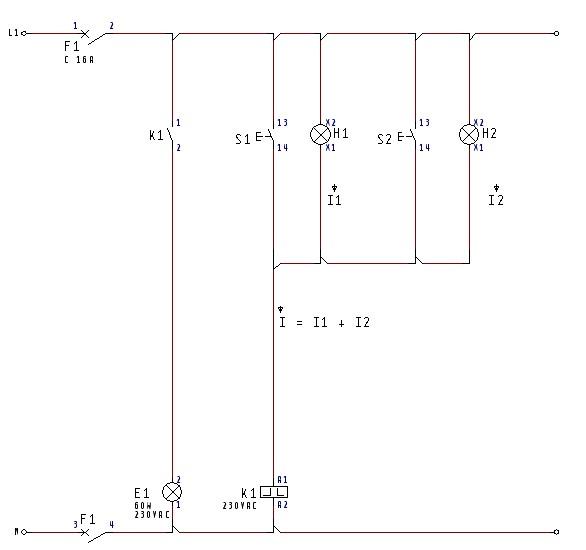
4.1.7 Voorbeeld schema op 230 V verlicht methode 2

4.1.8 Voorbeeld schema impulsrelais op verlaagde spanning.

4.1.9 Voorbeeld schema impulsrelais centrale bediening.

4.1.10 Trappenlicht 3 en 4 draads

4.2 Enkele bedenkingen :

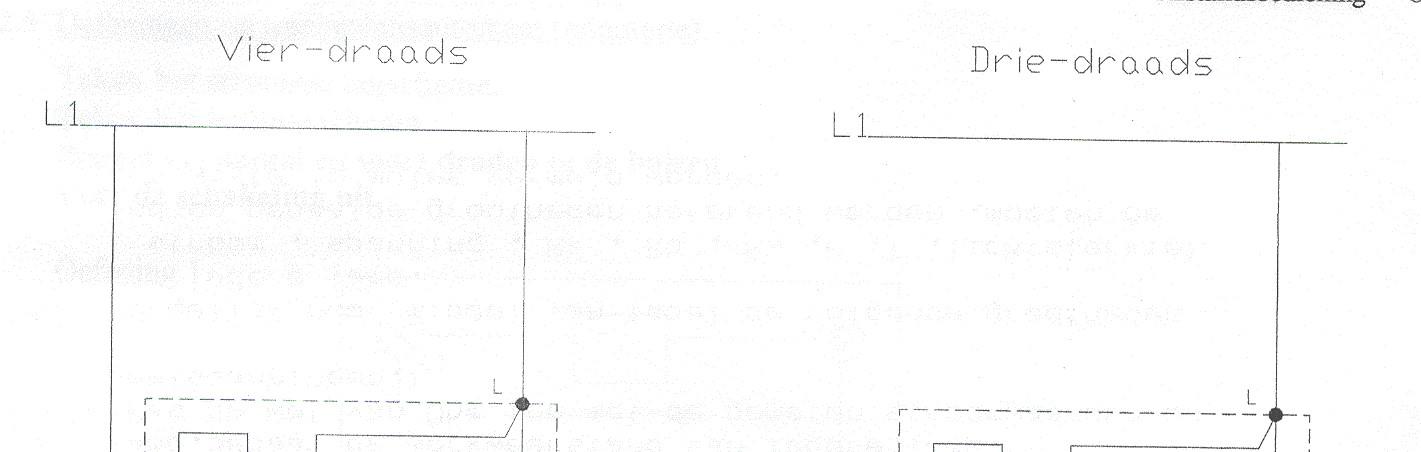
Bij het tekenen wordt rekening gehouden met de draadkleuren

De Europese kleurcodes voor de draden van het lichtnet:

bruin - fase (230 Volt)

blauw - nul

groen/geel - veiligheidsaarde

zwart of rood- schakeldraad; via een schakelaar

In oude huizen (voor ca. 1970) is voor de bedrading veelal de oude kleurcode gebruikt, de kleurcodering is onder meer vanwege rood–groen–kleurenblindheid veranderd.

groen - fase (230 Volt)

rood - nul

grijs - veiligheidsaarde

zwart - schakeldraad; via een schakelaar verbonden met fase

4.3 Opdrachten

Maak de volgende projecten.

Er wordt eerst een situatieschema gemaakt. Daarna volgt een stroombaan en een bedradingschema.

Dit wordt geschetst.

Met de schetsen wordt dit ook uitgevoerd.

4.3.1

Tuinhuis met dubbelpolige verlichting

Een nieuw tuinhuis werd geïnstalleerd doch de verlichting ontbreekt.

U wordt gevraagd om achter de deur, in de hoek, een kleine verdeelkast te plaatsen voor de zekeringen of automaten. De schakelaar komt op de meest handige plaats. De verbinding tussen verdeelkast en schakelaar gebeurt via de grond.

Twee lichtpunten worden geplaatst. De lampen worden met buizen verbonden naar de verdeelkast.

Aan de bovenzijde komt de spanning toe en vertrekken de leidingen naar de lichtpunten. De aansluitingen onderaan zijn voor de schakelaars en de later te plaatsen stopcontacten.

4.3.2

Garage met wisselschakeling

In de garage zijn twee toegangsdeuren. Aan beide deuren wordt een schakelaar geplaatst. Beide schakelaars bedienen twee lichtpunten.

4.3.3

Living met impulsrelais

Een living met 2 toegangen en 1 enkel verlichtingspunt wordt uitgevoerd met een impulsrelais in plaats van met de klassieke wisselschakeling.

5.1 Elektrische energie

Onderstaande schakeling vormt de basis van de elektriciteit.

Wanneer we de schakelaar S zullen sluiten dan zal de lamp branden.

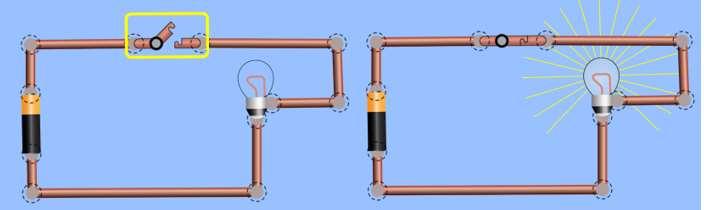
Maar hoe komt dit eigenlijk ?

Bij het sluiten van de schakelaar S zal er een elektrische stroom vloeien in de kring. Deze elektrische stroom vloeit van de plus-klem van de batterij door de schakelaar en de lamp naar de min-klem van de batterij. Op deze manier vormt men een gesloten kringloop. Deze elektrische stroom bezit energie om in de gloeilamp zowel licht als warmte te produceren.

Via volgende link kan dit basisschema kan het voorgaande schema gesimuleerd worden. https://phet.colorado.edu/sims/html/circuit-construction-kit-dc/latest/circuit-construction-kit-dc_nl.html

Een elektrische kring bestaat steeds uit 3 essentiële zaken, nl:

 een elektrische energiebron – in ons geval een batterij;

 een verbruiker – in ons geval een lampje;

 geleiders – transport van elektrische stroom.

Wanneer men de elektrische stroom willen onderbreken dan maken we gebruik van een schakelaar.

De elektrische energiebron of spanningsbron is in onze schakeling een batterij. We maken gebruik van een blokbatterij of 6LR61 batterij van 9 V. De waarde van de batterij(spanning) is zo laag, dat men niets kan voelen wanneer beide aansluitklemmen (polen) aangeraakt worden. Komt men echter

met de punt van de tong aan beide polen, dan voelt men een lichte kriebeling. De smaakzenuwen zijn een stuk gevoeliger dan de vingertoppen en zullen op deze kleine spanning reageren.

De verbruiker is in bovenstaand geval een gloeilamp. Gloeilampen waren een tientallen jaren terug de meest verkochte lichtbron. Door hun slechts rendement en korte levensduur werden ze vervangen door spaarlampen en later door LED-lampen.

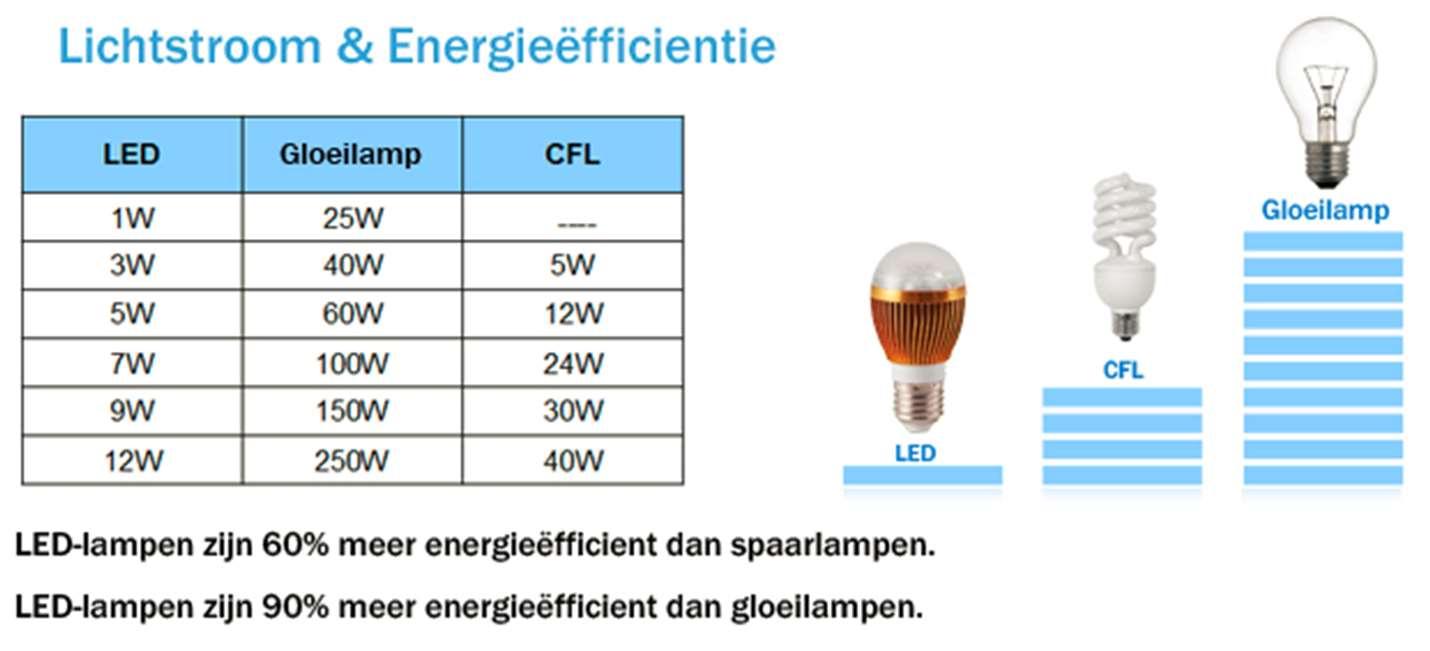
Tenslotte zijn er nog de geleiders. Zilver en koper zijn de beste geleider materialen. Aangezien zilver erg duur en zeldzaam is, wordt in de elektriciteit meestal koper gebruikt. Ook aluminium en staal worden gebruikt als geleider omwille van hun mechanische eigenschappen.

Voor de realisatie van opdrachten maken we gebruik van een breadboard. Dit bordje zal de verbindingen realiseren tussen voeding en componenten. De permanente verbindingen op het breadboard zien er als volgt uit:

5.2 Andere energievormen

Naast elektrische energie bestaan er ook heel wat andere energievormen, nl:

Mechanischeenergiebestaandeuit kinetischeenergieofbewegingsenergie(draaiende motor,draaiendwiel)enpotentiëleenergieofzwaartekrachtsenergie(stuwdam, opgespannenveer).

Warmte-energieofthermischeenergie,wanneerereenelektrischestroomdooreen weerstandvloeit,danwordterwarmteontwikkeldindieweerstand.Ditnoemtmenhet joule-effect.Toepassingenzijn:eenelektrischvuur,eenoven,eenkoffiezetapparaat,… Thermischeenergiebekomtmenookdoorhetverbrandenvansteenkool,aardgas, stookolie,benzine,enz.

Lichtenergie:Eenzonnecel(fotovoltaïschecelofPV-cel)zetlichtenergie(zonlicht)om inelektrischeenergie.PV-cellen(Photo-Voltaïsch)wordengemonteerdin zonnepanelen.

Scheikundigeofchemischeenergie:Eenkopereneneenzinkenplaatjeinverdund zwavelzuurgeplaatst,wekteenspanningop(batterij).

Kernenergie(nucleaireenergie)

Geluids-ofakoestischeenergie

Stralingsenergie(bijv.röntgenstralen)

Magnetischeenergie(bijv.aantrekkings-ofafstotingskrachtvaneenmagneet)

Je kan geen energie opwekken of doen verdwijnen. Energie kan dus niet worden “verbruikt”, alleen omgezet in een andere energievorm. In een kerncentrale zal nucleaire energie eerst omzet worden in thermischeenergie(stoom)omvervolgenstewordenomgezet inmechanischeenergie (stoomturbine) om tenslotte omgezet te worden in elektrische energie (wisselstroomgenerator). Hetzelfde geldt in een batterij waard chemische energie omgezet wordt in elektrische en thermische energie.

De energiehoeveelheid kan men eveneens niet wijzigen maar elke omvorming van energie gaat wel gepaard met een verlies. Een elektromotor zal elektrische energie opzetten naar mechanische energie, maar ook naar thermische energie.

5.3 Toepassingen van elektrische energie

Het omvormen van elektrische energie naar andere energievormen kent heel wat toepassingen :

Omvormennaarlichtenergie:gloeilamp,halogeenlamp,LEDlamp,…

Omvormingnaarwarmte-energie:strijkijzer,elektrischfornuis, verwarmingselementvaneenwasmachine

Omvormingnaarlicht-enwarmte-energie(vonken):lastoestel,bougie (ontstekingskaars).

Omzettingnaarchemischeenergie(elektrolyse):verkoperen,verzilveren,galvaniseren vanmaterialen

Omzettennaarmagnetischeenergie:bel,zoemer,hoorn,elektrischdeurslot, elektromagneten

Omgezetnaarmagnetischeenergieenmechanischeenergie:gelijkstroom-en wisselstroommotorenaccuboormachine,elektrischefiets,scooterofauto

Omzettenvanmagnetischeenergienaargeluid:luidspreker

Schokken:schrikdraad,defibrillator,stroomstootwapen

5.4 Voor- en nadelen van elektrische energie

Elektrische energie is eenvoudig te transporteren over grote afstanden en dit met heel weinig verlies.

Elektrische energie is ook heel snel te transporteren over grote afstanden (300 000 km/s). De toestellen om deze energie om te vormen zijn relatief eenvoudig waardoor de elektrische energie enorm veel toepassingen kent.

Grote hoeveelheden van elektrische energie is niet of moeilijk stockeerbaar. Deze energie is onzichtbaar wat heel veel gevaren met zich meebrengt.

6 Opbouw van de stof – Wat is elektriciteit

De hoofdzaak is, wat is elektriciteit. Om te weten wat elektriciteit is moeten we weten waaruit een stof is opgebouwd.

6.1 Elektriciteit

Elektriciteit kunnen we niet meer wegdenken uit ons leven. Als er geen elektriciteit was, zouden we 's nachts alleen maar kunnen zien door gebruik te maken van kaarslicht en zouden we onze levensmiddelen niet in de koelkast kunnen bewaren. Elektriciteit is een enorm handige manier om energie over te brengen. Maar waaruit bestaat dat nu eigenlijk, die elektriciteit?

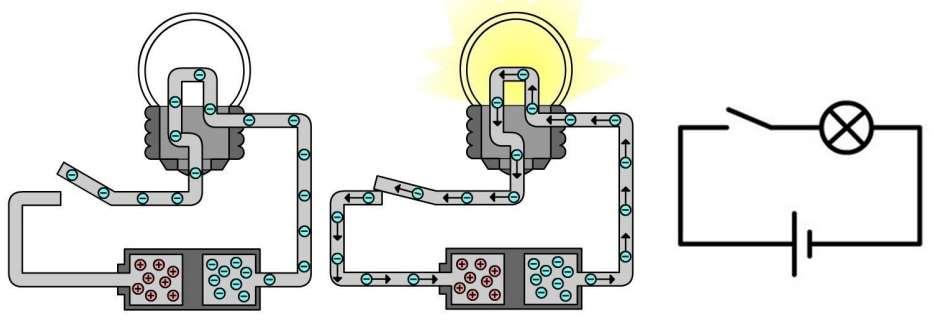
Elektriciteit kan omschreven worden als het verplaatsen van elektronen door een voorwerp (zoals bijvoorbeeld een elektriciteitsdraad).

Als de elektronen door de stroomkring stromen, zoals in Figuur 8, dan botsen ze voortdurend tegen de atomen waaruit de bedrading bestaat. In de gloeidraad van een gloeilamp zijn deze botsingen genoeg om de draad zo warm te maken dat deze gaat gloeien. Door ons te verdiepen in de opbouw van de stof, kunnen we begrijpen waarom elektronen in het éne materiaal wel kunnen stromen en in het andere niet.

6.2

Opbouw van een stof

In onze wereld komen stoffen voor met heel veel verschillende eigenschappen. De ene is hard, de andere zacht, de ene geleidt elektrische stroom, de andere niet. De eigenschappen van een stof zijn afhankelijk van hun opbouw.

6.2.1 Molecule

Elke stof bestaat uit moleculen. Een molecule is het kleinste deeltje van een stof dat nog alle eigenschappen (bv. geur, smaak, geleidbaarheid, hardheid, …) van die stof bezit.

Als men een molecule splitst, dan verandert de samenstelling, de bouwelementen of atomen worden gewijzigd en de eigenschappen worden veranderd.

Een voorbeeld van een molecule is bijvoorbeeld water.

Water bestaat uit:

- 2 atomen Waterstof, afgekort H

- 1 atoom Zuurstof, afgekort O

De chemische formule wordt dus H2O

Elke molecule bestaat uit één of meer atomen. Atomen zijn dus de bouwstenen voor de moleculen.

Een chemische stof is gedefinieerd door de atomen waaruit een molecule bestaat en de onderlinge verbindingen die tussen de atomen bestaan.

6.2.2

Atomen

Een atoom bestaat uit een kern en een elektronenmantel.

De kern bevat twee verschillende componenten, namelijk protonen en neutronen.

De protonen zijn positief geladen en de neutronen zijn neutraal geladen. Protonen

KERN

Neutronen

De elektronenmantel bestaat uit een aantal schillen waarop de elektronen bewegen met een grote snelheid via ellipsvormige banen rond de kern.

De elektronen zijn negatief geladen.

Elektronen

6.2.3 Atoomgetal

Het aantal elektronen dat rond de kern beweegt in normale toestand, is gelijk aan het aantal protonen in de kern. Dit aantal wordt weergegeven door het atoomgetal Z.

In de tabel van Mendeljev zijn de atomen volgens het aantal elektronen gerangschikt.

Schillen

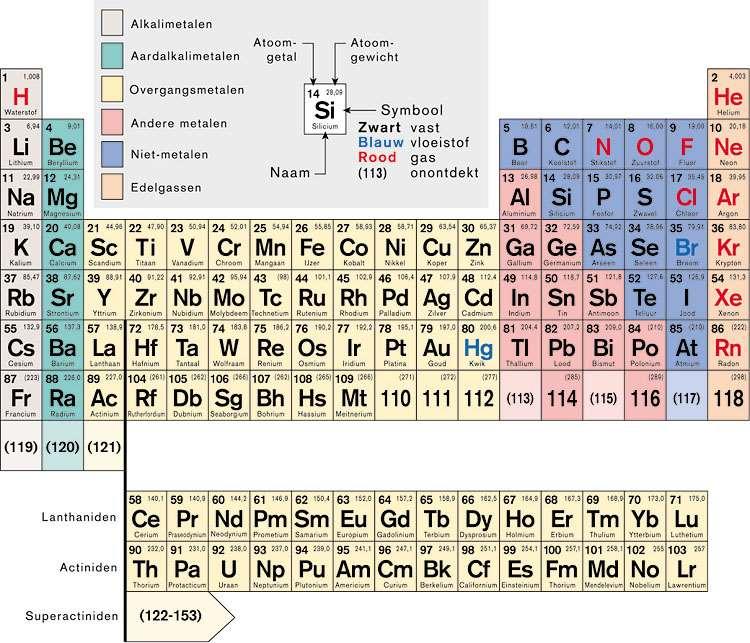
Voorbeeld Waterstof

Waterstof (H) heeft atoomgetal Z= 1. Dit wil zeggen dat waterstof één elektron heeft rond de kern en dat de kern één proton heeft.

Voorbeeld Koper

Koper (Cu) heeft atoomgetal Z = 29. Dit wil zeggen dat Koper 29 elektronen heeft rond de kern die zich als volgt over de schillen verdelen.

K = 2 (volledig bezet)

L = 8 (volledig bezet)

M = 18 (volledig bezet)

N = 1 (eenzaam en alleen)

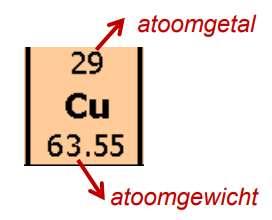
De kern heeft ook 29 protonen want het atoom is in normale toestand elektrisch neutraal.

6.3 De elektriciteit in de stof

6.3.1 De elektrische ladingen in een atoom

In de atomen van alle stoffen zit elektriciteit.

- Ieder elektron, onafhankelijk van het atoom waar het bij hoort, bevat eenzelfde zeer kleine hoeveelheid negatieve lading (-).

- Ieder proton, onafhankelijk van de kern waar het bij hoort, bevat eenzelfde hoeveelheid positieve lading (+). De negatieve lading van een elektron en de positieve lading van een proton zijn even groot.

- Een neutron is elektrisch niet geladen, het is neutraal.

Uit proeven blijkt dat een lading zich ten opzichte van een gelijknamige lading zich anders gedraagt dan ten opzichte van een ongelijknamige lading.

Gelijknamige ladingen stoten elkaar af en ongelijknamige ladingen trekken elkaar aan zoals in Figuur 15 is weergegeven.

6.3.2 Het vrij elektron

Op de elektronen van een atoom werken twee krachten in:

- De aantrekkingskracht tussen de atoomkern en de elektronen. Plus en min trekken elkaar aan die te vergelijken is met de zwaartekracht.

- Door de grote snelheid waarmee de elektronen rond de kern draaien, ontstaat op de elektronen een middelpuntvliedende kracht die de elektronen wil wegslingeren van de kern

Normaal houden de aantrekkingskracht en de middelpuntvliedende kracht elkaar in evenwicht en blijven de elektronen op hun baan draaien. Ze zijn gebonden aan de kern. De bindingskracht is niet voor alle elektronen even sterk. De elektronen op de binnenste baan worden sterker aangetrokken dan die op de buitenste baan.

Onder invloed van de kernen van aanliggende atomen kunnen de buitenste elektronen gemakkelijk overspringen naar de buitenste baan van een ander atoom. Dit betekent dat ze vrij en willekeurig bewegen tussen atomen. Het zijn vrije elektronen. Ze worden ook vrije ladingsdragers of valentie elektronen genoemd. De buitenste schil van een atoom noemt men ook de valentieschil. vrije elektronen kunnen ontstaan door verhitting, botsing met andere vrije elektronen, opvallen van licht, aanleggen van een spanning, ….

6.3.3 Ladingstoestand van een lichaam

Neutraal

Bij een atoom in neutrale toestand is de positieve kernlading even groot als de gezamenlijke negatieve lading van de elektronen. Het atoom heeft twee gelijke tegengestelde ladingen die elkaar neutraliseren of compenseren. Het atoom is hierdoor niet positief of negatief geladen. Het is ongeladen of neutraal zoals in Figuur 16.

Verliest een neutraal atoom een aantal elektronen of heeft het atoom een aantal elektronen opgenomen, dan is het evenwicht tussen de positieve en de negatieve lading verbroken. Het atoom is niet meer neutraal. Het is elektrisch geladen of geïoniseerd. Een geladen atoom heet een ion.

Positief

Verliest een neutraal atoom één of meer elektronen, dan is de positieve lading van de kern groter dan de gezamenlijke negatieve lading van de elektronen. De positieve lading overheerst.

Een atoom met te weinig elektronen is positief geladen en noemt een positief ion.

Negatief

Krijgt een neutraal atoom één of meer elektronen bij, dan is de gezamenlijke negatieve lading van de elektronen groter dan de positieve kernlading. De negatieve lading overheerst.

Een atoom met te veel elektronen is negatief geladen en heet een negatief ion.

Een lichaam heeft een elektrische lading als het minder of meer elektronen bezit dan in de neutrale toestand.

Positief, plus (+) betekent te weinig elektronen. Negatief, min (-) betekent te veel elektronen.

6.4 De elektrische stroom

Waar er in de natuur een evenwicht is verbroken, stel je een drang naar herstel van dit evenwicht vast.

- Bij geladen lichamen is het elektrisch evenwicht verbroken en ontstaat er een drang naar de neutrale toestand;

- Een positief lichaam heeft te weinig elektronen en zal daarom elektronen aantrekken;

- Een negatief lichaam heeft te veel elektronen en zal daarom elektronen afstoten

Om te begrijpen wat er met een elektrische bron gebeurt, vergelijk je een verplaatsing van elektronen met een verplaatsing van water.

Water

Teveel water

Teweinig water

Elektronen +

Ladingsverschil

Niveauverschil -

Buisleiding - +

Waterverplaatsing

- Door het verschil in waterniveau (communicerende vaten) ontstaat er een stuwkracht (druk) op het water.

Het gevolg is een verplaatsing van het water of waterstroom.

- De verplaatsing van water heet de waterstroom.

- Om een blijvende waterstroom te behouden is een waterpomp nodig die het verschil in waterniveau in stand houdt.

Elektronen verplaatsing Draadleiding Teweinig elektronen

Teveel elektronen

- Door het verschil in lading ontstaat elektrische stuwkracht op de elektronen.

Het gevolg is een elektronenverplaatsing of elektrische stroom.

- De verplaatsing van elektronen heet de elektrische stroom.

- Om een blijvende elektronenstroom te behouden is een elektronenpomp nodig die het verschil in lading in stand houdt. Die elektronenpomp is een elektrische bron

6.5 Geleiders, niet-geleider en halfgeleiders

De stoffen worden ingedeeld volgens hun geleidbaarheid.

6.5.1

Geleiders

Er bestaan geen volmaakte geleiders.

Geleiders zijn stoffen waarin een groot aantal vrije ladingdragers voorkomen. Hierdoor verplaatsen elektronen in geleiders zich gemakkelijk.

Indien een atoom de elektronen van de buitenste schil gemakkelijk vrijgeeft, spreken we van een geleider. In dergelijke stoffen is gemakkelijk verplaatsing van elektronen, m.a.w. een elektrische stroom, mogelijk.

Alle metalen (zilver, koper, aluminium, zink, lood, tin, ijzer, nikkel, enz.) zijn geleiders. Zilver is de beste geleider, zijn geleidbaarheid is het grootst.

Meest gebruikt:

Koper: atoomgetal Z = 29 (K = 2, L = 8, M = 18, N = 1)

Aluminium: atoomgetal Z = 13 (K = 2, L = 8, M = 3)

Er bestaan ook geleidende vloeistoffen, het zijn zout- en zuuroplossingen die men elektrolyten noemt. Ze worden gebruikt in cellen en accumulatoren.

Ook de aarde is, door het vele water waarin zout opgelost is, een goede geleider.

Goede geleiders gebruikt je waar je de stroom bijna ongehinderd wil doorlaten. bv. om elektrische energie te transporteren van de bron naar de verbruiker(s).

6.5.2 Supergeleiding

Supergeleider betekent: geen weerstand bieden aan de elektrische stroom.

Een supergeleider is dus een ideale geleider en kan daarom elektrische energie transporteren zonder energieverlies.

Er is echter een spelbreker: de temperatuur.

Supergeleiding is slechts mogelijk bij extreme lage temperaturen. Van koper is de nuldoorgang bij234,5 °C. Supergeleiding is dus niet mogelijk in normale omstandigheden.

De geschiedenis van de supergeleiding begon in 1911. De Nederlander Kamerlingh Onnes ontdekte dat de weerstand van kwik onmeetbaar klein werd, als het kwik afgekoeld (met vloeibaar helium) werd tot dicht bij het absolute nulpunt(-273°C). Supergeleiding voor dagelijks gebruik is echter nog niet voor vandaag. Geleerden over de hele wereld zoeken nog steeds koortsachtig naar een betaalbaar en gemakkelijk hanteerbaar materiaal dat bij kamertemperatuur supergeleidend is. Als dit ooit wordt ontdekt, zal het een onvoorstelbare verandering veroorzaken in de elektrotechniek en de elektronica.

6.5.3 Isolatoren en niet-geleiders

Niet-geleiders noem je ook isolatoren, isolatiestoffen of diëlektrische stoffen. Het zijn stoffen waarin bijna geen vrije elektronen voorkomen.

Dit zijn stoffen waarvan de elektronen van de buitenste baan sterk aan hun kern gebonden zijn waardoor ze moeilijk kunnen worden vrijgemaakt

De isolatoren geleiden bijna niet of bieden praktisch een oneindig grote weerstand.

Voorbeelden van isolatiestoffen zijn: rubber, PVC (polyvinylchloride), porselein, glas, olie, katoen, wol, droge lucht, praktisch alle gassen enz.

Isolatiestoffen worden gebruikt om geleiders af te zonderen, te ondersteunen of om af te schermen (bv. schakelaars, contactdozen). Dit heet isoleren.

Uit de praktijk. Isolatie van onder spanning staande delen

Een geïsoleerde geleider bevat een geleidende kern uit koper of aluminium (1), die bekleed is met pvc isolatiestof (2). De isolatie voor geleiders moet soepel, taai en gekleurd zijn.

Door isolatie met schillende kleuren te gebruiken zijn de draden gemakkelijk te herkennen.

L1 = bruin, N = blauw, PE = geel/groen

Isoleren van de geleiders biedt een bescherming tegen ongewenste aanraking (voorkomt dus elektrocutie). Tevens wordt belet dat de draden onderling contact zouden maken (voorkomt dus kortsluiting).

Water, aarde en lucht

Scheikundig zuiver (gedistilleerd) water is niet geleidend. Ons drink- en regenwater bevat mineralen en zouten (ionen) en is dus geleidend.

Het menselijk lichaam, dat voor een hoog percentage uit water bestaat, is geleidend.

Vochtige aarde is een geleider. (De samenstelling speelt een rol).

Lucht is een isolator. Daarom zijn hoogspanningsgeleiders niet geïsoleerd.

6.5.4 Halfgeleiders

Sommige stoffen gedragen zich, afhankelijk van de omstandigheden, soms als geleider en soms als isolator. Silicium en Germanium zijn halfgeleiders en zijn de belangrijkste grondstoffen waaruit elektronische componenten bestaan.

Silicium wordt het meest gebruikt.

Deze stoffen worden vooral gebruikt in elektronische componenten.

6.6 Weerstandsmaterialen

Weerstandsmaterialen hebben veel minder vrije elektronen dan de goede geleiders. Ze geleiden de stroom slechter dan de goede geleiders. Hun geleidbaarheid is kleiner, hun weerstand groter.

Voorbeelden zijn: wolfram, chroomnikkel, constantaan, nikkeline, manganine enz.

Van wolfram en nikkel-chroomlegeringen (nichroom) maakt men weerstandsdraad die bestand is tegen hoge temperaturen.

Weerstandsdraad wordt gebruikt om elektrische energie om te vormen in warmte en vindt zijn toepassing als verwarmingselement in elektrische straalkachels, haardrogers, ovens, soldeerbouten, broodroosters,…

Van weerstandsmaterialen worden ook componenten gemaakt om de doorgang van elektrische stroom te bemoeilijken en te verstoren (weerstand te bieden).

Een elektronische component die wordt ingezet voor zijn elektrische weerstand heet een weerstand.

Weerstanden worden gebruikt als onderdeel in elektrische schakelingen.

De soortelijke of specifieke weerstand r van een geleider is de weerstand van een geleider van 1 m lang en een doorsnede van 1 mm² bij een omgevingstemperatuur van 20 °C. Hierdoor wordt r uitgedrukt in W/m/mm2 of Wm

De soortelijke weerstand van halfgeleiders is de weerstand die tussen 2 evenwijdige vlakken van een kubus van 1 cm³ gemeten wordt. Hierdoor wordt  uitgedrukt in cm.

Goede geleiders Isolatoren

Cu Mica

ρCu = 0,0175x10-6Ωm ρMica = 1014Ωm

6.6.1 Overzicht

Goede geleiders Half/slechte geleiders Isolatoren

Aluminium Manganine Droge lucht

Koper Ijzer-Nikkel Zuiver water

Lood Wolfraam Mica

Goud

Nikkel

Constantaan Glas

Nikkeline Olie

Platina Chroomnikkel Papier

Ijzer Silicium Kwarts

Zilver Steatiet

Zink Porselein

Chroom Bakeliet

Tin Rubber

6.7 Soorten weerstanden

6.7.1 Draadgewonden weerstanden

Deze weerstanden worden vervaardigd door een weerstandsdraad te wikkelen rond een wikkellichaam. De weerstandsdraad wordt afgedekt door een afdeklaag.

Deze weerstanden, meestal kortweg aangeduid als draadweerstanden, bestaan uit een buisje of staafje van isolatiemateriaal waarop een laag weerstandsdraad is gewikkeld. De draad wordt daarbij stevig op de drager bevestigd. Bij de zgn. axiale weerstanden vindt dit plaats door over de uiteinden van de aldus gevormde weerstand een metalen kapje te klemmen. De aansluitdraden worden vervolgens aan deze kapjes gelast. Bij de zwaardere uitvoeringen wordt de weerstandsdraad met klemringen, die tevens zijn voorzien van aansluitlippen, op de drager bevestigd.

Een dergelijke uitvoering is afgebeeld in onderstaande figuur.

Figuur2:Vermogendraadgewondenweerstanden

Figuur1:Draadgewondenweerstanden

De draad die op de drager van keramiek of glasvezel wordt gewikkeld, is voorzien van een dun laagje oxide. Het betreffende oxide gedraagt zich elektrisch als een isolator en vormt zodoende een afscherming tussen de naast elkaar liggende wikkelingen. Belangrijk is echter dat de oxidefilm wel een tamelijk goede warmtegeleider is, mede waardoor een zekere spreiding van de ontwikkelde warmte over de gehele weerstand wordt verkregen. De aldus gefabriceerde weerstand wordt vervolgens bedekt met een laag vuurvast cement (gecementeerde weerstanden), dan wel bedekt met een bepaalde laksoorten (geëmailleerde weerstanden).

Bij de rechthoekige weerstanden wordt het weerstandslichaam (drager + draad) ondergebracht in een behuizing van keramiek, die verder nog is opgevuld met zand.

De weerstandswaarde en tolerantie worden meestal tekstueel op de afdeklaag gedrukt. Voorbeeld: 2R7 is 2,7 Ω, 2k7 is 2700 Ω en 10 kΩ is 10000 Ω

Deze weerstanden worden gebruikt waar een dissipatievermogen groter dan 2 W vereist is of als zeer nauwkeurige weerstandswaarden (precisie weerstanden) vereist zijn (meettechniek).

6.7.2

Koolfilmweerstanden

Deze weerstand worden vervaardigd door op een keramisch staafje een koolstoffilm aan te brengen. Demaximaleweerstandswaarde vanhetaldus bekomen weerstandbedraagtslechts enkeleduizenden ohm’s. De uiteindelijke correcte weerstandswaarde wordt bekomen door een gedeelte van de koolstoffilm spiraalvormigweg te slijpen. Voor een weerstandswaarde kleiner dan10 Ω bestaat de film uit nikkel. De koollaagweerstand behoort tot de groep van de filmweerstanden. Bij deze groep van weerstanden moet de ontwikkelde warmte van de weerstand hoofdzakelijk afgegeven worden via de aansluitdraden. Daarom gebruikt men een keramisch staafje met goede warmtegeleidingseigenschappen.

Figuur3:Koollaagweerstanden

De weerstandswaarde en tolerantie worden op de afdeklaag aangebracht in de vorm van een kleurencode die bestaat uit vier ringen. Om vergissingen te vermijden is de eerste ring dichter bij de

aansluitdraden aangebracht dan de laatste, dit volstaat niet altijd en om het nog duidelijker te maken wordt de laatste ring breder gemaakt.

1: eerste cijfer van de weerstandswaarde

2: tweede cijfer van de weerstandswaarde

3: vermenigvuldigingsfactor

4: tolerantie

Figuur4:Kleurencodekoollaagweerstand

De volgorde van de kleuren kan men gemakkelijk onthouden met het volgende ezelsbruggetje:

Zus  Zwart

Bracht  Bruin

Rozen  Rood

Op  Oranje

Geert’s  Geel

Graf  Groen

Bij  Blauw

Vies  Violet (Paars)

Grijs  Grijs

Weer  Wit

Voorbeeld:

Kleurencode oranje/zwart/bruin/goud = weerstand van 300 Ω met een tolerantie van 5 %

6.7.2.1 Oefeningen

Bepaal de weerstandswaarde en tolerantie.

1 Bruin Zwart bruin zilver

2 Blauw Grijs bruin Zilver

3 Bruin Groen zwart Goud

4 Bruin Zwart rood Zilver

5 Oranje Oranje bruin

6 Geel Violet oranje Goud

7 Rood Geel zwart Goud

8 Bruin zwart groen

9 Grijs rood zwart Goud

Bepaal de kleurringen en de tolerantiering

Weerstand 1ste ring 2de ring 3de ring 4de ring

1 470 Ω ± 10 % geel paars bruin Zilver

2 10 k Ω ± 10 %

3 47 k Ω ± 5 %

4 5,6 k Ω ± 20 %

5 680 k Ω ± 10 %

6 820 k Ω ± 5 %

7 3,9 k Ω ± 20 %

8 180 Ω ± 5 %

9 27 kΩ ± 20 %

10 1,2 M Ω ± 10 %

Bepaal de minimum- en maximumwaarde

1 4,7 k Ω ± 5 %

2 51 k Ω ± 5 %

3 330 Ω ± 5 %

4 1 M Ω ± 10 %

5 27k Ω ± 5 %

6 2,2 Ω ± 10 %

6.7.3 Metaalfilmweerstanden

Deze weerstanden worden vervaardigd door op een keramisch staafje een metaalfilm aan te brengen. De uiteindelijkecorrecteweerstandswaardewordt bekomendooreengedeeltevan demetaalfilm weg te slijpen. Metaalfilmweerstanden onderscheiden zich van koollaagweerstanden door een kleinere tolerantie, een kleinere afwijking bij temperatuursschommelingen en een kleinere afwijking van de waarde door veroudering.

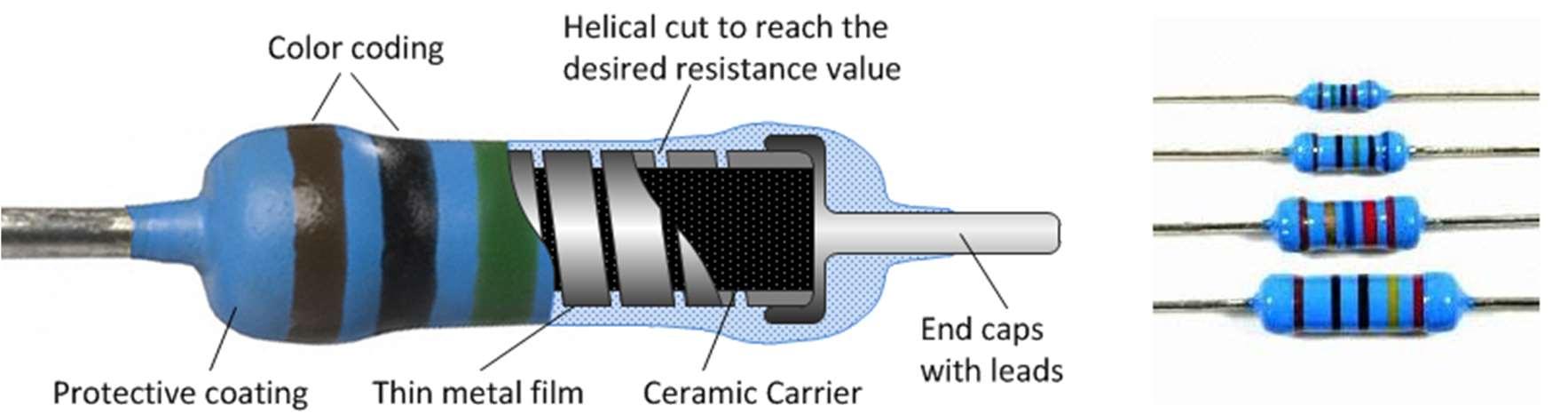
De weerstandswaarde en tolerantie wordt op de afdeklaag aangebracht onder de vorm van een kleurencode die bestaat uit vijf ringen.

Figuur5:Metaalfilmweerstanden

Figuur6:Kleurencodemetaalfilmweerstand

1: eerste cijfer van de weerstandswaarde

2: tweede cijfer van de weerstandswaarde

3: derde cijfer van de weerstandswaarde

4: vermenigvuldigingsfactor

5: tolerantie

Voorbeeld: Kleurencode oranje/zwart/bruin/oranje/bruin =weerstand van301000 Ωof301kΩ met eentolerantie van 1 %

7 SI-stelsel

7.1 Grootheden en eenheden

Je start elektriciteit met een kennismaking met de grootheden en eenheden zoals bepaald in het S.I.stelsel. Die grootheden en eenheden zal je ook in andere vakken leren gebruiken.

Alle grootheden en eenheden kan men herleiden tot een combinatie van 7 basisgrootheden en eenheden. De enige ‘elektrische’ basisgrootheid is de stroomsterkte

Het S.I.-stelsel (Système International d’unités) is een eenhedenstelsel dat in België en in Europa van kracht is sinds 1974. Het bevat 7 basisgrootheden en 7 eenheden.

De voordelen van het S.I.-stelsel zijn als volgt samen te vatten:

 Basisgrootheden zijn onderling onafhankelijk.

 De eenheden zijn onveranderlijk.

 Het is een coherent systeem. Alle grootheden vertrekken van 1.

Een grootheid is datgene waarmee een fysisch verschijnsel wordt benoemd.

Een grootheid wordt voorgesteld met een symbool.

Voorbeeld:

De grootheid lengte heeft als symbool l

De grootheid massa heeft als symbool m

De grootheid tijd heeft als symbool t.

Alle grootheden worden uitgedrukt in een eenheid.

Een eenheid is een maat voor een fysisch verschijnsel.

Het wordt ook voorgesteld door een symbool.

Voorbeeld:

De eenheid van lengte is de meter en heeft symbool m.

De eenheid van massa is de gram en heeft als symbool g.

De eenheid van tijd is de seconde en heeft als symbool s.

Voorbeeld:

De lengte van een voetbalveld is 100 meter.

l = 100 . 1m

Grootheid = getalwaarde . eenheid

7.2 Basiseenheden

Er zijn in het SI-stelsel 7 basiseenheden. Alle andere eenheden zijn hiervan afgeleid.

Basisgrootheid Eenheid

Lengte (l) meter (m)

Massa (m) gram (g)

Tijd (t) seconden (s)

Elektrische stroomsterkte (I) ampère (A)

Temperatuur (T) Kelvin (K)

Lichtsterkte (I) Candela (cd)

Hoeveelheid van stof (n) mol

7.3 Geschiedenis

Ieder land had vroeger zijn eigen eenheden. Dat was erg verwarrend. De Franse zeemijl was b.v. niet even lang als de Engelse zeemijl en die was op zijn beurt weer niet even lang als de Engelse landmijl.

In de tijd van Napoleon heeft men geprobeerd hier een eind aan te maken. Uit die tijd stammen de meter en de kilogram. De kilogram werd gelijk gesteld aan de massa van 1 liter water.

Voorbeeld: definitie lengte (l)

In 1790 besloot de Franse regering een standaardmeter te maken, gedefinieerd als het veertig miljoenste deel van de aardomtrek. Er werd een standaardmeter van platina vervaardigd, Deze wordt bewaard in het Franse staatsarchief. Internationaal werd deze meter in 1875 aanvaard.

(zo ziet de meter eruit)

Sinds oktober 1983 is de meter in het SI gedefinieerd als de lengte van de weg die het licht in vacuüm aflegt in een tijdsinterval van 1/299 792 458 seconde.

Voorbeeld: definitie tijd (t)

De eenheid van tijd is de duur van 9 192 631 770 perioden van de straling die overeenkomt met de overgang tussen de twee hyperfijne energieniveaus van de grondtoestand van het cesium-133atoom.

7.4 Omzetten van eenheden naar veelvouden

Een basiseenheid of afgeleide eenheid is niet altijd even praktisch in het gebruik.

Voorbeeld: een miljoenste van een meter wordt = 0,000001 m

 Door het gebruik van decimale voorvoegsels wordt het eenvoudiger.

 Decimale onderverdelingen verschillen normaal een factor 1000 of 10³

 Uitzonderingen die gebruikt worden bij lengte, oppervlakte en inhoudsmaten.

Omzettingsschema

7.5 Oefeningen op grootheden en eenheden

Bij de oefeningen en in de praktijk wil men getallen zoals 10000V en 0,01V vermijden.

Men zal 10000V schrijven als 10kV (=om van de eenheid V naar kV te gaan moet men vermenigvuldigen met 103 of 1000).

Men zal 0,01V schrijven als 10mV (=om van de eenheid V naar mV te gaan moet men vermenigvuldigen met 10-3 of 0,001).

Zorg ervoor dat je de veelvouden aanpast zodat de waarde nooit:

- Kleiner is dan 1;

- Groter is dan 999.

Zet om naar correcte veelvoud:

 17859 A = …………………………………………………………………………………..

 0.008 A =

 7891255 mA = …………………………………………………………………………………..

 0.000125 MA = …………………………………………………………………………………..

Zet om naar grondeenheid:

 875 mA = …………………………………………………………………………………..

 3.5 µg = …………………………………………………………………………………..

 879 Mm = …………………………………………………………………………………..

8 De elektrische stroomkring

8.1 Stroom en spanning

De op zich willekeurige beweging van de vrije elektronen laat zich van buitenaf goed beïnvloeden.

Brengt men aanhet begin van een koperdraadeen negatieve lading aan enaan het einde een positieve lading, dan lopen de vrije (negatieve) elektronen, afgestoten door de negatieve ladingen en aangetrokken door de positieve, naar het einde van de draad.

Het stromen van elektronen noemt men elektrische stroom. De hoeveelheid elektronen die per tijdseenheid door een draaddoorsnede, bijvoorbeeld op plaats B passeren, noemt men de stroomsterkte. Deze wordt in ampère (A) gemeten en in formules aangegeven met symbool I.

De kracht waarmee de elektronen verplaatst worden is afhankelijk van de ladingen waardoor ze aangetrokken respectievelijk afgestoten worden. Preciezer gezegd, van het verschil tussen de ladingssterkten (potentialen) aan het begin en einde van de draad. Dit verschil noemt men elektrische spanning of potentiaalverschil.

Stelt men een kogel die van een helling afrolt. De steilheid van de helling kan men met elektrische spanning vergelijken.

Figuur7:Potentiaalverschil

Hoe groter het hoogteverschil (spanning) tussen A en C is, des te sneller rolt de kogel (elektron), des te meer energie heeft de kogel (vermogen). De hoogte van de berg zelf speelt eigenlijk geen rol. Net zoals men een hoogteverschil alleen tussen twee punten kan meten, zo is ook de spanning alleen tussen twee punten te meten.

De spanning wordt in Volt (V) gemeten en in formules met symbool U aangegeven.

De stroom in bovenstaande figuur vloeit jammer genoeg maar gedurende een korte tijd, dan zijn alle elektronen naar rechts gelopen. Wanneer de stroom niet mag ‘uitsterven’, moet een ‘elektronenpomp’, een spanningsbron aangebracht worden.

Figuur8:Elektronenpomp

De spanningsbron trekt de elektronen rechts aan, net zoals in bovenstaande figuur noemt men deze kant de pluspool, en schuift ze er links, aan de minpool, weer uit. De leiding en de spanningsbron

moeten een gesloten kring vormen zodat de elektronen aan de uitgangszijde terugkomen. Aangezien een stroom alleen door een geleider kan vloeien – lucht bevat praktisch geen vrije elektronen – stopt hij onmiddellijk wanneer de stroomkring onderbroken wordt.

Stroom is dus alleen met behulp van een spanningsbron in een gesloten stroomkring mogelijk. De stroomsterkte is overal in de kring gelijk.

Elektronen kunnen zich dus alleen verplaatsen wanneer ze energie krijgen (aantrekking -afstoting).

8.2 Wet van Faraday

De wet van Faraday slaat dus op de hoeveelheid elektriciteit die er verplaatst wordt

De hoeveelheid elektriciteit die er verplaatst wordt is gelijk aan de stroomsterkte vermenigvuldigd met de tijd.

Q = I x t

Q is de lading in Coulomb (=C)

I is de stroom uitgedrukt in Ampère (=A)

t is de tijd uitgedrukt in seconden (=s)

8.3 Praktische eenheid van hoeveelheid elektriciteit

De Coulomb is vaak een te kleine eenheid. Dit is zeker het geval voor toepassingen in de sterkstroom. Daarom gebruikt men meestal de praktische eenheid Ampère-uur.

Je bekomt de hoeveelheid elektriciteit in ampère-uur (Ah), als je de stroomsterkte in ampère vermenigvuldigt met de tijd in uur (h).

Een ampère-uur (1Ah) is de hoeveelheid elektriciteit die verplaatst wordt als gedurende 1 uur (=1h) de stroom een constante waarde van 1 ampère (1A) heeft.

De opslagcapaciteit van een batterij wordt ook uitgedrukt in Ah. In Figuur 27 zie je dat de batterij een spanning levert van 12V en een capaciteit heeft van 30Ah. Dit wil zeggen als men een lamp aansluit op de batterij die 1A verbruikt dat een volle batterij de lamp 30 uur kan doen branden.

Als de lamp maar 500mA verbruikt dan zal de lamp tweemaal zo lang branden. Dus 60 uur.

Figuur9:Eenbatterijvan12Veneencapaciteitvan30Ah.

8.4 Afgeleide formules

De formule van de wet van Faraday is:

Als we de formule omvormen naar de stroom dan krijgen we:

Als we de formule omvormen naar de tijd dan krijgen we:

8.5 Hoeveelheid energie

Een veelgebruikte term bij elektriciteit is Watt-uur (Wh). Denk maar aan een fietsaccu (vb. Stromer ST1 – 983Wh – 48V). Dit drukt uit hoeveel energie geleverd kan worden voor een bepaalde tijdsduur.

De arbeid (energie) zal bepaalt worden door de spanning en de hoeveelheid elektriciteit of lading. ��=���� Waarbij: Q : hoeveelheid elektriciteit of lading - Coulomb (c) - [As]

U : spanning – Volt (V)

W : arbeid (energie) – joule (J) – [Ws]

8.6 Vermogen

Vermogen is de uitgewisselde energie per tijdseenheid.

Waarbij: P: Vermogen - Watt (W) - [J/s]

W: arbeid (energie) – joule (J) – [Ws]

t: tijd [s]

Het vermogen in een gelijkstroomkring is ook te bepalen uit het product van de spanning en de stroom. Dit wordt hier aangetoond:

8.7 Voorbeelden

1) Door een elektrisch verwarmingstoestel vloeit een stroomsterkte van 10 A gedurende een tijd van 3 h. We berekenen de totale hoeveelheid elektriciteit in coulomb, ampère- seconde en ampère-uur.

Q = I t = 10 A 3 h = 30 Ah

Q = I t = 10 A 3 3600 s = 108000 As = 108000 C= 108 kC

2) Een 12 V-accumulator stuurt door een gloeilamp een stroomsterkte van 1,5 A. We berekenen de hoeveelheid elektriciteit (in Ah en C) die door deze gloeilamp vloeit in 10 uur tijd.

Q=I t= 1,5 A l0 h= 15 Ah

Q=1,5 A l0 h 3600 s = 54000 As = 54.000 C = 54 kC

3) Een loodaccumulator is gemerkt: 6 V en 81 Ah Hoe lang kan hij een verbruiker voeden die een stroomsterkte van 3 A nodig heeft?

Q = I x t

t = Q/I = 81 Ah / 3 A = 27 h = 27x3600 s = 97.200 s

8.8 Oefeningen

1) Een elektrisch verwarmingselement van 1000 W en 200 V neemt een stroomsterkte van 5 A op gedurende een tijd van 12 uur. Bereken de hoeveelheid elektriciteit in Ah en C die gedurende die 12 uur door het verwarmingselement vloeide.

2) Hoe lang kan een accumulator van 12 V - 36 Ah een stroomsterkte leveren van 0,4 A?

3) Men wil een ontladen accumulator van 80 Ah opnieuw laden in een tijd van 16 uur. Hoe groot zal de stroomsterkte moeten zijn?

4) Door een lamp vloeit er gedurende 10 seconden een stroom van 0,45 A. Bereken de verplaatste hoeveelheid elektriciteit of lading in coulomb en in Ampèreuur.

5) Een accu van een autobatterij heeft een capaciteit van 3220 mAh. Hoelang kan deze accu een stroom leveren van 5 A?

6) Batterij met volgende gegevens:

Figuur10:AA-batterij

Bepaal de hoeveelheid stroom dat deze batterij kan leveren in 1 uur en de arbeid dat deze kan leveren.

7) Bepaal de hoeveelheid stroom dat deze laptopbatterij KT.0030G.001 kan leveren in 5 uur en de arbeid dat deze kan leveren.

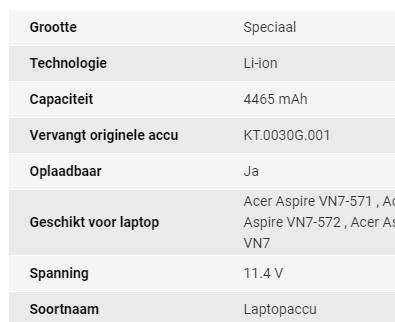
8) Batterij met volgende gegevens: DeWalt DCB184-XJ Li-Ion XR Slide Pack Battery. Hoeveel tijd kan deze batterij energie leveren bij een stroom van 500 mA. Bereken ook de arbeid dat deze batterij kan leveren

9) Bereken de stroomsterkte van de elektrische stroom die vloeit in een verbruiker van 1000W bij een spanning 24V.

10) Bij een potentiaalverschil van 60V wordt in een verbruiker een elektrische energie ontwikkeld van 72J, in een tijdspanne van 20s. Bereken de intensiteit van de stroom.

9 De elektrische stroomkring

9.1 De conventionele stroomzin

Vroeger, nog voor men het bestaan van elektronen kende, werd aangenomen dat de elektrische stroom buiten de bron vloeit van de pool met de hoger potentiaal (positief) naar de pool met de lager potentiaal (negatief).

De overeengekomen stroomzin die tegengesteld is aan de verplaatsing van de elektronen heet de conventionele stroomzin.

In de praktijk gaat men altijd gebruik maken van de conventionele stroomzin. Dit wil zeggen dat de stroom loopt van plus naar min. elektronenzin

gelijkspanningsbron

gelijkspanningsbron

Figuur11:Verschiltussenelektronenzinendeconventionelestroomzin.

9.2 De kleinst mogelijke elektrische stroomkring

Als je een lampje rechtsreeks verbindt op de klemmen van een batterij dan zal het lampje branden. Neem je de batterij weg dan brandt het lampje niet meer.

Figuur12:Eenbrandendeengedoofdelamp.

Zonder de spanning (stuwkracht op de elektronen) is er geen elektrische stroom. De spanning is de oorzaak, de stroom is het gevolg.

De twee noodzakelijke delen van de elektrische stroomkring zijn:

- De bron die de spanning (stuwkracht) onderhoudt op de polen (=aansluitingen) van de batterij;

- Een verbruiker die de elektrische energie omzet in een andere energievorm.

9.3 De elektrische stroomkring

In de meeste gevallen zal de verbruiker niet rechtstreeks op de bron worden aangesloten.

De verbruiker zal ook moeten in- en uitgeschakeld worden.

Bron

Heenleiding

Schakelaar Verbruiker

Middenleiding

Terugleiding

Figuur13:Onderdelenvaneenelektrischestroomkring.

Voor de elektrische stroomkring hebben we het volgende nodig:

- Een bron;

- Een schakelaar;

- Een verbruiker;

- Verbindingsdraden die de elektrische stroom leiden:

o Eén van de plusklem van de bron naar een aansluitklem van de schakelaar (heenleiding);

o Eén van de andere klem van de schakelaar naar de verbruiker (middenleiding);

o Eén van de andere aansluiting van de verbruiker naar de min-klem van de bron (terugleiding).

9.4 Het schema en de symbolen van een elektrische stroomkring

Een elektrische stroomkring opbouwen of een fout opsporen in een schakeling gaat gemakkelijker en vlugger als je beschikt over een schematische voorstelling van de schakeling. Op een elektrisch schema worden de onderdelen symbolisch voorgesteld zoals in Figuur 38.

Bron

Heenleiding Schakelaar Lamp (Verbruiker)

Middenleiding

Terugleiding

Figuur14:Schemavaneenelektrischestroomkring.

Als bron gebruiken we een gelijkspanningsbron. Hieronder worden de mogelijke symbolen voor een gelijkspanningsbron zijn afgebeeld.

Figuur15:Symboolgelijkspanningsbron

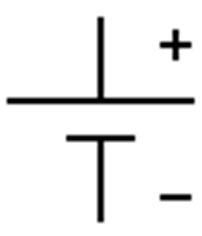
Figuur16:Symboolbatterij

Ezelsbruggetje symbool batterij: voor het plusteken is x zoveel streep nodig als het minteken.

Als verbruiker gebruiken we een lamp. Het symbool van een lamp is afgebeeld in Figuur 41.

Figuur17:Symboolvaneenlamp.

Het symbool van de leidingen zijn gewoon lijnen zoals de rode heenleiding, de groene middenleiding en de blauwe terugleiding in Figuur 38.

Het symbool van een schakelaar is afgebeeld in Figuur 42.

Figuur18:Symboolvaneenschakelaar.

9.5 De open stroomkring

Een stroomkring is open:

- Als de schakelaar open staat;

- Er ergens een onderbreking of een slecht contact is;

- De verbruiker (lampje) stuk is.

Schakelaar

Heenleiding

Middenleiding

Bron

Lamp (Verbruiker)

Terugleiding

Figuur19:Eenopenstroomkringwaardeschakelaaropenstaat.

Bij een open of onderbroken stroomkring is er geen geleidende verbinding tussen de aansluitingen van de bron. De bron levert wel spanning, maar er is GEEN STROOM. De bron is ONBELAST.

9.6 De gesloten stroomkring

De stroomkring is gesloten:

- Als de schakelaar gesloten is;

- Er geen onderbrekingen of slechte contacten zijn;

- De verbruiker (lampje) werkt of niet stuk is.

Schakelaar

Heenleiding

Middenleiding

Bron

Lamp (Verbruiker)

Terugleiding

Figuur20:Eengeslotenstroomkring.

Bij een gesloten stroomkring is er een geleidende verbinding tussen de aansluitingen van de bron

De bron levert spanning en er VLOEIT STROOM. De bron is BELAST.

10 Opmeten van de elektrische grootheden

Voor het opmeten van de elektrische grootheden maakt men vaak gebruik van een multimeter. Een multimeter is een toestel waarbij het mogelijk is om verschillende grootheden te meten. Klassiek kan je met een multimeter zeker volgende grootheden meten:

Grootheid Symbool grootheid Eenheid Symbool eenheid

Spanning U Volt V

stroom(sterkte) I Ampère A

weerstand R Ohm 

Men kan zowel gelijk- als wisselspanningen en -stromen opmeten. Het is dan wel belangrijk om je multimeter correct in te stellen.

 Wisselstroom wordt afgekort met de letters AC (alternating current) of kan je herkennen aan volgend symbool:

 Gelijkstroom wordt afgekort met de letters DC (direct current) of kan je herkennen aan volgend symbool:

Vaak komt men ook volgend symbool tegen: . Via een selectie of functieknop moet men nu de keuze maken tussen DC of AC.

Figuur 21: Types multimeter

10.1 Soorten multimeters

Men kan de multimeters,maar eigenlijkalle meetinstrumenten, onderverdelen intweegrote groepen. Men heeft er met eendigitale aflezing, men noemt ze digitale meetinstrumenten,maar er bestaanook analoge meetinstrumenten waar men naar de positie van de naald ten opzichte van een schaalverdeling moeten kijken wat de gemeten waarde is.

10.1.1 Digitale multimeter

De digitale multimeter is snel te herkennen aan het display en moet gevoed worden met een batterij (net omwille van het display). Digitale multimeters zorgen voor een snelle aflezing van het meetresultaat, let wel op dat je goed kijkt naar het gekozen meetbereik om je meetresultaat goed te interpreteren!

Figuur22:Digitalemultimeter

10.1.2 Analoge multimeter

Een analoge (multi)meter is te herkennen aan de wijzer/naald. Hier krijgen we dus niet rechtstreeks de gemeten waarde te zien, maar moeten we op de juiste schaalverdeling kijken en zelf nog de waarde bepalen. Zorg dat de naald steeds 0 aangeeft als hij uitgeschakeld is, enkel op die manier heb je een correcte meting.

Figuur23:Analogemultimeter

Vaak hebben analoge meters in de schaalverdeling een spiegel zitten, dit om de parallaxfout te voorkomen (die parallaxfout komt ook voor bij het aflezen van een schuifmaat). Je kan de correcte waarde aflezen als het spiegelbeeld van de naald, perfect achter de naald ligt (op die manier kijk je zelf recht op de schaalverdeling).

Figuur24:Parallaxfoutbijschuifmaat

10.2 Correct opmeten van de basisgrootheden

Een correcte meting uitvoeren is eenvoudig, zolang men een aantal stappen en regels respecteert. Het meettoestel zal in de meeste gevallen wel een waarde weergeven, ook al is de meter niet goed ingesteld. Hierdoor bekom je dus een foutieve meetwaarde.

Het is van cruciaal belang te weten welke grootheid men moet meten. Niet alleen de instellingen van het meettoestel moeten aangepast worden aan de te meten grootheid, ook de manier waarop men gaat meten is anders!

10.2.1 Het meten van de spanning

Spanning staat steeds over iets (potentiaalverschil), men moeten dus ook over een component meten (parallel) om de correcte spanningswaarde te krijgen. Men moet dus de elektrisch kring niet onderbreken om een spanningsmeting uit te voeren.

De zwarte meetpen steekt men steeds in de ‘COM’-poort, de rode meetpen steekt men in de ‘VHz’bus. Denk na over de waarde die men zou moeten uitkomen, dit om het correcte meetbereik in te stellen. Beschikt men over een automatische meetbereikinstelling dan zal het meettoestel altijd start bij het hoogste meetbereik. Daarna maken we een keuze uit AC of DC. Men plaatst vervolgens één meetpen voor en de andere meetpen na het component waarover men de spanning wil meten.

Figuur25:DC-meting

Figuur26:AC-meting

Symbool van een spanningsmeter ziet er als volgt uit:

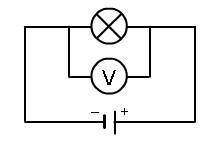
Figuur27:Symboolvaneenspanningsmeter

Om een voltmeter op een schema te plaatsen gebruik je het linkse symbool.Om specifiek aan te duiden dat je een gelijkspanning wil meten gebruik je het rechtse symbool.

V

V

HetalgemeensymboolvaneenVoltmeterenhetsymboolvaneenVoltmeterindestandDC.

Het schema om de spanning van een 9V batterij te meten wordt dus:

Schemavanhetmetenvaneengelijkspanningvaneenbatterij.

10.2.2 Oefeningen op het meten van spanning

10.2.2.1 Experimenteerset

Benodigdheden:

- Experimenteerset Velleman

o Breadboard

o Schakelaar

o Led lamp (groen)

o 2 kabels

- Knoopcelbatterij 2032

- Wasknijper

Opmeten van de spanning van volgende basisschakeling. Plaats op onderstaande schakeling een Voltmeter om de spanning over de batterij, de schakelaar en de lamp te meten.

Opdracht:

1. Wat is de spanning van de batterij?

2. Wat is het verband tussen de polariteit van de batterij en de kleur van de meetprobes op het meettoestel?

3. Teken het equivalent schema van het circuit.

4. Zorg ervoor dat het circuit werkt. Wat gebeurt er als de LED wordt omgedraaid?

5. Hoeveel bedraagt de spanning over de lamp wanneer deze brandt (schakelaar dicht)?

6. Hoeveel bedraagt de spanning over de lamp wanneer deze niet brandt (schakelaar open)?

7. Hoeveel bedraagt de spanning over de schakelaar wanneer de lamp brandt (schakelaar dicht)?

8. Hoeveel bedraagt de spanning over de schakelaar wanneer de lamp niet brandt (schakelaar open)?

10.2.2.2

AC-spanning

 Opmeten van de netspanning. Opgepast deze spanning is een stuk hoger dan de batterijspanning. Maak dus enkel contact met de meetpennen.

Hoeveel bedraagt de netspanning? ………… V

10.2.3

Het meten van de stroom

De elektrische stroom is een verplaatsing van elektronen. We moeten dus tellen hoeveel elektronen zich verplaatsen om een idee te krijgen over de waarde van de elektrische stroom. De stroom meten we in de kring (serie). We moeten de kring dus onderbreken om de stroom te meten.

Figuur28:Praktischeopstellingvoorhetopmetenvanspanning

Als men stroom meet dan meet men de stroom altijd door iets. In het schema loopt de stroom van de plus-klem door de schakeling naar de min-klem. De stroom is overal gelijk. Dit wil zeggen dat de ampèremeter gelijk waar mag staan in de kring.

Men onderbreekt dus de kring en plaatst er de Ampèremeter tussen. Vooraleer men de onderbreking maakt zorg men dat de installatie afgeschakeld is van de elektrische bron (men werkt spanningsloos). Daarna plaatst men de Ampèremeter in de kring, waarna men de installatie terug onder spanning plaatst. Doet men dit niet dan kan het gebeuren kan bij het onderbreken van de kring vlambogen ontstaan. Dit komt natuurlijk maar voor bij het onderbreken van zeer grote stromen.

https://www.youtube.com/watch?v=frHs-PwRUZ0

De zwarte meetpen steek men opnieuw in de ‘COM’-poort. De rode meetpen steekt men, afhankelijk van de grootte van de stroom in de ‘15A’ of ‘AmA’-bus. Denk dus na over de waarde die men zou moeten uitkomen, dit om het correcte meetbereik in te stellen. Verwacht je een stroom van 10A of van 2 mA?

Figuur29:Keuze15A-ofµAmA-bus

Heeft men geen idee van de stroomwaarde, dan stelt men het meettoestel in voor het grootste meetbereik. Indien nodig kan men afhankelijk van het meetresultaat het meetbereik verkleinen om de waarde nauwkeuriger op te meten.

Technischishet niet altijdmogelijkom de stroomkringteonderbreken. Dankunnen wegebruikmaken van een stroomtang om de stroom te meten in een kring.

Figuur30:Opmetenvanstroommetstroomtang

Symbool van een ampèremeter ziet er als volgt uit:

Figuur31:Symboolvanstroommeter

Om een ampèremeter op een schema te plaatsen gebruik je het linkse symbool Om aan te duiden dat je een gelijkstroom wil meten gebruik je het rechtse

A A

HetalgemeensymboolvaneenampèremeterenhetsymboolvaneenampèremeterindestandDC.

10.2.4 Oefeningen op het meten van stroom

10.2.4.1 Experimenteerset

Zelfde opstelling als in “6.2.2.1 Experimenteerset”.

Opmeten van de stroom van volgende basisschakeling. Plaats op de schakeling een Ampèremeter om de stroom door de batterij, de schakelaar en de lamp te meten.

1) Hoeveel bedraagt de stroom door de schakelaar als de schakelaar open staat?

2) Hoeveel bedraagt de stroom door de lamp als de schakelaar open staat?

3) Hoeveel bedraagt de stroom door de schakelaar als de schakelaar gesloten is?

4) Hoeveel bedraagt de stroom door de lamp als de schakelaar gesloten is?

5) Speelt de plaats van de Ampèremeter een rol in deze schakeling?

10.2.5 Het meten van de weerstand

Als men de weerstand wil meten, dan moet men dit spanningsloos doen. In het beste geval haalt men dus het component uit de elektrische kring om de meting uit te voeren. Het meettoestel zal zelf een stroom sturen door het component en meet gelijktijdig de spanning. Op die manier kan het, door gebruik te maken van de wet van ohm (zie verder in de cursus), de weerstandswaarde berekenen. De zwarte meetpen steekt men opnieuw in de ‘COM’-poort, de rode meetpen steekt men in de ‘VHz’bus. Men plaats de multimeter in de stand weerstand Ω en meet met de twee meetpennen over de weerstand.

Figuur32:Weerstandsmeting

Symbool van een weerstandsmeter ziet er als volgt uit:

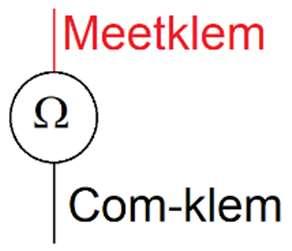
Figuur33:Symboolvanweerstandsmeter

Afhankelijk van het meetresultaat en het meetbereik wordt de weerstandswaarde uitgedrukt in:

 ohm (Ω)

 kilo-ohm (kΩ = 1000 Ω)

 Mega-ohm (MΩ = 1000 kΩ = 1000000Ω)

10.2.6 Oefeningen op het meten van weerstand

10.2.6.1 Experimenteerset

Zelfde opstelling als in “6.2.2.1 Experimenteerset”.

1) Hoeveel bedraagt de weerstand van de schakelaar als deze open staat?

2) Hoeveel bedraagt de weerstand van de schakelaar als deze gesloten is?

3) Hoeveel bedraagt de weerstand van de lamp?

Hoeveel bedraagt de weerstand van de schakelaar als deze gesloten is en de spanningsbron is ingeschakeld?

10.3 Voorwaarden voor een elektrische stroom

Om een elektrische stroom te krijgen is er in eerste instantie een bron nodig die een spanning levert. Er is dus spanning nodig.

Vervolgens is er een gesloten kring nodig met een verbruiker

Als beide voorwaarden voldaan zijn dan zal er een elektrische stroom vloeien of stromen.

10.4 Testen op een open of gesloten kring

Bij een defecte kring ga je altijd eerst kijken of er spanning aanwezig is. Dit kan je meten met een voltmeter en wordt in hoofdstuk 10.2.1 besproken.

Als er spanning aanwezig is ga je verder kijken wat de fout kan zijn. Je kijkt of er ergens een slecht contact, een onderbreking of een defecte schakelaar is.

10.4.1 Oefening op testen open of gesloten kring

10.4.1.1 Experimenteerset

Benodigdheden:

- Experimenteerset Velleman

o Breadboard

o 2x Schakelaar

o Led lamp (groen)

o 3 kabels

- Knoopcelbatterij 2032

- Wasknijper

Opmeten van de spanning op verschillende punten op volgende basisschakeling.

Figuur34:Praktischeopstellingvoorhettestenopeenopenofeengeslotenkring

Opdracht:

1) Teken het equivalent schema van het circuit.

2) Welke spanning denk je te meten? Zonder meettoestel oplossen!

Schakelaar 1 open Schakelaar 1 dicht Schakelaar 1 dicht

Schakelaar 2 open

Voor schakelaar 1

Voor schakelaar 2

Voor lamp

3) Welke spanning meet je?

Schakelaar 1 open

Schakelaar 2 open

Schakelaar 2 open

Schakelaar 2 dicht

Schakelaar 1 dicht

Schakelaar 2 open

Schakelaar 1 dicht

Schakelaar 2 dicht

Voor schakelaar 1

Voor schakelaar 2

Voor lamp

10.4.2 De doormeetstand van een multimeter.

De multimeter stel je in de doormeetstand door de draaiknop in te stellen in de stand met het symbool van het geluidssignaal zoals in Figuur 59.

Figuur 35: Instellen van de multimeter in de doormeetstand.

Een multimeter heeft meestal meer dan twee aansluitklemmen. De zwarte meetpen plaats je in de zwarte aansluiting of de aansluiting waar er COM bij staat.

COM is de afkorting van common wat gemeenschappelijk wil zeggen.

De rode en tweede aansluiting plaats je in de aansluiting waar het geluidssymbooltje bij staat.

De aansluitingen kan je zien zoals in Figuur 60.

Figuur36:Verbindenvanmeetprobesindemultimetervoorhetdoormeten.

Als je de twee meetprobes (de zwarte en de rode) tegen elkaar houdt dan zal je een geluidssignaal horen en zal de multimeter een kleine weerstandswaarde weergeven zoals in Figuur 61. Meer over weerstand wordt er besproken in hoofdstuk 8.

Figuur 37: Een multimeter in de doormeetstand waarvan de kring gesloten is.

Als je de meetprobes niet tegen elkaar houdt dan hoor je geen geluidssignaal en dan zal er op de display OL staan zoals in Figuur 62. OL staat voor Open loop wat open kring wil zeggen. Dit is een oneindig hoge weerstand.

Figuur38:Eenmultimeterindedoormeetstandwaarvandekringopenis.

Als je de meetprobes tegen elkaar hebt gehouden en je hoort geen signaal, dan is de multimeter defect, het meettoestel staat niet in de juiste stand, de meetprobes zitten niet in de juiste aansluitingen van het meettoestel of één of alle twee de meetsnoeren zijn defect.

Vooraleer je begint met testen controleer je eerst of je meettoestel werkt door de twee probes eens tegen elkaar te plaatsen en te controleren of je een geluidssignaal hoort. Als dit werk dan is je toestel in orde.

11 De elektrische spanning

11.1 Elektrische potentiaal

De drang van een geladen lichaam naar de neutrale toestand heet potentiaal

Potentiaal heeft als symbool U (=spanning) en wordt uitgedrukt in Volt (V).

Is die drang sterker, dan is de potentiaal groter:

- Neutrale lichamen en de aarde hebben geen potentiaal (=0V);

- Lichamen met te weinig elektronen of met andere woorden positief geladen lichamen bezitten een positief potentiaal;

- Lichamen met te veel elektronen of met andere woorden negatief geladen lichamen bezitten een negatief potentiaal

Potentiaal is de spanning ten opzichte van een referentie. Als referentie wordt de aarde gebruikt. Je kan dit vergelijken met de hoogte van het aardoppervlak. We gebruiken de zeespiegel als referentie. De hoogte van het strand is 0 meter omdat het strand aan de zee grenst en er geen niveauverschil is. Naarmate dat je meer naar het binnenland gaat de hoogte ten opzichte van de zeespiegel naar omhoog.

Bij elektrisch potentiaal wordt de aarde als referentie gezien. In een schema spreekt men over de aarding en stelt men de aarding voor door het symbool zoals in Figuur 63. In het Engels is deze term gekend als “ground” afgekort “GND”.

Symboolvandeaarding,groundofGND.

Men zal in een schema niet altijd één punt aan de aarde hangen maar men zal wel een referentie kiezen. Die referentie noemt men de massa. Het symbool van de massa wordt afgebeeld in Figuur 64. Enkele voorbeelden van toepassingen waarbij de massa die niet gelijk is aan de aarding zijn:

 Draadloze toestellen

 Auto’s

 Vliegtuigen

Symboolvandemassa.

In de meeste gevallen zal men de negatieve aansluiting van de spanningsbron nemen als ground

Het schema van de elektrische kring ziet er dan uit zoals in Figuur 65. Hierbij is de bron een geschakelde voeding waarvan de uitgang galvanisch gescheiden is van de ingang. Om problemen te vermijden wordt de min-klem gebruikt als ground.

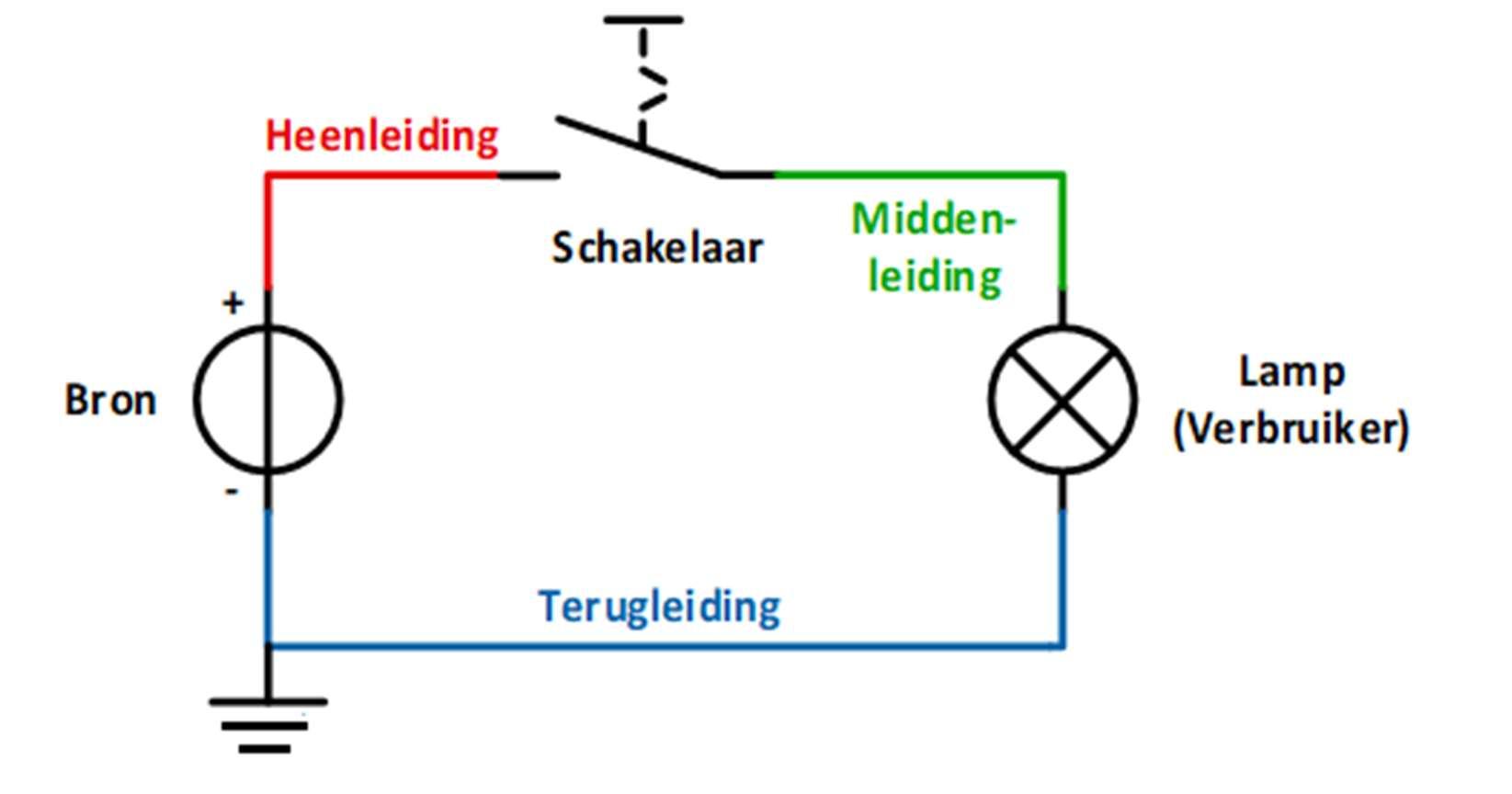
SchemavandeelektrischekringmetGND.

Belangrijk is om te onthouden dat het potentiaal de spanning is ten opzichte van de referentie.

11.2 Elektrisch potentiaalverschil

Het elektrisch potentiaalverschil is het ladingsverschil, de spanning tussen twee lichamen.

Je kan dit vergelijken door de hoogte van twee steden, bijvoorbeeld Brugge en Kortrijk.

De hoogte van Brugge ten opzichte van de zeespiegel is ongeveer 10m.

De hoogte van Kortrijk ten opzichte van de zeespiegel is ongeveer 20m.

Het hoogteverschil tussen de twee steden is 10m (20m-10m).

Het hoogteverschil kan je vergelijken met het potentiaalverschil.

We hebben twee lichamen A en B.

A is positief geladen en heeft een potentiaal van 5V (potentiaal is t.o.v. de GND). B is negatief geladen en heeft een potentiaal van -5V (potentiaal is t.o.v. de GND).

Het potentiaalverschil is 10V zoals voorgesteld in Figuur 66.

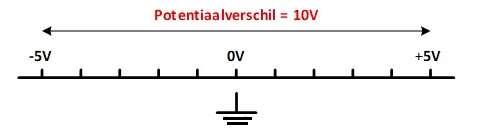
Voorstellingvanpotentiaalenpotentiaalverschil.

11.3 Soorten spanningen en stromen

We weten dat we in een elektrische kring een bron moeten hebben en dat die bron een bepaalde spanning moet hebben. Als op de bron een verbruiker wordt aangesloten dan zal er stroom vloeien en zal de verbruiker de elektrische energie omvormen in een andere energievorm. Een lamp zal de elektrische energie omvormen in lichtenergie.

Nu zijn er verschillende soorten spanningen en stromen.

Deze kunnen ingedeeld worden in twee grote groepen, namelijk:

- Gelijkspanning en gelijkstroom;

- Wisselspanning en wisselstroom.

11.3.1 Gelijkspanning en gelijkstroom

We spreken over een gelijkspanning als de bron vaste polariteiten heeft. Dit wil zeggen dat de éne klem van de bron de plus-klem is en de andere klem de min-klem zoals in Figuur 67.

De stroom die geleverd wordt door de gelijkspanningsbron vloeit steeds in dezelfde zin.

Die stroom wordt gelijkstroom genoemd.

Gelijkspanning en gelijkstroom worden afgekort door de letters DC. DC is de afkorting van Direct

Current. Men spreekt dan over DC-spanningen en DC-stromen.

Een9Vbatterij.

Er bestaan statische- en roterende gelijkspanningsbronnen

Statische spanningsbronnen zijn zoals batterijen

:Symbolenvanstatischegelijkspanningsbronnen.

Roterende gelijkspanningsbronnen zijn bronnen zoals een fietsdynamo hebben bewegende delen.

Een roterende spanningsbron is een generator

Eenfietsdynamo.

GSymboolvaneengenerator.

Een gelijkspanningsbron wordt ook symbolisch voorgesteld door het gelijkheidsteken (=).

Algemeensymboolvaneengelijkspanningsbron.

11.3.2 Soorten gelijkspanningen en -stromen

Als we een spanning of een stroom zouden meten in functie van de tijd dan komen we een aantal verschillende gelijkspanningen of -stromen tegen.

Als men het heeft over een gelijkspanning of -stroom, dan heeft men het meestal over de constante gelijkspanning of -stroom. t(s)

I(A)

U(V) t(s)

Eenconstantegelijkspanningen-stroom.

Een willekeurige gelijkspanning of -stroom ziet eruit zoals in volgende figuur. Dit is een typisch voorbeeld van een storing.

Eenwillekeurigegelijkspanningen-stroom.

Een periodieke gelijkspanning en -stroom ziet kan je herkennen met volgende figuur. Deze noemt periodiek omdat een stuk van het signaal voortdurend wordt herhaald.

Eenperiodiekegelijkspanningen-stroom.

Er zijn nog een aantal periodieke signalen die je kan tegenkomen. Een bloksignaal, een driehoek of zaagtand.

Eenblokgolfgelijkspanningen-stroom.

Eenzaagtand-ofdriehoeksignaal.

Het meten van gelijkspanningen en stromen in functie van de tijd zoals in bovenstaande afbeeldingen meet je met een oscilloscoop.

11.4 Opdracht meten spanning en stroom deel 1

11.4.1 Doel van de meting:

 Metenvanstromen

 Metenvanspanningen

 Elektrischeweerstand

 Dezemetinggebeurtgezamenlijkenonderbegeleiding.

11.4.2 Materiaal

 2 lamphouders

 2 lampen

 1 netsnoer

 1 multimeter.

11.4.3 Meetopstelling 1:

Jestartmethetaansluitenvan1lampaanhetnetsnoer.Jetestofdelampnogcorrect werkt.

Jemeetdespanningoverdezelamp.Enjenoteertdezewaarde.Jeneemteenfotovan dezeopstelling.

Jeverbindtnuuwmeettoestelalsampèremeteraan1kantvandelamp.Jemeeten noteertdewaardevandezestroom.Jeneemteenfotovandezeopstelling.

Jeverbindtnuuwmeettoestelalsampèremeteraandeanderekantvandelamp.Jemeet ennoteertdewaardevandezestroom.Jeneemteenfotovandezeopstelling.

11.4.4 Meetopstelling 2 serie:

Jestartmethetaansluitenvan2lampenaanhetnetsnoer.Hoejedezemoetaansluiten wordtophetborddoordedocentgetekend.Jetestofdelampennogcorrectwerken.

Jemeetdespanningoverdelampen.Enjenoteertdezewaarden.Jeneemteenfotovan dezeopstelling.

Jeverbindtnuuwmeettoestelalsampèremetertussenhetsnoerendeeerste lamp.Je meetennoteertdewaardevandezestroom.Jeneemteenfotovandezeopstelling.

Jeverbindtnuuwmeettoestelalsampèremetertussenbeidelampen.Jemeetennoteert dewaardevandezestroom.Jeneemteenfotovandezeopstelling.

Jeverbindtnuuwmeettoestelalsampèremetertussenhetsnoerendetweedelamp.Je meetennoteertdewaardevandezestroom.Jeneemteenfotovandezeopstelling.

11.4.5 Meetopstelling 3 parallel:

Jestartmethetaansluitenvan2lampenaanhetnetsnoer.Hoejedezemoetaansluiten wordtophetborddoordedocentgetekend.Jetestofdelampennogcorrectwerken.

Jemeetdespanningoverdelampen.Enjenoteertdezewaarden.Jeneemteenfotovan dezeopstelling.

Jeverbindtnuuwmeettoestelalsampèremetertussenhetsnoerendeeerste lamp.Je meetennoteertdewaardevandezestroom.Jeneemteenfotovandezeopstelling.

Jeverbindtnuuwmeettoestelalsampèremetertussenhetsnoerendetweedelamp.Je meetennoteertdewaardevandezestroom.Jeneemteenfotovandezeopstelling.

11.4.6 Besluit

Beschrijf hier hoe je deze eerste meting mocht ervaren

12 Basiswetten elektriciteit

12.1

Wet van Ohm

De tegenstand die stoffen bieden aan de elektrische stroom heet elektrische weerstand of weerstand. Het symbool van elektrische weerstand is de hoofdletter R (Resistance) en wordt uitgedrukt in Ohm. Het symbool van Ohm is de Griekse letter Omega (Ω).

Weerstand kan je vergelijken met fietsen in de bergen.

De berg op fietsen gaat heel moeilijk, de weerstand is groot.

De berg afdalen gaat heel gemakkelijk, de weerstand is klein.

Bergopfietsen = Veelweerstand

Bergaffietsen = Weinigweerstand

Niet alle stoffen hebben dezelfde geleidbaarheid. De vraag die je nu kan stellen is: ”Welke invloed heeft dat in een elektrische kring”?

Ook Georg Ohm, een Duits natuurkundige (1787 - 1854), stelde zich deze vraag. In 1827 legde hij proefondervindelijk de wet van Ohm vast.

12.1.1 Opdracht : labo wet van ohm

Je mag eerst eens meten. Je vindt deze opdracht op Toledo

12.1.2 Het verband tussen U en I bij constante weerstand

R1 = 25 Ω

R2 = 50 Ω

Met de schakelaar kan je een weerstand selecteren.

De bronspanning is regelbaar van 0 - 50 V.

Om geen misverstanden te creëren, nemen we aan dat de V-meter geen stroom opneemt (heeft dus een oneindig grote weerstand) en dat de A-meter en de draden geen weerstand hebben.

Stijgt de spanning over dezelfde weerstand tweemaal (van 10 V naar 20 V), dan stijgt de stroom door die weerstand in dezelfde mate (van 0,4 A naar 0,8 A).

Besluiten:

- De verhouding is recht evenredig:

- Door de stroomsterkte en spanning te meten kan je de weerstand bepalen.

- Je kan de stroom door de weerstand vergroten door de spanning te verhogen

- De stroomsterkte in een weerstand is recht evenredig met de spanning

12.1.3 Het verband tussen R en I bij constante bronspanning

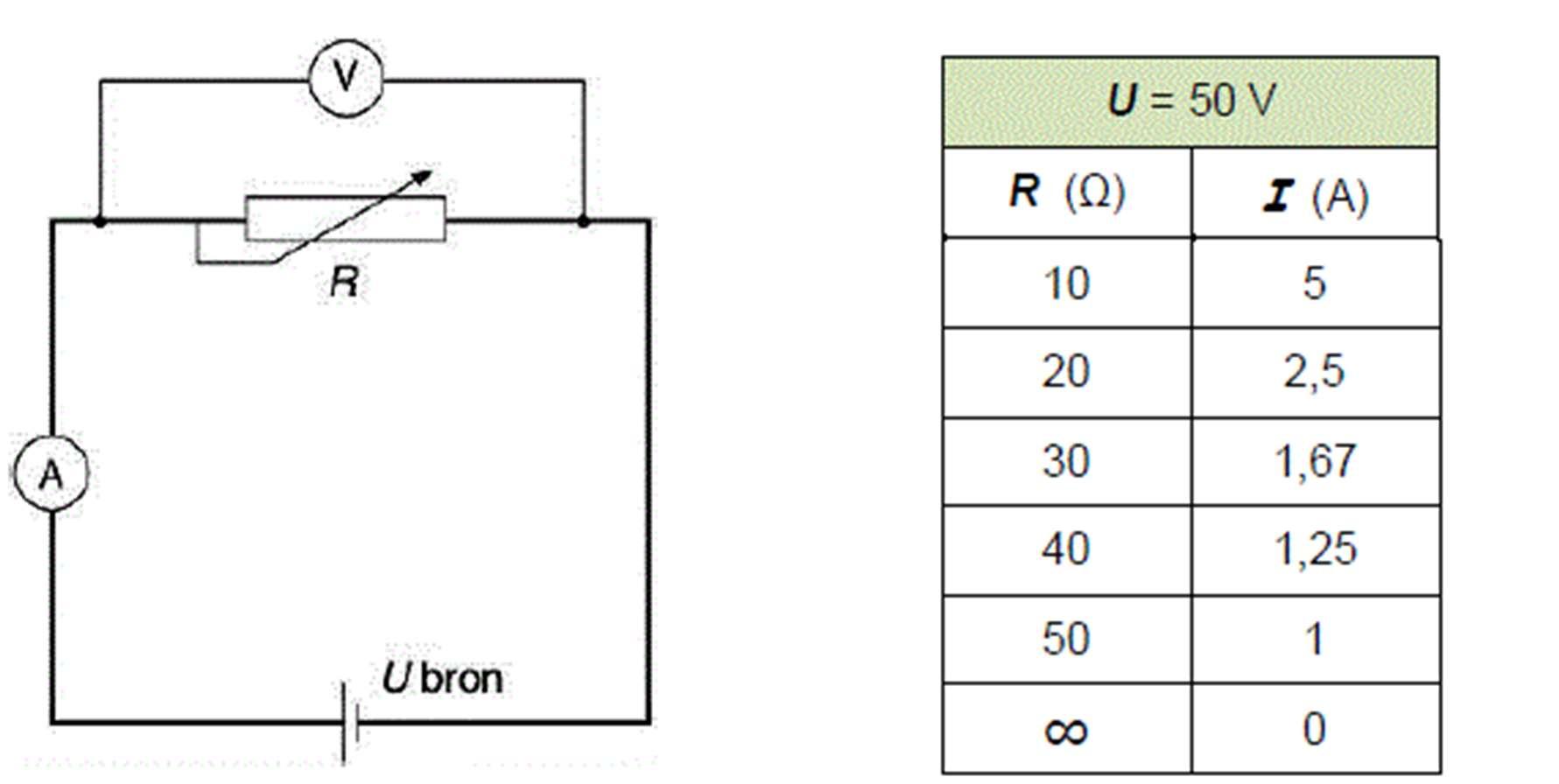
Vergroot de weerstand (vb. van 10 Ω naar 20 Ω) bij een constante spanning van 50 V, dan verkleint de stroom in dezelfde mate (van 5 A naar 2,5 A).

Besluiten:

- Stroomsterkte wordt bepaald door de verhouding spanning over weerstand.

- De stroomsterkte in een weerstand is omgekeerd evenredig met de weerstandswaarde.

12.1.4

Wet van ohm

De constante verhouding tussen spanning en stroomsterkte noemen we weerstand.

������������������= spanningoverdeweerstand stroomsterktedoordeweerstand

Bij een vaste weerstandswaarde: de stroom stijgt als de spanning over de weerstand stijgt. De stroom is evenredig met de spanning.

Bij een stijgende weerstand: de stroom daalt als de spanning constant blijft. De weerstand is omgekeerd evenredig met de stroom.

De weerstandswaarde is niet afhankelijk van de aangesloten spanning en is ook niet afhankelijk van de stroomsterkte die er door vloeit. De weerstandswaarde wordt enkel bepaald door zijn natuurkundige eigenschappen en zijn constructie.

Uit de wet van Ohm volgt dat de elektrische weerstand uitgedrukt wordt in volt per ampère. In technische taal gebruik je de naam “ohm” (1 V/A = 1 Ω).

Eén ohm is de weerstand tussen twee punten waarover een spanning van 1 volt nodig is om er een stroom van 1 ampère door te sturen.

12.1.5

Voorbeelden

1) Een voltmeter, parallel geschakeld over een weerstand, duidt 8 V aan. De ampèremeter, in serie met deze weerstand, duidt 4 A aan. Bereken de waarde van de weerstand.

Geg: U = 8 V en I = 4 A

Gev: R

Oplossing

2) Bereken de spanning die nodig is aan de klemmen van een verbruikstoestel met een weerstand van 500 Ω om er een stroomsterkte van 2 mA door te sturen.

Geg: R = 500  en I = 2 mA

Gev: U

Oplossing

R= of U = R I = 500 2 10-3= 1 V

3) Op het kenplaatje van een verwarmingstoestel vind je de volgende gegevens:

1000 W - 200 V - 5 A.

Hoe groot is de weerstand van het toestel?

Geg: U = 8 V en I = 4 A

Gev: R

Oplossing

R= = = 40 

12.1.6 Oefeningen

1) Een strijkijzer met weerstand van 40 Ω wordt aangesloten op een spanning van 230 V. Welke stroomsterkte zal het strijkijzer opnemen?

2) Welke weerstand is er nodig om bij een spanning van 220 V de stroomsterkte te beperken tot 10 mA?

3) Een weerstand van 400 Ω voert een stroomsterkte van 0,3 mA. Bereken de spanning aan de klemmen van de weerstand.

4) Welke spanning moet je aanleggen aan de klemmen van een weerstand van 15 Ω als men je een hoeveelheid elektriciteit van 40 C per seconde wil verplaatsen?

5) Een accumulator van 36 Ah – 12 V voedt een verbruiker met weerstand 200 Ω. Hoe lang kan hij deze verbruiker voeden?

6) Door een geleider vloeit een stroomsterkte van 10 A. Hoe groot is de verplaatste hoeveelheid elektriciteit gedurende 8 uur in Ah en C ?

7) Bereken de inwendige weerstand van een A-meter indien hij 2 A aanduidt en de spanning over de klemmen 0,8 V bedraagt.

8) Door een spoeltje van een relais mag maar 0,03 A vloeien. De weerstandmeting gaf als resultaat 400 W. Welke spanning mag men aanleggen?

9) Om een hoeveelheid koper vrij te maken, moet er een hoeveelheid elektriciteit van 7,2 MC worden verplaatst. Men beschikt over een stroomsterkte van 120 A. Hoe lang zal deze stroom moeten vloeien ?

10) Welke spanning zal men moeten aanleggen aan de klemmen van een weerstand van 15 W indien men er een hoeveelheid elektriciteit van 40 C per seconde in verplaatst?

12.2 Wet van Pouillet

12.2.1 Factoren die de weerstand van een geleider beïnvloeden

Je weet dat de elektronen om de kern sterk of minder sterk aan hun kern gebonden zijn. De elektrische geleidbaarheid van de stof hangt hiervan af. De elektronen van sommige stoffen kunnen gemakkelijk worden vrijgemaakt (bijv. metalen), bij andere stoffen is dat moeilijk. Hieruit besluiten we dat het soort van materiaal een grote invloed heeft op de weerstand van een geleider.

De lengte van een geleider zal eveneens van grote invloed zijn. Hoe langer de geleider is, hoe meer weerstand hij zal bieden aan de door gang van de elektrische stroom (vgl. lengte van de waterleidingbuizen).

De weerstand is recht evenredig met de lengte van de geleider.

De oppervlakte of doorsnede speelt eveneens een grote rol. Hoe groter de oppervlakte van de geleider, hoe gemakkelijker de elektrische, stroom erdoor kan. De weerstand van een geleider is omgekeerd evenredig met de doorsnede ervan.

Indien men aan een materiaal warmte (energie) toevoert, dan heeft dat invloed op de toestand van de elektronen om de kern, dus ook op de weerstand van het materiaal. Hier kan geen algemene regel worden toegepast. Bij de meeste stoffen (metalen) neemt de weerstand toe met de temperatuur, bij andere stoffen zoals silicium en koolstof neemt de weerstand af. Bij nog andere stoffen is de invloed van de temperatuur praktisch te verwaarlozen.

Andere invloeden

Buiten de bovengenoemde factoren, die de weerstand van vaste geleiders bepalen, zijn er materialen waarvan de weerstand ook beïnvloed wordt door de stroomzin, het invallende licht (L.D.R.), de spanning (V.D.R.),druk, enz.

12.2.2 Soortelijke weerstand 

Om een maatstaf te hebben bij het berekenen van weerstandswaarden heeft men de soortelijke weerstand of ‘resistiviteit’ ingevoerd.

De resistiviteit is de weerstand van een materiaal in kubusvorm van 1 m x 1 m x 1 m (m³) bij een bepaalde temperatuur. Je kan het zien als de weerstand van een ‘geleider’ met doorsnede 1 m² en lengte 1 m.

Voor koper bij 15 °C is dat: 0,0175. 10-6 Ωm. Voor aluminium is dat 0,028. 10-6 Ωm

De herkomst van de eenheid ohmmeter zal later duidelijk worden.

12.2.3

Wet van Pouillet

Claude Pouillet (1790 - 1868) was een Frans natuurkundige die verdere studie deed op de uitvinding van zijn tijdsgenoot Ohm. Hij onderzocht welke factoren de weerstand bepalen Uit het begrip soortelijke weerstand kunnen we nu, door eenvoudige redenering, de formule opbouwen die de weerstand van een willekeurige geleider bij een temperatuur van 15°C (eventueel 0°C) bepaalt.

Een geleider met een lengte van 1 m en een doorsnede van 1 m² van een willekeurige stof heeft, bij 15 °C (0 °C), een weerstand R = 

Een geleider met een lengte van 2 m en een doorsnede van 1m² van een willekeurige stof heeft, bij 15 °C (0 °C), een weerstand R =  2.

Als we een willekeurige lengte l meter nemen en een doorsnede van 1 m, bij 15 °C (0 °C), dan is R =  l.

Als de doorsnede verdubbeld wordt, zal de weerstand worden gehalveerd. Een lengte van l meter en een doorsnede van 2 m² bij 15 °C zal een weerstand: ��= geven.

Een lengte van l meter en een willekeurige doorsnede van A m² bij 15 °C zal een weerstand: ��= geven.

De weerstand van een willekeurige vaste geleider zal worden gegeven door de formule: ��= ook de wet van Pouillet genoemd

Toelichting

Eenheid van soortelijke weerstand in SI-stelsel

In de formule vullen we de eenheden van de gebruikte grootheden in:

m is dus de afgeleide eenheid van soortelijke weerstand in het SI-stelsel.

12.2.4 Oefeningen

1) Hoe groot is de weerstand van een rol koperdraad van 2,5 mm² doorsnede en 100 m lengte bij een temperatuur van 15°C?

2) Voor het vervaardigen van een weerstand van 2 W gebruikt men manganine met een doorsnede van 0,6 mm². Hoeveel meter draad zal men nodig hebben? (T =15°C)

3) Een weerstand van 700W is gemaakt van 4396 m draad met 2 mm diameter. Uit welk materiaal is deze weerstand vervaardigd?

4) Een koperdraad met een lengte van 160 m heeft een weerstand van 2W. We berekenen de diameter (T = 15 °C).

5) Een messingstrook van 180 cm lang moet een weerstand hebben van 1 mW. Het materiaal is 3 mm dik. Hoe breed wordt deze strook ?

6) Een aluminiumstaaf met afmetingen 2 x 30 mm als doorsnede heeft een weerstand van 10 mW. Wat is de lengte ervan? (T = 15 °C)

7) Hoe groot is de weerstand van een tweedradige koperen leiding met een lengte van 5 km en een doorsnede van 4.10-6 m² ? (T = 15°C)

Indien deze draad een stroomsterkte voert van 20 A, wat is dan het verlies door joule-effect? Hoeveel elektrische arbeid of energie zal in deze leiding in warmte worden omgezet gedurende 24 uur?

Bereken de kostprijs per 24 uur van deze verloren energie, als men weet dat 1 kWh € 0,15 kost.

8) Een kabel met 2 aders is 15 m lang. De aderdoorsnede is 1,5 mm². Uw verbruiker slorpt 10 A. Bereken de warmte die in 1 uur ontwikkeld wordt.

9) Een verwarmingstoestel, 1650 W, wordt aangesloten op het stopcontact. Bereken de weerstand van dit toestel. Wanneer dit toestel 24 u continu zou verwarmen, wat zal dit kosten aan € 0,15 / kWh?

10) Hoeveel elektrische arbeid wordt er gedurende 1 uur in een elektrisch fornuis met 20 Ω weerstand omgezet in warmte als de spanning 100 V bedraagt? Hoe groot is het vermogen van dat fornuis.

11) Een generator levert een vermogen van 60 kW. Hoeveel energie levert die generator in 5 uur?

12) Een strijkijzer aangesloten op 200 V neemt een stroomsterkte op van 5 A. Hoe lang zal het strijkijzer ingeschakeld moeten blijven om een elektrische energie van 54000 J om te vormen? Berekenen eveneens het toegevoerde vermogen

13) De lichten van een auto hebben een vermogen van 60 W. De 12 V autobatterij heeft een capaciteit van 30 Ah. Hoe lang zal het duren voor de batterij ontladen is? Berekenen ook de hoeveelheid omgevormde energie.

14) Een toestel zet in twee minuten een elektrische energie om van 4200 J terwijl men een stroomsterkte meet van 0,5 A. Welke spanning staat over de klemmen van het toestel?

15) Men beschikt over een accumulator met de volgende gegevens: 12 V - 36 Ah. Hoe groot moet het vermogen van het lampje (12 V) zijn zodat de accu in 24 uur tijd volledig ontlaadt? Hoeveel elektrische energie is gedurende die tijd omgevormd

16) Hoeveel elektrische energie kan een batterij omvormen in een zaklamp als de spanning op de klemmen 4,5 V bedraagt en de stroomsterkte 0,4 A is gedurende 3 uur? Bereken ook de hoeveelheid elektriciteit die verplaatst wordt.

17) Een motor van een freesmachine levert een nuttig vermogen van 3,6 kW terwijl het net 4,5 kW toevoert. De kostprijs van 1kWh bedraagt € 0,15. Bereken het rendement, en de kostprijs als de motor 10 uren draait.

18) Een waterverwarmer van 4 kW is gedurende 8 uren aangesloten op een spanning van 230 V. Bereken de stroomsterkte, de weerstand van het verwarmingselement en de kostprijs van het verbruik. (1 kWh kost € 0,15).

19) Een generator wordt aangedreven waardoor een mechanische energie wordt toegevoerd van 10 000 J. Deze generator heeft een rendement van 80%. De elektrische energie die deze generator afgeeft wordt gebruikt als voeding een verwarmingsapparaat. Dit apparaat zet deze energie om in warmte met een rendement van 90%. Hoe groot is de toegevoerde energie aan het verwarmingsapparaat? Wat is het totale rendement van deze installatie?

20) Een centrale levert een spanning van 150 kV, 400A aan een verbruiker. Welk vermogen ontvangt de verbruiker als je de weerstand van de leidingen tussen centrale en verbruiker = 20. Wat is het rendement van deze situatie?

21) We willen een boiler van 10 l water van 18°C naar 60° C te brengen in 20 minuten. Hoeveel energie moeten we hier toevoegen voor een boiler met een  = 90%.

22) Een zonneboiler brengt in 8 uur een vat van 250 l van 17°C naar 75°C op een zomerdag. Hoeveel energie ontwikkelde de zon. Hoeveel bespaarde je als je rekent aan € 0,17 /kWh?. Wat is het rendement als je bedenkt dat om dit alles te laten functioneren een circulatiepomp gebruikt wordt van 50W.

23) Een motor van 15 kW wordt aangesloten op een 230V net. De leiding is 40 m. Wat is de doorsnede van de geleiders indien je maximaal 5% vermogenverlies toestaat.

12.3 Joule-effect

Wanneer er door een weerstand een stroom vloeit, wordt de elektrische energie omgezet in warmte energie. Dit verschijnsel heet het joule-effect. De vermogen die wordt omgezet in warmte kan worden bepaalt met volgende formule:

met

P: het vermogen gedissipeerd in de weerstand of joule-effect [W]

I : stroomsterkte [A]

R: weerstand [Ω]

Het vermogenverlies dat in de vorm van warmte verloren gaat noemt men ‘vermogenverlies door joule-effect’ P. Het maximaal dissipatievermogen PD van een weerstand geeft het maximaal toegelaten gedissipeerde vermogen door joule-effect aan. PD is de maximale grens van P. Indien men dit vermogen overschrijdt, kan de weerstand doorbranden. Uit het dissipatievermogen leidt men de maximaal toegelaten stroomsterkte door de weerstand af. Indien de stroom door de weerstand groter wordt dan IMAX, kan er beschadiging van de weerstand optreden. De stroom door de weerstand mag dus nooit groter zijn dan IMAX

Het dissipatievermogen PD van een weerstand is een vaste waarde, het vermogen P is afhankelijk van de stroom door de weerstand en de weerstandswaarde.

�� = �� ��

Met IMAX = de maximale stroom door de weerstand [A]

PD = maximaal toegelaten gedissipeerde vermogen door joule-effect [W]

R = de weerstand [Ω]

12.3.1

Oefeningen

1) Wat is de maximale stroom die mag vloeien door een weerstand waarvan het dissipatievermogen ¼ Watt is en een weerstandswaarde van 100 Ω.

2) Een tweeaderige koperen leiding van 20m lengte en 2.5mm² doorsnede voert een stroom van 15A. Welk vermogen gaat er verloren onder de vorm van warmte?

12.4 Invloed van de temperatuur op de weerstand

12.4.1 Temperatuurscoëfficiënt

De weerstand van een geleider is in het algemeen afhankelijk van de temperatuur. De temperatuurscoëfficiënt van een geleider is de weerstandsverandering ∆R per ohm beginweerstand RT1 en per graad temperatuurverandering ∆T.

De temperatuurscoëfficiënt wordt voorgesteld door het symbool α (alfa) en uitgedrukt in ° of

Als de weerstand toeneemt bij stijging van de temperatuur, is de temperatuurscoëfficiënt positief (positieve temperatuurscoëfficiënt : PTC).

Indien de weerstand vermindert met een toename van de temperatuur dan is de temperatuurscoëfficiënt negatief (negatieve temperatuurscoëfficiënt : NTC).

PTC- en NTC-weerstanden worden toegepast voor het meten van temperaturen, voor temperatuurcompensatie in elektronische schakelingen, voor temperatuurcontrole, in beveiligingskringen van elektrische machines, …

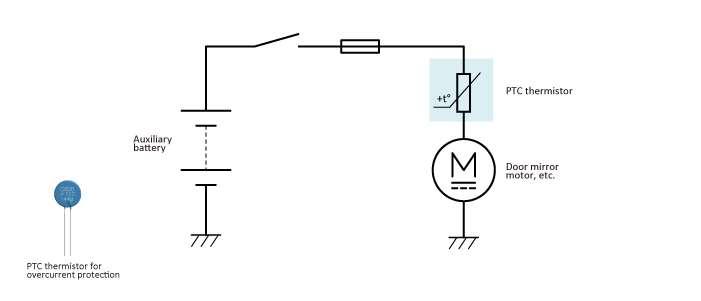
Beveiligingtegenoverstroom

12.4.2

Weerstand bij een bepaalde temperatuur

Als de temperatuur van een geleider of weerstand van 1Ω met 1 graad stijgt, is de weerstandsverandering ∆R gelijk aan α en bedraagt de eindwaarde 1 + α.

Indien de temperatuur stijgt met T graden bij een beginweerstand R0 bij 0K, dan zal de eindweerstand gelijk zijn aan:

Rt = R0 + R0 . α . (T – 0K)

Rt = R0 + R0 . α . T

Rt = R0 . (1 + α . T)

De weerstand Rt2 bij een temperatuur t2, in functie van de weerstand Rt1 bij een temperatuur t1 is:

Rt2 = Rt1 .

Voorbeeld:

Een geleider van zink heeft, bij 20 °C, een weerstand van 18 Ω. Bepaal de weerstand bij 60 °C bij een temperatuurscoëfficiënt α = 0,0039 .

R60 = 18Ω . , ° ° , ° °

R60 = 18Ω . , , = 20,605Ω

13 Schakelen van weerstanden

13.1 Soorten schakelingen

13.1.1 Serieschakeling

Twee of meer weerstanden staan in serie als het einde van de eerste weerstand verbonden wordt met het begin van de tweede weerstand en het einde van de tweede weerstand met het begin van de derde, enz.

Bij elke weerstand komt maar één draad toe en er vertrekt maar één draad uit.

De stroomsterkte is in de hele stroomkring gelijk.

13.1.2 Parallelschakeling

Twee of meer weerstanden staan in parallel wanneer je alle beginpunten met elkaar verbindt en ook alle eindpunten met elkaar verbindt.

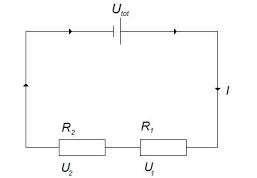
13.1.3

Gemengde schakeling

Dit is een combinatie van serie- en parallelschakelingen. Ze bevat altijd meer dan twee weerstanden.

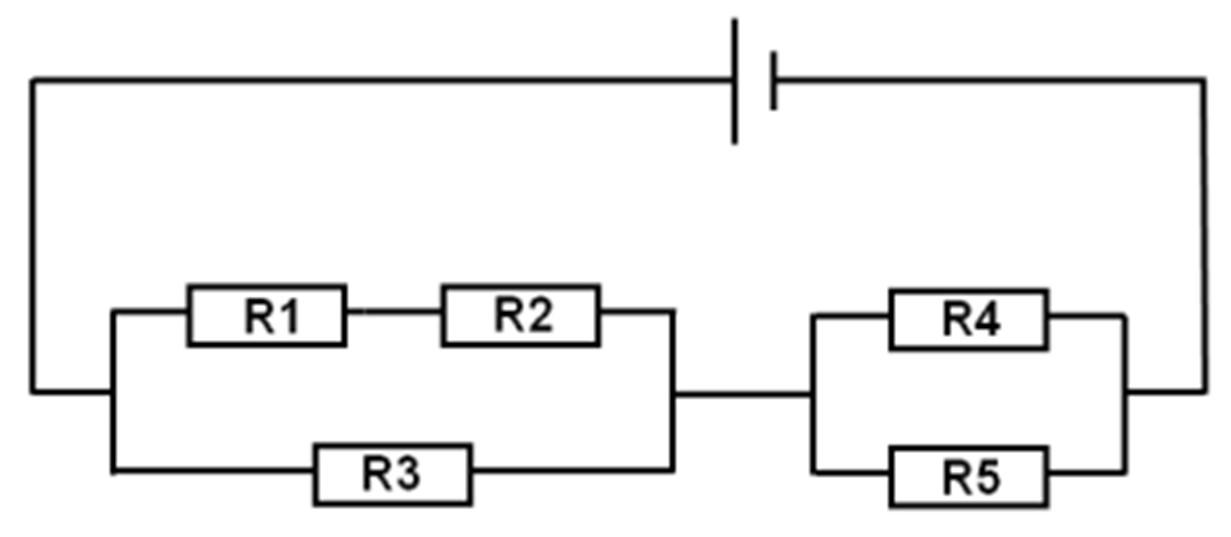
13.2 Vervangingsweerstand

Dit is één enkele weerstand die hetzelfde effect heeft als een de schakeling van meerdere weerstanden zonder de totale stroom en spanning verandert.

13.3 Spanningsverlies in een weerstand

Wanneer er stroom door een weerstand vloeit ontstaat er een spanningsverlies.

De stroom kan slechts vloeien ten koste van een spanningsverlies. Dit spanningsverlies is altijd gelijk aan: Uv = I x R

13.4 De serieschakeling

De verschillende weerstanden zijn hier in een onvertakte keten opgenomen

13.4.1 Labo

Je maakt opnieuw samen met jouw collega een labo waar we bepaalde zaken gaan meten.

De opdracht vindt je terug op Toledo.

13.4.2

Beschrijving en wetten

Als de kring gesloten is, vloeit er een stroom van de plus naar de min van de bron. Hij vloeit achtereenvolgens door al de weerstanden. De waarde van de stroomsterkte hangt af van de respectieve weerstanden. De stroomsterkte die aan de plus vertrekt, komt aan de min weer binnen. In de buitenketen is geen enkele splitsing (aftakking) mogelijk.

Bij een serieschakeling is de stroomsterkte overal constant.

Dat kan proefondervindelijk worden vastgesteld door een A-meter op verschillende punten in de keten te schakelen. De A-meter zal altijd dezelfde stroomwaarde aanduiden.

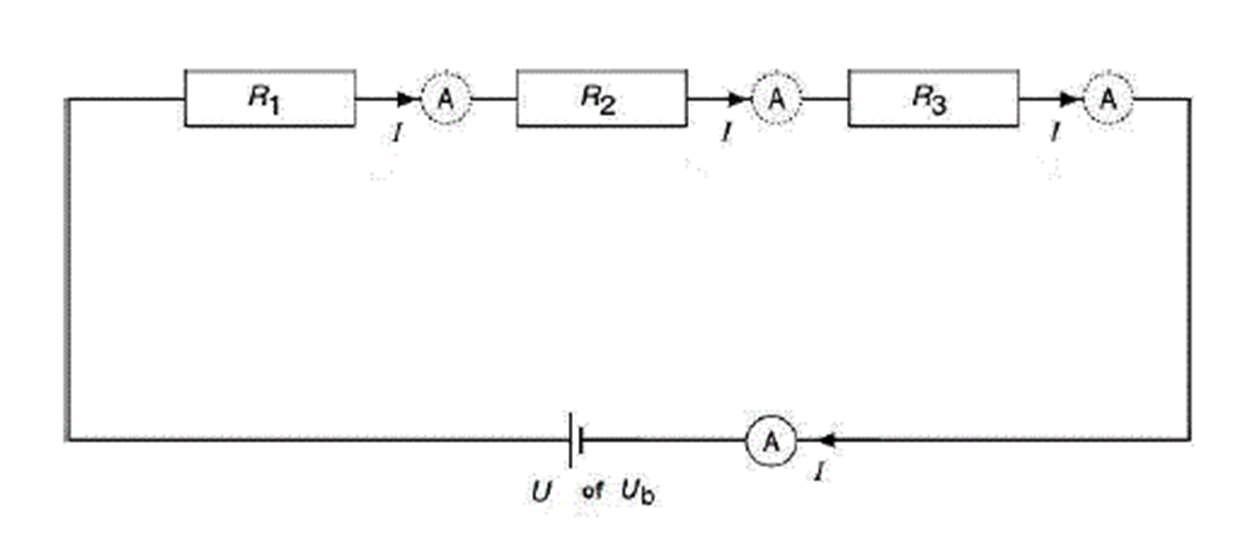
Om de stroomsterkte I door weerstand R, te sturen, is er een spanning U1 = R1.I nodig. Om diezelfde stroomsterkte door R2, R3... Rn te sturen, is er telkens een spanning U2 = R2.I, U3 = R3.I,... ,Un = Rn. I nodig (deelspanningen). Om de stroomsterkte door heel de serieketen te sturen, is er een totale spanning nodig die gelijk is aan

U = U1 + U2 + U3 +... + Un

Bij een serieschakeling is de totale spanning gelijk aan de som van de deelspanningen.

Dat kan proefondervindelijk gemakkelijk worden nagegaan door de totale spanning en al de deelspanningen met een voltmeter te meten.

U = U1 + U2 + U3 +.. + Un

U = R1.I + R2.I+ R3.I +... + Rn. I

U = I [R1 + R2 + R3 +... + Rn)

Die zelfde stroomsterkte, bij een spanning U wordt ook bekomen bij het plaatsen van 1 vervangingsweerstand Rv = R1 + R2 + R3 +... + Rn.

Deze weerstand is dan de vervangingsweerstand van de serieschakeling.

Bij een serieschakeling is de vervangingsweerstand gelijk aan de som van de in serie geschakelde weerstanden.

Bij gelijke weerstanden in serie geschakeld, is Rv = n. R1 en U = n. U1 (U1: de waarde van de spanning over een weerstand)

BasisElektrotechniek

13.4.3 Toepassingen

1) Vier weerstanden van respectievelijk 4 - 6 -10 en 12W, staan in serie geschakeld op een spanning van 230 V. Bereken de vervangingsweerstand, de stroomsterkte door elke weerstand en de spanning over elke weerstand.

2) Een gloeilamp met 120 W gloeiweerstand wordt in serie geschakeld met een R=30 W. Aan de klemmen van de gloeilamp heerst een potentiaalverschil van 48 V. Hoe groot is de stroomsterkte, de bronspanning en de vervangingsweerstand? Bereken het joule-effect dat in de weerstand ontwikkeld wordt.

3) Drie in serie geschakelde weerstanden van respectievelijk 5 - 10 en 15W worden doorlopen met een stroomsterkte van 2 A. Welke waarde duidt de V-meter, over de bron geschakeld, aan?

4) Een weerstand van 5 W is in serie geschakeld met een spoeltje van koperdraad dat 57 m draad van 0,3 mm² doorsnede bevat. De schakeling is aangesloten op een accumulator van 12 V. Bereken de stroomsterkte die de keten opneemt.

5) Voor een kerstboomverlichting worden een reeks lampjes van 6 V - 1 W geschakeld. Hoeveel lampjes moet je in serie schakelen deze verlichting aan te sluiten op de netspanning van 230 V? Welk vermogen zal de hele schakeling opnemen ? Bereken de stroomsterkte. Welk groot nadeel heeft zo een kerstboomverlichting ?

13.4.4 Voorschakelweerstand

Om de spanning over een toestel te verlagen door er een weerstand (voorschakelweerstand) mee in serie geplaatst.

Stel een verbruiker 8 V – 10 W moet worden aangeschakeld op een spanning van 12 V.

Om de spanning te verlagen, (12 V bron, 8V verbruiker) is het nodig er een weerstand Rv mee in serie te plaatsen.

De stroomsterkte ��= = = 0,8��

De spanning die de voorschakelweerstand zal moeten opnemen:

Uvoor = U - Uverb = 12 - 8 = 4 V

De voorschakelweerstand: �� = �� �� = 4 0,8 =5Ω

De voorschakelweerstand zal altijd voor een vermogenverlies zorgen (Joule-effect).

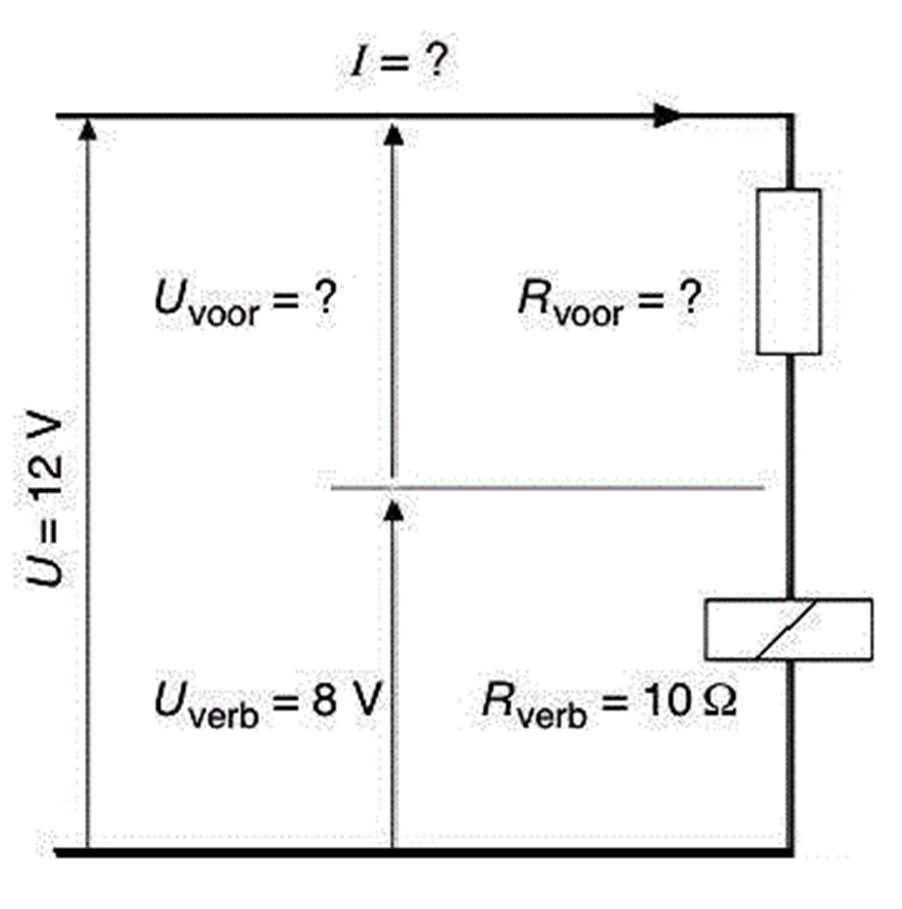
Meestal zal de voorschakelweerstand een relatief groot vermogen opnemen.

13.4.5 Schakelen met een voltmeter

Een voltmeter is een Ampèremeter met hoge voorschakelweerstand.

De V-meter meet het potentiaalverschil tussen de twee punten waarop hij aangesloten wordt en is gekenmerkt door zijn meetbereik. Het meetbereik is de maximumspanning die, zonder bijkomende hulpmiddelen op het toestel mag worden aangesloten.

Een A-meter zouden we als V-meter kunnen gebruiken tot een maximum meetbereik van

UA = RA. Ia. met Ia: max. meetstroom

Een A-meter moet een zo klein mogelijke weerstand moet hebben.

UA is ook een zeer kleine spanningswaarde.

Voor grotere spanningen wordt een weerstand mee in serie geplaatst.

De stroomsterkte Ia mag niet worden overschreden en bij maximum schaaluitslag zal de spanning: U = (Rv+RA).I

 Kies Rv = 9, 49, 99, 199... maal groter dan RA, dan worden spanningen gemeten tot U = (RA + 9 RA) Ia = 10 RA Ia = 10 UA 50 UA, 100 UA, 200 UA

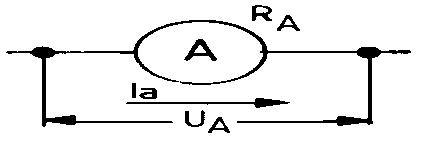
 Door de geschikte voorschakelweerstand te kiezen wordt het meetbereik van een voltmeter willekeurig groot gemaakt.

 Waarde van de inwendige weerstand:

Hoe groter het meetbereik, hoe groter de inwendige weerstand van een V-meter. Een Vmeter heeft altijd een hoge inwendige weerstand en wordt aangegeven in het aantal ohm (kW) per volt meetbereik (W/V).

 Meer meetbereik

De meeste V-meters bezitten verschillende meetbereiken. Dat wordt bekomen door verscheidene voorschakelweerstanden te gebruiken die met een keuzeschakelaar ingeschakeld worden.

 Ampéremeter

Een A-meter meet de stroomsterkte die door het toestel vloeit. Ook dit toestel is gekenmerkt door zijn meetbereik. Het is de maximumwaarde van de stroomsterkte die erdoor mag vloeien en waarmee de schaaleinduitslag overeenkomt.

Om de stroomsterkte die door een toestel gaat te meten, wordt de A-meter in serie met het toestel geschakeld. Hierdoor komt er een weerstand bij in de keten die de stroomsterkte doet dalen en een valse uitslag geeft.

Daarom moet de inwendige weerstand van een A-meter zo klein mogelijk zijn. Hoe groter het meetbereik, hoe kleiner de inwendige weerstand moet zijn.

13.4.6 Regelweerstanden

Dikwijls is het nodig de stroomsterkte in een keten te wijzigen of, wat op hetzelfde neerkomt, de spanning aan een toestel te verlagen. De regelweerstanden, die naar gelang van de toepassing van uitvoeringsvormenverschillen, worden in serie met de verbruiker geschakeld.

13.4.7 Schakelen van LED ’s

 Een LED is een lichtgevende diode die enorm frequent gebruikt wordt.

 Een LED heeft een hoge levensduur.

 De kleuren (rood, geel , groen, blauw, oranje) worden bepaald door het materiaal waaruit deze is opgebouwd.

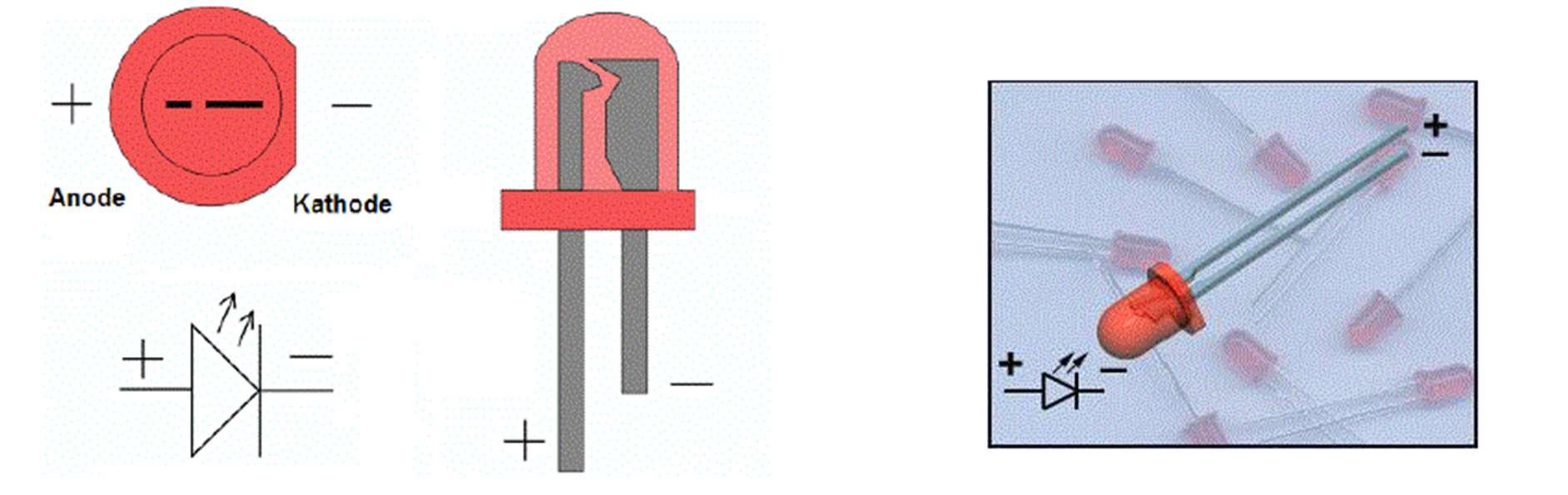
 Een LED geleidt de stroom enkel in de richting van de aangesloten pijl in het symbool. De aansluitklemmen: anode en kathode. De kathode (-) herken je aan de afgeplatte kant of aan de kortste aansluitdraad.

 Stroomverbruik is max 20 mA.

 De meest voorkomende spanning: Rood, Geel en Blauw: 2,3V.

Groen, Blauw en Wit 3,6 V. dit zijn geen courante spanningen waardoor altijd een voorschakelweerstand zal nodig zijn.

 Vb Rode LED aansluiten op 12V:

UR = 12 – 2,3 = 9,7 V

Rv = = , =485Ω

Praktisch wordt dit 560 

Het vermogen ontwikkeld in de Rv

I = = , =17,3����

PR = UR I = 9,7 V. 17,3 mA = 168 mW.

Het vermogen ontwikkeld in de LED

PL = UL I = 2,3 V. 17,3 mA = 40 mW. Nogmaals geldt dat een voorschakelweerstand het rendement naar beneden haalt.

 Bij tweekleurenLED s zijn in de LED -behuizing twee LED ’s geïntegreerd die een verschillende kleur, veelal rood en groen, hebben. Bij tweekleurenLEDs met twee pootjes verandert de kleur die de LED uitstraalt als je de polariteit van de spanning omdraait. Met drie pootjes kan elke mengkleur van rood en groen gemaakt worden door de stroom door de twee LED s apart te regelen (sturen).

 Er zijn ook LED s met meer dan twee kleuren op de markt, de RGB-LED . Door de Rode, Groene en Blauwe LED s aan te sturen kan je kleuren bepalen. (bv oplichting rood en groen geeft bruin licht) Ze worden toegepast in grote lichtkranten, in beeldschermen en in designmeubelen.

13.4.8 Oefeningen

1) Twee weerstanden R1 en R2 zijn in serie geschakeld tussen twee punten met een spanning van 108V. De spanning over R2 = 11W bedraagt 33V. Bereken R1 en de stroomsterkte door de keten.

2) Vier weerstanden staan in serie op een spanning van 150 V. R1: 18W, R2: zet in 20 s 40 J om in warmte, R3: lamp van 25 W opgenomen vermogen R4: onbekend.

De spanning aan de klemmen R2 is 10V. Bereken: R2, R3 en R4; de stroomsterkte, de vervangingsweerstand en het totaal ontwikkeld vermogen.

3) Een keten bevat vier weerstanden in serie. De eerste drie weerstanden zijn elk 32W. Als de totale spanning 80V is, vloeit er een stroom sterkte van 0,4A. Bereken de vierde weerstand.

4) Vijf weerstanden, respectievelijk 4- 5,5- 7- 8,5 en 10W zijn in serie geschakeld. De A-meter duidt een stroomsterkte aan van 3A.

Bereken:

De waarde van de deelspanningen.

De totale spanning.

Het vermogen in elke weerstand ontwikkeld.

5) Een voltmeter met 3 kW inwendige weerstand heeft een meetbereik van 3 V. Bereken de voorschakelweerstand nodig om het meetbereik uit te breiden tot 30 V.

6) De stroomsterkte door een weerstand van 2 W bedraagt 8 A. Deze wordt gemeten met een A-meter met 0,2 W Hoeveel zal de meetstroom bedragen? (De bronspanning is constant)

7) Drie weerstanden met de volgende karakteristieken staan in serie:

R1: 150 W - 50 mA, R2: 100 W - 75 mA en R3: 10 W-1 A. Welke spanning mag men aan heel de keten aanleggen? Bereken de spanningsverdeling.

8) Drie weerstanden R1= 22 W, R2 = 20,625 W en R3 zijn in serie geschakeld. De tweede weerstand geeft een hoeveelheid warmte van 99.104 joule af gedurende 50 minuten. De bronspanning bedraagt 200 V. Bereken de stroomsterkte, R3, de vervangingsweerstand en het totaal ontwikkelde vermogen.

9) Een voltmeter met Rv= 3 kW en een meetbereik van 3 V wil men met verschillende meetbereiken uitvoeren, namelijk voor 10 V – 30 V – 100 V – 300 V. Bereken de waarde van de respectieve voorschakelweerstanden.

Hoe zal men wordt de inwendige weerstand op het toestel aangegeven?

10) Om een motor van 3,2 kW nuttig vermogen aan te lopen, wordt een aanzetweerstand in serie geschakeld. De motor heeft een weerstand van 1 W en een rendement van 80 %. De aanzetstroom mag 2, 5 maal de nominale vollaststroom bedragen, terwijl de bronspanning 200 V is.

Hoe groot zal de aanzetweerstand zijn?

13.5 De parallelschakeling

De parallelschakeling is wellicht de meest gebruikte schakeling. Denk maar aan de stopcontacten op een zelfde kring in een huisinstallatie, de lampen van een luchter. Alle verbruikers in een woning staan parallel op het wisselstroomnet

Twee of meer weerstanden staan parallel als: Alle beginpunten liggen verbonden in een knooppunt langs de ene zijde. Alle eindpunten liggen verbonden langs de andere zijde.

13.5.1

Labo

Je maakt opnieuw samen met jouw collega een labo waar we bepaalde zaken gaan meten.

De opdracht vindt je terug op Toledo.

13.5.2

Beschrijving en wetten

Iedere weerstand staat over dezelfde bronspanning.

Bij een parallelschakeling is de spanning overal constant

U = U1 = U2 = U3

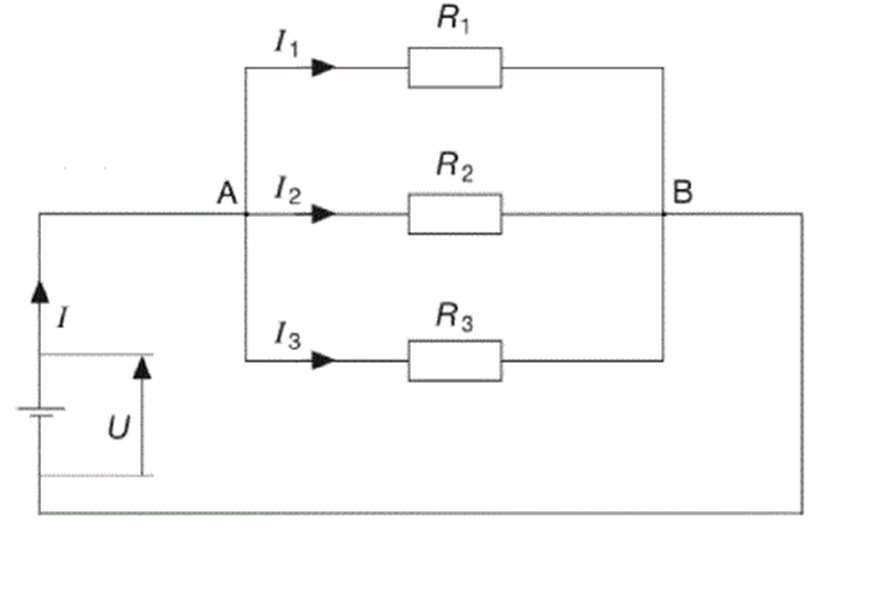
In knooppunt A zal de stroom I zich opsplitsen. Door iedere weerstand vloeit een gedeelte van de totale stroom I I1, I2 en I3 zijn de deelstromen.

In knooppunt B komen deze deelstromen weer samen en vormen terug de totale stroom.

I = I1 + I2 + I3

Bij een parallelschakeling is de totale stroom gelijk aan de som van de deelstromen.

Grootte van de deelstromen: �� = �� = �� =

Aangezien éénzelfde spanning staat over al de weerstanden, zal de grootste weerstand de kleinste stroom doorlaten. De deelstromen zijn omgekeerd evenredig met de waarde van de deelweerstanden.

M.a.w. als: R1 > R2 > R3 dan is I1 < I2 < I3

Hoe groot is de vervangingsweerstand ?

I = I1 + I2 + I3 +... In = + + +⋯..+

maar alle deelspanningen zijn gelijk = + + +⋯..+ alles delen door U levert

De vervangingsweerstand van een parallelschakeling is gelijk aan het omgekeerde van de som van de omgekeerden van de takweerstanden.

 Indien maar twee weerstanden in parallel staan, dan zullen de deelstromen zich verhouden als het omgekeerde van hun weerstandswaarden. = en ook = en =

 Indien maar twee weerstanden in parallel staan dan is �� = .

 Indien meerdere gelijke weerstanden parallel worden geschakeld dan is �� = met n het aantal weerstanden.

 Het bijschakelen van een weerstand zal de vervangingsweerstand altijd kleiner worden. De vervangingswaarde zal altijd kleiner zijn dan de kleinste weerstand. De totale stroom zal in altijd toenemen.

 De maximumspanning die over de klemmen van een weerstand mag staan is In R. Bij het parallel plaatsen van verschillende weerstanden in, met elk hun eigen nominale spanning.

De spanning die in dit geval aan de parallelschakeling mag worden aangelegd, is dan gelijk aan de kleinste nominale spanning van de weerstanden.

13.5.3 Oefeningen

1) Drie weerstanden, respectievelijk 2- 4 en 8  zijn in parallel geschakeld. De toegepaste spanning bedraagt 8 V. Bereken de vervangingsweerstand, de totale stroomsterkte en de stroomsterkte door elke weerstand.

Welk vermogen wordt er in het totaal ontwikkeld?

2) Vier weerstanden 18 - 12 - 6 en 20 W staan in parallel. Door de eerste vloeit 2 A. Bereken de vervangingsweerstand, de andere deelstromen, de totale stroomsterkte en de bronspanning.

3) De weerstanden van 60 - 40 en 15W staan parallel op een spanning van 75 V. Bereken deelstromen, hoofdstroom en vervangingsweerstand.

4) Drie weerstanden van 9 W zijn in parallel op een bron van 27 V geschakeld. Bereken vervangingsweerstand, deel- en hoofdstroom. Welk vermogen wordt hier omgezet in warmte?

5) Twee weerstanden, respectievelijk 6 en 3 W zijn in parallel geschakeld. De totaal opgenomen stroomsterkte bedraagt 10,5 A. Bereken de spanning over elke weerstand en de deelstromen.

6) Twee weerstanden, respectievelijk van 50 en 27,5 W worden parallel geschakeld op een spanning van 110 V. Er wordt een derde bijgeschakeld om een stroomsterkte van 10A af te nemen.

Hoe groot moet deze weerstand zijn?

7) Twee weerstanden R1 en R2 zijn in parallel geschakeld op een spanning van 12 V. De totale opgenomen stroomsterkte bedraagt 2,5 A en R1 = 8 W. Hoe groot is de tweede weerstand?

13.5.4 De ampèremeter met shunt of nevensluiting

Een shunt is het middel om het meetbereik van een A-meter uit te breiden. Door de A-meter mag niet meer stroom vloeien dan het meetbereik toelaat. Om een grotere stroom te meten met hetzelfde toestel, dan moet de overtollige stroom via een shunt (nevensluiting) worden afgevoerd.

De stroom Ish = I - Ia

 Hoe groter het meetbereik wordt, hoe kleiner Rsh moet zijn. Dat heeft voor gevolg dat het toestel met het grootste meetbereik de kleinste inwendige weerstand bezit.

 De nevensluitingen of shunts kunnen zowel inwendig als uitwendig zijn (een uitwendige shunt heeft zijn geijkte aansluitsnoeren).

 De inwendige weerstand van een A-meter is altijd zo klein mogelijk. Vandaar dat de weerstand van de aansluitsnoeren hier niet meer verwaarloosd mag worden. Elke A-meter heeft zijn eigen shunts en indien de Rsh uitwendig moet worden aangesloten, gebeurt dat met dezelfde snoeren waarmee het toestel geijkt werd.

 Een eenvoudige en goedkope manier om een grote stroom van een elektrisch net af te nemen bestaat uit een reeks gloeilampen (vermogen kan willekeurig worden gekozen) die in parallel geschakeld zijn en afzonderlijk kunnen worden in- en uitgeschakeld. Dit is een lampenweerstand.

Bij het bijschakelen zal de vervangingsweerstand telkens verkleinen, waardoor de totale stroomsterkte toeneemt.

 In een huisinstallatie worden alle stopcontacten in parallel geschakeld. De lampen van eenzelfde verlichtingsarmatuur staan praktisch altijd in parallel.

13.5.5 Oefeningen

1) Vier weerstanden 6 W - 400 mA, 30 W - 300 mA, 6 W - 200 mA en 25 W - 60 mA worden in parallel geschakeld. Wat is de grootste spanning voor deze schakeling?

2) Een luchter met zes gloeilampen van 60 W - 220 V staan in parallel. Bereken de vervangingsweerstand.

3) Twee weerstanden van 18 W en 40 W zijn in parallel geschakeld. De hoofdstroom is 12 A. Bereken de deelstromen.

4) Drie weerstanden R1 = 20 W, R2 = 40 W en R3 zijn in parallel geschakeld op een spanning van 230 V. De netstroom bedraagt 20 A. Bereken de deelstromen en R3.

5) Hoe zal een stroomsterkte van 10 A zich verdelen over drie weerstanden van 120, 300 en 500 W?

6) Van een A-meter met meetbereik 10 mA en 20 W inwendige weerstand wordt het meetbereik uitgebreid met een universele shunt. De shuntweerstanden zijn R1 = 4 W, R2 = 2 W en R3 = 5 W.

Hoe groot zullen de verschillende meetbereiken zijn?

7) Men wil een generator van 110 V - 3300 W nuttig vermogen volledig belasten. Een belastingsweerstand 4 x 20 W en lampenweerstanden met lampen van 40 W worden geschakeld.

Hoeveel lampen zijn er nodig?

8) Om een generator met klemspanning 230 V te belasten, worden 5 lampen van 200 W – 230 V, 5 lampen van 100 W - 230 V, 10 lampen van 60 W - 230 V, en 5 lampen van 40 W - 230 V geschakeld.

Het rendement van de generator is 83 %. Bereken het toegevoerd vermogen op de as van de generator.

13.6 De gemengde schakeling

 Een gemengde schakeling bevat meer dan twee weerstanden.

Het is een combinatie van serie- en parallelschakelingen. In dit schema staan R1 en R2 in serie. R3 staat ermee parallel.

 In principe zijn deze altijd te herleiden naar 5 basisconfiguraties:

 In elk van de gevallen zal de vervangingsweerstand en de stroomverdeling anders zijn.

 Voor het oplossen zijn geen bijkomende formules vereist. Enkel inzicht en kennis van de formules van serie- en parallel schakelen kunnen helpen bij het oplossen.

13.6.1 Labo

Je maakt opnieuw samen met jouw collega een labo waar we bepaalde zaken gaan meten.

De opdracht vindt je terug op Toledo.

13.6.2 Voorbeeld met berekeningen

 R1 = 600  , R2 = R3 = R4 = R5 = R6 = 100  en R7 = 200 . U = 90V

 Door iedere weerstand loopt een stroom, over iedere weerstand staat een spanning. De deelstromen en de -spanningen worden genummerd zoals de weerstand.

 R2 en R3 staan in serie. Ze worden vervangen door R23 = 200 

 Ook R4, R5 en R6 staan in serie , zij worden vervangen door R456 = 300  zodat het schema kan worden hertekend als:

 R1, R23 en R456 staan in parallel en worden vervangen door R123456 = 100  waardoor het schema wordt hertekend als.

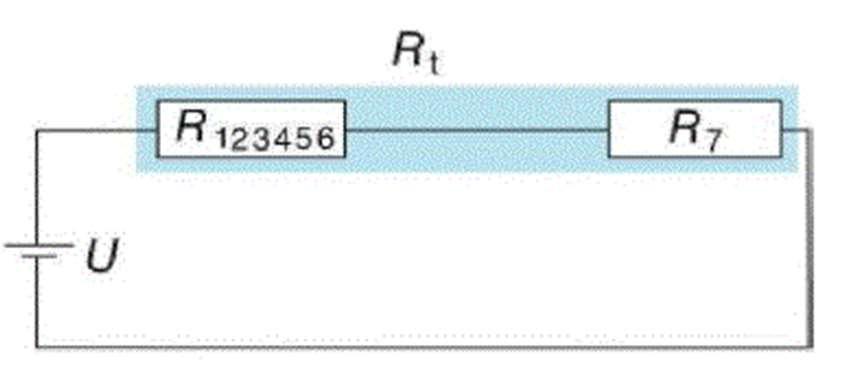
 R123456 en R7 staan in serie en worden vervangen door Rt = 300 Ω

 De stroom I vloeit door R123456 en R7 of I = I7 = 0,3 A.

 De spanning over R7 : U7 = 60 V.

 De spanning over het parallelle deel of over R123456 = 30V.

 U1 = U23 = U456 = 30V

 I1 = 50 mA.

 I2 = I3 = I23 = 150 mA

 I4 = I5 = I6 = I456 = 100 mA.

 U2 = U3 = 15V

 U4 = U5 = U6 = 10V.

 P1 = 1,5 W

 P2 = P3 = 2,25 W

 P4 = P5 = P6 = 1 W

 P7 = 18 W

 Totale vermogen P = 27 W

13.6.3 Toepassingen

1) Bereken voor deze schakeling de vervangingsweerstand. Alle stromen. De deelspanningen.

2) Een elektrisch verwarmingstoestel bevat vier parallel geschakelde weerstandsspiralen van chroomnikkeldraad met elk een weerstand van 32 W. De middellijn van de weerstandsdraad is 0,5 mm. Het toestel wordt aangesloten op een leiding (twee draden) die zelf 1 W totale weerstand heeft als de bronspanning 230 V is.

Bereken de stroomsterkte in de toevoerdraad, de lengte van de chroomnikkeldraad op elke spiraal (r = 1,4 x 10-6 Wm), de spanning aan de klemmen van het toestel en het vermogen

door het toestel opgenomen, de kostprijs van de totale omgezette elektrische energie gedurende 24 uur als 1 kWh € 0,15 kost.

3) 6 gloeilampen van elk 100 W - 220 V worden gebruikt als belasting van een generator. Bereken de generator (I en U) die nodig is om de lampen normaal te voeden voor volgende schakelingen:

3 parallel geschakelde groepen heeft van telkens 2 lampen in serie. of 2 parallel geschakelde groepen heeft van telkens 3 lampen in serie.

4) Bereken voor deze schakeling de vervangingsweerstand, alle stromen en alle deelspanningen.

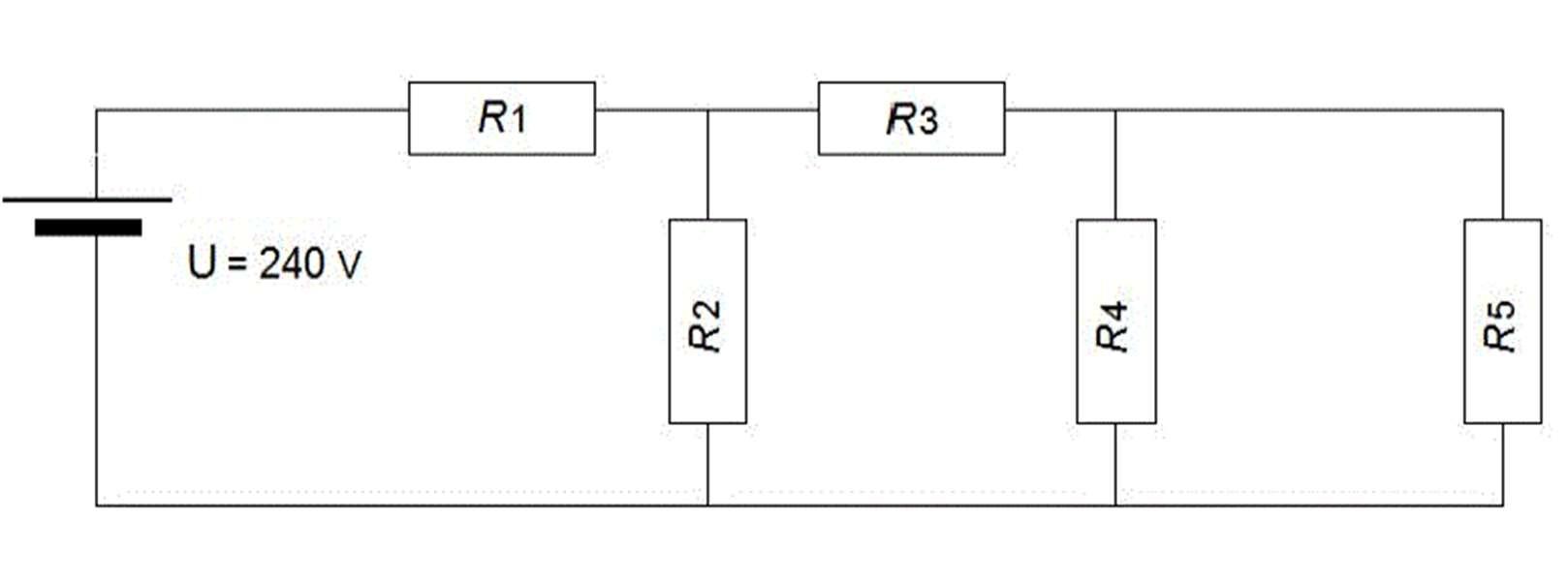
5) Bereken de bronspanning en de vervangingsweerstand.

6) Bereken de bronspanning, de vervangingsweerstand, deelstromen en deelspanningen.

Hoeveel seconden is de schakeling in gebruik om 6 Wh te verbruiken?

13.6.4 Weerstand meten met volt- en ampèremeter

Volgens de wet van Ohm geldt dat I U R  met

U: spanning over de weerstand; te meten met een V-meter.

I: stroomsterkte door de weerstand; te meten met een A-meter

Schakeling 1: Met de voltmeter de spanning U over de weerstand meten.

Met de A-meter wordt niet de stroom door de weerstand, maar wel de totale stroomsterkte I' gemeten.

Op deze manier bekom je niet de exacte R waarde.

De A-meter geeft I' = I + Iv, zodat I = I' – Iv Iv I U I U R   ' U en I' worden afgelezen op de toestellen.

Iv: de voltmeterstroom kan worden berekend wanneer de inwendige weerstand bekend is.

v v R U I 

De juiste waarde van de weerstand v R U I U R  '

 Als Rv groot is, zal Iv verwaarloosbaar zijn voor minder nauwkeurige gevallen. Mits het toestaan van een kleine fout worden beide meetwaarden gewoon door elkaar gedeeld ' I U R 

 De elektronische V-meters (analoge en digitale) hebben een zeer grote inwendige weerstand. Praktisch wordt dan met de V-meterstroom geen rekening gehouden.

 Hoe groter Rv is t.o.v. R, des te kleiner de fout wordt.

Schakeling 2

Met de A-meter de stroom door de weerstand meten.

De V-meter echter meet niet de spanning over R, wel over R + Ra namelijk U' = U + Ua, waaruit

U= U’ - Ua

Beide meetresultaten door elkaar delen levert opnieuw een foutief resultaat.

Het juiste resultaat

U' en I zijn de waarden op de toestellen, Ra: inwendige weerstand van de A-meter.

 Indien de meetwaarden gedeeld worden door elkaar is er een fout gemaakt. Ra is klein en kan in vele gevallen worden verwaarloosd.

 Een A-meter heeft altijd een weerstand, zodat er altijd een correctie (berekening) moet worden toegepast, als je het resultaat nauwkeurig wilt kennen.

 Hoe groter de meetweerstand R is, des te kleiner zal de foutieve invloed van Ra worden.(Bij grote weerstanden is de meetfout meestal verwaarloosbaar.)

13.6.5 Regelbare spanningsdeler (potentiometer)

Onbelaste spanningsdeler:

Onbelast is deze schakeling een in serie schakelen van 2 weerstanden. De spanning over R2 wordt gezien als de uitgangsspanning.�� =��

Voor �� =�� dit is de potentiometrische formule waaruit nogmaals blijkt dat de spanning zich evenredig verdeelt.

Stel nu dat U = 20V en over de uitgangsspanning met 12 V zijn (U2 = 12 V)

R1 = 1 k

Dan blijkt dat R2 = 1,5 k. en I = 8 mA.

Belast spanningsdeler

Over R2 wordt een extra weerstand geplaatst, de belastingsweerstand. Wat is het effect?

Stel dat er in vorige schakeling een belasting wordt geschakeld van Rb = 300 

Dan is R2b = 250 . waardoor Rv = 1250 

I = 16 mA.

U1 = 16 V en U2 = 4V

Wat als Rb = 1 k, 10 k , 0 ?

De volgende berekeningstabel tracht een duidelijk inzicht te geven in de spanningsregeling voor verschillende belastingsweerstanden.

Hoe groter de belasting hoe meer de uitgangsspanning daalt.

Onbelaste spanningsdeler met potentiometer

Bij een potentiometer sluit je de ingangsspanning aan op klemmen a en c,. Met de loper b ontstaat een regelbare spanning tussen a en b, maar ook tussen b en c. Als uitgangsspanning wordt gekozen voor b en c.

Dit levert een identiek schema als bij de onbelaste spanningsdeler. R1 = Rab en R2 = Rbc

Wanneer we deze schakeling belasten met Rb.

Dan geldt:

13.6.6 Oefeningen

1) Bereken de inwendige weerstand van de V- en A- meter bij deze situatie.

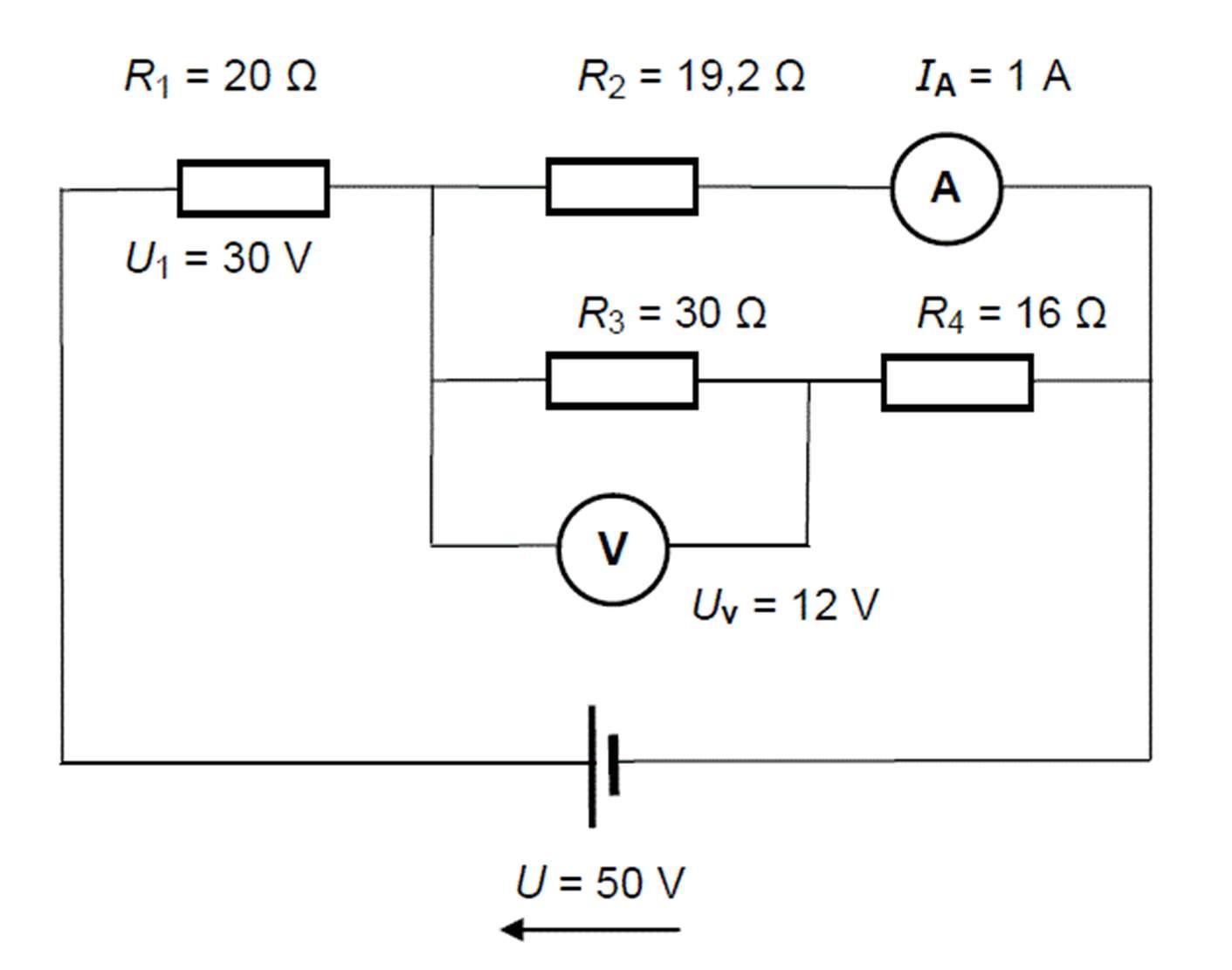
Bereken de totale

I5 en I6, U2 en U4 en Rv

2)

stroom,

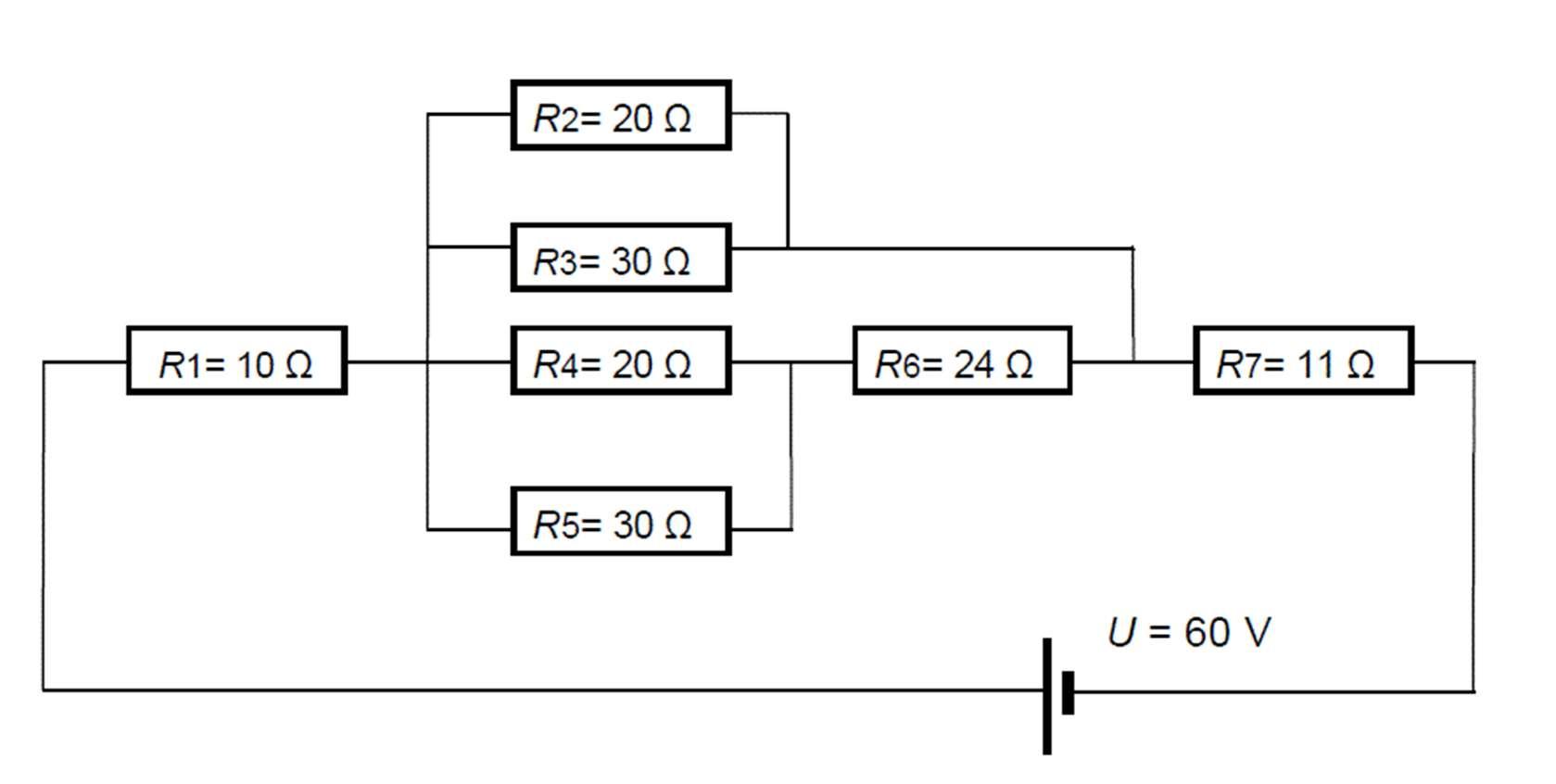
3) Bereken Rv, U en I

4) Bereken Rv, U, I en I5

5) Op een voedingsbron worden volgende verbruikers aangesloten: een kerstboomverlichting van 20 lampjes in serie, elk met een vermogen van 2 W onder een spanning van 10 V.

Een luchter met 15 lampen van 25 W - 200 V in parallel. Een verwarmingselement van 500 W - 200 V.

Bereken de vervangingsweerstand van de schakeling en de stroomsterkte die in het totaal door de bron moet worden geleverd.

6) Bereken voor de situatie U = 10 V en Rac = 1 k

De uitgangsspanning bij de stand 0, ¼, ½ , ¾ en 1. Voor de onbelaste situatie, en voor de belaste situatie met Rb= 1 k en Rb = 100 

Bibliografie

Basis elektronica

Geschreven door I. Maesen, R. Peeters, E. Vranken

Uitgegeven door Wolters Plantyn.

Elektriciteit 1 van de serie elektrotechniek

Geschreven door L. Claerhout

Uitgegeven door Wolters Plantyn.

Leerpakket elektriciteit leerboek A-1

Geschreven door K. Standaert en P. Hemelryck

Uitgegeven door De Boeck

Syllabus e-learning netsystemen van Volta

Brochure huishoudelijke elektrische installaties Editie 2020 uitgegeven door Vincotte.

Project huisinstallatie, Elektriciteit theorie en lab proefondervindelijk deel 1 en 2

Uitgeven door Plantyn

Project huisinstallatie, Naslagwerk

Uitgeven door Plantyn

Project huisinstallatie, Installatiemethoden en praktijk Elektriciteit projectmatig deel 1 en 2

Uitgeven door Plantyn

Elektrotechniek: Oefenenbundel geschreven door Ronny Mees & Tom Scharlaken (VIVES)

Basic Electricity 1 geschreven door Jurgen Boterberge (VIVES)

Basic Electricity 1 geschreven door Tom Deuninck (VIVES)

Sommige figuren komen van het internet.

Bijlagen