LIZENTZIA PROIEKTU DIGITALA DAUKA

BATXILERGOA 2
Ana
José Colera J., M.ª José Oliveira G., Ramón Colera C., Rosario García P.,
MATEMATIKA GIZARTE ZIENTZIETARA APLIKATUTA II Aicardo B.
Munduahelburu
12HILEKO

I.
1. Ekuazio linealen sistemak
2. Ekuazio linealen sistema baten soluzio posibleak
3. Sistema mailakatuak
4. Gaussen metodoa
5. Ekuazio-sistemen eztabaida
Ariketak eta problemak
Autoebaluazioa
2 Matrizeen aljebra
1. Nomenklatura. Definizioak
2. Eragiketak matrizeekin
3. Matrizeen arteko eragiketen propietateak
4. Matrize karratuak
5. Zenbaki errealen n-koteak
6. Matrize baten heina
7. Ekuazio-sistema baten forma matriziala
Ariketak eta problemak
Autoebaluazioa
3 Sistemak determinante en
1. Matrize karratu baten determinantea
2. Minor osagarria eta adjuntua
3. Determinantea lerro bateko
elementuetatik abiatuta garatu
4. Matrize baten heina, minorretatik abiatuta
5. Sistema bat bateragarria den jakiteko irizpidea
6. Cramerren erregela
7. Sistema homogeneoak
8. Sistemak determinanteen bidez eztabaidatu
9. Matrize baten alderantzizkoa kalkulatu
Ariketak eta problemak
Autoebaluazioa
4 Programazio lineala
1. Zer den programazio lineala. Adibide batzuk
2. Bi aldagairako programazio lineala. Enuntziatu orokorra
Ariketak eta problemak
Autoebaluazioa
Unibertsitatera sartzeko probarako: I. multzoa
I. multzoaren autoebaluazioa
II. MULTZOA. Analisia
5 F untzioen limiteak.
Jarraitutasuna
1. Funtzioen limiteen ideia grafikoa
2. Limiteen eragiketa errazak
3. Indeterminazioak
4. Infinituen konparazioa. Limiteetan erabiltzea x → ±∞ denean
5. Limiteen kalkulua x → +∞ denean
6. Limiteen kalkulua x → –∞ denean
7. Funtzio baten limitea puntu batean. Jarraitasuna
8. Limiteen kalkulua x → c denean
9. L’Hôpitalen erregela
Ariketak eta problemak
Autoebaluazioa
6 Deribatuak
1. Funtzio baten deribatua puntu batean
2. Funtzio deribatua
3. Deribazio-erregelak
Ariketak eta problemak
Autoebaluazioa
100
124
150
Aurkibidea Ikasturteko oinarrizko jakintzak I kaskuntza-egoeren aurkezpena 8 0 Problemak ebatzi 12 • Estrategia batzuen azterketa Praktikatzeko problemak
MULTZOA.
Ekuazio-sistemak. Gaussen metodoa 26
Aljebra 1
46
bidez ebaztea
74
7 Deribatuen erabilerak 168
1. Kurba batekiko zuzen ukitzailea
2. Funtzio baten goratzea eta beheratzea puntu batean
3. Funtzio baten maximo eta minimo erlatiboak
4. Bigarren deribatutik ateratako informazioa
5. Funtzioen optimizazioa
Ariketak eta problemak
Autoebaluazioa
8 Funtzioen adierazpena
1. Kurbak eraikitzeko oinarrizko elementuak
2. Balio absolutua funtzioen adierazpenean
3. Funtzio polinomikoen adierazpena
4. Funtzio arrazionalen adierazpena
5. Beste funtzio mota batzuen adierazpena
Ariketak eta problemak
Autoebaluazioa
11 La gin estatistikoak 268
1. Laginen zeregina
2. Zelakoak izan behar dira laginak?
3. Zorizko laginketa motak
4. Populazio finitu batetik zorizko laginketa bat lortzeko teknikak
5. Laginak eta estimatzaileak
Ariketak eta problemak
Autoebaluazioa
188
9 In tegral mugatua 214
1. Jatorrizkoak. Kalkulurako oinarrizko erregelak
2. Kurba baten azpiko azalera.
3. «Kurba baten azpiko azalera» funtzioa
4. Kurba baten eta X ardatzaren arteko azalera kalkulatzea
5. Bi kurbaren arteko azalera kalkulatzea
Ariketak eta problemak
Autoebaluazioa
Unibertsitatera sartzeko probarako: II. multzoa
II. multzoaren autoebaluazioa
III. MULTZOA. Estatistika eta probabilitatea
10 Zo ria eta probabilitatea 244
1. Zorizko saiakuntzak. Gertaerak
2. Maiztasuna eta probabilitatea
3. Laplaceren legea
4. Probabilitate baldintzatua. Gertaera askeak
5. Proba konposatuak
6. Probabilitate osoa
7. «A posteriori» probabilitateak. Bayesen formula
Ariketak eta problemak
Autoebaluazioa
12 Inferentzia estatistik oa.
1. Banaketa normala. Oinarrizko teknikak berrikusten
2. Tarte bereizgarriak
3. Lagin-batezbestekoen banaketa
4. Zer da estatistika inferentziala?
5. Batezbestekorako konfiantza-tartea
6. Konfiantza-mailaren, errore onargarriaren eta laginaren tamainaren arteko erlazioa
7. Zertan datza hipotesi estatistikoaren test bat?
Ariketak eta problemak
13
1. Banaketa binomiala. Laginketarako oinarrizko teknikak
2. Lagin-proportzioen banaketa
3. Proportzio edo probabilitate baterako konfiantza-tartea
4. Proportzio baterako hipotesi-egiaztatzea
Ariketak eta problemak
Autoebaluazioa
Unibertsitatera sartzeko probarako: III. multzoa
III. multzoa autoebaluazioa
Batezbestekoaren estimazioa 282
Autoebaluazioa
Inferentzia estatistik oa. Proportzio baten estimazioa 308
Eranskina A utoebaluazioen soluzioak 326
Honelakoa da zure liburua
Hasteko
Problemak ebatzi

Liburua hastean aurkituko duzun lehenengoa da problemak ebazte unitate bat.
Zer da benetako problema bat? Dagoeneko hainbat ikasturtetan ikusiko zenuenez, zure liburuan problemak ebatzi izeneko atala agertzen da. Atal horretan, problema berezi batzuk lantzen dira, problema bitxiak. Horiek ebazteko, garrantzitsuena ez da asko jakitea; horiek ebazteko, garrantzitsuena ondo pentsatzen jakitea da. Benetako problema horiek argi eta garbi bereizten dira ariketa soiletatik. Aurrean benetako problema bat daukagunean, gutxi gorabehera badakigu egoera horretan nora joan nahi dugun, baina ez dakigu nola iritsi. Hain zuzen ere, hori izango da zailtasunik handiena: egoera argitzea eta helburura eramango gaituen bide egokiren bat aurkitzea. Benetako problemak ebazten jakiteko, trebea izan behar da oso. Baina hori pazientzia eta ekina izanda lortzen da: ausarta izan eta hainbat eratako problemak landu behar dira, eta horietatik guztietatik ahalik eta onunarik handiena ateratzen ahalegindu behar dugu, ebaztea lortu zein lortu ez. Hurrengo orrialdeetan, problemak ebazten lagunduko dizuten pentsamenduestrategia batzuk emango dizkizugu. Lan horri begira emaitza onak izaten dituzten jokatzeko moduak dira. Horrez gainera, ageri diren ariketek estrategiak errazago landu eta barneratzen lagunduko dizute. Atal honetan proposatu diren problemetako batzuk errazak irudituko zaizkizu; beste batzuk, ez hain errazak; eta beste batzuk, berriz, oso-oso zailak. Baina denetatik aterako duzu probetxua eta, beharbada, probetxurik handiena zailenak iruditu zaizkizun horietatik lortuko duzu, pentsatzeko bide eta metodo gehiago saiatu beharko baitituzu. Ez dezazula pentsatu problemak ebazten egiten duzun denbora alperrekoa dela. Ebaztea lortzen ez baduzu ere, denbora hori ondo baino hobeto erabilitakoa izango da beti. Problemen ebazpenean ageri diren etapak Problema ulertzea Arretaz irakurri behar dugu. Zenbait kasutan, eskema bat erabiliko dugu. Argi izan behar dugu zer dakigun, zer eskatzen zaigun eta baldintzak zein diren. Ebazte-plan bat pentsatzea Hau da faserik zailena. Problema asko ebazteak ondorio argi bat du: baliabide egokiak bereganatuko ditugu problema berriak trebe ebazteko. Problemak ebazteko estrategiak atalean baliabide horietako batzuk deskribatzen dira. Pentsatutako plana gauzatzea Plana ondo pentsatuta badago, aurrera ateratzea eta emaitza lortzea nahiko erraza izaten da. Dena dela, normalena izaten da aldez aurretik pentsatutako bidea moldatu eta plana egokitu behar izatea.

Eduki-multzoak
sartzeko probarako
Estatistika eta probabilitatea
Eduki-multzo bakoitzaren amaieran unibertsitatera sartzeko proba prestatzeko argibideak aurkituko dituzu.
Badakizu estimatzen µ batezbestekoaren balioa – lagin-batezbestekotik abiatuta, banaketa normalaren bidez?
Problemei aurre egiteko jarraibideak eta urratsak emango dizkizugu.
Ariketen eta problemen adibideak Unibertsitatera sartzeko ebaluazio-proban hainbat zailtasun motatako ariketak eta problemak topatu ditzakezu.
Hainbat estrategia erakutsiko dizkizugu, eta estrategia horiek erabiltzeko problemak planteatuko dizkizugu.
dela ikusi dugu. Lortu pilates eskolen hileko batezbestekoa, μ, estimatzeko konfiantza-tartea % 99,2an. b. Zehaztu ausazko lagin sinple batek gutxienez izan beharko lukeen lagin-tamaina, batezbestekoaren estimazioan egindako errore maximoa, gehienez ere, 3 eurokoa izan dadin, % 95eko konfiantzarekin.
Eduki-multzo bakoitzaren amaieran autoebaluazio luze bat aurkituko duzu, multzoko unitate guztien edukiak berrikusteko.
Problema hauek ebazteko behar izan diren teknikak ezkerrean berrikusita ageri direnak dira. anayaharitza.es webgunean hau aurkituko duzu: Probabilitaterako oinarrizko teknikak ikasteko bide bat, arintasuna eskuratu dezagun teknika horiek ulertzeko, erabiltzeko eta aplikatzeko. Unibertsitatera sartzeko proben problema-bilduma bat, ebatzitakoak, proposatutakoak, laguntza eta guzti emanda, jarraibideak emanda…
Multzoko autoebaluazioa
Anek, Beak eta Nireak herentzia bat banatu behar
Hemen, unibertsitatera sartzeko probetan agertzen diren eduki batzuen azalpen labur bat ikusi ahal izango duzu, aurreko urteetako ariketa eta problema batzuekin batera.
€ gutxituz gero. 15 Hipermerkatu batek 6 kaxa sagar, 8 kaxa madari eta 10 kaxa laranja behar ditu gutxienez. Horretarako, fruta kontainerretan ekartzen dioten A eta B bi hornitzaile erabil ditzake. A-ko kontainer bakoitzean 1 kaxa sagar, 2 kaxa madari eta 1 kaxa laranja etortzen dira, eta 60 € balio du; B-ko kontainer bakoitzean, berriz, 1 kaxa sagar, 1 kaxa madari eta 5 kaxa laranja etortzen dira, eta 75 € balio du. Kalkulatu zenbat kontainer eskatu behar dizkion hipermerkatuak hornitzaile bakoitzari, behar duenari ahalik eta kosturik txikienarekin erantzuteko, eta zenbat izango den kostu hori.
Liburua hiru multzotan banatuta dago: Aljebra; Analisia; Estatistika eta probabilitatea.
Autoebaluazioa I. multzoa: Aljebra anayaharitza.es 5. Funtzioen limitea. Jarraitutasuna 6. Deribatuak. Deribazio teknikak 7. Deribatuen erabilerak 8. Funtzioen adierazpena 9. Integralak ANALISIA II. multzoa Egiaztatu honako sistema hauek bateragarriak diren, eta interpretatu geometrikoki: a) xy xy z xy 6 32 20 ––+= * b) xy xz yz 21 27 3 –2 Ebatzi eta interpretatu geometrikoki. a) xy xy 2 2 1 23 37 –– * b) xy z 2 23 4 –3 Kalkulatu -ren eta b-ren zer baliotarako egiaztatzen den M aM bI 0 berdintza, M 2 2 5 eo izanik; identitate-matrizea, eta 0 matrize nulua. 4 A 1 3 3 1 eo B xy 15 fp matrizeak izanda, aurkitu -ren eta -ren zer baliorekin diren matrizeak trukakorrak; hau da, zer baliorekin egiaztatzen duten A B B A 5 Aztertu M 1 2 4 2 3 1 3 0 6 0 1 ––fp matrizearen heina parametroaren balioen arabera. 6 Bakandu X matrizea BXB B X + A ekuazioan. 7 Matrize hau daukagu: A 1 1 –1 fp a) -ren zer baliorekin da alderantzikagarria? b) A bada hiru ezezaguneko hiru ekuazio dituen sistema homogeneo baten matrizea, ebatzi 0 kasurako. 8 M matrizea hiru ordenakoa da, horren errenkadak E E dira, eta det ( = –2 da. Zein izango da 2 E E3 errenkadak dituen matrizearen determinantea? Arrazoitu erantzuna. 9 Eztabaidatu sistema hau a-ren balioen arabera, ebatzi posible denean eta interpretatu geometrikoki kasu bakoitza: () 2 3 2 += * 10 Matrize hauek ditugu: A 1 2 0 0 eo B 1 1 0 2 eo C 10 11 7 eo a) Aurkitu B matrizearen alderantzizkoa. b) Aurkitu honako hau egiaztatzen duten X eta Y matrizeak: AX BY C AX Y * 11
dute, honela: Anek jaso behar du beste biek jasotakoaren batezbestekoa gehi 3 € Beak, beste biek jasotakoaren batezbestekoa, eta Nireak, beste biek jasotakoaren batezbestekoa ken 3 000 € a) Zenbat diru gehiago jaso behar du Anek Beak baino? b) Herentzia 99 000 €-koa bada, zenbat jasoko du bakoitzak? 12 Enpresa batek hiru autobus-linea ditu: A, B eta C. Astelehenean, A lineako 5 autobus irten ziren, B lineako 3, eta C lineako 4. Asteartean, A-ko 2, B-ko 1 eta C-ko 4. Asteazkenean, A lineako 1, B-ko 3, eta C-ko 5. a) Adierazi datuak matrize eran eta aurkitu alderantzizko matrizea, aurkitu badaiteke. b) D matrizea a) ataleko matrizea bada, ebatzi honako ekuazio-sistema hau, ebatz badaiteke: y fp = –33 1 1 fp 13 Inekuazio hauek mugatzen duten esparrua dugu: ≤ xy xy xy 20 35 70 00 + a) Arrazoitu (4,1; 11,7) koordenatuak dituen puntua esparru horretakoa den. b) Adierazi esparru hori eta kalkulatu horren erpinak. c) Adierazi non lortuko dituen F = 0,6 funtzioak muturretako balioak. Zein dira balio horiek? 14 olasak egiten dituen enpresa batek bi joko fabrikatzen ditu: Batailak Marrazkiak Hauek dira joko bakoitzaren unitate-onurak eta fabrikako atal bakoitzean behar diren orduak: 114 45 € Fabrikazioan 36 ordu, muntaketan 16 ordu eta paketatzean 10 ordu erabil badaitezke, zein da etekinak maximizatuko dituen ekoizpena? a) Ebatzi grafikoki. b) Aztertu, grafikoki, zer gertatzen den Batailak jokoaren irabaziak 15
4 323 Prestatu anayaharitza.es
Unibertsitatera
III. multzoa:
P A ∪ = A] + P [B P A ∪ B A/B = P A ∩ B P B Badakizu
interpretatzeko eta ebazteko? A A B –
webgunean
erabiltzen zuhaitzdiagrama probabilitate-problemak
Menderatzen
Badakizu
/2 /2
–Teknika
ditzakezu. a. Zuhaitz-diagrama batek datuak bistaratzeko eta horien gainean arrazoitzeko modua ematen digu. b. Kontuan izango dugu: P [hurb ∪ ekol] = P [hurb] + P [ekol] – P [hurb ∩ ekol] Azoka batean, merkaturatzen diren barazkien % 70 tokikoak dira eta, gainerakoak, ez. Tokiko barazkien % 30 ekologikoak dira; tokikoak ez direnen artean, berriz, % 10 baino ez dira ekologikoak. Ausaz aukeratutako bezero batek barazki bat erosi badu, kalkulatu probabilitate hauek: Erositako barazkia ekologikoa ez izateko probabilitatea. b. Erositako barazkia tokikoa edo ekologikoa izateko probabilitatea. Eskualde batean, pilates eskolen hileko kuota banaketa normala duen ausazko aldagai baten bidez hurbil daiteke, batezbestekoa euro eta bariantza 49 euro2 izanik. Mota horretako eskolak ematen dituzten 64 zentrotako ausazko lagin bat aztertu, eta hileko batezbesteko prezioa 34 eurokoa
N(μ,
–
34.
z
balio kritikoa. P[ = 0,996 → = 2,65 Tarte hau lortzen dugu: 34 2,65 64 7 0,992 0,992 0,5 = 0,996 C eta D dira ausazko esperimentu baten bi gertakari, eta P C = 0,3; P D = 0,6 eta P C ∪ D = 0,8 betetzen da. Kalkulatu: P C D b. P CD /C ] Ariketa hau aljebraikoki ere ebatzi daiteke, probabilitatearen propietateak erabiliz. Zer proportzio hartzen du C-k D-ren osotasunean? P C/D = 0 0 1 6 1 b. Zer proportzio betetzen du -k C ∩ D da C ∩ D multzotik kanpo dagoena, eta, beraz P C ∩ D C] 03 02 3 2 Lehenengo, P C ∩ D] lortu behar dugu: P C ∩ D = P C + P D – P C ∪ D = 0,3 + 0,6 0,8 = 0,1 b. ebatziko ditugu grafikoen gainean arrazoituta: Ezagutzen dituzu gertaeren propietateak eta horien probabilitateak? Badakizu erabiltzen adierazpen grafikoa gertaeren propietateak eta probabilitateak bistaratzeko? Probabilitatearen atala landu duzunean, hainbat problema mota ebazteko modua ematen duten oinarrizko kontzeptu eta teknikak ikasi dituzu. Gogoratu ditzagun horietako batzuk. 12 13
Erlazionatzen dituzu σ eta n parametroak xz ± v konfiantza-maila jakin bati lotutako tartearen tamainarekin?
duzu nola erabili kurba normala eta horren ezaugarriak?
lortzen probabilitate bati lotutako /2 balio kritikoa?
k
hauekin eta beste batzuekin, arazo asko ebatzi
7), laginaren tamaina = 64,
=
b. z 7 < 3 erlazioak ematen digu -ren balioa.
= 1,96, eta hori da p = 0,95-i dagokion
Lortutako soluzioari buruz hausnartzea Oso urrats garrantzitsua da problemen ebazpena hobetzeko. — Lortutako soluzioa zentzuzkoa eta arrazoizkoa den ziurtatu behar da. — Jarraitutako prozesuari buruzko gogoeta egin behar da, zertan hobetu daitekeen ikusi… Problema horrekin lotuta dauden beste batzuk planteatzea komeni izango da, agian: errazagoak, konplexuagoak… Problemak ebazteko aholku batzuk (jarrerak) Ondo ulertu problemako termino guztiak. Ziurtatu datu guztiak eta esaldi guztiak ulertzen dituzula. Zer eskatzen den, zertan oinarritu zaitezkeen... Enuntziatua zail samarra bada, saiatu zeure buruari edo beste pertsona bati azaltzen. Jarri lanean buruko baliabide guztiak Jarri zeure arreta oso-osoa egiten ari zaren horretan, problemak ebaztea buruzko jarduera konplexua baita. Pazientzia dosi handia beharko duzu eta ekina izan beharko duzu. Ez etsi lehenengo zailtasunarekin topo egiten duzunean. Problema bakoitzak bere denbora behar du Ebatzi berriro zailenak izan diren problemak. Problema bat ebazteko laguntza behar izan baduzu, saiatu problema hori berori zeure kabuz ebazten arratsalde horretan bertan. Eta berriro gero, handik egun batzuetara Egin ebazteko beste bide batzuei buruzko gogoeta. Zurea izan ez den beste ebazpide bat erakutsi badizute, agertu interesa eta saiatu bide hori ulertzen. Gero, saiatu beste bide horri jarraituta ebazten. Atera probetxua problema onei. Problema onak ikasteko iturri emankorra dira. Problema bat «berriro egitea», idazketa hobetuz, urratsen bat zehaztuz, laburbideren bat erabiliz... ez da inondik ere denbora alperrik galtzea, ariketa bikaina baizik Problema interesgarria bada, aukera izango duzu beharbada beste hauetarako: — Problema orokortzeko. — Antzeko beste bat asmatzeko (errazagoa zein zailagoa). Baldintza jakin bat ezabatuz gero, edo beste bat gehituz gero zer gertatuko litzatekeen galdetzeko… Trukatu ondorioak ikaskideekin. Problemak bakarka pentsatu beharrekoak dira. Kasu batzuetan bakarrik izango du zentzua taldean lantzeak; adibidez, soluziora heltzen lagunduko diguten ideien bila ari garenean. Baina hori ere bakarkako lanaren ondoren egin beharrekoa da (taldeari lagundu ahal izateko, prest egon beharra dago, eta prestakuntza horrek bakarkako saiakera eskatzen du). Baina behin problema ebatzi ondoren, ideiak trukatzea probetxu handikoa izango da. Eta oso onuragarria izango da ohitura hori sistematiko bihurtzea.
Unitateak epigrafe eta azpiepigrafeetan banatuta daude, eta horietan ikasi behar dituzun kontzeptuak eta tresnak erakusten dizkizugu.
Unitate bakoitzaren garapena
Proiektuaren GAKOekin erlazionatutako baliabideak
Epigrafe bakoitzean aurkituko dituzu ebatzitako ariketak eta ebazteko proposatzen dizkizugun beste batzuk.
Aurkezpen teorikoa osatzeko, ebatzitako ariketak eta problemak ematen dituzten zenbait orrialde daude.
Konfiantza-mailaren,
errore onargarriaren
betetzen du || /2 n v E v balioa errore maximo onargarria da ren araberakoa da, honela Zenbat eta handiagoa izan laginaren tamaina, orduan eta txikiagoa da E (orduan eta estuagoa da tartea; hau da, estimazioa zehatzagoa izango da). Zenbat eta handiagoa izan α hau da, gure estimaziotik zenbat eta ziurrago egon nahi dugun), orduan eta handiagoa da E Alboko taulan erabiltzen diren konfiantza-maila ohikoenak bildu ditugu Ikusten duzunez, zenbat eta handiagoa izan 1 – α orduan eta handiagoa da α/2 eta, beraz, handiagoa da E Laginaren tamaina eta α jakinda lortzea
dugu
eta laginaren tamainaren arteko erlazioa 6 0,90 0,95 0,99 0,10 0,05 0,01 1,645 1,96 2,575 /2 m 1 –ADI! zenbaki osoa izan behar da -ren balio moduan lortutako zenbakiaren hurrengo zenbaki osoa hartuko dugu 1 Prozesu baten iraupena kalkulatzeko egin diren neurketetan lortutako emaitzen desbideratze tipikoa σ = 0,5 segundo da. Zenbat neurketa egin behar dira, % 99ko konfiantzarekin, estimazioaren errorea ez dadin 0,1 segundotik gorakoa izan? A% 99ko konfiantza-mailari α = 0,01) hau dagokio /2 2,575 n lortzea 0,1 = 2,575 05 → 01 2575 05 = 12,875 → = 165,77 166 neurketa egin behar dira (165,77ren hurrengo osoa) Ebatzitako ariketa 1 Soldadu batzuen altueren desbideratze tipikoa 5,3 cm-koa da Zer tamaina izan behar du laginak, populazioaren μ batezbesteko altuera 0,5 cm baino gutxiagoko erroreaz eta % 95eko konfiantza-mailaz estimatzeko Pentsatu eta praktikatu 2 Badakigu oilaskoen pisuen desbideratze tipikoa 300 g dela. Granja bateko oilaskoen batezbesteko pisua estimatu nahi dugu 100 baino errore txikiagoa eginez; eta, horretarako, 50 indibiduoko lagina hartu dugu Zer konfiantza-mailaz egingo dugu estimazioa? Pentsatu eta praktikatu 0 1 Psikologo batek erreakzio-denborak neurtzen ditu, eta badaki neurketa guztien desbideratze tipikoa 0,5 segundokoa dela. Erreakzioen batezbesteko denbora estimatu nahi du, 0,1 segundoko errore maximoarekin. Horretarako 100 saiakuntza egin ditu Esan zer konfiantza-mailaz emango duen (x– – 0,1; – + 0,1) tartea. 0,1 = /2 100 05 /2 05 01 10 = 2 P /2 P < 2] = 0,9772 a P z 2] = 1 – 0,9772 0,0228 → = 0,0456 = 0,9544 /2 2 0,0228 1 100 saiakuntza eginda lortu den batezbesteko denbora – bada, % 95,44ko konfiantza-mailaz ziurtatuko dugu erreakzio-denbora –– 0,1 eta –+ 0,1 segundo artekoa dela 2 Koronel batek erregimentuko soldadu guztien batezbesteko altuera estimatu nahi du, egindako errorea 0,5 cm baino txikiagoa izanik eta 30 soldaduko lagina erabiliz. σ = 5,3 cm dela jakinda, zer konfiantza-mailaz egingo du estimazioa 0,5 = /2 30 53 /2 53 05 30 0,52 P /2 P < 0,52] 0,6985 a P z 0,52] = – 0,6985 = = 0,3015 = 0,6030 = 0,52 a 0,3015 –Konfiantza-maila – = 0,3970 Konfiantza-maila % 39,7koa izango da. Txikiegia! Horretarako, ez du merezi saiakuntza egitea Hain konfiantza-maila baxua lortzeak badu arrazoi bat: oso lagin txikia hartu da (30 indibiduo) zehaztasun handia lortu nahi izateko (erroreak zentimetro erdia baino txikiagoa izan behar zuen). Ebatzitako ariketak
Ikono horiek adierazten dute anayaharitza.es webgunean badagoela orrialdeko edukiekin lotutako jarduera bat, eta bi tresna digital hauetako batekin ebatzi ahal izango duzula:
GeoGebra oso tresna konpletoa da, eta matematikako ia disziplina guztietan lan egiteko erabili ahalko duzu.
Kalkulu-orriak aholkulariek, informatikariek, irakasleak… erabiltzen dituzte. Ezinbesteko tresna dira.
162
162
1. Jarraitutasuna eta deribagarritasuna
Aztertu funtzio honen jarraitutasuna eta deribagarritasuna: = x2x1 bada bada 0 – )
GJH konpromisoa
Hizkuntzaplana
Hezkuntza emozionala
Pentsamenduaren garapena
Orientazio akademikoa eta lanekoa
Lankidetzako ikaskuntza
Ebaluazioa IKTak
• Aurkitu alboko deribatuak x = 0 denean, eta aztertu bat datozen. Soluzioa: ) jarraitua da x 0 puntuan, izan ere, (0) lm x). Jarraitua da Á deribagarria da x 0 bada, baina ez da deribagarria = 0 puntuan, izan ere (0– = 0 ≠ (0 = 2.
2. Funtzioa deribagarri egingo duten bi parametroren balioak lortzea
Kalkulatu a eta b parametroak, funtzio hau deribagarria izateko = 1 puntuan: (x) = x a be bada bada 2 1 1
] ] ] ]
·≤ –Z [ \
Funtzioak jarraitua izan behar du deribagarria izateko. Horretarako, b parametroek baldintza jakin bat bete behar dute. Horrela, parametroak erlazionatzen dituen ekuazio bat lortuko dugu • deribagarria izateko, a eta parametroek ekuazio berri bat bete behar dute Hori eginda, ezezagunak dituzten bi ekuazioko sistema lortu dugu. Ebatzi Egiaztatu horrela lortutako funtzioa jarraitua eta deribagarria dela 1 puntuan
Soluzioa: 4 5 b 4 5

3. Funtzioak logaritmoen propietateak erabiliz sinplifikatzea deribatu aurretik
Kalkulatu funtzio hauen deribatuak:
a) = lnosx3 b) = ln x1 4 –



4. Deribatu nuluko puntuak
Kalkulatu zer puntutan den nulua funtzio honen deribatua: (x) = 2x x100– 2
Horrez gain, gidatutako ariketak eta problemak dituen orrialde bat ere ikusiko duzu, labur-labur adieraziko dizkizugun urrats batzuei jarraituta ebatzi ditzazun.
• Adierazi erroa berretura moduan Sinplifikatu funtzioak logaritmoen propietateak erabiliz ln ln ln ( b = ln ln b ln ( b = ln ln b Sinplifikatu ondoren, erraz deribatzen dira • Gogoan izan sin cos x eta tg x arteko erlazioak Soluzioa: a) y' ln tgx 2 3 2 3 – b) y' ln 4 –2

• Sartu 2 erro barruan eta deribatu • Berdindu emaitza hori zerorekin eta zehaztu -ren zer baliorekin baliogabetzen den zenbakitzailea. Kontuz ibili, izendatzailea ez baliogabetzeko • Aurkitu lehen lortu duzun -ren balio bakoitzari dagokion -ren balioa Soluzioa: (– 50 –100), 50 100)
5. Balio absolutudun funtzio baten deribatua 6. Parametro batek f deribagarri egiteko izan behar duen balioa zehaztea Aurkitu funtzio honen funtzio deribatua: (x) = – 3 + Adierazi zer puntutan ez den deribagarria. EGIN ZUK Kalkulatu funtzio honen funtzio deribatua eta adierazi ( = 2 – + + 1 tarteen bidez definituko dugu, honako hau kontuan hartuz: || ≥ x x x x 3 3 3 3 0 0 –––bad –bada bada bada < || ) ) – 3| =––2 + 332 ––3| + 30 x = ≤ 23 3 23 03 ––bada bada bada < * = 2 0 0 03 3 –bada bada bada * (0– = –2, (0 = 0 → ez da deribagarria 0 puntuan, (0– ≠ (0 baita. (3– = 0, (3 = 2 ez da deribagarria = puntuan, (3– ≠ (3 baita. f' Kalkulatu zer balio izan behar duen m parametroak (x) funtzioa deribagarria izateko = 1 puntuan. (x) = bada bada 3 2 1 EGIN ZUK Kalkulatu zein izan behar den balioa ( funtzioa deribagarria izateko Á osoan: = 22 2 0 0 –bad bada 2 * deribagarria izateko = 1 puntuan, jarraitua izan behar da = 1 puntuan. jarraitua bada = 1 puntuan, lm x = (1) = 3 – m. lm x () () () lm fx lm lm fx iilm 33 22 3 –2 jarraitua da = 1 puntuan, 1 edo = 2 badira. deribagarria izango da x = puntuan, (1– = (1 bada. = 1: = ≤ x 3 1 –bada bada x = ,bada '( ,bada' () x xf xf 2 2 11 2 11 2 ––≤–––*4 deribagarria da x = puntuan 1 bada. m = 2: x = 32 1 –bada bada = ,bada '( ,bada '( ) x xf xf 4 1 11 11 1 ––––< –*4 ez da deribagarria 1 puntuan = 2 bada. = → U 12 297 296 Konfiantza-maila E eta n jakinda lortzea E errore maximo onargarria eta laginaren tamaina zein diren badakigu, estimazioa egiteko konfiantza-maila honela lortuko dugu E z v ⇒ z En v /2 zein den jakinda, kurba normalaren taulak 2 -ren balioa emango digu Hortik 1 – α konfiantza-maila lortuko dugu Ikusi berri dugunez, laginen (1 – α % 100-ek hau
163
163
26 Aztertu funtzio hauen definizio-eremuak, asintotak eta muturrak, eta informazio horrekin, saiatu behean bakoitzaren grafikoa aurkitzen: a) y snix b) c) y sin x 2 d) y e) 1 y sin –2 02 26 –
2 –2 –2 –2–4 4 –224 –4 6 bada bada * ()ft urteak ehunka a) Adierazi funtzio hori. b) Zein izan da hasierako prezioa? Eta azkenekoa? c) Zenbat iraun du gai horren salmentak? Zein izan da pre-




Galdera teorikoak 37 x funtzio batek ezaugarri hauek ditu: Dom Á – {0} eta jarraitua eta deribagarria da bere definizio-eremu osoan. lm –) = – lm ) = + li –) = + li ) = –Honako baieztapen hauetatik, esan zein diren ziurrak, zein izan litezkeen eta zein diren ezinezkoak: a) bikoitia da. b) bakoitia da. c) Ez du ez maximorik ez minimorik. d) Maximo bat eta minimo bat ditu. e) X ardatza bi puntutan ebakitzen du. ) X ardatza gutxienez bi puntutan ebakitzen du. g) Asintota bertikal bat du gutxienez. h) Asintota bertikal bakarra du. i) Asintota zeihar bat du. j) Ahurra da < 0 denean, eta ganbila, x > 0 denean. 38 Irudikatu [0, 4] tartean jarraitua den funtzio bat, eta (2, 3) puntuan maximo erlatibo bat eta (3, 4) puntuan minimo erlatibo bat dituena gutxienez. Funtzio polinomikoa balitz, zer mailatakoa izan behar du gutxienez?
Sakontzeko 39 Konposatu baten nitrogeno-kontzentrazioa (%-tan) beheko funtzio horrek ematen du [0, +∞) denboraren funtzioan (segundotan neurtuta): N ) e12 60 –+ a) Frogatu nitrogeno-kontzentrazioa hazi egiten dela denborarekin. Zer -rekin da minimoa nitrogeno-kontzentrazioa, eta zenbatekoa da? b) Zer baliotara jotzen du nitrogeno-kontzentrazioak denboran infiniturantz jotzen duenean? 40
–
Partikula bat x 1

2 27 Zehaztu funtzio hauen asintotak: a) y x 3 1– b) y xx 1 28 Enpresa batek izandako irabaziak, ehunka mila eurotan, AUTOEBALUAZIOA ➜ anayaharitza.es Ariketa hauen ebazpena.
3 4 –dn puntuan, kurba utzi eta kurbarekiko ukitzailea den zuzenean zehar doa. a) Aurkitu ukitzaile horren ekuazioa. b) Eskuinetik ezkerrera badoa, esan zer puntutan aurkitzen duen partikulak P puntutik hurbilen dagoen asintota bertikala. c) Ezkerretik eskuinera badoa, esan zer puntutan aurkitzen duen partikulak X ardatza.
Unitatea ixteko, autoebaluazio bat ageri da, zure aurrerapenak egiaztatzen laguntzeko.
5 U 8 Proposatutako ariketak eta problemak Irudikatu funtzioaren grafikoa, honako hau jakinda: lm ) = + lm –) = –3, lm ) = –(–5) = 0; (0) = 0; (–5) = 0; (0) = 2 2 Deskribatu honako funtzio hau: 3 x = x x 3 – 3 – 4x + 4 funtzioak maximorik edota minimorik du? Eta inflexio-punturik? Aztertu kurba eta adierazi. 4 Aztertu hurrengo funtzioen asintotak eta puntu singularrak eta adierazi grafikoki:: a) ) = 4 6 b) = xx65 ––2 + 5 Adierazi x = 4 2 –funtzioa. Esan zein diren horren tarte gorakor eta beherakorrak eta muturrak 6 Aurkitu ( funtzioaren maximoak eta minimoak. Esan asintotarik duen eta adierazi grafiko bidez. 7 Irudikatu = + 3 + – 1 funtzioa. 8 ( bx da. Aurkitu zein diren b eta balioak,
jakinda ( funtzioak mutur erlatibo bat duela x = –3 abzisa-puntuan, eta x funtzioak x 0 abzisapuntuan duen zuzen ukitzailearen ekuazioa y 6 + 8 dela. 9 Adierazi ) () x 1 2 funtzioa. 10 Zein grafiko dagokio ) || funtzioari? zenbatekoak izan diren azken 5 urteetan, denboraren (urteetan) arabera adierazitako honako funtzio honek ematen dizkigu: ) = () [, (, 6 2 3 03 35 –– bada bada ! a) Adierazi noiz hazi den irabazia eta zehaztu zer unetan egon diren maximo eta minimo lokalak, eta zein balio dagozkien. b) Noiz izan du 500 000 €-ko irabazia? c) Irudikatu funtzioa. 29 = + zuzena ondorengo funtzio honen asintota zeiharra da: = xk 21 –Aurkitu -ren balioa eta adierazi horrela lortu duzun funtzioa. 30 = b funtzioa izanda, kalkulatu zein izan behardiren -ren eta b-ren balioak -ren grafikoa (–2, – 6) puntutik igaro eta puntu horretan ukitzaile horizontala izan dezan. Adierazi funtzioa -ren balio horietarako.
Ebazteko 31 Aurkitu a b eta parametroen zer baliorekin duen ( = ax bxc funtzioak asintota horizontal moduan y –1 zuzena eta minimo bat (0, 1) puntuan. 32 Egiaztatu funtzio honek bi asintota horizontal desberdin dituela: || x 33 ( = – funtzioak asintotarik du? Asintotarik badu, aurkitu. 34 Funtzio hau dugu: x): Adierazi zer grafiko dagokien beste funtzio hauei: (– (| |) –| a) b) c) d) 35 Funtzio honek hau adierazten du: gai jakin batek zer eskari izan duen urteetan zehar: = ≤≤ 1 2 84 02 bada bada + * ()ft urteak milakagai a) Adierazi funtzioa. b) Zenbatekoa da eskaria 2 urtera? Zer urtetik aurrera da eskaria 000 unitatetik gora? c) Eskariak zenbat unitatetik gora ez du sekula egingo, denbora asko igarota ere? 36 Gai jakin baten prezioaren aldakuntza funtzio honek ematen digu: ) = 2 5 2
ekuazio duen kurbak irudikatzen duen grafikoaren gainetik higitzen da > 1 denean.
Gidatutako ariketak eta problemak
Ebatzitako ariketak eta problemak
• Aztertu jarraitua den 0 puntuan. Eta gainerako balioetan?
• Aurkitu deribatua x ≠ 0 kasuan.
E errore maximo onargarria eta 1 – konfiantza-maila zenbatekoak diren zehazten badizkigute, baldintza horiek beteko dituen laginak gutxienez zer tamaina izan behar duen lortzeko, E-ren adierazpenean askatuko dugu E /2 v a ⇒ E /2 ⇒ E /2 2cm Ikusten duzunez, laginaren tamaina Zenbat eta handiagoa izan orduan eta handiagoa da tamaina. Hau da, zenbat eta txikiagoa izan eta handiagoa izan 1 – Beraz, konfiantza-maila handitzeko, laginaren tamaina ere handiagotu egin behar dugu Zenbat eta txikiagoa izan E orduan eta handiagoa da tamaina. Hau da, estimazioak zehatzagoak izateko, laginaren tamaina handiagotu behar
Ariketak eta autoebaluazioak
Unitatearen amaieran, ariketa eta problema mordoa proposatzen dizkizugu, eskuratutako ezagutza eta prozesu guztiak praktikan jar ditzazun.
Jarduera batzuetan ageri diren ikonoek iradokitzen dute kasu bakoitzean proiektuaren zer gako erabil daitekeen. Horrez gain, anayaharitza.es webgunean bideoak, orientabideak eta hainbat dokumentu ere aurkituko dituzu, gakoak aplikatzeko.
Ebatzitako eta gidatutako ariketak
Honelakoa da zure proiektu digitala

Proiektu honek ikasturteko eduki guztiak eskaintzen dizkizu, bai liburu digitalaren bidez, bai era askotako baliabideen bidez.
Ikasteko beste modu bat ezagutuko duzu, erraza, intuitiboa eta edozein plataforma eta gailurekin bateragarria.
Nola sartu?
Zure liburuko lehenbiziko orrialdearekin batera aurkituko dituzu proiektu digitalean sartzeko behar dituzun argibide guztiak.

2 3 5
30
2
3 5
Ekuazio linealen sistema baten soluzio posibleak
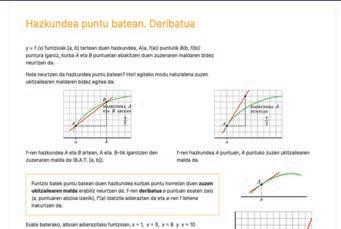
2 Ekuazio-sistema batek soluzioa izan dezake (bateragarria edo baliteke soluziorik ez izatea (bateraezina). Sistema bateragarriek soluzio bat izan dezakete determinatuak edo infinitu so- luzio izan ditzakete indeterminatuak). Bi ezezaguneko ekuazio-sistemak Honako sistema hauek eta horien interpretazio geometrikoak aztertuko ditugu:
2 3 3 5 9 4–+= 4 Ekuazio-sistema honen soluzioa = 3, = 1 da. Horrek esan nahi du bi zuzenek (3, 1) puntuan ebakitzen dutela elkar. Beraz, sistema bateragarria determinatua da.
x
KONTUAN IZAN Sistema bat bateragarria edo bateraezina dela esan beharrean, zuzenago izango litzateke zehaztea sistema eratzen duten ekuazioak bateragarriak direla (hau da, denek soluzio komun bat dutela) edo bateraezinak direla (ez dagoela denena den soluzio komunik). Dena dela, hemen erabilitako nomenklatura orokorrean onartuta dagoena da.
y y y
3 5
2

9 4 13 –– 4 Sistema hau aurrekoaren berdina da ia; izan ere, aurreneko bi ekuazioak berdinak dira, eta hirugarrena aurreko bi horiek atalez atal batuta lortzen da. Zuzen berria (marrazkian beltza dena) (3, 1) puntutik igarotzen da eta puntu ho- rretan ebakitzen dute elkar hiru zuzenek. Beraz, sistema hori ere bateragarria eta determinatua da.
• 2 4 3 6 9 184 Bi ekuazioek gauza bera diote. Horietako baten soluzio bakoitza bestearena ere bada. Bi zuzenak bat datoz. Hau da, zuzen bera dira Sistema bateragarria eta indeterminatua da.
x y y 2 4 3 6 9 12 + 4 Ekuazioek kontrakoa diote. Ez dute soluzio berdinik. Geometrikoki, bi zuzenak paraleloak dira, puntu batean ere ez baitute bat egiten. Sistema honek ez du soluziorik. Bateraezina da. Ebazten saiatzen garenean, zen- tzugabeko adierazpenak lortzen ditugu.


x y y y
3 5 2
9 4 6 – 4 Sistema hau bigarren sistemaren oso antzekoa da; hirugarren ekuazioko gai askea baino ez da aldatzen. Baina hori dela eta, ez da beste biek elkar ebakitzen duten (3, 1) puntutik igarotzen. Ez dago hiru puntuek bat egiten duten punturik. Beraz, sistema hau bateraezina da.
2 4 7
2 4 3 25
x
y
–
––
y y
11 20 8 3
Z [ ] ] Laugarren ekuazioak beste hiruren baturaren esaten du. Plano hori (horia) ez da beste hiruren puntutik igarotzen. Sistema bateraezina da. Ez du soluziorik.
––x y y y z z 2 32 11 20 9 ––––+= * Hirugarren ekuazioak, beste bien batura denez, telako informaziorik eransten sistemari. Sistema rri indeterminatua da. Soluzioa: Planoek elkar ebakitzen duten zuzeneko guztiak dira sistemaren soluzio. • 2 32 11 20 3 ––– + * Hirugarren ekuazioak kontra egiten dio beste lortzen denari. Sistema bateraezina da. Ez du soluziorik. Ebatzi eta interpretatu geometrikoki honako ekuazio-sis- tema hauek: a) x y y y 2 32 1 4 3 + * b) x y y y2 6 1 7 – * c) x y y z 6 0 0– * d) xy y z 6 1 1 –++ * 2 a) b) c) d) Pentsatu eta praktikatu



6
2 +3y=9 3x–5y=4 2 +3y=9 3x–5y=4 5 –2y = 13 2 +3y=9 4x+6y=18 2x+3y=9 4 +6y=12 2 +3y=9 3x–5y=4 5 –2y = –6
x
x x
y z 2 4 7 3 2 5 4 11 20
––+ + Z
Hiru ezezaguneko ekuazio-sistemak Azter ditzagun honako sistema hauek eta horiei dagozkien interpretazio koak:
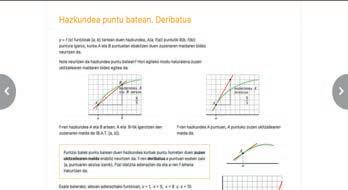
11 20 8 –
++ * Hiru planoek puntu batean ebakitzen dute elkar. bateragarri determinatua da. Soluzioa: = 1, y = 7, = –2
8 1 ––
[ \ ] ] ] ]
Laugarren ekuazioa beste hiruren batura da. kion planoa (horia) komunean duten puntutik da. Sistema bateragarri determinatua da. Soluzioa: = 1, y = 7, z = –2 x x
3 2 5 4
y = sin(x) f(x) = sin x
Zer eskaintzen dizu?
Era askotako baliabideak ditu; paperezko liburuaren erreprodukzioa baino askoz gehiago da.
Honakoak egiteko aukera izango duzu:
Ariketak egin
ariketa elkarreragileak
Aztertu
laburpen elkarreragileak, eskemak...
Ikasi
audioak, bideoak, Game Room-ak...
Ebaluatu
autoebaluazioa, portfolioa...
Nolakoa da?
Erantzun globala era askotako hezkuntza-ingurune baterako.
Intuitiboa
Zuk erraz erabiltzeko modukoa.
Gailu anitzekoa
Edozein gailu motatan (ordenagailuan, tabletan, smartphonean…) egokitzen eta ikusten da, pantailaren edozein tamaina eta bereizmenetan.
Deskargagarria


Aukera ematen du Interneteko konexiorik gabe lan egiteko eta gailu batean baino gehiagotan deskargatzeko.

Sinkronizagarria
Erabiltzaileak egiten dituen aldaketak berez sinkronizatzen dira, lan egiteko erabilitako edozein gailu konektatzean.
Unibertsala
Bateragarria da ikastetxeetan gehien erabiltzen diren sistema eragileekin, ikaskuntzako inguru birtualekin (IIB) eta hezkuntza-plataformekin (LMS).
7 U 1 31 interpretazio geometrielkar. Sistema Horri dagopuntutik igarotzen kontrakoa hiruren ebakiez dio besSistema bateragazuzeneko puntu biak batuta Ebatzi sistema hau: 23 4–* Erantsi hirugarren ekuazio bat sistema bateragarria izaten jarraitzeko. Erantsi hirugarren ekuazio bat sistema bateraezina izateko. Interpretatu geometrikoki kasu bakoitzean egin duzuna. Sortu mota desberdinetako ekuazio-sistemak.
IKASKUNTZA-EGOERAK ERRONKAK ITZALA UZTEN DUEN
Eta honek, zertarako balio du?
Galdera hori behin eta berriro egiten da Matematikako eskoletan, urtez urte. Eta atzetik etorri ohi den azalpena luzea izaten da: matematikak nonahi daude, baita naturan ere; denerako balio dute; ia edozein diziplinatan erabiltzen dira... Baina noiz erabiliko ditut benetako zerbaitetan?
Tira. Ikasgelan ikasten diren kontzeptuak eta tresnak erabilgarriak izan daitezen, ez dira beti arazo errealetan zuzenean aplikatzeko modukoak izan behar. Matematika ikasteak balio du, batez ere, egitura mentalak sortzeko, edozein motatako problemei aurre egiteko estrategiak sortzeko, eta, gainera, zentzu kritikoa garatzeko.


Eta gozatzeko ere bai. Bai, hala da. Baita problema on bat modu autonomoan ebazteak ematen duen poza sentitzeko ere.
Jarraian aurkezten diren ikaskuntza-egoeretan aurkituko dituzu problema errealak, sinplifikatuak, ezagutzen dituzun tresnekin ebatz daitezkeenak, edota ikasturtean zehar eskuratuko dituzunekin. Eta, jakina, ikerketak ere topatuko dituzu, landutako ezagutzak integratzeko, teoriak eraikitzen eta hipotesiak baieztatzen edo ezeztatzen parte hartzeko, dela eskuan boligrafoa hartuta, dela ordenagailu edo kalkulagailu erabilita.
Helburu horrekin. anayaharitza.es webgunean eduki-multzo desberdinekin lotutako erronkak aurkituko dituzu, hemen aurkezten dizkizugun hauek bezalakoak; eta horiei aurre egin beharko diezu, taldean edo banaka, zeure ikaskuntza propioa eraikitzeko. Horretarako, dagoeneko dakizunaren eta ezagutza berrien arteko beharrezko loturak ezarri beharko dituzu.
Piztu
Piztu zure burua eta ekarri gogora urte hauetan zehar eskuratu dituzun eduki guztiak. Eduki horiek izango dira erronka ebazteko beharko dituzun ikaskuntza berriak eraikitzen hasteko oinarria.
Planifikatu
Planifikatu zure ikaskuntza eraikitzeko eta gaitasunak garatzeko prozesua. Erabili eskura dituzun iturriak eta baliabideak.
Ebaluatu
Ebaluatu eta berrikusi jarraitu duzun prozesua, eta laburbildu ikasi duzun guztia. Lortu duzu zure helburura iristea? Nola sentitu zara?
Aurre egin

















Erronka hauei aurre egitea lagungarri izango duzu egitura mentalak sortzeko, egoeren ereduak egiten ikasteko, azaltzeko, argudiatzeko, arrazoitzeko, problema berriei modu sistematiko eta sendoan aurre egiteko, egungo mundua ulertzeko, eta matematikaz, bere metodoen, formen, egituren, sortze-prozesuen eta historiaren edertasunaz gozatzeko.

ZENBAT SALGAI EROSIKO DUGU ASTE HONETAN? NOLA KUDEATU JATETXE BATEKO GENEROA
Ikasturte honetan neurri txikiko matrizeak ikusiko dituzu; oro har, ez dira 5 errenkada edo zutabe baino handiagoak izango. Dena dela, matrizeen erabileretako bat da zenbakizko datu kopuru handiak erabiltzea, horietatik informazioa ateratzeko. Hori matrize-eragiketa soil batzuen bidez lor daiteke. Eragiketa horiek guk egin ditzakegu edo, atsegin handiz, ordenagailu batek egingo dizkigu.
ZERTARAKO JAKIN KURBA BATEN AZPIKO AZALERA
Auto batek t une bakoitzean daraman v abiaduraren funtzioa zein den jakinda, v = f (t) auto horrek ibilitako espazioa t0 unetik t1 unera da kurbaren azpiko azalera [t0, t1]. tartean
Matrizeak erabiliko ditugu hainbat gosariren osagaiak, astebetean zer kantitate kontsumitzea espero den edota prezioak zein diren. Azken batean, lortu nahi duguna da astean erabiltzen diren osagaien kopuru osoa, eta zenbat balio duten.

Matrizeak erabilita, prozesua egituratu eta sistematizatu egiten da; horrela, astero, kontsumitu nahi diren errazioak aldatuz, automatikoki lortzen da produktuen eta prezioen azken emaitza.

Propietate sinple horri esker, bi trenen posizioei buruzko problema oso era bitxian ebatziko dugu: trenen abiadurek deskribatzen dituzten kurben azpiko azalera kalkulatuta.
Ariketa hau garatzean, argi ikusiko duzu abiadurakurbaren azpiko azaleraren eta ibilitako espazioaren artean dagoen erlazioa. Eta beste funtzio batzuen kasuan aplikatu ahal izango duzu. Adibidez, etxebizitza batean kontsumitutako energia da une bakoitzean konektatutako potentzia deskribatzen duen kurbaren azpiko azalera. Erlazio hori etxeari dagozkion problemak zein zuk enuntziatutakoak ebazteko erabili ahal izango duzu.


9
t0 t1
abiadura denbora
KAFE HUTSA KAFESNEA KAKAOA TEA TEA ESNEAREKIN ESNEA ZUKUA
ASTELEHENA ASTEARTEA ASTEAZKENA OSTEGUNA OSTIRALA LARUNBATA IGANDEA
GOSARIA
FUNTZIO INFINITU BATZUEN AZTERKETA
Adierazpen horretan ez dago modurik Hego Korearen kurbak ezaugarririk hautemateko. Eta beste bi grafikoak oso zailak dira konparatzeko hasierako tarteetan. Funtzioen azterketak balio digu bi magnitude nola erlazionatzen diren ulertzeko. Beren grafikoek erlazio hori laburtzen eta interpretatzen laguntzen digute, baina adierazpena egokia bada soilik.
Kutsatzeek hazkunde esponentziala erakusten dute. Eskala logaritmikoak laguntzen digu horrelako hazkunde azkarrak ulertzen eta konparatzen.
Ikaskuntza-egoera honetan, funtzio esponentzialak zein bizkor hazten diren aztertuko dugu, eta, oso hazkunde azkarreko funtzioak aztertzeko eta konparatzeko, paper erdilogaritmikoa erabiltzen ikasiko dugu.
Funtzio logistikoa
51015202530354045505560657075 0
Grafiko horiek erakusten dute COVIDaren ondorioz, zenbait herrialdetan eta denboran zehar, izan diren hildakoen kopuru metatuaren bilakaera. Guztietan ageri da oso igoera azkarra, baina gero motelduz doa, eta, azkenean egonkortu egiten da.
Eskala logaritmikoa
Aztertu ardatz bertikaleko eskala: lehenengo kota 10 da, eta bigarrena, 20 izan beharrean, 100 da; eta horrela jarraitzen du, 10ekin biderkatuta. Eskala mota hau logaritmikoa da.
Eskala normala erabili izan balitz, normalean erabiltzen ditugunen modukoa, kurbak honela geratuko lirateke:
Kutsatzeei dagozkien funtzioak esponentzialak badira, nola liteke ez egotea guztiok gaixotasunen batekin kutsatuta? Bada, praktikan, eredu esponentzialak lehenengo fasea soilik deskribatzen duelako; gerora, kutsatzeen kopurua egonkortu egiten da, eta, azkenerako, balio konstante bat hartzen du. Funtzio esponentziala, beraz, funtzio logistikoa bihurtzen da.
Ikaskuntza-egoera honetan, hasierako funtzioa esponentziala, baina amaierako logistikoa daukaten kasu errealak aztertu eta deskribatuko ditugu.
Logaritmoen hazkunde mantsoa
Ondo dakigunez, bat baino oinarri handiagoa duten funtzio esponentzialak neurriz kanpo hazten dira. Eta kontrako muturrean funtzio logaritmikoak daude: funtzio logaritmikoen hazkundea hain da geldoa, non ezinezkoa baitirudi infinitura jotzea. Jokabide harrigarri horretaz behar bezala jabetzeko, aztertuko ditugun funtzioetan, x-ri Unibertsoaren diametroa adinako balioa eman, eta funtzioaren balioa milimetro batzuk baino ez dela hazten ikusiko dugu. Eta, hala ere, infinitura jotzeko joera erakusten duela!
10
10 000 1 000 100 10
0 102030405060708090 16 000 14 000 12 000 10 000 8 000 6 000 4 000 2 000
COVIDaren ondorioz hildakoen bilakaera Italian, Hego Korean, Alemanian
COVIDaren ondorioz hildakoen bilakaera Italian, Hego Korean, Alemanian
Esponentziala Logistikoa
ZENBAT ARRAIN DAUDE AINTZIRAN?
Ziur honelakoak irakurri izan dituzula albiste eta berrietan:
• Sardinen populazioak % 72ko beherakada izan du.
• Ozeano Atlantikoko hegalaburren populazioa % 90 ere murriztu da azkeneko urteetan.
Zenbatuta ote dituzte, bada, itsasoko arrain-ale guztiak? Nola zenbatu litezke sardinak, hainbeste egonda? Bada, itsasoa ikertzen duten zientzialarien zereginetako bat, hain zuzen ere, hori da: itsasoan bizi diren izaki bizidunen zenbaketa, populazio batzuetan eta besteetan dauden gorabeherak jakiteko. Eta animaliak zenbatzea ez da lan erraza.
Itsas biologoek markatzea/berriz harrapatzea teknikak erabili dituzte, itsas espezieen biologiaren alderdi garrantzitsuak ezagutzeko tresna gisa.

Teknika honetan, arrainak harrapatu eta markatu egiten dira, espezie bakoitzari egokitutako marka zientifiko jakin batzuekin; markatu ondoren, askatu egiten dira, eta handik gerora berriz harrapatu, besteak beste, espezie bakoitzeko ale kopurua kalkulatu ahal izateko.
HARA NON, JOLASTEAK ETA
KALKULATZEAK ZERBAITETARAKO BALIO DU
Egin dezagun jolas. Bota txanpona koadrikula gainera: marrarik ukitzen ez badu, irabazle; marraren bat ukitzen badu, galtzaile.
Zenbat jokatu nahi duzu?
Ikaskuntza-egoera honetan, markatzea/berriz harrapatzea prozesu osoa berregingo duzu, eremu sinpleago batean, bai eta gatzgabeagoan ere: poltsa batean dagoen txitxirio-kopurua kalkulatuko duzu. Era berean, ikasturte honetan ikasiko dituzun banaketa normala eta laginketa-teknikak erabiliko dituzu fikziozko egoera hori zorroztasun osoz ebazteko.
Horren ostean, zenbaketa interesgarriagoak proposatuko dizkizugu; esaterako, hiri batean dabiltzan autoen kopurua zenbatzea, edo zuri bururatzen zaizun beste edozer.
Jakina, emaitza izango da txanponaren erradioaren araberakoa, baita koadrikularen aldearen araberakoa ere. Baina horiek finkatu ondoren, irabazteko zer probabilitate dago? Ariketa honen bitartez ikusiko duzunez, probabilitate hori oso erraz kalkulatzen da azaleren kalkuluaren bidez. Emaitza teorikoa praktikoarekin kontrastatzeko, bota askotan txanpon bat neurri horretako koadrikula baten gainean eta kalkulatu «ez du marrarik ukitzen» gertaeraren maiztasun erlatiboa.
Aukera izango duzu probabilitateak esperimentazioaren bidez kalkulatzeko, guk eskainiko dizkizugun koadrikuletan, zein zuk asma ditzakezun beste batzuetan. Arrazoiketa geometrikoen bidez ebazten diren probabilitate hauek probabilitate geometrikoak deitzen dira, eta geometriarekin erlazionatuta ez dauden beste egoera batzuk ebazteko balio dute; adibidez, honelakoak:
Jakes eta Saioa kiosko baten ondora joango dira, 12:00etatik 13:00etara bitartean. Denbora-tarte horren barruan joan dira biak, baina zorian, eta joan aurretik 10 minutu itxaron dituzte. Zer probabilitate dago Jakes eta Saioa elkartzeko?


11
B A
1

Ekuazio-sistemak. Gaussen metodoa
Gaussek erabilitako metodoa
xix. mendearen hasieran, Gaussek Palas asteroidea behatu zuen. Eta lortutako neurketetatik abiatuta, sei ezezaguneko sei ekuazio zituen sistema batera heldu zen. Sistema hori ebazteko, gaur egun «Gaussen metodoa» esaten diogun prozedura diseinatu zuen.

Hogeita bat mende lehenago, Txinan Matematiken arteari buruzko bederatzi kapituluak liburua argitaratu zen. Zortzigarrenean, honako problema hau ageri da: Hiru zereal mota daude. Lehenengoaren hiru fardo, bigarrenaren bi fardo eta hirugarrenaren fardo bat hartuz gero, 39 neurri izango ditugu. Lehenengoaren bi fardo, bigarrenaren hiru eta hirugarrenaren bat hartuta, 34 neurri. Eta lehenengoaren fardo bat, bigarrenaren bi eta hirugarrenaren hiru hartuta, 26 neurri. Zenbat neurri zereal daude zereal mota bakoitzaren fardo batean?
Eta, ebazteko, honako hau egiten dute aipaturiko liburu horretan:
Zenbakiak taula batean jarri (ekuazio bakoitza zutabe batean deskribatzen da, enuntziatuko azkenengotik hasita):

Zutabeekin aldaketak eginez, ezkerreko taula beste hau bihurtzen da:
Eta eskuineko taulatik, berehala eta hurrenez hurren, fardo bakoitzeko zerealaren neurri-kopurua lortzen da.
Bi prozedurak zein antzekoak diren ikusita, gaur egun Gaussen metodo esaten diogun horri, beharbada, «Chui-Chang Suan-Shuren metodo» esan beharko genioke (hori baita egilea ezagun ez duen liburu horren izenburua txineraz).
26
1 2 3 2 3 2 3 1 1 26 34 39
0 0 3 0 5 2 36 1 1 99 24 39
«Matematiken arteari buruzko bederatzi kapituluak» liburuko orrialde bat
Gaussen egunkari zientifikoa
Carl Friedrich Gauss (1777-1855) historian izan den matematikaririk handiena da askorentzat, eta «matematikarien printzea» ezizenez ere esaten diote. Matematikaren arlo bat bera ere ez zuen utzi landu gabe. Baina bitxia badirudi ere, ez zen bere aurkikuntzak argitara ateratzeko zalea


19 urte zituela, Euklidesen garaitik ebatzi gabe zegoen geometriako problema bat ebazteko prozedura lortu zuen. Egiaztapen bikaina egin zuen, teknika aljebraikoak erabili baitzituen ebazteko (berrikuntza handia izan zen geometriako problema bat prozedura aljebraikoen bidez ebaztea).

20 markoko zilarrezko txanpona, Alemaniako Errepublika Demokratikoa zenekoa, Gaussen omenez
Gaussen zientzia-egunkariaren orrialdea
EBATZI
Zereal-fardoak
Aurkikuntza egin, eta berekin zeraman egunkari txikian zehaztu zuen egun horretan bertan, 19 orri baino ez zituen eskuliburu batean. Koadernotxo hori urte askotan erabili zuen, eta 146 ohar idatzi zituen guztira. Horietako azkena, 1814. urtean, oharrak egiten hasi eta 17 urtera. Bertan ageri diren ideien kopurua eta sakontasuna kontuan hartuz, matematiken historian izan den dokumentu baliotsuenetako bat dela esan dezakegu. Koadernotxo hori erabakigarria izan da jenio horren pentsaera ezagutzeko, baina ez zen argitaratu 1898. urtera arte; hau da, Gauss hil eta berrogeita hiru urte geroago arte
Zereal-fardoen problema txinatarrarekin batera zenbakien bi taula ageri dira. Lehenengoak enuntziatutik lortzen diren ekuazioak deskribatzen ditu. Ekuazioen koefizienteak zutabeetako zenbakiak direla kontuan izanda, sistema honela geratzen da:
a) Idatzi bigarren taulari dagokion ekuazio-sistema. Ikusten duzunez, sistema hau oso erraza da ebazten: 1. ekuaziotik z-ren balioa lortu, eta horrekin, bigarren ekuazioan, y lortzen da. Amaitzeko, 3. ekuaziotik x lortzen da. Soluzioa: x = 37/4, y = 17/4, z = 11/4.
b) Egiaztatu soluzio hau baliozkoa dela hasierako sisteman.
Zer aldaketa egin zioten ezkerreko taulari eskuinekoa lortzeko? Begira:
(2. taulako 1. zutabea) = 15 · (1.a) – 12 · (2.a) + 3 · (3.a)
(2. taulako 2. zutabea) = 3 · (2.a) – 2 · (1.a)
(1.a), (2.a) eta (3.a) lehenengo taulako zutabeak dira.
Lehenengo taulako zutabeekin bigarren taulakoak lortzeko hemen egiten diren eragiketek zailak badirudite ere, unitate honetan lan hori egiteko metodo errazago bat ikasiko duzu.
27
x x x y y y z z z3 2 3 2 3 2 326 34 39 3 + + + + + + = = = Z [ \ ] ] ] ] ] ] ] ]
Ekuazio linealen sistemak
Ekuazio lineala
Honako ekuazio hauek linealak dira:
2x – 3 = 0 5x + 4y = 20 3x + 2y + 6z = 6 5x – 3y + z – 5t = 0

Denek dute berezitasun bat: 1. mailako ekuazio polinomikoak dira. Hau da, ezezagunak ez daude berretzaileetara jasota, ez daude elkar biderkatzen, ez erro barruan, ez izendatzailean…
Beste ekuazio hauek, berriz, ez dira linealak:
2x – 3y + z = 5 3xy – 2z = 0 x + 2y – sen z = 1
Ekuazio lineala ezezagun bat edo gehiago dituen lehenengo mailako ekuazio polinomikoa da.
• Planoan mugitzen bagara, bi ezezagun izango ditugu: x, y. Bi ezezagun edo ezezagun bakarra dituen ekuazio lineal batek zuzen bat adierazten du planoan. Zuzeneko puntuak ekuazioaren soluzioak dira.
Adibidez, 5x + 4y = 20 da XY planoko zuzen bat. (4, 0), (0, 5), (–2; 7,5), (3; 1,25) puntuak zuzenekoak dira, eta, beraz, ekuazioaren soluzioak dira
x = 3 edo y = 5 ekuazioek ere zuzenak adierazten dituzte.
• Hiru ezezagun dituen (edo hiru ezezagunetakoren bat) ekuazio lineal batek plano bat adierazten du espazioan. Planoko puntuak ekuazioaren soluzioak dira.
Adibidez, 3x + 2y + 6z = 6 plano bat da hiru dimentsioko espazioan. (2, 0, 0), (0, 3, 0), (0, 0, 1), (1, 1, 1/6) puntuak planokoak dira, eta, beraz, ekuazioaren soluzioak dira.
5x + 4y = 20, x = 3 edo y = 5 ekuazioak ere planoak dira
Ekuazio baliokideak
Bi ekuazio baliokideak dira soluzio bera dutenean (edo soluzio berak dituztenean).
Ekuazio bateko bi atalak zero ez den zenbaki berarekin biderkatzen edo zatitzen baditugu, lortuko dugun ekuazioa eta hasierakoa baliokideak dira.
Adibidez:
x y 4 5 + = 1 eta 5x + 4y = 20 baliokideak dira (zuzen bera adierazten dute).

30x + 20y + 60z = 60 eta 3x + 2y + 6z = 6 baliokideak dira (plano bera adierazten dute).
Ekuazio linealen sistemak
Zenbait ekuazio batera ematen badira euren soluzio komuna edo komunak zehazteko, ekuazio-sistema bat eratzen dutela esaten dugu.
• Bi ezezaguneko ekuazio linealen sistema batek zuzen multzo bat adierazten du. Sistema ebazten badugu, zuzen horiek punturen bat berdina duten zehaztu eta puntu hori kokatuko dugu
• Sistema bateko ekuazioek hiru ezezagun badituzte, planoak adierazten dituzte. Sistema ebaztea da plano horiek guztiek berdina duten puntua edo puntuak aurkitzea.
SISTEMA
Ekuazio-sistemak oso interesgarriak dira, eta horiek landuko ditugu unitate honetan eta hurrengoetan. Horregatik, aurrerantzean, «ekuazio-sistema» edo, besterik gabe, «sistema» erabiltzen dugunean, «ekuazio linealen sistema» adierazi nahiko dugu.
28 1
bi ezezaguneko ekuazio linealak
Y X y =5 x =3 5x + 4y = 20 Y X Z 5x + 4y = 20 3x +2y + 6z = 6 Y X Z y =5 x =3
hiru ezezaguneko ekuazio linealak
➜ Marraztu planoak eta zuzenak.
Sistema baliokideak
Bi ekuazio-sistema baliokideak dira soluzio berdinak badituzte
Bi sistema baliokide izan daitezke, nahiz eta sistemak eratzen dituzten ekuazioak baliokideak izan ez
Adibidez: x x y y 52 3 16 3 ––= =+ 4 eta x x y y 513 1 + + = = 4 baliokideak dira, biek ere soluzio bakar
hau baitute: x = 3, y = –2
Aldaketak ekuazio-sistema batean
Sistema batetik beste sistema baliokide batera pasatzeko egindako aldaketa guztiak baliozkoak dira. Adibidez, honako hauek:
1 Ekuazioetako baten bi atalak zero ez den zenbaki batekin biderkatzea edo zatitzea
x xy z z y 3 25 53 ––+ + = = 4 (2.a) · 3

x x y y z z 3 3 5 63 3 15 ––+ + = = 4
2 Ageri diren ekuazioen konbinazio lineala den ekuazio bat eranstea, edo, aitzitik, ageri direnen konbinazio lineala den ekuazio bat kentzea.
x xy z z y 3 25 53 ––+ + = = 4 (1.a) – 3 · (2.a)

EKUAZIOEN KONBINAZIO LINEALA
x x y y y
35 2 114
3 5 12 –– + + = = = 4
z z z
3 Ekuazioetako baten ordez zenbaki batekin biderkaturiko beste ekuazio bat batzean lortzen den emaitza jartzea
Ekuazioen konbinazio lineala esaten diogu ekuazioetako bakoitza zenbaki batekin biderkatu eta atalez atal batzean lortzen dugun emaitzari.
ADI!
Sistemaren soluzioak aldatzen ez dituzten aldaketei baliozko aldaketa esaten zaie
Ekuazioen sistemak ebaztean, baliozkoak ez ezik «komenigarriak» ere badiren aldaketak egin behar ditugu; hau da, soluziora hurbilduko gaituzten aldaketak. Horretarako, batez ere, hemen deskribatu ditugun 1 eta 3 aldaketak erabiliko ditugu
1 Zuzena ala okerra?
a) (x, y) bi ezezagun dituen ekuazio-sistema batean, x + y = 4 ekuazioak, besteak beste, (3, 1) soluzioa du
b) (x, y, z) hiru ezezagun dituen sistema batean, x + y = 4 ekuazioak ez du zentzurik
c) (x, y, z) hiru ezezagun dituen sistema batean, x + y = 4 ekuazioak zentzua du. Plano bat adierazten du, eta sistema horren soluzio batzuk hauek dira: (3, 1, 0), (3, 1, 7), (3, 1, – 4).
d) Planoan bagaude (x, y bi ezezagunekin), y = 0 ekuazioak X ardatza adierazten du
e) Espazioan bagaude (x, y, z hiru ezezagunekin), y = 0 ekuazioak XZ planoa adierazten du
U 1 29
⎯⎯→
⎯⎯⎯⎯→ ←⎯⎯⎯⎯
x xy z z y 3 25 53 ––+ + =
4 ⎯⎯⎯⎯→ (1.a) – 3 · (2.a) x y y z z 11 2 412 5 – + = = 4
=
x + y = 1 5x + y = 13 x + 3y = –3 2x – 5y = 16
a) x x y y 27 5 –+= = ( x x y 3 5 12 + = = ) b) x x y y z 7 5 – + + = = ( x z y 2 7+ = = * c) x x x y y y z z 22 5 7 12 ––+ + + = = = * x z y 2 7+ = = * d) x x y y z z 2 11 7 ––+ + = = ( x y y z 11 4 ––+ = = ) Pentsatu eta praktikatu
2 Azaldu zergatik diren baliokideak sistema-pare hauek, ebazpena egin gabe:
➜ Bi eta hiru dimentsioko ekuaziosistemak.
Ekuazio-sistema batek soluzioa izan dezake (bateragarria) edo baliteke soluziorik ez izatea (bateraezina).
Sistema bateragarriek soluzio bat izan dezakete (determinatuak) edo infinitu soluzio izan ditzakete (indeterminatuak).
Bi ezezaguneko ekuazio-sistemak
Honako sistema hauek eta horien interpretazio geometrikoak aztertuko ditugu:
• x x y y 2 3 3 5 9 4–+= = 4
Ekuazio-sistema honen soluzioa x = 3, y = 1 da. Horrek esan nahi du bi zuzenek (3, 1) puntuan ebakitzen dutela elkar.
Beraz, sistema bateragarria eta determinatua da.
KONTUAN IZAN
Sistema bat bateragarria edo bateraezina dela esan beharrean, zuzenago izango litzateke zehaztea sistema eratzen duten ekuazioak bateragarriak direla (hau da, denek soluzio komun bat dutela) edo bateraezinak direla (ez dagoela denena den soluzio komunik). Dena dela, hemen erabilitako nomenklatura orokorrean onartuta dagoena da.
2 3 5
2 4
x x
3 5 2 –
+= = = 4 Sistema hau aurrekoaren berdina da ia; izan ere, aurreneko bi ekuazioak berdinak dira, eta hirugarrena aurreko bi horiek atalez atal batuta lortzen da
y y y
9 4 13 –
Zuzen berria (marrazkian beltza dena) (3, 1) puntutik igarotzen da eta puntu horretan ebakitzen dute elkar hiru zuzenek. Beraz, sistema hori ere bateragarria eta determinatua da. •
Bi ekuazioek gauza bera diote. Horietako baten soluzio bakoitza bestearena ere bada. Bi zuzenak bat datoz. Hau da, zuzen bera dira
4 3
2
• x x x y y y 2 3 5 3 5 2 9 4 6 –+= = = 4
Ekuazioek kontrakoa diote. Ez dute soluzio berdinik. Geometrikoki, bi zuzenak paraleloak dira, puntu batean ere ez baitute bat egiten
Sistema hau bigarren sistemaren oso antzekoa da; hirugarren ekuazioko gai askea baino ez da aldatzen. Baina hori dela eta, ez da beste biek elkar ebakitzen duten (3, 1) puntutik igarotzen. Ez dago hiru zuzenek bat egiten duten punturik.
Beraz, sistema hau bateraezina da.
2x+3y=9 3x–5y=4 2x+3y=9 3x–5y=4 5x –2y = 13 2x+3y=9 4x+6y=18 2x+3y=9 4x+6y=12 2x+3y=9 3x–5y=4 5x –2y = –6

30 2
• x x x
y y
3 6 9 18 + + = = 4
Sistema bateragarria eta indeterminatua da. • x x y y
6 9 12 + + = = 4
Sistema honek ez du soluziorik. Bateraezina da. Ebazten saiatzen garenean, zentzugabeko adierazpenak lortzen ditugu.
Ekuazio linealen sistema baten soluzio posibleak
Hiru ezezaguneko ekuazio-sistemak
Azter ditzagun honako sistema hauek eta horiei dagozkien interpretazio geometrikoak:
➜ Sortu mota desberdinetako ekuazio-sistemak.
Hiru planoek puntu batean ebakitzen dute elkar. Sistema bateragarri determinatua da
x = 1, y = 7, z = –2
Laugarren ekuazioa beste hiruren batura da. Horri dagokion planoa (horia) komunean duten puntutik igarotzen da. Sistema bateragarri determinatua da
x = 1, y = 7, z = –2
Laugarren ekuazioak beste hiruren baturaren kontrakoa esaten du. Plano hori (horia) ez da beste hiruren ebakipuntutik igarotzen. Sistema bateraezina da
Hirugarren ekuazioak, beste bien batura denez, ez dio bestelako informaziorik eransten sistemari. Sistema bateragarri indeterminatua da
Soluzioa: Planoek elkar ebakitzen duten zuzeneko puntu guztiak dira sistemaren soluzio.
Hirugarren ekuazioak kontra egiten dio beste biak batuta lortzen denari. Sistema bateraezina da
1 Ebatzi eta interpretatu geometrikoki honako ekuazio-sistema hauek:
2 a) Ebatzi sistema hau: x x y y 23 4–+= = *

b) Erantsi hirugarren ekuazio bat sistema bateragarria izaten jarraitzeko
c) Erantsi hirugarren ekuazio bat sistema bateraezina izateko
d) Interpretatu geometrikoki kasu bakoitzean egin duzuna
U 1 31
• x x x y y y z z 2 4 3 25 11 20 8 –––+ ++ = = = *
Soluzioa:
• x x x x y y y z z z 2 4 7 3 2 5 4 11 20 8 1 ––––+ + + + = = = = Z [ \ ] ] ] ]
Soluzioa:
• x x x x y y y z z z 2 4 7 3 2 5 4 11 20 8 3 –––+ + + + = = = = Z [ \ ] ] ] ]
Ez du soluziorik • x x x y y y z z 2 32 11 20 9 ––––+= = = + + *
• x x x y y y z z 2 32 11 20 3 –––+= = = + + *
Ez du soluziorik
a) x x x y y y 2 32 1 4 3 + + + = = = * b) x x y y y z z 2 6 1 7 –+ + += = = * c) x x x y y z z z 6 0 0–+ + += = = + * d) xy y z z z 6 1 1 –++ = = = *
Pentsatu eta praktikatu
Sistema mailakatuak
• Honako sistema hauek oso errazak dira ebazteko:
PROPOSAMENA
Ebatzi urratsez urrats honako hiru sistema hauetako bakoitza.
Behetik gora joanda, ezezagun bakoitzaren balioa lortuko dugu, eta aurreko ekuazioetan ordezkatzen badugu, prozesuarekin aurrera jarraitu ahal izango dugu. Sistema mota hauei mailakatu esaten zaie
• Beste sistema hau ere mailakatua da. Ekuazioak baino ezezagun gehiago dituenez, ezezagunetako bat bigarren atalera igaroko dugu, eta gainerakoak horren funtzioan kalkulatuko ditugu:
(3.a) z = 11 – 3t
(2.a) y = 8 – z = 8 – (11 – 3t) = –3 + 3t
(1.a) x = 5 + t – 2y = 5 + t – 2(–3 + 3t) = 11 – 5t

Ezezagun guztiak t-ren funtzioan jarrita daudenez, t parametrotzat hartuko dugu, balio aldakor bat emango diogu. t = λ esaten badiogu, honela geldituko da:
x = 11 – 5λ y = –3 + 3λ z = 11 – 3λ t = λ
λ-ri ematen diogun zenbakizko balio bakoitzerako, balio horri dagozkion x, y, z eta t-ren balioak lortuko ditugu. Adibidez:
λ = 0 denean, x = 11, y = –3, z = 11, t = 0 lortzen dugu.
λ = 1 denean, x = 6, y = 0, z = 8, t = 1 lortzen dugu.
• Hain agerikoa izan ez arren, honako sistema hau ere mailakatua da:
IDAZKERA
λ (lambda), μ (mu), ν (nu) parametro moduan erabiltzen diren letra grekoak dira.
x x
–++
y y yz
= = =
35 2 11 4 14
b b b b Argi dago 2. ekuazioan y bakandu dezakegula, 1. ekuazioan x, eta, azkenik, 3. ekuazioan z
_ ` a
Sistema hauei ere mailakatu esango diegu, nahiz eta itxura aldetik ematen ez duten
1 Identifikatu honako sistema hauek mailakatu gisa eta eba-
2 Mailakatuak dira sistema hauek? Ebatzi:
32 3
x y y 2 3 5 14 10 + = = * xy y z z z 3 5 2 3 7 6 12 ––+= = = * xy yz z t t t 2 3 2 5 8 11 6 –+ + + = = = = Z [ \ ] ] ] ] ]
–+
= = = 4 → xy yz z t t
+ + = = = + 4
xy yz z t t 2 3 5 8 11
+ +
25 8 113–
tzi: a) x xy 3 2 7 5–= = * b) x x x yz z 2 5 3 6 7 4–++ = = = * c) x x x yz z t t 2 5 3 26 7 4––++ + = = = * d) x x x y z z 2 4 3 30 7 4 –+ += = = *
a) x y y y z z 2 2 22 1 1 1 + + + = = = Z [ \ ] ] ] ] b) x x y z z 2 7 4–+ += = * c) x x y y z 3 2–+ + = = * d) x y z z z z t t t 3 2 2 2 3 4 2 5––+ + + = = = = Z [ \ ] ] ] ] ]
eta praktikatu
Pentsatu
Nola pasatu sistema batetik beste sistema baliokide mailakatu batera Ikus dezagun nola pasatu sistema batetik mailakatua den beste sistema baliokide batera, ebatzitako adibide batzuen bidez
Ebatzitako ariketa
1 Bihurtu sistema hauek sistema mai-
1

koefizienteak oso lagungarriak dira aldaketa errazak egiteko
Orain badaukagu sistema modu mailakatuan jarrita. Aldaketak(*) egin dira, argi dagoenez, y-ren koefizienteak berdintzeko, eta, horrela, zatikiak erabili beharrik gabe ezabatu ahal
Ebazpena:
3 Bihurtu sistema hauek mailakatu eta ebatzi
U 1 33
a) x x y y 2 3 321 4 –+ = = * b) x x x y y y z z z 2 34 2 6 –––+ + + + = = = * c) x x x y y y z z z 3 6 4 8 –+ + + + = = = * d) x x x x y y y y z z z z w w w 32 2 3 3 57 3 2 0 32 18 26 –––––––+ + + + + + = = = = Z [ \ ] ] ] ] ] Pentsatu
praktikatu
eta
lakatu: a) x x y y3 3 7 4 7 ––= = * b) x x x y y y z z z 2 4 5 3 3 4 7 11 3 –––+ + + = = = * c) x x x x y y y y z z z z t t t t 3 2 2 2 3 3 3 4 2 19 16 9 7 ––––––––+ + + + + + = = = = Z [ \ ] ] ] ] a) x x y y 3 3 7 4 7 ––= = * (1.a) (2.a) – 3 · (1.a) x y y 3 2 4 5 ––= = 4
diren
Ebazpena: (2.a) y = –2,5; (1.a) x = –3,5 b) x x x y y y z z z 2 4 5 3 3 4 7 11 3 –––+ + + = = = * (1.a) (2.a) – 2 · (1.a) (3.a) – 4 · (1.a) xy y y z z z 5 11 17 3 7 8 7 3 25 –––––+ + + = = = 4 (1.a) –17 · (2.a)(*) 11 · (3.a)(*) xy y y z z z 5 187 187 3 119 88 7 51 275 ––––+ + = = = 4 (1.a) (2.a)/17 –(3.a) – (2.a) xy y z z z 5 11 3 7 31 7 3 224 ––+= = = 4
izateko.
(1.a)
= 134/31 c) x x x x y y y y z z z z t t t t 3 2 2 2 3 3 3 4 2 19 16 9 7 ––––––––+ + + + + + = = = = Z [ \ ] ] ] ] (1.a) – 3 · (4.a) (2.a) – (4.a) (3.a) – 2 · (4.a) (4.a) x y y y y z z z t t t t 27 5 3 9 2 5 2 40 9 23 7 ––––––––+ + + = = = = _ ` a b b b b b (1.a) + 2 · (2.a) (2.a) (3.a) + (2.a) (4.a) x y y z z z t t t t 7 5 3 5 2 3 2 22 9 14 7 ––––––––+ + + = = = = _ ` a b b b b b 3 · (1.a) (2.a) –5 · (3.a) (4.a) x y y z z z t t t t 21 25 3 15 2 15 2 66 9 70 7 ––––– + + + + = = = = _ ` a b b b b b (1.a) + (3.a) (2.a) (3.a)/5 (4.a) x y y z z z t t t 4 5 3 2 3 2 4 9 14 7 ––––––+ + + + = = = = _ ` a b b b b b Ebazpena: (1.a) z = –1; (3.a) t = –3; (2.a) y = 3; (4.a) x = 5
(3.a) z = 224/31; (2.a) y = 151/31;
x
➜ Adierazi sistema mailakatu batera transformatzeko faseak.
Gaussen metodoa
Aurreko orrialdean ekuazio linealen sistema bat sistema mailakatu bihurtzeko ikusi eta erabili dugun prozedura Gaussen metodoa da. Metodo hori errazago erabiliko dugu ezezagunak alde batera utzi eta zenbakiak bakarrik erabiltzen baditugu (koefizienteak eta gai askeak), matrize eran jarrita
Ikus dezagun nola ebatz daitekeen aurreko orrialdeko bigarren adibidea:
MATRIZEAK
Zenbaki-kaxa hauek, matrize izenekoak, hurrengo unitatean landu eta ikasiko ditugu sakonago. Hemen ekuazio-sistema bateko koefizienteen euskarri moduan erabiliko ditugu, besterik gabe.
Prozesuan parte hartzen duten matrize horietako bakoitza ekuazio-sistema bati dagokio. Azkena mailakatua da eta, beraz, oso erraz ebazten da.
Gaussen metodoa da ekuazio linealen sistema bat sistema mailakatu bihurtzea. Horretarako, «zeroak egin» behar ditugu, ekuazioei oinarrizko bi aldaketa eginez:
• Ekuazio bat zero ez den zenbaki batekin biderkatzea.
• Ekuazio bat zenbaki batekin biderkatutako beste ekuazio batekin batzea.
Prozesu hori askoz errazagoa eta erosoagoa da ekuazioak erabili beharrean zenbakiak bakarrik erabiltzen baditugu —koefizienteak eta gai askeak— matrizetan egituratuta
Prozesuaren amaieran, edo tarteko urratsen batean, honako kasu hauetakoren bat aurki dezakegu:
a) Zeroen errenkada bat. Ekuazio hutsal bati dagokio eta, beraz, bazter utz dezakegu:
(0 0 … 0 0 ) ⇔ 0x + 0y + … + 0t = 0
b) Bi errenkada berdin edo proportzional. Ekuazio baliokideei dagozkie eta, beraz, horietako bat bazter utz dezakegu:
→ 015 26 ………… –…

18 –
c) Azkeneko zenbakia kenduta —gai askeari dagokiona— besteak zero dituen errenkada bat:
(0 0 … 0 ) ⇔ 0x + 0y + … + 0t =
( zero ez den zenbaki bat da)
Argi dago ekuazio hori ezinezkoa dela. Ebatzi ezin den ekuazio bat duten kasu hauek sistema bateraezintzat joko ditugu segituan
Pentsatu eta praktikatu
1 Zuzena ala okerra?
a) Sistema bateraezin batek sistema mailakatu bateragarria eman dezake, Gaussen metodoa aplikatu ondoren. Edo alderantziz
EKUAZIO HUTSALA
0x + 0y + 0z = 0 ekuazioak azalkeria bat, hutsaltasun bat adierazten du. Zenbakien edozein hirukote izango da ekuazio horren soluzio. Ekuazio hutsal esaten zaio.
b) Gaussen metodoa erabili ondoren azkenean lortzen dugun sistema mailakatua hasierako sistemaren mota berekoa da; izan ere, emandako urrats guztiek sistema bat beste sistema baliokide bat bihurtzen dute.
34 4
x x x y y y z z z 2 4 5 3 3 4 7 11 3 –––+ + + = = = * → f 1 2 4 5 1 3 3 1 4 7 11 3 ––– p → f 1 0 0 5 11 17 3 7 8 7 3 25 ––––– p → → f 1 0 0 5 187 187 3 119 88 7 51 275 –––– p → f 1 0 0 5 11 0 3 7 31 7 3 224 –– p → xy y z z z 5 11 3 7 31 7 3 224 ––+= = = *
f 0 0 1 3 5 15 2 6 6
cm
– p
Ekuazio-sistema motak
Gaussen metodoak modua ematen du ekuazio linealen edozein sistema horren baliokide izango den sistema mailakatu bat bihurtzeko
Hasierako sistema bateragarria den (determinatua zein indeterminatua) edo bateraezina den jakiteko, prozesuaren amaieran lortzen dugun sistema mailakatuaren itxurari begiratuko diogu. Honako kasu hauetako bat gerta daiteke:
I. f 0 0 0 0 0 0
zero ez den zenbaki bat edozein zenbaki
Ekuazio baliozkoak ezezagunak adina izango dira. Urratsez urrats joanda, ezezagun bakoitzerako zenbakizko balio bat lortuko dugu.
Beraz, sistema bateragarri determinatua da.
II.
SISTEMA HOMOGENEOAK
Sistema homogeneo bat da gai independente guztiak zero dituen sistema:
Ekuazio baliozkoak ezezagunak baino gutxiago dira. Sobera dauden ezezagunak bigarren atalera igaroko ditugu, eta, beraz, besteen balioa horien funtzioan emango dugu
Sistema bateragarri indeterminatua da. Sistema horren soluzio orokorra bigarren atalera igarotako ezezagunak adina parametroren bidez emango dugu.
III.
Adierazitako ekuazio hori ezin da inoiz bete Sistema bateraezina da.
Argi dago sistema homogeneo bateko ekuazio guztiek daukatela soluzio moduan, gutxienez, soluzio hutsala, x = 0, y = 0, z = 0. Beraz, sistema homogeneoak beti dira bateragarriak.
U 1 35
p
f 0 0 0 p
f … … … … … … 0 0 0 0 p
x x x y y z z y 35 2 0 0 0 –––+ + = = = *
bidez: x x x y y y z z z 2 5 5 2 3 7 4 3 11 ––+ + + + = = = * f 2 1 5 5 2 1 3 1 7 4 3 11 –– p (1.a) – 2 · (2.a) (2.a) (3.a) – 5 · (2.a) f 0 1 0 1 2 11 1 1 2 2 3 4 –––– p (1.a) (2.a) (3.a) – 2 · (1.a) f 0 1 0 1 2 13 1 1 0 2 3 0 ––– p Sistema modu mailakatuan jarrita dago. Sistema bateragarri determinatua da. Ebatzi egingo dugu: (3.a) 13y = 0 → y = 0 (1.a) –y + z = –2 → 0 + z = –2 → z = –2 (2.a) x – 2y + z = 3 → x – 0 – 2 = 3 → x = 5 Soluzioa: x = 5, y = 0, z = –2 Ebatzitako ariketak
1 Ebatzi honako sistema hau Gaussen
metodoaren
2
honako sistema hau Gaussen

36
metodoaren bidez: x x x y y y z z z 5 3 4 7 10 10 8 11 ––+ + + = = = * f 1 5 1 3 1 4 7 1 10 10 8 11 –– p (1.a) (2.a) – 5 · (1.a) (3.a) – (1.a) f 1 0 0 3 14 7 7 34 17 10 42 21 ––––– p (1.a) (2.a) Ezabatu egiten da (3.a) 1 0 3 7 7 17 10 21 –eo → x y y z z 3 7 7 17 10 21 – += = * Bigarren
bateragarri indeterminatua da. (2.a) 7y – 17z = –21 → y = z 7 2117 3 7 17 ––+ =+ z (1.a) x – 3y + 7z = 10 → x = 10 + 3 z 3 7 17 –+ cm – 7z = 1 + 7 2 z Soluzioa hau da: x = 1 + 7 2 λ; y = –3 + 7 17 λ; z = λ z = λ hartu beharrean z = 7λ hartzen badugu, soluzioa honela jarriko genuke: x = 1 + 2λ; y = –3 + 17λ; z = 7λ 3 Ebatzi sistema hau Gaussen metodoa erabiliz: x x x y y y z z z 2 3 8 2 15 21 7 3 11 –––––+ = = = * f 1 2 1 3 1 8 2 15 21 7 3 11 ––––– p (1.a) (2.a) – 2 · (1.a) (3.a) – (1.a) f 1 0 0 3 5 5 2 19 19 7 11 4 ––––– p (1.a) (2.a) (3.a) + (2.a) f 1 0 0 3 5 0 2 19 0 7 11 7 –– p (0 0 0 –7 ) errenkadak 0x + 0y + 0z = –7 ekuazioa adierazten du, eta horrek ez du soluziorik. Sistema bateraezina da Ebatzitako ariketak
Gaussen metodoa erabiliz : a) x x x y y y z z z 3 2 2 2 2 4 2 –+ + + + = = = * b) x x x y y y z z z 3 2 5 4 3 21 2 5 ––––+ + + = = = * c) x x x y y y z z 2 2 2 3 5 3 4 4 ––––+ + + = = = Z [ \ ] ] ] ] d) x x x y y y z z 35 2 0 0 0 ––+ + + = = = * e) x x x y y y z z z 5 3 9 0 0 0 – –++ = = = * f) x x x x y y y y z z z z 2 2 11 4 16 4 2 5 0 0 0 0 ––––+ + + + + = = = = Z [ \ ] ] ] ]
a) x x x y y y z z z 3 2 5 2 3 7 ––+ + + + + = = = * b) x x x x y y y y z z z w w w 2 5 5 2 22 0 0 0 0 –––+ + + + + = = = = Z [ \ ] ] ] ] ] c) x x x x y y y y z z z w w w 2 5 5 2 22 1 3 4 3 –––––––+ + + + + = = = = Z [ \ ] ] ] ] ] Pentsatu eta praktikatu ➜ Ekuazio-sistemen ebazpena.
Ebatzi
ekuazioa ezabatu egin dugu, hirugarrenarekin proportzionala baita. Hirugarren zutabea (z) gai askera igaroz gero, sistema mailakatuta izango dugu. Sistema
2 Ebatzi ekuazio-sistema hauek
3 Ebatzi Gaussen metodoaren bidez.
Ekuazio-sistemen eztabaida
Aztertu ekuazio linealen honako sistema hau:
Egia esan, ekuazio-sistema bat izan beharrean sistemen multzo bat da, k parametroaren balio bakoitzerako ekuazio-sistema desberdin bat baitago
Infinitu sistema horietatik, batzuk bateragarriak izango dira beharbada, eta beste batzuk, bateraezinak. Parametroaren «mendekoa» den sistema eztabaidatzea da sistema hori era batekoa edo bestekoa k-ren zer baliorekin izango den jakitea.
Parametro baten edo gehiagoren mendekoa den ekuazio-sistema bat eztabaidatzea hau da: sistema hori bateragarria edo bateraezina parametroen zer baliorekin izango den identifikatzea, determinatua edo indeterminatua zer kasuetan den ere bereiziz
1 Eztabaidatu sistema hau eta, ahal denean, ebatzi:
Gaussen metodoa erabiliko dugu:
• k = 1 bada, azkeneko errenkada (0 0 0 1 ) da. Sistema bateraezina da.
• k ≠ 1 bada, orduan: z = k k 1–y = (1 – k 2) k k 1–

Hau da, k ≠ 1 denean, sistema bateragarri determinatua da.
Soluzioa: ,, k kk k kk k k 1 21 1 – –32 2 + +
Kontuan hartu: Ez daude infinitu soluzio, infinitu sistema baizik: k-ren balio bakoitzerako sistema bat. Eta sistema horietako bakoitzak soluzio bakarra du, k = 1 kasuari dagokionak izan ezik. Horrek ez dauka soluziorik. Adibidez, k = 2 kasurako, hau da sistema:

U 1 37
() x kx x y ky y kz z z k k 1 1 1 –+ + + + + + = = =+ *
5
() x kx x y ky y kz z z k k 1 1 1 –+ + + + + + = = =+ *
f kk k k k 1 1 1 1 1 1 1 1 1 –+ p (1.a) (2.a) – k · (1.a) (3.a) – (1.a) f k k kk 1 0 0 1 1 0 1 1 1 0 –2 p
+ k
–
= k 2
x = k kk k 1 21
32 +
eo
x x x y y y z z z 2 21 2 3 + + + + + + = = = 4 Horren
hau da: x = –1, y = 6, z =
soluzioa
–2 Ebatzitako ariketa
k-ren funtzioan: a) x x kx y y y z z k 42 2 1 –+ + ++ = = = Z [ \ ] ] ] ] b) x x kx y y y z z k 42 2 0 –+ + ++ = = = Z [ \ ] ] ] ]
a) x y y z z z kx xk2 8 0 –+ ++ + = = = * b) x y y y z kz k x 2 1 1 + + + = = = + * Pentsatu eta praktikatu
1 Eztabaidatu ekuazio-sistema hauek
2 Eztabaidatu ekuazio-sistema hauek k-ren funtzioan:
➜ Adierazi parametro baten araberakoa den sistema bat.
Ebatzitako ariketak eta problemak
Ebatzi eta interpretatu geometrikoki honako ekuazio-sistema hauek:
a) Hiru aldagai daudenez, x, y, z, ekuazio bakoitza espazioko plano bat da. Lehenengo bi ekuazioen ordena aldatuko dugu, lehenengo koefizientea 1 izan dadin:
EGIN ZUK
Ebatzi eta interpretatu geometrikoki honako ekuazio-sistema hauek:
Soluzioak: (1 + λ, λ, –1 – λ)
Sistemak zuzen batean elkar ebakitzen duten lau plano adierazten ditu.
b) Ezezagunen koefiziente bat bera ere ez denez 1, erreferentzia moduan lehenengo ekuazioa hartuko dugu:
ezin da inoiz bete. Sistema bateraezina da, ez du soluziorik.
Sisteman ez dagoenez plano paraleloen bikoterik, binaka hiru zuzenetan elkar ebakitzen duten hiru plano adierazten ditu.
c) Bi aldagai baino ez daudenez, x eta y, ekuazio bakoitza planoko zuzen bat da. Erreferentzia moduan bigarren errenkada hartuko dugu:
errenkadak alde batera utzi, eta hau geratzen zaigu:
Soluzioa: (3/4, –1/4)
Sistemak (3/4, –1/4) puntuan elkar ebakitzen duten lau zuzen adierazten ditu.
38
a) 2 x x x y y y y z z z 2 13 3 15 1 1 2 13––––= + + + + + = = = Z [ \ ] ] ] ] b) x x x y y z z z 2 3 5 2 2 3 2 14 1 5 10 –– + + + = = = Z [ \ ] ] ] c) 2 x x x x y y y y 3 5 2 2 1 4 1 ––+ + = = = = Z [ \ ] ] ] ]
a) xy z xy z yz 0 22 1 1 –+= += += * b) y2 y11 x x x x2 5 2 23 1 ––+ + + = = = = y2 y *
2 2 13 3 15 1 –1 –2 13 x x x z y y y y z z –– = = = = + + + + + Z [ \ ] ] ] ] f 1 0 1 2 1 1 2 13 0 1 3 15 1 1 2 13 –––– p (1.a) (2.a) (3.a) – (1.a) (4.a) – 2 · (1.a) f 1 0 0 0 1 1 3 15 0 1 3 15 1 1 3 15 –––– p (1.a) (2.a) (3.a) – 3 · (2.a) (4.a) – 15 · (2.a) f 1 0 1 1 0 1 1 1 0 0 0 0 0 0 0 0 –– p → xy yz 1 1 ––= += * → x y z 1 1 m m m =+ = = Z [ \ ] ] ] Soluzioak parametro baten mendekoak dira; beraz, zuzen bat adierazten dute.
f 0 0 2 3 5 2 2 3 2 14 1 5 1 –– p (1.a) 2 · (2.a) – 3 · (1.a) 2 · (3.a) – 5 · (1.a) f 20 3 1 1 1 0 0 4 4 13 3 13 5 –– p (1.a) (2.a) (3.a) + (2.a) f 20 31 0 0 4 0 13 0 13 2 –– p Hirugarren ekuazioa
f 3 1 5 2 1 1 2 2 1 4 1 – p (1.a) – 3 · (2.a) (2.a) (3.a) – 5 · (2.a) (4.a) – 2 · (2.a) f 0 1 0 0 4 1 4 4 1 1 1 1 –––– p (1.a) (2.a) (3.a) – (1.a) (4.a) – (1.a) f 0 1 0 0 4 1 1 1 0 0 0 0 –– p
y xy 41 1 ––= = * → y = –1/4 → x = 3/4
Azkenengo bi
1 1 Y X
1. Gaussen metodoa
2. Gaussen metodoa ekuazio-sistema linealak eztabaidatzeko erabiltzea
Eztabaidatu eta ebatzi sistema hauek, beraietan ageri den parametroaren funtzioan, Gaussen metodoa erabilita. Eman, kasuetako bakoitzean, interpretazio geometriko bat:
EGIN ZUK
Eztabaidatu eta ebatzi, parametroaren funtzioan, Gaussen metodoa erabilita. Eman interpretazio geometrikoak.
• m = 1 bada, azkenengo errenkada (0 0 0 0) da eta kendu daiteke. Sistema bateragarri indeterminatua da, ezezagun gehiago dituelako ekuazioak baino. Parametro baten mendekoak diren infinitu soluzio ditu.
32 44 0
yz y 0
––= = = 4 Soluzioak: x = 2 – 3λ, y = 4 – 4λ, z = λ
Zuzen bat komunean duten hiru plano adierazten dituzte.
• m ≠ 1 bada, sistema bateragarri determinatua da.
xz yz ym
–––
32 44 01
= = = 4 Soluzioa: x = – 1, y = 0, z = 1
Hiru planoek (–1, 0, 1) puntuan ebakitzen dute elkar.
Bigarren ekuazioan y-ren koefizientea baliogabetzen duten balioak aurkituko ditugu: 1 – m 2 = 0 → m = ± 1
• m = –1 bada, bigarren ekuazioa 0 · y = 2 izango da. Sistema bateraezina da. Bi zuzen paralelo dira.
• m = 1 bada, bigarren ekuazioa, 0 · y = 0, ezabatu daiteke. Sistema bateragarri indeterminatua da. x + y = 0 ekuazioa baino ez zaigu geratzen, eta, ebazteko, y parametrotzat joko dugu. Soluzioak hauek dira: (–λ, λ). Bi zuzenak bat datoz.
• m ≠ ±1 bada, sistema bateragarri determinatua da. m-ren balio bakoitzerako, sistema bat daukagu, eta soluzio bakar bat:
puntu batean ebakitzen dute elkar.
a-ren balio bakoitzerako, sistema desberdin bat daukagu, soluzio bakar batekin: (0, 0, 0). Koordenatu ardatzean elkar ebakitzen duten hiru plano dira.
U 1 39
a) 22 2 2 0 x x x my y z z –––++ + = = = * b) x mx my y m m2 1 2 ––+ + = = * c) x x x y ay z az z 0 0 0 ––+ + + = = = Z [ \ ] ] ] ]
a) x x x y y y z z mz 2 3 2 3 3 5 7 + + + + + + = = = * b) x x x y y y z az z 3 2 2 0 5 3 + + + + + + = = = * c) mx y xmym 1 –+= = * a) Ekuazioen
aldatuko
f m 1 2 1 1 0 1 2 3 2 0 2 –––– p (3.a) (2.a) (1.a) f m 1 2 1 12 2 0 2 03 1 ––– p (1.a) (2.a) + 2 · (1.a) (3.a) – (1.a) f m 1 10 0 03 4 4 2 4 4 –––––– p (1.a) (2.a) (3.a) + (2.a) f m 1 0 0 1 0 0 1 3 4 0 2 4 ––––––– p
ordena
dugu.
xz
()
b) m mm m 1 1 1 22
–eo (1.a) (2.a) – m · (1.a) m m m mm 1 01 1 2 ––22 + eo
–
m mm m mm 1 21 1 2 – –2 2 2 2 + eo . Bi zuzenek
c) f a a 1 1 1 0 1 1 1 0 0 0 –– p (1.a) (2.a) – (1.a) (3.a) – (1.a) f a a 1 0 0 0 1 1 1 2 0 0 0 ––+ p (1.a) (2.a) (3.a) + a · (2.a) f a aa 1 0 0 0 1 0 1 1 2 0 0 0 ––2 + ++ p Sistema homogeneoa da. a 2 + a + 2 = 0 ekuazioak ez duenez
sistema beti da bateragarri determinatua.
,
soluziorik,
Ebatzitako ariketak eta problemak
3. Ekuazioak baino ezezagun gehiago dituzten sistemak
Ebatzi eta interpretatu geometrikoki honako sistema hauek:
a) xy z xy z 31 22 3 –+= += *
b) xy z xy z 24 62 23 1 ––+= +=
Sistema hauek (ekuazioak baino ezezagun gehiago dituztenak) ez daukate inoiz soluzio bakarra. Infinitu soluzio izan ditzakete, edo bat bera ere ez.
a) z bigarren atalera igaro eta z = λ egingo dugu (parametroa). Horrela, sistemak ekuazioak adina ezezagun izango ditu.
EGIN ZUK
Ebatzi eta interpretatu geometrikoki honako ekuazio-sistema hauek:
a) xy z yz 24 0 ––+= = *
b) xy z xy z 23 36 31 ––+= += *
Pertsona batek 60 000 € inbertitu ditu A, B eta C hiru enpresatan, eta 6 000 €-ko irabaziak lortu ditu. A eta B enpresetan inbertitu duenaren batura k aldiz izan da C enpresan inbertitutakoa, eta irabaziak % 5ekoak izan dira A-n, % 10ekoak B-n eta % 20koak C-n.
a) Planteatu ekuazio-sistema bat enpresa bakoitzean zenbat diru inbertitu duen jakiteko.
b) Aztertu bere bateragarritasuna eta ebatzi k = 5 kasurako, baldin eta ahal bada.
EGIN ZUK
A, B eta C-ren artean guztira daukaten dirua A eta B-ren artean daukatenaren % 150 da, eta A eta C-ren artean daukatenaren bikoitza. C-k duen dirua A-k duenaren bikoitza bada, jakin dezakegu zenbat diru duen bakoitzak?
xy
xy 31 23 2–m m += + += +
(1.a) (2.a) – 2 · (1.a) xy y 31 55––m += + = * → x y z
Sistemaren soluzioak (–2 + λ, 1, λ) dira. Parametro baten mendekoak direnez, zuzen bat eratzen duten infinitu soluzio daude.
λ-ren balio bakoitzerako soluzio bat lortzen dugu.
Zuzen batean elkar ebakitzen duten bi plano dira.
Soluzioen egiaztapena:
() 23 1 22 12 –3 mm mm ++ = ++ =
b) Bi ekuazioek plano bera adierazten dute, bata bestearen bikoitza baita. Bigarren ekuazioa baino ez dugu hartuko, eta hiru ezezagun dituenez, bi parametro behar ditugu ebazteko.
z eta y bigarren atalera igaroko ditugu, x = 1 + 2y – 3z, eta y = λ eta z = μ egingo dugu.
Sistemaren soluzioak (1 + 2λ – 3μ, λ, μ) dira. Sistemak infinitu soluzio ditu. Planoak bat datoz.
4. Problemak eztabaidatzea eta ebaztea
a) Ekuazio-sistema bat planteatuko dugu, problemako baldintzak aintzat hartuta. x da A enpresan inbertitutako dirua, y da B-n inbertitutakoa, eta z, C-n inbertitutakoa.
b) Bateragarritasuna aztertzeko, hirugarren ekuazioa sinplifikatuko dugu eta gai independenteak milaka eurotan adieraziko ditugu.
Bigarren ekuazioan ikusten dugunez, k = –1 bada, (0z = –60) ekuazioak ez du soluziorik. Beraz, k ≠ –1 izan behar da; eta k problema honetan zenbaki positibo bat izan behar denez (k aldiz), esango dugu sistema bateragarria dela baldin eta k > 0 bada.
40
*
*
1 –
*
2
m m =+ = =
*
,, , x x x y y y z z kz 2 0050 10 00 60000 6000 + + + + + = = = * → x x x y y y z kz z51020 60000 6000 0 00 –+ + + + + = = = *
x x x y y y z kz z 60 0 0 24 12 –+ + + + + = = = * → f k 1 11 1 0 1 1 24 60 120 – p (1.a) (2.a) – (1.a) (3.a) – (1.a) f k 1 0 0 1 0 1 1 1 3 60 60 60 – p
k = 5 bada → x y y z z z 660000 60000 60000 3 –+ + + = = = Z [ \ ] ] ] → z = 10 000 € → y = 30 000 € → x = 20 000 € 20 000 € inbertitu ditu A-n, 30 000 € inbertitu ditu B-n, eta 10 000 € inbertitu ditu C-n.
Ariketa eta problema gidatuak
1.
Parametro bateko
a) Eztabaidatu honako sistema hau m-ren balioen arabera:
+ + *
a) Gaussen metodoa ezartzean, sistema mailakatu bat lortuko duzu, eta hirugarren ekuazioa (m + 1)z = 8 da.
Zehaztu zer baldintza bete behar duen m-k ekuazio horrek soluzioa izan dezan.
–+ +
z z 2 2
y y y
= = =
22 1 3 5
b) Ebatzi sistema, bateragarri determinatua egiten duten m-ren balioetarako.
2. Sistema bateragarri
b) Adierazi z-ren balioa m-ren funtzioan, eta lortu x-ren eta y-ren balioak, horiek ere m-ren funtzioan
Soluzioa:
a) m ≠ −1 bada, sistema bateragarri determinatua da. m ≠ −1 den balio bakoitzerako, soluzio bakarra duen sistema desberdin bat daukagu.
b) x = –1; y = m m 1 7–+ ; z = m 1 8 +
indeterminatu baten soluzio berdinak dituen sistema bat
S: x x y y z z2 21 32 – += = * sistema izanda, kalkulatu zein izan behar den k-ren balioa, S sistemari x + y + kz = 1 formako hirugarren ekuazio bat erantsiz gero lortzen den sistema S-rekiko baliokidea izateko.
3. Sistema bateragarria
xy z xy z xy z xy az a 1 22 3 22 ––++ = ++ = ++ = += *
4. Sistema bateragarria
• Frogatu S sistema bateragarri indeterminatua dela, eta lortu bere soluzioak.
• Idatzi sistema berriaren matrizea eta ezarri Gaussen metodoa.
• Zehaztu zein izan behar den k-ren balioa ekuazio berria hutsala izan eta ezabatu ahal izateko.
• Egiaztatu S-ren soluzioek hirugarren ekuazioa egiaztatzen dutela lortu duzun k-ren baliorako.
Soluzioa: k = –8 denean, soluzioak dira (1 + 5λ, 3λ, λ) zuzeneko puntuak.
• Egiaztatu, Gaussen metodoa erabilita, lehenengo hiru ekuazioak soilik dituen sistema bateragarria dela, eta laugarrenarekin bateragarri izaten jarraitzen duela a-ren edozein baliotarako.
• Zein izan behar da a-ren balioa laugarren ekuazioa ekuazio hutsala izateko?
• Ezabatu ekuazio hutsalak eta ebatzi sistema, bateragarri indeterminatua eta bateragarri determinatua den kasuetan.
• Aukeratu egokiro parametro moduan hartuko duzun ezezaguna.
Soluzioa: a = –1 bada, bateragarri indeterminatua da, eta soluzioa ,, 3 1 3 4 – mm dn da.
a ≠ –1 bada, bateragarri determinatua da, eta soluzioa ,, 3 1 3 1 1 dn da.
• Ezarri Gaussen metodoa, eta 2. ekuaziorako (1 – m2)y = –(1 + m) lortuko duzu.
• Zer baldintza bete behar du m-k sistemak soluzioa izan dezan?
• Zehaztu m-ren zer baliok bihurtzen duten ekuazio hori bateraezin edo ekuazio hutsal bat.
y
xmy mx
• Sistemak planoko bi zuzen adierazten ditu, komunean puntu bat izan dezaketenak, puntu bat ere ez, edo infinitu puntu.
–
––
m ≠ ±1 balio bakoitzerako, puntu batean elkar ebakitzen duten bi zuzen lortzen ditugu.
m = 1 bada, sistema bateraezina da. Bi zuzen paralelo dira.
m = –1 bada, sistema bateragarri indeterminatua da. Zuzenak bat datoz.
41 U 1
x x x
eta soluzio bakarreko sistemak
Eztabaidatu honako sistema hau a-ren balioen arabera, eta ebatzi horretarako aukera dagoen kasu guztietan:
m
–––
= *
Aztertu m-ren zer baliotarako duen honako sistema honek soluzioa, ebatzi soluzio bakarra duen kasuan, eta interpretatu lortutako emaitzak geometrikoki:
10 10
+= ++
• Idatzi sistema adierazten duen hiru errenkadako eta hiru zutabeko matrizea.
Soluzioa: m ≠ ±1 bada, bateragarri determinatua da, eta soluzioa , mm 1 1 1 1 –
dn da.
Proposatutako ariketak eta problemak
Praktikatzeko
Ekuazio-sistema linealen ebazpena eta interpretazio geometrikoa

1 Ebatzi eta interpretatu geometrikoki honako sistema hauek:
Gaussen metodoa
7 Ebatzi Gaussen
2 Ebatzi eta interpretatu geometrikoki.
3 Arrazoitu honako sistema hauek soluziorik duten, eta interpretatu geometrikoki. Ebatzi, egin litekeen kasuetan.
9 Ebatzi, ahal izanez gero, honako sistema hauek:
6 Idatzi hiru ekuazioko eta bi ezezaguneko sistema bat, soluziorik ez duena, eta interpretatu geometrikoki.
10 Aztertu eta ebatzi Gaussen metodoaren bidez.
11 Sailkatu honako sistema hauek bateragarriak edo bateraezinak diren kontuan izanda:
12 Aztertu eta ebatzi Gaussen metodoaren bidez:
23
42
a) (/ ) (/) xy xy xy 20 25 32 30 32 –––+= += = * b) x x x y y y 3 2 2 4 5 1 0 –+ + = = = * c) x x x y y y 5 0 23 3–+ + = = = * d) x x x y y y 2 5 4 2 10 6 3 15 ––––+ = = = *
a) x x x y y y 32 0 32 6 1 + + + = = = * b) xy xy xy 21 23 58 ––+= = += * c) x x x yz yz 2 5 3 0 ––+ + = = = * d) x x y y y z z z 2 2 1 3 0 –––+ + = = = *
a) x x y y z z 23 2 ––+ + = = * b) (/ ) x x y y z z 23 3 2 6 4 3 2 – ++ = = *
mailakatu hauek: a) xy y x 27 2369 23 2 –– –= = * b) x y y z z z 3 9 1 2 3 ––+ + = = = * c) xy y z 2 5 –+ = = * d) xy y z z 24 2 ++ + = = *
Ebatzi
sistema mailakatu hauek: a) x x x yz z 20 9 2 –––+ = = = * b) x x y y y z 2 3 3 2 0 0 1 ––+= = = * c) xy y z z z t t t2 4 3 1 ––+ + + + = = = * d) xy y y t t z z 2 4 1 ––+ + + = = = *
4 Ebatzi honako sistema
5
honako
metodoa erabiliz. a) x x y yz z 1 2 3 –+ + + = = = * b) x x x y y y z z z 2 3 4 2 3 0 0 0 + + + + + + = = = * c) x x x y y y z z z 3 5 2 33 1 1 1 –+ + + + + = = = * d) xy z xy z xy z 34 3 66 216 26 2 66 –+= += += *
Ebatzi Gaussen metodoa erabiliz. a) xy xy z xz z y 25 16 32 2 4 2 2 25 2 –+= += += + * b) x x x y y y z z z 3 5 2 33 1 3 0 + + + + + + = = = * c) x x x y y z z 2 2 2 0––+= += = * d) x x x y yz z 2 3 3 1 4 –+ + + = = = *
8
a) xy z xy z xy z 29 10 25 2 22 2 ––++ = = += * b) xy z xy z 23 21 2 2 ++ = += * c) x x x y y y z z z 2 2 42 1 3 2 –––+ + + + = = = * d) x x x y y y z z 2 3 4 30 0 0 –––+ += = = *
a) xy z xy z xy z 32 42 5 24 71 2 3 ––++ = += += * b) yz xy xy z x z 1 1 23 2 23 23 –––– += = ++ = + * c) x x x y y y z z z 5 2 2 2 2 3 2 4 3 3 + + + + + = = =
d) x x x y y y z z z t t t 2 3 2 3 3 3 5 14 6 0 0 0 ––––+ + + + + = = =
*
*
x x y y z z z 3 3 0 –+ + += = =
b) x x x y y y z z z 2 3 2 1 ––++ + + = = =
a)
*
*
a) xy z xy z xy z 2 23 511 56 29
6 2 –++ = ++ = +=
b) x x x y y y z z z 2 4 3 2 0 0 0 –––+ + += = =
*
*
Ekuazio-sistemak eztabaidatzea
13 Eztabaidatu honako sistema hauek m parametroaren balioen arabera:
Ebazteko
19 Sailkatu honako sistema hauek, kontuan izanda a-ren balioen arabera zenbat soluzio dituzten, eta ebatzi a = 2 kasuan:
a) x x y y y z az 2 1 3 2 ––+ = =

14 Eztabaidatu honako sistema hauek eta ebatzi, egin litekeenean:
20 a) Zehaztu, a parametroaren balioen arabera, zer kasutan daukan edo ez daukan honako sistema honek soluzioa: x x x
15 Ebatzi honako sistema hauetako bakoitza bateragarri egingo
16 Eztabaidatu sistema hauek k-ren balioen arabera, eta ebatzi, egin litekeenean:
17 Eztabaidatu honako ekuazio-sistema hauek parametroaren balioen funtzioan:
18 Eztabaidatu eta ebatzi parametroaren funtzioan:
= = = *
+ +
1 2
y y y a a 2 4 4 10
b) Ebatzi bateragarri determinatua den kasuetan.
2 2 0 –m m + + *
z z 23
+ + = = =
b) Ebatzi λ = 3 kasurako.
x
a)
xy xy z xy z
= = = *
+ + +
y y y
+ + +
z z az 2 5 34 0 0 06
a) Ondorioztatu a-ren zer baliorekin daukan sistemak (0, 0, 0) soluzioa soilik.
b) Ebatzi sistema infinitu soluzio dituen kasuan.
25 Itsasontzi batek 400 ibilgailu (autoak, kamioiak eta motorrak) garraiatzen ditu. 5 kamioiko 2 motor daude. Eta autoak gainerako ibilgailuen 9/7 dira. Mota bakoitzeko zenbat ibilgailu garraiatzen ditu itsasontziak?
43 U 1
a) xy y ym 2 2 3 1 2–+= = = * b) xy y y z z zm 2 3 2 7 3 0 –+ + + = = = * c) xy y z z mz 28 1 3 1 ––+ + = = = * d) () x x y z mz 3 5 0 0 0 ––+ = = = *
a) x x x y y ky 24 2 2 2 –+ + = = = * b) x x x y y y z z zm 2 5 2 52 1 3 –––+ + + = = = *
duten m-ren balioetarako: a) x x x y y ym 2 4 2 3 3 1–+ + = = = * b) x x x x y y y z z z zm 2 3 2 2 3 5 2 1 3 + + + + + = = = = *
a) x x x y ky y z z z 2 5 3 2 3 0 0 0 ––+ += = = * b) x x x y y z z kz 3 2 2 2 1 1 0 ––+ ++ = = = *
a) x x x y y y z z kz k 2 21 0 –––+ + + = = = * b) x x x y y ay z z z 3 3 4 0 0 0 –+ + + + + = = = * c) xy z mx yz xy z m 21 1 34 23 2 22 ––+= += += * d) x x x y y y az z z 3 5 2 33 1 2 1–+ + + + + = = = *
a) xmyz xy z xz m my 2 22 0 32 2 ––– –++ = += = * b) x x x y y y z az z 3 2 2 0 5 3 + + + + + + = = = *
*
x x x y y y z z z a 2 2
0 1 ––+ += = = *
=
b)
0
21 a) Aztertu sistema λ-ren balioen arabera: x x x y y
x x y y y z z zm 2 5 2 52 1 3 –––+ + + = = =
b) () x mx x y y my z mz zm 1 1 2–+ + + + + + = = = *
22 Aztertu honako ekuazio-sistema hauek. Ebatzi bateragarriak direnean, eta interpretatu lortutako soluzioak geometrikoki.
*
b)
z 1 23
0 22 5 25 –––a = += +=
23 Eztabaidatu honako sistema hauek α-ren balioen arabera, eta interpretatu geometrikoki: a) xy xy 1 21 – a aa a a = = *
516
*
24 Honako ekuazio-sistema hau izanda: x x x
Proposatutako ariketak eta problemak

26 Gitarra elektrikoak egiten dituen enpresa batek 325 aleko eskaera bat bete behar du, eta hiru tamainatako kutxatan sartuta bidaliko ditu. 3 kutxa-modelo ditu (A, B eta C), eta kutxetan 5, 10 eta 15 ale sartzen dira, hurrenez hurren. Guztira 35 kutxa ditu. Gainera, A eta B modeloetako kutxen kopurua 6 aldiz handiagoa da C modelokoena baino.
a) Planteatu ekuazio-sistema bat eskariari erantzuteko modelo bakoitzeko zenbat kutxa erabil daitezkeen kalkulatzeko.
b) Aztertu sistema horren bateragarritasuna eta ebatzi.
27 Liburu-salatzaile batek 84 liburu saldu ditu, bi preziotan: batzuk, 5m euroan, eta beste batzuk, 4m euroan. Guztira, 3 105 euro bildu ditu.
a) Planteatu ekuazio-sistema bat, kontuan izanda x eta y ezezagunak direla mota bakoitzetik saldutako liburuen kopurua, eta aztertu bateragarritasuna.
b) Izan litezke liburuen prezioak 45 eta 36 euro, hurrenez hurren?
c) Ebatzi sistema m = 9 kasuan. Mota bakoitzeko zenbat liburu saldu ditu?
28 Talde batean 18 eta 25 urte bitarteko 288 pertsona daude, batzuk ikasleak, beste batzuk landunak, eta beste batzuk langabeak. Bost ikasleko hiru landun daude, eta lanik gabe daudenak gainerakoen % 80 dira.
a) Planteatu enuntziatu horri dagokion ekuazio-sistema.
b) Zenbat ikasle, landun eta langabe daude?
29 Euro bateko txanpon batzuk ditugu, hiru pilotan banatuta. Hirugarren pilotik hamabi txanpon pasatu ditugu bigarren pilora, eta, ondoren, bigarren horretatik hamar txanpon lehenengora. Azkenean, hiru piloak txanpon kopuru berarekin geratu dira.
a) Zehaz dezakegu zenbat txanpon zeuden pilo bakoitzean, emandako datu horiekin? Arrazoitu zure erantzuna.
b) Zehaztu zenbat txanpon zeuden hasieran pilo bakoitzean, guztira 51 txanpon zeudela jakinda.
30 Zenbaki baten hiru zifren batura 13 da. Unitateen eta ehunekoen zifrak trukatzen baditugu, zenbakia 495 unitate handitzen da. Ehunekoen zifra hamarrekoena baino m unitate handiagoa da.
a) Planteatu ekuazio-sistema bat, eta arrazoitu m-ren zer baliotarako den bateragarri determinatua.
b) Zein izan behar da m-ren balioa problemak soluzioa izateko? Kalkulatu soluzioa m = 4 kasurako.
31 Kafetegi batean, A mahaikoek 6 kafe eta 3 tostada eskatu dituzte eta 12 € ordaindu dute, eta B mahaikoek, 6 kafe eta m tostada eskatuta, 13,60 € ordaindu dute.
a) Planteatu ekuazio-sistema bat, x eta y ezezagunak kafearen prezioa eta tostadaren prezioa izanik, hurrenez hurren.
b) m-ren zer baliotarako dauka soluzioa aurreko sistemak? Soluziorik egonez gero, bakarra izango da beti? Eskatu ahal izan dituzte B mahaikoek 4 tostada? Erantzuna baietz bada, zenbat balio du kafe batek?

32 Lagun batzuek, atzo, 4 freskagarri, 3 ogitarteko eta 5 izozki eskatu zituen taberna batean, eta 30,60 € ordaindu zuten guztira. Aurreko egun batean, 2 freskagarri, ogitarteko bat eta 2 izozki erosita, 12,30 € ordaindu zuten.
a) Gaur ere taberna horretan izan dira, eta 6 freskagarri, 5 ogitarteko eta 8 izozki eskatu dituzte. Zenbat ordainduko dute? Arrazoitu zure erantzuna.
b) Freskagarri batek, ogitarteko batek eta izozki batek 8,20 € balio badute, zein da bakoitzaren prezioa banaka?
33 Lantegi batean, goizeko txandan kontsumitu dituzten erregai-tonak m aldiz dira arratsaldeko txandan kontsumitutako tonak.
Gainera, badakigu arratsaldeko txandan m tona gutxiago kontsumitzen dituztela goizeko txandan baino.
a) Planteatu eta eztabaidatu problema hori m-ren funtzioan.
b) Izan liteke goizeko txandan bi aldiz erregai gehiago kontsumitzea arratsaldeko txandan baino?
c) m = 2 dela pentsatuz gero, zenbat kontsumitzen da arratsaldeko txandan?
34 Herrialde batek A, B eta C hiru markatako 21 000 ibilgailu inportatu ditu, 10 000, 15 000 eta 20 000 euroan, hurrenez hurren. Ibilgailuak 322 milioi euro kostatu dira guztira. Badakigu 21 000 ibilgailu daudela, B markakoak eta k aldiz A markakoak zenbatuta.
a) Planteatu sistema bat problemaren baldintzekin, marka bakoitzeko ibilgailu-kopuruaren funtzioan.
b) Ebatzi sistema k = 3 kasurako.
c) Egiaztatu sistemak ez duela soluziorik k = 2 kasuan.
44
Galdera teorikoak
35 Zuzena ala okerra? Arrazoitu eta jarri adibideak.
a) Bi ezezaguneko bi ekuazio dituen eta bateragarri indeterminatua den sistema bati ekuazio bat erantsita, sistema hori bateragarri determinatua bihur dezakegu, edo bateraezina.
b) Hiru ezezaguneko hiru ekuazio dituen eta bateragarri determinatua den sistema bati ekuazio bat erantsita, sistema hori bateragarri indeterminatua bihur dezakegu.
c) xy za
xy za 2 24 22 1 22 ––+= += + * sistema bateraezina da a-ren balioa edozein dela ere
d) x x y y a b 32 –+= = * sistema bateragarri indeterminatua da a-ren
eta b-ren edozein baliotarako
e) Sistema bateragarri determinatu bat eta bateragarri indeterminatu bat baliokideak izan daitezke.
36 Erantsi ekuazio bat xy z xy z22 1 22 3––+= += * sistemari, bihurtu dadin:


a) bateraezina. b) bateragarri determinatua.
c) bateragarri indeterminatua.
1 Ebatzi eta interpretatu sistema hauek geometrikoki:
Sakontzeko
37 a-ren zer baliotarako da sistema hau bateraezina?
2 Eztabaidatu sistema hau eta ebatzi, ahal denean:
• Izan daiteke bateragarri indeterminatua a = 2 baliorako?
• Ebatzi a = 2 den kasuan.
• a ≠ 1 eta a ≠ 2 bada, izan daiteke bateragarri determinatua?
38 Ekuazio-sistema hau edukita:
a) Arrazoitu parametroen a = 0, b = 1, c = 2 balioetarako sistema bateragarria dela.
b) Zehaztu zein izan behar diren a, b eta c parametroen balioak (x, y, z) = (1, 2, 3) sistemaren soluzioa dela egiaztatzeko.
c) Arrazoitu soluzio hori bakarra den ala ez den.
4 Ekuazio hauek ditugu: xy z xy z
a) Erantsi ekuazio bat sistema bateraezina izan dadin.
b) Erantsi ekuazio bat bateragarri determinatua izan dadin.
c) Erantsi ekuazio bat bateragarri indeterminatua izan dadin.
Arrazoitu zer prozedura erabili duzun kasu bakoitzean.
5 Ekuazio linealen sistema hau daukagu:
3 Kutxazain automatiko batean 1 330 € daude, 10 €, 20 € eta m €-ko billeteetan. Badakigu guztira 97 billete daudela, eta 10 €-koak bi aldiz gehiago daudela 20 €-koak baino.
a) Planteatu ekuazio-sistema bat mota bakoitzeko zenbat billete dauden jakiteko.
b) Frogatu m ∈{5, 50, 100, 200} bada sistema bateragarri determinatua dela, eta ebatz ezazu m = 50 kasuan.
c) Arrazoitu kutxazainean 100 €-ko billeterik egon daitekeen.
a) Aurkitu sistema bateraezin egingo duen a -ren balio bat.
b) Eztabaidatu ba al dagoen sistema bateragarri determinatua egiten duen a-ren baliorik.
c) Ebatzi sistema a = 0 kasuan.
45 U 1
() () x ax x yz z az 1 2 3 2 0 1 2 0 ––++ + = = = =
*
a b
*
ax x ax by by y z cz cz c
2 3 5 2 2 2 3 4 – –++ + = = =
a) x x x y y y 2 3 6 2 3 0 11 0 ––+ + = = = * b) xy yz 25 3 ––= = *
xy
yz xmyz
z
23 2 37 ++ = += ++ = *
*
32 5 23 4 – += +=
() x x x y ay ay z z z 2 2 2 3 3 6 1 2 3 + + + + + ++ = = =
*
AUTOEBALUAZIOA ➜ anayaharitza.es Ariketa hauen ebazpena.
© GRUPO ANAYA, S.A., 2023 - C/ Valentín Beato, nº 21 - 28037 Madrid.
Reservados todos los derechos. El contenido de esta obra está protegido por la Ley, que establece penas de prisión y/o multas, además de las correspondientes indemnizaciones por daños y perjuicios, para quienes reprodujeren, plagiaren, distribuyeren o comunicaren públicamente, en todo o en parte, una obra literaria, artística o científica, o su transformación, interpretación o ejecución artística fijada en cualquier tipo de soporte o comunicada a través de cualquier medio, sin la preceptiva autorización.









































