EM2NY_GK_M1_Learn_25SPAA_122261_updated_04.24 by General

KUna historia de unidades®

Parte-parte-total

APRENDER ▸ Conteo y cardinalidad Módulo

Libro para estudiantes

¿Qué tiene que ver esta pintura con las matemáticas?

Piet Mondrian redujo los sujetos de sus obras a figuras geométricas coloridas. En esta pintura, gruesas líneas negras, horizontales y verticales, enmarcan los vibrantes cuadrados y rectángulos con el rojo, el negro y el amarillo, entre otros colores. ¿Crees que alguna de las figuras se parecen? ¿Observas que las figuras más pequeñas se juntan para crear figuras más grandes? ¿Cuántas figuras ves en total?

En la portada

Composition with Large Red Plane, Yellow, Black, Gray and Blue, 1921

Piet Mondrian, Dutch, 1872–1944

Oil on canvas

Kunstmuseum Den Haag, The Hague, Netherlands

Piet Mondrian (1872–1944), Composition with Large Red Plane, Yellow, Black, Gray and Blue, 1921.

Den Haag. Image credit: Bridgeman Images

Great Minds® is the creator of Eureka Math® , Wit & Wisdom® , Alexandria Plan™, and PhD Science® Published by Great Minds PBC. greatminds.org © 2025 Great Minds PBC. All rights reserved. No part of this work may be reproduced or used in any form or by any means—graphic, electronic, or mechanical, including photocopying or information storage and retrieval systems—without written permission from the copyright holder. Printed in the USA A-Print 1 2 3 4 5 6 7 8 9 10 XXX 29 28 27 26 25 ISBN 979-8-89012-226-1

Una historia de unidades®

Parte-parte-total

APRENDER

Módulo

Module 2

Conteo y cardinalidad

Module

Module 4

Figuras bidimensionales y tridimensionales Comparación

KModule

Module 6

Composición y descomposición

Suma y resta

Fundamentos del valor posicional

▸

Contenido

Conteo y cardinalidad

Tema A 5

Clasificar para formar categorías y contar

Lección 1 .

Comparar objetos según sus atributos

Lección 2

Esta lección aparece solo en el libro Enseñar.

Lección 3

Esta lección aparece solo en el libro Enseñar.

Lección 4

Clasificar objetos en tres categorías y contar

Lección 5

Clasificar objetos en tres categorías, contarlos y emparejarlos con un numeral

Tema B

Responder preguntas sobre cuántos hay con hasta 5 objetos

Lección 6

Organizar, contar y representar una colección de objetos

Lección 7

Practicar el conteo con precisión

Lección 8

Contar conjuntos en configuraciones lineales, de matrices y dispersas

Lección 9

Conservar el número de objetos en cualquier configuración

Escribir numerales y crear grupos de hasta 5 objetos

Lección 10

Contar un grupo de objetos para emparejarlos con un numeral

Lección

Escribir los numerales del 1 al 3 para responder preguntas sobre cuántos hay

Comprender el significado del cero y escribir el numeral

Lección 15

Clasificar el mismo grupo de objetos de más de una manera y contar

Lección 16

Descomponer un conjunto que se muestra en una imagen

Lección 17

Esta lección aparece solo en el libro Enseñar.

Lección 18

Esta lección aparece solo en el libro Enseñar.

2 K ▸ M1 EUREKA MATH2 New York Next Gen

. .

. . . . . . . . . . . . . . . . . . . . . . . . . . 7

. .

. . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

Tema C 31

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33

11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 Escribir los numerales 4 y 5 para responder preguntas sobre cuántos hay Lección 13 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 Contar suficientes objetos y escribir el numeral Tema D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45

14 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47

Lección 12

Descomponer números Lección

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

Responder preguntas sobre cuántos hay con hasta 10 objetos

Lección 19

Organizar, contar y representar una colección de objetos

Lección 20

Contar objetos en grupos de 5 y en configuraciones de matrices, y emparejarlos con un numeral

Lección 21

Contar objetos en configuraciones circulares y emparejarlos con un numeral

Lección 22

Esta lección aparece solo en el libro Enseñar

Lección 23

Conservar el número sin importar el orden en que los objetos se cuentan

Tema F

Escribir numerales y crear grupos de hasta 10 objetos

Lección 24

Contar un grupo de objetos para emparejarlos con un numeral

Lección 25 . . .

Escribir los numerales 6 y 7

Lección 26

Escribir el numeral 8

Lección 27

Escribir los numerales 9 y 10

Lección 28

Ordenar los numerales del 1 al 10 y razonar acerca de un número desconocido en una secuencia numérica Tema G

Analizar la secuencia de conteo

3 EUREKA MATH2 New York Next Gen K ▸ M1

E . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59

Tema

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75

. . . . . . . . . .

. . . . . . . . . . . . . . . . . 79

. .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99 Representar el patrón de 1 más en una secuencia de conteo hacia delante Lección 30 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101 Construir escaleras de números para mostrar el patrón de 1 más en una secuencia de conteo hacia delante Lección 31 103 Usar números ordinales para describir la posición y la magnitud de números enteros Lección 32 Esta lección aparece solo en el libro Enseñar. Lección 33 105 Dibujar escaleras de números para representar el patrón de 1 menos en una secuencia de conteo hacia atrás Lección 34 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107 Organizar, contar y representar una colección de objetos Recursos Créditos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109 Agradecimientos . . . . . . . . . . . . . . . . . . . . . . . . . 110 © Great Minds PBC

Lección 29 .

MATEMÁTICAS EN FAMILIA

Clasificar para formar categorías y contar

Estimada familia:

Este boletín informativo les mantendrá al día sobre lo que la clase está aprendiendo en matemáticas. Usen lo que lean como una ayuda para que su familia converse sobre matemáticas y practiquen en el hogar. Recibirán un boletín informativo de Matemáticas en familia cada vez que comencemos un tema nuevo.

Para comenzar el año, la clase está aprendiendo a clasificar objetos en grupos por color, tipo, forma o tamaño. Luego de clasificar, cuentan los objetos de cada grupo e indican cuántos hay.

Palabras que estamos aprendiendo clasificar contar

número

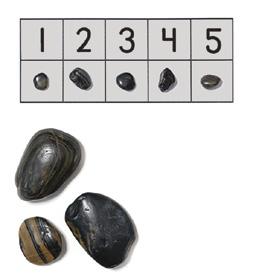
La clase clasifica por tamaño y, luego, cuenta cuántos objetos hay en cada grupo.

Actividades para completar en el hogar

Idea de actividad 1 Conteo en voz baja y en voz alta

La clase clasifica por tipo y, luego, empareja un número con cada grupo.

Cuenten simultáneamente desde el 1 hasta el 10 en voz baja. Luego, vuelvan a contar en voz alta. Cuenten hasta el 10 algunas veces más. Para variar el conteo, usen voces graciosas, túrnense, usen gestos como pistas para comenzar y detenerse o cuenten mientras marchan, brincan o hacen saltos de tijera. Cuando su estudiante esté listo o lista, cuenten hasta el 20 o más.

Idea de actividad 2 Clasificar

La clasificación permite a cada estudiante organizar su entorno al pensar en qué se parecen y en qué se diferencian las cosas. Dé a su estudiante un grupo de artículos domésticos que se puedan clasificar en diferentes categorías. Utensilios de cocina, ropa o alimentos son buenas opciones. Deje que su estudiante decida cómo clasificar los objetos. Puede clasificar por color, forma o tamaño. También podría usar categorías más personales, como alimentos que le gustan o que no le gustan.

5 Módulo 1 Tema A

A continuación, haga preguntas como las siguientes:

• ¿Cómo clasificaste?

• ¿Por qué clasificaste de esta manera?

• ¿Cuántos objetos hay en este grupo? ¿Puedes mostrarme cómo lo resolviste?

Ejemplos de clasificación

Clasificar calcetines por tamaño

Mis calcetines Otros calcetines

Cucharas

Clasificar utensilios por uso o tipo

Tenedores

Cuchillos

K ▸ M1 ▸ TA EUREKA MATH2 New York Next Gen 6 MATEMÁTICAS EN FAMILIA ▸ Módulo 1 ▸ Tema A

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TA ▸ Plantilla de dos manos 7 © Great Minds PBC

Dibuja tus grupos para mostrar cómo clasificaste.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TA ▸ Lección 4 9

Nombre 4

Great Minds PBC

Dibuja tus grupos para mostrar cómo clasificaste.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TA ▸ Lección 5 11

Nombre 5

Great Minds PBC

MATEMÁTICAS EN FAMILIA

Responder preguntas sobre cuántos hay con hasta 5 objetos

Estimada familia:

La clase está aprendiendo a contar grupos de hasta 5 objetos. Contar cada objeto una sola vez puede ser difícil, sobre todo si los objetos no están alineados. En clase, se usarán tres estrategias (tocar y contar, mover y contar, y marcar y contar) para organizar y contar de manera correcta. La clase aprenderá a usar estas estrategias para determinar si hay suficientes objetos cuando revisan los materiales del salón de clases.

Palabras que estamos aprendiendo estrategia

línea

suficientes

Tocar y contar

La clase toca los objetos mientras cuenta.

Mover y contar

La clase elige pegatinas y las mueve hacia la plantilla mientras cuentan.

Actividades para completar en el hogar

Idea de actividad 1 Emparejar números

Marcar y contar

La clase marca cada flor blanca para mostrar que la contaron.

Recorte las tarjetas de puntos y las tarjetas numéricas. Separe las tarjetas del 6 al 10 para usarlas después. Levante una tarjeta de puntos. Pida a su estudiante que diga cuántos puntos hay. Luego, pídale que halle y levante la tarjeta numérica que corresponda. Jueguen con el número: pida a su estudiante que se levante y salte, aplauda o toque los dedos de sus pies la cantidad de veces que indica el número. (¡Usted también puede hacerlo!). Cuando a su estudiante le resulten fáciles las tarjetas del 0 al 5, pasen a las tarjetas del 6 al 10.

DESAFÍO: Muestre la tarjeta de puntos solo dos segundos.

¿Su estudiante puede reconocer cuántos hay sin contar?

Idea de actividad 2 ¿Hay suficientes?

Como parte de las actividades diarias, a menudo preguntamos “¿Hay suficientes?”. Su estudiante puede usar esta pregunta cuando pone la mesa, juega a tomar el té con peluches o comparte algo con la familia o sus amigos o amigas. Cuando su estudiante participe en las tareas cotidianas, pídale que practique contar si hay suficientes con las estrategias que aprendió en clase.

13 Módulo 1 Tema B

Estrategias de conteo

La clase aprende tres estrategias de conteo para contar de manera correcta y descubrir cuántos objetos hay en un grupo.

Tocar y contar

Di el número mientras tocas el objeto.

Esta estrategia funciona mejor con objetos y dibujos alineados.

Mover y contar

Di el número mientras separas el objeto de los que todavía no se contaron.

Esta estrategia es buena para llevar el conteo de objetos que pueden moverse, sobre todo cuando están desordenados.

Marcar y contar

Di el número mientras tachas cada objeto.

Esta estrategia es buena para llevar el conteo de los objetos que ya se contaron, sobre todo cuando no están alineados y no pueden moverse.

K ▸ M1 ▸ TB EUREKA MATH2 New York Next Gen 14 MATEMÁTICAS EN FAMILIA ▸ Módulo 1 ▸ Tema B

“1” “1”

“1, 2, 3, 4, 5"

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB 15 Módulo 1 ▸ Tema B ▸ MATEMÁTICAS EN FAMILIA 0 1 2 3 4 5 6 7 8 9 10 © Great Minds PBC

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB 17 Módulo 1 ▸ Tema B ▸ MATEMÁTICAS EN FAMILIA © Great Minds PBC

Nombre

Dibuja tu colección para mostrar cómo contaste.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB ▸ Lección 6 19

Great Minds PBC

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB ▸ Lección 7 ▸ Tablero del Juego del oso 21

PARTIDA

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB ▸ Camino numérico 23 1 2 3 4 5 © Great Minds PBC

K ▸ M1 ▸ TB ▸ Camino numérico EUREKA MATH2 New York Next Gen 24 6 7 8 9 10 © Great Minds PBC

Nombre

Cuenta los animales. Encierra en un círculo el número que dice cuántos hay.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB ▸ Lección 8 25 8

1 2 3 4 5 1 2 3 4 5

PBC

K ▸ M1 ▸ TB ▸ Lección 8 EUREKA MATH2 New York Next Gen 26 GRUPO DE PROBLEMAS 1 2 3 4 5 1 2 3 4 5 © Great Minds PBC

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB ▸ Lección 8 27 GRUPO DE PROBLEMAS 1 2 3 4 5 1 2 3 4 5 © Great Minds PBC

Nombre 9

Coloca los cubos y cuenta. Encierra en un círculo el número.

Mueve los cubos para formar un diseño diferente. Luego, encierra en un círculo el número.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TB ▸ Lección 9 29

3 4 5 3 4 5 3 4 5 3 4 5 © Great Minds PBC

K ▸ M1 ▸ TB ▸ Lección 9 EUREKA MATH2 New York Next Gen 30 GRUPO DE PROBLEMAS 3 4 5 3 4 5 3 4 5 3 4 5 © Great Minds PBC

MATEMÁTICAS EN FAMILIA

Escribir numerales y crear grupos de hasta 5 objetos

Estimada familia:

La clase está aprendiendo a contar hasta 5 objetos de un grupo más grande. ¡Esto es más difícil de lo que parece! ¡Puede ser difícil dejar de contar en un número dado y no seguir contando todo el grupo!

Asimismo, la clase está aprendiendo a escribir los números del 1 al 5 con rectángulos de escritura y rimas de práctica. Encontrará más información acerca de esta importante destreza en el reverso de esta página.

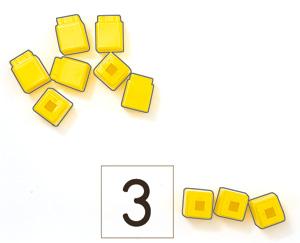
La clase cuenta 3 cubos de un grupo más grande para emparejar el número.

La clase sabe que hay cubos suficientes porque sobre cada punto hay un cubo.

Actividades para completar en el hogar

Idea de actividad 1 Contar un grupo

La clase muestra 4 con dibujos y números.

Dé a su estudiante un recipiente con objetos de la casa, como pasta, frijoles o pennies. Muestre un número del 1 al 5 y pídale que cuente el mismo número de objetos. Cuando los grupos de 5 le resulten fáciles, cuente grupos hasta el 10.

Consejo: Use las tarjetas numéricas del juego que se envió a casa junto con el módulo 1 del tema B de Matemáticas en familia, o bien escriba los números del 1 al 10 en tarjetas de índice o notas adhesivas.

Idea de actividad 2 Dibujar números

Pida a su estudiante que dibuje cada número con el dedo para practicar cómo escribir los números del 1 al 5. Use las rimas que están en el reverso de esta página para recordarle cómo escribir cada número. Luego, invente un juego en el que su estudiante deba dibujar con el dedo un número en su espalda y usted intentará adivinar el número que dibujó. Una vez que su estudiante haya practicado cada número, intercambien los roles para que pueda adivinar el número que usted le dibuje con el dedo en la espalda.

31 Módulo 1 Tema C

Rectángulo de escritura

El rectángulo de escritura es una guía para ayudar a escribir correctamente los números. El punto en la parte superior de cada rectángulo de escritura indica el lugar donde deben empezar. Es menos probable que su estudiante invierta los números cuando comienza desde el punto y mantiene la escritura dentro del rectángulo. Con el tiempo, podrá escribir los números sin el rectángulo de escritura, pero esta herramienta le brinda la estructura necesaria para formar correctamente los números desde el principio. Es normal y apropiado desde el punto de vista del desarrollo que las y los estudiantes de kindergarten inviertan los números, es decir, que los escriban al revés. La inversión de números no debe ser motivo de preocupación. En cambio, simplemente recuerde a su estudiante que comience desde el punto y que use el rectángulo de escritura, mientras repite la rima de los números (ver abajo), como ayuda para escribir el número.

Es importante que su estudiante incorpore en kindergarten el hábito de comenzar a escribir números y letras desde la parte superior, pues le ayudará a escribir de forma rápida y legible cuando las exigencias de escritura aumenten en grados posteriores. Un punto recuerda a sus estudiantes que deben comenzar a escribir los números desde arriba.

Rimas para escribir los números

1 “De arriba abajo, sin ningún atajo. El número 1 no da trabajo”.

2 “Ese cisne tiene pico y también un largo cuello. Luego, gira a la derecha y el 2 ya está hecho”.

3 “Hago un medio círculo una vez. Otro medio círculo y ya se formó el 3”.

4 “Una línea cortita y otra más a la derecha. Y para terminar el 4, una línea larga bien hecha”.

5 “Bajo de costado y en redondo doy un brinco. Pongo luego el techo y ya escribí el 5”.

K ▸ M1 ▸ TC EUREKA MATH2 New York Next Gen 32 MATEMÁTICAS EN FAMILIA ▸ Módulo 1 ▸ Tema C

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TC ▸ Plantilla de dos manos 33 © Great Minds PBC

Lista de compras

3 manzanas

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TC ▸ Lección 10 35 10

Nombre

2 5 1 ba n a n a zanahorias fresas

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TC ▸ Lección 11 37 11

PBC

Nombre

Great Minds

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TC ▸ Lección 12 39 12

Nombre

Cuenta y escribe cuántos objetos hay.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TC ▸ Lección 12 41 12

K ▸ M1 ▸ TC ▸ Lección 12 EUREKA MATH2 New York Next Gen 42 GRUPO DE PROBLEMAS © Great Minds PBC

Tacos Manzanas Pretzels

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TC ▸ Lección 13 43 13

Nombre Menú

Manza nas Pretzels Orden Tacos

K ▸ M1 ▸ TC ▸ Lección 13 EUREKA MATH2 New York Next Gen 44 LECCIÓN

MATEMÁTICAS EN FAMILIA

Descomponer números

Estimada familia:

Su estudiante está aprendiendo la relación entre los números mediante la clasificación de los objetos en más de una manera. Quizá se pregunte: ¿Por qué seguimos clasificando? La clasificación es una forma de ver cómo los números pueden dividirse en partes. Por ejemplo, 5 osos pueden clasificarse en 4 osos amarillos y 1 oso rojo. La oración numérica 5 es 4 y 1 representa esta situación. 5 osos también se pueden clasificar en 3 osos grandes y 2 osos pequeños. Su estudiante podría decir “5 es 3 y 2” para representar esta clasificación.

Invite a su estudiante a que le muestre cómo contar con el método matemático, una nueva forma que está aprendiendo de contar con los dedos.

Palabras que estamos aprendiendo oración numérica

Ordenar por color: 5 es 4 y 1.

Actividades para completar en el hogar

Idea de actividad 1 Clasificar de diferentes maneras

Ordenar por tamaño: 5 es 3 y 2.

Ofrezca a su estudiante un grupo de 4 o 5 objetos, como juguetes, marcadores o monedas, que pueda clasificar en diferentes categorías según el color, la forma o el tamaño. Deje que su estudiante decida cómo clasificar los objetos. A continuación, formule las siguientes preguntas para ayudar a su estudiante a pensar en el número total de objetos y en el número que hay en cada grupo.

• ¿Cuántos ______ hay?

• ¿Cuántos grupos formaste?

• ¿Cuántos objetos hay en este grupo?

Vuelva a colocar los objetos en una pila. Pida a su estudiante que clasifique de otra manera y, luego, vuelva a hacer las mismas preguntas. ¿Esta clasificación dio como resultado el mismo número de grupos? ©

Módulo 1 Tema D

Great Minds PBC

Idea de actividad 2 Búsqueda en la naturaleza

Pida a su estudiante que encuentre formas de clasificar o contar objetos mientras dan un paseo a pie o en auto. Por ejemplo: “Veo 4 árboles. 3 son grandes y 1 es pequeño”. Si es posible, recojan algunos objetos, como hojas, piñas o piedras, para clasificarlos en el momento y más tarde.

Contar con el método matemático

Usar los dedos para las matemáticas no es algo infantil. De hecho, los y las estudiantes de corta edad que son capaces de representar los números o los problemas con los dedos obtienen mejores resultados a la hora de contar, comparar números y hacer estimaciones en años posteriores. El trabajo temprano con los dedos desarrolla una parte del cerebro que se utiliza para la aritmética. La clase aprende a “ver” una representación de los dedos en el cerebro incluso cuando no utilizan los dedos para resolver los problemas.

Su estudiante está aprendiendo a contar del 1 al 5 con el método matemático, comenzando por el meñique izquierdo y levantando un dedo a la vez hasta llegar al pulgar.

Al contar con el método matemático, la clase puede ver y sentir cómo aumenta el número de dedos al contar del 1 al 10, pasando del meñique izquierdo al derecho sin interrupción. Este movimiento de izquierda a derecha les resultará conocido cuando empiecen a utilizar herramientas como el camino numérico y, en grados posteriores, la recta numérica. ¡Piense en este trabajo como si fueran flexiones para el cerebro!

K ▸ M1 ▸ TD EUREKA MATH2 New York Next Gen 46 MATEMÁTICAS EN FAMILIA ▸ Módulo 1 ▸ Tema D

1 2 3 4 5 6 7 8 9 10

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TD ▸ Lección 14 ▸ Plantilla de dos manos 47 © Great Minds PBC

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TD ▸ Lección 14 49 14 Nombre © Great Minds PBC

Nombre

Cuenta y escribe cuántos hay.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TD ▸ Lección 14 51 14

Great Minds PBC

¿Cuántas manzanas hay en cada árbol?

¿Cuántos gatos hay en los árboles?

K ▸ M1 ▸ TD ▸ Lección 14 EUREKA MATH2 New York Next Gen 52 GRUPO DE PROBLEMAS

Nombre

Crea una barra de 5 cubos.

Separa la barra en partes para que entre en los recuadros. Escribe las parejas de números que suman 5.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TD ▸ Lección 15 53 15

1 2 3 4 5 6 7 8 9 10 © Great Minds PBC

Crea una barra de 4 cubos.

Separa la barra en partes para que entre en los recuadros. Escribe las parejas de números que suman 4.

K ▸ M1 ▸ TD ▸ Lección 15 EUREKA MATH2 New York Next Gen 54 GRUPO DE PROBLEMAS

1 2 3 4 5 6 7 8 9 10 © Great Minds PBC

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TD ▸ Lección 16 55 16

es y . © Great Minds PBC

Nombre Dibuja los 4 crayones de Kia.

Nombre

Cuenta y escribe cuántos hay en total.

Colorea 1.

Colorea 2.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TD ▸ Lección 16 57 16

MATEMÁTICAS EN FAMILIA

Responder preguntas sobre cuántos hay con hasta 10 objetos

Estimada familia:

La clase está aprendiendo a contar grupos de hasta 10 objetos. Llevar la cuenta en estos grupos más grandes es más difícil, sobre todo cuando los objetos están dispersos o dispuestos en círculo. Asimismo, la clase practica las tres estrategias de conteo (tocar y contar, mover y contar, y marcar y contar) para llevar la cuenta de los objetos que ya contó.

CONFIGURACIONES DE CONTEO

Lineal Grupo de 5 Matriz

Circular Dispersa

Actividades para completar en el hogar

Idea de actividad 1 Juego del Número bip

Para jugar Número bip, diga algunos números en orden y reemplace uno de ellos con la palabra bip. Por ejemplo, si dice “2, 3, bip, 5”, su estudiante deberá responder “4”. Use las tarjetas numéricas (que se enviaron a casa junto con el tema B) como apoyo adicional para que su estudiante pueda tocar cada número mientras usted cuenta. Cuando su estudiante esté listo o lista, pídale que diga los números, mientras que usted adivina el número bip.

Idea de actividad 2 Contar juguetes

Use juguetes u otros objetos de la casa para hacer diferentes configuraciones de conteo como las que se muestran arriba. Anime a su estudiante a tocar y contar o a mover y contar los juguetes para averiguar cuántos hay.

Módulo 1 Tema E

Formación de grupos de 5

¿Por qué usamos grupos de 5? Habrán observado que las tarjetas de puntos (que se enviaron con el tema B) muestran 5 puntos en línea. Los grupos de 5 ayudan a su estudiante a visualizar los números que van del 6 al 10 (5 y 1, 5 y 2, etc.). Los puntos hacen que sea más fácil ver cada número como 5 puntos más algunos puntos más.

10 9 8 7 6

Los puntos no son la única manera de mostrar grupos de 5. El uso de los dedos para contar con el método matemático enfatiza la relación entre el 5 y los números que van del 6 al 10 (los 5 dedos de una mano y algunos de la otra). Organizar objetos y dibujos en grupos de 5 puede resultar útil para ver esta importante relación.

Dedos para contar con el método matemático

5 y 1

Imágenes de 5 y 5

Blue Orange

Cubos que cambian de color en el 5

5 y 2

K ▸ M1 ▸ TE EUREKA MATH2 New York Next Gen 60 MATEMÁTICAS EN FAMILIA ▸ Módulo 1 ▸ Tema E

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TE ▸ Plantilla de grupos de 5 61 © Great Minds PBC

Nombre

Dibuja tu colección para mostrar cómo contaste.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TE ▸ Lección 19 63 19

Great Minds PBC

Nombre

Encierra en un círculo un grupo de cinco en todas las imágenes.

Luego, cuenta y encierra en un círculo cuántos hay en total.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TE ▸ Lección 20 65 20

5 6 7 7 8 9 8 9 10 7 8 9 © Great Minds PBC

K ▸ M1 ▸ TE ▸ Lección 20 EUREKA MATH2 New York Next Gen 66 GRUPO DE PROBLEMAS 5 6 7 5 6 7 8 9 10 5 6 7 © Great Minds PBC

Nombre

Cuenta. Encierra en un círculo cuántos hay en el camino numérico.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TE ▸ Lección 21 67

1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 © Great Minds PBC

K ▸ M1 ▸ TE ▸ Lección 21 EUREKA MATH2 New York Next Gen 68 GRUPO DE PROBLEMAS 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 © Great Minds PBC

Cuenta. Encierra en un círculo para mostrar cuántos hay.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TE ▸ Lección 21 69 GRUPO DE PROBLEMAS

Nombre

Colorea el primer objeto. Cuenta y encierra en un círculo cuántos hay en el camino numérico.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TE ▸ Lección 23 71

K ▸ M1 ▸ TE ▸ Lección 23 EUREKA MATH2 New York Next Gen 72 GRUPO DE PROBLEMAS 2 3 4 5 6 7 8 9 10 1 1 2 3 4 5 6 7 8 9 10 © Great Minds PBC

MATEMÁTICAS EN FAMILIA

Escribir numerales y crear grupos de hasta 10 objetos

Estimada familia:

La clase está aprendiendo a contar hasta 10 objetos de un grupo más grande. Al igual que cuando cuentan de un grupo más pequeño, puede resultarles difícil dejar de contar al llegar a un número específico. ¡Hay quienes querrán seguir contando todo el grupo! Asimismo, la clase está aprendiendo a escribir los números del 6 al 10 usando rectángulos de escritura y rimas de práctica. Pida a su estudiante que comparta algunas de las razones por las que escribimos números, ¡y usted comparta las suyas!

La clase cuenta un grupo dibujando y encerrando en un círculo los objetos de una imagen.

¿Por qué escribimos números?

- jugar al restaurante

- recordar el conteo

- hacer la lista de compras

- compartir nuestro número de teléfono

- es más rápido que dibujar

- hacer un calendario

- números de habitaciones

- llevar un marcador

- jugar un juego

- hacer una tarjeta de cumpleaños

La clase responde la pregunta: “¿Por qué escribimos números?”. La clase ve sus ideas registradas en un afiche.

Actividades para completar en el hogar

Idea de actividad 1 Búsqueda y conteo

Muestre una tarjeta numérica del 1 al 10 (que se enviaron con el tema B) y pida a su estudiante que halle esa cantidad de bloques, cucharas, pennies o cualquier otro objeto divertido en casa. Una vez terminada la búsqueda, diviértanse con el número: pida a su estudiante que salte, aplauda o se toque la punta de los pies el mismo número de veces. (¡Usted también puede hacerlo!). Cuando a su estudiante ya le resulten fáciles estos números, use otros más grandes, como el 12, el 15 y, luego, el 20.

Idea de actividad 2 Escribir los números

Practiquen escribir los números del 0 al 10. Use las rimas ubicadas en el reverso de esta página para recordar a su estudiante cómo escribir cada número. Luego, convierta esta actividad en un juego pidiéndole que escriba el número en un rectángulo de espuma para afeitar (esparcida

Módulo 1 Tema F

en una bandeja para hornear o a un lado de la bañera). Con un dedo o un frijol, marque un punto en la parte superior para ayudar a su estudiante a saber por dónde comenzar.

Rectángulo de escritura

El rectángulo de escritura es una herramienta importante para aprender a escribir los números. El punto ubicado en la parte superior de cada rectángulo de escritura indica a su estudiante el lugar donde debe comenzar y ayuda a evitar que invierta los números.

Rimas para escribir los números

0 “Desde arriba arranco primero. Redondo como un agujero, ¡así se escribe el cero!”.

1 “De arriba abajo, sin ningún atajo. El número 1 no da trabajo”.

2 “Ese cisne tiene pico y también un largo cuello. Luego, gira a la derecha y el 2 ya está hecho”.

3 “Hago un medio círculo una vez. Otro medio círculo y ya se formó el 3”.

4 “Una línea cortita y otra más a la derecha. Y para terminar el 4, una línea larga bien hecha”.

5 “Bajo de costado y en redondo doy un brinco. Pongo luego el techo y ya escribí el 5”.

6 “Bajo recto y hago un rulito. El 6 parece el rabo de un cerdito”.

7 “Atravieso el cielo y luego bajo al suelo. Un aplauso para el 7, ¡qué gran vuelo!”.

8 “Hago una S que no se detiene. El trazo sube para que el 8 llegue”.

9 “Un rulo seguido de un palito breve. Bien hasta abajo, así se hace el 9”.

K ▸ M1 ▸ TF EUREKA MATH2 New York Next Gen 74 MATEMÁTICAS EN FAMILIA ▸ Módulo 1 ▸ Tema F

Lista de compras

7 zanahorias

6 fresas

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lección 24 77 24

Nombre

8 champiñones

10 arándanos

Great Minds PBC

9 guisantes ©

Encierra

7 en un círculo. Encierra

6 en un círculo.

Encierra

8 en un círculo. Encierra

10 en un círculo.

Encierra

9 en un círculo.

K ▸ M1 ▸ TF ▸ Lección 24 EUREKA MATH2 New York Next Gen 78 GRUPO DE PROBLEMAS

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lección 25 79 25

PBC

Nombre

Great Minds

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lección 26 81 26

PBC

Nombre

Minds

Nombre

Cuenta los brazos y las patas. Escribe cuántos o cuántas hay.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lección 26 83 26

Tablero de puntuación

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lección 27 ▸ Tablero de puntuación 85

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lección 27 87 27

Nombre

Escribe los números en el afiche de Puedo contar.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lección 27 89 27

Great Minds PBC

Nombre

Escribe los números en orden. Dibuja puntos en grupos de 5 para emparejarlos con los números.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TF ▸ Lección 28 91 28

MATEMÁTICAS EN FAMILIA

Analizar la secuencia de conteo

Estimada familia:

La clase está explorando la secuencia de números del 1 al 10. Las escaleras de números hacen que sea más fácil ver que el siguiente número de la secuencia de conteo es 1 más: “1; 1 más es 2”. Luego, “2; 1 más es 3…”. Cuando cuenta hacia atrás, la clase observa lo opuesto, es decir, que cada número es 1 menos.

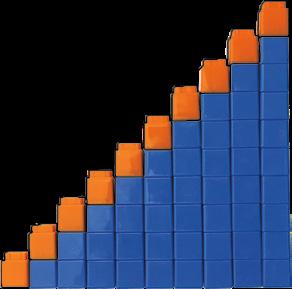
Escalera de números de 1 más Escalera de números de 1 menos

Actividades para completar en el hogar

Idea de actividad 1 Detective de números

1. Use las tarjetas numéricas del tema B o recorte las tarjetas numéricas que se incluyen en esta carta. Mézclelas y pida a su estudiante que las coloque en orden, del 0 al 10.

2. Una vez que estén en orden, dé vuelta a algunas tarjetas, de modo que algunos números queden ocultos. Señale una de las tarjetas volteadas y pida a su estudiante que use los números que se muestran para adivinar cuál es el número oculto.

Idea de actividad 2 Juego de emparejar números

Mezcle las tarjetas numéricas junto con las tarjetas de puntos (incluidas en esta carta) y coloque 6 tarjetas bocarriba. Túrnense para emparejar las tarjetas que muestran el mismo número. Reemplacen las tarjetas emparejadas con otras del juego. Continúen jugando hasta emparejar todas las tarjetas. Desafíe a su estudiante a que ordene las tarjetas emparejadas del 0 al 10.

93 Módulo 1 Tema G

Escaleras de números

En clase, las y los estudiantes construyen escaleras de números del 0 al 10 y hallan que el número que sigue en la secuencia de conteo es 1 más. Las escaleras de números les permiten visualizar, u observar, el patrón de 1 más en la secuencia de conteo hacia delante. También construirán escaleras de números del 10 al 0 para ver que, cuando se cuenta hacia atrás, cada número es 1 menos. A esto lo llamamos el patrón de 1 menos. Además, usan las escaleras de números para ver la relación entre los números ordinales (primero, segundo, tercero… , décimo) y la magnitud, o cuántos hay. Observan que la cuarta escalera tiene 4 cubos y la sexta escalera tiene 6 cubos.

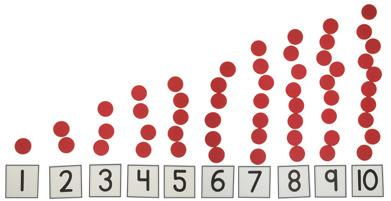
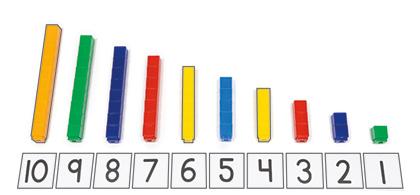
¿Por qué es necesario que las y los estudiantes comprendan el patrón de las secuencias de conteo hacia delante y hacia atrás? La comprensión de este concepto les ayuda a saber cuántos objetos hay en un grupo cuando suman 1 o quitan 1. De lo contrario, podrían sumar un penny a un grupo de 24 y, luego, contarían todo el grupo desde el 1.

La clase verá la secuencia numérica representada en un camino numérico y, en los grados siguientes, en una recta numérica.

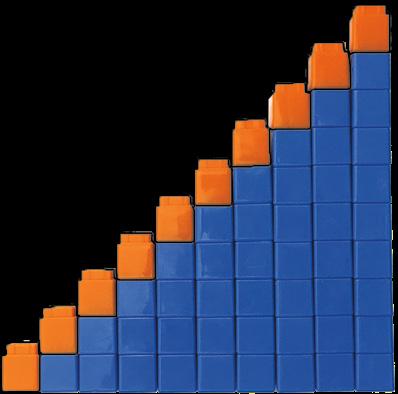
Escalera de números

Camino numérico

K ▸ M1 ▸ TG EUREKA MATH2 New York Next Gen 94 MATEMÁTICAS EN FAMILIA ▸ Módulo 1 ▸ Tema G

K K y 1 2 1 3 4 5 6 7 8 9 1 0 2 1 2 3 4 5 6 7 8 9 10

Great Minds PBC

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TG 95 Módulo 1 ▸ Tema G ▸ MATEMÁTICAS EN FAMILIA 0 1 2 3 4 5 6 7 8 9 10 © Great Minds PBC

Nombre

Escribe los números en orden. Colorea la escalera de números para que coincidan.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TG ▸ Lección 30 101

Nombre

Escribe los números en orden. Colorea la quinta escalera. Colorea la octava escalera.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TG ▸ Lección 31 103

Nombre

Escribe los números en orden del 10 al 1. Colorea la escalera de números para que coincidan.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TG ▸ Lección 33 105

Nombre

Dibuja tu colección para mostrar cómo contaste.

EUREKA MATH2 New York Next Gen K ▸ M1 ▸ TG ▸ Lección 34 107

Créditos

Great Minds® has made every effort to obtain permission for the reprinting of all copyrighted material. If any owner of copyrighted material is not acknowledged herein, please contact Great Minds for proper acknowledgment in all future editions and reprints of this module.

Cover, Piet Mondrian (1872–1944), Composition with Large Red Plane, Yellow, Black, Gray and Blue, 1921. Oil on canvas. Kunstmuseum Den Haag, The Hague, Netherlands. Image copyright

©Kunstmuseum Den Haag. Image credit: Bridgeman Images; page 13, Henri Rousseau, The Flamingos, 1907. Photo credit: Dennis Hallinan/Alamy Stock Photo; pages 43, 44, (composite image) julie deshaies/ Shutterstock.com, Khumthong/Shutterstock.com, Hong Vo/Shutterstock.com; page 68, loskutnikov/ Shutterstock.com; All other images are the property of Great Minds.

For a complete list of credits, visit http://eurmath.link/media-credits.

109 EUREKA MATH2 New York Next Gen K ▸ M1

Agradecimientos

Beth Barnes, Lauren Brown, Melissa Brown, Dawn Burns, Stella Chen, Mary Christensen-Cooper, Cheri DeBusk, Stephanie DeGiulio, Jill Diniz, Brittany duPont, Lacy Endo-Peery, Ryan Galloway, Krysta Gibbs, Melanie Gutierrez, Karen Hall, Eddie Hampton, Rachel Hylton, Travis Jones, Kelly Kagamas Tomkies, Alison Kenyon, Emily Koesters, Liz Krisher, Alicia Machuca, Ben McCarty, Kate McGill Austin, Cristina Metcalf, Ashley Meyer, Melissa Mink, Katie Moore, Bruce Myers, Marya Myers, Maximilian Peiler-Burrows, Shelley Petre, John Reynolds, Meri Robie-Craven, Robyn Sorenson, Julie Stoehr, James Tanton, Julia Tessler, DesLey V. Plaisance, Philippa Walker, MaryJo Wieland

Ana Alvarez, Lynne Askin-Roush, Stephanie Bandrowsky, Mariel Bard, Rebeca Barroso, Brianna Bemel, Rebecca Blaho, Charles Blake, Carolyn Buck, Lisa Buckley, Shanice Burton, Adam Cardais, Cindy Carlone, Gina Castillo, Ming Chan, Tatyana Chapin, Christina Cooper, Kim Cotter, Gary Crespo, Lisa Crowe, David Cummings, Brandon Dawley, Cherry dela Victoria, Timothy Delaney, Delsena Draper, Erin DuRant, Sandy Engelman, Tamara Estrada, Ubaldo Feliciano-Hernández, Soudea Forbes, Liz Gabbard, Diana Ghazzawi, Lisa Giddens-White, Laurie Gonsoulin, Adam Green, Sagal Hassan, Kristen Hayes, Tim Heppner, Marcela Hernandez, Sary Hernandez, Abbi Hoerst, Elizabeth Jacobsen, Ashley Kelley, Sonia Khaleel, Lisa King, Sarah Kopec, Drew Krepp, Jenny Loomis, Antonia López, Stephanie Maldonado, Christina Martire, Siena Mazero, Thomas McNeely, Cindy Medici, Ivonne Mercado, Sandra Mercado, Brian Methe, Sara Miller, Mary-Lise Nazaire, Corinne Newbegin, Tara O’Hare, Max Oosterbaan, Tamara Otto, Christine Palmtag, Laura Parker, Toy Parrish, Katie Prince, Neha Priya, Jeff Robinson, Nate Robinson, Gilbert Rodriguez, Todd Rogers, Karen Rollhauser, Neela Roy, Gina Schenck, Aaron Shields, Madhu Singh, Leigh Sterten, Mary Sudul, Lisa Sweeney, Tracy Vigliotti, Bruce Vogel, Charmaine Whitman, Glenda Wisenburn-Burke, Samantha Wofford, Howard Yaffe, Dani Zamora

K ▸ M1 EUREKA MATH2 New York Next Gen 110

Herramienta para la conversación

Puedo compartir mi razonamiento.

Puedo estar de acuerdo o en desacuerdo.

En mi dibujo, se ve...

Lo hice de esta forma porque...

Creo que porque...

Estoy de acuerdo porque...

No estoy de acuerdo porque...

Lo hice de otra forma. Yo...

Puedo hacer preguntas. ¿Cómo has...?

¿Por qué has...?

¿Puedes explicar...?

Puedo decirlo otra vez. Te escuché decir que... dijo que...

¿Lo puedes decir de otra manera?

LAS MATEMÁTICAS ESTÁN EN TODAS PARTES

¿Quieres comparar qué tan rápido corren tú y tus amigos y amigas?

¿Quieres estimar cuántas abejas hay en un panal?

¿Quieres calcular tu promedio de bateo?

Las matemáticas están detrás de muchas cosas maravillosas, de muchos acertijos y de muchos planes de la vida.

Desde tiempos remotos y hasta nuestros días, hemos usado las matemáticas para construir pirámides, para navegar los mares, para construir rascacielos, ¡y hasta para enviar naves espaciales a Marte!

Con tu curiosidad para comprender el mundo como combustible, las matemáticas te impulsarán en cualquier camino que elijas.

¿Todo listo para arrancar?

ISBN 979-8-89012-226-1

Módulo 1

Conteo y cardinalidad

Módulo 2

Figuras bidimensionales y tridimensionales

Módulo 3

Comparación

Módulo 4

Composición y descomposición

Módulo 5

Suma y resta

Módulo 6

Fundamentos del valor posicional

¿Qué tiene que ver esta pintura con las matemáticas?

En la portada

Composition with Large Red Plane, Yellow, Black, Gray and Blue, 1921

Piet Mondrian, Dutch, 1872–1944

Oil on canvas

Kunstmuseum Den Haag, The Hague, Netherlands

Piet Mondrian, Composition with Large Red Plane, Yellow, Black, Gray and Blue, 1921. Kunstmuseum Den Haag, The Hague, Netherlands.

Image credit: Bridgeman Images

9 798890 122261