1 A Story of Units® Units of Ten

TEACH ▸ Counting, Comparison, and Addition Module 1
What does this painting have to do with math?
American realist Edward Hopper painted ordinary people and places in ways that made viewers examine them more deeply. In this painting, we are in a restaurant, where a cashier and server are busily at work. What can you count here? If the server gave two of the yellow fruits to the guests at the table, how many would be left in the row? We will learn all about addition and subtraction within 10s in Units of Ten.

On the cover
Tables for Ladies, 1930
Edward Hopper, American, 1882–1967
Oil on canvas
The Metropolitan Museum of Art, New York, NY, USA
Edward Hopper (1882–1967), Tables for Ladies, 1930. Oil on canvas, H. 48 1/4, W. 60 1/4 in (122.6 x 153 cm). George A. Hearn Fund, 1931 (31.62). The Metropolitan Museum of Art. © 2020 Heirs of Josephine N. Hopper/Licensed by Artists Rights Society (ARS), NY. Photo credit: Image copyright © The Metropolitan Museum of Art. Image source: Art Resource, NY
Great Minds® is the creator of Eureka Math® , Wit & Wisdom® , Alexandria Plan™, and PhD Science®
Published by Great Minds PBC. greatminds.org
© 2025 Great Minds PBC. All rights reserved. No part of this work may be reproduced or used in any form or by any means—graphic, electronic, or mechanical, including photocopying or information storage and retrieval systems—without written permission from the copyright holder. Where expressly indicated, teachers may copy pages solely for use by students in their classrooms.
ISBN 979-8-89012-072-4
2 3 4 5
10
Printed in the USA A-Print 1
6 7 8 9
XXX 29 28 27 26 25
Module 1
2
Counting, Comparison, and Addition
Module 3
Module
4
Addition and Subtraction Relationships
Module 5
Properties of Operations to Make Easier Problems
Comparison and Composition of Length Measurements
Place Value Concepts to Compare, Add, and Subtract
Module 6
Attributes of Shapes · Advancing Place Value, Addition, and Subtraction
Units
▸ 1
A Story of Units®
of Ten
TEACH
Before This Module
Overview
Kindergarten Module 3
In kindergarten, students compare the number of objects in a set using language such as more than, fewer than, and the same as. They compare numbers to 10 using language such as greater than, less than, and equal to.
Kindergarten Module 5
Kindergartners represent composition and decomposition situations using number bonds and number sentences. They solve add to with result unknown and put together with total unknown problem types.
Kindergarten Module 6
At the end of kindergarten, students decompose teen numbers as ten ones and some more ones and write the decomposition as a 10+ fact.
Counting, Comparison, and Addition
Topic A Count and Compare with Data
Data contexts provide natural opportunities for counting. Students collect data by answering questions, sorting sets, and making observations. They create bar graphs, picture graphs, and tally charts to visually represent the data. As students count to find totals and visually compare quantities, they recognize that linear organizations are useful. Students compare what they see using language such as more than, fewer than, and equal to, and represent these statements numerically using the symbols >, <, and =. Number paths and tally marks provide students opportunities for counting on from 5.
There are 14 bears.
There are more medium bears than small bears.
6 > 4
There are fewer large bears than medium bears.
4 < 6
The number of small and large bears is equal.
4 = 4
© Great Minds PBC 2
4 6 4 4 6 4
Topic B Count On from a Visible Part
Students progress from finding totals by using the Level 1 strategy of counting all objects to using the Level 2 strategy of counting on from a known part. At first, objects are shown as two parts, such as the dots that appear on a pair of dice. Students choose a part they know, or can subitize, without counting one by one. They begin the count by naming the known part and then keep counting the objects in the second part to find the total:

Fooouuur, 5, 6, 7, 8, 9, 10. Students advance to counting on from a part embedded within a total. For example, given a collection of apples, students represent two parts (4 apples and 6 apples) and the total (10 apples) by using number bonds and number sentences. They realize they can count on from either part and get the same total.

EUREKA MATH2 New York Next Gen 1 ▸ M1 © Great Minds PBC 3
4 6 10 4 + 6 = 10
Fooouuur, 5, 6, 7, 8, 9, 10
Topic C Count On to Add



Now students count on to find totals for expressions (e.g., 4 + 6) rather than for sets of countable objects. Because the parts are no longer presented as sets of objects that can be counted, students must hold the first addend in mind and count on the second addend by tracking with fingers. Students experiment with counting on from both numbers by using a number path to determine the efficiency of starting with the larger addend. Recognizing this efficiency and knowing that starting with either addend results in the same total, students begin to find totals by strategically counting on from the larger part. Students also look for patterns when adding 0 and 1.


1 ▸ M1 EUREKA MATH2 New York Next Gen © Great Minds PBC 4
Fooouuur... 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 Siiix, 7, 8, 9, 10 4 + 6 = 6 + 4
Topic D
Make the Same Total in Varied Ways
This topic deepens understanding about the meaning of the equal sign, which earlier topics introduced through data and counting on. Students recognize that the expressions on both sides of the equal sign have the same total. In this topic, students reason about more complex number sentences to determine whether they are true or false. For example, 4 + 6 = 8 + 2 is true because 4 + 6 = 10 and 8 + 2 = 10. This work leads to decomposing numbers and finding the partners for each (e.g., 10 is 1 and 9, 2 and 8, 3 and 7, 4 and 6, etc.). Their burgeoning number sense allows students to decompose addends to make equivalent, often easier, problems.
After This Module
Grade 1 Module 2
Graphs provide context for adding to find the total of all the data points.
Students use counting strategies from this module to find unknown addends and to subtract.
Grade 1 Module 3
With Level 1 and Level 2 strategies well established in the first modules, module 3 focuses on Level 3 strategies that involve making easier problems. To access Level 3 strategies such as make ten, students practice
• decomposing numbers 5 through 9,
• finding the partner that makes 10 for any number,
• developing fluency with 10 + n facts, and
• working with three addend expressions.
Grade 1 Module 4 and 5
Students will use number paths as a measuring tool. They will also use >, <, and = symbols to compare measurements.
Students will use familiar >, <, and = symbols to compare two-digit numbers by using place value concepts.
EUREKA MATH2 New York Next Gen 1 ▸ M1 © Great Minds PBC 5
4 + 6 = 8 + 2 10 10 Partners to 10 10 10 10 10 10 10 0 10 1 9 2 8 3 7 4 6 5 5 4 + 4 + 2 = 10 4 + 6 4 2
total number of data points
compare categories in a picture graph.
© Great Minds PBC 6 Contents
Addition Why . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 Achievement Descriptors: Overview . . . . . . . . . . . . . . . 12 Topic A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 Count and Compare with Data Lesson 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 Organize to find how many and compare. Lesson 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 Organize and represent data to compare two categories. Lesson 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42 Sort to represent and compare data with three categories. Lesson 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 Find the
Lesson 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66 Organize and represent categorical data. Lesson 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78 Use tally marks to represent and compare data. Topic B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94 Count
Lesson 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98 Count
to
Lesson 8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114 Count on from a known part and identify both parts in a total. Lesson 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126 Count on from both parts and record part–total relationships. Lesson 10 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 140 Count on from 5 within a set. Lesson 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 154 See any part in a set and count on. Lesson 12 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 166 Count on from 10 to find an unknown total. Topic C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 178 Count On to Add Lesson 13 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 182 Count on from an addend in add to with result unknown situations. Lesson 14 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 194 Count on to find the total of an addition expression. Lesson 15 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206 Use the commutative property to count on from the larger addend. Lesson 16 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 218 Use the commutative property to find larger totals. Lesson 17 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 230 Add 0 and 1 to any number.
Counting, Comparison, and
and
On from a Visible Part
all or count on
solve put together with total unknown situations.
Make the Same Total in Varied Ways
Determine whether number sentences are true or false.
Organize, count, and record a collection of objects.
EUREKA MATH2 New York Next Gen 1 ▸ M1 © Great Minds PBC 7 Topic D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 245
Lesson 18 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 250
Lesson 19 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 264
Lesson 20 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 276
all two-part expressions
Lesson 21 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 286
all two-part expressions equal to
and 8. Lesson 22 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 298 Find all two-part expressions equal to 9 and 10. Lesson 23 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 308 Find the totals of doubles +1 facts. Lesson 24 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 320 Use known facts to make easier problems. Lesson 25 (Optional) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 332
Resources Module Assessment . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 341 Standards . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 346 Achievement Descriptors: Proficiency Indicators . . . . . . . . . . . 350 Observational Assessment Recording Sheet . . . . . . . . . . . . . . 356 Sample Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 358 Terminology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 362 Math Past . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 364 Materials . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 366 Works Cited . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 368 Credits . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 369 Acknowledgments . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 370
Reason about the meaning of the equal sign.
Find
equal to 6.
Find
7
Why
Counting, Comparison, and Addition
What are the 3 counting levels?
Students in K–2 advance through three strategy levels as they count, add, and subtract. All levels are valid strategies. However, each next level offers greater efficiency for problem solving.
• Level 1, Direct Modeling by Counting All or Taking Away: Students represent problems with groups of objects, fingers, or drawings. They model the action by composing or decomposing groups and then they count the result.

• Level 2, Counting On: Students count to solve, but they shorten the process of counting by starting with the number word of one part. They use different methods, such as fingers, to keep track of the count.
• Level 3, Convert to an Easier Equivalent Problem: Students work flexibly with numbers. They decompose and compose parts to create equivalent, easier problems.
What stages do students move through as they develop skills with counting on?
Counting on is foundational to more efficient addition strategies, mastery of facts within 20, and finding an unknown part. It takes practice for students to trust that counting all and counting on strategies each produce the same total. Several complexities are involved:
• When presented with two parts composed of discrete objects, students intuitively count the objects to find the total. Rather than count all the objects starting at 1, they subitize one part and say how many (the quantity). Then they point to each object in the second part to count on. They understand that the last number stated is the total. They recognize that counting on is addition, recording the parts and total in number bonds and number sentences.
© Great Minds PBC 8
6 3 9 6 + 3 = 9
• When given one set of discrete objects, students will subitize an embedded part and count on to find the total. Students may point to the remaining objects as they count on, or they may begin to use their fingers to keep track. Students begin to realize that they can count on from either part and get the same result.
• When presented with an addition expression, students state the first addend (possibly by making a fist). Then they count on the second addend, tracking with fingers. They stop when the number of fingers is the same as the second addend. The last number said is the unknown total.

• Students first experience using one hand to count on, when the addend is 5 or less, and using two hands to count on when the addend is 6 through 9.
• Students will see that the sums are the same, or equal, when counting on from either addend. They use number paths to show that counting on from the larger addend is more efficient. Finally, they choose to count on from the larger addend by thinking of 8 + 4 when presented with 4 + 8.
EUREKA MATH2 New York Next Gen 1 ▸ M1 © Great Minds PBC 9
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 4 + 8 8 + 4 Fiiiive 6 7
Which word problem types, or addition and subtraction situations, are used in this module?

The table shows examples of addition and subtraction situations.1 Darker shading in the table indicates the four kindergarten problem types. Students in grades 1 and 2 work with all problem types. Grade 2 students reach proficiency with the unshaded problem types.
Grade 1 students revisit the following problem types that were mastered in kindergarten. However, in grade 1, the problems may use numbers within 20 (not just within 10) and students solve them by using Level 2 and Level 3 strategies.
• Add to with result unknown: Both parts are given. An action joins the parts to form the total.
Hope has 7 rocks. She adds 3 more rocks. How many rocks does she have now?
(Lesson 13)
• Put together/take apart with total unknown: Both parts are given. No action joins or separates the parts. Instead, the parts are distinguished by an attribute such as type, color, size, or location.
5 markers are in the box. 3 markers are out of the box. How many markers are there in all? (Lesson 7)
• Put together/take apart with both addends unknown: Only the total is given. Students take apart the total to find both parts. This situation is the most open ended because the parts can be any combination of numbers that make the total.
There are 5 dogs. What are all the ways they can be inside the house or out in the yard?
(Lesson 18)
Students are invited to solve word problems intuitively. Each lesson presents an accessible problem that can also be extended. Some students may directly model all components of the problem with manipulatives or by drawing. Others may use their fingers, a number path, or drawing to count on from one part. This variety is important because it presents an opportunity for students to discuss their reasoning.
1 ▸ M1 EUREKA MATH2 New York Next Gen © Great Minds PBC 10
Count On: Drawing Count On: Number Path Count On: Fingers Count On: Number Facts 7 8 9 10 7 8 9 10 7 + 3 = 10 7 8 9 10 2 3 4 5 6 7 8 9 10 7
1 Common Core Standards Writing Team, Progressions for the Common Core (draft), Grades K–5, Counting and Cardinality & Operations and Algebraic Thinking, 9.
Teachers use students’ thinking to advance the class toward the objective. They watch how students solve the problem, select work to share, and ask questions that engage the class in others’ thinking. Observations about how students use counting on in these lessons may be useful for preparing to teach topics B and C. The Read–Draw–Write problem-solving routine begins in module 2.
Why is lesson 25 optional?
Students count a collection of objects in lesson 25. Counting collections lessons engage students in self-directed learning and provide opportunities for informal assessment. This lesson can be used in the module when the timing best meets the needs of the class. Note that counting collections lessons require preparation. Make sure to read the Lesson Preparation in advance.
Counting collections are best used as a frequent routine, as students benefit from opportunities to internalize the procedure, choose new collections, and try new counting strategies. They will be included in future lessons, however, consider doing them more often as time allows.



Why does this module include time?
Lesson 17 briefly introduces telling time to the hour. This initial exposure provides a starting place for ongoing informal practice before module 4, where telling time to the hour and to the half hour are directly addressed. Beginning with lesson 17, consider
• periodically pausing the class at the top of an hour to ask what time it is, and • pointing out the time when events regularly happen on the hour, such as lunch at 12:00 or dismissal at 3:00.



EUREKA MATH2 New York Next Gen 1 ▸ M1 11 © Great Minds PBC
Counting Collections
Achievement Descriptors: Overview
Counting, Comparison, and Addition
Achievement Descriptors (ADs) are standards-aligned descriptions that detail what students should know and be able to do based on the instruction. ADs are written by using portions of various standards to form a clear, concise description of the work covered in each module.
Each module has its own set of ADs, and the number of ADs varies by module. Taken together, the sets of module-level ADs describe what students should accomplish by the end of the year.
ADs and their proficiency indicators support teachers with interpreting student work on • informal classroom observations (recording sheet provided in the module resources),
• data from other lesson-embedded formative assessments, • Exit Tickets,
• Topic Tickets, and
• Module Assessments.
This module contains the nine ADs listed.
1.Mod1.AD1
Apply the commutative property of addition as a strategy to add. NY-1.OA.3
1.Mod1.AD2
Count on to find the total number of objects in a set and represent the total with an addition number sentence.
1.Mod1.AD3
Add within 20 by using strategies such as counting on or by creating an equivalent but easier problem.
12 © Great Minds PBC
356 This page may be reproduced for classroom use only. Great Minds PBC Observational Assessment Recording Sheet Student Name Grade 1 Module Counting, Comparing, and Adding Achievement Descriptors Dates and Details of Observations 1.Mod1.AD1 Apply the commutative property of addition as a strategy to add. 1.Mod1.AD2 Count on to find the total number of objects in set and represent the total with an addition number sentence. 1.Mod1.AD3 Add within 20 by using strategies such as counting on or by creating an equivalent but easier problem. 1.Mod1.AD4 Add fluently within 10. 1.Mod1.AD5 Fluently decompose totals within 10 in more than one way. 1.Mod1.AD6 Determine whether addition and/or subtraction number sentences are true or false. 1.Mod1.AD7 Count on from 10 to find totals between 11 and 19. 1.Mod1.AD8 Compare category totals in graphs by using the symbols >, =, and <. 1.Mod1.AD9 Organize and represent data with up to three categories and write how many are in each category. PP Partially Proficient P Proficient HP Highly Proficient Notes
NY-1.OA.5
NY-1.OA.5, NY-1.OA.6a
1.Mod1.AD4
Add fluently within 10. NY-1.OA.6b
1.Mod1.AD7
Count on from 10 to find totals between 11 and 19.
1.Mod1.AD5
Fluently decompose totals within 10 in more than one way.
1.Mod1.AD6
Determine whether addition and/or subtraction number sentences are true or false.
1.Mod1.AD8
Compare category totals in graphs by using the symbols >, =, and <.
1.Mod1.AD9
Organize and represent data with up to three categories and write how many are in each category. NY-1.MD.4
The first page of each lesson identifies the ADs aligned with that lesson. Each AD may have up to three indicators, each aligned to a proficiency category (i.e., Partially Proficient, Proficient, Highly Proficient). While every AD has an indicator to describe Proficient performance, only select ADs have an indicator for Partially Proficient and/or Highly Proficient performance.
An example of one of these ADs, along with its proficiency indicators, is shown here for reference. The complete set of this module’s ADs with proficiency indicators can be found in the Achievement Descriptors: Proficiency Indicators resource.
ADs have the following parts:
• AD Code: The code indicates the grade level and the module number and then lists the ADs in no particular order. For example, the first AD for grade 1 module 1 is coded as 1.Mod1.AD1.
• AD Language: The language is crafted from standards and concisely describes what will be assessed.
• AD Indicators: The indicators describe the precise expectations of the AD for the given proficiency category.
• Related Standard: This identifies the standard or parts of standards from the New York State Next Generation Mathematics Learning Standards (NGMLS) that the AD addresses.
EUREKA MATH2 New York Next Gen 1 ▸ M1 © Great Minds PBC 13
NY-1.OA.6b
NY-1.OA.7
NY-1.NBT.2, NY-1.NBT.2b
NY-1.NBT.3, NY-1.MD.4
1.Mod1.AD3 Add within 20 by using strategies such as counting on or by creating an equivalent but easier problem.
RELATED NGMLS
NY-1.OA.5 Relate counting to addition and subtraction.
NY-1.OA.6a Add and subtract within 20. Use strategies such as:
• counting on;
• making ten;
• decomposing a number leading to a ten;
• using the relationship between addition and subtraction; and
• creating equivalent but easier or known sums.
Partially Proficient Proficient
Add within 20 by representing with objects or a drawing and counting all

Add. Show how you know.
7 + 5 = 12
1.Mod1.AD4 Add fluently within 10.
RELATED NGMLS
NY-1.OA.6b Fluently add and subtract within 10.
Add within 20 by counting on Add. Show how you know.
7 + 5 = 12
I started with 7 and counted on with my fingers: Sevennnn, 8, 9, 1 0 , 1
,
Highly Proficient
Add within 20 by creating an equivalent but easier problem
Add. Show how you know. 6
Partially Proficient Proficient
Add fluently within 5.
Highly Proficient
1 ▸ M1 EUREKA MATH2 New York Next Gen 14 © Great Minds PBC EUREKA MATH2 New York Next Gen 1 ▸ M1 351 © Great Minds PBC
1
1 2.
7
+ 6 + 1 = 1 3
+
= 13 6
2 + 3 =
3 + 6 = AD Code Grade.Module.AD# AD Language
Add.
Add fluently within 10. Add.
Related Standards AD Indicators
Topic A Count and Compare with Data
Topic A gives students a chance to extend their kindergarten counting and comparing skills within real-life data contexts. These lessons provide opportunities for students to mathematize their world.
Students collect data by sorting sets, making choices, and tracking observations. They represent their data by using cubes, colored number paths, symbols, and tally marks. Students come to see that each piece of data can be represented by an object or mark. They also have opportunities to express which representations are most helpful to collect, represent, and interpret data.
As students interpret data, they see that organizing helps them find totals and compare categories. Students ask and answer questions such as How many animals are in the park? or Do more children ride the bus or walk to school? To answer, they may compare data by noticing that one category is longer than another or that there are “extras.” They may also compare numerically by noticing which total is greater.
At first, students use everyday words to share what they notice about the totals, and then they transition to more formal comparison terms. Finally, they connect the terms to the comparative symbols >, <, and =. Students write numbers to complete number sentence frames that use these symbols.
Students will progress from counting all to counting on to add in topic A and topic B. Representations such as the number path and tally marks, which use 5-groups, support the transition throughout topic A.
Comparison concepts are revisited later in module 1 as students explore equality; in module 2 when students find how many more; and in module 5 when students use place value reasoning.
Please note that lessons 1, 3, and 5 include sets of objects that students count. They require advance preparation, as described in the materials section of each lesson.
© Great Minds PBC 15
EUREKA MATH New York Next Gen M1 TA Lesson 6 © Great Minds PBC 35 See 6 9 9 6 Name How We Go X X X X X X X X X X X X X X X How We Go
Progression of Lessons
Lesson 1
Organize to find how many and compare.





Lesson 2
Organize and represent data to compare two categories.

Lesson 3
Sort to represent and compare data with three categories.
Organizing on a number path helps me count and compare.
I see my choice on the graph! More of us like to listen to music.
I can tell there are more blue cubes than red cubes. 8 is greater than 4.

16 1 ▸ M1 ▸ TA EUREKA MATH2 New York Next Gen © Great Minds PBC
Totals My Cubes Red Blue Yellow 4 8 10
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 13 14 15 16 17 18 19 20
Lesson 4
Find the total number of data points and compare categories in a picture graph.
Lesson 5
Organize and represent categorical data.
Lesson 6
Use tally marks to represent and compare data.
I counted the checkmarks to find out that there are 12 butterflies. There are the same number of small butterflies and large butterflies, 3 = 3.














Look! I have 41 cubes. I sorted them by color. I chose to show my collection by coloring a graph.
Tally marks show groups of 5. There are 5, 6, 7, 8, 9 animals! There are fewer stop signs than bridges, 6 < 9.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA 17 © Great Minds PBC
I See 6 9 9
Totals Cubes 11 18 12
Totals Butterfly Count ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 3 6 3
Organize to find how many and compare.
Lesson at a Glance
Students explore ways to organize by counting a set. With guidance, they organize their set on a number path. Students compare and reason about the totals on the number path and discover the usefulness of linear organization. Finally, they use color to represent and compare sets on number paths.
Key Question
• How can we show objects so they are easy to count and compare?
Achievement Descriptor
This lesson is foundational to the work of grade 1 and builds from NY-K.CC.6 and NY-K.CC.7. Lesson content is intended to serve as a formative assessment and is therefore not included on summative assessments in grade 1.
© Great Minds PBC 1 LESSON 1
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 1 © Great Minds PBC 7 1 Count out 8 cubes Color how many cubes 1 2 3 4 5 6 7 8 9 10 Count out 6 cubes. Color how many cubes. 1 2 3 4 5 6 7 8 9 10 Circle the number path with more cubes. Name
Agenda
Fluency 10 min
Launch 5 min
Learn 35 min
• Count a Set
• Organize to Count and Compare
• Problem Set
Land 10 min
Materials
Teacher
• 20-bead rekenrek
• Unifix® Cubes (16)
• Large number path
• Teacher computer or device*
• Projection device*
• Teach book*
Students
• Bag of Unifix® Cubes
• Large number path
• Pencil*
• Learn book*
• Personal whiteboard*
• Dry-erase marker*
• Whiteboard eraser*
* These materials are only listed in lesson 1. Ready these materials for every lesson.
Lesson Preparation
• Gather 16 Unifix Cubes: 7 of one color and 9 of a different color.
• Assemble one bag of 10–15 Unifix Cubes per student. Vary the number in each collection, but make sure that each bag contains only one color.
• Write a sentence frame for display: is greater than .
© Great Minds PBC 19 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 1
Fluency
Counting on the Rekenrek by Ones Within 5
Materials—T: Rekenrek
Students count by ones to prepare for work with the number path.
Show the rekenrek with the side panel attached. Start with all the beads behind the panel.
Say how many beads there are as I slide them over.
Slide the red beads from behind the panel, one at a time, as students count to 5.
1, 2, 3, 4, 5
Slide the red beads back behind the panel, one at a time, as students count down to 0.
5, 4, 3, 2, 1, 0
Watch closely! Say how many beads there are as I slide them over.
Slide the red beads, one at a time, to the left or to the right in the following sequence as students count:
Continue counting on the rekenrek within 5. Change directions occasionally, emphasizing where students hesitate or count inaccurately. Invite play and promote focus by varying the pace or inserting dramatic pauses.
1 ▸ M1 ▸ TA ▸ Lesson 1 EUREKA MATH2 New York Next Gen © Great Minds PBC 20
4 3 4 5 4 1 2 3 2 3
10 5 35 10
Student View
Ready, Set, Compare
Students compare values within 5 to prepare for comparing quantities by using the number path.
Let’s play Ready, Set, Compare. Have students form pairs and stand facing each other.
Model the action: Make a fist, and shake it on each word as you say, “Ready, set, compare.” At “compare,” open your fist, and hold up any number of fingers.
Tell students that they will make the same motion. At “compare,” they will show their partner any number of fingers. Consider doing a practice round with students.
Clarify the following directions:
• To show zero, show a closed fist at “compare.”
• Showing more fingers is not a win.
• Try to use different numbers each time to surprise your partner.
“I’m showing more fingers.” “4 is greater than 2.”
Each time partners show fingers, have them compare amounts. They might say, “I’m showing more fingers,” “I’m showing fewer fingers,” or “We’re showing the same number of fingers.” See the sample dialogue under the photograph.

Invite partners to use the word greater. For example, “ is greater than .”
Circulate as students play the game to ensure they are trying a variety of numbers within 5.
Differentiation: Support
If students need support with comparing, they can use the one-to-one matching strategy of touching fingertips to compare their numbers.
Consider also having students say their counts as they touch fingertips so that they experience the greater number being said last.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 1 © Great Minds PBC 21
Launch
Students recognize that organizing objects is useful for comparing the size of groups.
Gather students and display the scattered yellow bears and blue bears.
I will show you yellow bears and blue bears. See if you can tell just by looking whether there are more yellow bears or more blue bears.

Show the bears only for a few seconds.
Facilitate a brief discussion by using questions such as the following:
• Are there more yellow bears or blue bears?


• Is it easy or hard to tell which group has more? Why?
Repeat with the rows of blue bears and yellow bears.
Then display the scattered bears and rows of bears side by side.
Language Support
Consider using strategic, flexible grouping throughout the module.
• Pair students who have different levels of mathematical proficiency.
• Pair students who have different levels of English language proficiency.
• Join pairs of students to form small groups of four.
As applicable, complement any of these groupings by pairing students who speak the same native language.
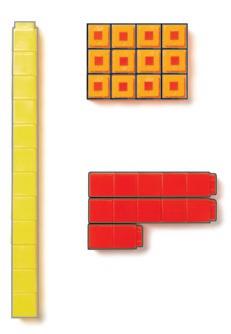
Draw attention to the usefulness of organization by asking the following question. Is it easier to compare the bears in the first picture or in the second? Why?
It is easier in the second picture, because there are extra yellow bears on the bottom line.
1 ▸ M1 ▸ TA ▸ Lesson 1 EUREKA MATH2 New York Next Gen © Great Minds PBC 22
10 5 35 10
Revoice the correct answer using the term organize in your response. The second picture makes comparing easier, because the bears are organized or lined up.
Transition to the next segment by framing the work. Today, we will organize Unifix Cubes to help us count and compare.
Learn Count a Set
Materials—S: Bag of Unifix Cubes
Students explore ways to organize and count a collection.
Distribute a bag of cubes to each student, and prompt them to count the items in their bags. Tell students that mathematicians take their time. Provide limited guidance so that you may circulate and informally assess the following counting behaviors:
• Do students show one-to-one correspondence (say one and only one number word per cube)?
• Do students understand that the last number said when counting is the total?
• Do students organize their count in some way?
• Do students say the counting sequence fluently?
Identify two or three students who have varied approaches to organizing and counting, such as organizing in a line or in an array or by using 5-groups, as shown.
Invite the students you identified to share their work with the class. Use prompts such as the following to show the value of organization.
Teacher Note
The following terms within this lesson are familiar from kindergarten:
• Organize
• Compare
• Is more than
• Is greater than
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 1 © Great Minds PBC 23
10 5 35 10
Tell us how you organized and counted.
How did organizing help our friend count?
It was easy for them to know what they already counted.
It helped them count each one (cube) only once. They didn’t skip any when they lined them up.
Organize to Count and Compare
Materials—T: Large number path, Unifix Cubes; S: Large number path Students use a number path to organize, count, and compare.
Distribute a number path, numbered side up, to each student.
Model counting to 5 by using a number path. Have students follow along on their own paths. Start at 1, place a cube on each number, and count out loud. When the class reaches 5, invite students to clear their number paths and repeat the process to organize and count their own collections.
Differentiation: Support
Consider making brief mention of incorrect counting behaviors, such as
• placing more than 1 cube in a space,
• skipping numbers on the number path as you place cubes, or
• starting at a number other than 1 when placing cubes.
Invite students to begin. As they finish, guide a class discussion.
Peek at the number under your last cube. That number is the total. Tell a partner your total.
How does the number path help you organize your cubes?
The cubes are in a line now. Each cube has its own spot.
How does using the number path make it easier to find the total?
The number under the last cube shows the total, so I don’t have to count. Have students set their work aside and turn their attention to the class number path. Place 9 cubes along the top and 7 cubes of another color along the bottom.
Promoting the Standards for Mathematical Practice
When students use the number path and are careful to start at 1, not skip any spaces, and only put 1 item in each space, they attend to precision (MP6).
Ask the following questions to promote MP6:
• When using the number path, what do you need to be extra careful with?
• What mistakes are easy to make when using the number path?
1 ▸ M1 ▸ TA ▸ Lesson 1 EUREKA MATH2 New York Next Gen © Great Minds PBC 24
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Ask students how many there are of each color. Then ask which color has more.
How can we tell there are more green cubes?
The green line of cubes is longer.
9 is more than 7.
We can match each blue cube with a green cube. 2 green cubes don’t have a match, or a partner, because there are more green cubes.
Tell students that we can also compare totals on the number path without using cubes. On the number path, circle the total of each color group, and then remove the cubes as shown. Point to the circled numbers as you refer to them.
Differentiation: Challenge
Consider asking the following questions:
• If you didn’t have a number path, how would you compare two amounts?
• Which numbers on the number path are greater than 7? Which numbers on the path are greater than 9?
7 is one total, and 9 is the other total.
Without cubes, how can we tell that 9 is more than 7?
9 comes after 7.
9 objects are more than 7 objects.
Display the prepared sentence frame and use it to compare the totals:
9 is greater than 7 .
We say 9 is greater than 7. Let’s say this statement together.
9 is greater than 7.
If students are ready, briefly introduce the greater than symbol (>) by recording a comparison on a whiteboard, such as 9 > 7.
Although the concept of difference is not taught until module 2, some students may notice how many more or how many fewer there are in one set than another.
For these students, ask the following questions:
• How many extra blue cubes are there?
• How many more green cubes would we need to make the groups the same?
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 1 © Great Minds PBC 25
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Green
Blue
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Have students return to their cubes and work with a partner to compare totals by using one or both of their number paths. Listen to student conversations, and prompt them to use the language more than or greater than as they discuss.
If time allows, consider having students trade bags of cubes to count and compare by using their number paths.
Problem Set
Differentiate the set by selecting problems for students to finish within the timeframe. Problems are organized from simple to complex.
In lesson 1, students may benefit from the support of guided practice, and the directions may be read aloud. Help students recognize the word count in print. Invite students to underline it as you read it aloud. Please note that students will continue to use their cubes and number path.
Teacher Note
The Problem Set transitions students from counting concretely with cubes to pictorial practice.
Notice that the image of the dogs adds the complexity of a scattered arrangement. If students need a strategy to organize and count accurately, suggest they use their pencils to mark and count each dog.
Some students may need to continue to organize and count cubes in lieu of counting static images.
1 ▸ M1 ▸ TA ▸ Lesson 1 EUREKA MATH2 New York Next Gen © Great Minds PBC 26
Land
Debrief 5 min
Objective: Organize to find how many and compare.
Display student work from page 2 of the Problem Set.
Facilitate a discussion within the given timeframe. Use some combination of the following questions to help students synthesize their experience from the lesson. Encourage students to build on one another’s ideas as they discuss the purpose of today’s lesson.
Which is easier to compare: the pictures or the number paths? Why?
The number paths are easier because you can see the numbers.
The number paths are easier because you can see which is longer.
How does organizing on the number path help us count?
We don’t forget to count anything.
We don’t count anything twice.
The number path shows the numbers in order.
I can look under the last cube to see the total.
How does organizing on the number path help us compare?
It makes it easy to see which group has extras. You can tell which group has more.
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
Teacher Note
Have students clean up their bags of cubes by making sticks of 10 and other sticks of the leftover cubes. This will aid with the preparation for the bags of cubes in lesson 3.
UDL: Representation
Consider making a graph in another format. Download the digital 1-20 Floor Number Path. Have students line up on either side of the Number Path based on their category choice.
UDL: Engagement
Allow students to choose what to count and compare. For example, students might suggest comparing information about their classmates, such as tied and non-tied shoes, siblings and no siblings, or other categories that they find interesting or familiar.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 1 © Great Minds PBC 27
5 35 10
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
1 ▸ M1 ▸ TA ▸ Lesson 1 EUREKA MATH2 New York Next Gen 28 © Great Minds PBC
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 1 © Great Minds PBC 5 1. Count out 7 cubes. Color how many cubes 1 2 3 4 5 6 7 8 9 10 Count out 9 cubes Color how many cubes 1 2 3 4 5 6 7 8 9 10 Circle the number path with more cubes. 1 Name 1 ▸ M1 ▸ TA ▸ Lesson 1 EUREKA MATH2 New York Next Gen © Great Minds PBC 6 PROBLEM SET 2. Color how many cats. 1 2 3 4 5 6 7 8 9 10 Color how many dogs. 1 2 3 4 5 6 7 8 9 10 Circle the number path with more cats or dogs.
Organize and represent data to compare two categories.
Lesson at a Glance
The class collects data about student preferences and makes a graph by representing each student choice with a cube on a number path. Students represent and compare a new set of data pictorially by coloring squares on a number path. Each time they represent data, students label categories and totals and use the graphs to answer questions. This lesson introduces the term graph and the symbol >.
Key Question
• What can we tell from a graph?
Achievement Descriptors
1.Mod1.AD8 Compare category totals in graphs by using the symbols >, =, and <. (NY-1.NBT.3, NY-1.MD.4)
1.Mod1.AD9 Organize and represent data with up to three categories and write how many are in each category. (NY-1.MD.4)
© Great Minds PBC 2 LESSON 2
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 2 © Great Minds PBC 13 Write the totals. Totals 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 We Like Rain or Sun 6 11 Which do more people like? Circle.
Name
2
Agenda
Fluency 10 min
Launch 5 min
Learn 35 min
• Represent Data with Cubes
• Represent Data by Coloring
• Problem Set
Land 10 min
Materials Teacher
• 20-bead rekenrek
• Large number path (2)
• Chart paper
• Sticky notes (8)
• T-chart
• Marker Students
• Unifix® Cube
• Crayon
Lesson Preparation
Using 2 of the sticky notes, prepare a T-chart with labels IN and OUT for display.
© Great Minds PBC 31 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 2
Fluency
Counting on the Rekenrek by Ones Within 10
Materials—T: Rekenrek
Students count by ones to prepare for work with the number path.
Show the rekenrek with the side panel attached. Start with all the beads behind the panel.
Say how many beads there are as I slide them over.
Slide the beads from behind the panel, one at a time, as students count to 10.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Slide the beads back behind the panel, one at a time, as students count down to 0.
10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0
Student View
Watch closely! Say how many beads there are as I slide them over.
Slide the beads, one at a time, to the left or to the right in the following sequence as students count:
Continue counting on the rekenrek within 10. Change directions occasionally, emphasizing where students hesitate or count inaccurately. Invite play and promote focus by varying the pace or inserting dramatic pauses.
1 ▸ M1 ▸ TA ▸ Lesson 2 EUREKA MATH2 New York Next Gen © Great Minds PBC 32
7 8 9 10 9 6 5 6 7 8
10 5 35 10
Ready, Set, Compare
Students compare values within 10 to prepare for comparing quantities by using the number path.
Let’s play Ready, Set, Compare. Today, we will use both hands. Have students form pairs and stand facing each other.

Model the action: Make two fists, and shake them on each word as you say, “Ready, set, compare.” At “compare,” open one or both fists, and hold up any number of fingers as shown.
Tell students that they will make the same motion. At “compare,” they will show their partner any number of fingers. Consider doing a practice round with students.
Clarify the following directions:
• To show zero, show closed fists at “compare.”
• Showing more fingers is not a win.
“I’m showing more fingers.” “6 is greater than 4.”
• Try to use different numbers each time to surprise your partner.
Each time partners show fingers, have them compare amounts. They might say, “I’m showing more fingers,” “I’m showing fewer fingers,” or “We’re showing the same number of fingers.”
Invite partners to use the word greater. For example, “ is greater than .”
Circulate as students play the game to ensure they are trying a variety of numbers within 10.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 2 © Great Minds PBC 33
Launch
Materials—T: Large number path
Students generate data by selecting one of two choices.
Gather students and invite them to get to know one another better through a survey. As you ask questions, acknowledge their responses, but do not record their choices. Explain to students that they should raise their hands only once.
Let’s collect information about the things we like. Which do you like better: listening to stories or listening to music?
Raise your hand if you like listening to stories.
Raise your hand if you like listening to music.
I’m getting so much good information, but I need a way to organize your choices so that we can remember them and talk about what we notice.
Display a number path. Help students recall that they used the number path to count and compare in lesson 1.
Let’s count and compare your choices by using the number path. Are we able to put ourselves on the number path just as we put the Unifix Cubes on the number path? Why?
UDL: Engagement
Sharing favorite activities through a class survey engages students by tapping into their interests and experiences. This also supports the development of a community of learners as students get to know their classmates and discover common interests.
Consider adjusting the questions to match the class’s interests.
No, because we’re too big (or it’s too small).
How can we use the number path to show your choices?
We can count our hands and then put cubes on two number paths.
Transition to the next segment by framing the work.
Today, we will use number paths to organize, show, and compare our choices.
1 ▸ M1 ▸ TA ▸ Lesson 2 EUREKA MATH2 New York Next Gen © Great Minds PBC 34
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
10 5 35 10
Learn
Represent Data with Cubes
Materials—T: Large number path, chart paper, sticky notes; S: Unifix Cube
Students graph and compare two categories of data by placing cubes on number paths.
Display two number paths on a piece of chart paper as shown. Distribute a cube to each student.
As I pass out the cubes, let’s count them together.
Why did we count up to (number of students present in class)?
That’s how many students we have.
Let’s use a cube to show each student’s choice. Use your cube instead of your hand this time to make your choice. Which do you like better: listening to stories or listening to music?
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 2 © Great Minds PBC 35
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
10 5 35 10
Use sticky notes to label the number paths with the words Music and Stories.
We will use two number paths: one to show who likes listening to music and the other to show who likes listening to stories.
Call up students who chose listening to music. Have them place their cubes one at a time, starting at 1, on the music number path. Emphasize the count by having the class say the number as each student places their cube. Have students reiterate the total and use a sticky note to label it as shown. Repeat the process with the stories number path for students who chose listening to stories.
When students finish, invite them to look at the final graph. If spaces are skipped or cubes are misaligned, work with students to make corrections.
As a class, discuss what each cube means: Each cube stands for one student choice.





When we organize our choices on number paths, line up the number paths, and add labels, we create a graph.
Label the representation with the word graph on a sticky note to connect the new term to the visual representation. Then add a sticky note to title the graph We Like Music or Stories as shown.
Adding a title to our graph tells us what the graph is about.

1 ▸ M1 ▸ TA ▸ Lesson 2 EUREKA MATH2 New York Next Gen © Great Minds PBC 36
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 13 14 15 16 17 18 19 20
Lead a class discussion about what students notice about the graph.
How does the graph help us organize our choices?
Our choices are shown in lines.
Each cube is on a square, so we make sure to count it.
What does the graph show us about our choices?
We can see if more students chose music or stories.
There are more cubes on the music path. Have students think–pair–share about the following question.
How do we know that more of us like listening to music than listening to stories?
The line of cubes for music is longer.
13 is more than 11.
Not all the cubes on the stories path have a match (or a partner). There are extra cubes on the music path.
Remember, we can say that 13 is more than 11 another way: 13 is greater than 11. Say that with me.
13 is greater than 11.
Write the comparison statement to describe the two totals. Write a comparison number sentence that includes the > symbol as shown.
Mathematicians draw a symbol to write is greater than.
Ask students to read the number sentence. Point to each part as they read.
Transition to the next segment of the lesson by framing the work.
Now we will answer a new question. This time, instead of showing our choices with cubes, we will collect our choices on a chart.
Teacher Note
When comparing objects such as cubes or apples, the correct term to use is more.
• There are more green apples than red apples.
When comparing numbers or expressions, the correct term to use is greater than.
• 12 is greater than 10.
Model correct language, but do not expect students to differentiate between these specific uses at this time.
Promoting the Standards for Mathematical Practice
When students use a cube to represent their choice, place it on the graph, and explain what the graph shows, they reason abstractly and quantitatively (MP2)
The following questions within the sample dialogue promote MP2:
• What does it mean when you put a cube on the graph?
• What does the graph tell you about our listening choices?
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 2 © Great Minds PBC 37
Represent Data by Coloring


Materials—T: Labeled T-chart, marker; S: Crayon
Students graph and compare two categories of data by coloring number paths. Collect a second set of data by asking a new question and inviting the class to raise their hands to make their choice.
Which do you like better: inside or outside recess?
Count raised hands, and then label and record the results by using a T-chart. Explain that the labels IN and OUT are simple ways to show choices for inside and outside recess.
Have students turn to the graph. Explain that they will use the number paths to show the student choices recorded on the T-chart. Have them color the number paths to show the choices instead of using cubes to count. Remind students to use a different number path to represent each choice from the T-chart. Students should not complete the comparison statements at the bottom of the page yet.
Differentiation: Challenge
Consider asking some of the following questions:
What do you notice?
• What true statements can you write as you look at the graph?
What do you wonder?
More people like in than out . 17 > 9
As students work, circulate and support the transition from cubes to coloring by asking students what each square stands for, or represents (one person’s choice). Also ask how they know the total of each category. Students may need support with labeling.
greater than
As they finish, gather students, and prompt them to notice what the graph shows. Discuss their observations, and close by comparing the categories.
• What questions can you write about the graph?
Consider allowing students to collect their own data by asking classmates to make one of two choices to answer a question, such as, “Do you like hot or cold lunch?” and graphing the results.
1 ▸ M1 ▸ TA ▸ Lesson 2 EUREKA MATH2 New York Next Gen © Great Minds PBC 38
Totals We Like or 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 17 9 IN OUT IN OUT EUREKA MATH 2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 2 © Great Minds PBC 9 2 Totals We Like or 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 17 9 IN OUT
IN OUT
Name
How can we use the graph to tell which choice our class likes better?
We colored more numbers on the IN path, which shows more of us like indoor recess. The number path for inside recess is longer.
17 is more, or greater, than 9.
Guide students to complete the two comparison statements at the bottom of the page. Read them aloud as a class.
Problem Set
Differentiate the set by selecting problems for students to finish within the timeframe. Problems are organized from simple to complex.
In this lesson, students may benefit from guided practice for more structured support. The directions may be read aloud. Help students recognize the word totals in print. Invite students to underline it as you read it aloud.
Consider providing context for the graphs shown. For example, “Some children answered a question about their favorite pets. This graph shows their choices.”
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 2 © Great Minds PBC 39
Land
Debrief 5 min
Materials—S: Completed student work
Objective: Organize and represent data to compare two categories. Show an accurately completed student graph from the Problem Set. Facilitate a discussion by using the following questions. Responses are samples only; students do not need to generate them all.
Why is the number path a helpful tool for making a graph?
We can color a box for each person’s choice.
The numbers are in a straight line. The longer line tells which one people like better.
What can you learn from this graph?
You can tell the two choices are hot dogs and pizza.
12 people chose hot dogs, and 9 people chose pizza.
Tell students that what we learn from graphs can help us make decisions.
Imagine that this class plans a picnic. How can the graph help them decide what food to bring?
They should bring hot dogs because 12 students chose hot dogs. 12 is more (greater) than 9, so they should bring hot dogs. 9 students like pizza. Maybe they should bring both.
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
Language Support
As students share ideas about the usefulness of the number path, reword their responses using precise terminology (indicated here in italic print). Consider the following scenarios:
• If a student says, “The longer line tells which one people like better,” reword the idea by clarifying, “Yes, the number path makes a straight line. When we compare number paths, the longer line shows more choices.”
• If a student says, “We can color a box for each person,” reword the idea by clarifying, “Yes, each box shows one student’s choice.”
1 ▸ M1 ▸ TA ▸ Lesson 2 EUREKA MATH2 New York Next Gen © Great Minds PBC 40
5 35 10
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
Which do more people like? Circle Write two totals. 12 > 9 greater than
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 2 41 © Great Minds PBC
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 2 © Great Minds PBC 11 1. Write the totals. Totals 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 We Like Rabbits or Snakes 12 15
2 Name 1 ▸ M1 ▸ TA ▸ Lesson 2 EUREKA MATH2 New York Next Gen © Great Minds PBC 12 PROBLEM SET 2. 12 people like hot dogs. 9 people like pizza Color Write the totals. Totals 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 We Like Hot Dogs or Pizza 12 9
Which do more people like? Circle. Write two totals. 15 > 12 greater than
Name
Sort to represent and compare data with three categories.
Lesson at a Glance
3
Students work in pairs to sort cubes into three categories and graph the data by coloring number paths. Using a completed graph, the class answers comparison questions about which category has more. Students read their comparisons as number sentences with the greater than symbol, >.
Key Question
• What can we tell from a graph?
Achievement Descriptors
1.Mod1.AD8 Compare category totals in graphs by using the symbols >, =, and <. (NY-1.NBT.3, NY-1.MD.4)
1.Mod1.AD9 Organize and represent data with up to three categories and write how many are in each category. (NY-1.MD.4)
There are more yellow apples than red apples .
There are more green apples than yellow apples .
There are more red apples than green apples .
© Great Minds PBC 3 LESSON 3
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 3 © Great Minds PBC 21 Write the totals. Totals Apple Count 12 6 3 Circle the true sentences.
Agenda
Fluency 10 min
Launch 5 min
Learn 35 min
• Sort and Represent Three Categories
• Compare Three Categories
• Problem Set
Land 10 min
Materials Teacher
• 20-bead rekenrek
• Bag of Unifix® Cubes
• Large number path Students
• Bag of Unifix® Cubes (1 per student pair)
• Crayons (3)
Lesson Preparation
• Prepare bags of Unifix Cubes. Each bag should contain 4 red cubes, 8 blue cubes, and 10 yellow cubes. Consider reusing the bags of cubes from lesson 1 to organize the bags.
• Match the color of the 3 crayons to the colors of the Unifix Cubes in each bag.
• Copy or print the student page (incomplete graph) to use for demonstration.
© Great Minds PBC 43 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 3
Fluency
Choral Response: Name the Shape
Students identify a two-dimensional shape to maintain shape terminology from kindergarten.
Display the picture of the circle.
What is the name of this shape? Raise your hand when you know.
Wait until most students raise their hands, and then signal for students to respond.
Circle
Repeat the process with the following sequence:
Circle Square Triangle Triangle Square Circle Square Hexagon Triangle Square
Counting on the Rekenrek by Ones Within 15
Materials—T: Rekenrek
Students count by ones to prepare for work with the number path.
Show the rekenrek with the side panel attached. Start with all beads behind the panel.
Say how many beads there are as I slide them over.
Slide the beads from behind the panel, one at a time, as students count to 10. 1,
Teacher Note
Use hand signals to introduce a procedure for answering choral response questions. For example, cup your hand around your ear for listen, lift your finger to your temple for think, and raise your own hand to remind students to raise theirs.
Teach the procedure by using general knowledge questions, such as the following:
• What grade are you in?
• What is the name of our school?
• What is your teacher’s name?
1 ▸ M1 ▸ TA ▸ Lesson 3 EUREKA MATH2 New York Next Gen © Great Minds PBC 44
10 5 35 10
2, 3, 4, 5, 6, 7, 8, 9, 10
Continue sliding the beads, one at a time, to the left or to the right in the following sequence as students count:
9 10 11 10 11
Continue counting on the rekenrek within 15. Change directions occasionally, emphasizing where students hesitate or count inaccurately. Invite play and promote focus by varying the pace or inserting dramatic pauses.
5-Groups to 5
Students recognize a group of dots to prepare for counting on beginning in topic B.
Display the 5-group card that shows 3.
How many dots? Raise your hand when you know.
Wait until most students raise their hands, and then signal for students to respond.
Repeat the process with the following sequence:
Offer more practice with recognizing 5-groups, skipping around within 5. As students are ready, challenge them to recognize the groups of dots more quickly by showing each image for less time.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 3 © Great Minds PBC 45
12 13 14 15 14
3
1
2 3 4 3 5
3
Launch
Materials—T: Bag of Unifix Cubes, large number path
Students notice the attributes of tools for collecting and representing data.
Gather the class and display a student bag of red, blue, and yellow Unifix Cubes.

Our bags of cubes are different today. What do you notice about them?
The cubes in the bag are different colors. Before they were all the same color.
Display the large number path, showing the side without numbers. Engage students in a discussion about how this number path differs from the tool they used in lesson 2. The following sample dialogue shows some likely observations.
What makes this number path different from other ones we’ve used?
There are no numbers.
Why do you think there are 5 gray and 5 white squares?
The colors show groups of 5 (or 10).
It makes it easier to count. You can start at 5 (or 10) and then count more.
Display the number path as shown.
How many squares are blue? How do you know?
6. I started at the first square and counted each square: 1, 2, 3, 4, 5, 6.
6. I started at 5 and counted 1 more: Fiiiive, 6.
Teacher Note
Counting on from 5, or even 10, by using the number path is a counting option. However, it is not expected at this point. Counting on from 5 will be further developed in later lessons.
Note that the spelling of a number is stretched out (fiiiive) to signify that students are counting on from that number.
1 ▸ M1 ▸ TA ▸ Lesson 3 EUREKA MATH2 New York Next Gen © Great Minds PBC 46
10 5 35 10
Close the discussion by transitioning to the next segment.
Today, we will sort cubes, show them on a graph, and compare totals.
Learn
Sort and Represent Three Categories
Materials—S: Bag of Unifix Cubes, crayons
Students generate data by sorting and counting, and then represent the data on a graph.
Partner students and distribute a bag of cubes to each pair.
Direct students to sort by color and count each group. Depending on the available workspace, consider having students sort their cubes on a personal whiteboard so they can easily move their cubes as needed.

Promoting the Standards for Mathematical Practice
When students create a graph to model their cubes and represent the totals using numerals, they are modeling with mathematics (MP4).
Ask the following questions to promote MP4:
• What can you do to represent, or show, 1 cube on the graph?
• How can you check that your graph shows the right number of cubes?
When most pairs are finished, ask students to turn to the My graph and get out crayons and a pencil. Display the incomplete graph to guide the class in graphing their own cube collections.
First, invite students to complete the title frame with a word or phrase that tells what they are graphing.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 3 © Great Minds PBC 47
10 5 35 10
EUREKA MATH2 1 M1 TA Lesson 3 Copyright Great Minds PBC 15 3 Name Totals My Cubes Red Blue Yellow 4 8 10
Then model graphing the first category.
How can we use these number paths to make a graph to show our color groups?
We can use one path for each color.
We can use our crayons to color how many cubes there are in each group.
How can we label this number path to show the red cubes?
We can write the word red or draw a red square next to it.
How can we show how many red cubes we have?
We can color the same number of squares as there are red cubes.
We can write the total in the box.
Have students use their cubes to complete their graphs independently. Observe and support as needed.
When students finish, ask them to put away their cubes. Use the following prompt to have them turn and talk about the graph.
What does the graph tell you about the cubes?
Listen for students to share the totals of each category and comparisons of categories. Some may even find the total of all their cubes.
Teacher Note
Consider printing the digital graph so that students can use it to graph data in other contexts:
• Sorting other collections
• Counting classroom items
• Recording classroom votes
The removable is also available with numbered number paths for students who need additional practice with counting and writing numbers.
Teacher Note
Students will count to graph in different ways:
• lining up the cubes with the number path, and then coloring to match (without counting the cubes first)
• counting the cubes, then counting each square to match
• counting the cubes, counting that many squares, and marking the last square they need to color before coloring the others
Consider having students discuss how they graphed their cubes.
1 ▸ M1 ▸ TA ▸ Lesson 3 EUREKA MATH2 New York Next Gen © Great Minds PBC 48
Compare Three Categories
Students find multiple ways to compare categories on a graph and practice reading the greater than symbol.
Display a completed student graph. Tell students that they can compare the groups on the graph, just as they compared their choices in lesson 2. Guide the class to compare by using the following prompts.
Which color has the most? How do we know? Yellow. It has more than red or blue.
How do we know there are more yellow cubes than blue cubes?
The yellow line is longer than the blue line. There are more yellow squares than blue squares.
10 is greater than 8.
Write the comparison statement: 10 is greater than 8. Then write it again as a number sentence, placing the greater than symbol below the word greater.
UDL: Representation
Consider color coding the phrase is greater than and the greater than symbol to help students make connections between the words and the symbolic representation.
Read this sentence with me: 10 is greater than 8.
Now read the number sentence with me: 10 > 8.
I wonder what else we can compare by using this graph.
Write the sentence frame: There are more cubes than cubes.
Read the sentence frame aloud. Then pause and allow a moment for students to consider how they might complete the statement. Have students share a way to complete the sentence frame and explain by stating the number comparison. For example:
There are more yellow cubes than red cubes. 10 is greater than 4.
There are more blue cubes than red cubes. 8 is greater than 4.
Teacher Note
Topic A lessons focus on greater than to minimize confusion about the direction of the < and > symbols. As needed, encourage students who are not yet meeting expectations with these symbols to use one of the following strategies to describe which group has more:
• Point to the total or count aloud to find the total that comes “after” in the counting sequence.
• Look for the line of colored squares that is longer.
• Draw lines to match the squares between number paths. See which number path has extra squares.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 3 © Great Minds PBC 49
As students share, record the corresponding number sentences (10 > 4, 8 > 4) and have students read them aloud chorally.
Problem Set
Differentiate the set by selecting problems for students to finish within the timeframe. Problems are organized from simple to complex. Help students recognize the word sentence in print. Invite students to underline it as you read it aloud.
UDL: Action and Expression
As students work independently, prompt them to monitor their progress by comparing their work to the graph made as a class and by asking questions such as the following:
• Have I labeled the number path to show the cubes I’m graphing?
• Did I show how many on my graph?
• Do I need to do anything differently?
Land Debrief 5 min
Objective: Sort to represent and compare data with three categories.
Display the Apple Count graph. Facilitate a discussion about what information graphs provide and what we can learn from them.
What does this graph tell us about? How does it show that?
The graph tells about counting apples. The title is Apple Count, and the labels are apples. It tells that there are three different groups of apples. The labels are red, yellow, and green apples. The colored number paths (graph) show how many apples are in each group.
1 ▸ M1 ▸ TA ▸ Lesson 3 EUREKA MATH2 New York Next Gen © Great Minds PBC 50
10 5 35 10 Apple Count Totals 10 6 7
Have students think–pair–share about the following question.
What can we learn from the graph?
There are more red apples than green or yellow apples. There are more green than yellow apples.
Students may incorrectly respond that the graph tells that most students like red apples. Refer students to the title to clarify that the graph tells about how many apples there are of each color. Consider using this type of mistake as an opportunity to brainstorm alternative titles that would change the meaning of the graph. For example: Apples We Like Best.
Close by telling sudents that mathematicians use graphs to ask and answer questions, just like the class did today.
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
Language Support
As students share what they notice, revoice their responses using precise terminology (e.g., title, label, total), but do not expect students to generate the terms independently.
For example, if a student says, “It shows that they were counting apples because there are pictures of apples,” revoice the idea, and point to the relevant parts: “Yes, they sorted and counted apples. Each number path is labeled with the apple color.”
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 3 © Great Minds PBC 51
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
There are more red apples than yellow apples
There are more yellow apples than red apples .
There are more red apples than green apples
1 ▸ M1 ▸ TA ▸ Lesson 3 EUREKA MATH2 New York Next Gen © Great Minds PBC 52
© Great Minds PBC 17 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 3 Apple Count 3 Name 1 ▸ M1 ▸ TA ▸ Lesson 3 EUREKA MATH2 New York Next Gen © Great Minds PBC 18 PROBLEM SET
Write the totals. Totals Apple Count 10 6 7
1. Color how many apples .
Circle the true sentences.
Circle the true sentences.
There are more red apples than yellow apples
There are more yellow apples than red apples .
There are more green apples than red apples
Write two totals.
Sample: 10 > 8 greater than
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 3 53 © Great Minds PBC EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 3 © Great Minds PBC 19 PROBLEM SET
Totals 8 10 14
2. Color the totals.
Apple Count
Find the total number of data points and compare categories in a picture graph.
Lesson at a Glance
4
Students sort a set by varied attributes. With guidance, they represent the sorted data by drawing pictures on a number path. Students use these picture graphs to compare categories with both the > and = symbols. Students also share strategies for finding the total number of data points. This lesson introduces the term represent.
Key Questions
• How can we find the total of all the groups in a graph?
• How can a graph help us compare groups?
Achievement Descriptors
1.Mod1.AD8 Compare category totals in graphs by using the symbols >, =, and <. (NY-1.NBT.3, NY-1.MD.4)
1.Mod1.AD9 Organize and represent data with up to three categories and write how many are in each category. (NY-1.MD.4)
© Great Minds PBC 4 LESSON 4
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 4 © Great Minds PBC 31 Write the totals. ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ We See Totals 2 5 8 There are 15 leaves total. Write two totals. Sample: 8 > 2 greater than
Name
Agenda
Fluency 10 min
Launch 10 min
Learn 30 min
• Sort and Represent Data
• Interpret a Picture Graph
• Problem Set
Land 10 min
Materials Teacher
• None Students
• Butterfly cards (1 set per student or student pair, in the student book)
• Sorting mat (1 per student pair, in the student book)
Lesson Preparation
• The butterfly cards and the sorting mat must be torn out of student books. In addition, the butterfly cards must be cut out. Consider whether to prepare these materials in advance or to have students prepare them during the lesson.
• Optional: small stickers or stamps of any shape (that fit in the squares on the number path)
© Great Minds PBC 55 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 4
Fluency
Choral Response: Name the Shape
Students name a two-dimensional shape and identify the number of sides to maintain shape terminology from kindergarten.
After asking each question, wait until most students raise their hands, and then signal for students to respond.
Raise your hand when you know the answer to each question. Wait for my signal to say the answer.
Display the picture of the triangle.
What is the name of this shape?
Triangle
How many sides does a triangle have? 3
Repeat the process with the following sequence:
1 ▸ M1 ▸ TA ▸ Lesson 4 EUREKA MATH2 New York Next Gen © Great Minds PBC 56
Triangle Rectangle Triangle Triangle Rectangle Hexagon Rectangle Triangle 10 10 30 10
5-Groups to 10
Students recognize a group of dots to prepare for counting on beginning in topic B.
Display the 5-group card that shows 5.
How many dots? Raise your hand when you know.
Wait until most students raise their hands, and then signal for students to respond. 5
Repeat the process with the following sequence:
Offer more practice with recognizing 5-groups, skipping around within 10. As students are ready, challenge them to recognize the groups of dots more quickly by showing each image for less time.
Counting the Math Way Within 10
Students construct a number line with their fingers while counting aloud to prepare for counting on beginning in topic B.
Let’s count the math way.
Face the students, and direct them to mirror you. Show a fist with your right hand, palm facing out.
Show me your left hand. Make a fist like me. That’s 0.
Now, raise your right pinkie.
Show me your left pinkie. That’s 1.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 4 © Great Minds PBC 57
6 5 10 5 7 3 5 8 5 9
Teacher Note
Student View of Your Hand Student View of Student’s Hand
Students, whether they’re looking at their own hands or your hands, will see a left-toright progression. The progression from one finger to the next mimics the number path and, eventually, the number line. To you, the progression will appear in reverse.
Let’s put up the very next finger.
Raise your right ring finger; students raise their left ring finger.







That’s 2.
Let’s put up the next one. That’s 3.
Close it up!
(Closes hands.)
Now let’s count to 5 the math way.
Count to 5 the math way with students, modeling the math way on your fingers.
Show me 6.
Demonstrate by extending your left thumb.





Let’s count up to 10.
Count to 10 the math way with the students, modeling the math way on your fingers.
Differentiation: Support
Students with fine motor delays may find it easier to use their fingers when they lay their hands on the desk or floor. The flat surface helps them hold out the fingers they want raised and keep the others tucked.
1 ▸ M1 ▸ TA ▸ Lesson 4 EUREKA MATH2 New York Next Gen © Great Minds PBC 58
Student View of Your Hands
Student View of Student’s Hands
Offer more practice counting the math way. Have students count the math way from 0 to 3, then 0 to 5, and then 0 to 10 and back down to 0. Show the math way on your own fingers, but do not count aloud.






Launch
Materials—S: Butterfly cards
Students notice various attributes within a set and use them to sort. Display the butterfly garden, and give students a moment to look at the image.











Mathematicians notice things about the world around them and ask lots of questions. Let’s look at this butterfly garden as mathematicians would.

EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 4 © Great Minds PBC 59
10 10 30 10
Have students think–pair–share about what they notice and what they wonder about the butterflies. Accept all responses, and consider writing them in a Notice and Wonder chart. Revoice student observations centered around attributes such as color, size, shape, and design.



I heard you say that some of the butterflies are the same in some ways. I wonder whether we can sort the butterflies like we sorted our cubes in the last lesson.
Partner students, and ensure that each pair has a set of cut butterfly cards.

Provide an opportunity for exploration by inviting partners to sort in ways that make sense to them.
As they finish, gather the class, and discuss various ways to sort. Reiterate that there are many ways to organize these butterflies into groups. Transition to the next segment.
Let’s use our sorts to create graphs and compare the groups of butterflies.
Differentiation: Support
If partners need help sorting, ask:
• What is the same and different about the butterflies?







• How could you make a group with butterflies that are the same?
Differentiation: Challenge
If partners are ready for a challenge, ask:
• How many ways are there to sort the cards?
• How do you know you have found all the ways?
1 ▸ M1 ▸ TA ▸ Lesson 4 EUREKA MATH2 New York Next Gen © Great Minds PBC 60
© Great Minds PBC 23 EUREKA MATH New York Next Gen 1 ▸ M1 ▸ TA ▸ Butterfly Sorting Cards
Learn
Sort and Represent Data
Materials—S: Butterfly cards, sorting mat


Students sort cards into three categories and represent the data with a picture graph.
Ensure that each student pair has a sorting mat. Ask partners to use the mat to sort their butterfly cards again, this time by size.
After students complete their sorts, direct them to the incomplete graph in their student books.
Guide students to graph their sorts. Begin by pointing out that the title of the graph uses a picture and a word to tell what the graph is about. Then discuss a new way to represent the butterflies on the number paths.

So far, we have used cubes or colored squares to make graphs. Today, we will show 1 butterfly by drawing a picture in 1 square on the number path.
Promoting the Standards for Mathematical Practice
As students carefully make the graph by putting 1 picture in 1 square without skipping any squares, they attend to precision (MP6)
Ask the following questions to promote MP6:
• When making a graph, what steps do you need to be extra careful with?
• What mistakes are easy to make when making a graph?
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 4 © Great Minds PBC 61
25 EUREKA MATH New York Next Gen M1 TA Sorting Mat EUREKA MATH New York Next Gen M1 TA Lesson 4 © Great Minds PBC 27 Totals Butterfly Count There are butterflies total. 4 Name
10 10 30 10
Invite students to generate ideas about a simple picture they could use (e.g., circle, check mark). As an additional engagement strategy, consider providing small stickers or mini stamps. Students will use the picture they choose to graph every category.
Let’s show each small butterfly on the graph. How many small butterflies are there?
Use the labels to help you find the number path for small butterflies. Draw 1 picture in 1 square until the number path represents, or shows, 3 butterflies.
Write the total number of small butterflies at the end of the number path.
Have students graph the other two categories independently or in pairs. Observe and support as needed.
The sentence frame at the bottom of the page that asks for the total number of data points is used in the next segment; do not complete it yet.
When students finish graphing, have them clean up their cards.
Interpret a Picture Graph
Students use a picture graph to find the total number of data points and compare categories.
Display a student graph, and have the class refer to their own completed graphs. Guide students to use the graph to answer questions about the data. If possible, begin with a wondering from the Notice and Wonder chart from the Launch.
Earlier I heard you ask, “How many butterflies are in the garden?” How could we use the graph to find the total number of butterflies?
We can count all the pictures.
How does counting all the pictures help us find the total number of butterflies? Each picture represents, or shows, 1 butterfly.
Have students count all the pictures and compare their answer with at least one partner.
This is the first use of the term represent. Support the term in future instances by revoicing it as a way to show something with a drawing, symbol, or letter. If more support is needed, consider sharing a common use of the word in students’ lives:
“You can represent, or show, there are 5 children by drawing 5 circles. Each circle represents 1 child.”
Teacher Note
Save the butterfly cards for students to sort and graph in a different way, at another time.
Consider combining sets of butterfly cards for use as a counting collection material in lesson 25.

1 ▸ M1 ▸ TA ▸ Lesson 4 EUREKA MATH2 New York Next Gen © Great Minds PBC 62
3
Support
Language
EUREKA MATH 2 1 M1 TA Lesson 4 Copyright © Great Minds PBC 27 4 Name Totals Butterfly Count ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ 3 6 3 There are 12 butterflies total.
Class, how many butterflies are there?
12 butterflies
Prompt students to write the total to complete the sentence frame. Continue interpreting the graph by using the following sequence of questions.
Compare the number of small and medium-sized butterflies. What do you notice?
There are more medium butterflies than small butterflies.
6 is greater than 3.
Model writing a number sentence to show the comparison: 6 > 3.
What do you notice when you compare the small and large butterflies?
There are 3 small butterflies and 3 large butterflies.
Revoice a student response to transition to the concept of equality.
The totals are the same, or equal.
Write the number sentence: 3 = 3.
Remember, mathematicians draw an equal sign like this (point to =) to show that 3 is the same as 3. Read this number sentence with me.
3 equals 3.
If time allows, have students discuss what else they notice about the graph.
Problem Set
Differentiate the set by selecting problems for students to finish within the timeframe. Problems are organized from simple to complex.
In problem 2, consider prompting students to cross off the animals in the park to support accurate counting.
Teacher Note
Most students will count all to find the total number of data points. They are not expected to count on from one category or add the totals of the three categories, but some students may use these strategies.
Allowing these students to share their thinking with the class will support the counting on and addition strategies that are presented later in module 1.
UDL: Representation
To reinforce the concept of equality, consider comparing other examples of quantities that are equal and not equal. For example, the total number of windows vs. doors, desks vs. chairs, etc. Post examples in a 3-column chart.
• We have 2 windows and 1 door. How can we compare them?
• Is 2 the same as 1? Why?
• Can we write 2 = 3? Why?
• There are 22 desks and 22 chairs. How can we compare them?
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 4 © Great Minds PBC 63
Land
Debrief 5 min
Objective: Find the total number of data points and compare categories in a picture graph.
Show a student’s completed graph from the Problem Set, and use the following questions to lead a discussion. Encourage a variety of responses, and ask, “How do you know?” to prompt students to share how they arrived at their conclusions.
What can you learn from this graph?
There are 7 birds, 5 frogs, and 5 snails. When you count them, there are 17 animals in all.
There are more birds than snails. I know because 7 is more than 5. Frogs and snails both have 5 check marks.
How do you think this student found the total of all the animals?
She counted all the check marks starting at the top and going down. She saw 5 and 5 are 10. Then she counted 7 more.
How does this graph help us compare the groups, such as birds and snails, just by looking?
More check marks (pictures) means more animals. Fewer check marks (pictures) means fewer animals.
We can see which animal has the most check marks (pictures) on its number path.
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
Language Support
Language development begins with everyday words, such as more, bigger, longer, and the big number. Then students transition to more formal math terms, such as greater than.
Support this transition by asking questions that invite students to translate between everyday words and formal math terms.
• Tell me a math word for bigger (or longer, or more).
• Tell me an everyday word for greater.
1 ▸ M1 ▸ TA ▸ Lesson 4 EUREKA MATH2 New York Next Gen © Great Minds PBC 64
10 30 10
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 4 65 © Great Minds PBC
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 4 © Great Minds PBC 29
totals. ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ We See Totals 6 7 2 There are 15 bugs total. Write two totals. Sample: 7 > 6 greater than 4 Name 1 ▸ M1 ▸ TA ▸ Lesson 4 EUREKA MATH2 New York Next Gen © Great Minds PBC 30 PROBLEM SET
the totals. ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ We See Totals 7 5 5 There are 17 animals total.
two
1. Write the
2. Write
Write
totals. 5 = 5 equal to
Organize and represent categorical data.
Lesson at a Glance
This student-driven lesson invites partners to sort a set of about 50 items into categories. The class shares and compares their strategies for organizing and counting each category. Students then choose either a chart or graph to represent their categories and discuss what their representation shows about the greater set. Because of the time needed to sort and count sets, the Problem Set and Exit Ticket are not included in this lesson. Use student representations as formative assessment.
Key Question
• Why can it be helpful to show sorted objects by using a graph or chart?
Achievement Descriptor
1.Mod1.AD9 Organize and represent data with up to three categories and write how many are in each category. (NY-1.MD.4)
Exit Ticket
There is no Exit Ticket for this lesson. Instead, use students’ recordings to analyze their work after the lesson.
© Great Minds PBC 5
LESSON 5
Agenda
Fluency 5 min
Launch 5 min
Learn 45 min
• Sort and Count a Set
• Share and Compare Strategies
• Represent a Set
Land 5 min
Materials
Teacher
• 100-bead rekenrek
• Three-category data set
Students
• Three-category data set (1 per student pair)
• Organizing tools
Lesson Preparation
• Prepare a three-category data set: Place a set of objects (per student pair or student group) in a bag or small box. Although this lesson uses three types of bears, cubes, and pattern blocks, you may incorporate other items of high interest, such as pom-poms, erasers, and buttons. Each set should have no more than 60 total items and no more than 20 items per category. Each set should include three categories that can be sorted by an attribute, such as color, shape, or type.
• Prepare and display tools for organizing, such as number paths, cups, and bags.
• Consider providing sticky notes or personal whiteboards for tracking the count.
• Consider posting a large, wall-mountable number path, 0–120.
© Great Minds PBC 67 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 5
Fluency
Counting the Math Way Within 10
Students construct a number line with their fingers while counting aloud to prepare for counting on beginning in topic B.
Let’s count the math way.
Face the students and direct them to mirror you.
Counting the math way looks like this: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. (Demonstrate.)
Raise your right fist, palm facing out.
Show me your left fist. That’s 0. Let’s keep counting to 10.
Show the math way on your own fingers while students count, but do not count aloud.

Have students count the math way to 10.
Stay here at 10. Now, count back down to 0. Ready?
Have students count the math way from 10 to 0.
Offer more practice counting the math way. Have students count the math way from 0 to 3, from 0 to 5, and from 0 to 10 and then back down to 0.
1 ▸ M1 ▸ TA ▸ Lesson 5 EUREKA MATH2 New York Next Gen © Great Minds PBC 68
1 2 3 4 5 6 7 8 9 10 0
5 5 45 5
Counting on the Rekenrek by Tens
Materials—T: Rekenrek
Students count by tens to prepare for counting a set of objects. Show students the rekenrek. Start with all beads to the right side. Say how many beads there are as I slide them over.
Slide the top row of beads to the left side.
10
Slide the second row of beads to the left side.
20
Slide the third row of beads to the left side.
30
Slide all the beads back to the right side.
Repeat the process, having students count by tens to 50 and then by tens to 100 as you slide rows of beads to the left side.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 5 © Great Minds PBC 69
Student View
Launch
Materials—T: Three-category data set
Students estimate the total of a set and then prepare to sort and count the set. Gather students and show them a three-category data set of cubes in a basket. Explain that they will choose a similar set of objects to sort, count, and then show on a graph or chart.

First, guide students to make a reasonable estimate of how many total objects are in the set. Encourage them to make estimates by using what they might already know. For example, they may guess based on the amounts in previous sets or the number that was too high for another estimate.
Mathematicians think about how many there might be before they count. Let’s make a good guess.
Turn to your partner and answer this question: How many cubes do you think there are?
What total is too low?
(somewhere between 0 and 20)
What total is too high?
(anything higher than 100)
We said is too low and is too high. What guess makes sense then?
(somewhere between 30 and 70)
Teacher Note
Estimating before counting or solving supports students’ sense of quantity and builds their number sense.
Asking for a number they know is too high and one that is too low early on establishes boundaries for a reasonable answer and encourages accuracy.
Consider using a mounted number path to direct and support students’ estimates.
Teacher Note
Plan for what student pairs should do when they finish counting and recording their set:
• Try another way to organize and count.
• Switch sets with another student pair, and count to confirm the total.
• Explain their recording to another student pair.
• Clean up and get another set.
1 ▸ M1 ▸ TA ▸ Lesson 5 EUREKA MATH2 New York Next Gen © Great Minds PBC 70
5 5 45 5
Use the suggested questions below to get students thinking about how they might sort, organize, and count.
How could we sort the objects into groups?
How could we organize the groups to count them?
How might we show these objects on a graph or chart?
Briefly orient students to the steps of the lesson:
• Choose a set of objects (and organizing tools).
• Make a good guess of how many objects there are.
• Sort the set into three groups.
• Count how many are in each group.
• Count how many are in the whole set.
Transition to the next segment by framing the work.
Today, we will organize, count, and represent a set of objects.
Learn
Sort and Count a Set
Materials—S: Three-category data sets, organizing tools
Students self-select a way to sort, organize, and count a set.
Pair students and invite them to find a workspace. Consider having students count on a work mat or chart paper to help them keep their materials in their own work area, allow for the organized objects to be moved and shared, and expedite clean-up. Have whiteboards or sticky notes available for students to track their counts.
Promoting the Standards for Mathematical Practice
When students select a set of objects, make a plan about how to count, carry out the plan, and adjust the plan as needed, they make sense of problems and persevere in solving them (MP1)
Ask the following questions to promote MP1:
• How could you explain your plan in your own words?
• Is your plan working? Is there something else you could try?
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 5 © Great Minds PBC 71
5 5 45 5
Circulate and ask questions such as the following that encourage organization and accuracy:
• What is your plan? Why did you choose that plan?
• Show or tell me how you are counting.
• How are you keeping track of what you already counted and what you still need to count?
• How can you organize to make counting easier?
As students work, notice how they organize and count after sorting. The following samples show possible ways to sort objects.
Teacher Note
The sample student work shows common responses. Look for similar work from your students and encourage authentic conversations about the key concepts.
If your students do not produce similar work, choose one piece to share. Highlight how it shows movement toward the goal of this lesson.
Select two work samples that demonstrate an accurate sorting method and one or more of these counting strategies to share in the next segment:


• Uses a strategy to keep track of the count (e.g., move and count)
• Uses a tool to group or organize (e.g., cups or number paths)


• Uses 5-groups to organize
Share and Compare Strategies
Materials—S: Three-category data sets, organizing tools
Students share and discuss their counting strategies.
Invite the selected pairs to share their work. Have the rest of the class leave their organized objects in place and gather to look at the work to be shared.
Then select the sample way shown that best advances your students’ thinking. Consider presenting the work by saying, “This is how another student sorted and counted. What do you think they did?”
1 ▸ M1 ▸ TA ▸ Lesson 5 EUREKA MATH2 New York Next Gen © Great Minds PBC 72
Count Groups by Ones Count Organized Groups by Ones Organize in 5-Groups, Count by Fives
Consider facilitating a discussion by asking some of the following questions:
• How did you sort your objects?
• How did you count each group?
• Why did you count that way?
• How did you find the total of all the objects?
• How else could you group or count the objects?
Use the three sample discussions below for reference.
Count Groups by Ones (Malik and Imani’s Way)
Invite the pair to share how they sorted and demonstrate their approach to counting: moving cubes and counting by ones. Stop them after they count about 10 cubes and ask the class to describe their strategy. Highlight the usefulness of keeping track of the count.

How did keeping track of the cubes help you find the total of each group?
We counted each cube only one time. We counted all the cubes and did not miss any.
Count Organized Groups by Ones (Jon and Zan’s Way)
Highlight this pair’s way of organizing shapes into groups. Ask questions such as the following to help them explain their strategy.
Please tell us how you sorted and counted your shapes. We put different shapes in cartons.
We counted how many were in each carton: 1, 2, 3, …
How did this tool help you?
The egg cartons made a place for each counter so that we didn’t miss any.


When we put the counters in, they were in a line. That helped us keep track of what we already counted.
UDL: Representation
Consider creating a two-column chart and, as partners share, record each organizational and counting strategy.
…
After all pairs have shared, have students reflect on the efficiency of the various ways to organize and count:
• How might you organize next time? Why?
• Which way of counting seemed most helpful to you? Why?
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 5 © Great Minds PBC 73
Organize in 5-Groups, Count by Fives (Liv and Kai’s Way)
This pair sorted bears by size and then used 5-groups to organize each category. Ask questions such as the following to help them explain their strategy.
How did organizing in 5-groups help you count?
We know 2 fives make 10.
It made it easy to count by fives.
How did you count to find the total?
We counted by fives: 5, 10, 15.
If students use groups such as twos, fives, and tens, ask them to explain how they counted any extras. For example, students may say, “I counted 5, 10, 15, and then I counted 16, 17, 18.”
Have students compare the work shared by using a variation of think–pair–share:
• Have students stand and find a new partner.
• Prompt students to talk about what was the same and different about the shared strategies. Listen in as partners discuss.
• Select students from different groups to share their responses. Close the discussion.
How does organizing help you count many objects?

It helps you keep track of what you already counted.
It helps because you make sure you don’t miss any.
You can make groups like fives or tens that help you count faster.
Teacher Note
Not all students will make the connection between seeing groups of 10 and skipcounting by tens yet. If students do happen to make this connection, invite them to share their thinking. Ten as a unit is formally introduced in module 3.
1 ▸ M1 ▸ TA ▸ Lesson 5 EUREKA MATH2 New York Next Gen © Great Minds PBC 74
Represent a Set
Students create and discuss a representation to show their set.
Briefly brainstorm how pairs might represent, or show, their grouped objects on paper. Entertain a variety of suggestions and encourage students to use the charts and graphs from lessons 1–4. Possible ideas include the following:
• Draw a picture of the groups.
• Make a chart with lines or numbers to show how many are in each group.
• Color number paths for each group to make a graph.
• Draw pictures on number paths to make a graph.
Display the two recording sheets from student books. Invite pairs to decide whether to make a chart, graph, or picture graph to represent their set (see completed student samples). Then show them how to select the corresponding recording sheet.
If students select the chart, they may decide how to represent their set in the chart. For example, they may use tally marks or lines, drawings of the objects in each group, numbers, or groups of 2, 5, or 10.
Allow partners to continue to work together, but have each student create their own representation.
Teacher Note
Watch as students complete their charts or graphs.
• Do they recount before recording?
• Do they need to count each square on the number path to find the total, or do they count on from 5 or 10 by using the shading on the number path?
• Do they count to find the total data points by counting all, or do they have another strategy such as counting on or adding?
Differentiation: Challenge
As students complete their recordings, consider having pairs look at each other’s work. Prompt them with some of the following questions:
• What do you notice?
• What true statements can you write as you look at the chart?
• What do you wonder?
• What questions can you write about the chart?
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 5 © Great Minds PBC 75
Have students clean up their objects and gather with their representations. Ask volunteers to share their representations with the class. If possible, select volunteers who made different types of representations. The following are samples of completed student work:
Use any combination of the following questions to facilitate a discussion:
• How did you represent, or show, your objects?
• Why is this a helpful way to show your objects?
• How can you use the graph or chart to find the total of all the objects?
• How is this graph or chart the same as or different from the ones we made in previous lessons?
Language Support
If students represent their groups on a graph, listen for and support the use of terms such as title, labels, and total(s).
Note that the word total may refer to the total of each group or to the total of all the data points. As needed, help clarify which total the term refers to.
1 ▸ M1 ▸ TA ▸ Lesson 5 EUREKA MATH2 New York Next Gen © Great Minds PBC 76
EUREKA MATH M1 TA Lesson Copyright © Great Minds PBC 37 10 20 Shapes Totals 15 There are 45 shapes total. 5 Name EUREKA MATH M1 TA Lesson 35 5 Cubes Totals 11 18 12 There are 41 cubes total. EUREKA MATH Lesson Copyright Great Minds PBC Totals 20 15 10 Bears There are 45 bears total. 5
Land
Debrief 5 min
Objective: Organize and represent categorical data.
Display a student’s representation that hasn’t been shared yet and use it to help the class summarize the lesson.
What can we learn by looking at the graph (or chart)?
Listen for students to articulate the following ideas:
• The categories used to sort
• The total of each group
• How the totals of the categories are different
• The total of the whole set
Why can it be helpful to show our objects by using a graph or chart?
We can share what we found out with someone who was not here.
We don’t have to count again to find how many or compare.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 5 77 © Great Minds PBC
5 45 5
© Great Minds PBC 6 LESSON 6 Use tally marks to represent and compare data. EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA © Great Minds PBC 41 1. Write the totals. Bugs We See 6 5 4 A Name 1 ▸ M1 ▸ TA EUREKA MATH2 New York Next Gen © Great Minds PBC 42 TOPIC TICKET 2. Color the totals. Write the totals. Totals Ways We Go 6 8 4
Which one has more? Circle
Lesson at a Glance
The class collects data from a video and represents the data concretely by placing craft sticks on a chart. Students form tallies by organizing the sticks into fives and ones. They then represent the tallies pictorially by drawing tally marks to complete their own tally charts. They continue to count and compare category totals. This lesson introduces the < symbol.
Key Question
Write two totals.
• How do tally marks make counting and comparing easier?
Achievement Descriptors
1.Mod1.AD8 Compare category totals in graphs by using the symbols >, =, and <. (NY-1.NBT.3, NY-1.MD.4)
1.Mod1.AD9 Organize and represent data with up to three categories and write how many are in each category. (NY-1.MD.4)
© Great Minds PBC 79 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 6
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA © Great Minds PBC 43 TOPIC TICKET
> 4
8
greater than Sample:
Agenda
Fluency 10 min
Launch 5 min
Learn 35 min
• Represent Data in a Tally Chart
• Compare Categories in a Tally Chart
• Problem Set
Land 10 min
Materials Teacher
• 20-bead rekenrek
• Chart paper
• Craft sticks (25) Students
• None
Lesson Preparation
Make a chart with three rows on chart paper.
1 ▸ M1 ▸ TA ▸ Lesson 6 EUREKA MATH2 New York Next Gen © Great Minds PBC 80
Fluency
Choral Response: Name the Shapes
Students name the two-dimensional shapes used to form a larger shape to maintain fluency with composition of shapes from kindergarten. Display the picture of the triangle on top of the square. Which shapes did I use to make the bigger shape? Raise your hand when you know.
Wait until most students raise their hands, and then signal for students to respond.
Triangle and square
Repeat the process with the following sequence:
Rectangle and triangle Square and square Triangle and triangle Triangle and triangle Triangle, rectangle, and triangle
Counting on the Rekenrek by Ones Within 20
Materials—T: Rekenrek
Students count by ones to maintain fluency counting within 20 from kindergarten.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 6 © Great Minds PBC 81
10 5 35 10
Show the rekenrek with the side panel attached. Start with all beads behind the panel.
Say how many beads there are as I slide them over.
Slide the beads from behind the panel, one at a time, as students count to 10.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Continue sliding the beads, one at a time, to the left or to the right in the following sequence as students count:
Continue counting on the rekenrek within 20. Change directions occasionally, emphasizing where students hesitate or count inaccurately.
5-Groups to 10
Students recognize a group of dots to prepare for counting on beginning in topic B.
Display the 5-group card that shows 5.
How many dots? Raise your hand when you know.
Wait until most students raise their hands, and then signal for students to respond.
1 ▸ M1 ▸ TA ▸ Lesson 6 EUREKA MATH2 New York Next Gen © Great Minds PBC 82
14 15 16 15 16 11 12 13 14 15
5
Repeat the process with the following sequence:
Offer more practice with recognizing 5-groups, skipping around within 10. As students are ready, challenge them to recognize the groups of dots more quickly by showing each image for less time.
Launch
Students watch a video to count and keep track of data points.
Gather students and prepare them to watch a video by setting the context. Briefly explain that in this video, two siblings take a long ride in the car. To help pass time, they play a game called I See. One child looks for and counts bridges, and the other child looks for and counts signs.
Before playing the video, have students discuss different ways the characters could keep track of their counts.
How could the children remember how many bridges or signs they count?
Invite the class to play the game with the children as they watch the video.
Partner students and assign one partner to count bridges and the other partner to count signs. Have students share with their partner how they will remember, or keep track of, their count. Do not provide guidance about the methods of tracking. Have students ready any tools they need, and then play the video.
Have partners turn and talk about how many bridges and signs they counted. Then ask them to reflect on the method they used to count.
Promoting the Standards for Mathematical Practice
When students choose their own tools and decide how they will count the objects in the video, they use appropriate tools strategically (MP5).
Ask the following questions to promote MP5:
• Which tools could you use to help you keep count?
• Why did you choose that tool? Did it work well?
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 6 © Great Minds PBC 83
6 5 10 5 7 3 5 8 5 9
10 5 35 10
Tell your partner: Would you remember, or keep track of, your count the same way next time? Why?
No. I tried counting in my head, but I forgot where I was.
Yes. I used my fingers, and it worked well.
No. I used lines, but I had to keep looking down so I may have missed one. Then transition to the next segment.
Let’s make a chart to show and compare what the children saw on their road trip.
Learn
Represent Data in a Tally Chart
Materials—T: Chart paper, craft sticks
Students make a tally chart to represent data.
Place the chart on a flat surface, such as a carpet area or table. Gather students around it and point out the title and labeled categories. Tell students that the class will use the chart to show the counts of signs and bridges.
I saw some of you keeping track by drawing a line (or putting up a finger) each time you saw a bridge or a sign.
Invite students to share their totals for the bridges and signs (9 and 6, respectively), bringing the class to consensus if there is disagreement. Then have volunteers lay sticks on the chart to represent each total. Have students place the sticks in the correct section. Do not expect neat organization.
1 ▸ M1 ▸ TA ▸ Lesson 6 EUREKA MATH2 New York Next Gen © Great Minds PBC 84
10 5 35 10
How could we organize our craft sticks to count totals more easily?
We could put them in a straight line. We could make groups.
Invite a volunteer to move the sticks in the Bridge category into a straight line. Then lead the class in a choral count to confirm the total. Stop the class after counting 4. Pick up the fifth stick and lay it across the first 4 to show a group of 5 as shown.
How do you see 4 and 1 more in this group? (Point to the group of 5.)
I see 4 sticks in a line and 1 stick laying across them.
What is 4 and 1 more? 5
Let’s keep counting, starting at 5.
5, 6, 7, 8, 9
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 6 © Great Minds PBC 85
Record the category total on the I See chart. Please note that the third category, Animal, will be created in the following segment.
We used tallies to represent, or show, 9 bridges. To make a group of 5 with tallies, draw 4 lines and then 1 more line across to make 5.
Use the following question to have students think–pair–share about how the sticks show the total.
Look at our tally chart. How did we show 9 with tallies?
We showed 9 as a group of 5 and 4 more.
A stick goes across 4 sticks to make 5. Then there are 4 more sticks.
Repeat the process with the Sign category. Reinforce the idea that placing 1 stick across 4 sticks makes a group of 5.
Write a third category on the chart: Animal. Using tally formation, place 9 sticks in the Animal category.
As he drove, Dad played too. He counted animals. How many animals did he count? He counted 9 animals.
UDL: Representation
Present multiple examples and nonexamples of the correct use of tally marks to emphasize the importance of groups of 5. For example, draw 5 lines and then make a sixth line across to form a group.
Ask students to show thumbs up or down to indicate whether they see an accurately formed group of tally marks. Invite the class to help identify and correct the mistake. Repeat the process with additional examples and nonexamples.
Note that students may place the fifth tally across in either direction. Mastery of written tally marks is not expected in this lesson. Students will have additional opportunities to practice.
1 ▸ M1 ▸ TA ▸ Lesson 6 EUREKA MATH2 New York Next Gen © Great Minds PBC 86
How did you find the total?
I counted the sticks: 1, 2, … , 8, 9.
I started with the group of 5 and then counted the rest: 5, 6, 7, 8, 9.
Have students turn to the I See chart in their book (see example). Tell them that they will make their own tally charts to show how many bridges, signs, and animals were in the video. Be sure to have students complete only the tally chart, not the comparison statements that follow.
Guide the class as they draw tally marks for each category, one at a time. Circulate and provide support, modeling if needed. Consider having partners compare their work. Then chorally count each category (starting at 5), and have students write the totals.
How do tally marks make counting easier?
You can easily see a group of 5 and then count more marks.
Compare Categories in a Tally Chart
Students use a tally chart to compare categories with >, <, and = signs.
Invite partners to use the I See tally chart to orally compare the categories. Display the following sentence frames for students:
• There are more than .
• There are fewer than .
• There are the same number of and .
See how many ways you can compare the numbers of bridges, signs, and animals. As students finish, gather the class to share, record, and display their responses:
There are more bridges than signs.
There are more animals than signs.
There are fewer signs than bridges.
There are fewer signs than animals.
There are the same number of bridges and animals.
Differentiation: Support
Create additional support by having students use craft sticks to make various totals and then draw tally marks on whiteboards to match.
Differentiation: Challenge
Create a challenge by asking students to find the total data points using strategies such as the following:
• Counting all by ones
• Counting by fives, then counting on by ones • Addition
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 6 © Great Minds PBC 87
EUREKA MATH New York Next Gen ▸ M1 ▸ TA ▸ Lesson 6 © Great Minds PBC 35 I See 6 9 9 6 Name ▸ M1 ▸ TA ▸ Lesson 6 EUREKA MATH2 New York Next Gen © Great Minds PBC 36 LESSON 9 > 6 greater than 6 < 9 less than 9 = 9 equal to
How do we know there are more bridges (or animals) than signs?
There are more tally marks.
9 is greater than 6.
Have students complete the number sentence 9 > 6 on the first line below the tally chart.
I heard you say there are fewer signs than bridges. How do we know this?
There are fewer tally marks.
6 is less than 9.
Write 6 is less than 9.
Then write it again as a number sentence, placing the < symbol below the word less. Explain that mathematicians turn the greater than symbol around when they want to show less than in a number sentence.
Teacher Note
The terms greater than and less than are used to compare numbers. For example:
• 5 is greater than 3, and 3 is less than 5.
The terms more than and less than are used to compare continuous (i.e., not counted) amounts:
• Edwin has more cake than Kit. Kit has less cake than Edwin.
The terms more than and fewer than are used to compare discrete (i.e., counted) amounts:
• Edwin has more cards than Kit. Kit has fewer cards than Edwin.
Read this sentence with me: 6 is less than 9.
Have students fill in the number sentence 6 < 9.
What number sentence can we write to show that there are the same number of bridges and animals?
9 equals 9.
Have students fill in the number sentence 9 = 9.
If time allows, add another craft stick to the Animal category. Have students consider the change in the data.
If Dad saw 1 more animal, what comparisons could we make then?
Animals would have a total of 10.
10 is greater than 9 and greater than 6.
Use the term equal to describe amounts that are the same:
• 3 is the same as, or equal to, 2 + 1.
Students may incorrectly use a term that has the right general meaning. For example, they may use less than and fewer than interchangeably. Although mastery is not expected at this stage, continue to model correct terminology.
1 ▸ M1 ▸ TA ▸ Lesson 6 EUREKA MATH2 New York Next Gen © Great Minds PBC 88
To close this segment, ask the following question.
The children wondered who saw the most objects on their trip. How can we use the chart to help them find out?
The chart shows the total objects each person in the car found. They can compare the totals to see who saw more.
Problem Set
Differentiate the set by selecting problems for students to finish within the timeframe. Problems are organized from simple to complex.
Help students recognize the word fewer in print. Invite students to underline it as you read it aloud.
Land
Debrief 5 min
Objective: Use tally marks to represent and compare data.
Display the totals for How We Go. Use the three representations to help students summarize topic A concepts.
Differentiation: Challenge
Some students may be ready to use comparisons to find differences between categories. Ask questions such as these:
• How many more signs does the family need to see to get to the same total as bridges or animals?
• How many more bridges than animals did the family see?
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 6 © Great Minds PBC 89
How We Go X X X X X X X X X X X X X X X How We Go How We Go
10 5 35 10
Have students think–pair–share to compare and connect the three representations.
What is the same or different about these ways to show totals?
They all show that more children take the bus to school.
They all show that 9 children take the bus and 6 children walk.
The two graphs have number paths.
Groups of 5 are shown in different ways. The tally chart has lines in groups of 5. The number path has squares in groups of 5.
Which graph is helpful for you to compare groups? Why?
The colored number paths are the easiest way to see a longer line.
The X’s make it easy to see how many extras there are.
What is helpful about each way of showing information?
Number paths are helpful because you can compare by seeing which line is longer.
Tallies are helpful because they are quick to make.
A graph with pictures is helpful because you can count all the pictures easily to find the totals.
Finally, preview the skill of counting on from the next lesson. Ask students to consider how the representations make use of groups of 5.
How do number paths and tallies both use groups of 5 to make counting easier?
Number paths start with 5 gray squares. You don’t have to start counting at 1.
Tallies group 5 lines together, so you can start counting at 5 instead of 1.
Topic Ticket 5 min
Provide 5–10 minutes for students to complete the Topic Ticket. It is possible to gather formative data even if some students do not complete every problem.
The ancient Chinese used rods to represent numbers, which is similar to the tally work in this lesson.

Students may find it interesting that mathematicians from long ago also used efficient ways to organize, group, and count.
Consider creating an extension to this lesson by referring to the Math Past Resource for a more in-depth discussion of ancient Chinese number systems and suggestions for how to use them with students.
1 ▸ M1 ▸ TA ▸ Lesson 6 EUREKA MATH2 New York Next Gen © Great Minds PBC 90
Math Past
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 6 © Great Minds PBC 91
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 6 © Great Minds PBC 37 1. Draw tallies for the totals. I See 5 7
Write two totals. 5
less than 6 Name 1 ▸ M1 ▸ TA ▸ Lesson 6 EUREKA MATH2 New York Next Gen © Great Minds PBC 38 PROBLEM SET 2. Write the totals. How We Go 6 9 6
There are fewer dogs than birds .
< 7
1 ▸ M1 ▸ TA ▸ Lesson 6 EUREKA MATH2 New York Next Gen 92 © Great Minds PBC EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TA ▸ Lesson 6 © Great Minds PBC 39 PROBLEM SET Write two totals for each. 9 > 6 greater than 6 < 9 less than 6 = 6 equal to
Topic B Count On from a Visible Part
This topic opens by inviting students to discover and verbalize that when finding a total of two parts, such as a box of 6 markers and 3 additional markers, using the Level 2 strategy of counting on from a known part is more efficient than counting all.


As topic B progresses, students use the Level 1 strategy of counting all less frequently. They learn to trust the cardinality of a part, seeing it as a unit from which they can count on. They select parts that they “just know,” or subitize. Subitizing a part and counting on the other part to find the total requires practice over time.
Students may find it difficult to represent the second part in number bonds or number sentences. For example, students might ask, “When we count on 2 more from 5, why do we write 2 when we counted 6 and 7?” Several representations help students make sense of these part–total relationships:
• numerical recordings of the count sequence (5, 6, 7)
• number bonds
• number sentences that relate counting on to addition
As they better understand part–total relationships, students count on from both parts and notice that the total remains the same. Students take note of special part–part–total relationships and doubles, and they continue to practice these in fluency activities throughout module 1.
Mid-topic, a subtle shift advances student learning. Students conceptually subitize, or isolate one part, within a visible set, such as those represented on dot cards, and count on from that part. Familiar 5 + n facts support the shift. Students move toward counting on from any known part to find the total. Their sense of efficiency and flexibility grows as they realize that some parts are more helpful to see and count on from, and that totals can be found in many ways.
© Great Minds PBC 94
“1,
“Fiiiive,
5 2 7
2, 3, 4, 5, 6, 7”
6, 7”
To prepare for addition expressions, students count on from 10. Because the second part is now shown as a numeral rather than a set of objects, students use fingers to track. Students learn that the term unknown refers to what needs to be figured out, and they use it to describe the total. Although students worked with 10 + n facts in kindergarten, fluency with these facts is essential to their success with Level 3 strategies.


EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB © Great Minds PBC 95
7 8 9 10 6 5 9 4 5 + 4 = 9
Progression of Lessons
Lesson 7
Count all or count on to solve put together with total unknown situations.
Lesson 8
Count on from a known part and identify both parts in a total.
Lesson 9
Count on from both parts and record part–total relationships.
I drew all the markers and counted them.
I know there are 6 markers in the box. I can start counting from 6.

Partner A: I see 4. I can point to the dots on the other die and count on.






Partner B: I see 6. I can count on by pointing to the dots on the other die.
We can count on from either part and get the same total. The parts are the same in the number bonds and the number sentences, but they are in a different order.
© Great Minds PBC 96 1 ▸ M1 ▸ TB EUREKA MATH2 New York Next Gen
6
5 2 7 5 + 2 = 7 2 5 7 2 + 5 = 7
Name
Circle a part.
Lesson 10
Count on from 5 within a set.
Fill in the number bond.
Lesson 11
See any part in a set and count on.
Write the number sentence.
Sample:
6 3 9
Lesson 12
Count on from 10 to find an unknown total. 4 14
I see 5. I don’t need to start at 1. I can say fiiiive, and then count on two more, 6, 7.
6 + 3 = 9
I see a part I can use to count on: Siiiix, 7, 8, 9. The parts are 6 and 3, and the total is 9.
I can say 10 and count on by using my fingers for the other part. I was looking for the total.

EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB 97 © Great Minds PBC
© Great Minds PBC 89 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 11 11
all or count on to solve put together with total unknown situations.
Lesson at a Glance
This lesson invites students to solve put together with total unknown situations by using strategies of their choice. Through discussion, the class compares and connects representations and strategies. Expect a range of student understanding at this stage, and advance student thinking from counting all toward counting on from a known, trusted part. This lesson provides an opportunity for formative assessment.
Key Question
• What is the same and what is different about counting all and counting on?
Achievement Descriptor
1.Mod1.AD2 Count on to find the total number of objects in a set and represent the total with an addition number sentence. (NY-1.OA.5)
© Great Minds PBC 7 LESSON 7
© Great Minds PBC 49 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 7 7 5 How many crayons in all? 7 Show how you know. Name
Count
Agenda
Fluency 10 min
Launch 5 min
Learn 35 min
• Represent and Solve: Marker Problem
• Share, Compare, and Connect
• How Many in All?
• Problem Set
Land 10 min
Materials
Teacher
• 20-bead rekenrek
• Marker box
• Markers (8)
• Small box
• Two-color counters (10)
• Sticky notes (2)
Students
• Two-color counters (10 per student pair)
• Hide Zero® cards (1 set per student pair)
• 10-Frame removable (1 per student pair, in the student book)
Lesson Preparation
• The 10-Frame removables must be torn out of student books and placed in personal whiteboards. Consider whether to prepare these materials in advance or to have students prepare them during the lesson. Consider saving these for use in lessons 8 and 9.
• Prepare bags of 10 two-color counters for each student pair. Pull out cards 0–10 from the Hide Zero cards for each student pair. Save for use in lessons 8 and 9.
• Have a variety of math tools, such as two-color counters, number paths, and cubes, available for students to use.
• Place 5 markers in a marker box and label with the number 5 by using a sticky note. Have 3 additional markers available.
• Put 7 counters in a small box and label with the number 7 by using a sticky note.
© Great Minds PBC 99 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 7
Fluency
10-Frame Fill-Up
Materials—S: Two-color counters, Hide Zero cards, 10-Frame removable
Students find the number that makes 10 to maintain fluency with partners to 10 from kindergarten.
Have students form pairs. Invite students to fill up the 10-frame by using the following procedure:
• Partner A picks a card and places the corresponding number of red counters on the 10-frame.
• Partner B completes the 10 by placing yellow counters on the 10-frame.
• Partner B states the 10-fact. For example, “3 and 7 make 10.”
Have students alternate roles as they play.
Circulate as students work and provide support as needed.
Counting the Math Way: 5 and Some More
Students represent 5 and some more the math way to prepare for counting on beginning in lesson 8.
Let’s count to 5 the math way.
Have students count the math way from 0 to 5. Show the math way on your own fingers, but do not count aloud.
1 ▸ M1 ▸ TB ▸ Lesson 7 EUREKA MATH2 New York Next Gen © Great Minds PBC 100
10 5 35 10 3
Close it up!
Now let’s start at 5.
Show me 5.
(Students show 5 on their fingers the math way.)
Show me 6.
(Students put up their right thumb to show 6.)


Close it up!
Show me 5.
Show me 7. Close it up!
Continue with the following sequence:
Student View of Your Hand
Show 5 Show 8
Show 9 Show 5
Show 10 Show 5
Continue skipping around to different numbers, always building from 5.
Differentiation: Support
If students count from 1 each time instead of unitizing the 5 fingers, playfully invite students to count all the fingers on one hand and ask how many. Repeat several times. Likewise, ask them to show 5 as fast as they can to build confidence in showing fingers without having to count.
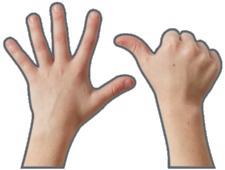











EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 7 © Great Minds PBC 101 a 0 1 2 3 4 5
Counting on the Rekenrek Within 20 the Say Ten Way
Materials—T: Rekenrek
Students count the Say Ten way to maintain fluency with the skill from kindergarten.
Show the rekenrek with the side panel attached. Start with all beads behind the panel.
Let’s count on the rekenrek the Say Ten way.
Say how many beads there are as I slide them over.
Slide the top row of beads to the side.
10
Here’s 1 more.
Slide over 1 bead on the bottom row.
This is ten 1. How many beads?
Ten 1
Slide over 1 more bead on the bottom row.
How many beads?
Ten 2
Slide the beads from behind the panel, one at a time, as students count the Say Ten way to ten 10.
Ten 3, ten 4, ten 5, ten 6, ten 7, ten 8, ten 9, ten 10
Slide the beads back behind the panel, one at a time, as students count the Say Ten way down to ten.
Ten 10, ten 9, ten 8, ten 7, ten 6, ten 5, ten 4, ten 3, ten 2, ten 1, ten
Teacher Note
In kindergarten, students learned to interpret teen numbers as 10 ones and some more ones, thinking of 20 as ten and ten. For now, twenty is “ten 10” the Say Ten way. When students learn to compose a ten later in grade 1, twenty becomes “2 ten.”
1 ▸ M1 ▸ TB ▸ Lesson 7 EUREKA MATH2 New York Next Gen © Great Minds PBC 102
“Ten” Student View “Ten” Student View “Ten 1” Student View “Ten 1” Student View
Launch
Materials—T: Marker box, additional markers
Students analyze a put together with total unknown situation in which the objects in each part are visible.
Gather students and show them the marker box. Point to the label and show that there are 5 markers in the box. Also show the 3 additional markers outside the box.

Place the box and markers to the side. Prompt students to retell the situation and use their responses to write the situation as the beginning of a word problem as shown.
What do we know about the markers I showed you?
Next have students consider what questions they could ask about the markers. Some possible responses include:
• Are there more markers in the box or out of the box?
• How many markers are there?
• How many more markers do we need to fill 2 boxes?
• How many markers would we have if we lost 2?
Great ideas! Today, we are going to answer this question.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 7 © Great Minds PBC 103
10 5 35 10
Write the put together with total unknown question as shown to finish the word problem. Read the whole word problem out loud to the class.
Transition to the next segment by framing the work.
Today, we will solve word problems and share strategies.
Learn
10 5 35 10
Represent and Solve: Marker Problem
Students independently represent and solve a put together with total unknown word problem.
Continue to display the word problem. Prompt students to think–pair–share about the following question.
How could we figure out how many markers there are in all?
We could count on a number path.
We could use our fingers.
We could draw the markers.
We could use two-color counters (or cubes).
Have students work independently to represent and solve the problem. Provide materials such as two-color counters, cubes, number paths, and personal whiteboards for student use. Encourage students to self-select their tools.
Teacher Note
Students may use a variety of representations to model and solve this problem including
• markers,
• manipulatives,
• fingers,
• number paths, or
• drawings.
1 ▸ M1 ▸ TB ▸ Lesson 7 EUREKA MATH2 New York Next Gen © Great Minds PBC 104
?
Circulate and observe student strategies. Select two or three students to share in the next segment. Look for work samples that help advance the lesson’s objective by using the count all and count on strategies to find a total.
Share, Compare, and Connect
Materials—T: Two-color counters
Students share solution strategies and make connections between counting all and counting on.
Gather the class and invite the selected students to share their work. If possible, order the work so that it shows a progression of thinking from counting all to counting on. The first strategy should be accessible to all students.
As each student shares, ask questions to elicit thinking, clarify the strategy, and make connections among different strategies. Increase engagement and promote student-tostudent discourse by encouraging students to use the Talking Tool as they compare the strategies.
Use the following sample discussions to guide the debrief of student work.

Highlight a student’s work that shows counting all with two groups.
Count All: Counters (Dan’s Way)
Dan, how did you find how many markers there are in all?
I put out 5 red counters and 3 yellow counters.
Class, how does Dan’s work show the problem?
Teacher Note
The sample student work shows common responses. Look for similar work from your students and encourage authentic conversations about the key concepts.
If students do not produce similar work, choose one or two pieces of their work to share. Highlight how these examples show movement toward the lesson objective. Then select one example from the chart to discuss that best advances the class’s thinking.
Consider presenting the work by asking the following question:
• This is how another student solved the problem. What do you think this student did?
Talking Tool
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 7 © Great Minds PBC 105
Count All: Counters Count All: Number Path Count On: Tallies Count On: Drawing Count On: Fingers 5 3 8 “1, 2, 3, 4, 5 (pause), 6, 7, 8.” 1 2 3 4 5 6 7 8 9 10 5 6 7 8 5
I Can Share My Thinking My drawing shows . I did it this way because . . I think because . I Can Agree or Disagree I agree because . I disagree because . I did it a different way. I . I Can Ask Questions How did you . ? Why did you . ? Can you explain . ? I Can Say It Again I heard you say . said . Can you say it another way?
© Great Minds PBC
The red counters show the 5 markers in the box, and the yellow counters show the 3 markers out of the box.
Dan made a group of 5 and a group of 3.
Dan, how did you count to find the total?
I counted each counter. 1, 2, … , 7, 8.
Class, how many markers are there in all? There are 8 markers.
Dan counted all the counters to find the total. Is there another way to count them?
You could start with the yellow ones instead of the red ones. You could start with 5 and keep counting.
Leave Dan’s counters displayed and take a moment to prepare students to transition from discussing counting all strategies to counting on strategies.
Let’s count just the red counters.
Circle the 5 red counters and label.
Let’s count all the counters again together, this time starting from 5. (Point to the group of 5 as students count: Fiiiive, 6, 7, 8.)
How many counters? 8
We got the same total as Dan: 8. He started at the beginning and counted all the counters, and we started at 5 and counted on.
Why did we get the same total both ways?
We already know there are 5 counters in the red group, so we don’t have to count them.
Promoting the Standards for Mathematical Practice
When students consider multiple strategies to find the total number of markers and notice that counting all and counting on both give the same total, they look for and express regularity in repeated reasoning (MP8).
Ask the following questions to promote MP8:
• When you count all and count on, what doesn’t change?
• How do you know counting on always works to find the total?
1 ▸ M1 ▸ TB ▸ Lesson 7 EUREKA MATH2 New York Next Gen © Great Minds PBC 106
Highlight the work of a student who counted on from 5 pictorially.
Count On: Drawing (Kioko’s Way)
Kioko, how did you find the total number of markers?
I wrote a 5 on the box of markers, and then I drew 3 more markers.
Class, Kioko didn’t draw every marker. How does her work show the problem?
The problem says there are 5 markers in the box. She drew the box of 5 and then the 3 other markers.
Kioko, show us how you counted to find the total.
Fiiiive, 6, 7, 8. (Points to the 5 and then each of the 3 markers.)
Let’s use Kioko’s way to count together. (Point to the drawing as students count chorally.)
Fiiiive, 6, 7, 8
We started with the group of 5 and counted on 3 more. Show thumbs-up if you found the total by counting on from 5, like Kioko did.
Have students think–pair–share about the following question.
Why did we start counting from 5 instead of 1?
We don’t have to start at 1 if we know there are 5 in the box.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 7 © Great Minds PBC 107
5
Highlight the work of a student who used fingers to count on from 5.
Count On: Fingers (Zoey’s Way)
Ask Zoey to demonstrate her strategy: She says 5 and counts on 3 more to 8, by using fingers to track.
Who can explain what strategy Zoey used?
She used her brain to think of 5 and then she used her fingers to count 3 more.
How did Zoey use her fingers to show the parts of the problem?
The problem has a box of 5 markers. Zoey just thought about 5. Then she showed 3 fingers to count the other 3 markers.
Zoey counted on from 5, just like Kioko did. Instead of drawing the box of 5 markers, Zoey imagined the box.
Record and display Zoey’s strategy.
Let’s use Zoey’s way to count together. Put a picture of the 5 markers in your mind and ready your fingers.
Point to the 5 as the class chorally says, “fiiiive.” Then model raising 3 fingers, one at a time, as the class chorally counts: 6, 7, 8.
Some students may find it helpful to make a fist to signal the group of 5 and then raise a finger to show the next number, 6.

Return to the word problem about the markers. Guide students to answer the question.
Differentiation: Support
Let’s answer the question in a complete sentence. How many markers are there in all?
There are 8 markers in all.
Some students may benefit from counting the actual markers used in Launch. Allow them to take the markers out of the box and count all.

Then put the markers back in the box and support them as they start with 5 markers and count on 3 more. Help students remember that because they know there are 5 markers in the box, they do not need to start at 1.
Consider changing the number of markers in the box to 3, 4, or 6 (change the label as well) and practicing counting all and counting on.
1 ▸ M1 ▸ TB ▸ Lesson 7 EUREKA MATH2 New York Next Gen © Great Minds PBC 108
?
5 6 7 8
How Many in All?
Materials—T: Two-color counters, small box, sticky note Partners solve a put together with total unknown situation in which some objects are hidden. Invite students to listen to another problem. As you present the problem, show students the box that contains 7 yellow counters and is labeled with a 7. Also show them 2 red counters in your hand.
There are 7 yellow counters in the box. There are 2 red counters in my hand. How many counters do I have in all?
Pair students, and prompt them to find the total by using the count on strategies shared earlier. Invite them to select their own tools (e.g., two-color counters, whiteboards, fingers).
Circulate as students solve the problem. If they use the counting all strategy, ask advancing questions such as the following:
• We know how many are in the box. What number can we start with?
• Would we get the same total if we counted on from 2 instead?
Notice how students count on to find the total. For example:
• The student makes a model that shows 7 as a group and then counts on from 7, pointing to the other counters.
• The student finds 7 on the number path and hops 2 more.
• The student holds 7 in mind and then counts on by using a gesture, such as head bobbing or tracking with fingers.
Conclude by revealing the 7 yellow counters in the box. Have the class chorally count all and count on from 7. Support students to see that both counting all and counting on result in the same answer because starting at 7 includes the count sequence from 1 to 7.
If time allows, vary the number of counters in the box and in your hand, such as 6 and 4.

Differentiation: Challenge
Show one or both of the following representations and invite students to discuss how they relate to the situation and to the strategy of counting on.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 7 © Great Minds PBC 109
8
3
+ 3 = 8
5
5
Problem Set
Differentiate the set by selecting problems for students to finish within the timeframe. Problems are organized from simple to complex.
In this lesson, consider providing structured support by reading the problem aloud, inviting students to work collaboratively, or providing tools to help them solve. Encourage them to represent their solution to the problem in the space provided.
Land
Debrief 5 min
Objective: Count all or count on to solve put together with total unknown situations.
Display the picture of Deb and Max’s thinking. Ask students to study how each student counted. Then have students think–pair–share about the following questions.
Talk with your partner about how Deb and Max counted. What is the same? What is different?
They got the same total.
Deb counted every counter. Max counted on from 3.
Why did they get the same total, even though Deb counted all and Max counted on?
They both still counted all the counters.
If we know there are 3 in the bowl, we can just say 3 and keep counting. You don’t have to say every number.




Is it easier for you to count all like Deb or count on like Max? Why?
Counting all is easier because I know I won’t miss any.
It’s easier to count on because sometimes you just know how many there are in a group, and you don’t need to count them all.
1 ▸ M1 ▸ TB ▸ Lesson 7 EUREKA MATH2 New York Next Gen © Great Minds PBC 110
10 5 35 10 Deb 1 2 3 4 5 Max 3 4 Deb 1 2 3 4 5 Max 3 4 5
Conclude the lesson by explaining why counting on and counting all result in the same total.
When we count all, we count each object: 1, 2, 3, 4, 5. When we count on, we know how many are in one part. We say the total of that part and keep counting the other objects one at a time. Either way, we are counting them all, either one by one or starting with a group.
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 7 © Great Minds PBC 111
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
1 ▸ M1 ▸ TB ▸ Lesson 7 EUREKA MATH2 New York Next Gen 112 © Great Minds PBC 1 ▸ M1 ▸ TB ▸ Lesson 7 EUREKA MATH2 New York Next Gen © Great Minds PBC 48 PROBLEM SET 4 8 6 10 10 14 © Great Minds PBC 47 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 7 7 How many crayons in all? Show how you know. 5 9 5 8 Name
Count on from a known part and identify both parts in a total.
Lesson at a Glance
Partners play a game, Roll a Total, to practice counting on from a known part to find a total. They record the parts and total in a number bond.
Key Question
• Why should we count on from a part we know?
Achievement Descriptor
1.Mod1.AD2 Count on to find the total number of objects in a set and represent the total with an addition number sentence. (NY-1.OA.5)
© Great Minds PBC 8 LESSON 8
© Great Minds PBC 59 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 8 8 Count on from a part. Fill in the number bond. 4 2 6 3 3 6 Name
Agenda
Fluency 10 min
Launch 10 min
Learn 30 min
• Roll a Total
• Record Two Parts and a Total
• Problem Set
Land 10 min
Materials
Teacher
• 20-bead rekenrek
• Roll a Total (digital download)
• 6-sided dot dice
Students
• Hide Zero® cards (1 set per student pair)
• Two-color counters (1 bag per student pair)
• 10-Frame removable (1 per student pair, in the student book)
• 6-sided dot dice (2 per student pair)
• Roll a Total (1 per student pair, in the student book)
Lesson Preparation
• Use the bags of 10 counters and Hide Zero cards 0–10 prepared in lesson 7.
• The 10-Frame removables must be torn out of student books and placed in personal whiteboards. Consider whether to prepare these materials in advance, to have students assemble them during the lesson, or to use the ones prepared in lesson 7. Consider saving these for use in lesson 9.
• Copy or print Roll a Total to use for demonstration.
• Roll a Total must be torn out of student books and placed in personal whiteboards. Consider whether to prepare these materials in advance or to have students prepare them during the lesson.
© Great Minds PBC 115 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 8
Fluency
10-Frame Fill-Up
Materials—S: Two-color counters, Hide Zero cards, 10-Frame removable Students find the number that makes 10 and complete a statement, number bond, and number sentence to maintain fluency with partners to 10 from kindergarten.
Have students form pairs. Invite students to fill up the 10-frame by using the following procedure:
• Partner A picks a card and places the corresponding number of red counters on the 10-frame.
• Partner B completes the 10 by placing yellow counters on the 10-frame.
• Partner B states the 10-fact. For example, “3 and 7 make 10.”
• Partner A writes the number sentence on the whiteboard and fills in the number bond as shown. For example, 3 + 7 = 10.
Have students alternate roles as they play. Circulate as students work and provide support as needed.
5-Groups: Imagine 1 More
Students recognize a group of dots and imagine 1 more to prepare for counting on.
After asking each question, wait until most students raise their hands, and then signal for students to respond.
Raise your hand when you know the answer to each question. Wait for my signal to say the answer.
1 ▸ M1 ▸ TB ▸ Lesson 8 EUREKA MATH2 New York Next Gen © Great Minds PBC 116
10 10 30 10 3 and + make 10. 10 = 10 3 3 7 7
Display the 5-group card that shows 5.
How many dots?
5
Imagine there is 1 more. What is the total?
6
Repeat the process with the following sequence:
Counting on the Rekenrek Within 20 the Say Ten Way
Materials—T: Rekenrek
Students count the Say Ten way to maintain fluency with the skill from kindergarten.
Show the rekenrek with the side panel attached. Start with all beads behind the panel.
Let’s count on the rekenrek the Say Ten way.
Say how many beads there are as I slide them over.
Slide the top row of beads to the side.
10
Here’s 1 more.
Slide over 1 bead on the bottom row.
This is ten 1. How many beads?
Ten 1
Slide 1 more bead over on the bottom row.
How many beads?
Ten 2
Differentiation: Support
If students need support to mentally add the dot, they can make a closed fist in the air to represent the extra dot. Align it, from their perspective, to the next empty space on the 5-group card. This way students can see what the 5-group card would look like with 1 more dot.

EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 8 © Great Minds PBC 117
6 5 10 5 7 3 5 8 5 9
“Ten” Student View “Ten” Student View “Ten 1” Student View “Ten 1” Student View
Slide beads, one at a time, to the left or to the right in the following sequence as students count:
Continue counting on the rekenrek the Say Ten way within 20. Change directions occasionally, emphasizing crossing over ten and ten 5 and where students hesitate or count inaccurately.
Launch
Students count on from one part and identify both parts within the total.
Display the picture of dice and ask the following question.



How many dots are there? How do you know?
Give students quiet think time. Ask them to give a silent signal to indicate that they know the total.
Pair students, and have them discuss how they found the total. Circulate and listen. If some students know that 6 and 4 is 10, ask them to show how they know.
Identify a student who counted on from 6 and a student who counted on from 4 to share their thinking with the class. Invite the student who counted on from 6 to share their way first. Record their strategy on the image: label the blue die 6, and circle it. Then label the four additional dots 7, 8, 9, and 10, and circle the yellow die as shown.
Teacher Note
Kindergarten students learn that the last number said tells how many. We apply that understanding to the known part to make sense of why counting on works.
For example, when we count 5 objects, the last number we say is 5. When we know a part is 5, we say the next number in the counting sequence (6) to start counting the next part.
Consider demonstrating this concept and making it explicit. This will support students who are still learning cardinality and those who are on the verge of understanding to see why it is that we can always say 5, 6, 7.
1 ▸ M1 ▸ TB ▸ Lesson 8 EUREKA MATH2 New York Next Gen © Great Minds PBC 118
Ten 6 Ten 7 Ten 8 Ten 9 Ten 10 Ten 3 Ten 4 Ten 5 Ten 4 Ten 5
10 10 30 10
Point to the labeled dots, and have all students chorally count on from 6. Then discuss the count on strategy by using the following dialogue as guidance.
What is the total of 6 and 4?
We started with the part that has 6. How did starting with that part help us count?
We could just say 6 and count on 4 more.
If we counted all the dots on the blue die, would the first dot we count on the yellow die still be 7? Let’s find out.
Invite the class to answer the question by chorally counting all. Begin with the blue die, and point to each dot as the class counts it. Ask students to confirm that the count starts at 7 when they switch to the yellow die.




We don’t need to count all the dots one by one. We know there are 6 in this part (gesture to the blue die). So we can keep counting on the dots on the yellow die, starting at 7 for the first dot.
Invite the student who counted on from 4 to share. Record the strategy, and then have the class chorally count on as well.
What is the total of 4 and 6?
We started with the part that has 4. How did starting with that part help us count?
We could just say 4 instead of starting at 1.
We counted on 6 more dots. When we count on to find a total, we start with how many are in one part. Then we continue counting by ones as we count the other part.
Transition to the next segment by framing the work.
Let’s play a game to practice counting on from a part.
Language Support
Counting on means to count up from one subitizable part, or addend, to find the total.
Consider creating an anchor chart to support use of the term count on. For example:
Count On
Start Count on from a part to get a total.
Fiiiive, 6, 7
It may be helpful to add to this anchor chart as students use varied tools, such as fingers or a number path, to count.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 8 © Great Minds PBC 119
10
10
5
7
Learn
Roll a Total
Materials—T/S: Dice, Roll a Total
Students practice counting on from one part to find the total.
Gather students, and display the Roll a Total recording sheet. Use the recording sheet and two dice to demonstrate how to play the game. Consider posting student-friendly directions for the game for students to refer to as they play.

Partner A rolls the dice, chooses a part (hold up or point to one die), and counts on from that part to find the total.


Threeee, 4
Partner B finds the total on the Roll a Total recording sheet and draws an X on it. If the total already has an X on it from an earlier turn, Partner B makes a tally mark in the space next to the total.
Partners switch roles for each turn. For the next turn, Partner B rolls the dice and counts on to find the total. Partner A marks the total on the Roll a Total page.
Twoooo, 3, 4
Pair students. Ensure that each pair has a copy of Roll a Total in a personal whiteboard and two dice.
Ready students to play by generating excitement and purpose.
Differentiation: Support
Support students who count all by asking them to notice which number they say as they start counting the second part. Prompt them to count again, this time starting with the last number they say on the first die. Ask:
• Do you get the same answer when you count all and count on from a part?
Differentiation: Challenge
Challenge students by asking them to count on another way before rolling the dice again. Some students may recognize that this is addition; invite them to write matching expressions or number sentences on a whiteboard.
Students may also use three dice, number cubes, or 1–9 dice.


1 ▸ M1 ▸ TB ▸ Lesson 8 EUREKA MATH2 New York Next Gen © Great Minds PBC 120
10 10 30 10 EUREKA MATH M1 TB Lesson 8 Sprint Roll a Total Copyright Great Minds PBC 53 Roll a Total 2 3 4 5 6 7 8 9 10 11 12
I wonder if we will cross off all the totals. Which total will we roll the most?
Let students play for 7 to 8 minutes as you circulate and listen. Then have them clean up their materials. Consider taking a moment to ask how many totals pairs crossed off and which totals had the most tallies.
Record Two Parts and a Total
Students count on to find the total and name the two parts.
Have students follow along in their student books as you introduce the three problems, each using a different pair of dice. Use the following questions to guide students through each problem.
As you played, I noticed a few different ways that rolling the dice made the same total. This picture shows one roll. What are the two parts?
4 and 2
Let’s count on to check the total.
Have students chorally count on from 4, recording the count on the dice.
Draw attention to how the counting sequence continues, rather than starts again, as you count on.
Why did we write 4, and then 5, 6, instead of writing 4, and then 1 and 2?
We already know we have 4, so we can keep counting instead of starting over.
Refer to the number bond as you activate prior knowledge about the model.
A number bond shows how parts come together to make a total. Let’s fill in this number bond to show the two parts and the total.
Guide students to complete the number bond.
Differentiation: Support
Some students may not understand why the second die is labeled with the numbers 5 and 6, but the corresponding part on the number bond is labeled 2.
Point to the dots on the dice to clarify the two parts. Then explain that the labels 5 and 6 show how they counted on from the first part to find the total.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 8 © Great Minds PBC 121
© Great Minds PBC 55 EUREKA MATH New York Next Gen M1 TB Lesson 8 4 5 6 4 2 6 Name Great Minds PBC 56 LESSON 1 M1 TB Lesson EUREKA MATH New York Next Gen 3 4 5 6 3 3 6 5 6 5 6
What are the two parts? (Point to the two part boxes above the arms.)
4 and 2
What is the total? (Point to the total box.)
6
Notice that in this number bond, the parts are on the top and the total is on the bottom.
Repeat the process with the next two problems. Release responsibility to the students as appropriate.
Problem Set
Differentiate the set by selecting problems for students to independently finish within the timeframe. Problems are organized from simple to complex.
Promoting the Standards for Mathematical Practice
When students start with the next number after the part they count on from and are careful to count on the correct number of objects, they attend to precision (MP6).
Ask the following questions to promote MP6:
• When counting on, what steps do you need to be extra careful with?
• What mistakes are easy to make when counting on?
Differentiation: Challenge
Some students may be ready to write number sentences. Ask students where the numbers on the dice appear in the number bond and in the number sentence.
1 ▸ M1 ▸ TB ▸ Lesson 8 EUREKA MATH2 New York Next Gen © Great Minds PBC 122
Land
Debrief 5 min
Objective: Count on from a known part and identify both parts in a total.
Gather students with their Problem Sets. Have students compare their work for the second problem. Then show a student’s work and invite the class to analyze what they see.
How do you think Beth found the total?
I think she counted on from the 3 dots: Threeee, 4, 5.
Is there another way to find the total?
You could count on from the 2 dots: Twoooo, 3, 4, 5.
You could count all the dots: 1, 2, 3, 4, 5.
Help students summarize the major learning from this lesson.
How is counting on the same and different as counting all?
We get the same total.
When we count all, we count each dot. But when we count on, we just say the whole first part and then count on the other part.
Why can we just say the first part?
We know how many are in that part already.
Yes, the last number you say is how many are in a part. If you know how many there are in that part, you can just start counting on from that number.
How is counting on from a part you know helpful?
It is quicker than counting all the dots.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 8 © Great Minds PBC 123
10 30 10
3 2 5 3
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
1 ▸ M1 ▸ TB ▸ Lesson 8 EUREKA MATH2 New York Next Gen © Great Minds PBC 124
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 8 125 © Great Minds PBC
© Great Minds PBC 57 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 8 8 1. Count on from a part. Fill in the number bond 2 2 4 3 2 5 3 3 6 3 4 7 Name 1 ▸ M1 ▸ TB ▸ Lesson 8 EUREKA MATH2 New York Next Gen © Great Minds PBC 58 PROBLEM SET 2. Count on from a part. Fill in the number bond. 5 3 8 6 3 9 5 5 10 6 5 11
Count on from both parts and record part–total relationships.
Lesson at a Glance
Students explore counting on from both parts and discover that either starting point will result in the same total. As partners play the familiar Roll a Total game, they count on from a part, make a number bond, and write a matching number sentence. Students are introduced to the term doubles, and they notice that counting on from either part is exactly the same.
Key Question
• Why do we get the same total no matter which part we count on from?
Achievement Descriptors
1.Mod1.AD1 Apply the commutative property of addition as a strategy to add. (NY-1.OA.3)
1.Mod1.AD2 Count on to find the total number of objects in a set and represent the total with an addition number sentence. (NY-1.OA.5)
© Great Minds PBC 9 LESSON 9
© Great Minds PBC 71 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 9 9 Count on two ways. Fill in the number bonds. Write the number sentences. 3 4 7 3 + 4 = 7 4 3 7 4 + 3 = 7 Name
Agenda
Fluency 10 min
Launch 5 min
Learn 35 min
• Record Counting On Two Ways
• Roll a Total
• Doubles Roll
• Problem Set
Land 10 min
Materials Teacher
• Number Bond removable (2, digital download)
Students
• Bag of two-color counters (1 per student pair)
• Hide Zero® cards (1 set per student pair)
• 10-Frame removable (1 per student pair, in the student book)
• Number Bond removable (in the student book)
• 6-sided dot dice (2 per student pair)
• Roll a Total (1 per student pair, in the student book)
Lesson Preparation
• Use the bags of 10 counters and Hide Zero cards 0–10 first prepared in lesson 7.
• The 10-Frame removables must be torn out of student books and placed in personal whiteboards. Consider whether to prepare these materials in advance, to have students assemble them during the lesson, or to use the ones first prepared in lesson 7.
• Copy or print the Number Bond removable to use for demonstration.
• The Number Bond removables must be torn out of student books and placed in personal whiteboards. Consider whether to prepare these materials in advance or to have students prepare them during the lesson. Consider saving these for use in lesson 12.
• Roll a Total must be torn out of student books and will need to be placed in personal whiteboards during the lesson. Consider whether to tear the pages out in advance or to have students tear them out during the lesson.
© Great Minds PBC 127 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 9
Fluency
10-Frame Fill-Up
Materials—S: Two-color counters, Hide Zero cards, 10-Frame removable
Students find the number that makes 10 and complete a statement, number bond, and number sentence to maintain fluency with partners to 10 from kindergarten.
Have students form pairs. Invite students to fill up the 10-frame by using the following procedure:
• Partner A picks a card and places the corresponding number of red counters on the 10-frame.
• Partner B completes the 10 by placing yellow disks on the 10-frame.
• Partner B states the 10-fact. For example, “3 and 7 make 10.”
• Partner A writes the number sentence on the whiteboard and fills in the number bond. For example, 3 + 7 = 10.
Have students alternate roles as they play.
Circulate as students work and provide support as needed.
Counting the Math Way: Count On from 5
Students count on from 5 with their fingers to develop fluency with counting on.
Let’s count to 5 the math way.
Have students count the math way from 0 to 5. Show the math way on your own fingers, but do not count aloud.
Close it up!
Now let’s start at 5.
1 ▸ M1 ▸ TB ▸ Lesson 9 EUREKA MATH2 New York Next Gen © Great Minds PBC 128
10 5 35 10 3 and + make 10. 10 = 10 3 3 7 7
Show me 5.
(Students show 5 on their fingers the math way.)
Show me 7.
(Students put up their right thumb and right index finger to show 7.)
Close it up!
(Students close up fingers.)
Count on from 5 to 7 the math way.
Fiiiive, 6, 7
Close it up!
Continue with the following sequence:
Offer more practice counting on, always starting from 5.
5-Groups: Imagine 0 More, 1 More
Students recognize a group of dots and imagine 0 more and 1 more to develop fluency with counting on.
After asking each question, wait until most students raise their hands, and then signal for students to respond.
Raise your hand when you know the answer to each question. Wait for my signal to say the answer.

Display the 5-group card that shows 5.
How many dots? 5
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 9 © Great Minds PBC 129
5 Show 8 Show 10 Show 5 Show 9 Show 5 Count on from 5 Count on from 5 Count on from 5
Show
5 7 6
Imagine there are 0 more. What is the total?
Imagine there is 1 more. What is the total?
Repeat the process with the following sequence:
Launch
Students count on two ways and see that both ways result in the same total.
Display the picture of dice. Tell students that the dice show a roll from Roll a Total, the game played in lesson 8. Ask students to turn and talk about the following question.




How would you count on to find the total?
Listen in as students share. They may describe and show strategies such as
• pointing at the dots or using fingers to count all,
• counting on from one part by pointing at dots as they bob their head, or
• counting on from one part and using fingers to track the second part.
Display the picture of the two sets of dice.
Have students use the first pair of dice to chorally count on from 5, using their fingers to track. Then repeat the process with the second pair of dice, starting with 2.
Differentiation: Support
Show counting all if students still need to see how the two strategies connect.
Counting all, starting with a different part (die) each time, supports the idea that we can start counting on from either part and get the same total or add in any order.
1 ▸ M1 ▸ TB ▸ Lesson 9 EUREKA MATH2 New York Next Gen © Great Minds PBC 130
5
6
3 5 10 5 9 8 5 6 5 7
10 5 35 10
Record both ways as shown. Use the displayed recordings to facilitate a class discussion. How is counting on from 2 like counting on from 5?
The parts are the same. The total is the same: 7.
Which way would you choose to count on? Why?
I would start with 2 because I know that part.
I would start with 5 because starting with 5 is faster.
Transition to the next segment by framing the work.
Let’s count on from both parts and show how we find the total.
Learn
Record Counting On Two Ways
Materials—T/S: Number Bond removable


Students record number bonds and number sentences to show the part–total relationships in their counts.
Continue to display the two recordings from Launch. For each recording, use the following sample dialogue to guide students to
• use the number bond to show the part–total relationship and
• express the count as a number sentence.
Teacher Note
Encourage students to track with their fingers as they count on. This becomes increasingly important in later lessons when the objects in one part are not visible. Note that some students may count the math way, but they may start with any finger that makes sense to them.


EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 9 © Great Minds PBC 131
6 3 4 5 6 7 7 Fiiiive Twoooo 10 5 35 10
Begin with the recording of dice that shows counting on from 5.


Let’s think about how we found the total. What part did we start with?
We started with 5.
Then we counted on 6 and 7. How many numbers did we count in the second part?
Two numbers
We have a part that is 5 and a part that is 2. Let’s show these parts on our number bond.
Demonstrate writing the parts.
When we count on, we add parts together to find the total. What is the total of 5 dots and 2 dots?
7 dots
Write the total on the number bond and 5 + 2 = 7 below the number bond.
We can write the number sentence 5 + 2 = 7 to show how we added the parts to find the total.
Ask students to complete the number bond and write the number sentence. Have the class read the number sentence chorally.
Repeat the same procedure for the recording of dice that shows counting on from 2. Have students erase their whiteboards to start again. Use the second number bond for demonstration so the two representations can be shown side-by-side.
Display both completed number bonds and number sentences. Have students think–pair–share to discuss the following question.
Teacher Note
Although the number bond is written here according to the part the students used to count on from (left to right), the order in which we write each part of the number bond doesn’t matter.
1 ▸ M1 ▸ TB ▸ Lesson 9 EUREKA MATH2 New York Next Gen © Great Minds PBC 132
EUREKA MATH M1 TB Lesson Number Bond Copyright Great Minds PBC 65 5 + 2 = 7 5 2 7
EUREKA MATH M1 TB Lesson Number Bond Copyright Great Minds PBC 65 2 + 5 = 7 2 5 7
What do you notice about the number bonds and number sentences?
Both totals (7) are in the same place.
The parts (5 and 2) switched places.
The total is the same. How does knowing that the total is the same help you choose a part to count on from?
You can start with any part you know.
You can start with the part that is easier for you.
Consider pausing here to provide students time to process. Encourage them to ask any questions they have about counting the parts in any order.
Roll a Total
Materials—S: Dice, Roll a Total, Number Bond removable Students relate counting on to number bonds and number sentences.

Tell students they are going to play Roll a Total, as they did in lesson 8, to practice counting on. Partner students and distribute a pair of dice to each group. Have partner A place the Roll a Total page into a personal whiteboard. Have partner B keep the Number Bond in a personal whiteboard.
Differentiation: Support
If students always count on from the smaller part, it may be that they are not yet able to subitize the larger number. Advance thinking by asking:
• What two parts do you see? Which part is bigger?
• How do you know those are the parts and the total?
• Where did you get the numbers in your number sentence?
Differentiation: Challenge
Consider increasing complexity by using three dice and encouraging students to use what they know about the total of two dice as the starting point for counting on. Also consider using dice with larger numbers to promote subitizing larger amounts from which to count on. Note the recording sheet will not reflect the resulting larger totals.
To further extend student thinking, invite students to notice which totals are coming up the most and least. Invite students to write down the combinations and discover that there are more combinations that make the middle value (7) than the largest and smallest values (2 and 12). Ask, “Why might this be happening?”
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 9 © Great Minds PBC 133
EUREKA MATH New York Next Gen M1 TB Lesson 9 Roll Total © Great Minds PBC 65 Roll a Total 2 3 4 5 6 7 8 9 10 11 12 EUREKA MATH New York Next Gen M1 TB Number Bond © Great Minds PBC 63
Review the following directions for Roll a Total. Note that in today’s game, each partner has a different job than they had in lesson 8.
• Partner A rolls the dice, chooses a part, and counts on from that part to find the total.
• Partner A finds the total on the Roll a Total page and draws an X on it. If the total already has an X on it from an earlier turn, partner A makes a tally mark in the space next to the total.
• Partner B completes the number bond to show the roll and writes a number sentence to show the count.
• Partners switch roles for each turn.
Students can choose to count on from either part. If they are unsure about which part to choose, encourage them to try both ways and decide.
Allow students to play for 5 or 6 minutes. Consider closing the game by having pairs share whether anyone drew an X on all the totals and which total had the most tally marks.
Doubles Roll
Students count on from doubles and see that the count is the same starting from either part.
Display the picture of two dice showing 5. Ask students to share what they notice about the dice. Have students raise their hands if they encountered a roll where the dice showed the same numbers.
Prompt the class to count on chorally to find the total, and then pose this question:
Are there two ways to count on when you roll two 5s? Why? No. You have to start at 5 no matter which part you choose first.
Promoting the Standards for Mathematical Practice
When students represent the roll and their counting using number bonds and number sentences, they reason abstractly and quantitatively (MP2).
Ask the following questions to help promote MP2:
• How does the number bond show your roll in the game?
• How does the number sentence show your counting?
1 ▸ M1 ▸ TB ▸ Lesson 9 EUREKA MATH2 New York Next Gen © Great Minds PBC 134
Display the picture of doubles 1–6.
When both parts are the same number, we call them doubles.
Point to each pair of dice as you name the doubles.
1 and 1, 2 and 2, … , 6 and 6 are all doubles.
As time allows, have students find the totals of each doubles fact shown by counting on chorally or with a partner. Share the totals as a class.
Look for doubles in your Problem Set today.
Problem Set
Differentiate the set by selecting problems for students to independently finish within the timeframe. Problems are organized from simple to complex.
Help students recognize the words number sentence in print. Invite students to underline it as you read it aloud.
Teacher Note
Students are not expected to master doubles facts in this lesson. Doubles practice will continue through fluency activities in module 1. In topic D, students will make problems easier by using doubles facts.
Teacher Note
Students do not need to record counting on by writing on the dice as long as they are counting on by pointing, counting aloud, or using their fingers.
Some students may count on from the same part for both pictures of the dice. Prompt these students to point to the die they started with, and then ask them to count on from the other part.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 9 © Great Minds PBC 135
Land
Debrief 5 min
Objective: Count on from both parts and record part–total relationships.
Gather the class and display a completed first page of the Problem Set. Have students think–pair–share about the following question.
The number bonds and number sentences for these two rolls are almost the same. Why are they so similar?
The parts are the same on the dice: 3 and 5.
The total is the same no matter which part you start with. 3 + 5 and 5 + 3 both make 8. The order doesn’t matter.
We can count on from either part and get the same total. Why do we get the same total no matter which part we count on from?
Because the parts are the same.
The total number of dots is the same, no matter if we start with 3 or 5.
If you rolled 3 and 5, which part would you choose to count on from? Why?
I would choose to count on from 3 because I can see 3 without counting those dots.
I would choose to count on from 5 because it’s the bigger part. There aren’t as many dots to count on.
At this time, focus on what works for each student rather than efficiency. Consider closing the segment by pointing out that mathematicians are flexible and know many ways to solve problems.
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
1 ▸ M1 ▸ TB ▸ Lesson 9 EUREKA MATH2 New York Next Gen © Great Minds PBC 136
5 35 10
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 9 © Great Minds PBC 137
1 ▸ M1 ▸ TB ▸ Lesson 9 EUREKA MATH2 New York Next Gen © Great Minds PBC 68 PROBLEM SET 2. Count on two ways. Fill in the number bonds. Write the number sentences. 6 + 4 = 10 4 + 6 = 10 6 4 10 4 6 10 © Great Minds PBC 67 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 9 9 1. Count on two ways. 5 + 3 = 8 3 + 5 = 8 Fill in the number bonds. Write the number sentences. 5 3 8 3 5 8 Name
1 ▸ M1 ▸ TB ▸ Lesson 9 EUREKA MATH2 New York Next Gen 138 © Great Minds PBC EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 9 © Great Minds PBC 69 PROBLEM SET 3. Count on from a part. Write the number sentence. 2 + 2 = 4 5 + 5 = 10 4 + 4 = 8 6 + 6 = 12
Lesson at a Glance
Students identify and count on from 5 by using hands, 5-groups, and dot patterns. They show the parts and total on a number bond and write a number sentence to record the count. Students apply counting on from 5 to find totals in graphs and charts. Students learn that seeing a part within a set, such as 5, and using it to count on makes finding the total easier.
Key Question
• How is seeing 5 within a set helpful for finding the total?
Achievement Descriptor
1.Mod1.AD2 Count on to find the total number of objects in a set and represent the total with an addition number sentence. (NY-1.OA.5)
© Great Minds PBC 10
© Great Minds PBC 81 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 10 10 Circle 5 and count on. Fill in the number bond. Write the number sentence. 5 4 9 5 + 4 = 9 Name
LESSON 10 Count on from 5 within a set.
Agenda
Fluency 10 min
Launch 5 min
Learn 35 min
• Find 5 and Count On
• Count On from 5 and Record
• Count On from 5 in Data Contexts
• Problem Set
Land 10 min
Materials Teacher
• None Students
• Dot Cards removable (in the student book)
Lesson Preparation
The Dot Cards removables must be torn out of student books and placed in personal whiteboards. Consider whether to prepare these materials in advance or to have students prepare them during the lesson.
© Great Minds PBC 141 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 10
Fluency
5-Groups: Count On from 5
Students recognize groups of dots and count on from 5 to develop fluency with counting on.
After asking each question, wait until most students raise their hands, and then signal for students to respond.
Raise your hand when you know the answer to each question. Wait for my signal to say the answer.
Display the 5-group card that shows 6.
How many total dots?
6
How many dots are in the top row? (Gesture to the top row.)
5
How many dots are in the bottom row? (Gesture to the bottom row.) 1
We can count on like this: Fiiiive (slide finger across the row of 5), 6 (point to the 1 dot on the bottom row). Try it with me. Ready?
Fiiiive, 6. (Mimics the sliding and pointing motions in the air.)
Repeat the process with the following sequence:
Teacher Note
As students become familiar with the routine, consider reducing the questions to as few words as possible (e.g., Top? Bottom?). Using this economy of language allows students to complete a greater volume of problems in a short time while maintaining an energetic pace.
1 ▸ M1 ▸ TB ▸ Lesson 10 EUREKA MATH2 New York Next Gen © Great Minds PBC 142
7 8 9 10 10 5 35 10
Ready, Set, Add
Students find a total and say addition number sentences to build addition fluency within 10.
Let’s play Ready, Set, Add. Have students form pairs and stand facing each other.
Model the action: Make a fist, and shake it on each word as you say, “Ready, set, add.” At “add,” open your fist, and hold up any number of fingers.
Tell students that they will make the same motion. At “add,” they will show their partners any number of fingers. Consider doing a practice round with students.
Clarify the following directions:
• To show zero, show a closed fist at “add.”
• Try to use different numbers each time to surprise your partner.
Each time partners show fingers, have them both say the total number of fingers. Then have each student say the addition sentence, starting with the number of fingers on their own hand. See the sample dialogue under the photograph.

Circulate as students play the game to ensure they are trying a variety of numbers within 5.
Partners A and B: “6”
Partner A: “2 + 4 = 6”
Partner B: “4 + 2 = 6”
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 10 © Great Minds PBC 143
Launch
Students use the fingers on one hand to count on from a known part, 5. Gather students and make a game of having them recognize 5 fingers on their hand.







Show me 5 the math way.
Do you need to count each finger to know that there are 5, or are there always 5?
There are always 5. Have all students show 7 fingers the math way.






Teacher Note
Remember, to count the math way, the teacher begins counting from the right pinkie. Students begin counting from their left pinkie. In this way, students see numbers from left to right.

Student counting on the math way: 5 6 7
Ask which part they know without counting. Students may respond with 5 or 2. Invite the class to chorally count on from both parts.
Both 5 and 2 are parts we can count on from. Which way is easier? Why? It is easier to count on from 5 because we only need to count on 2 more.
1 ▸ M1 ▸ TB ▸ Lesson 10 EUREKA MATH2 New York Next Gen © Great Minds PBC 144
1 2
5 6
3 4
7
10 5 35 10
5 6 7 “Fiiiive, 6, 7” 2 3 4 5 6 7 “Twoooo, 3, 4, 5, 6, 7”
Prompt students to show 8 the math way. Have students count on from 5 to find the total. Repeat for 9.
Is it easier to count on from 5 or count all our fingers? Why?
It is easier to count on from 5 because you don’t need to count all the fingers.
It is easier to start at 5 because it is faster.
Turn and talk with your partner. How did we count on from a part we know to find the total?
Transition to the next segment by framing the work.
Today, let’s look for 5 and count on from it.
Learn Find 5 and Count On
Students recognize a group of 5 within a set and use it to count on to find the total.
Invite students to look at another set of objects. Display the 7-dot card. Have students think–pair–share about the following question.
What are some ways to count on to find the total?
Invite a few students to share responses with the class. If possible, include a student who mentions counting on from 5. Circle the row of 5 dots on the image.
I circled 5. 5 is one part of the total. What is the other part?
The other part is 2.
Where do you see the parts of 5 and 2 in the picture?
There are 5 dots in the circled part on top and 2 on the bottom.
Teacher Note
This lesson advances counting from lessons 8 and 9 in how the parts are presented. Previously, parts were visually separated on two dice. Now students find a known part inside a larger set.
This helps students trust the known part: They come to see the part as a unit or addend rather than a set of discrete objects.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 10 © Great Minds PBC 145
10 5 35 10
Have the class chorally count on from 5 to find the total. Circle the 5 as the first part students counted on from. Then record the counting on sequence so students can see it as they voice it.
What is the total number of dots?
Ask students to share the parts and the total again. As they share, draw a number bond to represent the part–total relationship.
UDL: Representation
Recording helps students relate the parts in the dots image and the number bond to the parts in the counting sequence.
Consider explicitly asking students to make these connections.
• How do 6 and 7 in the count show this part (point to the 2) of the number bond and this part (point to the 2 dots) of the picture?
Use color to highlight the corresponding parts.
What number sentence could we write to show how we counted on?
5 + 2 = 7
1 ▸ M1 ▸ TB ▸ Lesson 10 EUREKA MATH2 New York Next Gen © Great Minds PBC 146
7
Count On from 5 and Record
Materials—S: Dot Cards removable
Students recognize a group of 5 within a set, count on to find the total, and record the corresponding number sentence. Ensure each student has a copy of the Dot Cards removable in a personal whiteboard. Be sure the red side of the whiteboard remains visible.
Prompt students to use the class recording from the previous segment to independently complete the first problem that shows the 5 and 2 dot card. Be sure students remember to circle 5 and record the count sequence, number bond, and number sentence.
Use the Whiteboard Exchange routine to review work and provide immediate feedback:
• Tell students to indicate they are ready by showing the red side of their boards. Say, “Red when ready!”
• When most are ready, prompt students to hold up their whiteboards to show you their work.
• Give quick individual feedback, such as Yes! or Check your count sequence. For each correction, return to validate the corrected work.
For the three remaining problems, have students find a part that makes 5 within the set, count on from it to find the total, and complete the number bond and number sentence. Use the Whiteboard Exchange routine to review and provide feedback after each problem.
Form pairs of students, and have partners follow the same process of counting and recording to complete the dot card problems in their student book. Consider using these strategies to increase engagement:
• Use a crayon or highlighter to circle 5.
• Count on from 5 out loud.
• Stand and find a new partner for each problem.
Differentiation: Challenge
Some students may know 5 + n facts from memory. Invite these students to express the part–total relationship by recording two different ways to write the number sentence. For example:
To extend the exploration of 5 as a group from which to count on, ask students to look around the room (as well as at themselves) to find things that come in fives, like their fingers. Students can make a list with drawings or words. What other groupings do they notice? Tables, cubbies, and table containers, for instance, may all be grouped in fours rather than fives. Invite students to consider how these repeated groups help with counting. Encourage them to choose a set of objects in the room and use the groupings to help them find the total of a set.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 10 © Great Minds PBC 147
EUREKA MATH New York Next Gen M1 TB Dot Cards © Great Minds PBC 73 7 2 5 8 3 5 5 4 9 5 6 5 + 2 = 7 5 + 3 = 8 5 + 4 = 9 5 + 1 = 6 © Great Minds PBC 75 EUREKA MATH New York Next Gen M1 TB Lesson 10 10 5 + 4 = 9 5 + 3 = 8 5 + 2 = 7 5 + 5 = 10 10 5 5 7 2 5 8 3 5 5 4 9 Name
5 + 2 = 7 and 2 + 5 = 7
Close the activity by sharing two or three student work samples. Pose questions such as the following to drive discussion:
• How does the dot picture match the number bond and number sentence?
• Why is counting on from 5 a helpful way to find the total?
Count On from 5 in Data Contexts
Students recognize 5 as a part within totals shown on graphs and tally charts.
We have groups of 5 on our hands. (Wiggle your fingers.) We also saw groups of 5 on the dot cards.
Prompt students to look carefully at the graph and tally chart and think–pair–share by using the following questions.
Where do you see groups of 5 in these pictures?
I see 5 gray boxes on the number paths.
I see groups of 5 in the tally marks. There are 4 lines and then 1 line across to make 5.
How can we use 5 to find the totals?
We can start at 5 and count on more squares or lines.
Invite students to count on from 5 to find the totals in the graph and in the chart. Have students compare their work with a partner’s. Circulate and observe counting on from 5 behaviors, and check for accuracy. Consider having students share their totals with the class or model counting on from 5, if needed.
Problem Set
Differentiate the set by selecting problems for students to independently finish within the timeframe. Problems are organized from simple to complex.
Differentiation: Support
Some students may need to circle 5 on the number path to help them isolate that group.
Promoting the Standards for Mathematical Practice
When students find 5 within a set and use it as a part from which to count on, they are looking for and making use of structure (MP7)
Ask the following questions to promote MP7:
• Why is it helpful to look for 5 in a set?
• Where do you see groups of 5? How do those groups help?
• How can counting on from 5 help you solve this problem?
1 ▸ M1 ▸ TB ▸ Lesson 10 EUREKA MATH2 New York Next Gen © Great Minds PBC 148
M1 TB Lesson 10 EUREKA MATH New York Next Gen © Great Minds PBC 76 LESSON Totals Baseball 8 9 Tennis 7 10
Land
Debrief 5 min
Objective: Count on from 5 within a set.
Is it easier to count all the objects in a set or to find a part of the set and count on? Why?
It’s easier to see a part and count on because then you don’t have to count all the dots.
It’s easier to see a part because it makes counting faster. Display the picture of 9 dots.
What parts do you see that you could use to count on?
Invite volunteers to share a variety of ideas, identifying where they see the parts. Have the class chorally count on by using a few different ideas, so they see that some parts are easier to see and use than others. Possible responses include:
There are 5 dots up and down on the right side. You could count on from 5: Fiiiive, 6, 7, 8, 9.
I see 2 dots across the top. You could count on from 2: Twoooo, 3, 4, 5, 6, 7, 8, 9.
There are 3 dots going across and down at the bottom. You could count on from 3: Threeee, 4, 5, 6, 7, 8, 9.
What makes 5 an easy group to see or know?
Lots of times you just know when there are 5. There are 5 fingers on our hands, and it’s easy to see 5 when there are 5 dots in a line. Some tools show 5 too. On a number path, there might be gray or white boxes to show 5. On dice or tally marks, 5 looks a special way.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 10 © Great Minds PBC 149
5 35 10
How does seeing 5 in a set help you find the total?
When you know a part, you can count on. You do not need to start at 1. 5 is a big part, so you don’t have to count on that many other dots. Lots of numbers have 5 as a part, so you can find it and use it a lot.
Summarize the lesson, and preview lesson 11 by telling students that some parts, like 5, are easier than others to see and count on from.
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
1 ▸ M1 ▸ TB ▸ Lesson 10 EUREKA MATH2 New York Next Gen © Great Minds PBC 150
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 10 © Great Minds PBC 151
© Great Minds PBC 77 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 10 10 1. Circle 5 and count on. Fill in the number bond Write the number sentence. 5 + 3 = 8 5 3 8 3 + 5 = 8 3 5 8 Name 1 ▸ M1 ▸ TB ▸ Lesson 10 EUREKA MATH2 New York Next Gen © Great Minds PBC 78 PROBLEM SET 2. Circle 5 and count on. Write a number sentence. 5 + 0 = 5 5 + 1 = 6 5 + 4 = 9 5 + 2 = 7
1 ▸ M1 ▸ TB ▸ Lesson 10 EUREKA MATH2 New York Next Gen 152 © Great Minds PBC EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 10 © Great Minds PBC 79 PROBLEM SET 3. Count on from 5. Write the totals. Totals Soccer 7 9 5 + 7 = 12 5 + 6 = 11 1 ▸ M1 ▸ TB ▸ Lesson 10 EUREKA MATH2 New York Next Gen © Great Minds PBC 80 PROBLEM SET 4. Count on from 5. Write the totals. Basketball 8 6
Lesson at a Glance
Students identify parts they know within a set and use them to count on. Through partner practice and discussion, students solidify the understanding that there are many ways to see parts within a set and to count on to find the total.
Key Questions
• How can we use number bonds to show how we find totals?
• How can we use number sentences to show how we find totals?
Achievement Descriptor
1.Mod1.AD2 Count on to find the total number of objects in a set and represent the total with an addition number sentence. (NY-1.OA.5)
© Great Minds PBC 11 LESSON 11
© Great Minds PBC 89 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 11 11 Circle a part. Fill in the number bond. Write the number sentence. 6 + 3 = 9 Sample: 6 3 9 Name
See any part in a set and count on.
Fluency 10 min
Launch 15 min
Learn 25 min
• Count On from a Part
• Problem Set
Land 10 min
• 20-bead rekenrek
• None
© Great Minds PBC 155 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 11
Agenda
Materials Teacher
Students
Lesson Preparation
None
Fluency
Counting the Math Way: Count On from 5
Students count on from 5 with their fingers to develop fluency with counting on.
Let’s count to 5 the math way.
Have students count the math way from 0 to 5. Show the math way on your own fingers, but do not count aloud.

Close it up!
Now let’s start at 5.
Show me 5.
(Students show 5 on their fingers the math way.)
Show me 7.
(Students put up their right thumb and right index finger to show 7.)
Close it up!
(Students close up fingers.)
Count on from 5 to 7 the math way.
Fiiiive, 6, 7
Close it up!
Continue with the following sequence: Show
Offer more practice counting on, always starting from 5.
1 ▸ M1 ▸ TB ▸ Lesson 11 EUREKA MATH2 New York Next Gen © Great Minds PBC 156
5 Show 6 Show 8 Show 5 Show 9 Show 5 Count on from 5 Count on from 5 Count on from 5
10 15 25 10 5 7 6
Counting on the Rekenrek Within 20 the Say Ten Way
Materials—T: Rekenrek
Students count the Say Ten way to maintain the skill from kindergarten.
Show the rekenrek with the side panel attached. Start with all beads behind the panel.
Let’s count on the rekenrek the Say Ten way.
Say how many beads there are as I slide them over.
Slide the top row of beads to the side.
10
Here’s 1 more.
Slide over 1 bead on the bottom row.
This is ten 1. How many beads?
Ten 1
Slide 1 more bead over on the bottom row.
How many beads?
Ten 2
Slide beads, one at a time, to the left or to the right in the following sequence as students count:
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 11 © Great Minds PBC 157
Ten 6 Ten 7 Ten 8 Ten 9 Ten 10 Ten 3 Ten 4 Ten 5 Ten 6 Ten 5 “Ten” Student View “Ten 1” Student View “Ten” Student View “Ten 1” Student View
Continue counting on the rekenrek the Say Ten way within 20. Change directions occasionally, emphasizing crossing over ten and ten 5 and where students hesitate or count inaccurately.
Ready, Set, Add
Students find a total and say addition number sentences to build addition fluency within 10.
Let’s play Ready, Set, Add.
Have students form pairs and stand facing each other.
Model the action: Make a fist, and shake it on each word as you say, “Ready, set, add.” At “add,” open your fist, and hold up any number of fingers.
Tell students that they will make the same motions. At “add,” they will show their partner any number of fingers. Consider doing a practice round with students.
Clarify the following directions:
• To show zero, show a closed fist at “add.”
• Try to use different numbers each time to surprise your partner.
Partners A and B: “6”
Partner A: “2 + 4 = 6”
Partner B: “4 + 2 = 6”
Each time partners show fingers, have them both say the total number of fingers. Then have each student say the addition sentence, starting with the number of fingers on their own hand. See the sample dialogue under the photograph.
Circulate as students play the game to ensure they are trying a variety of numbers within 5.

1 ▸ M1 ▸ TB ▸ Lesson 11 EUREKA MATH2 New York Next Gen © Great Minds PBC 158
Launch
Students share different ways to see parts within a total.
Gather students and tell them that you will quickly show a picture of apples. Prepare them to notice how many apples are in the picture. Flash the picture of 5 red apples for 2 or 3 seconds.
Show me with your fingers. How many apples?
How did you count them?
I just know there are 5.
I saw 2 and counted on 3 more.
I saw 3 and 2. I know 3 + 2 = 5.
Display the image of 10 green and red apples. Use the Math Chat routine to engage students in mathematical discourse. Give students silent think time to find the total number of apples. Have students give a signal to indicate they are ready.


How many apples? How did you know?
Have students discuss their thinking with a partner. Circulate and listen as they talk. Identify some students to share their thinking. Purposefully choose students who found the total by counting on from a part.
Invite the selected students to share their thinking with the whole group. Consider recording their strategies. Have students use the Talking Tool to help them share their thinking and engage with each other’s comments.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 11 © Great Minds PBC 159
10 15 25 10 I Can Share My Thinking My drawing shows . did it this way because . . think because . I Can Agree or Disagree agree because . disagree because . did it a different way. . . I Can Ask Questions How did you . ? Why did you . ? Can you explain ? I Can Say It Again heard you say . said Can you say it another way? Talking Tool © Great Minds PBC
Use the following sample discussion to guide your own discourse.
Class, how many apples are there?
10 apples
Nate, how do you know there are 10 apples?
I saw 5 red apples, and I counted on for the rest: Fiiiive, 6, 7, 8, 9, 10.
Who will show us how they counted on from a different part?
I saw 3 green apples together: Threeee, 4, 5, 6, 7, 8, 9, 10.
I saw 3 green and 3 red on the left. That is 6: Siiiix, 7, 8, 9, 10.
I heard Tam count on from 7. Tam, can you share where you see 7?
I see 5 red apples around the 2 green apples. 5 and 2 is 7.
Let’s all count on from 7 to find the total apples. (Point to the apples to track the count.)
Sevennnn, 8, 9, 10
We counted the apples in different ways, but the total is always 10.
Transition to the next segment by framing the work.
Let’s find totals by counting on from parts we know.
Teacher Note
Students are not expected to subitize 6, 7, 8, or 9. Focus on building confidence with the count on strategy by using any part the student can easily subitize.
Students may use more than two parts to find the total. For example:
• I see 3 and 1. That is 4. Fooouuur, 5, 6, 7, 8, 9, 10.
• I see threeee, 4, 5, 6. I see 3 more—siiiix, 7, 8, 9. I see 1 more. That is 10.
Some students may use three or four parts. For example:
1 ▸ M1 ▸ TB ▸ Lesson 11 EUREKA MATH2 New York Next Gen © Great Minds PBC 160
3 + 3 + 3 + 1 = 10 3 + 5 + 2 = 10
Learn
Count On from a Part
Students identify a part they can subitize and count on to find the total. Have students turn to the dot pictures in their student books.
Show the first problem (6-dot picture) and explain the following routine:
• Find and circle any part you know.
• Count on from that part to find the total number of dots.
• Write a number sentence that shows how you counted on.
• Fill in the number bond to show the parts and total.
Invite students to work independently on the first problem only. Then ask two or three students to share their thinking. Consider displaying student work as they share.
What part did you count on from? What did that sound like?
I saw 3 on top. I counted on: Threeee, 4, 5, 6. How do your number sentence and number bond show the way you counted on?
I saw 3 and circled it to make the first part. There are 3 dots left, so 3 is the other part. I counted on: Threeee, 4, 5, 6. The total is 6.
Class, show thumbs-up if you counted on from 3, too.
Who found a different part to count on from?
I see 5. I see 3 and 2. That makes 5, and 1 more is 6.
If students decompose the dot picture into more than two parts, support them in recording the corresponding number sentences and number bonds on a whiteboard.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 11 © Great Minds PBC 161
10 15 25 10 © Great Minds PBC 83 EUREKA MATH New York Next Gen M1 TB Lesson 11 11 3 + 3 = 6 5 + 1 = 6 4 + 3 = 7 2 + 5 = 7 3 3 6 6 5 4 3 7 7 5 2 Name © Great Minds PBC 84 LESSON ▸ M1 TB ▸ Lesson 11 EUREKA MATH New York Next Gen 5 + 3 = 8 4 + 4 = 8 6 + 3 = 9 5 + 4 = 9 5 4 9 6 3 9 4 4 8 5 3 8
Note
Teacher
Confirm the total number of dots. Then pair students, and have them complete the next 6-dot picture together.
Find two different ways to count the total of the next dot picture. You and your partner can each record one way that you find.
As partners finish, discuss their work.
Then invite partners to complete the remaining problems. Consider having students use one or more of the following strategies:
• Circle a part with a crayon or highlighter.
• Count on from the circled part in a whisper.
• Stand and find a new partner for each new total.
As partners finish, prompt a few students to share their work. Pose questions such as the following:
• How did this student count on to find the total?
• Why do you agree or disagree with this work?
• How could you do this problem differently?
• How does the dot picture match the number bond and number sentence?
Problem Set
Differentiate the set by selecting problems for students to finish independently within the timeframe. Problems are organized from simple to complex.
Teacher Note
Encourage students who work quickly to find other ways to break apart the given dot picture.
UDL: Engagement
As you listen to partners share thinking, provide students with feedback that emphasizes their application of strategies. For example, recognize when students explain that they saw a part they knew and counted on from that part, and validate the use of that strategy as contributing to their success.
Promoting the Standards for Mathematical Practice
When students analyze each other’s work to describe the strategy used and then explain why they agree or disagree with the strategy, they construct viable arguments and critique the work of others (MP3).
Ask the following questions to promote MP3:
• What questions can you ask about the strategy this student used?
• What don’t you understand about the student’s work?
1 ▸ M1 ▸ TB ▸ Lesson 11 EUREKA MATH2 New York Next Gen © Great Minds PBC 162
Land
Debrief 5 min
Objective: See any part in a set and count on.
Display the picture of fish. Ask students to count on from a part to find the total number of fish.
Have a few students share how they found the total number of fish. Some students may be able to subitize larger parts, such as 6, and count on to find the total. Others may see three or four separate parts and then need to count on more than once. For each student who shares, prompt the class to summarize the thinking by asking questions such as the following:
• What part did they count on from?
• What parts did they see?
• What number sentence could we write to match how they counted on?
Bring the class to agreement that there are 10 fish.
Reiterate that there are many valid ways to count on. Then have students reflect on their own preferences.
Which part is easiest for you to count on from? Why?
Students have answered variations on this question in previous lessons. Notice and point out any advancements, such as mentions of efficiency, in their responses.
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 11 © Great Minds PBC 163
15 25 10
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
1 ▸ M1 ▸ TB ▸ Lesson 11 EUREKA MATH2 New York Next Gen © Great Minds PBC 164
1 ▸ M1 ▸ TB ▸ Lesson 11 EUREKA MATH2 New York Next Gen © Great Minds PBC 86 PROBLEM SET 2. Circle a part. Fill in the number bond Write the number sentence. 3 4 7 3 + 4 = 7 7 2 9 7 + 2 = 9 7 + 3 = 10 7 3 10 Sample: © Great Minds PBC 85 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 11 11 1. Circle a part. Fill in the number bond Write the number sentence. Sample: 3 3 6 3 + 3 = 6 4 4 8 4 + 4 = 8 5 + 4 = 9 5 4 9 Name
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 11 165 © Great Minds PBC EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 11 © Great Minds PBC 87 PROBLEM SET
Count on two ways. Circle a part. Write the number sentence. Sample: 3 + 6 = 9 6 + 3 = 9
3.
12 © Great Minds PBC LESSON 12
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB © Great Minds PBC 95
1. Circle a part and count on. Fill in the number bond. 2 4 6 2. Circle a part and count on. Write the number sentence. 6 + 3 = 9 Sample: Name 1 ▸ M1 ▸ TB EUREKA MATH2 New York Next Gen © Great Minds PBC 96 TOPIC TICKET 3. Count on from 10. Write the number sentence. 5 10 + 5 = 15
Count on from 10 to find an unknown total.
B
Lesson at a Glance
Students count on from 10 to find a total when the objects in the second part are hidden or not visible. They use their fingers to keep track of the hidden part, and they record their count as a number bond and a number sentence. Partners practice these skills by playing a game. This lesson introduces the term unknown.
Key Question
• Why are fingers helpful tools for counting on when we can’t see a part?
Achievement Descriptors
1.Mod1.AD2 Count on to find the total number of objects in a set and represent the total with an addition number sentence. (NY-1.OA.5)
1.Mod1.AD7 Count on from 10 to find totals between 11 and 19. (NY-1.NBT.2, NY-1.NBT.2b)
Agenda
Fluency 10 min
Launch 10 min
Learn 30 min
• Missing Totals
• 10-Card Count
• Problem Set
Land 10 min
Materials
Teacher
• 20-bead rekenrek
Students
• Hide Zero® cards
• Number Bond removable (in the student book)
Lesson Preparation
The Number Bond removables must be torn out of student books and placed in personal whiteboards. Consider whether to prepare these materials in advance, to have students assemble them during the lesson, or to use the ones prepared in lesson 9.
© Great Minds PBC 167 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 12
Fluency
Counting on the Rekenrek Within 20 the Say Ten Way
Materials—T: Rekenrek
Students count the Say Ten way to maintain the skill from kindergarten.
Show the rekenrek with the side panel attached. Start with all beads behind the panel.
Let’s count on the rekenrek the Say Ten way.
Say how many beads there are as I slide them over.
Slide the top row of beads to the side.
10
Here’s 1 more.
Slide over 1 bead on the bottom row.
This is ten 1. How many beads?
Ten 1
Slide over 1 more bead on the bottom row.
How many beads?
Ten 2
Slide beads, one at a time, to the left or to the right in the following sequence as students count:
1 ▸ M1 ▸ TB ▸ Lesson 12 EUREKA MATH2 New York Next Gen © Great Minds PBC 168
Ten 8 Ten 9 Ten 10 Ten 9 Ten 10 Ten 3 Ten 4 Ten 5 Ten 6 Ten 7 10 10 30 10 “Ten” Student View “Ten” Student View “Ten 1” Student View “Ten 1” Student View
Continue counting on the rekenrek the Say Ten way within 20. Change directions occasionally, emphasizing crossing over ten and ten 5 and where students hesitate or count inaccurately.
Counting the Math Way: Count On from 5
Students count on from 5 with their fingers to develop fluency with counting on.
Let’s count to 5 the math way.
Have students count the math way from 0 to 5. Show the math way on your own fingers, but do not count aloud.

Close it up!
Now let’s start at 5.
Show me 5.
(Students show 5 on their fingers the math way.)
Show me 7.
(Students put up their right thumb and right index finger to show 7.)
Close it up!
(Students close up fingers.)
Count on from 5 to 7 the math way.
Fiiiive, 6, 7
Close it up!
Continue with the following sequence:
Offer more practice counting on, always starting from 5.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 12 © Great Minds PBC 169
Show 5 Show 8 Show 9 Show 5 Show 10 Show 5 Count on from 5 Count on from 5 Count on from 5
5 7 6
Ready, Set, Add
Students find a total and say addition sentences to build addition fluency within 10.
Let’s play Ready, Set, Add.
Have students form pairs and stand facing each other.
Model the action: Make a fist, and shake it on each word as you say, “Ready, set, add.” At “add,” open your fist, and hold up any number of fingers.
Tell students that they will make the same motion. At “add” they will show their partner any number of fingers. Consider doing a practice round with students.
Clarify the following directions:
• To show zero, show a closed fist at “add.”
• Try to use different numbers each time to surprise your partner.
Each time partners show fingers, have them both say the total number of fingers. Then have each student say the addition sentence, starting with the number of fingers on their own hand. See the sample dialogue under the photograph.

Circulate as students play the game to ensure they are trying a variety of numbers within 5.
Launch
Students share strategies for starting at 10 to count on and find the total.
Use the Math Chat routine to engage students in discussion. Gather the class and display the picture of 10 butterflies. Ask students to find the total number of butterflies. Allow a moment of silent think time.
Partners A and B: “6”
Partner A: “2 + 4 = 6”
Partner B: “4 + 2 = 6”
1 ▸ M1 ▸ TB ▸ Lesson 12 EUREKA MATH2 New York Next Gen © Great Minds PBC 170
10 10 30 10
How many butterflies do you see? How do you know?
10. I saw 5 blue butterflies, and I counted on.
10. I saw 5 blue and 5 orange. 5 and 5 make 10. Use the following prompt to have students think–pair–share.
Imagine 4 more butterflies came. What would the total be then?
As pairs discuss, identify two or three students to share their thinking with the class. Purposefully choose students whose thinking allows for making connections between strategies.
Invite the selected students to tell or show the class how they found the total. Guide students to express their ideas by using the sentence stems on the Talking Tool. Record and display strategies as they are shared and use the prompts below to facilitate a class discussion about them.
Count
• What was your strategy to find the total?
• Why did you choose that strategy?
• Did anyone do it a different way?
Display the picture of 14 butterflies, and ask the class to confirm that 14 is the total number of butterflies. Write 10 + 4 = 14, if not already recorded.
























Differentiation: Support
To prepare for topic C, students count on a second part where the objects are hidden.
Transition to the next segment by framing the work.
Today, we will count on from 10 when we cannot see all the objects.
Most students will be able to track the count for the second part with their fingers. If students are not yet able to track with fingers, allow them to use cubes or a drawing. They should use their representation to count on: Tennnn, 11, 12, 13, 14.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 12 © Great Minds PBC 171
I Can Share My Thinking My drawing shows . I did it this way because . I think because . I Can Agree or Disagree I agree because I disagree because . I did it a different way. I Can Ask Questions How did you ? Why did you ? Can you explain . ? Can Say It Again I heard you say said . . Can you say it another way? Talking Tool © Great Minds PBC 10 10 + 4 = 14 11 12 13 14
On: Fingers Know Number Facts
Learn
Missing Totals
Materials—S: Number Bond removable
Students count on from 10 to find a total and record the part–total relationship.
Gather students and display the picture of the number bond.
How many dots do you see?
Yes, one part is 10. What is the other part?
So, what is the missing total? How do you know?
14. I started at 10 and used my fingers to count on 4 more. I know there are 14 because 10 plus 4 is 14.
Display the next number bond to show 4 dots as the other part so that students can confirm their answer.
Ensure that each student has a copy of the Number Bond removable in a personal whiteboard. Make sure the red side of the whiteboard remains visible.
Have students record the appropriate numbers in the number bond and write the corresponding number sentence for the number bond. Use the Whiteboard Exchange routine to review work and provide feedback:
• Tell students to turn their boards over so the red side is up. When they are ready, say, “Red when ready!”
• When most are ready, tell students to hold up their whiteboards to show you their work. Give quick individual feedback, such as Yes! or Check your total. For each correction, return to validate the corrected work.
Differentiation: Support
If students count all starting at 1, help them notice that there are 10 dots they can see. Prompt them to count on by asking:
• What comes after 10?
• Can you start at 10 and count on by using your fingers (or by tapping)?
If students have trouble counting on because they cannot see the second set of dots, prompt them to use their fingers to show that part and count on.
• How many more do we need to count on?
• How many fingers do you need to count on?
Promoting the Standards for Mathematical Practice
When students understand that because the given part is always 10, they will not be able to count all on their fingers, but must instead count on from 10, keeping track of the other part on their fingers, they make use of structure (MP7).
Ask the following questions to promote MP7:
• Why is it helpful to say “10” without showing it on your fingers?
• How do you know how many fingers to use when finding the total?
1 ▸ M1 ▸ TB ▸ Lesson 12 EUREKA MATH2 New York Next Gen © Great Minds PBC 172
10
4
10 10 30 10
4 14
Display a complete recording and ask students to interpret the representations.
What did we need to figure out: a part or the total?
The total
Yes, in this problem the total was unknown. When we say unknown, we mean that we need to figure out that number.
What number tells the total in our number bond and number sentence? 14
Let’s all draw a box around 14 in the number bond and in the number sentence to help us remember that the total was unknown.
Repeat the procedure with three more number bond sets.
• Give students a moment to count on from 10 to find the total.
• Share a student strategy.
• Reveal the dots or fingers in both parts to confirm the total.
• Use the Whiteboard Exchange routine with the number bond.
Teacher Note
Unknown refers to a number or quantity in a problem that is not yet known.
In module 1, the unknown is always the total. In module 2, students find unknown parts as well as unknown differences.
As students make math drawings to represent word problems, consider encouraging students to use a question mark to show the unknown.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 12 © Great Minds PBC 173
EUREKA MATH M1 TB Lesson 12 Number Bond Copyright Great Minds PBC 93 10 4 14 10 + 4 = 14 15 5 7 17 10 9 10 19
Use the following questions to help students summarize their learning.
Why did we count on from 10 to find the total?
We know the first part is 10.
It is faster to start at 10.
How can we keep track of our count when we can’t see the dots or fingers in the second part?
You can use fingers. For each number you count, you put out 1 finger.
What did we need to figure out, or what was unknown, in each problem?
The total
10-Card Count
Materials—S: Hide Zero cards
Students practice counting on from 10 to find a total by working in pairs.
Gather students to demonstrate and give directions for the 10-Card Count game. Partners use one Number Bond inside a personal whiteboard. Distribute one pack of cards to each pair. Then share the following procedure for playing the game:
• Partners find the 10-dot card and set it in front of them. They put the other cards in a pile.
• Partner A takes a numeral card from the pile and sets it next to the 10-dot card.
• Partner A counts on from 10 to find the total of the two cards.
• Partner B writes a number bond and number sentence on the personal whiteboard to match the count.
• For the next turn, partners switch roles. They leave the 10-dot card in place and draw a new numeral card from the pile.
UDL: Action & Expression
Consider posting student-friendly directions for the 10-Card Count game for students to refer to as they play.
1 ▸ M1 ▸ TB ▸ Lesson 12 EUREKA MATH2 New York Next Gen © Great Minds PBC 174
5 EUREKA MATH M1 TB Lesson 12 Number Bond Copyright © Great Minds PBC 93 10 5 15 10 + 5 = 15
Consider pairing students with similar ability to allow for differentiating the activity. Allow students to play for 7 to 8 minutes, leaving them time to clean up their materials before the next segment.
Problem Set
Differentiate the set by selecting problems for students to finish independently within the timeframe. Problems are organized from simple to complex.
Differentiation: Support
• Support students who count all by having them use dots to represent both addends.
Differentiation: Challenge
• If students add without counting on, transition them to using numerals for both addends.
5 10
• Challenge students who are fluent with 10+ facts by having them count on from 20, 30, or 40 instead of 10. 20 5
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 12 © Great Minds PBC 175
Land
Debrief 5 min
Objective: Count on from 10 to find an unknown total. Gather students and display the picture of the person counting on from 10. Initiate a class discussion by using the following prompts.
How do you see Adrien counting on?
He is counting on from 10 to 14. I see 10 and then 11, 12, 13, 14.
10 is the first part, and he is using his fingers to keep track of the second part.
Think about finding the total for this problem. What is different about counting on and counting all?
You can count on faster because you don’t have to say all the numbers. With counting all you might run out of fingers. With counting on you only need fingers for the second part.
How is counting on helpful?
You can use parts to help you count faster. You can still use your fingers to help you count bigger numbers. If time allows, advance student thinking by asking the following question.
Would it be possible to use the count on strategy to add 10 and 11? Why?
Topic Ticket 5+ min
Provide 5–10 minutes for students to complete the Topic Ticket. It is possible to gather formative data even if some students do not complete every problem.
1 ▸ M1 ▸ TB ▸ Lesson 12 EUREKA MATH2 New York Next Gen © Great Minds PBC 176
10 30 10 10 11 12 13 14
Sample Solutions

Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.

EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 12 177 © Great Minds PBC
© Great Minds PBC 93 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TB ▸ Lesson 12 12 1. Count on from 10. Fill in the number bond Name 12 13 3 17 7 10 5 15 5 1 ▸ M1 ▸ TB ▸ Lesson 12 EUREKA MATH2 New York Next Gen © Great Minds PBC 94 PROBLEM SET 2. Count on from 10. Write the number sentence. 2 10 + 2 = 12 10 8 10 + 8 = 18 9 10 10 + 9 = 19 10 10 + 10 = 20 6 10 + 6 = 16
Topic C Count On to Add
Topic C advances the Level 2 strategy of counting on to find a total. Students move from counting on to find how many objects to counting on to add the numerals—or addends—in an expression. Students will find sums within 20, allowing them to apply counting on as a strategy for most addition facts and practice critical 10 + n facts.
The strategy of counting on to add efficiently is key to adding within 20. Counting on to add involves building these skills:
• Seeing one part, or addend, as a unit from which to count on
• Holding that addend in mind
• Tracking on fingers to count on the second part, or addend
Many students find it difficult to perform all three of these skills at once. At first, students hold actual objects to represent the first addend. Students may also use elongated pronunciation of the first addend—“threeee”—as they transition to holding the first addend in their minds. Some students may simply state the first addend—“three.”
By using fingers to count on the second addend—“4, 5, 6, 7, 8, 9”—students can track the count and know when to stop. The last finger raised also gives visual confirmation that the last number they say is the total.

Students become more efficient with counting on through work with the commutative property, which tells us that addends can be arranged in any order and the total stays the same. Through exploring part–part–total relationships (e.g., 6 and 3 make 9), students trust that 3 + 6 has the same total as, or is equal to, 6 + 3. Students practice finding totals by counting on from different addends and confirm the efficiency of counting on from the larger addend. With this knowledge in place, students use the commutative property to think of expressions like 3 + 6 as 6 + 3, so that the larger addend comes first.

© Great Minds PBC 178
Fiiiive, 6, 7, 8, 9 3 + 6 = 9 Threeee, 4, 5, 6, 7, 8, 9 3 + 6 = 9 6 + 3 6, 7, 8, 9
Students also use repeated reasoning to increase their efficiency with finding totals. They notice patterns with facts involving 0 and 1 to form a conjecture, or a statement they think is true. Then students try their idea on similar problems to validate their reasoning.
Topic D continues to develop the Level 2 strategy of counting on, and it introduces students to the Level 3 strategy of making an easier problem. Module 2 will advance counting on to find an unknown part or difference.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC © Great Minds PBC 179
Progression of Lessons
Lesson 13
Count on from an addend in add to with result unknown situations.

Lesson 14
Count on to find the total of an addition expression.
Lesson 15
Use the commutative property to count on from the larger addend.
I imagine holding 5 in my hand. Then I track on my fingers to count on 4 more: Fiiiive, 6, 7, 8, 9.




I don’t have to show or count the first part. If I know 4 frogs are in the pond, I can just count on: Fooouuur, 5, 6, 7, 8, 9.
1 + 6 and 6 + 1 have the same total. I can add in any order. It is helpful, or more efficient, to start with the larger part.
© Great Minds PBC 180 1 ▸ M1 ▸ TC EUREKA MATH2 New York Next Gen
4
6
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
Lesson 16
Use the commutative property to find larger totals.
Lesson 17
Add 0 and 1 to any number.
Teacher Note
I notice that when I add 1 to a number, I get the next number.
Note that lesson 17 introduces telling time to the hour as an extension of counting on and adding 1. Mastery is not expected in this lesson, as the skill of telling time benefits from distributed practice and classroom application.



It is more efficient to start with the larger part. So I can think of 4 + 8 as 8 + 4. I can use a number path or my fingers to count on past 10.
I notice that when I add 0 to a number, I get the same number.
Using these true statements helps me add 0 or 1 to any number!
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC 181 © Great Minds PBC
4 + 8 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
5 + 1 = 6 1 2 3 4 5 6 7 8 9 10
5 + 0 = 5 1 2 3 4 5 6 7 8 9 10
Count on from an addend in add to with result unknown situations.
Lesson at a Glance
Students solve add to with result unknown problems by using strategies of their choice. After solving independently, the class compares work and makes connections among representations and strategies. This lesson supports students as they transition from counting on from a part of a set to counting on from an addend.
Key Question
• What are some ways to represent counting on by using tools and numbers?
Achievement Descriptor
1.Mod1.AD2 Count on to find the total number of objects in a set and represent the total with an addition number sentence. (NY-1.OA.5)
© Great Minds PBC 13 LESSON 13
© Great Minds PBC 99 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 13 Listen to the story. Count on to find the total. 5 frogs are in the pond. 4 more frogs hop into the pond. How many frogs are in the pond now? 5 9
13 Name
frogs
Agenda
Fluency 10 min
Launch 5 min
Learn 35 min
• Represent and Solve: Rock Problem
• Share, Compare, and Connect
• Problem Set
Land 10 min
Materials Teacher
• None Students
• Hide Zero® cards (1 set per student pair)
Lesson Preparation
• Remove the 10 and the 20 from the Hide Zero cards for each pair of students. Keep cards available for lessons 14 and 15.
• Have a variety of math tools, such as two-color counters, number paths, and cubes, available for students to self-select.
© Great Minds PBC 183 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 13
Fluency
Happy Counting by Ones Within 10
Students count forward and backward by ones to prepare for the use of addition and subtraction strategies.
Invite students to participate in Happy Counting.
When I give this signal, count up. (Demonstrate.) When I give this signal, count down. (Demonstrate.)
The first number you say is 1. Ready?
Signal up or down accordingly for each count.
Now the first number you say is 3. Ready?
Signal up or down accordingly for each count.
Counting On with Numerals and 5-Groups
Materials—S: Hide Zero cards
Students practice counting on to prepare for noting the efficiency of starting with the larger addend beginning in lesson 15.
Have students form pairs. Distribute a set of cards to each pair and have them play according to the following rules. Consider doing a practice round with students.
Teacher Note
Choose signals you are comfortable with, such as thumbs-up and thumbs-down or two fingers pointing up and down. Show your signal and gesture up or down with each count. Gestures should be clear and crisp so that students count in unison. Avoid saying the numbers with the class; instead, listen for errors and hesitations.
1 ▸ M1 ▸ TC ▸ Lesson 13 EUREKA MATH2 New York Next Gen © Great Minds PBC 184
1 2 3 2 3 2 3 4 5 4 5
3 4 5 6 5 6 5 6 7 8 9 10 9 10
10 5 35 10
• Each partner draws a card.
• Partner A puts the card numeral side up.
• Partner B puts the card dot side up.
• Both partners count on the number of dots, starting with the numeral.
• Both partners flip their cards and count on from the other numeral.
• Draw two new cards and play again.
Circulate as students play the game and provide support as needed.
Launch
Students watch a video and make sense of an add to with result unknown situation.
Gather the class and set the context for the video. Briefly explain that a child named Hope collects rocks. She takes a walk to find new rocks for her collection.
As you watch, notice how many rocks are in Hope’s collection before she takes a walk. Play the first segment, which reveals 7 rocks in Hope’s collection to start.
Pause the video, and ask:
How many rocks are in Hope’s collection?
Continue to play the video to the end. The final segment shows Hope adding 3 more rocks to her collection. When the video finishes, have students think–pair–share to retell Hope’s story. Prompt students to share with the class by using the following questions. Record their summary of the story.
UDL: Engagement
If presenting a video is not an option or if students would benefit from a tactile experience, consider having them act out the story.
Partner students and provide each pair with 7 cubes and a cup or an opaque bag.
Have partner A represent Hope’s rock collection before the walk by counting out 7 cubes and placing them out of sight in a bag or under the overturned cup.
Have partner B go for a “walk” to visit the teacher. Give partner B 3 cubes to take back.
Partners add the 3 new rocks to their collection and talk about how many rocks they have in all.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 13 © Great Minds PBC 185
7
2 “Twoooo, 3, 4, 5, 6, 7, 8, 9” 10 5 35 10
“Sevennnn,
8, 9”
Show with your fingers: How many rocks does Hope have in her box before her walk?
(Shows 7 fingers)
Record the following sentence and read it aloud: Hope has 7 rocks.
Show with your fingers: How many rocks does Hope put in her box? (Shows 3 fingers)
Record and read aloud: She adds 3 more rocks.
What math questions could we ask about this story?
Does Hope have more rocks before or after her walk?
How many rocks does she have now?
Record a question that requires finding the total, and read it aloud. Then transition to the next segment by framing the work.
Today, we will solve problems like the one about Hope’s rocks and share our strategies.
Learn
Represent and Solve: Rock Problem
Students represent and solve an add to with result unknown problem.
Display the word problem:
Hope has 7 rocks.
She adds 3 more rocks.
How many rocks does she have now?
Prompt students to think–pair–share about how to represent and solve the problem. Consider charting their ideas.
Differentiation: Challenge
What if students know that 7 + 3 = 10?
Consider that even if students know the sum from memory, it may still be useful for them to practice representing a word problem situation and recording at least one solution strategy. If students need a challenge, however, change the problem to 7 + 7, 11 + 3, or 17 + 3.
Teacher Note
Word problem types such as add to with result unknown often feel more accessible than others because they involve action that students can visualize. The add to action gently suggests which operation or strategies might be helpful.
In this case, the action in the problem matches the action of counting on. Although not all students will count on to solve, the problem also encourages that strategy by using numbers (addends) to show parts rather than parts of sets, as in earlier lessons.
1 ▸ M1 ▸ TC ▸ Lesson 13 EUREKA MATH2 New York Next Gen © Great Minds PBC 186
10 5 35 10
How could we figure out how many rocks Hope has in her box now?
We could show rocks by drawing circles. Then we could count the circles. We could use a number path and count on from 7. We could start with 7 and count on 3 more with our fingers.
Have students work independently to represent and solve the problem. Provide materials, such as two-color counters, cubes, number paths, and personal whiteboards, for student use. Encourage students to self-select their tools.
No matter how they choose to represent and solve, encourage students to record their strategy (as shown in the strategy chart). For example, if students use cubes to directly model the situation, ask them to draw a picture of how they counted or arranged their cubes. Encourage students to label with numbers as they draw.
Circulate and observe student strategies. Select two or three students to share in the next segment. Look for work samples that help advance the lesson’s objective of counting on from a known part where the objects are not visible.
Differentiation: Support
The strategies that students select progress over time. They often begin by directly modeling the situation with concrete materials before moving to more abstract counting strategies that focus on the count rather than the physical manipulation of objects.
Support students who have difficulty recording their counting strategies pictorially by encouraging them to list the numbers they said in the counting sequence.

EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 13 © Great Minds PBC 187
Count On: Drawing Count On: Number Path Count On: Fingers Number Facts 7 1 2 3 4 5 6 7 8 9 10 7 8 9 10 7 8 9 10 7 8 9 10 7 + 3 = 10
Share, Compare, and Connect
Students discuss and reason about representations and solution strategies.
Gather the class and invite the selected students to share their work. Purposely order shared student work so it shows a progression of thinking (see the sample progression in the strategy chart). If possible, the first strategy should be accessible to all students.
As each student shares, ask questions to elicit their thinking, clarify the strategy, and make connections between different strategies. Encourage students to use the Talking Tool to increase engagement and promote student-to-student discourse. Students might use, in particular, “My drawing shows … ” and “I did it a different way ….”
Use the following sample discussions to guide the debrief of student work.
Count On: Drawing (Ming’s Way)
Class, how did Ming show the problem?
He drew each rock.
Ming circled a group of 7 because that’s how many rocks Hope had at first.
What are some things Ming did to make his drawing clear?
Ming labeled the group of 7.
He drew the 7 rocks like a dot card. He drew 5 on top and 2 on the bottom. He circled a part to make it easy to see the two parts in the problem.
Ming, how did you count to find the total?
I knew there were 7 rocks, so I started there and counted on: Sevennnn, 8, 9, 10. Have the class confirm that the total number of rocks is 10. Then ask students to show thumbs-up if they also solved by counting on starting from 7. Invite the class to practice counting on from 7 all together. Model by using fingers to track the second part.
Teacher Note
The sample student work shows common responses. Look for similar work from your students and encourage authentic classroom conversations about the key concepts.
If your students do not produce similar work, choose one or two pieces of their work to share, and highlight how each shows movement toward the goal of this lesson. Then select one sample work from the lesson that would best advance student thinking. Consider presenting the work by saying, “This is how another student solved the problem. What do you think this student did?”
Promoting the Standards for Mathematical Practice
When students choose how they will represent problems, they use appropriate tools strategically (MP5).
Ask the following questions to promote MP5:
• Why did you choose this tool to represent, or show, the problem?
• How was this tool helpful to you?
• What other tool might you use? Why?
1 ▸ M1 ▸ TC ▸ Lesson 13 EUREKA MATH2 New York Next Gen © Great Minds PBC 188
7
Count: Fingers (Kai’s Way)
Kai, how did you find the total?
I held 7 in my brain. Then I counted on 3 more with my fingers: Sevennnn, 8, 9, 10.
Draw a number bond to show the part–total relationship. Have students think–pair–share about the following question.
(Gesture to the number bond.) How do the numbers in this number bond show Kai’s count?

7 is the first part. That’s the part Kai held in her brain.
3 is the other part, so Kai counted 3 more on her fingers.
10 is the total. When Kai finished counting 7 and 3, the answer was 10.
Help students relate the number bond to the word problem.
Think about Hope’s rocks. In the word problem, what does the number 7 tell us about?
7 is how many rocks Hope has before her walk.
What does the number 3 tell us about?
3 tells us the number of rocks Hope finds on her walk.
What does the number 10 tell us about?
10 tells us how many rocks are in Hope’s collection now.
Return to the word problem text, and reread the question: How many rocks does she have now?
Let’s say a sentence to answer the question, like this: She has 10 rocks now. Say it with me.
She has 10 rocks now.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 13 © Great Minds PBC 189
7 8 9 10 7 8 9 10
Number Facts (Mel’s Way)
7 + 3 = 10
Let’s look at another way to find the total. How does this work match the problem?
It shows two parts, 7 and 3.
The number sentence puts 7 and 3 together to make 10.
Then have students think–pair–share about the following question.
What is the same about all the strategies we studied today?
They all started with 7.
They all showed the two parts of the problem. They all showed 10 as the total.
Problem Set
Differentiate the set by selecting problems for students to finish independently within the timeframe. Problems are organized from simple to complex. Problem 1 stories are intended to be read aloud. Customize the directions as needed. Problem 2 stories may also be read aloud.
Land
Debrief 5 min
Objective: Count on from an addend in add to with result unknown situations.
Display the student work example. Explain that this shows a student’s strategy.
1 ▸ M1 ▸ TC ▸ Lesson 13 EUREKA MATH2 New York Next Gen © Great Minds PBC 190
10 5 35 10 4 3 7 4 5 6 7
Take a moment to study this student’s work. She showed the same problem in two ways.
Turn and talk to a partner: What are the parts, and what is the total?
The parts are 4 and 3. The total is 7.
Where do you see the parts and total in her work?
I see them in the number bond.
She circled 4 to show the first part, and then she wrote three more numbers. The last number is the total.
Where do you see counting on in her work?
In the line of numbers, I can see that she started at 4 and counted on: 5, 6, 7.
Display the picture of the bus and share the following word problem.
Listen to the problem she solved: 4 students are on the bus. 3 students get on the bus. How many students are on the bus now?
This student solved the problem by counting on. Turn and talk to a partner: Why was counting on a helpful choice?
Because she didn’t have to start counting at 1.
The problem already tells you the parts: 4 and 3. You just have to pick a part to start.
You can start at 4, the number of students already on the bus, and then count on 3 fingers to find the total.
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 13 © Great Minds PBC 191
4
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
Name
1. Listen to the story.
Count on to find the total.
4 bees are in the hive.
2 more bees fly into the hive.
How many bees are in the hive now?
4
6 bees
6 squirrels are in the tree.
3 more squirrels run up the tree.
How many squirrels are in the tree now?
9 squirrels 6
4 frogs are in the pond.
5 more frogs hop into the pond.
How many frogs are in the pond now?
9 frogs
4
2. Count on to find the total.
Show how you know.
7 people are on the bus.
3 people get on the bus.
How many people are on the bus now?
10 people 7
10 people are on the bus.
5 people get on the bus.
How many people are on the bus now?
15 people 10
1 ▸ M1 ▸ TC ▸ Lesson 13 EUREKA MATH2 New York Next Gen 192 © Great Minds PBC
© Great Minds PBC 97 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 13
13
1 ▸ M1 ▸ TC ▸ Lesson 13 EUREKA MATH2 New York Next Gen © Great Minds PBC 98 PROBLEM SET
Count on to find the total of an addition expression.
Lesson at a Glance
Students count on to find the total of two addends. They practice “holding” the first addend and using their fingers to track as they count on the second addend. Then they relate counting on with fingers to counting on with hops on the number path. This lesson introduces the term expression.
Key Question
• Why are fingers helpful tools for counting on when we can’t see the parts?
Achievement Descriptor
1.Mod1.AD3 Add within 20 by using strategies such as counting on or by creating an equivalent but easier problem. (NY-1.OA.5, NY-1.OA.6a)
© Great Minds PBC 14 LESSON 14
© Great Minds PBC 103 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 14 Add. Count on with your fingers or the number path. 1 2 3 4 5 6 7 8 9 10 5 + 3 = 8 2 + 8 = 10 14 Name
Agenda
Fluency 10 min
Launch 10 min
Learn 30 min
• Track by using Fingers
• Count On with Fingers and the Number Path
• Problem Set
Land 10 min
Materials
Teacher
• Centimeter cubes (10)
Students
• Hide Zero® cards (1 set per student pair)
• Centimeter cubes (10)
• Centimeter number path
Lesson Preparation
Hide Zero cards should still have the 10 and 20 cards removed, as in lesson 13.
© Great Minds PBC 195 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 14
Fluency
Happy Counting by Ones Within 10
Students count forward and backward by ones to prepare for the use of addition and subtraction strategies.
Invite students to participate in Happy Counting. When I give this signal, count up. (Demonstrate.) When I give this signal, count down. (Demonstrate.)
The first number you say is 3. Ready? Signal up or down accordingly for each count.
Offer more practice counting by ones within 10. Change directions occasionally, emphasizing crossing over 5 and where students hesitate or count inaccurately.
Counting On with Numerals and 5-Groups
Materials—S: Hide Zero cards
Students practice counting on to prepare for noting the efficiency of starting with the larger addend, beginning in lesson 15. Have students form pairs. Distribute a set of cards to each pair and have them play according to the following rules. Consider doing a practice round with students.
• Each partner draws a card.
• Partner A puts the card numeral side up.
• Partner B puts the card dot side up.
1 ▸ M1 ▸ TC ▸ Lesson 14 EUREKA MATH2 New York Next Gen © Great Minds PBC 196
3 4 5 6 5 6 5 6 7 8 9 10 9 10 9 10
10 10 30 10 7
“Sevennnn, 8, 9”
• Both partners count on the number of dots, starting with the numeral.
• Both partners flip their cards and count on from the other numeral.
• Draw two new cards and play again. Circulate as students play the game and provide support as needed.
Green Light, Red Light
Students count from a given number to prepare for the use of addition and subtraction strategies.
Display the green and red dots with the numbers 1 and 3.
On my signal, start counting with the green light number. (Point to the 1 written below the green dot.)
Stop at the red light number. (Point to the 3 written below the red dot.)
Look at the numbers.
Think. Ready? Green light!
1, 2, 3
Repeat the process with the following sequence:
If more movement is desired, consider having students run in place, hop, or engage in another physical exercise while counting.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 14 © Great Minds PBC 197
3 1 green red 5 8 green red 10 8 green red 3 5 green red 2 “Twoooo, 3, 4, 5, 6, 7, 8, 9” 1 3
red
green
Teacher Note
Launch
Students share strategies for finding the total when the second part is not shown.
Gather the class and display the picture of 5 basketballs. Use the Math Chat routine to lead a discussion. Encourage the use of finger work, which is a focus in this lesson, and avoid offering number paths, cubes, or whiteboards.

Ask the following question:
How many basketballs do you see?
Have students share how they know the total is 5.
Suppose someone put 4 more basketballs on the rack. How many basketballs would there be?
Allow silent think time to find the total. Have students signal to indicate they are finished.
Pair students to discuss their thinking. Identify a few students to share their strategies, purposely selecting those who chose ways that involve using fingers to count on from 5.
Invite the selected students to share with the whole group. Use the following sample dialogue to facilitate a class discussion about their ideas.
Felipe, how did you find the total?
I put up 5 fingers and 4 fingers. I counted on: Fiiiive, 6, 7, 8, 9.

Violet, you used your fingers a different way. Show us how.
I knew there were 5 already, so I only put up 4 fingers.
1 ▸ M1 ▸ TC ▸ Lesson 14 EUREKA MATH2 New York Next Gen © Great Minds PBC 198
10 10 30 10 5 6 7 8 9
Fiiiive (makes a fist), 6, 7, 8, 9 (raises one finger for each number)





They used their hands differently. Why did they both get 9? They both counted the parts, 5 and 4.
Most of us used our fingers instead of the picture to find the total. Why didn’t we use the picture?
The picture only shows 5 basketballs, not the 4 more that someone puts on the rack.
We had to picture the 4 more basketballs in our minds. Using our fingers helped us keep track of those basketballs as we added them to the 5 on the rack.
Display the picture of all 9 basketballs to help students confirm the total. Point to the basketballs as students chorally count on from 5. Then ask students to share the corresponding number bond and number sentence as you record.
Transition to the next segment by framing the work. Today, let’s use our fingers to count on.

EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 14 © Great Minds PBC 199
6
Learn
Track by using Fingers
Materials—T/S: Centimeter cubes
Students find the total of an expression by counting on the second addend with their fingers.

Distribute 10 centimeter cubes to each student. Write the expression 4 + 3.
Instead of counting on to find a total with a picture, I will show you expressions like this. (Point.) It says 4 plus 3. An addition expression is like a number sentence because it shows the parts to add. An expression is different from a number sentence because it does not have an equal sign. We will use our fingers to add the parts to find the total.
Let’s start with the first part of the expression: 4. Put 4 cubes in one hand. (Demonstrate.)
Suppose we get 3 more cubes. How many cubes will we have then? Find the total. Watch how students track to add (mentally, raising fingers, head bobbing, tapping, etc.).
Some of you added 3 by using your fingers to keep track of how many you added.
Let’s all count on the second part in our expression, 3, with our fingers.
Language Support
Show students an expression and a number sentence:
Expression: 4 + 5
Number Sentence: 4 + 5 = 9
Ask them to notice what is the same and what is different about them.
Same: parts, 4 and 5
Different: = sign and the total, 9
Explain that a number sentence always has an equal sign or comparison symbol, and an expression does not.
Note that a subtraction expression, such as 10 – 7, has a total and a part with no equal sign.
1 ▸ M1 ▸ TC ▸ Lesson 14 EUREKA MATH2 New York Next Gen © Great Minds PBC 200
10 10 30 10
Guide students to hold out their fists with the 4 cubes and say, “Fooouuur.” Then have them count 3 more on their other hand, raising a finger for each number: “Five, six, seven.”
Why did we count on from 4?
It is the first part. I have 4 in my hand.
Why did we put up 3 fingers?
The 3 fingers helped us keep track of adding 3 more.
What is 4 + 3?
7
Have students open their hands and use cubes to count on and confirm the total.
Repeat the process with 6 + 3, 7 + 2, 9 + 3, and 10 + 5 without cubes to build confidence with
• trusting the first addend to start the count and • tracking with fingers to count on the second addend.
When students are ready, have them make a fist to represent the first part (instead of holding cubes). Students may use either hand. Many will transition to making the fist with the same hand they use to count on.
Collect the cubes and close the activity by helping students summarize the usefulness of counting on.
How does it help to say the first part when you count on?
If you say the first part, then you know which number comes next to keep counting on.
How are fingers helpful for keeping track of the second number?
Fingers give you a way to see the part if there is no picture. You stop on the answer.
Teacher Note
Students do not need to count on in a certain way. Students should extend one finger for each count in the sequence, but encourage them to do what feels right and makes sense to them. Students may use either hand and begin with their thumb, pinkie, or index finger.



Students may say the first part (without making or referring to a fist). Allow students to do what makes sense for them as they “hold” the first part and begin counting on with their fingers.
Fooouuur
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 14 © Great Minds PBC 201
Count On with Fingers and the Number Path
Materials—S: Centimeter number path
Students compare by using fingers and number paths to count on. Write 5 + 3. Prompt students to count on to find the total.
Did we count on to find a part or the total?
The total
What is the total of 5 and 3?
8

5
5 plus 3 is the same as, or equals, 8.
Add an equal sign to the expression, and record the total, 5 + 3 = 8. Draw a box around the total.
Display a number path, and distribute one to each student.
Model using the number path to count on 3 more than 5 by circling 5 and drawing 3 hops to 8. Record + 3 above the 3 hops or jumps.
UDL: Representation
The number sentence, hand count, and number path provide students with multiple formats to represent counting on.
Teacher Note
When hopping on the number path to add or subtract, circling the start number helps clarify which number to count on from. Later it will help clarify whether they are counting on to add or counting back to subtract.
Students may use their finger to “hop” or record their hops when the number path is provided on paper or put under a page protector. They should show their thinking in any way that makes sense to them.


Differentiation: Challenge
Have students use their fingers to practice hopping to count on by using their own number paths. Then ask students to think–pair–share by asking the following question.
How is counting on by using fingers the same as counting on by using the number path?
You start with the same part.
You count on the same number. With counting on, you put up fingers, and with the number path, you hop.

Many students may be ready to add larger numbers when tracking on fingers or using the number path. Use expressions such as these:
15 + 3, 12 + 5, 17 + 4, 11 + 6
Invite students to confirm the total in more than one way with tools like number paths, the rekenrek, or drawings. Some students will begin to discover the relationship between expressions, such as 5 + 3 and 15 + 3 or 2 + 5 and 12 + 5.
1 ▸ M1 ▸ TC ▸ Lesson 14 EUREKA MATH2 New York Next Gen © Great Minds PBC 202
1 2 3 4 5 6 7 8 9 10
Write 9 + 3.
How could we count on to find the total of 9 and 3?
We could make a fist for 9 and then count on 3 more. We could circle 9 on the number path and make hops. Consider having a student lead the class in counting on by using fingers. Model counting on and recording on the number path.
Differentiation: Support
If students are not able to track the second imagined addend, try showing it as a dot card.
Then have students
• track on their fingers as they count dots,
• point to the dots to count on, or
• tap on their desks for each dot they count.
Have students use their fingers to follow along on their number paths. Add an equal sign to the expression and record the total.
If time permits, continue with 11 + 4.
Problem Set
Differentiate the set by selecting problems for students to finish independently within the timeframe. Problems are organized from simple to complex. The directions may be read aloud.
Land
Debrief 5 min
Objective: Count on to find the total of an addition expression.
Gather students with their Problem Sets. Have partners discuss a selected problem. To support student-to-student conversation, pair students, and assign one student to be partner A and the other partner B. Prompt partner A to use the “I can share my thinking”
Students may draw 3 dots under the second addend.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 14 © Great Minds PBC 203
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
10 10 30 10 Can Share My Thinking My drawing shows did it this way because . think because . . Can Agree or Disagree agree because disagree because . did it a different way. . I Can Ask Questions How did you . ? Why did you ? Can you explain . ? I Can Say It Again heard you say said . Can you say it another way? Talking Tool © Great Minds PBC
section of the Talking Tool, and prompt partner B to use another section, such as “I can ask questions,” to respond.
Sakon: My strategy was to count on my fingers.
Val: How did you get 7?
Sakon: Fooouuuur, 5, 6, 7. (Holds up fist and then fingers.)
Val: I did it a different way. I used the number path. I started at 4, and I landed on 7 too. Then use any combination of the following questions to help students summarize their counting on understandings.
How can we count on when we cannot see all the parts?
We can use our fist for the first part and count on with our fingers for the second part.
Why is it helpful to track the second number with your fingers?
We will know when to stop and get the answer.
If time allows, pique curiosity by providing a glimpse into the next lesson with the following questions.
Can you count on starting at 6 to find the total of 2 and 6? Why?
Yes, you can add parts in any order.
In this expression, 6 is the second part. Why would we start counting on from that part?
Because it’s easy to count on 2 more. We only need one hand.
Because 6 is the bigger number.
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
Promoting the Standards for Mathematical Practice
As students communicate their strategies, respond to their partner’s thinking, and ask questions, they construct viable arguments and critique the reasoning of others (MP3).
If students need support, prompt them with the following questions:
• Tell (or show) your partner about your strategy. Why did you choose this strategy?
• What questions can you ask your partner about this strategy?
Teacher Note
Developing student-to-student dialogue takes practice and patience. Consider these helpful tips:
• Role-play with a student or guide two students to role-play as the class watches.
• Provide short, easy-to-read scripts.
• Instead of responding to students directly, consider cuing other students to agree or disagree, ask a question, or repeat an idea in their own words.
1 ▸ M1 ▸ TC ▸ Lesson 14 EUREKA MATH2 New York Next Gen © Great Minds PBC 204
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 14 205 © Great Minds PBC
© Great Minds PBC 101 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 14 1. Add. Count on with your fingers 14 Name 5 + 2 = 7 6 + 2 = 8 3 + 3 = 6 2 + 5 = 7 4 + 2 = 6 5 + 3 = 8 3 + 4 = 7 4 + 4 = 8 1 ▸ M1 ▸ TC ▸ Lesson 14 EUREKA MATH2 New York Next Gen © Great Minds PBC 102 PROBLEM SET 2. Add. Count on with the number path. 1 2 3 4 5 6 7 8 9 1 0 3 + 6 = 9 1 2 3 4 5 6 7 8 9 1 0 6 + 4 = 10 1 2 3 4 5 6 7 8 9 1 0 1 1 12 1 3 1 4 1 5 1 6 17 1 8 19 20 6 + 5 = 11 1 2 3 4 5 6 7 8 9 1 0 1 1 12 1 3 1 4 1 5 1 6 17 1 8 19 20 9 + 4 = 13
Use the commutative property to count on from the larger addend.
Lesson at a Glance
Students explore commutativity as they consider what statements are true. They notice that expressions with the same total are equal because the parts are the same and can be added in any order. With guidance, students use the number path and fingers to count on from either addend. The class discusses how it is more efficient to count on from the larger part. This lesson introduces the academic verb convince.
Key Question
• Why can we add numbers in any order?
Achievement Descriptor
1.Mod1.AD1 Apply the commutative property of addition as a strategy to add. (NY-1.OA.3)
© Great Minds PBC 15 LESSON 15
© Great Minds PBC 109 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 15 Circle the larger part. Count on. Fill in the number bond 1 2 3 4 5 6 7 8 9 1 0 15 Name 3 + 6 = 9 6 + 3 = 9 6 3 9
Agenda
Fluency 10 min
Launch 5 min
Learn 35 min
• Commutative Property
• Adding Efficiently
• Roll a Total
• Problem Set
Land 10 min
Materials Teacher
• Unifix® Cubes (5) Students
• Hide Zero® cards (1 set per student pair)
• Centimeter number path
• Roll a Total (in the student book)
• Number cubes (2 per student pair)
Lesson Preparation
• Prepare a stick of 2 yellow and 3 red Unifix Cubes.
• Roll a Total must be torn out of student books and placed in personal whiteboards. Consider whether to prepare these materials in advance or to have students assemble them during the lesson.
© Great Minds PBC 207 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 15
Fluency
Happy Counting by Ones Within 15
Students count forward and backward by ones to prepare for the use of addition and subtraction strategies.
Invite students to participate in Happy Counting. When I give this signal, count up. (Demonstrate.) When I give this signal, count down. (Demonstrate.)
The first number you say is 8. Ready? Signal up or down accordingly for each count.
Offer more practice counting by ones within 15. Change directions occasionally, emphasizing crossing over 10 and where students hesitate or count inaccurately.
Counting On with Numerals and 5-Groups
Materials—S: Hide Zero cards
Students practice counting on to prepare for noting the efficiency of starting with the larger addend, beginning in lesson 15. Have students form pairs. Distribute a set of cards to each pair and have them play according to the following rules. Consider doing a practice round with students.
• Each partner draws a card.
• Partner A puts the card numeral side up.
• Partner B puts the card dot side up.
Teacher Note
Remember to listen to student responses and be mindful of errors and hesitation and lack of full-class participation. If needed, adjust the tempo or sequence of numbers.
1 ▸ M1 ▸ TC ▸ Lesson 15 EUREKA MATH2 New York Next Gen © Great Minds PBC 208
8 9 10 11 10 11 12 13 14 15 14 15 14 15
10 5 35 10
7
“Sevennnn, 8, 9”
• Both partners count on the number of dots, starting with the numeral.
• Both partners flip their cards and count on from the other numeral.
• Draw two new cards and play again. Circulate as students play the game and provide support as needed.
Green Light, Red Light
Students count from a given number to prepare for the use of addition and subtraction strategies.
Display the green and red dots with the numbers 2 and 4.
On my signal, start counting with the green light number. (Point to the 2 written below the green dot.)
Stop at the red light number. (Point to the 4 written below the red dot.)
Look at the numbers.
Think. Ready? Green light!
2, 3, 4
Repeat the process with the following sequence:
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 15 © Great Minds PBC 209
8 6 green red 6 9 green red 4 1 green red 4 7 green red 2 “Twoooo, 3, 4, 5, 6, 7, 8, 9” 2 4 green red
Launch
Materials—T: Unifix Cubes
Students confirm that two parts can be put together in any order and result in the same total.
Hold up a stick of 5 Unifix Cubes: 2 yellow and 3 red as shown.



How many cubes are in each part?
2 and 3
What is the total?
5
Draw a blank number bond and invite students to complete it with you.
Help me fill in a number bond to show the parts and total in this stick.
Prompt students to say what each number refers to as you write it in the bond (i.e., yellow cubes, red cubes, total cubes).
Slowly turn the stick of cubes to show 3 red and 2 yellow.
Is the total the same now? Why?
Yes. The total is still 5 because you didn’t add more cubes, and you didn’t take any cubes away.
Draw and complete a second number bond next to the first one. Have students help by calling out each referent as you write the numbers.
You said the total is still 5. But now which part comes first?
The 3 red cubes
Have students think–pair–share to compare the number bonds.
The total is the same.
UDL: Representation
Consider providing an example of the commutative property in another format. Show students the dot side of a Hide Zero card in the traditional orientation, and then turn it upside down. Have students discuss whether the total changed to confirm that the order of the parts does not change the total.
Have students write the corresponding number bonds and number sentences on whiteboards.
1 ▸ M1 ▸ TC ▸ Lesson 15 EUREKA MATH2 New York Next Gen © Great Minds PBC 210
10 5 35 10
The parts are the same: 3 and 2. The parts are in different orders. Transition to the next segment by framing the work. Today, we’re going to try adding parts in different orders to see whether we get the same total and whether one way is easier.
Learn
Commutative Property
Materials—S: Centimeter number path
Students determine that counting on from the larger addend is more efficient.
Have students ready their whiteboards and tell them they will listen to a math story. Students will decide whether Wes, the brother in the story, is right. They may draw or make recordings as they listen.
Wes has 6 crackers. Mom gives Wes 1 more cracker. Val has 1 cracker. Mom gives Val 6 more crackers. Wes says, “That’s not fair! Val has more!”
Invite students to think–pair–share about the following question.
Is what Wes said true? Does Val have more? Why do you think so?
Display the expressions that represent each child’s crackers, and have students retell the important details of the story by using the numbers.
Have students use fingers or whiteboards to confirm whether Wes is right.
Does Val have more crackers than Wes?
No, they both have 7 crackers.
Wes
Val
Teacher Note
Although the number bond is written here according to the part the students used to count on, from left to right, the order in which students write each part of the number bond does not matter.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 15 © Great Minds PBC 211
10 5 35 10 6 + 1
1 + 6
How do you know that 6 + 1 is the same as 1 + 6?
I know because they both total 7.
Record the true number sentences 6 + 1 = 7 and 1 + 6 = 7.
What do you notice about these number sentences?
The total is the same for both.
The parts are in different orders.
Write 6 + 1 = 1 + 6.
Is this number sentence true? How do you know?
Yes, it is true because 6 + 1 is the same as 7, and 1 + 6 is the same as 7.
Yes. They’re the same numbers on each side of the equal sign, just switched around.
When the total on both sides of the equal sign is the same, we can say the number sentence is true.
Transition to the next segment by framing the work.
Now that we know 6 + 1 and 1 + 6 are equal, let’s decide which way of adding is more helpful.
Adding Efficiently
Materials—S: Centimeter number path
Students determine that counting on from the larger addend is more efficient.
Distribute a number path to each student. Have them use it to model counting on to find the total for each expression: 6 + 1 and 1 + 6. They should use their fingers to point and hop. Invite volunteers to show the strategy for each problem. Record the hops as shown starting with 1 + 6, followed by 6 + 1.
Confirm that the total is the same no matter which part students use to start counting from. Guide students to notice the more efficient approach by having them think–pair–share about the following question.
1 ▸ M1 ▸ TC ▸ Lesson 15 EUREKA MATH2 New York Next Gen © Great Minds PBC 212
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
Is it easier to count on starting with 1 or 6? Why?
It’s easier to start at 6 because you only have to hop once.
Since we know that 6 + 1 and 1 + 6 have the same total, when you’re asked to find 1 + 6, you can think of it as 6 + 1 in your head and then count on: Siiiix, 7.
We can say that starting with 6 is more efficient. An efficient strategy is the most helpful way to solve a problem correctly. An efficient strategy is one you know and understand. It is less work for you than another strategy. You may learn new, more efficient strategies that you do not know yet.
Display 2 + 7, and prompt students to consider how to add most efficiently.
Would it be more efficient to start counting on from 2 or from 7? Why?
Starting with 7 would be more efficient because you only count on 2 more.
If you start with 2, then you have to count on 7 more fingers.


7 is the second part. How do we know that we can start with 7?
2 + 7 has the same total as 7 + 2. You can add in any order.
Circle 7. Then prompt students to find the total by counting on from 7 by using fingers or number paths. Come to consensus on the solution and record the total.
So, to find 2 + 7, what other expression can I think about?
7 + 2
2 + 7
Teacher Note
If students choose not to count on starting with the larger number, they will need both hands to track.
“Twoooo, 3, 4, 5, 6, 7, 8, 9”
2 + 7
Yes, when we circle the 7 and count on (Sevennnn, 8, 9), we are thinking of this expression as 7 + 2 to count on more efficiently.
As time allows, continue with other expressions, such as 3 + 6, 8 + 2, 3 + 7, and 4 + 5. Consider partnering students: Have one partner count on by using a number path and the other partner count on by using fingers.
Promoting the Standards for Mathematical Practice
Students look for and make use of structure (MP7) when they choose to find the total of an expression by counting on from the larger addend.
Ask the following questions to promote MP7:
• How can you use 2 + 7 to help you find 7 + 2?
• Why is it helpful to count on from the larger part?
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 15 © Great Minds PBC 213
Roll a Total
Materials—S: Number cubes, Roll a Total

Students play a familiar game to count on from the larger part. Pair students. Ensure that each pair has a copy of Roll a Total in a personal whiteboard and two number cubes. Review the game directions:
• Partner A rolls the number cubes, chooses the larger addend, and counts on from that part to find the total. Partner A should consider which part is more efficient to start with as they choose it.
• Partner B looks for the total on the recording sheet and draws an X on top of the total. If there is already an X on the total from another turn, partner B draws a tally mark in the space next to the total instead.
• Partners switch jobs for the next turn.
As students play, ask them how they chose what number cube to count on from. If needed, help students remember that it is more efficient to count on from the larger addend.

After 6 or 7 minutes, collect the number cubes. Consider having pairs share whether they rolled all the totals and how many tally marks they had for the total that was rolled most often.
Problem Set
Differentiate the set by selecting problems for students to finish independently within the timeframe. Problems are organized from simple to complex. The directions may be read aloud.
Help students recognize the word larger in print. Invite students to underline it as you read it aloud.
Differentiation: Challenge
After 4–5 minutes of play, ask students what they noticed as they played. They may notice that it is easy to cross off the totals in the middle and that they reoccur frequently, but the very small and very large totals occur less frequently.
Differentiation: Support
All students should have access to solving the problem to create rich discussion. If needed, choose an expression card with a total less than 10.
1 ▸ M1 ▸ TC ▸ Lesson 15 EUREKA MATH2 New York Next Gen © Great Minds PBC 214
EUREKA MATH2 New York Next Gen M1 ▸ TC ▸ Lesson 15 ▸ Roll Total © Great Minds PBC 105 Roll a Total 2 3 4 5 6 7 8 9 10 11 12
Land
Debrief 5 min
Objective: Use the commutative property to count on from the larger addend. Show an expression card, such as 5 + 7. Invite students to turn and talk about how they would find the total.
We are going to play a game called Convince Me. When you convince someone, you explain or show why your idea is best. First, I am going to try to convince you!
I would start counting on from 5 because 5 comes first, and I have 5 on one hand. Do you agree, or do you think there is a better way? Convince me!
I disagree. It is more efficient to count on from the larger number.
Why is starting with 7 more efficient?
7 is the larger part, so you will count on fewer numbers. You will use fewer fingers.
It will be fewer hops on the number path.
Can someone show me how we would use fewer fingers if we start with 7?
Sevennnn, 8, 9, 10, 11, 12. (Puts up 5 fingers, one at a time.)
Fiiiive, 6, 7, 8, 9, 10, 11, 12. (Puts up 7 fingers, one at a time.)
You convinced me! We should think about 5 + 7 as 7 + 5 and start with 7.
Why can we change the order of the parts?
Changing the order of the parts doesn’t change the total; they will be the same.
Yes, the total of 5 and 7 is the same as, or equal to, the total of 7 and 5. To be more efficient, we can think of the parts of the addition expression in either order.
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
Language Support
This is the first use of the term convince. Support the term in future instances by revoicing it as a way to explain or show why an idea is best. If students need more support, consider sharing a common use of the word in their lives:
“You may convince someone to play a game you like.”
Teacher Note
Some students may share and use other strategies, such as the following:
• I agree because 5 and 5 is 10 and 2 more is 12.
• I have a different way: I can take 1 from 7 and give it to the 5 to make doubles: 6 + 6. That is 12.
It is important to honor all ideas. Efficiency is relative; it reflects what makes sense and is helpful to the student.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 15 © Great Minds PBC 215
5 35 10
5 + 7
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
Show how you know. Sample: It is true. You can add in any order.
1 ▸ M1 ▸ TC ▸ Lesson 15 EUREKA MATH2 New York Next Gen 216 © Great Minds PBC
© Great Minds PBC 107 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 15 15 Name 1. Circle the larger part. Count on. Fill in the number bond. 1 2 3 4 5 6 7 8 9 1 0 5 2 7 4 2 6 5 + 2 = 7 2 + 5 = 7 2 + 4 = 6 4 + 2 = 6 1 2 3 4 5 6 7 8 9 1 0 1 ▸ M1 ▸ TC ▸ Lesson 15 EUREKA MATH2 New York Next Gen © Great Minds PBC 108 PROBLEM SET 2. Circle the larger part. Count on. 10 + 3 = 13 2 + 9 = 11
this number
2 + 14 = 14 + 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
3. Is
sentence true?
Use the commutative property to find larger totals.
Lesson at a Glance
Students continue to count on from the larger addend, this time with totals greater than 10. With partners, students count on from both addends by using various tools. The class discusses strategies and confirms that it is easier to count on from the larger part because there are fewer numbers to count.
Key Question
• Is it easier to count on from the larger or smaller part? Why?
Achievement Descriptor
1.Mod1.AD1 Apply the commutative property of addition as a strategy to add. (NY-1.OA.3)
© Great Minds PBC 16 LESSON 16
© Great Minds PBC 113 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 16 Circle the larger part. Use your fingers or the number path to count on. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 8 + 3 = 11 11 = 3 + 8
Name
16
Agenda
Fluency 10 min
Launch 10 min
Learn 30 min
• Use the Commutative Property to Count on Efficiently
• Count On to Find an Unknown Total
• Problem Set
Land 10 min
Materials Teacher
• None Students
• Two-color counters (10 per student pair)
• Cup (1 per student pair)
Lesson Preparation
• Place 10 two-color counters in a cup for each student pair. At the end of the lesson, save them for lesson 17.
• Write the following sentence frames for display. Save them for lesson 17 as well. is greater than . is less than . is equal to .
• Have math tools, such as cubes or number paths, available for students to self-select.
© Great Minds PBC 219 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 16
Fluency
Shake Those Disks: Compare
Materials—S: Two-color counters, cup
Students compare different color counters to maintain work with comparing numbers from kindergarten.
Have students form pairs. Distribute cups of two-color counters.
Display the following sentence frames:
Have students play according to the following rules. Consider doing a practice round with students.
• Partner A shakes the cup and spills all the counters.
• Partners work together to organize the spilled counters into two groups by color.
• Partners count the number of counters in each color group.
• Partner A uses the sentence frames to make a comparison statement about the counters.
• Partners continue playing, switching roles each time.
Two ways to organize 6 red and 4 yellow counters.
Circulate as students play. Encourage students to organize their counters so that they are easier to count and compare.
1 ▸ M1 ▸ TC ▸ Lesson 16 EUREKA MATH2 New York Next Gen © Great Minds PBC 220
is
is less than . is equal to .
greater than .
10 10 30 10
Finger Flash: Doubles
Students represent a doubles fact on their fingers and say a number sentence to prepare for using doubles facts as a strategy for addition beginning in topic D.
Let’s use our fingers to show doubles facts.
Face the students, and direct them to copy you. Raise both pinkie fingers.
That’s 2. How many?
2
Raise both pinkie and ring fingers. Students do the same.

How many?
4
Continue by using your fingers to model doubles for 6, 8, and 10.
Let’s use our fingers to show doubles again. This time we will say the number sentence. Ready?
Raise both pinkie fingers. Students do the same.
This shows 1 + 1 = 2. What is the number sentence?
1 + 1 = 2
Raise both pinkie and ring fingers while students do the same.
What is the number sentence?
2 + 2 = 4
Continue modeling doubles with fingers and stating the facts as a class.




EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 16 © Great Minds PBC 221
Launch
Students count on two ways to confirm that parts can be added in any order and the total remains the same.
Display the puppy image and use the Math Chat routine to engage students in discussion.








































How many puppies are in the picture? How do you know?
Allow think time. Have students show a silent signal to indicate when they are ready.
Invite a few students to share their counting strategies and confirm the total with the class. See sample student strategies:
Count all:
1, 2, 3, 4, 5, 6, 7, 8
Doubles: 4 + 4 = 8
Count by twos: 2, 4, 6, 8
Count on:
Fooouuur, 5, 6, 7, 8
1 ▸ M1 ▸ TC ▸ Lesson 16 EUREKA MATH2 New York Next Gen © Great Minds PBC 222
10 10 30 10
Display the equation 8 + 3 = .
What if 3 more puppies join this group? What would be the total? How do you know?
Allow think time. Have students show a silent signal to indicate when they are ready. Then pair students to discuss their thinking. Circulate and listen. Invite a student who counted on from 8 and found the total to share with the class.
Ask students to think–pair–share about the following prompt.
Suppose there are 3 puppies at first. Then 8 more puppies join them. Could you still count on from 8 to find how many puppies? Why?
Listen for and revoice reasoning that draws on prior knowledge, such as the following:
• 8 + 3 is the same as, or equal to, 3 + 8.
• We can think of 3 + 8 as 8 + 3 to count on from 8 because they have the same total.
• Numbers can be added in any order.
• It is more efficient to count on from 8 because is it larger.
Have students count on from 3 to confirm that 3 + 8 has the same total as 8 + 3.
Transition to the next segment by framing the work.
Today, we are going to add efficiently by counting on from the larger part.
Teacher Note
All the totals in this lesson are greater than 10. Therefore, students cannot count all with their fingers. This provides practice with holding the first addend in mind and tracking the second addend with fingers.

EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 16 © Great Minds PBC 223
8
9 10 11
Learn
Use the Commutative Property to Count On Efficiently
Partners count on from both addends and decide which way is more efficient.
Pair students and have them ready their personal whiteboards. Students may also choose to use cubes or number paths during Learn. Have students use a variation of the Numbered Heads routine. Assign each partner a number: 1 or 2. Have students write their numbers in the corner of their whiteboards to help them remember.
Display the equation 4 + 8 = .
Partner 1, count on from 4 to find the total.
Partner 2, count on from 8 to find the total.
Provide quiet time for students to independently find the total. As needed, allow them to self-select tools, such as drawings, number paths, cubes, or fingers.
Have students stand and show their partners how they counted. Set expectations for productive group work:
Lean in, look at your partner, and listen carefully. Partner 1, go first. Partner 2, go second.
Have partners decide on the more efficient way to count on to find the total.
Now it’s time to put your heads together and decide: Is it more efficient to count on from 4 or from 8?
On your whiteboard, show how you and your partner chose to find the total. Be ready to share your thinking with the class.
Allow up to 2 minutes for pairs to select and record their thinking. Tell students that either partner could be called on to share, so they should both be prepared.
Before calling on students to share, return to the displayed equation, and agree on the total. Record it.
Promoting the Standards for Mathematical Practice
Students explain to a partner how they found the total, ask questions to make sure they understand their partner’s work, and work together to choose the more efficient way. As they do this, they construct viable arguments and critique the reasoning of others (MP3).
Ask the following questions to promote MP3:
• How did you find the total? Tell your partner.
• What questions can you ask your partner about how they found the total?
• Which way do you think is more efficient? Why?
1 ▸ M1 ▸ TC ▸ Lesson 16 EUREKA MATH2 New York Next Gen © Great Minds PBC 224
10 10 30 10
Decide whether to call on partner 1 or partner 2, and then select a few partners to share their pair’s idea about the most efficient number to count on from and the tool they used to find the total. See sample student responses.
As students share, ask the class to indicate whether their group had the same ideas by showing thumbs-up.
Why did so many of you count on from 8?
It’s more efficient to start with the bigger part because you only have to count on 4 more, not 8 more. Display both expressions.
4 + 8 8 + 4
Remember, we call these expressions because they do not have an equal sign. When we count on from 8 to find 4 + 8, what other expression are we thinking of to help us?
8 + 4
How do we know we can use 8 + 4 to help us figure out 4 + 8?
4 + 8 and 8 + 4 have the same total.
We can add parts in any order.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 16 © Great Minds PBC 225
4
Counting on from 4 with drawing Counting on from 8 with fingers Counting on from 8 with number path 1 2 3 4 5 1 1 12 13 4 1 5 6 7 8 9 10 16 17 1 8 19 20
8 9 10 11 12
Reiterate that 4 + 8 is the same as, or equal to, 8 + 4 because both expressions have a total of 12. Illustrate the point by circling 8 in each expression and drawing lines to record the totals as shown.
Teacher Note
Display the two number paths. Ask students to direct you as you record counting on, first from 4 and then from 8.
Fluency with addition facts that have a total greater than 10 is not expected in grade 1. Presenting problems with larger addends encourages students to hold the larger addend in their mind and count on because they can’t directly model the problem on their fingers.
If students “just know” the 10 + n facts from their kindergarten experience, encourage them to use counting on as a way to check their thinking or prove their solution.
Help students recall that there are fewer numbers to count on when you start from the larger part and that counting on from either addend produces the same total. Circle 12 on both number paths to reinforce that the total is the same.
Count On to Find an Unknown Total
Partners determine the more efficient way to count on as they find an unknown total that precedes the equal sign.
Display the equation = 2 + 9.
How is this problem different from 4 + 8 = ?
The parts are 2 and 9, not 8 and 4.
The line for the answer is first.
The equal sign comes before the two parts and the plus sign.
1 ▸ M1 ▸ TC ▸ Lesson 16 EUREKA MATH2 New York Next Gen © Great Minds PBC 226
4 + 8 8 + 4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
This time the unknown, or what we need to figure out, comes before the equal sign. What is the unknown: a part or the total?
The total
The parts and the total switched to different sides of the equal sign. We need to figure out the total for both problems, and we can figure it out the same way for each one.
Repeat the Numbered Heads routine variation:
• Both partners find the unknown total independently, this time choosing an addend to count on from.
• Partners discuss and agree on the most efficient addend to count on from.
• Decide whether to call on partner 1 or partner 2, and then call on those partners to share their thinking.
• Confirm as a class that it is easier to count on from the larger addend. If needed, display the two number paths again, have students guide counting on from both addends, and compare the number of jumps or hops.
• Record the total in the equation. Help students read the equation: 11 equals, or is the same as, 2 plus 9.
As time allows, repeat the Numbered Heads variation with any of the following equations:
Problem Set
Differentiate the set by selecting problems for students to finish independently within the timeframe. Problems are organized from simple to complex. The directions may be read aloud.
Teacher Note
In this lesson, students are asked to consider equations that include a blank for the unknown, such as 3 + 2 = . Because this equation uses a symbol for the unknown (the blank), it cannot be referred to as a number sentence. The term equation will not be formally introduced until module 2; the term problem is used with students until then. When an equation includes a total, such as in 3 + 2 = 5, it may still be referred to as a number sentence.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 16 © Great Minds PBC 227
• 5 + 7 = • = 3 + 11 • = 14 + 6
Land
Debrief 5 min
Objective: Use the commutative property to find larger totals.
Write 3 + 9 = .
Display the example of counting on from 3. Explain that this shows how one student found the total.
What do you notice about this student’s work?
She counted on.
She started with the smaller part instead of the larger one. She got the wrong answer. She only counted on 8 more, instead of 9.
If no one recognizes the error, say:
Count on from 3 yourself to make sure she found the correct total. Have students think–pair–share about the following question.
What would you show or tell this student?
I would show her how to count on by tracking 9 on her fingers. I would tell her to start from the bigger part, so she only has to count on 3 more.
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
UDL: Engagement
Emphasize that sustaining effort and persistence is a trait of mathematicians.
Consider expanding the conversation to discuss how we learn from mistakes and that we all make mistakes.
1 ▸ M1 ▸ TC ▸ Lesson 16 EUREKA MATH2 New York Next Gen © Great Minds PBC 228
3 4 5 6 7 8 9 10 11
10 30 10
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 16 229 © Great Minds PBC
© Great Minds PBC 111 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 16 1. Circle the larger part. Count on with your fingers or the number path 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 10 + 4 = 14 4 + 10 = 14 9 + 4 = 13 4 + 9 = 13 8 + 5 = 13 5 + 8 = 13 13 = 6 + 7 13 = 7 + 6 16 Name 1 ▸ M1 ▸ TC ▸ Lesson 16 EUREKA MATH2 New York Next Gen © Great Minds PBC 112 PROBLEM SET 2. Count on with your fingers or the number path 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 17 = 15 + 2 10 + 5 = 15 5 + 15 = 20 18 + 2 = 20 19 = 4 + 15 20 = 3 + 17 14 = 8 + 6 6 + 8 = 14
© Great Minds PBC 17 LESSON 17 Add 0 and 1 to any number. EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC © Great Minds PBC 117 1. Add. 4 + 0 = 4 7 + 1 = 8 2. Circle the larger part. Count on. Fill in the number bond. 3 + 5 = 8 5 + 3 = 8 8 5 3 C Name 1 ▸ M1 ▸ TC EUREKA MATH2 New York Next Gen © Great Minds PBC 118 TOPIC TICKET 3. Circle a part. Count on. 9 = 2 + 7 8 = 5 + 3 9 + 4 = 13 16 = 6 + 10
Lesson at a Glance
Students apply their counting skills to telling time to the hour by using an analog clock. They notice patterns in sequences of +1 and +0 problems. They generalize to make conjectures about the total for each type of problem. They test their ideas on different problems to see whether their conjectures hold true. Students are introduced to the terms hour hand, minute hand, and o’clock.
Key Questions
• What happens when we add 1 to any number?
• What happens when we add 0 to any number?
Achievement Descriptors
1.Mod1.AD3 Add within 20 by using strategies such as counting on or by creating an equivalent but easier problem. (NY-1.OA.5, NY-1.OA.6a)
1.Mod1.AD4 Add fluently within 10. (NY-1.OA.6b)
Agenda
Fluency 10 min
Launch 10 min
Learn 30 min
• Add 1 to Any Number
• Add 0 to Any Number
• Problem Set
Land 10 min
Materials Teacher
• Demonstration clock Students
• Two-color counters (10 per student pair)
• Cup (1 per student pair)
• Sticky notes (2)
Lesson Preparation
Have sentence frames from lesson 16 ready for display:
• is greater than .
• is less than .
• is equal to .
© Great Minds PBC 231 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 17
Fluency
Shake Those Disks: Compare
Materials—S: Two-color counters, cup
Students compare different color counters to maintain work with comparing numbers from kindergarten.
Have students form pairs. Distribute cups of two-color counters.
Display the sentence frames:
• is greater than .
• is less than .
• is equal to .
Have students play according to the following rules. Consider doing a practice round with students to refresh them on the procedure for the game.
• Partner A shakes the cup and spills all counters.
• Partners work together to organize the spilled counters into two groups by color.
• Partners count the number of counters in each color group.
• Partner A uses the sentence frames to make a comparison statement about the counters.
• Partners continue playing, switching roles each time.
Two ways to organize 6 red and 4 yellow counters
Circulate as students play. Encourage students to organize their counters so that they are easier to count and compare.
1 ▸ M1 ▸ TC ▸ Lesson 17 EUREKA MATH2 New York Next Gen © Great Minds PBC 232
10 10 30 10
Finger Flash: Doubles




Students represent a doubles fact on their fingers and say a number sentence to prepare for using doubles facts as a strategy for addition beginning in topic D.
Let’s use our fingers to show doubles facts.
Face the students, and direct them to copy you. Model doubles on your fingers and say the totals as students do the same.

2, 4, 6, 8, 10
Let’s use our fingers to show doubles again. This time, we will say the number sentence. Ready?
Model the doubles with fingers and state the facts as a class.
Green Light, Red Light
Students count from a given number to prepare for the use of addition and subtraction strategies.
Display the green and red dots with the numbers 3 and 5.
On my signal, start counting with the green light number. Stop at the red light number.
Look at the numbers.
Think. Ready? Green light!
green red
3, 4, 5 3 5
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 17 © Great Minds PBC 233
1 + 1 = 2, 2 + 2 = 4, 3 + 3 = 6, 4 + 4 = 8, 5 + 5 = 10
Repeat the process with the following sequence:
Launch
Materials—T: Demonstration clock
Students notice the features of a clock and compare telling time to the hour to counting on a number path.
Gather students. Display the image of two clocks and show a demonstration clock that reads one o’clock. Tell students that these are clocks and that clocks help us tell time.


Teacher Note
Lessons in module 5 directly address telling time to the hour and to the half hour, but frequent, distributed practice with telling time helps students learn the skill.
Fluency activities in upcoming lessons support such practice. In addition, consider
• periodically pausing the class at the top of an hour to ask “What time is it?”;
• assigning a student the job of “town crier” to pause the class at the top of an hour; or
Why do you think it is important to know how to tell time?
What do you notice about all these clocks?
• regularly pointing out times on the hour when the same event happens every day, such as lunch at twelve o’clock or dismissal at three o’clock.
1 ▸ M1 ▸ TC ▸ Lesson 17 EUREKA MATH2 New York Next Gen © Great Minds PBC 234
9 6 green red 6 10 green red 4 7 green red 5 2 green red
10 10 30 10
Use the demonstration clock to briefly introduce the following ideas. Mastery is not expected in this module.
• The large (red) numbers going around the clock tell the hour.
• The short hand points to the hour. We call it the hour hand.
• When the long minute hand points to the 12, we say o’clock.
When the hour hand points to 1 and the minute hand points to 12, we say that the time is one o’clock.
Have students read the time chorally. Then slowly move the hands on the clock to show two o’clock.
As the minute hand goes around the clock, the hour hand slowly moves to the next number. Once the minute hand goes all the way around, the hour hand points to the next number. 1 hour has passed.
Have students chorally read the time: two o’clock. Move the minute hand again to show three o’clock and have students chorally read the time.
Teacher Note
Demonstration clocks often use color coding as a scaffold. For example, the red hand may point to a red number that tells the hour. The blue hand may point to a blue number or tick mark that tells the minutes.
Each time the minute hand goes all the way around the clock and the hour hand goes to the next number, we count 1 more hour.
Move the minute hand around the clock to show four, five, six, seven, eight, nine, ten, eleven, and twelve o’clock. Have students chorally read each hour. As time allows, start at different hours, and move the hands on the clock as students read each new hour up to twelve o’clock.
Point out that on some clocks, the numbers look like a number path shaped as a circle.
How are numbers on a clock and numbers on a number path the same or different?
They both have numbers in order.
The clock has numbers in a circle. The number path has them in a line.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 17 © Great Minds PBC 235
How does reading hours on a clock remind you of counting on with the number path?
You don’t always start at 1. Sometimes you start at another number and keep counting. When you read hours, the numbers go in order. When you count on with the number path, the numbers go in order too.
Set the clock aside as you transition to Learn.
Let’s find out what happens when we add 1 and 0 to different numbers.
Learn
Add 1 to Any Number
Materials—S: Sticky note

Students find the totals in a sequence of +1 problems to make and test a conjecture about the totals.
Display the image that shows 5 + 1. Allow think time for students to find the total. Signal for students to chorally say the total.
Display the image that shows 5 + 1 = 6 to confirm the total. Point out that the number path shows 1 hop.
Differentiation: Support
Some students will benefit from using fingers and cubes to demonstrate the addition of 1 more.



Repeat with the sets of images for 3 + 1 and 9 + 1.

1 ▸ M1 ▸ TC ▸ Lesson 17 EUREKA MATH2 New York Next Gen © Great Minds PBC 236
5 + 1 1 2 3 4 5 6 7 8 9 10 5 + 1 = 6 1 2 3 4 5 6 7 8 9 10
10 10 30 10
1
6 +
= 7
Display the +1 number sentences made thus far.
We added 1 each time. Look at the first part and the total in each problem. What do you notice?
The total is the next number after the first part.
Why is the total the next number?
Because the total is just 1 more.
Have students think–pair–share about the following prompts to make a conjecture that the class can test.
Do you think it is always true that when we add 1, the total is just the next number?
What statement can we say to tell what we think happens when we add 1 to any number?
Then record and display the following statement:
Invite students to test the conjecture by continuing with the sets of images for 12 + 1, 1 + 5, 1 + 3, and 1 + 20.
Display the +1 number sentences made so far. Then reread the +1 statement chorally as a class.
Look carefully at our +1 number sentences. Do you still think our statement is true?
Yes, the totals are all the next number.
A conjecture is a statement or idea that you think is true. Even young students can form conjectures about math principles they notice. This lesson provides many examples of each principle so that students look for patterns to make their first conjectures. In addition, students are provided opportunities to create examples of their conjectures, essentially testing the accuracy and precision of the statements.
While checking numerous examples to support a conjecture is a good mathematical practice, it does not constitute a formal proof. A formal proof indisputably shows that the conjecture is true in every possible case. Without a formal proof, any statement is still only a conjecture. Therefore, avoid stating that a conjecture must be true simply because we have checked a variety of examples.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 17 © Great Minds PBC 237
5 + 1 = 6 3 + 1 = 4 9 + 1 = 10 Teacher Note
12 + 1 = 13 1 + 5 = 6 1 + 3 = 4 1 + 20 = 21
Display the image that shows 3 + 1 = 4 and 1 + 3 = 4.
Why do you think our statement is still true when 1 is the first part?
You can add numbers in any order. The total is still 1 more than the other number (part). As needed, show other examples of 1 + n problems to build students’ confidence.
What happens when we add 1 to any number?
When you add 1 to any number, you get the next number.
Distribute a sticky note to each student.

Write a number sentence that goes with our statement.
Have students post their number sentences near the recorded conjecture. Keep the display available for use during the Problem Set.
Promoting the Standards for Mathematical Practice
When students find +1 and +0 facts, use the answers to form a conjecture, and then support their conjecture by completing more examples, they look for and express regularity in repeated reasoning (MP8).
Ask the following questions to promote MP8:
• How can you use the statement we made to help find the total for 50 + 1?
• How do you know that adding 1 gives the next number?
• How can you use the statement we made to help find the total for 50 + 0?
• How do you know that adding 0 gives the same number?
1 ▸ M1 ▸ TC ▸ Lesson 17 EUREKA MATH2 New York Next Gen © Great Minds PBC 238
1 + 1 = 2 3 + 1 = 4 30 + 1 = 31 1 + 2 = 3 1 + 9 = 10 1 + 10 = 11 7 + 1 = 8 5 + 1 = 6 1 2 3 4 5 6 7 8 9 10 3 + 1 = 4 1 + 3 = 4
Add 0 to Any Number
Materials—S: Sticky note
Students find the totals in a sequence of +0 problems to make and test a conjecture about the totals.
Invite students to find the total where a part is 0. Display the image that shows 5 + 0. Allow think time for students to find the total. Signal for students to chorally say the total.
Differentiation: Support
Some students will benefit from using fingers and cubes to demonstrate the addition of 0.



Display 5 + 0 = 5 to confirm the total. Point out that the number path shows adding 0 (no hops).
Display the sets of images for 3 + 0 and 7 + 0. Repeat the same procedure.
What is the total when we add 0?
The total is the same number as the other part.
Why is that so?
Because 0 is none. You don’t add any more.
Display the +0 number sentences made thus far. Follow the same process as above to have students make and test a conjecture.
Do you think it is always true that when we add 0, the total will be the same as the other part?
What statement can we say to tell what we think happens when we add 0 to any number?
Record and display the following statement:
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 17 © Great Minds PBC 239
5 + 0 1 2 3 4 5 6 7 8 9 10 5 + 0 = 5 1 2 3 4 5 6 7 8 9 10
20 + 0 = 20 5 + 0 = 5 3 + 0 = 3 7 + 0 = 7
Display the sets of images for 13 + 0, 0 + 3, 0 + 8, and 20 + 0, and repeat the above procedure. Display the +0 number sentences the students just made.
Let’s reread our statement and look at our number sentences.
Do you still think our statement is true?
Yes, when we add 0 to any number, we get the same number.
Display the image that shows 3 + 0 = 3 and 0 + 3 = 3.
Why do you think our statement is still true when 0 is the first part?
You can add in any order.
We are still adding 0, or nothing.
What happens when we add 0 to any number?
When you add 0 to any number, you get the same number.
Distribute a sticky note to each student.

Write a number sentence that goes with our statement.
Have students post their number sentences near the recorded conjecture. Keep the display available for use during the Problem Set.
UDL: Engagement
Consider using a version of Simon Says for practice. Explain that in this version, no one is ever out.
• Simon says use your hands to clap 2 + 1 times. Go.
(Claps 3 times)
• Simon says tap your nose 1 + 0 times. Go. (Taps nose 1 time)
Have students whisper the total as they begin the action.
While Sitting:
• Tap your head 3 + 0 times.
• Touch your chin 4 + 1 times.
• Clap your hands 6 + 0 times.
• Touch your shoulder 1 + 5 times.
While Standing:
• Stomp a foot 4 + 1 times.
• Jump up 3 + 0 times.
• Bend and touch toes 1 + 3 times.
• Arms up and cheer 5 + 1 times.
With Room to Move:
• Take 2 + 0 steps forward.
• Hop forward 3 + 0 times.
• Turn around 1 + 0 times.
• Nod your head 5 + 1 times.
1 ▸ M1 ▸ TC ▸ Lesson 17 EUREKA MATH2 New York Next Gen © Great Minds PBC 240
2 + 0 = 2 12 + 0 = 12 6 + 0 = 6 0 + 9 = 9 14 + 0 = 14 5 + 0 = 5 1 + 0 = 1 0 + 100 = 100 13 + 0 = 13 0 + 3 = 3 0 + 8 = 8 20 + 0 = 20 3 + 0 = 3 1 2 3 4 5 6 7 8 9 10 0 + 3 = 3
Problem Set
Differentiate the set by selecting problems for students to finish independently within the timeframe. Problems are organized from simple to complex. The directions may be read aloud.
In this lesson, it is important for students to have an opportunity to apply what they have learned about adding 1 and adding 0, which are on either side of the Problem Set.
Land
Debrief 5 min
Objective: Add 0 and 1 to any number. Select two accurate number sentences (written on sticky notes) from each chart. Remove and display the four sticky notes in a random order as shown in this example.
Teacher Note
Consider using the + 0 and + 1 fact cards to support future distributed practice with adding 0 and 1.
Gather students and pose a problem.
What if these sticky notes fell off?




Point to one sticky note, for example 14 + 0 = 14, and facilitate a class discussion. Encourage students to build on one another’s ideas by saying, “Can anyone say more about that statement?”
Which chart does this number sentence belong on? How do you know?
I think it goes on the chart “When you add 0 to a number…,” because there is a +0 in the number sentence.
I agree, and when you add 14 to 0, you get the same number, 14.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 17 © Great Minds PBC 241
0 + 100 = 100
10 10 30 10
0 1 2 3 4 5 6 0 + 0 0 + 0 + 2 0 + 3 0 + 4 0 + 5 0 + 6 + 0 + + 2 1 + 3 1 + 4 1 + 5 2 + 0 2 + 1 3 + 1 4 + 5 + 3 + 0 4 + 0 5 + 0 6 + 0 7 8 9 10 0 + 7 0 + 8 0 + 9 0 + 10 + 6 + 7 + 8 + 9 6 + 7 + 8 + 1 9 + 1 7 + 0 8 + 0 9 + 0 10 + 0
Which other sticky note can we put back on the same chart? Why?
0 + 100 = 100, because you are still adding 0. And you get the same number, 100.
Why do we get the same number when we add 0? You are adding nothing.
If you have 5 pennies and you get 0 pennies, you still have 5 pennies!
Point to one of the two remaining sticky notes, for example 1 + 1 = 2.
Which chart does this number sentence go back on? How do you know?
I think it goes on the chart “When you add 1 to a number…,” because there is a plus 1 in the number sentence.
I agree, and when you add 1 to 1, you get the next number after 1, which is 2.
Can we put this last sticky note back on the same chart? Why?
Yes, because you are adding 1 to 10.
You get the next number, 11.
Why does that happen when we add 1?
You are adding just 1 more, just like when you are counting out loud (or looking at a number path).
It is the number you say (see) next.
Topic Ticket 5+ min
Provide 5–10 minutes for students to complete the Topic Ticket. It is possible to gather formative data even if some students do not complete every problem.
1 ▸ M1 ▸ TC ▸ Lesson 17 EUREKA MATH2 New York Next Gen © Great Minds PBC 242
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
Write two more number sentences like these.
Write two more number sentences like these.
2. How do you add 1 to any number?
Show how you know. Sample: The answer is the next number.
4. How do you add 0 to any number?
Show how you know. Sample: The number stays the same.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 17 243 © Great Minds PBC
© Great Minds PBC 115 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TC ▸ Lesson 17
Add.
1.
1 + 5 = 6 8 = 7 + 1 12 = 11 + 1 10 + 1 = 11 1 + 8 = 9 7 = 6 + 1 Sample: 17 Name 9 + 1 = 10 13 = 12 + 1 1 ▸ M1 ▸ TC ▸ Lesson 17 EUREKA MATH2 New York Next Gen © Great Minds PBC 116 PROBLEM SET
Add.
3.
2 + 0 = 2 5 = 0 + 5 0 + 7 = 7 9 = 9 + 0 10 + 0 = 10 1 1 + 0 = 11 Sample: 6 = 0 + 6 1 + 0 = 1
Topic D Make the Same Total in Varied Ways
Module 1 intentionally presents number sentences in various forms (figure 1) to promote understanding of the equal sign. Instead of reading the equal sign as a signal that the answer comes next, students learn that the equal sign tells about the relationship between the expressions on either side. For example, 2 + 3 = 3 + 2 means that the total of 2 and 3 is the same as the total of 3 and 2.
Topic D advances this understanding by presenting more complex number sentences (figure 2). Students use concrete and pictorial models to represent the expressions on either side of the equal sign and compare their totals to determine whether the number sentence is true or false. A true number sentence is one in which the totals on both sides of the equal sign are the same.
Students also study equality by finding all the two-part expressions for given totals within 10. This work happens over the course of several lessons, and day by day, the expressions they find are put together to make an Addition Totals chart. The class uses the chart to notice patterns that help them confirm that they found all the expressions for a total and to predict how many expressions can be generated for the next total.
Students use the chart to find examples of the commutative property and to identify doubles facts. From these expressions, they distill the “partners” that make each total. Whereas expressions contain symbols, such as the plus sign, partners are simply pairs of numbers that make a total. For example, partners to 5 are 1 and 4, 2 and 3, and 5 and 0. Students need fluency with partners of totals within 10 to access Level 3 strategies that involve making an easier problem. Work with Level 3 strategies begins in this topic. Students find the total of doubles +1 facts by decomposing one addend to create an equivalent, often easier, problem.
© Great Minds PBC 245
“ ” 7 = 6 + 1 7 2 + 5 because both sides have the same total. 6 + 1 = 2 + 5 is true 6 = 4 + 2 7 6 + 1 “ ” 6 is not the same total as, or equal to, 7. 4 + 2 = 6 + 1 is false.
0 2 3 4 5 6 0 + 0 0 + 1 0 + 2 0 + 3 0 + 4 0 + 5 0 + 6 + 0 + + 2 + 3 + 4 1 + 5 2 + 0 2 + 2 + 2 2 + 3 2 + 4 3 + 0 3 + 3 + 2 3 + 3 4 + 0 4 + 1 4 + 2 5 + 0 5 + 1 6 + 0 7 8 0 + 7 0 + 8 + 6 + 7 2 + 5 2 + 6 3 + 4 3 + 5 4 + 3 4 + 4 5 + 2 5 + 3 6 + 6 + 2 7 + 0 7 + 8 + 0 9 10 0 + 9 0 + 10 + 8 + 9 2 + 7 2 + 8 3 + 6 3 + 7 4 + 5 4 + 6 5 + 4 5 + 5 6 + 3 6 + 4 7 + 2 7 + 3 8 + 8 + 2 9 + 0 9 + 1 10 + 0 5 = 5 2 + 3 = 5 5 = 2 + 3 2 + 3 = 3 + 2 Figure 1 Figure 2 3 + 2 = 4 + 1 5 + 1 = 2 + 2 + 2 7 + 2 = 0 + 9
Progression of Lessons
Lesson 18
Determine whether number sentences are true or false.


Lesson 19
Reason about the meaning of the equal sign.
Lesson 20
Find all two-part expressions equal to 6.
The total of 1 and 4 is 5. The total of 2 and 3 is 5. 5 is the same total as, or equal to, 5, so this number sentence is true.
If the total is the same on both sides of the equal sign, we can say it is true. If the total is not the same on both sides of the equal sign, the number sentence is false.
I know that we found all the expressions that add to 6. We started with 0 red and ended with 6 red.
246 © Great Minds PBC 1 ▸ M1 ▸ TD EUREKA MATH2 New York Next Gen
1 + 4 = 2 + 3
2 + 5 = 3 +3 5 + 1 = 2 + 2 + 2
EUREKA MATH M1 TD Lesson 20 140 Ways to Make 6 Copyright © Great Minds PBC 0 + 6 1 + 5 2 + 4 3 + 3 4 + 2 5 + 1 6 + 0
Lesson 21
Find all two-part expressions equal to 7 and 8.
Lesson 22
Find all two-part expressions equal to 9 and 10.
Lesson 23
Find the totals of doubles +1 facts.
I see patterns in the expressions. I notice that there is 1 more expression than the total: 6 has 7 expressions, 7 has 8 expressions, and 8 has 9 expressions.
A total has 1 more expression than the last total. The total 8 had 9 expressions, so 9 will have 10 expressions, and 10 will have 11 expressions.
I can use doubles facts I know to add doubles +1 facts. It is just 1 more!
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD 247 © Great Minds PBC
EUREKA MATH M1 TD Lesson 21 Copyright Great Minds PBC 149 Ways to Make 7 0 + 7 1 + 6 2 + 5 3 + 4 4 + 3 5 + 2 6 + 7 + 0 21 Name M1 TD Lesson 21 EUREKA MATH 150 CLASS WORK Ways to Make 8 0 + 8 + 7 2 + 6 3 + 5 4 + 4 5 + 3 6 + 2 7 + 8 + 0
EUREKA MATH M1 TD Lesson 22 Copyright Great Minds PBC 22 Name Ways to Make 9 0 + 9 1 + 8 2 + 7 3 + 6 4 + 5 5 + 4 6 + 3 7 + 2 8 + 1 9 + 0 M1 TD Lesson 22 EUREKA MATH PROBLEM SET Ways to Make 10 0 + 10 + 9 2 + 8 3 + 7 4 + 6 5 + 5 6 + 4 7 + 3 8 + 2 9 + 10 + 0
2 + 3 = 4 5 2 + 2 + 1 = 5 2 + 2 =
Lesson 24
Use known facts to make easier problems.
Lesson 25 (Optional)
Organize, count, and record a collection of objects.

I can break up a part to make a problem easier.
We can organize our collection into groups of 5. This helps us find the total. We can show how we counted our collection by recording the groups by using tally marks.
248 1 ▸ M1 ▸ TD EUREKA MATH2 New York Next Gen © Great Minds PBC
+ 6 + + 2 = 10 2 + 6 + + 1 = 10 1
Determine whether number sentences are true or false.
Lesson at a Glance
Students represent a put together with both addends unknown situation by generating two-part expressions that total 5, which are familiar from kindergarten. They work in pairs to prove the equality of these expressions by using cubes and number bonds. Students determine whether number sentences are true or false and explain their reasoning.
Key Question
• What makes a number sentence true or false?
Achievement Descriptor
1.Mod1.AD6 Determine whether addition and/or subtraction number sentences are true or false. (NY-1.OA.7)
© Great Minds PBC 18 LESSON 18
© Great Minds PBC 125 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 18 18 Circle the number sentence if it is true. Draw an X on the number sentence if it is false. Name 5 = 1 + 3 3 + 2 = 2 + 3
Agenda
Fluency 10 min
Launch 10 min
Learn 30 min
• Equal Expressions of 5
• True or False?
• Problem Set
Land 10 min
Materials
Teacher
• Unifix® Cubes (10)
• Addition expression cards
Students
• Number Bond Dash: Make 5 (in the student book)
• Unifix® Cubes (10)
Lesson Preparation
• Number Bond Dash: Make 5 must be torn out of student books. Consider whether to prepare these materials in advance or to have students prepare them during the lesson.
• Prepare two 5-sticks of Unifix Cubes in two different colors (e.g., 5 red and 5 yellow) for each student.

• Pull the following cards from the set of Addition expression cards to create an Addition Totals chart: total cards 0–5, expression cards (for totals of 0–5).
• Copy or print the doggy door recording sheet to use for demonstration.
© Great Minds PBC 251 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 18
Fluency
Choral Response: Compare Numbers
Students determine which number is greater to maintain work with comparing numbers from kindergarten.
Display 7 and 3.
Which number is greater? Raise your hand when you know. Wait until most students raise their hands, and then signal for students to respond.
7
Display the sentence frame.
When I give the signal, say the comparison statement. Ready?
7 is greater than 3.
Display the completed sentence frame.
Repeat the process with the following sequence:
Number Bond Dash: Make 5
Materials—S: Number Bond Dash: Make 5
Students complete number bonds with totals of 5 to prepare for work with decompositions of 5.
Help students recall the meanings of part and total with a kinesthetic activity warm-up.
When I say the word total, make this signal.
Model two hands clasped together.
Teacher Note
The terms whole and total can be used interchangeably. Sample discussions suggest total to avoid confusing students who think hole when they hear whole. However, choose the word that resonates best with your students.
1 ▸ M1 ▸ TD ▸ Lesson 18 EUREKA MATH2 New York Next Gen © Great Minds PBC 252
8, 2 9, 5 1, 6 5, 10 7, 5 5, 6 9, 8 3, 1
10 10 30 10
is greater than 7 3
When I say the word parts, pull the total apart to make this signal.
Exaggerate with a facial expression as if straining while pulling the two hands apart.
Practice the signals for total and parts with students until they appear familiar with the routine.


Differentiation: Support
If some students need support with completing the number bonds, provide additional support by giving them a 5-stick of cubes. Students can break apart the cubes to find the unknown part of the number bond.
Direct students to the Number Bond Dash. Read aloud the directions. Invite students to use their finger to practice completing a number bond on their paper.
Tell students that if they finish early, they should count from 5 to the highest number they can, recording their count on the back of the paper.
Give a signal to begin.
Let students work for 60 seconds or until about 80% of the class nears completion of the page. Do not extend beyond 2 minutes of written work.
Call time. Have students put down their pencils. Read the number bonds aloud as students correct their own papers. When you have finished reading all problems, tell students to write the number they got correct in the star at the top of the page. Celebrate student success.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 18 © Great Minds PBC 253
5 4 Total
© Great Minds PBC 119 EUREKA MATH New York Next Gen M1 TD ▸ Number Bond Dash: Make 5 Number Bond Dash: Make 5 Fill in the number bonds 5 4 1 5 5 0 5 4 1 5 3 2 5 4 1 5 3 2 5 2 3 5 4 1 5 1 4 5 2 3 5 0 5 5 1 4 5 2 3 5 3 2 5 4 1 5 5 0 5 4 1 5 3 2 5 2 3 5 1 4
Parts
Show Me the Math Way
Students show a number the math way to prepare for work with decomposing numbers beginning in lesson 20.
Show me 0.
Show me 1.
Show me 2.
Show me 3.
Continue having students show fingers the math way up to 10. Next skip around to different numbers within 10.














Launch
Students draw and write expressions to represent a put together with both addends unknown situation.
Gather the class. Display the picture of the dog and read the problem aloud.
There are 5 dogs.
They have a doggy door.

The dogs can be inside the house or outside in the yard.
Draw all the different ways that 5 dogs might be inside or outside.
Teacher Note
The phrase math drawing refers to drawings that are efficient and focused on the math. For example, draw simple circles to represent the dogs.
1 ▸ M1 ▸ TD ▸ Lesson 18 EUREKA MATH2 New York Next Gen © Great Minds PBC 254
10 10 30 10
Clarify the context by asking questions, such as the following:
• What is the problem about?
• What do we need to figure out?
What is one way to think about how many dogs are inside and how many dogs are outside?
Have students share their thinking. Select one accurate response, such as 4 dogs inside and 1 dog outside.
Invite students to brainstorm math drawings they could sketch of the dogs. Highlight ideas that save time, such as drawing a circle to represent each dog. Select one drawing to demonstrate this technique.
Ask students to open their books to the doggy door recording sheet. Use the first In-Out box to demonstrate.
Use the In box to show the dogs that are inside. (Draw 4 circles.) Use the Out box to show the dogs that are outside. (Draw 1 circle.)
Pause for a moment, and ask students to do the same.
What expression can we write to match our drawing?
4 + 1
Have students draw more combinations and write matching expressions for another minute or two. Note the specific combinations students make. Be ready in the next segment to ask about the combinations not identified.
Transition to the next segment by framing the work.
Now let’s compare the expressions that you wrote to represent the 5 dogs.
Teacher Note
Students may not show all the dogs that are inside or outside (5 + 0 or 0 + 5). Prompt them to discover this possibility by asking the following questions:
• Can all the dogs be outside?
• If so, then how many dogs are inside?
• What expression can you write to show this?
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 18 © Great Minds PBC 255
Copyright © Great Minds PBC 123 EUREKA MATH2 M1 TD Lesson 18 18 Draw all the ways 5 dogs can be in or out. Write the expression. IN OUT + 4 IN OUT + 4 IN OUT + 2 3 IN OUT + 3 2 IN OUT + 5 0 IN OUT + 0 5 Name EM2_0101TE_D_L18_classwork_studentwork.indd 123 29/12/20 12:26 PM
Learn
Equal Expressions of 5
Students generate all two-part expressions with a total of 5. Invite students to share their drawings and expressions.
What is one way to draw how many dogs are inside and how many dogs are outside?
There could be 2 dogs inside and 3 dogs outside.
What expression matches your drawing?
2 + 3
Record and display the expression 2 + 3. Ask students to show thumbs-up if they also thought of this combination. Continue to elicit responses and record expressions until all responses from students are shared. If a possible expression is not shared, then ask a guiding question such as:
How many dogs are outside if 0 dogs are inside?
Have students turn and talk about the list of expressions.
What do you notice about these expressions?
Some are similar, like 2 + 3 and 3 + 2. The order of the numbers is different, but the parts are the same.
They all show ways of thinking about the 5 dogs. They are all equal to 5.
Students may comment that some expressions are the same (e.g., 2 + 3 and 3 + 2). Point out that the expressions do have the same parts and total, but they match different drawings. Use one situation to explain the difference: 1 dog is inside and 4 dogs are outside versus 4 dogs are inside and 1 dog is outside.
Have students put their books away in preparation for the next segment.
Promoting the Standards for Mathematical Practice
When students represent problems by using math drawings and then represent the math drawings by using expressions, they reason abstractly and quantitatively (MP2)
Ask the following questions to promote MP2:
• What does the expression 2 + 3 tell you about the dog story?
• What does “2 dogs are inside and 3 dogs are outside” tell you about which expression you should write?
Teacher Note
Students decomposed and composed 5 in kindergarten. The two-part expressions that equal 5 are intentionally used in this lesson so that students can extend their thinking to equality between expressions. Using familiar combinations will allow them to attend to new, more complex mathematical concepts.
1 ▸ M1 ▸ TD ▸ Lesson 18 EUREKA MATH2 New York Next Gen © Great Minds PBC 256
10 10 30 10
True or False?
Materials–T/S: Unifix Cubes
Students determine whether number sentences are equal (true) or not equal (false).
Partner students, and have them ready their whiteboards. Distribute one bag of Unifix Cubes to each student.
Guide partners through the following activity by modeling with cubes. Use one color for the first addend and another color for the second addend in each expression.
• Partner A uses cubes to show 2 + 3.
• Partner B uses cubes to show 4 + 1.
• Partners place their cube sticks one above the other, with the ends aligned.
What do you notice about the parts and totals?
The red and yellow parts are different.
Both sticks have a total of 5 cubes.
Since both sets have a total of 5 cubes, they are the same length. When we organize them this way, they look like an equal sign.
Draw the symbol for an equal sign, =, next to the cubes.
Let’s write a number sentence to show that both sets of cubes are equal in length and have the same total.
Record 2 + 3 = 4 + 1. Ask students to write this number sentence on their whiteboards.
How do we know that 2 + 3 is equal to, or has the same total as, 4 + 1?
The sticks are the same length.
Both sticks have the same total number of cubes.
Differentiation: Challenge
If students are ready, have them generate all the ways 6, 7, 8, 9, or 10 dogs can be inside and outside. Consider having them compare the expressions generated to explore equality.
Differentiation: Support
Students may think that the answer must come after the equal sign: 5 + 1 = 6 is true, but 3 + 3 = 4 + 2 and 6 = 1 + 5 are false. This thinking shows a misconception about the meaning of the equal sign.
Use the following sequence of number sentences to help students examine their ideas. Have them use cubes to construct arguments in support of their thinking.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 18 © Great Minds PBC 257
1 + 4 = 5 5 = 1 + 4 5 = 5 1 + 4 = 1 + 4 1 + 4 = 4 + 1 1 + 4 = 2 + 3 1 + 4 = 5 + 1 (false)
Write the total below each expression. Draw number bond arms to show the total for each expression.
Teacher Note
Each side of the number sentence has the same total. We can say that 2 + 3 = 4 + 1 is a true number sentence because the total on each side is equal to 5.
Write 5 = 5.
Is this number sentence true? Why?
Yes, it is true. Both sides are 5.
Both sides of the number sentence have the same total.
Have students erase their whiteboards and write 1 + 4 = 2 + 3. Prompt partners to use cubes or whiteboards to help them determine whether the number sentence is true.
Is this number sentence true? Why?
It’s true because 1 + 4 = 5 and 2 + 3 = 5.
Have partners repeat the process, this time by using the false number sentence 2 + 2 = 5 + 0. As students share, listen for thinking, such as:
It is not true. We showed 2 + 2 and 5 + 0 with cubes. One stick was longer than the other stick.
We drew lines to show the totals, and they were not the same length. 2 + 2 = 4 and 5 + 0 = 5.
We can say that 2 + 2 = 5 + 0 is false. The expression on each side of the equal sign has a different total. Draw an X over a number sentence to show that it is false. Do that with me. (Demonstrate.)
The similarity between the equal sign and cube sticks of the same length not only is helpful to students, but also has a historical basis. The equal sign we use today was first used in 1557 by Welsh mathematician Robert Recorde. He wrote that to avoid constantly repeating the phrase is equal to, he would instead use a pair of twin lines.
Differentiation: Support
If students do not see or evaluate the expression on each side of the equal sign, consider drawing a box around each expression for emphasis.
1 + 4 = 2 + 3
1 ▸ M1 ▸ TD ▸ Lesson 18 EUREKA MATH2 New York Next Gen © Great Minds PBC 258
As time allows, provide more practice by using the following number sentences. Have students show their reasoning: one partner with cubes and the other with a whiteboard (by writing the total of each expression). Remind students to draw an X over a false number sentence.
• 3 + 1 = 2 + 2 (true)
• 1 + 2 = 3 + 1 (false)
• 1 + 2 = 2 + 1 (true)
• 5 = 5 + 2 (false)
• 5 + 1 = 2 + 2 + 2 (true)
Problem Set
Differentiate the set by selecting problems for students to finish independently within the timeframe. Problems are organized from simple to complex.
Help students recognize the word expression in print. Invite students to underline it as you read it aloud.
Many students will need to model the expression on each side of the equal sign to determine whether the number sentence is true or false. Encourage students to show each expression with cubes, draw a picture, or draw number bonds to evaluate each expression.
UDL: Representation
Create a two-column chart, and record as students decide whether each number sentence is true or false.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 18 © Great Minds PBC 259
5 + 1 = 2 + 2 + 2 6 5 + 1 = 2 + 2 + 2 6
Land
Debrief 5 min
Objective: Determine whether number sentences are true or false.
Use your observation of students’ work during the lesson to select and display at least one of the following number sentences.
Teacher Note
Students explore equality by generating the full set of expressions that total 5. In kindergarten, students generated “partners” to 5, which are the number pairs in any order.
Ask students to use whiteboards, cubes, or other ways of reasoning to determine whether each number sentence is true or false. Lead a discussion about their work.
How can you tell whether this number sentence is true or false?
I can count on to find the total of each side to see if they are the same.
I can use cubes to see if one stick is longer than the other stick.
I can see the two numbers on both sides are the same, just in different orders.
Draw an X on each false number sentence that is displayed. Then guide students to verbalize their current understandings about equality.
What do we mean when we say that a number sentence is true?
Each side of the equal sign has the same total.
What do we mean when we say that a number sentence is false?
Each side of the equal sign has a different total.
What does the equal sign mean?
The expressions on both sides of the number sentence have the same total.
The work in both grade levels offers practice with decomposing numbers. This essential skill is necessary to access Level 3 strategies that involve making a problem easier.
Consider organizing the expressions chart made by the class in Learn to make a partners to 5 chart.
1 ▸ M1 ▸ TD ▸ Lesson 18 EUREKA MATH2 New York Next Gen © Great Minds PBC 260
10 30 10
0 + 5 2 + 2 9 + 1 5 + 5 2 + 5 5 + 2 = = =
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
Teacher Note
Begin the construction of the classroom wall display, Addition Totals chart. Place the totals cards (0–5) across the top row. Place the expression cards (for totals of 0–5) in the correct total columns, as shown.
Expression cards for totals of 6–10 will be added to the chart in lessons 20, 21, and 22.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 18 © Great Minds PBC 261
0 1 2 3 4 5 0 + 0 0 + 1 0 + 2 0 + 3 0 + 4 0 + 5 1 + 0 1 + 1 1 + 2 1 + 3 1 + 4 2 + 0 2 + 1 2 + 2 2 + 3 3 + 0 3 + 1 3 + 2 4 + 0 4 + 1 5 + 0
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
1. Circle the number sentence if it is true.
Draw an X on the number sentence if it is false
2. Circle the number sentence if it is true
Draw an X on the number sentence if it is false
3. Write a true number sentence.
Show how you know it is true.
Sample:
1 ▸ M1 ▸ TD ▸ Lesson 18 EUREKA MATH2 New York Next Gen 262 © Great Minds PBC
© Great Minds PBC 123 18 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 18
2 + 3 = 1 + 4 5 = 0 + 5 3 = 3 4 + 1 = 2 + 2 Name © Great Minds PBC 124 PROBLEM SET 1 ▸ M1 ▸ TD ▸ Lesson 18 EUREKA MATH2 New York Next Gen
4 + 1 = 1 + 4 4 = 3 + 1 6 = 5 2 + 5 = 7 + 1 3 + 1 = 4 + 0 4
4
Reason about the meaning of the equal sign.
Lesson at a Glance
Students practice matching equal expressions as a class and then in pairs. They reason about equality and the meaning of the equal sign as they evaluate whether a variety of number sentences are true or false.
Key Question
• What does the equal sign mean?
Achievement Descriptor
1.Mod1.AD6 Determine whether addition and/or subtraction number sentences are true or false. (NY-1.OA.7)
© Great Minds PBC 19 LESSON 19
© Great Minds PBC 133 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 19 19 Circle the number sentence if it is true Draw an X on the number sentence if it is false 3 + 3 6 + 2 = 7 + 1 6 + 2 = Name
Agenda
Fluency 5 min
Launch 10 min
Learn 35 min
• Class True or False?
• Partner True or False?
• Match: Expressions
• Problem Set
Land 10 min
Materials Teacher
• Addition expression cards
Students
• Number Bond Dash: Make 5 (in the student book)
• Match: Expressions (in the student book)
• Bag of Addition expression cards for Match: Expressions (21-card set per student pair)
• Unifix® Cubes (10)
Lesson Preparation
• Pull the following cards from the teacher set of Addition expression cards for teacher use: 3 + 3, 2 + 4, 6 + 0, 6 + 1.
• Use the Addition expression cards to make sets of 21 cards to play Match: Expressions. Pull out four cards (from the full set) per total 6, 7, 8, 9, and 10. Be sure to include a few cards that show the total on both sides of the card. Also include an equal sign card. Save the sets in a resealable plastic bag for use in lessons 20, 23, and 24. (Differentiate sets by pulling four cards for lower totals, such as 3, 4, 5, 6, and 7.)
• Number Bond Dash: Make 5 must be torn out of student books. Consider whether to prepare these materials in advance or to have students prepare them during the lesson.
• Match: Expressions must be torn out of student books and placed in personal whiteboards. Consider whether to prepare these materials in advance or to have students prepare them during the lesson.
• Have math tools, such as cubes or number paths, available for students to self-select.
© Great Minds PBC 265 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 19
Fluency
Number Bond Dash: Make 5
Materials—S: Number Bond Dash: Make 5
Students complete number bonds with totals of 5 to prepare for making an easier problem beginning in module 3.
Recall the meanings of part and total with a kinesthetic activity warm-up.
When I say the word total, make this signal.
Model two hands clasped together.
When I say the word parts, pull the total apart to make this signal.
Exaggerate with facial expression as if straining while pulling the two hands apart.
Practice the signals for total and parts with students until they appear familiar with the routine.
Direct students to the Number Bond Dash. Read aloud the directions. Invite students to use their fingers to practice completing a number bond on their paper.
Tell students that if they finish early, they should count from 5 to the highest number they can, recording their count on the back of the paper.
Give a signal to begin.
Let students work for 60 seconds or until about 80% of the class nears completion of the page. Do not extend beyond 2 minutes of written work.
Call time. Have students put down their pencils. Read the number bonds aloud as students correct their own papers. When you have finished reading all problems, tell students to write the number they got correct in the star at the top of the page. Celebrate student success.
1 ▸ M1 ▸ TD ▸ Lesson 19 EUREKA MATH2 New York Next Gen © Great Minds PBC 266
5 10 35 10 © Great Minds PBC 127 EUREKA MATH2 New York Next Gen ▸ M1 ▸ TD Number Bond Dash: Make 5 Number Bond Dash: Make 5 Fill in the number bonds 5 4 1 5 5 0 5 4 1 5 3 2 5 4 1 5 3 2 5 2 3 5 4 1 5 1 4 5 2 3 5 0 5 5 1 4 5 2 3 5 3 2 5 4 1 5 5 0 5 4 1 5 3 2 5 2 3 5 1 4
Launch
Materials—T: Addition expression cards (3 + 3, 2 + 4, 6 + 0, 6 + 1)
Students match expressions that are equal and explain their reasoning.
Gather students, and display the four expression cards shown. Distribute whiteboards, and have cubes and number paths available. Ask students to find at least two expression cards that are equal to one another. After about a minute of individual think time, allow students to turn and talk to a partner about their matches.
Invite volunteers to share a match, such as 3 + 3 and 2 + 4, and explain how they know the expressions are equal. Encourage students to build on each other’s ideas by using the Talking Tool.
A common mistake is to suggest that 3 + 3 and 6 + 1 match. Students see 3 + 3 and think it is equal to the 6, ignoring the + 1. Even if students do not share this match, invite the class to discuss these expressions.
Are 3 + 3 and 6 + 1 a match? Why?
They are not a match. 3 + 3 = 6, but there is a plus 1 after the 6.
6 + 1 = 7, but 3 + 3 = 6. They are not a match.
6 + 1
Display the 6 + 1 expression card.
I noticed you did not share a match for 6 + 1. Why? 6 + 1 = 7. None of the other cards equal 7.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 19 © Great Minds PBC 267
3 + 3 6 + 0 2 + 4 6 + 1
5 10 35 10 I Can Share My Thinking My drawing shows did it this way because think because I Can Agree or Disagree agree because disagree because did it a different way. I Can Ask Questions How did you ? Why did you ? Can you explain ? Can Say It Again heard you say said Can you say it another way? Talking Tool © Great Minds PBC
Transition to the next segment by framing the work.
Today, we will use what we know about the equal sign to decide if a number sentence is true or false.
Learn
Class True or False?
Materials—S: Unifix Cubes
Students reason about true and false number sentences to understand the meaning of the equal sign.
Have students ready their whiteboards. Distribute Unifix Cubes as needed. Display the following number sentence, and ask students to determine whether it is true or false. Encourage them to show their thinking by using whiteboards and cubes. Give students a moment of silent work time.
6 + 1 = 2 + 5
Is this number sentence true or false? How do you know?
It is true because 6 + 1 is the same as, or equal to, 2 + 5. True. Both sides of the number sentence equal 7.
Encourage students to be precise. For example, if they say that both sides of the number sentence are the same, tell them that you think both sides are different because 6 and 1 are not the same numbers as 2 and 5. Then ask them to clarify the meaning of the same as by asking how 6 + 1 and 2 + 5 are the same.
Some students say that 6 + 1 = 2 + 5 is false because you can’t write number sentences that way. What do you think they mean?
You need to have the two numbers and then the equal sign and then one number after the equal sign.
1 ▸ M1 ▸ TD ▸ Lesson 19 EUREKA MATH2 New York Next Gen © Great Minds PBC 268
5 10 35 10
The equal sign always goes between two amounts that are the same. Do the expressions on both sides of the equal sign have the same total?
Yes, 6 + 1 = 7 and 2 + 5 = 7.
What is another way to say that the equal sign always goes between two amounts that are the same?
The equal sign means that both sides have the same total.
Display the following false number sentence: 2 + 5 = 3 + 3
Is this number sentence true or false? Why?
False. 2 + 5 = 7, but 3 + 3 = 6.
False. 7 and 6 are not the same total.
Verify the total for each expression as a class.
2 + 5 = 3 + 3
2 + 5 = 3 + 3
Draw an X on the number sentence to show that it is false.
Partner True or False?
Students collaborate to evaluate and confirm whether number sentences are true or false.
Next, use a variation of the Numbered Heads routine. Form pairs of students (rather than groups of 4) to practice counting on independently. Assign each partner a number: 1 or 2.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 19 © Great Minds PBC 269
1 2
Help students remember their number by having them write it in the corner of their whiteboard.
Write 7 + 3 = 1 + 9.
Is this number sentence true or false? How do you know?
Allow quiet time for independent work. Encourage students to self-select tools, such as number sentences, number paths, cubes, or fingers. Then have students stand and share their work with their partner.
Set expectations for productive group work:
Lean in, look at your partner, and listen carefully. Partner 2 go first. Partner 1 go second.
After partners share, have them decide whether the number sentence is true or false. Now it is time to put your heads together to decide. Is the number sentence true or false? Why? Everyone should be ready to share their thinking with the class.
Circulate and listen. Tell students that either partner could be called on to share. Both students should be prepared to give an answer and show work that supports their thinking. Following are possible strategies:
Promoting the Standards for Mathematical Practice
Students self-select useful tools to represent the abstract number sentence and determine if a number sentence is true (MP5)
To promote MP5, ask the following question:
• Why did you choose that tool to figure out if the number sentence is true?
When students decide that a number sentence is true or false and create arguments to defend their thinking or challenge the thinking of other students, they construct viable arguments and critique the reasoning of others (MP3).
Ask the following questions to promote MP3:
Decide whether to call on partner 1 or partner 2, and then select a few partners to share their answers. Guide the discussion by asking questions that promote reasoning about equality, such as the following:
• How do you know the number sentence is true (or false)?
• Does anyone disagree? Why?
Circle the number sentence when the class agrees that the number sentence is true.
• Is your answer a guess, or do you know for sure? How do you know for sure?
• What questions can you ask your partner to make sure you understand their answer?
1 ▸ M1 ▸ TD ▸ Lesson 19 EUREKA MATH2 New York Next Gen © Great Minds PBC 270
10 9 8 7 6 5 4 3 2 1 10 9 8 7 6 5 4 3 2 1 7 8 9 10 9 10
Select a number sentence from the following options, and repeat the process. If the class agrees that a number sentence is false, draw an X over it during discussion.
Match: Expressions
Materials—S: Bag of Addition expression cards, Match: Expressions
Students match equal expressions to apply their understanding of equality and the equal sign.
Keep students in pairs, and demonstrate a game similar to the Launch activity.
Take six cards from your set and arrange them plain side up (no color border) as shown. Place the equal sign card out as well. Put the rest of your cards to the side in a pile.
Teacher Note
An expression is a number, or any combination of sums or differences, that can be evaluated. 10 is an expression, as are 8 + 2 and 5 + 5 + 5.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 19 © Great Minds PBC 271
5 4 + 1 5 + 2 8 + 0 2 + 3 7 6 + 1 3 + 7 = 4 + 5 0 = 0 + 7 6 = 2 + 2 + 2
Partner 1: Pick up two expression cards that you think are equal. Use the equal sign to make a true number sentence. Explain to your partner why you think the number sentence is true. You may use cubes or your whiteboard for support.
Turn the cards over to check if they are equal (side with the color border). The totals are equal, so this number sentence is true.
Partner 2: Write the true number sentence on the Match: Expressions recording sheet.
Partner 1: Keep your matching cards and draw two new cards from the pile. Place one card in each missing spot. Then switch jobs! Partner 2, it is now your turn to make a match.
Distribute a bag of Addition expression cards for Match: Expressions and a Match: Expressions recording sheet to each pair. Invite them to self-select tools, such as number paths, fingers, whiteboards, or cubes as needed.
Circulate and remind students to explain why they think two expressions make a true number sentence. Have students play until they find a match for all the cards.
Have students put the cards away. Save the card sets for lesson 20.
Differentiation: Challenge
If students finish quickly, have them write their own true or false number sentences and trade with their partner. Ask them to discuss how they know that their partner’s number sentences are true or false.
1 ▸ M1 ▸ TD ▸ Lesson 19 EUREKA MATH2 New York Next Gen © Great Minds PBC 272
5 = 4 + 1 = 2 + 3 4 + 1 OR
5 5 =
EUREKA MATH M1 TD Lesson 19 Match Copyright © Great Minds PBC 131 Write true number sentence. 5 4 + 1 2 + 4 1 + 5 3 + 4 2 + 5 6 4 + 2 4 + 4 5 + 3 10 + 0 0 + 10 = 4 + 0 2 + 2 = = = = = =
Problem Set
Differentiate the set by selecting problems for students to finish independently within the timeframe. Problems are organized from simple to complex.
Land
Debrief 5 min
Objective: Reason about the meaning of the equal sign.
Display the image of a blank number sentence. Challenge the class to generate a variety of true number sentences and record their thinking.
Let’s write different true number sentences with expressions that equal 6. How many can we think of?
6 = 6
6 = 5 + 1
3 + 3 = 4 + 2
4 + 2 = 2 + 4
1 + 1 + 1 + 1 + 1 + 1 = 6
What makes all these number sentences true?
The same total is on each side of the equal sign.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 19 © Great Minds PBC 273
=
5 10 35 10
Write 6 = 6 + 2.
A student says that 6 = 6 + 2 is true because 6 = 6. Why do you agree or disagree?
I disagree. 6 is equal to 6, but 6 + 2 = 8.
What do we know about the equal sign?
You can have two (or more) numbers on both sides.
The answer can come first.
It means that what is on both sides is the same total.
The total on both sides has to be the same if the number sentence is true.
If time allows, present a more difficult problem for partners to think–pair–share about.
How would you explain to a friend why 6 = 3 + 3 is true, but 6 = 2 + 2 is false?
6 is the same total as 3 and 3 put together, so it is true.
6 = 2 + 2 is not true because 2 + 2 = 4. 6 does not equal 4, so that number sentence is false.
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
1 ▸ M1 ▸ TD ▸ Lesson 19 EUREKA MATH2 New York Next Gen © Great Minds PBC 274
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
1. Circle the number sentence if it is true.
Draw an X on the number sentence if it is false 5 = 3 + 2
2. Circle the number sentence if it is true .
Draw an X on the number sentence if it is false
6 + 6 = 10 + 2
3. Write a true number sentence.
Show how you know it is true .
Sample: 5 5
= 4 1 + 5 0 +
4. Write a false number sentence and draw an X.
Show how you know it is false
Sample: 5 + 0 = 0 5 is not the same as 0.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 19 275 © Great Minds PBC
© Great Minds PBC 131 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 19 19
2
5
5
2 5
3
8
1
© Great Minds PBC 132 PROBLEM SET 1 ▸ M1 ▸ TD ▸ Lesson 19 EUREKA MATH2 New York Next Gen
+
=
+
+
=
+
Name
Name
Color three ways to make 6.
Fill in each number bond
Write each number sentence.
Sample:
Find all two-part expressions equal to 6.
Lesson at a Glance
Students study a picture of items with a variety of attributes and sort, graph, and write a two-addend expression that totals 6. They identify the finite set of two-part expressions that total 6 through a guided, systematic approach. They play a game to develop fluency with facts that total 6.
Key Question
• How can we use the pattern on the Addition Totals chart to be sure that we found all the ways to make 6?
Achievement Descriptors
1.Mod1.AD4 Add fluently within 10. (NY-1.OA.6b)
1.Mod1.AD5 Fluently decompose totals within 10 in more than one way. (NY-1.OA.6b)
© Great Minds PBC 20 LESSON 20
© Great Minds PBC 141 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 20 20
6 4 2 4 + 2 = 6 6 3 3 3 + 3 = 6 6 5 1 5 + 1 = 6
Agenda
Fluency 10 min
Launch 15 min
Learn 25 min
• Two-Part Expressions of 6
• Problem Set
Land 10 min
Materials Teacher
• Addition expression cards (totals of 6)
• Chart paper
• Two-color counters (6)
• Addition Totals chart
• Crayons to match the colors on the counters
• Cup
• Shake Those Disks: 6 (digital download) Students
• Bag of Addition expression cards for Match: Addition expressions (21-card set per student pair)
• Two-color counters (6)
• Crayons to match the colors on the counters
• Cup
• Shake Those Disks: 6 (in the student book)
Lesson Preparation
• Ready the bags of Addition expression cards used in lesson 19.
• Prepare to add expressions that total 6 to the Addition Totals chart that began in lesson 18.
• Put 6 counters in a cup for each student.
• Shake Those Disks: 6 must be torn out of student books and placed in personal whiteboards. Consider whether to prepare these materials in advance or to have students prepare them during the lesson.
• Copy or print Shake Those Disks: 6 to use for demonstration.
© Great Minds PBC 277 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 20
Fluency
Show Me the Math Way: Totals of 6
Students show numbers the math way and say an addition number sentence to prepare for work with decompositions of 6.
Show me 5.
Show me 6.
Show me 5.
How many more to make 6?
Say the addition sentence starting with 5. Ready?
5 + 1 = 6
Repeat the process of making 6 with the following sequence of starting numbers:


Match: Addition Expressions
Materials—S: Bag of Addition expression cards
Students identify equivalent expressions and use them to make a true number sentence to develop an understanding of equality.
Have students form pairs. Distribute a set of cards to each pair, and have them play according to the following rules. Consider doing a practice round with students.
• Lay out six cards expression side up.
• Match two expressions that have equal totals.
1 ▸ M1 ▸ TD ▸ Lesson 20 EUREKA MATH2 New York Next Gen © Great Minds PBC 278
1
10 15 25 10 5 6 1 3 6 0 4 2 4 + 1 = 2 + 3 Front
• Form a true number sentence by placing an equal sign card between equal expressions.
• Check that the number sentence is true. Turn over the cards to the side with the color border to see whether the totals on either side of the equal sign are the same.
• Place the matched cards to the side, and replace them with two new cards from the pile.
• Continue until all cards are matched.
Circulate as students play the game and provide support as needed.
Launch
Materials—T: Chart paper
Students sort and graph 6 items into two groups.
10
Gather students and display the picture of apples.
Look at the picture carefully. What do you notice?
Guide students toward noticing quantities and attributes. Possible observations to chart include the following:
• 3 green, 3 red
• 2 small, 4 large
• 4 stems, 2 no stems
• 1 worm, 5 no worm
• 3 leaves, 3 no leaves
• 6 apples, 0 other fruit
Display the following graph. Tell students that this is how another class sorted and represented the apples.
Differentiation: Support
If students need support with adding the totals, consider providing sets of cards with lower totals of 3, 4, 5, 6, and 7.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 20 © Great Minds PBC 279
5 = 5 Back
15 25
Copyright © Great Minds PBC 141 20 EUREKA MATH 2 M1 TD Lesson 20 Totals 3 3 Leaf No Leaf Apple Leaf 3 + 3 = 6 6 3 3 Name
10
Ask students to share their observations. Point to the elements of the graph (title, labels, etc.) as they discuss.
What can you tell about the apples from this graph?
It is about apple leaves.
3 apples have leaves, and 3 do not. There are 6 apples.
They made a number bond and number sentence to show the total number of apples. Display the apple picture again along with the chart of observations. Pair students and ask them to talk about ways to sort the apples. Encourage them to use the picture and chart to support their discussion.
Ask partners to select one attribute to sort and graph the apples. Have them represent their sort on the graph in their student books. As students work, circulate and notice the different ways they sorted. See the following samples.
UDL: Action & Expression
Consider having students take 1 minute to discuss the plan for their graph. Ask students to show thumbs-up when they have decided how to graph the apple information. Remind students that mathematicians take time to think and plan before starting to work.
Select two or three different graphs that represent common ways the class sorted and graphed (e.g., by size). Invite pairs to share their graphs, and facilitate a class discussion by asking the following questions.
How does your graph use two parts to show 6?
It shows 1 apple with a worm and 5 apples with no worms.
What other two parts could we use to show 6?
3 red apples and 3 green apples
Teacher Note
Encourage students to title and label their graphs by using the sounds they hear in the words they wish to write or by drawing simple pictures to represent those words. Students may choose picture graphs rather than bar graphs.
1 ▸ M1 ▸ TD ▸ Lesson 20 EUREKA MATH2 New York Next Gen © Great Minds PBC 280
139 20 Totals 5 Worm No Worm Apple Worms 6 5 1 Name Copyright © Great Minds PBC 141 20 EUREKA MATH M1 TD Lesson 20 Totals 2 4 Small Big Apple Size 2 + 4 = 6 6 4 2 Name 20 Totals 3 3 Red Green Apple Color 3 + 3 = 6 6 3 3 Name
Why do some graphs have different parts, but every graph shows a total of 6 apples?
The picture has 6 apples total. Different student groups sorted the apples into different parts.
Help students relate the graph, number sentence, and number bond in each work sample. Point out that each representation shows two parts that total 6.
Transition to the next segment.
Today, we will find all the expressions with two parts that make 6.
Learn
Two-Part Expressions of 6
Materials—T: Two-color counters, crayons; S: Two-color counters, crayons, cup
Students organize counters to find all expressions that total 6.
Distribute a cup with 6 two-color counters and crayons to match the colors to each student. Have the class turn to Ways to Make 6 in their student books.
Let’s organize our counters to find all the ways to make 6. Display 6 yellow counters in a line. Place 6 yellow counters in a line above your book.
How many counters are red? How many are yellow?
There are 0 red counters and 6 yellow counters.
Guide students to color the first row of circles yellow and to write the expression 0 + 6.

Turn the first counter in the line to red, and have students do the same.
How many of the 6 counters are red? How many are yellow?
There is 1 red counter and 5 yellow counters.
UDL: Action & Expression
If needed, to minimize the fine motor demands of placing and turning over the counters, display counters instead. Students may direct each turn of a counter and then color the new combinations.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 20 © Great Minds PBC 281
10 15 25 10 EUREKA MATH2 ▸ M1 ▸ TD ▸ Lesson 20 140 Ways to Make 6 Copyright © Great Minds PBC 0 + 6 + 5 2 + 4 3 + 3 4 + 2 5 + 1 6 + 0
How can we write that as an expression?
1 + 5
Continue turning over counters, coloring, and writing expressions for all the combinations of 6. Have students turn counters from left to right so they record expressions where the first addend represents the red counters.
As they clean up, have students place counters and crayons back in cups and set them aside for use in a game at the end of the lesson. Display a work sample and invite students to reflect on their work.
Have students think–pair–share about the following questions.
What do you notice about the counters we colored?
It looks like stairs.
Each time a yellow gets 1 less, a red gets 1 more.
We started at 6 yellow, and we ended with 6 red.
They have matches like 4 red and 2 yellow or 2 red and 4 yellow.
3 red and 3 yellow does not have a match.
What do you notice about our list of expressions?
I notice it goes 0, 1, 2, … , 6. (Points to the first addends.)
(Points to the second addends.) Here it is like you are counting backward. It starts with 0 and 6, and it ends with 6 and 0.
6 + 0 and 0 + 6 have the same parts, but in a different order. What are the two parts that make 6 in the expressions 6 + 0 and 0 + 6?
6 and 0
Create an anchor chart of partners to 6 by recording student responses as number bonds. Repeat with the other two pairs of expressions and then 3 + 3.
Teacher Note
In lessons 20, 21, and 22, students find all the ways to decompose 6, 7, 8, 9, and 10 into two whole number parts. Note that these lessons do not explicitly state that both parts must be whole numbers because grade 1 does not discuss other types of numbers (such as fractions and negative numbers).
Promoting the Standards for Mathematical Practice
Students attend to precision (MP6) when they are careful to color and list each expression that sums to 6 exactly once without skipping any expression that totals 6.
Ask the following questions to promote MP6:
• What do you need to be careful about when finding all the expressions that total 6?
• Where is it easy to make mistakes when you are writing all the expressions that total 6?
1 ▸ M1 ▸ TD ▸ Lesson 20 EUREKA MATH2 New York Next Gen © Great Minds PBC 282
These are all the partners to 6. They show all the ways to break 6 into two parts.
Tell your neighbor the partners to 6.
Display the anchor chart. Note that four similar charts are generated in lessons 21 and 22.
Problem Set
Materials—T/S: Cup, Shake Those Disks: 6, two-color counters
In lieu of asking students to complete a Problem Set, prompt them to play Shake Those Disks in pairs to practice the skills from this lesson. Ensure that each pair has a Shake Those Disks graph. Display the graph point to the title, and read it aloud.
Demonstrate how to play the game.
• Partner A shakes the 6 two-color counters in a cup and spills them out.
• Partner A counts how many counters landed on red and how many landed on yellow. They say the total and the parts they see. For example, 6 is 4 and 2, or 6 = 4 + 2.
• Partner B identifies the matching number bond on the graph and makes an X above it.
• Partners switch jobs.
Consider posting sentence frames to help students state the number sentence that represents their counters: is and . OR = +
Have students clean up by placing their counters back in the cup. Set these materials aside for use in lessons 21 and 22.

Teacher Note
Becoming comfortable with the partners to 5, 6, 7, 8, 9, and 10 directly supports students’ fluency with addition facts to 10.
Decomposing numbers fluently also plays a key role in two critical skills:
• Making problems easier
• Recognizing subtraction as an unknown addend problem
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 20 © Great Minds PBC 283
137 EUREKA MATH M1 TD Lesson 20 Shake Those Disks: 6 Shake Those Disks: 6 X X X X X X X X X X X 6 0 6 6 1 5 6 2 4 6 3 3 EM2_0101TE_D_L20_shake_and_spill6_studentwork.indd 137 29/12/20 12:07 PM
Land
Debrief 5 min
Materials—T: Addition expression cards (totals of 6), Addition Totals chart
Objective: Find all two-part expressions equal to 6.
Gather students and display the Addition Totals chart (with expressions for the totals 1–5). Help students recall that the number at the top of each column shows the total. The expressions for each total are listed below.
Invite students to share the expressions of 6 they found in this lesson. As students share, place the corresponding Addition expression cards on the chart in order. If students do not share all the expressions, then show the remaining expression cards, and ask the class to confirm that each card shows a total of 6.
Engage students in a discussion about the finite set of expressions of 6.
How do we know these are all the ways to make 6 with two parts?
The first part starts with 0 and goes up to 6.
I agree. 0, 1, 2, 3, 4, 5, 6. We did not miss any!
Draw attention to the other columns on the chart, and guide students to see that the 0 column has 1 expression, the 1 column has 2 expressions, the 2 column has 3 expressions, and so on.
How many expression cards do you think 7 and 8 will have? Why do you think so?
Entertain all responses and consider recording predictions for lesson 21.
1 ▸ M1 ▸ TD ▸ Lesson 20 EUREKA MATH2 New York Next Gen © Great Minds PBC 284
15 25 10 0 1 2 3 4 5 6 0 + 0 0 + 1 0 + 2 0 + 3 0 + 4 0 + 5 0 + 6 1 + 0 1 + 1 1 + 2 1 + 3 1 + 4 1 + 5 2 + 0 2 + 1 2 + 2 2 + 3 2 + 4 3 + 0 3 + 1 3 + 2 3 + 3 4 + 0 4 + 1 4 + 2 5 + 0 5 + 1 6 + 0
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 20 285 ©
PBC
Great Minds
© Great Minds PBC 21 LESSON 21
7 and 8. © Great Minds PBC 149 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 21 21 1. Color a way to make 7. Fill in the number bond Write the number sentence. Name 7 5 2 Sample: 5 + 2 = 7 © Great Minds PBC 150 EXIT TICKET 1 ▸ M1 ▸ TD ▸ Lesson 21 EUREKA MATH2 New York Next Gen 2. Color a way to make 8. Fill in the number bond. Write the number sentence. Sample: 8 4 4 4 + 4 = 8
Find all two-part expressions equal to
Lesson at a Glance
In this lesson students build upon the previous lesson by finding the expressions for a given total. They apply the same systematic approach by using two-color counters to model the parts that make totals of 7 and 8. They record the finite set of two-part expressions equal to 7 and 8 and play a game to develop fluency with these facts.
Key Question
• How can we use the patterns on the Addition Totals chart to be sure that we found all the ways to make 7? 8?
Achievement Descriptors
1.Mod1.AD4 Add fluently within 10. (NY-1.OA.6b)
1.Mod1.AD5 Fluently decompose totals within 10 in more than one way. (NY-1.OA.6b)
Agenda
Fluency 10 min
Launch 5 min
Learn 35 min
• Two-Part Expressions of 7
• Two-Part Expressions of 8
• Problem Set
Land 10 min
Materials
Teacher
• Chart paper
• Addition expression cards (totals of 7 and 8)
• Addition Totals chart (0–6)
Students
• Two-color counters (8)
• Crayons to match the colors on the counters
• Cup
• Shake Those Disks: 7 (in the student book)
• Shake Those Disks: 8 (in the student book)
Lesson Preparation
• Add 1 more counter to the cups of 6 counters used in lesson 20. Prepare to distribute 1 more counter to each student in the middle of the lesson.
• Prepare to add expressions of 7 and 8 to the Addition Totals chart that began in lesson 18.
• Shake Those Disks: 7 and Shake Those Disks: 8 must be torn out of student books and placed in personal whiteboards. Consider whether to prepare these materials in advance or to have students prepare them during the lesson.
© Great Minds PBC 287 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 21
Fluency
Choral Response: Compare Numbers
Students determine which number is less to maintain work with comparing numbers from kindergarten.
Display the numbers 7 and 3.
Which number is less? Raise your hand when you know.


3
Display the sentence frame.
When I give the signal, say the comparison statement. Ready?
3 is less than 7.
Display the completed sentence frame.
Repeat the process with the following sequence:
Show Me the Math Way: Totals of 7
Students show numbers the math way and say an addition number sentence to prepare for work with decompositions of 7.
Show me 6.
Show me 7.
Show me 6.
How many more to make 7?
1 ▸ M1 ▸ TD ▸ Lesson 21 EUREKA MATH2 New York Next Gen © Great Minds PBC 288
1 10 5 35 10
less than . 3 7 7 3 2, 9 6, 10 5, 1 9, 4 5, 8 7, 8 4, 3 1, 3 6 7
is
Say the addition sentence starting with 6. Ready?
6 + 1 = 7
Repeat the process of making 7 with the following sequence of starting numbers:
Show Me the Math Way: Totals of 8
Students show numbers the math way and say an addition number sentence to prepare for work with decompositions of 8.
Show me 7.
Show me 8.
Show me 7.
How many more to make 8?
1
Say the addition sentence starting with 7. Ready?
7 + 1 = 8
Repeat the process of making 8 with the following sequence of starting numbers:


EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 21 © Great Minds PBC 289
1 5 2 7 0 3 4 7 8 1 5 3 8 0 4 6 2
Launch
Materials—T: Addition Totals chart
Students analyze the Addition Totals chart to predict the number of two-part expressions that make 7 and 8.
Gather students and display the Addition Totals chart.
Point to the 0 column and activate prior knowledge by asking the following question.
How many expressions are there for 0?
1 expression
Point to totals 1–6 and repeat the same question for each total.
2, 3, 4, 5, 6, 7 (expressions)
Think about the number of expressions for each total. What patterns do you notice?
Every time the total is 1 more, there is 1 more expression.
There is 1 more expression than the total.
How many expressions do you think we can make for 7? Why?
8 expressions. There are 7 expressions for 6, so there are probably 8 expressions for 7.
8 expressions. The total is 7, and there is usually 1 more expression than the total.
How many expressions do you think we can make for 8? Why?
Record students’ predictions to validate later in the lesson. Transition to the next segment by framing the work.
Let’s see if we are right. Today, we will find all the expressions with two parts that make 7 or 8.
Promoting the Standards for Mathematical Practice
When students predict how many twoaddend expressions there will be with totals of 7 and 8, they look for and express regularity in repeated reasoning (MP8).
Students make use of their previous work with finding all the expressions with totals of 0–5 to make this prediction. They notice the repeated pattern that each total has 1 more expression than the previous total and express regularity to predict that the pattern will continue.
1 ▸ M1 ▸ TD ▸ Lesson 21 EUREKA MATH2 New York Next Gen © Great Minds PBC 290
10 5 35 10
0 1 2 3 4 5 6 0 + 0 0 + 1 0 + 2 0 + 3 0 + 4 0 + 5 0 + 6 1 + 0 1 + 1 + 2 1 + 3 1 + 4 1 + 5 2 + 0 2 + 1 2 + 2 2 + 3 2 + 4 3 + 0 3 + 1 3 + 2 3 + 3 4 + 0 4 + 1 4 + 2 5 + 0 5 + 1 6 + 0
Learn
Two-Part Expressions of 7
Materials—T: Chart paper; S: Two-color counters (7), crayons, cup
Students organize counters to find all expressions of 7.
Give each student a cup with 7 two-color counters and crayons to match the colors. Have the class turn to Ways to Make 7 in their books.
Help students recall the process to find two-part expressions used in lesson 20:
• Place 7 yellow counters in a line above your book.
• In your book, color the circles, and write the expression 0 + 7 to show 0 red counters and 7 yellow counters.
• Turn over the first counter on the left.
• Color the circles and write an expression to show how many red and how many yellow counters. (The first addend in the expression represents the red counters.)
Have students use this process to find and record all the two-part expressions of 7.
When students finish, display a work sample.
How many expressions are there for 7? Is our prediction correct?
There are 8 expressions. Our prediction was right.
Invite students to notice patterns in their work.
Have students think–pair–share about the following questions.
What do you notice about the counters we colored?
This looks just like our work when we found expressions of 6.
Each time yellow gets 1 less, and red gets 1 more.
We started at 7 yellow, and we ended with 7 red.
They have matches like 4 red and 3 yellow or 3 red and 4 yellow.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 21 © Great Minds PBC 291
10 5 35 10 EUREKA MATH M1 TD Lesson 21 Copyright Great Minds PBC 149 Ways to Make 7 0 + 7 1 + 6 2 + 5 3 + 4 4 + 3 5 + 2 6 + 1 7 + 0 21 Name
What do you notice about our list of expressions?
I notice it goes 0, 1, 2, … , 7. (Points to the first addends.) (Points to the second addends.) Here it is like you are counting backward. It starts with 0 and 7 and ends with 7 and 0.
7 + 0 and 0 + 7 have the same parts, but in a different order. What other expressions add the same numbers in a different order?
Create an anchor chart of partners to 7 by recording student responses as number bonds.
These are all the partners to 7. They show all the ways to break 7 into two parts. Share the partners to 7 with your classmate.
Display the chart next to the partners to 6 anchor chart from lesson 20.
If time allows, conclude this segment by displaying the picture of 7 birds. Have the class use partners to 7 to find various ways to sort the birds into two groups. Chart their responses. The sample chart shows possible responses.
We notice:
• 1 striped wings, 6 no stripes
• 2 on the ground, 5 in the air
• 3 grey, 4 blue
Differentiation: Challenge
Students may see a pattern in the expressions created for 6 and 7 and not need counters or coloring to generate expressions of 8. Have those students explain how they figured out the expressions and how they know they found them all.
1 ▸ M1 ▸ TD ▸ Lesson 21 EUREKA MATH2 New York Next Gen © Great Minds PBC 292
Two-Part Expressions of 8
Materials—T: Chart paper; S: Two-color counters, crayons, cup
Students organize counters to find all expressions of 8.
Distribute 1 more counter to each student. Invite students to find and record all the two-part expressions of 8 by using the same process they used for totals of 7.
As they clean up, have students place counters and crayons back in cups and set them aside for use in a game at the end of the lesson.
Display a work sample, and invite students to reflect on their work.
How many expressions are there for 8? Is our prediction correct?
There are 9 expressions. Our prediction was right.
As with 7, invite students to think–pair–share about the patterns in the counters and expressions. Then create an anchor chart of partners to 8 by recording number pairs as number bonds.
These are all the partners to 8. They show all the ways to break 8 into two parts. Share the partners to 8 with your classmate.
Display the anchor chart next to the anchor charts for partners to 6 and 7.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 21 © Great Minds PBC 293
M1 TD Lesson 21 EUREKA MATH Copyright © Great Minds PBC 150 CLASS WORK Ways to Make 8 0 + 8 1 + 7 2 + 6 3 + 5 4 + 4 5 + 3 6 + 2 7 + 1 8 + 0
If time allows, conclude this segment by displaying the picture of 8 animals at the pond. Have the class use partners to 8 to sort the animals similar to the previous picture of 7 birds. Chart their responses. The sample chart shows possible responses.
We notice:
• 1 standing, 7 not standing
• 2 big animals, 6 little animals
• 3 in pond, 5 out of pond
• 4 ducks, 4 frogs
• 8 animals, 0 people
Problem Set
Materials—S: Cup, Shake Those Disks: 7, Shake Those Disks: 8, two-color counters
Prompt students to play Shake Those Disks in pairs to practice partners to 7 then 8. As needed, remind students how to play the game.
• Partner A shakes the 7 two-color counters in a cup and spills them out.
• Partner A finds how many counters landed on red and how many on yellow. They say the total and the parts they see. For example, 7 is 4 and 3, or 7 = 4 + 3.
• Partner B identifies the matching number bond on the Shake Those Disks: 7 graph and makes an X above it.
• Partners switch jobs.
1 ▸ M1 ▸ TD ▸ Lesson 21 EUREKA MATH2 New York Next Gen © Great Minds PBC 294
EUREKA MATH M1 TD Lesson 21 Shake Those Disks: 7 Copyright © Great Minds PBC 143 Shake Those Disks: 7 X X X X X X X X X X 7 0 7 7 1 6 7 3 4 7 2 5 EM2_0101TE_D_L21_shake_and_spill7_8_studentwork.indd 143 M1 TD Lesson 21 Shake Those Disks: EUREKA MATH2 Copyright © Great Minds PBC 144 Shake Those Disks: 8 X X X X X X X X X X X X 8 0 8 8 1 7 8 3 5 8 2 6 8 4 4 EM2_0101TE_D_L21_shake_and_spill7_8_studentwork.indd 144 29/12/20 12:07 PM
Consider posting a sentence frame(s) to help students state the number sentence that represents their counters: is and . OR = +
Circulate and provide support. After about 3 or 4 minutes, have students use 8 two-color counters and the Shake Those Disks: 8 graph.
Have students clean up by placing their counters back in the cup. Set these materials to the side for use in lesson 22.
Differentiation: Challenge
At another time, consider creating deeper exploration by encouraging student pairs to graph their sorts for the 7 birds or 8 animals at the pond. The Launch in lesson 20 provides examples of sorting the items in a picture to create graphs. The sorting graph is located in the student book.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 21 © Great Minds PBC 295
Land
Debrief 5 min
Materials—T: Addition expression cards (totals of 7 and 8), Addition Totals chart
Objective: Find all two-part expressions equal to 7 and 8.
Gather students and display the Addition Totals chart.
Invite students to share the expressions of 7 they found in this lesson. As students share, place the corresponding Addition expression cards on the chart in order. If students do not share all the expressions of 7, show the remaining expression cards, and ask the class to confirm that the cards show a total of 7.
Engage students in a discussion about the finite set of expressions of 7.
How do we know these are all the ways to make 7 with two parts?
I see all the matches 0 + 7 and 7 + 0, … , 3 + 4 and 4 + 3. The total of 6 has 7 expression cards, and the total of 7 has 1 more. Repeat the process with expressions of 8.
Conclude by having students predict the number of expressions for totals of 9 and 10. Consider recording these predictions to use in lesson 22.
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
1 ▸ M1 ▸ TD ▸ Lesson 21 EUREKA MATH2 New York Next Gen 296 © Great Minds PBC
5 35 10 0 1 2 3 4 5 6 0 + 0 0 + 1 0 + 2 0 + 3 0 + 4 0 + 5 0 + 6 + 0 1 + + 2 + 3 1 + 4 + 5 2 + 0 2 + 1 2 + 2 2 + 3 2 + 4 3 + 0 3 + 3 + 2 3 + 3 4 + 0 4 + 4 + 2 5 + 0 5 + 1 6 + 0 7 8 0 + 7 0 + 8 + 6 1 + 7 2 + 5 2 + 6 3 + 4 3 + 5 4 + 3 4 + 4 5 + 2 5 + 3 6 + 6 + 2 7 + 0 7 + 8 + 0
© Great Minds PBC 22 LESSON 22
9 and 10. © Great Minds PBC 157 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 22 22 1. Color a way to make 9. Fill in the number bond Write the number sentence. Name Sample: 9 5 4 5 + 4 = 9 © Great Minds PBC 158 EXIT TICKET 1 ▸ M1 ▸ TD ▸ Lesson 22 EUREKA MATH2 New York Next Gen 2. Color a way to make 10. Fill in the number bond Write the number sentence. Sample: 6 + 4 = 10 10 6 4
Find all two-part expressions equal to
Lesson at a Glance
Students now decompose 9 and 10 to complete the lesson trio: 20, 21, and 22. As in earlier lessons, students use two-color counters to systematically model the finite set of two-part expressions equal to totals of 9 and 10. They record the expressions and develop fluency with the facts by playing a game.
Key Question
• How can we use the pattern on the Addition Totals chart to be sure that we found all the ways to make 9? 10?
Achievement Descriptors
1.Mod1.AD4 Add fluently within 10. (NY-1.OA.6b)
1.Mod1.AD5 Fluently decompose totals within 10 in more than one way. (NY-1.OA.6b)
Agenda
Fluency 10 min
Launch 5 min
Learn 35 min
• Two-Part Expressions of 9
• Two-Part Expressions of 10
• Problem Set
Land 10 min
Materials Teacher
• 20-bead rekenrek
• Chart paper
• Addition expression cards (totals of 9 and 10)
• Addition Totals chart (0–8)
Students
• Two-color counters (10)
• Crayons to match the colors on the counters
• Cup
• Shake Those Disks: 9 (in the student book)
• Shake Those Disks: 10 (in the student book)
Lesson Preparation
• Add 1 more counter to the cups of 8 counters used in lesson 21. Prepare to distribute 1 more counter to each student in the middle of the lesson.
• Prepare to add expressions of 9 and 10 to the Addition Totals chart that began in lesson 18.
• Shake Those Disks: 9 and Shake Those Disks: 10 must be torn out of student books and placed in personal whiteboards. Consider whether to prepare these materials in advance or to have students prepare them during the lesson.
© Great Minds PBC 299 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 22
Fluency
Show Me the Math Way: Totals of 9
Students show numbers the math way and say an addition number sentence to prepare for work with decompositions of 9.
Show me 8.
Show me 9.
Show me 8.
How many more to make 9?
Say the addition sentence starting with 8. Ready?



8 + 1 = 9
Repeat the process of making 9 with the following sequence of starting numbers:
Show Me the Math Way: Totals of 10
Students show numbers the math way and say an addition number sentence to prepare for work with decompositions of 10.
Show me 9.
Show me 10.
Show me 9.
How many more to make 10?
Say the addition sentence starting with 9. Ready?
9 + 1 = 10

1 ▸ M1 ▸ TD ▸ Lesson 22 EUREKA MATH2 New York Next Gen © Great Minds PBC 300
1
1
10 5 35 10 8 9 5 4 9 0 7 2 6 3 9 10
Repeat the process of making 10 with the following sequence of starting numbers:
Choral Response: Doubles on the Rekenrek
Materials—T: Rekenrek
Students count using an array configuration to prepare for noticing patterns when adding doubles beginning in lesson 23.
Show students the rekenrek with the side panel attached. Start with 2 beads to the left side, shown as 1 bead on the top row and 1 bead on the bottom row.
How many beads?
Show 4 on the rekenrek as 2 beads on the top and 2 beads on the bottom.
How many beads?
Continue the process with the following sequence:
Offer more practice with doubles on the rekenrek, skipping around within 10 in array configurations.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 22 © Great Minds PBC 301
2
4
6 8 10
1 2 8 3 7 4 6 5
Student View
Student View
Launch
Materials—T: Addition Totals chart
Students analyze the Addition Totals chart to predict the number of two-part expressions that make 9 and 10.
Gather students and display the Addition Totals chart. Help students recall that the numbers along the top show the totals, and the expressions of each total are listed below.
Invite students to use the chart to think–pair–share about the following questions.
What do we know about how many expressions there are for a total?
There is 1 more expression than the total. The total of 7 has 8 expressions.
Each new total has 1 more expression than the last one.
How many expressions do you think we can make for 9? Why?
How many expressions do you think we can make for 10? Why? Record students’ predictions to validate later in the lesson. Transition to the next segment by framing the work.
Let’s see if we are right. Today, we will find all the expressions with two parts that make 9 or 10.
Promoting the Standards for Mathematical Practice
Students look for and make use of structure (MP7) when they use previously noticed patterns to make a conjecture about how many expressions of 9 and 10 there will be and to help them list these expressions efficiently.
Ask the following questions to promote MP7:
• Why is it helpful to see the expressions of 6, 7, and 8 when trying to list the expressions of 9 and 10?
• How is finding all the expressions of 9 or 10 similar to finding the expressions of 6, 7, and 8?
1 ▸ M1 ▸ TD ▸ Lesson 22 EUREKA MATH2 New York Next Gen © Great Minds PBC 302
10 5 35 10 0 1 2 3 4 5 6 0 + 0 0 + 1 0 + 2 0 + 3 0 + 4 0 + 5 0 + 6 + 0 1 + + 2 + 3 1 + 4 + 5 2 + 0 2 + 1 2 + 2 2 + 3 2 + 4 3 + 0 3 + 3 + 2 3 + 3 4 + 0 4 + 4 + 2 5 + 0 5 + 1 6 + 0 7 8 0 + 7 0 + 8 + 6 1 + 7 2 + 5 2 + 6 3 + 4 3 + 5 4 + 3 4 + 4 5 + 2 5 + 3 6 + 6 + 2 7 + 0 7 + 8 + 0
Learn
Two-Part Expressions of 9
Materials—T: Chart paper; S: Two-color counters (9), crayons, cup
Students organize counters to find all expressions of 9.
Distribute a cup with 9 two-color counters and crayons to match the two colors to each student. Have the class turn to Ways to Make 9 in their books.
Help students recall the process that they used to find two-part expressions in lessons 20 and 21.
• Place 9 yellow counters in a line above your book.
• In your book, color the circles, and write the expression 0 + 9 to show 0 red counters and 9 yellow counters.
• Turn over the first counter on the left.
• Color the circles and write an expression to show how many red and yellow counters there are. (The first addend in the expression represents the red counters.)
Have students use the process to find and record all the two-part expressions of 9.
When students finish, display a work sample.
How many expressions are there for 9? Is our prediction correct?
There are 10 expressions. Our prediction was right.
Encourage students to notice patterns in their work.
Have them think–pair–share about the following questions.
What do you notice about the counters we colored?
This looks just like our work for totals of 6, 7, and 8.
What do you notice about our list of expressions?
I notice it goes 0, 1, 2, … , 9. (Points to the first addends.)
Differentiation: Challenge
Students may recognize the pattern from expressions of 6, 7, and 8 and not need counters or coloring to generate expressions of 9.
Consider having these students write all the expressions and then check with counters or a partner to confirm that they have all the expressions.
These students may also explore repeating this reasoning for larger numbers, such as 12, 16, or 20. Ask:
• How many two-part expressions that total 12 do you think there are? Test your guess!
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 22 © Great Minds PBC 303
10 5 35 10 EUREKA MATH M1 TD Lesson 22 Copyright Great Minds PBC 22 Name Ways to Make 9 0 + 9 + 8 2 + 7 3 + 6 4 + 5 5 + 4 6 + 3 7 + 2 8 + 9 + 0
(Points to the second addends.) Here it’s like you are counting backward.
It starts with 0 and 9 and ends with 9 and 0.
9 + 0 and 0 + 9 have the same parts, but in a different order. What other expressions add the same numbers in a different order?
Create an anchor chart of partners to 9 by recording student responses as number bonds.
These are the partners to 9. They show all the ways to break 9 into two parts. Tell your partner the partners to 9.
Display the chart next to the partners to 6, 7, and 8 anchor charts from lessons 20 and 21.
If time allows, conclude this segment by displaying the picture of 9 muffins. Have the class use partners to 9 to find various ways of sorting the muffins in the bakery. Chart their responses. The sample chart shows possible responses.
We notice:
• 1 jumbo size, 8 normal size
• 2 purple wrappers, 7 green wrappers
• 3 on the top shelf, 6 on the bottom shelf
• 4 with berries, 5 with no berries
Two-Part Expressions of 10
Materials—T: Chart paper; S: Two-color counters, crayons, cup
Students organize counters to find all expressions of 10.
Distribute 1 more counter to each student. Invite students to find and record all the two-part expressions of 10 by using the same process they used for totals of 9.
1 ▸ M1 ▸ TD ▸ Lesson 22 EUREKA MATH2 New York Next Gen © Great Minds PBC 304
M1 TD Lesson 22 EUREKA MATH Copyright Great Minds PBC 2 PROBLEM SET Ways to Make 10 0 + 10 + 9 2 + 8 3 + 7 4 + 6 5 + 5 6 + 4 7 + 3 8 + 2 9 + 1 10 + 0
As students finish, display a work sample, and invite students to reflect on their work.
How many expressions are there for 10? Is our prediction correct?
There are 11 expressions. Our prediction was right.
As they did with 9, invite students to think–pair–share about the patterns in the counters and expressions of 10. Then create an anchor chart of partners to 10 by recording number pairs as number bonds.
These are all the partners to 10. They show all the ways to break 10 into two parts. Tell your partner the partners to 10.
Display the anchor chart next to the anchor charts for partners to 6, 7, 8, and 9.
If time allows, conclude this segment by displaying the picture of 10 puppies at the dog park. Have the class use partners to 10 to sort the puppies, as with the picture of muffins. Chart their responses. The sample chart shows possible responses.
We notice:
• 1 sleeping, 9 awake
• 2 have a ball, 8 have no ball
• 3 wearing collars, 7 no collars
• 4 have spots, 6 have no spots
• 5 white, 5 brown
Teacher Note
Consider posting or saving the partners to 6–10 posters for use in module 2.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 22 © Great Minds PBC 305
Problem Set
Materials—S: Cup, Shake Those Disks: 9, Shake Those Disks: 10, two-color counters
Prompt students to play Shake Those Disks in pairs to practice partners to 9 and 10. As needed, remind students how to play the game.
• Partner A shakes the 9 two-color counters in a cup and spills them out.
• Partner A counts how many counters landed on red and how many on yellow. They say the total and the parts they see. For example, 9 is 4 and 5 or 9 = 4 + 5.
• Partner B identifies the matching number bond on the Shake Those Disks: 9 graph and makes an X above it.
• Partners switch roles.
Consider posting a sentence frame to help students state the number sentence that represents their counters:
Differentiation: Challenge
Point out to students that in the game Roll a Total, some totals are more likely than others. Ask:
• In Shake Those Disks, are any partners more likely to spill than others? Why?
Circulate and support students. After about 3 or 4 minutes, have students repeat the activity by using 10 two-color counters and the Shake Those Disks: 10 graph.
Differentiation: Challenge
After the lesson, consider creating deeper exploration by encouraging pairs to graph their sorts for the picture of the 9 muffins in the bakery or the 10 puppies at the dog park. The Launch in lesson 20 provides examples of how to sort the items in a picture to create information for a graph. The graph recording sheet is located in the student book.
1 ▸ M1 ▸ TD ▸ Lesson 22 EUREKA MATH2 New York Next Gen © Great Minds PBC 306
is and . OR = +
EUREKA MATH M1 TD Shake Those Disks: 9 Copyright © Great Minds PBC 151 Shake Those Disks: 9 X X X X X X X X X X 0 9 9 1 8 9 2 7 9 3 6 9 4 5 9 EM2_0101TE_D_L22_shake_and_spill_9_10_studentwork.indd 151 04/01/21 8:54 PM M1 TD ▸ Shake Those Disks: 10 EUREKA MATH Copyright © Great Minds PBC 152 Shake Those Disks: 10 X X X X X X X X X X X X X X 0 10 10 1 9 10 2 8 10 3 7 10 4 6 10 5 5 10 EM2_0101TE_D_L22_shake_and_spill_9_10_studentwork.indd 152
Land
Debrief 5 min
Materials—T: Addition expression cards (totals of 9 and 10), Addition Totals chart
Objective: Find all two-part expressions equal to 9 and 10.
Invite students to share the expressions of 9 and 10 they created in this lesson. As students share, place the corresponding Addition expression cards on the chart in order. If students do not share them all, show the remaining expressions, and ask the class to confirm that they show totals of 9 or 10.
Engage students in a discussion about the finite set of expressions of 9 and 10.
How many ways are there to make 9? 10?
There are 10 ways to make 9, and there are 11 ways to make 10.
How do we know these are all the ways to make 9 and 10 with two parts?
There is always 1 more expression than the total. The total of 10 has 11 expressions. Each next total has 1 more expression than the total before.
Invite students to think about the entire Addition Totals chart. As time allows, guide students to notice other patterns, such as the following:
• Doubles
• Rows show 0+, 1+, 2+, 3+, 4+, 5+, 6+, 7+, 8+, 9+, and 10+ facts
Leave the Addition Totals chart displayed for future lessons. Consider also displaying it throughout module 2 (or all year).
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
Differentiation: Challenge
• Which totals have a doubles fact? How might that pattern continue? Why?
• If the order of the parts does not matter, how many number bonds could we make for each total?
• Now that we have tested our predictions, what is the rule for how many two-part expressions there are for any total?
The number of two-part expressions is 1 more than the total.
If you add 1 to the total, that is how many there are.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 22 307 © Great Minds PBC
5 35 10 0 1 2 3 4 5 6 0 + 0 0 + 0 + 2 0 + 3 0 + 4 0 + 5 0 + 6 + 0 + 1 + 2 1 + 3 1 + 4 + 5 2 + 0 2 + 1 2 + 2 2 + 3 2 + 4 3 + 0 3 + 1 3 + 2 3 + 3 4 + 0 4 + 4 + 2 5 + 0 5 + 6 + 0 7 8 0 + 7 0 + 8 + 6 + 7 2 + 5 2 + 6 3 + 4 3 + 5 4 + 3 4 + 4 5 + 2 5 + 3 6 + 6 + 2 7 + 0 7 + 8 + 0 9 10 0 + 9 0 + 10 + 8 1 + 9 2 + 7 2 + 8 3 + 6 3 + 7 4 + 5 4 + 6 5 + 4 5 + 5 6 + 3 6 + 4 7 + 2 7 + 3 8 + 1 8 + 2 9 + 0 9 + 1 10 + 0
Find the totals of doubles +1 facts.
Lesson at a Glance
The introduction of doubles in topic B and continued fluency practice have prepared students for the concepts in this lesson. Students recognize doubles facts through analyzing a series of pictures. They discover that they can use doubles facts to help them find doubles +1 facts. They apply these understandings to a sequence of related doubles and doubles +1 problems.
Key Question
• How can a doubles fact help us find the total of a doubles +1 fact?
Achievement Descriptor
1.Mod1.AD3 Add within 20 by using strategies such as counting on or by creating an equivalent but easier problem. (NY-1.OA.5, NY-1.OA.6a)
© Great Minds PBC 23 LESSON 23
© Great Minds PBC 165 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 23 23 Add. Show how you know the total. Sample: Name 3 + 3 + 1 = 7 4 + 4 + 1 = 9 3 + 3 = 6 3 + 4 = 7 4 + 5 = 9
Agenda
Fluency 10 min
Launch 10 min
Learn 30 min
• Doubles +1
• Number String
• Problem Set
Land 10 min
Materials Teacher
• 20-bead rekenrek Students
• Bag of Addition expression cards for Match: Addition Expressions (21-card set per student pair)
Lesson Preparation
Ready the bags of Addition expression cards prepared in lesson 19.
© Great Minds PBC 309 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 23
Fluency
Match: Addition Expressions
Materials—S: Bag of Addition expression cards
Students identify equivalent expressions and use them to make a true number sentence to develop an understanding of equality. Have students form pairs. Distribute a set of cards to each pair, and have them play according to the following rules. Consider doing a practice round with students.
• Lay out six cards expression side up.
• Match two expressions that have equal totals.
• Form a true number sentence by placing an equal sign card between equal expressions.
• Check that the number sentence is true. Turn over the cards to the side with the color border to see whether the totals on both sides of the equal sign are the same.
• Place the matched cards to the side, and replace them with two new cards from the pile.
• Continue until all cards are matched. Circulate as students play the game, and provide support as needed.
Choral Response: Doubles on the Rekenrek
Materials—T: Rekenrek
Students count using an array configuration and say an addition sentence to prepare for noticing patterns when adding doubles and doubles +1.
Show students the rekenrek with the side panel attached. Start with 2 beads to the left side, shown as 1 bead on the top row and 1 bead on the bottom row.
1 ▸ M1 ▸ TD ▸ Lesson 23 EUREKA MATH2 New York Next Gen © Great Minds PBC 310
10 10 30 10 2 + 3 4 + 1 = Front 5 5 = Back
How many beads?
How many beads are on the top?
Student View
Teacher Note
How many beads are on the bottom?
Say the number sentence. (Point to the top and bottom rows as students respond.)
1 + 1 = 2
Repeat the process with the following sequence:
Launch
Students use doubles facts to write number sentences that represent groups of objects.
Display the picture of 8 fish, and use the Math Chat routine to engage students in discussion.
How many fish are there? How do you know?
Allow think time. Have students show a silent signal to indicate when they are ready. Then pair students to discuss their thinking. Students may count on from 4, count by twos, or know the doubles fact.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 23 © Great Minds PBC 311
2
1
1
2 + 2 = 4 3 + 3 = 6 4 + 4 = 8 5 + 5 = 10
As students become familiar with the routine, consider reducing the questions to as few words as possible (e.g., Top? Bottom?). Using this economy of language allows students to complete a greater volume of problems in a short time while maintaining an energetic pace. 10 10 30 10
Invite a student who sees the doubles fact 4 + 4 = 8 to share.
I see 4 green fish and 4 blue fish. 4 + 4 = 8.
Record 4 + 4 = 8 next to the picture.
How do you know that 4 + 4 = 8? It is a doubles fact I know. It is a partner to 8. I counted on.
Display the picture of 9 fish, and invite students to think–pair–share.
How many fish are there now? How do you know?
9. It is the same picture, just now there is a purple fish at the bottom of one side.
Record 4 + 5 = 9 next to the picture.
Here is another way to think about it. We can use 4 + 4, the doubles we already know, and add 1 more.
Circle two groups of 4 fish and a group of 1 fish in the picture. Have students think–pair–share about the following question.
What number sentence can we write to show this strategy?
4 + 4 + 1 = 9
1 ▸ M1 ▸ TD ▸ Lesson 23 EUREKA MATH2 New York Next Gen © Great Minds PBC 312
Record 4 + 4 + 1 = 9 below 4 + 5 = 9, leaving space between the number sentences. Next, draw a number bond to show decomposing the 5 in 4 + 5 = 9 as 4 and 1.
Teacher Note
Drawing a number bond is a way to show doubles embedded in a number sentence. The number bond model supports understanding of this concept. Exposure to this notation is foundational to work in module 3.
We can think of 4 + 5 as 4 + 4 + 1. Why might we want to do that?
It is easier. We know 4 + 4 and just have to add 1.
Display the picture of 9 fish with the number sentence 4 + 5 = 4 + 4 + 1.
How do we know that 4 + 5 is equal to 4 + 4 + 1?
We just circled the fish differently.
I see 4 and 5 on both sides. Both sides have the same total, 9.
To illustrate equality, draw number bonds to show that both expressions have the same total.
Because they have the same total, we can think of 4 + 5 as 4 + 4 + 1. We call 4 + 5 = 9 a doubles +1 fact.
Transition to the next segment by framing the work.
Today, we will find totals by thinking of the doubles facts we know.
Teacher Note
Students may reason about equality in several ways, including by:
• concretely modeling both expressions and seeing that they represent the same number of objects,
• calculating the sum on both sides of the equal sign to see that they have the same total, or
• relating the addends, or parts, on both sides of the equal sign without any calculations.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 23 © Great Minds PBC 313
Learn
Doubles +1
Students decompose an addend to make a doubles +1 problem. Use the following process to guide students through the first pair of equations in their book: 2 + 2 = and 2 + 3 = .
Have students write the total for 2 + 2.
What is the same and what is different about the cubes that show 2 + 2 and the cubes that show 2 + 3?
They both show 2 + 2 with red cubes. The cubes for 2 + 3 have 1 more blue cube.
How can the doubles 2 + 2 help us find 2 + 3? 2 + 2 = 4. So, 2 + 3 is just 1 more.
Guide students to show this idea by writing 2 + 2 + 1 = 5.
We can see the doubles 2 + 2 in this number sentence. But where do you see 2 + 2 in 2 + 3?
We can break 3 into 2 and 1.
Revoice the idea that we can decompose 3 into 2 and 1. Draw a number bond to show the decomposition. Tell students that modeling this way helps us see the doubles +1 fact. As needed, guide students through one more problem. Then invite them to continue by working in pairs.
Number String
Students use doubles facts to find the totals in a series of related problems. Have students ready their personal whiteboards. Display the following string of problems one at a time, and use the sample dialogue to guide the facilitation. Encourage students
1 ▸ M1 ▸ TD ▸ Lesson 23 EUREKA MATH2 New York Next Gen © Great Minds PBC 314
10 10 30 10 EUREKA MATH2 M1 TD Lesson 23 159 Copyright © Great Minds PBC 23 Name 2 + 2 = 4 2 + 3 = 5 3 + 3 = 6 3 + 4 = 7 4 + 4 = 8 4 + 5 = 9 5 + 5 = 10 5 + 6 = 11 2 1 2 + 2 + 1 = 5 3 + 3 + = 7 4 + 4 + = 9 5 + 5 + 1 =11
to find the first four totals by using mental math or fingers. Have them use whiteboards only for the last two problems.
3 + 3 = 3 + 3 + 1 = 3 + 4 = 4 + 4 = 4 + 5 = 5 + 6 =
What is 3 + 3? How do you know?
Give students a moment of silent think time. 6, I just know it. It’s a doubles fact.
I used my fingers to show 3 + 3. I saw 6 fingers.
Record the total.
What is 3 + 3 + 1? How do you know?
I already know that 3 and 3 make 6, so I just added 1 more. That’s 7.
Record the total.
Show 3 + 4 = and ask students to find the total. Record the total, and then have students turn and talk to share how they found the answer. Listen for thinking such as the following:
If 3 + 3 = 6, then 3 + 4 = 7. It’s just 1 more.
We just added 3 + 3 + 1, which has the same total as 3 + 4.
Record students’ ideas by drawing a number bond to decompose 4 into 3 and 1. Ask students where they see the doubles 3 + 3.
Show 4 + 4 = . After a moment of think time, have the class say the answer chorally. Record the total.
Show 4 + 5 = .
Teacher Note
An intentionally crafted sequence of related problems is commonly called a number string. A number string sequence begins with a problem that is accessible to all learners. Students consider how to apply a strategy— in this case, using doubles facts—as they move through the sequence, completing increasingly challenging problems.
The intentional sequence helps students use their thinking about one problem to solve another. Provide more explicit support by using the following prompts:
• How did the last problem help you figure out this one?
• Keep the last problem in your mind. Now find the total for this problem.
Promoting the Standards for Mathematical Practice
As students find the totals in the number string and notice patterns, they look for and express regularity in repeated reasoning (MP8).
Ask the following questions to promote MP8:
• What patterns do you notice in 3 + 3, 3 + 3 + 1, and 3 + 4?
• How do you know that using a doubles fact to make a doubles +1 fact gives you the right total?
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 23 © Great Minds PBC 315
Advance students’ thinking toward decomposing an addend to make a doubles +1 fact.
What doubles fact could help you find this total?
4 + 4 = 8
Prompt students to use their personal whiteboards to show their thinking. Invite a student who makes a doubles +1 problem to show their work. If no one uses this strategy, then model the strategy. Record the total.
Show 5 + 6 = . Encourage students to find the total by using the doubles +1 strategy. Have them show their work on personal whiteboards.
How did a doubles fact help you?
5 + 5 = 10. So, 5 + 6 is just 1 more.
Where did you see 5 + 5 in 5 + 6?
6 can be broken into 5 and 1.
Problem Set
Differentiate the set by selecting problems for students to finish independently within the timeframe. Problems are organized from simple to complex. The directions may be read aloud.
Some students may know doubles facts beyond 4 + 4 = 8. Consider letting them explore the doubles +1 strategy with the following expressions:
1 ▸ M1 ▸ TD ▸ Lesson 23 EUREKA MATH2 New York Next Gen © Great Minds PBC 316
1 4 4 + 5 4 + 4 + 1 = 9
Differentiation: Challenge
6 + 7 7 + 8 8 + 9 9 + 10 10 + 11
Land
Debrief 5 min
Objective: Find the totals of doubles +1 facts.
Display the picture of the dice and share a brief story that contextualizes using doubles to find a total.

My friend and I played a game. This was his roll. He knew the total without even counting!
Have students think–pair–share about the following question.
How do you think he figured out the total so easily?
He just knows 5 + 4.
He knows that 5 + 5 = 10, and 1 less is 4.
He knows a doubles fact. 4 + 4 = 8, and 1 more makes 9.
Where do you see the doubles 4 + 4 in 5 + 4?
There are a total of 4 dots on one die, and there are 4 dots on the outside of the other die. 5 can be broken into 4 and 1.
How can you use a doubles fact to help you find the total of a doubles +1 fact?
We can see a doubles fact in the doubles +1 fact. We can add 1 more.
As time allows, have students identify all the doubles and doubles +1 facts on the Addition Totals chart.
Exit Ticket 5 min
Provide up to 5 minutes for students to complete the Exit Ticket. It is possible to gather formative data even if some students do not complete every problem.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 23 © Great Minds PBC 317
10 30 10 0 1 2 3 4 5 6 0 + 0 0 + 0 + 2 0 + 3 0 + 4 0 + 5 0 + 6 + 0 + + 2 1 + 3 1 + 4 1 + 5 2 + 0 2 + 1 2 + 2 2 + 3 2 + 4 3 + 0 3 + 1 3 + 2 3 + 3 4 + 0 4 + 4 + 2 5 + 0 5 + 6 + 0 7 8 0 + 7 0 + 8 + 6 + 7 2 + 5 2 + 6 3 + 4 3 + 5 4 + 3 4 + 4 5 + 2 5 + 3 6 + 6 + 2 7 + 0 7 + 8 + 0 9 10 0 + 9 0 + 10 + 8 + 9 2 + 7 2 + 8 3 + 6 3 + 7 4 + 5 4 + 6 5 + 4 5 + 5 6 + 3 6 + 4 7 + 2 7 + 3 8 + 1 8 + 2 9 + 0 9 + 1 10 + 0
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
1 ▸ M1 ▸ TD ▸ Lesson 23 EUREKA MATH2 New York Next Gen © Great Minds PBC 318
© Great Minds PBC 161 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 23 23 1. Add. Circle doubles that help you. Name 3 + 3 = 6 3 + 4 = 7 5 + 5 = 10 5 + 6 = 11 2 + 2 = 4 2 + 3 = 5 © Great Minds PBC 162 PROBLEM SET 1 ▸ M1 ▸ TD ▸ Lesson 23 EUREKA MATH2 New York Next Gen 2. Add. 4 + 4 = 8 4 + 5 = 9 2 + 2 = 4 1 + 1 = 2 2 + 3 = 5 1 + 2 = 3 3 + 3 = 6 5 + 5 = 10 3 + 4 = 7 5 + 6 = 11
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 23 319 © Great Minds PBC © Great Minds PBC 163 PROBLEM SET EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 23 3. Add. Show how you know the total. Sample: 5 + 4 = 9 4 + 4 + 1 = 9 4 + 3 = 7 3 + 3 + 1 = 7 6 + 5 = 11 5 + 5 + 1 = 11 6 + 7 = 13 6 + 6 + 1 = 13
Use known facts to make easier problems.
Lesson at a Glance
DStudents apply the skill of breaking up an addend to use doubles for finding the totals of doubles +1 facts. They share and discuss various strategies for adding, including breaking up an addend to make the problem easier.
Key Question
• How can we be sure that when we make an easier problem the total stays the same?
Achievement Descriptors
1.Mod1.AD3 Add within 20 by using strategies such as counting on or by creating an equivalent but easier problem. (NY-1.OA.5, NY-1.OA.6a)
1.Mod1.AD6 Determine whether addition and/or subtraction number sentences are true or false. (NY-1.OA.7)
© Great Minds PBC 24 LESSON 24
© Great Minds PBC 171 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD
1. Add. 2. Write a true number sentence. Sample: 3. Write a false number sentence with an X. Sample: 4 + 4 = 6 + 1 6 + 1 4 + 3 = Name 2 + 2 = 4 8 = 4 + 4 2 + 3 = 5 9 = 4 + 5
Agenda
Fluency 10 min
Launch 10 min
Learn 30 min
• How Many Ways
• Make an Easier Problem
• Problem Set
Land 10 min
Materials Teacher
• 20-bead rekenrek
Students
• Bag of Addition expression cards for Match: Addition Expressions (21-card set per student pair)
Lesson Preparation
Ready the bags of Addition expression cards prepared in lesson 19.
© Great Minds PBC 321 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 24
Fluency
Match: Addition Expressions
Materials—S: Bag of Addition expression cards
Students identify equivalent expressions and use them to make a true number sentence to develop an understanding of equality. Have students form pairs. Distribute a set of cards to each pair, and have them play according to the following rules. Consider doing a practice round with students.
• Lay out six cards expression side up.
• Match two expressions that have equal totals.
• Form a true number sentence by placing an equal sign card between equal expressions.
• Check that the number sentence is true. Turn over the cards to the side with the color border to see if the totals on both sides of the equal sign are the same.
• Place the matched cards to the side, and replace them with two new cards from the pile.
• Continue until all cards are matched. Circulate as students play the game, and provide support as needed.
Choral Response: Doubles on the Rekenrek
Materials—T: Rekenrek
Students imagine 1 more and say an addition sentence to prepare for noticing patterns when adding doubles and doubles +1.
Show students the rekenrek with the side panel attached. Start with 2 beads to the left side, shown as 1 bead on the top row and 1 bead on the bottom row.
1 ▸ M1 ▸ TD ▸ Lesson 24 EUREKA MATH2 New York Next Gen © Great Minds PBC 322
10 10 30 10 2 + 3 4 + 1 = Front 5 5 = Back
How many beads?
Imagine 1 more. How many beads?
Say the number sentence.
As students respond, slide 1 additional bead over on the top to show that 2 and 1 more is 3.
2 + 1 = 3
Repeat the process with the following sequence: 4 6 8 10
Offer more practice with doubles and doubles +1 on the rekenrek, skipping around within 10 in array configuration.
Launch
Students use doubles facts to find the totals of doubles +1 problems.
Have students ready their personal whiteboards. Display the problems shown one at a time. For each problem, allow time for students to find the answer mentally or by using whiteboards. Have them show a silent signal when they are ready. Prompt the class to chorally share the answer and record the total.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 24 © Great Minds PBC 323
2
3
Student
Student View 10 10 30 10 2 + 3 3 + 4 4 + 5 5 + 6
View
Write 2 + 3. Ask students to think about a doubles fact they know, and encourage them to use it to find the total.
What is 2 + 3?
How did you use a doubles fact to find the total?
I know that 2 + 2 = 4 and 3 is 1 more than 2. The answer is just 1 more. Record 5 as the total.
Continue with the other three problems. If students break apart an addend with a number bond or write a three-part expression on their whiteboards, ask them to show their representation as they explain their strategy. For example:
Differentiation Support
Students may benefit from seeing doubles +1 facts modeled on a rekenrek. Ask students where they see the doubles fact and record the model two ways. For example:
Consider challenging students with 6 + 7 as appropriate.
Invite students to reflect on the sequence of problems.
What do you notice about all these problems?
The two parts are just 1 away from each other.
The second part is 1 more than the first part.
The totals get bigger by 2 each time.
Give the sequence of problems a title: Doubles +1 Facts.
Why are these all called doubles +1 facts?
We can break up one part to make doubles and then add 1 more. Then transition to the next segment by framing the work.
Let’s look at different ways we know that can make problems easier.
1 ▸ M1 ▸ TD ▸ Lesson 24 EUREKA MATH2 New York Next Gen © Great Minds PBC 324
3 + 4 3 1 3 + 3 + 1 = 7
Learn
How Many Ways
Materials—T: Rekenrek
Students self-select addition strategies and discuss their choices as a class.
Write 4 + 6. Tell students that their job is to use and share as many ways as possible to add 4 and 6.
Provide think time and ask students to record their work on their whiteboards. Have them give a silent signal to show when they are ready. Then prompt students to share their thinking with a partner.
As pairs talk, identify several students who can share their strategies in a later discussion. In particular, try to choose students who decompose an addend similar to Beth’s way or Nate’s way. If no one uses that strategy, then plan to present Beth’s way during discussion and ask the class to explain the strategy.
Engage students in a discussion about ways to add 4 and 6. Invite students to share their thinking with the class, and record their reasoning. Encourage students to use the Talking Tool to ask questions about their peers’ work.
Corey, how did you find the total?
I counted on from the bigger number. Siiiix, 7, 8, 9, 10.
Did anyone find the total a different way?
Beth: I broke 6 into 4 and 2. 4 + 4 = 8 and 2 more is 10.
Nate: I broke 6 into 5 and 1 because I know my 5 facts. 4 + 5 = 9 and 1 more is 10.
Senji: I thought of 4 + 6 as 5 + 5. I took 1 from 6 and added it to 4. I know 5 + 5 = 10.
As such strategies are shared, consider using the rekenrek to model the thinking.
10.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 24 © Great Minds PBC 325
10 10 30 10 Beth’s Way Nate’s Way Corey’s Way Peg’s Way 4 + 4 + 2 = 10 4 + 6 4 2 4 + 5 + 1 = 10 4 + 6 = 10 4 + 6 5 1 6 7 8 9 10 I know the partners that
Senji’s Way 5 + 5 = 10 4 + 6 1
add to
Teacher Note
Some students will begin to add by using more sophisticated strategies than counting on. For example, they may recognize that they can find totals by making easier, equivalent problems. They use the idea that smaller numbers are embedded within larger numbers to compose and decompose addends.
Strategies that involve making easier, equivalent problems are called Level 3 strategies. They are taught directly in module 3.
At this time, it is not critical for students to represent these strategies. It is more important that they can explain what they did and why it worked.
They are not expected to independently write equivalent three-part expressions or to draw number bonds to decompose an addend. These representations are primarily modeled during discussion to record students’ thinking.
Summarize the discussion by naming several strategies that the class talked about (e.g., using doubles, counting on, breaking apart numbers). Remind students that all these ways are strategies.
Close the discussion by inviting partners to turn and talk about the following questions.
What strategy did you learn to help you add 4 and 6?
Which strategy would you like to try next time? Why?
1 ▸ M1 ▸ TD ▸ Lesson 24 EUREKA MATH2 New York Next Gen © Great Minds PBC 326
Beth’s Way: Nate’s Way: Senji’s Way: 4 + 4 + 2 4 + 6 4 + 6 4 + 5 + 1 4 + 6 5 + 5
Make an Easier Problem
Materials—T: Rekenrek
Students break up an addend to make a problem easier. Some students added 4 and 6 by breaking up one part. Let’s try that strategy on another problem.
Write 5 + 7. Show the parts on the rekenrek by sliding to the left 5 beads on the top row and 7 beads on the second row.
What doubles do you see?
5 + 5
Where can we get another 5?
From the 7. We can break it into 5 and 2.
Model this by sliding the 2 white beads slightly to the right toward the center of the row. Prompt students to write 5 + 7 on their whiteboards. Guide them to draw a number bond to break 7 into 5 and 2. Point out the 2 rows of 5 red beads on the rekenrek.
What is 5 + 5?
How many more do we still need to add?
What is 10 + 2?
Then what is 5 + 7?
Is 5 + 7 or 10 + 2 easier? Why? 10 + 2. We know 5 + 5 = 10 and just 2 more is 12.
Write 5 + 5 + 2 = 12.
Promoting the Standards for Mathematical Practice
Students construct viable arguments (MP3) when they choose a strategy that makes sense to them and explain their thinking verbally.
Ask the following questions to promote MP3:
• Why does your strategy work?
• What questions can you ask about your classmate’s strategy?
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 24 © Great Minds PBC 327
10
2
12
12
Ask students to find 5 + 7 another way and then share their thinking with a partner. They may choose counting on or shifting 1 from 7 to 5 to make 6 + 6. Invite a few students to share their different strategies (see sample student thinking).
If time allows, write 5 + 3. Prompt students to work with a partner to find the total and show their thinking on their whiteboards. If they just know the fact, encourage them to record a strategy that validates that their total is correct. Lead a class discussion. Try to select at least one student who made the problem easier.
Problem Set
Differentiate the set by selecting problems for students to finish independently within the timeframe. Problems are organized from simple to complex. The directions may be read aloud.
All students should complete 6 + 7. As the class works, select two students to share their strategies. Have these students bring their books to the Debrief in Land.
1 ▸ M1 ▸ TD ▸ Lesson 24 EUREKA MATH2 New York Next Gen © Great Minds PBC 328
3 + 3 + 2 = 8 5 + 3 2 3 6, 7, 8 5 5 + 3 = 8 I know my 5+ facts! 4 + 4 = 8 5 + 3 1
Land
Debrief 5 min
Objective: Use known facts to make easier problems.
Gather students and remind them that mathematicians use different strategies to add. Call on two students who used different strategies for 6 + 7 to share their thinking. Students may use the following strategies:
• Counting on from 7
• Doubles +1 (6 + 6 + 1)
• Decompose 6 into 5 and 1 and 7 into 5 and 2, then add (5 + 5 + 1 + 2)
Adrien, how did you find the total?
I made the problem easier by thinking of 5 + 5 = 10. Then I just needed to add 1 and 2 more. That is 13.
Ren, how did you make this problem easier?
I know 6 + 6 = 12. It is a doubles fact. Then I added 1 more. These students used two different strategies. Both found the same correct answer.
Topic Ticket 5+ min
Provide 5–10 minutes for students to complete the Topic Ticket. It is possible to gather formative data even if some students do not complete every problem.
UDL: Action & Expression
Support students in monitoring their own progress by having them sort addition expressions on a chart. Provide students with expression cards (the sets can be differentiated). They should complete the cards one at a time, using a strategy of their choice, and place each card in the appropriate category. A sample strategy sorting mat is shown below.

EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 24 © Great Minds PBC 329
10 30 10
I Know It Doubles +1 Count On My Way 3 4 5
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
2. Add. Show how you know the total.
1 ▸ M1 ▸ TD ▸ Lesson 24 EUREKA MATH2 New York Next Gen © Great Minds PBC 330
© Great Minds PBC 167 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 24 24
2 + 3 = 5 3 + 4 = 7 5 + 6 = 11 4 + 3 = 7 6 + 5 = 11 5 + 4 = 9 Name 1 ▸ M1 ▸ TD ▸ Lesson 24 EUREKA MATH2 New York Next Gen © Great Minds PBC 168 PROBLEM SET
Sample: 2 + 4 = 6 5 + 3 = 8 4 + 6 = 10 4 + 4 + 2 = 10 13 = 7 + 6 6 + 6 + 1 = 13 12 = 7 + 5 5 + 5 + 2 = 12 14 = 6 + 8 6 + 6 + 2 = 14 6 + 7 = 13
1. Color the circles. Circle doubles that help you. Write the total.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 24 331 © Great Minds PBC EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 24 © Great Minds PBC 169 PROBLEM SET 3. Add. 6 + 6 = 12 9 + 1 = 10 0 + 17 = 17 14 = 8 + 6 11 = 7 + 4 14 = 7 + 7
Organize, count, and record a collection of objects. (Optional)
Lesson at a Glance
This student-driven lesson invites partners to count and record a collection of objects by using tools and strategies of their choice. Through comparing and connecting strategies, students recognize the value of organizing objects into groups to count efficiently. Students may display a range of abilities.
Due to the time needed to count collections, Fluency, Problem Set, and Exit Ticket are not included in this lesson. Use student recordings to analyze their work.
Key Question
• How can we use groups to help us organize and count?
Achievement Descriptor
This lesson is foundational to the work of NY-1.NBT.1. Lesson content is intended to serve as a formative assessment and is therefore not included on summative assessments in this module.
Exit Ticket
There is no Exit Ticket for this lesson. Instead, use students’ recordings to analyze their work after the lesson.
© Great Minds PBC 25 LESSON 25
Agenda
Launch 10 min
Learn 45 min
• Organize, Count, and Record
• Share, Compare, Connect
Land 5 min
Materials Teacher
• None Students
• Counting collection (1 per student pair)
• Organizing tools
Lesson Preparation
• Count, bag, and display collections. Prepare and display a counting collection in a bag or small box. Each collection should have up to 120 items. Although this lesson uses two types of bears, cubes, and pattern blocks, you may incorporate other items of high interest.
• Have whiteboards or sticky notes accessible.
• Prepare counting mats or chart paper for each student pair.
• Select tools that students can choose to organize their count, such as cups, plates, number paths, or 10-frames.
• Copy or print the recording sheet to use for demonstration.
© Great Minds PBC 333 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 25
Launch
Materials– T: Counting collection
Students estimate the total number of objects in a collection and prepare to organize and count.
Gather students, and show a counting collection. Explain that students will choose a similar set of objects to organize, count, record, and share.




Briefly orient students to the procedure of counting a collection. Consider making and displaying a chart.


• Choose a set of objects and organizing tools.
• Make a good guess about how many objects are in the collection.

• Plan how to count the collection, then count.
• Show how you counted the collection on paper.
• Share your work.
Using the demonstration collection, guide students to make a reasonable estimate of how many objects are in the collection.
Mathematicians think about how many there might be before they count. Let’s make a good guess.
How many do you think there are in my collection? Turn and talk to your partner.
What total is too low?
(Between 0 and 20)
What total is too high?
(Greater than 200)
Estimating before counting supports students’ sense of quantity. Asking for a number they know is too high and too low early on establishes boundaries for a reasonable answer and encourages accuracy. Consider using a mounted number path to support estimation.
1 ▸ M1 ▸ TD ▸ Lesson 25 EUREKA MATH2 New York Next Gen © Great Minds PBC 334
10 10 30 10 1 2 12 3 4 5 Choose a collection. Make a good guess Make a plan and count Record the collection. Share our work. We will... 8 1, 2, 3, 4, … Teacher
Note
We said is too low, and is too high. What guess makes sense?
(Between 25 and 150)
Model how to use a recording sheet. Show students how to name their collection and write their estimate. Then use the following questions to get students thinking about how they might organize, count, and record:
How could we organize the groups to count them?
How could we show the way we count the collection?
Transition to the next segment by framing the work.
Today, we will share and discuss how we count our collections.
Learn Organize, Count, and Record
Materials—S: Counting collection, organizing tools
Students use their own strategies to organize and count objects and record their process.
Partner students, and invite them to choose a collection, organizing tools (if they would like them), and space to work.
Circulate and notice how students organize, count, and record. (See possible student work in the chart below.)
• Counting strategies may include counting by ones or another familiar number (twos, fives, tens) or counting subgroups and adding them to find the total.
• Recordings may include drawings, tally charts, numbers, expressions, or number sentences.
Teacher Note
Plan for what student pairs should do when they finish counting and recording their collections:
• Try another way to organize and count.
• Switch collections with another student pair, and count to confirm the total.
• Explain their recording to another student pair.
• Clean up and get another collection.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 25 © Great Minds PBC 335
5 5 45 5
Use the following questions and prompts to assess and advance student thinking:
• What is your plan? Show (or tell) me how you are counting.
• How are you keeping track of what you already counted and what you still need to count?
• How does what you drew or wrote show how you counted your collection?
Differentiation: Support
If students sort by size, color, or other ways not related to number, help them transition to more efficient ways of organizing and counting. Use prompts such as the following:


• How can you organize your collection to help you count?

• What organizing tools can help you count?
• Let’s visit another group to see what helps them count their collection.
Teacher Note
The sample student work shows common responses. Look for similar work from your students and encourage authentic classroom conversations about the key concepts.
If your students do not produce similar work, choose one to share and highlight how it shows movement toward the goal of this lesson.
Then select a provided sample that advances your class’s thinking. Consider presenting the work by saying, “This is how another student counted the collection. What do you think this student did?”
1 ▸ M1 ▸ TD ▸ Lesson 25 EUREKA MATH2 New York Next Gen © Great Minds PBC 336 Move and Count by Ones Organize by 5-Groups Organize by 10-Groups Copyright © Great Minds PBC 175 How many do you think there are? 70 Total 52 bears EUREKA MATH ▸ M1 TD Lesson 25 25 10 10 10 10 10 2 Name 173 Copyright © Great Minds PBC EUREKA MATH ▸ M1 ▸ TD ▸ Lesson 25 How many do you think there are? 50 Total 40 big cubes 25 Name EUREKA MATH2 M1 TD Lesson 25 Copyright © Great Minds PBC 174 How many do you think there are? 25 Total 30 small cubes Name 25
If needed, prompt students to record their collection:
• Can you write or draw something on your paper to show how you counted?
• Can you write numbers or number sentences to show your collection?
Select student work that highlights the usefulness of organization in terms of the counting or recording to share in the next segment.
Share, Compare, Connect
Students discuss strategies for organizing and counting a collection.
Gather the class to discuss the selected work.
Move and Count by Ones (Logan and Deb’s Way)
Tell us what you did first.
We put our cubes on the mat, and then we moved each one as we counted it.

Invite the pair to briefly demonstrate their strategy.
What would happen if you lost count?
We would start over.
After they demonstrate their strategy for counting, ask for their total and how it compares to their estimate.
Then ask the pair to share their recording and explain how it matches their strategy. Facilitate a discussion to lead students toward recognizing that organizing objects into groups makes counting easier.
Could you make bigger groups that would be easy to count by?
You could make groups of 5 squares. You could circle two groups of tallies to make 10.
Move and Count by Ones
Teacher Note
How do I make student collections visible for sharing?
• Have students gather around the collection.
• Take a picture of the work and project it.
• Use a portable document camera to project.
• Carefully move the counting mat to a central area.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 25 © Great Minds PBC 337
173 Copyright © Great Minds PBC EUREKA MATH ▸ M1 TD Lesson 25 How many do you think there are? 50 Total 40 big cubes 25 Name
Turn and talk to your partner about what could help you organize so you don’t lose track of the count.
Listen for students to mention 5-groups, number paths, graphs, and any other organizing tools they have used in module 1.
Close the share by inviting the class to ask questions, compliment the work, or make suggestions. Then gather the class around the next sample.
Organize
by 5-Groups (Dan and Ben’s Way)
Class, what did Dan and Ben do?
They made 5-groups.
I think they counted by fives.
Invite the pair to confirm or correct responses and then briefly demonstrate their strategy.
Why is it useful to make groups of 5?
You can count more cubes at once, so it’s faster.

If you lose track, you don’t have to start over from 1.
Ask the pair to share their total and their estimate. Then have them display their recording.
How does their picture show the way they organized their cubes?
There’s a group of 5 tallies for every group of 5 cubes. There are 6 rows of 5 cubes, and there are 6 groups of 5 tally marks.
Invite the class to ask questions, give compliments, or make suggestions.
Allow 5 minutes at the end of this segment for cleanup. Collect student recordings to review as informal assessment after the lesson.
Promoting the Standards for Mathematical Practice
Students model with mathematics (MP4) when they choose to record their collection abstractly, for example using tally marks.
Ask the following questions to promote MP4:
• What can you write or draw to represent, or show, your collection?
• How does what you wrote or drew show how you counted your collection? How is it different?
1 ▸ M1 ▸ TD ▸ Lesson 25 EUREKA MATH2 New York Next Gen © Great Minds PBC 338
EUREKA MATH M1 TD Lesson 25 Copyright © Great Minds PBC 174 How many do you think there are? 25 Total 30 small cubes Name 25
Organize by 5-Groups
Land
Debrief 5 min
Objective: Organize, count, and represent a collection of objects. Support students in reflecting on their counting experience by selecting one of the following questions.
If you were to count your collection again, would you do it the same way?
I think I would try to group my cubes into tens and then count.
I think I want to try counting by fives.
How does organizing objects into groups make it easier to count them?
If you lose track, you don’t have to start all over again. It makes it easier to draw.
You can count faster.
What is a tool you might try next time we do counting collections?
I might use cups so I can group by fives.
I might try 5-groups so I can group by tens. Maybe I’ll try the number path to 20.
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ TD ▸ Lesson 25 339 © Great Minds PBC
5 45 5
1. Color the totals. Write the totals.
Which one has more? Circle . Write two totals.
EUREKA MATH 2 New York Next Gen 1 ▸ M1 ▸ Module Assessment © Great Minds PBC This page may be reproduced for classroom use only.
Module
341
Name
Assessment
I Count Totals
>
2. Circle a part and count on. Write the number sentence . 3. Circle a part. Count on. 5 8
EUREKA MATH 2 New York Next Gen 1 ▸ M1 ▸ Module Assessment 342 © Great Minds PBC This page may be reproduced for classroom use only.
4 = 2 + 10 = = 1 + 6 = 0 + 6
+
EUREKA MATH 2 New York Next Gen 1 ▸ M1 ▸ Module Assessment 343 © Great Minds PBC This page may be reproduced for classroom use only.
true .
an X on the number sentence if it is false .
how you know.
+ 2 = 7 + 1 3 + 4 = 4 + 3
4. Show two ways to make 9. 5. Circle the number sentence if it is
Draw
Show
5
EUREKA MATH 2 New York Next Gen 1 ▸ M1 ▸ Module Assessment 344 © Great Minds PBC This page may be reproduced for classroom use only.
=
6. Write a doubles number sentence. 7. Add. Circle doubles that help you. 5 + 4
EUREKA MATH 2 New York Next Gen 1 ▸ M1 ▸ Module Assessment 345 This page may be reproduced for classroom use only. © Great Minds PBC 8. Listen to the story . Count on to find the total. 7 frogs are in the pond. 2 more frogs hop into the pond. How many frogs are in the pond now?
7 frogs
Standards
Module Content Standards
Understand and apply properties of operations and the relationship between addition and subtraction.
NY-1.OA.3 Apply properties of operations as strategies to add and subtract. Add and subtract within 20.
NY-1.OA.5 Relate counting to addition and subtraction.
NY-1.OA.6a Add and subtract within 20. Use strategies such as:
• counting on;
• making ten;
• decomposing a number leading to a ten;
• using the relationship between addition and subtraction; and
• creating equivalent but easier or known sums.
NY-1.OA.6b Fluently add and subtract within 10. Work with addition and subtraction equations.
NY-1.OA.7 Understand the meaning of the equal sign, and determine if equations involving addition and subtraction are true or false.
© Great Minds PBC 346
Understand place value.
NY-1.NBT.2 Understand that the two digits of a two-digit number represent amounts of tens and ones.
b. Understand the numbers from 11 to 19 are composed of a ten and one, two, three, four, five, six, seven, eight, or nine ones.
NY-1.NBT.3 Compare two two-digit numbers based on meanings of the tens and ones digits, recording the results of comparisons with the symbols >, =, and <. Represent and interpret data.
NY-1.MD.4 Organize, represent, and interpret data with up to three categories; ask and answer questions about the total number of data points, how many in each category, and how many more or less are in one category than in another.
Standards for Mathematical Practice
MP1 Make sense of problems and persevere in solving them.
MP2 Reason abstractly and quantitatively.
MP3 Construct viable arguments and critique the reasoning of others.
MP4 Model with mathematics.
MP5 Use appropriate tools strategically.
MP6 Attend to precision.
MP7 Look for and make use of structure.
MP8 Look for and express regularity in repeated reasoning.
EUREKA MATH2 New York Next Gen 1 ▸ M1 347 © Great Minds PBC
Module Achievement Descriptors and Content Standards by Lesson
1.Mod1.AD5 NY-1.OA.6b
1.Mod1.AD6 NY-1.OA.7
1.Mod1.AD7 NY-1.NBT.2 NY-1.NBT.2b
1.Mod1.AD8 NY-1.NBT.3 NY-1.MD.4
1.Mod1.AD9 NY-1.MD.4
348 © Great Minds PBC This page may be reproduced for classroom use only. 1 ▸ M1 EUREKA MATH2 New York Next Gen
Focus content Supplemental content A Topic 1 Lesson Achievement Descriptor Aligned NGMLS A 1 A 2 A 3 A 4 A 5 A 6 B 7 B 8 B 9 B 10 B 11 B 12 C 13 C 14 C 15 C 16 C 17 D 18 D 19 D 20 D 21 D 22 D 23 D 24 D 25 1.Mod1.AD1 NY-1.OA.3 1.Mod1.AD2 NY-1.OA.5
1.Mod1.AD3 NY-1.OA.5 NY-1.OA.6a 1.Mod1.AD4 NY-1.OA.6b
Achievement Descriptors: Proficiency Indicators
1.Mod1.AD1 Apply the commutative property of addition as a strategy to add.
RELATED NGMLS
NY-1.OA.3 Apply properties of operations as strategies to add and subtract.
Partially Proficient Proficient Highly Proficient
Count on to add, always counting on from the first addend
Circle a part.
Count on to find the total.
Apply the commutative property of addition as a strategy to add, counting on from the larger addend regardless of its position. Circle a part. Count
Explain how to use the commutative property of addition to add.
How does knowing 5 + 2 = 7 help you know the answer to 2 + 5?
5 + 2 and 2 + 5 have the same total. I can add in any order.
1.Mod1.AD2 Count on to find the total number of objects in a set and represent the total with an addition number sentence.
RELATED NGMLS
NY-1.OA.5 Relate counting to addition and subtraction.
Partially Proficient Proficient
Count on from a known part to find the total number of objects in a set.
Circle a part.
Count on to find the total.
Count on from a known part to find the total number of objects in a set and represent the total with an addition number sentence.
Circle a part.
Count on to find the total.
5 Write a number sentence.
Highly Proficient
350 © Great Minds PBC
2 + 5 = 7
on to find the total. 2 + 5 = 7
5
1.Mod1.AD3 Add within 20 by using strategies such as counting on or by creating an equivalent but easier problem.
RELATED NGMLS
NY-1.OA.5 Relate counting to addition and subtraction.
NY-1.OA.6a Add and subtract within 20. Use strategies such as:
• counting on;
• making ten;
• decomposing a number leading to a ten;
• using the relationship between addition and subtraction; and
• creating equivalent but easier or known sums.
Partially Proficient Proficient
Add within 20 by representing with objects or a drawing and counting all.
Add. Show how you know.
Add within 20 by counting on. Add. Show how you know.
Highly Proficient
Add within 20 by creating an equivalent but easier problem.
Add. Show how you know.
I started with 7 and counted on with my fingers: Sevennnn, 8, 9, 10, 11 , 12
1.Mod1.AD4 Add fluently within 10.
RELATED NGMLS
NY-1.OA.6b Fluently add and subtract within 10.
Partially Proficient Proficient
Add fluently within 5
Add fluently within 10
Highly Proficient
EUREKA MATH2 New York Next Gen 1 ▸ M1 351 © Great Minds PBC
7 + 5 = 12
5
7 +
= 12
6 + 7 = 13 6 + 6 + 1 = 13
2 + 3 =
Add.
Add. 3 + 6 =
1.Mod1.AD5 Fluently decompose totals within 10 in more than one way.
RELATED NGMLS
NY-1.OA.6b Fluently add and subtract within 10.
Partially Proficient Proficient
Decompose totals within 10 in more than one way by using objects or pictures.
Use counters to show two ways to make 7. Fill in the number bond.
Fluently decompose totals within 10 in more than one way.
Show two ways to make 7.
Highly Proficient
Fluently name the partner to a number within 10.
1.Mod1.AD6 Determine whether addition and/or subtraction number sentences are true or false.
RELATED NGMLS
NY-1.OA.7 Understand the meaning of the equal sign, and determine if equations involving addition and subtraction are true or false.
Partially Proficient Proficient Highly Proficient
Determine whether addition and/or subtraction number sentences with one operation symbol (e.g., 3 + 4 = 7) are true or false.
Circle the number sentence if it is true.
Draw an X on the number sentence if it is false. 3 + 4 = 8
Determine whether number sentences involving two addition expressions or two subtraction expressions (e.g., 5 + 2 = 6 + 1 or 6 – 4 = 3 – 1) are true or false.
Circle the number sentence if it is true.
Draw an X on the number sentence if it is false.
5 + 3 = 2 + 6
Determine whether number sentences involving both addition and subtraction expressions (e.g., 4 + 1 = 7 – 2) or three addends (e.g., 2 + 2 + 1 = 3 + 2 + 0) are true or false.
Circle the number sentence if it is true.
Draw an X on the number sentence if it is false.
9 - 3 = 2 + 4
1 ▸ M1 EUREKA MATH2 New York Next Gen 352 © Great Minds PBC
10 6 10 8
1.Mod1.AD7 Count on from 10 to find totals between 11 and 19.
RELATED NGMLS
NY-1.NBT.2 Understand that the two digits of a two-digit number represent amounts of tens and ones. NY-1.NBT.2b Understand the numbers from 11 to 19 are composed of a ten and one, two, three, four, five, six, seven, eight, or nine ones.
Partially Proficient Proficient Highly Proficient
Count on from 10 to find the total number of objects in a set arranged as 10 ones and some more ones.
Find the total. Count on from 10.
Count on from 10 to find totals between 11 and 19.
Circle a part.
Count on to find the total.
Find the totals of 10+ facts fluently.
EUREKA MATH2 New York Next Gen 1 ▸ M1 353 © Great Minds PBC
10 + 6 =
Add. 10 + 4 = 10 + 6 = 10 + 8 =
1.Mod1.AD8 Compare category totals in graphs by using the symbols >, =, and <.
RELATED NGMLS
NY-1.NBT.3 Compare two two-digit numbers based on meanings of the tens and ones digits, recording the results of comparisons with the symbols >, =, and <. NY-1.MD.4 Organize, represent, and interpret data with up to three categories; ask and answer questions about the total number of data points, how many in each category, and how many more or less are in one category than in another.
Partially Proficient Proficient Highly Proficient
Compare category totals in graphs by using the words more than, fewer than, and the same number as.
Write the totals.
Compare category totals in graphs by using the symbols >, =, and <.
Write the totals.
Compare category totals in graphs and answer how many more or how many fewer questions.
Write the totals.
Write two totals.
Circle the true sentences.
There are more ladybugs than caterpillars. There are more ladybugs than flies. There are more caterpillars than flies.
We see more caterpillar than ladybugs.
1 ▸ M1 EUREKA MATH2 New York Next Gen 354 © Great Minds PBC
✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ We See Totals
✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ We See Totals
>
greater than
✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ We
See Totals
1.Mod1.AD9 Organize and represent data with up to three categories and write how many are in each category.
RELATED NGMLS
NY-1.MD.4 Organize, represent, and interpret data with up to three categories; ask and answer questions about the total number of data points, how many in each category, and how many more or less are in one category than in another.
Highly Proficient
Write how many are in each group in a graph or chart. Write the totals.
Organize and represent data with up to three categories by using a graph or chart and write how many are in each category.
Color how many animals. Write the totals.
We See Totals
EUREKA MATH2 New York Next Gen 1 ▸ M1 355 © Great Minds PBC
Partially Proficient Proficient
✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓
See Totals
We
Observational Assessment Recording Sheet
Grade 1 Module 1
Counting, Comparing, and Adding
Achievement
Descriptors
1.Mod1.AD1 Apply the commutative property of addition as a strategy to add.
1.Mod1.AD2 Count on to find the total number of objects in a set and represent the total with an addition number sentence.
1.Mod1.AD3 Add within 20 by using strategies such as counting on or by creating an equivalent but easier problem.
1.Mod1.AD4 Add fluently within 10.
1.Mod1.AD5 Fluently decompose totals within 10 in more than one way.
1.Mod1.AD6 Determine whether addition and/or subtraction number sentences are true or false.
1.Mod1.AD7 Count on from 10 to find totals between 11 and 19.
1.Mod1.AD8 Compare category totals in graphs by using the symbols >, =, and <.
1.Mod1.AD9 Organize and represent data with up to three categories and write how many are in each category.
Notes
Student Name
Dates and Details of Observations
PP Partially Proficient P Proficient HP Highly Proficient
356 This page may be reproduced for classroom use only. © Great Minds PBC
Sample Solutions
Expect to see varied solution paths. Accept accurate responses, reasonable explanations, and equivalent answers for all student work.
© Great Minds PBC 358
EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ Module Assessment © Great Minds PBC This page may be reproduced for classroom use only. Name Module Assessment 341 1. Color the totals. Write the totals. I Count Totals 5 6 3 Which
Circle. Write two totals. Sample: 6 > 5 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ Module Assessment 342 © Great Minds PBC This page may be reproduced for classroom use only. 2. Circle a part and count on. Write the number sentence. 5 + 4 = 9 3. Circle a part. Count on. 5 8 + 4 = 12 2 + 10 = 12 7 = 1 + 6 6 = 0 + 6
one has more?
4. Show two ways to make 9.
6. Write a doubles number sentence.
7. Add. Circle doubles that help you. 5 + 4 = 9
EUREKA MATH2 New York Next Gen 1 ▸ M1 © Great Minds PBC 359 EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ Module Assessment 343 © Great Minds PBC This page may be reproduced for classroom use only.
Sample:
Draw an X on
it is false Show how you know. 9 5 4 9 8 1 5 + 2 = 7 + 1 7 8 3 + 4 = 4 + 3
are in a different order. EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ Module Assessment 344 © Great Minds PBC This page may be reproduced for classroom use only.
5. Circle the number sentence if it is true
the number sentence if
They
4 + 4 = 8
1 ▸ M1 EUREKA MATH2 New York Next Gen 360 © Great Minds PBC EUREKA MATH2 New York Next Gen 1 ▸ M1 ▸ Module Assessment 345 This page may be reproduced for classroom use only. © Great Minds PBC 8. Listen to the story. Count on to find the total. 7 frogs are in the pond. 2 more frogs hop into the pond. How many frogs are in the pond now? 7 9 frogs
Terminology
The following terms are critical to the work of grade 1 module 1. This resource groups terms into categories of New, Familiar, and Academic Verbs. The lessons in this module incorporate terminology with the expectation that students work toward applying it during discussions and in writing.
Items in the New category are discipline-specific words that are introduced to students in this module. These items include the definition, description, or illustration as it appears in the lesson. At times, this resource also includes italicized language for teachers that expands on the wording used with students.
Items in the Familiar category are discipline-specific words introduced in prior modules or in previous grade levels.
Items in the Academic Verbs category are high-utility terms that are used across disciplines. These terms come from a list of academic verbs that the curriculum strategically introduces at this grade level.
New doubles
An addition number sentence or expression where both parts are the same number. Doubles can also be shown with objects. For example, 3 + 3 = 6, 2 + 2, 4 fingers on one hand and 4 on the other, or two dice showing 6 dots. (Lesson 9)
expression
An expression is like a number sentence, but there is no equal sign. (Lesson 14)
In grade 1, an expression is a number, or combination of sums and differences, that can be evaluated. For example, 10 + 2 is an expression that evaluates to 12. However, 10 + is not an expression because it cannot be evaluated. In later grades, expressions will include multiplication and division. Some or all of the numbers in an expression may be replaced with symbols that represent unknowns.
graph
A way of organizing and representing, or showing, information so that we can ask and answer questions. (Lesson 2)
In module 1, students make graphs by aligning number paths, titling the graph, and labeling categories with pictures, letters, or words.
hour hand
The short hand on a clock, which points to the hour. (Lesson 17)
minute hand
The long hand on a clock, which points to the minutes. (Lesson 17)
o’clock
We say “o’clock” to say the time when the minute hand points to 12. For example, when the hour hand points to 1 and the minute hand points to 12, we say that the time is one o’clock. (Lesson 17)
unknown
A number that we need to figure out. (Lesson 12)
© Great Minds PBC 362
Familiar compare is greater than is more than number path organize partners sort tally mark total Academic Verbs convince represent
EUREKA MATH2 New York Next Gen 1 ▸ M1 363 © Great Minds PBC
Math Past
Chinese Counting Rods
How did the ancient Chinese use rods to count?

Did they make tally groups like we do? Did they represent 5 in a special way like we do?
Tally the students in your class. Just make one vertical mark for every student. Let’s say your tally looks like this.
1 2 3 4 5 6 7 8 9
Can you tell at a glance that you have tallied 20 students?
Probably not! When there are 1, 2, 3, 4, or even 5 tally marks, most people can tell how many marks there are at a glance. After that, we need some way of grouping the marks to make it easier to count them.
Suppose you redo your tally, this time placing every fifth tally mark diagonally across the 4 preceding marks to make groups of 5. Then it would look like this.
The Chinese counted to 5 by using a single vertical rod for each 1. When they got to 5, they didn’t lay the fifth rod diagonally across the other 4 like we do with tally marks. Instead, they did something special when they formed numbers greater than 5.
Now how many students does the tally show? With groups of 5 we can easily count “5, 10, 15, 20.”
Around 2,400 years ago, the Chinese represented numbers by arranging rods that looked like tally marks to form certain patterns. These rods were made from bamboo, iron, ivory, jade, or animal bones. In China, they were used for counting for almost 2,000 years, and their use also spread to Korea and Japan.
Ask your students to look at the rods that form the number 6. The Chinese used a horizontal rod to represent 5, and they put a vertical rod underneath it to represent 1. Point out to your students that when you add 5 and 1, you get 6. Then look at the rod numbers for 7, 8, and 9. Help students notice that the horizontal rod representing 5 is in each of these numbers too.
This leads to an interesting question. We’ve seen that the Chinese didn’t use a diagonal rod to make a group of 5. But since they did use the horizontal rod to represent 5 in forming the numbers 6, 7, 8, and 9, why didn’t they just use instead of to represent 5?
© Great Minds PBC 364
Here is how the Chinese formed numbers from rods.
The answer lies in the fact that the Chinese used two styles of arranging rods to form numbers. Here are the Chinese rod numbers in the second style.
Let’s call the first style vertical because the 1 is vertical. We can call the second style horizontal because the 1 is horizontal.
The Chinese wanted to represent 1 in horizontal style. It would be pretty confusing if they also let it represent 5 in vertical style. If you didn’t know which style you were looking at, you wouldn’t know what the number was!
So in vertical style, the horizontal rod could only represent 5 when it was combined with vertical rods, as in 6, 7, 8, 9. It couldn’t represent 5 all by itself.
But why did the Chinese use two different styles of rod numbers? It helps to know that the earliest counting rods were round, so they sometimes rolled around when they were laid out.

A merchant or official who needed to compute something would pull out his bag of rods and lay them out on a counting board. The counting board might have been an actual table, or it could have just been the floor.
Suppose the merchant laid out rods to form the number 11 by using just the vertical style. What would happen if the board was jostled? The rod in the right-hand box might roll across the dividing line into the left-hand box. Then the merchant would end up with the number 20.
Any counting board had to have lines to divide it into boxes. The rods that formed a number went in one box. Numbers greater than 9 occupied two boxes next to each other, much like we write two-digit numbers today.
Whoops! To avoid this problem, the Chinese counting rod system switched between the vertical and horizontal styles, starting with the digit on the right in vertical style. The correct way to form 11 was like this.
Then, even if the rods rolled, the merchant knew what number they should be, and the merchant could gently roll the rods back where they belonged.
Have your class look again at the number 20. How did the Chinese display the number 0? Help your class to see that the Chinese just left a box blank. They had no special character for 0.
Now that you’ve had a brief look at Chinese rods, consider pointing out the similarities between the Chinese counting rod system and our number system. We both have 10 symbols for numbers. We both represent 0—the Chinese didn’t have a symbol for 0, but an empty box meant the same thing. And both number systems form larger numbers by using the same symbols in different positions—the tens place, the hundreds place, and so on. The ancient Chinese counting rod system was actually very modern!
EUREKA MATH2 New York Next Gen 1 ▸ M1 365 © Great Minds PBC
1 2 3 4 5 6 7 8 9
Materials
The following materials are needed to implement this module. The suggested quantities are based on a class of 24 students and one teacher.
1 100-bead demonstration rekenrek
1 20-bead rekenrek—wood
1 Centimeter cubes, set of 500
1 Craft sticks, box of 200
24 Crayon sets
24 Cups, 6–8 ounce
1 Demonstration clock
2 Dot dice, set of 12
24 Dry-erase markers
1 Eureka Math2™ Addition expression cards, 13 decks
25 Eureka Math2™ Centimeter number paths
1 Eureka Math2™ Hide Zero® cards, basic student set of 12
25 Eureka Math2™ Large number paths
24 Learn books
1 Markers, set of 8
2 Number cubes, wooden, set of 12
1 Pad of chart paper
2 Pads of sticky notes
24 Pencils
24 Personal whiteboards
24 Personal whiteboard erasers
1 Plastic pattern blocks set, 0.5 cm
1 Projection device
1 Small box
1 Teach book
1 Teacher computer or device
1 Teddy bear counters, set of 96
1
counters, 200 pieces
1 Unifix® Cubes, set of 1,000
Please see lesson 25 for a list of organizational tools (cups, rubber bands, graph paper, etc.) suggested for the counting collection.
366 © Great Minds PBC
Two-color
Works Cited
CAST. Universal Design for Learning Guidelines version 2.2. Retrieved from http://udlguidelines.cast.org, 2018.
Common Core Standards Writing Team. Progressions for the Common Core State Standards in Mathematics. Tucson, AZ: Institute for Mathematics and Education, University of Arizona, 2011–2015. http://math.arizona.edu/~ime /progressions.
National Governors Association Center for Best Practices, Council of Chief State School Officers (NGA Center, CCSSO).
Common Core State Standards for Mathematics.
Washington, DC: National Governors Association Center for Best Practices, Council of Chief State School Officers, 2010.
Zwiers, Jeff, Jack Dieckmann, Sara Rutherford-Quach, Vinci Daro, Renae Skarin, Steven Weiss, and James Malamut. Principles for the Design of Mathematics Curricula: Promoting Language and Content Development. Retrieved from Stanford University, UL/SCALE website: https:// ul.stanford.edu/resource/principles-design-mathematicscurricula, 2017.
368 © Great Minds PBC
Credits
Great Minds® has made every effort to obtain permission for the reprinting of all copyrighted material. If any owner of copyrighted material is not acknowledged herein, please contact Great Minds for proper acknowledgment in all future editions and reprints of this module.
From the New York State Education Department. New York State Next Generation Mathematics Learning Standards. Available from https://www.nysed.gov/sites/default/files/programs /curriculum-instruction/nys-next-generation-mathematics -p-12-standards.pdf; accessed 19 September, 2023.
For a complete list of credits, visit http://eurmath.link/media-credits.
Edward Hopper (1882–1967), Tables for Ladies, 1930. Oil on canvas, H. 48 1/4, W. 60 1/4 inches (122.6 x 153 cm.)
George A. Hearn Fund, 1931 (31.62). The Metropolitan Museum of Art. © 2020 Heirs of Josephine N. Hopper/Licensed by Artists Rights Society (ARS), NY. Photo Credit: Image copyright © The Metropolitan Museum of Art. Image source: Art Resource, NY; pages 17, 59, (composite image) Super Prin/Shutterstock. com, Vladimirkarp/Shutterstock.com, Metelitsa Viktoriya/ Shutterstock.com, Potapov Alexander/Shutterstock.com, Butterfly
Hunter/Shutterstock.com, elena09/Shutterstock.com, Kashtal/ Shutterstock.com; page 60, (composite image) Super Prin/ Shutterstock.com, Vladimirkarp/Shutterstock.com, Metelitsa Viktoriya/Shutterstock.com, Potapov Alexander/Shutterstock. com, Butterfly Hunter/Shutterstock.com, elena09/Shutterstock. com; page 61, 62, aodaodaodaod/Shutterstock.com; pages 72, 73, GraphicsRF/Shutterstock.com; pages 90, 365, The Picture Art Collection/Alamy Stock Photo; page 171, (composite image) Vladimirkarp/Shutterstock.com, Potapov Alexander/Shutterstock. com; pages 198, 199, Joe Robbins/Getty Images Sport/Getty Images; page 222, (composite image) BG-FOTO/Shutterstock. com, Elles Rijsdijk/EyeEm/Getty Images, Ermolaev Alexander/ Shutterstock.com, Eric Isselee/Shutterstock.com, Dorottya Mathe/ Shutterstock.com, Svetography/Shutterstock.com, Jagodka/ Shutterstock.com, 5 second Studio/Shutterstock.com; page 234, (left) pim pic/Shutterstock.com, (right) Sahara Prince/ Shutterstock.com; page 254, mikeledray/Shutterstock.com; page 329, Yayayoyo/Shutterstock.com; page 364, Korean Sangi Rods, late 19th century, Rare Book & Manuscript Library, Columbia University in the City of New York; All other images are the property of Great Minds.
369 © Great Minds PBC
Acknowledgments
Kelly Alsup, Lauren Brown, Melissa Brown, Dawn Burns, Jasmine Calin, Stella Chen, Mary Christensen-Cooper, Cheri DeBusk, Stephanie DeGiulio, Jill Diniz, Brittany duPont, Melissa Elias, Lacy Endo-Peery, Scott Farrar, Ryan Galloway, Krysta Gibbs, Melanie Gutierrez, Karen Hall, Eddie Hampton, Tiffany Hill, Robert Hollister, Christine Hopkinson, Rachel Hylton, Travis Jones, Kelly Kagamas Tomkies, Emily Koesters, Liz Krisher, Alicia Machuca, Ben McCarty, Maureen McNamara Jones, Cristina Metcalf, Ashley Meyer, Melissa Mink, Richard Monke, Bruce Myers, Marya Myers, Andrea Neophytou Hart, Kelley Padilla, Kim L. Pettig, Marlene Pineda, DesLey V. Plaisance, Elizabeth Re, John Reynolds, Meri Robie-Craven, Robyn Sorenson, Marianne Strayton, James Tanton, Julia Tessler, Philippa Walker, Lisa Watts Lawton, MaryJo Wieland
Trevor Barnes, Brianna Bemel, Adam Cardais, Christina Cooper, Natasha Curtis, Jessica Dahl, Brandon Dawley, Delsena Draper, Sandy Engelman, Tamara Estrada, Soudea Forbes, Jen Forbus, Reba Frederics, Liz Gabbard, Diana Ghazzawi, Lisa Giddens-White, Laurie Gonsoulin, Nathan Hall, Cassie Hart, Marcela Hernandez, Rachel Hirsh, Abbi Hoerst, Libby Howard, Amy Kanjuka, Ashley Kelley, Lisa King, Sarah Kopec, Drew Krepp, Crystal Love, Maya Márquez, Siena Mazero, Cindy Medici, Ivonne Mercado, Sandra Mercado, Brian Methe, Patricia Mickelberry, Mary-Lise Nazaire, Corinne Newbegin, Max Oosterbaan, Tamara Otto, Christine Palmtag, Andy Peterson, Lizette Porras, Karen Rollhauser, Neela Roy, Gina Schenck, Amy Schoon, Aaron Shields, Leigh Sterten, Mary Sudul, Lisa Sweeney, Samuel Weyand, Dave White, Charmaine Whitman, Nicole Williams, Glenda Wisenburn-Burke, Howard Yaffe
370 © Great Minds PBC
Exponentially Better
Knowledge2 In our tradition of supporting teachers with everything they need to build student knowledge of mathematics deeply and coherently, Eureka Math2 provides tailored collections of videos and recommendations to serve new and experienced teachers alike.
Digital2 With a seamlessly integrated digital experience, Eureka Math2 includes hundreds of clever illustrations, compelling videos, and digital interactives to spark discourse and wonder in your classroom.
Accessible2 Created with all readers in mind, Eureka Math2 has been carefully designed to ensure struggling readers can access lessons, word problems, and more.
Joy2 Together with your students, you will fall in love with math all over again—or for the first time—with Eureka Math2.
Module 1
Counting, Comparison, and Addition
Module 2
Addition and Subtraction Relationships
Module 3
Properties of Operations to Make Easier Problems
Module 4
Comparison and Composition of Length Measurements
Module 5 Place Value Concepts to Compare, Add, and Subtract
Module 6
Attributes of Shapes • Advancing Place Value, Addition, and Subtraction
What does this painting have to do with math?
American realist Edward Hopper painted ordinary people and places in ways that made viewers examine them more deeply. In this painting, we are in a restaurant, where a cashier and server are busily at work. What can you count here? If the server gave two of the yellow fruits to the guests at the table, how many would be left in the row? We will learn all about addition and subtraction within 10s in Units of Ten

On the cover Tables for Ladies, 1930
Edward Hopper, American, 1882–1967 Oil on canvas
The Metropolitan Museum of Art, New York, NY, USA
ISBN
Edward Hopper (1882–1967), Tables for Ladies, 1930. Oil on canvas, H. 48¼, W. 60¼ in (122.6 × 153 cm). George A. Hearn Fund, 1931 (31.62). The Metropolitan Museum of Art. © 2020 Heirs of Josephine N. Hopper/Licensed by Artists Rights Society (ARS), NY.
Photo credit: Image copyright © The Metropolitan Museum of Art.
Image source: Art Resource, NY
979-8-89012-072-4 9 798890 120724
A

























































































































































































































































