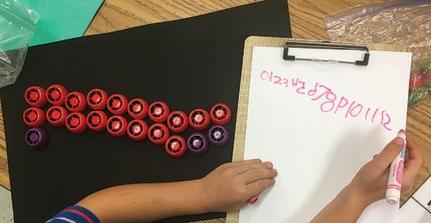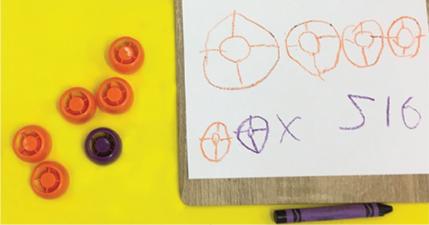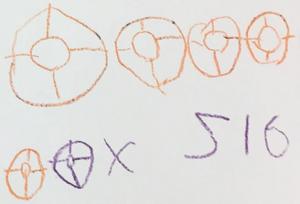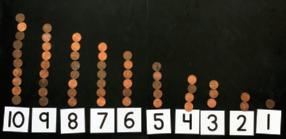Una historia de unidades®
Parte-parte-total
ENSEÑAR ▸ Módulo 1 ▸ Conteo y cardinalidad

K
¿Qué tiene que ver esta pintura con las matemáticas?
Piet Mondrian redujo los sujetos de sus obras a figuras geométricas coloridas. En esta pintura, gruesas líneas negras, horizontales y verticales, enmarcan los vibrantes cuadrados y rectángulos con el rojo, el negro y el amarillo, entre otros colores. ¿Crees que alguna de las figuras se parecen? ¿Observas que las figuras más pequeñas se juntan para crear figuras más grandes? ¿Cuántas figuras ves en total?
En la portada
Composition with Large Red Plane, Yellow, Black, Gray and Blue, 1921
Piet Mondrian, Dutch, 1872–1944
Oil on canvas
Kunstmuseum Den Haag, The Hague, Netherlands
Piet Mondrian (1872–1944), Composition with Large Red Plane, Yellow, Black, Gray and Blue, 1921. Oil on canvas. Kunstmuseum Den Haag, The Hague, Netherlands. Image copyright © Kunstmuseum Den Haag. Image credit: Bridgeman Images

Great Minds® is the creator of Eureka Math® , Wit & Wisdom® , Alexandria Plan™, and PhD Science® .
Published by Great Minds PBC. greatminds.org
© 2023 Great Minds PBC. All rights reserved. No part of this work may be reproduced or used in any form or by any means—graphic, electronic, or mechanical, including photocopying or information storage and retrieval systems—without written permission from the copyright holder. Where expressly indicated, teachers may copy pages solely for use by students in their classrooms.
ISBN 978-1-63898-654-6
A-Print 1 2 3 4 5 6 7 8 9 10 XXX 27 26 25 24 23
Printed in the USA
Módulo 1 Conteo y cardinalidad
2 Figuras bidimensionales y tridimensionales
3 Comparación
4 Composición y descomposición
5 Suma y resta
6 Fundamentos del valor posicional
Una historia de unidades® Parte-parte-total ▸ K ENSEÑAR
Antes de este módulo
Contenido general
Módulo 2 de kindergarten

Sus estudiantes de kindergarten no necesitan experiencia previa con Eureka Math ni ningún currículo preescolar para tener éxito con este módulo.
Sus estudiantes de kindergarten no necesitan experiencia previa con Eureka Math ni ningún currículo preescolar para tener éxito con este módulo.


Sin embargo, varios módulos de prekínder brindan un apoyo directo al trabajo de este módulo. Preparan a la clase para contar con éxito grupos de 0 a 10 objetos y hallar o escribir el numeral para emparejarlo. También sientan las bases para usar la correspondencia de uno a uno como manera de determinar si hay suficientes.
Sin embargo, varios módulos de prekínder brindan un apoyo directo al trabajo de este módulo. Preparan a la clase para contar con éxito grupos de 0 a 10 objetos y hallar o escribir el numeral para emparejarlo. También sientan las bases para usar la correspondencia de uno a uno como manera de determinar si hay suficientes.
Conteo y cardinalidad
Tema A
Clasificar para formar categorías y contar
Clasificar objetos en grupos por atributos crea un contexto natural para contar y trabajar con números. Se presenta a la clase cuatro ideas centrales sobre contar, que se conocen en su conjunto como fundamentos numéricos. (Ver la sección ¿Por qué?).
Tema B
Responder preguntas sobre cuántos hay con hasta 5 objetos
La clase integra los elementos de los fundamentos numéricos mientras considera distintas maneras y razones para contar. Aprenden tres estrategias para contar con precisión, sin importar la configuración: tocar y contar, mover y contar, y marcar y contar.
Tema C
Escribir numerales y crear grupos de hasta 5 objetos
La clase comienza a escribir numerales y experimenta situaciones de conteo más complejas, como contar sonidos y palabras que se pueden escuchar pero no se pueden ver. Cuentan objetos para emparejar con un número dado. También cuentan para averiguar si tienen suficientes.
© Great Minds PBC 2
Tema D
Descomponer números

La clase explora las relaciones numéricas. Comienzan con el contexto ya conocido de clasificar y, luego, trabajan con problemas con historia. Sus estudiantes comienzan a usar oraciones numéricas como 5 es 2 y 3. Estas primeras experiencias con la resolución de problemas sientan las bases para trabajar los conceptos de suma y resta en los módulos 4 y 5.
Tema E
Responder preguntas sobre cuántos hay con hasta 10 objetos
El tema E toma como base el trabajo realizado en el tema B, mientras la clase aplica los conceptos de los fundamentos numéricos a grupos que incluyen de 6 a 10 objetos. A medida que el grupo aumenta, llevar la cuenta del conteo se vuelve más difícil. La clase considera cómo elegir una estrategia de conteo adecuada.
Tema F
Escribir numerales y crear grupos de hasta 10 objetos
El tema F da lugar a practicar el conteo mientas la clase aprende a escribir 6, 7, 8, 9 y 10. Sus estudiantes cuentan cosas que suceden en un período de tiempo, como los saltos de una persona o las carreras en un partido de beisbol, y ven que escribir números es una buena manera de registrar y recordar la información.
Tema G
Analizar la secuencia de conteo
La clase analiza la secuencia de conteo, enfocándose en la noción de que cada número consecutivo es 1 más cuando contamos hacia delante y 1 menos cuando contamos hacia atrás. El modelo de las escaleras de números ilustra claramente estos patrones.

Después de este módulo
Módulo 2 de kindergarten
La clase aplica su capacidad para aislar y clasificar por atributos, incluidos los números, a medida que analiza y compara las figuras geométricas del módulo 2. Cuentan los lados y las esquinas a medida que mencionan, comparan, representan y componen figuras.

EUREKA MATH2 K ▸ M1 © Great Minds PBC 3
10 9 8 7 6 5 4 3 2 1
el mismo grupo de objetos de más de una manera y contar
© Great Minds PBC 4
Conteo y cardinalidad ¿Por qué? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 Criterios de logro académico: Contenido general . . . . . 10 Tema A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 Clasificar para formar categorías y contar Lección 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 Comparar objetos según sus atributos Lección 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 Clasificar objetos en dos categorías Lección 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 Clasificar objetos en dos categorías y contar Lección 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44 Clasificar objetos en tres categorías y contar Lección 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60 Clasificar objetos en tres categorías, contarlos y emparejarlos con un numeral Tema B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70 Responder preguntas sobre cuántos hay con hasta 5 objetos Lección 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74 Organizar, contar y representar una colección de objetos Lección 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86 Practicar el conteo con precisión Lección 8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94 Contar conjuntos en configuraciones lineales, de matrices y dispersas Lección 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104 Conservar el número de objetos
cualquier configuración Tema C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113 Escribir numerales
grupos
objetos Lección 10 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116 Contar un grupo de objetos
emparejarlos
numeral Lección 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124 Escribir
3
preguntas sobre cuántos hay Lección 12 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134 Escribir los numerales 4 y 5 para responder preguntas sobre cuántos hay Lección 13 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144 Contar suficientes objetos y escribir el numeral Tema D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 153 Descomponer números Lección 14 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156 Comprender el significado del cero y escribir el numeral Lección 15 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 166 Clasificar
Lección 16 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 178
Lección 17 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 188 Representar
Lección 18 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 200
numéricos
Contenido
en
y crear
de hasta 5
para
con un
los numerales del 1 al
para responder
Descomponer un conjunto que se muestra en una imagen
problemas con historia
Representar problemas con historia e identificar los referentes
objetos en grupos de 5 y en configuraciones de matrices, y emparejarlos con un numeral
Analizar la secuencia de conteo
Lección 29
Representar el patrón de 1 más en una secuencia de conteo hacia delante
Construir escaleras de números para mostrar el patrón de 1 más en una secuencia de conteo hacia delante
Representar el patrón de 1 menos en una secuencia de conteo hacia atrás Lección 32
en configuraciones dispersas y emparejarlos con un
Conservar el número sin importar el orden en que los objetos se
Escribir numerales y crear grupos de hasta 10 objetos
Contar un grupo de objetos para emparejarlos con un numeral
Escribir los numerales 6 y 7
Escribir el numeral 8
Escribir los numerales 9 y 10
Lección 28
Ordenar los numerales del 1 al 10 y razonar acerca de un número desconocido en una secuencia numérica
Dibujar escaleras de números para representar el patrón de 1 menos en una secuencia de conteo hacia atrás
EUREKA MATH2 K ▸ M1 © Great Minds PBC 5 Tema E . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 210
preguntas
cuántos
objetos Lección 19 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 214 Organizar,
Lección 20 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 224 Contar
Lección 21 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 236 Contar objetos
un numeral Lección 22 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 246
numeral Lección 23 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 284
cuentan Tema F . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 293
Responder
sobre
hay con hasta 10
contar y representar una colección de objetos
en configuraciones circulares y emparejarlos con
Contar objetos
Lección 24 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 296
Lección 25 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 304
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 312
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 320
Lección 26
Lección 27
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 330
Tema G . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 339
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 342
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 352
Lección 30
31 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 362
Lección
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 372
Lección 33 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 382 Organizar, contar y representar una colección de objetos Recursos Hoja de registro de la evaluación observacional . . . . . . . . . . . . 390 Evaluación del módulo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 392 Estándares . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 398 Criterios de logro académico: Indicadores de competencias . . . . 400 Vocabulario . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 406 Las matemáticas en el pasado . . . . . . . . . . . . . . . . . . . . . . . . 408 Materiales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 410 Obras citadas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 416 Créditos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 417 Agradecimientos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 418
¿Por qué?
Conteo y cardinalidad
¿Qué son los fundamentos numéricos? ¿De qué manera se relacionan con el conteo?
En este módulo, la clase tendrá una interacción permanente con los cuatro conceptos fundamentales para describir el número de objetos de un grupo. Estos conceptos se conocen en su conjunto como fundamentos numéricos.
• Lista de palabras numéricas: La clase dice los números en la secuencia de conteo adecuada (1, 2, 3, etc.).
• Correspondencia de uno a uno: Cuando cuentan, sus estudiantes emparejan un objeto con una palabra numérica, con cuidado de no contar ningún objeto dos veces ni dejar alguno sin contar.
• Cardinalidad: La clase dice un número para indicar cuántos hay en un grupo. Pueden decir cuántos hay por conteo súbito, conteo o al emparejar un grupo con una cantidad ya conocida. Cuando cuentan, reconocen que el último número que se dice representa el número total de objetos en el grupo.
• Numerales escritos: Sus estudiantes leen y escriben símbolos para representar números. También conectan el numeral escrito con el número de objetos de un conjunto.

Deben integrar todos los aspectos de los fundamentos numéricos para contar y usar los números con fluidez. La mayoría de las actividades de kindergarten deben incluir tres o más elementos de los fundamentos numéricos en conjunción. Los componentes de los fundamentos numéricos no se aprenden de manera aislada.
Sientan las bases para el trabajo con las relaciones numéricas, las operaciones y la comprensión del valor posicional; por ello, son una introducción fundamental durante el año de kindergarten.
La clase usa la correspondencia de uno a uno cuando dice una palabra numérica por cada araña que toca.
La clase muestra cuántos hay en un conjunto (cardinalidad) con numerales escritos.

© Great Minds PBC 6
¿Por qué no hay una lección para cada número del 1 al 10?
El módulo 1 se enfoca en las estrategias, más que en los números específicos. Cuando la clase aprende estrategias para contar correctamente, puede aplicarlas a distintos números organizados en distintas configuraciones.


Por ejemplo, cuando se cuenta en una configuración circular, el desafío es identificar los puntos de inicio y de finalización, para contar todos los objetos solo una vez. Una vez que la clase aprende la estrategia de marcar el inicio, esa estrategia puede ser útil para contar con éxito cualquier número de objetos en una configuración circular. La misma estrategia de marcar el inicio también se puede usar para contar los lados y las esquinas de las figuras.
Tan pronto como sea posible, queremos que la clase aborde la resolución de problemas con una estrategia que permita precisión y eficiencia. Cuando una lección se enfoca en un solo número, la clase aborda la tarea de conteo anticipando el total. Las tareas de conteo en las que la clase no sabe de antemano el total, sino que en verdad quiere descubrirlo, abren la puerta al proceso de elección de estrategias para resolver problemas (MP1). A través de preguntas eficaces, la clase comienza a evaluar si la estrategia elegida es efectiva.
El enfoque en las estrategias en lugar de en números específicos permite que el tamaño de un conjunto pueda variar para ofrecer tareas más complejas a estudiantes particulares. Este enfoque propicia accesibilidad y participación de la clase de kindergarten, con su rango de experiencias de conteo.
¿Qué es contar con el método matemático? ¿De qué manera influye en el aprendizaje?
Los dedos son materiales didácticos conocidos que la clase lleva consigo todo el día. Si se usan con un propósito, pueden apoyar la comprensión y resolución de problemas a lo largo de toda la escuela primaria. En todo el mundo, las personas usan los dedos para representar números de diferentes maneras. Según las experiencias culturales, sus estudiantes de corta edad pueden comenzar a contar desde el pulgar, desde el índice, el meñique o incluso desde una parte de un dedo. La clase aprende a contar con el método matemático en el módulo 1, comenzando con el 1 en el dedo meñique de la mano izquierda y llegando al 10 en el dedo meñique de la mano derecha.
La ventaja matemática de contar con el método matemático es que la clase cuenta de izquierda a derecha sin interrupción, al igual que lo hacen con el camino numérico y, eventualmente, con la recta numérica. También permite que la clase vea y sienta cómo aumenta la cantidad a medida que cuentan hacia delante. El aumento uniforme de la distancia desde el punto de partida es un modelo físico y visual para comprender la magnitud de un número.
EUREKA MATH2 K ▸ M1 © Great Minds PBC 7
Contar con el método matemático tiene ventajas para comprender las relaciones numéricas que serán importantes en kindergarten y en años posteriores.












• Formar una nueva unidad: Cuando la clase forma una nueva unidad, hace uso del cinco como entero, en lugar de pensar en 5 partes individuales. La estructura de las manos facilita que la clase forme una nueva unidad con el 5 cuando piensan en el 6 como 5 y 1, el 7 como 5 y 2, y así sucesivamente. Formar una nueva unidad es un paso clave para usar las estrategias de contar desde un número de nivel 2.
• Parejas de números que suman 10: La fluidez con las parejas de números que suman 10 es clave para usar las estrategias de resolución de problemas de nivel 3. Cuando cuentan con el método matemático, sus estudiantes pueden ver claramente que los dedos que están arriba y los que están abajo son parejas que suman 10. Otras formas de contar con los dedos no siempre mantienen los dedos que representan cada parte uno al lado del otro.
• Números incluidos en otros números: La capacidad para descomponer un número en partes incluidas es clave para muchas estrategias de nivel 3. Mostrar las partes dentro de un total es fácil cuando las dos partes suman 5 o menos. Para representar 2 + 3, su estudiante puede mostrar una parte en cada mano. Es más difícil ver las partes para representar 6 + 2. A la vez que desarrollan la motricidad fina, sus estudiantes pueden doblar los dedos para representar una parte mientras mantienen la otra parte quieta. Contar con el método matemático coincide con cómo se ven los números incluidos en otros números dentro del total.



K ▸ M1 EUREKA MATH2 © Great Minds PBC 8
10 5 9 4 8
7 2 6 1
3
Este es un módulo sobre números hasta el 10. ¿Por qué se sugieren las colecciones de conteo de hasta 25 objetos?
Las colecciones de conteo son tareas ricas que permiten a la clase explorar los números y participar en las prácticas matemáticas. También son oportunidades de evaluación auténticas para maestros y maestras.
La primera colección de conteo, en la lección 6, es una evaluación diagnóstica a la vez que una oportunidad de presentar las estrategias de conteo. Hay estudiantes de corta edad con acceso regular a experiencias matemáticas de alta calidad que llegan a kindergarten con la capacidad de organizar, contar y representar conjuntos de 50 o más objetos. Ofrecer colecciones de conteo más numerosas les permite compartir el rango completo de sus capacidades, para que usted pueda diferenciar la enseñanza y satisfacer sus necesidades.
Sugerimos comenzar con colecciones de entre 5 y 25 objetos por las siguientes razones:
• Las investigaciones indican que la clase puede contar más cuando se cuentan objetos que con el conteo repetitivo.1
• Cuando sus estudiantes pasen la veintena, verá si pueden usar el patrón repetitivo de los nombres de los números en español (p. ej., decir veintiuno en lugar de veintionce).
• Las y los estudiantes de corta edad son hábiles para elegir una colección acorde a su capacidad de conteo cuando las colecciones tienen menos de 25 objetos. Con colecciones más grandes, no podrán percibir la diferencia de tamaño con suficiente precisión para mantenerse en un rango que les sea cómodo.
• Experimentar el éxito en las primeras actividades de kindergarten es importante para desarrollar la autoestima de la clase y sentirse como expertas y expertos en matemáticas.

El número de objetos de una colección debe aumentar en las lecciones siguientes (lecciones 19 y 33) si hay estudiantes que demuestran dominio hasta el 25. Intente con 40 o 50 objetos y aumente de a poco el número hasta llegar al punto en el que sus estudiantes comiencen a necesitar ayuda con la lista de nombres de palabras numéricas o con la organización para mantener la correspondencia de uno a uno.
EUREKA MATH2 K ▸ M1 © Great Minds PBC 9
1 Carpenter, Thomas P., Young Children’s Mathematics, pág. 26
Criterios de logro académico: Contenido general Conteo y cardinalidad
Los Criterios de logro académico (CLA) son descripciones alineadas con los estándares que detallan lo que cada estudiante debe saber y poder hacer. Los criterios se escribieron usando secciones de distintos estándares para formar una descripción clara y precisa del trabajo cubierto en cada módulo.
Cada módulo tiene su propio conjunto de criterios y el número de criterios varía según el módulo. En conjunto, los grupos de criterios por módulo/nivel describen lo que cada estudiante debe haber aprendido al terminar el año escolar.
Los criterios y sus indicadores de competencias ayudan a las maestras y los maestros a interpretar el trabajo de cada estudiante a través de:
• observaciones informales en el salón de clases (hoja de registro que se proporciona en los recursos del módulo);
• los datos acumulados en evaluaciones formativas de otras lecciones;
• Evaluaciones de los módulos.
Este módulo contiene los 10 CLA que se indican.
K.Mód1.CLA1
Cuentan hasta el 10.
K.CC.A.1
K.Mód1.CLA2
Escriben los números del 0 al 10.
hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías. Notas PC Parcialmente competente Competente AC Altamente competente
K.CC.A.3
K.Mód1.CLA3
Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.CC.A.3
© Great Minds PBC 10
390 © Great Minds PBC This page may be reproduced for classroom use only. Hoja de registro de la evaluación observacional Estudiante Módulo 1 de kindergarten Conteo y cardinalidad Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones K.Mód1.CLA1 Cuentan
K.Mód1.CLA4
Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5
Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.CC.B.4.a
K.Mód1.CLA7
Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.CC.B.4.c
K.Mód1.CLA8
K.CC.B.4.b
Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.CC.B.5
K.Mód1.CLA6
Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.CC.B.4.b
K.Mód1.CLA9
Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.CC.B.5
K.Mód1.CLA10
Clasifican objetos en categorías.
K.MD.B.3
La primera página de cada lección identifica los Criterios de logro académico (CLA) alineados con esa lección. Cada criterio puede tener hasta tres indicadores, cada uno de estos alineado con una categoría de competencia (es decir, Parcialmente competente, Competente, Altamente competente). Cada criterio tiene un indicador para describir el rendimiento Competente, pero solo algunos criterios tienen un indicador para Parcialmente competente o Altamente competente.
Un ejemplo de uno de estos criterios, incluyendo sus indicadores de competencias, se muestra a continuación como referencia. El grupo completo de criterios de este módulo con los indicadores de competencias puede encontrarse en el recurso Criterios de logro académico: Indicadores de competencias.
EUREKA MATH2 K ▸ M1 © Great Minds PBC 11
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
Los Criterios de logro académico contienen las siguientes partes:
CCSSEE DE MATEMÁTICAS RELACIONADO
K.CC.B.5 Cuentan para responder preguntas sobre “¿cuántos hay?” sobre una serie de hasta 20 objetos, ordenados en línea, de forma rectangular o circular, o sobre una serie de 10 objetos que estén esparcidos; dado un número del 1 al 20, cuentan los objetos.
• Código del CLA: El código indica el grado y el número del módulo, y luego presenta los criterios sin un orden específico. Por ejemplo, el primer criterio para el módulo 1 de kindergarten se codifica como K.Mód1.CLA1.
• Texto del CLA: El texto se ha escrito a partir de los estándares y describe de manera concisa lo que se evaluará.
Parcialmente competente Competente Altamente competente
Cuentan un número dado de 1 a 5 objetos de un grupo más grande.
Cuentan un número dado de 6 a 10 objetos de un grupo más grande.
• Indicadores del CLA: Los indicadores describen las expectativas precisas del criterio para la categoría de competencia dada.
• Estándar relacionado: Identifica el estándar o las partes del estándar de los Estándares Estatales Comunes que el criterio aborda.
Encierra en un círculo 3 clips.
Encierra en un círculo 6 pelotas.
Código del CLA: Grado.Mód#.CLA# Texto del CLA
K.Mód1.CLA10 Clasifican objetos en categorías.
CCSSEE DE MATEMÁTICAS RELACIONADO
K.MD.B.3 Clasifican objetos en categorías determinadas; cuentan la cantidad de objetos en cada categoría y clasifican las categorías según su número.3
3Limitar las categorías a números menores que o iguales a 10.
Parcialmente competente Competente Altamente competente
Identifican si los objetos son iguales o diferentes.
¿Estas figuras geométricas son exactamente iguales?
Clasifican los objetos en categorías cuando hay un atributo dado.
Clasifica los objetos por color.
Clasifican los objetos en categorías cuando no hay un atributo dado.
Clasifica los objetos.
Estándar relacionado Indicadores del CLA
K ▸ M1 EUREKA MATH2 © Great Minds PBC 12
EUREKA MATH2 K ▸ M1 405 © Great Minds PBC
Tema A Clasificar para formar categorías y contar
El tema A capitaliza la energía y el entusiasmo de los y las estudiantes de corta edad que ingresan al kindergarten, ya que ofrece experiencias divertidas y activas con las matemáticas. Las lecciones brindan el tiempo que necesita la clase para explorar las herramientas y los procedimientos de matemáticas durante los primeros días de escuela.
En este tema, se entrelazan dos conceptos elementales de matemáticas: la clasificación y los fundamentos numéricos. Para sus estudiantes de kindergarten, la clasificación implica identificar los atributos de un objeto, usarlos para clasificar objetos y comentar las estrategias y reglas de clasificación: Esta cuenta pertenece al grupo rojo. Estoy clasificando por color. Estos conceptos básicos de clasificación son fundamentales para trabajar con geometría, datos y operaciones durante el año de kindergarten y en adelante.
Clasificar objetos en grupos crea un contexto natural para contar: ¿Cuántas cuentas azules hay en este grupo? ¿Cuántas cuentas rojas hay en ese grupo? Los contextos de clasificación brindan una forma significativa de presentar cuatro ideas principales sobre el conteo, que en su conjunto se conocen como fundamentos numéricos:
• la lista de palabras numéricas (la secuencia de conteo, es decir, 1, 2, 3…)
• la correspondencia de uno a uno (un objeto emparejado con una palabra numérica)
• la cardinalidad (cuántos objetos hay en un grupo)
• los numerales escritos
A lo largo del módulo 1, la clase experimenta situaciones que le ayudan a establecer conexiones importantes entre estos cuatros fundamentos. En el módulo 3, la clase amplía este conocimiento al comparar el conteo en cada grupo: ¿Qué grupo tiene más cuentas?

Primero, la clase clasifica los objetos según un único atributo.
Luego, aplica los fundamentos numéricos para contar cada grupo.
© Great Minds PBC 13
Progresión de las lecciones
Lección 1
Comparar objetos según sus atributos
Lección 2
Clasificar objetos en dos categorías
Lección 3
Clasificar objetos en dos categorías y contar

Los clasifiqué por color.
Las manzanas tienen el mismo color, pero diferente tamaño.


Los clasifiqué por tamaño. Hay 5 piedras pequeñas y 3 piedras grandes.

© Great Minds PBC 14 K ▸ M1 ▸ TA EUREKA MATH2
Lección 4
Clasificar objetos en tres categorías y contar
Lección 5
Clasificar objetos en tres categorías, contarlos y emparejarlos con un numeral


Los clasifiqué por color. Dibujé 3 cuentas negras, 2 rojas y 5 azules.
Los clasifiqué por nombre. Coloqué un número junto a cada grupo.
EUREKA MATH2 K ▸ M1 ▸ TA © Great Minds PBC 15
LECCIÓN 1
Comparar objetos según sus atributos
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
En esta lección, la clase considera varios atributos para comparar objetos. Si todos los atributos son iguales, los objetos son exactamente iguales. Si algunos atributos son iguales, pero otros son diferentes, la clase usa iguales pero… para describir las semejanzas y diferencias. Prestar atención a los atributos es fundamental para clasificar a lo largo de este tema.
Pregunta clave
• ¿De qué maneras las cosas pueden ser iguales?
Criterio de logro académico
K.Mód1.CLA10 Clasifican objetos en categorías.
(K.MD.B.3)
1
390 © Great Minds PBC This page may be reproduced for classroom use only.
© Great Minds PBC
Agenda
Fluidez 10 min
Presentar 10 min
Aprender 20 min
• Exactamente iguales o iguales pero…
• Grupo de problemas
Concluir 10 min
Materiales
Maestro o maestra
• guante numerado derecho
• computadora o dispositivo*
• proyector*
• edición para la enseñanza*
Estudiantes
• Plantilla de dos manos (en el libro para estudiantes)
• frijoles de dos colores (5)
• bolsita de plástico resellable
* Estos materiales solo se mencionan en la lección 1. Prepare estos materiales para cada una de las lecciones de este módulo.
Preparación de la lección
• Considere cómo incorporar rutinas y procedimientos a la lección. Se asignó tiempo adicional a cada componente de la lección de modo que haya tiempo para las rutinas y los procedimientos.
• Prepare bolsitas con 5 frijoles de dos colores para cada estudiante. Guarde las bolsitas de frijoles para usarlas en lecciones posteriores.
• Cree guantes numerados. Comience con el guante derecho. Escriba números en las puntas de los dedos, comenzando con el 1 en el meñique y terminando con el 5 en el pulgar. Continúe con el guante izquierdo, comenzando con el 6 en el pulgar y terminando con el 10 en el meñique. Guarde los guantes para usarlos en lecciones posteriores.
• Considere retirar la Plantilla de dos manos y colocarla en una pizarra blanca individual. La Plantilla de dos manos se usará varias veces a lo largo del módulo.
• Cree frijoles de dos colores pintando con aerosol rojo uno de los lados de los frijoles.
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 1
© Great Minds PBC 17
Fluidez
Contar con movimiento hasta el 10
La clase cuenta con movimientos del cuerpo para desarrollar fluidez con los nombres de los números y la correspondencia de uno a uno.
Aplaudamos 5 veces y contemos los aplausos. ¿Comenzamos?
Al principio, cuente y aplauda del 1 al 5 lentamente, haciendo énfasis en que para cada aplauso se dice un número. Repita el proceso hasta que la mayor parte de la clase esté aplaudiendo, contando o, idealmente, aplaudiendo y contando.
Repita el proceso, pero esta vez dé pisotones y cuente hasta el 5.
Ahora, aplaudamos 10 veces y contemos los aplausos. ¿Comenzamos?
Cuente y aplauda del 1 al 10 junto con la clase.
Repita el proceso, pero esta vez dé pisotones y cuente hasta el 10.
Contar en el guante numerado hasta el 3
Materiales: M) Guante numerado derecho

La clase cuenta en el guante numerado para desarrollar el reconocimiento numérico y familiarizarse con el conteo con el método matemático.
Observen mi guante numerado y cuenten en voz alta. ¿Comenzamos?
Comience con el puño cerrado y, después, muestre lentamente el dedo meñique, luego, el anular y, por último, el mayor.
1, 2, 3
Quédense aquí, en el 3. Vamos a contar hacia atrás hasta el 1. ¿Comenzamos?
Muestre los 3 dedos. Baje el dedo mayor y, luego, el anular.
3, 2, 1
Guante numerado visto desde la perspectiva de la clase
DUA: Participación
Ajuste la actividad de Contar con movimiento hasta el 10 para que participe la mayor cantidad de estudiantes posible. Considere sus capacidades físicas, contextos culturales e intereses cuando elija los movimientos. Estos son unos pocos ejemplos de movimientos que pueden contarse de forma sencilla:
• parpadeos
• movimientos para asentir con la cabeza
• percusiones en un tambor
• saltos de rana
• rebotes con la pelota de basquetbol
10 10 20 10
K ▸ M1 ▸ TA ▸ Lección 1 EUREKA MATH2 © Great Minds PBC 18
Facilite más práctica para contar del 1 al 3 y, luego, del 3 al 1.
¡Ahora pueden hacer algo más difícil! Esta vez, contaremos hacia arriba y hacia abajo, como si fuera una ola. Observen mi guante numerado y cuenten en voz alta.
Use el guante numerado para mostrar la siguiente secuencia mientras la clase cuenta en voz alta.
Nota para la enseñanza
Recuerde no contar junto con la clase para evitar que imiten sus movimientos en lugar de enfocarse en el orden de los números.
Marque el ritmo del conteo con las manos. Recuerde prestar atención a las respuestas de la clase para detectar errores, dudas y falta de participación. Si es necesario, ajuste el ritmo o la secuencia de los números.
Frijoles y plantilla de manos

Materiales: E) Plantilla de dos manos, frijoles de dos colores
La clase aprende las rutinas y los procedimientos como preparación para la distribución, el cuidado y la recopilación de los materiales.
• Distribución de los materiales: Establezca un procedimiento eficaz para la distribución de los frijoles y las plantillas. Enseñe y practiquen el procedimiento. Anticípese a los problemas antes de que ocurran. Deténgase para corregir y resolver los problemas de inmediato.
• Cuidado de los materiales: Demuestre de manera interactiva cómo guardar y manipular adecuadamente los frijoles.
• Exploración libre de los materiales: Dé tiempo para que la clase inspeccione, manipule, comente y, posiblemente, cuente los materiales sin objetivos de enseñanza.
• Recopilación de los materiales: Realice el procedimiento opuesto a la distribución.
1 2 3 2 1 2 1 2 3 2 3 2 3
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 1 © Great Minds PBC 19
Presentar
La clase identifica los atributos en un conjunto de imágenes y aísla un atributo para seleccionar lo que no pertenece.
Muestre el conjunto de imágenes para la rutina ¿Cuál no pertenece al grupo?
Usen los ojos para observar la imagen que no pertenece al grupo. Piensen cuál no se parece a las otras imágenes.
Usen la mente para imaginar por qué esa imagen no pertenece al grupo de las otras imágenes. ¿En qué se diferencia esa imagen?
Establezca rutinas que den tiempo a toda la clase para formular sus propias ideas. Una vez transcurrido el suficiente tiempo para pensar, señale la imagen de la rueda.
Si piensan que la rueda no pertenece al resto de las imágenes, pónganse de pie.
Reúna a quienes se pusieron de pie y pregúnteles en voz baja por qué piensan que la rueda no pertenece al grupo. Recabe tantas razones como sea posible de forma eficaz. Asegúrese de que participen todas las personas del grupo. Pida a la clase que regresen a sus asientos. Resuma el razonamiento del grupo pequeño a todo el grupo.
Este grupo dijo que la rueda no pertenece a las demás imágenes porque no es naranja. Repita estos pasos para cada imagen que elija la clase.
• Color: la rueda no pertenece porque no es naranja.
• Tamaño: la pelota de basquetbol no pertenece al grupo porque es más pequeña que las otras imágenes.
• Forma: el sombrero no pertenece al grupo porque no es redondo.
• Uso: la naranja no pertenece al grupo porque se puede comer y las demás no.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hicieron un buen trabajo al usar cosas como el color y el tamaño para hablar sobre los objetos. Hoy, vamos a usar palabras para comparar más cosas.
Nota para la enseñanza
En los primeros días de clase, es importante practicar rutinas de gestión que permitan un máximo aprendizaje. En la sección Presentar, hay dos ejemplos escritos.
Comenzar las oraciones con recordatorios discretos como “Usen los ojos” o “Usen la mente” promueve el tiempo para pensar de toda la clase.
El susurro dentro de un grupo llamará la atención de quienes están fuera porque, de forma innata, intentarán escuchar el “secreto” que se comenta.
Apoyo para la comprensión del lenguaje
Considere formar grupos de manera estratégica y flexible a lo largo del módulo.
• Forme parejas de estudiantes que tengan distintos niveles de competencia en matemáticas.
• Forme parejas de estudiantes que tengan distintos niveles de competencia en el idioma.
De ser posible, intente formar las parejas con estudiantes que tengan el mismo idioma materno.
10 10 20 10
K ▸ M1 ▸ TA ▸ Lección 1 EUREKA MATH2 © Great Minds PBC 20
Aprender
Exactamente iguales o iguales pero…
La clase usa atributos para determinar si dos objetos son exactamente iguales o si son iguales pero tienen una pequeña diferencia.
Muestre la imagen de los dos patos.
Observen los dos patos. ¿Son iguales? ¿Cómo saben que son iguales?


Sí. Los dos son amarillos.
Tienen el mismo tamaño.
Son iguales en todo. Podemos decir que son exactamente iguales.
Muestre la imagen de las manzanas.
Observen las dos manzanas. ¿Son exactamente iguales? No.
¿Qué tienen de igual las dos manzanas? Reúnanse y conversen en parejas para decir qué tienen de igual las dos manzanas.


Las dos son rojas.
Las dos son redondas.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante pone atención a la precisión (MP6) cuando usa las frases exactamente iguales e iguales pero… para describir dos objetos. Comunica con precisión atributos en común entre los objetos en vez de simplemente describirlos como iguales o diferentes.
Evaluación observacional
; Escuche las respuestas de sus estudiantes cuando se reúnan y conversen en parejas. ¿Pueden describir los atributos que son iguales y los que son diferentes?
10 10 20 10
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 1 © Great Minds PBC 21
¿Qué no es igual en las dos manzanas? ¿En qué se diferencian? Reúnanse y conversen en parejas para decir en qué se diferencian las manzanas.
Una es grande y la otra es pequeña.
Son iguales porque las dos son manzanas rojas y redondas, pero son diferentes porque una es grande y la otra es pequeña. Podemos decir que tienen el mismo nombre, el mismo color y la misma forma, pero su tamaño es diferente.
Repita la actividad con cada imagen: los vasos de jugo, los dados y los perros. Para apoyar a la clase, resuma sus ideas usando una estructura oracional repetitiva.



• Son iguales en todo. Son exactamente iguales.
• Son iguales porque , pero son diferentes porque .
• Tienen el mismo , pero su es diferente .
Grupo de problemas
Por lo general, los Grupos de problemas se reservan para que la clase trabaje de forma individual en el objetivo del día. No hay práctica independiente para la lección 1. Use este tiempo para establecer transiciones y rutinas de modo que, en los días siguientes, la clase se desplace por el salón de clases y manipule materiales de forma eficaz, por ejemplo, el libro para estudiantes.
Brindar oportunidades para que la clase practique y muestre lo aprendido a lo largo del trabajo independiente en clase es una parte integral de Una historia de unidades®. En kindergarten, esa práctica puede realizarse mediante experiencias prácticas, juegos o trabajo escrito.
Mediante la introducción gradual de los Grupos de problemas, cada estudiante de kindergarten adquiere la capacidad de representar su trabajo mediante los dibujos y la escritura. No todas las lecciones de kindergarten cuentan con Grupos de problemas.
Nota para la enseñanza
Las imágenes están ordenadas para establecer, primero, el significado de igual y diferente y, luego, para animar a la clase a considerar diversos atributos que puedan compararse.
El último par puede ser particularmente complicado porque el mismo perro está en distintas posiciones. ¿Por qué se introduce esta complejidad? La idea de que un objeto mantiene su nombre independientemente de su posición u orientación será importante en el módulo 2, cuando la clase considere los atributos de las figuras. Los triángulos que aparecen a continuación son la misma figura, pero están en diferentes posiciones.
Apoyo para la comprensión del lenguaje
Las y los estudiantes de corta edad están aprendiendo a elaborar oraciones complejas de forma independiente. Al usar una estructura oracional repetitiva para volver a expresar las respuestas de la clase, se proporciona un modelo de lenguaje que puede ser imitado.
En su lugar, la clase puede usar dos oraciones sencillas: “Es el mismo perro. Lo que es diferente es que una imagen muestra al perro sentado y la otra muestra al perro acostado”.


K ▸ M1 ▸ TA ▸ Lección 1 EUREKA MATH2 © Great Minds PBC 22
Concluir
Reflexión final 10 min
Objetivo: Comparar objetos según sus atributos
Muestre el conjunto de imágenes de la sección Presentar.
¿Qué imágenes son iguales pero un poco diferentes?
La naranja y la rueda son redondas, pero la rueda no se puede comer.
La naranja, la pelota de basquetbol y el sombrero son iguales porque todos son naranjas, pero son diferentes porque son todas cosas distintas.
Escuché que dijeron que la naranja, la pelota de basquetbol y el sombrero son iguales porque todos son naranjas. Todos tienen el mismo…
Color
¿De qué otras maneras las cosas pueden ser iguales?
Tamaño, nombre, forma, número
10 20 10 EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 1 © Great Minds PBC 23
Clasificar objetos en dos categorías
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
Una vez que la clase pueda comparar objetos según un atributo específico, podrá crear grupos de objetos que compartan un atributo (clasificación). Al principio, los grupos se clasifican por atributos simples y obvios, como el color. En esta lección, cada estudiante elige una manera de clasificar objetos y usa palabras para compartir cómo los clasificó. En esta lección se presenta el término clasificar.
Pregunta clave
• ¿De qué maneras podemos clasificar objetos?
Criterio de logro académico
K.Mód1.CLA10 Clasifican objetos en categorías. (K.MD.B.3)
2
LECCIÓN 2
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 5 min
Aprender 25 min
• Clasificar
• Nombrar una manera de clasificar
Concluir 10 min
Materiales
Maestro o maestra
• guante numerado derecho
• cubos Unifix® (5)
• papel de rotafolio
• bolsitas para clasificar
• marioneta o animal de peluche
Estudiantes
• Plantilla de dos manos
• frijoles de dos colores (3)
• bolsitas para clasificar (1 por estudiante o pareja de estudiantes)
• plantilla de trabajo (1 por estudiante o pareja de estudiantes)
Preparación de la lección
• Prepare las bolsitas de 5 frijoles de dos colores de la lección 1, para que ahora haya 3 frijoles en cada bolsita.
• Coloque 3 cubos Unifix rojos y 2 azules en una bolsita.
• Decida si la clase va a trabajar de manera individual o en parejas. Prepare las bolsitas para clasificar para cada estudiante o pareja de estudiantes. Cree bolsitas para clasificar de forma que los objetos puedan clasificarse en dos categorías. Consulte la sección Materiales de los recursos del módulo para obtener más información sobre cómo preparar un conjunto diferenciado de bolsitas para clasificar.
• La plantilla de trabajo puede ser una pizarra blanca individual, la parte de atrás de la Plantilla de dos manos o un trozo de papel de construcción, cualquier cosa que permita delimitar el área de trabajo.
• A lo largo del año se usará muchas veces una marioneta o un animal de peluche. Considere elegir algo que se pueda usar varias veces para que se convierta en algo conocido.
© Great Minds PBC 25 EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 2
Fluidez
Contar con movimiento hasta el 10
La clase cuenta con movimientos del cuerpo para desarrollar fluidez con los nombres de los números y la correspondencia de uno a uno.
Aplaudamos 5 veces y contemos los aplausos. ¿Comenzamos?
Al principio, cuente y aplauda del 1 al 5 lentamente, haciendo énfasis en que para cada aplauso se dice un número. Repita el proceso hasta que la mayor parte de la clase esté aplaudiendo, contando o, idealmente, aplaudiendo y contando.
Repita el proceso, pero esta vez dé pisotones y cuente hasta el 5.
Ahora, aplaudamos 10 veces y contemos los aplausos. ¿Comenzamos?
Cuente y aplauda del 1 al 10 junto con la clase.
Repita el proceso, pero esta vez dé pisotones y cuente hasta el 10.
Contar en el guante numerado hasta el 3
Materiales: M) Guante numerado derecho

La clase cuenta en el guante numerado para desarrollar el reconocimiento numérico y familiarizarse con el conteo con el método matemático.
Observen mi guante numerado y cuenten en voz alta. ¿Comenzamos?
Comience con el puño cerrado y, después, muestre lentamente el dedo meñique, luego, el anular y, por último, el mayor. 1, 2, 3
Quédense aquí, en el 3. Vamos a contar hacia atrás hasta el 1. ¿Comenzamos?
Muestre los 3 dedos. Baje el dedo mayor y, luego, el anular. 3, 2, 1
Guante numerado visto desde la perspectiva de la clase
Nota para la enseñanza
Las actividades de Fluidez, como Contar con movimiento hasta el 10, se pueden repetir a lo largo de la lección o de la jornada escolar siempre que la clase necesite moverse. Esto puede resultar de mucha utilidad durante las transiciones del trabajo independiente a las conversaciones de la clase o en lecciones que tienen un fuerte énfasis en el debate. El conteo a coro atrae la atención de la clase, y el movimiento impulsa la sangre al cerebro. Al final del conteo, la clase está atenta para escuchar los próximos pasos que diga el maestro o la maestra.
10 5 25 10
K ▸ M1 ▸ TA ▸ Lección 2 EUREKA MATH2 © Great Minds PBC 26
Facilite más práctica para contar del 1 al 3 y, luego, del 3 al 1.
¡Ahora pueden hacer algo más difícil! Esta vez, contaremos hacia arriba y hacia abajo, como si fuera una ola. Observen mi guante numerado y cuenten en voz alta.
Use el guante numerado para mostrar la siguiente secuencia mientras la clase cuenta en voz alta.
Frijoles y plantilla de manos
Materiales: E) Plantilla de dos manos, frijoles de dos colores
La clase empareja 1 frijol con 1 dedo para desarrollar la correspondencia de uno a uno.
¡Levanten el dedo índice! Toquen los puntos rojos que hay en la parte de abajo de la plantilla.
Abran sus bolsitas como lo practicamos.
Coloquen 1 frijol sobre 1 punto. 1 frijol, 1 punto. Continúen hasta que se queden sin frijoles.
Haga una pausa mientras la clase coloca los 3 frijoles sobre 3 de los puntos rojos.



Recojan 1 frijol. ¡Muéstrenlo! Colóquenlo sobre el meñique.
La clase coloca 1 frijol sobre el meñique en la Plantilla de dos manos.
Recojan 1 frijol. ¡Muéstrenlo! Colóquenlo sobre el siguiente dedo.
La clase coloca 1 frijol sobre el dedo anular en la Plantilla de dos manos.
Continúe el proceso con el tercer frijol sobre el dedo mayor en la Plantilla de dos manos.
1 2 3 2 1 2 1 2 3 2 3 2 3
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 2 © Great Minds PBC 27
Ahora, volvamos a colocar los frijoles sobre los puntos. 1 frijol, 1 punto. Díganlo conmigo mientras lo hacen.
1 frijol, 1 punto. (Deslizan 1 frijol hacia un punto).
Repita el proceso de mover los 3 frijoles desde los puntos hasta la punta de los dedos y otra vez hacia los puntos.
Presentar
Materiales: E) Bolsita para clasificar, plantilla de trabajo

La clase examina objetos y considera sus atributos.
Comience este segmento con la clase en el lugar donde hará su trabajo independiente. Van a moverse a un lugar central al comienzo de la sección Aprender.
Pida a la clase que vierta el contenido de sus bolsitas en las plantillas. Asigne un tiempo para que puedan explorar libremente: examinar, observar, organizar, conversar sobre los objetos y, posiblemente, contar.
¿Las cosas de sus bolsitas son exactamente iguales? Bueno, tienen el mismo color, pero diferente tamaño. Los míos son todos alimentos, pero tienen distintos colores. Yo tengo muchos animales, pero no el mismo tipo de animales.
Guíe la conversación a fin de presentar posibles atributos de clasificación. Si la clase no los menciona, usted podría preguntar: ¿todos tienen el mismo tamaño, color y forma? ¿Todos tienen el mismo nombre?
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hoy, vamos a pensar en qué se parecen y en qué se diferencian las cosas para ayudarnos a formar grupos.
10 5 25 10 K ▸ M1 ▸ TA ▸ Lección 2 EUREKA MATH2 © Great Minds PBC 28
Aprender
Clasificar
Materiales: M) Cubos Unifix; E) Bolsitas para clasificar

La clase clasifica objetos en dos grupos según un atributo.
Reúna a la clase en un lugar central del salón de clases, lejos de sus bolsitas para clasificar. Asegúrese de que puedan ver de forma clara el conjunto de cubos Unifix que está en una bolsita (3 rojos, 2 azules). Saque los cubos de la bolsita.
Yo también tengo algunas cosas. Observen cómo las clasifico en dos grupos.
Uno por uno, separe los cubos rojos y azules en dos grupos distintos. Señale los cubos rojos.
¿Qué nombre le pondrían a este grupo?
Grupo rojo

Repita con el grupo azul.
Los clasifiqué por color. Todas las cosas en este grupo son rojas. (Señale). Todas las cosas en este grupo son azules. (Señale). Cuando clasificamos, colocamos las cosas en grupos.
Ahora es su turno. Clasifiquen sus cosas en dos grupos. No es necesario que clasifiquen por color, como hice yo. Pueden elegir lo que funcione para sus cosas.
Pida a la clase que vuelva a sus áreas de trabajo y que comience a clasificar. Si necesitan ayuda, dé instrucciones puntuales. Dígales que clasifiquen los objetos por color, tamaño o nombre. Si es necesario, dé ejemplos o instrucciones explícitas, como “Formen un grupo de cosas moradas”.
Apoyo para la comprensión del lenguaje
La acción es clave para ayudar a la clase a comprender el vocabulario nuevo, como clasificar. No explique la actividad en detalle. En su lugar, ayude a sus estudiantes a entender cómo clasificar incentivando a que observen y razonen mientras usted representa. Luego, deje que pongan a prueba su comprensión y la perfeccionen a lo largo de su actividad de clasificación. Es más fácil usar y definir el vocabulario matemático como clasificar luego de haber tenido la experiencia de clasificar. Al final de la lección, la clase hará una lista de varias maneras de clasificar. Evaluación observacional
; Escuche las respuestas de la clase a la pregunta “¿Qué nombre le pondrían a este grupo?”. Observe mientras clasifican de forma independiente. ¿Pueden nombrar la manera en que clasifican cuando les pregunta?
10 5 25 10
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 2 © Great Minds PBC 29
Seleccione a un grupo pequeño de estudiantes para que compartan su clasificación en el siguiente segmento. Busque una clasificación obvia o probable y otra inusual o inesperada.
Pídales que se levanten cuando terminen. El simple acto de pararse es un claro indicador de que han terminado y crea una sensación de urgencia, además de ser una oportunidad propicia para moverse. Quienes terminen primero pueden pensar en otra forma de clasificar sus objetos o agarrar otra bolsita para clasificar.
Nombrar una manera de clasificar
Materiales: M) Papel de rotafolio
La clase comparte y representa mediante afiches el atributo que usaron para clasificar.
Cuando la mayoría de la clase esté de pie, pídale que unan las manos detrás de la espalda para volver a concentrarse.
Facilite la participación y seleccione a estudiantes para preguntarles cómo clasificaron. Ayúdeles a identificar y nombrar el atributo que usaron. Por ejemplo, responda a “Clasifiqué por amarillo y verde” con “Clasificaste por color”.
Represente cada respuesta nueva en un afiche. Acepte toda respuesta razonable con justificación, incluidas las preferencias personales como “cosas que considero bonitas y cosas que no considero bonitas”.
Nuestro afiche muestra distintas maneras de clasificar.
Pensemos en imágenes que nos ayuden a recordar estas maneras de clasificar.
El afiche de cada clase será único y variará según las respuestas de cada estudiante.
Use las ideas de la clase para agregar imágenes simples que sirvan de apoyo para quienes todavía no leen. La clase completará este afiche en las próximas lecciones.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante razona de forma abstracta (MP2) cuando elige un atributo para clasificar, nombra ese atributo e imagina un símbolo para representarlo.
K ▸ M1 ▸ TA ▸ Lección 2 EUREKA MATH2 © Great Minds PBC 30
Concluir
Reflexión final 10 min
Materiales: M) Bolsita para clasificar, marioneta o animal de peluche
Objetivo: Clasificar objetos en dos categorías
Seleccione una bolsita para clasificar de sus estudiantes. Presente una marioneta o animal de peluche que clasificará los objetos de forma silenciosa.

Haga que la marioneta clasifique los objetos en dos grupos. Presente la rutina Pensar-Trabajar en parejas-Compartir para que la clase pueda comentar cómo creen que la marioneta hace la clasificación.
Primero, pida a la clase que piense. Usen la mente para pensar cómo clasifica la marioneta.
Luego, pida a sus estudiantes que formen parejas y conversen. Comenten con su pareja cómo clasificó la marioneta.
Pida a un pequeño grupo de estudiantes que comparta sus respuestas.
¿Cómo clasificó la marioneta?
La marioneta hizo un grupo de piedras grandes y un grupo de piedras pequeñas. La marioneta clasificó por tamaño.
Nota para la enseñanza
La marioneta o el animal de peluche se usa a lo largo del año para ayudar a la clase a entender cómo resumir y sintetizar ideas. La marioneta puede desempeñar una relación de pares que el maestro o la maestra no puede. Por ejemplo, la marioneta puede cometer errores que la clase puede corregir. Además, la clase puede usar sus palabras para enseñar a la marioneta lo que aprendieron.
5 25 10
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 2 © Great Minds PBC 31
LECCIÓN 3
Clasificar objetos en dos categorías y contar
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
En esta lección, la clase continúa clasificando objetos en grupos y se enfoca en los atributos que suponen un desafío. Además, después de crear un grupo, hacen y responden la pregunta natural “¿Cuántos objetos hay en el grupo?”. La correspondencia de uno a uno y la comprensión de la cardinalidad son los temas de discusión y práctica. En esta lección se formaliza el término contar.
Pregunta clave
• ¿Qué podemos hacer para contar correctamente?
Criterios de logro académico
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas. (K.CC.B.5)
K.Mód1.CLA10 Clasifican objetos en categorías. (K.MD.B.3)
3
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 10 min
Aprender 20 min
• Contar cada grupo
• Clasificar y contar
Concluir 10 min
Materiales
Maestro o maestra
• guante numerado derecho
• cubos Unifix® (5)
• bolsita para clasificar
• Camino numérico (en la edición para la enseñanza)
• afiche de Maneras de clasificar
• marioneta o animal de peluche
• objetos clasificados
Estudiantes
• Plantilla de dos manos
• frijoles de dos colores (5)
• bolsita para clasificar (1 por estudiante o pareja de estudiantes)
• Camino numérico (1 por estudiante o pareja de estudiantes)
Preparación de la lección
• Prepare la bolsita para clasificar del maestro o la maestra con un lápiz, un marcador, un bolígrafo, un tenedor, una cuchara y palitos chinos.
• Use el afiche de Maneras de clasificar de la lección 2. Continúe agregando información en ese afiche en vez de crear una nueva.
• Cree las bolsitas para clasificar antes de comenzar la lección. Las bolsitas deben contener objetos que se puedan clasificar en dos categorías. Consulte la sección Materiales de los recursos del módulo para ver ejemplos de bolsitas para clasificar.
• Prepare las bolsitas de 3 frijoles de dos colores de la lección 2 de modo que ahora haya 5 frijoles en cada bolsita.
© Great Minds PBC 33 EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 3
Fluidez
Contar en el guante numerado hasta el 5
Materiales: M) Guante numerado derecho
La clase cuenta en el guante numerado para desarrollar el reconocimiento numérico y familiarizarse con el conteo con el método matemático. Observen mi guante numerado y cuenten en voz alta. ¿Comenzamos?
Comience con el puño cerrado. Después, muestre lentamente el dedo meñique y, luego, el resto de los dedos en orden. 1, 2, 3, 4, 5
Quédense aquí, en el 5. Vamos a contar hacia atrás hasta el 1. ¿Comenzamos?
Muestre los 5 dedos. Baje el dedo pulgar y, luego, el resto de los dedos en orden. 5, 4, 3, 2, 1

Ahora, contaremos hacia arriba y hacia abajo, como si fuera una ola. Observen mi guante numerado y cuenten en voz alta.
Use el guante numerado para mostrar la siguiente secuencia mientras la clase cuenta en voz alta.
Si la clase tiene dificultades con la secuencia hasta el 5, regrese a una secuencia hasta el 3 y, luego, suba gradualmente hasta el 5.
1 2 3 2 1 2 1 2 3 4 3 4 5 4 5 4 3
10 10 20 10 K ▸ M1 ▸ TA ▸ Lección 3 EUREKA MATH2 © Great Minds PBC 34
Frijoles y plantilla de manos
Materiales: E) Plantilla de dos manos, frijoles de dos colores
La clase empareja 1 frijol con 1 dedo y dice el número de frijoles para desarrollar la correspondencia de uno a uno y una comprensión de la cardinalidad.
¡Levanten el dedo índice! Toquen los puntos rojos que hay en la parte de abajo de la plantilla.
Abran sus bolsitas como lo practicamos.
Coloquen 1 frijol sobre 1 punto. 1 frijol, 1 punto. Continúen hasta completar todos los puntos rojos.
Haga una pausa mientras la clase coloca los 5 frijoles sobre los puntos rojos.





Recojan 1 frijol. ¡Muéstrenlo! Colóquenlo sobre el meñique.
¿Cuántos dedos tienen un frijol?
Recojan 1 frijol y colóquenlo sobre el dedo anular. ¿Cuántos dedos tienen un frijol ahora?
Continúe hasta el 5 y, luego, hacia atrás hasta el 1. Omita el 0 mientras no se haya presentado el concepto.
Si la clase subitiza, o sabe cuántos hay sin contar, no insista en que toquen y cuenten. Insistir en que toquen y cuenten puede hacer que piensen que cometieron un error y que no confíen en su habilidad de saber cuántos hay “a simple vista”.
Conteo en voz baja y en voz alta
Materiales: M) Cubos Unifix
La clase cuenta para decir el número de objetos y se enfoca en el nombre del último número que se dice para desarrollar una comprensión de la cardinalidad.
En esta actividad se utilizan los cambios en el tono de voz para dirigir la atención hacia la última palabra numérica que se dice. Antes de comenzar, establezca lo que significan el conteo en voz baja y en voz alta.
1
2
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 3 © Great Minds PBC 35
Quiero que digan 1, 2, 3 en voz baja. Díganlo lo suficientemente alto para que pueda escuchar. (Señale sus labios para enfatizar).
1, 2, 3 (en voz baja)
¡Excelente! Ahora, quiero que digan 1, 2, 3 en voz alta. No gritemos para no molestar a las demás clases. (Ahueque las manos alrededor de la boca y haga la expresión facial correspondiente para enfatizar).
1, 2, 3 (en voz alta)
Muestre una barra de 3 cubos Unifix. Use un marcador de borrado en seco para marcar un punto en el último cubo.



Yo toco y ustedes cuentan. Diremos los números en voz baja, pero, cuando lleguen al último (señálelo), ¡digan el número en voz alta!
1 (en voz baja), 2 (en voz baja), 3 (en voz alta)
Repita el proceso con una barra de 5 cubos.
Presentar
Materiales: M) Bolsita para clasificar
La clase clasifica según el uso, que es un atributo nuevo. Muestre uno de los objetos.
¿Qué hacemos con esto?
Pida a la clase que represente (o demuestre acciones correspondientes al uso de los objetos) los actos de comer, escribir o dibujar. Haga esto con algunos de los objetos. Esta simple pregunta brinda acceso inmediato, atrae la atención de toda la clase sin importar su compresión matemática, y prepara a la clase para pensar sobre su uso.

1 (contar en voz baja)
2 (contar en voz baja)
3 (contar en voz alta)
10 10 20 10 K ▸ M1 ▸ TA ▸ Lección 3 EUREKA MATH2 © Great Minds PBC 36
Voy a clasificar mis cosas. Vean si pueden decir cómo las estoy clasificando.
Haga un grupo de herramientas para dibujar y un grupo de utensilios para comer.


¿En qué se parecen todas las cosas de este grupo?
Dibujamos con ellas.
Bien. Digámoslo de otra forma. Digan para qué las usamos. Las usamos…
¡Las usamos para dibujar!
Repita con los utensilios para comer. Agregue uso al afiche de Maneras de clasificar de la lección 2. Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Me pregunto cuántas cosas hay en cada grupo. Hoy, vamos a contar para averiguarlo.
Aprender
Contar cada grupo
Materiales: M) Bolsita para clasificar, Camino numérico
La clase cuenta un grupo y se enfoca en usar la correspondencia de uno a uno y la cardinalidad.
Use los utensilios para comer y las herramientas para dibujar para representar cómo contar cada grupo usando el camino numérico. Al colocar cuidadosamente cada objeto en el camino numérico, la clase practica la correspondencia de uno a uno.
Contamos para hallar cuántos hay en cada grupo. El camino numérico es una herramienta que nos puede ayudar a contar. Vamos a contar las cosas que usamos para dibujar mientras las colocamos en el camino numérico, de esta forma.
Demuestre cómo hacerlo diciendo solo un número mientras mueve cada objeto al camino numérico.
Diferenciación: Desafío
Como desafío para sus estudiantes, pídales que consideren otras maneras en las que los objetos de la bolsita son parecidos y diferentes. En el ejemplo que se muestra aquí, la mayoría de los objetos tienen una forma similar (larga y con forma de bastón) y se pueden agarrar con la mano.
Nota para la enseñanza
El camino numérico apoya la correspondencia de uno a uno porque hay 1 espacio para cada objeto. También anima a la clase a mover y contar, lo que ayuda a llevar la cuenta de lo que ya se contó.
En la lección 5, hay una presentación formal de los numerales. En el camino numérico, se expone a la clase a los numerales, antes de su presentación formal.
10 10 20 10
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 3 © Great Minds PBC 37
Moví cada objeto para confirmar que solo lo conté una vez. Dijimos un número por cada objeto. Cuando hacemos esto, le decimos mover y contar.
Vamos a mover y contar otra vez, pero esta vez vamos a contar en voz baja y en voz alta como hicimos antes. ¿Quién recuerda cuándo contamos en voz alta?
En el último número
Despeje el camino numérico. Mueva cada herramienta para dibujar al camino numérico mientras la clase cuenta.
Reúnanse y comenten con su pareja cuántas herramientas para dibujar hay. Digan una oración completa como esta: Hay herramientas para dibujar en total. (Agite la mano sobre las herramientas para dibujar).
Hay 3 herramientas para dibujar en total.
Repita con el grupo de utensilios para comer; haga una pausa luego de que la clase cuente para confirmar que hayan comprendido.
Contaron 1, 2, 3, 4. ¿Qué número indica cuántos hay?
El número 4
El último número que dijo
El último número que dije, 4, me indica cuántos hay. ¿Tenemos 4 cosas que usamos para qué?
4 cosas que usamos para comer
Sí. 4 nos indica todas las cosas que usamos para comer, todo el grupo.
¿Por qué creen que sería importante saber cuántas cosas hay en un grupo? ¿Por qué querrían contarlas?
Para saber si hay suficientes para toda la clase
Para saber si perdimos algo
Nota para la enseñanza
Con pequeñas cantidades, parte de la clase va a tocar y contar, mientras que otra parte podrá subitizar (saber cuántas hay sin contar) o usar el camino numérico para saber cuántas hay.
Si la clase subitiza, no insista en que toquen y cuenten. Insistir en que toquen y cuenten puede hacer que piensen que cometieron un error y que no confíen en su habilidad de saber cuántos hay “a simple vista”.
K ▸ M1 ▸ TA ▸ Lección 3 EUREKA MATH2 © Great Minds PBC 38
Clasificar y contar
Materiales: M) Afiche de Maneras de clasificar; E) Bolsita para clasificar, Camino numérico

La clase clasifica objetos en dos grupos y cuenta cada grupo.
Distribuya bolsitas para clasificar y caminos numéricos a cada estudiante o pareja de estudiantes. Pídales que clasifiquen los objetos de sus bolsitas en dos grupos y que cuenten cada grupo. Dé tiempo a sus estudiantes para que consideren las diferencias entre los objetos y para que elijan una manera de clasificar. Apoye a la clase brindándole una manera de clasificar solo si es necesario.
Cuando recorra el salón de clases, pida a las parejas que respondan preguntas sobre sus grupos. Anime a la clase a nombrar la unidad cuando indiquen cuántas cosas hay en un grupo: “5 piedras” en vez de “5”.
¿Cómo clasificaron sus grupos?
¿Cuántos objetos hay en cada grupo? ¿Cómo lo saben?
Conté: 1, 2, 3, 4, 5.
Simplemente lo puedo ver.
El camino numérico está lleno hasta el 5.
Diga a la clase que se levanten cuando hayan terminado. Quienes terminen primero pueden pensar en otra manera de clasificar sus objetos o agarrar otra bolsita para clasificar.
Si alguien en la clase halla otra manera de clasificar, pídale que la comparta y agréguela al afiche de Maneras de clasificar que comenzaron en la lección 2.
Diferenciación: Apoyo y desafío
Si hay estudiantes que tienen dificultades para entender la cardinalidad, brinde apoyo mientras cuentan sus grupos. Coloque una nota adhesiva debajo del último objeto para recordarles que cuenten ese número en voz alta.
Para plantear un desafío, pida a sus estudiantes que muestren cómo funciona mover y contar sin usar el camino numérico.
Evaluación observacional
; Observe a la clase mientras hacen la transición hacia contar objetos de forma independiente. ¿Llevan el registro de su cuenta tocando y moviendo sus objetos? ¿Usan el camino numérico o un método diferente de organización?
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante busca estructuras (MP7) cuando identifica atributos compartidos por los objetos y elige una manera de clasificar. Identificar las relaciones entre los objetos sienta las bases para detectar relaciones y estructuras en números y expresiones.
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 3 © Great Minds PBC 39
Concluir
Reflexión final 10 min
Materiales: M) Marioneta o animal de peluche, objetos clasificados
Objetivo: Clasificar objetos en dos categorías y contar
Reúna a sus estudiantes en un lugar donde puedan ver la marioneta y un conjunto de objetos clasificados.
Observen a la marioneta mientras cuenta. Vean si pueden detectar el error.
Demuestre un error común en la correspondencia de uno a uno: saltee un objeto, toque un objeto más de una vez o deslice la mano de la marioneta de forma rápida mientras cuenta. Pida a la clase que use la rutina Pensar-Trabajar en parejas-Compartir para analizar el error de la marioneta.
Usen la mente para pensar en el error de la marioneta.
Junto con sus parejas, conversen sobre el error de la marioneta.
Pida a un pequeño grupo de estudiantes que compartan sus respuestas.
¿Qué error cometió la marioneta?
Hay 4, no 5.
La marioneta contó ese dos veces.
Pida a la clase que exprese el error de forma clara. “Hay 4, no 5.” no es una respuesta completa. Pida a la clase que marque con precisión el comportamiento que dio lugar al error.
Todo el mundo comete errores. Es parte del aprendizaje. ¿Qué puede hacer la marioneta para contar correctamente?
Contar más despacio
Usar el camino numérico para contar
Contar cada cosa una vez
Haga que la marioneta cuente otra vez usando las sugerencias de la clase.
Nota para la enseñanza
La clase generalmente observa a su maestra o maestro en busca de pistas sobre precisión. Cuando el maestro o la maestra comete errores de manera deliberada, la clase a veces se confunde y repite el error. Además, corregir a una persona adulta puede generarles incomodidad.
Cuando una marioneta o un animal de peluche comete un error, es más probable que la clase entienda que se cometió un error. Es posible que les resulte más fácil describir el error y cómo se puede corregir.
10 20 10
K ▸ M1 ▸ TA ▸ Lección 3 EUREKA MATH2 © Great Minds PBC 40
© Great Minds PBC 41 This page may be reproduced for classroom use only. EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 3 ▸ Camino numérico 1 2 3 4 5
© Great Minds PBC 42 This page may be reproduced for classroom use only. K ▸ M1 ▸ TA ▸ Lección 3 ▸ Camino numérico EUREKA MATH2 6 7 8 9 10
LECCIÓN 4
Clasificar objetos en tres categorías y contar
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
Después de adquirir experiencia con la clasificación, la clase puede clasificar en más de dos grupos. En esta lección, cada estudiante clasifica en tres grupos y cuenta el número de objetos de cada grupo. También registra su clasificación en papel, un ejemplo temprano de representación a través de las matemáticas (MP4).
Pregunta clave
• ¿Qué significa clasificar en grupos?
Criterios de logro académico
K.Mód1.CLA1 Cuentan hasta el 10. (K.CC.A.1)
K.Mód1.CLA10 Clasifican objetos en categorías. (K.MD.B.3)
4
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 5 min
Aprender 30 minutos
• Clasificar
• Nombrar la clasificación
• Grupo de problemas
Concluir 5 min
Materiales
Maestro o maestra
• guante numerado derecho
• cubos Unifix® (5)
• afiche de Maneras de clasificar
• Imágenes de transportes (en la edición para la enseñanza)
• papel de rotafolio
Estudiantes
• Plantilla de dos manos
• frijoles de dos colores (5)
• bolsitas para clasificar (1 por estudiante o pareja de estudiantes)
• libro para estudiantes
Preparación de la lección
• Muestre el afiche de Maneras de clasificar.
• Seleccione imágenes que muestren tres maneras en las que sus estudiantes puedan volver de la escuela o de la guardería a sus casas (p. ej., autobús, auto, a pie, bicicleta, tren). Asegúrese de que toda la clase pueda estar incluida en alguna de las tres categorías.
• Cree una tabla de clasificación de transportes con tres encabezados que coincidan con las imágenes.
• Ajuste las bolsitas para clasificar que se usaron en las lecciones anteriores para que los objetos se puedan clasificar en tres categorías (p. ej., agregar borradores a una bolsita con lápices y crayones). Las categorías no pueden tener más de 5 objetos.
© Great Minds PBC 45 EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 4
Fluidez





Contar en el guante numerado hasta el 5
Materiales: M) Guante numerado derecho

La clase cuenta en el guante numerado para desarrollar el reconocimiento numérico y familiarizarse con el conteo con el método matemático.
Observen mi guante numerado y cuenten en voz alta. ¿Comenzamos?
Use el guante numerado para mostrar la siguiente secuencia mientras la clase cuenta en voz alta.
Si la clase tiene dificultades con la secuencia hasta el 5, regrese a una secuencia hasta el 3 y, luego, suba gradualmente hasta el 5.
Frijoles y plantilla de manos
Materiales: E) Plantilla de dos manos, frijoles de dos colores
La clase empareja 1 frijol con 1 dedo y dice el número de frijoles para desarrollar la correspondencia de uno a uno y una comprensión de la cardinalidad.
¡Levanten el dedo índice! Toquen los puntos rojos que hay en la parte de abajo de la plantilla.
Coloquen 1 frijol sobre 1 punto. 1 frijol, 1 punto. Continúen hasta completar todos los puntos rojos.
1 2 3 2 1 2 1 2 3 4 3 4 5 4 5 4 3
10 5 30 5 K ▸ M1 ▸ TA ▸ Lección 4 EUREKA MATH2 © Great Minds PBC 46
Haga una pausa mientras la clase coloca los 5 frijoles sobre los puntos rojos.
Recojan 1 frijol. ¡Muéstrenlo! Colóquenlo sobre el meñique. ¿Cuántos dedos tienen un frijol?
Recojan 1 frijol y colóquenlo sobre el dedo anular. ¿Cuántos dedos tienen un frijol ahora?
Continúe hasta el 5 y, luego, hacia atrás hasta el 1. Omita el 0 mientras no se haya presentado el concepto.
Conteo en voz baja y en voz alta
Materiales: M) Cubos Unifix

La clase cuenta para decir el número de objetos y se enfoca en el nombre del último número que se dice para desarrollar una comprensión de la cardinalidad.
En esta actividad se utilizan los cambios en el tono de voz para dirigir la atención hacia la última palabra numérica que se dice. Antes de comenzar, establezca lo que significan el conteo en voz baja y en voz alta.
Quiero que digan 1, 2, 3 en voz baja. Díganlo lo suficientemente alto para que pueda escuchar. (Señale sus labios para enfatizar).
1, 2, 3 (en voz baja)
¡Excelente! Ahora, quiero que digan 1, 2, 3 en voz alta. No gritemos para no molestar a las demás clases. (Ahueque las manos alrededor de la boca y haga la expresión facial correspondiente para enfatizar).
1, 2, 3 (en voz alta)
Muestre una barra de 3 cubos Unifix. Use un marcador de borrado en seco para marcar un punto en el último cubo.


Yo toco y ustedes cuentan. Diremos los números en voz baja, pero, cuando lleguen al último (señálelo), ¡digan el número en voz alta!
1 (en voz baja), 2 (en voz baja), 3 (en voz alta)
Repita el proceso con una barra de 5 cubos.
1
2
1 (contar en voz baja)
2 (contar en voz baja)
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 4 © Great Minds PBC 47
3 (contar en voz alta)
Presentar
Materiales: M) Afiche de Maneras de clasificar
Esta actividad presenta la clasificación en tres categorías y anima a la clase a considerar cómo se clasifican los objetos.
Asegúrese de que el afiche de Maneras de clasificar esté a la vista. Muestre a la clase la imagen de un grupo de piedras clasificadas en tres grupos. A continuación, pida a la clase que use la rutina Pensar-Trabajar en parejas-Compartir para analizar la siguiente pregunta.
¿Cómo creen que están clasificadas estas piedras?

Por lo que pesan
Pequeñas, medianas y grandes
Brinde apoyo a sus estudiantes para explicar sus razonamientos al usar la imagen. Use las piedras para aclarar las respuestas que son evidentemente incorrectas, como clasificar por color.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición. Hoy, vamos a clasificar en tres grupos.
Aprender
Clasificar
Materiales: M) Imágenes de transportes, tabla de clasificación de transportes La clase clasifica a cada estudiante según un único atributo (cómo llegan a su casa) y cuentan cada categoría.
Muestre a la clase el papel en el que están representadas las tres maneras de volver de la escuela o de la guardería a sus casas. Coloque las imágenes de transportes en un área despejada del salón de clases ubicadas a unos pies de distancia entre sí.
Nota para la enseñanza
Este tipo de conversaciones abiertas es una oportunidad para enseñar en kindergarten qué es relevante matemáticamente y qué no lo es. Modere con amabilidad las respuestas de sus estudiantes, especialmente las historias personales, cuando no tengan que ver con la conversación matemática.
10 5 30 5
10 5 30 5 K ▸ M1 ▸ TA ▸ Lección 4 EUREKA MATH2 © Great Minds PBC 48
Pida a sus estudiantes que se clasifiquen y se dirijan hacia la imagen que muestra la manera en que vuelven a sus casas. Mientras la clase se clasifica, anticípese a la incertidumbre de dónde pararse y a las superposiciones en los espacios de los tres grupos. Exprese ideas sobre cómo organizar la clase para que sea más fácil ver a cada grupo.
¿Qué observan sobre nuestros tres grupos?
Muchos van a pie.
Quienes toman el autobús y el tren son números parecidos.
Me pregunto cuántas personas hay en cada grupo. ¿Cómo podríamos averiguarlo?
(La clase empieza). 1, 2, 3, 4… Podríamos contar.

Si la clase todavía no sugirió hacer una fila en cada grupo, pídales que lo hagan. Recuérdeles la estrategia de mover y contar que fue útil para contar en las lecciones anteriores.
Use los siguientes pasos para cada grupo. Primero seleccione el grupo con menos personas.
• Pídales que formen una línea recta para que puedan enumerarse de uno en uno.
• Mientras cada persona se enumera, dibuje un círculo en el afiche, debajo del encabezado adecuado. Ayude a la clase a contar, en especial si un grupo tiene más de 10 estudiantes.
• Pida a toda la clase que cuenten los círculos juntos, para asegurarse de que coinciden con el grupo.
• Escriba el numeral en el afiche.
Nota para la enseñanza
Esta es una oportunidad para hablar acerca de cómo hacer un dibujo matemático simple. “Llevaría mucho tiempo dibujar a cada persona. En su lugar, voy a hacer un dibujo matemático y usar un círculo para representar a cada persona”.
A pie Autobús Tren
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 4 © Great Minds PBC 49
Nombrar la clasificación
La clase nombra el atributo que usó para clasificar.
Converse con la clase acerca de la clasificación. Consulte el afiche de Maneras de clasificar o agregue información si es necesario.
¿Cómo clasificamos en grupos?
Tren, autobús y a pie
Clasificamos por cómo volvemos a casa.
Sí. Clasificamos por cómo volvemos de la escuela o de la guardería a nuestras casas.
Agregue un título a la tabla: Cómo volvemos a casa.
¿Por qué querríamos saber cuántas personas hay en cada grupo?
Para saber que la mayoría va a pie
Podemos contar para asegurarnos de que quienes van a pie se vayan cuando se les llame. Queremos que todas lleguen a sus hogares a salvo.
Grupo de problemas
Materiales: E) Bolsita para clasificar
Distribuya bolsitas para clasificar a cada estudiante o pareja de estudiantes. Tenga caminos numéricos disponibles para quienes quieran usarlos para contar.
Pida a la clase que clasifique los objetos de sus bolsitas en tres grupos. Dé tiempo para que consideren las diferencias entre los objetos de una bolsita y desarrollen su propia regla de clasificación. Apoye a la clase brindándoles una manera de clasificar solo si es necesario.
Cuando recorra el salón de clases, pida a las parejas que respondan preguntas sobre sus grupos. El siguiente diálogo muestra preguntas de ejemplo y oraciones incompletas.
¿Cómo clasificaron en grupos?
Clasificamos por…
Apoyo para la comprensión del lenguaje
Mientras sus estudiantes comparten sus observaciones, repita sus respuestas usando la terminología precisa (por ejemplo, clasificar, grupo, regla), pero no espere que generen los términos de forma independiente.
Por ejemplo, si alguien dice: “Tren, autobús y a pie”, vuelva a expresar la idea y señale las partes relevantes: “Sí, clasificó en tres grupos. Los grupos eran tren, autobús y a pie”.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante representa a través de las matemáticas (MP4) al dibujar su clasificación y comparar sus dibujos con los objetos físicos.
Evaluación observacional
; Observe a quienes clasifican en dos grupos y a quienes clasifican en tres grupos. (clasificación)
; Escuche a sus estudiantes decir la secuencia numérica en un orden convencional cuando cuenten sus grupos. (secuencia numérica)
K ▸ M1 ▸ TA ▸ Lección 4 EUREKA MATH2 © Great Minds PBC 50
¿Cómo decidieron dónde poner esto? (Muestre un objeto). ¿Por qué no puede ir en otros grupos?
Puede ir en este grupo porque…
No puede ir en ese grupo porque…
¿Cuántos hay en ese grupo?
Si hay tiempo suficiente, pida a la clase que dibuje sus grupos en la página de Grupo de problemas luego de que clasifiquen y cuenten.
Concluir
Reflexión final 5 min
Objetivo: Clasificar objetos en tres categorías y contar
Reúna a la clase en un lugar central del salón de clases y use la rutina Pensar-Trabajar en parejasCompartir para comenzar una conversación.
¿Qué significa clasificar en grupos?
Significa que pones algunas cosas en un grupo y otras cosas en otro grupo.
Piensas en una forma de clasificar, por ejemplo, por cómo llegas a tu casa. Luego, piensas qué cosas entran en ese grupo.
¿Pueden pensar en otras situaciones donde clasificar nos ayuda a responder preguntas importantes?
Cómo llegas a la escuela
El almuerzo: algunas personas traen su almuerzo y otras almuerzan en la cafetería.
DUA: Acción y expresión
Es posible que haya estudiantes que quieran escribir un numeral para registrar cuántos objetos hay en cada grupo. Si lo necesitan, sugiérales que usen el camino numérico o las tarjetas Hide Zero (que ocultan el cero) como ejemplos. La presentación formal a la escritura de numerales comienza en la lección 11.

10
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 4 © Great Minds PBC 51
5 30 5
K ▸ M1 ▸ TA ▸ Lección 4 ▸ Imágenes de transportes EUREKA MATH2 © Great Minds PBC 52 This page may be reproduced for classroom use only.
Bicicleta
Autobús Autobús escolar
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 4 ▸ Imágenes de transportes © Great Minds PBC 53 This page may be reproduced for classroom use only. Auto \ A pie Tren
K ▸ M1 ▸ TA ▸ Lección 4 ▸ Imágenes de transportes EUREKA MATH2 © Great Minds PBC 54 This page may be reproduced for classroom use only.
Autobús
Autobús escolar
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 4 ▸ Imágenes de transportes © Great Minds PBC 55 This page may be reproduced for classroom use only.
K ▸ M1 ▸ TA ▸ Lección 4 ▸ Imágenes de transportes EUREKA MATH2 © Great Minds PBC 56 This page may be reproduced for classroom use only. Bicicleta
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 4 ▸ Imágenes de transportes © Great Minds PBC 57 This page may be reproduced for classroom use only.
A pie
K ▸ M1 ▸ TA ▸ Lección 4 ▸ Imágenes de transportes EUREKA MATH2 © Great Minds PBC 58 This page may be reproduced for classroom use only. Tren
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 4 ▸ Imágenes de transportes © Great Minds PBC 59 This page may be reproduced for classroom use only. Auto
LECCIÓN 5
Clasificar objetos en tres categorías, contarlos y emparejarlos con un numeral
Vistazo a la lección
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Durante las primeras cuatro lecciones se exponen ante la clase los numerales escritos, pero se les presenta formalmente en la lección 5. La clase canta “Puedo contar”, una canción que les puede resultar conocida del prekínder, para nombrar a los numerales y asociar a cada uno de ellos con una cantidad. Continúan clasificando y contando objetos, y ahora emparejan un numeral con cada grupo. En esta lección se presenta el término número.
Pregunta clave
• ¿Cómo pueden ayudarnos los números?
Criterios de logro académico
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10. (K.CC.A.3)
K.Mód1.CLA10 Clasifican objetos en categorías. (K.MD.B.3)
5 © Great Minds PBC
390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 10 min
Aprender 25 min
• Adivina mi regla
• Contar y emparejar
• Grupo de problemas
Concluir 5 min
Materiales Preparación de la lección
Maestro o maestra
• guante numerado derecho
• cubos Unifix® (5)
• letra de la canción “Puedo contar” (en la edición para la enseñanza)
• hojas para recortar de Puedo contar (en la edición para la enseñanza)
• juguetes del salón de clases
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 1 al 5)
• marioneta o animal de peluche
• conjunto de objetos clasificados
Estudiantes
• Plantilla de dos manos
• frijoles de dos colores (5)
• tarjetas Hide Zero® (1 juego del 1 al 5 por estudiante o pareja de estudiantes)
• bolsitas para clasificar (1 por estudiante o pareja de estudiantes)
• libro para estudiantes
• Prepare un conjunto de juguetes del salón de clases que se pueda clasificar en tres categorías. Cada categoría debe tener de 1 a 5 objetos para que la clase pueda emparejar los numerales que se presentan formalmente. Idealmente, el conjunto de juguetes puede clasificarse de más de una manera.*
• Reserve la letra de la canción “Puedo contar” como referencia para la sección Presentar.
• Saque el juego para demostración de las tarjetas Hide Zero y prepare las tarjetas del 1 al 5.
• Saque el juego de la clase de las tarjetas Hide Zero y prepare las tarjetas del 1 al 5.
*Consulte la sección Materiales de los recursos del módulo para ver ejemplos de bolsitas para clasificar.
© Great Minds PBC 61 EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 5
Fluidez
Contar en el guante numerado hasta el 5
Materiales: M) Guante numerado derecho
La clase cuenta en el guante numerado como preparación para emparejar un numeral con un conjunto.

Observen mi guante numerado y cuenten en voz alta. ¿Comenzamos?
Use el guante numerado para mostrar la siguiente secuencia mientras la clase cuenta en voz alta.
Si la clase tiene dificultades con la secuencia hasta el 5, regrese a una secuencia hasta el 3 y, luego, suba gradualmente hasta el 5.
Frijoles y plantilla de manos
Materiales: M) Guante numerado derecho; E) Plantilla de dos manos, frijoles de dos colores
La clase dice y muestra cuántos dedos hay para desarrollar el reconocimiento numérico y familiarizarse con el conteo con el método matemático.
Muestre 1 dedo en el guante numerado.
¿Cuántos dedos hay?
¡Emparéjenlos! Coloquen 1 frijol exactamente en el mismo dedo.
Señale la plantilla de manos. Según sea necesario, ayude a sus estudiantes a colocar un frijol sobre el meñique de la mano izquierda.
1 2 3 2 1 2 1 2 3 4 3 4 5 4 5 4 3
1
10 10 25 5 K ▸ M1 ▸ TA ▸ Lección 5 EUREKA MATH2 © Great Minds PBC 62
Muestre 2 dedos en el guante numerado.
¿Cuántos dedos hay?
¡Emparéjenlos!
Asegúrese de que sus estudiantes coloquen un frijol en el anular de la mano izquierda. Continúe hasta el 5 y, luego, hacia atrás hasta el 1.
Conteo en voz baja y en voz alta
Materiales: M) Cubos Unifix

La clase cuenta para decir el número de objetos y se enfoca en el nombre del último número que se dice para desarrollar una comprensión de la cardinalidad.
En esta actividad se utilizan los cambios en el tono de voz para dirigir la atención hacia la última palabra numérica que se dice. Antes de comenzar, establezca lo que significan el conteo en voz baja y en voz alta.
Quiero que digan 1, 2, 3 en voz baja. Díganlo lo suficientemente alto para que pueda escuchar. (Señale sus labios para enfatizar).
1, 2, 3 (en voz baja)
¡Excelente! Ahora, quiero que digan 1, 2, 3 en voz alta. No gritemos para no molestar a las demás clases. (Ahueque las manos alrededor de la boca y haga la expresión facial correspondiente para enfatizar).
1, 2, 3 (en voz alta)
Muestre una barra de 3 cubos Unifix. Use un marcador de borrado en seco para marcar un punto en el último cubo.


Yo toco y ustedes cuentan. Diremos los números en voz baja, pero, cuando lleguen al último (señálelo), ¡digan el número en voz alta!
1 (en voz baja), 2 (en voz baja), 3 (en voz alta)
Repita el proceso con una barra de 5 cubos.
1 (contar en voz baja)
2 (contar en voz baja)
3 (contar en voz alta)
2
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 5 © Great Minds PBC 63
Materiales: M) Letra de la canción “Puedo contar”
La clase asocia la secuencia de palabras de conteo con los numerales del camino numérico.
Muestre el apoyo visual Puedo contar y tenga preparada la letra de “Puedo contar”.
Cante las dos primeras estrofas de la canción (hasta el 5) y avance la imagen a medida que canta. Al final de la primera estrofa, toque las flores mientras canta “1, 2, 3”. Haga lo mismo con los patos al final de la segunda estrofa “1, 2, 3, 4, 5”.
Muestre el numeral 1.
Este es el número 1. Señalen al grupo que tiene 1 cosa.
Pida a alguien en la clase que señale el grupo con 1 cosa (el ave azul) y que cuente para demostrar que hay 1 ave azul. Coloque el numeral debajo de la columna del ave azul. Repita con los otros numerales en orden.
Una vez que estén todos en su lugar, toque y cuente los numerales con toda la clase. Si hay tiempo suficiente, vuelva a cantar la canción y señale las partes correspondientes del apoyo visual.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hoy, vamos a usar números para mostrar cuántos objetos hay en un grupo.
DUA: Representación
El apoyo visual Puedo contar se puede presentar como un afiche de referencia interactivo. Se puede hacer usando las hojas para recortar de Puedo contar de la 1 a la 10, papel de rotafolio y cinta de dos caras.
Pida a la clase que interactúe con él y que elimine estratégicamente algunos numerales o imágenes. Mientras la clase ubica los lugares correctos para las piezas que faltan, pregunte cómo saben dónde poner las piezas.
Puedo contar
Cantar con la melodía de “Una vez pesqué un pez vivo” (Once I Caught a Fish Alive)
1 ave azul cantará.
2 abejas volarán.
3 flores crecen a la vez.
¡Puedo contar! 1, 2, 3
4 gatas duermen al sol.
5 patos tienen calor.
Al estanque entran de un brinco.
Cuento 1, 2, 3, 4, 5.
6 ardillas juntan semillas.
7 aves hacen rosquillas.
Preparan todas un gran banquete.
1, 2, 3, 4, 5, 6, 7
8 frijoles cuelgan de la rama.
9 caracoles se van a la cama.
1, 2, 3, 4, ¡salen cuando llueve!
5, 6, 7, 8 y 9.
10 autos pasean muy limpios.
Cuéntalos: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
¡Contemos todo otra vez!
Presentar
10 10 25 5
1
Great Minds PBC 68 This page may be reproduced for classroom use only.
2 3 4 5
K ▸ M1 ▸ TA ▸ Lección 5 EUREKA MATH2 © Great Minds PBC 64
Aprender
Adivina mi regla
Materiales: M) Juguetes del salón de clases

La clase razona sobre un conjunto de objetos clasificados para decir cómo se clasificaron.
Asegúrese de que la clase pueda ver el conjunto de juguetes del salón de clases de forma clara desde sus asientos. Dígale que tendrán una oportunidad para adivinar su regla de clasificación, o la manera en que clasificó. Establezca una señal silenciosa para que la clase muestre cuando tenga una respuesta. Luego, comience a clasificar el conjunto de juguetes del salón de clases en tres grupos.
Pida a la clase que use la rutina Pensar-Trabajar en parejas-Compartir para responder la siguiente pregunta.
¿Cómo creen que se clasificaron estos juguetes? ¿Cuál fue mi regla de clasificación?
Cosas que se mueven, cosas que son animales y bloques Van en contenedores diferentes. Clasificó por el lugar donde van. Brinde apoyo a sus estudiantes para explicar sus razonamientos al usar atributos de los tres grupos. Use los objetos para aclarar las respuestas que son evidentemente incorrectas, como clasificar por color.
Clasifiqué por el tipo de juguete. Este es el grupo de vehículos. (Señale). Este es el grupo de animales. (Señale). Este es el grupo de bloques. (Señale). Todos tienen su propio contenedor en nuestro salón de clases.

Promoción de los estándares para la práctica de las matemáticas
Cada estudiante construye argumentos viables (MP3) cuando nombra la regla de clasificación que usaron para los juguetes y explica su razonamiento.
10 10 25 5
EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 5 © Great Minds PBC 65
Contar y emparejar
Materiales: M) Juguetes del salón de clases; E) Tarjetas Hide Zero
La clase cuenta cada grupo clasificado y halla el numeral para emparejar.
Me pregunto cuántos objetos hay en cada grupo. ¿Cómo podríamos averiguarlo?
Contando
Movamos y contemos los animales.
Guíe a la clase en un conteo a coro del primer grupo, asegurándose de que el conteo coincida con el movimiento de cada objeto a una línea.
Pida a la clase que ordene las tarjetas Hide Zero del 1 al 5. Pida a alguien de la clase que encuentre el numeral que coincida con el primer grupo y que lo coloque al lado. Repita con los otros dos grupos.



Grupo de problemas
Materiales: E) Tarjetas Hide Zero y bolsitas para clasificar
Distribuya tarjetas Hide Zero a cada estudiante o pareja de estudiantes. Pídales que ordenen las tarjetas del 1 al 5 en la parte superior de su área de trabajo.
Distribuya bolsitas para clasificar. Pida a la clase que clasifique los objetos de sus bolsitas en tres grupos y que empareje un número con cada grupo.
Cuando recorra el salón de clases, pida a las parejas que respondan preguntas sobre sus grupos. Brinde apoyo con oraciones incompletas según sea necesario.
Use la clasificación de Adivina mi regla para crear un ejemplo típico del Grupo de problemas. Antes de pedir a sus estudiantes que dibujen sus grupos, comparta el modelo con la clase y explique que las expertas y los expertos en matemáticas dibujan imágenes matemáticas simples en lugar de imágenes detalladas. Muestre el modelo para que la clase lo pueda consultar mientras trabaja.
Después de que clasifiquen y cuenten, pídales que dibujen sus grupos en la sección Grupo de problemas. Recuerde a sus estudiantes que dibujen una imagen matemática simple con puntos, líneas o círculos en lugar de dibujar imágenes detalladas de sus objetos.
Diferenciación: Desafío
Si sus estudiantes necesitan un desafío, pídales que piensen en una nueva manera de clasificar juguetes. Sus categorías pueden ser únicas basadas en sus experiencias personales: “Este grupo tiene mis juguetes favoritos. Estos juguetes no son mis favoritos”. También es posible que creen más de tres categorías, como en el ejemplo que se muestra a continuación, donde eligieron clasificar por color.
Evaluación observacional
; ¿La clase empareja el numeral correcto con los grupos clasificados? ¿Ponen atención a la orientación de la tarjeta numérica? ¿Está dada vuelta o hacia un lado?
; ¿Nombran y clasifican en tres grupos?
K ▸ M1 ▸ TA ▸ Lección 5 EUREKA MATH2 © Great Minds PBC 66
Concluir
Reflexión final 5 min
Materiales: M) Marioneta, objetos clasificados, tarjetas Hide Zero
Objetivo: Clasificar objetos en tres categorías, contarlos y emparejarlos con un numeral


Reúna a la clase en un lugar donde puedan ver la marioneta, un conjunto de objetos clasificados y las tarjetas Hide Zero del 1 al 5. Haga que la marioneta cuente un grupo de forma correcta pero que olvide cómo era el número.
La marioneta clasificó estas cosas. ¿Cómo puede averiguar la marioneta qué número es el 5?
¡Yo sé! La marioneta me puede preguntar a mí.
La marioneta podría contar las tarjetas y elegir la que es el 5.
Puede dar vuelta a las tarjetas y contar los puntos.
Haga que la marioneta coloque la tarjeta 5 al lado del grupo. Cuente y empareje un numeral con los otros grupos.
Esconda los objetos de un grupo, pero deje el numeral a la vista.
¿Cuántos objetos hay en este grupo? ¿Cómo lo saben? No pueden ver el grupo.
Podemos ver el número 4.
¿Cómo pueden ayudarnos los números?
Podemos ver el número y saber cuántos hay. No tenemos que volver a contar. Solo hay que mirar el número.
10 25 5 EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 5 © Great Minds PBC 67
Puedo contar
Cantar con la melodía de “Una vez pesqué un pez vivo” (Once I Caught a Fish Alive)
1 ave azul cantará.
2 abejas volarán.
3 flores crecen a la vez.
¡Puedo contar! 1, 2, 3
Preparan todas un gran banquete.
1, 2, 3, 4, 5, 6, 7
4 gatas duermen al sol.
5 patos tienen calor.
Al estanque entran de un brinco.
Cuento 1, 2, 3, 4, 5.
8 frijoles cuelgan de la rama.
9 caracoles se van a la cama.
1, 2, 3, 4, ¡salen cuando llueve!
5, 6, 7, 8 y 9.
6 ardillas juntan semillas.
7 aves hacen rosquillas.
10 autos pasean muy limpios.
Cuéntalos: 1, 2, 3, 4, 5,
6, 7, 8, 9, 10.
¡Contemos todo otra vez!
K ▸ M1 ▸ TA ▸ Lección 5 ▸ Puedo contar EUREKA MATH2 © Great Minds PBC 68 This page may be reproduced for classroom use only.
© Great Minds PBC 69 This page may be reproduced for classroom use only. EUREKA MATH2 K ▸ M1 ▸ TA ▸ Lección 5 ▸ Puedo contar
Responder preguntas sobre cuántos hay con hasta 5 objetos

El tema B desarrolla conocimientos anteriores con fundamentos numéricos. La clase practica usando la lista de palabras numéricas, la correspondencia de uno a uno, la cardinalidad y los numerales escritos en distintos contextos reales. Construyen una caja de estrategias de conteo que incluye:
• tocar y contar (se dice una palabra numérica mientras se toca un objeto)
• mover y contar (se dice una palabra numérica mientras se mueve un objeto)
• marcar y contar (se dice una palabra numérica mientras se marca un objeto)
La clase considera cuándo y por qué cada una de estas estrategias es eficaz. Por ejemplo, tocar y contar sirve cuando los objetos ya están en una línea u ordenados de otra manera que brinde un recorrido de conteo claro. Puede ser una estrategia eficaz para objetos concretos y dibujos. Mover y contar es útil para llevar el conteo de los objetos que ya se contaron y los que no, en especial cuando los objetos están desordenados. Sin embargo, mover y contar no sirve para contar objetos en dibujos. La estrategia de marcar y contar permite a sus estudiantes llevar el conteo de los objetos desordenados en un dibujo. Tachan o colocan una ficha sobre cada objeto a medida que cuentan.
A medida que trabajen con conjuntos más grandes en los temas siguientes, las estrategias de conteo y organización tendrán cada vez más importancia para lograr eficiencia y precisión.
En el tema A, la clase comienza a pensar de qué manera les sirve contar en los contextos de clasificar objetos. En el tema B, se preguntan: ¿Por qué necesitamos contar? ¿De qué sirve? Descubren que contar les permite participar de un juego y asegurarse de que haya suficientes piezas para todo el grupo. Estas preguntas seguirán siendo un tema a lo largo del módulo 1.


© Great Minds PBC 70
Tema B
Tocar y contar
Mover y contar
Marcar y contar
La clase también tiene experiencias en las que saben cuántos objetos hay en un conjunto sin contar. Trabajar con pequeñas cantidades permite a sus estudiantes subitizar, o saber, el número de objetos de un conjunto sin contar. Experimentan con la conservación de números al contar un conjunto, mover objetos e indicar cuántos hay. Esta tarea refuerza la idea de que hay más de un camino para hallar la cardinalidad de un conjunto, es decir, el número de objetos que hay. También confirma que el número de objetos de un conjunto es igual sin importar su organización o el orden en el que se cuentan (K.CC.B.4.b).
© Great Minds PBC 71 EUREKA MATH2 K ▸ M1 ▸ TB
Progresión de las lecciones
Lección 6

Organizar, contar y representar una colección de objetos

Lección 7
Practicar el conteo con precisión
Lección 8
Contar conjuntos en configuraciones lineales, de matrices y dispersas
Hay 8 bloques. Los tocamos para contarlos.
Conté para emparejar las tarjetas.
Usamos la estrategia de marcar y contar con las flores blancas para que no falte ninguna.
© Great Minds PBC 72 K ▸ M1 ▸ TB EUREKA MATH2
Lección 9
Conservar el número de objetos en cualquier configuración
Sé que sigue habiendo 3 cubos después de moverlos. Si había 3 antes, seguirán siendo 3 después.

EUREKA MATH2 K ▸ M1 ▸ TB © Great Minds PBC 73
Organizar, contar y representar una colección de objetos
Vistazo a la lección
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten Conteo
y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Esta lección es una oportunidad para recopilar datos de evaluación formativa mientras la clase usa una colección de conteo para explorar maneras de contar y representar un grupo de objetos. Sus estudiantes deciden cómo contar, observan cómo cuentan los demás y comentan sobre las estrategias de conteo más eficaces. En esta lección se presenta el término estrategia.
Pregunta clave
• ¿Qué cosas podemos hacer o qué estrategias podemos usar como ayuda para contar?
Criterios de logro académico
K.Mód1.CLA1 Cuentan hasta el 10. (K.CC.A.1)
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10. (K.CC.B.4.a)
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron. (K.CC.B.4.b)
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas. (K.CC.B.5)
6
LECCIÓN 6
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 5 min
Presentar 10 min
Aprender 30 min
• Organizar, contar y registrar
• Compartir, comparar y conectar
Concluir 5 min
Materiales
Maestro o maestra
• cubos Unifix® (5)
Estudiantes
• colección de conteo (1 por pareja de estudiantes)
• herramientas de organización
• plantilla de trabajo
• libro para estudiantes
Preparación de la lección

• Cuente y coloque en bolsitas las colecciones (consulte la sección Materiales en los recursos del módulo).
• Decida si la clase trabajará en parejas o de manera individual. La lección está redactada para trabajar en parejas, pero puede adaptarse para que cada estudiante trabaje de manera individual.
• Seleccione las herramientas de organización que la clase pueda elegir para organizar su conteo, como cartones con marcos de 10, caminos numéricos (en la edición para la enseñanza) o marcos de 10 (en la edición para la enseñanza).
• Coloque la Lista de verificación de la evaluación observacional en un portapapeles para tomar notas de las observaciones.
© Great Minds PBC 75 EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 6
Fluidez
Dedos a la vista: El método matemático hasta el 3
La clase dice cuántos dedos ve para desarrollar la capacidad de subitizar cantidades que se muestran con el método matemático.
Voy a mostrarles algunos dedos con el método matemático, pero solo por un segundo. Ustedes me dirán el número que ven. Presten mucha atención, ¡o se lo perderán!

Inclínese hacia delante, establezca contacto visual, haga una pausa con teatralidad y, luego, muestre por un instante 3 dedos con el método matemático. Ocúltelos.
¿Cuántos dedos vieron?
Prepárense. Aquí viene el siguiente.
Continúe con la siguiente secuencia:
Capte el interés de la clase y cree un ambiente lúdico, con pausas teatrales, falsos comienzos y repeticiones.
Conteo en voz baja y en voz alta
Materiales: M) Cubos Unifix
La clase cuenta para decir el número de objetos y se enfoca en el nombre del último número que se dice para desarrollar una comprensión de la cardinalidad.
Quiero que digan 1, 2, 3 en voz baja. Díganlo lo suficientemente alto para que pueda escuchar. (Señale sus labios para enfatizar).
1, 2, 3 (en voz baja)
3
1 3 1 2 2 2 3 3 3 2 3 2
30 10 5 5 K ▸ M1 ▸ TB ▸ Lección 6 EUREKA MATH2 © Great Minds PBC 76
¡Excelente! Ahora, quiero que digan 1, 2, 3 en voz alta. No gritemos para no molestar a las demás clases. (Ahueque las manos alrededor de la boca y haga la expresión facial correspondiente para enfatizar).
1, 2, 3 (en voz alta)
Muestre una barra de 3 cubos Unifix. Use un marcador de borrado en seco para marcar un punto en el último cubo.

Yo toco y ustedes cuentan. (Señale el último cubo). Contaremos en voz baja, pero cuando lleguemos al último cubo, ¡diremos el número en voz alta!
1 (en voz baja), 2 (en voz baja), 3 (en voz alta)
¿Cuántos cubos hay?
3 Repita el proceso unas veces más con 3 cubos y, luego, con 5 cubos.
Presentar
1 (contar en voz baja)
Nota para la enseñanza
Si bien no se requiere una plantilla de trabajo, es útil para la clase por dos motivos. La plantilla brinda un área de trabajo clara para que cada pareja trabaje en su lugar. También delimita el trabajo de las parejas para organizar su colección, en especial cuando alinean objetos.
2 (contar en voz baja)
3 (contar en voz alta)
Materiales: E) Colección de conteo, plantilla de trabajo, herramientas de organización
La clase aprende el procedimiento para explorar las características de una colección de conteo.

Oriente brevemente a la clase acerca de los materiales y el procedimiento para la actividad de colección de conteo:
• Trabajarán en parejas para contar una colección.
• Las parejas elaborarán sus propios registros para mostrar cómo contaron.
Señale las herramientas de organización que la clase puede elegir. Las herramientas como los caminos numéricos, los cartones con marcos de 10 o los marcos de 10 facilitarán la correspondencia de uno a uno y pueden ser de ayuda.
Forme parejas de estudiantes. Pídales que elijan una colección y hallen un área de trabajo.
Nota para la enseñanza
En una lección sobre contar colecciones, la clase organiza, cuenta y registra todos los objetos de un conjunto. Cada conjunto se llama colección de conteo. Cada clase necesita una variedad de colecciones de objetos hechas de materiales cotidianos. Para esta lección, cada colección de conteo debe tener entre 5 y 25 objetos.

Es posible que la clase quiera organizar su conteo con herramientas como vasos, caminos numéricos o marcos de 10. Estos materiales deben exhibirse para que la clase pueda usarlos.

30 10 5 5
© Great Minds PBC 77 EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 6
Antes de sacar las colecciones de la bolsita, pida a las parejas que planifiquen cómo trabajarán en conjunto para contar toda la colección. Pida a algunas parejas que tengan planes razonables que compartan su razonamiento con la clase. Use preguntas y oraciones incompletas como las siguientes.
¿Cómo van a contar la colección con su pareja?
Vamos a contar…
¿Qué tarea deben hacer ustedes? ¿Qué tarea debe hacer su pareja?
Mi tarea es… La tarea de mi pareja es…
Si es necesario, dé un ejemplo de trabajo en parejas para que la clase comprenda que las matemáticas son una actividad colaborativa. Mientras dé el ejemplo, procure permanecer neutral sobre la manera de contar para que las decisiones de la clase sean válidas. A lo largo de la lección, busque y valore ejemplos de buen trabajo en parejas.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hoy, contaremos todos los objetos de nuestra colección y mostraremos nuestro trabajo en papel. Pueden empezar a contar con sus parejas.
Aprender
Organizar, contar y registrar
Materiales: E) Colección de conteo, plantilla de trabajo, herramientas de organización
La clase usa sus propias estrategias para contar objetos y registran el proceso.
Recorra el salón de clases y observe cómo la clase organiza, cuenta y registra.
• Como hace poco se hizo énfasis en la clasificación, es posible que haya estudiantes que clasifiquen sus colecciones antes de contar. Recuérdeles que deben contar todos los objetos de su colección. Las estrategias de organización pueden incluir tocar y contar o mover y contar con distintas configuraciones (lineales, de matrices o dispersas).

• Los registros pueden ser dibujos, sellos o números.
Nota para la enseñanza
Elabore un plan que establezca qué deberán hacer las parejas de estudiantes al finalizar de contar sus colecciones y registrar cómo contaron:
• Probar otra manera de organizar y contar
• Intercambiar las colecciones con otra pareja y contar para confirmar el total
• Explicar lo registrado a otra pareja
• Sacar todo y buscar otra colección
DUA: Acción y expresión
Hay estudiantes de corta edad que eligen colecciones grandes y pueden contarlas fácilmente, pero tienen dificultades para registrar. El desarrollo de la motricidad fina puede no estar a la par de las destrezas de conteo. Considere darles un sello y una almohadilla con tinta para que representen los objetos de su colección.
30 10 5 5
K ▸ M1 ▸ TB ▸ Lección 6 EUREKA MATH2 © Great Minds PBC 78
Use los siguientes planteamientos y preguntas para evaluar e incentivar el razonamiento matemático:
• Muestren o compartan lo que hicieron.
• ¿Funciona su plan? ¿Podrían intentar hacerlo de otra manera?
• ¿Cómo llevaron registro de lo que ya habían contado y lo que les faltaba contar?
• ¿Pueden escribir o dibujar algo en el papel para mostrarme cómo contaron?
Elija a algunas parejas para que compartan su trabajo de conteo en el siguiente segmento. Busque ejemplos que demuestren maneras adecuadas de llevar el registro del conteo, como tocar y contar y mover y contar. Si es posible, tome fotos para proyectar. Si no es posible, separe los trabajos seleccionados para compartirlos.
Pida a sus estudiantes que ordenen todo si no comparten su trabajo. Recoja las representaciones escritas para revisarlas como evaluación formativa después de la lección.
Compartir, comparar y conectar
Materiales: M) Ejemplos de trabajo de la clase; E) Colección de conteo
La clase comenta estrategias de conteo.
Reúna a la clase para ver y comentar los ejemplos de trabajo seleccionados. Invite a las parejas seleccionadas a compartir el proceso de conteo que usaron. Mencione las estrategias de conteo que usó cada pareja.
Use los siguientes ejemplos para guiar la conversación de la clase.
Tocar y contar (método de Oscar y Audrey)
Pida a una pareja que haya usado la estrategia de tocar y contar que la muestre usando su colección o una foto de su trabajo. Cuando la pareja haya terminado de contar, guíe la conversación de la clase sobre la estrategia.

¿Cuántos bloques hay en su colección? ¿Cómo lo saben?
El último número era 8.
Evaluación observacional
; Observe a sus estudiantes a medida que cuentan. Verifique si:
• mueven los objetos para llevar la cuenta de cada objeto que cuentan (uno a uno);
• dicen la secuencia numérica correcta;
• dicen el último número de su conteo para indicar el total (cardinalidad).
Promoción de los estándares para la práctica de las matemáticas

Cada estudiante da sentido a los problemas y persevera en su resolución (MP1) cuando cuenta una colección de objetos. Crea un plan para considerar cómo contar, llevar a cabo el plan y ajustarlo según sea necesario.

8
© Great Minds PBC 79 EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 6
¿Qué hicieron Oscar y Audrey para asegurarse de contar todos los bloques?
Tocaron todos los bloques. No se olvidaron de ningún número.
Hay varias maneras de asegurarnos de contar correctamente. Llamaremos a esas maneras estrategias. Oscar y Audrey usaron la estrategia de tocar y contar para asegurarse de decir un número por cada bloque.
Oscar y Audrey, ¿de qué manera les ayudó alinear los bloques para contar?
Comenzamos desde abajo y fuimos subiendo. Entonces, ¿la línea les ayudó a saber cuándo empezar y cuándo terminar de contar? Sí.
Mover y contar (método de Alaina y Campbell)

Invite a una pareja que haya usado la estrategia de mover y contar a que la muestre. Pídales que se detengan cuando hayan contado alrededor de 5 objetos y haga la siguiente pregunta.
Veo que algunos de sus caimanes están en línea. (Señale la línea). Otros de sus caimanes están en una pila. ¿Por qué?
Estos son los que contamos. Todavía no contamos los que están en la pila.
¡Ah! Mueven los caimanes a medida que los cuentan.
Permita que la pareja termine de contar sin interrumpir su trabajo.
¿De qué manera ayudó la estrategia de mover y contar a que Alaina y Campbell hallaran cuántos caimanes hay en su colección?
Contaron cada caimán solo una vez. Sabían cuántos ya habían contado.
K ▸ M1 ▸ TB ▸ Lección 6 EUREKA MATH2 © Great Minds PBC 80
Concluir
Reflexión final 5 min
Objetivo: Organizar, contar y representar una colección de objetos
Asigne a sus estudiantes una pareja nueva para la reflexión final. Considere la posibilidad de formar parejas de estudiantes de una manera que implique movimiento, de tal modo que la clase se revitalice para la conversación.
Siga mostrando el trabajo de sus estudiantes de la sección Compartir, comparar y conectar. Pida a la clase que consulte el trabajo mientras usan la rutina Pensar-Trabajar en parejas-Compartir para responder la siguiente pregunta.
¿Qué cosas podemos hacer o qué estrategias podemos usar como ayuda para contar?
Contar cada objeto una vez. No olvidar ningún objeto.
Podemos alinearlos.
Podemos mover y contar.
30 10 5 © Great Minds PBC 81 EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 6
K ▸ M1 ▸ TB ▸ Lección 6 ▸ Marco de 10 EUREKA MATH2 © Great Minds PBC 82 This page may be reproduced for classroom use only.
EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 6 ▸ Camino numérico © Great Minds PBC 83 This page may be reproduced for classroom use only. 1 2 3 4 5
K ▸ M1 ▸ TB ▸ Lección 6 ▸ Camino numérico EUREKA MATH2 © Great Minds PBC 84 This page may be reproduced for classroom use only. 6 7 8 9 10
Practicar el conteo con precisión
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten Conteo
y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
Sus estudiantes de corta edad necesitan mucha práctica para integrar los fundamentos numéricos y contar con precisión. A lo largo de este módulo, la clase considerará las razones para contar y usar números. Los juegos de esta lección brindan práctica de conteo y refuerzan la idea de que contar es útil y divertido a la vez. En esta lección se presenta el término suficientes.
Pregunta clave
• ¿Cómo sabemos que hemos contado correctamente?
Criterios de logro académico
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10. (K.CC.A.3)
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10. (K.CC.B.4.a)
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron. (K.CC.B.4.b)
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas. (K.CC.B.5)
7
7
LECCIÓN
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 5 min
Presentar 10 min
Aprender 30 min
• Juego del oso
• Juego de emparejar
Concluir 5 min
Materiales
Maestro o maestra
• guante numerado derecho
Estudiantes
• bolsita con osos para contar (1 por grupo de estudiantes)
• Tablero del Juego del oso (1 por pareja, en el libro para estudiantes)
• osos para contar (2 por pareja de estudiantes)
• frijoles de dos colores (5 por pareja de estudiantes)
• vaso (1 por pareja de estudiantes)
• tarjetas para emparejar (1 juego por pareja de estudiantes)
Preparación de la lección
• Prepare bolsitas con 3 a 5 osos para contar. En cada bolsita, escriba cuántos osos hay. El número de osos de cada bolsita no siempre debe coincidir con el número de estudiantes de cada grupo.
• Saque el Tablero del Juego del oso.
• Las tarjetas para emparejar tienen un conjunto de dibujos en un lado y un numeral en el otro. Use solo las tarjetas con numerales y configuraciones del 1 al 5. Guarde las tarjetas para volver a usarlas en la lección 9.
© Great Minds PBC 87 EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 7
Fluidez
Contar en el guante numerado hasta el 5
Materiales: M) Guante numerado derecho
La clase cuenta en el guante numerado para desarrollar el reconocimiento numérico y familiarizarse con el conteo con el método matemático.
Observen mi guante numerado y cuenten en voz alta. ¿Comenzamos?
Use el guante numerado para mostrar la siguiente secuencia mientras la clase cuenta en voz alta.
Si la clase tiene dificultades con la secuencia hasta el 5, regrese a una secuencia hasta el 3 y, luego, suba gradualmente hasta el 5.
Contar con movimiento hasta el 10
La clase cuenta con movimientos del cuerpo para desarrollar fluidez con los nombres de los números y la correspondencia de uno a uno.

Aplaudamos 5 veces y contemos los aplausos. ¿Comenzamos?
Al principio, cuente y aplauda del 1 al 5 lentamente, haciendo énfasis en que para cada aplauso se dice un número. Repita el proceso hasta que la mayor parte de la clase esté aplaudiendo, contando o, idealmente, aplaudiendo y contando.
Repita el proceso, pero esta vez dé pisotones y cuente hasta el 5.
Ahora, aplaudamos 10 veces y contemos los aplausos. ¿Comenzamos?
Cuente y aplauda del 1 al 10 junto con la clase.
Repita el proceso, pero esta vez dé pisotones y cuente hasta el 10.
1 2 3 2 1 2 1 2 3 4 3 4 5 4 5 4 3
30 10 5 5 K ▸ M1 ▸ TB ▸ Lección 7 EUREKA MATH2 © Great Minds PBC 88
Presentar
Materiales: E) Bolsita con osos para contar

La clase cuenta para ver si hay suficientes, con el fin de resaltar la importancia de contar con precisión.
Siente a sus estudiantes en grupos de 3 a 5. Muestre las bolsitas con osos con los numerales visibles. Diga a cada grupo que tome una bolsita. Pida a los grupos que cuenten cuántas personas hay en su grupo.
¿De qué manera contar cuántas personas hay en su grupo ayudó a saber qué bolsita debían elegir?
Queríamos que cada estudiante tuviera un oso.
Ahora, sabemos cuántos osos necesitamos.
Pida a una persona de cada grupo que elija una bolsita. Invite a cada grupo a comprobar si hay suficientes osos en la bolsita elegida. Si a un grupo le faltan o le sobran muchos osos, pídales que piensen cuántos osos más necesitan o cuántos deben devolver.
Tener suficientes significa que cada estudiante recibe 1 oso. ¿Qué hicieron para hallar si hay suficientes osos para cada estudiante del grupo?
Los repartimos y cada estudiante obtuvo un oso.
Sé que hay suficientes porque somos 5 estudiantes y hay 5 osos.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Contar es útil para comprobar si hay suficientes. Eso significa que cada persona obtiene un objeto. Contar también es útil cuando jugamos. Hoy, practicaremos cómo contar.
Nota para la enseñanza
Esta lección presenta más material que el que puede usarse adecuadamente en la mayoría de las clases de 50 minutos. Hay algunas maneras de adaptar la lección:
• Demuestre y jueguen uno de los juegos.
• Demuestre y jueguen los dos juegos, y deje que sus estudiantes elijan cuál jugar.
• Si dispone de ayuda, divida a la clase en dos y que cada adulto enseñe uno de los juegos. Luego, intercambien estudiantes.
• Jueguen a emparejar con toda la clase.
Una vez que la clase conozca bien los juegos, pueden jugar por su cuenta.
Apoyo para la comprensión del lenguaje
El enfoque de la sección Presentar está en la palabra suficientes. Sin embargo, puede haber oportunidades para usar no son suficientes y más de. Estos son algunos ejemplos:
• Hubo estudiantes que no recibieron un oso. Los osos no son suficientes.
• Cada estudiante recibió un oso y aún tenemos más. Hay más osos de los que necesitamos.
La clase tendrá más tiempo de desarrollar el lenguaje para estos conceptos en la lección 13.
30 10 5 5
EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 7 © Great Minds PBC 89
Aprender
Juego del oso
Materiales: E) Tablero del Juego del oso, osos para contar, frijoles de dos colores, vaso La clase practica el conteo de conjuntos para participar en un juego.
Proyecte la hoja extraíble del juego. Elija a una o un estudiante y muestre cómo jugar.
• Estudiante A: Vierte el vaso con frijoles y cuenta solo los frijoles rojos. Mueve su oso el mismo número de huellas de oso que el número de frijoles rojos. Por ejemplo, si arrojó 2 frijoles rojos y 3 frijoles blancos, debe mover el oso 2 huellas de oso.
• Estudiante B: Vierte el vaso con frijoles y cuenta solo los frijoles rojos. Mueve su oso el mismo número de huellas de oso que el número de frijoles rojos.
• Sigan jugando hasta que alguien llegue a la miel. La persona que llegue a la miel primero gana.
Dé tiempo a la clase para jugar en parejas. Camine por el salón de clases y observe cómo cuentan mientras juegan. Observe que quienes cuentan correctamente:
• usan la correspondencia de uno a uno;
• comprenden que el último número indica cuántos hay;
• comienzan a contar desde la siguiente huella de oso del camino, sin contar la huella sobre la que están; y
• cuentan solo los frijoles rojos y no dan vuelta a los frijoles blancos para obtener más rojos.
Diferenciación: Apoyo y desafío
Para apoyar a sus estudiantes con el conteo hasta el 3, reduzca el número de frijoles. Agregue un desafío al incluir los frijoles blancos en las reglas: los osos se pueden mover adelante según el número de frijoles rojos y hacia atrás según el número de frijoles blancos.
Nota para la enseñanza
Si bien puede resultar más fácil usar un dado o una rueda giratoria en el Juego del oso, usar frijoles o discos de dos colores enriquece la experiencia matemática. La clase crea dos grupos cada vez que arrojan frijoles (ven un grupo de 5 frijoles blancos como 5 blancos y 0 rojos) y separan los frijoles rojos. Esta experiencia apoyará su trabajo con la descomposición y los números incluidos en otros números en el tema D.

Evaluación observacional
; Observe a la clase mientras participa en el Juego del oso.
• ¿Mueven su oso tocando en vez de deslizándose sobre cada huella? (una a una)
• ¿Se detienen cuando llegan al número determinado?
30 10 5 5
K ▸ M1 ▸ TB ▸ Lección 7 EUREKA MATH2 © Great Minds PBC 90
Juego de emparejar
Materiales: E) Tarjetas para emparejar
La clase practica cómo contar conjuntos y emparejar un numeral con un conjunto.
Mezcle las tarjetas. Muestre seis tarjetas en dos hileras de tres, asegurándose de que algunas muestren objetos y otras, numerales.
Observen las tarjetas. Hallemos dos tarjetas que se emparejen.
Pida a un o una estudiante que elija una tarjeta para mostrar cómo tocar y contar cada objeto.
¿Cuántos insectos hay?
¿Pueden hallar otra tarjeta con el mismo número de objetos?
Elija a otra persona para que halle una tarjeta que pueda emparejarse.
¿Cómo pueden comprobar que las dos tarjetas se emparejan?
Podemos contarlas otra vez.
Hay números en la parte de atrás. Podemos ver si los números son iguales.
Gire las tarjetas y muestre los números. Pida a la clase que confirme si los números son exactamente iguales. Complete los espacios en blanco con tarjetas del juego. Sigan jugando hasta hallar todas las coincidencias.
Primera coincidencia
Evaluación observacional
; Observe a sus estudiantes mientras participan en el Juego de emparejar.
• ¿Dicen el último número de su conteo para indicar el total? (cardinalidad)
• ¿Emparejan los numerales con las cantidades correctas? (símbolo numérico)
Promoción de los estándares para la práctica de las matemáticas
En el Juego de emparejar, cada estudiante razona de forma abstracta y cuantitativa (MP2) cuando reconoce que los objetos del mundo real, las matrices de figuras y los numerales son distintas representaciones del mismo número.
Diferenciación: Desafío
Considere una de las siguientes adaptaciones del juego para aumentar el desafío a medida que la clase esté lista:
Segunda coincidencia
Organice a la clase en parejas o grupos y reparta conjuntos de tarjetas. Ayude a los grupos mientras ordenan las tarjetas en dos hileras de tres. A medida que sus estudiantes juegan, tome notas de su capacidad para contar haciendo uso de todos los fundamentos numéricos.
• Disponga ocho tarjetas en dos hileras de cuatro para desarrollar la capacidad de sus estudiantes de clasificar con más información visual.
• Incluya el 0.
• Use dos juegos de tarjetas con los números del 1 al 10. Limite el juego a 20 tarjetas para mayor facilidad.
• Invite a sus estudiantes a hallar tarjetas que formen 5.
3
Dos hileras de tres
EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 7 © Great Minds PBC 91
Concluir
Reflexión final 5 min
Objetivo: Practicar el conteo con precisión
¿Están mejorando con el conteo? ¿Cómo lo saben?
Sí. En el Juego de emparejar, conté el número de cosas en las tarjetas y miré los números en la parte de atrás. Hallé todos los números bien.
Piensen cómo podemos usar nuestro cuerpo para contar. ¿Usan el ombligo para contar?
¡No!
¿Y los dedos? ¿Cómo pueden usar los dedos para contar?
Sí, señalo y toco cada objeto con mi dedo.
¿Qué me dicen de los ojos? ¿Cómo pueden usar los ojos para contar?
Observo cada cosa a medida que cuento y señalo.
A veces, tan solo miro y sé cuántos objetos hay.
¿Cómo saben que han contado correctamente?
Puedo contar los cuadrados y, luego, dar vuelta a la tarjeta para comprobar si tengo razón.
Mi pareja y yo contamos los frijoles por separado. Obtuvimos el mismo número.
30 10 5 K ▸ M1 ▸ TB ▸ Lección 7 EUREKA MATH2 © Great Minds PBC 92
Contar conjuntos en configuraciones lineales, de matrices y dispersas
Vistazo a la lección
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
En esta lección, la clase explora maneras de contar dibujos cuando los objetos están en configuraciones lineales, de matrices o dispersas. Usan la estrategia de tocar y contar y aprenden una estrategia alternativa llamada marcar y contar para usar cuando no pueden mover objetos. En esta lección se presentan los términos línea y observar.
Pregunta clave
• ¿Qué estrategias podemos usar para contar correctamente?
Criterio de logro académico
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas. (K.CC.B.5)
8
8
LECCIÓN
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Estudiante
Agenda
Fluidez 10 min
Presentar 5 min
Aprender 25 min
• Tocar y contar
• Marcar y contar
• Grupo de problemas
Concluir 10 min
Materiales
Maestro o maestra
• Grupo de problemas (descarga digital)
• cubos Unifix® (5)
Estudiantes
• cubos Unifix® (5)
• Camino numérico (en el libro para estudiantes)
• plantilla de trabajo
• libro para estudiantes
Preparación de la lección
Imprima o haga una copia del Grupo de problemas para presentarlo como ejemplo para guiar a la clase a lo largo de la lección.
© Great Minds PBC 95 EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 8
Fluidez
Dedos a la vista: El método matemático hasta el 5
La clase dice cuántos dedos ve para desarrollar la capacidad de subitizar cantidades que se muestran con el método matemático.
Voy a mostrarles algunos dedos con el método matemático, pero solo por un segundo. Ustedes me dirán el número que ven. Presten mucha atención ¡o se lo perderán!

Inclínese hacia delante, establezca contacto visual, haga una pausa con teatralidad y, luego, muestre por un instante 3 dedos con el método matemático. Ocúltelos.
¿Cuántos dedos vieron?
Prepárense. Aquí viene el siguiente.
Continúe con la siguiente secuencia:
Facilite más práctica con el conteo súbito, haciendo énfasis en las cantidades 3, 4 y 5.
Capte el interés de la clase y cree un ambiente lúdico, con pausas teatrales, falsos comienzos y repeticiones.
Estacionamiento en el camino numérico
Materiales: E) Plantilla de trabajo, Camino numérico, cubos Unifix
La clase organiza y cuenta los cubos sobre un camino numérico para adquirir fluidez con la correspondencia de uno a uno y el reconocimiento de los numerales.
3
1 3 4 4 4 5 5 5 3 3 3 4
10 5
10 K ▸ M1 ▸ TB ▸ Lección 8 EUREKA MATH2 © Great Minds PBC 96
25
Agiten su varita mágica (lápiz, marcador o dedo) sobre los cubos. Digan unas palabras mágicas. Abracadabra... ¡Puf!
Ya no hay cubos. ¡Ahora hay autos! “Condúzcanlos” por la plantilla.
Dé tiempo a sus estudiantes para mover los cubos Unifix alrededor de la plantilla mientras hacen sonidos de auto.
Y... ¡deténganse! Para encender el motor, deben tocar cada auto.
Demuestre brevemente cómo tocar cada “auto” y, luego, invite a la clase a hacer lo mismo para encender sus autos.
Para llevar el auto hacia su estacionamiento, digan “ruuum” y hagan esto. (Demuestre cómo deslizar un cubo hacia dentro del espacio que hay en el camino numérico).
¡Ahora es su turno!
Ruuum, ruuum, ruuum (La clase empareja cada sonido con un auto).
¡Volvamos atrás! Saquen los autos del estacionamiento. Esta vez, vamos a contar los autos que vamos estacionando. Digan el número a medida que llevan cada auto al estacionamiento, de esta manera. (Demuéstrelo).
1, 2, 3 (La clase empareja cada palabra numérica con cada auto).
Repita el proceso con 4 y 5 cubos, comenzando desde el 1 cada vez.
Presentar
10
La clase analiza una obra de arte y observan objetos que se pueden contar.
25 10

5
Muestre la obra de Henri Rousseau Los flamencos (The Flamingos) (1907). Proyectar la pintura con una cámara de documentos facilitará el uso de cubos en la sección Aprender. Use la pintura para iniciar una conversación. EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 8 © Great Minds PBC 97
¿Qué observan, o ven, en la pintura?
Veo personas.
Veo flamencos.
Veo flores rosas, amarillas y blancas.
Guíe a sus estudiantes para que hagan preguntas sobre la obra. Dé ejemplos de enunciados interrogativos que sean matemáticamente relevantes. Espere enunciados y preguntas simples sobre la pintura.
Cuando veo las cosas que hay en la pintura, me pregunto cuántas flores hay. ¿Hay algo que les llame la atención de la pintura?
Me pregunto qué hacen las personas.
Me pregunto cuántos flamencos hay.
Me pregunto qué flor es la más larga.
Para generar un clima de entusiasmo, diga a la clase que aprenderán una nueva estrategia para contar los objetos de la pintura.
Aprender
Tocar y contar
La clase cuenta objetos en configuraciones lineales. Siga mostrando la pintura de Henri Rousseau, Los flamencos (1907).


Alguien preguntó cuántos flamencos hay en la pintura. Vamos a contar los flamencos rosas. ¿Cómo podemos contarlos? ¿Qué estrategia podemos usar?
Podemos tocar y contar.
Apoyo para la comprensión del lenguaje
Este es el primer uso del término observar. Apoye la comprensión usando el término observar para volver a expresar lo que ven: “Pueden observar, o ver, que hay flores rosas, amarillas y blancas”.
10 5 25 10
K ▸ M1 ▸ TB ▸ Lección 8 EUREKA MATH2 © Great Minds PBC 98
Toque los flamencos lentamente mientras la clase cuenta. Invite a la clase a señalar y llevar la cuenta junto con usted.
Muéstrenme el dedo para contar. (Levante el dedo índice). ¿De qué manera les ayuda usar el dedo para contar?
Nos permite tocar todos los objetos mientras contamos.
Los flamencos están en una línea. ¿Dónde comenzamos a contar? ¿Qué flamenco tocamos y contamos primero?
El más pequeño que está en el extremo ¿Qué flamenco contamos último?
El flamenco grande que está en el otro extremo
Nos movimos en una línea por la pintura, entonces no nos olvidamos de ningún flamenco ni contamos un flamenco dos veces. (Demuestre esto moviendo el dedo de un flamenco a otro).
Invite a la clase a buscar otros objetos de la pintura que estén en línea, como las personas o las flores rosas. Toque y cuente estos objetos con la clase.

Marcar y contar
Materiales: M) Cubos Unifix
La clase cuenta objetos en configuraciones dispersas.
Centre la atención de la clase en las flores blancas. Señale que las flores blancas no están en línea; entonces, podría ser difícil tocarlas y contarlas.
Voy a marcar cada flor con un cubo a medida que contamos. Comencemos con una flor blanca y sigamos hasta que contemos todas.
Coloque un cubo sobre cada flor blanca a medida que cuentan.
¿Cuántas flores blancas hay?
Acabamos de usar la estrategia de marcar y contar para hallar que hay 5 flores blancas.
DUA: Representación
Considere brindar varios ejemplos y ejemplos erróneos de objetos en una línea recta para verificar que la clase pueda diferenciar entre las distintas configuraciones.
Use la técnica de pulgares hacia arriba o pulgares hacia abajo, o una similar, para medir la comprensión de la clase. Refuerce la idea de usar la estrategia de tocar y contar cuando los objetos están en línea, y la estrategia de marcar y contar para llevar la cuenta cuando los objetos no están en línea.
5
EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 8 © Great Minds PBC 99
Demuestre que tachar objetos es otra manera de marcar y contar. Repita el mismo proceso y preguntas anteriores.
¿Por qué usamos la estrategia de marcar y contar para contar las flores?
Podríamos olvidarnos de contar alguna flor si usamos nuestro dedo, porque las flores no están en una línea.
Así no nos olvidamos de ninguna flor ni las contamos más de una vez.
¿Por qué contamos los flamencos de una manera diferente a la que usamos para contar las flores blancas?

Porque podemos usar el dedo cuando las cosas están en línea. Las flores no están en línea. No queremos olvidarnos de contar ninguna flor, entonces las tachamos para llevar la cuenta.
Grupo de problemas
Materiales: E) Cubos Unifix
Para establecer una transición al trabajo de este segmento, practique su rutina de repartir el libro para estudiantes y hallar la página correcta.
Pida a sus estudiantes que observen el primer grupo de caracoles. Demuestre cómo usar cubos para marcar y contar los caracoles. Invite a la clase a hacer lo mismo.
Mueva los cubos de los caracoles al camino numérico mientras cuentan otra vez. Haga una pausa y pida a la clase que haga lo mismo.
¿Cuántos caracoles hay? 3
¿Cómo sabemos que son 3?
Usamos cubos para contar y hay 3 cubos.
Hay 3 cubos en nuestro camino numérico.
Pida a la clase que encierren en un círculo el numeral 3. Si hay tiempo suficiente, pueden colorear los cuadrados del camino numérico.
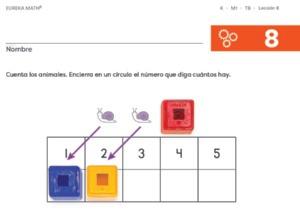

Nota para la enseñanza
Este Grupo de problemas está diseñado para la demostración sistemática. En el primer problema, usted representa el proceso de conteo a través de las preguntas interactivas, las respuestas a coro y conversación como “¿Qué dijo Mónica?”. Después de completar el primer problema en conjunto, la clase prueba resolver el problema del final de la página por su cuenta.
Siga usando la demostración sistemática con los Grupos de problemas de todo el módulo 1 hasta que la clase se sienta cómoda con lápiz y papel.

Diferenciación: Desafío
Quienes necesiten más desafío pueden contar todos los animales de la página. Anime a sus estudiantes a que representen su conteo. En el ejemplo de abajo, la persona continuó el camino numérico.
K ▸ M1 ▸ TB ▸ Lección 8 EUREKA MATH2 © Great Minds PBC 100
Invite a la clase a completar el siguiente problema por su cuenta.
Use una demostración sistemática (consulte la Nota para la enseñanza) en el segundo Grupo de problemas, pero esta vez demuestre cómo tachar las mariposas. Permita a sus estudiantes completar los dos problemas de la tercera página de práctica de manera independiente si ya pueden hacerlo. Anime a la clase a usar su estrategia de conteo preferida.
Evaluación observacional
; ¿Cómo lleva la cuenta la clase de sus conteos?
• Tachan los objetos que no pueden mover para marcarlos.
• Colocan fichas sobre los objetos que no pueden mover para contarlos.
• Usan los números del camino numérico.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante razona de forma abstracta y cuantitativa (MP2) con el Grupo de problemas cuando descontextualiza con cubos en lugar de animales y, luego, vuelve a contextualizar para reconocer que el número de cubos es igual que el número de animales.
© Great Minds PBC 25 EUREKA MATH K ▸ M1 ▸ TB ▸ Lección 8 Cuenta los animales. Encierra en un círculo el número que dice cuántos hay. 1 2 3 4 5 1 2 3 4 5 8 Nombre EUREKA MATH K ▸ M1 ▸ TB ▸ Lección 8 © Great Minds PBC 27 GRUPO DE PROBLEMAS 1 2 3 4 5 1 2 3 4 5 K M1 TB Lección EUREKA MATH © Great Minds PBC 26 GRUPO DE PROBLEMAS 1 2 3 4 5 1 2 3 4 5 EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 8 © Great Minds PBC 101
Concluir
Reflexión final 10 min
Objetivo: Contar conjuntos en configuraciones lineales, de matrices y dispersas
Reúna a la clase cerca de un papel de rotafolio en blanco. Durante la conversación, escriba las estrategias de conteo en el papel a medida que las mencionan. Si hay tiempo suficiente, agregue una ilustración para cada estrategia. Si no es posible, deje espacio para dibujarla después.
Cuando contamos nuestras colecciones, ¿qué estrategias de conteo usamos?
Puedes usar el dedo índice para tocar todos los objetos.
Esa estrategia se llama tocar y contar. ¿Qué otras estrategias usamos para contar cosas que se pueden mover?
Mover y contar, como con los autos del estacionamiento
Cuando contamos los objetos de un dibujo, no podemos moverlos. ¿Qué estrategia podemos usar para asegurarnos de contarlos correctamente?
Tocar y contar
Podemos tacharlos cuando contamos.
Marcar y contar
Invite a la clase a usar la rutina Pensar-Trabajar en parejas-Compartir para analizar la siguiente pregunta.
Cuando cuentan objetos de un dibujo que están en línea, ¿qué estrategia usarían? ¿Por qué?
Si hay tiempo suficiente, invite a estudiantes a compartir sus ideas.
Nota para la enseñanza
El afiche de Estrategias de conteo será útil a lo largo del módulo. En las próximas lecciones, anime a sus estudiantes a mencionar la estrategia de conteo que usan y a explicar por qué la eligieron. Puede usar el afiche de referencia como punto de referencia cuando conversen sobre estrategias de conteo.
5 25 10
K ▸ M1 ▸ TB ▸ Lección 8 EUREKA MATH2 © Great Minds PBC 102
LECCIÓN 9
Conservar el número de objetos en cualquier configuración
Vistazo a la lección
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
En esta lección, la clase considera si debe volver a contar un grupo de objetos después de moverlos. Las experiencias repetidas de este tipo ayudan a la clase a comprender la conservación, que significa que el número de objetos de un grupo permanece igual sin importar cómo están ordenados.
Pregunta clave
• ¿Debemos volver a contar cuando movemos un grupo?
Criterio de logro académico
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos. (K.CC.B.4.b)
PC Parcialmente competente C Competente AC Altamente competente
9
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Conteo y cardinalidad
Agenda
Fluidez 15 min
Presentar 10 min
Aprender 20 min
• ¿Debemos volver a contar?
• Grupo de problemas
Concluir 5 min
Materiales
Maestro o maestra
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 1 al 5)
• cubos Unifix® (5)
Estudiantes
• tarjetas para emparejar (1 juego por pareja de estudiantes)
• cubos Unifix® (5)
• libro para estudiantes
Preparación de la lección
• Prepare los juegos de tarjetas para emparejar con numerales y configuraciones del 1 al 5 de la lección 7.
• Prepare tarjetas del 1 al 5 del juego para demostración de las tarjetas Hide Zero.
© Great Minds PBC 105 EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 9
Fluidez
Emparejar: Conjuntos y numerales
Materiales: E) Tarjetas para emparejar
La clase cuenta conjuntos y empareja un numeral con un conjunto para adquirir fluidez con la correspondencia de uno a uno y una comprensión de la cardinalidad.
Pida a la clase que trabaje en parejas. Distribuya un juego de tarjetas a cada pareja y pídales que jueguen de acuerdo con las siguientes reglas. Considere hacer una ronda de práctica con la clase.
• Coloquen seis tarjetas.
• Estudiante A: Selecciona las tarjetas que coinciden.
• Estudiante B: Comprueba su trabajo y da una felicitación (p. ej., “¡Buen trabajo!”) o una sugerencia (p. ej., “Intenta usar la estrategia de tocar y contar”).
• Dejen las tarjetas emparejadas a un lado y reemplácenlas con dos tarjetas nuevas de la pila.
• Continúen hasta que todas las tarjetas estén emparejadas y cambien de roles en cada turno.
Recorra el salón de clases mientras se desarrolla el juego y proporcione apoyo según sea necesario. Por ejemplo, las parejas de estudiantes podrían necesitar apoyo para dar sugerencias adecuadas. En ese caso, pregunte si tienen una sugerencia, como usar la estrategia de tocar y contar.
Contar con movimiento hasta el 10
La clase cuenta con movimientos del cuerpo para desarrollar fluidez con los nombres de los números y la correspondencia de uno a uno.
Aplaudamos 5 veces y contemos los aplausos. ¿Comenzamos?
Al principio, cuente y aplauda del 1 al 5 lentamente, haciendo énfasis en que para cada aplauso se dice un número. Repita el proceso hasta que la mayor parte de la clase esté aplaudiendo, contando o, idealmente, aplaudiendo y contando.
Diferenciación: Desafío
Considere una de las siguientes adaptaciones del juego para aumentar el desafío a medida que la clase esté lista.
• Disponga ocho tarjetas en dos hileras de cuatro para desarrollar la capacidad de sus estudiantes de clasificar con más información visual.
• Incluya el 0.
• Use dos juegos de tarjetas con los números del 1 al 10. Limite el juego a 20 tarjetas para mayor facilidad.
• Invite a sus estudiantes a hallar tarjetas que formen 5.
15 10 20 5
K ▸ M1 ▸ TB ▸ Lección 9 EUREKA MATH2 © Great Minds PBC 106
Repita el proceso, pero esta vez dé pisotones y cuente hasta el 5.
Ahora, aplaudamos 10 veces y contemos los aplausos. ¿Comenzamos?
Cuente y aplauda del 1 al 10 junto con la clase.
Repita el proceso, pero esta vez dé pisotones y cuente hasta el 10.
Es posible que el ritmo del conteo repetitivo al unísono lleve a la clase hacia un estado cognitivo de relajación. Intente variar el ritmo para inducir a la clase a regresar al estado de alerta e incentivar el juego.
Presentar
La clase cuenta un conjunto que está ordenado en línea y, luego, considera cuántos hay después de que el conjunto se reordena (es decir, la conservación).
Muestre el dibujo de los niños y las niñas que miran una película.
¿Cómo podemos averiguar cuántas personas están viendo la película?
Podemos contarlas.
Vamos a contar en grupo. Voy a tocar y contar a cada persona desde el principio de la línea. Digamos un número por cada persona que cuente.
Cuenten en grupo. Para reforzar el principio de cardinalidad, pregunte cuántas personas hay cuando terminen de contar.
Muestre a los niños y las niñas sentados en un círculo.
¿Qué hacen estas personas?
Leen cuentos.
Están en el recreo.
DUA: Participación
Ajuste la actividad de Contar con movimiento para que participe la mayor cantidad de estudiantes posible. Considere sus capacidades físicas, contextos culturales e intereses cuando elija los movimientos. Estos son algunos ejemplos de movimientos que pueden contarse de forma sencilla:
• parpadeos
• movimientos para asentir con la cabeza
• percusiones en un tambor
• saltos de rana
• rebotes con una pelota de basquetbol
15 10 20 5 EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 9 © Great Minds PBC 107
Son las mismas personas que veían la película. No se fue ninguna persona, ni nadie llegó. Me pregunto cuántas personas hay ahora.
Cierren los ojos y piensen en su mente cuántas personas creen que hay ahora. Muéstrenme con sus dedos cuántos hay.
Pida a alguien que haya mostrado 5 dedos que explique su respuesta. Cuenten en grupo para confirmar la respuesta para quienes no están seguros.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hoy, contaremos todos los objetos de nuestra colección y mostraremos nuestro trabajo en papel. Pueden empezar a contar con sus parejas.
Aprender
¿Debemos volver a contar?
Materiales: M) Tarjetas Hide Zero, cubos Unifix

La clase cuenta y usa tarjetas numéricas para describir un conjunto antes y después de ordenarlo otra vez.
Muestre 3 cubos Unifix en una configuración lineal y tarjetas del 1 al 5.
¿Cuántos cubos hay?
3

¿Qué tarjeta numérica dice cuántos cubos hay?
La tarjeta del 3
Mueva la tarjeta del 3 debajo de los cubos.
Mueva los cubos lentamente para dar tiempo a la clase a ver cómo crea una configuración dispersa.
¿Cuántos hay ahora? ¿Cómo lo saben?
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante reconoce y expresa regularidad en la lógica de la repetición (MP8) cuando prueba que el número de objetos de un conjunto es igual sin importar su organización y cuando expresa esto verbalmente.
15 10 20 5
K ▸ M1 ▸ TB ▸ Lección 9 EUREKA MATH2 © Great Minds PBC 108
Habrá estudiantes que descubrirán de inmediato que sigue habiendo 3 cubos, y habrá estudiantes que necesitarán contar para comprobarlo. Para validar las dos estrategias, pida a estudiantes que compartan cómo saben que sigue habiendo 3 cubos.
Sé que sigue habiendo 3 cubos porque los conté otra vez.
Sé que sigue habiendo 3 cubos porque vi cómo los movía. Si había 3 antes, seguirán siendo 3 ahora.
¿Qué tarjeta numérica dice cuántos cubos hay?
Repita el ejercicio con 4 y 5 cubos. Considere usar variaciones de las cuatro configuraciones mostradas.
Grupo de problemas
Materiales: E) Cubos Unifix
Para establecer una transición al trabajo de este segmento, practique su rutina de pasar el libro para estudiantes y hallar la página correcta.
Es su turno de contar cubos y hallar el número que indica cuántos cubos contaron. Hagamos el primero en conjunto.
Muestre cómo colocar los cubos en las plantillas provistas, cuente y encierre en un círculo el número que coincida. Luego, mueva los mismos cubos en una configuración diferente en el espacio provisto y encierre en un círculo el mismo número. Si hay tiempo e interés suficiente, invite a estudiantes a trazar o dibujar su nueva configuración de cubos.
Nota para la enseñanza
No use más de 5 cubos. Con pequeñas cantidades, hay estudiantes que subitizarán, mientras que otros pueden tocar y contar.
Si hay estudiantes que subitizan, no insista con que toquen y cuenten. Podrían pensar que cometieron un error y no aprenderán a confiar en su capacidad de “solo ver” el número. El conteo súbito es importante a la hora de aprender a contar.
Nota para la enseñanza
Este Grupo de problemas está diseñado para la demostración sistemática (consulte la lección 8 para más detalles). Siga usando la demostración sistemática con los Grupos de problemas de todo el módulo 1 hasta que la clase se sienta cómoda con lápiz y papel.
Evaluación observacional
; Observe mientras la clase mueve los cubos en otra configuración. ¿Vuelven a contar los cubos o simplemente encierran en un círculo el mismo número del conteo anterior?
 Lineal Matriz Circular Dispersa
Lineal Matriz Circular Dispersa
EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 9 © Great Minds PBC 109
Diferenciación: Desafío
Anime a quienes necesiten más desafío a mostrar varias configuraciones para cada problema. Pídales que compartan cómo saben el número de cubos sin contar cada vez que cambian la configuración.
K M1 ▸ TB Lección EUREKA MATH © Great Minds PBC 30 GRUPO DE PROBLEMAS 3 4 5 3 4 5 3 4 5 3 4 5 © Great Minds PBC 29 EUREKA MATH K M1 TB Lección 9 Coloca los cubos cuenta. Encierra en un círculo el número. Mueve los cubos para formar un diseño diferente. Luego, encierra en un círculo el número. 3 4 5 3 4 5 3 4 5 3 4 5 9 Nombre K ▸ M1 ▸ TB ▸ Lección 9 EUREKA MATH2 © Great Minds PBC 110
Concluir
Reflexión final 5 min
Materiales: M) Cubos Unifix, tarjetas Hide Zero
Objetivo: Conservar el número de objetos en cualquier configuración
Muestre 4 cubos en una configuración de matriz como se muestra.
¿Cuántos cubos hay?
4
Rotule la matriz con la tarjeta del 4. Mueva los cubos como se muestra.
¿Cuántos cubos hay ahora?
4


¿Debo contar de nuevo porque moví los cubos?
No, porque movió los mismos cubos.
¿Tengo que cambiar la tarjeta numérica?
No, sigue habiendo 4 cubos.
Correcto. Si no se quitan ni se agregan cubos, el número de cubos permanecerá igual sin importar las veces que se muevan.
Mueva los cubos unas veces más y pregunte cuántos hay después de cada configuración nueva. Considere usar configuraciones lineales, circulares, dispersas e incluso algunas graciosas.
¿Puedo mover los cubos de cualquier manera?
¡Sí! Sigue habiendo 4 cubos.
Nota para la enseñanza
Habrá estudiantes que tal vez no demuestren conservación de números al final de esta lección. La conservación se desarrolla con la experiencia a lo largo del tiempo. Habrá más oportunidades para que la clase practique la conservación a lo largo del módulo.
10 20 5
EUREKA MATH2 K ▸ M1 ▸ TB ▸ Lección 9 © Great Minds PBC 111
Tema C
Escribir numerales y crear grupos de hasta 5 objetos
En el tema C, la clase continúa integrando los elementos de los fundamentos numéricos y explora las razones para contar. Comienzan a escribir numerales y consideran la pregunta ¿Por qué escribimos números?

Contar un grupo es una nueva razón para contar. Contar un grupo existente de objetos para responder una pregunta sobre cuántos hay es diferente a contar un número dado de objetos de un grupo más grande. Contar un grupo requiere hacer muchas tareas al mismo tiempo, ya que la clase debe recordar el número determinado, decir las palabras numéricas en orden y poner atención a la correspondencia de uno a uno, todo a la vez.
Contar objetos que se pueden oír pero no ver, como sonidos o palabras, es otra nueva razón para escribir numerales. La clase practica cómo dibujar y escribir numerales para representar el número de veces que escuchan una palabra. Pescado, pescado, pescado, pescado se puede representar dibujando 4 pescados o escribiendo el numeral 4. Este trabajo comienza a descubrir la eficiencia de nuestro sistema numérico escrito, que se verá más claro a medida que la clase maneje cantidades más grandes. Dibujar 100 pescados no es un método práctico para comunicar un número en la vida diaria.
Por último, la clase descubre que contar es útil para determinar si hay suficientes o no hay suficientes. Si hay suficientes platos para cada estudiante en la mesa, han contado correctamente. Si no hay suficientes o si hay platos adicionales, han cometido un error de conteo. Estos conceptos son básicos para el trabajo de comparación del módulo 3.
La clase cuenta un grupo para emparejar con el numeral.
La clase cuenta palabras y las representa con dibujos y numerales.
© Great Minds PBC 113
Progresión de las lecciones
Lección 10


Contar un grupo de objetos para emparejarlos con un numeral
Lección 11
Escribir los numerales del 1 al 3 para responder preguntas sobre cuántos hay
Lección 12
Escribir los numerales 4 y 5 para responder preguntas sobre cuántos hay
Lista de compras manzanas
Conté 3 manzanas.

Puedo escribir 1, 2 y 3.
Puedo escribir 4 y 5.
114 K ▸ M1 ▸ TC EUREKA MATH2 © Great Minds PBC
Lección 13
Contar suficientes objetos y escribir el numeral
Sé que hay suficientes porque hay 4 puntos y 4 cubos.

EUREKA MATH2 K ▸ M1 ▸ TC 115 © Great Minds PBC
Contar un grupo de objetos para emparejarlos con un numeral
Vistazo a la lección
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
Una vez que la clase puede contar un grupo para responder una pregunta de cuántos hay, está lista para crear un grupo con un número específico de objetos. En esta lección, la clase explora una nueva razón para contar: crear un grupo de un tamaño específico.
Pregunta clave
• ¿Cómo podemos recordar cuándo debemos dejar de contar?
Criterio de logro académico
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande. (K.CC.B.5)
PC Parcialmente competente C Competente AC Altamente competente
10 LECCIÓN 10
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 5 min
Aprender 25 min
• Contar un conjunto
• Grupo de problemas
Concluir 10 min
Materiales
Maestro o maestra
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 1 al 5)
• marioneta o animal de peluche
• frijoles de dos colores (10)
Estudiantes
• Plantilla de dos manos (en el libro para estudiantes)
• frijoles de dos colores (11)
• tarjetas Hide Zero® del 1 al 5 (1 por grupo de estudiantes)
• plato (1 por grupo de estudiantes)
• libro para estudiantes
Preparación de la lección
• Prepare las tarjetas del 1 al 5 del juego para demostración de las tarjetas Hide Zero. Conserve estas tarjetas para utilizarlas en las lecciones 11 a 13.
• Prepare las tarjetas del 1 al 5 de las tarjetas Hide Zero de estudiantes para cada grupo.
• Considere colocar 11 frijoles en bolsitas resellables para cada estudiante, a fin de facilitar su distribución.
• Revise el menú proporcionado en los recursos digitales de esta lección. Considere ajustarlo para incorporar alimentos culturalmente conocidos.
© Great Minds PBC 117 EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 10
Fluidez
Muéstrame frijoles hasta el 3
Materiales: M) Tarjetas Hide Zero; E) Plantilla de dos manos, frijoles de dos colores
La clase escucha un número o ve un numeral y cuenta un conjunto en voz alta como preparación para asociar un numeral con un conjunto.
Prepárense. Coloquen 3 frijoles sobre los puntos rojos que están en la parte de abajo.
Voy a decir un número. Ustedes moverán esa cantidad de frijoles hacia la punta de los dedos. Recuerden comenzar por el meñique, como lo practicamos. (Mueva el meñique para enfatizar). ¿Comenzamos?
Muéstrenme 1.
Haga una pausa mientras la clase mueve un frijol rojo hacia el meñique de la mano izquierda.
¡Rápidamente! Muéstrenme 2.
Haga una pausa mientras la clase mueve un frijol rojo hacia el dedo anular de la mano izquierda.
¡Muy bien! Muéstrenme 3.
Haga una pausa mientras la clase mueve un frijol rojo hacia el dedo mayor de la mano izquierda.
¡Volvamos atrás! Vuelvan a colocar los 3 frijoles sobre los puntos rojos que están en la parte de abajo.



(Muestre las tarjetas). Esta vez, voy a mostrarles un número. Ustedes moverán esa cantidad de frijoles hacia la punta de los dedos. Recuerden comenzar por el meñique, como lo hicieron antes. (Mueva el meñique para enfatizar). ¿Comenzamos?
Muestre la tarjeta del 1 y haga una pausa mientras la clase mueve un frijol rojo hacia el dedo meñique de la mano izquierda.
1 2 3
Repita el proceso con las tarjetas del 2 y del 3, mientras la clase mueve frijoles hacia el dedo anular y el dedo mayor.
10 5 25 10
K ▸ M1 ▸ TC ▸ Lección 10 EUREKA MATH2 © Great Minds PBC 118
Respuesta a coro: Conteo sorpresa hasta el 3
La clase subitiza cantidades pequeñas como preparación para responder con eficiencia las preguntas sobre cuántos hay hasta el 3.
Muestre la imagen de la carpeta.
¡Sorpresa! (Levante y baje la carpeta para dejar ver 2 pelotas de beisbol). Repita el proceso algunas veces.
Detrás de esta carpeta hay algunas cosas. ¿Las vieron?
Levante y baje la carpeta rápidamente.
¿Cuántas cosas vieron? Levanten la mano cuando sepan la respuesta.
Espere hasta que la mayor parte de la clase haya levantado la mano y, luego, dé la señal para que responda.
Juguemos Conteo sorpresa otra vez. Esta vez, podría haber
1 cosa, 2 cosas o 3 cosas.
Muestre la imagen de la carpeta. Levante y baje la carpeta para dejar ver una pelota de futbol y una pelota de beisbol.
¿Cuántas cosas vieron?
Repita el proceso con la siguiente secuencia:
Nota para la enseñanza
Haga señales con las manos a fin de presentar un procedimiento para responder las preguntas de la actividad Respuesta a coro. Por ejemplo, coloque la mano alrededor de la oreja para escuchar, lleve un dedo hacia la sien para pensar y levante la mano para recordar a sus estudiantes que deben levantar las suyas. Enseñe el procedimiento usando preguntas de conocimiento general, como las siguientes:
• ¿En qué grado están?
• ¿Cuál es el nombre de nuestra escuela?
• ¿Cómo se llama su maestro o maestra?
2
2
EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 10 © Great Minds PBC 119
Presentar
Materiales: M) Tarjetas Hide Zero 2, 3 y 5
La clase recuerda un número determinado mientras realiza muchas tareas al mismo tiempo.
Muestre a modo de juego la tarjeta del 2 el tiempo suficiente como para que la clase la reconozca, y, luego, retírela de la vista.
Digan el número.
2
Recuerden ese número en su mente y salten hasta que diga alto. ¿Comenzamos? ¡Adelante!
Deje que la clase salte varias veces antes de decir alto. Deberían saltar más de 2 veces.
¡Alto! ¿Cuál era el número?
2
Vamos a comprobarlo.
Levante la tarjeta para verificar el número y celebre.
Apláudanse 2 veces por haber recordado que el número era el 2.
Repita el proceso, pero esta vez pida a la clase que recuerde el número determinado mientras se mueve esa cantidad de veces. Por ejemplo, muestre la tarjeta del 3 y pida a la clase que salte 3 veces.
Juegue una tercera ronda para que la clase recuerde el número determinado mientras se mueve una cantidad diferente de veces. Por ejemplo, utilice el número determinado de 5 y pida a la clase que salte 3 veces.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hoy, jugaremos al restaurante para practicar el conteo.
Nota para la enseñanza
Contar un grupo requiere realizar muchas tareas al mismo tiempo. La clase debe recordar el número determinado mientras dice las palabras numéricas en orden y pone atención en la correspondencia de uno a uno. Este ejercicio proporciona práctica para recordar un número a pesar de las distracciones cada vez más complejas.
A lo largo de esta lección, la clase puede ver un numeral como apoyo mientras se acostumbra a retenerlo en su cabeza.
10 5 25 10
K ▸ M1 ▸ TC ▸ Lección 10 EUREKA MATH2 © Great Minds PBC 120
Aprender
Contar un conjunto

Materiales: E) Tarjetas Hide Zero, plato, frijoles de dos colores
La clase reconoce los numerales y cuenta un conjunto para emparejarlo con el numeral.
Presente una situación que se desarrolle en un restaurante de comida para llevar y represente los roles de empleada y cliente.
Muestre el menú donde toda la clase pueda verlo. La empleada necesita los frijoles (para representar la comida) y un plato. El cliente necesita las tarjetas Hide Zero del 1 al 5.
Considere utilizar la siguiente secuencia:
El cliente se acerca a la ventanilla del restaurante. La empleada saluda al cliente y le pregunta qué va a ordenar.
¿Cuántos tacos desea ordenar?

El cliente entrega una tarjeta Hide Zero a la empleada y dice su orden.
4 tacos, por favor.
La empleada cuenta 4 frijoles y los coloca en el plato. El cliente cuenta para comprobar. Prepare a quienes compran y quienes venden para hacer correcciones amables si fuera necesario.
Usted pidió 2. La tarjeta dice 5. Por favor, inténtalo de nuevo. Esto no es lo que ordené. Por favor, inténtalo de nuevo.
Forme parejas de estudiantes o pequeños grupos para hacer una dramatización. Cambie roles ocasionalmente para que cada estudiante tenga la oportunidad de contar un conjunto.
Recorra el salón de clases y observe. Según sea necesario, haga correcciones precisas como:
• Recuerden el número de la tarjeta. Dejen de contar cuando lleguen a ese número.
• Tienes demasiados tacos, cuenta otra vez.
• Necesitas 1 más para formar 4 tacos.

Apoyo para la comprensión del lenguaje
Como apoyo a esta dramatización, use esquemas de oraciones adecuados para cada estudiante. Relacione las matemáticas con el contexto al representar y animar el diálogo natural que la clase usaría en el mundo real. La longitud de las oraciones se puede modificar para cumplir con los objetivos lingüísticos de la clase.
• ¿Cuántos _____ desea ordenar?
• ¿Cuántos _____?
• ¿Cuántos son? (Señale un objeto en el menú).
• Llevaré 4 _____, por favor.
• 4 _____, por favor
• 4 (Señale un objeto en el menú).
Evaluación observacional
; Observe mientras las empleadas y los empleados cuentan la cantidad solicitada. ¿El número determinado coincide con la comida dada? ¿Necesitan volver a contar una o dos veces?
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante razona de forma cuantitativa y abstracta (MP2) cuando comprende que la palabra numérica cuatro, el numeral 4 y un grupo de 4 fichas para contar son distintas representaciones del número 4.
10 5 25 10
Menú Tacos Manzanas Pretzels
EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 10 © Great Minds PBC 121
Grupo de problemas
Materiales: E) Frijoles de dos colores
Invite a la clase a contar frijoles para emparejarlos con el número correspondiente de alimentos de la lista de compras. Si fuera necesario, represente cómo colocar los frijoles cerca de la imagen de cada alimento.
Prepárese para brindar apoyo a quienes cometan errores al contar. Comience con preguntas que les permitan considerar métodos para revisar su trabajo.
Tienen 4 manzanas. ¿Deberían quitar algunas o agregar más?
Dibujaron demasiadas manzanas. ¿Qué pueden hacer para tener 3 manzanas?
No hay suficientes manzanas. ¿Cómo pueden mostrar 3 manzanas?
Si hay tiempo suficiente, anime a la clase a representar los alimentos con dibujos, sellos o trazos.
DUA: Participación
Las actividades del restaurante de comida para llevar y de la lista de compras sirven para relacionar el conteo con contextos conocidos y hacer conexiones con el mundo real. Considere personalizar el menú con las comidas favoritas de la clase para lograr una mayor participación en la lección.
Para seguir practicando cómo contar un grupo, brinde menús personalizados y listas de compras para que cada estudiante escoja.
EUREKA MATH K ▸ M1 TC ▸ Lección 10 © Great Minds PBC 35 10 Lista de compras 3 manzanas 2 5 1 ba n a n a zanahorias fresas Nombre
K ▸ M1 ▸ TC ▸ Lección 10 EUREKA MATH2 © Great Minds PBC 122
Concluir
Reflexión final 10 min
Materiales: M) Marioneta o animal de peluche, tarjeta Hide Zero del 3, frijoles de dos colores
Objetivo: Contar un grupo de objetos para emparejarlos con un numeral
Reúna a la clase en un lugar donde cada estudiante pueda ver la marioneta, la tarjeta del 3 y una pila de frijoles.
La marioneta recibió una orden de 3 manzanas. Observen a la marioneta mientras cuenta las manzanas.
Haga que la marioneta cuente y se pase del 3; deténgase cuando haya contado todos los frijoles.

¡Ay no! ¿Qué sucede?
¡Hay demasiadas!
La marioneta no se detuvo en el 3.
Pida a la clase que use la rutina Pensar-Trabajar en parejas-Compartir para ayudar a la marioneta.
Usen la mente para pensar cómo la marioneta podría recordar cuándo dejar de contar.
Reúnanse con su pareja y comenten lo que podría hacer la marioneta.
Escoja estudiantes para que compartan sus respuestas.
¿Cómo puede recordar la marioneta cuándo debe dejar de contar?
La marioneta puede mirar el número de la tarjeta. Si dice 3, se detiene en el 3.
La marioneta puede recordar mentalmente el número que ordenaron y dejar de contar allí.
5 25 10 EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 10 © Great Minds PBC 123
Escribir los numerales del 1 al 3 para responder preguntas sobre cuántos hay
Vistazo a la lección
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
La clase considera por qué se escriben numerales mientras aprenden a escribir el 1, el 2 y el 3. En esta lección, cuentan palabras habladas, algo que no pueden ver o tocar, y representan el número de palabras escribiendo un numeral.
Pregunta clave
• ¿Por qué escribimos números?
Criterio de logro académico
K.Mód1.CLA2 Escriben los números del 0 al 10. (K.CC.A.3)
11
LECCIÓN 11
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 10 min
Aprender 25 min
• Escritura en el aire y en la alfombra
• Escribir los numerales
• Número bip
Concluir 5 min
Materiales
Maestro o maestra
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 1 al 5)
• juguetes de cocina surtidos o fichas para contar
• marioneta o pelota para escribir los números
• papel de rotafolio
Estudiantes
• frijoles de dos colores (3)
• Plantilla de dos manos
• pizarra blanca individual
• marcador de borrado en seco
• libro para estudiantes
Preparación de la lección
• Prepare las tarjetas del 1 al 5 del juego para demostración de las tarjetas Hide Zero. Separe estas tarjetas para utilizarlas en las lecciones 12 y 13.
• En lugar de juguetes de cocina surtidos, se pueden utilizar fichas para contar.
• En esta lección es necesario contar con capacidades auditivas y visuales para tomar órdenes de comida en la sección Aprender.
• Considere retirar la página de escritura de numerales y colocarla en una pizarra blanca individual.
© Great Minds PBC 125 EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 11
Fluidez
Muéstrame frijoles hasta el 3
Materiales: M) Tarjetas Hide Zero; E) Plantilla de dos manos, frijoles de dos colores
La clase escucha un número o ve un numeral y cuenta un conjunto en voz alta para desarrollar fluidez con la asociación de un numeral a un conjunto.
Prepárense. Coloquen 3 frijoles sobre los puntos rojos que están en la parte de abajo.
Voy a decir un número. Ustedes moverán esa cantidad de frijoles hacia la punta de los dedos. Recuerden comenzar por el meñique, como lo practicamos. (Mueva el meñique para enfatizar). ¿Comenzamos?
Muéstrenme 3.
Haga una pausa mientras la clase mueve los frijoles rojos hacia el meñique, el anular y el dedo mayor de la mano izquierda.
Repita el proceso con la siguiente secuencia:
Observe qué estudiantes deben volver a contar y quiénes pueden ajustar si agregan o quitan un frijol a la vez.
¡Volvamos atrás! Vuelvan a colocar los 3 frijoles sobre los puntos rojos que están en la parte de abajo.



25 5 1 2 3
(Muestre las tarjetas). Esta vez, voy a mostrarles un número. Ustedes moverán esa cantidad de frijoles hacia la punta de los dedos. Recuerden comenzar por el meñique, como lo hicieron antes. (Mueva el meñique para enfatizar). ¿Comenzamos?
2 1 2 3 2 3 2 1 2
10 10
K ▸ M1 ▸ TC ▸ Lección 11 EUREKA MATH2 © Great Minds PBC 126
Muestre la tarjeta del 3 y haga una pausa mientras la clase mueve frijoles rojos hacia el dedo meñique, el anular y el mayor de la mano izquierda.
Repita el proceso, y muestre las tarjetas en una secuencia similar a la anterior.
Respuesta a coro: Conteo sorpresa hasta el 5
La clase subitiza cantidades pequeñas como preparación para responder con eficiencia las preguntas sobre cuántos hay hasta el 5.
Muestre la imagen de la carpeta.
¡Sorpresa! (Levante y baje la carpeta para dejar ver 3 manzanas).
Repita el procedimiento algunas veces.
Detrás de esta carpeta hay algunas cosas. ¿Las vieron?
Levante y baje la carpeta rápidamente.
¿Cuántas cosas vieron? Levanten la mano cuando sepan la respuesta.
Espere hasta que la mayor parte de la clase haya levantado la mano y, luego, dé la señal para que respondan.
Juguemos Conteo sorpresa otra vez. Esta vez, podría haber 3 cosas, 4 cosas o 5 cosas.
Repita el proceso con la siguiente secuencia:
3
EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 11 © Great Minds PBC 127
Presentar
Materiales: M) Juguetes de cocina surtidos o fichas para contar La clase comenta maneras de contar cosas que se pueden escuchar pero que no se pueden ver.
Presente una situación que se desarrolle en un restaurante donde personas llaman para pedir sus órdenes. Elija a un o una estudiante para representar el papel de chef. Proporciónele fichas para contar o juguetes de cocina.
Represente el papel de la persona que toma las órdenes por teléfono. Muestre la imagen del pingüino.
Gracias por comunicarse con el restaurante Kindergarten. ¿Qué desea ordenar?
Reproduzca el audio del pingüino que ordena 6 pescados. Reprodúzcalo una vez más si fuera necesario. Diríjase a quien haga de chef y repita la orden con un error.
Necesito pescado, pescado, pescado, pescado.
Después de escuchar la orden, quien haga de chef puede reaccionar de muchas formas. Guíe una conversación de la clase con preguntas como las siguientes:
¿Cuál fue el problema con la orden que hice?
¿Cuál sería una forma más sencilla de decir la orden?
¿Cómo puedo llevar la cuenta de cuántos pescados se ordenaron?
Sugiera a la clase que intente algunas de sus ideas en el siguiente segmento para establecer una transición.
Hoy, usaremos dibujos y números como ayuda para preparar correctamente las órdenes.
Anticípese a que la clase presente dificultades para recordar la orden de comida. La orden larga es intencional para ilustrar la importancia de escribir los numerales.
Elija a alguien que se sienta a gusto representando el papel de chef, a pesar de la incertidumbre de la situación. Considere preparar a esta persona con anticipación.
10 10 25 5
enseñanza
Nota para la
K ▸ M1 ▸ TC ▸ Lección 11 EUREKA MATH2 © Great Minds PBC 128
Aprender
Escritura en el aire y en la alfombra
Materiales: M) Marioneta o pelota
La clase aprende los trazos básicos para escribir los numerales 1, 2 y 3.
Invite a la clase a representar el papel de la persona que toma las órdenes. Contestarán las llamadas telefónicas de sus clientes y clientas animales y escribirán las órdenes para la cocina del restaurante.
Muestre la imagen del perro y reproduzca el audio del perro que ordena un hueso.
Reprodúzcalo una vez más si fuera necesario.
¿Cuántas veces el perro dijo hueso?
Dibuje la imagen de 1 hueso y, luego, escriba el numeral 1.
Podemos hacer un dibujo de 1 hueso para recordar la orden o podemos escribir el número 1. Usen el dedo para contar y escriban el número 1 en el aire conmigo. Sigan la pelota.
Use la pelota para “escribir” el numeral en el aire. Ponga la pelota en alto para comenzar desde la parte superior. A medida que mueve la pelota hacia abajo, diga la siguiente rima.
De arriba a abajo, sin ningún atajo. El número 1 no da trabajo.
Pida a la clase que traslade sus dedos para contar a la alfombra o a otra superficie que pueda tocar.
Repita la rima mientras la clase escribe el 1 sobre la nueva superficie.
Muestre la imagen de la rana y reproduzca el audio de la rana que ordena 2 insectos.
Presente la escritura del 2 con el mismo proceso usado para el 1.
Ese cisne tiene pico y también un largo cuello. Luego, gira a la derecha y el 2 ya está hecho.
Nota para la enseñanza
La mayor parte del tiempo, los maestros y las maestras deben hacer dibujos matemáticos simples. En esta lección y en la próxima, cuando dibuje las órdenes, tómese el tiempo que necesite para hacer los detalles. El objetivo es ayudar a la clase a descubrir que escribir numerales es más eficaz que dibujar todos los objetos. En esto se enfoca la sección Concluir en la lección 12.
Nota para la enseñanza
Comenzar los numerales y las letras desde la parte superior es un hábito importante para que sus estudiantes aprendan en kindergarten. Les ayudará a no atrasarse cuando las demandas de escritura aumenten en grados superiores. Los numerales del 1 al 3 comienzan todos en la parte superior izquierda.
1
10 10 25 5
EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 11 © Great Minds PBC 129
Muestre la imagen del ave y reproduzca el audio del ave que ordena 3 gusanos.
A medida que los números aumentan, anticípese a algún desacuerdo o duda acerca de cuántas palabras se dijeron. Reproduzca el audio nuevamente y demuestre cómo usar los dedos para llevar la cuenta de cada palabra a medida que se dice.
Anime a la clase a usar estrategias intuitivas para seguir el conteo, como levantar los dedos o hacer marcas en un papel.
Presente la escritura del 3 con el mismo proceso usado para el 1 y el 2. Hago un medio círculo una vez. Otro medio círculo y ya se formó el 3.
Escribir los numerales
Materiales: E) Página de escritura de numerales
La clase dibuja y escribe los numerales 1, 2 y 3.
Distribuya el trabajo en clase y los utensilios de escritura. Muestre la imagen del perro y el hueso.
Invite a la clase a hallar el número que coincide con la orden del perro. Cuando tengan los dedos sobre el numeral 1, pida que digan la rima en conjunto mientras dibujan el numeral con los dedos.
Demuestre cómo escribir el 1. Luego, invite a la clase a usar un lápiz o crayón para escribir el 1 hasta completar la fila. Si terminan rápido, sugiera que dibujen la orden del perro dentro del recuadro.
Repita con los numerales 2 y 3 usando las imágenes de la rana con los insectos y del ave con los gusanos respectivamente.
Nota para la enseñanza
Considere retirar la página de escritura de numerales y colocarla en una pizarra blanca individual para que la clase pueda volver a usarla para practicar.
Nota para la enseñanza
La herramienta de rectángulo de escritura ayuda a la clase a escribir los numerales sistemáticamente. Los rectángulos de escritura tienen un punto que muestra dónde empezar el numeral. Es menos probable que la clase invierta los números cuando comienza desde el punto y mantiene la escritura dentro del rectángulo.
Primero, sus estudiantes dibujan el numeral. Luego, lo escriben dentro del rectángulo de escritura de forma independiente. Con el tiempo, podrán escribir los números sin el rectángulo de escritura, pero esta herramienta les brinda la estructura para formar los números en forma correcta desde el comienzo.
Evaluación observacional
; Observe a sus estudiantes mientras escriben. ¿Comienzan en el punto y se mantienen dentro del rectángulo de escritura?
K ▸ M1 ▸ TC ▸ Lección 11 EUREKA MATH2 © Great Minds PBC 130
Número bip
La clase practica la secuencia de los números hasta el 3.
Pida a la clase que se ponga de pie para jugar Número bip.
¡Juguemos Número bip! Voy a contar, pero, en lugar de decir uno de los números, voy a decir bip. Levanten la mano cuando sepan el número bip. ¿Comenzamos?
1, 2, bip. (Dé la señal).
3
1, bip, 3. (Dé la señal).
2 1, 2, bip, 4. (Dé la señal).
3 Bip, 2, 3. (Dé la señal).
1
Si hay tiempo suficiente, invite a la clase a completar las secuencias numéricas ubicadas en la parte inferior de la página de escritura de numerales. Trabajen en grupo en la primera secuencia, como si jugaran Número bip en el papel. Marque con el dedo y diga los números que se muestran. Diga bip para los espacios.
Diferenciación: Apoyo
Si hay estudiantes que tienen dificultades con la secuencia verbal en el número bip, considere pedirles que sigan el camino numérico con los dedos.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante pone atención a la precisión (MP6) cuando considera que usar números puede ayudarle a comunicarse con más claridad, en este caso, tomando órdenes de comida. Al principio, expresan esto verbalmente y, al final de la lección, pueden expresarlo escribiendo los numerales cuidadosamente.
Apoyo para la comprensión del lenguaje
La palabra orden tiene múltiples significados en esta lección. En el contexto del restaurante, la clase toma órdenes de comida. En esta actividad de secuencia numérica, la clase pone los números en orden
Si usa la palabra orden en la actividad de secuencia numérica, preste atención a las reacciones de la clase. Según sea necesario, comparta ambos significados e invite a la clase a pensar en otras maneras de usar la palabra orden
EUREKA MATH K M1 TC Lección 11 © Great Minds PBC 37 11 Nombre
EUREKA MATH K M1 TC Lección 11 © Great Minds PBC 37 11 Nombre
EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 11 © Great Minds PBC 131
Concluir
Reflexión final 5 min
Materiales: M) Papel de rotafolio
Objetivo: Escribir los numerales del 1 al 3 para responder preguntas sobre cuántos hay
Muestre la imagen de 3 manzanas, la letra M y el numeral 3.
Digan la letra. M
Digan el número. 3
¿Cuál nos dice cuántas manzanas hay?
El 3 nos dice cuántas hay.
El número 3 nos dice cuántas manzanas hay en la imagen. La letra M nos ayuda a escribir la palabra manzana.

¿Por qué escribimos números? Hagamos un afiche con todas las razones por las que las personas escriben números.
Para recordar cuántas cosas hay
Para que no tengan que contar de nuevo cada vez que alguien pregunta
Muestre el afiche donde toda la clase pueda verla. Agregue al afiche a medida que surjan oportunidades en las lecciones subsiguientes.
El afiche de la clase será única y estará basada en las respuestas de sus estudiantes.
10 25 5
3 M
¿ ? K ▸ M1 ▸ TC ▸ Lección 11 EUREKA MATH2 © Great Minds PBC 132
Escribir los numerales 4 y 5 para responder preguntas sobre cuántos hay
Vistazo a la lección
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
La clase continúa explorando razones para escribir los numerales a medida que aprenden a formar el 4 y el 5.
Pregunta clave
• ¿Por qué escribimos números?
Criterios de logro académico
K.Mód1.CLA1 Cuentan hasta el 10. (K.CC.A.1)
K.Mód1.CLA2 Escriben los números del 0 al 10. (K.CC.A.3)
12
LECCIÓN 12
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 5 min
Aprender 30 minutos
• Escritura en el aire y en la alfombra
• Escribir los numerales
• Número bip
• Grupo de problemas
Concluir 5 min
Materiales
Maestro o maestra
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 1 al 5)
• marioneta o pelota
• afiche de la lección 11
Estudiantes
• Plantilla de dos manos
• frijoles de dos colores (5)
• pizarra blanca individual
• marcador de borrado en seco
• libro para estudiantes
Preparación de la lección
• Prepare las tarjetas del 1 al 5 del juego para demostración de las tarjetas Hide Zero. Separe estas tarjetas para utilizarlas en la lección 13.
• En esta lección, es necesario contar con capacidades auditivas y visuales para tomar órdenes de comida en la sección Aprender.
• Considere retirar la página de escritura de numerales y colocarla en una pizarra blanca individual para un uso futuro.
© Great Minds PBC 135 EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 12
Fluidez
Contar hasta el 3: ¿Qué número sientes en la espalda?
Materiales: M) Tarjetas Hide Zero
Cada estudiante dibuja un número y adivina un numeral para desarrollar la memoria cinestésica necesaria para formar números. Juguemos ¿Qué número sientes en la espalda?
Pida a la clase que trabaje en parejas. Cada integrante de la pareja se colocará en fila, mirando hacia delante. Quien esté detrás será quien escriba. Quien esté delante será quien adivine.
Párese detrás de la clase, mirando hacia la espalda de cada estudiante, y muestre la tarjeta del 1.
Estudiantes que escriben, dense vuelta y observen mi número, pero no lo digan. ¡Guarden el secreto! Escriban este número con el dedo en la espalda de su compañero o compañera. Usen toda la espalda para que puedan escribir un número grande y bonito.
Estudiantes que adivinan, ¿se dieron cuenta de qué número les escribieron en la espalda?
Parejas de estudiantes, dense vuelta y observen mi número. Si acertaron, ¡denme 1 aplauso!
Continúe con el 2 y el 3, y, luego, los numerales 1 a 3 en orden aleatorio. Felicite a la clase con el número correspondiente de aplausos. Después de un tiempo, pida a las parejas que cambien los roles.
Muéstrame frijoles hasta el 5
Materiales: M) Tarjetas Hide Zero; E) Plantilla de dos manos, frijoles de dos colores
La clase escucha un número o ve un numeral y cuenta un conjunto en voz alta para desarrollar fluidez con la asociación de un numeral con un conjunto.
Prepárense. Coloquen 5 frijoles sobre los puntos rojos que están en la parte de abajo.
Voy a decir un número. Ustedes moverán esa cantidad de frijoles hacia la punta de los dedos. Recuerden comenzar por el meñique, como lo practicamos. (Mueva el meñique para enfatizar). ¿Comenzamos?
Diferenciación: Apoyo
Si hay estudiantes que necesitan apoyo para escribir, pueden decir la rima de formación de numerales mientras dibujan.
Si hay estudiantes que necesitan apoyo para adivinar, quienes escriben pueden hacerlo en las manos de quienes adivinan, para que puedan sentir y ver el numeral. Ajuste la disposición de los asientos según sea necesario.
Si alguien sintiera incomodidad con tocar, se puede jugar escribiendo en el aire o en la alfombra.
1
10 5 35 10
K ▸ M1 ▸ TC ▸ Lección 12 EUREKA MATH2 © Great Minds PBC 136
Muéstrenme 3.
Haga una pausa mientras la clase mueve frijoles rojos hacia el meñique, el anular y el dedo mayor de la mano izquierda.
¡Rápidamente! Muéstrenme 4.
Haga una pausa mientras la clase mueve un frijol rojo hacia el dedo índice de la mano izquierda.
¡Muy bien! Muéstrenme 5.
Haga una pausa mientras la clase mueve un frijol rojo hacia el pulgar de la mano izquierda.

¡Volvamos atrás! Vuelvan a colocar los 5 frijoles sobre los puntos rojos que están en la parte de abajo.





(Muestre las tarjetas). Esta vez, voy a mostrarles un número. Ustedes moverán esa cantidad de frijoles hacia la punta de los dedos. Recuerden comenzar por el meñique, como lo hicieron antes. (Mueva el meñique para enfatizar).
¿Comenzamos?
1 2 3 4 5
Muestre la tarjeta del 3 y haga una pausa mientras la clase mueve frijoles rojos hacia el meñique, el anular y el dedo mayor de la mano izquierda.
Repita el proceso con las tarjetas del 4 y del 5, mientras la clase mueve frijoles hacia el dedo índice y el pulgar izquierdos.
Dedos a la vista hasta el 3
La clase dice cuántos dedos ve para desarrollar la capacidad de subitizar cantidades en diversas configuraciones.
Voy a mostrarles algunos dedos, pero solo por un segundo. Ustedes dirán el número que ven. ¡Miren con atención!
Inclínese hacia delante, establezca contacto visual, haga una pausa con teatralidad y, luego, muestre por un instante 2 dedos cualesquiera. Ocúltelos.
¿Cuántos dedos vieron?
2
EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 12 © Great Minds PBC 137
Prepárense. Aquí viene el siguiente.
Continúe con la siguiente secuencia:



2 dedos cualesquiera, de la otra mano 2 dedos, 1 dedo de cada mano 3 dedos con el método matemático 3 dedos cualesquiera, de la otra mano 2 dedos de una mano, 1 dedo de la otra


Facilite más práctica con el conteo súbito, usando diversas configuraciones de dedos hasta el 3.
Capte el interés de la clase y cree un ambiente lúdico, con pausas teatrales, falsos comienzos y repeticiones.
Presentar
La clase halla números en el salón de clases.
Usen los ojos para mirar alrededor de nuestro salón de clases. Detengan la vista cuando vean un número.
Después de mirar durante aproximadamente 30 segundos, pida a la clase que camine hasta un numeral y lo señale. Nombre brevemente los diferentes lugares del salón de clases donde hallan los numerales.

Si la clase halló en el salón de clases un numeral escrito en más de una forma, utilice esos ejemplos para las preguntas siguientes (el 1, el 4 y el 9 son los ejemplos más comunes). De no ser así, reúna a la clase y muestre la imagen del numeral 1 escrito de dos formas.
Señale cada numeral y pida a la clase que lo nombre.
¿Estos números son iguales? ¿Por qué?

No, uno tiene una línea arriba.
Los dos tienen una línea como esta. (La clase mantiene el dedo arriba y lo mueve en forma recta hacia abajo).
10 5 30 5 K ▸ M1 ▸ TC ▸ Lección 12 EUREKA MATH2 © Great Minds PBC 138
Los unos están escritos de manera diferente. Se ven diferentes, pero los dos significan uno.
Muéstrenme 1 dedo. (Pausa). Muéstrenme el 1 de otra manera. (Pausa). Hay diferentes maneras de escribir los números, así como hay diferentes maneras de mostrar los números.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hicieron un buen trabajo al hallar números en el salón de clases. ¡Hoy, abriremos la cocina de nuestro restaurante y escribiremos las órdenes de los animales!
Aprender
Escritura en el aire y en la alfombra
Materiales: M) Marioneta o pelota
La clase aprende los trazos básicos para escribir los numerales 4 y 5.
Vuelva a presentar el contexto de la lección 11. La clase recibirá más llamadas telefónicas de animales y escribirá las órdenes para la cocina.
Muestre la imagen del pingüino y reproduzca el audio del pingüino ordenando 4 pescados.
¿Cuántas veces el pingüino dijo pescado?
Anticipe algún desacuerdo o alguna duda acerca de cuántas veces el pingüino dijo pescado. Reproduzca el audio nuevamente y demuestre cómo usar los dedos para llevar la cuenta de cada palabra a medida que se dice.
Dibuje 4 pescados y pida a la clase que los cuente. Guíe a la clase para que escriba el numeral 4 con el siguiente proceso.
Nota para la enseñanza
Comenzar a formar los números y las letras desde la parte superior es un hábito importante para que sus estudiantes aprendan en kindergarten. Les ayudará a no atrasarse cuando las demandas de escritura aumenten en grados superiores.
Puede parecer raro comenzar el 5 en la esquina izquierda y “poner el techo” al final. Sin embargo, si sus estudiantes aprenden a comenzar en la esquina izquierda, cuando tengan dudas estarán en la posición correcta para 7 de 10 numerales (0, 8 y 9 son las excepciones). Comenzar el 5 en la esquina izquierda refuerza este hábito.
10 5 30 5
EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 12 © Great Minds PBC 139
Podemos hacer un dibujo de 4 pescados para recordar la orden o podemos escribir el número 4. Usen el dedo para contar para escribir el 4 en el aire conmigo. Síganme.
Use la marioneta para “escribir” el numeral en el aire. Sostenga la marioneta en alto y escriba el 4 empezando desde arriba mientras dice la siguiente rima.
Una línea cortita y otra más a la derecha. Y para terminar el 4, una línea larga bien hecha.
Pida a la clase que traslade los dedos para contar a la alfombra o a otra superficie que pueda tocar. Repita la rima mientras la clase escribe el 4 sobre la nueva superficie.
Muestre la imagen de la ardilla y reproduzca el audio de la ardilla ordenando 5 nueces.
Presente la escritura del 5 con el mismo proceso usado para el 4.
Bajo de costado y en redondo doy un brinco. Pongo luego el techo y ya escribí el 5.
Escribir los numerales
Materiales: E) Página de escritura de numerales
La clase dibuja y escribe los numerales 4 y 5.
Distribuya el trabajo en clase y los utensilios de escritura. Muestre la imagen del pingüino con los pescados.
Invite a la clase a hallar el número que coincide con la orden del pingüino. Cuando tengan los dedos sobre el numeral 4, pida que digan la rima en conjunto mientras dibujan el numeral con los dedos.
Demuestre cómo escribir el 4. Luego, invite a la clase a usar un lápiz o crayón para escribir el 4 hasta completar la fila. Si terminan rápido, sugiera que dibujen la orden del pingüino adentro del recuadro.
Repita con el numeral 5 usando la imagen de la ardilla con las nueces.
Nota para la enseñanza
Considere retirar la página de escritura de numerales y colocarla en una pizarra blanca individual para que la clase pueda volver a usarla para práctica.
Evaluación observacional
; ¿La clase puede formar numerales con precisión?
; ¿La clase puede completar correctamente los números que faltan? (secuencia numérica)
DUA: Acción y expresión
La clase puede beneficiarse del dibujo de los números hechos con una variedad de texturas (p. ej., pintura inflable, papel de lija o hilo), mientras repiten las rimas. Esta práctica les ayuda a desarrollar la memoria motora para formar cada número.
Construir los numerales con plastilina suave también ayuda en la formación de los numerales y desarrolla la fuerza en la motricidad fina. Dé a cada estudiante plastilina suave y una bandeja rectangular poco profunda (las tapas de las cajas de calzado infantil funcionan bien). La bandeja rectangular imita el rectángulo de escritura y ayuda a evitar las inversiones. Muestre un numeral y anime a la clase a usar la plastilina suave para hacer el numeral en la bandeja.
K ▸ M1 ▸ TC ▸ Lección 12 EUREKA MATH2 © Great Minds PBC 140
Número bip
La clase practica la secuencia de los números hasta el 5.
Pida a la clase que se ponga de pie para jugar Número bip.
Juguemos Número bip. Voy a contar, pero en lugar de decir uno de los números, voy a decir bip. Levanten la mano cuando sepan el número bip. ¿Comenzamos?
1, 2, 3, 4, bip. (Dé la señal).
5 1, 2, bip, 4, 5. (Dé la señal).
3
1, bip, 3, 4, 5. (Dé la señal).
2 Bip, 2, 3, 4, 5. (Dé la señal).
1
Si hay tiempo suficiente, invite a la clase a completar las secuencias numéricas ubicadas en la parte inferior de la página de escritura de numerales. Trabajen en grupo en la primera secuencia, como si jugaran Número bip en el papel. Marque con el dedo y diga los números que se muestran. Diga bip para los espacios.
EUREKA MATH K M1 TC Lección 12 © Great Minds PBC 39 12 Nombre EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 12 © Great Minds PBC 141
Grupo de problemas
La práctica de hoy brinda una oportunidad de observar y apoyar las estrategias de la clase para responder preguntas sobre cuántos hay, como tocar y contar, marcar y contar y el conteo súbito. Use la representación sistemática para que la clase se ponga en marcha.
Nota para la enseñanza
Este Grupo de problemas está diseñado para usar la representación sistemática (ver lección 8 para conocer más detalles). Continúe usando la representación sistemática para los Grupos de problemas en todo el módulo 1 hasta que la clase se sienta cómoda trabajando con lápiz y papel.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante razona de forma cuantitativa y abstracta (MP2) al contar los objetos en la imagen, escribir el numeral correspondiente y reconocer que el numeral representa la cardinalidad del conjunto de objetos.
Concluir
Reflexión final 5 min
Materiales: M) Marioneta, afiche de la lección 11
Objetivo: Escribir los numerales 4 y 5 para responder preguntas sobre cuántos hay
Elija a estudiantes que sientan seguridad para escribir el numeral 5. Presente el contexto de la siguiente manera:
¡El ave volvió y quiere más gusanos! La marioneta dibujará la orden del ave. Kaliya escribirá el número.
© Great Minds PBC 41 EUREKA MATH K M1 TC Lección 12 Cuenta y escribe cuántos objetos hay. 12 Nombre K M1 TC Lección 12 EUREKA MATH © Great Minds PBC 42 GRUPO DE PROBLEMAS
10 5 30 5 K ▸ M1 ▸ TC ▸ Lección 12 EUREKA MATH2 © Great Minds PBC 142
Muestre la imagen del ave y reproduzca el audio del ave ordenando 5 gusanos.
Pida a la clase que se ponga de acuerdo con la orden del ave.
Dé la señal para empezar a dibujar y escribir. Use la marioneta para dibujar gusanos con mucho detalle mientras su estudiante escribe el 5. Asegúrese de que su estudiante escriba mucho más rápido que la marioneta.
Mmm… ¿qué fue más sencillo: dibujar 5 gusanos o escribir el 5?
Escribir el 5
Escribir fue más rápido.
Escribir el 5 me resulta difícil. Prefiero dibujar.
¿Y si el ave ordenara 100 gusanos? ¿Tendría sentido dibujar esa cantidad de gusanos para la cocina?
No. Eso llevaría mucho tiempo. Se necesitaría mucho papel.
¿Por qué escribimos números?
Es más fácil que dibujar.
Para tomar órdenes
Para hacer un calendario
Agregue las nuevas ideas al afiche ¿Por qué escribimos números? de la lección 11. Muestre el afiche donde toda la clase pueda verla. Habrá oportunidades para agregar ideas al afiche cuando la clase aprenda a escribir los numerales del 6 al 10 en el tema F.
Parte de la clase seguirá hallando más sencillo dibujar. De ser así, señale que el dibujo de la marioneta llevó mucho tiempo porque incluyó demasiados detalles. Los dibujos matemáticos son más rápidos porque son simples.
Con tiempo y práctica, escribir los numerales será más fácil. A medida que se agranden los grupos de conteo, la clase verá la eficiencia del sistema numérico escrito.
¿ ?
Nota para la enseñanza
EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 12 © Great Minds PBC 143
Contar suficientes objetos y escribir el numeral
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
En esta lección, la clase piensa en el concepto de suficientes y lo usa para ver si ha contado correctamente un grupo. Reparten platos y sirven alimentos de mentira para razonar y asegurarse de que tienen suficientes.
Pregunta clave
• ¿Cómo sabemos que hemos contado los suficientes?
Criterios de logro académico
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10. (K.CC.B.4.a)
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron. (K.CC.B.4.b)
13
13
LECCIÓN
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 10 min
Aprender 25 min
• ¿Hay suficientes?
• Contar los suficientes
Concluir 5 min
Materiales
Maestro o maestra
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 1 al 5)
Estudiantes
• Plantilla de dos manos
• frijoles de dos colores (5)
• cubos Unifix® (10 por pareja de estudiantes)
• plato con puntos
• menú y bloc de órdenes (1 por pareja de estudiantes, en el libro para estudiantes)
• pizarra blanca individual
• marcador de borrado en seco
• libro para estudiantes
Preparación de la lección
• Prepare las tarjetas del 1 al 5 del juego para demostración de las tarjetas Hide Zero.
• La clase necesita platos con diferentes configuraciones de puntos hasta el 5. Prepare uno para cada estudiante (más 6 a 8 adicionales) con platos de papel y un marcador. Vea ejemplos en el libro Aprender.
• Considere retirar el menú y el bloc de órdenes y colocarlos en una pizarra blanca individual.
© Great Minds PBC 145 EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 13
Fluidez
Contar hasta el 5: ¿Qué número sientes en la espalda?
Materiales: M) Tarjetas Hide Zero
Cada estudiante dibuja un número y adivina un numeral para desarrollar la memoria cinestésica necesaria para formar números.
Juguemos ¿Qué número sientes en la espalda?
Pida a la clase que trabaje en parejas. Cada integrante de la pareja se colocará en fila, mirando hacia delante. Quien esté detrás será quien escriba. Quien esté delante será quien adivine.
Párese detrás de la clase, mirando hacia la espalda de cada estudiante, y muestre la tarjeta del 3.
Estudiantes que escriben, dense vuelta y observen mi número, pero no lo digan. ¡Guarden el secreto! Escriban este número con el dedo en la espalda de su compañero o compañera. Usen toda la espalda para que puedan escribir un número grande y bonito.
Estudiantes que adivinan, ¿se dieron cuenta de qué número les escribieron en la espalda?
Parejas de estudiantes, dense vuelta y observen mi número. Si acertaron, ¡denme 3 aplausos!
Continúe con el 4 y el 5 y, luego, los numerales 1 a 5 en orden aleatorio. Felicite a la clase con el número correspondiente de aplausos. Después de un tiempo, pida a las parejas que cambien los roles.
Muéstrame frijoles hasta el 5
Materiales: M) Tarjetas Hide Zero; E) Plantilla de dos manos, frijoles de dos colores
La clase escucha un número o ve un numeral y cuenta un conjunto en voz alta para desarrollar fluidez con la asociación de un numeral con un conjunto.
Prepárense. Coloquen 5 frijoles sobre los puntos rojos que están en la parte de abajo.
Voy a decir un número. Ustedes moverán esa cantidad de frijoles hacia la punta de los dedos. Recuerden comenzar por el meñique, como lo practicamos. (Mueva el meñique para enfatizar). ¿Comenzamos?
Muéstrenme 3.
3
10 5 35 10 K ▸ M1 ▸ TC ▸ Lección 13 EUREKA MATH2 © Great Minds PBC 146
Haga una pausa mientras la clase mueve frijoles rojos hacia el meñique, el anular y el dedo mayor de la mano izquierda.
¡Rápidamente! Muéstrenme 4.
Haga una pausa mientras la clase mueve un frijol rojo hacia el dedo índice de la mano izquierda.
¡Muy bien! Muéstrenme 5.
Haga una pausa mientras la clase mueve un frijol rojo hacia el pulgar de la mano izquierda.
Continúe con la siguiente secuencia: 4 3 4 5 4 3 2
¡Volvamos atrás! Vuelvan a colocar los 5 frijoles sobre los puntos rojos que están en la parte de abajo.





(Muestre las tarjetas). Esta vez, voy a mostrarles un número. Ustedes moverán esa cantidad de frijoles hacia la punta de los dedos. Recuerden comenzar por el meñique, como lo hicieron antes. (Mueva el meñique para enfatizar).
¿Comenzamos?
1 2 3 4 5
Muestre la tarjeta del 3 y haga una pausa mientras la clase mueve frijoles rojos hacia el dedo meñique, el anular y el mayor de la mano izquierda.
Repita el proceso y muestre las tarjetas en una secuencia similar a la anterior.
Dedos a la vista hasta el 5
La clase dice cuántos dedos ve para desarrollar la capacidad de subitizar y reconocer cantidades en diversas configuraciones.
Voy a mostrarles algunos dedos, pero solo por un segundo. Ustedes dirán el número que ven. ¡Miren con atención! EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 13 © Great Minds PBC 147
Inclínese hacia delante, establezca contacto visual, haga una pausa con teatralidad y, luego, muestre por un instante 3 dedos cualesquiera. Ocúltelos.
¿Cuántos dedos vieron? 3
Prepárense. Aquí viene el siguiente. Continúe con la siguiente secuencia:
4 dedos con el método matemático
4 dedos cualesquiera de la otra mano

4 dedos, 2 de cada mano
3 dedos cualesquiera
3 dedos de una mano, 1 dedo de la otra
3 dedos de una mano, 2 dedos de la otra





Facilite más práctica con el conteo súbito, usando diversas configuraciones de dedos hasta el 5. Capte el interés de la clase y cree un ambiente lúdico, con pausas teatrales, falsos comienzos y repeticiones.

K ▸ M1 ▸ TC ▸ Lección 13 EUREKA MATH2 © Great Minds PBC 148
Presentar
La clase razona si hay suficientes objetos en un grupo.
Muestre la imagen de las mesas y las sillas para preparar la escena de un restaurante.
Miren las mesas de este restaurante. Hay que servir los platos en las mesas.
Muestre la imagen con 5 platos.
Acá están los platos. ¿Necesitamos contar cuántos platos hay?
No, porque allí está la tarjeta del 5. Hay 5 platos.
Me pregunto… ¿hay suficientes para que cada silla del restaurante tenga un plato?
Pida a la clase que aplique la rutina Pensar-Trabajar en parejas-Compartir para calcular si hay platos suficientes. Escuche a sus estudiantes compartir ideas como las siguientes:
Podemos contar las sillas para ver si hay suficientes platos.
Podemos comenzar a repartir los platos para ver si hay suficientes.
Veo que no hay platos suficientes porque hay más de 5 sillas.
Para las tres preguntas siguientes, señale la imagen mientras pregunta acerca de las mesas. Dé tiempo para pensar, para que la mayoría de la clase cuente o subitice antes de pedir que respondan cada pregunta.
Nota para la enseñanza
A lo largo de la lección, parte de la clase podrá necesitar emparejar objetos usando la correspondencia de uno a uno para averiguar si hay suficientes. Parte de la clase puede estar preparada para comparar números, como “5 es más grande que 3; entonces, eso no es suficiente”.
Si lo considera apropiado, brinde apoyo para la comprensión del lenguaje; represente el lenguaje matemático: “5 es más que 3”. El lenguaje de comparación es el enfoque del módulo 3.
10 10 20 10
5 EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 13 © Great Minds PBC 149
¿Hay platos suficientes para la mesa rosa?
Sí.
¿Qué mesa necesita exactamente 5 platos?
La mesa verde
¿Hay platos suficientes para la mesa rosa y la mesa verde?
No.
No hay suficientes.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hoy, comprobaremos si hay suficientes objetos mientras trabajamos en nuestro restaurante.
10
Aprender
¿Hay suficientes?
15 25 10
Materiales: E) Plato con puntos
La clase cuenta suficientes platos para servir la mesa. Forme grupos de tres o cuatro (posiblemente sentados a la mesa). Identifique a un o una ayudante por grupo y, de manera intencional, no entregue suficientes platos para repartir al grupo.

Preparemos nuestro restaurante en el salón de clases. Ayudantes, repartan los platos a su grupo.
¿El grupo tiene suficientes platos?
No.
Necesitamos más platos.
Intentemos nuevamente. Por favor, reúnan los platos y tráiganlos. K ▸ M1 ▸ TC ▸ Lección 13 EUREKA MATH2 © Great Minds PBC 150
Hablen con su grupo. ¿Cómo pueden asegurarse de que cada uno reciba un plato?
Pida que aporten ideas para comenzar una conversación de la clase. Si es necesario, guíe el razonamiento hacia el conteo del número de participantes del grupo para enfatizar que podemos contar para saber cuántos son suficientes. Elija a otro u otra ayudante.
Cuenten las personas de su grupo. Pidan al nuevo o la nueva ayudante que consiga platos suficientes para todo el mundo.
Pida a quienes hagan de ayudantes que repartan los platos a sus grupos. Pregunte a cada grupo si tienen suficientes platos.


¡Ahora, tenemos suficientes platos! ¡Podemos abrir nuestro restaurante y tomar órdenes!

Contar los suficientes
Materiales: E) Cubos Unifix, plato con puntos, menú y bloc de órdenes


La clase practica cómo contar y escribir los numerales para emparejar.
Asegúrese de que cada pareja de estudiantes tenga un menú, una página del bloc de órdenes y un conjunto de 10 cubos Unifix. Cada integrante de la pareja necesita un plato con puntos.
Pida a la clase que represente los roles de quien vende y quien compra en un restaurante, como en las lecciones anteriores. Forme parejas de estudiantes y asígneles el rol de cliente o clienta, o de empleado o empleada.
Luego, muestre el menú.
Clientes y clientas, miren el menú. Elijan un elemento. Cuenten los puntos de su plato y ordenen esa cantidad de ______.
Apoyo para la comprensión
del lenguaje
Relacione las matemáticas con el contexto al representar y animar a formar oraciones que los clientes y clientas de un restaurante usarían en el mundo real. Apoye esta dramatización con esquemas de oraciones apropiados para la clase.
• Llevaré 4 _____, por favor.
• Hay demasiadas/demasiados _____.
• No hay suficientes _____.
Evaluación observacional
; Observe cómo los clientes y clientas emparejan la “comida” con los puntos del plato. Pregunte cuántos tacos tienen. Observe y escuche para ver si cuentan nuevamente o simplemente dicen el número.


Promoción de los estándares para la práctica de las matemáticas
Cada estudiante construye argumentos viables y ofrece valoraciones sobre el razonamiento de otros y otras (MP3) cuando empareja los cubos con los puntos del plato, observa si le sirvieron la cantidad incorrecta y comunica el problema.
EUREKA MATH K M1 ▸ TC ▸ Lección 13 © Great Minds PBC 43 13 Menú Nombre Tacos Manzanas Pretzels © Great Minds PBC 44 K M1 TC Lección 13 EUREKA MATH LECCIÓN Manzanas Tacos Pretzels Orden
EUREKA MATH2 K ▸ M1 ▸ TC ▸ Lección 13 © Great Minds PBC 151
Empleadas y empleados, usen el bloc de órdenes para escribir el número que escucharon al lado del elemento que se ordenó. Luego, cuenten esa cantidad de cubos y sírvanles la “comida”.
Clientes y clientas, asegúrense de que les dan la cantidad correcta. Hagan saber al empleado si no tienen suficientes o si tienen más de lo que han ordenado.
Cambien roles para que cada estudiante tenga la oportunidad de practicar las diferentes destrezas. Repita, si hay tiempo suficiente, y cambie ocasionalmente los platos entre las parejas.
Grupo de problemas
En esta lección, no se incluye Grupo de problemas. Si hay tiempo suficiente después de la dramatización, considere usar la página de escritura de los numerales de las lecciones 11 y 12 para practicar cómo formar los numerales del 1 al 5.
Concluir
Reflexión final 5 min
Objetivo: Contar suficientes objetos y escribir el numeral
¿Cómo supieron que tenían platos suficientes? ¿Y comida?
Contamos el número de personas de nuestro grupo y tomamos esa cantidad de platos.
Emparejé la comida simulada con los puntos del plato.
¿Cómo te ayudó escribir números cuando eras quien vendía comida?
Me ayudó a recordar cuánta comida servir.
Miré mi bloc de órdenes y, luego, conté la comida para emparejarla con el número.
10 5 30 5 K ▸ M1 ▸ TC ▸ Lección 13 EUREKA MATH2 © Great Minds PBC 152
Tema D Descomponer números


En los temas anteriores, la clase utilizó números para contar y responder preguntas sobre cuántos hay. El tema D dirige la atención de la clase a las relaciones entre los números.
Al inicio del tema, la clase considera la relación conocida entre algo y nada. La mayor parte de la clase llega al kindergarten con una comprensión informal de este concepto y puede describirlo utilizando palabras como ninguno, no queda nada o no hay más. Con una sólida comprensión de los números del 1 al 5, la clase está preparada para aprender que un número, el 0, describe un grupo sin objetos.
La clase también explora las relaciones numéricas a través de la descomposición. La descomposición es el proceso de dividir algo (un grupo, un número, una forma) en partes. Cuando sus estudiantes clasifican los objetos en grupos, están descomponiendo. Las actividades de clasificación del tema D difieren de las del tema A en dos aspectos:
• La clase cuenta todos los objetos antes de clasificarlos. También encuentran el número de objetos en cada grupo después de la clasificación. Clasifiqué 5 osos. 4 son amarillos y 1 es rojo.
• La clase clasifica los objetos más de una vez, usando un atributo diferente en cada ocasión. En primer lugar, clasifiqué mis osos por color. Luego, clasifiqué mis osos por tamaño.
Estos factores animan a la clase a empezar a pensar en las diferentes formas de descomponer, o separar en partes, los números. Ven que el 5 se puede dividir en 4 y 1, así como en 3 y 2. Algunas personas pueden incluso ver 5 como 2 y 2 y 1.
Los problemas con historia proporcionan un contexto para pensar en la descomposición y su operación inversa, la composición. La composición es el proceso de reunir cosas (grupos, números, formas). Los problemas con historia utilizan las ideas intuitivas de la clase sobre la composición y la descomposición para explorar la suma y la resta. La atención se centra en dar sentido al problema más que en encontrar una respuesta o escribir una ecuación. En los módulos 4 y 5, la clase aprenderá a representar los problemas con historia mediante enlaces numéricos y oraciones numéricas.
© Great Minds PBC 153
Ordenar por color: 5 es 4 y 1.
Ordenar por tamaño: 5 es 3 y 2.
Progresión de las lecciones
Lección 14
Comprender el significado del cero y escribir el numeral

Lección 15
Clasificar el mismo grupo de objetos de más de una manera y contar
Lección 16
Descomponer un conjunto que se muestra en una imagen
Puedo escribir el 0. Cero significa ninguno.
Primero, clasifiqué mis osos por tamaño. Luego, clasifiqué mis osos por color.
Veo 2 perros con manchas y 2 perros sin manchas. 4 es 2 y 2.
154 K ▸ M1 ▸ TD EUREKA MATH2 © Great Minds PBC
Lección 17
Representar problemas con historia
Lección 18
Representar problemas con historia e identificar los referentes numéricos

Estas son las 4 personas en el autobús. 1 persona se baja del autobús. Ahora, hay 3 personas.
4 representa los cachorros que había al principio. Llegó 1 cachorro. 5 representa todos los cachorros juntos. 4 y 1 es 5.
EUREKA MATH2 K ▸ M1 ▸ TD 155 © Great Minds PBC
Comprender el significado del cero y escribir el numeral
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
La clase aprende a utilizar el cero para describir un grupo sin objetos. Ven un video en el que se muestra cómo se retiran los objetos, uno a la vez, hasta que no queda ninguno y utilizan frijoles para representar lo que ven. La clase también aprende a escribir el numeral 0.
Pregunta clave
• ¿Qué significa el cero?
Criterios de logro académico
K.Mód1.CLA2 Escriben los números del 0 al 10. (K.CC.A.3)
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10. (K.CC.A.3)
14
LECCIÓN 14
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 5 min
Aprender 30 min
• Historia de los globos
• Escritura en el aire y en la alfombra
• Escribir numerales
• Número bip
• Grupo de problemas
Concluir 5 min
Materiales
Maestro o maestra
• marioneta o pelota
• zanahorias (3)
• plato
Estudiantes
• Plantilla de dos manos
• frijoles de dos colores (5)
• libro para estudiantes
Preparación de la lección
• Considere colocar los 5 frijoles en una bolsita o vaso pequeño para facilitar su distribución.
• Considere retirar la página de escritura de numerales del libro para estudiantes y colocarla en una pizarra blanca individual para volver a usarla para practicar.
© Great Minds PBC 157 EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 14
Fluidez
Contar hasta el 3 con el método matemático
Materiales: E) Plantilla de dos manos, frijoles de dos colores
La clase hace una transición del conteo en la Plantilla de dos manos al conteo con el método matemático.
¡Levanten el dedo índice! Toquen los puntos rojos que hay en la parte de abajo.
¡Levanten las dos manos! Averigüen cuál de sus propias manos coincide con la mano que tiene los puntos rojos.



Dé tiempo para la experimentación mientras cada estudiante determina qué mano debe colocar en la plantilla. La clase debe colocar la mano izquierda sobre la mano izquierda dibujada en la plantilla.
Prepárense. Coloquen 3 frijoles sobre los puntos rojos que están en la parte de abajo.
Voy a decir un número. Ustedes moverán esa cantidad de frijoles hacia la punta de los dedos. Recuerden comenzar por el meñique, como lo practicamos. (Mueva el meñique para enfatizar). ¿Comenzamos?
Muéstrenme 1.
Haga una pausa mientras la clase mueve un frijol rojo hacia el meñique izquierdo.
¿Cuántos dedos tienen un frijol?
¿Qué dedo es?
El meñique
Muéstrenme su propio dedo meñique. Este es el dedo con el que empezaremos a contar cuando contemos con el método matemático.
Nota para la enseñanza
En todo el mundo, los números se representan con las manos de muchas maneras. La ventaja matemática de contar con el método matemático es que la clase cuenta de izquierda a derecha sin interrupción, al igual que lo hace con el camino numérico y, eventualmente, con la recta numérica. También permite que la clase vea y sienta cómo aumenta la cantidad a medida que cuentan hacia delante.
La clase seguirá usando este método hasta 5.o grado para representar conceptos de valor posicional y realizar operaciones con números enteros y fracciones decimales.
Nota para la enseñanza
Cada estudiante, tanto si observa sus propias manos como las de usted, verá una progresión de izquierda a derecha. Para usted, la progresión aparecerá en orden inverso.
1
10 5 30 5
K ▸ M1 ▸ TD ▸ Lección 14 EUREKA MATH2 © Great Minds PBC 158
Póngase de frente a la clase y pida a sus estudiantes que copien los movimientos. Levante el meñique derecho.
Muéstrenme el meñique izquierdo. Eso es 1.
Coloquen un frijol junto al dedo siguiente. ¿Cuántos dedos tienen frijoles ahora?
Muéstrenme qué dedos tienen frijoles. Usen la plantilla como ayuda. el salón de clases y proporcione apoyo). Vamos a contar hasta el 2 con el método matemático. ¿Comenzamos?
Levante el meñique derecho y, luego, el anular derecho; cada estudiante levanta el meñique izquierdo y, luego, el anular izquierdo.

1, 2

Manos del maestro o de la maestra
Coloquen un frijol junto al dedo siguiente. ¿Cuántos dedos tienen frijoles ahora? 3
Muéstrenme qué dedos tienen frijoles. Usen la plantilla como ayuda. y proporcione apoyo). Vamos a contar hasta el 3 con el método matemático. ¿Comenzamos?
Levante el meñique derecho, luego, el anular derecho y, luego, el mayor derecho; cada estudiante levanta el meñique izquierdo, luego, el anular izquierdo y, luego, el mayor izquierdo.




1, 2, 3
Vean si pueden hacerlo sin mirar la plantilla. ¡Cierren las manos! (Muestre un puño cerrado).
¿Comenzamos?
Cuente hasta el 3 con el método matemático junto con la clase, representando el método con los dedos.
Deténganse aquí en el 3. Ahora, cuenten hacia atrás hasta el 1. ¿Comenzamos?
Cuente del 3 al 1 con el método matemático junto con la clase, representando el método con los dedos.
Facilite más práctica para contar hasta el 3 con el método matemático.
DUA: Acción y expresión
La clase no siempre contará, ni mostrará con los dedos, el método matemático. Anime a sus estudiantes a seguir utilizando los dedos como lo harían de forma natural mientras añaden a su repertorio el contar con el método matemático.
Representar los números con las manos de diversas maneras ayuda al trabajo de descomposición y conservación del número. La actividad de fluidez Muéstramelo de otra manera: El 2 y el 3 es un ejemplo.
Diferenciación: Apoyo
Colocar las manos sobre el escritorio o el piso puede ayudar a sus estudiantes que aún no tienen completo dominio de la motricidad fina a usar los dedos. La superficie plana les ayuda a mantener algunos dedos estirados y los demás doblados.
1
2
EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 14 © Great Minds PBC 159
Muéstramelo de otra manera: El 2 y el 3
La clase representa un número con los dedos de diferentes maneras como preparación para trabajar con la descomposición de números a partir de la lección 16.
Muéstrenme el 2 con el método matemático.
(La clase muestra el 2 con los dedos usando el método matemático).
Ahora, muéstrenme otra manera de formar el 2. ¡La que más les guste!
(La clase muestra el 2 con los dedos de otra manera).
¡Cierren las manos! Muéstrenme el 2 de otra manera.
Continúe pidiendo a la clase que muestre el 2 con los dedos de diversas maneras algunas veces más.
Repita el proceso con el 3.
Presentar

Materiales: M) Marioneta, zanahorias, plato
La clase aprende que cero es la palabra matemática para ninguno.
Use una cámara de documentos para mostrar las zanahorias sobre un plato u otro fondo. Reúna a sus estudiantes y pídales que escuchen su historia.
La mamá de la marioneta le dijo que se comiera todas las zanahorias antes de salir a jugar.
¿Cuántas zanahorias tiene que comer la marioneta?
Haga que la marioneta finja comer una zanahoria. Esconda la zanahoria.
¿Puede salir ahora la marioneta? ¿Por qué?

No, la marioneta todavía tiene que comerse algunas zanahorias.

3
10 5 30 5 K ▸ M1 ▸ TD ▸ Lección 14 EUREKA MATH2 © Great Minds PBC 160
Repita con la segunda y tercera zanahoria. A continuación, guíe una conversación planteando las siguientes preguntas.
¿Puede salir ahora la marioneta? ¿Por qué?
Sí, porque se comió todas las zanahorias.
¿Cuántas zanahorias le faltan comer a la marioneta?
Ninguna
Cero es la palabra matemática para ninguno. 0 es el número que indica cuántas zanahorias quedan.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hoy, veremos una historia y practicaremos la escritura del número 0.
Aprender
Historia de los globos
Materiales: E) Frijoles de dos colores
La clase ve y representa un video que muestra la descomposición de un número hasta que queda 0.
Prepárese para reproducir el video, en el que se ve a Malik caminando con globos que el viento hace volar de uno en uno.
Entregue a cada estudiante 5 frijoles. Dígales que van a usar sus frijoles para representar el video. Reproduzca brevemente el video y póngalo en pausa para mostrar a Malik caminando con 5 globos.
¿Cuántos globos hay en total? Muestren el mismo número con sus frijoles.
0
5 10 5 30 5 EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 14 © Great Minds PBC 161
Reanude la reproducción del video. Pause después de que se vuele un globo.
¿Qué ha pasado?
1 globo se voló.
Diga a la clase que muestre lo que ha pasado con sus frijoles.
¿Cuántos globos hay ahora? ¿Cómo lo saben?
Hay 4 globos. Lo sé porque conté mis frijoles.
Continúe reproduciendo el video y pausando cada vez que se vuele un globo. Cuando se haya volado el último globo, ayude a la clase a utilizar cero para describir la situación.
¿Cuántos globos hay ahora?
¿Cuál es la palabra matemática para ninguno?
Repitan conmigo: Hay 0 globos.
¿Cuántos frijoles quedan?
Escritura en el aire y en la alfombra
Materiales: M) Marioneta o pelota
La clase aprende el trazo básico para escribir el numeral 0.
Invite a la clase a practicar la escritura del 0 en el aire.
Usen el dedo de contar para escribir el 0 en el aire conmigo. Sigan a la marioneta.
Sostenga la marioneta en el aire y escriba 0 empezando por arriba mientras dice la rima.
Desde arriba arranco primero. Redondo como un agujero, ¡así se escribe el 0!
Pida a la clase que traslade los dedos que usan para contar a la alfombra o a otra superficie que puedan tocar. Repita la rima mientras la clase escribe el 0 en la nueva superficie.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante razona de forma abstracta y cuantitativa (MP2) cuando usa el numeral 0 para representar que no hay globos y cuando determina por el contexto que significa ninguno o nada.
K ▸ M1 ▸ TD ▸ Lección 14 EUREKA MATH2 © Great Minds PBC 162
Escribir numerales
Materiales: E) Página de escritura de numerales
La clase traza y escribe el numeral 0.
Distribuya el trabajo en clase y los útiles de escritura. Muestre cómo se escribe el 0 mientras la clase repite la rima del número.
Invite a la clase a hallar el 0 en su papel. Una vez que tengan los dedos en el numeral 0, digan en grupo la rima mientras trazan el numeral con un dedo. Luego, invite a la clase a escribir con un lápiz o crayón el 0 hasta completar la fila.
Número bip
La clase practica la secuencia de los números hasta el 5, incluido el 0.
Pídales que se pongan de pie para jugar Número bip.
Juguemos Número bip. Voy a contar, pero en lugar de decir uno de los números, voy a decir bip. Levanten la mano cuando sepan el número bip. ¿Comenzamos?
3, 2, bip, 0 (Dé la señal).
1
3, 2, 1, bip (Dé la señal).
3, bip, 1, 0 (Dé la señal).
5, 4, 3, 2, 1, bip (Dé la señal).
Si hay tiempo suficiente, invite a la clase a completar las secuencias numéricas ubicadas en la parte inferior de la página de escritura de numerales. Trabajen en grupo en la primera secuencia, como si jugaran Número bip en el papel. Marque con el dedo y diga los números que se muestran. Diga bip para los espacios.
Nota para la enseñanza
Considere retirar la página de escritura de numerales y colocarla en una pizarra blanca individual para volver a usarla para practicar.
Nota para la enseñanza
La clase ve más fácilmente el 0 como parte de la secuencia cuando cuentan hacia atrás que cuando cuentan hacia delante porque tienen el hábito de empezar por el 1. Empezar con 0 es difícil, sobre todo si están contando un grupo de objetos.
0
2
0
EUREKA MATH K ▸ M1 TD ▸ Lección 14 Great Minds PBC 49 14 Nombre EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 14 © Great Minds PBC 163
Grupo de problemas
Use la demostración sistemática para que la clase se inicie en el Grupo de problemas. Considere el mejor momento para leer las preguntas. Puede ser más fácil leer todas las instrucciones al grupo antes de que comiencen con su trabajo independiente.
Evaluación observacional
; ¿La clase entiende que el cero es un número que representa nada?
; ¿La clase forma correctamente el numeral 0?
EUREKA MATH ▸ M1 ▸ TD ▸ Lección 14 © Great Minds PBC 51 Cuenta y escribe cuántos hay. 14 Nombre K M1 ▸ TD ▸ Lección 14 EUREKA MATH2 © Great Minds PBC 52 GRUPO DE PROBLEMAS ¿Cuántas manzanas hay en cada árbol? ¿Cuántos gatos hay en los árboles?
K ▸ M1 ▸ TD ▸ Lección 14 EUREKA MATH2 © Great Minds PBC 164
Concluir
Reflexión final 5 min
Objetivo: Comprender el significado del cero y escribir el numeral
Reúna e invite a sus estudiantes a mirar alrededor del salón de clases mientras hace las siguientes preguntas:
• ¿Cuántas alfombras hay en nuestro salón de clases?
• ¿Cuántas ventanas hay?
• ¿Cuántos elefantes hay?
A continuación, use las siguientes preguntas para ayudar a la clase a resumir el objetivo del día.
¿Qué palabra matemática nueva hemos aprendido hoy?
Cero
¿Qué significa el cero?
Ninguno
Nada No hay más
Usen su dedo de contar para escribir el 0 en el aire.
Las matemáticas en el pasado
Si el cero significa nada, ¿por qué lo necesitamos?
¿Alguien inventó el cero?
¿El cero siempre se dibujó como 0?
Quienes tengan curiosidad quizá quieran saber más sobre el cero. Proporcióneles algunos datos divertidos sobre la historia del cero de la sección Las matemáticas en el pasado: El cero.
Muestre los símbolos del cero en las antiguas culturas maya, india y árabe. Pida a la clase que compare los símbolos antiguos con el que aprendieron a escribir hoy.
5 30 5
EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 14 © Great Minds PBC 165
Clasificar el mismo grupo de objetos de más de una manera y contar
Vistazo a la lección
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
La clase cuenta para hallar el número total de objetos de un conjunto y, luego, clasifica el conjunto en grupos. Expresan la relación entre el total y los grupos (o partes) mediante una oración numérica, como 5 es 4 y 1. Clasifican los conjuntos de objetos más de una vez, usando un atributo diferente en cada ocasión. En esta lección se presenta la frase oración numérica.
Pregunta clave
• ¿El número de objetos cambia si clasificamos el mismo grupo de manera diferente?
Criterio de logro académico
K.Mód1.CLA10 Clasifican objetos en categorías. (K.MD.B.3)
15
LECCIÓN 15
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 5 min
Aprender 30 min
• Clasificar osos
• Compartir, comparar y conectar
• Clasificar de otra manera
• Grupo de problemas
Concluir 5 min
Materiales
Maestro o maestra
• tarjetas 5-group™ (grupos de 5), juego para demostración (del 1 al 3)
• cubos Unifix® (5)
• Rompecabezas de barra de 5 (en la edición para la enseñanza)
Estudiantes
• osos para contar (5 por pareja de estudiantes)
• platos de papel (3 por pareja de estudiantes)
• tarjetas Hide Zero® (que ocultan el cero) (1 juego de 1 a 5 por pareja de estudiantes)
• cubos Unifix® (5)
• libro para estudiantes
Preparación de la lección
• Prepare las tarjetas del 1 al 3 del juego para demostración de los grupos de 5.
• Para cada pareja de estudiantes, prepare una bolsita de 5 osos usando dos colores y tamaños diferentes. Por ejemplo, una bolsita puede contener 3 osos amarillos grandes, 1 oso amarillo pequeño y 1 oso rojo pequeño.
• Cree barras de 5 con los cubos Unifix, una para cada estudiante y una para usted.
• Considere retirar las páginas del libro para estudiantes con antelación para ahorrar tiempo.
• Imprima o haga una copia del Rompecabezas de barra de 5 de la edición para la enseñanza.
© Great Minds PBC 167 EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 15
Fluidez
Contar hasta el 3 con el método matemático
La clase hace una recta numérica con los dedos mientras cuentan en voz alta para desarrollar un sentido de cantidad y orden.




Vamos a contar con el método matemático.
Póngase de frente a la clase y pida a sus estudiantes que copien los movimientos.
Contar con el método matemático es así: 1, 2, 3. (Demuéstrelo).
Levante el meñique derecho.
Muéstrenme el meñique izquierdo. Eso es 1.
Levantemos el dedo que sigue.
Levante el dedo anular derecho; la clase levanta el anular izquierdo.
Eso es 2.
Vamos con el que sigue. Eso es 3. ¡Cierren las manos!
Vamos a contar hasta el 3 con el método matemático.
Muestre el método matemático con los dedos mientras la clase cuenta, pero no cuente en voz alta.
Manos del maestro o de la maestra
Pida a la clase que cuente del 1 al 3 con el método matemático.
Deténganse aquí en el 3. Ahora, cuenten hacia atrás hasta el 0. ¿Comenzamos?


Pida a la clase que cuente del 3 al 0 con el método matemático y que baje todos los dedos para mostrar 0.
Facilite más práctica para contar hasta el 3 con el método matemático.
Diferenciación: Apoyo
Si sus estudiantes necesitan apoyo, vuelva a los frijoles y la plantilla de manos que se usan para presentar esta actividad en la lección 14.
10 5 30 5
K ▸ M1 ▸ TD ▸ Lección 15 EUREKA MATH2 © Great Minds PBC 168
Grupos de 5 hasta el 3
Materiales: M) Tarjetas de grupos de 5
La clase reconoce un grupo de puntos para desarrollar la capacidad de subitizar cantidades que se muestran con grupos de 5.
La configuración de grupos de 5 se volverá conocida con el tiempo, lo que permitirá a la clase subitizar. Sin embargo, en la rutina se incorpora tiempo de espera para permitir el conteo si es necesario. Los y las estudiantes que respondan rápidamente se beneficiarán de retener un número en la memoria y practicar la autorregulación mientras esperan a que el resto termine.
Recuerden escuchar, pensar, levantar la mano y esperar la señal. (Enfatice con gestos cada paso).
Levanten la mano cuando sepan la respuesta a la pregunta. Esperen mi señal para decir la respuesta.
Muestre la tarjeta de grupos de 5 que muestra 1.
¿Cuántos puntos hay?
Espere hasta que la mayor parte de sus estudiantes haya levantado la mano y, luego, dé la señal para que respondan.
Repita el proceso con la siguiente secuencia:
Cuando la clase esté preparada, muestre cada tarjeta durante menos tiempo como desafío para que sus estudiantes reconozcan los grupos de puntos más rápidamente.
Nota para la enseñanza
Las tarjetas digitales de grupos de 5 son prácticas y fáciles de ver para toda la clase. Sin embargo, las tarjetas de grupos de 5 físicas ofrecen la flexibilidad de cambiar la secuencia en función de las respuestas de la clase.
1
2 3 2 1 3 2 3 1 3 2
EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 15 © Great Minds PBC 169
Contar con movimiento hasta el 10
La clase cuenta con movimientos del cuerpo para adquirir fluidez con los nombres de los números y la correspondencia de uno a uno.
Aplaudamos 5 veces y contemos los aplausos. ¿Comenzamos?
Al principio, cuente y aplauda del 1 al 5 lentamente, haciendo énfasis en que para cada aplauso se dice un número. Repita el proceso hasta que la mayor parte de la clase esté aplaudiendo, contando o, idealmente, aplaudiendo y contando.
Repita el proceso, pero esta vez dé pisotones y cuente hasta el 5.
Ahora, aplaudamos 10 veces y contemos los aplausos. ¿Comenzamos?
Cuente y aplauda del 1 al 10 junto con la clase.
Repita el proceso, pero esta vez dé pisotones y cuente hasta el 10.
Es posible que el ritmo del conteo repetitivo al unísono lleve a la clase hacia un estado cognitivo de relajación. Intente variar el ritmo para inducir a la clase a regresar al estado de alerta e incentivar el juego.
Presentar
La clase considera los atributos que podrían utilizarse para clasificar.
Muestre la imagen de 5 osos en un plato.
¿Qué observan sobre los osos?
Son azules y verdes.
Hay 5 osos en un plato.
Hay osos grandes y osos pequeños.
Invite a la clase a usar la rutina Pensar-Trabajar en parejasCompartir para analizar la siguiente pregunta.
Apoyo para la comprensión del lenguaje
Apoye el desarrollo del lenguaje señalando los osos cuando utilice las palabras que la clase necesita para describir los atributos. Hágalo cuando repita las ideas de la clase sobre la forma de clasificar. Por ejemplo:
• Este oso es azul. (Señale). Este oso es verde. (Señale). Estos son de diferentes colores.
• Este oso es grande. (Señale). Este oso es pequeño. (Señale). Estos son de diferentes tamaños.

10 5 30 5
K ▸ M1 ▸ TD ▸ Lección 15 EUREKA MATH2 © Great Minds PBC 170
Piensen sin decirlo en voz alta: ¿Cómo podríamos clasificar estos osos?
Díganselo a su pareja de trabajo. Empiecen así: Podríamos clasificar los osos por…
Seleccione un grupo pequeño de estudiantes para que compartan sus ideas y asegúrese de que mencionen el tamaño y el color.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Me pregunto si la forma de clasificar cambiará el número de cosas. Hoy, probaremos diferentes formas de clasificar y veremos qué ocurre.
Aprender
Clasificar osos
Materiales: E) Tarjetas Hide Zero, bolsita de osos, platos de papel
La clase clasifica los osos y cuenta cuántos hay en cada grupo.
Forme parejas de estudiantes y distribuya los materiales.
Coloquen sus tarjetas numéricas en orden del 1 al 5.
Una vez que las parejas tengan las tarjetas del 1 al 5 en orden, muestre cómo colocar el 0 antes del 1.
A continuación, pida a la clase que saque los osos de la bolsita, los coloque en un plato de papel y cuente cuántos hay.
Levanten la tarjeta numérica que dice cuántos osos hay.
Coloquen la tarjeta en el plato.
Piensen en una forma de clasificar sus osos. Luego, clasifíquenlos en los dos platos vacíos.
Una vez que sus estudiantes hayan clasificado los objetos, pídales que cuenten cada grupo y encuentren la tarjeta Hide Zero correspondiente a los osos de cada plato.
Evaluación observacional
; ¿La clase puede clasificar los osos al menos de una manera, por tamaño o por color?
Nota para la enseñanza
Los platos de papel hacen visible la relación de parte-total. La clase utiliza los enlaces numéricos para explorar la descomposición y la composición en el módulo 4. Los platos de papel sirven como un anticipo del trabajo con vínculos numéricos que se planteará más adelante, por lo que su organización es importante para representar.

10 5 30 5
1 2 3 4 5 0
EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 15 © Great Minds PBC 171
Seleccione a dos parejas para que compartan su clasificación en el siguiente segmento. Si es posible, elija ejemplos de trabajo que muestren uno o los dos siguientes aspectos:
• dos maneras diferentes de clasificar, como por color y por tamaño
• dos formas diferentes de descomponer el 5, como 5 es 4 y 1 y 5 es 3 y 2

Compartir, comparar y conectar
La clase comenta las formas de clasificar y aprende a hacer una oración numérica.
Reúna a la clase para comentar los ejemplos de trabajo seleccionados. Considere alejar al resto de la clase de sus materiales de clasificación para que puedan concentrarse.
Clasificar por color (método de Ainsley y Theo)
Díganme, ¿cómo clasificó este grupo sus osos?
Los clasificaron por color.
¿Cuántos osos hay en el grupo amarillo?
4 osos
¿Cuántos osos hay en el grupo rojo?
1 oso
¿Cuántos osos tenían al comenzar?
5 osos
Clasificaron los 5 osos en un grupo de 4 amarillos y otro grupo de 1 rojo.
Podemos decir que en una oración numérica: 5 es 4 y 1. (Señale los osos correspondientes al decir cada número. Señale a todos los osos al decir el 5).
Repitan conmigo: 5 es 4 y 1.
5 es 4 y 1.

Nota para la enseñanza
El ejemplo de trabajo muestra respuestas típicas. Busque trabajos similares entre sus estudiantes y promueva conversaciones auténticas sobre los conceptos clave.
Si la clase clasifica los objetos de manera diferente a la que se muestra aquí, ayúdeles a nombrar el atributo elegido y a utilizar la clasificación para decir una oración numérica.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante pone atención a la precisión (MP6) cuando usa oraciones numéricas como 5 es 4 y 1 para describir clasificaciones y cuando procura decir cada número una vez y en el orden correcto.
K ▸ M1 ▸ TD ▸ Lección 15 EUREKA MATH2 © Great Minds PBC 172
Clasificar por tamaño (método de Sammy y Rosie)
Díganme, ¿cómo clasificó este grupo sus osos? Los clasificaron por tamaño.
¿Cuántos osos hay en el grupo de osos grandes?
3 osos
¿Cuántos osos hay en el grupo de osos pequeños?
2 osos
¿Cuántos osos tenían al comenzar?
5 osos
Clasificaron los 5 osos en un grupo de 3 osos grandes y otro grupo de 2 osos pequeños.
Digamos eso en forma de oración numérica. Repitan conmigo: 5 es 3 y 2. (Señale a los osos al decir cada número).
5 es 3 y 2.

Indique a las parejas de estudiantes que vuelvan a sus clasificaciones y que formulen oraciones numéricas.
Miren sus clasificaciones. Es su turno de hablar de sus osos usando números: 5 es ...
Recorra el salón de clases y escuche a sus estudiantes mientras dicen sus oraciones numéricas entre sí.
Clasificar de otra manera
La clase clasifica sus osos de una forma nueva y dice la oración numérica correspondiente.
Vuelvan a poner los osos en el plato junto al 5. Con su pareja, piensen en una forma diferente de clasificar.
Las parejas vuelven a clasificar, cuentan cuántos osos hay en cada grupo y rotulan con las tarjetas Hide Zero. Cuando las parejas hayan terminado, pídales que digan la oración numérica correspondiente.
Nota para la enseñanza
En la lección 18 se presenta una descripción sencilla de la oración numérica. Para ese momento, la clase ha explorado las oraciones numéricas en diferentes contextos y tiene una comprensión más profunda de su uso.
EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 15 © Great Minds PBC 173
Grupo de problemas
Materiales: M) Rompecabezas de barra de 5, cubos Unifix; E) Cubos Unifix
Reúna a la clase, muestre el rompecabezas y sostenga una barra de 5 cubos Unifix.
¿Cuántos cubos hay?
5
Coloque la barra de cubos sobre el contorno del Rompecabezas de barra de 5.
Tengo que separar la barra de 5 cubos para que entre en el rompecabezas azul.
Separe la barra en 2 y 3. Intente colocar las partes sobre el rompecabezas. Anime a la clase a que participe en una conversación sobre cómo se podría separar la barra en partes para que entre.
Separe la barra en 1 y 4. Coloque el cubo individual y la barra de 4 cubos en el rompecabezas.
¿Cuántos cubos hay aquí? (Señale el cubo individual).
1
Escriba 1 en la casilla gris debajo del cubo.
¿Cuántos cubos hay en esta barra? (Señale la barra de 4).
4
Escriba 4 en la casilla gris debajo de la barra de 4.
Separamos 5 en 1 y 4. Terminen mi oración numérica: 5 es ... (Señale cada barra para que la clase diga los números).


1 y 4
Entregue a la clase una barra de 5 y pídales que la separen en partes para que entre en los rompecabezas del Grupo de problemas. Anime a la clase a decir una oración numérica para cada rompecabezas.
K ▸ M1 ▸ TD ▸ Lección 15 EUREKA MATH2 © Great Minds PBC 174
Si la clase está preparada para una mayor independencia, muéstreles cómo empezar con una barra de 4 cubos en la página siguiente para que puedan trabajar a su propio ritmo.
Concluir
Reflexión final 5 min
Objetivo: Clasificar el mismo grupo de objetos de más de una manera y contar
Muestre la imagen de 5 osos y 3 platos.

La marioneta clasificó los osos que vimos antes. ¿Cuántos osos tenía la marioneta al comenzar?
5 osos
© Great Minds PBC 53 EUREKA MATH K M1 TD Lección 15 15 Nombre Crea una barra de 5 cubos. Separa la barra para que entre en los recuadros. Escribe las parejas de números que suman 5. 1 2 3 4 5 6 7 8 9 10 K M1 TD Lección 15 EUREKA MATH © Great Minds PBC 54 GRUPO DE PROBLEMAS Crea una barra de 4 cubos. Separa la barra para que entre en los recuadros. Escribe las parejas de números que suman 4. 1 2 3 4 5 6 7 8 9 10 10 5 30 5 EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 15 © Great Minds PBC 175
Muestre la imagen de 5 osos ordenados por tamaño.
Primero, la marioneta los ordenó por tamaño. Terminen mi oración numérica: 5 es ... (Señale cada plato para que la clase diga los números).
3 y 2

Muestre la segunda clasificación.
Luego, la marioneta los ordenó por color. Terminen mi oración numérica: 5 es ... (Señale cada plato para que la clase diga los números).
2 y 3
Invite a la clase a usar la rutina Pensar-Trabajar en parejas-Compartir para analizar la siguiente pregunta.
¿La clasificación de los osos de una manera diferente cambia el número de osos que tiene la marioneta?
No lo sé. Esa imagen tiene 3 y 2. La otra imagen tiene 2 y 3.
No. La marioneta comenzó con 5 las dos veces.
No. Hay 5 osos en ambas imágenes.
Nota para la enseñanza
Al final de esta lección, no toda la clase verá que el número total de osos sigue siendo el mismo independientemente de cómo se ordenen. Esta comprensión se desarrolla con la experiencia a lo largo del tiempo. La clase tendrá más oportunidades de explorar esta idea a lo largo del tema y en el módulo 4.
K ▸ M1 ▸ TD ▸ Lección 15 EUREKA MATH2 © Great Minds PBC 176
de barra de 5
EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 15 ▸ Rompecabezas de barra de 5 © Great Minds PBC 177 This page may be reproduced for classroom use only.
Rompecabezas
LECCIÓN 16
Descomponer un conjunto que se muestra en una imagen
Vistazo a la lección
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
La clase clasifica objetos de imágenes seleccionando un atributo y describiendo cuántos objetos corresponden a cada grupo. Este es un nuevo nivel de abstracción, ya que la clase no puede mover los objetos para formar grupos. La clase enfoca la atención en los números en preparación para el trabajo de parte-total del módulo 4.
Preguntas clave
• ¿Cómo podemos descomponer un conjunto en grupos?
• ¿Cómo podemos formar una oración numérica para emparejar con un grupo?
Criterio de logro académico
K.Mód1.CLA10 Clasifican objetos en categorías. (K.MD.B.3)
16
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 5 min
Aprender 30 min
• Imagen de perros
• Los crayones de Kia
• Grupo de problemas
Concluir 5 min
Materiales
Maestro o maestra
• ninguno
Estudiantes
• crayón rojo
• crayón azul
• libro para estudiantes
Preparación de la lección
No se necesita.
© Great Minds PBC 179 EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 16
Fluidez
Contar hasta el 5 con el método matemático
La clase hace una recta numérica con los dedos mientras cuenta en voz alta para desarrollar el sentido de la cantidad y del orden.






Vamos a contar con el método matemático.
Póngase de frente a la clase y pida a sus estudiantes que copien los movimientos.
Así contamos con el método matemático: 1, 2, 3, 4, 5. (Demuéstrelo).
Levante el meñique derecho.
Muéstrenme el meñique izquierdo. Eso es 1. Sigamos contando hasta el 5.

Muestre el método matemático con los dedos mientras la clase cuenta, pero no cuente en voz alta.
Pida a la clase que cuente del 1 al 5 con el método matemático.
Deténganse aquí en el 5. Ahora, cuenten hacia atrás hasta el 0. ¿Comenzamos?



Pida a la clase que cuente del 5 al 0 con el método matemático y que baje todos los dedos para mostrar 0.
Manos del maestro o de la maestra
Manos de la clase
Facilite más práctica para contar hasta el 5 con el método matemático.
10 5 30 5
K ▸ M1 ▸ TD ▸ Lección 16 EUREKA MATH2 © Great Minds PBC 180
Muéstramelo de otra manera: El 3, el 4 y el 5
La clase representa un número con los dedos de diferentes maneras como preparación para trabajar con la descomposición de números.
Muéstrenme el 3 con el método matemático.
(La clase muestra el 3 con los dedos usando el método matemático).
Ahora, muéstrenme otra manera de formar el 3. ¡La que más les guste!
(La clase muestra el 3 con los dedos de otra manera).
Cierren las manos. Muéstrenme el 3 de otra manera.
Continúe pidiendo a la clase que muestre el 3 con los dedos de diversas maneras algunas veces más. Repita el proceso con el 4 y el 5.
Contar con movimiento hasta el 10
La clase cuenta con movimientos del cuerpo para adquirir fluidez con los nombres de los números y la correspondencia de uno a uno.


Aplaudamos 5 veces y contemos los aplausos. ¿Comenzamos?
Al principio, cuente y aplauda del 1 al 5 lentamente, haciendo énfasis en que para cada aplauso se dice un número. Repita el proceso hasta que la mayor parte de la clase esté aplaudiendo, contando o, idealmente, aplaudiendo y contando.
Repita el proceso, pero esta vez dé pisotones y cuente hasta el 5.
Ahora, aplaudamos 10 veces y contemos los aplausos. ¿Comenzamos?
Cuente y aplauda del 1 al 10 junto con la clase.
Repita el proceso, pero esta vez dé pisotones y cuente hasta el 10.
Es posible que el ritmo del conteo repetitivo al unísono lleve a la clase hacia un estado cognitivo de relajación. Intente variar el ritmo para inducir a la clase a regresar al estado de alerta e incentivar el juego.

EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 16 © Great Minds PBC 181
Presentar
La clase comenta lo que observa en la imagen.
Muestre a la clase la imagen de los perros.
¿Qué observan en los perros de la imagen?
Hay 4 perros.
2 perros corren, 1 está sentado y 1 está acostado.
1 perro está jugando con una pelota y 3 perros no están jugando con una pelota.
¿Cuántos perros hay sobre la banca?
Ninguno
¿Qué número es ninguno? 0
A medida que la clase participa, anime a sus estudiantes a que encuentren varias maneras de descomponer 4.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hoy, vamos a buscar diferentes maneras de clasificar lo que vemos en la imagen.
10 5 30 5 K ▸ M1 ▸ TD ▸ Lección 16 EUREKA MATH2 © Great Minds PBC 182
Aprender
Imagen de perros
La clase analiza la imagen de 4 y comenta más de una manera de clasificar.
Continúe mostrando la imagen de perros de la sección Presentar.
¿Cuántos perros hay en la imagen? Muéstrenme con los dedos.
(La clase muestra 4 dedos).
Vamos a clasificar los perros en dos grupos. ¿Cuántos perros tienen collar? Muéstrenme con los dedos.
(La clase muestra 3 dedos).
Mantengan esos dedos arriba. (Mueva la mano abierta). Muéstrenme la otra mano: ¿cuántos perros no tienen collar?
(La clase muestra 1 dedo).
Levante 3 dedos en una mano y 1 dedo en la otra.
Muéstrenme cuántos perros tienen collar.
(La clase mueve la mano mostrando 3 dedos).
Muéstrenme cuántos perros no tienen collar.
(La clase mueve la mano mostrando 1 dedo).
Ahora, junten las dos manos.
(La clase mueve las manos juntas).
¿Cuántos perros muestran ahora sus dedos?
Los 4 perros
Evaluación observacional
; ¿La clase puede usar la imagen para clasificar y formar dos grupos razonables?
; ¿La clase puede dibujar dos grupos en el segmento Los crayones de Kia de la sección Aprender?
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante utiliza las herramientas apropiadas estratégicamente (MP5) cuando usa sus dedos para clasificar y contar los perros de la imagen y también cuando usa los dibujos para representar el problema con historia de los crayones.
10 5 30 5
EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 16 © Great Minds PBC 183
Terminen mi oración numérica: 4 es… (Mueva las manos mostrando 3 y 1 por separado).
3 y 1 (La clase mueve las manos por separado).
¿De qué otra forma podemos clasificar los perros de la imagen?
Podemos clasificarlos por color.
Veo algunos perros con manchas y otros sin manchas.
Use la idea de una persona de la clase para clasificar a los perros de una manera diferente y muestre ambos grupos con los dedos, tal como se muestra arriba. Ayude a la clase para que diga una oración numérica que corresponda a su clasificación (p. ej., 4 es y ) mientras separa las dos manos para representar la descomposición.
Si ningún estudiante propone una clasificación que incluya cero, pídales que clasifiquen los perros que están sobre la banca y los que no están sobre la banca.
Los crayones de Kia
Materiales: E) Crayones
La clase hace un dibujo donde los dos sumandos son desconocidos para reforzar la idea de que 4 puede descomponerse en múltiples formas.
Distribuya libros para estudiantes y crayones entre la clase. De ser posible, distribuya solamente crayones rojos y azules.

Escuchen la historia que voy a contarles.
Kia tiene un vaso con crayones rojos y azules. Saca 4 crayones.
Pida a la clase que dibujen los 4 crayones de Kia. Anime a la clase para que hagan dibujos matemáticos simples. Si la clase está lista, pídales que completen la oración numérica al pie de la página.
Nota para la enseñanza
Espere que algunas personas dibujen más de 4 crayones. Si esto sucede, dé a la persona la posibilidad de reconocer el error y pensar en una solución. ¿Cómo podrían cambiar la imagen para mostrar 4 crayones?
Si necesitan apoyo, sugiérales encerrar en un círculo un grupo de 4 crayones. ¿Pueden encerrar en un círculo los 4 crayones de Kia? Quizás quieran tachar los crayones sobrantes. ¡Tienes demasiados crayones! Tachemos los que sobran.
EUREKA MATH K M1 TD Lección 16 © Great Minds PBC 55 Dibuja los 4 crayones de Kia es y 16 Nombre K ▸ M1 ▸ TD ▸ Lección 16 EUREKA MATH2 © Great Minds PBC 184
Cuando terminen, pídales que usen la rutina Pensar-Trabajar en parejas-Compartir para analizar las siguientes preguntas:
Observen la imagen de su pareja. ¿En qué se parecen sus imágenes? ¿En qué se diferencian?
Los colores son diferentes.
Ambos tenemos 4 crayones. Es igual.



Somos iguales porque tenemos 4 crayones, pero somos diferentes porque ella tiene 3 rojos y yo tengo 1 rojo.
Dé a la clase tiempo para conversar y, luego, pídales que compartan sus ideas. A medida que comparten, use la oración numérica 4 es ___ y ___ para reforzar la comprensión de que hay múltiples maneras de descomponer 4.
Diferenciación: Desafío
Desafíe a sus estudiantes a que piensen en todas las combinaciones posibles de crayones rojos y azules. Inicie la reflexión registrando algunas de las combinaciones compartidas en clase. ¿Encontramos todas las maneras posibles de combinar los crayones de Kia? ¿Cómo lo saben?


Grupo de problemas
Use la demostración sistemática para que la clase se inicie en el Grupo de problemas. Demuestre cómo contar y, luego, escriba el número total de objetos en la caja gris. Luego, muéstreles el crayón que está sobre la palabra Color y el número junto a él. Pídales que coloreen esa misma cantidad de objetos y que digan una oración numérica que corresponda a la imagen. Por ejemplo, 3 es 1 y 2.
Recorra el salón de clases mientras la clase trabaja. Desafíe a sus estudiantes a decir una oración numérica para cada problema.
© Great Minds PBC 57 EUREKA MATH K M1 TD Lección 16 Cuenta y escribe cuántos hay en total. Colorea 1. Colorea 2. 16 Nombre EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 16 © Great Minds PBC 185
Concluir
Reflexión final 5 min
Materiales: E) Grupo de problemas
Objetivo: Descomponer un conjunto que se muestra en una imagen
Reúna a la clase y pídales que tengan a mano su Grupo de problemas.
Miren el primer problema del Grupo de problemas. (Señale). ¿Cuántos círculos hay?
Invite a la clase a usar la rutina Pensar-Trabajar en parejas-Compartir para analizar las siguientes preguntas usando el Grupo de problemas que colorearon como inspiración.
¿Cómo podrían clasificar o desarmar los 3 círculos en grupos?
Podrían tener un grupo gris y un grupo blanco.
Podría haber 2 círculos que no estén coloreados y 1 círculo que esté coloreado.
Yo haría tres grupos. ¡1 círculo en cada grupo!
¿Qué oración numérica empareja con sus grupos?
Ayude a la clase a usar oraciones numéricas como 3 es y , para describir sus grupos. Destaque que podemos buscar números más pequeños dentro de números más grandes. Enfatice esto mientras la clase analiza uno o dos problemas más del Grupo de problemas utilizando las mismas preguntas.
3
5 30 5 © Great Minds PBC 57 EUREKA MATH K M1 TD Lección 16 Cuenta y escribe cuántos hay en total. Colorea 1. Colorea 2. 16 Nombre K ▸ M1 ▸ TD ▸ Lección 16 EUREKA MATH2 © Great Minds PBC 186
Representar problemas con historia
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
La clase representa intuitivamente los problemas con historia como parte de su vida cotidiana. Esta lección aprovecha su forma natural de pensar en los problemas de suma y resta. Aprenden que, cuando llegan más cosas, el grupo se hace más grande y, cuando las cosas se van, el grupo se hace más pequeño. El módulo 5 explora las convenciones formales de la suma y la resta. En esta lección se presentan los términos explicar y resolver.
Preguntas clave
• ¿Qué sucede con un grupo cuando algunas cosas llegan?
• ¿Qué sucede con un grupo cuando algunas cosas se van?
Criterio de logro académico
Esta lección es fundacional para el trabajo de K.OA.A.1. El contenido de la lección está destinado a servir de evaluación formativa y, por lo tanto, no se incluye en las evaluaciones acumulativas de este módulo.
17
LECCIÓN 17
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 10 min
Aprender 25 min
• ¿Más grande o más pequeño?
• Representar una historia de sumar
• Representar una historia de restar
• Resolver problemas con historia
Concluir 5 min
Materiales
Maestro o maestra
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 1 al 5)
• sillas (5)
• cubos Unifix® (5)
• Marco de 5 (en la edición para la enseñanza)
Estudiantes
• cubos Unifix® (5)
Preparación de la lección
• Prepare las tarjetas del 1 al 5 del juego para demostración de las tarjetas Hide Zero.
• Coloque sillas en la parte delantera del salón de clases, imitando los asientos de un autobús.
• El Marco de 5 está incluido en la edición para la enseñanza. Prepare una copia del Marco de 5 para que cada estudiante lo coloque en una pizarra blanca individual.
• Cree barras de 5 con los cubos Unifix, una para cada estudiante y una para usted.
© Great Minds PBC 189 EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 17
Fluidez
Contar hasta el 5 con el método matemático
La clase hace una recta numérica con los dedos mientras cuenta en voz alta para desarrollar el sentido de la cantidad y del orden.
Muestre el método matemático con los dedos mientras la clase cuenta, pero no cuente en voz alta.
Vamos a contar con el método matemático.
Póngase de frente a la clase y pida a sus estudiantes que copien los movimientos.
Pida a la clase que cuente del 1 al 5 con el método matemático y, luego, hacia atrás del 5 al 0.
Miren con atención y cuenten en voz alta. ¿Comenzamos? (Levante el meñique derecho).
1 (La clase levanta el meñique izquierdo).
Levante el dedo anular derecho.
2 (La clase levanta el dedo anular izquierdo).
Levante el dedo mayor derecho.
3 (La clase levanta el dedo mayor izquierdo).
Baje el dedo mayor derecho.
2 (La clase levanta el dedo mayor izquierdo).
Continúe el proceso con la siguiente secuencia:













Mano











Nota para la enseñanza
En esta lección, contar con el método matemático se vuelve más complejo al invertir el sentido de la cuenta con frecuencia. Esta complejidad ayuda a la clase a interiorizar la recta numérica.
Mano de la clase


Nota para la enseñanza
Mantenga un ritmo lento pero sostenido. Recuerde prestar atención a las respuestas de la clase para detectar errores, dudas y falta de participación. Si es necesario, ajuste el ritmo o la secuencia de números.
del maestro o de la maestra
10 10 25 5
K ▸ M1 ▸ TD ▸ Lección 17 EUREKA MATH2 © Great Minds PBC 190
Contar hasta el 5: ¿Qué número sientes en la espalda?
Materiales: M) Tarjetas Hide Zero
Cada estudiante dibuja un número y adivina un numeral para desarrollar la memoria cinestésica necesaria para formar números.
Juguemos ¿Qué número sientes en la espalda?
Pida a la clase que trabaje en parejas. Cada integrante de la pareja se colocará en fila, mirando hacia delante. Quien esté detrás será quien escriba. Quien esté delante será quien adivine.
Párese detrás de la clase, mirando hacia la espalda de cada estudiante, y muestre la tarjeta del 3.
Estudiantes que escriben, dense vuelta y observen mi número, pero no lo digan. ¡Guarden el secreto! Escriban este número con el dedo en la espalda de su compañero o compañera. Usen toda la espalda para que puedan escribir un número grande y bonito.
Estudiantes que adivinan, ¿se dieron cuenta de qué número les escribieron en la espalda?
Parejas de estudiantes, dense vuelta y observen mi número. Si acertaron, ¡denme 3 aplausos!
Continúe con el 4, el 5 y el 0, y, luego, los numerales hasta el 5 en orden aleatorio. Felicite a la clase con el número correspondiente de aplausos. Después de un tiempo, pida a las parejas que cambien los roles.
Presentar
Materiales: M) Sillas
La clase representa la incorporación y la separación con acciones.
Haga un autobús colocando 5 sillas en fila.
Diferenciación: Apoyo
Si hay estudiantes que necesitan apoyo para escribir, pueden decir la rima de formación de numerales mientras dibujan.
Si hay estudiantes que necesitan apoyo para adivinar, quienes escriben pueden hacerlo en las manos de quienes adivinan, para que puedan sentir y ver el numeral. Ajuste la disposición de los asientos según sea necesario.
Si alguien sintiera incomodidad con tocar, se puede jugar escribiendo en el aire o en la alfombra.
3
10 10 25 5 EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 17 © Great Minds PBC 191
¡Miren el autobús! ¿Cuántas personas pueden viajar en nuestro autobús?
5
Todo el mundo podrá viajar en el autobús hoy. Cuenten conmigo mientras doy un toque a 3 personas para que suban al autobús.
Toque a 3 estudiantes para que suban al autobús. Asegure a la clase que todas las personas viajarán en el autobús.
1, 2, 3
¿Cuántas personas subieron al autobús?
3
Toque a 2 estudiantes más para que suban al autobús.
¿Cuántas personas hay ahora en el autobús?
5
Toque a 1 estudiante para que baje del autobús.
¿Cuántas personas bajaron del autobús? 1
¿Cuántas personas hay ahora en el autobús?
4
Continúe todo el tiempo que sea necesario para dar a cada estudiante la oportunidad de viajar en el autobús y responder a las preguntas sobre cuántos hay. Varíe el número de estudiantes que suben y bajan del autobús. Use las siguientes preguntas para que la clase piense en sumar o restar.
¿Cuántas personas subieron al autobús?
¿Cuántas personas bajaron del autobús?
¿Cuántas personas hay ahora en el autobús?
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hoy, vamos a pensar en otros problemas con historia.
K ▸ M1 ▸ TD ▸ Lección 17 EUREKA MATH2 © Great Minds PBC 192
Aprender
¿Más grande o más pequeño?
Materiales: M) Cubos Unifix, Marco de 5, pizarra blanca individual
La clase se da cuenta de lo que ocurre cuando las cantidades se unen y cuando se separan.
Invite a la clase a escuchar una historia sobre el autobús.
Algunas personas están en el autobús. Otra persona sube al autobús.
Pida a la clase que recuerde la historia y que la cuenten en parejas. Luego, haga la siguiente pregunta.
¿El grupo de personas en el autobús se volvió más grande o más pequeño?
Más grande
Ahora, hay más personas.
Invite a la clase a escuchar una segunda historia sobre el autobús. Después de la historia, pídales que se la cuenten a su pareja.
Algunas personas están en el autobús. Alguien se baja del autobús.
¿El grupo de personas en el autobús se volvió más grande o más pequeño?
Más pequeño
Muestre una barra de 5 de cubos Unifix, un Marco de 5 y una pizarra blanca individual. Estas son herramientas matemáticas. También tienen herramientas matemáticas en sus manos. (Mueva los dedos).
¿De qué manera se pueden usar estas herramientas matemáticas para mostrar las historias del autobús? Reúnanse y conversen en parejas.
Escuche cómo hablan las parejas y seleccione ideas útiles para compartirlas con la clase. Destaque las ideas que muestran cómo los cubos, los dedos o los dibujos pueden representar a las personas que suben o bajan del autobús.
Apoyo para la comprensión del lenguaje
En el módulo 3 se enseña lenguaje de comparación preciso como más y menos. Por ahora, el uso informal de más grande y más pequeño permite a la clase considerar cómo sumar o restar elementos de un grupo cambia su tamaño.
Evite el error de enseñar a la clase a usar palabras clave como más y menos al resolver problemas verbales. A medida que la clase avanza en el aprendizaje de las matemáticas en cursos posteriores, estas palabras se convierten en formas poco fiables de elegir una operación.
10 10 25 5
EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 17 © Great Minds PBC 193
Representar una historia de sumar
Materiales: E) Cubos Unifix, Marco de 5, pizarra blanca individual
La clase elige herramientas para representar y resolver un problema con historia de sumar.
Invite a la clase a escuchar otro problema con historia.
Hay 4 personas en el autobús. 1 persona sube al autobús.
¿Cuántas personas hay ahora en el autobús?
Dé tiempo para que sus estudiantes seleccionen las herramientas matemáticas y representen la historia. Considere hacer preguntas como las siguientes para ayudar a la clase mientras trabaja.
¿Cuántas personas hay en el autobús al principio?
¿Cuántas personas hay ahora en el autobús?
Cuando alguien sube al autobús, ¿el número se hace más grande o más pequeño?
Luego de que hayan tenido suficiente tiempo para trabajar, pida a la clase que se ponga de acuerdo sobre el total.
¿Cuántas personas hay en el autobús? 5
Elija a dos o tres estudiantes que puedan explicar su razonamiento con palabras, números o materiales. Comparta los trabajos para que la clase pueda comparar semejanzas y diferencias y establecer conexiones. El siguiente diálogo representa un ejemplo de conversación.
Representar con los dedos (método de Jacob)
Jacob usó sus dedos para mostrar el autobús. Vamos a escucharlo explicar, o contar, su pensamiento.
Levanto 4 dedos porque es la cantidad de personas que hay en el autobús. Luego, otra persona sube al autobús, así que levanto otro dedo. Y, luego, hay 5 dedos porque hay 5 personas en el autobús.
Nota para la enseñanza
Esta lección invita intencionalmente a la elección de la clase. Es una oportunidad de evaluación formativa para ver cómo la clase representa y resuelve problemas básicos de sumar y restar
Parte de la clase puede saber que 5 es 1 más que 4. Anime a sus estudiantes a que muestren cómo lo saben utilizando materiales didácticos o dibujos.
Promoción de los estándares para la práctica de las matemáticas

Cada estudiante utiliza las herramientas apropiadas estratégicamente (MP5) cuando decide qué herramientas matemáticas va a utilizar para representar la historia del autobús. Cada estudiante representa a través de las matemáticas (MP4) cuando utiliza las herramientas para representar la historia del autobús, explica su pensamiento a la clase y vuelve a expresar las estrategias de otras personas.
Apoyo para la comprensión del lenguaje
Este es el primer uso del término explicar. Apoye la comprensión usando el término explicar para expresar formas de volver a expresar el razonamiento de la clase:
“Puedes usar palabras, números, dibujos u objetos para explicar o contar tu pensamiento”.


K ▸ M1 ▸ TD ▸ Lección 17 EUREKA MATH2 © Great Minds PBC 194
Invite a un grupo de estudiantes a utilizar sus propias palabras para explicar cómo resolvió Jacob el problema.
Representar con cubos (método de Noah)
Noah usó cubos para mostrar la historia. Escuchemos a Noah.
Los cubos son las personas. Las cajas son el autobús. Puse 4 personas en el autobús. Luego, puse 1 cubo más para la persona que sube al autobús. Conté a todas las personas y había 5.
¿Qué es igual en los métodos de Jacob y de Noah?
Ambos tienen 5 personas en el autobús.
Empezaron con 4 personas y subieron a 1 persona más al autobús.
¿Qué es diferente en los métodos de Jacob y de Noah?
Jacob usó sus dedos. Noah usó los cubos.
Noah tenía un autobús con 5 asientos.
Cuando alguien sube al autobús, ¿el número se hace más grande o más pequeño?
Más grande
Representar una historia de restar
Materiales: E) Cubos Unifix, Marco de 5, pizarra blanca individual
La clase elige herramientas para representar y resolver un problema con historia de restar.
Invite a la clase a escuchar otro problema con historia.
Hay 4 personas en el autobús. 1 persona baja del autobús. ¿Cuántas personas hay ahora en el autobús?
Dé tiempo para que sus estudiantes seleccionen las herramientas matemáticas que quieren usar para resolver el problema. Considere hacer preguntas como las siguientes para ayudar a la clase mientras trabaja.
Diferenciación: Desafío
Las oraciones numéricas, o ecuaciones, que incluyen signos como +, – e = se presentan en el módulo 4. Si hay estudiantes que usan una frase numérica como 4 + 1 = 5 en esta lección, reconozca su trabajo y sondee para evaluar su comprensión de los números y los símbolos.
• ¡Escribiste una oración numérica! ¿Me la puedes leer?
• ¿Qué nos indica el número 4? ¿El 1? ¿El 5?
• (Señale el signo más). ¿Qué significa esto?
• (Señale el signo igual). ¿Qué significa esto?
Si gran parte de la clase utiliza símbolos, considere la posibilidad de seleccionar un ejemplo para compartir después de compartir un modelo concreto. Si solo un pequeño grupo de estudiantes intenta este tipo de oraciones numéricas o su comprensión de los símbolos está en desarrollo, limítese a mostrar representaciones concretas y pictóricas del problema.
EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 17 © Great Minds PBC 195
¿Cuántas personas hay en el autobús al principio?
¿Cuántas personas hay ahora en el autobús?
Luego de que hayan tenido suficiente tiempo para trabajar, elija a dos o tres estudiantes que puedan explicar su razonamiento con palabras, números o materiales. A continuación, un ejemplo de conversación.
Representar con cubos (método de Vivi)
Vivi usó cubos para resolver o para encontrar la respuesta. Escuchemos a Vivi. Estas son las 4 personas del autobús. Luego, 1 persona se baja. (La clase aleja un cubo). Ahora, hay 3 personas.
¿Cómo sabes que hay 3 personas en el autobús ahora?
Conté 1, 2, 3.
¿Quién puede decirnos por qué Vivi se llevó un cubo?
Una persona se bajó del autobús. Se fue.
Representar con un dibujo (método de Tilly)
Tilly dibujó la historia. Escuchemos a Tilly.
Hice un dibujo matemático. (La clase señala los círculos). Estas son las 4 personas. (Señala el círculo tachado). Esta es la persona que se fue.
Miren el dibujo de Tilly. ¿Cómo demostró que una persona se fue?
Tachó un círculo.
¿Qué círculos muestran a las personas que están en el autobús ahora?
(La clase señala los 3 círculos). Estos 3
¿Qué ocurre cuando alguien abandona el autobús? ¿El número se vuelve más grande o más pequeño?
Más pequeño
Apoyo para la comprensión del lenguaje
Este es el primer uso del término resolver. Apoye la comprensión utilizando el término resolver para expresar las ideas sobre la búsqueda de la respuesta:
“Puedes encontrar la respuesta, o resolver, usando cubos o dibujando”.
DUA: Acción y expresión
Considere mostrar un ejemplo como el dibujo de Tilly para recordar que deben usarse dibujos matemáticos en lugar de dibujos artísticos más detallados para representar los problemas con historia.

“¡Tilly se acordó de hacer un dibujo matemático! Usó círculos para mostrar a las 4 personas. Hizo el dibujo en poco tiempo, pero puedo ver todas las partes de la historia”.
Anime a la clase a verificar su propio trabajo consultando el ejemplo cuando dibujen historias a lo largo del año.
K ▸ M1 ▸ TD ▸ Lección 17 EUREKA MATH2 © Great Minds PBC 196
Resolver problemas con historia
Si hay tiempo suficiente, use los siguientes problemas con historia como guía y repita la actividad de aprendizaje usando un intercambio de ideas con la clase. Invente más historias de matemáticas según sea necesario, asegurándose de mantener los totales en 5.
Problemas con historia Complejidades
3 niñas están jugando en los columpios.
2 niños vienen a columpiarse. ¿Cuántas personas se columpian ahora?
5 niños y niñas están jugando en los columpios.
2 niñas se van a jugar balonmano. ¿Cuántas personas se columpian ahora?
2 niñas están nadando en la piscina.
2 niñas más saltan a la piscina. ¿Cuántas niñas hay ahora en la piscina?
4 niños están nadando en la piscina. Todos salen de la piscina. ¿Cuántos niños están nadando ahora?
Las historias del patio de recreo implican la entrada o salida de 2 niños o niñas. Es poco probable que la mayor parte de la clase conozca los patrones de 2 más o 2 menos.
Ambas partes, o sumandos, son iguales. Esto puede dificultar a la clase llevar la cuenta de los referentes de la historia.
Esta historia requiere que la clase reconozca que todos los niños que salen de la piscina dejan 0 niños en la piscina.
EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 17 © Great Minds PBC 197
Concluir
Reflexión final 5 min
Objetivo: Representar problemas con historia
Piensen en las dos historias del autobús que les conté hoy.
Después de darle a la clase la oportunidad de recordar las historias del autobús, repítalas.
Hay 4 personas en el autobús. 1 persona sube al autobús. (Escriba los números 4 y 1 mientras cuenta la historia).
Hay 4 personas en el autobús. 1 persona baja del autobús. (Señale los números 4 y 1 cuando los diga).
Usamos el 4 y el 1 en las dos historias del autobús. ¿Tenía el autobús el mismo número de personas al final de ambas historias?
No. Había 5 personas en el autobús al final de la primera historia y 3 personas en el autobús al final de la segunda historia.
Si usamos los mismos números, ¿por qué tenemos un número diferente de personas al final de cada historia?
En la primera historia, alguien subió al autobús y, en la segunda, alguien se bajó.
¿Qué sucede con un grupo cuando se agregan personas?
Se hace más grande. Hay más personas.
¿Qué sucede con un grupo cuando algunas personas se van?
Se hace más pequeño. Hay menos personas.
10 25 5 K ▸ M1 ▸ TD ▸ Lección 17 EUREKA MATH2 © Great Minds PBC 198
EUREKA MATH2 K ▸ M1 ▸ TD ▸ Marco de 5 © Great Minds PBC 199 This page may be reproduced for classroom use only.
Representar problemas con historia e identificar los referentes numéricos
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
Esta lección amplía la representación intuitiva de los problemas con historia al ayudar a la clase a relacionar los números con el contexto de la historia. Comprender a qué se refieren los números en las historias matemáticas es clave para resolver problemas con historia con éxito. La presentación gradual de las habilidades para resolver problemas a lo largo del año es intencional. Los problemas con historia se retoman en los módulos 4 y 5.
Preguntas clave
• ¿Qué es un problema con historia?
• ¿Qué nos dicen las oraciones numéricas sobre un problema con historia?
Criterio de logro académico
Esta lección es fundamental para el trabajo de K.OA.A.1. El contenido de la lección está destinado a servir de evaluación formativa y, por lo tanto, no se incluye en las evaluaciones acumulativas de este módulo.
18
LECCIÓN 18
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 10 min
Aprender 25 min
• Referentes del problema con historia
• Representar problemas con historia
Concluir 5 min
Materiales
Maestro o maestra
• tarjetas 5-group™ (grupos de 5), juego para demostración (del 1 al 5)
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración
• papel de rotafolio
Estudiantes
• cubos Unifix® (5)
• plantilla de trabajo
• Marco de 5
Preparación de la lección
Prepare las tarjetas del 1 al 5 del juego para demostración de las tarjetas de grupos de 5.
© Great Minds PBC 201 EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 18
Fluidez










Contar hasta el 7 con el método matemático
La clase hace una recta numérica con los dedos mientras cuenta en voz alta para desarrollar el sentido de la cantidad y del orden.





Muestre el método matemático con los dedos mientras la clase cuenta, pero no cuente en voz alta.
Vamos a contar con el método matemático.
Póngase de frente a la clase y pida a sus estudiantes que copien los movimientos.
Así contamos con el método matemático: 1, 2, 3, 4, 5, 6, 7. (Demuéstrelo).
Levante el meñique derecho.
Muéstrenme el meñique izquierdo. Eso es 1. Sigamos contando hasta el 7.



Pida a la clase que cuente del 1 al 7 con el método matemático.
Manos del maestro o de la maestra Manos de la clase
Repita la cuenta una vez más.
Deténganse aquí en el 7. Ahora, cuenten hacia atrás hasta el 0. ¿Comenzamos?
Pida a la clase que cuente del 7 al 0 con el método matemático.
Facilite más práctica para contar hasta el 7 con el método matemático.
10 10 25 5 K ▸ M1 ▸ TD ▸ Lección 18 EUREKA MATH2 © Great Minds PBC 202
Grupos de 5 hasta el 5
Materiales: M) Tarjetas de grupos de 5
La clase reconoce un grupo de puntos para desarrollar la capacidad de subitizar cantidades que se muestran con grupos de 5.
La configuración de grupos de 5 se volverá conocida con el tiempo, lo que permitirá a la clase subitizar. Sin embargo, en la rutina se incorpora tiempo de espera para permitir el conteo si es necesario. Los y las estudiantes que respondan rápidamente se beneficiarán reteniendo un número en la memoria y practicando la autorregulación mientras esperan a que el resto termine.
Recuerden escuchar, pensar, levantar la mano y esperar la señal. (Enfatice con gestos cada paso).
Levanten la mano cuando sepan la respuesta a la pregunta. Esperen mi señal para decir la respuesta.
Muestre la tarjeta de grupos de 5 que muestra 3.
¿Cuántos puntos hay?
Espere hasta que la mayor parte de la clase haya levantado la mano y, luego, dé la señal para que respondan.
Repita el proceso con la siguiente secuencia:
Cuando la clase esté preparada, muestre cada tarjeta durante menos tiempo como desafío para que reconozcan los grupos de puntos más rápidamente.
3
4 5 3 2 1 3 5 4 2 3
EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 18 © Great Minds PBC 203
Contar con movimiento hasta el 10
La clase cuenta con movimientos del cuerpo para adquirir fluidez con los nombres de los números y la correspondencia de uno a uno.
Aplaudamos 5 veces y contemos los aplausos. ¿Comenzamos?
Al principio, cuente y aplauda del 1 al 5 lentamente, haciendo énfasis en que para cada aplauso se dice un número. Repita el proceso hasta que la mayor parte de la clase esté aplaudiendo, contando o, idealmente, aplaudiendo y contando.
Repita el proceso, pero esta vez dé pisotones y cuente hasta el 5.
Ahora, aplaudamos 10 veces y contemos los aplausos. ¿Comenzamos?
Cuente y aplauda del 1 al 10 junto con la clase.
Repita el proceso, pero esta vez dé pisotones y cuente hasta el 10.
Es posible que el ritmo del conteo repetitivo al unísono lleve a la clase hacia un estado cognitivo de relajación. Intente variar el ritmo para inducir a la clase a regresar al estado de alerta e incentivar el juego.
Presentar
Materiales: M) Papel de rotafolio; E) Cubos Unifix y plantilla de trabajo
La clase usa herramientas matemáticas para representar de forma abstracta el personaje, el escenario y la acción.
Distribuya los materiales y favorezca el intercambio de ideas para plantear objetos y contextos para los problemas con historia. Levante cinco dedos. Baje un dedo por cada idea compartida. Un puño cerrado indica que la exposición de ideas ha concluido.
Muestren 3 cubos en su plantilla de trabajo. Usen su imaginación. ¿Qué podría ser esto? Tomaré cinco ideas.
Represente las ideas con palabras o dibujos sencillos de rebus para utilizarlos a lo largo de la lección. Aproveche las cinco ideas para desarrollar escenarios y acciones relacionadas.
Nota para la enseñanza
Usar los dedos para guiar la lluvia de ideas matematiza el intercambio de ideas y refuerza el concepto de cero.
Este intercambio de ideas proporciona contextos atractivos y culturalmente relevantes. A lo largo de la sección Aprender, ajuste los contextos de los problemas de la historia para que resuenen con la clase.
10 10 25 5
K ▸ M1 ▸ TD ▸ Lección 18 EUREKA MATH2 © Great Minds PBC 204
¿Quién? ¿Dónde? ¿Qué?
¡Miren el autobús! Usen su imaginación. ¿Qué lugar podría ser este?
¿Qué podrían estar haciendo estas cosas?
Después de compartir ideas, haga que la clase use los cubos Unifix y las plantillas de trabajo para representar quién, dónde y qué imaginaron.
Vuelva a reunir a la clase y representen en grupo algunos escenarios.
Imaginen que sus cubos son peces. ¡Háganlos saltar! ¡Ahora, hagan que naden!
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hoy, vamos a usar nuestros cubos para representar problemas con historia.
DUA: Participación
Este intercambio de ideas pretende que la clase comparta contextos que les resulten atractivos y relevantes. A lo largo de la sección Aprender, ajuste los contextos de los problemas con historia para que interesen a la clase. Use los números sugeridos y haga que tanto personajes como acciones se ajusten a los intereses de la clase.
EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 18 © Great Minds PBC 205
Aprender
Referentes del problema con historia
Materiales: M) Tarjetas Hide Zero; E) Cubos Unifix y plantilla de trabajo
La clase relaciona los números con los problemas con historia.
Use una idea generada durante la sección Presentar para el siguiente intercambio.
Muestren 3 cubos en su plantilla de trabajo.
Agite la mano sobre sus cubos y diga una palabra tonta... ¡puf! La plantilla es ahora un parque. ¡Sus cubos son cachorros! Haga que jueguen en el parque.
Pida a la clase que escuchen atentamente y que muevan sus cubos para mostrar lo que ocurre mientras usted les cuenta una historia.
Vamos a contar una historia. 3 cachorros están en el parque.
Llegan 2 cachorros más. Muéstrenlo con sus cubos.
Observe cómo la clase añade 2 cubos a su plantilla de trabajo.
¿Cuántos cachorros hay ahora en el parque?
Ayúdenme a volver a contar la historia. Contaremos la misma historia usando nuestras propias palabras.
Levante la tarjeta del 3 y pida a la clase que repitan después de usted la siguiente afirmación.
3 cachorros están en el parque. (Señale los 3 cachorros).
Levante la tarjeta del 2 y pida a la clase que repita.
Llegan 2 cachorros más. (Mueva 2 cachorros más para que se unan a los demás).
Levante la tarjeta del 5 y pida a la clase que repita.
5 cachorros están jugando en el parque en total. (Señale a todos los cachorros).
3
Nota para la enseñanza
La omisión de oraciones numéricas con símbolos como 4 + 1 = 5 es deliberada. El objetivo de esta lección es que la clase se mueva con flexibilidad entre su modelo y el contexto de la historia.
La clase aprende a separar momentáneamente las matemáticas de la historia cuando formulan oraciones numéricas como “4 y 1 forman 5”. Recontextualizan los números cuando se les hacen preguntas como: “¿Qué nos indica el 4?”.

2 K ▸ M1 ▸ TD ▸ Lección 18 EUREKA MATH2 © Great Minds PBC 206



5
10 10 25 5
El módulo 5 contiene lecciones completas sobre la suma y la resta y el uso de símbolos para representar problemas con historia. 5
Escriba que 3 y 2 forman 5.
Estos son los números de nuestra historia. Podemos decirlos en una oración numérica como esta: 3 y 2 forman 5. ¡Inténtenlo ustedes!
3 y 2 forman 5.
¿De qué parte de la historia nos habla el número 3? (Señale el 3 en la oración numérica).
Los cachorros que hay al principio.
¿De qué parte de la historia nos habla el número 2? (Señale).
Los cachorros que llegan después.
¿De qué parte de la historia nos habla el número 5? (Señale).
Todos los cachorros que hay al final de la historia.
Invierta la acción de la historia.
5 cachorros juegan en el parque. 2 cachorros se van a casa. ¿Cuántos cachorros están jugando ahora en el parque?
Pida a la clase que representen y vuelvan a contar la historia. Presente y escriba la oración numérica si a 5 le quitamos 2 es 3. Use la anterior secuencia de preguntas para que la clase comparta el referente de cada número de la historia.
Representar problemas con historia
Materiales: E) Cubos Unifix, plantilla de trabajo, marco de 5, pizarra blanca individual
La clase representa problemas con historia e identifica los referentes numéricos.
Los siguientes problemas abordan diferentes complejidades en problemas con historia de sumar con resultado desconocido y restar con resultado desconocido. Elija los problemas en función de las necesidades de su clase. Ajuste los contextos para incorporar las ideas que la clase generó durante la sección Presentar.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante razona de forma abstracta y cuantitativa (MP2) a medida que se mueve con fluidez entre las historias y las representaciones abstractas como los cubos y los números, representando las historias con cubos, volviendo a contar historias con oraciones numéricas y contextualizando al identificar lo que cada número representa en la historia.
EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 18 © Great Minds PBC 207
Ofrezca a sus estudiantes acceso a los materiales utilizados para la representación en la lección 17. Mientras la clase representa los problemas, anime a sus estudiantes a usar oraciones numéricas y a decir a qué se refiere cada número en la historia.
Problemas Complejidades
Tienes 2 crayones. Tu amiga te da 2 más.
¿Cuántos crayones tienes ahora?
Tienes 4 crayones. Le das 2 a tu amiga.
¿Cuántos crayones tienes ahora?
La agricultora recoge 1 manzana. Luego, recoge 1 cereza. Luego, recoge 1 melocotón.
¿Cuántas frutas tiene ahora?
La agricultora tiene 3 frutas. La agricultora tiene hambre y se come 1 manzana. Sigue teniendo hambre y se come 1 cereza. También se come 1 melocotón. ¿Cuántas
frutas tiene ahora?
2 gaviotas están en la playa. Llegan 0 más.
¿Cuántas gaviotas hay en total?
Las historias de crayones presentan a la clase la idea de que los referentes pueden ser el mismo número pero que remiten a diferentes partes de la historia.
Las historias de la fruta muestran que puede haber más de dos partes. El problema con historia de resta incluye el 0 en una estructura accesible de conteo regresivo.
La historia de la gaviota presenta a la clase el 0 como sumando. La clase debe determinar cómo representar la acción, o la falta de ella, con sus materiales.
K ▸ M1 ▸ TD ▸ Lección 18 EUREKA MATH2 © Great Minds PBC 208
Concluir
Reflexión final 5 min
Objetivo: Representar problemas con historia e identificar los referentes numéricos

¿Cuáles son algunos de los problemas con historia con los que hemos trabajado?
La historia del cachorro
Trabajamos en las historias del autobús.
¿Qué es un problema con historia?
Los problemas con historia suelen tener números.
Cuentan algo que está sucediendo.
Muestre la imagen de los cubos.
Usamos oraciones numéricas con nuestras historias. Una oración numérica indica cómo juntamos o separamos los números. Cuando contamos lo de los 3 cachorros en el parque y los 2 que vienen al parque, nuestra frase numérica fue 3 y 2 forman 5.
¿Qué nos dicen las oraciones numéricas sobre los problemas con historia?
Nos cuentan cuántos cachorros hay al principio y cuántos cachorros más llegan al parque. Cuentan sobre cuántos hay.
10 25 5
EUREKA MATH2 K ▸ M1 ▸ TD ▸ Lección 18 © Great Minds PBC 209
3 y 2 forman 5.
Responder preguntas sobre cuántos hay con hasta 10 objetos
El tema E se basa en el trabajo realizado en el tema B, a medida que la clase amplía los conceptos sobre fundamentos numéricos y las estrategias de conteo a grupos de entre 6 y 10 objetos. A medida que el tamaño del grupo aumenta, llevar la cuenta del conteo se vuelve más difícil. La clase considera dos preguntas clave para elegir una estrategia de conteo:
• ¿Puedo mover los objetos que quiero contar?
• ¿Cuál es la organización, o configuración, de los objetos?
El primer factor, el movimiento, depende de si la clase cuenta objetos concretos o si los objetos forman parte de una imagen. La estrategia de mover y contar funciona bien para objetos concretos con cualquier configuración. El movimiento permite llevar la cuenta de lo que contaron y de lo que no contaron. Cuando los objetos son imágenes en papel, se necesita una estrategia alternativa, como la de tocar y contar o la de marcar y contar.



La complejidad de la configuración influye en la elección de la estrategia y en cómo se usa. ¿Qué es lo que hace que una configuración sea más o menos compleja? Las configuraciones menos complejas tienen un camino de conteo directo y los puntos donde empieza y termina el conteo son claros. Las configuraciones lineales son las más fáciles para contar, porque tienen todas estas características. Las configuraciones de matriz, donde los objetos están alineados en filas y columnas iguales, son un poco más complejas. La clase debe contar cada fila o columna de la matriz sin repetir ninguna. Las configuraciones circulares son todavía más difíciles, porque no tienen puntos claros donde empezar o terminar el conteo, y existe el riesgo de repetición al continuar contando alrededor del círculo. Las configuraciones dispersas son las más difíciles. Sin un camino de conteo claro, se debe usar una estrategia como la de marcar y contar para asegurarse de que cada objeto se haya contado exactamente una vez.

© Great Minds PBC 210
Tema E
Circular Matriz
Dispersa Lineal
La estructura de grupos de 5 es importante para ayudar a las y los estudiantes de corta edad a visualizar cantidades del 6 al 10. Primero, la clase experimenta la formación de grupos de 5 en el tema E. Empiezan a formar una nueva unidad con cinco y ven el 6 como 5 y 1, el 7 como 5 y 2, y así sucesivamente. Con tiempo y experiencia, la clase puede subitizar de 6 a 10 objetos en una formación de grupos de 5. También llegan a ver cada número en relación con el diez. Con la estructura de la formación de grupos de 5 es más fácil ver cuántos se necesitan para completar la matriz y formar diez. La clase usa formaciones de grupos de 5 hasta 5.o grado.
Grupo de 5

EUREKA MATH2 K ▸ M1 ▸ TE 211 © Great Minds PBC
Progresión de las lecciones
Lección 19
Organizar, contar y representar una colección de objetos
Lección 20
Contar objetos en grupos de 5 y en configuraciones de matrices, y emparejarlos con un numeral

Lección 21
Contar objetos en configuraciones circulares y emparejarlos con un numeral
Usamos la estrategia de mover y contar para llevar la cuenta de nuestros bastones de caramelo.

Todos los grupos de 5 tienen cinco en la parte de arriba.
Usamos la estrategia de marcar y contar para averiguar que 8 personas pueden subir a la rueda de la fortuna.
212 K ▸ M1 ▸ TE EUREKA MATH2 © Great Minds PBC
Lección 22
Contar objetos en configuraciones dispersas y emparejarlos con un numeral

Lección 23
Conservar el número sin importar el orden en que los objetos se cuentan
Contamos para jugar bingo.
Comenzamos a contar en lugares diferentes, pero toda la clase contó 9 fichas cuadradas.

EUREKA MATH2 K ▸ M1 ▸ TE 213 © Great Minds PBC
LECCIÓN 19
Organizar, contar y representar una colección de objetos
Vistazo a la lección
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
En esta lección, se invita a la clase a usar herramientas y estrategias de su preferencia para contar y registrar una colección de objetos. Durante esta segunda experiencia con colecciones de conteo, la clase tiene la oportunidad de demostrar y celebrar el crecimiento con los conceptos de conteo mientras las maestras y los maestros recopilan datos para la evaluación formativa. En esta lección, no hay actividades de fluidez.
Pregunta clave
• ¿Qué cosas podemos hacer o qué estrategias podemos usar como ayuda para contar?
Criterios de logro académico
K.Mód1.CLA1 Cuentan hasta el 10. (K.CC.A.1)
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10. (K.CC.B.4.a)
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron. (K.CC.B.4.b)
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas. (K.CC.B.5)
19
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Presentar 10 min
Aprender 35 min
• Preparar
• Organizar, contar y registrar
• Compartir, comparar y conectar
Concluir 5 min
Materiales
Maestro o maestra
• letra de la canción “Puedo contar” (en la edición para la enseñanza)
• hojas para recortar de Puedo contar (en la edición para la enseñanza)
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 6 al 10)
Estudiantes
• colección de conteo (1 por pareja de estudiantes)
• plantilla de trabajo
• herramientas de organización
• libro para estudiantes
Preparación de la lección
• Prepare las tarjetas del 6 al 10 del juego para demostración de las tarjetas Hide Zero.
• Deje a un lado la letra de la canción “Puedo contar” como referencia.
• Use el trabajo de sus estudiantes de la lección 6 para determinar si en las colecciones de conteo recopiladas para esa lección hay suficientes objetos para la lección de hoy. Adáptelo según sea necesario.
• Decida si la clase trabajará en parejas o de manera individual. La lección está redactada para trabajar en parejas, pero puede adaptarse para que cada estudiante trabaje de manera individual.
• Seleccione las herramientas de organización que puedan usarse para organizar el conteo, como cartones con marco de 10, caminos numéricos o marcos de 10.
• Coloque la Lista de verificación de la evaluación observacional en un portapapeles para tomar notas de las observaciones.
© Great Minds PBC 215 EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 19
Materiales: M) Letra de la canción “Puedo contar”, tarjetas Hide Zero
La clase asocia la secuencia de palabras de conteo con los numerales del camino numérico.
Muestre el apoyo visual Puedo contar y tenga preparada la letra de “Puedo contar”.
Cante “Puedo contar” (hasta el 10) y avance la imagen a medida que canta. Al final del primer verso, toque las flores mientras canta “1, 2, 3”. Repita al final de cada verso, y toque y cuente la última columna de imágenes.
Muestre la tarjeta del 6.
Este es el número 6. Señalen el grupo que contiene 6 cosas.
Pida a un o una estudiante que señale al grupo con 6 cosas (las ardillas) y que cuente para demostrar que hay 6 ardillas. Coloque el numeral debajo de la columna de las ardillas. Repita el proceso con los otros numerales en orden.
Una vez que todos los numerales estén en la posición correcta, toque y cuente los numerales con la clase. Si hay tiempo suficiente, vuelva a cantar la canción y señale las partes correspondientes del apoyo visual.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hoy, volveremos a contar las colecciones. Quizá quieran usar algunos de estos números en sus registros.
DUA: Representación
Si presentó el apoyo visual Puedo contar como un afiche de referencia interactivo en la lección 5, invite a la clase a interactuar con él. Retire estratégicamente algunos numerales o imágenes de las láminas del 1 al 5 y, a medida que sus estudiantes ubican los lugares correctos de las piezas que faltan, pregunte cómo saben dónde colocar las piezas.
Puedo contar
Cantada con la melodía de “Una vez pesqué un pez vivo”
(Once I Caught a Fish Alive)
1 ave azul cantará.
2 abejas volarán.
3 flores crecen a la vez.
¡Puedo contar! 1, 2, 3.
4 gatas duermen al sol.
5 patos tienen calor.
Al estanque entran de un brinco.
Cuento 1, 2, 3, 4, 5.
6 ardillas juntan semillas.
7 aves hacen rosquillas.
Preparan todas un gran banquete. 1,
8 frijoles cuelgan de la rama.
9 caracoles se van a la cama.
1, 2, 3, 4; ¡salen cuando llueve!
5, 6, 7, 8 y 9.
10 autos pasean muy limpios.
Cuéntalos: 1, 2, 3, 4, 5,
6, 7, 8, 9, 10.
¡Contemos todo otra vez!
Presentar
5 35 10
2 3 5 6 7 8 9 10 4 K ▸ M1 ▸ TE ▸ Lección 19 ▸ Puedo contar EUREKA MATH © Great Minds PBC 222 This page may be reproduced for classroom use only.
2, 3, 4, 5, 6, 7.
K ▸ M1 ▸ TE ▸ Lección 19 EUREKA MATH2 © Great Minds PBC 216
Aprender
Preparar
Materiales: E) Colección de conteo, plantilla de trabajo, herramientas de organización
La clase repasa los procedimientos y se prepara para contar colecciones.
Vuelva a orientar brevemente a la clase sobre los materiales y el procedimiento para la colección de conteo:
• Las parejas colaboran para contar una colección.
• Cada estudiante hace un registro individual para mostrar cómo contó la pareja.
Presente las herramientas de organización que cada estudiante puede elegir usar. Herramientas como un camino numérico, un cartón con marco de 10 o un marco de 10 favorecerán la correspondencia de uno a uno y pueden ser útiles sobre todo para las colecciones más grandes.
Forme parejas de estudiantes. Pídales que elijan una colección y que hallen un área de trabajo.
Antes de sacar las colecciones de la bolsita, invite a las parejas de estudiantes a planificar cómo trabajarán en conjunto para contar toda la colección. Recorra el salón de clases y pida a sus estudiantes que expliquen brevemente sus planes. Pida a algunas parejas con planes razonables que compartan su razonamiento con la clase haciendo las siguientes preguntas:
¿Cómo van a contar su colección?
Contaremos …
¿Cuál es tu tarea? ¿Cuál es la tarea de la otra persona?
Mi tarea es…
La tarea de la otra persona es…
Si es necesario, dé un ejemplo de trabajo en parejas para que la clase comprenda que las matemáticas son una actividad colaborativa. Durante el ejemplo, procure no dar su opinión sobre maneras de contar a fin de que las decisiones de la clase sean genuinas. A lo largo de la lección, busque y elogie ejemplos de buen trabajo en parejas.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Pueden empezar a contar con sus parejas. Recuerden contar todas las cosas de la colección y mostrar su trabajo en una hoja de papel.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante utiliza las herramientas apropiadas estratégicamente (MP5) cuando planea cómo contar su colección, selecciona las herramientas necesarias y usa su plan y las herramientas para contar.
Nota para la enseñanza
Elabore un plan que establezca qué deberá hacer la clase al finalizar de contar sus colecciones y registrarlas.
• Probar otra manera de organizar y contar
• Intercambiar las colecciones con otra pareja de estudiantes y contar para confirmar el total
• Explicar lo registrado a otra pareja de estudiantes
• Guardar la colección usada y buscar otra
5 35 10
EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 19 © Great Minds PBC 217
Organizar, contar y registrar
Materiales: E) Colección de conteo, plantilla de trabajo, herramientas de organización

La clase usa sus propias estrategias para organizar y contar objetos y para registrar su proceso.
Recorra el salón de clases y observe cómo organizan, cuentan y registran información.
• Las estrategias de organización pueden incluir tocar y contar o mover y contar para diferentes configuraciones (lineales, de matriz o dispersas).
• Los registros pueden ser dibujos, sellos o números.
Use los siguientes planteamientos y preguntas para evaluar e incentivar el razonamiento matemático:
Muestren (o expliquen) lo que hicieron.
¿Cómo llevan la cuenta de lo que ya contaron y de lo que aún les falta contar?
¿Pueden escribir o dibujar algo en una hoja de papel para mostrar cómo contaron?

Elija algunas parejas para que compartan su trabajo de conteo en el siguiente segmento. Busque ejemplos que demuestren con precisión maneras de llevar la cuenta, como las estrategias de mover y contar y tocar y contar. Si es posible, tome fotografías para proyectar. De no ser así, separe los trabajos seleccionados para compartirlos.
Pida a quienes no estén compartiendo su trabajo que ordenen los materiales. Después de la lección, reúna representaciones escritas para repasar como evaluación formativa.
Nota para la enseñanza
Al comienzo del año escolar, las representaciones de la clase varían de manera significativa. Algunos dibujos muestran claramente objetos individuales de una colección, mientras que otros apenas se distinguen. Con el tiempo y la experiencia, la clase desarrolla la comprensión de los números y lo que significa representar un grupo, así como las destrezas de la motricidad fina.
Tomar fotografías mientras la clase trabaja facilita el registro de ese desarrollo. Por ejemplo, en la imagen que se muestra a continuación, se dibujó el contorno de toda la colección. En la fotografía que se tomó durante la clase se muestra cómo esta representación se relaciona con la colección.
Evaluación observacional
; Mire a la clase mientras cuenta. Compruebe si se realiza lo siguiente:
• Mueven los objetos para llevar la cuenta de las cosas que ya han contado (uno a uno).
• Dicen la secuencia numérica correcta.
• Dicen el último número del conteo para indicar el total (cardinalidad).
Mover y contar Tocar y contar
K ▸ M1 ▸ TE ▸ Lección 19 EUREKA MATH2 © Great Minds PBC 218
Compartir, comparar y conectar
Materiales: M) Ejemplos de trabajo; E) Colección de conteo
La clase comenta estrategias para contar y registrar una colección.
Reúna a la clase para ver y comentar los ejemplos de trabajo seleccionados. Invite a las parejas seleccionadas a compartir el proceso de conteo que usaron. Nombre las estrategias de conteo que usó cada pareja.

Mover y contar (método de Colin y Tsega)
Invite a una pareja que haya usado la bolsita como parte de una estrategia de mover y contar para demostrar su proceso. Cuando la pareja haya terminado el conteo, ayude a la clase a comentar su estrategia.
¿Cómo llevaron Colin y Tsega la cuenta de lo que ya habían contado y de lo que aún les faltaba contar?
Usaron la bolsita.
Sacaron los bastones de caramelo de la bolsita cuando contaron.
Los bastones de caramelo que están sobre la plantilla ya habían sido contados. Los que estaban en la bolsita todavía estaban sin contar.
¿Cómo ayudó a Colin y Tsega la estrategia de mover y contar para contar todos los bastones de caramelo?
No contaron ninguno dos veces.
Cuando la bolsita estaba vacía, se dieron cuenta de que habían terminado.
Tocar y contar (método de Dashay y Oscar)
Invite a una pareja que haya usado una estrategia de tocar y contar a demostrar su proceso. Cuando la pareja haya terminado el conteo, ayude a la clase a comentar su estrategia.
¿Cuántas tapas hay en la colección? ¿Cómo lo saben? 6
El último número fue el 6.
Nota para la enseñanza
Si una pareja de estudiantes tiene una colección más grande (15 elementos o más), pídales que cuenten una parte de su colección para mantener el interés del resto de la clase.
 Mover y contar
Mover y contar
EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 19 © Great Minds PBC 219
Tocar y contar
¿Qué hicieron Dashay y Oscar para asegurarse de que contaron todas las tapas?
Contaron todas las tapas sin que faltara ninguna. Tocaron y contaron.
La estrategia de tocar y contar les ayudó a contar todas las tapas.
Si la pareja tiene registros que coinciden claramente con su colección, compártalos brevemente.
Oscar, veo que escribiste el 6 sobre tu dibujo de 6 tapas. ¿Qué usaste como ayuda para escribir el 6?

El camino numérico. Conté 1, 2, 3, 4, 5, 6. (Señala el camino numérico). Entonces, vi cómo hacer un 6.
Dashay, veo que escribiste el 6 para indicar todas las tapas. (Señale). También escribiste el 5 y el 1. (Señale). ¿Por qué escribiste el 5?
Hay 5 tapas naranjas.
¿Por qué escribiste el 1?
Hay una tapa morada.
Ya veo. Escribiste números para mostrar que 5 tapas y 1 tapa forman 6 tapas.
K ▸ M1 ▸ TE ▸ Lección 19 EUREKA MATH2 © Great Minds PBC 220
Concluir
Reflexión final 5 min
Objetivo: Organizar, contar y representar una colección de objetos
Asigne nuevas parejas para la reflexión final. Considere usar una estrategia que incluya movimiento para formar las parejas de estudiantes, de modo que la clase recupere energías para la conversación.
Continúe mostrando ejemplos de trabajo de la sección Compartir, comparar y conectar. Invite a la clase a mencionar el trabajo al usar la rutina Pensar-Trabajar en parejas-Compartir para analizar la siguiente pregunta.
¿Qué cosas podemos hacer o qué estrategias podemos usar como ayuda para contar?
Podemos mover cosas cuando las contamos.
Pongo mis borradores en línea sobre mi plantilla para no saltearme ninguno.
Podemos usar la bolsita para poner los que todavía no hemos contado.
5 35 10 EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 19 © Great Minds PBC 221
Puedo contar
Cantada con la melodía de “Una vez pesqué un pez vivo”
(Once I Caught a Fish Alive)
1 ave azul cantará.
2 abejas volarán.
3 flores crecen a la vez.
¡Puedo contar! 1, 2, 3.
Preparan todas un gran banquete.
1, 2, 3, 4, 5, 6, 7.
4 gatas duermen al sol.
5 patos tienen calor.
Al estanque entran de un brinco.
Cuento 1, 2, 3, 4, 5.
8 frijoles cuelgan de la rama.
9 caracoles se van a la cama.
1, 2, 3, 4; ¡salen cuando llueve!
5, 6, 7, 8 y 9.
6 ardillas juntan semillas.
7 aves hacen rosquillas.
10 autos pasean muy limpios.
Cuéntalos: 1, 2, 3, 4, 5,
6, 7, 8, 9, 10.
¡Contemos todo otra vez!
K ▸ M1 ▸ TE ▸ Lección 19 ▸ Puedo contar EUREKA MATH2 © Great Minds PBC 222 This page may be reproduced for classroom use only.
© Great Minds PBC 223 This page may be reproduced for classroom use only. EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 19 ▸ Puedo contar
Contar objetos en grupos de 5 y en configuraciones de matrices, y emparejarlos con un numeral
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
La clase relaciona cómo contar con el método matemático usando los dedos con las formaciones de grupos de 5 pictóricas. Estos modelos permiten que la clase vea los números del 6 al 10 en relación con el 5, que sirve de apoyo para la visualización y el conteo súbito. También crearán y contarán configuraciones de matrices. En esta lección, se presenta el término grupo de 5.
Pregunta clave
• ¿Por qué el 5 es un número importante?
Criterios de logro académico
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron. (K.CC.B.4.b)
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas. (K.CC.B.5)
20 LECCIÓN 20
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 5 min
Aprender 30 min
• 5 dedos
• Relacionar el conteo con el método matemático con grupos de 5
• Construir y contar matrices
• Grupo de problemas
Concluir 5 min
Materiales
Maestro o maestra
• guantes numerados derecho e izquierdo
• tarjetas 5-group™ (grupos de 5), juego para demostración (del 1 al 5)
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 6 al 10)
• cubos Unifix® (10)
• Plantilla de grupos de 5 (descarga digital)
Estudiantes
• cubos Unifix® (10)
• Plantilla de grupos de 5 (en el libro para estudiantes)
• libro para estudiantes
Preparación de la lección
• Prepare las tarjetas del 1 al 5 del juego para demostración de las tarjetas de grupos de 5.
• Considere retirar la Plantilla de grupos de 5 y colocarla en una pizarra blanca individual. La plantilla se usará varias veces a lo largo del módulo.
• Prepare las tarjetas del 6 al 10 del juego para demostración de las tarjetas Hide Zero.
• Imprima o haga una copia de la Plantilla de grupos de 5 para usarla en la demostración.
© Great Minds PBC 225 EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 20
Fluidez
Contar hasta el 7 en el guante numerado
Materiales: M) Guantes numerados derecho e izquierdo
La clase cuenta en el guante numerado como preparación para formar una nueva unidad con cinco y familiarizarse con el conteo con el método matemático.
Observen mi guante numerado y cuenten en voz alta. ¿Comenzamos?
Use el guante numerado para mostrar la siguiente secuencia mientras la clase cuenta en voz alta.
Nota para la enseñanza
Hoy, es la primera vez que la clase comenzará a contar un número distinto de 1 en el guante numerado. Si la clase duda, considere indicarles el número inicial antes de mostrar 3 dedos.
Facilite más práctica para contar en el guante numerado hasta el 7, haciendo énfasis cuando pasen por el 5. Haga hincapié en el cinco mostrando y escondiendo la mano izquierda (detrás de la espalda).
Si la clase tiene dificultades con una secuencia hasta el 7, regrese a una secuencia hasta el 5 y, luego, suba gradualmente hasta el 7.
Contar hasta el 7 con el método matemático
La clase hace una recta numérica con los dedos mientras cuenta en voz alta para desarrollar el sentido de la cantidad y del orden.
Para cada conteo, muestre el método matemático con los dedos mientras la clase cuenta, pero no cuente en voz alta.
Vamos a contar con el método matemático.
Párese de frente a la clase y pida a sus estudiantes que copien los movimientos.
Pida a la clase que cuente con el método matemático del 1 al 7 y, luego, del 7 al 0.
“Observen mi guante numerado y cuenten en voz alta. Empiecen diciendo el 3. ¿Comenzamos?”.
3
4 5 6 5 6 5 6 7 6 7
10 5 30 5
K ▸ M1 ▸ TE ▸ Lección 20 EUREKA MATH2 © Great Minds PBC 226
Miren con atención y cuenten en voz alta. ¿Comenzamos? (Levante el dedo meñique derecho).
1 (La clase levanta el dedo meñique izquierdo).
Levante el dedo anular derecho.
2 (La clase levanta el dedo anular izquierdo).
Levante el dedo mayor derecho.
3 (La clase levanta el dedo mayor izquierdo).
Baje el dedo mayor derecho.
2 (La clase baja el dedo mayor izquierdo).
Continúe con la siguiente secuencia: 6 6 6 7 6 7

Facilite más práctica para contar hasta el 7 con el método matemático, haciendo énfasis cuando pasen por el 5. La clase puede desarrollar la memoria cinestésica para el cinco colocando la mano derecha detrás de la espalda cuando no la necesite para contar.





Grupos de 5 hasta el 5
Materiales: M) Tarjetas de grupos de 5
La clase reconoce un grupo de puntos para desarrollar la capacidad de subitizar cantidades que se muestran con grupos de 5.
Levanten la mano cuando sepan la respuesta a la pregunta. Esperen mi señal para decir la respuesta.











Muestre la tarjeta de grupos de 5 que muestra 3.
¿Cuántos puntos hay?
EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 20 © Great Minds PBC 227
Espere hasta que la mayor parte de la clase haya levantado la mano y, luego, dé la señal para que respondan.
Repita el proceso con la siguiente secuencia:

Cuando la clase esté preparada, muestre cada tarjeta durante menos tiempo como desafío para que reconozcan los grupos de puntos más rápidamente.
Presentar
Materiales: E) Plantilla de grupos de 5, cubos Unifix
Hallar un cinco en imágenes de objetos cotidianos y en representaciones matemáticas.

Muestre la colección de imágenes. Invite a la clase a usar la rutina Pensar-Trabajar en parejas-Compartir para analizar dónde ven cinco en cada imagen.
¿Dónde ven cinco en estas imágenes?
La estrella de mar tiene 5 brazos.

Hallé 5 anillos.

El papá y el bebé tienen 5 dedos en cada pie.
Hay 5 dedos en cada guante.
3
4
4
5 3 2 1 3
5 2 3
10 5 30 5 K ▸ M1 ▸ TE ▸ Lección 20 EUREKA MATH2 © Great Minds PBC 228
¡Hallemos cinco también en nuestro cuerpo!
Pida a la clase que muestre una mano y cuente los dedos. Luego, pídales que muestren la otra mano y cuenten los dedos.
5 dedos en esta mano (moviendo una mano) y 5 dedos en esta otra (moviendo la otra mano). ¿Es el mismo número?
Sí.
Hallemos cinco en algunas de nuestras herramientas matemáticas.
Distribuya plantillas de grupo de 5. Primero, pida a la clase que cuente los puntos de la línea superior y que, luego, cuente los de la línea inferior. Enfatice que tanto la línea superior como la inferior tienen el mismo número de puntos (5).
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hoy, busquemos métodos para hallar cinco en herramientas matemáticas.
Aprender
5 dedos
Materiales: E) Plantilla de grupos de 5, cubos Unifix
La clase halla un cinco en una configuración lineal conocida: sus manos.
Distribuya cubos Unifix y una plantilla a cada estudiante. Luego, presente un contexto imaginario: Los dedos de cada estudiante son personas y los cubos son sombreros. Dé a la clase un momento para jugar, deje que las personas bailen, hablen y se muevan.
Apoyo para la comprensión del lenguaje
Para facilitar el uso de las plantillas de grupos de 5, considere presentar las palabras de posición arriba, medio y abajo, que pueden resultarles conocidas de los programas de aprendizaje o de escritura.
Empiece con una actividad simple de “Muéstrame”. Use gestos para indicar las posiciones en el espacio y en la plantilla como apoyo para el uso de estos términos. Empiece con un patrón predecible: muéstrame arriba, abajo, arriba, abajo. Luego, cambie e incorpore una repetición lúdica: arriba, arriba, arriba, abajo.
Use gestos a lo largo de la lección para reforzar la adquisición del lenguaje.
EUREKA MATH K M1 ▸ TE ▸ 5-Group Mat Copyright Great Minds PBC 61
10 5 30 5
EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 20 © Great Minds PBC 229
Plantilla de grupos de 5
Cuenten 5 sombreros. Colóquenlos sobre la plantilla.
Pida a la clase que coloque los sombreros en los dedos. Diga que comiencen con el meñique izquierdo y que cuenten con el método matemático. Luego, cada estudiante puede poner un sombrero en el dedo anular, seguido por el dedo mayor, y así sucesivamente. Continúe hasta que los 5 dedos tengan sombreros, hasta terminar con el pulgar.
¿Cuántos sombreros pusieron?
5
¿Cuántas personas llevan sombreros?
5
Recordemos por un momento que no son personas de verdad, sino que son sus dedos.
¿Cuántos dedos hay en esa mano?
5

Vuelvan a imaginar que sus dedos son personas. ¿Y si 1 persona más quiere usar un sombrero? ¿Qué harían?
Tendríamos que usar la otra mano.
Podríamos ponerlo en el otro pulgar.
¡Bien pensado! Veámoslo.
Después de que se coloquen el sexto cubo en un dedo, repita la serie de preguntas acerca del número de sombreros, las personas y los dedos.
Relacionar el conteo con el método matemático con grupos de 5
Materiales: M) Tarjetas Hide Zero, cubos Unifix, Plantilla de grupos de 5; E) Plantilla de grupos de 5, cubos Unifix
La clase representa los números del 6 al 10 con las manos y con grupos de 5.
Muestre 6 cubos sobre una plantilla: 5 en la parte superior y 1 en la parte inferior.
Quítense los cubos de los dedos y hagan que se vean así.
Muestre la tarjeta Hide Zero del 6.
K ▸ M1 ▸ TE ▸ Lección 20 EUREKA MATH2 © Great Minds PBC 230
Solo con los dedos, muéstrenme 6 con el método matemático.
Observen sus dedos. Observen sus cubos. ¡Dedos, cubos, dedos, cubos!
Repita el procedimiento algunas veces de manera entretenida y, luego, guarde la tarjeta Hide Zero del 6.
¿Dónde está el cinco en las manos? Levanten las manos bien arriba.
(La clase levanta la mano izquierda y muestra los 5 dedos).
¿Dónde está el cinco en la plantilla? Enciérrenlo en un círculo con los dedos.
(La clase encierra en un círculo la fila de arriba).
(Muestre la tarjeta Hide Zero del 6). Muéstrenme 6 con el método matemático.
¿Dónde ven el 1 en las manos? Levanten las manos bien arriba.
(La clase levanta la mano derecha y muestra el pulgar).
¿Dónde ven el 1 en la plantilla? Enciérrenlo en un círculo con los dedos.
(La clase encierra en un círculo el único cubo que está en la fila inferior).
Observen sus cubos. Levanten la mano cuando sepan cuántos hay en la plantilla.
Dé tiempo para contar y, luego, dé la señal para que respondan a coro.
(Señale la fila superior). Mostramos 6 como 5 y 1 más. (Señale la fila inferior). A esto lo llamamos grupo de 5. ¿Cómo lo llamamos?
Grupo de 5
Si hay tiempo suficiente, continúe con los números del 7 al 10 y haga una pausa para relacionar los modelos e incorporar el vocabulario nuevo.
Promoción de los estándares para la práctica de las matemáticas

Cada estudiante reconoce y utiliza estructuras (MP7) cuando busca el cinco como ayuda para contar. Por ejemplo, ve cinco en sus manos, en grupos de 5 y en otras organizaciones de objetos en el salón de clases.
Si bien sería más sencillo dejar que cada estudiante cuente como quiera, anime a la clase a buscar y hacer uso del cinco. Plantar esta semilla ahora ayudará a garantizar que tengan una base adecuada cuando les toque contar desde un número en 1.er grado.
EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 20 © Great Minds PBC 231
Construir y contar matrices

Materiales: M) Plantilla de grupos de 5, cubos Unifix; E) Plantilla de grupos de 5, cubos Unifix
La clase construye configuraciones de matrices para emparejar una imagen y contar.

Indique a la clase que coloque la Plantilla de grupos de 5 del lado que está en blanco. Muestre la imagen del 10 como una matriz de 2 por 5.
Hagan que sus cubos se parezcan a los míos. Pónganse de pie cuando hayan terminado.
El simple acto de ponerse de pie es un claro indicador de que han completado la actividad y crea una sensación de urgencia, además de ser una buena oportunidad para moverse. Una vez que la mayoría esté de pie, pida a cada estudiante que comente con el resto cuántos cubos hay en la plantilla para volver a enfocar a la clase.
Díganme, ¿cuántos cubos hay en sus plantillas? 10
Esta manera de mostrar 10 se llama… ¡Grupo de 5!
Muestre la imagen del 8 como una matriz de 2 por 4. Repita la secuencia anterior, pero esta vez con la clase sentada y después de que hayan organizado sus cubos.
Díganme, ¿cuántos cubos hay en sus plantillas?
¿Este es un grupo de 5?
No.
¿Hay 5 arriba?
No.
Diferenciación: Desafío
Las matrices se pueden descomponer fácilmente en partes. Como desafío, pida a sus estudiantes que creen enunciados numéricos para emparejar cada matriz. Las partes que forman 10 pueden inspirar algunos de los siguientes enunciados numéricos:
• 10 es 5 y 5.
• 5 y 5 forman 10.
• 10 es 2 y 2 y 2 y 2 y 2.
• 4 y 6 forman 10.
Evaluación observacional
; Observe cómo la clase mueve y cuenta los cubos.
• ¿Cuentan de una manera organizada (p. ej., de izquierda a derecha o de arriba a abajo)?
• Cuando pregunta “¿cuántos hay?”, ¿pueden repetir con seguridad el último número dicho? (cardinalidad)
8
K ▸ M1 ▸ TE ▸ Lección 20 EUREKA MATH2 © Great Minds PBC 232
Repita el proceso con la siguiente secuencia. Cuando sea posible, permita que la clase construya la matriz sin guía. Recuérdeles que cero significa ninguno.
Grupo de problemas
Dé las indicaciones en dos partes. Primero, pida a la clase que encierre en un círculo un grupo de cinco en cada imagen. Considere pedirles que encierren en un círculo un grupo de cinco con un dedo antes de usar útiles de escritura. Después de que hayan encerrado cinco en un círculo en todas las imágenes, pídales que cuenten y encierren en un círculo el número que indica cuántos hay en total.

Nota para la enseñanza
Este Grupo de problemas está diseñado para usar la representación sistemática (consulte la lección 8 para conocer más detalles). Continúe usando la representación sistemática para los Grupos de problemas hasta que la clase se sienta cómoda trabajando con lápiz y papel.



© Great Minds PBC 65 EUREKA MATH K M1 TE Lección 20 Encierra en un círculo un grupo de cinco en todas las imágenes. Luego, cuenta y encierra en un círculo cuántos hay en total. Nombre 5 6 7 7 8 9 8 9 10 7 8 9 20 K M1 TE Lección 20 EUREKA MATH2 © Great Minds PBC 66 GRUPO DE PROBLEMAS 5 6 7 5 6 7 8 9 10 5 6 7
EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 20 © Great Minds PBC 233
Concluir
Reflexión final 5 min
Objetivo: Contar objetos en grupos de 5 y en configuraciones de matrices, y emparejarlos con un numeral

Muestre las imágenes que muestren 7. Registre las respuestas mientras la clase comenta en qué se parecen y en qué se diferencian las imágenes.
¿En qué se parecen las herramientas matemáticas de esta imagen? ¿En qué se diferencian?
Se parecen en que las dos muestran 7.
Se parecen en que las dos tienen 5 y 2. Se diferencian en que en una hay puntos y en la otra hay dedos.
Muestre la imagen de las tarjetas Hide Zero del 6 al 10.
Cada imagen muestra un grupo de 5. ¿Por qué creen que los llamamos grupos de 5?
Todos tienen 5 en la parte de arriba.
El 10 tiene 5 en la fila superior y 5 en la fila inferior.
Hay 5 y algunos más.
¿Por qué el 5 es un número importante?
Tenemos 5 dedos en cada mano.
Hay 5 puntos en la parte de arriba del grupo de 5.
5 30 5 K ▸ M1 ▸ TE ▸ Lección 20 EUREKA MATH2 © Great Minds PBC 234
Contar objetos en configuraciones circulares y emparejarlos con un numeral
Vistazo a la lección
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Las y los estudiantes de corta edad necesitan mucha práctica para integrar los componentes de los fundamentos numéricos para contar correctamente. Esta es la primera lección en la que la clase considera cómo contar objetos correctamente en una configuración circular. Comentan estrategias para registrar, comenzar y terminar sus conteos.
Pregunta clave
• ¿Qué cosas podemos hacer o qué estrategias podemos usar como ayuda para contar cosas que están en un círculo?
Criterios de logro académico
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10. (K.CC.A.3)
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas. (K.CC.B.5)
21 LECCIÓN 21
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 5 min
Aprender 30 min
• Marcar y contar
• Marcar el comienzo
• Grupo de problemas
Concluir 5 min
Materiales
Maestro o maestra
• guantes numerados
• tarjetas 5-group™ (grupos de 5), juego para demostración (del 5 al 7)
• notas adhesivas (8)
• marioneta o animal de peluche
Estudiantes
• libro para estudiantes
Preparación de la lección
Prepare las tarjetas del 5 al 7 del juego para demostración de las tarjetas de grupos de 5.
© Great Minds PBC 237 EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 21
Fluidez










Contar hasta el 10 con el método matemático
La clase hace una recta numérica con los dedos mientras cuenta en voz alta para desarrollar el sentido de la cantidad y el orden.



Vamos a contar con el método matemático.
Párese de frente a la clase y pida a sus estudiantes que copien los movimientos.
El método matemático es así: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. (Demuestre).

















Levante el meñique derecho.
Muéstrenme el meñique izquierdo. Eso es 1. Sigamos contando hasta el 10.
Muestre el método matemático con los dedos mientras la clase cuenta, pero no cuente en voz alta.
Pida a la clase que cuente del 1 al 10 con el método matemático.
Repita el conteo dos veces más.
Deténganse aquí en el 10. Ahora, cuenten hacia atrás hasta el 0. ¿Comenzamos?
Pida a la clase que cuente del 10 al 0 con el método matemático.
10 5 30 5 K ▸ M1 ▸ TE ▸ Lección 21 EUREKA MATH2 © Great Minds PBC 238
Grupos de 5 hasta el 7
Materiales: M) Tarjetas de grupos de 5
La clase reconoce un grupo de puntos para desarrollar la comprensión de los números del 6 al 10 como 5 y algunos más.
Levanten la mano cuando sepan la respuesta a cada pregunta. Esperen mi señal para decir la respuesta.
Muestre la tarjeta de grupos de 5 que muestra 5.
¿Cuántos puntos hay?
Espere hasta que la mayor parte de la clase haya levantado la mano y, luego, dé la señal para que respondan.
5
Repita el proceso con la siguiente secuencia:
6 5 7 5 6 7 5
Observe que la secuencia vuelve deliberadamente al 5 con frecuencia, de modo que la clase pueda ver al cinco como una unidad. Cuando la clase esté preparada, muestre cada tarjeta durante menos tiempo como desafío para que reconozcan los grupos de puntos más rápidamente.
EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 21 © Great Minds PBC 239
Presentar
Materiales: M) Marioneta o animal de peluche
La clase reconoce la necesidad de llevar la cuenta cuando los objetos están organizados en una configuración circular.
Muestre la rueda de la fortuna.
¿Cuántas personas pueden subir a la rueda de la fortuna al mismo tiempo?
Pida a la clase que use la rutina Pensar-Trabajar en parejas-Compartir.
Piensen cómo podríamos resolver esto. Comenten sus ideas en parejas.
Tenemos que contar todas las cabinas.
Podríamos hacer de cuenta que en cada cabina entra 1 persona y luego contar las personas.
Escucho que muchos de ustedes dicen que contarían las cabinas. A la marioneta le encanta contar, así que vamos a pedirle que nos ayude.
Use la marioneta para contar las cabinas sin detenerse. Continúe contando alrededor de la rueda hasta que la clase detenga a la marioneta.
¿Qué sucede? ¿Por qué hicieron que la marioneta dejara de contar?
La marioneta contó demasiadas cabinas y no se detuvo en la parte de abajo.
La marioneta no sabe dónde dejar de contar.
La marioneta no lleva la cuenta de las cabinas contadas.
Ayudemos a la marioneta a contar cosas que están en un círculo.
Diferenciación: Desafío
Sugiera que hay 2 personas a bordo de cada cabina e invite a sus estudiantes a plantear una estrategia. Algunas posibilidades son:
• Ilevar la cuenta con los dedos
• contar alrededor del círculo dos veces
• contar de dos en dos
Si hay tiempo suficiente, pídales que exploren otras opciones con números con los que sepan contar salteado, como de cinco en cinco o de diez en diez.
10 5 30 5
K ▸ M1 ▸ TE ▸ Lección 21 EUREKA MATH2 © Great Minds PBC 240
Aprender
Marcar y contar
Materiales: M) Notas adhesivas
La clase usa la estrategia de marcar y contar para hallar cuántos objetos hay en una configuración circular.
Pienso que si usamos la estrategia de marcar y contar ayudaremos a la marioneta a saber cuántas personas pueden subir a la rueda de la fortuna.
Marquemos cada cabina a medida que contamos para llevar la cuenta. Cuenten conmigo.
Coloque una nota adhesiva en cada cabina a medida que la clase cuenta.
Vamos a contar una vez más. Esta vez escribiré el número en cada nota adhesiva para que podamos recordar cuántas personas pueden subir al mismo tiempo.
A medida que la clase cuenta, escriba cada número y quite las notas adhesivas de la rueda de la fortuna para colocarlas en una formación lineal.
¿Cuántas personas pueden subir a la rueda de la fortuna al mismo tiempo?
8 personas
Levante o señale las 8 notas adhesivas para reforzar la cardinalidad: el último número mencionado indica la cantidad.
10 5 30 5 EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 21 © Great Minds PBC 241
Marcar el comienzo
La clase marca la posición de inicio y cuenta cuántos hay en una configuración circular.
Marcar la posición de inicio en una configuración circular es una manera más simple de marcar y contar que es eficiente para una parte de la clase. Otra parte preferirá hacer una marca por cada objeto que cuentan.
Muestre la flor.
Miren esta flor. Quiero saber cuántos pétalos tiene, pero ya no me quedan notas adhesivas.
¿Cómo podemos marcar la imagen para asegurarnos de que contamos correctamente?
Podemos tachar cada pétalo después de contarlo.
Podemos poner una marca donde comenzamos a contar para saber dónde terminar de contar.
¡Excelentes ideas! Intentemos marcar el primer pétalo que contamos para recordar dónde comenzamos.
Tache el primer pétalo y toque los otros mientras la clase cuenta.
¿Cuántos pétalos hay en esta flor?
6 pétalos
Escriba el 6 para reforzar que el último número que dijeron indica la cantidad.
Ahora es su turno de contar algunas otras cosas que están en un círculo.
Promoción
Cada estudiante pone atención a la precisión (MP6) cuando marca el primer pétalo y procura contar todos los pétalos sin contar dos veces el pétalo tachado.
de los estándares para la práctica de las matemáticas
K ▸ M1 ▸ TE ▸ Lección 21 EUREKA MATH2 © Great Minds PBC 242
Grupo de problemas
La clase cuenta objetos en configuraciones circulares y encierran en un círculo el numeral que coincida. Use la representación sistemática para comenzar la clase y luego recorra el salón de clases o trabaje con un grupo pequeño de estudiantes que necesiten de apoyo adicional.

Evaluación observacional

; Observe a la clase mientras trabaja en el Grupo de problemas.
• ¿Puede escuchar a la clase decir la secuencia numérica mientras usan una estrategia para contar (p. ej., marcar el comienzo o tachar)?
• ¿La clase reconoce y encierra en un círculo el número correcto del camino numérico sin contar desde el 1 para hallar el número?
Great Minds PBC 67 EUREKA MATH K M1 TE Lección 21 Nombre Cuenta. Encierra en un círculo cuántos hay en el camino numérico. 2 3 4 5 6 7 8 9 10 2 3 4 5 6 7 8 9 10 21 K M1 TE Lección 21 EUREKA MATH © Great Minds PBC 68 GRUPO DE PROBLEMAS 2 3 4 5 6 7 8 9 10 2 3 4 5 6 7 8 9 10 EUREKA MATH K M1 TE Lección 21 © Great Minds PBC 69 GRUPO DE PROBLEMAS Cuenta. Encierra en un círculo para mostrar cuántos hay. 8 9 10 2 3 4 5 6 7 8 9 10 8 9 10 EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 21 © Great Minds PBC 243
Concluir
Reflexión final 5 min
Materiales: M) Marioneta o animal de peluche

Objetivo: Contar objetos en configuraciones circulares y emparejarlos con un numeral
Vamos a enseñarle a la marioneta cómo contar objetos que están en un círculo.
Piensen en las estrategias que usaron en la clase de hoy. ¿Qué estrategias podemos usar para enseñarle a la marioneta?
Podemos usar notas adhesivas para marcar las cosas que estamos contando.
Podemos mover los objetos y formar una línea para que sea más fácil contarlos.
Si marcamos dónde comenzamos a contar, sabremos dónde detenernos.
Cuando contamos imágenes, podemos tachar cada cosa que contamos.
5 30 5 K ▸ M1 ▸ TE ▸ Lección 21 EUREKA MATH2 © Great Minds PBC 244
Contar objetos en configuraciones dispersas y emparejarlos con un numeral
Vistazo a la lección
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
La clase cuenta objetos en configuraciones dispersas, para lo cual usan la estrategia de mover y contar, para los objetos concretos, y la estrategia de marcar y contar, para las imágenes. Emparejan tarjetas numéricas con grupos en configuraciones dispersas, circulares, lineales y de matrices. Luego, juegan bingo, lo que proporciona práctica para reconocer números aislados.
Pregunta clave
• ¿Qué estrategias usaríamos para contar en un grupo disperso?
Criterios de logro académico
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10. (K.CC.A.3)
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas. (K.CC.B.5)
22 LECCIÓN 22
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 10 min
Aprender 25 min
• Emparejar números
• Bingo
Concluir 5 min
Materiales
Maestro o maestra
• osos para contar (7)
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración
• tarjetas 5-group™ (grupos de 5), juego para demostración (del 5 al 10)
Estudiantes
• tarjetas Hide Zero®
• Tablero de Bingo (en la edición para la enseñanza)
• pizarra blanca individual
• cubos Unifix® o frijoles de dos colores (9)
Preparación de la lección
• Prepare las tarjetas del 5 al 10 del juego para demostración de las tarjetas de grupos de 5.
• Considere colocar los tableros de bingo en las pizarras blancas individuales para que la clase pueda usar la estrategia de marcar y contar.
• Organice grupos de cubos Unifix o de frijoles para que la clase use como marcadores en los espacios del Tablero de Bingo.
© Great Minds PBC 247 EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22
Fluidez
Contar hasta el 10 con el método matemático
La clase hace una recta numérica con los dedos mientras cuenta en voz alta para desarrollar el sentido de la cantidad y el orden.
Muestre el método matemático con los dedos mientras la clase cuenta, pero no cuente en voz alta. Vamos a contar con el método matemático.
Párese de frente a la clase y pida a sus estudiantes que copien los movimientos.
Pida a la clase que cuente con el método matemático del 1 al 10 y, luego, del 10 al 0.
Miren con atención y cuenten en voz alta. ¿Comenzamos? (Levante el meñique derecho).
1 (La clase levanta el meñique izquierdo).
Levante el dedo anular derecho.
2 (La clase levanta el dedo anular izquierdo).
Levante el dedo mayor derecho.
3 (La clase levanta el dedo mayor izquierdo).
Baje el dedo mayor derecho.
2 (La clase baja el dedo mayor izquierdo).
Continúe con la siguiente secuencia:

























Facilite más práctica para contar hasta el 10 con el método matemático, haciendo énfasis cuando pasen por el 5.

10 10
10 10 25 5 K ▸ M1 ▸ TE ▸ Lección 22 EUREKA MATH2 © Great Minds PBC 248
Grupos de 5 hasta el 10
Materiales: M) Tarjetas de grupos de 5
La clase reconoce un grupo de puntos para desarrollar la comprensión de los números del 6 al 10 como 5 y algunos más.
Levanten la mano cuando sepan la respuesta a la pregunta. Esperen mi señal para decir la respuesta.
Muestre la tarjeta de grupos de 5 que muestra 5.
¿Cuántos puntos hay?
Espere hasta que la mayor parte de la clase haya levantado la mano y, luego, dé la señal para que respondan.
5
Repita el proceso con la siguiente secuencia:
Observe que la secuencia vuelve deliberadamente al 5 con frecuencia, de modo que la clase pueda ver al cinco como una unidad. Cuando la clase esté preparada, muestre cada tarjeta durante menos tiempo como desafío para que reconozcan los grupos de puntos más rápidamente.
8 5 9 5 10 5 5 9 8 7 5
EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 © Great Minds PBC 249
Presentar
Materiales: M) Osos para contar
La clase usa diferentes estrategias de conteo para contar un grupo de objetos concretos y un grupo que aparece en una imagen.
Muestre 7 osos para contar en una configuración dispersa. Considere usar dos colores para resaltar un grupo de 5.


Me pregunto cuántos osos hay. ¿Qué podemos hacer para averiguarlo?
Podemos contarlos.
¿Cómo debemos contar los osos para no cometer un error?
Podemos tocar y contar.
Podemos moverlos mientras contamos.
Podemos moverlos para formar una línea.
Buenas ideas. Voy a moverlos para formar una línea mientras los contamos a coro.
Forme una línea con los osos mientras la clase cuenta a coro hasta el 7.
¿Cuántos osos hay?
7 osos
Correcto. Mover y contar los osos hace que sea más fácil contar sin olvidarnos de ningún oso ni contar un oso dos veces.
Reserve los osos para contar para usarlos en la sección Concluir. Muestre la imagen de los osos en el bosque.
Observen la imagen de los osos. Me pregunto cuántos osos hay en esta imagen.
10 10 25 5 K ▸ M1 ▸ TE ▸ Lección 22 EUREKA MATH2 © Great Minds PBC 250
¿Podemos moverlos y contarlos, como hicimos antes?
No. Están pegados en la imagen.
¿Cómo debemos contar los osos de la imagen para no cometer un error?
Podemos marcar el primer oso que contemos, seguir contando y detenernos cuando volvamos al primero que marcamos.
Podemos tachar cada oso a medida que los contamos.
Buenas ideas. Tachemos los osos. Cuenten a medida que tacho cada oso.
¿Cuántos osos hay?
7 osos
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hoy, observemos las imágenes y usemos nuestras estrategias de conteo para hallar cuántos hay.
Aprender
Emparejar números
La clase cuenta conjuntos de objetos y los empareja con tarjetas numéricas.
Materiales: M) Tarjetas Hide Zero; E) Tarjetas Hide Zero, Tablero de Bingo
Distribuya los tableros de bingo y las tarjetas Hide Zero. Pida a sus estudiantes que ordenen las tarjetas Hide Zero del 0 al 10 debajo del Tablero de Bingo.
Observen sus tableros de bingo. Cuenten las cosas que hay en el primer recuadro.
Hallen la tarjeta numérica que coincide y colóquenla en el recuadro.
Los tableros de bingo están agrupados según su complejidad. En el primer nivel tienen 4 o 5 espacios con numerales y pueden ser útiles para estudiantes que necesitan más tiempo para contar. Los tableros del quinto nivel no tienen numerales y tienen algunas configuraciones que son un desafío.
Todos los tableros contienen grupos de entre 0 y 10 objetos en diferentes configuraciones. En cada tablero hay al menos una oportunidad para contar objetos en una configuración dispersa.
10 10 25 5
Diferenciación
EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 © Great Minds PBC 251
Haga una demostración si fuera necesario. Recorra el salón de clases mientras sus estudiantes cuentan y emparejan sus tarjetas con los grupos que hay en el tablero.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante razona de forma abstracta y cuantitativa (MP2) cuando empareja las tarjetas numéricas con los recuadros, para lo cual reconoce organizaciones de objetos y numerales como diferentes representaciones del mismo número.
Evaluación observacional
Pídales que dejen las tarjetas Hide Zero sobre los tableros y que se preparen para jugar bingo en el siguiente segmento.
Bingo

Materiales: M) Tablero de Bingo, cubos Unifix o frijoles de dos colores; E) Tablero de Bingo, tarjetas Hide Zero, cubos Unifix o frijoles de dos colores
La clase reconoce números en forma aislada y fuera de una secuencia.
Muestre un Tablero de Bingo con tarjetas Hide Zero. Represente y explique cómo jugar:

• El maestro o la maestra dice un número del 0 al 10.
• Sus estudiantes hallan ese número en sus tableros.
• Sus estudiantes usan un cubo Unifix o un frijol para marcar el número dicho.
• La primera persona que tenga tres números en una fila horizontal, vertical o diagonal gana.
Mientras juegan, recorra el salón de clases para asegurarse de que la clase identifica y marca el número correcto.
; Observe a la clase mientras trabaja con el Tablero de Bingo.
• ¿La clase usa una estrategia de conteo para contar las imágenes? ¿Algunas configuraciones son más difíciles de contar?
• ¿La clase puede reconocer números en forma aislada? (símbolo del número)
Nota para la enseñanza
Mantener las tarjetas Hide Zero en la parte superior del tablero da a la clase práctica para reconocer numerales en forma aislada. También hace que el juego se desarrolle a un ritmo que mantiene el interés. Cuando hace una pausa para que una parte de la clase vuelva a contar los grupos, el resto se dispersa.
Considere pedir a alguien de la clase que diga los números. Cuando la clase haya aprendido a jugar bingo de manera independiente, se puede agregar a los centros o estaciones.
K ▸ M1 ▸ TE ▸ Lección 22 EUREKA MATH2 © Great Minds PBC 252
Concluir
Reflexión final 5 min
Materiales: M) Osos para contar
Objetivo: Contar objetos en configuraciones dispersas y emparejarlos con un numeral
Muestre los 7 osos para contar de la sección Presentar y la imagen de los osos en el bosque.
¿Cómo contamos cada grupo de osos?
Movimos los osos azules y los rojos. Tachamos los osos en el bosque.
¿Cuál es la diferencia en el conteo de estos grupos de osos?
Podemos mover estos osos para formar una línea. No podemos mover los osos de la imagen porque están en el papel.
Usamos estrategias diferentes para contar los osos que pudimos mover y los osos que estaban en la imagen. Podemos usar las estrategias de mover y contar y de marcar y contar como ayuda para saber cuántos hay.
Muestre la imagen de los ositos de peluche.
Imaginen que este grupo de osos está en su tarjeta de bingo.
¿Qué estrategias usarían para contar este grupo?
Usaría la estrategia de marcar y contar. Cubriría con la mano los osos que ya conté.
10 25 5 EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 © Great Minds PBC 253
K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo EUREKA MATH2 © Great Minds PBC 254 This page may be reproduced for classroom use only.
10 0 9 5
BINGO
EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo © Great Minds PBC 255 This page may be reproduced for classroom use only. BINGO 3 5 0 8 1
K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo EUREKA MATH2 © Great Minds PBC 256 This page may be reproduced for classroom use only.
10 0 2
BINGO 4
EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo © Great Minds PBC 257 This page may be reproduced for classroom use only. BINGO 0 9 5 8
K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo EUREKA MATH2 © Great Minds PBC 258 This page may be reproduced for classroom use only.
3
0
BINGO 1
2
EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo © Great Minds PBC 259 This page may be reproduced for classroom use only.
4 7 10 2
BINGO 8
K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo EUREKA MATH2 © Great Minds PBC 260 This page may be reproduced for classroom use only.
4 7 8
BINGO

EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo © Great Minds PBC 261 This page may be reproduced for classroom use only.
7 1
BINGO 3
K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo EUREKA MATH2 © Great Minds PBC 262 This page may be reproduced for classroom use only.
3 5 7
BINGO

EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo © Great Minds PBC 263 This page may be reproduced for classroom use only. BINGO 1 10 9
K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo EUREKA MATH2 © Great Minds PBC 264 This page may be reproduced for classroom use only.
6 10
BINGO 1

EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo © Great Minds PBC 265 This page may be reproduced for classroom use only.
6 8
BINGO 5
K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo EUREKA MATH2 © Great Minds PBC 266 This page may be reproduced for classroom use only.
1 3
BINGO

EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo © Great Minds PBC 267 This page may be reproduced for classroom use only.
BINGO 4 2
K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo EUREKA MATH2 © Great Minds PBC 268 This page may be reproduced for classroom use only.
0 2
BINGO
EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo © Great Minds PBC 269 This page may be reproduced for classroom use only.
9 6
BINGO

K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo EUREKA MATH2 © Great Minds PBC 270 This page may be reproduced for classroom use only.
7 5
BINGO

EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo © Great Minds PBC 271 This page may be reproduced for classroom use only.
8 10
BINGO

K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo EUREKA MATH2 © Great Minds PBC 272 This page may be reproduced for classroom use only.
BINGO 4

EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo © Great Minds PBC 273 This page may be reproduced for classroom use only.
BINGO 6


K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo EUREKA MATH2 © Great Minds PBC 274 This page may be reproduced for classroom use only.
9
BINGO

EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo © Great Minds PBC 275 This page may be reproduced for classroom use only.
BINGO 8

K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo EUREKA MATH2 © Great Minds PBC 276 This page may be reproduced for classroom use only.
BINGO 2


EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo © Great Minds PBC 277 This page may be reproduced for classroom use only.
BINGO 5

K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo EUREKA MATH2 © Great Minds PBC
BINGO

EUREKA MATH2 Tablero de
© Great Minds PBC 279 This page may be reproduced for classroom use only. BINGO
Bingo


K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo EUREKA MATH2 © Great Minds PBC 280 This page may be reproduced for classroom use only.
BINGO

EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo © Great Minds PBC 281 This page may be reproduced for classroom use only.
BINGO

K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo EUREKA MATH2 © Great Minds PBC 282 This page may be reproduced for classroom use only.
BINGO


EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 22 ▸ Tablero de Bingo 283 This page may be reproduced for classroom use only. BINGO
Conservar el número sin importar el orden en que los objetos se cuentan
Vistazo a la lección
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
La clase cuenta grupos de objetos dispersos de diferentes maneras. Observan que el número de objetos se mantiene igual. La clase usa experiencias repetidas para poner a prueba la idea y confirmar que el número de objetos se mantiene igual sin importar el orden en que se cuentan.
Pregunta clave
• ¿Tiene importancia por dónde comenzaron a contar?
Criterio de logro académico
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos. (K.CC.B.4.b)
PC Parcialmente competente C Competente AC Altamente competente
23
23
LECCIÓN
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Conteo y cardinalidad
Agenda
Fluidez 5 min
Presentar 10 min
Aprender 25 min
• Punto de partida
• Volcar y contar
• Grupo de problemas
Concluir 10 min
Materiales
Maestro o maestra
• guantes numerados derecho e izquierdo
• página de Demostración (en la edición para la enseñanza)
• crayón
Estudiantes
• vaso (por pareja de estudiantes)
• frijoles de dos colores (entre 6 y 10 por pareja de estudiantes)
• plantilla de trabajo
• libro para estudiantes
• crayón
Preparación de la lección
• Cada pareja de estudiantes necesita 1 vaso con 6 a 10 frijoles. Varíe el número de frijoles de los vasos para que las parejas puedan intercambiarlos y practicar cómo contar diferentes cantidades.
• Prepare la página de Demostración para usar en la actividad Grupo de problemas.
© Great Minds PBC 285 EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 23
Fluidez
Contar hasta el 10 en el guante numerado
Materiales: M) Guantes numerados derecho e izquierdo
La clase cuenta en el guante numerado para desarrollar fluidez con la formación de una nueva unidad con cinco y para familiarizarse con el conteo con el método matemático.
Observen mi guante numerado y cuenten en voz alta. ¿Comenzamos?
Use el guante numerado para mostrar la siguiente secuencia mientras la clase cuenta en voz alta:


Facilite más práctica para contar en el guante numerado hasta el 10, haciendo énfasis cuando pasen por el 5. Haga hincapié en el cinco mostrando y escondiendo la mano izquierda (detrás de la espalda).
Si la clase tiene dificultades con la secuencia hasta el 10, regrese a una secuencia hasta el 5 y, luego, suba gradualmente hasta el 10.
Muéstramelo de otra manera: El 6 y el 7
La clase representa números con los dedos de diferentes maneras como preparación para el trabajo con conservación.
Muéstrenme 6 con el método matemático. (La clase muestra 6 con los dedos usando el método matemático).
3 4 5 6
5 6 7 8 7 8
9 10 9 10
5 10 25
K ▸ M1 ▸ TE ▸ Lección 23 EUREKA MATH2 © Great Minds PBC 286
10
Ahora, muéstrenme otra manera de formar 6. ¡La que más les guste!
(La clase muestra 6 con los dedos de otra manera).
Cierren las manos. Muéstrenme 6 de otra manera.
Continúe pidiendo a la clase que muestre 6 con los dedos de diversas maneras algunas veces más.
Repita el proceso con 7.
A medida que el total aumenta más allá del 6, las combinaciones posibles con las manos son cada vez menos. Por ejemplo, no se puede mostrar 7 con 6 en una mano y 1 en la otra. La actividad Muéstramelo de otra manera no continúa más allá del 8 porque solo es posible una combinación numérica para los totales de 9 y 10.
Presentar
La clase analiza dos imágenes para determinar si contienen el mismo número de objetos.
Reúna a la clase y muestre las imágenes de fichas cuadradas.
La marioneta hizo esta figura con fichas cuadradas. (Señale el cuadrado grande). Muestren los pulgares hacia arriba cuando sepan cuántas fichas cuadradas usó la marioneta.
Espere a que la mayor parte de la clase muestre los pulgares hacia arriba y, luego, pida que respondan a coro.
¿Cuántas fichas cuadradas hay en la figura que hizo la marioneta?
9 fichas cuadradas
La marioneta se alejó por un momento de la plantilla de trabajo. Cuando regresó, encontró esta figura. (Señale la imagen de la derecha).
DUA: Acción y expresión


Considere brindar cubos Unifix para construir figuras y que la clase pueda explorar la pregunta. El color del cubo es clave para responder la pregunta. Proporcione 3 cubos azules, 3 verdes y 3 rojos.


5 10 25 10
EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 23 © Great Minds PBC 287
¿Qué les parece que sucedió? ¿Piensan que alguien sacó o agregó algunas fichas cuadradas?
¿O tal vez el número de fichas no cambió para nada?
Invite a la clase a usar la rutina Pensar-Trabajar en parejas-Compartir para analizar las siguientes preguntas.
(Señale la imagen de la derecha). ¿Podrían hacer la segunda figura usando las fichas cuadradas de la marioneta? ¿Cómo lo saben?
Escuche y promueva todas las explicaciones sin reconocer la respuesta correcta. Una parte de la clase quizá vea que ambas figuras están hechas con las mismas fichas cuadradas, ya sea porque se enfocaron en el número de fichas que hay en cada figura o porque visualizaron el movimiento de las fichas para formar la segunda figura. Otra parte quizá se enfoque en la longitud del lado o el aspecto y piense que la segunda figura no se puede crear usando las fichas cuadradas de la marioneta.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición. Sus explicaciones me ayudan a comprender su razonamiento. Hoy, pensemos un poco más sobre cuántas fichas cuadradas hay en la nueva figura.
Aprender
Punto de partida
10

25 10
La clase usa diferentes estrategias de conteo y observa que el número de objetos es el mismo.
Muestre la imagen de la nueva figura.
Muestren los pulgares hacia arriba cuando sepan cuántas fichas cuadradas hay en esta figura.
Espere a que la mayoría muestre los pulgares hacia arriba y luego pida que respondan a coro.
¿Cuántas fichas cuadradas hay en esta figura?
9 fichas cuadradas
Nota para la enseñanza
Esta lección se enfoca en diferentes puntos de partida, porque son fáciles de marcar. Si la clase comienza a contar en diferentes lugares, toman diferentes estrategias de conteo. Para las y los estudiantes de corta edad puede ser complicado llevar la cuenta y comparar estrategias de conteo.
Gran parte de la conservación es comprender que el número de objetos es el mismo, sin importar cómo se organizan o el orden en el que se cuentan. La idea de que se puede llegar a la misma respuesta con estrategias diferentes es clave en las matemáticas de la escuela primaria. Esta lección da a la clase una de sus primeras oportunidades para experimentar ese concepto.
5
K ▸ M1 ▸ TE ▸ Lección 23 EUREKA MATH2 © Great Minds PBC 288
Invite a diferentes estudiantes a mostrar cómo contaron las fichas. Marque los puntos de partida.
Pregunte quiénes comenzaron a contar desde una ficha diferente. Invite a un par de estudiantes para que muestren cómo contaron y marque sus puntos de partida.
Tres personas diferentes comenzaron a contar las fichas desde tres lugares diferentes. ¿Cómo llegaron al mismo número de fichas?
El número de fichas era el mismo.
Las fichas no cambiaron. Eran las mismas para toda la clase.
Entonces, ¿el número de fichas es el mismo, sin importar dónde comenzamos a contar?
Sí.
Vamos a poner a prueba nuestra idea con un juego.

Volcar y contar
Materiales: E) Frijoles de dos colores, vaso, plantilla de trabajo
La clase pone a prueba la idea de que pueden usar diferentes estrategias de conteo y hallar que el número de objetos es el mismo.
Pida a la clase que ayude a representar cómo participar del juego Volcar y contar.
• Estudiante A: Vuelca todos los frijoles que están en el vaso en la plantilla de trabajo. Estudiante A: Cuenta los frijoles y dice cuántos hay.
• Estudiante B: Cuenta los frijoles comenzando con un frijol diferente y dice cuántos hay.
• Vuelven a colocar los frijoles en el vaso. Intercambian los vasos con otro grupo.

• Cambian los roles y repiten el juego.
Las parejas pueden mover los frijoles mientras cuentan. Esta práctica refuerza la idea de que mover los frijoles no cambia el número.
Una vez que hayan contado sus frijoles, pídales que los vuelvan a colocar en el vaso y que intercambien los vasos con otro grupo.
Evaluación observacional
; Observe mientras la clase cuenta frijoles desde un punto de partida y luego vuelve a contar desde un punto de partida diferente. Cuando pregunta “¿cuántos hay?”, ¿la clase puede simplemente decir el último número que contó las dos veces, o tiene que volver a contar una tercera vez?
EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 23 © Great Minds PBC 289
Después de que la clase haya intercambiado los vasos un par de veces, ayude a recordar la idea que han puesto a prueba.
Estamos poniendo a prueba la idea de que el número es el mismo, sin importar dónde comenzamos a contar. ¿Es esta afirmación verdadera para sus frijoles?
Sí. Marisol comenzó con estos frijoles y yo comencé con aquellos, pero los dos contamos 10 frijoles.
Grupo de problemas
Materiales: M) Página de Demostración, crayón
Para establecer una transición al Grupo de problemas, practique su rutina de repartir el libro para estudiantes y hallar la página correcta.
Use la página de Demostración para mostrar la actividad Grupo de problemas. Represente colorear el punto de partida, contar los peces y encerrar en un círculo el número relacionado en el camino numérico.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante reconoce y expresa regularidad en la lógica de la repetición (MP8) cuando pone a prueba que el número de frijoles es el mismo, sin importar dónde comienza a contar.
K M1 TE Lección 23 ▸ Demostración EUREKA MATH © Great Minds PBC 292 This page may be reproduced for classroom use only. 2 3 4 5 6 7 8 9 10 EUREKA MATH K ▸ M1 TE ▸ Lección 23 Great Minds PBC 71 Nombre Colorea el primer objeto. Cuenta encierra en un círculo cuántos hay en el camino numérico. 2 3 4 5 6 7 8 9 10 2 3 4 5 6 7 8 9 10 23
K ▸ M1 ▸ TE ▸ Lección 23 EUREKA MATH2 © Great Minds PBC 290
Concluir
Reflexión final 10 min
Materiales: E) Grupo de problemas
Objetivo: Conservar el número sin importar el orden en que los objetos se cuentan
Reúna a la clase y pídales que tengan a mano su Grupo de problemas. Pídales que señalen el primer círculo que contaron. Pida a la clase que use la rutina Pensar-Trabajar en parejas-Compartir para analizar las siguientes preguntas.
¿Comenzaste tu conteo en el mismo círculo que tu pareja?
¿Contaron el mismo número de círculos?
¿Tiene importancia por dónde comenzaron a contar? ¿Por qué?
No. No importa porque los círculos son los mismos sin importar de qué manera los cuentes. No lo creo. Contamos 8 círculos.
Seleccione estudiantes para que compartan sus respuestas. Si lo necesitan, use estas preguntas con los otros ejercicios de la actividad Grupo de problemas para consolidar la idea de que el número es el mismo, sin importar dónde comenzamos a contar.
10 25 10 EUREKA MATH K M1 TE Lección 23 Great Minds PBC 71 Nombre Colorea el primer objeto. Cuenta y encierra en un círculo cuántos hay en el camino numérico. 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 23 EUREKA MATH2 K ▸ M1 ▸ TE ▸ Lección 23 © Great Minds PBC 291
K ▸ M1 ▸ TE ▸ Lección 23 ▸ Demostración EUREKA MATH2 © Great Minds PBC 292 This page may be reproduced for classroom use only. 1 2 3 4 5 6 7 8 9 10
Tema F
Escribir numerales y crear grupos de hasta 10 objetos
El tema F brinda a la clase el ámbito para practicar cómo contar mientras aprenden a escribir los números 6, 7, 8, 9 y 10. La mezcla de contextos conocidos y nuevos anima a cada estudiante a desarrollar su independencia y, al mismo tiempo, participar activamente.
La estructura sistemática que tienen las lecciones en las que se aprende a escribir numerales ofrece un ámbito para practicar tipos de conteo nuevos. La clase cuenta cosas que suceden durante un determinado tiempo, como los saltos que realiza una persona o las carreras en un partido de beisbol, y observa que escribir números es una buena manera de registrar y recordar esa información. Después de preguntarles por qué escribimos números y de desarrollar una amplia lista de razones durante varias semanas, sus estudiantes comparten su razonamiento como una manera de celebrar que pueden escribir los numerales del 0 al 10.
Hacer secuencias y ordenar los números es un tema subyacente en todo el módulo. Al final del tema F, la clase está lista para aplicar su conocimiento sobre una secuencia numérica y razonar acerca de cómo se relacionan los números entre sí. Esto sienta las bases para el tema G, en el que la clase descubre patrones en la lista de palabras numéricas, y comprende específicamente que el nombre de cada número consecutivo se refiere a una cantidad que es uno más grande que la cantidad anterior (K.CC.B.4.c).
Sus estudiantes cuentan un grupo dibujando y encerrando en un círculo los objetos de una imagen.
Lista de compras 7 zanahorias Encierra 7 en un círculo. ¿ ?
La clase responde la pregunta: “¿Por qué escribimos números?”.
© Great Minds PBC 293
Progresión de las lecciones
Lección 24
Contar un grupo de objetos para emparejarlos con un numeral Lista de compras 7 zanahorias
Dibujé 7 zanahorias.
Lección 25
Escribir los numerales 6 y 7
Lección 26
Escribir el numeral 8
Puedo escribir el 6 y el 7.
Puedo escribir el 8.
294 K ▸ M1 ▸ TF EUREKA MATH2 © Great Minds PBC
Lección 27
Escribir los numerales 9 y 10
Lección 28
Ordenar los numerales del 1 al 10 y razonar acerca de un número desconocido en una secuencia numérica
1 2 3 5
Sé cuál es el número que falta porque los números están en orden.
Puedo escribir el 9 y el 10.
EUREKA MATH2 K ▸ M1 ▸ TF 295 © Great Minds PBC
Contar un grupo de objetos para emparejarlos con un numeral
Vistazo a la lección
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
En esta lección se repasa la dramatización de la escena del restaurante de la lección 10, en la que la clase contó un grupo de objetos para emparejarlos con un número del 1 al 5. En esta lección se extiende el trabajo hasta el 10. Ahora que la clase puede contar un grupo de hasta 10 objetos con precisión y reconocer los numerales del 6 al 10, está lista para crear grupos más grandes.
Pregunta clave
• ¿Cómo podemos recordar cuándo debemos dejar de contar?
Criterio de logro académico
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande. (K.CC.B.5)
24
LECCIÓN 24
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 15 min
Presentar 5 min
Aprender 25 min
• Contar un conjunto
• Grupo de problemas
Concluir 5 min
Materiales
Maestro o maestra
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 6 al 10)
Estudiantes
• Plantilla de grupos de 5 (en el libro para estudiantes)
• cubos Unifix® (10)
• tarjetas para emparejar (1 juego por pareja de estudiantes)
• tarjetas Hide Zero® (1 juego del 6 al 10 por pareja de estudiantes)
• plato (1 por pareja de estudiantes)
• libro para estudiantes
Preparación de la lección
• Prepare las plantillas de grupos de 5.
• Prepare los juegos de tarjetas para emparejar. Haga juegos de 22 tarjetas por pareja de estudiantes que incluyan dos tarjetas de cada cantidad, del 0 al 10.
• Prepare las tarjetas del 6 al 10 del juego para demostración de las tarjetas Hide Zero.
• Revise el menú proporcionado en los recursos digitales de esta lección. Considere ajustarlo para incorporar alimentos culturalmente conocidos.
© Great Minds PBC 297 EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 24
Fluidez
Muéstrame grupos de 5: Del 5 al 10
Materiales: E) Plantilla de grupos de 5, cubos Unifix
La clase coloca cubos en grupos de 5 para desarrollar la comprensión de los números del 6 al 10 como 5 y algunos más.

A lo largo de esta actividad, anime a la clase a añadir cubos Unifix de izquierda a derecha para que puedan ver la formación de grupos de 5.
Juguemos Muéstrame grupos de 5. Yo digo un número y ustedes lo muestran con cubos. Usen la plantilla como ayuda para formar un grupo de 5.
Muéstrenme 5.
(La clase coloca 5 cubos sobre la plantilla y completa la fila superior).
Muéstrenme 6.
(La clase coloca un cubo sobre el punto inferior izquierdo).
Muéstrenme 7.
(La clase coloca otro cubo sobre la plantilla, sin saltearse ningún punto, para obtener un total de 2 cubos en la fila inferior).
Continúe hasta el 10, en orden.
Nota para la enseñanza
La primera vez que la clase participe de Muéstrame grupos de 5, habrá quienes cuenten desde el 1 cada vez que diga un número nuevo. La secuencia sugerida en esta lección requiere que agreguen 1 cubo más cada vez. Observe quiénes descubrieron este patrón y pídales que expliquen por qué no necesitaron contar desde el 1.
15 5 25 5
K ▸ M1 ▸ TF ▸ Lección 24 EUREKA MATH2 © Great Minds PBC 298
Emparejar: Conjuntos y numerales
Materiales: E) Tarjetas para emparejar
La clase cuenta conjuntos y empareja un numeral con un conjunto para conservar la fluidez con la correspondencia de uno a uno y una comprensión de la cardinalidad.

Pida a la clase que trabaje en parejas. Distribuya un juego de tarjetas a cada pareja y pídales que jueguen de acuerdo con las siguientes reglas. Considere hacer una ronda de práctica con la clase.
• Coloquen seis tarjetas.
• Estudiante A: Selecciona las tarjetas que coinciden. Si las tarjetas no coinciden, use un procedimiento eficiente para resolver la situación (p. ej., sacar una tarjeta adicional hasta lograr que coincidan).
• Estudiante B: Comprueba su trabajo y da una felicitación (p. ej., “¡Buen trabajo!”) o una sugerencia (p. ej., “Intenta usar la estrategia de tocar y contar”).
• Dejen las tarjetas emparejadas a un lado y reemplácenlas con dos tarjetas nuevas de la pila.
• Continúen hasta que todas las tarjetas estén emparejadas y cambien de roles en cada turno. Recorra el salón de clases mientras se desarrolla el juego y proporcione apoyo según sea necesario. Por ejemplo, las parejas de estudiantes podrían necesitar apoyo para dar sugerencias adecuadas. En ese caso, pregunte si tienen una sugerencia, como usar la estrategia de tocar y contar.
Presentar
Materiales: M) Tarjetas Hide Zero
La clase recuerda un número determinado mientras realiza muchas tareas al mismo tiempo.
Muestre a modo de juego la tarjeta del 7 el tiempo suficiente como para que la clase la reconozca y, luego, retírela de la vista.
Diferenciación: Desafío
Cuando la clase esté lista, considere hacer cualquiera de las siguientes adaptaciones al juego para aumentar el desafío:
• Disponga ocho tarjetas en dos filas de cuatro para desarrollar la capacidad de clasificar con más información visual.
• Invite a sus estudiantes a hallar dos tarjetas que formen 5 u otro número determinado.
EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 24 © Great Minds PBC 299
0 9 15 5 25 5
Digan el número.
7
Recuerden ese número y salten hasta que diga alto. ¿Comenzamos? ¡Salten! ¡Alto! ¿Cuál era el número?
7
Vamos a comprobarlo.
Levante la tarjeta para verificar el número y celebre. Apláudanse 7 veces por haber recordado que el número era el 7.
Repita el proceso. Esta vez, muestre la tarjeta del 8 y pida a la clase que salte 8 veces.
Continúe con el 6, el 9 y el 10 usando diversos ejercicios (p. ej., dar pisotones, ponerse en cuclillas, saltar en un pie) para mantener una participación activa.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición. Vamos a practicar cómo contar cubos para emparejar con los números de las tarjetas.
Aprender
Contar un conjunto
Materiales: E) Cubos Unifix, tarjetas Hide Zero, plato
La clase reconoce los numerales y cuenta un conjunto para emparejarlo con el numeral.
Muestre el menú. Recuerde a la clase la situación en el restaurante de la lección 10 y dramatice un diálogo entre una clienta y un empleado. Use el siguiente intercambio como guía.
La clienta se acerca a la ventanilla del restaurante. El empleado saluda a la clienta y le pregunta qué va a ordenar.
Nota para la enseñanza
Contar un grupo requiere realizar muchas tareas al mismo tiempo. La clase debe recordar el número determinado mientras dice las palabras numéricas en orden y pone atención a la correspondencia de uno a uno. Este ejercicio ofrece la oportunidad de practicar cómo recordar un número a pesar de diversas distracciones.
Desarrollo del lenguaje
Brinde apoyo durante la dramatización con esquemas de oraciones que sean adecuados para cada estudiante. Relacione las matemáticas con el contexto al representar y animar el diálogo natural que la clase usaría en el mundo real. La longitud de las oraciones se puede modificar para cumplir con los objetivos lingüísticos.
• ¿Cuántas desea ordenar?
• ¿Cuántas ?
• Llevaré 8 , por favor.
• 8 , por favor.
15 5 25 5
Uvas Galletas Zanahorias K ▸ M1 ▸ TF ▸ Lección 24 EUREKA MATH2 © Great Minds PBC 300
Menú
¿Cuántas uvas desea ordenar?
La clienta entrega da una tarjeta Hide Zero y dice qué va a ordenar. Quisiera 8 uvas, por favor.
El empleado cuenta un conjunto de 8 cubos y los coloca sobre el plato. La clienta cuenta para comprobar. Prepare a quienes compran y quienes venden para hacer correcciones amables.
Usted pidió 8. Esta tarjeta dice 6. Por favor, inténtelo de nuevo. Eso no es lo que ordené. Por favor, inténtelo de nuevo.
Después de esta representación, invite a la clase a realizar una dramatización. Forme parejas de estudiantes y distribuya los materiales. Cambie los roles ocasionalmente para que cada estudiante tenga la oportunidad de contar un conjunto.
Recorra el salón de clases y observe. Según sea necesario, haga correcciones precisas:
• Recuerden el número de la tarjeta. Dejen de contar cuando lleguen a ese número.
• Tienes demasiadas uvas; cuenta otra vez.
• Necesitas 2 más para llegar a 8 uvas.
Grupo de problemas
Materiales: E) Cubos Unifix
Los primeros ejercicios del Grupo de problemas requieren que la clase represente un número de alimentos. Pueden dibujar o usar sellos. Si fuera necesario, permita que, para empezar, usen o dibujen fichas para contar. Brinde apoyo a quienes dibujen una cantidad equivocada al principio; empiece haciendo preguntas que les permitan considerar distintas maneras de resolver el problema:
• Tienen 8 zanahorias. ¿Deben tachar algunas o dibujar más?
• Dibujaron demasiadas zanahorias. ¿Qué pueden hacer para que su dibujo muestre 7 zanahorias?
• No hay suficientes zanahorias. ¿Cómo pueden mostrar 7?
Evaluación observacional
; Observe cómo quienes venden cuentan la cantidad necesaria.
• ¿El número determinado coincide con la cantidad de alimentos que reciben quienes compran?
• ¿Quienes venden necesitan volver a contar una o dos veces?
EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 24 © Great Minds PBC 301
Los problemas de la segunda página del Grupo de problemas requieren que la clase cuente y encierre en un círculo un grupo para emparejarlo con el número que se muestra. Por ejemplo, deben encerrar en un círculo un grupo de 7 zanahorias. Si necesitan apoyo para encerrar en un círculo la cantidad correcta, sugiera usar la estrategia de marcar y contar para que los objetos que forman parte del grupo sean fáciles de ver.
Encierra 7 en un círculo.
Encierra 6 en un círculo.
Encierra 8 en un círculo.
Encierra 10 en un círculo.
Encierra 9 en un círculo.
Concluir
Reflexión final 5 min
Objetivo: Contar un grupo de objetos para emparejarlos con un numeral
Reúna a la clase y pídales que tengan a mano su Grupo de problemas. Muestre la primera página y pídales que pongan un dedo sobre las zanahorias.
¿Qué dibujaron para mostrar las zanahorias?
Círculos
Nota para la enseñanza
Este Grupo de problemas está diseñado para usar la representación sistemática (consulte la lección 8 para obtener más detalles).
Considere ofrecer a la clase sellos o pegatinas como alternativa a hacer dibujos en la primera página.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante representa a través de las matemáticas (MP4) cuando hace dibujos para mostrar 7 zanahorias, 6 fresas, etc. Pedir a la clase que modifique sus dibujos si muestran el número incorrecto les ayuda a desarrollar el importante hábito de revisar un modelo.
© Great Minds PBC 77 EUREKA MATH K ▸ M1 TF ▸ Lección 24
Nombre Lista de compras 7 zanahorias 6 fresas 8 champiñones 10 arándanos 9 guisantes K ▸ M1 ▸ TF ▸ Lección 24 EUREKA MATH2 © Great Minds PBC 78 GRUPO DE PROBLEMAS
24
5
5 K ▸ M1 ▸ TF ▸ Lección 24 EUREKA MATH2 © Great Minds PBC 302
Líneas 15
25
Vamos a contar las zanahorias. A medida que contamos, digamos qué estamos contando. Como estamos contando zanahorias, diremos 1 zanahoria, 2 zanahorias y así sucesivamente hasta que las hayamos contado todas.
1 zanahoria, 2 zanahorias, 3 zanahorias, 4 zanahorias, 5 zanahorias, 6 zanahorias, 7 zanahorias
¿Cómo supieron cuándo dejar de dibujar zanahorias?
Las conté mientras dibujaba cada una.
Miré el número 7 y conté mis zanahorias para asegurarme de que hubiera 7.
Si completaron ambas páginas, invite a la clase a que se reúna y converse en parejas acerca de las siguientes preguntas.
¿Qué fue más fácil: dibujar 7 zanahorias o encerrar en un círculo 7 zanahorias? ¿Por qué?
¿Qué hicieron para asegurarse de encerrar en un círculo el número correcto de zanahorias? Muéstrenselo
a su pareja de trabajo. Great Minds PBC 77 EUREKA MATH K M1 ▸ TF Lección 24 24 Nombre Lista de compras 7 zanahorias 6 fresas 8 champiñones 10 arándanos 9 guisantes K ▸ M1 TF ▸ Lección 24 EUREKA MATH © Great Minds PBC 78 GRUPO DE PROBLEMAS Encierra 7 en un círculo. Encierra 6 en un círculo. Encierra 8 en un círculo. Encierra 10 en un círculo. Encierra 9 en un círculo. EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 24 © Great Minds PBC 303
Escribir los numerales 6 y 7
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
La clase considera por qué se escriben los numerales mientras aprenden a escribir el 6 y el 7. Se enfocan en escribir los numerales para recordar cuántas veces sucede algo.
Pregunta clave
• ¿Por qué escribimos los números?
Criterio de logro académico
K.Mód1.CLA2 Escriben los números del 0 al 10. (K.CC.A.3)
25
LECCIÓN 25
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 5 min
Presentar 10 min
Aprender 25 min
• Escritura en el aire y en una alfombra
• Escribir los numerales
• Número bip
Concluir 10 min
Materiales
Maestro o maestra
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 0 al 7)
• papel de rotafolio
• marioneta o pelota
• afiche de ¿Por qué escribimos los números?, de la lección 11
Estudiantes
• Plantilla de grupos de 5
• cubos Unifix® (10)
• libro para estudiantes
Preparación de la lección
• Prepare las plantillas de grupos de 5.
• Prepare las tarjetas del 0 al 7 del juego para demostración de las tarjetas Hide Zero.
• Considere retirar la página de escritura de numerales y colocarla en una pizarra blanca individual.
© Great Minds PBC 305 EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 25
Fluidez
Muéstrame grupos de 5: Del 10 al 5
Materiales: E) Plantilla de grupos de 5, cubos Unifix
La clase coloca cubos en grupos de 5 para desarrollar la comprensión de los números del 6 al 10 como 5 y algunos más.


A lo largo de la actividad, anime a la clase a añadir cubos Unifix de izquierda a derecha para que puedan ver la formación de grupos de 5.
Juguemos Muéstrame grupos de 5. Yo digo un número y ustedes lo muestran con cubos. Usen la plantilla como ayuda para formar un grupo de 5.
Muéstrenme 10.
(La clase coloca 10 cubos sobre la plantilla y completa las filas superior e inferior).
Muéstrenme 9.
(La clase retira un cubo del punto inferior derecho).
Muéstrenme 8.
(La clase retira el siguiente cubo de la fila inferior sin saltearse ninguno).
Continúe hasta el 5 en orden. Observe a la clase para ver quiénes deben contar desde el 1 cada vez.
Dedos a la vista: El método matemático con el 5, el 6 y el 7
La clase dice cuántos dedos ve para desarrollar la capacidad de reconocer cantidades del 6 al 10 como 5 y algunos más.
Voy a mostrarles algunos dedos con el método matemático, pero solo por un segundo. Ustedes me dirán el número que ven. ¡Miren con atención!
Inclínese hacia delante, establezca contacto visual, haga una pausa con teatralidad y, luego, muestre por un instante 5 dedos con el método matemático. Ocúltelos.
Nota para la enseñanza
Habrá quienes cuenten desde el 1 cada vez que diga un número nuevo. La secuencia sugerida en esta lección requiere que muestren 1 cubo menos cada vez. Observe quiénes descubrieron este patrón y pídales que expliquen por qué no necesitaron contar desde el 1.
5 10 25 10
K ▸ M1 ▸ TF ▸ Lección 25 EUREKA MATH2 © Great Minds PBC 306
¿Cuántos dedos vieron?
Prepárense. Aquí viene el siguiente.
Muestre por un instante 6 dedos con el método matemático. Ocúltelos.
¿Cuántos dedos vieron?
Continúe el proceso con la siguiente secuencia:

Presentar
Materiales: M) Tarjetas Hide Zero, papel de rotafolio
La clase desarrolla la necesidad de escribir los numerales.
Comparta el procedimiento del juego Saltar el número secreto:
• El maestro o la maestra muestra a un o una estudiante un número secreto.
• El o la estudiante salta esa cantidad de veces mientras el resto de la clase cuenta.
• Cuando el maestro o la maestra da una señal, la clase dice el número secreto.
Invite a tres o cuatro estudiantes a jugar. Haga una pausa para ver si la clase recuerda cuántas veces saltó cada estudiante.
¿Cuántas veces saltó Jahari? ¿Y Neelia?
Creo que 3. ¿O fueron 4?
No lo recordamos.
Se está haciendo más difícil recordarlo. Escribamos cuántas veces salta cada persona. Cuando debemos recordar muchos números, podemos escribirlos como ayuda.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante razona de forma abstracta y cuantitativa (MP2) al descontextualizar el uso de numerales para representar cuántas veces saltan sus pares. Luego, contextualizan los numerales al recordar que se refieren a cuántas veces saltó cada estudiante.

5
6
7 5 7 5 7 5 6 5 6 5
5 10 25 10
EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 25 © Great Minds PBC 307
Escriba en el papel de rotafolio los nombres de quienes saltaron. Use la memoria de la clase y las tarjetas Hide Zero para escribir el número de veces que saltó cada persona.
Invite a saltar a más estudiantes hasta que se hayan usado todas las tarjetas. Esta vez, registre sus nombres y el número de saltos en el papel de rotafolio.
Miren el afiche. ¿Cuántas veces saltó Amyra? (Señale el nombre de la persona en el afiche).
¿Por qué es importante escribir el número después de que cada persona salte?
Para poder recordar los números fácilmente.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición. Ya tienen experiencia en escribir la mayoría de los números en nuestro afiche: el 0, el 1, el 2, el 3, el 4 y el 5. Hoy, aprenderemos cómo escribir los números 6 y 7.
Cubra el afiche o retírela de la vista, pero téngala a disposición para mostrarla nuevamente en la sección Concluir.
Aprender
Escritura en el aire y en una alfombra
Materiales: M) Marioneta o pelota
La clase aprende los trazos básicos para escribir los numerales 6 y 7.
Sostenga la pelota en el aire y escriba el numeral 6. Empiece desde arriba mientras dice la rima. Anime a la clase a seguir sus movimientos sin doblar el brazo.
Bajo recto y hago un rulito. El 6 parece el rabo de un cerdito.
Pida a la clase que traslade los dedos que usan para contar a la alfombra o a otra superficie que puedan tocar. Repita la rima mientras la clase escribe el 6 sobre la nueva superficie.
DUA: Representación
Pedir a la clase que mueva un brazo en el aire o que mueva los dedos sobre una alfombra u otra superficie que pueda tocar para simular que escriben numerales presenta la información de diversos modos. Esto brinda maneras adicionales de procesar y retener la información.
5 10 25 10
K ▸ M1 ▸ TF ▸ Lección 25 EUREKA MATH2 © Great Minds PBC 308
Repita el mismo proceso con el numeral 7.
Atravieso el cielo y luego bajo al suelo. Un aplauso para el 7, ¡qué gran vuelo!
Escribir los numerales
Materiales: E) Página de escritura de numerales
La clase dibuja y escribe los numerales 6 y 7.
Distribuya el trabajo en clase y los útiles de escritura. Invite a la clase a hallar el numeral 6 en la página. Una vez que hayan colocado los dedos sobre el numeral 6, pídales que digan la rima en conjunto, mientras dibujan el numeral con los dedos.
Demuestre cómo escribir el 6. Luego, invite a la clase a usar un lápiz o un crayón para escribir el 6 hasta completar la fila. Si hay tiempo suficiente, pídales que dibujen 6 círculos dentro del recuadro.
Repita el proceso con el numeral 7.
Número bip
La clase practica la secuencia de los números hasta el 7.
Pida a la clase que se ponga de pie para jugar Número bip.
¡Juguemos Número bip! Voy a contar, pero, en lugar de decir uno de los números, voy a decir bip. Levanten la mano cuando sepan el número bip. ¿Comenzamos?
3, 4, 5, bip (Dé la señal).
6
4, 5, 6, bip (Dé la señal). 7
3, 4, bip, 6 (Dé la señal). 5
4, 5, bip, 7 (Dé la señal).
Nota para la enseñanza
Considere retirar la página de escritura de numerales y colocarla en una pizarra blanca individual para volver a usarla para practicar.
Evaluación observacional
; Observe a sus estudiantes mientras escriben.
• ¿Comienzan en el punto y se mantienen dentro del rectángulo de escritura?
Diferenciación: Apoyo
Si sus estudiantes tienen dificultades con la secuencia verbal en Número bip, considere pedirles que sigan el camino numérico con los dedos.
6
EUREKA MATH K ▸ M1 TF ▸ Lección 25 Great Minds PBC 79 Nombre 25
EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 25 © Great Minds PBC 309
Si hay tiempo suficiente, invite a la clase a completar las secuencias numéricas ubicadas en la parte inferior de la página de escritura de numerales. Trabajen en grupo en la primera secuencia, como si jugaran Número bip en el papel. Marque con el dedo y diga los números que se muestran. Diga bip para los espacios.
Concluir
Reflexión final 10 min
Materiales: M) Afiche de ¿Por qué escribimos números?
Objetivo: Escribir los numerales 6 y 7
Reúna a sus estudiantes y recuérdeles el juego del número secreto que jugaron en la sección Presentar. Sin mostrar el afiche, haga la siguiente pregunta.
¿Cuántas veces saltó Tyler?
No lo recordamos.
Creo que 4 o 5 veces.
¿Qué hicimos para ayudarnos a recordar?
Lo anotamos.
Muestre el afiche de la sección Presentar. Pregunte cuántas veces saltaron diferentes estudiantes. Deje que la clase consulte el afiche para responder.
Muestre o señale el afiche de ¿Por qué escribimos números?, que comenzaron en la lección 11.
¿Por qué escribimos números?
Para ayudarnos a recordar cosas
Es más fácil que dibujar 6 o 7 cosas.
Agregue ideas nuevas al afiche.
¿ ?
5 10 25 10
K ▸ M1 ▸ TF ▸ Lección 25 EUREKA MATH2 © Great Minds PBC 310
LECCIÓN 26
Escribir el numeral 8
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
La clase sabe que los numerales escritos nos indican cuántos o cuántas hay, son más eficientes que los dibujos y nos ayudan a recordar cantidades. Continúan explorando las razones por las que las personas escriben los numerales mientras aprenden a escribir el 8. Descubren que, cuando cuentan los brazos y las patas de los animales, es útil escribir el número de extremidades en lugar de contarlos muchas veces.
Pregunta clave
• ¿Por qué escribimos números?
Criterios de logro académico
K.Mód1.CLA1 Cuentan hasta el 10. (K.CC.A.1)
K.Mód1.CLA2 Escriben los números del 0 al 10. (K.CC.A.3)
© Great Minds PBC 26
390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 10 min
Aprender 25 min
• Escritura en el aire y en una alfombra
• Escribir los numerales
• Número bip
• Grupo de problemas
Concluir 5 min
Materiales
Maestro o maestra
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 0 al 7)
• papel de rotafolio
• marioneta o pelota
• afiche de ¿Por qué escribimos números?
Estudiantes
• Plantilla de grupos de 5
• cubos Unifix® (10)
• libro para estudiantes
Preparación de la lección
• Prepare las plantillas de grupos de 5.
• Prepare las tarjetas del 0 al 7 del juego para demostración de las tarjetas Hide Zero.
• Prepare una bolsita resellable con 10 cubos Unifix del mismo color para cada estudiante.
• Considere retirar la página de escritura de numerales y colocarla en una pizarra blanca individual.
© Great Minds PBC 313 EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 26
Fluidez
Muéstrame grupos de 5: El 5 y el 10
Materiales: E) Plantilla de grupos de 5, cubos Unifix
La clase coloca cubos en grupos de 5 para desarrollar la comprensión de los números del 6 al 10 como 5 y algunos más.

A lo largo de la actividad, anime a la clase a añadir cubos Unifix de izquierda a derecha para que puedan ver la formación de grupos de 5.
Juguemos Muéstrame grupos de 5. Yo digo un número y ustedes lo muestran con cubos. Usen la plantilla como ayuda para formar un grupo de 5.
Muéstrenme 5.
(La clase coloca 5 cubos sobre la plantilla y completa la fila superior).
Muéstrenme 10.
(La clase coloca 5 cubos más sobre la plantilla y completa la fila inferior).
Muéstrenme 5.
(La clase retira los 5 cubos de la fila inferior).
Muéstrenme 10.
(La clase vuelve a colocar 5 cubos en la fila inferior).
Para que sea entretenido, alterne entre el 5 y el 10 para retirar o completar una fila de 5 de una vez.
Nota para la enseñanza
Muéstrame grupos de 5: El 5 y el 10 hace énfasis en la estructura de los grupos de 5. Esta estructura ayuda a las y los estudiantes de corta edad a visualizar cantidades del 6 al 10.
Esta actividad sencilla ayuda a sus estudiantes a formar una nueva unidad con 5 o a trabajar con un grupo de 5 cubos como una unidad en lugar de trabajar con cubos individuales. Pueden ver el 10 como dos filas, o unidades, de 5. Este razonamiento promueve la comprensión de la relación de parte-total y sienta las bases para las estrategias de nivel 2 de contar desde un número.
K ▸ M1 ▸ TF ▸ Lección 26 EUREKA MATH2 © Great Minds PBC 314
10 10 25 5
Contar hasta el 7: ¿Qué número sientes en la espalda?
Materiales: M) Tarjetas Hide Zero
Cada estudiante dibuja un número y adivina un numeral para desarrollar la memoria cinestésica necesaria para formar números.
Juguemos ¿Qué número sientes en la espalda?
Pida a la clase que trabaje en parejas. Cada integrante de la pareja se colocará en fila, mirando hacia delante. Quien esté detrás será quien escriba. Quien esté delante será quien adivine. Párese detrás de la clase, mirando hacia la espalda de cada estudiante, y muestre la tarjeta del 6.
Estudiantes que escriben, dense vuelta y observen mi número, pero no lo digan. ¡Guarden el secreto! Escriban este número con el dedo en la espalda de su compañero o compañera. Usen toda la espalda para que puedan escribir un número grande y bonito.
Estudiantes que adivinan, ¿se dieron cuenta de qué número les escribieron en la espalda?
Parejas de estudiantes, dense vuelta y observen mi número. Si acertaron, ¡denme 6 aplausos!
Continúe con los numerales recién aprendidos, el 6 y el 7, y con cualquier otro que presente un desafío para sus estudiantes. Felicite a la clase con el número correspondiente de aplausos. Ahora que los números son más altos, invite a sus estudiantes a contar mientras aplauden. Después de un tiempo, pida a las parejas que cambien los roles.
Diferenciación: Apoyo
Si hay estudiantes que necesitan apoyo para escribir, pueden decir la rima de formación de numerales mientras dibujan.
Si hay estudiantes que necesitan apoyo para adivinar, quienes escriben pueden hacerlo en las manos de quienes adivinan, para que puedan sentir y ver el numeral. Ajuste la disposición de los asientos según sea necesario. Si alguien sintiera incomodidad con tocar, se puede jugar escribiendo en el aire o en la alfombra.
EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 26 © Great Minds PBC 315
6
Presentar
Materiales: M) Papel de rotafolio
La clase cuenta las patas y los brazos de los animales y dicen cuántos y cuántas hay.
Reúna a sus estudiantes y dígales que harán un viaje imaginario al zoológico. Si hay tiempo suficiente, pídales que se sienten como si estuviesen viajando en un tren.
Mientras viajamos en tren por el zoológico, deben contar el número de brazos y patas que tiene cada animal.
Muestre la imagen del avestruz.
Levanten la mano si saben el nombre de este animal. Avestruz

¿Cuántos brazos y cuántas patas tiene el avestruz?
2
Registre el nombre del animal y el número total de brazos y patas en el papel de rotafolio. Pida a sus estudiantes que digan las rimas para escribir los números mientras escribe cada numeral.
Continúe contando y registrando el número de patas con las imágenes de la jirafa, la garza negra, el mono, la víbora, la estrella de mar y el pulpo.
Cuando llegue a la imagen del pulpo, exprese la necesidad de escribir el numeral 8 para establecer una transición al siguiente segmento.
Necesitamos aprender cómo escribir el número 8 para poder escribir que el pulpo tiene 8 brazos.
Diferenciación: Desafío
Anime a sus estudiantes a clasificar los animales según el número de brazos y patas que tengan. Una vez que hayan clasificado una docena de animales o más, pídales que busquen patrones. En anatomía, la simetría es muy común y muchos animales tienen un número par de brazos y patas. Anime a sus estudiantes a investigar y aprender más acerca de la anatomía de los animales para comprender mejor los patrones que hallan.
K ▸ M1 ▸ TF ▸ Lección 26 EUREKA MATH2 © Great Minds PBC 316
10 10 25 5
Aprender
Escritura en el aire y en una alfombra
Materiales: M) Marioneta o pelota
La clase aprende los trazos básicos para escribir el numeral 8.
Sostenga la pelota en el aire y escriba el numeral 8. Empiece desde arriba mientras dice la rima. Anime a la clase a seguir sus movimientos sin doblar el brazo.
Hago una S que no se detiene. El trazo sube para que el 8 llegue.
Pida a la clase que traslade los dedos que usan para contar a la alfombra o a otra superficie que puedan tocar. Repita la rima mientras la clase escribe el 8 sobre la nueva superficie.
Si sus estudiantes necesitan más práctica con los numerales del 1 al 7, cuando tenga tiempo adicional practique o repase las rimas para escribir esos numerales.
Escribir los numerales
Materiales: E) Página de escritura de numerales
La clase dibuja y escribe el numeral 8.
Distribuya el trabajo en clase y los útiles de escritura. Invite a la clase a hallar el numeral 8 en la página. Una vez que hayan colocado los dedos sobre el numeral 8, pídales que digan la rima en conjunto, mientras dibujan el numeral con los dedos.
Demuestre cómo escribir el 8. Luego, invite a la clase a usar un lápiz o un crayón para escribir el 8 hasta completar la fila. Si hay tiempo suficiente, pida a sus estudiantes que dibujen un animal que tenga 8 brazos u ocho patas dentro del rectángulo.
Evaluación observacional
; Observe a sus estudiantes mientras escriben.
• ¿Pueden escribir los numerales con precisión?
• ¿Pueden completar los números que faltan correctamente? (secuencia numérica)
EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 26 © Great Minds PBC 317
10 10 25 5 EUREKA MATH M1 TF Lección 26 © Great Minds PBC 81 Nombre 26
Número bip
La clase practica la secuencia de los números hasta el 8. Pida a la clase que se ponga de pie para jugar Número bip.
¡Juguemos Número bip! Voy a contar, pero, en lugar de decir uno de los números, voy a decir bip. Levanten la mano cuando sepan el número bip. ¿Comenzamos?
5, 6, 7, bip (Dé la señal).
8
5, 6, bip, 8 (Dé la señal).
7
5, bip, 7, 8 (Dé la señal).
6 Bip, 6, 7, 8 (Dé la señal).
5 Si hay tiempo suficiente, invite a la clase a completar las secuencias numéricas ubicadas en la parte inferior de la página de escritura de numerales. Trabajen en grupo en la primera secuencia, como si jugaran Número bip en el papel. Marque con el dedo y diga los números que se muestran. Diga bip para los espacios.
Grupo de problemas
Para establecer una transición al Grupo de problemas, practique su rutina de repartir el libro para estudiantes y hallar la página correcta.
Invite a sus estudiantes a contar el número de brazos y patas en cada recuadro y a escribir el numeral en el rectángulo de escritura. Anticipe las preguntas sobre los problemas de la vaca y la gaviota. Anime a la clase a contar las patas de todos los animales de cada recuadro.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante reconoce y utiliza estructuras (MP7) cuando usa los numerales dados en la secuencia de conteo como ayuda para calcular qué numerales necesita escribir en los recuadros vacíos de la página de escritura de numerales.
Diferenciación: Desafío
Las imágenes del Grupo de problemas se pueden usar para la descomposición o la composición. Desafíe a sus estudiantes a crear enunciados numéricos sobre las imágenes.
• Araña: 8 patas son 4 patas y 4 patas.
• Vacas: 4 patas y 4 patas hacen 8 patas.
• Gaviotas: 2 patas y 2 patas y 2 patas y 2 patas hacen 8 patas.
K ▸ M1 ▸ TF ▸ Lección 26 EUREKA MATH2 © Great Minds PBC 318
Great Minds PBC 83 EUREKA MATH K M1 TF Lección 26 26 Nombre Cuenta los brazos y las patas. Escribe cuántos o cuántas hay.
Concluir
Reflexión final 5 min
Materiales: M) Afiche de ¿Por qué escribimos números?
Objetivo: Escribir el numeral 8
Reúna a la clase y pídale que tenga a mano su Grupo de problemas. Muestre el Grupo de problemas. Pida a sus estudiantes que señalen la araña.
Muestren a su pareja de trabajo cómo contaron las patas de la araña.
Haga una pausa para que las parejas de trabajo compartan cómo contaron las patas de la araña. Preste atención a las estrategias de conteo organizadas. Elija dos estrategias de conteo para compartir con la clase.
Escuché que hubo quienes dijeron que marcaron cada pata mientras contaban para llevar la cuenta.
También hubo quieres tocaron y contaron cada pata. Contaron todas las patas en uno de los lados de la araña y, luego, todas las del otro lado. Alguien dijo: “4 patas y 4 patas son 8 patas”.
A pesar de que usamos diferentes estrategias para contar las patas, todos escribimos el número 8.
Muestre o señale el afiche de ¿Por qué escribimos números? Agregue ideas nuevas al afiche.
EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 26 © Great Minds PBC 319
10 25 5 © Great Minds PBC 83 EUREKA MATH2 K M1 TF Lección 26 26 Nombre Cuenta
los brazos y las patas. Escribe cuántos o cuántas hay.
Escribir los numerales 9 y 10
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
La clase concluye su experiencia con la escritura de los numerales del módulo 1 al aprender cómo escribir el 9 y el 10. Para celebrar sus nuevas destrezas, escriben los numerales del 1 al 10 en orden y comparten sus ideas sobre por qué se escriben los números.
Pregunta clave
• ¿Por qué escribimos números?
Criterio de logro académico
K.Mód1.CLA2 Escriben los números del 0 al 10. (K.CC.A.3)
27
LECCIÓN 27
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 10 min
Aprender 20 min
• Escritura en el aire y en una alfombra
• Escribir los numerales
• Grupo de problemas
Concluir 10 min
Materiales
Maestro o maestra
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 0 al 8)
• marioneta o pelota
• letra de la canción “Puedo contar” (en la edición para la enseñanza)
• afiche de ¿Por qué escribimos números?
Estudiantes
• Plantilla de grupos de 5
• cubos Unifix® (10)
• Tablero de puntuación (en el libro para estudiantes)
• pizarra blanca individual
• marcador de borrado en seco
• libro para estudiantes
Preparación de la lección
• Prepare las plantillas de grupos de 5.
• Prepare las tarjetas del 0 al 8 del juego para demostración de las tarjetas Hide Zero.
• El Tablero de puntuación debe colocarse en las pizarras blancas individuales. Considere retirar los tableros de puntuación de los libros para estudiantes y colocarlos en las pizarras blancas antes de comenzar la lección.
• Considere retirar la página de escritura de numerales y colocarla en una pizarra blanca individual.
© Great Minds PBC 321 EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 27
Fluidez
Muéstrame grupos de 5: Contar a partir de 5
Materiales: E) Plantilla de grupos de 5, cubos Unifix
La clase coloca cubos en grupos de 5 para desarrollar la comprensión de los números del 6 al 10 como 5 y algunos más.

A lo largo de la actividad, anime a la clase a añadir cubos Unifix de izquierda a derecha para que puedan ver la formación de grupos de 5.
Juguemos Muéstrame grupos de 5. Yo digo un número y ustedes lo muestran con cubos. Usen la plantilla como ayuda para formar un grupo de 5.
Muéstrenme 5.
(La clase coloca 5 cubos sobre la plantilla y completa la fila superior).
Muéstrenme 6.
(La clase coloca un cubo sobre el punto inferior izquierdo).
Muéstrenme 5.
(La clase retira un cubo de la fila inferior).
Muéstrenme 7.
(La clase coloca 2 cubos en la fila inferior, comenzando desde la izquierda).
Continúe el proceso con la siguiente secuencia: 105 95 85
Observe a la clase para ver quiénes usan la estructura de grupos de 5 en lugar de contar desde el 1 cada vez.
Nota para la enseñanza
Muéstrame grupos de 5: Contar a partir de 5 enfatiza la estructura de los grupos de 5. Esta simple actividad les ayuda a formar una nueva unidad con 5, al ver el 6 como 5 y 1, el 7 como 5 y 2, y así sucesivamente. Formar una nueva unidad con 5 de esta manera sienta las bases para las estrategias de nivel 2 de contar desde un número.
10 10 20 10
K ▸ M1 ▸ TF ▸ Lección 27 EUREKA MATH2 © Great Minds PBC 322
Dedos a la vista: El método matemático hasta el 10
La clase dice cuántos dedos ve para desarrollar la capacidad de reconocer cantidades del 6 al 10 como 5 y algunos más.

Voy a mostrarles algunos dedos con el método matemático, pero solo por un segundo. Ustedes me dirán el número que ven. ¡Miren con atención!
Inclínese hacia delante, establezca contacto visual, haga una pausa con teatralidad y luego muestre por un instante 5 dedos con el método matemático. Ocúltelos.
¿Cuántos dedos vieron? 5
Prepárense. Aquí viene el siguiente.
Muestre por un instante 6 dedos con el método matemático. Ocúltelos.
¿Cuántos dedos vieron?
Continúe el proceso con la siguiente secuencia:
Contar hasta el 8: ¿Qué número sientes en la espalda?
Materiales: M) Tarjetas Hide Zero
Cada estudiante dibuja un número y adivina un numeral para desarrollar la memoria cinestésica necesaria para formar números.


Juguemos ¿Qué número sientes en la espalda?
Pida a la clase que trabaje en parejas. Cada integrante de la pareja se colocará en fila, mirando hacia delante. Quien esté detrás será quien escriba. Quien esté delante será quien adivine.
Párese detrás de la clase, mirando hacia la espalda de cada estudiante, y muestre la tarjeta del 8.
6
10 5 9 5 8 5 7 5
EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 27 © Great Minds PBC 323
Estudiantes que escriben, dense vuelta y observen mi número, pero no lo digan. ¡Guarden el secreto! Escriban este número con el dedo en la espalda de su compañero o compañera. Usen toda la espalda para que puedan escribir un número grande y bonito.
Estudiantes que adivinan, ¿se dieron cuenta de qué número les escribieron en la espalda?
Parejas de estudiantes, dense vuelta y observen mi número. Si acertaron, ¡denme 8 aplausos!
Continúe con los numerales recién aprendidos, el 6, el 7 y el 8, y con cualquier otro que presente un desafío para sus estudiantes. Felicite a la clase con el número correspondiente de aplausos. Ahora que los números son más altos, invite a sus estudiantes a contar mientras aplauden. Después de un tiempo, pida a las parejas que cambien los roles.
Presentar
Materiales: E) Tablero de puntuación, pizarra blanca individual, marcador de borrado en seco La clase practica escribir los numerales del 0 al 8 y establece un propósito para la escritura de los numerales.
10
Muestre la actividad digital interactiva de Osos de beisbol.
Los ositos de peluche azules y rojos organizan una competencia de cuadrangulares. Obtienen 1 punto por cada jonrón que hacen.
Nuestro trabajo es llevar un registro de la puntuación. ¿Qué podemos hacer para mostrar cuántos puntos anota cada osito?
Tablero de puntuación
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante utiliza las herramientas apropiadas estratégicamente (MP5) cuando elige escribir los numerales para llevar la cuenta de la puntuación. También podrían usar dibujos o hacer marcas para anotar la puntuación, pero observan que, si usan numerales, no tienen que contar repetidamente.
Escuche las ideas de sus estudiantes. Si nadie sugiere escribir los numerales, muestre una copia del Tablero de puntuación y describa cómo usarlo para llevar la cuenta de las carreras en beisbol. Distribuya un Tablero de puntuación a cada estudiante.
Haga las siguientes preguntas para promover el estándar MP5:
• ¿Podemos dibujar círculos cada vez que un equipo anota un punto?
8
10 10 20
K ▸ M1 ▸ TF ▸ Lección 27 EUREKA MATH2 © Great Minds PBC 324
Los ositos no han marcado ningún punto todavía. ¿Qué palabra usamos en matemáticas para referirnos a ninguno?
Cero
Pida a la clase que escriba un 0 para cada osito en el tablero de puntuación. Si fuera necesario, demuestre cómo se forma el numeral mientras dice la rima para escribir ese número.
Comenzará el equipo azul. En la actividad digital interactiva, permita que uno de los ositos tenga un turno para batear. Si el osito hace un jonrón, pida a sus estudiantes que cambien sus tableros de puntuación. Si el osito no hace un jonrón, está out.
¡El osito azul anotó un punto! ¿Qué cambio debemos hacer en nuestros tableros de puntuación?
Debemos cambiar el puntaje de los ositos azules de 0 a 1.
Considere pedir a sus estudiantes que sostengan sus pizarras blancas individuales en alto para poder validar rápidamente si el trabajo que hicieron es preciso.
Continúe con el osito azul hasta que tenga 3 out. Automáticamente, será el turno de batear de un osito rojo.
Repita el proceso. Si es necesario, demuestre cómo escribir los numerales hasta que sus estudiantes deban escribir el 9.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Debemos cambiar la puntuación a 9, pero no hemos practicado cómo escribir el 9 o el 10. Vamos a aprender esos números ahora.
© Great Minds PBC 85 EUREKA MATH 2 K ▸ M1 ▸ TF ▸ Lección 27 ▸ Tablero de puntuación
Equipo rojo EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 27 © Great Minds PBC 325
Tablero de puntuación
Aprender
Escritura en el aire y en una alfombra
Materiales: M) Marioneta o pelota
La clase aprende los trazos básicos para escribir los numerales 9 y 10.
Sostenga la pelota en el aire y escriba el numeral 9. Empiece desde arriba mientras dice la rima. Anime a la clase a seguir sus movimientos sin doblar el brazo.
Un rulo seguido de un palito breve. Bien hasta abajo, así se hace el 9.
Pida a la clase que traslade los dedos que usan para contar a la alfombra o a otra superficie que puedan tocar. Repita la rima mientras escriben el 9 en la nueva superficie.
No hay una rima para el numeral 10.
Para escribir 10 usamos el 1 y el 0. Ya sabemos cómo escribir el 1 y el 0.
Practique escribir el 10, primero en el aire y, luego, en la alfombra.
Escribir los numerales
Materiales: E) Página de escritura de numerales
La clase dibuja y escribe los numerales 9 y 10.
Distribuya el trabajo en clase y los útiles de escritura. Invite a la clase a hallar el numeral 9 en la página. Una vez que hayan colocado los dedos sobre el numeral 9, pídales que digan la rima en conjunto, mientras trazan el numeral con los dedos.
Demuestre cómo escribir el 9. Luego, invite a la clase a usar un lápiz o un crayón para escribir el 9 hasta completar la fila. Si hay tiempo suficiente, pídales que dibujen 9 círculos dentro del recuadro.
Repita el proceso con el numeral 10.
Nota para la enseñanza
El diez es el primer numeral de dos dígitos que sus estudiantes aprenden a escribir. Evite hacer comentarios como “el diez es un 1 y un 0”, que la clase podría malinterpretar como un enunciado numérico. El diez es un único número compuesto por dos dígitos. Esta precisión resulta especialmente importante cuando sus estudiantes desarrollen las bases para comprender el valor posicional en el módulo 6.
Nota para la enseñanza
Considere retirar la página de escritura de numerales y colocarla en una pizarra blanca individual para volver a usarla para practicar.
10 10 20 10 EUREKA MATH K M1 TF Lección 27 © Great Minds PBC 87 Nombre 27
K ▸ M1 ▸ TF ▸ Lección 27 EUREKA MATH2 © Great Minds PBC 326
Grupo de problemas
Materiales: M) Letra de la canción “Puedo contar”
Muestre el apoyo visual Puedo Contar y tenga preparada la letra de “Puedo contar”.
Cante la canción y muestre cada una de las columnas de imágenes a medida que se mencionan. Cuando termine la canción, pida a la clase que se dirija al Grupo de problemas. Invite a sus estudiantes a escribir los numerales del 1 al 10 de manera que coincidan con las imágenes y con la canción.
Evaluación observacional
; Observe a sus estudiantes mientras escriben.
• ¿Comienzan en el punto y se mantienen dentro del rectángulo de escritura?
2 3 5 6 7 8 9 10 4 © Great Minds PBC 89 EUREKA MATH 2 K M1 TF Lección 27 Escribe los números en el afiche de Puedo contar. 27 Nombre EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 27 © Great Minds PBC 327
Concluir
Reflexión final 10 min
Materiales: M) Afiche de ¿Por qué escribimos números?
Objetivo: Escribir los numerales 9 y 10
¡Hoy es un gran día para nuestra clase! Después de mucho trabajo y práctica, hemos aprendido a escribir los números del 1 al 10.
¿Cómo nos ayudó escribir los números a llevar la cuenta de la puntuación durante el partido de beisbol?
Nos ayudó a recordar cuántos puntos tenía cada equipo.
Durante las últimas semanas, hemos conversado mucho acerca de las diferentes razones por las que escribimos los números. ¿Qué ideas no hemos registrado en el afiche?
¿ ? Nota para la enseñanza
Considere diversas maneras de convertir esta conversación en la celebración de un hito.
• Tome una foto de la clase sosteniendo sus Grupos de problemas en alto.
• Invite a un integrante especial de la comunidad educativa para que les pregunte por qué se escriben los números.
• Envíe una nota a casa animando a las familias a felicitar a sus estudiantes por el logro obtenido y a preguntarles por qué se escriben los números.
• Escriban una carta al director o la directora de la escuela, indicando las razones por las que las personas escriben los números.
10 20 10
K ▸ M1 ▸ TF ▸ Lección 27 EUREKA MATH2 © Great Minds PBC 328
Puedo contar
Cantada con la melodía de “Una vez pesqué un pez vivo”
(Once I Caught a Fish Alive)
1 ave azul cantará.
2 abejas volarán.
3 flores crecen a la vez.
¡Puedo contar! 1, 2, 3.
Preparan todas un gran banquete.
1, 2, 3, 4, 5, 6, 7.
4 gatas duermen al sol.
5 patos tienen calor.
Al estanque entran de un brinco.
Cuento 1, 2, 3, 4, 5.
8 frijoles cuelgan de la rama.
9 caracoles se van a la cama.
1, 2, 3, 4, ¡salen cuando llueve!
5, 6, 7, 8 y 9.
6 ardillas juntan semillas.
7 aves hacen rosquillas.
10 autos pasean muy limpios.
Cuéntalos: 1, 2, 3, 4, 5
6, 7, 8, 9, 10.
¡Contemos todo otra vez!
EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 27 ▸ Puedo contar © Great Minds PBC 329 This page may be reproduced for classroom use only.
Ordenar los numerales del 1 al 10 y razonar acerca de un número desconocido en una secuencia numérica
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
Hacer una secuencia de números ayuda a sus estudiantes a empezar a entender la relación que existe entre ellos. La clase explora esta relación al ordenar tarjetas numéricas del 1 al 10. Se convierten en detectives de números al identificar números en una secuencia que no pueden ver.
Pregunta clave
• ¿De qué manera el orden de los números nos ayuda a calcular el número que falta?
Criterio de logro académico
K.Mód1.CLA1 Cuentan hasta el 10. (K.CC.A.1)
28
LECCIÓN 28
© Great Minds PBC 390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Fluidez 10 min
Presentar 10 min
Aprender 25 min
• Ordenar los números del 1 al 10
• Detective de números
• Grupo de problemas
Concluir 5 min
Materiales
Maestro o maestra
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 1 al 10)
• notas adhesivas (12)
• tarjetas numéricas de Eureka Math2 (del 1 al 10)
Estudiantes
• Plantilla de grupos de 5
• cubos Unifix® (10)
Preparación de la lección
• Prepare las plantillas de grupos de 5.
• Prepare las tarjetas del 0 al 10 del juego para demostración de las tarjetas Hide Zero.
• Escriba los números del 1 al 12 en las notas adhesivas.
• Prepare las tarjetas del 1 al 10 del juego de tarjetas numéricas. Si no tiene tarjetas numéricas, considere usar tarjetas de índice. Numere las tarjetas del 1 al 10.
© Great Minds PBC 331 EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 28
Fluidez
Muéstrame grupos de 5: Del 6 al 10
Materiales: E) Plantilla de grupos de 5, cubos Unifix
La clase coloca cubos en grupos de 5 para desarrollar la comprensión de los números del 6 al 10 como 5 y algunos más.

A lo largo de la actividad, anime a la clase a añadir cubos Unifix de izquierda a derecha para que puedan ver la formación de grupos de 5.
Juguemos Muéstrame grupos de 5. Yo digo un número y ustedes lo muestran con cubos. Usen la plantilla como ayuda para formar un grupo de 5.
Muéstrenme 5.
(La clase coloca 5 cubos sobre la plantilla y completa la fila superior).
Continúe con los números del 6 al 10 en cualquier orden.
Si la clase está lista, considere retirar la Plantilla de grupos de 5.
Contar hasta el 10: ¿Qué número sientes en la espalda?
Materiales: M) Tarjetas Hide Zero
Cada estudiante dibuja un número y adivina un numeral para desarrollar la memoria cinestésica necesaria para formar números.
Juguemos ¿Qué número sientes en la espalda?
Pida a la clase que trabaje en parejas. Cada integrante de la pareja se colocará en fila, mirando hacia delante. Quien esté detrás será quien escriba. Quien esté delante será quien adivine.
Párese detrás de la clase, mirando hacia la espalda de cada estudiante, y muestre la tarjeta del 9.
Estudiantes que escriben, dense vuelta y observen mi número, pero no lo digan. ¡Guarden el secreto! Escriban este número con el dedo en la espalda de su compañero o compañera.
Usen toda la espalda para que puedan escribir un número grande y bonito.
Diferenciación: Apoyo
Si sus estudiantes necesitan apoyo, consulte las lecciones anteriores. Así podrá brindar más apoyo en las secuencias. Observe a sus estudiantes para ver quiénes usan la estructura de grupos de 5 en lugar de contar desde el 1 cada vez.
10 10 25 5
K ▸ M1 ▸ TF ▸ Lección 28 EUREKA MATH2 © Great Minds PBC 332
Estudiantes que adivinan, ¿se dieron cuenta de qué número les escribieron en la espalda?
Parejas de estudiantes, dense vuelta y observen mi número. Si acertaron, ¡denme 9 aplausos!
Continúe con los numerales recién aprendidos, el 9 y el 10, y con cualquier otro que presente un desafío para sus estudiantes. Felicite a la clase con el número correspondiente de aplausos. Ahora que los números son más altos, invite a sus estudiantes a contar mientras aplauden. Después de un tiempo, pida a las parejas que cambien los roles.
Presentar
Materiales: M) Notas adhesivas
La clase corrige una secuencia de números que está desordenada.
Pida a la clase que mire un reloj y preste atención a los números. Luego, muestre el reloj con los números mezclados.
Miren este reloj. ¿Hay algo malo en él?
Sí, los números están mezclados.
Sí, no dice la hora.
Vamos a arreglarlo en grupo; pongamos los números en orden.
Muestre el reloj que no tiene números y coloque las notas adhesivas numeradas de manera desordenada en un lugar donde sus estudiantes puedan verlas fácilmente.
Vamos a usar estas notas adhesivas para poner los números en orden.
¡Pongamos el 1 primero! ¿Dónde debe ir?
Nota para la enseñanza
El objetivo de esta lección no es decir la hora, sino mostrar a la clase un ejemplo conocido de una secuencia de números del mundo real para crear curiosidad sobre la razón detrás del orden de los números.
9
10 10 25 5
3 8 911 12 2 7 10 65 4 1 EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 28 © Great Minds PBC 333
Halle la nota adhesiva con el número 1 y siga las instrucciones que le den sus estudiantes para colocarlo en el lugar adecuado en el reloj.
¿Qué número va después?
El 2
Pida a alguien de la clase que halle el 2 y señale el lugar adecuado para colocarlo en el reloj. Continúe hasta que se hayan agregado todos los números en orden.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hoy, vamos a explorar otras maneras en las que el orden de los números nos ayuda a calcular cosas.
Aprender
Ordenar los números del 1 al 10
Materiales: M) Tarjetas numéricas
Ordenar los numerales del 1 al 10 y razonar acerca de un número desconocido en una secuencia numérica
Tengo un juego de tarjetas numéricas. Están desordenadas. Vamos a ponerlas en orden.
Coloque 10 tarjetas numéricas grandes en una línea recta, desordenadas, de manera que toda la clase pueda verlas.
¿Cómo deberíamos ordenar estos números?
Podemos moverlos y contarlos.
Podemos hallar el número 1 y pasarlo al principio.
¡Buenas ideas! Vamos a tomar la tarjeta del 1 y pasarla al principio en una nueva fila.
5 6
9 4 3 1 2 10
8 7
10 10 25 5 K ▸ M1 ▸ TF ▸ Lección 28 EUREKA MATH2 © Great Minds PBC 334
Mueva la tarjeta del 1 para empezar otra fila y continúe haciendo una secuencia de los números con la clase. 5 6 8 7 9 4 3 1 2
Evaluación observacional
10
; ¿La clase puede ordenar las tarjetas con precisión y eficiencia?
; ¿La clase puede nombrar el número que falta? ¿Cuentan las tarjetas desde el principio o simplemente dicen el número?
Ahora, todos los números están en orden. Vamos a contarlos para asegurarnos de que sea así. (Señale las tarjetas numéricas mientras la clase cuenta a coro).
Detective de números
Materiales: M) Tarjetas numéricas
La clase razona sobre los números según el lugar que ocupan en una secuencia.
Use las tarjetas numéricas secuenciadas y dé vuelta una tarjeta por medio, comenzando con el 1. 10 8 6 4 2
Señale una de las tarjetas que está bocabajo. Por ejemplo, el número 1.
Seamos detectives de números y usemos pistas para calcular este número. Cuando crean que sepan cuál es el número, pónganse de pie.
Dé a sus estudiantes tiempo para pensar y espere a que la mayoría esté de pie. Pida a alguien de la clase que diga el número.
Si están de acuerdo, muestren los pulgares hacia arriba. Demos vuelta a la tarjeta y veamos si hicimos un buen trabajo como detectives.
Dé vuelta a la tarjeta y revele el número 1.
Variaciones para Detective de números
Hay muchas maneras de hacer variaciones a este juego. Use las sugerencias a continuación para brindar apoyo o desafiar a la clase.
Apoyo
• Use menos tarjetas (del 1 al 5).
• Use tarjetas Hide Zero con puntos en la parte de atrás.
• Digan la secuencia numérica a coro y, luego, pida a alguien de la clase que identifique uno de los números escondidos.
Desafío
• Use la tarjeta del 0.
• Coloque las tarjetas en una secuencia descendente, empezando con el 10.
• Ordene las tarjetas en grupos de 5 en vez de ordenarlas en una formación lineal.
EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 28 © Great Minds PBC 335
¡Bien! ¡Estaban en lo correcto! ¿Qué pistas usaron para calcular que este número era el 1?
El 1 está el principio.
El 1 va antes del 2.
Juegue algunas veces más con otras tarjetas que se encuentren bocabajo. Asegúrese de preguntar a sus estudiantes qué pistas usaron para calcular el número escondido.
Seamos detectives por un rato más. Esta vez, todas las tarjetas están bocabajo.
Promoción de los estándares para la práctica de las matemáticas
Invite a alguien de la clase a elegir una tarjeta sin mostrársela al resto de la clase. Deles tiempo para usar la rutina Pensar-Trabajar en parejas-Compartir para analizar la siguiente pregunta.
¿Qué número hay en la tarjeta que falta? ¿Cómo lo saben?
El 4; lo sé porque conté 1, 2, 3, 4. (Toca las tarjetas y el espacio vacío).
Continúe el juego; invite a más estudiantes a elegir una tarjeta. Use las sugerencias del recuadro Variaciones para Detective de números para personalizar esta actividad y satisfacer las necesidades de su clase.
Grupo de problemas
Use la representación sistemática para que la clase empiece con el Grupo de problemas. Recorra el salón de clases o trabaje con un grupo pequeño de estudiantes que necesite apoyo adicional.
Cada estudiante reconoce y utiliza estructuras (MP7) cuando usa los numerales que puede ver en la secuencia de conteo como ayuda para calcular los números escondidos. Pedirles que expliquen qué pistas observan les ayuda a revelar qué partes de la estructura observan y usan.
© Great Minds PBC 91 EUREKA MATH M1 TF Lección 28 Escribe los números en orden. Dibuja puntos en grupos de 5 para emparejarlos con los números. 28 Nombre K ▸ M1 ▸ TF ▸ Lección 28 EUREKA MATH2 © Great Minds PBC 336
Concluir
Reflexión final 5 min
Materiales: M) Tarjetas numéricas
Objetivo: Ordenar los numerales del 1 al 10 y razonar acerca de un número desconocido en una secuencia numérica
Sostenga en alto la tarjeta del 4 de manera tal que la clase no pueda ver el número.
¡Hoy hicimos un muy buen trabajo como detectives de números!
¿Saben qué número es este?
¿El 5? ¿El 1? ¿El 3?
No lo sabemos porque la tarjeta está separada del resto.
Debe ponerla en una fila para que podamos calcular qué número es.
Muestre las tarjetas del 1, el 2, el 3 y el 5 en una fila, dejando un espacio entre el 3 y el 5. Luego, dé vuelta a las tarjetas para esconder los números.
Veamos si pueden usar pistas como los detectives para calcular cuál es el número que falta. El número que falta va en este espacio. (Señale el espacio). ¿Qué número es?
El 4
Coloque la tarjeta para que toda la clase pueda ver el número 4.
¿Cómo podemos usar el orden de los números para saber qué número está en la tarjeta que falta?
Podemos contar desde el principio. Si la tarjeta que falta está al principio, sabemos que es el 1 porque ese es el primer número.
10 25 5 1 2 3 5 EUREKA MATH2 K ▸ M1 ▸ TF ▸ Lección 28 © Great Minds PBC 337
Tema G Analizar la secuencia de conteo
El Tema G celebra el avance de la clase de kindergarten con los conceptos de conteo, a la vez que abre la puerta a métodos más sofisticados para usar el sistema numérico. El trabajo de la clase para descubrir el patrón de 1 más y el patrón de 1 menos en la secuencia de conteo es el primer paso conceptual en el camino hacia las estrategias de contar hacia delante desde un número en 1.er grado.
El orden de los números es un tema que se desarrolla a lo largo de todo el módulo 1 y es el tema principal de la lección 29. Allí, la clase combina su comprensión de la lista de palabras numéricas con los numerales escritos para ordenar los números del 1 al 10. Ahora, tienen la capacidad de analizar la secuencia de conteo y descubrir dos patrones complementarios.
• El patrón de 1 más en una secuencia de conteo hacia delante
• El patrón de 1 menos en una secuencia de conteo hacia atrás
El modelo de las escaleras de números brinda la mejor representación visual del patrón cuando la clase muestra los patrones de 1 más y 1 menos de distintas maneras. Sus estudiantes de kindergarten usan las escaleras de números para mostrar los dos patrones a medida que adquieren el vocabulario para describirlos. La práctica de conteo con 1 más y 1 menos (1; 1 más es 2. 2; 1 más es 3) ayuda a desarrollar el lenguaje y la comprensión del concepto. Con apoyo, sus estudiantes usan sus propias palabras para compartir que el nombre de cada número sucesivo se refiere a una cantidad que es uno más que la cantidad anterior (K.CC.B.4.c): los números aumentan de 1 en 1 cuando se cuenta hacia delante.
¿Por qué es tan importante comprender estos patrones en la secuencia de conteo? Sin esta comprensión de base, sus estudiantes podrían volver a contar toda la colección cuando agreguen o quiten 1 objeto. El vocabulario de más y menos es clave para la comparación del módulo 3, donde las escaleras de números son un modelo importante. Estos patrones también tienen un papel clave en el desarrollo de estrategias eficientes de suma y resta, incluidos los patrones con más o menos 1, más o menos 10 y el conteo hacia delante desde un número en 1.er grado.
La lección final de cada módulo es una actividad de cierre. En el módulo 1, la actividad de cierre es una colección de conteo. Es una oportunidad para que sus estudiantes reflexionen y celebren su progreso en el conteo. También es una oportunidad para que maestros y maestras evalúen los conceptos de conteo a través de una tarea real.
La clase practica cómo contar 1 más: 1; 1 más es 2. 2; 1 más es 3. 3…
Este trabajo muestra el patrón de 1 más en la secuencia numérica con el dibujo de una diagonal que sube por la escalera de números.
© Great Minds PBC 339
10 9 8 7 6 5 4 3 2 1
Progresión de las lecciones
Lección 29
Representar el patrón de 1 más en una secuencia de conteo hacia delante 10
Lección 30
Construir escaleras de números para mostrar el patrón de 1 más en una secuencia de conteo hacia delante
Lección 31
Representar el patrón de 1 menos en una secuencia de conteo hacia atrás 0
La escalera es pequeña al comienzo y se vuelve más grande.
Construí una escalera de números. El número que sigue es 1 más.
La escalera es grande al comienzo y se vuelve más pequeña.
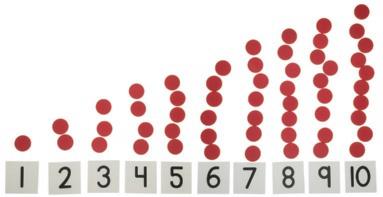
340 K ▸ M1 ▸ TG EUREKA MATH2 © Great Minds PBC
Lección 32
Dibujar escaleras de números para representar el patrón de 1 menos en una secuencia de conteo hacia atrás


Lección 33
Organizar, contar y representar una colección de objetos
Cuando cuentas hacia atrás, el número que sigue es 1 menos.
Sé que mi colección y mi dibujo coinciden, porque coloqué las bolas de algodón sobre el dibujo.
EUREKA MATH2 K ▸ M1 ▸ TG 341 © Great Minds PBC
LECCIÓN 29
Representar el patrón de 1 más en una secuencia de conteo hacia delante
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
La clase visualiza el patrón de 1 más en una secuencia de conteo hacia delante a través de una serie de modelos. Las escaleras de números son un recurso visual de alto impacto para ayudar a sus estudiantes a ver que, cuando cuentan hacia delante, cada número que dicen es 1 más que el número anterior.
Pregunta clave
• ¿Qué observan o escuchan cuando contamos del 1 al 10?
Criterio de logro académico
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10. (K.CC.B.4.c)
390 © Great Minds PBC
This page may be reproduced for classroom use only.
29
© Great Minds PBC
Agenda
Fluidez 10 min
Presentar 10 min
Aprender 25 min
• Representar la “Canción de los gatos bailarines”
• Contar 1 más
• Escaleras de números
Concluir 5 min
Materiales
Maestro o maestra
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 1 al 7)
• cubos Unifix® (10)
• letra de la “Canción de los gatos bailarines”
Estudiantes
• Plantilla de dos manos (en el libro para estudiantes)
• frijoles de dos colores (7)
• tarjetas numéricas de Eureka Math2 (1 juego del 1 al 10 por pareja de estudiantes)
• cubos Unifix® (10)
Preparación de la lección
• Prepare las tarjetas del 1 al 7 del juego para demostración de las tarjetas Hide Zero.
• Durante la sección Presentar, la clase representa la “Canción de los gatos bailarines”. Halle o cree un espacio en el salón de clases para representar una pista de baile.
• Prepare las tarjetas del 1 al 10 del juego de tarjetas numéricas. Si no tiene tarjetas numéricas, considere usar tarjetas de índice. Numere las tarjetas del 1 al 10.
© Great Minds PBC 343 EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 29
Fluidez













Muéstrame frijoles hasta el 7
Materiales: M) Tarjetas Hide Zero; E) Plantilla de dos manos, frijoles de dos colores La clase escucha un número o ve un numeral y cuenta en voz alta un conjunto para adquirir fluidez con la asociación de un numeral a un conjunto.
Prepárense. Coloquen 5 frijoles rojos sobre los puntos rojos que están en la parte de abajo.
Coloquen 2 frijoles blancos sobre los puntos blancos que están en la parte de abajo.
Voy a decir un número. Ustedes moverán esa cantidad de frijoles hacia la punta de los dedos. Recuerden comenzar por el meñique, como lo practicamos. (Mueva el meñique para enfatizar). ¿Comenzamos?
Muéstrenme 5.
Haga una pausa mientras la clase mueve los frijoles rojos para completar la mano izquierda, desde el meñique hasta el pulgar.
¡Rápidamente! Muéstrenme 6.
Haga una pausa mientras la clase mueve un frijol blanco hacia el pulgar de la mano derecha.
¡Muy bien! Muéstrenme 5.
Haga una pausa mientras la clase quita un frijol blanco del pulgar de la mano derecha.
Continúe con la siguiente secuencia:
5 5 6 7 6 7 6 5 6 10 10 25 5 K ▸ M1 ▸ TG ▸ Lección 29 EUREKA MATH2 © Great Minds PBC 344
Pida a la clase que vuelva atrás y que mueva los 7 frijoles en sus plantillas hacia los puntos que están en la parte de abajo.
Repita la actividad; esta vez, use una tarjeta para mostrar cuántos frijoles deben mover. Comience con la tarjeta del 5 y siga con la del 6. Continúe mostrando las tarjetas en una secuencia similar a la anterior.
Detective de números
Materiales: E) Tarjetas numéricas
La clase secuencia los números hasta el 10 como preparación para trabajar con el patrón de 1 más.
Pida a la clase que trabaje en parejas. Distribuya un juego de tarjetas a cada pareja y pídales que jueguen de acuerdo con las siguientes reglas:
• Las parejas trabajan en equipo para colocar las tarjetas en orden con los números bocarriba.
• Las parejas ponen las tarjetas bocabajo. A medida que lo hacen, colocan con cuidado cada tarjeta nuevamente en posición dentro de la secuencia.
• Estudiante A: Toma una tarjeta. Estudiante B: Usa pistas para determinar el número.
• Estudiante A: Muestra el número. Estudiante A: Determina si la pareja acertó y responde con una felicitación o con una sugerencia (por ejemplo: “Intenta usar la estrategia de tocar y contar”).
• Las parejas cambian de rol y vuelven a jugar, comenzando con todas las tarjetas bocabajo.
Recorra el salón de clases mientras se desarrolla el juego y proporcione apoyo según sea necesario. Por ejemplo, recuerde a sus estudiantes que cuenten a coro mientras tocan las tarjetas, si es necesario.
Diferenciación: Apoyo
• Use menos tarjetas (del 1 al 5).
• Use las tarjetas Hide Zero con puntos en la parte de atrás.
• Digan la secuencia numérica a coro y, luego, pida a alguien de la clase que identifique uno de los números escondidos.
Diferenciación: Desafío
• Use la tarjeta del 0.
• Coloque las tarjetas en una secuencia descendente, empezando con el 10.
• Ordene las tarjetas en grupos de 5 en vez de ordenarlas en una formación lineal.
1 2 3 4 5 6 7 8 9 10
EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 29 © Great Minds PBC 345
Materiales: M) Letra de la “Canción de los gatos bailarines”
La clase representa el patrón de 1 más a través del movimiento y el canto.
Antes de comenzar, seleccione un espacio del salón de clases para representar una pista de baile. Debe tener un ancho suficiente para que 10 estudiantes bailen en línea.
Elija a alguien de la clase para que sea el primer gato. Prepare a su estudiante para que represente el primer verso de la canción.
Repite después de mí: Un gato baila con zapatos. ¡Ahora es tu turno!
Un gato baila con zapatos.
Elija a alguien que represente el segundo y el tercer verso.
Uno más se unió. Ahora son… (Haga una pausa y señale con un gesto a quienes actúan).
Continúe hasta el 10. Pida a más estudiantes que se unan a los gatos siguiendo la letra de la canción. Anticipe que se unirán más estudiantes para cantar mientras reconocen el patrón.
¿Qué pasó con el grupo de gatos a medida que cantábamos la canción?
Se hizo más grande.
Llenaron la pista de baile.
Haga la transición al siguiente segmento.
Hoy, hallaremos otras maneras de mostrar lo que pasa cuando 1 más se une a un grupo.
Canción de los gatos bailarines
Un gato baila con zapatos. 6 Seis gatos bailan con zapatos.
Uno más se unió. Uno más se unió.
Ahora son dos. Ahora son siete.
2 Dos gatos bailan con zapatos. 7 Siete gatos bailan con zapatos.
Uno más se unió. Uno más se unió.
Ahora son tres. Ahora son ocho.
3 Tres gatos bailan con zapatos. 8 Ocho gatos bailan con zapatos.
Uno más se unió. Uno más se unió.
Ahora son cuatro. Ahora son nueve.
4 Cuatro gatos bailan con zapatos. 9 Nueve gatos bailan con zapatos.
Uno más se unió. Uno más se unió.
Ahora son cinco. Ahora son diez.
5 Cinco gatos bailan con zapatos.
Uno más se unió.
Ahora son seis.
DUA: Acción y expresión
Apoye a sus estudiantes para que, de formas flexibles, expresen lo que aprendieron. Pídales que lleven la cuenta con los dedos mientras repiten la canción. Si cuentan con el método matemático, verán que la cantidad crece en forma sostenida de izquierda a derecha.
Presentar
2
10 10 25 5
© Great Minds PBC 351 This page may be reproduced for classroom use only. EUREKA MATH2 K ▸ M1 ▸ TG Lección 29 ▸ Canción de los gatos bailarines
K ▸ M1 ▸ TG ▸ Lección 29 EUREKA MATH2 © Great Minds PBC 346
Aprender
Representar la “Canción de los gatos bailarines”
Materiales: E) Cubos Unifix
La clase usa cubos para representar el patrón de 1 más de la canción.
Para este segmento, sus estudiantes pueden unir cubos Unifix de manera horizontal para imitar las acciones de la canción o apilarlos de manera vertical para formar una torre. Anime a sus estudiantes a representarlo de cualquier manera que entiendan. Pídales que comiencen con una pila de cubos en vez usar barras de cubos conectados.


Hagamos de cuenta que estos cubos son los gatos. ¿Cómo empieza la canción?
Un gato baila con zapatos.
Veamos. ¡Hagan que parezca que está bailando!
Haga una pausa para permitir a la clase que haga bailar un cubo por toda la mesa.
¿Qué pasó después?
1 más se unió. (La clase agrega otro cubo). Ahora, son 2. Continúe hasta el 10 a un ritmo sostenido. Recorra el salón de clases para brindar apoyo a quienes necesiten ayuda para que sus cubos coincidan con la canción.
Cuando termine la canción, pida a la clase que separe sus cubos otra vez. Pida que se pongan de pie al finalizar. El simple acto de ponerse de pie brinda la oportunidad de tomarse unos momentos para moverse e indica que la clase está lista para la siguiente tarea.
10 10 25 5 EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 29 © Great Minds PBC 347
Contar 1 más
Materiales: M/E) Cubos Unifix
La clase construye una torre para representar el patrón de 1 más en la secuencia de conteo hacia delante.
Para este segmento, forme una torre vertical para que sus estudiantes observen la correspondencia entre 1 más y el crecimiento de la torre. Trabajar de manera vertical establecerá una relación con la imagen de las escaleras de números del siguiente segmento.
En la “Canción de los gatos bailarines” hay palabras matemáticas que se repiten: 1 más, 1 más, 1 más. Asientan con la cabeza si escuchan eso.
Podemos contar hacia delante con las palabras 1 más.
Para lograr más participación de sus estudiantes al contar, pida que canten después de usted para enseñar a contar 1 más. La cadencia del canto animará a sus estudiantes a mover el cuerpo y a internalizar la frase 1 más.
Tengo 1. (Levante 1 cubo).
Tengo 1.
1 más es 2. (Agregue un cubo).
1 más es 2.
Continúe hasta el 10 con las respuestas a coro. Luego, repita el proceso. Esta vez, pida a sus estudiantes que usen sus cubos para construir torres a medida que cuentan con la frase 1 más.
Nota para la enseñanza
Enunciar el patrón de 1 más puede ser un desafío lingüístico. Sus estudiantes tenderán a apresurarse y omitir la cantidad inicial: 1 más es 2, 1 más es 3, 1 más es 4, y así sucesivamente.
Ayude a la clase a mantener el ritmo e introduzca el número inicial con frases como “estamos en el 5” o “tengo 6” antes de decir el siguiente enunciado de 1 más.
Del mismo modo, si usted acompaña con movimientos claros y distintivos, refuerza la comprensión conceptual del patrón. La mayoría de sus estudiantes imitará sus acciones naturalmente.
Evaluación observacional
; Escuche y observe mientras la clase construye las torres. ¿Usan la frase 1 más a medida que agregan un cubo a la torre? ¿Hablan demasiado lento o demasiado rápido? ¿Hacen coincidir la frase 1 más con 1 cubo?

K ▸ M1 ▸ TG ▸ Lección 29 EUREKA MATH2 © Great Minds PBC 348
Escaleras de números
La clase analiza el patrón de 1 más con el modelo de las escaleras de números.
Muestre el dibujo de 1 cubo (la primera escalera de números).
Hice un dibujo de sus torres para cada número. Cuenten conmigo. 1; 1 más es 2. 2; 1 más es 3…
Avance con los siguientes dibujos de la escalera de números mientras cuentan hasta el 10 con la frase 1 más. Deje la imagen de las 10 escaleras de números a la vista para una conversación con la clase.
Estas se llaman escaleras de números. ¿Por qué creen que se llaman así?
Porque van hacia arriba, suben y suben
Parecen escaleras.
¿Qué nos muestran las escaleras de números sobre el número 1?
El 1 es pequeño. Es muy pequeño.
Solo necesitamos 1 cubo. No es una torre.
¿Qué nos muestran las escaleras de números sobre el número 10?
El 10 tiene la torre más grande; entonces, es el número más grande de la imagen.
El número más grande de la imagen, así es. Qué bueno que lo mencionaron. ¿Los números se detienen en el 10?
No.
¿Qué pasa con los números cuando contamos del 1 al 10?
Al principio son pequeños y se van haciendo más grandes.
Nota para la enseñanza
Sus estudiantes, por su corta edad, a menudo usan términos generales como grande, pequeño y chiquito para describir los atributos medibles. Si usan términos genéricos para describir las escaleras de números, puede volver a expresar su razonamiento con sutileza, con términos más específicos como alto, largo o bajo, pero sin centrarse en el vocabulario en este momento.
La comparación de los atributos medibles y el vocabulario preciso se verán en profundidad en el módulo 3. En esta lección, el énfasis está puesto en la magnitud y el patrón de 1 más en la secuencia de conteo.
1
10 EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 29 © Great Minds PBC 349
Concluir
Reflexión final 5 minutos
Objetivo: Representar el patrón de 1 más en una secuencia de conteo hacia delante
¿Qué pasó con el grupo de gatos a medida que repetíamos la canción?
Se hizo más grande.
¿Quién puede decir lo que pasó usando las palabras 1 más?
Se unió 1 persona más cada vez que cantamos.
1 gato más se unió a la pista de baile hasta llegar a 10 gatos.
¿Qué pasó con las torres cuando contamos del 1 al 10?
Las torres se hicieron cada vez más grandes.
¿Quién puede hablar sobre las torres usando las palabras 1 más?
Colocamos 1 cubo más cada vez que cantamos.
El número que sigue es 1 más.
¿Qué pasa con los números cuando contamos del 1 al 10?
Se hacen más grandes.
¿Quién puede hablar sobre los números usando las palabras 1 más?
Cada número es 1 más.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante reconoce y expresa regularidad en la lógica de la repetición (MP8) cuando observa que, si suma 1 más a un grupo, siempre obtiene el número siguiente. Expresar este concepto verbalmente ayudará a sus estudiantes a pensarlo como una regla en la que pueden confiar y usar para contar hacia delante.
10 25 5
K ▸ M1 ▸ TG ▸ Lección 29 EUREKA MATH2 © Great Minds PBC 350
Canción de los gatos bailarines
1 Un gato baila con zapatos. 6 Seis gatos bailan con zapatos.
Uno más se unió. Uno más se unió.
Ahora son dos. Ahora son siete.
2 Dos gatos bailan con zapatos. 7 Siete gatos bailan con zapatos.
Uno más se unió. Uno más se unió.
Ahora son tres. Ahora son ocho.
3 Tres gatos bailan con zapatos. 8 Ocho gatos bailan con zapatos.
Uno más se unió. Uno más se unió.
Ahora son cuatro. Ahora son nueve.
4 Cuatro gatos bailan con zapatos. 9 Nueve gatos bailan con zapatos.
Uno más se unió. Uno más se unió.
Ahora son cinco. Ahora son diez.
5 Cinco gatos bailan con zapatos.
Uno más se unió.
Ahora son seis.
© Great Minds PBC 351 This page may be reproduced for classroom use only. EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 29 ▸ Canción de los gatos bailarines
Construir escaleras de números para mostrar el patrón de 1 más en una secuencia de conteo hacia delante
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
La clase construye y dibuja escaleras de números para mostrar el patrón de 1 más en una secuencia de conteo hacia delante. Usan su trabajo para mostrar que cada número consecutivo es 1 más que el anterior y desarrollan vocabulario para describir el patrón.
Pregunta clave
• ¿Qué observan cuando contamos del 1 al 10?
Criterio de logro académico
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10. (K.CC.B.4.c)
30
LECCIÓN 30
390 © Great Minds PBC This page may be reproduced for classroom use only.
© Great Minds PBC
Agenda
Fluidez 10 min
Presentar 5 min
Aprender 30 min
• Contar con escaleras de números
• Construir escaleras de números
• Paseo por la galería
• Grupo de problemas
Concluir 5 min
Materiales
Maestro o maestra
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 1 al 10)
Estudiantes
• Plantilla de dos manos
• frijoles de dos colores (10)
• fichas para contar (55)
• tarjetas Hide Zero® (del 1 al 10)
Preparación de la lección
• Prepare las tarjetas del 1 al 10 del juego para demostración de las tarjetas Hide Zero.
• Decida si la clase construirá las escaleras de números de manera individual o en grupos.
• La clase usa fichas para contar para construir escaleras de números. Las fichas pueden ser cualquier material del salón de clases, como cubos, fichas cuadradas de colores, pegatinas, osos para contar, cuadrados de papel o pennies. Asegúrese de que cada estudiante o cada grupo tenga 55 objetos del mismo material. Cada estudiante o grupo puede tener un material diferente.
• Asegúrese de que todas las fichas del modelo de escalera de números de un grupo tengan el mismo tamaño. Si hay variaciones en el tamaño de las unidades, el patrón de 1 más no se apreciará. Por ejemplo, la diferencia de tamaño entre estas piedras hace que el modelo de escaleras de números no sea efectivo.

© Great Minds PBC 353 EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 30
Fluidez










Muéstrame frijoles hasta el 10
Materiales: M) Tarjetas Hide Zero; E) Plantilla de dos manos, frijoles de dos colores
La clase escucha un número o ve un numeral y cuenta en voz alta un conjunto para adquirir fluidez con la asociación de un numeral a un conjunto.
Prepárense. Coloquen 5 frijoles rojos sobre los puntos rojos que están en la parte de abajo.
Coloquen 5 frijoles blancos sobre los puntos blancos que están en la parte de abajo.
Voy a decir un número. Ustedes moverán esa cantidad de frijoles hacia la punta de los dedos. Recuerden comenzar por el meñique, como lo practicamos. (Mueva el meñique para enfatizar). ¿Comenzamos?
Muéstrenme 5.
Haga una pausa mientras la clase mueve los frijoles rojos para completar la mano izquierda, desde el meñique hasta el pulgar.
¡Rápidamente! Muéstrenme 6.
Haga una pausa mientras la clase mueve un frijol blanco hacia el pulgar de la mano derecha.
¡Muy bien! Muéstrenme 7.
Haga una pausa mientras la clase mueve un frijol blanco hacia el dedo índice de la mano derecha.
Continúe con la siguiente secuencia:
Pida a la clase que vuelva atrás y que mueva los 10 frijoles en sus plantillas hacia los puntos que están en la parte de abajo.
Repita la actividad, pero, esta vez, use una tarjeta para mostrar cuántos frijoles deben mover.
Comience con la tarjeta del 5 y siga con la del 6. Continúe mostrando las tarjetas en una secuencia similar a la anterior.
8 8 9 10 9 10 9 7
10 5 30 5 K ▸ M1 ▸ TG ▸ Lección 30 EUREKA MATH2 © Great Minds PBC 354
Muéstrame el método matemático: 1 más
La clase muestra un número y 1 más con el método matemático para desarrollar fluidez con el patrón de 1 más.
Muéstrenme 3 con el método matemático.
(La clase muestra el dedo meñique, el anular y el mayor de la mano izquierda).
Muéstrenme 1 más. Para hacerlo, pueden levantar
1 dedo más.
(La clase levanta el índice de la mano izquierda).
¿Cuántos dedos muestran ahora?
4
¡Cierren las manos! Prepárense para el siguiente.
Muéstrenme 5 con el método matemático.
(La clase muestra la mano izquierda completa).
Muéstrenme 1 más.
(La clase levanta el pulgar de la mano derecha).





¿Cuántos dedos muestran ahora?
6
¡Cierren las manos! Prepárense para el siguiente.
Repita el proceso con el 9 y, luego, con cualquier otro número y 1 más.
EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 30 © Great Minds PBC 355
La clase representa el patrón creciente de 1 más con su cuerpo.
Demuestre la acción de una semilla que brota y se convierte en un árbol para que sus estudiantes puedan imitar. Comience por mostrar cómo ponerse en cuclillas de manera segura para imitar la semilla.
Hagan de cuenta que son una semilla pequeña que está en el suelo. Lentamente, crezcan hasta convertirse en un árbol. Primero, serán una planta pequeña, que irá creciendo y creciendo hasta que sus ramas lleguen al cielo.
Permita a la clase que practique los movimientos antes de comenzar a contar. Para lograr más participación, describa una escena de jardín. Considere reforzar los objetivos de ciencias usando las luces del salón de clases y simulando que la lluvia da a las semillas lo que necesitan para crecer.
Esta vez, serán una semilla de conteo. Para que la semilla de conteo crezca y se convierta en un árbol, contaremos con la frase 1 más.
Estamos en el 1. 1 más es…
Anime a sus estudiantes a que se unan al conteo mientras crecen lentamente hasta convertirse en un árbol.
Estamos en el 2. 1 más es 3.
Estamos en el 3. 1 más es 4. Continúe hasta el 10.
Nota para la enseñanza
Enunciar el patrón de 1 más puede ser un desafío lingüístico. Además, sus estudiantes tenderán a apresurarse y omitir la cantidad inicial: 1 más es 2, 1 más es 3, 1 más es 4, y así sucesivamente.
Ayude a la clase a mantener el ritmo e introduzca el número inicial con frases como “estamos en el 5” o “tengo 6” antes de decir el siguiente enunciado de 1 más.
DUA: Representación
Considere presentar la información en otro formato. Si hay una escalera real disponible, invite a la clase a subir por turnos mientras cuentan con la frase 1 más. Se puede hacer esta actividad en lugar de la sección Presentar o en otro momento del día.
Presentar
2
10 5 30 5
K ▸ M1 ▸ TG ▸ Lección 30 EUREKA MATH2 © Great Minds PBC 356
Aprender
Contar con escaleras de números
La clase usa escaleras de números para contar hacia delante con la frase 1 más.
Muestre el dibujo de 1 cubo (la primera escalera de números). Avance con las imágenes de la escalera de números mientras sus estudiantes repiten el canto que aprendieron en la lección anterior.
Intentemos usar nuestro conteo de 1 más con las escaleras de números.
Tengo 1.
Tengo 1.
1 más es 2. (Avance la lámina).
1 más es 2.
Continúe hasta el 10. Deje la imagen de las 10 escaleras de números a la vista mientras sus estudiantes las construyen en el siguiente segmento. Como el modelo es relativamente nuevo, la imagen es una referencia visual importante mientras la clase cuenta los grupos y los alinea para formar las escaleras.
Construir escaleras de números
Materiales: E) Tarjetas Hide Zero, fichas para contar La clase ordena los números y construye escaleras de números para emparejarlos.
Organice si sus estudiantes trabajarán en parejas o en grupos. Asigne un área de trabajo con espacio para los materiales y, de ser posible, que incluya una guía natural para alineación (p. ej., una alfombra, una baldosa o el borde de una mesa). Distribuya las tarjetas Hide Zero.
Diferenciación: Apoyo
Considere la cantidad de andamiaje necesario cuando elija los materiales para construir las escaleras de números. Los cubos brindan la mejor estructura y son fáciles de alinear en la parte de abajo para mostrar claramente el patrón de 1 más. Hay otros materiales conectables que pueden brindar una estructura similar, si bien algunos, como los eslabones, pueden ser difíciles de alinear en una superficie horizontal.
Un camino numérico preimpreso puede servir de apoyo a quienes necesiten reforzar la secuencia de conteo. También puede ayudar a que sus estudiantes organicen y alineen sus escaleras de números.
10 5 30 5 1
10 9 8 7 6 5 4 3 2 1 EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 30 © Great Minds PBC 357
Hoy, haremos escaleras de números con distintos tipos de fichas. Toda la clase tendrá los mismos números. Comiencen poniendo las tarjetas en orden.
Recorra el salón de clases para comprobar la precisión. Cuando un grupo haya ordenado sus números de manera correcta, entréguele una bolsita de fichas para que comience a construir las escaleras.
Mientras la clase trabaja, use las siguientes preguntas para evaluar e incentivar el razonamiento matemático. Pídales que usen gestos o movimientos para acompañar sus explicaciones.
¿Cómo hicieron la escalera para el número 6?
¿Cómo pueden usar la escalera del número 7 como ayuda para hacer la escalera del 8?
¿Qué pasa con sus escaleras de números cuando van del 1 al 2? ¿Y del 2 al 3? ¿Y del 3 al 4?


¿Cómo muestran sus escaleras de números el patrón de 1 más?
¿Cómo se vería una escalera para el número 11? ¿Hacia dónde iría?
¿Dónde estaría el número 0 en las escaleras de números?
Cuando sus estudiantes terminen de construir las escaleras, pídales que usen su trabajo para contar usando la frase 1 más. Asegúrese de que dejen las escaleras de números en su lugar para dar un paseo por la galería.
Paseo por la galería
La clase examina el trabajo de sus pares y aprende los protocolos para dar un paseo por la galería.
Reúna a sus estudiantes lejos de las escaleras de números para presentar la rutina del paseo por la galería. Este es el primero de los tres paseos por la galería de este tema. Cada uno de ellos introduce una parte nueva de la rutina.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante reconoce y utiliza estructuras (MP7) cuando observa y usa el patrón de 1 más para construir la siguiente escalera. En lugar de contar todos los objetos de cada escalera, usan el patrón para comprender que esta escalera es 1 número más alta que la anterior. Las preguntas de esta lección propician esta práctica matemática al ayudar a la clase a conversar sobre la estructura de la secuencia numérica.
Evaluación observacional
; Escuche y observe mientras sus estudiantes construyen las escaleras. ¿Dicen la secuencia numérica a medida que construyen cada escalera, o usan el patrón de 1 más para construir las escaleras y dicen la secuencia después de construirlas?
K ▸ M1 ▸ TG ▸ Lección 30 EUREKA MATH2 © Great Minds PBC 358
Hagamos de cuenta que estamos en un museo de matemáticas y demos un paseo por la galería. Esta es una oportunidad para apreciar el trabajo de la clase y aprender del resto
Establezcamos reglas para caminar por el salón de clases y observar los trabajos.
Observen pero no toquen, como haríamos en un museo o galería de arte. Mantengan las manos detrás de la espalda a modo de recordatorio. (Una las manos detrás de la espalda).
Manténganse en silencio mientras recorren la galería, para que toda la clase pueda pensar en lo que ve.
En este paseo por la galería, enfóquese en el procedimiento de caminar en silencio con las manos unidas para observar los trabajos. En las lecciones 32 y 33, la clase practicará cómo dar una retroalimentación positiva sobre el trabajo de un par.
Grupo de problemas
Use la representación sistemática para que la clase se inicie en el Grupo de problemas. Recorra el salón de clases mientras la clase trabaja. Tome nota de quiénes colorean y cuentan cada cuadrado (sin usar el patrón de 1 más) y de quiénes usan la estructura de las escaleras de números para colorear 1 cuadrado más cada vez (usando el patrón de 1 más).
DUA: Participación
Considere ofrecer retroalimentación que reconozca el esfuerzo de sus estudiantes para cumplir las reglas durante el paseo por la galería. Estudiar el trabajo de otras personas sin hablar ni tocar puede ser difícil en kindergarten; por ello, es importante elogiar a quienes hagan un gran esfuerzo para cumplir con la rutina. Por ejemplo: “Me doy cuenta de que David en verdad aprecia el trabajo de la clase, porque observa todo en silencio y sin tocar”.
Este elogio alienta el tipo de conducta necesaria para que los paseos por la galería sean un intercambio útil de ideas en el futuro.
Great Minds PBC 101 EUREKA MATH K M1 TG Lección 30 30 Nombre Escribe los números en orden. Colorea la escalera de números para que coincidan.
EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 30 © Great Minds PBC 359
Concluir
Reflexión final 5 min
Objetivo: Construir escaleras de números para mostrar el patrón de 1 más en una secuencia de conteo hacia delante
Reúna a la clase y pídales que tengan a mano su Grupo de problemas.
¿En qué se parecen sus imágenes de las escaleras de números a las escaleras de números que construyeron con objetos? ¿En qué se diferencian?

Las dos crecen 1, 2, 3..., 10. Las dos agregan 1 más, 1 más, 1 más. Una está hecha de cosas y la otra está pintada.
¿Cómo decidieron qué colorear?
Primero, escribí todos los números. Luego, observé cada número y coloreé esa cantidad de espacios.
Primero, coloreé un grupo de unos en el fondo y, luego, 1 más y 1 más hasta llegar al número correcto.
¿Qué observan cuando contamos del 1 al 10?
Los números aumentan de 1 en 1. El número que sigue es 1 más.
Diferenciación: Desafío
Si sus estudiantes comprenden claramente el patrón de 1 más, profundice su razonamiento mostrándole las variaciones de las escaleras de números para su análisis.
Guíe a sus estudiantes para que observen características como el cambio de color en el 5 o de qué manera el modelo indica 1 más.
Una manera simple de llamar la atención sobre esas características es a través del conteo a coro: Vamos a contar los cubos azules de cada escalera.
Entregue a sus estudiantes copias en blanco del Grupo de problemas para que experimenten con distintas representaciones en otro momento.
5 30 5
K ▸ M1 ▸ TG ▸ Lección 30 EUREKA MATH2 © Great Minds PBC 360
Representar el patrón de 1 menos en una secuencia de conteo hacia atrás
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
La clase observa el patrón de 1 menos mientras cuenta hacia atrás a través de una serie de modelos. El modelo final son las escaleras de números invertidas que comienzan en el 10. Usar un modelo conocido ayuda a la clase a ver que el patrón de 1 menos es complementario al patrón de 1 más y que, al contar hacia atrás, cada número es 1 menos que el anterior.
Pregunta clave
• ¿Qué observan cuando contamos hacia atrás del 10 al 0?
Criterio de logro académico
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10. (K.CC.B.4.c)
31
LECCIÓN 31
390 © Great Minds PBC This page may be reproduced for classroom use only.
©
Minds PBC
Great
Agenda
Fluidez 10 min
Presentar 10 min
Aprender 25 min
• Las manzanas de José
• Contar 1 menos
• Escaleras de números
Concluir 5 min
Materiales
Maestro o maestra
• guantes numerados derecho e izquierdo
• marioneta o animal de peluche
• letra de la canción “Había 10 manzanas en el árbol de José”
• álbum Growing Up with Ella Jenkins (Creciendo con Ella Jenkins)
• cubos Unifix® (10)
Estudiantes
• tarjetas numéricas de Eureka Math2 (1 juego del 1 al 10 por pareja de estudiantes)
• cubos Unifix® (10)
• tapete de trabajo
Preparación de la lección
• Si fuera posible, busque el álbum Growing Up with Ella Jenkins, de Ella Jenkins, para usar en la sección Presentar.
• Considere pedir a la clase que dibuje un árbol fuera del bloque de matemáticas. Podrán usar sus dibujos cuando representen “Había 10 manzanas en el árbol de José”, en la sección Aprender.
• Prepare las tarjetas del 1 al 10 del juego de tarjetas numéricas.
© Great Minds PBC 363 EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 31
Fluidez
Contar en el guante numerado
Materiales: M) Guantes numerados derecho e izquierdo
La clase cuenta hacia abajo en el guante numerado como preparación para trabajar con el patrón de 1 menos.
Observen mi guante numerado y cuenten en voz alta. ¿Comenzamos?
Use el guante numerado para mostrar la siguiente secuencia mientras la clase cuenta en voz alta:
• Cuenten hacia abajo del 3 al 0.
• Cuenten hacia abajo del 5 al 0.
• Cuenten hacia abajo del 10 al 0.
Facilite más práctica para contar hacia abajo desde el 10 en el guante numerado, siempre terminando en el 0.
Detective de números
Materiales: E) Tarjetas numéricas
La clase secuencia los números hasta el 10 como preparación para trabajar con el patrón de 1 menos.
Pida a la clase que trabaje en parejas. Distribuya un juego de tarjetas a cada pareja y pídales que jueguen de acuerdo con las siguientes reglas:
• Las parejas trabajan en equipo para colocar las tarjetas en orden con los números bocarriba.
• Las parejas ponen las tarjetas bocabajo. A medida que lo hacen, colocan con cuidado cada tarjeta nuevamente en posición dentro de la secuencia.
• Estudiante A: Toma una tarjeta. Estudiante B: Usa pistas para determinar el número.
• Estudiante A: Muestra el número. Estudiante A: Determina si la pareja acertó y responde con una felicitación o con una sugerencia (por ejemplo: “Intenta usar la estrategia de tocar y contar”).
• Las parejas cambian de rol y vuelven a jugar, comenzando con todas las tarjetas bocabajo.
10 10 25 5 K ▸ M1 ▸ TG ▸ Lección 31 EUREKA MATH2 © Great Minds PBC 364
Recorra el salón de clases mientras se desarrolla el juego y proporcione apoyo según sea necesario.
Apoyo para la comprensión del lenguaje
Use acciones para ayudar a la clase a comprender el vocabulario nuevo. Por ejemplo, cada vez que sus estudiantes escuchen la palabra cayó, pídales que hagan de cuenta que recogen algo del suelo.
Presentar
Materiales: M) Letra de la canción “Había 10 manzanas en el árbol de José”, marioneta, Growing Up with Ella Jenkins, de Ella Jenkins
La clase cuenta hacia atrás cantando una canción y observa el patrón de 1 menos.
Muestre la imagen del árbol con 10 manzanas. Muestre la marioneta y explique que representa a José. José quiere que se caiga una manzana para comerla. Cante el primer verso de manera individual.
Había 10 manzanas en el árbol de José.
Había 10 manzanas en el árbol de José.
Se cayó 1 manzana y José se la comió; quedan 9 manzanas en el árbol de José.
DUA: Representación
Coloque un camino numérico en la pizarra blanca para que sus estudiantes lo consulten mientras cantan la canción. El camino numérico les da la oportunidad de ver qué número sigue en la secuencia de conteo regresivo. Es posible que la clase deba hacer una pausa después de que se cae cada manzana para evaluar cuántas manzanas quedan en el árbol.
1
2 3 4 5 6 7 8 9 10
10 10 25 5
EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 31 © Great Minds PBC 365
Anime a la clase a cantar en conjunto. Comience otra vez desde el 10 para ayudarles a recordar el ritmo de la canción. Invite a sus estudiantes a mostrar con los dedos las manzanas del árbol de José mientras cantan.
Continúe con la canción hasta que haya 0 manzanas en el árbol.
¿Qué pasó con el grupo de manzanas mientras cantábamos?
Se hizo más pequeño.
José siguió comiendo manzanas hasta que no quedó ninguna.
Para terminar, haga la transición al siguiente segmento.
Hoy, hallaremos maneras de mostrar qué sucede cuando quitamos 1 de un grupo.
Aprender
Las manzanas de José
Materiales: E) Cubos Unifix, tapete de trabajo
La clase usa cubos para representar el patrón de 1 menos de la canción.
Distribuya cubos Unifix y tapetes de trabajo. Sus estudiantes pueden comenzar con los cubos unidos o separados. Pídales que hagan una representación de cualquier manera que tenga sentido para cada estudiante.
Hagamos de cuenta que estos cubos son las manzanas. ¿Cómo empieza la canción?
Había 10 manzanas en el árbol de José.
Invite a la clase a tomar 10 cubos y colocarlos en sus tapetes de trabajo para crear sus árboles.


Había 10 manzanas en el árbol de José
Había 10 manzanas en el árbol de José (Repetir)
Se cayó 1 manzana y José se la comió; quedan 9 manzanas en el árbol de José.
Había 9 manzanas en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; quedan 8 manzanas en el árbol de José.
Había 8 manzanas en el árbol de José. (Repetir) Se cayó 1 manzana y José se la comió; quedan 7 manzanas en el árbol de José.
Había 7 manzanas en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; quedan 6 manzanas en el árbol de José.
Había 6 manzanas en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; quedan 5 manzanas en el árbol de José.
Había 5 manzanas en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; quedan 4 manzanas en el árbol de José.
Había 4 manzanas en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; quedan 3 manzanas en el árbol de José.
Había 3 manzanas en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; quedan 2 manzanas en el árbol de José.
Había 2 manzanas en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; queda 1 manzana en el árbol de José.
Había 1 manzana en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; quedan 0 manzanas en el árbol de José.
Nota para la enseñanza
En esta lección, no hay previsto tiempo para hacer dibujos de árboles, pero tal vez a sus estudiantes les guste usar dibujos que hayan hecho antes de la lección.
10 10 25 5
K M1 TG Lección 31 Había 10 manzanas en el árbol de José EUREKA MATH2 © Great Minds PBC 370 This page may be reproduced for classroom use only.
K ▸ M1 ▸ TG ▸ Lección 31 EUREKA MATH2 © Great Minds PBC 366
Letra de la canción “Había 10 manzanas en el árbol de José”
¿Qué sucedió a continuación?
Se cayó 1 manzana.
¡Correcto! Saquemos 1 manzana de nuestro árbol. (Quite 1 cubo).
¿Cuántas manzanas quedan en el árbol?
9
Canten la canción y quiten 1 cubo a la vez hasta que haya 0 manzanas en el árbol. Recorra el salón de clases para brindar apoyo a quienes necesiten ayuda para hacer que sus cubos coincidan con la canción.
Cuando termine la canción, pida a la clase que construya una torre con sus cubos. Pídales que se pongan de pie cuando terminen. El simple acto de ponerse de pie brinda un momento propicio para moverse e indica que la clase está preparada para la siguiente tarea.
Contar 1 menos
Materiales: M/E) Cubos Unifix

La clase usa cubos para representar el patrón de 1 menos en una secuencia de conteo hacia atrás.
Cuando cantamos la “Canción de los gatos bailarines”, repetimos 1 más. Cuando cantamos la canción del árbol de José y se cae 1 manzana, hay 1 menos.
Podemos contar hacia atrás usando las palabras 1 menos.
Pida a sus estudiantes que canten a coro después de usted para enseñarles a contar 1 menos. Demuestre el concepto con una torre de cubos en posición vertical para que sus estudiantes observen la correspondencia entre 1 menos y la torre que se hace cada vez más baja. Trabajar en forma vertical estable una relación con el modelo de las escaleras de números del siguiente segmento.

Tengo 10. (Muestre una barra de 10 cubos).
Tengo 10.
EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 31 © Great Minds PBC 367
1 menos es 9. (Quite un cubo).
1 menos es 9.
Continúe hasta el 0 con las respuestas a coro. Luego, repita el proceso. Esta vez pida a la clase que quite los cubos de sus propias torres, uno a la vez, mientras cuentan hacia atrás en conjunto usando la frase 1 menos.
Escaleras de números
La clase analiza el patrón de 1 menos con el modelo de las escaleras de números.
Muestre la imagen de 10 cubos (la última escalera de números). Continúe con las demás escaleras de números mientras cuentan hacia atrás hasta el 0.
Aquí hay una imagen de sus torres para cada número. Cuenten hacia atrás conmigo. 10; 1 menos es 9. 9; 1 menos es 8...
Sigan contando hacia atrás hasta el 0 usando la frase 1 menos. Deje la imagen de las 10 escaleras de números a la vista para una conversación con la clase.
¿En qué se diferencian estas escaleras de números?
Siguen pareciendo escaleras, pero ahora van hacia abajo en vez de hacia arriba. Se hacen cada vez más cortas.
¿Qué observan cuando contamos hacia atrás del 10 al 0?
Los números se hacen más pequeños. Cada torre tiene 1 menos.
Cuando contamos hacia abajo, ¿qué número viene después del 1?
El 0
Evaluación observacional
; Escuche y observe mientras la clase quita cubos de sus torres. ¿Sus estudiantes usan la frase 1 menos al quitar cada cubo de sus torres, sin hablar demasiado lento ni demasiado rápido y relacionando la frase 1 menos con 1 cubo?
Nota para la enseñanza
Las y los estudiantes de corta edad suelen usar términos generales, como grande, pequeño o pequeña, para describir atributos medibles. Si usan términos genéricos para describir las escaleras de números, puede volver a expresar sutilmente el concepto con términos más específicos, como bajas, largas o altas, pero sin centrarse por ahora en ese vocabulario.
La comparación de los atributos medibles y el vocabulario preciso se verá en profundidad en el módulo 3. El énfasis de esta lección está puesto en la magnitud y el patrón de 1 menos en la secuencia de conteo.
10
0 K ▸ M1 ▸ TG ▸ Lección 31 EUREKA MATH2 © Great Minds PBC 368
Concluir
Reflexión final 5 minutos
Objetivo: Representar el patrón de 1 menos en una secuencia de conteo hacia atrás
¿Qué sucedió con el grupo de manzanas a medida que se cayeron del árbol?
El grupo se hizo más pequeño.
¿Quién puede contarnos sobre esto usando las palabras 1 menos?
Cuando se cayó una manzana, había 1 manzana menos en el árbol.
Quitamos 1 cubo a la vez para que haya 1 menos.
¿Qué sucedió con las escaleras de números a medida que contamos hacia atrás del 10 al 0?
Las escaleras se hicieron cada vez cortas.
¿Quién puede contarnos sobre esto usando las palabras 1 menos?
Quitamos 1 cubo a la vez para que haya 1 cubo menos.
1 menos es el número que sigue cuando contamos hacia atrás.
¿Qué sucede con los números cuando contamos hacia atrás del 10 al 0?
Se hacen más pequeños.
¿Quién puede contarnos sobre esto usando las palabras 1 menos?
Cada número es 1 menos.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante reconoce y expresa regularidad en la lógica de la repetición (MP8) cuando observa que, cuando un grupo tiene 1 menos, siempre obtiene el número que está justo antes. Expresar este concepto verbalmente ayuda a sus estudiantes a pensar en el patrón como una regla en la que pueden confiar y usar de aquí en adelante.
10 25 5
EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 31 © Great Minds PBC 369
Había 10 manzanas en el árbol de José
Había 10 manzanas en el árbol de José (Repetir)
Se cayó 1 manzana y José se la comió; quedan 9 manzanas en el árbol de José.
Había 9 manzanas en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; quedan 8 manzanas en el árbol de José.
Había 8 manzanas en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; quedan 7 manzanas en el árbol de José.
Había 7 manzanas en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; quedan 6 manzanas en el árbol de José.
Había 6 manzanas en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; quedan 5 manzanas en el árbol de José.
Había 5 manzanas en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; quedan 4 manzanas en el árbol de José.
Había 4 manzanas en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; quedan 3 manzanas en el árbol de José.
Había 3 manzanas en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; quedan 2 manzanas en el árbol de José.
Había 2 manzanas en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; queda 1 manzana en el árbol de José.
Había 1 manzana en el árbol de José. (Repetir)
Se cayó 1 manzana y José se la comió; quedan 0 manzanas en el árbol de José.
K ▸ M1 ▸ TG ▸ Lección 31 ▸ Había 10 manzanas en el árbol de José EUREKA MATH2 © Great Minds PBC 370 This page may be reproduced for classroom use only.
Dibujar escaleras de números para representar el patrón de 1 menos en una secuencia de conteo hacia atrás
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Vistazo a la lección
La clase construye y dibuja escaleras de números del 10 al 1 para representar el patrón de 1 menos en una secuencia de conteo hacia atrás. Usan su trabajo para mostrar que el número que sigue es 1 menos que el anterior y desarrollan el vocabulario para describir el patrón.
Pregunta clave
• ¿Qué observan cuando contamos hacia atrás del 10 al 0?
Criterio de logro académico
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10. (K.CC.B.4.c)
32 LECCIÓN 32
390 © Great Minds PBC This page may be reproduced for classroom use only.
© Great Minds PBC
Agenda
Fluidez 5 min
Presentar 5 min
Aprender 35 min
• Contar con escaleras de números
• Construir escaleras de números
• Paseo por la galería
• Grupo de problemas
Concluir 5 min
Materiales
Maestro o maestra
• ninguno
Estudiantes
• tarjetas Hide Zero® (que ocultan el cero), juego para demostración (del 1 al 10)
• fichas para contar (55)
Preparación de la lección
• Decida si la clase construirá las escaleras de números de manera individual o en grupos.
• La clase usa fichas para contar para construir escaleras de números. Las fichas pueden ser cualquier material del salón de clases, como cubos Unifix, fichas cuadradas de colores, pegatinas, osos para contar, cuadrados de papel o pennies. Asegúrese de que cada estudiante o cada grupo tenga 55 objetos del mismo material. Cada estudiante o grupo puede tener un material diferente.
© Great Minds PBC 373 EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 32
Fluidez
Contar hasta el 10 con el método matemático
La clase hace una recta numérica con los dedos mientras cuenta en voz alta para desarrollar fluidez con el patrón de 1 menos.
Muestre el método matemático con los dedos mientras la clase cuenta, pero no cuente en voz alta. Vamos a contar con el método matemático.
Párese de frente a la clase y pida a sus estudiantes que copien los movimientos.
Pida a la clase que cuente con el método matemático del 3 al 0.
Continúe el proceso con la siguiente secuencia:

• Cuenten hacia abajo del 5 al 0.
• Cuenten hacia abajo del 10 al 0.
Muéstrame el método matemático: 1 menos
La clase muestra un número y 1 menos con el método matemático para desarrollar fluidez con el patrón de 1 menos.
Muéstrenme 3 con el método matemático. (La clase muestra el dedo meñique, el anular y el mayor de la mano izquierda).

Muéstrenme 1 menos. Para hacerlo, pueden bajar 1 dedo. (La clase baja el dedo mayor de la mano izquierda).
¿Cuántos dedos muestran ahora?
¡Cierren las manos! Prepárense para el siguiente.
2
5 5 35 5 K ▸ M1 ▸ TG ▸ Lección 32 EUREKA MATH2 © Great Minds PBC 374
Muéstrenme 5 con el método matemático.
(La clase muestra la mano izquierda completa).
Muéstrenme 1 menos.
(La clase baja el pulgar de la mano izquierda).


¿Cuántos dedos muestran ahora?
4
¡Cierren las manos! Prepárense para el siguiente.
Repita el proceso con el 10 y, luego, con cualquier otro número y 1 menos.
Presentar
La clase representa el patrón de 1 más y el patrón de 1 menos contando hacia delante y hacia atrás con movimientos.
Represente la acción del sol cuando sale y cuando se oculta para que la clase imite. Comience por mostrar cómo ponerse en cuclillas de manera segura para simular el sol que comienza a elevarse.
Hagan de cuenta que es la mañana y sale el sol. Levántense un poco más y más alto hasta que sus brazos se eleven al cielo.
Dé tiempo a la clase para que practique los movimientos antes de comenzar a contar. Una vez que sus estudiantes se hayan estirado del todo, pídales que muestren cómo se oculta el sol inclinándose lentamente hasta volver a estar en cuclillas.
Esta vez, serán un sol de conteo. Para hacer que el sol se eleve, haremos nuestro conteo de 1 más.
Estamos en el 1. 1 más es…
Anime a sus estudiantes a que se unan al conteo mientras se elevan lentamente. Deténganse cuando lleguen al 10.
Enunciar el patrón de 1 menos puede ser un desafío lingüístico. Existe una tendencia a apresurarse y omitir el número anterior: 1 menos es 9, 1 menos es 8, 1 menos es 7, y así sucesivamente.
Ayude a la clase a mantener el ritmo e introduzca el número inicial con frases como “estamos en el 9” o “tengo 8” antes de decir el siguiente enunciado de 1 menos.
2
5 5 35 5 Nota para la enseñanza
EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 32 © Great Minds PBC 375
Ahora que estamos en el 10, contaremos con 1 menos para que el sol se oculte.
Estamos en el 10. 1 menos es…
Continúe hasta el 0. Practique contar hacia delante y hacia atrás hasta que la clase pueda recitar la secuencia con facilidad.
Aprender
Contar con escaleras de números
La clase usa escaleras de números para contar hacia atrás con la frase 1 menos.
Muestre el dibujo de 10 cubos (la última escalera de números). Avance con las imágenes de las escaleras de números mientras la clase repite la canción que aprendieron en la lección anterior.
Intentemos usar nuestro conteo de 1 menos con las escaleras de números.
Tengo 10.
Tengo 10.
1 menos es 9. (Avance la lámina).
1 menos es 9.
Continúen contando hacia atrás hasta el 0 con la frase 1 menos. Deje la imagen de las 10 escaleras de números a la vista mientras sus estudiantes las construyen en el siguiente segmento.
DUA: Acción y expresión
Como el modelo es relativamente nuevo, la imagen es una referencia visual importante mientras la clase cuenta los grupos y los alinea para formar las escaleras.
9
5 5 35 5 10 1 2 3 4 5 6 7 8 9 10 0
K ▸ M1 ▸ TG ▸ Lección 32 EUREKA MATH2 © Great Minds PBC 376
Construir escaleras de números
Materiales: E) Tarjetas Hide Zero, fichas para contar
La clase ordena los números del 10 al 1 y construye escaleras de números para emparejarlos.
Organice si sus estudiantes trabajarán en parejas o en grupos. Asigne un área de trabajo con espacio para los materiales y, de ser posible, que incluya una guía natural para alineación (p. ej., una alfombra, una baldosa o el borde de una mesa).
Distribuya las tarjetas Hide Zero.
Hoy, volveremos a hacer escaleras de números con distintos tipos de fichas. Pero esta vez, en vez de contar del 1 al 10, vamos a contar hacia atrás, del 10 al 1. Comencemos por colocar las tarjetas en orden del 10 al 1.
Recorra el salón de clases para comprobar la precisión. Cuando una pareja o grupo haya ordenado sus números de manera correcta, entrégueles una bolsita de fichas para que comiencen a construir las escaleras de números.

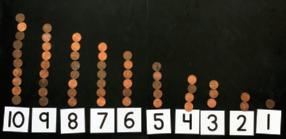

Mientras la clase trabaja, use las siguientes preguntas para evaluar e incentivar el razonamiento matemático. Pídales que usen gestos o movimientos para acompañar sus explicaciones.
• ¿Qué sucede con sus escaleras de números cuando van del 10 al 9? ¿Y del 9 al 8? ¿Y del 8 al 7?

• ¿Cómo pueden usar la escalera del número 7 como ayuda para hacer la escalera del 6?
Nota para la enseñanza
Los espacios no uniformes entre los objetos dificultan que se observe el patrón de 1 menos o el de 1 más en las escaleras de números.
Si los espacios son un problema, considere lo siguiente:
• Pida a sus estudiantes que hagan que los objetos se toquen. Dígales que el objeto de la parte de abajo debe tocar la tarjeta Hide Zero.
• Deles cubos para unir en lugar de materiales sueltos.
Promoción de los estándares para la práctica de las matemáticas
Cada estudiante reconoce y utiliza estructuras (MP7) cuando observa y usa el patrón de 1 menos para construir la siguiente escalera. Usa el patrón para construir la escalera 1 número más corta que la escalera anterior, en lugar de contar todos los objetos cada vez. Las preguntas de esta lección propician esta práctica matemática al ayudar a la clase a conversar sobre la estructura de la secuencia numérica.
EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 32 © Great Minds PBC 377
• ¿Cómo muestran sus escaleras de números el patrón de 1 menos?
• ¿Cómo harían la escalera para el número 0? ¿Hacia dónde iría?
• ¿Dónde estaría el número 11 en las escaleras de números?
Cuando sus estudiantes terminen de construir las escaleras, pídales que usen su trabajo para contar usando la frase 1 menos. Asegúrese de que las dejen en su lugar para dar un paseo por la galería.
Paseo por la galería
La clase examina el trabajo de sus pares y aprende los protocolos para dar un paseo por la galería.
Reúna a la clase lejos de las escaleras de números para presentar una nueva parte de la rutina del paseo por la galería.
Diga a sus estudiantes que darán otro paseo por la galería. Recuerde las siguientes reglas:
• Recuerde a la clase que observe pero sin tocar, como haría en un museo o una galería de arte. Pueden mantener las manos atrás de la espalda como recordatorio.
• Pida a sus estudiantes que observen los trabajos en silencio. Pídales que piensen en lo que observan sobre las escaleras de números.
Observe a sus estudiantes mientras recorren la galería. Una vez que hayan terminado el paseo, reúna a la clase. Use los siguientes planteamientos y pida a la clase que use la rutina Pensar-Trabajar en parejas-Compartir para responder.
Reúnanse y conversen con sus pares sobre qué observaron sobre las escaleras de números. Pueden decir “Observé…” para empezar la oración.
¿Qué observaron sobre las escaleras de números mientras daban el paseo?
Observé que las torres se hacían más pequeñas.
Observé que las escaleras se veían diferentes porque los materiales eran diferentes.
Evaluación observacional
; Escuche y observe mientras sus estudiantes construyen las escaleras.
• ¿Comienzan a construir sus escaleras desde el 10 o desde el 1?
• ¿Dicen la secuencia de 1 menos o construyen en silencio?
• ¿Cuentan claramente y con confianza?
K ▸ M1 ▸ TG ▸ Lección 32 EUREKA MATH2 © Great Minds PBC 378
Grupo de problemas
Use la representación sistemática para que la clase se inicie en el Grupo de problemas. Mientras sus estudiantes trabajan, observe si pueden usar el patrón para colorear 1 menos en cada escalera.
Great Minds PBC 103 EUREKA MATH K ▸ M1 ▸ TG Lección 32 32 Nombre Escribe los números en orden del 10 al 1. Colorea la escalera de números para que coincidan. EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 32 © Great Minds PBC 379
Concluir
Reflexión final 5 min
Objetivo: Dibujar escaleras de números para representar el patrón de 1 menos en una secuencia de conteo hacia atrás
Reúna a la clase y pídales que tengan a mano su Grupo de problemas.
¿En qué se parece la imagen de las escaleras de números a las escaleras de números que construyeron con objetos? ¿En qué se diferencia?
La imagen y los objetos empiezan con 10 y bajan como escaleras. Usé la estrategia de mover y contar con los objetos, pero coloreé la imagen.
¿Cómo decidieron qué colorear?
Primero, escribí todos los números. Luego, observé cada número y coloreé esa cantidad de cuadrados para que coincidiera.
No tuve que contar; tan solo coloreé 1 menos cada vez.
Comencemos con 10 y digamos el patrón de 1 menos. Pueden usar el Grupo de problemas como ayuda.
10; 1 menos es 9. 9; 1 menos es 8…
Ahora, empiecen el conteo en otro número que no sea el 10. Dé a la clase tiempo para hallar el número inicial en sus Grupos de problemas antes de comenzar a contar.
¿Qué pasa con los números cuando contamos hacia atrás del 10 al 0?
Bajan de 1 en 1.
El número que sigue es 1 menos.
5 35 5 K ▸ M1 ▸ TG ▸ Lección 32 EUREKA MATH2 © Great Minds PBC 380
Organizar, contar y representar una colección de objetos
Vistazo a la lección
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
Esta lección de conteo de colecciones sirve como tarea de cierre del módulo. La clase demuestra y celebra su crecimiento en los conceptos de conteo y los registros escritos, mientras que los maestros y las maestras recopilan datos de evaluación formativa. La conversación de la clase se enfoca en los registros de sus estudiantes. En esta lección, no hay actividades de fluidez. En esta lección, se presenta el término registrar.
Pregunta clave
• ¿De qué manera pueden ahora contar mejor o registrar mejor la información?
Criterios de logro académico
K.Mód1.CLA1 Cuentan hasta el 10. (K.CC.A.1)
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10. (K.CC.B.4.a)
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron. (K.CC.B.4.b)
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas. (K.CC.B.5)
© Great Minds PBC
33
LECCIÓN 33
390 © Great Minds PBC This page may be reproduced for classroom use only.
Agenda
Presentar 10 min
Aprender 35 min
• Organizar, contar y registrar
• Compartir, comparar y conectar
• Paseo por la galería
Concluir 5 min
Materiales
Maestro o maestra
• ninguno
Estudiantes
• colección de conteo (1 por pareja de estudiantes, en el libro para estudiantes)
• plantilla de trabajo
• herramientas de organización
• libro para estudiantes
Preparación de la lección
• Use el trabajo de sus estudiantes de la lección 19 para determinar si las colecciones de conteo recopiladas en esa lección tienen suficientes objetos para la lección de hoy. Ajústelas según sea necesario.
• Decida si la clase trabajará en parejas o de manera individual. La lección está redactada para parejas, pero se puede adaptar al trabajo individual.
• Seleccione las herramientas de organización que la clase pueda elegir para organizar su conteo, como cartones con marcos de 10, caminos numéricos o marcos de 10.
• Coloque la Lista de verificación de la evaluación observacional en un portapapeles para tomar notas de las observaciones.
© Great Minds PBC 383 EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 33
Materiales: E) Colección de conteo, plantilla de trabajo, herramientas de organización
La clase repasa los procedimientos y prepara sus colecciones de conteo.
Oriente brevemente a la clase acerca de los materiales y el procedimiento para la actividad:
• Las parejas colaboran para contar una colección.

• Cada estudiante hace un registro individual para mostrar cómo contó la pareja.
Señale las herramientas de organización que la clase puede elegir. Las herramientas como los caminos numéricos o los cartones con marcos de 10 facilitarán la correspondencia de uno a uno y pueden ser de ayuda. Anime a la clase a elegir una herramienta diferente a la que haya usado en lecciones de conteo de colecciones anteriores.
Forme parejas de estudiantes. Pídales que elijan una colección y hallen un área de trabajo.
Antes de sacar las colecciones de la bolsita, pida a las parejas que planifiquen cómo trabajarán en conjunto para contar toda la colección. Recorra el salón de clases y pida a sus estudiantes que expliquen brevemente sus planes. Pida a algunas parejas con planes razonables que compartan su razonamiento con la clase.
A lo largo de la lección, busque y valore ejemplos de buen trabajo en parejas.
Presente el trabajo que van a hacer en el siguiente segmento para establecer una transición.
Hoy, contaremos nuestras colecciones y mostraremos el trabajo en papel.
Nota para la enseñanza
Los caminos numéricos de distinta longitud son excelentes herramientas. Brindan apoyo para la correspondencia de uno a uno y pueden permitir que sus estudiantes trabajen con colecciones más grandes de las que podrían contar sin ayuda. Sus estudiantes también usan los caminos numéricos para hallar y copiar numerales por su cuenta.

Presentar
5 35 10
K ▸ M1 ▸ TG ▸ Lección 33 EUREKA MATH2 © Great Minds PBC 384
Aprender
Organizar, contar y registrar
Materiales: E) Colección de conteo, trabajo en clase con la colección de conteo, plantilla de trabajo, herramientas de organización
La clase usa sus propias estrategias para contar objetos y registrar el proceso. Anime a sus estudiantes a comenzar a contar.
Recorra el salón de clases y observe cómo organizan, cuentan y registran sus estudiantes.
• Recuérdeles que deben contar todos los objetos de su colección. Las estrategias de organización pueden incluir tocar y contar o mover y contar para diferentes configuraciones (lineales, de matrices o dispersas).
• Los registros pueden ser dibujos, sellos o números.
Use las siguientes preguntas para evaluar e incentivar el razonamiento de la clase:
¿Qué estrategia de conteo usaron? ¿Funciona? ¿Podrían intentar hacerlo de otra manera?
¿Cómo mostrarán los objetos que contaron en el papel? ¿Qué dibujarán o escribirán?
¿Su dibujo coincide con la colección? ¿Cómo lo saben?
Elija algunas parejas para que compartan su trabajo de conteo en el siguiente segmento. Busque ejemplos que demuestren distintas maneras de registrar, como los dibujos y los numerales. Si es posible, tome fotos para proyectar. De no ser así, separe los trabajos seleccionados para compartirlos.
Nota para la enseñanza
A medida que sus estudiantes cuentan sus colecciones, es posible que quieran escribir números de dos dígitos. Evite decir enunciados como: “El catorce es un 1 y un 4.” Esto dará la impresión errónea de que el catorce está compuesto por dos números, 1 y 4, cuando en realidad es un solo número compuesto por dos dígitos.
Cuando sus estudiantes pregunten cómo escribir números de dos dígitos, muéstreles un ejemplo que puedan copiar. Desarrollarán el conocimiento del valor posicional que necesitan para comprender la composición de estos números en el módulo 6. Evaluación observacional
; Observe a sus estudiantes a medida que cuentan. Controle si:
• mueven los objetos para llevar la cuenta de las cosas que ya han contado (de uno a uno);
• dicen la secuencia numérica correcta y
• dicen el último número de su conteo para indicar el total (cardinalidad).
5 35 10
EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 33 © Great Minds PBC 385
Pida a quienes no compartan su trabajo que lo dejen en el lugar para usarlo en el paseo por la galería. Pídales que sea fácil para los demás ver sus colecciones y dibujos.
Promoción de los estándares para la práctica de las matemáticas
Compartir, comparar y conectar
Materiales: M) Ejemplos de trabajo de la clase La clase comenta estrategias para contar y registrar una colección.
Reúna a la clase para ver y comentar los ejemplos de trabajo seleccionados. Invite a cada pareja seleccionada a compartir sus registros junto con su colección.
Registro incompleto (método de Ellie y Theo)
Invite a una pareja que haya usado la estrategia de mover y contar para que la comparta.
(Señale las filas horizontales). Veo que sus dinosaurios están en filas. ¿Por qué decidieron ponerlos en filas?

Queríamos alinearlos, pero no entraban en el papel, así que tuvimos que poner los demás arriba.
¿Los pusieron en filas primero, o antes los movieron y contaron? Los movimos y contamos.
Cada estudiante representa a través de las matemáticas (MP4) cuando usa dibujos, números u otra información escrita para representar su colección. La revisión es un paso importante en la representación matemática. Asegúrese de animar a pensar cómo solucionar su trabajo a quienes cometieron errores en su registro.
K ▸ M1 ▸ TG ▸ Lección 33 EUREKA MATH2 © Great Minds PBC 386
Dirija la atención a los registros de la pareja.
Ellie, ¿cómo registraste, o mostraste, tu colección en la hoja?
Comencé a dibujar los dinosaurios, pero me llevaba mucho tiempo. Entonces, escribí 14 en vez de eso.
Theo, vi que dibujaste dinosaurios en tu registro. ¿Qué averiguaste sobre dibujar dinosaurios?
Es difícil. Tienen muchas partes puntiagudas. Me hicieron sentir frustrado.
No es divertido sentirse frustrado. Queremos mostrar toda la colección. Pidamos ideas al resto de la clase. Díganme, ¿cómo sería más fácil dibujar los 14 dinosaurios?
¿Tal vez dibujar círculos?
Sí, podrían dibujar círculos y, luego, poner un dinosaurio sobre el círculo hasta que todos los dinosaurios tengan un círculo.
Si sus estudiantes no sugieren hacer dibujos matemáticos, como círculos, busque la oportunidad de representar o hablar de los dibujos matemáticos. Para favorecer el desarrollo de una comunidad que se apoye en el aprendizaje matemático, invite a la clase a escuchar e intentar las ideas de sus pares.
Dibujos y numerales (método de Mila y Campbell)

Muestre los registros de otra pareja. Si es posible, elija registros que incluyan dibujos y numerales.
Tóquense la nariz con un dedo si pueden decirme cuántas arañas hay en la colección de Mila y Campbell.
Elija un par de estudiantes que se ofrezcan para decir cuántas arañas hay y expliquen cómo lo saben. Resalte los elementos de los registros que facilitan ver el número de arañas. Pueden ser el uso de números, dibujos claros de objetos individuales o la organización de los objetos en el papel.
Apoyo para la comprensión del lenguaje
En este segmento, se presenta el término registrar como vocabulario nuevo. Brinde apoyo en el uso de este término en el futuro; vuelva a expresarlo y describirlo como una manera de mostrar algo con un dibujo, una letra o números. “Pueden registrar, o dibujar, para mostrar cómo contaron y cuántos elementos hay en su colección”.
EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 33 © Great Minds PBC 387
Mila, veo que escribiste 25 arañas en tu registro. Escribir el rótulo, arañas, fue muy útil porque ahora sabemos qué contaste. ¿Cómo supiste cómo debías escribir el número 25?
Usé el camino numérico y conté hasta el 25.
Campbell, veo que escribiste 25. Hay una flecha que apunta desde el número 25 hasta esta araña. (Señale la flecha). ¿Qué nos muestra la flecha?
Dibujé demasiadas arañas, entonces conté las arañas y puse el número en mi dibujo. Esa es la última araña. Ahí es donde hay 25 arañas.
Poner las arañas arriba del dibujo fue una buena manera de comprobar que tu dibujo coincide con la colección. Hallaste una manera de hacer que tu dibujo coincida, aunque al principio dibujaste de más.
¿Alguien más dibujó elementos de más al principio? ¿Cómo hicieron para cambiar su dibujo?
Invite a un par de estudiantes más para compartir su solución por dibujar objetos de más.
Paseo por la galería
La clase da un paseo por la galería para examinar el trabajo del resto de la clase.
Diga que darán otro paseo por la galería. Recuerde las siguientes reglas:
• Recuerde a sus estudiantes que observen pero sin tocar, como harían en un museo o una galería de arte. Pueden mantener las manos atrás de la espalda como recordatorio.
• Pida a la clase que observe los trabajos en silencio. Pídales que piensen en lo que observaron sobre las colecciones y los registros.
Mientras damos el paseo por la galería, piensen en algo que observan o que les gusta sobre alguno de los trabajos.
Observe a la clase mientras recorre la galería. Una vez que haya terminado el paseo, reúna a la clase.
Hablemos de lo que observaron o lo que les gustó sobre los trabajos. Pueden decir “Observé…” o “Me gustó…” para empezar la oración.
K ▸ M1 ▸ TG ▸ Lección 33 EUREKA MATH2 © Great Minds PBC 388
Concluir
Reflexión final 5 min
Materiales: M) Trabajo de la clase
Objetivo: Organizar, contar y representar una colección de objetos
Continúe mostrando el trabajo de sus estudiantes del paseo por la galería. Enfoque la conversación en lo que la clase aprendió desde que empezaron la escuela.
¿Cómo ha cambiado su forma de contar desde la primera colección de conteo?
Me gusta mover mi colección y ponerla en filas para contar. Al principio, tiraba los objetos en la mesa y contaba.
No sabía contar más de 10. Ahora, puedo contar hasta 20.
¿Cómo ha cambiado su manera de registrar, o dibujar, su colección en una hoja?
Intenté dibujar los objetos la primera vez que registré. Ahora, dibujo círculos para mostrar cuántos hay. Es mucho más rápido.
No sabía cómo dibujar mi colección al principio. Ahora, lo sé.
Han aprendido mucho sobre matemáticas desde el comienzo del año escolar. ¿Qué tareas de matemáticas han aprendido a hacer?
¡Aprendí a contar y escribir números!
Ahora, sé cómo clasificar.
¡Puedo contar una colección grande!
Puedo hablar de mi razonamiento matemático.
Celebre todas las tareas que sus estudiantes saben hacer. Si hay tiempo suficiente, haga una lista de todas las tareas que mencionan y exhíbala en el salón de clases.
5 35 10 EUREKA MATH2 K ▸ M1 ▸ TG ▸ Lección 33 © Great Minds PBC 389
Hoja de registro de la evaluación observacional
Módulo 1 de kindergarten
Conteo y cardinalidad
Estudiante
Criterios de logro académico Criterios de logro académico Fechas y detalles de las observaciones
K.Mód1.CLA1 Cuentan hasta el 10.
K.Mód1.CLA2 Escriben los números del 0 al 10.
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
K.Mód1.CLA10 Clasifican objetos en categorías.
Notas
PC Parcialmente competente C Competente AC Altamente competente
390 © Great Minds PBC This page may be reproduced for classroom use only.
Criterios de logro académico del módulo y estándares de contenido por lección
Contenido de enfoque Contenido suplementario
CCSSee de matemáticas alineados
K.Mód1.CLA1 K.CC.A.1
K.Mód1.CLA2 K.CC.A.3
K.Mód1.CLA3 K.CC.A.3
K.Mód1.CLA4 K.CC.B.4.a
K.Mód1.CLA5 K.CC.B.4.b
K.Mód1.CLA6 K.CC.B.4.b
K.Mód1.CLA7 K.CC.B.4.c
K.Mód1.CLA8 K.CC.B.5
K.Mód1.CLA9 K.CC.B.5
K.Mód1.CLA10 K.MD.B.3
391 © Great Minds PBC This page may be reproduced for classroom use only. EUREKA MATH2 K ▸ M1 ▸ Hoja de registro de la evaluación observacional
Criterio de logro académico Lección Lección Lección Lección Lección Lección Lección Tema A Tema B Tema C Tema D Tema E Tema F Tema G 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
Evaluación del módulo
Módulo 1 de kindergarten
Conteo y cardinalidad
Administre esta evaluación únicamente a estudiantes que muestren competencia inconsistente a lo largo del módulo según los registros de las evaluaciones observacionales. Dé por terminada la evaluación si la o el estudiante no es capaz de responder las primeras preguntas.
Materiales
• bolsita con 10 cubos Unifix® sueltos
• colección de útiles de escritura para clasificar: lápices de colores, crayones, marcadores
• tarjeta Hide Zero® (que ocultan el cero) del 7
• camino numérico (proporcionado en hoja extraíble)
• imagen de una flor (proporcionada en hoja extraíble)
• página de escritura de numerales (proporcionada en hoja extraíble)
© Great Minds PBC 392
Criterios de logro académico y estándares Pregunta de evaluación
K.Mód1.CLA1 Cuentan hasta el 10. (K.CC.A.1)
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10. (K.CC.A.3)
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10. (K.CC.B.4.a)
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron. (K.CC.B.4.b)
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas. (K.CC.B.5)
K.Mód1.CLA10 Clasifican objetos en categorías. (K.MD.B.3)

1. Dé a su estudiante una bolsita con útiles de escritura. Coloque el camino numérico enfrente.
Puedes clasificar estos objetos como quieras. Si es necesario, pídale que clasifique por tamaño. Señale el grupo más pequeño de la clasificación.
¿Cuántos objetos hay en este grupo?
Señala el número que diga cuántos hay.
¿Cuántos cubos hay en el grupo?
Si su estudiante dice ninguno, pregunte por el número que muestra ninguno (0).
EUREKA MATH2 K ▸ M1 © Great Minds PBC 393
1 2 3 4 5 6 7 8 9 10
Criterios de logro académico y estándares Pregunta de evaluación
K.Mód1.CLA1 Cuentan hasta el 10. (K.CC.A.1)
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10. (K.CC.A.3)
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10. (K.CC.B.4.a)
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron. (K.CC.B.4.b)
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos. (K.CC.B.4.b)
K.Mod1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas. (K.CC.B.5)
2. Muestre la imagen de la flor. Cuenta los pétalos. Coloca 1 cubo sobre cada pétalo mientras cuentas.

¿Cuántos cubos hay?
Señala el número que dice cuántos hay. Disperse los cubos.
¿Cuántos cubos hay?
394
K ▸ M1 EUREKA MATH2 © Great Minds PBC
1 2 3 4 5 6 7 8 9 10
Criterios de logro académico y estándares Pregunta de evaluación
K.Mód1.CLA1 Cuentan hasta el 10. (K.CC.A.1)
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10. (K.CC.A.3)
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10. (K.CC.B.4.a)
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron. (K.CC.B.4.b)
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10. (K.CC.B.4.c)
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande. (K.CC.B.5)
K.Mód1.CLA2 Escriben los números del 0 al 10. (K.CC.A.3)
3. Dé a su estudiante la bolsita de 10 objetos. Muestre la tarjeta Hide Zero del 7. (Muestre la tarjeta del 7). Cuenta esta cantidad. Si consigues 1 más, ¿cuántos hay?

Señala el número que muestra 1 más que 7.
4. Quite el camino numérico. Coloque la página de escritura de numerales frente a su estudiante.
Escribe los números del 1 al 10 en orden.

EUREKA MATH2 K ▸ M1 © Great Minds PBC 395
1 2 3 4 5 6 7 8 9 10

EUREKA MATH 2 K ▸ M1 ▸ Evaluación del módulo 396 © Great Minds PBC This page may be reproduced for classroom use only.
EUREKA MATH 2 K ▸ M1 ▸ Evaluación del módulo 397 © Great Minds PBC This page may be reproduced for classroom use only.
Estándares
Estándares de contenido del módulo
Conocen el nombre de los números y la secuencia de conteo.
K.CC.A.1 Cuentan hasta 100 de uno en uno y de diez en diez.
K.CC.A.3 Escriben números del 0 al 20. Representan un número de objetos con un número escrito del 0-20 (en donde el número 0 representa la ausencia de objetos).
Cuentan para expresar el número de objetos.
K.CC.B.4 Comprenden la relación entre números y cantidades; relacionan el conteo y la cardinalidad.
a. Al contar objetos, dicen los nombres de los números en el orden convencional, emparejando cada objeto con un solo número y cada número con un solo objeto.
b. Comprenden que el último número que se dice indica la cantidad de objetos contados. La cantidad de objetos no cambia independientemente de la manera en que se les organiza si se les reorganiza o si se cambia el orden en que se contaron.
c. Comprenden que cada número sucesivo se refiere a una cantidad que es uno más que la cantidad anterior.
K.CC.B.5 Cuentan para responder preguntas sobre “¿cuántos hay?” sobre una serie de hasta 20 objetos, ordenados en línea, de forma rectangular o circular, o sobre una serie de 10 objetos que estén esparcidos; dado un número del 1 al 20, cuentan los objetos.
© Great Minds PBC 398
Clasifican objetos y cuentan la cantidad de objetos en cada categoría.
K.MD.B.3 Clasifican objetos en categorías determinadas; cuentan la cantidad de objetos en cada categoría y clasifican las categorías según su número.3
Estándares para la práctica de las matemáticas
MP1 Dan sentido a los problemas y perseveran en su resolución.
MP2 Razonan de forma abstracta y cuantitativa.
MP3 Construyen argumentos viables y ofrecen valoraciones sobre el razonamiento de otros y otras.
MP4 Representan a través de las matemáticas.
MP5 Utilizan las herramientas apropiadas estratégicamente.
MP6 Ponen atención a la precisión.
MP7 Reconocen y utilizan estructuras.
MP8 Reconocen y expresan regularidad en la lógica de la repetición.
EUREKA MATH2 K ▸ M1 © Great Minds PBC 399
3 Limitar las categorías a números menores que o iguales a 10.
Criterios de logro académico: Indicadores de competencias
K.Mód1.CLA1 Cuentan hasta el 10.
CCSSEE DE MATEMÁTICAS RELACIONADO
K.CC.A.1 Cuentan hasta 100 de uno en uno y de diez en diez.
Parcialmente competente Competente
Cuentan hasta el 5.
Cuenta lo máximo que puedas.
1, 2, 3, 4, 5, 8, 7, 10
Cuentan hasta el 10.
Cuenta lo máximo que puedas.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Altamente competente
Cuentan hasta números mayores que 10.
Cuenta lo máximo que puedas.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
K.Mód1.CLA2 Escriben los números del 0 al 10.
CCSSEE DE MATEMÁTICAS RELACIONADO
K.CC.A.3 Escriben números del 0 al 20. Representan un número de objetos con un número escrito del 0-20 (en donde el número 0 representa la ausencia de objetos).
Parcialmente competente Competente
Escriben algunos números del 0 al 10.1
Escribe los números del 1 al 10.
Escriben todos los números del 0 al 10.2
Escribe los números del 1 al 10.
Altamente competente
1 Las inversiones ocasionales son comunes al principio del año y no representan falta de competencias.
2 Las inversiones ocasionales son comunes al principio del año y no representan falta de competencias.
400 © Great Minds PBC
K.Mód1.CLA3 Representan un grupo de objetos con un numeral escrito del 0 al 10.
CCSSEE DE MATEMÁTICAS RELACIONADO
K.CC.A.3 Escriben números del 0 al 20. Representan un número de objetos con un número escrito del 0-20 (en donde el número 0 representa la ausencia de objetos).
Parcialmente competente Competente Altamente competente
Representan un grupo de objetos con un numeral escrito del 0 al 5.




Cuenta los cubos. Señala el número que muestra cuántos hay.
Representan un grupo de objetos con un numeral escrito del 6 al 10.
Cuenta los cubos. Señala el número que muestra cuántos hay.
K.Mód1.CLA4 Dicen el nombre de un número con cada objeto que cuentan hasta el 10.
CCSSEE DE MATEMÁTICAS RELACIONADO
K.CC.B.4.a Al contar objetos, dicen los nombres de los números en el orden convencional, emparejando cada objeto con un solo número y cada número con un solo objeto.
Parcialmente competente Competente Altamente competente
Dicen el nombre de un número con cada objeto que cuentan hasta el 10 con la ayuda de una herramienta, como el camino numérico.
Cuenta los cubos. ¿Cuántos cubos hay?
Dicen el nombre de un número con cada objeto que cuentan hasta el 10 usando estrategias como tocar y contar, mover y contar, o marcar y contar.
Cuenta las mariposas. ¿Cuántas mariposas hay?
Dicen el nombre de un número con cada objeto que cuentan hasta más de 10 objetos.
Cuenta los puntos. ¿Cuántos puntos hay?
EUREKA MATH2 K ▸ M1 401 © Great Minds PBC
1 2 3 4
6
5
7 8 9 10
1 2
3 4 10
K.Mód1.CLA5 Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
CCSSEE DE MATEMÁTICAS RELACIONADO
K.CC.B.4.b Comprenden que el último número que se dice indica la cantidad de objetos contados. La cantidad de objetos no cambia independientemente de la manera en que se les organiza si se les reorganiza o si se cambia el orden en que se contaron.
Parcialmente competente Competente Altamente competente
Usan el último número de un conteo para decir cuántos hay, independientemente de la organización de los objetos o el orden en el que contaron.
Cuenta los puntos.
K ▸ M1 EUREKA MATH2 402 © Great Minds PBC
2, 3, 4, 5, 6, 7
7
1,
¿Cuántos puntos hay?
K.Mód1.CLA6 Dicen cuántos hay sin volver a contar cuando se reorganizan los objetos.
CCSSEE DE MATEMÁTICAS RELACIONADO
K.CC.B.4.b Comprenden que el último número que se dice indica la cantidad de objetos contados. La cantidad de objetos no cambia independientemente de la manera en que se les organiza si se les reorganiza o si se cambia el orden en que se contaron.
Parcialmente competente Competente Altamente competente
Dicen cuántos hay sin volver a contar cuando se reorganizan de 1 a 5 objetos.
Cuenta los cubos.
1, 2, 3
¿Cuántos cubos hay? 3
El maestro o la maestra dispersa los cubos.
¿Cuántos cubos hay ahora?
Dicen cuántos hay sin volver a contar cuando se reorganizan de 6 a 10 objetos.
Cuenta los cubos.
1, 2, 3, 4, 5, 6, 7
¿Cuántos cubos hay?
7
El maestro o la maestra dispersa los cubos.
¿Cuántos cubos hay ahora?
7
Dicen cuántos hay sin volver a contar cuando se reorganizan más de 10 objetos.
Cuenta los cubos.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
¿Cuántos cubos hay?
15
El maestro o la maestra reorganiza los cubos.
¿Cuántos cubos hay ahora? 15
EUREKA MATH2 K ▸ M1 403 © Great Minds PBC
3
K.Mód1.CLA7 Comprenden que cada número consecutivo es uno más que la cantidad anterior cuando cuentan hasta el 10.
CCSSEE DE MATEMÁTICAS RELACIONADO
K.CC.B.4.c Comprenden que cada número sucesivo se refiere a una cantidad que es uno más que la cantidad anterior.
Parcialmente competente Competente Altamente competente
Cuentan desde el 1 para decir el número que es uno más, hasta el 10.
Tengo 3 cubos. Uno más es…
1, 2, 3, 4. 4.
Dicen el número que es uno más, hasta el 10.
Tengo 3 cubos. Uno más es…
4.
K.Mód1.CLA8 Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en configuraciones lineales, de matriz rectangular, circulares o dispersas.
CCSSEE DE MATEMÁTICAS RELACIONADO
K.CC.B.5 Cuentan para responder preguntas sobre “¿cuántos hay?” sobre una serie de hasta 20 objetos, ordenados en línea, de forma rectangular o circular, o sobre una serie de 10 objetos que estén esparcidos; dado un número del 1 al 20, cuentan los objetos.
Parcialmente competente Competente Altamente competente
Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en línea o en una matriz rectangular.
Cuenta los puntos. ¿Cuántos puntos hay?
Cuentan para responder preguntas sobre cuántos hay con hasta 10 objetos organizados en un círculo o una configuración dispersa.
Cuenta los osos. ¿Cuántos osos hay?
Cuentan para responder preguntas sobre cuántos hay con hasta 20 objetos organizados en una línea, en una matriz rectangular o en un círculo.
Cuenta los cerdos. ¿Cuántos cerdos hay?
K ▸ M1 EUREKA MATH2 404 © Great Minds PBC
K.Mód1.CLA9 Cuentan un número dado de 1 a 10 objetos de un grupo más grande.
CCSSEE DE MATEMÁTICAS RELACIONADO
K.CC.B.5 Cuentan para responder preguntas sobre “¿cuántos hay?” sobre una serie de hasta 20 objetos, ordenados en línea, de forma rectangular o circular, o sobre una serie de 10 objetos que estén esparcidos; dado un número del 1 al 20, cuentan los objetos.
Parcialmente competente Competente
Cuentan un número dado de 1 a 5 objetos de un grupo más grande.
Encierra en un círculo 3 clips.
Cuentan un número dado de 6 a 10 objetos de un grupo más grande.
Encierra en un círculo 6 pelotas.
K.Mód1.CLA10 Clasifican objetos en categorías.
CCSSEE DE MATEMÁTICAS RELACIONADO
Altamente competente
K.MD.B.3 Clasifican objetos en categorías determinadas; cuentan la cantidad de objetos en cada categoría y clasifican las categorías según su número.3
3Limitar las categorías a números menores que o iguales a 10.
Parcialmente competente
Identifican si los objetos son iguales o diferentes.
¿Estas figuras geométricas son exactamente iguales?
Competente
Clasifican los objetos en categorías cuando hay un atributo dado.
Clasifica los objetos por color.
Altamente competente
Clasifican los objetos en categorías cuando no hay un atributo dado.
Clasifica los objetos.
EUREKA MATH2 K ▸ M1 405 © Great Minds PBC
Vocabulario
Los siguientes términos son sumamente importantes para el trabajo en el módulo 1 de kindergarten. Este recurso agrupa el vocabulario en las siguientes categorías: Nuevo y Verbos académicos. Las lecciones del módulo incorporan el vocabulario con la expectativa de que la clase emplee el vocabulario durante las discusiones y en sus escritos.
Los elementos en la categoría Nuevo son palabras específicas de la disciplina que se presentan a la clase en este módulo. Estos elementos incluyen la definición, la descripción o una ilustración como aparece en la lección. En ocasiones, este recurso incluye también explicaciones en cursiva para las maestras y los maestros destinadas a ampliar la terminología usada con la clase.
Los elementos de la categoría Verbos académicos son términos de gran utilidad que pueden usarse en otras disciplinas. Los términos provienen de una lista de verbos académicos que se presentan estratégicamente en el currículo para este grado.
Nuevo clasificar
Colocar un conjunto de objetos en diferentes grupos. Podemos organizarlos por color, tamaño o de otra manera. (Lección 2) contar
Cuando queremos saber cuántos hay, contamos. (Lección 3)
estrategia
Plan para resolver un problema. Podemos usar una estrategia para asegurarnos de estar contando correctamente. (Lección 6)
En el módulo 1, la clase aprende varias estrategias de conteo, como tocar y contar, y mover y contar. Más adelante, la clase aprenderá otros tipos de estrategias, como estrategias de suma y de resta.
línea
Cuando los objetos se organizan de manera recta en forma vertical u horizontal, están en línea. (Lección 8)
número
Cuántas cosas hay. Escribimos números para mostrar cuántas cosas hay. (Lección 5)
En kindergarten, el término número se usa comúnmente para referirse a un número (el concepto del 5), a su numeral (5) y a la palabra en español que designa a ese número (cinco). En kindergarten, no se requiere que la clase distinga entre estos conceptos.
oración numérica
Las oraciones numéricas nos indican cómo juntar o separar un número en partes. Por ejemplo, 5 es igual a 3 y 2, y si a 3 le quitamos 1 es 2.
(Lección 15 y Lección 18)
En el módulo 4, también usaremos el término oración numérica para describir una ecuación en la que se usan signos como +, – e =. Por ejemplo, 5 = 2 + 3 y 3 – 1 = 2 son oraciones numéricas.
suficientes
Cuando hay suficientes, no necesitamos más. Por ejemplo, cada perro recibe 1 golosina, cada persona recibe 1 par de zapatos, hay 1 tenedor para cada plato. (Lección 7)
Verbos académicos
© Great Minds PBC 406
explicar observar registrar resolver
Las matemáticas en el pasado
El cero
Si el cero significa “nada”, ¿por qué lo necesitamos?
¿Alguien inventó el número cero?
¿El cero siempre se dibujó como 0?
Invite a la clase a imaginar un mundo sin el número cero. Aquí se presentan situaciones que podrían resultarles entretenidas. ¡Intente pensar en otras!
Sin el cero…
…podrías contar hacia atrás: 3, 2, 1. ¡Pero no podrías lanzar un cohete! Los cohetes necesitan un conteo regresivo que vaya hasta el cero: 3… 2… 1… ¡despegue! El lanzamiento ocurre cuando el conteo regresivo llega al cero.
• En un mundo sin el cero, ¡el cohete se quedaría ahí!
…podrías caminar, porque un pie siempre estaría en el suelo. Pero no podrías saltar ni brincar. Si lo hicieras, tendrías cero pies tocando el suelo.
• En un mundo sin el cero, ¡no podrías saltar ni brincar!
…podrías tener una galleta en la mano, ¡pero no podrías comerla! Si comieras la galleta, tendrías cero galletas en la mano.
• En un mundo sin el cero, ¡no podrías comer la galleta!
Es muy bueno que el mundo tenga el número cero. ¡Necesitamos el cero!
Las personas cuentan 1, 2, 3, etc., desde hace mucho tiempo. Las cantidades como 1 piedra, 2 ramitas y 3 flores representan cosas que podemos ver y tocar. Pero no podemos ver ni tocar cero piedras.

Con el tiempo, las personas se dieron cuenta de que nuestro sistema numérico necesitaba un símbolo para representar el cero. Como escribió un historiador de los símbolos numéricos:
El cero es algo que debe estar ahí para que podamos decir que ahí no hay nada.1
© Great Minds PBC 408
de
1 Traducido
Karl Menninger, Number Words and Number Symbols, 400.
Los mayas fueron una de las primeras civilizaciones en escribir un símbolo para el cero. Vivieron en lo que hoy es México y Centroamérica hace más de 3,000 años. Su símbolo para el cero parecía una concha llamativa: Los hindúes de la antigua India también crearon un símbolo para el cero. Su símbolo era mucho más parecido al cero moderno y se veía así:
La idea de dar un marcador de posición al cero llegó hasta Irán e Irak. Su símbolo para el cero al principio se veía así:
Por último, el símbolo del cero evolucionó hasta llegar al que usamos hoy:
¡Nuestro símbolo del cero se parece al cero hindú y al árabe!
EUREKA MATH2 K ▸ M1 © Great Minds PBC 409
• ₀ o
Materiales
Se necesitan los siguientes materiales para implementar este módulo. Las cantidades sugeridas se basan en una clase de 24 estudiantes y una maestra o un maestro.
1 bloc de notas adhesivas
48 bolsitas de plástico resellables pequeñas
25 borradores para las pizarras blancas individuales
25 bolsitas para clasificar
25 colecciones de conteo
1 computadora o dispositivo para la enseñanza
1 cubos Unifix®, set de 1,000
275 frijoles de dos colores, rojos y blancos
25 lápices
1 libro Enseñar
24 libros Aprender
1 marioneta o animal de peluche
25 marcadores de borrado en seco
3 osos para contar, set de 96
1 papel blanco, paquete
1 papel de rotafolio, bloc
Visite http://eurmath.link/materials para saber más.
1 par de guantes numerados, izquierdo y derecho
25 paquetes de crayones
25 pizarras blancas individuales
96 platos de papel
1 proyector
25 vasos
1 tarjetas 5-group™ (grupos de 5) de Eureka Math2™, juego para demostración
25 tableros de Bingo de Eureka Math2™
24 tarjetas Hide Zero® (que ocultan el cero) de Eureka Math2™, juego básico para estudiantes, set de 12
1 tarjetas Hide Zero® de Eureka Math2™, juego para demostración
12 tarjetas para emparejar de Eureka Math2™, juego de 12
12 tarjetas numéricas de Eureka Math2™
3 zanahorias
Por favor, consulte la lección 6 para obtener una lista de herramientas de organización (vasos, bandas elásticas, papel cuadriculado, etc.) sugerida para la colección de conteo.
© Great Minds PBC 410
Kits de herramientas diarias
En el módulo 1, la clase trabaja con materiales prácticos para explorar los conceptos matemáticos presentados en cada lección. La lista de materiales a continuación incluye los elementos utilizados con más frecuencia en el módulo 1. Considere crear un kit de herramientas para cada estudiante para minimizar la preparación de materiales para cada lección. Tener a la mano kits de herramientas de matemáticas para estudiantes y para maestras y maestros permite transiciones suaves y disminuye drásticamente el tiempo de preparación de la lección.
Para obtener mejores resultados, comience el módulo 1 con 5 cubos Unifix®, 5 frijoles de dos colores, tarjetas Hide Zero® del 0 al 5, un lápiz y un crayón. Aumente el número de cubos, frijoles y tarjetas Hide Zero® a 10 antes de comenzar el tema E.
Kit de herramientas diarias para estudiantes
• cubos Unifix® (10)
• frijoles de dos colores en bolsita resellable (10)
• tarjetas Hide Zero® (que ocultan el cero) de Eureka Math2TM , juego para estudiantes (del 0 al 10)

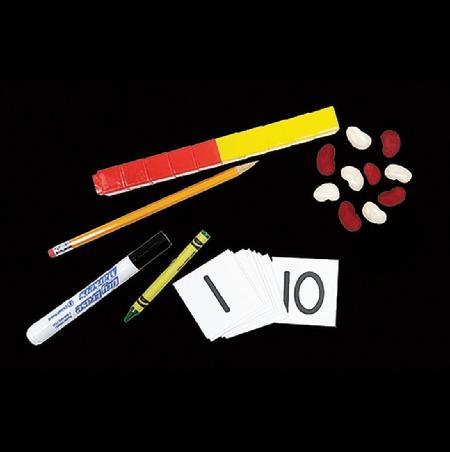
• lápiz
• crayón
Kit de herramientas diarias para la enseñanza
• par de guantes numerados, izquierdo y derecho
• frijoles de dos colores en bolsita resellable (10)
• cubos Unifix® (10)
• tarjetas Hide Zero® de Eureka Math2™, juego para demostración (del 0 al 10)
EUREKA MATH2 K ▸ M1 © Great Minds PBC 411
Materiales de creación propia
Guantes numerados
Para crear los guantes numerados, necesitará un par nuevo de guantes de limpieza y un marcador permanente. Ponga los guantes con las palmas hacia arriba. Comience con el guante derecho y escriba números en las puntas de los dedos, comenzando con el 1 en el meñique. Siga hasta terminar con el 5 en el pulgar. Continúe con el guante izquierdo, comenzando con el 6 en el pulgar y terminando con el 10 en el meñique. Conserve los guantes en su kit de herramientas para usar varias veces en el módulo 1.

Frijoles de dos colores
Para crear los frijoles de dos colores, necesitará frijoles de tipo pallar y una lata de pintura roja en aerosol. Coloque los frijoles sobre papel de periódico o una superficie protegida. Rocíe un lado de los frijoles con la pintura y deje secar. El otro lado quedará con el color original de los frijoles. Conserve los frijoles en un lugar fresco y seco de su kit de herramientas para usar varias veces en el módulo 1.

K ▸ M1 EUREKA MATH2 © Great Minds PBC 412
Bolsitas para clasificar
En el tema A, sus estudiantes clasifican objetos de distintas maneras y explora atributos como número, tamaño, forma y color. Usan las bolsitas para clasificar, o bolsitas con objetos seleccionados estratégicamente, que pueden clasificarse por atributo. Use estas bolsitas para brindar práctica adicional en las estaciones, enseñar a grupos pequeños o en otros momentos del módulo 1.
Use la tabla para crear bolsitas para clasificar que varíen de atributo y complejidad. Arme una o más bolsitas por cada atributo. No es necesario
armar conjuntos por cada tipo de bolsita, porque sus estudiantes eligen cada día entre todas.
La clase no está limitada a clasificar los objetos de la bolsita de una sola manera, aun cuando la bolsita esté diseñada con un atributo específico en mente. Por ejemplo, pueden clasificar una bolsita de botones por color, forma o tamaño. También pueden clasificar por categorías únicas, en base a sus experiencias personales. Dar a la clase autonomía para clasificar objetos como quieran les permite explorar las categorías y los atributos de manera independiente.
Atributos
Dificultad Color Tamaño Nombre o tipo Forma Ubicación Uso o actividad
Alta Distintos objetos con el mismo patrón
Distintos objetos con dimensiones contrastantes (p. ej., objetos largos y delgados; objetos cortos y anchos; objetos largos y anchos; objetos cortos y delgados)
Objetos similares con distintos atributos (p. ej., insectos y arañas)
Distintos objetos, de dos y tres dimensiones
Objetos similares, 3 tipos de transporte (p. ej., estudiantes que toman el autobús, caminan o andan en bicicleta)
Objetos con múltiples usos, 3 usos (p. ej., uso para jugar, uso para escribir, uso para construir)
Intermedia Distintos objetos, 3 colores
Baja Mismo objeto, 2 colores
Distintos objetos, 3 tamaños (pequeño, mediano, grande)
Mismo objeto, 2 tamaños
Distintos objetos, 3 tipos (p. ej., mosca, gato y pez)
Distintos objetos, 2 tipos obvios (p. ej., mosca y gato)
Distintos objetos, 3 formas
Distintos objetos, 3 ubicaciones Distintos objetos, 3 usos
Mismo objeto, 2 formas (p. ej., botón redondo y botón cuadrado)
Distintos objetos, 2 ubicaciones obvias (p. ej., manzana en la caja del almuerzo, auto en la caja de juguetes)
Distintos objetos, 2 usos obvios (p. ej., usar para comer, usar para escribir)
EUREKA MATH2 K ▸ M1 © Great Minds PBC 413
Las bolsitas que puedan clasificarse en más de una manera son especialmente interesantes para la clase. También pueden usarse para actividades de descomposición desde el tema D del módulo 1 hasta el módulo 4. En los siguientes ejemplos, el número de objetos
de cada grupo y el número de grupos posibles puede variar según el atributo que se use para clasificar. Esto mantiene la atención de la clase para contar en el tema A y para considerar distintas maneras de descomponer un número en el tema D y siguientes.
Baja • osos amarillos grandes, osos amarillos pequeños, osos azules grandes, osos azules pequeños (tamaño, color)
• banana amarilla, autobús escolar amarillo, limón amarillo, marcador amarillo, manzana roja, camión de bomberos rojo, marcador rojo, lechuga verde, auto verde (color, tipo, uso)
• manzana verde, guisante, melón, banana, calabaza amarilla, maíz, manzana roja, frambuesa, cereza (color, forma, tipo, tamaño)
Intermedia
• piedras blancas pequeñas, piedras negras pequeñas, rocas negras medianas, rocas grises grandes (tamaño, color, forma)
• botones marrones redondos y pequeños, botones marrones redondos y grandes, botones rosas redondos y medianos, botones rosas con forma de corazón y pequeños, botones azules cuadrados y grandes, botones verdes redondos y pequeños (color, tamaño, forma)
• ave, insecto, avión, bote, pato, flotador (transporte, aire o agua; tipo, vivo o no vivo; uso, volar o flotar)
Alta • pollera a lunares, pantalones a lunares, plato a lunares, chaqueta a rayas, taza a rayas, calcetines a cuadros, servilleta a cuadros (color, uso)
• pez, perro, ballena, buey, burro, tiburón, toro, tigre, tortuga (nombre, primer sonido; ubicación, agua o tierra)
• tijeras, lápiz, crayón, marcador, borrador, cepillo de dientes, peine, sandalias, sombrilla, traje de baño (uso, ubicación)
K ▸ M1 EUREKA MATH2 © Great Minds PBC 414
Colecciones de conteo
Durante el año de kindergarten, la clase organizará, contará y registrará colecciones de objetos. Cada clase necesita una variedad de colecciones de objetos hechas de materiales cotidianos. Al comienzo del año es apropiado usar colecciones de 4 a 25 objetos para la mayoría de estudiantes. Al finalizar el año, cada estudiante de kínder puede contar colecciones de 100 o más objetos. ¿Cree que será mucho trabajo administrar los materiales? Establecer rutinas y un sistema de organización para contar las colecciones hace que el proceso sea mucho más manejable, y los logros en el aprendizaje de cada estudiante valdrán la pena.

Materiales de rutina
Desarrolle un conjunto de materiales de rutina que cada pareja de estudiantes necesite para contar en las lecciones de conteo. Se necesita una colección de conteo y dos trozos de papel por pareja de estudiantes, pero proporcionar un tapete de trabajo y dos portapapeles les ayudará a mantenerse organizados. Un trozo de papel de 11" × 17" es un buen tapete de trabajo. Las lecciones de colecciones de conteo son una gran oportunidad para la evaluación formativa, por lo que recomendamos que se tenga disponible una lista de verificación de observaciones.
Selección de materiales y herramientas de organización
26 a 45 objetos
46 a 100 objetos
101 a 150 objetos
Crear y organizar colecciones
Las colecciones de conteo se pueden recopilar utilizando materiales que se encuentran fácilmente en los salones de clase o los hogares. Botones, frijoles, tapas de botellas, pompones, gomas de borrar, palitos, crayones... casi cualquier cosa puede ser parte de una colección de conteo. Coloque cada colección en una bolsa o recipiente resellable.
Sugerimos ordenar y almacenar colecciones en contenedores codificados por colores según el número de objetos en la colección. Coloque una etiqueta adhesiva del color correspondiente en cada colección para que se pueda devolver fácilmente al contenedor adecuado. Comience el año con un inventario escrito de cuántos objetos hay en cada bolsa para ayudar a medir la precisión de conteo de la clase, especialmente con colecciones más grandes. Considere tener un contenedor designado para los artículos que se perdieron durante la limpieza.
La clase puede elegir usar herramientas de organización mientras cuentan y registran. Los vasos, los tazones, los cartones con marcos de 10, los caminos numéricos, los marcos de 10 y las plantillas de dos manos pueden ayudar a organizar, contar y registrar la colección. Las notas para la enseñanza proporcionan ideas específicas para usar herramientas de organización para apoyar o desafiar a la clase. Muestre y ponga a disposición de la clase este tipo de materiales para que los usen como lo deseen.
EUREKA MATH2 K ▸ M1 © Great Minds PBC 415
Contenedores de colecciones de conteo
4 a 10 objetos 11 a 25 objetos
Obras citadas
Boaler, Jo and Lang Chen. “Why Kids Should Use Their Fingers in Math Class.” The Atlantic. April 13, 2016. https://www .theatlantic.com/education/archive/2016/04/why-kids should-use-their-fingers-in-math-class/478053/.
CAST. Universal Design for Learning Guidelines version 2.2. Retrieved from http://udlguidelines.cast.org, 2018.
Carpenter, Thomas P., Megan L. Franke, Nicholas C. Johnson, Angela C. Turrou, and Anita A. Wager. Young Children’s Mathematics: Cognitively Guided Instruction in Early Childhood Education. Portsmouth, NH: Heinemann, 2017.
Common Core Standards Writing Team. Progressions for the Common Core State Standards in Mathematics. Tucson, AZ: Institute for Mathematics and Education, University of Arizona, 2011–2015. https://www.math.arizona.edu/~ime/progressions/.
Menninger, Karl. Number Words and Number Symbols: A Cultural History of Numbers. New York: Dover Publications, 1992.
National Governors Association Center for Best Practices, Council of Chief State School Officers (NGA Center, CCSSO). 2013. Common Core State Standards English/Spanish Language Version. Estándares Estatales Comunes de Matemáticas. Translated by San Diego County Office of Education. San Diego, CA: San Diego County Office of Education.
Zaslavsky, Claudia. Number Sense and Nonsense: Games, Puzzles, and Problems for Building Creative Math Confidence. Chicago: Chicago Review Press Incorporated, 2019.
© Great Minds PBC 416
Créditos
Great Minds® has made every effort to obtain permission for the reprinting of all copyrighted material. If any owner of copyrighted material is not acknowledged herein, please contact Great Minds for proper acknowledgment in all future editions and reprints of this module.
Common Core State Standards Spanish Language Version © Copyright 2013. San Diego County Office of Education, San Diego, California. All rights reserved.
For a complete list of credits, visit http://eurmath.link/media-credits.
Cover, Piet Mondrian (1872–1944), Composition with Large Red Plane, Yellow, Black, Gray and Blue, 1921. Oil on canvas. Kunstmuseum Den Haag, The Hague, Netherlands. Image copyright ©Kunstmuseum Den Haag. Image credit: Bridgeman Images; pages 22 (top), (composite image) Alex Staroseltsev/Shutterstock.com, Elena Elisseeva/Shutterstock.com;
pages 14, 21 (bottom), Tim UR/Shutterstock.com; page 21, (top) Becky Stares/Shutterstock.com; page 22, (bottom) Jan Havlicek/Shutterstock. com; pages 70, 72, 98, 99, 100, Henri Rousseau, The Flamingos, 1907. Photo credit: Dennis Hallinan/Alamy Stock Photo; pages 121, 151 (composite image) julie deshaies/Shutterstock.com, Khumthong/ Shutterstock.com, Hong Vo/Shutterstock.com; page 228, (composite image) Nataliia K/Shutterstock.com, Suzanne Puttman Photography/ Moment/Getty Images, 5 second Studio/Shutterstock.com, YAY Media AS/ Alamy Stock Vector; page 243, loskutnikov/Shutterstock.com; page 316, Radek Borovka/Shutterstock.com; pages 366, 370, Words by Ella Jenkins, music traditional, adapted by Ella Jenkins/Ell-Bern Publishing Co. ASCAP; page 408, hobbit/Shutterstock.com; All other images are the property of Great Minds.
© Great Minds PBC 417
Agradecimientos
Beth Barnes, Dawn Burns, Mary Christensen-Cooper, Cheri DeBusk, Stephanie DeGiulio, Jill Diniz, Brittany DuPont, Lacy Endo-Peery, Krysta Gibbs, Melanie Gutiérrez, Eddie Hampton, Rachel Hylton, Travis Jones, Kelly Kagamas Tomkies, Liz Krisher, Ben McCarty, Kate McGill Austin, Cristina Metcalf, Ashley Meyer, Melissa Mink, Katie Moore, Bruce Myers, Marya Myers, Maximilian Peiler-Burrows, Shelley Petre, John Reynolds, Meri Robie-Craven, Robyn Sorenson, Julie Stoehr, James Tanton, Julia
Tessler, Philippa Walker
Ana Álvarez, Lynne Askin-Roush, Trevor Barnes, Rebeca Barroso, Brianna Bemel, Carolyn Buck, Lisa Buckley, Shanice Burton, Adam Cardais, Christina Cooper, Kim Cotter, Gary Crespo, Lisa Crowe, David Cummings, Jessica Dahl, Brandon Dawley, Julie Dent, Delsena Draper, Sandy Engelman, Tamara Estrada, Ubaldo Feliciano-Hernández,
Soudea Forbes, Jen Forbus, Reba Frederics, Liz Gabbard, Diana Ghazzawi, Lisa Giddens-White, Laurie Gonsoulin, Adam Green, Dennis Hamel, Cassie Hart, Sagal Hasan, Kristen Hayes, Abbi Hoerst, Libby Howard, Elizabeth Jacobsen, Amy Kanjuka, Ashley Kelley, Lisa King, Sarah Kopec, Drew Krepp, Stephanie Maldonado, Siena Mazero, Alisha McCarthy, Cindy Medici, Ivonne Mercado, Sandra Mercado, Brian Methe, Patricia Mickelberry, Mary-Lise Nazaire, Corinne Newbegin, Max Oosterbaan, Tara O’Hare, Tamara Otto, Christine Palmtag, Laura Parker, Jeff Robinson, Gilbert Rodríguez, Todd Rogers, Karen Rollhauser, Neela Roy, Gina Schenck, Amy Schoon, Aaron Shields, Leigh Sterten, Rhea Stewart, Mary Sudul, Lisa Sweeney, Karrin Thompson, Cherry dela Victoria, Tracy Vigliotti, Dave White, Charmaine Whitman, Glenda Wisenburn-Burke, Howard Yaffe
© Great Minds PBC 418
Exponencialmente mejor
Conocimientos2 Siguiendo con la tradición de ayudar a los maestros y maestras con todo lo que necesiten para que sus estudiantes desarrollen un conocimiento profundo y coherente de las matemáticas, Eureka Math2 ofrece colecciones de videos y recomendaciones hechas a medida de los y las profesionales con más y con menos experiencia.
Digital2 A través de una experiencia digital perfectamente integrada, Eureka Math2 incluye cientos de imágenes inteligentes, videos cautivadores y actividades digitales interactivas que encienden la chispa de la conversación y el asombro en su salón de clases.
Accesible2 Siempre con nuestros lectores y lectoras en mente, Eureka Math2 se ha diseñado cuidadosamente para que quienes tengan dificultades con la lectura puedan acceder a las lecciones, los problemas verbales, ¡y más!
Sonrisas2 Con Eureka Math2, usted y sus estudiantes se enamorarán de las matemáticas, o recordarán qué era lo que les hizo enamorarse de ellas.
¿Qué tiene que ver esta pintura con las matemáticas?
Piet Mondrian redujo los sujetos de sus obras a figuras geométricas coloridas. En esta pintura, gruesas líneas negras, horizontales y verticales, enmarcan los vibrantes cuadrados y rectángulos con el rojo, el negro y el amarillo, entre otros colores. ¿Crees que alguna de las figuras se parecen? ¿Observas que las figuras más pequeñas se juntan para crear figuras más grandes?
¿Cuántas figuras ves en total?
En la portada
Composition with Large Red Plane, Yellow, Black, Gray and Blue, 1921
Piet Mondrian, Dutch, 1872–1944
Oil on canvas
Kunstmuseum Den Haag, The Hague, Netherlands
Piet Mondrian, Composition with Large Red Plane, Yellow, Black, Gray and Blue, 1921, Kunstmuseum Den Haag, The Hague, Netherlands. Image credit: Bridgeman Images

Módulo 1
Conteo y cardinalidad
Módulo 2
Figuras bidimensionales y tridimensionales
Módulo 3
Comparación
Módulo 4
Composición y descomposición
Módulo 5
Suma y resta
Módulo 6
Fundamentos del valor posicional
ISBN 978-1-63898-654-6
9 7 8 1 6 3 8 9 8 6 5 4 6
B