Tree Physiology 25, 929–938
© 2005 Heron Publishing—Victoria, Canada
A case study of forest management planning using a new heuristic algorithm
JEONG-HOSEO,1,2 FRANTIŠEKVILÈKO,1 SOFÍASÁNCHEZOROIS,1 STEPHANKUNTH,1 YEONG-MOSON3 and KLAUS VON GADOW1
1 InstitutfürWaldinventurundWaldwachstum,Georg-August-Universität, Göttingen, Germany
2 Corresponding author(jseo@uni-forst.gwdg.de)
3 Korea Forest Research Institute, 207,Cheongyangni-2dongdongdaemun-gu, Seoul, 130-712, Korea
Received June 9, 2004; accepted February 6, 2005; published online May 2, 2005
Summary
Wepresentanapproachtogenerateandevaluate differentsilviculturaldevelopmentpathsandtooptimizethe developmentofaNorwaysprucestand,usingalong-termplanninghorizon.Togenerateasilviculturalpath,themaximum standdensitywasapplied.Ateachthinningevent,threepossiblethinningintensities(10,20,30%ofthestemnumberperha) wererandomlychosen.Asearchalgorithmknownasmodified AcceleratedSimulatedAnnealing(mASA)wasusedtoestimatetheoptimumcombinationofstandpathsforagivenforest asawhole.Productionandeconomicmanagementobjectives wereconsideredandthencompared.Theeconomiccriterion wastheExpectedStandValue(ESV)witha4%discountrate.
Thegenerateddatasetof38Norwaysprucestands(comprisingatotalof123.8ha)wasusedinthecasestudy.Theresult withthebestcombinationofpathswaspresentedinadigitized forestmap.Forestmanagementsimulationwasperformedusingaspeciallydevelopedcomputerprogram,foraplanning horizonof20years.ThemASAprovedtobeaneffective search method for identifying optimum paths.
Keywords:expectedstandvalue,Norwayspruce,searchalgorithm,silviculturalpath.
Introduction
Amajorchallengeinforestmanagementisintegratingstandlevelandforest-levelobjectives.Astandisageographicalunit withinaforestedlandscapewithdefinedboundariesandattributes.Neighboringstandsmaydifferinspeciescomposition,stageofdevelopment,densityandstructure.Stand-level planningisconcernedwiththespecificationofdevelopment paths,i.e.,atimeseriesofsilviculturalactivitiesforagiven stand.Forest-levelplanningdeterminesthebestcombination ofdevelopmentpathsinallstands,consideringconstraintsand objectivesfortheenterpriseortheforestedlandscapeasa whole(Clutteretal.1983,vonGadow1991,Wikström2000).
Theobjectiveofforestmanagementistoensuresustainability ofthedifferentforestfunctionsandtoimplementthesilviculturalandeconomicgoalsoftheenterprise.Animportant
prerequisiteforachievingthisobjectiveistheabilityto generateoptimumpaths,usingsuitablegrowthmodelsandalgorithmsthatmimicspecificharvestoperationsdescribedin termsofstandardforestryterminology.Optimumforestmanagementcanbeachievedonlywhensufficientandrealistic stand-levelpathsarespecified.Therefore,theprocessofgenerating paths is a crucial element in forest planning.
Inforestmanagementplanning,spatialgoals,suchasadjacencyrestrictions,arecombinatorialproblemsbynature.Thus astheproblemsizeincreases,thesolutionspacealsoincreases,butatadisproportionatelygreaterrate(Lockwood andMoore1993).Mixedintegerprogrammingandinteger programmingtechniqueshavebeenusedtoproducemanagementplanswithadjacencyconstraints,butthesetechniques havelimitations,directlyrelatedtoproblemsize,whenappliedtolargecombinatorialproblems(LockwoodandMoore 1993).Theuseofheuristictechniquesforforestmanagement planningisbecomingmorecommon.Manytypesofcomplex, nonlineargoals(e.g.,spatialandtemporaldistributionofelk habitat,asdescribedbyBettingeretal.1997),whichhavetraditionallybeenconsideredtoocomplextosolvewithtraditionaloptimizationtechniques,arenowbeingconsidered.In recentyears,heuristicprogrammingtechniqueshavebeen appliedtotraditionalforestharvestschedulingproblems(HogansonandRose1984)aswellastoforesttransportationproblems(Pulkki1984,NelsonandBrodie1990,Weintraubetal. 1994,1995,MurrayandChurch1995),wildlifeconservation andmanagement(ArthaudandRose1996,Bettingeretal. 1997,HaightandTravis1997),aquaticsystemmanagement (Bettingeretal.1998),andtheachievementofbiologicaldiversity goals (KangasandPukkala1996).
ThemethodknownasSimulatedAnnealingisoneofthe heuristictechniquescommonlyusedinforestmanagement planning.NelsonandLiu(1994)developedaSimulatedAnnealingalgorithmfora431-unitwithadjacencyconstraints. TheyshowedthattheirSimulatedAnnealingtechniquecould generatesuperiorsolutionstoarandomstarthill-climbingalgorithm.LockwoodandMoore(1993)developedaSimulated Annealingalgorithmtosolveatacticalschedulingproblemfor
by guest on October 13, 2011 treephys.oxfordjournals.org Downloaded from
a6148-unitinnortheasternOntario(Canada).Dahlinand Sallnäs(1993)alsousedSimulatedAnnealingtosolveplanningproblemswithadjacencyconstraintsinthesub-alpine region in Sweden.
TheobjectiveofthisstudyistopresentamethodofgeneratingsilviculturalpathsforaNorwayspruceforest,andtoapply aheuristicsearchmethodbasedonSimulatedAnnealingto identify an optimum path combination for the entire forest.
Materials and methods
Datafrom38NorwaysprucestandsatWinnefeldSüdinthe SollingforestofnorthwesternGermanywereusedinthiscase
study.Table1showstheinitialdataforeachstand.Thetotal forestareawas123.8ha.Topresenttheoptimizedforestmanagementplan,adigitalizedforesttypemapcontainingstand growthinformationwaspreparedwithreferencetoageographical information system (GIS).
Growth model
AbasalareamodeldevelopedbyVilèkoandvonGadow (unpublishedresults)onthebasisofstudiesbySchübeler (1997),Gurjanovetal.(2000)andSánchezOroisetal.(2001) wasusedtoestimatemeanstemdiametergrowth.Toestimate thedominantheightgrowth,asimplepolymorphicheight model(Sloboda1971)wasused.Themeanheightwasesti-
930
TREE PHYSIOLOGY VOLUME 25, 2005
SEO,VILÈKO,SÁNCHEZOROIS,KUNTH, SON AND VONGADOW
Age ComSubComArea (ha)Ho (m)SI Dg (cm)BA (m2 ha –1) N ha –1 7 219 e 2.2 0* 0* 2 1.88 6010 7 221 c3 1.3 0* 0* 2 1.91 6050 7 221 d 3.5 0* 0* 2 1.89 6020 7 222 b2 4.0 0* 0* 2 1.89 6030 14 220 b2 0.7 3.6 38 4 6.53 5200 15 219 d2 0.7 4.3 38 4 6.35 5050 17 219 a2 0.4 5.4 37 5 9.82 5000 17 220 c 2.5 5.4 37 6 14.14 5000 17 223 a 1.9 5.8 38 5 9.82 5000 23 219 d1 2.1 11.4 40 9 26.99 4244 23 220 b1 1.3 13.8 43 10 31.99 4074 27 225 b 5.0 13.8 39 10 31.99 4074 29 224 a 5.0 16.5 41 12 34.09 3012 32 226 d 4.3 16.5 38 12 30.60 2706 37 224 b2 1.9 17.9 37 13 30.39 2290 38 225 a 4.2 21.9 40 16 32.89 1636 40 220 d 7.2 21.9 39 16 36.59 1820 40 222 a 9.0 21.9 39 16 32.89 1636 41221b15.320.4371531.591788 41223b13.421.9391636.591820 41223b23.821.9391632.891636 42221c21.221.9381636.591820 44221b22.824.4401822.69892 44226a3.724.4401834.091340 45221a7.224.4391841.611635 46224b14.722.8371736.791621 47219c6.922.8371736.791621 50222c2.024.9381942.181488 50223c1.324.9381938.381354 52219a14.524.9371930.711083 63219a34.629.5382547.42966 65220b30.628.1362325.09604 68226b5.029.2362525.82526 68226c2.329.2362530.09613 72219b2.824.8303628.09276 83220a2.028.0313924.36204 86221c10.728.8312629.31552 116222b11.834.6323834.59305 Sum123.8 by guest on October 13, 2011 treephys.oxfordjournals.org Downloaded from
Table1.Datasetfor38Norwaysprucestands.Abbreviations:Com=compartment;SubCom=sub-compartment;Ho=dominantheight;SI=site index; Dg =quadaticmean diameter; BA = basal area; N ha –1 = stem number per hectare; and * = no data.
A HEURISTIC ALGORITHM FOR LONG-TERM FOREST MANAGEMENT 931
Table2.Basicfunctionsofthegrowthmodelusedtoestimatedthechangeinstandparameters.Abbreviations: G1 =basalareaatpresent; G2 = basalareaatthenextperiod; A1 =standageatpresent; A2 =standageatthenextperiod;SI=siteindex; N1 =stemnumberperhectareatpresent; N2 =stemnumberperhectareatthenextperiod; A100 =referenceyear(Year100); A =standageatpresent; G =basalarea;FZ=formfactor;dg = quadratic mean diameter at breast height; N
= maximum stand density index.
matedfromtheestimateddominantheight,withasimplenonlinearregressionfunction.Aformfunctiondevelopedby Bergel(1973)wasusedtoestimatestandvolume.Amaximum densityfunctionbasedonthestanddensityindex(SDI)conceptwasusedtoestimatemaximumstemnumberperhaasa thinningcontrolfunction.Theparametersofeachmodelwere fittedtotheNorwaysprucestanddataset.Thesemodelswere appliedtoestimatestandgrowthtothenextthinningevent(Table 2).
Table3.Equationsforestimatingthechangeofstandafterthinning.
Abbreviation:DBH=diameteratbreastheight;dga =quadraticmean DBHafterthinning;dgb =quadraticmeanDBHbeforethinning; NG=NGindex;hga =meanheightafterthinning;andhgb =mean height before thinning.
TheequationsshowninTable3wereusedtoestimatethe changeinstandparameters(thequadraticmeandiameterat breastheight(DBH)andmeanheight)afterthinning.ParametersinbothequationswereestimatedfromtheNorwayspruce data set.
Thinning model
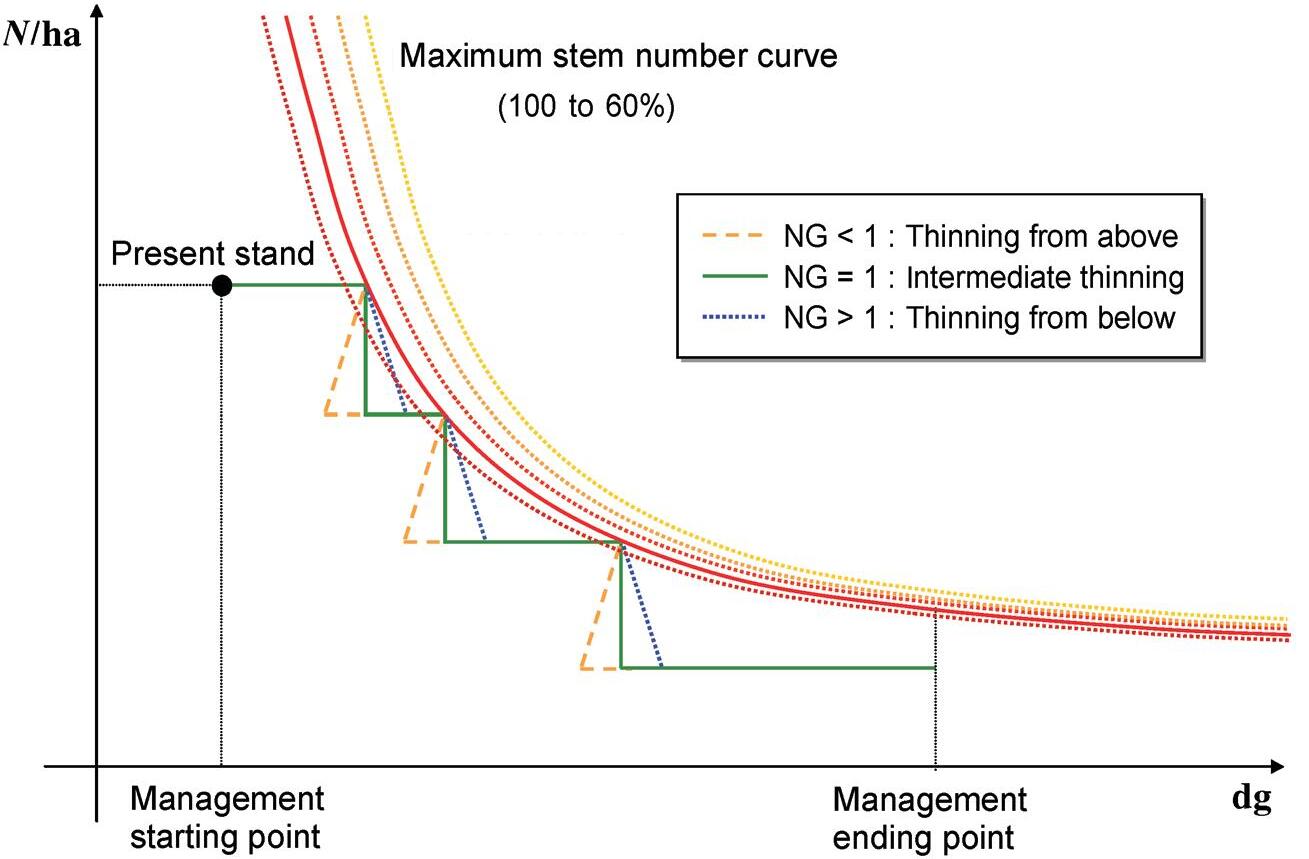
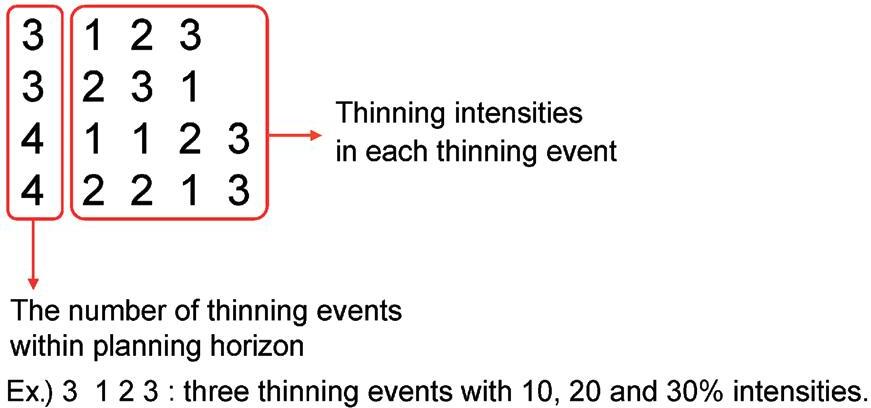
Thebasicruleofmanagementinthisstudywastothinahead ofmortality.Thethinningmodelisbasedonstanddensity (Seoetal.,unpublishedresults).Threethinningintensities wererandomlyselectedateachthinningevent(10,20,30%of stemnumberperha).Thetimingofathinningeventwasdefinedbythemaximumdensity.Ifthesimulatedstemnumber ofastandisclosetoorequaltothemaximumstemnumber, thethinningwillbecarriedout1yearbefore,otherwisethe stemnumberwillremainconstantuntilthenextthinningevent (Figure 1).
Inthisthinningmodel,themaximumstemnumbercurveis animportantfactorfordeterminingthetimeofathinning event.Therefore,itwasnamedthe“ThinningControlFactor” (TCF).Toapplyadditionalthinningsequences,notonlythe
TREE PHYSIOLOGY ONLINE at http://heronpublishing.com
maximum stem number per hectare; andSDImax
Model Functions Basal area G A A G A A 2 1 2 1 1 2 557191001191 = +− expln.–.SI A A N A A N 1 2 2 1 2 1 00091.lnln Dominant height H100 1782423 12881611 976623 = exp (. SI 97.6623 ) (.) AA 100 1288161112881611 1782423 12881611 + Mean height HH m = 061026 100 1123689 Volume VGH = m FZ Form factor FZ dg dg dg m =−++ 0040167562111361950057654 2 .././ln./ H Nmax NN maxmax ,,maxmax = == SDI dg SDI 25 125139 17857 1932668 17857 dg
max =
Model Functions Quadratic meanDBH dgdg NG ab = 10364 0007900583 A Mean height hghgNG ab=−1019200045 00232 A
DBH= diameter
n
n
by guest on October 13, 2011 treephys.oxfordjournals.org Downloaded from
Figure 1. Timing a thinning event and defining thinning intensities. Abbreviations:
at breast height; t = stand age at present; and
=
th year.
maximumstemnumber(100%),butalso90,80,70and60% ofthemaximumwereusedasTCF(Figure2).ThusalltheapplicablepathsforastandcanbecalculatedwithEquation1. Threekindsofthinningtype(thinningfrombelow,thinning fromaboveandindifferentthinning)wereapplied,according tostandage.ThethinningtypewasspecifiedbasedontheNG index(Equation2)(Staupendahl1999,vonGadowandHui 1999):
Animportantpartofpathgenerationisaplausibilitytest. Thetestisperformedusingtworulesforallinitializedpaths. Thefirstruleisa mortalitypreemption rulethatstatesthata thinningeventisinvalidifthestemnumberhasexceededthe maximumstemnumbercurve.Thesecondrule,knownasthe thinningevent rule,eliminatesallpathswherethenumberof specifiedthinningeventscannottakeplacewithinthespecifiedtimewindow.Onlyvalidpathsareselectedandtheirobjectivefunctionvaluescalculated(Figure4).Thelaststepof thegenerationinvolvestheselectionofthe10bestpathsin eachstand,accordingtotheobjectivefunctionvalues.This data set is used in the forest-wide optimization.
whereTIisthenumberofthinningintensities,nTCFisthe numberofthinningcontrolfactors,maxisthemaximumnumberofthinningfrequencies,andministheminimumnumber of thinning frequencies:
(2)
where Nr and Nt areremovedandtotalstemnumber,respectively,and Gr and Gt areremovedandtotalbasalarea, respectively.
Forexample,aminimumofoneandamaximumof10thinningeventswithfiveTCFcurveswilltheoreticallygive 442,860 paths for one stand:
(3)
Objective function
Twoobjectiveswereappliedinthisstudy.Thefirstwasmaximumvolumeproduction(Equation4);thesecondwasmaximumExpectedStandValue(ESV)(Equation5),representing thesumofnetpresentvalue,stumpagevalueandlandexpectationvalueofeachstand(Equation6).ToestimatethenetpresentvalueinESV,theso-calledtime-windowmethodwasused (Hilleetal.1999,SánchezOroisandVilèko2002):
Generatingsiviculturalpaths
Togeneratesilviculturalpathsforeachofthe38stands,acomputerprogramwasdevelopedinVisualBasic6.0.Beforethe startofthegenerationprocess,allpossiblepathsareinitialized (Figure3).
where z1 istheobjectivefunctionvalueofthefirstobjective, n isthenumberofstands, hi , j istheremovedvolumeha –1 atthe i ththinninginstand j, F isthenumberofthinnings, TE , j isthe volumeha –1 attheendoftheplanningperiodinstand j,and Aj is the areaofstand j (ha):
TInTCF i i = ∑ min max
(1)
NG rt rt = NN GG / /
1 10 i i = = ∑ ,
35442860
Max: zhTA ijEj i F j j n 1 11 =+ == ∑∑ ,, (4)
Max:ESV z ttj j n 2 1 0 = = ∑ –, (5) 932 SEO,VILÈKO,SÁNCHEZOROIS,KUNTH, SON AND VONGADOW TREE PHYSIOLOGY VOLUME 25, 2005
by guest on October 13, 2011 treephys.oxfordjournals.org Downloaded from
Figure 2. Thinning process by thinning type with maximum stem number curve. Abbreviations: N/ha = stem number per hectare; and dg = quadratic mean diameter at breast height.
where z2 istheobjectivefunctionvalueofthesecondobjective, ESVttj 0 , istheexpectedstandvalueofstand j, t isstandageat theendoftheplanningperiod, t0 isstandageatthebeginning oftheplanningperiod, ti isstandageatthinning i, r israteof interest,CFi iscashflowatthinningevent i,SVt isstumpage valueattheendoftheplanningperiod,LEVt islandexpectation value at the end of the planning period.
Thelandexpectationvalueofeachpathwasassumedtobea constant,becausetheplanninghorizonisthesame.Therefore, theexpectedstandvaluewascalculatedwithoutthelandexpectationvalue.Tocalculateestimatedcashflow,product pricesandharvestingcostsarebasedonmeanstemdiameter.
Constraint
Therearemanywaystospecifyharvestconstraints.Onepossibilityistodefineaso-calledeven-flowconstraintthatisoften usedtoensuremoreorlessequalharvestvolumesovertime. Sometimesitisdesirablethatthetotalharvestshouldincrease fromyeartoyear,forexamplebyatleast p percent,which could be implemented using the following constraint:
where hijt isthesumofthefellingvolumes(thinningsplus clearfelling)perhaatyear t ifalternative j ( jthtreatmentoptiononstand i )isusedand Xij isthecorrespondingarea(ha)of
ESV CF SV ttj i tt it t tt t r r i –, () () 0 0 0 1 1 = + + + = ∑ ()() 1100 LEV + + + rr tt t tt (6)
hX p hX ijt j J ij i I ijtij j J ii + = == ∑ ∑∑ ≥+ 1 1 11 1 100 i I t = ∑ ∀ 1 , (7)
TREE PHYSIOLOGY ONLINE at http://heronpublishing.com A HEURISTIC ALGORITHM FOR LONG-TERM FOREST MANAGEMENT 933
Figure 3. Initializing all possible alternatives.
Figure4.Plausibilitytestbasedontworules:(a)themortalitypreemptionruleand(b)thethinningevenrule.(c)Plausibleandpossible alternative after the test.
by guest on October 13, 2011 treephys.oxfordjournals.org Downloaded from
Figure 5. The algorithm of accelerated simulated annealing.
stand i (i =1... I ).Ourcurrentmodelformulationspecifiesthat at least 100m3 must be harvested each year, thus
Thetaskistofindthecombinationoffinalfelling,thinning agesandthinningintensitiesinthedifferentstandsthatmaximizestheobjectivefunctionvalueandsatisfiestheconstraints.
Optimization method
SimulatedAnnealing(SA;Kirkpatricketal.1983,Lockwood
hXt ijt j J ij i I i == ∑∑ ≥∀ 11 100, (8)
934 SEO,VILÈKO,SÁNCHEZOROIS,KUNTH, SON AND VONGADOW TREE PHYSIOLOGY VOLUME 25, 2005
Figure 6. Comparison of convergence between standard SA (A) andmASA(B).
by guest on October 13, 2011 treephys.oxfordjournals.org Downloaded from
Figure 7. Overview of the optimized forest plan.
andMoore1993,ChenandvonGadow2002,2003)isaheuristicsearchtechniquethatiscommonlyusedtosolvespatial harvestschedulingproblems.BostonandBettinger(1999)reportedthatSAisabletolocatethebestsolutionvaluestoproblemswhencomparedwithotherheuristictechniques(Monte CarloIntegerProgrammingandTabusearch).Bettingeretal. (2002)comparedeightheuristictechniques.Theyclassified thetechniquesintothreeclasses(verygood,adequateandless thanadequate).TheSAmethodwasfoundtobe“verygood.” Therefore, we used SA as a search method.
AcceleratedSimulatedAnnealing(ASA)hasbeenproposedandtestedempiricallybyYoonandCho(1996).Itis fasterthanstandardSAandyetmaintainstheconvergence propertybecauseitdoesnotalterthebasicSAstructure.The mainfeatureofASAisthatitincreasesthespeedofconvergencebymakingthesizeoftheinnerloopsmallerthanSA. ThisismadepossiblebycheckingiftheMarkovchaindescribingtheevolutionmadeintheinnerloopofSAreachesthe steadystatebydecreasingthetemperature T onlywhenthe
Markovchainisjudgedtoreachthesteadystate.Ofcourse, thereareotherconsiderationsadaptedtomakeASAmoreefficient:theautomaticinitialtemperaturesettingmechanismand carefulstoppingcriteriatoavoidanunnecessarilylongwanderingperiodatthefinalstageoftheconvergence.TheASA algorithm is given inFigure5.
ThemodifiedASA(mASA,developedbythefirstauthor)is animprovementfeaturinganadditionalfunction.Thisfunctioncontrolsandteststhenextsolution(combinationof paths),whichisrandomlyselectedtocomparetheobjective values,sothatwhenaparticularcombinationhasbeenrandomlyselected,itwillnotbeselectedagain.Asaresultofthis function,thewholeprocessingtimecanbereducedby50% (cf.Hajek1988).
ToevaluatethemASA,asimpleoptimizationwasperformedusing100objectivevaluesand100iterations.Theoptimalsolutionwasknown.Apracticalwaytoevaluatethe performanceofaheuristicistocomparetheresultsofaheuristicprocedurewithaknownoptimalsolution.Heuristictech-
TREE PHYSIOLOGY ONLINE at http://heronpublishing.com
935
A HEURISTIC ALGORITHM FOR LONG-TERM FOREST MANAGEMENT
by guest on October 13, 2011 treephys.oxfordjournals.org Downloaded from
Figure8.Comparisonofmanagementschedulebetweenobjectives.Thinningwillbecarriedoutincompartmentsthatareindicatedbythecolors.
936 SEO,VIL
ÈKO,SÁNCHEZOROIS,KUNTH, SON AND VONGADOW
niqueshavethedisadvantagethatonecannotguaranteetheir performance;thus,thereisnoguaranteethatanoptimalsolutionwillbefound(BostonandBettinger1999).Figure6 showstheconvergencebetweenstandardSA(a)andmASA (b)forthesameproblem.UsingmASA,theoptimalsolution canbesuccessfullyandrapidlyestimatedwithonly14itera-
tions,whereasusingstandardSA,theoptimalsolutionwas foundafter78iterations.BecausetheresultsofSAarenotalwaysclosetothetrueoptimum,moreiterationsarerequiredto obtaintheoptimalsolutionneartheglobalextreme.Numerous runsusingmASAproducedasimilarresult,indicatingthatthe mASAalgorithm is more efficient than standard SA.
Table4.Estimatedoptimumtreatmentalternativeforwholestandsandestimatedobjectivefunctionvalues.Abbreviations:St.No.=standnumber;TCF= thinning control factor; Vol. = volume (m 3 ); Th.-Freq. = thinning frequency; andESV= expected stand value (Euro).
TREE PHYSIOLOGY VOLUME 25, 2005
St. No.AgeVolume maximizing ESVmaximizing TCFTh.-Freq.OptimumVol. ha –1 ESVTCFTh.-Freq.OptimumVol. ha –1 ESV 170No thinning293433100310(17), 10(18),277438 10(19) 270No thinning325553100130(19)316558 370No thinning293430100310(17), 10(18),277436 10(19) 470No thinning265317100210(17), 30(19)252324 5140No thinning3871,4690No thinning3871,469 6150No thinning3901,5470No thinning3901,547 7170No thinning4332,1040No thinning4332,104 8170No thinning4832,8270No thinning4832,827 9170No thinning4672,3600No thinning4672,360 1023100210(13), 20(16)1 7937,429100210(13), 20(16)7937,429 1123100220(10), 20(15)99110,549100220(10), 20(15)99110,549 1227100310(11), 20(14),8608,704100310(10), 20(14),8568,712 10(19)30(19) 1329100310(12), 10(15),95415,536100210(12), 20(15)95015,575 10(18) 1432100110(16)82813,051100120(16)81913,053 15370No thinning77612,51190130(15)74512,513 1638100110(19)91216,50690130(19)90816,662 1740100110(16)95617,27690130(11)91117,458 18401000No thinning88815,96180130(10)98616,087 19410No thinning80613,98680130(11)75714,075 2041100110(16)94817,17880120(6), 30(13)86517,311 21410No thinning88015,81980130(10)82315,950 2242100110(16)92816,68880120(6), 30(14)85316,904 23440No thinning66512,82760130(13)63412,962 24440No thinning92417,44170220(5), 30(12)83117,822 2545100210(13), 10(18)1,04319,92760330(1), 20(3),86020,582 30(10) 2646100110(19)89816,38470220(2), 30(9)79416,820 2747100110(19)89216,26860330(1), 20(7),74316,730 30(14) 2850100110(15)1,00819,38560330(1), 30(3),82920,556 30(15) 2950100110(19)93717,89160320(1), 20(3),79318,868 30(10) 30520No thinning76414,63960220(4), 30(12)69215,181 3163100110(16)1,07822,81260230(1), 30(6)95828,256 326560110(18)60612,56260130(18)60112,707 336860110(19)60912,85260130(19)60612,925 34680No thinning69214,46860130(10)66415,932 35720No thinning4089,2940No thinning4089,294 36830No thinning3858,9520No thinning3858,952 378660110(17)58912,50860130(17)58412,770 3811660110(18)66515,48360130(18)66215,729 Sum27,017436,92125,584450,429 1 120(16): 20% of stem number per ha will be thinned at 16th year. by guest on October 13, 2011 treephys.oxfordjournals.org Downloaded from
Optimization system
AnoptimizationsystembasedonmASAwasdeveloped.The estimatedresultoftheoptimizationissavedintheMicrosoft Excelformatandalsoinadatabaseformattolinktheprocess withaGISdatabase.TheMapObjectcomponentwasincluded inthissystem.Thiscomponentoffersthepossibilitythata shapefile(digitizedmap)includingattributedataofeach polygoncanbeusedbythesystem.Thisoffersthepossibility ofpresentingoptimizationresultsasamapthatshowsthespatialarrangementofthemanagementactivitiesinthedifferent time periods (Figure7).
Results
Atotalof609,948pathsweregeneratedforthe38Norway sprucestands,butonly380paths(the10bestpathsineach stand×38stands)wereusedintheoptimizingprocess.Table4 showstheoptimalcombinationofpathsforthe38Norway sprucestandsandtheobjectivefunctionvalue,consideringan even-flowconstraint.Theplanninghorizonwas20yearsand therateofinterestwas4%.Thetotalharvestvolumewas 27,017m3 andthetotalESVwas450,429€.TheselectedTCF inthevolumemaximizationwasalmostalways100%,which istobeexpectedbecausevolumegrowthishigherathigher densities.IntheESVmaximization,100%ofTCFwasselectedformostoftheyoungstands,becausethehigherTCF suggestsalaterthinningtime,producingmorevaluableharvestedtimber.Inmostofthematureandolderstands,alower TCF(60%)wasgenerallyselectedbecausetheyielddifferencesbetweenharvesteventsinolderstandsaresmallandearlierpositivecashflowsarepreferablewhenthevaluesofthe cash flows are similar.
Figure8presentsaseriesofmapsshowingtheresultofthe optimization;thatis,thespatialarrangementofthemanagementschedulefor20yearsinaccordancewiththespecified objectives.
Conclusions
Wedevelopedamethodforgeneratingallpossiblepathsfor onestand.Outofagreatnumberofpaths,onlythebest10 wereselectedtoparticipateintheoptimizationprocess,toreducetheotherwiseprohibitiveprocessingtime.Thedifference intheobjectivefunctionvaluesbetweenpathswasrather small.Thenewsearchalgorithm,knownasmASA,provedto besuperiortothestandardSA.WeconcludethatmASAis usefulwhenoneneedstosolvelargeforestmanagement problems.
Theapplicationsystemcanbeusedtogenerateamanagementplanforanentireforestenterprise,basedoncurrentstand attributesandspecifiedobjectives.Amajoradvantageofthe multiplepathsapproachisthatanychangeinthecurrentstand attributesorintheobjectivescanbeeasilyimplemented.Althoughalltheotherdataandspecificationsremainasthey havebeendefined,anewoptimalplancanbeproducedalmost instantaneously.Thisflexibilityisanimportantadvantage.
Theoptimalplancanbeusedtoformulatepracticaloperationalschedulesthatcanbechangedeasilyasconditions change.Therefore,theconceptofmultiplepathsisasuitable theoreticalbasisfordesigningthedevelopmentofaforested landscape.
References
Arthaud,G.J.andD.Rose.1996.Amethodologyforestimatingproductionpossibilityfrontiersforwildlifehabitatandtimbervalueat the landscape level. Can. J. For. Res. 26: 2191–2200.
Bergel,D.1973.FormzahluntersuchunganBuche,Fichte,EuropächerLärcheundJapanischerLärchezurAufstellungneuer Massentafel.Allg.ForstJagdztg. 117–124.
Bettinger,P.,J.Sessions,andK.Boston.1997.UsingTabusearchto scheduletimberharvestssubjecttospatialwildlifegoalsforbig game. Ecol. Model. 94:111–123.
Bettinger,P.,J.SessionsandK.N.Johnson.1998.Ensuringthecompatibilityofaquatichabitatandcommodityproductiongoalsin easternOregonwithaTabusearchprocedure.For.Sci.44:96–112.
Bettinger,P.,D.Graetz,K.Boston,J.SessionsandW.Chung.2002. Eightheuristicplanningtechniquesappliedtothreeincreasingly difficult wildlife planning problems. SilvaFenn. 36:561–584.
Boston,K.andP.Bettinger.1999.AnanalysisofMonteCarlointeger programming,simulatedannealing,andTabusearchheuristics. For. Sci. 45:292–301.
Chen,B.W.andK.vonGadow.2002.Timberharvestplanningwith spatialobjectives,usingthemethodofsimulatedannealing. Forstwiss.Centralbl. 121:25–34.
Chen,B.W.andK.vonGadow.2003.Acasestudyofsimulatedannealing,geneticalgorithm,Tabusearchandlinearprogramming for solving forest planning problems.Forstachiv74:26–31.
Clutter,J.L.,J.C.Fortson,L.V.Pienaar,G.H.BristerandR.L.Bailey. 1983.Timbermanagement—aquantitativeapproach.Wileyand Sons, New York, pp 238–252.
Dahlin,B.andO.Sallnas.1993.Harvestschedulingunderadjacency constraints—acasestudyfromtheSwedishsub-alpineregion. Scand. J. For. Res. 8:281–290.
Gurjanov,M.,S.SanchezOroisandJ.Schröder.2000.GrundflächenmodellefürgleichaltrigeFichtenreinbestände.EinevergleichendeAnalyse.Centralbl.gesamteForstwes. 117:187–198.
Haight,R.G.andL.E.Travis.1997.Wildlifeconservationplanning usingstochasticoptimizationandimportancesampling.For.Sci. 43:129–139.
Hajek,B.1988.Coolingschedulesforoptimalannealing.Math.Oper. Res. 13:311–329.
Hille,M.,D.Hessenmöller,B.MöhringandK.vonGadow.1999. BewertungwaldbaulicherMassnahmenmitHilfederZeitfenstermethodeamBeispieleines110-järigenBuchenbestandes. In IUFROProc., Prague, Czech Republic, pp 94–100.
Hoganson,H.M.andD.Rose.1984.Asimulationapproachforoptimal timber management scheduling. For. Sci. 30:220–238.
Kangas,J.andT.Pukkala.1996.Operationalizationofbiologicaldiversityasadecisionobjectiveintacticalforestplanning.Can.J. For. Res. 26:103–111.
Kirkpatrick,S.,C.D.GellatandM.P.Vecchi.1983.Optimizationby simulated annealing. Science 220:671–680.
Lockwood,C.andT.Moore.1993.Harvestschedulingwithspatial constraints:asimulatedannealingapproach.Can.J.For.Res.23: 468–478.
Murray,A.T.andR.L.Church.1995.Heuristicsolutionapproachesto operationalforestplanningproblems.Oper.Res.Spektrum17: 193– 203.
TREE PHYSIOLOGY ONLINE at http://heronpublishing.com A HEURISTIC ALGORITHM FOR LONG-TERM FOREST MANAGEMENT 937 by guest on October 13, 2011 treephys.oxfordjournals.org Downloaded from
938SEO,VILÈKO,SÁNCHEZOROIS,KUNTH, SON AND VONGADOW
Nelson,J.andJ.D.Brodie1990.Comparisonofarandomsearchalgorithmandmixedintegerprogrammingforsolvingarea-based forest plans. Can. J. For. Res. 20:934–942.
Nelson,J.andG.Liu.1994.Schedulingcutblockswithsimulated annealing. In ProceedingsoftheInternationalSeminaronForest OperationsUnderMountainousConditions.Ed.J.Sessions.
Harbin, P.R. of China, pp 29–36.
Pulkki,R.1984.Aspatialdatabase—heuristicprogrammingsystem foraidingdecision-makinginlong-distancetransportofwood.
Acta For.Fenn. 188, 89 p.
SánchezOrois,S.andF.Vilèko.2002.BewertungundOptimierung vonVornutzungeninFichtenbeständen.Forstwiss.Centralbl.121: 250–264.
SánchezOrois,S.,M.GurjanovandJ.Schröder.2001.Analysedes GrundflächenzuwachsesgleichaltrigerFichtenbestände.Allg. ForstJagdztd. 172:51–60.
Schübeler,D.1997:UntersuchungenzurstandortabhängigenWachstumsmodellierungbeiderFichte.Diss.zurErlangungdes DoktorgradesderForstlichenFakultätderGeorg-AugustUniversitätGöttingen, 155 p.
Sloboda,B.1971.ZurDarstellungvonWachstumsprozessenmit HilfevonDifferentialgleichungenersterOrdnung.Mitt.Bad.Württemb.Forstl. Vers. u.Forsch.Anst. 32.
Staupendahl,K.1999.BestandesbezogeneModelierungvonDurchforstungeninBuchenreinbeständenaufderBasisdesStammzahl-Grundflächen-Verhältnisses.VortraganlässlichderJahrestagungderSektionErtragskundedesDeutschenVerbandes ForstlicherForschungsanhalteninVolprehausen/Sollingam 17.-19.Mai1999.
vonGadow,K.1991.IntegrationvonEinzel-undGesamtnutzungsplannunginderForsteinrichtung.Allg.ForstJagdztg.162:72–75. vonGadow,K.andG.Y.Hui.1999.Modelingforestdevelopment. KluwerAcademic Publisher, Dordrecht, 213 p.
Weintraub,A.,G.Jones,A.Magendzo,M.MeachamandM.Kirby, M.1994.Aheuristicsystemtosolvemixedintegerforestplanning models.Oper. Res. 42:1010–1024.
Weintraub,A.,G.Jones,M.Meacham,A.MagendzoandD.Malchuk.1995.Heuristicproceduresforsolvingmixed-integerharvest scheduling—transportationplanningmodels.Can.J.For.Res.25: 1618–1626.
Wilkström,P.2000.Solvingstand-levelplanningproblemsthatinvolvemultiplecriteriaandasingle-treegrowthmodel.Doctoral Thesis, Swedish Univ. Agric. Sci., Umeå, 167 p.
Yoon,B.S.andG.Y.Cho.1996.Accelerationofsimulatedannealing antitsapplicationforvirtualpathmanagementinATMnetworks.
J. Korean Operation Res. Manage. Sci. Soc. 20:125–140.
TREE PHYSIOLOGY VOLUME 25, 2005 by guest on October 13, 2011 treephys.oxfordjournals.org Downloaded from View publication stats
