FINLAY DOUGLAS PORTFOLIO Selected Works
TABLE OF CONTENTS
Introduction 02
Unwind 03
Duplex 10
Dwelling 14
Market 18
INTRODUCTION
In this portfolio I examine interaction in many and various forms. I have become fascinated by the way in which forms interact, as well as the way in which we interact with the spaces around us. While this portfolio mainly consists of my academic work, I start this portfolio with a personal piece in which I formally examine the way in which code interacts with each other.
1
PIECE ONE
Unwind Personal Project
In the course, McGill COMP 502: Programming Languages and Paradigms, I was tasked to program an original computing language. The goal of this language was to understand and compute relatively simple tasks. This included expression evaluation, type checking (checking the type of an input variable; an integer, fraction, true/ false statement, etc), and type inferencing. My code contains five main components: free_vars, unused_vars, subst, infer, and eval. The components, or sub-programs, interact to produce a result. Unwind, explores the rhythm of the code and the nature in which each subprogram interacts with all other sub-programs.
RHYTHM OF SUBST
# P.parse "let val x = 4 in y + 3 end;" ;; - : (string, exp) either = Right (Let ([Val (Int 4, "x")], Primop (Plus, [Var "y"; Int 3])))
This diagram depicts a cross-section of the sub program subst.
Each line represents a step in the computation of data.
Data passing through embedded programs within subst are represented by thicker lines. The time complexity of the embedded program is represented in the thickness of the line.
When an outside function is called to assist in the computation, a space is found. The time complexity of the outside function is represented in the size of the space.
A recursive call is when the programs calls itself to compute a substrata of the data.
calling the function: # subst (Int 4, "y") ((Let ([Val (Int 4, "x")], Primop (Plus, [Var "y"; Int 3])))) if ... then ... else ...
List.mem a [set]
match (e) with
program interating through choices
subst (e', x) (e) recursive call
calling free_vars (e)
List.map f [a1; ...; an]

4
4
end of program; "let val x =
in
+ 3 end;"
Origional sketch of rhyhm graph
String, acrylic panes, and fishing line
x 1 x 8 feet
A QUICK EXPLANATION
Below is a rhythm diagram of the sub-program free_vars (e) and the code itself. Free_vars is used to find variables within an expression that are not captured. For example, with "let x = 4 in y + 3", "y" has no defined value and is therefore free. The code below outlines how each type of variable is computed in free_vars. For example, "| int _ -> []" means if the expression called is an integer, the returning value is nothing.
RHYTHM OF FREE_VARS
free_vars (e)
let rec free_vars (e : exp) : name list = match e with
| Int _ -> []
| Bool _ -> []
| If (e1, e2, e3) -> union (free_vars e1) (union (free_vars e2) (free_vars e3))
| Primop (p, args) -> List.fold_right (fun e1 -> union (free_vars e1)) args []
| Tuple args -> List.fold_right (fun e1 -> union (free_vars e1)) args []
| Fn (name, t, e1) -> delete [name] (free_vars e1)
| Rec (name, t, e1) -> delete [name] (free_vars e1)
| Let (args, e1) -> match args with
[] -> free_vars e1
y::ys -> (match y with
Val (e2, name) | ByName (e2, name) -> (union (free_vars e2) (delete [name] (union (free_vars (Let (ys, e1))) (free_vars e1))))
Valtuple (e3, name_l) -> (union (free_vars e3) (delete name_l (union (free_vars (Let (ys, e1))) (free_vars e1)))))
| Apply (e1, e2) -> union (free_vars e1) (free_vars e2)
| Var e1 -> [e1]
| Anno (e1, typ) -> free_vars e1
This diagram depicts a cross-section of the sub program free_vars. Each line represents a step in the computation of data.
The code uses the 'match' call to look for the type of variables in the expression and computes accordingly. When iterating through choices, a line is made in the diagram.
In order for my lanaguage to understand the expression, it is broken down into a list of sub-components that can be individually examined; the given expression becomes: (Let ([Val (Int 4, "x")], Primop (Plus, [Var "y"; Int 3])))
calling the function: # free_vars (Let ([Val (Int 4, "x")], Primop (Plus, [Var "y"; Int 3]))
program interating through choices match (e) with free_vars (e) recursive call delete call union call List.fold_right f [a1; ... ; an] []
free_vars (e) recursive call
# P.parse "let val x = 4 in y + 3 end;" ;; - : (string, exp) either = Right (Let ([Val (Int 4, "x")], Primop (Plus, [Var "y"; Int 3]))) end of program; "[y]"
let lexer_to_stream lexer lexbuf in try let ) parse_exp_semi in ignore tok_match EOF ); Right with Error err Left err end ;; module sig val parse string -> string exp either end Print sig val exp_to_string exp -> string val typ_to_string typ -> string end struct let rec separate separator match with [] -> "[]" f x1 :: xs f x1 separator separate separator xs let paren lvl oplvl string if oplvl lvl then "(" string ")" else string let po_prec match with Or -> And Equals -> NotEquals -> LessThan GreaterThan LessEqual -> GreaterEqual -> Plus Minus Times -> Div -> Negate let po_to_str match with "||" And -> "&&" Equals -> NotEquals "!=" GreaterThan -> ">" LessEqual -> "<=" GreaterEqual ">=" Plus Minus -> Times -> "*" Div "/" Negate let typ_to_string ty let ref in let freshVar () counter := !counter "a" string_of_int counter in let rec typstr lvl ty match ty with TArrow domain range typstr in let l'' t' typstr l' range in l'' paren lvl -> " t')) TProduct [] "()" TProduct [x typstr lvl TProduct (t :: ts -> let fun -> let (l' t' typstr in l' t t' in let l' t' List fold_left (typstr ts in l' paren lvl t' TInt l "int" TBool -> (l "bool" TVar -> with None -> begin match List assq_opt l with None let freshVar () in (( Some end Some t -> typstr in snd typstr [] ty let exp_to_string let expstr lvl match with Int -> string_of_int Bool -> string_of_bool If ef paren lvl "if expstr ec then expstr et else " expstr ef Primop []) -> "(bad primop)" Primop ]) paren lvl po_to_str expstr Primop :: es -> let expstr' po_to_str expstr po_prec in paren lvl po_prec List fold_left expstr' expstr (po_prec es Tuple -> "(" separate ", expstr ")" Fn begin match with None -> paren lvl "fn x => expstr Some -> paren lvl "fn ": " typ_to_string t => expstr end Rec ff ftype -> paren lvl ff typ_to_string ftype => expstr Let decs -> "let separate "\n decstr decs in expstr end" Apply paren lvl ((expstr e1 expstr e2)) Var -> Anno t) paren lvl expstr 1 typ_to_string and decstr match with Val Rec (ff ftype Fn body)), gg when ff gg "fun ff typ_to_string ftype expstr body Val e1 ) -> "val expstr ByName e1 "name expstr e1 Valtuple (e1 -> "val (" separate ", fun ") expstr in expstr end ;; sig val exp_to_string exp -> string val typ_to_string typ -> string end let print_exp_list list begin if list [] then Printf printf "[] else List iter fun -> Printf printf "%s )) list end ;; val print_exp_list string list unit fun let rec union xs ys match xs with [] -> ys if member x ys then union else union ys ;; val union 'a list -> 'a list -> 'a list fun let union_list sets List fold_right union sets [] ;; val union_list 'a list list 'a list fun let rec delete ds set match set with [] -> [] if member h ds then delete ds t else delete ds ;; val delete 'a list 'a list 'a list fun let parse_tests : (string string exp either list (* Provide your tests for the parser *) "69;" Right )); "true;" Right (Bool true)); "y 1" Left "Expected SEMICOLON token")); "let val in end;" Right ([Val )], Primop (Plus ])))); ;; val parse_tests (string string exp either list [("69;" Right (Int 69)); "true;" Right (Bool true)); "y 1" Left "Expected SEMICOLON token"); "let val 8 in end;" Right Let ([Val Int "x")], Primop (Plus Var "x" Int ]))))] let free_vars exp list match with Int -> [] Bool -> [] If ) union free_vars e1 union free_vars e2 free_vars e3)) Primop -> List fold_right fun e1 -> union free_vars e1)) args [] Tuple args List fold_right fun e1 -> union free_vars e1)) args [] Fn e1 -> delete ] free_vars e1 delete name] free_vars e1 Let args e1) -> begin match args with [] -> free_vars e1 ys -> match with Val ( union free_vars e2 delete name union free_vars Let ys e1))) (free_vars e1)))) ByName union free_vars e2 delete name union free_vars Let e1))) (free_vars e1)))) Valtuple name_l union free_vars e3 delete name_l union free_vars Let e1))) (free_vars e1)))) end Apply e1 e2) -> union free_vars free_vars e2 Var e1 e1] Anno e1 typ) -> free_vars e1 ;; val free_vars exp -> list fun let unused_vars exp list match with If e1 e2 e3) -> union unused_vars e1 union unused_vars e2 unused_vars e3)) Primop exp_list List fold_right fun e1 union unused_vars e1)) exp_list [] Tuple exp_list -> List fold_right fun e1 -> union unused_vars e1)) exp_list [] if member name free_vars e1 then delete unused_vars e1)) else union unused_vars e1)) Rec e1 if member name free_vars e1 then delete name unused_vars e1)) else union name unused_vars e1)) Let args e1) -> begin match args with [] -> unused_vars e1 ys -> begin match with Val e2 name ByName e2 name -> if member free_vars e2 || member free_vars e1 then delete name union union unused_vars Let ys e1))) (unused_vars e2)) unused_vars e1)) else union union unused_vars )) union unused_vars (Let ys e1))) unused_vars e1)) Valtuple e3 name_l -> List fold_right fun free_variable if member name free_vars e1 || member name free_vars e3 then union delete ] union union unused_vars e3 (unused_vars Let ys e1)))) unused_vars e1))) free_variable else union union union [name unused_vars e3)) union unused_vars Let e1))) unused_vars e1))) free_variable name_l [] end end Apply e1 e2) union unused_vars e1) unused_vars e2 if free_vars )) then [] else e1 Anno e1 typ) unused_vars e1 Int Bool [] (* Q3 Substitute variable *) let subst ((e' exp exp exp if not member x free_vars )) then else match with if then e' else Int Bool -> Primop po Primop po List map subst e' )) If If subst (e' e1 subst e' ) e2 subst e' e3 Tuple -> Tuple List map subst e' )) Anno Anno ((subst e' ), Let ds e2) -> begin let check ds_o e_h ds_a begin match ds_o with [] -> Let ((ds_a), subst (e' e_h)) ys match with Val e3 name ByName (e3 name if then Let ((ds_a), e2 check ys e_h ds_a Valtuple e4 namelist -> if member namelist then Let ((ds_a), e2 else check ys e_h ds_a end in let helper_fun ds_origional ds_helper e_helper ds_acc begin match ds_helper with
RHYTHM OF ALL SUB-PROGRAMS
In asking the program to evaluate "let val x = 4 in y + 3 end;", each sub-program is called at separate points in time. Given the structure of their code, the role each sub-program plays in executing the expression results in varying rhythms. Below, ordered from called first to last, are the sub-programs and their rhythm. The size of each diagram directly correlates to the time complexity; the larger the diagram, the more time and computing power is required.
subst (e', x) (e) infer (ctx) (e) eval (e) free_vars (e)
unused_vars (e)
Format: name (input 1) (intput 2)
Type: integer, floating integer (fraction), bool (true/false), etc
Legend: infer the type of the expression, e, given the list of possible types outlined in ctx. evaluate the expression, e. return the free variables found in expression, e. substitute the expression, e', for variable name, x, in expression, e. return the variables not used in expression, e.
infer (ctx) (e): eval (e): free_vars (e): subst (e', x) (e): unused_vars (e):
ts -> match with Val e3 name if member name free_vars e' then let fn fresh_var in helper_fun ds_origional (subst ((Var fn), name e_helper (ds_acc Val ((subst (e' e3), fn)]) else helper_fun ds_origional e_helper (ds_acc Val ((subst (e' e3), name)]) ByName e4 -> if member free_vars e' then let fresh_var name in helper_fun ds_origional ts (subst ((Var fn), e_helper (ds_acc ByName ((subst e' ), fn)]) else helper_fun ds_origional ts e_helper (ds_acc ByName ((subst e' ), )]) Valtuple e5 namelist let rec namelist_check nl_h e_h nl_a begin match nl_h with | [] -> helper_fun ds_origional ts e_h ds_acc Valtuple ((subst e' ) ), nl_a)]) | ::ys -> if member free_vars e' then let fn fresh_var in namelist_check ys subst ((Var fn), e_h nl_a fn]) else namelist_check ys e_h nl_a ]) end in namelist_check namelist e_helper [] end in helper_fun ds ds e2 [] end | Apply e1 e2 Apply ((subst e' e1), subst e' e2)) | Fn -> if then Fn else if member free_vars e' then let fv fresh_var in ((fv), ( fv ))) else Fn subst e' e)) | Rec -> if then Rec y else if member free_vars e' then let fv fresh_var in ((fv), subst e' subst fv ))) else Rec subst e' )) let eval exp -> exp (* do not change the code from here *) let bigstep_depth ref 0 in fun -> if debug >= then print_endline String make (!bigstep_depth ' "eval (" Print exp_to_string ")\n"); incr bigstep_depth (* to here *) let result match with Int Bool Tuple es Tuple (List map eval es If e1 e2 e3 -> begin match eval e1 with Bool if then eval e2 else eval stuck "Condition for if expression should be of the type bool" Anno _) -> eval (* types are ignored in evaluation *) Var stuck "Free variable \"" "\" during evaluation" Fn t -> Fn Apply e2 begin match eval e1) with Fn -> eval subst ((eval e2), stuck "Condition for Apply expression should be of the type Fn" end eval subst (( )), Primop (And -> begin with Bool Bool -> Bool && -> stuck "Condition for Primop AND should be of the type Bool" end Primop (Or es -> begin match with Bool Bool Bool || -> stuck "Condition for Primop OR should be of the type Bool" end Primop (op es let List eval in begin match eval_op op with stuck "Bad arguments to primitive operation" Some -> end let rec helper ds1 e_acc begin match ds1 with [] eval e_acc ::ys -> begin match y with Val (e3 name ByName e3 name helper ys subst ((eval e3), name e_acc Valtuple ((Tuple e4), namelist -> let namelist_helper e_h namelist_h eh_acc begin match e_h namelist_h with (_, []) | ([], _) eh_acc (( ::xs), ::ns)) -> namelist_helper subst ((eval ), eh_acc) in helper ys namelist_helper e4 namelist -> stuck "Valtuple must take in tuple and namelist" end end in helper ds in (* do not change the code from here *) decr bigstep_depth if debug >= then print_endline String make (!bigstep_depth ' "result of eval (" Print exp_to_string ") " Print exp_to_string result "\n"); (* to here *) result (* Q5 Type an expression *) (* Q7* Implement the argument type inference For this question, move this function below the "unify" *) let infer exp) typ match with Int -> TInt Bool -> TBool If if (typ_eq infer ctx e2 infer ctx e3)) && typ_eq infer ctx e1 TBool then infer ctx e3 else type_fail "type error" Primop args -> begin match with Plus | Minus Times Div Negate if List for_all fun -> typ_eq infer ctx infer ctx List hd args))) args then TInt else type_fail "your primop requries two TInts." And Or LessThan LessEqual GreaterThan GreaterEqual Equals NotEquals -> if List for_all fun typ_eq infer infer List hd args))) args then TBool else type_fail "you can only compare two values of the same type." end Tuple args -> TProduct (List map infer ctx args let ctx' extend ctx name in TArrow infer ctx' e1)) Fn None e1 infer ctx e1 Rec name t e1 -> let ctx' extend ctx in infer ctx' Let args e1 -> let extend_ctx_dec arg ctx match arg with [] ctx :: -> begin match with Val e2 name ByName e2 name) -> let ctx' extend ctx infer ctx e2)) in extend_ctx_dec ys ctx' Valtuple ((Tuple ), let rec ctx_namelist_helper e_h namelist_h ctx_acc begin match e_h namelist_h with (_, []) ([], _) ctx_acc ((x::xs), ::ns)) -> let ctx' extend ctx_acc infer ctx_acc )) in ctx_namelist_helper xs ns ctx' end in extend_ctx_dec ys ctx_namelist_helper e3 namelist type_fail "valtuple must take in tuple and namelist" end in infer extend_ctx_dec args ctx e1 Apply e1 e2 begin let inf_e1 infer ctx e1 in match inf_e1 with TArrow t2)) t2 type_fail "first argument must be a function of: TArrow (t1, t2)" end Var n1 ctx_lookup ctx n1 Anno e1 typ -> if typ_eq infer ctx e1 typ then typ else type_fail "Anno's expression and type should be of same type." (* find the next function for Q5 *) (* Q6 Unify two types *) let rec unify ty1 typ (ty2 typ : unit let check_type t1 t2 begin match t1 with TInt -> false TBool -> false TVar begin match with Some ty -> ty t2 false end TArrow ( -> t2 || t2 TProduct ty_l -> begin match ty_l with [] -> false ys if t2 then check_type TProduct ys)) end end in match ty1 ty2 with TInt TInt | TBool TBool () ty TVar ) TVar ), ty -> begin if || check_type ty then type_fail "Unify does not work with the given types" else := Some ty end TProduct t_l1), TProduct t_l2 begin match t_l1 t_l2 with t1 t1s), t2 t2s -> if (unify ()) then unify TProduct )) TProduct t2s)) else type_fail "Unify does not work with the given types" [], [] () type_fail "Unify does not work with the given types" end TArrow t1 t2), TArrow t3 t4 -> unify t1 t3 unify t2 t4 type_fail "Unify does not work with the given types" (* Now you can play with the language that you've implemented! *) let execute string unit match parse with Left print_endline "parsing failed: Right -> try (* first we type check the program *) ignore (infer Ctx []) ); let result eval in print_endline "program is evaluated to: " Print exp_to_string result with NotImplemented -> print_endline "code is not fully implemented" Stuck print_endline "evaluation got stuck: s NotFound -> print_endline "variable lookup failed" TypeError -> print_endline "type error: print_endline "unknown failure: Printexc to_string ;;
INTERACTION PROCESS
At different points in time, the examined sub-programs call each other to assist in the task. The data walk through different rooms of the code, each room impacting the data and directing them to the exit. Each room has a different purpose, and its doors directly connect to other rooms. I examine the nature in which the sub-programs call each other; the orientation of the rooms and their doors.
The coloured lines signify the data types within the expression; Let, Val, Rec, Fn, Primop, and Apply
The diagram outlines the computation of the expression: 32

The expression is written in a language, however, that my program cannot understand. Meaning, my program does not have the vocabulary to compute to the power of. The solution is to create an expression that will teach my program.
Let valid_program1 = ”let fun power (x : int) (y: int) : int = if x = 0 then 0 else if y = 0 then 1 else x * power (x)(y-1) in power 3 2 end;“ ;;
Essentially, the expression above is a function that acts as a loop; computing 3 x 3. In order for this to work with my program, it must be translated (P.parse) into my language:
P.parse valid_program1 ;; - : (string, exp) either = (Let ([Val (Rec ("power", TArrow (TInt, TArrow (TInt, TInt)), Fn ("x", Some TInt, Fn ("y", Some TInt, If (Primop (Equals, [Var "x"; Int 0]), Int 0, If (Primop (Equals, [Var "y"; Int 0]), Int 1, Primop (Times, [Var "x"; Apply (Apply (Var "power", Var "x"), Primop (Minus, [Var "y"; Int 1]))])))))), "power")], Apply (Apply (Var "power", Int 3), Int 8))))
The result proves to be a detailed description of the expression that my program can understand.
START
FINISH
in tok_match SEMICOLON (* parse_factors: Recursively consume adjacent atomic factors (parse_factora), forming them into chain of applications. *) and parse_factors match parse_factor_option with | Some -> begin match with parse_factors Some -> parse_factors (Some Apply ))) end | None match eo with None -> raise Error "Expected expression" Some -> and parse_factor es parse_factors es None and parse_tuple let parse_exp in let s' next_msg MSGS rparen_or_comma in if COMMA then let s' parse_tuple s' in else ([ ], s parse_factora tok match tok with | TRUE -> Some Bool true | FALSE Some Bool false | NUM Some Int | VAR -> Some Var | IF -> let parse_exp in let tok_match THEN in let et parse_exp in let tok_match ELSE in let ef parse_exp in Some If ec et ef), | LPAREN -> let parse_exp in let next_msg rparen_or_comma in begin match with RPAREN -> Some COMMA parse_tuple in Some Tuple ( :: es), tok_match RPAREN -> raise Error MSGS rparen_or_comma end | let parse_var in let s' next_msg "expect colon or =>" in let if COLON then let parse_type s' in Some else ( in let tok_match DARROW in let in Some Fn ), | let ds parse_decs in let tok_match IN in let parse_exp in tok_match in Some Let ds ), | NEGATE -> begin match parse_factora next_msg "expect operand after ~" with None -> None Some -> Some Primop Negate [ ]), end | None and parse_dec match with | VAL let s' next_msg "expect variable or left parenthesis" in if let xs parse_tup_vars s' in let tok_match RPAREN in let tok_match EQUAL in let e parse_exp in Valtuple xs), else let parse_var in let tok_match EQUAL in let e parse_exp in Val ( ), | let parse_var in let tok_match EQUAL in let parse_exp in ByName ), | FUN -> let in let parse_args in tok_match in let parse_type in let tok_match EQUAL in let parse_exp in let ts match with Some -> TArrow ts None -> TArrow TVar ref None), ts in let ft List fold_right xs t in let e' List fold_right fun ( -> Fn )) in Val ft e'), ), | raise Error "shouldn't occur" and parse_decs let next_msg "expect val, name, fun or in" in match with | VAL NAME FUN -> let parse_dec s' in parse_decs in :: ds | -> ([], and parse_args let s' next_msg "expect variable, left parenthesis or colon" in match with | VAR let xs parse_args s' in None | let parse_var s' in let tok_match COLON in let parse_type in let tok_match in let xs parse_args in Some | [], and parse_var let next_msg MSGS variable in match with | VAR ( | -> raise Error MSGS variable and parse_tup_vars' let parse_var in let s' next_msg MSGS rparen_or_comma in if COMMA then let parse_tup_vars' s' in :: xs else ([ ], parse_tup_vars let parse_var in let tok_match COMMA in let parse_tup_vars' in ( :: xs ) and parse_factor_option match force with | Nil None | Cons res -> parse_factora res and parse_or_aux let relop match next with OR -> Some Or -> None in match relop with | Some op -> let parse_and in parse_or_aux [(op )]) | and parse_or let parse_and in let exp's parse_or_aux [] in (build_primops exp's and parse_exp let parse_or s in match next s with | COLON -> let parse_type in Anno e ), | -> and parse_and_aux let relop match next with AND ) -> Some And None in relop with | Some op -> let parse_and in parse_and_aux [(op )]) | None acc and parse_and let parse_comp in let ands s parse_and_aux [] in build_primops ands s and parse_comp_aux let relop match next with EQUAL -> Some Equals NEQUAL -> Some NotEquals LessThan LE -> Some LessEqual GT -> Some GreaterThan GE Some GreaterEqual in match relop with | Some op -> let parse_comp in parse_comp_aux (acc [(op )]) | None -> acc and parse_comp let parse_exp' in let comps parse_comp_aux [] in build_primops comps and parse_exp'_aux acc let addop match next with PLUS -> Some (Plus Minus -> None in match addop with | Some addop let parse_term in parse_exp'_aux acc [(addop )]) | None -> and parse_exp' es let parse_term es in let terms parse_exp'_aux [] in build_primops and parse_term_aux acc let mulop match next with Times DIV ) -> Some Div -> None in match mulop with | mulop let parse_factor in parse_term_aux [(mulop )]) | None and parse_term es let parse_factor in let factors parse_term_aux [] in build_primops factors and parse_basetype ) match with | INT TInt | BOOL -> TBool | LPAREN -> let parse_type in let tok_match RPAREN in | raise Error "expect type" and parse_type_tup let next_msg "expect base type" in let parse_basetype in let s' next_msg "expect tuple type" in if TIMES then let ts parse_type_tup s' in else ([ ], s and parse_type let next_msg "expect base type" in let domain parse_basetype t in let s' next_msg "expect ->, *, or nothing" in match with | let range parse_type s' in TArrow domain range), | TIMES parse_type_tup in TProduct domain :: ts), | -> domain let parse_exp_semi let parse_exp in let tok_match SEMICOLON in ( let parse_exps let helper try let parse_exp_semi in let helper in with Error -> ([], in let parse_exp_semi in let es helper in ( :: es ) let __ocaml_lex_tables Lexing lex_base

 Left: Unwind, string through plexiglass detail.
Right: Unwind, image taken looking up through the sculpture detail, 2021, 1' x 1' x 8'. String, plexiglass, fishing wire.
Left: Unwind, string through plexiglass detail.
Right: Unwind, image taken looking up through the sculpture detail, 2021, 1' x 1' x 8'. String, plexiglass, fishing wire.
INTERACTION PROCESS
In displaying the nature of how code interacts, found in the top right, I begin by outlining the entirety of each sub-program mapped in relation to its time complexity (x-axis) and to the time the sub-program is called (y-axis). Within this graph, I depict how/when a sub-program may be called, either through the process of another sub-program, or recursively within the sub-program itself.
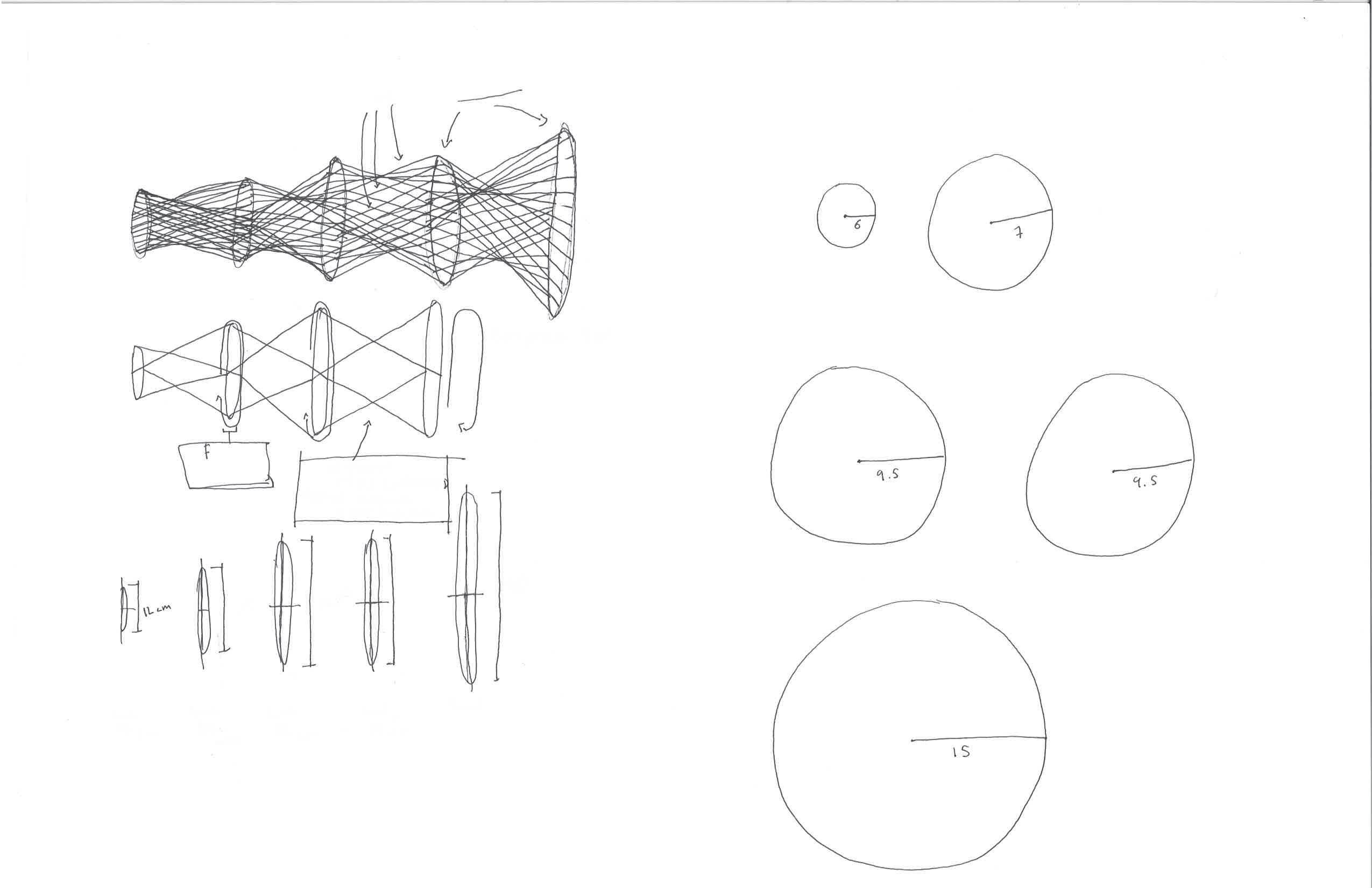


Before an expression is evaluated, it is made up of a collection of "strings". These strings are data, that pass through, are analyzed, and manipulated by each sub-program. When the data passes through, it is calculated and condensed, then called to another sub-program (if required) to finish the calculation. Through displaying each sub-program as a ring on a plate, I can twist each plate 90 degrees to convey the idea of sub-program interaction through said data manipulation and calculation. The final piece was constructed by weaving string through CNC routered clear acrylic panes. Each pane was suspended by fishing wire and rotated 90˚, creating the planned concave effect.

let rec unused_vars exp) name list match with If (e1, e2, e3) union (unused_vars e1) (union (unused_vars e2) (unused_vars e3)) Primop (p, exp_list) -> List.fold_right (fun -> union (unused_vars e1)) exp_list [] Tuple exp_list List.fold_right (fun -> union (unused_vars e1)) exp_list [] Fn (name, t, e1) -> if member name (free_vars e1) then (delete [name] (unused_vars e1)) else (union [name] (unused_vars e1)) Rec (name, t, e1) -> if member name (free_vars e1) then (delete [name] (unused_vars e1)) else (union [name] (unused_vars e1)) Let (args, e1) begin match args with -> unused_vars y::ys -> begin match with Val (e2, name) ByName (e2, name) -> if member name (free_vars e2) || member name (free_vars e1) then delete [name] (union (union (unused_vars (Let (ys,e1))) (unused_vars e2)) (unused_vars e1)) union (union [name] (unused_vars e2)) (union (unused_vars (Let (ys,e1))) (unused_vars e1)) Valtuple (e3, name_l) -> List.fold_right (fun name free_variable -> if member name (free_vars e1) || member name (free_vars e3) union (delete [name] (union (union (unused_vars e3) (unused_vars (Let (ys,e1)))) (unused_vars e1))) free_variable union (union (union [name] (unused_vars e3)) (union (unused_vars (Let (ys, e1))) (unused_vars e1))) free_variable name_l [] end Apply (e1, e2) union (unused_vars e1) (unused_vars e2) Var e1 if member e1 (free_vars (Var e1)) then else [e1] Anno (e1, typ) unused_vars e1 Int Bool [] let rec subst ((e', x) exp name) (e exp) exp update_3 if not (member (free_vars e)) then Var -> if then else Var Int Bool -> Primop (po, es) -> Primop (po, List.map (subst (e', x)) es) (e1, e2, e3) -> If (subst (e', x) e1, subst (e', e2, subst (e', e3) Tuple es Tuple (List.map (subst (e', x)) es) Anno (e, -> Anno ((subst (e', x) e), t) Let (ds, e2) -> begin let rec check ds_o e_h ds_a begin match ds_o with [] -> Let ((ds_a), (subst (e', x) e_h)) y::ys -> match with Val (e3, name) ByName (e3, name) -> Let ((ds_a), e2) else check ys e_h ds_a Valtuple (e4, namelist) if member namelist then Let ((ds_a), e2) else check ys e_h ds_a end in let rec helper_fun ds_origional ds_helper e_helper ds_acc begin match ds_helper with [] -> check ds_origional e_helper ds_acc h::ts -> match with Val (e3, name) -> if member name (free_vars e') then let fn fresh_var name in helper_fun ds_origional ts (subst ((Var fn), name) e_helper) (ds_acc [Val ((subst (e', x) e3), fn)]) else helper_fun ds_origional ts e_helper (ds_acc [Val ((subst (e', x) e3), name)]) ByName (e4, name) -> if member name (free_vars e') then let fn fresh_var name in helper_fun ds_origional ts (subst ((Var fn), name) e_helper) (ds_acc [ByName ((subst (e', x) e4), fn)]) else helper_fun ds_origional ts e_helper (ds_acc [ByName ((subst (e', x) e4), name)]) Valtuple (e5, namelist) -> let rec namelist_check nl_h e_h nl_a begin match nl_h with [] -> helper_fun ds_origional e_h (ds_acc [Valtuple ((subst (e', x) e5), nl_a)]) y::ys -> if member (free_vars e') then let fn fresh_var in namelist_check ys (subst ((Var fn), e_h) (nl_a [fn]) else namelist_check (e_h) (nl_a [y]) end in namelist_check namelist e_helper [] end in helper_fun ds e2 [] end Apply (e1, e2) -> Apply ((subst (e', x) e1), (subst (e', x) e2)) (y, t, e) -> if then Fn (y, t, e) else if member (free_vars e') then let fresh_var in Fn ((fv), t, (subst (e', x) (subst (Var fv, y) e))) else Fn (y, t, (subst (e', x) e)) Rec (y, e) -> if then Rec (y, t, e) else if member (free_vars e') then let fresh_var in Rec ((fv), t, (subst (e', x) (subst (Var fv, y) e))) else Rec (y, t, (subst (e', x) e)) let rec eval exp -> exp let bigstep_depth ref in fun -> !debug >= then print_endline (String.make (!bigstep_depth) "eval (" Print.exp_to_string ")\n"); incr bigstep_depth; let result update_4 Int Bool -> Tuple es -> Tuple (List.map eval es) If (e1, e2, e3) -> begin match eval e1 with Bool eval e2 else -> stuck "Condition for expression should be of the type bool" end Anno (e, _) -> eval (* types are ignored in evaluation *) Var -> stuck ("Free variable \"" "\" during evaluation") Fn (x, t, e) Fn (x, e) Apply (e1, e2) -> begin match (eval e1) with Fn (x, e) -> eval (subst ((eval e2), x) -> stuck "Condition for Apply expression should be the type Fn" Rec (f, t, e) eval (subst ((Rec (f, t, e)), f) Primop (And, es) -> begin match es with [Bool x; Bool y] Bool (x&&y) -> stuck "Condition for Primop AND should of the type Bool" end Primop (Or, es) -> begin match es with [Bool x; Bool y] Bool (x||y) -> stuck "Condition for Primop OR should of the type Bool" end Primop (op, es) -> let vs List.map eval es in begin match eval_op vs with None -> stuck "Bad arguments to primitive operation" Some end Let (ds, e) -> let rec helper ds1 e_acc begin match ds1 with [] -> eval e_acc y::ys begin match with Val (e3, name) ByName (e3, name) helper (subst ((eval e3), name) e_acc) Valtuple ((Tuple e4), namelist) -> let rec namelist_helper e_h namelist_h eh_acc begin match (e_h, namelist_h) with (_, []) ([], _) eh_acc ((x::xs), (n::ns)) namelist_helper ns (subst ((eval x), n) eh_acc) in helper ys (namelist_helper (e4) namelist e) -> stuck "Bad arguments let; valtuple must take tuple and namelist" end in helper ds decr bigstep_depth; !debug >= then print_endline (String.make (!bigstep_depth) "result of eval (" Print.exp_to_string ") Print.exp_to_string result "\n"); result let rec infer (ctx context) (e exp) typ match with Int TInt Bool TBool If (e1, e2, e3) if (typ_eq (infer ctx e2) (infer ctx e3)) && (typ_eq (infer ctx e1) TBool) then (infer ctx e3) else type_fail "Bad arguments If; both e2 and should be of same type an if expression and e1 should be type Primop (p, args) -> begin match with Plus Minus Times Div Negate if List.for_all (fun -> typ_eq (infer ctx x) (infer ctx (List.hd args))) args else type_fail "your primop requries two TInts." And Or LessThan LessEqual GreaterThan GreaterEqual Equals NotEquals -> if List.for_all (fun -> typ_eq (infer ctx x) (infer ctx (List.hd args))) args then TBool else type_fail "you can only compare two values of the same type." Tuple args -> TProduct (List.map (infer ctx) args) Fn (name, Some e1) -> let ctx' extend ctx (name, t) in TArrow (t, (infer ctx' e1)) Fn (name, None, e1) -> infer ctx e1 Rec (name, t, e1) -> let ctx' extend ctx (name, t) in infer ctx' e1 Let (args, e1) let rec extend_ctx_dec arg ctx match arg with -> ctx y::ys -> begin match with Val (e2, name) ByName (e2, name) -> let ctx' extend ctx (name, (infer ctx e2)) extend_ctx_dec ys ctx' Valtuple ((Tuple e3), namelist) -> let rec ctx_namelist_helper e_h namelist_h ctx_acc begin match (e_h, namelist_h) with (_, []) ([], _) -> ctx_acc ((x::xs), (n::ns)) -> let ctx' extend ctx_acc (n, (infer ctx_acc x)) in ctx_namelist_helper ns ctx' in extend_ctx_dec (ctx_namelist_helper e3 namelist ctx) -> type_fail "Bad arguments let; valtuple must take tuple and namelist" in infer (extend_ctx_dec args ctx) e1 Apply (e1, e2) begin let inf_e1 infer ctx e1 in match inf_e1 with (TArrow (t1, t2)) t2 -> type_fail "Applys first argument must be function of type: TArrow (t1, t2)" end Var n1 ctx_lookup ctx Anno (e1, typ) if typ_eq (infer ctx e1) typ then typ else type_fail "Anno's expression and type should be of same type." let execute (s: string) unit match P.parse with Left print_endline ("parsing failed: s) Right try (* first we type check the program *) ignore (infer (Ctx []) e); print_endline ("program is evaluated to: Print.exp_to_string result) NotImplemented -> print_endline "code is not fully implemented" Stuck -> print_endline ("evaluation got stuck: s) NotFound -> print_endline "variable lookup failed" TypeError print_endline ("type error: s) -> print_endline ("unknown failure: Printexc.to_string e)
Left: Sketch of string passing through outer diameter of rhythm graphs. Right: Process of depicting the interaction among sub-programs through data.
type name string ;; type name string type primop Equals (* v1 v2 *) NotEquals (* v1 != v2 *) LessThan (* i1 i2 *) LessEqual (* i1 <= i2 *) GreaterThan (* i1 i2 *) GreaterEqual (* i1 >= i2 *) And (* b1 && b2 *) Or (* b1 || b2 *) (* i1 i2 *) Minus (* i1 i2 *) Times (* i1 i2 *) Div (* i1 i2 *) Negate ;; type primop Equals NotEquals LessThan LessEqual GreaterThan GreaterEqual And Or Plus Minus Times Div Negate exception TypeError string ;; exception TypeError of string let type_fail message raise TypeError message ;; val type_fail string 'a fun type typ TArrow of typ typ (* -> *) TProduct of typ list (* *) (* int *) TBool (* bool *) TVar of typ option ref ;; type typ of typ typ TProduct of typ list TInt TBool of typ option ref let fresh_tvar () TVar ref None ;; val fresh_tvar unit -> typ fun let typ_eq t1 e2 match t1 e2) with (TArrow domain1 range1), TArrow (domain2 range2)) -> typ_eq domain1 domain2 && typ_eq range1 range2 (TProduct TProduct ts2 List length ts1 List length ts2 && List for_all2 typ_eq ts1 ts2 (TInt TInt) -> true (TBool TBool false ;; val typ_eq typ -> typ -> bool fun> exception Stuck of string ;; exception Stuck of string let stuck message raise (Stuck message ;; val stuck string -> 'a fun type exp of int (* ... *) Bool of bool (* true | false *) If of exp exp exp (* if then e1 else e2 *) Primop of primop exp list (* e1 <op> e2 or <op> *) Tuple of exp list (* (e1, ..., eN) *) Fn of name typ option exp) (* fn => *) Rec of typ exp (* rec => *) Let of dec list exp (* let decs in end *) Apply of exp exp (* e1 e2 *) Var of name (* *) Anno of exp typ (* *) and dec Val of (* val *) Valtuple of exp list (* val (x1,...,xN) *) ByName of exp ;; type exp Int of int Bool of bool If exp exp exp Primop of primop exp list Tuple of exp list Fn of typ option exp Rec of name typ exp Let of dec list exp Apply of exp exp of Anno of exp typ and dec Val of exp Valtuple of exp list ByName of exp name let eval_op match op args with (Equals i1; i2]) Bool i1 i2)) (NotEquals Int i1; Int i2]) -> Some Bool i1 <> i2)) (LessThan Int i1; Int i2]) -> Some Bool i1 i2)) (LessEqual Int i1; Int i2]) Some Bool i1 i2)) ( ; ]) )) (GreaterEqual Int i1; Int i2]) -> Some Bool i1 >= i2)) (Plus Int i1; Int i2]) -> Some Int i1 i2)) (Minus Int i1; Int i2]) Some Int i1 - i2)) (Times Int i1; Int i2]) Some Int i1 i2)) (Div Int i1; Int i2]) -> Some Int i1 i2)) (Negate Int ]) -> Some Int (- )) ;; val eval_op primop exp list exp option fun type context Ctx of name typ list ;; type context Ctx of typ list exception NotFound ;; exception NotFound let ctx_lookup ctx let with | [] -> raise NotFound | rest -> if y then else rest in let Ctx list ctx in assoc list ;; val ctx_lookup : context -> name -> typ fun let extend ctx ( let Ctx list ctx in Ctx (( )::list ;; val extend typ fun let rec extend_list ctx match with [] -> ctx ( pairs extend_list extend )) pairs ;; val extend_list context -> name typ list -> context fun type 'a 'b either Left of 'a Right of 'b ;; type 'a 'b either Left of 'a Right of 'b let member List ;; val member 'a 'a list bool fun let (fresh_var reset_ctr let counter ref in ((fun -> string_of_int (!counter ), fun () -> counter ;; val fresh_var string string fun val reset_ctr unit unit fun let debug ref ;; val debug int ref contents module sig val parse string -> string exp either end struct exception Error of string type token | VAR of string | VAL | TRUE | TIMES | THEN | SEMICOLON | RPAREN | PLUS | NUM of int | | NAME | MINUS | DIV | | LET | INT | IN | | FUN | FN | FALSE | EQUAL | NEQUAL | LT | GT | LE | GE | AND | | EOF | END | ELSE | | COMMA | COLON | BOOL | ARROW let token_to_str tok match tok with | VAR Format sprintf "VAR %s" | VAL -> "VAL" | TRUE -> "TRUE" | "TIMES" | THEN "THEN" | SEMICOLON -> "SEMICOLON" | RPAREN -> "RPAREN" | | NUM -> Format sprintf "NUM %d" | NEGATE -> "NEGATE" | NAME -> "NAME" | | DIV -> "DIV" | LPAREN -> "LPAREN" | LET "LET" | | IN -> "IN" | IF -> "IF" | FUN "FUN" | FN "FN" | FALSE -> "FALSE" | EQUAL -> "EQUAL" | NEQUAL "NEQUAL" | LT "LT" | GT -> "GT" | LE -> "LE" | | AND -> "AND" | OR -> "OR" | EOF "EOF" | | ELSE -> "ELSE" | DARROW -> "DARROW" | COMMA "COMMA" | COLON "COLON" | BOOL -> "BOOL" | ARROW -> "ARROW" module struct type 'a Stream of (unit -> 'a front and 'a front Nil Cons of 'a 'a ) let delay let memo ref None in let memof () match with g None -> let () in begin memo := Some end in Stream memof let force Stream () let iterate delay fun () match () with None -> Nil iterate )) end module MSGS struct let rparen_or_comma "expect right parenthesis or comma" let variable "expect variable" end let lexer_to_stream lexer lexbuf Lexing lexbuf S iterate fun () Some lexer lexbuf)) let next_msg msg match force with | Nil -> raise Error msg | Cons -> (* next (x,s'), where is the head of s, s' the tail of raises Error if stream is empty *) let next next_msg "Unexpected end of stream" (* match tok s s', s' is the tail of raises Error if head of does not match tok *) let tok_match tok let msg Format sprintf "Expected %s token" (token_to_str tok in let s' next_msg msg in if tok then s' else raise (Error msg let build_primop e' primop Primop primop ]) let build_primops List fold_left build_primop exp op_exps (* parse_program (e,s') where is the result of parsing the beginning of and s' the unprocessed tail of *) let rec parse_program let parse_exp delay fun () -> Cons )) TIME COMPLEXITY: DIAMETER OF RHYTHM GRAPH TIME SUB-PROGRAM IS CALLED START FINISH
The final piece is an abstract interpretation of code interaction. With each pass through a sub-program, the data is twisted and condensed for the next sub-program to understand.


PIECE TWO
Duplex
Academic Project
ARCH 200A: Core Studio I - Fall 2022

Partner Work
Instructor: Amy Louie
With the analysis of the Shah Houses by Anupama Architects, I extracted the formal syntax of push and pull. As a continuation, I deployed this formal logic to design a new architecture.
In tandem with my partner's formal logic of mirror and split, we created a duplex intended to house a gardener and musician. There is no site or context; this project continued our formal exploration while introducing the complexities that come with homeowner preferences.
 Initial Sketches of Design
Exploration into the pushing of a rectangle through another
Initial Sketches of Design
Exploration into the pushing of a rectangle through another
FORMAL OPERATIONS
The formal operations employed were pushing, mirroring, splitting, and filleting. Initially, there were two mirrored rectilinear forms that were capped with off-set gabled roofs. One of the forms was rotated and then pushed into the other. The result: an exploration into the subsequent space when the two forms intersect.
The syntax of splitting was employed to create a cohesive dwelling, merging the two intersecting volumes into a singular form. The manipulation of the house silhouette fosters a sense of familiarity with an otherwise uncommon structure.

INTERIOR ORGANIZATION

The roof was used as construction lines to break up the floor plan. On the ground floor, there are two entrances to each dwelling and a common area covering large functions and utilities. On the first floor, each dwelling has its own private kitchen, bathroom, and balcony.
The left unit is intended for the gardener, with a lot of transparency between the indoor and outdoor areas, as shown in the windows fragmenting the wall. The common area is intended to be a performative space. The double-heighted space gives a stronger sense of performance and introduces the gabled roof to amplify the acoustics.
Back View Digital Render Floor Plan 01 Floor Plan 02 Short Seciton 01 Short Section 02 Cut Axonometric Composite
 Back view with double height area exposed.
Digital Render
Back view with double height area exposed.
Digital Render
PIECE THREE
Single Dwelling With Community Garden
Academic Project
ARCH 200A: Core Studio I - Fall 2022
Individual Work
Instructor: Amy Louie
Award: Design Excellence Award
As a continuation of my formal syntax, I further explored the resulting spaces found from two intersecting rectilinear forms with gabled roofs. When one is pushed through the other, a fillet is created, as though the form pushing through is dragging with it some of the other. The final form is a private dwelling for a gardener and a communal greenhouse and garden space coupled with public washrooms and storage.

The gardener can be considered as one who enjoys the outdoors and requires a lot of open space and natural light. With that in mind, the house is angled to catch as much natural light as possible, particularly in the morning, as noted in the left rendering. To further complement the characteristics of the gardener, the bottom floor is set in the ground and formally generated once again by the intersection of two rectilinear forms. The bottom floor is shifted from the top, creating offset moments that allow for skylights and circulation decks.
 Initial Sketches of Design Exploration into roofline over intersecting volumes.
Initial Sketches of Design Exploration into roofline over intersecting volumes.
INTERIOR ORGANIZATION
The left side of the first floor plan is the public space with an outdoor garden. Above, the interior space is private for the gardener. The detached greenhouse is connected via a public path around the house. Through its roof and orientation, the greenhouse expresses formal continuity while remaining a detached form. As expressed in the facade study, this results in a facade reading that, at moments, resembles one continuous form.
 Floor Plan 00
Floor Plan 01
Section 01
Section 02
Facade and Roof Composite
Floor Plan 00
Floor Plan 01
Section 01
Section 02
Facade and Roof Composite
When one form is pushed through the other, it drags the other with it. This operation generates a fillet at the corner that takes the form of an arc; a segment of a circle. The tangents of these circles connect the roof lines and are used as generative tools for interior division.








As shown in the diagram in the bottom right, the roofline and circle extend through to the detached greenhouse. The overlapping volumes and roofline generate the void for the double-height space. The interior perspective to the left shows the main entrance that follows this doubleheight space and subsequently, the roofline. This space allows natural light to fall into the space below, including the dweller's bedroom. With the continuation of the roof through to the greenhouse, the roof splits above the double-height space. As demonstrated in the light study render to the right, the split presents an opportunity for the roof to open up, filling the double-height space with morning light, influenced by the volume below. The interior walls remain cohesive through both floors, expressing further continuity in this public/private dwelling.

In the space below, the dweller has their bedroom which is open to the community garden and morning light. Staying true to this persona, the private dwelling has been designed to fully service the gardener's preferences. Their bedroom is grounded within the earth but remains open for morning light. The dweller has their own private garden with direct access from their kitchen. While the dweller's private area remains separated from the public space with limited windows, their space is completely open to their garden. The fragmentation of the walls lining the garden begins to dissolve the separation between outside and in.

FACADES
Though detached, the greenhouse remains formally relevant. The curvature of the roof, formed by tangent circles, is continuous through to the greenhouse, leaving a familiar yet distorted gabled roof silhouette on the side. The greenhouse stays accessible due to the deck created by offsetting the forms making up the basement level. While the greenhouse formally resembles the home, its materiality begins to contribute to its separation. This separation allows the public to affirm its public intention as it has no connection to the private. It remains cohesive, yet separate.




 Left: Unwind, string through plexiglass detail.
Right: Unwind, image taken looking up through the sculpture detail, 2021, 1' x 1' x 8'. String, plexiglass, fishing wire.
Left: Unwind, string through plexiglass detail.
Right: Unwind, image taken looking up through the sculpture detail, 2021, 1' x 1' x 8'. String, plexiglass, fishing wire.







 Initial Sketches of Design
Exploration into the pushing of a rectangle through another
Initial Sketches of Design
Exploration into the pushing of a rectangle through another



 Back view with double height area exposed.
Digital Render
Back view with double height area exposed.
Digital Render

 Initial Sketches of Design Exploration into roofline over intersecting volumes.
Initial Sketches of Design Exploration into roofline over intersecting volumes.
 Floor Plan 00
Floor Plan 01
Section 01
Section 02
Facade and Roof Composite
Floor Plan 00
Floor Plan 01
Section 01
Section 02
Facade and Roof Composite



















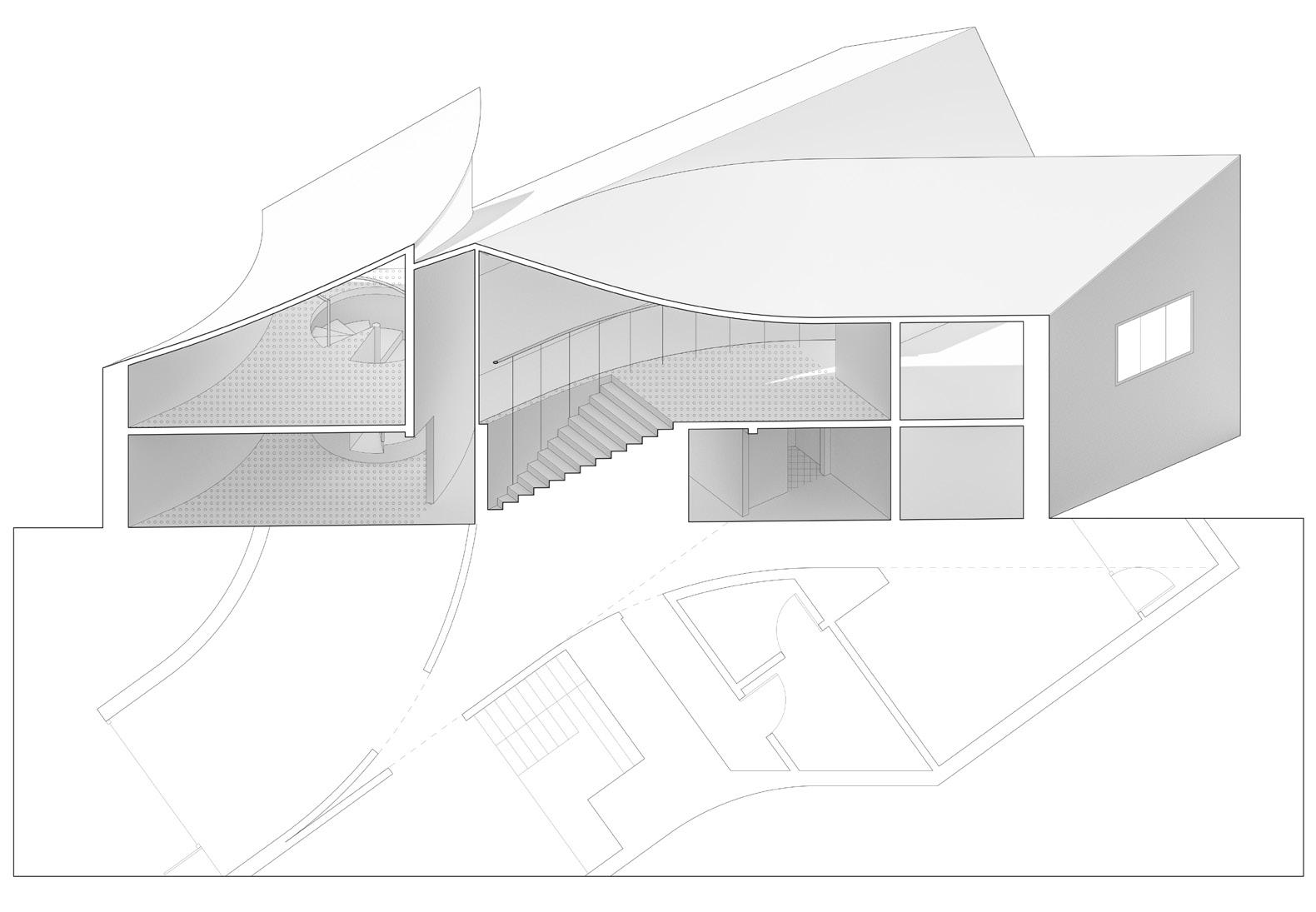
 Short Section 01
Long Section 01
Short Section 01
Long Section 01