PIECE FOUR

Market Core

Academic Project

ARCH 200B: Core Studio II - Spring 2023

Individual Work

Instructor: Allisa Chastain

Site: 20th st. and Tennessee st. San Francisco, CA

Structure can be understood in at least two ways. First, it describes the physical parts of a building that support all other parts of the building. Second, it describes the organizational ideas that bring order and hierarchy to a building’s form, space, programs, and materiality. For this project, I explored how these two ideas work to support each other as well as order and structure the spaces and programs within the four-storey building.

Starting with two structural column grids provided, the challenge was to orient the grids in such a way that would lead the form and function of the building. The placement and orientation of the two systems begin to form spatial relations and programs. All subsequent design decisions related to programs and site were in response to the initial decisions about structure.

Site Context

The site is found within the Dogpatch area in San Francisco. Historically, the neighborhood was a ship-building zone due to its proximity to the water. Historic buildings in the area are, therefore, factory-style buildings with steel and glass structure. The 1990s brought gentrification to the area, making adaptive reuse of the industrial buildings. Nowadays, Dogpatch is mainly industrial and residential, with residents communiting to either San Francisco or South San Francisco.

The site is situated in a busy area, where the main rail station towards Downtown San Francisco is a street away to the east. The freeway entrance ramp is a block away west. The intersection of these two streams of traffic make the south-west corner of the site ver visible by both cars and pedestrians. The site is surrounded by multiple forms of transit and new residential buildings.

Designing The Void

For this project, there were two types of assigned program: fixed and flexible. The fixed program included the market’s infrastructural core; the spaces that support or otherwise make possible the places of commerce and exchange that populate the flexible program. The flexible program was considered to be the outdoor market spaces. It was required that the fixed program remained - more or less - in the center of the building.

When considering the form of the core, I took it quite literally. My core started as a solid rectangular prism, similar in proportion to the building but reduced to its maximum allotted size. Understanding that the building's southwest corner would see the most foot traffic, the core and the grid structure were rotated to face that corner, allowing the structure to direct people to the center.

To promote vertical circulation and interaction within the building, I treated the core as a multi-level social hub that nested within the staircases. The core was sculpted through the subtraction of resized rectangular forms. The forms rest on two axes, either one in line with the shift towards the corner or parallel with the building. The void was sculpted to maximize light throughout the day, creating a light tunnel through the middle of the building. The light falling through to the bottom floor of the building further encourages movement towards the center and then up.

The layering that occurs with the carve provides a sculptural interior; almost monolithic. As one vertical moves through the core, they are presented with multi-layer seating decks provided by the layering. People are able to circulate up through the building without leaving natural light.

Interior Organization

The supporting core provides multiple facilities: restaurant and seating on the first floor, administrative offices and snack bar on the second, employee break room and rented offices on the third, and a daycare on the fourth floor. The carved core is a place to gather, interact, and move. No windows ever connect these facilities to the core, keeping the circulation and seating decks private.

At moments, the carvings cut through the floor plates as well, opening the center even more. The stairs remain a part of the monolithic block and wind along the interior walls of the core. Though simple, the stairs and the space they create become the centerpiece of the building.

Vertical Carves

The rectilinear forms used to carve vary in size both horizontally and vertically. At moments, the floor plate is voided out due to a heightened carve and the subsequent seating deck is slightly lowered. These variations provide dynamic spaces in section and further contribute to the layering of platforms and spaces found within the core.

Piece Five

Unwind Personal Project

In the course, McGill COMP 502: Programming Languages and Paradigms, I was tasked to program an original computing language. The goal of this language was to understand and compute relatively simple tasks. This included expression evaluation, type checking (checking the type of an input variable; an integer, fraction, true/ false statement, etc), and type inferencing. My code contains five main components: free_vars, unused_vars, subst, infer, and eval. The components, or sub-programs, interact to produce a result. Unwind, explores the rhythm of the code and the nature in which each subprogram interacts with all other sub-programs.

Rhythm Of Subst

# P.parse "let val x = 4 in y + 3 end;" ;; - : (string, exp) either = Right (Let ([Val (Int 4, "x")], Primop (Plus, [Var "y"; Int 3]))) calling the function: # subst (Int 4, "y") ((Let ([Val (Int 4, "x")], Primop (Plus, [Var "y"; Int 3])))) if ... then ... else ...

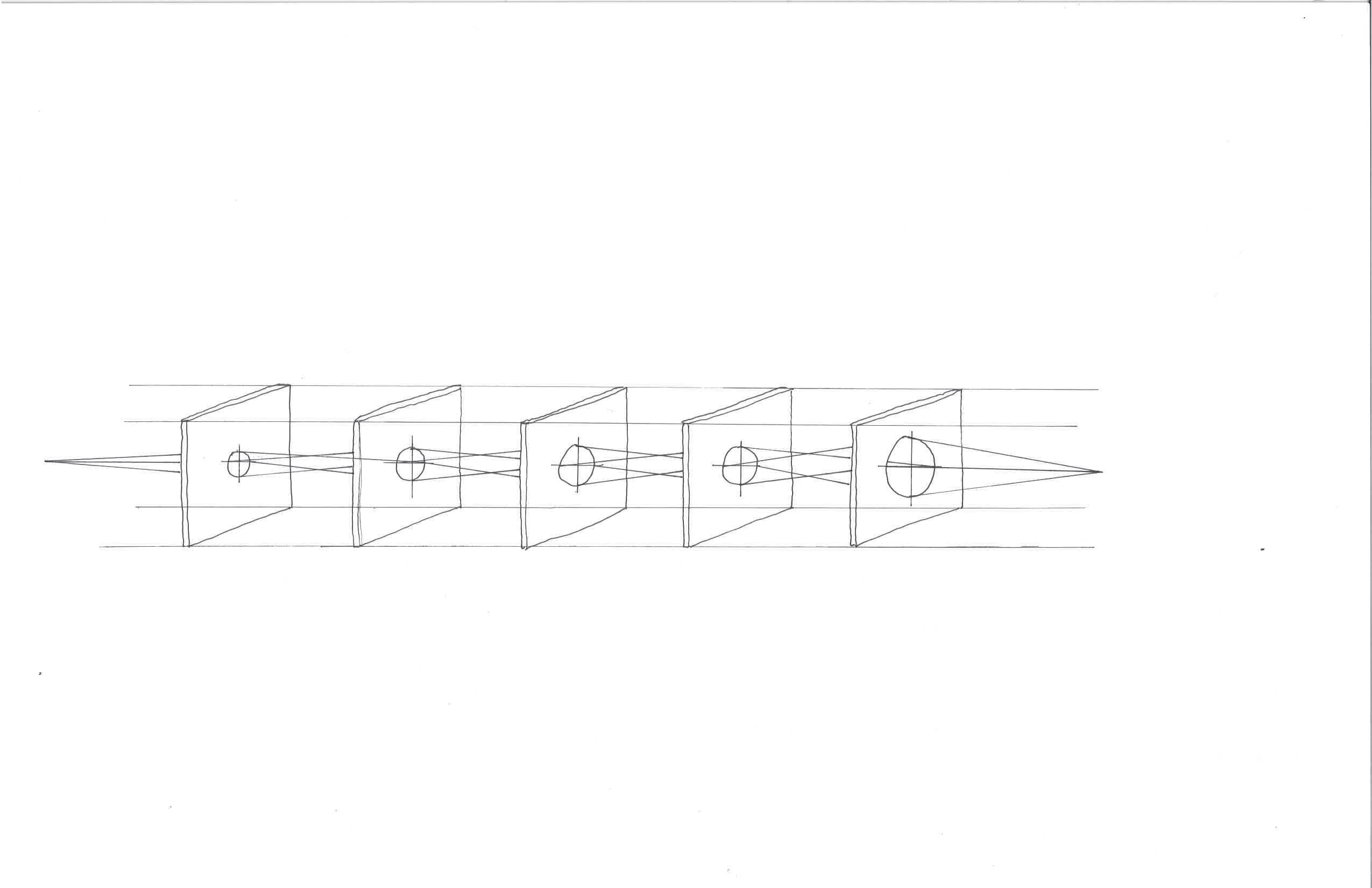
This diagram depicts a cross-section of the sub program subst.

Each line represents a step in the computation of data.

Data passing through embedded programs within subst are represented by thicker lines. The time complexity of the embedded program is represented in the thickness of the line.

When an outside function is called to assist in the computation, a space is found. The time complexity of the outside function is represented in the size of the space.

A recursive call is when the programs calls itself to compute a substrata of the data.

List.mem a [set] match (e) with program interating through choices subst (e', x) (e) recursive call calling free_vars (e)

List.map f [a1; ...; an]

A Quick Explanation

Below, is a rhythm diagram of the sub-program free_vars (e) and the code itself. Free_vars is used to find variables within an expression that are not captured. For example, with "let x = 4 in y + 3", "y" has no defined value and therefore is free. The code below outlines how each type of variable is computed in free_vars. For example, "| int _ -> []" means if the expression called is an integer, the returning value is nothing.

RHYTHM OF FREE_VARS

free_vars (e) let rec free_vars (e : exp) : name list = match e with

| Int _ -> []

| Bool _ -> []

| If (e1, e2, e3) -> union (free_vars e1) (union (free_vars e2) (free_vars e3))

| Primop (p, args) -> List.fold_right (fun e1 -> union (free_vars e1)) args []

| Tuple args -> List.fold_right (fun e1 -> union (free_vars e1)) args []

| Fn (name, t, e1) -> delete [name] (free_vars e1)

| Rec (name, t, e1) -> delete [name] (free_vars e1)

| Let (args, e1) -> match args with

[] -> free_vars e1 y::ys -> (match y with

Val (e2, name) | ByName (e2, name) -> (union (free_vars e2) (delete [name] (union (free_vars (Let (ys, e1))) (free_vars e1))))

Valtuple (e3, name_l) -> (union (free_vars e3) (delete name_l (union (free_vars (Let (ys, e1))) (free_vars e1)))))

| Apply (e1, e2) -> union (free_vars e1) (free_vars e2)

| Var e1 -> [e1]

| Anno (e1, typ) -> free_vars e1

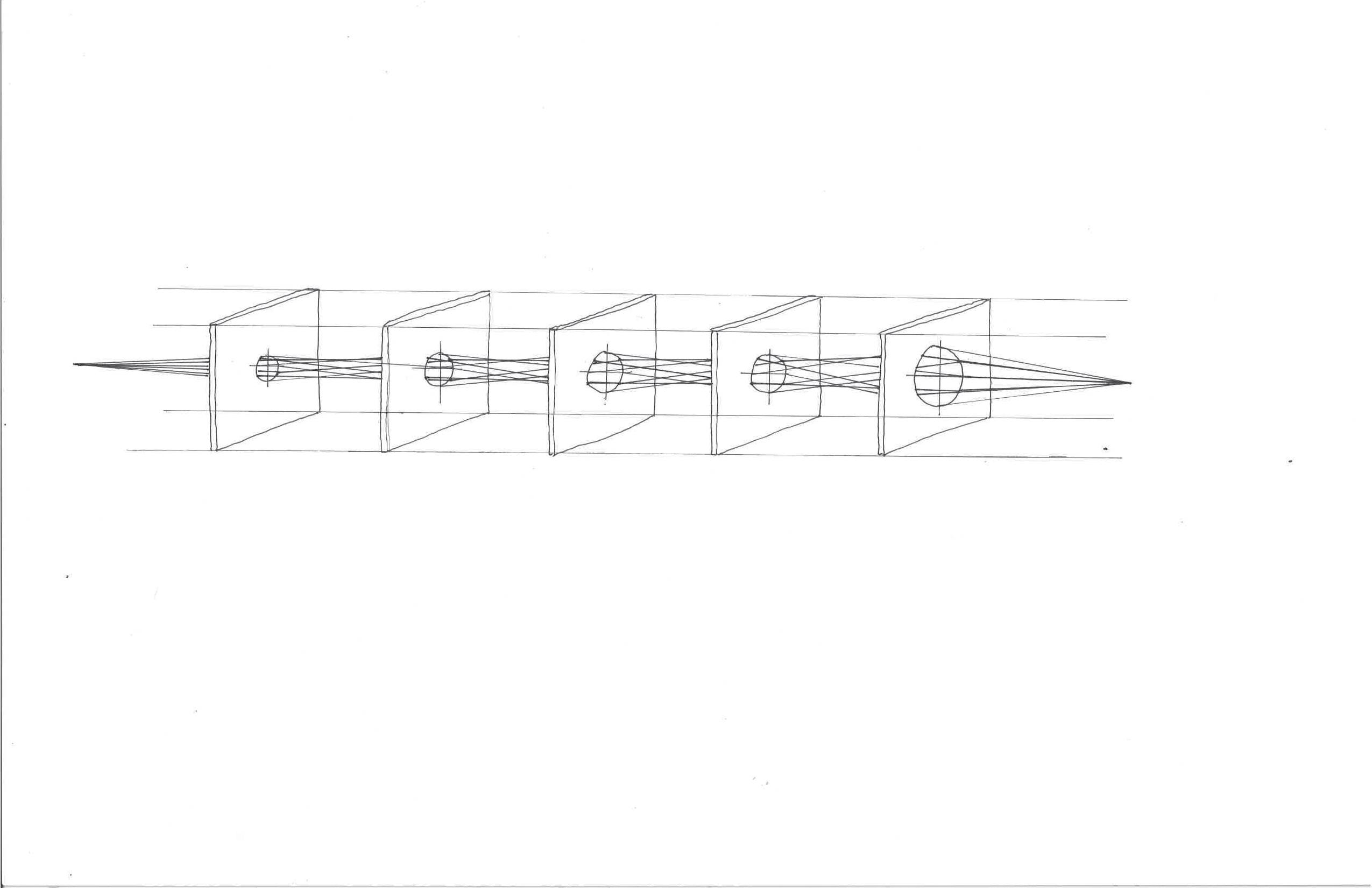
This diagram depicts a cross-section of the sub program free_vars. Each line represents a step in the computation of data.

The code uses the 'match' call to look for the type of variables in the expression and computes accordingly. When iterating through choices, a line is made in the diagram.

In order for my lanaguage to understand the expression, it is broken down into a list of sub-components that can be individually examined; the given expression becomes: (Let ([Val (Int 4, "x")], Primop (Plus, [Var "y"; Int 3]))) calling the function: # free_vars (Let ([Val (Int 4, "x")], Primop (Plus, [Var "y"; Int 3])) program interating through choices match (e) with free_vars (e) recursive call delete call union call List.fold_right f [a1; ... ; an] [] free_vars (e) recursive call

# P.parse "let val x = 4 in y + 3 end;" ;; - : (string, exp) either = Right (Let ([Val (Int 4, "x")], Primop (Plus, [Var "y"; Int 3]))) end of program; "[y]"

RHYTHM OF ALL SUB-PROGRAMS

In asking the program to evaluate "let val x = 4 in y + 3 end;", each sub-program is called at separate points in time. Given the structure of their code, the role each sub-program plays in executing the expression results in varying rhythms. Below, ordered from called first to last, are the sub-programs and their rhythm. The size of each diagram directly correlates to the time complexity; the larger the diagram, the more time and computing power is required.

subst (e', x) (e) infer (ctx) (e) eval (e) free_vars (e) unused_vars (e)

Format: name (input 1) (intput 2)

Type: integer, floating integer (fraction), bool (true/false), etc infer (ctx) (e): eval (e): free_vars (e): subst (e', x) (e): unused_vars (e):

Legend: infer the type of the expression, e, given the list of possible types outlined in ctx. evaluate the expression, e. return the free variables found in expression, e. substitute the expression, e', for variable name, x, in expression, e. return the variables not used in expression, e.

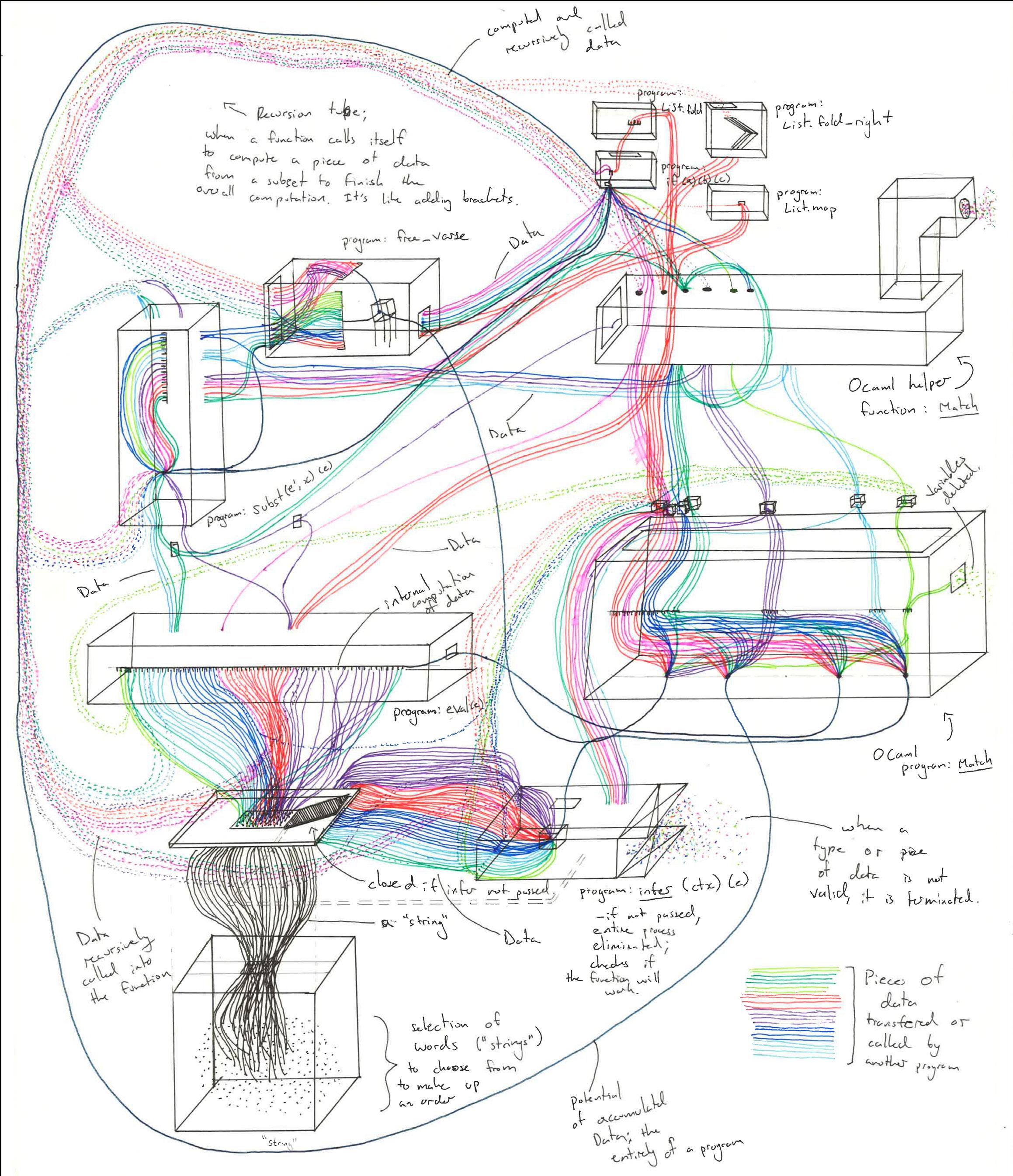
Interaction Process

At different points in time, the examined sub-programs call each other to assist in the task. The data walk through different rooms of the code, each room impacting the data and directing them to the exit. Each room has a different purpose, and its doors directly connect to other rooms. I examine the nature in which the sub-programs call each other; the orientation of the rooms and their doors.

The coloured lines signify the data types within the expression; Let, Val, Rec, Fn, Primop, and Apply

The diagram outlines the computation of the expression: 32

The expression is written in a language, however, that my program cannot understand. Meaning, my program does not have the vocabulary to compute to the power of. The solution is to create an expression that will teach my program.

Let valid_program1 = ”let fun power (x : int) (y: int) : int = if x = 0 then 0 else if y = 0 then 1 else x * power (x)(y-1) in power 3 2 end;“ ;;

Essentially, the expression above is a function that acts as a loop; computing 3 x 3, twice. In order for this to work with my program, it must be translated (P.parse) into my language:

P.parse valid_program1 ;; - : (string, exp) either = (Let ([Val (Rec ("power", TArrow (TInt, TArrow (TInt, TInt)), Fn ("x", Some TInt, Fn ("y", Some TInt, If (Primop (Equals, [Var "x"; Int 0]), Int 0, If (Primop (Equals, [Var "y"; Int 0]), Int 1, Primop (Times, [Var "x"; Apply (Apply (Var "power", Var "x"), Primop (Minus, [Var "y"; Int 1]))])))))), "power")], Apply (Apply (Var "power", Int 3), Int 8))))

The result proves to be a detailed description of the expression that my program can understand.

Interaction Process

In displaying the nature of how code interacts, found in the top right, I begin by outlining the entirety of each sub-program mapped in relation to its time complexity (x-axis) and to the time the sub-program is called (y-axis). Within this graph, I depict how/when a sub-program may be called, either through the process of another sub-program, or recursively within the sub-program itself.

Before an expression is evaluated, it is made up of a collection of "strings". These strings are data, that pass through, are analyzed, and manipulated by each sub-program. When the data passes through, it is calculated and condensed, then called to another sub-program (if required) to finish the calculation. Through displaying each sub-program as a ring on a plate, I can twist each plate 90 degrees to convey the idea of sub-program interaction through said data manipulation and calculation.

TIME COMPLEXITY: DIAMETER OF RHYTHM GRAPH