PROYECTO FINAL

4372-21-20149

MANUEL FERNANDO ESTRADA GARCÍA
Introducción
¿Qué es lógica?
Principios de lógica matemática
Conjuntos Solución de problemas de conjuntos Calculo proposicional Secuencia Lógica
Leyes Proposicionales
Razonamiento Deductivo E
Inductivo
Silogismo categórico Leyes de Inferencia
Tablas de Verdad
Cuantificadores
Falacias
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. INDICE
¡Bienvenidos a la fascinante revista de matemáticas, donde los números y las formas se convierten en una apasionante aventura para todos! Aquí encontrarás un universo de conocimiento que te llevará más allá de lo imaginable, desvelando los misterios y maravillas que se esconden detrás de los números y las ecuaciones. Prepárate para descubrir cómo las matemáticas gobiernan el mundo que nos rodea, desde la música y el arte hasta la tecnología y la ciencia. Te invitamos a embarcarte en un viaje asombroso, donde cada página revelará secretos ocultos y te sorprenderá con sus sorprendentes aplicaciones en la vida cotidiana. ¡Sumérgete en este apasionante viaje y despierta tu mente a la magia de las matemáticas!
1.
INTRODUCCIÓN
¿QUÉ ES LA LÓGICA?
La lógica matemática es la ciencia que estudia el razonamiento, a través de proposiciones que se evalúan únicamente de dos maneras: verdadero o falso. Se parte de una o varias afirmaciones, llamadas
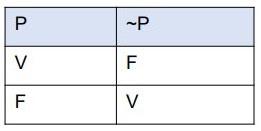
“premisas”, y de ellas se obtienen otras afirmaciones, que constituyen la “conclusión”.

2.
EXTRA: JUEGO DE LOGICA

2. EJEMPLOS DE LÓGICA
Ejemplo: Proposiciones y operaciones lógicas:
.p: La tierra es plana.
Sabemos que pueden tomar un valor de falso o verdadero; por lo tanto son proposiciones validas. Y en el caso de p la proposición es falsa.
3. PRINCIPIOS DE LÓGICA MATEMATICA

Unos de los principales principios de la Lógica Matemática son los siguientes:
Lógica proposicional: en la cual una proposición es un enunciado que tienen un valor de verdad, en otras palabras, puede que sea falso o verdadero.
Estructuras: matemáticas relacionados con las diferentes teorías axiomáticas y la lógica matemática.
3. PRINCIPIOS DE LÓGICA MATEMATICA
Reglas de deducción formales:
así como de las diferentes capacidades expresivas que se encuentran presentes en los lenguajes formales y en las propiedades metodológicas. los conectores son los encargados de unir o conectar dos diferentes proposiciones los cuales deben de estar presentes para poder así obtener un resultado verdadero. Si símbolo es: {Ù , un punto (.), un paréntesis}.
Conectivos lógicos y proposiciones compuestas:
4. CONJUNTOS
Los conjuntos son una colección de elementos considerada en sí misma como un objeto. Los elementos de un conjunto, pueden ser cualquier elemento que sea imaginable, como lo son personas, animales, automóviles, marcas registradas etc.
El contenido del conjunto se escribe dentro de llaves "{ }", paréntesis "( )" o corchetes "[ ]".
Ejemplos:
EXTRA: DATOS CURIOSOS

¿Sabías que el número 9 se considera mágico? Esto se debe a que si multiplicas cualquier número por 9, añádele todos los dígitos al resultado y su suma siempre da 9.
¡Pruébalo y verás como es cierto!
¡Magia!
5. SOLUCIÓN DE PROBLEMAS CON CONJUNTOS
Para aprender a desarrollar de mejor manera la solución a problemas de conjuntos la manera más apropiada es realizarlo por medio de un ejemplo el cual se puede ejemplificar de manera muy fácil.
Para el siguiente ejemplo, se plantea el problema relacionado al conjunto y se da solución y el seguimiento lógico para llegar a una respuesta.
El ejemplo se plantea en las próximas paginas
5. SOLUCIÓN DE PROBLEMAS CON CONJUNTOS
Una farmacia rebajó el precio de una loción y el de una crema. La contabilidad al final de un día indicó que 66 personas habían comprado crema; 21 compraron loción y 21 ambos productos a. ¿Cuántas personas aprovecharon la oferta? b. ¿Cuántas compraron solamente la loción. ¿Cuántas compraron solamente la crema?
Solución
Consideremos los siguientes conjuntos:
C = {x/x compró crema}
L = {x/x compró loción}
De acuerdo al problema tenemos que:
η (C∩L) = 21
Este será nuestro elemento clave para resolver el problema, para ello la herramienta más práctica para solucionar elejercicio es mediante el uso de los diagramas de Venn-Euler
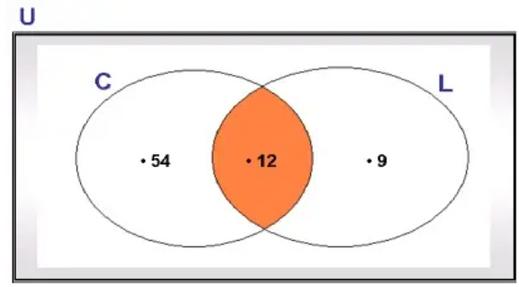
Este será el diagrama que utilizaremos para darle solución al problema.
dentro del total de personas que adquirieron las
cremas (66) se están contabilizando las que compraron cremas y lociones (12), de esta manera se tiene que, para saber cuántas personas compraron SOLAMENTE
cremas realizamos el siguiente cálculo:
η (Solamente Crema) =η (C) -η (C∩L)
η (Solamente Crema) =66-12= 54
De la misma manera, para conocer la cantidad de personas que adquirieron SOLAMENTE lociones:
η(Solamente Lociones) =η(L) -η(C∩L)
η(Solamente Crema) =21-12= 9

De esta forma, ¿Cuántas personas aprovecharon la oferta?
η(C∪L)=η(C) +η(L) -η(C∩L).
η(C∪L)=66+21-12
η(C∪L)= 75
Gráficamente se observa la solución del ejercicio planteado:
6. CALCULO PROPOSICIONAL
Sistema lógico que formaliza los razonamientos basados en relaciones de verdad entre proposiciones que se examinan haciendo abstracción de su estructura interna de sujetopredicado.
Las proposiciones son las unidades básicas del cálculo proposicional y pueden ser verdaderas o falsas. Las proposiciones se combinan mediante conectivas lógicas como “y”, “o” y “no” para formar fórmulas más complejas.

Ejemplos:
Las computadoras trabajan más rápido que los hombres.
No tengo un auto azul.
Marcela estudia en Quito y Pablo en Loja.
7. SECUENCIA LÓGICA

Una secuencia lógica es una sucesión ordenada de ideas o acciones que guardan alguna relación entre sí. Una secuencia lógica tiene sentido y coherencia, y facilita la comprensión de un texto o de un proceso. No tiene que ser una secuencia fija o única, pero cualquier otro orden posible tiene menos sentido lógico que el que se le presenta
Ejemplos:
Las leyes proposicionales son equivalencias lógicas que nos permiten reducir esquemas moleculares complejos y expresarlos en formas más sencillas. La lógica proposicional, también llamada lógica de enunciados, lógica de orden cero o cálculo proposicional, es un sistema formal cuyos elementos más simples representan proposiciones o enunciados, y cuyas constantes lógicas, llamadas conectivas lógicas, representan operaciones sobre proposiciones, capaces de formar otras proposiciones de mayor complejidad.

8. LEYES PROPOSICIONALES
9. RAZONAMIENTO DEDUCTIVO E INDUCTIVO
El método inductivo y deductivo son diferentes tipos de razonamiento. La gran diferencia entre razonamiento inductivo y deductivo está en que el inductivo tiene como objetivo desarrollar una teoría; mientras que el deductivo, probar una teoría existente.
Por otra parte, el razonamiento inductivo va de lo micro a lo macro. Es decir, se mueve desde observaciones específicas hacia generalizaciones más amplias. El razonamiento deductivo, mientras tanto, lo hace al revés.
Ambos enfoques, tanto el método inductivo y deductivo, se utilizan ampliamente en las investigaciones científicas y en diversos tipos de investigación. De hecho, hoy no es para nada extraño que en estudios científicos muy grandes se apliquen ambos a la vez.
9. RAZONAMIENTO DEDUCTIVO E INDUCTIVO

Ejemplos:
Razonamiento Deductivo:
Los lácteos aportan calcio.
El yogur es un lácteo.
El yogur aporta calcio.
El 12 de octubre es feriado.
Hoy es 12 de octubre.
Hoy es feriado.
Razonamiento Inductivo:
En mi departamento hace calor.
En el departamento de mi vecino hace calor.
Hace calor en todo el edificio en el que vivo.
Felipe es dulce y trabajador.
Fernanda es una persona dulce y trabajadora.
Las personas cuyo nombre empieza con F son dulces y trabajadoras.
Un silogismo categórico es un argumento deductivo que consta de tres proposiciones categóricas (dos premisas y una conclusión); colectivamente, estas tres proposiciones presentan exactamente tres clases; cada una de las tres clases ocurre exactamente en dos de las proposiciones.
Ejemplo:
Todas las ardillas son republicanas. Algunos republicanos son golfistas. Por lo tanto, algunas ardillas son golfistas.
Cada uno de los tres términos de clase tiene una designación especial. El llamado término mayor es el término que aparece en posición predicada en la conclusión; en nuestro tonto ejemplo, ese es 'golfistas'. El término menor es el término que aparece en posición sujeto en la conclusión; en nuestro ejemplo, eso es 'ardillas'. El término medio es el otro, el que aparece en cada una de las premisas; en nuestro ejemplo, se trata de 'republicanos'.
10. SILOGISMO CATEGORICO
EXTRA: VIDEO PROPOSICIONES CATEGORICAS

11. LEYES DE INFERENCIA
Las reglas de inferencia son reglas de misa sión

Silogismo disyuntivo
11. LEYES DE INFERENCIA


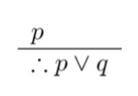
Adición
Simplificación
Conjunción
Resolución
Ejemplo:
p: Está nublado.
q: Llueve.
r: El suelo está mojado.
12. TABLAS DE VERDAD
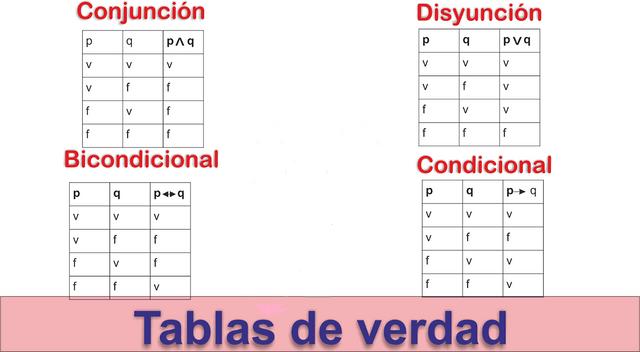
Es una estrategia de la lógica simple que permite establecer la validez de varias propuestas en cuanto a cualquier situación, es decir, permite determinar las condiciones necesarias para que sea verdadero un enunciado propuesto, permitiendo clasificarlos en tautológicos.
Funciones de las tablas de verdad
Las tablas de verdad lógicas permiten el análisis de cualquier fórmula para encontrar los valores que la hagan verdad. Determinan si una fórmula es satisfactoria, así como la validez de un razonamiento
Ejemplo:
EXTRA: VIDEO EXPLICATIVO POR MANUEL ESTRADA

13. CUANTIFICADORES
En lógica formal, un cuantificador es una expresión que indica la cantidad de veces que un predicado o propiedad P se satisface dentro de una determinada clase (por ejemplo, pertenencia, equivalencia u orden). Existen muchos tipos de cuantificadores, entre los más utilizados están:1

Cuantificador universal
∀x, y…
Para todo x, y...
Cuantificador existencial
∃x, y…
Existe al menos un x, y...
Cuantificador existencial único
∃!x, y…
Existe exactamente un x, y...
Negación del cuantificador existencial
∄x, y…
No existe ningún x, y...
Ejemplo:
EXTRA: INFOGRAFIA CUANTIFICADORES

14. FALACIAS
Una falacia es un razonamiento incorrecto pero con apariencia de razonamiento correcto. Es un argumento engañoso o erróneo (falaz), pero que pretende ser convincente.
Tipos de Falacias:
Falacia ad ignorantiam
Falacia ad verecundiam
Argumento ad consequentiam
Generalización apresurada
Falacia del hombre de paja
Falacia ad hominem
Estos son solo uno de los tipos de falacias que existen.
Ejemplo:
No puedo estar embarazada, si lo estuviera papá
me mataría.
Este es un argumento ad consequentiam ya que esta falacia consiste en evaluar la veracidad de una premisa a partir de lo deseables o indeseables
EXTRA: DATOS CURIOSOS
¿Sabías que en algunas escuelas israelíes, se enseña álgebra evitando usar el símbolo «+» porque recuerda a una cruz? En lugar de usar este símbolo, prefieren emplear una «T» invertida. Una de las curiosidades matemáticas más particulares del mundo.
Se ha observado que aquellos estudiantes que durante un examen de matemáticas mastican goma de mascar, son los que consiguen mejores calificaciones
 Creado en 2023. Manuel Fernando Estrada García. 4372-21-20149. UMG
Creado en 2023. Manuel Fernando Estrada García. 4372-21-20149. UMG


















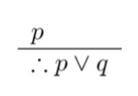



 Creado en 2023. Manuel Fernando Estrada García. 4372-21-20149. UMG
Creado en 2023. Manuel Fernando Estrada García. 4372-21-20149. UMG