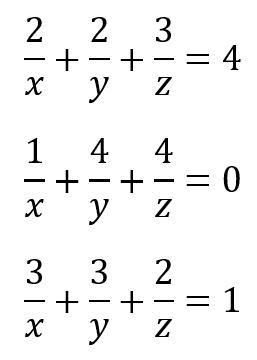Tiga Variabel

Kelas/ Semester : X. ..... /Ganjil
Nama Kelompok : .........................................................
Nama Tutor : .........................................................

Nama Anggota : 1. .....................................
IDENTITAS STIMULUS
2. .....................................
7. .....................................
Masih ingatkah kalian tentang materi sistem persamaan linear dua variabel (SPLDV) ? Pada jenjang SMP, anda telah mempelajarinya dan mengetahui bagaimana cara menyelesaikan SPLDV. Di jenjang SMA/MA ini, kita akan mempelajari tentang sistem persamaan linear tiga variabel (SPLTV) dan sistem pertidaksamaan linear dua variabel (SPtLDV).

KEGIATAN 2
Jika ketiga struk di atas diubah ke dalam model matematikanya, dengan x menyatakan harga 1 , y menyatakan harga 1 , dan z menyatakan harga 1 , maka diperoleh ..
Struk pertama membeli , , dan seharga
Rp. . Model matematikanya : x + y + z =
Struk kedua membeli , , dan seharga
Rp. . Model matematikanya : x + y + z =
Struk ketiga membeli , , dan seharga
Rp. . Model matematikanya : x + y + z =
DEFINISI SISTEM PERSAMAAN LINEAR TIGA VARIABEL
Ketiga model matematika di atas mempunyai variabel dengan masing-masing variabelnya berderajat . Jika ketiga persamaan linear digabungkan, akan diperoleh sistem persamaan linear tiga variabel, yaitu :
x + y + z =
x + y + z =
x + y + z =
DISKUSIKAN DAN RUBAH KETIGA STRUK TERSEBUT KE DALAM MODEL MATEMATIKA ! SMA NEGERI

Langkah-langkah dalam menyelesaikan SPLTV menggunakan metode ini adalah sebagai berikut :
Langkah (1) : Amatilah persamaan tersebut. Kita lihat bahwa variabel

mempunyai bentuk yang sederhana (koefisiennya kecil), sehingga kita akan mengeliminasi variabel terlebih dahulu.
Langkah (2) : Buatlah SPLDV tanpa variabel , dengan mengeliminasi dua
pasang persamaan
Eliminasi variabel dari persamaan ( ) dan ( )
Eliminasi variabel dari persamaan ( ) dan ( )
Langkah (3) : Selesaikan SPLDV tersebut, sehingga kita peroleh salah satu nilai variabel, yaitu .
Eliminasi variabel dari persamaan ( ) dan ( )
Langkah (4) : Substitusikan nilai ke salah satu persamaan dua variabel sehingga diperoleh nilai variabel lainnya, yaitu Substitusikan = ke persamaan ( ), diperoleh

Langkah (5) : Substitusikan nilai dan ke salah satu persamaan tiga variabel sehingga diperoleh nilai variabel .
Substitusikan = dan = ke persamaan ( ), diperoleh
Jadi, himpunan penyelesaiannya adalah {( , , )}.