Learning Digital Electronics
With 20+ Practical Projects in Logic and Circuit Design
● This is an Elektor Publication. Elektor is the media brand of Elektor International Media B.V. PO Box 11, NL-6114-ZG Susteren, The Netherlands Phone: +31 46 4389444
● All rights reserved. No part of this book may be reproduced in any material form, including photocopying, or storing in any medium by electronic means and whether or not transiently or incidentally to some other use of this publication, without the written permission of the copyright holder except in accordance with the provisions of the Copyright Designs and Patents Act 1988 or under the terms of a licence issued by the Copyright Licencing Agency Ltd., 90 Tottenham Court Road, London, England W1P 9HE. Applications for the copyright holder's permission to reproduce any part of the publication should be addressed to the publishers.
● Declaration
The material in this publication is of the nature of general comment only, and does not represent professional advice. It is not intended to provide specific guidance for particular circumstances and it should not be relied on as the basis for any decision to take action or not take action on any matter which it covers. Readers should obtain professional advice where appropriate, before making any such decision. To the maximum extent permitted by law, the author and publisher disclaim all responsibility and liability to any person, arising directly or indirectly from any person taking or not taking action based on the information in this publication.
● ISBN 978-3-89576-700-5 Print
ISBN 978-3-89576-701-2 eBook
● © Copyright 2025 Elektor International Media www.elektor.com
Editor: Glaucileine Vieira
Elektor is the world's leading source of essential technical information and electronics products for pro engineers, electronics designers, and the companies seeking to engage them. Each day, our international team develops and delivers high-quality content - via a variety of media channels (including magazines, video, digital media, and social media) in several languages - relating to electronics design and DIY electronics. www.elektormagazine.com
5.6
9.5
Preface
The world around us is becoming increasingly digital. From the smartphones in our hands to the embedded systems controlling industrial processes, digital electronics form the backbone of modern technology. At the heart of this transformation lies a fundamental toolkit—logic gates and sequential logic systems. This book is written for students, hobbyists, and engineers who wish to gain a clear, practical understanding of how these systems are designed, built, and applied.
This book is not merely an introduction to digital electronics. It walks through the core ideas of digital logic, aiming to build solid knowledge and support hands-on skills. The focus is on understanding through design: each chapter progresses logically from theory to application, with carefully crafted examples and projects that highlight real-world relevance.
The first part of the book introduces basic concepts such as binary systems, Boolean algebra, and the operation of individual logic gates. From there, we move into combinational logic— including multiplexers, decoders, and adders—and eventually transition into sequential systems, including flip-flops, counters, registers, and state machines.
The real strength of digital systems lies in their ability to remember and react over time, and this is where sequential logic becomes key. Designing these systems requires both creative thinking and analytical precision. In this book, readers will learn how to design and build systems that operate synchronously and asynchronously. Special attention is given to design methodology, helping readers learn how to think in terms of states, transitions, and control logic.
What sets this book apart is its project-based approach. Each major topic is reinforced through hands-on exercises and practical design challenges—from simple binary counters to more complex systems. These projects are intended not just to reinforce learning but also to encourage experimentation, critical thinking, and creativity.
I wrote this book with a deep appreciation for both the elegance and utility of digital design. Whether you’re an undergraduate student exploring this field for the first time, a selftaught enthusiast, or a professional looking to refresh your knowledge, my goal is to make these concepts both accessible and engaging.
You are encouraged to read with curiosity and build with confidence. The most effective learning happens when theory meets practice—when you wire up your first circuit, troubleshoot a misbehaving flip-flop, or see a state machine operate exactly as intended. Through this book, I hope to bridge the gap between understanding and application, and to equip you with the tools to explore digital systems on your own.
I hope this book is a useful step in your journey into digital electronics. Let’s get started.
Dogan Ibrahim 2025, London
Chapter 1 • Number Systems and Base Conversions
1.1 Overview
Digital systems use various number systems such as Decimal, Binary, Octal, and Hexadecimal. For example, the hexadecimal number system is commonly used in microcontroller-based applications. In this chapter, we will learn the commonly used number systems, and also learn how to convert from one number system to another system.
1.2
Number Systems
Table 1.1 shows the commonly used number systems from decimal 0 to decimal 15.
Decimal number system: This is a base-10 number system used in everyday counting and calculations. It uses ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Each digit is a power of 10, e.g., 100, 101, 102, 103, etc. For example, the decimal number 2518 has the following digits:
2518 = 2 x 103 + 5 x 102 + 1 x 101 + 8 x 100
Binary number system: This is a base-2 number system used in digital electronics. It uses two digits: 0 and 1. Each digit is a power of 2, e.g., 20, 21, 22, 23, etc. For example, the binary number 00101011 has the following digits:
00101011 = 0 x 27 + 0 x 26 + 1 x 25 + 0 x 24 + 1 x 23 + 0 x 21 + 1 x 20
Octal number system: This is a base-8 number system used in digital electronics. It uses eight digits: 0, 1, 2, 3, 4, 5, 6, and 7. Each digit is a power of 8, e.g., 80, 81, 82, 83, etc. For example, the octal number 2317 has the following digits:
2317 = 2 x 83 + 3 x 82 + 1 x 81 + 7 x 80
Hexadecimal number system: This is a base-16 number system commonly used in microcontroller and digital logic applications. It uses 16 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Each digit is a power of 16, e.g., 160, 161, 162, 163, etc. For example, the hexadecimal number A1B2 has the following digits:
A1B2 = 10 x 163 + 1 x 162 + 11 x 161 + 2 x 160
1.3 Number System Conversions
Decimal to binary conversion
The steps are:
• Divide the decimal number by 2.
• Record the remainder (0 or 1).
• Continue dividing the quotient by 2 until the quotient is 0.
• The binary equivalent is the remainders read from bottom to top
For example, let us convert the decimal number 41 to binary.
Therefore, the answer is, reading from bottom to top: 101001
Binary to decimal conversion
The steps are:
• Write down the binary number.
• Multiply each digit (0 or 1) by 2 raised to the power of its position, starting from 20 at the rightmost digit.
• Add the result of all the multiplications.
• The sum is the decimal equivalent.
For example, let us convert the binary number 01101001 into decimal
Decimal to octal conversion
The steps are:
• Divide the decimal number by 8.
• Record the remainder (from 0 to 7).
• Continue dividing the quotient by 8 until the quotient becomes 0.
• The octal equivalent is the remainders read from bottom to top.
For example, let us convert the decimal number 285 to octal.
Therefore, the answer is, reading from bottom to top is: 435
Octal to decimal conversion
The steps are:
• Write down the octal number.
• Multiply each digit by 8 raised to the power of its position, starting from 80 at the rightmost digit.
• Add the result of the multiplications.
• The sum is the decimal equivalent.
For example, let us convert the octal number 271 into decimal.
Decimal = 2 x 82 + 7 x 81 + 1 x 80 = 185
Decimal to hexadecimal conversion
The steps are:
• Divide the decimal number by 16.
• Record the remainder (0-9 or A-F).
• Continue dividing the quotient by 16 until the quotient becomes 0.
• The hexadecimal equivalent is the remainders read from bottom to top.
For example, let us convert the decimal number 2481 to hexadecimal.
Therefore, the hexadecimal equivalent of 2481 is, reading from bottom to top: 9B1
Hexadecimal to decimal conversion
The steps are:
• Write down the hexadecimal number.
• Multiply each digit by 16 raised to the power of its position, starting from 160 at the rightmost digit.
• Add the results of the multiplications.
• The sum is the decimal equivalent.
For example, let us convert the hexadecimal number A1B2 into decimal.
Decimal = 10 x 163 + 1 x 162 + 11 x 161 + 2 x 160 = 40960 + 256 + 176 + 2 = 41394
Hexadecimal to binary conversion
The steps are:
• Each hexadecimal number corresponds to a 4-bit binary number.
• Write the 4-bit binary number corresponding to each hexadecimal digit.
For example, let us convert the hexadecimal number AB12 to binary.
A B 1 2 1010 1011 0001 0010
Therefore, the binary number is: 1010101100010010.
Binary to hexadecimal number conversion
The steps are:
• Each 4-bit binary numbers correspond to a hexadecimal digit
• Divide the binary numbers into groups of 4 bits starting from the rightmost bit
• If the number of bits is not a multiple of 4, add leading zeroes to the leftmost group
• Write the equivalent hexadecimal digit for each 4-bit group
For example, let us convert the binary number 1001110001100001 to hexadecimal.
1001 1100 0110 0001
9 C 6 1
Therefore, the hexadecimal number is 9C61
Octal to binary conversion
The steps are:
• Each octal number corresponds to a 3-bit binary number
• Write the 3-bit binary number corresponding for each octal digit.
For example, let us convert the octal number 277 to binary.
2 7 7
010 111 111
Therefore, the binary number is 010111111.
Binary to octal conversion
The steps are:
• Each 3-bit binary group correspond to an octal digit
• Divide the binary numbers into groups of 3 bits starting from the rightmost bit
• If the number of bits is not a multiple of 3, add leading zeroes to the leftmost group
• Write the equivalent octal number for each group
For example, let us convert the binary number 111101101 to octal.
111 101 101 7 5 5
Therefore, the octal number is 755.
1.4 Signed Binary Numbers, 1’s Complement, 2’s Complement, Signed Magnitude
Both signed and unsigned numbers are represented by a string of bits on a digital computer. It is up to the user to determine whether a number is positive or negative. If the binary number is signed, then the leftmost bit represents the sign. A zero represents that the number is positive, while a one represents that the number is negative. For example, the number 01001 can be considered as an unsigned or a positive signed number since the most significant bit is zero. The number 11001 represents the binary number 25 when considered as an unsigned number, or -9 when considered as a signed number since the top bit is negative.
The representation of signed numbers in the last example is known as the signed magnitude format. Here, the number consists of a magnitude with the most significant bit representing the sign of the number. When arithmetic operations are performed on a digital computer, negative numbers are represented using the 2’s complement notation. This is done by complementing each bit of the number (known as 1’s complement) and then adding one to the number. Some examples are given below by considering the decimal number 9, assuming 8-bit representation:
Signed magnitude format: 00001001 +9
Signed magnitude format: 10001001 -9
1’s complement: 11110110
2’s complement: 11110111 -9
Using the 2’s complement notation, arithmetic operations can easily be done with binary numbers.
1.5 Binary Coded Decimal (BCD)
This is a commonly used encoding system where each decimal digit is represented by 4 bits ranging from 0 to 9. BCD is used in calculators and clocks where decimal displays are required. Some examples of BCD numbers are given here.
Let us consider the decimal number 3467. This is represented in BCD format as follows:
3 4 6 7 0011 0100 0110 0111
Therefore, the BCD representation of decimal number 3467 is 0011 0100 0110 0111.
Chapter 2 • Logic Gates
Chapter 2 • Logic Gates
2.1 Overview
Logic gates are the fundamental building blocks of digital electronics. They operate on one or more digital input signals to produce a digital output signal. Logic circuits respond to two distinct voltage levels at their inputs, which represent logic 0 or logic 1.
For example, a particular digital system may operate at +5 volts, where any voltage lower than 2 volts may represent logic 0 and any voltage higher than 3 volts may represent logic 1. As shown in Figure 2.1, the voltage range and its logical equivalent have an acceptable range. The intermediate region (here between 2 volts and 3 volts) is only crossed during a state transition, and no input or output remains in this transition region.
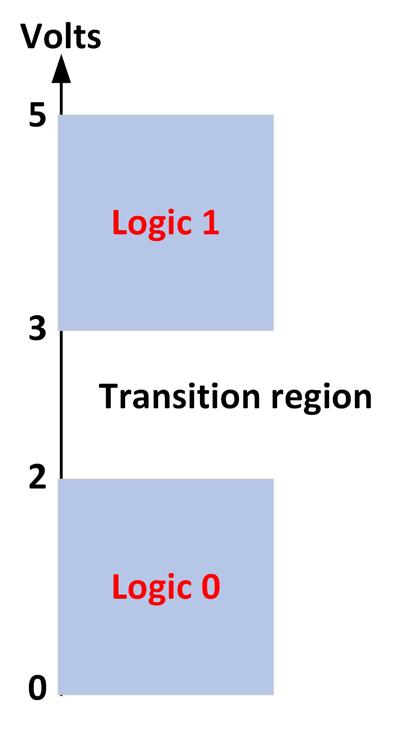
Figure 2.1 Digital voltage levels for the example
In this chapter, you will learn the input-output relationships (known as Truth Tables) for commonly used logic gates.
2.2 AND Gate
The AND gate can have two, three or more inputs and one output. The output state of the AND gate is logic 1 if all its inputs are at logic 1, otherwise, the output state is 0 if any of its inputs is 0. Figure 2.2 shows the logic diagram of a two input AND gate and its Truth Table. Assuming the inputs are A and B and the output is Y, the AND gate input-output relationship
is represented using one of the following notations. In this book we will use the notation without any symbols between the gate inputs:
Y = A.B or Y = A and B or Y = A & B or Y = AB (preferred)

2.2 Two-input AND gate
2.3 OR Gate
The OR gate can have two, three, or more inputs and one output. The output state of the OR gate is logic 1 if at least one of its inputs is at logic 1, otherwise, the output state is 0 if all its inputs are 0. Figure 2.3 shows the logic diagram of a two input OR gate and its Truth Table. Assuming inputs are A and B and the output is Y, the OR gate input-output relationship is represented using one of the following notations:
Y = A or B or Y = A | B or Y = A+B (preferred)

2.3
2.4 NOT Gate
The NOT gate has one input and one output. It is also known as an inverter or an inverting buffer. When the input signal is 0, the output is 1 and vice versa. Figure 2.4 shows the logic diagram and the truth table of a NOT gate. Assuming the input is A and the output is Y, the NOT gate input-output relationship is represented using one of the following notations:
Y = NOT A or Y = A’ or Y =

Sometimes a bar is placed on top of the input as shown in the figure.

2.5 Exclusive-OR Gate
The Exclusive-OR gate (also called the XOR gate) is commonly used to perform modulo additions in digital circuits. This gate has two inputs and one output. The output is logic 0 if both inputs are the same; otherwise, the output is logic 1. Figure 2.5 shows the logic diagram and truth table of the XOR gate. Assuming the inputs are A and B and the output is C, the XOR gate input-output relationship is represented using one of the following notations.
C = A XOR B or C = A’B + AB’ or C= �� ⊕ ��
Sometimes a small circle with a + symbol inside is used to denote an XOR gate as shown in the Figure.

2.5 Exclusive-OR gate
2.6 Exclusive-NOR Gate
The Exclusive-NOR gate (also called the XNOR gate) has two inputs and one output. The output is logic 1 if both inputs are the same; otherwise, the output is logic 0. Figure 2.6 shows the logic diagram and truth table of the XNOR gate. Assuming the inputs are A and B and the output is Y, the XNOR gate input-output relationship is represented using one of the following notations.
Y = A XNOR B or Y = AB + A’B’ or Y = A ⊙ B
Sometimes a small circle with a dot symbol inside is used to denote an XNOR gate.

Figure 2.6 Exclusive-NOR gate
2.7 Universal Logic Gates
Any digital logic expression can be realised by using two types of gates: the NAND gate and the NOR gate. These gates are also known as the universal logic gates. You will learn in later chapters how to realize logic circuits using these universal logic gates.
2.7.1 NAND gate
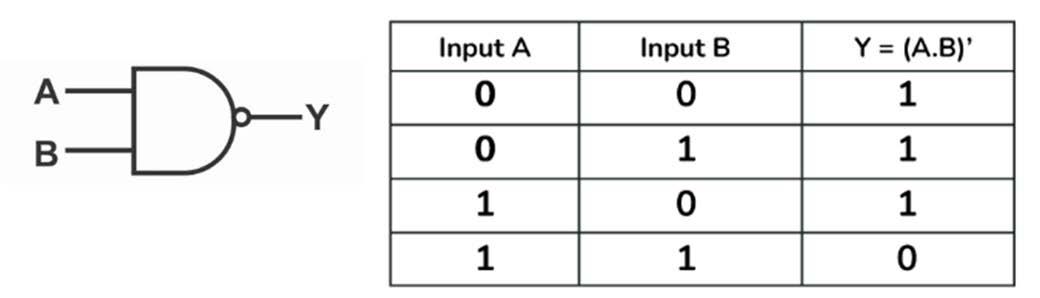
The NAND gate is a combination of an AND gate followed by a NOT gate. It can have two or more inputs and a single output. The output of a NAND gate is 1 when either of its inputs is 1 or both of its inputs are 0. Figure 2.7 shows the logic diagram of a two-input NAND gate and its truth table. Assuming A and B are the inputs and Y is the output of a NAND gate, the input-output relationship is represented using one of the following notations:
Y = (AB)’ or Y = A NAND B or Y =

2.7.2 NOR gate
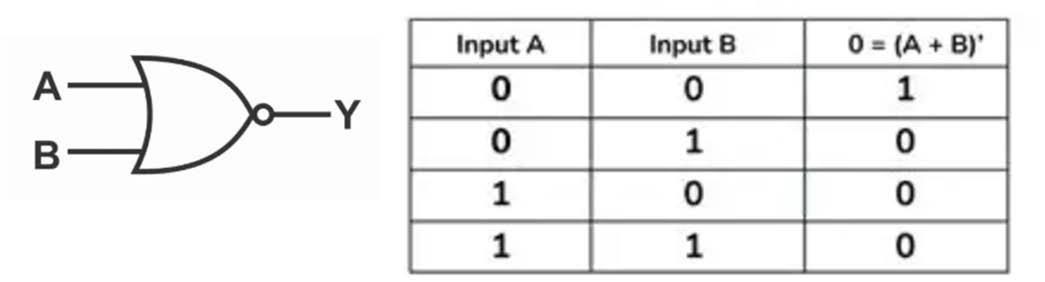
The NOR gate is a combination of an OR gate followed by a NOT gate. It can have two or more inputs and a single output. The output of a NOR gate is 1 when all of its inputs are 0. Figure 2.8 shows the logic diagram of a two-input NOR gate and its truth table. Assuming A and B are the inputs and Y is the output of a NOR gate, the input-output relationship is represented using one of the following notations:
Y = (A+B)’ or Y = A NOR B or Y =
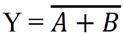
Learning Digital Electronics
With 20+ Practical Projects in Logic and Circuit Design
This book is a practical guide to digital electronics, covering the essential components of modern digital systems: number systems, logic gates, Boolean algebra, combinational and sequential logic, and more.
Through more than 20 structured projects, you’ll design and build digital systems using real-world components such as logic gates, multiplexers, decoders, flip-flops, counters, and shift registers. The projects range from basic LED logic circuits to digital locks, display systems, tra ic light controllers, and timing-based designs.
Selected projects introduce the use of tools such as CircuitVerse for circuit simulation, while several designs make use of 74HC-series logic devices, commonly used in digital hardware prototyping.
Inside, you’ll find:
> Clear coverage of number systems and binary arithmetic
> Logic gate fundamentals and universal gate implementations
> Step-by-step projects using flip-flops, counters, and registers
> Real-world design with 74HC-series logic chips
> Techniques for designing combinational and sequential systems
This book takes a design-first, application-driven approach to digital electronics—built around working circuits, tested logic, and hands-on experimentation.



Prof Dr Dogan Ibrahim holds a BSc degree in Electronic Engineering, an MSc degree in Automatic Control Engineering, and a PhD in Digital Signal Processing. He worked in numerous industrial organizations before returning to academic life. Prof. Ibrahim is the author of over 60 technical books and over 200 technical articles on microcontrollers, microprocessors, and related fields. He is a Chartered Electrical Engineer and a Fellow of the Institution of Engineering and Technology.
