https://ebookmass.com/product/the-black-book-of-quantum-
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
Models of Quantum matter : a first course on integrability and the Bethe Ansatz First Edition. Edition Eckle
https://ebookmass.com/product/models-of-quantum-matter-a-first-courseon-integrability-and-the-bethe-ansatz-first-edition-edition-eckle/
ebookmass.com
Quantum Computing: A New Era of Computing Kuldeep Singh Kaswan
https://ebookmass.com/product/quantum-computing-a-new-era-ofcomputing-kuldeep-singh-kaswan/
ebookmass.com
An Introduction to quantum optics and quantum fluctuations First Edition. Edition Milonni
https://ebookmass.com/product/an-introduction-to-quantum-optics-andquantum-fluctuations-first-edition-edition-milonni/
ebookmass.com
Perceiving Things Divine: Towards a Constructive Account of Spiritual Perception Frederick D. Aquino (Editor)
https://ebookmass.com/product/perceiving-things-divine-towards-aconstructive-account-of-spiritual-perception-frederick-d-aquinoeditor/
ebookmass.com
The Physical Universe Sixteenth Edition Konrad Krauskopf https://ebookmass.com/product/the-physical-universe-sixteenth-editionkonrad-krauskopf/
ebookmass.com
Biogeochemical Cycles and Climate Han Dolman
https://ebookmass.com/product/biogeochemical-cycles-and-climate-handolman/
ebookmass.com
Killer Visual Strategies: Engage Any Audience, Improve Comprehension, And Get Amazing Results Using Visual Communication 1st Edition Amy Balliett
https://ebookmass.com/product/killer-visual-strategies-engage-anyaudience-improve-comprehension-and-get-amazing-results-using-visualcommunication-1st-edition-amy-balliett/ ebookmass.com
My Unwilling Bodyguard: A Mafia Romance Novel Stacey Ortel
https://ebookmass.com/product/my-unwilling-bodyguard-a-mafia-romancenovel-stacey-ortel/
ebookmass.com
Twisted In Obsession (Marchetti Family Series Book 2)
Kelly Kelsey
https://ebookmass.com/product/twisted-in-obsession-marchetti-familyseries-book-2-kelly-kelsey/
ebookmass.com
Getting the Message: A History of Communications, Second Edition Laszlo Solymar
https://ebookmass.com/product/getting-the-message-a-history-ofcommunications-second-edition-laszlo-solymar/
ebookmass.com
THEBLACKBOOKOFQUANTUMCHROMODYNAMICS TheBlackBookofQuantum Chromodynamics APrimerfortheLHCEra JohnCampbell
TheoreticalPhysicsDepartment,Fermilab,Batavia,Illinois,USA
JoeyHuston DepartmentofPhysicsandAstronomy,MichiganStateUniversity,EastLansing, Michigan,USA
FrankKrauss InstituteforParticlePhysicsPhenomenology,DurhamUniversity,Durham,UK
GreatClarendonStreet,Oxford,OX26DP, UnitedKingdom
OxfordUniversityPressisadepartmentoftheUniversityofOxford. ItfurtherstheUniversity’sobjectiveofexcellenceinresearch,scholarship, andeducationbypublishingworldwide.Oxfordisaregisteredtrademarkof OxfordUniversityPressintheUKandincertainothercountries ©JohnCampbell,JoeyHuston,andFrankKrauss2018
Themoralrightsoftheauthorshavebeenasserted FirstEditionpublishedin2018 Impression:1
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedin aretrievalsystem,ortransmitted,inanyformorbyanymeans,withoutthe priorpermissioninwritingofOxfordUniversityPress,orasexpresslypermitted bylaw,bylicenceorundertermsagreedwiththeappropriatereprographics rightsorganization.Enquiriesconcerningreproductionoutsidethescopeofthe aboveshouldbesenttotheRightsDepartment,OxfordUniversityPress,atthe addressabove
Youmustnotcirculatethisworkinanyotherform andyoumustimposethissameconditiononanyacquirer PublishedintheUnitedStatesofAmericabyOxfordUniversityPress 198MadisonAvenue,NewYork,NY10016,UnitedStatesofAmerica BritishLibraryCataloguinginPublicationData Dataavailable
LibraryofCongressControlNumber:2017943893
ISBN978–0–19–965274–7 DOI10.1093/oso/9780199652747.001
LinkstothirdpartywebsitesareprovidedbyOxfordingoodfaithand forinformationonly.Oxforddisclaimsanyresponsibilityforthematerials containedinanythirdpartywebsitereferencedinthiswork. Printedandboundby CPIGroup(UK)Ltd,Croydon,CR04YY
Toourfamilies,withlove.
Tocolleaguesandfriends, whoshapedourunderstandingof particlephysics,withgratitude.
Acknowledgements Wearegreatlyindebtedtoalargenumberofpeople,whoinspiredustodoparticle physics,whodidtheirbesttoteachussomething,whocollaboratedwithus,andwho, byfarandlarge,shapedourviewofQCDattheLHC andothercolliderexperiments: wetrulyarestandingontheshouldersofgiants.
WealsooweadebtofgratitudetoourfriendsandcolleaguesfromCTEQand MCnetwhoputupwithouranticswhilefurtherhelpingourunderstandingofscience incountlessnight-timediscussionsduringgraduateschoolsandothermeetings.We wouldliketothankStefanoCatani,DanieldeFlorian,KeithHamilton,StefanH¨oche, SimonPl¨atzer,StefanPrestel,andMarekSch¨onherrforpatientlyansweringourmany questionsconcerningsomeofthemorespecializedaspectsinthisbook.Youhavebeen ahugehelp!Anyinaccuracyorerrorisnotareflectionofyourexplanationsbutof ourlimitedunderstandingofthem.
WeareextremelygratefultoJoshIsaacson,PavelNadolsky,PetarPetrov,and AlessandroTricoliforcarefullyreadingpartsofthebookwhileitwasbeingwritten, pointingoutconceptualshortcomingsandmisunderstandingsfromourside,thetypical errorswithfactorsoftwo,unfortunateformulations,andmuchmore.Howevergood, forallmistakesleftinthebook,thebuckstopswithus.Alistofupdates,clarifications, andcorrectionsismaintainedatthefollowingwebsite: http://www.ippp.dur.ac.uk/BlackBook
Wewouldliketothankthefollowingforusefulconversationsandforproviding figuresforthebook:SimonBadger,JohannesBellm,KeithEllis,SteveEllis,RickField, JunGao,NigelGlover,StefanH¨oche,SilvanKuttimalai,GionataLuisoni,Matthew Mondragon,IvanPogrebnyak,StefanPrestel,MarekSch¨onherr,CiaranWilliams,Jan Winter,andUn-kiYang.
Thegenesisofthisbookwasareviewarticleco-writtenbytwoofus[320]and wethankbothourco-author,JamesStirling,andtheIOPfortheircollaborationand support.Somepartsofthisbookbenefittedtremendouslyfromusbeingallowedto testthemonunsuspectingstudentsinlecturesduringregularcourses,atgraduate schools,orsummerinstitutes,andonourcolleaguesduringtalksatconferencesand workshops.Thankyou,foryourpatiencewithusandyourfeedback!
Manyoftheplotsinthisbookhavebeencreatedusingthewonderfultoolsapfelweb[331],JaxoDraw[249],RIVET [291],MATPLOTLIB [638],xmGRACE,andXFIG. OnthatoccasionwewouldalsoliketothankAndyBuckley,HolgerSchulzandDavid Grellscheidfortheircontinuoussupportandingenioushelpwithsomeofthefiner issueswithRIVET andLATEX.
Wearealsogratefulforthegreatsupportbyourpublisher,andinparticularbythe teamtakingcareofthismanuscript:SonkeAdlung,HarrietKonishiandHemalatha Thirunavukkarasu.
Finally,ofcoursewewouldliketothankourfamiliesforputtingupwithuswhile weassembledthismanuscript.Surely,wewerenotalwaysthemostprettytowatch ortheeasiestpeopletohavearound.
Introduction 1.1ThephysicsoftheLHC era 1.1.1ParticlephysicsintheLHC era Theturn-onoftheLHC in2008culminatedanalmost20-yeardesignandconstruction effort,resultinginthelargestparticleaccelerator(actuallythelargestmachine)ever built.AtitsinceptionacompetitionstillexistedwiththeTEVATRON which,although operatingatamuchlowerenergy,hadadatasamplewithalargeintegratedluminosityandwell-understooddetectorsandphysics-analysissoftware.TheTEVATRON haddiscoveredthetopquarkandwascontinuingitssearchfortheHiggsboson.Asis wellknown,theLHC sufferedconsiderabledamagefromacryogenicquenchsoonafter turn-onthatresultedinashut-downforabout1.5years.Its(re)turn-onin2010was atamuchlowerenergy(7TeVratherthan14TeV)andatmuchlowerintensities.The smalldatasampleatthelowerenergycanbeconsideredinretrospectasablessingin disguise.TherewasnotenoughdatatoevenconsiderasearchfortheHiggsboson(or evenformuchinthewayofnewphysics),buttherewasenoughdatatoproduce W and Z bosons,topquarks,photons,leptonsandjets—inotherwords,alloftheparticlesoftheStandardModelexceptfortheHiggsboson.Theresultwasthe re-discovery oftheStandardModel (acoinageforwhichoneoftheauthorstakescredit)andthe developmentoftheanalysistoolsandthedetailedunderstandingofthedetectorsthat allowedforthediscoveryoftheHiggsbosononJuly4,2012,withdatafrom7TeV in2011and8TeVin2012.TheLHC turnedoffagaininearly2013forrepairsand upgrades(toavoidthetypeofcatastrophicquenchthatoccurredin2008).TheLHC detectorsalsousedthistwo-yearperiodforrepairsandupgrades.TheLHC ranagain in2015,atanenergymuchclosertodesign(13TeV).Theincreasedenergyallowedfor moredetailedstudiesoftheHiggsboson,butmoreimportantlyofferedamuchgreater reachforthediscoveryofpossiblenewphysics.Atthetimeofcompletionofthisbook, agreatdealofphysicshasbeenmeasuredattheoperatingenergyof13TeV.Given thenewresultscontinuallypouringoutatthisnewenergy,thedecisionwasmadeto concentrateinthisbookonresultsfrom7and8TeVrunning.Thisissufficientfor thedatacomparisonsneededtoillustratethetheoreticalmachinerydevelopedhere.
TheBlackBookofQuantumChromodynamics:APrimerfortheLHCEra. JohnCampbell,JoeyHuston,andFrankKrauss. ©JohnCampbell,JoeyHuston,andFrankKrauss2018.Publishedin2018byOxfordUniversityPress. DOI10.1093/oso/9780199652747.001.0001
1.1.2ThequestfortheHiggsboson—andbeyond
1.1.2.1FindingtheHiggsboson
TheLHC wasdesignedasadiscoverymachine,withadesigncentre-of-massenergya factorofsevenlargerthanthatoftheTEVATRON.Thishighercollisionenergyopened upawidephasespaceforsearchesfornewphysics,buttherewasonediscoverythat theLHC was guaranteed tomake;thatoftheHiggsboson,oranequivalentmechanism forpreventing WW scatteringfromviolatingunitarityathighmasses.
TheHiggsbosoncouplesdirectlytoquarks,leptonsandto W and Z bosons,and indirectly(throughloops)tophotonsandgluons.ThustheHiggsbosonfinalstates arejustthebuildingblocksoftheSMwithwhichwehavemuchexperience,bothat theTEVATRON andtheLHC.TheATLAS andCMS detectorsweredesignedtofindthe Higgsbosonandtomeasureitspropertiesindetail.
Thecross-sectionforproductionofaHiggsbosonisnotsmall.However,thefinal statesforwhichtheHiggsbosonbranchingratioislarge(suchas bb)havebackgrounds whicharemuchlargerfromothermorecommonprocesses.Thefinalstateswithlow backgrounds(suchas ZZ∗ → + + )sufferfrompoorstatistics,primarilydue tothe Z branchingratiotoleptons.TheHiggs→ γγ finalstatesuffersfromasmall branchingratioandalargeSMbackground.Thusonemightnotexpectthisfinalstate tobepromisingforaHiggsbosonsearch.However,duetotheintrinsicnarrowwidth oftheHiggsboson,adiphotonsignalcanbeobservableiftheexperimentalresolution ofthedetectorisgoodenoughthatthesignalstandsoutoverthebackground.
ThemeasurablefinalstatesoftheHiggsbosondecayswerefurthersubdividedinto differenttopologiessothatoptimizedcutscouldbeusedtoimproveonthesignalto-backgroundratioforeachtopology(forexample,inATLAS thediphotonchannel wasdividedinto12topologies).Theextractedsignalwasfurtherweightedbythe expectationsoftheSMHiggsbosoninthosetopologies.Inthissense,theHiggsboson thatwasdiscoveredin2012wasindeedtheStandardModelHiggsboson.However,as willbediscussedinChapter9,detailedstudieshavedeterminedthepropertiesofthe newparticletobeconsistentwiththisassumption.
1.1.2.2ThetriumphoftheGaugePrinciple ThediscoveryoftheHiggsbosonbytheATLAS andCMS collaboration,reportedin July2012andpublishedin[15,368],isundoubtedlythecrowningachievementofthe LHC endeavoursofar.Itishardtooverestimatetheimportanceofthisdiscoveryfor thefieldofparticlephysicsandbeyond.
TheHiggsbosonistheonlyfundamentalscalarparticleeverfound,whichinitself makesitunique;allotherscalarsuptonowwereboundstates,andthefundamental particlesfoundsofarhavebeenalleitherspin-1/2fermionsorspin-1vectorbosons. Thisdiscoveryisevenmoresignificantasitmarksatriumphofthehumanmind:the HiggsbosonisthepredictedvisiblemanifestationoftheBrout–Englert–Higgs(BEH) mechanism[516,601,619–621,675],whichallowsthegenerationofparticlemassesin agauge-invariantway[580,835,888].Ultimately,thisdiscoveryprovestheparadigm ofgaugeinvarianceasthegoverningprincipleofthesub-nuclearworldatthesmallest
distancesandlargestenergiestestedinalaboratorysofar.Withthisdiscoverya 50-year-oldpredictionconcerningthecharacterofnaturehasbeenproven
ThequestionnowisnotwhethertheHiggsbosonexistsbutinsteadwhatare itsproperties?IstheHiggsbosonperhapsaportaltosomenewphenomena,new particles,orevennewdynamics?Therearesomehintsfromtheoryandcosmology thatthediscoveryoftheHiggsbosonisnotthefinallegofthejourney.
1.1.2.3BeyondtheStandardModel Byfindingthelastmissingparticleandtherebycompletingthemostaccurateand precisetheoryofnatureatthesub-nucleareverconstructed,theparadigmsbywhich ithasbeenconstructedhaveprovedoverwhelminglysuccessful.Despitethisthereare stillfundamentalquestionsleftunanswered.Thesequestionsgobeyondtherealmof theSM,buttheyremainofutmostimportanceforanevendeeperunderstandingof theworldaroundus.
Observationsofmatter—Earth,otherplanetsintheSolarSystemorbeyond, otherstars,orgalaxies—suggestthatthesymmetrybetweenmatterandanti-matter isbroken.Thisisauniversefilledbymatterandpracticallydevoidofanti-matter. Whilenaivelythereisnoobviousreasonwhyoneshouldbepreferredovertheother, atsomepointinthehistoryoftheUniverse—andpresumablyveryearly—this asymmetryhadtoemergefromwhatisbelievedtohavebeenasymmetricinitialstate. Inorderforthistohappen,asetofconditions,thefamous Sakharovconditions [710, 834]hadtobemet.Oneoftheseintricateconditionsistheviolationof CP,which demandsthatthesymmetryunderthecombinedparityandcharge–conjugation(CP) transformationmustbebroken.Experimentally,theexistenceof CP violationhas beenconfirmedandistightlyrelatedtotheexistenceofatleastthreegenerations ofmatterfieldsintheSM.DuetotheBEHmechanism,particlesacquiremasses, andtheirmassandelectroweakinteractioneigenstatesarenolongeralignedafter EWSB.TheexistenceofacomplexphaseintheCKMmatrix,whichparametrizesthe interrelationbetweenthesetwosetofeigenstates,ultimatelytriggers CP violationin thequarksector.However,theamountof CP violationestablishedissubstantially smallerthannecessarytoexplainhowtheuniverseevolvedfromaninitialsymmetric configurationtothematter-dominatedconfigurationseentoday[358].
Likewise,theexistenceofdarkmatter(DM)isnowwellestablished,firstevidenced bytherotationalcurvesofgalaxies[831].DMdenotesmatterwhichinteractsonlyvery weaklywithnormalmatter(describedbytheSM)andthereforecertainlydoesnot interactthroughelectromagnetismorthestrongnuclearforce.Despitenumerousattemptsithasnotbeendirectlydetected.DMinteractsthroughgravityandthereby hasinfluencedtheformationoflarge-scalestructuresintheUniverse.Cosmological precisionmeasurementsbytheWMAP andPLANCK collaborations[125,623,862]concludethatdarkmatterprovidesabout80%ofthetotalmattercontentoftheUniverse. Thisinturncontributesabout25%oftheoverallenergybalance,withtherestofthe energycontentoftheUniverseprovidedbywhatisknownasdarkenergy(DE),which isevenmoremysteriousthanDM.TheonlythingknownisthattheinterplayofDM andDEhasbeencrucialinshapingtheUniverseasobservedtodayandwillcontinue todetermineitsfuture.OnepossibleavenueinsearchesforDMparticlesatcolliderex-
perimentsisthattheyhavenocouplingtoordinarymatterthroughgaugeinteractions butinsteadcouplethroughtheHiggsboson.
TheseexamplesindicatethattheSM,asbeautifulasitis,willdefinitelynotprovide theultimateanswertothequestionsconcerningthefundamentalbuildingblocksofthe worldaroundusandhowtheyinteractattheshortestdistances.TheSMwillhavetobe extendedbyatheoryencompassingatleastenhancedCPviolation,darkmatter,and darkenergy.Anysuchextensionisalreadyseverelyconstrainedbytheoverwhelming successofthegaugeprinciple:thegaugesectoroftheSMhasbeenscrutinizedto incrediblyhighprecision,passingeverytestuptonowwithflyingcolours.Seefor example[179]forarecentreview,combiningdatafrom e e+ andhadroncollider experiments.TheHiggsbosonhasbeenfoundonlyrecently,anditisevidentthatthis discoveryanditsimplicationswillcontinuetoshapeourunderstandingofthemicro–worldaroundus.Thediscoveryitself,andevenmoresothemassofthenewparticle andourfirst,imprecisemeasurementsofitsproperties,alreadyruleoutorplacesevere constraintsonmanynewphysicsmodelsgoingbeyondthewell-establishedSM[515].
Rightnow,wearemerelyatthebeginningofanextensiveprogrammeofprecision testsintheHiggssectoroftheSMorthetheorythatmayrevealitselfbeyondit.It canbeanticipatedthatattheendoftheLHC era,eithertheSMwillhaveprevailed completely,withnewphysicseffectsandtheirmanifestationasnewparticlespossibly beyonddirecthumanreach,oralternatively,wewillhaveforgedanew,evenmore beautifulmodelofparticlephysics.
1.1.3LHC:Acceleratoranddetectors 1.1.3.1LHC,themachine
TheLHC notonlyistheworld’slargestparticleacceleratorbutitisalsotheworld’s largestmachine,at27kmincircumference.TheLHC isaproton-protoncollider(althoughitalsooperateswithcollisionsofprotonsonnuclei,andnucleionnuclei), locatedapproximately100mundergroundandstraddlingtheborderbetweenFrance andSwitzerland.TheLHC occupiesthetunnelformerlyusedfortheLEP accelerator inwhichelectronsandpositronscollidedatcentre-of-massenergiesupto209GeV. TheLHC contains9593magnets,including1232superconductingdipolemagnets,capableofproducingmagneticfieldsoftheorderof8.3T,andamaximumprotonbeam energyof7TeV(trillionelectron-volts),leadingtoamaximumcollisionenergyof14 TeV.Thusfar,theLHC hasrunatcollisionenergiesof7TeV(2010,2011),8TeV (2012)and13TeV(2015,2016),greatlyexceedingthepreviousrecordoftheFermilabTEVATRON of1.96TeV.1 ThelargeradiusoftheLHC isnecessitatedbecauseof thedesiretoreachashighabeamenergyaspossible(7TeV)usingdipoleswiththe largestmagneticfieldspossible(inanaccelerator).Runningatfullenergy,thepower consumption(includingtheexperiments)is750GWhperyear.Atfullpower,theLHC willcollide2808protonbunches,eachapproximately30cmlongand16micronsin diameterandcontaining1 15 × 1011 protons,leadingtoaluminosityof1034cm 2/s andabillionproton-protoncollisionspersecond.Thespacingbetweenthebunchesis 25nsleadingtocollisionsoccurringevery25ns;thus,atfull luminosity therewill
1UnliketheLHC,theTEVATRON wasaproton-antiprotoncollider.
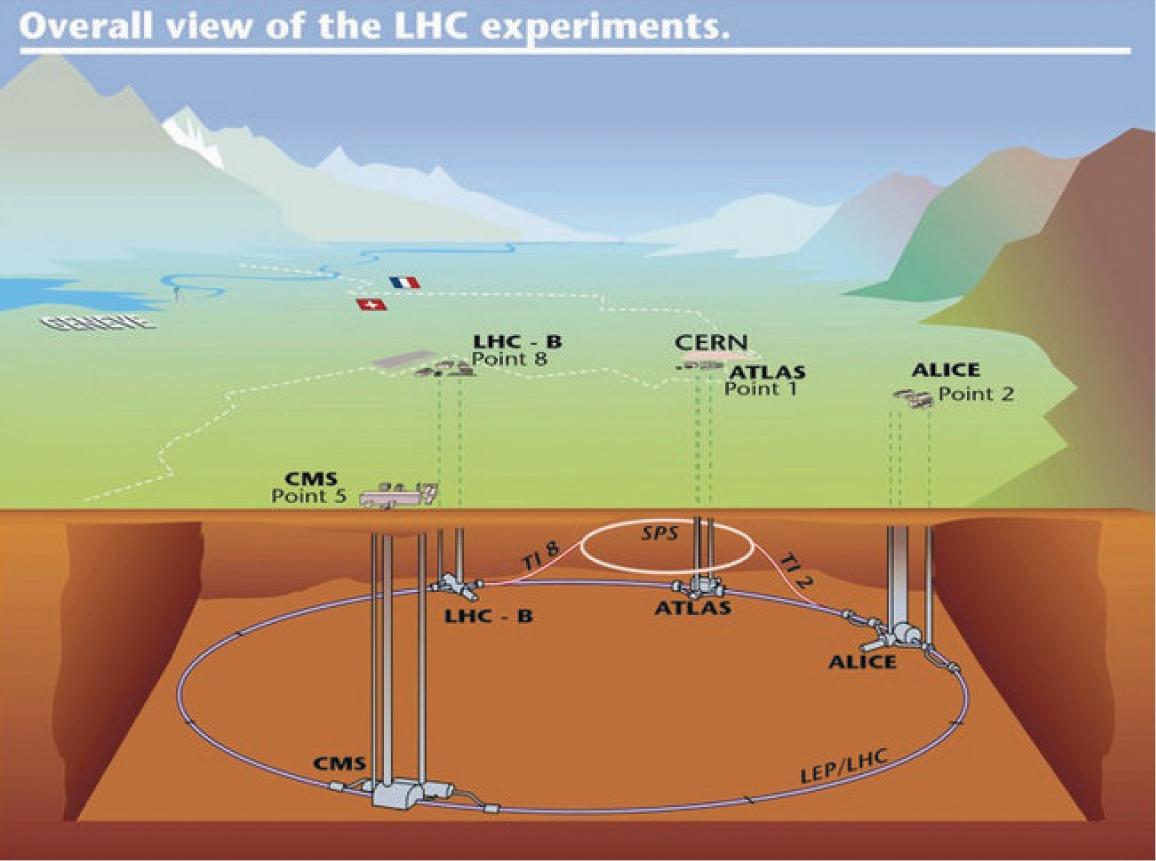
Fig.1.1 A3DlayoutoftheLHC,showingthelocationofthefourmajor experiments.ReprintedwithpermissionfromCERN. beonaverage25interactionseverybeamcrossing,mostofwhichwillberelatively uninteresting.Thehighluminosityforthemachineisneededtoproduceeventsfrom processeswithsmallcross-sections,forexampleinvolvingphysicsattheTeVscale.
TherearesevenexperimentsrunningattheLHC (ATLAS,CMS,LHCB,ALICE, TOTEM,LHCfandMoEDAL),withATLAS andCMS beingthetwogeneral-purpose detectors.AschematicdrawingoftheLHC,indicatingthepositionofthefourlarger experimentsisshowninFig.1.1.
1.1.3.2Thedetectors Itseemsparadoxicalthatthelargestdevicesareneededtoprobethesmallestdistance scales.TheATLAS detector,forexample,is46mlong,25mindiameterandweighs 7000tonnes.TheCMS detector,althoughsmallerthanATLAS at15mindiameter and21.5minlength,istwiceasmassive,at14, 000tonnes.Thiscanbecompared totheCDFdetectorattheTEVATRON whichwas only 12m×12m×12m(and5000 tonnes).ThekeytothesizeandcomplexityoftheLHC detectorsistheneedto measurethefour-vectorsofthelargenumberofparticlespresentinLHC events,whose momentacanextendtotheTeVrange.Thelargeparticlemultiplicityrequiresvery finesegmentation;theATLAS detector,forexample,has160millionchannelstoread out,halfofwhichareinthepixeldetector.Thelargeenergies/momentarequire,in additiontofinesegmentation,largemagneticfieldsandtrackingvolumesandthick calorimetry.
BothATLAS andCMS arewhatareknownasgeneral-purpose4π detectors,meaning thattheyattempttocoverasmuchofthesolidanglearoundthecollisionpointas
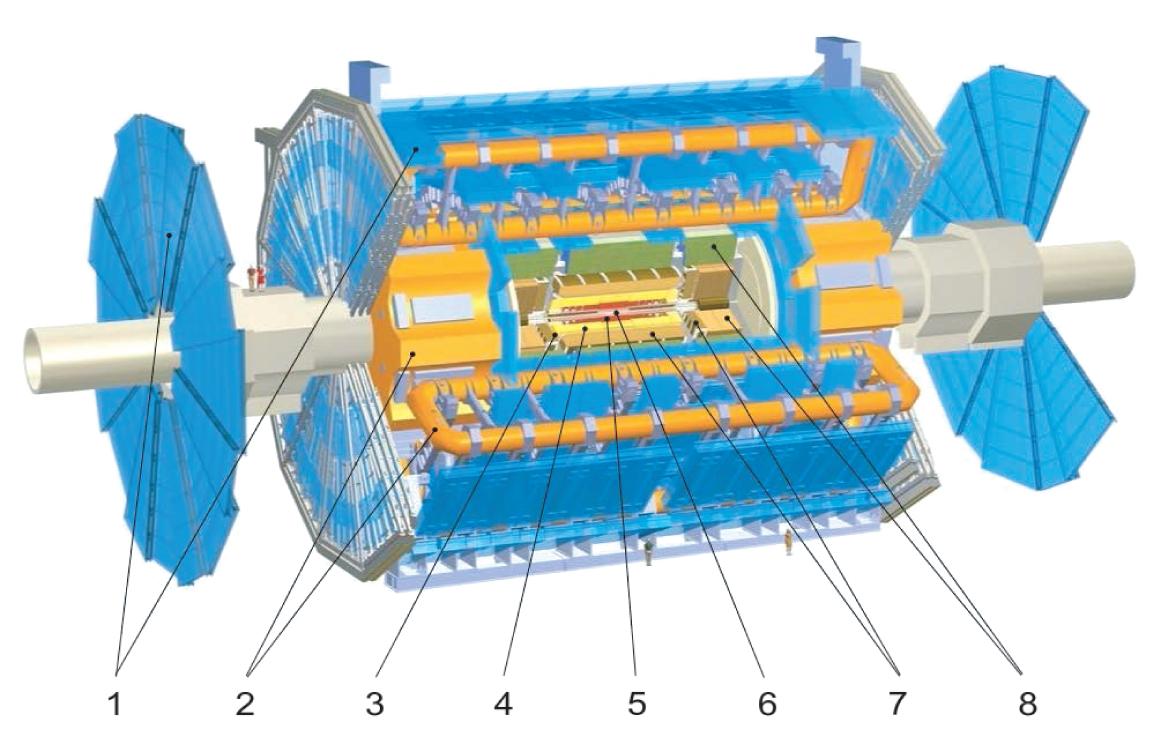
possible,inordertoreconstructasmuchinformationabouteacheventaspossible.2 Thereisa universal cylindricallysymmetricconfigurationfora4π detector,embodied, forexample,intheATLAS detector,asshowninFig.1.2.Collisionstakeplaceinthe centreofthedetector.Particlesproducedineachcollisionfirstencounterthepixel detector(6)andthesilicontrackingdetector(5).Thefirstlayerofthepixeldetector isactuallymountedonthebeam-pipeinordertobeasclosetotheinteractionpoint aspossible.Thebeam-pipeitself,intheinteractionregion,iscomposedofberylliumin ordertopresentaslittlematerialaspossibletotheparticlesproducedinthecollision. Theproximityofthepixelandsilicondetectorstothecollisionpointandtheveryfine segmentation(50×400 µm forthepixeldetectorand70 µm forthesilicondetector) allowforthereconstructionofsecondaryverticesfrombottomandcharmparticles, whichcantraveldistancesofafewmmfromtheinteractionpointbeforedecaying. Thenexttrackingdevice(4),thetransitionradiationdetector,isastraw-tubedetector thatprovidesinformationnotonlyonthetrajectoryofthechargedparticlebutalso onthelikelihoodoftheparticlebeinganelectron.Allthreetrackingdevicessitinside thecentralmagneticfieldof2Tproducedbythesolenoid(3).
Theenergiesoftheparticlesproducedinthecollision(bothneutralandcharged) aremeasuredbytheATLAS calorimeters,thelead-liquidargonelectromagneticcalorimeter(7)andtheiron-scintillatorhadroniccalorimeter(Tilecal)(8).BoththeATLAS and CMS electromagneticcalorimeterdesignsemphasizedgoodresolutionforthemeasurementoftheenergiesofphotonsandelectrons,primarilytobeabletodistinguishthe Higgsbosonto γγ signalfromthemuchlargerdiphotonbackground.Thewidthofa lightHiggsbosonismuchlessthantheexperimentalresolution,soanyimprovement intheresolutionwillleadtoabetterdiscriminationoverthebackground.
Energeticmuonscanpassthroughthecalorimetry,whileotherparticlesareabsorbed.Thetoroidalmagnets(2),inboththecentralandforwardregions,producean additionalmagneticfield(4T)inwhichasecondmeasurementofthemuonmomentumcanbecarriedoutusingthemuontrackingchambers(1),usingseveraldifferent technologies.OneoftheuniquecharacteristicsoftheATLAS detector(andpartofits acronym)isthepresenceoftheair-coretoroidalmuonsystem.Therelativelysmall amountofmaterialinthetrackingvolumeleadstolessmultiplescatteringandthus amoreprecisemeasurementofthemuon’smomentum.Themuonmomentumcanbe measuredtoaprecisionof10%atatransversemomentumvalueof1TeV.
1.1.3.3Challenges Touseapopularanalogy,samplingthephysicsattheLHC issimilartotryingtodrink fromafirehose.Over1billionproton-protoncollisionsoccureachsecond,butthe limitofpracticaldatastorageisontheorderofhundredsofeventspersecondonly. Thus,theexperimentaltriggershavetoprovideareductioncapabilityofafactorofthe orderof107,whilestillrecording bread-and-butter signaturessuchas W and Z boson production.Thisrequiresahighlevelofsophisticationfortheon-detectorhardware triggersandaccesstolargecomputingresourcesforthehigher-leveltriggering.Timing
2Themainlimitationforthesolid-anglecoverageisintheforward/backwarddirections,wherethe instrumentationiscutoffbythepresenceofthebeampipe.
Fig.1.2 AlayoutoftheATLAS detector,showingthemajordetector components,from en.wikipedia.org/wiki/ATLAS experiment.Original imagefromCERN.ReprintedwithpermissionfromCERN.
isalsoanimportantissue.TheATLAS detectoris25mindiameter.Withabunchcrossingtimeof25ns,thismeansthatasnewinteractionsareoccurringinonebunch crossing,theparticlesfromthepreviousbunchcrossingarestillpassingthroughthe detector.Eachcrossingproduces25interactions.Experimentalanalysesthusfaceboth in-timepileupandout-of-timepileup.Thelattercanbelargelycontrolledthroughthe readoutelectronics(modulosubstantialvariationsinthepopulationoftheindividual bunches),whiletheformerrequiressophisticatedtreatmentinthephysicsanalyses.
ThedynamicrangesattheLHC arelargerthanattheTEVATRON.Leptonsfrom W bosondecaysontheorderoftensofGeVarestillimportant,butsoaremulti-TeV leptons.Precisecalibrationandthemaintenanceoflinearityarebothcrucial.Tosome extent,theTEVATRON hasservedasabootcamp,providingalearningexperiencefor physicsattheLHC,albeitatlowerenergiesandintensities.Cominglater,theLHC has benefitedfromadvancesinelectronics,incomputing,andperhapsmostimportantly, inphysicsanalysistools.Thelattercomprisebothtoolsfortheoreticalpredictionsat higherordersinperturbativeQCDandtoolsforthesimulationofLHC finalstates.
Despitethedifficulties,theLHC hashadgreatsuccessduringitsinitialrunning, culminatinginthediscoveryoftheHiggsboson,but,alas,notinthediscoveryofnew physics.Theresultsobtainedsofarcompriseasmallfractionofthetotaldatataking plannedfortheLHC.Newphysicsmaybefoundwiththismuchlargerdatasample, butdiscoveringitmayrequirepreciseknowledgeofSMphysics,includingQCD.
1.2Aboutthisbook ThereaderisassumedtobealreadyfamiliarwithtextbookmethodsforthecalculationofsimpleFeynmandiagramsattreelevel,theevaluationofcross-sectionsthrough phase-spaceintegrationwithanalyticterms,andtheideasunderlyingtheregularizationandrenormalizationofultravioletdivergenttheories;however,forashortreview,
readersarereferredtoAppendixB.1,andforamorepedagogicalintroductiontothese issuestoawealthofoutstandingtextbooksonvariouslevels,includingthebooksby PeskinandSchr¨oder[803],HalzenandMartin[606],Ramond[822],Field[525]and others.ForareviewofQCDatcolliderexperiments,thereaderisreferredtothe excellentbooksbyEllis,Stirling,andWebber[504]andbyDissertori,Knowles,and Schmelling[467].Ofcourse,forarealunderstandingofvariousaspectsitishardto beattheoriginalliterature,andreadersareencouragedtousethereferencesinthis bookasastartingpointfortheirjourneythroughparticlephysics.
Thisbookaimstoprovideanintuitiveapproachastohowtoapplytheframework ofperturbativetheoryinthecontextofthestronginteractiontowardspredictionsat theLHC andultimatelytowardsanunderstandingofthesignalsandbackgroundsat theLHC.Thus,evenwithoutthebackgrounddiscussedatthebeginningofthissection, thisbookshouldbeusefulforanyonewishingforabetterunderstandingofQCDat theLHC.
Theideasforthisbookhavebeendevelopedovervariouslectureseriesgivenat graduatelevellecturesoratadvancedschoolsonhigh-energyphysicsbytheauthors. Theauthorshopethatthisbookturnsouttobeusefulinsupportingtheself-study ofyoungresearchersinparticlephysicsatthebeginningoftheircareeraswellas moreadvancedresearchersasaresourcefortheiractualresearchandasmaterialfor agraduatecourseonhigh-energyphysics.
1.2.1Contents Chapter2providesafirstoverviewofthecontentofthisbookandaimsatputting varioustechniquesandideasintosomecoherentperspective.Firstofall,aphysical pictureunderlyinghadronicinteractions,andespeciallyscatteringreactionsathadron colliders,isdeveloped.Toarriveatthispicture,theideasunderlyingtheall-important factorizationformalismareintroducedwhich,intheend,allowstheuseofperturbative conceptsinthediscussionofthestronginteractionathighenergiesandthecalculation ofcross-sectionsandotherrelatedobservables.Theseconceptsarethenusedina specificexample,namelytheinclusiveproductionof W bosonsathadroncolliders. There,theirproductioncross-sectioniscalculatedatleadingandatnext-to-leading orderinthestrongcouplingconstant,therebyremindingthereaderoftheingredients ofsuchcalculationsandfixingthenotationandconventionsusedinthisbook.This partalsoincludesafirstdiscussionofobservablesrelevantforthephenomenologyof stronginteractionsathadroncolliders.Inaddition,somegenericfeaturesandissues relatedtosuchfixed-ordercalculationsaresketched.Inasecondpart,theperturbative conceptsalreadyemployedinthefixed-ordercalculationsareextendedtoalsoinclude dominanttermstoallordersthroughtheresummationformalism.Genericfeaturesof analyticalresummationareintroducedthereandsomefirstpracticalapplicationsfor W productionathadroncollidersarebrieflydiscussed.Asasomewhatalternativeuse ofresummationtechniques,jetproductioninelectron–positronannihilationsandin hadroniccollisionsisalsodiscussedand,especiallyinthelatter,somecharacteristic patternsaredeveloped.
Thenextchapter,Chapter3,isfairlytechnical,asitcomprisesapresentationof mostofthesometimesfairlysophisticatedtechnologythatisbeingusedinorderto
evaluatecross-sectionatleadingandnext-toleadingorderintheperturbativeexpansionofQCD.Italsoincludesabriefdiscussionofemergingtechniquesforevenhigher ordercorrectionsinQCD.Inaddition,theinterplaybetweenQCDandelectroweak correctionsistoucheduponinthischapter.Startingwithadiscussionofgenericfeatures,suchasameaningfuldefinitionofperturbativeordersforvariouscalculations, thecorrespondingtechnologyisintroduced,representingthecurrentstateoftheart. Assimpleillustrativeexamplesforthemethodsemployedinsuchcalculations,again inclusive W bosonproductionanditsproductioninassociationwithajetareemployed.Thecalculationsareworkedoutinsomedetailatbothleadingandnext-to leadingorderintheperturbativeexpansioninthestrongcoupling.
Theoverallpictureandphenomenaencounteredinhadron–hadroncollisions,developedinChapter2,isdiscussedinthecontextofspecificprocessesinChapter4. Theprocessesdiscussedhererangefromthecommonplace(e.g.jetproduction)to someofthemostrare(e.g.productionofHiggsbosons).Ineachcasetheunderlying theoreticaldescriptionoftheprocessisdescribed,typicallyatnext-toleadingorder precision.Specialemphasisisplacedonhighlightingphenomenologicallyrelevantobservablesandissuesthatariseinthetheoreticalcalculations.Thechaptercloseswith asummaryofwhatisachievablewithcurrenttechnologyandanoutlookofwhatmay becomeimportantandrelevantinthefuturelifetimeoftheLHC experiments.
FollowingthelogicoutlinedinChapter2,inChapter5thediscussionoffixed-order technologyisextendedtotheresummationofdominantterms,connectedtolargelogarithms,toallorders.Afterreviewinginmoredetailstandardanalyticresummation techniques,anddiscussingtheirsystematicimprovementtogreaterprecisionbythe inclusionofhigher-orderterms,theconnectiontootherschemesishighlighted.Inthe secondpartofthischapter,numericalresummationasencodedinpartonshowersisdiscussedinsomedetail.Thephysicalpictureunderlyingtheirconstructionisintroduced, somestraightforwardimprovementsbyintroducingsomegenerichigh–ordertermsare presentedanddifferentimplementationsarediscussed.Sincethepartonshowersare attheheartofmoderneventsimulation,bridgingthegapbetweenfixed-orderperturbationtheoryathighscalesandphenomenologicalmodelsforhadronizationand thelikeatlowscales,theirimprovementhasbeeninthefocusofactualresearchin thepastdecade.Therefore,somespaceisdevotedtothediscussionofhowthesimple partonshowerpictureissystematicallyaugmentedwithfixed-orderprecisionfromthe correspondingmatrixelementsinseveralschemes.
InChapter6,animportantingredientforthesuccessofthefactorizationformalismunderlyingtheperturbativeresultsintheprevioustwochaptersisdiscussedin moredetail,namelythepartondistributionfunctions.Havingbrieflyintroducedthem, mostlyatleadingorder,inChapter2,andpresentedsomesimpleproperties,inthis chapterthefocusshiftsontheirscalingbehaviouratvariousordersandhowthiscan beemployedtoextractthemfromexperimentaldata.Variouscollaborationsperform suchfitswithslightlydifferentmethodologiesandslightlydifferentbiasesinhowdata areselectedandtreated,leadingtoavarietyofdifferentresultingpartondistributions.Theyarecomparedforsomestandardcandlesinthischapteraswell,witha specialemphasisonhowtheintrinsicuncertaintiesinexperimentaldataandthemore theoreticalfittingproceduretranslatesintosystematicerrors.
Thetourofingredientsforacompletepictureofhadronicinteractionsterminatesin Chapter7,wheredifferentnon-perturbativeaspectsarediscussed.Mostoftheideasto addressthemarefairlyqualitativeandcanbeembeddedinphenomenologicalmodels only.Therefore,ratherthanpresentingindetailalldevelopmentsinthisfield,the bookfocusesmoreongenericfeaturesandbasicstrategiesunderlyingtheirtreatment indifferentcontexts.Issuesdiscussedthereincludehadronization,thetransitionfrom thepartonsofperturbationtheoryofthestronginteraction,quarksandgluons,tothe experimentallyobservablehadrons,andtheirdecaysintostableones,theunderlying event,whichisduetosofterfurtherinteractionsbetweenthehadronicstructuresof theincidentparticles,anditsconnectiontoveryinclusiveobservablessuchastotal andelasticcross-sections.
InChapters8and9theoreticalresultsfromanalyticcalculationsandsimulation toolsarecomparedwithahostofexperimentaldata.Chapter8focusesondataespeciallyfromtheTEVATRON,3 wherethefoundationsofourcurrentunderstandingof theSMandinparticularthedynamicsofthestronginteractionhavebeenshaped. InChapter9themostsophisticatedcalculationsandsimulationsarecomparedwith themostrecent,mostpreciseandmostchallengingdatasofar,takenattheLHC duringRun I.Thiscomparisonrangesfrominclusiveparticleproductionoverevent shapeobservablestodatatestingthedynamicsoftheSM—andpotentiallybeyond —overscalesrangingovertwoorderofmagnitudeinthesameprocess.Thisisthe mostchallengingtestofourunderstandingofnatureatitsmostfundamentallevel everperformed.Itisfairtostatethatwhileourmostup-to-datetools,analyticalcalculationsandsimulationsfareamazinglywellinthiscomparison,somefirstcracksare showingthatwillmotivatethecommunitytopushevenfurtherintheyearstocome.
1.2.2Auser’sguide ThisbookismeanttoprovidePhDstudentsinexperimentalparticlephysicsworking attheLHC whohaveakeeninterestintheoreticalissues,aswellasPhDstudents workinginparticletheorywithanemphasisonphenomenologyatcolliders,astarting pointfortheirresearch.Itismeanttointroduceandexposethereadertoallrelevant conceptsincurrentcolliderphenomenology,introduceandexplainthetechnologythat bynowisroutinelyusedintheperturbativetreatmentofthestronginteraction,and provideanintegratedperspectiveontheresultsofsuchcalculationsandsimulations andthecorrespondingdata.
Thebookconsistsofthreeparts.Thefirstpartisanoverviewoftherelevant terminologyandtechnology,workedoutthroughonestandardexampleandproviding acoherentperspectiveonhadronicinteractionsathighenergies.Readersandteachers, usingthisbookforlectures,areinvitedtostudyChapter2firstbeforeembarkingon amorein-depthdiscussionofvarioustheoreticalorexperimentalaspects.Theother twopartsconsistofamoredetaileddiscussionofvariousaspectsoftheperturbative treatmentofthestronginteractioninhadronicreactionsinthesecondpartofthebook, inChapters3–7.Whilethesechaptersfrequentlyreferbacktotheoverviewchapter, Chapter2,theyarefairlyindependentfromeachotherandcouldinprinciplebeusedin
3ExperiencesfromLEP andHERA havealsobeenimportantbutarenotincludedduetospace limitations.
anysequencethereaderorteacherfindsmostbeneficial.Thethirdpart,Chapters8and 9,wherecoreexperimentalfindingsareconfrontedwiththeoreticalpredictions,again isindependentofthesecondpart,althoughforabetterunderstandingoftheoretical subtletiesitmaybeadvantageoustobeacquaintedwithcertainaspectsthere.
Finally,alistofupdates,clarificationsandcorrectionstothisbookismaintained atthefollowingwebsite:
http://www.ippp.dur.ac.uk/BlackBook
HardScatteringFormalism Beforeembarking,inthischapter,onafirstdiscussionofthefactorizationformula andsomeofitsimmediateconsequencesintermsofactualphenomenaandcalculations,inSection2.1anintuitivepictureofhigh-energyreactionsinvolvinghadronsin theinitialstatewillbedeveloped.Thispictureinfactformsthephysicalbackground ofthefactorizationformalism,whichinturnprovidesthetheoreticalfoundationsof thisbook.
Inthenextsection,Section2.2,theideasformulatedintheprevioussectionwill befurtherformalizedandcondensedintoadiscussionoftheperturbativetreatmentof high-energyreactionsathadroncollidersatfixedorder.Toillustratethefactorization formalisminaction,thecaseofinclusive W -bosonproductionwillbeanalysedat leadingandatnext-to-leadingorder.
InSection2.3theperturbativeformalismdevelopedsofarwillbefurtherexpanded toincludethemostimportanteffectstoallperturbativeorders.Thisisachieved throughtheidentificationandsubsequentresummationofthecorrespondingleading terms.Again,thecaseof W bosonproductionservesasthemainillustrativeexample.
Finally,inSection2.4,somegeneralthoughtsandissuesrelatedtothedescription ofhardprocessesthroughperturbationtheorywillbedeepened.
2.1Physicalpictureofhadronicinteractions 2.1.1Electromagneticanalogy
Toillustratethephysicalpictureunderlyingfactorizationinprocessesinitiatedbycollidingstronglyinteractingparticlessuchasprotonsathighenergies,thesimplercase ofcollisionswithleptonsintheinitialstateisconsideredfirst.Inthis,anintuitive understandingofthetheoryofstronginteractions,QCD,quantumchromodynamics, willbedevelopedincloseanalogywiththesimplertheoryofQED,quantumelectrodynamics.Inbothcases,althoughultimatelyverydifferent,thecollidingparticleswill emitsecondaryquantainanintricateradiationpattern,whichmustbetakeninto accounttogainfulltheoreticalcontroloverthecollisiondynamics.
Experimentally,forexampleincollisionsofelectron–positronpairs,itisofcourse typicallynotdifficulttorequirethattheenergyintheactualcollisionisclosetothe
TheBlackBookofQuantumChromodynamics:APrimerfortheLHCEra. JohnCampbell,JoeyHuston,andFrankKrauss. ©JohnCampbell,JoeyHuston,andFrankKrauss2018.Publishedin2018byOxfordUniversityPress. DOI10.1093/oso/9780199652747.001.0001
centre-of-massenergyofthecollidingbeams,thuseffectivelyreducingtheamount ofenergycarriedawayfromtheleptonsthroughelectromagneticradiation.However, mostofthetime,especiallywhentheircombinedinitialinvariantmassisabovethe massofaresonance,suchasthe Z boson,theleptonswillreactwithactualenergies thatarereducedwithrespecttotheirfullavailableenergy.Thiseffectissometimes called“radiativereturn”Thecorrespondingenergylossisduetotheemissionof photonsfromtheincidentleptons,aprocessdenotedasQEDinitial-stateradiation (ISR)..
WhileinQEDthetreatmentofISRpotentiallyisatediousbutessentiallystraightforwardexercise,tractablewithperturbationtheory,inQCDtheproblemismuchmore involvedandfundamentallydifferent.ThisisbecauseinQCD,thecollidingparticles cannotbeinterpretedasthefundamentalquantaofthetheorybutratherasbound states,hadronssuchasprotons,whichcannotbequantitativelyunderstoodanddescribedthroughthelanguageofperturbationtheory.Thisconceptualgapnecessitates theconstructionofaframeworktoprovidedirectandsystematicallyimprovablecontactbetweentheprovenlanguageofperturbativecalculationsofcorrespondingcrosssectionsandthenon-perturbativestructureofthehadronicboundstates.Thissection isdevotedtodevelopinganintuitivepictureofhowthis factorization framework actuallyworks,bydwellingonthelimitedanalogywiththeemissionsofsecondary quantainQEDandthedifferencesbetweenelectromagneticandstronginteractions whenconsideringsuchcollisionsingreaterdetail.
2.1.1.1Equivalentquanta Classically,thephenomenonofinitial-stateradiationcanbeunderstoodwiththe equivalentphotonpicture [523,884,892].Initsownrestframe,theleptonactsas thepoint-likesourceofapurelyradialelectricfield,withnomagneticfieldpresent. ThissituationisdepictedintheleftpanelofFig.2.1.Boostingtheleptonintoany framewhereitisnotatrestand,inparticular,intothelaboratoryframetransforms thestaticsourceofanelectricfieldintoanelectromagneticcurrent,whichinturn producesalsoamagneticfield.Withincreasingleptonvelocity, v → c,thetwofields becomeincreasinglyconfinedtoaplaneperpendiculartotheaxisofmotionandthey alsobecomemoreandmoreperpendiculartoeachother,withtheelectricalfieldradialandthemagneticfieldcirculararoundtheaxisofmotion, cf. themiddlepanelof Fig.2.1.Thisorthogonalityallowstheidentification,inastraightforwardway,ofthis classicalconfigurationwithquantaoftheelectromagneticinteraction,thephotons, shownintherightpanelofFig.2.1.Theaccumulatedenergyflux–thatis,thetotal energycarriedbythefieldsaccompanyingthelepton–isobtainedbyintegratingthe Poyntingvectorovertheplaneorthogonaltothelepton’saxisofmotion.Itisthus paralleltothelepton’smotion.Interpretingthecontinuousenergyfluxwithaflux ofequivalentquanta,thephotons,thenumberdensityofaccompanyingphotonsper energyintervalanddistancefromtheleptoncanbededucedas
Fig.2.1 Electricalandmagneticfieldsinblueandgreenofaleptonat rest(v =0,leftpanel)andwithavelocity v ≈ c (middlepanel).The equivalentphotonsaredepictedontherightpanel.
Here ω istheenergyoftheequivalentphoton,andtheconstantofproportionality isobtainedbyintegratingoverthetransverseplane,parameterizedbytheimpact factor b⊥,andbytheelectromagneticcouplingconstant.Thelattergetsmodifiedby therelativechargeoftheelectron, ee,whichofcourseequals-1.Thereisamaximal energyavailablefortheseequivalentphotons;naivelyitisgivenby ωmax = E,the energyofthelepton.
Inamorequantumfield-theoreticalwayofthinkingaboutthis,theimpactparameterisreplacedwiththetransversemomentum, b⊥ ←→ k⊥,throughaFourier transform,andtheequivalentphotonsareconsideredtobepartofthelepton’swave function.Theirspectrumthenreads
Insuchapicture,thephysicalleptonisgivenbyasuperpositionofstateswithvarying photonmultiplicity,
wherethephotonshavedifferentenergiesandtransversemomenta.Duetomomentum conservation,theyaretypicallyofftheirmassshell.Thislimitsthelifetimeofthe quantum-fluctuationslike |eγ or |eγγ
Toseehowthisworksinsomewhatmoredetail,considerthecaseofthe |eγ Fock state.Assumingmasslesson-shellelectronsintheinitialandfinalstate,butallowing thephotonstogooff-shell,thekinematicsofasplitting e(P ) → e(p)+ γ(k)canbe writtenas
Parameterizingthesplittingoftheenergy, E of P suchthat ω ≡ Eγ = xE and therefore Ee =(1 x)E fortheenergyoftheoutgoingelectron,leadsto
inthecasewhere x issmall, i.e.,forthebulkofthephotons.Thisalsoimpliesthat inthislimitthemomentumcomponentofthephotonparalleltotheelectronisabout k ≈ ω,theenergyofthephoton.Thefactthattheemittedphotons(ortheelectrons orboth)areoff-shellisequallytrueformassiveelectrons,anditlimitsthelifetimeof the(eγ)-componentofthewavefunctionthroughtheuncertaintyprinciple.Withthe photonmomentumgivenby kµ ≈ (ω, k⊥,ω),theenergyshiftnecessarytomoveiton itsmassshellisgivenby δω ≈ k2 ⊥/2ω yielding
asthe lifetimeofthefluctuation.Thisimpliesthatsuchfluctuationslivelonger, astheenergyofthephotonincreasesandtherelativetransversemomentumofthe photonandtheelectrondecrease.Notethatinthisbooknaturalunitsarebeingused, soeffectively = c =1.
Inaddition,ofcourse,thephotonscansplitintoafermion–anti-fermionpair,asyet anotherquantumfluctuation,whichinturnmayemitfurtherphotons.Thiscomplicatesthewave-functionpictureevenmore.However,altogether,thedistancefromthe originalleptonandthelifetimeofallthesevirtualparticles,thequantumfluctuations whichtheymanifest,aregivenbytheamounttheyareofftheirmassshellandbythe amountofenergytheycarry.
2.1.1.2Dokshitser–Gribov–Lipatov–Altarelli–Parisiequations
Thewave-functionideacanberelated,atleadingorder,byprobabilitiesoffinding theoriginallepton,thephotons,orsecondaryleptonsatgivenenergiesandtransverse momenta.Duetothenatureoftheelectromagneticinteraction,theseprobabilities (or,theleptonwavefunction),canbecalculatedfromfirstprinciples.Inthefollowing theprobabilityoffindingaleptonorphotonatenergyfraction x (withrespectto theoriginallepton)andattransversemomentum k⊥ willbedenotedas (x,k⊥)and γ(x,k⊥),respectively.At leading orderin α,thatiswithoutanyemissionofsecondary quanta,theyareofcoursegivenby
(x,k2 ⊥ =0)= δ(1 x)and γ(x,k2 ⊥ =0)=0 (2.7)
Theradiationthatactuallygivesrisetotheaforementionedsecondaryparticlescan nowbedescribed,toallorders,byequationsthatareknownas evolutionequations, sincetheyrelatetheprobabilitytofindquantawithcertainkinematics x and k2 ⊥ to similarprobabilitiesatotherscales,throughemissionofsecondaries.Ingeneral,they canbeobtainedindifferentapproximationsrelatedtodifferentkinematicalsituations, whichcanbeintimatelyrelatedtodifferent factorizationschemes.Inthe collinear factorizationscheme,whichwillbeemployedinmostoftheremainderofthis
book,theenergyandespeciallytransversemomentumofthesecondaryparticlesare consideredtobesmallwithrespecttotheenergyoftheoriginallepton,andtherefore thekinematicaleffectmerelyamountstoasuccessivereductionoftheoriginallepton energy.Inthisscheme,theprobabilitydensitiesevolvewiththelogarithmofthe transversemomentum, cf. Eq.(2.2),as
(2.8)
wheretheeffectofphotonssplittingintovirtuallepton–anti-leptonpairshasbeen omitted.Thefirstlineoftheseequationsexhibithowtheprobabilitydensityofleptons withsmallerenergyfraction x isdrivenbyleptonswithalargerenergyfraction x/ξ> x,whichcanbeinterpretedastheleptonsontherighthandsideoftheequationlosing anenergyfraction1 ξ intheemissionofaphoton.Inthekinematicalapproximation employedhere,termslike P (x/ξ,α),thesplittingkernels,canbeunderstoodas reducedmatrixelementsfortheemissionofonephotonoffthelepton.Ingeneral, Pba denotessuchkernelsforatransitionofaparticleoftype a toaparticleoftype b,while emittingaparticleoftype c,whichisnotbeenmadeexplicit.Thesekernelshavebeen takenatleadingorder,asmanifestbytheexplicitorderin α infront,butofcourse theycanalsobeevaluatedtohigherordersinaperturbativeexpansioninpowersof thecouplingwithcorrespondingcoefficientfunctions.
Closerinspectionrevealsthatthissetofequationsisnothingbutthecelebrated Dokshitser–Gribov–Lipatov–Altarelli–Parisi(DGLAP)equation,specifiedfor QED.Inthisequation,the splittingkernels atleadingorderareindependentofthe couplingconstantandread
Here,thenotationof“+”–functionshasbeenemployed,whichwillcropupagain atvariousplaces,especiallyinconjunctionwithsplittingkernelssuchastheones discussedhere.Theyaredefinedthroughtheirintegraltogetherwithatestfunction g(z)suchthat
Forfurtherdetails,thereaderisreferedtoAppendixA.1.2.Togainamoreintuitive understanding,considerthisprescriptiontoworkinsuchawaythatthepolefor z → 1in P isexcludedinthe+-functionandreinsertedthroughthesecondpartof
thesplittingkernel,proportionaltothe δ-function.Itwillbeseenlater,howsuchterms becomenecessarytoensurethecorrectphysicalbehaviourofthesplittingfunctions, suchassatisfyingmomentumconservation.
However,theseequationswillberevisitedanddiscussedinmoredetailinlater chaptersofthebook.Tofollowthereasoninginthismoreintroductorychapterit shouldsufficetomentionthatthe1/ω polepresentinthenaiveclassicalpicturehas itscounterpartinthe1/(1 z)or1/z termsappearinginthesplittingfunction.
2.1.1.3Initial-stateradiation Turningawayfromthedetailsofhowtheleptonwavefunctionisevaluatedandback tothephysicalconsequencesoftheexistenceofthefluctuations,theobviousquestion is:whathappensinacollision?Cantheemergingpicturebeputtostringenttests andcantheexistenceofsuchfluctuationsbequantifiedbysuitableprobes?
Toanswerthis,atleastqualitatively,andtogainsomeinsightintothephysical processestakingplaceinacollision,considerfirstthecaseofnocollisionatall.There, thefluctuationshaveafinitelifetimeanddistancetotheoriginallepton,relatedto thekinematicsofthevirtualparticles.Four-momentumconservationthusforcesthese fluctuationstoeventuallycollapsebackintotheoriginallepton,guaranteeingthequantumcoherenceofthelepton–itmustremainintact.If,ontheotherhand,acollision takesplace,oneormoreofthequantumexcitations,theparticlesformingthelepton’s Fockstate,may,throughtheexchangeoffour-momentumwiththeincidentprojectile, goontheirmassshell.Inthiswaytheyacquireaninfinitelifetime.Insuchasituation, thecorrespondingparticleswillnotfallbackontotheoriginalleptonandthecoherenceofthefluctuationsisthereforebroken.Inthisway,oneormoreofthehitherto virtualparticlesmaybecomerealandhencephysicallyobservableinthefinalstateof thecollision.
Toillustratethis,considerthecaseof e+e collisions,whichhavebeeninvestigated ingreatdetailforexampleatLEP,andassumethatitistheelectronandpositronthat takepartinthecollision.Thenthecentre-of-massenergy ˆ Ec m ofthisactualreaction maybereducedwithrespecttotheenergyobtainedfromthenominalbeamenergies, ˆ Ec m <Ec m =2Ebeam. 1 Thedifferenceisstoredintheenergiesofthephotons accompanyingtheelectron–positronpair;theirdistributionintransversemomenta andenergiesisgivenapproximatelybyEq.(2.2).Inmoremodernlanguagethese photonswouldbeattributedto initial-stateradiation offtheincident“original” pair,ratherthantothequantummanifestationofthebreakdownofcoherenceof theFockstatesdescribingtheleptonsandtheiraccompanyingelectromagneticfields. Nevertheless,thisradiationwould,ofcourse,bedescribedbyequationsverysimilar totheapproximateone.
Itshouldbestressed,however,that,takenonitsown,thisinitial-stateradiationis amanifestationofthebreakdownofquantumcoherenceofcomplicatedFockstates, bindingthephotonstotheoriginalleptons.
1Here,andthroughoutthebook,kinematicalquantities q relatedtothecollidingpartonsare supplementedwithaˆ q,whilethoserelatedtothe(beam-)particlesareleftwithoutitas q
2.1.1.4Final-stateradiation
Asimilarpicturealsoemergeswhenchargedparticlesareproducedinthefinalstate. Asanexample,considerthecaseof,say,muonpairproductioninelectron-positron annihilations, e+e → µ+µ .Classically,theproductionofthemuonscanbeunderstoodastheirinstantaneousaccelerationafteremergingfromafiniteenergydensity relatedtothepreviousannihilationoftheelectronandpositronintoelectromagnetic fields,theintermediatephotoninquantumfieldtheory.Inclassicalelectrodynamics suchanaccelerationofchargedparticlestriggerstheradiationofadditionalphotons offthecharges,knownas Bremsstrahlung 2 Interpretingthemuonpairasacurrentgoingfromavelocity v to v attheoriginofthecoordinatesystem,thedouble differentialclassicalradiationspectrum I inthedirection n(Ω)withpolarization reads
inthedominantregionofsmallenergies,wherethesquaredtermisknownasthe radiationfunction W[645].Formasslessparticlestravellingatthespeedoflight, theradiationfunctioncanberewrittenas
Castinitscovariantformandinterpretedasaphotonspectrumandtacitlyinserting α = e2/(4π),theradiationspectrumbecomes
forthenumberofphotons N emittedintheprocess.Here, k and denotethephoton’s four-momentumandpolarizationfour-vector,while p and p denotethefour-momenta ofthemuons.Theformabove,
isalsoknownasthe eikonal form,anditisidenticalwiththeresultofafull-fledged calculationinquantumfieldtheory,asfollows.
Forthecaseathand,considerthephotonemissionpartoffthemuons,whichare assumedtobemassless.ThemuonsareproducedthroughavertexfactorcalledΓ.The leading-orderFeynmandiagramsaredepictedinFig.2.2.Thecorrespondingmatrix elementfor X → µ (p)µ+(
)γ(k)isgivenby
2Inthequantumpicture,equivalently,thistranslatesintotheradiationofBremsstrahlungphotons.