Tensorsfor DataProcessing Theory,Methods,andApplications
Editedby YipengLiu
SchoolofInformationandCommunicationEngineering
UniversityofElectronicScienceandTechnology ofChina(UESTC) Chengdu,China
AcademicPressisanimprintofElsevier 125LondonWall,LondonEC2Y5AS,UnitedKingdom 525BStreet,Suite1650,SanDiego,CA92101,UnitedStates 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom
Copyright©2022ElsevierInc.Allrightsreserved.
MATLAB® isatrademarkofTheMathWorks,Inc.andisusedwithpermission. TheMathWorksdoesnotwarranttheaccuracyofthetextorexercisesinthisbook. Thisbook’suseordiscussionofMATLAB® softwareorrelatedproductsdoesnotconstitute endorsementorsponsorshipbyTheMathWorksofaparticularpedagogicalapproachorparticularuse oftheMATLAB® software.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronic ormechanical,includingphotocopying,recording,oranyinformationstorageandretrievalsystem, withoutpermissioninwritingfromthepublisher.Detailsonhowtoseekpermission,further informationaboutthePublisher’spermissionspoliciesandourarrangementswithorganizationssuch astheCopyrightClearanceCenterandtheCopyrightLicensingAgency,canbefoundatourwebsite: www.elsevier.com/permissions
Thisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythe Publisher(otherthanasmaybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperience broadenourunderstanding,changesinresearchmethods,professionalpractices,ormedicaltreatment maybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluating andusinganyinformation,methods,compounds,orexperimentsdescribedherein.Inusingsuch informationormethodstheyshouldbemindfuloftheirownsafetyandthesafetyofothers,including partiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assume anyliabilityforanyinjuryand/ordamagetopersonsorpropertyasamatterofproductsliability, negligenceorotherwise,orfromanyuseoroperationofanymethods,products,instructions,orideas containedinthematerialherein.
LibraryofCongressCataloging-in-PublicationData
AcatalogrecordforthisbookisavailablefromtheLibraryofCongress
BritishLibraryCataloguing-in-PublicationData
AcataloguerecordforthisbookisavailablefromtheBritishLibrary
ISBN:978-0-12-824447-0
ForinformationonallAcademicPresspublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: MaraConner
AcquisitionsEditor: TimPitts
EditorialProjectManager: CharlotteRowley
ProductionProjectManager: PremKumarKaliamoorthi
Designer: MilesHitchen
TypesetbyVTeX
Listofcontributors .............................................xiii Preface......................................................xix
CHAPTER1Tensordecompositions:computations, applications,andchallenges .................... 1 YingyueBi,YingcongLu,ZhenLong,CeZhu,and YipengLiu
1.1 Introduction ......................................1
1.1.1Whatisatensor?............................1
1.1.2Whydoweneedtensors?. ....................2
1.2 Tensoroperations .................................3
1.2.1Tensornotations............................3
1.2.2Matrixoperators ............................4
1.2.3Tensortransformations.......................6
1.2.4Tensorproducts .............................7
1.2.5Structuraltensors............................11
1.2.6Summary..................................13
1.3 Tensordecompositions .............................13
1.3.1Tuckerdecomposition ........................13
1.3.2Canonicalpolyadicdecomposition ...............14
1.3.3Blocktermdecomposition. ....................16
1.3.4Tensorsingularvaluedecomposition.. ...........18
1.3.5Tensornetwork.............................19
1.4 Tensorprocessingtechniques .........................24
1.5 Challenges. ......................................25 References. ......................................26
CHAPTER2Transform-basedtensorsingularvalue decompositioninmultidimensionalimagerecovery 31 Tai-XiangJiang,MichaelK.Ng,andXi-LeZhao
2.1 Introduction ......................................32
2.2 Recentadvancesofthetensorsingularvaluedecomposition..34
2.2.1Preliminariesandbasictensornotations...........34
2.2.2Thet-SVDframework........................35
2.2.3Tensornuclearnormandtensorrecovery ..........38
2.2.4Extensions.................................41
2.2.5Summary..................................44
2.3 Transform-basedt-SVD.............................44
2.3.1Linearinvertibletransform-basedt-SVD ..........45
2.3.2Beyondinvertibilityanddataadaptivity ...........47
2.4 Numericalexperiments .............................49
2.4.1Exampleswithinthet-SVDframework...........49
2.4.2Examplesofthetransform-basedt-SVD..........51
2.5 Conclusionsandnewguidelines... ....................53 References. ......................................55
CHAPTER3Partensor 61
ParisA.Karakasis,ChristosKolomvakis,GeorgeLourakis, GeorgeLykoudis,IoannisMariosPapagiannakos, IoannaSiaminou,ChristosTsalidis,and AthanasiosP.Liavas
3.1 Introduction ......................................62
3.1.1Relatedwork...............................62 3.1.2Notation..................................63
3.2 Tensordecomposition. .............................64
3.2.1Matrixleast-squaresproblems ..................65
3.2.2Alternatingoptimizationfortensordecomposition...69
3.3 Tensordecompositionwithmissingelements.. ...........70
3.3.1Matrixleast-squareswithmissingelements ........71
3.3.2Tensordecompositionwithmissingelements:the unconstrainedcase ...........................74
3.3.3Tensordecompositionwithmissingelements:the nonnegativecase ............................75
3.3.4Alternatingoptimizationfortensordecomposition withmissingelements........................75
3.4 Distributedmemoryimplementations...................75
3.4.1SomeMPIpreliminaries......................75
3.4.2Variablepartitioninganddataallocation ...........77
3.4.3Tensordecomposition ........................79
3.4.4Tensordecompositionwithmissingelements .......81
3.4.5Someimplementationdetails...................82
3.5 Numericalexperiments .............................83
3.5.1Tensordecomposition ........................83
3.5.2Tensordecompositionwithmissingelements .......84
3.6 Conclusion ......................................87 Acknowledgment ..................................88 References. ......................................88 CHAPTER4ARiemannianapproachtolow-ranktensor
4.1 Introduction ......................................91
4.2 AbriefintroductiontoRiemannianoptimization ..........93
4.2.1Riemannianmanifolds ........................94
4.2.2Riemannianquotientmanifolds .................95
4.3 RiemannianTuckermanifoldgeometry .................97
4.3.1Riemannianmetricandquotientmanifoldstructure..97
4.3.2Characterizationoftheinducedspaces. ...........100
4.3.3Linearprojectors ............................102
4.3.4Retraction.................................103
4.3.5Vectortransport.............................104
4.3.6Computationalcost ..........................104
4.4 Algorithmsfortensorlearningproblems................104
4.4.1Tensorcompletion...........................105
4.4.2Generaltensorlearning... ....................106
4.5 Experiments .....................................107
4.5.1Choiceofmetric............................108
4.5.2Low-ranktensorcompletion...................109
4.5.3Low-ranktensorregression....................113
4.5.4Multilinearmultitasklearning ..................115
4.6 Conclusion ......................................116 References. ......................................117
CHAPTER5Generalizedthresholdingforlow-ranktensor
recovery:approachesbasedonmodeland learning 121
FeiWen,ZhonghaoZhang,andYipengLiu
5.1 Introduction ......................................121
5.2 Tensorsingularvaluethresholding. ....................123
5.2.1Proximityoperatorandgeneralizedthresholding....123
5.2.2Tensorsingularvaluedecomposition.. ...........126
5.2.3Generalizedmatrixsingularvaluethresholding.....128
5.2.4Generalizedtensorsingularvaluethresholding ......129
5.3 Thresholdingbasedlow-ranktensorrecovery.............131
5.3.1Thresholdingalgorithmsforlow-ranktensorrecovery132
5.3.2Generalizedthresholdingalgorithmsforlow-rank tensorrecovery.............................134
5.4 Generalizedthresholdingalgorithmswithlearning .........136
5.4.1Deepunrolling. .............................137
5.4.2Deepplug-and-play ..........................140
5.5 Numericalexamples...............................141
5.6 Conclusion ......................................145 References. ......................................147
CHAPTER6Tensorprincipalcomponentanalysis ............. 153 PanZhou,CanyiLu,andZhouchenLin
6.1 Introduction ......................................153
6.2 Notationsandpreliminaries..........................155
6.2.1Notations..................................156
6.2.2DiscreteFouriertransform.....................157
6.2.3T-product .................................159
6.2.4Summary..................................160
6.3 TensorPCAforGaussian-noisydata...................161
6.3.1Tensorrankandtensornuclearnorm.. ...........161
6.3.2AnalysisoftensorPCAonGaussian-noisydata.....165 6.3.3Summary..................................166
6.4 TensorPCAforsparselycorrupteddata.................166 6.4.1RobusttensorPCA..........................167
6.4.4Summary..................................191
6.5 TensorPCAforoutlier-corrupteddata ..................191
6.5.1OutlierrobusttensorPCA. ....................192
6.5.2ThefastOR-TPCAalgorithm..................196
6.6 OthertensorPCAmethods ...........................207
6.7 Futurework......................................208 6.8 Summary........................................208 References. ......................................209
CHAPTER7Tensorsfordeeplearningtheory
215 YoavLevine,NoamWies,OrSharir,NadavCohen,and AmnonShashua
7.1 Introduction ......................................215
7.2 Boundingafunction’sexpressivityviatensorization ........217
7.2.1Ameasureofcapacityformodelinginput dependencies.. .............................218
7.2.2Boundingcorrelationswithtensormatricizationranks220
7.3 Acasestudy:self-attentionnetworks ...................223
7.3.1Theself-attentionmechanism ..................223
7.3.2Self-attentionarchitectureexpressivityquestions....227
7.3.3Resultsontheoperationofself-attention ..........230
7.3.4Boundingtheseparationrankofself-attention ......235
7.4 Convolutionalandrecurrentnetworks ..................242
7.4.1Theoperationofconvolutionalandrecurrentnetworks243
7.4.2Addressedarchitectureexpressivityquestions ......243
7.5 Conclusion ......................................245 References. ......................................245 CHAPTER8Tensornetworkalgorithmsforimageclassification 249 CongChen,KimBatselier,andNgaiWong
8.1 Introduction ......................................249
8.2 Background ......................................251
8.2.1Tensorbasics...............................251
8.2.2Tensordecompositions... ....................253
8.2.3Supportvectormachines.. ....................256
8.2.4Logisticregression..........................257
8.3 Tensorialextensionsofsupportvectormachine ...........258
8.3.1Supervisedtensorlearning. ....................258
8.3.2Supporttensormachines.. ....................260
8.3.3Higher-ranksupporttensormachines.. ...........263
8.3.4SupportTuckermachines.. ....................265
8.3.5Supporttensortrainmachines ..................269
8.3.6Kernelizedsupporttensortrainmachines ..........275
8.4 Tensorialextensionoflogisticregression................284
8.4.1Rank-1logisticregression. ....................285
8.4.2Logistictensorregression.....................286
8.5 Conclusion ......................................288 References. ......................................289
CHAPTER9High-performancetensordecompositionsfor compressingandacceleratingdeepneural networks ....................................... 293 Xiao-YangLiu,YimingFang,LiuqingYang,ZechuLi,and AnwarWalid
9.1 Introductionandmotivation ..........................294
9.2 Deepneuralnetworks. .............................295
9.2.1Notations..................................295
9.2.2Linearlayer... .............................295
9.2.3Fullyconnectedneuralnetworks ................298
9.2.4Convolutionalneuralnetworks ..................300
9.2.5Backpropagation ............................303
9.3 Tensornetworksandtheirdecompositions ...............305
9.3.1Tensornetworks............................305
9.3.2CPtensordecomposition.. ....................308
9.3.3Tuckerdecomposition ........................310
9.3.4HierarchicalTuckerdecomposition... ...........313
9.3.5Tensortrainandtensorringdecomposition ........315
9.3.6Transform-basedtensordecomposition ...........318
9.4 Compressingdeepneuralnetworks ....................321
9.4.1Compressingfullyconnectedlayers... ...........321
9.4.2CompressingtheconvolutionallayerviaCP decomposition. .............................322
9.4.3CompressingtheconvolutionallayerviaTucker decomposition. .............................325
9.4.4CompressingtheconvolutionallayerviaTT/TR decompositions .............................327
9.4.5Compressingneuralnetworksviatransform-based decomposition. .............................330
9.5 Experimentsandfuturedirections. ....................333
9.5.1PerformanceevaluationsusingtheMNISTdataset...333
9.5.2PerformanceevaluationsusingtheCIFAR10dataset.336
9.5.3Futureresearchdirections.....................337 References. ......................................338
CHAPTER10Coupledtensordecompositionsfordatafusion 341 ChristosChatzichristos,SimonVanEyndhoven, EleftheriosKofidis,andSabineVanHuffel
10.1 Introduction ......................................341 10.2 Whatisdatafusion?...............................342
10.2.1Contextanddefinition
10.2.2Challengesofdatafusion..
10.2.3Typesoffusionanddatafusionstrategies
10.3.3Coupledtensordecompositions
10.4 Applicationsoftensor-baseddatafusion................355 10.4.1Biomedicalapplications.......................355 10.4.2Imagefusion...............................357 10.5 FusionofEEGandfMRI:acasestudy..................358
10.6 Datafusiondemos.................................361
Conclusionandprospects
TatsuyaYokota,CesarF.Caiafa,andQibinZhao
11.1 Low-levelvisionandsignalreconstruction
11.1.1Observationmodels ..........................372
11.1.2Inverseproblems............................374
11.2 Methodsusingrawtensorstructure
Methodsusingtensorization ..........................409
11.4 Examplesoflow-levelvisionapplications...............415
11.4.1Imageinpaintingwithrawtensorstructure .........415
11.4.2Imageinpaintingusingtensorization.. ...........416
11.4.3Denoising,deblurring,andsuperresolution ........417
11.5 Remarks........................................419 Acknowledgments .................................420 References. ......................................420
CHAPTER12Tensorsforneuroimaging
....................... 427
AybükeErolandBorbálaHunyadi
12.1 Introduction ......................................427
12.2 Neuroimagingmodalities ............................429
12.3 Multidimensionalityofthebrain.. ....................431
12.4 Tensordecompositionstructures.. ....................433
12.4.1Productoperationsfortensors ..................434
12.4.2Canonicalpolyadicdecomposition ...............435
12.4.3Tuckerdecomposition ........................435
12.4.4Blocktermdecomposition. ....................437
12.5 Applicationsoftensorsinneuroimaging ................437
12.5.1Fillinginmissingdata ........................438
12.5.2Denoising,artifactremoval,anddimensionality reduction ..................................441
12.5.3Segmentation...............................444
12.5.4Registrationandlongitudinalanalysis. ...........445
12.5.5Sourceseparation ...........................447
12.5.6Activityrecognitionandsourcelocalization ........451
12.5.7Connectivityanalysis .........................456
12.5.8Regression.................................462
12.5.9Featureextractionandclassification... ...........463
12.5.10Summaryandpracticalconsiderations. ...........468
12.6 Futurechallenges ..................................471
12.7 Conclusion ......................................472 References. ......................................473
CHAPTER13Tensorrepresentationforremotesensingimages 483
YangXu,FeiYe,BoRen,LiangfuLu,XudongCui, JocelynChanussot,andZebinWu
13.1 Introduction ......................................483
13.2 Opticalremotesensing:HSIandMSIfusion.............488
13.2.1Tensornotationsandpreliminaries...............488
13.2.2Nonlocalpatchtensorsparserepresentationfor HSI-MSIfusion.............................488
13.2.3High-ordercoupledtensorringrepresentationfor HSI-MSIfusion.............................496
13.2.4JointtensorfactorizationforHSI-MSIfusion.......504
13.3 Polarimetricsyntheticapertureradar:featureextraction.....517
13.3.1BriefdescriptionofPolSARdata................518
13.3.2Thetensorialembeddingframework.. ...........519
13.3.3Experimentandanalysis.. ....................522 References. ......................................532
CHAPTER14Structuredtensortraindecompositionforspeeding
upkernel-basedlearning ........................ 537 YassineZniyed,OuafaeKarmouda,RémyBoyer, JérémieBoulanger,AndréL.F.deAlmeida,and GérardFavier
14.1 Introduction ......................................538
14.2 Notationsandalgebraicbackground ....................540
14.3 Standardtensordecompositions... ....................541
14.3.1Tuckerdecomposition ........................542
14.3.2HOSVD..................................542
14.3.3TensornetworksandTTdecomposition ...........543
14.4 Dimensionalityreductionbasedonatrainoflow-ordertensors545
14.4.1TD-trainmodel:equivalencebetweenahigh-orderTD andatrainoflow-orderTDs...................546
14.5 Tensortrainalgorithm..............................548
14.5.1DescriptionoftheTT-HSVDalgorithm...........548
14.5.2Comparisonofthesequentialandthehierarchical schemes ...................................549
14.6 Kernel-basedclassificationofhigh-ordertensors..........551
14.6.1FormulationofSVMs........................552
14.6.2PolynomialandEuclideantensor-basedkernel ......553
14.6.3KernelonaGrassmannmanifold................553
14.6.4Thefastkernelsubspaceestimationbasedontensor traindecomposition(FAKSETT)method ..........554
14.7 Experiments .....................................555
14.7.1Datasets...................................555
14.7.2Classificationperformance. ....................557
14.8 Conclusion ......................................558 References. ......................................560
Listofcontributors
KimBatselier
DelftCenterforSystemsandControl,DelftUniversityofTechnology,Delft, TheNetherlands
YingyueBi
SchoolofInformationandCommunicationEngineering,UniversityofElectronic ScienceandTechnologyofChina(UESTC),Chengdu,China
JérémieBoulanger
CRIStAL,UniversitédeLille,Villeneuved’Ascq,France
RémyBoyer
CRIStAL,UniversitédeLille,Villeneuved’Ascq,France
CesarF.Caiafa
InstitutoArgentinodeRadioastronomía–CCTLaPlata,CONICET/CIC-PBA/ UNLP,VillaElisa,Argentina
RIKENCenterforAdvancedIntelligenceProject,Tokyo,Japan
JocelynChanussot
LJK,CNRS,GrenobleINP,Inria,UniversitéGrenoble,Alpes,Grenoble,France
ChristosChatzichristos
KULeuven,DepartmentofElectricalEngineering(ESAT),STADIUSCenterfor DynamicalSystems,SignalProcessingandDataAnalytics,Leuven,Belgium
CongChen
DepartmentofElectricalandElectronicEngineering,TheUniversityofHong Kong,PokfulamRoad,HongKong
NadavCohen
SchoolofComputerScience,HebrewUniversityofJerusalem,Jerusalem,Israel
XudongCui
SchoolofMathematics,TianjinUniversity,Tianjin,China
AndréL.F.deAlmeida
DepartmentofTeleinformaticsEngineering,FederalUniversityofFortaleza, Fortaleza,Brazil
AybükeErol
CircuitsandSystems,DepartmentofMicroelectronics,DelftUniversityof Technology,Delft,TheNetherlands
YimingFang
DepartmentofComputerScience,ColumbiaUniversity,NewYork,NY, UnitedStates
GérardFavier
LaboratoireI3S,UniversitéCôted’Azur,CNRS,SophiaAntipolis,France
BorbálaHunyadi
CircuitsandSystems,DepartmentofMicroelectronics,DelftUniversityof Technology,Delft,TheNetherlands
PratikJawanpuria
Microsoft,Hyderabad,India
Tai-XiangJiang
SchoolofEconomicInformationEngineering,SouthwesternUniversityof FinanceandEconomics,Chengdu,Sichuan,China
ParisA.Karakasis
SchoolofElectricalandComputerEngineering,TechnicalUniversityofCrete, Chania,Greece
OuafaeKarmouda
CRIStAL,UniversitédeLille,Villeneuved’Ascq,France
HiroyukiKasai
WasedaUniversity,Tokyo,Japan
EleftheriosKofidis
Dept.ofStatisticsandInsuranceScience,UniversityofPiraeus,Piraeus,Greece
ChristosKolomvakis
SchoolofElectricalandComputerEngineering,TechnicalUniversityofCrete, Chania,Greece
YoavLevine
SchoolofComputerScience,HebrewUniversityofJerusalem,Jerusalem,Israel
ZechuLi
DepartmentofComputerScience,ColumbiaUniversity,NewYork,NY, UnitedStates
AthanasiosP.Liavas
SchoolofElectricalandComputerEngineering,TechnicalUniversityofCrete, Chania,Greece
ZhouchenLin
KeyLab.ofMachinePerception,SchoolofEECS,PekingUniversity,Beijing, China
Xiao-YangLiu
DepartmentofComputerScienceandEngineering,ShanghaiJiaoTong University,Shanghai,China
DepartmentofElectricalEngineering,ColumbiaUniversity,NewYork,NY, UnitedStates
YipengLiu
SchoolofInformationandCommunicationEngineering,UniversityofElectronic ScienceandTechnologyofChina(UESTC),Chengdu,China
ZhenLong
SchoolofInformationandCommunicationEngineering,UniversityofElectronic ScienceandTechnologyofChina(UESTC),Chengdu,China
GeorgeLourakis
Neurocom,S.A,Athens,Greece
CanyiLu
CarnegieMellonUniversity,Pittsburgh,PA,UnitedStates
LiangfuLu
SchoolofMathematics,TianjinUniversity,Tianjin,China
YingcongLu
SchoolofInformationandCommunicationEngineering,UniversityofElectronic ScienceandTechnologyofChina(UESTC),Chengdu,China
GeorgeLykoudis
Neurocom,S.A,Athens,Greece
BamdevMishra
Microsoft,Hyderabad,India
MichaelK.Ng
DepartmentofMathematics,TheUniversityofHongKong,Pokfulam, HongKong
IoannisMariosPapagiannakos
SchoolofElectricalandComputerEngineering,TechnicalUniversityofCrete, Chania,Greece
BoRen
KeyLaboratoryofIntelligentPerceptionandImageUnderstandingofMinistryof EducationofChina,XidianUniversity,Xi’an,China
OrSharir
SchoolofComputerScience,HebrewUniversityofJerusalem,Jerusalem,Israel
AmnonShashua
SchoolofComputerScience,HebrewUniversityofJerusalem,Jerusalem,Israel
IoannaSiaminou
SchoolofElectricalandComputerEngineering,TechnicalUniversityofCrete, Chania,Greece
ChristosTsalidis
Neurocom,S.A,Athens,Greece
SimonVanEyndhoven
KULeuven,DepartmentofElectricalEngineering(ESAT),STADIUSCenterfor DynamicalSystems,SignalProcessingandDataAnalytics,Leuven,Belgium icometrix,Leuven,Belgium
SabineVanHuffel
KULeuven,DepartmentofElectricalEngineering(ESAT),STADIUSCenterfor DynamicalSystems,SignalProcessingandDataAnalytics,Leuven,Belgium
AnwarWalid
NokiaBellLabs,MurrayHill,NJ,UnitedStates
FeiWen
DepartmentofElectronicEngineering,ShanghaiJiaoTongUniversity,Shanghai, China
NoamWies
SchoolofComputerScience,HebrewUniversityofJerusalem,Jerusalem,Israel
NgaiWong
DepartmentofElectricalandElectronicEngineering,TheUniversityofHong Kong,PokfulamRoad,HongKong
ZebinWu
SchoolofComputerScienceandEngineering,NanjingUniversityofScience andTechnology,Nanjing,China
YangXu
SchoolofComputerScienceandEngineering,NanjingUniversityofScience andTechnology,Nanjing,China
LiuqingYang
DepartmentofComputerScience,ColumbiaUniversity,NewYork,NY, UnitedStates
FeiYe
SchoolofComputerScienceandEngineering,NanjingUniversityofScience andTechnology,Nanjing,China
TatsuyaYokota
NagoyaInstituteofTechnology,Aichi,Japan
RIKENCenterforAdvancedIntelligenceProject,Tokyo,Japan
ZhonghaoZhang
SchoolofInformationandCommunicationEngineering,UniversityofElectronic ScienceandTechnologyofChina(UESTC),Chengdu,China
QibinZhao
RIKENCenterforAdvancedIntelligenceProject,Tokyo,Japan GuangdongUniversityofTechnology,Guangzhou,China
Xi-LeZhao
SchoolofMathematicalSciences/ResearchCenterforImageandVision Computing,UniversityofElectronicScienceandTechnologyofChina,Chengdu, Sichuan,China
PanZhou
SEAAILab,Singapore,Singapore
CeZhu
SchoolofInformationandCommunicationEngineering,UniversityofElectronic ScienceandTechnologyofChina(UESTC),Chengdu,China
YassineZniyed
UniversitédeToulon,Aix-MarseilleUniversité,CNRS,LIS,Toulon,France
Preface
Thisbookprovidesanoverviewoftensorsfordataprocessing,coveringcomputing theories,processingmethods,andengineeringapplications.Thetensorextensions ofaseriesofclassicalmultidimensionaldataprocessingtechniquesarediscussed inthisbook.Manythanksgotoallthecontributors.Studentscanreadthisbookto getanoverallunderstanding,researcherscanupdatetheirknowledgeontherecent researchadvancesinthefield,andengineerscanrefertoimplementationsonvarious applications.
Thefirstchapterisanintroductiontotensordecomposition.Inthefollowing,the bookprovidesvariantsoftensordecompositionswiththeirefficientandeffectivesolutions,includingsomeparallelalgorithms,Riemannianalgorithms,andgeneralized thresholdingalgorithms.Sometensor-basedmachinelearningmethodsaresummarizedindetail,includingtensorcompletion,tensorprincipalcomponentanalysis, supporttensormachine,tensor-basedkernellearning,tensor-baseddeeplearning,etc. Todemonstratethattensorscaneffectivelyandsystematicallyenhanceperformance inpracticalengineeringproblems,thisbookgivesimplementaldetailsofmanyapplications,suchassignalrecovery,recommendersystems,climateforecasting,image clustering,imageclassification,networkcompression,datafusion,imageenhancement,neuroimaging,andremotesensing.
Isincerelyhopethisbookcanservetointroducetensorstomoredatascientists andengineers.Asanaturalrepresentationofmultidimensionaldata,tensorscanbe usedtosubstantiallyavoidtheinformationlossinmatrixrepresentationsofmultiway data,andtensoroperatorscanmodelmoreconnectionsthantheirmatrixcounterparts. Therelatedadvancesinappliedmathematicsallowustomovefrommatricestotensorsfordataprocessing.Thisbookispromisingtomotivatenoveltensortheoriesand newdataprocessingmethods,andtostimulatethedevelopmentofawiderangeof practicalapplications.
Chengdu,China Aug.10,2021
YipengLiu
YingyueBi,YingcongLu,ZhenLong,CeZhu,andYipengLiu SchoolofInformationandCommunicationEngineering,UniversityofElectronicScienceand TechnologyofChina(UESTC),Chengdu,China
CONTENTS
1.1 Introduction
1.1.1
1.1.2
1.2
1.3
1.3.1
1.3.2
1.3.3
1.3.4
1.1 Introduction
1.1.1 Whatisatensor?
Thetensorcanbeseenasahigher-ordergeneralizationofvectorandmatrix,which normallyhasthreeormoremodes(ways)[1].Forexample,acolorimageisathirdordertensor.Ithastwospatialmodesandonechannelmode.Similarly,acolorvideo isafourth-ordertensor;itsextramodedenotestime.
TensorsforDataProcessing. https://doi.org/10.1016/B978-0-12-824447-0.00007-8
2CHAPTER1 TDs:computations,applications,andchallenges
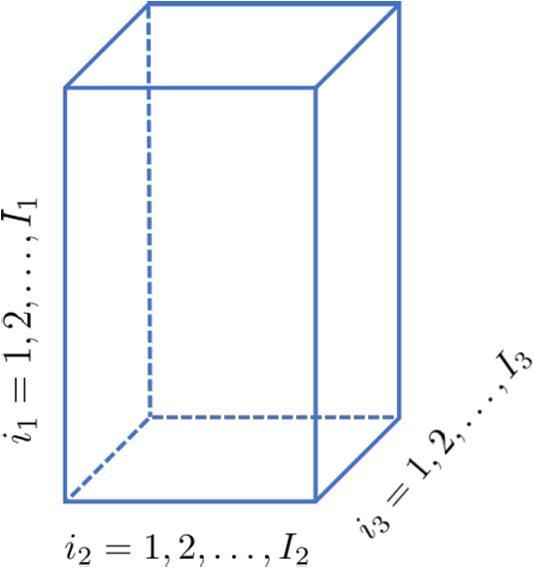
Asspecialformsoftensors,vector a ∈ RI isafirst-ordertensorwhose i -th entry(scalar)is ai andmatrix A ∈ RI ×J isasecond-ordertensorwhose (i,j)thelementis ai,j .Ageneral N -th-ordertensorcanbemathematicallydenotedas A ∈ RI1 ×I2 ×···×IN andits (i1 ,i2 , ,iN )-thentryis ai1 ,i2 , ,iN .Forexample,athirdordertensor A ∈ RI1 ×I2 ×I3 isillustratedinFig. 1.1.
FIGURE1.1
Athird-ordertensor A ∈ RI1 ×I2 ×I3
1.1.2 Whydoweneedtensors?
Tensorsplayimportantrolesinanumberofapplications,suchassignalprocessing, machinelearning,biomedicalengineering,neuroscience,computervision,communication,psychometrics,andchemometrics.Theycanprovideaconcisemathematical frameworkforformulatingandsolvingproblemsinthosefields.
Hereareafewcasesinvolvingtensorframeworks:
•Manyspatial-temporalsignalsinspeechandimageprocessingaremultidimensional.Tensorfactorization-basedtechniquescaneffectivelyextractfeaturesfor enhancement,classification,regression,etc.Forexample,nonnegativecanonical polyadic(CP)decompositioncanbeusedforspeechsignalseparationwherethe firsttwocomponentsofCPdecompositionrepresentfrequencyandtimestructure ofthesignalandthelastcomponentisthecoefficientmatrix[2].
•Thefluorescenceexcitation–emissiondata,commonlyusedinchemistry,medicine, andfoodscience,hasseveralchemicalcomponentswithdifferentconcentrations. Itcanbedenotedasathird-ordertensor;itsthreemodesrepresentsample,excitation,andemission.TakingadvantageofCPdecomposition,thetensorcanbe factorizedintothreefactormatrices:relativeexcitationspectralmatrix,relative emissionspectralmatrix,andrelativeconcentrationmatrix.Inthisway,tensor decompositioncanbeappliedtoanalyzethecomponentsandcorrespondingconcentrationsineachsample[3].
•Socialdataoftenhavemultidimensionalstructures,whichcanbeexploitedby tensor-basedtechniquesfordatamining.Forexample,thethreemodesofchat dataareuser,keyword,andtime.Tensoranalysiscanrevealthecommunication patternsandthehiddenstructuresinsocialnetworks,andthiscanbenefittasks likerecommendersystems[4].
1.2 Tensoroperations
Inthissection,wefirstintroducetensornotations,i.e.,fibersandslices,andthen demonstratehowtorepresenttensorsinagraphicalway.Beforewediscusstensor operations,severalmatrixoperationsarereviewed.
1.2.1 Tensornotations
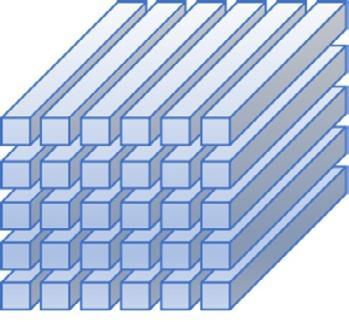
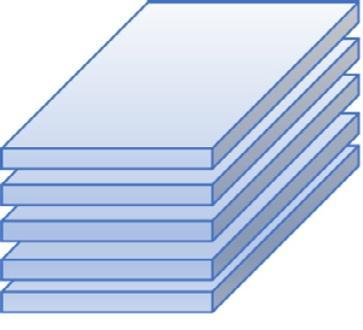
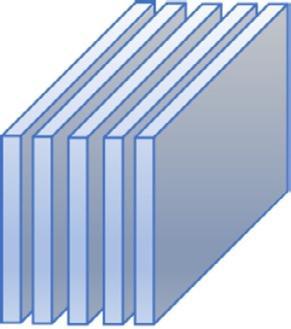
Subtensors,suchasfibersandslices,canbeformedfromtheoriginaltensor.Afiber isdefinedbyfixingalltheindicesbutoneandasliceisdefinedbyfixingallbut twoindices.Forathird-ordertensor AI1 ×I2 ×I3 ,itsmode-1,mode-2,andmode-3 fibersaredenotedby A(:,i2 ,i3 ), A(i1 , :,i3 ),and A(i1 ,i2 , :),where i1 = 1, ··· ,I1 , i2 = 1, ··· ,I2 and i3 = 1, ··· ,I3 ,whichareillustratedinFig. 1.2.Itshorizontal slices A(i1 , :, :),i1 = 1, ··· ,I1 ,lateralslices A(:,i2 , :),i2 = 1, ··· ,I2 ,andfrontal slices A(:, :,i3 ),i3 = 1, ··· ,I3 ,areshowninFig. 1.3.Foreaseofdenotation,we refertothefrontalsliceof A as A(·) insomeformulas.
FIGURE1.2
Theillustrationofmode-1fibers A(:,i2 ,i3 ),mode-2fibers A(i1 , :,i3 ),andmode-3fibers A(i1 ,i2 , :) with i1 = 1, ,I1 , i2 = 1, ,I2 and i3 = 1, ,I3 .
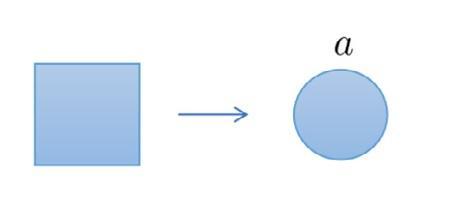
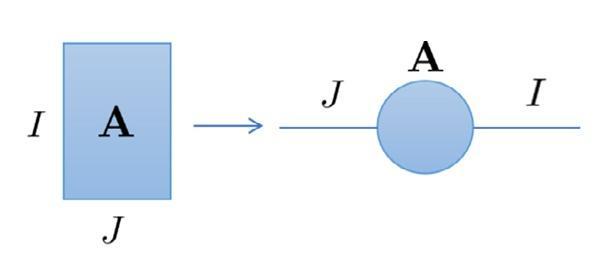
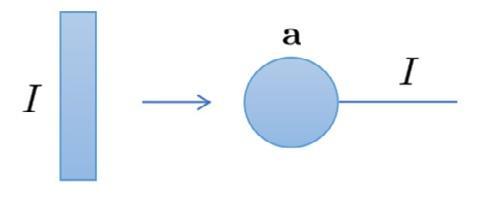
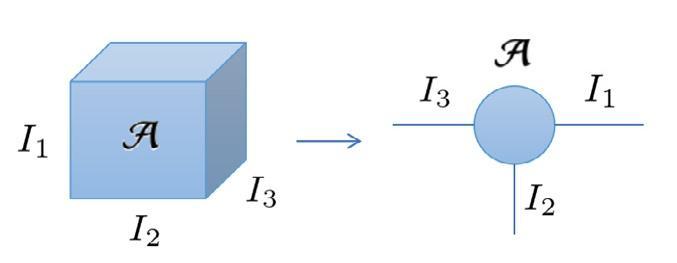
Otherthantheaforementionednotations,thereisanotherwaytodenotetensors andtheiroperations[5].Takingadvantageofgraphicalrepresentations,tensorscan bedenotedbynodesandedgesinastraightforwardway.Graphicalrepresentations forscalars,vectors,matrices,andtensorsareshowninFig. 1.4.Thenumbernextto theedgerepresentstheindicesofthecorrespondingmode.
FIGURE1.3
Theillustrationofhorizontalslices A(i1 , :, :)i1 = 1, ··· ,I1 ,lateralslices A(:,i2 , :) i2 = 1, ··· ,I2 ,andfrontalslices A(:, :,i3 )i3 = 1, ··· ,I3
FIGURE1.4
Graphicalrepresentationsofscalar,vector,matrixandtensor.
1.2.2 Matrixoperators
Definition1.2.1. (Matrixtrace[6])Thetraceofmatrix A ∈ RI ×I isobtainedby summingallthediagonalentriesof A,i.e.,tr(A) = I i =1 ai,i .
Definition1.2.2. ( p -norm[6])Formatrix A ∈ RI ×J ,its p -normisdefinedas
Definition1.2.3. (Matrixnuclearnorm[7])Thenuclearnormofmatrix A isdenoted as A ∗ = i σi (A),where σi (A) isthe i -thlargestsingularvalueof A
Definition1.2.4. (Hadamardproduct[8])TheHadamardproductformatrices A ∈ RM ×N and B ∈ RM ×N isdefinedas A B ∈ RM ×N with
Definition1.2.5. (Kroneckerproduct[9])TheKroneckerproductofmatrices A
RMP ×NQ ,whichcanbewrittenmathematicallyas
BasedontheKroneckerproduct,alotofusefulpropertiescanbederived.Given matrices A, B, C, D,wehave (A ⊗ B)(C ⊗ D) = AC ⊗ BD
where AT and A† representthetransposeandMoore–Penroseinverseofmatrix A.
Definition1.2.6. (Khatri–Raoproduct[10])TheKhatri–Raoproductofmatrices A ∈ RM ×N and B ∈ RL×N isdefinedas
SimilartotheKroneckerproduct,theKhatri–Raoproductalsohassomeconvenientproperties,suchas