https://ebookmass.com/product/peridynamic-modeling-
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
Multiphysics Modeling: Numerical Methods and Engineering Applications: Tsinghua University Press Computational Mechanics Series 1st Edition Cen
https://ebookmass.com/product/multiphysics-modeling-numerical-methodsand-engineering-applications-tsinghua-university-press-computationalmechanics-series-1st-edition-cen/ ebookmass.com
Advances in Engineered Cementitious Composite Materials, Structures, and Numerical Modeling Y. X. Zhang
https://ebookmass.com/product/advances-in-engineered-cementitiouscomposite-materials-structures-and-numerical-modeling-y-x-zhang/
ebookmass.com
Deterministic Numerical Modeling of Soil Structure Interaction 1st Edition Stephane Grange
https://ebookmass.com/product/deterministic-numerical-modeling-ofsoil-structure-interaction-1st-edition-stephane-grange/
ebookmass.com
Undercover Wolf Paige Tyler
https://ebookmass.com/product/undercover-wolf-paige-tyler-3/
ebookmass.com
Her Ruthless Duke: A Guardian Ward Regency Romance (Rogue's Guild Book 1) Scarlett Scott
https://ebookmass.com/product/her-ruthless-duke-a-guardian-wardregency-romance-rogues-guild-book-1-scarlett-scott/
ebookmass.com
Spacecraft Systems Engineering 4th Edition – Ebook PDF Version
https://ebookmass.com/product/spacecraft-systems-engineering-4thedition-ebook-pdf-version/
ebookmass.com
Radio-Frequency Capacitive Discharges 1st Edition – Ebook PDF Version
https://ebookmass.com/product/radio-frequency-capacitivedischarges-1st-edition-ebook-pdf-version/
ebookmass.com
Foundation Engineering: Geotechnical Principles and Practical Applications 1st Edition Handy
https://ebookmass.com/product/foundation-engineering-geotechnicalprinciples-and-practical-applications-1st-edition-handy/
ebookmass.com
Macroeconomic Policy in Fragile States Ralph Chami
https://ebookmass.com/product/macroeconomic-policy-in-fragile-statesralph-chami/
ebookmass.com
https://ebookmass.com/product/etextbook-978-0205992126-evolutionarypsychology-the-new-science-of-the-mind-5th-edition/
ebookmass.com
TheMechanicsofAdvancedMaterials bookseriesfocusesonmaterials-andmechanics-relatedissuesaroundthebehaviorofadvancedmaterials,includingthemechanicalcharacterization,mathematical modeling,andnumericalsimulationsofmaterialresponsetomechanicalloads,variousenvironmental factors(temperaturechanges,electromagneticfields,etc.),aswellasnovelapplicationsofadvanced materialsandstructures.
Volumesintheseriescoveradvancedmaterialstopicsandnumericalanalysisoftheirbehavior,bringing togetherknowledgeofmaterialbehaviorandthetoolsofmechanicsthatcanbeusedtobetterunderstand,and predictmaterialsbehavior.Itpresentsnewtrendsinexperimental,theoretical,andnumericalresultsconcerningadvancedmaterialsandprovidesregularreviewstoaidreadersinidentifyingthemaintrendsin researchinordertofacilitatetheadoptionofthesenewandadvancedmaterialsinabroadrangeofapplications.
Serieseditor-in-chief:VadimV.Silberschmidt
VadimV.SilberschmidtisChairofMechanicsofMaterialsandHeadoftheMechanicsofAdvanced MaterialsResearchGroup,LoughboroughUniversity,UnitedKingdom.HewasappointedtotheChairof MechanicsofMaterialsattheWolfsonSchoolofMechanicalandManufacturingEngineeringatLoughboroughUniversity,UnitedKingdomin2000.Priortothis,hewasaSeniorResearcherattheInstituteAfor MechanicsatTechnischeUniversitatMuncheninGermany.EducatedintheUSSR,heworkedattheInstitute ofContinuousMediaMechanicsandInstituteforGeosciences[both theUSSR(later Russian)Academy ofSciences].In1993 94,heworkedasavisitingresearcher,FellowoftheAlexander-von-Humboldt FoundationatInstituteforStructureMechanicsDLR(GermanAerospaceAssociation),Braunschweig, Germany.In2011 14,hewasAssociateDean(Research).HeisaChartedEngineer,FellowoftheInstitution ofMechanicalEngineersandInstituteofPhysics,wherehealsochairedAppliedMechanicsGroupin 2008 11.HeservesasEditor-in-Chief(EiC)oftheElsevierbookserieson MechanicsofAdvancedMaterials.He isalsoEiC,associateeditor,and/orservesontheboardofanumberofrenownedjournals.Hehascoauthoredfourresearchmonographsandover550peer-reviewedscientificpapersonmechanicsandmicromechanicsofdeformation,damage,andfractureinadvancedmaterialsundervariousconditions.
Serieseditor:ThomasBo ¨ hlke
ThomasBo ¨ hlkeisProfessorandChairofContinuumMechanicsattheKarlsruheInstituteofTechnology(KIT),Germany.HepreviouslyheldprofessorialpositionsattheUniversityofKasselandatthe Otto-von-GuerickeUniversity,Magdeburg,Germany.HisresearchinterestsincludeFE-basedmultiscale methods,homogenizationofelastic,brittle-elastic,andvisco-plasticmaterialproperties,mathematical descriptionofmicrostructures,andlocalizationandfailuremechanisms.Hehasauthoredover130peerreviewedpapersandhasauthoredorcoauthoredtwomonographs.
Serieseditor:DavidL.McDowell
DavidL.McDowellisRegents’ProfessorandCarterN.Paden,Jr.DistinguishedChairinMetalsProcessingatGeorgiaTechUniversity,UnitedStates.HejoinedGeorgiaTechin1983andholdsadual appointmentintheGWWSchoolofMechanicalEngineeringandtheSchoolofMaterialsScienceandEngineering.HeservedastheDirectoroftheMechanicalPropertiesResearchLaboratoryfrom1992to2012.In 2012hewasnamedFoundingDirectoroftheInstituteforMaterials(IMat),oneofGeorgiaTech’sInterdisciplinaryResearchInstituteschargedwithfosteringaninnovationecosystemforresearchandeducation. HehasservedasExecutiveDirectorofIMatsince2013.Hisresearchfocusesonnonlinearconstitutive modelsforengineeringmaterials,includingcellularmetallicmaterials,nonlinearandtime-dependent fracturemechanics,finitestraininelasticityanddefectfieldmechanics,distributeddamageevolution, constitutiverelations,andmicrostructure-sensitivecomputationalapproachestodeformationanddamage ofheterogeneousalloys,combinedcomputationalandexperimentalstrategiesformodelinghighcyclefatigueinadvancedengineeringalloys,atomisticsimulationsofdislocationnucleationandmediationatgrain boundaries,multiscalecomputationalmechanicsofmaterialsrangingfromatomisticstocontinuum,and system-basedcomputationalmaterialsdesign.AFellowofSES,ASMInternational,ASME,andAAM,heis therecipientofthe1997ASMEMaterialsDivisionNadaiAwardforcareerachievementandthe2008Khan InternationalMedalforlifelongcontributionstothefieldofmetalplasticity.Hecurrentlyservesonthe editorialboardsofseveraljournalsandiscoeditorofthe InternationalJournalofFatigue
Serieseditor:ZhongChen
ZhongChenisaProfessorintheSchoolofMaterialsScienceandEngineering,NanyangTechnological University,Singapore.InMarch2000,hejoinedNanyangTechnologicalUniversity(NTU),Singaporeasan AssistantProfessorandhassincebeenpromotedtoAssociateProfessorandProfessorintheSchoolofMaterials ScienceandEngineering.SincejoiningNTU,hehasgraduated30PhDstudentsand5MEngstudents.Hehas alsosupervisedover200undergraduateresearchprojects(FYP,URECA,etc.).Hisresearchinterestincludes(1) coatingsandengineerednanostructuresforcleanenergy,environmental,microelectronic,andotherfunctional surfaceapplicationsand(2)mechanicalbehaviorofmaterials,encompassingmechanicsandfracturemechanicsofbulk,compositeandthinfilmmaterials,materialsjoining,andexperimentalandcomputational mechanicsofmaterials.Hehasservedasaneditor/editorialboardmemberforeightacademicjournals.Hehas alsoservedasareviewerformorethan70journalsandanumberofresearchfundingagenciesincludingthe EuropeanResearchCouncil(ERC).Heisanauthorofover300peer-reviewedjournalpapers.
ELSEVIERSERIESINMECHANICS OFADVANCEDMATERIALS
Contributors
SundaramVinodK.AnicodeDepartmentofAerospaceandMechanical Engineering,TheUniversityofArizona,Tucson,AZ,UnitedStates
AtilaBarutDepartmentofAerospaceandMechanicalEngineering,The UniversityofArizona,Tucson,AZ,UnitedStates
TinhQuocBuiDepartmentofCivilandEnvironmentalEngineering,Tokyo InstituteofTechnology,Tokyo,Japan
CaganDiyarogluDepartmentofNavalArchitecture,OceanandMarine Engineering,UniversityofStrathclyde,Glasgow,UnitedKingdom
MehmetDorduncuMechanicalEngineeringDepartment,ErciyesUniversity, Kayseri,Turkey
YakubuKasimuGaladimaDepartmentofNavalArchitecture,Oceanand MarineEngineering,UniversityofStrathclyde,Glasgow,UnitedKingdom
UgoGalvanettoIndustrialEngineeringDepartment,UniversityofPadova, Padova,Italy;CISAS“G.Colombo”,UniversityofPadova,Padova,Italy
XiaoqiaoHeDepartmentofArchitectureandCivilEngineering,CityUniversity ofHongKong,HongKongSAR,China
MasakiHojoDepartmentofMechanicalEngineeringandScience,Kyoto University,Kyoto,Japan
MichiyaImachiGraduateSchoolofAdvancedScienceandEngineering, HiroshimaUniversity,Higashihiroshima,Japan
AliJaviliDepartmentofMechanicalEngineering,BilkentUniversity,Ankara, Turkey
LeiJuCollegeofShipBuildingEngineering,HarbinEngineeringUniversity, China
EmmaLejeuneDepartmentofMechanicalEngineering,BostonUniversity, Boston,MA,UnitedStates
ChristianLinderDepartmentofCivilandEnvironmentalEngineering,Stanford University,Stanford,CA,UnitedStates
XuefengLiuDepartmentofMechanicsandAerospaceEngineering,Southern UniversityofScienceandTechnology,Shenzhen,Guangdong,China
ChunLuDepartmentofMechanicsandAerospaceEngineering,Southern UniversityofScienceandTechnology,Shenzhen,Guangdong,China
ErdoganMadenciDepartmentofAerospaceandMechanicalEngineering,The UniversityofArizona,Tucson,AZ,UnitedStates
NaokiMatsudaDepartmentofMechanicalEngineeringandScience,Kyoto University,Kyoto,Japan
AndrewMcBrideGlasgowComputationalEngineeringCentre,Schoolof Engineering,UniversityofGlasgow,Glasgow,UnitedKingdom
CodyMittsDepartmentofAerospaceandMechanicalEngineering,The UniversityofArizona,Tucson,AZ,UnitedStates
CongTienNguyenDepartmentofNavalArchitecture,OceanandMarine Engineering,UniversityofStrathclyde,Glasgow,UnitedKingdom
MasaakiNishikawaDepartmentofMechanicalEngineeringandScience,Kyoto University,Kyoto,Japan
ErkanOterkusDepartmentofNavalArchitecture,OceanandMarine Engineering,UniversityofStrathclyde,Glasgow,UnitedKingdom
SeldaOterkusDepartmentofNavalArchitecture,OceanandMarine Engineering,UniversityofStrathclyde,Glasgow,UnitedKingdom
MuratOzdemirDepartmentofNavalArchitectureandMarineEngineering, OrduUniversity,Ordu,Turkey
AnilPathrikarCentreofExcellenceinAdvancedMechanicsofMaterials,Indian InstituteofScience,Bangalore,Karnataka,India
TimonRabczukInstituteofStructuralMechanics,BauhausUniversityWeimar, Weimar,Germany
DebasishRoyCentreofExcellenceinAdvancedMechanicsofMaterials,Indian InstituteofScience,Bangalore,Karnataka,India
PraneshRoyCentreofExcellenceinAdvancedMechanicsofMaterials,Indian InstituteofScience,Bangalore,Karnataka,India
ArmanShojaeiInstituteofMaterialSystemsModeling,Helmholtz-Zentrum Geesthacht,Geesthacht,Germany
StewartA.SillingSandiaNationalLaboratories,Albuquerque,NewMexico, UnitedStates
PaulSteinmannGlasgowComputationalEngineeringCentre,Schoolof Engineering,UniversityofGlasgow,Glasgow,UnitedKingdom;Instituteof AppliedMechanics,Friedrich-Alexander-UniversitatErlangen-Nurnberg, Erlangen,Germany
SatoyukiTanakaGraduateSchoolofAdvancedScienceandEngineering, HiroshimaUniversity,Higashihiroshima,Japan
BozoVazicDepartmentofNavalArchitecture,OceanandMarineEngineering, UniversityofStrathclyde,Glasgow,UnitedKingdom
QingWangCollegeofShipBuildingEngineering,HarbinEngineering University,China
WenxuanXiaDepartmentofNavalArchitecture,OceanandMarine Engineering,UniversityofStrathclyde,Glasgow,UnitedKingdom
YanzhuoXueCollegeofShipBuildingEngineering,HarbinEngineering University,China
ZhenghaoYangDepartmentofNavalArchitecture,OceanandMarine Engineering,UniversityofStrathclyde,Glasgow,UnitedKingdom
MircoZaccariottoIndustrialEngineeringDepartment,UniversityofPadova, Padova,Italy;CISAS“G.Colombo”,UniversityofPadova,Padova,Italy XiaoyingZhuangChairofComputationalScienceandSimulationTechnology, InstituteofPhotonics,LeibnizUniversityHannover,Hannover,Germany; DepartmentofGeotechnicalEngineering,CollegeofCivilEngineering,Tongji University,Shanghai,China
Preface
AlthoughperidynamicswasoriginallyintroducedbyDr.StewartA. SillingfromSandiaNationalLaboratoriesin2000forpredictingand simulatingthefailureresponseofstructures,ithasbeenextendedand appliedtomanychallengingproblemsfromdifferentdisciplines.Ithas becomeauniqueapproachformultiphysicsanalysiswithdamagepredictioncapabilityacrossvaryinglengthscales.Sinceitsinception,peridynamicsisgrowingexponentiallybycontributionsandpublicationsof researchersfromdifferentpartsoftheworld.
Thisbookbringstogetherawiderangeofrecentcontributionsinthe areaofperidynamics.Wehopethatitoffersnewideasandmotivatesperidynamicresearcherstoexplorenewapplications.Thebookstartswithan introductorychapterauthoredbyDr.StewartSilling.Theremainingnineteenchaptersinthebookaredividedintotwosections:newconceptsin peridynamicsandnewapplicationsinperidynamics.Itpresentsnewtechniquessuchasdualhorizonperidynamics,damagemodelingusingthe phase-fieldapproach,peridynamicsforaxisymmetricanalysis,beam andplatemodelsinperidynamics,coupledperidynamicsandXFEM,fracturemechanicsevaluationwithperidynamics,andcontactanalysisof rigidanddeformablebodies.Also,itpresentscutting-edgeapplications ofperidynamicssuchasicemodeling,compositesdelaminationanddamageinceramics,modelingatnanoscale,andmore.
Weprofuselyappreciateandthanktherenownedauthorsfortheircontributionsandcommitmentfordifferentchaptersofthisbook.Wehope thatthisbookfurtheracceleratesthegrowthofperidynamicsbyproviding thebeginneraswellasthecurrentperidynamicresearcherswithrecent progressandnovelapplicationsofperidynamics.
Lastly,weappreciatetheencouragementandsupportofmanycolleaguesinthefieldofperidynamicsinthepreparationofthisbook,programmanagersatAFOSRfortheMURICenterforMaterialFailure PredictionthroughPeridynamicsattheUniversityofArizona(AFOSR GrantNo.FA9550-14-1-0073),andprogrammanagersatEOARDforthe financialsupporttotheUniversityofStrathclyde(AFOSRGrantNo. FA9550-18-1-7004).
ErkanOterkus, SeldaOterkus, and ErdoganMadenci
1.Whatisperidynamics?2
2.Peridynamicsobtainedfromthesmoothingofanatomicsystem3
3.Materialmodels5
3.1Linearmicroelasticmodel6
3.2Prototypemicroelasticbrittlemodel8
3.3Microelasticnucleationandgrowthmodel10
3.4Nonlinearandrate-dependentbond-basedmodels11
3.5Ordinarystate-basedmaterialmodels12
3.6Non-ordinarystate-basedmaterialsandthecorrespondencemodel15
4.Relationtothelocaltheory18
5.Simplemeshlessdiscretization19
6.Someresearchtrendsintheperidynamictheory20 6.1Specialpurposematerialmodels21 6.2Wavedispersion21 6.3Materialstability21 6.4Micropolartheories22
1.Whatisperidynamics?
Theperidynamictheoryisanalternativeformofcontinuummechanics thatismorecompatiblethanthestandard(local)theorywithdiscontinuitiessuchasgrowingcracks.Intheperidynamictheory,theequationof motionandmaterialmodelsuseintegralsratherthanpartialdifferential equations.Thisallowstheperidynamicequationstobeapplieddirectly onthesurfaceofacrack.Theequationofmotionreplacestheterminthe localtheorythatcharacterizestheinternalforceswithinamaterial.
where s isthestresstensorand f(q,x,t)isaforcedensity(perunitvolume squared)thataneighboringpoint q exertson x.Thisforcedensityis determinedbythedeformationaccordingtothematerialmodel.Itis alwaysrequiredasaconsequenceofNewton’slawsthat
forall x, q, t.Theregionofintegrationin Eq.(1.1) isthe family of x,which isaneighborhoodwhoseradius d > 0iscalledthe horizon (Fig.1.1).
Thehorizonisacutoffdistanceforforceinteractions.
Using Eq.(1.1),theperidynamicequationofmotionisasfollows:
where r isthemassdensity, y isthedeformationmap,and b isthe externalbodyforcedensityfield.Theattributeofthetheorythatallows interactionsbetweenpointssuchas x and q directlyacrossafinitedistanceissometimescalled strongnonlocality.
Inintroducingperidynamics,thebasic Eq.(1.3) isusuallypresentedas anassumptionthatiselaboratedupontoshowthatithasdesirable properties,suchasbeingabletosustaingrowingcracks,andnotviolating anylawsofphysics(Silling,2000).Thisleavessomepeoplewondering, “Wheredoesthiscomefrom?”Inparticular,thestronglynonlocalnature of Eq.(1.3) isperceivedaslackingmotivation.Withthisinmind,Ihope
thatthediscussioninthenextsectionhelpstomotivatetheperidynamic continuumtheoryespeciallywithregardtononlocality.
2.Peridynamicsobtainedfromthesmoothingofanatomic system
Afundamentalconceptincontinuummechanicsistherepresentation ofamaterialasamathematicallycontinuousfield,eventhoughinreality anymaterialismadeofatomsandmolecules.Onewaytojustifythe assumptionofacontinuumistoapplyasmoothingfunctiontothesystem ofparticles.Inthefollowing,wedefineacontinuousdisplacementfieldin thiswayandinvestigatetheevolutionequationthatthiscontinuousfield obeys.Theevolutionequationturnsouttobetheperidynamicequationof motion.
Consideranassemblyofmutuallyinteractingparticles(pointmasses) inacrystalwithmass Mk, k ¼ 1,2, ,N.Letthereferencepositionsofthese particlesbedenoted xk,andthedisplacementvectors uk(t).Forsimplicity, thermaloscillationswillbeneglectedinthefollowingdiscussion.
Supposeanyparticle [ exertsaforceFk[ ðtÞ onanyparticle k.Asa notationalconvenience,set Fkk ¼ 0 forany k.Theseforcesareassumedto havetheantisymmetrygivenby
Bond
ℋ = family of
FIGURE1.1 Thehorizonandfamilyofamaterialpoint x
forall k, [,and t.Itisalsoassumedthatthereisacutoffdistance d forthe atomicinteractionssuchthat Fk[ ¼ 0if jx[ xk j > d.
Additionally,particle k issubjecttoaprescribedexternalforce Bk(t).For any x˛R3,defineasmoothingfunction U(x, $)suchthatthefollowing normalizationholds:
foranypoint p.Itisconvenienttoassumethatatany x, U(x, $)vanishes outsideaneighborhoodofradius R,where R isapositivenumber.Define thesmoothedmassdensityandbodyforcedensityfieldsby
Definethesmootheddisplacementfieldby
Nowweinvestigatetheevolutionequationfor u.Theparticlesobey Newton’ssecondlaw, Mk € uk ðtÞ¼ X [ Fk[ ðtÞþ Bt ðtÞ.(1.8)
Differentiating Eq.(1.7) twicewithrespecttotimeyields rðxÞuðx; tÞ¼ X k Uðx; xk ÞMk uk ðtÞ (1.9)
From Eqs.(1.6),(1.8),and(1.9),
rðxÞ € uðx; tÞ¼ X k Uðx; xk Þ"X [ Fk[ ðtÞþ Bk ðtÞ# ¼ X k X [ Uðx; xk ÞFk[ ðtÞþ bðx; tÞ (1.10)
From Eqs.(1.5)and(1.10),
rðxÞuðx; tÞ¼ X k X [ Uðx; xk ÞFk[ ðtÞ Z Uðq; x[ Þdq þ bðx; tÞ (1.11)
Eq.(1.11) canberewrittenasfollows:
rðxÞuðx; tÞ¼ Z fðq; x; tÞdq þ bðx; tÞ (1.12)
where
and b isgivenby Eq.(1.6).Itiseasilyshownfrom Eqs.(1.4)and(1.13) that f hastheantisymmetry Eq.(1.2).Thevectordefinedby x ¼ q x (1.14) iscalleda bond.(Whentalkingaboutbonds,itisalwaysassumedthat x s 0,withoutexplicitlystatingthis.)Thefunction f iscalledthe pairwise bondforcedensity andhasdimensionsofforce/volume2.From Eq.(1.13), thepoints x and q interactonlyif
Thelength d isthehorizonforthecontinuummodel(Fig.1.1).
Insummary,wedefinedaweightingfunction U andusedittodefine smoothedfields r, b,and u.Withthesedefinitions,andNewton’ssecond lawappliedtotheparticles,thesmootheddisplacementfieldwasfound toobeytheperidynamicequationofmotion Eq.(1.12).Theperidynamic bondforcesthatappearinthisequationofmotionaredefinedby Eq. (1.13).Conceptually,theequationofmotionis,andshouldbe,nonlocal becausechangingthedisplacementofasingleparticle k directlyaffects thesmootheddisplacementsatallthepoints x whosesmoothingfunction U(x, $)havenonzerovaluesat xk.Amorecompletederivationofthe peridynamicequationswasobtainedfromstatisticalmechanicsby LehoucqandSears(2011).
Thedefinitionofthepairwisebondforcedensity Eq.(1.13) isnotvery practicalasamaterialmodelbecauseitdoesnotdirectlyrelatethevalues of u near x tothebondforces f.Morepracticalmethodsofdetermining f arediscussedin Section3.
3.Materialmodels
Thepurposeofamaterialmodelinperidynamicsistodeterminethe valuesofthepairwisebondforcedensity f(q,x,t)intermsofthesmoothed displacementsinthevicinityof x and q andanyotherphysicallyrelevant fieldssuchastemperature.(Theword“smoothed”willbeomittedfrom nowon,sincewearenolongerconcernedwiththeunderlyingatomic system.)Itisassumedthatthereisahorizon d,suchthat
forall x,q,t.Thefollowingdiscussionstartswiththeconceptually simplestmaterialmodelandprogressestomoreadvancedmodels.
3.1Linearmicroelasticmodel
Thesimplesttypeofmaterialmodeliscalled linearmicroelastic.Inthis model,eachbondactslikealinearspring,andthebodycanbethoughtof asanetworkcomposedofaninfinitenumberofthesesprings.Todefine thepairwisebondforcedensityinalinearmicroelasticmaterial,wefirst definetheunitvector M inthedirectionofadeformedbond x ¼ q x:
Alsodefinethe bondelongatione andthe bondstrains by
Thebondelongationisthereforethechangeinlengthofabondasit deforms.Thepairwisebondforcedensityisthengivenby
where c(x)isthe springconstant forthebond x and b f isascalarvalued functionthatgivesthemagnitudeoftheforcedensity.
Thelinearmicroelasticmaterialmodeliselasticintheusualsenseof continuummechanics.Abodycomposedoflinearmicroelasticmaterial storesstrainenergyduetoquasi-staticloadingfromexternalforces.This energystorageisreversible,sinceitcanallberecoveredbyreversingthe externalforcesandunloadingthebodytoitsoriginalcondition.Inother words,thereisnoenergydissipation.
Thestoredenergycanbeidentifiedwithindividualbonds.Eachbond x hasa micropotentialw(s)suchthat
Hence,forthelinearmicroelasticmaterial,
Themicropotentialisrelatedtothestrainenergydensityatanypoint x bysummingupthecontributionsfromallthebondsconnectedto x:
Thefactorof1/2appearsin (1.22) becauseeachendpointofabond “owns”onlyhalfofthebonds’smicropotential.
Thestrainenergydensitygivenby (1.22) hasthesamemeaningasin thelocaltheory,sinceitrepresentsthepotentialenergyperunitvolume thatisstoredat x duetodeformationofthenearbymaterial.Ifthematerialisisotropicaswellaslinearmicroelastic,thisinterpretationprovidesaneasywaytocalibrate c(x)ifthegeneralformofthedependenceof c onbondlengthisgiven.Foranisotropicmaterial, c(x)dependsonlyon thebondlength, x ¼ |x|.Byrequiringtheperidynamicstrainenergy densitygivenby (1.22) toequalitsvalueinthelocaltheoryforanisotropic expansion,itiseasilyshownthat c isrelatedtothebulkmodulus k bythe followingexpression(SillingandAskari,2005):
Asaspecialcase,if c(x)hastheform
ðxÞ¼
forany0 <x d,where c0 isaconstant,then Eq.(1.23) yields
Thus,withthesimplifyingassumption Eq.(1.24),ifthehorizon d is given,theonlyparameterinthelinearmicroelasticmaterialmodelis easilycomputedfromthebulkmodulus.
Thelinearmicroelasticisanexampleof bond-based peridynamicmaterialmodels.Thisclassofmaterialmodelshasthepropertythatthe pairwiseforcedensityinthebond x ¼ q x isfullydeterminedbythe deformationofthatparticularbond,anddoesnotdependonwhathappensinotherbonds.
Bond-basedmaterialshavetheadvantageofbeingsimpletounderstandandcalibrate.Theyallowforgeometricnonlinearity,becausethe bondsrotatealongwiththebondsastheydeform.Theyconserveangular momentum,becauseregardlessofthedeformation,eachpairwisebond forceexertszeromomentontheendpointsofthebond.Bond-based materialmodelscanincludematerialnonlinearity,aswellasgeometric nonlinearity,byusingafunction b f in Eq.(1.19) thatincludesnonlinear dependenceonthebondstrain.
3.2Prototypemicroelasticbrittlemodel
Bond-basedmaterialsalsolendthemselvestoasimplewaytomodel damage. Eq.(1.19) ismodifiedtoincludeahistory-dependenttermthat reflects bondbreakage:
where m isabinary-valuedfunctionthatstartsat1anddropsto0accordingtosomeprescribeddamagecriterion.Thesimplestsuchcriterion breaksabondwhenitsstrainexceedssomepredefinedvalue s0:
where H istheHeavisidestepfunctionand tbreak istheearliesttimeat which s(x,t) s0.Thelinearmicroelasticmaterialusing Eq.(1.24) and equippedwiththebondbreakagecriteriongivenby Eqs.(1.26)and(1.27) iscalledthe prototypemicroelasticbrittle (PMB)materialmodel.
WiththePMBmodel,thecriticalbondstrain s0 canbecalibratedto matchagivencriticalenergyreleaserateforarealbrittlematerial.Thisis donebysumminguptheworkrequiredtobreakallthebonds(which equalsthemicropotentialatbreakage)amongallthebondsthatinitially connectedonsideofacracksurfacetotheother.Thisprocedureallows s0 tobecomputedexplicitlytoreproduceagivencriticalenergyreleaserate G0,thebulkmodulus,andthehorizonforthePMBmaterialmodel.Detailsofthiscalculationaregivenin SillingandAskari(2005).
Theresultinthreedimensionsisgivenby
ThePMBmodelislimitedinthetypesofmaterialsitcanrepresent(see Section3.5);notablythePoissonratioisrestrictedto1/4inthreedimensions.Nevertheless,thePMBmodelhasfoundmanyapplications andoftengivesgoodresultsforproblemsinwhichthisrestrictionis tolerable.Forexample, Fig.1.2 showsasimulationoftheimpactofa brittlecylinderagainstarigidwall. Fig.1.3 showsthecross-sectionofa glassrodthatundergoesfractureintension.Thefracturestartsatasmall defectattheloweredgeofthecross-section.Asthefracturegrowsand speedsup,itstrajectorybecomesunstable,resultinginfeaturesresemblingthefamous“mirror-mist-hackle”transitionindynamicbrittle fracture.Thesefiguresillustrate autonomouscrackgrowth inperidynamics, whichmeansthatcracks“dowhattheywant”:theirevolutionisnot controlledbyanysupplementalmathematicalrelations.
FIGURE1.2 Peridynamicsimulationoftheimpactofabrittlecylinderonarigidwall.
FIGURE1.3 Simulatedsurfaceofadynamicallyfracturedglassrod,showingfeatures similartothemirror-mist-hackletransition.Colorsrepresenttheaxialpositionofthesurfacemodelisobtained(WecknerandMohamed,2013).
3.3Microelasticnucleationandgrowthmodel
Recallfrom Section3.2 thatwiththePMBmodel,thecriticalbond breakagestrain s0 iscalibratedtoreproduceagivencriticalenergyrelease rate G0.So,ifahomogeneousbodyisstretched,thestrainatwhich damagefirstoccurs(“nucleates”)isthissame s0.Sincethis s0 dependson d accordingto Eq.(1.28),thestrainatnucleationalsodependson d.Thisis frequentlyanunsatisfactorysituationformodelingrealmaterials, becausewewouldliketobeabletospecifybothanucleationstrainand thecriticalenergyreleaseforanyvalueof d and k.
Fortunately,afurtherrefinementofthePMBmaterialallowsboththe strainatnucleationand G0 tobeprescribed.Ifthereisnodamageattime t withinthehorizonofapoint x,thenthecriticalstrainistakentobea constant snuc,whichisaninputparameter.Thisis,ineffect,thestrainat nucleation,andisindependentof d.If,ontheotherhand,damageis presentwithinthehorizonof x,thenthecriticalstrainisdeterminedby Eq.(1.28).Theresultingmodeliscalledthe microelasticnucleationand growth (MNG)model(SillingandFermen-Coker,2020).
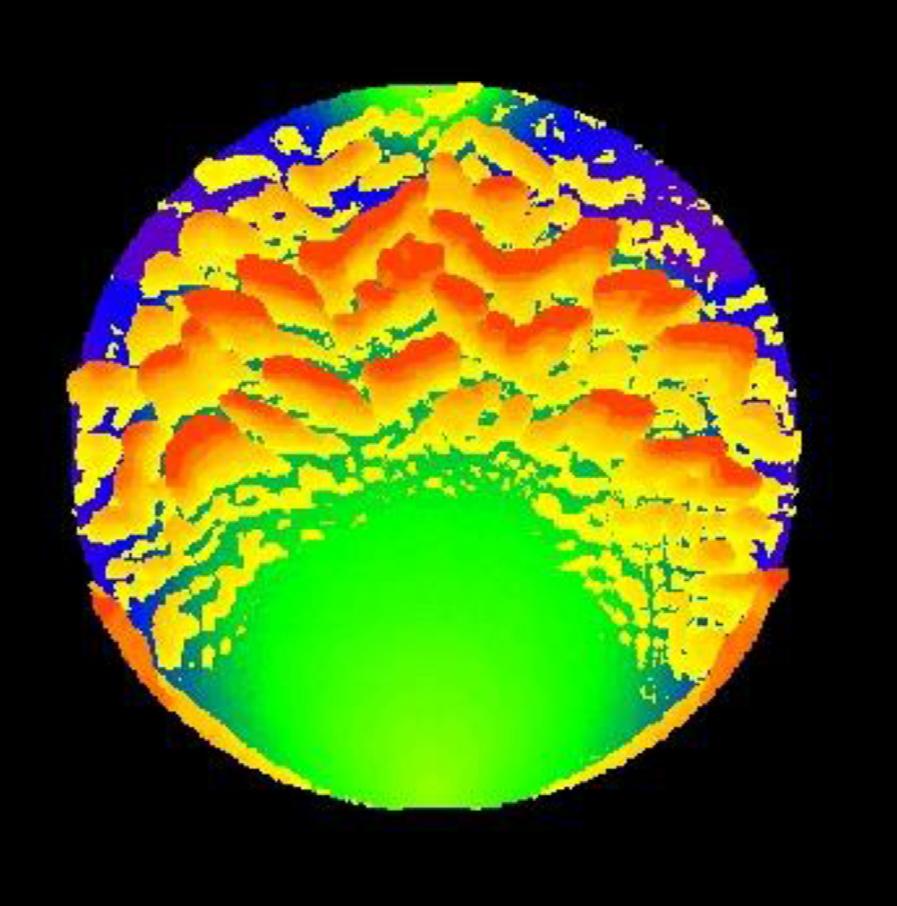
AnexampleusingtheMNGmodelisshownin Fig.1.4.Ahardsphere impactsabrittleelasticmembrane.Theinitialfailureoccursnearthepoint ofimpact.Thestoredstrainenergyinthemembranepriortothisinitial failureissuddenlyreleasedandcreatesafamilyofradialdynamiccracks.
FIGURE1.4 PerforationofamembranebyaspheremodeledwiththeMNGmaterial model.
ThegrowthofthesecracksfollowstheGriffithcriterion,whichisbuilt into Eq.(1.28).Thisexamplealsoillustratesthecapabilityofbond-based peridynamicmaterialmodelstotreatgeometricnonlinearity,duetothe largeout-of-planedisplacements.
3.4Nonlinearandrate-dependentbond-basedmodels
Thematerialmodelsdiscussedintheprecedingsectionsassumea lineardependenceofthebondforceonthebondextension(orequivalentlythebondstrain).Avarietyofusefulbond-basedmodelscanbe obtainedbyincludingnonlinearityorotherphysicalfields.Byincluding therateofbondstrainin Eq.(1.19),aviscoelasticperidynamicmaterial.
where c1(x)isamaterialpropertythatcontrolstheratedependence.
Thebondforcemagnitude b f ðsÞ canalsoincludehistorydependence. Onewaytomodelplasticityistointroduceyieldphenomenaintothe individualbondresponses(MacekandSilling,2007).Inthe microplastic model,thereisahistory-dependentyieldstrainineachbond,denotedby sy(x,t).Thebondforcemagnitudeisthengivenby
Theyieldstrainevolvesasfollows:
Thermalexpansioniseasilyincludedinthebasiclinearmicroelastic model Eq.(1.19) bysubtractingoffatemperature-dependentexpansion strainfromtheexpressionforbondforcedensity:
where q isthetemperature, q0 isroomtemperature,and a isthecoefficient ofthermalexpansion(CTE)(MadenciandOterkus,2013).Thesimple treatmentofthermalexpansionin Eq.(1.32) hasbeenappliedtocrack growthdrivenbytemperaturegradientsinbrittlematerialssuchasglass (KilicandMadenci,2009; Xuetal.,2018),rock(Wangetal.,2018b),and ceramicnuclearfuelpellets(MellaandWenman,2015; Chenetal.,2016; OterkusandMadenci,2017; Wangetal.,2018c).
Recently,XuandFosterappliedreasoninginvolvingasmoothed displacementfielddefinedsimilarlyto Eq.(1.7),togetherwithamultiscalemodel,toderiveaperidynamicmodelforwavesinlayeredelastic media(XuandFoster,2020).Thismodelwasdemonstratedtoreproduce aspectsofwavepropagationinthesemedia.
3.5Ordinarystate-basedmaterialmodels
Bond-basedelasticmaterialsalwayshaveaPoissonratioof1/4inthree dimensions(TrageserandSeleson,2020).Thisrestrictionisunacceptable formanyapplications.Themicroplasticmodel,becauseeachbondrespondsindependentlyofalltheotherbondsinthefamily,cannotenforce plasticincompressibility.Thisrestrictionisunsatisfactoryformostmetals atmoderatepressure.
Toovercometheseandotherlimitationsofbond-basedmaterial models,analternativeapproachcalled state-based materialmodelingwas developed(Sillingetal.,2007).Instate-basedmaterialmodels,the assumptionthateachbondrespondsindependentlyoftheothersis dropped.Instead,theforcedensityineachbondcanbedeterminednot onlybythedeformationofthatbondbutalsobyanyotherbondinthe family.ThisallowsanyadmissiblePoissonratiotobemodeled,andit allowssuchfeaturesasplasticincompressibilitytobeenforced.Theprice thatispaidforthisgreatergeneralityistheneedtousemoreabstractand complicatedmathematicaltools.Thesetoolsarestatesandtheiraccompanyingnotionoffirstderivatives,calledFre ´ chetderivatives.
Informulatingastate-basedmaterialmodel,weneedtospecifyhow theforcedensityinabond x dependsonthedeformationofallthebonds inthefamilyof x,whichareingeneralinfiniteinnumber.Tokeeptrackof thesemanybonddeformations,itisnecessarytointroducenonlocaloperatorscalled states.Astate A[x,t]CxD isamappingfromthebond x tosome otherquantity,eitheravectororscalar.Thenotation[x,t]isusedifthe stateitselfisafunctionofpositionandtime.
Statesformalinearvectorspaceandcanbemanipulatedwithmanyof theusualalgebraicoperators.Forexample,thesumoftwostates A and B isthestatedefinedby
forall x.Theinnerproductassociatedwithstatesiscalledthe dotproduct andisthescalardefinedby
forallstates A and B.
Thebasickinematicalquantityforpurposesofstate-basedmaterial modelingisthe deformationstate Y definedby
forany x,q,t.Thedeformationstatemapsanybondtoitsimageunderthe deformation.Internalforcesamongbondsarecontainedinthe forcestate T suchthat
Thetwotermsontherighthandsideof (1.36) aretheforcestatesdueto thematerialmodelsat x and q.Amaterialmodel b T fora simple materialis astate-valuedfunctionofastate:
Formoregeneralmaterials,thematerialmodelcanincludedependenceonothervariablessuchastemperature.
Howistheforcestaterelatedtothestresstensorinlocaltheory?Fora uniformdeformationofahomogeneousmaterial,theapplicableconcept ofstressisgivenbythe partialstresstensor (Sillingetal.,2015):
Thepartialstresstensor,forauniformdeformationofahomogeneous material,ismechanicallysimilartothefirstPiolastresstensorsince npn equalstheforceperunitareainthereferenceconfigurationthrougha planewithunitnormal n.Thepartialstresstensorisaspecialcaseofthe peridynamicstresstensor,whichisapplicabletomoregeneraldeformations andheterogeneousmaterials(LehoucqandSilling,2008)butismuch moreburdensometocomputeinpractice.
Anexampleofwhatstate-basedmaterialmodelshavetoofferisprovidedbythenonlocaldilatation.Toexplainthis,firstletthe extensionstate e andthe bondlengthstatex bedefinedby
foranybond x.Let u beaweightingfunctioncalledthe influencestate. Thendefinethe nonlocaldilatation by
Itiseasilyconfirmedthatforasmallisotropicstrain,thenonlocal dilatationdefinedby Eq.(1.40) hasthesamevalueastheconventional localdilatationinthreedimensions.
Withthehelpofthenonlocaldilatation,ageneralizationofthelinear microelasticmaterialiseasilydefined.Recallfrom Eqs.(1.21)and(1.22)
thatforanydeformationinalinearmicroelasticmaterial,thestrainenergydensityatapointisgiven(usingstatenotation)by
where C isthestatedefinedby
Toovercometherestrictionof n ¼ 1/4forthelinearmicroelasticmaterial,anewtermisaddedto Eq.(1.41) thatdependsonlyonthevolume change:
where w isthenonlocaldilatationdefinedby Eq.(1.40) and g isaconstant. Toderivethebondforcesfromastate-basedexpressionforstrainenergydensitysuchas Eq.(1.43),aconceptofdifferentiationwithrespectto statesmustbeintroducedanalogoustothetensorgradientinthelocal theory.Thisconceptisprovidedbythe Fre ´ chetderivative,whichisatypeof functionalderivative.If J(A)isascalar-valuedfunctionofastate,then theFre ´ chetderivative JA(A)isthestatesuchthatforanyincrement DA, thechangein J obeys
Inanelasticstate basedmaterialmodel,theforcestateisrelatedtothe strainenergydensityby
foranydeformationstate Y.Applying Eq.(1.45) totheexpressionfor strainenergydensity Eq.(1.43),theforcestateisgivenby
where M isthestatedefinedby
forall x.Byrequiringthestrainenergydensityin Eq.(1.43) toequalits localcounterpartforbothisotropicexpansionanduniaxialstrain,itis straightforwardtoshowthat
(1.48) where l and m aretheLame ´ moduliand
UsingthestandardidentityforthePoissonratio n ¼ l/2(l þ m),one findsthat
(1.50)
In Eq.(1.50),ifweset g ¼ 0,then n ¼ 1/4,aswithabond-basedmaterial.Ifweset b ¼ 0,then n ¼ 1/2,aswithafluidinthelocaltheory.Thus, thestate-basedmaterialmodel Eq.(1.46) canreproduceanyadmissible Poissonratio.Thematerialmodel Eq.(1.46) iscalledthe linearperidynamic solid (LPS),anditistheworkhorseofperidynamicmodeling.Itisusually combinedwithabondbreakagecriterionsimilarto Eq.(1.26).Moredetailscanbefoundin(Sillingetal.,2007).
IntheforcestatefortheLPS,givenby Eq.(1.46),thebondforceisalwaysparalleltothedeformedbonddirection.Thismeansthatthereis alwayszeronetmomentonanymaterialpoint,soconservationofangular momentumissatisfiedtrivially.State-basedmaterialmodelswiththis propertyarecalled ordinary state-basedmodels.Allothermodelsare called non-ordinary state-basedmaterialmodels.
Ordinarystate-basedmodelshavebeendevelopedforviscoelasticity (Mitchell,2011; MadenciandOterkus,2017; Delormeetal.,2017)and elastic-plasticresponse(MadenciandOterkus,2016; Liuetal.,2020; Zhou etal.,2018; AsgariandKouchakzadeh,2019).Compositesandother anisotropicmaterialmodelshavebeensuccessfullydeveloped.Mostof thesecompositemodelsintroduceanisotropybychangingthebond propertiesaccordingtothebonddirection.Boththeelasticpropertiesand thebondfailurecriteriacanbeafunctionoftheinitialbondangle.For example,abondparalleltothedirectionofareinforcingfibercanbegiven propertiesthatarestifferelasticallyandstrongerwithrespecttobond breakagethantheotherbonds.Asummaryofperidynamicapproachesto compositemodelingcanbefoundin Askarietal.(2015).
3.6Non-ordinarystate-basedmaterialsandthecorrespondence model
Innon-ordinarymodels,thebondforcevectorisnotnecessarilyparalleltothedeformedbonddirection,sothebalanceofangular
momentumisnottriviallysatisfied,asitiswithbond-basedandordinary state-basedmaterialmodels.Instead,itmustbeenforcedasaseparate conditiononthemodel:
foralldeformationstates Y.Nevertheless,non-ordinarymodelscanbe veryusefulinapplications.
Theclassofnon-ordinarystate-basedmodelsthathasgainedthemost attentionistheclassof correspondence materials.Inthesemodels,theforce stateisobtainedfromaPiolastresstensor s thatiscomputedfromany constitutivemodelinthelocaltheory.Theresultingforcestateisgivenby
where K isthesymmetric shapetensor definedby
Forpurposesoffinding s fromalocalconstitutiverelation,the followingnonlocalapproximationtothedeformationgradienttensoris used:
Thecorrespondencematerialshavesomedesirableproperties, includingthattheyallowperidynamicstouselocalmaterialmodels directly.If s obeysthebalanceofangularmomentum,thatis,ifthe Cauchystresstensorissymmetric,thentheforcestategivenby Eq.(1.52) doessoaswell.Ifthelocalmaterialmodelishyperelastic,thentheperidynamicmodelisaswell,inthesenseof Eq.(1.45).
Undesirabletraitsofthecorrespondencemodelsincludethefactthat theycansustain“waveswithzerovelocity”(inadditiontophysically reasonablewavesatfinitevelocity).Thisimpliesthatinequilibrium, perturbationscanbefoundtothedisplacementthatdonotchangethe potentialenergyinabody.Thisphenomenongivesrisetotroublesome “zeroenergymode”instabilitiesinnumericalimplementations.Fortunately,thereareeffectivewaysofstabilizingthesematerialsbyadding termstotheenergythatpenalizethezeroenergymodes.Onesuchstabilizationmethodassociatesastrainenergypenaltywithdeparturesofa deformationstatefromauniform(affine)deformation(Silling,2017).An exampleofplasticdeformationusingthismethodisshownin Fig.1.5, whichillustratestheneckingofanelastic-plasticbar.
Bonddamageisusuallyimplementedincorrespondencemodelsby setting uCxD ¼ 0ifthebond x isbroken.Whenusingthisapproachto
damage,anadditionalsofteningtermmustbeincludedinthestress tensorthatreflectsthetotaldamageamongallthebondsconnectedtoany x.Withoutthisterm,theterm K 1 in Eq.(1.52) increasesasdamage progresses,causingthebondforcestoincreasenonphysicallyamongthe unbrokenbonds.Tupek,Rimoli,andRadovitzkyproposedamethodfor treatingbonddamageusingalocalcontinuumdamagemodelappliedto theconditionsandbothendpointsofthebond(Tupeketal.,2013).
Statesprovidetoolstotailorthedamageresponseofmaterialsto reproducemanycharacteristicsofrealmaterialfailure.Recallthatthe mostbasicbondbreakagecriterioncomparesthecurrentstraininabond toapredefinedcriticalstrain s0.Thebondbreakswhen s s0.AMohrCoulombtypeoffailureresponsecanbeobtainedbyincreasingthe criticalstrainasthehydrostaticpressureincreases(andthereforethe dilatationdecreases):
where w isgivenby Eq.(1.40) and a and b areconstants. Manyothertypesofdamagecriteriaarepossiblewithstate-based concepts.Forexample,theHashincriterionforcompositescanbe applied(Shangetal.,2019).Aversionofcontinuumdamagemechanics hasbeenproposedthatisconsistentwithnonlocalmechanicsand
s0 ¼ a bw
(1.55)
FIGURE1.5 Neckingofanelastic-plasticbarusingastabilizedcorrespondencemodel. Colorsrepresentequivalentplasticstrain,red ¼ 1.4.
thermodynamics(Silling,2019).Fatiguefracturecanbesimulatedwitha bondbreakagelawthattakesintoaccountthenumberofloadingcyclesin abondaswellastheamplitudeofthecyclesateachmaterialpoint,for example(Zhangetal.,2016).
4.Relationtothelocaltheory
Intheperidynamictheory,allinternalforcesaretreatedasstrongly nonlocal,thatis,theyactacrossafinitedistance.Theseforcesarecharacterizedthroughbondinteractions,asdescribedabove.Thehorizonacts asacutoffdistanceforthesebondinteractions.Ingeneral,foranyvalueof thehorizon,materialmodelscanbecalibratedtomatchtheusualbulk materialproperties,asdemonstratedabovefortheLPSmaterial.
Whathappensifthehorizonisreducedtonearlyzero?Itisreasonable toexpectthatthelocaltheoryshouldberecoveredinthislimit.This convergenceisindeedwhathappens,withcertainrestrictions.
Oneaspectofthisconvergenceisthataperidynamicmaterialmodel calibratedtoreproducethebulkelasticpropertiesofmaterialhasthe followingproperty.Supposethematerialiselastic,andforany d,the strainenergydensity c W d iscalibratedsuchthatforanydeformation gradienttensor F,
Thenthepartialstressdensitygivenby Eq.(1.38) hasthepropertythat foranysmoothdeformation,atany x,
0(1.56) where s isthefirstPiolastresstensor,givenby sðxÞ¼ Wlocal vF ðFðxÞÞ; F ¼ vy vx .
Severalstrongerresultsaboutconvergencealsoappearintheliterature.Manyofthesepertaintotheconvergenceofperidynamicdisplacementfieldstosolutionofdisplacementequationofequilibrium(Navier’s equation)inthelocaltheory(EmmrichandWeckner,2007a,b,c; Duetal., 2013; MengeshaandDu,2014a,b).Ithasalsobeendemonstratedmany timesthatasapracticalmatter,peridynamicsolutionsagreecloselywith finiteelementsolutionswhencomparablematerialmodelsareused.
Theaboveremarksaboutconvergenceapplywhenthedeformationis smooth.Butremarkably,Liptonandcoworkers(Lipton,2014, 2016; Liptonetal.,2018a,b, 2019; JhaandLipton,2018)haveproventhatwitha certainclassof nonconvex elasticperidynamicmaterials,thesolution convergestoadeformationthatcontainscracksbutisclassicallysmooth offofthecracks.Awayfromthecracks,thedeformationconvergestoa fieldthatsatisfiesthelocalPDEswithasuitabledefinedlocalmaterial modelthatemergesfromtheanalysis.Evenmoreremarkably,under loadingconditionsthatcausethesecrackstogrow,thecracksconsumea definiteamountofenergyperunitofaddedsurfaceareaonthecrack faces.Inotherwords,theyareGriffithcracks.Thecracksgrowwithout theuseofaseparatebondbreakagecriterion.
5.Simplemeshlessdiscretization
Recallfrom Eq.(1.12) thelinearmomentumbalanceforperidynamics:
forall x,t.Thesimplestnumericaldiscretizationof Eq.(1.57) dividesthe referenceconfigurationofacontinuousbodyintoLagrangiannodeswith positions xi,eachofwhichhasadefinitevolume Vi inthereference configuration(SillingandAskari,2005).Theintegralin Eq.(1.57) is approximatedbyafinitesum:
where a n i istheaccelerationofnode i attimestep n.Thediscretized pairwisebondforcedensities fij n arefoundfromtheoriginalmaterial modelin Eq.(1.58):
Thevelocitiesanddisplacementsareupdatedusinganexplicitfinite differenceapproximationintime:
where h isthetimestepsize.
Thediscretizationdescribedaboveismeshlessinthesensethatthere arenoelementsorothergeometricalconnectionsbetweenthenodes.The methodsuffersfromsomeknownproblems,includingthatitfailsthe patchtestunlessthegridspacingisconstant.Thatis,ifthenodesare