https://ebookmass.com/product/multivariate-frequencyanalysis-of-hydro-meteorological-variables-a-copula-basedapproach-fateh-chebana/
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
Time-frequency Analysis of Seismic Signals Yanghua Wang
https://ebookmass.com/product/time-frequency-analysis-of-seismicsignals-yanghua-wang/
ebookmass.com
Multivariate Data Analysis 8th Edition Edition Joseph F. Hair
https://ebookmass.com/product/multivariate-data-analysis-8th-editionedition-joseph-f-hair/
ebookmass.com
Practical Radiology: A Symptom-Based Approach 1st Edition
https://ebookmass.com/product/practical-radiology-a-symptom-basedapproach-1st-edition/
ebookmass.com
Sell Yourself: How to Create, Live, and Sell a Powerful Personal Brand Cindy Mcgovern
https://ebookmass.com/product/sell-yourself-how-to-create-live-andsell-a-powerful-personal-brand-cindy-mcgovern/
ebookmass.com
A Song for the Dead: A totally addictive edge-of-your-seat crime thriller (Detectives Kane and Alton Book 21) D.K. Hood
https://ebookmass.com/product/a-song-for-the-dead-a-totally-addictiveedge-of-your-seat-crime-thriller-detectives-kane-and-altonbook-21-d-k-hood/ ebookmass.com
The War Within: Private Interests and the Fiscal State in Early-Modern Europe 1st ed. Edition Joël Félix
https://ebookmass.com/product/the-war-within-private-interests-andthe-fiscal-state-in-early-modern-europe-1st-ed-edition-joel-felix/ ebookmass.com
Comparative study of Chronic Ulcerative Dermatopathy in cultured meagre, Argyrosomus regius M.I. Tsertou
https://ebookmass.com/product/comparative-study-of-chronic-ulcerativedermatopathy-in-cultured-meagre-argyrosomus-regius-m-i-tsertou/
ebookmass.com
Coptic Interference in the Syntax of Greek Letters from Egypt Victoria Beatrix Maria Fendel
https://ebookmass.com/product/coptic-interference-in-the-syntax-ofgreek-letters-from-egypt-victoria-beatrix-maria-fendel/ ebookmass.com
Morphology effect of MnO2 promoter to the catalytic performance of Pt toward methanol electrooxidation reaction Yuan-Yuan Feng & Gui-Hua Song & Qiang Zhang & Jian-Ning Lv & Xi-Yu Hu & Yu-Long He & Xin Shen
https://ebookmass.com/product/morphology-effect-of-mno2-promoter-tothe-catalytic-performance-of-pt-toward-methanol-electrooxidationreaction-yuan-yuan-feng-gui-hua-song-qiang-zhang-jian-ning-lv-xi-yuhu-yu-long-he-xin/ ebookmass.com
Thirst Trapp Farms (Big Timber Book 1) Christina Hill
https://ebookmass.com/product/thirst-trapp-farms-big-timberbook-1-christina-hill/
ebookmass.com
MULTIVARIATEFREQUENCYANALYSISOF HYDRO-METEOROLOGICALVARIABLES Thispageintentionallyleftblank
MULTIVARIATE VARIABLES ACOPULA-BASEDAPPROACH
FATEH CHEBANA Water,EarthandEnvironmentCentre,NationalInstituteofScientificResearch, UniversityofQuebec,Quebec,Canada
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands
TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright©2023ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans, electronicormechanical,includingphotocopying,recording,oranyinformationstorageand retrievalsystem,withoutpermissioninwritingfromthepublisher.Detailsonhowtoseek permission,furtherinformationaboutthePublisher’spermissionspoliciesandourarrangements withorganizationssuchastheCopyrightClearanceCenterandtheCopyrightLicensingAgency, canbefoundatourwebsite: www.elsevier.com/permissions
Thisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythe Publisher(otherthanasmaybenotedherein).
Notices Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperience broadenourunderstanding,changesinresearchmethods,professionalpractices,ormedical treatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgein evaluatingandusinganyinformation,methods,compounds,orexperimentsdescribedherein.In usingsuchinformationormethodstheyshouldbemindfuloftheirownsafetyandthesafetyof others,includingpartiesforwhomtheyhaveaprofessionalresponsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors, assumeanyliabilityforanyinjuryand/ordamagetopersonsorpropertyasamatterofproducts liability,negligenceorotherwise,orfromanyuseoroperationofanymethods,products, instructions,orideascontainedinthematerialherein.
ISBN:978-0-323-95908-7
ForInformationonallElsevierpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: CandiceG.Janco
AcquisitionsEditor: MariaElekidou
EditorialProjectManager: AndraeAkeh
ProductionProjectManager: RashmiManoharan
CoverDesigner: HarrisGreg
TypesetbyMPSLimited,Chennai,India
Acknowledgmentsix
1. Introduction1
1.1Context1 1.2Purposeandaims2 1.3Readership4 1.4Structureandcontent5 1.5Howtoreadthisbook?7 1.6Finalpoints7 References8
2. Multivariatehydrologicalfrequencyanalysis,overview11
2.1Generalaimsofhydrologicalfrequencyanalysis11
2.2Fromunivariatetomultivariatehydrologicalfrequencyanalysis14
2.2.1Mainstepsofacompletemultivariatehydrologicalfrequencyanalysis17
2.2.1.1Exploratoryanalysis
2.2.1.3Modelingandparameterestimation
2.3Hydrologicaleventsandtheirmainfeatures21
2.3.1Floodfeatures21
2.3.2Illustrativeexample23
2.3.3Droughtfeatures23
2.3.4Rainfallstormfeatures25
2.3.5Sedimentfeatures26 References26
3. Multivariatepreliminaryanalysis31 3.1Contextandmotivation31 3.2Visualization33 3.3Cross-dependencemeasures36 3.4Outliers39 3.4.1Outlyingness40 3.4.2Threshold40 3.5Locationmeasures42
3.5.1Samplemean43
3.5.2Component-wisemedian43
3.5.3Depth-basedmedian43
3.5.4Spatialmedian44
3.5.5 α depth-trimmedmean44
3.6Scalemeasures45
3.6.1 α-trimmedsampledispersionmatrix47
3.6.2Scalarformofscale47
3.7Asymmetry49
3.7.1Sphericalsymmetry49
3.7.2Ellipticalsymmetry50
3.7.3Antipodalsymmetry50
3.7.4Angularsymmetry50
3.8Kurtosis51
3.8.1LorenzcurveofMahalanobisdistance52
3.8.2Shrinkageplot53
3.8.3Fanplot53
3.8.4Quantile-basedmeasure54 References56
4. Checkingbasicassumptionsformultivariatehydrological frequencyanalysis57
4.1Introductionandgeneralconsiderations57
4.2Stationarity60
4.2.1Multivariatetrendtests61
4.2.1.1Mann Kendalltypetests
4.2.1.2Thecovarianceinversiontest
4.2.1.3Thecovariancesumtest 63
4.2.1.4Thecovarianceeigenvaluetest 63
4.2.1.5Spearman’srhotypetests 64
4.2.2Performanceevaluation65
4.2.3Furtherdiscussion67
4.2.3.1Example 67
4.3Homogeneity69
4.3.1Multivariateshiftdetectiontests71
4.3.1.1TheCrame ´ rtest
4.3.1.2TheM-test
4.3.1.3TheT-test 73
4.3.1.4TheWilcoxontest 74
4.3.1.5Thequalityindextest 74
4.3.1.6TheZhangtest 75
4.3.2Comparisonsandotherapproaches75
4.3.3Example76
4.4Serialindependence77
4.4.1Serialempiricalcopulatest79
4.4.2Illustrativeexample82
4.5Completeillustrativeexample83 References86
5. Modelinginmultivariatehydrologicalfrequencyanalysiswith copula89
5.1Introduction89
5.2Descriptionofcopulamodels93
5.3Classesofcopula96
5.3.1Archimedeancopulas97
5.3.2Extreme-valuecopulas100
5.3.3Meta-ellipticalcopulas102
5.3.4Otherclassesofcopulas103
5.4Dependencemeasures104
5.4.1Overalldependencemeasures105
5.4.2Taildependencemeasures109
5.5Copulaparameterestimation111
5.5.1Inferencefunctionsformarginsmethod112
5.5.2MaximumPseudo-likelihoodmethod112
5.5.3Moment-basedmethod113
5.5.4Multi-parametercopulaestimation113
5.6Copulaselection114
5.6.1Preliminarystep115
5.6.2Copulagoodness-of-fittesting119
5.6.3Selectioncriteriaforcopula123
5.6.4Marginmodeling125
References129
6. Multivariatereturnperiodandquantile133
6.1Riskassessmentinhydrology133
6.2Multivariatereturnperiodsandmultivariatequantile:generalities134
6.2.1Definitionsandpresentation135
6.2.2Illustrativeexample1139
6.3Methodstoselectcombinations140
6.3.1Mostlikelydesignrealizationapproach143
6.3.2Structure-basedapproach144
6.3.3Kendallreturnperiodapproach145
6.3.4Conditionaldistributionapproach146
6.3.5Regression-basedapproach147
6.3.6Multivariatequantilecurve,properpartapproach147
6.3.7Alpha-regionapproach148
6.3.8Ilustrativeexample2149 References152
7. Multivariatenonstationaryfrequencyanalysis155
7.1Nonstationaryhydrologicalfrequencyanalysis155
7.2Multivariatenonstationaryhydrologicalfrequencyanalysisliterature156
7.3Multivariatenonstationarymodels158
7.3.1Modelingdescription158
7.3.2Covariate-varyingcopulas160
7.3.3Covariate-varyingmargins161
7.3.4Nonstationarymodelselection162
7.3.5Bayesianmultivariatenonstationarymodel163
7.3.6Modelingproceduresteps164
Step1:descriptivestudy 164
Step2:testingtrends 164
Step3:jointdistributionselection 164
Step4:nonstationarymultivariatequantileandreturnperiod 166
7.3.7Dataserieslengthandmovingwindowseries168
7.4Illustrativeexample168 References172
8. Multivariateregionalfrequencyanalysis175
8.1Regionalhydrologicalfrequencyanalysis175
8.2Multivariateregionalfrequencyanalysis177
8.3Delineation179
8.3.1Multivariatediscordancy179
8.3.2Multivariatehomogeneity181
8.4Multivariateestimation(index-floodmodel)184
8.5Discussion187 References188
AppendixA:Tiesinthecopula-basedframeworkand inhydrology191
AppendixB:Statisticaldepthfunctions193
AppendixC:Multivariate L-moments197
AppendixD: p-Valuecomputation201 Index203
Acknowledgments Iwouldliketoacknowledgeallthosewhohavecontributedtothe preparationandcompletionofthisbook.Iamgratefultomycolleagues andfriends,fromINRSandotherinstitutionsfromCanadaandabroad, whogavecommentsdirectlyorindirectlyrelatedtothetopicofthis book,inparticular,theSTAHY(InternationalCommissiononStatistical Hydrology)members.Ihavebeengreatlyinfluencedbythediscussions andsupportofAbdelhameedEl-Shaarawi,founderandformerEditorin-ChiefofEnvironmetrics.
Iwouldliketoexpressmygratitudetomystudentsandteammembers,especiallyDorsafGoutali,forallofherhelpduringthelastyear. Allefforts,commitments,andpatiencefromElsevierteamaregreatly appreciated.
I’mgratefultomyfamily,especiallymywife,Narimane,andour kids,fortheirpatience,support,andencouragementovertheyears. Iexpressmysincerethankstoeachpersonconcerned. Idedicatethisbooktomyparents,AchourandLaatra!!
FatehChebana QuebecCity,Canada
Thispageintentionallyleftblank
1 Introduction 1.1Context Extremehydro-meteorologicalevents,includingfloods,droughts, andstorms,mayhaveseriouseconomicandsocialconsequences.Given theimportanceofdealingwithsuchadverseevents,severalstudies havefocusedspecificallyoneachoftheseevents.Inwaterresource management,oneofthechallengingtopicsisrelatedtodroughts, whereasthedesignofhydraulicstructuresisbasedonfloods.Anaccurateestimationoftheriskcausedbytheseeventsisessential.Inthis regard,hydrologicalfrequencyanalysis(HFA),asasetofstatistical methodsandtechniques,iscommonlyconsidered.HFAismainlycomposedofthefollowingsteps:(1)performingexploratoryanalysisand outlierdetection,(2)testingthebasicassumptions(stationarity,homogeneityandserialindependence),(3)modelingandestimatingmodel parameters,and(4)makinginference,includingriskevaluation.Inthe univariateHFAframework,allthesestepsareextensivelystudiedand usuallyconsideredintheanalysis.
Environmentalandhydro-meteorologicalprocesses,suchasfloods, droughts,rainstorms,hurricanes,tornadoes,windstorms,weather extremes,andtides,aregenerallycomplex.Theyareoftendescribed bymorethanonecorrelatedvariable(e.g.,floodvolume,peak,and duration),whichinvolvessimultaneousconsiderationofthesevariablesusingmultivariatemodelsandmethods(seee.g., Barnett,2012). Inparticular,dealingwithextremehydro-meteorologicalevents requiresmultivariateHFA.Tradit ionalmultivariateHFAmethodsare toorestrictiveanddonotevenapplyinmanycases.Consequently,over thelasttwodecades,copulafunctionshaveemergedasapreferred methodinavarietyofapplications,especiallyhydro-meteorologyand inmultivariateHFA.
AdoptingthemultivariateHFAframeworkinhydro-meteorologyin preferencetounivariateHFAwasextensivelyjustifiedintheliterature. Indeed,univariateHFAcanonlyprovidelimitedrepresentativityand understandingofextremeeventsandtheirprobabilityofoccurrence.In addition,theunivariateframeworkofeacheventcharacteristicseparatelydoesnottakeintoaccounttheirdependencestructure,leadingto potentiallylessaccurateriskestimation.Nevertheless,univariateHFA canbeusefulinsomesituationssuchaswhenonlyonevariableissignificantfordesignpurposesorwhenthedependencebetweenthese variablesisnotsignificant.However,multivariateHFAismorereliable formodelinghydro-meteorologicalvariables,leadstobetterriskassessment,andisamoreflexibleframework(see Chapter2 formoredetails).
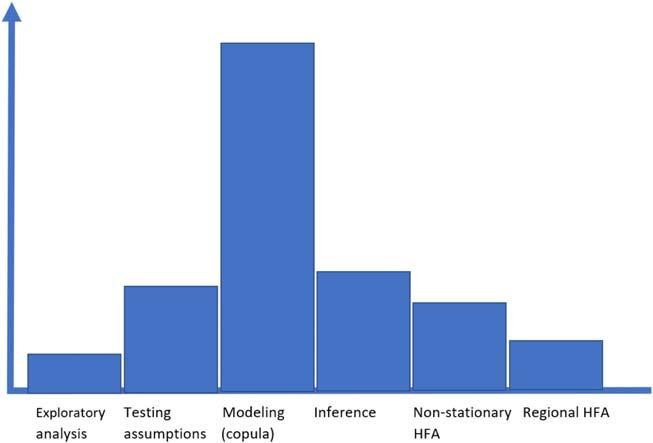
1.2Purposeandaims MultivariateHFAisaveryactiveresearchtopicinstatisticalhydrometeorology.Arelativelylargebodyofliterature,dealingwithmultivariateHFA,isavailablemostlyasjournalpapers(theoreticaldevelopments,casestudies,etc.).Ingeneral,thesepaperstreatspecificaspects suchasahydrologicalevent(e.g.,flood,drought),aparticularstepof theanalysis(e.g.,modeling,testing,exploratoryanalysis),oragiven statisticalapproachortechnique(e.g.,copulas,L-moments).Inaddition, mostoftheliteraturefocusesonthemodelingstepmainlybasedonthe copulafunction. Fig.1.1 illustratessomeoftheaspectsofmultivariate HFAhighlightedintheliteratureandtheirimportanceandthevolume ofstudiesfocusedonthis.Itshowsthatthemodelingstep,especially basedoncopulas,ismostprevalenttheliterature.Althoughcopulaand modelingareimportantandessential,manyotheraspectsandsteps alsoneedtobeconsideredtoperformacompleteandappropriateanalysis.MultivariateHFAassociatedliteratureaspapersandreportsisnot easilyaccessibletopractitionersandstudents.Hence,thishasledtoan increasinggapbetweenresearchandpracticeinthisfield.Therefore, thedesperateneedofareferencebookwherethereadercanfindallthe relevantmaterialcoveringthedifferentstepsandsituationsofamultivariateHFAinasimplifiedandaccessiblepresentation,theconnections betweenthemaswellasacompleteoverviewofallstepsoftheanalysis hasbeenfelt.
Thisbookattemptstoreduceoreliminatesomeofthechallengesand difficultiesfacedbypractitionersinmultivariateHFA.Thisbookcompilesalltherelevantbackgroundmaterialandnewdevelopmentsin oneplaceandalsopresentsthismaterialinahomogeneousandpedagogicalwayinordertoallowstudents,engineers,practitioners,and researcherstoaccessanduseefficientlyalltheinformationaboutthis
topic.Inaddition,giventheadvancednatureoftheapproachesinmultivariateHFAandtheongoingdevelopments,eventhoughusefuland necessary,theyarecomplexforamajorityofpractitionersandstudents, especiallyreaderswithoutstatisticalbackground.Therefore,thisbook triestosimplifythepresentationoftheseconceptsandhenceaimstofill thegapbetweentheoryandpractice.Also,amajorpartoftheliterature neglectssomeofstepsoftheanalysis(Fig.1.1),potentiallyleadingto incompleteanalysisorevenwrongconclusions.Consequently,this bookhighlightstheimportanceofthosestepsandprovidestherecent andadvancedapproachestodealwiththemasalongwithexamples fromreal-lifesituations.
Tothebestoftheauthor’sknowledge,thereisnosuchexistingbook thatdealsspecificallyanddirectlywiththetopicofmultivariateHFAas awholeandinanintegratedmanner.Indeed,theexistingbooksmainly covercopulafunctionseitherinhydrologyorstatistics,suchas Salvadori etal.(2007), ZhangandSingh(2019),and ChenandGuo(2019) inwater sciencesand Joe(2014) and Hofertetal.(2018) instatistics.ThisbookprovidesasolidplatformbringingtogethermultivariateHFAtoolsinhydrometeorologicalpracticeandcontributestofillingthegapbetweentheory andpracticeandtheadvancementofthefieldofstatisticalhydrometeorology.Thisbookenablesthereadertoperformawell-justified multivariateHFAcoveringallrelevantstepsandaspectsoftheanalysis,
FIGURE1.1 Illustrationoftheimportance/volumeofstudiesintheliteratureoneach step/topicinmultivariatehydrologicalfrequencyanalysis.
includingthepreliminaryimportantsteps(e.g.,testingtheassumptions) andusefulextensions(nonstationary,regional).Thisbookprovides detailedandcomprehensivedescriptionsofthetechniquesandallsteps involvedinperformingacompletemultivariateHFA.
Inthisbook,thecopula-basedapproachisgivendueimportanceand alargechapter(Chapter5)isdedicatedtothistopic,alongwithcoveringotherimportanttopics,includinghypothesistestingofthebasic assumptions,thereturnperiodandquantile,andpreliminaryanalysis suchasoutliersanddescriptivestatistics.Whereappropriate,some examplesbasedonthesamedatasetsarepresentedacrossseveralchapterstoshowhowtoperformtheanalysisandthestepsinvolved.
1.3Readership Thisbookisaimedtobeareferenceforresearchers,practitioners,and graduatestudentsinthefieldofmultivariateHFA,withaclearandcomprehensivepresentationofallrelevantapproachesandstepsinvolvedin performingacompleteanalysis.Italsoservesasanidealmultidisciplinaryintroductorybookforhydrologists,climatologists,andengineersto makethemselvesfamiliarwiththemostup-to-dateandadvancedmultivariatemethodologiesinhydrologicaldesign,planning,andmanagement,tomentionsome,andtheirpracticalapplications.Thisbookalso servesasaguideforthereadersinapplyingthemostrecentapproaches availabletowardevaluatinghydro-meteorologicalrisks,designing hydraulicstructures,andteaching(facultymembers),andasstate-of-the artmethodologiestomoverapidlytothenextlevelintheirresearchprojects(graduatestudentsandpostdocs).
Avarietyofreadersfromindustry,governmentagencies,oracademia (forresearchandgraduateteaching)aswellasstatisticiansandnonstatisticianreaderscanbenefitfromthisbook.Advancedapproachesare presentedinaneasy-to-understandmannerandwithanappropriatelevel ofdetail.Eventhoughtheprimarytargetreadersarehydrologists,climatologists,engineersandstatisticians,giventhatsomematerialisinterdisciplinary,itcanbeusedforreferenceby practitionersfromotherapplication fieldssuchasfinancialinstitutions, insurancecompanies(damagescaused byfloodsanddroughts),earthsciences,environmentalmodeling,andgovernmentagencies(e.g.,publicsafety,environmentandtransportation). Readersinterestedinunderstanding theoreticalconceptsandpractical aspectsrelatedtocopula-basedmodernmultivariateHFAcanfindthis bookwithin-depthtechnicaldetails extremelyhelpful,whereadvanced andcomplexmathematics/statistics havebeenavoidedtotheextentpossible.Nevertheless,basicknowledgeof probabilityandstatistics,suchas randomvectors,estimationmethods, andstatisticaltests,isexpected.
Overthelasttwodecades,multivariateHFAhasgainedicreasingattentioninbothapplicationsandtheoreticaldevelopments.ThisbookiscomposedofsevenotherchaptersandanAppendix. Chapter2 introducesHFA andbrieflymakestheconnection betweenthesubsequentchapters.
Chapters3 6 discussthemainHFAstepsinvolvedinastandardmultivariateHFA. Chapters7and8 arededicatedtoadvancedanalysisaswellas extensionsofthestandardanalysis,dealingwithmultivariatenonstationary modelingandmultivariateregionalanalysis.Tomaintainthefluencyofthe content,sometechnicalconceptsarepresentedintheAppendix.
Chapter2 providesanoverviewandthebasicsofHFA.Itstartswith describingthegeneralaimsandgoalsofHFAaswellastheessential conceptsofreturnperiodandquantileforhydrologicalriskassessment. Then,itbrieflyintroducesthemainstepsinvolvedinperformingthe wholeHFA.Thischapteralsodiscussestheadvantagesandchallenges facedwhiletransitioningfromunivariatetomultivariateHFAframeworks,especiallyusingcopulafunctions.Themultivariatecharacterof anumberofhydrologicalphenomena,suchasfloods,droughts,rainfall storms,andsediments,isdescribedasalongwiththeirmainfeaturesto betreatedinthemultivariateHFAframework.
Chapter3 treatsthepreliminaryanalysiswithintheframeworkofthe multivariateHFA.Severalstatisticalpropertiesofthemultivariatesamplearediscussed,suchaslocation,scale,skewness,kurtosisaswellas outlierdetection.Thisstepcanbeusefulinsummarizing,describing, andunderstandingtheinformationcontainedinthedataseries.Onthe otherhand,thispreliminaryanalysisisusefulformodelinghydrologicalvariablesandhenceforriskevaluation.Thepresentedmethodsare generalandcanbeadaptedandappliedtoavarietyofhydrometeorologicaleventssuchasfloods,droughts,storms,andsediment transportalongwithotherfields.
Chapter4 addressesthetestingstepwithintheframeworkofmultivariateHFA.Inthischapter,thecorrespondingtechniquesandmethods arepresentedinmoredetailwithafewexamples.Nonstationarity,heterogeneity,andserialdependenceneedtobetestedbeforethemodeling stepinamultivariateHFA.Thetestingstepisimportanttoensurethe basicassumptionsaremetandthustheselectedmodelsareappropriate. Thesestatisticaltestsaregenericandcanbeadaptedandappliedtoa varietyofhydro-meteorologicalvariablesaswellastootherfields.
Chapter5 introducesthemodelingstepofmultivariateHFAbased oncopulafunctions.Eventhoughcopulamodelingistheheartofthe multivariateHFA,thepreliminaryanalysisandtestingofthebasic assumptionsshouldbeperformedfirst(presented,respectively,in
Chapters3and4).Here,thebasicassumptionsareassumedtobefulfilled(see Chapter4).Thischapteralsopresentsanoverviewofthestatisticalapproachesandmethodsregardingcopulamodeling,including parameterestimationandgoodness-of-fittestingaswellasmodelselectioncriteriawithillustrations.
Chapter6 examinesthelaststepofmultivariateHFA,whichdeals withtheinference,inparticularriskassessmentintermsofreturnperiods orquantiles.Thisstepisperformedbasedontheanalysisanddecisions madeinallprevioussteps(describedinpreviouschapters),especiallythe modelingstep(Chapter5).Here,riskassessmentinhydrologyisbriefly presented,followedbythebasicsregardingmultivariatereturnperiod andquantile,and,finally,anoverviewofthestatisticalapproachesand methodsregardingtheselectionofthemultivariatecombinationsfora givenreturnperiodwithillustrativeexamples.
Chapter7 treatsnonstationarityinthemultivariatesetting.Combining thosetwoaspects(nonstationarityandmultivariate)leadstothemultivariatenonstationaryHFA,whichaimsatestimatinghydro-meteorological quantiles(risks)inthepresenceofnonstationarity(caused,forinstance,by climatechange).Priortoperformingnonstationaryanalysis,appropriate testsshouldbeaccomplished(Chapter4).Hydro-climatologyphenomena arenaturallymultivariatewithstationarityassumptioneitherfulfilledor not.Therefore,itismorerealisticandrepresentativetoconsiderthejoint multivariateandnonstationaryHFAsetting.ThischapterbrieflyintroducesthebasicsofnonstationarityinHFAfollowedbypresentingthe multivariatenonstationarycontext.Then,themodelingmethodologyof thelatterisdescribedfollowedbyanillustrativeexample.
ThelastchapterbrieflyintroducesthebasicsofregionalHFAfollowedbypresentingthemultivariatecontextofregionalfrequencyanalysis(RFA).Then,thedelineationandtheregionalestimation,asthetwo maincomponentsofRFA,arepresented.Thischapteralsodealswith RFAinthemultivariatesetting.Combiningregionalandmultivariate aspectsleadstothemultivariateRFA,whichaimsatestimatinghydrometeorologicalquantiles(risks)at ungauged sites.Usually,inthelatter, nohydrologicaldataareavailableunliketheat-site(local)HFAanalysis seeninthepreviouschapters.RFAintheunivariatesettingiswidely usedbyhydrologists.Themultivariatenatureofhydro-meteorological phenomenaispresentatsiteseithergaugedorungauged.Therefore,it ismorerealistic/usefultoconsidermultivariateRFA.
Inordertofacilitatereadability,someofthetechnicalstatistical conceptsandtoolsneededinthepreviouschaptersareoutlinedin theAppendix,whichincludestiesinthemultivariateframeworkand inhydrology,statisticaldepthfunctions,multivariateL-moments,and p-valuecomputation.Thesetoolsarealsogenericandcanbeuseful inotherfieldsanddisciplinesaswell.
1.5Howtoreadthisbook?
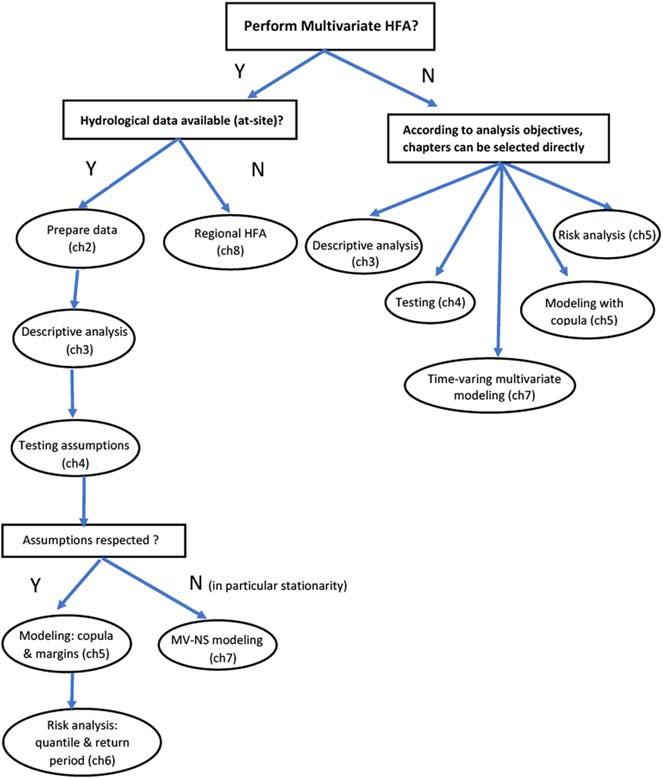
Ononehand,chapterscanbefollowedindependentlybasedonthe requirementsofthereader.Forinstance,iftheobjectiveistostudy trends,thereadercandirectlygoto Chapter4 orifthereaderisinterestedinmultivariatemodeling,includingmodelselectionandparameterestimation,thenthereadercanfindtheappropriatematerialin Chapter5.Ontheotherhand,ifthereaderaimstoperformacomplete multivariateHFA,itisrecommendedtoreadthechaptersinasequentialorderstartingfrom Chapter2 to Chapter6 forastandardHFA. Since Chapters7and8 presentadvancedmaterial,itisrecommendedto startwiththechaptersdealingwiththestandardanalysis(Chapters 2 6).Thisisillustratedin Fig.1.2,whichprovideslinksbetweenall chaptersasadiagramshowinghowtheyareconnectedandreading pathoptions.
1.6Finalpoints Eventhoughthebookattemptstoaddressmostofthepractical issuesandmethodologicalfacetsrelatedtomultivariateHFA,itdoes notpretendtocoverallworksinthefield.Inparticular,theapplications andcasestudiesarefocusedonfloodseventhoughthepresentedmaterialandapproachesarevalidforotherhydro-meteorologicalapplicationsorinotherfieldsaswell.Indeed,floodsarethemostcommon naturalhazardsthataccountforclosetohalfofthetotalworldwidedisasters,affectinghundredsofmillionsofpersons(NDRR,2020).Inaddition,multivariateHFAislargelyusedtostudyfloods.Asregards theory,focuswasmadeonthebivariatesettingwhilethehighdimensionsituationsarediscussedbriefly.Thebivariatesettingisopted forsinceitisthemoststudiedcaseandsimpleaswell.Someother topicsliketheuncertaintyintheestimationaswellasvinecopulasare onlymentionnedmainlybecausethisbookisafirstofitskindinthis field,andmostofthetheseconceptsarestillindevelopmentinhydrometeorology.
Eventhoughreasonableeffortshavebeenmadetopublishreliable data,illustrations,andinformation,theauthorandpublisherarenot responsibleforthevalidityofallthepresentedmaterialsortheconsequencesoftheiruse.
Thebookisentirelybasedonthesubjectknowledgeoftheauthor. Yet,asinanyotherpublication,itmaycontainsomeerrors.Comments, corrections,andsuggestionsfromthereadersaboutthematerialpresentedinthebookandrelatedmattersarewelcome.
FIGURE1.2 Illustrationofthedifferentpathoptionsthatcanbetakenbythereader.
References Barnett,V.(2012).Outliers,multivariate. EncyclopediaofEnvironmetrics. https://doi.org/ 10.1002/9780470057339.vao020
Chen,L.,&Guo,S.(2019). Copulasanditsapplicationinhydrologyandwaterresources (p.290)Singapore:Springer.
Hofert,M.,Kojadinovic,I.,Machler,M.,&Yan,J.(2018). ElementsofcopulamodelingwithR (pp.9 79).Springer.
Joe,H.(2014). Dependencemodelingwithcopulas.CRCPress. NDRR.(2020).Humancostofdisasters:Anoverviewofthelast20years(2000 2019). https://www.undrr.org/publication/human-cost-disasters-overview-last-20-years2000-2019
Salvadori,G.,DeMichele,C.,Kottegoda,N.T.,&Rosso,R.(2007). Extremesinnature:An approachusingcopulas.Springer. Zhang,L.,&Singh,V.P.(2019). Copulasandtheirapplicationsinwaterresourcesengineering CambridgeUniversityPress.
Thispageintentionallyleftblank
Multivariatehydrological frequencyanalysis,overview Inthischapter,wepresentanoverviewandthebasicsofhydrologicalfrequencyanalysis(HFA).Westartfirstbydescribingthegeneral aimsandgoalsofHFAaswellastheessentialnotionsofreturnperiod andquantileforhydrologicalriskassessment.Then,webrieflyintroducethemainstepstoperformthewholeHFAandrefertothecorrespondingchapterwhereeachstepisfullypresented.Wecoverthe advantagesandchallengeswhenpassingfromunivariatetomultivariateHFAframeworks,especiallyusingcopulafunction.Wedescribethe multivariatecharacterofanumberofhydrologicalphenomena,suchas droughts,rainfallstorms,andsediments,aswellastheirmainfeatures tobetreatedinthemultivariateHFAframework.
2.1Generalaimsofhydrologicalfrequencyanalysis Seriouseconomicandsocialconsequencesmaybecausedbyextreme hydrologicalevents,suchasfloods,droughts,andstorms.Severalstudies focusspecificallyoneachoftheseeventswithdifferentmethodologies andfordifferentregions.Forinstance,inwaterresourcesmanagement, droughtsisoneofthechallengingtopicswhereasextremerainfalland floodestimatesrepresentthebasisforthedesignofhydraulicandhydrologicstructures.Agoodknowledgeconcerningthefeaturesassociated withtheseextremehydrologicaleventsisimportantforaccurateestimationoftheriskassociatedwithwaterinfrastructuresintheirdesignand operation.Indeed,ononehand,anunderestimationofdesignfloods leadstomaterialdamagesandlossofhumanlives.Ontheotherhand, anoverestimationleadstoanover-sizingofhydraulicstructuresinvolvingsupplementarycosts.Hence,itiscrucialtoconsidertheappropriate modelsforthemostaccuratepredictionoftheseevents.Tothisend,
HFA,asanensembleofstatisticalmethodsandtechniques,isthemost consideredapproachbyhydrologistsandcivilengineers.
Theoccurrenceofextremeeventsinhydrologycannotbeestimated, predicted,orforecastedonthebasisof deterministicinformationwithsufficientskillandleadtime(e.g., Rao&Hamed,2000).Alternatively,aprobabilisticapproachisrequiredtoincorporatetheeffectsofsucheventsinto decisions.Basedontheassumptionthatoccurrencesareindependentof time,thatis,successiveeventshavenorelationintheirtimingandmagnitude,HFAcanbeemployedasadecisiontoolbyassessingthelikelihood ofaneventoracombinationofevents.AnumberofengineeringapplicationsmakeuseofHFAsuchashydraulicandmunicipalstructuredesign (culverts,stormsewers)andlandslidehazardevaluation.
Formally,forarandomvariable X,themainobjectiveofHFAof extremeeventsistheassessmentoftheprobabilityPr X $ xT ðÞ ofan event xT tobeexceeded.Instatistics,theevent xT isthequantileof probabilityofexceedance p with p 5 Pr X $ xT ðÞ,whereasinHFApractice, xT correspondstothereturnperiod T inyears.Bothnotions,quantileandreturnperiod,areequivalentsincewehave
where θ isthevectorofparametersassociatedtothedistributionfunction F.Notethat p correspondstothehydrologicalriskand xT isthequantile oforder1 p ofthedistribution F.Becauseofthevariabilityoftimearrivalsbetweenevents,areturnperiodisdefinedastheaverageofthe intereventtimesbetweenhydrologicalevents.Largereturnperiodsare naturallyassociatedtolargeeventsandviceversa(Rao&Hamed,2000).
From Eq.(2.1),fittingaprobabilitydistribution F toaseriesof observedvalues,suchasmaximumannualflow,isessentialtoperform anHFA.SeveraldistributionshavebeenproposedtofithydrometeorologicalvariablesandarecommonlyusedinHFAsuchasthe GeneralizedExtremeValue(GEV),Lognormal(LN),andthePearson type3family.Specificdistributionsarerecommendedinsomecountries,suchastheGEVintheUnitedKingdomforfloodsandinthe UnitedStatesforprecipitation;theLNinChina;andtheLog-Pearson type3distribution(LP3)intheUnitedStatesforannualpeakflowdata. However,theuseoftheGEVdistributionislargelyconsideredbecause ofthesimplicityofitsquantilefunction,theoreticalresultsandthe availabilityofsoftwareforparameterestimation(ElAdlounietal., 2010).In(Singh,2017,Chapter21),alargenumberof(univariate)distributionsarepresentedanddiscussedinahydrologicalcontext.
Therighttailportionisthemostimportantpartofthesedistributions. Indeed,thehydrologicalextremesoccurforhighvaluesofthevariable andwithverylowfrequencies.Therefore, ElAdlounietal.(2008)
presentedanoverviewregardingthetailbehaviorofthemainprobability distributionfamiliesusedinHFA.Theauthorsprovidedaclassification ofanumberofdistributionsusedinHFAaccordingtotheirtailssincea numberofdistributionscouldbeverysimilarintheircentralparts.
BeforecarryingoutastandardHFA,thedataseriesmustbeindependent andidenticallydistributed(iid)(e.g., Rao&Hamed,2000).Inotherwords, thedataseriesshouldmeetstatistical conditionsincludingindependence, homogeneity,andstationarity.Inabriefandsimpleway,independence meansthatthedataseriesdonotpresentanysignificantautocorrelation. Whenalltheelementsofthedataseriesoriginatefromasinglepopulation, thenthehomogeneityisrespected.Tomeetstationarity,exceptforfluctuations,thedataseriesshouldbeinvariantwithrespecttotimeanddonot havepatternssuchastrends,jumps,andcycles.InHFAapplications,the lattercanoccurinavarietyofsituationwhereforinstancejumpsaredueto achangeinstationlocation,whereas long-termclimaticfluctuationsmay leadtotrendsandcycles.Foreachofthethreeassumptions,appropriate statisticaltestsareusuallyemployed:intheunivariatesetting,the Wald Wolfowitztestforindependence,theMann Whitneytestforhomogeneity,andtheMann Kendallforstationarity.
Basedonalltheabovediscussedelements,themainandbasicsteps involvedtoperformanHFAareasfollows:(1)preliminaryanalysis includinganexplanatoryanalysisfordatacheckingandoutlierdetection;(2)testingthatthedataseriessatisfiesthehypothesesofindependence,homogeneity,andstationarity;(3)fittingofthebesttheoretical probabilitydistributiontorepresentthedataseries;and(4)estimating thequantilesandreturnperiodeventsusingtheselecteddistribution. Thesestepsaredescribedinmoredetailin Section2.3.
In Eq.(2.1),theparametervector θ shouldbeestimated.Tothisend,a numberofmethodshavebeendevelopedandareavailableinthehydrologicalandstatisticalliterature.Themethodofmomentsisamongthe simplestandmostdirectones,whichprovidesparameterestimatessuch thatthetheoreticalmomentsareequaltothecomputedsamplemoments. Anothermethodforestimatingparametersisbasedonthesample L-momentswhichiswidelyusedinhydrology,especiallyintheestimationofGEVdistributionparameters.Indeed,sampleL-momentsareless biasedthantraditionalmomentestimators,andthusarebettersuitedfor usewithsmallsamplesizescommonlyencounteredinHFA.Themethod ofmaximumlikelihood(ML)providesestimatorsthatmaximizethe likelihoodfunctionwithveryinterestingstatisticalpropertiesforlarge sampleswhichisusuallynotthecaseinHFA.Intheparticularcaseof theGEV,ageneralizedMLversioncanbeconsideredwhereaprior distributionfortheshapeparameteroftheGEVisinvolved.
ToperformacompleteandstructuredmultivariateHFA,thestatistical tools,techniques,methods,andmodelspresentedinthisbookshouldbe
takenasawhole,respectingtheirsequentialorder.However,iftaken separately,thesestatisticaltoolsarealsousefultootherhydrometeorologicalandwaterresourcesapplications,suchassimulation,forecasting, downscaling,andweathergeneration.Theyarealso,inasense,useful forotherboarderapplicationssuchasfinanceandinsurance.
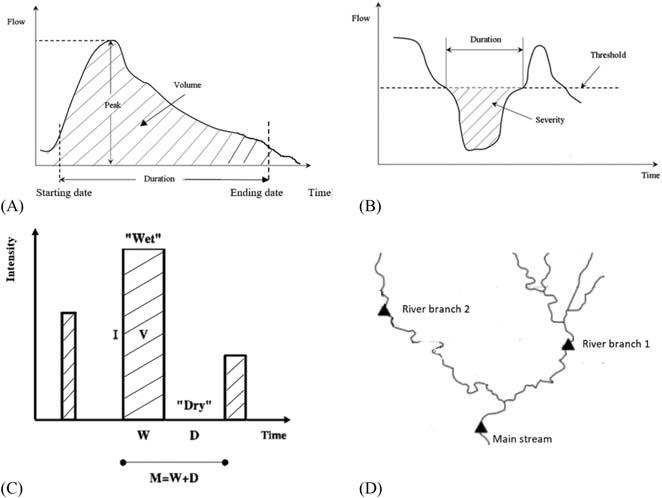
2.2Fromunivariatetomultivariatehydrologicalfrequency analysis Intheprevioussection,wemostlydiscussedthebasiccaseinHFA whereonly one feature(variableorcharacteristic)ofthehydrologicalevent isinvolved.ItistheunivariateHFA.However,generally,hydrological eventsarecharacterizedbyseveralcorrelatedfeatures,suchaspeak,volume,anddurationforfloods;severity,magnitude,anddurationfor droughts;andstormdurationandintensity.Indeed,rivermanagement maystronglydependuponthejointfeaturesoffloodpeakandfloodvolume;thecharacterizationofdroughtsrequiresthejointanalysisofduration magnitude intensity;anddifferentcombinationsofrainfallintensity andstormdurationmaygeneratedifferentstorms.Therefore,itisoftenof fundamentalimportancetobeabletolinkthemarginaldistributionsofdifferentvariablesinordertoobtainajointlawdescribingthemainfeatures ofthehydrologicalevents.Theaim ofthemultivariateHFAframeworkis totreatingthefeaturesofeachoftheseeventsjointly.Themultivariate settingisalsoofinteresttostudyagivenfeature,forexample,floodpeak, fortwoormoredifferentlocations(multisite).Asaspecificexample, ElAdlouniandOuarda(2008) estimatedthecombinedriskassociated withtheflowintheChateauguayRiverandtheSt-LouisLakeinQuebec, Canada. Fig.2.1 presentsanillustrationofthevariablesassociatedwith floods,droughts,andstorms,aswellasthemultisitecase.
MultivariateHFAhasrecentlyattractedincreasingattentionwhereseveralstudiespointedouttheimportanceofconsideringdifferentvariables thatcharacterizeahydrologicalevent(see,e.g., Genest&Chebana,2017; Hao&Singh,2016).Severalotherstudiesfocusedonthejointtreatmentof theseeventvariablesbasedonmultivariatetechniquessuchasmultivariate distributionsorcopulas(see,e.g., Chebana&Ouarda,2011a; DeMichele &Salvadori,2003; Sharma&Mujumdar,2019; Yueetal.,1999).
Inrecentyears,severalstudiesandreviewpaperswerepublishedcoveringmultivariateapplicationsrelatedtoextremeeventsinhydroclimatology(Chebana,2013;Genest&Chebana,2017;Hao&Singh,2016).It wasalsoshownintheliteraturethatunivariateHFAprovidesalimited assessmentofanextremeeventprobabilityofoccurrence.Often,amultivariateanalysisisnecessaryinordertoavoidunder/overestimationof therisk,asshownbelow.Ifagivenhydrologicaleventismultivariate,
FIGURE2.1 Differenthydrologicalfeaturesinthemultivariatesettingfortheconsideredevents:(A)floods,(B)droughts,(C)rainfallstorms,and(D)multisiteforfloodpeak. Source:(C)Adaptedfrom(Salvadori&DeMichele,2006).Elsevier
thenunivariateHFAisnotabletoprovidecompleteassessmentofthe probabilityofoccurrencewhichreducestheaccuracyoftheriskestimation.TheunivariateHFAignoresthedependencestructurebetweenthe eventfeaturesandhenceitislessrepresentativeofthephenomenon. However,univariateanalysisisusefulinsituationswhereonlyonevariableissignificantinthedesignprocess,orwhentherandomvariables haveanegligibledependence.TheunivariateHFAcanbeconsideredas asteptobeincludedinthemultivariateHFA.
Inhydrology,themultivariateframeworkgoesbackbefore2000(e.g., Ashkaretal.,1998)whereanumberofmultivariatedistributionssuchas multivariateversionsofNormal,Gamma,GEV,andExponentialwere developedoremployed.Traditionally,themultivariatedistributionsused inhydrologyhavenormal,log-normal,orexponentialmargins(Salvadori &DeMichele,2004).However,multivariatedistributionsarenotenough flexibleandhaveanumberoflimitations.Indeed,availableclassicalmultivariatedistributionsrequirethatthemarginstobewithinthesameclass andarelessflexibleregardingthedependencestructure.Inaddition,the usualdistributionswhichcanbeextendedtothemultivariatesettingare verylimited,includingforinstancenormalandgamma(e.g., Hao&