INTELLIGENT NANOTECHNOLOGY
Editedby YUEBINGZHENG
WalkerDepartmentofMechanicalEngineeringandTexas MaterialsInstitute,TheUniversityofTexasatAustin, Austin,TX,UnitedStates
ZILONGWU
WalkerDepartmentofMechanicalEngineeringandTexas MaterialsInstitute,TheUniversityofTexasatAustin, Austin,TX,UnitedStates
Elsevier
Radarweg29,POBox211,1000AEAmsterdam,Netherlands
TheBoulevard,LangfordLane,Kidlington,OxfordOX51GB,UnitedKingdom 50HampshireStreet,5thFloor,Cambridge,MA02139,UnitedStates
Copyright©2023ElsevierInc.Allrightsreserved.
Nopartofthispublicationmaybereproducedortransmittedinanyformorbyanymeans,electronicormechanical, includingphotocopying,recording,oranyinformationstorageandretrievalsystem,withoutpermissioninwriting fromthepublisher.Detailsonhowtoseekpermission,furtherinformationaboutthePublisher’spermissionspolicies andourarrangementswithorganizationssuchastheCopyrightClearanceCenterandtheCopyrightLicensingAgency, canbefoundatourwebsite: www.elsevier.com/permissions.
ThisbookandtheindividualcontributionscontainedinitareprotectedundercopyrightbythePublisher(otherthanas maybenotedherein).
Notices
Knowledgeandbestpracticeinthisfieldareconstantlychanging.Asnewresearchandexperiencebroadenour understanding,changesinresearchmethods,professionalpractices,ormedicaltreatmentmaybecomenecessary.
Practitionersandresearchersmustalwaysrelyontheirownexperienceandknowledgeinevaluatingandusingany information,methods,compounds,orexperimentsdescribedherein.Inusingsuchinformationormethodsthey shouldbemindfuloftheirownsafetyandthesafetyofothers,includingpartiesforwhomtheyhaveaprofessional responsibility.
Tothefullestextentofthelaw,neitherthePublishernortheauthors,contributors,oreditors,assumeanyliabilityfor anyinjuryand/ordamagetopersonsorpropertyasamatterofproductsliability,negligenceorotherwise,orfrom anyuseoroperationofanymethods,products,instructions,orideascontainedinthematerialherein.
ISBN:978-0-323-85796-3
ForinformationonallElsevierpublications visitourwebsiteat https://www.elsevier.com/books-and-journals
Publisher: MatthewDeans
AcquisitionsEditor: StephenJones
EditorialProjectManager: ClodaghHolland-Borosh
ProductionProjectManager: KameshR
CoverDesigner: MarkRogers
TypesetbySTRAIVE,India
Contributors
TrevonBadloe
DepartmentofMechanicalEngineering,PohangUniversityofScienceandTechnology (POSTECH),Pohang,RepublicofKorea
YijunBao
DepartmentofBiomedicalEngineering,DukeUniversity,Durham,NC,UnitedStates
KeithA.Brown
DepartmentofMechanicalEngineering;PhysicsDepartmentandDivisionofMaterialsScience& Engineering,BostonUniversity,Boston,MA,UnitedStates
QianChen
DepartmentofMaterialsScienceandEngineering;DepartmentofChemistry;BeckmanInstitute forAdvancedScienceandTechnology;MaterialsResearchLaboratory,UniversityofIllinoisat Urbana-Champaign,Urbana,IL,UnitedStates
HongruiCheng
CollegeofChemistry,FuzhouUniversity,Fuzhou;FujianScience&TechnologyInnovation LaboratoryforOptoelectronicInformation,China
LiuChen-Xu
BeijingJiaotongUniversity,SchoolofCivilEngineering,Beijing,China
FrankCichos
LeipzigUniversity,MolecularNanophotonicsGroup,Leipzig,Germany
ZhengyangDuan
DepartmentofElectronicEngineering,TsinghuaUniversity,Beijing,China
ZheyuFang
SchoolofPhysics,AcademyforAdvancedInterdisciplinaryStudies,PekingUniversity,Beijing, China
PaulS.Francis
SchoolofLifeandEnvironmentalSciences,FacultyofScience,EngineeringandBuilt Environment,DeakinUniversity,WaurnPonds,VIC,Australia
ShengGao
DepartmentofElectronicEngineering,TsinghuaUniversity,Beijing,China
YiGao
DepartmentofElectronicEngineering,TsinghuaUniversity,Beijing,China
YiyangGong
DepartmentofBiomedicalEngineering;DepartmentofNeurobiology,DukeUniversity, Durham,NC,UnitedStates
AldairE.Gongora
DepartmentofMechanicalEngineering,BostonUniversity,Boston,MA,UnitedStates
GraceX.Gu
MechanicalEngineering,UniversityofCalifornia,Berkeley,Berkeley,CA,UnitedStates
YuGui-Lan
BeijingJiaotongUniversity,SchoolofCivilEngineering,Beijing,China
Che-LunHung InstituteofBiomedicalInformatics,NationalYangMingChiaoTungUniversity,Taipei,Taiwan
SantiagoMuin ˜ osLandin
AIMENTechnologyCentre,SmartSystemsandSmartManufacturing–ArtificialIntelligenceand DataAnalyticsLaboratory,Pontevedra,Spain
ChihunLee
DepartmentofMechanicalEngineering,PohangUniversityofScienceandTechnology (POSTECH),Pohang,RepublicofKorea
FushanLi
InstituteofOptoelectronicTechnology,FuzhouUniversity,Fuzhou,China
YuLi
SchoolofPhysics,AcademyforAdvancedInterdisciplinaryStudies,PekingUniversity,Beijing; SiliconPhotonicsR&DCenter,CUMEC,Chongqing,China
XingLin
DepartmentofElectronicEngineering,TsinghuaUniversity,Beijing,China
ZhengchangLiu
SchoolofPhysics,AcademyforAdvancedInterdisciplinaryStudies,PekingUniversity,Beijing, China
CuicuiLu
BeijingInstituteofTechnology,Beijing,China
YongfengLu
CollegeofChemistry,FuzhouUniversity,Fuzhou;FujianScience&TechnologyInnovation LaboratoryforOptoelectronicInformation,China
G.Milano
AdvancedMaterialsMetrologyandLifeSciencesDivision,ItalianNationalInstituteofMetrology Research,Torino,Italy
JaebumNoh
DepartmentofMechanicalEngineering,PohangUniversityofScienceandTechnology (POSTECH),Pohang,RepublicofKorea
RaviPradip
UniversitatPolite ` cnicaDeCatalunya,Barcelona,Spain
JunsukRho
DepartmentofMechanicalEngineering;DepartmentofChemicalEngineering,Pohang UniversityofScienceandTechnology(POSTECH),Pohang,RepublicofKorea
C.Ricciardi
AppliedScienceandTechnologyDepartment(DISAT),PolitecnicodiTorino,Torino,Italy
VerdaSaygin
DepartmentofMechanicalEngineering,BostonUniversity,Boston,MA,UnitedStates
KelseyL.Snapp
DepartmentofMechanicalEngineering,BostonUniversity,Boston,MA,UnitedStates
SunaeSo
DepartmentofMechanicalEngineering;GraduateSchoolofArtificialIntelligence,Pohang UniversityofScienceandTechnology(POSTECH),Pohang,RepublicofKorea
ZhongweiXu InstituteofOptoelectronicTechnology,FuzhouUniversity,Fuzhou,China
CharlesYang
MechanicalEngineering,UniversityofCalifornia,Berkeley,Berkeley,CA,UnitedStates
LehanYao
DepartmentofMaterialsScienceandEngineering,UniversityofIllinoisatUrbana-Champaign, Urbana,IL,UnitedStates
HongyiYuan
BeijingInstituteofTechnology,Beijing,China
JooyeongYun
DepartmentofMechanicalEngineering,PohangUniversityofScienceandTechnology (POSTECH),Pohang,RepublicofKorea
NianenZhang
BeijingInstituteofTechnology,Beijing,China
ZhizhouZhang MechanicalEngineering,UniversityofCalifornia,Berkeley,Berkeley,CA,UnitedStates
YuanhuiZheng
CollegeofChemistry,FuzhouUniversity,Fuzhou;FujianScience&TechnologyInnovation LaboratoryforOptoelectronicInformation,China
Preface
Nanosciencehasbeenanactiveresearchfieldoverthepastseveraldecades,triggered bytherisinginterestinexploringnewscienceandtechnologieswithmaterialsatthe nanoscale.Artificialintelligence(AI)hasledtorevolutionarydevelopmentinmany applicationssuchascommunication,computervision,andspeech/imagerecognition. BridgingthelinkbetweennanoscienceandAIcanprovideanewgenerationoftechnologiesthatwillhavelargeimpactsonoursociety.SomeoftheAItoolsarebeing implementedbyresearcherstoadvancenanoscienceandnanotechnologythrough AI-enhanceddesign,manufacturing,measurements,andapplicationsofnanomaterials andnanodevices.Meanwhile,nanotechnologyprovidesenormousdatasetsandnew hardwareplatformstoadvancethetrainingofAlmodelsandtheimplementationof AIalgorithms.
Withgreatcontributionsfromsomeofthetopresearchersworkingintheinterdisciplinaryfield,IntelligentNanotechnology:MergingNanoscienceandArtificialIntelligence providesanoverviewoftheadvancesinscienceandtechnologymadepossiblebythe convergenceofnanoscienceandAI.Section1focusesonAI-enhanceddesign,characterizationandmanufacturingofnanomaterials,andtheuseofAItoimproveimportant materialproperties,withanemphasisonmechanical,photonic,phononic,electronic, andmagneticproperties.TheuseofAIintheacquisitionandanalysisofdatainexperimentsisexploredaswell.Section2includeschaptersonAItechnologiesthathavebeen enhancedthroughnanotechnologyplatforms.Forexample,memristors,neuromorphic computing,andartificialneuralnetworksareincluded.Finally,Section3reviewsthe advancesinapplicationsenabledbythemergingofnanotechnologyandartificial intelligence,includingexamplesfrombiomedicine,chemistry,anticounterfeiting,and automatedresearch.Wehopethatthisbookwillprovideabridgetofurthercollaborationsamongresearchersfromdifferentfields.
YuebingZheng
ZilongWu
Acknowledgments
TheeditorsacknowledgethefinancialsupportfromtheNationalScienceFoundation (NSF-ECCS-2001650)andtheNationalInstituteofGeneralMedicalSciencesofthe NationalInstitutesofHealth(DP2GM128446).
Inversedesignmeetsnanophotonics: Fromcomputationaloptimizationto artificialneuralnetwork
JaebumNoha,*,TrevonBadloea,*,ChihunLeea,*,JooyeongYuna,*,SunaeSoa,b,* , andJunsukRhoa,c
aDepartmentofMechanicalEngineering,PohangUniversityofScienceandTechnology(POSTECH),Pohang, RepublicofKorea
bGraduateSchoolofArtificialIntelligence,PohangUniversityofScienceandTechnology(POSTECH),Pohang, RepublicofKorea
cDepartmentofChemicalEngineering,PohangUniversityofScienceandTechnology(POSTECH),Pohang,RepublicofKorea
1.Computationalinversedesign
Themethodsfordiscoveringoptimizeddesignsforphotonicplatformsusingcomputationalalgorithmsbroadlyfallintooneoftwocategories,namely,gradient-basedor evolutionary-basedalgorithms.Indeed,neuralnetworksaretrainedusinggradients andbackpropagation,soarefundamentallyrelatedinthisway.However,akeydifference occursinthefactthattraditionalcomputationinversedesignmethodsaregenerally definedbyaspecificobjectivefunctiontobeoptimized.Thiscouldbeanyrequiredopticalproperty,forexample,aresonanceataspecificwavelengthormaximizingthebroadbandefficiencyofadevice.Thedesignspacecanbeasfreeoraslimitedastheresearcher requires,whichcouldbedirectlyrelatedtothefabricationconstraintsofcertainmaterials ortechniques.Inthissection,wewillfocusontheapplicationofcomputationaloptimizationwithouttheintegrationofneuralnetworksasanintroductiontocomputational methods.Wewilldescribetheoverallgoalsandmethodologiesofgradientand evolutionary-basedalgorithmsandprovideexamplesofrecentresultsthatshowcase thepowerofnumericaloptimizationtechniquesinthedesignofnanophotonicdevices. Asimplevisualdescriptionofeachmethodisprovidedin Fig.1.
1.1Gradient-based
Gradient-basedoptimizationtechniquesrelyonthecomputationofthelocalgradientof theobjectivefunctioninrelationtothedesignateddesignparameters.Thisgradientthen guidestheoptimizationalgorithminacertaindirectiontowardaminimum(ormaximum)fortheobjectivefunction.Aproblemarisesinthatthereisnoguaranteethatthis localpointofinflectioninthegradientsoftheobjectivefunctionistheglobalminimum,
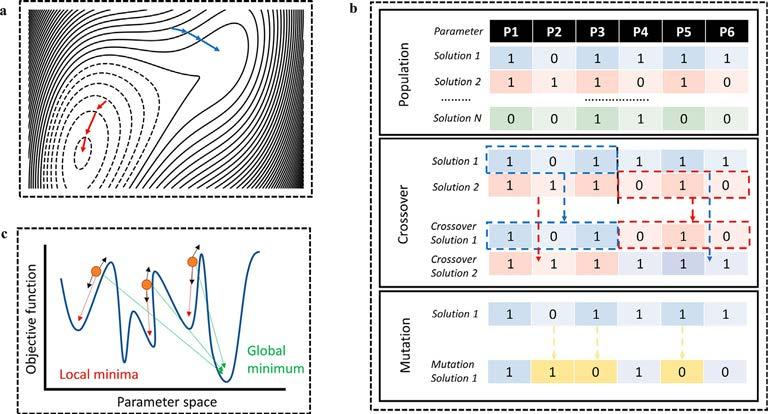
Fig.1 Visualrepresentationsofnumericaloptimizationmethods.(A)Gradientdescentmethod.The blue (grayintheprintversion)and red (darkgrayintheprintversion) arrows representoptimization pathsfromdifferentstartingpoints,leadingtodifferentlocalminima.(B)Geneticalgorithm.The populationismadeupof N uniquesolutionstotheproblem,herewithsixdifferentparameters. Aftereachhasbeengivenascoreandrankedintermsofthefitnessfunction,thebestsolutions areusedtoperformcrossover,wherethegenesoftwo-parentsolutionsaresplicedtogetherto createanewchildsolution.Withaspecifiedrandomchance,somesolutionsalsoundergo mutationtocreatenewsolutions.Thisallowsfortheoptimizationtohavesomechanceof escapinglocalminima.(C)Particleswarm.Threeparticles(orangecircles (grayintheprintversion)) withacertainpositionandmomentumexploretheparameterspaceindependentlyandare updatedbasedontheirlocalinformationaswellastheinformationofthepopulationasawhole, tohopefullyendintheglobalminimum,i.e.,theoptimalsolutiontotheproblem.(For interpretationofthereferencestocolorinthisfigurelegend,thereaderisreferredtotheweb versionofthisarticle.)
whichis,ingeneral,whatwewishtouncovertoproducethemostoptimizeddesign.If theobjectivefunctionisconvex,however,alllocalminimaarealsoglobalminima, meaningthatgloballyoptimizedsolutionscanbefound.Asdescribedin Fig.1A,after thegradienthasbeencalculatedataspecificlocation,theoptimizationalgorithmtakes astepinthatdirection.Weneedtodeterminehowbigofasteptotakeinthegiven direction,andhowfrequentlytomeasurethegradient.Thesizeofthestepisanimportantfactor,astoolargeofastepcouldleadtoovershootingtheminimum,whilethefrequencyofmeasuringthegradientisdeterminedbycomputationallimitations.Ofcourse, ideally,wewouldliketoknowthegradientateverypointwithinfinitesimallysmallsteps inordertouncovertheoptimumglobalsolution,butthisofobviouslyunrealisticinpractice.Anotherimportantfactoringradient-basedoptimizationmethodsisthestarting guessintheparameterspace.Duetotheselimitations,itiscommontodomultipleruns
withdifferentstartingpointsandstepsizes,increasingthecomputationalload.Inan attempttolightenthecomputationalloadoncalculatingthegradientsoftheobjective functionofhigh-dimensionalparameter’sspaces,theadjointmethodhasbeenintroduced.Thisallowsthegradientstobecalculatedusingonlyasingularadditionaladjoint simulation,significantlyreducingthecomputationalload [1,2].
1.1.1Adjointoptimization
Sincethegoalofoptimizationistofindtheparametersinthedesignspacethatmaximizes theachievableperformanceofthegivenobjective,thetraditionalmethodofdesigning individualstructuresandarrangingtheminperiodicarraysisunnecessary.Inaddition,by treatingthedeviceasawhole,withtheonlyconstraintbeingonthefinaloutputobjective,issuessuchascouplingandinteractionsbetweenneighboringstructuresareeradicated.Thiscanallowadjointoptimizationtofindstructuresandlayoutsthatavoid suboptimaldesigns.Therehavebeenvariousapplicationsofadjointoptimizationin thefieldofnanophotonicsfordesigninglarge-scaleandmultilayereddevicesforapplicationssuchaswaveguides [3–5] andgratingcouplers [6,7].Someoftherecentdemonstrationswillbeintroducedandtheresultsofthedevicesdesignedusingadjoint optimizationwillbediscussedinthissection.
Adjointoptimizationallowsforonlyoneadditionalsimulationinordertocalculate thegradientsoftheobjectivefunctionwithregardtothedesignparameters.Thisallows fornumerousstructurestobeoptimizedinasinglepass.Usingthisframework,Backer numericallydesignedadoublemetalenssystem,holographicelement,andanall-optical neuralnetwork,provingtheversatilityandrobustnessofadjointoptimization(Fig.2A andB) [8].UsingasquareTiO2 nanostructureontheglasslibrary,alloftheaforementionedapplicationswererealized.Theachromatic,polarization-independent,doublet metalenswasdesignedwithanapertureof800 μmandabackfocallengthof2mm.It showedabandwidthof160nmacrossthevisiblespectrum.Toconfinethedesignparameterspacetoensurethatthenanostructurescanberealisticallyfabricated,limitsofthe minimumandmaximumsizeofthenanostructureswereenforced.Iftheoptimization gradientspecifiedanunrealisticstructurethatisoutsideofthedesignatedlimits,then itwastruncatedtothelimit.Full-wave3DsimulationswithFDTDarecomputationally expensive,soallthepropagationsinboththeforwardandadjointsimulationswerecarriedoutina2Dcrosssectionofthetotalmetalenstoproducealibraryofresults,and Fourieropticswasusedtopropagatetheresultingwavestothefarfield.Sincetheconcept oftheadjointmethodissimilartobackpropagationmethodsusedinconventional machinelearningalgorithms,thesystemcanalsoproduceopticalneuralnetworks.Using anarrayof10detectors,itwasshownthatanadjointoptimizedmetasurfacecansuccessfullyclassifyimagesofnumberswithanaccuracyof84%.Unfortunately,theseresults werepurelynumerical;however,thepowerthatadjointoptimizationcanbringtomultipletaskswithlargeparameterspaceswasclearlyproven.
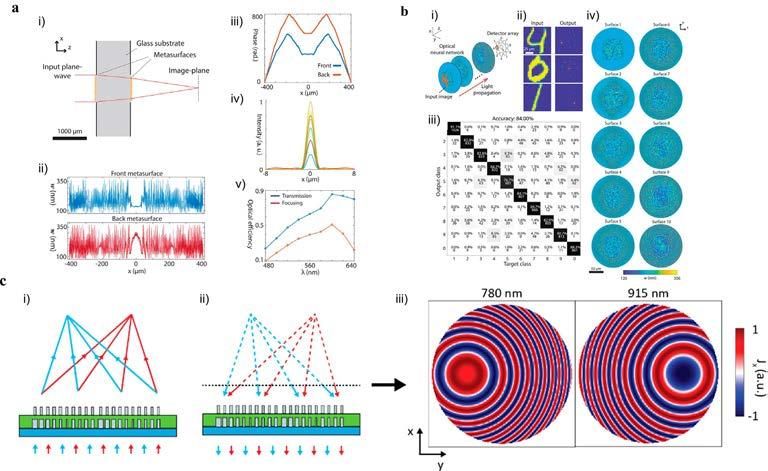
Fig.2 Examplesofnanophotonicdevicesdesignedusingtheadjointmethod.(A)Inversedesignofan achromaticdoubletmetalens.(i)Schematicofthedesign.(ii)Thewidthsofthestructuresthatmakeup themetalens.(iii)Phaseprofileacrossmetasurfaceaperturesat λ ¼ 640nm.(iv)Crosssectionoffocal planeintensityatalldesignedwavelengths.(v)Theopticalefficiencyofthemetalens.(B)Opticalneural networkforhandwrittendigitclassification.(i)Schematicofthedesign.(ii)Simulatedtestinputsand outputsoftheoptimizeddesign.(iii)ConfusionmatrixfortheMNISTdataset.(iv)Theoptimized metasurfacedesigns.(C)Amultiwavelengthmetalensdesign.(i)Schematicrepresentationofthe forward,(ii)theadjointsimulationsintheadjointoptimizationtechnique,and(iii)colormapsof thesurfaceelectriccurrentdensitiesusedasexcitationsourcesintheadjointsimulations. Panels AandBareadaptedwithpermissionfromMansouree,M.,etal.,Multifunctional2.5Dmetastructures enabledbyadjointoptimization.Optica7(2020)77–84,copyright2020OpticalSocietyofAmerica. PanelCisadaptedwithpermissionfromBacker,A.S.,Computationalinversedesignforcascaded systemsofmetasurfaceoptics.Opt.Express27(2019)30308–30331,copyright2019OpticalSocietyof America.
Inanotherdemonstrationoftheadjointoptimizationtechnique,thedesignspacesof metasurfaceshavebeenincreasedfromtheirgeneraltwo-dimensionallimitations,into 2.5Ddevices [9].A2.5Dmetalensthatfocusesdifferentwavelengthsoflightatdifferent focalpointswasdesignedandfabricated.Byincludingthelayersofmetasurfacesintothe design,thecomplexityisincreaseddramatically,asinteractionsbetweenneighboring nanostructuresinthesameplanearealsojoinedbyinteractionswiththelayersabove andbelow.Thiscouldbeanextremelyarduousdesigntooptimizeforaresearcherto optimizebyhand;however,despitetheincreaseddegreesoffreedomandcomplexity ofthedesignspace,utilizationoftheadjointoptimizationtechniqueproduceddevices withconsiderablyhigherefficienciesthanthosedesignedusingconventionalmethods.
AnFDTDsolverwasusedtosimulatetheelectricfieldsofplanewavesofthedesired wavelengthsincidentonthemetasurfaceandthecorrespondingadjointsimulations, whicharedefinedasthesamestructureilluminatedbysourcesthatareequaltothecomplexconjugateofthedesiredoutputfields(Fig.2C).Thiscanbeunderstoodaspropagatingthedesiredoutputfieldsbacktowardthemetasurface.Throughthecalculated gradients,thedimensionsofnanopostsweremanipulatedtofindtheoptimizedparameters.Thiswasprovedforbothtwoandthreelayersofmetasurfaces,withfocusingefficienciesofover50%.Asthefabricationprocessofmultilayermetasurfacesismuchmore involved,theperformanceincreasemustbeworthwhileinpractice.Here,theincreaseof focusingefficiencyfrom35%to48%,to60%forthesingle,bilayer,andtrilayermetasurfacesprovedtheaddedcomplexityoffabricationisindeedworththeextraeffortin ordertoproduceoptimizeddevices.
Expansionsofadjointoptimizationincludeusingimprovedupdaterules [10,11], automaticdifferentiation [12],andextensionintothenonlinearregime [13].Limitations ofadjointoptimizationcomefromthediscretizationofthestructureandthemeshing accuracyofthefull-wavesimulations.Higheraccuracycomeswithahighercomputationalcostforboththeforwardandadjointsimulations.Althoughthisoptimization techniquedoesindeedsimultaneouslyoptimizethewholedeviceateachupdatestep, full-wavesimulationsoflarge-scaledevicesrequireserversorclusterswithlargeenough memory,orothersimulationtricksmustbeutilized,suchasmakinguseofsymmetryor simulatinga2Dcrosssection.
1.1.2Topologyoptimization
Topologyoptimization(TO)hasrecentlybeenintroducedtothefieldofnanophotonics, afterbeingwidelyusedinnumerousfieldsforthedesignofphysicalsystemsandmechanicalstructures [14,15].Itisdefinedbytheallocationofmaterialeitherexistingornotat specificpointsinadefinedarea,inordertosatisfyanobjectivefunction.Thismeansthat eachgridpointisadesignparameter,leadingtothegeometrybeingoptimizedinapixellikefashion.Again,inordertoupdatethedesignovereachiteration,agradientneedsto becalculatedinrelationtotheparameterspace,soTOisoftencoupledwiththecomputationallyefficientadjointmethod,asdescribedintheprevioussection.TOwasintroducedtothefieldofnanophotonicstodesignlow-losswaveguidebends [16] andisnowa staplemethodfortheoptimizationofamagnitudeofdifferentnanophotonicdevices [17].SeeRef. [18] foranin-depthreviewanddescriptionofthefundamentalsandproceduresoftheoptimizationmethod,andRef. [19] forarecenttutorialthatincludesFEM modelexamples.
UsingTO,Ref. [20] designedreconfigurablemetalensesthatfocuslightatwavelengths thatareanorderofmagnitudeapart,andalsoanactivemetalensthatshiftstheirfocallength dependingonthestateofanactivematerial.Thiswasachievedusinga10-layer,multiheightTOmethodthathasaround10 [4] degreesoffreedom(Fig.3A).Bymodeling
theprobleminanaxisymmetricdomainusingMaxwell’sequationswithatime-harmonic behavior,thefull3Dequationswerereplacedwiththeirsimpler2Dcounterparts.This allowsthecomputationalcomplexitytobereducedatthesacrificeofrestrictingthe geometricfreedomofthedevice.Tofurthersimplifytheprocedure,far-fieldtransformationswereappliedratherthansimulatingtheentirespatialdomainbetweenthelensandthe focalpoint.Thefigureofmeritwasdefinedastheintensityoftheelectricfieldatthefocal point,andthegradientswerecalculatedusingadjointsensitivityanalysis [21].Asan experimentalvalidationofthetechnique,asingle-layermetalensmadeupofvariable heightswasfabricated.Thefinaldesignfocusedlightwithawavelengthof1550nmwith anumericalapertureof0.4withanabsolutepowertransmissionofaround93%.Although thisworkshowsthepromiseofTO,inreality,thefabricationofa10-layermetasurface withvariableheightsisagreatchallenge,butonethatcouldbecomearealitywith improvednanofabricationmethodssuchas2.5Dlithographyormulti-photon polymerization.
OtherworkhasshownthatTOcanbeusedtotailorthephasefrontofthelightat will.Inparticular,usingfreeformoptimization,Selletal.,provednumericallyandexperimentallythattheoptimizationofadeviceformultiplewavelengthsatthesametimeis possible [22] (Fig.3B).Inprinciple,thetechniquecanbescaledtoalargenumberof wavelengthsatthecostofaddedcomputationaleffort.Usingsilicon,abeamsteering devicecapableofsteering N wavelengthsinto N uniquediffractionorders,withanefficiencythatscalesas1/N0.5 wasdesigned.Theoptimizationiscarriedoutoverthewhole periodicityofthemetasurface,meaningthatthespacethatisbeingoptimizedismuch largerthanthewavelengthitisbeingdesignedfor.Thisisinstarkcontrasttotheconventionalmethodofdesigningsubwavelengthnanoantennastobuildthetotalsurface. Thisalsoallowsthefreedomofthestructurestobeofanyshapethatisrequired,without anyconstraintonlocalperiodicities.Thisfreedomindesignspaceallowsforcurvesand interconnectedgeometriesthatproduceopticalcouplingandresonancesthatwouldotherwisebenearlyimpossibletodesign.Onelimitationofthisworkwastheuseofrigorous coupled-waveanalysis(RCWA)solverforthesimulations,asitrequiresthestructuresto beperiodic.Thiscouldeasilybeovercomethroughtheuseofothermethodsofsolving Maxwell’sequationsthatdonotrelyonperiodicboundaryconditions [23].Examplesof multiwavelengthandlarge-angleaberration-freemetalenseshavealsobeendemonstrated usingTO [24].
TOisabletouncoverdesignsforopticalpropertiesthatareveryraretofindinnature. Inparticular,Shietal.producedsingle-layeredopticalelementsthatshowaconsiderable birefringencefordifferentpolarizationsofincidentlight [25] (Fig.3C).UsingTOallows thedevicetohavearbitrarygeometries,whichallowthedegreesoffreedomtobeasbigas theresolutionoftheindividualpixelstobeoptimized.Ellipticalbirefringenceisachieved inasingleplanardevicebyexploitingtheincidentangleofthelighttobreakthesymmetryofthestructure.
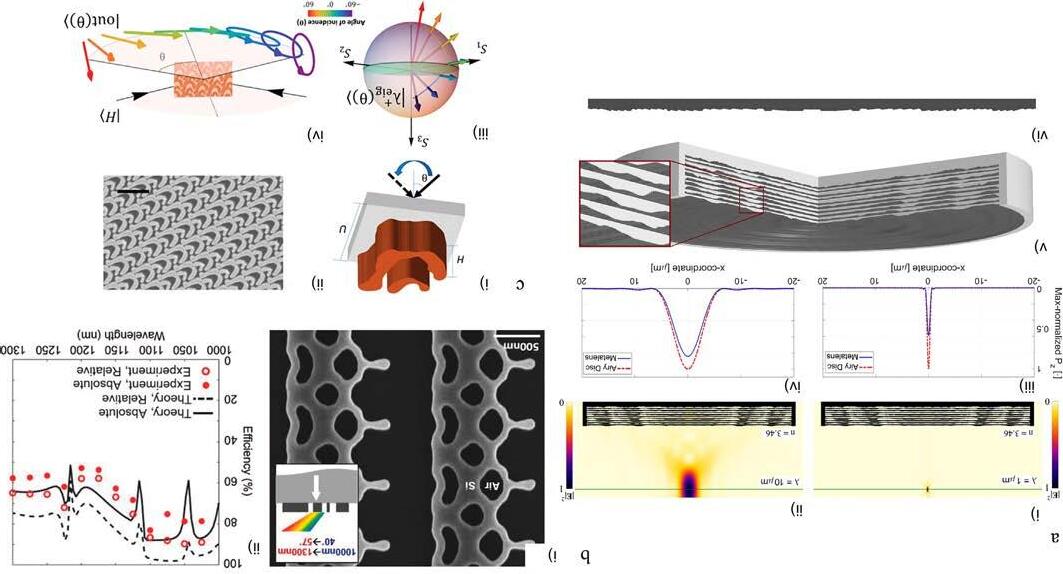
Fig.3 Examplesofnanophotonicdevicesdesignedusingtopologyoptimization.(A)Normalizedelectricfieldinthe x–z planethroughthecenter ofthemetalensfor(i) ¼ 1 μmand(ii) ¼ 10 μm.(iii)Thepowerinthe z-directionthroughthefocalplanenormalizedtothemaximumoftheAiry discfor ¼ 1 μmand(iv) ¼10 μm.(v)A3Dillustrationofthe10-layermetalensdesign.(vi)Crosssectionofsingle-layerreferencedesign. (B)Experimentalcharacterizationofthebroadbandblazedmetagrating.(i)Scanningelectronmicroscopyimageoftheblazedmetagrating operatingbetween1000and1300nmforTM-polarizednormallyincidentwaves.(ii)Plotofthetheoreticalandexperimentalefficienciesvs wavelengthforthedevice.(C)(i)Schematicoftheoptimizedunitstructure.(ii)SEMimageofafabricatedsample.Scalebar,1 μm.(iii)The arrows representtheangle-dependenteigen-polarizationstatesofthedevice. Differentcolors correspondtodifferentanglesofincidence.As theangleofincidencevaries,thedevicecanbecontinuouslytunedbetweenlinearandellipticalbirefringence.(iv)Angle-dependent polarizationgeneration.Forafixedincidentpolarization,theoutputpolarizationstatechangescontinuouslyfromrightcircularpolarization throughhorizontallinearpolarizationto45degreelinearpolarizationforvaryinganglesofincidence. PanelAisadaptedwithpermission fromChristiansen,R.E.,etal.,Fullwavemaxwellinversedesignofaxisymmetric,tunable,andmulti-scalemulti-wavelengthmetalenses.Opt. Express.28(2020)33854–33868,copyright2020OpticalSocietyofAmerica.PanelBisadaptedwithpermissionfromSell,D.,Yang,J.,Doshay,S., Fan,J.A.,Periodicdielectricmetasurfaceswithhigh-efficiency,multiwavelengthfunctionalities.Adv.Opt.Mater.5(2017)1700645,copyright2017 JohnWileyandSons.PanelCisadaptedwithpermissionfromShi,Z.,etal.,Continuousangle-tunablebirefringencewithfreeformmetasurfaces forarbitrarypolarizationconversion.Sci.Adv.6(2020)eaba3367,copyright2020CCBY-NC.
Contrarytointuition,ithasbeenshownthatrandominitialgeometriesproducebetterresultsthanusingexistingnanophotonicdesignsasthestartingpoint [26].TOusually hasnoconstraintsontheconstituentpartsofthefinaldesign,whichcouldpossiblyleadto unrealisticdesigns.Forexample,iftherearevoidsorfloatingelements,thismayproduce anoutputthatmaximizestheobjectivefunction,butitwouldbeimpossibletorealize experimentally.Therefore,considerationoffabricationfeasibilityhasalsobecomea keypointofimprovingdevicesdesignedusingTO [27].
1.2Evolutionaryalgorithms
Incontrasttogradient-basedoptimizationmethods,evolutionaryalgorithmstakeinspirationfromnaturetoreachdesignsthatmeetacertaindesignobjective.Themostwellknownandoftenusedexamplesofevolutionaryalgorithmsarethegeneticalgorithm (GA)andparticleswarmoptimization(PSO).Bothareknownasmetaheuristic approaches,meaningthattheyareabletofindareasonablesolutiontoanoptimization problemwithlimitedinformationorcomputationalcost.Althoughthereislimited mathematicalevidencethatevolutionaryalgorithmsconvergetoglobaloptima,they dooftenreachextremelygoodresults [28,29]
1.2.1Geneticalgorithm
TheGAisinspiredbyCharlesDarwin’stheoryofnaturalevolution,byfocusingonthe selection, mutation,and crossover ofapopulationofsolutions.Avisualrepresentationis shownin Fig.1B.Theoptimizationreliesontheknowledgeofgoodsolutionswithin thepopulation,inordertoreachbettersolutions,whilealsokeepinganamountofrandommutationtoallowfornewsolutionsoutsideofthecurrentdirectiontobeaccessible. TheGAstartswithapopulationofpossiblesolutions,innanophotonicdesign,thiscould beasetofgeometricparametersforeachindividual.Followingtheleadofnaturalselection,theparametersarecalledgenes,whileasetofgenesthatformthesolutionforone individualisknownasachromosome.Eachsolutionisthenrankedintermsofitsperformance,withhigherscoreshavingahigherchanceofbeing selected forthenextiteration orgeneration. Crossover isanotherimportantpartoftheGA,wherebythegenesofparent solutionsaremixedtogethertoformnewsolutions.Thisallowsnewchildsolutionstobe formedfromhigh-performancesolutions,whichshouldresultinnew,bettersolutions. Mutation relatestosomegenesbeingchangedatrandom,allowingforameasureofdiversityinthepopulation,andavoidingprematureconvergencetoapossiblesuboptimal solution.TheimportantparametersoftheGAarethepopulationsize,informativefitness function,andtheamountofmutationandcrossover.Thepopulationsizeisusuallylimitedbytheavailablecomputationalresources,soitneedstobechosentoappropriately findagoodsolutioninareasonableamountoftime.Thissimpleyetintuitivetechnique hasbeenappliedtothefieldofnanophotonicswithgreatsuccesstodesignwaveguides andphotoniccrystals [30],andsomeexamples [31] willbediscussedhere.
InRef. [32] theGAwasutilizedwithsomemodificationsinordertodesignphasecontrolledmetasurfaces.Inthiswork,theconceptofthecrossoverwasomitted completely,initsplaceonlymutationensued.Inordertoreachanoptimalsolution, theamountofmutationwascontrolledtobesmallerandsmallerastheiterationswere concluded.Anelaboratefitnessfunctionwasproducedtocreatetheexactdesired responseforthefinalsolution.Furthermore,physicalconstraintswereincludedtoensure thatunphysicalresultswereeradicatedduringtheoptimizationprocess.Thiskindof supervisionofthemutationisessentialtokeeptheresultsinthedesireddomain.In anotherwork,strongchiraldichroisminaplasmonicmetasurfacewasdemonstrated, usingamicro-geneticalgorithm [33].Thekeyfeatureofthisadaptationisthatinstead ofhavingmutation,thereisacompleterepopulationoftheworst-performingsolutions withcompletelynewrandomsolutionsforfasterconvergence.SincetheGAhasno boundsintermsofthenumberofparametersthatitcanoptimizeinasingleiteration, itoweswelltofreeformdesignswherethesurfaceisdiscretizedintoindividualpixels thatcanbechosentoincludeorexcludematerial,similartotheTOmethod [34] Butsincenogradientsareneeded,thereisnolimitationonthefitnessfunctionto bedifferentiable.Here,thesurfacewasdiscretizedintoabinarypatternasshownin Fig.4A.Circulardichroismof0.63and0.60wasreportedforfabricatedsamples.The GAhasalsobeenusedtochoosethephotonicelementsfromalibraryinordertoproduce thedesiredresponse [35].Thedesignoftheindividualstructureswasdonebyhand,but thephaseprofilewasachievedusingtheoptimizationpoweroftheGA.UsinganadaptiveGAallowsfortheproblemtobesplitintosubproblemsthataresolvedinsequence,to reachthefinalsolution [36].Theauthorsnotethatthelargenumberofsolutionsthatare producedwithresultsthatareclosetothedesignedfitnessfunctioncouldalsobe employedlaterindatahungrymethodssuchasadeeplearningmodels.Inafinalexample ofusingtheGAtooptimizetheperformanceofnanophotonicapplications,itwasusedto designperfectabsorbersandcolorfiltersforsinglenanostructuresandunitcellswithmultiplenanostructures(Fig.4B) [37].Thisstudyshowedthelimitationsthatsinglenanoparticleshavewhentryingtooptimizeasolutionwithlimiteddegreesoffreedom.The colorsachievedafterincreasingtheunitcelltoincludemultiplestructuresweregreatly improved,aswerethebroadbandabsorptionproperties.Foralloftheexamplespresented here,itisinterestingforresearcherstodelveintotheunderlyingphysicsoftheoptimized solutiontounderstandwhycertaindesignsarebetterthanothers,whichinturn,helps researcherstouncovernewideasthatcanbeappliedsuccessfullyinnewapplications.
1.2.2Particleswarmoptimization
Particleswarmoptimizationgetsitsinfluencefromthemovementofbirdsandschoolsof fish.Eachsolutionistreatedasaparticlethathasapositionandamomentumthatis updatedateachiteration.Theupdatedependsontheparticularsolution’slocaloptimum, aswellastheoptimaofthewholepopulationasawhole,asdemonstratedin Fig.1C [38]
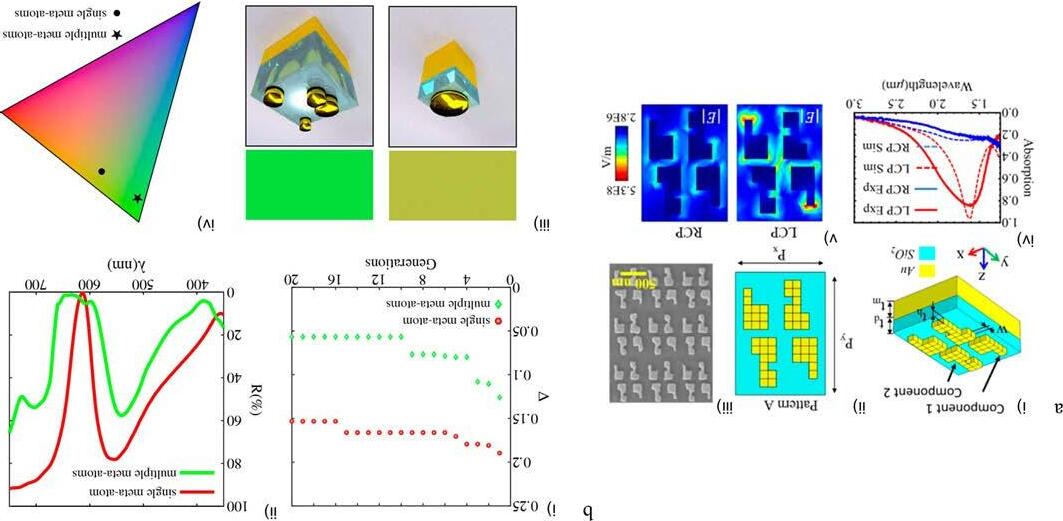
Fig.4 Examplesofnanophotonicdevicesdesignedusinggeneticalgorithms.(A)(i)Schematicofthebinarypatternforthechiralplasmonic metasurface.(ii)Topviewofthepattern.(iii)SEMimageofthefabricatedchiralmetasurface.(iv)Experimentalandsimulatedabsorption spectraunderLCPandRCPatnormalincidence.(v)Normalizedelectricfielddistributionsattheresonantwavelengthof1.62 μmunderLCP andRCPincidence.(B)(i)ThedistancebetweenthetargetanddesignedcolorgeneratedintheCIEdiagramasafunctionofgenerations. Redcircles (darkgrayintheprintversion)representthesingle-unitcell, greendiamonds (grayintheprintversion)representtheunitcell withmultiplenanostructures.(ii)Comparisonofreflectionspectrabetweentheoptimizedsamplesofsingle(green (grayintheprint version))andextended(red (darkgrayintheprintversion))unitcells.(iii)Comparisonofthegeneratedcolorsandcorresponding configurations.(iv)ThegeneratedcolorsontheCIEdiagram. Circles denotethesinglenanostructureand stars representthemultiple nanoparticles.(Forinterpretationofthereferencestocolorinthisfigurelegend,thereaderisreferredtothewebversionofthisarticle.) PanelAisadaptedwithpermissionfromLi,Z.,Rosenmann,D.,Czaplewski,D.A.,Yang,X.,Gao,J.Strongcirculardichroisminchiralplasmonic metasurfacesoptimizedbymicro-geneticalgorithm.Opt.Express27(2019)28313–28323,copyright2019OpticalSocietyofAmerica.PanelBis adaptedwithpermissionfromLiu,C.,Maier,S.A.,Li,G.,Genetic-algorithm-aidedmeta-atommultiplicationforimprovedabsorptionand colorationinnanophotonics.ACSPhotonics7(2020)1716–1722,copyright2020AmericanChemicalSociety.
Theupdatesaregovernedbyalearningratethatdetermineshowmuchthevelocityofthe particleischangedateachupdate.This,alongwiththenumberofparticlesprovidesthe mostimportantparametersthatneedtobeoptimizedforeachproblemandconsidered withregardtotheavailablecomputingpower.
InoneexampleofusingPSOfornanophotonicapplications,Ref. [39] produceda freestandingmetasurfaceofsiliconforhigh-performancebeamsteering(Fig.5A). Aparticleswarmalgorithmwascoupledwithafull-wavesimulationthroughtheFDTD method.Afteroptimization,boththeforwardtransmissionsweregreatlyincreased,and thepowerofthedeflectedbeaminthedesireddirectionwasimproveddramatically. However,itwasnotedthatthecombinationof3Dsimulationsisahugebottleneck inthistypeoftechnique,asthetotaltimeneededforasingleoptimizationwasaround 850h.InanotherworkusingthePSOmethod,asiliconnitride Y-junctionwasdevelopedwiththegoalofconvertinglinearlypolarizedlightintoitsoppositepolarization (Fig.5B) [40].Conversionefficienciesofover97%forbothpolarizationswerereported andconfirmedwithnumericalsimulations.Manyotherexampleshavealsobeendemonstrated,suchaswaveguides [41],andpixelatedsurfaces [42] withmultipleobjective functions [43].
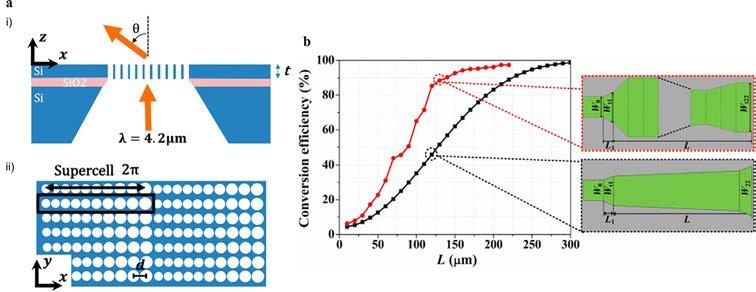
Fig.5 Examplesofnanophotonicdevicesdesignedusingparticleswarm.(A)(i)Schematicofa freestandingsiliconnanoholearraymetasurfaceactingasabeamdeflectorwithadeflectionangle θ . (ii)Top-downviewofthesiliconnanoholearraybeamdeflectormetasurfaceconstructedusing repeatingsupercells.(B)Conversionefficiencyasafunctionofthelength L forthedesignedmodeconversionsectionandtheadiabatictaperstructure. PanelAisadaptedwithpermissionfromOng,J.R., Chu,H.S.,Chen,V.H.,Zhu,A.Y.,Genevet,P.Freestandingdielectricnanoholearraymetasurfacefor mid-infraredwavelengthapplications.Opt.Lett.42(2017)2639–2642,copyright2017OpticalSocietyof America.PanelBisadaptedwithpermissionfromZhang,B.,etal.,Particleswarmoptimizedpolarization beamsplitterusingmetasurface-assistedsiliconnitrideY-junctionformid-infraredwavelengths.Opt. Commun.451(2019)186–191,copyright2019Elsevier.
2.Deeplearning-basedinversedesign
Despitetheachievementsofcomputationaloptimizationmethods,asthedesigncomplexityincreases,newchallengestoinversedesignarise.Specifically,solvinghighlycomplexproblemsmayrequirenumerousiterationstoapproachtheoptimumsolution.In parallel,thesuddenriseofartificialintelligence(AI),inparticularmachinelearning (ML),overthepastdecadehashadprofoundimpactsonvariousfieldsofscience.DL, poweredbyneuralnetworks,hasrisenasoneofthemostwidelyusedmachinelearning architectures [44].ThecombinationofthenanophotonicsinversedesignandDLisa notableapproachthatcansolvethechallengingproblemsofinversedesigninnanophotonicbasedondata-drivenways.
Neuralnetworkscomputationallymodelhowlearninghappensintheneuronsofthe brain.Asneuronsinbiologicalbrainsareconnectedinacomplexmannerwiththe strengthoftheconnectionsbeingdeterminedbycertainexternalstimuli,theneurons computationallyimitatethisfunction.Thesimplestnetwork,knownasaperceptron, consistsofseveralinputneuronsandoneoutputneuron.Everyadjacentneuronsareconnectedbyweight.Eachnodeinthepreviouslayerismultipliedbytheweightand summedasonevalue.Next,bycomparingtheoutputofnetworkandtheoutputof actualdata,theweightsareadjustedinadirectiontoreducethisdistance.Thedistance functionbetweentheperditionvalueofthenetworkandtheactualtruevalueisnamed thecostfunction,andthemethodofupdatingtheweightsbasedondifferentiatingis namedbackpropagation.ThedetailedmathematicalmethodsofforwardingandbackpropagationareshowninRef. [45].Astheconnectionsarelinear,onlysimpleproblems canbesolved.Throughtheintroductionofanon-linearactivationfunction,which decideswhetheraneuronisactivatedornotbycalculatingtheweightedsumofprevious neurons,itbecomespossibletolearnnonlinearrelationships.
Tosolveincreasinglymorecomplexproblems,deepandwidemultilayerperceptrons (MLPs)wereintroduced,knownasDL.Theadjective“deep”inDLreferstotheuseof multiplelayersandnodes.Ingeneral,themoredeepstructure,themorecomplexrelationshipscanbecarried.DramaticimprovementsinDLalgorithmshavebeenrealizedin recentyearsbyovercomingchroniclimitationssuchasvanishinggradients [46] andoverfitting [47].Alongwiththegrowthofaccessiblebigdataandadvancementsincomputing power,MLhasemergedasanextremelyusefultoolinvariousfieldsofcomputerscience, includinglanguageprocessing [48],computervision [44],imagegeneration [49],and speechrecognition [50].TherehavealsobeenattemptstocombineDLwithotherdisciplines,includingmanufacturing [51],microscopy [52],andnanophotonics [53–58]
DLmodelseffectivelylearntoapproximatethecomplexnonlinearrelationships betweeninputandoutputdata,evenwithoutananalyticphysicalmodel.MostapplicationsofDLinnanophotonicsrelatethedesignparametersofthenanostructures,suchas thematerial,spatiallocation,andgeometrywiththeiropticalresponsessuchasthephase,
transmittance,orscatteringpower.Predictingtheopticalpropertiesfromthedesign parametersisknownasforwardmodeling,whichisgenerallycalculatedthroughcomputationallyexpensivefull-wavesimulationsbasedonMaxwell’sequations.Aftera modelhasbeenwelltrained,itlearnstoapproximatetheseequationsandcanachieve extremelyfastcalculationtimeswithconsiderableaccuracy.Ontheotherhand,inverse designhasalsobeenproveninnanophotonicsusingDL,byacquiringthegeometric parametersthatproducethedesiredopticalproperties.Forinversedesignusinganalytic ornumericalmethods,acompromisemightbemadebetweenhigh-designfeasibilityand highspectralcomplexity;however,usingDLcanactasabridgebetweenthetwo,as shownin Fig.6A [55].Inthissection,wereporttherecentprogressinDL-basedinverse designinnanophotonics.TheDLmodelsusedforinversedesigncanbedividedintotwo types,deterministicandgenerative.Theformeralwaysproducesthesameoutputfora giveninput,whilethelattergeneratesanoutputbasedonaprobabilisticmodelwhichcan openthepossibilitytodesignbeyondtheintuitionoftheresearcher.Inthissection,we focusonthemethodologyofdeterministicmodelsandpresentthelatestresearch.We thenintroduceexamplesofgenerativemodelssuchasautoencodersandgenerative adversarialnetworksfornanophotonicinversedesign.
2.1Deterministicneuralnetwork-basedinversedesign
Deterministicmodelisaneuralnetworkthatdoesnotcontainrandomness,onceithas beentrained,itactsasafunctionwhichproducestheoutputforthegiveninput.RepresentativedeterministicneuralnetworksareMLP,convolutionneuralnetwork(CNN), andrecurrentneuralnetwork(RNN).Eachnetworkhasaspecializeddatatypebasedon itsstructureandalgorithms.Forexample,CNNisusedtoanalyzeimages,andRNNis mainlyusedtoanalyzetime-seriesdata.Inthisway,researchersselectthebestnetwork thatcanproperlydescribethegivenpaireddata.Beforesolvingtheinversedesignproblem,researchersevaluatewhetherthenetworkcansimulateMaxwell’sequationproperly throughaforwardmodel.Inthissection,wereportthelatestexamplesofforwardand inversemodelsusingMLPsandCNNsinnanophotonics.
2.1.1Multilayerperceptron
MLPsconsistoffullyconnectedlayerswhereeverynodeofeachadjacentlayerisconnected.Itisthemostbasicarchitectureofartificialneuralnetwork(ANN).InRef. [59],it wasdemonstratedthatMLPscanbeusedtopredictthescatteringspectraofmultilayered nanoparticleswithvariablethicknesses [60].Therelationshipbetweentheparticledesign andthescatteringspectrumwassufficientlytrainedusingasimpleshallownetworkwitha datasetof50,000samples.Thisresearchshowedthatwell-trainedMLPscanbeindeed utilizedasanapproximatorofMaxwell’sequationstoareasonableaccuracywithan increaseinthespeed,comparedtoconventionalanalyticsimulations.
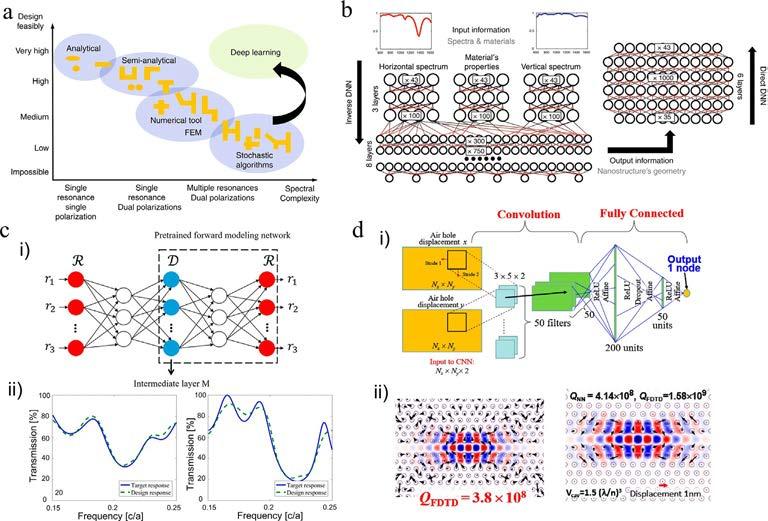
Fig.6 Advantagesofdeeplearninginphotonicsandphotonicdesignsbydeterministicneural networks.(A)Computationaltoolsgenerallydecreasethedesignfeasibilityastheopticalresponse becomesmorecomplex.Inversedesignmethodsthroughdeeplearningcanovercomethisgap. (B)Two-phasenetworkfindsandverifiestheinversedesignfromspectrumandmaterial informationtodesireddesignparameters.Theinversenetworkmergedtheexpandedfeaturesof spectrumandmaterialpropertiestoconsidercorrespondinggeometry.Afterthat,thedirect networkisalsotrainedtoimprovetheaccuracyoftheinversenetwork.(C)(i)Thestructureof tandemnetworkwhichconnectstheinversenetworkandforwardnetworksequentially. R denotes theopticalresponseand D indicatesthedesignparameters.Totrainthetandemnetwork,apretrainedforwardnetworkisnecessary.(ii)Theresultsoftestdataforthetandemnetworkmethod. (D)2DphotoniccrystaloptimizationbyCNN.(i)Theschematicofneuralnetworkwhichcanlearn betweenairholedisplacementandQfactors.(ii)Theheterostructureof2Dphotoniccrystal nanocavity. Circle denotestheairhole(110nmradius)and vectorarrows indicatethe displacementsofairholes.The Q factorbeforeimprovedfrom3.8 108(left)and1.58 109(right) bydeeplearningoptimization.TheestimatedMSEsare2.64 10–3 (left)and1.10 10–4 (right). PanelsAandBareadaptedwithpermissionfromMalkiel,I.,etal.,Plasmonicnanostructuredesign andcharacterizationviadeeplearning.Light:Sci.Appl.7(2018)60,copyright2018CCBY4.0.Panel CisadaptedwithpermissionfromLiu,D.,Tan,Y.,Khoram,E.,Yu,Z.,Trainingdeepneuralnetworks fortheinversedesignofnanophotonicstructures.ACSPhotonics5(2018)1365–1369,ACS.PanelDis adaptedwithpermissionfromAsano,T.,Noda,S.,Optimizationofphotoniccrystalnanocavitiesbased ondeeplearning.Opt.Express26(2018)32704–32717,copyright2018CCBY4.0.
Beyondforwardmodeling,MLPswereappliedtoinversedesign.InRef. [61],an inversedesignmethodusingadeepandwidewasdeveloped.Theinputwassettothree typesofseriesdataconsistingof43samplingpointsandtheoutputtoeightdesignfeatures ofanH-shapedantenna,includingtheexistenceofaleg,theangleofthestructure,and thelengthsofeachpart(Fig.6B).With15,000simulatedsamples,thetrainednetwork wasabletosuccessfullydesignstructurestosatisfythedesiredspectrum,whichwereverifiedusingfull-wavesimulations.
AlthoughMLPshavebeenshowntoproducesuitablecandidatedesigns,without properrestrictions,theinversedesignmaybedifficulttorealizeexperimentallydueto featuresthataretoosmallorlarge,orhaveanunrealisticallyhighaspectratio [62].This canbeovercomebyincludingextraconstraintsintotheMLPcostfunction [63].Before proceedingtheinversedesign,reasonablegeometrydesignparameterswerespecified. Afterthat,thecostfunctionincludesnotonlythedifferencebetweentheprediction valueandthetruevalue,butalsothedifferencebetweentherecommendedgeometric parametersandpre-setgeometricparameters.Throughthiscostfunctionwithgeometricalconstraint,itwaspossibletosuggestanoptimaldesignwhichwasnottoodifferent fromthepre-setgeometry.Thegeometryvectorincludesthethickness,radius,andgap betweenthemeta-atoms.Asaresult,thetrainednetworkwasabletoquicklyrecommendphysicallyfeasiblemeta-atomsthatproducetherequiredopticalproperties.
AfundamentalissueofinversedesignusingDLoccursfromthenon-uniquenessof solutions;wherebyvariousstructurescanproducethesameopticalproperties.Thishindersthetrainingofthemodelasdifferentsolutionsaregivenforthesameinputs.InRefs. [64,65],tandemnetworkswereintroduced.Thisworksbycombiningapre-trainedforwardmodelingnetworkwithaninversenetworktoovercometheone-to-manyproblem [64,65].Asshownin Fig.6C,theinversenetworkissequentiallyconnectedtothe pre-trainedforwardmodel.Totraintheinversemodel,theinversemodelerroriscombinedwiththeerrorbetweentheforwardnetworkresultandtheoriginaltargetresponse. Tofindthepropermultilayerfilmwhichcansatisfythedesiredtransmissionspectrum, thethicknessesof20layerswereusedasthedesignparameters,and200transmissionspectralpointswereusedastheopticalproperties [66].Themodelwasabletoproduceinverse designsthatcloselymatchthedesiredspectra,demonstratingthattandemnetworkscan overcometheproblemofnon-uniquenessforinversedesigninnanophotonics.
Inparallel,researchersdemonstratedthatMLPscanbeusedtosolveinversedesign problemsofvariousapplicationsincludingintegratednanophotonicdevices [67],color generation [68,69],photonicpowersplitters [70],absorbers [71],andcore-shellparticles [59,72].InRef. [72],aninversedesignmodelwasdevelopedwhichconsidersboththe thicknessandmaterialofcore-shellnanoparticlesusingtandemnetworks.Thisresultalso demonstratesthatDN-basedmethodscanhandlethemultifunctionaldesignbysimply consideringmulti-designparameters(e.g.,length,thickness,andmaterialtypes)and
responses(e.g.,amplitude,phase,andpolarization)whichishardtoachievewithpurely guidedbyphysicalintuition.
2.1.2Convolutionalneuralnetworks
Earlystudiesexpressedthedesignofnanostructuresusingseveraldesignfeaturessuchas height,width,length,andangle.Whilethisreducesthenumberofinputfeaturesand promotestraining,thereisalsoalimitationthattheresultsthatinversedesignsare restrictedwithinthedefinedformat.Therefore,tobreaktheserestrictions,thedesign canbeconsideredasanimage.TheintroductionofCNNcaneffectivelyconsiderspatial andtemporaldata [73].Moreover,bysharingtheweightwiththefilter,itcanachieve betterperformancewithfewerweightsthanMLPs.Morespecifically,theconvolution layers,whichcalculatetheconvolutionvaluesofimagesandfilters,wereusedtoextract thekeyfeatures.Generalconventionalimagefiltershavepre-definedvaluesdepending ontheirspecificgoalssuchasedgedetectionblurring,anddenoising,butthefiltersin CNNdonothaveaspecificformanditupdatesitselffromtherandomstatetoreduce theerrorsofthecostfunction.Withthesetrainablefilters,itextractsthecriticalfeatures fromrawimagedataandusesitasaninputforthefollowingfullyconnectedlayers.This makesCNNsusefultoanalyzeimagedataofnanophotonicstructuresoroptical responses.
ThecombinedCNN-basedforwardmodelandcomputationaloptimizationmethods wereconductedtoreducethesimulationtime.InRef. [74],polarization-insensitiveplasmonicmetasurfacewith90%absorptionwasdevelopedbycombiningGAandCNN. Anotherapplicationisanexampleofmaximizingthe Q factorofphotoniccrystal [75].Tosolvethis Q factormaximizeproblem,morethan1000,000simulationswere needed.However,byreplacingthesimulationwithapre-trainedCNNforwardmodel, only1000simulationswereconductedforgatheringthetrainingdata(Fig.6D).
Therewerealsoattemptstoinversedesigndirectlybyusingspectrumsasinput,and designparametersasoutput [76].Tooptimizetheplasmonicmetasurface,25,000samples wereusedtodescribetherelationshipbetween300spectralpointsandsixdesignparameters.Particularly,thisstudyalsocomparestheeffectsofDLalgorithmsbychangingnetworkstructures(MLPorCNN),andnormalizationmethods(batchnormalizationisused ornot).Asaresult,CNN-basedmodelcanrecommendthepropergeometrywhichsatisfiestheusersuggestedtargetabsorptionspectrum.ItalsodemonstratesthattheCNN withbatchnormalizationhassuperiorperformancecomparedtotheMLP-basedmodel.
Findingtheproperthin-multilayer-filmmetamaterial’sthickness,whichrepresents thedesiredspectralresponse,aninverseCNNmodelwasapplied [77].Thisresearchused multiplespectraincludingreflectanceandtransmittanceatvariousanglesasinputandthe thicknessofthefilmasoutput.Todescribetherelationshipbetweeninputandoutput, CNNwasdevelopedwith200,000samples.Moreover,bycomparingCNNandcomputationaloptimizationmethodssuchastheleastsquaremethodandGA,thisstudy



















